2012第四届两岸四地精英赛二试试题(小学高年级组)
2012年海峡两岸数学邀请赛初赛试题及答案(四年级)

四年级 第1页 四年级 第2页绝密★启用前2012年奥林匹克数学竞赛海峡两岸邀请赛试题(2012年5月)四年级(初赛)(本试卷满分120分 ,考试时间90分钟 )一、填空。
(该大题共15小题,每题5分,共计75分)1、凌浩是龙年的前一年出生的宝宝,凌浩算了一下,到今年龙年,他和爸爸、妈妈的年龄和刚好是91岁,爸爸说他的年龄是凌浩的3倍还多2岁,那么凌浩的妈妈今年 岁。
2、按规律填数:0.012、1.2、0.12、12、1.2、120、 、 。
3、灰太狼自认为儿子小灰灰智力远远高于那些吃草的羊羊们,一天他出了一道这样的题给儿子做:狼大叔一次买菜回来,发现找回的钱多了10元4角4分,仔细一算,他把买肉的钱的小数点点错了一位,那么买肉实际用了多少钱。
小灰灰想了很久也没有一点头绪,最后还是被路过的喜洋洋算出来了,喜洋洋算出的结果是 元。
4、杨阳是班里有名的小马虎,这次在做(200×9-□)÷25+13时,又没看到题里的括号,算的结果是1788,正确的结果应该是 。
5、20.16平方米= 平方分米 50元6分= 元 300平方米= 公顷。
6、《泰坦尼克号》是一部经典欧美电影,如今它又披上3D 面纱向人们款款走来,4月10日这天,思思和静香说好一起去影院看电影。
已知思思家在影院南偏东30°方向1600米处,静香说从她家要先向北走400米到邮局,再向东偏北30°走1200米才到影院,静香家在影院 方向,思思在静香家 方向。
(横线上同时写上度数)7、魔术师有一根神奇的橡皮筋,每拉动一次长度就变为原来的100倍,每收回一次就缩小原来的1100。
橡皮筋原来的长度只有1.4厘米,他拉动四次,再收回三次后橡皮筋是 厘米。
8、采石师傅发现一种铁矿石,每10克里含铁6.02克,每克铁矿石不含铁 克。
9、A 、B 、C 三个人,一位是老师,一位是营业员, 一位是医生,你能确定他们的职业吗? A 说:C 比医生大 B 说:A 与营业员不同岁 C 说:营业员比B 小 A : B : C : 10、对于自然数a 和b 规定运算“※”为:a ※b=a ×2+b ×5,那么2※5+10= 。
2012杯赛真题汇编 四年级 by王刚
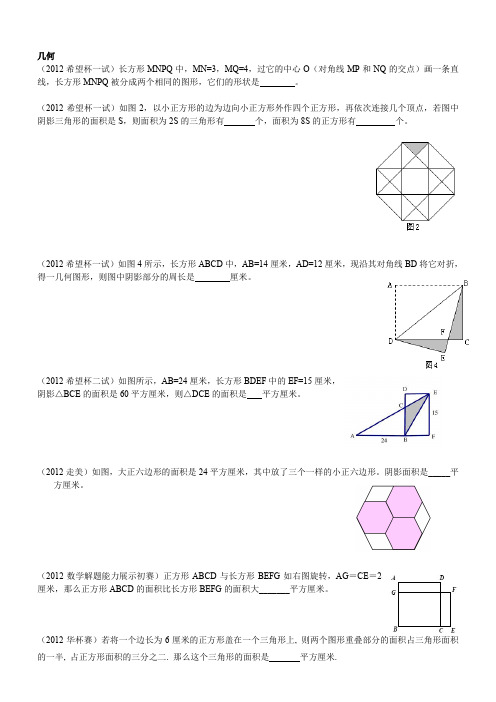
几何(2012希望杯一试)长方形MNPQ中,MN=3,MQ=4,过它的中心O(对角线MP和NQ的交点)画一条直线,长方形MNPQ被分成两个相同的图形,它们的形状是。
(2012希望杯一试)如图2,以小正方形的边为边向小正方形外作四个正方形,再依次连接几个顶点,若图中阴影三角形的面积是S,则面积为2S的三角形有个,面积为8S的正方形有个。
(2012希望杯一试)如图4所示,长方形ABCD中,AB=14厘米,AD=12厘米,现沿其对角线BD将它对折,得一几何图形,则图中阴影部分的周长是厘米。
(2012希望杯二试)如图所示,AB=24厘米,长方形BDEF中的EF=15厘米,阴影△BCE的面积是60平方厘米,则△DCE的面积是平方厘米。
(2012走美)如图,大正六边形的面积是24平方厘米,其中放了三个一样的小正六边形。
阴影面积是_____平方厘米。
(2012数学解题能力展示初赛)正方形ABCD与长方形BEFG如右图旋转,AG=CE=2厘米,那么正方形ABCD的面积比长方形BEFG的面积大_______平方厘米。
(2012华杯赛)若将一个边长为6厘米的正方形盖在一个三角形上, 则两个图形重叠部分的面积占三角形面积(2012华杯赛)有一个长方形, 如果它的长和宽同时增加6厘米, 则面积增加了114平方厘米. 则这个长方形的周长等于厘米.(2012华杯赛)右图中的一个长方形纸板每个角上都被切掉了一个小长方形(含正方形),如果被切掉的小长方形的8对对边的长度分别是一个1, 四个2, 两个3和一个4, 那么纸板剩下部分的面积最大是多少?(2012IMC新加坡决赛)选择对应的展开图。
数论(2012希望杯一试)只能被1和它本身整除的自然数叫做质数,如:2,3,5,7,等。
那么,比40大并且比50小的质数是,小于100的最大的质数是。
(2012希望杯一试)有一筐桃子,4个4个地数,多2个;6个6个地数,多4个;8个8个地数,少2个,已知这筐桃子的个数不少于120,也不多于150,则这筐桃子共有个。
2012年少年奥林匹克数学竞赛海峡两岸邀请赛复赛参考答案

2012年奥林匹克数学竞赛海峡两岸邀请赛试题参考答案三年级:一、填空。
1、7 31 13 8、22、北400 9、243、6 5 10、644、20 32 11、4505、35 12、浙A79366、5 13、1607、.丙14、58015、4064二、解答题。
16、=42÷2-55÷5-48÷6=21-11-8=10-8=217、(241+3×90)÷7=73(页)18、19、(97+2)×4=396(分)97×3=291(分)396-291=105(分)20、80-20=60(元)60+2×10=80(元)赔了80元四年级:一、填空1、695007.6万2、45或503、8.04 7.954、10 1005、125×(100-2)6、827、52 8、6 60 5.79、普通票32 10、2011、0.38 12、803000.313、17 9 14、2815、60二、解答题。
16、=46.53-6.53-4.96+427-27×10=40-4.96+427-270=35.04+157=192.0417、∠6=∠1+∠4=41°+29°=70°∠2=120°—∠6=120°—70°=50°18、(450.5—30.7×7—30.5)÷7=29.3(米/分)19、800÷4=200(棵)200×3=600(棵)20、周、钱、赵、孙、李依次入住106、109、105、107、103,所以ABCDE是69573一、填空题1、20072、93、84、65、246、43 7、6 8、9043 9、1911 10、3 81 11、5 12、2413、11 14、12、36、77和18、56、33 15、31216、21+61+121+201+301+……+99001 =1-21+21-31+31-41+41-51+51-61+……+991-1001=1-1001=10099二、解答题 17、 45.6÷4=11.4(平方厘米) 11.4÷3.8=3(厘米) 3+3.8=6.8(厘米) (3×3+3×6.8+3×6.8)×2=99.6(平方厘米)18、 1×2÷4=0.5(平方厘米) 0.5÷(4×2)=16119、 乙车:(1800+200)÷(2+1+1)=500(千克) 甲车:500×2=1000(千克) 丙车:500-200=300(千克)20、 一头牛和一只羊每天共吃:(136+106)÷(8+3)=22(千克) 三头牛和三只羊每天共吃:22×3=66(千克) 一头牛一天吃:(136-66)÷(8-3)=14(千克) 一只羊一天吃:22-14=8(千克)一、填空题:1、432、83、404、4005、366、5:67、45.5 25.5 8、39、95 10、8:6:15 11、8 12、3:1 13、40 14、360 15、20二、解答题:16、设每包书X本。
第四届两岸四地精英赛一试试题和答案(小学高年级组)

第四届两岸四地华罗庚金杯少年数学精英邀请赛笔试一试卷和答案(小学高年级组)共12题,每题10分1. 计算185292[(4.32 1.681)]162511735+--⨯-÷= .2. 今天是13日,如果将若干自然数按下表排列,那么这个表中所有自然数的总和是 . 12 3 4 … 12 13 23 4 5 … 13 14 3 4 5 6 … 14 15 … … … … … … …13 14 15 16 ... (25)3. 一只油桶,装的油占全桶装油量的35,卖出18千克后,还剩原有油的60%。
那么这只油桶能装 千克油.4. 在ABC △中,123D D D 、、为AB 边的内分点,123E E E 、、为AC 边的内分点,那么下图中有 个三角形.5. 两个带小数相乘,将得到的积四舍五入可得27.6 . 现已知这两个小数都是一位小数,且它们个位上都是5,那么这两个小数相乘所得的准确积是 .6. A 、B 两地共有学生81人,其中A 地的第一个学生与B 地的10个学生联系过,第二个学生与B 地的11个学生联系过,第三个学生与B 地的12个学生联系过,…,第n 个学生与B 地的所有学生都联系过. 那么A 、B 两地各有学生.7.有一种八边形,它的每条边的长度都是一个整厘米数. 若从该八边形中取出任意三条边的都不能构成三角形. 则符合这些条件的八边形周长最短是cm.8.在小于2012的所有正整数n中,使得2-能被7整除的n共有2n n个.9.三角形ABC中,1,6,2,2====,三角形BE EF FC BD ADAHG的面积是4.86,三角形GFC的面积是2,则四边形BEHD的面积是.⨯的矩形棋盘(其中,m n为不超过10的正整数),10.由单位正方形组成的m n在棋盘的左下角单位正方形里放有一枚棋子,甲乙两人轮流行棋. 规则是:或者向上走任意多格,或者向右走任意多格,但是不能走出棋盘或者不走. 若规定不能再走者为负(即最先将棋子移至右上角者获胜). 那么能使先行棋的甲m n共有个.有必胜策略的正整数对(,)11.将自然数2、3、4……、n分成两组,满足①同一组任意两个数的乘积不在这个组;②任意一个数与它的平方不在同一组. 则n最大是. 12.一个棱长为4的正方形盒子放一个半径为1的球,球在盒子里随意移动,盒子也可以随意翻动. 则球接触不到的正方体内表面的面积是.答案:1、2—2、21973、754、645、27.566、36,457、548、5769、2.86 10、90 31、31 12、725 12。
2012年秋四校联考期中考试思品试题2

10000 6000 4000 2000思 品 试 题一、单项选择题:(本大题共10小题,每小题2分,共20分。
在各题的四个选项中,只有一项是最符合题意要求的答案。
请将正确的答案写在答题卡相应的位置上)1、一次记者招待会上,有人问杨利伟如何看待航天员这个职业,杨利伟说:“在飞天的征程中充满着风险,但征服太空是航天员的神圣使命,为了国家的航天事业,我们要时刻准备奉献和牺牲。
”这体现了杨利伟:①面对责任不言代价与回报 ②主动为国分忧,勇担重任③信守承诺,勇担过错 ④具有强烈的社会责任感A 、①②③B 、②③④C 、①②④D 、①②③④2、“我愿是一片晶莹剔透的雪花,在寒冷的夜空中飞舞,停留在你心灵的窗户,为你的梦添上绚丽的色彩;我愿是一滴轻柔的雨滴,为你荒漠的心灵送去甘露,滋润你孜孜的期盼,为你的梦送上甜美的祝愿。
”诗的寓意给我们以下启示A 、中学生要学会负责,在承担责任中健康成长B 、中学生要学会负责,承担关爱集体的责任C 、中学生学会负责,有助于实现远大的理想D 、中学生学会负责,有助于获得幸福的生活和有意义的人生3. 经过30多年的不懈努力,深圳迅速从一个边陲小镇发展成为一个现代化大城市,综合经济实力跃居全国大中城市前列。
这充分证明了A .改革开放是发展进步的活力源泉B .经济特区制度是我国的基本经济制度C .对外开放是我国一切工作的中心D .“一国两制”方针具有强大的生命力4. “70年代吃饱,80年代吃味道,90年代吃品质,今天我们吃健康。
”这一时代变迁反映了我国人民生活水平的不断提高。
这得益于我国①坚持改革开放,走富国强民之路 ②大力引进外资,立足国外谋发展③实施科教兴国战略和人才强国战略 ④坚持以经济建设为中心,大力发展社会生产力A .①②③B .②③④C .①③④D .①②④5. 2011年4月28 日,我国第六次全国人口普查结果公布,右图是 “历次普查每10万人拥有的大学文化程度人口”的有关数据,从中可以看出A .我国是世界上人口最多的国家B .我国的人口素质有了较大的提高C .我国的人口形势己发生根本性的变化D.我国的人口增速趋缓,计划生育基本国策取得显著成效6. 2011年4月某市开展“五治三化”(治路、治尘、治污、治水、治乱,绿化、亮化、美化)为重点的城乡环境综合治理,为招商引资营造良好的环境,加快经济发展。
2012月12月四级考试真题(第二套)作文及听力答案解析

2012年12月四级考试真题(第二套)作文及听力答案解析Part I WritingPart III Listening Comprehension Section A11. W: I just heard about a really beautiful park in theeast end of the town. There are a lot of rosesin bloom.M: Why don’t we walk over there and see for ourselves?Q: What will the speakers probably do? 11.【听前预测】选项描述的都是人的行为动作,由重复出现的to the park推测,本题可能考查去公园做某事。
【解析】选D)。
对话中女士说城市东头有一座漂亮的公园,很多玫瑰花正盛开,男士回答:“我们为什么不走过去欣赏一下呢”。
由此可知,男士和女士将去公园赏花,故答案为D)。
Why don’t we…?是提建议的常用句式。
12. M: My presentation is scheduled for 9:30tomorrow morning at the lecture hall. I hopeto see you there.W: Oh, sorry. I was about to tell you that I have an appointment with my dentist at 9:00o’clock tomorrow.Q: What do we learn about the woman? 12.【听前预测】选项中的talk和presentation提示,对话与演讲有关。
选项均以She开头,结合She is going to meet the man推测,本题考查的是女士的情况,女士的话为听音重点。
【解析】选C)。
第四届“两岸四地”少年儿童数学邀请赛

第四屆“兩岸四地”少年兒童數學邀請賽四年級個人賽決賽詴題(時間:2008年6月28日9∶00~10∶30)一、填空題:(將正確答案填在每題的括弧裏,每題6分,共60分。
)1、七個小隊共種樹100棵,各小隊種的棵數都不同,其中種樹最多的小隊種了18棵,種樹最少的小隊至少種了()棵。
2、如果一個整數與1、2、3這三個數通過加、減、乘、除運算組成算式(可以添加括弧),結果等於24,那麼這個整數就稱為“可用整數”,那麼在4、5、6、7、8、9、10這七個整數中,有()個“可用整數”。
3、有八個球編號是①至⑧,其中有六個球一樣重,另外兩個球都輕1克,為了找出這兩個輕球,用天平稱了三次,結果如下:第一次:①+②比③+④重;第二次:⑤+⑥比⑦+⑧輕,第三次: ①+③+⑤與②+④+⑧一樣重.那麼,兩個輕球的編號是( )和( )。
4、每次考詴滿分是100分,小明4次考詴的平均成績是89分,為了使平均成績儘快達到94分(或更多),他至少要再考( )次。
5、用0、5、1、2這四個數位,可以組成很多個不同的四位數,將這些四位數從大到小排列,2105是第()個。
6、一個國家的居民不是騎士就是無賴,騎士不說謊,無賴永遠說謊。
我們遇到該國A 與B兩位居民,B對我們說:“A和我不同;一個是騎士,一個是無賴。
”請問A是騎士還是無賴?答:()7、歡歡沿長和寬相差10米的長方形花壇跑了3圏,共跑了480米,問這個花壇的面積是()平方米。
8、將一盒餅乾平均分給三個小朋友,每人吃了八塊後,這時三個小朋友共剩的餅乾數正好和開始1個人分到的同樣多,那麼每個小朋友分到()塊。
9、三個人外出野炊,甲買了4千克食物,乙買了5千克食物,丙沒有買食物,假設平均每千克食物的價錢一樣,為了使三個人平均分擔這次費用,丙拿出了18元錢。
那麼在這些錢中,甲應得()元;乙得()元。
10、根據下式寫出除法算式:( )÷( )=( )。
二、簡答題:(要求寫出簡要的解答過程,每題8分,共16分。
2008年第4届“两岸四地”少年儿童数学邀请赛夏季赛决赛试卷(六年级个人赛)

2008年第4届“两岸四地”少年儿童数学邀请赛夏季赛决赛试卷(六年级个人赛)2008年第4届“两岸四地”少年儿童数学邀请赛夏季赛决赛试卷(六年级个人赛)一、填空题:(将正确答案填在每题的括号里,每题6分,共60分.)1.(6分)÷2=_________.2.(6分)一个同学把他的生日的月份乘以31,日期乘以12,然后加起来的和是170,那么,这位同学的生日是_________月_________日.3.(6分)有一列数、、、、、…,请问第2008个数是_________.4.(6分)18世纪末,有人提出十进制钟的想法,这种钟每天有10“小时”,每小时有100“分钟”.假定这种钟从午夜0:00开始转动,在我们常见的钟到达早上9点时,它显示的时间是_________.5.(6分)有一个数除以5余数是2,除以7余数是3,这个数除以35的余数是_________.6.(6分)有一天,唐僧师徒四人来到一个被称为“长寿岛”的地方,迎面走来一位青年,他自称有101岁了,孙悟空灵机一动,出了几道算术题给他算:1+1=?;1+1+1=?;1+1+1+1=?;2×3=?.这位青年的计算结果是:1+1=2,1+1+1=3,1+1+1+1=4,2×3=10.孙悟空仰天一笑,大声说,我知道你是_________岁.7.(6分)从1~16这16个数中挑出15个数填入图中的小方格中,使每一横行五数之和相等,使每一竖列三数之8.(6分)有三个数字能组成6个不同的三位数.这6个三位数的和是2442,则这6个三位数中最小的三位数是_________.9.(6分)在长方形ABCD中,E是AD边上的三等分点,DE=2AE,BD、CE将长方形分成四部分,两个三角形的面积已给出,则阴影部分的面积是_________.10.(6分)某校六年级原有两个班,现在要重新编为三个班.将原一班的与原二班的组成新一班,将原一班的与原二班的组成新二班,余下的30人组成新三班.如果新一班的人数比新二班的人数多10%,那么原一班人数有_________人.二、简答题:(要求写出简要的解答过程,每题8分,共16分.)11.(8分)在桌面上摆有一些大小一样的小正方体木块,从前往后看如图1,从右往左看如图2,要摆出这样的图形,最多能用多少块小正方体木块?最少需要多少块小正方体木块?12.(8分)某城市南北走向的地铁1号线与东西走向的地铁2号线恰好相互垂直,如图,某时刻甲列车恰好从B 站出发向北开去,乙列车恰好从A站出发向西开去,4分钟后,它们离A站的距离相等;如果它们不停顿地继续行驶,再过24分钟它们离A站的距离又会相等,已知乙列车的速度是每分钟1.5千米,问AB两站的距离是多少千米?三、详解或论述题:(要求写出详细的解答或论述过程,每题12分,共24分.)13.(12分)如图,若规定对图1中任意一行或一列中的数字都同时加1或减1算作一次操作,如果经过若干次操作后,图1变成了图2,问图2中“育”字代表什么数?14.(12分)一个正三角形ABC的边长为10厘米,现将相邻的两条边各平均分成20等份,然后把对应的等分点连起来,请问连起来的线段总长是多少厘米?2008年第4届“两岸四地”少年儿童数学邀请赛夏季赛决赛试卷(六年级个人赛)参考答案与试题解析一、填空题:(将正确答案填在每题的括号里,每题6分,共60分.)1.(6分)÷2=.÷故答案为:2.(6分)一个同学把他的生日的月份乘以31,日期乘以12,然后加起来的和是170,那么,这位同学的生日是2月9日.y=3.(6分)有一列数、、、、、…,请问第2008个数是.故答案为:4.(6分)18世纪末,有人提出十进制钟的想法,这种钟每天有10“小时”,每小时有100“分钟”.假定这种钟从午夜0:00开始转动,在我们常见的钟到达早上9点时,它显示的时间是3:75.5.(6分)有一个数除以5余数是2,除以7余数是3,这个数除以35的余数是17.6.(6分)有一天,唐僧师徒四人来到一个被称为“长寿岛”的地方,迎面走来一位青年,他自称有101岁了,孙悟空灵机一动,出了几道算术题给他算:1+1=?;1+1+1=?;1+1+1+1=?;2×3=?.这位青年的计算结果是:1+1=2,1+1+1=3,1+1+1+1=4,2×3=10.孙悟空仰天一笑,大声说,我知道你是37岁.7.(6分)从1~16这16个数中挑出15个数填入图中的小方格中,使每一横行五数之和相等,使每一竖列三数之8.(6分)有三个数字能组成6个不同的三位数.这6个三位数的和是2442,则这6个三位数中最小的三位数是128.+++9.(6分)在长方形ABCD中,E是AD边上的三等分点,DE=2AE,BD、CE将长方形分成四部分,两个三角形的面积已给出,则阴影部分的面积是11.ADAD×=AD10.(6分)某校六年级原有两个班,现在要重新编为三个班.将原一班的与原二班的组成新一班,将原一班的与原二班的组成新二班,余下的30人组成新三班.如果新一班的人数比新二班的人数多10%,那么原一班人数有48人.﹣)()二、简答题:(要求写出简要的解答过程,每题8分,共16分.)11.(8分)在桌面上摆有一些大小一样的小正方体木块,从前往后看如图1,从右往左看如图2,要摆出这样的图形,最多能用多少块小正方体木块?最少需要多少块小正方体木块?12.(8分)某城市南北走向的地铁1号线与东西走向的地铁2号线恰好相互垂直,如图,某时刻甲列车恰好从B 站出发向北开去,乙列车恰好从A站出发向西开去,4分钟后,它们离A站的距离相等;如果它们不停顿地继续行驶,再过24分钟它们离A站的距离又会相等,已知乙列车的速度是每分钟1.5千米,问AB两站的距离是多少千米?①×﹣三、详解或论述题:(要求写出详细的解答或论述过程,每题12分,共24分.)13.(12分)如图,若规定对图1中任意一行或一列中的数字都同时加1或减1算作一次操作,如果经过若干次操作后,图1变成了图2,问图2中“育”字代表什么数?14.(12分)一个正三角形ABC的边长为10厘米,现将相邻的两条边各平均分成20等份,然后把对应的等分点连起来,请问连起来的线段总长是多少厘米?菁优网 ©2010-2014 菁优网参与本试卷答题和审题的老师有:xuetao ;似水年华;languiren ;王亚彬;WX321;whgcn ;林清涛;李斌;nywhr ;齐敬孝(排名不分先后)菁优网2014年7月4日。
小高第五届两岸四地赛答案详解

如图,连结点 A,F,易知四边形 ABEF 为长方形。对角线 AE 被 DH 平分,即 AO=OE.
作 OI 垂直 BE,垂足为点 I. 可得 OI 为长方形宽的一半,为 60÷2=30,即 OI=30.(高)
正八边形中,每个内角是(8-2)×180°÷8=135°,长方形中∠BEF=90°,所以∠JED=135° -90°=45°,∠JDE=135°÷2=67.5°,∠DJE=180°-45°-67.5°=67.5°,所以△JDE 为等腰三角形,JE=DE=60.(底)
,化简之后可得
,其中
.
因为
都为质数,所以 r 不可能为 p 的因数,所以 r 为 291 的因数。291 因式分解得 ,然后分类讨论:
12
A3=3+
6
6
32 52
=3.145
6
12
A4=3+
6
6
32 52
6 72
=3.139
6
12
A5=3+
6
6
6
32
52
6
7
2
92
=3.143
6
12
A6=3+
6
6
6
32
52
72
6
6
92 112
6
=3.141
观察发现,每两个数字都是上下波动的,但是波动的幅度逐渐减小,A1、A2 介于 3.167 与 3.133 之间,A3、A4 介于 3.145 与 3.139 之间,A5、A6 介于 3.143 与 3.141 之间,由此可以 得出规律 A7、A8 一定是 3.141 与 3.143 之间。所以 An×100 最接近的整数是 314。
2012年秋四校联考期中考试物理试题2

2012秋季九年级第五次月考物理试题一、选择题(3×9=27)1.张亮收看电视直播北京奥运会百米赛跑决赛,看到运动员跑到终点后,不能立即停下来,这是因为运动员A.失去了惯性B.具有惯性C.不受力的作用D.惯性大于阻力2.我们常用“鸡蛋碰石头”来形容对立双方的势力悬殊非常大,鸡蛋(弱者)很容易被碰的“头破血流”,而石头(强者)却完好无损,对此现象的正确解释是()A.鸡蛋受到力的作用,而石头没有受到力的作用B.鸡蛋受到较大的力的作用,石头受到较小力的作用C.它们相互作用力大小一样,只是石头比鸡蛋硬D.以上说法都不对3.图3所示的四种情境中,所使用的杠杆属于费力杠杆的是()4、用托盘天平测量物体质量时,向右移动游码的作用是()A相当于向左调节平衡螺母 B可代替指针用来指示平衡C相当于在右盘中加小砝码 D移动游码,使指针指在分度盘中线5.质量相等的两只降落伞,甲以3m/s的速度匀速下降,乙以5m/s的速度匀速下降,在下降的过程中()A.甲伞受到的阻力大B.乙伞受到的阻力大C.两只伞受到的阻力一样大D.无法确定6.铅笔盒静止在水平桌面上,以下属于一对平衡力的是A.铅笔盒受到的重力与地面对桌子的支持力B.铅笔盒受到的重力与铅笔盒对桌面的压力C.铅笔盒对桌面的压力与桌面对它的支持力D.铅笔盒受到的重力与桌面对铅笔盒的支持力7、下列关于力的说法中正确的是( )A、水往低处流说明重力的方向是垂直向下的B、如果物体只受一对平衡力的作用,则物体只能沿力的方向运动C、投球时,手的推力使篮球在空中继续飞行D、用力提起一桶水感到手臂被向下拉说明物体间力的作用是相互的8、如图所示的简单机械,忽略各种摩擦及杠杆和滑轮的重力,当提起相同的重物时,最省力的是()9.水平放在水平地面上的一块砖,沿竖直方向切去一半,则剩下的半块【】A.质量减少一半,密度减少一半,对地压强减半;B.质量减少一半,密度不变,对地压强不变;C.密度减少一半,对地压力减少一半,对地压强不变;D.以上的说法均不正确;二、填空与作图(10——14题每空1分,15、16题每题3分,共17分)10.推土机它的履带做得宽大是为了对地面的压强,土铲做得锋利是为了对被铲物体的压强.(填增大或减少)11、和大多数物质一样,汽油也有热胀冷缩的性质,随着气温的下降,汽油密度会_______________(选填“变大”或“变小”),受此因素影响,在每吨汽油价格不变的情况下,每升(每立方分米)汽油的价格会______________(选填“上调”或“下调”)。
第四届两岸四地“华罗庚金杯”少年数学精英邀请赛试卷(小高组一试)

2012年第四届两岸四地“华罗庚金杯”少年数学精英邀请赛试卷(小高组一试)一.填空题(每题10分)1.(10分)计算:2+[(4.32﹣1.68﹣1)×﹣]÷1=.2.(10分)今天是13日,如果将若干自然数按下表排列,那么这个表中所有自然数的总和是.1 2 3 4 …12 132 3 4 5 …13 143 4 5 6 …14 15…………………13 14 15 16 (25)3.(10分)一只油桶,装的油占全桶装油量的,卖出18千克后,还剩原有油的60%.那么这只油桶能装千克油.4.(10分)在△ABC中,D1、D2、D3为AB边的内分点,E1、E2、E3为AC边的内分点,那么图中有个三角形.5.(10分)两个带小数相乘,将得到的积四舍五入可得27.6.现已知这两个小数都是一位小数,且它们个位上都是5,那么这两个小数相乘所得的准确积是.6.(10分)A、B两地共有学生81人,其中A地的第一个学生与B地的10个学生联系过,第二个学生与B地的11个学生联系过,第三个学生与B 地的12个学生联系过,…,第n个学生与B地的所有学生都联系过.那么A、B两地各有学生.7.(10分)有一种八边形,它的每条边的长度都是一个整厘米数.若从该八边形中取出任意三条边的都不能构成三角形.则符合这些条件的八边形周长最短是cm.8.(10分)在小于2012的所有正整数n中,使得2n﹣n2 能被7整除的n共有个.9.(10分)三角形ABC中,BE=1,EF=6,FC=2,BD=2AD,三角形AHG 的面积是4.86,三角形GFC的面积是2,则四边形BEHD的面积是.10.(10分)由单位正方形组成的m×n的矩形棋盘(其中m,n为不超过10的正整数),在棋盘的左下角单位正方形里放有一枚棋子,甲乙两人轮流行棋.规则是:或者向上走任意多格,或者向右走任意多格,但是不能走出棋盘或者不走.若规定不能再走者为负(即最先将棋子移至右上角者获胜).那么能使先行棋的甲有必胜策略的正整数对(m,n)共有个.11.(10分)将自然数2、3、4…、n分成两组,满足①同一组任意两个数的乘积不在这个组;②任意一个数与它的平方不在同一组.则n最大是.12.(10分)一个棱长为4的正方形盒子放一个半径为1的球,球在盒子里随意移动,盒子也可以随意翻动.则球接触不到的正方体内表面的面积是.2012年第四届两岸四地“华罗庚金杯”少年数学精英邀请赛试卷(小高组一试)参考答案与试题解析一.填空题(每题10分)1.(10分)计算:2+[(4.32﹣1.68﹣1)×﹣]÷1=2.【分析】先把小括号里面的算式,根据减法的性质简算;然后再根据四则混合运算的运算顺序计算即可.【解答】解:2+[(4.32﹣1.68﹣1)×﹣]÷1=2+{[4.32﹣(1.68﹣1)]×﹣}÷1=2+{[4.32﹣3]×﹣}÷1=2+{1.32×﹣}÷1=2+{0.6﹣}÷1=2+÷=2+=2;故答案为:2.2.(10分)今天是13日,如果将若干自然数按下表排列,那么这个表中所有自然数的总和是2197 .1 2 3 4 …12 132 3 4 5 …13 143 4 5 6 …14 15…………………13 14 15 16 (25)【分析】根据高斯求和公式可知,第一列的数和是(1+13)×13÷2=7×13,第二行的数和是(14+2)×13÷2=8×13,第三行的数和是(3+15)×13÷2=9×13,由于可发现,n行的数和是(7+n﹣1)×13,所以13行所有数的和是7×13+8×12+…+(7+13﹣1)×13=[7+8+9+…+(7+13﹣1)]×13=[(7+13﹣1)+7)×13÷2×13.据此完成【解答】解:(1+13)×13÷2+(14+2)×13÷2+(3+15)×13÷2+…+(13+25)×13÷2=14×13÷2+16×13÷2+18×12÷2+…+38×13÷2=7×13+8×13+9×13+…+19×13=(7+8+9+…+19)×13=(7+19)×13÷2×13=26×13÷2×13=13×13×13=2197答:那么这个表中所有自然数的总和是2197.故答案为:2197.3.(10分)一只油桶,装的油占全桶装油量的,卖出18千克后,还剩原有油的60%.那么这只油桶能装75 千克油.【分析】先把原来油的质量看成单位“1”,卖出18千克后,还剩原有油的60%,那么卖出的质量就是原来油质量的(1﹣60%),它对应的数量是18千克,根据分数除法的意义,用18千克除以(1﹣60%)即可求出原来油的质量,这又是全桶装油量的,再把全桶装油量看成单位“1”,再根据分数除法的意义,用原来油的质量除以即可求出这个油桶能装多少千克油.【解答】解:18÷(1﹣60%)=18÷40%=45(千克)45÷=75(千克)答:这只油桶能装 75千克油.故答案为:75.4.(10分)在△ABC中,D1、D2、D3为AB边的内分点,E1、E2、E3为AC边的内分点,那么图中有64 个三角形.【分析】在三角形BCD1中有4+3+2+1=10个三角形;如果不看CD3,在BCD2中也有10个三角形;如果不看CD3、CD2,在BCD1中同样有10个三角形;如果不看CD3、CD2、CD1在BCA有10个三角形;在D2D3C中有4个三角形;在D2D1C中有4个三角形;在D1CA中4个三角形;在D1D3C中除了前面数出的还有4个三角形;在D2AC中除了前面数出的还有4个三角形;在D3AC 除了前面数出的还有4个三角形.【解答】解:4×10+4×6=64(个)故填645.(10分)两个带小数相乘,将得到的积四舍五入可得27.6.现已知这两个小数都是一位小数,且它们个位上都是5,那么这两个小数相乘所得的准确积是27.55 .【分析】首先根据个位数字是5,那么两个5乘积的结果个位也一定是5,再根据四舍五入的规律即可求解.【解答】解:依题意可知:首先根据两个小数的结果是2位小数,个位数字都是5,那么原来结果的尾数一定是5;根据四舍五入的结果是27.6,那么只能是27.55满足条件.故答案为:27.556.(10分)A、B两地共有学生81人,其中A地的第一个学生与B地的10个学生联系过,第二个学生与B地的11个学生联系过,第三个学生与B 地的12个学生联系过,…,第n个学生与B地的所有学生都联系过.那么A、B两地各有学生36人、45人.【分析】按题意,显然A地的第一个学生与B地的10个学生联系过,第二个学生与B地的11个学生联系过,第三个学生与B地的12个学生联系过,…,第n个学生与B地的所有学生都联系过,A地的学生比B地的学生要少9人,而总数是81人,可以用总数减去9,就是A地学生人数的两倍,不难求得A地和B地的学生人数.【解答】解:根据分析,A地的学生比B地的学生要少9人,而总数是81人,可以用总数减去9,就是A地学生人数的两倍,故A地有:(81﹣9)÷2=36(人);B地有:81﹣36=45(人),故答案是:36人、45人.7.(10分)有一种八边形,它的每条边的长度都是一个整厘米数.若从该八边形中取出任意三条边的都不能构成三角形.则符合这些条件的八边形周长最短是54 cm.【分析】斐波那契数列,这个数列从第三项开始,每一项都等于前两项之和,任意取3个数为三条边的都不能构成三角形,即可得出结论.【解答】解:由题意,八边形的边长满足斐波那契数列,符合这些条件的八边形周长最短时,边长为1,1,2,3,5,8,13,21,周长为54cm.故答案为54.8.(10分)在小于2012的所有正整数n中,使得2n﹣n2 能被7整除的n共有576 个.【分析】2n﹣n2 被7除的余数随着n变化的最小周期是3,这个你可以直接计算试一试知道.n从1开始,2n﹣n2 被7除的余数是2,4,1,2,4,1,…2n﹣n2 被7除的余数随着n变化的最小周期显然是7.n从1开始,2n﹣n2 被7除的余数是1,4,2,2,4,1,0,.总的来说,因为3和7互质,所以2n﹣n2 2被7除的余数以3×7=21为周期.在一个周期中,3除n余1的,7除n可以余3和4,分别对应数10和4;3除n余2的(此时2n﹣n2 被7除余4),7除n可以余2和5,分别对应数2和5;3除n余0的(此时2n﹣n2 被7除余1),7除n可以余1和6,分别对应数15和6.由上面的讨论,所有使得2n﹣n2能被7整除的正整数n为2,4,5,6,10,15以及它们加上整数倍的21.有了这个结果后不难得出在小于2012的所有正整数中,因为2012=21×95+17这样的n有95×6+6=576个,据此解答.【解答】解:因为2n﹣n2 被7除的余数随着n变化的最小周期是3,n从1开始,2n﹣n2 被7除的余数是2,4,1,2,4,1因为3和7互质,所以2n﹣n2 被7除的余数以3×7=21为周期.7除n可以余2和5,分别对应数2和5;3除n余0的(此时2n﹣n2 被7除余1),7除n可以余1和6,分别对应数15和6综上所述:所有使得2n﹣n2能被7整除的正整数n为2,4,5,6,10,15以及它们加上整数倍的21.有了这个结果后不难得出在小于2012的所有正整数中,因为2012=21×95+17这样的n有95×6+6=576个,故答案为:576.9.(10分)三角形ABC中,BE=1,EF=6,FC=2,BD=2AD,三角形AHG 的面积是4.86,三角形GFC的面积是2,则四边形BEHD的面积是 2.86 .【分析】连接BH,FH,分析各个三角形之间的面积关系,求出各个面积大小.【解答】解:连接BH,FH,由题意△BEH、△EFH、△CFH之间的面积比是2:6:1由BD=2AD,可得△CBD的面积是△CAD的2倍,△DBH的面积是△DAH的2倍,由这两个条件可得△BHC的面积是△AHC的面积的2倍.把△BHC的面积看成9份,那△AHC的面积就是9÷2=4.5份如果把△AHC看成底边是AG的两个三角形面积和,把△CHF看成底边是FG 的两个三角形之和,那么△AHC与△CHF的面积比就等于AG:FG,也就是4.5:2=9:4根据AG:FG=9:4和△AHG的面积是4.86,可以求出△HGF的面积是4.86÷9×4=2.16因为△CFG的面积是2.16+2=4.16,所以△BEH的面积是4.16÷2=2.08AH:HE=4.5:8=9:16所以三角形ABD的面积就是2.08÷16×9=1.17根据AD:BD=1:2得到BDH的面积=1.17÷3×2=0.78所以四边形BEHD的面积是0.78+2.08=2.8610.(10分)由单位正方形组成的m×n的矩形棋盘(其中m,n为不超过10的正整数),在棋盘的左下角单位正方形里放有一枚棋子,甲乙两人轮流行棋.规则是:或者向上走任意多格,或者向右走任意多格,但是不能走出棋盘或者不走.若规定不能再走者为负(即最先将棋子移至右上角者获胜).那么能使先行棋的甲有必胜策略的正整数对(m,n)共有90 个.【分析】当M=N时,先走的甲必须会败;当M不等于N,甲可以通过独到的策略回到棋盘一,导致乙先,乙会败.有10种甲会败,有100﹣10=90种甲会胜利.【解答】解:假设甲先走,乙后走,首先容易知道M=N=1时,甲必败,下面我们归纳证明当M=N时,甲必败,首先M=N=1的情形是显然的.假设M=N≤K时,甲必败,则当M=N=K+1时,假设甲第一步往任意一个方向走X步,则乙便往另外一个方向走X步.若X=K+1,易知此时已经走到右上角,所以甲已经败了,否则X<K+1,这样就就变成了重新在一个(K+1﹣X,K+1﹣X)的棋盘上行棋.这里1≤K+1﹣X≤K,而此时刚好也轮到甲行棋,由归纳假设知此时甲必败,所以结果仍然是甲必败.这样就完成了证明.下面看当M不等于N时的情形,假设M>N (M<N同理),甲可以第一步直接将棋子沿长为M的方向走M﹣N步这样就变成了重新在一个(N,N)棋盘上行棋,且此时轮乙行棋,由上面的结论知此时乙必败,即甲必胜.综上知要使先走的甲必胜,那么只需要M不等于N即可.即满足这样的正整数对有10×10﹣10=90对.故答案为90.11.(10分)将自然数2、3、4…、n分成两组,满足①同一组任意两个数的乘积不在这个组;②任意一个数与它的平方不在同一组.则n最大是31 .【分析】若2在第一组,则4在第二组,16在第一组,8只能在第二组,此时32既不能在第一组,也不能在第二组,故n的最大值不超过31,即可得出结论.【解答】解:若2在第一组,则4在第二组,16在第一组,8只能在第二组,此时32既不能在第一组,也不能在第二组,故n的最大值不超过31.当n=31时构造如下:(2,3,5,7,11,13,16,17,19,23,24,29,31)和(4,6,8,9,10,12,14,15,18,20,21,22,25,26,27,28,30),所以n最大为31.故答案为31.12.(10分)一个棱长为4的正方形盒子放一个半径为1的球,球在盒子里随意移动,盒子也可以随意翻动.则球接触不到的正方体内表面的面积是72 .【分析】先单独看一个面,因为球半径1,所以这个面最外1单位长度宽的一圈,球是接触不到的,球只能接触到中间的2单位长度的正方部分,接触到的面积4平方分米,接触不到的部分是16﹣4=12,由此即可解决问题.【解答】解:先单独看一个面,因为球半径1,所以这个面最外1单位长度宽的一圈,球是接触不到的,球只能接触到中间的2单位长度的正方部分,接触到的面积4平方单位,接触不到的部分是16﹣4=12,六个面一共12×6=72平方单位,故答案为:72.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/7 10:44:13;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
2020年第四届两岸四地“无悔金杯”少年数学精英邀请赛小学组试卷(五年级)

2012年第四届两岸四地“华罗庚金杯”少年数学精英邀请赛小学组试卷(五年级)一、填空题:(把答案填入括号内,不用写过程.每题7分,共63分.)1.(7分)计算:123×32×125=.2.(7分)爱尔兰作家刘易斯曾写过一篇反讽寓言,文中描述了一个名为尼亚特泊的野蛮国家.在这个国家里使用西巴巴数字.西巴巴数字的形状与通用的阿拉伯数字相同,但含义相反.如“0”表示“9”,“1”表示“8”,以次类推.他们写数字是从左到右,使用的运算符号也与我们使用的一样.例如,他们用62代表我们所写的37.按照尼亚特泊人的习惯,应怎样写837+742的和是.3.(7分)7×17×27×37×47×57×67×77×87×97积的个位数字是.4.(7分)后羿朝三个箭靶分别射了三支箭,如图:他在第一个箭靶上得了29分,第二个箭靶上得了43分.请问他在第三个箭靶上得了分.5.(7分)有一行数:1,1,2,3,5,8,13,21,…,从第三个数开始,每个数都是前两个数的和,问在前2007个数中,有是偶数.6.(7分)今年小翔和爸爸、妈妈的年龄分别是5岁、48岁、42岁.年后爸爸、妈妈的年龄和是小翔的6倍.7.(7分)用1,2,3,4,5,6,7,8这八个数字组成两个不同的四位数(每个数字只用一次)使他们的差最小,那么这个差是.8.(7分)将偶数按下图进行排列,问:2008排在第列.2468161412101820222432302826…9.(7分)棱长都是1厘米的63个白色小正方体和1个黑色小正方体,可以拼成一个大正方体,问:一共可以拼成种不同的含有64个小正方体的大正方体.二、简答题:(需要写出简要过程及理由,每小题10分)10.(10分)幼儿园给小朋友派礼物,如果有2人各派4个,其余各派3个,则还剩余11个,如果4人各派3个,其余各派6个,则剩余10个,问一共有多少件礼物?11.(10分)请把12、15、33、44、51、85这六个数平均分成两组,使每组四个数的乘积相等.三、详答或论述题:(写出详细过程、方法及结果.本题17分)12.(17分)一块长方形木板,如果按长、短不同的两组边分别截去4分米,则面积减少了168平方分米,请问:原来长方形的周长是多少分米?2012年第四届两岸四地“华罗庚金杯”少年数学精英邀请赛小学组试卷(五年级)参考答案与试题解析一、填空题:(把答案填入括号内,不用写过程.每题7分,共63分.)1.(7分)计算:123×32×125=492000.【分析】32=4×8,然后再根据乘法交换律和结合律进行简算.【解答】解:123×32×125=123×(4×8)×125=(123×4)×(8×125)=492×1000=492000.故答案为:492000.2.(7分)爱尔兰作家刘易斯曾写过一篇反讽寓言,文中描述了一个名为尼亚特泊的野蛮国家.在这个国家里使用西巴巴数字.西巴巴数字的形状与通用的阿拉伯数字相同,但含义相反.如“0”表示“9”,“1”表示“8”,以次类推.他们写数字是从左到右,使用的运算符号也与我们使用的一样.例如,他们用62代表我们所写的37.按照尼亚特泊人的习惯,应怎样写837+742的和是419.【分析】“0”表示“9”,0+9=9,“1”表示“8”,1+8=9,由此可知西巴巴数字,表示的数字与正常数字的和都是9;由此找出837、742表示的数字,然后相加即可.【解答】解:西巴巴数字8表示阿拉伯数字9﹣8=1,西巴巴数字3表示阿拉伯数字9﹣3=6,西巴巴数字7表示阿拉伯数字9﹣7=2,西巴巴数字4表示阿拉伯数字9﹣4=5,西巴巴数字2表示阿拉伯数字9﹣2=7,所以837+742表示的正常算式为:162+257=419.故答案为:419.3.(7分)7×17×27×37×47×57×67×77×87×97积的个位数字是9.【分析】因为该算式的这10个数的个位都是7,只要判断出10个7相乘的个位数是几即可,先分别求出71、72、73、74、75、76的数值可得出个位数成规律变化,继而可得出答案.【解答】解:71=7,72=49、73=343、74=2401、75=16807、76=117649,所以可得出个位数分别为7、9、3、1且黑豆网https://黑豆网涵盖电影,电视剧,综艺,动漫等在线观看资源!金马医药招商网:金马医药招商网是专业提供医药代理招商的资讯信息发布平台,科技新闻网:科技新闻网每天更新最新科技新闻,这里有最权威的科技新闻资料。
最新首届两岸四地华罗庚金杯少年数学精英邀请赛决赛试题笔试(二)及答案

首届两岸四地华罗庚金杯少年数学精英邀请赛决赛试题笔试(二)及答案一、填空题(每题12分,满分60分)1. 如下数表由从1开始的连续自然数写成,并且每行最右边的一个数都是平方数:则表中第10行所写出的各数的和等于.解:第10行是从82 ~ 100共19个自然数之和:82 + 83 + 84 + …… + 99 + 100 = 808449010451001729⨯++⨯++=.注:计算82 + 83 + 84 + ……+ 99 + 100的方法很多,比如:82 + 83 + 84 + …… + 99 + 100{}1(82100)(8399)(8498)(10082)2=++++++++ 172991182019911918221=-=⨯=⨯⨯= 或 82 + 83 + 84 +…… + 99 +100(118)1810019(1218)19002+⨯=⨯-++=- 190019919001711729.=-⨯=-=2. 图1中,长方形ABCD 的长BC = 10厘米,宽AB = 6厘米. 在BC 上取点M ,在AD 上取点N ,使得四边形BMDN 是一个菱形. 则菱形BMDN 的面积是平方厘米.解:因为BMDN 是一个菱形,可设(图1)BM MD ND BN x ====,则10AN x =-. 在直角三角形ABN 中,由勾股定理得 2226(10)x x +-=,即13620x =,解得 6.8x =. 菱形BMDN 的面积 = 6.8×6 = 40.8(平方厘米).3.100名少年运动员胸前的号码分别是1,2,3,……,99,100. 选出其中的k 名运动员,使得他们的号码数之和等于2008. 那么k 的最大值是.解:显然,选号码越小的,可以使选出的人数越多. 因此,考虑先选前n 名运动员,他们的号码是1~n 的连续自然数,并且号码数之和不超过2008.由于 (1)12320082n n n +++++=≤, 得(1)2008,(1)40162n n n n +≤+≤. ,49007070,36006060=⨯=⨯ 故 n 是二位数,其十位数字是6. 从小到大,逐一试算)1(+n n ,得到401640326463,401639066362>=⨯<=⨯,即选出的运动员不可能多于62人.又因为5519532008,195326362=-=⨯,可以选如下号码的运动员: 1,2,3,…,7,9,…,62,63,这些号码数的和是(1953-8+63)=2008,所以,k 的最大值是62.4. 自然数b 与175的最大公约数记为d . 如果 176(111)51b d d ⨯-⨯+=⨯+, 则b =.解:由于(175,)d b =,d 必为175的约数,而175=5×5×7,所以d 只能取1,5,7,25,35,175中的某一个. 另外由176(111)51b d d ⨯-⨯+=⨯+ 可知 111b d -+为非0自然数, 即1111b d -+≥,因此 5117635.d d +≥⇒≥ 所以d =35或175.将d =35代入176(111)51b d d ⨯-⨯+=⨯+,得b = 385. 将d =175代入176(111)51b d d ⨯-⨯+=⨯+,得 176(111751)51751876b ⨯-⨯+=⨯+=,即44(111751)219b ⨯-⨯+=,左边是偶数,右边是奇数,矛盾!所以d =175不合要求. 所以b = 385.5.华罗庚爷爷说:数学是我国人民所擅长的学科.请小朋友求解《九章算术》中的一个古代问题:“今有木长二丈,围之三尺,葛生其下,缠木七周,上与木齐.问葛长几何?”白话译文:如图2,有圆柱形木棍直立地面,高20尺,圆柱底面周长3尺. 葛藤生于圆柱底部A 点,等距缠绕圆柱七周恰好长到圆柱上底面的B 点. 则葛藤的长度是________ 尺.解:设想从A 点将葛藤剪断,顶点处B 不动,将缠绕的葛藤解开拉直,如图2-1所示:A 点变为地面上的C 点. 则葛藤长为Rt BAC ∆的斜边BC . 由AB =20,AC =21和勾股定理得:2222021BC =+400441=+ = 841=222230601302301(301)29-+=-⨯+=-=. 所以BC =29(尺).答:葛长29尺.二、解答下列各题,要求写出简要过程(每小题15分,满分45分)6. 如图3,摆放2×2的“4宫格”要用12根火柴棍; 摆放3×3的“9宫格”要用24根火柴棍. 小明用1300根火柴棍,恰好摆放成一个m ×m 的“m 2宫格”,问m =?解:在“m 2宫格”中,横向的火柴棍有1+m 行,每行有m 根,共有)1(+m m 根. 同样,纵向的火柴棍有1+m 列,每列有m 根,也共有)1(+m m 根. 所以,摆放“m 2宫格”共用了2m (m +1)根火柴. ……(10分)由2(1)1300m m +=, 得到2(1)65025132526m m +==⨯⨯=⨯,因此25.m =(图3)(图2-1)……(15分)7. 图4中,M 是AB 的中点, N 是BC 上一点,CN= 2BN . 连接AN 交MC 于O 点. 若四边形BMON的面积为14平方厘米, 求:(1)CO ︰OM =?(2)三角形ABC 的面积 = ?解:8. 在1 ~ 30m (其中m 是非零自然数)这些自然数中,(1)能被2整除的合数共有多少个?能被3整除的合数共有多少个?(2)请说明:在1 ~ 30m 这些自然数中,质数的个数不超过10m .解:(1)在1 ~ 30m (其中m 是非零自然数)这些自然数中,被2整除的数有15m个,由于2是质数,所以偶合数共有15m – 1个; ……(3分)被3整除的数有10m 个,由于3是质数,其中的合数有10m – 1个.……(6分)(2)由(1)的结果可知:在1 ~ 30m (其中m = 1,2,3,……)这些自然数中,被2整除的合数有15m – 1个;被3整除的合数有10m – 1个;既被2整除同时又被3整除的数有5m 个,每一个都是合数. ……(9分)(图4)在1 ~ 30m(其中m = 1,2,3,……)这些自然数中,减去15m – 1个偶合数;再减去10m – 1个被3整除的合数,其中被6整除的数减重复了,注意再补回5m个重复减掉的被6整除的合数. 注意,1不是质数也不是合数;此外,对任意非零自然数m,在1 ~ 30m中,25是既不被2整除也不被3整除的一个合数,因而尚未被除去. 所以,再除掉1与25这两个数后,质数包含在剩下部分的数中,因此,质数的个数不会超过剩下部分的数的个数,也就是质数的个数不会超过30(151)(101)5210----+-=……(15分)m m m m m另一解法:从1到30m中,能被2整除的数共有15m个,能被3整除的数共有10m 个,能被5整除的数共有6m个;能被2和3整除的数共有5m个,能被2和5整除的数共有3m个,能被3和5整除的数共有2m个;能被2、3和5整除的数共有m 个.由“包含排除”原理,1到30m中不能被2或3或5整除的数共有(30=)106-+++++-(个)15mmmm5(mm)23m8mm设1到30m中质数的个数为z,因为2、3和5都是质数,1既不是质数也不是合数,因此2m≤mz. 由8210+≤m m,得到1 ~ 30m中,质数的个数-3818+=+不超过10m .三. 解答下列各题,要求写出详细过程(第9题20分,第10题25分,满分45分)9.在A到B的公路段上,每30千米设一个慢车站,每50千米设一个快车站,如果相邻两个车站间的路程大于15千米,则在这段路程的中点设一个维修点. 如果一个车站既是慢车站也是快车站,则在这个车站设一家商店. 已知从A到B共设有7家商店,A和B既是慢车站也是快车站.问:(1)从A到B的路程有多少千米? (2)从A到B的途中共设有多少个维修点?解:(1)计算从A 到B 的路程和快车站、慢车站的站数. 易知A 是第1个商店,其余各商店到A 的路程是30和50的公倍数,而[30,50]=150,B 是第7个商店,所以,从A 到B 的路程是(71)1506150900-⨯=⨯=(千米). ……(8分)(2)途中的5个商店将全路程等分成6等份,每个等份中快车站、慢车站的设置完全相同. 由于A 是第1个商店,因此只要考虑从A 到第2个商店这一段150千米的路程上的快车站与慢车站的分布情况就可以了.设第2个商店为C 点,则AC =150千米. 在AC 这一段上(不包括A,C ),有4个慢车站,2 个快车站,如图所示:绿色□表示快车站,△表示慢车站. 从图上可以看出:相邻两站的路程为30千米的路段有3段;相邻两站的路程为20千米的路段有2段;相邻两站的路程为10千米的路段也有2段. 其中相邻两站的路程大于15千米的路段共有5段,因此在AC 这一路段上应该设有5个维修站点. 从A 到B 全路程上应该设有5630⨯=个维修站点. ……(18分)答:从A 到B 的路程为900千米;途中共设有30个维修站点. ……(20分) 另解:若学生按比例画出示意图,从图中标出A ,B 及快车站、慢车站,商店和维修点,从图中数出全程长900千米;一共设有30个维修站点. 也给满分20分.10. 图5是由16个面积为1的等边三角形组成的一个大的等边三角形,这个大的等边三角形内部及边上共有15个交叉点. 请回答:(1)以这些交叉点为顶点,可以连成多少个等边三角形?(2)所连成的全部等边三角形的面积的总和是多少?解:(1)总计可以连成35个等边三角形.其中:面积是1的等边三角形有16个;面积是4的等边三角形有7个;面积是9的等边三角形有3个;面积是16的等边三角形有1个;……(10分) 利用对称的性质,如图5-1,红色等边三角形的面积是由6个面积是1的等边三角形组成的正六边形面积的一半,等于3,面积是3的等边三角形共有6个;利用对称的性质,如图5-2,蓝色等边三角形的面积是7362116=⨯⨯-, 面积是7的等边三角形共有2个; ……(18分)此外,不能再连成别的等边三角形了.因此,可以连成的等边三角形总计有 16 + 7 + 3 + 1 + 6 + 2 = 35个.……(20分)(2)所连成的全部等边三角形面积的总和等于11647931613672119⨯+⨯+⨯+⨯+⨯+⨯=. ……(25分) 答:可以连成35个等边三角形;所有等边三角形的面积总和是119.(图5-2)。
第四届“两岸四地”少年儿童数学邀请赛六年级

第四届“两岸四地”少年儿童数学邀请赛六年级个人赛决赛试题(时间:2008年6月28日9∶00~10∶30)一、填空题:(将正确答案填在每题的括号里,每题6分,共60分。
)1.718 ×412 +16 1313 -334 ÷3516 ÷278 =( )。
2.小熊把他生日的月份乘以31,日期乘以12,然后加起来的和是170,小熊的生日是( )月( )日。
3.有一列数13 、16 、111 、118 、127、……,请问第2008个数是( )。
4.18世纪末,有人提出十进制钟的想法,这种钟每天有10“小时”,每小时有100“分钟”。
假定这种钟从午夜0∶00开始转动,在我们常见的钟到达早上9点时,它显示的时间是( )。
5.有一个数除以5余数是2,除以7余数是3,这个数除以35的余数是( )。
6.有一天,唐僧师徒四人来到一个被称为“长寿岛”的地方,迎面走来一位青年,他自称有101岁了,孙悟空灵机一动,出了几道算术题给他算:1+1=? 1+1+1=? 1+1+1+1=? 2×3=? 这位青年的计算结果是:1+1=2, 1+1+1=3, 1+1+1+1=4, 2×3=10。
孙悟空仰天一笑,大声说,我知道你是( )岁。
7.从1~16这16个数中挑出15个数填入图中的小方格中,使每一横行五数之和相等,使每一竖列三数之和相等。
8.有三个数字能组成6个不同的三位数。
这6个三位数的和是2442,则这6个三位数中最小的三位数是( )。
9.在长方形ABCD 中,E 是AD 边上的三等分点,DE =2AE , BD 、CE 将长方形分成四部分,两个三角形的面积已给出,则阴影部分的面积是( )。
10.联合学校六年级原有两个班,现在要重新编为三个班。
如将原来一班的13 与原二班的14组成新的一班,将原来一班的14 与原二班的13组成新的二班,余下的30人组成新的三班。
如果新一班的人数比新二班人数多10%,那么原来一班有( )人。
第4届精英赛笔试二试题解答

第四届两岸四地“华罗庚金杯”少年数学精英邀请赛笔试二试题及解答(小学中年级组 )一、填空题(每题 20 分, 共 60 分)1. 某次小学生高年级数学比赛的满分为100 分,小明和小光在比赛中获得了优异成绩 .当小记者采访他们时,小明说:“我的名次、年纪和分数的乘积等于 1067”,小光说:“我的名次、年纪和分数的乘积等于3135”.那么小明和小光两人的均匀分是分.答案:96.解答:1067=11 97 1 11 97.所以小明名次序一,年纪11,得分 97.而 3135=3×5×11×19=3×11×95=5×11×57,只闻名次 3、年纪 11、分数 95 与获得优秀成绩符合 . 所以小光名次序三,年纪 11,得分 95.小明和小光两人的均匀分是96 分.2.右图由 4 个正六边形构成,每个面积都是 6. 以这4 个正六边形的极点为极点,能够连结面积为3的等边三角形的个数共有个.答案:12 个.解答:见下列图,共有 12 个等边三角形,它们的极点是4 个正六边形的极点,而面积为 3.3.小红和小明两人都带了钱想买《兴趣数学》这本书 . 到书店一看,小红带的钱缺 2 元 2 角,小明带的钱缺 1 元 8 角. 而两人带的钱合起来恰巧买一本 . 则《兴趣数学》每本订价元.答案:4 元.解答:依题意,书价 = 小红带的钱+2元2角书价 = 小明带的钱+1元8角书价 = 小红带的钱+ 小明带的钱三个式子比较可知,小红缺的钱,正是小明带的钱;小明缺的钱,也正是小红带的钱 . 所以,小红带钱 1 元 8 角,小明带钱 2 元 2 角 .《兴趣数学》的书价是4元 .二、解答题(每题 20 分, 共 60 分)4.如右图所示,小正方形 EFGH 在大正方形 ABCD 的内部 , 暗影部分的总面积为 124 平方厘米 , E, H 在边 AD上, O 为线段 CF 的中点 . 求四边形 BOGF 的面积,并简述原因 .答案:31 平方厘米 .解答:连结 CG, 设小正方形边长为 a, 大正方形边长为 b.则梯形 BCGF 的面积1(a b)(b a). 2梯形 ABFE 的面积 +梯形 CDHG 的面积1b) AE 1(a (a b) DH2 21( a b) ( A E D H) 1(a b) (b a).2 2所以梯形 BCGF 的面积=梯形 ABFE 的面积 +梯形 CDHG 的面积但梯形 BCGF 的面积 +(梯形 ABFE 的面积 +梯形 CDHG 的面积) =124 所以梯形 BCGF 的面积 =62(平方厘米)但梯形 BCGF 的面积 =△BCF 的面积 +△CGF 的面积=2×△BOF 的面积 +2×△OGF 的面积=2×(△ BOF 的面积 +△ OGF 的面积 )=2 ×四边形 BOGF 的面积所以四边形 BOGF 的面积 = 1梯形BCGF 的面积= 1 62 31 (平方厘米).2 25.设M 772 73 74 75 72009 72010 72011 72012. 试说明:M是100的倍数,并指出 M 倒数第一个非 0 数字是几?( 注:同样的n个自然数的乘积叫做这个自然数的n 次方,如1×1=12,4 6类推)2×2×2×2=2 , 7×7×7×7×7×7=7 ,答案:倒数第一个非0 数字是 4..解答:计算得 71 7, 72 7 7 49, 73 49 7 343, 74 343 7 2401.所以717273747 49 343 2401 2800.末端连续两个0.而M77273747572009720107201172012.(7 727374 ) 74(7 727374)72008(7 727374 ).2800 147872 0 07 2800 2800 28002800 1 74 78 72008,因为1 74 78 72008每一项个位503项503 项数是 1,所以其和是 503 个个位是 1 的数相加,和的个位是 3.M2800 一个个位等于 3的数一个百位为 4十位与个位都为 0 的数 .所以 M 是 100 的倍数, M 倒数第一个非 0 数字是 4.6.安排男女共 10 名学生坐在长椅上 . 能够使得每两个男同学之间坐着偶数个学生,而每两个女同学之间坐着奇数个学生吗?假如能,请举出一例;假如不可以,试说明原因 .答案:不可以 .解答:假定男女共十个学生能实现题设要求的排坐法 . 因为两个女同学之间坐着奇数个学生,可见两个女孩不可以相邻 . 这样一来,至多能坐 5 个女同学 . 又两个相邻的男同学之间有偶数个学生,假如再有第 3 名男同学,则第 3 名男同学与第二名男同学之间有偶数个学生,但与第一个男同学之间却有奇数个学生. 所以,男孩的数目至多 2 人. 总计起来,男女生一同最多排5+2=7 人,与 10 个学生不符 .第四届两岸四地“华罗庚金杯”少年数学精英邀请赛笔试二试题及解答(小学高年级组 )一、填空题(每题 20 分, 共 60 分)1.小红和小明两人都带了钱想买《兴趣数学》这本书 .到书店一看,小红带的钱缺 2 元 2 角,小明带的钱缺 1 元 8 角. 而两人带的钱合起来恰巧买一本 . 则《兴趣数学》每本订价元 .答案:4.解答:依题意,书价 = 小红带的钱+2元2角书价 = 小明带的钱+1元8角书价 = 小红带的钱+ 小明带的钱三个式子比较可知,小红缺的钱,正是小明带的钱;小明缺的钱,也正是小红带的钱 .所以,小红带钱 1 元 8 角,小明带钱 2 元 2 角.《兴趣数学》的书价是4元 .2.如右图所示,小正方形EFGH 在大正方形ABCD 的内部 , 暗影部分的总面积为 124 平方厘米 , E, H 在边积为平方厘米 .答案:31.解答:连结 CG.,设小正方形边长为a, 大正方形边长为 b.则梯形 BCGF 的面积1(a b)(b a). 2梯形 ABFE 的面积 +梯形 CDHG 的面积1(a b) AE 1(a b) DH2 21( a b) ( A E D H) 1(a b) (b a).2 2所以梯形BCGF 的面积=梯形ABFE 的面积 +梯形CDHG的面积但梯形BCGF 的面积 +(梯形ABFE 的面积 +梯形CDHG的面积)=124 所以梯形BCGF 的面积 =62(平方厘米)但梯形BCGF 的面积 =△BCF的面积 +△CGF的面积=2×△ BOF 的面积 +2×△OGF 的面积=2×(△ BOF 的面积 +△ OGF 的面积 )=2 ×四边形 BOGF 的面积所以四边形 BOGF 的面积 =1梯形 BCGF 的面积 = 1(平方厘米) .2 62 3123. 一些边长是 1 的小正方体码放成一个立体, 从上向下看这个立体, 如左下列图,从正面看这个立体,如右下列图 . 在这个立体的体积最大时 , 将这些小正方体码放成一个底面积为 4 的长方体 , 则这个长方体的高是.从上向下看从正面看答案:3.解答 . 体积最大的立体图为共有 12 个小小正方体 , 将这些小正方体码放成一个底面积为 4的长方体时 , 长方体的高是 3.二、 解答题 (每题 20 分, 共 60 分)4.已知两个正整数之和为 432,这两个正整数的最小公倍数与最大条约数之和为 7776. 则这两个正整数的乘积是多少 ?答案:46620解答:设 a 和 b 的最大条约数为 d,且 a=dm,b=dn,则 m 与 n 互质,且 a 和 b 的最小公倍数为 dmn. 由题目的条件可知dm+dn=d(m+n)=432, dmn+d= d(mn+1)=7776.由上边这两个式子可得mn+1=18(m+n),或 mn-18(m+n)+1=0.所以 (m-18)(n-18)=182-1=17 ×19. 不如设 m > n,所以m-18=17 ×19=323,n-18=1,或 m-18=19,n-18=17. 若 m=341,n=19,则 m+n=360,不存在正整数 d 使得 d(m+n)=432 ,所以这组解不切合要求. 若 m=37, n=35,则d=432/(37+35)=6. 所以 a=dm=222,b=dn=210,a 与 b 的乘积为 46620.5.设不一样的字母代表不一样的非零数码,同样的字母代表同样的数码,若AB CB DDD ,且 AB CB,求A,B,C,D.答案:A=2,B=7,C=3,D=9解答:第一AB CB D 111 D 3 37.(*) 因为AB CB 且37 37 1369 是个四位数, 所以37 只好是CB 的因数. 因为CB 是个两位数, CB 只可能是37 或74.AB D 3 且B=7, 得出D=9, A=2. 而A=2,B=7,C=3, 若CB为37,则D = 9 知足题目要求.若CB为74, 则AB 2 D 3,B=4, AB 2 30 . 从而推出 A 只好为1. 而14 不是 3 的倍数 , 所以CB为 74 时, 没有知足题目要求的A, B, C, D.6.奥运会男子足球小组赛,每组四个队进行单循环比赛 . 每场比赛胜队得 3 分,败队得 0 分. 平手时两队各得 1 分. 小组赛所有赛完此后,每组取积分最高的两个队出线进入下轮比赛 (对积分同样的队,按更细规则排序 ). 那么在所有能够出线的状况中 , 一个出线队的得分最少是多少 ? 请说明原因 . 答案:2解答:记四个队为 A, B, C, D.有这样的可能 , A 队的 3 场比赛全胜 , 得 9 分 . 此外三队互相之间的比赛都是平手 , 每队各得 2 分 . 在此种状况下 , 有一个得 2 分的队出线 .另一方面 , 因为共有 6 场比赛 , 四个队的得分之和起码为 12 分, 必有一个队得分许多于 2 分. 假定得分许多于 2 分的队为 D, 因为 A, B, C 三个队之间的比赛共 3 场, 所以这 3 个队的得分之和许多于 6 分 , 此中必有一个队得分许多 2 分, 也就是说 , 起码有两个队得分许多于 2 分. 所以 , 少于 2 分的队不可以能出线 .第四届两岸四地“华罗庚金杯”少年数学精英邀请赛笔试二试题及解答(初一组 )一、填空题 (每题 20 分, 共 60 分)1. 一列数b0, b1, b2, ,拥有下边的规律, b2n 1 b n , b2 n 2 b n b n 1,若 b0 =1.则b2013 的值为.答案 29解答:这道题目主假如依据给定的规则,把后边的数用前方的数来表示出来。
第4届精英赛笔试二试卷初一简E

第四届两岸四地华罗庚金杯少年数学精英邀请赛笔试二试卷 (初一组)(2012年8月14日,60分钟) Fourth Hua Luogeng Golden Cup Juvenile Talents Mathematics Competition Final Test (Junior Middle School) (August 14, 2012,60 minutes) 题号 Number 1 2 3 4 5 6 总成绩 Score 得分 Points 一、填空题(每题20分, 共60分) Fill Blanks (20 points for each, 60 point in total ) 1. 一列数 ,,,210b b b ,具有下面的规律,12212,++++==n n n n n b b b b b ,若0b =1. 则 2013b 的值为 . A sequence of numbers, ,,,210b b b ,has the property: ,2,1,0,,12212=+==+++n b b b b b n n n n n . If 0b =1 then ______2013=b . 2. 甲、乙、丙三个车队于某日共行驶了21600 公里,其中甲车队每辆车平均行驶了325 公里,乙车队每辆车平均行驶了250 公里,丙车队每辆车平均行驶了150公里. 已知丙车队车辆恰好是甲乙两个车队车辆总数的三分之一,则丙车队最多有 辆车. There are three teams of cars A, B and C. In some a day, sum of all distances three teams ran is 21600 km, in which each car of team A ran 325 km in average, 250 km for team B and 150 km for team C. If the number of cars of team C is just one third of the total of teams A and B, then team C has at least _______ cars.学校____________ 姓名_________ 参赛证号 联系电话 电子邮件密 封 线 内 请 勿 答 题 学校____________ 姓名_________ 参赛证号 联系电话 电子邮件 密 封 线 内 请 勿 答 题3.已知两个正整数之和为432,这两个正整数的最小公倍数与最大公约数之和为7776. 则这两个正整数的乘积为_______.Assume that sum of two positive integers is 432, sum of their least common multiple (LCM) and greatest common divisor (GCD) is 7776. Then product of these two positive integers is _______ .二、解答题(每题20分, 共60分)Solve Problems (20 points for each, 60 points in total)4.右图中, 正方形ABCD的面积为1,长方形ABFE,GFCH,IJHD,EKLI的面积分别是长方形ABCD,EFCD,EGHD,EGJI的面积的三分之一,连接,JDKB,,,求四边形BJDK的面积.JBKDIn the figure, area of the square ABCD is 1, areas of the rectangles ABFE,GFCH,IJHD and EKLI are equal to one third of areas of the rectanglesABCD,EFCD, EGHD and EGJI respectively, connect segments KB, JB,BJDK Find the area of BJDK.KD and HD to form a quadrilateral .5. 设不同的字母代表不同的非零数码,相同的字母代表相同的数码,若DDD CB AB =⨯, 且CB AB <, 求 A , B , C , D .Let distinct letters represent distinct nonzero digits, and the same letters the same digits. If DDD CB AB =⨯ and CB AB < hold, find the digits represented by A , B , C , D . 6. 求 |2013||2012|||)1(|3||2||1|1-+--+--++-+---+x x k x x x x k 的最小值. Find the minimum of the algebraic expression |2013||2012|||)1(|3||2||1|1-+--+--++-+---+x x k x x x x k .学校____________ 姓名_________ 参赛证号 联系电话 电子邮件 密 封 线 内 请 勿 答 题。
小高-2014第五届两岸四地华罗庚金杯少年数学精英邀请赛

第五届两岸四地华罗庚金杯少年数学精英邀请赛笔试一解析(小学高年级,时间:60分)一、填空题Ⅰ(每题8分,共32分)1. 算式()()()213579101214161856789⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯ 的计算结果是 . 答案:2供题:桦树湾教育 成俊峰解析:()()()21357910121416185678935733253222722222335522337722222233332⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=2. 今年是2014年,2014不是完全平方数,但可以将它的各位数字改变顺序,使得到的新四位数是完全平方数.例如1024=322.已知用数字2、0、1、4各一个还能组成另一个四位完全平方数,那么这个新的四位完全平方数是 .答案:2401供题:华杯赛北京管委会 陈 平解析:2492401=3. 在不同的历史时期,“斤”和“两”之间的进制不同.成语“半斤八两”就是由16进制而来的.为方便计算,我们认为古代16两是1斤,每斤为现代的600克;现代10两是1斤,每斤为现代的500克.现有一批药品,有一部分按古制称,另一部分按现制称,统计发现,“斤”数和是5,“两”数和是68.那么,这批药品共有 克. 答案:2800供题:桦树湾教育 成俊峰解析:假设全是按照古制称量,5斤是:16580⨯=(两)实际“两”数和是68,所以按现制称量的“斤”数是:(80-68)÷(16-10)=2(斤)所以,这批药品共有:600×3+500×2=2800(克)4. 两个完全相同的正三角形可以拼成一个菱形,如果正三角形的边长为10,则这个菱形内部最大的正方形面积为 .答案:50供题:巨人教育 居思远解析:当正方形如图摆放时,面积最大.面积最大为:1010250⨯÷=二、填空题Ⅱ(每题10分,共40分)5.+++++=6765636132222A ,与A ×100最接近的整数是 . 答案:314供题:学而思培优 孙佳俊 解析:设222221=336567696x+++++原式 , ++=61162x >6, ++=61162x <61162+<27 当x =6时,2222222222221111=3333 3.1429963336666975989556663327766399626+=+=+=+=++++++++++原式当x =27时,222211=33 3.1408927366843564969+=+=++++原式所以与算式计算结果100倍最接近的整数是314.6. 如图所示,由75个小方格组成了15×5的图案,图中一些小方格已经被涂上了阴影,现在要继续把一些空白的小方格涂上阴影,保证任意2×2的方格中阴影小方格的数量都多于一半,那么最少需要再把________个空白小方格涂上阴影.答案:17供题:顺天府学 石 键解析:不存在右图四种情况的相连空白格(即任意两个空白格不存在公共顶点)将空白格分成如图不相连的7块. 其中D 、G 两块为5×1,每块至少需要涂其中2个格子;同理,C 、F 两块,每块至少需要涂其中1个格子.而对于A 块,可分为1块5×1和1块2×1,所以至少需要涂其中2+1=3个格子.B 块与A 块完全相同.而对于E 块,可分为1块5×1和1块2×2,2×2中不能有任何2块空白,所以2×2中至少需要涂上三个格子,这样E 块至少需要涂其中2+3=5个格子.综上所述,A 、B 、C 、D 、E 、F 、G 这7块依次分别至少需要涂上3、3、1、2、5、1、2个格子,那么一共至少涂上3+3+1+2+5+1+2=17(个) 格子.右图,给出了一种构造(实际上只有E 、F 这2块各有2种选择,其它阴影格子都是惟一选择).7. 自然数A 除本身以外最大的约数是d ,自然数A +2除本身以外最大的约数是d +2,那么A 的值是 .答案:7供题:学而思培优 胡 浩解析:如果A 是偶数,2A d =, 222A d ++=,矛盾. 所以A 是奇数,A 和A +2互质,d 和d +2互质.若A 不是质数,设A =md ,m 是A 最小的质因数,则:2|2d md ++∴2|222d md m m +++- ∴2|22d m +-∴2|1d m +-与m 是A 最小的质因数矛盾 ∴A 是质数 ∴d =1,d +2=3∵d +2是A +2除本身以外的最大约数∴A +2=9 ∴A =7路口,A,B,C,D,E五位警察在其中5个不同的路口站岗.如果两个警察在同一条街道上,那么他们就能互相看到.他们各自说了如下的一句话:A:“我能看到另4位警察”.B:“我能看到另4位警察中的3位”.C:“我能看到另4位警察中的2位”.D:“我只能看到B”.E:“我谁也看不到”.已知他们恰有1人说谎,且说慌的警察所在路口的编号是五位警察中最小的.那么,A,B,C,D,E所在路口编号依次组成的五位数是.答案:25496供题:华杯赛北京管委会陈平解析:A说的话与D、E矛盾,所以A说的是错的,B、C、D、E说的是对的.如果有人站在1号位置,他可以看到2、4、8、3、6号,共5个位置,所以E不能站在1号位置,否则2、4、8、3、6号位置均不能站人,则位置不够.同理,3号能看到6个位置,4号能看到6个位置,5号能看到5个位置,7号能看到6个位置,8号能看到6个位置,这些位置E都不能站.所以E只能站在2、6、9.如果E站在2号位置,1、4、5、7不能站人,剩下的3、6、8、9这4个位置中没人能同时看到另外3个位置,与B可以看到3个人矛盾;如果E站在9号位置,3、5、7、8不能站人,剩下的1、2、4、9这4个位置中能同时看到另外3个位置的只有1,那么B在1,而1是最小编号,A所在位置的编号一定比1大,这与题意中“说慌的警察所在路口的编号是五位警察中最小的”矛盾;所以E在6号位置,1、3、7、8不能站人,剩下的2、4、5、9中能同时看到另外3个位置的只有5,那么B在5;说慌的A所在路口的编号是五位警察中最小的,所以A在2;4能看到在2的A与在5的B,据“D只能看到B”,所以D不在4,D在9;剩下的C在4.所以,答案为25496.三、填空题Ⅲ(每题12分,共48分)9.四个小伙伴想办“亲情套餐”,即缴纳一定金钱后,四人之间发短信免费.但是尴尬的是,当地只有10元的“三人间免费”的A套餐和5元的“两人间免费”的B套餐.四人想了一下,觉得可以开几个这种套餐,使得小伙伴们可以通过由中间人转发做到互相之间都可以免费发短信.那么在花钱最少的情况下,他们有种开通套餐的方式.答案:28供题:学而思培优韩旭东解析:4人如果想相互之间免费发短信,最少花15元.可以办1个三人套餐1个两人套餐,或3个两人套餐.第一种情况,办1个三人套餐和1个两人套餐,从4个人选出3个人办套餐共有4种方法,3人中选出1人跟没办3人套餐的人办两人套餐,所以,共有4×3=12种方法; 第二种情况,办3个两人套餐,A 和B 、B 和C 、C 和D ,共有4×3×2×1÷2=12种方法;第三种情况,办3个两人套餐,A 和B 、C 、D 办,共有4种方法.综上所述,共有12+12+4=28种方法.10. 如图,正八边形中连出3条对角线围成一个三角形(图中阴影部分),如果该正八边形的边长为60,那么阴影部分的面积是__________.答案:900供题:桦树湾教育 成俊峰 解析:以AB 为底,做△OAB 的高OH . 据对称性,H 是中点,∴ OH 是△BEF 的中位线∴OH =30 根据正八边形的对称性,ABCD 是菱形∴AB =BC =60∴△ABC 的面积为60×30÷2=90011. AB 两地相距291千米,甲、乙两人同时从A 地出发匀速前往B 地,与此同时丙从B 地出发匀速前往A 地.当乙走了p 千米与丙相遇时,甲走了q 千米;又过了一段时间,当甲、丙相遇时,乙共走了r 千米.如果p 、q 、r 均是质数,那么,p 、q 、r 的和是__________. 答案:221供题:学而思培优 赵璞铮解析:当乙走了p 千米时,甲和丙共走了291-p +q 千米;当乙走了r 千米时,甲和丙共走了291千米; ∴291291p r p q =-+ 化简,得 ()291291p r p q =-+∵p <r ,p 、r 均是质数∴ (),1p r = ∴ |291r ,r =3或97 r =3时,据质数p <r ,∴p =2,代入()291291p r p q =-+得 194=291-2+q ,矛盾! ∴97r =代入()291291p r p q =-+,得4291p q =+∵4293p >,p >73,又据p <r =97且p 的尾数不能是9(否则q 尾数是5),∴83p =,代入后可得,41q =综上述,,,p q r 的和是834197221++=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四届两岸四地华罗庚金杯二试高年级组得分日期
一、填空题(每题20分,共60分)
1.小红和小明两人都带了钱想买《趣味数学》这本书,到书店一看,小红带的钱缺2元2角,小明带的
钱缺1元8角. 而两人带的钱合起来刚好买一本. 则《趣味数学》每本定价元.
2.如右图所示,小正方形EFGH在大正方形ABCD的内部,阴影
、在边AD上,O为线段
部分的总面积为124平方厘米,E H
CF的中点. 则四边形BOGF的面积为平方厘米.
3.一些边长是1的小正方体码放成一个立体,从上向下看这个立体,如左下图,从正面看这个立体,如
右下图. 在这个立体的体积最大时,将这些小正方体码放成一个底面积为4的长方体,则这个长方体的高是.
二、解答题(每题20分,共60分)
4.已知两个正整数之和为432,这两个正整数的最小公倍数与最大公约数之和为7776. 则这两个正整数的
乘积是多少?
5、设不同的字母代表不同的非零数码,相同的字母代表相同的数码,若AB CB DDD
⨯=
、、、.
且AB CB
<,求A B C D
6、奥运会男子足球小组赛,每组四个队进行单循环比赛. 每场比赛胜队得3分,败队得0分,平局时
两队各得1分. 小组赛全部赛完以后,每组取积分最高的两个队出线进图下轮比赛(对积分相同的队,按更细规则排序). 那么在所有能够出线的情况中,一个出现对的得分最少是多少?请说明理由.
1.。
