2005年武汉市中考数学试题及答案
2005年湖北省武汉市初中毕业升学考试(理化课改卷)及答案

2005武汉市初中毕业升学考试物理、化学综合试卷(课改实验区)亲爱的同学,在你答题前,请认真阅读下面的注意事项:1.本试卷分第Ⅰ卷和第Ⅱ卷。
第Ⅰ卷为选择题;第Ⅱ卷为非选择题,分为化学部分和物理部分。
2.请将你的姓名、准考证号和座位号填写在试卷的指定位置内。
3.第Ⅰ卷的答案分别填写在第Ⅱ卷前的化学部分和物理部分的答题卡上,第Ⅱ卷的答案直接答在试卷上,请用蓝、黑圆珠笔或钢笔答题。
4.答卷时间为120分钟,化学大约50分钟,物理大约70分钟。
你可以按顺序答题,也可以自选顺序答题,但一定要控制时间,以免影响后面的答题。
预祝你取得优异成绩!可能用到的相对原子质量: H:1 S:32 O:16 Zn:65第Ⅰ卷(选择题)一、选择题(本题共20小题,每题只有一个正确答案。
)1、下列变化不属于化学变化的是A.燃烧B.钢铁生锈C.湿衣服经太阳晒后变干D.食物腐烂2、地壳中含量最多的金属元素是A.铁 B.铝C.硅 D.钙3、原子核A.由电子和质子构成 B.由质子和中子构成C.由电子和中子构成 D.由质子、中子和电子构成4、某工地发生多人食物中毒,经化验为误食工业用盐亚硝酸钠(NaNO2)所致。
NaNO2中氮元素的化合价是A.+2 B.+3 C.+4 D.+55、从环境保护的角度考虑,下列燃料中最理想的是A.氢气 B.天然气 C.酒精 D.汽油6、铅蓄电池中含有硫酸,如果不慎将硫酸漏到大理石地面上,会发出嘶嘶声,并有气体产生。
这种气体是A.二氧化硫 B.氧气 C.氢气 D.二氧化碳7、下列关于氢氧化钠的描述中错误的是A.易溶于水,溶解时放出大量的热B.对皮肤有强烈的腐蚀作用C.水溶液能使石蕊试液变红D.能去除油污,可作厨房的清洁剂8、某学生测定的下列数据中,不合理的是A.用10mL量筒量取7.5mL的水B.用pH试纸测得某地水的pH为5.2C.用托盘天平称得某小苏打样品的质量为16.7gD.测的某粗盐中氯化钠的质量分数为90.5%9、一壶水烧开后,壶盖被顶开,这是因为A.水分子变大B.水分解生成了氢气和氧气C.水由液态变为气态,体积膨胀D.构成物质的粒子数目增多10、为了防止病虫害,常对生长过程中的蔬菜喷洒农药。
2005年湖北省武汉中考试题

2005年武汉市中考语文试题亲爱的同学,在你答题前,请认真阅读下面的注意事项:1.本试卷分A、B两卷,全卷21题,共8页,考试时间150分钟。
2.请将你的姓名、准考证号和座位号填写在试卷的指定位置。
3.请用钢笔或圆珠笔将答案直接写在试卷上,不要在密封线内答题。
预祝你取得优异成绩!A卷(共60分)一、基础知识(32分)1.根据拼音在括号里填写汉字。
(5分)①“富贵不能yín( ),贫贱不能移,威武不能屈”表现了大丈夫的英雄气ɡai( )。
②白杨树是在北方风雪的压迫下仍然保持着juéjiànɡtǐnɡ( )立的一种树。
2.下列每组词语中各有一个错别字,请将改正后的字填写在括号里。
(6分)①煦暖相形见拙拮据阔绰( )②恻隐无遐顾及逶迤脊梁( )③潮汛不屑置辩魁梧祈愿( )3.与下面的句子衔接最恰当的一句是( )(6分)梅花和雪花都是文学作品中经常描写的对象,它们各有所长:A.梅花没有雪花那么素雅,雪花没有梅花那么芬芳。
B.雪花没有梅花那么芬芳,但它比梅花素雅。
C.梅花比雪花芬芳,雪花比梅花素雅。
D.雪花比梅花素雅,但它没有梅花那么芬芳。
4.依据相关课文,将下面诗文中的名言名句补充完整。
(15分,每小题3分)①山重水复疑无路,。
(陆游《游山西村》)②,化作春泥更护花。
(龚自珍《己亥杂诗》)③江流天地外,。
(王维《汉江临眺》)④,直挂云帆济沧海。
(李白《行路难》)⑤先天下之忧而忧,。
(范仲淹《岳阳楼记》)二、语段阅读(28分)(一)阅读下面的文字,回答5—7题(14分)有几回,邻居孩子听得笑声,也赶热闹,围住了孔乙己。
他便给他们茴香豆吃,一人一颗。
孩子吃完豆,仍然不散,眼睛都望着碟子。
孔乙己着了慌,伸开五指将碟子①住,弯腰下去说道,“不多了,我已经不多了。
”直起身又看一看豆,自己摇头说:“不多不多!多乎哉?不多也。
”于是这一群孩子都在笑声里走散了。
……有一天,大约是中秋前的两三天,掌柜正在慢慢的结账,取下粉板,忽然说:“孔乙己长久没有来了。
四边形性质探索典型中考题 - 副本

四边形yi、填空题1.(2005年福州市)如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式___________________________.2.(2005年黑龙江省)如图,E,F是ABCD对角线BD上的两点,请你添加一个适当的条件:____________________,使四边形AECF是平行四边形.3.(2005年黑龙江省)已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内一点,且PB=PD=2,那么AP的长为_______________.4.(2004年重庆市北碚区)有一个直角梯形零件ABCD,AD∥BC,斜腰DC的长为10cm,∠D=120°,则该零件另一腰AB的长是_________cm,(结果不取近似值)5.(2004年黑龙江省宁安市)如图,矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积是_________.6.(2004年黑龙江省宁安市)某面粉厂要制1万条长1米,宽0.5米的矩形包装用袋,已知一匹布长50米,宽1米,至少需要_________匹布.7.(2004年四川·成都·郫县)如图,四边形ABCD的两条对角线AC、BD互相垂直,A1B1C1D1是四边形ABCD的中点四边形.如果AC=8,BD=10,那么四边形A1B1C1D1的面积为_________.8.(2004年贵阳市)如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是__________.9.(2004年潍坊市)如图,请写出等腰梯形ABCD(AB∥CD)特有而一般梯形不具有的三个特征:_______________;_____________;______________.10.如图,等腰梯形ABCD中对角线AC、BD相交于点O,那么图中的全等三角形最多有_____对.三、解答题1.(2005年海淀区)如图,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F.求证:BE=CF.2.(2005年海淀区)如图,梯形ABCD中,AB∥DC,∠B=90°,E为BC上一点,且AE⊥ED.若BC=12,DC=7,BE:EC=1:2,求AB的长.3.(2005年青岛市)已知:如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.⑴试猜想AE与BF有何关系?说明理由;⑵若△ABC的面积为3cm2,求四边形ABFE的面积;⑶当∠ACB为多少度时,四边形ABFE为矩形?说明理由.4.(2005年潍坊市)如图,菱形ABCD中,AB=4,E为BC中点,AE⊥BC于点E,AF⊥CD 于点F,CG∥AE,CG交AF于点H,交AD于点G.⑴求菱形ABCD的面积;⑵求∠CHA的度数.5.(2005年潍坊市)(A题)某市经济开发区建有B、C、D三个食品加工厂,这三个工厂和开发区A处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且AB=CD=900米,AD=BC =1700米.自来水公司已经修好一条自来水主管道AN,B、C两厂之间的公路与自来水管道交于E处,EC=500米.若修建自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.⑴要使修建自来水管道的造价最低,这三个工厂的自来水管道路线应怎样设计?并在图中画出;⑵求出各厂所修自来水管道的最低造价各是多少元?(B题)如图,已知平行四边形ABCD及四边形外一直线m,四个顶点A、B、C、D到直线m的距离分别为a、b、c、d.⑴观察图形,猜想得出a、b、c、d满足怎样的关系式?证明你的结论;⑵现将m向上平移,你得到的结论还一定成立吗?请分情况写出你的结论.6.(2005年曲沃、灵武)如图,已知E、F分别是矩形ABCD的边BC、CD上两点,连结AE、BF.请你再从下面四个反映图中边角关系的式子:①AB=BC;②BE=CF;③AE=BF;④∠AEB =∠BFC中选两个作为已知条件,一个作为结论,组成一个命题,并证明这个命题是否正确(只需写出一种情况).已知:求证:证明:7.(2005年曲沃、灵武)O点是△ABC所在平面内一动点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,如果DEFG能构成四边形.⑴如图,当O点在△ABC内时,求证四边形DEFG是平行四边形;⑵当O点移动到△AB C外时,⑴的结论是否成立?画出图形并说明理由;⑶若四边形DEFG为矩形,O点所在位置应满足什么条件?试说明理由.8.(2005年广州市)如图,点E、F分别是菱形ABCD的边CD与CB延长线上的点,且DE=BF.求证:∠E=∠F.9.(2005年广州市)如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.⑴求边AD的长;⑵设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;⑶若S=3300m2,求PA的长(精确到0.1m).10.(2005年广东省)设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去……⑴记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,a n,请求出a1,a2,a3,a4的值;⑵根据以上规律写出a n的表达式.11.(2005年广东省)如图,等腰梯形ABCD中,AD∥BC,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点.⑴求证:四边形MENF是菱形;⑵若四边形MENF是正方形,请探索等腰梯形ABCD的高和底边BC的数量关系,并证明你的结论.12.(2005年浙江省)请将四个全等直角梯形(如图)拼成一个平行四边形,并画出两种不同的拼法示意图(拼出的两个图形只要不全等就认为是不同的拼法).13.(2005年浙江省)一个矩形,两边长分别为xcm和10cm,如果它的周长小于80cm,面积大于100cm2,求x的取值范围.14.(2005年徐州市)如图,已知AC是平行四边形ABCD的对角线.⑴用直尺和圆规作AC的垂直平分线与边AD、BC分别相交于点E、F,垂足为O,连结AF、CE(保留作图痕迹,不写作法);⑵判断四边形AFCE是否为菱形,并说明理由.15.(2005年武汉市)如图,在四边形ABCD中,对角线AC、BD相交于点O,已知∠ADC =∠BCD,AD=BC.求证:AO=BO.16.(2005年河北省)已知线段AC=8,BD=6.⑴已知线段AC垂直于线段BD.设图甲、图乙和图丙中的四边形ABCD的面积分别为S1、S2和S3,则S1=__________,S2=_________,S3=___________;⑵如图丁,对于线段AC与线段BD垂直相交(垂足O不与点A,C,B,D重合)的任意情形,请你就四边形ABCD面积的大小提出猜想,并证明你的猜想;⑶当线段BD与AC(或CA)的延长线垂直相交时,猜想顺次连结A,B,C,D,A所围成的封闭图形的面积是多少?17.(2005年河北省)如图甲和乙,四边形ABCD是正方形,M是AB延长线上一点.直角三角形的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.⑴如图甲,当点E在AB边的中点位置时:①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是_____________;②连结点E与AD边的中点N,猜想NE与BF满足的数量关系是______________;③请证明你的上述两个猜想.⑵如图乙,当点E在AB边上的任意位置时,请你在AD边上找到一点N使得NE=BF,进而猜想此时DE与EF有怎样的数量关系.18.(2005年河南省)如图,梯形ABCD中,AD∥BC,AB=DC,P为梯形ABCD外一点,PA、PD分别交线段BC于点E、F,且PA=PD.⑴写出图中三对你认为全等的三角形(不再添加辅助线);⑵选择你在⑴中写出的全等三角形中的任意一对进行证明.19.(2005年辽宁省11市)如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC 和BD相交于点O,E是BC边上一个动点(点E不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.⑴求证:四边形EFOG的周长等于2OB;⑵请你将上述题目的条件“梯形ABCD中,AD∥BC,AB=DC”改为另一种四边形,其他条件不变,使得结论“四边形EFOG的周长等于2OB”仍成立,并将改编后的题目画出图形,写出已知、求证,不必证明.20.如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.⑴求证:△BCF≌△DCE;⑵若BC=5,CF=3,∠BFC=90°,求DG:GC的值.21.(2005年黑龙江省)已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+S△PCD.理由:过点P作EF⊥BC,分别交AD、BC于E、F两点.∵S△PBC+S△PAD=BC·PF+AD·PE=BC(PF+PE)=BC·EF=S矩形ABCD,又∵S△PAC+S△PCD+S PAD=S矩形ABCD,∴S△PBC+S△PAD=S△PAC+S△PCD+S PAD.∴S△PBC=S△PAC+S△PCD.请你参照上述信息,当点P分别在图2、图3中的位置时,S△PBC、S△PAC、S△PCD又有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.22.(2005年大连市)在数学活动中,小明为了求的值(结果用n表示),设计如图1所示的几何图形.⑴请你利用这个几何图形求的值为___________;⑵请你利用图形2,再设计一个能求的值的几何图形.23.(2005年济南市)如图,已知ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F.⑴求证:CD=FA;⑵若使∠F=∠BCF,ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并进行证明(不要再增添辅助线).24.(2004年重庆市北碚区)如图,有一块塑料矩形模板ABCD,长为10cm,宽为4cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P.⑴能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时AP的长;若不能,请说明理由;⑵再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH始终通过点B,另一直角边PF与DC的延长线交于点Q,与BC交于点E,能否使CE=2cm?若能,请你求出这时AP的长;若不能,请你说明理由.25.(2004年青海省湟中县)有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米,求这个矩形的面积.26.(2004年青海省湟中县)阅读材料:如图1,在四边形ABCD中,对角线AC⊥BD,垂足为P.求证:S四边形ABCD=AC·BD.∴S四边形ABCD=S△ACD+S△ACB=AC·PD+AC·BP =AC(PD+PB)=AC·BD解答问题:⑴上述证明得到的性质可叙述为______________________________________________;⑵已知:如图2,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,AD=3cm,BC=7cm,利用上述的性质求梯形的面积.27.(2004年黑龙江省宁安市)如图,四边形ABCD中,点E在边CD上,连结AE、BE. 给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.⑴用序号写出一个真命题(书写形式如:如果×××,那么×××),并给出证明;⑵用序号再写出三个真命题(不要求证明);⑶真命题不止以上四个,想一想,就能够多写出几个真命题,请再写出两个真命题.28.(2004年四川·成都·郫县)已知:如图,梯形ABCD中,AB∥DC,E是BC的中点,AE、DC的延长线相交于点F,连接AC、BF.⑴求证:AB=CF;⑵四边形ABFC是什么四边形,并说明你的理由.29.(2004年河北省)用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.⑴当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时(如图1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;⑵当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在⑴中得到的结论还成立吗?简要说明理由.30.(2004年贵阳市)如图,四边形ABCD中,AC=6,BD=8且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1;再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去得到四边形A n B n C n D n.⑴证明:四边形A1B1C1D1是矩形;⑵写出四边形A1B1C1D1和四边形A2B2C2D2的面积;⑶写出四边形A n B n C n D n的面积;⑷求四边形A5B5C5D5的周长.31.(2004年南宁市)某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10m,20m的梯形空地上种植花木(如图).⑴他们在△AMD和△BMC地带上种植太阳花,单价为8元/m2,当△AMD地带种满花后(图中阴影部分),共花了160元,请计算种满△BMC地带所需的费用;⑵若其余地带要种的有玫瑰和茉莉花两种花木可供选择,单价分别为12元/m2和10元/m2,应选择种哪种花木,刚好用完所筹集的资金?32.(2004年北京市)已知:如图,DC∥AB,且DC=AB,E为AB的中点.⑴求证:△AED≌△EBC;⑵观察图形,在不添加辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形(直接写出结果,不要求证明).中考四边形试题集锦参考答案或提示一、1.C 2.A 3.D 4.A 5.B 6.B 7.B 8.B 9.C10.C 11.C 12.A 13.A 14.D二、1.(a2-b2)=(a+b)(a-b) 2.BE=DF等 3.2或4 4.55. 6.200 7.20 8.9.如∠A=∠B,∠C=∠D,AD=BC等10.3三、1.提示:证△BOE≌△COF2.提示:由BC=12,BE:EC=1:2求得BE=4,EC=8.证△EAB~△DEC可求得AB=3. ⑴由旋转易证△ACE≌△BCF,∴AE=BF,∠1=∠2.∴AE∥BF.即AE与BF的关系为AE BF ⑵∵△ACE≌△BCF,∴S△ACE=S△BCF.又∵BC=CE,∴S△ABC=S△ACE.同理,S△CEF=S△BCF. ∴S△CEF=S△BCF=S△ACE=S△ABC=3.∴S四边形ABFE=3×4=12(cm2)⑶当∠ACB =60°时,四边形ABFE为矩形.理由是:∵BC=CE,AC=CF,∴四边形ABFE为平行四边形.当∠ACB=60°时,∵AB=AC,∴△ABC为等边三角形.∴BC=AC.∴AF=BE.∴四边形ABFE为矩形.即当∠ACB=60°时,四边形ABFE为矩形4.⑴S菱形ABCD=8⑵∠CHA=120°5.A题⑴过B、C、D分别作AN的垂线段BH、CF、DG,交AN于H、F、G,PH、CF、DG 即为所求的造价最低的管道路线,图形如图所示⑵易求BE=1200(米),AE=1500(米).由△A BE~△CFE求得CF=300(米).由△BHE~△CFE求得BH=720(米).由△ABE~△DGA求得DG=1020(米).所以,B、C、D三厂所建自来水管道的最低造价分别是:720×800=576000(元),300×800=240000(元),102.×800=816000(元)B题⑴a+c=b+d.证明:连结AC、BD,且AC、BD相交于点O,OO1为点O到直线m的距离,∴OO1为直角梯形BB1D1D的中位线.∴2OO1=DD1+BB1=b+d;同理,2OO1=AA1+CC1=a+c.∴a+c=b+d⑵不一定成立.分别有以下情况:直线m过A点时,c=b+d;直线m过A点与B点之间时,c-a=b+d;直线m过B点时,c-a=d;直线m过B点与D点之间时,a-c=b-d;直线m过D点时,a-c=b;直线m过C点与D点之间时,a-c=b+d;直线m过C点时,a=b+d;直线m过点C上方时,a+c=b+d.6.如,已知:E、F分别是矩形ABCD的边BC、CD上两点,连结AE、BF,AB=BC,AE=BF.求证:∠AEB=∠BFC.证Rt△ABE≌Rt△BCF,可得∠AEB=∠BFC.7.⑴利用三角形中位线定理证⑵图略,证法同⑴⑶若四边形DEFG是矩形,O点应在过A点且垂直于BC的直线上(A点除外).理由:如图,过A作BC的垂线MN交BC于K点.设O是MN上任一点(A点除外).连结OB、OC,由⑴得DEFG是平行四边形.在△ABO中,DE∥OA.在△ABC中,DG∥BC,AK⊥BC.∴DE⊥DG,即∠EDG=90°.∴平行四边形DEFG是矩形8.提示:证△ADE≌△ABF可得∠E=∠F9.⑴过点D作DE⊥AB.AD=100米⑵证△APM∽△ADE,得,即.∴PM=x,AM=x,MB=AB-AM=100-x,S=PM·MB=x·(100-x)=-x2+80x.由PM=x≥36,得x≥45.∴自变量x的取值范围是45≤x≤100⑶当S=3300m2时,-x2+80x=3300.解这个方程,得x1=,x2=75.即当S=3300m2时,PA的长为m或75m10.⑴a2=,a3=2,a4=2⑵a n=()n-111.⑴由证△ABM≌△DCM,得BM=CM.再由三角形中位线定理及已知条件可证得EN=FN =FM=EM.∴四边形ENFM是菱形⑵结论:等腰梯形ABCD的高是底边BC的一半.可证MN是梯形ABCD的高.由四边形MENF是正方形知△BMC是直角三角形,又N是BC 的中点,∴MN=BC12.例如:13.根据题意,得解这个不等式组,得10<x<30.所以x的取值范围是10<x<3014.⑴略⑵四边形AFCE是菱形.提示:先说明四边形AFCE是平行四边形,再由AC⊥EF,得四边形AFCE是菱形15.证△ADC≌△BCD,得AC=BD,∠ACD=∠BDC,∴OD=OC.∴AC-0C=BD-OD,即AO=BO16.⑴24,24,24 ⑵S四边形ABCD=24.证明略⑶顺次连结点A、B、C、D、A所围成的封闭图形的面积仍为2417.⑴①DE=EF ②NE=BF ③证△DNE≌△EBF,可得DE=EF,NE=BF⑵在DA边上截取DN=EB(或截取AN=AE),连结NE,点N就使得NE=BF成立(图略).此时,DE=EF18.⑴①△ABP≌△DCP②△ABE≌△DCF③△BEP≌△CFP④△BFP≌△CEP⑵可就△ABP≌△DCP证明,证明略19.⑴如图1,证△ABC≌△DCB可得∠1=∠2,由GE∥AC可得∠2=∠3,∴∠1=∠3.∴EG =BG.由EG∥OC,EF∥OB,得四边形EGOF是平行四边形.∴EG=OF,EF=OG.∴四边形EGOF 的周长=2(OG+GE)=2(OG+GB)=2OB⑵方法1:如图2,已知矩形ABCD中,对角线AC、BD相交于点O,E为BC上一个动点(点E不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.求证:四边形EFOG 的周长等于2OB.方法1:如图3,已知正方形ABCD中,……其余略20.⑴略⑵可求得DE=4,可证得DE∥FC,∴△DGE∽△CGF.∴DG:GC=DE:CF=4:321.猜想结果:图2结论S△PBC=S△PAC+S△PCD,图3结论S△PBC=S△PAC-S△PCD.证明结论S△PBC=S△PAC+S△PCD:如图2,过点P作EF⊥AD,分别交AD、BC于E、E两点.∵S△PBC=BC·PF=BC·PE+BC·EF=AD·PE+BC·EF=S△PAD+S矩形ABCD,S△PAC+S△PCD=S△PAD+S△ADC=S△PAD+S矩形ABCD,∴S△PBC=S△PAC+S△PCD证明S△PBC=S△PAC-S△PCD:如图3,过点P作EF⊥AD,分别交AD、BC于E、E两点.∵S△PAD=AD·PE=AD·PF+AD·EF=BC·PF+AD·EF=S△PBC+S矩形ABCD,S△PAC+S△ADC=S△PAC+S矩形ABCD=S△PAD+S△PCD=S△PBC+S矩形ABCD+S△PCD,∴S△PBC=S△PAC-S△PCD22.⑴1-⑵如图1或图2或图3或图4等23.⑴证△DCE∽△AFE,得CD=FA ⑵在平行四边形ABCD中,只要BC=2AB,就能使∠F =∠BCF,证明略24.⑴能.证△ABP∽△DPC,可求得AP=2cm或8cm⑵能.设AP=xcm,CQ=ycm.由于ABCD是矩形,∠HPF=90°,∴△BAP~△ECQ,△BAP∽△PDQ.∴AP·CE=AB·CQ,AP·PD=AB·DQ.∴2x=4y,即y=.① x(10-x)=4(4+y).②消去y,得x2-8x+16=0.解得x1=x2=4,即AP=4cm25.证△ADG∽△AB C,可求得矩形的长为50米.∴S矩形ABCD=40×50=2000米226.⑴对角线互相垂直的四边形的面积等于对角线乘积的一半⑵由证△ABC≌△DCB,得BP=CP;再由证△BPC是等腰直角三角形得BP=PC=BC=.同理DP=AP=AD=.∴BD=BP+DP=.∴S梯形=AC·BD=BD2=25(cm2)27.⑴如果①②③,那么④⑤.证明:如图,延长AE交BC的延长线于F.证△ADE≌△FCE易得结论.⑵如果①②④,那么③⑤如果①③④,那么②⑤如果①③⑤,那么②④⑶如果①②⑤,那么③④如果①④⑤,那么②③28.⑴证△CEF≌△BEA,得AB=CF⑵四边形ABFC是平行四边形.由⑴证明可知,AB与CF平行且相等,所以四边形ABFC 是平行四边形29.⑴BE=CF.证△ABE≌△ACF可得⑵BE=CF仍然成立.证△ABE≌△ACF即可30.⑴略⑵四边形A1B1C1D1的面积为12,四边形A2B2C2D2的面积为6⑶四边形A n B n C n D n的面积为24×⑷∵矩形A5B5C5D5∽矩形A1B1C1D1,∴矩形A5B5C5D5的面积/矩形A1B1C1D1的面积=(矩形A5B5C5D5的周长)2/(矩形A1B1C1D1的周长)2,即×24:12=(矩形A5B5C5D5的周长)2:142,∴矩形A5B5C5D5的周长=31.⑴由证△AMD∽△CMB,得.求得S△AMD=160÷8=20(m2),∴S△CMB =80(m2).∴△CMB地带的花费为80×8=640(元)⑵易求得梯形的高为12,S梯形ABCD=180(m2),∴S△AMB+S△DMC=180-20-80=80(m2).∴160+640+80×12=1760(元),而160+640+80×10=1600(元),∴⑶如图,点P在AD、BC的中垂线上,此时易证△APB≌△DPC.设△APD的高为x,则△BPC的高为(12-x).当S△APD=S△BPC时,×10x=×20(12-x).解得x=8.∴当点P在AD、BC的中垂线上且与AD的距离为8m时,S△APD=S△BPC32.⑴略⑵△ACD,△ACE,△CDE中的两个。
2005年武汉中考真题大纲卷

2005年武汉市初中毕业、升学考试英语参考试卷第I卷[含听力测试;A卷;BI卷]笔试部分A 卷(二)基础知识(共20小题,满分60分)从A、B、C三个选项中,选出可以填入空白处的最佳答案。
(共20小题,每小题3分,满分60分)21. My eyes are green and are blue.A. youB. yourC. yours.选择C,考查形容词性物主代词和名词性物主代词。
22. -I’ve made some coffee. Would you like ?-That would be fine.A. someB. anyC. no选择A,考查表示数量的不定代词。
23. Mary is now in .A. the four gradeB. Grade FourC. Grade Second选择B,考查序数词和基数词。
24. We went to their English Corner its opening night.A. atB. inC. on选择C,考查介词的用法。
25. I’d like to go with you I’m too busy.A. andB. orC. but选择C,考查连词的用法。
26. The street hasn’t changed much. It is still it used to be.A. as quieter asB. so quiet thanC. as quiet as选择C,考查as…as…的用法。
27. Smith has three cars. The black one is of the three.A. most goodB. the bestC. better选择B,考查形容词good的最高级形式。
28. I’ll go to the bank this morning. There’s very money left.A. littleB. a littleC. much选择A,考查形容词的用法。
2005年湖北省宜昌市中考数学试题及答案(课改区)

2005年湖北省宜昌市中考数学试题及答案(课改区)第 2 页 共 26 页2005年湖北省宜昌市初中毕业生学业考试数 学 试 卷(课改实验区使用)(考试形式:闭卷 全卷共五大题25小题 卷面分数:120分 考试时限:120分钟)考生注意:1.本试卷分为两卷,解答第I 卷(1~2页)时请将解答结果填写在第II 卷(3~8页)上指定的位置,否则答案无效,交卷时只交第II 卷.2.答卷时允许使用科学计算器.以下数据和公式供参考:二次函数y =ax 2+bx +c 图象的顶点坐标是)44,2(2ab ac a b -- ;扇形面积S =3602r n π.第Ⅰ卷(选择题、填空题 共45分)一、选择题:(下列各小题都给出了四个选项,II 卷上指定的位置. 本大题共103分,计30分)!立体图形的认识与三视图1.图中物体的形状类似于( A ).(第1题)第 3 页 共 26 页题目简单更要仔细哟!A .棱柱B .圆柱C .圆锥D .球!二次根式及其运算 2.化简20的结果是( B ).A .25B .52C.D .54!图形的相似(包含相似多边形的概念)3.如图所示,BC =6,E 、F 分别是线段AB 和线段AC 的中点,那么线段EF 的长是( D ).A .6B .5C .4.5D .3 !简单事件的概率计算4.4.有6张背面相同的扑克牌,正面上的数字分别是4,5,6,7,8,9.若将这六张牌背面朝上洗匀后,从中任意抽取一张,那么这张牌正面上的数字是9的概率为( A ) A .23B .12C .13D .16. !图形的三种基本变换5.在5×5方格纸中将图(1)中的图 1F E CBA(第3图形N平移后的位置如图(2)中所示,那么正确的平移方法是(C).A.先向下移动1格,再向左移动1格B.先向下移动1格,再向左移动2格C.先向下移动2格,再向左移动1格D.先向下移动2格,再向左移动2格!实数6.三峡大坝坝顶从2005年7月到9月共92天将对游客开放,每天限接待1000人,在整个开放期间最多能接待游客的总人数用科学记数法表示为(B)人.A.92×103B.9.2×104 Array C.9.2×103D.9.2×105!统计图表7.如图,希望中学制作了学生选择棋类、武术、摄影、刺绣四门校本课程情况的扇形统计图. 从图中可以看出选择刺绣的学生为( C ).A.11%B.12%C.13%D.14%第 4 页共 26 页第 5 页 共 26 页!多边形的基本认识(包含正多边形的概念) 8.某城市进行旧城区人行道的路面翻新,准备对地面密铺彩色地砖, 有人提出了4种地砖的形状供设计选用:①正三角形,②正四边形,③正五边形,④正六边形.其中不能进行密铺的地砖的形状是( C )A .①B .②C .③D .④ . !一元一次不等式(组)及其解法9.实数m 、n 在数轴上的位置如图所示,则下列不等关系正确的是( A ). A .n <m B .n 2<m 2C .n 0<m 0D .| n |<| m |!反比例函数10.如图所示的函数图象的关系式可能是( D ). A .y = xB .y =x1 C .y = x 2D .y = 1x(第9四川省资中县重龙中学 刘之平编辑第 6 页 共 26 页二、填空题:(请将答案填写在第II 卷上指定的位置.本大题共5小题,每小题3分,计15分)!实数11.如果收入15元记作+15元,那么支出20元记作 -20 元. !相交线与平行线12.如图,直线AB 、CD 相交于点O ,若∠1=28°,则∠2= 28° .!解直角三角形13.已知,在Rt △ABC 中∠C =90°,∠BAC =30°,AB =10,那么BC = 5 . !数据的汇总与数据代表的计算14.甲、乙、丙三台包装机同时分装质量为400克的茶叶.从它们各自分装的茶叶中分别随机抽取了10盒,测得它们的实际质量的方差如下表所示:!规律探索性问题15.如图,时钟的钟面上标有1,2,3,……,(第15题)甲包装机乙包装机丙包装机根据表中数据,可以认为三台包装(第12题)21ODCBA12共12个数,一条直线把钟面分成了两部分.请你再用一条直线分割钟面,使钟面被分成三个不同的部分且各部分所包含的几个数的和都相等,则其中的两个部分所包含的几个数分别是1,2,11,12和3,4,9,10;或5,6,7,8。
2005年武汉市中考数学试卷

4.方茴说:“可能人总有点什么事,是想忘也忘不了的。
”5.方茴说:“那时候我们不说爱,爱是多么遥远、多么沉重的字眼啊。
我们只说喜欢,就算喜欢也是偷偷摸摸的。
”6.方茴说:“我觉得之所以说相见不如怀念,是因为相见只能让人在现实面前无奈地哀悼伤痛,而怀念却可以把已经注定的谎言变成童话。
”7.在村头有一截巨大的雷击木,直径十几米,此时主干上唯一的柳条已经在朝霞中掩去了莹光,变得普普通通了。
8.这些孩子都很活泼与好动,即便吃饭时也都不太老实,不少人抱着陶碗从自家出来,凑到了一起。
9.石村周围草木丰茂,猛兽众多,可守着大山,村人的食物相对来说却算不上丰盛,只是一些粗麦饼、野果以及孩子们碗中少量的肉食。
1.“噢,居然有土龙肉,给我一块!”2.老人们都笑了,自巨石上起身。
而那些身材健壮如虎的成年人则是一阵笑骂,数落着自己的孩子,拎着骨棒与阔剑也快步向自家中走去。
2005年武汉市中考数学试卷参考公式:在半径为R 的圆中,圆心角为n °的扇形面积的计算公式是:2360R n S π=扇形第I 卷(A 卷第1~20题)一、判断题(共10小题,每小题2分,共20分)请你判断下列各题的正误,若是正确的,请在括号内打“√”,若是错误的,请在括号内打“×”。
1. 一元二次方程02342=-+x x 的二次项系数为4,一次项系数为3。
( )2. 直角坐标系中,第三、四象限的点的纵坐标都小于零。
( )3. 当x=2时,函数53-=x y 的值为1。
( )4. 反比例函数xy 6-=的图像在第二、四象限。
( ) 5. 数据4,5,5,3,5的众数是5。
( )6. sin30°+cos60°=1。
( )7. 任何一个三角形有且只有一个外接圆。
( )8. 相等的圆心角所对的弧相等。
( )9. 三角形的内心到三边的距离相等。
( )10. 圆既是轴对称图形,又是中心对称图形。
( )二、选择题(共10小题,每小题4分,共40分)下列各题均有四个备选答案,其中有且只有一个是正确的,请将正确的答案的序号填在题后的括号内。
2005年湖北省宜昌市中考数学试题及标准答案(课改区)

题目简单更要仔细哟!2005年湖北省宜昌市初中毕业生学业考试数 学 试 卷(课改实验区使用)(考试形式:闭卷 全卷共五大题25小题 卷面分数:120分 考试时限:120分钟)考生注意:1.本试卷分为两卷,解答第I 卷(1~2页)时请将解答结果填写在第II 卷(3~8页)上指定的位置,否则答案无效,交卷时只交第II 卷. 2.答卷时允许使用科学计算器.以下数据和公式供参考:二次函数y=ax 2+b x+c图象的顶点坐标是)44,2(2ab ac a b -- ;扇形面积S =3602r n π.第Ⅰ卷(选择题、填空题 共45分)一、选择题:(下列各小题都给出了四个选项,其中只有一项是符合题目要求的,请将符合要求的选项前面的字母代号填写在第II 卷上指定的位置. 本大题共10小题,每小题3分,计30分)!立体图形的认识与三视图错误!未定义书签。
.图中物体的形状类似于( A ).A .棱柱B .圆柱 C.圆锥 ﻩ D.球!二次根式及其运算错误!未定义书签。
.化简20的结果是( B ). A.25 B.52ﻩ C. D.54ﻩ !图形的相似(包含相似多边形的概念)错误!未定义书签。
.如图所示,BC =6,E、F分别是线段AB 和线段AC的中点,那么线段EF 的长是( D ).A.6ﻩB.5 C .4.5 D .3 !简单事件的概率计算错误!未定义书签。
.4.有6张背面相同的扑克牌,正面上的数字分别是4,5,6,7,8,9.若将这六张牌背面朝上洗匀后,从中任意抽取一张,那么这张牌正面上的数字是9的概率为( A ) A.23B.12ﻩ C.13D.16ﻩ. !图形的三种基本变换错误!未定义书签。
.在5×5方格纸中将图(1)中的图形N 平移(第5题)FECBA(第3题)(第1题)后的位置如图(2)中所示,那么正确的平移方法是( C ). A .先向下移动1格,再向左移动1格 B .先向下移动1格,再向左移动2格 C .先向下移动2格,再向左移动1格ﻩ D .先向下移动2格,再向左移动2格 !实数错误!未定义书签。
2005宜昌市中考数学试题及答案(课改区)

题目简单更要仔细哟!2005年湖北省宜昌市初中毕业生学业考试数 学 试 卷(课改实验区使用)(考试形式:闭卷 全卷共五大题25小题 卷面分数:120分 考试时限:120分钟)考生注意:1.本试卷分为两卷,解答第I 卷(1~2页)时请将解答结果填写在第II 卷(3~8页)上指定的位置,否则答案无效,交卷时只交第II 卷. 2.答卷时允许使用科学计算器.以下数据和公式供参考:二次函数y =ax 2+bx +c 图象的顶点坐标是)44,2(2ab ac a b -- ;扇形面积S =3602r n π.第Ⅰ卷(选择题、填空题 共45分)一、选择题:合要求的选项前面的字母代号填写在第II 卷上指定的位置. 本大题共10小题,每小题3分,计30分)1. 图中物体的形状类似于( ).(A )棱柱 (B )圆柱 (C )圆锥 (D )球(第1题)2.化简20的结果是( ).(A)25 (B)52(C) . (D)543. 如图所示,BC =6,E 、F 分别是线段AB 和线段AC 的中点,那么线段EF 的长是( ). (A )6 (B )5 (C )4.5 (D )34.有6张背面相同的扑克牌,正面上的数字分别是4,5,6,7,8,9.若将这六张牌背面朝上洗匀后,从中任意抽取一张,那么这张牌正面上的数字是9的概率为( ).(A)23 (B) 12 (C) 13 (D) 165.在5×5方格纸中将图(1)中的图形N 平移后的位置如图(2)中所示,那么正确的平移方法是( ).(A)先向下移动1格,再向左移动1格 (B)先向下移动1格,再向左移动2格 (C)先向下移动2格,再向左移动1格 (D)先向下移动2格,再向左移动2格(第5题) F E CBA(第3题)6. 三峡大坝坝顶从2005年7月到9月共92天将对游客开放,每天限接待1000人,在整个开放期间最多能接待游客的总人数用科学记数法表示为( )人. (A )92×103 (B )9.2×104 (C )9.2×103 (D )9.2×1057.如图,希望中学制作了学生选择棋类、武术、摄影、刺绣四门校本课程情况的扇形统计图. 从图中可以看出选择刺绣的学生为( ). (A)11% (B)12% (C) 13% (D) 14%8.某城市进行旧城区人行道的路面翻新,准备对地面密铺彩色地砖, 有人提出了4种地 砖的形状供设计选用:①正三角形,②正四边形,③正五边形,④正六边形.其中不 能进行密铺的地砖的形状是( ).(A) ① (B) ② (C) ③ (D) ④9.实数m 、n 在数轴上的位置如图所示,则下列不等关系正确的是( ). (A )n <m (B ) n 2<m 2(C )n 0<m 0(D )| n |<| m | (第9题) 10.如图所示的函数图象的关系式可能是( ). (A )y = x (B )y =x 1(C )y = x 2 (D) y = 1x二、填空题:(请将答案填写在第II 卷上指定的位置.本大题共5小题,每小题3分,计15分)11.如果收入15元记作+15元,那么支出20元记作 元. 12.如图,直线AB 、CD 相交于点O ,若∠1=28°,则∠2= .13.已知,在Rt △ABC 中∠C =90°,∠BAC =30°,AB =10,那么BC = .14.甲、乙、丙三台包装机同时分装质量为400克的茶叶.从它们各自分装的茶叶中分别随机抽取了10盒,测得它们的实际质量的方差如下表所示:15.如图,时钟的钟面上标有1,2,3,……,12共12个数,一条 直线把钟面分成了两部分.请你再用一条直线分割钟面,使钟面被 分成三个不同的部分且各部分所包含的几个数的和都相等,则其 中的两个部分所包含的几个数分别是 和. 。
中考规律题集锦

规律题1.(2005年海淀区)把编号为1,2,3,4…的若干盆花按如图所示摆放,花盆中的花按红、黄、蓝、紫的颜色依次循环排列,则第8行从左边数第6盆花的颜色为______色.2.(2005年武汉市)下面是一个有规律排列的数表:第1行第2行第3行3.(2005年福州市)瑞士中学教师巴尔末成功地从光谱数据……中得到巴尔末公式,从而打开了光谱奥妙的大门.请你按这种规律写出第七个数据是________.4.(2005年南宁市)如图是与杨辉三角有类似性质的三角形垒,a,b,c,d是相邻两行的前四个数,那么当a=8时,c=____,d=_____.5.(2005年重庆市)如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在第n个图形中,互不重叠的三角形共有________个(用含n 的代数式表示).6.(2005年甘肃省)用黑白两种颜色的正六边形地板砖按如图所示的规律,拼成如图所示若干地板图案,则第n个图案中,白色的地板砖有__________块.7.(2005年济南市)把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行、…中间用虚线围的一列从上至下依次为1、5、13、25、…则第10个数为________.8.(2005年武汉市)在计算机程序中,二叉树是一种表示数据结构的方法,如图,一层二叉树的结点总数为1;二层二叉树的结点总数为3;三层二叉树的结点总数为7;四层二叉树的结点总数为15;……照此规律,七层二叉树的结点总数为__________.9.(2005年昆明市)用火柴棒搭如图所示的图形,照这样的规律搭下去,那么搭第n个(n为正整数)这样的图形需要______根火柴棒.10.(2004年重庆市北碚区)如图所示,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察图形,则第n个图形中需用黑色瓷砖_________块(用含n的代数式表示).12.(2004年哈尔滨市)观察下列等式9-1=8 16-4=12 25-9=16 36-16=20 ……这些等式反映自然数间的某种规律,设n(n≥1)表示自然数,用关于n的等式表示这个规律为_______. 14.(2003年河北省)如图所示,是用火柴棍摆出的一系列三角形图案.按这种方式摆下去,当每边上摆20(即n=20)根时,需要的火柴棍总数为_________根.15.(2003年济南市)请你观察思考下列计算过程:∵112=121,∴=11;同样:∵1112=12321,∴=111;……由此猜想=_____________________.16.(2003年武汉市)已知:…,若10+(a,b为整数),则a+b=______.17.(2003年潍坊市)小明在阅览时发现这样一个问题:“在某次聚会中,共有6人参加,如果每两人都握一次手,共握几次手?”小明通过努力得出了答案.为了解决更一般的问题,小明设计了下列图表进行探究:请你在图表右下角的横线上填上你归纳出的一般结论.三、解答题1.(2005年海淀)印制一本书,为了使装订成书后页码恰好为连续的自然数,可按如下方法操作:先将一张整版的纸,对折一次为4页,再对折一次为8页,连续对折三次为16页,……;然后再排页码.如果想设计一本16页的毕业纪念册,请你按图甲、图乙、图丙(图中的1,16表示页码)的方法折叠,在图丁中填上按这种折叠方法得到的各页在该面相应位置上的页码.2.(2005年河北省)观察下面的图形(每个正方形的边长均为1)和相应的等式,探究其中的规律:⑴写出第五个等式,并在给出的正方形上画出与之对应的图示;⑵猜想并写出与第n个图形相对应的等式.3.(2005年安徽省)如图⑴,是一个扇形AOB,将其作如下划分:第一次划分:如图⑵所示,以OA的一半OA1为半径画弧,再作∠AOB的平分线,得到扇形的总数为6个,分别为扇形AOB、扇形AOC、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB1;第二次划分:如图⑶所示,在扇形C1OB1中,按上述划分方式继续划分,可以得到扇形的总数为11个;第三次划分:如图⑷所示;……依次划分下去.⑴根据题意,完成下表:划分次数扇形总个数1 62 1134… …n⑵根据上表,请你判断按上述划分方式,能否得到扇形的总数为2005个?为什么?4.(2005年河南省)观察下表,填表后再解答问题.⑴完成下列表格:⑵试求第几个图形中“◎”的个数和“☆”的个数相等?5.(2004年河北省)观察下面的点阵图和相应的等式,探究其中的规律:⑴在④和⑤后面的横线上分别写出相应的等式:1=12;②1+3=22;③1+3+5=32;④_______________;⑤________________;……⑵通过猜想写出与第n个点阵相对应的等式.6.(2004年广东省)阅读材料:多边形边上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图A给出了四边形的具体分割方法,分别将四边形分割成了2个、3个、4个小三角形.请你按照上述方法将图B中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至n边形.中考探索规律试题集锦参考答案一、1.规律:从第一个数起,依次连续3个数相加得下一个数,即2+2+4=8,2+4+8=14,4+8+14=26,8+14+26=48,14+26+48=88,26+48+88=162.故应选C.二、1.规律:第1行1盆花,第2行2盆花,第3行3盆花,…,第8行8盆花,前8行总共1+2+3+…+8=36盆花.因为4分盆花一个循环,且按红、黄、蓝、紫的顺序从左到右依次排列,而39÷4=9,所以第8行从左边数第6盆花的颜色是黄色.故填黄.2.依据前3行各列数的排列规律知第9行各列数据为第9行第7列的数是.故应填3.这列数的排列规律:.所以第7个数是.故应填4.观察图形我们发现,每行的第一个数与行数相同,a=8,即说明a是第八行的第一个数,而c是与a相邻行的第一个数,即第九行的第一个数,故c=9;从第三行起,每行第二个数都是它上行第一个数与第二个数的和,因此,第六行第二个数是16,第7行第二个数是22,第八行第二个数是29,第九行第二个数是37,即d=375.第一个图形有4=3×1+1个三角形;第二个图形有7=3×2+1个三角形;第三个图形有10=3×3+1个三角形;…;第n个图形有3n+1个三角形.故填3n+16.第一个图案白色的地板砖有4×1+2块;第二个图案白色的地板砖有4×2+2块;第三个图案白色的地板砖有4×3+2块;…;第n个图案白色的地板砖有(4n+2)块.故填4n+27.到第10个数共排到了19行,因每行数的个数与行数相同,所以19行共有1+2+3+…+19=190个数,这190个数从第一行1开始由小到大从左到右蛇形排列,至第19行,第19行应从右到左从172起一直排列到190,中间一个数为181.故填1818.规律:从二层二叉树开始,后面二叉树的结点总数比前面二叉树增加的结点数依次为2,4,8,16,32,64,…因此一,五层二叉树结点总数、六层二叉树结点总数、七层二叉树结点总数依次为31,63,127.故填1279.规律:第一个图形有2×1+1根火柴棒;第二个图形有2×2+1根火柴棒;第三个图形有2×3+1根火柴棒;第四个图形有2×4+1根火柴棒;…;第n个图形有2n+1根火柴棒.故填2n+110.规律:第⑴个图形中需用黑色瓷砖4×1+8块;第⑵个图形中需用黑色瓷砖4×2+8块;第⑶个图形中需用黑色瓷砖4×1+8块;…;第(n)个图形中需用黑色瓷砖4n+8块.故填4n+811.由珠子排列的规律知,被盒子遮住部分的黑珠子有5+6+7+6=24颗,白珠子有3颗,共27颗.故填2712.观察所给等式发现:第1个等式可以表示为:(1+2)2-12=4(1+1);第2个等式可以表示为:(2+2)2-22=4(2+1);第3个等式可以表示为:(3+2)2-32=4(3+1);第4个等式可以表示为:(4+2)2-42=4(4+1);………………………………………………依此规律,第n个等式可以表示为:(n+2)2-n2=4(n+1).故填(n+2)2-n2=4(n+1)13.从“苹果图”中苹果的摆放规律看出:第一行有1个苹果可以表示为:第一行有21-1=20个苹果;第二行有2个苹果可以表示为:第一行有22-1=21个苹果;第三行有4个苹果可以表示为:第一行有23-1=22个苹果;第四行有8个苹果可以表示为:第一行有24-1=23个苹果;………………………………………………………………第十行的苹果数可以表示为:第十行有210-1=29个苹果.29=512.故可填29或51214.图案的摆放规律是:当n=1时,有1个三角形;当n=2时,有1+2=3个三角形;当n=3时,有1+2+3=6个三角形;当n=4时,有1+2+3+4=10个三角形;……当n=20时,有1+2+3+…+20=210个三角形.因为每个三角形摆放3根火柴棍,所以摆210个三角形需要的火柴棍总数为3×210=630根.故填63015.观察所给的计算过程发现:把被开方数由右向左每两位数分成一节,最后若剩一位数也为一节,那么分成多少节,算术平方根就有几个1.121能分成1,21两节,算术平方根就是11;12321能分成1,23,21三节,算术平方根就是111.因12345678987654321能分成1,23,45,67,89,87,65,43,21九节,算术平方根应是111111111.故填11111111116.由所给等式呈现的规律可知:a=10,b=102-1=99,所以a+b=10+99=109.故填10917.从图表中可以发现这样的规律:2人参加握手握手次数1可以表示为:;3人参加握手握手次数3可以表示为:;4人参加握手握手次数6可以表示为:;5人参加握手握手次数10可以表示为:;由此可以归纳出:n人参加握手握手次数可以表示为:.故填三、1.8 9 16 15 12 13 42.⑴5×=5-<------>⑵n×=n-3.⑴ ⑵不能够得到2005个扇形,因为满足5n+1=2005的正整数n不存在划分次数扇形总个数1 62 113 164 21… …n 5n+14.⑴第一行空格处填16,第二行空格处填9⑵设第n个图形中“◎”的个数和“☆”的个数相等. 观察图形的规律可知,第n个图形中“◎”的个数为8n个,“☆”的个数为n2个,当n2=8n时,求得n=0(不合题意,舍去)或n=8.所以,第8个图形中“◎”的个数和“☆”的个数相等5.⑴④1+3+5+7=42⑤1+3+5+7+9=52⑵我们把⑴中的五个等式做适当的变形:①1=(2×1-1)=12;②1+3=1+(2×2-1)=22;③1+3+5=1+3+(2×3-1)=32;④1+3+5+7=1+3+5+(2×4-1)=42;⑤1+3+5+7+9=1+3+5+7+(2×5-1)=52.观察这五个等式发现,括号中2乘以几,相应等式的右边就是几的平方,因而猜想出与第n个点阵相对应的等式是1+3+5+…+(2n-1)=n26.将六边形进行分割的结果及得到小三角形的个数如图推广结论至n边形,分割后得到的小三角形的个数分别为n-2,n-1,n(3)(2)(1)C 3B 3A 3A 2C 1B 1A 1C B AC 2B 2B 2C 2A B C A 1B 1C 1A 2C 1B 1A 1C B A … 图4(2010哈尔滨)1.观察下列图形:它们是按一定规律排列的,依照此规律,第9个图形中共有 个★2815. 如图4,在图(1)中,A 1、B 1、C 1分别是△ABC 的边BC 、CA 、AB 的中点,在图(2)中,A 2、B 2、C 2分别是△A 1B 1C 1的边B 1C 1、C 1 A 1、 A 1B 1的中点,…,按此规律,则第n 个图形中平行四边形的个数共有 3n 个.(2010遵义市)小明玩一种的游戏,每次挪动珠子的颗数与对应所得的分数如下表:挪动珠子数(颗)2 3 4 5 6 …… 对应所得分数(分)26122030……当对应所得分数为132分时,则挪动的珠子数为 ▲ 颗. 答案:1(2010台州市)如图,菱形ABCD 中,AB =2 ,∠C =60°,菱形ABCD 在直线l 上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O 所经过的路径总长为(结果保留π) ▲ .答案:83+4)π玉溪市2010)22. 平面内的两条直线有相交和平行两种位置关系.(1)AB 平行于CD .如图a ,点P 在AB 、CD 外部时,由AB ∥CD ,有∠B=∠BOD ,又因∠BOD 是△POD 的外角,故∠BOD=∠BPD +∠D ,得∠BPD=∠B-∠D .如图b ,将点P 移到AB 、CD 内部,以上结论是否成立?,若不成立,则∠BPD 、∠B 、∠D 之间有何数量关系?请证明你的结论;(2)在图b 中,将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ,图aO图b OB(第16题)lD第17题ABCA 1A 2A 3B 1 B 2 B 3 如图c ,则∠BPD ﹑∠B ﹑∠D ﹑∠BQD 之间有何数量关系?(不需证明); (3)根据(2)的结论求图d 中∠A+∠B+∠C+∠D+∠E+∠F 的度数.解:(1)不成立,结论是∠BPD=∠B+∠D. 延长BP 交CD 于点E, ∵AB ∥CD. ∴∠B=∠BED.又∠BPD=∠BED+∠D ,∴∠BPD=∠B+∠D. …………4分 (2)结论: ∠BPD=∠BQD+∠B+∠D. …………7分(3)由(2)的结论得:∠AGB=∠A+∠B+∠E. 又∵∠AGB=∠CGF.∠CGF+∠C+∠D+∠F=360°∴∠A+∠B+∠C+∠D ∠E+∠F=360°. …………11分(桂林2010)18.如图:已知AB =10,点C 、D 在线段AB 上且AC =DB =2; P 是线段CD 上的动点,分别以AP 、PB 为边在线段AB 的同侧作等边△AEP 和等边△PFB ,连结EF ,设EF 的中点为G ;当点P 从点C 运动到点D 时,则点G 移动路径的长是________.3(2010年连云港)17.如图,△ABC 的面积为1,分别取AC 、BC 两边的中点A 1、B 1,则四边形A 1ABB 1的面积为34,再分别取A 1C 、B 1C 的中点A 2、B 2,A 2C 、B 2C 的中点A 3、B 3,依次取下去….利用这一图形,能直观地计算出3 4+3 42+3 43+…+34n =________.(2010济宁市)18.(6分)观察下面的变形规律:211⨯ =1-12; 321⨯=12-31;431⨯=31-41;…… 解答下面的问题:(1)若n 为正整数,请你猜想)1(1+n n = ;(2)证明你猜想的结论; (3)求和:211⨯+321⨯+431⨯+…+201020091⨯ . O图c图dGA B C D PE F G……图③图②图①(2010宁波市)25.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V )、面数(F )、棱数(E )之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:(1)根据上面多面体的模型,完成表格中的空格:多面体 顶点数(V )面数(F )棱数(E )四面体 4 4 长方体 8 6 12 正八面体 8 12 正十二面体201230你发现顶点数(V )、面数(F )、棱数(E )之间存在的关系式是________; (2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是;(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面三角形的个数为x 个,八边形的个数为y ,求x +y 的值. (2010年成都)24.已知n 是正整数,111222(,),(,),,(,),n n n P x y P x y P x y 是反比例函数ky x=图象上的一列点,其中121,2,,,n x x x n ===.记112A x y =,223A x y =,1n n n A x y +=,,若1A a =(a 是非零常数),则12n A A A 的值是________________________(用含a 和n 的代数式表示). 答案:(2)1na n +(2010年眉山)16.如图,将第一个图(图①)所示的正三角形连结各边中点进行分割,得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割,……,则得到的第五个图中,共有________个正三角形.答案:17北京12. 右图为手的示意图,在各个手指间标记字母A 、B 、C 、D 。
2005年湖北黄冈市中考数学试题及答案(实验区)-推荐下载

D.16
500
200
E
Q(升)
O5 B
O5
Q(升)
120%
83%
D
9 D
F
50 t(分钟) 3
95 t(分钟)
100
95%
C
13、(本题满分 7 分)你喜欢玩游戏吗?现请你玩一个转盘游戏。如图所示的两个转盘中 指针落在每一个数字上的机会均等,现同时自由转动甲乙两个转盘,转盘停止后,指针各 指向一个数字,用所指的两个数字作乘积。
⑵
D.– 1
B. x3 x5 x8
1
你学习
1
D.( 2x – 3 y) (– 2x + 3y ) = 4x 2 – 9 y 2
,将 x – xy 2 分解因式
祝
进步
1
;
个空心圆;
9、不等式组 2x 1 3
3x 1 x 3 8
1 2
x
1
的解集应为( )
A、 x 2 B、 2 x 2 C、 2 x 1 D、 x 2 或 7
2.反比例函数 y = x的图象经过点(tan45°,cos60°),则 k =
3、水平放置的正方体六个面分别用“前面、后面、上面、下面、左面、右面”表示。
如图是一个正方体的平面展开图,若图中的“进”表示正方体的前面,“步”表示右面,
“习”表示下面,则“祝”、“你”、“学”分别表示正方体的________。
3
12、某超市购进了一批不同价格的皮鞋,下表是该超市在近几年统计的平均数据。
皮鞋价(元) 160
销售百分率
60%
要使该超市销售皮鞋收入最大,该超市应多购( )的皮鞋。
140%
75%
A、160 元 B、140 元 C、120 元 D、100 元
2000年湖北省武汉市中考数学试卷及答案(word版)

2000年武汉市中考数学试卷一、选择题(本大题共12小题,每小题3分,共36分)1.计算所得正确结果是(A)(B)1 (C)(D)-12.若a<0,则化简后为(A) (B) (C) (D)3.一元二次方程x2+px+q=0的两根为3,那么二次三项式x2+pX+q可分解为(A)(x+3)(x-4) (B)(x-3)(x+4) (C)x-3)(x-4)(D)(x+3)(x+4)4.数据5,7,4,0,5,4,9,7,6,4的中位数和众数分别为(A)5和5 (B)4和5 (C)5和4 (D)4.5和55.如图,A、C是函数的图象上的任意两点,过A作x的垂线,垂足为B,过垂C作y的线,垂足为D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则(A)S1>S2(B)S1<S2(C)S1=S2(D)S1和S2的大小关系不能确定6.已知直线y=kx+b(k≠0)与x轴的交点在x轴的正半轴,下列结论:①k>0,b>0;②k>0,b<0;③k<0,b>0;④k<0,b<0.其中正确结论的个数是(A)1 (B)2 (C)3 (D)47.二次函数y=ax2+bx+c的图象如图所示,则a、b、c的大小关系是(A)a>b>c (B)a>c>b(C)a>b=c (D)a、b、c的大小关系不能确定8.过⊙O内一点M的最长的弦长为4cm最短的弦长为2cm,则OM的长为(A) (B) (C)1cm (D)3cm9.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以BC上一点O为圆心作⊙O 与AC、AB都相切,又⊙O与BC的另一个交点为D,则线段BD的长为(A)1 (B)(C)(D)10.如图,三个半径为r的等圆两两外切,且与△AB C的三边分别相切,则△ABC 的边长为(A)2r (B) (C)3r (D)11.如图,在直角梯形ABCD中,AB⊥BC,AD=1,BC=3,CD=4,EF为梯形的中位线,DH为梯形的高。
中考中跨学科试题
中考中跨学科试题江苏省盐城市射阳县实验初级中学 朱丰胜数学课程标准倡导学科整合,主张学科渗透,要求学生能够解决带有实际意义的和相关学科中的数学问题。
因此,近几年各地的中考数学试卷中涌现了一批立意新颖、结构合理的跨学科试题。
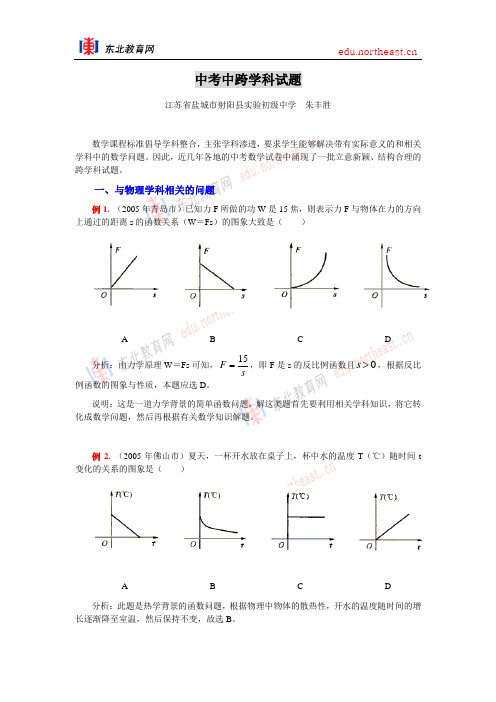
一、与物理学科相关的问题例1. (2005年青岛市)已知力F 所做的功W 是15焦,则表示力F 与物体在力的方向上通过的距离s 的函数关系(W =Fs )的图象大致是( )ABCD分析:由力学原理W =Fs 可知,F s=15,即F 是s 的反比例函数且s >0,根据反比例函数的图象与性质,本题应选D 。
说明:这是一道力学背景的简单函数问题,解这类题首先要利用相关学科知识,将它转化成数学问题,然后再根据有关数学知识解题。
例2. (2005年佛山市)夏天,一杯开水放在桌子上,杯中水的温度T (℃)随时间t 变化的关系的图象是( )ABCD分析:此题是热学背景的函数问题,根据物理中物体的散热性,开水的温度随时间的增长逐渐降至室温,然后保持不变,故选B 。
例3. (2005年河北省)某闭合电路中,电源的电压为定值,电流I (A )与电阻R (Ω)成反比例,图1表示的是该电路中电流I 与电阻R 之间的图象,则用电阻R 表示电流I 的函数解析式为( )图1A. I R=2B. I R=3C. I R=6D. I R=-6 分析:图中点B (3,2)坐标的意义是,当电阻R =3()Ω时,电流I =2(A )。
将R 、I 的值代入I U R =,易得U =6(V ),所以用电阻R 表示电流I 的函数解析式为I R=6,故选C 。
例4. (2005年桂林市)已知矩形ABCD 中,AB =2,BC =3,F 是CD 的中点,一束光线从点A 出发,通过BC 边反射,恰好落在F 点(如图2),那么,反射点E 与点C 的距离为__________。
图2分析:由光学知识“入射角等于反射角”知,∠AEB =∠FEC ,则Rt △AEB ∽Rt △FEC ,再根据相似三角形的性质进行求解。
湖北省武汉市课改实验区中考数学试卷及答案

2005年武汉市初中毕业、升学考试数学试卷(课改实验区)亲爱的同学,在你答题前,请认真阅读下面的注意事项:1. 本试卷由第I 卷和第II 卷组成,全卷26题,共12页,考试时间120分种;2. 请将你的姓名,准考证号和座位号填写在时间的指定位置内;3. 请用钢笔或圆珠笔答题,答案写在指定的位置上。
预祝你考试取得优异成绩!第I 卷(选择题)一、选择题(本答题共10小题,在每小题给出的四个选项中,只有一项是符合题目要求的,请将你选取的答案的英文字母填写在下面的表格内)A .74.010.⨯B .64010.⨯C .84010.⨯D .80.410.⨯ 1、由几个相同的小正方体搭成的几何体的视图如图所示,则搭成这个几何体的小正方体的个数是 A .4. B .5. C .6. D .7.2、将矩形ABCD 沿AE 折叠,得到如图所示的图形,已知∠CED '=60°,则∠AED 的大小是A .60°.B .50°.C .75°. D .55°. 3、下列运算中,计算结果正确的是A .236a a a .=B .2a +3b =5abC .523a a a .÷=D .224a b a b ()=. 4、不等式组x x ⎧⎨⎩>1,>3的解集在数轴上可以表示为5、如图,一电线杆AB 高为10米,当太阳光线与地面的夹角为60°时,其影长AC 1.732,结果保留3个有效数字) A. 5.00米. B. 8.66米 C. 17.3米 D. 5.77米6、一个暗箱里装有10个黑球,8个白球,12个红球,每个球除颜色外都相同,从中任意摸出一个球,摸到白球的概率是A.13 B. 18 C. 415 D. 4117、如图,⊙O 是△ABC 的外接圆,且∠BAO =25°,则∠C 的大小为A. 25°B. 50°C. 60°D. 65° 9、已知二次函数2y ax bx c =++(a ≠0)的图象如图所示,则 下列结论: ①a 、b 同号;②当x =1和x =3时,函数值相等; ③4a +b =0;④当y =-2时,x 的值只能取0.其中正确的个数是A. 1个B. 2个C. 3个D. 4个10、下表选自北京师范大学出版社出版的《数学》课本(九年级下册)。
2005年武汉市中考数学试卷

2005年武汉市中考数学试卷参考公式:在半径为R 的圆中,圆心角为n °的扇形面积的计算公式是:2360R n S π=扇形第I 卷(A 卷第1~20题)一、判断题(共10小题,每小题2分,共20分)请你判断下列各题的正误,若是正确的,请在括号内打“√”,若是错误的,请在括号内打“×”。
1. 一元二次方程02342=-+x x 的二次项系数为4,一次项系数为3。
( )2. 直角坐标系中,第三、四象限的点的纵坐标都小于零。
( )3. 当x=2时,函数53-=x y 的值为1。
( )4. 反比例函数xy 6-=的图像在第二、四象限。
( ) 5. 数据4,5,5,3,5的众数是5。
( )6. sin30°+cos60°=1。
( )7. 任何一个三角形有且只有一个外接圆。
( )8. 相等的圆心角所对的弧相等。
( )9. 三角形的内心到三边的距离相等。
( )10. 圆既是轴对称图形,又是中心对称图形。
( )二、选择题(共10小题,每小题4分,共40分)下列各题均有四个备选答案,其中有且只有一个是正确的,请将正确的答案的序号填在题后的括号内。
11. 一元二次方程092=-x 的根为( )A. x=3B. x=-3C. 3321-==x x ,D. 3021==x x ,12. 一元二次方程05752=+-x x 的根的情况是( )A. 有两个相等的实数根B. 有两个不相等的实数根C. 只有一个实数根D. 没有实数根13. 函数2-=x x y 中,自变量x 的取值范围是( ) A. x ≠0 B. x>2 C. x ≠2 D. x ≠-214. 下列函数:①y=2x ;②2x y =;③y=2x+1;④y=2x 2+1其中一次函数的个数是( )A. 4B. 3C. 2D. 115. 已知:如图,圆心角∠AOB=100°,则圆周角∠ACB 等于( )A. 130°B. 120°C. 110°D. 100°16. 已知圆O 的半径为8cm ,如果一条直线和圆心O 的距离为8cm ,那么这条直线和这个圆的位置关系为( )A. 相离B. 相切C. 相交D. 相交或相离17. 圆O 1与圆O 2的半径分别是4cm 和5cm ,若O 1O 2=10cm ,则这两圆的位置关系为( )A. 外离B. 外切C. 相交D. 内切18. 若两圆只有一个公共点,则公切线的条数为( )A. 1B. 2C. 3D. 1或319. 半径为2cm 的圆中,有一条长为2cm 的弦,则圆心到这条弦的距离为( )A. 1cmB. 2cmC. 3cmD. 2cm20. 关于x 的一元二次方程02=--n x x 没有实数根,则抛物线n x x y --=2的顶点在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限第I 卷(BI 卷第21~32题)三、选择题(共12小题,每小题3分,共36分)下列各题中均有四个备选答案,其中有且只有一个是正确的,请将正确的答案的序号填在题后的括号内。
2005年宜昌市中考数学试题及答案(课改区)-推荐下载

b 二次函数 y=ax2+bx+c 图象的顶点坐标是 (-
,
4ac b2
2a 4a
第Ⅰ卷(选择题、填空题 共45分)
一、选择题:(下列各小题都给出了四个选项,其中只有一项是符合题目要求的,请将符合
要求的选项前面的字母代号填写在第II卷上指定的位置. 本大题共10小题,每小题3
分,计30分)
1. 图中物体的形状类似于(
(A)棱柱 (B)圆柱 (C)圆锥
2.化简 20 的结果是( ).
(A) 5 2
(B) 2 5
).
(C) 2 10 .
3. 如图所示,BC=6,E、F 分别是线段 AB 和线段 AC 的中点,
那么线段 EF 的长是( ). (A)6 (B)5 (C)4.5
(D)3
不
能进行密铺的地砖的形状是( ).
(A) ①
(B) ②
(C) ③
9.实数 m、n 在数轴上的位置如图所示,则下列不等关系正确的是( ).
(A)n<m
(C)n0<m0
(B) n2<m2
(D)| n |<| m |
10.如图所示的函数图象的关系式可能是( ).
(A)y = x
1
(B)y =
x
1
(C)y = x2 (D) y =
4.有 6 张背面相同的扑克牌,正面上的数字分别是 4,5,6,7,8,9.若将这六张牌背
面朝上洗匀后,从中任意抽取一张,那么这张牌正面上的数字是 9 的概率为(
Байду номын сангаас
).
2
(A)
3
1
(B)
2
1
(C)
黄冈中考数学试题及答案2005
二00五年湖北省黄冈市初中升学统一考试数 学 试 题<课改区)<满分:120分 考试时间:120分钟)一、填空题<每空3分,共24分)1.错误!的相反数是 ,立方等于– 64的数是 ,将x – xy 2分解因式的结果是 ;iKzaInL3ic 2.反比例函数y = 错误!的图象经过点<tan45°,cos60°),则k = ;iKzaInL3ic 3、水平放置的正方体六个面分别用“前面、后面、上面、下面、左面、右面”表示。
如图是一个正方体的平面展开图,若图中的“进”表示正方体的前面,“步”表示右面,“习”表示下面,则“祝”、“你”、“学”分别表示正方体的________。
iKzaInL3ic4某一时刻测得一棵小树的高为1.5M 这棵大树的影长为3M ,则这棵大树的实际高度为 M ;iKzaInL3ic5.某同学在电脑中打出如下排列的若干个圆<图中●表示实心圆,○表示空心圆):● ○●●○●●●○●●●●○●●●●●○●●●●●●○若将上面一组圆依此规律复制得到一系列圆,那么前2005个圆中有 个空心圆;6、图⑴中的梯形符合____条件时,可以经过旋转和翻折形成图案⑵。
号里,不填、错填或多填均不得分,每小题3分,共18分)iKzaInL3ic 7.已知y x ,为实数,且()02312=-+-y x ,则y x -的值为< )A .3B .– 3C .1D .– 18.下列运算中正确的是< ) A .10552x x x =+B .()()853x x x -=-∙--C .(– 2x 2y> 3·4x – 3 = – 24x 3y 3D .( 错误!x – 3 y> (– 错误!x + 3y > = 错误!x 2 – 9y 2iKzaInL3ic 9、不等式组()()⎪⎩⎪⎨⎧≤--+<--+-1213128313xx x x 的解集应为< ) ⑴ ⑵A 、2-<xB 、722≤<-x C 、12≤<-x D 、2-<x 或x ≥110、如图,在平行四边形ABCD 中,EF ∥AB ,DE ∶EA = 2∶3,EF = 4,则CD 的长为< )iKzaInL3icA .错误!B .8C .1011是一定的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2005年武汉市中考数学试题及答案A卷一、判断题(共10小题,每小题2分,共20分)1. 方程的二次项系数为3,一次项系5。
2. 函数中,自变量x的取值范围是。
3. 直角坐标系中,点P(6,-7)在第四象限。
4. 函数是反比例函数。
5. 数据5,3,7,8,2的平均数是5。
6. 。
7. 在同圆或等圆中,相等的圆心角所对的弧相等。
8. 长度相等的两弧是等弧。
9. 三角形的外心到三角形各顶点的距离都相等。
10. 两圆相外切,这两个圆的公切线共有三条。
二、选择题(共10小题,每小题4分,共40分)下列各题均有四个备选答案,其中且只有一个是正确的。
请在答题卡中将正确答案的代号涂黑。
11.一元二次方程的根为().(A)x=1 (B)x=-1 (C),(D)12.不解方程,判别方程5-7x+5=0的根的情况是().(A)有两个相等的实数根(B)有两个不相等的实数根(C)只有一个实数根(D)没有实数根13.函数中自变量x的取值范围是().(A)x≠-1 (B)x>-1 (C)x≠1 (D)x≠014.下列函数中,一次函数是().(A)(B)(C)(D)15.一次函数y=x+1的图象在().(A)第一、二、三象限(B)第一、三、四象限(C)第一、二、四象限(D)第二、三、四象限16.如图,已知圆心角∠BOC=,则圆周角∠BAC的度数为().(A)(B)(C)(D)17.已知圆的半径为6.5cm,如果一条直线和圆心的距离为9cm,那么这条直线和这个圆的位置关系是(A)相交(B)相切(C)相离(D)相交或相离18.已知⊙和⊙的半径分别为3cm和4cm,圆心距=10cm,那么⊙和⊙的位置关系是(A)内切(B)相交(C)外切(D)外离19.过⊙内一点M的最长弦长为10cm,最短弦长为8cm,那么OM的长为().(A)3cm (B)6cm (C)cm (D)9cm20.若二次函数,当x取,(≠)时,函数值相等,则当x取+时,函数值为(A)a+c (B)a-c (C)-c (D)cB卷三、选择题: 下列各题中均有四个备选答案,其中有且只有一个是正确的。
请在答题卡上将正确答案的代号涂黑。
21.计算的结果为().(A)1 (B)x+1 (C)(D)22.(1,3)关于原点过对称的点的坐标是().(A)(-1,3)(B)(-1,-3)(C)(1,-3)(D)(3,1)23.若a≤1,则化简后为().(A)(B)(C)(D)24.小明家装修房屋,用同样的正多边形瓷砖铺地,顶点连着顶点,为铺满地面而不重叠,瓷砖的形状可能有().(A)正三角形、正方形、正六边形(B)正三角形、正方形、正五边形(C)正方形、正五边形(D)正三角形、正方形、正五边形、正六边形25.若点(3,4)是反比例函数图象上一点,则此函数图象必须经过点().(A)(2,6)(B)(2,-6)(C)(4,-3)(D)(3,-4)26.如图,△ABC中,AB=AC,AD=DE,∠BAD=,∠EDC=。
则∠DAE的度数为(A)(B)(C)(D)27.在一次科技知识竞赛中,两组学生成绩统计如下表,通过计算可知两组的方差为,。
下列说法:①两组的平均数相同;②甲组学生成绩比乙组学生成绩稳定;③甲组成绩的众数>乙组成绩的众数;④两组成绩的中位数均为80,但成绩≥80的人数甲组比乙组多,从中位数来看,甲组成绩总体比乙组好;⑤成绩高于或等于90分的人数乙组比甲组多,高分段乙组成绩比甲组好。
其中正确的共有().28.如图,外切于P点的⊙⊙和⊙是半径为3cm的等圆,连心线交⊙于点A,交⊙于点B,AC与⊙相切于点C,连结PC,则PC的长为().(A)cm (B)cm (C)cm (D)cm29.某商店把一商品按标价的九折出售(即优惠10%),仍可获利20%,若该商品的标价为每件28元,则该商品的进价为().(A)21元(B)19.8元(C)22.4元(D)25.2元30.抛物线的图角如图,则下列结论:①>0;②;③>;④<1.其中正确的结论是().(A)①②(B)②③(C)②④(D)③④31.小明早晨从家骑车到学校,先上坡后下坡,行程情况如图,若返回时上、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是()。
(A)37.2分钟(B)48分钟(C)30分钟(D)33分钟32.已知:如图,中,,BC为定长,以BC为直径的⊙O分别交AB、AC于点D、E。
连结DE、OE。
下列结论:①BC=2DE;②D点到OE的距离不变;③BD+CE=2DE;④OE为外接圆的切线。
其中正确的结论是()。
(A)①②(B)③④(C)①②③(D)①②④28题30题31题32题四、填空题(共4小题,每小题2分,共8分)33.(本题共有A、B两小题,请你只选择一题作答)A.请你写出一个能分解的二次四项式并把它分解。
B.用计算器计算:。
(精确到0.01)34.在同一平面上,1条直线把一个平面分成个部分,2条直线把一个平面最多分成个部分,3条直线把一个平面最多分成个部分,那么8条直线把一个平面最多分成部分。
35.如图,AB是⊙O的直径,⊙O交BC于D,,垂足为E,要使DE是⊙O的切线,则图中的线段应满足的条件是或。
36.如图,中,,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为。
五、证明与解答题(本大题共3小题,共22分)37.(本题6分)武汉市教育局在中学开展的“创新素质实践行”中,进行了小论文的评比。
各校交论文的时间为5月1日至30日,评委会把各校交的论文的件数按5天一组分组统计,绘制了频率分布直方图,已知从左至右各长方形的高的比为2:3:4:6:4:1,第二组的频数为18。
请回答下列问题:(1)本次活动共有多少篇论文参加评比?(2)哪组上交的论文数量最多?有多少篇?(3)经过评比,第四组和第六组分别有20篇、4篇论文获奖,问这两组哪组获奖率较高?38.(本题8分)如图,已知:⊙、⊙外切于点P,A是⊙上一点,直线AC切⊙于点C交⊙于点B,直线AP交⊙于点D。
(1)请你判断是否成立(不需证明);(2)将“⊙、⊙外切于点P”改为“⊙、⊙内切于点P”,其他条件不变。
(1)中的结论是否仍然成立?画出图形并证明你的结论。
39.(本题8分)2004年8月中旬,我市受14号台风“云娜”的影响后,部分街道路面积水比较严重。
为了改善这一状况,市政公司决定将一总长为1200m的排水工程承包给甲、乙两工程队来施工。
若甲、乙两队合做需12天完成此项工程;若甲队先做了8天后,剩下的由乙队单独做还需18天才能完工。
问甲、乙两队单独完成此项工程各需多少天?又已知甲队每施工一天需要费用2万元,乙队每施工一天需要费用1万元,要使完成该工程所需费用不超过35万元,则乙工程队至少要施工多少天?六、综合题(本题10分)40.已知抛物线交,交轴的正半轴于C点,且。
(1)求抛物线的解析式;(2)是否存在与抛物线只有一个公共点C的直线。
如果存在,求符合条件的直线的表达式;如果不存在,请说明理由。
七、综合题(本题14分)41.已知:如图,直线交轴于,交轴于,⊙与轴相切于O点,交直线于P点,以为圆心P为半径的圆交轴于A、B两点,PB交⊙于点F,⊙的弦BE=BO,EF的延长线交AB于D,连结PA、PO。
(1)求证:;(2)求证:EF是⊙的切线;(3)的延长线交⊙于C点,若G为BC上一动点,以为直径作⊙交于点M,交于N。
下列结论①为定值;②线段MN的长度不变。
只有一个是正确的,请你判断出正确的结论,并证明正确的结论,以及求出它的值。
参考答案A卷共60分三、选择题(共12小题,每小题3分,共36分)33.A如 B 2.35 34.37 35. AB=AC或BD=DC 36.五、证明与解答题(本大题共3小题,共22分)37.(本题6分)答:(1)本次活动共有120篇论文参评;(2)第四组上交的论文数量最多,有36篇;(3)第六组获奖率最高。
38.(本题8分)(1)∠BPC=∠CPD成立。
(2)解:(1)中的结论仍然成立。
过点P作两圆的公切线PM,则∠MPB=∠A,∠MPC=∠BCP。
∴∠BPC=∠MPC-∠MPB=∠BCP-∠A=∠CPA。
∴∠BPC=∠CPD39.解:设甲、乙两队单独完成此项工程分别需要x天,y天。
依题意得解之得经检验知它们适合方程组和题意。
则甲队每天施工1200÷20=60m,乙队每天施工1200÷30=40m.设甲、乙两队实际完成此项工程分别需要a天,b天.依题意得解之得b≥35.答:甲、乙两队单独完成此项工程分别需要20天,30天;要使完成该工程所需费用不超过35万元,则乙工程队至少要施工15天。
六、综合题(本题10分)40.解:(1)由条件知AO=||=-,OB=||=,OC=3(m+1).∵,,得:.∵<,||>||,∴<=m-2<0,∴m=1. ∴函数的解析式为(2)存在与抛物线只有一个公共点C的直线. C点的坐标为(0,6).①当直线过C(0,6)且与x轴垂直时,直线也抛物线只有一个公共点,∴直线。
②过C点的直线,与抛物线只有一个公共点C,即只有一个实数解。
∴,,∴,∴。
∴。
∴符合条件的直线的表达式为或。
七、综合题(本题14分)41.证明:(1)连结。
∵。
∴,,∴.∴,得,∴。
又AB为直径,∴, ∴。
(2)延长ED交⊙于点H,连结PE。
BO为切线,∴。
又∵BE=BO,∴。
而,∴∽,∴, ∴BE=BH, 有。
又由(1)知,∴,∴EF为⊙的切线。
(3)MN的长度不变。
过N作⊙的直径NK,连结MK。
则,且,又NK=,∴≌,∴MN=ED。
而,,∴=5,∴。
AB=16,且OD=,∴AD=7,BD=9。
,∴。
故MN的长度不会发生变化,其长度为。
