泵与风机课后习题参考答案(完整版)
流体力学泵与风机_课后题答案详解

流体力学泵与风机部分习题答案 2-15解:(1)当1γ为空气 21p p = ()A B p h z p =++γ ()h z p p p B A +=-=∆γ 3.010008.9⨯⨯= kpa pa 94.22940== (2)当1γ为油 31p p =()z H h p p A +++=γ1 ()H h p p B γγ++=13H h z H h p p p p p B A γγγγγ--+++-=-=∆131h z h 1γγγ-+=1.090002.010008.91.010008.9⨯-⨯⨯+⨯⨯= kpa pa 04.22040== 2-16 解:21p p =()211h h H p p M +++=水γ 212h h p p a 汞油γγ++=()2121h h p h h H p a M 汞油水γγγ++=+++()2.010008.96.1378502.05.110008.998011⨯⨯⨯+⨯=++⨯⨯+-h h 26656785098002.098005.1980098011+=+⨯+⨯+-h h 1960147009802665619501--+=hm h 63.51= 2-28解:()21h h p -=γ()()()b h h h b h h h h P 02210212145sin 45sin 21-+--=γγ ()()145sin 22310008.9145sin 232310008.92100⨯-⨯⨯+⨯-⨯-⨯⨯⨯= kN N 65.343465022510008.9==⨯⨯=()()()Pbl h h h bl h h h h l D D D 2022110212145sin 45sin 21-+--=γγ m 45.222510008.9222210008.92322210008.9=⨯⨯⨯⨯⨯+⨯⨯⨯=2-32 解:b h h b h h P 02202145sin 2145sin γγ+= 2222210008.9212222110008.9⨯⨯⨯⨯⨯+⨯⨯⨯⨯=kN N 8576.1106.1108572810008.9==⨯⨯=Ph h b h h h h b h h l D 02102202102145sin 3245sin 2145sin 245sin ⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=γγ 2810008.92372410008.9222410008.9⨯⨯⨯⨯⨯+⨯⨯⨯=2613= 26722613=-=p lT P G l T l P l G ⨯=⨯+⨯22672810008.9162.19⨯=⨯⨯⨯+⨯T kN T 31.10134.27481.9=+= 2-41解:245sin 0=⨯=r hb h h P x ⨯⨯⋅⋅=21γ 4212210008.9⨯⨯⨯⨯⨯=kN N 2.3939200==V P z γ=b r r r⎪⎭⎫⎝⎛⨯⨯⨯-=00245cos 45sin 2136045πγ 4212281214.310008.92⨯⎪⎭⎫ ⎝⎛⨯⨯-⨯⨯⨯⨯= kN N 344.2222344==kN P 1.45344.222.3922=+=03057.0arctan 2.39344.22arctan arctan≈===x z P P α3-3解:(1)s m v d Q /0049.010025.04432323=⋅⋅=⋅=ππs kg Q /9.4=ρ(2)s m v d d v /625.032131=⎪⎪⎭⎫⎝⎛= s m v d d v /5.232232=⎪⎪⎭⎫ ⎝⎛=3-5解:s m h m Q /778.2/1000033==s m d Qv /2042≤=π所以,177.04=≥πv Qd 所以,mm m d 45045.0== 此时,s m d Q d Qv /4.1763585.0112.114422====ππ3-6解:22543212054d d A A A A A ππ======22114012021d d A A ππ=⋅="=' 22224012021d d A A ππ=⋅="='22334012021d d A A ππ=⋅="='22444012021d d A A ππ=⋅="='22554012021d d A A ππ=⋅="='2214014d d ππ=d d 1011=d r 10211= 2224034d d ππ=d d 1032= d r 10232= 2234054d d ππ=d d 1053= d r 10253= 2244074d d ππ=d d 1074= d r 10274=2254094d d ππ=d d 1035=d r 10235= ()()54321254321220240u u u u u d u u u u u d Q G ++++=++++==πρπρρ3-7解:干管前端的质量流量为:42562.2211111d A v Q πρρ⨯⨯==()s kg /128544.005.042562.22=⨯⨯⨯=πs kg Q Q Q /064272.02132===ρρρ ()s m A Q v /247.2204.043.2064272.022222=⋅⋅==πρρ()s m A Q v /05.18045.0424.2064272.023333=⋅⋅==πρρ 3-10解:将基准面建立在B 点经过的水平面上,列能量方程:gv p z gv p z 222222221111αγαγ++=++其中,m z 2.11= m p 5.11=γ s m v /21= s m v d d v /5.4122212== 121==αα gp g 25.40225.12.1222++=++γ871.125.4225.12.1222=-++=gg p γ 3-11解:将2点所在的水平面作为基准面,列能量方程: gv p z gv p z 222222221111αγαγ++=++31=z 02=zγγ21p p =s m v /31=gv p g p 2023322221++=++γγ s m gh v /2.83222=+=32.822112=⎪⎪⎭⎫ ⎝⎛=d d v v 所以,m d 12.02= 3-14解:以水面为基准面,列0-0和D-D 的能量方程:gv p z gv p z DD DD 22220000αγαγ++=++00=z00=γp02200=gv α 4-=D z0=γDpgv DD 2040002α++-=++ 所以,422=gv DD α,即,s m v D /85.88.924=⋅⋅=所以,s m v d Q D /017368.085.805.044322=⋅⋅==ππ81:1:2:24422==A D DD A A d d gv gv αα列0-0和A-A 断面的能量方程:gv p z gv p z AA AA 22220000αγαγ++=++8147000++-=++γAp 所以,8147-=γAp 所以,kpa p A 1.68= 列0-0和B-B 断面的能量方程:gv p z gv p z BB BB 22220000αγαγ++=++kpa p B 484.08.9814-=⋅-= 列0-0和C-C 断面的能量方程:gv p z gv p z CC CC 22220000αγαγ++=++kpa p C 1.208.98142-=⨯⎪⎭⎫ ⎝⎛+-=0=D p3-18解:将基准面建在管道所在的水平面上,列能量方程:21222222111122-+++=++l h gv p z gv p z αγαγ128.998.0008.9490222+++=++g v α9.3222=gv s m v /74.82= 3-19 解:(1)(a )将基准面建在A 所在的水平面上,列0-0和C-C 断面的能量方程:gv p z gv p z CC CC 2222000αγαγ++=++gv CC 2000042α++=++422=gv CC α s m v C /85.88.98=⨯=1:4:2:22222==B C CC B B s s gv gv αα122=gv BB α s m v /43.48.921=⨯= 且 B A v v =(b )(c )gv p z gv p z AA AA 22220000αγαγ++=++10004++=++γAp3=γAp kpa p A 4.29=(2)(a )2122000022-+++=++l CC CC h gv p z gv p z αγαγ其中,gv g v h l 2324222121+=-g v g v g v 223200004222222++++=++54222=g v 所以,s m v /96.32= s m v v /96.12121==(b )(c )gv g v p z g v p z 2222212111120000+++=++αγαγ 5300041++=++γp5341-=γp kpa p 32.331= gv g v g v p z g v p z 223242222222222220000++++=++αγαγ5423545400042⋅++++=++γp kpa p 76.112=3-20 解:()()212221221122-++=--++l a p v p z z v p ργγρs m d Qv /38.2005.014.34202.042221=⨯⨯⨯==πs m d Qv /19.1005.014.3402.04222=⨯⨯==π2423222121v v p l ρρ+=-()()242322222122212211v v v p z z v p a ρρργγρ+++=--++22214v v =()()8.930306.02.1224232300212221221⨯+---+++=v v v v p ρρρρ()()8.930306.02.12424212230022222222⨯+---+++=v v v v ρρρρ8.9606.019.1026.0133002⨯⨯-⨯⨯+= pa 16.352= mm p h 6.449.716.3521===γ3-22解:s kN h kN G /048944.0/2.176==s m GQ /1347.77.08.910048944.033=⨯⨯==γs m d Q d Qv /09.914.31347.7444222=⨯===ππ()2122221122-++=-++l a p v p H v p ργγρ其中,01≈v ,pa h p 988.9101010331=⨯⨯⨯==-γ()γgv d H H 2035.0209.97.008.97.02.1098222+⨯+=⨯⨯-++-()8.97.08.9209.9035.0209.97.008.97.02.109822⨯⨯⨯+⨯+=⨯⨯-++-H HH H 0122.19.289.498+=+-所以,m H 64.32=()212211212212-++=-++l M M a p v p H v p ργγρ()8.97.08.9209.9164.322035.0209.97.064.328.97.02.12109822⨯⨯⨯+⨯+=⨯⨯-++-M p 科技52.169.28968.7998++=+-M p 所以,pa p M 45.63-=3-263-28解:列连续性方程:s m D Qv /18.34.014.344.04221=⨯⨯==π s m d Q v /96.501.014.344.04222=⨯⨯==π列能量方程: g v p z g v p z 222222221111αγαγ++=++ g v g v p 222112221ααγ-=m 98.1318.9218.396.5022=⨯-= kpa p 404.12938.998.1311=⨯=列动量方程:()12v vQ F -=∑ρ ()12222144v v Q R d p D p -=-⨯-⨯ρππ()18.396.504.04.04404.12932-⨯=-⨯⨯R πkN R 339.14378.474.04.04404.12932=⨯-⨯⨯=π kN R 94.1112=3-33解:列能量方程:g v p z g v p z 222222221111αγαγ++=++ 其中,5321=v v 2221259v v = g v g v 209.0205.1222211αα++=++gv g v 225926.02222-= s m v /3.42= s m v /58.21=()12v v Q F -=∑ρ()1222212121v v Q R b h b h -=--ργγ 其中,s m Q /644.45.12.158.23=⨯⨯= 72.1644.410009.0108.9215.1108.9212323⨯⨯=-⨯⨯⨯-⨯⨯⨯R N R 2.480=4-2 (1) m mm d 1.0100== s kg Q /10=ρs m Q Q /01.03==ρρs m d Q v /274.11.014.301.04422=⨯⨯==π s m /10519.126-⨯=ν 8387110519.11.0274.1Re 6=⨯⨯==-νvd (紊流) (2) s kg Q /10=ρ s m Q Q /011765.0850103===ρρ s m d Q v /4987.11.014.3011765.04422=⨯⨯==π s m /1014.124-⨯=ν 13151014.11.04987.1Re 4=⨯⨯==-νvd 4-3 解:m d 3.0= C T 020= s m /107.1526-⨯=νs m d v /1067.1043.0107.152000Re 36max --⨯=⨯⋅=⋅=ν s m A v Q /103947.743.014.31067.1043323max max --⨯=⨯⨯⨯=⋅= h kg Q /9.3136002.1103947.73=⨯⨯⨯=-ρ4-4 解:212=d d 4212221==d d v v 222111Re 2214Re ===ννd v d v 所以,2Re Re 21= 4-12 紊流粗糙区,5106Re ⨯> νvd=Re ,所以,s m d v /14.325.010308.1106Re 65=⨯⨯⨯==-ν s m d v Q /154.0425.014.314.34322=⨯==π 4-13 s m s L Q /2.0/20031==s m d Q v /076433.44211==π 661107791.010308.125.0076433.4Re ⨯=⨯⨯==-νvd s L Q /202= s m v /4076433.02=4210791.7Re ⨯=s L Q /53= s m v /1019.03= 43109478.1Re ⨯=查尼氏图,得到, 5106Re ⨯=u 4104Re ⨯=l123Re Re Re Re Re <<<<u l ,所以,1Q 属于紊流粗糙区,2Q 属于紊流过渡区,3Q 属于紊流光滑区,(1) 对于1Q ,采用希弗林松公式,02326.025.0105.011.011.025.0325.01=⎪⎪⎭⎫ ⎝⎛⨯=⎪⎭⎫ ⎝⎛=-d K λm g v d l h f 888.78.92076433.425.010002326.0222111=⨯⨯⨯==λ (2) 对于2Q ,采用阿公式,02547.010791.76825.0105.011.0Re 6811.025.04325.02=⎪⎪⎭⎫ ⎝⎛⨯+⨯=⎪⎭⎫ ⎝⎛+=-d K λ m g v d l h f 086.08.924076433.025.010002547.0222222=⨯⨯⨯==λ(3) 对于3Q ,采用布公式02678.05.194773164.0Re 3164.025.025.03===λ m g v d l h f 005676.08.9244076433.025.010002678.0222333=⨯⎪⎭⎫ ⎝⎛⨯⨯==λ 4-15 5102Re ⨯=u 4000Re =lm d 05.0= m K 31025.0-⨯= s m d v u /028.405.010007.1102Re 65max =⨯⨯⨯==-νs L d v Q /905.7405.014.3028.4422max max =⨯==π 26min 10056.805.010007.14000Re --⨯=⨯⨯==d v l ν s L s m d v Q /1581.0/1001581.0405.014.310056.8432222min min =⨯=⨯⨯==--π 4-21 (1) a d d =21 2211av v = gv d l d v g v d l g v d l h f 2642Re 64221111211121111νλ=== 4212221211ad d v v h h f f == 19.1=a (2)75.425.12275.12122225.0225.0225.021125.0125.0125.021123164.023164.0a d d v v gv d l d v g v d l d v h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==νν 16.1=a (3)25.525.11222122225.0221125.01211211.0211.0a d d v v g v d l d K g v d l d K h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛= 14.1=a 4-24 解:s m Q /002742.0602329.03=⨯=s m d Q v /3972.105.014.3002742.04422=⨯⨯==π 629.022=⎪⎭⎫ ⎝⎛+g v d l ζλ ()629.08.923972.162=⨯+ζ 3151.0=ζ 4-26 解:(1) 突然缩小375.03145.7815.015.0121=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζmm m g v h j 5.760765.08.922375.022211==⨯==ζ (2)5.02=ζmm m g v h j 102102.08.9225.022222==⨯==ζ (3)1693145.781122213=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζ mm m h j 115115.08.92216923==⨯= (4)14=ζ mm m h j 204204.08.922124==⨯= 4-27 解:()()gv v g v v h h m m j j 222121-+-=''+' ()()()()02212221=-+--=''+'gv v g v v h h m m vm j j 所以,221v v v m += 此时,()j j j h gv v g v v v g v v v h h 2221222222121212211=-=⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛+-=''+' 4-29 解:s m h m Q /1044.4/16333-⨯== s m d Q v /2624.205.014.31044.44423211=⨯⨯⨯==-π s m d Q v /5656.01.014.31044.44423222=⨯⨯⨯==-π m g v v p p h j 140674.08.925656.02624.28.910001739.522222121=⨯-+⨯⨯-=-+-=γ g v h j 2211ζ= 5387.01=ζ gv h j 2222ζ= 619.82=ζ5-17 解:5.6082.014.32.12.01002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 7.30422.014.32.12.05002.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 973671.014.32.11.05002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 3.101018973677.30425.608321=++=++=p p p p S S S S 22211/91.227215.03.101018m N Q S p p =⨯==22222/1.258616.03.101018m N Q S p p =⨯==5-25 解:()()⎪⎩⎪⎨⎧=++=++=1021520232322223221SQ Q Q S SQ Q Q S SQ 610=S解得,s m Q /10472.4331-⨯= s m Q /1041.2332-⨯= s m Q /1063.0333-⨯=5-27 解:94.10348.92.014.32.020002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 8.206988.91.014.31.0100025.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 78.37258.92.014.32.072002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 038035.087.14311705.321111211=+=+='S S S 所以,25.6911='S 1)()H Q S S =+'231s m S S H Q /10186.604417163331-⨯==+'=2)H SQ =2 H Q S =⎪⎭⎫ ⎝⎛'221 1325133831432=+'=-'=S S S S gd πζ ()1.25688.92.014.31325142=⨯⨯⨯=ζ 5-28 解:286.1368.93.014.383.020002.084242=⨯⨯⨯⨯==g d d l S AB AB AB AB πλ 029.1098.93.014.383.016002.084242=⨯⨯⨯⨯==g d d l S AC AC AC AC πλ 34.328.94.014.384.020002.084242=⨯⨯⨯⨯==g d d l S AD AD AD AD πλ 772.818.93.014.383.012002.084242=⨯⨯⨯⨯===g d d l S S BC BC BC CD BC πλ 5108.2⨯=A p2AB AB A Q S p γ= s m S p Q AB A AB /457868.08.91000286.136108.235=⨯⨯⨯==γ 2AD AD A Q S p γ= s m S p Q AD A AD /93993.08.9100034.32108.235=⨯⨯⨯==γ ()()222BC BC BC AC A Q S Q S p += ()s m S S p Q Q BC AC A CD BC /23488.043=+==γs m Q Q Q BC AB /69275.022=+= s m Q Q Q CD AD /17481.123=+=s m Q Q Q /86756.13321=+= 22/2.44m kN Q S p BC BC C ==γ。
泵与风机课后习题答案(完整版)

流量qv :单位时间内通过风机进口的气体的体积。
全压p :单位体积气体从风机进口截面到风机出口截面所获得的机械能。
轴向涡流的定义:容器转了一周,流体微团相对于容器也转了一周,其旋转角速度和容器的旋转角速度大小相等而方向相反,这种旋转运动就称轴向涡流。
影响:使流线发生偏移从而使进出口速度三角形发生变化。
使出口圆周速度减小。
叶片式泵与风机的损失:(一)机械损失:指叶轮旋转时,轴与轴封、轴与轴承及叶轮圆盘摩擦所损失的功率。
(二)容积损失:部分已经从叶轮获得能量的流体从高压侧通过间隙向低压侧流动造成能量损失。
泵的叶轮入口处的容积损失,为了减小这部分损失,一般在入口处都装有密封环。
(三),流动损失:流体和流道壁面生摸差,流道的几何形状改变使流体产生旋涡,以及冲击等所造成的损失。
多发部位:吸入室,叶轮流道,压出室。
如何降低叶轮圆盘的摩擦损失:1、适当选取n 和D2的搭配。
2、降低叶轮盖板外表面和壳腔内表面的粗糙度可以降低△Pm2。
3、适当选取叶轮和壳体的间隙。
轴流式泵与风机应在全开阀门的情况下启动,而离心式泵与风机应在关闭阀门的情况下启动。
泵与风机(课后习题答案)第一章1-1有一离心式水泵,其叶轮尺寸如下:1b =35mm, 2b =19mm, 1D =178mm,2D =381mm, 1a β=18°,2a β=20°。
设流体径向流入叶轮,如n=1450r/min ,试画出出口速度三角形,并计算理论流量,V T q 和在该流量时的无限多叶片的理论扬程T H ∞。
解:由题知:流体径向流入叶轮 ∴1α=90° 则:1u =1n60D π=317810145060π-⨯⨯⨯=13.51 (m/s )1V =1m V =1u tg 1a β=13.51⨯tg 18°=4.39 (m/s )∵1V q =π1D 1b 1m V =π⨯0.178⨯4.39⨯0.035=0.086 (3m /s ) ∴2m V =122Vq D b π=0.0860.3810.019π⨯⨯=3.78 (m/s ) 2u =2D 60n π=338110145060π-⨯⨯⨯=28.91 (m/s )2u V ∞=2u -2m V ctg 2a β=28.91-3.78⨯ctg20°=18.52 (m/s )T H ∞=22u u V g∞=28.9118.529.8⨯=54.63 (m )1-2有一离心式水泵,其叶轮外径2D =220mm,转速n=2980r/min ,叶片出口安装角2a β=45°,出口处的轴面速度2m v =3.6m/s 。
泵与风机-何川主编-第四版-课后习题+思考题(全7章)答案

绪论思考题1.在火力发电厂中有那些主要的泵与风机其各自的作用是什么答:给水泵:向锅炉连续供给具有一定压力和温度的给水。
循环水泵:从冷却水源取水后向汽轮机凝汽器、冷油器、发电机的空气冷却器供给冷却水。
凝结水泵:抽出汽轮机凝汽器中的凝结水,经低压加热器将水送往除氧器。
疏水泵:排送热力系统中各处疏水。
补给水泵:补充管路系统的汽水损失。
灰渣泵:将锅炉燃烧后排出的灰渣与水的混合物输送到贮灰场。
送风机:向锅炉炉膛输送燃料燃烧所必需的空气量。
\引风机:把燃料燃烧后所生成的烟气从锅炉中抽出,并排入大气。
2.泵与风机可分为哪几大类发电厂主要采用哪种型式的泵与风机为什么答:泵按产生压力的大小分:低压泵、中压泵、高压泵风机按产生全压得大小分:通风机、鼓风机、压气机泵按工作原理分:叶片式:离心泵、轴流泵、斜流泵、旋涡泵容积式:往复泵、回转泵其他类型:真空泵、喷射泵、水锤泵风机按工作原理分:叶片式:离心式风机、轴流式风机容积式:往复式风机、回转式风机发电厂主要采用叶片式泵与风机。
其中离心式泵与风机性能范围广、效率高、体积小、重量轻,能与高速原动机直联,所以应用最广泛。
轴流式泵与风机与离心式相比,其流量大、压力小。
故一般用于大流量低扬程的场合。
目前,大容量机组多作为循环水泵及引送风机。
3.@4.泵与风机有哪些主要的性能参数铭牌上标出的是指哪个工况下的参数答:泵与风机的主要性能参数有:流量、扬程(全压)、功率、转速、效率和汽蚀余量。
在铭牌上标出的是:额定工况下的各参数5.水泵的扬程和风机的全压二者有何区别和联系答:单位重量液体通过泵时所获得的能量增加值称为扬程;单位体积的气体通过风机时所获得的能量增加值称为全压联系:二者都反映了能量的增加值。
区别:扬程是针对液体而言,以液柱高度表示能量,单位是m。
全压是针对气体而言,以压力的形式表示能量,单位是Pa。
6.离心式泵与风机有哪些主要部件各有何作用!答:离心泵叶轮:将原动机的机械能传递给流体,使流体获得压力能和动能。
工程流体力学泵与风机课后答案

⼯程流体⼒学泵与风机课后答案第1章绪论1.1 试从⼒学分析的⾓度,⽐较流体与固体对外⼒抵抗能⼒的差别。
答:固体在承受⼀定的外⼒后才会发⽣形变;⽽流体只要承受任何切⼒都会发⽣流动,直到切⼒消失;流体不能承受拉⼒,只能承受压⼒。
1.2 何谓连续介质模型?为了研究流体机械运动的规律,说明引⽤连续介质模型的必要性和可能性。
答:把流体当做是由密集质点构成的、内部⽆空隙的连续体来研究,这就是连续介质模型。
建⽴连续介质模型,是为了避开分⼦运动的复杂性,对流体物质的结构进⾏简化,建⽴连续介质模型后.流体运动中的物理量都可视为空间坐标和时间变址的连续函数.这样就可⽤数学分析⽅法来研究流体运动。
1.3 按作⽤⽅式的不同,以下作⽤⼒:压⼒、重⼒、引⼒、摩擦⼒、惯性⼒,哪些是表⾯⼒?哪些是质量⼒?答:压⼒、摩擦⼒是表⾯⼒;重⼒、引⼒、惯性⼒是质量⼒。
1.4 为什么说流体运动的摩擦阻⼒是内摩擦阻⼒?它与固体运动的摩擦⼒有何不同?答:上平板带动与其相邻的流层运动,⽽能影响到内部各流层运动,说明内部各流层间存在切向⼒,即内摩擦⼒,这就是黏滞性的宏观表象。
也就是说,黏滞性就是流体的内摩擦特性。
摩擦阻⼒存在于内部各流层之间,所以叫内摩擦阻⼒。
固体运动的摩擦⼒只作⽤于固体与接触⾯之间,内摩擦阻⼒作⽤于流体各流层之间。
1.5 什么是流体的粘滞性?它对流体流动有什么作⽤?动⼒粘滞系数µ和运动粘滞系数v有何区别及联系?答:黏滞性的定义⼜可表⽰为流体阻抗剪切变形的特性。
由于流体具有黏性,在流动时存在着内摩擦⼒,便会产⽣流动阻⼒,因⽽为克服流动阻⼒就必然会消耗⼀部分机械能。
消耗的这部分机械能转变为热,或被流体吸收增加了流体的内能,或向外界散失,从⽽使得推动流体流动的机械能越来越⼩。
运动黏滞系数是动⼒黏滞系数与密度的⽐。
1.6 液体和⽓体的粘度随着温度变化的趋向是否相同?为什么?答:⽔的黏滞系数随温度升⾼⽽减⼩,空⽓的黏滞系数则随温度升⾼⽽增⼤。
泵与风机(课后习题答案))

泵与风机学习指导书第一章练习题名词解释1)泵(2)泵的扬程(3)风机的全压(4)轴功率2.简答题(1)简述热力发电厂锅炉给水泵的作用和工作特点。
(2)简述热力发电厂锅炉引风机的作用和工作特点。
3)按照风机产生的全压大小,风机大致可分为哪几类?(4)叶片泵大致可分为哪几类?第二章练习题1.名词解释(1)排挤系数(2)基本方程式(3)轴向旋涡运动(4)反作用度2.选择题[请在四个备选的答案中选择一个正确答案填至()内](5)(1)由于叶轮中某点的绝对速度是相对速度和圆周速度的向量合成,所以()A. 绝对速度总是最大的;B. 绝对速度的径向分速度总是等于相对速度的径向分速度;C. 绝对速度流动角α 总是大于相对速度流动角β ;C. 流动效率η h 总是小于1;D. 有实际意义的叶轮,其反作用度τ总是小于1。
3.简答题(1)简述离心式泵与风机的工作原理。
(2)简述流体在离心式叶轮中的运动合成(3)在推导基本方程式时采用了哪些假设?(4)有哪些方法可以提高叶轮的理论扬程(或理论全压)(5)叶轮进口预旋和轴向旋涡运动会对叶轮扬程(或全压)产生如何影响?(6)离心式泵与风机有哪几种叶片型式?各有何优点?(7)为什么离心泵都采用后弯式叶片?(8)在其它条件不变的情况下,叶片出口安装角对叶轮扬程(或全压)有何影响?4.计算题(1)有一离心式水泵,其叶轮的外径D2=22cm,转速n=2980r/min,叶轮出口安装角β 2 a =45 °,出口处的径向速度v 2 r∞ = 3.6m/s。
设流体径向流入叶轮,试按比例画出出口速度三角形,并计算无限多叶片叶轮的理论扬程H T∞ ,若滑移系数K=0.8,叶轮流动效率η h =0.9,叶轮的实际扬程为多少?(2)某离心式风机的转速为1500r/min,叶轮外径为600mm,内径为480mm,设叶轮有无限多叶片且叶片厚度为无限薄,叶片进、出口处的安装角分别为60°、120°,进、出口处空气的相对速度分别为25m/s、22m/s,空气密度为 1.2kg/m3。
流体力学泵与风机_课后题答案

流体力学泵与风机部分习题答案2-15解:(1)当1γ为空气 21p p = ()A B p h z p =++γ ()h z p p p B A +=-=∆γ3.010008.9⨯⨯= k p a pa 94.22940== (2)当1γ为油 31p p = ()z H h p p A +++=γ1()H h p p B γγ++=13H h z H h p p p p p B A γγγγγ--+++-=-=∆131h z h 1γγγ-+=1.090002.010008.91.010008.9⨯-⨯⨯+⨯⨯= k p a pa 04.22040== 2-16 解:21p p =()211h h H p p M +++=水γ 212h h p p a 汞油γγ++=()2121h h p h h H p a M 汞油水γγγ++=+++()2.010008.96.1378502.05.110008.998011⨯⨯⨯+⨯=++⨯⨯+-h h 26656785098002.098005.1980098011+=+⨯+⨯+-h h 1960147009802665619501--+=hm h 63.51= 2-28解:()21h h p -=γ()()()b h h h b h h h h P 02210212145sin 45sin 21-+--=γγ()()145sin 22310008.9145sin 232310008.9210⨯-⨯⨯+⨯-⨯-⨯⨯⨯=kN N 65.343465022510008.9==⨯⨯=()()()Pbl h h h bl h h h h l D D D 222110212145sin 45sin 21-+--=γγm 45.222510008.9222210008.92322210008.9=⨯⨯⨯⨯⨯+⨯⨯⨯=2-32 解:b h h b h h P 0222145sin 2145sin γγ+=2222210008.9212222110008.9⨯⨯⨯⨯⨯+⨯⨯⨯⨯=kN N 8576.1106.1108572810008.9==⨯⨯= Ph h b h h h h b h h l D 02102202102145sin 3245sin 2145sin 245sin ⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=γγ2810008.92372410008.9222410008.9⨯⨯⨯⨯⨯+⨯⨯⨯=2613= 26722613=-=p l T P G l T l P l G ⨯=⨯+⨯ 22672810008.9162.19⨯=⨯⨯⨯+⨯TkN T 31.10134.27481.9=+=2-41解:245sin 0=⨯=r hb h h P x ⨯⨯⋅⋅=21γ4212210008.9⨯⨯⨯⨯⨯=kN N 2.3939200== V P z γ=b r r r ⎪⎭⎫⎝⎛⨯⨯⨯-=00245cos 45sin 2136045πγ 4212281214.310008.92⨯⎪⎭⎫⎝⎛⨯⨯-⨯⨯⨯⨯= kN N 344.2222344== kN P 1.45344.222.3922=+=3057.0arctan 2.39344.22arctanarctan ≈===xz P P α3-3解:(1)s m v d Q /0049.010025.04432323=⋅⋅=⋅=ππs kg Q /9.4=ρ(2)s m v d d v /625.032131=⎪⎪⎭⎫⎝⎛= s m v d d v /5.232232=⎪⎪⎭⎫ ⎝⎛= 3-5解:s m h m Q /778.2/1000033==s m dQv /2042≤=π所以,177.04=≥πv Q d所以,mm m d 45045.0== 此时,s m dQdQv /4.1763585.0112.114422====ππ3-6解:22543212054d d A A A A A ππ======22114012021d d A A ππ=⋅="='22224012021d d A A ππ=⋅="='22334012021d d A A ππ=⋅="='22444012021d d A A ππ=⋅="='22554012021d d A A ππ=⋅="='2214014d d ππ=d d 1011=d r 10211=2224034d d ππ=d d 1032=d r 10232=2234054d d ππ=d d 1053=d r 10253=2244074d d ππ=d d 1074=d r 10274=2254094d d ππ=d d 1035=d r 10235=()()54321254321220240u u u u u d u u u u u d Q G ++++=++++==πρπρρ3-7解:干管前端的质量流量为:42562.2211111d A v Q πρρ⨯⨯==()s kg /128544.005.042562.22=⨯⨯⨯=πs kg Q Q Q /064272.02132===ρρρ()s m A Q v /247.2204.043.2064272.022222=⋅⋅==πρρ()s m A Q v /05.18045.0424.2064272.023333=⋅⋅==πρρ3-10解:将基准面建立在B 点经过的水平面上,列能量方程:gv p z gv p z 222222221111αγαγ++=++其中,m z 2.11=m p 5.11=γs m v /21= s m v d d v /5.4122212==121==ααgp g25.40225.12.1222++=++γ871.125.4225.12.1222=-++=ggp γ3-11解:将2点所在的水平面作为基准面,列能量方程: gv p z gv p z 222222221111αγαγ++=++31=z 02=zγγ21p p =s m v /31=gv p gp 2023322221++=++γγs m gh v /2.83222=+=32.822112=⎪⎪⎭⎫ ⎝⎛=d d v v 所以,m d 12.02= 3-14解:以水面为基准面,列0-0和D-D 的能量方程: gv p z gv p z D D DD 22220000αγαγ++=++00=z00=γp02200=gv α 4-=D z0=γDpgv D D 2040002α++-=++ 所以,422=gv D D α,即,s m v D /85.88.924=⋅⋅=所以,s m v d Q D /017368.085.805.044322=⋅⋅==ππ81:1:2:24422==A D D D A A d d gv gv αα列0-0和A-A 断面的能量方程: gv p z gv p z A A AA 22220000αγαγ++=++8147000++-=++γAp所以,8147-=γAp 所以,kpa p A 1.68=列0-0和B-B 断面的能量方程: gv p z gv p z B B BB 22220000αγαγ++=++kpa p B 484.08.9814-=⋅-=列0-0和C-C 断面的能量方程:gv p z gv p z C C CC 22220000αγαγ++=++kpa p C 1.208.98142-=⨯⎪⎭⎫ ⎝⎛+-=0=D p3-18解:将基准面建在管道所在的水平面上,列能量方程:21222222111122-+++=++l h gv p z gv p z αγαγ128.998.0008.9490222+++=++gv α9.3222=gv s m v /74.82=3-19 解:(1)(a )将基准面建在A 所在的水平面上,列0-0和C-C 断面的能量方程:gv p z gv p z C C CC 22220000αγαγ++=++gv C C 2000042α++=++422=gv C C α s m v C /85.88.98=⨯=1:4:2:22222==B C C C B B s s gv gv αα122=gv B B α s m v /43.48.921=⨯= 且 B A v v =(b )(c )gv p z gv p z A A AA 22220000αγαγ++=++10004++=++γAp3=γAp k p a p A 4.29=(2)(a )2122000022-+++=++l C C CC h gv p z gv p z αγαγ其中,gv gv h l 2324222121+=-gv gv gv 223200004222222++++=++54222=gv 所以,s m v /96.32=s m v v /96.12121==(b )(c )gv gv p z gv p z 2222212111120000+++=++αγαγ5300041++=++γp5341-=γp k p a p 32.331=gv gv gv p z gv p z 223242222222222220000++++=++αγαγ5423545400042⋅++++=++γp kpa p 76.112=3-20 解:()()212221221122-++=--++l a p v p z z v p ργγρs m d Qv /38.2005.014.34202.042221=⨯⨯⨯==πs m dQv /19.1005.014.3402.04222=⨯⨯==π2423222121v v p l ρρ+=-()()242322222122212211v v v p z z v p a ρρργγρ+++=--++22214v v =()()8.930306.02.1224232300212221221⨯+---+++=v v v v p ρρρρ()()8.930306.02.12424212230022222222⨯+---+++=v v v v ρρρρ8.9606.019.1026.0133002⨯⨯-⨯⨯+=pa 16.352=mm p h 6.449.716.3521===γ3-22解:s kN h kN G /048944.0/2.176==s m G Q /1347.77.08.910048944.033=⨯⨯==γs m dQdQv /09.914.31347.7444222=⨯===ππ()2122221122-++=-++l a p v p H v p ργγρ其中,01≈v ,pa h p 988.9101010331=⨯⨯⨯==-γ ()γgv d H H 2035.0209.97.008.97.02.1098222+⨯+=⨯⨯-++-()8.97.08.9209.9035.0209.97.008.97.02.109822⨯⨯⨯+⨯+=⨯⨯-++-HHH H 0122.19.289.498+=+-所以,m H 64.32= ()212211212212-++=-++l M M a p v p Hv p ργγρ()8.97.08.9209.9164.322035.0209.97.064.328.97.02.12109822⨯⨯⨯+⨯+=⨯⨯-++-M p 52.169.28968.7998++=+-M p所以,pa p M 45.63-= 3-263-28解:列连续性方程:s m DQv /18.34.014.344.04221=⨯⨯==πs m dQv /96.501.014.344.04222=⨯⨯==π列能量方程: gv p z gv p z 222222221111αγαγ++=++gv gv p 222112221ααγ-=m 98.1318.9218.396.5022=⨯-=kpa p 404.12938.998.1311=⨯=列动量方程:()12v v Q F-=∑ρ()12222144v v Q R d p D p -=-⨯-⨯ρππ()18.396.504.04.04404.12932-⨯=-⨯⨯R πkN R 339.14378.474.04.04404.12932=⨯-⨯⨯=πkN R 94.1112=3-33解:列能量方程:gv p z gv p z 222222221111αγαγ++=++其中,5321=v v 2221259v v =gv gv 209.0205.1222211αα++=++gv gv 225926.02222-=s m v /3.42= s m v /58.21=()12v v Q F-=∑ρ()1222212121v v Q R b h b h -=--ργγ其中,s m Q /644.45.12.158.23=⨯⨯=72.1644.410009.0108.9215.1108.9212323⨯⨯=-⨯⨯⨯-⨯⨯⨯RN R 2.480=4-2 (1) m mm d 1.0100== s kg Q /10=ρs m Q Q /01.03==ρρs m dQv /274.11.014.301.04422=⨯⨯==πs m /10519.126-⨯=ν 8387110519.11.0274.1Re 6=⨯⨯==-νvd(紊流) (2) s kg Q /10=ρs m Q Q /011765.0850103===ρρs m dQv /4987.11.014.3011765.04422=⨯⨯==π s m /1014.124-⨯=ν13151014.11.04987.1Re 4=⨯⨯==-νvd4-3 解:m d 3.0= C T 020= s m /107.1526-⨯=νs m dv /1067.1043.0107.152000Re 36max --⨯=⨯⋅=⋅=νs m A v Q /103947.743.014.31067.1043323max max --⨯=⨯⨯⨯=⋅=h kg Q /9.3136002.1103947.73=⨯⨯⨯=-ρ4-4 解:212=d d 4212221==d d v v222111Re 2214Re ===ννd v d v 所以,2ReRe 21=4-12 紊流粗糙区,5106Re ⨯>νvd=Re ,所以,s m dv /14.325.010308.1106Re 65=⨯⨯⨯==-νs m d vQ /154.0425.014.314.34322=⨯==π4-13 s m s L Q /2.0/20031==s m dQ v /076433.44211==π 661107791.010308.125.0076433.4Re ⨯=⨯⨯==-νvds L Q /202= s m v /4076433.02=4210791.7Re ⨯=s L Q /53= s m v /1019.03= 43109478.1Re ⨯=查尼氏图,得到, 5106Re ⨯=u 4104Re ⨯=l123Re Re Re Re Re <<<<u l ,所以,1Q 属于紊流粗糙区,2Q 属于紊流过渡区,3Q 属于紊流光滑区, (1) 对于1Q ,采用希弗林松公式,02326.025.0105.011.011.025.0325.01=⎪⎪⎭⎫ ⎝⎛⨯=⎪⎭⎫ ⎝⎛=-d K λm gv d l h f 888.78.92076433.425.010002326.0222111=⨯⨯⨯==λ(2) 对于2Q ,采用阿公式, 02547.010791.76825.0105.011.0Re 6811.025.04325.02=⎪⎪⎭⎫⎝⎛⨯+⨯=⎪⎭⎫⎝⎛+=-dK λm g v d l h f 086.08.924076433.025.010002547.0222222=⨯⨯⨯==λ(3) 对于3Q ,采用布公式 02678.05.194773164.0Re3164.025.025.03===λm g v d l h f 005676.08.9244076433.025.010002678.0222333=⨯⎪⎭⎫ ⎝⎛⨯⨯==λ4-15 5102Re ⨯=u 4000Re =lm d 05.0= m K 31025.0-⨯=s m dv u /028.405.010007.1102Re 65max =⨯⨯⨯==-νs L d v Q /905.7405.014.3028.4422maxmax =⨯==π26m i n 10056.805.010007.14000Re --⨯=⨯⨯==dv l νs L s m d v Q /1581.0/1001581.0405.014.310056.8432222minmin =⨯=⨯⨯==--π4-21 (1)a d d =212211av v =gv d l d v gv d l gv d l h f 2642Re 64221111211121111νλ===4212221211add v v h h f f ==19.1=a(2)75.425.12275.12122225.0225.0225.021125.0125.0125.021123164.023164.0ad d v v g v d l d v gv d l dvh h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==νν16.1=a(3)25.525.11222122225.0221125.01211211.0211.0ad d v v gvd l d K gv d l d K h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛=14.1=a4-24 解:s m Q /002742.0602329.03=⨯= s m dQv /3972.105.014.3002742.04422=⨯⨯==π629.022=⎪⎭⎫ ⎝⎛+g vd l ζλ ()629.08.923972.162=⨯+ζ 3151.0=ζ4-26 解:(1) 突然缩小375.03145.7815.015.0121=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζmm m gvh j 5.760765.08.922375.022211==⨯==ζ(2)5.02=ζ mm m gvh j 102102.08.9225.022222==⨯==ζ(3)1693145.781122213=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζ mm m h j 115115.08.92216923==⨯=(4)14=ζmm m h j 204204.08.922124==⨯=4-27 解:()()gv v gv v h h m m j j 222121-+-=''+'()()()()02212221=-+--=''+'gv v gv v h h m m vmj j所以,221v v v m +=此时,()j j j h gv v g v v v g v v v h h 2221222222121212211=-=⎪⎭⎫⎝⎛-++⎪⎭⎫ ⎝⎛+-=''+'4-29 解:s m h m Q /1044.4/16333-⨯==s m dQv /2624.205.014.31044.44423211=⨯⨯⨯==-πs m dQv /5656.01.014.31044.44423222=⨯⨯⨯==-πm gv v p p h j 140674.08.925656.02624.28.910001739.522222121=⨯-+⨯⨯-=-+-=γgv h j 2211ζ= 5387.01=ζ gv h j 2222ζ= 619.82=ζ5-17 解:5.6082.014.32.12.01002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 7.30422.014.32.12.05002.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 973671.014.32.11.05002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 3.101018973677.30425.608321=++=++=p p p p S S S S22211/91.227215.03.101018m N Q S p p =⨯== 22222/1.258616.03.101018m N Q S p p =⨯==5-25 解:()()⎪⎩⎪⎨⎧=++=++=1021520232322223221SQ Q Q S SQ Q Q S SQ 610=S解得,s m Q /10472.4331-⨯= s m Q /1041.2332-⨯= s m Q /1063.0333-⨯=5-27 解:94.10348.92.014.32.020002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 8.206988.91.014.31.0100025.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 78.37258.92.014.32.072002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 038035.087.14311705.321111211=+=+='S S S 所以,25.6911='S1)()H Q S S =+'231s m S S H Q /10186.604417163331-⨯==+'=2)H SQ=2H Q S =⎪⎭⎫⎝⎛'2211325133831432=+'=-'=S S S S gd πζ()1.25688.92.014.31325142=⨯⨯⨯=ζ5-28 解:286.1368.93.014.383.020002.084242=⨯⨯⨯⨯==g d d l S AB ABABABπλ029.1098.93.014.383.016002.084242=⨯⨯⨯⨯==g dd l S ACACAC AC πλ34.328.94.014.384.020002.084242=⨯⨯⨯⨯==g d d l S AD ADADADπλ772.818.93.014.383.012002.084242=⨯⨯⨯⨯===g dd l S S BCBCBC CD BC πλ5108.2⨯=A p2ABAB A Q S p γ= s m S p Q AB A AB /457868.08.91000286.136108.235=⨯⨯⨯==γ2ADAD A QS p γ= s m S p Q AD A AD /93993.08.9100034.32108.235=⨯⨯⨯==γ()()222BC BC BC AC A Q S Q S p +=()s m S S p Q Q BC AC ACD BC /23488.043=+==γs m Q Q Q BC AB /69275.022=+= s m Q Q Q CD AD /17481.123=+= s m Q Q Q /86756.13321=+= 22/2.44m kN Q S p BC BC C ==γ。
泵与风机课后习题参考答案(完整版)
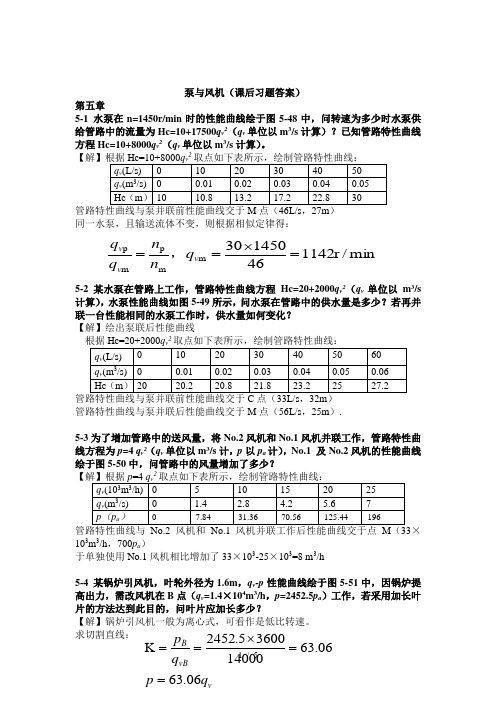
泵与风机(课后习题答案)第五章5-1 水泵在n=1450r/min 时的性能曲线绘于图5-48中,问转速为多少时水泵供给管路中的流量为Hc=10+17500q v 2(q v 单位以m 3/s 计算)?已知管路特性曲线方程Hc=10+8000q v 2(q v 单位以m 3/s 计算)。
2同一水泵,且输送流体不变,则根据相似定律得:5-2 某水泵在管路上工作,管路特性曲线方程Hc=20+2000q v 2(q v 单位以m 3/s 计算),水泵性能曲线如图5-49所示,问水泵在管路中的供水量是多少?若再并联一台性能相同的水泵工作时,供水量如何变化? 【解】绘出泵联后性能曲线2管路特性曲线与泵并联后性能曲线交于M 点(56L/s ,25m ).5-3为了增加管路中的送风量,将No.2风机和No.1风机并联工作,管路特性曲线方程为p =4 q v 2(q v 单位以m 3/s 计,p 以p a 计),No.1 及No.2风机的性能曲线绘于图5-50中,问管路中的风量增加了多少?2×103m 3/h ,700p a )于单独使用No.1风机相比增加了33×103-25×103=8 m 3/h5-4 某锅炉引风机,叶轮外径为1.6m ,q v -p 性能曲线绘于图5-51中,因锅炉提高出力,需改风机在B 点(q v =1.4×104m 3/h ,p =2452.5p a )工作,若采用加长叶片的方法达到此目的,问叶片应加长多少?【解】锅炉引风机一般为离心式,可看作是低比转速。
求切割直线:B p 36005.2452⨯min /r 114246145030m m p m p =⨯==v v v q n n q q ,a A 点与B 点为对应工况点,则由切割定律得m 8.1)1114(D D )(22222==''=',D D q q v v 则应加长1.8-1.6=0.2m5.5 略5-6 8BA-18型水泵的叶轮直径为268mm ,车削后的8BA-18a 型水泵的叶轮直径为250mm ,设效率不变,按切割定律计算qv 、H 、P 。
泵与风机-何川主编-第四版-课后习题+思考题(全7章)答案

绪论思考题1.在火力发电厂中有那些主要的泵与风机?其各自的作用是什么?答:给水泵:向锅炉连续供给具有一定压力和温度的给水。
循环水泵:从冷却水源取水后向汽轮机凝汽器、冷油器、发电机的空气冷却器供给冷却水。
凝结水泵:抽出汽轮机凝汽器中的凝结水,经低压加热器将水送往除氧器。
疏水泵:排送热力系统中各处疏水。
补给水泵:补充管路系统的汽水损失。
灰渣泵:将锅炉燃烧后排出的灰渣与水的混合物输送到贮灰场。
送风机:向锅炉炉膛输送燃料燃烧所必需的空气量。
引风机:把燃料燃烧后所生成的烟气从锅炉中抽出,并排入大气。
2.泵与风机可分为哪几大类?发电厂主要采用哪种型式的泵与风机?为什么?答:泵按产生压力的大小分:低压泵、中压泵、高压泵风机按产生全压得大小分:通风机、鼓风机、压气机泵按工作原理分:叶片式:离心泵、轴流泵、斜流泵、旋涡泵容积式:往复泵、回转泵其他类型:真空泵、喷射泵、水锤泵风机按工作原理分:叶片式:离心式风机、轴流式风机容积式:往复式风机、回转式风机发电厂主要采用叶片式泵与风机。
其中离心式泵与风机性能范围广、效率高、体积小、重量轻,能与高速原动机直联,所以应用最广泛。
轴流式泵与风机与离心式相比,其流量大、压力小。
故一般用于大流量低扬程的场合。
目前,大容量机组多作为循环水泵及引送风机。
3.泵与风机有哪些主要的性能参数?铭牌上标出的是指哪个工况下的参数?答:泵与风机的主要性能参数有:流量、扬程(全压)、功率、转速、效率和汽蚀余量。
在铭牌上标出的是:额定工况下的各参数4.水泵的扬程和风机的全压二者有何区别和联系?答:单位重量液体通过泵时所获得的能量增加值称为扬程;单位体积的气体通过风机时所获得的能量增加值称为全压联系:二者都反映了能量的增加值。
区别:扬程是针对液体而言,以液柱高度表示能量,单位是m。
全压是针对气体而言,以压力的形式表示能量,单位是Pa。
5.离心式泵与风机有哪些主要部件?各有何作用?答:离心泵叶轮:将原动机的机械能传递给流体,使流体获得压力能和动能。
(完整word版)泵与风机课后思考题答案

思考题答案绪论思考题1.在火力发电厂中有那些主要的泵与风机?其各自的作用是什么?答:给水泵:向锅炉连续供给具有一定压力和温度的给水。
循环水泵:从冷却水源取水后向汽轮机凝汽器、冷油器、发电机的空气冷却器供给冷却水。
凝结水泵:抽出汽轮机凝汽器中的凝结水,经低压加热器将水送往除氧器。
疏水泵:排送热力系统中各处疏水。
补给水泵:补充管路系统的汽水损失。
灰渣泵:将锅炉燃烧后排出的灰渣与水的混合物输送到贮灰场。
送风机:向锅炉炉膛输送燃料燃烧所必需的空气量。
引风机:把燃料燃烧后所生成的烟气从锅炉中抽出,并排入大气。
2.泵与风机可分为哪几大类?发电厂主要采用哪种型式的泵与风机?为什么?答:泵按产生压力的大小分:低压泵、中压泵、高压泵风机按产生全压得大小分:通风机、鼓风机、压气机泵按工作原理分:叶片式:离心泵、轴流泵、斜流泵、旋涡泵容积式:往复泵、回转泵其他类型:真空泵、喷射泵、水锤泵风机按工作原理分:叶片式:离心式风机、轴流式风机容积式:往复式风机、回转式风机发电厂主要采用叶片式泵与风机。
其中离心式泵与风机性能范围广、效率高、体积小、重量轻,能与高速原动机直联,所以应用最广泛。
轴流式泵与风机与离心式相比,其流量大、压力小。
故一般用于大流量低扬程的场合。
目前,大容量机组多作为循环水泵及引送风机。
3.泵与风机有哪些主要的性能参数?铭牌上标出的是指哪个工况下的参数?答:泵与风机的主要性能参数有:流量、扬程(全压)、功率、转速、效率和汽蚀余量。
在铭牌上标出的是:额定工况下的各参数4.水泵的扬程和风机的全压二者有何区别和联系?答:单位重量液体通过泵时所获得的能量增加值称为扬程;单位体积的气体通过风机时所获得的能量增加值称为全压联系:二者都反映了能量的增加值。
区别:扬程是针对液体而言,以液柱高度表示能量,单位是m。
全压是针对气体而言,以压力的形式表示能量,单位是Pa。
5.离心式泵与风机有哪些主要部件?各有何作用?答:离心泵叶轮:将原动机的机械能传递给流体,使流体获得压力能和动能。
泵与风机_何川主编_第四版_课后习题+思考题(全7章)答案

绪论思考题1.在火力发电厂中有那些主要的泵与风机?其各自的作用是什么?答:给水泵:向锅炉连续供给具有一定压力和温度的给水。
循环水泵:从冷却水源取水后向汽轮机凝汽器、冷油器、发电机的空气冷却器供给冷却水。
凝结水泵:抽出汽轮机凝汽器中的凝结水,经低压加热器将水送往除氧器。
疏水泵:排送热力系统中各处疏水。
补给水泵:补充管路系统的汽水损失。
灰渣泵:将锅炉燃烧后排出的灰渣与水的混合物输送到贮灰场。
送风机:向锅炉炉膛输送燃料燃烧所必需的空气量。
引风机:把燃料燃烧后所生成的烟气从锅炉中抽出,并排入大气。
2.泵与风机可分为哪几大类?发电厂主要采用哪种型式的泵与风机?为什么?答:泵按产生压力的大小分:低压泵、中压泵、高压泵风机按产生全压得大小分:通风机、鼓风机、压气机泵按工作原理分:叶片式:离心泵、轴流泵、斜流泵、旋涡泵容积式:往复泵、回转泵其他类型:真空泵、喷射泵、水锤泵风机按工作原理分:叶片式:离心式风机、轴流式风机容积式:往复式风机、回转式风机发电厂主要采用叶片式泵与风机。
其中离心式泵与风机性能范围广、效率高、体积小、重量轻,能与高速原动机直联,所以应用最广泛。
轴流式泵与风机与离心式相比,其流量大、压力小。
故一般用于大流量低扬程的场合。
目前,大容量机组多作为循环水泵及引送风机。
3.泵与风机有哪些主要的性能参数?铭牌上标出的是指哪个工况下的参数?答:泵与风机的主要性能参数有:流量、扬程(全压)、功率、转速、效率和汽蚀余量。
在铭牌上标出的是:额定工况下的各参数4.水泵的扬程和风机的全压二者有何区别和联系?答:单位重量液体通过泵时所获得的能量增加值称为扬程;单位体积的气体通过风机时所获得的能量增加值称为全压联系:二者都反映了能量的增加值。
区别:扬程是针对液体而言,以液柱高度表示能量,单位是m。
全压是针对气体而言,以压力的形式表示能量,单位是Pa。
5.离心式泵与风机有哪些主要部件?各有何作用?答:离心泵叶轮:将原动机的机械能传递给流体,使流体获得压力能和动能。
流体力学泵与风机蔡增基课后习题答案

绪论1. 流体的容重及密度有何区别及联系?解: © = 〉 g 〉是流体的本身属性。
© 还与g 有关。
2.已知水的密度 〉 = 1000kg/m 3 ,求其容重。
若有这样的水1L,它的质量和重力各是多少?解: © = 〉 g=1000×9.807=9807N/m 3m= 〉 v=1000×0.001=1kg G=mg=1×9.807=9.807N3.什么是流体的粘滞性?它对流体流动有什么作用?动力粘滞系数 ∝和运动粘滞系数⎠有何区别及联系?答:流体内部质点间或流层间因为相对运动的性质叫粘滞性,它使流动的能量减少。
∝表征单位速度梯度作用下的切应力,反映粘滞性的动力性质。
⎠是单位速度梯度作用下的切应力对单位体积质量作用产生的阻力加速度。
⎠ = ∝ / 〉 4.水的容重 © =9.17kN/ m 3 , ∝ =0.599×10 3 pa.s 求它的运动粘滞系数⎠解:⎠ = ∝= ∝ g/ © =6.046×10 5 m 2 /s〉5.空气容重 © =11.5N/ m 3,⎠ =0.157cm 2 /s,求它的动力粘滞系数 ∝。
解: ∝ = 〉⎠ = ©⎠= 11.5 ⋅ 0.157 ⋅10 4 / 9.807 = 1.841⋅10 5 pa.sg6.当空气从0℃增加到20℃时, ⎠增加15%,容重减少10%,问此时 ∝增加多少?解: ∝ = 〉⎠ = ©⎠g = (1 10%)(1 + 15%)© 0⎠ 0g© ⎠= 1.035 0 0g所以 ∝增加了3.5%7.水平方向运动的木板,其速度为1m/s,平板浮在油面上,™ = 10mm ,油的 ∝ =0.09807pa.s。
求作用于平板单位面积上的阻力。
解:⎜ = ∝ du = 0.09807 ⋅1/ 0.01 = 9.807 N / m 2dy8.温度为20℃的空气,在直径为2.5cm 管中流动,距管壁上1mm 处的空气速度为3cm/s。
泵与风机课后习题答案

泵与风机课后习题答案泵与风机课后习题答案一、选择题1. A2. C3. B4. D5. A6. B7. C8. D9. B10. A二、判断题1. 错误。
泵是将液体输送到高处的装置,而风机是将气体输送到高处的装置。
2. 正确。
3. 错误。
泵和风机的工作原理不同,泵是通过旋转叶轮来产生压力,而风机是通过旋转叶片来产生气流。
4. 错误。
泵和风机都可以用来输送液体或气体,只是工作原理和用途不同。
5. 正确。
三、填空题1. 泵和风机的共同点是:都是通过旋转装置来产生流体的运动。
2. 泵和风机的区别是:泵主要用于输送液体,而风机主要用于输送气体。
3. 泵和风机的分类方法有:按工作原理分为离心泵和容积泵;按用途分为给水泵、排水泵、化工泵等。
4. 泵和风机在工程中的应用:泵主要用于给水供排、冷却循环等;风机主要用于通风换气、烟气排放等。
四、简答题1. 离心泵和容积泵的工作原理有何不同?离心泵是利用叶轮的旋转产生离心力,将液体从低压区域输送到高压区域。
液体进入泵后,被叶轮的旋转力推动,产生离心力,使液体获得动能,然后通过泵壳的出口管道排出。
容积泵是通过容积变化来输送液体的。
容积泵的工作腔内有一个可变容积的工作元件,当工作元件容积变大时,液体被吸入工作腔内;当工作元件容积变小时,液体被压出工作腔。
2. 泵和风机在工程中的应用有哪些?泵在工程中的应用非常广泛。
常见的应用包括给水供排、冷却循环、污水处理、石油化工、空调系统等。
不同类型的泵有不同的用途,如离心泵适用于输送清水、污水、化工液体等;容积泵适用于输送高粘度液体、含固体颗粒的液体等。
风机主要用于通风换气、烟气排放、空气净化等。
在建筑工程中,风机用于排除室内污浊空气,保持室内空气新鲜;在工业生产中,风机用于排放烟气、废气,保持生产环境清洁。
3. 泵和风机的选择应考虑哪些因素?选择泵和风机时需要考虑以下因素:- 流量要求:根据需要输送的液体或气体的流量确定泵和风机的型号和规格。
泵与风机课后习题答案(第5章)

泵与风机(课后习题答案)第五章5-1 水泵在n=1450r/min 时的性能曲线绘于图5-48中,问转速为多少时水泵供给管路中的流量为30L/s ?已知管路特性曲线方程Hc=10+8000q v 2(q v 单位以m 3/s 计算)。
【解】根据Hc=20+8000q v 2取点如下表所示,绘制管路特性曲线:管路特性曲线与泵并联前性能曲线交于M 点(46L/s ,27m ) 同一水泵,且输送流体不变,则根据相似定律得:5-2 某水泵在管路上工作,管路特性曲线方程Hc=20+2000q v 2(q v 单位以m 3/s 计算),水泵性能曲线如图5-49所示,问水泵在管路中的供水量是多少?若再并联一台性能相同的水泵工作时,供水量如何变化? 【解】绘出泵联后性能曲线根据Hc=20+2000q v 2取点如下表所示,绘制管路特性曲线:管路特性曲线与泵并联前性能曲线交于C 点(33L/s ,32m ) 管路特性曲线与泵并联后性能曲线交于M 点(56L/s ,25m ).5-3为了增加管路中的送风量,将No.2风机和No.1风机并联工作,管路特性曲线方程为p =4q v 2(q v 单位以m 3/s 计,p 以p a 计),No.1 及No.2风机的性能曲线绘于图5-50中,问管路中的风量增加了多少?【解】根据p =4 q v 2取点如下表所示,绘制管路特性曲线:min/r 114246145030mmp mp =⨯==v v v q n n q q ,管路特性曲线与No.2风机和No.1风机并联工作后性能曲线交于点M (33×103m 3/h ,700p a ) 于单独使用No.1风机相比增加了33×103-25×103=8 m 3/h5-4 某锅炉引风机,叶轮外径为1.6m ,q v -p 性能曲线绘于图5-51中,因锅炉提高出力,需改风机在B 点(q v =1.4×104m 3/h ,p =2452.5p a )工作,若采用加长叶片的方法达到此目的,问叶片应加长多少?【解】锅炉引风机一般为离心式,可看作是低比转速。
泵与风机课后习题答案 标准版

又叶轮出口相对速度沿半径方向 2a =90°
u
2
=
D2n 60
=
0.3 60
2980
=46.79(m/s)
由图知 u2 =V2u =46.79m/s
∴ pT = u2V2u =1.2 46.79 46.79=2626.7(Pa)
1-5 有一离心式风机,转速 n=1500r/min,叶轮外径 D2 =600mm,内径 D1 =480mm,
解:流体径向流入叶轮 1 =90°
u2
=
D2n 60
=
0.361480 60
=27.88
(m/s)
v2m
=
qV ,T A
= 83.8103 0.023
=3.64
(m/s)
v2u = u2 - v2m ctg2a =27.88-3.64 3 =21.58 (m/s)
HT
=
u2V2u g
= 27.88 21.58 =61.39 9.8
3600 0.6 0.15
w2
=
V2m sin 2a
= 9.83 sin 30
=19.66(m/s)
V2 = w22 u22 2w2u2 cos 2a = 19.662 45.532 219.66 45.53 cos 30 =30.15(m/s)
(2)∵ u2 =45.53m/s V2m =9.83m/s
(m)
HT = K HT =0.82 61.39=50.34 (m)
1-4 有一叶轮外径为 300mm 的离心式风机,当转速为 2890r/min 时。无限多叶片 叶轮的理论全压 pT 是多少?设叶轮入口气体沿径向流入,叶轮出口的相对速
度,设为半径方向。空气密度ρ=1.2kg/ m3 。
泵与风机课后习题答案及思考题.第四版

新浪微博:@孟得明扬程:单位重量液体从泵进口截面到泵出口截面所获得的机械能。
流量qv :单位时间内通过风机进口的气体的体积。
全压p :单位体积气体从风机进口截面到风机出口截面所获得的机械能。
轴向涡流的定义:容器转了一周,流体微团相对于容器也转了一周,其旋转角速度和容器的旋转角速度大小相等而方向相反,这种旋转运动就称轴向涡流。
影响:使流线发生偏移从而使进出口速度三角形发生变化。
使出口圆周速度减小。
叶片式泵与风机的损失:〔一〕机械损失:指叶轮旋转时,轴与轴封、轴与轴承及叶轮圆盘摩擦所损失的功率。
〔二〕容积损失:局部已经从叶轮获得能量的流体从高压侧通过间隙向低压侧流动造成能量损失。
泵的叶轮入口处的容积损失,为了减小这局部损失,一般在入口处都装有密封环。
〔三〕,流动损失:流体和流道壁面生摸差,流道的几何形状改变使流体产生旋涡,以及冲击等所造成的损失。
多发部位:吸入室,叶轮流道,压出室。
如何降低叶轮圆盘的摩擦损失:1、适中选取n 和D2的搭配。
2、降低叶轮盖板外外表和壳腔内外表的粗糙度可以降低△Pm2。
3、适中选取叶轮和壳体的间隙。
轴流式泵与风机应在全开阀门的情况下启动,而离心式泵与风机应在关闭阀门的情况下启动。
泵与风机〔课后习题答案〕第一章1-1有一离心式水泵,其叶轮尺寸如下:1b =35mm, 2b =19mm, 1D =178mm,2D =381mm, 1a β=18°,2a β=20°。
设流体径向流入叶轮,如n=1450r/min ,试画出出口速度三角形,并计算理论流量,V T q 和在该流量时的无限多叶片的理论扬程T H ∞。
解:由题知:流体径向流入叶轮 ∴1α=90° 那么:1u =1n60D π=317810145060π-⨯⨯⨯=13.51 〔m/s 〕1V =1m V =1u tg 1a β⨯tg 18°=4.39 〔m/s 〕 ∵1V q =π1D 1b 1m V =π⨯⨯⨯0.035=0.086 〔3m /s 〕 ∴2m V =122V q D b π=0.0860.3810.019π⨯⨯=3.78 〔m/s 〕 2u =2D 60n π=338110145060π-⨯⨯⨯=28.91 〔m/s 〕 2u V ∞=2u -2m V ctg 2a β⨯ctg20°=18.52 〔m/s 〕T H ∞=22u u V g∞=28.9118.529.8⨯=54.63 〔m 〕1-2有一离心式水泵,其叶轮外径2D =220mm,转速n=2980r/min ,叶片出口安装角2a β=45°,出口处的轴面速度2m v =3.6m/s 。
泵与风机答案何川

泵与风机(课后习题答案)2-3有一离心式水泵,转速为480r/min,总扬程为136m时,流量q V=5.7m3/s, 轴功率为P=9860KW,其容积效率与机械效率均为92%,求流动效率。
设输入的水温度及密度为:t=20C,T =1000kg/m3。
解:H = pe = Pgq v H =1°°°7 27 Ml36—”? P 1000 P 1000X9860又•••= h V m••• h =——= 077=0.91=91%V m0.92 0.922-4用一台水泵从吸水池液面向50m高的水池输送q, =0.3m3/s的常温清水(t=20C, P=1000kg/m3),设水管的内径为d =300m m,管道长度L=300m,管道阻力系数■ =0.028,求泵所需的有效功率。
2 2解:根据伯努利方程z"R +虫+ H =Z2 +止+里+ h wPg 2g Pg 2g由题知:乙-乙=50; p1 = p2 =0; v1 = v2V1 = V2= V :-d2 4h. l v2 m= =d 2g0.3= =4.246 (m/s)0.3242300 4.2462代入方程得H =75.76(m)P光0H=10009・8°3了5.76 = 222.7 (kW)10002-5设一台水泵流量q v =25 L/s,出口压力表读数为323730Pa入口真空表读数为39240PQ两表位差为0.8m,(压力表高,真空表低),吸水管和排水管直径为1000mm和750mm,电动机功率表读数为12.5kW,电动机效率g=0.95,求轴功率、有效功率、泵的总效率(泵与电动机用联轴器直接连接)。
解:由题知:P2e =323730Pa R v=39240Pa R e = - P v = -39240Paz2-Z!=0.8m, d1 =1000mm=1m , d2=750mm=0.75mP g=12.5kW, g=0.95, tm=0.98^25厂 0.032 m/s1000 3.14 122=0.057 m/s1000 3.14 0.7522 2+牛2g+H=z 2+卸备得.2 2 2 2H = Z 2 - 乙 ++ ◎ =0.8+ 323730一( 一39240)°.057一°.°32=37.84mPg2g1000 汉 9.82 疋 9.8沁=10009.8 25 10‘ 羿84-?©( KW ) 1000P = P g tm g =12.5 0.980.95=11.64 ( KW )P 9 3 =」 100%= 100%=79.6% P 11.642-6有一送风机,其全压是1962Pa 时,产生q , =40m 3/min 的风量,其全压效率为50%,试求其轴功率。
泵与风机课后习题答案及思考题.第四版

新浪微博:@孟得明扬程:单位重量液体从泵进口截面到泵出口截面所获得的机械能。
流量qv :单位时间内通过风机进口的气体的体积。
全压p :单位体积气体从风机进口截面到风机出口截面所获得的机械能。
轴向涡流的定义:容器转了一周,流体微团相对于容器也转了一周,其旋转角速度和容器的旋转角速度大小相等而方向相反,这种旋转运动就称轴向涡流。
影响:使流线发生偏移从而使进出口速度三角形发生变化。
使出口圆周速度减小。
叶片式泵与风机的损失:(一)机械损失:指叶轮旋转时,轴与轴封、轴与轴承及叶轮圆盘摩擦所损失的功率。
(二)容积损失:部分已经从叶轮获得能量的流体从高压侧通过间隙向低压侧流动造成能量损失。
泵的叶轮入口处的容积损失,为了减小这部分损失,一般在入口处都装有密封环。
(三),流动损失:流体和流道壁面生摸差,流道的几何形状改变使流体产生旋涡,以及冲击等所造成的损失。
多发部位:吸入室,叶轮流道,压出室。
如何降低叶轮圆盘的摩擦损失:1、适当选取n 和D2的搭配。
2、降低叶轮盖板外表面和壳腔内表面的粗糙度可以降低△Pm2。
3、适当选取叶轮和壳体的间隙。
轴流式泵与风机应在全开阀门的情况下启动,而离心式泵与风机应在关闭阀门的情况下启动。
泵与风机(课后习题答案)第一章1-1有一离心式水泵,其叶轮尺寸如下:1b =35mm, 2b =19mm, 1D =178mm, 2D =381mm, 1a β=18°,2a β=20°。
设流体径向流入叶轮,如n=1450r/min ,试画出出口速度三角形,并计算理论流量,V T q 和在该流量时的无限多叶片的理论扬程T H ∞。
解:由题知:流体径向流入叶轮 ∴1α=90° 则:1u = 1n60D π= 317810145060π-⨯⨯⨯=13.51 (m/s )1V =1m V =1u tg 1a β=13.51⨯tg 18°=4.39 (m/s )∵1V q =π1D 1b 1m V =π⨯0.178⨯4.39⨯0.035=0.086 (3m /s )∴2m V =122V q D b π=0.0860.3810.019π⨯⨯=3.78 (m/s ) 2u =2D 60n π=338110145060π-⨯⨯⨯=28.91 (m/s )2u V ∞=2u -2m V ctg 2a β=28.91-3.78⨯ctg20°=18.52 (m/s )T H ∞=22u u V g ∞=28.9118.529.8⨯=54.63 (m ) 1-2有一离心式水泵,其叶轮外径2D =220mm,转速n=2980r/min ,叶片出口安装角2a β=45°,出口处的轴面速度2m v =3.6m/s 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
泵与风机(课后习题答案)第五章5-1 水泵在n=1450r/min 时的性能曲线绘于图5-48中,问转速为多少时水泵供给管路中的流量为Hc=10+17500q v 2(q v 单位以m 3/s 计算)?已知管路特性曲线方程Hc=10+8000q v 2(q v 单位以m 3/s 计算)。
【解】根据Hc=10+8000q v 2取点如下表所示,绘制管路特性曲线:q v (L/s) q v (m 3/s) 0 0.01 0.02 0.03 0.04 0.05 Hc (m ) 10 10.8 13.2 17.2 22.8 30管路特性曲线与泵并联前性能曲线交于M 点(46L/s ,27m ) 同一水泵,且输送流体不变,则根据相似定律得:5-2 某水泵在管路上工作,管路特性曲线方程Hc=20+2000q v 2(q v 单位以m 3/s 计算),水泵性能曲线如图5-49所示,问水泵在管路中的供水量是多少?若再并联一台性能相同的水泵工作时,供水量如何变化? 【解】绘出泵联后性能曲线根据Hc=20+2000q v 2取点如下表所示,绘制管路特性曲线:q v (L/s) 60 q v (m 3/s) 0 0.01 0.02 0.03 0.04 0.05 0.06Hc (m ) 20 20.2 20.8 21.8 23.2 25 27.2 管路特性曲线与泵并联前性能曲线交于C 点(33L/s ,32m ) 管路特性曲线与泵并联后性能曲线交于M 点(56L/s ,25m ).5-3为了增加管路中的送风量,将No.2风机和No.1风机并联工作,管路特性曲线方程为p =4 q v 2(q v 单位以m 3/s 计,p 以p a 计),No.1 及No.2风机的性能曲线绘于图5-50中,问管路中的风量增加了多少?【解】根据p =4 q v 2取点如下表所示,绘制管路特性曲线:q v (103m 3/h) 0 5 10 15 20 25 q v (m 3/s) 0 1.4 2.8 4.2 5.6 7p (p a )0 7.84 31.36 70.56 125.44 196 管路特性曲线与No.2风机和No.1风机并联工作后性能曲线交于点M (33×103m 3/h ,700p a )于单独使用No.1风机相比增加了33×103-25×103=8 m 3/h5-4 某锅炉引风机,叶轮外径为1.6m ,q v -p 性能曲线绘于图5-51中,因锅炉提高出力,需改风机在B 点(q v =1.4×104m 3/h ,p =2452.5p a )工作,若采用加长叶片的方法达到此目的,问叶片应加长多少?【解】锅炉引风机一般为离心式,可看作是低比转速。
求切割直线:B p 36005.2452⨯min /r 114246145030m m p m p =⨯==v v v q n n q q ,描点做切割直线 q v (104m 3/h) 2 4 6 8 10 12 14 q v (m 3/s) 5.56 11.11 16.67 22.22 27.78 33.36 38.89p (p a )350.6 700.6 1051.2 1401.2 1751.8 2103.7 2452.4 切割直线与泵性能曲线交于A (11 m 3/h ,2000 p a ) A 点与B 点为对应工况点,则由切割定律得m 8.1)1114(D D )(22222==''=',D D q q v v 则应加长1.8-1.6=0.2m5.5 略5-6 8BA-18型水泵的叶轮直径为268mm ,车削后的8BA-18a 型水泵的叶轮直径为250mm ,设效率不变,按切割定律计算qv 、H 、P 。
如果把8BA-18a 型水泵的转速减至1200r/min ,假设效率不变,其qv 、H 、P 各为多少?8BA-18型水泵额定工况点的参数为:n=1450r/min ,q v =7.9L/s ,H=18m ,P=16.6kW ,η=84%。
【解】根据公式得:可知该泵为低比转速,可用如下切割定律求出切割后的qv 、H 、P ,其值如下:对8BA-18a 型水泵只改变转速,可根据相似定律计算泵的qv 、H 、P ,其值如下:64.2218109.71450H n 4/334/3s =⨯==-v q n kW35.156.16)260250()(64.1681)260250()(L/s 3.77.9)260250()(442222222222=⨯=''='=⨯=''='=⨯=''='P D D PP mH D D H H q D D q q vv v,,,kW 51.1035.1514501200m 4.1164.1614501200/04.6145012003.722m p 22m p m m p m p =⨯===⨯===⨯==)(,)()(,)(,m mp m m p v v v P n n P P H n n H H s L q n n q q5-7有两台性能相同的离心式水泵(其中一台的性能曲线绘于图5-12上),并联在管路上工作,管路特性曲线方程Hc=0.65q v 2(q v 单位以m 3/s 计算)。
问当一台水泵停止工作时,管路中的流量减少了多少?【解】根据Hc=0.65q v 2取点如下表所示,绘制管路特性曲线:q v (m 3/h) 0 10×103 20×103 30×103 40×103 q v (m 3/s) 0 2.78 5.56 8.33 11.12 Hc (m ) 0 5.02 20.09 45.10 80.38 同时绘出两台性能相同的泵并联后的性能曲线画图得管路特性曲线与泵并联后性能曲线交于M 点(36×103 m 3/h ,65m ). 与单独一台泵运行时的交于C 点(28×103 m 3/h ,40m ) 管路中的流量减少了36×103-28×103=8×103 m 3/h5-8 n 1=950r/min 时,水泵的特性曲线绘于图5-53上,试问当水泵转速减少到n 2=750r/min 时,管路中的流量减少多少?管路特性曲线方程为Hc=10+17500q v 2(q v 单位以m 3/s 计算)。
【解】根据Hc=10+17500q v 2取点如下表所示,绘制管路特性曲线:q v (L/s) q v (m 3/s) 0 0.01 0.02 0.03 0.04 0.05 Hc (m ) 10 11.75 17 25.75 38 53.75管路特性曲线与泵性能曲线交于M 点(39.8L/s ,37m ). 同一台泵,输送相同流体有减少量为:39.8-31.4=8.4(L/s )5-9在转速n 1=2900r/min 时,ISI25-100-135型离心水泵的q v -H 性能曲线绘于图5-54所示。
管路性能曲线方程式Hc=60+9000q v 2(q v 单位以m 3/s 计算)。
若采用变速调节,离心泵向管路系统供给的流量q v =200m 3/h ,这时转速n 2为多少? 【解】根据Hc=60+9000q v 2取点如下表所示,绘制管路特性曲线: q v (m 3/h) 200 240 280 q v (m 3/s) 0 0.011 0.022 0.033 0.044 0.055 0.066 0.077 Hc (m ) 60 61.11 64.44 7 77.78 87.78 100 114.44 管路特性曲线与泵性能曲线交于M 点(246.7 m 3/h ,101.7m ) 采用变速调节,可根据相似定律5-11 4-13-11No.6型风机在n=1250r/min 时的实测参数如下表所示: (1)求各测点效率。
(2)绘制性能曲线。
(3)写出该风机最高效率点的参数。
【解】p q v =ηm in /r 23517.246200290022121=⨯==n n n q q v v ,s L q n n q q v v v /4.319507508.3922121=⨯==,(1)根据公式, 求得各测点效率如下表所示。
(2)绘制性能曲线如图1所示500100015002000250052906640736081008800950010250110000.10.20.30.40.50.60.70.80.91全压功率效率(3)最高效率为0.9118,对应各参数为红色标记数值。
5-12 由上题已知n=1250r/min ,D 2=0.6m 时的性能曲线,试绘出4-13-11系列风机的无因次性能曲线。
【解】根据公式 得A 2=0.2826m 2根据公式 得u 2=39.25根据无因次系数公式得出V q 、p 、P 和η填入下表中: q v (m 3/h)529025011000q v (m 3/h) 529 0250 11000 q v (m 3/s) 1.47 1.84 2.04 2.25 2.44 2.64 2.85 3.06 p (p a )843.4823.8 814 794.3 755.1 696.3 637.4 578.6 P (kW) 16920 2150 η 0.73330.85840.89470.91180.90930.88340.85600.8223ηηρρ====效率系数:功率系数:全压系数:流量系数:23222221000A u P P u p p A u q q shVV)m (42222D A π=s)/m 6022(n D u π=q v (m 3/s) 1.47 1.84 2.04 2.25 2.44 2.64 2.85 3.06p (p a ) 843.4 823.8 814 794.3 755.1 696.3 637.4 578.6 P (kW) 169202150流量系数/V q 0.132 0.166 0.184 0.203 0.220 0.238 0.257 0.275 全压系数/p 0.4560.4460.4400.4300.4080.377 0.345 0.313功率系数/P 0.0824 0.0863 0.0907 0.0956 0.0989 0.102 0.103 0.105 效率系数/η0.7330.8590.8950.9120.9090.883 0.856 0.822以流量为横坐标绘制无因次性能曲线如下图所示:0.10.20.30.40.50.60.70.80.910.1324770.1662850.1843160.2028480.2203780.2379080.256690.275473全压功率效率5-13由4-13-11系列风机的无因次性能曲线查得最高效率点的参数为:η=91.4%,无因次参数为:V q =0.212,p =0.416,P =0.0965,求当风机的叶轮直径D 2=0.4m ,n=2900r/min 时,该风机的比转速n y 为多少?【解】将参数D 2=0.4m ,n=2900r/min ,V q =0.212,p =0.416带入下述公式:V V q nD q 32.2432=流量:,p p 304D n 222=全压:求得最高效率点时的流量q v =1.62m 3/s ,全压p =1841.35p a根据公式:4/320y n p q n v =,带入n ,q v ,和p 得出:n y =13.13。
