勾股定理(毕达哥拉斯定理)及各种证明方法
勾股定理的六种证明方法

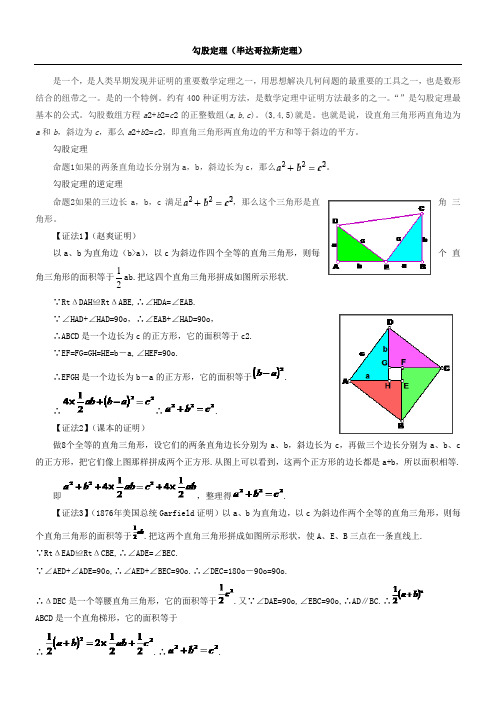
勾股定理的证明方法【证法1】(传说中毕达哥拉斯的证明)图1 图2如图所示,作8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图2所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2. 四边形ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴ 222c b a =+. 【证法3】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状. ABCD 是一个边长为c 的正方形,它的面积等于c 2. EFGH是一个边长为b―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+.图4【证法4】(Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上. 则 ΔDEC是一个等腰直角三角形,它的面积等于221c . ABCD 是一个直角梯形,它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+∴ 222c b a =+. 【证法5】(马永庆证明方法1)对任意的符合条件的直角三角形绕其锐角顶点旋转90°得图5,该图是旋转90°得到的,所以∠BAE=90°,且四边形ACFD 是一个正方形,它的面积和四边形ABFE 面积相等,而四边形ABFE 面积等于Rt ⊿BAE 和Rt ⊿BFE 的面积之和,所以:S 正方形ACFD =S ⊿BAE +S ⊿BFE即:()()a b a b 21c 21b 22-++=. 整理:()()a b a b c 2b 22-++=∴a 2+b 2=c 2.图5 图6 【证法6】(马永庆证明方法2)对任意的符合条件的两个全等的Rt ⊿BEA 和Rt ⊿ACD 拼成图6(此图也可以看成Rt ⊿BEA 绕其直角顶点顺时针旋转90°,再向下平移得到)。
勾股定理(毕达哥拉斯定理)及各种证明方法
勾股定理(毕达哥拉斯定理) 是一个,是人类早期发现并证明的重要数学定理之一,用思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
是的一个特例。
约有400种证明方法,是数学定理中证明方法最多的之一。
“”是勾股定理最基本的公式。
勾股数组方程a 2+b 2=c 2的正整数组(a ,b ,c )。
(3,4,5)就是。
也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a 2+b 2=c 2,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1如果的两条直角边长分别为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2如果的三边长a ,b ,c 满足,那么这个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ),以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于21ab.把这四个直角三角形拼成如图所示形状. ∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB.∵∠HAD+∠HAD=90o,∴∠EAB+∠HAD=90o,∴ABCD 是一个边长为c 的正方形,它的面积等于c2.∵EF=FG=GH=HE=b―a,∠HEF=90o.∴EFGH 是一个边长为b―a 的正方形,它的面积等于.∴∴.【证法2】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a+b ,所以面积相等.即,整理得.【证法3】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于.把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上. ∵RtΔEAD≌RtΔCBE,∴∠ADE=∠BEC.∵∠AED+∠ADE=90o,∴∠AED+∠BEC=90o.∴∠DEC=180o―90o=90o.∴ΔDEC 是一个等腰直角三角形,它的面积等于.又∵∠DAE=90o,∠EBC=90o,∴AD∥BC.∴ABCD 是一个直角梯形,它的面积等于 ∴.∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
勾股定理的推导和证明方法

勾股定理的推导和证明方法勾股定理是数学中的一个重要定理,它描述了直角三角形边长之间的关系。
这个定理被广泛应用于各个领域,包括物理学、工程学等。
本文将介绍勾股定理的推导和证明方法。
勾股定理的推导始于古希腊,最著名的是毕达哥拉斯定理,即a²+b²=c²,其中a、b为直角三角形的两条直角边,c为斜边。
以下是勾股定理的推导和证明方法的详细解析。
1. 推导过程:假设存在一个直角三角形,其中直角边分别为a和b,斜边为c。
用几何方法进行推导如下:首先,假设一个正方形,边长为a+b,将其平分成两个等腰直角三角形。
如下图所示:(图)根据正方形的性质,两个等腰直角三角形的面积相等。
因此,每个等腰直角三角形的面积为(a+b)²/4。
接下来,我们将这个正方形旋转,并将两个等腰直角三角形组合在一起,形成一个更大的正方形,边长为c。
如下图所示:(图)根据旋转后的正方形的性质,其面积为c²。
而这个正方形由两个等腰直角三角形组成,因此其面积为2*(a²/2)=(a²+b²)。
综上所述,我们可以得到等式(a+b)²/4=c²,即推导出了勾股定理。
2. 证明方法:除了几何方法外,还有代数方法用于证明勾股定理。
下面我们将介绍一种基于几何方法的证明。
首先,我们假设一个直角三角形,其中直角边分别为a和b,斜边为c。
我们可以构造一个以c为直径的圆,如下图所示:(图)根据圆的性质,半径为c/2的圆的面积为π(c/2)²=πc²/4。
另一方面,根据直角三角形的面积公式,可以得到三角形的面积为ab/2。
现在我们将这个圆分成四个相等的部分,并按下图进行排列:(图)由于四个部分的面积相等,我们可以得到每个部分的面积为πc²/16。
将三角形面积和圆的四个部分的面积相比较,可以得到ab/2=πc²/16。
进一步化简可得a²+b²=c²。
勾股定理(毕达哥拉斯定理)及各种证明方法

勾股定理(毕达哥拉斯定理)勾股定理是一个初等几何定理,是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
勾股定理是余弦定理的一个特例。
勾股定理约有400种证明方法,是数学定理中证明方法最多的定理之一。
“勾三股四弦五”是勾股定理最基本的公式。
勾股数组方程a ² + b ²= c ²的正整数组(a ,b ,c )。
(3,4,5)就是勾股数。
也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a ²+b ²=c ² ,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1 如果直角三角形的两条直角边长分别为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2 如果三角形的三边长a ,b ,c 满足,那么这个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于21ab. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE,∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º,∴ ∠EAB + ∠HAD = 90º, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c2. ∵ EF = FG =GH =HE = b―a ,∠HEF = 90º. ∴ EFGH 是一个边长为b―a 的正方形,它的面积等于.∴ ∴.【证法2】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等.即, 整理得 .【证法3】(1876年美国总统Garfield证明)以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形,它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴AD∥BC.∴ABCD是一个直角梯形,它的面积等于∴ .∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
勾股定理及其证明方法

勾股定理及其证明方法勾股定理是数学中的重要定理之一,也是几何学中最基本的定理之一。
它是指直角三角形中,直角边的平方和等于斜边的平方。
勾股定理的形式化表达为:设直角三角形的两条直角边长分别为a、b,斜边长为c,则有a² + b² = c²。
勾股定理最早可以追溯到古希腊数学家毕达哥拉斯提出,因此也被称为毕达哥拉斯定理。
在古代,毕达哥拉斯学派将勾股定理作为其教义的核心内容之一,认为宇宙万物的运行都遵循着数学规律,而勾股定理则是这种规律的具体体现。
证明勾股定理有多种方法,下面将介绍几种常见的证明方法:1. 几何法证明:最经典的勾股定理证明方法就是几何法。
通过构造直角三角形,利用几何图形的性质和几何关系,可以清晰地展示出直角三角形中各边之间的关系。
其中最著名的一种构造方法就是利用正方形的四个顶点构造直角三角形,通过对角线的长度关系来证明勾股定理。
2. 代数法证明:代数法证明勾股定理则是通过代数运算来完成。
将直角三角形的三条边长代入勾股定理的公式中,进行平方运算和等式推导,最终得到等式两边相等的结果,从而证明了勾股定理的成立。
3. 数学归纳法证明:数学归纳法是一种数学证明方法,通过证明当n=k时命题成立,再证明n=k+1时命题也成立,从而推导出对于所有自然数n命题都成立的结论。
在证明勾股定理时,可以采用数学归纳法来证明直角三角形边长为任意正整数时勾股定理都成立。
4. 向量法证明:利用向量的性质和运算规律,也可以证明勾股定理。
通过向量的加法、数量积等运算,可以得到直角三角形中各边向量的关系,从而推导出勾股定理的成立。
以上是几种常见的勾股定理证明方法,每种方法都有其独特的思路和推导过程。
勾股定理作为数学中的基础定理,不仅在几何学中有着重要的应用,也在物理学、工程学等领域有着广泛的应用。
深入理解和掌握勾股定理及其证明方法,有助于提升数学思维能力和解决实际问题的能力。
勾股定理(毕达哥拉斯定理)及各种证明方法

勾股定理(毕达哥拉斯定理)勾股定理是一个初等几何定理,是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
勾股定理是余弦定理的一个特例。
勾股定理约有400种证明方法,是数学定理中证明方法最多的定理之一。
“勾三股四弦五”是勾股定理最基本的公式。
勾股数组方程a ² + b ²= c ²的正整数组(a ,b ,c )。
(3,4,5)就是勾股数。
也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a ²+b ²=c ² ,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1 如果直角三角形的两条直角边长分别为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2 如果三角形的三边长a ,b ,c 满足,那么这个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于21ab. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE,∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º,∴ ∠EAB + ∠HAD = 90º, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c2. ∵ EF = FG =GH =HE = b―a ,∠HEF = 90º. ∴ EFGH 是一个边长为b―a 的正方形,它的面积等于.∴ ∴.【证法2】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等.即, 整理得 .【证法3】(1876年美国总统Garfield证明)以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形,它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴AD∥BC.∴ABCD是一个直角梯形,它的面积等于∴ .∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
10种勾股定理的证明方法

10种勾股定理的证明方法1什么是勾股定理勾股定理,又称勾股论,是基督教神学家和物理学家第乌里希(Pythagoras)在公元前6世纪提出的一个名言:在给定一个直角三角形中,直角两边的平法相加,等于直角边的平方。
也就是说,在一个直角三角形中,腰边的平方等于两个斜边的平方和。
2勾股定理的表示形式勾股定理可以用一下式子表示:a²+b²=c²,其中a和b是直角三角形的两个斜边,c是这个直角三角形的直角腰边。
3关于勾股定理的10种证明方法1.构造法:构造带有两个相等斜边a和b的两个直角三角形,以证明a²+b²=c²。
2.投影定理:利用投影定理将这些斜边投影,使两个三角形等同,从而证明勾股定理。
3.物理四边形法:采用正方形,梯形和菱形将这三角形组合成一个完整的四边形,证明了勾股定理。
4.三角不等式:根据直角三角形的三角不等式来证明a²+b²>c²。
5.毕达哥拉斯定理:该定理指出,在给定一个直角三角形时,斜边的平方和等于两个斜边相乘再乘以直角边的任何一个数字。
6.幂法:将a²+b²和c²都改写成几次幂的形式,然后将两个完整的当作可以对等的数字比较,从而证明勾股定理。
7.等差数列法:分别建立一个等差数列和一个等比数列,将它们相加,可以得到勾股定理的完整证明。
8.泰勒公式:根据勾股定理,a²+b²=c²,用泰勒公式解析勾股定理,就能得出正确的结论。
9.三角函数法:将勾股定理表示为正弦、余弦和正切的函数关系,根据不同的三角函数的关系证明勾股定理。
10.几何图表法:将斜边a、b、c绘制成一个两个直角三角形的示意图,并且两个三角形的直角边的和是刚好相等的,可以读出完整的证明。
4结论勾股定理是一个经典的定理,已被证明是绝对正确的,而证明它的方法也分多种。
从上面这10种证明方法中,我们可以看出,勾股定理可以通过计算、构造、投影和其它几何变换理论来证明。
勾股定理500种证明方法

勾股定理500种证明方法勾股定理是数学中一条非常重要的定理,它以毕达哥拉斯学派的希腊数学家毕达哥拉斯的名字命名。
勾股定理的数学表达式为a²+b²=c²,其中a、b、c分别代表一个直角三角形的两个短边和斜边的长度。
然而,勾股定理有许多不同的证明方法,超过500种的说法是不准确的。
这里我会介绍一些著名的证明方法,希望能给你一个对这个定理的全面认识。
1.几何证明法:通过利用几何图形中的属性和关系,可以推导出勾股定理。
其中最著名的几何证明方法是欧几里得的证明,他使用了面积相等和相似三角形的概念。
2.代数证明法:通过代数运算和方程的推导,可以证明勾股定理。
其中一种代数证明方法是使用平方差公式展开等式,然后化简并比较系数。
3.三角函数证明法:通过三角函数的性质和恒等式,可以得到勾股定理。
其中一种三角函数证明方法是使用正余弦函数的定义,将斜边的平方表示为两个边的平方和。
4.拆分法:通过将直角三角形拆分成若干个子三角形,然后通过这些子三角形的边长关系来推导勾股定理。
这种证明方法的关键是找到合适的子三角形。
5.向量证明法:通过向量的定义和运算,可以证明勾股定理。
其中一种向量证明方法是使用点乘和模的关系,将勾股定理转化为向量的相等关系。
还有许多其他的证明方法,如数学归纳法、复数证明法、递推证明法等等。
每一种证明方法都有其独特的思路和技巧,它们都可以用来证明勾股定理。
尽管有许多不同的证明方法,但它们都可以追溯到同一个基本的原理,即三角形的几何属性和数学关系。
通过不同的角度和方法来证明这个定理,可以加深我们对这个定理的理解,并且展示数学的多样性和美妙之处。
总结起来,勾股定理是一个有着丰富证明方法的重要定理。
尽管不存在500种证明方法,但每一种证明方法都是通过不同的思路和工具来推导这个定理。
通过学习这些证明方法,我们可以更加深入地理解和欣赏数学。
勾股定理(毕达哥拉斯定理)及各种证明方法

勾股定理(毕达哥拉斯定理) 是一个,是人类早期发现并证明的重要数学定理之一,用思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
是的一个特例。
约有400种证明方法,是数学定理中证明方法最多的之一。
“”是勾股定理最基本的公式。
勾股数组方程a ² + b ²= c ²的正整数组(a ,b ,c )。
(3,4,5)就是。
也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a ²+b ²=c ² ,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1 如果的两条直角边长分别为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2 如果的三边长a ,b ,c 满足,那么这个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于21ab. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE,∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º,∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c2.∵ EF = FG =GH =HE = b―a ,∠HEF = 90º.∴ EFGH 是一个边长为b―a 的正方形,它的面积等于.∴∴ .【证法2】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等.即, 整理得 .【证法3】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形,它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴AD∥BC.∴ABCD是一个直角梯形,它的面积等于∴ .∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
勾股定理十种证明

勾股定理十种证明勾股定理是数学历史上最有名的定理之一,它表明三角形的斜边之和等于其他两边的平方和,即:a2 + b2 = c2它的出现可追溯到古希腊,其中由毕达哥拉斯提出了该定理的最早对应,而后经由许多人的活跃研究,最终由哥白尼、笛卡尔等最终完善和形成了现在的标准形式。
一般来说,无论在什么地方,都有专家们提出这个定理的证明方法,并把它带入教学之中。
然而,大多数时候,专家们提出的证明方法是有限的,因为每个数学家都有自己喜欢的证明方法,他们并不一定能够知道其他专家提出的证明方法。
本文将介绍十种证明勾股定理的方法,以提高读者对勾股定理的理解。
二、十种证明勾股定理的方法1、几何法这是最常用的证明方法,它借助两个直角三角形构成的边构建的矩形的四边,由此可以证明勾股定理。
2、矩阵法这是一种更先进的方法,它借助矩阵相乘来证明勾股定理。
3、物理法这是一种利用物理定律、电磁定律等来证明勾股定理的方法,它充分利用物理定律中相关性的概念,从而证明勾股定理。
4、代数法这是一种运用代数计算证明勾股定理的方法,它把对勾股定理的证明拆分为两个小问题,包括求和等式的求解以及证明两个等式的等价性,从而证明勾股定理。
5、统计法这是一种利用统计理论、概率论等来证明勾股定理的方法,它借助描述性统计学、抽样分布等来说明勾股定理。
6、微积分法这是一种利用微积分来证明勾股定理的方法,它利用微积分的思想,分别定义勾股定理的三个边,并利用微积分中各种概念,从而证明勾股定理。
7、证明归纳法这是一种以归纳法证明勾股定理的方法,它运用归纳法的思想和归纳准则,从而证明勾股定理。
8、几何性质法这是一种利用几何性质来证明勾股定理的方法,它充分利用几何性质的概念,从而证明勾股定理。
9、变形法这是一种利用计算机上图形变形来证明勾股定理的方法,它通过利用计算机上图形变换的思想,从而证明勾股定理。
10、数学归纳法这是一种利用数学归纳法来证明勾股定理的方法,它运用数学归纳法的思想和归纳准则,从而证明勾股定理。
勾股定理的10种证明

5.《周髀算经》中勾股定理的公式与证明
“故折矩①,以为勾广三,股修四,径隅五。”:开始做图——选择一个 勾三(圆周率三)、股四(四方) 的矩,矩的两条边终点的连线应为5(径隅五)。
“②既方之,外半其一矩,环而共盘,得成三四五。”:这就是关键的证明过程——以矩的两条边画正方形(勾方、股方),根据矩的弦外面再画一个矩(曲尺,实际上用作直角三角),将“外半其一矩”得到的三角形剪下环绕复制形成一个大正方形,可看到其中有 边长三勾方、边长四股方、边长五弦方 三个正方形。
7.希腊人的方法
作四个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c.把它们拼成如图那样的一个多边形,使D、E、F在一条直线上。过点C作AC的延长线交DF于点P.于是便不难得出
8.欧几里德(Euclid)射影定理证法
Rt△ABC中,∠ABC=90°,BD是斜边AC上的高
通过证明三角形相似则有射影定理如下:
由△CAD∽△BAC可得AC2=AD×AB。②
我们发现,把①、②两式相加可得
BC2+AC2=AB(AD+BD),
而AD+BD=AB,
因此有BC2+AC2=AB2,这就是a2+b2=c2。
4.课本方法:画两个边长为(a+b)的正方形,如图,其中a、b为直角边,c为斜边。这两个正方形全等,故面积相等。
勾股定理的证明方法十种过程

勾股定理的证明方法十种过程全文共四篇示例,供读者参考第一篇示例:勾股定理,又称毕达哥拉斯定理,是几何学中最基础的定理之一。
它表明在直角三角形中,直角的两边的平方和等于斜边的平方。
勾股定理的证明方法有很多种,下面我将介绍十种常用的证明过程。
一、几何证明法1. 利用相似三角形的性质,构造辅助线,将直角三角形分割成两个直角三角形,再利用勾股定理的定义证明斜边的平方等于直角两边的平方和。
2. 利用平行线的性质,构造辅助线,形成四边形,再利用四边形的性质推导出勾股定理。
二、代数证明法1. 利用代数方法将直角三角形的三边长度表示成a,b,c,利用勾股定理的定义列出等式a^2 + b^2 = c^2,再进行变形推导得到结论。
2. 利用向量法,将三角形的三个顶点表示成二维向量,用向量的性质证明直角三角形满足勾股定理。
三、三角函数证明法1. 利用正弦、余弦、正切等三角函数的关系,将直角三角形的三条边长和角度联系起来,通过三角函数的计算推导出勾股定理。
2. 利用三角函数的定义,将角度和边长关系转换成三角函数的等式,再通过化简和运算得到勾股定理。
五、解析几何证明法1. 利用直角三角形在坐标平面上的表示,用坐标的差和平方和表达斜边和直角两边之间的关系,进行运算保证两边相等。
2. 利用解析几何的方法,利用两直线间的距离公式和直线的斜率关系,推导出勾股定理成立的条件。
七、数学归纳法证明法1. 从一个特殊的直角三角形出发,比如3-4-5直角三角形,验证勾股定理成立。
然后假设勾股定理对于n=1的情况成立,推导出n=k+1的情况也成立,利用数学归纳法证明定理的普遍性。
2. 从勾股数列的性质入手,证明勾股定理的普遍性。
十、几何变换证明法1. 利用几何变换,比如平移、旋转等,将直角三角形变换成其他几何形状,再通过形状不变性证明勾股定理。
2. 利用相似性和对称性的变换,将直角三角形转化成其他几何形状,结合几何形状的性质证明勾股定理的成立。
勾股定理(毕达哥拉斯定理)及各种证明方法

勾股定理(毕达哥拉斯定理)及各种证明方法勾股定理(毕达哥拉斯定理)勾股定理是一个初等几何定理,是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
勾股定理是余弦定理的一个特例。
勾股定理约有400种证明方法,是数学定理中证明方法最多的定理之一。
“勾三股四弦五”是勾股定理最基本的公式。
勾股数组方程a² + b²= c ²的正整数组(a,b,c)。
(3,4,5)就是勾股数。
也就是说,设直角三角形两直角边为a和b,斜边为c,那么a²+b²=c²,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么。
勾股定理的逆定理命题2 如果三角形的三边长a,b,c满足,那么这个三角形是直角三角形。
为a、b、c的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b,所以面积相等.即,整理得.【证法3】(1876年美国总统Garfield证明)以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形,它的面积等于.又∵ ∠DAE = 90º, ∠EBC= 90º,∴AD∥BC.∴ABCD是一个直角梯形,它的面积等于∴ .∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
勾股定理的九种证明方法(附图)

勾股定理的九种证明方法(附图)勾股定理的证明方法一、传说中毕达哥拉斯的证法(图1)左边的正方形是由1个边长为的正方形和1个边长为的正方形以及4个直角边分别为、,斜边为的直角三角形拼成的。
右边的正方形是由1个边长为的正方形和4个直角边分别为、,斜边为的直角三角形拼成的。
因为这两个正方形的面积相等(边长都是),所以可以列出等式,化简得。
二、美国第20任总统茄菲尔德的证法(图3)这个直角梯形是由2个直角边分别为、,斜边为 的直角三角形和1个直角边为的等腰直角三角形拼成的。
因为3个直角三角形的面积之和等于梯形的面积,所以可以列出等式,化简得。
三、相似三角形的证法:4.相似三角形的方法:在学习了相似三角形以后,我们知道在直角三角形中,斜边上的高把这个直角三角形所分成的两个三直角角形与原三角形相似。
CAD∴ BCPM是一个矩形,即∠MBC = 90°.∵∠QBM + ∠MBA = ∠QBA =90 °,∠ABC + ∠MBA = ∠MBC = 90°,∴∠QBM = ∠ABC,又∵∠BMP = 90°,∠BCA = 90°,BQ = BA = c,∴ RtΔBMQ ≌ RtΔBCA.同理可证RtΔQNF ≌ RtΔAEF.即a^2+b^2=c^2六、欧几里德射影定理证法:如图,Rt△ABC中,∠ABC=90°,AD是斜边BC上的高,通过证明三角形相似则有射影定理如下:1)(BD)^2;=AD·DC,(2)(AB)^2;=AD·AC ,(3)(BC)^2;=CD·AC 。
由公式(2)+(3)得:(AB)^2;+(BC)^2;=AD·AC+CD·AC =(AD+CD)·AC=(AC)^2;,即(AB)^2;+(BC)^2;=(AC)^2七、杨作玫证法:做两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a),斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形. 过A作AF⊥AC,AF交GT于F,AF交DT于R. 过B作BP⊥AF,垂足为P. 过D 作DE与CB的延长线垂直,垂足为E,DE交AF于H.∵∠BAD = 90º,∠PAC = 90º,∴∠DAH = ∠BAC.又∵∠DHA = 90º,∠BCA = 90º,AD = AB = c,∴RtΔDHA ≌RtΔBCA.∴DH = BC = a,AH = AC = b.由作法可知,PBCA 是一个矩形,所以RtΔAPB ≌RtΔBCA. 即PB = CA = b,AP= a,从而PH = b―a.987654321PQR HG Dabcaccc∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA. ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a . ∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为 543212S S S S S c ++++= ① ∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+=812SS b -- . ② 把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +. ∴ 222c b a =+.八、陈杰证法:设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c. 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a ,连结DA 、DC , 则 AD = c. ∵ EM = EH + HM = b + a , ED = a , ∴ DM = EM ―ED = ()a b +―a = b. 又∵ ∠CMD = 90º,CM = a , ∠AED = 90º, AE = b , ∴ Rt ΔAED ≌ Rt ΔDMC. ∴ ∠EAD = ∠MDC ,DC = AD = c.∵ ∠ADE + ∠ADC+ ∠MDC =180º, ∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE.连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE.BD F Gab ca b cac a b c 1234567∴ ∠AFB = ∠AED = 90º,BF = DE = a. ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中, ∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG.∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=, 76451S S S S S +===, ∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.九、辛卜松证法:设直角三角形两直角边的长分别为a 、b ,斜边的长为c. 作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为 ()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.ab 21ab 21ab 21ab 212c 2b 2aAD B Bab aba bb a ccccb a ab ab ba b a。
勾股定理500种证明方法

勾股定理500种证明方法
勾股定理,又称毕达哥拉斯定理,是数学几何中最著名的定理之一、它表明,在一个直角三角形中,直角边的平方之和等于斜边的平方,即$a^2+b^2=c^2$。
据说有许多不同的证明方法,至少有500种不同的证明方法。
下面将简单介绍几种常见的证明方法:
1.欧几里得的证明:这是最早的证明方法之一,通过构造相似三角形和利用平行线的性质,证明三角形的内角和为180度。
由此可以得到
$a^2+b^2=c^2$。
2.利用面积的证明:可以将直角三角形划分成两个直角三角形,然后利用面积的性质证明等式的成立。
3.利用复数的证明:可以利用复数的平方模等于平方和的性质,将直角三角形的顶点表示为复数,然后利用复数运算的性质进行计算,最终得到$a^2+b^2=c^2$。
4.利用向量的证明:将三边向量化,将向量的长度平方与向量的点积进行计算,最终得到$a^2+b^2=c^2$。
5.利用相似三角形的证明:通过构造相似的三角形,可以通过比较对应边长的比例关系,推导出$a^2+b^2=c^2$。
这只是其中几种比较常见的证明方法,实际上还有很多其他的证明方法,包括利用解析几何、三角函数、几何画法等等。
每一种证明方法都有自己的特点和逻辑,通过研究和理解这些不同的证明方法,可以更好地理解勾股定理的本质和几何背后的原理。
证明勾股定理的16种方法

勾股定理证明十六种方法方法一:赵爽弦图证法
方法二:毕达哥拉斯证法
方法三:书本证明方法
法四:利用三角形相似推导
方法五:切割线定理证明
方法六:托勒密定理证明
方法七:利用切线长定理
方法八:总统证法
方法九:八法变式
方法十和方法十一:
总结:上述方法是非常常见的方法,当然同学们可以总结出,用到最多的还是面积法,对于面积法无论证明方法如何变化,图形如何变化,方法都有一种熟悉感。
同时,还有很多其它与圆相关的定理应用,要理解它们,同学们要掌握更多的相关知识。
以下方法,只展示图片,同学们可以自行感悟。
方法十二:
方法十三:面积法
方法十四:拼接法1
方法十五:拼接法2
方法十六:射影定理。
勾股定理(毕达哥拉斯定理)及各种证明方法

勾股定理(毕达哥拉斯定理)勾股定理是一个初等几何定理,是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
勾股定理是余弦定理的一个特例。
勾股定理约有400种证明方法,是数学定理中证明方法最多的定理之一。
“勾三股四弦五”是勾股定理最基本的公式。
勾股数组方程a ² + b ²= c ²的正整数组(a ,b ,c )。
(3,4,5)就是勾股数。
也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a ²+b ²=c ² ,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1 如果直角三角形的两条直角边长分别为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2 如果三角形的三边长a ,b ,c 满足,那么这个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于21ab. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE,∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º,∴ ∠EAB + ∠HAD = 90º, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c2. ∵ EF = FG =GH =HE = b―a ,∠HEF = 90º. ∴ EFGH 是一个边长为b―a 的正方形,它的面积等于.∴ ∴.【证法2】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等.即, 整理得 .【证法3】(1876年美国总统Garfield证明)以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形,它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD∥BC.∴ABCD是一个直角梯形,它的面积等于∴ .∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
勾股定理 毕达哥拉斯

勾股定理毕达哥拉斯勾股定理,又称毕达哥拉斯定理,是数学中的一条基本定理,是与坐标系有关的,被广泛应用于几何、三角学等领域。
一、勾股定理的定义与证明勾股定理的定义是指:在直角三角形中,直角边两条边的平方和等于斜边边的平方。
勾股定理的证明较为复杂,有多种方法。
其中一个较为简单而易懂的证明方法如下:设直角三角形的两直角边分别为a和b,斜边为c,如下图所示。
以直角边a为底,以直角边b为高,可以构造一个面积为S1的直角三角形。
同理,以直角边b为底,以直角边a为高,可以构造一个面积为S2的直角三角形。
因此,直角三角形的面积可以表示为S1+S2。
又因为斜边长度为c,以斜边c为底,以直角边a为高,可以构造一个面积为S3的三角形。
同理,以斜边c为底,以直角边b为高,可以构造一个面积为S4的三角形。
因此,直角三角形的面积也可以表示为S3+S4。
根据勾股定理,可以知道斜边c上的高等于直角边a和直角边b构成的两个三角形的高之和。
因此,S3和S4的和等于S1和S2之和,即S3+S4=S1+S2。
综上,直角三角形的面积可以表示为S1+S2或S3+S4,因此S1+S2=S3+S4,即a²+b²=c²。
二、勾股定理的应用勾股定理广泛应用于几何、三角学等领域,下面列举一些常见的应用:1. 求直角三角形的斜边长度设直角三角形的两直角边长度分别为a和b,斜边长度为c,则根据勾股定理可以得到c²=a²+b²。
因此,当已知两个直角边长度时,可以利用勾股定理求解斜边长度。
2. 判断一个三角形是否为直角三角形当一个三角形的三边长度分别为a、b、c时,若满足a²+b²=c²,则该三角形为直角三角形;反之,若不满足该条件,则该三角形不是直角三角形。
3. 求解两直角边当已知斜边长度c和其中一条直角边长度a时,可以利用勾股定理求解另一条直角边的长度b,即b=√(c²-a²)。
证明勾股定理的方法

证明勾股定理的方法勾股定理,也被称为毕达哥拉斯定理,是数学中的一条基本定理,它描述了直角三角形中直角边与斜边之间的关系。
证明勾股定理的方法有很多种,下面将介绍其中几种常见的方法。
方法一:几何证明法几何证明法是最常见的证明勾股定理的方法之一。
它通过构造几何图形,利用几何性质来证明定理的正确性。
下面以一种简单的几何证明法为例进行说明。
设直角三角形的两条直角边分别为a和b,斜边为c。
我们可以构造一个正方形,边长为a+b,如图所示。
[图1]根据正方形的性质,它的对角线相等,即对角线AC的长度等于对角线BD的长度。
又因为AC的长度等于a+b,BD的长度等于c,所以a+b=c。
这就证明了勾股定理。
方法二:代数证明法代数证明法是另一种常见的证明勾股定理的方法。
它通过代数运算和方程推导来证明定理的正确性。
下面以一种代数证明法为例进行说明。
设直角三角形的两条直角边分别为a和b,斜边为c。
根据勾股定理,我们有a²+b²=c²。
我们可以将这个方程转化为等价的形式进行证明。
首先,我们将c²展开,得到c²=a²+b²。
然后,我们将a²和b²分别展开,得到a²=(c-b)(c+b)和b²=(c-a)(c+a)。
将这两个等式代入c²=a²+b²中,得到c²=(c-b)(c+b)+(c-a)(c+a)。
我们可以进行简化运算,得到c²=2ac+2bc-2ab。
继续简化运算,得到c²+2ab=2ac+2bc。
再将等式两边同时除以2,得到(c²+2ab)/2=(2ac+2bc)/2。
化简得到c²+ab=ac+bc。
根据等式两边的相等性,我们可以得到a(c-b)=b(c-a)。
再将等式两边同时除以c-a,得到a=b。
同样的方法,我们可以得到b=a。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理(毕达哥拉斯定理)
勾股定理是一个初等几何定理,是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
勾股定理是余弦定理的一个特例。
勾股定理约有 400 种证明方法,是数学定理中证明方法最多的定理之一。
“ 勾三股
四弦五”是勾股定理最基本的公式。
勾股数组方程
a 2 +2=
c
2的正整数组 (,,
c
) 。
(3,4,5)
b a b
就是勾股数。
也就是说,设直角三角形两直角边为 a 和 b,斜边为 c,那么 a2+b2=c2,即
直角三角形两直角边的平方和等于斜边的平方。
勾股定理
命题 1 如果直角三角形的两条直角边长分别为a, b,斜边长为 c,那么。
勾股定理的逆定理
命题 2 如果三角形的三边长 a,b,c 满足,那么这个三角形是直角三角形。
【证法 1】(赵爽证明)
以 a、 b 为直角边( b>a),以 c 为斜边作四个全等的直角三角形,则每个直角三角形的面
积等于1
ab. 把这四个直角三角形拼成如图所示形状. 2
∵ Rt DAH ≌ Rt ABE,∴ ∠HDA = ∠EAB.
∵ ∠HAD + ∠HAD = 90o,∴∠EAB + ∠HAD = 90o,
∴ ABCD 是一个边长为 c 的正方形,它的面积等于c2.
∵EF = FG =GH =HE = b ―a , ∠HEF = 90o.
∴ EFGH 是一个边长为b―a的正方形,它的面积等于.
∴∴
【证法 2】(课本的证明)
.
做8个全等的直角三角形,设它们的两条直角边长分别为
分别为 a、 b、 c 的正方形,把它们像上图那样拼成两个正方形方形的边长都是 a + b ,所以面积相等.a、 b,斜边长为c,再做三个边长
. 从图上可以看到,这两个正
即,整理得.
【证法 3】( 1876年美国总统 Garfield证明)以a、b 为直角边,以 c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于.把这两个直角三角形拼成如图所示形
状,使 A、E、 B 三点在一条直线上.
∵ Rt EAD ≌ Rt CBE,∴ ∠ADE = ∠BEC.
∵ ∠AED + ∠ADE = 90o, ∴ ∠AED + ∠BEC = 90o. ∴ ∠DEC = 180o―90o= 90o.
∴DEC是一个等腰直角三角形,它的面积等于. 又∵∠DAE = 90o, ∠EBC = 90o, ∴
AD∥BC.∴
ABCD是一个直角梯形,它的面积等于
∴. ∴.
【趣闻】:在 1876年一个周末的傍晚,在美国华盛顿的郊外,
有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。
由于好奇心驱使伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。
只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。
于是伽菲尔德便问他们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和 4,那么斜边长为多少呢?”伽菲尔德答到:“是 5呀。
”小男孩又问道:“如果两条直角边分别为 5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不加思
索地回答到:“那斜边的平方一定等于5的平方加上 7的平方。
”小男孩又说道:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心理很不是滋味。
于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题。
他经过反复的思考与演算,终于弄
清楚了其中的道理,并给出了简洁的证明方法。
1876年 4月 1日,伽菲尔德在《新英格兰教育
日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第二十任总统后来,
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统。
”
证法。
【证法 4】(欧几里得证明)做三个边长分别为a、 b、 c 的
正方形,把它们拼成如图所示形状,使H、 C、 B 三点在一
条直线上,连结BF、CD. 过 C作 CL⊥DE,交 AB于点 M,交
DE于点 L. ∵ AF = AC , AB = AD,∠ FAB = ∠GAD,
∴FAB ≌GAD,
∵FAB 的面积等于,GAD的面积等于矩形ADLM的
面积的一半,
∴矩形 ADLM的面积 =. 同理可证,矩形MLEB的面积 =.
∵正方形 ADEB的面积= 矩形 ADLM的面积 +矩形 MLEB的面积
∴,即.
【证法 5】(利用相似三角形性质证明)
如图,在 Rt ABC中,设直角边 AC、 BC的长度分别为a、b,斜边 AB
的长为 c,过点 C 作 CD⊥AB,垂足是 D.在ADC和ACB中,
∵ ∠ADC = ∠ACB = 90o,∠ CAD = ∠BAC,∴ADC ∽ACB.
∴AD∶AC = AC ∶AB,即.
同理可证,CDB ∽ACB,
从而有. ∴,即
【证法 6】(邹元治证明)
以 a、b 为直角边,以 c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于.把这四个直角三角形拼成如图所示形状,使A、E、 B 三点在一条直
线上, B、 F、 C 三点在一条直线上,C、 G、 D 三点在一条直线上 .
∵ Rt HAE ≌ Rt EBF,∴ ∠AHE = ∠BEF.
∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o.
∴ ∠HEF = 180o―90o= 90o.
∴四边形 EFGH是一个边长为 c 的正方形 .它的面积等于 c2.
∵ Rt GDH≌ Rt HAE,∴ ∠HGD = ∠EHA.
∵ ∠HGD + ∠GHD = 90o,∴ ∠EHA + ∠GHD = 90o.
又∵∠GHE = 90o,∴ ∠DHA = 90o+ 90o= 180o.
∴ ABCD 是一个边长为 a + b 的正方形,它的面积等于.
∴. ∴.
【证法 7】(利用切割线定理证明)
在 Rt ABC中,设直角边 BC = a , AC = b ,斜边 AB = c.
如图,以 B 为圆心 a 为半径作圆,
交AB及 AB的延长线分别于 D、E,则 BD = BE = BC = a.
因为∠ BCA = 90o,点 C 在⊙B上,
所以 AC是⊙ B 的切线 .由切割线定理,得
===,
即,∴.【证法 8】(作直角三角形的内切圆证明)
在 Rt ABC中,设直角边BC = a , AC = b ,斜边 AB = c.
内切圆⊙ O,切点分别为D、 E、 F(如图),设⊙O 的半径为作
r.
Rt ABC的
∵AE = AF , BF = BD,CD = CE,
∴
== r + r = 2r,即,∴.
∴,
即,
∵,
∴,又∵== ==,∴,
∴,
∴,
∴.。
