九年级数学平行四边形的判定同步练习
北师大版九年级数学上册第一章特殊平行四边形《正方形的性质与判定》同步练习

正方形的性质与判定(典型题)第1课时正方形及其性质1.如图1,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠ACP的度数是()图1A.45°B.22.5°C.67.5°D.75°2.正方形的一条对角线的长为4,则这个正方形的面积是()A.8 B.4 2C.8 2D.163.如图2,四边形ABCD是正方形,E,F分别是AB,AD上的一点,且BF⊥CE,垂足为G.求证:AF=BE.图24.如图,在正方形ABCD的外侧作等边三角形ADE,AC,BE交于点F,则∠BFC的度数为()A.45°B.55°C.60°D.75°5.如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为()A.23a2B.14a2C.59a2D.49a26.如图5,正方形ABCD的边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,F A⊥AE,交CB的延长线于点F,则EF的长为________.图57.如图6,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC相交于点G,连接AE,CF.(1)求证:AE=CF;(2)若∠ABE=55°,求∠EGC的大小.图68.如图7,正方形ABCD绕点A逆时针旋转45°与正方形AEFG重合,EF与CD交于点M,得四边形AEMD,正方形ABCD的边长为2,则两正方形重合部分(阴影部分)的面积为()图7A.4 2-4 B.4 2+4 C.8-4 2 D.2+19.如图8,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG 绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=()图8A.2+6B.3+1C.3+2D.3+610.如图9,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为________.图911.如图10所示,在正方形ABCD中,点E,F分别在边AD,CD上,且∠EBF=45°.(1)求证:EF=FC+AE;(2)若AB=2,求△DEF的周长.图1012.如图11,在正方形ABCD中,点E,F分别在BC,CD上移动,但点A到EF的距离AH始终保持与AB的长相等,则在点E,F移动的过程中:(1)∠EAF的大小是否发生变化?请说明理由;(2)△ECF的周长是否发生变化?请说明理由.图1113.如图12,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作C1;再作第二个正方形A2B2C2A3,周长记作C2;继续作第三个正方形A3B3C3A4,周长记作C3;点A1,A2,A3,A4,…在射线ON上,点B1,B2,B3,B4,…在射线OM上……依此类推,则第n个正方形的周长C n=________.图1214.如图13①,在正方形ABCD中,E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.(1)请判断:FG与CE的数量关系是________,位置关系是________;(2)如图②,若E,F分别是边CB,BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请做出判断并给予证明;(3)如图③,若E,F分别是边BC,AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断.参考答案1.B2.A3.证明:∵四边形ABCD是正方形,∴AB=BC,∠A=∠CBE=90°.∵BF⊥CE,∴∠BCE+∠CBG=90°.∵∠ABF+∠CBG=90°,∴∠BCE=∠ABF.在△BCE和△ABF中,∠BCE=∠ABF,BC=AB,∠CBE=∠A,∴△BCE≌△ABF(ASA),∴AF=BE.4.C5.D6.6 2[解析]7.解:(1)证明:∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°.∵BE⊥BF,∴∠EBF=90°,∴∠ABE=∠CBF.∵AB=BC,∠ABE=∠CBF,BE=BF,∴△ABE≌△CBF,∴AE=CF.(2)∵BE=BF,∠EBF=90°,∴∠BEF=45°.∵∠ABC=90°,∠ABE=55°,∴∠GBE=35°,∴∠EGC=∠GBE+∠BEF=80°.8.A9.A10.3211.解:(1)证明:将△ABE绕点B顺时针旋转90°得到△CBM,则BA=BC,AE=CM,BE=BM,∠ABE=∠CBM,∠A=∠BCM.∵四边形ABCD是正方形,∴∠A=∠ABC=∠BCD=90°,∴F,C,M三点共线,∠EBM=90°.∵∠EBF=45°,∴∠FBM=45°.在△BEF与△BMF中,BE=BM,∠EBF=∠MBF,BF=BF,∴△BEF≌△BMF,∴EF=FM=FC+CM=FC+AE.(2)由(1)知EF=FC+AE,∴△DEF的周长=DE+DF+EF=DE+DF+AE+CF=AD+CD=2AB=4. 12.解:(1)∠EAF的大小不发生变化.理由如下:根据题意,知AB=AH,∠B=∠AHE=90°.又∵AE=AE,∴Rt△BAE≌Rt△HAE,∴∠BAE=∠HAE.同理,Rt△HAF≌Rt△DAF,∴∠HAF=∠DAF,∴∠EAF=12∠BAH+12∠HAD=12(∠BAH+∠HAD)=12∠BAD.又∵∠BAD=90°,∴∠EAF=45°,∴∠EAF的大小不发生变化.(2)△ECF的周长不发生变化.理由如下:C△ECF=EF+EC+FC.由(1),得Rt△BAE≌Rt△HAE,∴EB=HE.同理,HF=DF.∴C△ECF=EF+EC+FC=EB+DF+EC+FC=2BC,∴△ECF的周长不发生变化.13.2n+114.解:(1)相等互相平行(2)成立.证明:如图,过点G作GH⊥CB交其延长线于点H.∵EG⊥DE,∴∠GEH+∠DEC=90°.∵∠GEH+∠HGE=90°,∴∠DEC=∠HGE.在△HGE与△CED中,∠GHE=∠DCE=90°,∠HGE=∠DEC,EG=DE,∴△HGE≌△CED,∴GH=CE,HE=CD.∵CE=BF,∴GH=BF.又∵GH∥BF且∠GHE=90°,∴四边形GHBF是矩形,∴FG=BH,FG∥CH,∴FG∥CE.∵四边形ABCD是正方形,∴CD=BC,∴HE=BC,∴HE+EB=BC+EB,∴BH=CE,∴FG=CE.(3)成立.FG=CE,FG∥CE.第2课时正方形的判定(典型题)1.下列说法不正确的是()A.一组邻边相等的矩形是正方形B.对角线相等的菱形是正方形C.对角线互相垂直的矩形是正方形D.有一个角是直角的平行四边形是正方形2.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是________.3.如图14,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA 的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=()时,则四边形AECF是正方形.图14A.30°B.45°C.60°D.90°4.已知四边形ABCD各边的中点分别是E,F,G,H,如果四边形ABCD满足____________________,那么四边形EFGH是正方形.5.如图15,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC 交BE的延长线于点F,连接CF.(1)求证:AD=AF;(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.图156.如图16,在Rt△ABC中,∠BAC=90°,AD=CD,E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF,CG.(1)求证:AF=BF;(2)如果AB=AC,求证:四边形AFCG是正方形.图167.⑥如图17,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是()图17A.7 B.8 C.7 2D.7 38.2017·宜昌如图18,正方形ABCD的边长为1,O是BC边上的一个动点(与B,C不重合),以O为顶点在BC所在直线的上方作∠MON=90°.(1)当OM经过点A时,请直接填空:ON________(填“可能”或“不可能”)过点D;(图①仅供分析)(2)如图②,在ON上截取OE=OA,过点E作EF垂直于直线BC,垂足为F,作EH⊥CD 于点H,求证:四边形EFCH为正方形.图189.如图19,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.(1)求证:四边形EDFG是正方形;(2)当点E在什么位置时,四边形EDFG的面积最小?并求出四边形EDFG面积的最小值.图1910.矩形的四个内角平分线围成的四边形是()A.正方形B.矩形C.菱形D.一般平行四边形11.如图0,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是________.图012.如图1,E是矩形ABCD的边BC的中点,P是边AD上的一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形?并证明;(2)在(1)的条件下,动点P运动到什么位置时,矩形PHEF变为正方形?为什么?图113.如图2,AC,BD是正方形ABCD的对角线,将△DCB绕点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.(1)求证:△AED≌△GED;(2)求证:四边形AEGF是菱形;(3)若AC=1,求BC+FG的值.图214.如图3①,△ABC中,AD平分∠BAC交BC于点D,在线段AB上截取AE=AC,过点E作EF∥BC交AD于点F.连接DE,DF.(1)试判断四边形CDEF是何种特殊的四边形.(2)当AB>AC,∠ABC=20°时,四边形CDEF能是正方形吗?如果能,求出此时∠BAC 的度数;如果不能,请说明理由.(3)若AD平分∠BAC的外角交直线BC于点D,在直线AB上截取AE=AC,过点E作EF∥BC交直线AD于点F,如图②”,设∠ABC=x,其他条件不变,四边形CDEF能是正方形吗?如果能,求出此时∠BAC关于x的关系式;如果不能,试说明理由.图3参考答案1.D2.①③④3.D.4.对角线互相垂直且相等5.解:(1)证明:∵AF∥BC,∴∠EAF=∠EDB.∵E是AD的中点,∴AE=DE.在△AEF和△DEB中,∠EAF=∠EDB,AE=DE,∠AEF=∠DEB,∴△AEF≌△DEB(ASA),∴AF=BD.∵在△ABC中,∠BAC=90°,AD是中线,∴AD=BD=DC=12BC,∴AD=AF.(2)四边形ADCF是正方形.证明:∵AF=BD=DC,AF∥BC,∴四边形ADCF是平行四边形.∵AB=AC,AD是中线,∴AD⊥BC.又∵AD=AF,∴四边形ADCF是正方形.6.证明:(1)∵AD=CD,E是边AC的中点,∴DE⊥AC,∴DE是线段AC的垂直平分线,∴AF=CF,∴∠F AC=∠ACB.在Rt△ABC中,由∠BAC=90°,得∠B+∠ACB=90°,∠F AC+∠BAF=90°,∴∠B=∠BAF,∴AF=BF.(2)∵AG∥CF,∴∠AGE=∠CFE.又∵E是边AC的中点,∴AE=CE.在△AEG和△CEF中,∠AGE=∠CFE,∠AEG=∠CEF,AE=CE,∴△AEG≌△CEF(AAS),∴AG=CF.又∵AG∥CF,∴四边形AFCG是平行四边形.又∵AF=CF,∴四边形AFCG是菱形.在Rt△ABC中,由AF=CF,AF=BF,得BF=CF,即F是边BC的中点.又∵AB=AC,∴AF⊥BC,即∠AFC=90°,∴四边形AFCG是正方形.7.C8.解:(1)不可能.理由如下:若ON过点D,则OA>AB,OD>CD,∴OA2>AD2,OD2>AD2,∴OA2+OD2>2AD2≠AD2,∴∠AOD≠90°,这与∠MON=90°矛盾,∴ON不可能过点D,故答案为:不可能.(2)证明:∵EH⊥CD,EF⊥BC,∴∠EHC=∠EFC=90°.又∠HCF=90°,∴四边形EFCH为矩形.∵∠MON=90°,∴∠EOF=90°-∠AOB.在正方形ABCD中,∠BAO=90°-∠AOB,∴∠EOF=∠BAO.在△OFE和△ABO中,∠EOF=∠BAO,∠EFO=∠B,OE=AO,∴△OFE≌△ABO(AAS),∴EF=OB,OF=AB.又OF=CF+OC,AB=BC=BO+OC,∴CF=BO=EF,∴四边形EFCH为正方形.9.解:(1)证明:连接CD,如图①所示.∵△ABC为等腰直角三角形,∠ACB=90°,D是AB的中点,∴∠A=∠DCF=45°,AD=CD.在△ADE和△CDF中,AE=CF,∠A=∠DCF,AD=CD,∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF.∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,∴△EDF为等腰直角三角形.∵O为EF的中点,GO=OD,∴GD⊥EF,且GD=2OD=EF,∴四边形EDFG是正方形.(2)过点D作DE′⊥AC于点E′,如图②所示.∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC=4,∴DE′=12BC=2,AB=42,点E′为AC的中点,∴2≤DE<22(点E与点E′重合时取等号),∴4≤S四边形EDFG=DE2<8.∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4.10.A11.3212.解:(1)当矩形ABCD的长是宽的2倍时,四边形PHEF是矩形.证明:∵四边形ABCD是矩形,∴AD=BC,AB=CD.∵E是BC的中点,∴AB=BE=EC=CD,则△ABE,△DCE均是等腰直角三角形,∴∠AEB=∠DEC=45°,∴∠AED=90°.在四边形PHEF中,∵∠PFE=∠FEH=∠EHP=90°,∴四边形PHEF是矩形.(2)当点P是AD的中点时,矩形PHEF变为正方形.理由如下:由(1)可得∠BAE=∠CDE=45°,∴∠F AP=∠HDP=45°.又∵∠AFP=∠DHP=90°,AP=DP,∴Rt△AFP≌Rt△DHP,∴PF=PH,∴矩形PHEF是正方形.13.解:(1)证明:由旋转可知DG=DC,∠DGH=∠DCB=90°. ∵AD=CD,∴AD=DG.又∵ED=ED,∴Rt△AED≌Rt△GED(HL).(2)证明:由(1)知△AED≌△GED,∴AE=EG,∠ADE=∠GDE=12∠BDA=22.5°,∴∠CDF=67.5°,∠CFD=67.5°,∴∠CDF=∠CFD,∴CF=CD.又∵AC=BD,CD=DG,∴AF=BG=EG.由旋转知∠H=∠DBC=45°.又∵∠DAC=45°,∴AF∥EG,∴四边形AEGF是平行四边形.又∵AE=EG,∴▱AEGF是菱形.(3)由(2)知四边形AEGF是菱形,∴AF=FG.由(2)知CF=CD,∴BC=CF,∴BC+FG=CF+AF=AC=1.。
2021年九年级中考数学一轮复习《平行四边形》基础复习卷

2021年中考数学一轮复习《平行四边形》基础复习卷一、选择题1.能判定四边形是平行四边形的条件是( )A.一组对边平行,另一组对边相等;B.一组对边相等,一组邻角相等;C.一组对边平行,一组邻角相等;D.一组对边平行,一组对角相等。
2.如图,在▱ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为()A.4cm B.5cm C.6cm D.8cm3.如图,□ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为()A.16B.14C.12D.104.如图,将边长为2cm的菱形ABCD沿边AB所在的直线翻折得到四边形ABEF.若∠DAB=30°,则四边形CDFE的面积为( )A.2cm2B.3cm2C.4cm2D.6cm25.如图,菱形ABCD周长为20,对角线AC、BD相交于点O,E是CD的中点,则OE的长是( )A.2.5 B.3 C.4 D.56.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )A.28°B.52°C.62°D.72°7.如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE长是()A.1.6B.2.5C.3D.3.48.如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为()A.14B.16C.17D.189.如图,矩形ABCD中,E在AD上,EF⊥EC,EF=EC,DE=2,矩形周长为16,则AE长是( )A.3B.4C.5D.710.如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长为2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为 ( )A.3a+2bB.3a+4bC.6a+2bD.6a+4b11.菱形、矩形、正方形都具有的性质是()A.对角线相等B.对角线互相垂直C.对角线互相平分D.对角线平分一组对角12.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD 上有一点P,使PC+PE的和最小,则这个最小值为()A.4B.2C.2D.2二、填空题13.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件________(只添一个即可),使四边形ABCD是平行四边形.14.如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是(只填一个你认为正确的即可).15.如图,要使平行四边形ABCD是矩形,则应添加的条件是__________(添加一个条件即可).16.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加条件,才能保证四边形EFGH是矩形.17.如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是.18.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD 和EFGH都是正方形,如果AB=10,EF=2,那么AH为a,BH为b,则ab= .三、解答题19.如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上(1)给出以下条件:①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;(2)在(1)条件中你所选条件的前提下,添加AE=CF。
初中数学,特殊的平行四边形同步练习题

特殊的平行四边形同步练习题基础练习题1.下列条件中,能判定一个四边形为菱形的条件是A.对角线互相平分的四边形B.对角线互相垂直且平分的四边形C.对角线相等的四边形D.对角线相等且互相垂直的四边形2.菱形的对角线长分别为3和4,则该菱形的面积是A.6 B.8 C.12 D.243.在四边形中,能判定这个四边形是正方形的条件是A.对角线相等,对边平行且相等B.一组对边平行,一组对角相等C.对角线互相平分且相等,对角线互相垂直D.一组邻边相等,对角线互相平分4.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC=A.5 B.4 C.3.5 D.35.如图,已知在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,若∠DAE∶∠BAE=3∶1,则∠EAC的度数是A.18°B.36°C.45°D.72°6.在一个直角三角形中,已知两直角边分别为6 cm,8 cm,则下列结论不正确的是A.斜边长为10 cm B.周长为25 cmC.面积为24 cm2 D.斜边上的中线长为5 cm7.在四边形ABCD 中,对角线,AC BD 互相平分,若添加一个条件使得四边形ABCD 是矩形,则这个条件可以是A .90ABC ∠=︒B .AC BD ⊥C .AB CD =D .AB CD ∥8.如图,在长方形ABCD 中,AB =3,BC =4,若沿折痕EF 折叠,使点C 与点A 重合,则折痕EF 的长为A .158B .154C .152D .159.如图,菱形ABCD 的对角线交于点O ,AC =8 cm ,BD =6 cm ,则菱形的高为A .485cm B .245cm C .125cm D .105cm 10.如图,在菱形ABCD 中,P 、Q 分别是AD 、AC 的中点,如果PQ =3,那么菱形ABCD 的周长是A .30B .24C .18D .611.在菱形ABCD 中,AE ⊥BC 于点E ,AF ⊥CD 于点F ,且E 、F 分别为BC 、CD 的中点,则∠EAF 等于A .60°B .55°C .45°D .30°12.如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是A.75°B.60°C.54°D.67.5°13.如图,平行四边形ABCD中,AD=5,AB=3,若AE平分∠BAD交边BC于点E,则线段EC的长度为_________.14.如图是一个平行四边形,当∠α的度数为________度时,两条对角线长度相等.15.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6 cm,BC=8 cm,则△AEF的周长为________cm.16.如图,在菱形ABCD中,AB=4,线段AD的垂直平分线交AC于点N,△CND的周长是10,则AC的长为__________.17.如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为__________.18.如图,等边三角形EBC在正方形ABCD内,连接DE,则ADE∠=__________.19.已知菱形ABCD中,对角线AC=16 cm,BD=12 cm,BE⊥DC于点E,求菱形ABCD的面积和BE的长.20.如图,已知四边形ABCD是正方形,延长BC到E,在CD上截取CF=CE,BF交DE于G,求证:BG⊥DE.21.已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点.(1)求证:△BED是等腰三角形:学-科网(2)当∠BCD=________°时,△BED是等边三角形.22.如图,四边形ABCD 中,90A ABC ∠=∠=︒,1AD =,3BC =,E 是边CD 的中点,连接BE 延长与AD 的延长线相交于点F ,连接CF . (1)求证:四边形BDFC 是平行四边形. (2)已知CB CD =,求四边形BDFC 的面积.23.如图,在矩形ABCD 中,AD =12,AB =7,DF 平分∠ADC ,AF ⊥EF .(1)求证:AF =EF ; (2)求EF 长.24.如图,在矩形ABCD 中,M ,N 分别是边AD ,BC 的中点,E ,F 分别是线段BM ,CM 的中点. (1)求证:△ABM ≌△DCM ;(2)当AB ∶AD =__________时,四边形MENF 是正方形,并说明理由.能力拓展25.如图,矩形ABCD 沿着AE 折叠,使D 点落在BC 边上的F 点处,如果60BAF ∠=︒,则DAE ∠等于A .15°B .30°C .45°D .60°26.如图,在△ABC 中,∠BAC =90°,AD 是BC 边上的高,E 、F 分别是AB 、AC 边的中点,若AB =8,AC =6,则△DEF 的周长为A .12B .13C .14D .1527.如图,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,DH ⊥AB 于H ,连接OH ,∠DHO =20°,则∠CAD 的度数是A .20°B .25°C .30°D .40°28.如图,以A 点为圆心,以相同的长为半径作弧,分别与射线AM ,AN 交于B ,C 两点,连接BC ,再分别以B ,C 为圆心,以相同长(大于12BC )为半径作弧,两弧相交于点D ,连接AD ,BD ,CD .则下列结论错误的是A.AD平分∠MAN B.AD垂直平分BCC.∠MBD=∠NCD D.四边形ACDB一定是菱形29.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=2∶1,则线段CH的长是A.3 B.4 C.5 D.630.如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为A.2B.22C.2+1 D.22+131.如图,在矩形ABCD中,E是AB边上的中点,将△BCE沿CE翻折得到△FCE,连接AF.若∠EAF=75°,那么∠BCF的度数为__________.32.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为____________.33.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=2EC.其中正确结论的序号是____________.34.如图,正方形ABCD中,AB=3,点E、F分别在BC、CD上,且∠BAE=30°,∠DAF=15°.(1)求证:DF+BE=EF;(2)求∠EFC的度数;(3)求△AEF的面积.35.如图1,四边形ABCD是平行四边形,BD是它的一条对角线,过顶点A、C分别作AM⊥BD,CN⊥BD,M,N为垂足.(1)求证:AM=CN;(2)如图2,在对角线DB的延长线及反向延长线上分别取点E,F,使BE=DF,连接AE、CF,试探究:当EF满足什么条件时,四边形AECF是矩形?并加以证明.真题实战36.(2018·浙江台州)下列命题正确的是A.对角线相等的四边形是平行四边形B.对角线相等的四边形是矩形C.对角线互相垂直的平行四边形是菱形D.对角线互相垂直且相等的四边形是正方形37.(2018·江苏淮安)如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是A.20 B.24 C.40 D.4838.(2018·山东烟台)对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O 折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为A.7 B.6 C.5 D.439.(2018·四川内江)如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为A.31°B.28°C.62°D.56°40.(2018·湖北宜昌)如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥A B.EI ⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于A.1 B.12C.13D.1441.(2018·黑龙江牡丹江)如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为A.6 B.5 C.4 D.342.(2018·广西贵港)如图,在菱形ABCD 中,AC =62,BD =6,E 是BC 边的中点,P ,M 分别是AC ,AB 上的动点,连接PE ,PM ,则PE +PM 的最小值是A .6B .33C .26D .4.543.(2018·湖南湘潭)如图,已知点E 、F 、G .H 分别是菱形ABCD 各边的中点,则四边形EFGH 是A .正方形B .矩形C .菱形D .平行四边形44.(2018·浙江嘉兴)用尺规在一个平行四边形内作菱形ABCD ,下列作法中错误的是A .B .C .D .45.(2018·四川甘孜州)如图,在菱形ABCD 中,对角线AC 与BD 相交于点86O AC BD ==,,, OE AD ⊥于点E ,交BC 于点F ,则EF 的长为__________.46.(2018·辽宁锦州)如图,菱形ABCD 的对角线AC ,BD 相交于点O ,过点A 作AH ⊥BC 于点H ,连接OH .若OB =4,S 菱形ABCD =24,则OH 的长为__________.47.(2018·四川攀枝花)如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=1 3 S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为__________.48.(2018·辽宁葫芦岛)如图,在菱形OABC中,点B在x轴上,点A的标为(2,3),则点C的坐标为__________.49.(2018·四川广安)如图,四边形ABCD是正方形,M为BC上一点,连接AM,延长AD至点E,使得AE=AM,过点E作EF⊥AM,垂足为F,求证:AB=EF.50.(2018·湖南郴州)如图,在ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.51.(2018·辽宁沈阳)如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,ABCD的面积是__________.参考答案1. B2. A3. C4. B5. C6. B7. A8. B9. B 10. B 11. A 12. B 13. 2 14. 90 15. 9 16. 617. (18. 15°19. 485(cm ).20. ∵BC =CD ,∠BCF =∠DCE =90°,CF =CE , ∴△BCF ≌△DCE ,∴∠FBC =∠EDC . 又∵∠BFC =∠DFG ,∴∠DGF =∠BCF =90°, 即BG ⊥DE .21. (1)等腰三角形;(2)150° 22. (1)∵90A ABC ∠=∠=︒,∴∥BC AF ,∴CBE DFE ∠=∠, 又∵DE CE =,DEF BEC ∠=∠, ∴△BEC ≌△FED ,∴BE EF =,又∵CE DE =,∴四边形BDFC 是平行四边形. (2)如图,过D 作DH CB ⊥于H ,∴∠DHB =∠A =∠ABH =90°,∴四边形ADHB 是矩形,∴1BH AD ==, ∵3CB CD ==,∴2CH =,在Rt △CDH 中,∵90CHD ∠=︒,∴22325DH =-= ∴平行四边形BDFC S BC DH =⋅35= 23.(1)∵四边形ABCD 是矩形,∴∠B =∠C =∠ADC =90°,AB =DC =7,BC =AD =12,∴∠BAF +∠AFB =90°, ∵DF 平分∠ADC ,∴∠ADF =∠CDF =45°,∴△DCF 是等腰直角三角形, ∴FC =DC =7,∴AB =FC ,∵AF ⊥EF ,∴∠AFE =90°,∴∠AFB +∠EFC =90°,∴∠BAF =∠EFC , 在△ABF 和△FCE 中,BAF EFCAB FC B C ∠=∠=∠=∠⎧⎪⎨⎪⎩,∴△ABF ≌△FCE (ASA ),∴EF =AF ;(2)BF =BC –FC =12–7=5,在Rt △ABF 中,由勾股定理得: AF 22227574AB BF +=+则EF =AF 7424.【解析】(1)∵四边形ABCD 是矩形, ∴AB=DC ,∠A =∠D =90°. ∵M 为AD 的中点,∴AM=MD ,∴△ABM ≌△DCM . (2)1∶2,理由:∵AB ∶AD =1∶2,∴AB =12AD . ∵AM =12AD ,∴AB=AM ,∴∠ABM =∠AMB . ∵∠A =90°,∴∠AMB =45°. ∵△ABM ≌△DCM ,∴BM=CM,∠DMC=∠AMB=45°,∴∠BMC=90°.∵E,F,N分别是BM,CM,BC的中点,∴EN∥CM,FN∥BM,EM=MF,∴四边形MENF是菱形.∵∠BMC=90°,∴菱形MENF是正方形.25.A26.A27.A28.D29.B30.B31.30°32.3.533.①②④⑤34.(1)如图,延长EB至G,使BG=DF,连接AG,∵正方形ABCD,∴AB=AD,∠ABG=∠ADF=∠BAD=90°,∵BG=DF,∴△ABG≌△ADF,∴AG=AF,∵∠BAE=30°,∠DAF=15°,∴∠FAE=∠GAE=45°,∵AE=AE,∴△FAE≌△GAE,∴EF=EG=GB+BE=DF+BE;(2)∵在△ADF中,∠D=90°,∠DAF=15°,∴∠AFD=90°–15°=75°,∵△ABG≌△ADF,△AGE≌△AFE,∴∠AFE=∠AGE=∠AFD=75°,∴∠EFC=180°–∠DFA–∠AFE=180°–75°–75°=30°;(3)∵AB=BC3∠BAE=30°,∴BE=1,CE31,∵∠EFC=30°,∴CF=3S△CEF=12CE•CF3,由(1)知,△ABG≌△ADF,△FAE≌△GAE,∴S△AEF=S正方形ABCD–S△ADF–S△AEB–S△CEF=S正方形ABCD–S△AEF–S△CEF,∴S△AEF=12(S正方形ABCD–S△CEF)=2111)(3322-=35.(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∠ADM=∠CBN.∵AM⊥BD,CN⊥BD,∴∠AMD=∠CNB=90°,在△AMD和△CNB中,===ADM CENAMD CNBAD BC∠∠∠∠⎧⎪⎨⎪⎩,∴△AMD≌△CNB.∴AM=CN.(2)猜想:当EF=AC时,四边形AECF是矩形.证明:由(1)得△AMD≌△CNB,∴DM=BN.∵BE=DF,∴DM+DF=BN+BE,即MF=NE.在△AMF和△CNE中,===MF NEAMF CNE AM CN∠∠⎧⎪⎨⎪⎩,∴△AMF≌△CNE.∴AF=CE,∠AFE=∠CEF.∴AF∥CE且AF=CE.即四边形AECF是平行四边形.又EF=AC,∴四边形AECF是矩形.36.C37.A38.D39.D40.B41.B42.C43.B44.C45.24 546.347.48.(2,﹣3)49.∵四边形ABCD为正方形,∴∠B=90°,AD∥BC,∴∠EAF=∠BMA,∵EF⊥AM,∴∠AFE=90°=∠B,在△ABM和△EFA中,EAF BMAAFE BAE AM∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABM≌△EFA(AAS),∴AB=EF.50.∵在ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO,在△EOD和△FOB中,EOD FBO OD OBEOD FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△DOE≌△BOF(ASA),∴OE=OF,又∵OB=OD,∴四边形EBFD是平行四边形,∵EF⊥BD,∴四边形BFDE为菱形.51.(1)∵四边形ABCD是菱形,∴AC⊥BD,∴∠COD=90°.∵CE∥OD,DE∥OC,∴四边形OCED是平行四边形,又∠COD=90°,∴平行四边形OCED是矩形.学-科网(2)由(1)知,平行四边形OCED是矩形,则CE=OD=1,DE=OC=2.∵四边形ABCD是菱形,∴AC=2OC=4,BD=2OD=2,∴菱形ABCD的面积为:12AC·BD=12×4×2=4,故答案为:4.。
江苏省苏州市中考数学一轮复习 第22讲《平行四边形》练习-人教版初中九年级全册数学试题

2017年中考数学一轮复习第22讲《平行四边形》【考点解析】知识点一、求多边形的边数【例1】(2015某某某某)一个多边形的每个外角都等于60°,则这个多边形的边数为()A.8 B.7 C.6 D.5【答案】C.【分析】根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.【解析】360°÷60°=6.故这个多边形是六边形.故选C.【点评】根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握.【变式】(2016·某某·3分)请从以下两个小题中任选一个作答,若多选,则按第一题计分.A.一个多边形的一个外角为45°,则这个正多边形的边数是8 .B.运用科学计算器计算:3sin73°52′≈11.9 .(结果精确到0.1)【考点】计算器—三角函数;近似数和有效数字;计算器—数的开方;多边形内角与外角.【分析】(1)根据多边形内角和为360°进行计算即可;(2)先分别求得3和sin73°52′的近似值,再相乘求得计算结果.【解答】解:(1)∵正多边形的外角和为360°∴这个正多边形的边数为:360°÷45°=8(2)3知识点二、求多边形的内角和【例2】(2015某某某某)八边形的内角和等于()A.360° B.1080° C.1440° D.2160°【答案】B.【分析】直接根据多边形内角和定理计算即可.【解析】(8﹣2)×180°=1080°,故选B.【点评】本题主要考查了多边形的内角和定理,是基础题,熟记定理是解题的关键.【变式】(2016·某某某某)如果一个正六边形的每个外角都是30°,那么这个多边形的内角和为1800°.【考点】多边形内角与外角.【分析】根据正多边形的性质,边数等于360°除以每一个外角的度数,然后利用多边形的内角和公式计算内角和即可.【解答】解:∵一个多边形的每个外角都是30°,∴n=360°÷30°=12,则内角和为:(12﹣2)•180°=1800°.故答案为:1800°.【点评】本题主要考查了利用外角求正多边形的边数的方法以及多边形的内角和公式,解题的关键是掌握任意多边形的外角和都等于360度.知识点三、平行四边形的性质【例3】(2016·某某某某)如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD 于点E,AB=6,EF=2,则BC长为()A.8B.10C.12D.14【考点】平行四边形的性质.【分析】由平行四边形的性质和角平分线得出∠ABF=∠AFB,得出AF=AB=6,同理可证DE=DC=6,再由EF的长,即可求出BC的长.【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC,DC=AB=6,AD=BC,∴∠AFB=∠FBC,∵BF平分∠ABC,∴∠ABF=∠FBC,则∠ABF=∠AFB,∴AF=AB=6,同理可证:DE=DC=6,∵EF=AF+DE﹣AD=2,即6+6﹣AD=2,解得:AD=10;故选:B.【变式】如图,在▱ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为__________.【答案】8.【解析】根据平行四边形的性质知:AO=OC,∵OE⊥AC,∴OE为AC的垂直平分线,即:AE=EC,∴△CDE的周长为:CD+AD=5+3=8.知识点四、平行四边形的判定【例4】(2016·某某省某某市)如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC 的中点D、E、F、G依次连结,得到四边形DEFG.(1)求证:四边形DEFG是平行四边形;(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.【考点】平行四边形的判定与性质.(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC,【分析】DG∥BC且DG=BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;(2)先判断出∠BOC=90°,再利用直角三角形斜边的中线等于斜边的一半,求出EF即可.【解答】解:(1)∵D、G分别是AB、AC的中点,∴DG∥BC,DG=BC,∵E、F分别是OB、OC的中点,∴EF∥BC,EF=BC,∴DE=EF,DG∥EF,∴四边形DEFG是平行四边形;(2)∵∠OBC和∠OCB互余,∴∠OBC+∠OCB=90°,∴∠BOC=90°,∵M为EF的中点,OM=3,∴EF=2OM=6.由(1)有四边形DEFG是平行四边形,∴DG=EF=6.【点评】此题是平行四边形的判定与性质题,主要考查了平行四边形的判定和性质,三角形的中位线,直角三角形的性质,解本题的关键是判定四边形DEFG是平行四边形.【变式】(2016·某某省滨州市·10分)如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.(1)请判断四边形EBGD的形状,并说明理由;(2)若∠ABC=30°,∠C=45°,ED=2,点H是BD上的一个动点,求HG+HC的最小值.【考点】平行四边形的判定与性质;角平分线的性质.【分析】(1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.【解答】解:(1)四边形EBGD是菱形.理由:∵EG垂直平分BD,∴EB=ED,GB=GD,∴∠EBD=∠EDB,∵∠EBD=∠DBC,∴∠EDF=∠GBF,在△EFD和△GFB中,,∴△EFD≌△GFB,∴ED=BG,∴BE=ED=DG=GB,∴四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2,∴EM=BE=,∵DE∥BC,EM⊥BC,DN⊥BC,∴EM∥DN,EM=DN=,MN=DE=2,在RT△DNC中,∵∠DNC=90°,∠D=45°,∴∠NDC=∠NCD=45°,∴DN=NC=,∴MC=3,在RT△EMC中,∵∠EMC=90°,EM=.MC=3,∴EC===10.∵HG+HC=EH+HC=EC,∴HG+HC的最小值为10.【点评】本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识,解题的关键是利用对称找到点H的位置,属于中考常考题型.【典例解析】【例题1】(2016·某某)如图,在▱ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.求证:AF∥CE.【考点】平行四边形的性质;全等三角形的判定与性质.【分析】由平行四边形的性质得出AD∥BC,AD=BC,证出∠1=∠2,DF=BE,由SAS证明△ADF≌△CBE,得出对应角相等,再由平行线的判定即可得出结论.【解答】证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠1=∠2,∵BF=DE,∴BF+BD=DE+BD,即DF=BE,在△ADF和△CBE中,,∴△ADF≌△CBE(SAS),∴∠AFD=∠CEB,∴AF∥CE.【例题2】(2016·某某某某·3分)如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=45 度.【考点】切线的性质;平行四边形的性质.【分析】连接OD,只要证明△AOD是等腰直角三角形即可推出∠A=45°,再根据平行四边形的对角相等即可解决问题.【解答】解;连接OD.∵CD是⊙O切线,∴OD⊥CD,∵四边形ABCD是平行四边形,∴AB∥CD,∴AB⊥OD,∴∠AOD=90°,∵OA=OD,∴∠A=∠ADO=45°,∴∠C=∠A=45°.故答案为45.【例题3】(2016·某某·7分)图1,图2都是8×8的正方形网格,每个小正方形的顶点成为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点(1)请在图1,图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等);(2)图1中所画的平行四边形的面积为 6 .【考点】作图—应用与设计作图;平行四边形的性质.【分析】(1)根据平行四边形的判定,利用一组对边平行且相等的四边形为平行四边形可在图1和图2中按要求画出平行四边形;(2)根据平行四边形的面积公式计算.【解答】解:(1)如图1,如图2;(2)图1中所画的平行四边形的面积=2×3=6.故答案为6.【例题4】(2016·某某某某)已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F.(1)求证:△ABF≌△CDE;(2)如图,若∠1=65°,求∠B的大小.【考点】平行四边形的性质;全等三角形的判定与性质.【分析】(1)由平行四边形的性质得出AB=CD,AD∥BC,∠B=∠D,得出∠1=∠DCE,证出∠AFB=∠1,由AAS证明△ABF≌△CDE即可;(2)由(1)得∠1=∠DCE=65°,由平行四边形的性质和三角形内角和定理即可得出结果.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AD∥BC,∠B=∠D,∴∠1=∠DCE,∵AF∥CE,∴∠AFB=∠ECB,∵CE平分∠BCD,∴∠DCE=∠ECB,∴∠AFB=∠1,在△ABF和△CDE中,,∴△ABF≌△CDE(AAS);(2)解:由(1)得:∠1=∠ECB,∠DCE=∠ECB,∴∠1=∠DCE=65°,∴∠B=∠D=180°﹣2×65°=50°.【中考热点】【热点1】(2016·某某)如图所示,在▱ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为50°.【考点】平行四边形的性质.【分析】由“平行四边形的对边相互平行”、“两直线平行,同位角相等”以及“直角三角形的两个锐角互余”的性质进行解答.【解答】解:∵四边形ABCD是平行四边形,∴DC∥AB,∴∠C=∠ABF.又∵∠C=40°,∴∠ABF=40°.∵EF⊥BF,∴∠F=90°,∴∠BEF=90°﹣40°=50°.故答案是:50°.【热点2】(2016·某某某某)如图,平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF(1)根据题意,补全原形;(2)求证:BE=DF.【考点】平行四边形的性质;全等三角形的判定与性质.【分析】(1)如图所示;(2)由全等三角形的判定定理SAS证得△BEO≌△DFO,得出全等三角形的对应边相等即可.【解答】(1)解:如图所示:(2)证明:∵四边形ABCD是平行四边形,对角线AC、BD交于点O,∴OB=OD,OA=OC.又∵E,F分别是OA、OC的中点,∴OE=OA,OF=OC,∴OE=OF.∵在△BEO与△DFO中,,∴△BEO≌△DFO(SAS),∴BE=DF.【热点3】(2016·某某某某)如图,在□ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E 处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为_______.【考点】平行四边形的性质【答案】36°【解析】∵四边形ABCD为平行四边形,∴∠D=∠B=52°,由折叠的性质得:∠EAD,=∠DAE =20°,∠AED,=∠AED=180°-∠DAE-∠D=180°-20°-52°=108°,∴∠AEF=∠D+∠DAE=52°+20°=72°,∴∠FED′=108°-72°=36°.【热点4】(2016·某某随州·3分)如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=BD,连接DM、DN、MN.若AB=6,则DN= 3 .【考点】三角形中位线定理;直角三角形斜边上的中线;平行四边形的判定与性质.【分析】连接CM,根据三角形中位线定理得到NM=CB,MN∥BC,证明四边形DCMN是平行四边形,得到DN=CM,根据直角三角形的性质得到CM=AB=3,等量代换即可.【解答】解:连接CM,∵M、N分别是AB、AC的中点,∴N M=CB,MN∥BC,又CD=BD,∴MN=CD,又MN∥BC,∴四边形DCMN是平行四边形,∴DN=CM,∵∠ACB=90°,M是AB的中点,∴CM=AB=3,∴DN=3,故答案为:3.。
九年级中考数学专题复习-平行四边形专题
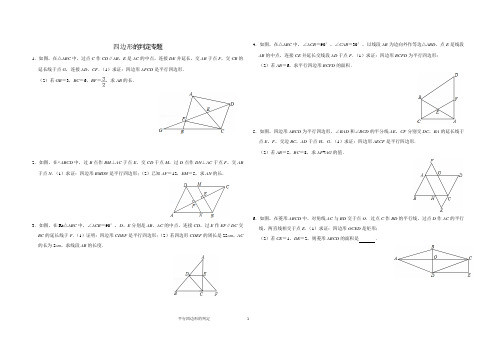
四边形的判定专题1.如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.(1)求证:四边形AFCD是平行四边形.(2)若GB=3,BC=6,BF =,求AB的长.2.如图,在▱ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB 于点N.(1)求证:四边形BMDN是平行四边形;(2)已知AF=12,EM=5,求AN的长.3.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.(1)证明:四边形CDEF是平行四边形;(2)若四边形CDEF的周长是25cm,AC 的长为5cm,求线段AB的长度.4.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形BCFD的面积.5.如图,四边形ABCD为平行四边形,∠BAD和∠BCD的平分线AE,CF分别交DC,BA的延长线于点E,F,交边BC,AD于点H,G.(1)求证:四边形AECF是平行四边形.(2)若AB=5,BC=8,求AF+AG的值.6.如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,则菱形ABCD的面积是.7.如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD 的平分线于点E、F.(1)若CE=8,CF=6,求OC的长;(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.8.如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)若∠A=50°,则当∠BOD =°时,四边形BECD 是矩形.9.如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.(1)求tan∠DBC的值;(2)求证:四边形OBEC是矩形.10.如图,在△ABC中,AB=BC,BD平分∠ABC.四边形ABED是平行四边形,DE交BC于点F,连接CE.求证:四边形BECD是矩形.11.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.12.如图,矩形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E、F.(1)求证:四边形BEDF是平行四边形;(2)只需添加一个条件,即,可使四边形BEDF为菱形.13.如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.14.如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD、AC、BC于点E、O、F,连接CE 和AF.(1)求证:四边形AECF为菱形;(2)若AB=4,BC=8,求菱形AECF的周长.15.如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.(1)求证:四边形ABCD是菱形;(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.16.如图,在△ABC中,∠ACB=90°,O、D分别是边AC、AB的中点,过点C作CE∥AB交DO的延长线于点E,连接AE.(1)求证:四边形AECD是菱形;(2)若四边形AECD的面积为24,tan∠BAC =,求BC的长.17.如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.(1)求证:四边形AECD是菱形;(2)若AB=6,BC=10,求EF的长.18.如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.(1)求证:四边形AEBD是菱形;(2)若DC =,tan∠DCB=3,求菱形AEBD 的面积.19.如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.20.如图,在▱ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.21.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.22.如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.(1)求证:AF=CE;(2)若DE=2,BE=4,求sin∠DAF的值.23.如图,已知▱ABCD中,AB=AC,CO⊥AD,垂足为点O,延长CO、BA交于点E,联结DE.(1)求证:四边形ACDE是菱形;(2)联结OB,交AC于点F,如果OF=OC,求证:2AB2=BF•BO.24.如图,在▱ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,且AE=AF.(1)求证:▱ABCD是菱形;(2)若∠EAF=60°,CF=2,求菱形ABCD的面积.25.如图,菱形ABCD 的边长为,对角线AC、BD交于O,且DE∥AC,AE∥BD.(1)判断四边形AODE的形状并给予证明;(2)若四边形AODE的周长为14,求四边形AODE的面积.26.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,F是AD的中点,连接EC.(1)求证:四边形ADCE是平行四边形;27.如图,矩形ABCD的对角线AC,BD交于点O,以OC,OD为邻边作平行四边形OCED,连接OE.(1)求证:四边形OBCE是平行四边形;(2)连接BE交AC于点F.若AB=2,∠AOB=60°,求BF的长.。
中考数学总复习《45多边形与平行四边形》试题训练及解析.doc

第五节多边形与平行四边形基础训练1.(2017苏州中考)如图,在正五边形ABCDE中,连接BE,贝iJZABE的度数为(B)A.30°B.36°C.54°D.72°“(第1题图)2.(湘西屮考)下列说法错误的是(D)A.对角线互相平分的四边形是平行四边形2两组对边分别相等的四边形是平行四边形C 一组对边平行冃相等的四边形是平行四边形D.一组对边相等,另一组对边平行的四边形是平行四边形3・(2015石家屮四十三屮模拟)如图,在口ABCD屮,延长AB到点E,使BE = AB,连接DE交BC于点F,则下列结论不一定成立的是(D)A. ZE=ZCDF B・ EF=DFC. AD = 2BFD. BE=2CF4.(2017 丽水中考)如图,在口ABCD 中,连接AC, ZABC= ZCAD=45° , AB =2,则BC的长是(C)A.y[2B. 2C. 2^2 D・ 45.(荷泽中考)在口ABCD中,AB = 3, BC=4,当口ABCD的面积最大时,下列结论正确的有(B)①AC = 5;②ZA+ZC=180° ;③AC丄BD;④AC=BD.A.①②③B.①②④C.②③④D.①③④6・(孝感中考)在口ABCD中,AD = 8, AE平分ZBAD交BC于点E” DF平分ZADC 交BC于点F,且EF=2,则AB的长为(D)儿 3 B. 5C 2或3 〃・3或57.平行四边形ABCD与等边AAEF如图放置,如果ZB = 45° ,那么ZBAE 的大小是(A)A.75°B.70°C.65°D.60°8.(北京中考)如图是由射线AB, BC, CD, DE, EA组成的平面图形,则Z1 + Z2+Z3+Z4+Z5= 360°9・(江西中考)如图所示,在oABCD中,ZC = 40° ,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则ZBEF的度数为§0。
中考数学模拟题汇总《平行四边形的判定与证明》专项练习(附答案解析)

中考数学模拟题汇总《平行四边形的判定与证明》专项练习(附答案解析)一、综合题1.如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.(1)求证:DE=CF;(2)若AC=6cm,AB=10cm,求四边形DCFE的面积.2.已知△ABC内接于⊙O,AB是⊙O的直径,OD∥AC,AD=OC.(1)求证:四边形OCAD是平行四边形;(2)若AD与⊙O相切,求∠B.3.已知:如图,点D在ΔABC的边AB上,CF//AB,DF交AC于E,EA=EC.(1)如图1,求证:CD=AF;(2)如图2,若AD=BD,请直接写出和ΔBDC面积相等的三角形.4.如图,在四边形ABCD中,点E和点F是对角线AC上的两点,AE=CF,DF=BE,且DF//BE,过点C作CG⊥AB交AB的延长线于点G.(1)求证:四边形ABCD是平行四边形;(2)若tan∠CAB=25,∠CBG=45°,BC=4√2,则▱ABCD的面积是.5.已知,如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.(1)求证:△AFD≌△CEB;(2)四边形ABCD是平行四边形吗?请说明理由.6.如图,▱ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.(1)求证:BE=DF;(2)设ACBD=k,当k为何值时,四边形DEBF是矩形?请说明理由.7.如图,在ΔABC中,点D、E、F分别在AB、AC、BC上,DE // BC,EF // AB.(1)求证:ΔADE∽ΔEFC;(2)如果AB=6,AD=4,求SΔADESΔEFC的值.8.如图,已知平行四边形ABCD,过A点作AM⊥BC于M,交BD于E,过C点作CN⊥AD于N,交BD于F,连接AF、CE.(1)求证:四边形AECF为平行四边形;(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值.BC,9.如图,等边△ABC的边长是4,D、E分别为AB、AC的中点,延长BC至点F,使CF=12连接CD和EF .(1)求证:DE=CF;(2)求EF的长.10.如图,在四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD交于点H.(1)求证:四边形DEBC是平行四边形;(2)若BD=9,求DH的长.11.已知锐角△ABC内接于⊙O,AD⊥BC于点D,连接AO.(1)如图1,求证:∠BAO=∠CAD;(2)如图2,CE⊥AB于点E,交AD于点F,过点O作OH⊥BC于点H,求证:AF=2OH;,BC=2√15,求AC的长.(3)如图3,在(2)的条件下,若AF=AO,tan∠BAO=1312.如图,抛物线y=x2+bx+c与x轴交于点A(−1,0),B(5,0),与y轴交于点C.(1)求抛物线的解析式和顶点D的坐标.(2)连结AD,点E是对称轴与x轴的交点,过E作EF∥AD交抛物线于点F(F在E的右侧),过点F作FG∥x轴交ED于点H,交AD于点G,求HF的长.13.如图,CD是⊙O的直径,点A是⊙O外一点,AD与⊙O相切于点D,点B是⊙O上一点(点B不与点C,D重合),连接AO,AB,BC .(1)当BC与AO满足什么位置关系时,AB是⊙O的切线?请说明理由;(2)在(1)的条件下,当∠DAO=度时,四边形AOCB是平行四边形.(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足14.如图,已知函数y= kx为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点EOD,求a、b的值;(1)若AC= 32(2)若BC∥AE,求BC的长.15.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.16.如图.在一次数学研究性学习中,小华将两个全等的直角三角形纸片Rt△ABC和Rt△DEF拼在一起,使点A与点F重合,点C与点D重合(如图),其中∠ACB=∠DFE=90°,发现四边形ABDE是平行四边形.如图,小华继续将图中的纸片Rt△DEF沿AC方向平移,连结AE,BD,当点F与点C重合时停止平移.(1)请问:四边形ABDE是平行四边形吗?说明理由.cm时,请判断四边形ABDE的形(2)如图,若BC=EF=6cm,AC=DF=8cm,当AF=92状,并说明理由.参考答案与解析1.【答案】(1)证明:在△CDE 和△ECF 中,∵∠ACB=∠ECF=90°,点D 、E 是分别是AB 、BC 的中点.∴CD=BD=AD ,∴∠B=∠DCE ,∠CED=∠ECF=90°, 又∵∠FEC=∠B ..∠FEC=∠DCE ,又∵CE=EC .∴△CDE ≌△ECF (ASA ),∴DE=CF ;(2)解:在Rt △ABC 中,∵∠ACB=90°,∴BC=√AB 2−AC 2=√102−62=8cm , ∵点D 、E 分别是AB 、BC 的中点,∴DE ∥CF ,又DE=CF , ∴四边形DCFE 是平行四边形,∴DE=12AC=12×6=3cm ,CE=12BC=12×8=4cm , ∴S 四边形DCFE =DE ×CE=3×4=12cm . 2.【答案】(1)证明:∵OA =OC =AD , ∴∠OCA =∠OAC ,∠AOD =∠ADO , ∵OD ∥AC , ∴∠OAC =∠AOD ,∴180°﹣∠OCA ﹣∠OAC =180°﹣∠AOD ﹣∠ADO , 即∠AOC =∠OAD , ∴OC ∥AD , ∵OD ∥AC ,∴四边形OCAD 是平行四边形;(2)解:∵AD 与⊙O 相切,OA 是半径, ∴∠OAD =90°, ∵OA =OC =AD , ∴∠AOD =∠ADO =45°,∵OD∥AC,∴∠OAC=∠AOD=45°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠B=45°.3.【答案】(1)证明:∵CF//AB∴∠DFC=∠ADF,∠DAC=∠ACF又∵EA=EC∴ΔADE≌ΔCFE(AAS)∴CF=AD又∵CF//AD∴四边形ADCF为平行四边形∴DC=AF(有一组对边平行且相等的四边形为平行四边形)(2)解:ΔADC,ΔADF,ΔCFD,ΔCFA∵AD=BD,∴SΔADC=SΔBDC (等底等高面积相等)∵四边形ADCF是平行四边形,∴SΔADC=SΔCDF=SΔADF=SΔACFF (等底等高面积相等) .故与ΔBDC面积相等的三角形为:ΔADC,ΔADF,ΔCFD,ΔCFA.4.【答案】(1)证明:∵AE=CF,∴AE+EF=CF+EF,即AF=CE,∵DF//BE,∴∠DFA=∠BEC,∵DF=BE,∴ΔADF≅ΔCBE(SAS),∴AD=CB,∠DAF=∠BCE,∴AD//CB,四边形ABCD是平行四边形(2)245.【答案】(1)证明:∵DF∥BE,∴∠DFA=∠BEC,在△ADF和△CBE中{DF=BE∠DFA=∠BECAF=CE,∴△AFD≌△CEB(SAS).(2)解:四边形ABCD是平行四边形,理由如下:∵△AFD≌△CEB,∴AD=CB,∠DAF=∠BCE,∴AD∥BC,∴四边形ABCD是平行四边形.6.【答案】(1)证明:如图,连接DE,BF,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵E,F分别是OA,OC的中点,∴OE=12OA=12OC=OF,∴四边形DEBF是平行四边形,∴BE=DF .(2)解:由(1)已证:四边形DEBF是平行四边形,要使平行四边形DEBF是矩形,则BD=EF,∵OE=12OA=12OC=OF,∴EF=OE+OF=12OA+12OC=OA=12AC,即AC=2EF,∴k=ACBD =2EFEF=2,故当k=2时,四边形DEBF是矩形. 7.【答案】(1)证明:∵DE//BC,EF//AB,∴∠A=∠CEF,∠AED=∠C,∴△ADE∽△EFC.(2)解:∵AB=6,AD=4,∴DB=6-4=2,∵DE//BC,EF//AB,∴四边形DBFE是平行四边形,∴EF=DB=2,∵△ADE∽△EFC,SΔADE SΔEFC =(ADEF)2=(42)2=4.8.【答案】(1)证明∵四边形ABCD是平行四边形(已知),∴BC∥AD(平行四边形的对边相互平行)。
北师大版数学初三上册第一章特殊平行四边形菱形的性质与判定同步练习题含答案

北师大版数学初三上册第一章特殊平行四边形菱形的性质与判定同步练习题含答案1. 下列说法正确的是( )A.对角线相等的平行四边形是菱形B.有一组邻边相等的平行四边形是菱形C.对角线相互垂直的四边形是菱形D.有一个角是直角的平行四边形是菱形2.若顺次相连四边形的各边中点所得的四边形是菱形,则该四边形一定是( )A.矩形 B.等腰梯形C.对角线相等的四边形 D.对角线互相垂直的四边形3.如图,将△ABC沿BC偏向平移得到△DCE,相连AD,下列条件能够鉴定四边形ACED为菱形的是( )A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°4. 用直尺和圆规作一个以线段AB为边的四边形,作图痕迹如图所示,能得到四边形ABCD是菱形的依据是( )A.一组邻边相等的平行四边形是菱形B.四边相等的四边形是菱形C.对角线互相垂直的平行四边形是菱形D.每条对角线中分一组对角的平行四边形是菱形5. 如图,在▱ABCD中,AE、CF分别是∠BAD和∠BCD的中分线,增加一个条件,仍无法鉴别四边形AECF为菱形的是( )A.AE=AF B.EF⊥ACC.∠B=60° D.AC是∠EAF的中分线6. 在△ABC中,AB≠AC,D是边BC上的一点,DE∥CA交AB于点E,DF∥BA交AC于点F,要使四边形AEDF是菱形,只需增加条件( )A.AD⊥BC B.∠BAD=∠CAD C.BD=DC D.AD=BC7. 如图,菱形ABCD中,E是AD的中点,将△CDE沿CE折叠后,点D和点A恰恰重合.若AB=4,则菱形ABCD的面积为( )A.2 3 B.4 3 C.8 2 D.8 38. 已知▱ABCD,对角线AC、BD相交于点O,请你增加一个适当的条件,使▱ABCD 成为一个菱形,你增加的条件是___________.9.如图,在等腰梯形ABCD中,AB∥DC,AD=BC=CD,点E为AB上一点,相连CE,请增加一个你以为合适的条件_________________________________,使四边形AECD为菱形.10. 如图,在四边形ABCD中,对角线AC、BD交于点O,OA=OC,OB=OD,增加一个条件使四边形ABCD是菱形,那么所增加的条件可以是_______________________(写出一个即可).11. 如图,点E、F、G、H分别是恣意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足____________条件时,四边形EFGH是菱形.12. 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;从中选择一个条件使四边形BECF是菱形,你以为这个条件是____ (只填写序号).13. 已知:如图,在▱ABCD中,E、F分别是边AD、BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G、H,交BD于点O.(1)求证:△ABE≌△CDF;(2)相连DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.14. 如图所示,▱ABCD的对角线AC的垂直中分线与边AD、BC分别交于E、F.求证:四边形AFCE是菱形.参考答案;1---7 BCBBC BD8. AD=DC9. 可增加的条件为AE =AD 或∠CEB =∠B 等(答案不唯一)10. 不唯一,AB =AD 等11. AB =CD12. ③13. (1)证明:∵四边形ABCD 是平行四边形,∴AB =CD ,∠BAE =∠DCF ,在△ABE 和△CDF 中,⎩⎪⎨⎪⎧ AB =CD ∠BAE =∠DCFAE =CF,∴△ABE ≌△CDF(SAS);(2)解:四边形BEDF 是菱形;理由如下:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∵AE =CF ,∴DE =BF ,∴四边形BEDF 是平行四边形,∴OB =OD ,∵DG =BG ,∴EF ⊥BD ,∴四边形BEDF 是菱形.14. 证明: ∵四边形ABCD 是平行四边形,∴AE ∥CF ,∴∠CAE =∠ACB ,又∵∠AOE =∠COF ,OA =OC ,∴△AOE ≌△COF ,∴AE =CF ,∴四边形AFCE 是平行四边形,又∵EF ⊥AC ,∴▱AFCE 是菱形.。
2021年九年级数学中考复习分类专题:平行四边形的判定与性质(四)

2021年九年级数学中考复习分类专题:平行四边形的判定与性质(四)一.选择题1.平行四边形ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得到四边形AECF 一定为平行四边形的是()A.BE=DF B.AF∥CE C.AE=CF D.∠BAE=∠DCF 2.如图,E是▱ABCD的边AD延长线上一点,连接BE,CE,BD,BE交CD于点F,添加以下条件,不能判定四边形BCED为平行四边形的是()A.∠AEB=∠BCD B.EF=BF C.∠ABD=∠DCE D.∠AEC=∠CBD 3.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下=5.正列结论中.①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD 确的个数是()A.1个B.2个C.3个D.4个4.如图,在▱ABCD中,点E,F分别在边BC,AD上.若从下列条件中只选择一个添加到图中的条件中;①AE∥CF;②AE=CF;③BE=DF;④∠BAE=∠DCF.那么不能使四边形AECF是平行四边形的条件相应序号是()A.①B.②C.③D.④5.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列五个条件:①∠ADB=∠CBD②DE=BF③∠EDF=∠EBF④∠DEB=∠DFB⑤AE=CF.其中不能判定四边形DEBF是平行四边形的有()A.1个B.2个C.3个D.4个6.在平行四边形ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不能是()A.AF=CE B.AE=CF C.∠BEA=∠ECF D.∠BAE=∠FCD 7.如图,▱ABCD中,E,F分别是AB,CD的中点,则图中有()个平行四边形.A.7个B.8个C.9个D.10个8.如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点.下列结论:①S△ADE =S△EOD;②四边形BFDE也是菱形;③△DEF是轴对称图形;④∠ADE=∠EDO;⑤四边形ABCD面积为EF×BD.其中正确的结论有()A.5个B.4个C.3个D.2个9.下列说法中:①一组对边平行且一组对角相等的四边形是平行四边形;②平行四边形对角线的交点到一组对边的距离相等;③对角线互相垂直的四边形面积等于对角线乘积的一半;④一组对边平行,另一组对边相等的四边形是平行四边形;其中正确的个数为()个.A.1 B.2 C.3 D.410.如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足()A.BD<2 B.BD=2C.BD>2 D.以上情况均有可能二.填空题11.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有次.12.如图,四边形ABCD中,AD∥BC,作AE∥DC交BC于E.△ABE的周长是25cm,四边形ABCD的周长是37cm,那么AD=cm.13.如图,平行四边形ABCD的对角线AC,BD相交于点O,E、F是对角线AC上的两点,给出下列4个条件:①OE=OF;②DE=BF;③∠ADE=∠BCF;④∠ABE=∠CDF;其中不能判定四边形DEBF是平行四边形的是.(只填序号)14.有甲、乙两张纸条,甲纸条的宽度是乙纸条的2倍,如图,将这两张纸条交叉重叠地放在一起,重合部分为四边形ABCD,则AB与BC的数量关系为.15.如图,在△ABC中,AB=4,AC=3,BC=5,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为.16.如图,直角三角形ABC中,∠ABC=90°,E为BC上的一点,BE=,CD∥AE,且DE=CE,连接AD,∠EDA=2∠ACB,则AD=.三.解答题17.如图,在平行四边形ABCD中,E、F分别是DA、BC延长线上的点,且∠ABE=∠CDF.求证:(1)△ABE≌△CDF;(2)四边形EBFD是平行四边形.18.如图,已知AC垂直平分BD,∠ABC=∠DAF,DF⊥BD(1)证明:四边形ACDF是平行四边形;(2)若AF=DF=5,AD=6,试求CD和BD的长.19.如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=2,CE=4;(1)求证:四边形ACED是平行四边形.(2)求BC的长.20.已知,如图,在▱ABCD中,延长AB到点E,延长CD到点F,使得BE=DF,连接EF,分别交BC,AD于点M,N,连接AM,CN.(1)求证:△BEM≌△DFN;(2)求证:四边形AMCN是平行四边形.21.如图,在四边形ABCD中,AD∥BC,E为AD的中点,延长CE交BA的延长线上于点F,CE=EF.(1)如图1,求证:四边形ABCD是平行四边形;(2)如图2,若CE⊥AD,连接AC、DF,请直接写出图中和线段CD相等的所有线段.22.如图,在▱ABCD中,点E、F分别在BC、AD上,AC与EF相交于点O,且AO=CO.(1)求证:△AOF≌△COE;(2)连接AE、CF,则四边形AECF(填“是”或“不是”)平行四边形.23.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD的中点.(1)试说明四边形AECF是平行四边形.(2)若AC=8,AB=6.若AC⊥AB,求线段BD的长.24.如图,在平行四边形ABCD中,对角线AC,BD交于点O,E是AD上任意一点,连接EO 并延长,交BC于点F,连接AF,CE.(1)求证:四边形AFCE是平行四边形;(2)若∠DAC=60°,∠ADB=15°,AC=6.求出平行四边形ABCD的边BC上的高h的值.25.如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.(1)求证:四边形MNCD是平行四边;(2)求证:BD=CD.参考答案一.选择题1.解:如图,连接AC与BD相交于O,在▱ABCD中,OA=OC,OB=OD,要使四边形AECF为平行四边形,只需证明得到OE=OF即可;A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;B、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;C、若AE=CF,则无法判断OE=OE,故本选项符合题意;D、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,然后同A,故本选项不符合题意;故选:C.2.解:A、∵AE∥BC,∴∠AEB=∠CBF,∵∠AEB=∠BCD,∴∠CBF=∠BCD,∴CF=BF,同理,EF=DF,∴不能判定四边形BCED为平行四边形;故A错误;∵DE∥BC,∴∠DEF=∠CBF,在△DEF与△CBF中,,∴△DEF≌△CBF(ASA),∴DF=CF,∵EF=BF,∴四边形BCED为平行四边形,故B正确;∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴DE∥BC,∠ABD=∠CDB,∵∠ABD=∠DCE,∴∠DCE=∠CDB,∴BD∥CE,∴四边形BCED为平行四边形,故C正确;∵AE∥BC,∴∠DEC+∠BCE=∠EDB+∠DBC=180°,∵∠AEC=∠CBD,∴∠BDE=∠BCE,∴四边形BCED为平行四边形,故D正确,故选:A.3.解:∵32+42=52,∴AB2+AC2=BC2,∴∠BAC=90°,∴AB⊥AC,故①正确;∵△ABD,△ACE都是等边三角形,∴∠DAB=∠EAC=60°,∴∠DAE=150°,∵△ABD和△FBC都是等边三角形,∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,∴∠DBF=∠ABC,在△ABC与△DBF中,,∴△ABC≌△DBF(SAS),∴AC=DF=AE=4,同理可证:△ABC≌△EFC(SAS),∴AB=EF=AD=3,∴四边形AEFD是平行四边形,故②正确;∴∠DFE=∠DAE=150°,故③正确;∴∠FDA=180°﹣∠DFE=180°﹣150°=30°,∴S▱AEFD=AD•(DF•sin30°)=3×(4×)=6,故④不正确;∴正确的个数是3个,故选:C.4.解:①∵AF∥EC,AE∥CF,∴四边形AECF是平行四边形;②∵AE=CF不能得出四边形AECF是平行四边形,∴条件②符合题意;③∵四边形ABCD平行四边形,∴AD=BC,AD∥BC,又∵BE=DF,∴AF=EC.又∵AF∥EC,∴四边形AECF是平行四边形.④∵四边形ABCD是平行四边形,∴∠B=∠D,∵∠BAE=∠DCF,∴∠AEB=∠CFD.∵AD∥BC,∴∠AEB=∠EAD.∴∠CFD=∠EAD.∴AE∥CF.∵AF∥CE,∴四边形AECF是平行四边形.综上所述,不能使四边形AECF是平行四边形的条件有1个.故选:B.5.解:③可以判断四边形DEBF是平行四边形.理由:将△EFB沿AC法则得到△EFT,∵∠EDF=∠EBF=ETF,∴D,E,F,T四点共圆,由题意点D,点T到AC的距离线段,∴DT∥AC,∴∠TDF=∠DFE,∴=,∴=,∴DE=TF,DF=TE,∵BE=DT,BF=TF,∴DF=BE,DE=BF,∴四边形DEBF是平行四边形.④可以判断四边形DEBF是平行四边形.理由:在OA上取一点E′,使得OE′=OF,连接DE′,BE′.∵OD=OB,OF=OE′,∴四边形DE′BF是平行四边形,∴∠DFB=∠DE′B,∵∠DEB=∠DFB,∴∠DEB=∠DE′B,∴点E与点E′重合,∴四边形DEBF是平行四边形.⑤可以判断四边形DEBF是平行四边形.理由:∵四边形ABCD是平行四边形,∴OD=OB,OA=OC,∵AE=CF,∴OE=OF,∴四边形DEBF是平行四边形,故选:B.6.解:A、∵四边形ABCD是平行四边形,∴AF∥EC,∵AF=EC,∴四边形AECF是平行四边形.故选项A不符合题意.B、根据AE=CF,所以四边形AECF可能是平行四边形,有可能是等腰梯形,故选项B符合题意.C、错误.∵∠BEA=∠FCE,∴AE∥CF,∵AF∥EC,∴四边形AECF是平行四边形.故选项C不符合题意.D、由∠BAE=∠FCD,∠B=∠D,AB=CD可以推出△ABE≌△CDF,∴BE=DF,∵AD=BC,∴AF=EC,∵AF∥EC,∴四边形AECF是平行四边形.故选项D不符合题意.故选:B.7.解:E,F分别是AD,BC的中点,则有AE=FC=ED=BF=AD=BC ∴四边形AECF,EDFB,是平行四边形,有∠FBE=∠EDF=∠AEB∵AE∥BF∴EAF=∠AFB∴根据ASA得出△MAE≌△MFB,∴AM=MF,即点M是AF的中点.同理,点N是FD的中点,∴MN是△EBC和△AFD的中位线,∴MN=AE=FC=ED=BF=AD =BC∴四边形AENM,DEMN,BMNF,FCNM是平行四边形∵EN∥MF,ME∥FN∴四边形ENFM是平行四边形,而四边形ABCD也是平行四边形,共8个平行四边形.故选:B.8.解:①正确∵E、F分别是OA、OC的中点.∴AE=OE.∵S△ADE =×AE×OD=×OE×OD=S△EOD∴S△ADE =S△EOD.②正确∵四边形ABCD是菱形,E,F分别是OA,OC的中点.∴EF⊥OD,OE=OF.∵OD=OD.∴DE=DF.同理:BE=BF∴四边形BFDE是菱形.③正确∵菱形ABCD的面积=AC×BD.∵E、F分别是OA、OC的中点.∴EF=AC.∴菱形ABCD的面积=EF×BD.④不正确由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.⑤正确∵EF⊥OD,OE=OF,OD=OD.∴△DEO≌△DFO.∴△DEF是轴对称图形.∴正确的结论有四个,分别是①②③⑤,故选:B.9.解:①一组对边平行且一组对角相等的四边形是平行四边形;正确;②平行四边形对角线的交点到一组对边的距离相等;正确;③对角线互相垂直的四边形面积等于对角线乘积的一半;正确;④一组对边平行,另一组对边相等的四边形是平行四边形;不正确;故选:C.10.证明:∵AE=AB,∴∠ABE=∠AEB,同理∠CBD=∠CDB∵∠ABC=2∠DBE,∴∠ABE+∠CBD=∠DBE,∵∠ABE=∠AEB,∠CBD=∠CDB,∴∠AEB+∠CDB=∠DBE,∴∠AED+∠CDE=180°,∴AE∥CD,∵AE=CD,∴四边形AEDC为平行四边形.∴DE=AC=AB=BC.∴△ABC是等边三角形,∴BC=CD=1,在△BCD中,∵BD<BC+CD,∴BD<2.故选:A.二.填空题(共6小题)11.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,∵以点P、D、Q、B为顶点组成平行四边形,∴DP=BQ,分为以下情况:①点Q的运动路线是C﹣B,方程为12﹣4t=12﹣t,此时方程t=0,此时不符合题意;②点Q的运动路线是C﹣B﹣C,方程为4t﹣12=12﹣t,解得:t=4.8;③点Q的运动路线是C﹣B﹣C﹣B,方程为12﹣(4t﹣24)=12﹣t,解得:t=8;④点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣36=12﹣t,解得:t=9.6;⑤点Q的运动路线是C﹣B﹣C﹣B﹣C﹣B,方程为12﹣(4t﹣48)=12﹣t,解得:t=16,此时P点走的路程为16>AD,此时不符合题意.∴共3次.故答案为:3.12.解:∵AD∥BC,AE∥DC,∴四边形AECD是平行四边形,∴AE=CD,AD=EC,又∵△ABE的周长=AB+BE+AE=13cm,梯形ABCD的周长=AB+BC+CD+AD=37cm,∴AD=(梯形ABCD的周长﹣△ABE的周长)=6cm,故答案为:6.13.解:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,AD∥BC,AD=BC,OB=OD,OA=OC,①OE=OF,则四边形DEBF是平行四边形;故①能判定四边形DEBF是平行四边形;②DE=BF时,不能证明OE=OF,故②不能判定四边形DEBF是平行四边形;③∠ADE=∠BCF时,不能证明OE=OF,故③不能判定四边形DEBF是平行四边形;④∵AB∥CD,∴∠BAE=∠DCF,在△ABE和△CDF中,,∴△ABE≌△CDF(ASA),∴AE=CF,∴OA﹣AE=OC﹣CF,即OE=OF,又∵OB=OD,∴四边形DEBF是平行四边形;故④能判定四边形DEBF是平行四边形;故答案为:②③.14.解:过A作AE⊥BC于E、作AF⊥CD于F,∵甲纸条的宽度是乙纸条宽的2倍,∴AE=2AF,∴AB×AF=BC×AE=BC×2AF=BC×AF,∴AB=2BC,故答案为:AB=2BC15.解:∵在△ABC中,AB=3,AC=4,BC=5,∴BC2=AB2+AC2,∴∠BAC=90°,∵△ABD,△ACE都是等边三角形,∴∠DAB=∠EAC=60°,∴∠DAE=150°,∵△ABD和△FBC都是等边三角形,∴∠DBF+∠FBA=∠ABC+∠ABF=60°,∴∠DBF=∠ABC,在△ABC与△DBF中,∴△ABC≌△DBF(SAS),∴AC=DF=AE=3,同理可证△ABC≌△EFC,∴AB=EF=AD=4,∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).∴∠FDA=180°﹣∠DAE=30°,过F作FM⊥AD于M,∵DF=3,∠FDA=30°,∴FM=DF=1.5,∴S▱AEFD=AD•FM=4×1.5=6.即四边形AEFD的面积是6.故答案为:6.16.解:过点A作AF∥BC交CD于点F,连接EF交AC于点G,连接BG,∴四边形AECF是平行四边形,∴AE∥CD,AG=CG,EF=2EG,∵∠ABC=90°,∴BG=CG,∴∠CBG=∠ACB,∵平行四边形AECF,∴AE=CF,∵CE=DE,∴∠ECF=∠EDC,∵AE∥CD,∴∠AED=∠EDC=∠ECF,∴△ADE≌△FEC(SAS),∴∠CEF=∠ADE=2∠ACB=2∠EBG,∵∠CEF=∠EBG+∠EGB,∴∠EBG+∠EGB=2∠EBG,∴∠EBG=∠EGB,∴EG=BE=,∴AD=EF=2EG=,故答案为:.三.解答题(共9小题)17.证明:(1)∵四边形ABD是平行四边形,∴AB=CD,∠BAD=∠DCB,∴∠BAE=∠DCF,在△ABE和△CDF中,,∴△ABE≌△CDF(ASA);(2)∵△ABE≌△CDF,∴AE=CF,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴AD+AE=BC+CF,即DE=BF,∴四边形EBFD是平行四边形.18.(1)证明:∵AC垂直平分BD,∴AB=AD,BC=DC,又∵AC=AC,在△ABC与△ADC中,,∴△ABC≌△ADC(SSS),∴∠ABC=∠ADC,∵∠ABC=∠DAF,∴∠ADC=∠DAF,∴AF∥CD,∵AC⊥BD,DF⊥BD,∴DF∥AC,∴四边形ACDF是平行四边形;(2)解:∵四边形ACDF是平行四边形,AF=DF=5,∴▱ACDF是菱形,∴CD=AC=5,∵AD=6,设CE=x,则AE=5﹣x,∴CD2﹣CE2=AD2﹣AE2即52﹣x2=62﹣(5﹣x)2解得:x=,即CE=,∴DE=,∴BD=2DE=.19.解:(1)证明:∵∠ACB=90°,DE⊥BC,∴AC∥DE又∵CE∥AD∴四边形ACED是平行四边形.(2)∵四边形ACED是平行四边形.∴DE=AC=2.在Rt△CDE中,由勾股定理得CD===2.∵D是BC的中点,∴BC=2CD=4.20.证明:∵四边形ABCD是平行四边形,∴∠BAD=∠BCD,AB∥CD,∴∠BAD=∠ADF,∠EBC=∠BCD,∠E=∠F,∴∠ADF=∠EBC,在△DFN和△BEM中∴△DFN≌△BEM(ASA);(2)四边形ANCM是平行四边形,理由是:∵由(1)知△DFN≌△BEM,∴DN=BM,∵四边形ABCD是平行四边形,∴AD=BC,且AD∥BC,∴AD﹣DN=BC﹣BM,∴AN=CM,AN∥CM,∴四边形ANCM是平行四边形.21.(1)证明:∵E是AD的中点,∴DE=AE,在△DEC和△AEF中,,∴△DEC≌△AEF(SAS),∴∠D=∠EAF,∴CD∥AB,又∵AD∥BC,∴四边形ABCD是平行四边形;(2)解:图中和线段CD相等的所有线段为AC、AF、DF、AB,理由如下:∵四边形ABCD是平行四边形,CE⊥AD,∴AB=CD,四边形ABCD是菱形,∴AC=AF=DF=CD,∴AC=AF=DF=CD=AB.22.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠OAF=∠OCE,在△AOF和△COE中,,∴△AOF≌△COE(ASA)(2)解:四边形AECF是平行四边形,理由如下:由(1)得:△AOF≌△COE,∴FO=EO,又∵AO=CO,∴四边形AECF是平行四边形;故答案为:是.23.(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵E,F为OB,OD的中点,∴OE=OF,∴AC与EF互相平分,∴四边形AECF为平行四边形;(2)解:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,∵AC=8,∴AO=4,∵AB=6,AC⊥AB,∴BO===2,∴BD=2BO=4.24.证明:(1)∵四边形ABCD是平行四边形∴AD∥BC,AO=CO∴∠AEF=∠CFE,∠EAC=∠FCA,且AO=CO ∴△AOE≌△COF(AAS)∴OF=OE,且AO=CO∴四边形AFCE是平行四边形;(2)∵∠DAC=60°∴sin∠DAC=,∴h=×AC=3.25.证明:(1)∵ABCD是平行四边形,∴AD=BC,AD∥BC,∵M、N分别是AD、BC的中点,∴MD=NC,MD∥NC,∴MNCD是平行四边形;(2)如图:连接ND,∵MNCD是平行四边形,∴MN=DC.∵N是BC的中点,∴BN=CN,∵BC=2CD,∠C=60°,∴△NCD是等边三角形.∴ND=NC,∠DNC=60°.∵∠DNC是△BND的外角,∴∠NBD+∠NDB=∠DNC,∵DN=NC=NB,∴∠DBN=∠BDN=∠DNC=30°,∴∠BDC=90°.∵tan,∴DB =DC.31 / 31。
2023年中考九年级数学高频考点 专题训练--平行四边形的判定

2023年中考九年级数学高频考点专题训练--平行四边形的判定一、综合题1.如图,在□ ABCD中,点E、F在对角线BD上,且BE=DF.(1)求证:AE=CF;(2)求证:四边形AECF是平行四边形.2.如图,E、F是平行四边形ABCD对角线AC上两点,且AE=CF.(1)求证:四边形BFDE是平行四边形.(2)如果把条件AE=CF改为BE⊥AC,DF⊥AC,试问四边形BFDE是平行四边形吗?为什么?(3)如果把条件A E=CF改为BE=DF,试问四边形BFDE还是平行四边形吗?为什么?3.如图,平行四边形ABCD 中,AB=8 cm,BC=12 cm,⊥B=60°,G 是CD 的中点,E 是边AD 上的动点,EG 的延长线与BC 的延长线交于点F,连接CE,DF.(1)求证:四边形CEDF 是平行四边形;(2)①AE=cm 时,四边形CEDF 是矩形,请写出判定矩形的依据(一条即可);②AE=cm 时,四边形CEDF 是菱形,请写出判定菱形的依据(一条即可).4.如图,四边形ABCD中,AD⊥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.(1)求证:四边形ABCD是平行四边形.(2)若⊥BAE=⊥BDC,AE=3,BD=9,AB=4,求四边形ABCD的周长.5.如图,直线y=−2x+10与x轴交于点A,点B是该直线上一点,满足OB=OA.(1)求点B的坐标;(2)若点C是直线上另外一点,满足AB=BC,且四边形OBCD是平行四边形,试画出符合要求的大致图形,并求出点D的坐标.6.如图,在⊥ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)若⊥A=50°,则当⊥BOD= °时,四边形BECD是矩形.7.如图,在⊥AFC中,⊥FAC=45°,FE⊥AC于点E,在EF上取一点B,连接AB、BC,使得AB=FC,过点A作AD⊥AF,且AD=BC,连接CD。
九年级最新数学中考一轮复习测试题初三数学复习检测题带图文答案100篇一轮复习9期四边形同步练习

中考一轮复习:四边形同步练习平行四边形同步练习(答题时间:30分钟)1.(广东)如图,平行四边形ABCD 中,下列说法一定正确的是( )A. AC =BDB. AC ⊥BDC. AB =CDD. AB =BC2.(新疆)四边形ABCD 中,对角线AC 与BD 交于点O ,下列条件不能判定这个四边形是平行四边形的是( )A. OA =OC ,OB =ODB. AD ∥BC ,AB ∥DCC. AB =DC ,AD =BCD. AB ∥DC ,AD =BC*3.(孝感)如图,在平行四边形ABCD 中,对角线AC 、BD 相交成的锐角为α,若AC =a ,BD =b ,则平行四边形ABCD 的面积是( )A. 21ab sinαB. ab sinαC. ab cosαD. 21ab cosα **4.(浙江湖州)在连接A 地与B 地的线段上有四个不同的点D 、G 、K 、Q ,下列四幅图中的实线分别表示某人从A 地到B 地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )A BC D**5.(襄阳)在平行四边形ABCD 中,BC 边上的高为4,AB =5,AC =25,则平行四边形ABCD 的周长等于__________。
**6. (安徽)如图,在平行四边形ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF 、CF ,则下列结论中一定成立的是__________。
(把所有正确结论的序号都填在横线上)①∠DCF=12∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF。
7. (广西贺州)如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2。
(1)求证:BE=DF;(2)求证:AF∥CE。
8. (广东汕尾)如图,在平行四边形ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F。
中考数学总复习《平行四边形的判定与性质》练习题及答案

中考数学总复习《平行四边形的判定与性质》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.如图在四边形ABCD中AB=CD,对角线AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,若DE=BF,则下列结论不一定正确的是()A.CF=AE B.OE=OFC.△CDE为直角三角形D.四边形ABCD是平行四边形2.如图四边形ABCD中AB∥CD,∥B=∥D点E为BC延长线上一点,连接AE,AE交CD于点H,∥DCE的平分线交AE于点G.若AB=2AD=10,点H为CD的中点,HE=6,则AC的值为()A.9B.√97C.10D.3 √103.如图在Rt∥ABC中∥ACB=90°,分别以AB、AC为腰向外作等腰直角三角形∥ABD和∥ACE,连结DE,CA的延长线交DE于点F,则与线段AF相等的是()A.AC B.AB C.BC D.AB4.如图在菱形ΑΒCD中∠Α=60∘,AD=8,F是ΑΒ的中点.过点F作FΕ⊥ΑD,垂足为Ε.将ΔΑΕF沿点Α到点Β的方向平移,得到ΔΑ′Ε′F ′.设Ρ、Ρ′分别是ΕF、Ε′F ′的中点,当点Α′与点Β重合时,四边形ΡΡ′CD的面积为()A.28√3B.24√3C.32√3D.32√3−85.下列说法中错误的是()A.平行四边形的对角线互相平分B.对角线互相垂直的四边形是菱形C.菱形的对角线互相垂直D.对角线互相平分的四边形是平行四边形6.如图.若要使平行四边形ABCD成为菱形.则需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD7.如图点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∥ABC+∥ADC=120°,则∥A的度数是()A.100°B.110°C.120°D.125°8.如图在∥ABC中AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则∥BED与∥DFC的周长的和为()A.34B.32C.22D.209.如图在平面直角坐标系中点A(1,5),B(4,1),C(m,−m),D(m−3,−m+4),当四边形ABCD 的周长最小时,则m 的值为().A.√2B.32C.2D.310.如图分别在四边形ABCD的各边上取中点E,F,G,H,连接EG,在EG上取一点M,连接HM,过F作FN∥HM,交EG于N,将四边形ABCD中的四边形①和②移动后按图中方式摆放,得到四边形AHM′G′和AF′N′E,延长M′G′,N′F′相交于点K,得到四边形MM′KN′.下列说法中错误的是()A.S四边形MM′KN′=S四边形ABCD B.HM=NFC.四边形MM′KN′是平行四边形D.∠K=∠AHM′11.如图,已知∥ABC与∥CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD 是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤∥AOE与∥COF成中心对称.其中正确的个数为()A.2B.3C.4D.512.如图P为平行四边形ABCD内一点,过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点,若S四边形AHPE=3,S四边形PFCG=5,则S∥PBD为()A.0.5B.1C.1.5D.2二、填空题13.如图在平行四边形ABCD中点E,F分别在BC,AD上,请添加一个条件,使四边形AECF是平行四边形(只填一个即可).14.如图在Rt△ABC中AC=2√3,BC=2,点P是斜边AB上任意一点,D是AC的中点,连接PD并延长,使DE=PD.以PE,PC为边构造平行四边形PCQE,则对角线PQ的最小值为.15.如图▱ABCD中∥BAD=120°,E、F分别在CD和BC的延长线上,AE∥BD,EF∥BC,EF=5√3,则AB的长是16.如图在∥ABC中∥ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD= 13BD,连接DM、DN、MN.若AB=6,则DN=.17.若AC=10,BD=8,那么当AO=DO=时,四边形ABCD是平行四边形。
中考数学复习专题之平行四形的性质与判定,考点过关与基础练习题

24.平行四边形➢考点分类考点1平行四边形的性质例1如图所示,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:AB=CF(2)连接DE,若AD=2AB,求证:DE⟂AF.考点2平行四边形的判定例2如图所示,DE是ABC的中位线,延长DE至F,使EF=DE,连接BF.(1)求证:BF=DC(2)求证:四边形ABFD是平行四边形.考点3平行四边形综合探究例3如图1,在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于F.(1)当∠ABC=90°时,G是EF的中点,联结DB,DG(如图2),请直接写出∠BDG 的度数(2)当∠ABC=120°时,FG∥CE,且FG=CE,分别联结DB、DG(如图3),求∠BDG 的度数.➢真题演练1.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是()A.20B.21C.22D.232.在平行四边形ABCD中,已知∠A+∠C=200°,则∠A=()A.40°B.60°C.80°D.100°3.如图,平行四边形ABCD的对角线AC,BD相交于点O.点E为BC的中点,连接EO 并延长交AD于点F,∠ABC=60°,BC=2AB.下列结论:①S▱ABCD=AB•AC;②AD=4OE;③EF⊥AC;④S△BOE=14S△ABC.其中正确结论的个数是()A.4B.3C.2D.14.如图,在Rt △ABC 中,∠B =90°,BC =4,AC =5,点D 在BC 上,以AC 为对角线的所有平行四边形ADCE 中,DE 的最小值是( )A .3B .6C .8D .105.如图,在▱ABCD 中,AD =BD ,∠ADC =105°,点E 在AD 上,∠EBA =60°,则ED AE的值是( )A .23B .√3C .√32D .√336.如图,⟂ABCD 的对角线AC ,BD 交于点O ,AE 平分⟂BAD ,交BC 于点E ,且⟂ADC =60°,AD =2AB ,连接OE ,下列结论:⟂⟂CAD =30°;⟂OD =AB ;⟂S 平行四边形ABCD =AC •CD ;⟂S 四边形OECD =32S ⟂AOD :⟂OE =14AD .其中成立的个数是( )A .1个B .2个C .3个D .4个7.如图,点O 是平行四边形ABCD 对角线的交点,EF 过点O 分别交AD ,BC 于点E ,F .下列结论:①OE =OF ;②AB =BF ;③∠DOC =∠OCD ;④∠CFE =∠DEF ,其中正确结论的个数是( )A .4个B .3个C .2个D .1个8.如图,平行四边形ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=3,AO=2,BC=5,则AE的长为.9.如图,在平行四边形ABCD中,AD=5,AB=3,∠BAD的平分线AE交BC于E点,则EC的长为.10.如图,在▱ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=3BG,S▱BEPG =1.5,则S▱AEPH=.11.如图,在平行四边形ABCD中,E,F分别是AB,BC的中点,EH⊥AC,垂足为H,与AF交于点G,若AC=24,GF=6√5,则EG的长为.12.在平行四边形ABCD中,∠C=45°,AD=BD,点P为边CD上的动点(点P不与点D重合),连接AP,过点P作EP⊥AP交直线BD于点E.(1)如图①,当点P为线段CD的中点时,求证:P A=PE;(2)如图②,当点P在线段CD上时,求证:DE﹣DA=√2DP.13.已知:如图,▱ABCD 中,F 是AB 中点,连接DF ,DF 延长线交CB 的延长线于点E ,连接AE . 求证:(1)△AFD ≌△BFE ;(2)若BF =BC ,∠EDC =60°,判断四边形AEBD 的形状,并证明你的结论.➢ 课后练习1.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,AE 平分∠BAD ,分别交BC ,BD 于点E 、P .连接OE ,∠ADC =60°,AB =12BC =1,则下列结论: ①∠CAD =30°;②BD =2√3;③S 平行四边形ABCD =AB •AC ; ④AD =4OE .其中结论正确的个数是( )A .1个B .2个C .3个D .4个2.如图,平行四边形ABCD 中,对角线AC 、BD 相交于O ,过点O 作OE ⊥AC 交AD 于点E ,若AE =4,DE =3,AB =5,则AC 的长为( )A .3√2B .4√2C .5√2D .5√223.如图,已知在▱ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列结论正确的有()个.①F A:FB=1:2;②BE:CF=1:2;③AE:BC=1:2;④S△ABE:S△FBC=1:4.A.1个B.2个C.3个D.4个4.如图,在平行四边形ABCD中,CE平分∠BCD,交AB于点E,AE=3,EB=5,ED=4.则CE的长是()A.2√2B.6√2C.5√5D.4√55.如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E 不与A、B重合),连接EF、CF,则下列结论中正确个数是()①∠DCF=12∠BCD;②EF=CF;③S△BEC<2S△CEF;④∠DFE=4∠AEFA.4B.3C.2D.16.如图,在平行四边形ABCD中,E为CD上一点,且CE=BC,AE=DE,AE=4,∠DAE =60°,则下列结论:①∠AEB=90°;②平行四边形ABCD周长是24;③∠ABE=∠EBC=30°;④BE2=48;⑤E为CD中点.正确的结论有()A.2个B.3个C.4个D.5个7.如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于G,交AD延长线于F,若BC=6,DF=4,EF=2AE,则△ABE的面积为.8.如图,在▱ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,BE=1,平行四边形ABCD面积为6√3.则AF=.9.如图,在▱ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有(填序号).10.如图,在平行四边形ABCD中,AD=12,AB=6,以AD为底边向右作腰长为10的等腰△ADP,Q为边BC上一点,BQ=4,连接PQ,则PQ的最小值为.11.在平面直角坐标系中,O为原点,点A(√3,0),点B(0,1),点E是边AB中点,把△ABO绕点A顺时针旋转,得△ADC,点O,B旋转后的对应点分别为D,C.记旋转角为α.(1)如图①,当点D恰好在AB上时,求点D的坐标;(2)如图②,若α=60°时,求证:四边形OECD是平行四边形.12.如图,在▱ABCD中,AE平分∠BAD交对角线BD于点E,CF平分∠DCB交对角线BD 于点F,连接AF,CE.(1)若∠BCF=50°,求∠ADC的度数;(2)求证:四边形AECF为平行四边形.➢冲击A+如图,在△ABC中,AB=BC,AB为⊙O的直径,AC与⊙O相交于点D,过点D做DE⊥BC于点E,CB延长线交⊙O于点F.(1)求证:DE为⊙O的切线;(2)若BE=1,BF=2,求AD的长.。
九年级数学平行四边形的判定

பைடு நூலகம்
皇冠买球提不了款怎么办
[填空题]对于极易溶的气体,气相一侧的界面浓度yI接近于(),而液相一侧的界面浓度xI接近于()。 [名词解释]绕射波 [问答题,案例分析题]阅读下列说明,回答问题1至问题3【说明】某学校见到其他学校都陆续建立了多媒体网站作为学校的一个窗口,也想自己建立一个,就请一个计算机公司帮助建立。在公司人员和学校负责人讨论需求时,学校负责人并不能清晰表达,只能简要表达要满足学校教学和办公需求 [单选,A2型题,A1/A2型题]术后发生深静脉血栓,其处理措施不正确的是()A.患肢抬高B.禁忌经患肢静脉输液C.勤按摩D.溶栓治疗E.抗凝治疗 [单选]流体即物质实体,具有()A.物质属性与流动属性B.自然属性与社会属性C.物质属性与社会属性D.物质属性与流动属性 [单选]建设工程质量保证金(保修金)是从应付的工程款中预留,用以保证承包人对建设工程出现的缺陷进行维修的资金。该缺陷出现的时间应在()内。A.缺陷责任期B.保修期C.竣工验收期D.工程使用期 [填空题]()是指两枚邮票(或多枚邮票)之间相连着一段非邮票的特殊连票。 [多选]建设项目决策阶段环境影响评价管理的主要内容有()等。A.环境影响评价的确立和委托B.环境影响评价文件的编制C.环境影响评价文件的评估D.环境影响评价项目的分析E.环境影响评价文件的审批 [单选]厨房人员在厨房内的占地面积不得小于()平方米。A、1.8B、1.5C、1.7D、1.4 [问答题,简答题]过氧乙酸 [单选]洞门墙应根据实际需要设置泄水孔和()。A.施工缝或伸缩缝B.施工缝或沉降缝C.施工缝或结构缝D.沉降缝和伸缩缝 [判断题]WLANAP可以采用带POE功能的以太网交换机进行供电,可串接POE供电器。()A.正确B.错误 [单选]尺骨的构造是()。A、分为一体两端,上端称尺骨冰,下端称尺骨茎突B、分为一体两端,上端钩状突出的是鹰咀,下端称尺骨头C、分为一体两端,上端钩状突出的是鹰咀,下端有滑车切迹D、分为一体两端,上端粗大有滑车切迹,下端有尺骨鹰咀 [单选]对易燃易爆化学物品经营单位扩建工程竣工时未经消防验收或者经验收不合格擅自使用的,经公安消防机构责令限期改正后逾期不改的,应当()。A、责令立即改正B、责令停止施工C、责令停止使用,可以并处罚款D、处罚款 [单选,A2型题,A1/A2型题]螺旋CT技术的实现主要是因为采用了()A.滑环与电刷技术B.电缆与高压发生器技术C.球管与准直器技术D.信号放大技术E.图像处理技术 [单选,A2型题,A1/A2型题]女性,66岁,糖尿病病史10余年,长期口服降糖药治疗,血糖控制差。查体:身高158cm,体重76kg,给予人胰岛素(总量60U/d)治疗2周后,血糖仍为11.3~18.6mmol/L。目前首先考虑患者存在()。A.胰岛素抵抗B.胰岛素抗药性C.胰岛素过敏D.胰岛素过量E.黎明 [单选]工程上规定把发生()残余伸长的应力作为屈服强度。A.0.3%B.0.4%C.0.2%D.0.1% [单选]SDH日常维护项目的周期?()A.每日一次B.每周一次C.每月一次D.每季一次 [单选,A1型题]根据水解产物不同来分类,五倍子鞣质属于()A.咖啡鞣质B.逆没食子鞣质C.可水解鞣质低聚体D.缩合鞣质E.没食子鞣质 [单选,共用题干题]患者,女,29岁,白化病。欲与一患白化病男性结婚,婚前前来进行咨询。如已结婚并妊娠,以下恰当的处理是()。A.产前诊断B.男胎、女胎均可保留C.建议终止妊娠D.保留男胎E.保留女胎 [问答题,案例分析题]B企业拟在A市郊区原A市卷烟厂厂址处(现该厂已经关闭)新建屠宰量为120万头猪/年的项目(仅屠宰,无肉类加工),该厂址紧临长江干流,A市现有正在营运的日处理规模为3万t的城市污水处理厂,距离B企业1.5km。污水处理厂尾水最终排入长江干流(长江干流在A市段 [单选,A2型题,A1/A2型题]关于甲状旁腺功能减退症所致外胚层组织营养变化,下列说法错误的是()。A.纠正低钙血症可使白内障不再发展B.患者可有皮肤干燥、脱屑C.纠正低钙血症可使白内障恢复正常D.患者易患念珠菌感染E.白内障颇为常见 [单选]根据系统论的理论,物流系统可分为四个层次,错误的是()A.上级系统B.下级系统C.本级系统D.外级系统 [单选]21岁男性,体检发现肝右叶6cm占位,CT及MRI扫描除病灶中央可见放射状低密度/低信号影外,病灶实体未见显示,应首先考虑()。A.原发性肝癌B.局灶性结节增生C.肝血管瘤D.介入后致密斑E.肝脏炎性假瘤 [问答题,简答题]已知:某汽油机的气缸数目i=6,冲程数t=4,气缸直径D=100[mm],冲程S=115[mm],转速n=3000[r/min],有效功率Ne=100[kW],每小时耗油量Gt=37[kg/h],燃料低热值hu=44100[kJ/kg],机械效率hm=0.83。求:平均有效压力,有效扭矩,有效燃料消耗率,有效热效率,升功率 [名词解释]收货人 [单选]〈HR〉在HTML中是标记()A.标题B.空格C.换行D.水平线 [名词解释]需要 [多选]一般网络地址由哪几部分组成()A.逻辑地址B.链路地址C.网络地址D.主机地址 [单选]下列关于情报分析意义的说法不正确的是()。A、情报来源的合法性是情报分析结论合法性的前提B、情报来源的可靠性和情报的确实性对情报分析结论的可靠性有重要影响C、情报的秘密等级是情报分发范围的依据D、情报分析的过程是通过对情报资料之间关系的认识来认识情报所代表的 [单选]纳税人申请印花税核定调整或取消,基本规范规定的办理时限为()。A、15个工作日B、10个工作日C、20个工作日D、30个工作日 [问答题,简答题]什么叫花卉园艺? [单选]下列()法律法规不是保安押运公司员工需要重点掌握的。A.《中华人民共和国道路交通管理条例》B.《中华人民共和国枪支管理法》C.《专职守护押运人员枪支使用管理条例》D.《社会治安管理条例》 [单选]《灵枢.百病始生》所言的“虚邪”是指()。A.正气虚弱B.致病性不强的邪气C.四时不正之气D.泛指一切致病因素E.情志失调 [单选,A1型题]下列哪种检查,不适合于泌尿系统新鲜损伤()A.大剂量静脉肾盂造影B.逆行肾盂造影C.B超检查D.CT检查E.肾动脉造影 [单选]游乐园的()应该执行国家有关标准和规范。A、计划、设计、施工B、引进、安装C、制造、安装D、规划、设计、施工 [单选]男性,35岁,6h前因意外事故受挤压伤入院,体检:神志清醒,双下肢因断离已做初期手术处理,切口处仍有多量渗血,血压10/8kPa(75/60mmHg),心率150次/min,右侧第四肋骨骨折,已做胶布固定,右血气胸已作闭式引流,腹部无伤口,压痛(-),腹水征(-),B超腹内器官探 [问答题,简答题]激励明星销售人员的方法有几种? [单选]高压供电系统中,当时,计算短路电流可以只考虑()。A.系统短路电阻B.系统短路阻抗C.系统短路电抗D.系统短路电压 [单选,A2型题,A1/A2型题]关于β2-微球蛋白叙述错误的是().A.存在于所有有核细胞表面尿液B.患炎症及肿瘤时血浆中浓度可降低C.β2-微球蛋白主要用于监测肾小管功能D.急性白血病有神经浸润时,脑脊液中β2-微球蛋白可增高E.肾移植后如排斥反应影响肾小管功能时,尿液&beta
北师大版九年级上册数学同步培优第一章特殊平行四边形 正方形的判定

又∵∠AEC+∠AME=90°,∠AME=∠BMC, ∴∠ABG+∠BMC=90°.∴CE⊥BG. ∴四边形CGEB是垂美四边形. 由(2)得CG2+BE2=CB2+GE2. ∵AC=4,AB=5,∴BC=3,CG=4 2 ,BE=5 2 . ∴GE2=CG2+BE2-CB2=73.∴GE= 73 .
在△BEA和△DFA中,∠BEA=∠DFA,∠B=∠D,
AE=AF,∴△BEA≌△DFA(AAS),
∴AB=AD,∴矩形ABCD是正方形.
返回
9.【教材P27复习题T8拓展】【2021·兴安盟】如图,AD是 △ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是 E,F,连接EF,EF与AD相交于点H.
(2)已知BH=7,BC=13,求DH的长.
解:∵四边形AFHE和四边形ABCD都是正方形,
∴AE=EH=FH,AB=BC=13.
设AE=x,则BE=x+7.
在Rt△AEB中,AB2=AE2+BE2,即132=x2+(x+7)2,
整理,得(x+12)(x-5)=0. ∴x+12=0或x-5=0.
解得x=5(x=-12舍去),
解:△ABC满足∠BAC=90°时,四边形AEDF是正方形. 理由:∵∠AED=∠AFD=∠BAC=90°, ∴四边形AEDF是矩形. 又∵EF⊥AD,∴矩形AEDF是正方形.
返回
提优分类练
10.【2021·扬州】如图,在△ABC中,∠BAC的平分线交BC 于点D,DE∥AB,DF∥AC.
(1)试判断四边形AFDE的形状,并说明理由;
【点方法】由正方形的性质可得四边形
BEDF为平行四边形,且BD⊥EF,可证
得四边形BEDF为菱形,再根据勾股定理
计算DE的长,可得结论.
北师大版九年级数学上学期第一章:特殊的平行四边形 同步练习题 (含答案)

第一章特殊的平行四边形一.选择题(共10小题)1.若菱形的两条对角线长分别是6和8,则它的周长为()A.20 B.24 C.40 D.482.如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是()A.5B.2C.D.3.如图,已知菱形ABCD的周长为24,对角线AC、BD交于点O,且AC+BD=16,则该菱形的面积等于()A.6 B.8 C.14 D.284.如图,在四边形ABCD中,AC与BD相交于点O,∠OAB=∠OAD,BO=DO,那么下列条件中不能判定四边形ABCD是菱形的为()A.OA=OC B.BC=DC C.AD=BC D.AD=DC5.如图,菱形ABCD中,∠BAD=60,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①2OG=AB;②与△EGD 全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形,其中正确的是()A.①④B.①③④C.①②③D.②③④6.如图,矩形ABCD中,AB>AD,AN平分∠DAB,DM⊥AN,CN⊥AN,MN为垂足若AB=a,则DM+CN的值为()A.a B.a C.D.7.如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E.已知AB=2,△DOE的面积为,则AE的长为()A.B.2 C.1.5 D.8.在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是矩形的是()A.∠ABC=90°B.AC⊥BD C.AC=BD D.∠ACD=∠CDB 9.正方形ABCD的一条对角线长为8,则这个正方形的面积是()A.4B.32 C.64 D.12810.在正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF,则添加下列哪一个条件可以判定四边形BEDF是菱形()A.∠1=∠2 B.BE=DF C.∠EDF=60°D.AB=AF二.填空题(共10小题)11.已知,菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠EAF=60°,∠BAE=23°.则∠FEC=度.12.在菱形ABCD中,AD=10,AC=12,则菱形ABCD的面积是.13.如图在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=时,平行四边形CDEB为菱形.14.如图,在▱ABCD中,对角线AC,BD相交于点O,添加一个条件判定▱ABCD是菱形,所添条件为(写出一个即可)15.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成了一个四边形ABCD,当线段AD=5时,线段BC的长为.16.如图1,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,我们把的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:.如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=,则S△A′E′F′=.17.如图所示,长方形纸片上画有两个完全相同的灰色长方形,那么剩余白色长方形的周长为(用含a,b的式子表示).18.如图,将边长为6cm的正方形ABCD先向下平移2cm,再向左平移1cm,得到正方形A'B'C'D',则这两个正方形重叠部分的面积为cm2.19.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快s后,四边形ABPQ成为矩形.20.如图所示,直线经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E.若DE=5,BF=3,则EF的长为.三.解答题(共7小题)21.如图,菱形ABCD的对角线AC和BD相交于点O,AB=,OA=a,OB=b,且a,b满足:.(1)求菱形ABCD的面积;(2)求的值.22.如图,点A、B、C、D依次在同一条直线上,点E、F分别在直线AD的两侧,已知BE ∥CF,∠A=∠D,AE=DF.(1)求证:四边形BFCE是平行四边形;(2)填空:若AD=7,AB=2.5,∠EBD=60°,当四边形BFCE是菱形时,菱形BFCE的面积是.23.已知:AC,BD为菱形ABCD的对角线,∠BAD=60°,点EF分别在AD,CD边上,且∠EBF=60°.(1)求证:△BEF是等边三角形;(2)当∠ABE=15°时,AB=1+,求BE.24.同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).(1)证明:四边形AECF是菱形;(2)求菱形AECF的面积.25.(1)如图1,已知正方形ABCD,点E在BC上,点F在DC上,且∠EAF=45°,则有BE+DF =.若AB=4,则△CEF的周长为.(2)如图2,四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.26.在正方形ABCD的外侧作等腰△ABE,已知∠EAB=a,连接ED交等腰△ABE底边上的高AF所在的直线于点G.(1)如图1,若a=30°,求∠AGD的度数;(2)如图2,若90°<a<180°,BE=8,DE=14,则此时AE的长为.27.如图,在矩形ABCD中,AB=4cm,AD=12cm;P点在AD边上以每秒1cm的速度从A向D运动,点Q在BC边上,以每秒4cm的速度从C点出发,在CB间往返运动,两点同时出发,待P点到达D点为止,求经过多长时间四边形ABQP为矩形?参考答案与试题解析一.选择题(共10小题)1.【解答】解:如图所示,根据题意得AO=×8=4,BO=×6=3,∵四边形ABCD是菱形,∴AB=BC=CD=DA,AC⊥BD,∴△AOB是直角三角形,∴AB====5,∴此菱形的周长为:5×4=20.故选:A.2.【解答】解:∵四边形ABCD是菱形,AC=6cm,BD=8cm,∴AO=CO=3cm,BO=DO=4cm,∠BOC=90°,∴BC==5(cm),∴AE×BC=BO×AC故5AE=24,解得:AE=.故选:C.3.【解答】解:∵四边形ABCD是菱形,∴AC⊥BD,AB=BC=CD=DA,∵菱形ABCD的周长为24,∴AD=AB=6,∵AC+BD=16,∴AO+BO=8,∴AO2+BO2+2AO•BO=64,∵AO2+BO2=AB2,∴AO•BO=14,∴菱形的面积=4×三角形AOD的面积=4××14=28,故选:D.4.【解答】解:A、若AO=OC,且BO=DO,∴四边形ABCD是平行四边形,∴AB∥CD∴∠BAO=∠OCD,且∠OAB=∠OAD∴∠OAD=∠OCD∴AD=CD,∴四边形ABCD是菱形故A选项不符合题意B、若BC=DC,BO=DO∴AC是BD的垂直平分线∴AB=AD则不能判断四边形ABCD是菱形故B选项符合题意,C、∵∠OAB=∠OAD,BO=DO,∴AB=AD,且BO=DO∴AC垂直平分BD∴BC=CD,且AD=BC∴AB=AD=BC=CD∴四边形ABCD是菱形故C选项不符合题意D、∵∠OAB=∠OAD,BO=DO,∴AB=AD,且BO=DO∴AC垂直平分BD∴BC=CD,且AD=CD∴AB=AD=BC=CD∴四边形ABCD是菱形故D选项不符合题意故选:B.5.【解答】解:∵四边形ABCD是菱形,∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,∵CD=DE,∴AB=DE,在△ABG和△DEG中,,∴△ABG≌△DEG(AAS),∴AG=DG,∴OG是△ACD的中位线,∴OG=CD=AB,∴2OG=AB,①正确;∵AB∥CE,AB=DE,∴四边形ABDE是平行四边形,∵∠BCD=∠BAD=60°,∴△ABD、△BCD是等边三角形,∴AB=BD=AD,∠ODC=60°,∴OD=AG,四边形ABDE是菱形,④正确;∴AD⊥BE,由菱形的性质得:△ABG≌△DEG(SAS),△BDG≌△DEG(SAS),在△ABG和△DCO中,,∴△ABG≌△DCO(SAS),∴△ABO≌△DEG(SAS),△BCO≌△DEG(SAS),△CDO≌△DEG(SAS),△AOD≌△DEG(AAS),△ABG≌△DEG(SAS),△BDG≌△DEG(SAS),∴②不正确;∵OB=OD,AG=DG,∴OG是△ABD的中位线,∴OG∥AB,OG=AB,∴△GOD∽△ABD(ASA),△ABF∽△OGF(ASA),∴△GOD的面积=△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,∴△AFG的面积=△OGF的面积的2倍,又∵△GOD的面积=△AOG的面积=△BOG的面积,∴S四边形ODGF=S△ABF;③不正确;正确的是①④.故选:A.6.【解答】解:如图所示:∵四边形ABCD是矩形,∴∠ADC=∠DAB=90°,CD=AB=a,∴AN平分∠DAB,∴∠DAM=45°,∴∠CEN=∠DEM=45°,∵DM⊥AN,CN⊥AN,∴△DME和△CNE是等腰直角三角形,∴DM=DE,CN=CE,∴DM+CN=(DE+CE)=CD=a;故选:C.7.【解答】解:连接BE,如图所示:由题意可得,OE为对角线BD的垂直平分线,∴BE=DE,S△BOE=S△DOE=,∴S△BDE=2S△BOE=.∴DE•AB=,又∵AB=2,∴DE=,∴BE=在Rt△ABE中,由勾股定理得:AE===1.5.故选:C.8.【解答】解:A、∵四边形ABCD是平行四边形,∠ABC=90°,∴四边形ABCD是矩形,故本选项不符合题意;B、根据四边形ABCD是平行四边形和AC⊥BD不能推出四边形ABCD是矩形,故本选项符合题意;C、∵四边形ABCD是平行四边形,AC=BD,∴四边形ABCD是矩形,故本选项不符合题意;D、∵∠ACD=∠CDB,∴OD=OC,∵四边形ABCD是平行四边形,∴AO=OC,BO=OD,∴AC=BD,∴四边形ABCD是矩形,故本选项不符合题意;故选:B.9.【解答】解:在正方形中,对角线相等,所以正方形ABCD的对角线长均为8,∵正方形又是菱形,菱形的面积计算公式是S=ab(a、b是正方形对角线长度)∴S=×8×8=32,故选:B.10.【解答】解:由正方形的性质知,∠ACD=∠ACB=45°,BC=CD,CF=CF,∴△CDF≌△CBF(SAS),∴BF=FD,同理,BE=ED,∴当BE=DF,有BF=FD=BE=ED,四边形BEDF是菱形.故选:B.二.填空题(共10小题)11.【解答】解:连接AC,∵四边形ABCD是菱形,∴AB=BC=CD=AD,∵∠B=∠EAF=60°,∴△ABC是等边三角形,∠BCD=120°,∴AB=AC,∠B=∠ACF=60°,∵∠BAE+∠EAC=∠FAC+∠EAC,∴∠BAE=∠FAC,且AB=AC,∠B=∠ACF∴△ABE≌△ACF(ASA),∴AE=AF,又∵∠EAF=∠D=60°,∴△AEF是等边三角形,∴∠AEF=60°,又∠AEC=∠B+∠BAE=83°,∴∠CEF=83°﹣60°=23°.故答案为:2312.【解答】解:如图,连接AC,BD交于点O.∵四边形ABCD是菱形,∴AC⊥BD,OA=OC=6,∴∠AOD=90°,∴OD==8,∴BD=2OD=16,∴S菱形ABCD=×AC×BD=×12×16=96,故答案为96.13.【解答】解:如图,连接CE交AB于点O.∵Rt△ABC中,∠ACB=90°,AC=4,BC=3,∴AB==10若平行四边形CDEB为菱形时,CE⊥BD,OD=OB,CD=CB.∵AB•OC=AC•BC,∴OC=.∴OB==∴AD=AB﹣2OB=故答案为:14.【解答】解:根据一组邻边相等的平行四边形是菱形,则可添加条件为:AB=AD(AD=CD,BC=CD,AB=BC)也可添加∠1=∠2,根据平行四边形的性质,可求AD=CD.根据对角线互相垂直的平行四边形是菱形,则可添加条件为:AC⊥BD.故答案为:AB=AD(答案不唯一)15.【解答】解:由条件可知AB∥CD,AD∥BC,∴四边形ABCD为平行四边形,∴BC=AD=5.故答案为:5.16.【解答】解:如图,在图2中,形变前正方形的面积为:a2,形变后的菱形的面积为:a•a=a2,∴菱形形变前的面积与形变后的面积之比:a2:a2=2:,∵这个菱形的“形变度”为2:.∴菱形形变前的面积与形变后的面积之比=这个菱形的“形变度”,S△AEF=×2×2+×2×2=4,∵若这个菱形的“形变度”k=,∴=,即=,∴S△A′E′F′=.故答案为:.17.【解答】解:剩余白色长方形的长为b,宽为(b﹣a),所以剩余白色长方形的周长=2b+2(b﹣a)=4b﹣2a.故答案为4b﹣2a.18.【解答】解:如图,向下平移2cm,即AE=2,则DE=AD﹣AE=6﹣2=4cm向左平移1cm,即CF=1,则DF=DC﹣CF=6﹣1=5cm则S矩形DEB'F=DE•DF=4×5=20cm2故答案为:2019.【解答】解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得3x=20﹣2x.解得x=4,故答案为:4.20.【解答】解:∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴∠BAF+∠EAD=90°,∵BF⊥a,DE⊥a,∴∠AED=∠AFB=90°∴∠BAF+∠ABF=90°,∴∠ABF=∠EAD,∴△AFB≌△DEA,∴AF=ED=5,AE=BF=3,∴EF=AF+AE=5+3=8,故答案为:8三.解答题(共7小题)21.【解答】解:(1)∵四边形ABCD是菱形,∴BD垂直平分AC,∵OA=a,OB=b,AB=,∴a2+b2=5,,∵a,b满足:.∴a2b2=4,∴ab=2,∴△AOB的面积=ab=1,∴菱形ABCD的面积=4△AOB的面积=4;(2)∵a2+b2=5,ab=2,∴(a+b)2=a2+b2+2ab=9,∴a+b=3,∴=.22.【解答】(1)证明:∵BE∥CF,∴∠EBC=∠FCB,∴∠EBA=∠FCD,在△ABE和△DCF中,,∴△ABE≌△DCF(AAS),∴BE=CF,AB=CD,∴四边形BFCE是平行四边形.(2)解:连接EF交BC于O,如图所示:∵AD=7,AB=DC=2.5,∴BC=AD﹣AB﹣DC=2,∵四边形BFCE是菱形,∠EBD=60°,EF⊥BC,OB=BC=1,OE=OF,∴△CBE是等边三角形,∠BEO=30°,∴BC=EC=2,∴OE=OB=,∴EF=2,∴菱形BFCE的面积=BC×EF=×2×2=2;故答案为:2.23.【解答】证明:(1)∵四边形ABCD是菱形∴AB=AD=BC=CD,且∠BAD=60°∴△ABD是等边三角形,∠ADC=120°∴AB=AD=BD,∠ABD=∠ADB=60°∴∠ABD=∠EBF=60°=∠BDC,∴∠ABE=∠DBF,∠BAD=∠BDF=60°,且AB=BD∴△ABE≌△DBF(ASA)∴BE=BF,且∠EBF=60°.∴△BEF是等边三角形(2)如图,过点E作EH⊥AB于H,作∠GEB=∠ABE=15°,∴∠EGH=30°,GE=GB,设HE=x,在Rt△GHE中,∠EGH=30°∴GE=2x=BG,HG=x,在Rt△AHE中,∠BAD=60°∴AH=x,∵AB=AH+HG+BG=1+∴x+x+2x=1+∴x=∴HE=∴BH=∵BE2=HE2+BH2,∴BE2=()2+()2,∴BE=24.【解答】(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠FAC=∠ACE,∵∠CAE=∠DAC,∠ACF=∠ACB,∴∠EAC=∠ACF,∴AE∥CF,∵AF∥EC,∴四边形AECF是平行四边形,∵∠FAC=∠FCA,∴AF=CF,∴四边形AECF是菱形.(2)解:∵四边形AECF是菱形,∴AE=EC=CF=AF,设菱形的边长为a,在RT△ABE中,∵∠B=90°,AB=12,AE=a,BE=18﹣a,∴a2=122+(18﹣a)2,∴a=13,∴BE=DF=5,AF=EC=13,∴S菱形AECF=S矩形ABCD﹣S△ABE﹣S△DFC=216﹣30﹣30=156cm2.25.【解答】解:(1)延长EB至H,使BH=DF,连接AH,如图1,∵在正方形ABCD中,∴∠ADF=∠ABH,AD=AB,在△ADF和△ABH中,,∴△ADF≌△ABH(SAS),∴∠BAH=∠DAF,AF=AH,∴∠FAH=90°,∴∠EAF=∠EAH=45°,在△FAE和△HAE中,,∴△FAE≌△HAE(SAS),∴EF=HE=BE+HB,∴EF=BE+DF,∴△CEF的周长=EF+CE+CF=BE+CE+DF+CF=BC+CD=2AB=8.故答案为:EF;8.(2)EF=BE+DF,理由如下:延长CB至M,使BM=DF,连接AM,如图2,∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,∴∠D=∠ABM,在△ABM和△ADF中,,∴△ABM≌△ADF(SAS),∴AF=AM,∠DAF=∠BAM,∵∠BAD=∠C=90°,∠EAF=45°,即∠BAD=2∠EAF,∴∠DAF+∠BAE=∠EAF,∴∠EAB+∠BAM=∠EAM=∠EAF,在△FAE和△MAE中,,∴△FAE≌△MAE(SAS),∴EF=EM=BE+BM=BE+DF,即EF=BE+DF.26.【解答】解:(1)∵AE=AB,AF⊥BE,∠EAB=30°∴∠FAE=15°∵∠EAB=30°,∠BAD=90°∴∠EAD=120°,且AE=AD∴∠AED=∠ADE=30°∴∠AGD=∠AED+∠EAF=45°(2)如图,连接AC,BD交于点O,连接FO,∵四边形ABCD是正方形∴BO=DO,BD=AB,∠ABD=∠ADB=45°∵AE=AB,AF⊥BE∴∠AEB=∠ABE,EF=BF=4,且BO=DO∴FO=DE=7,FO∥DE∵AE=AD∴∠AED=∠ADE∵∠ABD+∠ADB+∠AED+∠ADE+∠AEB+∠ABE=180°∴2(∠AEB+∠AED)=90°∴∠DEB=45°∵FO∥DE∴∠BFO=45°,且BM⊥FO∴FM=BM,∴BF=BM=4∴BM=FM=4∴MO=3∴BO==5∴BD=2BO=10∴AB=5=AE故答案为:527.【解答】解:∵在矩形ABCD中,AD=12cm,∴AD=BC=12cm.当四边形ABQP为矩形时,AP=BQ.①当0<t<3时,t=12﹣4t,解得,t=;②当3≤t<6时,t=4t﹣12,解得t=4;③当6≤t<9时,t=36﹣4t,解得t=;④当9≤t≤12时,t=4t﹣36,解得,t=12.综上所述,当t为或4或或12时,四边形ABQP为矩形.。
数学:1.3平行四边形,矩形,菱形,正方形的性质和判定(2)平行四边形的判断同步练习(苏科版九年级上)

平行四边形的判定练习题
1.下面几组条件中,能判定一个四边形是平行四边形的是().
A.一组对边相等; B.两条对角线互相平分
C.一组对边平行; D.两条对角线互相垂直
2.BD是平行四边形ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需要添加的一个条件是_________.
3.如图所示,在平行四边形ABCD中,P
1、P
2
是对角线BD的三等分点,求证:•
四边形AP
1CP
2
是平行四边形.
4.已知如图所示,点O为平行四边形ABCD的对角线BD的中点,直线EF经过点O,分别交BA、DC的延长线于E、F两点,求证:AE=CF.
5.已知:如图所示,平行四边形ABCD的对角线AC、BD•相交于点O,EF经过点O 并且分别和AB、CD相交于点E、F,又知G、H分别为OA、OC的中点.求证:四边形EHFG是平行四边形.。
九年级数学平行四边形的判定

[单选]下列()方法可以减小渠道整体受冲刷的程度。A、用混凝土衬砌,取代土渠B、多采用弯道,降低流速C、拆除跌水、采用明渠直连D、拆除衬砌,采用土渠 [配伍题,B型题]是运用物理化学原理、方法和手段,研究药剂学中有关处方设计、制备工艺、剂型特点、质量控制等内容的边缘科学。</br>是研究药物在体内的吸收、分布、代谢与排泄的机理及过程,阐明药物因素、剂型因素和生理因素与药效之间关系的边缘科学。</br>是研究药物制剂工业生 [单选]紫花地丁来源于()A.菊科B.豆科C.毛茛科D.堇菜科E.唇形科 [名词解释](司空图的)“四外”说 [单选]学生为了就学由个人或家庭直接承担的各种费用及机会成本称为()A.教育的社会成本B.教育的个人成本C.教育的直接成本D.教育的间接成本 [填空题]各类油泵吊至检修平台过程中应注意油泵内的()。不得在运输途中发生漏油。如在途中有漏油,应及时做好(),防止人员()。 [单选,A2型题,A1/A2型题]关于孤独症的治疗,错误的是()A.异常行为的改变和变更B.对孩子行为的宽容和理解C.特别能力的发现、培养和转化D.应用行为分析疗法是高强度的行为疗法E.采用以药物治疗为主、教育和训练为辅的办法 [单选]一般平版胶印的润版液组成为()。A.纯水B.酒精C.水+少量药品D.酒精+少量药品 [单选]铁路平面无线调车B型号调车长台,直接发三车信号时用()A.黄(0.5)B.黄(1.5)C."黄绿"D."黄红" [填空题]1487年,葡萄牙人的船队,沿非洲西岸南行,到达非洲的最南端,葡萄牙国王把这里命名为()。 [单选]对母线充电时,下列哪种措施不能消除谐振()?A.先将线路接入母线B.先将变压器中性点及消弧线圈接地C.在母线电压互感器二次侧开口三角并接消谐电阻D.用刀闸进行操作 [单选]下面哪部歌剧是瓦格纳的作品:()A.《茶花女》(威尔第)B.《纽伦堡的名歌手》C.《塞维利亚理发师》(罗西尼)D.《费加罗的婚礼》(莫扎特) [填空题]“说”就是和客户保持(),向客户提供(),给客户创造更多价值。 [单选]一条高速公路的通信系统由()子系统构成。A.光纤数字传输系统、数字程控交换系统、会议电视系统、通信电源系统、光电缆工程及通信管道工程B.光纤数字传输系统、数字程控交换系统、有线广播系统、通信电源系统、光电缆工程及通信管道工程C.光纤数字传输系统、数字程控交换系 [单选,A1型题]既有肠燥便秘,又有水肿腹满者应选用的药物是()A.火麻仁B.杏仁C.桃仁D.郁李仁E.商陆 [名词解释]人格结构 [多选]通航安全水上水下施工作业涉及的范围包括()。A.设置、拆除水上水下设施B.架设桥梁、索道,构筑水下隧道C.救助遇难船泊,或紧急清除水面污染物、水下污染源D.渔船捕捞作业E.清除水面垃圾 [问答题,简答题]什么是“投资单位”、“买入价”、“卖出价”? [单选,A2型题,A1/A2型题]使肾病综合征病情加重的最常见诱因是()A.感染B.焦虑C.活动增多D.暴饮暴食E.蛋白质摄入不足 [填空题]乙炔装置AR476分析仪参比气是()。 [判断题]海洋中的岛屿图形只能选取或舍弃,任何时候都不能把几个小岛合成一个大的岛屿。A.正确B.错误 [问答题,简答题]世界第一大半岛? [问答题,计算题]B-2857号飞机从广州飞往北京,该飞机起飞全重、落地全重、无油全重分别为97650kg,89961kg,83456kg,修正后飞机基本重量为52350kg,飞机起飞油量12000kg,其中航段耗油量4000kg,飞机最大业载限额为31500kg,从广州到北京的旅客人数为176/02/00,行李750kg,邮件 [单选]某孕妇,26岁,孕1产0,妊娠40周。检查:胎方位枕左前,有规律宫缩已18小时,宫颈扩张3cm,胎心140次/分,产妇一般情况良好。宫缩较初期间歇延长,为5~10分,持续30秒,宫缩高峰时子宫不硬。经详细检查无头盆不称、骨盆狭窄。该产妇除有宫缩乏力外,还应诊断()A.第二产程 [单选]为了对计算机信息系统的安全威胁有更全面、更深刻的认识,信息应用系统安全威胁的分类方法一般用()3种"综合分类"方法。A.高、中、低B.对象的价值、实施的手段、影响(结果)C.按风险性质、按风险结果、按风险源D.自然事件、人为事件、系统薄弱环节 [单选,A1型题]病例对照研究与队列研究的主要相同点是()A.均是分析性研究B.均是前瞻性研究C.均是回顾性研究D.均是实验性研究E.均是描述性研究 [单选,A2型题,A1/A2型题]《实验室认可管理办法》规定的中国实验室认可原则,不包括()。A.自愿申请原则B.非歧视原则C.国家强制原则D.专家评审原则E.国家认可原则 [单选]胶结物充填于颗粒之间的孔隙中,颗粒呈()接触,这种胶结称为孔隙胶结。A、稀疏B、紧密C、点状D、支架状 [判断题]液体气化的方法有蒸发和沸腾。()A.正确B.错误 [单选,A1型题]脓血症最具特征性的临床表现是()。A.寒战后高热B.白细胞计数达(20~30)×109/L以上C.可出现感染性休克D.转移性脓肿E.病情重而病程短 [单选]凯恩斯认为,在()情况下,对新的实物资本进行投资是不值得的。A.新投资的预期利润率大于为购买这些资产而必须借进的款项所要求的利率B.新投资的预期利润率小于为购买这些资产而必须借进的款项所要求的利率C.新投资的预期利润率等于为购买这些资产而必须借进的款项所要求的 [单选]按临床分类,中度吸入性损伤指()A.伤及肺泡B.伤及咽部以上C.伤及细支气管D.伤及气管以上E.伤及喉部以上 [单选,A2型题,A1/A2型题]男性雄激素的作用不包括()A.皮脂腺分泌多,有痤疮B.腋毛多C.阴毛呈菱形分布D.声音高调E.睾丸和阴茎的发育 [名词解释]GPS [单选,A2型题,A1/A2型题]对于术后尿潴留患者,首先应采取的处理措施为()A.在严格无菌操作下,进行导尿B.肌注卡巴胆碱0.25mgC.诱导患者自行排尿D.下腹部热敷E.针刺治疗 [问答题,简答题]屈曲肢体加垫止血法。 [单选]货位管理就是指货品进入仓库之后,对货品如何处理、如何放置、放置在何处等进行合理有效的()。A.计划和管理B.养护和管理C.规划和管理D.筹划和管理 [单选]刮片细胞学检查时,常用的固定液是()A.甲醛B.丙酮C.乙醇D.冰醋酸E.甲醇 [名词解释]地球化学背景 [单选]间接维持子宫前倾位置的子宫韧带是()。A.圆韧带B.阔韧带C.主韧带D.骨盆漏斗韧带E.宫骶韧带
2023年九年级中考数学一轮复习小题狂练-平行四边形的判定

2023届一轮复习小题狂练-平行四边形的判定一、选择题(共20小题)1. 根据图中所给的边长及角度,下列四边形中,为平行四边形的是( )A. B.C. D.2. 下列语句中,是假命题的是( )A. 若a∥b,b∥c,则a∥cB. 若a=b,b=c,则a=cC. 若a⊥b,b⊥c,则a⊥cD. 若a>b,b>c,则a>c3. 下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )A. 1:2:3:4B. 2:2:3:3C. 2:3:2:3D. 2:3:3:24. 下列命题中,假命题是( )A. 对顶角相等B. 等角的补角相等C. 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行D. 如果一个角的两边分别平行于另一个角的两边,那么这两个角相等5. 能判定四边形为平行四边形的是( )A. 一组对角相等B. 两条对角线互相垂直C. 两条对角线互相平分D. 一对邻角互补6. 下列命题是真命题的是( )A. 一个角的补角一定大于这个角B. 平行于同一条直线的两条直线平行C. 等边三角形是中心对称图形D. 旋转改变图形的形状和大小7. 四边形ABCD中,AD∥BC,当满足下列哪个条件时,可以得出四边形ABCD是平行四边形( )A. ∠A+∠C=180∘B. ∠B+∠D=180∘C. ∠A+∠B=180∘D. ∠A+∠D=180∘8. 如图,在平行四边形ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )A. BO=DOB. AC=BDC. CD=ABD. ∠BAD=∠BCD9. 已知平行四边形ABCD中,∠A+∠C=200∘,则∠B的度数是( )A. 100∘B. 160∘C. 80∘D. 60∘10. 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )A. ①②B. ①④C. ③④D. ②③11. 在四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )A. 3种B. 4种C. 5种D. 6种12. 在四边形ABCD中,对角线AC,BD相交于点O,且AO=CO,如果要使四边形ABCD是平行四边形,可以再添加的条件是( )A. AC⊥BDB. AO=BOC. OB=ODD. OC=OD13. 下列命题中,假命题( )A. 在同一平面内,垂直于同一条直线的两直线平行B. 到线段两端点距离相等的点在这条线段的垂直平分线上C. 一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等D. 一边长相等的两个等腰直角三角形全等14. 下列说法正确的有( )①对角线互相平分且垂直的四边形是菱形;②一组对边平行,一组对边相等的四边形是平行四边形;③有一个角是直角的四边形是矩形;④对角线相等且垂直的四边形是正方形.A. 1B. 2C. 3D. 415. 平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )A. AB=BCB. AC=BDC. AC⊥BDD. AB⊥BD16. 如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )A. AD=BCB. CD=BFC. ∠A=∠CD. ∠F=∠CDF17. 下列命题中,真命题的个数是( )①对角线互相平分的四边形是平行四边形;②两组对角分别相等的四边形是平行四边形;③一组对边平行,另一组对边相等的四边形是平行四边形.A. 3B. 2C. 1D. 018. 如图,在四边形ABCD中,下列条件不能判定四边形ABCD是平行四边形的是( )A. AB∥DC,AD∥BCB. AB=DC,AD=BCC. AD∥BC,AB=DCD. AB∥DC,AB=DC19. 不能判断四边形ABCD是平行四边形的是( )A. AB∥CD,AD∥BCB. AB=CD,AD=BCC. AB=CD,AB∥CDD. AB=CD,AD∥BC20. 【测试2】下列命题中,是真命题的有( )①同位角相等;②对顶角相等;③同一平面内,如果直线l1∥l2,直线l2∥l3,那么l1∥l3;④同一平面内,如果直线l1⊥l2,直线l2⊥l3,那么l1∥l3.A. 0个B. 1个C. 2个D. 3个二、填空题(共8小题)21. 下列四边形中,是平行四边形的是(请填写序号).22. 如图,在四边形ABCD中,AC,BD相交于点O.(1)若AD=8cm,AB=4cm,那么BC=cm,CD=cm时,四边形ABCD为平行四边形;(2)若AC=8cm,BD=10cm,那么当AO=cm,DO=cm时,四边形ABCD为平行四边形.23. 如图,DE∥BC,DF∥AC,EF∥AB,图中共有个平行四边形.24. 如图,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件(写一个即可),使四边形ABCD是平行四边形.25. 如图,在四边形ABCD中,∠A=∠C=130∘,要使四边形ABCD成为平行四边形,则∠B=∘.26. 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90∘,若AB=6,BC=8,则EF的长为.27. 在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是.28. 如图所示,点D,E分别是△ABC的边AB,AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=3,则DE的长为.三、解答题(共5小题)29. 如图,在四边形ABCD中,AO=3,BO=2,CO=3,DO=2.判断四边形ABCD是否为平行四边形.30. 如图,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.31. 如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD,求证:四边形ABCD是矩形.32. 如图,四边形ABCD中,AB=CD,E,F分别为AD,BC的中点,延长BA,FE交于M,延长FE,CD交于N.求证:∠AME=∠N.33. 如图,在平行四边形ABCD中,DM⊥AC,BN⊥AC,M,N为垂足.求证:DM=BN.答案1. B2. C【解析】A选项:若a∥b,b∥c,则a∥c是真命题,故A错误;B选项:若a=b,b=c,则a=c是真命题,故B错误;C选项:若a⊥b,b⊥c,则a∥c是假命题,故C正确;D选项:若a>b,b>c,则a>c是真命题,故D错误.3. C4. D5. C6. B 【解析】A、一个角的补角不一定大于这个角,故A错误;B、平行于同一条直线的两条直线平行,故B正确;C、等边三角形是轴对称图形,不是中心对称图形,故C错误;D、旋转不改变图形的形状和大小,故D错误;故选:B.7. D8. B9. C10. D【解析】因为只有②③两块角的两边互相平行,角的两边的延长线的交点就是平行四边形的顶点,所以带②③两块碎玻璃,就可以确定平行四边形的大小.11. B12. C13. D【解析】A.在同一平面内,垂直于同一条直线的两直线平行,本选项说法是真命题;B.到线段两端点距离相等的点在这条线段的垂直平分线上,本选项说法是真命题;C.一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等,本选项说法是真命题;D.当一个等腰直角三角形的直角边长等于另一个等腰直角三角形的斜边长时,两个等腰直角三角形不全等,故一边长相等的两个等腰直角三角形全等是假命题.故选:D.14. A【解析】①对角线互相平分且垂直的四边形是菱形,故符合题意;②一组对边平行,一组对边相等的四边形不一定是平行四边形,故不符合题意;③有一个角是直角的平行四边形是矩形,故不符合题意;④对角线相等且垂直的平行四边形是正方形,故不符合题意.故选:A.15. B16. D17. B【解析】分别利用平行四边形的判定方法:(1)两组对边分别平行的四边形是平行四边形;(2)两组对角分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形,进而得出①,②是真命题,③是假命题.18. C19. D【解析】根据平行四边形的判定:A,B,C可判定为平行四边形,而C不具备平行四边形的条件,A.∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形),满足;B.∵AB=CD,AD=BC,∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形),满足;C.∵AB=CD,AB∥CD,∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形),满足;D.∵AB=CD,AD∥BC,∴四边形ABCD等腰梯形,不一定是平行四边形,不满足.20. D【解析】①两直线平行,同位角相等,原命题是假命题;②对顶角相等,是真命题;③同一平面内,如果直线l1∥l2,直线l2∥l3,那么l1∥l3;是真命题;④同一平面内,如果直线l1⊥l2,直线l2⊥l3,那么l1∥l3.是真命题;故选:D.21. ①②③22. 8,4,4,523. 324. AB=CD或AD∥BC等25. 5026. 127. ①②③【解析】在矩形ABCD中,对角线AC,BD相交于点O,连接PM,QN,若PM与QN均经过点O,则四边形MNPQ为平行四边形,此时若PM=QN,则四边形MNPQ为矩形;若PM⊥QN,则四边形MNPQ为菱形.有的矩形不存在以点M,N,P,Q为顶点的正方形.故正确的结论是①②③.28. 3229. 四边形ABCD是平行四边形.∵AO=3,CO=3,BO=2,DO=2,∴AO=CO,BO=DO,∴四边形ABCD是平行四边形.30. ∵∠BAE=∠DAC,∴∠BAE+∠CAE=∠DAC+∠CAE,∴∠CAB=∠EAD,且AB=AD,AC=AE,∴△ABC≌△ADE(SAS),∴∠C=∠E.31. ∵四边形ABCD中,AB=CD,AD=BC,∴四边形ABCD是平行四边形,∴AC=2AO,BD=2OD,∵OA=OD,∴AC=BD,∴四边形ABCD是矩形.32. 如图,连接BD,取BD的中点G,连接EG,FG.∵DE=EA,DG=GB,∴EG为△DAB的中位线,∴EG∥AB,EG=12AB,∴∠GEF=∠AME,同理,FG∥CD,FG=12CD,∴∠GFE=∠N,∵AB=CD,∴EG=FG,∴∠GEF=∠GFE,∴∠AME=∠N.33. ∵DM⊥AC,BN⊥AC,∴∠AMD=∠CNB=90∘,∵四边形ABCD为平行四边形,∴AD=BC且AD∥BC,∴∠DAM=∠BCN.在△ADM与△CBN中,{∠AMD=∠CNB,∠DAM=∠BCN, AD=BC,∴△ADM≌△CBN(AAS),∴DM=BN。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2平形四边形的判定
一、试试你的身手(每小题3分,共24分)
1.在□ABCD中,已知AB+BC=20,且AD=8,则BC= ,CD= .
2.用20cm长的铁丝围成一个平行四边形,使长边比短边长2cm,则它的长边长为,短边长为.
3.如图1,□ABCD的对角线AC和BD相交于点O,那么图中的全等三角形共有对.
4.□ABCD中,∠A的2倍与∠B的补角互为余角,那么∠A= .5.在□ABCD中,已知∠B+∠D=280°,则它的各角度数是.6.在平行四边形ABCD中,E、F分别是AD、BC的中点,则四边形EBFD 是.
7.四边形ABCD中,已知AB=7cm,BC=5cm,CD=7cm,当AD= 时,四边形ABCD是平行四边形.
8.如图2,在□ABCD中,对角线AC、BD相交于点O,E、F分别在OB、OD上,且OE=OF,又因为OC= ,所以四边形AECF 是,理由是.
二、相信你的选择(每小题3分,共24分)
1.如图3,平行四边形ABCD中,∠B-∠A=20°,则∠D的度数是()A.80°B.90°C.100°D.110°
2.平行四边形的一边长为6cm,周长为28cm,则这条边的邻边长是()
A.22cm B.16cm C.11cm D.8cm 3.已知平行四边形的一组邻边分别为a、b,且a边上的高为h,那么b边上的高为()
A.ah
b B.ab
h
C.bh
a
D.abh
4.如图4,AC、BD是□ABCD的对角线,AC和BD相交于点O,AC=4,BD=5,BC=3,则△BOC的周长是()
A.7.5 B.12 C.8.5 D.9
5.如果平行四边形有一组对角互补,那么这个平行四边形的四个角一定都是()
A.直角B.钝角C.锐角D.不确定
6.下列条件中,能判定四边形是平行四边形的条件是()A.两条对角线互相垂直
B.两条对角线互相垂直且相等
C.两条对角线相等且交角为60°
D.两条对角线互相平分
7.下列说法属于平行四边形判定方法的有()
①两组对边分别平行的四边形是平行四边形
②平行四边形的对角线互相平分
③两组对边分别相等的四边形是平行四边形
④平行四边形的每组对边平行且相等
⑤两条对角线互相平分的四边形是平行四边形
A.5个B.4个C.3个D.2个
8.下列条件中能判定四边形ABCD是平行四边形的是()A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
三、挑战你的技能(共41分)
1.(10分)如图5,四边形ABCD是平行四边形,DB⊥AD,AD=8cm,BD=12cm,求BC,AC的长.
2.(10分)如图6,在□ABCD中,对角线AC与BD相交于点O,已知∠OAB=90°,OC=3cm,AB=4cm,求BD、AD的长度.
3.(10分)如图7,在△ABC中,AD是角平分线,DE∥AC交AB于E,EF∥BC交AC于F.请猜想AE与CF的关系,并说明你的理由.
4.(11分)如图8,延长□ABCD的边BA到E,延长DC到F,使BE=DF.则AC与EF互相平分吗?请说明理由.
四、拓广探索(11分)
如图9,□ABCD中,AC是对角线,B M⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?为什么?
提升能力题:
1.如图1,在四边形ABCD中,AB∥DC,对角线AC、BD交于点O,EF 过O点交AB于E,交CD于F,且OE=OF,则四边形ABCD是平行四边形,试说明理由.
2.如图2,在□ABCD中,E、F分别为AD、BC的中点,AF与BE交于G,DF与CE交于H.则四边形EGFH能够是平行四边形吗?请说明理由.
3.如图3,在□ABCD中,点E、F在对角线AC上,且AE=CF.请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想
并说明它和图中已知的某一线段相等(只需说明一组线段相等即可)
(1)连接.
(2)猜想:= .
(3)试说明理由.
参考答案
一、1.8,12
2.6cm,4cm
3.4
4.30°
5.∠A=∠C=40°,∠B=∠D=140°
6.平行四边形
7.5cm
8.OA,平行四边形,两条对角线互相平分的四边形是平行四边形
二、1.C 2.D 3.A 4.A 5.A 6.D 7.C 8.C
三、1.BC=8cm,AC=20cm.
2.BD=10cm,AD=
3.AE=CF.
理由略.
4.AC与EF互相平分.理由略.
四、解:四边形BMDN是平行四边形.
理由:因为DN⊥AC,BM⊥AC,所以DN∥BM.
因为四边形ABCD是平行四边形,所以AD=BC,AD∥BC,所以∠DAN=∠BCM.
又因为∠AND=∠BMC=90°,所以△ADN≌△CBM.所以DN=BM.
所以四边形BMDN是平行四边形.
提升能力题答案:
1.四边形ABCD是平行四边形.
2.四边形EGFH是平行四边形.理由略.
3.(1)BF;
(2)BF=DE;
(3)理由:因为四边形ABCD是平行四边形,所以AD=BC,AD∥BC.所以∠DAE=∠BCF.
又因为AE=CF,所以△ADE≌△CBF.所以BF=DE.。
