考研三角函数公式
考研数学必备公式不看后悔

考研数学必备公式不看后悔IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】一. 三角公式1. 倍角公式与半角公式x x x cos sin 22sin =; x x x x x 2222sin 211cos 2sin cos 2cos -=-=-= 2cos 2cos 12x x =+, 或2cos 12cos 2x x += 2sin 2cos 12xx =-, 或2cos 12sin 2x x -=2. 三角函数定义与恒等式sin α=对边/斜边; cos α=邻边/斜边; tan α=对边/邻边; 1cos sin 22=+x x ; 22sec tan 1x x =+, 22tan sec 1x x =-xxx cos sin tan =; xx cos 1sec =3. 特殊角的三角与反三角函数值, 三角函数在四个象限中的符号arctan()/2π+∞=; arctan()/2π-∞=-,0e e +∞-∞=+∞=, ln(),ln 0++∞=+∞=-∞-- 1 -- 3. 诱导公式sin()cos 2παα-=; cos()sin 2παα-=; tan()cot 2παα-=;sin()sin παα-=; cos()cos παα-=-; tan()tan παα-=- ααsin )sin(-=-; ααcos )cos(=-; ααtan )tan(-=- 二.代数公式1.2)1(321+=+⋅⋅⋅⋅+++n n n (等差数列求和公式)2.21111n n a a aaa--+++⋅⋅⋅+=- (等比数列求和公式,1a <)或 )1)(1(121++⋅⋅⋅++-=---a a a a a n n n3.2222)(b ab a b a +±=± (和差的平方公式)3223333)(b ab b a a b a ±+±=± (和差的立方公式) ))((22b a b a b a -+=- (平方差公式)))((2233b ab a b a b a +±=± (立方和、立方差公式)4.指数运算: c b c b a a a +=⋅; /b c b c a a a -=; bc c b a a =)(;()c c c a b a b ⋅=⋅; (/)/c c c a b a b =; 10=a ; 11/a a -=5. 对数运算: c b bc a a a log log )(log +=;log log log aa ab bc c=-; b b a a log 1log -=log log c a a b c b =; log b a b a =; 特别 ln b b e =log 10a =; log 1a a =; 特别 ln10=,ln 1e =;6. 基本不等式: x a a x a <⇔-<< (其中0a >)222a b ab +≥, 也可写成当,0a b >时成立a b +≥-- 2--7. 一元二次方程20ax bx c ++=求根公式: 有解1,22b x a-=三.极限 四. 平面解析几何 1.直线方程:y kx b =+ (斜截式:斜率为k ,y 轴上截距为b );00()y y k x x -=- (点斜式: 过点00(,)x y ,斜率为k );1x ya b+= (截距式: x 与y 轴上截距分别为a 与b )0ax by c ++= (一般式) 两直线垂直⇔它们的斜率为负倒数关系 121/k k =-。
整理高数微积分公式+三角函数公式考研

高数微积分公式三角函数公式考研整理表姓名:职业工种:申请级别:受理机构:填报日期:A4打印/ 修订/ 内容可编辑高等数学公式导数公式:基本积分表:三角函数的有理式积分:一些初等函数:两个重要极限:三角函数公式:·诱导公式:·和差角公式:·和差化积公式:·倍角公式:·半角公式:·正弦定理:·余弦定理:·反三角函数性质:高阶导数公式——莱布尼兹(Leibniz)公式:中值定理与导数应用:曲率:定积分的近似计算:定积分应用相关公式:空间解析几何和向量代数:文件编号:F8-65-23-08-CC 多元函数微分法及应用微分法在几何上的应用:文件编号:F8-65-23-08-CC 方向导数与梯度:多元函数的极值及其求法:重积分及其应用:柱面坐标和球面坐标:曲线积分:曲面积分:高斯公式:斯托克斯公式——曲线积分与曲面积分的关系:常数项级数:级数审敛法:绝对收敛与条件收敛:幂级数:函数展开成幂级数:一些函数展开成幂级数:欧拉公式:三角级数:傅立叶级数:周期为的周期函数的傅立叶级数:微分方程的相关概念:一阶线性微分方程:全微分方程:二阶微分方程:二阶常系数齐次线性微分方程及其解法:二阶常系数非齐次线性微分方程整理丨尼克本文档信息来自于网络,如您发现内容不准确或不完善,欢迎您联系我修正;如您发现内容涉嫌侵权,请与我们联系,我们将按照相关法律规定及时处理。
考研数学公式大全(考研必备)

高等数学公式篇·平方关系:sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系:sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·三角函数恒等变形公式:·两角和与差的三角函数:cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·辅助角公式:Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B·倍角公式:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]·三倍角公式:sin(3α)=3sinα-4sin^3(α)cos(3α)=4cos^3(α)-3cosα·半角公式:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))·万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-c osβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0三角函数的角度换算[编辑本段]公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=c osαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-t anαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)部分高等内容[编辑本段]·高等代数中三角函数的指数表示(由泰勒级数易得):sinx=[e^(ix)-e^(-ix)]/(2i) cosx=[e^(ix)+e^(-ix)]/2 tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)] 泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n !+… 此时三角函数定义域已推广至整个复数集。
详细的三角函数公式分类表-考研必备
万能公式
sin 2 tan( / 2) 1 tan 2( / 2) 1 tan 2( / 2) 1 tan 2( / 2) 2 tan( / 2) 1 tan 2( / 2)
cot( ) cot
sin(2 ) sin cos(2 ) cos tan(2 ) tan cot(2 ) cot
(其中 k∈Z)
2
) cos ) sin ) cot ) tan ) cos ) sin ) cot ) tan
cos( tan( cot(
2 2
2
sin(
2
cos( tan( cot(
2 2
sin(
sin( ) sin cos( ) cos tan( ) tan cot( ) cot
sin(2 ) sin cos(2 ) cos tan(2 ) tan cot(2 ) cot
二倍角的正弦、余弦和正切公式
sin 2 2sin cos cos 2 cos 2 sin 2 2 cos 2 1 1 2sin 2
三倍角的正弦、 余弦和正切公式
sin 3 3sin 4sin 3 cos 3 4 cos 3 3cos . tan 3 3 tan tan 3 1 3 tan 2
பைடு நூலகம்
cos
考研数学三公式大全

高等数学公式导数公式:基本积分表:ax x a a a x x x x x x x x x x a x x ln 1)(log ln )(cot csc )(csc tan sec )(sec csc )(cot sec )(tan 22='='⋅-='⋅='-='='222211)cot (11)(arctan 11)(arccos 11)(arcsin x x arc x x x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx xdx x Cx dx x x Cx xdx x dx C x xdx x dx xx)ln(ln csc cot csc sec tan sec cot csc sin tan sec cos 22222222Ca x x a dx C x a xa a x a dx C a x ax a a x dx C a xa x a dx Cx x xdx C x x xdx Cx xdx C x xdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 21arctan 1cot csc ln csc tan sec ln sec sin ln cot cos ln tan 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ三角函数的有理式积分:222212211cos 12sin ududx x tg u u u x u u x +==+-=+=, , , A 。
考研数学公式大全(考研同学必备)

考研数学公式(全) ·平方关系:sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系:sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·三角函数恒等变形公式·两角和与差的三角函数:cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tan α)·辅助角公式:Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B·倍角公式:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]·三倍角公式:sin(3α)=3sinα-4sin^3(α)cos(3α)=4cos^3(α)-3cosα·半角公式:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))·万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)] tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)] cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)] cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)] sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2] cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2] cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0 cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0三角函数的角度换算[编辑本段]公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)部分高等内容[编辑本段]·高等代数中三角函数的指数表示(由泰勒级数易得):sinx=[e^(ix)-e^(-ix)]/(2i) cosx=[e^(ix)+e^(-ix)]/2tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+…此时三角函数定义域已推广至整个复数集。
考研数学三角函数公式

sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα
sin(3π/2-α)= sin(2π-α)=-
-cosα
sinα
cos(3π/2-α)= cos(2π-α)=
sin(-α)=-sinα
诱导公式(口诀:奇变偶不变,符号看象限)
cos(-α)=cosα
tan(-α)=-tanα cot(-α)=-cotα
sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα
sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα
cosα+cosβ=2cos———·cos——— 2 α+β
cosα-cosβ=-2sin———·sin——— 2
2 α-β
2
1
cosα ·cosβ=-[cos(α+β)+
cos(α-β)]
2
2
1
sinα ·sinβ=- -[cos(α+β)
-cos(α-β)]
2
化 asinα ±bcosα 为一个角的一个三角函数的形式(辅助角的三角函数的公式)
tanα+tanβ tan(α+β)=——————
1-tanα ·tanβ
tanα-tanβ tan(α-β)=——————
1+tanα ·tanβ
半角的正弦、余弦和正切公式
1+tan2(α/2) 1-tan2(α/2) cosα=—————— 1+tan2(α/2) 2tan(α/2) tanα=—————— 1-tan2(α/2)
考研数学三知识点总结

重要极限 lim
x →0
sinx =1 x
1 x lim ( 1 + ) = e x x →∞
lim ( 1 + x ) =e
x →0
1 x
x 趋向于 0 时的等价无穷小
sinx ∼ x tanx ∼ x arcsinx ∼ x arctanx ∼ x 1 2 1− cosx∼ x 2
ln ( 1 + x )∼ x
n 1+ x − 1 ∼ √
log a ( x +1 )∼
x lna
e x −1∼ x
a x −1∼ xlna
x n
( 1+bx )a−1 ∼abx
导数公式 ( a x )' = a x lna ( tanx )' = sec 2 x ( arcsinx )' = 1 √1− x 2
( log a x ) =
1 2 圆锥体积 V = π r h 3
4 3 球体积 V = π r 3
交点坐标 (
p ,0) 2
准线 x =−
p 2Βιβλιοθήκη ∣ax 0+by 0+ c∣
√a 2 +b2
第一类间断点:包括可去间断点和跳跃间断点。 可去间断点:间断点处左右极限存在但不等于该点函数值。 f ( x 0+ 0 )= f ( x 0− 0 )≠ f ( x 0) 跳跃间断点:间断点处左右极限存在但不相等。 f ( x 0+ 0 )≠ f ( x 0−0 ) 第二类间断点:间断点处左右极限至少有一个是∞
cos ( A+ B)=cosAcosB + sinAsinB sin ( A+ B )= sinAcosB + cosAsinB 1 sinxcosx = sin2x 2
考研高数必背公式

对于考研高等数学,以下是一些常见的必背公式:1. 导数公式:- $(c)'=0$(常数的导数为零)- $(x^n)'=nx^{n-1}$(幂函数的导数)- $(e^x)'=e^x$(指数函数的导数)- $(\ln x)'=\frac{1}{x}$(自然对数函数的导数)- $(\sin x)'=\cos x$(正弦函数的导数)- $(\cos x)'=-\sin x$(余弦函数的导数)- $(\tan x)'=\sec^2 x$(正切函数的导数)2. 积分公式:- $\int k \,dx=kx+C$(常数的积分)- $\int x^n \,dx=\frac{1}{n+1}x^{n+1}+C$(幂函数的积分)- $\int e^x \,dx=e^x+C$(指数函数的积分)- $\int \frac{1}{x} \,dx=\ln |x|+C$(倒数函数的积分)- $\int \sin x \,dx=-\cos x+C$(正弦函数的积分)- $\int \cos x \,dx=\sin x+C$(余弦函数的积分)- $\int \sec^2 x \,dx=\tan x+C$(正切函数的积分)3. 三角函数关系:- $\sin^2 x + \cos^2 x = 1$(三角恒等式)- $\sin (2x) = 2\sin x \cos x$(双角正弦公式)- $\cos (2x) = \cos^2 x - \sin^2 x$(双角余弦公式)- $\tan x = \frac{\sin x}{\cos x}$(正切的定义)这些是考研高等数学中的一些常见公式,但并非全部。
在复习过程中,建议根据自己的教材和课程重点,对相关公式进行系统性的整理和复习。
不仅要记住公式,还要了解其推导和应用方法,以便在解题过程中能够熟练运用。
同时,还要注重理解概念和原理,培养灵活的思维和解题能力。
考研三角函数公式大全

三角函数相关公式大全一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=,正弦:r y =αsin 余弦:r x=αcos 正切:xy=αtan 余切:y x =αcot正割:xr=αsec 余割:yr =αcsc 注:我们还可以用单位圆中的有向线段表示任意角的三角函数:如图,与单位圆有关的有向..线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线。
二、同角三角函数的基本关系式倒数关系:1csc sin =⋅αα,1sec cos =⋅αα,1cot tan =⋅αα。
商数关系:αααcos sin tan =,αααsin cos cot =。
平方关系:1cos sin22=+αα,αα22sec tan 1=+,αα22csc cot 1=+。
三、诱导公式⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
(口诀:函数名不变,符号看象限)⑵απ+2、απ-2、απ+23、απ-23的三角函数值,等于α的异名函数值,前面加上一个把α看成..锐角时原函数值的符号。
(口诀:函数名改变,符号看象限) 四、和角公式和差角公式βαβαβαsin cos cos sin )sin(⋅+⋅=+βαβαβαsin cos cos sin )sin(⋅-⋅=-βαβαβαsin sin cos cos )cos(⋅-⋅=+ βαβαβαsin sin cos cos )cos(⋅+⋅=-βαβαβαtan tan 1tan tan )tan(⋅-+=+βαβαβαtan tan 1tan tan )tan(⋅+-=-五、倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=ααα2tan 1tan 22tan -=ααα3sin 4sin 33sin -= αααcos 3cos 43cos 3-=二倍角的余弦公式)(*有以下常用变形:(规律:降幂扩角,升幂缩角) αα2cos 22cos 1=+ αα2sin 22cos 1=-1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )22)cos (sin 2sin 1ααα+=+ 2)cos (sin 2sin 1ααα-=- 22cos 1cos 2αα+=,22sin 1sin 2αα+=,ααααα2cos 12sin 2sin 2cos 1tan +=-=。
考研-三角函数公式大全
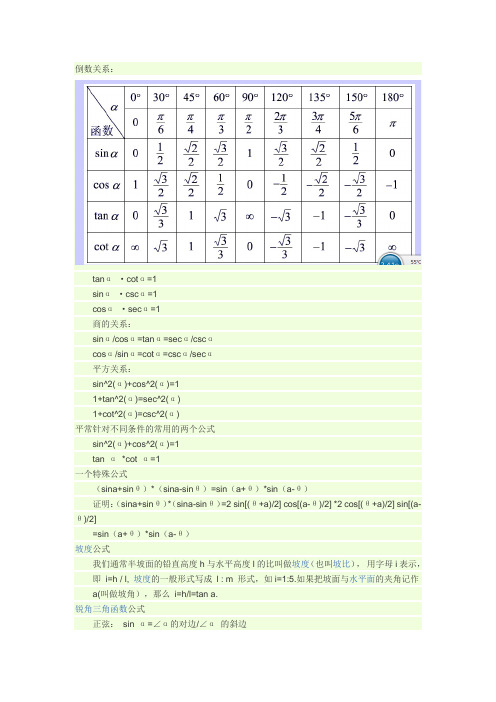
倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系:sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α*cot α=1一个特殊公式(sina+sinθ)*(sina-sinθ)=sin(a+θ)*sin(a-θ)证明:(sina+sinθ)*(sina-sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2]=sin(a+θ)*sin(a-θ)坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比),用字母i表示,即i=h / l, 坡度的一般形式写成l : m 形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角),那么i=h/l=tan a.锐角三角函数公式正弦:sin α=∠α的对边/∠α的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.k3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a)正切tan2A=(2tanA)/(1-tan^2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a ·tan(π/3+a)·tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2] =4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)^2]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下: sin2α=2sinαcosαtan2α=2tanα/(1-tan^2(α)) cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用。
考研数学三公式大全

考研数学三公式大全1.二项式定理二项式定理是数学中常用的公式之一,它表达了两个数之和的n次幂的展开式。
二项式定理的公式如下:(a+b)^n=C(n,0)*a^n+C(n,1)*a^(n-1)*b+C(n,2)*a^(n-2)*b^2+...+C(n,n)*b^n其中C(n,k)表示组合数,可以通过以下公式计算:C(n,k)=n!/(k!*(n-k)!)2.三角函数的和差公式三角函数的和差公式是在三角函数的加减情况下,将两个三角函数用一个三角函数表示的公式。
常用的三角函数的和差公式如下:sin(A±B) = sinA*cosB ± cosA*sinBcos(A±B) = cosA*cosB ∓ sinA*sinBtan(A±B) = (tanA ± tanB) / (1 ∓ tanA*tanB)3.倍角公式和半角公式倍角公式和半角公式是将一个角的倍数或一半角表示为其他角的公式。
常用的倍角公式和半角公式如下:sin2A = 2*sinA*cosAcos2A = cos^2A - sin^2A = 2*cos^2A - 1 = 1 - 2*sin^2Atan2A = (2*tanA) / (1 - tan^2A)sin^2(A/2) = (1 - cosA) / 2cos^2(A/2) = (1 + cosA) / 24.位移公式位移公式是描述一个物体运动过程中的位移与时间、初速度、加速度之间的关系公式。
常用的位移公式如下:s = vt + (1/2)*a*t^2v=u+a*tv^2=u^2+2*a*s其中s表示位移,v表示末速度,u表示初速度,t表示时间,a表示加速度。
5.高中几何常用公式高中几何常用公式是在解决几何题目时经常用到的公式,包括三角形的面积公式、直角三角形的勾股定理等。
常用的高中几何常用公式如下:三角形面积公式:S = (1/2)*a*b*sinC直角三角形勾股定理:a^2+b^2=c^2正弦定理:a/sinA = b/sinB = c/sinC余弦定理:a^2 = b^2 + c^2 - 2bc*cosA6.概率公式概率公式用于计算事件发生的可能性。
考研数学必备三角函数转换

y arctgx
R
增
, 2 2
arctg(-x) - arctgx 奇
y arcctgx
R
减
0,
arcctg( x ) arcctgx
⒗最简单的三角方程 方程
sin x a
方程的解集
a 1 a 1
x | x 2k arcsin a, k Z
sec 2 x tan 2 x 1
csc 2 x cot 2 x 1
⑷ a sin b cos a 2 b 2 sin( ) 一象限,且 tg )
b a
(其中辅助角 与点(a,b)在同
⒍函数 y= A sin( x ) k 的图象及性质: ( 0, A 0 )
3
② cos 3 3 cos 4 cos3 4 cos cos(60 ) cos(60 ) ③ tg 3
3tg tg 3 tg tg (60 ) tg (60 ) 1 3tg 2
⒓半角公式: (符号的选择由 所在的象限确定) ① sin
a 2 sin B sin C b 2 sin A sin C c 2 sin A sin B = = =pr= p ( p a )( p b)( p c ) 2 sin A 2 sin B 2 sin C
1 2
(其中 p ( a b c ) , r 为三角形内切圆半径) ⒌同角关系: ⑴商的关系: ① tg = =
1 cos 2 2
1 cos 2 2
2
② sin 2
1 cos 2 2 2
③ cos
考研三角函数公式大全

三角函数相关公式大全一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=,正弦:r y =αsin 余弦:r x=αcos 正切:x y =αtan 余切:y x=αcot正割:x r =αsec 余割:yr=αcsc注:我们还可以用单位圆中的有向线段表示任意角的三角函数:如图,与单位圆有关的有向..线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线。
二、同角三角函数的基本关系式倒数关系:1csc sin =⋅αα,1sec cos =⋅αα,1cot tan =⋅αα。
商数关系:αααcos sin tan =,αααsin cos cot =。
平方关系:1cos sin 22=+αα,αα22sec tan 1=+,αα22csc cot 1=+。
三、诱导公式⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
(口诀:函数名不变,符号看象限)⑵απ+2、απ-2、απ+23、απ-23的三角函数值,等于α的异名函数值,前面加上一个把α看成..锐角时原函数值的符号。
(口诀:函数名改变,符号看象限) 四、和角公式和差角公式βαβαβαsin cos cos sin )sin(⋅+⋅=+βαβαβαsin cos cos sin )sin(⋅-⋅=- βαβαβαsin sin cos cos )cos(⋅-⋅=+ βαβαβαsin sin cos cos )cos(⋅+⋅=-βαβαβαtan tan 1tan tan )tan(⋅-+=+ βαβαβαtan tan 1tan tan )tan(⋅+-=-五、倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=ααα3sin 4sin 33sin -= αααcos 3cos 43cos 3-=二倍角的余弦公式)(*有以下常用变形:(规律:降幂扩角,升幂缩角) αα2cos 22cos 1=+ αα2sin 22cos 1=-1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )22 2六、半角公式七、万能公式(可以理解为二倍角公式的另一种形式)ααα2tan 1tan 22sin +=,ααα22tan 1tan 12cos +-=,ααα2tan 1tan 22tan -=。
考研反三角函数公式

考研反三角函数公式
在考研数学中,反三角函数是一个常考的知识点,其中包含了很多重要的公式。
这些公式需要我们熟练掌握,才能在考试中得心应手。
以下是一些常见的反三角函数公式:
1. $sin^{-1}x+cos^{-1}x=frac{pi}{2}$,其中$-1le xle 1$。
2. $tan^{-1}x+cot^{-1}x=frac{pi}{2}$,其中$x>0$。
3. $sin^{-1}x=cos^{-1}sqrt{1-x^2}$,其中$-1le xle 1$。
4. $cos^{-1}x=sin^{-1}sqrt{1-x^2}$,其中$-1le xle 1$。
5.
$tan^{-1}x=sin^{-1}frac{x}{sqrt{1+x^2}}=cos^{-1}frac{1}{sqr t{1+x^2}}$,其中$xin R$。
6. $sin(tan^{-1}x)=frac{x}{sqrt{1+x^2}}$,其中$xin R$。
7. $cos(tan^{-1}x)=frac{1}{sqrt{1+x^2}}$,其中$xin R$。
以上这些公式是我们在考研数学中需要掌握的反三角函数公式。
我们需要通过不断地练习和总结,来提高我们的数学水平,顺利通过考试。
- 1 -。
考研极限公式范文

考研极限公式范文1.常见的基本极限:- $\lim_{n\to\infty}(1+\frac{1}{n})^n=e$- $\lim_{n\to\infty}{\frac{1}{n^p}}=0$ ($p>0$)- $\lim_{n\to\infty}{\sqrt[n]{a}}=1$ ($a>0$)2.三角函数的极限:- $\lim_{x\to0}\frac{\sin x}{x}=1$- $\lim_{x\to0}\frac{\tan x}{x}=1$- $\lim_{x\to0}\frac{1-\cos x}{x^2}=\frac{1}{2}$3. $e^x$和$\ln x$的极限:- $\lim_{x\to0}\frac{e^x-1}{x}=1$- $\lim_{x\to+\infty}(1+\frac{1}{x})^x=e$- $\lim_{x\to0}\frac{\ln(1+x)}{x}=1$4.可用洛必达法则求解的一些极限:- $\lim_{x\to0}\frac{\sin x}{x}=1$- $\lim_{x\to+\infty}\ln x=x$- $\lim_{x\to0}\frac{\ln(1+x)}{x}=1$5.无穷小形式:- $\sin x \sim x$- $\tan x \sim x$- $1-\cos x \sim \frac{1}{2}x^2$需要说明的是,这些极限公式只是考研数学中的一部分公式,掌握它们可以帮助我们在解题时更快地得到结果,但并不是解题的核心。
在考研数学中,重要的是掌握解题的思路和方法,理解题目的要求,合理运用公式和定理。
综合运用各种公式和解题方法,灵活解决各种题目才是最关键的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
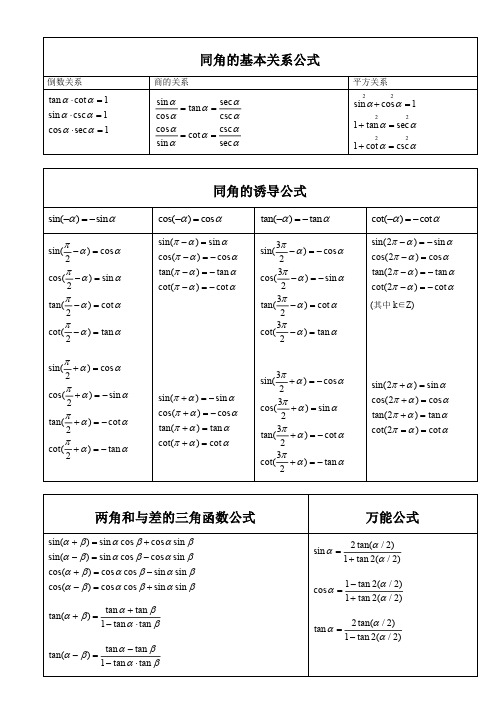
【2012考研必备资料】三角函数公式表
同角三角函数的基本关系式
倒数关系: 商的关系:平方关系:
tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 sinα/cosα=tanα=secα/cscα
cosα/sinα=cotα=cscα/secα
sin2α+cos2α=1
1+tan2α=sec2α
1+cot2α=csc2α
(六边形记忆法:图形结构“上弦中切下割,左正右余
中间1”;记忆方法“对角线上两个函数的积为1;阴影
三角形上两顶点的三角函数值的平方和等于下顶点的三
角函数值的平方;任意一顶点的三角函数值等于相邻两
个顶点的三角函数值的乘积。
”)
诱导公式(口诀:奇变偶不变,符号看象限。
)
sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα
sin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanα
sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sin(3π/2-α)=-
cosα
cos(3π/2-α)=-
sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
sin(3π/2+α)=-
cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-
cotα
cot(3π/2+α)=-
tanα
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
(其中k∈Z)
两角和与差的三角函数公式万能公式
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
tanα+tanβ
tan(α+β)=——————
1-tanα ·tanβ
2tan(α/2) sinα=——————
1+tan2(α/2)
1-tan2(α/2) cosα=——————
1+tan2(α/2)
2tan(α/2) tanα=——————
tanα-tanβ
tan(α-β)=——————
1+tanα ·tanβ
1-tan2(α/2)
半角的正弦、余弦和正切公式三角函数的降幂公式
二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式
sin2α=2sinαcosα
cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α
2tanα
tan2α=—————
1-tan2αsin3α=3sinα-4sin3α
cos3α=4cos3α-3cosα
3tanα-tan3αtan3α=——————
1-3tan2α
三角函数的和差化积公式三角函数的积化和差公式
α+βα-β
sinα+sinβ=2sin———·cos———
2 2
α+βα-β
sinα-sinβ=2cos———·sin———
2 2
α+βα-β
cosα+cosβ=2cos———·cos———
2 2
α+βα-β
cosα-cosβ=-2sin———·sin———
2 2 1
sinα·cosβ=-[sin(α+β)+sin(α-β)]
2
1
cosα·sinβ=-[sin(α+β)-sin(α-β)]
2
1
cosα·cosβ=-[cos(α+β)+cos(α-β)]
2
1
sinα·sinβ=—-[cos(α+β)-cos(α-
β)]
2
化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)。
