SPSS课件第11章
合集下载
《SPSS统计分析》第11章 回归分析
返回目录
多元逻辑斯谛回归
返回目录
多元逻辑斯谛回归的概念
回归模型
log( P(event) ) 1 P(event)
b0
b1 x1
b2 x2
bp xp
返回目录
多元逻辑斯谛回归过程
主对话框
返回目录
多元逻辑斯谛回归过程
参考类别对话框
保存对话框
返回目录
多元逻辑斯谛回归过程
收敛条件选择对话框
创建和选择模型对话框
返回目录
曲线估计
返回目录
曲线回归概述
1. 一般概念 线性回归不能解决所有的问题。尽管有可能通过一些函数
的转换，在一定范围内将因、自变量之间的关系转换为线性关 系，但这种转换有可能导致更为复杂的计算或失真。 SPSS提供了11种不同的曲线回归模型中。如果线性模型不能确 定哪一种为最佳模型，可以试试选择曲线拟合的方法建立一个 简单而又比较合适的模型。 2. 数据要求
线性回归分析实例1输出结果2
方差分析
返回目录
线性回归分析实例1输出结果3
逐步回归过程中不在方程中的变量
返回目录
线性回归分析实例1输出结果4
各步回归过程中的统计量
返回目录
线性回归分析实例1输出结果5
当前工资变量的异常值表
返回目录
线性回归分析实例1输出结果6
残差统计量
返回目录
线性回归分析实例1输出结果7
返回目录
习题2答案
使用线性回归中的逐步法，可得下面的预测商品流通费用率的回归系数表：
将1999年该商场商品零售额为36.33亿元代入回归方程可得1999年该商场 商品流通费用为：1574.117-7.89*1999+0.2*36.33=4.17亿元。
《统计分析与SPSS的应用》课后练习答案(第11章)
《统计分析与SPSS的应用（第五版）》（薛薇）课后练习答案第11章SPSS的因子分析1、简述因子分析的主要步骤是什么因子分析的主要步骤：一、前提条件：要求原有变量之间存在较强的相关关系。
二、因子提取。
三、使因子具有命名解释性：使提取出的因子实际含义清晰。
四、计算样本的因子得分。
2、对“基本建设投资分析.sav ”数据进行因子分析。
要求：1）利用主成分方法，以特征根大于1为原则提取因子变量，并从变量共同度角度评价因子分析的效果。
如果因子分析效果不理想，再重新指定因子个数并进行分析，对两次分析结果进行对比。
2）对比未旋转的因子载荷矩阵和利用方差极大法进行旋转的因子载荷矩阵，直观理解因子旋转对因子命名可解释性的作用。
“基本建设投资分析”因子分析步骤：分析降维因子分析导入全部变量到变量框中详细设置描述、抽取的设置如下: -相黄性舸阵［3□逆模型迥）显1F 性水平逞）□再生迟） □柠別式也）上厦映象追）V 邕M 。
和Bartiettm 形度橙验旋转、得分、选项的设置如下:./丘示圜子卷敘粗胖I 』［ai~J匚淙存n 欝童海© BarJet瞅■!圖丽药亟T 矗匸Q 脚dii*A3R 迟》0晰平即口甘描因亶除■£洞&式E 卜曲/ 牺削'■:诩|型J®J（3S1T ；■■ ■昌同子分疔信辻统计Statistics(1)表一是原有变量的相关系数矩阵。
由表可知，一些变量的相关系数都较高，呈较强的线由表二可知，巴特利特球度检验统计量的观测值为，相应的概率 性水平为，由于概率P-值小于显著性水平a,则应拒绝原假设，认为相关系数矩阵与单位P-值接近0.如果显著阵有显著差异，原有变量适合做因子分析。
同时, 量可以进行因子分析。
KMO 直为，根据KMC 度量标准可知原有变由表三可知，利用外资、自筹资金、其他投资等变量的绝大部分信息（大于 因子解释，这些变量的信息丢失较少。
但国家预算内资金这个变量的信息丢失较为严重（近80%。
11+++参数估计 spss课件 教学课件
• 置信度，即置信概率，是作出某种推断时 正确的可能性（概率）。
2020/6/17
显著性水平
• 对总体平均数进行区间估计时，置信概率表 示做出正确推断的可能性，但这种估计还是 会有犯错误的可能。显著性水平 (significance level)就是指估计总体参数落 在某一区间时，可能犯错误的概率，用符号 α表示。 P＝１-α
pq pq
S
P1P2
n1 n2
(n1p1n2p2)(n1q1n2q2) n1n（ 2 n1n2）
2020/6/17
当两个样本的容量相等时，上式可以化简为：
S 2pq (p1p2)q (1q2)
P 1P 2
n
2n
2020/6/17
2020/6/17
二．总体平均数的区间估计
1．总体平均数区间估计的基本步骤 ①．根据样本的数据，计算样本的平均数和标
准差；
②．计算平均数抽样分布的标准误；
③．确定置信概率或显著性水平；
④．根据样本平均数的抽样分布确定查何种统 计表；
2020/6/17
2．平均数区间估计的计算
①总体正态，σ已知（不管样本容量大小），
2020/6/17
例2
• 从某区随机抽取100个中学生，查得正常视力有65人， 若用样本比率p=0.65来估计全区中学生正常视力的比率，那么 全区中学生正常视力的比率0.95和0.99的置信区间各是什么？
2020/6/17
查表法
• 例1：有研究者从7岁儿童中随机抽取了100名被试进行了 一项智力测查，结果发现，IQ在70分以下的（弱智）有2人，试 估计7岁儿童从总体上看弱智的发生率是多少？
第十一讲 参数估计
2020/6/17
2020/6/17
显著性水平
• 对总体平均数进行区间估计时，置信概率表 示做出正确推断的可能性，但这种估计还是 会有犯错误的可能。显著性水平 (significance level)就是指估计总体参数落 在某一区间时，可能犯错误的概率，用符号 α表示。 P＝１-α
pq pq
S
P1P2
n1 n2
(n1p1n2p2)(n1q1n2q2) n1n（ 2 n1n2）
2020/6/17
当两个样本的容量相等时，上式可以化简为：
S 2pq (p1p2)q (1q2)
P 1P 2
n
2n
2020/6/17
2020/6/17
二．总体平均数的区间估计
1．总体平均数区间估计的基本步骤 ①．根据样本的数据，计算样本的平均数和标
准差；
②．计算平均数抽样分布的标准误；
③．确定置信概率或显著性水平；
④．根据样本平均数的抽样分布确定查何种统 计表；
2020/6/17
2．平均数区间估计的计算
①总体正态，σ已知（不管样本容量大小），
2020/6/17
例2
• 从某区随机抽取100个中学生，查得正常视力有65人， 若用样本比率p=0.65来估计全区中学生正常视力的比率，那么 全区中学生正常视力的比率0.95和0.99的置信区间各是什么？
2020/6/17
查表法
• 例1：有研究者从7岁儿童中随机抽取了100名被试进行了 一项智力测查，结果发现，IQ在70分以下的（弱智）有2人，试 估计7岁儿童从总体上看弱智的发生率是多少？
第十一讲 参数估计
2020/6/17
第十一章SPSS的时间序列分析
3.1 AR（自回归）模型
一般地，如果和p个过去值有关则是p阶自回归模型， 记为AR（p），表达式为： xt 0 1 xt 1 2 xt 2 p xt p t
(B) xt t
或者
其中， (B) 1 1 B 2 B 2 p B p
1 - 12
第三节 时间序列的图形化观察
4、互相关图（CCF） 对两个互相对应的时间序列进行相关性分 析，检验一个序列与另一个序列的滞后 序列之间的相关性 Analyze>Forecasting>Cross Correlations 举例： GDP与通信业务收入，0阶滞后相关性最显 著
1 - 13
3.2 MA模型
（Moving Average Model）
3.3 ARMA模型
（Auto Regression Moving Average model）
3.4 ARIMA模型
（ Autoregressive Integrated Moving Average Model ）
1 - 22
3.1 AR（自回归）模型
1 - 15
第六节 ARIMA模型
ARIMA模型全称为自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA)，是由博克 思(Box)和詹金斯(Jenkins)于70年代初提出的著名时间序列 预测方法，所以又称为box-jenkins模型、博克思-詹金斯法。
第十一章 SPSS的时间序列分析
1-1
第一节 时间序列分析概述
一、相关概念 时间序列：有序的数列：y1,y2,y3,…yt 理解： 1、有先后顺序且时间间隔均匀的数列； 2、随机变量族或随机过程的一个“实现” ，即在每一个固定时间点t上，现象yt看 作是一个随机变量， y1,y2,y3,…yt是一系 列随机变量所表现的一个结果。
SPSS数据分析问题提出与实例导学 第11章 效度检验因素分析.ppt
SPSS数据分析： 问题提出与实例导学
（第十一部分）
主讲：赵小军（安庆师范学院） 祁禄（广州大学）
第十一章 效度检验――因素分析
第一节 因素分析统计知识简介
一、R型因子分析与Q型因子分析
R型因子分析是针对变量所做的因子分析，其 基本思想是通过对变量的相关系数矩阵内部结构 的研究，找出能够控制所有变量的少数几个随机 变量去描述多个随机变量之间的相关关系。但这 少数几个随机变量是不能直接观测的，通常称为 因子。然后再根据相关性的大小把变量分组，使 同组内的变量之间的相关性较高，不同组变量之 间的相关性较低。Q型因子分析是针对样品所做 的因子分析。
具体来讲，探索性因素分析与验证性因素分析模型假设有一些区分: 【探索性因素分析的假设】
（1）所有的公共因素都相关（或都无关）； （2）所有的公共因素直接影响所有的观测变量； （3）特殊因素之间相互独立； （4）所有观测变量只受一个特殊因素的影响； （5）公共因素和特殊因素相互独立 ； （6） 观测变量与潜在变量之间的关系不是事先假定的； （7）潜在变量的个数不是在分析前确定的； （8）模型通常是不可识别的。 【验证性因素分析的假设】
correlation matrix框： coefficients:相关系数矩阵 significance level:显著性水平 determinant:相关系数矩阵的行列式 inverse:相关系数矩阵的逆矩阵 reproduced:由k（k≤m）个主成分再生的原变量相关系数矩阵 anti-image:反映象相关矩阵 KMO and Bartlett’s test of sphericity ：KMO检验和Bartlett检 验，它是对分析模型的适宜程度的检验。（必选）
（1）正交旋转：正交，指旋转过程中，因子之间 的轴线夹角为90度，即因子之间的相关设定为0。 有最大变异法，四方最大法，均等变异法。 （2）斜交旋转：先求得在正交因素模型下的因素 负荷矩阵B，然后对因素负荷矩阵A作斜交变换T*， 求得斜交负荷矩阵A*=BT*。这种方法因子与因子 之间具有一定的相关性。有最小斜交法，最大斜 交法和四方最小法。 至于采用何种转轴法，研究者可以根据文献探究 与理论基础分析结果作为依据，如果相关理论上 显示共同因素层面间是彼此独立，没有关系存在 的，则应采取正交转轴法；如果依理论研究所得， 因素层面间，彼此有相关并且非独立的，则应采 取斜交转轴法。在心理学与教育学中，更多的可 能应该选择斜交旋转。
（第十一部分）
主讲：赵小军（安庆师范学院） 祁禄（广州大学）
第十一章 效度检验――因素分析
第一节 因素分析统计知识简介
一、R型因子分析与Q型因子分析
R型因子分析是针对变量所做的因子分析，其 基本思想是通过对变量的相关系数矩阵内部结构 的研究，找出能够控制所有变量的少数几个随机 变量去描述多个随机变量之间的相关关系。但这 少数几个随机变量是不能直接观测的，通常称为 因子。然后再根据相关性的大小把变量分组，使 同组内的变量之间的相关性较高，不同组变量之 间的相关性较低。Q型因子分析是针对样品所做 的因子分析。
具体来讲，探索性因素分析与验证性因素分析模型假设有一些区分: 【探索性因素分析的假设】
（1）所有的公共因素都相关（或都无关）； （2）所有的公共因素直接影响所有的观测变量； （3）特殊因素之间相互独立； （4）所有观测变量只受一个特殊因素的影响； （5）公共因素和特殊因素相互独立 ； （6） 观测变量与潜在变量之间的关系不是事先假定的； （7）潜在变量的个数不是在分析前确定的； （8）模型通常是不可识别的。 【验证性因素分析的假设】
correlation matrix框： coefficients:相关系数矩阵 significance level:显著性水平 determinant:相关系数矩阵的行列式 inverse:相关系数矩阵的逆矩阵 reproduced:由k（k≤m）个主成分再生的原变量相关系数矩阵 anti-image:反映象相关矩阵 KMO and Bartlett’s test of sphericity ：KMO检验和Bartlett检 验，它是对分析模型的适宜程度的检验。（必选）
（1）正交旋转：正交，指旋转过程中，因子之间 的轴线夹角为90度，即因子之间的相关设定为0。 有最大变异法，四方最大法，均等变异法。 （2）斜交旋转：先求得在正交因素模型下的因素 负荷矩阵B，然后对因素负荷矩阵A作斜交变换T*， 求得斜交负荷矩阵A*=BT*。这种方法因子与因子 之间具有一定的相关性。有最小斜交法，最大斜 交法和四方最小法。 至于采用何种转轴法，研究者可以根据文献探究 与理论基础分析结果作为依据，如果相关理论上 显示共同因素层面间是彼此独立，没有关系存在 的，则应采取正交转轴法；如果依理论研究所得， 因素层面间，彼此有相关并且非独立的，则应采 取斜交转轴法。在心理学与教育学中，更多的可 能应该选择斜交旋转。
11、spss第十一章_主成分分析和因子分析
将上表因子载荷矩阵中的数据输入SPSS数据编辑窗口中，将 3个变量名分别命名为a1,a2和a3。 用公式 e a / 计算出标准化特征向量。其步骤为：打开 Analyze→ Compute Variable，计算过程如下图所示。
ij ij i
11
西南财经大学出版社
SPSS16.0与统计数据分析
11.1 主成分析
计算结束后得到的特征向量矩阵如下表所示。
变量 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 t1 0.17 0.24 -0.06 0.36 0.25 0.34 0.11 0.26 0.25 0.22 0.27 0.27 0.35 0.30 0.24 t2 0.33 -0.30 0.01 -0.14 0.32 -0.05 -0.26 0.29 0.29 0.32 -0.29 -0.28 -0.08 -0.26 0.32 t3 0.25 0.20 0.77 -0.17 0.03 -0.26 0.17 0.04 0.01 0.18 0.16 0.16 -0.28 0.13 0.00
.268 .209 .821 -.181 .028 -.281 .184 .041 .008 .196 .172 .166 -.297 .144 .005
10
西南财经大学出版社
SPSS16.0与统计数据分析
11.1 主成分析
第5步 利用因子分析的结果进行主成分分析：上表是旋转 前的因子载荷矩阵，并不是主成分分析中所需要的标准化的 正交向量，要得到标准化正交向量还需作如下运算：
118.4
120.6 132.9 104.5 58.6 94.5 110.5
0.497
1.84 2.252 0.321 1.533 0.502 0.218
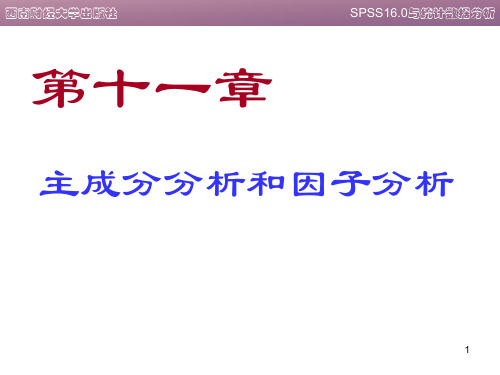
ij ij i
11
西南财经大学出版社
SPSS16.0与统计数据分析
11.1 主成分析
计算结束后得到的特征向量矩阵如下表所示。
变量 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 t1 0.17 0.24 -0.06 0.36 0.25 0.34 0.11 0.26 0.25 0.22 0.27 0.27 0.35 0.30 0.24 t2 0.33 -0.30 0.01 -0.14 0.32 -0.05 -0.26 0.29 0.29 0.32 -0.29 -0.28 -0.08 -0.26 0.32 t3 0.25 0.20 0.77 -0.17 0.03 -0.26 0.17 0.04 0.01 0.18 0.16 0.16 -0.28 0.13 0.00
.268 .209 .821 -.181 .028 -.281 .184 .041 .008 .196 .172 .166 -.297 .144 .005
10
西南财经大学出版社
SPSS16.0与统计数据分析
11.1 主成分析
第5步 利用因子分析的结果进行主成分分析：上表是旋转 前的因子载荷矩阵，并不是主成分分析中所需要的标准化的 正交向量，要得到标准化正交向量还需作如下运算：
118.4
120.6 132.9 104.5 58.6 94.5 110.5
0.497
1.84 2.252 0.321 1.533 0.502 0.218
SPSS入门讲义 ppt课件
医学课件 3
SPSS软件的特点
①集数据录入、资料编辑、数据管理、统 计分析、报表制作、图形绘制为一体。从 理论上说，只要计算机硬盘和内存足够大， SPSS可以处理任意大小的数据文件，无论 文件中包含多少个变量，也不论数据中包 含多少个案例
医学课件
4
②统计功能囊括了《教育统计学》中所有的项 目，包括常规的集中量数和差异量数、 相关 分析、回归分析、方差分析、卡方检验、t检 验和非参数检验；也包括近期发展的多元统计 技术，如多元回归分析、聚类分析、判别分析、 主成分分析和因子分析等方法，并能在屏幕 (或打印机)上显示(打印)如正态分布图、直方 图、散点图等各种统计图表。从某种意义上讲， SPSS软件还可以帮助数学功底不够的使用者学 习运用现代统计技术。使用者仅需要关心某个 问题应该采用何种统计方法，并初步掌握对计 算结果的解释，而不需要了解其具体运算过程， 可能在使用手册的帮助下定量分析数据。
医学课件 2
目前，世界上最著名的数据分析软件是SAS和 SPSS。SAS由于是为专业统计分析人员设计的， 具有功能强大，灵活多样的特点，为专业人士 所喜爱。而SPSS是为广大的非专业人士设计， 它操作简便，好学易懂，简单实用，因而很受 非专业人士的青睐。此外，比起SAS软件来， SPSS主要针对着社会科学研究领域开发，因而 更适合应用于教育科学研究，是国外教育科研 人员必备的科研工具。1988年，中国高教学会 首次推广了这种软件，从此成为国内教育科研 人员最常用的工具。
医学课件 47
示例1
某物质在处理前与处理后分别抽样分析其 含脂率如下 处理前(Xi) 0.19 0.18 0.21 0.30 0.41 0.12 0.27 处理后(Yi) 0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12
SPSS软件的特点
①集数据录入、资料编辑、数据管理、统 计分析、报表制作、图形绘制为一体。从 理论上说，只要计算机硬盘和内存足够大， SPSS可以处理任意大小的数据文件，无论 文件中包含多少个变量，也不论数据中包 含多少个案例
医学课件
4
②统计功能囊括了《教育统计学》中所有的项 目，包括常规的集中量数和差异量数、 相关 分析、回归分析、方差分析、卡方检验、t检 验和非参数检验；也包括近期发展的多元统计 技术，如多元回归分析、聚类分析、判别分析、 主成分分析和因子分析等方法，并能在屏幕 (或打印机)上显示(打印)如正态分布图、直方 图、散点图等各种统计图表。从某种意义上讲， SPSS软件还可以帮助数学功底不够的使用者学 习运用现代统计技术。使用者仅需要关心某个 问题应该采用何种统计方法，并初步掌握对计 算结果的解释，而不需要了解其具体运算过程， 可能在使用手册的帮助下定量分析数据。
医学课件 2
目前，世界上最著名的数据分析软件是SAS和 SPSS。SAS由于是为专业统计分析人员设计的， 具有功能强大，灵活多样的特点，为专业人士 所喜爱。而SPSS是为广大的非专业人士设计， 它操作简便，好学易懂，简单实用，因而很受 非专业人士的青睐。此外，比起SAS软件来， SPSS主要针对着社会科学研究领域开发，因而 更适合应用于教育科学研究，是国外教育科研 人员必备的科研工具。1988年，中国高教学会 首次推广了这种软件，从此成为国内教育科研 人员最常用的工具。
医学课件 47
示例1
某物质在处理前与处理后分别抽样分析其 含脂率如下 处理前(Xi) 0.19 0.18 0.21 0.30 0.41 0.12 0.27 处理后(Yi) 0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12
统计学实验—SPSS与R软件应用与实例-第11章参数估计-R
最后点击Continue→单击OK。
2019/11/1
《统计学实验》第11章参数估计
11-26
【软件操作】
R软件采用prop.test( )函数来进行总体比例 之差的区间估计，具体程序如下。
opinion=c(822,690) #两个城市认为该城市的 住房价格高的人数
people=c(1000,800) #两个样本的样本容量 prop.test(opinion,people) #总体比例之差的区
(3.2)
2019/11/1
《统计学实验》第11章参数估计
11-9
【软件操作】
采用t.test( )函数来进行总体均值的估计 setwd(“D:/R-Statistics/data/chap-11”) #设定
工作路径 dat=read.table("li11.1.txt",header=T) #从
2019/11/1
《统计学实验》第11章参数估计
11-3
二、实验环境
1. 系统软件Windows2000或WindowsXP或 Windows7；
2. 统计软件R2.13.2或更高版本。
2019/11/1
《统计学实验》第11章参数估计
11-4
三、实验内容
1. 一个正态总体均值的点估计和区间估计 2. 两个正态总体均值差的点估计和区间估计 3. 总体比例的估计 4. 总体比例之差的估计
2019/11/1
《统计学实验》第11章参数估计
11-7
【统计理论】
当总体方差已知时，可以采用以下由Z统计 量（即标准正态统计量）构造的置信区间
xZ/2 n
(3.1)
2019/11/1
SPSS第11章聚类分析
•e.“Number of Cluster”选项区提供了两种确定分类组数的方法，一种是由 SPSS自动提供，这里需要给出最大的分类组数；另一种是人为确定分类组 数，这里需要给出最终的分类组数。
• ③在图11.2中单击“Plots”按钮，进入对话框，如图11.2示。
• 选择“Variable Importance Plot”中“Rank Variable”的“by variable”，以便显示在两步聚类中各个变量重要性的图形， 再选择“Continue”按钮，回到原来菜单。
学习目标
解释聚类分析的基本概念
熟悉系统聚类分析方法 分析“Classify”菜单，阐述聚类分析与判别分析的基本原理和基本操作。用 实例说明5种方法的具体实现过程，解释其主要功能、背景知识及其主要选择 项。
第11章 聚类分析和判别分析
• 11.1 聚类分析和判别分析过程综述 • 11.2 两步聚类
11.4 分层聚类分析 11.6 判别分析
• ⑤单击“OK”按钮，在Output窗口和“Data View”中显示计算 结果。
2）基本输出结果与解释
•①首先，给出了最终的聚类结果（3类），并且给出了各类的 每个变量的均值与标准差（图略）。
•②其次，给出了3个分类中男女性、经济收入、教育水平变量 的分布状况图11.4。 •③给出了变量均值的95%置信区间在3类中的对比图图11.5。 •④图11.6所示，给出了一系列图形（本例中有6张图）表示给 个变量在聚类中的重要性。
预先并不知道类的特征，甚至不知道类的数目，因此要选择聚类的基 础变量、距离测量标准以及聚类标准。
11.1.3 Classify的功能
•SPSS的“Classify”菜单中提供了5种分类分析。 •① 两步聚类（TwoStep Cluster）提供了可以同时 根据连续变量和分类变量进行聚类的功能。
• ③在图11.2中单击“Plots”按钮，进入对话框，如图11.2示。
• 选择“Variable Importance Plot”中“Rank Variable”的“by variable”，以便显示在两步聚类中各个变量重要性的图形， 再选择“Continue”按钮，回到原来菜单。
学习目标
解释聚类分析的基本概念
熟悉系统聚类分析方法 分析“Classify”菜单，阐述聚类分析与判别分析的基本原理和基本操作。用 实例说明5种方法的具体实现过程，解释其主要功能、背景知识及其主要选择 项。
第11章 聚类分析和判别分析
• 11.1 聚类分析和判别分析过程综述 • 11.2 两步聚类
11.4 分层聚类分析 11.6 判别分析
• ⑤单击“OK”按钮，在Output窗口和“Data View”中显示计算 结果。
2）基本输出结果与解释
•①首先，给出了最终的聚类结果（3类），并且给出了各类的 每个变量的均值与标准差（图略）。
•②其次，给出了3个分类中男女性、经济收入、教育水平变量 的分布状况图11.4。 •③给出了变量均值的95%置信区间在3类中的对比图图11.5。 •④图11.6所示，给出了一系列图形（本例中有6张图）表示给 个变量在聚类中的重要性。
预先并不知道类的特征，甚至不知道类的数目，因此要选择聚类的基 础变量、距离测量标准以及聚类标准。
11.1.3 Classify的功能
•SPSS的“Classify”菜单中提供了5种分类分析。 •① 两步聚类（TwoStep Cluster）提供了可以同时 根据连续变量和分类变量进行聚类的功能。
《SPSS培训教程》课件
01
02
03
宏观经济分析
对国民生产总值、财政收 支、货币供应量等宏观经 济指标进行分析，了解经 济运行的基本情况。
产业经济分析
对各产业的发展状况、产 业结构、产业政策等进行 分析，评估产业发展的趋 势和存在的问题。
微观经济分析
对企业经营状况、市场供 需、消费者行为等进行分 析，了解微观经济的运行 情况。
可视化与交互性
增强数据可视化的效果和交互性，提供更加直观 和易用的界面设计，提升用户体验。
THANKS
感谢观看
总结词
通过SPSS分析品牌形象数据，评估品牌形象对消费者选择的影响。
详细描述
本案例将介绍如何使用SPSS软件对品牌形象调查数据进行统计分析，包括描述性 统计、因子分析和回归分析等，以评估品牌形象对消费者选择的影响，为品牌管 理和营销策略提供指导。
案例三：市场细分研究
总结词
通过SPSS分析市场细分数据，识别不同消费群体的特征和需求。
支持多种数据格式导入，如Excel 、CSV、数据库等。
数据整理
对数据进行清洗、筛选、排序等 操作，确保数据质量。
变量处理与数据转换
变量转换
支持变量类型转换、变量计算、变量 重新编码等功能。
数据转换
对数据进行拆分、合并、重塑等操作 ，满足数据分析需求。
描述性统计分析
频数统计
统计各变量的频数、频率、百分比等。
04
SPSS在社会科学研究中的应用
问卷调查数据分析
描述性统计分析
因子分析
对问卷调查数据进行描述性统计分析 ，如求平均值、标准差、频数等，以 了解数据的基本特征和分布情况。
通过因子分析找出问卷中潜在的结构 ，简化数据，便于后续的深入分析。
SPSS课件第11章
第11章聚类分析和判别分析聚类分析和判别分析都是研究事物分类的多元统计方法，两者紧密联系又有所区别。
随着多元统计方法的快速发展和计算机的普遍应用，这两种方法在许多领域得到了大量的应用，理论和软件也越来越成熟。
已经成为研究事物分类的最常用的方法之一。
俗话说：“物以类聚，人以群分。
”在现实世界中，存在着大量的分类问题。
例如，某学校学生按德智体全方位发展分成几个等级；在经济学中，根据人均国民收入、人均工农业产值等多项指标将全球各国家分成几类；在金融应用中，按照经每股收益、每股利润、每股净资产、市盈率、市净率等指标将上市公司进行分类；银行按照客户的收入、职业、信用情况、抵押品等指标将客户分成几类。
这些问题都是聚类分析和判别分析可以发挥的用武之地。
判别分析和聚类分析都是研究事物分类的基本方法，它们有着不同的分类目的。
各种判别方法都要求对类的情况事先了解，根据已有的分类数据提取出类的特征，在根据提取的特征对新的还没有分类的数据进行分类。
如果类别情况事先不了解，那么就可以通过聚类得到分类情况，聚类分析的目的是把分类对象按照相似性的大小分成若干类，类的数目不必确定，分类完全根据数据自身的特点来完成，在分类结束以后，要求同类的对象相似，而不同类的对象差别大。
根据两种方法的关系，如果数据没有分类信息，就应该先进行聚类，待得到类别信息以后，就可以用判别分析提取类别的特征（通常是判别函数或判别准则），然后就建立了数据的一套“分类机制”，新的数据获取以后可以迅速进行分类。
因此对于两种方法，我们按照顺序先介绍聚类分析，再介绍判别分析。
SPSS中，聚类分析和判别分析都集成在菜单Cassify中，如图11-1所示，其中Two-Step Cluster、K-Means Cluster和Herarchical Cluste是聚类分析菜单，而Tress和Discriminant是判别分析菜单，还有一个Nearest Neighbor最近邻居法菜单是新增的非参数功能菜单。
第11章 统计分析—双变量
第三步：显示统计结果 1、分组统计概要
10- 13 10-
社会 统计学
2、方差齐性检验和t检验结果 、方差齐性检验和t
F值>F 0.025 (n 1-1,n 2-1), 说明方差不齐。
10- 14 10-
P值小于给定的显著性水平α, 说明方差不齐。
P值小于给定的显著性水平α, 拒绝原假设。
社会 统计学
社会 统计学
10- 44 10-
社会 统计学
10- 45 10-
社会 统计学
【例2】“年龄段”与“忙碌程度”
10- 46 10-
社会 统计学
10- 47 10-
社会 统计学
10- 48 10-
社会 统计学
10- 49 10-
社会 统计学
斯皮尔曼等级相关系数（spearman）在这: 斯皮尔曼等级相关系数（spearman）在这: Analyze Correlate Bivariate
2、 比较重要 3、 一般 5、 很不重要 6 、说不清楚
10- 40 10-
社会 统计学
1、将被访者学历与“读书的地位”都看成 定类变量，作列联相关的检验。 2、被访者学历与“读书的地位”均为定序 量，作等级相关检验。
10- 41 10-
社会 统计学
10- 42 10-
社会 统计学
10- 43 10-
社会 统计学
二、独立样本T 检验 独立样本T
Analyze Compare Means
IndependentIndependent-Samples检验变量栏 T Test,
打开Independent-Samples T Test对 IndependentTest对
分组变量栏, 话框 只能有一个分 组变量
10- 13 10-
社会 统计学
2、方差齐性检验和t检验结果 、方差齐性检验和t
F值>F 0.025 (n 1-1,n 2-1), 说明方差不齐。
10- 14 10-
P值小于给定的显著性水平α, 说明方差不齐。
P值小于给定的显著性水平α, 拒绝原假设。
社会 统计学
社会 统计学
10- 44 10-
社会 统计学
10- 45 10-
社会 统计学
【例2】“年龄段”与“忙碌程度”
10- 46 10-
社会 统计学
10- 47 10-
社会 统计学
10- 48 10-
社会 统计学
10- 49 10-
社会 统计学
斯皮尔曼等级相关系数（spearman）在这: 斯皮尔曼等级相关系数（spearman）在这: Analyze Correlate Bivariate
2、 比较重要 3、 一般 5、 很不重要 6 、说不清楚
10- 40 10-
社会 统计学
1、将被访者学历与“读书的地位”都看成 定类变量，作列联相关的检验。 2、被访者学历与“读书的地位”均为定序 量，作等级相关检验。
10- 41 10-
社会 统计学
10- 42 10-
社会 统计学
10- 43 10-
社会 统计学
二、独立样本T 检验 独立样本T
Analyze Compare Means
IndependentIndependent-Samples检验变量栏 T Test,
打开Independent-Samples T Test对 IndependentTest对
分组变量栏, 话框 只能有一个分 组变量
第11章spss21教程完整版
11.3.2 实例分析 1．参数设置
选择菜单“分析→相关→偏相关”，弹出如图11-12所示对话框，此对话框用来设 置偏相关分析相关参数。选中变量Health care funding和Reported disease rate并选入到 “变量”选项栏中，选中变量Visits to health care providers并选入到“控制”选项栏中。 然后单击图11-12中的“选项”按钮，弹出如图11-13所示对话框，选中“零阶相 关系数”选项栏和“按列表排除个案”选项栏，接着单击“继续”按钮返回主界面。 返回到偏相关主界面，单击“确定”按钮运行偏相关分析过程。
选择菜单“分析→相关→偏相关”，弹出如图11-9所示对话框，此对话框用来设置偏相 关分析相关参数。 1．变量选择设置 图11-9中左边为变量列表，变量框用于选择要进行偏相关分析的变量，至少选入 两个变量，如果选入的变量个数大于两个，则系统会分别进行两两相关分析。控制变 量框用于选择偏相关分析中的控制变量，如果不选的话，则等同于进行一般的相关分 析。 2．显著性检验栏 此栏用于定义相关系数的检验方法。 • 双侧检验； • 单侧检验。 • 3．显示实际显著性水平栏 选择是否给出真实的显著性水平值。
11.4 距离过程
11.4.1 距离过程的参数设置
选择菜单“分析→相关→距离”，弹出如图11-13所示对话框，此对话框用来设置 距离分析相关参数。 • 1．变量选择设置 图11-15的左边是变量列表框，变量选项框用于选择要进行距离分析的变量，至少 要选入两个变量。标注个案选项栏用来选择标识变量。 2．计算距离选项栏 • 个案间：定义对观测值进行距离分析； 变量间：定义对变量进行距离分析。 3．度量标准（Measure）选项栏 • 选择距离分析的测度类型。 • 不相似性：计算不相似性测度； • 相似性：计算相似性测度； • 度量按钮：如果要选择不相似性，单击此 按钮，则弹出如图11-16所示的“度量”对话 框，用于定义距离分析的测度类型。如果要 选择相似性，单击此按钮，则弹出如图11-17 所示的“度量”对话框。
【课件】SPSS 10~11
502
498
522
2、依次单击Analyze → Regression → Linear，打开回归 分析主对话框。 3、指定因变量和自变量。指定 “穗”、“粒”作为自变量； 指定“产量”作为因变量。在Method中选择Stepwise项。 4 、 单 击 Statistics 按 钮 ， 打 开 统 计 量 选 项 对 话 框 ， 选 中 Descriptives，要求显示描述统计量；在Residuals方框中，选中 Casewise diagnostics 中 的 Outlies outside 3 standard deviations项。该选项的作用是，当标准化残差超过3时，显示 具体观测量的标准化残差以帮助发现奇异值。 5、单击Save按钮，打开保存对话框，在Predicted Values 方 框 中 选 择 Unstandardized 项 ， 在 Residuals 方 框 中 选 中 Unstandardized项。要求将标准化的预测值和残差作为新变量 保存在数据文件中。 6、其余使用默认选项，单击OK，提交系统执行。结果如 图10-19~图10-23所示。
在主对话框中选择了因变量和自变量后，单击Plots按钮， 打开图形对话框。 从左侧列表框中选择标准化预测值*ZPRED作为横轴变 量进入X框中；选择因变量DEPENDENT作为纵轴进入Y框 中。 在Standardized Residual Plots方框中选中Histogram及 Normal probability plot项，要求作标准化残差的直方图及标 准化残差的正态概率图。 再运行一次程序，结果如图10-15~图10-17所示。
图10-15标准化残差直方图
图10-16 标准化残差的正态概率图
图10-17 散点图
SPSS的时间序列分析ppt课件
·自相关函数图和偏自相关函数图〔ACF＆PACF〕
所谓自相关是指序列与其本身经过某些阶数滞后构成的序列之间存 在某种程度的相关性。对自相关的测度往往采用自协方差函数和自相关 函数。偏自相关函数是在其他序列给定情况下的两序列条件相关性的度 量函数。
自相关函数图和偏自相关函数图将时间序列各阶滞后的自相关和偏 自相关函数值以及在一定置信程度下的置信区间直观的展现出来。
各统计量在不同序列之间不应有显著差别。假设差
值大于检验值，那么以为序列具有非平稳性。
• 11.3.4 时间序列的图形化察看和检验的根本操作 • 11.3.4.1 绘制序列图的根本操作 • 〔1〕选择菜单Graph→Sequence。
〔2〕将需绘图的序列变量选入Variables框中。
〔3〕在Time Axis Labels框中指定横轴〔时间轴〕标志变量。该标志 变量默许的是日期型变量。
那么概率空间〔W，F，P〕上随机过程｛y〔t〕，t∈T｝称为平稳过
程。具有时间上的平稳不变性。实际当中是非常困难甚至是不能够的。
•
宽平稳：宽平稳是指随机过程的均值函数、方差函数均为常数，自协方 差函数仅是时间间隔的函数。如二阶宽平稳随机过程定义为：E〔yt〕
= E〔yt+h〕为常数，且对 t，t+h∈T都使协方差E［yt- E〔yt〕
第十章
SPSS的时间序列分析
11.1 时间序列分析概述
• 11.1.1时间序列的相关概念
•
通常研讨时间序列问题时会涉及到以下记号和概念：
• 1.目的集T
•
目的集T可了解为时间t的取值范围。
• 2.采样间隔△t
•
采样间隔△t可了解为时间序列中相邻两个数的时间间隔。
• 3.平稳随机过程和平稳时间序列
所谓自相关是指序列与其本身经过某些阶数滞后构成的序列之间存 在某种程度的相关性。对自相关的测度往往采用自协方差函数和自相关 函数。偏自相关函数是在其他序列给定情况下的两序列条件相关性的度 量函数。
自相关函数图和偏自相关函数图将时间序列各阶滞后的自相关和偏 自相关函数值以及在一定置信程度下的置信区间直观的展现出来。
各统计量在不同序列之间不应有显著差别。假设差
值大于检验值，那么以为序列具有非平稳性。
• 11.3.4 时间序列的图形化察看和检验的根本操作 • 11.3.4.1 绘制序列图的根本操作 • 〔1〕选择菜单Graph→Sequence。
〔2〕将需绘图的序列变量选入Variables框中。
〔3〕在Time Axis Labels框中指定横轴〔时间轴〕标志变量。该标志 变量默许的是日期型变量。
那么概率空间〔W，F，P〕上随机过程｛y〔t〕，t∈T｝称为平稳过
程。具有时间上的平稳不变性。实际当中是非常困难甚至是不能够的。
•
宽平稳：宽平稳是指随机过程的均值函数、方差函数均为常数，自协方 差函数仅是时间间隔的函数。如二阶宽平稳随机过程定义为：E〔yt〕
= E〔yt+h〕为常数，且对 t，t+h∈T都使协方差E［yt- E〔yt〕
第十章
SPSS的时间序列分析
11.1 时间序列分析概述
• 11.1.1时间序列的相关概念
•
通常研讨时间序列问题时会涉及到以下记号和概念：
• 1.目的集T
•
目的集T可了解为时间t的取值范围。
• 2.采样间隔△t
•
采样间隔△t可了解为时间序列中相邻两个数的时间间隔。
• 3.平稳随机过程和平稳时间序列
SPSS11
Algorithm for learning ANN
Initialize the weights (w0, w1, …, wk)
Adjust the weights in such a way that the output of ANN is
consistent with class labels of training examples – Objective function:
中国科 学院自 动化研 究所
2012.12.07 DATAGURU专业数据分析网站
线性方法的缺点
线性方法对于很多数据不能进行有效的处理.
20
15
10
5
0 1 0.5 0 -0.5 -1 -1 -0.5 0.5 0 1
现实中数据的有用特性往往不是特征的线性组合.
中国科 学院自 动化研 究所
2012.12.07 DATAGURU专业数据分析网站
2012.12.07 DATAGURU专业数据分析网站
15
线性判别分析(LDA)
LDA是一种监督的维数约简方法.
1
LDA的思想: 寻找最能把两类样本分开的投影直线. LDA的目标: 使投影后两类样本的均值之差与投影样本的总类散布的 比值最大 . Best projection direction for classification
Y
Output Y is 1 if at least two of the three inputs are equal to 1.
2012.12.07 DATAGURU专业数据分析网站
Artificial Neural Networks (ANN)
Input nodes
第11章SPSS对应分析ppt课件
运用纯汉字的点和最好的数学成绩A最接近，而不会汉字只会英文 的点与最差的数学成绩F（或者D，虽然在纵坐标稍有差距）最接 近，而用部分汉字的和数学成绩B接近。
对应分析的数学原理是什么？
结果解释
▪ 根据SPSS对数据ChMath.sav的计算，得到一些表格。 ▪ 其中第一个就是下面的各维的汇总表。这里所涉及的是行与列因
对应分析
▪ 在对应分析中，根据各行变量的因子载荷和各列变量的因子载荷 之间的关系，行因子载荷和列因子载荷之间可以两两配对。
▪ 如果对每组变量选择前两列因子载荷，则两组变量就可画出两因 子载荷的散点图。
▪ 由于这两个图所表示的载荷可以配对，于是就可以把这两个因子 载荷的两个散点图画到同一张图中，并以此来直观地显示各行变 量和各列变量之间的关系。
对应分析
▪ 由于列联表数据形式和一般的连续变量的数据形式类似， 所以也可以用对应分析的数学方法来研究行变量各个水 平和列变量各个水平之间的关系；
▪ 虽然对不同数据类型所产生结果的解释有所不同，数学 的原理是一样的。下面通过对ChMath.txt数据的计算和 结果分析来介绍对应分析。
首先看对应分析结果的一个主要SPSS展示，然后 再解释该图的来源和解释。
M
L O
u2mM lmGv21M l1
l v22 2
M
L v2m lm
O M
up1 l1 l up2 2 L vpm lm vn1 l1 vn2 l2 L vnm lm
可以对变量和样品作两两因子载荷图. 返回
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
▪ 两表中的概念不必记；其中Mass为行与列的边缘概率；Score in Dimension是各维度的分值 (二维图中的坐标)；Inertia:就是前面 所提到的惯量，为每一行/列到其重心的加权距离的平方。
对应分析的数学原理是什么？
结果解释
▪ 根据SPSS对数据ChMath.sav的计算，得到一些表格。 ▪ 其中第一个就是下面的各维的汇总表。这里所涉及的是行与列因
对应分析
▪ 在对应分析中，根据各行变量的因子载荷和各列变量的因子载荷 之间的关系，行因子载荷和列因子载荷之间可以两两配对。
▪ 如果对每组变量选择前两列因子载荷，则两组变量就可画出两因 子载荷的散点图。
▪ 由于这两个图所表示的载荷可以配对，于是就可以把这两个因子 载荷的两个散点图画到同一张图中，并以此来直观地显示各行变 量和各列变量之间的关系。
对应分析
▪ 由于列联表数据形式和一般的连续变量的数据形式类似， 所以也可以用对应分析的数学方法来研究行变量各个水 平和列变量各个水平之间的关系；
▪ 虽然对不同数据类型所产生结果的解释有所不同，数学 的原理是一样的。下面通过对ChMath.txt数据的计算和 结果分析来介绍对应分析。
首先看对应分析结果的一个主要SPSS展示，然后 再解释该图的来源和解释。
M
L O
u2mM lmGv21M l1
l v22 2
M
L v2m lm
O M
up1 l1 l up2 2 L vpm lm vn1 l1 vn2 l2 L vnm lm
可以对变量和样品作两两因子载荷图. 返回
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
▪ 两表中的概念不必记；其中Mass为行与列的边缘概率；Score in Dimension是各维度的分值 (二维图中的坐标)；Inertia:就是前面 所提到的惯量，为每一行/列到其重心的加权距离的平方。
SPSS实用教程第11章
SPSS实用教程第十一章因子分析11.1 主要功能11.2 实例操作11.1 主要功能多元分析处理的是多指标的问题。
由于指标太多，使得分析的复杂性增加。
观察指标的增加本来是为了使研究过程趋于完整，但反过来说，为使研究结果清晰明了而一味增加观察指标又让人陷入混乱不清。
由于在实际工作中，指标间经常具备一定的相关性，故人们希望用较少的指标代替原来较多的指标，但依然能反映原有的全部信息，于是就产生了主成分分析、对应分析、典型相关分析和因子分析等方法。
调用Data Reduction菜单的Factor过程命令项，可对多指标或多因素资料进行因子分析。
因子分析的基本目的就是用少数几个因子去描述许多指标或因素之间的联系，即将相关比较密切的几个变量归在同一类中，每一类变量就成为一个因子（之所以称其为因子，是因为它是不可观测的，即不是具体的变量，这与上一章的聚类分析不同），以较少的几个因子反映原资料的大部分信息。
返回目录返回全书目录11.2 实例操作[例11-1]下表资料为25名健康人的7项生化检验结果，7项生化检验指标依次命名为X1至X7，请对该资料进行因子分析。
11.2.1 数据准备激活数据管理窗口，定义变量名：分别为X1、X2、X3、X4、X5、X6、X7，按顺序输入相应数值，建立数据库，结果见图11.1。
图11.1 原始数据的输入11.2.2 统计分析激活Statistics 菜单选Data Reduction 的Factor...命令项，弹出Factor Analysis 对话框（图11.2）。
在对话框左侧的变量列表中选变量X1至X7，点击 钮使之进入Variables 框。
图11.2 因子分析对话框点击Descriptives...钮，弹出Factor Analysis:Descriptives对话框（图11.3），在Statistics中选Univariate descriptives项要求输出各变量的均数与标准差，在Correlation Matrix栏内选Coefficients项要求计算相关系数矩阵，并选KMO and Bartlett’s test of sphericity项，要求对相关系数矩阵进行统计学检验。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
图11-13
Step06 ：相关分析
选择菜单栏中的【Analyze(分析)】→【Forecasting(预测)】→ 【Autocorrelations(自相关)】命令，弹出【Autocorrelation s(自相关) 】对话框。将【VAR00001】移入【Variables(变量)】 列表框中,在【Display(显示)】选项组中勾选所以复选框，即展示 自相关函数图、又偏相关函数图。单击【OK(确认)】按钮即可绘制 自相关函数图和偏相关函数图。
如果选择月度数据或季度数据，将会出现【Periodicity at highe r level(更高级别的周期)】。在其下方将显示数据的最大周期长度， 月度数据默认周期长度为12，季度数据默认周期长度为4。
单击【OK(确认)】按钮，此时完成时间的定义，SPSS将在当前数据 编辑窗口中自动生成标志时间的变量。
（2）样本自相关系数的图形 在SPSS中画出了样本自相关系数图。图中的横轴为 滞后期（Lag Number），纵轴为样本自相关系数 （ACF）。图中用条形形状来表示样本自相关系数， 并画出了95%的置信上下限的线条。从下图可以看出 该时间序列的自相关系数并不呈负指数收敛到零，其 衰减速度比较慢，不是平稳时间序列。
3 实例结果及分析
（1）直观分析的输出结果 我国2000年1月到2009年12月社会商品零售总额的线图，从图上 可以看出该序列有明显的趋势性或周期性这说明该序列，而且无离 群点和缺失值．
（2）特征分析结果
我国2000年1月到2009年12月社会商品零售总额的直方图，如图1 1-16所示。从图上可以看出该序列的样本均值为5655.5333，样本 标准差为2559.27829，样本容量为120个。
⑶特征分析 所谓特征分析就是在对数据序列进行建模之前，通过从时间序 列中计算出一些有代表性的特征参数，用以浓缩、简化数据信 息，以利数据的深入处理，或通过概率直方图和正态性检验分 析数据的统计特性。通常使用的特征参数有样本均值、样本方 差、标准偏度系数、标准峰度系数等。 ⑷相关分析 所谓相关分析就是测定时间序列数据内部的相关程度，给出相 应的定量度量，并分析其特征及变化规律。 理论上，自相关系数序列与时间序列具有相同的变化周期．所 以，根据样本自相关系数序列随增长而衰减的特点或其周期变 化的特点判断序列是否具有平稳性，识别序列的模型，从而建 立相应的模型。
Step05 ：相关分析
选择菜单栏中的【Analyze(分析)】→【Forecasting(预测)】 →【Autocorrelations(自相关)】命令，弹出【Autocorr elations(自相关)】对话框。
在左侧的候选变量列表框中选择一个变量，将其移入【Variables (变量)】列表框中。 单击【Options】按钮，弹出【Options(选项)】对话框。
（2）季节分解法
季节分解的一般步骤如下： 第一步，确定季节分解的模型； 第二步，计算每一周期点（每季度，每月等等）的季节指数 （乘法模型）或季节变差（加法模型）； 第三步，用时间序列的每一个观测值除以适当的季节指数（或 减去季节变差），消除季节影响； 第三步，对消除了季节影响的时间序列进行适当的趋势性分析； 第四步，剔除趋势项，计算周期变动； 第五步，剔除周期变动，得到不规则变动因素； 第六步，用预测值乘以季节指数（或加上季节变差），乘以周 期变动，计算出最终的带季节影响的预测值。
（3）相关分析结果
（1）样本自相关系数的值 在SPSS中给出了不同滞后期（Lag列）的样本自相关系数的 值（Autocorrelation列），样本自相关系 数的标准误差 （Std Error列），以及Box-ljung Statistic的值、自由 度（d f列）和相伴概率（Sig）。通过标准误差值以及Box-l jung Statistic的相伴概率都可以说该时间序列不是白噪声， 是具有自相关性的时间序列，可以建立ARIMA等模型。Box-l jung Statistic的相伴概率是在近似认为Box-ljung Statis tic服从卡方分布得到。
Step04 ：直观分析
选择菜单栏中的【Data(数据)】→【Forecasting(预测)】→【S equence Charts(序列图)】命令，弹出【Sequence Charts (序列图)】对话框，在该对话框左侧的候选变量列表框中选择【VA R00001】选项，将其移入【Variables(变量)】列表框中, 选择 【Year, not periodic】将其移入【Time Axis Labels(时间轴 标签)】列表框，单击【OK(确认)】按钮即可生成线图。
Step02：标志时间的变量出现 单击【OK(确认)】按钮，此时完成时间的定义，SPSS将在当前数据 编辑窗口中自动生成标志时间的变量，同时在输出窗口中将会出现 一个简明的日志，说明时间标志变量及其格式和包含的周期等。
Step03 ：数据采样 选择菜单栏中的【Data(数据)】→【Select Cases(选择个案)】 命令，弹出【Select Cases (选择个案) 】对话框，点选【Base d on time or case range(基于时间或个案全距) 】单选钮，并 单击【range(范围)】按钮，此时会出现新的对话框，在【First c ase(第一个个案)】选项组的【Year(年)】文本框中输入“2000”， 在【month(月)】文本框中输入“1”，在【First case(最后个个 案)】选项组的【Year(年)】文本框中输入“2009”，在【month (月)】文本框中输入“12” 。单击【Continue(继续)】按钮，然后 单击【Select Cases (选择个案)】对话框中的【OK(确认)】按钮， 此时在输出窗口中将会出现一个简明的日志，说明此时只对2000 年1月都2009年12月的数据做分析与建模。
11.2.2 指数平滑法的SPSS操作详解
Step01 ：打开【Create Models(创建模型)】对话框 当时间序列的数据已经准备好以后，选择菜单栏中的【Analyze(分 析)】→【Forecasting(预测)】→【Create Models(创建模型)】 命令，弹出【Create Models(创建模型)】对话框。
11.1.3 实例图文分析：社会商品零售总 额的预处理
1. 实例内容 为了分析社会商品零售总额的变动趋势，收集了我国2000年1月到 2010年5月社会商品零售总额的数据，现在对数据进行时间序列的 预处理。
2 实例操作
Step01：数据准备输入社会商品零售总额的数据，然后选择菜单栏 中的【Data(数据)】→【Define Dates(定义日期)】命令，弹出 【Define Dates(定义日期) 】对话框，选择【Years, month(年， 月)】选项,并在【First Case is 】选项组的【Year(年)】文本框 中输入“2000”，在【month(月)】文本框中输入“1” 。
（3）样本偏相关系数的值 在SPSS中给出了不同滞后阶（Lag列） 的样本偏相关系数的值（Partial Aut ocorrelations 列），样本偏相关系 数的标准误差（Std Error列）。从 表10-3样本偏相关系数的数据表可以 看出该时间序列不是白噪声。
（4）样本偏相关系数的图形 图中的横轴为滞后期（Lag Number），纵轴为样本偏相关系数 （PACF）。图中用条形形状来表示样本偏相关系数，并画出了95 %的置信上下限的线条。从下图可以看出该时间序列的偏相关系数 在一阶滞后期、12阶滞后期比较大，说明该时间序列具有周期性， 不是平稳时间序列。
第11章 SPSS在时间序列 预测中的应用
时间序列分析(Time Series Analyze)是概率统计学科中 应用性较强的一个分支，在金融经济、气象水文、信号 处 理、机械振动等众多领域有从所采用的数学工具和理论， 时间序列分析分为时域分析和谱分析两大类分析方法 预测的间序列的确定性分析
11.2.1 确定性分析的基本原理 1、使用目的 传统时间序列分析认为长期趋势变动、季节性变动、周期变动 是依一定的规则而变化的，不规则变动因素在综合中可以消除。 基于这种认识，形成了确定性时间序列分析。 通过确定性时间序列分析，一方面能够使序列的长期趋势变动 特征、季节效应、周期变动体现得更加明显；另一方面能确立 模型，从而成功捕捉数据的随“时间”变化的、“动态”的、 “整体”的统计规律。因此，对时间序列进行确定分析，从而 建立模型是非常必要的。
11.1 时间序列的预处理
11.1.1预处理的基本原理 1.使用目的 通过预处理，一方面能够使序列的随“时间”变化的、“动态” 的特征体现得更加明显，利用模型的选择；另一方面也使得数 据满足与模型的要求。 2.基本原理 ⑴数据采样 采样的方法通常有直接采样、累计采样等。 ⑵直观分析 时间序列的直观分析通常包括离群点的检验和处理、缺损值的 补足、指标计算范围是否统一等一些比较简单的，可以采用比 较简单手段处理的分析。
2、基本原理
（1）指数平滑法 指数平滑法有助于预测存在趋势和（或）季节的序列。指数平 滑法分为两步来建模，第一步确定模型类型，确定模型是否需 要包含趋势、季节性，创建最适当的指数平滑模型，第二步选 择最适合选定模型的参数。 指数平滑模法一般分为无季节性模型、季节性模型。无季节性 模型包括简单指数平滑法、布朗单参数线性指数平滑法等，季 节性模型包括温特线性和季节性指数平滑法。 指数平滑法，又称指数加权平均法，实际是加权的移动平均法， 它是选取各时期权重数值为递减指数数列的均值方法。
3.其他注意事项 进行时间序列预处理的时候，常常需要对数据一些变换，例如， 取对数，做一阶差分，做季节差分等。
11.1.2 时间序列预处理的SPSS操作详解
Step01:数据准备 选择菜单栏中的【Data(数据)】→【Define Dates(定义日期)】 命令，弹出【Define Dates(定义日期) 】对话框。