0282答案(临)
高一入学心理测试题及答案

高一入学心理测试题及答案一、选择题请根据自己的实际情况,从每题给出的选项中选择最符合自己的答案,将答案填写在题后的括号内。
1. 你对高一的学习压力感受如何?A. 非常大 ( )B. 有一点大 ( )C. 一般般 ( )D. 没有压力 ( )2. 你对新环境的适应能力如何?A. 非常差 ( )B. 有些困难 ( )C. 适应能力一般 ( )D. 很强 ( )3. 你与同学之间的相处状况如何?A. 喜欢独自行动 ( )B. 有些害羞,不太会交流 ( )C. 和大部分同学能友好相处 ( )D. 和大部分同学都关系很好 ( )4. 你对高中生活的期望如何?A. 担心无法适应 ( )B. 对未来充满期待 ( )C. 比较理智,有实际期望 ( )D. 对高中生活没什么期待 ( )5. 你在学习中的主动性如何?A. 想尽一切办法去学习 ( )B. 有时候会主动学习 ( )C. 需要老师的督促才能学习 ( )D. 没有学习的主动性 ( )二、判断题请根据自己的实际情况,判断下列说法是否符合自己的情况,将答案填写在题后的括号内。
1. 对于未来高中生活,我感到害怕和不安。
( )2. 我喜欢结交新朋友,对于与陌生人的交流比较擅长。
( )3. 我相信自己有足够的能力来应对高一的学习压力。
( )4. 我通常会主动参与到学校的各类活动中。
( )5. 对于自己的学习目标,我已经有了清晰的规划和计划。
( )三、简答题请简要回答下列问题,用1-2句话概括你的答案。
1. 你对高中的期待是什么?()2. 你认为你具备适应新环境的哪些能力?()3. 你觉得自己在学习中存在哪些优点和不足?()4. 你是否主动参与到学校活动中,为什么?()5. 你是否对自己的未来规划有清晰的目标和计划?()答案解析:一、选择题答案:1. ()2. ()3. ()4. ()5. ()二、判断题答案:1. ()2. ()3. ()4. ()5. ()三、简答题答案:1. ()2. ()3. ()4. ()5. ()注意:以上题目仅供心理测试使用,结果及解析仅为参考,个人具体情况请结合实际情况做出判断和决策。
(完整word版)七年级生物下册导学案及答案(全册),推荐文档

七年级生物下册第四单元生物圈中的人第一章人的由来导学1 第一节人类的起源和发展【学习目标】:1.说出人类起源于森林古猿,人类是在与自然环境的斗争中逐渐进化来的。
2.对比观察四种现代类人猿和人类起源与示意图,概述人类在起源和发展过程中自身形态和使用工具等方面的变化。
【学习重、难点】:1.运用比较的方法找出人类与类人猿的异同点。
2.认同现代人类是在与自然环境的长期斗争中进化来的观点。
【学习过程】:一、自主学习1、现代类人猿和人类的共同祖先是。
2、在人类的进化过程中,“露西”时代的古人类适于下地生活的特点是:上肢___________,下肢___________。
3、我国的古人类化石非常丰富,著名的北京人化石发现于______________。
1929年,________ 发现了第一个北京猿人头盖骨的化石。
4、人类和类人猿有共同的祖先,但在发展进化的过程中,人类不仅能适应环境,而且能够不断地改变环境,成为地球的强者,其主要原因是:_____________ ____。
二、合作探究任务一:认真阅读教材P2至P3思考:5、教材中的四种现代类人猿今天分布在地球的那些地方 ?它们的生活方式的共同点是。
其中与人亲缘关系最近的是。
6、今天人类的数量在急剧增加,而类人猿的数量日益减少,原因是什么?7、类人猿在形态结构上确实与人有许多相似,但与人的根本区别是什么?任务二:认真阅读分析教材P4至P5内容思考8、“露西”少女的化石与现代人类较为相似,想象一下他的运动方式会是什么?9、“东非人用图中的石块做什么?它们已经具有能力。
三、系统总结现代类人猿和人类的共同祖先是:人类的起源和发展自然条件:人类的起源和发展自身的变化:创造和使用。
四、生活链接现代的类人猿是否有一天会进化为人类?五、反馈检测10、许多生活的森林古猿,由于使前肢解放出来,臂和手变得灵巧,为使用、制造工具提供了前提;随着制造的工具越来越来复杂,并且使用了火,也越来越发达,在群体生活中产生了,因此相互之间能更好地交流与合作。
初级会计师经济法试题及答案

初级会计师经济法试题及答案一、单项选择题(每题1分,共10分)1. 根据《中华人民共和国企业所得税法》,企业所得税的税率为:A. 10%B. 20%C. 25%D. 30%2. 以下哪项不属于会计要素?A. 资产B. 负债C. 所有者权益D. 利润3. 会计核算的基本原则不包括:A. 真实性原则B. 合法性原则C. 及时性原则D. 可比性原则4. 根据《中华人民共和国增值税暂行条例》,增值税的一般税率为:A. 6%B. 10%C. 13%D. 17%5. 会计年度的起止日期是:A. 1月1日至12月31日B. 4月1日至次年3月31日C. 7月1日至次年6月30日D. 任意选择6. 会计凭证的保管期限一般为:A. 3年B. 5年C. 10年D. 永久7. 以下哪项不是会计报表的组成部分?A. 资产负债表B. 利润表C. 现金流量表D. 预算表8. 根据《中华人民共和国会计法》,会计档案的保管期限不得少于:A. 3年B. 5年C. 10年D. 15年9. 会计核算的基本原则包括:A. 权责发生制B. 收付实现制C. 现金制D. 预算制10. 会计年度的确定依据是:A. 企业自行决定B. 国家规定C. 行业惯例D. 企业章程答案:1. C2. D3. B4. C5. A6. C7. D8. C9. A10. B二、多项选择题(每题2分,共10分)11. 会计核算的基本原则包括以下哪些选项?A. 真实性原则B. 合法性原则C. 及时性原则D. 可比性原则E. 权责发生制12. 会计报表的组成部分包括:A. 资产负债表B. 利润表C. 现金流量表D. 预算表E. 所有者权益变动表13. 以下哪些属于会计档案的保管范围?A. 会计凭证B. 会计账簿C. 会计报表D. 预算表E. 会计档案目录14. 会计年度的确定可以依据:A. 企业自行决定B. 国家规定C. 行业惯例D. 企业章程E. 会计年度的起止日期15. 会计核算的基本原则不包括:A. 真实性原则B. 合法性原则C. 及时性原则D. 收付实现制E. 预算制答案:11. ABCDE12. ABCE13. ABCE14. BCD15. DE三、判断题(每题1分,共5分)16. 会计档案的保管期限不得少于10年。
2022年中国科学院大学高分子化学与物理考研试题

2022年中国科学院大学高分子化学与物理考研试题中国科学院高校2022年招收攻读硕士学位讨论生入学统一考试试题科目名称科目名称::高分子化学与物理考生须知考生须知:1.本试卷满分为150分,所有考试时光总计180分钟。
2.全部答案必需写在答题纸上,写在试题纸上或草稿纸上一律无效。
3. 可以使用无字典存储和编程功能的电子计算器。
高分子化学部分高分子化学部分((75分)一.名词解释名词解释((每小题2分,共10分)1. 官能团等活性2. 引发剂效率3. 聚硫橡胶4. 高分子功能化5. 缓聚二.挑选题挑选题((每题选一最佳答案每题选一最佳答案,每小题每小题2分,共20分)1. 二烯类橡胶的硫化机理是(a )离子机理;(b )自由基机理;(c )配位机理2. 对获得诺贝尔化学奖的高分子科学家讲述错误的是(a )Ziegler 和Natta 发明白有机金属引发体系,合成了高密度聚乙烯和等规聚丙烯(b )Heeger 、De Gennes 和Shirakawa 在导电高分子方面做出了特别贡献(c )Staudinger 建立了高分子学说(d )Flory 在缩聚反应理论、高分子溶液的统计热力学和高分子链的构象统计等方面做出了一系列杰出贡献。
3. 聚甲醛合成后加入醋酸酐处理的目的是(a )洗除低聚物;(b )除去引发剂;(c )提高热稳定性;(d )提高相对分子质量4. 下列最不易举行直接光引发的单体是(a )丙烯腈;(b )丙烯酰胺;(c )乙烯;(d )丙烯酸5. 以下讲述不正确的是(a )甲基丙烯酸甲酯的本体聚合为均相体系(b )悬浮聚合的单体-介质体系为非均相体系(c )丙烯腈在水相中的溶液聚合为均相体系(d )苯乙烯聚合时在甲苯中的溶液聚合为均相体系。
6. 甲基丙烯酸甲酯在下列哪种溶剂中以萘钠引发聚合时聚合速率最大?(a )苯;(b )四氢呋喃;(c )硝基苯;(d )丙酮科目名称:高分子化学与物理第1页共4页7. 下列属于热塑性弹性体的聚合物是(a )SBS ;(b )BSB ;(c )BS ;(d )ABS8. 下列环烃开环聚合能力大小次序正确的是(a )三元环烃>七元环烃>八元环烃(b )八元环烃八元环烃>四元环烃(d )五元环烃<八元环烃<三元环烃。
2008年(全国卷II)(含答案)高考文科数学

2007年普通高等学校招生全国统一考试(2全国Ⅱ卷)数学(文)试题一、选择题 ( 本大题 共 12 题, 共计 60 分) 1.cos330= ( )A .12B .12-C .32D .32-2.设集合{1234}{12}{24}U A B ===,,,,,,,,则()U A B = ð( ) A .{2}B .{3}C .{124},,D .{14},3.函数sin y x =的一个单调增区间是( )A .ππ⎛⎫- ⎪44⎝⎭,B .3ππ⎛⎫ ⎪44⎝⎭,C .3π⎛⎫π ⎪2⎝⎭,D .32π⎛⎫π ⎪2⎝⎭,4.下列四个数中最大的是( ) A .2(ln 2) B .ln(ln 2)C .ln 2D .ln 25.不等式203x x ->+的解集是( ) A .(32)-, B .(2)+∞, C .(3)(2)-∞-+∞ ,, D .(2)(3)-∞-+∞ ,,6.在ABC △中,已知D 是AB 边上一点,若123AD DB CD CA CB λ==+,,则λ=( )A .23B .13C .13-D .23-7.已知三棱锥的侧棱长的底面边长的2倍,则侧棱与底面所成角的余弦值等于( ) A .36B .34C .22D .328.已知曲线24x y =的一条切线的斜率为12,则切点的横坐标为( )A .1B .2C .3D .49.把函数e x y =的图像按向量(23)=,a 平移,得到()y f x =的图像,则()f x =( ) A .e 2x +B .e 2x -C .2e x -D .2e x +10.5位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有( ) A .10种B .20种C .25种D .32种11.已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于( )A .13B .33C .12D .3212.设12F F ,分别是双曲线2219y x +=的左、右焦点.若点P 在双曲线上,且120PF PF =,则12PF PF += ( )A .10B .210C .5D .25二、填空题:本大题共4小题,每小题5分,共20分.13.一个总体含有100个个体,以简单随机抽样方式从该总体中抽取一个容量为5的样本,则指定的某个个体被抽到的概率为 .14.已知数列的通项52n a n =-+,则其前n 项和n S = .15.一个正四棱柱的各个顶点在一个直径为2cm 的球面上.如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为 cm 2.16.821(12)1x x ⎛⎫++ ⎪⎝⎭的展开式中常数项为 .(用数字作答)三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)设等比数列{}n a 的公比1q <,前n 项和为n S .已知34225a S S ==,,求{}n a 的通项公式.18.(本小题满分12分)在ABC△中,已知内角Aπ=3,边23BC=.设内角B x=,周长为y.(1)求函数()y f x=的解析式和定义域;(2)求y的最大值.19.(本小题满分12分)从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率()0.96P A=.(1)求从该批产品中任取1件是二等品的概率p;(2)若该批产品共100件,从中任意抽取2件,求事件B:“取出的2件产品中至少有一件二等品”的概率()P B.20.(本小题满分12分)如图,在四棱锥S ABCD-中,底面ABCD为正方形,侧棱SD⊥底面ABCD E F,,分别为AB SC,的中点.(1)证明EF∥平面SAD;(2)设2SD DC=,求二面角A EF D--的大小.A EB CF SD21.(本小题满分12分)在直角坐标系xOy 中,以O 为圆心的圆与直线:43=-y x 相切 (1)求圆O 的方程(2)圆O 与x 轴相交于A 、B 两点,圆内的动点P 使|P A |、|PO |、|PB |成等比数列,求PA PB ∙的取值范围。
2019秋 西南大学0282《 教育统计学》在线作业答案

[0282]《教育统计学》讲师:周玲判断题1、两个变量之间精确和稳定的变化关系称为相关关系。
. A.√. B.×2、标准分数的数值大小和正负,可以反映其原始数据在团体中的位置。
. A.√. B.×3、通过计算所搜集数据的算术平均数来反映变量分布的离散趋势。
. A.√. B.×4、假设检验一般有两个相互对立的假设。
. A.√. B.×5、算术平均数是所有观察值的总和除以总频数所得之商。
. A.√. B.×6、学生某科考试成绩属于随机变量。
. A.√. B.×7、几何平均数是不同比重数据的平均数。
. A.√. B.×8、t分布是一种标准正态分布。
. A.√. B.×9、直方图是表示间断变量的统计图。
. A.√. B.×10、统计图由标题、图号和标目构成。
. A.√. B.×11、推断统计的内容包括参数估计和假设检验。
. A.√. B.×12、样本上的数字特征称为样本容量。
. A.√. B.×13、统计表由标题、表号、标目、线条、数字、表注等项目构成。
. A.√. B.×14、用同一测验对同一组被试在实验前后进行两次测验,所获得的两组测验结果属于相关样本。
. A.√. B.×15、点估计是直接用样本统计量的值估计相应总体参数的值。
. A.√. B.×16、数据60、45、90、66、80的中位数是90。
. A.√. B.×17、标准差越小,说明数据分布的范围越广,分布越不整齐。
. A.√. B.×18、两个变量之间的变化方向相反时,它们之间的关系称为正相关。
. A.√. B.×19、分层抽样是按照与研究内容有关的因素或指标把总体划分成几部分(即几个层),然后从各层中进行单纯随机抽样或机械抽样. A.√. B.×20、机械抽样是把总体中所有的个体按一定顺序编号,然后依固定的间隔取样的抽样方法。
201606_计算机基础选择题(含答案)

D0179、信息科学的主要研究对象是()。
P3A.通讯技术B.算法C.计算机技术D.信息A0180、信息论的创始人是()。
P1A.香农B.维纳C.冯·诺依曼D.爱因斯坦D0181、信息技术不包括()。
P2A.控制技术B.计算机技术C.通讯技术D.生物技术D0182、()不属于信息素养。
P6A.信息意识B.信息技能C.文化素养D.体能素质C0183、以下关于数据和信息的叙述中,不正确的是()。
P2A.数据是信息的具体表现形式B.信息是有意义的数据C.信息是数据的素材D.一条信息可以表示为多种形式的数据C0279、目前使用的微型计算机属于()计算机。
P9-10A.智能时代B.新一代C.第四代D.第五代A0280、“虚拟现实”技术英文缩写是()。
A.VRB.OAC.AID.CATD0281、由于计算机采用了()的原理,使其能实现自动连续运行。
P8A.布尔逻辑运算B.集成电路工作C.串行运算D.存储程序,顺序控制A0282、计算机主频的单位是()。
P30A.MHzB.MIPSC.MbpsD.KB/SD0283、计算机指令不包括()。
A.操作码和操作数B.指令码和操作数C.操作码和地址码D.循环编码和操作数D0379、下列字符中,ASCII码值最大的是()。
P19A.EB.8C.bD.eC0380、与十进制数16相等的十六进制数是()。
A.16HB.FHC.10HD.20HC0381、设逻辑“真”记为1,逻辑“假”记为0,分别用×和 + 表示“逻辑与”和“逻辑或”运算,则()逻辑运算式的结果为假。
P28A.1+0B.1×1C.0×1D.1+1D0382、2KB等于()比特。
A.16×1000B.2×1024C.8×1024D.16×1024D0383、存储1024个48×48点阵汉字,存储空间大约需要()。
A.2304BB.288BC.2304KBD.288KBD0479、微型计算机中()的宽度通常与微处理器的字长一致。
机械设计(第八版)课后习题答案及解析(最新_参考答案及解析)
3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
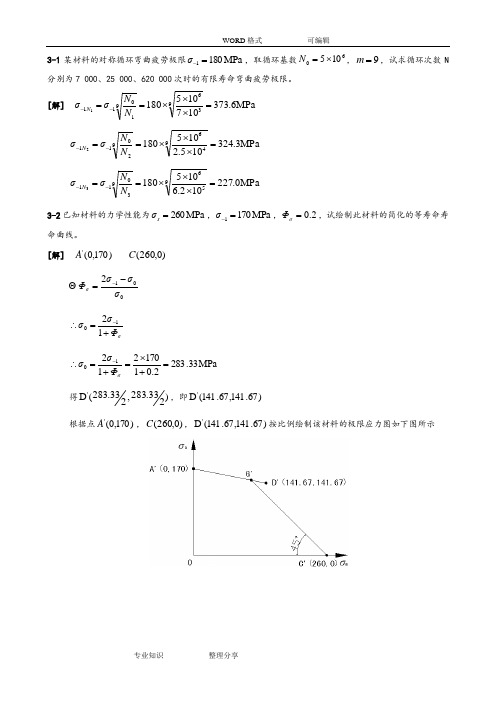
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB =420MPa ,精车,弯曲,βq =1,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。
江苏省东台市八校八年级数学下学期第二次质量检测试题

江苏省东台市八校2015-2016学年八年级数学下学期第二次质量检测试题(试卷满分120分 考试时间100分钟)一、选择题(每小题3分,共24分.请将唯一正确选项的字母代号填涂在答题卡相应位置上) 1.下列电视台的台标,是中心对称图形的是( )A .B .C .D .2.在分式b a b2+中,如果a 、b 都扩大为原来的3倍,则分式的值将 ( )A .扩大3倍B .不变C .缩小3倍D .缩小6倍 3.下列根式中,不能与3合并的是( )A .31 B .33 C .32D .27 4.如图,小红在作线段AB 的垂直平分线时,是这样操作的:分别以点A ,B 为圆心,大于线段AB 长度一半的长为半径画弧,相交于点C ,D ,则直线CD 即为所求。
连结AC ,BC ,AD ,BD ,根据她的作图方法可知,四边形ADBC 定是..( ) A. 矩形 B. 正方形 C.菱形 D. 平行四边形 5.对于函数y =6x,下列说法错误的是( ) A .它的图像分布在第一、三象限 B .它的图像与直线y =-x 无交点C .当x>0时,y 的值随x 的增大而增大D .当x<0时,y 的值随x 的增大而减小6.某一景点改造工程要限期完成,甲工程队独做可提前一天完成,乙工程队独做要误期6天,现由两工程队合做4天后,余下的由乙工程队独做,正好如期完成,若设工程期限为x 天,则下面所列方程正确的有( ) 个 ①1614=-++x x x ② 6614+=-x x ③611+=-x x x ④1614=++-x x x A. 1 B. 2 C.3 D. 47.若实数a 满足a a a =-+-20172016,则22016-a =( ) A. 2016 B. 2017 C.4033 D. 18.如图所示,正方形ABCD 的顶点B ,C 在x 轴的正半轴上,反比例函数)0(≠=k xky 在第一象限的图象经过顶点A (m ,m +3)和CD 上的点E ,且OB -CE =1,过点E 的直线l 交 x 轴于点F ,交y 轴于点G (0,-3),则OF 的长为( )A .4.5B .5C .5.4D .6二、填空题(本大题共有10小题,每小题3分,共30分.请将答案直接写在答题卡相应位置上) 9.写出一个根为2-的一元二次方程 10.若反比例函数ky x=的图像经过点(一2,3),则k = 11.等腰三角形,腰长为5cm ,它的周长是12cm ,则它的中位线长为 cm ; 12.如果m 为整数,那么使分式13++m m 的值为整数的m 的值为 (写出两个即可) 13.如果15-+x x 有意义,那么字母x 的取值范围是 14.若矩形ABCD 的两邻边长分别为一元二次方程x 2﹣7x +12=0的两个实数根,则矩形ABCD 的对角线长为15.已知023=-+-b a ,则b a61+的值为16.若一元二次方程020162=--bx ax 有一根为1-=x ,则b a +=________17.已知关于x 的分式方程112=+-x ax 的解为负数,则字母a 的取值范围是 18.若一元二次方程ax 2=b (ab >0)的两个根分别是2+m 与52-m ,则ab =三、解答题(本大题共有8小题,共66分.请在答题卡指定区域内作答,解答时应写出文字说明、推理过程或演算步骤)19.(本题满分8分,每题4分)计算 (1) 12214253532-++ (2)8143124⨯-⨯ 20. (本题满分8分,每题4分)解方程(3))1(3)1(2-=-x x (4)0142=+-x x21.(本题满分6分)已知132-=x ,求322-+x x 的值22.(本题满分6分)先化简再求值:)1121(122+---÷--a a a a a ,其中a 是方程20162=-x x 的解23.(本题满分8分)我市恒丰蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.下图是某天恒温系统从开启到关闭及关闭后,大棚内温度y (℃)随时间x (小时)变化的函数图象,其中BC 段是双曲线xky =的一部分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时? (2)求k 的值;(3)当x =16时,大棚内的温度约为多少度?24.(本题满分8分)如图,正方形ABCD 中,点E ,F 分别在边AB ,BC 上,AF =DE ,AF 和DE 相交于点G .(1)观察图形,写出图中所有与∠AED 相等的角.(2)选择图中与∠AED 相等的任意一个角,并加以证明.25.(本题满分10分)一次作业中,小明做了这样一题,以下是他的解题过程: 题目:当m 为何值时,关于x 的方程012)2(2=-+++m x m x 的两根互为相反数? 解:因为:关于x 的方程012)2(2=-+++m x m x 的两根互为相反数; 所以:设这个方程的两个根为k 与k -;所以:⎪⎩⎪⎨⎧=-+-++-=-+++)2(012))(2()()1(012)2(22m k m k m k m k (1)式减(2)式得:所以:2-=m 或0=k ;把0=k 0)2(2=+k m 代入(1)式,得1=m x (时)y (℃)18212 OA BC所以:2-=m 或21=m 老师批语:呵呵,你代入试试!请你代入原方程进行检验;说明小明同学解题过程是否正确?如果解题过程正确,请你给予适当的评价,如果不正确,请指出错误,并给予纠正.26.(本题满分12分)如图,直线l :y=x+1与x 轴、y 轴分别交于A 、B 两点,点C 与原点O 关于直线l 对称.反比例函数y=的图象经过点C ,点P 在反比例函数图象上且位于C 点左侧,过点P 作x 轴、y 轴的垂线分别交直线l 于M 、N 两点. (1)求ABO ∠的度数(2)求反比例函数的解析式; (3)求AN•BM 的值.初二数学试卷答题纸题号 1 2 3 4 5 6 7 8 选项二、填空题9. 10. 11. 12. 13. 14. 15. 16. 17. 18.三、解答题19.(本题满分8分,每题4分)计算 (1) 12214253532-++ (2)8143124⨯-⨯20. (本题满分8分,每题4分)解方程(3))1(3)1(2-=-x x (4)0142=+-x x21.(本题满分6分)已知132-=x ,求322-+x x 的值22.(本题满分6分)先化简再求值:)1121(122+---÷--a a a a a ,其中a 是方程20162=-x x 的解 班级_____________ 姓名___________ 考号__________________………………………………密…………封…………线…………内…………不…………得…………答…………题………………………………23. (本题满分8分)(1)(2)(3)24. (本题满分8分)(1)(2)25. (本题满分10分)(1)x(时) y(℃)182 12OA BC(2)26.(本题满分12分)(1)(2)(3)1.D2.B3.C4.C5.C6.B7.B8.C9.略 10.-6 11.1 12.0,1,-2,-3(写两个即可) 13.15≠-≥x x 且 14.5 15.33416.2016 17. 21-≠-a a 且π 18.9 19—21略 22.原式=)1(1-a a ;……………………4分当20162=-a a 时,上式=20161……………………6分 23.(1)恒温系统在这天保持大棚温度18℃的时间为10小时.………………2分(2)∵点B (12,18)在双曲线xky =上, ∴1218k =, ∴216=k .……………………5分(3)当x =16时,5.1316216==y , 所以当x =16时,大棚内的温度约为13.5℃.……………………8分24.(1)由图可知,∠DAG ,∠AFB ,∠CDE 与∠AED 相等;……………3分 (2)选择∠DAG =∠AED ,证明如下: ∵正方形ABCD ,∴∠DAB =∠B =90°,AD =AB , ∵AF =DE ,在△DAE 与△ABF 中,,∴△DAE ≌△ABF (SAS ), ∴∠ADE =∠BAF ,∵∠DAG +∠BAF =90°,∠GDA +∠AED =90°, ∴∠DAG =∠AE D .……………………8分 25.(1)小明解答不正确 (2)略26.(1)连接AC ,BC ,由题意得:四边形AOBC 为正方形,对于一次函数y=x+1,令x=0,求得:y=1;令y=0,求得:x=﹣1, ∴OA=OB=1,∴︒=∠45ABO ……………………4分 (2)∵OA=OB=1 ∴C (﹣1,1), 将C (﹣1,1)代入y=得:1=,即k=﹣1,则反比例函数解析式为y=﹣;……………………8分(3)过M作ME⊥y轴,作ND⊥x轴,设P(a,﹣),可得ND=﹣,ME=|a|=﹣a,∵△AND和△BME为等腰直角三角形,∴AN=×(﹣)=﹣,BM=﹣a,则AN•BM=﹣•(﹣a)=2.……………………12分。
2008年高考文科数学试题及答案-四川卷【解析版】

2008年普通高等学校招生全国统一考试(四川卷)数 学(文科)及参考答案本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3至第4页。
全卷满分150分,考试时间120分钟。
考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的座位号、姓名,并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致。
2. 答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动、用橡皮擦干净后,再选涂其他答案标号。
3. 答第Ⅱ卷时,必须用0.5毫米黑色墨水签字笔在答题卡上.....书写。
在试题卷上作答无效.........。
4. 考试结束,监考员将试题卷和答题卡一并收回。
参考公式:如果事件A 、B 互斥,那么 球的表面积公式()()()P A B P A P B +=+ 24S R π=如果事件A 、B 相互独立,那么 其中R 表示球的半径()()()P A B P A P B ⋅=⋅ 球的体积公式如果事件A 在一次实验中发生的概率是p ,那么 343V R π=n 次独立重复实验中事件A 恰好发生k 次的概率 其中R 表示球的半径()()()1,0,1,2,,n kk kn n P k C p p k n -=-=L第Ⅰ卷一.选择题:1.设集合{}{}{}1,2,3,4,5,1,2,3,2,3,4U A B ===,则()U A B =I ð( B )(A){}2,3 (B){}1,4,5 (C){}4,5 (D){}1,5 【解】:∵{}{}1,2,3,2,3,4A B == ∴{}2,3A B =I 又∵{}1,2,3,4,5U = ∴(){}1,4,5U A B =I ð 故选B ; 2.函数()1ln 212y x x ⎛⎫=+>- ⎪⎝⎭的反函数是( C ) (A)()112xy e x R =-∈ (B)()21x y e x R =-∈ (C)()()112xy e x R =-∈ (D)()21xy e x R =-∈【解】:∵由()ln 21y x =+反解得()112y x e =- ∴()112x y e =- 从而淘汰(B)、(D) 又∵原函数定义域为12x >- ∴反函数值域为12y >- 故选C ;【考点】:此题重点考察求反函数的方法,考察原函数与反函数的定义域与值域的互换性;【突破】:反解得解析式,或利用原函数与反函数的定义域与值域的互换对选项进行淘汰;3.设平面向量()()3,5,2,1a b ==-r r,则2a b -=r r ( A )(A)()7,3 (B)()7,7 (C)()1,7 (D)()1,3【解】:∵()()3,5,2,1a b ==-r r ∴()()()()23,522,1345273a b -=--=+-=r r,,故选C ; 【考点】:此题重点考察向量加减、数乘的坐标运算; 【突破】:准确应用向量的坐标运算公式是解题的关键; 4.()2tan cot cos x x x +=( D )(A)tan x (B)sin x (C)cos x (D)cot x【解】:∵()22222sin cos sin cos tan cot cos cos cos cos sin sin cos x x x x x x x x x x x x x +⎛⎫+=+=⋅ ⎪⎝⎭cos cot sin xx x== 故选D ; 【点评】:此题重点考察各三角函数的关系;【突破】:熟悉三角公式,化切为弦;以及注意22sin cos sin cos 1,tan ,cot cos sin x xx x x x x x+===; 5.不等式的解集为( A )(A)()1,2- (B)()1,1- (C)()2,1- (D)()2,2-【解】:∵22x x -< ∴222x x -<-< 即222020x x x x ⎧-+>⎨--<⎩,12x Rx ∈⎧⎨-<<⎩, ∴()1,2x ∈- 故选A ;【点评】:此题重点考察绝对值不等式的解法; 【突破】:准确进行不等式的转化去掉绝对值符号为解题的关键,可用公式法,平方法,特值验证淘汰法;6.直线3y x =绕原点逆时针旋转090,再向右平移1个单位,所得到的直线为( A )(A)1133y x =-+ (B)113y x =-+ (C)33y x =- (D)113y x =+【解】:∵直线3y x =绕原点逆时针旋转090的直线为13y x =-,从而淘汰(C),(D ) 又∵将13y x =-向右平移1个单位得()113y x =--,即1133y x =-+ 故选A ;【点评】:此题重点考察互相垂直的直线关系,以及直线平移问题;【突破】:熟悉互相垂直的直线斜率互为负倒数,过原点的直线无常数项;重视平移方法:“左加右减”; 7.ABC ∆的三内角,,A B C 的对边边长分别为,,a b c ,若,2a A B ==,则cos B =( B )【解】:∵ABC ∆中2a A B ⎧=⎪⎨⎪=⎩∴sin sin sin 22sin cos A B A B B B⎧=⎪⎨⎪==⎩∴cos B = 故选B ; 【点评】:此题重点考察解三角形,以及二倍角公式;【突破】:应用正弦定理进行边角互化,利用三角公式进行角的统一,达到化简的目的;在解三角形中,利用正余弦定理进行边角转化是解题的基本方法,在三角函数的化简求值中常要重视角的统一,函数的统一,降次思想的应用。
2020 成都中考数学密押卷(二)参考答案及评分意见

&
&'
&(
&$
'
'&
'(
'$
(
(&
('
($
$
$&
$'
$(
由上表可知出现等可能性的结果共有!&种其中同时选中小红小燕的结果有&种
3)同 时 选 中 小 红 小 燕 1!&&1 !) !
" 分
!)! 本 小 题 满 分 !$ 分
&&$$$0!&$$$1'$$名! 3 该 校 约 有 '$$ 名 学 生 喜 爱 打 乒 乓 球 !
%将小薇小燕小红小梅分别用字母 &'($ 表示! 依题意画树状图如下
( 分
数学密押卷二参考答案及评分意见第!& 页共"页
或列表如下
结果 第二次
&
'
(
$
第一次
%将 ,!1$ 代 入 ,!1 /#2'得 #1' 3点 ' 的坐标为'$!
将
,&1$
代
入
,&1
% '#2
+ '
得
2024届四川省成都市彭州市八年级数学第二学期期末联考试题含解析

2024届四川省成都市彭州市八年级数学第二学期期末联考试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每题4分,共48分)1.下列二次根式中,最简二次根式是( )A .12B .4C .6D .82.一个正多边形的内角和为1080,则这个正多边形的每一个外角的度数是( )A .45B .60C .90D .1353.下列四组线段中,能组成直角三角形的是( )A .a 1=,b 2=,c 3=B .a 2=,b 3=,c 4=C .a 2=,b 4=,c 5=D .a 3=,b 4=,c 5=4.如图,在方格纸中,以AB 为一边作△ABP ,使之与△ABC 全等,从P 1,P 2,P 3,P 4四个点中找出符合条件的点P ,则点P 有( )A .1个B .2个C .3个D .4个5.在四边形ABCD 中:①AB ∥CD ②AD ∥BC ③AB=CD ④AD=BC ,从以上选择两个条件使四边形ABCD 为平行四边形的选法共有( )A .3种B .4种C .5种D .6种6.生物学家发现了一种病毒,其长度约为0.00000032mm ,将数据0. 00000032用科学记数法表示正确的是( ) A .73.210⨯ B .73.210-⨯ C .83.210⨯ D .83.210-⨯7.如图,Rt △ABC 中,∠ACB =90°,若AB =15,则正方形ADEC 和正方形BCFG 的面积之和为( )A .150B .200C .225D .无法计算8.下列二次根式是最简二次根式的是A .13B .15C .15D .189.下列二次根式中,是最简二次根式的是( ).A .2B .0C .1D .910.若y =x +2–b 是正比例函数,则b 的值是( )A .0B .–2C .2D .–0.511.下列等式成立的是( )A .235+=B .2(4)2-=C .2323+=D .258102⨯=12.当x=2时,函数y=-12x 2+1的值是( ) A .-2 B .-1C .2D .3 二、填空题(每题4分,共24分)13.如图,以正方形ABCD 的BC 边向外作正六边形BEFGHC ,则∠ABE =___________度.14.在盒子里放有三张分别写有整式a+1、a+2、2的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是_____.15.将长为10米的梯子斜靠在墙上,若梯子的上端到梯子的底端的距离为6米,则梯子的底端到墙的底端的距离为_____.16.①_________;②_________;③_________.17.已知方程组122x y x y +=⎧⎨-=⎩的解为10x y =⎧⎨=⎩,则一次函数y =﹣x+1和y =2x ﹣2的图象的交点坐标为_____. 18.如图,正方形ABCD 中,AB =6,E 是CD 的中点,将△ADE 沿AE 翻折至△AFE ,连接CF ,则CF 的长度是_____.三、解答题(共78分)19.(8分)如图,在矩形ABCD 中,AD nAB =,,E F 分别在AB ,BC 上.(1)若1n =,AF DE ⊥.①如图1,求证:AE BF =;②如图2,点G 为CB 延长线上一点,DE 的延长线交AG 于H ,若AH AD =,求证:AE BG AG +=; (2)如图3,若E 为AB 的中点,ADE EDF ∠=∠.则CF BF的值为 (结果用含n 的式子表示) 20.(8分)求证:一组对边平行且相等的四边形是平行四边形.(要求:画出图形,写出已知、求证和证明过程)21.(8分)ABC 中,AD 是BAC ∠的平分线,AE BC ⊥,垂足为E ,作CF//AD ,交直线AE 于点F.设B α∠=,ACB β∠=.()1若B 30∠=,ACB 70∠=,依题意补全图1,并直接写出AFC ∠的度数;()2如图2,若ACB ∠是钝角,求AFC ∠的度数(用含α,β的式子表示);()3如图3,若B ACB∠∠∠的度数(用含α,β的式子表示).>,直接写出AFC22.(10分)如图,四边形ABCD中,AC⊥BD交BD于点E,点F、M分别是AB、BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF求证:(1)BN=2MN;(2)△MFN∽△BDC.23.(10分)小李在学校“青少年科技创新比赛”活动中,设计了一个沿直线轨道做匀速直线运动的模型.甲车从A处出发向B处行驶,同时乙车从B处出发向A处行驶.如图所示,线段1l、2l分别表示甲车、乙车离B处的距离y(米)与已用时间x(分)之间的关系.试根据图象,解决以下问题:(1)填空:出发_________(分)后,甲车与乙车相遇,此时两车距离B处________(米);(2)求乙车行驶1.2(分)时与B处的距离.24.(10分)为了了解某校七年级男生的体能情况,体育老师随即抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2尚不完整的统计图.(1)本次抽测的男生有人;(2)请你将图1的统计图补充完整;(3)若规定引体向上5次以上(含5次)为体能达标,则该校350名九年级男生中,估计有多少人体能达标?25.(12分)用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:四边形ABCD求作:点P,使∠PBC=∠PCB,且点P到AD和DC的距离相等.26.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.两车行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:(1)慢车的速度为km/h,快车的速度为km/h;(2)解释图中点C的实际意义并求出点C的坐标;(3)求当x为多少时,两车之间的距离为500km.参考答案一、选择题(每题4分,共48分)1、C【解题分析】根据最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式,结合选项求解即可.【题目详解】解:A =B =2不是最简二次根式,本选项错误;C 是最简二次根式,本选项正确;D =.【题目点拨】本题考查了最简二次根式的知识,解答本题的关键在于掌握最简二次根式的概念,对各选项进行判断.2、A【解题分析】根据多边形的内角和公式求出边数,从而求得每一个外角的度数.【题目详解】多边形的内角和为1080,即()18021080n ⨯-=解得:8n =∴该多边形为正八边形 ∴正八边形的每一个外角为:360458= 故选:A【题目点拨】本题考查了多边形的内角和与外角和公式,解题的关键在于根据内角和求出具体的边数.3、D【解题分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.【题目详解】A.1²+2²≠3²,故不是直角三角形,故本选项错误;B.2²+3²≠4²故不是直角三角形,故本选项错误;C.2²+4²≠5²,故不是直角三角形,故本选项错误;D.3²+4²=5 ²,故是直角三角形,故本选项正确.故选D.【题目点拨】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.4、C【解题分析】要使△ABP与△ABC全等,必须使点P到AB的距离等于点C到AB的距离,即3个单位长度,所以点P的位置可以是P1,P2,P4三个,故选C.5、B【解题分析】【分析】根据平行四边形的判定方法即可找到所有组合方式:(1)两组对边平行①②;(2)两组对边相等③④;(3)一组对边平行且相等①③或②④,所以有四种组合.【题目详解】(1)①②,利用两组对边平行的四边形是平行四边形判定;(2)③④,利用两组对边相等的四边形是平行四边形判定;(3)①③或②④,利用一组对边平行且相等的四边形是平行四边形判定;共4种组合方法,故选B.【题目点拨】本题主要考查了平行四边形的判定方法,熟练掌握平行四边形的判定方法是解题的关键.平行四边形的判定方法共有五种,在四边形中如果有:1、四边形的两组对边分别平行;2、一组对边平行且相等;3、两组对边分别相等;4、对角线互相平分;5、两组对角分别相等.则四边形是平行四边形.6、B【解题分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【题目详解】0.00000032=3.2×10-1.故选:B.【题目点拨】本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.7、C【解题分析】小正方形的面积为AC的平方,大正方形的面积为BC的平方,两正方形面积的和为AC2+BC2,对于Rt△ABC,由勾股定理得AB2=AC2+BC2,AB=15,故可以求出两正方形面积的和.【题目详解】正方形ADEC的面积为: AC2 ,正方形BCFG的面积为:BC2;在Rt△ABC中,AB2 = AC2+ BC2,AB=15,则AC2 + BC2 = 225cm2,故选:C.【题目点拨】此题考查勾股定理,熟记勾股定理的计算公式是解题的关键.8、B【解题分析】化简得到结果,即可作出判断.【题目详解】A. 被开方数含分母,故错误;B. 正确;C. 被开方数含分母,故错误;D. ,故错误;故选:B.【题目点拨】此题考查最简二次根式,解题关键在于检查最简二次根式的两个条件是否同时满足9、A【解题分析】检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.【题目详解】A、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故正确;B,故错误;C=1,故错误;D故错误;故选:A.【题目点拨】考查最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.10、C【解题分析】根据正比例函数的定义可得关于b的方程,解出即可.【题目详解】解:由正比例函数的定义可得:2-b=0,解得:b=2.故选C.【题目点拨】考查了正比例函数的定义,解题关键是掌握正比例函数的定义条件:正比例函数y=kx的定义条件是:k为常数且k≠0,自变量次数为2.11、D【解题分析】根据二次根式的混合运算法则进行求解即可.【题目详解】A. .B. 4=,故此选项错误;C. 2D.【题目点拨】本题主要考查了二次根式的混合运算,熟练掌握运算法则是解题关键.12、B【解题分析】把x=2代入函数关系式进行计算即可得解.【题目详解】x=2时,y=−12×22+1=−1.故选:B.【题目点拨】本题考查了函数值求解,把自变量的值代入进行计算即可,比较简单.二、填空题(每题4分,共24分)13、1【解题分析】分别求出正方形ABCD的内角∠ABC和正六边形BEFGHC的内角∠CBE的度数,进一步即可求出答案.【题目详解】解:∵四边形ABCD是正方形,∴∠ABC=90°,∵六边形BEFGHC是正六边形,∴∠CBE=()621801206-⋅︒=︒,∴∠ABE=360°-(∠ABC+∠CBE)=360°-(90°+120°)=1°.故答案为:1.【题目点拨】本题主要考查了正多边形的内角问题,属于基础题型,熟练掌握多边形的内角和公式是解题的关键.14、23.【解题分析】解:画树状图得:∴一共有6种等可能的结果,把两张卡片上的整式分别作为分子和分母,能组成分式的有4个,∴能组成分式的概率是42 63 =故答案为23.【题目点拨】此题考查了列表法或树状图法求概率.注意树状图法与列表法可以不重不漏的表示出所有等可能的结果.用到的知识点为:概率=所求情况数与总情况数之比.15、8米.【解题分析】在Rt△ABC中,利用勾股定理即可求出BC的值.【题目详解】在Rt△ABC中,AB1=AC1+BC1.∵AB=10米,AC=6米,∴BC22=-=8米,即梯子的底端到墙的底端的距离为8米.AB AC故答案为8米.【题目点拨】本题考查了勾股定理的应用,解答本题的关键是掌握勾股定理在直角三角形中的表达式.16、①, ②, ③.【解题分析】①根据二次根式的性质化简即可解答②根据立方根的性质计算即可解答③根据积的乘方,同底数幂的除法,进行计算即可解答【题目详解】①=②=-3③=4x=4x【题目点拨】此题考查二次根式的性质,同底数幂的除法,解题关键在于掌握运算法则17、(1,0)【解题分析】试题分析:二元一次方程组是两个一次函数变形得到的,所以二元一次方程组的解,就是函数图象的交点坐标试题解析:∵方程组1{22x yx y+=-=的解为1{xy==,∴一次函数y=-x+1和y=2x-2的图象的交点坐标为(1,0).考点:一次函数与二元一次方程(组).18、【解题分析】连接DF交AE于G,依据轴对称的性质以及三角形内角和定理,即可得到∠AGD=∠DFC=90°,再根据面积法即可得出DG=,最后判定△ADG≌△DCF,即可得到CF=DG=.【题目详解】解:如图,连接DF交AE于G,由折叠可得,DE=EF,又∵E是CD的中点,∴DE=CE=EF,∴∠EDF=∠EFD,∠ECF=∠EFC,又∵∠EDF+∠EFD+∠EFC+∠ECF=180°,∴∠EFD+∠EFC=90°,即∠DFC=90°,由折叠可得AE⊥DF,∴∠AGD=∠DFC=90°,又∵ED=3,AD=6,∴Rt△ADE中,又∵∴DG=∵∠DAG+∠ADG=∠CDF+∠ADG=90°,∴∠DAG=∠CDF,又∵AD=CD,∠AGD=∠DFC=90°,∴△ADG≌△DCF(AAS),∴CF=DG=,故答案为:.【题目点拨】本题主要考查了正方形的性质,折叠的性质以及全等三角形的判定与性质,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.三、解答题(共78分)19、(1)①见解析;②见解析;(2)241n【解题分析】(1)①由“ASA”可证△ADE ≌△BAF 可得AE=BF ;②过点A 作AF ⊥HD 交BC 于点F ,由等腰三角形的性质和平行线的性质可得∠HAF=∠AFG=∠DAF ,可得AG=FG ,即可得结论;(2)过点E 作EH ⊥DF 于H ,连接EF ,由角平分线的性质可得AE=EH=BE ,由“HL”可证Rt △BEF ≌Rt △HEF ,可得BF=FH ,由勾股定理可求解.【题目详解】证明(1)①∵四边形ABCD 是矩形,AD=AB,∴四边形ABCD 是正方形,∴AD=AB ,∠DAB=90°=∠ABC , ∴∠DAF+∠BAF=90°,∵AF ⊥DE ,∴∠DAF+∠ADE=90°,∴∠ADE=∠BAF ,且AD=AB ,∠DAE=∠ABF=90°,∴△ADE ≌△BAF (ASA ),∴AE=BF ;②如图,过点A 作AF ⊥HD 交BC 于点F ,由(1)可知AE=BF ,∵AH=AD ,AF ⊥HD ,∴∠HAF=∠DAF.∵AD ∥BC ,∴∠DAF=∠AFG ,∴∠HAF=∠AFG ,∴AG=GF ,∴AG=GB+BF=GB+AE ;(3)如图,过点E 作EH ⊥DF 于H ,连接EF ,∵E 为AB 的中点,∴AE=BE=12AB , ∵∠ADE=∠EDF ,EA ⊥AD ,EH ⊥DF ,∴AE=EH ,AD=DH=nAB ,∴BE=EH ,EF=EF ,∴Rt △BEF ≌Rt △HEF (HL ),∴BF=FH ,设BF=x=FH ,则FC=BC-BF=nAB-x ,∵DF 2=FC 2+CD 2,∴(nAB+x )2=(nAB-x )2+AB 2,∴x=4AB n=BF ,∴FC=2414n n-AB , ∴CF BF=4n 2-1. 【题目点拨】本题是四边形综合题,考查了正方形的性质,矩形的性质,全等三角形的判定和性质,勾股定理,等腰三角形的性质,添加恰当辅助线构造全等三角形是本题的关键.20、见解析.【解题分析】先根据题意画出图形,写出已知,求证,然后通过平行线的性质得出∠1=∠2,再利用SAS 证明△ABC ≌△CDA ,则有∠3=∠4,进一步得出AD ∥BC ,最后利用两组对边分别平行的四边形为平行四边形即可证明.【题目详解】已知:如图,在四边形ABCD 中,AB ∥CD ,AB=CD .求证:四边形ABCD 是平行四边形.证明:连接AC ,如图所示:∵AB ∥CD ,∴∠1=∠2,在△ABC 和△CDA 中,12AB CD AC CA =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△CDA (SAS ),∴∠3=∠4,∴AD ∥BC ,∴四边形ABCD 是平行四边形(两组对边分别平行的四边形是平行四边形).【题目点拨】本题主要考查平行四边形的判定,全等三角形的判定及性质,平行线的判定及性质,掌握全等三角形和平行线的判定及性质是解题的关键.21、(1)补图见解析,AFC 20∠=;(2) ()1AFC 180βα2∠=--;(3) ()1AFC αβ2∠=-. 【解题分析】(1)先根据三角形内角和定理求出∠BAC 和∠CAE ,根据角平分线定义求出∠CAD ,即可求出答案;(2)先根据三角形内角和定理求出∠BAC ,根据角平分线定义求出∠BAD ,根据三角形外角性质求出∠ADC ,根据三角形内角和定理求出∠DAE ,根据平行线的性质求出即可; (3)求出∠DAE 度数,根据平行线的性质求出即可.【题目详解】解:()1如图1,B 30∠=,ACB 70∠=,BAC 180B ACB 80∠∠∠∴=--=,AD 是BAC ∠的平分线,1CAD CAB 402∠∠∴==, AE BC ⊥,AEC 90∠∴=,ACB 70∠=,EAC 180907020∠∴=--=,DAE CAD CAE 402020∠∠∠∴=-=-=,CF//AD ,AFC DAE 20∠∠∴==;()2如图2,ABC 中,BAC B ACB 180∠∠∠++=,()BAC 180B ACB ∠∠∠∴=-+.()180αβ=-+, AD 是BAC ∠的平分线, ()11BAD BAC 90αβ22∠∠∴==-+, ()()11ADE B BAD α90αβ90βα22∠∠∠∴=+=+-+=--, AE BC ⊥,DAE ADE 90∠∠∴+=,()1DAE 90ADE βα2∠∠∴=-=-, CF//AD ,DAE AFC 180∠∠∴+=,()1AFC 180βα2∠∴=--; ()3如图3,ABC 中,BAC B ACB 180∠∠∠++=,()BAC 180B ACB ∠∠∠∴=-+,()180αβ=-+, AD 是BAC ∠的平分线, ()11CAD BAC 90αβ22∠∠∴==-+, AE BC ⊥,AEC 90∠∴=,ACB β∠=, EAC 18090β90β∠∴=--=-,()()()11DAE CAE CAD 90β90αβαβ22∠∠∠⎡⎤∴=-=----=-⎢⎥⎣⎦. 【题目点拨】本题考查了三角形内角和定理、三角形角平分线定义、三角形的高、平行线的性质等,熟练掌握相关的性质与定理是解题的关键.22、(1)见解析;(2)见解析【解题分析】(1)根据等腰三角形的性质,可得AM 是高线、顶角的角平分线,根据直角三角形的性质,可得90EAB EBA ∠+∠=︒,根据三角形外角的性质,可得45MNB ∠=︒,进而可知BMN ∆是等腰直角三角形,即得BN =.(2)根据三角形中位线的性质,可得MF 与AC 的关系,根据等量代换,可得MF 与BD 的关系,根据等腰直角三角形,可得BM 与NM 的关系,根据等量代换,可得NM 与BC 的关系,根据同角的余角相等,可得CBD ∠与NMF ∠的关系,根据两边对应成比例且夹角相等的两个三角形相似,可得答案.【题目详解】(1)证明:∵AB AC =,点M 是BC 的中点∴AM BC ⊥,AM 平分BAC ∠∵BN 平分ABE ∠∴EBN ABN ∠=∠∵AC BD ⊥∴90AEB =︒∠∴90EAB EBA ∠+∠=︒∴()1452MNB NAB ABN BAE ABE ∠=∠+∠=∠+∠=︒ ∴BMN ∆是等腰直角三角形∴BN =(2)证明:∵点F ,M 分别是AB ,BC 的中点,∴//FM AC ,12FM AC =∵AC BD = ∴12FM BD =,即12FM BD = ∵BMN ∆是等腰直角三角形 ∴12NM BM BC ==,即12NM BC = ∴FM NM BD BC= ∵AM BC ⊥∴90NMF FMB ∠+∠=︒∵//FM AC∴ACB FMB ∠=∠∵90CEB ∠=︒∴90ACB CBD ∠+∠=︒∴90CBD FMB ∠+∠=︒∴NMF CBD ∠=∠∴MFN BDC ∆∆∽【题目点拨】本题考查了相似三角形的判定和性质、等腰直角三角形的判定和性质、三角形的内角外角中位线相关性质,综合性较强,难度较大.23、(1)0.6,2.4;(2)4.8米【解题分析】(1)甲乙相遇即图象交点(0.6,2.4)(2)根据图象解出两条直线的解析式,再由题意得到乙车行驶1.2(分)时与B 处的距离.【题目详解】(1)甲乙相遇即图象交点(0.6,2.4)∴出发0.6(分)后,甲车与乙车相遇,此时两车距离B 处2.4(米);故答案为0.6和2.4(2)假设直线l2的解析式为y=kx,将点(0.6,2.4)代入得,y=4x当x=1.2时,y=4.8∴乙车行驶12(分)时与B处距离为4.8米.【题目点拨】本题主要考查一次函数的应用,熟练掌握一次函数是解答本题的关键.24、(1)50;(2)5次的人数有16人(3)252【解题分析】(1)由引体向上的次数为4次的人数除以所占的百分比即可求出抽测的男生数;(2)求出次数为5次的人数,补全统计图即可;(3)求出5次以上(含5次)人数占的百分比,乘以350即可得到结果.【题目详解】(1)根据题意得:10÷20%=50(人),则本次抽测的男生有50人;故答案为50人;(2)5次的人数为50-(4+10+14+6)=16(人),补全条形统计图,如图所示:(3)根据题意得:3635025250⨯=人,则该校350名九年级男生中估计有252人体能达标.【题目点拨】此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.25、图形见解析.【解题分析】作∠ADC的平分线和BC的垂直平分线便可.【题目详解】解:如图所示,点P即为所求.【题目点拨】考查线段垂直平分线和角平分线的作图运用.26、80120【解题分析】(1)由图象可知,两车同时出发.等量关系有两个:3.6×(慢车的速度+快车的速度)=720,(9-3.6)×慢车的速度=3.6×快车的速度,设慢车的速度为akm/h,快车的速度为bkm/h,依此列出方程组,求解即可;(2)点C表示快车到达乙地,然后求出快车行驶完全程的时间从而求出点C的横坐标,再求出相遇后两辆车行驶的路程得到点C的纵坐标,从而得解;(3)分相遇前相距500km和相遇后相遇500km两种情况求解即可.【题目详解】(1)设慢车的速度为ak m/h,快车的速度为bkm/h,根据题意,得()3.67205.4 3.6a ba b==⎧+⎨⎩,解得80120ab=⎧⎨=⎩,故答案为80,120;(2)图中点C的实际意义是:快车到达乙地;∵快车走完全程所需时间为720÷120=6(h),∴点C的横坐标为6,纵坐标为(80+120)×(6﹣3.6)=480,即点C(6,480);(3)由题意,可知两车行驶的过程中有2次两车之间的距离为500km.即相遇前:(80+120)x=720﹣500,解得x=1.1,相遇后:∵点C(6,480),∴慢车行驶20km两车之间的距离为500km,∵慢车行驶20km需要的时间是2080=0.25(h),∴x=6+0.25=6.25(h),故x=1.1 h或6.25 h,两车之间的距离为500km.【题目点拨】考查了一次函数的应用,主要利用了路程、时间、速度三者之间的关系,(3)要分相遇前与相遇后两种情况讨论,这也是本题容易出错的地方.。
内镜黏膜下剥离术治疗消化道早癌术后出血的风险模型构建

医学研究生学报2021年2月第34卷第2期J Mee Posmo,VP.34,Nc.2,Fedruary,202)-195•论著(临床研究)内镜黏膜下剥离术治疗消化道早癌术后出血的风险模型构建吴江,吴涛,庞澜,阿里木江•阿不都热合曼,马秀英,陈鹏,朱勇荷[摘要]目的构建消化道早癌患者应用内镜黏膜下剥离术(ESD)治疗后术后出血的预测模型。
方法回顾性分析2018年5月-2020年3月新疆医科大学第二附属医院内镜中心治疗的504例消化道早癌患者临床资料,并依据ESD术后是否出血分为出血组(g=25)、对照组(a=535)o采用/putu回归分析ESD术后出血的危险因素,根据筛选的危险因素构建ESD术后出血风险预测模型,并采用ROC曲线对预测模型进行评价。
结果多因素/putu回归分析显示,有高血压(OR= 3.eo,95%CI:).57~5.85,P=0.000)、操作时间>90min(OR=).67,95%CI:).I8~3.53,P=0.008)、最大病灶直径&3cm (OR=1.55,95%CI:).53~3.I9,P=0.002)、病灶位于直肠(OR=).7),95%CI:).55~3.58,P=0.019)为消化道早癌患者ESD 术后出血的危险因素。
ROC曲线分析显示,模型预测消化道早癌患者ESD术后出血的AUC为0.865(95%CI:0.849~0.976, P=0.000),准确率82.32%、敏感度84.00%、特异度82.24%、临界值为0.545。
结论消化道早癌患者ESD术后出血与高血压、操作时间、病灶直径及病灶部位有关,预测模型可有效预测个体ESD术后出血风险。
[关键词]消化道早癌;内镜黏膜下剥离术;术后出血;预测模型[中图分类号]R735[文献标志码]A[文章编号]1008-8199(202))02-0155-06[DOI]10.1657)/ki.l008N199.202).02.008Constrochon of risk model of endoscopic submucosal dissection in the treatment of postoperohve bleeding of early gastrointestinal04^X0WU Jiang1,WU Tua2,PANG Lon1,ALIMUJIANG•AOdui RaPmon1,MA Xiu-ying1,CHEN Peng1,ZHU Yong-Sa1(1:Deeartmegi O EnUoscofy,Oe SecooU人甘辽血畝Hospitcd O Xiniang Meetcal UrgRpPy,Urumqi336573,Xinjiang ,China;2.Deeartmegi O Oncolofy,Chirgsc Meeicige Hospital4^,0to Xigiang MeUcal Uniersim,Uo-mq336005,Xiniang,China)[Abstract]Objective The pre s ect stupp aims to coxstruct a predictive model for posmperative O/eding io paPests with early gastrointestinal cancer after treatmest with epdoscopic suUmucosol dissecdox(ESD).Methods A retrospective analysis was used to ana/ze the clinical data of504paPests with early gastrointestinal cancer from Map2013to March2020.According to whether06111(0-rhaae after ESD,the paPests were divideP into posmperative O/eding基金项目:新疆维吾尔自治区自然科学基金(2515 D51C251)作者单位:83/53乌鲁木齐,新疆医科大学第二附属医院内镜诊治科[吴江(医学硕士)、庞澜、阿里木江•阿不都热合曼、马秀英、陈鹏、朱勇荷];830/5乌鲁木齐,新疆医科大学附属中医医院肿瘤一科(吴涛)group25cases and coxtroi group537cases.Mul/variato/pistic ro-gressiox was used to idestiU the UsP factors of posmperative O/eding after ESD.ROC carve was used to evaluate the predictive moded ReseUs Mul/variato/nstic repressiox analysis sPowed that hypef-tessiox(OR=3.59,95%CI:1.72-6.86,P=0.000),operatiox time> 90mir(OR=).57,95%CI:518-3.73,P=0.008),the largest/-siox diameter^3cm(OR=1.55,95%CI:).23-3.I5,P二0.002), the lesiox located ir the rectum(OR=).71,95%CI:1.26-3.98,P=7.012)were the Ush factors of pos/peotive bleeding in patients with early gastroinmsdnxl cancer after ESD.ROC curve analysis showedhhnhhheAUCoipeednchntgioeposhopeenhneebeeedntgntpnhnethswnhheneetgnsheontheshntnecntceeniheeESD wns02865(95% CI:7242-7277,P=7.007),the accuracy rate was8222%,wnWPmm was84.07%,and specificity was8224%with the cut-off vu I uc was7245.Conclusion HemorOage after ESD in paPests with early gastroinmsdnxl canceOpocanceops lesions are related to hypeOession,operaPon Pmo,lesion diameter,and lesion location.The podict/n model can ehectively predict the Ush of individual beeedntgnheeESD2[Key worOs]early gastroinmsdnxl canceoesdoscopic submucosal dissect/n;pos/peotive bleeding;predictive model0引言近年来随着生活方式及饮食习惯的改变,消化道肿瘤发病率虽然呈不同的变化,但总体趋于年轻化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称【编号】:教育统计学【0282】A卷
大作业满分:100分
一、论述题(2道题,每道题35分,共70分。请根据题目要求对要点展开充分论述)
1.联系实际阐述教育统计学的任务和主要内容。(35分)
答:教育统计学的主要任务是研究如何搜集、整理、分析有关教育研究和教育实践工作中的数字资料,并以此为依据进行科学推断,揭示教育现象所蕴涵的客观规律。教育统计学的主要内容包括描述统计、推断统计和实验设计。
4答案:
第一点:大班的平均分比中班高,说明大班的整体实力高于中班。第二点:大班的标准差低于中班,反映大班的小朋友成绩较为稳定,偏离平均分的波动不大。
二、应用题(下面两道题中选做1道,30分。必须有完整的解题过程)
3.将下列20个教师的考评成绩以5分为组距编制一个完整的频数分布表。(30分)
72 70 83 94 67 65 72 88 94 72
69 75 85 79 86 98 79 76 70 65
4.在某幼儿园随机抽取了40名大班和60名中班小朋友进行一项心理测试,测查结果:大班小朋友的平均分是83.2分,标准差是4分;中班小朋友的平均分是81.5分,标准差是6分。请检验大班和中班小朋友的测试结果有无显著性差异。(30分)
2.结合实例阐述相关关系的含义和类型。(35分)
相关关系:是两个变量之间的不确定关系,它反映的是变量之间不十分严格,但却存在的依存关系。(举例)相关关系包括正相关、负相关和零相关。正相关是两个变量的变化方向一致的相关。负相关是两个变量的变化方向相反的相关。零相关是两个变量的变化方向无一定的规律的相关。(举例)
