HeapSort
C语言八大排序算法
C语⾔⼋⼤排序算法C语⾔⼋⼤排序算法,附动图和详细代码解释!来源:C语⾔与程序设计、⽵⾬听闲等⼀前⾔如果说各种编程语⾔是程序员的招式,那么数据结构和算法就相当于程序员的内功。
想写出精炼、优秀的代码,不通过不断的锤炼,是很难做到的。
⼆⼋⼤排序算法排序算法作为数据结构的重要部分,系统地学习⼀下是很有必要的。
1、排序的概念排序是计算机内经常进⾏的⼀种操作,其⽬的是将⼀组“⽆序”的记录序列调整为“有序”的记录序列。
排序分为内部排序和外部排序。
若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。
反之,若参加排序的记录数量很⼤,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。
2、排序分类⼋⼤排序算法均属于内部排序。
如果按照策略来分类,⼤致可分为:交换排序、插⼊排序、选择排序、归并排序和基数排序。
如下图所⽰:3、算法分析1.插⼊排序*直接插⼊排序*希尔排序2.选择排序*简单选择排序*堆排序3.交换排序*冒泡排序*快速排序4.归并排序5.基数排序不稳定排序:简单选择排序,快速排序,希尔排序,堆排序稳定排序:冒泡排序,直接插⼊排序,归并排序,奇数排序1、插⼊排序将第⼀个和第⼆个元素排好序,然后将第3个元素插⼊到已经排好序的元素中,依次类推(插⼊排序最好的情况就是数组已经有序了)因为插⼊排序每次只能操作⼀个元素,效率低。
元素个数N,取奇数k=N/2,将下标差值为k的数分为⼀组(⼀组元素个数看总元素个数决定),在组内构成有序序列,再取k=k/2,将下标差值为k的数分为⼀组,构成有序序列,直到k=1,然后再进⾏直接插⼊排序。
3、简单选择排序选出最⼩的数和第⼀个数交换,再在剩余的数中⼜选择最⼩的和第⼆个数交换,依次类推4、堆排序以升序排序为例,利⽤⼩根堆的性质(堆顶元素最⼩)不断输出最⼩元素,直到堆中没有元素1.构建⼩根堆2.输出堆顶元素3.将堆低元素放⼀个到堆顶,再重新构造成⼩根堆,再输出堆顶元素,以此类推5、冒泡排序改进1:如果某次冒泡不存在数据交换,则说明已经排序好了,可以直接退出排序改进2:头尾进⾏冒泡,每次把最⼤的沉底,最⼩的浮上去,两边往中间靠16、快速排序选择⼀个基准元素,⽐基准元素⼩的放基准元素的前⾯,⽐基准元素⼤的放基准元素的后⾯,这种动作叫分区,每次分区都把⼀个数列分成了两部分,每次分区都使得⼀个数字有序,然后将基准元素前⾯部分和后⾯部分继续分区,⼀直分区直到分区的区间中只有⼀个元素的时候,⼀个元素的序列肯定是有序的嘛,所以最后⼀个升序的序列就完成啦。
用Java实现常见的8种内部排序算法

⽤Java实现常见的8种内部排序算法⼀、插⼊类排序插⼊类排序就是在⼀个有序的序列中,插⼊⼀个新的关键字。
从⽽达到新的有序序列。
插⼊排序⼀般有直接插⼊排序、折半插⼊排序和希尔排序。
1. 插⼊排序1.1 直接插⼊排序/*** 直接⽐较,将⼤元素向后移来移动数组*/public static void InsertSort(int[] A) {for(int i = 1; i < A.length; i++) {int temp = A[i]; //temp ⽤于存储元素,防⽌后⾯移动数组被前⼀个元素覆盖int j;for(j = i; j > 0 && temp < A[j-1]; j--) { //如果 temp ⽐前⼀个元素⼩,则移动数组A[j] = A[j-1];}A[j] = temp; //如果 temp ⽐前⼀个元素⼤,遍历下⼀个元素}}/*** 这⾥是通过类似于冒泡交换的⽅式来找到插⼊元素的最佳位置。
⽽传统的是直接⽐较,移动数组元素并最后找到合适的位置*/public static void InsertSort2(int[] A) { //A[] 是给定的待排数组for(int i = 0; i < A.length - 1; i++) { //遍历数组for(int j = i + 1; j > 0; j--) { //在有序的序列中插⼊新的关键字if(A[j] < A[j-1]) { //这⾥直接使⽤交换来移动元素int temp = A[j];A[j] = A[j-1];A[j-1] = temp;}}}}/*** 时间复杂度:两个 for 循环 O(n^2)* 空间复杂度:占⽤⼀个数组⼤⼩,属于常量,所以是 O(1)*/1.2 折半插⼊排序/** 从直接插⼊排序的主要流程是:1.遍历数组确定新关键字 2.在有序序列中寻找插⼊关键字的位置* 考虑到数组线性表的特性,采⽤⼆分法可以快速寻找到插⼊关键字的位置,提⾼整体排序时间*/public static void BInsertSort(int[] A) {for(int i = 1; i < A.length; i++) {int temp = A[i];//⼆分法查找int low = 0;int high = i - 1;int mid;while(low <= high) {mid = (high + low)/2;if (A[mid] > temp) {high = mid - 1;} else {low = mid + 1;}}//向后移动插⼊关键字位置后的元素for(int j = i - 1; j >= high + 1; j--) {A[j + 1] = A[j];}//将元素插⼊到寻找到的位置A[high + 1] = temp;}}2. 希尔排序希尔排序⼜称缩⼩增量排序,其本质还是插⼊排序,只不过是将待排序列按某种规则分成⼏个⼦序列,然后如同前⾯的插⼊排序⼀般对这些⼦序列进⾏排序。
【十大经典排序算法(动图演示)】 必学十大经典排序算法

【十大经典排序算法(动图演示)】必学十大经典排序算法0.1 算法分类十种常见排序算法可以分为两大类:比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
0.2 算法复杂度0.3 相关概念稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后a 可能会出现在b 的后面。
时间复杂度:对排序数据的总的操作次数。
反映当n变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
1、冒泡排序(Bubble Sort)冒泡排序是一种简单的排序算法。
它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
1.1 算法描述比较相邻的元素。
如果第一个比第二个大,就交换它们两个;对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;针对所有的元素重复以上的步骤,除了最后一个;重复步骤1~3,直到排序完成。
1.2 动图演示1.3 代码实现1.unction bubbleSort(arr) {2. varlen = arr.length;3. for(vari = 0; i arr[j+1]) {// 相邻元素两两对比6. vartemp = arr[j+1];// 元素交换7. arr[j+1] = arr[j];8. arr[j] = temp;9. }10. }11. }12. returnarr;13.}2、选择排序(Selection Sort)选择排序(Selection-sort)是一种简单直观的排序算法。
8种排序算法

J=2(38) [38 49] 65 97 76 13 27 49
J=3(65) [38 49 65] 97 76 13 27 49
J=4(97) [38 49 65 97] 76 13 27 49
J=5(76) [38 49 65 76 97] 13 27 49
2. 堆的定义: N个元素的序列K1,K2,K3,...,Kn.称为堆,当且仅当该序列满足特性:
Ki≤K2i Ki ≤K2i+1(1≤ I≤ [N/2])
堆实质上是满足如下性质的完全二叉树:树中任一非叶子结点的关键字均大于等于其孩子结点的关键字。例如序列10,15,56,25,30,70就是一个堆,它对应的完全二叉树如上图所示。这种堆中根结点(称为堆顶)的关键字最小,我们把它称为小根堆。反之,若完全二叉树中任一非叶子结点的关键字均大于等于其孩子的关键字,则称之为大根堆。
(6)基数排序
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序,最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以其是稳定的排序算法。
2. 排序过程:
【示例】:
初始关键字 [49 38 65 97 76 13 27 49]
第一趟排序后 13 [38 65 97 76 49 27 49]
第二趟排序后 13 27 [65 97 76 49 38 49]
第三趟排序后 13 27 38 [97 76 49 65 49]
其次,说一下稳定性的好处。排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。基数排序就是这样,先按低位排序,逐次按高位排序,低位相同的元素其顺序再高位也相同时是不会改变的。另外,如果排序算法稳定,对基于比较的排序算法而言,元素交换的次数可能会少一些(个人感觉,没有证实)。
matlab数据排序的方法

matlab数据排序的方法【原创实用版2篇】目录(篇1)1.MATLAB 数据排序概述2.MATLAB 数据排序方法2.1 默认排序2.2 数组排序2.3 矩阵排序2.4 列表排序2.5 字符串排序2.6 结构体排序3.MATLAB 数据排序应用实例4.MATLAB 数据排序的优缺点正文(篇1)一、MATLAB 数据排序概述MATLAB 是一种广泛应用于科学计算、数据分析、可视化等领域的编程语言。
在数据处理过程中,排序是一个常见的操作。
MATLAB 提供了多种数据排序方法,可以满足不同类型的数据排序需求。
二、MATLAB 数据排序方法1.默认排序默认情况下,MATLAB 会对数字进行升序排序,对字符串进行字典序排序。
例如,对于数组 x = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5],使用命令`sort(x)`进行排序,结果为:```x =1 123 345 5 56 9```2.数组排序MATLAB 提供了`sort`函数对数组进行排序。
除了默认升序排序,还可以通过`sort`函数的`descend`参数进行降序排序。
例如:```x = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5];y = sort(x, "descend");```结果为:```y =9 6 5 5 5 4 3 3 2 1 1```3.矩阵排序MATLAB 提供了`sort`函数对矩阵进行排序。
需要注意的是,矩阵的每一列都需要单独排序。
例如:```A = [3, 1; 4, 1; 1, 5];B = [1, 9; 1, 6; 5, 2];C = sort(A, 2); % 对矩阵 A 的第二列进行排序D = sort(B, 1); % 对矩阵 B 的第一列进行排序```结果为:```C =1 53 14 1D =1 51 65 2```4.列表排序MATLAB 中的列表以元组的形式存储,可以使用`sort`函数对列表进行排序。
各种排序算法的实现以及思考

冒泡排序(Bubble sort)原理冒泡排序是一种简单的排序算法。
它重复访问要排序的数列,每一次比较两个元素,如果前一个大于后一个元素,则交换数据。
那么在一次全部访问过程中,最大的元素就’浮’动到数列的最后。
然后重复进行方法,知道再没有数据交换,也就是数列已经排序完成。
步骤1.比较相邻的元素。
如果第一个比第二个大,就交换他们两个。
2.对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。
这步做完后,最后的元素会是最大的数。
3.针对所有的元素重复以上的步骤,除了最后一个。
4.持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
实现void BubbleSort(int arr[], int n) {int i, j;i = n;bool flag = true;while (flag) {flag = false;for (j = 1; j < i; j++) {if (arr[j-1] > arr[j]) {swap(arr[j-1],arr[j]);flag = true;}}i--;}}在上面的代码中加入了一个flag来标记是否有数据交换,如果在排序过程中没发生数据交换,则表示已经排列好了,后面就不需要在遍历了。
冒泡排序算是最简单的排序算法了,但毕竟是一种效率低下的排序算法,再数据量不大的情况下可以使用。
插入排序(Insertion sort)原理插入排序是一种直观的排序算法。
它通过构建有序数列,对未排序的数据,在已排序的数列中从后往前扫描,找到相应的位置插入。
在排序的实现上,从后向前的扫描过程中,需要反复把已排序的元素逐步向后移动,为要插入的元素留空间。
步骤1.从第一个元素开始,该元素可以认为已经被排序2.取出下一个元素,在已经排序的元素序列中从后向前扫描3.如果该元素(已排序)大于新元素,将该元素移到下一位置4.重复步骤3,直到找到已排序的元素小于或者等于新元素的位置5.将新元素插入到该位置后6.重复步骤2~5实现void InsertSort(int arr[], int n) {int i, j;for (i = 1; i < n; i++) {if (arr[i] < arr[i-1]) {int temp = arr[i];for (j = i - 1; j >= 0 && arr[j] > temp; j--){arr[j+1] = arr[j];}arr[j+1] = temp;}}}插入排序不适合对于数据了比较大的排序应用。
Python常用数据结构之heapq模块
Python常⽤数据结构之heapq模块阅读⽬录Python数据结构常⽤模块:collections、heapq、operator、itertools 堆是⼀种特殊的树形结构,通常我们所说的堆的数据结构指的是完全⼆叉树,并且根节点的值⼩于等于该节点所有⼦节点的值 heappush(heap,item)往堆中插⼊⼀条新的值heappop(heap)从堆中弹出最⼩值heapreplace(heap,item)从堆中弹出最⼩值,并往堆中插⼊itemheappushpop(heap,item)Python3中的heappushpop更⾼级heapify(x)以线性时间将⼀个列表转化为堆merge(*iterables,key=None,reverse=False)合并对个堆,然后输出nlargest(n,iterable,key=None)返回可枚举对象中的n个最⼤值并返回⼀个结果集listnsmallest(n,iterable,key=None)返回可枚举对象中的n个最⼩值并返回⼀个结果集list常⽤⽅法⽰例 #coding=utf-8import heapqimport randomdef test():li = list(random.sample(range(100),6))print (li)n = len(li)#nlargestprint ("nlargest:",heapq.nlargest(n, li))#nsmallestprint ("nsmallest:", heapq.nsmallest(n, li))#heapifyprint('original list is', li)heapq.heapify(li)print('heapify list is', li)# heappush & heappopheapq.heappush(li, 105)print('pushed heap is', li)heapq.heappop(li)print('popped heap is', li)# heappushpop & heapreplaceheapq.heappushpop(li, 130) # heappush -> heappopprint('heappushpop', li)heapq.heapreplace(li, 2) # heappop -> heappushprint('heapreplace', li) >>> [15, 2, 50, 34, 37, 55] >>> nlargest: [55, 50, 37, 34, 15, 2] >>> nsmallest: [2, 15, 34, 37, 50, 55] >>> original list is [15, 2, 50, 34, 37, 55] >>> heapify list is [2, 15, 50, 34, 37, 55] >>> pushed heap is [2, 15, 50, 34, 37, 55, 105] >>> popped heap is [15, 34, 50, 105, 37, 55] >>> heappushpop [34, 37, 50, 105, 130, 55] >>> heapreplace [2, 37, 50, 105, 130, 55]堆排序⽰例 heapq模块中有⼏张⽅法进⾏排序: ⽅法⼀:#coding=utf-8import heapqdef heapsort(iterable):heap = []for i in iterable:heapq.heappush(heap, i)return [heapq.heappop(heap) for j in range(len(heap))]if__name__ == "__main__":li = [30,40,60,10,20,50]print(heapsort(li)) >>>> [10, 20, 30, 40, 50, 60] ⽅法⼆(使⽤nlargest或nsmallest):li = [30,40,60,10,20,50]#nlargestn = len(li)print ("nlargest:",heapq.nlargest(n, li))#nsmallestprint ("nsmallest:", heapq.nsmallest(n, li)) >>> nlargest: [60, 50, 40, 30, 20, 10] >>> nsmallest: [10, 20, 30, 40, 50, 60] ⽅法三(使⽤heapify):def heapsort(list):heapq.heapify(list)heap = []while(list):heap.append(heapq.heappop(list))li[:] = heapprint (li)if__name__ == "__main__":li = [30,40,60,10,20,50]heapsort(li) >>> [10, 20, 30, 40, 50, 60]堆在优先级队列中的应⽤ 需求:实现任务的添加,删除(相当于任务的执⾏),修改任务优先级pq = [] # list of entries arranged in a heapentry_finder = {} # mapping of tasks to entriesREMOVED = '<removed-task>'# placeholder for a removed taskcounter = itertools.count() # unique sequence countdef add_task(task, priority=0):'Add a new task or update the priority of an existing task'if task in entry_finder:remove_task(task)count = next(counter)entry = [priority, count, task]entry_finder[task] = entryheappush(pq, entry)def remove_task(task):'Mark an existing task as REMOVED. Raise KeyError if not found.'entry = entry_finder.pop(task)entry[-1] = REMOVEDdef pop_task():'Remove and return the lowest priority task. Raise KeyError if empty.'while pq:priority, count, task = heappop(pq)if task is not REMOVED:del entry_finder[task]return taskraise KeyError('pop from an empty priority queue') 。
排序(sort)或分类排序

排序(sort)或分类所谓排序,就是要整理文件中的记录,使之按关键字递增(或递减)次序排列起来。
其确切定义如下:输入:n个记录R1,R2,…,R n,其相应的关键字分别为K1,K2,…,K n。
输出:R il,R i2,…,R in,使得K i1≤K i2≤…≤K in。
(或K i1≥K i2≥…≥K in)。
1.被排序对象--文件被排序的对象--文件由一组记录组成。
记录则由若干个数据项(或域)组成。
其中有一项可用来标识一个记录,称为关键字项。
该数据项的值称为关键字(Key)。
注意:在不易产生混淆时,将关键字项简称为关键字。
2.排序运算的依据--关键字用来作排序运算依据的关键字,可以是数字类型,也可以是字符类型。
关键字的选取应根据问题的要求而定。
【例】在高考成绩统计中将每个考生作为一个记录。
每条记录包含准考证号、姓名、各科的分数和总分数等项内容。
若要惟一地标识一个考生的记录,则必须用"准考证号"作为关键字。
若要按照考生的总分数排名次,则需用"总分数"作为关键字。
排序的稳定性当待排序记录的关键字均不相同时,排序结果是惟一的,否则排序结果不唯一。
在待排序的文件中,若存在多个关键字相同的记录,经过排序后这些具有相同关键字的记录之间的相对次序保持不变,该排序方法是稳定的;若具有相同关键字的记录之间的相对次序发生变化,则称这种排序方法是不稳定的。
注意:排序算法的稳定性是针对所有输入实例而言的。
即在所有可能的输入实例中,只要有一个实例使得算法不满足稳定性要求,则该排序算法就是不稳定的。
排序方法的分类1.按是否涉及数据的内、外存交换分在排序过程中,若整个文件都是放在内存中处理,排序时不涉及数据的内、外存交换,则称之为内部排序(简称内排序);反之,若排序过程中要进行数据的内、外存交换,则称之为外部排序。
注意:①内排序适用于记录个数不很多的小文件②外排序则适用于记录个数太多,不能一次将其全部记录放人内存的大文件。
内部排序和外部排序
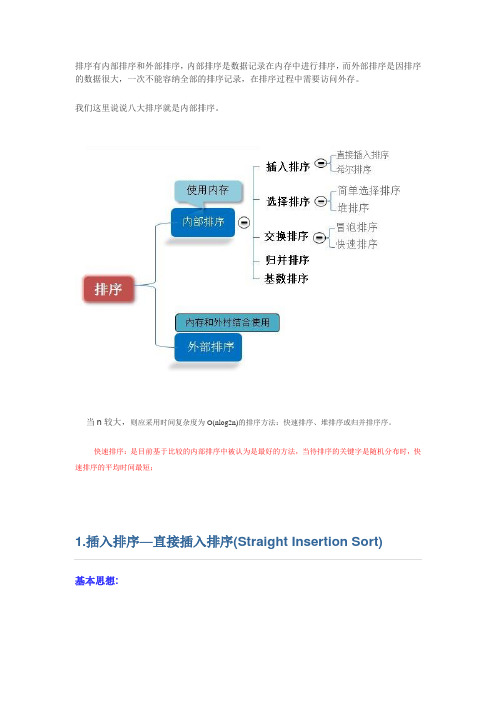
排序有内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
我们这里说说八大排序就是内部排序。
当n较大,则应采用时间复杂度为O(nlog2n)的排序方法:快速排序、堆排序或归并排序序。
快速排序:是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;基本思想:将一个记录插入到已排序好的有序表中,从而得到一个新,记录数增1的有序表。
即:先将序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插入,直至整个序列有序为止。
要点:设立哨兵,作为临时存储和判断数组边界之用。
直接插入排序示例:如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。
所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
算法的实现:1.void print(int a[], int n ,int i){2. cout<<i <<":";3.for(int j= 0; j<8; j++){4. cout<<a[j] <<" ";5. }6. cout<<endl;7.}8.9.10.void InsertSort(int a[], int n)11.{12.for(int i= 1; i<n; i++){13.if(a[i] < a[i-1]){ //若第i个元素大于i-1元素,直接插入。
小于的话,移动有序表后插入14.int j= i-1;15.int x = a[i]; //复制为哨兵,即存储待排序元素16. a[i] = a[i-1]; //先后移一个元素17.while(x < a[j]){ //查找在有序表的插入位置18. a[j+1] = a[j];19. j--; //元素后移20. }21. a[j+1] = x; //插入到正确位置22. }23. print(a,n,i); //打印每趟排序的结果24. }25.26.}27.28.int main(){29.int a[8] = {3,1,5,7,2,4,9,6};30. InsertSort(a,8);31. print(a,8,8);32.}效率:时间复杂度:O(n^2).其他的插入排序有二分插入排序,2-路插入排序。
排序算法总结

排序算法总结【篇一:排序算法总结】1、稳定排序和非稳定排序简单地说就是所有相等的数经过某种排序方法后,仍能保持它们在排序之前的相对次序,我们就说这种排序方法是稳定的。
反之,就是非稳定的。
比如:一组数排序前是a1,a2,a3,a4,a5,其中a2=a4,经过某种排序后为a1,a2,a4,a3,a5,则我们说这种排序是稳定的,因为a2排序前在a4的前面,排序后它还是在a4的前面。
假如变成a1,a4,a2,a3,a5就不是稳定的了。
2、内排序和外排序在排序过程中,所有需要排序的数都在内存,并在内存中调整它们的存储顺序,称为内排序;在排序过程中,只有部分数被调入内存,并借助内存调整数在外存中的存放顺序排序方法称为外排序。
3、算法的时间复杂度和空间复杂度所谓算法的时间复杂度,是指执行算法所需要的计算工作量。
一个算法的空间复杂度,一般是指执行这个算法所需要的内存空间。
功能:选择排序输入:数组名称(也就是数组首地址)、数组中元素个数算法思想简单描述:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
选择排序是不稳定的。
【篇二:排序算法总结】在计算机科学所使用的排序算法通常被分类为:计算的复杂度(最差、平均、和最好性能),依据列表(list)的大小(n)。
一般而言,好的性能是O(nlogn),且坏的性能是O(n2)。
对于一个排序理想的性能是O(n)。
仅使用一个抽象关键比较运算的排序算法总平均上总是至少需要O(nlogn)。
内存使用量(以及其他电脑资源的使用)稳定度:稳定排序算法会依照相等的关键(换言之就是值)维持纪录的相对次序。
也就是一个排序算法是稳定的,就是当有两个有相等关键的纪录R和S,且在原本的列表中R出现在S之前,在排序过的列表中R也将会是在S之前。
一般的方法:插入、交换、选择、合并等等。
交换排序包含冒泡排序和快速排序。
排序算法(比较类和非比较类)
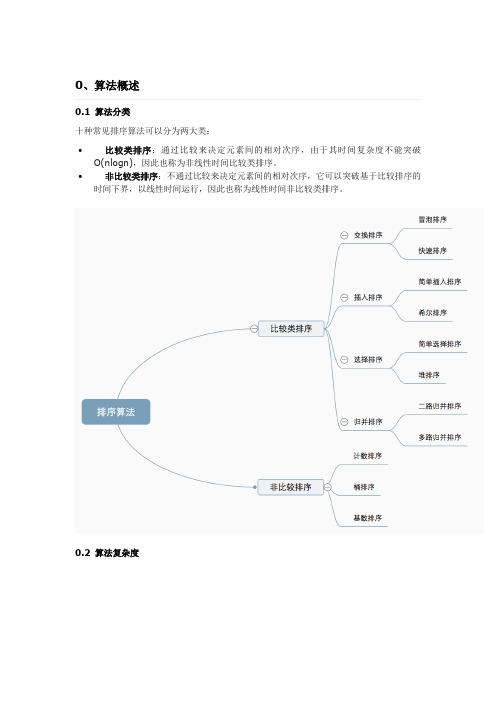
0、算法概述0.1 算法分类十种常见排序算法可以分为两大类:∙比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
∙非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
0.2 算法复杂度0.3 相关概念∙稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
∙不稳定:如果a原本在b的前面,而a=b,排序之后a 可能会出现在b 的后面。
∙时间复杂度:对排序数据的总的操作次数。
反映当n变化时,操作次数呈现什么规律。
∙空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
1、冒泡排序(Bubble Sort)冒泡排序是一种简单的排序算法。
它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
1.1 算法描述∙比较相邻的元素。
如果第一个比第二个大,就交换它们两个;∙对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;∙针对所有的元素重复以上的步骤,除了最后一个;∙ 重复步骤1~3,直到排序完成。
1.2 代码实现 12 345678 910111213 function bubbleSort(arr) { var len = arr.length; for (var i = 0; i < len - 1; i++) { for (var j = 0; j < len - 1 - i; j++) { if (arr[j] > arr[j+1]) { // 相邻元素两两对比 var temp = arr[j+1]; // 元素交换 arr[j+1] = arr[j]; arr[j] = temp; } } } return arr; }2、选择排序(Selection Sort )选择排序(Selection-sort)是一种简单直观的排序算法。
堆排序实例演示3

91
16
47
85
36
24
24 36 53 30
85 47 30 53
16
91
如果该序列是一个堆,则对应的这棵完全二叉树的特点是: 所有分支结点的值均不小于 (或不大于)其子女的值,即每棵子 树根结点的值是最大(或最小)的。
堆特点:堆顶元素是整个序列中最大(或最小)的元素。
2022/9/1
数据结构
2
2.堆排序
足堆,继续调 整。
将 堆 顶 元 素 R1 比根小,交换。
与Rn交换)。
2022/9/1
数据结构
d.到了叶子结 点,调整结束, 堆建成。
6
85
30
53
47
53
47
53
47
30
24 36 16 30
24 36 16 85
24 36 16 85
91
91
91
堆调整结束。
R1 与 Rn-1 交 换 , 堆被破坏。 对 R1 与 Rn-2 调 整。
16
b.调整结束后,以R4为 根的子树满足堆特性。 再将以R3结点为根的 子树调整为堆;
16
c. 以 R3为根的子树满足 堆特性。 再将以R2结点为根的子树 调整为堆;
30
91
91
47
91
47
30
47
85
24 36 53 85 16
24 36 53 85 16
24 36 53 30 16
以 R2 为 根 的 子 树 满 足 堆特性。 再 将 以 R1 结 点 为 根 的 子树调整为堆
d. 调整结束后,整棵树为堆。
建堆过程示例
❖ 例如,图中的完全二叉树表示一个有8个元素的无序序列: {49,38,65,97,76,13,27,49}(相同的两个关 键字49,其中后面一个用49表示),则构造堆的过程如 图3(b)~(f)所示。
各种排序方法的比较与讨论

各种排序方法的比较与讨论现在流行的排序有:选择排序、直接插入排序、冒泡排序、希尔排序、快速排序、堆排序、归并排序、基数排序。
一、选择排序1.基本思想:每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
2. 排序过程:【示例】:初始关键字[49 38 65 97 76 13 27 49]第一趟排序后13 [38 65 97 76 49 27 49]第二趟排序后13 27 [65 97 76 49 38 49]第三趟排序后13 27 38 [97 76 49 65 49]第四趟排序后13 27 38 49 [49 97 65 76]第五趟排序后13 27 38 49 49 [97 97 76]第六趟排序后13 27 38 49 49 76 [76 97]第七趟排序后13 27 38 49 49 76 76 [ 97]最后排序结果13 27 38 49 49 76 76 973.void selectionSort(Type* arr,long len){long i=0,j=0;/*iterator value*/long maxPos;assertF(arr!=NULL,"In InsertSort sort,arr is NULL\n");for(i=len-1;i>=1;i--){maxPos=i;for(j=0;jif(arr[maxPos]if(maxPos!=i)swapArrData(arr,maxPos,i);}}选择排序法的第一层循环从起始元素开始选到倒数第二个元素,主要是在每次进入的第二层循环之前,将外层循环的下标赋值给临时变量,接下来的第二层循环中,如果发现有比这个最小位置处的元素更小的元素,则将那个更小的元素的下标赋给临时变量,最后,在二层循环退出后,如果临时变量改变,则说明,有比当前外层循环位置更小的元素,需要将这两个元素交换.二.直接插入排序插入排序(Insertion Sort)的基本思想是:每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子文件中的适当位置,直到全部记录插入完成为止。
10种常用典型算法

什么是算法?简而言之,任何定义明确的计算步骤都可称为算法,接受一个或一组值为输入,输出一个或一组值。
(来源:homas H. Cormen, Chales E. Leiserson 《算法导论第3版》)可以这样理解,算法是用来解决特定问题的一系列步骤(不仅计算机需要算法,我们在日常生活中也在使用算法)。
算法必须具备如下3个重要特性:[1]有穷性。
执行有限步骤后,算法必须中止。
[2]确切性。
算法的每个步骤都必须确切定义。
[3]可行性。
特定算法须可以在特定的时间内解决特定问题,其实,算法虽然广泛应用在计算机领域,但却完全源自数学。
实际上,最早的数学算法可追溯到公元前1600年-Babylonians有关求因式分解和平方根的算法。
那么又是哪10个计算机算法造就了我们今天的生活呢?请看下面的表单,排名不分先后:1. 归并排序(MERGE SORT),快速排序(QUICK SORT)和堆积排序(HEAP SORT)哪个排序算法效率最高?这要看情况。
这也就是我把这3种算法放在一起讲的原因,可能你更常用其中一种,不过它们各有千秋。
归并排序算法,是目前为止最重要的算法之一,是分治法的一个典型应用,由数学家John von Neumann于1945年发明。
快速排序算法,结合了集合划分算法和分治算法,不是很稳定,但在处理随机列阵(AM-based arrays)时效率相当高。
堆积排序,采用优先伫列机制,减少排序时的搜索时间,同样不是很稳定。
与早期的排序算法相比(如冒泡算法),这些算法将排序算法提上了一个大台阶。
也多亏了这些算法,才有今天的数据发掘,人工智能,链接分析,以及大部分网页计算工具。
2. 傅立叶变换和快速傅立叶变换这两种算法简单,但却相当强大,整个数字世界都离不开它们,其功能是实现时间域函数与频率域函数之间的相互转化。
能看到这篇文章,也是托这些算法的福。
因特网,WIFI,智能机,座机,电脑,路由器,卫星等几乎所有与计算机相关的设备都或多或少与它们有关。
堆排序算法详解

堆排序算法详解1、堆排序概述堆排序(Heapsort)是指利⽤堆积树(堆)这种数据结构所设计的⼀种排序算法,它是选择排序的⼀种。
可以利⽤数组的特点快速定位指定索引的元素。
堆分为⼤根堆和⼩根堆,是完全⼆叉树。
⼤根堆的要求是每个节点的值都不⼤于其⽗节点的值,即A[PARENT[i]] >= A[i]。
在数组的⾮降序排序中,需要使⽤的就是⼤根堆,因为根据⼤根堆的要求可知,最⼤的值⼀定在堆顶。
2、堆排序思想(⼤根堆)1)先将初始⽂件Array[1...n]建成⼀个⼤根堆,此堆为初始的⽆序区。
2)再将关键字最⼤的记录Array[1](即堆顶)和⽆序区的最后⼀个记录Array[n]交换,由此得到新的⽆序区Array[1..n-1]和有序区Array[n],且满⾜Array[1..n-1].keys≤Array[n].key。
3)由于交换后新的根R[1]可能违反堆性质,故应将当前⽆序区R[1..n-1]调整为堆。
然后再次将R[1..n-1]中关键字最⼤的记录R[1]和该区间的最后⼀个记录R[n-1]交换,由此得到新的⽆序区R[1..n-2]和有序区R[n-1..n],且仍满⾜关系R[1..n-2].keys≤R[n-1..n].keys,同样要将R[1..n-2]调整为堆。
这样直到⽆序区中剩余⼀个元素为⽌。
3、堆排序的基本操作1)建堆,建堆是不断调整堆的过程,从len/2处开始调整,⼀直到第⼀个节点,此处len是堆中元素的个数。
建堆的过程是线性的过程,从len/2到0处⼀直调⽤调整堆的过程,相当于o(h1)+o(h2)…+o(hlen/2) 其中h表⽰节点的深度,len/2表⽰节点的个数,这是⼀个求和的过程,结果是线性的O(n)。
2)调整堆:调整堆在构建堆的过程中会⽤到,⽽且在堆排序过程中也会⽤到。
利⽤的思想是⽐较节点i和它的孩⼦节点left(i),right(i),选出三者最⼤者,如果最⼤值不是节点i⽽是它的⼀个孩⼦节点,那边交互节点i和该节点,然后再调⽤调整堆过程,这是⼀个递归的过程。
heapsort

Pack to the left
Sorting III / Slide 10
1
2 5 2
4
5
4
3
6
1
3
6
A heap
Not a heap
Heap-order property: the value at each node is less than or equal to the values at both its descendants --- Min Heap
Sorting III / Slide 21
class Heap { public: Heap(); Heap(const Heap& t); // constructor
~Heap();
bool empty() const; double root(); // access functions Heap& left(); Heap& right(); Heap& parent(double x); // … update …
Total number of nodes of a complete binary tree of depth d is 1 + 2 + 4 +…… 2d = 2d+1 - 1 3. Thus 2d+1 - 1 = N 4. d = log(N+1)-1 = O(logN)
2.
Side notes: the largest depth of a binary tree of N nodes is O(N)
Heaps, Heap Sort, and Priority Queues
np.sort用法 -回复

np.sort用法-回复每个人都知道,排序是计算机科学中最重要的操作之一。
排序是将一组元素按照特定的顺序重新排列的过程。
在实际应用中,经常需要对数据进行排序,因为这样可以使数据更易于查找和使用。
在Python中,我们可以使用np.sort()函数来对数组进行排序。
在本文中,我们将探讨np.sort()函数的使用方法,以及它在不同情况下的应用。
首先,让我们来了解一下np.sort()函数的基本用法。
np.sort()函数可以接受一个数组作为参数,并返回一个排序后的数组。
这意味着原始数组的顺序不会改变,而是返回一个新的已排序的数组。
下面是一个简单的示例:pythonimport numpy as nparr = np.array([3, 1, 5, 2, 4])sorted_arr = np.sort(arr)print(sorted_arr)输出结果为:[1 2 3 4 5]正如上面的例子展示的那样,通过调用np.sort()函数,我们得到了一个按照升序排列的新数组。
注意,这里返回的是一个新的数组,而不是对原始数组进行了修改。
除了对一维数组进行排序外,np.sort()函数还可以对多维数组进行排序。
当对多维数组进行排序时,默认情况下是按照最后一个轴进行排序。
如果需要指定其他轴进行排序,可以通过axis参数来实现。
让我们来看一个例子:pythonimport numpy as nparr = np.array([[3, 1, 5], [2, 4, 6]])sorted_arr = np.sort(arr, axis=1)print(sorted_arr)输出结果为:[[1 3 5][2 4 6]]在上面的例子中,我们传递了axis=1参数来指定按照第二个轴(即列)进行排序。
这样,我们得到了按照每一行进行升序排序的结果。
除了对整数数组进行排序外,np.sort()函数还可以对字符串数组进行排序。
当对字符串数组进行排序时,按照字母顺序进行排序。
排序方法

排序方法一、需求分析排序是计算机程序设计中的一种重要操作,其功能是对一个数据元素集合或序列重新排列成一个按数据元素某个相知有序的序列。
排序分为两类:内排序和外排序。
内部排序是指待排序列完全存放在内存中所进行的排序过程,适合不太大的元素序列。
其中快速排序的是目前排序方法中被认为是最好的方法。
内部排序方法:1.插入排序(直接插入排序);2.快速排序;3.选择排序(简单选择排序);4.归并排序;5.冒泡排序;6.希尔排序;希尔排序是对直接插入排序方法的改进。
7.堆排序;二、概要设计1.直接插入排序(Straiht Insertion Sort)算法描述:如果有一个已经排好序的序列 {R(20),R(35),R(88)},当要插入一个R(66)时,需要与各个元素进行比较,R(35)<R(66)<R(88),所以应该插在R(35)与R(88)直接。
算法开始时,取一个元素为原序列,然后重复执行上面的方法,将每个元素插入到序列中。
(1).直接插入排序(Straiht Insertion Sort)算法描述:如果有一个已经排好序的序列 {R(20),R(35),R(88)},当要插入一个R(66)时,需要与各个元素进行比较,R(35)<R(66)<R(88),所以应该插在R(35)与R(88)直接。
算法开始时,取一个元素为原序列,然后重复执行上面的方法,将每个元素插入到序列中。
//插入排序void InsertSort(int a[], int n){int i, j;int temp;for(i = 1; i < n; i++){temp = a[i];j = i-1;while(j >= 0 && a[j] > temp;){a[j+1] = a[j];--j;}a[j+1] = temp;}}//递归的插入排序void RecursiveInsertSort(int a[], int n){int i, j, key;if(n > 1){RecursiveInsertSort(a,n-1);}key = a[n-1];i = n-2;while(i >= 0 && a[i] > key){a[i+1] = a[i];i--;}a[i+1] = key;}//折半插入排序void BinInsertSort(int a[], int n){int i,j;for(i = 1; i < n; i++){// 在a[0..i-1]中折半查找插入位置使a[high]<=a[i]<a[high+1..i-1]int low = 0, high = i-1, m = 0;while(low <= high){m = m + (high-low)/2;if (a[i] < a[m]) high = m-1;else low = m+1;}// 向后移动元素a[high+1..i-1],在a[high+1]处插入a[i]int x = a[i];for (j = i-1; j > high; j--)a[j+1] = a[j];a[high+1] = x; // 完成插入}}此算法的时间复杂度为O(n2)2.快速排序快速排序是一种基于交换的排序方法,最常见的有冒泡排序(BubbleSort),快速排序(改进的冒泡排序)(QuickSort)下面先说冒泡排序:冒泡排序的基本思想是在一次排序中,将最大的元素沉入底部,然后缩小范围,继续进行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
In this chapter, we introduce another sorting algorithm—heapsort which combines the better attributes of the two sorting algorithms we have already discussed. Heapsort also introduces another algorithm design technique: the use of a data structure—”heap”
MAX-HEAPIFY(A, i ) 1 L ←LEFT(i) 2 r ←RIGHT(i) 3 if (l≤heap-size[A] && A[L] > A[i]) 4 largest←L 5 else largest←i 6 if (r≤heap-size[A] && A[r] > A[largest] ) 7 largest←r 8 if (largest≠i ) 9 A[i] ←→A[largest] // exchange 10 MAX-HEAPIFY(A,largest)
n n n k T (n) log n 2log 4log ... 2 log k , 2 4 2 其中 k=logn, =logn+2(logn-1)+2 (log n 2) ... 2 (log n k )
2 k
=(2 -1)logn - (2 1+2 2 2 3 ... 2 k ) =2nlogn-logn-(2nlogn-2n-2) =2n - logn + 2
2 3 k
k 1
=O(n)
6.4 The heapsort algorithm
HEAPSORT(A) 1 BUILD-MAX-HEAP(A) 2 for i←length[A] downto 2 3 do exchange A[1]←→A[i] 4 heap-size[A]←heap-size[A] -1 5 MAX-HEAPIFY(A, 1) The HEAPSORT procedure takes time O(n)+nO(lg n)=O(n lg n).
HEAP-MAXIMUM(A) 1 return A[1] HEAP-EXTRACT-MAX(A) 1 if heap-size[A] < 1 2 then error "heap underflow" 3 max←A[1] 4 A[1]←A[heap-size[A]] 5 heap-size[A]←heap-size[A]-1 6 MAX-HEAPIFY(A, 1) 7 return max
6.2 Maintaining the heap property
MAX-HEAPIFY is an important subroutine for manipulating heaps. Its inputs are an array A and an index i into the array. When HEAPIFY is called, it is assumed that the binary trees rooted at LEFT(i) and RIGHT(i) are heaps, but that A[i] may be smaller than its children, thus violating(违 反) the max-heap property. The function of MAX-HEAPIFY is to let the value at A[i] "float down" in the heap so that the subtree rooted at index i becomes a heap.
lg n n h T (n) h1 O(h) O n h1 2 h 0 2 h 0 lg n
h O n h1 O(n) h 0 2
Running time of BUILD-MAX-HEAP
6.5 Priority queues
A priority queue is a data structure for maintaining a set S of elements, each with an associated value called a key. A priority queue supports the following operations. INSERT(S, x) inserts the element x into the set S. This operation could be written as S←S∪{x}. MAXIMUM(S) returns the element of S with the largest key. EXTRACT-MAX(S) removes and returns the element of S with the largest key.
The root of the tree is A[1], and given the index i of a node, the indices of its parent PARENT(i), left child LEFT(i), and right child RIGHT(i) can be computed simply: PARENT(i) return i / 2 LEFT(i) return 2i RIGHT(i) return 2i+1
HEAP-INCREASE-KEY(A,i,key) 1 if key<A[i] 2 then error “new key is smaller than current key” 3 A[i]←key 4 while i > 1 and A[PARENT(i)] < key 5 do A[i]←→A[PARENT(i)] 6 i←PARENT(i) MAX-HEAP-INSERT(A,key) 1 heap-size[A]←heap-size[A]+1 2 A[heap-size[A]]←-∞ 3 HEAP-INCREASE-KEY(A,heap-size[A],key) The running time of them is O(lgn).
Heap property
Max-heap: For every node i other than the root, A[PARENT(i)]≥A[i], the largest element is stored at root. Min-heap: For every node i other than the root, A[PARENT(i)]≤A[i], the smallest element is stored at root.
6.1 Heaps
The (binary) heap data structure is an array object that can be viewed as a complete binary tree. The tree is completely filled on all levels except possibly the lowest, which is filled from the left up to a point. An array A that represents a heap is an object with two attributes: length[A], which is the number of elements in the array, and heap-size[A], the number of elements in the heap stored within array A. That is, although A[1 . . length[A]] may contain valid numbers, no element past A[heap-size[A]], where heap-size[A]≤length[A], is an element of the heap.
Running time of BUILD-MAX-HEAP
The time required by MAX-HEAPIFY when called on a node of height h is O(h), so we can express the total cost of BUILD-MAX-HEAP as
Running time of MAX-HEAPIFY
The running time of MAX-HEAPIFY on a subtree of size n rooted at given node i is theΘ(1) time to fix up the relationships among the elements A[i], A[LEFT (i)], and A[RIGHT (i)], plus the time to run MAX-HEAPIFY on a subtree rooted at one of the children of node i. The children's subtrees each have size at most 2n/3--the worst case occurs when the last row of the tree is exactly half full--and the running time of HEAPIFY can therefore be described by the recurrence T(n)≤T(2n/3)+Θ(1). The solution to this recurrence, by case 2 of the master theorem is T(n) = O(lg n).
