30量子6-XS
曾谨言量子力学第一卷习题答案解析3第三章.docx

第三章:一维定态问题[1]对于无限深势阱屮运动的粒子(见图3・1)证明…上(1—亠212 / 兀 2并证明当"T 00时上述结果与经典结论一致。
[解]写出归一化波函数:(1)先计算坐标平均值:x=「|屮「曲=「dn 2竺曲显「(l — cos 込)xdx Jo X a agJo a 利用公式:. xcos px sin px xs in pxax — --------------------- 1 -------- ;—P P—f 1T/ 2 2 / f 2 2 - 2 MX J 1 f" 2/1 2勿才、, x - 屮才 ax- —x sin 〜 ---------- ax-— 才Pl — cos ---------- ) axJo J a a a利用公式 [才2cos pxdx-—x 1 sin /zr +丄7才cos/zr —— sin pxJp矿p2/77LV(2)才 cos pxdx -xs in px cos px(3)(5) nnx得计算均方根值用s-$2 = 7-pj 2 J 以知,可计算7/__/ 12 ~ 2/72^2在经典力学的一维无限深势阱问题中,因粒子局限在(0, a )范围中运动,各点的几率密度看作 相同,由于总几率是1,几率密度CD=-.a_ f" 」r z, 1 , a x - coxar = —xax=—Jo Jo a 2[解](甲法):根据波函数标准条件,设定各区间的波函数如下:(x<0 区):屮=(x>a 区):H 7 = De~kyX但仏三寸2腻人一Q 丨Hk 、三 J2同匕 _ Z )/ 1i 写出在连接点x=0处连续条件(0<x<a 区):屮=BdJC 沙(2) (1) (3)/c 2 三 J2/〃Z7力故当/?—> oo 时二者相一致。
#[2]试求在不对称势力阱屮粒子的能f 4= B+CI k\A = ikAB—C} x=a处连续条件Be ikl<i + Ce ikia = De kyi (6)Bd® - C严=竺De kyi(7)(4)(5)二式相除得k x B-Cik[ B + C(6)(7)二式相除得ik、_ B" _ C严石一Bd^ + C严从这两式间可消去B, C,得到一个k&出间的关系ik、_ (心 + 右 + ik石+%2)/"+(一£ +%2)才®k、cos k^a-k2 sin k、a/(心sin k’a* k z cos k z a\解出tgkg得tgk、a = /"J + ")+ 〃兀(〃=0,1,2,...)〜k;-心最后一式用E表示吋,就是能量得量子化条件:個〃〃 + 一夕)tg --------- a -- ------ -- 彳、,〜卉夕-JW-勾“一刀(乙法)在0<x<a区间屮波函数表示为(8)屮(才)=2?sin (禺才+§)现在和前一法相同写出边界条件:力=2?sin 5(在x=0处) (9)(在x=a处) k x A-局〃cos5 (10)(11) 一(2 方cos/a+M = k^De(12)(9) (10)相除得加 3+»)=写出(13) (14)的反正切关系式,得到:E------- + mn V x -E EF Z77T V x -EE V z -E前述两法的结果形式不同,作为一种检验,可以用下述方法来统一。
红、绿CdSe@ZnS量子点配比对三波段标准白光LED器件的影响

红、绿CdSe@ZnS量子点配比对三波段标准白光LED器件的影响陈赟汉,张雪,周洁,曹进*,张建华,殷录乔,朱文清(1. 上海大学材料科学与工程学院,上海,200072;2. 上海大学新型显示技术及应用集成教育部重点实验室, 上海,200072)摘要:将一步法合成的具有梯度合金结构的红光、绿光CdSe@ZnS量子点,与硅胶均匀混合后作为光转换层涂覆到蓝色InGaN LED芯片上,制备了不含荧光材料的三波段白光LED器件。
研究了峰值为650nm和550nm的高效率红、绿量子点在硅胶中的含量及配比对白光LED色坐标以及效率的影响。
结果表明,当红:绿量子点配比为2:3时,可得到正白光QD-LED器件色坐标为(0.3228, 0.3359)、色温为5725K、功率效率为26.61 lm/W、显色指数为72.7;并且器件光谱中红、蓝、绿三色半高宽分别为30 nm、25 nm、38 nm,具有很好的单色性和高色纯度,在照明以及显示背光源领域有很好的应用前景。
关键词:量子点;核壳;白光LED;光转换层中图分类号:TN383+.2 文献标识码: AThe influence of red, green CdSe @ ZnS quantum dots ratios on standard three-band white LED devices CHEN Yun-han, ZHANG Xue, ZHOU Jie, CAO Jin*, ZHANG Jian-hua, YINLu-qiao, ZHU Wen-qing(1. Shanghai University School of Materials Science and Engineering, Shanghai, 2000722. Key Laborary of Advanced Display and System Applications, Shanghai University, Ministry ofEducation, Shanghai, 200072)Abstract:Highly-fluorescent green and red CdSe/ZnS core/ shell gradient alloy quantum dots (QDs) were successfully synthesized through one-step method, and we also fabricated phosphine-free three-band white light LED by directly incorporating QDs/epoxy composites with blue InGaN chip. The influences of the content and proportion of red and green QDs with peak wavelengths of 650 nm and 550 nm respectively on the color coordinates and efficiency of white LED are researched. The results showed that three-band RGB standard white light QD-WLED with a CIE-1931 color coordinates of (0.3228,0.3359), CCT 5725K, CRI 72.7 and the power efficiency of 26.61 lm/W can be achieved when the red:green QDs ratio is 2:3. And the FWHM of the red, blue and green in the white QD-LED is 30 nm, 25 nm and 38 nm respectively which indicate high color purity, so the three-band white light has a promising application in the field of lighting and the display backlight.Key words: quantum dot; core-shell; White-LED; light conversion layerCLC number: TN383+.2Document code: A1基金项目:上海自然科学基金(NO.09ZR1411900);上海市科委项目(NO.11100703200)资助项目作者简介:陈赟汉(1989-),男,硕士,山东泰安人,主要从事半导体器件的研究。
巡检机器人 维护使用手册说明书

巡检机器人维护使用手册版本:2.0北京眸视科技有限公司目录1.产品概述 (4)1.1.产品概述 (4)1.2.履带式机器人 (5)1.3.轮式机器人 (5)2.机器人开机 (6)2.1.机器人开机 (6)2.2.遥控器使用 (6)2.3.遥控器高级使用 (7)2.4.注意事项 (9)3.平板控制 (10)3.1.Wifi连接 (10)3.2.运行APP (10)3.3.自启动功能 (10)3.4.License更新功能 (11)3.5.参数配置 (14)3.6.状态检查 (15)3.7.开启巡检 (16)4.制图 (17)4.1.制图 (17)4.2.地图编辑 (20)4.3.地图备份与切换 (25)4.4.注意事项 (27)4.4.1.制图之前的准备 (28)4.4.2.建图操作原则 (28)4.4.3.建图结果检查 (30)5.导航 (31)5.1.导航到指定点 (31)5.2.导航到指定坐标 (32)5.3.取消导航 (32)6.1.准备工作 (34)6.2.工具安装 (34)6.2.1.开启root ssh权限 (34)6.2.2.JDK的安装 (35)6.2.3.TOMCAT安装 (35)6.2.4.MySQL数据库在线安装 (36)6.2.5.Redis安装 (37)6.2.6.Nginx安装 (37)6.3.程序部署 (38)6.3.1.前端web程序部署 (38)6.3.2.后端jar包部署 (39)6.4.系统参数配置 (41)6.4.1.域名地址映射 (41)6.4.2./etc/profile确认 (41)6.5.启动管理云平台系统程序 (41)6.5.1.后台java程序启动 (42)6.5.2.前台tomcat启动 (42)6.5.3.确认后台程序是否启动成功 (42)6.5.4.访问系统url (42)7.云平台使用 (43)7.1.系统登录 (43)7.1.1.系统首页 (44)7.1.2.个人中心 (45)7.2.实时监控 (45)7.3.数据查询 (47)7.3.1.巡检报表 (47)7.3.2.巡检点 (48)7.3.3.环境数据 (48)7.4.巡检任务 (49)7.4.1.任务管理 (49)7.4.2.任务日历 (51)7.5.1.巡检点管理 (52)7.5.2.地图管理 (53)7.5.3.机器人管理 (54)7.5.4.告警设置 (55)7.6.系统管理 (56)7.6.1.用户管理 (56)7.6.2.角色管理 (57)7.6.3.菜单管理 (59)7.6.4.场站管理 (59)7.6.5.字典管理 (60)7.6.6.车体状态 (61)7.6.7.版本信息 (62)8.巡检 (63)8.1.启动检查 (63)8.2.云平台操作 (64)9.注意事项 (66)9.1.常规检查 (66)9.2.维护保养 (66)9.3.长期储存 (67)10.快速故障排除 (69)10.1.机器人故障排查 (69)10.2.云端服务故障排查 (71)10.3.遥控器故障排查 (72)附录1:充电桩安装说明 (75)附录2、传感器清洁 (76)附录3、产品参数 (77)1.产品概述1.1.产品概述眸视机器人定位和导航系统,是一个集激光雷达、视觉(双目相机、深度相机)、超声波、惯性测量单元(IMU)等多种传感器于一体的定位和导航系统。
量子可逆逻辑电路综合

Ab ta t Th inf a c n r g e so e e sb elg cs n h sso u n u crut r n lz d sr c : esg ii n ea d p o r s fr v ri l o i y t ei fq a t m ic i a ea ay e . c s S v r l t o so y t e i o e e sb e cru ta e p e e td i cu ig t e ta so m ain b s d e e a meh d fs n h ss far v ri l ic i r r s n e ,n l dn h r n f r to a e ag rt m ,h x a sin me h d t eRM x a so eh d,n h eh d b s d o r u h o y lo i h t ee h u to t o ,h e p n i nm t o a d t em t o a e n g o p t e r . Th i c a a t rsis y t e i r ls to g a d we k p it r n l z d er h r ce itc ,s n h ss ue ,sr n n a on sa ea ay e .Th u t e e eo me t ef rh rd v lp n o h xsig me h d n h e e r h o e s l t n n e aih eisa ed su s d ft ee itn t o sa d t er s a c n n w ou i sa d n w rt m t r ic s e . o c
量子 电路成 为研究 的重 点 。
算过程 中的不可逆操作 , 例如 , 对于 2 个比特的异
量子统计理论

Fermion System 巨配分函数
BEIJING NORMAL UNIVERSITY
配分函数
三种系统公式比较
内能的统计表达式 外界对系统广义力的统计表达式
BEIJING NORMAL UNIVERSITY
配分函数的全微分
BEIJING NORMAL UNIVERSITY
若将N表达为:
∫ ∫ N =
∞
dN
=
0
∞ D (ε )d ε 0 e β(ε −μ ) − 1
∫ =
2π h3
(2m)32Fra bibliotek∞ε1 2d ε
0 e β(ε −μ) − 1
此式没有计入基态能级对粒子数的贡献是不合理的。
应修正为: N = N0(T ) + N ′(T )
( ) ∫ 其中:N ' = 2 π g V
热力学量的统计表达式
Boson System 定义巨配分函数
BEIJING NORMAL UNIVERSITY
内能的统计表达式 外界对系统广义力的统计表达式
BEIJING NORMAL UNIVERSITY
例 在无穷小的准静态过程中,当外参量有dy的改变
时,外界对系统所作的功为
在无穷小的准静态过程中,外界对系统所作的功 是粒子分布不变时由于能级改变而引起的内能变化.
2m kT h2
3 2 e −α ⎡⎢⎣ Γ
3 2
∓ e−α 1 Γ 22
3 2
⎤⎥⎦
( ) ( ) ∴
N = gV
2 πmkT h2
3 2 e−α
1 ∓ e−α 22
(a)
( ) ( ) U = gV
量子随机循环移位交织器的设计模型

信息处理 方面的 巨大 潜力 。随着 量子信息 处理技术 的发 展, 量子信息 处理技术 已逐渐 从理论走 向实验 , 向实用化方 向 并
发 展 。
即 m 个量子码字经交织后能够纠 正所有 的长度 小于等于 b m
的连 续 突 发 性 错 误 , 因此 量 子 交织 器 的研 究和 设 计对 量 子 纠
功率控制 中引入 成本 函数 ,来使各个用户有 效地利用 系统 资
源 ,代价 函数 的存在 可以促使各用 户选择服 从全 局最优 的发
射功率 。
21 非合 作功 率控 制 博弈 .
无线环境 中, 号会 受到诸如多径效应 、 信 边缘效应 、 路径 衰耗和加性 噪声等 因素的影响而逐渐 失真导致恶化 ,再加上 系统 中码 分多址干扰的影响 ,这些 因素都会对接收端信 号质 量产 生极其 显著的影响 。我们一般还是采用用户信干 比作 为 变量 的函数式来表 示。 WC DMA系统 中用户 i 以功率 发射信 号时,其效度 函
数表示 为:
1 博弈 论基 础
11 博弈 论基 本 概念 .
博弈 理论又可 以称为对策论 ,它最初是用来研 究决策者 在 已知信 息的情况下如何来决策 并最大化 自己的效益,并在 各个 决策 者之 间取得一个均衡 的理论 。它主要有 四个 因素组 成: 博弈者 、 策略空间、 博弈 的顺序 、 博弈 的信 息。
对 应 的 映射 函数 进 行 重 新 排 序 后 输 出 。利 用 交织 器 ,可 以将
量子计算的每一步都不产生错误和误差 ,因此量子纠错编码 成为克服 这一 困难 的有效手段 ,目前量子纠错 的方法有量子
重 复码 、 子 C S 和 量 子稳 定子 码 , 子 纠 错 主 要 是 通 过 增 量 S码 量
量子绝热定理(Ⅱ):近似和适用条件

rve e .T e ic n i e ce f h e rm n da ai a p o i t n d su s d i er c n trt r ed - e iw d h o s tn iso et oe a d a ib t p rxmai i se t e t i au ea e n s t h c o c n h e le rபைடு நூலகம்
治的结果 . J量子绝热定理 和量子绝热近似是不应
混淆的两个概念 , 在本文作者 的另一 篇评述 中u 已
r 相位的不正确的陈述 , y 文献 [ ] 了分析和改正 , 4作 文献[ ] 2 又宣称 M S的不 自 治性是可以化解 的, 但却
2 0 0 — 7收到初稿 , 0 0 — 2收到修改稿 0 6— 3 2 2 6- 9 1 0
现行共识的量子绝热条件不是绝热 近似 的充足条
件.
应用. 量子绝热定理 自12 年建立 以来 , 93 至今 8 O余
年已经过许多研究 和应用…. 但是令人讶异 的是直
至最近(0 4 ) 20 年 却有人发现 , 一般教科书和应用文
参考文献[ ] 记为 M )是最先指 出绝热近似 2( S
L a Z o g IHu ・ h n
( da cdR sac et ,Z ogh n( “一 f e )U irt,G agh u50 7 , hn A vne eer C n r h nsa S —Sn nv sy u nzo 12 5 C i h e ei a)
Ab t a t s c r
s rb d.Th u h rSp it f iw ep ee t di y df rn r m h s n tec re t i rt r .T ee it c e i ea t o on so e a r s ne n awa i e e t o t o ei h ur n t au e h xs v r f f le e c ft eic n itn y i c n r d, iet ec n itn y o eS -aldv n s i gq a t m e mercp a ei n eo h n o sse c s o f me whl h o sse c ft O c l a ih n u nu g o t h s s i h e i
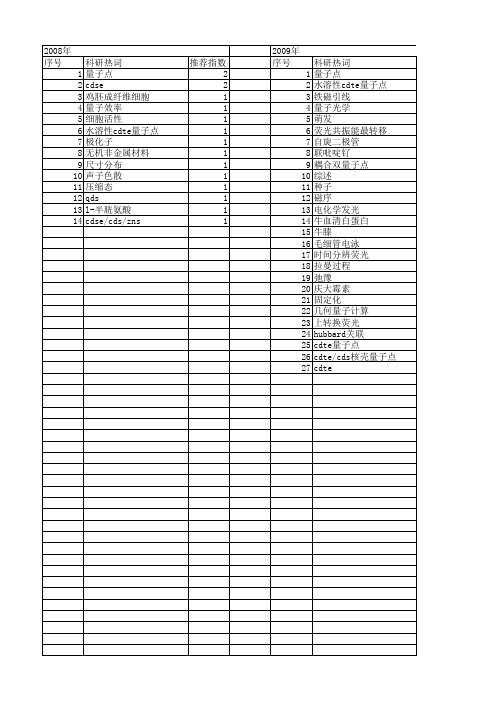
【国家自然科学基金】_双量子点_基金支持热词逐年推荐_【万方软件创新助手】_20140731
推荐指数 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
推荐指数 6 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
2014年 科研热词 量子点(qd) 量子点 超辐射发光管(sld) 荧光量子点 荧光猝灭 荧光探针 结构参数 粒子辐射 碘酸根离子 散粒噪声 器件模型 双注入区结构 全计数统计 cdte量子点 a549细胞 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
科研热词 量子点 cdse 鸡胚成纤维细胞 量子效率 细胞活性 水溶性cdte量子点 极化子 无机非金属材料 尺寸分布 声子色散 压缩态 qds l-半胱氨酸 cdse/cds/zns
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
科研热词 量子点 水溶性cdte量子点 铁磁引线 量子光学 萌发 荧光共振能最转移 自旋二极管 联吡啶钌 耦合双量子点 综述 种子 磁序 电化学发光 牛血清白蛋白 牛膝 毛细管电泳 时间分辨荧光 拉曼过程 弛豫 庆大霉素 固定化 几何量子计算 上转换荧光 hubbard关联 cdte量子点 cdte/cds核壳量子点 cdte
(完整word版)量子力学中有关角动量及其耦合问题的讨论.

量子力学中有关角动量及其耦合问题的讨论(陇东学院电气工程学院, 甘肃庆阳 745000)摘要:轨道角动量在直角坐标系与球极坐标系下的算符表示及相关推导,同时通过对易关系,得出轨道角动量并不能描写一个可观察量.然后运用力学量算符和波函数的矩阵表示,在给定表象下,讨论电子自旋算符的表示及自旋波函数的构造。
接着讨论角动量的LS耦合,其中主要计算总角动量与角动量分量的共同本征态,并且通过介绍耦合表象与非耦合表象,以及在展开耦合基矢的基础上规定量子数j的取值,进而分析角动量的JJ耦合关键词:角动量;算符;对易关系;自旋;角动量耦合The Disscussion of Angular Momentum and ItsCoupling Question in Quantum Mechemics(Electrical Engineering College, Longdong University, Qingyang 745000, Gansu,China)Abstract:First,using a basic assumption that the mechanical quantities in Quantum Mechanics is the appropriate operatorthe, it discuss the representation of orbital angular momentum optrator in both rectangular and spherical systems and related deduction in the text,at the same time it gets that orbital angular momentum optrator does not describe an observable quantity through the communication relations.Then useing mechanical quantity operator and matrix representation of wave funtion, it discusse the reprentation of the electronic spin operators and retructrue of spin wave funtion in a given reprentation.Nextit discusse the LS coupling of angular momentum, in which it mainly calculate the common eigenstates of the total angular momentum and angular momentum component,and through introdution the coupling and the non—coupling reprentation and determine the values of quantum number j on the basis of expand the coupling vectors, analyzeing the JJ coupling of angular momentum.Key words:angular momentum;operator;commutation relation;spin;angular momentum coupling; clebsh—gordan cofficient0 引言量子力学中有关角动量及其耦合的问题,在很多量子力学教材和文献[1,2,3,4,5,6]中都作过比较简明的阐述,但在许多文献中都是就某一方面进行分析的,并且由于角动量耦合的克莱布希—高登系数计算比较繁琐,大多数教材和文献中都是直接给出或查表得到,只有在一些高等量子力学教材中出现过较简明扼要的计算.本文对量子力学中的角动量及其耦合的问题进行了比较系统的阐述,首先详细讨论轨道角动量在直角坐标系下的算符表示向球极坐标系下的算符表示的推导,进而通过角动量的对易关系得出了轨道角动量的一些重要性质。
固体电子近自由电子近似优秀课件

时不为零,此时:
k'H ˆ(1) kL 1L 0U(x)ei2m axdx um
8
证明:
1
L
Lei(kk')xU(x)dxum
0
0
k'km2π a
k'km2π
a
当 k'k m2π
a
L 10 Lei(k k')xU (x)d xL 10 Le i m 2 a xU (x)dxu m
当 k'k m2π
固体电子近自由电子近似优秀 课件
紧束缚近似适用于近邻原子波函数相互交叠较小,电子在一个原子附近, 主要受到该原子势场作用的情形。因此特别适用于固体内层电子。
紧束缚近似模型中,以孤立原子势场作为零级近似,其它原子势场的 作用作为微扰项。
金属的价电子很容易脱离原子核的束缚,其行为很接近自由电子,主 要受到一个起伏很小的晶格周期势场的作用。此时,紧束缚近似不再是 一个好的近似,因为此时价电子并不是束缚在原子附近,孤立原子的电 子轨道不是好的零级近似。需采用近自由电子近似。
单电子哈密顿算符记做:
H ˆ 2 d2 U(x) 2me dx2
令:
H ˆ(0)
2
2me
d2 d x2
U0
则有:
H ˆ(1) U(x)U0
i2mx
ume a
m0
H ˆH ˆ(0)H ˆ(1)
当周期势场的起伏很小时(近自由电子近似的适用条件), H(1)代表周期势场的起伏,比起H(0)来很小,可以作为微扰项。
当 k 取 值 m/a 附 近 时 , 在 -m/a 附 近 有 一 状 态 , 二 者 相 差 m2/a,能量又非常接近,简并微扰的结果使原来能级高的更
纳米技术在光学领域的应用

纳米技术在光学领域的应用王蒙(长春工程学院理学院吉林省长春市邮编130026)摘要:随着科学技术的不断发展,纳米技术在日趋成熟。
纳米技术在许多领域都发挥着重要的作用,如应用纳米科学技术可以引发光电子、微电子、环保等诸多领域的革命,推动社会经济的腾飞;而纳米电子学、纳米光电子学和纳米光子学将成为21世纪信息时代的关键技术。
由于纳米半导体光电子材料蕴藏着许多新的物理信息和可资利用的独特功能而具有极其广阔的发展前景。
它是半导体光电子材料的一颗新星。
它的出现,意味着半导体光电子材料向低维化方向发展。
关键词:纳米技术;光学;纳米材料;光电材料;半导体。
引言半导体光电子材料经过几十年的发展,已经成为在国民经济和军事等领域得到广泛应用、充满生机的一类电子信息材料。
在信息化时代加速了该材料的升级,使它更加异彩纷呈,引人瞩目。
在20世纪90年代全球掀起的纳米科技浪潮推动下,纳米半导体光电子材料、纳米磁性材料、纳米陶瓷材料和纳米生物材料等纳米材料应运而生。
纳米材料是指尺寸为1~100nm的各种固体材料。
纳米半导体光电子材料是纳米材料家族中的重要成员,它的崛起是光电子材料发展的一次新的飞跃,成为发展新特性、新效应、新原理和新器件的基础。
当半导体光电子材料的尺寸减小到纳米量级时,其物理长度与电子自由程相当,载流子的输运将呈现量子力学特性,宏观固定的准连续能带消失而表现出分裂的能级,因而传统的理论和技术已不再实用。
纳米半导体光电子材料技术是一种多学科交叉的科学和技术,该领域充满了巨大的创新机会和广阔的发展前景。
1.关于纳米的概述1.1:纳米的概念纳米是一种长度度量单位,1纳米等于10亿分之一米( 1nm=10-3μm=10-9m)相当于头发丝直径的10万分之一。
1.2:纳米技术纳米技术是指在原子分子层次上对物质精细的观测识别与控制的研究与应用,它将对于21世纪的信息科学、生命科学、分子生物学、新材料科学和生态系统可持续发展科学提供一个新的技术基础,这将引起一场产业革命,其深远的意义堪与世纪的工业革命相媲美,它包括的领域甚为宽广。
论文全文翻译

刮刀沉积量子点在低损耗大面积发光元件的标准玻璃窗中的应用从减少更昂贵的光伏(PV)材料的使用和减少多电池PV模块的复杂性的方向,我们可以考虑使用发光太阳能集中器(LSC)以降低太阳能电力的成本。
LSC能够实现一些非常规的太阳能转换装置,例如在高人口城市区域作用明显的PV窗户。
在这里,我们试着用胶体核/壳量子点(量子点)制作的低损失,大面积(约90⇥30cm2)LSCs,其光谱是定制的,以最小化波导辐射的自吸收。
为了改善与聚合物基质的相容性和增强的稳定性,将QD封装到二氧化硅壳中。
使用标准刮涂沉积将QD /聚合物复合材料加工沉积到商业窗玻璃上,制造出的半透明器件对于几十厘米的尺寸显示出大于10%的内部量子效率。
发光太阳能聚光器(LSC)是可以用作光伏(PV)电池的大面积太阳光收集器的光管理器件。
LSC由浸渍或涂覆有高发射性荧光团的透明材料板(例如玻璃塑料)组成。
在吸收入射到板的较大面积表面上的太阳光后,LSC荧光团以较低能量再发射光子,这些光子被全内反射引导到器件边缘,在那里它们被PV收集。
如果LSC的成本远低于相当面积的PV电池的成本,并且LSC的效率足够高,则应用这些设备可以实现太阳能电力的成本的显着降低。
半透明LSCs的应用也可以应用于新型设备,如太阳能或PV窗户,可以将当前被动建筑立面转换为电力发电单元。
胶体量子点(QD)已经在利用QD性质的LSC应用的方面有了很多积极的探索,例如广泛可调的吸收和发射光谱,高光稳定性和溶液加工性。
这些结构也可以通过使用通过形状控制,异质结构或杂质掺杂实现的“斯托克斯频移工程”的概念,以大大减少导引光的再吸收(自吸收)的损失的方式来定制。
演示的方法包括使用核/厚壳“巨型”量子点(g-QDs),锰和铜掺杂QDs,II型异质结构和三元I-III-VI2 QDs。
在大多数报道的情况下,LSC荧光团已经嵌入聚合物,例如通过本体聚合制备的聚(甲基丙烯酸甲酯)(PMMA)9,16,17或聚(甲基丙烯酸月桂酯)12,18。
量子化学习题集

(2) x, x2, 3x21; (3) sinx, cosx;
(4) sinx, cosx, tanx;
(5)
sin2x, cos2x, 1;
(6) sinx, cosx, eix (7) sin2x, cos2y, 1
2.2 三维势箱中一粒子的波函数是下列那些算符的本征函数?
ˆ x (2)p ˆx (1) p
2ˆ2 ˆ2ˆ2ˆ2 ˆ xS ˆ y, S ˆy ˆ xS (2) 化简下面算符:S S z, S xS yS z
3.7 计算下列积分: ˆ z|0,0; (1)0,0|M ˆ +M ˆ |2,0; (4) 2,0|M 3.8 计算下列积分: ˆ z|py; (1) px|M ˆ +|py; (2) px|M ˆ y|px; (3) pz|M ˆ x|py (4)pz|M ˆ x|px (5) pz|M ˆ +|2,0; (2)2,1|M ˆ +|2,0 ˆ M (5) 2,0|M
x e
0
n qx
dx
n! q n 1
n 1, q 0 b0 b 0, n 1, 2,3... a 0, n 0,1, 2, ...
e
0 0
bx 2
dx
1 2 b
x
t
2 n bx 2
e
dx
(2n)! 2 n 1 2 n 1 2 n! b
判断下列函数那些是偶函数,那些是奇函数?
(1) sinx (2) cosx (3) tanx
(4) ex
(5) 12
(6)22x
2.6 对谐振子 v=1 的态,求粒子最可能的位置 2.7 对氢原子的基态,求(1) r 的平均值;(2) r 的最可几值;(3)求 2p 态的r 2.8 证明对于定态,T+V=E 2.9 计算氢原子基态的T,V 2.10 已知,力学量 A 的不确定度为A, A
基于蓝光量子点的发光器件的研究现状综述

基于蓝光量子点的发光器件的研究现状综述摘要:量子点是一类纳米级低维半导体材料的总称,这种材料具有激发波长范围宽、发射的光波长可连续调控以及荧光发射峰窄且对称等突出优势,因此量子点也被大多数科研人员认为是新一代最具有潜力的荧光粉材料。
由于量子点具有这些特殊的优点,所以导致量子点可以广泛地应用于发光二极管、医学成像和量子计算以及太阳能电池等众多重要的领域。
而在这之中,蓝光量子点及其发光器件的研究对白光照明和全色域显示都有着十分重要的意义。
关键词:量子点;蓝光量子点;发光器件1.引言随着我国科学创新技术的不断稳定健康发展,我国大多数人民对生活环境的舒适度等方面的要求越来越髙,其中与生活环境息息相关的便是照明,白光发光二极管在照明领域有着重要的应用。
然而一般常见的有机二极管也有很多不足之处,因为普通二极管所用的质料为有机物,不但生产成本髙, 而且受水氧影响较大,这些因素的存在都导致了发光器件的稳定性很差;又由于现存的大部分发光质料都存在色纯度不髙,很难显示出鲜艳的色彩等显著的不足,所以致使人们也在探求新的发光材料来满足人们越来越高的生活工作等日常需求。
30年前,科学家在培育纳米晶的半导体溶液中发现了量子约束效应,比如常见的一种胶体量子点。
在量子点中,由于电子和空穴的波函数在空间上的尺寸远远小于本体材料的激子玻尔半径,所以将会导致能级的量子化,量子点的离散能级产生了窄线宽的原子类发射,这就使得研究人员可以通过调节粒子的大小来调节发光的波长,其发光波长的范围很大,足以满足紫外光、可见光和近红外光波段等波长[1]。
相比于普通有机发光二极管,量子点有其本身特有的优势:首先可以在不改变器件构造的条件下通过调整粒子的直径来改变发光波长,这种方法使得发光器件的制备更简单;其次,是溶液法加工,不像普通有机发光二极管那样必须使用热蒸镀制备,量子点发光器件制备的材料利用率很高,同时成本较低;最后,量子点本身是一种无机半导体材料,这种无机半导体材料相对于有机材料,不容易受水氧侵蚀,这就是量子点发光器件性能更稳定,寿命更长的原因所在。
深圳市宏电技术 H7118 GPRS DTU 说明书

6,0 5„K
6,0 7RRO.LWV
Eg{#A
7UDQVPLVVLR&QRQWUR3OURWRFRO
˚
7LPH ’LYLVLRQ0XOWLSO$FHFHVV
+1u)5%4
7HOHFRPPXQLFDWLR0QDQDJHG 1HWZRUN
*7œˇC#A
8VHU’DWDJUDP 3URWRFRO
*Aı+
8VHU,GHQWLI0\ RGXOH
E*/ˇ|+2ˇ4‡ 6\VWHP
8QLYHUVD0ORELOH7HOHFRPPXQLFDWLRQ
M24§XŒ>9uDB ’DWD
8QVWUXFWXU6HXGSSOHPHQWDU6\HUYLFH
8,0 5„K
8,0 7RRO.LWV
AK´"…‘< 9LVLWR/RUFDWLRQ5HJLVWHU
D9A<´;
’˙9
S*A¨:,XY«("',X–x¨4£#¯c+T ¥L$@,X:M6\¨ˇ)44‘Æk„ˇ)6ªŒ!˝HA¨ :‘F…YEfl> Æ‘E@EQ˜
:m(
ˆ /K+ ˆ +RQJGLDQ +RQJGLDQˆ *356 ’78 ˆ 0’78 ˆc+ˆc+Tˆ#¯c
+
1#¯c+T¥L$@,X‘¨A¨:⁄,XJ
/ˇ|DB40ˆ)
0RELOH’DWD7HUPLQDO8QLW
1u)Cg
0DQDJHPHQW ,QIRUPDWLRQ%DVH
/ˇ|˜ 0RELOH6WDWLRQ
/ˇ|x6
0RELOH6ZLWFKLQ&J HQWHU
基于Matlab的量子激光雷达稳频通信模拟系统设计

赵炳炎等:基于Matlab的量子激光雷达稳频通信模拟系统设计《激光杂志》2021年第42卷第2期LASER JOURNAL(Vol.42,No.2,2021)161基于Matlab的量子激光雷达稳频通信模拟系统设计赵炳炎,陈宗华,赵刘英玉林师范学院物理与电信工程学院,广西玉林537000摘要:传统通信模拟系统设计较为复杂,导致模拟过程消耗能量较大,不能准确模拟稳频通信质量。
因此,提出基于Matlab的量子激光雷达稳频通信模拟系统。
由于振荡器是雷达形成初始信号源的基础,通过分析振荡电路与相位噪声,获得相位噪声函数与通信频率存在的关系;为确保通信过程的稳定,将准确性与稳定性作为信号质量的评价指标,并采用锁频环稳频技术计算频率偏移程度,根据PID控制算法控制频率,量子激光雷达稳频通信;利用Matlab确定激光器、探测器等硬件组成结构,通过时序与数字阵列的设置完成模拟系统设计。
仿真结果表明所提系统结构简便、性能稳定,能够真实模拟出稳频通信的信号质量。
关键词:量子激光雷达;稳频通信;模拟系统;PID控制算法;相位噪声中图分类号:TN929文献标识码:A doi:10.14016/ki.jgzz.2021.02.161The design of the simulation system of frequency stabilisationcommunication of quantum lidar based on MatlabZHAO Bingyan,CHEN Zonghua,ZHAO LiuyingSchool of Physics and Telecommunication Engineering,Yulin Normal University,Yulin537000,ChinaAbstract:The design of traditional communication simulation system is more complex,which leads to a large consumption of energy in the simulation process and can not accurately simulate the quality of frequency stabilisation communication.Therefore,this paper proposes a Matlab based simulation system of quantum-lidar frequency stabilisation communication.Because the oscillator is the basis of the radar x s initial signal source,the relationship between the phase noise function and the communication frequency is obtained by analysing the oscillation circuit and the phase noise.To ensure the stability of the communication process,accuracy and stability are taken as the evaluation index of the signal quality.Through the use of Frequency-locking loop frequency stabilisation technology calculates the frequency shift degree,and the PID control algorithm controls the frequency to stabilise the frequency communication of quantum lidar.By using the MATLAB to determine the structure of laser,detector and other hardware,through the timing and digital array settings to complete the simulation system design.The simulation results show that the proposed system is simple in structure and stable in performance and can simulate the frequency stabilised communication x s signal quality.Key words:quantum lidar;frequency stabilisation communication;simulation system;PID control algorithm;phase noise1引言量子激光雷达具有灵敏度高,不可克隆性和超强的反隐身性能;拥有较高角分辨率与距离分辨率等优收稿日期;2020-07-10基金项目:国家自然科学基金(理论物理专项)(No.11847144)作者简介:赵炳炎(1981-),男,硕士,讲师,研究方向:理论物理与计算物理。
XS原理及分析PPT课件

壳层都将分裂成两个能级XPS出现双峰
自旋——轨道劈裂
自旋-轨道劈裂
l=1 l=3
l=0
l=2
3、电子结合能
一个自由原子或离子的结合能,等于将此电子从所 在的能级转移到无限远处所需的能量。
4、XPS信息深度
5、化学位移
同种原子由于处于不同的化学环境,引起内壳层电子结 合能的变化,在谱图上表现为谱线的位移,这种现象称为化 学位移。
旋转取向;与上述3个量子数无关。
–电子的轨道运动和自旋运动间存在电磁相互作用, 即:自旋-轨道耦合作用的结果使其能级发生分
裂,对l >0的内壳层来说,这种分裂可用内量子 数j表示(j =| l+ ms |= | l ± 1/2 |) • 若l =0,则j = 1/2 ;
• 若l =1,则j = l ± 1/2 = 3/2或1/2 ;
1、光电效应
当一束能量为hν的单色光与原子发生相互作用 ,而入射光量子的能量大于原子某一能级电子的结合 能时,发生电离:
M + hν= M*+ + e光电效应过程同时满足能量守恒和动 量守恒,入射光子和光电子的动量之间的差额是由原 子的反冲来补偿的。 光电效应的几率随着电子同原子核结合的加紧 而很快的增加,所以只要光子的能量足够大,被激发 的总是内层电子。外层电子的光电效应几率就会很小 ,特别是价带,对于入射光来说几乎是“透明”的。
光电效应截面s与原子序数Z的关系 Z 3 4 5 6 7 8 9 11 12
元素 Li Be B C N O F Na Mg
s 1.1 4.2 11 22 40 64 100 195 266
2、原子能级的划分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多电子原 每个电子所处状态相应的(定态)波函数 子系统: (r , , ) 重要!
n ,l ,m ,ms l
100 1
例如: n =1
100
2
1 2
200 1
n =2
2
211 1
200
210 1 210
1 2
2 1
2 211 1 2 21-1 1 2 21-1 1
C. 不能表示原子的状态,也不是一个定态
课堂练习
设态
1 3 (r, , ) 1 1 2 3112 2 2102
以下哪个物理量有确定值?
A.能量 B. 角动量 √
C.角动量在z方向的投影值
D. 电子自旋角动量在外场方向的投影值 √
课堂练习
设态
1 3 (r, , ) 1 1 2 3112 2 2102
3
8
常规
2 .粒子数的正常分布
根据玻尔兹曼分布,具有能量Ei的原子数
N i Ae Ei / kT
E1
在能级E1和E2的原子数之比:
N2 e ( E 2 E1 ) / kT N1
在能级E1-E2的=1eV,T=300K,则原子数之比约为10-40.
可见高能级上原子数目极少.
34
解: n=3 l =( 0 , 1 ,2) ml =(0,±1,±2)
ms= 1/2
Zn = 2n2 2 X 3 2 18 共有18个量子态.
最多可容纳18个电子.
提问:
若有两个电子处于第二激发态,每个 电子趋向占有哪个态呢?
27
二、 能量最小原理 每个电子趋向占有能量最小的状态.
一般讲n 越小,能量越小。但是有时受l 影响, n壳层尚 未填满, n+1壳层已经开始有电子填入了.
A.只有(1)和(3); B.只有(2)和(4); √ C.只有(1)、(3)和(4); D.只有(2)、(3)和(4)。
课堂 练习
试写出n =3 时的各个量子态的四个量子数, 最 多有几个量子态? 最多可容纳多少个电子? l = 0, 1, 2,…, (n–1) ml = 0, 1, 2,… , l . ms= 1/2
E f f d d p p s s
f d
d p s s N= 1 2
d p s
p s
p s
E3 d E4 s
3
4
5
6
7
28
课堂练习
求下列量子态中可填充的最大电子数
1 (1) n 3 ms ; (2) n 3 l ml 3 2
1 解: (1)n 3 ms ; 2 1 缺少 m s 的9个电子. 2
原子发光的三种跃迁过程
E2 E2 h E1 h E1 发光前 发光后 受激辐射 光放大 相干光 E2 h h
h
E1 吸收前 吸收后 发光前 发光后 受激吸收 自发辐射 (原子的光激发)
*等几率假设: 入射光产生受激 辐射和受激吸收的几率相同
33
二. 相关物理概念
E2
1. 亚稳态能级 10 S 10 S
原子中每个壳层所能容纳的电子数
l n 1,K 2,L 3,M 4,N 5,O 6,P 7,Q 0 s 2(1s) 2(2s) 2(3s) 2(4s) 2(5s) 2(6s) 2(7s) 1 p 6(2p) 6(3p) 10(3d) 6(4p) 10(4d) 14(4f) 6(5p) 10(5d) 14(5f) 18(5g) 6(6p) 10(6d) 14(6f) 18(6g) 22(6h) 2 d 3 f 4 g 5 h 6 i Zn 2 8 18 32 50 72
3. 粒子数反转分布
能级E2 >E1时,
N2 1 N1
E2(N2)
实现粒子数反转的办法:
E1(N1)
具有亚稳态的三能级结构系统
E3 激发态 无辐射跃迁 E2 亚稳态
具有亚稳态的四能级系统
, 2, 3 D. L 3;L z 0,
E. 以上都不对
课堂练习 设原子的电子处于n=4,l=3的状态,此时角动量与 z轴的夹角有几个可能值?
A. 5个
B. √7个
C. 3个
D. 2个
E. 以上都不对
课堂练习
#1a1301040c
设原子的电子处于n=4,l=3的状态,此时角动量与 z轴的夹角的可能值中最小的角为多少?
一、 泡利不相容原理
在一个原子系统内不可能有两个或两个以上 的电子具有相同的状态,亦即不可能具有相 同的 4 个量子数 (n,l,ml ,ms ) 。
主量子数n : n =1, 2, 3,…
角量子数l : l =0,1,2,…,(n –1)
磁量子数ml : ml = 0,1,2,… ,l.
自旋磁量子数ms : ms=1/2
最大可填充的电子数为 9.
(2)n 3
l ml 3
没有此量子态!
29
应有l n; ml n
原子序数56的多电子原子的能级高低可用经验公式:
n 0.7l
提问:
2
越大,能级越高
重要!
K原子,核外有19个电子的排布 2 2 6 2 6 1 1s 2s 2 p 3s 3 p 3d 对吗?
16
原子壳层和支壳层的符号表示
n
壳层
1 K 0
2 L 1
3 M 2
4 N 3
5 O 4
6 P 5
l
支壳层
s
p
d
f
g
h
17
课堂练习
#1a1301027c
在氢原子的K壳层中,电子可能具有的量子数(n, l,ml,ms)是 A.(1,0,0,1/2); √
B.(1,0,-1,1/2);
C.(1,1,0,-1/2); D.(2,1,0,-1/2)。
当n、l一定时,不同的量子态数目为 2(2l+1) ; 当n一定时,不同的量子态数目为 2n2 .
22
课堂练习-填空
原子内电子的量子态由四个量子数(n,l,ml ,ms ) 表征.
1 2 n m n 当 一定, s 时,不同的量子态数目为 ; 2
ml 0,ms 当n一定, 1 2
6(7p) 10(7d) 14(7f) 18(7g) 22(7h) 26(7i) 98
思考: *同一支壳层(角动量量子数l)最多可容纳电子数? 19 *同一主量子数n的可容纳的最多电子数?
2 (2l 1) *同一支壳层(角动量量子数l)最多可容纳电子数:
对同一 l
ml 0、 1、 2 l
2、角量子数l 角动量量子化
l 0, 1, 2(n 1)
ml 0,1,2,... l
L l (l 1)
3、磁量子数 ml 角动量空间取向量子化
Lz ml
4、自旋磁量子数
自旋角动量空间取向量子化
自旋量子数
自旋角动量
2
课堂练习
#1a1301026a
直接证实了电子自旋存在的最早的实验之一是
共 (2l 1)个
再考虑自旋, 同一支壳层最多可容纳电子数:
(2l+1) X2
*同一主量子数n的可容纳的最多电子数:
2n
2
Z n 2(2l 1)
i 0
n 1
2 2(2n 1) n 2
2n
2
20
课堂 练习
第一激发态共有几个量子态? 2 2 2 8个 每个态对应的量子数?
n ,l ,m ,ms l
(r , , )
是否为原子的一个可能态?是否为一个定态? A.是一个可能的态,也是一个定态 √
B. 是一个可能的态,但不是一个定态
C. 不能表示原子的状态,也不是一个定态
课堂练习-填空
态函数
3, 2, 2,
1 2
角动量:
6
2
角动量在z方向的投影值: 2
L l (l 1)
课堂练习-填空
Lz ml
2
ml 0, 1, 2 l
当 n 4, l 2;3 时角动量为 L 6; L3 12 ; l 2 时角动量空间量子化的值可为 Lz 0, ,2 磁量子数可为 ml 0, 1 ,2 课堂练习-填空
100 1 100
1 2
2
24
课堂练习
#1a1301027b
在一个原子系统中,同一个主量子数为n的壳层上,最 多可容纳电子的个数是 A. 2n2; √
B. 2n; C. n2;
D. n。
课堂练习
#1a1301027d
下列四组量子数 (1)n=3,l=2, ml=0, ms=1/2; (2)n=3,l=3, ml=1, ms=1/2; (3)n=3,l=1, ml=-1, ms=-1/2; (4)n=3,l=0, ml=0, ms=-1/2。 其中可以描述原子中电子状态的
角动量和角动量的平均值是多少? A.
,
2 ,
2, 2
B. √
C.
2
D.
2, 2
E. 以上都不对
课堂练习 设原子的电子处于n=4,l=3的状态,此时角动量和 在z方向的投影值分别是:
A. L 6;L z 3
B. L 12;L z 3
, 2, 3 C. √ L 12;L z 0,
电子自旋角动量在外场方向的投影值:
课堂练习
设态函数表示形式
n ,l ,m ,ms l
(r , , )
1 3 (r, , ) 1 1 2 3112 2 2102
