200202一级笔试试题A卷
2002年国家公务员考试行政职业能力测试真题及详细解析

2002年中央、国家机关公务员录用考试《行政职业能力测验》试题(卷)(A 类)第一部分 数量关系(共15题,参考时限15分钟)本部分包括两种类型的试题,均为单项选择题。
一、数字推理共5题。
给你一个数列,但其中缺少一或二项,要求你仔细观察数列的排列规律,然后从四个选项中选出你认为最合理的一项来填补空缺项。
请开始答题:1.2,6,12,20,30,( )A .38B .42C .48D .562.20,22,25,30,37,( )A .39B .45C .48D .513.2,5,11,20,32,( )A .43B .45C .47D .494.1,3,4,7,11,( )A .14B .16C .18D .205.34,36,35,35,( ),34,37,( )A .36,33B .33,36C .37,34D .34,37二、数学运算共10题。
你可以在草稿纸上运算,遇到难题,你可以跳过不做,待你有时间再返回来做。
请开始答题:6.1998年,甲的年龄是乙的年龄的4倍。
2002年,甲的年龄是乙的年龄的3倍。
问甲、乙二人2000年的年龄分别是多少岁?A .34岁,12岁B .32岁,8岁C .36岁,12岁D .34岁,10岁7.一项工作,甲单独做10天完成,乙单独做15天完成。
问:两人合作3天完成工作的几分之几?A .1/2B .1/3C .1/5D .1/68. 15.025.053÷⨯的值是: A .1 B .1.5 C .1.6 D .2.09.某学校学生排成一个方阵,最外层的人数是60人,问这个方阵共有学生多少人?A .256人B .250人C .225人D .196人10.一根长18米的钢筋被锯成两段。
短的一段是长的一段的4/5,问短的一段有多少米长?A .7.5米B .8米C .8.5米D .9米11.1.1^2+1.2^2+1.3^2+1.4^2的值是:A .5.04B .5.49C .6.06D .6.3012.一个正方形的边长增加20%后,它的面积增加百分之几?A .36%B .40%C .44%D .48%13.一块三角地,在三个边上植树,三个边的长度分别为156米、186米、234米,树与树之间的距离均为6米,三个角上都必须栽一棵树,问共需植树多少棵?A.90棵B.93棵C.96棵D.99棵14.甲乙两名工人8小时共加736个零件,甲加工的速度比乙加工的速度快30%,问乙每小时加工多少个零件?A.30个B.35个C.40个D.45个15.如下图,一个正方形分成了五个大小相等的长方形。
2002年基础考试题及答案(下午)

2002年一级注册结构工程师考试基础课试题及答案(下午)1.下列关于计算机存储器的叙述是错误的?(A)任何计算机都必须要有内存储器(B)ROM、RAM都是内存储器(C)CD-ROM是外存储器的一种(D)CPU可以直接访问硬盘2.不允许出现无名公用区的程序块是:(A)数据块子程序(B)函数子程序(C)子例行程序(D)主程序3.当a=4,执行完下列语句后,b的值为:if(a.gt.3) thenif (a .eq. 3)b =3b =2else if (a. lt . 4) thenb = 1if ( a .eq .4) b =4endif(A) 4 (B) 3 (C) 2 (D) 14.对于INTEGER A(2,2),下列答案中能达到完全相同的输入效果的一对是:(1) read (*, *) A (1, 1), A (1, 2) , A (2, 1), A (2, 2,)(2 ) read (*, *) A(3 ) do 10 I =1, 2do 10 J =1, 210read (*, *) A (J, I )(4 ) read (*, * ) ( (A (I ,j ), J= 1, 2 ), I= 1 , 2 )(A)( 1 )和( 2 ) (B) ( 1 ) 和 ( 3 )(C) ( 1 ) 和 ( 4 ) (D) ( 3 ) 和 ( 4 )5. 下列程序的输入结果为:common T (4)data T/1.0, 2.0, 3.0, 4.0/external Pcall sub ( 3, 4, P, m )write ( *, * ) mendsubroutinue sub (m, n, t, k)k = t (m) + t (n)end(A) 18.0 (B) 7.0 (C) 7 (D) 186. 设ωi 是用f (x )的(n ≥1)次Lagrange 插值公式近似代替f (x )来计算定积分()ba f x dx ⎰的数值求积公式的求积系数,即:0()()nbi a i f x dx f x ω=≈∑⎰,则有:(A ) ωi >0 (B )0n i i b a ω=≡-∑(C ) 0n i i b a ω=≡-∑ (D ) 0n i i b a ω=≡-∑. 7.解非线性方程f (x )=0的牛顿-雷扶生(Newton-Raphson )迭代方法在单根x*附近具有:(A )平方收敛 (B )线性收敛(C )3阶收敛 (D )非局部线性收敛8.若A 为下列何项,则A 一定右以分解为A=LL T,其中L 为非奇异下三角阵。
2002年国家公务员考试行测真题及答案A类试卷:判断推理部分
石家庄:/邯郸站:/保定站:/沧州站:/唐山站:/秦皇岛:/判断推理(共30题,参考时限30分钟)本部分包括三种类型的试题,均为单项选择题。
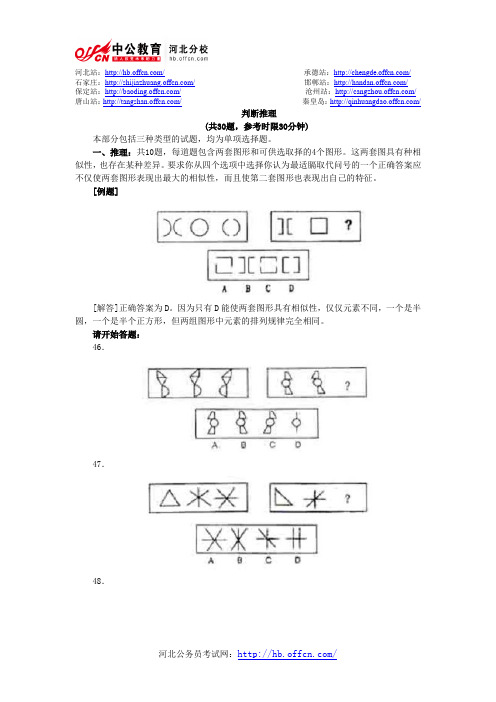
一、推理:共10题,每道题包含两套图形和可供选取择的4个图形。
这两套图具有种相似性,也存在某种差异。
要求你从四个选项中选择你认为最适膈取代问号的一个正确答案应不仅使两套图形表现出最大的相似性,而且使第二套图形也表现出自己的特征。
[例题][解答]正确答案为D。
因为只有D能使两套图形具有相似性,仅仅元素不同,一个是半圆,一个是半个正方形,但两组图形中元素的排列规律完全相同。
请开始答题:46.47.48.石家庄:/邯郸站:/保定站:/沧州站:/唐山站:/秦皇岛:/49.50.51.52.53.石家庄:/邯郸站:/保定站:/沧州站:/唐山站:/秦皇岛:/54.55.二、演绎推理:共10题,每题给出一段陈述,这段陈述被假设是正确的,不容置疑的。
要求你根据这段陈述,选出一个答案。
注意,正确答案应与所给的陈述相符合,不需要任何附加说明即可以从陈述中直接推出。
[例题] 某厂有五种产品:甲、乙、丙、丁、戊。
它们的年销售额之间的关系为:丙没有丁高,甲没有乙高,戊高于丁,而乙不如丙高。
请问,哪种产品的年销售额最高?A.甲 B.乙 C.丁 D.戊[解答] 从所给条件可以知道:戊>丁>丙>乙>甲。
因此,正确答案为D。
请开始答题:56.刑警队需要充实缉毒组的力量,关于队中有哪些人来参加该组,已商定有以下意见:(1)如果甲参加,则乙也参加;(2)如果丙不参加,则丁参加;(3)如果甲不参加而丙参加,则队长戊参加;(4)队长戊和副队长己不能都参加;(5)上级决定副队长己参加。
根据以上意见,下列推理完全正确的是:A.甲、丁、己参加B.丙、丁、己参加C.甲、丁、己参加D.甲、乙、丁、己参加57.中国移动通讯公司曾经投入巨资扩大移动通讯服务覆盖区,结果当年用户增加了石家庄:/邯郸站:/保定站:/沧州站:/唐山站:/秦皇岛:/ 25%,但是总利润却下降了10%。
02年职称英语考试理工类(A级)试题及答案6

02年职称英语考试理工类(A级)试题及答案6第二篇HackingPeople tend to think of computers as isolated machines,working away all by themselves.Some do-personal computer without an outside link,like Someone’s hideaway(隐蔽的)cabin in the woods.But just as most homes are tied to a community by streets,bus routes and electric lines.computers that exchange intelligence are part of a community-local,national and even global network joined by telephone connections.The computer network is a creation of the electric age,but it is based on old-fashioned trust. It cannot work without trust.A rogue loose(为所欲为的无赖)in a computer system called hacker (黑客) is worse than a thief entering your house.He could go through anyone’s electronic mail or add to,change,distort or delete anything in t he information stored in the computer’s memory.He could even take control of the entire system by placing his own instructions in the software that runs it.He could shut the computer down whenever he wished,and no one could stop him.Then he could program the computer to erase any sign of his ever having been there.Hacking,our electronic-age term for computer break-in,is more and more in the news-brainy kids vandalizing university records,even pranking(胡闹)about in supposedlyline14safeguarded systems.To those who understand how computer networks are increasingly regulating life in the late 20th century,these are not laughing matters.A potential for disaster isbuilding:A dissatisfied former insurance-company employee wipes out information trom payroll (工资表) files.A student sends out a”virus”,a secret anddestructive command,over a national network.The virus copies itself at lightning speed,jamming the entire network-thousands of academic,commercial and govemment computer systems.Such disastrous cases have already occurred.Now exists the possibility of terrorism by computer.Spoiling a system responsible for air.traffic control at a busy airport,or knocking out the telephones of a major city,is a relatively easy way to spread panic.Yet neither business nor government has done enough to toughen its defenses against attack.For one thing,such defenses are expensive;for another,they may interrupt communication -the main reason for using computers in the first place.36 The wr iter mentions’’a thief’in the second paragraphA to show that a hacker is more dangerous than a thief.B to tell people that thieves like to steal computers nowadays.C to demand that a protective computer system should be set up against thieves.D to demonstrate that hackers and thieves are the same people.37 The word”vandalizing”in Line 14 meansA “stealing”.B “creating”.C “destroying”.D “updating”.38 According to the passage.which of the following statements is NOT true?A Hacking is also known as computer break-in.B Experts on computer networks consider hacking nothing serious.C Hacking is a widespread concern.D Hacking is potentially disastrous.39 Which of the following is NOT mentioned in the passage as an instance of attack by a hacker?A Deleting information in the computer’s memory.B Shutting down the computer whenever he wishes.C Entering your house to steal.D Spoiling a system for air traffic.40 One of the reasons why business or government has not taken tough measures to stop hacking is thatA it will cause fear among tile public.B hacking has not caused much damage.C tough measures are illegal.D communication may be interrupted.。
2002年国家公务员录用考试《行测》真题(A卷)

2002年国家公务员录用考试《行测》真题(A卷)第一部分常识判断1:单选、计算机系统的下列设备中,既可作输入设备又可作输出设备的是()。
A、扫描仪B、磁盘驱动器C、键盘D、显示器2、单选、香烟点燃后,冒出的烟雾看上去是蓝色的,这是因为()。
A、烟雾的颗粒本身是蓝色的B、烟雾将光线中其他色光滤掉,只有蓝光透射出来C、烟雾的颗粒对蓝色光散射强烈D、烟雾的颗粒吸收光线后,发出蓝色荧光3、单选、在电磁波谱中,红外线、可见光和紫外线三个波段的频率大小关系是()。
A、红外线频率最高,可见光频率最低B、紫外线频率最高,红外线频率最低C、可见光频率最高,红外线频率最低D、紫外线频率最高,可见光频率最低4、单选、DNA是人类进行亲子鉴定的主要依据。
就DNA的组成,下面说法正确的是()。
A、DNA由核糖、碱基和磷酸组成B、DNA由脱氧核糖、磷酸和碱基组成C、DNA由脱氧核糖、磷酸、碱基和蛋白质组成D、DNA由脱氧核糖、磷酸、碱基和脂肪组成5、单选、多数鱼类背部发黑、腹部发白,其原因是()。
A、长期进化形成的保护色B、背部比腹部接受光线多,导致色素沉淀C、背部比腹部粘膜厚,吸收光线多D、背部鱼鳞多,吸收光线多6、单选、地球表面的绿色植物通过光合作用,将太阳的辐射能量转化成能被其他生物利用的有机化合能。
下面的说法错误的是()。
A、光合作用吸收的主要是太阳光中的绿光B、植物的绿色是反射了太阳光中的绿光C、不同植物的光合作用效率是不一样的D、植物在不同时间的光合作用效率不一样7、单选、温室效应将引起全球气温上升,导致气候异常、海平面上升、生态恶化。
引起温室效应的最主要的气体是()。
A、氮氧化合物B、二氧化碳C、臭氧D、氟利昂8、单选、下列电池中不能充电的()。
A、镍镉电池B、银锌电池C、普通干电池D、铅蓄电池9、单选、远程电力传输一般采用50-100万伏的高电压,其主要原因是()。
A、确保远程电力传输的安全B、减少传输线路上的电能损失C、节约传输线路上的设备和材料D、减少雷电对传输线路的破坏10、单选、盛水的烧杯里有一只盛水的试管,加热烧杯使水沸腾。
职称英语真题-综合类A级2002年

2002年职称英语考试综合类(A级)真题下面共有15个句子,每个句子中均有1个词或短语画有底横线,请从每个句子后面所给的4个选项中选择1个与画线部分意义最相近的词或短语。
答案一律涂在答题卡相应的位置上。
1 The price of vegetables fluctuates according to the weather.A jumpsB risesC fallsD changes2 Did you do that to irritate her?A teaseB attractC annoyD protect3 Mary looked pale and weary.A illB tiredC worriedD peaceful4 The water in this part of the river has been contaminated by sewage(污水).A pollutedB downgradedC mixedD blackened5 Her treatment of the subject is exhaustive.A very boringB verythoroughC very interestingD very touching6 Alice is a fascinating girl.A a beautifulB a prettyC an attractiveD a pleasant7 Her mood can be gauged by her reaction to the most trivial of incidents.C provedD assessed8 The old lady let her flat to an English couple.A offeredB rentedC providedD sold9 She stood there crying and trembling with fear.A shakingB staggeringC strugglingD murmuring10 They strolled around the lake for an hour or so.A ranB rolledC walkedD raced11 The conclusion can be deduced from the premises.A arguedB derivedC permittedD come12 I can no longer tolerate his actions.A put up withB acceptC takeD suffer from13 Our plan is to a11ocate one member of staff to handle appointmentsA askB persuadeC assignD order14 She has been the subject of massive media coverage.A extensiveB negativeC responsiveD explosive15 I expect that she will be able to cater for your particular needs.C provideD meet第2部分:阅读判断(第16~22题,每题1分,共7分)阅读下面这篇短文,短文后列出7个句子,请根据短文的内容对每个句子做出判断。
2002考研数学一真题及答案解析

2002年全国硕士研究生入学统一考试数学一试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.) (1)⎰∞+exx dx2ln =.(2)已知函数()y y x =由方程0162=-++x xy e y 确定,则(0)y ''=. (3)微分方程02='+''y y y 满足初始条件0011,'2x x yy ====的特解是.(4)已知实二次型323121232221321444)(),,(x x x x x x x x x a x x x f +++++=经正交变换x Py =可化成标准型216y f =,则a =.(5)设随机变量X 服从正态分布2(,)(0)N μσσ>,且二次方程042=++X y y 无实根的概率为12,则μ= .二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)考虑二元函数),(y x f 的下面4条性质: ①),(y x f 在点),(00y x 处连续; ②),(y x f 在点),(00y x 处的两个偏导数连续; ③),(y x f 在点),(00y x 处可微;④),(y x f 在点),(00y x 处的两个偏导数存在.若用“P Q ⇒”表示可由性质P 推出性质Q ,则有(A ) ②⇒③⇒①. (B ) ③⇒②⇒①. (C ) ③⇒④⇒①.(D ) ③⇒①⇒④.(2)设0(1,2,3,)n u n ≠=L ,且lim1n nnu →∞=,则级数11111(1)()n n n n u u ∞+=+-+∑ (A ) 发散. (B ) 绝对收敛.(C ) 条件收敛.(D ) 收敛性根据所给条件不能判定.(3)设函数()y f x =在(0,)+∞内有界且可导,则 (A ) 当0)(lim =+∞→x f x 时,必有0)(lim ='+∞→x f x .(B ) 当)(lim x f x '+∞→存在时,必有0)(lim ='+∞→x f x .(C ) 当0lim ()0x f x +→=时,必有0lim ()0x f x +→'=. (D ) 当0lim ()x f x +→'存在时,必有0lim ()0x f x +→'=.(4)设有三张不同平面的方程123i i i i a x a y a z b ++=,3,2,1=i ,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为(5)设1X 和2X 是任意两个相互独立的连续型随机变量,它们的概率密度分别为1()f x 和2()f x ,分布函数分别为1()F x 和2()F x ,则(A ) 1()f x +2()f x 必为某一随机变量的概率密度. (B ) 1()f x 2()f x 必为某一随机变量的概率密度. (C ) 1()F x +2()F x 必为某一随机变量的分布函数. (D ) 1()F x 2()F x 必为某一随机变量的分布函数.三、(本题满分6分) 设函数)(x f 在0x =的某邻域内具有一阶连续导数,且(0)0,(0)0f f '≠≠,若()(2)(0)af h bf h f +-在0→h 时是比h 高阶的无穷小,试确定b a ,的值.四、(本题满分7分) 已知两曲线)(x f y =与⎰-=x t dt e yarctan 02在点(0,0)处的切线相同,写出此切线方程,并求极限)2(lim nnf n ∞→.五、(本题满分7分) 计算二重积分dxdy e Dy x⎰⎰},max{22,其中}10,10|),{(≤≤≤≤=y x y x D .六、(本题满分8分)设函数)(x f 在(,)-∞+∞内具有一阶连续导数,L 是上半平面(y >0)内的有向分段光滑曲线,其起点为(b a ,),终点为(d c ,).记2221[1()][()1],L xI y f xy dx y f xy dy y y=++-⎰(1)证明曲线积分I 与路径L 无关; (2)当cd ab =时,求I 的值.七、(本题满分7分)(1)验证函数333369()1()3!6!9!(3)!n x x y x x n =++++++-∞<<+∞L L 满足微分方程x e y y y =+'+'';(2)利用(1)的结果求幂级数30(3)!nn x n ∞=∑的和函数.八、(本题满分7分)设有一小山,取它的底面所在的平面为xOy 坐标面,其底部所占的区域为2{(,)|D x y x =275}y xy +-≤,小山的高度函数为),(y x h xy y x +--=2275.(1)设),(00y x M 为区域D 上一点,问),(y x h 在该点沿平面上什么方向的方向导数最大?若记此方向导数的最大值为),(00y x g ,试写出),(00y x g 的表达式.(2)现欲利用此小山开展攀岩活动,为此需要在山脚下寻找一上山坡最大的点作为攀登的起点.也就是说,要在D 的边界线2275x y xy +-=上找出使(1)中),(y x g 达到最大值的点.试确定攀登起点的位置.九、(本题满分6分)已知四阶方阵),,,(4321αααα=A ,4321,,,αααα均为4维列向量,其中432,,ααα线性无关,3212ααα-=,如果4321ααααβ+++=,求线性方程组β=Ax 的通解.十、(本题满分8分) 设,A B 为同阶方阵,(1)若,A B 相似,证明,A B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当,A B 均为实对称矩阵时,证明(1)的逆命题成立.十一、(本题满分7分) 设维随机变量X 的概率密度为10,cos ,()220,x x f x π⎧≤≤⎪=⎨⎪⎩其他.对X 独立地重复观察4次,用Y 表示观察值大于3π的次数,求2Y 的数学期望.十二、(本题满分7分)其中1(0)2θθ<<是未知参数,利用总体X 的如下样本值3,1,3,0,3,1,2,3,求θ的矩估计值和最大似然估计值.2002年考研数学一试题答案与解析一、填空题 (1)【分析】 原式2ln 11.ln ln eed x x x+∞+∞==-=⎰(2)【分析】 方程两边对x 两次求导得'6'620,y e y xy y x +++=① 2'''6''12'20.y y e y e y xy y ++++=②以0x =代入原方程得0y =,以0x y ==代入①得'0,y =,再以'0x y y ===代入②得''(0) 2.y =-(3)【分析】 这是二阶的可降阶微分方程.令'()y P y =(以y 为自变量),则'''.dy dP dPy P dx dx dy=== 代入方程得20dP yPP dy +=,即0dPy P dy +=(或0P =,但其不满足初始条件01'2x y ==). 分离变量得0,dP dy P y+= 积分得ln ln ',P y C +=即1C P y=(0P =对应10C =); 由0x =时11,',2y P y ===得11.2C =于是又由01x y==得21,C =所求特解为y =(4)【分析】 因为二次型TxAx 经正交变换化为标准型时,标准形中平方项的系数就是二次型矩阵A 的特征值,所以6,0,0是A 的特征值.又因iiia λ=∑∑,故600, 2.a a a a ++=++⇒=(5)【分析】 设事件A 表示“二次方程042=++X y y 无实根”,则{1640}{A X X =-<=>4}.依题意,有1(){4}.2P A P X =>=而 4{4}1{4}1(),P X P X μΦσ->=-≤=-即414141(),(),0. 4.22μμμΦΦμσσσ----===⇒=二、选择题(1)【分析】 这是讨论函数(,)f x y 的连续性,可偏导性,可微性及偏导数的连续性之间的关系.我们知道,(,)f x y 的两个偏导数连续是可微的充分条件,若(,)f x y 可微则必连续,故选(A ).(2)【分析】 由1lim 101n n un n →+∞=>⇒充分大时即,N n N ∃>时10n u >,且1lim 0,n nu →+∞=不妨认为,0,n n u ∀>因而所考虑级数是交错级数,但不能保证1nu 的单调性. 按定义考察部分和111111111111(1)()(1)(1)nn nk k k n k k k k k k k S u u u u +++===++=-+=-+-∑∑∑1111111(1)11(1)1(1)(),k n nn l k l k l n n u u u u u ++==+--=-+-=+→→+∞∑∑⇒原级数收敛.再考察取绝对值后的级数1111()n nn u u ∞=++∑.注意111112,11nn n n u u n n n u u n n++++=+⋅→+ 11n n ∞=∑发散⇒1111()n n n u u ∞=++∑发散.因此选(C ).(3)【分析】 证明(B )对:反证法.假设lim ()0x f x a →+∞'=≠,则由拉格朗日中值定理,(2)()'()()f x f x f x x ξ-=→∞→+∞(当x →+∞时,ξ→+∞,因为2x x ξ<<);但这与(2)()(2)()2f x f x f x f x M -≤+≤矛盾(()).f x M ≤(4)【分析】 因为()()23r A r A ==<,说明方程组有无穷多解,所以三个平面有公共交点且不唯一,因此应选(B ).(A )表示方程组有唯一解,其充要条件是()() 3.r A r A ==(C )中三个平面没有公共交点,即方程组无解,又因三个平面中任两个都不行,故()2r A =和()3r A =,且A 中任两个平行向量都线性无关.类似地,(D )中有两个平面平行,故()2r A =,()3r A =,且A 中有两个平行向量共线.(5)【分析】 首先可以否定选项(A )与(C ),因121212[()()]()()21,()()112 1.f x f x dx f x dx f x dx F F +∞+∞+∞-∞-∞-∞+=+=≠+∞++∞=+=≠⎰⎰⎰对于选项(B ),若121,21,1,01,()()0,0,x x f x f x -<<-<<⎧⎧==⎨⎨⎩⎩其他,其他,则对任何(,),x ∈-∞+∞ 12()()0f x f x ≡,12()()01,f x f x dx +∞-∞=≠⎰因此也应否定(C ),综上分析,用排除法应选(D ).进一步分析可知,若令12max(,)X X X =,而~(),1,2,i i X f x i =则X 的分布函数()F x 恰是12()().F x F x1212(){max(,)}{,}F x P X X x P X x X x =≤=≤≤1212{}{}()().P X x P X x F x F x =≤≤=三、【解】 用洛必达法则.由题设条件知lim[()(2)(0)](1)(0).h af h bf h f a b f →+-=+-由于(0)0f '≠,故必有10.a b +-=及(0)0f '≠,则有20a b +=. 综上,得2, 1.a b ==-四、【解】 由已知条件得(0)0,f =22arctan arctan 02'(0)()'1,1xx t xx x e f e dt x --=====+⎰故所求切线方程为y x =.由导数定义及数列极限与函数极限的关系可得五、【分析与求解】 D 是正方形区域如图.因在D 上被积函数分块表示2222,,max{,}(,),,,x x y x y x y D y x y ⎧≥⎪=∈⎨≤⎪⎩于是要用分块积分法,用y x =将D 分成两块:1212,{},{}.D D D D D y x D D y x ==≤=≥U I I⇒I 222212max{,}max{,}xy xy D D e dxdy e dxdy =+⎰⎰⎰⎰2221212x y x D D D e dxdy e dxdy e dxdy =+=⎰⎰⎰⎰⎰⎰(D 关于y x =对称)2102xx dx e dy =⎰⎰(选择积分顺序)221102 1.x xxe dx e e ===-⎰六、【分析与求解】(1)易知Pdx Qdy +∃原函数,2211()()()()()x Pdx Qdy dx yf xy dx xf xy dy dy ydx xdy f xy ydx xdy y y y+=++-=-++ 0()()()[()].xy x xd f xy d xy d f t dt y y =+=+⎰⇒在0y >上Pdx Qdy +∃原函数,即0(,)()xy xu x y f t dt y =+⎰. ⇒积分I 在0y >与路径无关.(2)因找到了原函数,立即可得(,)(,)(,).c d a b c a I u x y d b==-七、【证明】 与书上解答略有不同,参见数三2002第七题(1)因为幂级数3693()13!6!9!(3)!nx x x x y x n =++++++L L的收敛域是()x -∞<+∞,因而可在()x -∞<+∞上逐项求导数,得25831'()2!5!8!(31)!n x x x x y x n -=+++++-L L ,4732''()4!7!(32)!n x x x y x x n -=+++++-L L ,所以2'''12!!nx x x y y y x e n ++=+++++=L L ()x -∞<+∞.(2)与'''xy y y e ++=相应的齐次微分方程为'''0y y y ++=,其特征方程为210λλ++=,特征根为1,212λ=-±.因此齐次微分方程的通解为212(cossin )22x Y eC x C x -=+. 设非齐次微分方程的特解为xy Ae *=,将y *代入方程'''xy y y e ++=可得13A =,即有13x y e *=.于是,方程通解为2121(sin )3xx y Y y eC x C x e -*=+=++. 当0x =时,有112121(0)1,23,0.311'(0)0.223y C C C y C ⎧==+⎪⎪⇒==⎨⎪==-++⎪⎩于是幂级数30(3)!n n x n ∞=∑的和函数为221()33x x y x e x e -=+()x -∞<+∞八、【分析与求解】(1)由梯度向量的重要性质:函数),(y x h 在点M 处沿该点的梯度方向0000(,)(,)0000(,){,}{2,2}x y x y h h h x y x y y x x y∂∂==-+-+∂∂grad方向导数取最大值即00(,)(,)x y h x y grad 的模,00(,)g x y ⇒=(2)按题意,即求(,)g x y 求在条件22750x y xy +--=下的最大值点⇔22222(,)(2)(2)558g x y y x x y x y xy =-+-=+-在条件22750x y xy +--=下的最大值点.这是求解条件最值问题,用拉格朗日乘子法.令拉格朗日函数 2222(,,)558(75),L x y x y xy x y xy λλ=+-++--则有 22108(2)0,108(2)0,750.L x y x y x L y x y x yL x y xy λλλ⎧∂=-+-=⎪∂⎪∂⎪=-+-=⎨∂⎪⎪∂=+--=⎪∂⎩解此方程组:将①式与②式相加得()(2)0.x y x y λ++=⇒=-或 2.λ=-若y x =-,则由③式得2375x =即5, 5.x y =±=m 若2,λ=-由①或②均得y x =,代入③式得275x=即x y =±=±于是得可能的条件极值点1234(5,5),(5,5),(M M M M ----现比较222(,)(,)558f x y g x y x y xy ==+-在这些点的函数值:1234()()450,()()150.f M f M f M f M ==== 因为实际问题存在最大值,而最大值又只可能在1234,,,M M M M 中取到.因此2(,)g x y 在12,M M 取到在D 的边界上的最大值,即12,M M 可作为攀登的起点.九、【解】 由432,,ααα线性无关及3212ααα-=知,向量组的秩1234(,,,)3r αααα=,即矩阵A 的秩为3.因此0Ax =的基础解系中只包含一个向量.那么由123412312(,,,)2010ααααααα⎡⎤⎢⎥-⎢⎥=-+=⎢⎥⎢⎥⎣⎦知,0Ax =的基础解系是(1,2,1,0).T- 再由123412341111(,,,)1111A βαααααααα⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+++==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦知,(1,1,1,1)T 是β=Ax 的一个特解.故β=Ax 的通解是1121,1101k ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦其中k 为任意常数.十、【解】(1)若,A B 相似,那么存在可逆矩阵P ,使1,P AP B -=故 111E B E P AP P EP P AP λλλ----=-=-11().P E A P P E A P E A λλλ--=-=-=-(2)令0100,,0000A B ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦那么2.E A E B λλλ-==- 但,A B 不相似.否则,存在可逆矩阵P ,使10P AP B -==.从而100A P P -==,矛盾,亦可从()1,()0r A r B ==而知A 与B 不相似.(3)由,A B 均为实对称矩阵知,,A B 均相似于对角阵,若,A B 的特征多项式相等,记特征多项式的根为1,,,n λλL 则有A 相似于1,n λλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦O B 也相似于1.n λλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦O 即存在可逆矩阵,P Q ,使111.n P AP Q BQ λλ--⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦O 于是111()().PQ A PQ B ---=由1PQ -为可逆矩阵知,A 与B 相似.十一、【解】 由于311{}cos ,3222x P X dx πππ>==⎰依题意,Y 服从二项分布1(4,)2B ,则有2222111()()4(4) 5.222EY DY EY npq np =+=+=⨯⨯+⨯= 十二、【解】 22012(1)23(12)34,EX θθθθθθ=⨯+⨯-+⨯+⨯-=-1(3).4EX θ=- θ的矩估计量为1ˆ(3),4X θ=-根据给定的样本观察值计算1(31303123)8x =+++++++ 2.=因此θ的矩估计值11ˆ(3).44x θ=-= 对于给定的样本值似然函数为624()4(1)(12),ln ()ln 46ln 2ln(1)4ln(12),L L θθθθθθθθ=--=++-+-2ln ()62824286.112(1)(12)d L d θθθθθθθθθθ-+=--=---- 令ln ()0d L d θθ=,得方程2121430θθ-+=,解得712θ-=(1,2θ=>不合题意). 于是θ的最大似然估计值为ˆθ=。
2002考研数学一试卷及答案

2002考研数学一试卷及解答一、填空题(本题共5小题,每小题3分,满分15分.把解答填在题中横线上.)(1)⎰∞+ex x dx2ln =.(2)已知函数()y y x =由方程0162=-++x xy e y 确定,则(0)y ''= .(3)微分方程02='+''y y y 满足初始条件11,'2x x yy ====的特解是.(4)已知实二次型323121232221321444)(),,(x x x x x x x x x a x x x f +++++=经正交变换x Py =可化成标准型216y f =,则a =.(5)设随机变量X 服从正态分布2(,)(0)N μσσ>,且二次方程042=++X y y 无实根的概率为12,则μ=.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.) (1)考虑二元函数),(y x f 的下面4条性质:①),(y x f 在点),(00y x 处连续;②),(y x f 在点),(00y x 处的两个偏导数连续;③),(y x f 在点),(00y x 处可微;④),(y x f 在点),(00y x 处的两个偏导数存在.若用“P Q ⇒”表示可由性质P 推出性质Q ,则有 (A) ②⇒③⇒①. (B) ③⇒②⇒①. (C) ③⇒④⇒①.(D) ③⇒①⇒④.(2)设0(1,2,3,)n u n ≠=,且lim 1n n n u →∞=,则级数11111(1)()n n n n u u ∞+=+-+∑ (A) 发散.(B) 绝对收敛.(C) 条件收敛. (D) 收敛性根据所给条件不能判定.(3)设函数()y f x =在(0,)+∞内有界且可导,则 (A) 当0)(lim =+∞→x f x 时,必有)(lim ='+∞→x f x . (B) 当)(lim x f x '+∞→存在时,必有)(lim ='+∞→x f x .(C) 当0lim ()0x f x +→=时,必有0lim ()0x f x +→'=. (D) 当0lim ()x f x +→'存在时,必有0lim ()0x f x +→'=.(4)设有三张不同平面的方程123i i i i a x a y a z b ++=,3,2,1=i ,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为(5)设1X 和2X 是任意两个相互独立的连续型随机变量,它们的概率密度分别为1()f x和2()f x,分布函数分别为1()F x和2()F x,则(A) 1()f x+2()f x必为某一随机变量的概率密度.(B) 1()f x2()f x必为某一随机变量的概率密度.(C) 1()F x+2()F x必为某一随机变量的分布函数.(D) 1()F x2()F x必为某一随机变量的分布函数.三、(本题满分6分)设函数)(xf在0x=的某邻域内具有一阶连续导数,且(0)0,(0)0f f'≠≠,若()(2)(0)af h bf h f+-在0→h时是比h高阶的无穷小,试确定ba,的值.四、(本题满分7分)已知两曲线)(xfy=与⎰-=x t dtey arctan2在点(0,0)处的切线相同,写出此切线方程,并求极限)2(limnnfn∞→.五、(本题满分7分)计算二重积分dxdyeDyx⎰⎰},max{22,其中}10,10|),{(≤≤≤≤=yxyxD.六、(本题满分8分)设函数)(xf在(,)-∞+∞内具有一阶连续导数,L是上半平面(y>0)内的有向分段光滑曲线,其起点为(b a ,),终点为(d c ,).记2221[1()][()1],L xI y f xy dx y f xy dy y y =++-⎰(1)证明曲线积分I 与路径L 无关; (2)当cd ab =时,求I 的值.七、(本题满分7分)(1)验证函数333369()1()3!6!9!(3)!nx x y x x n =++++++-∞<<+∞满足微分方程xe y y y =+'+'';(2)利用(1)的结果求幂级数30(3)!n n x n ∞=∑的和函数.八、(本题满分7分)设有一小 ,取它的底面所在的平面为xOy 坐标面,其底部所占的区域为2{(,)|D x y x =275}y xy +-≤,小 的高度函数为),(y x h xy y x +--=2275.(1)设),(00y x M 为区域D 上一点,问),(y x h 在该点沿平面上什么方向的方向导数最大?若记此方向导数的最大值为),(00y x g ,试写出),(00y x g 的表达式.(2)现欲利用此小 开展攀岩活动,为此需要在 脚下寻找一上 坡最大的点作为攀登的起点.也就是说,要在D 的边界线2275x y xy +-=上找出使(1)中),(y x g 达到最大值的点.试确定攀登起点的位置.九、(本题满分6分) 已知四阶方阵),,,(4321αααα=A ,4321,,,αααα均为4维列向量,其中432,,ααα线性无关,3212ααα-=,如果4321ααααβ+++=,求线性方程组β=Ax 的通解.十、(本题满分8分) 设,A B 为同阶方阵,(1)若,A B 相似,证明,A B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当,A B 均为实对称矩阵时,证明(1)的逆命题成立.十一、(本题满分7分) 设维随机变量X 的概率密度为10,cos ,()220,x x f x π⎧≤≤⎪=⎨⎪⎩其他.对X 独立地重复观察4次,用Y 表示观察值大于3π的次数,求2Y 的数学期望.十二、(本题满分7分) 设总体X 的概率分布为其中1(0)2θθ<<是未知参数,利用总体X 的如下样本值 3,1,3,0,3,1,2,3,求θ的矩估计值和最大似然估计值.参照解答 一、填空题(1)【解析】 原式2ln 11.ln ln eed x x x+∞+∞==-=⎰(2)【解析】 方程两边对x 两次求导得 '6'620,y e y xy y x +++=①2'''6''12'20.y y e y e y xy y ++++=②以0x =代入原方程得0y =,以0x y ==代入①得'0,y =,再以'0x y y ===代入②得''(0) 2.y =-(3)【解析】 这是二阶的可降阶微分方程.令'()y P y =(以y 为自变量),则'''.dy dP dPy P dx dx dy ===代入方程得20dP yPP dy +=,即0dPy P dy +=(或0P =,但其不满足初始条件01'2x y ==).分离变量得 0,dP dy P y +=积分得ln ln ',P y C +=即1C P y =(0P =对应10C =);由0x =时11,',2y P y ===得11.2C =于是1',2,2y P ydy dx y ===积分得22y x C =+.又由01x y ==得21,C =所求特解为y =(4)【解析】 因为二次型Tx Ax 经正交变换化为标准型时,标准形中平方项的系数就是二次型矩阵A 的特征值,所以6,0,0是A 的特征值. 又因iiia λ=∑∑,故600, 2.a a a a ++=++⇒=(5)【解析】 设事件A 表示“二次方程042=++X y y 无实根”,则{1640}{A X X =-<=> 4}.依题意,有1(){4}.2P A P X =>=而4{4}1{4}1(),P X P X μΦσ->=-≤=-即414141(),(),0. 4.22μμμΦΦμσσσ----===⇒=二、选择题(1)【解析】 这是讨论函数(,)f x y 的连续性,可偏导性,可微性及偏导数的连续性之间的关系.我们知道,(,)f x y 的两个偏导数连续是可微的充分条件,若(,)f x y 可微则必连续,故选(A).(2)【解析】 由1lim 101n n un n →+∞=>⇒充分大时即,N n N ∃>时10n u >,且1lim0,n n u →+∞=不妨认为,0,n n u ∀>因而所考虑级数是交错级数,但不能保证1n u 的单调性.按定义考察部分和111111111111(1)()(1)(1)nn nk k k n k k k k k k k S u u u u +++===++=-+=-+-∑∑∑1111111(1)11(1)1(1)(),k n nn l k l k l n n u u u u u ++==+--=-+-=+→→+∞∑∑⇒原级数收敛.再考察取绝对值后的级数1111()n n n u u ∞=++∑.注意111112,11n n n n u u n n nu u n n ++++=+⋅→+11n n ∞=∑发散⇒1111()n nn u u ∞=++∑发散.因此选(C).(3)【解析】 证明(B)对:反证法.假设lim ()0x f x a →+∞'=≠,则由拉格朗日中值定理,(2)()'()()f x f x f x x ξ-=→∞→+∞(当x →+∞时,ξ→+∞,因为2x x ξ<<);但这与(2)()(2)()2f x f x f x f x M-≤+≤矛盾(()).f x M ≤(4)【解析】 因为()()23r A r A ==<,说明方程组有无穷多解,所以三个平面有公共交点且不唯一,因此应选(B).(A)表示方程组有唯一解,其充要条件是()() 3.r A r A ==(C)中三个平面没有公共交点,即方程组无解,又因三个平面中任两个都不行,故()2r A =和()3r A =,且A 中任两个平行向量都线性无关.类似地,(D)中有两个平面平行,故()2r A =,()3r A =,且A 中有两个平行向量共线.(5)【解析】 首先可以否定选项(A)与(C),因121212[()()]()()21,()()112 1.f x f x dx f x dx f x dx F F +∞+∞+∞-∞-∞-∞+=+=≠+∞++∞=+=≠⎰⎰⎰对于选项(B),若121,21,1,01,()()0,0,x x f x f x -<<-<<⎧⎧==⎨⎨⎩⎩其他,其他,则对任何(,),x ∈-∞+∞12()()0f x f x ≡,12()()01,f x f x dx +∞-∞=≠⎰因此也应否定(C),综上解析,用排除法应选(D).进一步解析可知,若令12max(,)X X X =,而~(),1,2,i i X f x i =则X 的分布函数()F x 恰是12()().F x F x1212(){max(,)}{,}F x P X X x P X x X x =≤=≤≤1212{}{}()().P X x P X x F x F x =≤≤=三、【解】 用洛必达法则.由题设条件知lim[()(2)(0)](1)(0).h af h bf h f a b f →+-=+-由于(0)0f '≠,故必有10.a b +-=又由洛必达法则 00()(2)(0)'()2'(2)limlim 1h h af h bf h f af h bf h h →→+-+=(2)'(0)0,a b f =+=及(0)0f '≠,则有20a b +=.综上,得2, 1.a b ==-四、【解】 由已知条件得(0)0,f =22arctan arctan 02'(0)()'1,1x x t xx x e f e dt x --=====+⎰故所求切线方程为y x =.由导数定义及数列极限与函数极限的关系可得02()(0)2()(0)lim ()2lim 2lim 2'(0) 2.2n n x f f f x f n nf f n xn →∞→∞→--====五、【解析与求解】D 是正方形区域如图.因在D 上被积函数分块表示2222,,max{,}(,),,,x x y x y x y D y x y ⎧≥⎪=∈⎨≤⎪⎩于是要用分块积分法,用y x =将D 分成两块:1212,{},{}.D D D D D y x D D y x ==≤=≥⇒I222212max{,}max{,}xy xy D D e dxdy e dxdy=+⎰⎰⎰⎰2221212x y x D D D e dxdy e dxdy e dxdy=+=⎰⎰⎰⎰⎰⎰(D 关于y x =对称)2102xx dx e dy=⎰⎰(选择积分顺序)22112 1.x xxe dx e e ===-⎰六、【解析与求解】 (1)易知Pdx Qdy +∃原函数,2211()()()()()x Pdx Qdy dx yf xy dx xf xy dy dy ydx xdy f xy ydx xdy y y y+=++-=-++()()()[()].xy x xd f xy d xy d f t dt y y =+=+⎰⇒在0y >上Pdx Qdy +∃原函数,即0(,)()xy xu x y f t dty =+⎰.⇒积分I 在0y >与路径无关.(2)因找到了原函数,立即可得(,)(,)(,).c d a b c a I u x y d b ==-七、【证明】 与书上解答略有不同,参见数三2002第七题(1)因为幂级数3693()13!6!9!(3)!n x x x x y x n =++++++的收敛域是()x -∞<+∞,因而可在()x -∞<+∞上逐项求导数,得25831'()2!5!8!(31)!n x x x x y x n -=+++++-,4732''()4!7!(32)!n x x x y x x n -=+++++-,所以2'''12!!n xx x y y y x e n ++=+++++=()x -∞<+∞.(2)与'''xy y y e ++=相应的齐次微分方程为'''0y yy ++=,其特征方程为210λλ++=,特征根为1,2122λ=-±.因此齐次微分方程的通解为212()xY e C x C x -=+.设非齐次微分方程的特解为x y Ae *=,将y *代入方程'''x y y y e ++=可得13A=,即有13xy e *=.于是,方程通解为2121()3xx y Y y e C x C x e -*=+=++.当0x =时,有112121(0)1,23,0.311'(0)0.23y C C C y C ⎧==+⎪⎪⇒==⎨⎪==-+⎪⎩于是幂级数30(3)!nn x n ∞=∑的和函数为221()cos 323xxy x e x e -=+()x -∞<+∞八、【解析与求解】 (1)由梯度向量的重要性质:函数),(y x h 在点M 处沿该点的梯度方向0000(,)(,)0000(,){,}{2,2}x y x y h hh x y x y y x x y∂∂==-+-+∂∂grad方向导数取最大值即00(,)(,)x y h x y grad 的模,00(,)g x y ⇒=(2)按题意,即求(,)g x y 求在条件22750x y xy +--=下的最大值点⇔ 22222(,)(2)(2)558g x y y x x y x y xy =-+-=+-在条件22750x y xy +--=下的最大值点. 这是求解条件最值问题,用拉格朗日乘子法.令拉格朗日函数2222(,,)558(75),L x y x y xy x y xy λλ=+-++--则有22108(2)0,108(2)0,750.Lx y x y x Ly x y x y L x y xy λλλ⎧∂=-+-=⎪∂⎪∂⎪=-+-=⎨∂⎪⎪∂=+--=⎪∂⎩解此方程组:将①式与②式相加得()(2)0.x y x y λ++=⇒=-或2.λ=-若y x =-,则由③式得2375x =即5, 5.x y =±=若2,λ=-由①或②均得y x =,代入③式得275x =即x y =±=±于是得可能的条件极值点1234(5,5),(5,5),(M M M M ----现比较222(,)(,)558f x y g x y x y xy ==+-在这些点的函数值:1234()()450,()()150.f M f M f M f M ====因为实际问题存在最大值,而最大值又只可能在1234,,,M M M M 中取到.因此2(,)g x y 在12,M M 取到在D 的边界上的最大值,即12,M M 可作为攀登的起点.九、【解】 由432,,ααα线性无关及3212ααα-=知,向量组的秩1234(,,,)3r αααα=,即矩阵A 的秩为3.因此0Ax =的基础解系中只包含一个向量.那么由123412312(,,,)2010ααααααα⎡⎤⎢⎥-⎢⎥=-+=⎢⎥⎢⎥⎣⎦知,0Ax =的基础解系是(1,2,1,0).T- 再由123412341111(,,,)1111A βαααααααα⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+++==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦知,(1,1,1,1)T是β=Ax 的一个特解.故β=Ax 的通解是1121,1101k ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦其中k 为任意常数.十、【解】 (1)若,A B 相似,那么存在可逆矩阵P ,使1,P AP B -=故111E B E P AP P EP P APλλλ----=-=-11().P E A P P E A P E A λλλ--=-=-=-(2)令0100,,0000A B ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦那么2.E A E B λλλ-==-但,A B 不相似.否则,存在可逆矩阵P ,使10P AP B -==.从而100A P P -==,矛盾,亦可从()1,()0r A r B ==而知A 与B 不相似.(3)由,A B 均为实对称矩阵知,,A B 均相似于对角阵,若,A B 的特征多项式相等,记特征多项式的根为1,,,n λλ则有A 相似于1,n λλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦B 也相似于1.n λλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦即存在可逆矩阵,P Q ,使111.n P AP Q BQ λλ--⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦于是111()().PQ A PQ B ---=由1PQ -为可逆矩阵知,A 与B 相似.十一、【解】 由于311{}cos ,3222x P X dx πππ>==⎰依题意,Y 服从二项分布1(4,)2B ,则有2222111()()4(4) 5.222EY DY EY npq np =+=+=⨯⨯+⨯=十二、【解】22012(1)23(12)34,EX θθθθθθ=⨯+⨯-+⨯+⨯-=-1(3).4EX θ=-θ的矩估计量为1ˆ(3),4X θ=-根据给定的样本观察值计算1(31303123)8x =+++++++2.=因此θ的矩估计值11ˆ(3).44x θ=-=对于给定的样本值似然函数为624()4(1)(12),ln ()ln 46ln 2ln(1)4ln(12),L L θθθθθθθθ=--=++-+-2ln ()62824286.112(1)(12)d L d θθθθθθθθθθ-+=--=----令ln ()0d L d θθ=,得方程2121430θθ-+=,解得712θ=(71,122θ=>不合题意).于是θ的最大似然估计值为7ˆ12θ-=。
2002年-2014年数学一历年真题

2002 年全国硕士研究生入学统一考试 数学(一)试卷
一、填空题(本题共 5 小题,每小题 3 分,满分 15 分.把答案填在题中横线上) (1)
e
dx = _____________. x ln 2 x
(2)已知 e y 6 xy x2 1 0 ,则 y(0) =_____________. (3) yy y 2 0 满足初始条件 y (0) 1, y(0)
(C) FX ( x) + FY ( y) 必为某一随机变量的分布函数 (D) FX ( x) FY ( y) 必为某一随机变 量的分布函数. 三、(本题满分 6 分) 设函数 f ( x) 在 x 0 的某邻域具有一阶连续导数 , 且 f (0) f (0) 0 , 当 h 0 时 , 若
02-03年日语一级考试真题

2002年能力考1级真题语法详解:問題IV次の文の____にはどんな言葉をいれたらよいか。
1・2・3・4から最も適当なものを一つ選びなさい。
1出席欠席の____、同封した葉書にてお返事くださるようお願いいたします。
1.そばから2.ないまでも3.次第にしては4.いかんによらず●考点解析:测试点为句型「~いかんによらず」的用法。
「いかん」是文语词汇,意思是“如何”“怎样”。
句型「~いかんによらず」前接体言或「体言+の」的形式,表示不管或无论前项如何,后项都可以成立,译为“无论……”“不管……”。
○事情のいかんによらず、欠席は欠席だ。
/无论有什么理由,缺席就是缺席。
○試験の結果いかんによらず、試験中の不正行為のあったこの学生は絶対に認められない。
/不管考试结果如何,在考试中作弊的这个学生的入学资格绝对不能承认。
参考:「~そばから~」前接动词连体形,表示前后两项间几乎没有时间间隔,译为“刚刚……就……”“随着……就……”。
「~ないまでも~」前接动词连用形,表示从较高的程度退一步考虑,译为“即使不……也罢……”。
「~次第にしては~」为非正确形式。
正解为选项4。
译文:无论出席还是缺席,请您用附在信封中的明信片给予回复。
2私は、彼の失礼____態度に我慢ならなかった。
1.きわまった2.きわまりない3.きわめた4.きわめない●考点解析:测试点为「~きわまりない」的用法。
「~きわまりない」前接形容动词词干,表示程度极高,语气郑重,译为“极其……”。
○その探検旅行は危険きわまりないものと言えた。
/可以说,那次探险旅行极其危险。
○彼の生活は徹夜マージャンに深酒と不健康極まりない。
/通宵打麻将,外加过量饮酒,他的生活极不健康。
参考:「~きわまった」「~きわめた」「~きわめる」是三种错误形式。
正解为选项2。
译文:我无法忍受他那种极不礼貌的态度。
3田中さんは、この1週間と____、仕事どころではないようだ。
1.いうもの2.いっては3.いえず4.いうのに●考点解析:测试点为句型「~というもの」的用法。
2002年全国一级注册结构工程师资格考试基础考试真题及答案

1. 设直线 L:
2x-y+5=0 , 则 L 的一个方向向量 S 是: x+3z+1=0
(A) {2,-1,0} (B){1,0.3} (C) {-3,-6,1} (D){-3,6,1} 2. 设平面Ⅱ通过球面 x2+y2+z2=4(x-2y-2z)的中心,且垂直于直线:
(A) 2 (C)
(B)
2 3
(D)
2 3 3
1p 2 p n p 等于: n n p 1
2 3 9
9.设 p>0,则 lim
(A)
1 p 1
(B)
1 p2
(C)
2 3 3
(D)
2 3 9
10.设 D={(x, y)|x2+y2≤2y},则下列等式中正确的是: (A)
f ( x, y)dxdy
(C)
(D)
lim 5.极限 x 2, y 0
的值是: (B) 1
n 2n n
(A) 0
(C) 2 连续性的结论,正确的是: (B)除 x= 1 外处处连续 (D)处处连续
(D) ∞
6.下列关于函数 f ( x) lim 1 2 (A)除 x=0 外处处连续 (C)除 x=0, 1 外处处连续 7.设函数 f x
(D)
f ( x, y)dxdy
D
0
d
2sin
0
f (r cos , r sin )rdr
11.设有一物体,占有空间闭区域 {(x, y, z)| 0≤ x ≤1, 0≤ y ≤ 1, 0 ≤ z ≤ 1},其在点 (x,y,z)处的体密度为 p (x, y, z )=2(x +y +z),则该物体的质量为: (A) 1 (B) 2 (C) 3 (D) 4 2 2 12. 两条抛物线 y = x , y = x 所围成的图形的面积为:
2002年全国普通高等学校招生统一考试英语全国卷

2002年全国普通高等学校招生统一考试英语第一卷(三部分, 共115分)第一部分:听力(共两节, 满分30分)第一节(共5小题;每小题15分, 满分75分)听下面5段对话。
每段对话后有一个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。
听完每段对话后, 你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£19. 15.B. £9. 15.C. £9. 18.答案是B。
1. Who is Chris Paine?A. A computer engineer.B. A book seller.C. A writer.2. What are the two speakers talking about?A. A football player.B. A football team.C. A football match.3. Why did the woman buy a heavy coat for Jimmy?A. Winter is coming soon.B. Jimmy'll go into the mountains.C. Jimmy has caught a cold.4. Where is the woman?A. In a soap factory.B. In her house.C. At an information desk.5. When is the man checking in?A. Friday.B. Thursday.C. Tuesday.第二节(共15小题;每小题1.5分, 满分分)听下面5段对话或独白。
每段对话或独白后有几个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。
听每段对话或独白前, 你将有时间阅读各个小题, 每小题5秒钟;听完后, 各小题将给出5秒钟的作答时间。
2002级《高等数学》(1)期末考试试卷

附件十高等数学2002~2005学年历年期末考试题2002级《高等数学》(I )期末考试试卷(A)专业: 姓名: 学号: 考试日期:2003.1.21.2. 答案必须写在该题后的横线上或写在该题下方空白处,不得写在草稿纸中,否则该题答案无效.一、填空题(本题共10小题,每小题3分,满分30分): 1.=--+∞→xx x e e xsin lim.2. =⎪⎭⎫⎝⎛-∞→xx x 321lim .3. ⎰=+dx x x 221 . 4. 曲线⎪⎩⎪⎨⎧=+=321ty tx 在2=t 处的切线斜率为 .5.()=+⎰-2243cos 2sinππdx x x .6. 已知向量()k j i b a3,1,3,2--=-=,则=⋅b a ,=⨯b a .7. 要使函数()()⎪⎩⎪⎨⎧≤->+=0,cos 70,1ln 2sin x x e x ax xx f x 在0=x 处连续,则=a .8. 设()()()32321+++=x x x y ,则()=6y.9. 设()x f 在),0[+∞上连续,且()()x x dt t f xcos 10+=⎰,则=⎪⎭⎫⎝⎛π2f .10. 由曲线22x y =和直线1,2,1-===y x x 所围成的图形绕直线1-=y 旋转所得旋转体体积的定积分表达式是 .二、求解下列各题(本题共6小题,每小题6分,满分36分):1. 设3sin11ln2cos 1π+++=x xy x,求.dy 2. 求xx xx x 2sin sin lim -→. 3. 计算()()0,222>-⎰-b dx x b x b b.4. 求⎰-+dx x x 2)1()1ln(.5.设()x f 在0x x =处可导,求()000)(limx x x f x x xf x x --→.6.设()⎰-π=xdt t tx f 0sin ,求()⎰π0dx x f .三、(本题满分7分) 过点)0,1(-作曲线x y =的切线,求此切线与曲线x x y ,=轴所围成图形的面积.四、(本题满分7分) 求函数()()⎰-=2220x t dt e x f 在区间)3,0(内的极值,并判断曲线()x f y =在区间)3,0(内是否有拐点.五、(本题满分8分)一底为8 m 、高为6 m 的等腰三角形片,铅直地沉没在水中,顶在上,底在下且与水面平行,而顶离水面3 m ,试求它每面所受的压力. 六、(本题满分6分) 已知函数()x f 在区间)2,1(-内具有二阶导数,且()()01,0lim 0==→f xx f x ,试证在区间)1,0(内至少存在一点ξ,使得()0=ξ''f . 七、(本题满分6分) 证明方程2(121≥=++++-n x x x x n n的正整数)在区间)1,0(内必有唯一根n x ,并求数列{}n x 的极限n n x ∞→lim .2002级《高等数学》(I )期末考试试卷(B)专业: 姓名: 学号: 考试日期:2003.1.21.2. 答案必须写在该题后的横线上或写在该题下方空白处,不得写在草稿纸中,否则该题答案无效.一、填空题(本题共10小题,每小题3分,满分30分):1. =⎪⎭⎫ ⎝⎛-∞→xx x 221lim .2. =--+∞→xx x e e xcos lim.3. ()⎰=++dx x x x 222121 . 4. 曲线⎪⎩⎪⎨⎧=+=321ty tx 在4=t 处的切线斜率为 .5.()=+⎰-2245sin sinππdx x x .6. 已知向量()k j i b a--=-=3,2,3,1,则=⋅b a ,=⨯b a .7. 要使函数()()⎪⎩⎪⎨⎧≤->+=0,cos 70,1ln 3sin x x e x ax x x f x 在0=x 处连续,则=a8. 设()()4221++=x x x y ,则()=7y.9. 设()x f 在),0[+∞上连续,且()()x x dt t f x cos 210+=⎰,则=⎪⎭⎫⎝⎛π2f .10. 由曲线32x y =和直线2,3,1-===y x x 所围成的图形绕直线2-=y 旋转所得旋转体体积的定积分表达式是 .二、求解下列各题(本题共6小题,每小题6分,满分36分): 1. 设3cos 11ln2sin 1π+++=x xy x,求.dy2. 求xx xx x 2sin sin lim -→. 3. 计算()()0,222>-⎰-a dx x a x a a.4. 求()⎰-dx x x21ln .5.设()x f 在0x x =处可导,求()000)(limx x x f x x xf x x --→.6.设()⎰-π=xdt t tx f 0sin ,求()⎰π0dx x f .三、(本题满分7分) 求函数()()⎰-=2210x t dt e x f 在区间)2,0(内的极值,并判断曲线()x f y =在区间)2,0(内是否有拐点.四、(本题满分8分)一底为8 m 、高为6 m 的等腰三角形片,铅直地沉没在水中,顶在上,底在下且与水面平行,而顶离水面3 m ,试求它每面所受的压力. 五、(本题满分7分) 过点)0,1(-作曲线x y =的切线,求此切线与曲线x x y ,=轴所围成图形的面积.六、(本题满分6分) 证明方程2(121≥=++++-n x x x x n n的正整数)在区间)1,0(内必有唯一根n x ,并求数列{}n x 的极限n n x ∞→lim .七、(本题满分6分)已知函数()x f 在区间)2,1(-内具有二阶导数,且()()01,0lim 0==→f xx f x ,试证在区间)1,0(内至少存在一点ξ,使得()0=ξ''f .2002级《高等数学》(I )期末考试试卷(A)答案及评分标准一、填空题(本题共10小题,每小题3分,满分30分): 1.0; 2. 6-e ; 3. C x x +-arctan ; 4. 3; 5.43π; 6. =⋅b a 2,=⨯b a (10,7,1); 7. =a 31;8. ()=6y6!; 9. =⎪⎭⎫⎝⎛π2f 1-2π; 10. ⎰⎪⎪⎭⎫ ⎝⎛+=212212dx x V π. 二、求解下列各题(本题共6小题,每小题6分,满分36分): 1. 设3sin11ln2cos 1π+++=x xy x,求.dy 011sin ln 1cos 122cos 1++-⎪⎭⎫ ⎝⎛+='x x x x x x x xy x, (5分,前两项每项2分,后一项1分) dx x x x x x x x x dy x ⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+=22cos 11sin ln 1cos 11. (6分) 2. 3020sin lim sin sin limxxx x x x x x x -=-→→ (2分) 203cos 1limx xx -=→ (4分) 61321lim 220==→x xx . (6分) 3.()⎰⎰-=--bb bdx x b x dx x b x 0222222 (2分)⎰---=b x b d x b 02222)( (4分)()3023223232b x b b=⎥⎦⎤⎢⎣⎡--=. (6分) 4.⎰⎰⎪⎭⎫⎝⎛-+=-+x d x dx x x 11)1ln()1()1ln(2 (1分) ⎰+⋅--+-=dx xx x x 1111)1ln(11 (3分)⎰⎪⎭⎫⎝⎛++---+=dx x x x x 1111211)1ln( (4分)C xxx x +-+--+=11ln 211)1ln( (6分)5.()()()()0000000000)(lim )(lim00x x x f x x f x x f x x xf x x x f x x xf x x x x --+-=--→→ (3分)⎥⎦⎤⎢⎣⎡---=→0000)()()(lim 0x x x f x f x x f x x (4分) )()(000x f x x f '-=. (6分) 6.()[]()⎰⎰'-=πππ)(dx x f x x xf dx x f (2分)⎰⎰-⋅--=πππππ00sin sin dx xxx dt t t (4分)dx x x x x x⎰⎪⎭⎫ ⎝⎛-⋅--=ππππ0sin sin (5分) []2cos sin 00=-==⎰ππx dx x (6分)三、(本题满分7分) 过点)0,1(-作曲线x y =的切线,求此切线与曲线x x y ,=轴所围成图形的面积.解 设切点为()00,x x ,切线方程为:()00021x x x x y -=-, (2分) 因为过点)0,1(-,得()112121000000=⇒+=⇒--=-x x x x x x (4分) ⎰-⋅⋅=101221dx x A (6分)31321=-= (7分)四、(本题满分7分) 求函数()()⎰-=2220x t dt e x f 在区间)3,0(内的极值,并判断曲线()x f y =在区间)3,0(内是否有拐点.解 0)2(2)(4)2(令=-⋅='-x ex f x ,得2=x , (2分)0])2(82[)(4)2(4>-+=''-x e x f x , (4分)0)2(,02)2(=∴>=''f f 为极小值, (5分)又∴>'',0)(x f 曲线)(x f y =在)3,0(内无拐点. (7分)五、(本题满分8分)一底为8 m 、高为6 m 的等腰三角形片,铅直地沉没在水中,顶在上,底在下且与水面平行,而顶离水面3 m ,试求它每面所受的压力.解 建立坐标系为:取三角形的顶为坐标原点,铅直向下为x 轴,水平向右为y 轴.直线方程为 x y 32=, (2分) xdx x g ydx x g dP 34)3(2)3(+=+=ρρ (4分)⎰+=6034)3(xdx x g P ρ (6分)⎰+=602)3(34dx x x g ρ)(4.1646168233134623KN g x x g ==⎥⎦⎤⎢⎣⎡+=ρρ (8分)六、(本题满分6分)已知函数()x f 在区间)2,1(-内具有二阶导数,且()()01,0lim 0==→f xx f x ,试证在区间)1,0(内至少存在一点ξ,使得()0=ξ''f . 证 0)0(0)(lim=⇒=→f xx f x , (1分)由条件)(x f 具有二阶导数,且0)1(=f ,则)(x f 在]1,0[上连续,在)1,0(内可导,且()()10f f =,由Rolle 定理),1,0(1∈∃ξ使0)(1='ξf , (3分)又0)(lim )0()(lim)0(00==-='→→xx f x f x f f x x , (5分) 则)1()0(f f '=',对)(x f '在],0[1ξ上应用Rolle 定理,有)1,0(),0(1⊂∈∃ξξ,使0)(=''ξf . (6分)七、(本题满分6分) 证明方程2(121≥=++++-n x x x x n n的正整数)在区间)1,0(内必有唯一根n x ,并求数列{}n x 的极限n n x ∞→lim .证 设1)(21-++++=-x x xx x f n n ,则)(x f 在]1,0[上连续,又01)1(,01)0(>-=<-=n f f ,由零点定理,至少存在一点)1,0(∈n x ,使0)(=n x f , (2分) 又)1,0(,012)1()(21∈>+++-+='--x x x n nxx f n n)(x f ∴在]1,0[上单调增加,故至多存在一点)1,0(∈n x ,使0)(=n x f ,综上所述,存在唯一一点)1,0(∈n x ,使0)(=n x f , 即方程121=++++-x x xx n n在区间)1,0(内必有唯一根n x . (3分)101111211111121<<<⇒⎪⎭⎪⎬⎫=+++++=+++++++-++++-n n n n n n nn n n n n n nn n x x x x x x x x x x x , 即 数列{}n x 单调有界,故必有极限,设a x n n =∞→lim . (5分)而 11)1(21=--=++++-nnn n n n n n nn x x x x x x x ,取极限,得 2111=⇒=-a a a , 即21lim =∞→n n x . (6分)2002级《高等数学》(I )期末考试试卷(B)答案及评分标准一、填空题(本题共10小题,每小题3分,满分30分):1. 4-e ;2. 0;3. C x x ++-arctan 1; 4. 6; 5. π83; 6. =⋅b a 4;=⨯b a (5,6,8); 7. =a 21; 8. ()=7y 7!;9. =⎪⎭⎫⎝⎛π2f π-1; 10. ⎰⎪⎪⎭⎫ ⎝⎛+=312223dx x V π. 二、求解下列各题(本题共6小题,每小题6分,满分36分): 1. 设3cos 11ln2sin 1π+++=x xy x,求.dy011cos ln 1sin 122sin 1++-⎪⎭⎫ ⎝⎛-='x x x x x x x x y x , (5分,前两项每项2分,后一项1分) dx x x x x x x x x dy x ⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛-=22sin 11cos ln 1sin 11. (6分) 2.3020sin limsin sin limx xx x x x x x x -=-→→ (2分) 203cos 1limx xx -=→ (4分) 61321lim 220==→x xx . (6分)3.()⎰⎰-=--aa adx x a x dx x a x 0222222 (2分)⎰---=a x a d x a 02222)( (4分)()3023223232a x a a=⎥⎦⎤⎢⎣⎡--=. (6分) 4.⎰⎰⎪⎭⎫⎝⎛-=-x xd dx x x 11ln )1(ln 2 (1分) ⎰⋅---=dx x x x x 1111ln (3分) ⎰⎪⎭⎫ ⎝⎛-+--=dx x x x x 1111ln (4分)C xxx x +---=1ln 1ln (6分) 5.()()()()0000000000)(lim )(lim00x x x f x x f x x f x x xf x x x f x x xf x x x x --+-=--→→ (3分)⎥⎦⎤⎢⎣⎡---=→0000)()()(lim 0x x x f x f x x f xx (4分))()(000x f x x f '-=. (6分) 6.()[]()⎰⎰'-=πππ00)(dx x f x x xf dx x f (2分)⎰⎰-⋅--=πππππ00sin sin dx xxx dt t t (4分)dx x x x xx⎰⎪⎭⎫ ⎝⎛-⋅--=ππππ0sin sin (5分)[]2cos sin 00=-==⎰ππx dx x (6分)三、(本题满分7分) 求函数()()⎰-=2210x t dt e x f 在区间)2,0(内的极值,并判断曲线()x f y =在区间)2,0(内是否有拐点.解 0)1(2)(4)1(令=-⋅='-x ex f x ,得1=x , (2分)0])1(82[)(4)1(4>-+=''-x e x f x , (4分)0)1(,02)1(=∴>=''f f 为极小值, (5分)又∴>'',0)(x f 曲线)(x f y =在)2,0(内无拐点. (7分)四、(本题满分8分)一底为8 m 、高为6 m 的等腰三角形片,铅直地沉没在水中,顶在上,底在下且与水面平行,而顶离水面3 m ,试求它每面所受的压力.解 建立坐标系为:取三角形的顶为坐标原点,铅直向下为x 轴,水平向右为y 轴.直线方程为 x y 32=, (2分) xdx x g ydx x g dP 34)3(2)3(+=+=ρρ (4分)⎰+=6034)3(xdx x g P ρ (6分) ⎰+=602)3(34dx x x g ρ )(4.16461682331346023KN g x x g ==⎥⎦⎤⎢⎣⎡+=ρρ (8分)五、(本题满分7分)过点)0,1(-作曲线x y =的切线,求此切线与曲线x x y ,=轴所围成图形的面积. 解 设切点为()00,x x , 切线方程为:()00021x x x x y -=-, (2分) 因为过点)0,1(-,得()112121000000=⇒+=⇒--=-x x x x x x (4分) ⎰-⋅⋅=101221dx x A (6分) 31321=-= (7分)六、(本题满分6分)证明方程2(121≥=++++-n x x xx n n 的正整数)在区间)1,0(内必有唯一根n x ,并求数列{}n x 的极限n n x ∞→lim . 证 设1)(21-++++=-x x x x x f n n ,则)(x f 在]1,0[上连续,又01)1(,01)0(>-=<-=n f f ,由零点定理, 至少存在一点)1,0(∈n x ,使0)(=n x f , (2分) 又)1,0(,012)1()(21∈>+++-+='--x x x n nx x f n n)(x f ∴在]1,0[上单调增加,故至多存在一点)1,0(∈n x ,使0)(=n x f ,综上所述,存在唯一一点)1,0(∈n x ,使0)(=n x f ,即方程121=++++-x x x x n n 在区间)1,0(内必有唯一根n x . (3分)101111211111121<<<⇒⎪⎭⎪⎬⎫=+++++=+++++++-++++-n n n n n n n n n n n n n nn n x x x x x x x x x x x , 即 数列{}n x 单调有界,故必有极限,设a x n n =∞→lim . (5分)而 11)1(21=--=++++-n n n n n n n nn n x x x x x x x , 取极限,得2111=⇒=-a a a , 即 21lim =∞→n n x . (6分)七、(本题满分6分)已知函数()x f 在区间)2,1(-内具有二阶导数,且()()01,0lim0==→f x x f x ,试证在区间)1,0(内至少存在一点ξ,使得()0=ξ''f .证 0)0(0)(lim 0=⇒=→f x x f x , (1分)由条件)(x f 具有二阶导数,且0)1(=f ,则)(x f 在]1,0[上连续,在)1,0(内可导,且()()10f f =,由Rolle 定理 ),1,0(1∈∃ξ使0)(1='ξf , (3分) 又0)(lim )0()(lim )0(00==-='→→xx f x f x f f x x , (5分) 则)1()0(f f '=',对)(x f '在],0[1ξ上应用Rolle 定理,有)1,0(),0(1⊂∈∃ξξ,使0)(=''ξf . (6分)。
2002年国家公务员录用考试《行测》真题(A卷)参考答案及解析

1、【答案】B【解析】A项扫描仪是在影像处理过程中将照片图案等扫描输入到电脑的一项输入设备。
B项磁盘驱动器既可读盘,又能将数据写入,因此既可算做输入设备,又可看成输出设备。
C项键盘是电脑主要的输入设备,可以用来接收使用者的指令和外界的资料等。
D项显示器是电脑最主要的输出设备,可以将电脑处理后的结果如文字或影像显示出来。
A、C、D三项均功能单一,只有B项既可以作输入设备又可以作输出设备。
故正确答案为B2、【答案】C【解析】实际上,烟雾中的颗粒物是肉眼不易察觉的,A项错误;香烟冒出的蓝色烟雾实际上是香烟的颗粒对蓝色光有较强的散射效应。
按照光的散射定律,白光中的短波成分蓝紫色遭到散射比长波成分红黄色强烈,散射光因短波富集而呈蓝色。
与光的吸收和透射没有关系,BD项错误。
故答案为C【拓展】每当大雨初霁、澄清了尘埃的时候,天空总是呈美丽的蔚蓝色,其道理也是蓝紫光的散射。
旭日和夕阳呈红色,则是由于白光中蓝紫色成分被更多散射掉了,在直射的日光中剩余较多的是红黄色的长波成分3、【答案】B【解析】电磁波谱是一系列不同频率辐射的总称。
波段频率从低到高排列的顺序依次是:无线电波、微波、红外光、可见光、紫外光、X-射线、γ-射线。
所以ACD错误。
因此,正确答案为B【拓展】电磁波谱中,频率越高,波长越小。
所以,波长由高到低的排序依次是:无线电波、微波、红外光、可见光、紫外光、X-射线、γ-射线4、【答案】B【解析】DNA每条单链由脱氧核糖、核苷酸和磷酸构成,而核苷酸由碱基构成。
所以ACD错误,故正确答案为B 【拓展】DNA是一种长链聚合物,组成单位为四种脱氧核苷酸,即腺嘌呤脱氧核苷酸(dAMP脱氧腺苷)、胸腺嘧啶脱氧核苷酸(dTMP脱氧胸苷)、胞嘧啶脱氧核苷酸(dCMP脱氧胞苷)、鸟嘌呤脱氧核苷酸(dGMP脱氧鸟苷)5、【答案】A【解析】由于自然界的竞争十分激烈,所以很多动物都会形成保护色,这样能够与自然环境混为一体,有助于躲避其他动物天敌的捕食。
2002考研数学一试卷及答案

2002考研数学一试卷及答案一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1)⎰∞+ex x dx2ln =.(2)已知函数()y y x =由方程0162=-++x xy e y 确定,则(0)y ''= .(3)微分方程02='+''y y y 满足初始条件11,'2x x yy ====的特解是.(4)已知实二次型323121232221321444)(),,(x x x x x x x x x a x x x f +++++=经正交变换x Py =可化成标准型216y f =,则a =.(5)设随机变量X 服从正态分布2(,)(0)N μσσ>,且二次方程042=++X y y 无实根的概率为12,则μ=.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.) (1)考虑二元函数),(y x f 的下面4条性质:①),(y x f 在点),(00y x 处连续;②),(y x f 在点),(00y x 处的两个偏导数连续;③),(y x f 在点),(00y x 处可微;④),(y x f 在点),(00y x 处的两个偏导数存在.若用“P Q ⇒”表示可由性质P 推出性质Q ,则有 (A) ②⇒③⇒①. (B) ③⇒②⇒①. (C) ③⇒④⇒①.(D) ③⇒①⇒④.(2)设0(1,2,3,)n u n ≠=,且lim 1n n n u →∞=,则级数11111(1)()n n n n u u ∞+=+-+∑ (A) 发散.(B) 绝对收敛.(C) 条件收敛. (D) 收敛性根据所给条件不能判定.(3)设函数()y f x =在(0,)+∞内有界且可导,则 (A) 当0)(lim =+∞→x f x 时,必有)(lim ='+∞→x f x . (B) 当)(lim x f x '+∞→存在时,必有)(lim ='+∞→x f x .(C) 当0lim ()0x f x +→=时,必有0lim ()0x f x +→'=. (D) 当0lim ()x f x +→'存在时,必有0lim ()0x f x +→'=.(4)设有三张不同平面的方程123i i i i a x a y a z b ++=,3,2,1=i ,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为(5)设1X 和2X 是任意两个相互独立的连续型随机变量,它们的概率密度分别为1()f x和2()f x,分布函数分别为1()F x和2()F x,则(A) 1()f x+2()f x必为某一随机变量的概率密度.(B) 1()f x2()f x必为某一随机变量的概率密度.(C) 1()F x+2()F x必为某一随机变量的分布函数.(D) 1()F x2()F x必为某一随机变量的分布函数.三、(本题满分6分)设函数)(xf在0x=的某邻域内具有一阶连续导数,且(0)0,(0)0f f'≠≠,若()(2)(0)af h bf h f+-在0→h时是比h高阶的无穷小,试确定ba,的值.四、(本题满分7分)已知两曲线)(xfy=与⎰-=x t dtey arctan2在点(0,0)处的切线相同,写出此切线方程,并求极限)2(limnnfn∞→.五、(本题满分7分)计算二重积分dxdyeDyx⎰⎰},max{22,其中}10,10|),{(≤≤≤≤=yxyxD.六、(本题满分8分)设函数)(xf在(,)-∞+∞内具有一阶连续导数,L是上半平面(y>0)内的有向分段光滑曲线,其起点为(b a ,),终点为(d c ,).记2221[1()][()1],L xI y f xy dx y f xy dy y y =++-⎰(1)证明曲线积分I 与路径L 无关; (2)当cd ab =时,求I 的值.七、(本题满分7分)(1)验证函数333369()1()3!6!9!(3)!nx x y x x n =++++++-∞<<+∞满足微分方程xe y y y =+'+'';(2)利用(1)的结果求幂级数30(3)!n n x n ∞=∑的和函数.八、(本题满分7分)设有一小山,取它的底面所在的平面为xOy 坐标面,其底部所占的区域为2{(,)|D x y x =275}y xy +-≤,小山的高度函数为),(y x h xy y x +--=2275.(1)设),(00y x M 为区域D 上一点,问),(y x h 在该点沿平面上什么方向的方向导数最大?若记此方向导数的最大值为),(00y x g ,试写出),(00y x g 的表达式.(2)现欲利用此小山开展攀岩活动,为此需要在山脚下寻找一上山坡最大的点作为攀登的起点.也就是说,要在D 的边界线2275x y xy +-=上找出使(1)中),(y x g 达到最大值的点.试确定攀登起点的位置.九、(本题满分6分) 已知四阶方阵),,,(4321αααα=A ,4321,,,αααα均为4维列向量,其中432,,ααα线性无关,3212ααα-=,如果4321ααααβ+++=,求线性方程组β=Ax 的通解.十、(本题满分8分) 设,A B 为同阶方阵,(1)若,A B 相似,证明,A B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当,A B 均为实对称矩阵时,证明(1)的逆命题成立.十一、(本题满分7分) 设维随机变量X 的概率密度为10,cos ,()220,x x f x π⎧≤≤⎪=⎨⎪⎩其他.对X 独立地重复观察4次,用Y 表示观察值大于3π的次数,求2Y 的数学期望.十二、(本题满分7分) 设总体X 的概率分布为其中1(0)2θθ<<是未知参数,利用总体X 的如下样本值 3,1,3,0,3,1,2,3,求θ的矩估计值和最大似然估计值.参照答案 一、填空题(1)【解析】 原式2ln 11.ln ln eed x x x+∞+∞==-=⎰(2)【解析】 方程两边对x 两次求导得 '6'620,y e y xy y x +++=①2'''6''12'20.y y e y e y xy y ++++=②以0x =代入原方程得0y =,以0x y ==代入①得'0,y =,再以'0x y y ===代入②得''(0) 2.y =-(3)【解析】 这是二阶的可降阶微分方程.令'()y P y =(以y 为自变量),则'''.dy dP dPy P dx dx dy ===代入方程得20dP yPP dy +=,即0dPy P dy +=(或0P =,但其不满足初始条件01'2x y ==).分离变量得 0,dP dy P y +=积分得ln ln ',P y C +=即1C P y =(0P =对应10C =);由0x =时11,',2y P y ===得11.2C =于是1',2,2y P ydy dx y ===积分得22y x C =+.又由01x y ==得21,C =所求特解为y =(4)【解析】 因为二次型Tx Ax 经正交变换化为标准型时,标准形中平方项的系数就是二次型矩阵A 的特征值,所以6,0,0是A 的特征值. 又因iiia λ=∑∑,故600, 2.a a a a ++=++⇒=(5)【解析】 设事件A 表示“二次方程042=++X y y 无实根”,则{1640}{A X X =-<=> 4}.依题意,有1(){4}.2P A P X =>=而4{4}1{4}1(),P X P X μΦσ->=-≤=-即414141(),(),0. 4.22μμμΦΦμσσσ----===⇒=二、选择题(1)【解析】 这是讨论函数(,)f x y 的连续性,可偏导性,可微性及偏导数的连续性之间的关系.我们知道,(,)f x y 的两个偏导数连续是可微的充分条件,若(,)f x y 可微则必连续,故选(A).(2)【解析】 由1lim 101n n un n →+∞=>⇒充分大时即,N n N ∃>时10n u >,且1lim0,n n u →+∞=不妨认为,0,n n u ∀>因而所考虑级数是交错级数,但不能保证1n u 的单调性.按定义考察部分和111111111111(1)()(1)(1)nn nk k k n k k k k k k k S u u u u +++===++=-+=-+-∑∑∑1111111(1)11(1)1(1)(),k n nn l k l k l n n u u u u u ++==+--=-+-=+→→+∞∑∑⇒原级数收敛.再考察取绝对值后的级数1111()n n n u u ∞=++∑.注意111112,11n n n n u u n n nu u n n ++++=+⋅→+11n n ∞=∑发散⇒1111()n nn u u ∞=++∑发散.因此选(C).(3)【解析】 证明(B)对:反证法.假设lim ()0x f x a →+∞'=≠,则由拉格朗日中值定理,(2)()'()()f x f x f x x ξ-=→∞→+∞(当x →+∞时,ξ→+∞,因为2x x ξ<<);但这与(2)()(2)()2f x f x f x f x M-≤+≤矛盾(()).f x M ≤(4)【解析】 因为()()23r A r A ==<,说明方程组有无穷多解,所以三个平面有公共交点且不唯一,因此应选(B).(A)表示方程组有唯一解,其充要条件是()() 3.r A r A ==(C)中三个平面没有公共交点,即方程组无解,又因三个平面中任两个都不行,故()2r A =和()3r A =,且A 中任两个平行向量都线性无关.类似地,(D)中有两个平面平行,故()2r A =,()3r A =,且A 中有两个平行向量共线.(5)【解析】 首先可以否定选项(A)与(C),因121212[()()]()()21,()()112 1.f x f x dx f x dx f x dx F F +∞+∞+∞-∞-∞-∞+=+=≠+∞++∞=+=≠⎰⎰⎰对于选项(B),若121,21,1,01,()()0,0,x x f x f x -<<-<<⎧⎧==⎨⎨⎩⎩其他,其他,则对任何(,),x ∈-∞+∞12()()0f x f x ≡,12()()01,f x f x dx +∞-∞=≠⎰因此也应否定(C),综上解析,用排除法应选(D).进一步解析可知,若令12max(,)X X X =,而~(),1,2,i i X f x i =则X 的分布函数()F x 恰是12()().F x F x1212(){max(,)}{,}F x P X X x P X x X x =≤=≤≤1212{}{}()().P X x P X x F x F x =≤≤=三、【解】 用洛必达法则.由题设条件知lim[()(2)(0)](1)(0).h af h bf h f a b f →+-=+-由于(0)0f '≠,故必有10.a b +-=又由洛必达法则 00()(2)(0)'()2'(2)limlim 1h h af h bf h f af h bf h h →→+-+=(2)'(0)0,a b f =+=及(0)0f '≠,则有20a b +=.综上,得2, 1.a b ==-四、【解】 由已知条件得(0)0,f =22arctan arctan 02'(0)()'1,1x x t xx x e f e dt x --=====+⎰故所求切线方程为y x =.由导数定义及数列极限与函数极限的关系可得02()(0)2()(0)lim ()2lim 2lim 2'(0) 2.2n n x f f f x f n nf f n xn →∞→∞→--====五、【解析与求解】D 是正方形区域如图.因在D 上被积函数分块表示2222,,max{,}(,),,,x x y x y x y D y x y ⎧≥⎪=∈⎨≤⎪⎩于是要用分块积分法,用y x =将D 分成两块:1212,{},{}.D D D D D y x D D y x ==≤=≥⇒I222212max{,}max{,}xy xy D D e dxdy e dxdy=+⎰⎰⎰⎰2221212x y x D D D e dxdy e dxdy e dxdy=+=⎰⎰⎰⎰⎰⎰(D 关于y x =对称)2102xx dx e dy=⎰⎰(选择积分顺序)22112 1.x xxe dx e e ===-⎰六、【解析与求解】 (1)易知Pdx Qdy +∃原函数,2211()()()()()x Pdx Qdy dx yf xy dx xf xy dy dy ydx xdy f xy ydx xdy y y y+=++-=-++()()()[()].xy x xd f xy d xy d f t dt y y =+=+⎰⇒在0y >上Pdx Qdy +∃原函数,即0(,)()xy xu x y f t dty =+⎰.⇒积分I 在0y >与路径无关.(2)因找到了原函数,立即可得(,)(,)(,).c d a b c a I u x y d b ==-七、【证明】 与书上解答略有不同,参见数三2002第七题(1)因为幂级数3693()13!6!9!(3)!n x x x x y x n =++++++的收敛域是()x -∞<+∞,因而可在()x -∞<+∞上逐项求导数,得25831'()2!5!8!(31)!n x x x x y x n -=+++++-,4732''()4!7!(32)!n x x x y x x n -=+++++-,所以2'''12!!n xx x y y y x e n ++=+++++=()x -∞<+∞.(2)与'''xy y y e ++=相应的齐次微分方程为'''0y yy ++=,其特征方程为210λλ++=,特征根为1,2122λ=-±.因此齐次微分方程的通解为212()xY e C x C x -=+.设非齐次微分方程的特解为x y Ae *=,将y *代入方程'''x y y y e ++=可得13A=,即有13xy e *=.于是,方程通解为2121()3xx y Y y e C x C x e -*=+=++.当0x =时,有112121(0)1,23,0.311'(0)0.23y C C C y C ⎧==+⎪⎪⇒==⎨⎪==-+⎪⎩于是幂级数30(3)!nn x n ∞=∑的和函数为221()cos 323xxy x e x e -=+()x -∞<+∞八、【解析与求解】 (1)由梯度向量的重要性质:函数),(y x h 在点M 处沿该点的梯度方向0000(,)(,)0000(,){,}{2,2}x y x y h hh x y x y y x x y∂∂==-+-+∂∂grad方向导数取最大值即00(,)(,)x y h x y grad 的模,00(,)g x y ⇒=(2)按题意,即求(,)g x y 求在条件22750x y xy +--=下的最大值点⇔ 22222(,)(2)(2)558g x y y x x y x y xy =-+-=+-在条件22750x y xy +--=下的最大值点. 这是求解条件最值问题,用拉格朗日乘子法.令拉格朗日函数2222(,,)558(75),L x y x y xy x y xy λλ=+-++--则有22108(2)0,108(2)0,750.Lx y x y x Ly x y x y L x y xy λλλ⎧∂=-+-=⎪∂⎪∂⎪=-+-=⎨∂⎪⎪∂=+--=⎪∂⎩解此方程组:将①式与②式相加得()(2)0.x y x y λ++=⇒=-或2.λ=-若y x =-,则由③式得2375x =即5, 5.x y =±=若2,λ=-由①或②均得y x =,代入③式得275x =即x y =±=±于是得可能的条件极值点1234(5,5),(5,5),(M M M M ----现比较222(,)(,)558f x y g x y x y xy ==+-在这些点的函数值:1234()()450,()()150.f M f M f M f M ====因为实际问题存在最大值,而最大值又只可能在1234,,,M M M M 中取到.因此2(,)g x y 在12,M M 取到在D 的边界上的最大值,即12,M M 可作为攀登的起点.九、【解】 由432,,ααα线性无关及3212ααα-=知,向量组的秩1234(,,,)3r αααα=,即矩阵A 的秩为3.因此0Ax =的基础解系中只包含一个向量.那么由123412312(,,,)2010ααααααα⎡⎤⎢⎥-⎢⎥=-+=⎢⎥⎢⎥⎣⎦知,0Ax =的基础解系是(1,2,1,0).T- 再由123412341111(,,,)1111A βαααααααα⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+++==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦知,(1,1,1,1)T是β=Ax 的一个特解.故β=Ax 的通解是1121,1101k ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦其中k 为任意常数.十、【解】 (1)若,A B 相似,那么存在可逆矩阵P ,使1,P AP B -=故111E B E P AP P EP P APλλλ----=-=-11().P E A P P E A P E A λλλ--=-=-=-(2)令0100,,0000A B ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦那么2.E A E B λλλ-==-但,A B 不相似.否则,存在可逆矩阵P ,使10P AP B -==.从而100A P P -==,矛盾,亦可从()1,()0r A r B ==而知A 与B 不相似.(3)由,A B 均为实对称矩阵知,,A B 均相似于对角阵,若,A B 的特征多项式相等,记特征多项式的根为1,,,n λλ则有A 相似于1,n λλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦B 也相似于1.n λλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦即存在可逆矩阵,P Q ,使111.n P AP Q BQ λλ--⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦于是111()().PQ A PQ B ---=由1PQ -为可逆矩阵知,A 与B 相似.十一、【解】 由于311{}cos ,3222x P X dx πππ>==⎰依题意,Y 服从二项分布1(4,)2B ,则有2222111()()4(4) 5.222EY DY EY npq np =+=+=⨯⨯+⨯=十二、【解】22012(1)23(12)34,EX θθθθθθ=⨯+⨯-+⨯+⨯-=-1(3).4EX θ=-θ的矩估计量为1ˆ(3),4X θ=-根据给定的样本观察值计算1(31303123)8x =+++++++2.=因此θ的矩估计值11ˆ(3).44x θ=-=对于给定的样本值似然函数为624()4(1)(12),ln ()ln 46ln 2ln(1)4ln(12),L L θθθθθθθθ=--=++-+-2ln ()62824286.112(1)(12)d L d θθθθθθθθθθ-+=--=----令ln ()0d L d θθ=,得方程2121430θθ-+=,解得712θ=(71,122θ=>不合题意).于是θ的最大似然估计值为7ˆ12θ-=。
2002年一级结构专业上午真题word版

题1—4:有一承受非恒载为主的钢筋混凝土框架柱,安全等级II级,矩形截面尺寸b×h =300×500(mm),对称配筋,每则各配有322钢筋(A=942mm2)ξ b=0.544,混凝土强度等级为C25,纵向受拉钢筋合力点至载面近边矩离a =40mm,该柱的计算长度L0=4.5m.1.偏心矩增大系数ŋ与下列何项数值最为接近?提示:ζ1可按给出的近似公式计算:ζ1=0.2+2.7e i /h 。
(A)1.181 (B)1.205(C)1.177 (D)1.2072.该柱在某荷载效应组合状态下,其正截面受压承载力图如图2所示,受压区高度x=290mm 。
试问在该组合内力作用下,柱的受拉主筋的钢筋应力σs最接近于下列何项数值?(A)205.33N/mm 2(B )192.08N /mm2(C )310.00N /mm2(D )221.48N /mm 23.柱正截面受压承载力图同图2,已知该柱为小偏心受压,其轴向力对截面重心的偏心矩e0=150mm ,受压区高度x=293mm,受拉主筋压力σs =197N/mm2。
试问在已给出的配筋量的情况下,该柱所能承受的内力设计值M及N,与下列何项数值最为接近?(A)195KN·m, 130K N (B ) 222K N ·m , 1478K N(C ) 178K N·m , 1186KN (D ) 194K N ·m , 1293K N4.柱正截面受压承载力图同图2,已知该柱为小偏心受压。
假定该框架柱偏听偏心受压时作用有轴向压力设计值N=600KN,柱两配有双肢箍Ø8@150,计算截面的剪跨比λ=3,试问该柱斜截面受剪承载力设计值与下列何项数值最为接近?(A)176.9KN (B)240。
9KN(C)197KN (D)238KN5.某钢筋混凝土简支大梁,矩形截面,混凝土采用C30。
根据《混凝土结构设计规范》公式求出梁的挠度和裂缝稍大,需调整设计,但荷载和截面不能改变。
全真试题与参考答案

全真试题与参考答案2002年9月全国计算机等级考试一级笔试试卷(考试时间:90分钟,满分100分)一、选择题((1)—(30)每题1分,(31)—(55)每题2分,共80分)下列各题A)、B)、C)、D)四个选项中,只有一个选项是正确的,请将正确选项涂写在答题卡相应位置上,答在试卷上不得分。
(1) 第一台电子计算机是1946年在美国研制的,该机的英文缩写名是A) ENIAC B) EDVAC C) DESAC D) MARK-II(2) 运算器的组成部分不包括A) 控制线路B) 译码器C) 加法器D) 寄存器(3) 用高级程序设计语言编写的程序称为A) 目标程序B) 可执行程序C) 源程序D) 伪代码程序(4) 在微机的硬件设备中,既可以做输出设备,又可以做输入设备的是A) 绘图仪B) 扫描仪C) 手写笔D) 磁盘驱动器(5) 把内存中的数据传送到计算机的硬盘,称为A) 显示B) 读盘C) 输入D) 写盘(6) RAM具有的特点是A) 海量存储B) 存储在其中的信息可以永久保存C) 一旦断电,存储在其上的信息将全部消失且无法恢复D) 存储在其中的数据不能改写(7) Windows 98操作系统是一个真正32位系统,它可以管理的内存是A) 32M B) 64M C) 1GB D) 4GB(8) 在Windows98中,下列叙述正确的是A) “开始”菜单只能用鼠标单击“开始”按钮才能打开B) Windows任务栏的大小是不能改变的C) “开始”菜单是系统生成的,用户不能再设置它D) Windows任务栏可以放在桌面四个边的任意边上(9) 如果在Windows98的资源管理器底部没有状态栏,那么增加状态栏的操作是A) 单击“编辑”菜单中的“状态栏”命令B) 单击“工具”菜单中的“状态栏”命令C) 单击“查看”菜单中的“状态栏”命令D) 单击“文件”菜单中的“状态栏”命令(10) 在Windows 98缺省状态下,下列关于文件复制的描述不正确的是A) 利用鼠标左键拖动可实现文件复制B) 利用鼠标右键拖动不能实现文件复制C) 利用剪贴板可实现文件复制D) 利用组合键Ctrl+C和Ctrl+V可实现文件复制(11) 在Windows 98中创建启动盘,要使用控制面板的A)“添加/删除程序”模块B) “添加新硬件”模块C) “系统”模块D) “用户”模块(12) 在Windows 98中,全角方式下输入的数字应占的字节数是A) 1 B) 2 C) 3 D) 4(13) 在Windows 98缺省状态下,进行全角/半角切换的组合键是A)Alt+ B)Shift+空格C)Alt+空格D)Ctrl+.(14) 下列选项中不能用于启动Word 97的操作是A)双击Windows桌面上的Word快捷方式图标B) 单击“开始”→“程序”→“Microsoft Word”C) 单击任务栏中的Word快捷方式图标D)单击Windows桌面上的Word快捷方式图标(15) 在Word 97编辑状态下,若要把选定的文字移到其它文档中,首先应选用的按钮是A)B)C)D)(16) 在Word 97编辑状态下,给当前打开的文档加上页码,应使用的下拉菜单是A)编辑B)插入C) 格式D)工具(17) 在Word 97编辑状态下,要将文档中的所有“E-mail”替换成“电子邮件”,应使用的下拉菜单是A)编辑B)视图C)插入D)格式(18) 在Word 97编辑状态下,如果要在当前窗口中隐藏(或显示)格式工具栏,应选择的操作是A) 单击“工具”→“格式”B) 单击“视图”→“格式”C)单击“视图”→“工具栏”→“格式”D)单击“编辑”→“工具栏”→“格式”(19) 在Word 97编辑状态下,若要调整光标所在段落的行距,首先进行的操作是A)打开“编辑”下拉菜单B) 打开“视图”下拉菜单C)打开“格式”下拉菜单D) 打开“工具”下拉菜单(20) 在Word 97编辑状态下绘制图形时,文档应处于A) 普通视图B) 主控文档C) 页面视图D) 大纲视图(21) 在Word 97中,页眉和页脚的作用范围是A) 全文B)节C)页D)段(22) 当一个Word窗口被关闭后,被编辑的文件将A)被从磁盘中清除B)被从内存中清除C)被从内存或磁盘中清除D)不会从内存和磁盘中被清除(23)在Excel 97工作簿中,至少应含有的工作表个数是A) 1 B) 2 C) 3 D) 4(24) 在Excel 97工作表中,不正确的单元格地址是A) C$66 B) $C66 C) C6$6 D) $C$66(25) 在Excel 97 工作表中,在某单元格内输入数字123,不正确的输入形式是A) 123 B) =123 C) +123 D) *123(26) Excel 97 工作表可以进行智能填充时,鼠标的形状为A) 空心粗十字B) 向左上方箭头C) 实心细十字D) 向右上方前头(27) 在Excel 97工作表中,正确的Excel公式形式为A) =B3*Sheet3!A2 B) =B3*Sheet3$A2C) =B3*Sheet3:A2 D) =B3*Sheet3%A2(28) 在PowerPoint 97演示文稿中,将某张幻灯片版式更改为“垂直排列文本”,应选择的菜单是A)视图B)插入C)格式D)幻灯片放映(29) 浏览Web网站必须使用浏览器,目前常用的浏览器是A)Hotmail B)Outlook ExpressC)Inter Exchange D)Internet Explorer(30) 根据域名代码规定,域名为表示的网站类别应是A)教育机构B) 军事部门C) 商业组织D) 国际组织(31) 计算机硬件的组成部分主要包括:运算器、存储器、输入设备、输出设备和A)控制器B) 显示器C)磁盘驱动器D)鼠标器(32) 下列关于计算机病毒的叙述中,正确的选项是A)计算机病毒只感染.exe或.com文件B)计算机病毒可以通过读写软件、光盘或Internet网络进行传播C)计算机病毒是通过电力网进行传播的D)计算机病毒是由于软件片表面不清洁而造成的。
2002年一注结构工程师基础考试试题

2002年一级注册根底考试试题及答案〔答案见文档最下方〕1. 设直线L: 2x-y+5=0x+3z+1=0⎧⎨⎩, 那么L 的一个方向向量S 是: (A) {2,-1,0} (B){1,0.3}(C) {-3,-6,1} (D){-3,6,1}2. 设平面Ⅱ通过球面x 2+y 2+z 2=4(x-2y-2z)的中心,且垂直于直线:0:0,x L y z =⎧⎨+=⎩ 那么平面的方程是: (A) y-z=0 (B)y+z=0(C)4x+y+z=0 (D)2x+2y-z=03.将双曲线224x 9z 36,0z ⎧-=⎨=⎩绕x 曲线旋转一周所生成的旋转曲面的方程是: (A) 4〔x 2+z 2〕-9y 2=36 (B)4x 2-9〔y 2+z 2〕=36(C)4x 2-9y 2=36 (D)4〔x 2+y 2〕-9z 2=364. 空间曲线 222222216,0x y z x z y ⎧++=⎨+-=⎩在xoy 平面的投影的方程是: (A) 22222160x y x y ⎧+=⎨-=⎩ (B) 222160x y z ⎧+=⎨=⎩(C) 2216x y += (D) 222160x y z ⎧+=⎨=⎩ 5.极限sin()lim 2,0xy x y y →→的值是:(A) 0 (B) 1 (C) 2 (D) ∞6.以下关于函数()n f x =连续性的结论,正确的选项是:(A)除x=0外处处连续 (B)除x=±1外处处连续(C)除x=0, ±1外处处连续 (D)处处连续7.设函数 ()()2,ln 11,x e f x x λ-⎧⎪=⎨++⎪⎩ 00x x ≤>假设f 〔x 〕在x=0 处可导,那么λ的值是:(A) 1 (B) -2(C) 0 (D) -18.假设函数1()sin sin 33f x a x x =+在3x π=处取得极值,那么a 的值是:(A) 2 (B) 23(C)(D) 9.设 p>0,那么112lim p p pp n n n +→∞+++等于: (A) 11p +(B) 12p + (C)(D) 10.设D={〔x, y 〕|x 2+y 2≤2y},那么以下等式中正确的选项是: 〔A 〕22sin 00(,)(cos ,sin )D f x y dxdy d f r r dr πθθθθ=⎰⎰⎰⎰〔B 〕2sin 00(,)(cos ,sin )D f x y dxdy d f r r dr πθθθθ=⎰⎰⎰⎰〔C 〕22sin 00(,)(cos ,sin )D f x y dxdy d f r r rdr πθθθθ=⎰⎰⎰⎰〔D 〕2sin 00(,)(cos ,sin )D f x y dxdy d f r r rdr πθθθθ=⎰⎰⎰⎰11.设有一物体,占有空间闭区域Ω={〔x, y, z 〕| 0≤ x ≤1, 0≤ y ≤ 1, 0 ≤ z ≤ 1},其在点〔x ,y,z〕处的体密度为p (x, y, z )=2(x +y +z),那么该物体的质量为:(A) 1 (B) 2(C) 3 (D) 412. 两条抛物线y 2= x , y = x 2 所围成的图形的面积为:(A) 16 (B) 13 (C) 23(D)1 13. 幂级数()111n n n x n∞-=-∑的收敛区间是: (A) [-1 , 1 ] (B) (-1 ,1 )(C) [ -1 , 1 ] (D) ( -1 , 1 )14. 设0≤ a n <1n ( n = 1 ,2 , ),以下级数中必定收敛的是:(A) 1n ∞= (B) 1n n a ∞=∑(C) 21(1)n n n a ∞=-∑ (D) 1(1)n n n a ∞=-∑15. 前n 项局部和数列{S n }有界是正项级数1n n u∞=∑收敛的条件是:(A)充分必要条件 (B)充分条件,但不是必要条件(C)必要条件,但不是充分条件 (D)既不是充分条件,也不是必要条件16. 方程250y y y '''++=的通解是:(A) 12cos 2x c e x c -+ (B) 1cos 2sin 2c c x c x +(C) 12cos 2sin 2)x c x c x e -+ (D) 12sin 2x c e x c -+17. 10把钥匙中有3把能翻开门,今任取两把,那么能翻开门的概率是: (A)715 (B) 815(C) 615 (D) 91518. 随机变量x 满足P(│x -Ex │≥2 ) = 116, x 的方差记为D( x ),那么以下结果中一定正确 的是: (A)D( x ) =14 (B)D( x ) > 14(C) P(│x – Ex │<2)= 1516 (D)D( x ) < 14 19. 设 〔1,2,10,X X X 〕是抽自正态总体2(,)N μσ的一个容量为10的样本,其中 2,0σ-∞<+∞>,记55115i i X X ==∑,那么5102252161()()i i i i X X X μσ-==⎡⎤-+-⎢⎥⎣⎦∑∑服 从x 2 分布,其自由度为:(A) 9 (B) 8(C) 7 (D) 1020.如果随机变量X 与Y 满足D 〔X+Y 〕=D 〔X-Y 〕,那么以下结论中正确的选项是:(A)X 与Y 独立 (B) D 〔Y 〕=0(C) D 〔X 〕•D 〔Y 〕= 0 (D) X 与Y 不相关21.设P -1AP= ∧,其中P 为2阶可逆方阵,1002-∧=,那么10A 的值是:(A) -2 (B)210(C) -29 (D)2922.4阶方阵A 的秩为2,那么其伴随矩阵A*的秩为:(A) 0 (B) 1(C) 2 (D) 323.设A 为m n ⨯矩阵,齐次线性方程组Ax = 0仅有零解的充分必要条件是:(A) A 的行向量组线性无关 (B)A 的行向量组线性相关(C)A 的列向量组线性相关 (D)A 的列向量组线性无关24.一质沿一曲线2cos32sin 2t r e i tj tk -=++运动,其中t 为时间,那么在t=0时质点的速度大小为:(A) (B) (C)5 (D)325.一定量的理想气体,在温度不变的条件下,当容积增大时,分子的平均碰撞次数Z 和平均自由程λ的变化情况是: (A) Z 减小而λ不变 (B) Z 减小而λ增大 (C) Z 增大而λ减小 (D) Z 不变而λ增大26.温度相同的氦气和氧气,它们分子的平均动能ε和平均平动动能W 有如下关系: (A) ε和W 都相等 (B) ε相等,而W 不相等 (C) W 相等,而 ε不相等 (D) ε和W 都不相等27.在温度分别为2370C 和270C 的高温热源和低温热源之间工作的热机,理论上最大效率为:(A)25% (B)50 %(C)75 % (D) 91.74%28. 根据热力学第二定律可知:(A) 功可以全部转换为热,但热不能全部转换为功(B) 热可以从高温物体传到低温物体,但不能从低温物体传到高温物体 〔C 〕不可逆过程就是不能向相反方向进行的过程〔D 〕一切自发过程都是不可逆的29.“理想气体和单一热源接触作等温膨胀时,吸收的热量全部用来对外作功。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一级笔试练习题
(共100分)
一、单向选择题(每题1.5分,共30分)
1.下列设备中,只能作为输出设备的是()
(A)磁盘存储器(B)键盘(C)鼠标器(D)打印机
2.微型计算机中存储数据的最小单位是()
(A)字(B)字节(C)位(D)KB
3.二进制数01100100转换成十六进制数是()
(A)64 (B)63 (C)100 (D)144
4.计算机能自动工作,主要是用了()
(A)二进制数制(B)高速电子元件
(C)存储程序控制原理(D)程序设计语言
5.一座办公大楼各个办公室中的微机进行联网,这个网络属于()
(A)WAN (B)MAN (C)LAN (D)internet
6.HTTP是一种()
(A)高级程序设计语言(B)域名
(C)超文本传输协议(D)网址
7.多媒体计算机的英文缩写是()
(A)CAI (B)CAD (C)ROM (D)MPC
8.在Windows资源管理器右窗格中,同一文件夹下,用鼠标单击了第一个文件,按住Ctrl键再单击了第五个文件,则选中了()个文件。
(A)0 (B)5 (C)1 (D)2
9.下面关于Windows文件名的叙述,错误的是()
(A)文件名允许使用汉字(B)文件名允许使用多个圆点分隔符
(C)文件名允许使用空格(D)文件名允许使用竖线“|”
10.删除文件的命令是()
(A)CD (B)DEL (C)MD (D)RD
11.Windows中的窗口和对话框比较,窗口可移动和改变大小,而对话框()
(A)既不能移动,也不能改变大小(B)仅可以移动,不能改变大小
(C)仅可以改变大小,不能移动(D)既能移动也能改变大小
12.Word编辑状态下,鼠标在某行行首,若仅选择光标所在行应选用()
(A)单击鼠标左键(B)将鼠标左键击三下
(C)双击鼠标左键(D)单击鼠标右键
13.Word模板文件的扩展名为()
(A).DOC (B) .DOT (C).WPS (D).TXT
14.Word编辑状态下当前编辑的文档是C盘根目录下的d1.doc,要将该文档拷贝到软盘,应当使用()
(A)“文件”菜单中的“另存为”命令(B)“文件”菜单中的“保存”命令
(C)“文件”菜单中的“新建”命令(D)插入菜单中的命令
15.在E中,新建一个工作薄缺省的工作表有()个
(A)1 (B)2 (C)0 (D)3
16.数字字符“1”的ASCII码的十进制数表示为49,数字字符“8”的ASCII码的十进制数表示应为()
(A)56 (B)58 (C)60 (D)54
17.具有多媒体功能的微型计算机系统,常用CD—ROM作为外存储器,它是()
(A)只读存储器(B)可读可写存储器
(C)只读硬盘(D)只读大容量软盘
18.办公自动化是计算机的一项应用,按计算机应用的分类它属于( )
(A)科学计算 (B)实时控制 (C)数据处理 (D)辅助设计
19. 在Excel中,默认情况下,单元格名称使用的是( )
(A)相对引用 (B)绝对引用 (C)混合应用 (D)三维相对引用
20. Powerpoint演示文档存盘时,其默认的扩展年名为( )
(A) . ppt (B).pnt (C).pot (D).doc
二. 多选题(每题2分,共20分)
1. 微型计算机中,运算器的主要功能是( )
(A)逻辑运算(B)算术运算(C)分析指令并译码
(D)按主频指标规定发出时钟脉冲(E)保存指令信息供系统各部件使用
2. 静态RAM的特点是()
(A)在不断电的条件下,其中的信息保持不变
(B)在不断电的条件下,其中的不能长时间保持
(C)其中信息只能读不能写
(D)其中的信息断电后也不会丢失
(E)其中的信息断电后会丢失
3.下列叙述中,正确的有()
(A)内存容量是指微型计算机硬盘所能容纳信息的字节数
(B)微处理器的主要性能指标是字长和主频
(C)微型计算机应避免强磁场的干扰
(D)微型计算机机房湿度不宜过大
(E)用MIPS为单位来衡量计算机的性能,它指的是传输速率
4.计算机信息系统安全保护技术包括()
(A)运行安全(B)实体安全(C)信息安全
(D)操作安全(E)网络安全
5. 图表是Windows的一个重要元素,下列有关图标的描述中,正确的是()(A)图标只能代表某个应用程序或应用程序组
(B)图标可以代表任何快捷方式
(C)图标可以代表包括文档在内的任何文件
(D)图标可以代表文件夹
(E)图标可以重新排列
6. Windows中,“粘贴”和“剪切”操作描述正确的是()
(A)“粘贴”是将“剪切板”中的内容复制到指定位置
(B)“粘贴”是将“剪切板”中的内容移动到指定的位置
(C)“剪切”操作后可以进行多次“粘贴”操作
(D)“剪切”操作的结果是将选定的信息复制到“剪切板”中
(E)“剪切”操作的结果是将选定的信息移动到“剪切板”中
7. Word中的查找和替换功能可以()
(A)替换文字(B)替换格式(C)不能替换格式
(D)只替换格式不替换文字(E)格式和文字可以一起替换
8.Word中的文档“格式”工具中设置的对齐方式有()
(A)分散对齐(B)上下对齐(C)两端对齐
(D)居中对齐(E)右对齐
9.下面关于显示器的叙述正确的是()
(A)显示器的分辨率与微处理器的型号有关
(B)显示器的分辨率与微处理器的型号无关
(C)分辨率是1024*768,表示一屏的水平方向每行1024点,垂直方向每列768点(D)显示卡是驱动,控制计算机显示文本,图形,图象信息的硬件配置
(E)像素是显示屏上能独立赋予颜色和亮度的最小单位
10.下面关于系统软件的叙述中,错误的是()
(A)系统软件与具体应用领域无关
(B)系统软件与具体应用领域有关
(C)系统软件是在应用软件基础上开发的
(D)系统软件并不提供人机界面
(E)系统软件提供人机界面
三、判断题(每题1.5分,共30分)
1.计算机病毒可以通过电子邮件传播。
2.多媒体计算机可以处理图象和声音信息,但不能处理文字。
3.计算机系统是指计算机的软件系统,不包括硬件。
4.Windows支持长文件名,Dos不支持长文件名。
5.正版软件能用于生产和商业目的。
6.计算机与其他计算工具的本质区别是它能够存储和控制程序。
7.汉字“中”的区位码与国标码是相同的。
8.可以用软件和硬件技术来检测与消除计算机病毒。
9.任何程序不需进入内存,直接在硬盘上就可以了。
10.Windows中,剪切板使用的是内存的一部分空间。
11.Windows中,文档窗口组成与应用程序窗口组成的不同,是文档窗口不含菜单。
12.在Windows及其应用程序中,当拉下一个菜单时,如果某些命令是灰色,表示命令永远不能用。
13.Word中,对字符进行格式设置在字符键入的前后都可以进行。
14. Word的打印预览模式下,不能检查分页符,调整页边距。
15.用Word “插入”菜单中的“页码”命令在文档中标注页码,该命令对文档的第一页不标注页码号。
16.Internet中广泛使用的是TCP/IP协议。
17.多媒体技术具有集成性,实时性和交互性3个基本特性。
18.在Excel中,公式相对引用的单元格地址,在进行公式复制时会自动发生改变。
19.在Excel的工作表中不能插入来自其他文件的图片。
20.PowerPoint中的幻灯片的“切换效果”指的是幻灯片在放映时出现的方式
四.填空题(每空2分,共20分)
1.按目前的划分方式,微型计算机属于第()代计算机。
2.20G的硬盘相当于()M(兆)。
3.Windows中,通过“开始”菜单的“程序”项进入MS-DOS方式,可使用()命令再返回Windows.
4.长文件名“计算机文化基础.DOC”对应的短文件名是()。
5.当Word文档中含有页眉,页脚,图形等复杂格式内容时,应采用()方式进行显示。
6.Excel工作薄文件的扩展名是()。
7.在Internet中,用字符串表示的IP地址称为()。
8.计算机网络设备中,HUB是指()。
9.文件型病毒传染的对象主要是.COM和()。
10.在Excel工作表中,若当前活动单元格在H列11行上,该单元格的绝对地址表示形式是()。
