连云港市田家炳中学高三数学基础训练
连云港市田家炳中学高三数学专项练习三角与向量

解答题:解答须写出文字说明、证明过程和演算步骤.1.如图,渔船甲位于岛屿A 的南偏西60方向的B 处,且与岛屿A 相距12海里,渔船乙以10海里/小时的速度从岛屿A 出发沿正北方向航行,若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上. (1)求渔船甲的速度; (2)求sin α的值.1.解:(1)依题意,120BAC ∠=,12AB =,10220AC =⨯=,BCA α∠=.在△ABC 中,由余弦定理,得2222cos BC AB AC AB AC BAC =+-⨯⨯∠22122021220cos120784=+-⨯⨯⨯= .解得28BC =.所以渔船甲的速度为142BC=海里/小时. 答:渔船甲的速度为14海里/小时.(2)方法1:在△ABC 中,因为12AB =,120BAC ∠=,28BC =, BCA α∠=,由正弦定理,得sin sin120AB BCα=.即312sin120332sin 2814AB BC α⨯===. 答:sin α的值为3314. 方法2:在△ABC 中,因为12AB =,20AC =,28BC =,BCA α∠=,由余弦定理,得222cos 2AC BC AB AC BC α+-=⨯.即22220281213cos 2202814α+-==⨯⨯. α为锐角∴所以2213sin 1cos 114αα⎛⎫=-=-=⎪⎝⎭3314.答:sin α的值为3314. 2.在ABC △中,5cos 13A =-,3cos 5B =. (1)求sinC 的值;(2)设5BC =,求ABC △的面积.2.解:(1)由5cos 13A =-,得12sin 13A =, 60ABC东南西 北 α由3cos 5B =,得4sin 5B =.所以16sin sin()sin cos cos sin 65C A B A B A B =+=+=. (2)由正弦定理得45sin 13512sin 313BC B AC A ⨯⨯===. 所以ABC △的面积1sin 2S BC AC C =⨯⨯⨯1131652365=⨯⨯⨯83=. 3.在ABC ∆中,角,,A B C 所对的边分别是,,a b c ,又4cos 5A =. (1)求2cos cos 22AA +的值; (2)若2b =,ABC ∆的面积3S =,求a 的值.3.解:(1)221cos cos2(1cos )2cos 122A A A A +=++- =21116141592cos cos 2222525250A A +-=⨯+⨯-=(2)133sin ,2,sin ,3,5255S bc A b A c c ===∴⨯=∴=由余弦定理22242cos 425225135a b c bc A =+-=+-⨯⨯⨯= ∴13a = 4.已知向量(sin ,cos ),(cos ,3cos )3333x x x x a b == ,函数()f x a b = ,(1)求函数()f x 的单调递增区间;(2)如果△ABC 的三边a 、b 、c 满足2b ac =,且边b 所对的角为x ,试求x 的范围及函数()f x 的值域.4.解(1)()sincos 3cos cos 3333x x x x f x a b =⋅=+1232sin (1cos )2323x x =++ 1232323sin cos sin()23232332x x x π=++=++ 令2222332x k k πππππ-≤+≤+,解得,533,()44k x k k Z ππππ-≤≤+∈.故函数()f x 的单调递增区间为5[3,3],()44k k k Z ππππ-+∈ 22222221(),cos .2222a cb ac ac ac ac b ac x ac ac ac +-+--===≥= 2125cos 10,233339x x x ππππ∴≤<<≤∴<+≤,, 2sinsin()1333x ππ∴<+≤,2333sin()13322x π∴<++≤+即()f x 的值域为3(3,1]2+.综上所述,(0,],()3x f x π∈的值域为3(3,1]2+. 5.已知函数)6cos(sin )(π-+=x x x f ,R ∈x (1)求)(x f 的最大值;(2)设△ABC 中,角A 、B 的对边分别为a 、b ,若A B 2=且)6(2π-=A f a b ,求角C 的大小.5.解:(1))6cos(sin )(π-+=x x x f x x x sin 21cos 23sin ++= ⎪⎪⎭⎫ ⎝⎛+=x x cos 21sin 233)6sin(3π+=x .(注:也可以化为)3cos(3π-x )所以)(x f 的最大值为3.(2)因为)6(2π-=A f a b ,由(1)和正弦定理,得A B 2sin 32sin =.又A B 2=,所以A A 2sin 322sin =,即A A A 2sin 3cos sin =,而A 是三角形的内角,所以0sin ≠A ,故A A sin 3cos =,33tan =A , 所以6π=A ,32π==A B ,2ππ=--=B A C .6.如图,在平面直角坐标系xoy 中,以ox 轴为始边做两个锐角βα,,它们的终边分别与单位圆相交于A 、B 两点,已知A 、B 的横坐标分别为552,102 (1)求)tan(βα+的值; (2)求βα2+的值。
连云港市田家炳中学高三数学小题训练(1)

一、填空题:1.已知集合{|3,},{1,2,3,4}A x x x R B =>∈=,则()R A B = ð . 2.已知复数1(1)az i =+-,若复数z 为纯虚数,则实数a 的值为 . 3.已知角α的终边经过点(2,1)P --,则cos()3πα+的值为 .4.已知数据a ,4,2,5,3的平均数为b ,其中a ,b 是方程2430x x -+=的两个根,则这组数据的标准差是 . 5.已知函数()f x 是以5为周期的奇函数,且(3)2f -=,则(2)f -= . 6.以下程序运行后结果是__________. 1i ← 8While i <2233i i S i i i ←+←⨯+←+End While Pr int S7.如图,一个正四面体的展开图是边长为22的正三角形ABC ,则该四面体的外接球 的表面积为 .8.已知||1,(1,3)==-a b ,||3+=a b ,则a 与b 的夹角为 .9.已知数列{}n a 的前n 项和为n S ,11=a ,且3231=++n n S a (n 为正整数)则数列{}n a 的通项公式为 .10.命题:“存在实数x ,满足不等式2(1)10m x mx m +-+-≤”是假命题,则实数m 的取值范围是 .11.已知直线20ax by --=(,)a b R ∈与曲线3y x =过点(1,1)的切线垂直,则ba= . 12.如果椭圆)0(12222>>=+b a by a x 上存在一点P ,使得点P 到左准线的距离等于它到右焦点的距离的两倍,那么椭圆的离心率的取值范围为 . 13、(已知函数2()2sin 23sin cos 13f x x x x =--+的定义域为0,2π⎡⎤⎢⎥⎣⎦,求函数()y f x =的值域和零点.CBA(第7题)江苏省连云港田家炳2013届高三周练(12)1.已知集合{}2320A x x x =-+=,{}log 42x B x ==,则A B =2、已知等差数列{}n a ,22a =-,64a =,则4a = .3、方程2250x x -+=的复数根为 .4、已知集合{}4|1|2,lg(1)A x x B x y x⎧⎫=-≤==-⎨⎬⎩⎭,则A B = . 5、已知复数z 满足21z z i=++,则_________z =. 6、如右图,若执行程序框图,则输出的结果是 . 7、方程组125112x y ⎛⎫⎛⎫⎛⎫+= ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭的解是⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽. 8、某科技小组有6名同学,现从中选出3人参观展览,至少有1名女生入选的概率为45,则小组中女生人数为 .9、过抛物线22y x =的焦点F ,倾斜角为4π的直线l 交抛物线于,A B (A B x x >),则AF BF的值⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.10、若奇函数()y f x =的定义域为[4,4]-,其部分图像如图所示,则不等式()ln(21)0x f x -<的解集是 .11、已知ABC ∆三条边分别为,,a b c ,,,A B C 成等差数列,若2b =,则a c +的最大值为⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.12、在直三棱柱111C B A ABC -中, AB BC ⊥, D 为棱1CC 上任一点.(1)求证:直线11A B ∥平面ABD ;(2)求证:平面ABD ⊥平面11BCC B .开始1,1n A ==1n n =+1000A <是否 21A A =+ 输出n结束。
连云港市田家炳中学高三数学《数列》练习(2)

1.在等比数列{}n a 中,如果9,696==a a ,那么3a 等于2.如果9,,,,1--c b a 成等比数列,那么=b3.在等比数列{}n a 中,若11a =,418a =,则该数列的前10项和为4.等比数列{}n a 中,=3S 263,276=S ,则=n a ______5.在等比数列{}n a 中,12a =,前n 项和为n S ,若数列{}1n a +也是等比数列,则n S = __6.等差数列{}n a 的首项11=a ,公差0≠d ,若521,,a a a 成等比数列,则=d7.c b a ,,成等比数列,且公比为3,又c b a ,8,+成等差数列,则三数为_______8.在等比数列中,已知首项为89,末项为31,公比为32,则项数n 等于______. 9.等差数列{}n a 中,21=a ,公差不为零,且1131,,a a a 恰好为某等比数列的前三项,则等比数列的公比为 ______________10.已知在等比数列{}n a 中,1,0≠>q a n ,且132,21,a a a 成等差数列,则5443a a a a ++= . 11.n +⋅⋅⋅++⋅⋅⋅++++++21132112111= ___________________12.在等差数列{}n a 中,已知公差21=d ,且6099531=+⋅⋅⋅⋅⋅⋅+++a a a a ,则=+⋅⋅⋅⋅⋅⋅+++100321a a a a ____________13.设数列{}n a 的前n 项和为n S ,点(,)(*)N n S n n n∈均在函数23-=x y 的图象上.则数列{}n a的通项公式为 ____________14.设等比数列{}n a 的公比为q ,前n 项和为n S ,若12,,n n n S S S ++成等差数列,则q 的值_ ____15.有四个数,前三个数成等比数列,后三个数成等差数列,首末两项和为21,中间两项和为18,求这四个数.16.成等差数列的三个正数之和为15,若这三个数分别加上1,3,9后又成等比数列,求这三个数.17.已知数列{}n a 满足11=a ,)1(1++=+n S a n n .(1) 证明数列{}1+n a 成等比数列; (2)求n a 和n S .。
江苏省连云港市田家炳中学高三数学《立体几何线面平行》练习

江苏省连云港市田家炳中学高三数学《立体几何线面平行》练习1.下列命题,其中真命题的个数为 .①直线l平行于平面α内的无数条直线,则l∥α;②若直线a在平面α外,则a∥α;③若直线a∥b,直线b⊂α,则a∥α;④若直线a∥b,b⊂α,那么直线a就平行于平面α内的无数条直线.2. 对于不重合的两个平面α与β,给定下列条件:①存在平面γ,使得α,β都垂直于γ;②存在平面γ,使得α,β都平行于γ;③存在直线l⊂α,直线m⊂β,使得l∥m;④存在异面直线l、m,使得l∥α,l∥β,m∥α,m∥β.其中,可以判定α与β平行的条件有(写出符合题意的序号).3. (2008·海南,宁夏文,12)已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,一定成立的是 .①AB∥m ②AC⊥m③AB∥β④AC⊥β4.(2008·湖南理,5)设有直线m、n和平面α、β.下列命题不正确的是(填序号).①若m∥α,n∥α,则m∥n②若m⊂α,n⊂α,m∥β,n∥β,则α∥β③若α⊥β,m⊂α,则m⊥β④若α⊥β,m⊥β,m⊄α,则m∥α5下列关于互不相同的直线m,l,n和平面α,β的四个命题:①若m⊂α,l∩α=A,点A∉m,则l与m不共面;②若m,l是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α;③若l∥α,m∥β,α∥β,则l∥m;④若l⊂α,m⊂α,l∩m=A,l∥β,m∥β,则α∥β.其中假命题的序号是 .6 如图所示,正方体ABCD—A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F,且B1E=C1F.求证:EF∥平面ABCD.7如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E,F分别在线段AB,CD上,且AE∶EB=CF∶FD.(1)求证:EF∥β;(2)若E,F分别是AB,CD的中点,AC=4,BD=6,且AC,BD所成的角为60°,求EF的长.8如图所示,在正方体ABCD—A1B1C1D1中,E、F、G、H分别是BC、CC1、C1D1、A1A的中点.求证:(1)BF∥HD1;(2)EG∥平面BB1D1D;(3)平面BDF∥平面B1D1H.9正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ.求证:PQ∥平面BCE.。
连云港市田家炳中学高三数学专项练习向量的数量积

教学目标:1.理解平面向量数量积的概念;2.掌握两向量夹角的概念及其取值范围[0,]π; 3.掌握两向量共线及垂直的充要条件; 4.掌握向量数量积的性质. 教学过程: 一、【自学质疑】 引入:物理课中,物体所做的功的计算方法: ||||cos W F s θ= (其中θ是F 与s的夹角).二、【探究交流】 1.向量的夹角: 已知两个向量a 和b (如图2),作OA a = ,OB b = ,则AOB θ∠=(0180θ≤≤)叫做向量a 与b 的夹角. 当0θ=时,a 与b 同向;当180θ=时,a 与b 反向;当90θ= 时,a 与b 的夹角是90,我们说a 与b 垂直,记作a ⊥b .2.向量数量积的定义:已知两个非零向量a 和b ,它们的夹角为θ,则数量||||cos a b θ⋅⋅叫做a 与b 的数量积(或内积),记作a b ⋅ ,即||||cos a b a b θ⋅=⋅⋅.说明:①两个向量的数量积是一个数量,这个数量的大小与两个向量的长度及其夹角有关;②实数与向量的积与向量数量积的本质区别:两个向量的数量积是一个数量;实 数与向量的积是一个向量; ③规定,零向量与任一向量的数量积是0. 3.数量积的几何意义: (1)投影的概念:如图,OA a = ,,过点B 作1BB 垂直于直线OA ,垂足为1B ,则1||cos OB b θ= .||cos b θ叫做向量b 在a 方向上的投影,当θ为锐角时,它是正值;当θ为钝角时,它是一负值;当90θ= 时,它是0;当0θ= 时,它是||b ;当180θ=时,它是||b - . (2)a b ⋅ 的几何意义:数量积a b ⋅ 等于a 的长度||a 与b 在a 的方向上的投影||cos b θ的乘积.O ABabθ (图2) aO ABbθ 1B OABb a1B θ O ABb1()Bθ【自主空间】【练习】:①已知||5a = ,||4b = ,a 与b 的夹角120θ=,则a b ⋅= ;②已知||4b = ,a 在b 上的投影是1||2b,则a b ⋅= ;③已知||5a = ,||4b =, 32a b ⋅=- ,则a 与b 的夹角θ= .(3)数量积的性质:设a 、b 都是非零向量,θ是a 与b的夹角,则①cos ||||a ba b θ⋅= ;②当a 与b 同向时,||||a b a b ⋅= ;当a 与b 反向时,||||a b a b ⋅=- ;特别地:2||a a a ⋅= 或||a a a =⋅ ;③||||||a b a b ⋅≤ ; ④a b ⊥ 0a b ⇔⋅=; 若e 是与b方向相同的单位向量,则 ⑤||cos e a a e a θ⋅=⋅=.三、【精讲点拨】 例1 已知正ABC ∆的边长为2,设BC a = ,CA b = ,AB c = ,求a b b c c a ⋅+⋅+⋅.例2 已知||3a = ,||3b = ,||23c =,且0a b c ++= ,求a b b c c a ⋅+⋅+⋅ .四、课后练习:1.若非零向量a 与b 满足||||a b a b +=-,则a b ⋅= .2.已知|a |=2,|b |=3,a 与b 的夹角为90°,求a ·b .【教学反思】【自主空间】。
连云港市田家炳中学高三数学周练试题(3)

一、填空题:(每题5分,共14题)1.函数3sin(2)3y x π=+的振幅为 周期 当x= 有最小值 2.若tan 2α=,则22sin 3sin cos ααα-=3.定义在R 上的函数()f x 满足(4)()f x f x +=,当26x <≤时,()3f x x =-,则(1)f = .4.计算t a n10°t a n20°+3(t a n10°+t a n20°)= 。
5.函数5sin(2)4y x π=+的图像最靠近y 轴的一条对称轴方程是 6.在ABC Rt ∆中,斜边AB 的长为2,则ABC ∆的面积的最大值为___________。
7.设函数⎪⎩⎪⎨⎧≥-<=-2),1(log 2,2)(231x x x e x f x 则))2((f f 的值为 . 8.若411sin 3,cos()714ααβ=+=-,若,αβ是锐角,则β=___________.9.已知方程1sin cos -=-m x x 无实数解,则实数m 的取值范围10.已知α为锐角,且1sin cos 2αα=,则111sin 1cos αα+=++__________. 11.如果函数sin 2cos 2y x a x =+的图象关于直线8x π=-对称,那么a 等于 12.函数2sin(2)3y x π=-([0,])x π∈的递增区间是 13. 把函数x x y sin cos 3-=的图像向左平移)0(>m m 个单位,所得的图像关于y 轴对称,则m 的最小值是14.给出下列四个命题,其中正确的命题有 ①函数2sin(2)3y x π=-有一条对称轴方程是512x π=; ②函数()4sin(2) ()3f x x x R π=+∈,可改写成4cos(2)6y x π=+; ③若x x f 6cos )(sin =,则(cos15)0f ︒=;④正弦函数在第一象限为增函数.二、解答题:(请写出解题过程。
江苏省连云港市田家炳中学高三数学 基础训练

江苏省连云港市田家炳中学高三数学 基础训练一、填空题1.已知集合{}{}4,2,0,2,4,|13=--=-<<P Q x x ,则P Q = .2.若复数12,1z a i z i =-=+(i 为虚数单位),且12z z ⋅为纯虚数,则实数a 的值为 .3.如图所示的流程图中,输出的结果是 .4.在学生人数比例为2:3:5的A ,B ,C 三所学校中,用分层抽样方法招募n 名志愿者,若在A 学校恰好选出了6名志愿者,那么n = . 5.若)232cos(,31)6sin(απαπ+=-则的值为 . 6.已知等差数列}{n a 的前13项之和为413π,则)tan(876a a a ++等于 . 7.袋中装有2个红球, 2个白球, 这四个小球除颜色外其余均相同, 现从中任意摸出2个小球, 则摸出的两球颜色不同的概率为 8.若双曲线221y x k -=的焦点到渐近线的距离为k 的值是 .9.如图,在△ABC 中,∠ABC=900,AB=6,D 在斜边BC 上,且CD=2DB , 则AD AB ∙的值为 .10.已知命题p :|43|x -≤1;命题q :2(21)(1)x a x a a -+++≤0.若q ⌝是p ⌝的充分不必要条件,则实数a 的取值范围是 .11. 已知圆22x y m +=与圆2268110x y x y ++--=相交,则实数m 的取值范围为 .12.若直线y=x 是曲线y=x 3—3x 2+px 的切线,则实数p 的值为 .13. (本题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且A ,B ,C 成等差数列. (1)若32AB BC ⋅=-,且b =a +c 的值; (2)若存在实数m ,使得2sin sin A C m -=成立,求实数m 的取值范围.(第3题图)。
连云港市田家炳中学高三数学《三角函数》练习(1)

1、若角α的终边经过点)2,1(-P ,则=α2tan 。
2、.若,(0,)2παβ∈,53)2sin(=-βα,1sin()22αβ-=-,则2c o s βα+的值等于 。
3、将函数sin (0)y x ωω=>的图象向左平移6π后的图象如图所示,则平移后的图象所对应函数的解析式是 。
4、为了得到函数R x x y ∈+=),63sin(2π的图像,只需把函数R x x y ∈=,sin 2的图像上所有的点 。
5、.求︒-︒+︒40cos 2)10sin 310(cos 70tan 0的值。
6、.已知34παπ<<,23tan 10tan 30αα++= (Ⅰ)求tan α的值; (Ⅱ)求225sin 8sin cos 11cos 822222sin 2ααααπα++-⎛⎫- ⎪⎝⎭的值。
7、已知函数.3cos )4cos()4sin(32sin )(22---++=x x x x x f ππ(I )求函数)(x f 的最小正周期和单调递减区间;(II )求函数)(x f 在]32,12[ππ-上的最大值和最小值并指出此时相应的x 的值。
键。
8、如图,位于A 处的信息中心获悉:在其正东方向相距40海里的B 处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西︒30、相距20海里的C 处的乙船,现乙船朝北偏东θ的方向沿直线CB 前往B 处救援,求θcos 的值.9、在ABC ∆中,a 、b 、c 分别是三个内角A 、B 、C 的对边,且a 、b 、c 互不相等,设a =4,c =3,2A C =.(Ⅰ)求cos C 的值;(Ⅱ)求b 的值.10、,,,,,,ABC a b c A B C ∆在中分别是的对边且满足(2)cos cos a c B b C -=.(I)求角B 的大小; (II)若7,4,b a c ABC =+=∆求的面积.。
江苏省连云港市田家炳中学高三数学《直线和圆》练习

江苏省连云港市田家炳中学高三数学《直线和圆》练习【自我测试】1. (2009上海青浦区)直线013=+-y x 的倾斜角为 .2.(全国Ⅱ卷文3)原点到直线052=-+y x 的距离为 .3. (上海市青浦区2008调研)直线12:10:20l x my l x y ++=-+=与垂直,则m =_ .4. 过点(1,4)A ,且纵横截距的绝对值相等的直线共有_ __条5.【江苏·常州】8.直线l 与两直线1,70y x y =--=分别交于,A B 两点,若直线AB 的中点是(1,1)M -,则直线l 的斜率为 .6.【江苏·南通】3. 经过点(-2,3),且与直线250x y +-=平行的直线方程为 .7.光线从点P (-3,5)射到直线0443:=+-y x l 上,经过反射,其反射光线过点Q (3,5),则光线从P 到Q 所走过的路程为 .8.若直线mx+y+2=0与线段AB 有交点,其中A(-2, 3),B(3,2),求实数m 的取值范围 .9. 已知圆C :22(4)16x y -+=,若过点(2,6)的直线l 被圆C 所截得的弦长为34,则直线l 的方程为10.方程052422=+-++m y mx y x 表示圆的充要条件是 .11.(重庆卷文15)已知圆C : 22230x y x ay +++-=(a 为实数)上任意一点关于直线l :x -y +2=0的对称点都在圆C 上,则a = .14.(广东卷文6)经过圆2220x x y ++=的圆心C ,且与直线0x y +=垂直的直线方程是 .15.(上海市宝山区2008学年高三年级第一次质量调研4)设P 为圆221x y +=的动点,则点P 到直线34100x y --=的距离的最小值为 . 16.(四川延考理9)过点(1,1)的直线与圆22(2)(3)9x y -+-=相交于,A B 两点,则||AB 的最小值为 . 17.已知点P(2,1)在圆C :2220x y ax y b ++-+=上,点P 关于直线10x y +-=的对称点也在圆C 上,则圆C 的圆心坐标为 、半径为 .18..已知圆C 的方程为2210x y ax ++-=,若(1,2)A ,(2,1)B 两点一个在圆C 的内部,一个在圆C 的外部,则实数a 的取值范围是 .19.过点)1,0(P 与圆03222=--+x y x 相交的所有直线中,被圆截得的弦最长时的直线方程是 .20.过(1,2)总能作出两条直线和已知圆2222150x y kx y k ++++-=相切,求k 的取值范围 .22.点()4,4P ,圆C :22(1)5x y -+=与椭圆E :221182x y +=有一个公共点()3,1A ,12F F 、分别是椭圆左、右焦点,直线1PF 与圆C 相切.设Q 为椭圆E 上的一个动点,求AP AQ ⋅的取值范围.。
江苏省连云港市田家炳中学高三数学《集合与逻辑用语》练习(1)

江苏省连云港市田家炳中学高三数学《集合与逻辑用语》练习(1)1.用列举法表示集合D={2(,)8,,x y y x x N y N =-+∈∈}为 . 2.下列四个命题:①Φ={0};②空集没有子集;③任何一个集合必有两个或两个以上的子集;④空集是任何一个集合的子集.其中正确的有_____________________________3.集合A ={x |x 2+x -6=0},B ={x |mx +1=0},若B A ,则实数m 的值是 .4.已知集合{}{}{}2220,0,2M x x px N x x x q M N =++==--=⋂=且,则q p ,的值为________5.设集合A ={(x ,y )|4x +y =6},B ={(x ,y )|3x +2y =7},则满足C ⊆A ∩B 的集合C 的个数是_____________6.已知集合M={y|y=-x 2+1,x ∈R},N={y|y=x 2,x ∈R},则M ∪N 等于____________________7.设x,y ∈R,A={}(,)x y y x =,B= {}(,)1y x y x=,则A 、B 间的关系为____________________ 8.已知集合M={a,0},N={1,2},且M ∩N={1},那么M ∪N 的真子集有 个.9.已知A={-1,2,3,4};B={y|y=x 2-2x+2,x ∈A},若用列举法表示集合B ,则B= .10.已知全集U={0,1,2,…,9},若(C U A)∩(C U B)={0,4,5},A ∩(C U B)={1,2,8},A ∩B={9},试求A ∪B=_________________________________ 11.已知集合{}{}220,60,,A xx bx c B x x mx A B B A =++==++=⋃=且B ⋂={}2,求实数b,c,m 的值.12.已知集合A=}{240x Rx x ∈+=,B=}{222(1)10x R x a x a ∈+++-=,且A ∪B=A ,试求a 的取值范围.13.已知集合A={2210,,x ax x a R x R ++=∈∈}.(1)若A 中只有一个元素,求a 的值; (2)若A 中至多有一个元素,求a 的取值范围.14.已知集合A={}20,xx x -= B={}2240,x ax x -+=且A ⋂B=B ,求实数a 的取值范围.15.设全集U=R,集合A={}14x x -<<,B={}1,y y x x A =+∈,试求C U B, A ∪B, A ∩B,A ∩(C U B), ( C U A) ∩(C U B).16.已知集合A={x|x 2-3x+2=0},B={x|x 2-ax+3a -5},若A ∩B=B ,求实数a 的值.。
江苏省连云港市田家炳中学高三数学专项练习:向量的数量积(缺
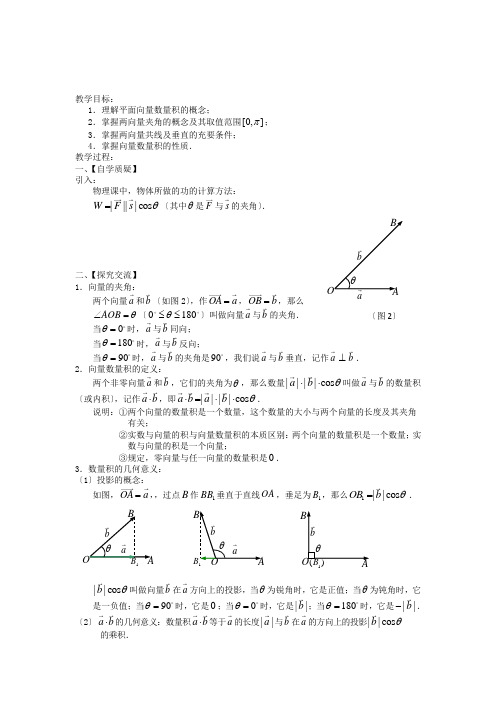
教学目标:1.理解平面向量数量积的概念;2.掌握两向量夹角的概念及其取值范围[0,]π;3.掌握两向量共线及垂直的充要条件;4.掌握向量数量积的性质.教学过程:一、【自学质疑】引入:物理课中,物体所做的功的计算方法:||||cos W F s θ=〔其中θ是F 与s 的夹角〕.二、【探究交流】1.向量的夹角:两个向量a 和b 〔如图2〕,作OA a =,OB b =,那么AOB θ∠=〔0180θ≤≤〕叫做向量a 与b 的夹角. 当0θ=时,a 与b 同向;当180θ=时,a 与b 反向;当90θ=时,a 与b 的夹角是90,我们说a 与b 垂直,记作a ⊥b .2.向量数量积的定义: 两个非零向量a 和b ,它们的夹角为θ,那么数量||||cos a b θ⋅⋅叫做a 与b 的数量积〔或内积〕,记作a b ⋅,即||||cos a b a b θ⋅=⋅⋅.说明:①两个向量的数量积是一个数量,这个数量的大小与两个向量的长度及其夹角有关;②实数与向量的积与向量数量积的本质区别:两个向量的数量积是一个数量;实 数与向量的积是一个向量;③规定,零向量与任一向量的数量积是0.3.数量积的几何意义:〔1〕投影的概念:如图,OA a =,,过点B 作1BB 垂直于直线OA ,垂足为1B ,那么1||cos OB b θ=.||cos b θ叫做向量b 在a 方向上的投影,当θ为锐角时,它是正值;当θ为钝角时,它 是一负值;当90θ=时,它是0;当0θ=时,它是||b ;当180θ=时,它是||b -. 〔2〕a b ⋅的几何意义:数量积a b ⋅等于a 的长度||a 与b 在a 的方向上的投影||cos b θ的乘积. A a b θ 〔图2〕 a B b θ 1B O b a 1θ b 1()B θ【练习】:①||5a =,||4b =,a 与b 的夹角120θ=,那么a b ⋅= ;②||4b =,a 在b 上的投影是1||2b ,那么a b ⋅= ;③||5a =,||4b =, 32a b ⋅=-a 与b 的夹角θ= . 〔3〕数量积的性质: 设a 、b 都是非零向量,θ是a 与b 的夹角,那么①cos ||||a b a b θ⋅=; ②当a 与b 同向时,||||a b a b ⋅=;当a 与b 反向时,||||a b a b ⋅=-; 特别地:2||a a a ⋅=或||a a a =⋅; ③||||||a b a b ⋅≤;④a b ⊥0a b ⇔⋅=;假设e 是与b 方向相同的向量,那么⑤||cos e a a e a θ⋅=⋅=.三、【精讲点拨】例1 正ABC ∆的边长为2,设BC a =,CA b =,AB c =,求a b b c c a ⋅+⋅+⋅.例2 ||3a =,||3b =,||23c =,且0a b c ++=,求a b b c c a ⋅+⋅+⋅.四、课后练习:1.假设非零向量a 与b 满足||||a b a b +=-,那么a b ⋅= .2.|a |=2,|b |=3,a 与b 的夹角为90°,求a ·b .。
江苏省连云港市田家炳中学高三数学周练试题(1)

江苏省连云港市田家炳中学高三数学周练试题(1)一、填空题1.已知集合{}11M =-,,11242x N xx +⎧⎫=<<∈⎨⎬⎩⎭Z ,,则M N =I __ . 2.设向量a ϖ与b ϖ的夹角为θ,)3,3(=a ϖ,)1,1(2-=-a b ϖϖ,则cos θ= .3.8.若向量b a ,满足2||,1||==b a ,且a 与b 的夹角为3π,则||b a += . 4.函数322)1()(-+--=m m x m m x f 是幂函数,且在),0(+∞上为减函数,则实数m 的值为 .5.设31sin (), tan(),522πααππβ=<<-=则tan ()βα-的值等于__ . 6.函数122-=x y 的最小值是 .7.在ABC ∆中,如果7:5:3sin :sin :sin =C B A ,那么C ∠等于 .8.已知(sin ,2)α=-a ,(1,cos )α=b ,且⊥a b . 2cos sin cos ααα-=9.设2)12(sin π=a ,12tan 2π=b ,)12(cos log 2π=c ,则c b a ,,由小到大的顺序为 . 10.已知函数⎩⎨⎧≤>=)0(3)0(log )(2x x x x f x 则)]41([f f 的值是 . 11.已知角α的终边经过点)6,(--x P ,且135cos -=α,则=+ααtan 1sin 1 . 12.已知函数()f x 是定义在实数集R 上的奇函数,且在区间[)+∞,0上是单调递增,若0)2(lg ))5(lg 50lg 2(lg 2<-++⋅x f f ,则x 的取值范围为 .14.若)21(log )(2+-=ax ax x f a 在]23,1[上恒正,则实数a 的取值范围是 . 15.奇函数()[3,7]f x 在区间上是增函数,在区间[3,6]上的最大值为8,最小值为-1,则2(6)(3)f f -+-= .16.若函数()21f x ax x =++在区间[)2,-+∞上为单调增函数,则实数a 的取值范围是17.不等式2(2)2(2)40a x a x -+--<对一切x R ∈恒成立,则a 的取值范围是_____18. 已知函数)sin(2θω+=x y 为偶函数(0,0)θπω<<>,其图像与直线y =2的某两个交点横坐标为1x ,2x ,||12x x -的最小值为π,则=ω ,=θ 。
江苏省连云港市田家炳中学高三数学周练试题(4)

江苏省连云港市田家炳中学高三数学周练试题(4)一、填空题:⒈若集合}2,1{-=m A ,且}2{=B A I ,则实数m 的值为 。
⒉若复数z 满足2)1(=-z i (为虚数单位),则=z 。
⒊现有在外观上没有区别的5件产品,其中3件合格,2件不合格,从中任意抽检2件,则一件合格,另一件不合格的概率为 。
⒋已知正六棱锥的底面边长是3,侧棱长为5,则该正六棱锥的体积是 。
⒌若1e ,2e 是两个单位向量,212e e a -=,2145e e b +=,且a ⊥b ,则1e ,2e 的夹角为 。
⒍如图,该程序运行后输出的结果为 。
⒎函数⎪⎭⎫ ⎝⎛-=4sin 2)(πx x f ,[]0,π-∈x 的单调递增区间为 。
⒏若等比数列{}n a 满足43=-m a 且244a a a m m =-(*N m ∈且4>m ),则51a a 的值为 。
⒐过点)3,2(且与直线1l :0=y 和2l :x y 43=都相切的所有圆的半径之和为 。
⒑设函数)(x f y =满足对任意的R x ∈,0)(≥x f 且9)()1(22=++x f x f 。
已知当]1,0[∈x 时,有242)(--=x x f ,则⎪⎭⎫ ⎝⎛62013f 的值为 。
⒒椭圆12222=+by a x (0>>b a )的左焦点为F ,直线m x =与椭圆相交于A ,B 两点,若FAB ∆的周长最大时,FAB ∆的面积为ab ,则椭圆的离心率为 。
⒓若函数()2ln 2f x mx x x =+-在定义域内是增函数,则实数m 的取值范围是 .⒔若点G 为ABC ∆的重心,且AG ⊥BG ,则C sin 的最大值为 。
14.设OM u u u u r =112⎛⎫ ⎪⎝⎭,,ON u u u r =(0,1),O 为坐标原点,动点P (x ,y )满足0≤OP OM ⋅u u u r u u u u r ≤1,0≤OP ON ⋅u u u r u u u r ≤1,则z =y -x 的最小值是 .二、解答题:本大题共6小题,计90分。
江苏省连云港市田家炳中学高三数学周练试题(6)

江苏省连云港市田家炳中学高三数学周练试题(6)一、填空题.本大题共10小题,每小题5分,共50分.把正确答案填在相应位置.1.若直线1+=kx y 与直线042=-+y x 垂直,则=k .2.已知集合{}m P ,1-=,⎭⎬⎫⎩⎨⎧<<-=431x x Q ,若∅≠⋂Q P ,则整数=m . 3.一根绳子长为6米,绳上有5个节点将绳子6等分,现从5个节点中随机选一个将绳子剪断,则所得的两段绳长均不小于2米的概率为 .4.2000年级 高一 高二 高三人数 800 600 600现用分层抽样的方法在全校抽取120名学生,则应在高三年级抽取的学生人数为 .5.若命题“R x ∈∀,02≥+-a ax x ”为真命题,则实数a 的取值范围是 .6.某程序框图如图所示,若输出的10=S ,则自然数=a .7.若复数z 满足1=-i z (其中i 为虚数单位),则z 的最大值为 .8.已知向量a 的模为2,向量e 为单位向量,)(e a e -⊥,则向量a 与e 的夹角大小为 .9.在等比数列{}n a 中,已知1235a a a =,78940a a a =,则567a a a = .10.函数65cos 2cos 6sin 2sin )(ππx x x f -=在⎥⎦⎤⎢⎣⎡-2,2ππ上的单调递增区间为 .11.已知f (x )是定义在R 上的奇函数,且f (x +4)=f (x ),当x ∈(0,2)时,f (x) =x +2,则f (7)=____12.过圆922=+y x 内一点)2,1(P 作两条相互垂直的弦AC ,BD ,当BD AC =时,四边形ABCD 的面积为 .13.若)(x f y =是定义在R 上周期为2的周期函数,且)(x f 是偶函数,当[]1,0∈x 时,12)(-=x x f ,则函数x x f x g 3log )()(-=的零点个数为 .14.设)(x f 是定义在R 上的可导函数,且满足0)()('>+x xf x f .则不等式)1(1)1(2-->+x f x x f 的解集为 .二、解答题.本大题共2小题,共30分.解答时要求写出必要的文字说明、证明过程或推理步骤.14.(本小题满分14分)在四棱锥ABCD P -中,⊥PA 底面ABCD ,CD AB //,BC AB ⊥,1==BC AB ,2=DC ,点E 在PB 上.(1)求证:平面⊥AEC 平面PAD ;(2)当//PD 平面AEC 时,求PE :EB 的值.15.(本小题满分14分)设ABC ∆的内角A ,B ,C 的对边长分别为a ,b ,c ,且.212ac b =(1)求证:43cos ≥B ; (2)若1cos )cos(=+-B C A ,求角B 的大小.17、 已知椭圆)0(12222>>=+b a b y a x 的离心率为22,且过点)21,22(P ,记椭圆的左顶点为.A(1)求椭圆的方程;(2)设垂直于y 轴的直线l 交椭圆于B ,C 两点,试求ABC ∆面积的最大值;(3)过点A 作两条斜率分别为1k ,2k 的直线交椭圆于D ,E 两点,且221=k k ,求证:直线DE 恒过一个定点.18、在数列{}n a 中,11a =,且对任意的*k N ∈,21221,,k k k a a a -+成等比数列,其公比为k q .(1)若k q =2(*k N ∈),求13521...k a a a a -++++;(2)若对任意的*k N ∈,k a 2,12+k a ,22+k a 成等差数列,其公差为k d ,设11k k b q =-. 求证:{}k b 成等差数列,并指出其公差;。
江苏省连云港市田家炳中学高三数学《指数函数、对数函数、幂函数》练习

江苏省连云港市田家炳中学高三数学《指数函数、对数函数、幂函数》练习一、填空题1.已知a =133()4-,b =143()4-,c =343()2-,则a 、b 、c 的大小关系为______________. 2.(2011·镇江模拟)函数f (x )=⎩⎪⎨⎪⎧ -x +3a ,x <0,a x , x ≥0 (a >0且a ≠1)是R上的减函数,则a 的取值范围为________.3.若函数f (x )=a x -1(a >0且a ≠1)的定义域和值域都是[0,2],则实数a 的值为________.4.设a =log 32,b =ln 2,c =125-,则a ,b ,c 大小关系为________ .5.2lg 5+23lg 8+lg 5·lg 20+lg 22=________. 6.函数f (x )=ln 1+ax 1+2x(a ≠2)为奇函数,则实数a 等于________. 7.已知函数f (x )=a x +log a x (a >0,a ≠1)在[1,2]上的最大值与最小值之和为log a 2+6,则a 的值为________.8.若函数f (x )=⎩⎪⎨⎪⎧ log 2x , x >0,log 12-x ,x <0,若f (a )>f (-a ),则实数a 的取值范围为______________.9.若函数f (x )是幂函数,且满足f f =3,则f (12)的值为________. 10.若幂函数y =222(33)m m m m x ---+的图象不经过原点,则实数m 的值为________.11.已知函数f (x )=x α(0<α<1),对于下列命题:①若x >1,则f (x )>1;②若0<x <1,则0<f (x )<1;③当x >0时,若f (x 1)>f (x 2),则x 1>x 2;④若0<x 1<x 2,则f x 1x 1<f x 2x 2. 其中正确的命题序号是______________.12. 已知n ∈{-1,0,1,2,3},若(-12)n >(-15)n ,则n =________. 二、解答题13、已知f (x )=2123n n x -++(n =2k ,k ∈Z )的图象在 [0,+∞)上单调递增,解不等式f (x 2-x )>f (x +3).14.已知f (x )=2+log 3x ,x ∈[1,9],求y =[f (x )]2+f (x 2)的最大值及y 取最大值时x的值.15.已知函数f (x )=log a (x +1)-log a (1-x ),a >0且a ≠1.(1)求f (x )的定义域;(2)判断f (x )的奇偶性并予以证明;(3)若a >1时,求使f (x )>0的x 的解集.16、已知定义域为R 的函数f (x )=-2x +b 2x +1+a是奇函数. (1)求a ,b 的值; (2)若对任意的t ∈R ,不等式f (t 2-2t )+f (2t 2-k )<0恒成立,求k 的取值范围.17.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x 的定义域为[0,1]. (1)求a的值.(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.18.函数y =1+2x +4x a 在x ∈(-∞,1]上y >0恒成立,求a 的取值范围.。
田家炳中学高三数学试卷

一、选择题(每题5分,共50分)1. 若函数f(x) = ax^2 + bx + c在x=1时取得最小值,则下列选项中正确的是()A. a > 0,b = 0,c = 0B. a > 0,b = 0,c ≠ 0C. a < 0,b ≠ 0,c ≠ 0D. a > 0,b ≠ 0,c ≠ 02. 下列不等式中正确的是()A. |x - 1| > 0B. x^2 + 1 > 0C. x^3 > 0D. x^2 - 1 > 03. 已知等差数列{an}的前n项和为Sn,若a1 = 3,S10 = 55,则公差d的值为()A. 1B. 2C. 3D. 44. 下列命题中正确的是()A. 若函数f(x)在区间(a, b)内单调递增,则f(a) < f(b)B. 若函数f(x)在区间(a, b)内单调递减,则f(a) > f(b)C. 若函数f(x)在区间(a, b)内单调递增,则f(a) < f(b)D. 若函数f(x)在区间(a, b)内单调递减,则f(a) > f(b)5. 已知复数z = a + bi(a, b ∈ R),若|z - 1| = |z + 1|,则a的值为()B. 1C. -1D. 26. 已知函数f(x) = x^3 - 3x,若函数f(x)在区间(0, 1)内存在两个零点,则下列选项中正确的是()A. f(0) < 0,f(1) > 0B. f(0) > 0,f(1) < 0C. f(0) < 0,f(1) < 0D. f(0) > 0,f(1) > 07. 已知等比数列{an}的前n项和为Sn,若a1 = 2,S5 = 32,则公比q的值为()A. 2B. 4C. 1/2D. 1/48. 下列命题中正确的是()A. 若函数f(x)在区间(a, b)内连续,则f(a) < f(b)B. 若函数f(x)在区间(a, b)内连续,则f(a) > f(b)C. 若函数f(x)在区间(a, b)内连续,则f(a) ≤ f(b)D. 若函数f(x)在区间(a, b)内连续,则f(a) ≥ f(b)9. 已知复数z = a + bi(a, b ∈ R),若|z - 1| = |z + 1|,则b的值为()A. 0B. 1C. -110. 已知函数f(x) = x^3 - 3x,若函数f(x)在区间(0, 1)内存在两个零点,则下列选项中正确的是()A. f(0) < 0,f(1) > 0B. f(0) > 0,f(1) < 0C. f(0) < 0,f(1) < 0D. f(0) > 0,f(1) > 0二、填空题(每题5分,共25分)11. 若函数f(x) = ax^2 + bx + c的图像开口向上,且顶点坐标为(1, 2),则a = __________,b = __________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
一、填空题
1.已知集合{}{}4,2,0,2,4,|13=--=-<<P Q x x ,则P Q = .
2.若复数12,1z a i z i =-=+(i 为虚数单位),且12z z ⋅为纯虚数,则实数a 的值为 .
3.如图所示的流程图中,输出的结果是 .
4.在学生人数比例为2:3:5的A ,B ,C 三所学校中,用分层抽样方
法招募n 名志愿者,若在A 学校恰好选出了6名志愿者,那么
n = . 5.若)232cos(,31)6sin(απαπ
+=-则的值为 . 6.已知等差数列}{n a 的前13项之和为413π,则)tan(876a a a ++等 于 . 7.袋中装有2个红球, 2个白球, 这四个小球除颜色外其余均相同, 现从中任意摸出2个小球, 则摸出的两球颜色不同的概率为 8.若双曲线2
21y x k -=的焦点到渐近线的距离为22,则实数k 的值 是 .
9.如图,在△ABC 中,∠ABC=900,AB=6,D 在斜边BC 上,且CD=2DB , 则AD AB ∙的值为 .
10.已知命题p :|43|x -≤1;命题q :2(21)(1)x a x a a -+++≤0.若q ⌝是p ⌝的充分不
必要条件,则实数a 的取值范围是 .
11. 已知圆22x y m +=与圆2268110x y x y ++--=相交,则实数m 的取值范围
为 .
12.若直线y=x 是曲线y=x 3—3x 2+px 的切线,则实数p 的值为 .
13. (本题满分14分)
在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且A ,B ,C 成等差数列.
(1)若32
AB BC ⋅=- ,且3b =,求a +c 的值; (2)若存在实数m ,使得2sin sin A C m -=成立,求实数m 的取值范围.
a ←5,S ←1
S ←S ×a
a ←a -1 结束 a ≥2 否 是
开始 输出S (第3题图)。
