第04讲__运算符及应用
九年级上第04讲 一元二次方程的应用 讲义+练习

类型三利润问题
某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
当3<x≤4时,S= ×2×(12-3x)=12-3x= ,∴x= (舍去),∴此时不存在.
综上所述,x= 或2+ 时,S= .
(3)当△AQP为锐角三角形时,2<x<6-2 .
1.受“减少税收,适当补贴”政策的影响,某市居民购房热情大幅提高.据调查,2017年1月该市宏鑫房地产公司的住房销售量为100套,3月份的住房销售量为169套.假设该公司这两个月住房销售量的增长率为x,根据题意所列方程为_____.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
【答案】(1)苗圃园与墙平行的一边长为(30-2x)米.依题意可列方程
(1)填表:(不需化简)
时间
第一个月
第二个月
清仓时
单价(元)
80
40
销售量(件)
200
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
【答案】
(1)80-x,200+10x,800-200-(200+10x);
(2)根据题意,得80×200+(80-x)(200+10x)+40[800-200-(200+10x)]-50×800=9000,
第04讲乘法运算定律推广到分数-(五升六)2023年六年级上册数学暑假衔接课(人教版)

第04讲乘法运算定律推广到分数【知识梳理】1、分数混合运算和简便计算。
(1)分数混合运算的运算顺序和整数混合运算的运算顺序相同,都是没有括号的,先算乘除法,再算加减法;有括号的先算括号里面的。
(2)整数乘法的交换律、结合律和分配律对于分数乘法同样适用。
【典型例题】例1两根木棒共长63米,第一根用去它的27,第二根用去后余下它的57,两根木棒一共用去________米。
【分析】第一根用去了27×第一根木棒长,第二根用去了517⎛⎫⎪⎝⎭-×第二根木棒长,据此解答。
【详解】2 7×第一根木棒长+517⎛⎫⎪⎝⎭-×第二根木棒长=27×第一根木棒长+27×第二根木棒长=27×(第一根木棒长+第二根木棒长)=27×63=18(米)【点睛】解答本题关键在于求出第一根和第二根都用去了各自长度的27,用乘法分配律表示出一共用去的。
例2某洗衣机厂五月份计划生产洗衣机504台,实际上半月完成了59,下半月完成了23,这个月实际生产洗衣机多少台? 【分析】我们把计划的生产量看成单位“1”,先求上下半月生产的对应分率和,再用单位“1”的量乘上全月对应分率和就是实际生产的台数。
【详解】 504×(59+23)=504×119=616(台)答:这个月实际生产了洗衣机616台。
【点睛】找出单位“1”,看实际的是单位“1”的几分之几,进而求出实际的量。
例3“十一国庆”过后,快递小张10月9日上午送快递73件,下午送快递155件,如果平均送一件快递要72分钟,小张这一天工作了多长时间? 【分析】首先用快递员小张11月9日上午送快递的数量加上下午送快递的数量,求出小张这一天一共送快递多少件;然后用它乘平均送一件快递要用的时间,求出小张这一天工作了多长时间即可。
【详解】 7731552⨯(+)72282⨯=798=(分钟)答:小张这一天工作了798分钟。
04第四讲 直方图及点运算

第 四 讲 直 方 图 及 点 运 算
4.1 灰度直方图
5. 直方图的作用:边界阈值选择
第 四 讲 直 方 图 及 点 运 算
频率
0
100
阈值 T
200
255 灰度
双峰直方图与阈值的确定
4.1 灰度直方图
5. 直方图的作用:边界阈值选择
第 四 讲 直 方 图 及 点 运 算
int iWidth = pDib->GetWidth(); int iHeight = pDib->GetHeight(); int iBitsWidth = pDib->GetBitsWidth(); unsigned char * lpPixel; LPSTR lpStartBit = pDib->GetPixelBit(); int i,j; // 获取图像宽度 // 获取图像高度 // 获取图像存储宽度 // 指向像素的指针 // 图像数据起始位置 // 循环变量
b
c
f
4.3 线性变换
6. 线性变换五 分段线性变换
第 四 讲 直 方 图 及 点 运 算
4.3 线性变换
7. 线性变换六
g
锯齿波变换
第 四 讲 直 方 图 及 点 运 算
d
灰度区间[0,a]变换为[0,d] ; 灰度区间[a,b]变换为[0,d] ; 灰度区间[b,c]变换为[0,d] 。
图像数据
内容回顾
位图文件头 位图信息头 调色板
调色板:颜色查找表,Look Up Table (LUT),由若干个颜色表项构成,每个 表项长度为4bit。 单色DIB:2个表项; 16色DIB:16个表项; 256色DIB:256个表项; 真彩色DIB:无调色板。 Typedef struct tag RGBQUAD { BYTE rgbBlue; //该颜色的蓝色分量 BYTE rgbGreen; //该颜色的绿色分量 BYTE rgbRed; //该颜色的红色分量 BYTE rgbReserved; //保留值,不考虑 } RGBQUAD;
第04讲 对数与对数函数(含对数型糖水不等式的应用)(学生版) 备战2025年高考数学一轮复习学案

第04讲 对数与对数函数(含对数型糖水不等式的应用)(8类核心考点精讲精练)1. 5年真题考点分布2. 命题规律及备考策略【命题规律】本节内容是新高考卷的命题常考内容,设题多为函数性质或函数模型,难度中等,分值为5-6分【备考策略】1.理解对数的概念和运算性质,熟练指对互化,能用换底公式能将一般对数转化成自然对数或常用对数2.了解对数函数的概念,能画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点3.熟练掌握对数函数x y a log =0(>a 且)1≠a 与指数函数x a y =0(>a 且)1≠a 的图象关系【命题预测】本节内容通常会考查指对幂的大小比较、对数的运算性质、对数的函数模型等,需要重点备考复习1.对数的运算(1)对数的定义如果,那么把叫做以为底,的对数,记作N x a log =,其中叫做对数的底数,叫做真数(2)对数的分类一般对数:底数为,,记为N a log 常用对数:底数为10,记为,即:xx lg log 10=自然对数:底数为e (e ≈2.71828…),记为,即:x x e ln log =(3)对数的性质与运算法则①两个基本对数:①01log =a ,②1log =a a ②对数恒等式:①N a N a =log ,②N a Na =log 。
③换底公式:aba b a b b c c a ln ln lg lg log log log ===;推广1:对数的倒数式ab b a log 1log =1log log =⋅⇒a b b a 推广2:d d c b a c b a c b a c b a log log log log 1log log log =⇒=。
④积的对数:()N M MN a a a log log log +=;(01)xa N a a =>≠且x a N a N a 0,1a a >≠且lg N ln N⑤商的对数:N M NMa a alog log log -=;⑥幂的对数:❶b m b a ma log log =,❷b nb a a n log 1log =,❸b n mb a ma n log log =,❹mna ab b nm log log =2.对数函数(1)对数函数的定义及一般形式形如:()0,10log >≠>=x a a x y a 且的函数叫做对数函数(2)对数函数的图象和性质图象定义域:()∞+,0值域:R当1=x 时,0=y 即过定点()0,1当时,;当时,当时,;当时,性质在()∞+,0上为增函数(5)在()∞+,0上为减函数3.对数型糖水不等式(1) 设 n N +Î, 且 1n >, 则有 12log log (1)n n n n ++<+ (2) 设 1,0a b m >>>, 则有 log log ()a a m b b m +<+(3) 上式的倒数形式:设 1,0a b m >>>, 则有 log log ()b b ma a m +>+1.(2024·重庆·三模)已知2log 5,85ba ==,则ab =.1a >01a <<01x <<(,0)y Î-∞1x >(0,)y Î+∞1x >(,0)y Î-∞01x <<(0,)y Î+∞2.(2024·青海·模拟预测)若3log 5a =,56b =,则3log 2ab -=( )A .1B .-1C .2D .-23.(2024·四川·模拟预测)若实数m ,n ,t 满足57m n t ==且112m n+=,则t =( )A.B .12CD1.(2024·河南郑州·三模)已知log 4log 4a b b a +=,则22a b 的值为.2.(2024·全国·高考真题)已知1a >且8115log log 42a a -=-,则=a .3.(2024·辽宁丹东·一模)若23a=,35b =,54c =,则4log abc =( )A .2-B .12CD .11.(2024·河南·三模)函数()f x = )A .(,0]-∞B .(,1)-∞C .[0,1)D .[0,)+∞1.(2023·广东珠海·模拟预测)函数()lg(21)f x x =-的定义域是( )A .1,2æö-∞ç÷èøB .1,2æö+∞ç÷èøC .1,2æù-∞çúèûD .1,2éö+∞÷êëø2.(2024·青海海南·二模)函数()2lg 10()x f x x-=的定义域为( )A.(B.(,)-∞+∞U C.[D.(È1.(2024高三·全国·专题练习)已知函数① y =log ax ;② y =log bx ;③ y =log cx ;④ y =log dx 的大致图象如图所示,则下列不等关系正确的是( )A .a +c <b +aB .a +d <b +cC .b +c <a +dD .b +d <a +c2.(2024·广东深圳·二模)已知0a >,且1a ≠,则函数1log a y x a æö=+ç÷èø的图象一定经过( )A .一、二象限B .一、三象限C .二、四象限D .三、四象限3.(2024·陕西渭南·二模)已知直线240mx ny +-=(0m >,0n >)过函数()log 12a y x =-+(0a >,且1a ≠)的定点T ,则26m n+的最小值为 .1.(2024高三·全国·专题练习)在同一平面直角坐标系中,函数y =1x a,y =log a (x +12)(a >0,且a ≠1)的图象可能是( )A .B .C .D .2.(2024·全国·模拟预测)若函数()log 21(0a y x a =-+>,且1)a ≠的图象所过定点恰好在椭圆221(0,0)x y m n m n+=>>上,则m n +的最小值为 .1.(辽宁·高考真题)函数212log (56)y x x =-+的单调减区间为( )A .52,æö+∞ç÷èøB .(3)+∞,C .52æö-∞ç÷èø,D .()2-∞,2.(2024·江苏南通·模拟预测)已知函数()ln(2)f x ax =+在区间(1,2)上单调递减,则实数a 的取值范围是( )A .a<0B .10a -£<C .10a -<<D .1a ³-3.(2024·全国·高考真题)已知函数22,0()e ln(1),0x x ax a x f x x x ì---<=í++³î在R 上单调递增,则a 的取值范围是( )A .(,0]-∞B .[1,0]-C .[1,1]-D .[0,)+∞4.(2024·北京·高考真题)已知()11,x y ,()22,x y 是函数2x y =的图象上两个不同的点,则( )A .12122log 22y y x x ++<B .12122log 22y y x x ++>C .12212log 2y y x x +<+D .12212log 2y y x x +>+1.(23-24高三下·青海西宁·开学考试)已知函数()()2lg 1f x x ax =++在区间(),2-∞-上单调递减,则a 的取值范围为 .2.(2022高三·全国·专题练习)函数()()215log 232f x x x =-++的单调递减区间为 .3.(23-24高三上·甘肃白银·阶段练习)已知()()312,1log ,1a a x a x f x x x ì-+£=í>î是R 上的单调递减函数,则实数a 的取值范围为.1.(山东·高考真题)函数2()log 31()xf x =+的值域为( )A .(0,)+∞B .[0,)+∞C .(1,)+∞D .[1,)+∞2.(22-23高三上·河北·阶段练习)已知函数()()2lg 65f x ax x =-+的值域为R ,那么a 的取值范围是 .3.(23-24高一下·上海闵行·阶段练习)函数()[]212log 2,2,6y x x x =+-Î的最大值为 .1.(2024高三·全国·专题练习)函数()[]ln ,1,e f x x x x =+Î的值域为.2.(2023高一·全国·课后作业)函数()212log 617y x x =-+的值域是 .3.(2024高三·全国·专题练习)已知函数()()2log 14f x x x =££,则函数()()()221g x f x f x éù=++ëû的值域为 .1.(2024高三·全国·专题练习)已知函数)2()log f x x =-是奇函数,则=a.2.(23-24高一上·安徽阜阳·期末)若函数()()(e e ln 1x x m n f x x -=-++(m ,n 为常数)在[]1,3上有最大值7,则函数()f x 在[]3,1--上( )A .有最小值5-B .有最大值5C .有最大值6D .有最小值7-3.(2024·江苏泰州·模拟预测)已知函数()21log 1f x a b x æö=-+ç÷+èø,若函数()f x 的图象关于点()1,0对称,则log a b =( )A .-3B .-2C .12-D .13-1.(22-23高二下·江西上饶·阶段练习)已知函数())3ln3f x x x =--+,[2023,2023]x Î-的最大值为M ,最小值为m ,则M m += .2.(2024·宁夏银川·二模)若()1ln 1f x a b x++-=是奇函数,则b = .1.(2024·天津·高考真题)若0.30.34.24.2 4.2log 0.2a b c -===,,,则a b c ,,的大小关系为( )A .a b c >>B .b a c >>C .c a b>>D .b c a>>2.(2022·天津·高考真题)已知0.72a =,0.713b æö=ç÷èø,21log 3c =,则( )A .a c b >>B .b c a >>C .a b c >>D .c a b>>3.(2022·全国·高考真题)设0.110.1e ,ln 0.99a b c ===-,则( )A .a b c <<B .c b a <<C .c<a<bD .a c b<<4.(2021·全国·高考真题)设2ln1.01a =,ln1.02b =,1c =.则( )A .a b c<<B .b<c<aC .b a c<<D .c<a<b1.(2021·天津·高考真题)设0.3212log 0.3,log 0.4,0.4a b c ===,则a ,b ,c 的大小关系为( )A .a b c <<B .c<a<bC .b<c<aD .a c b<<2.(2021·全国·高考真题)已知5log 2a =,8log 3b =,12c =,则下列判断正确的是( )A .c b a<<B .b a c<<C .a c b <<D .a b c<<3.(2024·全国·模拟预测)若log 4a =,14log 7b =,12log 6c =,则( )A .a b c >>B .b c a >>C .c b a>>D .a c b>>4.(23-24高三上·河北保定·阶段练习)设3log 4a =,0.8log 0.7b =,511.02c =,则a ,b ,c 的大小关系为( )A .a c b <<B .a b c <<C .b a c<<D .c<a<b5.(2024·山西·二模)设202310121011a æö=ç÷èø,202510131012b æö=ç÷èø,则下列关系正确的是( )A .2e a b <<B .2e b a <<C .2e a b <<D .2e b a <<1.(2022·全国·统考高考真题)已知910,1011,89m m m a b ==-=-,则( )A .0a b>>B .0a b >>C .0b a >>D .0b a>>1. 比较大小: 7log 4 与 9log 6?2.(2024·重庆·模拟预测)设2024log 2023a =,2023log 2022b =,0.2024log 0.2023c =,则( )A .c<a<b B .b<c<a C .b a c<<D .a b c<<一、单选题1.(2024·河北衡水·三模)已知集合{}()11,2,3,4,51lg 12A B x x ìü==-£-£íýîþ,,则A B =I ( )A .11510x x ìü££íýîþB .{2,3,4}C .{2,3}D .11310x x ìü££íýîþ2.(2024·贵州贵阳·三模)已知()()40.34444,log ,log log a b a c a ===,则( )A .a b c>>B .a c b>>C .b c a>>D .c a b>>3.(2024·天津滨海新·三模)已知2log 0.42a =,0.4log 2b =,031log 0.4c =.,则( )A .a b c>>B .b a c>>C .c a b>>D .a c b>>4.(2024·江苏宿迁·三模)已知函数()f x 为R 上的奇函数,且当0x >时,22()log 13f x x =-,则(f =( )A .59B .59-C .49D .49-5.(2024·河北沧州·模拟预测)直线4x =与函数()()12log (1),log a f x x a g x x =>=分别交于,A B 两点,且3AB =,则函数()()()h x f x g x =+的解析式为( )A .()2log h x x =-B .()4log h x x =-C .()2log h x x=D .()4log h x x=6.(2024·江苏盐城·模拟预测)函数cos y x =与lg y x =的图象的交点个数是( )A .2B .3C .4D .67.(2024·四川成都·模拟预测)已知定义在R 上的奇函数()f x 满足(3)(1)f x f x +=-,且当(2,0)x Î-时,2()log (3)f x x =+,则(2021)(2024)f f -=( )A .1B .1-C .21log 3-D .21log 3--二、填空题8.(2024·湖北·模拟预测)若函数()()()2ln e R x f x a x x =--Î为偶函数,则=a.9.(2024·吉林·模拟预测)若函数()ln(1)f x ax =+在(1,2)上单调递减,则实数a 的取值范围为.10.(2024·四川成都·三模)函数()ln 2m x f x x -=+的图象过原点,且()()e e 2x x g x f x m l l --=++,若()6g a =,则()g a -=.一、单选题1.(2024·黑龙江·模拟预测)设函数()ln ||f x x a =-在区间(2,3)上单调递减,则a 的取值范围是( )A .(,3]-∞B .(,2]-∞C .[2,)+∞D .[3,)+∞2.(2024·山东菏泽·模拟预测)已知函数()()()2e 1ln 2013mx f x m x+=->-是定义在区间(),a b 上的奇函数,则实数b 的取值范围是( )A .(]0,9B .(]0,3C .20,3æùçúèûD .10,3æùçúèû3.(2024·河北·三模)已知(),,1,a b c Î+∞,8ln ln10a a =,7ln ln11b b =,6ln ln12cc =,则下列大小关系正确的是( )A .c b a>>B .a b c>>C .b c a>>D .c a b>>4.(2024·广西贵港·模拟预测)已知函数41()log (41)2xf x x =+-,若(1)(21)-£+f a f a 成立,则实数a 的取值范围为( )A .(,2]-∞-B .(,2][0,)-∞-È+∞C .4[2,]3-D .4(,2][,)3-∞-+∞U 5.(2024·湖北黄冈·模拟预测)已知7ln 5a =,2cos 5b =,25c =,则,,a b c 的大小关系为( )A .a b c >>B .b c a >>C .c b a >>D .c a b>>6.(2024·陕西安康·模拟预测)已知函数()13,4443log (4)1,4a x x f x x x ì-£ïï-=íï->ïî是R 上的单调函数,则实数a 的取值范围是( )A .()0,1B.(C.(D .()1,37.(2024·河北衡水·模拟预测)设0,1a a >≠,若函数())23log 1a x a f x a x a æö-=+ç÷-èø是偶函数,则=a ( )A .12B .32C .2D .38.(2024·湖北黄冈·二模)已知a b c d ,,,分别满足下列关系:1715161731615,log 16,log ,tan 162a b c d ====,则a b c d ,,,的大小关系为( )A .a b c d<<<B .c a b d <<<C .a c b d <<<D .a d b c<<<二、多选题9.(2024·山东菏泽·模拟预测)已知函数()0,01ln ,1x f x x x <<ì=í³î,若0a b >>,且1³ab ,则下列关系式一定成立的为( )A .()()b f a bf a =B .()()()f ab f a f b =+C .()()a f f a f b b æö³-ç÷èøD .()()()ln2f a b f a f b +<++三、填空题10.(2024·陕西西安·模拟预测)函数1log 2x a y x a -=++(0a >且1a ≠)的图象恒过定点(),k b ,若m n b k +=-且0m >,0n >,则91m n +的最小值为 .1.(2024·全国·高考真题)已知1a >且8115log log 42a a -=-,则=a .2.(2024·全国·高考真题)设函数()()ln()f x x a xb =++,若()0f x ³,则22a b +的最小值为( )A .18B .14C .12D .13.(2023·北京·高考真题)已知函数2()4log x f x x =+,则12f æö=ç÷èø.4.(2023·全国·高考真题)(多选)噪声污染问题越来越受到重视.用声压级来度量声音的强弱,定义声压级020lgp p L p =´,其中常数()000p p >是听觉下限阈值,p 是实际声压.下表为不同声源的声压级:声源与声源的距离/m 声压级/dB 燃油汽车1060~90混合动力汽车105060:电动汽车1040已知在距离燃油汽车、混合动力汽车、电动汽车10m 处测得实际声压分别为123,,p p p ,则( ).A .12p p ³B .2310p p >C .30100p p =D .12100p p £5.(2022·天津·高考真题)化简()()48392log 3log 3log 2log 2++的值为( )A .1B .2C .4D .66.(2022·浙江·高考真题)已知825,log 3a b ==,则34a b -=( )A .25B .5C .259D .537.(2022·全国·高考真题)若()1ln 1f x a b x ++-=是奇函数,则=a ,b = .8.(2021·天津·高考真题)若2510a b ==,则11a b+=( )A .1-B .lg 7C .1D .7log 109.(2021·全国·高考真题)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L 和小数记录表的数据V 满足5lg LV =+.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为( ) 1.259»)A .1.5B .1.2C .0.8D .0.610.(2020·全国·高考真题)已知55<84,134<85.设a=log53,b=log85,c=log138,则()A.a<b<c B.b<a<c C.b<c<a D.c<a<b。
C语言数据结构_第04讲 栈

while(n); printf("转换后的二进制数值为:"); while(s.top) // 余数出栈处理 { printf("%d",s.top->data); // 输出栈顶的余数 stacknode* p=s.top; // 修改栈顶指针 s.top=s.top->next; delete p; // 回收一个结点,C语言中用free p } }
3-3-2 表达式求值
表达式是由运算对象、运算符、括号等组成的有意义的式子。 1.中缀表达式(Infix Notation) 一般我们所用表达式是将运算符号放在两运算对象的中 间,比如:a+b,c/d等等,我们把这样的式子称为中缀表达 式。 2.后缀表达式(Postfix Notation) 后缀表达式规定把运算符放在两个运算对象(操作数) 的后面。在后缀表达式中,不存在运算符的优先级问题,也 不存在任何括号,计算的顺序完全按照运算符出现的先后次 次序进行。 3.中缀表达式转换为后缀表达式 其转换方法采用运算符优先算法。转换过程需要两个栈: 一个运算符号栈和一个后缀表达式输出符号栈。
(4)读栈顶元素
datatype ReadTop(SeqStack *s) { if (SEmpty ( s ) ) return 0; // 若栈空,则返回0 else return (s->data[s->top] );
// 否则,读栈顶元素,但指针未移动
}
(5)判栈空
int SEmpty(SeqStack *s) { if (s->top= = –1) return 1; else return 0; }
2.顺序栈运算的基本算法 (1)置空栈 首先建立栈空间,然后初始化栈顶指针。 SeqStack *Snull() { SeqStack *s; s=new (SeqStack);
计算机运算符号大全及意义

计算机运算符号大全及意义计算机运算符是计算机语言中的基本元素,用于进行各种运算操作。
计算机运算符可以分为数学运算符、逻辑运算符和位运算符等多种类型。
在本文中,将详细介绍计算机运算符的种类及其意义。
一、数学运算符1. + 运算符:用于执行加法操作,将两个数相加并返回结果。
2. - 运算符:用于执行减法操作,将一个数减去另一个数并返回结果。
3. * 运算符:用于执行乘法操作,将两个数相乘并返回结果。
4. / 运算符:用于执行除法操作,将一个数除以另一个数并返回结果。
5. % 运算符:用于执行取模操作,返回两个数相除的余数。
6. ** 运算符:用于执行幂运算,将一个数的值提高到另一个数的幂次方。
7. // 运算符:用于执行整数除法操作,返回两个数相除的整数部分。
二、逻辑运算符1. and 运算符:用于执行逻辑与操作,当两个条件都为真时返回真,否则返回假。
2. or 运算符:用于执行逻辑或操作,当两个条件至少有一个为真时返回真,否则返回假。
3. not 运算符:用于执行逻辑非操作,对一个条件取反,如果条件为真,则返回假,否则返回真。
三、位运算符1. & 运算符:用于执行按位与操作,对两个数的二进制进行按位与运算。
2. | 运算符:用于执行按位或操作,对两个数的二进制进行按位或运算。
3. ^ 运算符:用于执行按位异或操作,对两个数的二进制进行按位异或运算。
4. ~ 运算符:用于执行按位取反操作,对一个数的二进制进行按位取反运算。
5. << 运算符:用于执行左移操作,将一个数的二进制向左移动指定的位数。
6. >> 运算符:用于执行右移操作,将一个数的二进制向右移动指定的位数。
四、赋值运算符1. = 运算符:用于将右边的值赋给左边的变量。
2. += 运算符:将右边的值加到左边的变量上,并将结果赋给左边的变量。
3. -= 运算符:将右边的值减去左边的变量,并将结果赋给左边的变量。
第04讲 空间向量及其运算的坐标表示 2024年新高二暑假数学专题化复习与重点化预习(解析版)

【典题1】在空间直角坐标系0-xyz中,点(1,-2,3)关于x轴对称的点的坐标为( )
A.(-1,2,-3) B.(1,2,-3)
C.(1,-2,-3) D.(-1,-2,-3)
【答案】B
【分析】根据给定条件,利用关于坐标轴对称的特点求出坐标即可.
【详解】点(1,-2,3)关于x轴对称的点的坐标为(1,2,-3).
λā=(λa? ,λa?,λa?) (λ∈R)
a·b=a? b?+a? b?+a? b?,
a ||b = a?=λb?,az=λb?,a?= λb?(λ∈ R)
a1b=a·b=0= a?b?+a? b?+a? b?=0,
②若A(x?,y?,z?), B(x?,y?,z?),则 AB=(x?-x?,y?-y?,Z?-z?).
交于点D,
则BD,BB?,BA三线两两垂直,可建立空间直角坐标系得各个点的坐标. 【详解】在平面BB?C?C上过B点作垂直BB?的直线,与CC?相交于点D,
如图所示,AB1侧面BB?C?C,BDc侧面BB?C?C,BB?c侧面BB?C?C,∴ ABIBD,ABIBB?,
又∵BB?IBD,所以BD,BB?,BA两两垂直,以B为原点,
0yz平面,它们把空间分成八个部分.
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,
则称这个坐标系为右手直角坐标系.
2
;
y
x
(2)空间直角坐标系中的坐标
在空间直角坐标系0-x y z中,对空间任一点A,存在唯一的有序实数组(x ,y,z),使OA=xi+yj+
求解. 【详解】法一:设点M在x轴、y轴、z轴上的射影分别为M?,M?,M?,
运算符的用法 -回复

运算符的用法-回复运算符是编程语言中的基本组成部分之一,用于对数据进行操作和处理。
在不同的编程语言中,运算符的用法会有所差异,但其基本功能是相似的。
本文将以运算符的用法为主题,详细讨论算术运算符、关系运算符、逻辑运算符和赋值运算符等几种常见的运算符。
1. 算术运算符:用于执行常见的数学计算,包括加法、减法、乘法和除法。
常见的算术运算符有:- 加法运算符:用符号“+”表示,用于将两个值相加。
例如:2 + 3 = 5。
- 减法运算符:用符号“-”表示,用于将一个值减去另一个值。
例如:5 - 3 = 2。
- 乘法运算符:用符号“*”表示,用于将两个值相乘。
例如:2 * 3 = 6。
- 除法运算符:用符号“/”表示,用于将一个值除以另一个值。
例如:6 / 3 = 2。
在某些编程语言中,还包括其他算术运算符,如求模运算符(用符号“”表示,用于求两个数相除的余数)和自增自减运算符(用于将变量的值增加1或减去1)。
2. 关系运算符:用于比较两个值之间的关系,返回一个布尔值(真或假)。
常见的关系运算符有:- 相等运算符:用符号“==”表示,用于判断两个值是否相等。
例如:2 == 3,返回false。
- 不等运算符:用符号“!=”表示,用于判断两个值是否不相等。
例如:2 != 3,返回true。
- 大于运算符:用符号“>”表示,用于判断一个值是否大于另一个值。
例如:3 > 2,返回true。
- 小于运算符:用符号“<”表示,用于判断一个值是否小于另一个值。
例如:2 < 3,返回true。
- 大于等于运算符:用符号“>=”表示,用于判断一个值是否大于或等于另一个值。
例如:3 >= 3,返回true。
- 小于等于运算符:用符号“<=”表示,用于判断一个值是否小于或等于另一个值。
例如:2 <= 3,返回true。
关系运算符在条件语句和循环语句中经常被使用,用于控制程序的流程。
C语言运算符详解

C语言运算符详解C语言是一种流行的编程语言,广泛应用于软件开发和系统编程领域。
在C语言中,运算符是一种非常重要的语法元素,用于对数据进行各种操作和计算。
本文将详细介绍C语言中常用的运算符及其使用方法,以帮助读者更好地理解和应用C语言。
一、算术运算符算术运算符用于执行基本的数学运算,包括加法、减法、乘法、除法和求余等操作。
常见的算术运算符包括加号(+)、减号(-)、乘号(*)、除号(/)和模运算符(%)。
下面将具体介绍这些运算符的使用。
1. 加法运算符(+):用于执行两个数值相加的操作。
例如,表达式a + b将返回a和b的和。
2. 减法运算符(-):用于执行两个数值相减的操作。
例如,表达式a - b将返回a减去b的结果。
3. 乘法运算符(*):用于执行两个数值相乘的操作。
例如,表达式a * b将返回a和b的乘积。
4. 除法运算符(/):用于执行两个数值相除的操作。
例如,表达式a / b将返回a除以b的结果。
需要注意的是,如果除数为0,则会出现错误。
5. 模运算符(%):用于计算两个数值相除的余数。
例如,表达式a % b将返回a除以b的余数。
二、赋值运算符赋值运算符用于将一个值赋给一个变量。
常见的赋值运算符是等号(=)。
下面将介绍赋值运算符的使用。
1. 等号赋值符(=):用于将右边的数值赋给左边的变量。
例如,a = b将把b的值赋给a。
除了普通的赋值运算符,还有一些复合赋值运算符,它们可以简化代码并实现特定的功能。
2. 加法赋值运算符(+=):用于将右边的数值与左边的变量相加,并将结果赋给左边的变量。
例如,a += b等效于a = a + b。
3. 减法赋值运算符(-=):用于将右边的数值从左边的变量中减去,并将结果赋给左边的变量。
例如,a -= b等效于a = a - b。
4. 乘法赋值运算符(*=):用于将右边的数值与左边的变量相乘,并将结果赋给左边的变量。
例如,a *= b等效于a = a * b。
c语言的34种运算符

c语言的34种运算符C语言是一种广泛使用的编程语言,它的运算符非常丰富,共有34种。
本文将详细介绍C语言的34种运算符及其应用。
一、算术运算符(共9种)1. 加法运算符:+2. 减法运算符:-3. 乘法运算符:*4. 除法运算符:/5. 取余运算符:%6. 递增运算符:++7. 递减运算符:--8. 求幂运算符:^9. 复合赋值运算符:a = a + b、a = a - b、a = a * b、a = a / b、a = a % b、a = a++、a = a--、a = a^b二、关系运算符(共6种)1. 等于运算符:==2. 不等于运算符:!=3. 小于关系运算符:<4. 大于关系运算符:>5. 小于等于关系运算符:<=6. 大于等于关系运算符:>=三、逻辑运算符(共3种)1. 与运算符:&&(双与)2. 或运算符:||(双或)3. 非运算符:!(单引号)四、赋值运算符(共6种)1. 简单赋值运算符:=2. 复合赋值运算符:+=、-=、*=、/=、%=、++、--、^=3. 指针赋值运算符:= *ptr、*p1 = p2、p1 = &p24. 数组赋值运算符:a[i] = value5. 结构体赋值运算符:struct_name.member = value6. union赋值运算符:union_name.member = value五、逗号运算符(共1种),,用于变量列表,每个变量先初始化再使用六、指针与地址运算符(共7种)1. &(取地址符号):获取变量的地址2. *(解引用符号):访问地址指向的值3. (类型) *ptr:获取ptr指向的变量的类型和值4. ptr1 ++:移动ptr1指向的地址,ptr1指向下一个地址5. ptr1 --:移动ptr1指向的地址,ptr1指向前一个地址6. ptr1 = ptr2:将ptr2指向的地址赋给ptr17. &variable_name:获取变量名的内存地址(注意:获取的是字符在内存中的地址,不是变量的值)七、三目运算符(共1种):条件表达式八、sizeof运算符(共1种)sizeof(变量或类型),用于计算变量或类型在内存中占用的字节数以上就是C语言中的34种运算符的详细介绍。
北师大版三年级上册小学数学第6单元 乘法_第04讲_连乘的计算和应用(教师版讲义)

【答案】25×2×3=150(箱) 【解析】25×2×3=150(箱) 随练 2、说一说下图中的信息,再计算. 一共有多少本书?
每层放了 108 本书.
【答案】108×4×2=864(本) 【解析】108×4×2=864(本) 随练 3、说一说下图中的信息,再计算. 一共有多少棵树?
【答案】18×5×2=180(袋)250>180 答:两次不能运完. 【解析】18×5×2=180(袋)250>180 答:两次不能运完. 拓展 8、某次大型舞蹈表演中舞蹈队分成了 4 个方阵,每个方阵有 81 人,每人需 2 把扇子,一共需要多少把扇子? 【答案】81×4×2=648(把)答:一共需要 648 把扇子. 【解析】81×4×2=648(把)答:一共需要 648 把扇子. 拓展 9、看谁跑得快.
每层有 5 间教室.
每个教室放 7 盆花.
【答案】4×5×7=140(盆) 【解析】4×5×7=140(盆) 例题 3、一瓶果汁 4 元,3 箱果汁一共多少元?
【答案】12×3×4=144(元) 【解析】12×3×4=144(元) 例题 4、一共有多少块积木?
【答案】8×4×3=96(块) 【解析】8×4×3=96(块)
________
________
________
【答案】元元:8×3×2=48(块) 龙龙:2×6×4=48(块) 小小:4×4×3=48(块) 【解析】元元:8×3×2=48(块) 龙龙:2×6×4=48(块) 小小:4×4×3=48(块)
随练 6、暑假里,小军去游泳池游泳,游泳池泳道长 50 米,他在泳道内游了 8 个来回,他一共游了多少米? 【答案】50×2×8=800(米)答:他一共游了 800 米. 【解析】50×2×8=800(米)答:他一共游了 800 米.
第04讲 有理数的加减法(解析版)

第4讲有理数的加减法1.掌握有理数加法的意义,法则及运算律,并会使用运算律简算;2.掌握有理数减法的法则和运算技巧,认识减法与加法的内在联系;3.熟练将加减混合运算统一成加法运算,理解运算符号和性质符号的意义,运用加法运算律合理简算,并会解决简单的实际问题.考点01有理数的加法1.定义:把两个有理数合成一个有理数的运算叫作有理数的加法.2.法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0;(3)一个数同0相加,仍得这个数.要点诠释:利用法则进行加法运算的步骤:(1)判断两个加数的符号是同号、异号,还是有一个加数为零,以此来选择用哪条法则.(2)确定和的符号(是“+”还是“-”).(3)求各加数的绝对值,并确定和的绝对值(加数的绝对值是相加还是相减).3.运算律:要点诠释:交换加数的位置时,不要忘记符号.考法01有理数的加法运算1.计算:(1)(+20)+(+12); (2)1223⎛⎫⎛⎫-+-⎪ ⎪⎝⎭⎝⎭; (3)(+2)+(-11);(4)(-3.4)+(+4.3); (5)(-2.9)+(+2.9); (6)(-5)+0.【答案】(1)(2)属于同一类型,用的是加法法则的第一条;(3)(4)属于同一类,用的是加法法则的第二条;(5)用的是第二条:互为相反数的两个数相加得0;(6)用的是法则的第三条.(1)(+20)+(+12)=+(20+12)=+32=32;(2)121211 23236⎛⎫⎛⎫⎛⎫-+-=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(3)(+2)+(-11)=-(11-2)=-9(4)(-3.4)+(+4.3)=+(4.3-3.4)=0.9(5)(-2.9)+(+2.9)=0;(6)(-5)+0=-5.【总结】绝对值不等的异号两数相加,是有理数加法的难点,在应用法则时,一定要先确定符号,再计算绝对值.2.计算:11 3343⎛⎫⎛⎫-++⎪ ⎪⎝⎭⎝⎭【答案】11111 3333433412⎛⎫⎛⎫⎛⎫-++=+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭3计算:(1) (+10)+(-11);(2)⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭12 -1+-23【答案】(1) (+10)+(-11)=﹣(11-10)=﹣1;(2)⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭1212341 -1+-=-1+=-1+=-2 2323666考点02有理数的减法1.定义:已知两个数的和与其中一个加数,求另一个加数的运算,叫做减法,例如:(-5)+?=7,求?,减法是加法的逆运算.要点诠释:(1)任意两个数都可以进行减法运算.(2) 几个有理数相减,差仍为有理数,差由两部分组成:①性质符号;②数字即数的绝对值.2.法则:减去一个数,等于加这个数的相反数,即有:()a b a b -=+-.要点诠释: 将减法转化为加法时,注意同时进行的两变,一变是减法变加法;二变是把减数变为它的相反数”.如:考法02有理数的减法计算:(1)(-32)-(+5); (2)(+2)-(-25).【思路】此题是有理数的减法运算,先按照减法法则将减法转化为加法,再按照有理数的加法进行计算. 【答案】法一:法二:(1)原式=-32-5=-32+(-5)=-37;(2)原式=2+25=27【总结】算式中的“+”或“-”既可以看作运算符号按法则进行计算,也可以看作是性质符号按多重符号化简进行计算.考点03有理数加减混合运算将加减法统一成加法运算,适当应用加法运算律简化计算.考法03有理数的加减混合运算1.计算:3.8+441﹣(+654)+(﹣832) 【思路】根据有理数的加减混合运算的方法:有理数加减法统一成加法,求解即可. 【答案】解:原式=(3.8﹣6.8)+(441﹣832) =﹣3﹣4125=﹣7125, 【总结】本题考查了有理数的加减混合运算的知识,如果在一个式子里,有加法也有减法,根据有理数减法法则,把减法都转化成加法,并写成省略括号的和的形式. 2.用简便方法计算:(1)(-2.4)+(-4.2)+(-3.8)+(+3.1)+(+0.8)+(-0.7) (2) 2)324(83)65()851(43-++-+-+ 【答案】 (1) 原式=[(-3.8)+ (-4.2)]+[ (-2.4)+ (-0.7) +(+3.1)]+(+0.8)=-8+0.8=-7.2 (2) 原式=(2-1-4)+(34-58-56+38-23)=-3+[68-58+38+(-56-46)]=-3-1=-4 考法04有理数加减法在实际生活中的应用1.邮递员骑车从邮局出发,先向南骑行2km 到达A 村,继续向南骑行3km 到达B 村,然后向北骑行9km 到C 村,最后回到邮局.(1)以邮局为原点,以向北方向为正方向,用1cm 表示1km ,画出数轴,并在该数轴上表示出A 、B 、C 三个村庄的位置; (2)C 村离A 村有多远? (3)邮递员一共骑了多少千米?【思路】(1)以邮局为原点,以向北方向为正方向用1cm 表示1km ,按此画出数轴即可; (2)可直接算出来,也可从数轴上找出这段距离;(3)邮递员一共骑了多少千米?即数轴上这些点的绝对值之和. 【答案】解:(1)依题意得,数轴为:;(2)依题意得:C 点与A 点的距离为:2+4=6(千米); (3)依题意得邮递员骑了:2+3+9+4=18(千米).【总结】本题主要考查了学生有实际生活中对数轴的应用能力,只要掌握数轴的基本知识即可.2.华英中学七年级(14)班的学生分成五组进行答题游戏,每组的基本分为100分,答对一题加50分,答错一题扣50分,游戏结束后各组的得分如下表:(1)第一名超过第二名多少分? (2)第一名超过第五名多少分?【答案】由表看出:第一名350分,第二名150分,第五名-400分.(1) 350-150=200(分)(2) 350-(-400)=350+400=750(分)答:第一名超过第二名200分;第一名超过第五名750分. 3.某产粮专业户出售粮食8袋,每袋重量(单位:千克)如下:197,202,197,203,200,196,201,198. 计算出售的粮食总共多少千克?【答案】法一:以200(千克)为基准,超过的千克数记作正数,不足的千克数记作负数,则这8个数的差的累计是:(-3)+(+2)+(-3)+(+3)+0+(-4)+(+1)+(-2)=-6200×8+(-6)=1594(千克) 答:出售的粮食共1594千克.法二:197+202+197+203+200+196+201+198=1594(千克) 答:出售的粮食共1594千克.考向01计算拆项法阅读下题的计算方法. 计算⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+-2134317329655解:原式=()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛++⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+-+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+-2134317329655=()()()[]⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+-++-+-2143326531795=0+(﹣45)=﹣45 上面这种解题方法叫做拆项法,按此方法计算:⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-211324022322010652011【思路】根据拆项法,可把整数结合在一起,分数结合在一起,再根据有理数的加法,可得答案. 【答案】解:原式=[(﹣2011)+(﹣65)]+[(﹣2010)+(﹣32)]+[4022+32]+[(﹣1)+(﹣21)] =[(﹣2011)+(﹣2010)+4022+(﹣1)]+[(﹣65)+(﹣32)+32+(﹣21)]=0+(﹣34)=﹣34.【总结】本题考查了有理数的加法,拆项法是解题关键.考向02凑整凑分(1)11(6)( 3.3)(3)(6)(0.3)(8)(6)(16)644⎛⎫⎛⎫++++-+++-+++++++-+- ⎪ ⎪⎝⎭⎝⎭. 【答案】解法一:11(6)( 3.3)(3)(6)(0.3)(8)(6)(16)644⎛⎫⎛⎫++++-+++-+++++++-+- ⎪ ⎪⎝⎭⎝⎭11(6)(3)(0.3)(8)(6)( 3.3)(6)(16)644⎡⎤⎡⎤⎛⎫⎛⎫=++++++++++++-+-+-+- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦→同号的数一起先加(23.55)(31.55)8=++-=-.解法二:11(6)( 3.3)(3)(6)(0.3)(8)(6)(16)644⎛⎫⎛⎫++++-+++-+++++++-+- ⎪ ⎪⎝⎭⎝⎭11(6)6[( 3.3)(3)(0.3)][(6)(6)][(16)(8)]44⎡⎤⎛⎫⎛⎫=++++-+-+++++-+++-++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦→同分母,互为相反数的数,或几个数可以凑整的数分别结合相加000(8)8=+++-=-.【总结】计算多个有理数相加时,必须先审题,分析特点,寻找规律,然后再去计算.注意在交换加数的位置时,要连同符号一起交换. (2)1113.7639568 4.7621362--+--+ 【答案】仔细观察各个加数,可以发现两个小数的和是-1,两个整数的和是29,三个分数通分后也不难算.故把整数、分数、小数分别分为一组. 解:1113.7639568 4.7621362--+--+ 111(3.76 4.76)(521)(3968)362=-+--++-+1(6)2922=-+-+=【总结】计算多个有理数相加时,必须先审题,分析特点,寻找规律,然后再去计算.注意在交换加数的位置时,要连同符号一起交换. (3)51133.464 3.872 1.54 3.376344+---+++ 【答案】3.46和1.54的和为整数,把它们分为一组;-3.87与3.37的和为-0.5,把它们分为一组;546与13-易于通分,把它们分为一组;124-与34同分母,把它们分为一组. 解:51133.464 3.872 1.54 3.376344+---+++5113(3.46 1.54)( 3.87 3.37)(4)(2)6344=++-++-+-+115(0.5)4(1) 4.537.522=+-++-=+=【总结】计算多个有理数相加时,必须先审题,分析特点,寻找规律,然后再去计算.注意在交换加数的位置时,要连同符号一起交换. (4)1355354624618-++- 【答案】先把整数分离后再分组.解:1355354624618-++- 1355354624618=--++++--1355(3546)()24618=-++-+-++-182********-++-=+2936= 注:带分数中的整数与分数分离时,如果这个数是负数,那么分离得到的整数与分数都是负数,例如 113322-=--. 【总结】计算多个有理数相加时,必须先审题,分析特点,寻找规律,然后再去计算.注意在交换加数的位置时,要连同符号一起交换. (5)132.2532 1.87584+-+ 【答案】如果按小数、整数分组,效果似乎不是很好.可先将小数和分数统一后再考虑分组.解:132.25321.87584+-+ (2.25 2.75)(3.125 1.875)=-++ 0.55 4.5=-+=【总结】计算多个有理数相加时,必须先审题,分析特点,寻找规律,然后再去计算.注意在交换加数的位置时,要连同符号一起交换.考向03特殊技巧计算-3.72-1.23+4.18-2.93-1.25+3.72; 【答案】观察各个加数,可以发现-3.72与3.72互为相反数,把它们分为一组;4.18、-2.93与-1.25的和为0,把它们分为一组可使计算简便. 解:-3.72-1.23+4.18-2.93-1.25+3.72 =(-3.72+3.72)+(4.18-2.93-1.25)-1.23 =0+0-1.23=-1.23【总结】计算多个有理数相加时,必须先审题,分析特点,寻找规律,然后再去计算.注意在交换加数的位置时,要连同符号一起交换.考向04凑正凑负11-12+13-15+16-18+17【答案】把正数和负数分别分为一组.解:11-12+13-15+16-18+17=(11+13+16+17)+(-12-15-18)=57+(-45)=12【总结】计算多个有理数相加时,必须先审题,分析特点,寻找规律,然后再去计算.注意在交换加数的位置时,要连同符号一起交换.考向05应用1.“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话.(1)现有1,2,3,4,5,6,7,8,9共九个数字,请将它们分别填入图1的九个方格中,使得第行的三个数、每列的三个数、斜对角的三个数之和都等于15;(2)通过研究问题(1),利用你发现的规律,将3,5,﹣7,1,7,﹣3,9,﹣5,﹣1这九个数字分别填入图2的九个方格中,使得横、竖、斜对角的所有三个数的和都相等.【答案】解:(1)15÷3=5,∴最中间的数是5,其它空格填写如图1;(2)如图2所示.【总结】本题考查了有理数加法,熟知“九宫图”的填法是解题的关键.2.某产粮专业户出售粮食8袋,每袋重量(单位:千克)如下:197,202,197,203,200,196,201,198.计算出售的粮食总共多少千克?【答案】法一:以200(千克)为基准,超过的千克数记作正数,不足的千克数记作负数,则这8个数的差的累计是:(-3)+(+2)+(-3)+(+3)+0+(-4)+(+1)+(-2)=-6200×8+(-6)=1594(千克) 答:出售的粮食共1594千克.法二:197+202+197+203+200+196+201+198=1594(千克) 答:出售的粮食共1594千克.【易错01】对括号使用不当导致错误(1)计算:-7-5.【答案】解:原式=-7+(-5)=-12. (2)计算:⎪⎭⎫⎝⎛-+--2141512 【答案】解:原式=2+15-14+12=2920.(1)3401(1)(5)|4|77⎡⎤⎛⎫⎛⎫+-----+--+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦;(2)212102133434⎛⎫⎛⎫⎛⎫-++---+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(3)4444499999999999999955555++++(4)1+(-2)+(-3)+4+5+(-6)+(-7)+8+…+97+(-98)+(-99)+100的值. (5)111118244880120++++; (6)2312()()3255---+--+-【解析】(1)原式341[15]45(5)1077=--+-++=--= (2)原式212102133434⎛⎫⎛⎫⎛⎫=-+++++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭21212133434=-++- 2211213213183344⎛⎫⎛⎫=-++-=-+=- ⎪ ⎪⎝⎭⎝⎭(3)原式=1111101001000100005555⎡⎤⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+-++-++-++- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦⎣⎦11000005⎡⎤⎛⎫++- ⎪⎢⎥⎝⎭⎣⎦11111(10100100010000100000)55555⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++++-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦111110(1)111109=+-=.(4)1+(-2)+(-3)+4+5+(-6)+(-7)+8+…+97+(-98)+(-99)+100=[1+(-2) + (-3)+4]+[5+(-6) + (-7)+8]+…+[97+(-98) + (-99)+100] =0+0++…+0=0.(5)111111111182448801202446688101012++++=++++⨯⨯⨯⨯⨯ 111111*********()()22446688101012221224=-+-+-+-+-=-= (6)原式23122312231283[()][()]32553255325530=------=--------=----=-1.某地一天的最高气温是12℃,最低气温是2℃,则该地这天的温差是( ) A . ﹣10℃ B . 10℃ C . 14℃D . ﹣14℃【答案】B2.比﹣1小2015的数是( )A .﹣2014B .2016C .﹣2016D .2014 【答案】C【解析】解:根据题意得:﹣1﹣2015=﹣2016,故选C.3.如果三个数的和为零,那么这三个数一定是( ).A .两个正数,一个负数B .两个负数,一个正数C .三个都是零D .其中两个数之和等于第三个数的相反数 【答案】D【解析】若0a b c ++=,则a b c +=-或b c a +=-或a c c +=-,所以D 正确. 4. 若0,0a b ><,a b <, 则a 与b 的和是 ( ) A. B.C.D..【答案】D【解析】(a b +)的符号与绝对值较大的b 一致为负的,并用较大的绝对值减去较小的绝对值,即有()b a --. 5.下列判断正确的是( ) A .两数之差一定小于被减数.六、对点通关训练B .若两数的差为正数,则两数都为正数.C .零减去一个数仍得这个数.D .一个数减去一个负数,差一定大于被减数. 【答案】D【解析】A 错误,反例:2-(-3)=5,而5>2;B 不对,反例:2-(-3)=5,而-3为负数;C 错误,0-2=-2,0-(-2)=2,所以零减去一个数得这个数的相反数.6.某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg ,(25±0.2)kg ,(25±0.3)kg 的字样,从中任意拿出两袋,它们的质量最多相差 ( )A .0.8kgB .0.6kgC .0.5kgD .0.4kg 【答案】B【解析】因为最低重量为24.7kg ,最大重量为25.3kg ,故质量最多相差25.3-24.7=0.6kg . 7.有理数,,a b c 在数轴上对应点位置如图所示,用“>”或“<”填空:(1)|a |______|b |;(2)a +b +c ______0: (3)a -b +c ______0; (4)a +c ______b ; (5)c -b ______a . 【答案】<,<,>,>,>【解析】由图可知:b a c >>,且0,0b a c <<>,再根据有理数的加法法则可得答案. 8.小明存折中原有450元,取出260元,又存入150元,现在存折中还有______元. 【答案】340【解析】450﹣260+150=290+150=340(元).9. 若a ,b 为整数,且|a-2|+| a -b|=1,则a+b =________. 【答案】2,6,3或5【解析】当|a-2|=1,| a -b|=0时,得:a+b =6或2;当|a-2|=0,| a -b|=1时,得:a+b =3或5;10.某地的冬天,半夜的温度是-5︒C ,早晨的温度是-1︒C ,中午的温度是4︒C.则 (1)早晨的温度比半夜的温度高________度; (2)早晨的温度比中午的温度低________度. 【答案】(1)4 (2) 5【解析】 (1)-1-(-5)=4 (2) -1-(+4)= -511.北京与纽约的时差为-13(负号表示同一时刻纽约时间比北京时间晚).如果现在是北京时间15:00,那么纽约时间是______________【答案】2:00【解析】15:00+(-13)=2:00.12. 数学活动课上,王老师给同学们出了一道题:规定一种新运算“☆”对于任意两个有理数a和b,有a☆b=a-b+1,请你根据新运算,计算(2☆3)☆2的值是 .【答案】 -1【解析】(2☆3)☆2=(2☆3)-2+1=2-3+1-2+1=-113.数轴上到原点的距离小于3的整数的个数为x,不大于3的正整数的个数为y,绝对值等于3的整数的个数为z,求:x+y+z的值.【解析】解:根据数轴,到原点的距离小于3的整数为0,±1,±2,即x=5,不大于3的正整数为1,2,3,即y=3,绝对值等于3的整数为3,﹣3,即z=2,所以x+y+z=10.14.股民李星星在上周星期五以每股11.2元买了一批股票,下表为本周星期一到星期五该股票的涨跌情况求:(1)本周星期三收盘时,每股的钱数.(2)李星星本周内哪一天把股票抛出比较合算,为什么?星期一二三四五每股涨跌/元+0.4 +0.45 ﹣0.2 +0.25 ﹣0.4【解析】解:(1)根据题意得:11.2+0.4+0.45+(﹣0.2)=11.85(元),则本周星期三收盘时,该只股票每股为11.85元;(2)根据题意得:11.2+0.4+0.45+(﹣0.2)+0.25=12.1(元),则本周该只股票最高价12.1元出现在周四,李星星本周四把股票抛出比较好.1.某市一天的最高气温为2℃,最低气温为﹣8℃,那么这天的最高气温比最低气温高()A.﹣10℃ B.﹣6℃ C.10℃D.6℃【答案】C【解析】解:2﹣(﹣8)=2+8=10℃.故选C.2.若等式0□1=﹣1成立,则□内的运算符号为()A. + B.﹣C.×D.÷【答案】B3.两个有理数相加,和小于其中一个加数而大于另一个加数,需满足()A.两个数都是正数 B.两个数都是负数C.一个是正数,另一个是负数 D.至少有一个数是零【答案】C【解析】举例验证.4.下列说法中正确的是A.正数加负数,和为0B.两个正数相加和为正;两个负数相加和为负C.两个有理数相加,等于它们的绝对值相加D.两个数的和为负数,则这两个数一定是负数【答案】B【解析】举反例:如5+(-2)=+3≠0,故A错;如:(-2)+(-3)≠|-2|+|-3|,故C错;如(+2)+(-8)=-6,故D错误.5.下列说法正确的是( )A.零减去一个数,仍得这个数B.负数减去负数,结果是负数C.正数减去负数,结果是正数D.被减数一定大于差【答案】C【解析】举反例逐一排除.6.某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差( )A .0.8kgB .0.6kgC .0.5kgD .0.4kg 【答案】B【解析】因为最低重量为24.7kg ,最大重量为25.3kg ,故质量最多相差25.3-24.7=0.6kg . 7. -3+5的相反数是( ).A .2B .-2C .-8D .8 【答案】B8.有理数,,a b c c 在数轴上对应点位置如图所示,用“>”或“<”(1)|a |______|b |;(2)a +b +c______0: (3)a -b +c______0;(4)a +c______b ; (5)c -b______a . 【答案】<,<,>,>,>【解析】由图可知:b a c >>,且0,0b a c <<>,再根据有理数的加法法则可得答案. 9.计算:|﹣2|+2=________. 【答案】4.10.某月股票M 开盘价20元,上午10点跌1.6元,下午收盘时又涨了0.4元,则股票这天的收盘价是_______. 【答案】18.8元【解析】跌1.6元记为-1.6元,涨0.4元记为+0.4元,故有收盘价为20+(-1.6)+0.4-18.8. 11.列出一个满足下列条件的算式:(1)所有的加数都是负数,和为-5,________;(2)一个加数是0,和是-5________;(3)至少有一个加数是正整数,和是-5,________. 【答案】(1)(-2)+(-3)=-5 (2)(-5)+0=-5 (3)2+(-7)=-5 【解析】答案不唯一.12. 数学活动课上,王老师给同学们出了一道题:规定一种新运算“☆”对于任意两个有理数a 和b ,有a ☆b =a-b+1,请你根据新运算,计算(2☆3)☆2的值是 . 【答案】-1【解析】(2☆3)☆2=(2☆3)-2+1=2-3+1-2+1=-1 13.计算(﹣3)+(﹣9)的结果为 . 【答案】-12.【解析】同号两数相加的法则是取相同的符号,并把绝对值相加. 原式=﹣(3+9)=﹣12.14.计算题(1)232(1)(1)( 1.75)343-----+-(2)132.1253(5)(3.2)58-+---+(3)21772953323+---(4)231321234243--++-+(5)2312()() 3255 ---+--+-(6)123456782001200220032004 -+-+-+-+--+-+【解析】(1)原式22(1)( 1.75 1.75)133=-++-+=;(2)原式131 [3( 3.2)][(5) 2.125]3 584 =+-++---=(3)原式21729771 9)533326 =+---=-(4)原式223311 ()()12334422 =-++-++-=-(5)原式23122312231283[()][()]32553255325530 =------=--------=----=-(6)原式=12342001200220032004 -+-++-+-+ (12)(34)(20032004)110021002 =-++-+++-+=⨯=15.已知:|a|=2,|b|=3,求a+b的值.【解析】由题意知:a=±2, b=±3,所以要分四种情况代入求值.∵|a|=2, ∴ a=±2, ∵|b|=3, ∴b=±3.当a=+2, b=+3时, a+b=(+2)+(+3)=+5;当a=+2, b=-3时, a+b=(+2)+(-3)=-1;当a=-2,b=+3时, a+b=(-2)+(+3)=+1;当a=-2, b=-3时, a+b=(-2)+(-3)=-5.16.某人用400元购买了8套儿童服装,准备以一定价格出售,如果以每套儿童服装55元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,﹣3,+2,+1,﹣2,﹣1,0,﹣2.(单位:元)(1)当他卖完这八套儿童服装后是盈利还是亏损?(2)盈利(或亏损)了多少钱?【解析】解:根据题意得(1)2﹣3+2+1﹣2﹣1+0﹣2=﹣3,55×8+(﹣3)=437元,∵437>400,∴卖完后是盈利;(2)437﹣400=37元,故盈利37元.。
关系运算符

关系运算符关系运算符是用于比较两个值之间关系的运算符。
在编程语言中,关系运算符常用于条件语句和循环结构中,用于判断条件是否成立。
在本文中,我们将介绍常用的关系运算符,并举例说明其使用方法和功能。
1. 相等运算符(==)相等运算符用于判断两个值是否相等。
如果两个值相等,则返回True;否则返回False。
相等运算符可以用于比较数值、字符串和其他数据类型。
例如:a = 5b = 5print(a == b) # 输出True2. 不等运算符(!=)不等运算符用于判断两个值是否不相等。
如果两个值不相等,则返回True;否则返回False。
不等运算符可以用于比较数值、字符串和其他数据类型。
例如:a = 5b = 7print(a != b) # 输出True3. 大于运算符(>)大于运算符用于判断一个值是否大于另一个值。
如果第一个值大于第二个值,则返回True;否则返回False。
大于运算符可以用于比较数值和字符串(按字典顺序)。
例如:a = 5b = 3print(a > b) # 输出True4. 小于运算符(<)小于运算符用于判断一个值是否小于另一个值。
如果第一个值小于第二个值,则返回True;否则返回False。
小于运算符可以用于比较数值和字符串(按字典顺序)。
例如:a = 3b = 5print(a < b) # 输出True5. 大于等于运算符(>=)大于等于运算符用于判断一个值是否大于等于另一个值。
如果第一个值大于等于第二个值,则返回True;否则返回False。
大于等于运算符可以用于比较数值和字符串(按字典顺序)。
例如:a = 5b = 5print(a >= b) # 输出True6. 小于等于运算符(<=)小于等于运算符用于判断一个值是否小于等于另一个值。
如果第一个值小于等于第二个值,则返回True;否则返回False。
小于等于运算符可以用于比较数值和字符串(按字典顺序)。
第04讲逻辑函数的公式化简

第04讲逻辑函数的公式化简逻辑函数是由逻辑变量和逻辑运算符组成的表达式。
在实际应用中,对逻辑函数进行简化通常是非常重要的,因为简化后的逻辑函数更容易理解和分析。
本文将介绍逻辑函数的公式化简方法,包括代数化简、卡诺图方法和奎因-麦克拉斯基方法。
一、代数化简代数化简是一种通过应用逻辑等式和等价变换来简化逻辑函数的方法。
逻辑等式是逻辑函数之间的等式关系,可以用来表示逻辑函数的等价性。
常见的逻辑等式包括德摩根定律、分配律、吸收律等。
1.1德摩根定律德摩根定律包括两个等式:1)非(A和B)等于非A或非B:~(A∧B)=~A∨~B2)非(A或B)等于非A和非B:~(A∨B)=~A∧~B通过应用德摩根定律,可以将逻辑函数中的与或非运算转化为或与非的运算,从而简化逻辑函数。
1.2分配律分配律包括两个等式:1)A和(B或C)等于(A和B)或(A和C):A∧(B∨C)=(A∧B)∨(A∧C)2)A或(B和C)等于(A或B)和(A或C):A∨(B∧C)=(A∨B)∧(A∨C)通过应用分配律,可以将逻辑函数中的与或运算关系转化为或与运算关系,从而简化逻辑函数。
1.3吸收律吸收律包括两个等式:1)A或(A和B)等于A:A∨(A∧B)=A2)A和(A或B)等于A:A∧(A∨B)=A通过应用吸收律,可以将逻辑函数中的与或运算关系进行简化。
通过应用上述逻辑等式和等价变换,可以将逻辑函数进行代数化简。
例如,假设有一个逻辑函数F=A∧(B∨C),我们可以应用分配律将其化简为F=(A∧B)∨(A∧C)。
二、卡诺图方法卡诺图是一种通过图形化表示逻辑函数的方法,可以帮助我们更好地理解和分析逻辑函数。
对于每个逻辑变量,卡诺图使用一个格子来表示该变量的取值,格子的数目等于变量的取值数。
逻辑函数的值则通过在卡诺图中填写格子来表示。
根据逻辑函数的真值表,我们可以绘制对应的卡诺图。
卡诺图的优势在于能够直观地观察逻辑函数的特点,并以此进行化简。
化简的原则是找出卡诺图中连续的1所对应的格子,并构建出尽可能简单的表达式。
应用题第04讲_植树问题(学生版)A4
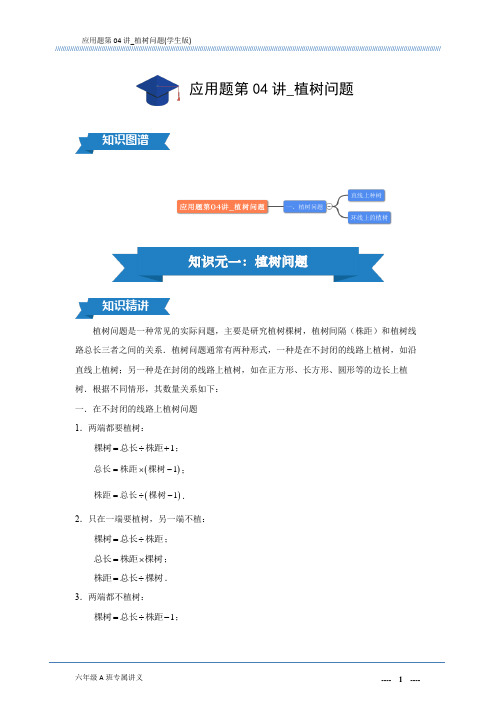
植树问题是一种常见的实际问题,主要是研究植树棵树,植树间隔(株距)和植树线路总长三者之间的关系.植树问题通常有两种形式,一种是在不封闭的线路上植树,如沿直线上植树;另一种是在封闭的线路上植树,如在正方形、长方形、圆形等的边长上植树.根据不同情形,其数量关系如下: 一.在不封闭的线路上植树问题 1.两端都要植树:1=÷+棵树总长株距;()1=⨯-总长株距棵树; ()1=÷-株距总长棵树.2.只在一端要植树,另一端不植:=÷棵树总长株距; =⨯总长株距棵树; =÷株距总长棵树.3.两端都不植树:1=÷-棵树总长株距;应用题第04讲_植树问题()1=⨯+总长株距棵树; ()1=÷+株距总长棵树.二.在封闭路线上植树问题在封闭路线上植树问题中,植树的棵树与段数相等.=÷棵树总长株距; =⨯总长株距棵树; =÷株距总长棵树.三.解决植树问题,要根据实际问题的具体情形,正确分析总长、株距、棵树之间的数量关系.多条线段上的间隔问题,注意线段间的公共点.重难点:植树问题相关公式及应用.题模一:直线上种树例1.1.1在一条长50米的马路的两侧种树,且两端都要种.每隔5米种一棵树,一共要种_______________棵树.例1.1.2一条路的一边种树,并且两头都不种树,如果每隔12米种一棵树,若马路长120米,则种了__________棵树. 例1.1.3马路的一侧安路灯.(1)一端有路灯,另一端没有.若每隔4米安一盏灯,马路长40米,问有几盏灯? (2)两端都没有路灯.若每隔6米安一盏灯,共有12盏,问马路有多长?例1.1.4有如图2条马路.现在要在马路的一侧种树,且每条马路的两端都种树.已知横向的路长45米,纵向的路长50米.每隔5米种一棵树,问共种几棵树?50米45米例 1.1.516个男生沿着300米的马路站成一排,两端都站人,相邻两人之间的距离都相等.现在,每相邻两个男生之间又加入了3个女生,相邻两人之间的距离还是相等.请问:一共加入了多少个女生?加入女生后,相邻两人之间的距离又是多少米?题模二:环线上的植树例1.2.1用蜡烛摆成一个周长60厘米圆形的造型,如果共有20根蜡烛,且相邻两个蜡烛间隔相同,那么相邻的两根蜡烛间的距离是__________厘米.例1.2.2鸟巢外一周共有1000米,绕着鸟巢的一周有灯和树木.(1)如果两盏灯之间的距离是5米,问鸟巢外一周有几盏灯?(2)如果鸟巢外共有250棵树,且相邻两棵树的距离相等,问相邻两棵树的距离是多少?例1.2.3一块长方形草地,长120米,宽100米.现在它的四周种树,四个角和各边中点都要求种树,且相邻两棵树之间的距离相等.请测算:最少要种______棵树.例1.2.4同学12人围着长480米的操场玩游戏,每两名同学间距离相等.如果在每两名同学间插入3名老师,使每两人间距离相等,那么每两人间距离是__________米.例1.2.5如图,有一个长方形的“田”字道路,整个长方形的长为100米,宽为70米.现在需要在所有道路上种树,相邻两棵树之间的距离都相等,而且拐弯的地点(顶点或中点)都要种上树.那么最少要种______棵树.A.108B.104C.102D.99随练1.1在马路一边插旗子,两端都插,每隔5米插一面,一共插了10面,这条马路长50米.()随练1.210名学生从左至右站成一排,相邻两名学生的间隔都是1米.排头和排尾的距离是_______米.A.11B.10C.9D.21随练 1.3有如图三条马路.现在要在马路的一侧种树,且每条马路的两端都种树.已知北路长40米,东路和西路分别长80米.每隔5米种一棵树,则共种__________棵树.随练1.4学校有一个圆形水池.水池内的周长为30米.如果绕着水池内共有10个换水孔,且相邻两个换水孔的距离相等,问相邻的两个换水孔间的距离是多少米?随练1.5有如图三条马路,长度都是100米.现在要在马路的一侧种树,且每条马路的两端都种树.每隔5米种一棵树,问共种__________棵树.随练1.630个男生沿着240米的跑道站成一圈,并且相邻两人之间的距离都相等.在每相邻两个男生之间又加入了同样多个女生,这时相邻两人之间的距离都是4米.请问:加入女生前,相邻两人之间的距离是多少米?一共加入了多少个女生?随练1.7有一块三角形土地,三条边的长度分别为120米、150米、80米.如果在边界上每隔10米种一棵树,三角形的每个顶点都必须种,一共要种多少棵树?作业1一条长500米的路的两边都要种树,并且两头都要种,如果每隔5米种一棵树,一共要种__________棵树.作业2马路的两侧种树,且两端不种.若每隔3米种一棵树,马路长30米,问有几棵树?西路北路东路作业3(1)马路的一侧种树,且两端种树.若每隔5米种一棵树,马路长30米,问有几棵树?(2)马路的两侧种树,且两端种树.若每隔5米种一棵树,共有20棵树,问马路有多长?作业4学校门前有条长100米的马路,马路两侧一共种了42棵树,每侧相邻两棵树之间的距离都相等,而且马路的两端都种了.相邻两棵树之间的距离是_______米. A .10 B .9 C .5 D .4作业5有如图三条马路.现在要在马路的一侧种树,且每条马路的两端都种树.已知北路长30米,东路和西路分别长60米.每隔3米种一棵树,则共种__________棵树.作业6学校有一个圆形水池,周长为48米,若绕着水池每隔6米种一棵树,则共种__________棵树.作业7有一块三角形土地,三条边的长度分别为120米、150米、80米.如果在边界上每隔10米种一棵树,三角形的每个顶点都必须种,一共要种______棵树. A .38 B .35 C .32 D .18作业850个男生沿着300米的跑道站成一圈,并且相邻两人之间的距离都相等.现在,每相邻两个男生之间又加入了两个女生,相邻两人之间的距离还是相等.一共加入了______个女生.加入女生后,相邻两人之间的距离又是______米. A .100,2 B .98,2 C .98,3 D .102,2西路北路东路。
九年级上册第04讲_一元二次方程的应用(教师版)

第04讲_一元二次方程的应用知识图谱一元二次方程的应用知识精讲一.面积问题解应用题的一般步骤(1)找出题中的等量关系;(2)设未知数;(3)根据等量关系列出方程;(4)解一元二次方程;(5)将方程的解代入原方程检验,回到实际问题中检验;(6)作答结论注意:求出x 值后需要检验是否符合实际意义草坪问题在一个长30m 、宽20m 的长方形ABCD 上修建三条同样宽的通道,剩余部分面积为468m 2,那么通道的宽应设计成多少m ?设通道的宽为x m ,列方程(30-2x )(20-x )=468篱笆问题利用围墙的一段,砌成一个矩形花园ABCD (围墙MN 最长可利用25m ),现在已备足可以砌50m 长墙的材料,恰好用完,试求AB 的长,使矩形花园的面积为300m 2设m AB x =,则()502m BC x =-由题意,()502m 25mBC x =-≤列方程,()502300x x -=解得:110x =(舍去)215x =15x ∴=二.经济问题增长率某商品经过两次降价,每盒零售价由168元降为128元,求两次降价的平均百分率设降价的平均百分率为x ,列方程()21681=128x -降价销售核桃进价为40元/kg ,售价为60元/kg ,平均每天售出100千克,单价每降低2元,平均每天销量增加20kg ,若想平均每天获利2240元,每千克核桃应降价多少元?设每千克核桃应降价x 元降价后售价:60-x单价降2元,销量增加20kg单价降x 元,销量增加202x⋅kg(60-x -40)(100+2x×20)=2240三.其他问题比赛问题有x 支球队参加篮球比赛,共比赛了45场,已知每两队之间都比赛一场,求x∵有x 支球队参加篮球比赛,每两队之间都比赛一场,∴共比赛场数为x (x ﹣1),∴(1)2x x -=45传染问题有一人患了流感,经过两轮传染后共有64人患了流感。
求每轮传染中平均一个人传染了几个人?设每轮传染中平均每人传染了x 人,一轮传染:1x⋅此时共有()1+x 人得病二轮传染:()1+x x ⋅∴1+x +x (x +1)=64x =7或x =-9(舍去)三点剖析一.考点:一元二次方程的应用.二.重难点:列一元二次方程解应用题.三.易错点:建立一元二次方程解决实际问题时一定要注意检验是否符合实际意义.面积问题例题1、公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为()A.(x+1)(x+2)=18B.x2﹣3x+16=0C.(x﹣1)(x﹣2)=18D.x2+3x+16=0【答案】C【解析】设原正方形的边长为xm,依题意有(x﹣1)(x﹣2)=18,例题2、如图是一无盖长方体铁盒的平面展开图,若铁盒的容积为3m3,则根据图中的条件,可列出方程:【答案】x(x+1)=3【解析】长方体的高是1,宽x,长是x+1,根据题意得x(x+1)=3.例题3、如图,某小区规划在一个长30m、宽20m的矩形ABCD上,修建三条同样宽的通道,使其中两条与AB 平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78㎡,那么通道的宽应设计成________m.【答案】2【解析】暂无解析例题4、在美化校园的活动中,某综合实践小组的同学借如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形的花圃ABCD(篱笆只围AB、BC两边)设AB=xm.(1)若想围得花圃面积为192cm2,求x的值;(2)若在点P处有一棵小树与墙CD、AD的距离分别为15m和6m,要将这棵树围在花圃内(含边界,不考虑树干的粗细),求花圃面积S的最大值.【答案】(1)12m或16m(2)195(m2)【解析】(1)∵AB=xm,则BC=(28-x)m,∴x(28-x)=192,解得:x1=12,x2=16,答:x的值为12m或16m;(2)设花园的面积为S,由题意得:S=x(28-x)=-x2+28x=-(x-14)2+196,∵62815 xx⎧⎨-⎩≥≥,∴6≤x≤13,6≤x≤13的范围内,S随x增大而增大,∴当x=13时,S最大值=-(13-14)2+196=195(m2)随练1、有一块长方形铁皮,长100cm,宽50cm,在它的四周各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3600cm2,设铁皮各角应切去的正方形边长为xcm,则下面所列方程正确的是()A.4x2=3600B.100×50﹣4x2=3600C.(100﹣x)(50﹣x)=3600D.(100﹣2x)(50﹣2x)=3600【答案】D【解析】设切去的小正方形的边长为x.根据题意得(100﹣2x)(50﹣2x)=3600.随练2、如图,在一块长为22米、宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米.若设道路宽为x米,则根据题意可列出方程为.【答案】(22-x)(17-x)=300【解析】设道路的宽应为x米,由题意有(22﹣x)(17﹣x)=300,随练3、如图是一张长100cm,宽50cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,然后将四周突出部分折起,可制成底面积是3600cm2的一个无盖长方形纸盒,求剪去的正方形边长.【答案】5cm【解析】设剪去的正方形边长为xcm,则纸盒底面长为(100-2x)cm,宽为(50-2x)cm,根据题意得:(100-2x )(50-2x )=3600,整理,得:x 2-75x +350=0,解得:x 1=5,x 2=70(不合题意,舍去).故:剪去的正方形边长为5cm .经济问题例题1、某种药品原价为36元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x ,根据题意所列方程正确的是()A.36(1-x )2=36-25 B.36(1-2x )=25C.36(1-x )2=25 D.36(1-x 2)=25【答案】C【解析】第一次降价后的价格为36×(1-x ),两次连续降价后售价在第一次降价后的价格的基础上降低x ,为36×(1-x )×(1-x ),则列出的方程是36×(1-x )2=25.例题2、某商场销售一批真丝围巾,平均每天可售出20条,每条盈利40元,为了扩大销售,增加盈利,尽量减少库存,商场决定适当降价。
第04讲 勾股定理的应用(解析版)

第04讲勾股定理的应用类型一:勾股定理解决路径问题类型二:勾股定理解决折叠问题类型三:勾股定理解决实际问题类型四:勾股定理探究动点问题中的直角三角形存在问题【类型一:勾股定理解决路径问题】1.(2023春•分宜县期末)如图,在长方体ABCD﹣EFGH盒子中,已知AB=4cm,BC=3cm,CG=5cm,长为10cm的细直木棒IJ恰好从小孔G处插入,木棒的一端I与底面ABCD接触,当木棒的端点Ⅰ在长方形ABCD内及边界运动时,GJ长度的最小值为()A.(10﹣5)cm B.3cm C.(10﹣4)cm D.5cm【分析】当GI最大时,GJ最小,当I运动到点A时,GI最大,根据勾股定理求解即可.【解答】解:当GI最大时,GJ最小,当I运动到点A时,GI最大,此时GI=cm,而AC2=AB2+BC2=42+32=25,∴GI===5(cm),∴GJ长度的最小值为(10﹣5)cm.故选:A.2.(2022秋•永州期末)如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D点,AB=12,BD =13,点P是线段BC上的一动点,则PD的最小值是()A.6B.5C.13D.12【分析】过点D作DE⊥BC于点E,则PD的最小值是DE的长,根据角平分线的性质定理可得AD=DE,再由勾股定理求出AD的长,即可求解.【解答】解:如图,过点D作DE⊥BC于点E,则PD的最小值是DE的长,∵∠A=90°,BD平分∠ABC,∴AD=DE,∵AB=12,BD=13,∴,∴DE=5,即PD的最小值是5.故选:B.3.(2023秋•北仑区校级期中)如图,△ABC中,∠C=90°,AC=8,BC=6,线段DE的两个端点D、E 分别在边AC,BC上滑动,且DE=6,若点M、N分别是DE、AB的中点,则MN的最小值为()A.2B.2.5C.3D.3.5【分析】根据勾股定理得到AB=10,根据直角三角形斜边中线的性质求得CN=AB=5,CM==3,由当C、M、N在同一直线上时,MN取最小值,即可求得MN的最小值为2.【解答】解:如图,连接CM、CN,∵∠C=90°,AC=8,BC=6,∴AB==10,∵DE=6,点M、N分别是DE、AB的中点,∴CN=AB=5,CM=DE=3,当C、M、N在同一直线上时,MN取最小值,∴MN的最小值为:5﹣3=2.故选:A.4.(2022秋•绵阳期末)如图,在△ABO中,∠AOB=90°,∠BAO=30°,BO=6,⊙O的面积为12π,点M,N分别在⊙O、线段AB上运动,则MN长度的最小值等于()A.B.C.D.【分析】过点O作OC⊥AB,交⊙O于点P,当点M与点P重合,点N与点C重合时,MN长度的最小即为线段PC的长度,利用含30度角的直角三角形的性质及勾股定理得出,再由等面积法确定,由圆的面积得出,结合图形即可得出结果.【解答】解:过点O作OC⊥AB,交⊙O于点P,当点M与点P重合,点N与点C重合时,MN长度的最小即为线段PC的长度,∵∠AOB=90°,∠BAO=30°,BO=6,∴AB=2BO=12,∴,∴,解得:,∵⊙O的面积为12π,设半径为r,∴πr2=12π,,即MN长度的最小值为,故选:C.5.(2023春•廊坊期末)在△ABC中,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是()A.5B.6C.4D.4.8【分析】根据点到直线的连线中,垂线段最短,得到当BP垂直于AC时,BP的长最小,过A作等腰三角形底边上的高AD,利用三线合一得到D为BC的中点,在直角三角形ADC中,利用勾股定理求出AD 的长,进而利用面积法即可求出此时BP的长.【解答】解:根据垂线段最短,得到BP⊥AC时,BP最短,过A作AD⊥BC,交BC于点D,∵AB=AC,AD⊥BC,∴D为BC的中点,又BC=6,∴BD=CD=3,在Rt△ADC中,AC=5,CD=3,根据勾股定理得:AD==4,=BC•AD=BP•AC,又∵S△ABC∴BP===4.8.故选:D.6.(2023秋•桐柏县期中)如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD⊥BC.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是.【分析】连接BP,利用等腰三角形的对称性得BP=PC,则PC+PQ=BP+PQ=BQ,当B,P,Q共线时,PC+PQ的值最小,当BQ⊥AC时,BQ的值最小,利用勾股定理列方程即可解决问题.【解答】解:如图,连接BP,在△ABC中,AB=AC=10,BC=12,AD=8,∴BD=DC,∴BP=PC,∴PC+PQ=BP+PQ=BQ,∴当B,P,Q共线时,PC+PQ的值最小,∴当BQ⊥AC时,BQ的值最小,令AQ'=a,则CQ'=10﹣a,∵BQ'⊥AC,∴AB2﹣AQ'2=BC2﹣CQ'2,即102﹣a2=122﹣(10﹣a)2,解得a=,∴BQ'==,∴PC+PQ的最小值为,故答案为:.7.(2023秋•吴中区期中)如图,一支铅笔放在圆柱笔筒中,笔筒的内部底面直径是9cm,内壁高12cm.若铅笔长为18cm,则这只铅笔露在笔筒外面的长度h的最小值是3cm.【分析】由勾股定理求出AC=15cm,即可解决问题.【解答】解:如图,由题意可得:AB=12cm,BC=9cm,AB⊥BC,∴∠ABC=90°,在Rt△ABC中,由勾股定理得:AC===15(cm),∴这只铅笔露在笔筒外面的长度h的最小值是:18﹣15=3(cm),故答案为:3cm.8.(2023秋•大冶市期中)如图,在△ABC中,∠ABC=45°,AB=,AC=6,BC>4,点E,F分别在BC,AC边上,且AF=CE,则AE+BF的最小值为2.【分析】过A点作AG∥BC,截取AG=AC,连接FG,BG,过B作BR⊥AG,交AG的反向延长线于R,则∠RBC=∠BRA=90°,利用SAS证明△AFG≌△CEA可求得AE+BF的最小值即为BG的长,再结合等腰直角三角形的性质及勾股定理可求解.【解答】解:过A点作AG∥BC,截取AG=AC,连接FG,BG,过B作BR⊥AG,交AG的反向延长线于R,则∠RBC=∠BRA=90°,∴∠GAF=∠ACE,在△AFG和△CEA中,,∴△AFG≌△CEA(SAS),∴GF=AE,∴AE+BF的最小值,即为BG的长,∵∠ABC=45°,∴∠RAB=∠EBA=45°,∵AB=4,∴BR=AR=4,∵AC=6,∴AG=AC=6,∴RG=AR+AG=4+6=10,∴BG===2,即AE+BF的最小值为2.故答案为:2.【类型二:勾股定理解决折叠问题】9.(2023春•息县月考)已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.3cm2B.4cm2C.6cm2D.12cm2【分析】根据折叠的条件可得:BE=DE,在直角△ABE中,利用勾股定理就可以求解.【解答】解:将此长方形折叠,使点B与点D重合,∴BE=ED.∵AD=9cm=AE+DE=AE+BE.∴BE=9﹣AE,根据勾股定理可知AB2+AE2=BE2.解得AE=4.∴△ABE的面积为3×4÷2=6.故选:C.10.(2023春•岳麓区校级期末)如图,△ABC中,∠ACB=90°,AC=4,BC=3,将△ADE沿DE翻折,使点A与点B重合,则AE的长为()A.B.3C.D.【分析】在Rt△BCE中,由BE2=CE2+BC2,得到(8﹣x)2=x2+62,即可求解.【解答】解:设AE=BE=x,则CE=4﹣x,在Rt△BCE中,BE2=CE2+BC2,即x2=(4﹣x)2+32,解得x=,故选:D.11.(2022秋•西峡县期末)如图,在长方形ABCD中,AB=3cm,BC=4cm.将长方形沿对角线AC折叠,点D落在了D′位置,AD′与BC相交于点E.则BE的长等于()A.B.C.D.【分析】设BE=x cm,则EC=(4﹣x)cm,根据题意可证得Rt△ABE≌Rt△CED′,可得BE=ED′=x cm,根据EC2=ED′2+CD′2可得到关于x的方程,求解即可得到答案.【解答】解:设BE=x cm,则EC=(4﹣x)cm.根据图形折叠的性质可知CD=CD′,∠D=∠D′.∵四边形ABCD为长方形,∴AB=CD=3cm,∠B=∠D=90°.∴AB=CD′=3cm,∠B=∠D′=90°.在△ABE和△CED′中∴△ABE≌△CED′(AAS).∴BE=ED′=x cm.在Rt△CED′中EC2=ED′2+CD′2,即(4﹣x)2=x2+32.解得.∴cm.故选:A.12.(2023秋•九台区期末)如图,Rt△ABC中,∠B=90°,AB=4,BC=6,将△ABC折叠,使点C与AB的中点D重合,折痕交AC于点M,交BC于点N,则线段CN的长为()A.B.C.3D.【分析】由折叠的性质可得DN=CN,根据勾股定理可求DN的长,即可求CN的长.【解答】解:∵D是AB中点,AB=4,∴AD=BD=2,∵将△ABC折叠,使点C与AB的中点D重合,∴DN=CN,∴BN=BC﹣CN=6﹣DN,在Rt△DBN中,DN2=BN2+DB2,∴DN2=(6﹣DN)2+4,∴DN=,∴CN=DN=,故选:D.13.(2022秋•东坡区期末)如图,将长方形纸片ABCD的边沿折痕AE折叠,使点D落在BC上的点F处,若AB=5,AD=13,则EF的长为()A.B.C.1D.【分析】先由长方形的性质得到BC=AD=13,∠B=∠C=90°,CD=AB=5,再由折叠的性质得到AF =AD=13,EF=DE,利用勾股定理求出BF=12,则CF=1,设EF=DE=x,则CE=CD﹣DE=5﹣x,利用勾股定理建立方程x2=12+(5﹣x)2,解方程即可得到答案.【解答】解:由长方形的性质可得BC=AD=13,∠B=∠C=90°,CD=AB=5,由折叠的性质可得AF=AD=13,EF=DE,在Rt△ABF中,由勾股定理得,∴CF=BC﹣BF=1,设EF=DE=x,则CE=CD﹣DE=5﹣x,在Rt△CEF中,由勾股定理得EF2=CE2+CF2,∴x2=12+(5﹣x)2,解得,∴,故选:B.14.(2023秋•银川期中)如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿直线AD对折,使它落在斜边AB上,且与AE重合,求CD的长.【分析】先由勾股定理求AB=10.再用勾股定理从△DEB中建立等量关系列出方程即可求CD的长.【解答】解:∵两直角边AC=6cm,BC=8cm,在Rt△ABC中,由勾股定理可知AB=10,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD=DE,AE=AC=6,∴BE=10﹣6=4,设DE=CD=x,BD=8﹣x,在Rt△BDE中,根据勾股定理得:BD2=DE2+BE2,即(8﹣x)2=x2+42,解得x=3.即CD的长为3cm.15.(2023秋•青岛期中)如图,平面直角坐标系中,点D的坐标为(15,9),过点D作DA⊥y轴,DC⊥x 轴,点E为y轴上一点,将△AED沿直线DE折叠,点A落在边BC上的点F处.(1)请你直接写出点A的坐标;(2)求FC,AE的长;(3)求四边形EOFD的面积.【分析】(1)证明四边形AOCD是矩形,再结合D的坐标即可得出结果;(2)根据折叠的性质得出DF的长,再根据勾股定理求出CF的长,即可得出OF的长,设AE=x,在Rt△OEF中根据勾股定理得出等式求解得出AE的长即可;+S△EFD=S△EOF+S△AED,再根据三角形的面积(3)根据折叠的性质可知,四边形EOFD的面积=S△EOF公式求解即可.【解答】解:(1)∵DA⊥y轴,DC⊥x轴,∠AOC=90°,∴四边形AOCD是矩形,∵D的坐标为(15,9),∴AD=OC=15,CD=AO=9,∴A(0,9);(2)∵将△AED沿直线DE折叠,点A落在边BC上的点F处.∴DF=AD=15,∴CF==12,∴OF=OC﹣CF=15﹣12=3,设AE=x,则EF=x,OE=9﹣x,在Rt△OEF中,由勾股定理得,OE2+OF2=EF2,即(9﹣x)2+32=x2,解得x=5,∴AE=5;(3)由(2)知AE=5,∴OE=9﹣5=4,=S△DFE,由折叠的性质可知,S△AED+S△EFD=S△EOF+S△AED∴四边形EOFD的面积=S△EOF===.【类型三:勾股定理解决实际问题】16.(2022秋•辉县市校级期末)如图1,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根12米处,图2是这棵大树折断的示意图,则这棵大树在折断之前的高是()A.20米B.18米C.16米D.15米【分析】利用勾股定理进行求解即可.【解答】解:设大树在折断之前的高是x m,由勾股定理得:(x﹣5)2=122+52,解得:x=18或x=﹣8(不符合题意,舍去),∴大树在折断之前的高是18m;故选:B.17.(2022秋•古县期末)如图,为了测量池塘的宽度DE,在池塘周围的平地上选择了A,B,C三点,且A,D,E,C四点在同一条直线上,∠C=90°,已测得AB=100m,BC=60m,AD=20m,EC=10m,则池塘的宽度DE是()A.80m B.60m C.50m D.40m【分析】根据已知条件在直角三角形ACB中,利用勾股定理求得AC的长,用AC减去AD、CE求得DE 即可.【解答】解:在Rt△ABC中,∠C=90°,AB=100m,BC=60m,∴AC===80(m),∴DE=AC﹣AD﹣EC=80﹣20﹣10=50(m),∴池塘的宽度DE为50米.故选:C.18.(2022秋•万荣县期末)山西地形较为复杂,境内有山地、丘陵、高原、盆地、台地等多种地貌类型,整个地貌是被黄土广泛覆盖的山地型高原.如图,在A村与B村之间有一座大山,原来从A村到B村,需沿道路A→C→B(∠C=90°)绕过村庄间的大山,打通A,B间的隧道后,就可直接从A村到B村.已知AC=9km,BC=12km,那么打通隧道后从A村到B村比原来减少的路程为()A.7km B.6km C.5km D.2km【分析】由勾股定理求出AB==15(km),因此AC+BC﹣AB=6(km),即可得到答案.【解答】解:∵∠C=90°,AC=9km,BC=12km,∴AB==15(km),∴AC+BC﹣AB=9+12﹣15=6(km),∴从A村到B村比原来减少的路程为6km.故选:B.19.(2023秋•尤溪县期中)如图,一架25m长的梯子AB,斜靠在竖直的墙AC上,这时梯子的底部B到墙底端C的距离为7m.(1)这个梯子的顶端距地面有多高?(2)如果梯子的底部B在水平方向滑动了8m至D,那么梯子的顶端A沿墙垂直也下滑了8m吗?【分析】(1)根据勾股定理即可得到结论;(2)根据勾股定理,求出EC即可解答.【解答】解:(1)根据题意得:AB=25,BC=7,∴AC==24(m),答:这个梯子的顶端距地面有24m;(2)梯子的顶端A沿墙垂直不是下滑了8m,∵BC=7,BD=8,∴CD=15m,∴CE==20(m),∴AE=AC﹣CE=24﹣20=4(m),∴梯子的顶端A沿墙垂直也下滑了4m.20.(2023秋•左权县期中)在学校组织的研学活动中,辰星小组合作搭建帐篷.图是他们搭建帐篷的支架示意图.在△ABC中,两根支架从帐篴顶点A支撑在水平的支架上,一根支架AD⊥BC于点D,另一根支架AE的端点E在线段BD上,且AE=BE.经测量,知BD=1.6m,AD=1.2m,AC=1.5m.根据测量结果,解答下列问题:(1)求AE的长;(2)按照要求,当帐篷支架AB与AC所夹的角度为直角时,帐篷最为稳定.请通过计算说明辰星小组搭建的帐篷是否符合要求.【分析】(1)设AE=x m,则BE=AE=x m,ED=(1.6﹣x)m,在Rt△ADE中,利用勾股定理即可求解;(2)利用勾股定理求出AB与CD的长,从而得出BC的长,再利用勾股定理逆定理得出△ABC是直角三角形,∠BAC=90°,进而得出结论.【解答】解:(1)设AE=x m,则BE=AE=x m,ED=(1.6﹣x)m,∵AD⊥BC,∴∠ADB=∠ADC=90°,在Rt△ADE中,AD2+ED2=AE2,1.22+(1.6﹣x)2=x2,解得.∴AE的长为;(2)帐篷符合要求.理由如下:在Rt△ABD中,BD=1.6m,AD=1.2m,∴,在Rt△ADC中,AD=1.2m,AC=1.5m,∴,∴BC=BD+CD=2.5m,∵AB2+AC2=22+1.52=6.25,BC2=2.52=6.25,∴AB2+AC2=BC2.∴△ABC是直角三角形,∠BAC=90°.∴帐篷符合要求.21.(2023秋•二道区期末)某实践探究小组在放风筝时想测量风筝离地面的垂直高度,通过勘测,得到如下记录表:测量示意图测量数据边的长度①测得水平距离BC的长为15米.②根据手中剩余线的长度计算出风筝线AB的长为17米.③小明牵线放风筝的手到地面的距离为1.7米.数据处理组得到上面数据以后做了认真分析,他们发现根据勘测组的全部数据就可以计算出风筝离地面的垂直高度AD.请完成以下任务.(1)已知:如图,在Rt△ABC中,∠ACB=90°,BC=15,AB=17.求线段AD的长.(2)如果小明想要风筝沿DA方向再上升12米,BC长度不变,则他应该再放出多少米线?【分析】(1)根据勾股定理求出AC,进而求出AD;(2)先根据勾股定理求出风筝线的长,再根据题意计算,得到答案.【解答】解:(1)在Rt△ABC中,∠ACB=90°,BC=15,AB=17,由勾股定理得:AC===8,则AD=AC+CD=8+1.7=9.7;(2)风筝沿DA方向再上升12米后,风筝的高度为20米,则此时风筝线的长为:=25(米),25﹣17=8(米),答:他应该再放出8米线.【类型四:勾股定理探究动点问题中的直角三角形存在问题】22.(2023秋•新吴区期中)如图,点A是射线BC外一点,连接AB,若AB=5cm,点A到BC的距离为3cm,动点P从点B出发沿射线BC以2cm/s的速度运动.设运动的时间为t秒,当t为()秒时,△ABP 为直角三角形.A.B.C.2或D.2或【分析】过点A作AH⊥BC于点H,由勾股定理求得BH=4cm,当∠APB=90°时,此时点P与点H重合,求出t=2;当∠BAP=90°时,HP=(2t﹣4)cm,由勾股定理得AP2=BP2﹣AB2=AH2+HP2,列出方程,解方程即可.【解答】解:如图1,过点A作AH⊥BC于点H,∵点A到BC的距离为3cm,∴AH=3cm,在Rt△AHB中,由勾股定理得:BH===4(cm),分两种情况:①当∠APB=90°时,此时点P与点H重合,由题意得:2t=4,解得:t=2;②如图2,当∠BAP=90°时,∵AB=5cm,BP=2t cm,AH=3cm,BH=4cm,∴HP=(2t﹣4)cm,由勾股定理得:AP2=BP2﹣AB2=(2t)2﹣25,AP2=AH2+HP2=32+(2t﹣4)2,∴(2t)2﹣25=32+(2t﹣4)2,解得:t=,综上所述,当t为(2或)秒时,△ABP为直角三角形,故选:D.23.(2022秋•泌阳县期末)如图,在Rt△ABC中,∠ACB=90°,BC=40cm,AC=30cm,动点P从点B 出发沿射线BA以2cm/s的速度运动.则当运动时间t=25或16s时,△BPC为直角三角形.【分析】首先根据勾股定理求出斜边AB的长度,利用三角形的面积求出斜边上的高CD,再分两种情况进行讨论:①当∠BCP为直角时,②当∠BPC为直角时,分别求出此时的t值即可.【解答】解:在Rt△ABC中,∠ACB=90°,BC=40cm,AC=30cm,∴AB===50(cm).如图,作AB边上的高CD.=AB•CD=AC•BC,∵S△ABC∴CD===24(cm).①当∠BCP为直角时,点P与点A重合,BP=BA=50cm,∴t=50÷2=25(秒).②当∠BPC为直角时,P与D重合,BP=2t cm,CP=24cm,BC=40cm,在Rt△BCP中,∵BP2+CP2=BC2,∴(2t)2+242=402,解得t=16.综上,当t=25或16秒时,△BPC为直角三角形.故答案为:25或16.24.(2023秋•乐平市期中)如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以每秒1cm的速度运动,设运动时间为t秒.当t为6或13或12或10.8时,△ACP是等腰三角形.【分析】分CA=CP、PA=PC、AC=AP、AC=CP四种情况,根据等腰三角形的性质解答.【解答】解:∵∠ACB=90°,AC=6cm,BC=8cm,∴AB==10,当CA=CP时,如图:∴CP=6cm,∴t=6÷1=6;当PA=PC时,如图:∴∠PAC=∠PCA,∵∠PAC+∠B=90°,∠ACP+∠PCB=90°,∴∠PCB=∠PBC∴PA=PC=PB=AB=5cm,∴t=(CB+BP)÷1=13;当AC=AP时,如图:AP=6cm,AB=10cm,∴PB=AB﹣AP=4cm,∴t=(CB+BP)÷1=12;当AC=CP时,如图:作CD⊥AB于点D△ABC的面积=×AC×BC=×AB×CD,即×6×8=×10×CD,解得,CD=4.8,在Rt△ACD中,AD==3.6,∴AP=2AD=7.2,∴BP=AB﹣AP=2.8,∴t=(CB+BP)÷1=10.8;综上所述,当t为6或13或12或10.8时,△ACP是等腰三角形.25.(2023秋•阜宁县期中)如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发,沿射线BC以2cm/s的速度移动设运动的时间为ts当t=2s或s时,△ABP为直角三角形.【分析】首先根据勾股定理求出BC的长度,再分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时的t值即可.【解答】解:∵∠C=90°,AB=5cm,AC=3cm,∴BC=4cm.①当∠APB为直角时,点P与点C重合,BP=BC=4cm,∴t=4÷2=2s.②当∠BAP为直角时,BP=2tcm,CP=(2t﹣4)cm,AC=3cm,在Rt△ACP中,AP2=32+(2t﹣4)2,在Rt△BAP中,AB2+AP2=BP2,∴52+[32+(2t﹣4)2]=(2t)2,解得t=s.综上,当t=2s或s时,△ABP为直角三角形.故答案为:2s或s.26.(2022秋•南阳期末)如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若动点P从点A出发,以1cm/s的速度沿折线A﹣C﹣B﹣A运动.设运动时间为t(t>0)s.当点P运动到恰好到点A和点B的距离相等的位置时,t的值为或19.【分析】设存在点P,使得PA=PB,此时PA=PB=t cm,PC=(8﹣t)cm,根据勾股定理列方程即可得到结论;【解答】解:在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,则由勾股定理得到:AC===8(cm)当点P在AC上时,设存在点P,使得PA=PB,此时PA=PB=t cm,PC=(8﹣t)cm,在Rt△PCB中,PC2+CB2=PB2,即:(8﹣t)2+62=t2,解得:t=,∴当t=时,PA=PB;当点P在AB上时,此时AC+BC+BP=8+6+5=19cm,∴当t=19时,PA=PB;故答案为:或19.27.(2023春•陈仓区期末)如图,在Rt△ABC中,∠ACB=90°,AB=10cm,AC=6cm,动点P从B出发沿射线BC以1cm/s的速度运动,设运动时间为t(s).(1)求BC边的长.(2)当△ABP为等腰三角形时,求t的值.【分析】利用勾股定理求解BC的长,再分3中情况讨论:当AP=BP时,当AB=BP时,当AB=AP 时,分别计算可求解.【解答】解:在Rt△ABC中,∠ACB=90°,AB=10cm,AC=6cm,∴BC=,当AP=BP时,如图1,则AP=t,PC=BC﹣BP=8﹣t,在Rt△ACP中,AC2+CP2=AP2,∴62+(8﹣t)2=t2,解得t=;当AB=BP时,如图2,则BP=t=10;当AB=AP时,如图3,则BP=2BC;∴t=2×8=16,综上,t的值为或10或16.28.(2023春•乳山市期末)如图,在△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以每秒1cm的速度运动,设运动的时间为t秒.(1)若△ABP是以BP为斜边的直角三角形,求t的值;(2)若△ABP是以BP为腰的等腰三角形,求t的值.【分析】(1)依题意,AP=t,利用勾股定理即可求得t的值;(2)分情况讨论:AB=BP时,直接可得t的值;BP=AP时,在Rt△APC中,利用勾股定理求解即可.【解答】解:(1)∵∠ACB=90°,AB=5cm,AC=3cm,∴,∴CP=t﹣4,由∠ACP=∠BAP=90°,可得AP2=t2﹣25=(t﹣4)2+9,解得,所以t的值为;(2)当AB=BP时,t=5.当BP=AP时,∴CP=4﹣t,在Rt△APC中,可得9+(4﹣t)2=t2,。
运算符号的运用与理解

运算符号的运用与理解运算符号是编程语言中非常重要的元素之一,它们用于执行各种数学和逻辑操作。
正确的使用和理解运算符号对于编写高效且具有逻辑可读性的代码至关重要。
本文将介绍常见的运算符号及其用法,并探讨如何正确理解和应用运算符号。
一、算术运算符算术运算符用于执行基本的数学运算,如加、减、乘、除等。
以下是常见的算术运算符及其使用方法:1. 加法运算符(+):用于将两个值相加。
2. 减法运算符(-):用于从一个值中减去另一个值。
3. 乘法运算符(*):用于将两个值相乘。
4. 除法运算符(/):用于将一个值除以另一个值。
5. 取余运算符(%):用于计算两个数相除的余数。
例如,在计算两个数的和时可以使用加法运算符:“a + b”。
通过正确使用这些算术运算符,我们可以轻松实现各种数学计算。
二、比较运算符比较运算符用于比较两个值之间的关系,并返回一个布尔值(True 或False)。
以下是常见的比较运算符及其使用方法:1. 相等运算符(==):用于判断两个值是否相等。
2. 不等运算符(!=):用于判断两个值是否不相等。
3. 大于运算符(>):用于判断一个值是否大于另一个值。
4. 小于运算符(<):用于判断一个值是否小于另一个值。
5. 大于等于运算符(>=):用于判断一个值是否大于等于另一个值。
6. 小于等于运算符(<=):用于判断一个值是否小于等于另一个值。
比较运算符常用于条件语句和循环控制,通过对比运算符的返回值,我们可以根据条件的满足与否来执行不同的代码逻辑。
三、逻辑运算符逻辑运算符用于对布尔值进行运算,判断多个条件的关系。
以下是常见的逻辑运算符及其使用方法:1. 与运算符(&&或and):用于判断多个条件是否同时为真。
2. 或运算符(||或or):用于判断多个条件是否至少一个为真。
3. 非运算符(!或not):用于对布尔值进行取反操作。
逻辑运算符常用于条件判断和循环控制语句中,通过组合多个条件可以实现更加复杂的逻辑运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010-5-20
7
注意事项: 注意事项
<,>,<=和>=只能用来比较两个数值类 , , 和 只能用来比较两个数值类 型数据(numbers含characters)的大小; 的大小; 型数据 含 的大小 – 不能用于 不能用于Strings,booleans,arrays或 , , 或 其他类型的比较; 其他类型的比较;
2010-5-20 17
运算符的优先级与结合性
优先级 1 2 3 4 5 6 7 8 9 10 11 12 13 14
2010-5-20
运算符 .,[],() -,~,!,+ +,- - ,类型强制 , ,, , *,/,% ,,
结合性 左/右 右 右 左 左 左 左 左 左 左 左 左 左 右 右
2010-5-20
15
7 表达式
由操作数和运算符按照一定的语法格式 组成表达式. 例如, (a+b)*(c-d) 表达式不是语句; 某些表达式加分号 分号可以成为语句,如: 分号 c=a+b;
2010-5-20 16
运算符的优先级与结合性
不同的运算符具有不同的优先顺序; 不同的运算符具有不同的优先顺序; 可以用( )来改变优先顺序或使表达式更 可以用 来改变优先顺序或使表达式更 容易理解; 容易理解; 例如 例如: –a + b + c / 3 – (a + b + c ) / 3
例如, double d = 3.14159; int a = ( int ) d; // 变量d类型不变
2010-5-20 19
Java中的数据类型转换规则 中的数据类型转换规则
在赋值运算中,不同数据类型是可以互相转换的; 弱的数据类型数据一般可以直接转换为强的数据类型, 也称为隐式类型转换 隐式类型转换.将强的数据类型数据转换为弱 隐式类型转换 的数据类型数据称为强制类型转换 强制类型转换,需要采用显式类 强制类型转换 型转换; 布尔类型数据不能与其它基本类型数据相互转换; 强制类型转换可能会造成丢失数据精度 丢失数据精度,如浮点型数 丢失数据精度 据转换成整型数据是用舍入取整而不是四舍五入方法 的.如果需要用四舍五入方法取整,可以用如下格式: 定点类型变量=(定点类型)(浮点表达式+0.5)
11
注意区别条件与&&( )和逻辑与&( ) 注意区别条件与 (或||)和逻辑与 (或|) 例如, 例如,int a=6, b=8, c=10, d=12; boolean x=++a>b++&&c++>d--; (a=7,b=9,c=10,d=12,x=false) , , , ,
&,不管其前面的表 , 达式为什么, 达式为什么,都计算 其后面表达式 &&,如果其前 , 面的表达式为 假,则不再计 算其后面的表 达式
2010-5-20
8
3.布尔逻辑运算符 布尔逻辑运算符
运算符 & | ! ^ && || 运算 逻辑与AND 逻辑与 逻辑或OR 逻辑或 逻辑非NOT 逻辑非 逻辑异或XOR 逻辑异或 条件与AND 条件与 条件或OR 条件或
逻辑运算是针对布尔型数据进行的运算,运算结果仍为 布尔型值,即:true false true和false true false;
第四讲 运算符及应用
教学目标:
1. 2. 3. 4. 5. 6. 掌握算术运算符及应用; 掌握算术运算符及应用; 掌握关系运算符及应用; 掌握关系运算符及应用; 掌握布尔逻辑运算符及应用; 掌握布尔逻辑运算符及应用; 掌握赋值类运算符及应用; 掌握赋值类运算符及应用; 掌握条件运算符及其它运算符的应用; 掌握条件运算符及其它运算符的应用; 理解运算符的优先级与结合性; 理解运算符的优先级与结合性;
2010-5-20 20
Java中的数据类型转换规则 中的数据类型转换规则
2010-5-20
21
总结: 总结
回顾了Java语言的基本语法,特别是标识符 的定义规则; 回顾了四大种(八小种)数据类型.整型, 字符型,浮点型,布尔型; 各种运算符的使用方法和优先级;
2010-5-20
22
a) b) c) d) e) f) g) h) i) j)
– op1:布尔表达式 布尔表达式
例如: 例如
int k= ( (i>=0) ? 1 : -1);
2010-5-20
14
6. 其他运算符
其他运算符包括:(类型 ,.,[ ],( ), 其他运算符包括: 类型 类型), , , , instanceof和new 和 例如: 例如:
int a=51; char c=(char)a;
2010-5-20
2
单目运算符: 单目运算符:
运算符 ++ -运算 自增 自减 取反 例子 a++或++a 或 a—或—a 或 -a 功能 a=a+1 a=a-1
这里特别要注意的是:++和--,它们若放在前面,是先执行单目运算符, 这里特别要注意的是:++和--,它们若放在前面,是先执行单目运算符, 然后再执行其它运算,否则相反. 然后再执行其它运算,否则相反.如: x=2; y=(++x)*3; int x=2; int y=(++x)*3;与 x=2; y=(x++)*3;就不一样. int x=2; int y=(x++)*3;就不一样.
2010-5-20
1
1. 算术运算符
双目运算符: 双目运算符:
运算符 + * / % 运算 加 减 乘 除 取余 例子 a+b a-b a*b a/b a%b 功能 求a与b的和 与 的和 a与b的差 求a与b的差 求a与b的积 与 的积 求a与b的商 与 的商 求a与b相除的余数 与 相除的余数
请模仿程序Javalogic.java,上机验证计算结果;2010- Nhomakorabea-20 23
�
课堂练习: 课堂练习0;则表达式j = 8+3*9/7-6计算之后j的值是______. 已知int i = 10,j =
已知int i = 10,j = 0;则表达式j = i+3*9%i-4计算之后j的值是______. 已知int i = 8,j = 0;则表达式j = 5+ ++i计算之后j的值是______,再计算 表达式j = 5 + i + +之后j的值是______. 已知int i = 5,j = 2;则表达式j = 5 - - - i计算之后j的值是______,再计 算表达式j = 5 + i - -之后j的值是______. 已知int i = 3,j = 9;则表达式j + = + + i计算之后j的值是_______,再计 算表达式 j - = 5 + i + +之后j的值是_____. 已知int i = 5,j = 8;则表达式j + = - - i计算之后j的值是_______,再计 算表达式 j - = 5 + i - -之后j的值是____. 已知int i = 5,j = 8;则表达式j*=j+3*i*j-- 计算后j的值是_____. 已知int i = 5,j = 8;则表达式j+=j-=j*=j 计算后j的值是_____. 已经 int i=11,j = 19, k = 28;则表达式(i<10&&j>10&&k!=10)的值是___, 表达式( i<10 || j>10 || k!=10 )的值是_____. 已经 int i=10,j = 18, k = 9;则表达式(i<9&&j>9&&k!=9)的值是____,表达 式( i<9 || j>9 || k!=9 )的值是______.
2010-5-20
3
前缀++:变量首先进行操作在自身进行加. 例如, int a=2; int b = a ++; (a=3,b=2) 后缀++:变量自身首先加然后再进行操作. 例如, int a=2; int b = ++ a; (a=3,b=3)
2010-5-20
4
算术运算符要注意: 算术运算符要注意:
2010-5-20
10
逻辑运算(&和 逻辑运算 和| )
两个操作数均会被运算 (即不采用短路规则 ; 即不采用短路规则); 即不采用短路规则 用不用短路规则,副作用不同; 用不用短路规则,副作用不同; 例如, 例如
(birthday == true) | (++age >= 65)
2010-5-20
– 没有指数运算,但是可以引用 没有指数运算, Math.pow(2.0, 3.0); // 2.03.0 – 整数除法:截去余数 整数除法: 7 / 5 结果为 1 – 取模:返回余数 取模: 7 % 5 结果为 2
2010-5-20
5
2. 关系运算符
运算符 == != > < >= <= 运算 等于 不等于 大于 小于 大于等于 小于等于
18
+,,
>>,<<,>>> , , <,<=,>,>= ,instanceof , , , ==,!= , & ^ | && || ?: =,<op>= ,
