未知单价
四年级上册数学 购物问题

一、解决问题:最多能买几件?类型一:有余数的。
用去尾法。
例1、文具盒每个12元,李老师带900元钱,最多能买多少个文具盒?解:200÷12=16(个)…8(元)答:最多能买16个文具盒。
类型二:有买有送的,先算买的,再算送的,最后合起来。
例2、李老师为学校买文具盒作为体育比赛的奖品,他带900元钱,最多能买多少个文具盒?买:900÷12=75(个)送:75÷8=9(个)…3(个)共:75+9=84(个)答:最多能买84个文具盒。
类型三:组合销售。
分方案计算,最后比较。
例3-1、运动鞋店开展促销活动,王老师,带330元,最多可以买几双运动鞋,还剩多少钱?方案一:185÷29=6(件)…11(元)方案二:185÷49=3(组)…38(元)38÷29=1(件)…9(元)3×2+1=7(件)答:最多可以买7件,还剩9元钱。
二、解决问题:每个便宜多少钱?类型一:已知买的件数和送的件数,算出现在单价,最后用原单单价-现单价。
例1、一条被子原价80元,五一期间商场举行优惠活动,买一送三,爸爸用原来买3条裤子的钱买裤子,每条裤子便宜多少元?解:80-80×3÷(3+1)=20(元)答:每条裤子便宜20元。
类型二:未知买多少件,要先求出件数。
然后算出现在单价,最后用原单单价-现单价。
例2、商店搞促销活动,一套乐高积木售价54元,买3套送1套。
王老师如果为班里6名同学1人置办1套,每套将便宜多少钱?6÷(3+1)=1(组)…2(套)现在单价:54×(3+5)÷6=45(元)便宜:54-45=9(元)答:便宜了9元。
三、解决问题:一共要花多少钱?例1、李伯伯准备买50棵树苗,应花多少钱?送:50÷(3+1)=12(组)…2(棵)买:50-12=38(棵)钱:16×38=608(元)答:应花608元。
投标报价之不平衡报价

随着我国建筑工程市场的逐步规范,《建设工程工程量清单计价规范》也在不断地充实和完善中,这标志着建筑工程招投标市场逐步走向一个有序、健康的运行轨道,同时也对造价人员也提出了更高的工作要求。
作为一名优秀的造价工作人员,在投标过程中如何采取有效的报价策略,在众多的投标单位中脱颖而出,最终中标,既为公司带来了生产任务又实现了公司的最大盈利价值这是我们追求的最终目标。
投标报价竞争的胜负和中标与否,不仅取决于竞争者的经济实力和技术水平,更主要取决于竞争策略是否正确。
投标报价策略是指投标单位在合法竞争条件下,依据自身的实力和条件决定投标报价行为的决策思维和行动。
投标策略作为投标取胜的方式、手段和艺术,贯穿于投标竞争的始终,内容十分丰富。
在工程投标过程中,投标报价是整个过程的核心,报价过高,则可能因为超出“最高限价”而失去中标机会;报价过低,则可能因为低于“合理低价”而废标,或者即使中标,也可能会给企业带来亏本的风险。
在市场竞争如此激烈的今天,施工企业想要在市场中站稳脚跟,就必须及时抓住市场转瞬即逝的契机,在追求利润最大化的同时,还要保证报价的竞争性,那么不平衡报价无疑是施工企业首选的投标报价策略。
一、不平衡报价的概念不平衡报价就是在一个工程项目的投标总价基本确定后,根据招标文件规定的付款条件及工程量清单的内容,合理地调整投标文件中子项目的报价,在不抬高总价以免影响中标的前提下,实施项目时能够尽早、更多地结算工程款,并能够赢得更多利润的一种投标报价方法。
二、不平衡报价的目的不平衡报价是在保持投标总价不变的前提下,通过增加工程量清单中的一些项目的单价;同时降低另外一些项目的单价来使工程所需要资金达到最小的方法。
它的目的并不是靠降低报价来提高投标的竞争力,也不是靠提高报价而期望中标后能取得较好的经济效益,而是:(一)改善工程项目的资金流动。
(二)赚取由于工程量改变而引起的额外收入。
(三)给二次经营工作开辟良好的索赔空间。
五年级数学上册用字母表示数练习题

五年级数学上册用字母表示数练习题篇一:人教版五年级上册数学用字母表示数练习题用字母表示数练习题1.储蓄罐里旧有n元钱,现在又重新加入两个一元的和两个五角的,现在存有()元。
2.车上原来有x人,下了5人后现在有()人。
3.桌子上加3个鱼缸,每缸里存有a条鱼,一共存有()条。
4.锅里有m个饺子(m为整十数),每盘装10个,可以装()盘。
5.我国青少年(7-17岁)在1980年平均体重xcm,至2000年,平均值体重快速增长了6cm。
2000年我国青少年平均值体重()cm。
6.人的骨骼约是体重的0.18倍,一个人重akg,骨骼约是()kg。
7.人的体重早晚可能会差距2cn,在早上最低,晚上最老。
一个人早上体重bcm,晚上体重可能将就是()cm。
8.小英家本月的用电量是80千瓦时,交电费c元,那么电费每千瓦时是()元。
9.昨天买进48个足球,今天比昨天多买进m个,今天买进足球()个。
当m=10时,今天买进()个。
当m=()时,今天买进60个。
10.我每分钟骑vm,2分钟骑()m,t分钟骑()m。
用v表示速度,t表示时间,s表示路程。
s=()如果每分钟行260m,时间是30分,路程是()米。
11.王红的每分钟踢x个字,她工作了5分钟,共踢了()个字。
12.商店原有120kg苹果,又运来了10箱苹果,每箱重akg。
这个商店里苹果的总质量是()。
当a等于25时,商店一共有()千克苹果。
13.仓库里存有货物96吨,运出了12车,每车运b吨。
用式子则表示仓库里剩货物的吨数为()。
当b等同于5时,仓库里剩的货物存有()吨。
14.动车的速度为220千米/时,普通列车的速度为120千米/时。
行驶x小时,动车和普通列车一共行了()千米。
行驶x小时,动车比普通列车多行了()千米。
15.一天早晨的温度就是b℃,中午比早晨低8℃。
b+8则表示()。
某班共有50名学生,女生有(50-c)名。
这里的表示()。
16.在一场篮球比赛中,小姚叔叔相继投过了x个3分球,3x则表示()。
小学三年级数学应用题分类及解法

小学三年级数学应用题分类及解法一、引言小学三年级是学生们开始接触数学应用题的初始阶段。
这一阶段的学习对于学生来说至关重要,因为它不仅为学生打下了数学基础,还培养了他们解决问题的能力。
本文将数学应用题分为几类,并给出相应的解题方法。
二、分类1、计算类应用题:这类应用题主要考察学生的计算能力,如加减乘除、分数、小数等。
例如:“小明有5个苹果,小红有3个苹果,他们一共有多少个苹果?”这类问题的解决方法主要是通过正确的计算步骤得出答案。
2、比较类应用题:这类应用题通过比较两个或多个数量或数值来考察学生的比较能力。
例如:“一斤苹果的价格是5元,一斤香蕉的价格是3元,哪种水果更便宜?”解决这类问题,学生需要掌握比较的方法,并能够确定哪个数量或数值更大或更小。
3、图形类应用题:这类应用题通过图形或几何问题来考察学生的空间观念和推理能力。
例如:“一个长方形的长是5厘米,宽是3厘米,请问这个长方形的面积是多少?”解决这类问题,学生需要理解图形的性质和相关的几何公式。
4、逻辑推理类应用题:这类应用题通过一系列的信息或条件,要求学生推断出某种结论或结果。
例如:“在1,2,3,4,5,6,7,8,9中,不重复的三个数字可以组成一个三位数,请问有多少种可能的组合方式?”解决这类问题,学生需要运用逻辑推理的能力,从给定的信息中推导出正确的答案。
三、解题方法对于每一类应用题,我们都有相应的解题方法:1、计算类应用题:首先要理解题目中的数学表达式或方程,然后使用正确的计算步骤得出答案。
如果遇到困难,可以重新阅读题目或寻求帮助。
2、比较类应用题:首先需要确定哪个数量或数值更大或更小,然后通过比较得出答案。
如果遇到困难,可以重新阅读题目或寻求帮助。
3、图形类应用题:首先需要理解图形的性质和相关的几何公式,然后使用这些公式来解决问题。
如果遇到困难,可以借助模型或重新阅读题目。
4、逻辑推理类应用题:首先需要仔细阅读题目,理解所有的信息和条件,然后使用逻辑推理的方法得出答案。
人教版四年级数学上册第四单元《第04课时_单价数量总价》(教案)

人教版四年级数学上册第四单元《第04课时_单价数量总价》(教案)一. 教材分析人教版四年级数学上册第四单元《单价数量总价》是本单元的第四课时,本节课主要让学生理解单价、数量和总价之间的关系,掌握用字母表示单价、数量和总价的方法,学会通过已知两个量来求第三个量的方法。
教材通过生动的例题和丰富的练习,让学生在实际操作中掌握单价、数量和总价之间的计算方法。
二. 学情分析学生在学习本节课之前,已经掌握了加减法、乘除法等基本运算,对数学符号有一定的认识。
但部分学生对单价、数量和总价的概念可能还比较模糊,需要通过实际操作和练习来加深理解。
此外,学生可能对用字母表示数的方法还不够熟悉,需要教师在教学中进行引导和讲解。
三. 教学目标1.让学生理解单价、数量和总价之间的关系,掌握用字母表示单价、数量和总价的方法。
2.培养学生通过已知两个量来求第三个量的能力。
3.提高学生的数学思维能力和解决问题的能力。
四. 教学重难点1.掌握单价、数量和总价之间的关系。
2.用字母表示单价、数量和总价的方法。
3.通过已知两个量来求第三个量的方法。
五. 教学方法采用启发式教学法、情境教学法、小组合作学习法等多种教学方法,引导学生通过观察、思考、操作、讨论等方式,自主探索单价、数量和总价之间的关系,提高学生的学习兴趣和参与度。
六. 教学准备教师准备教案、课件、练习题等教学资源;学生准备笔记本、笔等学习用品。
七. 教学过程1.导入(5分钟)教师通过创设情境,如购物场景,引导学生思考单价、数量和总价之间的关系。
提问:“请大家想一想,我们在购物时,如何计算要支付的总价呢?”让学生发表自己的看法。
2.呈现(10分钟)教师通过课件展示单价、数量和总价之间的关系,并用字母表示单价、数量和总价。
讲解单价、数量和总价之间的关系,让学生理解并掌握用字母表示单价、数量和总价的方法。
3.操练(10分钟)教师给出几个例子,让学生运用所学的知识,计算总价。
例如:一件商品的单价是20元,买了3件,求总价。
《单价、数量和总价》说课稿四年级上册数学人教版

《单价、数量和总价》说课稿一、说教材《单价、数量和总价》出自人教版小学数学四上第四单元三位数乘两位数的第四课时。
(一)地位和作用整体来看,本单元教学内容主要有三位数乘两位数笔算、积的变化规律以及常见的数量关系。
不难看出,本单元内容涉及的知识背景比较广,与学生的现实生活联系也较密切。
数学学习基于生活,高于生活,并从中习得数学知识与技能,体会数学思想方法的应用,积累数学学习的基本活动经验,最终形成良好的数学素养。
因此,数学教学应为学生研究数量关系提供了更丰富的材料,增加了经历、体验数量关系,对一些常见的数量关系进行适时适度地提炼、归纳与应用。
(二)内容编排接下来,我将从教材编排角度出发,对所执教课程内容进行分析:1、典型问题明概念教材首先提供两个典型购物问题:已知每件商品的价格和购买商品的件数,求商品的总价。
解决后,通过“这两个问题有什么共同点”来引导学生从两个问题的相关性入手,提炼出共同点:两个问题中都是知道每件商品的价格,也就是单价;还知道商品的件敦,也就是数量;要求的都是共花的钱也就是总价。
2、具体问题寻关系结合具体问题情境,分析“单价、数量与总价”三量之间的关系。
教材以“你知道单价、数量与总价之间的关系吗”为问题,引导学生结合自己的生活经验,自主探索、总结出数量关系。
3、习题练习固知识做一做部分有两道题。
第一道题让学生举例说明单价、数量、总价,检验学生是否理解单价、数量、总价的含义,加强学生对其概念的理解。
第二道题结合生活实际,将数学联系到生活,解决实际问题,通过分析已知得出未知,复习乘法模型,再次强调单价×数量=总价的数量关系。
总的来看,单价、数量、总价之间的数量关系,是学生在日常生活中经常接触到的数量关系。
由于学生具备一定的知识经验,理解起来也就轻松自如,教学只要提供学生熟悉的生活情景,就能使学生能从生活经验和已有的知识背景出发,主动探究数学问题,培养了应用意识。
二、说学情(一)学生的知识基础在二、三年级,学生已学习过乘法问题,“倍”的问题,掌握了乘法运算。
工程造价材料单价及直接工程费计算案例

作业: 作业: 1. 某工地运输钢材,运距36公里 运价率0.45元/t.km,求 公里, 某工地运输钢材,运距 公里,运价率 元 求 单位运费 2. 某工地运输电焊条,运距24公里 运价率0.48元/t.km, 公里, 某工地运输电焊条,运距 公里,运价率 元 求单位运费 3. 人工挑抬运粘土,运距20米 已知人工单价18元 工日 工日, 人工挑抬运粘土,运距 米,已知人工单价 元/工日 求单位运费 4. 4吨以内自卸汽车运碎石 吨以内自卸汽车运碎石6KM,已知汽车台班单价为 吨以内自卸汽车运碎石 , 319.53元/台班,求单位运费 台班, 元 台班 5. 某料厂机械轧碎石( 厘米),已知人工单价 厘米),已知人工单价18元 工日 工日, 某料厂机械轧碎石(4厘米),已知人工单价 元/工日, 片石21元 立方米 立方米, 电动碎石机120元/台班,求 台班, 片石 元/立方米,400*250电动碎石机 电动碎石机 元 台班 碎石的预算原价。 碎石的预算原价。 6. 某工地距料厂350米,采用人工装卸手扶拖拉机运输片 某工地距料厂 米 已知拖拉机41.20元/台班,人工单价 元/工日,钢 台班, 工日, 石,已知拖拉机 元 台班 人工单价17元 工日 钎8.4元/kg,硝铵炸药 元 ,硝铵炸药3.8 元/kg,导火线 ,导火线0.35 元/米,普 米 通雷管0.3 元/个,煤150 元/吨,求片石预算价格。 通雷管 个 吨 求片石预算价格。
建筑材料预算单价
Байду номын сангаас
材料规格式名称 汽油 柴油 空心钢钎 合金钻头
单 位 kg Kg Kg 个
预算单价 3 2.9 3.5 20
材料规格式名称 硝铵炸药 导火线 普通雷管 煤
单 位 kg m 个 t
预算单价 6 1 0.8 200
用方程和用算术方法解应用题的比较(说课稿)

用方程和用算术方法解应用题的比较(说课稿)我和大家探讨的题目是第八册第三单元中的《用方程和用算术方法解应用题的比较》。
用方程解应用题是小学数学教学的重要内容之一,它既是数学联系实际的一个重要方面,又是初中学习代数等初等数学的基础,通过它的教学既可以复习用字母表示数、简易方程等以前学过的基础知识,又可以培养学生分析问题、解决问题的能力,拓宽学生思维,发展学生的智力。
因此,这部分内容在中小学数学教学中起着十分明显的渗透、衔接、孕伏作用。
本节课是在掌握用方程解应用题的基础上,结合用算术方法解,进行数量关系解析等解题技巧的梳理、概括和提高,使学生知道用方程和用算术方法解应用题的区别,并能根据题目中“数量关系的特点”进行灵活选择解题方法,培养学生灵活、敏捷的思维能力,体现了大纲的培养目的。
教学中,我依据大纲、教材的要求,结合小学生的年龄、心理特点,遵循小学生的认知规律,采用“教学中,以教师为主导,学生为主体,训练为主线”的教学构思,通过对已有知识的深化,来巩固和发展学生的能力,抓住数量之间的内在联系,掌握好教师的“导”,导在问题上,导在知识的关键处,使学生有所思、有所得,同时以基本的数量关系为主线,进行发散与聚合的创造性思维训练,构建学生整体的认知结构,突破两种不同的解题思路相互干扰的难点,使学生积极主动地获取知识,并在获取知识、渗透“对立统一”唯物主义观点的过程中全面发展。
如何在教学中发挥好学生的主体作用呢?我拟设计以下三个阶段:第一个阶段:筑实基础,重视结构训练。
教育家布鲁纳提出的结构原则启发我们:“重视结构训练,才能打好解题基础”。
我用小黑板设计了两道复习题:(一)说出下面每组三个量之间的等量关系。
(1)单价、总价和数量。
(2)计划生产数、已经生产数和还要生产数。
(3)付出的钱、购物总价和找回的钱。
(二)用式子表示下面的数量关系。
商店运来500千克水果,其中有8筐苹果,剩下的是梨,梨有300千克,每筐苹果重多少千克?通过这样的数量关系结构训练,使学生清晰数量间的相互关系,回顾用方程解应用题的基本方法,沟通条件与问题之间的联系,理解其数量关系结构,促进学生解题思路的发展,为进一步的学习打下扎实的基础。
第二章 考点9 不等式的综合应用

例1 变1 例2 变2 例3 变3 例4 变4
解:设使用x年的平均费用为y万元,由题意得
10 0.9x 0.2 0.2x x
y
2
1 10
x
1 2
x 10 3,
x
x 10
10 x
当10 x 即x=10时,取等号. x 10
∴使用10年报废最划算.
【回顾反思】 解不等式的应用题,关键是构造不等式模型,即分析题目
例1 变1 例2 变2 例3 变3 例4 变4
【解】 设床价提高10x元/床,则床位减少10x张,由题意得 (50+10x)(200-10x)>15 000⇒5<x<10, 5×10+50=100(元/床),10×10+50=150(元/床).∴价格应定 为100~150元/床.
例1 变1 例2 变2 例3 变3 例4 变4
【提示】
∵ 3a 2b a b 6a 4b 5a 5b a b 0 ,
5
2
10
10
∴a>b.
A组 1 2 3 4 5 6 7 8 9 10 11 12 B组 1 2 3
2.设矩形的长为a,宽为b(a>b),面积为S1,与此矩形周长相
等的正方形的面积为S2,则( A )
A.S1<S2
例1 变1 例2 变2 例3 变3 例4 变4
【例3】 设计一个面积为800 cm2的矩形广告牌,要求左右均 留2 cm的空白,上下边均留1 cm的空白.问:怎样设计使中 间的文字面积最大?并求此最大值.
【思路点拨】 本题是求最值问题,一般选用“基本不等式” 模型或“一元二次函数”模型来解决.
例1 变1 例2 变2 例3 变3 例4 变4
2.常见的应用题类型 (1)分配问题、速度和时间问题、工程问题等一般用一元一次 不等式(组)模型解决. (2)价格问题、面积问题等一般用一元二次不等式(组)模型解 决. (3)最值问题等一般用基本不等式模型(均值定理)解决.
四年级上册数学教案-4 单价、数量和总价 - 人教版

四年级上册数学教案-4 单价、数量和总价 - 人教版一、教学目标1. 让学生掌握单价、数量和总价的概念。
2. 培养学生运用单价、数量和总价进行计算的能力。
3. 培养学生的逻辑思维能力和解决实际问题的能力。
二、教学内容1. 单价、数量和总价的概念。
2. 单价、数量和总价之间的关系。
3. 运用单价、数量和总价进行计算。
三、教学重点与难点1. 教学重点:单价、数量和总价的概念,单价、数量和总价之间的关系。
2. 教学难点:运用单价、数量和总价进行计算。
四、教学方法1. 讲授法:讲解单价、数量和总价的概念。
2. 演示法:通过实例演示单价、数量和总价之间的关系。
3. 练习法:通过练习题巩固单价、数量和总价的计算方法。
五、教学过程1. 导入新课通过生活中的购物实例,引出单价、数量和总价的概念。
2. 讲解单价、数量和总价的概念单价:每件商品的价格。
数量:购买商品的数量。
总价:购买商品所需支付的总金额。
3. 讲解单价、数量和总价之间的关系总价 = 单价× 数量单价 = 总价÷ 数量数量 = 总价÷ 单价4. 演示实例以购买水果为例,讲解单价、数量和总价之间的关系。
5. 练习题1. 计算题:根据给定的单价和数量,计算总价。
2. 应用题:根据给定的总价和单价,计算数量。
6. 总结总结单价、数量和总价的概念及其关系。
7. 作业布置1. 课后练习题。
2. 收集生活中的购物小票,分析单价、数量和总价。
六、课后反思本节课通过讲解单价、数量和总价的概念,使学生掌握了三者之间的关系。
通过实例演示和练习题,培养了学生运用单价、数量和总价进行计算的能力。
在今后的教学中,应注重联系实际生活,提高学生的实际问题解决能力。
重点关注的细节是“讲解单价、数量和总价之间的关系”,因为这是本节课的核心内容,也是学生容易混淆的地方。
下面将详细补充和说明这一部分。
单价、数量和总价之间的关系是数学中的基本概念,它们在日常生活中广泛应用,尤其是在购物、计费等场景中。
(教案)第三单元 常见的数量关系-四年级数学下册 (苏教版)

教案:第三单元常见的数量关系-四年级数学下册(苏教版)一、教学目标1. 知识与技能目标:理解并掌握速度、时间和路程的关系,能够运用速度×时间=路程、路程÷时间=速度、路程÷速度=时间进行计算。
2. 过程与方法目标:通过观察、实验、推理等方法,发现和理解单价、数量和总价的关系,能够运用单价×数量=总价、总价÷数量=单价、总价÷单价=数量进行计算。
3. 情感态度与价值观目标:培养学生对数学的兴趣,激发学生探索数量关系的欲望,提高学生解决问题的能力。
二、教学内容1. 速度、时间和路程的关系。
2. 单价、数量和总价的关系。
三、教学重点与难点1. 教学重点:掌握速度、时间和路程的关系,能够运用相关公式进行计算;掌握单价、数量和总价的关系,能够运用相关公式进行计算。
2. 教学难点:理解速度、时间和路程的关系,以及单价、数量和总价的关系,并能将其应用于解决实际问题。
四、教学过程1. 导入新课:通过展示一些与速度、时间和路程相关的实例,引发学生对数量关系的思考,激发学生的学习兴趣。
2. 讲解速度、时间和路程的关系:通过讲解、举例、练习等方式,使学生理解并掌握速度×时间=路程、路程÷时间=速度、路程÷速度=时间的关系。
3. 讲解单价、数量和总价的关系:通过讲解、举例、练习等方式,使学生理解并掌握单价×数量=总价、总价÷数量=单价、总价÷单价=数量的关系。
4. 练习与应用:设计一些与速度、时间和路程,以及单价、数量和总价相关的练习题,让学生独立完成,巩固所学知识。
5. 总结与反思:对本节课所学内容进行总结,引导学生反思自己在学习过程中的收获和不足,提高学生的学习效果。
五、教学评价1. 课堂表现:观察学生在课堂上的参与程度、思维活跃度、合作交流情况等,评价学生对本节课知识的掌握程度。
2. 练习完成情况:检查学生完成的练习题,评价学生对速度、时间和路程,以及单价、数量和总价关系的理解和运用能力。
结算表
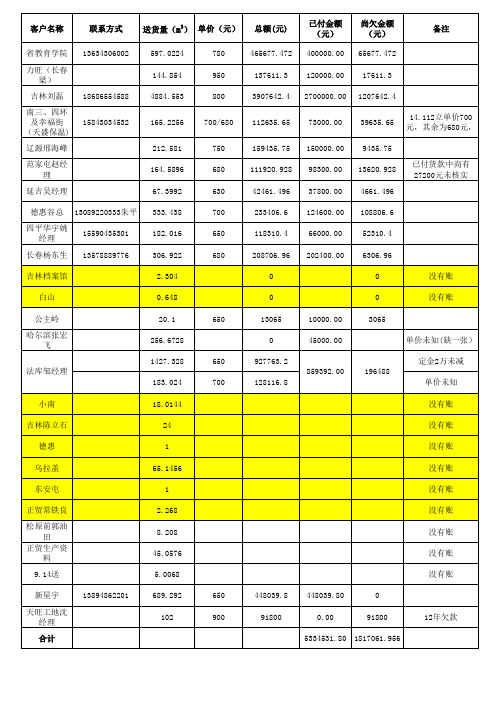
14.112立单价700 元,其余为680元,
已付货款中尚有 27200元未核实
13089220333朱平 15590435301 13578889776
333.438 182.016 306.922 2.304 0.648 20.1 256.6728 1427.328 183.024
没有账 没有账
650
13065 0
10000.00 45000.00
3065 单价未知(缺一张) 定金2万未减
650 700
927763.2 859392.00 128116.8 196488
单价未知 没有账 没有账 没有账 没有账 没有账 没有账 没有账 没有账 没有账
小南 吉林陈立石 德惠 乌拉盖 东安屯 正贸常铁良 松原前郭油 田 正贸生产资 料 9.14送 新星宇 天旺工地沈 经理 合计 13894862201
尚欠金额 (元) 65677.472 611.3 1207642.4 39635.65 9435.75 13620.928 4661.496 108806.6 52310.4 6306.96 0 0
备注
18686554588 15843034532
4884.553 165.2256 212.581 164.5896 67.3992
客户名称 省教育学院 力旺(长春 梁) 吉林刘磊 南三、四环 及幸福街 (天盛保温) 辽源邢海峰 范家屯赵经 理 延吉吴经理 德惠谷总 四平华宇姚 经理 长春杨东生 吉林档案馆 白山 公主岭 哈尔滨张宏 飞 法库邹经理
联系方式 13634306002
送货量(m3) 单价(元) 597.0224 144.854 780 950 800 700/680 750 680 630 700 650 680
北师大版六年级数学上册第七单元:百分数乘除法应用题“进阶版”(量率对应问题)专项练习(原卷版+解析)

2023-2024学年六年级数学上册典型例题系列第七单元:百分数乘除法应用题“进阶版”(量率对应问题)2023-2024学年六年级数学上册典型例题系列第七单元:百分数乘除法应用题“进阶版”(量率对应问题)(50%-40%),再根据百分数除法的意义解答即可。
【详解】5÷(50%-40%)=5÷10%=50(名);答:学校舞蹈队一共有50名学生。
【点睛】明确已知量5人对应的百分比是解答本题的关键,再根据百分数除法的意义解答。
7.某食品加工厂有三个运送小组运送面包,第一组运送全部面包的28%,第二小组运送全部面包的30%,两组共运送面包87箱,第三组要运送多少箱面包?【答案】63箱【分析】把面包总箱数看作单位“1”,根据:单位“1”=对应量÷对应量的分率,用87除以它的分率(28%+30%)计算出总数,然后减去87即可。
【详解】87÷(28%+30%)-87=87÷58%-87=150-87=63(箱)答:第三组要运送63箱面包。
【点睛】此题考查了百分数的应用,关键掌握:单位“1”=对应量÷对应量的分率。
8.水果店运来橘子350千克,运来苹果250千克,运来的香蕉比苹果少20%,运来的香蕉是运来水果总量的百分之几?【答案】25%【分析】运来香蕉的质量=运来苹果的质量×(1-20%),运来香蕉的质量占水果总质量的百分率=运来香蕉的质量÷水果的总质量×100%,据此解答。
【详解】250×(1-20%)=250×0.8=200(千克)200÷(350+250+200)×100%=200÷800×100%40%x-30%x=610%x=60.1x÷0.1=6÷0.1x=60答:这袋大米原有60千克。
【点睛】解题关键是找到题目中的等量关系。
18.一个书包和一个文具盒的价格相差12元,文具盒的价格是书包的60%。
2、《单价、数量、总价》说课稿(数学)

如何说课——以《单价、数量、总价》为例说课是在备课的基础上,在规定的时间内,针对具体课题,采用讲述为主的教研方式。
为了参加上学期的区教师教学评选活动,我首先根据教学进度选定了说课内容为《单价、数量、总价》,因为它是三年级上册用一位数除单元中的新增内容,说明它在教材中的位置是比较重要的,而且同行间说过的人也相对较少,能说出自己的亮点来。
选定内容后我就开始精心准备我的说课内容,主要包括七个部分,分别是说教材、说学生、说教学理念、说教学目标、说教学重难点,说教法,说教学过程。
一、说教材《单价、数量、总价》是二期课改小学数学九年义务教育课本第五册第四单元用一位数除单元中的新增内容,在教材中的位置是比较重要的。
学好这一课将为学习更复杂的应用题奠定基础。
单价、数量、总价这一组常用数量关系是学生在日常生活中,接触最多的。
将它放在学习了用一位数乘除法的后面,一方面是对乘除法含义的一个拓展,另一方面也体现新课标提出的“人人都能获得必要的数学”这一理念。
这是本单元的一个难点内容,主要难在要掌握“单价×数量=总价”这个数量关系式及其变式,并运用这个数量关系式解决实际问题,而且还要让学生理解单价和总价的相对性,学会灵活运用。
这就需要教师实施“基于课程标准的教学与评价”,能结合学生的实际情况,根据不同学生的态度倾向和能力,帮助他们达到课程学习的要求。
课时安排为2课时。
说教材就是要说明自己对教材的理解,确定教什么?如何教?可以将之后的教学目标和重难点也放在这个部分。
二、说学生在学习本课知识前学生已熟练掌握用一位数乘除法的计算,日常生活中也经常接触得到数量关系,只是没有用数学的语言去规范而已。
而三年级学生正处于瑞士儿童心理学家皮亚杰提出的“认知发展阶段论”中的具体运算阶段(7岁-1 1岁);他们在学习概念时可以直接把概念的关键属性同他们的认知结构相联系,从而获得意义。
但他们的思维仍有具体性,在学习概念时还要凭借表象的支持,规则学习更需要具体经验支持。
列方程(组)中设未知数的方法与技巧

列方程(组)中设未知数的方法与技巧作者:陈德前来源:《初中生世界(初一年级)》2008年第06期列方程(组)解决实际问题一直是中考命题的热点之一,而列方程(组)的关键步骤之一是设好未知数,那么解决中考中方程(组)问题设未知数有哪些方法与技巧呢?一、设直接未知数即求什么设什么,这是最常用的设未知数的方法.例1(2007年甘肃省白银市中考试题)某同学在A、B两家超市发现他看中的英语学习机的单价相同,书包单价也相同,英语学习机和书包单价之和是452元,且英语学习机的单价比书包单价的4倍少8元.(1)求该同学看中的英语学习机和书包单价各是多少元?(2)该同学上街,恰好赶上商家促销,超市A所有商品打7.5折;超市B全场购物满100元返购物券30元(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的英语学习机、书包,那么在哪一家购买更省钱?分析:(1)由“英语学习机和书包单价之和是452元,且英语学习机的单价比书包单价的4倍少8元”可以列方程组求出英语学习机和书包单价;(2)分别计算在A、B两个超市购买英语学习机与书包各一件所需花费的现金并与400元比较,再比较在A、B两个超市购买英语学习机与书包各一件所需花费的现金,来确定在哪家超市购买更省钱.解:(1)设书包的单价为x元,英语学习机的单价为y元.根据题意,得x+y=452,y=4x-8.解得x=92,y=360.答:该同学看中的英语学习机单价为360元,书包单价为92元.(2)在超市A购买英语学习机与书包各一件,需花费现金:452×75%=339(元),因为339<400,所以可以选择在超市A购买.在超市B可先花费现金360元购买英语学习机,再利用得到的90元购物券,加上2元现金购买书包,总计共花费现金:360+2=362(元);因为362<400,所以也可以选择在超市B购买.但是,由于362>339,所以在超市A购买英语学习机与书包更省钱.点悟:设直接未知数的方法应该是我们思考问题时的首选,当设直接未知数思考感到困难时,再考虑下文中设未知数的方法与技巧.二、设间接未知数即所设的未知数不是所求的未知量,但可以较为方便地求出所求的未知量.例2(2007年山东省临沂市中考试题)“种粮补贴”惠农政策的出台,大大激发了农民的种粮积极性,某粮食生产专业户去年计划生产小麦和玉米共18吨,实际生产了20吨,其中小麦超产12%,玉米超产10%,该专业户去年实际生产小麦、玉米各多少吨?分析:问题要求专业户去年实际生产小麦、玉米各多少吨,而已知的是小麦、玉米超产的百分率,设直接未知数求解比较困难,而设间接未知数——原计划生产小麦和玉米的吨数比较简便.解:设原计划生产小麦x吨,生产玉米y吨,根据题意得:x+y=18,12%x+10%y=20-18.解得x=10,y=8.10×(1+12%)=11.2(吨),8×(1+10%)=8.8(吨).答:该专业户去年实际生产小麦11.2吨,玉米8.8吨.点悟:当设直接未知数求解比较困难时,可考虑设间接未知数来解题.同学们可以用设直接未知数的方法来解决本题,再比较一下,从中体会设间接未知数的妙用.三、设辅助未知数当题目中缺少某些量时,可以增设一些量为辅助未知数(视为已知量),参与列方程,已知量多了,列方程(组)就方便了.例3(2007年四川省资阳市中考试题)陈老师为学校购买运动会的奖品后,回学校向后勤处王老师交账说:“我买了两种书,共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元. ”王老师算了一下,说:“你肯定搞错了.”(1)王老师为什么说他搞错了?试用方程的知识给予解释.(2)陈老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本. 但笔记本的单价已模糊不清,只能辨认出应为小于10元的整数,笔记本的单价可能为多少元?分析:(1)用方程的知识求出书的本数即可判断;(2)设出辅助未知数——笔记本的单价,列出含字母系数方程,利用整除的有关知识求解.解:(1)设单价为8元的课外书为x本,得:8x+12(105-x)=1500-418.解之得:x=44.5(不符合题意) . 所以王老师肯定搞错了.(2)设单价为8元的课外书为y本,设笔记本的单价为a元,依题意得:8y+12(105-y)=1500-418-a.解之得:178+a=4y. 因为a、y都是整数,且178+a应被4整除,所以a为偶数,又因为a为小于10元的整数,所以a可能为2,4,6,8 .当a=2时,4y=180,y=45,符合题意;当a=4时,4y=182,y=45.5,不符合题意;当a=6时,4y=184,y=46,符合题意;当a=8时,4y=186,y=46.5,不符合题意 .所以笔记本的单价可能为2元或6元 .点悟:本题中似乎缺少一些量,引进辅助未知数以后,“已知”条件增加了,列方程就方便多了,再利用题目中的特殊要求——问题的解是正整数,就可以解决问题了.。
四年级数学下册《单价数量总价的数量关系》教案、教学设计

1.认真审题,确保理解题意;
2.规范计算,避免粗心大意;
后,及时复习巩固,查找不足,为下次课做好准备。
(三)学生小组讨论
在学生小组讨论环节,我会将学生分成若干小组,每组4-6人。针对本节课所学内容,设计以下讨论话题:
1.单价、数量和总价在实际生活中的应用案例;
2.运用代入法、消元法等方法解决含有两个未知数的单价数量总价问题;
3.讨论如何检查计算结果是否正确。
在讨论过程中,我会鼓励学生积极发言,分享自己的观点和做法。同时,我会巡回指导,关注每个小组的讨论情况,并及时给予指导和帮助。
4.注重课堂反馈,及时调整教学策略
在教学过程中,我将密切关注学生的学习反馈,根据学生的实际表现,及时调整教学节奏、难度和策略。针对学生在学习中遇到的问题,给予个性化的指导,帮助他们克服困难,提高学习效果。
5.培养学生的合作意识和团队精神
通过小组合作、讨论交流等形式,培养学生的合作意识和团队精神。让学生在合作中学会倾听、尊重他人意见,发挥集体智慧,共同解决问题。
针对本章节“单价数量总价的数量关系”,教学设计将围绕以上三个部分展开。在教学过程中,注重激发学生的学习兴趣,引导学生主动探究,培养学生运用数学知识解决实际问题的能力。同时,关注学生的情感态度和价值观的培养,使他们在掌握知识的同时,形成良好的学习品质和价值观。
二、学情分析
在本章节的教学中,考虑到学生已处于四年级下册阶段,他们在数学学习方面已具备一定的知识基础和技能。学生对单价、数量和总价的概念已有初步的认识,但在具体的数量关系和实际应用上,可能还存在一定的困难。因此,在教学过程中,应关注以下几点:
2.采用启发式教学,引导学生自主探究和解决问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单位 台
单价
台
台 台
台
m m 套 个 个 个 个 个 个 个 个 个 个 个 个 75 18.74 1.5 m m m m m
m3 m3 m3 Φ90 Φ75 Φ75 Φ75 Φ63
35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57
3 3 3 3 3 3 3
面积为3×3m2 干管、分干管,1.6MPa 干管,0.8MPa 干管、分干管,1.6MPa 干管,1.0MPa 支管
毛管 毛管 毛管,0.6MPa
Φ75和63管道埋深0.7m,Φ32管道埋深0.1m,
PE PE PE PE
内镶式
规格 IS65-40-250 IS100-65-315C型 IS100-65-200型 IS80-65-250型 IS60-40-250型 100D-16×7型 IS65-40-200A型 I100-65-250A型 IS80-50-200型(2台) IS80-50-200A型(4台) IS65-40-250A型(2台) ISA125-100-315型(4 DN90 0.95m /h
3
个 个 个 个 个 个 个 个 m m 个 个 个
合价
备注 流量85.8m3/h,扬程92m,电机功率45kw 流量120m /h,扬程47m,电机功率22kw 流60m3/h,扬程87m,功率37kw 流量30m /h,扬程78m,功率15kw 流量54m /h,扬程123.2m,电机功率30kw 流量23.4m /h,扬程44m,电机功率7.5kw 流量93.5m /h,扬程70m,电机功率30kw 流量30m /h,扬程53m,电机功率15kw 流量46.8m3/h,扬程44m,电机功率11kw 流量23.4m3/h,扬程70m,电机功率11kw 流量60m /h,扬程33.5m,电机功率15kw 钢管 钢管 砂+网式配套 砂+网式配套
序号 项目名称 1 水泵 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 水泵 水泵 水泵 水泵 水泵 水泵 水泵 水泵 水泵 水泵 水泵 吸水管 吸水管 过滤器 3''网式过滤器 逆止阀 DN160逆止阀 DN110逆止阀 DN75逆止阀 压力表 16kg压力表 水表 排气阀 DN160排气阀 DN110排气阀 DN75排气阀 土方回填 C20砼 C15砼 PE管 PE管 PE管 PE管 PE管
PE管 PE管 PE管 滴箭 阀门井 控制阀门 泄水井 泄水阀 管网安装 宣传标志牌 报警设备 闸阀 闸阀 闸阀 闸阀 喷头 5022-2摇臂式喷头 DN20滴灌带 DN20镀锌钢管 DN旁通 DN堵头 控制阀 管材附件
Φ32 Φ20 Φ20 9L/h
m m m 套 个 个 个 个 m m
3 3
土方开挖 土方回填
