求解支座反力专题训练
理论力学期末复习题

1、如图所示结构,求支座反力。
2、组合梁AC和CE用铰链C相连,支承和荷载情况如图所示,已知跨度l=8m,F=5kN,均布荷载q=2.5kN/m,力偶矩M=5kNm。
求各支座的约束反力。
3、如图所示结构,求支座反力。
4、如图所示结构,q=10kN/m,求支座反力1、如图所示机构,杆OC与轮Ⅰ在轮心O处铰接,并以匀速v水平向左平移,起始时点O与点A相距l,AB杆可绕A轴定轴转动,与轮Ⅰ在D点接触,接触处有足够的摩擦使之不打滑,轮Ⅰ的半径为r。
求:θ=30°时,轮Ⅰ的角速度ω1和AB杆的角速度ω。
2、图示半径R=3r的凸轮以匀速v沿水平面向右移动,其中r为顶杆滚轮半径,顶杆O1O2沿铅直导轨滑动,假设滚轮与凸轮接触处无相对滑动,求当θ=30°,且B,O1,O2在同一直线上时,滚轮的角速度以及轮缘边上B点的速度。
3、图示机构,曲柄OA长为r,绕O轴转动,连杆AB=3r 始终与角点D保持接触,在图示位置时,曲柄的角速度为ω0,角加速度为α0,方向如图,求这时AB杆的:(1)角速度ωAB;(2)B点的速度v B。
)4、图示机构中,曲柄OA以匀角速度ω0绕O轴转动,通过齿条AB带动齿轮O1。
已知OA=R,齿轮O1半径r=0.5R,求当θ=60°时,齿条AB的角速度和齿轮O1的角速度。
1、如图所示,半径为r的均质圆盘,在半径为R的圆弧面上只滚不滑。
初瞬时θ=θ0,圆盘由静止开始纯滚动。
求均质圆盘脱离圆弧之前:(1)圆盘的角加速度(表示为θ的函数);(2)圆弧面作用于圆轮上的法向反力和摩擦力(表示为θ的函数)。
2、均质圆盘半径为r,质量为m,在初始角度θ0时静止释放后,在半径为R的圆弧轨道上做纯滚动。
求圆盘在任意位置θ时:(1)圆盘滚动的角加速度;(2)圆弧轨道的法向反力和摩擦力。
3、如图所示,均质杆AB长度为l,放在铅锤平面内,在角φ0时杆由静止状态倒下,墙与地面均光滑。
求(1)杆在脱离墙前之前的任意位置时的角速度和角加速度;(2)杆脱离墙面时与水平面的夹角。
求支座反力

解:1) 求支座反力2) 用截面依次在1-1,2-2 截面处截开,取左段为研究对象; 图(b):P Q F F -=11Q 1M c)(b 1 用截面法计算如图所示外伸梁1-1,2-2, 截面上的内力,其中:pa F M 21=C(a )解得:)(45↑=p Ay F F )(41↓=p By F F 校核:4145=--=-+=∑P P P P By Ay y F F F F F F F ∑=0B M 023=⨯--⨯a F M a F Ay p ∑=0A M2=⨯+-⨯a F M a F By P ∑=0yF1=--Q P F F ∑=-011M1=+M F pa paF M -=12.悬臂梁AB,在自由端受集中力偶M 作用,试绘出此梁的剪力图和弯矩图解:1)列剪力方程和弯矩方程• 将坐标 x 的原点取在A 端,由直接法可得3.作剪力图和弯矩图FQ22Q F Ay)(c (a)AF∑=0yF2=--Q P Ay F F F PQ F F 412=∑=-022M2=+M F pa paF M -=2Amx M L x Q =≤≤)(,0FQ(x)= Fp左=F AY=bFp /L (0<x<a)(a)FQ(x) = Fp右=- FBY =-aFp /L,(a<x<l) (c)Mc(x)= Mc(Fp左)= F AY x=bFpx/L(0<x<a) (b)M(x)= MZ(Fp右) = FBY (L-x)=aFp (L-x) /L, (a<x<L) (d)AC段和BC段的弯矩均为直线,分别由二控制点确定:M•AC段:•在x= 0,处,M(0)=MA= 0•在x= a处,M(a)=MC=abFp /l,•CB段:在x=a处, M(a)= MC =abFp /l,在x=0处, M(l)=MB=0,当a<b时,则在AC段的任一截面上的剪力值最大,|FQ|max=bFp /L在x=a处, Mmax =M(a)= MC =abFp /L4.简支梁受力如图所示,试作出该梁的剪力图和弯矩图。
应用力学习题
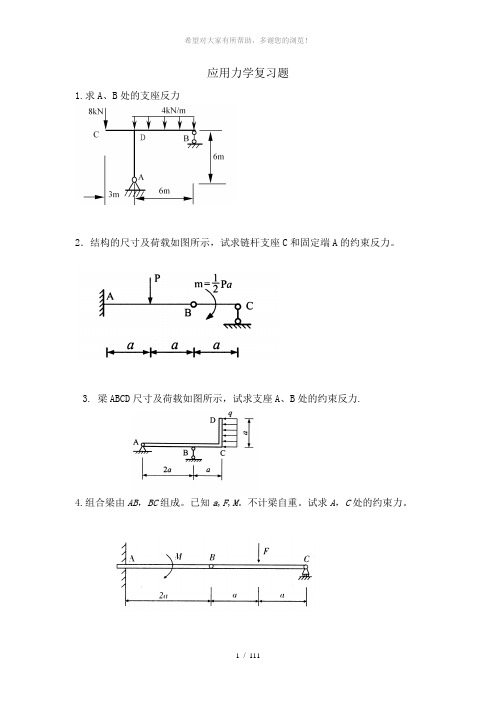
应用力学复习题1.求A、B处的支座反力2.结构的尺寸及荷载如图所示,试求链杆支座C和固定端A的约束反力。
3. 梁ABCD尺寸及荷载如图所示,试求支座A、B处的约束反力.4.组合梁由AB,BC组成。
已知a,F,M。
不计梁自重。
试求A,C处的约束力。
5.求图示多跨静定梁的支座反力。
α=。
,6.悬臂梁承受有均布荷载q和一集中力P,如图所示。
已知P=ql,45梁的自重不计,求支座A的反力。
7.计算刚架的支座反力。
8. 组合梁由AC,CD组成。
已知a,q。
不计梁自重。
试求A,B,D 处的约束力。
9.连续梁由AB、BC组成。
已知a,q。
不计梁自重。
试求AC处的约束力。
10.梁ABCD尺寸AB=BD=4m,CB=2m, C点作用有集中力偶40kN.m,D点作用有10kN 的集中力,AB梁作用有均布荷载10 kN/m,试求支座A、B处的约束反力。
11.按图示结构的尺寸和荷载求链杆支座A、B、C的约束反力。
12.结构如图所示,折杆CD 在C 处与简支梁AB 铰接,在D 处与斜面为光滑接触,已知F=100kN ,q=40kN/m ,斜面与水平面夹角为α=60°.求A 和B 处的支座反力.13、图示结构中的AB 杆可视为刚体,斜杆CD 为直径d=20mm 的圆形杆,许用应力[σ]=160MPa 。
试求结构的许可载荷[P]。
( 16 分) (阅卷人: )13. 图中,如果P =50KN, AB 杆为直径D =20mm 的圆截面钢杆,[σ]=160MPa ;AC 杆为边长b=100mm 的正方形木杆,木材的[σ]=10MPa 。
试校核各杆强度。
P100010001500ABCD14.图示结构中,AB和BC均为直径d=20mm的钢杆,钢杆的容许应力为[σ]=160MPa,求该结构的容许荷载[P]。
15. 图示桁架,受铅垂载荷P=50kN作用,杆1,2的横截面均为圆形,其直径分别为d1=15mm、d2=20mm,材料的容许应力均为[σ]=150MPa.试校核桁架的强度。
工程力学2习题课优选课堂
Me2
Me3 2
Me1
Mx 0
B C2 A
Me2 Me3 T2 0
Me2
T2 Me2 Me3 9560 N m
Me3 T2 x
结果为负号,说明T 2 应是负值扭矩 同理,在 BC 段内
BC
T1 Me2 4780 N m
简易辅导
Me2 T1 x
Me4 D
16
同理,在 BC 段内
ΔlAD ΔlAB ΔlBC 简易Δ辅lC导D -0.47 10-4mm
12
2、扭矩符号的规定 (Sign convention for torque)
Me
采用右手螺旋法则,当力偶矩矢的指
n Me
•
x
向背离截面时扭矩为正,反之为负.
3、扭矩图( Torque diagram)
Me
用平行于杆轴线的坐标 x 表示横
( Mea 2Mea ) 180 1
GIp GIp
π 简易辅导
aa
2M M
2a
3M +
18
例题12 作梁的内力图.
解 (1)支座反力为
RA
F1=2kN
F2=2kN RBm=10kN.m
A
C
D
4m
4m
4m
BE 3m
简易辅导
19
例题2 矩形截面铸铁梁的荷载和截面尺寸如图所示.铸铁的抗拉
许用应力为 [t] = 30MPa ,抗压许用应力为[c] =160MPa.,
FN3
=-
50kN
(-) 10
Ⅲ
R
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
Ⅰ
F2
F1
三跨连续梁支座反力计算例题

三跨连续梁支座反力计算例题三跨连续梁是一种常见的桥梁结构形式,其支座反力计算是桥梁设计中非常重要的一环。
下面我们来看一个三跨连续梁支座反力计算的例题。
假设有一座三跨连续梁,每跨长度均为20米,总长为60米,宽度为10米,梁高为2.5米,混凝土强度等级为C50,设计活载荷为25kN/m2,自重为25kN/m3。
该梁的支座形式为简支-悬臂-简支,其中第一跨和第三跨为简支,第二跨为悬臂,悬臂长度为5米。
现在需要计算该梁的支座反力。
首先,我们需要计算该梁的自重。
根据梁的尺寸和混凝土强度等级,可以计算出每米梁长的自重为:自重= 宽度×梁高×混凝土密度= 10 ×2.5 ×25 = 625 kN/m因此,整座梁的自重为:自重= 自重×梁长= 625 ×60 = 37500 kN接下来,我们需要计算设计活载荷的作用力。
根据设计活载荷和梁的宽度,可以计算出每米梁长的活载荷为:活载荷= 活载荷×宽度= 25 ×10 = 250 kN/m因此,整座梁的活载荷作用力为:活载荷作用力= 活载荷作用力×梁长= 250 ×60 = 15000 kN接下来,我们需要计算悬臂跨的支座反力。
由于该悬臂跨是单跨梁,其支座反力只有一个,即支座反力等于该跨的重力和作用力之和。
因此,悬臂跨的支座反力为:支座反力= 自重+ 活载荷作用力= 37500 + 15000 = 52500 kN最后,我们需要计算简支跨的支座反力。
由于简支跨是双跨梁,其支座反力需要分别计算。
对于第一跨,其支座反力等于该跨的重力和作用力之和。
因此,第一跨的支座反力为:支座反力= 自重+ 活载荷作用力= 37500 + 15000 = 52500 kN对于第三跨,其支座反力等于该跨的重力和作用力之和,再加上第二跨的支座反力。
因此,第三跨的支座反力为:支座反力= 自重+ 活载荷作用力+ 第二跨支座反力= 37500 + 15000 +52500 = 105000 kN综上所述,该三跨连续梁的支座反力分别为52500 kN、52500 kN和105000 kN。
工程中常见静定结构的支座反力计算—平面力系平衡计算总结

4
2
4
10
பைடு நூலகம்
FB
12
2
15
0
FB 5kN
Fy 0 FA 18 2 FB 2 0 FA 7kN
MO 0
平面力系平衡计算总结
平面 力系
平面汇交力系 平面
基本力系
平面力偶系
平面 特殊力系
平面平行力系
平面一般力系
平面力偶系
5 kN m
M =8 +5 7 6kN m
7 kN m
6 kN m
M M 1 M 2 M n M i 代数和
8 kN m
平面力偶系平衡的充要条件: M 0
所有各力偶矩的代数和等于零.
【例题】 求A、B处的支座反力?
M1 225 kN m M2 130 kN m
FA FB
练习
有一个二力构 件的物体系统
M 0
FA 2 2a M 0
平面平行力系
Fx 0
Fy 0
M O (F ) 0
平衡方程
永远自然满足!
1 平面汇交力系
平面特殊力系 2 平面力偶系
3 平面平行力系
FN1 FN2
4 平面一般力系
平面力系平衡方程
平面汇交力系 平面力偶系 平面平行力系
平面一般力系
平衡方程的理解:物体静止不动
平面上 物体的运动
y
x
O
平面一般 力系
水平方向不动,向左、向右的力合力为零 竖直方向不动,向上、向下的力合力为零
绕任何一个点不转,逆、顺时针力矩之合为零
练习1 求简支梁A、B处的支座反力?
0kN 1kN
绕A点不转
上下不动
1kN
各梁的支座反力习题答案

各梁的支座反力习题答案各梁的支座反力习题答案在学习结构力学的过程中,各梁的支座反力是一个重要的概念。
通过计算支座反力,我们可以了解到梁在不同位置的受力情况,进而分析和设计各种结构。
本文将通过几个习题来讲解各梁的支座反力的计算方法。
首先,我们来看一个简单的悬臂梁习题。
假设有一根长度为L的悬臂梁,其左端固定支座反力为R1,右端自由端的受力为R2。
我们需要计算出这两个支座反力的大小。
解答这个问题的关键是应用力平衡条件。
根据力平衡条件,我们可以得出以下方程:∑Fx = 0 (横向受力平衡)∑Fy = 0 (纵向受力平衡)∑M = 0 (力矩平衡)由于这是一个简单的悬臂梁,我们可以将力矩平衡的方程选择在左端支座上进行计算。
根据力矩平衡的原理,我们可以得到以下方程:R2 * L = 0由于右端是自由端,所以R2的大小为0。
因此,左端支座反力R1的大小为0。
接下来,我们来看一个更复杂一点的梁习题。
假设有一根长度为L的简支梁,其两个支座反力分别为R1和R2。
在梁的中点处有一个集中力F作用在上面。
我们需要计算出这两个支座反力的大小。
同样,我们可以应用力平衡条件来解答这个问题。
根据力平衡条件,我们可以得出以下方程:∑Fx = 0∑Fy = 0∑M = 0根据梁的简支条件,我们可以得到以下方程:R1 + R2 = F由于这是一个简支梁,所以梁的两个支座反力的大小之和等于集中力F的大小。
因此,我们可以通过这个方程来计算出R1和R2的大小。
最后,我们来看一个更复杂的梁习题。
假设有一根长度为L的悬臂梁,其左端固定支座反力为R1,右端固定支座反力为R2。
在梁的中点处有一个集中力F作用在上面,距离悬臂梁左端的距离为a。
我们需要计算出这两个支座反力的大小。
同样,我们可以应用力平衡条件来解答这个问题。
根据力平衡条件,我们可以得出以下方程:∑Fx = 0∑Fy = 0∑M = 0根据悬臂梁的条件,我们可以得到以下方程:R1 + R2 = FR2 * L - F * a = 0通过解这个方程组,我们可以得到R1和R2的大小。
弯矩剪力支反力计算例题

第三章静定梁与静定刚架目的要求:熟练掌握静定梁和静定刚架的力计算和力图的绘制方法,熟练掌握绘制弯矩图的叠加法与力图的形状特征,掌握绘制弯矩图的技巧。
掌握多跨静定梁的几何组成特点和受力特点。
能恰当选取隔离体和平衡方程计算静定结构的力。
重点:截面法、微分关系的应用、简支梁叠加法。
难点:简支梁叠加法,绘制弯矩图的技巧§3-1 单跨静定梁1.反力常见的单跨静定梁有简支梁、伸臂梁和悬臂梁三种,如图3-1(a)、(b)、(c)所示,其支座反力都只有三个,可取全梁为隔离体,由三个平衡条件求出。
图3-12.力截面法是将结构沿所求力的截面截开,取截面任一侧的局部为隔离体,由平衡条件计算截面力的一种根本方法。
〔1〕力正负号规定轴力以拉力为正;剪力以绕隔离体有顺时针转动趋势者为正;弯矩以使梁的下侧纤维受拉者为正,如图3-2(b)所示。
〔2〕梁的力与截面一侧外力的关系图3-21) 轴力的数值等于截面一侧的所有外力(包括荷载和反力)沿截面法线方向的投影代数和。
2) 剪力的数值等于截面一侧所有外力沿截面方向的投影代数和。
3) 弯矩的数值等于截面一侧所有外力对截面形心的力矩代数和。
3.利用微分关系作力图表示结构上各截面力数值的图形称为力图。
力图常用平行于杆轴线的坐标表示截面位置(此坐标轴常称为基线),而用垂直于杆轴线的坐标(亦称竖标)表示力的数值而绘出的。
弯矩图要画在杆件的受拉侧,不标注正负号;剪力图和轴力图将正值的竖标绘在基线的上方,同时要标注正负号。
绘力图的根本方法是先写出力方程,即以变量x表示任意截面的位置并由截面法写出所求力与x之间的函数关系式,然后由方程作图。
但通常采用的是利用微分关系来作力图的方法。
〔1〕荷载与力之间的微分关系在荷载连续分布的直杆段,取微段dx为隔离体,如图3-3所示。
假如荷载以向下为正,x 轴以向右为正,如此可由微段的平衡条件得出微分关系式〔3-1〕〔2〕力图形的形状与荷载之间的关系由上述微分关系的几何意义可得出以下对应关系:图3-31) 在均布荷载作用的梁段,q(x) = q(常数),FS图为斜直线,M图为二次抛物线,其凸向与q的指向一样。
工程中常见静定结构的支座反力计算(工程力学课件)

静定、超静定的概念
静定、超静定
未知量数目
平衡方程数目
未知量数目
静定 平衡方程数目
超静定 需要考虑结构变形等情况建立补充方程求解!
单个物体: 静定、超静定的判断
汇交力系
静定
超静定
平行力系
静定
超静定
一般力系
静定
超静定
物体系统:静定、超静定的判断
静定
数物体n 方程个数3n 数约束 未知数个数
一次超静定
练习
Fy ? MO (q) ?
用合力求!
a Fy -qa MO (q) qa 2
Fy -qb
M
O
(q)
qb
(a
b 2
)
Fy
- q0a 2
M
O
(q)
q0 a 2
2a 3
Fy
-
q0b 2
M
O
(q)
q0b 2
(a
2b 3
)
平面一般力系的简化
力的平移定理
作用在刚体上点 A 的力 F, 可以平行移 到任一点 B,但必须同时附加一个力偶, 这个附加力偶的矩等于原来的力 F 对 新作用点 B 的矩.
FA
Fx Fy
0 0
MFx Fy
O00 0
MO 0
FBx FBy
平面力系平衡计算总结
平面 力系
平面汇交力系 平面
基本力系
平面力偶系
平面 特殊力系
平面平行力系
平面一般力系
平面力偶系
5 kN m
M =8 +5 7 6kN m
7 kN m
6 kN m
M M 1 M 2 M n M i 代数和
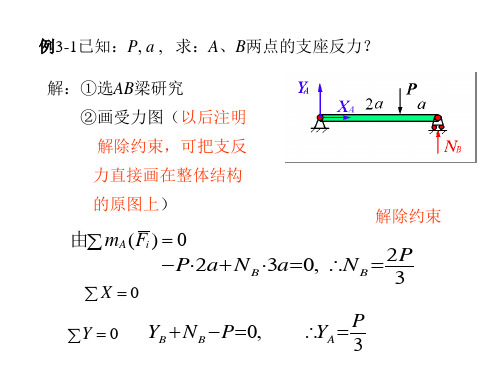
例3-1已知P
(a) (b)
∑ Y=0,
A
∑ M (F)=0,
MA-M-2qL•2L+FBsin60 º • 3L-Fcos30 º • 4L=0 (c)
q Fcx C Fcy B 。6030。 FD FB
∑
MC(F)=0, FBsin60°•L-q•L/2-Fcos30°•2L=0 FB=45.77kN FAX=32.89kN, FAY=-2.32kN MA=10.37kN.m
M
q C B 。
60
30
。 F
A
D
L
L
L
L
解:如图所示,组合梁在M,F,q,Fax,Fay,MA,FB下 平衡 M q 。 F FAy 30 MA 。 D A 60 FAx C B FB
∑
X=0, FAx - FBcos60º - Fsin30 º = 0 FAy-FBsin60 º -2qL-Fcos30 º =0
例3-5 已知:a、m、q(载荷集度)。 求:A、B、C 处约束力。 解:(1)先考虑BC
∑M = 0 →Y ∑F = 0 → X ∑F = 0 →Y
B x
y B
C
B
(2)再考虑整体AC
∑M = 0 → m ∑F = 0 → X ∑F = 0 →Y
A
x
y A
A
A
2.截面法 截面法 例3-6.已知:桁架尺寸、载荷。 求:杆4、5、6的内力。 解:先由整体平衡求出A、B 处的约束力;再作截面II, 考虑左半部平衡。
(d)
由式(d)可得 代入式(a),(b),(c)求得
已知:a、P、Q。求A、B 的约束反力。 例3-4 已知
解:(1)考虑整体 1 1 1 M A = 0 → YB ⋅ 2a + Q ⋅ a − P ⋅ a = 0 得:B = ( P − Q) Y ∑ 2 2 4 3 1 M B = 0 → YA = P + Q ∑ Fx = 0 → X A + X B − Q = 0 ∑ 4 4 (2)考虑左半部 1 M C = 0 → X A = ( P + Q) ∑ 4 1 代入得: X B = (3Q − P) 4
支座反力的计算反力怎么计算

支座反力计算简单的静定结构可以通过力的平衡与力矩的平衡来建立两个方程式,每个方程就是可以求一个未知量,就就是说,简单的静定结构只能求两个未知力;对于超静定结构计算就复杂了,不过还就是要用到平衡与力矩的平衡来建立方程,此外根据具体的情况增加其她方程联合求解,就就是说,有多少个未知力就需要多少个方程式;例如:一条简支梁长为L,两头AB简支,从左到右在1/3L处有个P向下的集中力,求两端支座反力。
这就就是简单的静定结构,解题如下:设两端的支座反力分别为:Ra与Rb根据垂直方向力的平衡条件得:Ra + Rb = P根据垂直方向力矩的平衡条件,以A为原点,得:Rb*L=P*1/3L(顺时针力矩等于逆时针力矩,A的支座反力过原点,力矩为零)联立两个方程组解得:Ra =2/3PRb =1/3P图解在这里就是用不上,所有结构力学的书都有计算的方法的,最好就就是找来瞧瞧,比我们在这里费尽心思的讲解要好得多。
例题: 简支梁的支座反力计算杆件长5米,离A端头1、5米有集中荷载为100N,问A,B两支座的反力为多少最佳答案RA=70KN RB=30KN1.1.5支座反力计算在静定结构的受力分析中,通常须预先求出支座反力,再进行内力计算。
求支座反力时,首先应根据支座的性质定出支座反力(包括个数与方位),然后假定支座反力的方向,再由整体或局部的平衡条件确定其数值与实际指向。
以图1-6a所示多跨刚架为例,讨论支座反力计算。
图1-6此刚架有五个支座反力:、、、与。
由整体的三个平衡方程,加上铰D与铰C处弯矩分别为零的平衡条件,即可求出这五个支座反力。
从几何组成的角度瞧,D 以右部分为三铰刚架,就是基本部分;D以左部分就是支承在地基与三铰刚架上的附属部分。
首先,取附属部分为隔离体(图1-6b),由平衡方程求、与。
(a)然后,将D铰处的约束反力反向加在基本部分上,取D以右三铰刚架为隔离体(图1-6c),利用平衡方程求与。
(b)(c)再取C以右半刚架为隔离体(图1-6d),由铰C处弯矩为零的平衡方程求。
