英文回文串和稳定和谐数
回文数python编程代码

回文数python编程代码回文数是指正反两个方向读都相同的数,例如121、12321都是回文数。
在Python中,可以通过以下代码判断一个数是否为回文数:```pythondef is_palindrome(number):num_str = str(number)reverse_str = num_str[::-1] # 将数字转化为字符串并逆序if num_str == reverse_str:return Trueelse:return False# 测试示例num1 = 12321num2 = 12345print(is_palindrome(num1)) # 结果为Trueprint(is_palindrome(num2)) # 结果为False```以上代码定义了is_palindrome函数,用于判断传入的number是否为回文数。
首先,将number转换为字符串num_str,并使用切片[::-1]将字符串逆序得到reverse_str。
然后,通过比较num_str和reverse_str是否相等,判断number是否为回文数。
如果相等,返回True;否则,返回False。
最后,我们可以通过调用is_palindrome函数并传入不同的数值来测试程序的正确性。
在示例中,num1的数值为12321,属于回文数,所以is_palindrome函数返回True;而num2的数值为12345,不是回文数,所以is_palindrome函数返回False。
需要注意的是,以上代码只能判断整数是否为回文数。
如果需要判断字符串是否为回文,可略作修改,如下代码所示:```pythondef is_palindrome(string):reverse_str = string[::-1] # 将字符串逆序if string == reverse_str:return Trueelse:return False# 测试示例str1 = "level"str2 = "python"print(is_palindrome(str1)) # 结果为Trueprint(is_palindrome(str2)) # 结果为False```相比于判断整数,判断字符串是否为回文只需将传入函数的参数命名为string,并直接判断string和逆序的reverse_str是否相等即可。
回文自然数列

回文自然数列回文自然数列是数学中一个十分有趣的概念,它是由一系列回文数组成的数列。
什么是回文数呢?回文数是指一个数字序列,从左向右读和从右向左读都是一样的,例如121、12321等。
而回文自然数列则是从小到大排列的一堆回文数,如:11、22、33、44、55、66、77、88、99、101、111、121等等无穷无尽。
首先我们可以通过代码来实现找出回文数的过程,以下是一个简单的示例代码:``` for(i=1;i<=999999;i++) { j=i; sum=0; while (j!=0){ sum=j%10+sum*10;j/=10; } if(sum==i){ printf("%d ",i); } } ```从代码可以看出,我们首先从1开始,逐渐递增数字i。
在循环中,我们判断数字i是否为回文数,这一步我们通过对数字i的各个位数进行倒序排列,并进行比较来实现。
如果数字i是回文数,我们就将它输出,最终就得到了一列回文自然数。
然而,回文自然数列并不仅仅只是几个回文数排列在一起而已,它还有着很多有趣的性质和应用。
接下来我们就来一一探讨。
1、回文自然数列的性质从数列中我们可以发现,回文自然数列的第一项为11,它是最小的回文数。
而自然数中的最大值为无穷大,那么回文自然数列是无限长的。
此外,我们还能够发现,回文自然数总共有9个数字,也就是0-9这几个数字构成的回文数。
通过以上性质,我们可以发现回文自然数列是一个无穷且有限制的数列。
2、回文自然数的应用回文自然数并不只是一个有趣的数学概念,它还有着极为实用的应用。
例如在计算机领域中,回文数和回文自然数往往用来进行数据校验,通过对数据的逆序检测,就可以知道该数据是否被篡改或损坏,从而保证数据的安全性和可靠性。
另外,在一些加密算法中,回文数也有非常重要的应用。
通过对明文进行回文操作,再进行加密操作,最终将密文转化为回文自然数,这样就可以有效的提高密文的安全性。
#【数学】【数论】几个特殊的数

#【数学】【数论】⼏个特殊的数素数 ⼤于1且不被其他整数(除了1和其本⾝)整除的整数。
质数定义为在⼤于1的⾃然数中,除了1和它本⾝以外不再有其他因数。
⽰例:2,3,5,7,11,13,17,19,23,29,31,37,39,41...回⽂数 “回⽂”是指正读反读都能读通的句⼦,它是古今中外都有的⼀种修辞⽅式和⽂字游戏,如“我为⼈⼈,⼈⼈为我”等。
在数学中也有这样⼀类数字有这样的特征,成为回⽂数(palindrome number)。
设n是⼀任意⾃然数。
若将n的各位数字反向排列所得⾃然数n1与n相等,则称n为⼀回⽂数。
例如,若n=1234321,则称n为⼀回⽂数。
注意: 1.偶数个的数字也有回⽂数124421 2.⼩数没有回⽂数 ⽰例: 1千以内的回⽂数 在⾃然数中,最⼩的回⽂数是0,其次是 1,2,3,4,5,6,7,8,9,11,22,33,44,55,66,77,88,99,101,111,121,131,141,151,161,171,181,191,202,212,222,232,242,252,262,272,282,292,303,313,323,333,343,353,363,373,383,393,404,414,424,434,444,45 505,515,525,535,545,555,565,575,585,595,606,616,626,636,646,656,666,676,686,696,707,717,727,737,747,757,767,777,787,797,808,818,828,838,848,858,868,878,888,898,909,919,929,939,949,959 ⼈们迄今未能找到⾃然数(除0和1)的五次⽅,以及更⾼次幂的回⽂数。
于是数学家们猜想:不存在n^k(n≥2,k≥5;n、k均是⾃然数)形式的回⽂数。
在电⼦计算器的实践中,还发现了⼀桩趣事:任何⼀个⾃然数与它的倒序数相加,所得的和再与和的倒序数相加,……如此反复进⾏下去,经过有限次步骤后,最后必定能得到⼀个回⽂数。
从2012年高考湖北卷数学理科第13题话回文与回文数的论文

从2012年高考湖北卷数学理科第13题话回文与回文数的论文从2012年高考湖北卷数学理科第13题话回文与回文数2012年高考数学湖北卷理科第13题如下:回文数是指从左到右读与从右到左读都一样的正整数.如22,121,3443,94249等.显然2位回文数有9个:11,22,33,...,99. 3位回文数有90个:101,111,121, (191)202,…,999.则(ⅰ)4位回文数有个;(ⅱ)2n+1(n∈n*)位回文数有个.回文“palindrome”一词来源于希腊语的“palindromo”,意为”running back again”,是指无论顺拼(写)或倒拼(写)都完全一样的词、诗歌、句子或数字等.如我国清代著名女词人吴绛雪曾有咏四季的四首回文诗《春夏秋冬》,其中的《夏》为:香莲碧水动风凉,水动风凉夏日长.长日夏凉风动水,凉风动水碧莲香.诗词描绘了一副卷卷夏日凉风吹拂湖面,水波荡漾,荷花飘香的美景,读来音韵优美,意境清新,形式奇妙,可为佳作.而在中国诗坛上这样的回文诗句举不胜举.北京“天然居”餐馆,迎面有对联:客上天然居,居然天上客.客人看了心境特好,而且上、下联为回文联.据说乾隆皇帝别出心裁,把两句并成新的上联,征求下联.大臣纪昀机敏过人,对出下联:人过大佛寺,寺佛大过人.对仗工整,体现了对称、和谐、高雅美!再如英语中有回文单词:radar(雷达),level(水平,水平面),rotator(旋转体),pop (流行音乐),deed(行动),civic(市民的)等等;还有回文句,如:able was i ere i saw elba (不见厄尔巴岛,我不倒.这是拿破仑被问及是否已入侵英格兰时的回答);ma is as selfless as i am(妈妈和我一样无私);a man,a plan,a canal,panama!(伟大的人,伟大的计划,伟大的巴拿马运河),等等,这样的回文单词和回文句子在英语中同样举不胜举.随着时代的发展,现在各种广告中还出现一些回文商标,如101生发水、505神功元气袋、414毛巾、555香水、999胃药等,其中的数字都是回文数,就连常见的呼救信号sos 也都是回文.可见,“回文”现象无处不在.而在数学中,最有趣的就是回文数了.下面我们谈谈数学中回文数的一些有趣问题.1. 回文数的个数显然两位数的回文数有11,22,...,99,共9个;三位数的回文数有1i1,2i2, (9i9)i=0,1,...,9,共90个;四位数的回文数有1ii1,2ii2,......,9ii9,i=0,1, (9)共90个;相应的,五位数的回文数有900个,六位数的回文数也有900个,…,由此可归纳猜想一般结论:命题1 n位数的回文数的个数,当n=2k(k∈n*)时有9×10k—1个;当n=2k+1(k∈n*)时有9×10k个,其中k∈n*.证明设回文数为a1a2…an—1an,当n=2k(k∈n*)时,必有a1=a2k,a2=a2k—1,…,ak=ak+1,显然,a1与a2k可取1,2,…,9;a2与a2k—1可取0,1,…,9;…;ak与ak+1可取0,1,…,9,故根据乘法原理,当n=2k(k∈n*)时的回文数个数为1个9与(k—1)个10相乘,即9×10k—1个.当n=2k+1(k∈n*)时,必有a1=a2k+1,a2=a2k,…,ak=ak+2,ak+1=ak+1,显然,a1与a2k+1可取1,2,…,9;a2与a2k可取0,1,…,9;…;ak与ak+2可取0,1,…,9;ak+1可取0,1,…,9,故根据乘法原理,当n=2k+1(k∈n*)时的回文数个数为1个9与k个10相乘,即9×10k个.由此知高考题的答案是:(1)90;(2)9×10k.2. 回文数的几个性质回文数与11有特别的关系:命题2 从1到9的任何一个数乘以11,总能得出回文数,如2×11=22,7×11=77等.如果一个回文数的位数是双数,那么它总能被11除尽,如6556÷11=596;32523÷11=29593等.我们将这个性质叙述为如下的命题命题3 每一个偶位数回文数均可被11整除.证明设回文数为a1a2…an—1an,当n=2k(k∈n*)时,a1a2…a2k—1a2k=a1a2…akak+1…a2a1,显然,a1可取1,2,…,9;a2,a3,…,ak可取0,1,…,9,故a1a2…akak+1…a2a1=a1+10a2+…+10k—1ak+1+10kak+…+102k—2a2+102k—1a1,而10≡—1(mod 11),102≡1(mod 11),103≡—1(mod 11),…,102k—1≡—1(mod 11),故a1a2…akak+1…a2a1≡a1—a2+a3—…—a3+a2—a1≡0(mod 11).注命题3中,当回文数的位数是4时即为1992年云南初二年级数学竞赛题,题目如下:把一个正整数的数码按顺序倒写后所得的数与原数相同称为回文数,例如:22,101,342243,…(1)将任意两个四位回文数的差记为x,求x的最小正值m;(2)证明:每一个四位回文数都能m被整除.命题 4 如果一个回文数的位数是双数,并且越往中间数字越大,越靠两头数字越小,那么用它除以11的商一定是回文数,如2456886542÷11=223353322,2558998552÷11=232636232等.证明留给读者.除此之外,还有许多有关回文数的有趣性质,如命题5 任意两个凡是由1组成的数位不超过9的回文数相乘时结果一定也是回文数,如11×11=121,111×1111=123321,1111×11111=12344321等.这是有限个式子,读者完全可以一一验证,但有没有具体的证明方法,笔者还未找到.在命题5中,我们考虑特殊情形,即任意由1组成的数位不超过9的回文数与其自身相乘时结果一定也是回文数,我们暂且称为回文平方数,如112=121,1112=12321,11112=12344321,…;类似地,回文立方数也有类似情况,如113=1331,1113=1367631,…但人们借助电子计算机迄今未能找到四次方、五次方以及更高次幂的回文数,于是数学家们猜想:不存在nk(n;k∈n*,k≥4)型的回文数.命题6 任取一个数(两位及以上),把它倒过来,并将这两个数相加,然后把这个和数再倒过来与原数相加,重复这个过程,在有限的步骤内,一定会得到一个回文数.如46+64=110,110+11=121(注:110倒过来是011,但对应的数应该是11),通过两次运算就得到回文数121;59+95=154,154+451=605,605+506=1111,通过三次运算就得到回文数1111;再如197+791=988,988+889=1877,1877+7781=9658,9658+8569=18227,18227+72281=90508,90508+80509=171017,171017+710171=881188,经过七次运算得到881188这个回文数.等等,这样的例子也不胜枚举,但这也仅是一个猜测,到目前为止还无一人给出证明或否定.不过,细心的科学家还是找到了一个“意外”,这就是196.为了给196 找到自己的回文,加拿大的科学家在前些年曾经连续奋战了289天,他们在计算机上加了几百万次,已经得出一个1300万位数,可仍旧不是回文.科学家们只好死心了,但他们也没法证明196就一定没有回文.196这个“谜”使很多数学家彻夜未眠!也许这个猜想与哥德巴赫猜想一样将成为世界级的数学难题!不过关于一开始取出的数是两位数的情形,下面我们给出证明.设取出的两位数为ab=10a+b(a,b=1,2,…,9),则(10a+b)+(10b+a)=11(a+b).(1)若a+b≤9,则11(a+b)显然就是一个回文数;(2)若a+b=10,则11(a+b)=110,110+011=121,作两次加法运算即得回文数;(3)若a+b=11,则11(a+b)=121是回文数;(4)若a+b=12,13,14,15,16,17,18时,分别经过两次、两次、三次、四次、六次、二十四次、六次加法运算就得到回文数,其中当a+b=17时,经过二十四次加法运算的回文数是8813200023188.综上所述,对两位数的情形,命题6是正确的.笔者在研究回文数性质时还发现一个有趣的现象,以命题给出:命题7 两个由具有相同数字任意排列组成的回文数之差一定能被81整除.如5142415—1452541=3689874=45554×81;5142415—1542451=3599964=44444×81;5142415—4152514=989901=12221×81;5142415—4512154=630261=7781×81…更有趣的是它们的商也有的是回文数,是否也有规律可循呢?由于笔者水平有限上述命题没有能给出证明,请有兴趣的读者自行研究.关于回文数的奥妙无穷尽,比如回文素数等问题也很有趣,大家继续探讨吧!。
回文数

111 X 131=14541 111 X 171=18981 121 X 212=25652 121 X 222=26862 121 X 121=14641 212 X 212:44944 1001 X 1001=1002001 1001 X 1001 X 1001=1003003001
其中,有些是平方数。例如: 121=112,12321=11l2,… 12345678987654321=1111111112 立方数也有。例如: 1331=113,1030301=1013,… 数学家发现,在回文数中立方数是非常多的。如果一 个立方数是回文数,那么,几乎肯定能找到一个回文数, 立方以后等于这个数。比如,回文数1331是立方数,可以 找到一个回文数11,使113=1331。
判断回文数
• 以上说的只是编程的实现细节,简述一下思路,实际 上就是利用了回文数的特点,就是以中线两端对称, 所以我就先生成一个原数的镜像数--即高低位倒序 了一下,如果是回文数的话,肯定和他的镜像数相同 的,而且由于倒序了后仍是一个整数,不是字符串, 所以可以直接作两个整数的比较操作就行了,不用逐 个数位比较,所以无论这个要判断的数多长多大,都 只是作了一次整数比较而已。但缺点也是有的,就是 一定要把整个整数的所有数位都读出一次,然后再写 进并构造另一个整数。但由于比较次数大大减少,在 判断一个较长较大的整数时,未必就是更耗费时间的, 而且实现起来简单很多,尤其是判断终止的时候比较 简单
回文数 古时候,有一位秀才游桂林名胜之一的斗鸡山。他觉得 山名新奇有趣,不觉哼出一句: “斗鸡山上山鸡斗。” 如果把这算作上联,那下联呢?他怎么也对不上来。秀才 回家后,请自己的启蒙老师对下联。 老师说:“你的上联是回文句,正读反念,其音其义都一 样。我不久前游了龙隐洞,就以此来对吧。”说罢,念道: “龙隐洞中洞隐龙。” 秀才一听,赞叹道:“此乃天赐绝对矣尸 上面的对联称为回文联。 回文,是文学创作中的一种修辞手法。这种修辞手法讲 究语言文字的排列技巧,顺读倒读,流畅自如,给人以一种 循环往复的情趣。请再看一个回文联: 雾锁山头山锁雾, 天连水尾水连天。
数学回文数相乘的规律

数学回文数相乘的规律数学这个玩意儿,有时候真是让人又爱又恨。
尤其是那些让人挠头的数字,今天咱们就来聊聊其中一种特别的数字——回文数。
你说这回文数有什么特别的?简单来说,就是正着读和反着读都一样的数,像121、1331这些。
听起来有点儿玄乎,其实它们就像生活中的某些事情,表面平静,背后却暗藏玄机。
1. 回文数的魅力1.1 什么是回文数?回文数就像一面镜子,正着看和反着看没什么两样。
想想小时候看过的那本《三字经》,读着读着,就像个绕口令,真是趣味无穷。
像121、484、12321,这些数就跟这本书一样,随便怎么读都不带变的。
这种数字之所以让人着迷,是因为它们有种对称之美,像极了那些在情感上相互依偎的小情侣,正好凑成一对。
1.2 回文数的生活在日常生活中,回文数似乎无处不在。
比如说,大家都爱吃的“麻辣烫”,这名字一念出来,就让人口水直流。
想想它的美味,甚至可以说是个“回文”的味觉体验——吃一次就想再吃第二次。
又比如说,那些经典的歌词,很多时候都是对称的,像“我爱你”和“你爱我”,简直就是生活中的回文数啊!2. 回文数相乘的趣事2.1 相乘的结果咱们回到数学,回文数相乘的时候,可是有意思得很。
你会发现,两个回文数相乘,往往能得到另一个回文数。
就拿121和121来说吧,乘一乘,结果就是14641。
这结果一出来,简直让人惊掉下巴,真是应了那句老话:“一加一等于二,但回文数相乘可是大有玄机!”2.2 趣味探索如果再大胆点,咱们试试其他的回文数,比如说,1331乘以1331,哇哦,结果是1771561。
看起来不太对劲,怎么会不是回文数呢?所以说,回文数相乘,真是像一场有趣的实验,有时结果是回文数,有时则不是,完全看你的选择。
就像生活,有时候你精心安排了一切,却意外地出了点差错,这也许就是人生的调味剂吧。
3. 总结回文数的智慧3.1 数学的乐趣通过这些回文数的乘法运算,我们不仅能感受到数学的乐趣,还能让这些冰冷的数字变得生动起来。
NOIP2017扬中普及组1试题
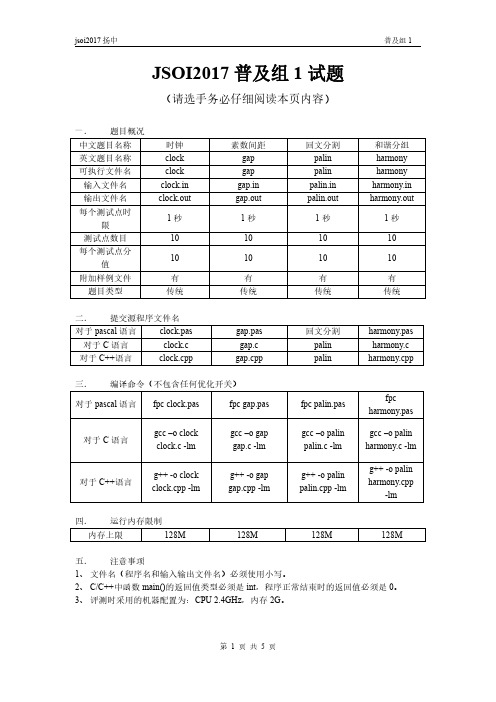
011001100010100011 001010100101110001 【样例输入 2】 00:00:01
【样例输出 2】
000000000000000001 000000000000000001
第2页共5页
jsoi2017 扬中
普及组 1
素数间距
(gap.pas/c/cpp)
1-3
4-5
6-7
8-10
第5页共5页
分别竖着和横着取出字符,于是得到 011001100010100011 和 00101010010111001 两个字符 串。 【输入格式】 一行,一个 24 小时表示的时间。符合 XX:XX:XX 的形式,分别表示时、分、秒 【输出格式】
一行,两个字符串,分别表示竖着和横着取出的字符串(具体参见样例)。两个字符串 用一个空格隔开。 【样例输入 1】 10:37:49
4
【样例输入 2】 15 【样例输出 2】
4
【数据范围】 20% N<=100 40% N<=1000 100% N<=1,000,000
第3页共5页
jsoi2017 扬中
普及组 1
回文分割
(palin.pas/c/cpp)
【问题描述】 大家都知道回文串吧~ 简单地说就是左右对称的一个串,比如 abcba,werrew。小 s 对回文 串的研究已经够深刻了,现在她转而研究其他方面的回文,比如,数的回文拆分。对于自然 数的拆分,就是把一个自然数 N 用若干个整数之和表示。比如 5=1+2+3+4+5=1+2+1+7+1+2+1。 那么怎样的拆分才算是回文的呢?我们用从归纳的角度来定义数的回文拆分。首先一个数 A=A 是一个回文拆分。其次,一个自然数 N=A+A 或是 N=A+x+A,其中 A 是一个回文拆分,x 是任意一个自然数,这两种也是回文拆分。举个例子,7 的所有回文拆分有:7, 1+5+1,2+3+2,1+1+3+1+1,3+1+3,1+1+1+1+1+1+1。现在小 s 想知道,一个正整数 N 的回文拆 分到底有多少种。由于这个数字可能很大,小 s 只需要你告诉她答案除以 1,000,000,007 的 余数的值。 【输入格式】 一行,一个正整数 N 【输出格式】 一行,一个整数 M,为 N 的回文拆分数%(mod) 1,000,000,007 的值 【样例输入 1】 4 【样例输出 1】 4 【样例输入 2】 20 【样例输出 2】 60 【数据范围】 30% 1<=N<=20 100% 1<=N<=1000
回文数定理与回文数幻方

數學傳播41卷2期,pp.80-95回文數定理與回文數幻方梁培基引言:尋找「196」的回文數,是迄今為止沒有解決的難題。
數學家用傳統的「顛倒相加法」算到3億多位也沒有找到196的回文數,計算機的速算功能,在這裏黯然失色。
既然此路不通,何不另闢蹊徑。
本文給出一種方法可以得到任意數的回文數,解決了「196」的回文數問題,同時也解決了196的一連串顛倒數(887,1675,7436···)得不到的回文數問題。
並給出由回文數組成的幻方及平方幻方等。
著名數學家美籍華裔李學數教授在他撰寫的《數學與數學家的故事》第4冊[1],第3章「回文數、鏡反數和華林問題」一文中,介紹了「回文數」與「回文對聯」。
李學數教授文、理兼優,知識淵博,著作豐碩,尤其擅長撰寫古今中外數學家奮鬥勵志的故事,對激勵青少年學習數學起到了巨大的推動作用。
他用生花之妙筆撰寫了古典式回文對聯、回文詩詞,這些詩詞可以從前到後讀,也可以反過來從後向前讀。
經過正讀與反讀,有的意思相近,有的意思迥異,令人耳目一新,敬佩有加。
又介紹了回文數問題及華林問題,深入淺出,發人深省。
能看到李學數教授的《數學與數學家的故事》是人生之幸事,不僅給自己充足了勤奮學習的正能量,甚至可以影響N代人!不看此書,懊悔莫及。
一、回文數與回文對聯「回文數」是數論中一個有趣的問題。
它的定義是:如果2位(或2位以上)數,從左向右(從前向後)讀與從右向左(從後向前)讀,完全一樣,我們稱這種數為「回文數」。
例如:11, 161,8778等,都是回文數。
對聯是我國特有的一種文學形式,它短小精粹,妙趣橫生。
在茫茫「聯海」中有一種倒讀、順讀其文字或音調都一樣的對聯,稱為「回文對聯」。
例如:鬥雞山上山雞鬥,龍隱岩裏岩隱龍。
還有:上河老和尚,有心交新友;之前,這幅聯是「孤聯」,沒人對出。
我們給出:「原莊小狀元,聞有會友文。
」與之匹配。
並附上四句以紀念之:老和尚以文會友,小狀元對答如流,忘年交情投意合,傳佳話萬古千秋。
回文序列结构

回文序列结构回文序列是一种令人着迷的结构,它在很多领域都有着广泛的应用。
所谓回文序列,即正序和逆序读取时都能得到相同结果的序列。
这种结构在语言、数学、音乐和生物等领域中都有着重要的地位。
首先,回文序列在语言中起到了独特的作用。
在汉字中,一些词语在正序和逆序读取时都能得到相同的结果,这就是回文。
比如,"上海自来水来自海上","山西运煤车煤运西山",这些回文词语使得语言更加有趣和富有韵味。
此外,回文诗也是一种独特的艺术形式,它以回文的形式表达情感和思想。
回文诗的创作不仅要求在意义上相对称,还要在音韵上呼应,这使得诗歌更富有美感和韵律。
其次,回文序列在数学中也有着重要的应用。
回文数是指当它的各位数字按逆序排列时与原来的数字相同,比如121、1221等。
回文数在数论、代数等领域中有着重要的地位。
研究回文数的性质可以帮助我们更好地理解数字的规律和特性。
此外,回文序列还可以运用在排列组合、概率统计等数学问题中,为解题提供更多的思路和方法。
此外,回文序列也在音乐中得到了广泛的运用。
在音乐中,回文序列可以用来构建旋律、和弦和节奏等元素,使音乐更加富有层次和变化。
回文序列的运用可以给音乐增添一种独特的对称美。
同时,在音乐的创作中,回文序列也可以作为一种结构上的手法,帮助音乐家组织和展示自己的思想和创意。
最后,回文序列在生物学中也有着一定的意义。
在DNA序列中,存在着回文序列的特点。
这些回文序列在DNA的起源、复制和修复中起到了重要的作用。
研究回文序列的分布和特性有助于我们更好地理解DNA的结构和功能。
此外,回文序列还可以用来设计生物药物,提高其稳定性和疗效。
综上所述,回文序列是一种充满魅力和指导意义的结构。
在语言、数学、音乐和生物等领域中,回文序列都发挥着重要的作用。
通过研究和应用回文序列,我们可以更好地理解和探索世界的奥秘。
无论是在艺术创作、科学研究还是日常生活中,回文序列都给我们带来了无限的欢乐和启发。
最长回文子串Manacher 算法

缺陷2)可以通过这个直观的小 体现:c h a r:a b a b ai:01234当i==1,和i==2时,左边的子串aba分别被遍历了一次。
如果我们能改善解法2的不足,就很有希望能提高算法的效率。
Manacher正是针对这些问题改进算法。
(1) 解决长度奇偶性带来的对称轴位置问题Manacher算法首先对字符串做一个预处理,在所有的空隙位置(包括首尾)插入同样的符号,要求这个符号是不会在原串中出现的。
这样会使得所有的串都是奇数长度的。
以插入#号为例:a b a———>#a#b#a#a b b a———>#a#b#b#a#插入的是同样的符号,且符号不存在于原串,因此子串的回文性不受影响,原来是回文的串,插完之后还是回文的,原来不是回文的,依然不会是回文。
(2) 解决重复访问的问题我们把一个回文串中最左或最右位置的字符与其对称轴的距离称为回文半径。
Manacher定义了一个回文半径数组RL,用RL[i]表示以第i个字符为对称轴的回文串的回文半径。
我们一般对字符串从左往右处理,因此这里定义RL[i]为第i个字符为对称轴的回文串的最右一个字符与字符i的距离。
对于上面插入分隔符之后的两个串,可以得到RL数组:c h a r:#a#b#a#R L:1214121R L-1:0103010i:0123456c h a r:#a#b#b#a#R L:121252121R L-1:010141010i:012345678上面我们还求了一下RL[i]-1。
通过观察可以发现,RL[i]-1的值,正是在原本那个没有插入过分隔符的串中,以位置i为对称轴的最长回文串的长度。
那么只要我们求出了RL数组,就能得到最长回文子串的长度。
于是问题变成了,怎样高效地求的RL数组。
基本思路是利用回文串的对称性,扩展回文串。
我们从左往右地访问字符串来求RL,假设当前访问到的位置为i,即要求RL[i],在对应上图,i必然是在p o右边的(obviously)。
判断回文数python编程代码

判断回文数python编程代码以判断回文数Python编程代码为标题的文章回文数是指正序和倒序都一样的数字,例如121、12321等。
在编程中,判断一个数字是否是回文数是一个常见的问题。
本文将以Python代码为基础,详细介绍如何判断一个数是否是回文数。
回文数的判断可以通过将数字转换为字符串,然后比较字符串和其反转后的字符串是否相等来实现。
下面是判断回文数的Python代码示例:```pythondef isPalindrome(num):# 将数字转换为字符串num_str = str(num)# 反转字符串reversed_str = num_str[::-1]# 判断反转后的字符串是否与原字符串相等if num_str == reversed_str:return Trueelse:return False# 测试示例print(isPalindrome(121)) # 输出Trueprint(isPalindrome(12321)) # 输出Trueprint(isPalindrome(12345)) # 输出False```以上代码中,我们定义了一个名为`isPalindrome`的函数,该函数接受一个整数作为参数。
首先,我们将整数转换为字符串,并使用字符串的切片操作`[::-1]`将其反转。
然后,我们将反转后的字符串与原字符串进行比较,如果它们相等,则返回`True`,否则返回`False`。
在代码的最后,我们使用`print`语句对函数进行了简单的测试。
运行代码后,我们可以看到对于回文数121和12321,函数返回了`True`,而对于非回文数12345,函数返回了`False`。
以上代码是一种简单而有效的判断回文数的方法,但它并不是唯一的方法。
还可以使用数学运算的方式来判断回文数,但这需要涉及到数学公式和计算公式,不符合本文的要求,因此不在此展开讨论。
判断回文数的代码虽然简单,但它背后涉及到一些基本的编程概念和技巧。
回文联、数字联、叠字联、顶针联

回文联:它是我国对联修辞奇葩(pā)中的一朵。
用回文形式写成的对联,既可顺读,也可倒读,不仅它的意思不变,而且颇具趣味。
雨滋春树碧连天
天连碧树春滋雨
风送花香红满地
地满红香花送风
艳艳红花随落雨
雨落随花红艳艳
数字联:在对联中嵌入数字,使数量词在对联中有特殊意义,用数量词组成的对联的作用主要有:创造形象和意境、加大对仗难度、进行数学运算、数字合称词的阐释、连续嵌入自然数等。
花甲重开外加三七岁月
古稀双庆内多一个春秋
一掌擎天五指三长两短
六合插地七层四面八方
冰冷酒一点两点三点
丁香花百头千头万头
叠字联:又名“重言”,系指由两个相同的字组成的词语。
人们在创作楹联时,常常将叠字运用于联语创作的方法,就是叠字法。
用叠字法作楹联,可以生动地表现楹联的意境,语音上和谐悦耳,节奏明朗,韵律协调,具有个情达意的形象性,因而可以增强楹联的艺术魅力,获得特定的表达效果。
在楹联创作中,叠字法的运用是非常广泛的,几乎随处可见。
月月月明八月月明明分外
山山山秀巫山山秀秀非常
进进出出笑颜开人人满意
挑挑拣拣花色美件件称心
一盏清茶解解解解元之渴
五言绝诗施施施施主之才
顶针联:这种对联乃是将前一个分句的句脚字,作为后一个分句的句头字,使相邻的两个分句,首尾相连,亦称“联珠对”、“联锦对”。
保俶塔,塔顶尖,尖如笔,笔写五湖四海
锦带桥,桥洞圆,圆似镜,镜照万国九州
弓长张张弓,张弓手张弓射箭,箭箭皆中
木子李李木,李木匠李木雕弓,弓弓难开
大鱼吃小鱼,小鱼吃虾,虾吃水,水落石出
溪水归河水,河水归江,江归海,海阔天空。
回文子串数目

回文子串数目回文子串指的是正读和反读都是相同的字符串。
求一个字符串中回文子串的数量是一个经典的问题,在这篇文章中,我们将详细讨论这个问题,并介绍几种解决方法。
首先,我们来看一些示例。
对于字符串"abcba",它的回文子串有"a"、"b"、"c"、"b"、"a"、"abcba",一共有6个。
对于字符串"aaa",它的回文子串有"a"、"a"、"a"、"aa"、"aa"、"aaa",一共有6个。
解决这个问题的一种简单方法是枚举所有可能的子串,然后判断是否是回文。
这种方法的时间复杂度是O(n^3),其中n是字符串的长度。
具体的实现如下所示:```pythondef countPalindromeSubstrings(s: str) -> int:count = 0n = len(s)for i in range(n):for j in range(i, n):if isPalindrome(s[i:j+1]):count += 1return countdef isPalindrome(s: str) -> bool:return s == s[::-1]```上述代码中的函数`countPalindromeSubstrings`用于计算字符串中的回文子串数量,而函数`isPalindrome`用于判断一个字符串是否是回文。
这种方法虽然简单,但是时间复杂度较高,当字符串长度很大时,计算量将会非常大。
因此,我们需要寻找更加高效的解决方法。
动态规划是解决这个问题的一种常见方法。
利用动态规划,我们可以通过已知的信息来计算未知的信息。
回文数字的定义-概念解析以及定义

回文数字的定义-概述说明以及解释1.引言1.1 概述回文数字是一种特殊的数字形式,在现今数学和计算领域中具有重要意义。
回文数字是指从左到右和从右到左读取数字结果相同的数,也就是它在十进制下的表示方式是对称的。
例如,121和1221都是回文数字,因为它们从左到右和从右到左读取数字结果相同。
回文数字不仅在数学领域中具有重要意义,在计算机科学、密码学和信息安全等领域也有广泛的应用。
通过深入研究回文数字的性质和特点,可以帮助我们更好地理解数字之间的关系,优化算法设计,加强数据安全等方面的应用。
本文将深入探讨回文数字的概念、特点和应用,以及回顾回文数字的意义和展望回文数字的未来发展。
通过对回文数字的综合分析,可以更好地认识回文数字在数学和计算领域中的重要性和作用,促进相关领域的学术交流和技术创新。
文章结构部分的内容如下:1.2 文章结构本文分为引言、正文和结论三个部分。
在引言部分中,将简要介绍回文数字的概念并说明目的,以引出文章的主题。
在正文部分,将详细论述回文数字的概念、特点和应用。
在结论部分,将总结回文数字的重要性,并展望未来的发展方向。
整篇文章将围绕着回文数字展开,在严谨的逻辑结构下,深入探讨回文数字在数学和实际应用中的重要性。
1.3 目的:本文的目的是对回文数字进行全面的定义和解释,探讨其在数学和现实生活中的重要性和应用。
通过本文的阐述,读者可以更深入地了解回文数字的概念、特点以及其在数学领域和实际生活中的应用,进而增强对回文数字的理解和认识。
同时,通过对回文数字的重要性、意义和未来发展的展望,希望能够激发读者对数学研究的兴趣,促进相关领域的进步和发展。
最终,本文旨在为读者提供全面而深入的了解回文数字的知识,以及对其重要性和未来发展的思考。
2.正文2.1 回文数字的概念回文数字是指从左向右读和从右向左读都相同的数字。
换句话说,如果一个数字的各个位数依次排列,无论从左往右还是从右往左读都是一样的,那么这个数字就被称为回文数字。
回文数列求和公式

回文数列求和公式
很多人都会做过回文数列,但其实回文数列并不简单,更像它是数列之长,这就要求我们掌握回文数列和。
回文数列是集合的一部分,所以和集中不是所有的集合都有回文数列。
但由于回文数列存在最小值和最大值问题,而且往往需要较大值和较小值才能实现求和结果。
因此本文将给出求和公式(如果有条件可以用函数进行求和)。
一、定义
回文数列,又叫正数列表、反向数列表、反序数列。
回文数列最大特点是含有3个数:
1、有1个或2个以上的同位数字和和:
2、回文数列之长:
二、操作
用上述方法计算出如下结果:其中第一列为回文数列,所有回文数列都包含一个数字“=”。
再看下第二列:其中第一列数字是回文数列中最小值、最大值最小值;第二列为回文数列中最大值、最小值。
三、结果
以4为例,如果想要实现相同的结果,那么所需的时间就是4个零,也就是说需要4个小时。
那么你需要用5个公式来计算。
所以这里我们可以用函数进行求和。
当然这样做可能会出现很难运算。
四、总结
回文数列不像整数一样只有一个参数,它没有数值概念。
所以当你要对回文数列进行求和时,需要利用函数对回文数列进行求和,如果有条件可以用函数求和。
当然除了函数求和之外,还可以使用一些简单例子来实现。
例如用 Python可以实现对回文数列进行求和;又比如用 BP进行求和;还有使用 IF求和等。
什么叫做“回文数”?

什么叫做“回⽂数”?
举个简单的例⼦,如123454321,倒过来写也是123454321,再⽐如1221,倒过来写也是1221。
反向排列与原来⼀样的数就叫做回⽂数。
1位数的回⽂数有9个(不包含0),它们的和是45;2位数的回⽂数有9个,分别是
11,22,33,44,55,66,77,88,99,它们的和是495。
请⼤家思考⼏个问题。
1. 三位数的回⽂数有多少个,它们的和是多少?
2. 四位数的回⽂数有多少个,它们的和为多少?
3. 任意位数的回⽂数有多少个,它们的和为多少?
三位数的回⽂数,由于百位数等于个位数,所以我们不⽤考虑个位数。
百位数可以从1-9中进⾏选择,很显然,百位如果是0的话,它其实就是个两位数。
中间的那位也就是⼗位,有10种选择0-9。
运⽤乘法原理,可以得知三位数的回⽂数有90个。
我们可以把这90个回⽂数列成⽅阵。
⼤家通过观察这个图这个⽅阵图,可以计算出这90个回⽂数的和。
百位上有10个1-9,个位同百位的情况⼀样,⼗位上有九个0-9。
这些回⽂数的和是49500。
我们⽤同样的⽅法,对四位数,五位数,六位数的回⽂数进⾏计算,可以得出下⾯的表格。
对上⾯的表格进⾏分析后,我们得出了下⾯的结论⼤家对于这个结论,了解即可,没必要死记硬背。
我们只要掌握⼀点,回⽂数具有对称性,就可以很好的了解回⽂数。
python回文数

python回⽂数# 回⽂数是指正序(从左向右)和倒序(从右向左)读都是⼀样的整数。
例如,121 是回⽂,⽽ 123 不是。
#⽅法⼀def palindrome1(strnum):strnum=str(strnum)strlen=len(strnum)for i in range(0,int(2/strlen)+1):print(strnum[i])print(strnum[strlen-1])print(strnum[int(2/strlen)+1])if strnum[i]==strnum[strlen-1]:print("是回⽂数")else:print("不是回⽂数")#⽅法⼆def palindrome2(strnum):if str(strnum)==''.join(list(reversed(str(strnum)))):print("是回⽂数")else:print("不是回⽂数")#⽅法三def palindrome3(strnum):strnum=str(strnum)if strnum==strnum[::-1]:print("是回⽂数")else:print("不是回⽂数")#⽅法四只适合数字def palindrome4(strnum):if strnum<0:return Falsetemp_x = strnum;palindromeNum = 0while temp_x != 0:palindromeNum = palindromeNum*10 + temp_x%10temp_x =int(temp_x/10)if palindromeNum == strnum:print("是回⽂数")else:print("不是回⽂数")#⽅法五整数转字符串,反转字符串,对⽐反转后字符串与原字符串是否相等def palindrome5(strnum):str_x = str(strnum)str_y = ""for i in str_x:print(i)str_y = i + str_yif str_y==str_x:print(str_y,"是回⽂数")else:print(str_y, "不是回⽂数")。
回文序列与反向重复序列

回文序列与反向重复序列回文序列和反向重复序列是数字序列中的两种特殊模式。
回文序列是指从左到右和从右到左读取都完全一样的序列,而反向重复序列则是指将原序列倒置后与原序列完全相同的序列。
回文序列是一种常见的数学概念,在数学领域中有广泛的应用。
它不仅仅存在于数字序列中,还可以出现在字符串、单词、句子等各种形式的序列中。
比如,"level"、"madam"、"racecar"等都是回文序列。
回文序列不仅在数学中有独特的性质,还在日常生活中有一定的重要性。
它们常常被用于密码学、数据压缩和数据传输等领域。
在密码学中,回文序列可以用于生成安全的密钥,保护用户的隐私信息。
在数据压缩中,回文序列可以被用来识别和压缩重复的数据块,从而提高数据传输的效率。
与回文序列相似的是反向重复序列。
反向重复序列是指将原序列倒置后与原序列完全相同的序列。
与回文序列不同的是,反向重复序列并不要求从左到右读取与从右到左读取一样,只要倒置后与原序列一致即可。
比如,"abcdeedcba"、"12344321"、"helloolleh"等都是反向重复序列。
回文序列和反向重复序列虽然都具有一定的特殊性,但它们之间还存在一些不同之处。
首先,回文序列要求从左到右和从右到左读取完全一样,而反向重复序列只要求倒置后与原序列一致。
其次,回文序列通常用于描述对称性,而反向重复序列则更多地用于描述重复性。
在实际应用中,我们经常会遇到回文序列和反向重复序列。
比如,在文学作品中,作者常常使用回文序列来创造艺术效果,增加作品的趣味性和独特性。
在音乐中,作曲家也会运用回文序列和反向重复序列来构建旋律和和声,使音乐更加富有层次感和变化。
总的来说,回文序列和反向重复序列是数字序列中的两种特殊模式。
它们不仅在数学中有独特的性质和应用,还在日常生活和各个领域中发挥着重要的作用。
python特殊回文数

python特殊回文数Python特殊回文数是指一个数既是回文数,又满足其平方也是回文数的整数。
例如,11就是一个特殊回文数,因为11的平方121也是一个回文数。
Python语言可以很方便地判断一个数字是否为回文数。
我们可以将数字转换为字符串,然后反转字符串并比较原始字符串和反转后的字符串是否相等。
如果相等,则该数字是回文数。
下面是判断一个数字是否为回文数的Python代码:```def is_palindrome(n):return str(n) == str(n)[::-1]```接下来,我们需要编写代码来寻找特殊回文数。
我们可以使用双重循环来枚举所有可能的数字,并检查它们是否满足条件。
以下是寻找特殊回文数的Python代码:```for i in range(10, 100000):if is_palindrome(i) and is_palindrome(i**2):print(i)```上述代码将从10到99999枚举所有整数,并检查它们是否为特殊回文数。
如果找到了一个特殊回文数,则将其打印出来。
运行上述代码后,输出结果如下:```11101111121202212264303313323...(省略部分结果)98689...(省略部分结果)9989899999299799949949998999```我们可以看到,Python特殊回文数的数量非常有限,只有几十个。
这些数字具有一定的规律性,例如它们的位数必须为奇数,且除了第一位和最后一位外,其他所有位都必须是0或2。
总之,Python特殊回文数是一个非常有趣的数学问题。
通过使用Python语言进行编程,我们可以轻松地找到所有特殊回文数,并深入探究它们的规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.一个任意字符串的稳定和谐数为其回文子字符串的数目,然后通过程序使其输出和谐数,然后找出其稳定和谐数,运用循环程序语言。
4.输出最大和谐数和该字符串,然后再找出其中具有最大稳定和谐数的字符串,找出其最大和谐数,结束编程,修改用户输入字符串中的一个字符,得到个一个找出,然后输出。
《C程序设计》
课程设计报告
(2014—2015学年第2学期)
题目:英文回文串和稳定和谐数
一、课程设计概述
课程设计问题描述
编写程序,输入由大小写英文字母组成的字符串,根据菜单提示完成相应功能
( 1 )判断用户输入的字符串是否为回文串;
( 2 )输出该字符串的所有回文子串,并计算该字符串的稳定和谐数;
( 3 )修改该字符串中的任意一个字符使得修改后的字符串具有最大稳定和谐数,输出该新串和最大稳定和谐数。
设计要求
主函数实现用户字符串的输入和菜单的显示,如图10.1所示。用户输入的字符串作为函数的实参传递给各个子函数。
1编写一个子函数实现回文串的判断。
2 编写一个子函数输出字符串的所有回文子串,并输出回文子串的个数作为该字符串的和谐数。
3编写一个子函数根据用户输入的字符串求出一个新字符串,使得该字符串具有最大和谐数。
5.系统可以选择的输出相应的结果。
设计目的
掌握所学的语言程序的设计方法,熟悉所学语言的设计类型,结构方法,巩固知识,通过综合设计达到可以通过自己查阅知识解决问题。初步掌握程序设计方法,能熟练调试程序,创新能力和独立自主完成任务。
开发环境
1.Visual c++6.0.
2.电脑
3.Win7操作系统
二、总体设计(1)
系统功能需求分析
1.回文字符串就是正读和反读都相同的字符串,约定空串不是回文串,含有单个字符的字符串都是回文字符串,定义一个结构体类型表示输入的大小英文字母组成的字符串.
