2018深圳二模文综pdf
最新-2018年深圳中学高三年级第二次阶段考试文科综合(地理)试题及答案 精品
试卷类型:A深圳中学2018届高三年级第二次阶段考试文科综合(地理)试题本试卷共12页,41小题,满分300分。
考试用时150 分钟。
一、选择题:本大题共35 小题,每小题4 分,共140 分。
在每小题列出的四个选项中。
只有一项是符合题目要求的。
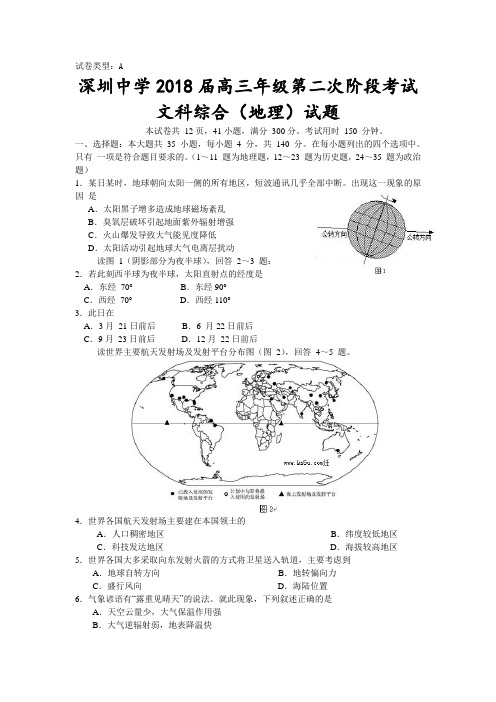
(1~11 题为地理题,12~23 题为历史题,24~35 题为政治题)1.某日某时,地球朝向太阳一侧的所有地区,短波通讯几乎全部中断。
出现这一现象的原因是A.太阳黑子增多造成地球磁场紊乱B.臭氧层破坏引起地面紫外辐射增强C.火山爆发导致大气能见度降低D.太阳活动引起地球大气电离层扰动读图1(阴影部分为夜半球),回答2~3 题:2.若此刻西半球为夜半球,太阳直射点的经度是A.东经70o B.东经90oC.西经70o D.西经110o3.此日在A.3月21日前后B.6 月22日前后C.9月23日前后D.12月22日前后读世界主要航天发射场及发射平台分布图(图2),回答4~5 题。
4.世界各国航天发射场主要建在本国领土的A.人口稠密地区B.纬度较低地区C.科技发达地区D.海拔较高地区5.世界各国大多采取向东发射火箭的方式将卫星送入轨道,主要考虑到A.地球自转方向B.地转偏向力C.盛行风向D.海陆位置6.气象谚语有“露重见晴天”的说法。
就此现象,下列叙述正确的是A.天空云量少,大气保温作用强B.大气逆辐射弱,地表降温快C.空气中水汽少,地表降温慢D.地面辐射强,地表降温慢图3 为某海岛等高线图(单位:米),读图判断7~8 题。
7.下列关于该岛的叙述正确的是A.位于东半球、南半球B.降水西多东少C.径流季节变化大D.南北长约10 千米8.该岛最高处的海拔可能是A.96 米B.118米C.152米D.175米9.造成澳大利亚大陆1月和7 月气温分布状况的原因分析,错误的是A.1 月气温分布受海陆热力性质差异影响大B.7 月气温分布受纬度因素影响大C.1 月,大陆东岸气温受暖流影响大D.7 月,大陆东岸气温受暖流影响大10.通常情况下,风浪最大的海域是A.赤道附近海域B.南北纬30°附近海域C.40°~60°N 海域D.40°~60°S 海域11.图5 是我国气温年较差分布图。
2018年届深圳二模文综试题和答案解析

深圳市2018届高三年级第二次调研考试文科综合本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共16页,满分300分。
考试用时150分钟。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,写在本试卷上无效。
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
第Ⅰ卷一、选择题:本题共35个小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
江苏无锡是中国光伏产业最为集中的地区。
自2001年首家中澳合资光伏企业成立至2011年,无锡光伏产业发展实行两头在外的发展模式(关键零部件、生产设备和销售市场主要依赖国外)参与国际市场竞争。
2 016年,无锡市太阳能电池产能占全国总规模的50%以上,已形成包括光伏材料、电池原件、光伏组件、逆变器、运维服务、数据管理等各生产环节的全产业链竞争优势。
光伏制造设备的本地化率已经超过50%;企业在为客户提供电子化学品原料的同时,还针对单晶硅和多晶硅生产中的化学品污染问题,主动研发废化学品的回收再利用技术;开发了可以通过互联网实现对遥远地区的风能、光伏等发电装置的远程监控、运行管理和维护技术。
据此完成1~3题。
1.与发达国家相比,2001-2011年间无锡光伏产业参与国际市场竞争的主要有利条件是A.生产成本较低 B.原料资源丰富C.交通位置优越 D.市场需求量大2.无锡光伏产业在短短10多年间,从两头在外发展模式到形成全球性竞争优势,主要得益于A.生产规模不断扩大B.智能化的运行管理和维护服务C.披术研发和创新D.废化学品的回收再利用3. 2016年,江苏省光伏累计装机容量列全国第五,仅次于4个太阳能资源一类地区——新疆、甘肃、青海和内蒙古。
深圳市2018年高三年级第二次调研考试(语文)(1)

深圳市2018年高三年级第二次调研考试2018.4注意事项:1.答卷前,考生务必将自己的姓名和座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
新媒介是一把双刃剑,在方便人们的日常生活、拓展人的行为能力以及提供各种超感官体验时,其产生的负面效应也不容忽视。
每天各种无用信息占据人们的大量时间,使人们非理性冲动增多,人际关系变得越来越淡薄,也更容易产生紧张和焦虑情绪。
要解决这一问题,就必须从媒体与受众两方面入手,积极寻求对策。
从媒体角度看,媒体可以利用信息智能匹配技术降低受众的信息接收成本。
这项技术以数据分析为依托,使信息更加智能化、个性化,从而与受众的需求相匹配。
比如,一些媒体机构根据用户个人需求方面的关键词、以往浏览的相关数据以及学历、职业、爱好等特征信息,进行汇集、整理、跟踪和分析,并根据用户充值、消费、反馈等数据信息,了解和掌握不同用户的个性化潜在需求,进行精准的信息推送。
虽然公司主要以推广自己服务项目为目的,但这种技术更注重用户的体验和选择,会大大减少许多有意无意强加于受众的信息,从而降低了受众进行信息处理的时间成本,使其在轻松愉悦的状态中接收自己需要的各种信息。
这样的智能匹配模式会越来越精细化、个性化和特色化。
比如,有的技术可以根据手机定位,确定用户是在办公场所、家里还是旅途中来推送合适的视听内容;还可以根据用户手机的睡眠模式、工作模式等确定推送时间,以及根据某一信息关注度的高低确定是否推送。
从信息受众角度看,受众需要提高理性使用新媒介的能力。
受众首先要提升自己的媒介素养,即对媒介本身带来的危害及个人在媒介使用过程中存在的问题保持清醒认识的能力。
高三政治-2018年深圳第二次调研考试 最新

广州省深圳市2018年高三年级第二次调研考试政治试题2018.5 本试卷分选择题和非选择题(含选做题)两部分,满分150分,考试用时120分钟。
注意事项:1.答卷前,考生首先检查答题卡是否整洁无缺损,监考教师分发的考生信息条形码是否正确;之后务必用0.5毫米黑色字迹答字笔在答题卡指定位置填写自己的学校、姓名和考生号,同时,将监考教师发放的条形码正向准确粘巾在答题卡的贴条形码区,请保持条形码整洁、不污损。
2.选择题每小题选出答案后,用2B铅笔把答题卡对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。
不按要求填涂的,答案无效。
3.非选择题必须用0.5毫米黑色字迹的签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,请注意每题答案空间,预先合理安排;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将答题卡交回。
第Ⅰ卷(选择题,共76分)一、选择题I:在各题的备选答案,请选出一个最符合题意的答案。
本大题共26小题,每小题2分,共52分。
1.2018年3月16日上午十届全国人大五次会议高票通过。
这部法律历经13年酝酿和广泛讨论,创造了中国立法史上单部法律草案审议次数最多的记录。
这部法律自2018年10月1日起施行A.《企业所得税法》B.《义务教育法》(修订)C.《物权法》D.《就业促进法》2.2018年11月8日,国家税务总局发布了《个人所得税自行纳税申报办法(试行)》,规定年所得12万元以上的纳税人,要在规定时间内自行向税务机关办理纳税申报。
此举有利于()①强化对高收入者的税收征管②彻底杜绝偷漏税行为的发生,促进财政收入的增长③培养纳税人依法诚信纳税的意识④更好地发挥个人所得税调节收入分配的作用,有利于构建社会主义和谐社会A.①②③B.②③④C.①②④D.①③④3.2018年2月27日,获得2018年度国家最高科学技术奖。
2018年深圳市高三年级第二次调研考试文综历史答案(水印)
市 在一定程度上导致了国际恐怖主义的形成;世界朝多极化方向发展,逐渐形成
“一超多强”的世界格局。(答出 1 点得 2 分,共 6 分。)
圳 启示:我们要坚持和平发展道路,推动构建人类命运共同体;要牢固树立共商共建共享 的全球治理观;各国人民要同心协力,建设持久和平、普遍安全、共同繁荣、
深 开放包容的新世界;要摒弃冷战思维和强权政治,走对话而不对抗、结伴而不
2分
2分
2分 每个角度 2 分
共4分
结论
圳 论,全面、客观地论述历史问题。
2分
示例: 角度:
深 古代中国人对古罗马帝国政治概况的认识
观点: 古代中国人对古罗马帝国政治概况的认知,既有其合理的成分,也存在与现实脱
节的臆想。(2 分) 论证: 东晋人对大秦国政治方面的记载散见于《后汉纪》与《抱朴子》。其中“国人谈
2018 年深圳市高三年级第二次调研考试
文科综合(历史部分)参考答案及评分意见
一、选择题。(每题 4 分,共 48 分)
题号 24 答案 C25源自D26 C27 C
28 B
29 B
院 30 31 32
BAD
33 B
34 B
35 A
二、非选择题。(共 52 分)
究
41.(25 分) (1)背景:中国沦为半殖民地半封建社会(或答清政府沦为帝国主义统治中国的工具);民
市等方面的环保水平。(答出 1 点得 2 分,共 6 分。) 究 启示:人与自然是生命共同体,我们要牢固树立社会主义生态文明观,实现人与自然和 圳 谐共生的现代化,建设美丽中国;推进绿色发展,加快建立绿色生产和消费的
研 法律制度和政策导向;着力解决突出环境问题,坚持全民共治,源头防治;加
2018年广东省深圳市高考数学二模试卷(文科)

2018年广东省深圳市高考数学二模试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合A={x∈N|x2−2x≤0},B={x|1≤x≤2},则A∩B=()A.{1, 2}B.{0, 1, 2}C.{x|1≤x≤2}D.{x|0≤x≤2}2. 设i为虚数单位,则复数|1−√3i|1+i=()A.−1+iB.−2+2iC.1−iD.2−2i3. 袋中装有外形相同的四个小球,四个球上分别标有2,3,4,6四个数,现从袋中随机取出两个球,则两球上数字之差的绝对值不小于2的概率为()A.1 3B.12C.23D.564. 如图,在三棱柱ABC−A′B′C′中,侧棱AA′⊥底面A′B′C′,且△A′B′C′是正三角形,若点P是上底面ABC内的任意一点,则三棱锥P−A′B′C′的正视图与侧视图的面积之比为()(注:以垂直于平面ACC′A′的方向为正视图方向)A.1 2B.√32C.1D.2√335. 设S n为等差数列{a n}的前n项和,已知a1=S3=3,则S4的值为()A.−3B.0C.3D.66. 九连环是我国一种传统的智力玩具,其构造如图1:要将9个圆环全部从框架上解下(或套上),无论是哪种情形,都需要遵循一定的规则.解下(或套上)全部9个圆环所需的最少移动次数可由如图2所示的程序框图得到,执行该程序框图,则输出结果为( )A.170B.256C.341D.6827. 设函数f(x)=x +1x +b ,若曲线y =f(x)在点(a, f(a))处的切线经过坐标原点,则ab =( ) A.1 B.0C.−1D.−28. 设F 2为双曲线T:x 2a2−y 2b 2=1(a >0, b >0)的右焦点,P 是双曲线T 右支上一点,且满足|PF 2|=2,线段PF 2的垂直平分线经过坐标原点,设M 是线段PF 2的中点,若|OM|=3,则双曲线T 的离心率为( )A.√104B.32C.√102D.√109. 已知f(x)=1sinx +1cosx ,则函数y =f(x −π4)为( ) A.奇函数B.偶函数C.既是奇函数又是偶函数D.既非奇函数也非偶函数10. 已知直线y =kx −3经过不等式组{x +y −2≥02x −y ≤4y ≤4 所表示的平面区域,则实数k 的取值范围是( ) A.[−72,32]B.(−∞,−72]∪[32,+∞) C.[−72,74]D.(−∞,−72]∪[74,+∞)11. 如图,在矩形ABCD 中,AB =4,AD =2,E 、F 分别为边CD 、AD 的中点,M 为AE 和BF 的交点,则以A 、B 为长轴端点,且经过M 的椭圆的标准方程为( )A.x 24+y 25=1 B.x 24+y 23=1C.x 24+y 22=1D.x 24+y 2=112. 对∀x >0,不等式lnx ≥ax −ex +2恒成立,则实数a 的取值范围为( ) A.(−∞,−2e ) B.(−∞,−2e ] C.(−∞, 2−e) D.(−∞, 2−e] 二、填空题(每题5分,满分20分,将答案填在答题纸上)已知向量m →=(3, k),n →=(2, 4),若m → // n →,则m →∗n →=________.在Rt △ABC 中,∠C =90∘,∠B =60∘,BC =1,以AC 为轴将Rt △ABC 旋转一周,所得几何体的外接球的表面积为________.已知数列{a n }是一个各项均为正数的等比数列,且a 1009⋅a 1010=10,若b n =lga n ,则数列{b n }的前2018项的和为________.如图,A ,B 为某市的两个旅游中心,海岸线l 可看做一条直线,且与AB 所在直线平行,现计划将两个旅游中心与海岸线连接起来,由于地势原因,需在以AB 为直径的半圆上选定一点P ,修建PA ,PB ,PQ 三段公路,其中PQ ⊥l ,AB =20km ,两平行直线AB 与l 之间的距离为20km ,公路PA 和PB 段的造价均为6千万元/km ,公路PQ 段的造价为5千万元/km ,为便于筹备充足资金,需要计算该项工程的最大预算,根据以上信息,这三段公路总造价的最大值为________千万.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)在△ABC 中,记内角A ,B ,C 所对的边分别为a ,b ,c ,已知B 为锐角,且acosB +bsinB =c .(1)求角C 的大小;(2)若B =π3,延长线段AB 至点D ,使得CD =√3,且△ACD 的面积为3√34,求线段BD 的长度.耐盐碱水稻俗称“海水稻”,是一种可以长在滩涂和盐碱地的水稻.海水稻的灌溉是将海水稀释后进行灌溉.某试验基地为了研究海水浓度x(‰)对亩产量y (吨)的影响,通过在试验田的种植实验,测得了某种海水稻的亩产量与海水浓度的数据如表: 绘制散点图发现,可用线性回归模型拟合亩产量y 与海水浓度x 之间的相关关系,用最小二乘法计算得y 与x 之间的线性回归方程为y ^=b ^x +0.88. (1)求b ^,并估计当浇灌海水浓度为8‰时该品种的亩产量;(2)(i)完成下列残差表:(ii)统计学中常用相关指数R 2来刻画回归效果,R 2越大,模型拟合效果越好,如假设R 2=0.8,就说明预报变量y 的差异有80%是由解释变量x 引起的.请计算相关指数R 2(精确到0.01),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的? (附:残差公式ei ^=y i −y i ^,相关指数R 2=1−∑ n i=1(y i −y i ^)2∑ n i=1(y i −y)2)在四棱锥P −ABCD 中,侧棱PA ⊥底面ABCD ,AB // CD ,∠BAD =90∘,M 是PC 的中点,N 在线段AB 上,且AB =3AN ,已知CD =AD =PA =2,AB =3. (1)证明:MN ⊥平面PCD ;(2)将过D ,M ,N 三点的平面α与侧棱PB 的交点记为Q , (i)确定点Q 的位置,并说明理由; (ii)求四棱锥P −DMQN 的体积.直线l 经过抛物线C:x 2=4y 的焦点F ,且与抛物线C 交于A ,B 两点,抛物线C 在A ,B 两点处的切线分别与x 轴交于点M ,N . (1)证明:AM ⊥MF ;(2)记△AFM 和△BFN 的面积分别为S 1和S 2,求S 1⋅S 2的最小值.设函数f(x)=e x−1−alnx ,其中e 为自然对数的底数. (1)若a =1,求f(x)的单调区间;(2)若0≤a ≤e ,求证:f(x)无零点.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]在平面直角坐标系中,直线l 的参数方程为{x =√32ty =12t(t 为参数),圆C 1的参数方程为{x =1+cosαy =sinα (α为参数),圆C 2的参数方程为{x =4cosαy =4+4sinα (α为参数).若直线l 分别与圆C 1和圆C 2交于不同于原点的点A 和B .(1)以直角坐标系的原点为极点,x 轴的正半轴为极轴,建立极坐标系,求圆C 1和圆C 2的极坐标方程;(2)求△C 2AB 的面积. [选修4-5:不等式选讲]已知函数f(x)=|x +1|+|x −1|,g(x)=x 2−x . (1)求不等式f(x)<g(x)的解集;(2)若f(x)+g(x)>a 恒成立,求a 的取值范围.参考答案与试题解析2018年广东省深圳市高考数学二模试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【答案】A【考点】交集及其运算【解析】解不等式求得集合A,根据交集的定义写出A∩B.【解答】集合A={x∈N|x2−2x≤0}={x∈N|0≤x≤2}={0, 1, 2},B={x|1≤x≤2},则A∩B={1, 2}.2.【答案】C【考点】复数的运算【解析】直接利用复数代数形式的乘除运算化简得答案.【解答】|1−√3i| 1+i =21+i=2(1−i)(1+i)(1−i)=1−i,3.【答案】C【考点】古典概型及其概率计算公式【解析】现从袋中随机取出两个球,基本事件总数n=C42=6,利用列举法求出两球上数字之差的绝对值不小于2包含的基本事件有4个,由此能求出两球上数字之差的绝对值不小于2的概率.【解答】袋中装有外形相同的四个小球,四个球上分别标有2,3,4,6四个数,现从袋中随机取出两个球,基本事件总数n=C42=6,两球上数字之差的绝对值不小于2包含的基本事件有:(2, 4),(2, 6),(3, 6),(4, 6),共4个,∴两球上数字之差的绝对值不小于2的概率为p=46=23.4.【答案】D【考点】简单空间图形的三视图【解析】分别求出则S正视图=12aℎ,S侧视图=12×√32aℎ,即可求出.【解答】设△A′B′C′的边长为a,三棱柱ABC−A′B′C′的高为ℎ,则三棱锥P−A′B′C′的正视图的底是△A′B′C′是正三角形的边长,高为三棱柱ABC−A′B′C′的高,则S正视图=12aℎ,则三棱锥P−A′B′C′的侧视图底是△A′B′C′是正三角形高,高为三棱柱ABC−A′B′C′的高,则S侧视图=12×√32aℎ,则三棱锥P−A′B′C′的正视图与侧视图的面积之比为12aℎ1 2×√32aℎ=2√33,5.【答案】B【考点】等差数列的通项公式【解析】此题暂无解析【解答】解:设数列{a n}的公差为d,则S3=3a1+3×22×d=9+3d=3,解得d=−2,所以S4=4a1+4×32×d=12+(−12)=0.故选B.6.【答案】C【考点】程序框图【解析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【解答】解:模拟程序的运行,可得i=1,S=1i=2,满足条件i为偶数,S=2不满足条件i>8,执行循环体,i=3,不满足i为偶数,S=5;不满足条件i>8,执行循环体,i=4,满足i为偶数,S=10;不满足条件i>8,执行循环体,i=5,不满足i为偶数,S=21;不满足条件i>8,执行循环体,i=6,满足i为偶数,S=42;不满足条件i>8,执行循环体,i=7,不满足i为偶数,S=85;不满足条件i>8,执行循环体,i=8,满足i为偶数,S=170;不满足条件i>8,执行循环体,i=9,不满足i为偶数,S=341;此时,满足条件i>8,退出循环,输出S的值为341.故选C.7.【答案】D【考点】利用导数研究曲线上某点切线方程【解析】求出切线方程,得到b=−2a ,故ab=a(−2a)=−2,从而求出答案.【解答】f(x)=x+1x +b,f(a)=a+1a+b,f′(x)=1−1x2,f′(a)=1−1a2,故切线方程是:y−a−1a −b=(1−1a2)(x−a),代入(0, 0)得:−a−1a −b=(1−1a2)(−a),故b=−2a,故ab=a(−2a)=−2,8.【答案】C【考点】双曲线的特性【解析】根据已知得到△F1PF2是直角三角形,根据双曲线的定义结合直角三角形的勾股定理建立方程关系进行求解即可..【解答】如图,设F1为双曲线T:x2a2−y2b2=1(a>0, b>0)的左焦点,依题意可得OM是△PF1F2的中位线,PF1=6,PF1⊥PF2,∴PF12+PF22=4c2,即c=√10.2a=PF1−PF2=4,a=2,则双曲线T的离心率为ca =√102.9.【答案】 A【考点】函数奇偶性的性质 【解析】可根据两角和的正弦公式及二倍角的正弦公式将f(x)=1sinx +1cosx 变成f(x)=2√2sin(x+π4)sin2x,然后可求出y =f(x −π4)=−2√2sinxcos2x,从而可判断y =f(x −π4)的奇偶性.【解答】 f(x)=1sinx+1cosx =sinx+cosx sinxcosx =√2sin(x+π4)12sin2x =2√2sin(x+π4)sin2x;∴ y =f(x −π4)=2√2sinxsin(2x−π2)=−2√2sinxcos2x; ∴ y =f(x −π4)为奇函数. 10.【答案】 B【考点】简单线性规划【解析】画出不等式组所表示的平面区域,利用数形结合法求出最优解的坐标, 计算对应k 的值,从而写出k 的取值范围. 【解答】画出不等式组{x +y −2≥02x −y ≤4y ≤4 所表示的平面区域,如图所示,直线y =kx −3是过定点M(0, −3)的直线, 由{y =4x +y −2=0 ,解得A(−2, 4), 当直线过点A 时,k =−3−40+2=−72;由{2x −y =4x +y −2=0 ,解得B(2, 0), 当直线过点B 时,k =−3−00−2=32; 由图形知,实数k 的取值范围是(−∞, −72]∪[32, +∞). 11.【答案】 D【考点】 椭圆的定义 【解析】建立坐标系,求得A ,B ,F 及E 点坐标,求得AE 及BF 的方程,即可求得M 点坐标,设椭圆方程,代入即可求得b 的值,即可求得椭圆方程. 【解答】以AB 为x 轴,AB 的垂直平分线为y 轴,建立平面直角坐标系,则A(−2, 0),B(2, 0),F(−2, 1),E(0, 2),则直线AE:y =x +2,直线BF 的方程:y =−14(x −2), 联立{y =x +2y =−14(x −2) ,解得:{x =−65y =45 ,则M(−65, 45), 设椭圆方程:x 24+y 2b 2=1(0<b <2),将M 代入椭圆方程,解得:b =1,∴ 椭圆的标准方程:x 24+y 2=1,12.【答案】 B【考点】利用导数研究函数的单调性 【解析】分类参数得出a ≤xlnx +ex 2−2x ,利用导数判断右侧函数的单调性,求出其最小值即可得出a 的范围. 【解答】由lnx ≥ax −ex +2(x >0)恒成立可得a ≤xlnx +ex 2−2x(x >0)恒成立, 令f(x)=xlnx +ex 2−2x(x >0),则f′(x)=lnx +2ex −1, 显然f′(x)在(0, +∞)上单调递增,又f′(1e )=−1+2−1=0, ∴ 当0<x <1e 时,f′(x)<0,当x >1e 时,f′(x)>0, ∴ 当x =1e 时,f(x)取得最小值f(1e )=−2e . ∴ a ≤−2e .二、填空题(每题5分,满分20分,将答案填在答题纸上) 【答案】 30【考点】平面向量共线(平行)的坐标表示 【解析】由已知条件求出k 的值,再利用向量的数量积的坐标运算求解即可. 【解答】∵ 向量m →=(3, k),n →=(2, 4),且m → // n →, ∴ 2k =12,即k =6. 则m →∗n →=(3, 6)⋅(2, 4)=3×2+6×4=30. 【答案】 16π3【考点】球的体积和表面积 【解析】所得几何体为底面半径r =BC =1,高为ℎ=AC =√3的圆锥,从而所得几何体的外接球半径R =ℎ2+r 22ℎ=√3【解答】∵ 在Rt △ABC 中,∠C =90∘,∠B =60∘,BC =1,以AC 为轴将Rt △ABC 旋转一周, ∴ 所得几何体为底面半径r =BC =1,高为ℎ=AC =√3的圆锥, ∴ 所得几何体的外接球半径R =ℎ2+r 22ℎ=2√3=√3,∴ 所得几何体的外接球的表面积为: S =4πR 2=4π×43=16π3.【答案】1009 【考点】 数列的求和 【解析】运用等比数列的性质和对数的运算性质,化简整理即可得到所求和. 【解答】数列{a n }是一个各项均为正数的等比数,且a 1009⋅a 1010=10, 可得a 1a 2018=a 2a 2017=...=a 1009⋅a 1010=10, 若b n =lga n ,可得数列{b n }的前2018项的和为b 1+b 2+b 3+...+b 2018=lga 1+lga 2+lga 3+...+lga 2018=lg(a 1a 2a 3...a 2018) =lg101009=1009. 【答案】 222【考点】函数的最值及其几何意义 根据实际问题选择函数类型 【解析】根据题意,设∠PAD =θ,则0≤θ≤π2,过点P 作PD ⊥AB ,则P 、D 、Q 三点共线,设这三段公路总造价为y ,用θ表示PA 、PB 和PQ 的长,进而可得y =6×(20sinθ+20cosθ)+5×(20−20cosθsinθ)=120(sinθ+cosθ)+100(1−sinθcosθ),设sinθ+cosθ=t ,则sinθcosθ=t 2−12,进而可得y =120t +100(1−t 2−12),结合二次函数的性质分析可得答案. 【解答】根据题意,设∠PAD =θ,则0≤θ≤π2,过点P 作PD ⊥AB ,则P 、D 、Q 三点共线,设这三段公路总造价为y ,又由AB =20km ,则AP =20cosθkm ,BP =20sinθkm ,则PD =20cosθsinθkm , 又由两平行直线AB 与l 之间的距离为20km ,则PQ =(20−20cosθsinθ)km ,则y =6×(20sinθ+20cosθ)+5×(20−20cosθsinθ)=120(sinθ+cosθ)+100(1−sinθcosθ),设sinθ+cosθ=t ,则t =√2sin(θ+π4),则有1≤t ≤√2, 则sinθcosθ=t 2−12,则y =120t +100(1−t 2−12)=120t +100(3−t 22)=−50t 2+120t +150,1≤t ≤√2,分析可得:t =65时,y 取得最大值,且y max =222;三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 【答案】解:(1)由题意及正弦定理可知sinAcosB +sin 2B =sinC , ∵ sinC =sin(A +B)=sinAcosB +cosAsinB , ∴ sin 2B =cosAsinB .∵ B ∈(0,π2),∴ sinB >0,∴ sinB =cosA ,即cos (π2−B)=cosA ,∵ A ∈(0,π),π2−B ∈(0,π2),∴ π2−B =A ,即A +B =π2, ∴ C =π2.(2)设BD =x,CB =a , ∵ ∠ABC =π3,∠ACB =π2, ∴ A =π6,∠DBC =2π3,且AC =√3a,AB =2a,AD =2a +x ,∴ S △ACD =12AC ⋅AD ⋅sinA =12×√3a ×(2a +x)×12=3√34, 即a(2a +x)=3在△BCD 中,由余弦定理可得CD 2=BC 2+BD 2−2BC ⋅BD ⋅cos∠DBC , 即x 2+a 2+ax =3联立可解得x =a =1,即BD =1. 【考点】 三角形求面积 【解析】 此题暂无解析 【解答】解:(1)由题意及正弦定理可知sinAcosB +sin 2B =sinC , ∵ sinC =sin(A +B)=sinAcosB +cosAsinB , ∴ sin 2B =cosAsinB .∵ B ∈(0,π2),∴ sinB >0,∴ sinB =cosA ,即cos (π2−B)=cosA , ∵ A ∈(0,π),π2−B ∈(0,π2),∴ π2−B =A ,即A +B =π2, ∴ C =π2.(2)设BD =x,CB =a , ∵ ∠ABC =π3,∠ACB =π2,∴ A =π6,∠DBC =2π3,且AC =√3a,AB =2a,AD =2a +x ,∴ S △ACD =12AC ⋅AD ⋅sinA =12×√3a ×(2a +x)×12=3√34, 即a(2a +x)=3在△BCD 中,由余弦定理可得CD 2=BC 2+BD 2−2BC ⋅BD ⋅cos∠DBC , 即x 2+a 2+ax =3联立可解得x =a =1,即BD =1. 【答案】计算x =15×(3+4+5+6+7)=5,y =15×(0.62+0.58+0.49+0.4+0.31)=0.48;代入线性回归方程y ^=b ^x +0.88中,解得b ^=0.48−0.885=−0.08,∴ y 与x 之间的线性回归方程为y ^=−0.08x +0.88; x =8时,y ^=−0.08×8+0.88=0.24,即估计当浇灌海水浓度为8‰时该品种的亩产量0.24(吨); (i)根据题意填写残差表如下:(ii)计算相关指数R 2=1−∑ n i=1(y i −y i ^)2∑ n i=1(y i −y)2=1−(−0.02)2+0.022+0.012+02+(−0.01)20.142+0.12+0.012+(−0.08)2+(−0.17)2≈0.98,由R 2=0.98,说明预报变量y 的差异有98%是由解释变量x 引起的, 即亩产量的变化98%的是由浇灌海水浓度引起的. 【考点】求解线性回归方程 【解析】(1)计算x 、y ,代入线性回归方程求得b ^的值,写出回归方程, 再利用回归方程计算x =8时y ^的值;(2)(i)根据公式计算并填写残差表;(ii)由公式计算相关指数R 2,结合题意得出统计结论. 【解答】计算x =15×(3+4+5+6+7)=5,y =15×(0.62+0.58+0.49+0.4+0.31)=0.48;代入线性回归方程y ^=b ^x +0.88中,解得b ^=0.48−0.885=−0.08,∴ y 与x 之间的线性回归方程为y ^=−0.08x +0.88;x=8时,y^=−0.08×8+0.88=0.24,即估计当浇灌海水浓度为8‰时该品种的亩产量0.24(吨);(i)根据题意填写残差表如下:(ii)计算相关指数R2=1−∑ni=1(y i−y i^)2∑n i=1(y i−y)2=1−(−0.02)2+0.022+0.012+02+(−0.01)20.142+0.12+0.012+(−0.08)2+(−0.17)2≈0.98,由R2=0.98,说明预报变量y的差异有98%是由解释变量x引起的,即亩产量的变化98%的是由浇灌海水浓度引起的.【答案】证明:由PA⊥底面ABCD,得平面PAD⊥平面ABCD,又CD // AB,AB⊥AD,得CD⊥AD,∴CD⊥平面PAD,则平面PCD⊥平面PAD,取PD中点F,由PA=AD,得AF⊥PD,则AF⊥平面PCD,连接MF,AF,可得MF // CD,MF=12CD,∵AN // CD,AN=12CD,∴AN // MF,AN=MF,则四边形ANMF为平行四边形,可得MN // AF.∴MN⊥平面PCD;(i)过D,M,N三点的平面α与侧棱PB的交点记为Q,Q为PB的中点.事实上,取PB中点Q,连接MQ,NQ,则MQ // BC,∵BN // CD,BN=CD,∴四边形BCDN为平行四边形,则BC // DN,∴MQ // DN,则四边形DMQN为平面四边形,即过D,M,N三点的平面α与侧棱PB的交点记为Q,Q为PB的中点;(ii)∵MQ=12BC=12DN,且MQ // DN,∴S△DMN=2S△QMN,则V P−MQN=12V P−MND,而V P−MND=V N−PMD,又CD=AD=PA=2,AB=3,AB=3AN,∴PD=2√2,MN=√(√5)2−(√3)2=√2.∴V P−DMQN=V P−MQN+V P−MDN=32V P−MDN=32V N−PMD=32×13×12×12×CD×PD×MN=18×2×2√2×√2=1.【考点】柱体、锥体、台体的体积计算【解析】(1)由PA⊥底面ABCD,得平面PAD⊥平面ABCD,再由已知可得CD⊥AD,得到CD⊥平面PAD,则平面PCD⊥平面PAD,取PD中点F,则AF⊥PD,可得AF⊥平面PCD,进一步证明MN // AF,得到MN⊥平面PCD;(2)(i)取PB中点Q,连接MQ,NQ,则MQ // BC,又BN // CD,BN=CD,可得四边形BCDN为平行四边形,则BC // DN,得到MQ // DN,则四边形DMQN为平面四边形,即过D,M,N三点的平面α与侧棱PB的交点记为Q,Q为PB的中点;(ii)由MQ=12BC=12DN,且MQ // DN,可得S△DMN=2S△QMN,则V P−MQN=12V P−MND,结合V P−MND=V N−PMD,可得V P−DMQN=V P−MQN+V P−MDN=32V P−MDN=32V N−PMD,则答案可求.【解答】证明:由PA⊥底面ABCD,得平面PAD⊥平面ABCD,又CD // AB,AB⊥AD,得CD⊥AD,∴CD⊥平面PAD,则平面PCD⊥平面PAD,取PD中点F,由PA=AD,得AF⊥PD,则AF⊥平面PCD,连接MF,AF,可得MF // CD,MF=12CD,∵AN // CD,AN=12CD,∴AN // MF,AN=MF,则四边形ANMF为平行四边形,可得MN // AF.∴MN⊥平面PCD;(i)过D,M,N三点的平面α与侧棱PB的交点记为Q,Q为PB的中点.事实上,取PB中点Q,连接MQ,NQ,则MQ // BC,∵BN // CD,BN=CD,∴四边形BCDN为平行四边形,则BC // DN,∴MQ // DN,则四边形DMQN为平面四边形,即过D,M,N三点的平面α与侧棱PB的交点记为Q,Q为PB的中点;(ii)∵MQ=12BC=12DN,且MQ // DN,∴S△DMN=2S△QMN,则V P−MQN=12V P−MND,而V P−MND=V N−PMD,又CD=AD=PA=2,AB=3,AB=3AN,∴PD=2√2,MN=√(√5)2−(√3)2=√2.∴ V P−DMQN =V P−MQN +V P−MDN =32V P−MDN =32V N−PMD =32×13×12×12×CD ×PD ×MN =18×2×2√2×√2=1.【答案】设A ,B 两点的坐标为(x 1, y 1),(x 2, y 2), ∴ y =14x 2, ∴ y′=12x , ∴ k AM =12x 1,则直线AM 的方程为y −y 1=12x 1(x −x 1), 令y =0,则x =x 1−2y 1x 1=x 1−12x 12x 1=x 1−12x 1=12x 1,∴ M(12x 1, 0), ∴ k MF =1−00−12x 1=−2x 1,∴ k AM ⋅k MF =12x 1(−2x 1)=−1,∴ AM ⊥MF ;由(1)可得|AM|=√(x 1−12x 1)2+y 12=14|x 1|⋅√x 12+4,|FM|=√(12x 1)2+1=12√x 12+4, ∴ S 1=12|AM|⋅|FM|=116|x 1|⋅(x 12+4), 同理可得S 2=116|x 2|⋅(x 22+4), ∴ S 1⋅S 2=1256|x 1x 2|(x 12+4)⋅(x 22+4)=1256|x 1x 2|[x 12x 22+4(x 1+x 2)2−8x 1x 2+16], 设直线AB 的方程为y =kx +1,联立方程组可得{y =kx +1x 2=4y ,消y 可得x 2−4kx −4=0, ∴ x 1+x 2=4k ,x 1x 2=−4, ∴ S 1⋅S 2=14k 2+1,当k =0时,S 1⋅S 2有最小值,最小值为1【考点】 抛物线的求解 【解析】(1)设A ,B 两点的坐标为(x 1, y 1),(x 2, y 2),根据导数的几何意义求出k AM =12x 1,可得直线AM 的方程,求出点M 的坐标,再根据斜率公式可得k MF =−2x 1,即k AM ⋅k MF =−1,问题得以证明,(2)由(1)求出|AM|,|FM|,可得S 1=12|AM|⋅|FM|=116|x 1|⋅(x 12+4),同理可得S 2=116|x 2|⋅(x 22+4),即可得到S 1⋅S 2,再设设直线AB 的方程为y =kx +1,联立方程组可得{y =kx +1x 2=4y ,根据根与系数的关系,即可求出. 【解答】设A ,B 两点的坐标为(x 1, y 1),(x 2, y 2), ∴ y =14x 2, ∴ y′=12x , ∴ k AM =12x 1,则直线AM 的方程为y −y 1=12x 1(x −x 1), 令y =0,则x =x 1−2y 1x 1=x 1−12x 12x 1=x 1−12x 1=12x 1,∴ M(12x 1, 0), ∴ k MF =1−00−12x 1=−2x 1,∴ k AM ⋅k MF =12x 1(−2x 1)=−1,∴ AM ⊥MF ;由(1)可得|AM|=√(x 1−12x 1)2+y 12=14|x 1|⋅√x 12+4, |FM|=√(12x 1)2+1=12√x 12+4,∴ S 1=12|AM|⋅|FM|=116|x 1|⋅(x 12+4), 同理可得S 2=116|x 2|⋅(x 22+4), ∴ S 1⋅S 2=1256|x 1x 2|(x 12+4)⋅(x 22+4)=1256|x 1x 2|[x 12x 22+4(x 1+x 2)2−8x 1x 2+16], 设直线AB 的方程为y =kx +1,联立方程组可得{y =kx +1x 2=4y ,消y 可得x 2−4kx −4=0, ∴ x 1+x 2=4k ,x 1x 2=−4, ∴ S 1⋅S 2=14k 2+1,当k =0时,S 1⋅S 2有最小值,最小值为1【答案】a =1时,f(x)=e x−1−lnx(x >0), f′(x)=e x−1−1x =xe x−1−1x,令g(x)=xe x−1−1(x >0),则g(x)在(0, +∞)上单调递增,又g(1)=0,∴ 当x ∈(0, 1)时,g(x)<0,即f′(x)<0,当x ∈(1, +∞)时,g(x)>0,即f′(x)>0,∴ f(x)的单调递减区间为(0, 1),单调递增区间为(1, +∞). 当a =0时,f(x)=e x−1>0,显然f(x)没有零点. 当0<a ≤e 时,f′(x)=e x−1−ax=xe x−1−ax,令ℎ(x)=xe x−1−a(x >0),则ℎ(x)在(0, +∞)上单调递增, 又ℎ(0)=−a <0,ℎ(2)=2e −a >0,∴ ℎ(x)在(0, 2)上存在唯一一个零点,不妨设为x 0,则x 0e x 0−1=a ,∴ 当x ∈(0, x 0)时,ℎ(x)<0,即f′(x)<0,当x ∈(x 0, +∞)时,ℎ(x)>0,即f′(x)>0,∴ f(x)在(0, x 0)上单调递减,在(x 0, +∞)上单调递增, ∴ f(x)的最小值为f(x 0)=e x 0−1−alnx 0, ∵ x 0ex 0−1=a ,∴ ex 0−1=ax 0,两边取对数可得x 0−1=lna −lnx 0,即lnx 0=lna +1−x 0,∴ f(x 0)=ax 0−a(lna +1−x 0)=ax 0+ax 0−alna −a ≥2a −alna −a =a −alna ,(当且仅当x 0=1时取等号),令m(a)=a−alna,则m′(a)=−lna,∴当a∈(0, 1)时,m′(a)>0,当a∈(1, e]时,m′(a)<0,∴m(a)在(0, 1)上单调递增,在(1, e]上单调递减.又m(e−n)=(e−n−1)(1−n)>0,m(e)=0,∴当0<a≤e时,m(a)≥0,当且仅当a=e时取等号,由(1)可知当a=1时,x0=1,故当a=e时,x0≠1,故f(x0)>m(a)≥0,∴f(x0)>0.∴当0≤a≤e时,f(x)没有零点.【考点】利用导数研究函数的单调性【解析】(1)令g(x)为f′(x)的分子部分,根据g(x)单调性和符号得出f(x)的单调性;(2)令ℎ(x)为f′(x)的分子部分,设x0为ℎ(x)的零点,求出f(x)的最小值f(x0),根据x0的性质和基本不等式得出f(x0)关于a的函数m(a),再根据m(a)的单调性求出m(a)的最小值即可得出结论.【解答】a=1时,f(x)=e x−1−lnx(x>0),f′(x)=e x−1−1x =xe x−1−1x,令g(x)=xe x−1−1(x>0),则g(x)在(0, +∞)上单调递增,又g(1)=0,∴当x∈(0, 1)时,g(x)<0,即f′(x)<0,当x∈(1, +∞)时,g(x)>0,即f′(x)> 0,∴f(x)的单调递减区间为(0, 1),单调递增区间为(1, +∞).当a=0时,f(x)=e x−1>0,显然f(x)没有零点.当0<a≤e时,f′(x)=e x−1−ax =xe x−1−ax,令ℎ(x)=xe x−1−a(x>0),则ℎ(x)在(0, +∞)上单调递增,又ℎ(0)=−a<0,ℎ(2)=2e−a>0,∴ℎ(x)在(0, 2)上存在唯一一个零点,不妨设为x0,则x0e x0−1=a,∴当x∈(0, x0)时,ℎ(x)<0,即f′(x)<0,当x∈(x0, +∞)时,ℎ(x)>0,即f′(x)>0,∴f(x)在(0, x0)上单调递减,在(x0, +∞)上单调递增,∴f(x)的最小值为f(x0)=e x0−1−alnx0,∵x0e x0−1=a,∴e x0−1=ax0,两边取对数可得x0−1=lna−lnx0,即lnx0= lna+1−x0,∴f(x0)=ax0−a(lna+1−x0)=ax0+ax0−alna−a≥2a−alna−a=a−alna,(当且仅当x0=1时取等号),令m(a)=a−alna,则m′(a)=−lna,∴当a∈(0, 1)时,m′(a)>0,当a∈(1, e]时,m′(a)<0,∴m(a)在(0, 1)上单调递增,在(1, e]上单调递减.又m(e−n)=(e−n−1)(1−n)>0,m(e)=0,∴当0<a≤e时,m(a)≥0,当且仅当a=e时取等号,由(1)可知当a=1时,x0=1,故当a=e时,x0≠1,故f(x0)>m(a)≥0,∴f(x0)>0.∴当0≤a≤e时,f(x)没有零点.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程] 【答案】圆C 1的参数方程为{x =1+cosαy =sinα (α为参数),转换为直角坐标方程为:(x −1)2+y 2=1, 转换为极坐标方程为:ρ=2cosθ.圆C 2的参数方程为{x =4cosαy =4+4sinα (α为参数).转换为直角坐标方程为:x 2+(y −4)2=16, 转换为极坐标方程为:ρ=8sinθ, 直线l 的参数方程为{x =√32ty =12t (t 为参数), 转换为极坐标方程为:θ=π6. 则:{ρ=2cosθθ=π6,解得:ρ1=√3. 由{ρ=8sinθθ=π6, 解得:ρ2=4.则:|AB|=|ρ1−ρ2|=4−√3,由于:圆C 1和圆C 2的公共弦的直线方程为:x −4y =0, 则:圆C 2的圆心(0, 4)到直线x −4y =0的距离为:d =√1+16=16√1717. 则:S △ABC 2=12∗3√3∗16√1717=24√5117. 【考点】参数方程与普通方程的互化 【解析】(1)利用转换关系,把参数方程和极坐标方程与直角坐标方程进行转化. (2)利用圆与圆的位置关系,极径和三角形的面积求出结果. 【解答】圆C 1的参数方程为{x =1+cosαy =sinα (α为参数),转换为直角坐标方程为:(x −1)2+y 2=1, 转换为极坐标方程为:ρ=2cosθ.圆C 2的参数方程为{x =4cosαy =4+4sinα (α为参数).转换为直角坐标方程为:x 2+(y −4)2=16, 转换为极坐标方程为:ρ=8sinθ, 直线l 的参数方程为{x =√32ty =12t (t 为参数), 转换为极坐标方程为:θ=π6.试卷第21页,总22页 则:{ρ=2cosθθ=π6 ,解得:ρ1=√3.由{ρ=8sinθθ=π6, 解得:ρ2=4.则:|AB|=|ρ1−ρ2|=4−√3,由于:圆C 1和圆C 2的公共弦的直线方程为:x −4y =0,则:圆C 2的圆心(0, 4)到直线x −4y =0的距离为:d =√1+16=16√1717. 则:S △ABC 2=12∗3√3∗16√1717=24√5117. [选修4-5:不等式选讲]【答案】当x ≤−1时,不等式为−x −1+1−x <x 2−x ,解得:x <−1或x >0(舍); 当−1<x <1时,不等式为x +1+1−x <x 2−x ,解得:x <−1(舍)或x >2(舍) 当x ≥1时,不等式为x +1+x −1<x 2−x ,解得:x <0(舍)或x >3. 综上,不等式的解集为:(−∞, −1)∪(3, +∞).令ℎ(x)=f(x)+g(x)={x 2−3x,x ≤−1x 2−x +2,−1<x <1x 2+x,x ≥1,∴ ℎ(x)在(−∞, 12)上单调递减,在(12, +∞)上单调递增,∴ ℎ(x)的最小值为ℎ(12)=74.∴ a <74.即a 的取值范围为(−∞, 74).【考点】绝对值三角不等式【解析】(1)讨论x 的范围,去掉绝对值符号解不等式;(2)化简f(x)+g(x)的解析式,根据其单调性求出最小值,得出a 的范围.【解答】当x ≤−1时,不等式为−x −1+1−x <x 2−x ,解得:x <−1或x >0(舍); 当−1<x <1时,不等式为x +1+1−x <x 2−x ,解得:x <−1(舍)或x >2(舍) 当x ≥1时,不等式为x +1+x −1<x 2−x ,解得:x <0(舍)或x >3. 综上,不等式的解集为:(−∞, −1)∪(3, +∞).令ℎ(x)=f(x)+g(x)={x 2−3x,x ≤−1x 2−x +2,−1<x <1x 2+x,x ≥1,∴ ℎ(x)在(−∞, 12)上单调递减,在(12, +∞)上单调递增,∴ ℎ(x)的最小值为ℎ(12)=74.∴ a <74.).即a的取值范围为(−∞, 74试卷第22页,总22页。
广东省深圳市2018届高三第二次(4月)调研考试语文试卷(含答案)

深圳市2018年高三年级第二次调研考试语文2018.4注意事项:1.答卷前,考生务必将自己的姓名和座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
新媒介是一把双刃剑,在方便人们的日常生活、拓展人的行为能力以及提供各种超感官体验时,其产生的负面效应也不容忽视。
每天各种无用信息占据人们的大量时间,使人们非理性冲动增多,人际关系变得越来越淡薄,也更容易产生紧张和焦虑情绪。
要解决这一问题,就必须从媒体与受众两方面入手,积极寻求对策。
从媒体角度看,媒体可以利用信息智能匹配技术降低受众的信息接收成本。
这项技术以数据分析为依托,使信息更加智能化、个性化,从而与受众的需求相匹配。
比如,一些媒体机构根据用户个人需求方面的关键词、以往浏览的相关数据以及学历、职业、爱好等特征信息,进行汇集、整理、跟踪和分析,并根据用户充值、消费、反馈等数据信息,了解和掌握不同用户的个性化潜在需求,进行精准的信息推送。
虽然公司主要以推广自己服务项目为目的,但这种技术更注重用户的体验和选择,会大大减少许多有意无意强加于受众的信息,从而降低了受众进行信息处理的时间成本,使其在轻松愉悦的状态中接收自己需要的各种信息。
这样的智能匹配模式会越来越精细化、个性化和特色化。
比如,有的技术可以根据手机定位,确定用户是在办公场所、家里还是旅途中来推送合适的视听内容;还可以根据用户手机的睡眠模式、工作模式等确定推送时间,以及根据某一信息关注度的高低确定是否推送。
从信息受众角度看,受众需要提高理性使用新媒介的能力。
受众首先要提升自己的媒介素养,即对媒介本身带来的危害及个人在媒介使用过程中存在的问题保持清醒认识的能力。
2018广东二模文综试题和答案

广东省2018届普通高校招生全国统一考试模拟试卷(二)文科综合第Ⅰ卷一、选择题:本题共35小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
圩田是古代中国劳动人民在利用濒河滩地、湖泊淤地过程中发展起来的一种农田,是一种筑堤挡水护田的土地利用方式。
XX省巢湖的圩田,可追溯到三国时代的曹魏江淮屯田时期,以后历代开垦不断,尤其在北宋年间发展较快。
《宋史·叶衡传》记载,合肥濒湖有圩田四十里衡奏:“募民以耕,岁可得谷数十万…··…,”据此完成1~3题。
1.对巢湖圩田建设影响较弱的自然因素是A.气候B.地质C.土壤D.水源2.巢湖圩田建设可A.改善土壤水分条件B.根除湖区水旱灾害C.提高巢湖的调蓄能力D.改变湖区作物熟制3.宋朝时期,巢湖圩田上种植的粮食作物主要是A.谷子B.小麦C.水稻D.玉米图1示意世界范围内某地区的传统民居和当地气候资料。
据此完成4~5题。
4.当地传统民居为木质角楼的主要原因是A.冬季寒冷,木质结构利于保温B.避免地质灾害的侵袭C.气候湿热,有利于通风散热D.为了顺应地形地势5.该地可能位于A.东非高原B.云贵高原C.伊朗高原D.圭亚那高原甘肃省西部红柳峡位于酒西盆地西段,地表为砂岩夹泥岩层,岩层中间有粗玄岩(即颗粒较粗的玄武岩)、角岩、玄武岩等。
地貌上凸显出一个椭圆形筒状高地M周边发育有环状和放射状节理,如图2所示。
据此完成6~8题。
6.M椭圆形筒状高地属于A.风力堆积地貌B.流水侵蚀地貌C.流水堆积地貌D.火山地貌7.该筒状高地放射状节理发育最明显的方向是A.西南B.东南C.东北D.西北8.下列属于地质学家研究该区域地质地貌科学价值的是A.探明该地区丰富的地下淡水资源B.探明该地区丰富的煤炭、油气资源C.推断该地区地质时期的地质构造演化D.通过粗玄岩中的生物化石证明海陆变迁贡嘠山(29°35′N,101°52′E)位于四川省西部,为大雪山的主峰,被誉为“蜀山之王”。
2018届广东省深圳市高三第二次(4月)调研考试文综政治试题(解析版)

2018 年深圳市高三年级第二次调研考试政治试题一、选择题1. 大数据、人工智能等先进技术手段的运用使零售业在线上、线下的全渠道融合进一步加强,实体门店逐步成为商品的售货、自提和配送中心,顾客的社交和体验中心。
这种新零售模式能够()①发挥需求引领作用,精准定位赢得市场②降低企业生产成本,减少商品流通环节③促进商业模式创新,增强发展的新动力④影响居民消费方式,优化社会消费结构A. ①②B. ③④C. ①③D. ②④【答案】C【解析】此题考查企业经营的相关知识。
大数据、人工智能等先进技术手段的运用可以及时了解市场需求状况,发挥需求引领作用,从而更精准定位赢得市场。
①符合题意;零售业在线上、线下的全渠道融合进一步加强,这种商业模式创新增强了零售业的发展动力,③符合题意;材料强调的是销售环节的模式创新,不会带来生产成本下降,②说法错误;零售业商业模式的创新会使居民消费方式发生变化,但这并不意味着消费结构的优化,④说法错误。
故本题选C。
2. 2018 年《国务院政府工作报告》指出,提高个人所得税起征点,增加子女教育、大病医疗等专项费用扣除,合理减负,鼓励人民群众通过劳动增加收入,迈向富裕。
当前我国适当提高个人所得税起征点()①体现出我国税收“取之于民,用之于民”的性质②是国家财税体制改革,优化税种结构的重要举措③是国家运用财政政策,调节个人收入分配的体现④有利于实现社会公平,增强广大人民群众幸福感A. ①②B. ①③C. ②④D. ③④【答案】D【解析】此题考查个人所得税的相关知识。
我国适当提高个人所得税起征点,增加子女教育、大病医疗等专项费用扣除,合理减负,鼓励人民群众通过劳动增加收入,迈向富裕。
这是国家运用财政政策,调节个人收入分配的具体体现,有利于实现社会公平,增强广大人民群众幸福感。
③④符合题意;材料未体现税收“用之于民”,①排除;材料只是对个税起征点的调整,不是对税种的调整,②与材料无关。
故本题选D。
2018届深圳二模文综试题及答案.pdf

深圳市2018届高三年级第二次调研考试文科综合(地理部分)江苏无锡是中国光伏产业最为集中的地区。
自2001年首家中澳合资光伏企业成立至2011年,无锡光伏产业发展实行两头在外的发展模式(关键零部件、生产设备和销售市场主要依赖国外)参与国际市场竞争。
2 016年,无锡市太阳能电池产能占全国总规模的50%以上,已形成包括光伏材料、电池原件、光伏组件、逆变器、运维服务、数据管理等各生产环节的全产业链竞争优势。
光伏制造设备的本地化率已经超过50%;企业在为客户提供电子化学品原料的同时,还针对单晶硅和多晶硅生产中的化学品污染问题,主动研发废化学品的回收再利用技术;开发了可以通过互联网实现对遥远地区的风能、光伏等发电装置的远程监控、运行管理和维护技术。
据此完成1~3题。
1.与发达国家相比,2001-2011年间无锡光伏产业参与国际市场竞争的主要有利条件是A.生产成本较低B.原料资源丰富C.交通位置优越D.市场需求量大2.无锡光伏产业在短短10多年间,从两头在外发展模式到形成全球性竞争优势,主要得益于A.生产规模不断扩大B.智能化的运行管理和维护服务C.披术研发和创新D.废化学品的回收再利用3.2016年,江苏省光伏累计装机容量列全国第五,仅次于4个太阳能资源一类地区——新疆、甘肃、青海和内蒙古。
在东部沿海各省区中,江苏省光伏累计装机容量居首位的比较优势是A.太阳能资源丰富B.国家新能源政策的扶持C.清洁能源市场需求量大D.光伏全产业链的强力支撑玛纳斯河山麓冲积扇是天山北麓规模最大的冲积扇,由南向北发育有多期冲积扇,不同时期形成的冲积扇之间有明显的阶梯状陡坎。
玛纳斯河山前冲积扇地区第四纪活动断层发育。
图1示意玛纳斯河山麓冲积扇的发展演变。
据此完成4~6题。
4.下列关于玛纳斯河山麓冲积扇特点的描述,错误..的是A.地势由南向北倾斜B.组成物质从南到北总体由粗变细C.耕地分布南多北少D.扇体边缘有大量地下水溢出5.从各期冲积扇的位置和形态变化推测,诱发该冲积扇发生Fl至F4四期演变的地质作用,最可能是A.风力搬运、沉积作用B.变质作用C.冰川搬运、沉积作用D.地壳运动6.玛纳斯县境内的F2冲积扇耕地上的灌溉干渠水流方向大多由A.东北流向西南B.西南流向东北C.东南流向西北D.西北流向东南在全球范围内,云层分布面积、纬度或高度的变化将影响全球的温度。
(全国卷1地区)2018深圳高考二模试卷及答案解析(精心排版,精心校对,含范文)

深圳市2018年高三年级第二次调研考试语文2018.4 注意事项:1.答卷前,考生务必将自己的姓名和座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
新媒介是一把双刃剑,在方便人们的日常生活、拓展人的行为能力以及提供各种超感官体验时,其产生的负面效应也不容忽视。
每天各种无用信息占据人们的大量时间,使人们非理性冲动增多,人际关系变得越来越淡薄,也更容易产生紧张和焦虑情绪。
要解决这一问题,就必须从媒体与受众两方面入手,积极寻求对策。
从媒体角度看,媒体可以利用信息智能匹配技术降低受众的信息接收成本。
这项技术以数据分析为依托,使信息更加智能化、个性化,从而与受众的需求相匹配。
比如,一些媒体机构根据用户个人需求方面的关键词、以往浏览的相关数据以及学历、职业、爱好等特征信息,进行汇集、整理、跟踪和分析,并根据用户充值、消费、反馈等数据信息,了解和掌握不同用户的个性化潜在需求,进行精准的信息推送。
虽然公司主要以推广自己服务项目为目的,但这种技术更注重用户的体验和选择,会大大减少许多有意无意强加于受众的信息,从而降低了受众进行信息处理的时间成本,使其在轻松愉悦的状态中接收自己需要的各种信息。
这样的智能匹配模式会越来越精细化、个性化和特色化。
比如,有的技术可以根据手机定位,确定用户是在办公场所、家里还是旅途中来推送合适的视听内容;还可以根据用户手机的睡眠模式、工作模式等确定推送时间,以及根据某一信息关注度的高低确定是否推送。
从信息受众角度看,受众需要提高理性使用新媒介的能力。
受众首先要提升自己的媒介素养,即对媒介本身带来的危害及个人在媒介使用过程中存在的问题保持清醒认识的能力。
2018年深圳高三第二第二次调研考试语文评卷之标杆作文纯文字版新

实用文档2018年深圳高三第二次调研考试语文评卷之标杆作文(纯文字版)【原题目】60分)(22.阅读下面的材料,根据要求写作。
他说自己子思受邀回到高中母校宣讲成长经历及学习心得。
他正跟着研究生导在母校学习期间就非常喜欢儒家文化;现在,师进行更深入的学习和研究。
‘约之“对儒家文化,我们有所了解,像有位同学向他提问:可是,之类的道理,我也很认可;‘推己及人'以礼'‘以德服人' 在生活中真要那样做,会不会连公交车都挤不上去?”如果你是子思,你将怎样回应这样的提问?要求选好角度,确定立意;明确文体,自拟标题;不要套作,不得抄袭;不少于800字。
1号文儒家文化与当下生活间无鸿沟必但我认为运海抟扶,这位同学认为若践行儒家文化,我们将在当今生活中寸步难行。
借垂天之羽,乘流击汰,必用飞云之楫。
儒家文化,也离不开日常生活。
正如同“圣人之道,无非百姓日用”。
儒家文化传承千年,离不开许多人的身体力行,而到了今天,人们却把它看作煌煌道德律例,而弃之迤逦。
实际上儒家文化教人谦逊知礼,使人聚魂凝魄,劝人奋发向上,而这些,不正是我们在日常生活中渴求的吗?大全.实用文档,哄抢热”行儒家之道却挤不上公交,何解?现代社会物欲横流,人人只注重自身利益,“这样就能说明儒家文化与当代生活之间存也都说明了这个问题。
然而,“无人扶”等现象,,在人人都基本能维持饱暖的现代,在着鸿沟天堑了吗?非也。
古人云“实仓廪而知礼节”正是“大道之行”的好时候。
试想,若人人都能行儒家之道,又岂会有一哄而上式的排队抢位,冷漠无情的见死不救呢?这正是我们要做的。
”儒家文化是道金斯曾说“自从文化出现,人类的终极任务就从生存变为了传承文化。
中华文化之根,之所以如今社会人人为己、礼崩乐坏,是因为人民为了求生而挣扎得太久,必是君子但当我们将儒家文化变为精神家园的沃土时,下一代长出的,而将儒道弃置不顾,之树。
这并非一日之功,一人所能为,需要一代人甚至几代人付出努力,身体力行,才能让”君子之风成为社会的底蕴,到了那时,则“振本而末存,行一而万毕矣。
2018深圳高三年级第二第二次调研考试语文评卷之标杆作文(纯文字版)新

2018年深圳高三第二次调研考试语文评卷之标杆作文(纯文字版)【原题目】22.阅读下面的材料,根据要求写作。
(60分)子思受邀回到高中母校宣讲成长经历及学习心得。
他说自己在母校学习期间就非常喜欢儒家文化;现在,他正跟着研究生导师进行更深入的学习和研究。
有位同学向他提问:“对儒家文化,我们有所了解,像‘约之以礼’‘以德服人’‘推己及人’之类的道理,我也很认可;可是,在生活中真要那样做,会不会连公交车都挤不上去?”如果你是子思,你将怎样回应这样的提问?要求选好角度,确定立意;明确文体,自拟标题;不要套作,不得抄袭;不少于800字。
1号文儒家文化与当下生活间无鸿沟这位同学认为若践行儒家文化,我们将在当今生活中寸步难行。
但我认为运海抟扶,必借垂天之羽,乘流击汰,必用飞云之楫。
儒家文化,也离不开日常生活。
正如同“圣人之道,无非百姓日用”。
儒家文化传承千年,离不开许多人的身体力行,而到了今天,人们却把它看作煌煌道德律例,而弃之迤逦。
实际上儒家文化教人谦逊知礼,使人聚魂凝魄,劝人奋发向上,而这些,不正是我们在日常生活中渴求的吗?行儒家之道却挤不上公交,何解?现代社会物欲横流,人人只注重自身利益,“哄抢热”,“无人扶”等现象,也都说明了这个问题。
然而,这样就能说明儒家文化与当代生活之间存在着鸿沟天堑了吗?非也。
古人云“实仓廪而知礼节”,在人人都基本能维持饱暖的现代,正是“大道之行”的好时候。
试想,若人人都能行儒家之道,又岂会有一哄而上式的排队抢位,冷漠无情的见死不救呢?这正是我们要做的。
道金斯曾说“自从文化出现,人类的终极任务就从生存变为了传承文化。
”儒家文化是中华文化之根,之所以如今社会人人为己、礼崩乐坏,是因为人民为了求生而挣扎得太久,而将儒道弃置不顾,但当我们将儒家文化变为精神家园的沃土时,下一代长出的,必是君子之树。
这并非一日之功,一人所能为,需要一代人甚至几代人付出努力,身体力行,才能让君子之风成为社会的底蕴,到了那时,则“振本而末存,行一而万毕矣。
广东省深圳市2018届高三第二次调研考试文科综合试题及答案 精品

2018年深圳市高三第二次调研考试文科综合能力测试2018.4.26第Ⅰ卷本卷共35个小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
“胡焕庸线”指我国黑龙江黑河和云南腾冲的连线,是划分我国东南、西北半壁及人口分布差异的界线(表1);人口分布和国土区域严重不匹配的现象被称为“胡焕庸现象”。
读表1,完成1~2题。
表11.“胡焕庸线”两侧的人口比重一直稳定少变,主要取决于A.计划生育政策 B.人口迁移方向C.自然地理环境 D.地域开放程度2.下列国家中,“胡焕庸现象”最不明显...的是A.巴西 B.加拿大C.澳大利亚 D.德国图1是我国华北平原地下水位埋藏深度空间分布图。
读图1,完成3~5题。
3.图示甲、乙、丙、丁四个区域中,土壤盐碱化最为严重的是A.甲 B.乙 C.丙D.丁4.华北平原土壤盐碱化程度加重的季节是A.春季和秋季 B.春季和夏季 C.夏季和秋季D.秋季和冬季5.不能..缓解华北平原土壤盐碱化的做法是A.地膜覆盖 B.增施熟石灰 C.农田开挖排水沟D.喷灌和滴灌图2是某岛屿的遥感影像。
该岛屿面积10458平方千米,岛屿东北部降水丰富,植被茂密;西南部降水很少,植被稀疏。
读图2,完成6~8题。
6.该岛屿位于A.北大西洋 B.南大西洋C.北太平洋 D.南太平洋7.该岛屿成因类型属于A.大陆岛 B.珊瑚岛C.冲积岛 D.火山岛8.该岛屿东北部山麓的自然植被属于A.亚热带常绿阔叶林B.亚热带常绿硬叶林C.热带雨林D.热带草原图3中的铁路曾多次因大风导致列车脱轨、倾覆及设备损毁。
读图3,完成9~11题。
9.受大风危害最严重的路段是A.十三间房附近 B.三间房附近C.了墩附近D.哈密附近10.通过该铁路输往我国东部地区的货物主要是A.钢铁和机械 B.石油和天然气C.小麦和甜菜 D.棉花和瓜果11.该段铁路没有沿虚线走向修建,主要是因为虚线线路 A.风灾危害大 B.修建成本高C.洪涝灾害多 D.占用耕地多12.通过社会化网络平台,资源所有者将自己闲置的资源拿出来,供那些需要的人有偿使用,这便是当前所说的“分享经济”。
【文科综合模拟】广东省深圳市2018届高三第二次调研考试文综

2018年深圳市高三第二次调研考试文科综合能力测试一、选择题K群岛各岛屿地势崎岖高峻,每年有330多天是晴天。
夏半年,在盛行风的吹拂和阳光的照耀下,海浪在每座小岛的一侧海面呈现出条带状银白色的波纹,岛屿犹如行驶在海洋上的巨轮。
图1是K 群岛的卫星照片。
据此完成1-3题。
1.该群岛夏半年盛行A.东南风B.西南风C.东北风D.西北风2.导致该群岛每年晴朗日数特别多的主导因素是A.海陆位置B.地形C.大气环流D.洋流3.该群岛中的特内里费岛被评为全球某种观赏活动的最佳岛屿,这种活动是观赏A.星空B.冰山漂浮C.极光D.高山冰川植被生长季是指植被开始复苏返青(生长季始期)到植被枯黄落叶(生长季末期)之间的时段。
伏牛山位于我国河南省西部,大致呈东西走向,面积2万多平方千米。
图2表示伏牛山地区各时段植被进入生长季始期和生长季末期的面积比例。
据此完成4-6题。
4.伏牛山地区大部分植被的生长季是A.3月至11月B.4月至9月C.5月至10月D.6月至8月5.伏牛山地区的植被出现六个时段的生长季始期,说明伏牛山A.跨纬度大B.跨经度大C.水热充足D.垂直起伏大6.对伏牛山大多数植物种类而言,同一种植物A.分布在海拔较高处的生长季始期较早B.分布在海拔较高处的生长季末期较晚C.同一海拔高度上北坡的生长季始期较早D.同一海拔高度上南坡的生长季末期较晚图3示意我国华北平原西部某区域等高线图,图中低山、丘陵地带以荒山草坡为主,正在打造“太阳山”——建设大型山坡集中式光伏发电站。
光伏发电站的发电效率主要与日照强度、日照时间和太阳能面板清洁度有关。
据此完成7-9题。
7.在甲、乙、丙、丁四个荒山草坡安置太阳能板,发电效率最高的是A.甲B.乙C.丙D.丁8.与甘肃河西走廊相比,该地建设大型集中式光伏发电站的比较优势是A.太阳辐射强B.日照时数多C.用地成本低D.面板清扫频次少9.①②③④四条支流的特点及其比较,正确的是A.①河落差超过1400米B.②河流域多年平均的雨水补给量最多C.③河春季流量比夏季大D.④河有凌汛现象黑龙江黑河—云南腾冲一线是反映我国东南地狭人稠、西北地广人稀这一显著差异的人口地理分界线。
最新-广东省深圳市2018届高三文综第二次调研考试 精品

绝密★启用前试卷类型:A2018年深圳市高三年级第二次调研考试文科综合本试卷共12页,41小题,满分300分。
考试用时150分钟。
注意事项:1.答卷前,考生首先检查答题卡是否整洁无缺损,监考教师分发的考生信息条形码是否正确;之后务必用0.5毫米黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号。
同时,将监考教师发放的条形码正向准确粘贴在答题卡的贴条形码区。
请保持条形码整洁、不污损。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案。
答案不能答在试卷上。
不按要求填涂的,答案无效。
3.非选择题必须用0.5毫米黑色字迹的签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上。
请注意每题答题空间,预先合理安排。
如需改动,先划掉原来的答案,然后再写上新的答案。
不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将答题卡交回。
一、单项选择题(每小题4分,满分140分。
在每小题给出的四个选项中,只有一个选项最符合题目要求。
)1.下表是某地(22°N,114°E)不同日期正午太阳高度。
据此判断,一年中该地在M日出现的现象是A.白昼最长B.正午影长最短C.气温最高D.气压最低2.图1所示的手机功能主要运用的地理信息技术是A.RS B.RS和GPSC.GPS和GIS D.RS和GIS图13.图2是某国人口增长走势及预测图,下列说法正确的是A.①时期人口平均寿命最长B.②时期社会养老负担最重C.③时期人口总量开始减少D.④时期人口总量达到最多图24.下面是两幅卫星云图(箭头表示气流方向),根据云层运动状态判断正确的是甲图3 乙A.图甲——北半球反气旋B.图乙——北半球气旋C.图甲——南半球反气旋D.图乙——南半球气旋5.图4是四地传统民居景观,最能反映当地高温潮湿气候特点的是,①②③④图4A.①B.②C.③D.④读2018年我国部分省区人均产粮和人口数量坐标图(图5),完成6~7题。
