概念复习卷

合集下载

2022-2023学年中考物理真题复习——物理常识概念专题训练(含答案)

—物理常识概念专题训练1.（2022锦州）下列对物理量的估测最接近实际的是（）A.蚂蚁的爬行速度约为2m/sB.冰箱冷藏室的温度约为-5℃C.比赛用篮球的质量约为6gD.日光灯的额定功率约为20W2.（2022广元）下列叙述与实际相符的是（）A.手机的质量约为5kgB.人的正常体温是37℃左右（口腔温度）C.我国海域深处蕴藏的大量“可燃冰”属于可再生能源D.LED灯的核心元件是发光二极管，二极管主要材料是超导体3.（2022锦州）对北京的一些比赛情景的描述，下列说确的是（）A.掷出去的冰壶能继续向前运动，是由于冰壶具有惯性B.单板滑雪运动员踩在滑雪板上，减小了对雪地的压强C.短道速滑运动员在匀速转弯过程中，运动状态没有变D.跳台滑雪运动员在空中下落的过程中，重力势能减小4.(2022宿迁)实践证明：“测体温”“勤洗手”“要消毒”及“戴口罩”等措施可以有效预防的传播对这些措施宁相关数据的估测，实际的是（）A.“测体温”：人体正常体温约为39℃B.“要消毒”：一张酒精消毒湿纸巾厚度约为0.4mmC.“勤洗手”：要取得好的清洁，洗手时间没有能超过20sD.“戴口罩”：一只性医用外科口罩质量约为50g5.（2022广元）下面几个实验探究中，采用了相同研究方法的是（）①“探究压力的作用与受力面积的关系”时，保持压力没有变，改变受力面积②“比较没有同物质吸热的情况”时，用加热时间的长短表示吸收热量的多少③“探究电流与电压的关系”时，保持电阻的阻值没有变，改变电阻两端的电压④在研究“阻力对物体运动的影响”实验中，运用科学推理得出牛顿定律A.①和④B.②和③C.①和③D.②和④6.(2022宿迁)关于粒子和宇宙，下列说确的是（）A.“日心说”认为地球是宇宙的B.汤姆生发现电子说明原子核是没有可分的C.起电的实质是电子发生了转移D.柳絮飞舞说明分子是运动的7.（2022锦州）目前我国在能源、材料和航天等领域都取得了巨大成就。

新概念新概念英语青少版1A Unit1-Unit15总复习试卷

♣Art is long, life is short. 人生短暂，学艺无穷。

♣1新概念英语青少版1A 总复习试卷一、听录音，选出你所听到的内容。

（）1、A. cook B. foot C. food（）2、A. sleep B. sheep C. cheap（）3、A. hurry up B. in a hurry C. don ’t worry（）4、A. How are you? B. How is he? C. How is she?（）5、A. No harm down! B. Better safe than sorry! C. Never mind!二、根据听到的内容选择正确的答案。

（）1、Whose book is it?A. Tim ’sB. John ’sC. Mike ’s（）2、What does Cindy ’s mother job?A. She ’s a singer.B. She ’s a waitress.C. She ’s an actress（）3、What colour is the cat?A. BrownB. WhiteC. Black（）4、What ’s on the shelf?A. A MP3playerB. A cameraC. A mobile（）5、What does Lily want?A. A bagB. A coatC. A watch三、请选出与其他三个划线部分发音不同的选项。

( )1、A. now B. how C. house D. coat( )2、A. old B. over C. on D. go( )3、A. boy B. open C. toy D. noise( )4、 A. my B. fish C. tie D. five( )5、 A. elegant B. wait C. play D. name( )6、 A. three B. thanks C. they D. thirty( )7、 A. sorry B. please C. house D. socks( )8、 A. gate B. girl C. orange D. give( )9、 A. father B. are C. car D. but( )10、 A. do B. woman C. who D. too四、选择填空。

《第三章函数的概念和性质》章节复习及单元检测试卷

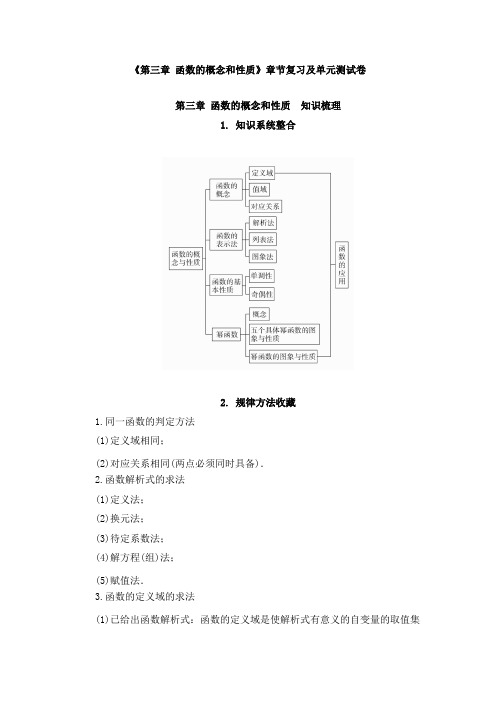
《第三章函数的概念和性质》章节复习及单元测试卷第三章函数的概念和性质知识梳理1. 知识系统整合2. 规律方法收藏1.同一函数的判定方法(1)定义域相同；(2)对应关系相同(两点必须同时具备)．2.函数解析式的求法(1)定义法；(2)换元法；(3)待定系数法；(4)解方程(组)法；(5)赋值法．3.函数的定义域的求法(1)已给出函数解析式：函数的定义域是使解析式有意义的自变量的取值集合．(2)实际问题：求函数的定义域既要考虑解析式有意义，还应考虑使实际问题有意义．(3)复合函数问题①若函数f(x)的定义域为[a，b]，函数f[g(x)]的定义域应由a≤g(x)≤b 解出；②若函数f[g(x)]的定义域为[a，b]，则函数f(x)的定义域为函数g(x)在[a，b]上的值域．注意：①函数f(x)中的x与函数f[g(x)]中的g(x)地位相同．②定义域所指永远是x的范围．4.函数值域的求法(1)配方法(二次或四次)；(2)判别式法；(3)换元法；(4)函数的单调性法．5.判断函数单调性的步骤(1)设x1，x2是所研究区间内任意两个自变量的值，且x1<x2；(2)判定f(x1)与f(x2)的大小：作差比较或作商比较；(3)根据单调性定义下结论．6.函数奇偶性的判定方法首先考查函数的定义域是否关于原点对称，再看函数f(－x)与f(x)之间的关系：①若函数f(－x)＝f(x)，则f(x)为偶函数；若函数f(－x)＝－f(x)，则f(x)为奇函数；②若f(－x)－f(x)＝0，则f(x)为偶函数；若f(x)＋f(－x)＝0，则f(x)为奇函数；③若f(x)f(－x)＝1(f(－x)≠0)，则f(x)为偶函数；若f(x)f(－x)＝－1(f(－x)≠0)，则f(x)为奇函数．7.幂函数的图象特征(1)幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限内，图象最多只能同时出现在两个象限内，至于是否在第二、三象限内出现，则要看幂函数的奇偶性．(2)幂函数的图象在第一象限内的变化规律为：在第一象限内直线x ＝1的右侧，图象从下到上，相应的指数由小到大，直线x ＝1的左侧，图象从下到上，相应的指数由大到小．8.函数的应用解决函数应用题关键在于理解题意，提高阅读能力．一方面要加强对常见函数模型的理解，弄清其产生的实际背景，把数学问题生活化；另一方面，要不断拓宽知识面，增加间接的生活阅历，诸如了解一些物价、行程、产值、利润、环保等实际问题，及有关角度、面积、体积、造价的问题，培养实际问题数学化的意识和能力．3 学科思想培优一、函数的定义域函数的定义域是指函数y ＝f (x )中自变量x 的取值范围．确定函数的定义域是进一步研究函数其他性质的前提，而研究函数的性质，利用函数的性质解决数学问题是中学数学的重要组成部分．所以熟悉函数定义域的求法，对于函数综合问题的解决起着至关重要的作用．[典例1] (1)函数f (x )＝x x -132＋(3x －1)0的定义域是( )A.)31,(-∞B.)131(，C.)3131(，-D.)31,(-∞∪)131(，(2)已知函数y ＝f (x ＋1)的定义域是[－2,3]，则y ＝f (2x －1)的定义域是( )A.]25,0[ B ．[－1,4]C.[－5,5] D ．[－3,7] 【答案】(1)D (2)A【解析】(1)由题意，得⎩⎨⎧≠->-01301x x ，解得x <1且x ≠31.(2)设u ＝x ＋1，由－2≤x ≤3，得－1≤x ＋1≤4，所以y ＝f (u )的定义域为[－1,4]．再由－1≤2x －1≤4，解得0≤x ≤25，即函数y ＝f (2x －1)的定义域是]25,0[ 二、分段函数问题所谓分段函数是指在定义域的不同子区间上的对应关系不同的函数．分段函数是一个函数而非几个函数，其定义域是各子区间的并集，值域是各段上值域的并集．分段函数求值等问题是高考常考的问题．[典例2] 已知实数a ≠0，函数f (x )＝⎩⎨⎧≥--<+1,21,2x a x x a x 若f (1－a )＝f (1＋a )，则a 的值_____．【答案】－43【解析】①当1－a <1，即a >0时，此时a ＋1>1，由f (1－a )＝f (1＋a )，得2(1－a )＋a ＝－(1＋a )－2a ，解得a ＝－23(舍去)； ②当1－a >1，即a <0时，此时a ＋1<1，由f (1－a )＝f (1＋a )，得－(1－a )－2a ＝2(1＋a )＋a ，解得a ＝－43，符合题意．综上所述，a ＝－43. 三、函数的单调性与奇偶性单调性是函数的一个重要性质，某些数学问题，通过函数的单调性可将函数值间的关系转化为自变量之间的关系进行研究，从而达到化繁为简的目的，特别是在比较大小、证明不等式、求值或求最值、解方程(组)等方面应用十分广泛．奇偶性是函数的又一重要性质，利用奇偶函数图象的对称性可以缩小问题研究的范围，常能使求解的问题避免复杂的讨论．[典例3]设函数()y f x =的定义域为R ，并且满足()()()f x y f x f y +=+，112f ⎛⎫= ⎪⎝⎭，当0x >时，()0f x >. （1）求(0)f 的值；（2）判断函数的奇偶性；（3）如果()(2)2f x f x ++<，求x 的取值范围.【解析】（1）令0x y ==，则(0)(0)(0)f f f =+，∴(0)0f =.（2）令y x =-，得(0)()()0f f x f x =+-=， ∴()()f x f x -=-，故函数()f x 是R 上的奇函数. （3）任取12,R x x ∈且12x x <，则210x x ->. ∵()()21f x f x -()()2111f x x x f x =-+- ()()()2111f x x f x f x =-+- ()210f x x =->，∴()()12f x f x <.故()f x 是R 上的增函数.∵112f ⎛⎫= ⎪⎝⎭，∴()1111122222f f f f ⎛⎫⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ()(2)2f x f x ++<∴[]()(2)((2)(22)(1)f x f x f x x f x f ++=++=+<.又由()y f x =是定义在R 上的增函数，得221x +<，解得21x <-四、函数图象及应用函数的图象是函数的重要表示方法，它具有明显的直观性，通过函数的图象能够掌握函数重要的性质，如单调性、奇偶性等．反之，掌握好函数的性质，有助于函数图象正确地画出．函数图象广泛应用于解题过程中，利用数形结合解题具有直观、明了、易懂的优点．[典例4] 设函数f (x )＝x 2－2|x |－1(－3≤x ≤3)． (1)证明：函数f (x )是偶函数； (2)画出这个函数的图象；(3)指出函数f (x )的单调区间，并说明在各个单调区间上f (x )的单调性； (4)求函数的值域．【解析】(1)证明：∵函数f (x )的定义域关于原点对称，且f (－x )＝(－x )2－2|－x |－1 ＝x 2－2|x |－1＝f (x )，即f (－x )＝f (x )，∴f (x )是偶函数． (2)当0≤x ≤3时，f (x )＝x 2－2x －1＝(x －1)2－2.当－3≤x <0时，f (x )＝x 2＋2x －1＝(x ＋1)2－2.即f (x )＝⎪⎩⎪⎨⎧<≤--+≤≤--)03(2)1()30(,2)1(22x x x x 根据二次函数的作图方法，可得函数图象如下图．(3)函数f (x )的单调区间为[－3，－1)，[－1,0)，[0,1)，[1,3]．f (x )在区间[－3，－1)和[0,1)上单调递减，在[－1,0)和[1,3]上单调递增．(4)当0≤x ≤3时，函数f (x )＝(x －1)2－2的最小值为－2，最大值为f (3)＝2；当－3≤x <0时，函数f (x )＝(x ＋1)2－2的最小值为－2，最大值为f (－3)＝2.故函数f (x )的值域为[－2,2].五、幂函数的图象问题对于给定的幂函数图象，能从函数图象的分布、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性等性质．注意图象与函数解析式中指数的关系，能够根据图象比较指数的大小．[典例5] 如图是幂函数y ＝x a ，y ＝x b ，y ＝x c ，y ＝x d 在第一象限内的图象，则a ，b ，c ，d 的大小关系为( )A.a <b <c <dB.a <b <d <cC.b <a <c <dD.b <a <d <c 【答案】A【解析】由幂函数的图象特征可知，在第一象限内直线x ＝1的右侧，图象从下到上，相应的指数由小到大．故选A.六、函数模型及其应用建立恰当的函数模型解决实际问题的步骤：(1)对实际问题进行抽象概括，确定变量之间的主被动关系，并用x ，y 分别表示；(2)建立函数模型，将变量y 表示为x 的函数，此时要注意函数的定义域； (3)求解函数模型，并还原为实际问题的解．[典例6] 已知A ，B 两城市相距100 km ，在两地之间距离A 城市x km 的D 处修建一垃圾处理厂来解决A ，B 两城市的生活垃圾和工业垃圾．为保证不影响两城市的环境，垃圾处理厂与市区距离不得少于10 km.已知垃圾处理费用和距离的平方与垃圾量之积的和成正比，比例系数为0.25.若A 城市每天产生的垃圾量为20 t ，B 城市每天产生的垃圾量为10 t ．(1)求x 的取值范围；(2)把每天的垃圾处理费用y 表示成x 的函数；(3)垃圾处理厂建在距离A 城市多远处，才能使每天的垃圾处理费用最少？【解析】(1)由题意可得x ≥10,100－x ≥10. 所以10≤x ≤90.所以x 的取值范围为[10,90]．(2)由题意，得y ＝0.25[20x 2＋10(100－x )2]，即y ＝215x 2－500x ＋25000(10≤x ≤90)． (3)由y ＝215x 2－500x ＋25000＝350000)3100(2152+-x (10≤x ≤90)，则当x ＝3100时，y 最小．即当垃圾处理厂建在距离A 城市3100km 时，才能使每天的垃圾处理费用最少．《第三章函数的概念和性质》单元测试卷（一）基础测评卷(时间：120分钟，满分：150分)一、单选题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知f (x )＝－3x ＋2，则f (2x ＋1)等于( B ) A ．－3x ＋2 B ．－6x －1 C ．2x ＋1 D ．－6x ＋5【答案】B【解析】在f (x )＝－3x ＋2中，用2x ＋1替换x ，可得f (2x ＋1)＝－3(2x ＋1)＋2＝－6x －3＋2＝－6x －1.2．函数1()f x x=的定义域是( )A ．RB ．[1,)-+∞C ．(,0)(0,)-∞+∞D ．[1,0)(0,)-+∞【答案】D【解析】由题意可得：10x +≥，且0x ≠，得到1x ≥-，且0x ≠，故选：D3．已知21,[1,0),()1,[0,1],x x f x x x +∈-⎧=⎨+∈⎩则函数()y f x =-的图象是（） A ．B ．C ． D ．【答案】A【解析】当0x =时，依函数表达式知2(0)(0)011f f -==+=，可排除B ；当1x =时，(1)(1)10f -=-+=，可排除C 、D ．故选A4．已知函数y ＝21,02,0x x x x ⎧+≤⎨->⎩，则使函数值为5的x 的值是（）A ．2-或2B ．2或52-C ．2-D ．2或2-或52- 【答案】C【解析】当0x ≤时，令5y =，得215x +=，解得2x =-；当0x >时，令5y =，得25x -=，解得52x =-，不合乎题意，舍去.综上所述，2x =-，故选C.5．某学校要召开学生代表大会，规定各班每10人推选一名代表，当各班人数除以10的余数大于6时再增选一名代表，那么，各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y=[x]([x]表示不大于x 的最大整数)可以表示为（）A ．y 10x ⎡⎤=⎢⎥⎣⎦B ．3y 10x +⎡⎤=⎢⎥⎣⎦C ．4y 10x +⎡⎤=⎢⎥⎣⎦D ．5y 10x +⎡⎤=⎢⎥⎣⎦【答案】B【解析】根据规定每10人推选一名代表，当各班人数除以10的余数大于6时增加一名代表，即余数分别为7,8,9时可以增选一名代表，也就是x 要进一位，所以最小应该加3，因此利用取整函数可表示为310x y +⎡⎤=⎢⎥⎣⎦，也可以用特殊取值法，若56,5x y ==，排除C ，D ，若57,6x y ==，排除A ，故选B ．6．设函数f (x )(x ∈R)为奇函数，f (1)＝21，f (x ＋2)＝f (x )＋f (2)，则f (5)等于( C )A ．0B ．1C ．25D ．5【答案】C【解析】令x ＝－1，得f (1)＝f (－1)＋f (2)．∵f (x )为奇函数，∴f (－1)＝－f (1)，∴f (1)＝－f (1)＋f (2)，∴21＝－21＋f (2)，∴f (2)＝1.令x ＝1，得f (3)＝f (1)＋f (2)＝21＋1＝23.令x ＝3，得f (5)＝f (2)＋f (3)＝257．已知函数()f x 是定义在R 上的偶函数,当0x ≥时,2()4f x x x =-,则不等式(2)5f x +<的解集为（）A ．(3,7)-B ．()4,5-C ．(7,3)-D ．()2,6-【答案】C【解析】当0x ≥时,2()45f x x x =-<的解为05x <≤；当0x <时，根据偶函数图像的对称性知不等式()5f x <的解为5x 0-<<，所以不等式()5f x <的解集为{}55x x -<<，所以不等式(2)5f x +<的解集为{}{}52573x x x x -<+<=-<<.故选：C 8．已知定义在R 上的奇函数f (x )满足f (x －4)＝－f (x )，且在区间[0,2]上是增函数，若方程f (x )＝m (m >0)在区间[－8,8]上有四个不同的根x 1，x 2，x 3，x 4，则x 1＋x 2＋x 3＋x 4等于( C )A ．－6B ．6C ．－8D ．8【答案】C【解析】f (x )在R 上是奇函数，所以f (x －4)＝－f (x )＝f (－x )，故f (x )关于x ＝－2对称，f (x )＝m 的根关于x ＝－2对称，∴x 1＋x 2＋x 3＋x 4＝4×(－2)＝－8.二、多选题(本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多个选项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得3分)9．下列各组函数表示的是同一个函数的是( BD )A ．f (x )＝32x -与g (x )＝x ·x 2-B ．f (x )＝|x |与g (x )＝x 2C ．f (x )＝x ＋1与g (x )＝x ＋x 0D ．f (x )＝x x与g (x )＝x 0【答案】BD【解析】对于A ，f (x )＝32x -与g (x )＝x ·x 2-的对应关系不同，故f (x )与g (x )表示的不是同一个函数；对于B ，f (x )＝|x |与g (x )＝x 2的定义域和对应关系均相同，故f (x )与g (x )表示的是同一个函数；对于C ，f (x )的定义域为R ，g (x )的定义域为{x |x ≠0}，故f (x )与g (x )表示的不是同一个函数；对于D ，f (x )＝x x与g (x )＝x 0的对应关系和定义域均相同，故f (x )与g (x )表示的是同一个函数．10．下列函数既是定义域上的减函数又是奇函数的是( BD )A ．f (x )＝x 1B ．f (x )＝－x 3C ．f (x )＝x |x |D ．f (x )＝－3x【答案】BD【解析】A ．f (x )＝x 1在定义域(－∞，0)∪(0，＋∞)上是奇函数，且在每一个区间上是减函数，不能说函数在定义域上是减函数，∴不满足题意；对于B ，f (x )＝－x 3在定义域R 上是奇函数，且是减函数，∴满足题意，对于C ，f (x )＝x |x |＝⎪⎩⎪⎨⎧<-≥0,0,22x x x x ，在定义域R 上是奇函数，且是增函数，∴不满足题意；对于D ，f (x )＝－3x 在定义域R 上是奇函数，且是减函数，∴满足题意．故选BD ．11．已知函数f (x )＝31++-x x ，则( ABD ) A ．f (x )的定义域为[－3,1] B ．f (x )为非奇非偶函数 C ．f (x )的最大值为8 D ．f (x )的最小值为2【答案】ABD【解析】由题设可得函数的定义域为[－3,1]，f 2(x )＝4＋2×322+--x x＝4＋2×2)1(4+-x ，而0≤2)1(4+-x ≤2，即4≤f 2(x )≤8，∵f (x )＞0，∴2≤f (x )≤22，∴f (x )的最大值为22，最小值为2，故选ABD ．12．下列说法正确的是( )A ．若方程x 2＋(a －3)x ＋a ＝0有一个正实根，一个负实根，则a ＜0B ．函数f (x )＝2211x x -+-是偶函数，但不是奇函数C ．若函数f (x )的值域是[－2,2]，则函数f (x ＋1)的值域为[－3,1]D ．曲线y ＝|3－x 2|和直线y ＝a (a ∈R)的公共点个数是m ，则m 的值不可能是1【答案】AD【解析】设方程x 2＋(a －3)x ＋a ＝0的两根分别为x 1，x 2，则x 1·x 2＝a <0，故A 正确；函数f (x )＝2211x x -+-的定义域为⎪⎩⎪⎨⎧≥-≥-010122x x ，则x ＝±1，∴f (x )＝0，所以函数f (x )既是奇函数又是偶函数，故B 不正确；函数f (x ＋1)的值域与函数f (x )的值域相同，故C 不正确；曲线y ＝|3－x 2|的图像如图，由图知曲线y ＝|3－x 2|和直线y ＝a 的公共点个数可能是2,3或4，故D 正确．三、填空题(本大题共4小题，每小题5分，共20分．将答案填在题中横线上)13．若函数()(31)4,1,1a x a x f x ax x -+<⎧=⎨-≥⎩，是定义在R 上的减函数，则a 的取值范围【答案】11,83⎡⎫⎪⎢⎣⎭【解析】因为函数()f x 是定义在R 上的减函数，所以3100314a a a a a -<⎧⎪-<⎨⎪-+≥-⎩，解得1183a ≤<. 14．函数f (x )＝x x+-11的定义域为___，单调递减区间为___.【答案】(－∞，－1)∪(－1，＋∞)，(－∞，－1)【解析】函数f (x )的定义域为(－∞，－1)∪(－1，＋∞)．任取x 1，x 2∈(－1，＋∞)且x 1＜x 2，则f (x 1)－f (x 2)＝)1)(1()22121x x x x ++-（＞0，即f (x 1)＞f (x 2)，故f (x )在(－1，＋∞)上为减函数；同理，可得f (x )在(－∞，－1)上也为减函数．15．函数y ＝f (x )是R 上的增函数，且y ＝f (x )的图像经过点A (－2，－3)和B (1,3)，则不等式|f (2x －1)|<3的解集为____.【答案】1(,1)2-【解析】因为y ＝f (x )的图像经过点A (－2，－3)和B (1,3)，所以f (－2)＝－3，f (1)＝3.又|f (2x －1)|<3，所以－3<f (2x －1)<3，即f (－2)<f (2x －1)<f (1)．因为函数y ＝f (x )是R 上的增函数，所以－2<2x －1<1，即⎩⎨⎧<-->-112212x x ，即⎪⎩⎪⎨⎧<->121x x ，所以－21<x <1.16．对于任意定义在R 上的函数f (x )，若实数x 0满足f (x 0)＝x 0，则称x 0是函数f (x )的一个不动点．现给定一个实数a ∈(4,5)，则函数f (x )＝x 2＋ax ＋1的不动点共有___个．【答案】2【解析】由定义，令x 2＋ax ＋1＝x ，则x 2＋(a －1)x ＋1＝0，当a ∈(4,5)时，Δ＝(a －1)2－4>0，所以方程有两根，相应地，函数f (x )＝x 2＋ax ＋1(a ∈(4,5))有2个不动点．四、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(10分)已知幂函数39*()m y x m N -=∈的图象关于y 轴对称且在()0,∞+上单调递减，求满足()()33132mm a a +<-－－的a 的取值范围.【解析】因为函数39*()m y x m N -=∈在()0,∞+上单调递减，所以390m -<，解得3m <.又因为*m N ∈，所以1m =，2；因为函数的图象关于y 轴对称，所以39m -为偶数，故1m =. 则原不等式可化为()()1133132a a +<-－－，因为13y x－＝在(),0-∞，()0,∞+上单调递减，所以1320a a +>->或3210a a -<+<或1032a a +<<-，解得2332a <<或1a <-. 故a 的取值范围是1a <-或2332a <<. 18．(10分)已知函数21()1x f x x -=+（1）试判断函数在（-1，+∞）上的单调性，并给予证明；（2）试判断函数在[3,5]x ∈的最大值和最小值【解析】（1）∵()213211x y f x x x -===-++， ∴函数()f x 在()1，-+∞上是增函数，证明：任取1x ，()21x ∈-+∞，，且12x x <，则()()1212213333221111f x f x x x x x ⎛⎫⎛⎫-=---=- ⎪ ⎪++++⎝⎭⎝⎭()()()1212311x x x x -=++， ∵121x x -<<，∴120x x -<，()()12110x x ++>， ∴()()120f x f x -<，即()()12f x f x <，∴()f x 在()1，-+∞上是增函数. （2）∵()f x 在()1，-+∞上是增函数， ∴()f x 在[3]5，上单调递增，它的最大值是()25135512f ⨯-==+，最小值是()23153314f ⨯-==+． 19．(12分)设函数f (x )＝ax 2＋(b －8)x －a －ab 的两个零点分别是－3和2.(1)求函数f (x )；(2)当函数f (x )的定义域是[0,1]时，求函数f (x )的值域．【解析】(1)∵f (x )的两个零点是－3和2，∴－3和2是方程ax 2＋(b －8)x －a －ab ＝0的两根，∴有9a －3(b －8)－a －ab ＝0，① 4a ＋2(b －8)－a －ab ＝0.② ①－②得b ＝a ＋8.③将③代入②得4a ＋2a －a －a (a ＋8)＝0，即a 2＋3a ＝0.∵a ≠0，∴a ＝－3，∴b ＝a ＋8＝5，∴f (x )＝－3x 2－3x ＋18.(2)由(1)得f (x )＝－3x 2－3x ＋18＝－3(x ＋21)2＋43＋18.图像的对称轴是直线x ＝－21.∵0≤x ≤1，∴f (x )min ＝f (1)＝12，f (x )max ＝f (0)＝18，∴此时函数f (x )的值域是[12,18]．20．(12分)已知函数())1f x a =≠. （1）若0a >，求()f x 的定义域；（2）若()f x 在区间(]0,1上是减函数，求实数a 的取值范围. 【解析】(1)当0a >且1a ≠时，由30ax -≥得3x a≤，即函数()f x 的定义域是3,a ⎛⎤-∞ ⎥⎝⎦.(2)当10a ->即1a >时，令3t ax =-要使()f x 在(]0,1上是减函数，则函数3t ax =-在(]0,1上为减函数，即0a -<，并且且310a -⨯≥，解得13a ；当10a -<即1a <时，令3t ax =-要使()f x 在(]0,1上是减函数，则函数3t ax =-在(]0,1为增函数，即0a -> 并且310a -⨯≥，解得0a <综上可知，所求实数a 的取值范围是()(],01,3-∞.21．(12分)已知函数f （x ）＝x mx+，且此函数图象过点（1，2）．（1）求实数m 的值；（2）判断函数f （x ）的奇偶性并证明；（3）讨论函数f （x ）在（0，1）上的单调性，并证明你的结论．【解析】（1）∵函数f （x ）＝x mx+，且此函数图象过点（1，2）， ∴2＝1+m ， ∴m ＝1；（2）f （x ）＝x 1x +，定义域为：()()00-∞⋃+∞，，，又f （﹣x ）＝﹣x 1x+=--f （x ）， ∴函数f （x ）是奇函数；（3）函数f （x ）在（0，1）上单调递减，设0＜x 1＜x 2＜1，则()()()()211212121212121212111x x x x f x f x x x x x x x x x x x x x ---=+--=-+=-⋅⋅⋅， ∵0＜x 1＜x 2＜1，∴x 1﹣x 2＜0，0＜x 1x 2＜1，x 1x 2﹣1＜0， ∴()()()1212121210x x f x f x x x x x --=-⋅＞，即f （x 1）＞f （x 2），∴f （x ）在（0，1）上的单调递减．22.(12分)某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元．该厂为了鼓励销售商订购，决定每一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降0.02元，但实际出厂单价不能低于51元．(1)当一次订购量为多少个时，零件的实际出厂单价恰好为51元？ (2)当销售商一次订购x 个零件时，该厂获得的利润为P 元，写出P ＝f (x )的表达式．【解析】(1)设每个零件的实际出厂价格恰好为51元时，一次订购量为x 0个，则60－0.02(x 0－100)＝51，解得x 0＝550，所以当一次订购量为550个时，每个零件的实际出厂价恰好为51元．(2)设一次订量为x 个时，零件的实际出厂单价为W ，工厂获得利润为P ，由题意P ＝(W －40)·x ，当0<x ≤100时，W ＝60；当100<x <550时，W ＝60－0.02(x －100)＝62－50x；当x ≥550时，W ＝51.当0<x ≤100时， f (x )＝(60－40)x ＝20x ；∴当100<x <550时， f (x )＝(22－50x )x ＝22x －501x 2；当x ≥550时， f (x )＝(51－40)x ＝11x .故f (x )＝⎪⎪⎩⎪⎪⎨⎧∈≥∈<<-∈≤<+++),550(,11),550100(5022),1000(202N x x x N x x x x N x x x《第三章函数的概念和性质》单元测试卷（二）能力测评卷(时间：120分钟，满分：150分)一、单项选择题(本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．下列函数中，既是奇函数又是在其定义域上是增函数的是( )A ．y ＝x ＋1B ．y ＝－x 3C ．y ＝x 1D ．y ＝x |x |【答案】D【解析】选项A 中，函数为非奇非偶函数，不符合题意；选项B 中，函数为奇函数，但在定义域为减函数，不符合题意；选项C 中，函数为奇函数，但在定2．已知幂函数y ＝f (x )的图象过点2，则下列结论正确的是( )A ．y ＝f (x )的定义域为[0，＋∞)B ．y ＝f (x )在其定义域上为减函数C ．y ＝f (x )是偶函数D ．y ＝f (x )是奇函数3．函数f (x )＝x x 2的定义域为( )A ．(0,1)B ．[0,1]C ．(－∞，0]∪[1，＋∞)D ．(－∞，0)∪(1，＋∞)【答案】D【解析】：由题意知：x 2－x >0，解得x <0或x >1，∴函数f (x )的定义域为(－∞，0)∪(1，＋∞)．4．已知函数f (3x ＋1)＝x 2＋3x ＋1，则f (10)＝( ) A ．30 B ．19 C ．6 D ．20 【答案】B【解析】令x ＝3得f (10)＝32＋3×3＋1＝19.5．已知函数f (x )＝|x ＋a |在(－∞，－1)上是单调函数，则a 的取值范围是( )A．(－∞，1] B．(－∞，－1) C．[1，＋∞) D．(－∞，1)【答案】A【解析】由于f(x)＝|x＋a|的零点是x＝－a，且在直线x＝－a两侧左减右增，要使函数f(x)＝|x＋a|在(－∞，－1)上是单调函数，则－a≥－1，解得a≤1.故选A.6．为了节约用电，某城市对居民生活用电实行“阶梯电价”，计费方法如下：( ) A．475度 B．575度 C．595.25度 D．603.75度【答案】D【解析】不超过230度的部分费用为：230×0.5＝115；超过230度但不超过400度的部分费用为：(400－230)×0.6＝102,115＋102<380；设超过400度的部分为x，则0.8x＋115＋102＝380，∴x＝203.75，故用电603.75度．7．已知函数y＝x2－4x＋5在闭区间[0，m]上有最大值5，最小值1，则m 的取值范围是( )A．[0,1] B．[1,2] C．[0,2] D．[2,4]【答案】D【解析】∵函数f(x)＝x2－4x＋5＝(x－2)2＋1的对称轴为x＝2，此时，函数取得最小值为1，当x＝0或x＝4时，函数值等于5.又f(x)＝x2－4x＋5在区间[0，m]上的最大值为5，最小值为1，∴实数m的取值范围是[2,4]，故选D.8．已知定义域为R的函数y＝f(x)在(0,4)上是减函数，又y＝f(x＋4)是偶函数，则( )A．f(2)<f(5)<f(7) B．f(5)<f(2)<f(7)C．f(7)<f(2)<f(5) D．f(7)<f(5)<f(2)【答案】B【解析】因为y＝f(x＋4)是偶函数，所以f(x＋4)＝f(－x＋4)，因此f(5)＝f(3)，f(7)＝f(1)，因为y＝f(x)在(0,4)上是减函数，所以f(3)<f(2)<f(1)，f(5)<f(2)<f(7)，选B.二、多项选择题(本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分)9．若函数y＝xα的定义域为R且为奇函数，则α可能的值为( )A．－1 B．1 C．2 D．3【答案】BD【解析】当α＝－1时，幂函数y＝x－1的定义域为(－∞，0)∪(0，＋∞)，A不符合；当α＝1时，幂函数y＝x，符合题意；当α＝2时，幂函数y＝x2的定义域为R且为偶函数，C不符合题意；当α＝3时，幂函数y＝x3的定义域为R且为奇函数，D符合题意．故选BD.10．某工厂八年来某种产品总产量y(即前x年年产量之和)与时间x(年)的函数关系如图，下列五种说法中正确的是( )A．前三年中，总产量的增长速度越来越慢B．前三年中，年产量的增长速度越来越慢C．第三年后，这种产品停止生产D．第三年后，年产量保持不变【答案】AC【解析】由题中函数图象可知，在区间[0,3]上，图象是凸起上升的，表明总产量的增长速度越来越慢，A正确；由总产量增长越来越慢知，年产量逐年减小，因此B错误；在[3,8]上，图象是水平直线，表明总产量保持不变，即年产量为0，因此C正确，D错误，故选AC.11．对于实数x，符号[x]表示不超过x的最大整数，例如[π]＝3，[－1.08]＝－2，定义函数f (x )＝x －[x ]，则下列命题中正确的是( )A ．f (－3.9)＝f (4.1)B ．函数f (x )的最大值为1C ．函数f (x )的最小值为0D ．方程f (x )－21＝0有无数个根值可能是( )A ．2B ．3C ．4D ．5 【答案】ABC【解析】函数y ＝x 2－4x －4的部分图象如图，f (0)＝f (4)＝－4，f (2)＝－8.因为函数y ＝x 2－4x －4的定义域为[0，m ]，值域为[－8，－4]，所以m 的取值范围是[2,4]，故选ABC.三、填空题(本题共4小题，每小题5分，共20分．请把正确答案填在题中横线上)13．若函数f (x )＝12+++bx x a x 在[－1,1]上是奇函数，则f (x )的解析式为________．14．已知幂函数()221()33mm f x m m x--=-+在(0,)+∞上单调递增，则m 值为_____.【答案】2【解析】由题意可知2233110m m m m ⎧-+=⎪⎨-->⎪⎩，解得2m =，故答案为：215．若定义在R 上的奇函数()f x 满足()()4f x f x +=，()11f =，则()()()678f f f ++的值为_______．【答案】1-【解析】由于定义在R 上的奇函数()y f x =满足()()4f x f x +=，则该函数是周期为4的周期函数，且()11f =，则()()800f f ==，()()()7111f f f =-=-=-，()()()622f f f =-=，又()()22f f -=-，()20f ∴=，则()60f =，因此，()()()6781f f f ++=-. 16.已知函数()(),f x g x 分别是定义在R 上的偶函数和奇函数，()()23x f x g x +=⋅.则函数()f x =__________；关于x 不等式()()2240g x x g x ++->的解集__________．【答案】33x x -+ ()(),41,-∞-+∞【解析】函数()f x 、()g x 分别是定义在R 上的偶函数和奇函数， ∴()()f x f x -=，()()g x g x -=-，又()()23xf xg x +=⋅，…①∴()()23xf xg x --+-=⋅，即()()23xf xg x --=⋅，…②由①②求得函数()33x x f x -=+，()33x xg x -=-. 易知()33x xg x -=-是定义域R 上的单调增函数，所以不等式()()2240g x x g x ++->可化为()()()2244g x x g x g x +>--=-，即224x x x +>-，整理得2340x x +->，解得4x <-或1x >，所以不等式的解集为()(),41,-∞-+∞，故答案为33x x -+，()(),41,-∞-+∞四、解答题(本题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(10分)已知函数f(x)＝61x -，(1)求函数f(x)的定义域； (2)求f(－1), f(12)的值．【解析】(1)根据题意知x －1≠0且x ＋4≥0，∴x≥－4且x≠1，即函数f(x)的定义域为[－4,1)∪(1，＋∞)．(2) ()6132f -==---f(12)＝66412111-=--＝3811-. 18.(12分)已知幂函数f (x )＝(m 2－5m ＋7)·x m －1为偶函数．(1)求f (x )的解析式；(2)若g (x )＝f (x )－ax －3在[1,3]上不是单调函数，求实数a 的取值范围．【解析】(1)由题意得m 2－5m ＋7＝1，即m 2－5m ＋6＝0，解得m ＝2或m ＝3. 又f (x )为偶函数，所以m ＝3，此时f (x )＝x 2.(2)由(1)知，g (x )＝x 2－ax －3，因为g (x )＝x 2－ax －3在[1,3]上不是单调19．(12分)已知函数()2f x x =+， (1)若该函数在区间()-2∞，+上是减函数，求a 的取值范围. (2)若1a =-，求该函数在区间[1,4]上的最大值与最小值．【解析】（1）因为函数()212112()222a x a ax af x a x x x ++-+-===++++在区间(2,)-+∞上是减函数,所以120a ->,解得12a <, 所以a 的取值范围1,2⎛⎫-∞ ⎪⎝⎭.（2）当1a =-时，13()122x f x x x -+==-+++，则()f x 在(),2-∞-和()2,-+∞上单调递减，因为[](),,421⊆-+∞，所以()f x 在[]1,4的最大值是()111012f -+==+，最小值是()4114422f -+==-+，所以该函数在区间[]1,4上的最大值为0，最小值为12-．20.已知函数f （x ）是定义在R 上的奇函数，且当x ≤0时，f （x ）＝x 2+2x ．（1）现已画出函数f （x ）在y 轴左侧的图象，如图所示，请补全函数f （x ）的图象；（2）求出函数f （x ）（x ＞0）的解析式；（3）若方程f （x ）＝a 恰有3个不同的解，求a 的取值范围．【解析】函数f(x)的图象如下：（2）因为f(x)为奇函数，则f(-x)=- f(x)∴当x 0>时，x 0-<∴f(-x)=- f(x)=()()2222x x x x ⎡⎤-+-=-⎣⎦故f(x)()220x x x =-+>（3）由（1）中图象可知：y=f(x)与y=a 的图象恰好有三个不同的交点1a ∴-<<121．已知函数2()4f x x =+. （1）设()()f x g x x=，根据函数单调性的定义证明()g x 在区间[2,)+∞上单调递增；（2）当0a >时，解关于x 的不等式2()(1)2(1)f x a x a x >-++.【解析】（1）由题意得，124(),,[2,)g x x x x x=+∀∈+∞，且12x x <，则()()()()()121212121212121244444x x x x g x g x x x x x x x x x x x --⎛⎫⎛⎫⎛⎫-=+-+=-+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.由212x x >≥，得12120,40x x x x -<->.于是()()120g x g x -<，即()()12g x g x <所以函数()g x 在区间[2,)+∞上单调递增（2）原不等式可化为22(1)40ax a x -++>.因为0a >，故2(2)0x x a ⎛⎫--> ⎪⎝⎭. （i ）当22a <,即1a >时，得2x a <或2x >. （ii ）当22a=,即1a =时，得到2(2)0x ->,所以2x ≠；（iii ）当22a >，即01a <<时，得2x <或2x a >.综上所述，当01a <<时，不等式的解集为2(,2),a ⎛⎫-∞⋃+∞ ⎪⎝⎭；当1a =时，不等式的解集为(,2)(2,)-∞⋃+∞；当1a >时，不等式的解集为2,(2,)a ⎛⎫-∞⋃+∞ ⎪⎝⎭22． 2018年10月24日，世界上最长的跨海大桥—港珠澳大桥正式通车。

函数的概念及表示方法专题复习卷(含答案详解)

三、解答题（共 6 题，共 70 分） 17．求下列函数的解析式：（1）已知 f (x)是二次函数且满足 f (0) = 1，f (x + 1) − f (x) = 2x，求 f (x)；（2）设 f ( − ) = x，求 f (x)； x （3）若 f (x) + 2f (−x) = 3x + 2，求 f (x)．
11．下列函数： ①y = x＋|x|；②y = x－|x|；③y = x|x|；④y = 考点函数的最值及其几何意义题点由函数图像求最值答案 2
0，x<0，解析 y = x + |x| = ymin＝0. 2x，x≥0，
x .其中有最小值的函数有________个． |x|
0，x>0， y = x − |x| = 无最小值． 2x，x≤0， x2，x>0， y = x|x| = 2 无最小值．－x ，x≤0，
y=
1，x>0， x = ymin = −1. |x| －1，x<0，
12．函数 f ( x) = 2 x + x 2 + 2 x ( x 0,1) 的值域为答案 [1, 5]．
22．已知 a R，函数 f ( x) = x 2 − 2ax + 5 ．（1）若不等式 f ( x) 0 对任意 x (0, +) 恒成立，求实数 a 的取值范围；（2）若 a 1 ，且函数 f ( x) 的定义域和值域均为[1, a]，求实数 a 的值．
参考答案
一、选择题 1．下列各组函数中表示相等函数的是（ A．f (x) = x 与 g(x) = ( x)2 B．f (x) = |x|与 g(x) = x(x > 0) C．f (x) = 2x－1 与 g(x) = 2x + 1(x∈N*) D．f (x) = x2－1 与 g(x) = x + 1(x ≠ 1) x－1 ）

新概念一97—108课复习题

新概念97—108课复习题答案一、单词：遗留leave 描述（V.）describe 描述（n.）description 拉链zip=zipper标签label提手把手handle地址address penny的复数pence 属于belong 错误的wrong哎哟ow滑倒滑了一脚slip落下跌倒（原形、过去式、过去分词）fall/fell/fallen下楼downstairs伤伤害疼痛（原形、过去式、过去分词）hurt/hurt/hurt 背back帮助help 一次once 一定的确信的sure X光透视X-ray执照licence认为想think 让let 有用的helpful无用的helpless 后门backdoor双肩包（2种）backbag = packbag苏格兰Scotland明信片card 青年youth招待所旅馆hostel 协会association不久soon写(原形过去式过去分词) write / wrote / written青年的young 明信片 a postcard公交卡IC card身份证ID card考试exam=examination及格通过pass数学mathematics = maths问题question容易的easy足够地enough考卷paper未及格失败fail回答answer分数mark其他的东西rest困难的difficult讨厌hate低的low振作振奋cheer家伙人guy上方顶部top聪明的clever笨的stupid便宜的cheap贵的expensive新鲜的fresh变馊的stale低的矮的low大声的loud高的high硬的hard甜的sweet软的soft酸的sour政治课politics物理physics困难（名词）difficulty不同的different困难（同义词）hard困难（反义词）easy讨厌（反义词）hate low（反义词）high干杯cheers测验test 持续(动词) last拼写(原形过去式过去分词) spell / spelt / spelt聪明的有智慧的intelligent错误mistake 礼物present 词典dictionary携带carry 改正纠正correct保存保留keep 夫人女士madam 漂亮的smart适于suit 漂亮的pretty 拼写(名词) spelling一套suit英俊潇洒handsome二、词组：一个绿色的小房子a small green house属于我belong to me 属于某人belong to sb取回某物get sth back在火车上on the train前几天the other day = a few days ago坐火车去某地the train to +地点坐火车去北京the train to Beijing让某人做某事let sb do sth 不属于我not belong to me 表示伴随状态，用with引导with + n. +介词9短语落到楼下fall downstairs伤害某人hurt sb伤害自己hurt oneself救我help me帮助某人某事help sb with sth(n.)帮助某人干某事help sb ( to) do sth谢谢你的帮助（2种）Thanks for your help. / Thanks for helping me驾照driving licence立即马上at once 起立站起来stand up 看病go to see the doctor最好干… had better do给某人读… read sth to sb. …中的一员 a member of…其它的什么what else给某人写信(2种) write to sb = write a letter to sb. 大声地说speak up青年招待所协会the Y.H.A. = the Youth Hostels Association到达某地（4个）arrive at +小地点/ arrive in + 大地点/ get to + 地点/ reach + 地点参加考试（2个）take an exam / have an exam 通过考试pass the exam通过英语考试pass in English 通过某个学科pass in + 学科回答问题answer the questuon回答我的问题answer my question 放松别紧张Take it easy! 法语不及格fail the French paper 一张纸a piece of paper一张试卷 a paper三张试卷three papers接电话answer the phone得满分get a full mark得高分get a high mark得低分get a low mark剩下的….the rest of…休息一下have a rest剩下的苹果是坏的The rest of apples are bad小家伙little guy我去开门了Let me answer the door低音in a low voice振作精神cheer up足够的钱enough money试卷的顶端at the top of the paper 足够地快quickly enough足够的容易（简单）easy enough适可而止Enough is enough在…顶部at the top of …知足常乐Enough is as good as a feast做的糟糕do too badly 邻近我next to me最后at last紧挨着某人next to sb.在明信片上on a card淡水fresh water大一学生fresh man聪明的女孩clever girl 对我来说不难easy enough for me对他来说太难了too difficult for him智力测试intelligent test犯错误make a mistake知识渊博的人working dictionary 充满了… be full of想要(某人)干…want sb to do sth 告诉(某人)干…tell sb to do sth要求(某人)干… ask sb to do sth 想要(某人)不要干… want sb not to do sth告诉(某人)不要干… tell sb not to do sth要求(某人)不要干… ask sb not to do sth这里有….给… Here is a …for sb 改作业correct the exercise-books好漂亮How nice ! 流行be in fashion 根本不not …at all你想干…吗？Would you like to do sith ?三、语法：（1）形容词性物主代词和名词性物主代词的特点：adj物主代词没有独立性，后面一定有名词；n.物主代词有独立性，后面没有名词。

2024成都中考数学第一轮专题复习圆的有关概念及性质知识精练(含答案)

2024成都中考数学第一轮专题复习圆的有关概念及性质知识精练基础题1. (2023江西)如图，点A，B，C，D均在直线l上，点P在直线l外，则经过其中任意三个点，最多可画出圆的个数为()A. 3B. 4C. 5D. 6第1题图2. (2023广东省卷)如图，AB是⊙O的直径，∠BAC＝50°，则∠D＝()第2题图A. 20°B. 40°C. 50°D. 80°3. (2023广元)如图，AB是⊙O的直径，点C，D在⊙O上，连接CD，OD，A C.若∠BOD＝124°，则∠ACD的度数是()A. 56°B. 33°C. 28°D. 23°第3题图4. (2023山西)如图，四边形ABCD内接于⊙O，AC，BD为对角线，BD经过圆心O.若∠BAC ＝40°，则∠DBC的度数为()第4题图A. 40°B. 50°C. 60°D. 70°5. (2023安徽)如图，正五边形ABCDE内接于⊙O，连接OC，OD，则∠BAE－∠COD＝()A. 60°B. 54°C. 48°D. 36°第5题图6. (2023赤峰)如图，圆内接四边形ABCD中，∠BCD＝105°，连接OB，OC，OD，BD，∠BOC ＝2∠COD，则∠CBD的度数是()第6题图A. 25°B. 30°C. 35°D. 40°7. [新考法—数学文化](2023岳阳)我国古代数学名著《九章算术》中有这样一道题：“今有圆材，径二尺五寸．欲为方版，令厚七寸，问广几何？”结合下图，其大意是：今有圆形材质，直径BD为25寸，要做成方形板材，使其厚度CD达到7寸，则BC的长是() A. 674寸 B. 25寸C. 24寸D. 7寸第7题图8. (2023杭州)如图，在⊙O中，半径OA，OB互相垂直，点C在劣弧AB上．若∠ABC＝19°，则∠BAC＝()第8题图A. 23°B. 24°C. 25°D. 26°9. (2023广西)赵州桥是当今世界上建造最早，保存最完整的中国古代单孔敞肩石拱桥．如图，主桥拱呈圆弧形，跨度约为37 m，拱高约为7 m，则赵州桥主桥拱半径R约为()第9题图A. 20 mB. 28 mC. 35 mD. 40 m10. (2023凉山州)如图，在⊙O中，OA⊥BC，∠ADB＝30°，BC＝23，则OC＝()A. 1B. 2C. 2 3D. 4第10题图11. 如图，点A，B，D在⊙O上，CD垂直平分AB于点C.现测得AB＝CD＝16，则圆形宣传图标的半径为()第11题图A. 12B. 10C. 8D. 612. 如图，在平面直角坐标系中，⊙O的半径为4，弦AB的长为3，过O作OC⊥AB于点C，则OC的长度是________；⊙O内一点D的坐标为(－2，1)，当弦AB绕O点顺时针旋转时，点D到AB的距离的最小值是________．第12题图13. (2023武汉)如图，OA，OB，OC都是⊙O的半径，∠ACB＝2∠BA C.(1)求证：∠AOB＝2∠BOC；(2)若AB＝4，BC＝5，求⊙O的半径．第13题图拔高题14. (2023吉林省卷)如图，AB，AC是⊙O的弦，OB，OC是⊙O的半径，点P为OB上任意一点(点P不与点B重合)，连接CP.若∠BAC＝70°，则∠BPC的度数可能是()A. 70°B. 105°C. 125°D. 155°第14题图15. 如图，正方形ABCD 内接于⊙O ，点E 为弧AB 的中点，连接DE 与AB 交于点F .若AB＝1，记△ADF 的面积为S 1，△AEF 的面积为S 2，则S 1S 2的值为________．第15题图16. 如图，以原点O 为圆心的圆交x 轴于A ，B 两点，交y 轴的正半轴于点C ，且点A 的坐标为(－2，0)，D 为第一象限内⊙O 上的一点，若∠OCD ＝75°，则AD 的长为________．第16题图参考答案与解析1. D 【解析】本题考查了确定圆的条件及圆的有关定义及性质．∵过不在同一直线上的三个点一定能作一个圆，∴要经过题中所给的3个点画圆，除选定直线l 外的点P 外，再在直线l 上的A ，B ，C ，D 四个点中任选其中2个即可画圆．∵从A ，B ，C ，D 四个点中任选其中2个点的方法可以是AB ，AC ，AD ，BC ，BD ，CD ，共6种，∴最多可以画出圆的个数为6.2. B 【解析】∵AB 是⊙O 的直径，∠BAC ＝50°，∴∠ACB ＝90°，∠B ＝180°－50°－90°＝40°.∵AC ＝AC ，∴∠D ＝∠B ＝40°.3. C 【解析】∵∠BOD ＝124°，∴∠AOD ＝180°－124°＝56°，∴∠ACD ＝12∠AOD ＝28°. 4. B 【解析】∵BD 经过圆心O ，∴∠BCD ＝90°.∵∠BDC ＝∠BAC ＝40°，∴∠DBC ＝90°－∠BDC ＝50°.5. D 【解析】∵五边形ABCDE 是正五边形，∴∠BAE ＝（5－2）×180°5＝108°，∠COD ＝360°5＝72°，∴∠BAE －∠COD ＝108°－72°＝36°. 6. A 【解析】∵∠BCD ＝105°，∴∠BAD ＝180°－105°＝75°，∴∠BOD ＝150°.∵∠BOC＝2∠COD ，∴∠COD ＝13 ∠BOD ＝50°，∴∠CBD ＝12∠COD ＝25°. 7. C 【解析】∵BD 是圆的直径，∴∠BCD ＝90°.∵BD ＝25，CD ＝7，∴在Rt △BCD 中，由勾股定理得，BC ＝252－72 ＝24(寸).8. D 【解析】如解图，连接OC ，∵∠ABC ＝19°，∴∠AOC ＝2∠ABC ＝38°.∵半径OA ，OB 互相垂直，∴∠AOB ＝90°，∴∠BOC ＝90°－38°＝52°，∴∠BAC ＝12∠BOC ＝26°.第8题解图9. B 【解析】如解图，在Rt △OAB 中，由勾股定理，得AO 2＋AB 2＝OB 2，即(R －7)2＋(372)2＝R 2，解得R ≈28(m).第9题解图10. B 【解析】如解图，连接OB ，设OA 交BC 于点E ，∵∠ADB ＝30°，∴∠AOB ＝60°.∵OA ⊥BC ，BC ＝23 ，∴BE ＝12 BC ＝3 .在Rt △BOE 中，sin ∠AOB ＝BE OB，∴sin 60°＝3OB ＝32，∴OB ＝2，∴OC ＝2.第10题解图11. B 【解析】如解图，连接OA ，设圆形宣传图标的半径为R ，∵CD 垂直平分AB ，AB＝CD ＝16，∴CD 过点O ，AC ＝BC ＝12 AB ＝12×16＝8，∠DCA ＝90°.∵AO ＝OD ＝R ，∴在Rt △AOC 中，由勾股定理，得OC 2＋AC 2＝OA 2，即(16－R )2＋82＝R 2，解得R ＝10，即圆形宣传图标的半径为10.第11题解图 12. 552 ；552 －5 【解析】如解图，连接OB ，∵OC ⊥AB ，∴BC ＝12 AB ＝32.由勾股定理，得OC ＝OB 2－BC 2 ＝552.当OD ⊥AB 时，点D 到AB 的距离最小，由勾股定理，得OD ＝22＋12 ＝5 ，∴点D 到AB 的距离的最小值为552 －5 .第12题解图13. (1)证明：由圆周角定理，得∠ACB ＝12 ∠AOB ，∠BAC ＝12∠BOC . ∵∠ACB ＝2∠BAC ，∴∠AOB ＝2∠BOC ；(2)解：如解图，过点O 作半径OD ⊥AB 于点E ，连接BD .则∠DOB ＝12∠AOB ，AE ＝BE . ∵∠AOB ＝2∠BOC ，∴∠DOB ＝∠BOC .∴BD ＝BC .∵AB ＝4，BC ＝5 ，∴BE ＝2，DB ＝5 .在Rt △BDE 中，∵∠DEB ＝90°，∴DE ＝BD 2－BE 2 ＝1.在Rt △BOE 中，∵∠OEB ＝90°，∴OB 2＝(OB －1)2＋22，∴OB ＝52，即⊙O 的半径是 52.第13题解图14. D 【解析】如解图，连接BC ，∵∠BAC ＝70°，∴∠BOC ＝2∠BAC ＝140°.∵OB ＝OC ，∴∠OBC ＝∠OCB ＝180°－140°2＝20°.∵点P 为OB 上任意一点(点P 不与点B 重合)，∴0°<∠OCP <20°.∵∠BPC ＝∠BOC ＋∠OCP ＝140°＋∠OCP ，∴140°<∠BPC <160°，故选D.第14题解图15. 2(2 ＋1) 【解析】如解图，连接OE 交AB 于点G ，连接AC .根据垂径定理的推论，得OE ⊥AB ，AG ＝BG .由题意可得，AC 为⊙O 的直径，AC ＝2 ，则圆的半径是22.根据正方形的性质，得∠OAF ＝45°，∴OG ＝12 ，EG ＝2－12.∵OE ∥AD ，∴△ADF ∽△GEF ，∴FE FD ＝EG DA ＝2－12 .∵△ADF 与△AEF 等高，∴S 1S 2 ＝S △ADF S △AEF＝DF EF ＝2(2 ＋1).第15题解图16. 23 【解析】如解图，连接OD ，BD .∵A (－2，0)，∴OA ＝OB ＝2，∴AB ＝4.∵OC ＝OD ，∴∠OCD ＝∠ODC ＝75°，∴∠DOC ＝180°－2×75°＝30°，∴∠DOB ＝90°－30°＝60°，∴∠DAB ＝12∠DOB ＝30°.∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴AD ＝AB ·cos 30°＝23 .第16题解图。

九年级上册物理总复习试卷【含答案】

九年级上册物理总复习试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪种现象属于光的反射？A. 彩虹B. 镜子中的倒影C. 太阳光直线传播D. 眼镜的放大效果2. 关于能量守恒定律，下列哪项是正确的？A. 能量可以从一个物体转移到另一个物体，但总能量不变B. 能量可以从一种形式转换为另一种形式，但总能量减少C. 能量可以从一个物体转移到另一个物体，但总能量增加D. 能量可以从一种形式转换为另一种形式，但总能量增加3. 下列哪种物质的比热容最大？A. 水B. 铝C. 铜D. 铁4. 关于电阻的计算公式，下列哪项是正确的？A. R = V/IB. R = I/VC. R = V^2/ID. R = I^2/V5. 下列哪种现象属于光的折射？A. 镜子中的倒影B. 彩虹C. 太阳光直线传播D. 眼镜的放大效果二、判断题（每题1分，共5分）1. 力可以改变物体的运动状态。

（）2. 光的传播速度在真空中是最慢的。

（）3. 电流的方向是由正电荷向负电荷流动的。

（）4. 物体的质量越大，其惯性越小。

（）5. 在串联电路中，电流在各个电阻上是相等的。

（）三、填空题（每题1分，共5分）1. 力的单位是______。

2. 光在真空中的传播速度是______。

3. 电流的单位是______。

4. 热量的计算公式是______。

5. 电阻的单位是______。

四、简答题（每题2分，共10分）1. 简述牛顿第一定律。

2. 简述光的反射定律。

3. 简述串联电路和并联电路的区别。

4. 简述能量守恒定律。

5. 简述电阻的定义及其计算公式。

五、应用题（每题2分，共10分）1. 一个物体质量为2kg，受到一个10N的力作用，求其加速度。

2. 一束光从空气斜射入水中，入射角为45度，求折射角。

3. 一个电阻为10Ω的电阻器，通过它的电流为0.5A，求其电压。

4. 一个物体吸收了100J的热量，其比热容为0.2J/(g·℃)，质量为200g，求其温度变化。

小学奥数之几何概念复习

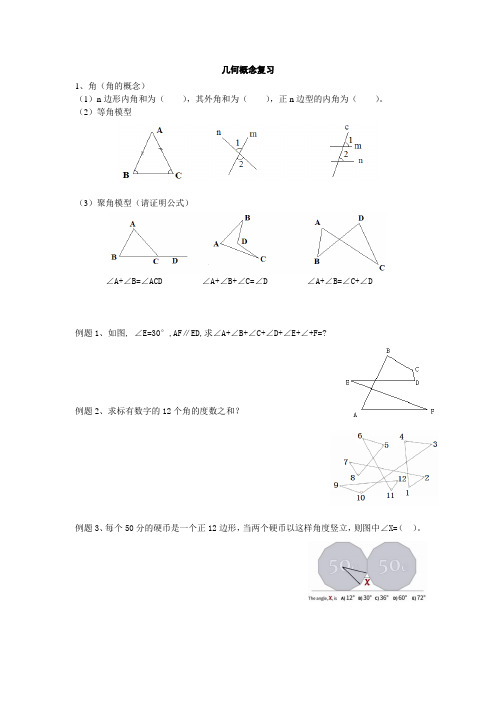
几何概念复习1、角（角的概念）（1）n边形内角和为（），其外角和为（），正n边型的内角为（）。

（2）等角模型（3）聚角模型（请证明公式）∠A+∠B=∠ACD ∠A+∠B+∠C=∠D ∠A+∠B=∠C+∠D例题1、如图, ∠E=30°,AF∥ED,求∠A+∠B+∠C+∠D+∠E+∠+F=?例题2、求标有数字的12个角的度数之和？例题3、每个50分的硬币是一个正12边形，当两个硬币以这样角度竖立，则图中∠X=（）。

2、求面积图形的若干一半模型（用阴影画出）3、求复杂图形的面积（1）、毕克定理正方形格点S=(N+L/2-1)·单三角形格点S=(2N+L-2)·单例1、例题1、正方形格点的面积为1，求⊿ACD的面积。

（2）平移和旋转（全等三角形）（3）空白和阴影对比法，结合和差公式。

（4）特殊四边形的面积例2、如图，如果长方形ABCD的面积为56 cm2，那么四边形MNPQ的面积为（）cm2。

例3、如图，甲乙丙丁四个长方形拼成一个正方形EFGH，中间阴影为正方形。

已知甲乙丙丁四个长方形的面积和为54 cm2，四边形ABCD的面积为37 cm2，求正方形EFGH的面积及甲、乙、丙、丁四个长方形的周长总和。

2、三角形三角形的内角和为（），外角和为（）。

等腰三角形的特点：（1）（2）（3）直角三角形：（1）、勾股定理：。

（2）、勾股定理逆定理：。

（3）、特殊直角三角形：【巩固1】、如图，RTΔABC，AB=AC,AD=BD,斜边AB=a，则ΔABC的面积为多少？【巩固2】如图，RTΔABC，∠A=30°, AD=BD,斜边AB=a，则ΔABC的面积为多少？【巩固3】已知一个直角三角形的两边长分别为5和12，则第三边长的平方是多少？巧求多边形的周长和面积【巩固3】正方形的边长为10，E、F、G、H分别是边长的中点，则阴影部分的面积为（）。

【巩固4】一个正方形，边长增加8 cm，其面积就增加256 cm2，问原来这个正方形的面积是多少？【巩固5】如图，RT⊿ABC中，AB=3，AC=4，点D、E、F、G、N、I都在长方形KLMJ上，且ABED、ACNI、BCGF都是正方形，则KLMJ面积为( ).【巩固5】有一个正方形（如图），把它分成8个小长方形，它们的周长之和为120cm，那么这个正方形的面积是多少？【巩固6】3.用4个相同的等腰直角三角形相互交迭拼成下图，阴影正方形的面积是（）平方厘米。

6年级上册数学复习试卷【含答案】

6年级上册数学复习试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个数字是偶数？A. 3B. 4C. 5D. 62. 一个正方形的四条边相等，那么它的周长是？A. 边长的两倍B. 边长的三倍C. 边长的四倍D. 边长的五倍3. 下列哪个图形是平行四边形？A. 矩形B. 三角形C. 圆形D. 正方形4. 下列哪个数是质数？A. 12B. 13C. 15D. 185. 一个长方形的长是10厘米，宽是5厘米，那么它的面积是？A. 50平方厘米B. 60平方厘米C. 70平方厘米D. 80平方厘米二、判断题（每题1分，共5分）1. 1+1=3 （）2. 9是3的平方。

（）3. 圆的周长等于直径的两倍。

（）4. 长方形的长和宽相等时，它就是一个正方形。

（）5. 0是最小的自然数。

（）三、填空题（每题1分，共5分）1. 一个正方形的边长是6厘米，那么它的周长是____厘米。

2. 2的立方是____。

3. 一个长方形的长是8厘米，宽是4厘米，那么它的面积是____平方厘米。

4. 下列哪个数是偶数？____。

5. 下列哪个数是质数？____。

四、简答题（每题2分，共10分）1. 请简述长方形和正方形的区别。

2. 什么是质数？请举例说明。

3. 什么是偶数？请举例说明。

4. 请简述平行四边形的特征。

5. 请简述圆的周长和面积的计算公式。

五、应用题（每题2分，共10分）1. 一个长方形的长是10厘米，宽是5厘米，求它的面积。

2. 一个正方形的周长是24厘米，求它的边长。

3. 请计算下列数的和：2+3+4+5+6。

4. 请计算下列数的差：9-4。

5. 请计算下列数的乘积：3×4。

六、分析题（每题5分，共10分）1. 小明有10个苹果，他吃掉了3个，然后又买了5个，请问他现在有多少个苹果？2. 一个长方形的长是8厘米，宽是4厘米，求它的周长和面积。

七、实践操作题（每题5分，共10分）1. 请画出一个边长为6厘米的正方形，并计算它的周长和面积。

八上物理期末复习(概念总汇)

八上物理期末复习卷（概念总汇）第一章声现象第一课时声音是什么1.声音是由物体______产生的。

正在发生的物体叫作______.2.声音可以在______、______和______中传播，但不能在______中传播。

3.声音是一种______,我们把它叫作______.当______传入人耳时，引起鼓膜______,进而人就听到了声音，而回声是由于____________形成的。

4.声音在不同的物体中传播的速度是______(相同/不同)的。

通常情况下，声音在______中传播的最快，在______中次之，在______中传播得最慢，空气中的声速大约是______m/s。

5.声音具有______，这种能量叫作______。

第二课时乐音的特性1.音乐悦耳动听、令人愉快，被称为___音，它是由声源做______振动产生的，可以用______、______和______来描述它的特性。

2.物理学中，把声音的______叫作响度，响度与声源的______有关，振幅越大，响度越___。

3.声音的______叫作音调。

音调与声源振动的______有关，频率越高，音调越___。

4.频率表示声源振动的______，声源______振动的次数叫作频率。

频率的单位是______，简称___，符号为____。

5.______是人们能够分辨声音的依据。

它是由发声体的______，______等因素决定的。

第三课时噪声及其控制1.噪声通常是指那些刺耳难听、令人______的声音。

它是声源做_________振动产生的。

从环境保护的角度看，凡是影响人们正常__________________的声音都属于噪声。

2.噪声的四大主要来源是______噪声、______噪声、______噪声和______噪声。

3.在声学上人们用_________为单位表示声音的强弱。

人耳刚刚能听到的声音为______，要使人感觉安静舒适，应控制噪声不超过______；为了不对他人交谈造成干扰，应控制噪声不超过______；为了保护听力，应控制噪声不超过______。

六年级英语复习试卷【含答案】

六年级英语复习试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个单词的发音与其他不同？A. catB. dogC. fishD. bird2. 选择正确的时态填空：I _______ to the park yesterday.A. goB. wentC. goesD. will go3. “She _______ her homework every day.” 选择正确的词组。

A. doB. doesC. doingD. to do4. 下列哪个单词表示“快乐”？A. sadB. happyC. angryD. tired5. 选择正确的单词填空：My mother is a _______. She works in a hospital.A. doctorB. teacherC. driverD. cook二、判断题（每题1分，共5分）1. “He likes playing football.” 这个句子是正确的。

（）2. “She don’t have a pen.” 这个句子是正确的。

（）3. “Can I help you?” 是一个疑问句。

（）4. “I am read a book.” 这个句子是正确的。

（）5. “They are watching TV now.” 表示过去进行时。

（）三、填空题（每题1分，共5分）1. I _______ (be) a student. I _______ (go) to school every day.2. She _______ (like) _______ (read) books.3. _______ (This) is my mother. _______ (She) is a teacher.4. We _______ (watch) a movie last night. It _______ (be) very interesting.5. They _______ (not have) any classes tomorrow.四、简答题（每题2分，共10分）1. 写出五种常见的交通工具。

高考数学模拟复习试卷试题模拟卷第01节集合的概念及其基本运算1 3

高考模拟复习试卷试题模拟卷第01节集合的概念及其基本运算A 基础巩固训练1.【高考新课标1，文1】已知集合{32,},{6,8,10,12,14}A x x n n N B ==+∈=，则集合A B 中的元素个数为( )（A ） 5 （B ）4 （C ）3 （D ）22.【高考浙江，文1】已知集合{}223x x x P =-≥，{}Q 24x x =<<，则Q P =（）A ．[)3,4B ．(]2,3C ．()1,2-D ．(]1,3- 3.【福州市三中模拟】已知集合，，若，则实数的取值范围是（） A ．B ．C ．D ．4.【冀州中学高三上学期第一次月考，文1】若集合{}0P y y =≥，P Q Q =，则集合Q 不可能是（）A ．∅B ．{}2,R y y x x =∈C ．{}2,R xy y x =∈D ．{}2log ,0y y x x =>5.【重点中学高三上学期第三次月考，理1】已知全集{}1,2,3,4,5,6,7,8,9U = 集合{}1,2,3,4,5,6A = 集合{}3,4,5,6,7,8B =，则集合B C A C U U ⋂为（）A ． {}3,4,5,6B ． {}1,2,7,8,9C ． {}1,2,3,4,5,6,7,8D ． {}9 B 能力提升训练1.定义集合A 与B 的运算“*”为:{A B x x A *=∈或x B ∈,但}x A B ∉.设X 是偶数集,{1,2,3,4,5}Y =,则()X Y Y **=（） A.X B.Y C.XY D.X Y2．下列四个集合中，是空集的是（）A ．{}3|3x x +=B ．22{|}x y y x x y R =∈（，）﹣，， C ．21{|0}x x x x R +=∈﹣， D ．2{|}0x x ≤3．设集合{}1,0,2A =-，集合{}2B x x A x A =-∈-∉且，则B =（）（A ）{}1 （B ）{}2- （C ）{}1,2-- （D ）{}1,0-4．【·海安中学模拟】已知集合A ＝{(x ，y)|x2＋y2＝1}，B ＝{(x ，y)||x|＋|y|＝λ}，若A ∩B ≠∅，则实数λ的取值范围是________．5．已知集合A ＝{x|4≤x2≤16}，B ＝[a ，b]，若A ⊆B ，则实数a －b 的取值范围是（） A. (－∞，－2]B.[)+∞-,2 C. (－∞，2]D.[)+∞,2 C 思维拓展训练1．【湖北八校联考文】已知M=3(,)|3,{(,)|20}2y x y N x y ax y a x -⎧⎫==++=⎨⎬-⎩⎭且M N =∅，则a =（）A ．6或2B ．6C ．2或6D ．22．【广东汕头市二模】设非空集合M 同时满足下列两个条件： ①{}1,2,3,,1M n ⊆⋅⋅⋅⋅⋅⋅-；②若a M ∈，则n a M -∈，(2,)n n N +≥∈．则下列结论正确的是（） A ．若n 为奇数，则集合M 的个数为122n - B ．若n 为奇数，则集合M 的个数为122n +C ．若n 为偶数，则集合M 的个数为22n D ．若n 为偶数，则集合M 的个数为221n - 3．设数集M 同时满足条件①M 中不含元素1,0,1-，②若a M ∈，则11aM a+∈-. 则下列结论正确的是 ( )（A ）集合M 中至多有2个元素；（B ）集合M 中至多有3个元素；（C ）集合M 中有且仅有4个元素；（D ）集合M 中有无穷多个元素. 4．【其中总动员】设集合(){}(){},|||||1,,()()0A x y x y B x y y x y x =+≤=-+≤，M AB =，若动点(,)P x y M ∈，则22(1)x y +-的取值范围是（）A ．15[,]22B ．25[,]22 C ．110[,]22 D ．210[,]225．已知集合()(){},M x y y f x ==，若对于任意()11,x y M∈，存在()22,x y M ∈，使得12120x x y y +=成立，则称集合M 是“垂直对点集”.给出下列四个集合：①()1,M x y y x ⎧⎫==⎨⎬⎩⎭； ②(){},sin 1M x y y x ==+；则以下选项正确的是（）(A)①是“垂直对点集” ，②不是“垂直对点集” (B)①不是“垂直对点集”，②是“垂直对点集” (C)①②都是“垂直对点集” (D) ①②都不是“垂直对点集”高考模拟复习试卷试题模拟卷第八章直线与圆一．基础题组1.（重庆市巴蜀中学高三月考数学、文、1）若直线210ax y ++=与直线20x y +-=互相垂直，那么a 的值等于( )A ．1B ．13-C ．23-D ．2- 2.（文昌中学高三模拟考试、文、15）圆心在直线x －2y ＝0上的圆C 与y 轴的正半轴相切，圆C 截x 轴所得弦的长为23，则圆C 的标准方程为________________．3.（重庆市巴蜀中学高三月考数学、文、15）在平面直角坐标系xOy 中，以点)0,1(为圆心且与直线)(012R m m y mx ∈=---相切的所有圆中，半径最大的圆的标准方程为.4.（重庆市部分区县高三上学期入学考试、文、16）若实数c b a ,,成等差数列，点)0,1(-P 在动直线0:==+c by ax l 上的射影为M ，点)3,0(N ，则线段MN 长度的最小值是．二．能力题组1.(五校协作体高三上学期期初考试数学、文、9)曲线21y x =+在点（1，2）处的切线为l ，则直线l 上的任意点P 与圆22430x y x +++=上的任意点Q 之间的最近距离是（）A.4515- B.2515- C.51- D.2 2.(示范高中高三第一次联考、文、14）已知圆的方程为()2214x y +-=。

信息论复习题

信息论概念复习题一、填空1、 1948 年，美国数学家香农发表了题为“通信的数学理论”的长篇论文，从而创立了信息论。

2、人们研究信息论的目的是为了高效、可靠、安全地交换和利用各种各样的信息。

3、信息的可度量性是建立信息论的基础。

4、统计度量是信息度量最常用的方法。

5、熵是香农信息论最基本最重要的概念。

6、事物的不确定度是用时间统计发生概率的对数来描述的。

7、单符号离散信源一般用随机变量描述，而多符号离散信源一般用随机矢量描述。

8、一个随机事件发生某一结果后所带来的信息量称为自信息量，定义为其发生概率对数的负值。

9、自信息量的单位一般有比特、奈特和哈特。

10、必然事件的自信息是 0 。

11、不可能事件的自信息量是∞ 。

12、两个相互独立的随机变量的联合自信息量等于两个自信息量之和。

13、当消息经过多级处理后，随着处理器数目的增多，输入消息与输出消息之间的平均互信息量趋于变小。

14、离散平稳无记忆信源 X 的 N 次扩展信源的熵等于离散信源 X 的熵的 N 倍。

15、离散平稳有记忆信源的极限熵，H = lim H(X N / X1 X2 …X N 1)N 。

16、对于 n 元 m 阶马尔可夫信源，其状态空间共有 n m 个不同的状态。

17、一维连续随即变量 X 在[a，b]区间内均匀分布时，其信源熵为 log2 (b-a ) 。

118、平均功率为 P 的高斯分布的连续信源，其信源熵， H c () = 2 log 2 2eP 。

19、对于限峰值功率的连续信源，当概率密度均匀分布时连续信源熵具有最大值。

20、对于限平均功率的一维连续信源，当概率密度高斯分布时，信源熵有最大值。

22、根据输入输出信号的特点，可将信道分成离散信道、连续信道、半离散或半连续信道。

23、信道的输出仅与信道当前输入有关，而与过去输入无关的信道称为无记忆信道。

24、具有一一对应关系的无噪信道的信道容量 C= log 2 n 。

25、对称信道的信道容量 C= log 2 m-H mi 。

2024届新高考数学复习：专项(导数的概念及运算)历年好题练习(附答案)

2024届新高考数学复习：专项（导数的概念及运算）历年好题练习[基础巩固]一、选择题1．若f (x )＝2xf ′(1)＋x 2，则f ′(0)等于( )A ．2B ．0C ．－2D ．－42．已知函数f (x )＝g (x )＋2x 且曲线y ＝g (x )在x ＝1处的切线方程为y ＝2x ＋1，则曲线y ＝f (x )在x ＝1处的切线的斜率为( )A ．2B ．4C ．6D ．83．已知曲线y ＝a e x ＋x ln x 在点(1，a e)处的切线方程为y ＝2x ＋b ，则( )A ．a ＝e ，b ＝－1B ．a ＝e ，b ＝1C ．a ＝e －1，b ＝1D ．a ＝e －1，b ＝－14．在等比数列{a n }中，a 1＝2，a 8＝4，函数f (x )＝x (x －a 1)ꞏ(x －a 2)ꞏ…ꞏ(x －a 8)，则f ′(0)＝( )A ．26B ．29C ．212D ．2155．设函数f (x )＝x 3＋(a －1)x 2＋ax ，若f (x )为奇函数，则曲线y ＝f (x )在点(0，0)处的切线方程为( )A ．y ＝－2xB ．y ＝－xC ．y ＝2xD ．y ＝x6．已知曲线y ＝x 24 －3ln x 的一条切线的斜率为－12 ，则切点的横坐标为( )A ．3B ．2C ．1D ．127．f ′(x )是f (x )＝sin x ＋a cos x 的导函数，且f ′⎝⎛⎭⎫π4 ＝2 ，则实数a 的值为( ) A ．23 B ．12C ．34D ．18．已知曲线y ＝x ＋ln x 在点(1，1)处的切线与二次曲线y ＝ax 2＋(a ＋2)x ＋1相切，则a 等于( )A ．－2B ．0C ．1D ．89．函数f (x )的定义域为R ，f (－1)＝2，对于任意x ∈R ，f ′(x )>2，则f (x )>2x ＋4的解集为( )A ．(－1，1)B ．(－1，＋∞)C ．(－∞，－1)D ．(－∞，＋∞)二、填空题10．已知物体运动的位移s与时间t之间的函数关系式为s＝12t3－t，则当t＝2时，该物体的瞬时速度为________．11．已知函数f(x)＝e x ln x，f′(x)为f(x)的导函数，则f′(1)的值为________．12．若曲线y＝e－x在点P处的切线与直线2x＋y＋1＝0平行，则点P的坐标是________．[强化练习]13．函数f(x)＝x4－2x3的图象在点(1，f(1))处的切线方程为()A．y＝－2x－1 B．y＝－2x＋1C．y＝2x－3 D．y＝2x＋114．(多选)已知函数f(x)＝－x3＋2x2－x，若过点P(1，t)可作曲线y＝f(x)的三条切线，则t的取值可以是()A．0 B．1 27C．128D．12915．已知e是自然对数的底数，函数f(x)＝(x－1)e x＋3e的图象在点(1，f(1))处的切线为l，则直线l的横截距为________．16．[2022ꞏ新高考Ⅰ卷]若曲线y＝(x＋a)e x有两条过坐标原点的切线，则a的取值范围是________．参考答案1．D ∵f (x )＝2xf ′(1)＋x 2，∴f ′(x )＝2f ′(1)＋2x ，∴f ′(1)＝2f ′(1)＋2，∴f ′(1)＝－2，∴f (x )＝－4x ＋x 2，∴f ′(x )＝－4＋2x ，∴f ′(0)＝－4.2．B ∵曲线y ＝g (x )在点(1，g (1))处的切线方程为y ＝2x ＋1，∴g ′(1)＝2.∵函数f (x )＝g (x )＋2x ，∴f ′(x )＝g ′(x )＋2＝g ′(1)＋2，∴f ′(1)＝2＋2＝4，即曲线y ＝f (x )在x ＝1处的切线的斜率为4.故选B.3．D 因为y ′＝a e x ＋ln x ＋1，所以当x ＝1时，y ′＝a e ＋1，所以曲线在点(1，a e)处的切线方程为y －a e ＝(a e ＋1)(x －1)，即y ＝(a e ＋1)x －1，所以⎩⎪⎨⎪⎧a e ＋1＝2，b ＝－1，解得⎩⎪⎨⎪⎧a ＝e －1b ＝－1. 4．C ∵函数f (x )＝x (x －a 1)(x －a 2)ꞏ…ꞏ(x －a 8)，∴f ′(x )＝(x －a 1)(x －a 2)ꞏ…ꞏ(x －a 8)＋x [(x －a 1)(x －a 2)ꞏ…ꞏ(x －a 8)]′，∴f ′(0)＝a 1a 2…a 8＝(a 1a 8)4＝84＝212.5．D ∵f (x )＝x 3＋(a －1)x 2＋ax 为奇函数，∴a －1＝0，得a ＝1，∴f (x )＝x 3＋x ，∴f ′(x )＝3x 2＋1，∴f ′(0)＝1，则曲线y ＝f (x )在点(0，0)处的切线方程为y ＝x ，故选D.6．B 令y ′＝2x 4 －3x ＝－12 ，解得x ＝－3(舍去)或x ＝2.故切点的横坐标为2，故选B.7．B ∵f ′(x )＝cos x －a sin x ，∴f ′⎝⎛⎭⎫π4 ＝22 －22 a ＝24 ，得a ＝12 . 8．D 由y ＝x ＋ln x ，得y ′＝1＋1x ，∴当x ＝1时，y ′＝2，∴切线方程为y －1＝2(x －1)，即y ＝2x －1，由⎩⎪⎨⎪⎧y ＝2x －1，y ＝ax 2＋（a ＋2）x ＋1，得ax 2＋ax ＋2＝0，由题意得⎩⎪⎨⎪⎧a ≠0，Δ＝a 2－8a ＝0，得a ＝8. 9．B 设g (x )＝f (x )－2x －4，g ′(x )＝f ′(x )－2，由题意得g ′(x )>0恒成立，∴g (x )在(－∞，＋∞)上单调递增，又g (－1)＝f (－1)－2×(－1)－4＝0，又f (x )>2x ＋4等价于g (x )>0，∴原不等式的解为x >－1.10．5答案解析：由题知s ′＝32 t 2－1，故当t ＝2时，该物体的瞬时速度为32 ×22－1＝5.11．e答案解析：f ′(x )＝e x ꞏln x ＋e x x ，∴f ′(1)＝e.12．(－ln 2，2)答案解析：∵y ＝e －x ，∴y ′＝－e －x ，设P (x 0，y 0)，由题意得－e －x 0＝－2，∴e －x 0＝2，∴－x 0＝ln 2，x 0＝－ln 2，∴P (－ln 2，2).13．B f ′(x )＝4x 3－6x 2，则f ′(1)＝－2，易知f (1)＝－1，由点斜式可得函数f (x )的图象在(1，f (1))处的切线方程为y －(－1)＝－2(x －1)，即y ＝－2x ＋1.故选B.14．CD ∵f (x )＝－x 3＋2x 2－x ，∴f ′(x )＝－3x 2＋4x －1.由已知得，过点P (1，t )作曲线y ＝f (x )的三条切线，情况如下：①点P (1，t )在曲线上，此时切点为P (1，t )，把P 点坐标代入函数答案解析式可得P (1，0)，利用切线公式得y ＝f ′(1)(x －1)，所以切线为x 轴，但此时切线只有一条，不符合题意．②点P (1，t )不在曲线上，设切点为(x 0，y 0)，又切线经过点P (1，t )，所以切线方程为y －t ＝f ′(x 0)(x －1). 因为切线经过切点，所以y 0－t ＝(－3x 20 ＋4x 0－1)(x 0－1).又因为切点在曲线上，所以y 0＝－x 30 ＋2x 20 －x 0.联立方程得化简得t ＝2x 30 －5x 20 ＋4x 0－1. 令g (x )＝2x 3－5x 2＋4x －1，即t ＝g (x )有三个解，即直线y ＝t 与y ＝g (x )的图象有三个交点．令g ′(x )＝6x 2－10x ＋4＝2(x －1)(3x －2)＝0，可得两极值点为x 1＝1，x 2＝23 .所以x ∈⎝⎛⎭⎫－∞，23 和(1，＋∞)时，g (x )单调递增，x ∈⎝⎛⎭⎫23，1 时，g (x )单调递减，所以当g (1)＝0＜t ＜127 ＝g ⎝⎛⎭⎫23 时，满足直线y ＝t 与y ＝g (x )的图象有三个交点，而0＜129 ＜128 ＜127 ，故选CD.15．－2答案解析：因为f ′(x )＝e x ＋(x －1)e x ＝x e x ，所以切线l 的斜率为f ′(1)＝e ，由f (1)＝3e 知切点坐标为(1，3e)，所以切线l 的方程为y －3e ＝e(x －1).令y ＝0，解得x ＝－2，故直线l 的横截距为－2.16．(－∞，－4)∪(0，＋∞)答案解析：设切线的切点坐标为(x 0，y 0).令f (x )＝(x ＋a )e x ，则f ′(x )＝(x ＋1＋a )e x ，f ′(x 0)＝(x 0＋1＋a )e x 0.因为y 0＝(x 0＋a )e x 0，切线过原点，所以f ′(x 0)＝y 0x 0，即(x 0＋1＋a )ꞏe x 0＝（x 0＋a ）e x 0x 0.整理，得x 20 ＋ax 0－a ＝0.由题意知该方程有两个不同的实数根，所以Δ＝a 2＋4a ＞0，解得a ＜－4或a ＞0.。

人工智能基础概念复习题(含参考答案)

人工智能基础概念复习题（含参考答案）一、单选题（共60题，每题1分，共60分）1、以下（）的说法是正确。

A、术语NOSQ1可以理解为"NotOn1ySQ1,,的缩写B、NOSQ1数据库属于关系数据库技术C、术语NOSQ1是"No!SQ1”的缩写D、NOSQ1数据库始终遵循ACID原则正确答案：A2、输入32*32的图像，用大小5*5的卷积核做步长为1的卷积计算,输出图像的大小是A、29*29B、28*28C、23*23D、28*23正确答案：B3、绝大多数统计和数据挖掘算法是按照（）来实现的。

A、关系型B、实践型C、参考型D、互联型正确答案：A4、（）模型是一种生成式有向图模型，主要用于处理离散型的数据，在信息检索、自然语言处理等领域有广泛应用。

A、话题模型B、数据模型C、信息模型D、语言模型正确答案：A5、（）是一类用图来表达变量相关关系的概率模型。

A、概率图模型B、变量图模型C、隐马尔可夫模型D、以上都不对正确答案：A6^2019年，DeepMind开发出一种()来近似计算薛定谓方程，在精度和准确性上都满足科研标准，为深度学习在量子化学领域的发展奠定了基础，A、费米神经网络B、深度神经网络C、卷积神经网络D、循环神经网络正确答案：A7、()是规则的置信度与先导的置信度之间的绝对差。

A、置信度值Bs标准差C、信息差D、置信度差正确答案：D8、标准正态分布的均数与标准差是()。

A、0,0B、1,1C、0,1D、1,0正确答案：C9、对于线性不可分的数据，支持向量机的解决方式是()A、核函数B、软间隔C、以上选项均不正确D、硬间隔正确答案：A10、HadooP的作者是下面哪一位()。

A、DougcuttingBsMartinFow1erC、GraceHopperD^KentBeck正确答案：A11、关于用4V来表示大数据的主要特征，描述错误的是A、大数据的时间分布往往不均匀，近几年生成数据的占比最高B、数据类型的多样性往往导致数据的异构性，进而加大数据处理的复杂性，对数据处理能力提出了更高要求C、数据价值与数据量之间存在线性关系D、“如何从海量数据中洞见（洞察）出有价值的数据”是数据科学的重要课题之一正确答案：C12、如果一个SVM模型出现欠拟合，那么下列哪种方法能解决这一问题？OA、增大惩罚参数C的值B、减小惩罚参数C的值C、减小核系数（gamma参数）正确答案：A13、以下卷积神经网络模型中，最早用于手写数字识别的是OA^A1exNetB、R esNet50C、ResNet152D^1eNet-5正确答案：D14、O作为第四次工业革命的核心，其前沿算法和基础理论正在发生巨大变化。

人工智能基础概念复习题含参考答案

人工智能基础概念复习题含参考答案一、单选题（共60题，每题1分，共60分）1、决策树中，同一路径上的所有属性之间是()关系A、逻辑与B、因果C、逻辑或D、相关正确答案：A2、CRISP-DM将数据挖掘的过程抽象为四个层次：阶段、一般任务、（）和过程实例A、分析B、建模C、具体任务D、规划正确答案：C3、智能机器人可以根据（）得到信息。

A、感知能力B、学习能力C、思维能力D、行为能力正确答案：A4、学习器的实际预测输出与样本的真实输出之间的差异称为A、精度B、误差C、查准率D、错误率正确答案：B5、（）是将人类语言经过处理转化为机器所能理解语言的一门技术。

A、大数据B、自然语言处理C、语音识别D、计算机视觉正确答案：B6、大数据的最显著特征是()A、数据价值密度高B、数据处理速度快C、数据类型多样D、数据规模大正确答案：D7、假设你在卷积神经网络的第一层中有5个卷积核，每个卷积核尺寸为7×7，具有零填充且步幅为1。

该层的输入图片的维度是224×224×3。

那么该层输出的维度是多少？()A、217x217x3B、218x218x5C、220x220x7D、217x217x8正确答案：B8、图像灰度的方差表示图像的哪种属性A、图像细节B、图像饱和度C、图像整体亮度D、图像对比度正确答案：D9、专用人工智能的简称是（）。

A、AIGB、AINC、ANID、AGI正确答案：C10、数据管理以()活动为基础。

A、数据预处理B、数据处理C、数据分析D、数据可视化正确答案：A11、避免由于过拟合造成貌似线性可分的结果，一个解决的办法是允许支持向量机在一些样本上出错，为此引入()的概念。

A、正则化B、软间隔C、核函数D、硬间隔正确答案：B12、有三种方法可以帮助决策者确定决策的作用：（）、场景分析和What-If分析A、回归分析B、测试C、建模D、假设分析正确答案：B13、关于表述数据可视化在数据科学中重要地位说法中，下列不正确的是()。

专题3 函数概念与性质(解析版)

2020-2021学年高一数学期末复习专题强化卷（人教A版2019必修第一册）专题3 函数概念与性质一、选择题：（本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1.函数f(x)=ln2−x2+x的图象关于（）对称．A.x轴B.y轴C.原点D.y=x【答案】C【解析】解：要使函数有意义，则2−x2+x>0，即（x﹣2）（x+2）＜0，解得﹣2＜x＜2，则定义域关于原点对称．又f（﹣x）=ln 2+x2−x =﹣ln 2−x2+x=−f(x)，∴函数f（x）是奇函数，图象关于原点对称，故选：C．2.设函数f(x)={2x,x<0g(x),x>0若f（x）是奇函数，则g（2）的值是（）A.−14B.﹣4 C.14D.4【答案】A【解析】解：∴f（x）为奇函数，x＜0时，f（x）=2x，∴x＞0时，f（x）=﹣f（﹣x）=﹣2﹣x= −12x，即g(x)=−12x ，g(2)=−14．故选A．3.下列函数中，既是奇函数，又是增函数是（）A.f（x）=x|x|B.f（x）=﹣x3C.f（x）= sinx(x∈[0,π2]) D.f（x）= lnxx【答案】A【解析】解：由f（﹣x）=﹣x|﹣x|=﹣x|x|=﹣f（x），知函数f（x）=x|x|为奇函数，又f（x）=x|x|= {x2(x>0)−x2(x<0)当x＞0时，f（x）=x2在（0，+∞）上为增函数，根据奇函数图象关于原点中心对称，所以当x＜0时，f （x）=﹣x2在（﹣∞，0）上也为增函数，所以函数f（x）=x|x|在定义域内既是奇函数，又是增函数，故A 正确．∴2＞1，而﹣23＜﹣13，所以函数f（x）=x3在定义域内不是增函数，故B不正确．∴ x∈[0,π2]不关于原点对称，∴f（x）=sinx (x∈[0,π2])在给定的定义域内不是奇函数，故C不正确．∴f（x）= lnxx 的定义域为{x|x＞0}，不关于原点对称，所以函数f（x）= lnxx在定义域内不是奇函数，故D不正确．故选A．4.已知函数y=f（x）在R上为奇函数，且当x≥0时，f（x）=x2﹣2x，则当x＜0时，f（x）的解析式是（）A.f（x）=﹣x（x+2）B.f（x）=x（x﹣2）C.f（x）=﹣x（x﹣2）D.f（x）=x（x+2）【答案】A【解析】解：任取x＜0则﹣x＞0，∴x≥0时，f（x）=x2﹣2x，∴f（﹣x）=x2+2x，①又函数y=f（x）在R上为奇函数∴f（﹣x）=﹣f（x）②由①②得x＜0时，f（x）=﹣x（x+2）故选A5.若幂函数y=f(x)的图象过点(3,13)，则f(1)为（）A.13B.12C.1D.2【答案】C【解析】设,因为幂函数的图象过点,所以所以,所以.选C。

复习验收卷(二)函数概念与基本初等函数Ⅰ

复习验收卷(二) 函数概念与基本初等函数Ⅰ(时间：120分钟满分：150分)一、单项选择题(本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.已知函数y ＝2x ＋1，x ∈{x ∈Z|0≤x ＜3}，则该函数的值域为( )A.{y |1≤y ＜7}B.{y |1≤y ≤7}C.{1，3，5，7}D.{1，3，5}答案 D解析由题意可知，函数的定义域为{0，1，2}，把x ＝0，1，2代入函数解析式可得y ＝1，3，5，所以该函数的值域为{1，3，5}，故选D.2.定义在R 上的奇函数f (x )满足f (x )＝x 2－2x (x ≥0)，则函数f (x )的零点个数为( )A.0B.1C.2D.3答案 D解析依题意，当x ＞0时，由f (x )＝x 2－2x ＝0得x ＝2，即函数f (x )的一个零点为x ＝2.又函数f (x )为奇函数，于是－2也是函数f (x )的一个零点，又f (0)＝0，因此函数f (x )的零点个数为3，故选D.3.已知偶函数f (x )在区间[0，＋∞)上单调递增，则满足f (2x －1)＜f ⎝ ⎛⎭⎪⎫13的x 的取值范围是( )A.⎝ ⎛⎭⎪⎫13，23 B.⎣⎢⎡⎭⎪⎫13，23 C.⎝ ⎛⎭⎪⎫12，23 D.⎣⎢⎡⎭⎪⎫12，23答案 A解析由于函数f (x )在区间[0，＋∞)上单调递增，且f (x )为偶函数，则由f (2x －1)＜f ⎝ ⎛⎭⎪⎫13得f (|2x －1|)＜f ⎝ ⎛⎭⎪⎫13，即有－13＜2x －1＜13，解得13＜x ＜23.故x 的取值范围是⎝ ⎛⎭⎪⎫13，23.4.(2020·北京海淀区一模)形如22n ＋1(n 是非负整数)的数称为费马数，记为F n ，数学家费马根据F 0，F 1，F 2，F 3，F 4都是质数提出了猜想：费马数都是质数.多年之后，数学家欧拉计算出F 5不是质数，那F 5的位数是( )(参考数据：lg 2≈0.301 0) A.9 B.10C.11D.12答案 B解析 F 5＝232＋1，设m ＝232，则两边取常用对数得lg m ＝lg 232＝32lg 2＝32×0.301 0＝9.632.m ＝109.632＝109×100.632，所以F 5＝109×100.632＋1，又1＜100.632＜10，故F 5是10位数.5.将甲桶中的a 升水缓慢注入空桶乙中，t min 后甲桶剩余的水量符合指数衰减曲线y ＝a e nt .假设过5 min 后甲桶和乙桶的水量相等，若再过m min 甲桶中的水只有a4升，则m 的值为( )A.5B.6C.8D.10答案 A解析根据题意知，因为5 min 后甲桶和乙桶的水量相等，所以函数f (t )＝a e nt 满足f (5)＝a e 5n ＝12a ，可得n ＝15ln 12，设当k min 后甲桶中的水只有a4升，所以f (k )＝a 4，即15ln 12·k ＝ln 14，所以15ln 12·k ＝2ln 12，解得k ＝10，所以k －5＝5，即m ＝5，故选A.6.(2021·安徽联盟联考)已知函数f (x )＝10（x 2＋1）x ·e |x |，则函数f (x )的图象大致为( )答案 A解析函数f (x )的定义域为(－∞，0)∪(0，＋∞)，又f (－x )＝10[（－x ）2＋1]－x ·e |－x |＝－10（x 2＋1）x ·e |x |＝－f (x )，故函数f (x )为奇函数，则函数f (x )的图象关于原点对称，排除B ，因为f (1)＝20e >0，且f (5)＝52e 5<1，所以排除C ，D ，选A.7.设函数f (x )＝x 3＋bx 2＋cx ＋d ，若2f (2)＝3f (3)＝4f (4)，则f (5)－13f (1)的值等于( )A.8B.12C.20D.36答案 A解析设2f (2)＝3f (3)＝4f (4)＝k ，则xf (x )－k ＝(x －2)(x －3)(x －4)·(x －p ).令x ＝0，得p ＝－k 24，于是f (1)＝－6＋3k 4，f (5)＝6＋k 4，即f (5)－13f (1)＝8，故选A.8.已知函数f (x )＝⎩⎨⎧ln （x ＋1）（x ≥0），x 3－3x （x <0），若函数y ＝f (x )－k 有三个不同的零点，则实数k 的取值范围是( ) A.(－2，2) B.(－2，1)C.(0，2)D.(1，3)答案 C解析当x <0时，f (x )＝x 3－3x ，则f ′(x )＝3x 2－3，令f ′(x )＝0，所以x ＝－1(舍去正根)，故f (x )在(－∞，－1)上单调递增，在(－1，0)上单调递减，又f (x )＝ln(x ＋1)在[0，＋∞)上单调递增，则函数f (x )的图象如图所示.当x <0时，f (x )极大值＝f (－1)＝2，且f (0)＝0，故当k ∈(0，2)时，y ＝f (x )－k 有三个不同的零点.二、多项选择题(本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分)9.在下列四组函数中，f (x )与g (x )表示同一函数的是( )A.f (x )＝x －1，g (x )＝x 2－1x ＋1B.f (x )＝|x ＋1|，g (x )＝⎩⎨⎧x ＋1，x ≥－1，－1－x ，x <－1C.f (x )＝1，g (x )＝(x ＋1)0D.f (x )＝（x ）2x ，g (x )＝x（x ）2答案 BD解析对于A ，函数f (x )的定义域为R ，g (x )的定义域为{x |x ≠－1}，f (x )与g (x )的定义域不相同，则不是同一函数；对于B ，函数f (x )的定义域为R ，g (x )的定义域为R ，f (x )与g (x )的定义域相同，f (x )＝|x ＋1|＝⎩⎪⎨⎪⎧x ＋1，x ≥－1，－1－x ，x <－1，对应关系相同，则f (x )与g (x )是同一函数；对于C ，函数f (x )的定义域为R ，g (x )的定义域为{x |x ≠－1}，f (x )与g (x )的定义域不相同，则不是同一函数；对于D ，函数f (x )＝（x ）2x ＝1(x >0)，g (x )＝x（x ）2＝1(x >0)的定义域与对应法则均相同，是同一函数，故选BD.10.关于函数f (x )＝－x 2＋2x ＋3的结论正确的是( )A.定义域、值域分别是[－1，3]，[0，＋∞)B.单调增区间是(－∞，1]C.定义域、值域分别是[－1，3]，[0，2]D.单调增区间是[－1，1] 答案 CD解析由－x 2＋2x ＋3≥0，可得x 2－2x －3≤0，解得－1≤x ≤3，即函数的定义域是[－1，3]，由二次函数的性质可知，y ＝－x 2＋2x ＋3＝－(x －1)2＋4∈[0，4]， ∴函数的值域为[0，2]，结合二次函数的性质可知，函数在[－1，1]上单调递增，在[1，3]上单调递减. 故选CD.11.设x ，y ，z 为正实数，且log 2x ＝log 3y ＝log 5z >0，则下列关系式可能成立的是( )A.x 2<y 3<z5B.z 5<y 3<x 2C.y 3<z 5<x 2D.x 2＝y 3＝z 5答案ABD解析令log2x＝log3y＝log5z＝k>0，则x＝2k>1，y＝3k>1，z＝5k>1，故x 2＝2k－1，y3＝3k－1，z5＝5k－1，若0<k<1时，f(x)＝x k－1在(0，＋∞)上单调递减，则z 5<y3<x2，B项成立.若k＝1时，x2＝y3＝z5＝1，D项成立.若k>1时，则f(x)＝x k－1在(0，＋∞)上单调递增，∴x2<y3<z5，选项A成立.C不成立.12.(2021·福州质检)已知f(x)是定义在R上的偶函数，其图象关于点(1，0)对称.以下关于f(x)的结论正确的有()A.f(x)是周期函数B.f(x)满足f(x)＝f(4－x)C.f(x)在(0，2)上单调递减D.f(x)＝cos πx2是满足条件的一个函数答案ABD解析因为f(x)为偶函数，所以f(－x)＝f(x).又其图象关于点(1，0)对称，所以f(－x)＝－f(2＋x)，所以f(x＋2)＝－f(x)，所以f(x＋4)＝－f(x＋2)＝f(x)，所以函数f(x)是以4为周期的周期函数，故A正确；由题意知，f(－x)＝f(x)＝f(x＋4).又f(x＋4)＝f(－x＋4)，所以f(x)＝f(4－x)，故B正确；函数f(x)＝cos πx2是定义在R上的偶函数，且由πx2＝kπ＋π2(k∈Z)，得x＝2k＋1(k ∈Z)，所以(1，0)是它的一个对称中心，故D 正确；又f (x )在(0，2)上不能确定单调性，故C 错误.综上所述，故选ABD. 三、填空题(本题共4小题，每小题5分，共20分) 13.求值：log 315－12log 325＝________. 答案 1解析 log 315－12log 325＝log 315－log 32512 ＝log 315－log 35＝log 33＝1.14.若函数f (x )＝⎩⎨⎧2x ＋2，x ≤1，2x －1，x ＞1，则f (f (0))＝________.答案 5解析 ∵f (0)＝3，∴f (f (0))＝f (3)＝5.15.已知函数f (x )的定义域为(0，1)，则y ＝f [log 12(2x －1)]的定义域为______.答案 ⎝ ⎛⎭⎪⎫34，1解析 ∵函数f (x )的定义域为(0，1)，∴0<log 12(2x －1)<1，即12<2x －1<1，解得34<x <1，∴函数y ＝f ⎣⎢⎡⎦⎥⎤log 12（2x －1）的定义域为⎝ ⎛⎭⎪⎫34，1. 16.已知函数f (x )＝m ·9x －3x ，若存在非零实数x 0，使得f (－x 0)＝f (x 0)成立，则实数m 的取值范围是________. 答案 ⎝ ⎛⎭⎪⎫0，12解析由题意得关于x 的方程m ·9－x －3－x ＝m ·9x －3x 有非零实数解，整理得到m ＝3x （3x ）2＋1＝13x ＋13x＜12，又m ＞0，所以实数m 的取值范围是0＜m ＜12. 四、解答题(本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)已知幂函数f (x )＝(m －1)2x m2－4m ＋2在(0，＋∞)上单调递增，函数g (x )＝2x －k . (1)求m 的值；(2)当x ∈[1，2)时，记f (x )，g (x )的值域分别为集合A ，B ，设p ：x ∈A ，q ：x ∈B ，若p 是q 成立的必要条件，求实数k 的取值范围. 解 (1)依题意得：(m －1)2＝1⇒m ＝0或m ＝2，当m ＝2时，f (x )＝x －2在(0，＋∞)上单调递减，与题设矛盾，舍去，∴m ＝0. (2)由(1)得，f (x )＝x 2，当x ∈[1，2)时，f (x )∈[1，4)，即A ＝[1，4)，当x ∈[1，2)时，g (x )∈[2－k ，4－k )，即B ＝[2－k ，4－k )，因p 是q 成立的必要条件，则B ⊆A ，则⎩⎪⎨⎪⎧2－k ≥1，4－k ≤4，即⎩⎪⎨⎪⎧k ≤1，k ≥0，得0≤k ≤1. 故实数k 的取值范围是[0，1].18.(本小题满分12分)已知函数f (x )＝x 2－4x ＋a ＋3，a ∈R. (1)若函数y ＝f (x )的图象与x 轴无交点，求a 的取值范围； (2)若函数y ＝f (x )在[－1，1]上存在零点，求a 的取值范围. 解 (1)若函数y ＝f (x )的图象与x 轴无交点，则f (x )＝0的根的判别式Δ＜0，即16－4(a ＋3)＜0，解得a ＞1. 故a 的取值范围为(1，＋∞).(2)因为函数f (x )＝x 2－4x ＋a ＋3图象的对称轴是直线x ＝2，所以y ＝f (x )在[－1，1]上单调递减. 又y ＝f (x )在[－1，1]上存在零点，所以⎩⎪⎨⎪⎧f （1）≤0，f （－1）≥0，即⎩⎪⎨⎪⎧a ≤0，a ＋8≥0，解得－8≤a ≤0.故实数a 的取值范围为[－8，0].19.(本小题满分12分)已知定义在R 上的奇函数f (x )和偶函数g (x )满足12f (x )－g (x )＝x －1x 2＋1. (1)求f (x )，g (x )的解析式；(2)若g (x ＋5)＋g ⎝ ⎛⎭⎪⎫1x －1＜g (x )＋g ⎝ ⎛⎭⎪⎫1x ，求x 的取值范围.解 (1)因为12f (x )－g (x )＝x －1x 2＋1，所以12f (－x )－g (－x )＝－x －1x 2＋1，即－12f (x )－g (x )＝－x －1x 2＋1，所以f (x )＝x －1x 2＋1－－x －1x 2＋1＝2x x 2＋1，g (x )＝1x 2＋1. (2)因为g (x )＋g ⎝ ⎛⎭⎪⎫1x ＝1x 2＋1＋11x 2＋1＝1，所以由g (x ＋5)＋g ⎝⎛⎭⎪⎫1x －1＜g (x )＋g ⎝ ⎛⎭⎪⎫1x ，得1（x ＋5）2＋1＋（x －1）21＋（x －1）2＜1，整理得1（x ＋5）2＋1＜11＋（x －1）2，解得x ＞－2. 结合分母不为零得x 的取值范围是(－2，0)∪(0，1)∪(1，＋∞). 20.(本小题满分12分)已知定义在区间(－1，1)上的函数f (x )＝x ＋ax 2＋1为奇函数. (1)求函数f (x )的解析式，并判断函数f (x )在区间(－1，1)上的单调性； (2)解关于t 的不等式f (t －1)＋f (t )＜0. 解 (1)∵f (x )是在区间(－1，1)上的奇函数，∴f (0)＝a ＝0，∴f (x )＝x 1＋x 2(经验证f (x )为奇函数).设－1＜x 1＜x 2＜1，则f (x 1)－f (x 2)＝x 11＋x 21－x 21＋x 22＝（x 1－x 2）（1－x 1x 2）（1＋x 21）（1＋x 22）， ∵－1＜x 1＜x 2＜1，∴x 1－x 2＜0，1－x 1x 2＞0，(1＋x 21)(1＋x 22)＞0，∴f (x 1)－f (x 2)＜0，即f (x 1)＜f (x 2)， ∴函数f (x )在区间(－1，1)上单调递增. (2)∵f (t －1)＋f (t )＜0，且f (x )为奇函数， ∴f (t )＜－f (t －1)＝f (1－t ).又函数f (x )在区间(－1，1)上单调递增， ∴⎩⎪⎨⎪⎧t ＜1－t ，－1＜t ＜1，－1＜1－t ＜1，解得0＜t ＜12， ∴关于t的不等式的解集为⎩⎨⎧⎭⎬⎫t |0＜t ＜12. 21.(本小题满分12分)已知函数g (x )＝ax 2－2ax ＋1＋b (a ＞0)在区间[2，3]上有最大值4和最小值1.设f (x )＝g （x ）x .(1)求a ，b 的值；(2)若不等式f (2x )－k ·2x ≥0在x ∈[－1，1]上有解，求实数k 的取值范围. 解 (1)g (x )＝a (x －1)2＋1＋b －a ，因为a ＞0，所以g (x )在区间[2，3]上是增函数，故⎩⎪⎨⎪⎧g （2）＝1，g （3）＝4，解得⎩⎪⎨⎪⎧a ＝1，b ＝0.(2)由(1)可得g (x )＝x 2－2x ＋1，所以f (x )＝x ＋1x －2，所以f (2x )－k ·2x ≥0可化为2x ＋12x －2≥k ·2x ，即1＋⎝ ⎛⎭⎪⎫12x 2－2·12x ≥k . 令t ＝12x ，则k ≤t 2－2t ＋1.因为x ∈[－1，1]，所以t ∈⎣⎢⎡⎦⎥⎤12，2. 记h (t )＝t 2－2t ＋1，因为t ∈⎣⎢⎡⎦⎥⎤12，2，所以h (t )max ＝1，所以实数k 的取值范围是(－∞，1].22.(本小题满分12分)已知定义在R 上的奇函数f (x )，当x ≥0时，f (x )＝⎝ ⎛⎭⎪⎫12x －x ＋33. (1)求f (x )的解析式；(2)若对任意的t ∈R ，不等式f (t 2－2t )＋f (2t 2－k )＜0恒成立，求实数k 的取值范围.解 (1)当x ＜0时，－x ＞0，则f (－x )＝⎝ ⎛⎭⎪⎫12－x －－x ＋33＝2x ＋x －33. 又f (x )为奇函数，所以－f (x )＝2x＋x －33，所以f (x )＝－2x ＋3－x 3，所以f (x )＝⎩⎨⎧⎝ ⎛⎭⎪⎫12x－x ＋33，x ≥0，－2x ＋3－x 3，x ＜0.(2)因为当x ≥0时，f (x )＝⎝ ⎛⎭⎪⎫12x －x ＋33，y ＝⎝ ⎛⎭⎪⎫12x 单调递减，y ＝－x ＋33也单调递减，所以f (x )在[0，＋∞)上单调递减. 又f (x )是定义在R 上的奇函数，所以f (x )在(－∞，0]上单调递减，所以f (x )在R 上单调递减.因为f (t 2－2t )＋f (2t 2－k )＜0在t ∈R 上恒成立，所以f (t 2－2t )＜－f (2t 2－k ).又f (x )为奇函数，所以f (t 2－2t )＜f (k －2t 2)，所以t 2－2t ＞k －2t 2在t ∈R 上恒成立，即3t 2－2t －k ＞0在t ∈R 上恒成立，所以4＋12k ＜0，即k ＜－13.所以实数k 的取值范围是⎝ ⎛⎭⎪⎫－∞，－13.。

新概念第二册Lesson1-12复习题

新概念第二册Lesson1-Lesson12目标测试卷Name Mark(Total Mark：120'）一、单词:（每空0。

5分,总计10分)（A）翻译1.私人的2.事，商业3.容忍4。

决定 5.接受，收到 6.比赛,竞赛7.拒绝8.损坏9.震惊(B）同音词/字母填写two_______ _______ son_______ see_______I_______ u________ b ________ ________pear _______ write _______ aunt _______二、写出下列单词的过去式和过去分词：（每题1分，总计10分）1。

steal ———- 2。

bear -—-—3。

send -—-— 4. lend ———-5. write ——-—6。

take —- ——7。

make ———- 8. leave —- ——9。

go -- -—10.be -- --三、单选：(每题1分，总计28分）1。

The writer looked at the man and the woman angrily。

He was very _____。

A。

sad B。

unhappy C。

cross D。

pleased2. The writer could not bear it。

He could not _____ it。

A. carryB. suffer C。

stand D。

lift3. He calls at every house in the street。

He _____ everyone.A。

shouts at B。

calls C。

cries out at D。

visits4. ______ does he call？Once a month.A. How seldom B。

How long C。

How soon D. How often5。

Two men took the parcel off the plane。