计算方法与实习作业
数值分析报告计算实习作业一

数值分析计算实习题一学号:姓名:院系:2015年11月5日一、分析1.1算法分析题目要求求出:1)特征值从小到大排列的最小特征值1λ和最大特征值501λ。
2)特征值中模最小的特征值s λ。
3)靠近一组数k μ的一组特征值k i λ。
4)矩阵A 的条件数cond(A)2。
5)行列式detA 。
解决方法:1)若将所有行列式按模的大小排列则模最大的特征值一定是1λ和501λ中的一个,因此利用幂法求出模最大的特征值1m λ。
然后利用带原点平移的幂法,将系数矩阵变为1m A I λ-即将所有特征值都减去1m λ,则特征值按大小顺序排列的次序不变,模最大的特征值依然在整个排列的两端,再用一次幂法得到模最大的特征值21=m m λλλ-,其中λ为带原点平移的幂法求出的特征值,最后两个特征值1m λ、2m λ比较大小,大的为501λ,小的为1λ。
2)因为s λ为按模最小的特征值,因此用反幂法可求的其特征值。
3)因为k i λ靠近数k μ,因此k i k λμ-一定是所有的k λμ-中模最小的,因此可利用带原点平移的反幂法求出特征值k i λ,此时的系数矩阵变为k A I μ-。
4)条件数cond(A)2为模最小的特征值与模最大的特征值的比的绝对值,因此利用1和2中求出的1m λ和s λ可解出条件数。
5)可对矩阵A 进行LU 分解,即A LU =则det()det()det()A L U =⨯,又因为矩阵L 对角线元素为1,则det()L =1,所以det()det()A U =,U 为上三角阵,行列式为对角线元素的乘积,因此可得A 的行列式。
1.2程序分析1.2.1 因为A 为拟三角阵,储存时零元素不储存,因此将矩阵A 压缩为5*501的矩阵CA 的带内元素ij a =C 中的元素1,i j s j c -++ 程序中A[5][501]即为压缩后的矩阵。
1.1.2 程序中的B[5][501]为过渡矩阵,在幂法迭代、反幂法迭代以及LU 分解中均用矩阵B 来计算,计算之间对B 进行适当的赋值。
东南大学计算方法与实习上机实验一

东南大学计算方法与实习实验报告学院:电子科学与工程学院学号:06A*****姓名:***指导老师:***实习题14、设S N=Σ(1)编制按从大到小的顺序计算S N的程序;(2)编制按从小到大的顺序计算S N的程序;(3)按两种顺序分别计算S1000,S10000,S30000,并指出有效位数。
解析:从大到小时,将S N分解成S N-1=S N-,在计算时根据想要得到的值取合适的最大的值作为首项;同理从小到大时,将S N=S N-1+ ,则取S2=1/3。
则所得式子即为该算法的通项公式。
(1)从大到小算法的C++程序如下:/*从大到小的算法*/#include<iostream>#include<iomanip>#include<cmath>using namespace std;const int max=34000; //根据第(3)问的问题,我选择了最大数为34000作为初值void main(){int num;char jus;double cor,sub;A: cout<<"请输入你想计算的值"<<'\t';cin>>num;double smax=1.0/2.0*(3.0/2.0-1.0/max-1.0/(max+1)),temps;double S[max];// cout<<"s["<<max<<"]="<<setprecision(20)<<smax<<'\n';for(int n=max;n>num;){temps=smax;S[n]=temps;n--;smax=smax-1.0/((n+1)*(n+1)-1.0);}cor=1.0/2.0*(3.0/2.0-1.0/num-1.0/(num+1.0)); //利用已知精确值公式计算精确值sub=fabs(cor-smax); //double型取误差的绝对值cout<<"用递推公式算出来的s["<<n<<"]="<<setprecision(20)<<smax<<'\n';cout<<"实际精确值为"<<setprecision(20)<<cor<<'\n';cout<<"则误差为"<<setprecision(20)<<sub<<'\n';cout<<"是否继续计算S[N],是请输入Y,否则输入N!"<<endl;cin>>jus;if ((int)jus==89||(int)jus==121) goto A;}(2)从小到大算法的C++程序如下:/*从小到大的算法*/#include<iostream>#include<iomanip>#include<cmath>using namespace std;void main(){int max;A: cout<<"请输入你想计算的数,注意不要小于2"<<'\t';cin>>max;double s2=1.0/3.0,temps,cor,sub;char jus;double S[100000];for(int j=2;j<max;){temps=s2;S[j]=temps;j++;s2+=1.0/(j*j-1.0);}cor=1.0/2.0*(3.0/2.0-1.0/j-1.0/(j+1.0)); //利用已知精确值公式计算精确值sub=fabs(cor-s2); //double型取误差的绝对值cout<<"用递推公式算出来的s["<<j<<"]="<<setprecision(20)<<s2<<'\n';cout<<"实际精确值为"<<setprecision(20)<<cor<<'\n';cout<<"则误差为"<<setprecision(20)<<sub<<'\n';cout<<"是否继续计算S[N],是请输入Y,否则输入N!"<<endl;cin>>jus;if ((int)jus==89||(int)jus==121) goto A;}(3)(注:因为程序中setprecision(20)表示输出数值小数位数20,则程序运行时所得到的有效数字在17位左右)ii.选择从小到大的顺序计算S1000、S10000、S30000的值需要计算的项S1000S10000S30000计算值0.74900049950049996 0.74966672220370571 0.74996666722220728实际精确值0.74900049950049952 0.74990000499950005 0.74996666722220373误差 4.4408920985006262*10-16 5.6621374255882984*10-15 3.5527136788005009*10-15有效数字17 17 17附上部分程序运行图:iii.实验分析通过C++程序进行计算验证采用从大到小或者从小到大的递推公式算法得到的数值基本稳定且误差不大。
计算方法与实习 第四版 (孙志忠 著) 东南大学出版社 课后答案

2
ww
w.
kh
da
w.
co
∗ − y | → ∞, 计算过程不稳定。 注 :此题中,|yn n
m
× 10−3 .
w.
n = 1, 2, · · ·
co m
e2 e2 r r = . 1 + er 1 − er
w.
课后答案网
aw . kh d
∗ − y | = 510 e ≤ n = 10时,|yn n 0
√ 计算到y100 , 若取 783 ≈ 27.982 (5位有效数字),试问计算到y100 将有多大误差? √ 答 :设x∗ = 783, x = 27.982, x∗ = x + e.
−2 ∗ = y∗ yn n−1 − 10 (x + e), yn = yn−1 − 10−2 x,
1 √ 783, 100
概率与数理统计 第二, C语言程序设计教程 第 西方经济学(微观部分) C语言程序设计教程 第 复变函数全解及导学[西 三版 (浙江大学 三版 (谭浩强 张 (高鸿业 著) 中 二版 (谭浩强 张 安交大 第四版]
社区服务
社区热点
进入社区
/
2009-10-15
ww
er − er = er −
e2 e e 1 r = . = e − = e − r r x∗ e+x 1 + er 1 + e1 r ·········
7. 设y0 = 28, 按递推公式
案 答
yn = yn−1 −
网 课 后
1 2
6. 机器数–略。
w. kh da
∗ −y |=e≤ n = 100时,|yn n
课后答案网
初一数学实践作业

初一数学实践作业
以下是一个简单的初一数学实践作业的示例,旨在帮助学生复习和巩固他们所学的数学知识:
作业题目:测量并计算一个房间的面积
任务:
1. 选择一个房间,可以是你的卧室、客厅或其他任何房间。
2. 使用测量工具(如卷尺或激光测距仪)测量房间的长度和宽度。
3. 计算房间的面积,使用公式:面积 = 长度× 宽度。
4. 将测量和计算结果记录在表格中。
5. 根据测量和计算结果,估计房间的面积与其他物品(如地毯、床、沙发等)的面积之间的关系。
请注意,这只是一个简单的示例,您可以根据学生的学习情况和兴趣进行调整和扩展。
通过实践作业,学生可以更好地理解数学概念,提高他们的数学技能和解决问题的能力。
计算方法与实习大作业

计算方法与实习大作业班级:021011班学号:02101091姓名:师梦艳插值法:拉格朗日插值多项式在数值分析中,拉格朗日插值法是以法国十八世纪数学家约瑟夫·路易斯·拉格朗日命名的一种多项式插值方法。
许多实际问题中都用函数来表示某种内在联系或规律,而不少函数都只能通过实验和观测来了解。
如对实践中的某个物理量进行观测,在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。
这样的多项式称为拉格朗日(插值)多项式。
数学上来说,拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。
拉格朗日插值法最早被英国数学家爱德华·华林于1779年发现,不久后(1783年)由莱昂哈德·欧拉再次发现。
1795年,拉格朗日在其著作《师范学校数学基础教程》中发表了这个插值方法,从此他的名字就和这个方法联系在一起。
数据建模有两大方法:一类是插值方法,另一类是拟合函数一般的说,插值法比较适合数据准确或数据量小的情形。
然而Lagrange 插值有很多种,1阶,2阶,…n 阶。
我们可以利用拉格朗日插值求方程,根据它的程序求原方程的图像。
下面我具体介绍分析一下拉格朗日插值的算法设计及应用。
具体算法1、基本概念 已知函数y=f(x)在若干点i x 的函数值i y =()i x f (i=0,1,⋅⋅⋅,n )一个差值问题就是求一“简单”的函数p(x):p(i x )=i y ,i=0,1,⋅⋅⋅,n, (1) 则p(x)为f(x)的插值函数,而f(x)为被插值函数会插值原函数,0x ,1x ,2x ,...,n x 为插值节点,式(1)为插值条件,如果对固定点-x 求f(-x )数值解,我们称-x 为一个插值节点,f(-x )≈p(-x )称为-x 点的插值,当-x ∈[min(0x ,1x ,2x ,...,n x ),max(0x ,1x ,2x ,...,n x )]时,称为内插,否则称为外插式外推,特别地,当p(x)为不超过n 次多项式时称为n 阶Lagrange 插值。
计算方法上机实习作业
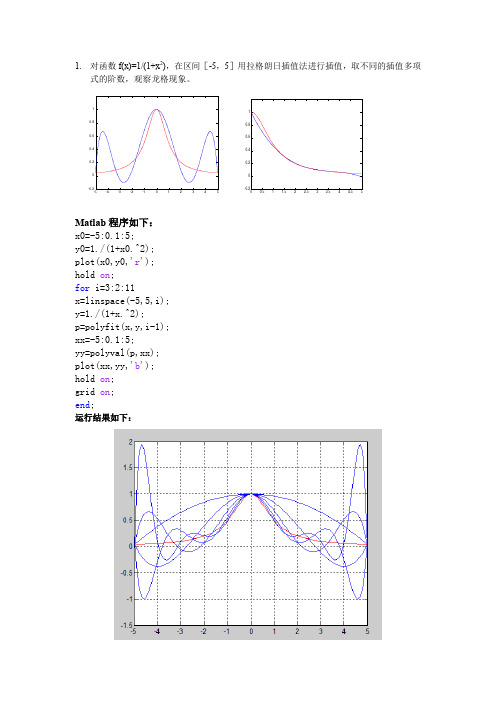
如图所示,在两端出现龙格现象,并且阶数越高龙格现象越明显。 若在区间[0,5]进行插值,是否还存在龙格现象?
Matlab 程序如下: x0=0:0.1:5; y0=1./(1+x0.^2); plot(x0,y0,'r'); hold on; for i=3:2:11 x=linspace(-0,5,i); y=1./(1+x.^2); p=polyfit(x,y,i-1); xx=0:0.1:5; yy=polyval(p,xx); plot(xx,yy,'b'); hold on; grid on; end;
0
1
2
3
4
Matlab 程序如下: clear;clc; x=0:0.1:2.5; y=sin(x); y1=x; y2=x-x.^3/6; y3=x-x.^3/6+x.^5/120; plot(x,y,'b',x,y1,'g',x,y2,'r',x,y3,'k')
输出结果如图:
1.500000000000000 1.414213562374690 1.414213562373095
1.416666666666667 1.414213562373095
2.000000000000000 1.732050810014727 1.732050807568877
1.750000000000000 1.732050807568877
x 2 n 1 ,编写程序实 ( 2n 1)! k 1 现如下功能:对 n=1,2,3,绘制出区间[0,2.5 ]上的近似函数的图形以及 sin x 本身的图
4.由正弦函数的 Tylor 展开式取前 n 项,得 sin x ( 1) n1
数值计算方法实习作业模板小

2.1函数图形与极限2.1.1 实验目的1.熟悉Mathematica 基本绘图语句。
2.掌握函数极限的有关操作命令。
3.学会利用Mathematica 软件对函数进行分析研究。
4.熟悉Mathematica 二元函数绘图语句。
2.1.2 实验内容【基本语句】1.Plot[f[x],{x,xmin,xmax},选项]; 功能: 画出函数f[x] 从min 到max 间的图形;2.Plot[{f1[x],f2[x],...},{x,xmin,xmax},选项]; 功能: 在同一坐标系下画出函数f1,f2,...的图形。
3. ParametricPlot[{fx,fy},{t,tmin,tmax}]; 功能: 画出参数方程fx=x(t),fy=y(t)的图形;ParametricPlot[{{f1x,f1y},{f2x,f2y}},{t,tmin,tmax}]; 功能:在同一坐标系下画出用参数方程表示的两幅函数图形。
【备注】fx,fy 的给出方式:⑴fx=x(t) , fy=y(t)⑵fx=x ,fy=f(x)与fx=f(x) ,fy=x 构成反函数的图形关系⑶r=r(t) , fx=r(t)Cos(t) , fy=r(t)Sin(t)4. Show[tu1,tu2]功能:将tu1及tu2两幅函数图形重叠在一起,将两个函数图形一起显示。
5. Plot3D[f[x,y],{x,x0,x1},{y,y0,y1}] 功能:作出函数f[x,y]在区域[x0,x1]×[y0,y1]上的图形; ParametricPlot3D[{x[u,v],y[u,v],z[u,v]},{u,u0,u1},{v,v0,v1}] 功能:作出参数方程表示的曲面。
6. Limit[f[x],x->x0] 功能:求函数f[x]在x0处的极限。
7. Limit[f[x],x->x0,Direction->+1] 功能:求函数f[x]在x0处的左极限。
计算方法与实习报告

Difference(x,y,N);
b=y[N];
for(i=N-1;i>=0;i--)
b=b*(varx-x[i])+y[i];
printf("Nn(%f)=%f",varx,b);
(3)如果 ,则交换第k行与第 行对应元素位置
(4)消元,对i=k+1,........,n计算 ,对j=k+1,..........,n+1计算
回代过程
(1)若 ,则矩阵A奇异,程序结束;否则执行(2)
(2) ;对i=n-1,......2,1计算
(1)程序代码为:
#include<iostream>
void main()
{
float sum=0;
int n=1;
while(n<=10000){
sum=sum+(float)1/(n*n);
n++;
}
cout<<"The sum that from min to max is:"<<sum;
}
(2)运行输出的结果为:
The sum that from max to min is:=1.64473
}
while(fabs(d)>eps&&fabs((*f)(x1))>eta);
return x1;
}
float f(float x)
{
return float(x*x-exp(x));
计算方法与实习上机题答案
实习题11用两种不容的顺序计算644834.1100012≈∑=-n n,分析误差的变化〔1〕顺序计算 源代码:#include<stdio.h> #include<math.h> void main() { double sum=0; int n=1; while(1) { sum=sum+(1/pow(n,2)); if(n%1000==0)printf("sun[%d]=%-30f",n,sum); if(n>=10000)break; n++; } printf("sum[%d]=%f\n",n,sum); }结果:〔2〕逆序计算 源代码:#include<stdio.h> #include<math.h> void main() { double sum=0; int n=10000; while(1) { sum=sum+(1/pow(n,2));if(n%1000==0) printf("sum[%d]=%-30f",n,sum); if(n<=1)break; n--; } printf("sum[%d]=%f\n",n,sum); }结果:2连分数))//(.../(322101n n b a a b a b a b f ++++=利用下面的方法计算f:11)0,...,2,1(,d f n n i d a b d b d i i i i n n =--=+==++写一个程序,读入n,n n b a ,,计算并打印f 源代码:#include<stdio.h> #include<math.h> void main() { int i=0,n; float a[1024],b[1024],d[1024]; printf("please input n,n="); scanf("%d",&n); printf("\nplease input a[1] to a[n]:\n"); for(i=1;i<=n;i++) { printf("a[%d]=",i); scanf("%f",&a[i]);} printf("\nplease input b[0] to b[n]:\n"); for(i=0;i<=n;i++) { printf("b[%d]=",i); scanf("%f",&b[i]); } d[n]=b[n]; for(i=n-1;i>=0;i--) d[i]=b[i]+a[i+1]/d[i+1]; printf("\nf=%f\n",d[0]); }结果:3给出一个有效的算法和一个无效的算法计算积分⎰=+=10)10,...1,0(14n dx x x y n n 源代码:#include<stdio.h> #include<math.h> main() { double y_0=(1/4.0)*log(5),y_1; double y_2=(1.0/55.0+1.0/11.0)/2,y_3; int n=1,m=10; printf("有效算法输出结果:\n"); printf("y[0]=%-20f",y_0);while(1) { y_1=1.0/(4*n)+y_0/(-4.0); printf("y[%d]=%-20f",n,y_1); if(n>=10) break; y_0=y_1; n++; if(n%3==0) printf("\n"); } printf("\n 无效算法的输出结果:\n"); printf("y[10]=%-20f",y_2); while(1) { y_3=1.0/n-4.0*y_2; printf("y[%d]=%-20f",m-1,y_3); if(m<=1) break; y_2=y_3; m--; if(m%2==0) printf("\n"); } }结果:4设∑=-=Nj N j S 2211,其准确值为)11123(21+--N N (1)编制按从小到大顺序计算N S 的程序 (2)编制按从小到达的顺序计算N S 的程序(3)按两种顺序分别计算30000100001000,,S S S ,并指出有效位数源代码:#include<stdio.h> main() { int N; double SN[30000]; SN[30000]=(3.0/2.0-1.0/30000.0-1/30001.0)/2.0; for(N=30000;N>=2;N--) SN[N-1]=SN[N]-1.0/(N*N-1); printf("从大到小顺序计算:\nSN[1000]=%f\nSN[10000]=%f\nSN[30000]=%f\n",SN[1000],SN[10000],SN[30000]); SN[2]=(3.0/2-1.0/2.0-1/3.0)/2.0; for(N=3;N<=30000;N++) SN[N]=SN[N-1]+1.0/(N*N-1); printf("从小到大顺序计算:\nSN[1000]=%f\nSN[10000]=%f\nSN[30000]=%f\n",SN[1000],SN[10000],SN[30000]); }结果:实习题21.用牛顿法求以下方程的根2=-x e x01=-x xe 02lg =-+x x源代码:#include <stdio.h> #include <math.h>typedef float (*p)(float ); float ff1(float x) { return x*x-exp(x); }float ff2(float x) { return x*exp(x)-1; }float ff3(float x) { return log(x)+x-2; }float answer(float(*p)(float)) { int k=2; float m=1,n=-1,x2,a,b,c; if (p==ff3)n=2; printf("x[0] = %.4f, x[1] = %.4f, ",m,n); while (1) { if (fabs(m-n)<1e-4) break; a=p(n)*(n-m); b=p(n)-p(m); c=a/b; x2=n-c; m = n; n = x2; printf("x[%d] = %.4f, ",k,x2); k++; if (k%3==0) printf("\n"); }if (k%3!=0) printf("\n");printf("iteration times: %d, roots: %.4f\n ",k-2,n);return 0;}main(){printf("x*x-exp(x),\n");answer(ff1);printf("x*exp(x)-1,\n");answer(ff2);printf("lg(x)+x-2,\n");answer(ff3);return 0;}结果:2.编写一个割线法的程序,求解上述各方程源代码:#include<stdio.h>#include<math.h>float gexian(float,float);float f(float);main(){int i,j;float x1=2.2;float x2=2,x3;scanf("%d",&i);if(i==1)printf("%f",x1); else if(i==2) printf("%f",x2); else { for(j=3;j<=i;j++) { x3=gexian(x1,x2); x1=x2; x2=x3; } printf("%f",gexian(x1,x2)); } }float f(float x) { return (x*x-exp(x)); }float gexian(float x1,float x2) { return (x2-(f(x2)/(f(x2)-f(x1)))*(x2-x1)); }结果:实习题31用列主元消去法解以下方程组;⎪⎪⎩⎪⎪⎨⎧=++=-++--=+--=--+43443233312)1(421432143214321x x x x x x x x x x x x x x x ⎪⎪⎩⎪⎪⎨⎧=++--=++-=-+--=-+-4341220332282)2(432132143214321x x x x x x x x x x x x x x x 源程序:#include<stdio.h>#include<math.h>void ColPivot(float*,int,float[]);void ColPivot(float*c,int n,float x[]){int i,j,t,k;float p;for(i=0;i<=n-2;i++){k=i;for(j=i+1;j<=n-1;j++)if(fabs(*(c+j*(n+1)+i))>(fabs(*(c+k*(n+1)+i))))k=j;if(k!=i)for(j=i;j<=n;j++){p=*(c+i*(n+1)+j);*(c+i*(n+1)+j)=*(c+k*(n+1)+j);*(c+k*(n+1)+j)=p;}for(j=i+1;j<=n-1;j++){p=(*(c+j*(n+1)+i))/(*(c+i*(n+1)+i));for(t=i;t<=n;t++)*(c+j*(n+1)+t)-=p*(*(c+i*(n+1)+t));}}for(i=n-1;i>=0;i--){for(j=n-1;j>=i+1;j--)(*(c+i*(n+1)+n))-=x[j]*(*(c+i*(n+1)+j));x[i]=*(c+i*(n+1)+n)/(*(c+i*(n+1)+i));}}void main(){int i;float x[4];float c[4][5]={1,1,0,3,4,2,1,-1,1,1,3,-1,-1,3,-3,-1,2,3,-1,4};ColPivot(c[0],4,x);for(i=0;i<=3;i++)printf("x[%d]=%f\n",i,x[i]);}结果:第〔1〕题第〔2〕题2、源代码:#include<stdio.h>void main(){float x[4];int i;float a[4][5]={48,-24,0,-12,4,-24,24,12,12,4,0,6,20,2,-2,-6,6,2,16,-2};void DirectLU(float*,int,float[]);DirectLU(a[0],4,x);for(i=0;i<=3;i++)printf("x[%d]=%f\n",i,x[i]);}void DirectLU(float*u,int n,float x[]){int i,r,k;for(r=0;r<=n-1;r++){for(i=r;r<=n;i++)for(k=0;k<=r-1;k++)*(u+r*(n+1)+i)-=*(u+r*(n+1)+k)*(*(u+k*(n+1)+i));for(i=r+1;i<=n-1;i++){for(k=0;k<=r-1;k++)*(u+i*(n+1)+r)-=*(u+i*(n+1)+k)*(*(u+k*(n+1)+r));*(u+i*(n+1)+r)/=*(u+r*(n+1)+r);}}for(i=n-1;i>=0;i--){for(r=n-1;r>=i+1;r--)*(u+i*(n+1)+n)-=*(u+i*(n+1)+r)*x[r];x[i]=*(u+i*(n+1)+n)/(*(u+i*(n+1)+i));}}实习题41、源代码:#include<stdio.h>float Lagrange(float x[],float y[],float xx,int n) //n为〔n+1〕次插值;{int i,j;float *a,yy=0;a=new float[n];for(i=0;i<=n-1;i++){a[i]=y[i];for(j=0;j<=n-1;j++)if(j!=i)a[i]*=(xx-x[j])/(x[i]-x[j]);yy+=a[i];}delete a;return yy;}void main(){float x[5]={-3.0,-1.0,1.0,2.0,3.0};float y[5]={1.0,1.5,2.0,2.0,1.0};float xx1=-2,xx2=0,xx3=2.75,yy1,yy2,yy3;yy1=Lagrange(x,y,xx1,3);yy2=Lagrange(x,y,xx2,3);yy3=Lagrange(x,y,xx3,3);printf("x1=%-20f,y1=%f\n",xx1,yy1);printf("x2=%-20f,y2=%f\n",xx2,yy2);printf("x3=%-20f,y3=%f\n",xx3,yy3);}结果:2、源代码:#include<stdio.h>float Lagrange(float x[],float y[],float xx,int n) //n为〔n+1〕次插值;{int i,j;float *a,yy=0;a=new float[n];for(i=0;i<=n-1;i++){a[i]=y[i];for(j=0;j<=n-1;j++)if(j!=i)a[i]*=(xx-x[j])/(x[i]-x[j]);yy+=a[i];}delete a;return yy;}void main(){float x[6]={0.30,0.42,0.50,0.58,0.66,0.72};float y[6]={1.04403,1.08462,1.11803,1.15603,1.19817,1.23223};float xx1=0.46,xx2=0.55,xx3=0.60,yy1,yy2,yy3;yy1=Lagrange(x,y,xx1,6);yy2=Lagrange(x,y,xx2,6);yy3=Lagrange(x,y,xx3,6);printf("x1=%-20f,y1=%f\n",xx1,yy1);printf("x2=%-20f,y2=%f\n",xx2,yy2);printf("x3=%-20f,y3=%f\n",xx3,yy3);}结果:源代码:#include<stdio.h>#define N 3void Difference(float y[],float f[4][4],int n){int k,i;f[0][0]=y[0];f[1][0]=y[1];f[2][0]=y[2];f[3][0]=y[3];for(k=1;k<=n;k++)for(i=0;i<=(N-k);i++)f[i][k]=f[i+1][k-1]-f[i][k-1];return;}void main(){int i,k=1;float a,b=1,m=21.4,t=1.4,f[4][4]={0};float x[5]={20,21,22,23,24};float y[5]={1.30103,1.32222,1.34242,1.36173,1.38021};Difference(y,f,N);a=f[0][0];for(i=1;i<=N;i++){k=k*i;b=b*(t-i+1);a=a+b*f[0][i]/k;}printf("x(k)\n");for (i=0;i<=4;i++)printf( "%-20f",x[i]);printf("\ny(k)\n");for (i=0;i<=4;i++)printf("%-20f",y[i]);for(k=1;k<=3;k++){printf("\nF(%d)\n ",k);for(i=0;i<=(3-k);i++){printf("%-20f",f[i][k]);}}printf ("\n");printf("f(%f)=%-20f",m,a);printf ("\n");结果:实习题52、源代码:#include<stdio.h>#include<math.h>void main(){int i,n;float a[2];float x[15]={1,1.5,2,2.5,3,3.5,4,4.5,5,5.5,6,6.5,7,7.5,8},z[15];floaty[15]={33.4,79.50,122.65,159.05,189.15,214.15,238.65,252.50,267.55,280.50,296.65,301.40,310. 40,318.15,325.15};for(n=0;n<=14;n++) //增加了数组z;{z[n]=log(y[n]/x[n]);}void Approx(float[],float[],int,int,float[]);Approx(x,z,15,1,a); //变成一次拟合;//for(i=0;i<=1;i++)//printf("a[%d]=%f\n",i,a[i]);printf("a=exp(a[0])=%f\n",exp(a[0]));printf("b=-a[1]=%f\n",-a[1]); }void Approx(float x[],float y[],int m,int n,float a[]){int i,j,t;float *c=new float[(n+1)*(n+2)];float power(int,float);void ColPivot(float *,int,float[]);for(i=0;i<=n;i++){for(j=0;j<=n;j++){*(c+i*(n+2)+j)=0;for(t=0;t<=m-1;t++)*(c+i*(n+2)+j)+=power(i+j,x[t]);}*(c+i*(n+2)+n+1)=0;for(j=0;j<=m-1;j++)*(c+i*(n+2)+n+1)+=y[j]*power(i,x[j]);}ColPivot(c,n+1,a);delete c;}void ColPivot(float *c,int n,float x[]){int i,j,t,k;float p;for(i=0;i<=n-2;i++){k=i;for(j=i+1;j<=n-1;j++)if(fabs(*(c+j*(n+1)+i))>(fabs(*(c+k*(n+1)+i))))k=j;if(k!=i)for(j=i;j<=n;j++){p=*(c+i*(n+1)+j);*(c+i*(n+1)+j)=*(c+k*(n+1)+j);*(c+k*(n+1)+j)=p;}for(j=i+1;j<=n-1;j++){p=(*(c+j*(n+1)+i))/(*(c+i*(n+1)+i));for(t=i;t<=n;t++)*(c+j*(n+1)+t)-=p*(*(c+i*(n+1)+t));}}for(i=n-1;i>=0;i--){for(j=n-1;j>=i+1;j--)(*(c+i*(n+1)+n))-=x[j]*(*(c+i*(n+1)+j));x[i]=*(c+i*(n+1)+n)/(*(c+i*(n+1)+i));}float power(int i,float v){float a=1;while(i--)a*=v;return a;}结果:实习题61、源代码:〔1〕#include<stdio.h>#include<math.h>float Cotes(float(*f)(float),float a,float b,int n){int k;float c,c1=0,c2,c3,c4;float h=(b-a)/n;c2=(*f)(a+h/4);c3=(*f)(a+h/2);c4=(*f)(a+3*h/4);for(k=1;k<=n-1;k++){c1+=(*f)(a+k*h);c2+=(*f)(a+k*h+h/4);c3+=(*f)(a+k*h+h/2);c4+=(*f)(a+k*h+3*h/4);}c=h/90*(7*((*f)(a)+(*f)(b))+14*c1+32*c2+12*c3+32*c4);return c;}float f(float x){return 1/sqrt(1+x*x*x);}void main()int i,n=4;float c;for(i=0;i<=4;i++){c=Cotes(f,0,1,n);printf("C(%d)=%f\n",n,c);n*=2;}}〔2〕#include<stdio.h>#include<math.h>float Cotes(float(*f)(float),float a,float b,int n){int k;float c,c1=0,c2,c3,c4;float h=(b-a)/n;c2=(*f)(a+h/4);c3=(*f)(a+h/2);c4=(*f)(a+3*h/4);for(k=1;k<=n-1;k++){c1+=(*f)(a+k*h);c2+=(*f)(a+k*h+h/4);c3+=(*f)(a+k*h+h/2);c4+=(*f)(a+k*h+3*h/4);}c=h/90*(7*((*f)(a)+(*f)(b))+14*c1+32*c2+12*c3+32*c4);return c;}float f(float x){ // return 1/sqrt(1+x*x*x);if (x==0)return 1;else return sin(x)/x;}void main(){int i,n=4;float c;for(i=0;i<=4;i++){// c=Cotes(f,0,1,n);c=Cotes(f,0,5,n);printf("C(%d)=%f\n",n,c);n*=2;}}结果:〔1〕〔2〕实习题7 一、改良欧拉法1、#include<stdio.h>#include<iostream>double Adams (double (*f)(double x, double y),double x0,double y0,double h,int N) {for(int n=0; n<N; ++n) {double x1=x0+h;double yp=y0+h*f(x0,y0);double y1=y0+h*f(x1,yp);y1=(yp+y1)/2.0;printf("ty=%f\n",y1);x0=x1;y0=y1;}}int main(void){double f(double x, double y); double x0=0,y0=0;double x,y,step;long i;step=0.1;Adams(f,x0,y0,0.1,10);}double f(double x, double y) {double r;r=x*x+y*y;return(r);}2、int main(void){double f(double x, double y); double x0=0,y0=0;double x,y,step;long i;step=0.1;Adams(f,x0,y0,0.1,10);}double f(double x, double y) {double r;r=1/(1+y*y);return(r);}3、int main(void){double f(double x, double y); double x0=0,y0=1;double x,y,step;long i;step=0.1;Adams(f,x0,y0,0.1,10);}double f(double x, double y) {double r;r=y-2*x/y;return(r);}四阶龙格库塔法1、#include<iostream>#include<stdio.h>using namespace std;//f为函数的入口地址,x0、y0为初值,xn为所求点,step为计算次数double Runge_Kuta( double (*f)(double x, double y), double x0, double y0, double xn, long step ) {double k1,k2,k3,k4,result;double h=(xn-x0)/step;if(step<=0)return(y0);if(step==1){k1=f(x0,y0);k2=f(x0+h/2, y0+h*k1/2);k3=f(x0+h/2, y0+h*k2/2);k4=f(x0+h, y0+h*k3);result=y0+h*(k1+2*k2+2*k3+k4)/6;}else{double x1,y1;x1=xn-h;y1=Runge_Kuta(f, x0, y0, xn-h,step-1);k1=f(x1,y1);k2=f(x1+h/2, y1+h*k1/2);k3=f(x1+h/2, y1+h*k2/2);k4=f(x1+h, y1+h*k3);result=y1+h*(k1+2*k2+2*k3+k4)/6;}printf("%lg\n",result);return(result);}int main(void){double f(double x, double y);double x0=0,y0=0,k;double x,y,step;long i;step=0.1;cout.precision(10);//for(i=0;i<=10;i++)//{// x=x0+i*step;// cout<<x<<" - "<<Runge_Kuta(f,x0,y0,x,i)<<endl; //}//cout<<Runge_Kuta(f,x0,y0,1,10);k= Runge_Kuta(f,x0,y0,1,10);}double f(double x, double y){double r;r=x*x+y*y;return(r);}2、int main(void){double f(double x, double y);double x0=0,y0=0,k;double x,y,step;long i;step=0.1;cout.precision(10);//for(i=0;i<=10;i++)//{// x=x0+i*step;// cout<<x<<" - "<<Runge_Kuta(f,x0,y0,x,i)<<endl; //}//cout<<Runge_Kuta(f,x0,y0,1,10);k= Runge_Kuta(f,x0,y0,1,10);}double f(double x, double y){double r;r=1/〔1+y*y〕;return(r);}3、int main(void){double f(double x, double y);double x0=0,y0=0,k;double x,y,step;long i;step=0.1;cout.precision(10);//for(i=0;i<=10;i++)//{// x=x0+i*step;// cout<<x<<" - "<<Runge_Kuta(f,x0,y0,x,i)<<endl; //}//cout<<Runge_Kuta(f,x0,y0,1,10);k= Runge_Kuta(f,x0,y0,1,10);}double f(double x, double y){double r;r=1/〔1+y*y〕;return(r);}二、int main(void){double f(double x, double y);double x0=0,y0=1,k;double x,y,step;long i;step=0.1;cout.precision(10);//for(i=0;i<=10;i++)//{// x=x0+i*step;// cout<<x<<" - "<<Runge_Kuta(f,x0,y0,x,i)<<endl;//}//cout<<Runge_Kuta(f,x0,y0,1,10);k= Runge_Kuta(f,x0,y0,1,10);}double f(double x, double y){double r;r=y-2*x/y;return(r);}三、1、void Runge_Kutta(float(*f)(float x,float y),float a,float b,float y0,int N,float yy[]) {float x=a,y=y0,K1,K2,K3,K4;float h=(b-a)/N;int i;for(i=1;i<=3;i++){K1=(*f)(x,y);K2=(*f)(x+h/2,y+h*K1/2);K3=(*f)(x+h/2,y+h*K2/2);K4=(*f)(x+h/2,y+h*K3);y=y+h*(K1+2*K2+2*K2+2*K3+K4)/6;x=a+i*h;yy[i-1]=y;}}void Adams (float a,float b,int N,float(*f)(float x,float y),float y0){int i;float y1,y2,y,yp,yc,yy[3],h,x;printf("x[0]=%f\ty[0]=%f\n",a,y0);Runge_Kutta(f,a,b,y0,N,yy);y1=yy[0];y2=yy[1];y=yy[2];h=(b-a)/N;for(i=1;i<=3;i++)printf("x[%d]=%f\ty[%d]=%f\n",i,a+i*h,i,yy[i-1]);for(i=3;i<N;i++){x=a+i*h;yp=y+h*(55*f(x,y)-59*f(x-h,y2)+37*f(x-2*h,y1)-9*f(x-3*h,y0))/24;yc=y+h*(9*(*f)(x+h,yp)+19*(*f)(x,y)-5*(*f)(x-h,y2)+(*f)(x-2*h,y1))/24;printf("x[%d]=%f\ty[%d]=%f\n",i+1,x+h,i+1,yc);y0=y1;y1=y2;y2=y;y=yc;}}float f(float x,float y){return y*y;void Runge_Kutta(float(*f)(float x,float y),float a,float,float b,float y0,int N,float yy[]); void Adams (float a,float b,int N,float(*f)(float x,float y),float y0);float f(float x,float y);int main (void){float a=0,b=1,y0=1;int N=10;Adams(a,b,N,f,y0);}2、#include<stdio.h>void Runge_Kutta(float(*f)(float x,float y),float a,float b,float y0,int N,float yy[]) {float x=a,y=y0,K1,K2,K3,K4;float h=(b-a)/N;int i;for(i=1;i<=3;i++){K1=(*f)(x,y);K2=(*f)(x+h/2,y+h*K1/2);K3=(*f)(x+h/2,y+h*K2/2);K4=(*f)(x+h/2,y+h*K3);y=y+h*(K1+2*K2+2*K2+2*K3+K4)/6;x=a+i*h;yy[i-1]=y;}}void Adams (float a,float b,int N,float(*f)(float x,float y),float y0)int i;float y1,y2,y,yp,yc,yy[3],h,x;printf("x[0]=%f\ty[0]=%f\n",a,y0);Runge_Kutta(f,a,b,y0,N,yy);y1=yy[0];y2=yy[1];y=yy[2];h=(b-a)/N;for(i=1;i<=3;i++)printf("x[%d]=%f\ty[%d]=%f\n",i,a+i*h,i,yy[i-1]);for(i=3;i<N;i++){x=a+i*h;yp=y+h*(55*f(x,y)-59*f(x-h,y2)+37*f(x-2*h,y1)-9*f(x-3*h,y0))/24;yc=y+h*(9*(*f)(x+h,yp)+19*(*f)(x,y)-5*(*f)(x-h,y2)+(*f)(x-2*h,y1))/24;printf("x[%d]=%f\ty[%d]=%f\n",i+1,x+h,i+1,yc);y0=y1;y1=y2;y2=y;y=yc;}}float f(float x,float y){return 0.1*(x*x*x+y*y);}void Runge_Kutta(float(*f)(float x,float y),float a,float,float b,float y0,int N,float yy[]); void Adams (float a,float b,int N,float(*f)(float x,float y),float y0);float f(float x,float y);int main (void){float a=0,b=1,y0=1;int N=10;Adams(a,b,N,f,y0);}。
计算方法大作业(第一次)

数值计算第一次大作业实验目的 以Hilbert 矩阵为例,研究处理病态问题可能遇到的困难。
内容 Hilbert 矩阵的定义是,()11/21/31/1/21/31/41/(1)1/31/41/51/(2)1/1/(1)1/(2)1/(21)n i j H h nn n n n n n =⎡⎤⎢⎥+⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥++-⎣⎦它是一个对称正定矩阵,而且()n cond H 随着n 的增加迅速增加,其逆矩阵1,()n i j H α-=,这里,2(1)(1)!(1)!(1)[(1)!(1)!]()!()!i j i jn i n j i j i j n i n j α+-+-+-=+----- 1) 画出ln(())~n cond H n 之间的曲线(可以用任何的一种范数)。
你能猜出ln(())~n cond H n 之间有何种关系吗?提出你的猜想并想法验证。
用行范数for n=1:50 for i=1:n for j=1:nA(i,j)=1/(i+j-1);B(i,j)=factorial(n+i-1)*factorial(n+j-1)/((i+j-1)*(factorial(i-1)*factorial(j-1))^2*factorial(n-i )*factorial(n-j));end endresult1=0; for j=1:nresult1=result1+A(1,j); endresult1=log(result1); result2=0; for i=1:n for j=1:nresult2=B(i,j)+result2; endresult(i)=log(result2); endm=max(result);x(n)=result1+m; end plot([1:50],x)对于更大的n 值,由于Hilbert 逆矩阵中的元素过大,溢出,故在此取50以内的n 。
图1 ln(())~n cond H n 关系曲线图猜想ln(())~n cond H n 之间存在线性关系 验证:设ln(()n cond H an b ∞=+ 在以上程序基础上,再添加>>;>> y=x'; >> l=1:40; >> k=l';>> p=polyfit(k,y,1) %一次多项式拟合 p =3.5446 -3.0931% P=polyfit(k,y,2) %二次多项式拟合 p =-0.0008 3.5778 -3.3253 % P=polyfit(k,y,3) %三次多项式拟合0.0000 -0.0033 3.6198 -3.4777% P=polyfit(k,y,4) %四次多项式拟合-0.0000 0.0002 -0.0082 3.6654 -3.5815 % P=polyfit(k,y,5) %五次多项式拟合 p =0.0000 -0.0000 0.0007 -0.0156 3.7107 -3.6542 从上式可以看出,高次项系数相对于一次项和常数项系数要小很多, 所以取ln(() 3.5446 3.0931n cond H n ∞=-2)设D 是n H 的对角线元素开方构成的矩阵。
《计算方法与实习》实验报告

迭代9500次时,和为:S=1.644829误差为:i=5.19077e-006
迭代10000次时,和为:S=1.644834误差为:i=7.184807e-008
Press any key to continue
(2)从10000叠加到1的源代码如下:
迭代1000次时,和为:S=1.643935误差为:i=0.0008994333
迭代1500次时,和为:S=1.644268误差为:i=0.0005663776
迭代2000次时,和为:S=1.644434误差为:i=0.0003998082
迭代2500次时,和为:S=1.644534误差为:i=0.0002998532
4 -0.709834 -0.703483 0.00635069
5 -0.703483 -0.703467 1.59816e-005
6 -0.703467 -0.703467 1.0107e-010
算法成功,迭代次数为:n=6
Press any key to conΒιβλιοθήκη inue第三章第1题(1):
编写用追赶法解三对角线性方程组的程序,并解下列方程组:
a=i;
if(a%500==0)cout<<setprecision(7)<<"迭代"<<a<<"次时,和为:S="<<n<<'\t'<<"误差为:i="<<fabs(S-n)<<endl<<endl;
}
return 0;
计算方法与实习答案

计算方法与实习答案【篇一:《基础会计学习指导、习题与实训》答案】名词解释1.会计:是以货币为主要计量单位,以凭证为依据,运用专门的技术方法,对一定主体的经济活动进行连续、系统、全面的核算与监督,以提高经济效益为目标,向有关方面提供会计信息的一种经济管理活动。
2.会计职能:是指会计在经济管理中所具有的功能,即会计在经济管理中能发挥什么作用。
3.会计核算职能:是指以货币为主要计量单位,对企事业单位一定时期的经济活动进行真实、连续、系统、完整的记录、计量和报告。
4.会计监督职能:是指依据监督标准,利用会计核算所提供的会计信息对各单位的经济活动全过程的合法性、合理性和有效性进行的指导、控制和检查。
5.会计对象:是指会计所要核算和监督的内容,即会计工作的内容。
6.会计要素:是对会计对象按经济特性所做的基本分类,是会计对象的具体内容。
7.资产:是指企业过去的交易或者事项形成的、由企业拥有或者控制的、预期会给企业带来未来经济利益的资源。
8.负债:是指企业过去的交易或者事项形成的、预期会导致经济利益流出企业的现时义务。
9.所有者权益:是指企业资产扣除负债后由所有者享有的剩余权益,包括实收资本、资本公积、盈余公积和未分配利润。
10.收入:是指企业在日常活动中形成的、会导致所有者权益增加的、与所有者投入资本无关的经济利益的总流入,包括销售商品收入、劳务收入、利息收入等。
11.费用:是指企业在日常活动中发生的、会导致所有者权益减少的、与向所有者分配利润无关的经济利益的总流出。
12.利润:是指企业在一定会计期间的经营成果,包括收入减去费用后的净额、直接计入当期利润的利得和损失等。
13.会计方法:是为实现会计核算、进行会计管理和完成会计任务所采用的手段。
14.会计核算方法:是对单位已经发生的经济活动进行连续、系统、全面的核算所采用的方法,包括设置账户、复式记账、审核和填制会计凭证、登记账簿、成本计算、财产清查和编制财务会计报告。
2021年计算实习报告三篇

2021年计算实习报告三篇计算实习报告篇1一、实习目的通过理论联系实际,巩固所学的知识,提高处理实际问题的能力,为顺利毕业进行做好充分的准备,并为自己能顺利与社会环境接轨做准备。
通过这次实习,使我们进一步理解和领会所学的基本理论,了解计算机技术和信息管理技术的发展及应用,较为系统地掌握计算机应用技能和信息管理技能,把所学知识与解决实际问题相联系,能够利用计算机处理工作中的各种信息,培养我们发现问题、分析问题和解决问题的能力,从而提高我们从事实际工作的能力。
通过理论联系实际,巩固所学的知识,提高处理实际问题的能力,了解设计专题的主要内容,使学生能够了解社会、学校的需要,在实习单位领导的帮助,对自己今后所从事的事业有一个实习了解的过程。
为毕业设计的顺利进行做好充分的准备,并为自己能顺利与社会环境接轨做准备。
二、实习意义通过实习,使学生在社会实践中接触与本专业相关的实际工作,增强感性认识,培养和锻炼学生综合运用所学的基础理论、基本技能和专业知识,去独立分析和解决实际问题的能力,把理论和实践结合起来,提高实践动手能力,为学生毕业后走上工作岗位打下一定的基础;同时可以检验教学效果,为进一步提高教育教学质量,培养合格人才积累经验。
计算机是一门对实践要求较高的学科,通过专业实习,使学生能熟悉有关计算机专业的各个领域,使学生毕业后能胜任与本专业相关的工作。
大学四年学习了很多,经历了很多,得到的是学习能力、处事能力和一些专业知识。
可面对社会,我们经验太少,思想单纯!毕业实习,给了我们一个了解社会,增加经验,熟悉工作单位的机会。
锻炼自己的动手能力,将学习的理论知识运用于实践当中,反过来还能检验书本上理论的正确性,有利于融会贯通。
同时,也能开拓视野,完善自己的知识结构,达到锻炼能力的目的。
一切都是为了让实践者对本专业知识形成一个客观,理性的认识,从而不与社会现实相脱节。
此外通过理论联系实际,巩固所学的知识,提高处理实际问题的能力,了解设计专题的主要内容,为毕业设计的顺利进行做好充分的准备,并为自己能顺利与社会环境接轨做准备。
实用的计算实习报告3篇

实用的计算实习报告3篇计算实习报告篇1[实习目的]通过理论联系实际,巩固所学的知识,提高处理实际问题的能力,了解设计专题的主要内容,为毕业设计的顺利进行做好充分的准备,并为自己能顺利与社会环境接轨做准备。
[实习任务]对计算机在人事管理方面的应用进行归纳总结,并查阅资料为毕业设计作准备.[实习内容]计算机在人事管理中的应用随着社会的发展,科技的进步,作为信息载体的计算机日益显露出其举足轻重的地位。
当今社会已步入了信息社会,知识经济将成为新世纪的主导产业。
伴随计算机的逐步推广和使用,计算机已在科研、生产、商业、服务等许多方面创造了提高效率的途径,与此同时,单位技术成本也逐年有了明显的下降,然而办公室里的人事费用却不断增加。
在国外,花费在专业、管理和行政人员上的成本占了办公室总成本的2/3—4/5,这一现象使人们对办公室自动化的要求与日俱增。
我们必须在进行机构改革的同时,尽快使用现代化管理设备、管理手段、管理方法。
计算机在人事部门的广泛使用,改进了统计手段,改革了统计方法,提高了统计工计算机在人事部门的广泛应用,将为我国的人事管理工作,提供现代化的管理手段和科学的管理方法,并将为开创人事管理工作的新局面创造条件。
目前,计算机在我国的人事管理工作中,主要可用来进行报表处理,档案管理,文书编辑,信息查询,综合分析。
干部统计作为人事管理的一个重要组成部分,是通过对干部情况的调查,整理和分析,了解干部队伍的发展趋势,为各级领导机关制定干部工作的方针,政策,加强干部管理,改革干部制度提供准确数字的依据。
其工作除涉及到干部的基本情况统计之外,还包括干部的工资统计,干部编制情况统计,干部奖惩情况统计,军转干部安置情况统计,老干部情况统计等方面,其涉及的面之广,数据量之大可想而知,若利用手工进行干部的统计工作,大致要经过干部统计调查,干部统计资料的整理,干部统计分析三个过程,但这种手工统计过程,存在着几个明显的问题,比如说统计资料缺乏准确性,及时性,需要花费大量的人力,物力,财力等。
有关计算实习报告模板集合六篇

有关计算实习报告模板集合六篇计算实习报告篇1一实习目的理论联系实际,巩固所学知识,提高处理实际问题的能力,大学生计算机实习报告总结。
为自己能顺利与社会环境接轨做准备。
二实习任务计算机基础理论在实践中的应用三实习内容1.mysql数据库的安装。
配置和使用2.java基础,java网络编程3. linux基础命令,linux bash shell编程,linux服务器的配置,linux常用软件的安装配置使用4.网络安全5.计算机的日常维护四实习过程1.网络基础的实践20__年1月6日,我把电脑从学校搬回家里。
20__年1月13日,家里的网络通了。
在这段时间内,我和家人去网通的代理商那里报装了adsl 1m包年的套餐。
我在代理商那里观察了他们的网络布线情况。
那里有一个modem和一个交换机,上面密密麻麻地布满了许多网线和一些电话线。
20__年1月13日,安装人员终于来到我家,帮助我们接通了网络。
家里电脑的上网方式是虚拟拨号上网,使用的ppp协议。
线路连接方式是:电话线——modem——电脑网卡的rj45接口,实习总结《大学生计算机实习报告总结》。
电脑在学校上网的线路连接方式是:电话线——分离器——电话机——路由器——电脑主机的rj45接口。
在学校,提供服务的运营商是中国电信;在家里,提供服务的运营商是中国网通。
使用中国电信的打开南方的网页快,例如打开qq 空间;使用中国网通的打开北方的网页快,例如看央视的视频。
我的电脑在家里出现的问题有:1.打开不了qq空间(在学校可以)2.linux上不了网(在学校可以)。
2.数据库的学习20__年2月,我开始做毕业设计。
数据库sql 200在xp2安装过程中失败。
失败的原因本人至今不知道。
大二时曾经安装过sql __,后来使用出现问题,我把它卸载掉。
本人重装系统后发现:原来重装前的系统可以安装sql __,从那一次开始,安装都失败了。
有一次,安装sql __过程中出现系统蓝屏。
计算方法作业集范文

计算方法作业集范文一、整数加减法计算问题(300字)整数加减法是我们学习数学的基础,也是我们日常生活中经常遇到的计算问题。
在整数加减法计算中,我们经常会遇到减法绝对值大于被减数的情况,这时我们需要进行借位操作。
例如,计算-9-7的结果时,我们可以先将问题转化为-9+(-7),再利用加法的逆元性质进行计算,即-9+(-7)=-(9+7)=-16在整数加减法计算中,还需要注意进位的问题。
例如,计算-15+8的结果时,我们可以先进行取反运算,得到15+(-8),然后进行正数加法运算,即15+(-8)=7另外,在整数加减法计算中,我们还可以利用拆分法进行计算。
例如,计算-13+5的结果时,我们可以将-13拆分成-10和-3,然后进行分别计算,即-10+5=-5,-3+5=2,最后将两个结果相加得到-13+5=-5+2=-3在实际应用中,整数加减法计算经常会涉及到财务、经济、物理等领域。
例如,在财务账目上进行损益计算时,需要准确计算各项收入和支出的总和,以确定损益情况。
在物理实验中,使用质量、长度、时间等量进行计算时,也需要进行整数加减法运算。
总之,整数加减法计算是我们学习数学的基础,也是我们日常生活中经常遇到的计算问题。
通过掌握加减法的计算方法,我们可以更好地解决实际生活和学习中遇到的各种计算问题。
二、小数乘除法计算问题(300字)小数乘除法是数学中较为复杂的计算问题之一、在小数乘法计算中,我们需要注意小数点的位置和小数位数的处理。
例如,计算2.5×0.3的结果,我们可以先去掉小数点,将2.5和0.3都乘以10,得到25和3,再进行乘法运算,即25×3=75,最后将结果除以100得到最终结果0.75在小数除法计算中,我们需要注意除数为0的情况。
除数为0时,计算结果是无穷大或无解。
例如,计算8.4÷0的结果时,我们可以得知结果为无穷大,表示该除法运算没有意义。
另外,在小数乘除法计算中,我们还可以利用科学计数法进行计算。
