胚优课件第四天

合集下载

五年级上册奥数培优第四讲小数除法的应用

小数除法的应用循环小数的应用例1、求3÷7商的小数点后面第2021个数字是几？练一练1、5÷7商的小数点后面第2000数字是几?2、23÷13商的小数点后面第1000数字是几?3、34÷11商的小数点后面第2020个数字是几?例2、求32÷37商的小数点后面前125个数字之和是多少？练一练4化成小数，它的小数部分的第38位上的数字是几?小数部分1、把7的前100个数字之和是多少?6化成小数，小数点后面第1000位的数字是几?这1000个数字2、把7之和是多少？3、11÷13商的小数点后面2020个数之和是多少？解决问题（一）例1、五(1)班45名同学合影留念，拍6寸合影照片并冲印两张照片，费用为15元，如果需加印，每张加收3元1现在每人各要一张照片，平均每人需付多少元?练一练1、静静前4次英语测验的平均成绩是93分，今天她超常发挥，得了99分.静静5次英语测验的平均成绩是多少分?2、佳美超市有45千克奶糖，每千克115元，还有55千克水果糖，每千克9.5元。

把这两种糖混合起来成为什锦糖，至少每千克多少元卖出不亏本?3、五(1)班45位同学集体合影，收费方式是，拍摄并冲印5张照片，收25元。

另外加印，每张2.5元.如果全班每人要一张照片，平均每人需付多少钱?(结果保留两位小数)例2、欢欢有12.8元，贝贝有51.2元，欢欢想买一本《中国少年童百科全书》，发现身上钱不够贝贝借了若干元给欢欢后，欢欢的钱数是贝贝的3倍，问贝贝借了多少元给欢欢?练一练1、欢欢有38.4元，贝贝有768元.他俩各买了一本《唐诗三百首》，贝贝剩下的钱是欢欢剩下的钱的4倍，你知道一本《唐诗三百首》多少元吗?2、某城市地铁2号线的建设工地原来有3台搅拌机，8小时可以搅拌混凝28.8吨.现在因为工期紧张，又增加了2台同样的搅拌机，20小时可以比原来8小时多搅拌出多少吨混凝土?(每台搅拌机工作效率一样)3、一个服装店购进80件服装，开始的60件以每件68.5元售出，剩下的服装采用“买一赠一”的方式售出.这批服装一共卖得多少元?解决问题（二）例1、朝晖小学五(2)班同学数学期中测试的平均成绩为91.5分，事后复查发现计题成绩时将一位同学的98分误作89分计算了.经重新计算，全班的平均成绩是91.7分，五(2)班有多少名同学?练一练1、五(1)班有42名同学，期中数学测验有2名同学因病缺考，这时班级平均分为85分，缺考的同学补考各得95、96分.这个班的期中测验平均分是多少?2、某班在一次语文测验中的平均成绩是85.1分，后来发现李蓉的成绩是97分，被误看成79分，重新计算后平均成绩是85.5分.该班共有多少名学生?3、小敏、非菲和童童是好朋友，下午放学后，她们三人一起买了12片面包，平均分着吃，不巧的是非菲忘了带钱，于是小敏付了5块面包的钱，童童付了7块面包的钱回家后，非菲拿了12元分给她们俩，小敏和童童应各拿多少元?例2、“十ー”黄金周期间，小洁有兴趣地读了《未来科学家》，第一天读了83页，第二天读了74页，第三天读了71页，第四天读了64页，第五天读的页数比五天中所读页数的平均数还多3.2页。

人教版七年级上册数学同步培优课件第4章第3课时点、线、面、体

略
返回
数学
精典范例
3.【例1】观察图形，回答下列问题：
(1)图①是由几个面组成的？这些面有什么特征？ (2)图②是由几个面组成的？这些面有什么特征？ (3)图①中共形成了多少条线？这些线都是直的吗？图②呢？ (4)图①和图②中各有几个顶点？
返回
数学
解：(1)图①是由6个面组成的，这些面都是平面． (2)图②是由2个面组成的，1个平面和1个曲面． (3)图①中共有12条线，这些线都是直的；图②中有1条线，是曲线． (4)图①中有8个顶点，图②中只有1个顶点．小结：解答此类问题要联系实物的形状与面的形状作对比，然后作出判断，平面与平面相交成直线，曲面与平面相交成曲线.
3．养成学生积极主动的学习态度和自主学习的方式.
返回
数学
知识要点知识点一：点、线、面、体的概念及构成图形的元素 (1)几何体也简称体，包围着体的是面，面有平面和曲面两种． (2)面和面相交的地方是线，线有直线和曲线两种． (3)线和线相交的地方是点． (4)几何图形都是由点、线、面、体组成的，点是构成图形的基本元素.
返回
数学
变式练习 6.观察下列立体图形，并把下表补充完整．
名称三棱柱四棱柱五棱柱六棱柱
图形
顶点数 6
8
10 12
棱数 9
12 15
18
面数 5
6
7
8
返回
数学
4.【例2】把如图所示的图形绕着给定的直线旋转一周后形成
的几何体是( D )
小结：此题考查了点、线、面、体，重在体现面动成体，需
要发挥立体图形的空间想象能力及提高分析问题、解决问题
返回

初一培优记录

初一培优记录第一天今天是我初一培优班的第一天，我对这个班级充满了期待。

早上，我提前到达了学校，看到了许多同学也在等待开班。

我们迎来了班主任老师的介绍，她是一位非常和蔼可亲的老师。

她告诉我们，在这个班级里，我们将会学习很多有趣的知识，并且会有一些有趣的活动和实践。

听到这些，我的心情更加激动了。

上午的第一节课是语文课，老师给我们讲解了课本中的一篇文章。

这篇文章是关于大自然的美好景色的描述，我被其中的细节所吸引。

老师还带我们进行了一些课堂讨论，让我们发表自己的想法和感受。

我觉得这种交流的方式非常有效，能够提高我们的思维能力和表达能力。

下午的课程比较丰富多样，我们学习了数学、英语和科学。

虽然没有使用数学公式或计算公式，但我们学习了一些基本的数学概念和方法。

英语课上，我们进行了一些口语练习，通过模拟对话和角色扮演，提高了我们的口语表达能力。

科学课上，老师带我们进行了一次有趣的实验，我们通过实践观察到了一些现象，加深了对科学知识的理解。

第二天今天是我初一培优班的第二天，我对今天的课程也非常期待。

上午的第一节课是美术课，老师带我们学习了一些绘画技巧。

我们用铅笔画了一幅风景画，我尽力将大自然的美景表现出来。

虽然我的画并不完美，但我觉得这是一个很好的开始。

接下来是音乐课，老师教我们唱了一首经典的歌曲。

我们学习了歌曲的歌词和旋律，通过集体合唱，我们感受到了音乐的魅力。

下午的课程包括了体育、地理和历史。

体育课上，我们进行了一些有趣的运动项目，锻炼了身体的同时也增强了团队合作能力。

地理课上，老师给我们讲解了地球的形状和地理分布，我对地理知识有了更深的了解。

历史课上，我们学习了一些历史事件和人物，并进行了小组讨论，交流了自己的观点和思考。

第三天今天是我初一培优班的第三天，我对今天的课程充满了期待。

上午的第一节课是生物课，老师带我们进行了一次动物观察活动。

我们来到学校的花园里，观察了花朵上的蜜蜂和蝴蝶。

通过观察和讨论，我们学习到了一些关于昆虫的知识。

培优训练人教版七年级数学下册5ppt

B．－3<b≤－2
解：解不等式①得x＞＜－a－2，1. 解不等式②得x≤4＋a.
∴类不型等三式组已的知解不集等是式－组2有＜、x≤无4＋解a求. 字母系数的取值范围
谢谢！解请不根等据式上②述得定义x＞解－决6问. 题：若a＜2※x＜7，且解集中有两个整数解，则a的取值范围是____________．
10．若关于 x 的不等式组x3＋x＋1<5>a① x－，7② 有解，求实数 a 的取值范围. 解：解不等式①得x＜a－1.解不等式②得x＞－6. ∵不等式组有解，∴－6＜a－1.∴a＞－5.
∴一不元等一式次组不的等解式集(组是)中－含2＜字x母≤4＋a.
解 A．：－解3不<b等<－式2①得x＜式x＞(组－式)6中. 含组字母的解集是－2＜x≤4＋a.
解不等式②得x＞－6.
类型三已知不等式组有、无解求字母系数的取值范围
∵不等式组恰好有两个整数解，类型一已知解集求字母系数的值或取值范围
解：解不等式①得x＜a－1.
5．关于x的不等式x－b>0恰有两个负整数解，则b的取值范围是( )
6.对于任意实数m，n，定义一种新运算m※n＝mn－m －n＋3，等式的右边是通常的加减和乘法运算，例如： 3※5＝3×5－3－5＋3＝10.请根据上述定义解决问题：若a＜2※x＜7，且解集中有两个整数解，则a的取值范围是___4_≤__a_＜__5___．
5x＋1＞3（x－1）①，
A．－3<b<－2
解不等式②得x＞－6.
类型一已知解集求字母系数的值或取值范围
类型二已知整数解的情况求字母系数的取值范围
解：解不等式①得x＞－2，解不等式②得x≤4＋a. ∴不等式组的解集是－2＜x≤4＋a.

人教版四年级数学下册培优公开课课件4.15 最佳策略 (共13张PPT)

我们可以把题中的关键数称为获胜的“制胜点”。要获胜关键是占领 “制胜点”。
用什么方法占领每次的“制胜点”？两人一轮取数的和=允许取的最小值+最大值和÷（较小数+较大数）=商……余数余数就是第一个“制胜点”；如果没有余数，除数就是第一个“制胜点”。
例3：四（1）班和四（2）班比赛乒乓球。每班选出打乒乓球最好的3名同学参赛，共打3场球，3盘2胜。如果你是四（2）班的同学，你将怎样安排本班的3名选手出场比赛，才可能打赢比赛？
后拿者 2 1
Hale Waihona Puke 获胜者后拿者甲在某一时刻留下3个球不管乙怎么拿，甲接下去和乙拿的球数和为3，甲必胜。
所以甲必须拿到第10、7、4、1个球，才能保证获胜。
规律：1、倒着往前推； 2、两人一轮拿的球数和=允许拿的最小值+最大值。
例2：有30根火柴，甲、乙两人玩轮流取火柴的游戏，规定每人每次可取出不超过3根的火柴，但不可不取，谁最后把火柴取玩，谁就获胜，问如何能确保获胜？
15 、常胜将军
——最佳策略
例1：有13个乒乓球，甲乙两人轮流拿，每人每次可以拿1个或者2个，不能不拿，拿到最后一个的为胜。甲有保证获胜的方法吗？
① ② ③ ④ ⑤ ⑥⑦ ⑧⑨ ⑩ 11 12 1133
剩下1-2个球，先拿的可以一次性拿完取胜;
剩下3个球，先拿的不能一次性拿完，后拿者取胜。
先拿者 1 2
1班
第一场
A
第二场
B
第三场
C
胜2班
C
A B
结果
1班胜 2班胜 2班胜
假设按技术从高到低把3位选手分为A、B、C号同学
例4：196个空格排成一排，第一格中放有一枚棋子，现有两人做游戏，轮流移动棋子，每人每次可前移1格、2格、3格或4格。谁先移到最后一格，谁为胜者。问怎样的移法才能确保获胜？

培优辅差4

A组材料一：1825年9月的一天，“旅行者号”机车拖着30多节小车厢正式试车，车厢载有450名乘客和90吨货物。

当时，铁路两旁人山人海，许多人兴奋地跟着火车跑材料二：1885年本茨制成一辆三轮汽车，此后汽车发展迅速，成为陆上主要交通工具。

1903年12月的一天，莱特兄弟制成飞机并试飞成功。

1、材料一中的火车是哪次工业革命的成果?它以什么为动力?它是谁发明的？2、材料二中的汽车和飞机中哪次工业革命的重要成果？它们都以什么为动力？3、试联系实际谈谈火车、汽车和飞机的发明对人类生活的影响B组材料一到了工业革命差不多结束的时候，英国在当时煤的产量占了世界的三分之二，铁的产量占了二分之一，棉织品的产量是整个世界所有其他国家加在一起的总和。

材料二一些工业发展的城市和工矿区人口密集、物流量大，煤的燃烧量急剧增加，大气污染的环境问题不断发生。

如1873、1880、1882、1891、1892年，英国伦敦多次发生可怕的有毒烟雾事件。

———刘少康编著《环境与环境保护导论》(1)材料一反映了工业革命使英国拥有怎样的国际地位?(2)材料二反映了英国伦敦出现了怎样的问题?依据材料二，分析出现这种问题的原因。

（3）根据以上材料和所学知识，你认为在发展经济时应该注意些什么?C组1、美国独立之后，北方和南方都发展起来。

两种制度水火不容。

19世纪中期，围绕着问题，北方和南方之间的矛盾再也无法调合。

2、1861年3月，就任美国总统，成为南方奴隶主发动叛乱的借口。

南方的一些州联合起来，宣布组成一个独立国家，号称“”。

年4月，挑起内战，美国南北战争爆发。

3、美国南北战争爆发后，北方由于和缺乏，北方军队虽然士气高昂，作战勇敢，在战争初期却一再失利。

4、年9月，林肯颁布了《》，规定从1863年元旦起，废除叛乱各州的，并允许奴隶作为参加北方军队。

发表意义：。

5、年，美国南北战争以的胜利告终，美国的统一最终得到维护。

6、南北战争结束后不久，拥护奴隶制的狂热分子在剧院刺杀了林肯。

2016年八年级下学期数学培优第4课时

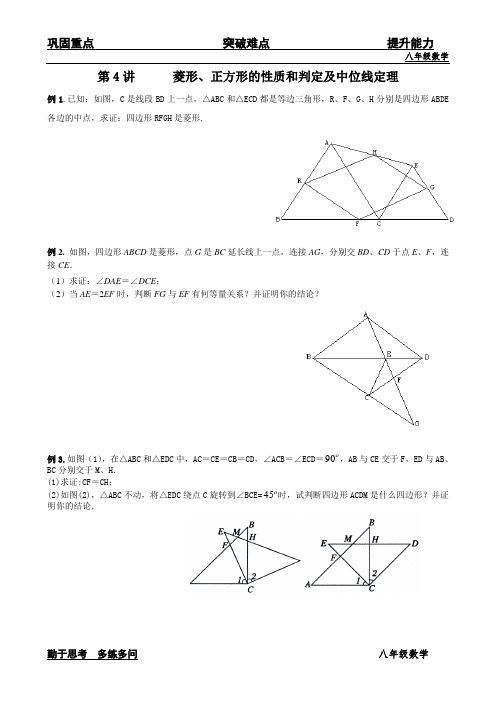
第4讲菱形、正方形的性质和判定及中位线定理例1.已知：如图，C是线段BD上一点，△ABC和△ECD都是等边三角形，R、F、G、H分别是四边形ABDE 各边的中点，求证：四边形RFGH是菱形.例2. 如图，四边形ABCD是菱形，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F，连接CE．（1）求证：∠DAE＝∠DCE；（2）当AE＝2EF时，判断FG与EF有何等量关系？并证明你的结论？90，AB与CE交于F，ED与AB、例3.如图（1），在△ABC和△EDC中，AC＝CE＝CB＝CD，∠ACB＝∠ECD＝BC分别交于M、H．(1)求证:CF＝CH；45时，试判断四边形ACDM是什么四边形？并证(2)如图(2)，△ABC不动，将△EDC绕点C旋转到∠BCE=明你的结论．（） A ．35° B ．45° C ．50° D ．55°2. 如图，将一个长为10cm ，宽为8cm 的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到的菱形的面积为（）A ．210cmB ．220cmC ．240cmD ．280cm3.如图将矩形纸片ABCD 按如图所示的方式折叠，得到菱形AECF ．若AB ＝3，则BC 的长为（）. A ．1 B ．2 C ．2 D ．34.如图，菱形ABCD 中，∠B ＝60°，AB ＝2，E 、F 分别是BC 、CD 的中点，连接AE 、EF 、AF ，则△AEF 的周长为（）A ．32B ．33C ．34 D．35．如图，菱形ABCD 的两条对角线分别长6和8，点P 是对角线AC 上的一个动点，点M 、N 分别是边AB 、BC 的中点，则PM +PN 的最小值是_____________．6. 如图，菱形ABCD 的边长为2，45ABC ∠=，则点D 的坐标为．7．如图，菱形ABCD 中，对角线AC BD 、相交于点O ，H 为AD 边中点，菱形ABCD 的周长为24，则OH 的长等于．8．如图，菱形ABCD 中，AE 垂直平分BC ，垂足为E ，AB ＝4cm ．那么，菱形ABCD 的面积是，对角线BD 的长是．9.如图，菱形ABCD 的对角线AC 、BD 相交于点O ，且AC=8，BD=6，过点O 作OH AB ⊥,垂足为H ，则点O 到边AB 的距离OH= .第5题图BAHCO 第7题图BCAM NP FE 10.在边长为6的菱形ABCD 中，动点M 从点A 出发，沿A →B →C 向终点C 运动，连接DM 交AC 于点N ．（1）如图1，当点M 在AB 边上时，连接BN ．①求证：ABN ADN △≌△；②若∠ABC = 60°，AM = 4，∠ABN = ，求点M 到AD 的距离；（2）如图2，若∠ABC = 90°，记点M 运动所经过的路程为x （6≤x ≤12）．试问：x 为何值时，△ADN 为等腰三角形．11.如图，△ABC 中，点P 是边AC 上的一个动点，过P 作直线MN ∥BC ，设MN 交∠BCA 的平分线于点E ，交∠BCA 的外角平分线于点F ． (1)求证：PE ＝PF ；(2)当点P 在边AC 上运动时，四边形BCFE 可能是菱形吗？说明理由；(3)若在AC 边上存在点P ，使四边形AECF 是正方形，且AP BC ＝32．求此时∠A 的大小．专题二、正方形与平行四边形例4.如图所示，E 是正方形ABCD 的边BC 延长线上的点，且BC=CE. （1）四边形ACED 是平行四边形吗？说明理由；（2）如果AC=2，请求出四边形ACED 的面积.CBMND （图1）CMBNA D（图2）例5.如图，四边形ABCD 为平行四边形，四边形DFEC 和BCGH 是正方形.求证：.练习：12.如图，已知正方形ABCD ，点E 是BC 上一点，以AE 为边作正方形AEFG . （1）连接GD ，求证：ADG ABE ≅（2）请在AB 边上找一点Q ，使得四边形DQEF 是平行四边形，并说明理由.13.（1）如图①，在ABCD 的形外作等腰直角ABF 和等腰直角ADE ，090FAB EAD ∠=∠=,连接AC 、EF.在图中找一个与FAE 全等的三角形，并加以证明.说明EF 与AC 的位置关系，并加以证明. （2）以ABCD 的四边为边，在其形外分别做正方形，如图②,连接EF 、GH 、IJ 、KL.若ABCD 的面积为5，则图中阴影部分（四个三角形的面积和）为 .专题三、正方形与菱形例6.如图，以正方形ABCD 的对角线AC 为一边，延长AB 到E ，使AE=AC ，以AE 为边作菱形AEFC ，若菱形AEFC 的面积为.例7.如图，已知平行四边形ABCD 中，对角线AC 、BD 交于点O ，E 是DB 延长线上一点，且ACE 是等边三角形.（1）求证：四边形ABCD 是菱形；（2）若2AEB EAB ∠=∠，求证：四边形ABCD 是正方形CD 、DA 上，且AH=2,连接CF.（1）当DG=2时，求证：菱形EFGH 为正方形；（2）设DG=x ，试用含x 的代数式表示FCG 的面积.专题四、正方形的综合应用例8.如图1，在正方形ABCD 中，点O 是对角线的交点，045MON ∠=.（1）如图1，当点M 在BC 边上，ON 与CD 的延长线交于点N ，写出BM 、MN 、CN 之间的数量关系并证明你的结论；（2）如图2，当点M 在BC 边上，ON 与CD 交于点N ，写出BM 、MN 、CN 之间的数量关系并证明你的结论；（3）在（2）中，若正方形的边长为4，MC=1，求CN 的长.例9.如图，正方形ABCD 中，对角线AC 、BD 交于点O ，直线a 经过点A ，过D 作DE a ⊥于E 点，连接OE.（1）如图1，当直线a 在正方形的内部时，求证：AE DE -（2）如图2，当直线a 在正方形的外部时，DE a ⊥于E 点，连接OE ，写出AE 、DE 、OE 三者之间的数量关系：；（不证明）（3）如图3，在（2）的条件下，若2OE =,:4:3AE DE =.连接BE ，求线段BE 的长.练习15.如图，已知点D 为正方形ACBF 内一点，015CAD CBD ∠==. （1）求证：AD=BD ；（2）E 为AD 延长线上的一点，且CE=CA ，求证：AD+CD=DE;（3）当BD=2时，AC 的长为 .（直接写出结果，不要求写过程）练习16．如图，正方形ABCD ，AB =点E 、F 分别在BC 、CD 上，且030BAE ∠=，015DAF ∠=，求AEF 的面积.17．如图，在正方形ABCD 中，E 是AB 上一点，F 是AD 延长线上的一点，且DF BE =. （1）求证：CE=CF;（2）在图①中，若G 在AD 上，且045GCE ∠=，则GE BE GD =+成立吗？为什么？（3）运用（1）（2）解答中所积累的经验和知识，完成下题：如图②,在直角梯形ABCD 中，AD ∥BC （BC>AD ），∠B=090，AB=BC=12，E 是AB 上一点，45DCE ∠=，BE=4，求DE 的长.B18．正方形ABCD 中，E 为直线AB 上任意一点，交直线BC 的延长线于点F ，直线EF 、AC 交于点H ，连接DH.（1）如图①,当点E 在AB 上时，①判断线段DH 与EF 之间的位置关系与数量关系，证明你的结论；②AH HC -与AE 之间的数量关系，并证明你的结论；（2）如图②,当点E 在AB 的反向延长线上时，①判断线段DH 与EF 之间的位置关系与数量关系，证明你的结论；②AH HC -与AE 之间的数量关系，并证明你的结论；专题五、直角三角形和中位线例7.已知AD 是△ABC 的中线，E 是AD 的中点，求证：FC=2AF.练习：、如图，在△ABC 中，D 、E 、F 分别为三边中点，AG 是BC 边上的高，求证：四边形DGEF 是等腰梯形。

2013 夏四培优第四讲

6
一试身手：
• 计算：7＋11＋15＋19＋23＋27＋31
• 计算：(1＋3＋5＋…＋199)＋(2＋4＋6＋ …＋198) • 计算：2＋3＋4＋5＋……＋100＋101
100个数
例4．计算自然数中所有三位数的和
一试身手：
• 求自然数中所有两位数的和
例5. 求下面等差数列的和．
文本
文本
文本
文本
文本
• (1) 1＋4＋7＋10……；
100个
• (2) 1＋4＋7＋10＋…＋100．
一试身手：
• 1.计算： • (1)13＋17＋21＋25＋29……
80个
• (2)1＋5＋9＋13＋…＋1993
• 2．已知一等差数列的首项是1，末项是99 ，公差是7，求这个等差数列的和？ • 3．若A＝1＋3＋5＋7＋…＋1991，B＝2＋ 4＋6＋8＋…＋1990，试比较A与B的大小？并求差
2013 夏四培优第四讲
例1．计算 1＋2＋3＋……＋49＋50
例2．有一堆粗细均匀的圆木，堆成下图的形状，最上面一层有6根，每向下一层增加一根，共堆了25层。问：这堆圆木共有多少根？
一试身手：
• 1．有一堆粗细均匀的圆木，堆成如图的形状，最上面一层有6根，每向下一层增加一根，若最下面一层有 94根，那么这堆圆木共多少根？

【数学暑期培优课程】第3册 JA 第04讲运算顺序(下) 教师版

第04讲
运算顺序（下）
教学目标：
1.掌握混合运算中只有一级运算时的运算规律；掌握混合运算中有两级混合运算时的运算规律；学会用两步计算解决简单的实际问题；
2.培养学生的计算力、推理力和分析力；
3.通过理解用两步计算解决简单的实际问题的过程，获得解决问题的实际体验，为变身理财师做准备。

教学重点：
能够正确应用混合运算中的运算顺序；
教学难点：
熟练掌握在不同级运算中的运算顺序；
教学过程：
场景1：虎博士为了让大家都能够熟练地掌握正确的运算顺序，出了很多题目，我们和至慧宝贝们一起看一看吧！
【复习与提升】
【层层高1】
参考答案：
略。

【层层高2】
解析部分：
1、结合场景解题过程如下：教师引导学生审题，理解题目的意思。

观察算式的运算顺
序，发现其中运算顺序的错误，能够说一说为什么错了，应该怎样算，并改正。

2、本题的重点、难点：熟练掌握混合运算中的运算顺序；
【层层高3】
参考答案：
略。

【层层高4】
参考答案：
略。

【层层高5】
参考答案：
略。

【作业与预习】
【作业1】
参考答案：
略。

【作业2】
参考答案：
略。

【预习】
请你说说，在前四次课中你学习了哪些内容？。

2019-2020学年人教版高中数学必修四培优新方案浙江专用课件：第一章 1.4 1.4.2 第一课

第十八页，编辑于星期六：二十三点四十三分。
题型三三角函数的奇偶性与周期性的应用
[典例] 定义在R上的函数ƒ(x)既是偶函数又是周期函数，若ƒ(x)
的最小正周期是π，且当x∈0，π2时，ƒ(x)＝sin x，求ƒ53π的值． [解] ∵ƒ(x)的最小正周期是π，
∴ƒ53π＝ƒ53π－2π＝ƒ－π3 ∵ƒ(x)是R上的偶函数，
由图象可知 T＝π.
第十一页，编辑于星期六：二十三点四十三分。
[方法技巧]
求三角函数的周期的方法 (1)正弦函数和余弦函数的周期性实质是由终边相同的角所具有的周期性决定的． (2)求三角函数的周期，通常有三种方法： ①定义法． ②公式法．对于 y＝Asin(ωx＋φ)或 y＝Acos(ωx＋φ)(A， ω，φ 是常数，且 A≠0，ω≠0)，T＝|2ωπ|； ③观察法(图象法)．三种方法各有所长，要根据函数式的结构特征，选择适当方法求解，为了避免出现错误，求周期之前要尽可能将函数化为同名同角三角函数，且函数的次数为 1.
第八页，编辑于星期六：二十三点四十三分。
题型一三角函数的周期
[典例] 求下列函数的最小正周期． (1)ƒ(x)＝cos2x＋π3；(2)ƒ(x)＝|sin x|. [解] (1)[法一定义法] ∵ƒ(x)＝cos2x＋π3＝cos2x＋π3＋2π ＝cos2x＋π＋π3＝ƒ(x＋π)，
第九页，编辑于星期六：二十三点四十三分。
函数
y＝sin x
y＝cos x
周期
2kπ(k∈Z且k≠0)
2kπ(k∈Z且k≠0)
最小正周期
2π
2π
奇偶性
奇函数
偶函数
第五页，编辑于星期六：二十三点四十三分。
二、基本小题检验

2019-2020学年人教版高中数学必修四培优新方案浙江专用课件：第一章 1.3 第一课时诱导公式

第六页，编辑于星期六：二十三点四十三分。
2．已知 cos(π＋θ)＝ 63，则 cos θ＝( )
3 A. 6
B．－
3 6
C.
33 6
D．－
33 6
答案：B
第七页，编辑于星期六：二十三点四十三分。
3．下列式子中正确的是( A．sin(π－α)＝－sin α C．cos α＝sin α 答案：D
第十四页，编辑于星期六：二十三点四十三分。
[方法技巧] 利用诱导公式一～四化简应注意的问题 (1)利用诱导公式主要是进行角的转化，从而达到统
一角的目的； (2)化简时函数名没有改变，但一定要注意函数的符
号有没有改变； (3)同时有切(正切)与弦(正弦、余弦)的式子化简，一
般采用切化弦，有时也将弦化切．
第五页，编辑于星期六：二十三点四十三分。
二、基本小题检验
1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)
(1)诱导公式中角 α 是任意角．
(× )
(2)公式 sin(－α)＝－sin α，α 是锐角才成立．
(× )
(3)公式 tan(α－π)＝tan α 中，α＝π2不成立．
(√ )
[解]
(1)sin－73π＝－sin73π＝－sin2π＋π3＝－sinπ3＝－
3 2.
(2)cos176π＝cos2π＋56π＝cos56π＝cosπ－π6＝－cosπ6＝－ 23. (3)tan－855°＝－tan 855°＝－tan2×360°＋135°＝－tan 135°
＝－tan(180°－45°)＝－tan(－45°)＝tan 45°＝1.
1.3 三角函数的诱导公式第一课时诱导公式(一)

培优训练课件人教版七年级数学下册

∴∠FPB＝∠3，∠FPA＝∠1.
∴(180－3x)＋(180－4x)＋2x＝180，解得x＝36.
1 1 儿童有无抱负，这无关紧要，可成年人则不可胸无大志。
x＋90 °，∠DBF＝∠CBF－∠DBC＝ 90－ x °. 8．如图，已知直线l1∥l2，直线l3交l1于C点，交l2于D点，P是直线CD上的一个动点．当P在直线CD上运动时，请你探究∠1，∠2，∠3
类型三 (转化思想)利用平移进行转化求图形的
少年心事当拿云。死犹未肯输心去，贫亦其能奈我何!
周长或面积胸有凌云志，无高不可攀。
沧海可填山可移，男儿志气当如斯。男儿不展同云志，空负天生八尺躯。心随朗月高，志与秋霜洁。
胸生9无无．大一志锥，土如枉，活常图一有世四，。海心。直角三角形ABC的周长为100，在其内部有6个
类型一方程思想
1．如图，直线AB，CD相交于点O，∠AOC＝60°，OE
把∠BOD分成两部分，且∠BOE∶∠EOD＝1∶2，则
∠AOE的度数为( B )
A．180°
B．160°
C．140°
D．120°
2．如图，直线AB，CD相交于点O，OE平分∠BOD，OF 平分∠COB，∠AOD∶∠EOD＝4∶1，则∠AOF的度数为__1_2_0_°___．
类型四从特殊到一般的思想
13．如图①，三条直线两两相交，且不共点，则图中同旁内角有___6___对；如图②，四条直线两两相交，任三条直线不经过同一点，则图中的同旁内角有___2_4__对．
14.(2019·丛台区期末)如图，AB∥CD，∠ABE与∠CDE两个角的平分线相交于点F. (1)如图①，若∠E＝80°，求∠BFD的度数；
4．如图，AD∥BC，BE平分∠ABC交AD于点E，BD平分 ∠EBC. (1)若∠DBC＝30°，求∠A的度数； (2)若点F在线段AE上，且7∠DBC－2∠ABF＝180°，请问图中是否存在与∠DFB相等的角？若存在，请写出这个角，并说明理由；若不存在，请说明理由．