江苏省苏州市2015年中考数学试卷(解析版)

合集下载

江苏省苏州市2015年中考数学真题试题(含答案)

2015年苏州市初中毕业暨升学考试试卷数学本试卷由选择题、填空题和解答题三大题组成，共28小题，满分130分，考试时间120分钟．注意事项：1．答题前，考生务必将自己的姓名、考点名称、考场号、座位号用0.5毫米黑色墨水签字笔填写在答题卡相应位置上，并认真核对条形码上的准考号、姓名是否与本人的相符； 2．答选择题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，请用橡皮擦干净后，再选涂其他答案；答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题；3．考生答题必须答在答题卡上，保持卡面清洁，不要折叠，不要弄破，答在试卷和草稿纸上一律无效．一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将选择题的答案用2B 铅笔涂在答题卡相应位置上．．．．．．．．． 1．2的相反数是 A ．2B ．12C ．-2D ．-122．有一组数据：3，5，5，6，7，这组数据的众数为 A ．3B ．5C ．6D ．73．月球的半径约为1 738 000m ，1 738 000这个数用科学记数法可表示为 A ．1.738×106B ．1.738×107C ．0.1738×107D ．17.38×1054．若()222m =⨯-，则有 A ．0＜m ＜1 B ．-1＜m ＜0 C ．-2＜m ＜-1 D ．-3＜m ＜-25．小明统计了他家今年5月份打电话的次数及通话时间，并列出了频数分布表：通话时间x /min 0＜x ≤5 5＜x ≤10 10＜x ≤1515＜x ≤20频数（通话次数）201695则通话时间不超过15min 的频率为 A ．0.1B ．0.4C ．0.5D ．0.96．若点A （a ，b ）在反比例函数2y x=的图像上，则代数式ab -4的值为 A ．0 B ．-2C ． 2D ．-67．如图，在△ABC 中，AB =AC ，D 为BC 中点，∠BAD =35°，则∠C 的度数为 A ．35°B ．45°C ．55°D ．60°8．若二次函数y =x 2+bx 的图像的对称轴是经过点（2，0）且平行于y 轴的直线，则关于x 的方程x 2+bx =5的解为A ．120,4x x ==B ．121,5x x ==C ．121,5x x ==-D ．121,5x x =-=9．如图，AB 为⊙O 的切线，切点为B ，连接AO ，AO 与⊙O 交于点C ，BD 为⊙O 的直径，连接CD ．若∠A =30°，⊙O 的半径为2，则图中阴影部分的面积为 A ．433π- B ．4233π- C ．3π- D ．233π-10．如图，在一笔直的海岸线l 上有A 、B 两个观测站，AB =2km ，从A 测得船C 在北偏东45°的方向，从B 测得船C 在北偏东22.5°的方向，则船C 离海岸线l 的距离（即CD 的长）为 A ．4kmB ．()22+kmC ．22kmD ．()42-km二、填空题：本大题共8小题，每小题3分，共24分．把答案直接填在答题卡相应位置上．．．．．．．．． 11．计算：2a a ⋅= ▲ ．12．如图，直线a ∥b ，∠1=125°，则∠2的度数为 ▲ °．DCB A（第7题）（第9题）DC BAO（第10题）l北西南东CDBA45°22.5°cba21（第12题）（第13题）20%10%30%40%其他乒乓球篮球羽毛球13．某学校在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为 ▲ 名． 14．因式分解：224a b -= ▲ ．15．如图，转盘中8个扇形的面积都相等．任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为 ▲ ．16．若23a b -=，则924a b -+的值为 ▲ ．17．如图，在△ABC 中，CD 是高，CE 是中线，CE =CB ，点A 、D 关于点F 对称，过点F 作FG ∥CD ，交AC 边于点G ，连接GE ．若AC =18，BC =12，则△CEG 的周长为 ▲ ．18．如图，四边形ABCD为矩形，过点D 作对角线BD 的垂线，交BC 的延长线于点E ，取BE 的中点F ，连接DF ，DF =4．设AB =x ，AD =y ，则()224x y +-的值为 ▲ ．三、解答题：本大题共10小题，共76分．把解答过程写在答题卡相应位置上．．．．．．．．，解答时应写出必要的计算过程、推演步骤或文字说明．作图时用2B 铅笔或黑色墨水签字笔．19．（本题满分5分）计算：()9523+---．（第17题）GF E D CBA F EDC B A （第18题）（第15题）8765432120．（本题满分5分）解不等式组：()12,31 5.x x x +≥⎧⎪⎨-+⎪⎩＞21．（本题满分6分）先化简，再求值：2121122x x x x ++⎛⎫-÷⎪++⎝⎭，其中31x =-．22．（本题满分6分）甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问甲、乙每小时各做多少面彩旗？23．（本题满分8分）一个不透明的口袋中装有2个红球（记为红球1、红球2）、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．（1）从中任意摸出1个球，恰好摸到红球的概率是 ▲ ；（2）先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．24．（本题满分8分）如图，在△ABC 中，AB =AC ．分别以B 、C 为圆心，BC 长为半径在BC 下方画弧，设两弧交于点D ，与AB 、AC 的延长线分别交于点E 、F ，连接AD 、BD 、CD ．（1）求证：AD 平分∠BAC ；（2）若BC =6，∠BAC ＝50︒，求DE 、DF 的长度之和（结果保留π）．25．（本题满分8分）如图，已知函数ky x=（x ＞0）的图像经过点A 、B ，点B 的坐标为（2，2）．过点A 作AC ⊥x 轴，垂足为C ，过点B 作BD ⊥y 轴，垂足为D ，AC 与BD 交于点F ．一次函数y=ax +b 的图像经过点A 、D ，与x 轴的负半轴交于点E ．（1）若AC =32OD ，求a 、b 的值；（2）若BC ∥AE ，求BC 的长．26．（本题满分10分）如图，已知AD 是△ABC 的角平分线，⊙O 经过A 、B 、D 三点，过点B 作BE∥AD ，交⊙O 于点E ，连接ED ．（1）求证：ED ∥AC ；（2）若BD =2CD ，设△EBD 的面积为1S ，△ADC 的面积为2S ，且2121640S S -+=，求△ABC 的面积．（第24题）FEDCBAy xF OE D CBA（第25题）EBCDAO（第26题）27．（本题满分10分）如图，已知二次函数()21y x m x m =+--（其中0＜m ＜1）的图像与x轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，对称轴为直线l ．设P 为对称轴l 上的点，连接PA 、PC ，PA =PC ．（1）∠ABC 的度数为 ▲ °；（2）求P 点坐标（用含m 的代数式表示）；（3）在坐标轴上是否存在点Q （与原点O 不重合），使得以Q 、B 、C 为顶点的三角形与△PAC 相似，且线段PQ 的长度最小？如果存在，求出所有满足条件的点Q 的坐标；如果不存在，请说明理由．28．（本题满分10分）如图，在矩形ABCD 中，AD =a cm ，AB =b cm （a ＞b ＞4），半径为2cm 的⊙O在矩形内且与AB 、AD 均相切．现有动点P 从A 点出发，在矩形边上沿着A →B →C →D 的方向匀速移动，当点P 到达D 点时停止移动；⊙O 在矩形内部沿AD 向右匀速平移，移动到与CD 相切时立即沿原路按原速返回，当⊙O 回到出发时的位置（即再次与AB 相切）时停止移动．已知点P 与⊙O 同时开始移动，同时停止移动（即同时到达各自的终止位置）．（1）如图①，点P 从A →B →C →D ，全程共移动了 ▲ cm （用含a 、b 的代数式表示）；（2）如图①，已知点P 从A 点出发，移动2s 到达B 点，继续移动3s ，到达BC 的中点．若点P 与⊙O 的移动速度相等，求在这5s 时间内圆心O 移动的距离；y x O P C B A l （第27题）（3）如图②，已知a =20，b =10．是否存在如下情形：当⊙O 到达⊙O 1的位置时（此时圆心O 1在矩形对角线BD 上），DP 与⊙O 1恰好相切？请说明理由．2015年苏州市初中毕业暨升学考试数学试题答案一、选择题 1．C 2．B 3．A 4．C 5．D 6．B7．C8．D9．A10．B二、填空题 11．3a 12．55 13．60 14．()()22a b a b +- 15．1416．317．2718．16三、解答题19.解：原式＝ 3+5-1 ＝ 7． 20.解：由12x +≥，解得1x ≥，由()315x x -+＞，解得4x ＞， ∴不等式组的解集是4x ＞．（第28题）O 1ABCDOP（图②）（图①）PO DCBA21.解：原式＝()21122x x x x ++÷++ ＝()2121211x x x x x ++⨯=+++．当31x =-时，原式＝11333113==-+． 22.解：设乙每小时做x 面彩旗，则甲每小时做（x +5）面彩旗．根据题意，得60505x x=+．解这个方程，得x =25．经检验，x =25是所列方程的解． ∴x +5=30．答：甲每小时做30面彩旗，乙每小时做25面彩旗．23.解：（1）12．（2）用表格列出所有可能的结果：第二次第一次红球1 红球2白球黑球红球1（红球1，红球2）（红球1，白球）（红球1，黑球）红球2 （红球2，红球1）（红球2，白球）（红球2，黑球）白球（白球，红球1）（白球，红球2）（白球，黑球）黑球（黑球，红球1）（黑球，红球2）（黑球，白球）由表格可知，共有12种可能出现的结果，并且它们都是等可能的，其中“两次都摸到红球”有2种可能．∴P （两次都摸到红球）=212=16．24.证明：（1）由作图可知BD =CD ．在△ABD 和△ACD 中，,,,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACD （SSS ）．∴∠BAD ＝∠CAD ，即AD 平分∠BAC ．解：（2）∵AB =AC ，∠BAC =50°，∴∠ABC ＝∠ACB=65°．∵BD = CD = BC ，∴△BDC 为等边三角形． ∴∠DBC ＝∠DCB=60°． ∴∠DBE ＝∠DCF=55°． ∵BC =6，∴BD = CD =6．∴DE 的长度=DF 的长度=556111806ππ⨯⨯=． ∴DE 、DF 的长度之和为111111663πππ+=． 25．解：（1）∵点B （2，2）在ky x=的图像上，∴k =4，4y x=． ∵BD ⊥y 轴，∴D 点的坐标为（0，2），OD =2．∵AC ⊥x 轴，AC =32OD ，∴AC =3，即A 点的纵坐标为3．∵点A 在4y x=的图像上，∴A 点的坐标为（43，3）．∵一次函数y =ax +b 的图像经过点A 、D ，∴43,3 2.a b b ⎧+=⎪⎨⎪=⎩ 解得3,42.a b ⎧=⎪⎨⎪=⎩ （2）设A 点的坐标为（m ，4m），则C 点的坐标为（m ，0）． ∵BD ∥CE ，且BC ∥DE ，∴四边形BCED 为平行四边形． ∴CE = BD =2．∵BD ∥CE ，∴∠ADF =∠AEC ．∴在Rt △AFD 中，tan ∠ADF =42AF mDF m -=，在Rt△ACE 中，tan ∠AEC =42AC mEC =， ∴4422m m m -=，解得m =1． ∴C 点的坐标为（1，0），BC =5．26．证明：（1）∵AD 是△ABC 的角平分线， ∴∠BAD =∠DAC ．∵∠E=∠BAD ，∴∠E =∠DAC ． ∵BE ∥AD ，∴∠E =∠EDA ． ∴∠EDA =∠DA C ． ∴ED ∥AC ．解：（2）∵BE ∥AD ，∴∠EBD =∠ADC ．∵∠E =∠DAC ，∴△EBD ∽△ADC ，且相似比2BDk DC==．······· ∴2124Sk S ==，即124S S =． ∵2121640S S -+=，∴222161640S S -+=，即()22420S -=．∴212S =． ∵233ABC S BC BD CD CDS CD CD CD +====，∴32ABCS =． 27．解：（1）45．理由如下：令x =0，则y =-m ，C 点坐标为（0，-m ）．令y =0，则()210x m x m +--=，解得11x =-，2x m =．∵0＜m ＜1，点A 在点B 的左侧， ∴B 点坐标为（m ，0）．∴OB =OC =m ．∵∠BOC ＝90°，∴△BOC 是等腰直角三角形，∠OBC ＝45°．（2）解法一：如图①，作PD ⊥y 轴，垂足为D ，设l 与x 轴交于点E ，由题意得，抛物线的对称轴为12mx -+=．设点P 坐标为（12m-+，n ）． ∵PA = PC ， ∴PA 2= PC 2，即AE 2+ PE 2=CD 2+ PD 2．∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭．解得12m n -=．∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．解法二：连接PB ．由题意得，抛物线的对称轴为12mx -+=． ∵P 在对称轴l 上，∴PA =PB ． ∵PA =PC ，∴PB =PC ．∵△BOC 是等腰直角三角形，且OB =OC ， ∴P 在BC 的垂直平分线y x =-上．∴P 点即为对称轴12mx -+=与直线y x =-的交点． ∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭． y xy x图①图②O PE D CBAl Q Ql ABC D E PO（3）解法一：存在点Q 满足题意．∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭， ∴PA 2+ PC 2=AE 2+ PE 2+CD 2+ PD2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． ∵AC 2=21m +，∴PA 2+ PC 2=AC 2．∴∠APC ＝90°．∴△PAC 是等腰直角三角形．∵以Q 、B 、C 为顶点的三角形与△PAC 相似，∴△QBC 是等腰直角三角形．∴由题意知满足条件的点Q 的坐标为（-m ，0）或（0，m ）． ①如图①，当Q 点的坐标为（-m ，0）时，若PQ 与x 轴垂直，则12m m -+=-，解得13m =，PQ =13．若PQ 与x 轴不垂直，则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ 取得最小值1010． ∵1010＜13， ∴当25m =，即Q 点的坐标为（25-，0）时， PQ 的长度最小． ②如图②，当Q 点的坐标为（0，m ）时，若PQ 与y 轴垂直，则12m m -=，解得13m =，PQ =13．若PQ 与y 轴不垂直，则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ 取得最小值1010． ∵1010＜13， ∴当25m =，即Q 点的坐标为（0，25）时， PQ 的长度最小．综上：当Q 点坐标为（25-，0）或（0，25）时，PQ 的长度最小．解法二：如图①，由（2）知P 为△ABC 的外接圆的圆心．∵∠APC 与∠ABC 对应同一条弧AC ，且∠ABC ＝45°，∴∠APC ＝2∠ABC ＝90°．下面解题步骤同解法一．28．解：（1）a +2b ．（2）∵在整个运动过程中，点P 移动的距离为()2a b +cm ，圆心O 移动的距离为()24a -cm ，由题意，得()224a b a +=-． ①∵点P 移动2s 到达B 点，即点P 用2s 移动了b cm ，点P 继续移动3s ，到达BC 的中点，即点P 用3s 移动了12a cm ． ∴1223a b =． ② 由①②解得24,8.a b =⎧⎨=⎩∵点P 移动的速度与⊙O 移动的速度相等，∴⊙O 移动的速度为42b =（cm/s ）． ∴这5s 时间内圆心O 移动的距离为5×4=20（cm ）．（3）存在这种情形．解法一：设点P 移动的速度为v 1cm/s ，⊙O 移动的速度为v 2cm/s ，由题意，得()()1222021052422044v a b v a ++⨯===--． HG F E P O DCB A O 1如图，设直线OO 1与AB 交于点E ，与CD 交于点F ，⊙O 1与AD 相切于点G ．若PD 与⊙O 1相切，切点为H ，则O 1G =O 1H ．易得△DO 1G ≌△DO 1H ，∴∠ADB =∠BDP ．∵BC ∥AD ，∴∠ADB =∠CBD ．∴∠BDP =∠CBD ．∴BP =DP ．设BP =x cm ，则DP =x cm ，PC =（20-x ）cm ，在Rt △PCD 中，由勾股定理，可得222PC CD PD +=，即()2222010x x -+=，解得252x =． ∴此时点P 移动的距离为25451022+=（cm ）． ∵EF ∥AD ，∴△BEO 1∽△BAD ．∴1EO BE AD BA =，即182010EO =． ∴EO 1=16cm ．∴OO 1=14cm ．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ，∴此时点P 与⊙O 移动的速度比为454521428=． ∵455284≠， ∴此时PD 与⊙O 1不可能相切．②当⊙O在返回途中到达⊙O1的位置时，⊙O移动的距离为2×(20-4)-14=18（cm），∴此时点P与⊙O移动的速度比为45455218364==．∴此时PD与⊙O1恰好相切．解法二：∵点P移动的距离为452cm（见解法一），OO1=14cm（见解法一），125 4vv=，∴⊙O应该移动的距离为4541825⨯=（cm）．①当⊙O首次到达⊙O1的位置时，⊙O移动的距离为14cm≠18 cm，∴此时PD与⊙O1不可能相切．②当⊙O在返回途中到达⊙O1的位置时，⊙O移动的距离为2×(20-4)-14=18（cm），∴此时PD与⊙O1恰好相切．解法三：点P移动的距离为452cm，（见解法一）OO1=14cm，（见解法一）由125 4vv=可设点P的移动速度为5k cm/s，⊙O的移动速度为4k cm/s，∴点P移动的时间为459252k k=（s）．①当⊙O首次到达⊙O1的位置时，⊙O移动的时间为1479 422k k k=≠，∴此时PD与⊙O1不可能相切．②当⊙O在返回途中到达⊙O1的位置时，⊙O移动的时间为2(204)14942k k⨯--=，∴此时PD与⊙O1恰好相切．。

2015年苏州市中考数学试卷与答案

2015 年苏州市初中毕业暨升学考试试卷数学本试卷由选择题、填空题和解答题三大题组成，共28 小题，满分130 分，考试时间120 分钟．注意事项：1．答题前，考生务必将自己的姓名、考点名称、考场号、座位号用0.5 毫米黑色墨水签字笔填写在答题卡相应位置上，并认真核对条形码上的准考号、姓名是否与本人的相符；2．答选择题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，请用橡皮擦干净后，再选涂其他答案；答非选择题必须用0.5 毫米黑色墨水签字笔写在答题卡指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题；3．考生答题必须答在答题卡上，保持卡面清洁，不要折叠，不要弄破，答在试卷和草稿纸上一律无效．一、选择题：本大题共10 小题，每小题 3 分，共30 分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将选择题的答案用2B 铅笔涂在答．题．卡．相．应．位．置．上．．1．2 的相反数是A．2 B．12C． 2 D．122．有一组数据：3，5，5，6，7，这组数据的众数为A．3 B．5 C．6 D．73．月球的半径约为1 738 000m ，1 738 000 这个数用科学记数法可表示为6 B．1.738×107 C．0.1738×107 D．17.38×105A．1.738×104．若2m 2 ，则有2A．0＜m＜1 B．- 1＜m＜0 C．- 2＜m＜-1D．- 3＜m＜- 2 5．小明统计了他家今年 5 月份打电话的次数及通话时间，并列出了频数分布表：通话时间x/min 0＜x≤ 5 5＜x≤10 10＜x≤15 15＜x≤20频数（通话次数）20 16 9 5 则通话时间不超过15min 的频率为A．0.1 B．0.4 C．0.5 D．0.96．若点A（a，b）在反比例函数y 2x的图像上，则代数式a b- 4 的值为A ．0 B．- 2 C． 2 D．- 67．如图，在△ABC 中，AB= A C，D 为BC 中点，∠BAD =35°，则∠ C 的度数为A．35°B．45°C．55°D．60°ABD C（第7 题）8．若二次函数y=x2+bx 的图像的对称轴是经过点（2，0）且平行于y 轴的直线，则关于x 的方程x2+ b x=5 的解为A ．x1 0, x2 4 B．x1 1, x2 5 C．x1 1, x2 5 D．x1 1, x2 5 9．如图，AB 为⊙O 的切线，切点为B，连接AO，AO 与⊙O 交于点C，BD 为⊙O 的直径，连接CD．若∠A=30°，⊙O 的半径为2，则图中阴影部分的面积为A ．433 B．432 3 C． 3 D．233北C B西东南22.5 °OC A45°lAB DD（第9 题）（第10 题）10．如图，在一笔直的海岸线l 上有A、B 两个观测站，AB=2km，从 A 测得船 C 在北偏东45°的方向，从 B 测得船 C 在北偏东22.5°的方向，则船 C 离海岸线l 的距离（即CD 的长）为A ．4 km B． 2 2 km C．2 2 km D． 4 2 km二、填空题：本大题共8 小题，每小题 3 分，共24 分．把答案直接填在答题．卡．相．应．位．置．上．．．11．计算： 2a a = ▲．12．如图，直线a∥b，∠1=125°，则∠2 的度数为▲°．a1c羽毛球30%其他10%乒乓球篮球20% 240%b（第12 题）（第13 题）13．某学校在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少 6 人，则该校被调查的学生总人数为▲名．14．因式分解： 2 4 2a b = ▲．15．如图，转盘中8 个扇形的面积都相等．任意转动转盘 1 次，当转盘停止转动时，指针指向大于 6 的数的概率为▲．1 82 73 64 5（第15 题）16．若a 2b 3 ，则9 2a 4b 的值为▲．17．如图，在△ABC 中，CD 是高，CE 是中线，CE=CB，点A、D 关于点 F 对称，过点 F 作FG∥CD，交AC 边于点G，连接GE．若AC =18，BC=12，则△CEG 的周长为▲．CA DGA B C F EF E D B（第18 题）（第17 题）18．如图，四边形ABCD 为矩形，过点 D 作对角线BD 的垂线，交BC 的延长线于点E，取BE 的中点F，连接DF ，DF =4．设AB= x，AD =y，则 22 4x y 的值为▲．三、解答题：本大题共10 小题，共76 分．把解答过程写在答题．卡．相．应．位．置．上．．，解答时应写出必要的计算过程、推演步骤或文字说明．作图时用2B 铅笔或黑色墨水签字笔．19．（本题满分5分）计算：0 9523．20．（本题满分5分）解不等式组：x12,3x1＞x 5.21．（本题满分6分）先化简，再求值：121x2x1x2x2，其中x31．22．（本题满分6分）甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问甲、乙每小时各做多少面彩旗？23．（本题满分8分）一个不透明的口袋中装有2个红球（记为红球1、红球2）、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．（1）从中任意摸出1个球，恰好摸到红球的概率是▲；（2）先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．24．（本题满分8分）如图，在△ABC中，AB=A C．分别以B、C为圆心，BC长为半径在BC下方画弧，设两弧交于点D，与AB、AC的延长线分别交于点E、F，连接AD、BD、CD．（1）求证：AD平分∠BAC；（2）若BC=6，∠BAC＝50，求D?E、D?F的长度之和（结果保留）．ABCED（第24题）F25．（本题满分8分）如图，已知函数y kx（x＞0）的图像经过点A、B，点B的坐标为（2，2）．过点A作AC⊥x轴，垂足为C，过点B作BD⊥y轴，垂足为D，AC与BD交于点F．一次函数y=ax+b的图像经过点A、D，与x轴的负半轴交于点E．（1）若AC=32OD，求a、b的值；y（2）若BC∥AE，求BC的长．AD F BxE OC（第25题）26．（本题满分10分）如图，已知AD是△ABC的角平分线，⊙O经过A、B、D三点，过点B作BE∥AD，交⊙O于点E，连接ED．（1）求证：ED∥AC；（2）若BD=2CD，设△EBD的面积为S，△ADC的面积为S2，且12S116S240，求△ABC的面积．EAOB D C（第26题）27．（本题满分10分）如图，已知二次函数21y x m x m（其中0＜m＜1）的图像与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，对称轴为直线l．设P 为对称轴l上的点，连接PA、PC，PA=PC．（1）∠ABC的度数为▲°；（2）求P点坐标（用含m的代数式表示）；（3）在坐标轴上是否存在点Q（与原点O不重合），使得以Q、B、C为顶点的三角形与△PAC相似，且线段PQ的长度最小？如果存在，求出所有满足条件的点Q的坐标；如果不存在，请说明理由．ylPxA O BC（第27题）28．（本题满分10分）如图，在矩形ABCD中，AD=acm，AB=bcm（a＞b＞4），半径为2cm 的⊙O在矩形内且与AB、AD均相切．现有动点P从A点出发，在矩形边上沿着A→B →C→D的方向匀速移动，当点P到达D点时停止移动；⊙O在矩形内部沿AD向右匀速平移，移动到与CD相切时立即沿原路按原速返回，当⊙O回到出发时的位置（即再次与AB相切）时停止移动．已知点P与⊙O同时开始移动，同时停止移动（即同时到达各自的终止位置）．（1）如图①，点P从A→B→C→D，全程共移动了▲cm（用含a、b的代数式表示）；（2）如图①，已知点P从A点出发，移动2s到达B点，继续移动3s，到达BC的中点．若点P与⊙O的移动速度相等，求在这5s时间内圆心O移动的距离；（3）如图②，已知a=20，b=10．是否存在如下情形：当⊙O到达⊙O1的位置时（此时圆心O1在矩形对角线BD上），DP与⊙O1恰好相切？请说明理由．B P CPB CO O O1A D A D（图①）（图②）（第28题）2015 年苏州市初中毕业暨升学考试数学试题答案一、选择题1．C 2．B 3．A 4．C 5．D6．B 7．C 8．D 9．A 10．B二、填空题11． 3a 12．55 13．60 14． a 2b a 2b15．1416．3 17．27 18．16三、解答题22.6解：原式＝3+5 1 ＝7．22.7解：由x 1 2，解得x 1，由 3 x 1 ＞x 5 ，解得x＞4 ，∴不等式组的解集是x＞4 ．x1x 1 x 2 x 2 2＝x 1 x 2 12x 2 x 1 x 122.8解：原式＝．当x 3 1时，原式＝1 1 33 1 1 3 3．22.9解：设乙每小时做x 面彩旗，则甲每小时做（x+5）面彩旗．根据题意，得60 50x 5 x．解这个方程，得x=25．经检验，x=25 是所列方程的解．∴x+5=30．答：甲每小时做30 面彩旗，乙每小时做25 面彩旗．22.10解：（1）12．（2）用表格列出所有可能的结果：第二次红球1 红球2 白球黑球第一次红球 1 （红球1，红球2）（红球1，白球）（红球1，黑球）红球 2 （红球2，红球1）（红球2，白球）（红球2，黑球）白球（白球，红球1）（白球，红球2）（白球，黑球）黑球（黑球，红球1）（黑球，红球2）（黑球，白球）由表格可知，共有12 种可能出现的结果，并且它们都是等可能的，其中“两次都摸到红球”有 2 种可能．∴P（两次都摸到红球）= 212 = 16 ．22.11证明：（1）由作图可知B D =C D．在△ABD 和△ACD 中，AB AC,BD CD ,AD AD,∴△ABD≌△ACD（SSS）．∴∠BAD＝∠CAD，即AD 平分∠BAC．解：（2）∵AB=AC，BAC =50°，∴∠ABC＝∠ACB= 65°．∵BD= CD = BC，∴△BDC 为等边三角形．∴∠DBC＝∠DCB= 60°．∴∠DBE＝∠DCF= 55°．∵BC=6，∴BD= CD =6．∴D?E的长度= D?F的长度= 55 6 11180 6 ．∴D?E、D?F的长度之和为11 11 116 6 3 ．25．解：（1）∵点B（2，2）在y kx的图像上，∴k=4，y 4x ．∵BD⊥y 轴，∴D 点的坐标为（0，2），OD =2．∵AC⊥x 轴，AC= 32OD，∴AC =3，即 A 点的纵坐标为3．∵点A 在y 4x 的图像上，∴ A 点的坐标为（43，3）．∵一次函数y=ax+b 的图像经过点A、D，∴43a b 3, a解得34, b 2. b 2.（2）设A点的坐标为（m， 4m ），则C点的坐标为（m，0）．∵BD∥CE，且BC∥DE，∴四边形B CED 为平行四边形．∴CE= BD =2．∵BD∥CE，∴∠ADF =∠AEC．4AF m2∴在Rt△AFD 中，tan∠ADF =，DF m4在Rt△ACE 中，tan∠AEC= AC m EC 2，∴4 42m mm 2，解得m=1．∴C 点的坐标为（1，0），BC= 5 ．26．证明：（1）∵AD 是△ABC 的角平分线，∴∠BAD =∠DAC．∵∠E=∠BAD，∴∠E =∠DAC．∵BE∥AD，∴∠E =∠EDA．∴∠EDA =∠DA C．∴ED∥AC．解：（2）∵BE∥AD，∴∠EBD =∠ADC．∵∠E =∠DAC，∴△EBD∽△ADC，且相似比k BD 2DC ．··················∴S1S22k 4 ，即S1 4S2 ．∵ 2S1 16 S2 4 0 ，∴216S 16S 4 0 ，即2 224S 2 0 ．2∴ 1S ．22∵S BC BD CD 3CDV ，∴ 3ABC3S V ．ABCS CD CD CD 2 227．解：（1）45．理由如下：令x=0，则y=- m，C 点坐标为（0，- m）．2 1 0令y=0，则x m x m ，解得x1 1 ，x2 m．∵0＜m＜1，点A 在点B 的左侧，∴B 点坐标为（m，0）．∴OB =OC= m．∵∠BOC＝90°，∴△BOC 是等腰直角三角形，∠OBC＝45°．（2）解法一：如图①，作P D⊥y 轴，垂足为D，设l 与x 轴交于点E，由题意得，抛物线的对称轴为1 m x ．2设点P 坐标为（ 12m ，n）．∵PA= PC，∴PA2= PC2，即AE2+ PE2=CD2+ PD2．∴2 21 m 1 m221 n n m ．2 2解得1 mn ．∴P 点的坐标为21 m 1 m,2 2．解法二：连接P B．由题意得，抛物线的对称轴为1 m x ．2∵P 在对称轴l 上，∴PA=PB．∵PA=PC，∴PB=PC．∵△BOC 是等腰直角三角形，且OB=OC，∴P 在BC 的垂直平分线y x上．∴P 点即为对称轴 1 mx 与直线y x的交点．2∴P 点的坐标为1m 1 m,2 2．y yl lPDPQDx xA Q EB A E O BOC C图①图②（3）解法一：存在点Q 满足题意．∵P 点的坐标为1m 1 m,2 2，∴PA2+ PC2=AE2+ PE2+CD2+ PD2=2 2 2 21 m 1 m 1 m 1 m21 m 1 m ．2 2 2 22∵AC2=1 m ，∴PA2+ PC2= A C2．∴∠APC＝90°．∴△PAC 是等腰直角三角形．∵以Q、B、C 为顶点的三角形与△PAC 相似，∴△QBC 是等腰直角三角形．∴由题意知满足条件的点Q 的坐标为（- m，0）或（0，m）．①如图①，当Q 点的坐标为（- m，0）时，若PQ 与x 轴垂直，则 1若PQ 与x 轴不垂直，2 mm ，解得1m ，PQ=313．则2 2 22 2 2 1 m 1 m 5 2 1 5 2 1 PQ PE EQ m m 2m m ．2 2 2 2 2 5 10∵0＜m＜1，∴当2m 时，52PQ 取得最小值110，PQ 取得最小值1010．∵1010＜13，∴当2m ，即Q 点的坐标为（525，0）时，PQ 的长度最小．②如图②，当Q 点的坐标为（0，m）时，若PQ 与y 轴垂直，则 1若PQ 与y 轴不垂直，2mm ，解得1m ，PQ=313．则2 2 22 2 2 1 m 1 m 5 2 1 5 2 1 PQ PD DQ m m 2m m ．2 2 2 2 2 5 10∵0＜m＜1，∴当 2m 时，52PQ 取得最小值110，PQ 取得最小值1010．10 1 ∵＜，10 3∴当2m ，即Q 点的坐标为（0，525）时，PQ 的长度最小．综上：当Q 点坐标为（25 ，0）或（0，25）时，PQ 的长度最小．解法二：如图①，由（2）知P 为△ABC 的外接圆的圆心．∵∠APC 与∠ABC 对应同一条弧A?C，且∠ABC＝45°，∴∠APC＝2∠ABC＝90°．下面解题步骤同解法一．28．解：（1）a+2b．（2）∵在整个运动过程中，点P 移动的距离为 a 2b cm，圆心O 移动的距离为 2 a 4 cm，由题意，得 a 2b 2 a 4 ．①∵点P 移动2s 到达B 点，即点P 用2s 移动了bcm，点P 继续移动3s，到达BC 的中点，即点P 用3s移动了12a cm．∴1ab22 3．②由①②解得ab24,22.12∵点P 移动的速度与⊙O 移动的速度相等，b∴⊙O 移动的速度为 42（cm/s）．∴这5s时间内圆心O 移动的距离为5×4=20（cm）．（3）存在这种情形．解法一：设点P 移动的速度为v1cm/s，⊙O 移动的速度为v2cm/s，由题意，得v a 2b 20 2 10 51v 2 a 4 2 20 4 42．PB CHEO O1FA DG如图，设直线OO1与AB 交于点E，与CD 交于点F，⊙O1 与AD 相切于点G．若PD 与⊙O1 相切，切点为H，则O1G=O1H．易得△DO1G≌△DO1H，∴∠ADB =∠BDP．∵BC∥AD，∴∠ADB =∠CBD．∴∠BDP =∠CBD ．∴BP=DP．设BP=xcm，则D P =xcm，PC =（20- x）cm，在Rt△PCD 中，由勾股定理，可得 2 2 2PC CD PD ，即 2 2 220 x 10 x ，解得25 x ．2∴此时点P 移动的距离为10 25 452 2∵EF ∥AD，∴△BEO1∽△BAD．（cm）．∴EO1 BEAD BA ，即E O1 820 10．∴EO1=16cm．∴OO1=14cm．①当⊙O 首次到达⊙O1 的位置时，⊙O 移动的距离为14cm，45452∴此时点P 与⊙O 移动的速度比为14 28．∵45 528 4 ，∴此时PD 与⊙O1不可能相切．②当⊙O 在返回途中到达⊙O1 的位置时，⊙O 移动的距离为2×(20- 4)- 14=18 （cm），4545 52∴此时点P 与⊙O 移动的速度比为18 36 4．∴此时PD 与⊙O1恰好相切．解法二：∵点P 移动的距离为452 cm（见解法一），OO1=14cm（见解法一），v1v254，45 4 2 5∴⊙O 应该移动的距离为18（cm）．①当⊙O 首次到达⊙O1 的位置时，⊙O 移动的距离为14cm≠18 cm，∴此时PD 与⊙O1不可能相切．②当⊙O 在返回途中到达⊙O1 的位置时，⊙O 移动的距离为2×(20- 4)- 14=18 （cm），∴此时PD 与⊙O1恰好相切．解法三：点P 移动的距离为452 cm，（见解法一）OO1=14cm，（见解法一）由v1v254可设点P 的移动速度为5k cm/s，⊙O 的移动速度为4k cm/s，45∴点P 移动的时间为925k 2k（s）．①当⊙O 首次到达⊙O1 的位置时，⊙O 移动的时间为∴此时PD 与⊙O1不可能相切．14 7 94k 2k 2k，②当⊙O 在返回途中到达⊙O1 的位置时，⊙O 移动的时间为2 (20 4) 14 94k 2k，∴此时PD 与⊙O1 恰好相切．。

苏州市中考数学试卷及答案

2015年苏州市初中毕业暨升学考试试卷数学一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将选择题的答案用2B 铅笔涂在答题卡相应位置上．．．．．．．．． 1．2的相反数是 A ．2B ．12C ．-2D ．-122．有一组数据：3，5，5，6，7，这组数据的众数为 A ．3B ．5C ．6D ．73．月球的半径约为1 738 000m ，1 738 000这个数用科学记数法可表示为A ．1.738×106B ．1.738×107C ．0.1738×107D ．17.38×1054．若()2m =-，则有 A ．0＜m ＜1 B ．-1＜m ＜0 C ．-2＜m ＜-1 D ．-3＜m ＜-25．小明统计了他家今年5月份打电话的次数及通话时间，并列出了频数分布表：则通话时间不超过15min 的频率为 A ．0.1B ．0.4C ．0.5D ．0.96．若点A （a ，b ）在反比例函数2y x=的图像上，则代数式ab -4的值为 A ．0 B ．-2C ． 2D ．-67．如图，在△ABC 中，AB =AC ，D 为BC 中点，∠BAD =35°，则∠C 的度数为 A ．35° B ．45°C ．55°D ．60°DCBA8．若二次函数y =x 2+bx 的图像的对称轴是经过点（2，0）且平行于y 轴的直线，则关于x 的方程x 2+bx =5的解为 A ．120,4x x ==B ．121,5x x ==C ．121,5x x ==-D ．121,5x x =-=9．如图，AB 为⊙O 的切线，切点为B ，连接AO ，AO 与⊙O 交于点C ，BD 为⊙O 的直径，连接CD ．若∠A =30°，⊙O 的半径为2，则图中阴影部分的面积为 A．43πB．43π-C．π D．23π10．如图，在一笔直的海岸线l 上有A 、B 两个观测站，AB =2km ，从A 测得船C 在北偏东45°的方向，从B 测得船C 在北偏东22.5°的方向，则船C 离海岸线l 的距离（即CD 的长）为 A ．4kmB．(2+kmC．D．(4km二、填空题：本大题共8小题，每小题3分，共24分．把答案直接填在答题卡相应位置上．．．．．．．．． 11．计算：2a a ⋅= ▲ ．12．如图，直线a ∥b ，∠1=125°，则∠2的度数为 ▲ °．13．某学校在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛（第9题）（第10题）lba（第13题）20%10%30%40%其他乒乓球篮球羽毛球球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为 ▲ 名． 14．因式分解：224a b -= ▲ ．15．如图，转盘中8个扇形的面积都相等．任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为 ▲ ．16．若23a b -=，则924a b -+的值为 ▲ ．17．如图，在△ABC 中，CD 是高，CE 是中线，CE =CB ，点A 、D 关于点F 对称，过点F作FG ∥CD ，交AC 边于点G ，连接GE ．若AC =18，BC =12，则△CEG 的周长为 ▲ ．18．如图，四边形ABCD 为矩形，过点D 作对角线BD 的垂线，交BC 的延长线于点E ，取BE 的中点F ，连接DF ，DF =4．设AB =x ，AD =y ，则()224x y +-的值为 ▲ ．三、解答题：本大题共10小题，共76分．把解答过程写在答题卡相应位置上．．．．．．．．，解答时应写出必要的计算过程、推演步骤或文字说明．作图时用2B 铅笔或黑色墨水签字笔． 19．（本题满分5分）(052---． 20．（本题满分5分）解不等式组：()12,31 5.x x x +≥⎧⎪⎨-+⎪⎩＞（第17题）GF E D CBA F EDC B A （第18题）（第15题）21．（本题满分6分）先化简，再求值：2121122x x x x ++⎛⎫-÷⎪++⎝⎭，其中1x ．22．（本题满分6分）甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问甲、乙每小时各做多少面彩旗？23．（本题满分8分）一个不透明的口袋中装有2个红球（记为红球1、红球2）、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．（1）从中任意摸出1个球，恰好摸到红球的概率是 ▲ ；（2）先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．24．（本题满分8分）如图，在△ABC 中，AB =AC ．分别以B 、C 为圆心，BC 长为半径在BC 下方画弧，设两弧交于点D ，与AB 、AC 的延长线分别交于点E 、F ，连接AD 、BD 、CD ．（1）求证：AD 平分∠BAC ；（2）若BC =6，∠BAC ＝50︒，求DE 、DF 的长度之和（结果保留π）．CBA25．（本题满分8分）如图，已知函数ky x=（x ＞0）的图像经过点A 、B ，点B 的坐标为（2，2）．过点A 作AC ⊥x 轴，垂足为C ，过点B 作BD ⊥y 轴，垂足为D ，AC 与BD 交于点F ．一次函数y=ax +b 的图像经过点A 、D ，与x 轴的负半轴交于点E ．（1）若AC =32OD ，求a 、b 的值；（2）若BC ∥AE ，求BC 的长．26．（本题满分10分）如图，已知AD 是△ABC 的角平分线，⊙O 经过A 、B 、D 三点，过点B 作BE ∥AD ，交⊙O 于点E ，连接ED ．（1）求证：ED ∥AC ；（2）若BD =2CD ，设△EBD 的面积为1S ，△ADC 的面积为2S ，且2121640S S -+=，求△ABC 的面积．27．（本题满分10分）如图，已知二次函数()21y x m x m =+--（其中0＜m ＜1）的图像与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，对称轴为直线l ．设P 为对称轴l 上的点，连接P A 、PC ，P A =PC ．（1）∠ABC 的度数为 ▲ °；（2）求P 点坐标（用含m 的代数式表示）；（3）在坐标轴上是否存在点Q （与原点O 不重合），使得以Q 、B 、C 为顶点的三角形与△P AC 相似，且线段PQ 的长度最小？如果存在，求出所有满足条件的点Q 的坐标；如果不存在，请说明理由．28．（本题满分10分）如图，在矩形ABCD 中，AD =a cm ，AB =b cm （a ＞b ＞4），半径为2cm的⊙O 在矩形内且与AB 、AD 均相切．现有动点P 从A 点出发，在矩形边上沿着A →B →C →D 的方向匀速移动，当点P 到达D 点时停止移动；⊙O 在矩形内部沿AD 向右匀速平移，移动到与CD 相切时立即沿原路按原速返回，当⊙O 回到出发时的位置（即再次与AB 相切）时停止移动．已知点P 与⊙O 同时开始移动，同时停止移动（即同时到达各自的终止位置）．（1）如图①，点P 从A →B →C →D ，全程共移动了 ▲ cm （用含a 、b 的代数式表示）；（2）如图①，已知点P 从A 点出发，移动2s 到达B 点，继续移动3s ，到达BC 的中点．若点P 与⊙O 的移动速度相等，求在这5s 时间内圆心O 移动的距离；（3）如图②，已知a =20，b =10．是否存在如下情形：当⊙O 到达⊙O 1的位置时（此时圆心O 1在矩形对角线BD 上），DP 与⊙O 1恰好相切？请说明理由．2015年苏州市初中毕业暨升学考试数学试题答案一、选择题 1．C2．B3．A4．C5．D（第28题）（图②）（图①）6．B7．C8．D9．A10．B 二、填空题 11．3a 12．55 13．60 14．()()22a b a b +- 15．1416．317．2718．16三、解答题19.解：原式＝ 3+5-1 ＝ 7． 20.解：由12x +≥，解得1x ≥，由()315x x -+＞，解得4x ＞， ∴不等式组的解集是4x ＞．21.解：原式＝()21122x x x x ++÷++ ＝()2121211x x x x x ++⨯=+++．当1x==． 22.解：设乙每小时做x 面彩旗，则甲每小时做（x +5）面彩旗．根据题意，得60505x x=+．解这个方程，得x =25．经检验，x =25是所列方程的解． ∴x +5=30．答：甲每小时做30面彩旗，乙每小时做25面彩旗． 23.解：（1）1．（2）用表格列出所有可能的结果：到红球”有2种可能．∴P （两次都摸到红球）=212=16． 24.证明：（1）由作图可知BD =CD ．在△ABD 和△ACD 中，,,,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩∴△ABD≌△ACD（SSS）．∴∠BAD＝∠CAD，即AD平分∠BAC．解：（2）∵AB=AC，∠BAC=50°，∴∠ABC＝∠ACB=65°．∵BD= CD = BC，∴△BDC为等边三角形．∴∠DBC＝∠DCB=60°．∴∠DBE＝∠DCF=55°．∵BC=6，∴BD= CD =6．∴DE的长度=DF的长度=556111806ππ⨯⨯=．∴DE、DF的长度之和为111111 663πππ+=．25．解：（1）∵点B（2，2）在kyx=的图像上，∴k=4，4yx =．∵BD⊥y轴，∴D点的坐标为（0，2），OD=2．∵AC⊥x轴，AC=32OD，∴AC=3，即A点的纵坐标为3．∵点A在4yx=的图像上，∴A点的坐标为（43，3）．∵一次函数y=ax+b的图像经过点A、D，∴43,32.a bb⎧+=⎪⎨⎪=⎩解得3,42.ab⎧=⎪⎨⎪=⎩（2）设A点的坐标为（m，4m），则C点的坐标为（m，0）．∵BD∥CE，且BC∥DE，∴四边形BCED为平行四边形．∴CE= BD=2．∵BD∥CE，∴∠ADF=∠AEC．∴在Rt△AFD中，tan∠ADF=42 AF mDF m-=，在Rt△ACE中，tan∠AEC=42 AC m EC=，∴4422m mm-=，解得m=1．∴C点的坐标为（1，0），BC．26．证明：（1）∵AD是△ABC的角平分线，∴∠BAD =∠DAC．∵∠E=∠BAD，∴∠E =∠DAC．∵BE∥AD，∴∠E =∠EDA．∴∠EDA =∠DA C ． ∴ED ∥AC ．解：（2）∵BE ∥AD ，∴∠EBD =∠ADC ．∵∠E =∠DAC ，∴△EBD ∽△ADC ，且相似比2BDk DC==． ··················· ∴2124S k S ==，即124S S =． ∵2121640S S -+=，∴222161640S S -+=，即()22420S -=．∴212S =． ∵233ABC S BC BD CD CD S CD CD CD +====，∴32ABCS=． 27．解：（1）45．理由如下：令x =0，则y =-m ，C 点坐标为（0，-m ）．令y =0，则()210x m x m +--=，解得11x =-，2x m =．∵0＜m ＜1，点A 在点B 的左侧，∴B 点坐标为（m ，0）．∴OB =OC =m ．∵∠BOC ＝90°，∴△BOC 是等腰直角三角形，∠OBC ＝45°．（2）解法一：如图①，作PD ⊥y 轴，垂足为D ，设l 与x 轴交于点E ，由题意得，抛物线的对称轴为12mx -+=．设点P 坐标为（12m-+，n ）． ∵P A = PC ， ∴P A 2= PC 2，即AE 2+ PE 2=CD 2+ PD 2．∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭．解得12m n -=．∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．解法二：连接PB ．由题意得，抛物线的对称轴为12m x -+=． ∵P 在对称轴l 上，∴P A =PB ． ∵P A =PC ，∴PB =PC ．∵△BOC 是等腰直角三角形，且OB =OC ， ∴P 在BC 的垂直平分线y x =-上．∴P 点即为对称轴12mx -+=与直线y x =-的交点． ∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．图①图②（3）解法一：存在点Q 满足题意．∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭， ∴P A 2+ PC 2=AE 2+ PE 2+CD 2+ PD 2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． ∵AC 2=21m +，∴P A 2+ PC 2=AC 2．∴∠APC ＝90°． ∴△P AC 是等腰直角三角形．∵以Q 、B 、C 为顶点的三角形与△P AC 相似， ∴△QBC 是等腰直角三角形．∴由题意知满足条件的点Q 的坐标为（-m ，0）或（0，m ）． ①如图①，当Q 点的坐标为（-m ，0）时，若PQ 与x 轴垂直，则12mm -+=-，解得13m =，PQ =13．若PQ 与x 轴不垂直，则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+⎪⎪ ⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ ．＜13， ∴当25m =，即Q 点的坐标为（25-，0）时， PQ 的长度最小．②如图②，当Q 点的坐标为（0，m ）时，若PQ 与y 轴垂直，则12mm -=，解得13m =，PQ =13．若PQ 与y 轴不垂直，则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ．＜13， ∴当25m =，即Q 点的坐标为（0，25）时， PQ 的长度最小．综上：当Q 点坐标为（25-，0）或（0，25）时，PQ 的长度最小．解法二：如图①，由（2）知P 为△ABC 的外接圆的圆心． ∵∠APC 与∠ABC 对应同一条弧AC ，且∠ABC ＝45°，∴∠APC ＝2∠ABC ＝90°．下面解题步骤同解法一．28．解：（1）a +2b ．（2）∵在整个运动过程中，点P 移动的距离为()2a b +cm ，圆心O 移动的距离为()24a -cm ，由题意，得()224a b a +=-． ①∵点P 移动2s 到达B 点，即点P 用2s 移动了b cm ，点P 继续移动3s ，到达BC 的中点，即点P 用3s 移动了12a cm ．∴1223a b =． ② 由①②解得24,8.a b =⎧⎨=⎩∵点P 移动的速度与⊙O 移动的速度相等， ∴⊙O 移动的速度为42b=（cm/s ）．∴这5s 时间内圆心O 移动的距离为5×4=20（cm ）．（3）存在这种情形．解法一：设点P 移动的速度为v 1cm/s ，⊙O 移动的速度为v 2cm/s ，由题意，得()()1222021052422044v a b v a ++⨯===--．FE如图，设直线OO 1与AB 交于点E ，与CD 交于点F ，⊙O 1与AD 相切于点G ．若PD 与⊙O 1相切，切点为H ，则O 1G =O 1H ．易得△DO 1G ≌△DO 1H ，∴∠ADB =∠BDP ．∵BC ∥AD ，∴∠ADB =∠CBD ．∴∠BDP =∠CBD ．∴BP =DP ．设BP =x cm ，则DP =x cm ，PC =（20-x ）cm ，在Rt △PCD 中，由勾股定理，可得222PC CD PD +=，即()2222010x x -+=，解得252x =．∴此时点P 移动的距离为25451022+=（cm ）． ∵EF ∥AD ，∴△BEO 1∽△BAD ． ∴1EO BE AD BA =，即182010EO =． ∴EO 1=16cm ．∴OO 1=14cm ．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ， ∴此时点P 与⊙O 移动的速度比为454521428=．∵455284≠， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ）， ∴此时点P 与⊙O 移动的速度比为45455218364==． ∴此时PD 与⊙O 1恰好相切．解法二：∵点P 移动的距离为452cm （见解法一），OO 1=14cm （见解法一），1254v v =， ∴⊙O 应该移动的距离为4541825⨯=（cm ）． ①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ≠18 cm ， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ），∴此时PD 与⊙O 1恰好相切．解法三：点P 移动的距离为452cm ，（见解法一） OO 1=14cm ，（见解法一）由1254v v =可设点P 的移动速度为5k cm/s ，⊙O 的移动速度为4k cm/s ， ∴点P 移动的时间为459252k k=（s ）．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的时间为1479422k k k=≠， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的时间为2(204)14942k k⨯--=， ∴此时PD 与⊙O 1恰好相切．。

江苏苏州中考数学真题测试卷有答案

2015年江苏省苏州市中考数学试卷一、选择题（本大题共共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将选择题的答案用2B铅笔涂在答题卡相应位置上）1．2的相反数是（）A ．2 B．C．﹣2 D．﹣2．有一组数据：3，5，5，6，7，这组数据的众数为（）A． 3 B． 5 C． 6 D． 73．月球的半径约为1738000m，1738000这个数用科学记数法可表示为（）A ．1.738×106B．1.738×107C．0.1738×107D．17.38×1054．若m=×（﹣2），则有（）A． 0＜m＜1 B．﹣1＜m＜0 C．﹣2＜m＜﹣1 D．﹣3＜m＜﹣25．小明统计了他家今年5月份打电话的次数及通话时间，并列出了频数分布表：通话时间x/min 0＜x≤55＜x≤1010＜x≤1515＜x≤20频数（通话次数）20 16 9 5则通话时间不超过15min的频率为（）A． 0.1 B． 0.4 C． 0.5 D． 0.96．若点A（a，b）在反比例函数y=的图象上，则代数式ab﹣4的值为（）A． 0 B．﹣2 C． 2 D．﹣67．如图，在△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为（）A． 35°B． 45°C． 55°D． 60°8．若二次函数y=x2+bx的图象的对称是经过点（2，0）且平行于y轴的直线，则关于x的方程x2+bx=5的解为（）A ．x1=0，x2=4 B．x1=1，x2=5 C．x1=1，x2=﹣5 D．x1=﹣1，x2=59．如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD．若∠A=30°，⊙O的半径为2，则图中阴影部分的面积为（）A ．﹣B．﹣2C．π﹣D．﹣10．如图，在一笔直的海岸线l上有A、B两个观测站，AB=2km、从A测得船C在北偏东45°的方向，从B测得船C在北偏东22.5°的方向，则船C离海岸线l的距离（即CD的长）为（）A ．4km B．（2+）km C．2km D．（4﹣）km二、填空题（本大题共8小题，每小题3分，满分24分，把答案直接填在答题卡相应位置上）11．计算：a•a2=．12．如图，直线a∥b，∠1=125°，则∠2的度数为．13．某学校“你最喜爱的球类运动”调查中，随机调查了若干名学生（每个学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为名．14．分解因式：a2﹣4b2=．15．如图，转盘中8个扇形的面积都相等，任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为．16．若a﹣2b=3，则9﹣2a+4b的值为．17．如图，在△ABC中，CD是高，CE是中线，CE=CB，点A、D关于点F对称，过点F 作FG∥CD，交AC边于点G，连接GE．若AC=18，BC=12，则△CEG的周长为．18．如图，四边形ABCD为矩形，过点D作对角线BD的垂线，交BC的延长线于点E，取BE的中点F，连接DF，DF=4．设AB=x，AD=y，则x2+（y﹣4）2的值为．三、解答题（本大题共10小题，满分76分按解答过程写在答题卡相应位置上，解答时应写出必要的计算过程，推演步骤或文字说明，作图时用2B铅笔会黑色墨水签字笔）19．计算：+|﹣5|﹣（2﹣）0．20．解不等式组：．21．先化简，再求值：（1﹣）÷，其中x=﹣1．22．甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问：甲、乙每小时各做多少面彩旗？23．一个不透明的口袋中装有2个红球（记为红球1、红球2），1个白球、1个黑球，这些球除颜色外都相同，将球搅匀．（1）从中任意摸出1个球，恰好摸到红球的概率是（2）先从中任意摸出一个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表），求两次都摸到红球的概率．24．如图，在△ABC中，AB=AC，分别以B、C为圆心，BC长为半径在BC下方画弧．设两弧交于点D，与AB、AC的延长线分别交于点E、F，连接AD、BD、CD（1）求证：AD平分∠BAC；（2）若BC=6，∠BAC=50°，求DE、DF的长度之和（结果保留π）．25．如图，已知函数y=（x＞0）的图象经过点A、B，点B的坐标为（2，2）．过点A作AC⊥x轴，垂足为C，过点B作BD⊥y轴，垂足为D，AC与BD交于点F．一次函数y=ax+b 的图象经过点A、D，与x轴的负半轴交于点E（1）若AC=OD，求a、b的值；（2）若BC∥AE，求BC的长．26．如图，已知AD是△ABC的角平分线，⊙O经过A、B、D三点．过点B作BE∥AD，交⊙O于点E，连接ED（1）求证：ED∥AC；（2）若BD=2CD，设△EBD的面积为S1，△ADC的面积为S2，且S12﹣16S2+4=0，求△ABC 的面积．27．如图，已知二次函数y=x2+（1﹣m）x﹣m（其中0＜m＜1）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，对称轴为直线l．设P为对称轴l上的点，连接PA、PC，PA=PC（1）∠ABC的度数为；（2）求P点坐标（用含m的代数式表示）；（3）在坐标轴上是否存在着点Q（与原点O不重合），使得以Q、B、C为顶点的三角形与△PAC相似，且线段PQ的长度最小？如果存在，求出所有满足条件的点Q的坐标；如果不存在，请说明理由．28．如图，在矩形ABCD中，AD=acm，AB=bcm（a＞b＞4），半径为2cm的⊙O在矩形内且与AB、AD均相切，现有动点P从A点出发，在矩形边上沿着A→B→C→D的方向匀速移动，当点P到达D点时停止移动．⊙O在矩形内部沿AD向右匀速平移，移动到与CD相切时立即沿原路按原速返回，当⊙O回到出发时的位置（即再次与AB相切）时停止移动，已知点P与⊙O同时开始移动，同时停止移动（即同时到达各自的终止位置）．（1）如图①，点P从A→B→C→D，全程共移动了cm（用含a、b的代数式表示）；（2）如图①，已知点P从A点出发，移动2s到达B点，继续移动3s，到达BC的中点，若点P与⊙O的移动速度相等，求在这5s时间内圆心O移动的距离；（3）如图②，已知a=20，b=10，是否存在如下情形：当⊙O到达⊙O1的位置时（此时圆心O1在矩形对角线BD上），DP与⊙O1恰好相切？请说明理由．参考答案一、选择题（本大题共10小题） 1.C解析：a 的相反数是-a ，所以2的相反数是-2.点评：本题考查了相反数的概念，解题的关键掌握相反数的概念． 2.B解析：5出现的次数最多，所以这组数据的众数是5.点评：本题考查了众数的概念，解题的关键掌握众数概念． 3.A解析：用科学记数法表示1 738 000，先确定a =1.738，再确定10的指数．点评：本题考查了科学记数法，根据概念求解最重要，解题的关键是要正确确定a 的值以及n 的值． 4.C解析：m=-2，所以-2＜m ＜-1.点评：本题考查了二次根式的运算和估值，解题的关键是要正确的运算和掌握无理数的估值方法． 5.D解：样本容量为20+16+9+5=50，而通话时间不超过15min 的频数和为45，所以通话时间不超过15min 的频率为0.9.点评：本题考查了数据的频数和频率. 6.B将A 点的坐标代入解析式，得ab =2，则ab -4=-2. 点评：本题考查了反比例函数，求代数式的值. 7.C解：因为AB =AC ，D 为BC 中点，所以∠BAC =2∠BAD =70°，所以∠C 的度数为55°. 点评：本题考查了等腰三角形的性质和三角形的内角和定理. 8.D解：由题意知此抛物线的对称轴是直线x =2，故b =-4，得方程x 2+4x =5，解之，得121,5x x =-=. 点评：本题考查了二次函数的图像的对称轴和一元二次方程的解法. 9.A解：由AB 为⊙O 的切线，∠A =30°，得∠D =∠OCD =30°，则∠COD =120°，因为⊙O 的半径为2，故点O 到CD 的距离为3，所以扇形OCD 的面积为120443603ππ⨯=，△COD 的面积为3，所以阴影部分的面积为433π-. 点评：本题考查了直线和圆的位置关系、垂径定理、三角形的面积、扇形的面积.根据图形间的位置关系得到图形面积之间的数量关系求解. 10.B过点B 作BE ⊥AD 交AC 于点E .则BE =AB =2，AE =22；CE =BE =2，所以AC =22+2，所以CD =()22+km.点评：本题考查了解直角三角形的应用——方向角问题.二、填空题(本大题共8小题) 11.a 3解：根据同底数幂的乘法法则，底数不变，指数相加，得a 3. 点评：本题考查了同底数幂的乘法. 12.55根据平行线的性质得∠2的补角的度数为1250，故∠2的度数为550. 点评：本题考查了平行线的性质，将线的位置关系转化为角的数量关系. 13.60最喜欢羽毛球的人数所占百分率比最喜欢乒乓球的人数所占百分率少10%，故被调查总人数为6÷10%=60（人）.点评：本题考查了扇形统计图. 14.()()22a b a b +-直接用平方差公式分解，得()()22a b a b +-. 点评：本题考查了多项式的因式分解.15.14解：一共有8个等可能的结果，其中大于6的结果有2个，所以指针指向大于6的数的概率为14. 点评：本题考查了 16.3解：9-2a +4b =9-2(a -2b )=9-6=3.点评：本题考查了求代数式的值，运用整体思想求值. 17.27点A 、D 关于点F 对称，则AF=DF ，因为FG ∥CD ，所以AG=CG =9；因为AE=BE ，所以EG =12BC =6；而CE=CB =12，所以△CEG 的周长为CG+EG+CE =9+6+12=27. 点评：本题考查了图形的中心对称、平行线的性质、平行线分线段成比例定理的推论，三角形中位线定理. 18.16在矩形ABCD 中，CD =AB =x ，在R t △BDE 中，∠BDE =900，点F 为BE 的中点，所以BF=EF=DF =4，所以()224x y +-=CD 2+CF 2=DF 2=16.点评：本题考查了矩形的性质、直角三角形中线的性质、勾股定理. 三、解答题：本大题共10小题19．解析：原式第一项是利用算术平方根的定义计算，第二项利用绝对值的代数意义化简，最后一项是利用零指数幂法则计算. 原式＝ 3+5-1 ＝ 7．点评：利用算术平方根的定义，绝对值的意义和零指数幂的法则进行计算. 20.解析：先求出两个不等式的解集，再求其公共解.由12x +≥，解得1x ≥，由()315x x -+＞，解得4x ＞， ∴不等式组的解集是4x ＞．21．解析：先运用分式的减法法则和除法法则对分式进行化简，然后将x 的值代入，在对二次根式进行化简. 原式＝()21122x x x x ++÷++ ＝()2121211x x x x x ++⨯=+++．当31x =-时，原式＝ 11333113==-+．点评：本题考查了分式的化简求值和二次根式的化简.22．解析：可设乙每小时做x 面彩旗，则甲每小时做（x +5）面彩旗．根据等量关系“甲做60面彩旗与乙做50面彩旗所用时间相等”列出方程求解.设乙每小时做x 面彩旗，则甲每小时做（x +5）面彩旗．根据题意，得60505x x=+．解这个方程，得x =25．经检验，x =25是所列方程的解． ∴x +5=30．答：甲每小时做30面彩旗，乙每小时做25面彩旗．点评：本题考查了列分式方程解应用题. 23．解析：（1）根据4个小球中红球的个数，即可确定出从中任意摸出1个球，恰好是红球的概率；（2）列表（或画树状图），得到所有等可能的情况，找出两次都摸到红球的情况数，即可求出所有求得概率.（1）12．（2）用表格列出所有可能的结果：第二次第一次红球1 红球2白球黑球红球1（红球1，红球2）（红球1，白球）（红球1，黑球）红球2 （红球2，红球1）（红球2，白球）（红球2，黑球）白球（白球，红球1）（白球，红球2）（白球，黑球）黑球（黑球，红球1）（黑球，红球2）（黑球，白球）由表格可知，共有12种可能出现的结果，并且它们都是等可能的，其中“两次都摸到红球”有2种可能． ∴P （两次都摸到红球）=212=16．点评：本题考查了等可能情况下的概率. 24．解析：（1）根据题意得BD =CD ．由SSS 证明△ABD ≌△ACD ，得出∠BAD ＝∠CAD 即可.（2）由等腰三角形的性质得出∠ABC ＝∠ACB=65°，由等边三角形的性质得出∠DBC ＝∠DCB=60°，再由角平分线的定义求出∠DBE ＝∠DCF=55°，然后根据弧长公式求出DE 、DF 的长度，即可得出结论.（1）由作图可知BD =CD ．在△ABD 和△ACD 中，,,,A B A CB DC DA D A D =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACD （SSS ）．∴∠BAD ＝∠CAD ，即AD 平分∠BAC ．（2）∵AB =AC ，∠BAC =50°，∴∠ABC ＝∠ACB=65°． ∵BD = CD = BC ，∴△BDC 为等边三角形．∴∠DBC ＝∠DCB=60°． ∴∠DBE ＝∠DCF=55°． ∵BC =6，∴BD = CD=6．∴DE 的长度=DF 的长度=556111806ππ⨯⨯=． ∴DE 、DF 的长度之和为111111663πππ+=点评：本题考查了全等三角形的判定与性质、等边三角形的判定与性质、弧长的计算. 25．解析：（1）首先利用反比例函数图像上点的坐标性质求出k 的值，再得出A 、D 点的坐标，进而求出a 、b 的值.（2）设A 点的坐标为（m ，4m），则C 点的坐标为（m ，0）．得出tan ∠ADF =42AF m DF m -=，tan ∠AEC =42AC mEC =，进而求出m 的值，即可得到答案. （1）∵点B （2，2）在k y x =的图像上，∴k =4，4y x=． ∵BD ⊥y 轴，∴D 点的坐标为（0，2），OD =2． ∵AC ⊥x 轴，AC =32OD ，∴AC =3，即A 点的纵坐标为3． ∵点A 在4y x=的图像上，∴A 点的坐标为（43，3）．∵一次函数y =ax +b 的图像经过点A 、D ，∴43,3 2.a b b ⎧+=⎪⎨⎪=⎩解得3,42.a b ⎧=⎪⎨⎪=⎩（2）设A 点的坐标为（m ，4m），则C 点的坐标为（m ，0）．∵BD ∥CE ，且BC ∥DE ，∴四边形BCED 为平行四边形． ∴CE = BD =2． ∵BD ∥CE ，∴∠ADF =∠AEC ． ∴在Rt △AFD 中，tan ∠ADF =42AF m DF m -=，在Rt △ACE 中，tan ∠AEC =42AC mEC =，∴4422m m m -=，解得m =1． ∴C 点的坐标为（1，0），BC =5．点评：本题考查了反比例函数和一次函数的交点问题，以及锐角三角函数关系等知识.解题关键是求出A 、D 两点的坐标. 26．解析：（1）由AD 是△ABC 的角平分线，得到∠BAD =∠DAC ，由于∠E=∠BAD ，等量代换得到∠E =∠DAC ，再根据平行线的性质与判定即可解决问题.（2）由BE ∥AD 得到∠EBD =∠ADC ，再由∠E =∠DAC 证明出△EBD ∽△ADC ，个呢局相似三角形的性质：相似三角形的面积比等于相似比的平方即可得到结果. （1）∵AD 是△ABC 的角平分线，∴∠BAD =∠DAC ． ∵∠E=∠BAD ，∴∠E =∠DAC ． ∵BE ∥AD ，∴∠E =∠EDA ．∴∠EDA =∠DA C ． ∴ED ∥AC ．（2）∵BE ∥AD ，∴∠EBD =∠ADC ． ∵∠E =∠DAC ， ∴△EBD ∽△ADC ，且相似比2BDk DC==．∴2124S k S ==，即124S S =． ∵2121640S S -+=，∴222161640S S -+=，即()22420S -=． ∴212S =． ∵233ABC S BC BD CD CD S CD CD CD +====，∴32ABCS=．点评：本题考查了相似三角形的判定与性质，解一元二次方程，圆周角定理.解题的关键是熟练的运用图形的性质，数形结合思想、转化思想，最后运用方程来解决问题.27．解析：（1）首先求出B 点坐标，进而得出OB=OC=m ，再利用等腰直角三角形的性质求出即可.（2）作PD ⊥y 轴于D ，设l 与x 轴交于点E ，利用勾股定理得AE 2+ PE 2=CD 2+ PD 2进而达到方程求出P 点的坐标.（3）根据题意得出△QBC 是等腰直角三角形，可得满足条件的点Q 的坐标为（-m ，0）或（0，m ），进而分别分析求出符合题意得答案. （1）45．理由如下：令x =0，则y =-m ，C 点坐标为（0，-m ）．令y =0，则()210x m x m +--=，解得11x =-，2x m =．∵0＜m ＜1，点A 在点B 的左侧，∴B 点坐标为（m ，0）．∴OB =OC =m ．∵∠BOC ＝90°，∴△BOC 是等腰直角三角形，∠OBC ＝45°．（2）解法一：如图①，作PD ⊥y 轴，垂足为D ，设l 与x 轴交于点E ，由题意得，抛物线的对称轴为12mx -+=．设点P 坐标为（12m -+，n ）．∵P A = PC ， ∴P A 2= PC 2，即AE 2+ PE 2=CD 2+ PD 2．∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭．解得12m n -=．∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．解法二：连接PB ．由题意得，抛物线的对称轴为12mx -+=． ∵P 在对称轴l 上，∴P A =PB ．∵P A =PC ，∴PB =PC ．∵△BOC 是等腰直角三角形，且OB =OC ，∴P 在BC 的垂直平分线y x =-上． ∴P 点即为对称轴12mx -+=与直线y x =-的交点．∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭． y xy x图①图②O PE D CBAl Q Ql ABC D E PO（3）解法一：存在点Q 满足题意．∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭，∴P A 2+ PC 2=AE 2+ PE 2+CD 2+ PD 2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭．∵AC 2=21m +，∴P A 2+ PC 2=AC 2．∴∠APC ＝90°． ∴△P AC 是等腰直角三角形．∵以Q 、B 、C 为顶点的三角形与△P AC 相似，∴△QBC 是等腰直角三角形． ∴由题意知满足条件的点Q 的坐标为（-m ，0）或（0，m ）．①如图①，当Q 点的坐标为（-m ，0）时，若PQ 与x 轴垂直，则12mm -+=-，解得13m =，PQ =13．若PQ 与x轴不垂直，则2222222115152122222251m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+⎪⎪ ⎪⎝⎭⎝⎭⎝⎭．∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ 取得最小值1010．∵1010＜13，∴当25m =，即Q点的坐标为（25-，0）时， PQ 的长度最小．②如图②，当Q 点的坐标为（0，m ）时，若PQ 与y 轴垂直，则12mm -=，解得13m =，PQ =13．若PQ 与y 轴不垂直，则2222222115152122222251m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ 取得最小值1010．∵1010＜13，∴当25m =，即Q点的坐标为（0，25）时， PQ 的长度最小．综上：当Q 点坐标为（25-，0）或（0，25）时，PQ 的长度最小．解法二：如图①，由（2）知P 为△ABC 的外接圆的圆心．∵∠APC 与∠ABC 对应同一条弧AC ，且∠ABC ＝45°，∴∠APC ＝2∠ABC ＝90°．下面解题步骤同解法一．点评：本题是一道二次函数的综合题.主要考查了二次函数的图像与性质、等腰直角三角形的性质、勾股定理、相似三角形的性质等.解题的关键是根据有关性质，熟练的运用数形结合思想、转化思想、分类讨论思想和方程思想解题. 28．解析：（1）根据有理数的加法，可得答案；（2）根据圆O 移动的距离与P 点移动的距离相等，P 点移动的速度相等，可得方程组，根据解方程组，可得a 、b 的值，根据速度与时间的关系，可得答案；（3）根据相同时间内速度的比等于路程的比，可得的值，根据相似三角形的性质，可得∠ADB=∠BDP ，根据等腰三角形的判定，可得BP 与DP 的关系，根据勾股定理，可得DP 的长，根据有理数的加法，可得P 点移动的距离；根据相似三角形的性质，可得EO 1的长，分类讨论：当⊙O 首次到达⊙O 1的位置时，当⊙O 在返回途中到达⊙O 1位置时，根据的值，可得答案．（1）a +2b ．（2）∵在整个运动过程中，点P 移动的距离为()2a b +cm ，圆心O 移动的距离为()24a -cm ，由题意，得()224a b a +=-． ① ∵点P 移动2s 到达B 点，即点P 用2s移动了b cm ，点P 继续移动3s ，到达BC 的中点，即点P 用3s 移动了12a cm ．∴1223a b =． ②由①②解得24,8.a b =⎧⎨=⎩ ∵点P 移动的速度与⊙O 移动的速度相等，∴⊙O 移动的速度为42b=（cm/s ）．∴这5s 时间内圆心O 移动的距离为5×4=20（cm ）．（3）存在这种情形．解法一：设点P 移动的速度为v 1cm/s ，⊙O 移动的速度为v 2cm/s ，由题意，得()()1222021052422044v a b v a ++⨯===--．HGFE PODCBA O 1如图，设直线OO 1与AB 交于点E ，与CD 交于点F ，⊙O 1与AD 相切于点G ．若PD 与⊙O 1相切，切点为H ，则O 1G =O 1H ．易得△DO 1G ≌△DO 1H ，∴∠ADB =∠BDP ．∵BC ∥AD ，∴∠ADB =∠CBD ．∴∠BDP =∠CBD ．∴BP =DP ．设BP =x cm ，则DP =x cm ，PC =（20-x ）cm ，在Rt △PCD 中，由勾股定理，可得222PC CD PD +=，即()2222010x x -+=，解得252x =．∴此时点P 移动的距离为25451022+=（cm ）．∵EF ∥AD ，∴△BEO 1∽△BAD ．∴1EO BE AD BA =，即182010EO =．∴EO 1=16cm ．∴OO 1=14cm ．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ，∴此时点P 与⊙O 移动的速度比为454521428=．∵455284≠，∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ），∴此时点P 与⊙O 移动的速度比为45455218364==．∴此时PD 与⊙O 1恰好相切．解法二：∵点P 移动的距离为452cm （见解法一），OO 1=14cm （见解法一），1254v v =，∴⊙O 应该移动的距离为4541825⨯=（cm ）． ①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ≠18 cm ，∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ），∴此时PD 与⊙O 1恰好相切．解法三：点P移动的距离为452cm，（见解法一），OO1=14cm，（见解法一），由1254vv=可设点P的移动速度为5k cm/s，⊙O的移动速度为4k cm/s，∴点P移动的时间为459252k k=（s）．①当⊙O首次到达⊙O1的位置时，⊙O移动的时间为1479422k k k=≠，∴此时PD与⊙O1不可能相切．②当⊙O在返回途中到达⊙O1的位置时，⊙O移动的时间为2(204)14942k k⨯--=，∴此时PD与⊙O1恰好相切．点评：本题是一道圆的综合题，主要考查了图形的运动、直线与圆的位置关系、全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的性质等.运用数形结合思想、转化思想、方程思想和分类讨论思想来解题.。

【初中数学】江苏省苏州市2015年初中毕业暨升学考试数学试卷(解析版) 苏科版

【解析】给2 添上一个负号即可，故选C。

2．有一组数据：3，5，5，6，7，这组数据的众数为A．3 B．5 C．6 D．7【难度】★【考点分析】考查众数的概念，是中考必考题型，难度很小。

【解析】众数是一组数据中出现次数最多的数值，5 出现了两次，其它数均只出现一次，故选B。

3．月球的半径约为1 738 000m，1 738 000这个数用科学记数法可表示为A．1.738×106B．1.738×107C．0.1738×107D．17.38×105【难度】★【考点分析】考查科学记数法，是中考必考题型，难度很小。

【解析】科学记数法的表示结果应满足：a⨯10n（1≤ a <10）的要求，C,D 形式不满足，排除，通过数值大小（移小数点位置）可得A 正确，故选A。

4．若()2m=-，则有A．0＜m＜1 B．-1＜m＜0 C．-2＜m＜-1 D．-3＜m＜-2【难度】★☆【考点分析】考察实数运算与估算大小，实数估算大小往年中考较少涉及，但难度并不大。

苏州市中考数学试卷及答案

2015年苏州市初中毕业暨升学考试试卷数学一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将选择题的答案用2B 铅笔涂在答题卡相应位置上．．．．．．．．． 1．2的相反数是A ．2B ．12C ．?2D ．?122．有一组数据：3，5，5，6，7，这组数据的众数为A ．3B ．5C ．6D ．73．月球的半径约为1 738 000m ，1 738 000这个数用科学记数法可表示为 A ．1.738×106 B ．1.738×107 C ．0.1738×107 D ．17.38×1054．若()2m =-，则有 A ．0＜m ＜1 B ．-1＜m ＜0 C ．-2＜m ＜-1 D ．-3＜m ＜-25．小明统计了他家今年5月份打电话的次数及通话时间，并列出了频数分布表：则通话时间不超过15min 的频率为 A ．0.1B ．0.4C ．0.5D ．0.96．若点A （a ，b ）在反比例函数2y x=的图像上，则代数式ab -4的值为 A ．0B ．-2C ． 2D ．-67．如图，在△ABC 中，AB =AC ，D 为BC 中点，∠BAD =35°，则∠C 的度数为 A ．35° B ．45°C ．55°D ．60°8．若二次函数y =x 2+bx 的图像的对称轴是经过点（2，0）且平行于y 轴的直线，则关于x 的方程x 2+bx =5的解为A ．120,4x x ==B ．121,5x x ==C ．121,5x x ==-D ．121,5x x =-=9．如图，AB 为⊙O 的切线，切点为B ，连接AO ，AO 与⊙O 交于点C ，BD为⊙O 的直径，连接CD ．若∠A =30°，⊙O 的半径为2，则图中阴影部分的面积为DCB A（第7题）A．43πB．43π-C．π D．23π10．如图，在一笔直的海岸线l 上有A 、B 两个观测站，AB =2km ，从A 测得船C 在北偏东45°的方向，从B 测得船C 在北偏东22.5°的方向，则船C 离海岸线l 的距离（即CD 的长）为 A ．4kmB．(2+kmC．D．(4km二、填空题：本大题共8小题，每小题3分，共24分．把答案直接填在答题卡相应位置上．．．．．．．．． 11．计算：2a a ⋅= ▲ ．12．如图，直线a ∥b ，∠1=125°，则∠2的度数为 ▲ °． 13．某学校在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为 ▲ 名．14．因式分解：224a b -= ▲ ．15．如图，转盘中8个扇形的面积都相等．任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为 ▲ ．16．若23a b -=，则924a b-+的值为 ▲ ．（第9题）（第10题）lba（第13题）20%10%30%40%其他乒乓球篮球羽毛球（第15题）17．如图，在△ABC 中，CD 是高，CE 是中线，CE =CB ，点A 、D 关于点F 对称，过点F作FG ∥CD ，交AC 边于点G ，连接GE ．若AC =18，BC =12，则△CEG 的周长为 ▲ ．18．如图，四边形ABCD 为矩形，过点D 作对角线BD 的垂线，交BC 的延长线于点E ，取BE 的中点F ，连接DF ，DF =4．设AB =x ，AD =y ，则()224x y +-的值为 ▲ ．三、解答题：本大题共10小题，共76分．把解答过程写在答题卡相应位置上．．．．．．．．，解答时应写出必要的计算过程、推演步骤或文字说明．作图时用2B 铅笔或黑色墨水签字笔． 19．（本题满分5分）(052---． 20．（本题满分5分）解不等式组：()12,31 5.x x x +≥⎧⎪⎨-+⎪⎩＞21．（本题满分6分）先化简，再求值：2121122x x x x ++⎛⎫-÷⎪++⎝⎭，其中1x ． 22．（本题满分6分）甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问甲、乙每小时各做多少面彩旗？23．（本题满分8分）一个不透明的口袋中装有2个红球（记为红球1、红球2）、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．（1）从中任意摸出1个球，恰好摸到红球的概率是 ▲ ；（2）先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．24．（本题满分8分）如图，在△ABC 中，AB =AC ．分别以B 、C 为圆心，BC 长为半径在BC 下方画弧，设两弧交于点D ，与AB 、AC 的延长线分别交于点E 、F ，连接AD 、BD 、（第17题）GF E D CBA F EDC B A （第18题）CD ．（1）求证：AD 平分∠BAC ；（2）若BC =6，∠BAC ＝50?，求DE 、DF 的长度之和（结果保留π）．25．（本题满分8分）如图，已知函数k y x=（x ＞0）的图像经过点A 、B ，点B 的坐标为（2，2）．过点A 作AC ⊥x 轴，垂足为C ，过点B 作BD ⊥y 轴，垂足为D ，AC 与BD 交于点F ．一次函数y=ax +b 的图像经过点A 、D ，与x 轴的负半轴交于点E ．（1）若AC =32OD ，求a 、b 的值；（2）若BC ∥AE ，求BC 的长．26．（本题满分10分）如图，已知AD 是△ABC的角平分线，⊙O 经过A 、B 、D 三点，过点B 作BE ∥AD ，交⊙O 于点E ，连接ED ．（1）求证：ED ∥AC ；（2）若BD =2CD ，设△EBD 的面积为1S ，△ADC的面积为2S ，且2121640S S -+=，求△ABC 的面积．27．（本题满分10分）如图，已知二次函数()21y x m x m =+--（其中0＜m ＜1）图像与x 轴交于A 、B 两点（点A 在点B 的侧），与y 轴交于点C ，对称轴为直线l ．设为对称轴l 上的点，连接P A 、PC ，P A =PC ．（1）∠ABC 的度数为 ▲ °；（2）求P 点坐标（用含m 的代数式表示）；（3）在坐标轴上是否存在点Q （与原点O 不重合），使得以Q 、B 、C 为顶点的三角形与△P AC 相似，且线段PQ 的长度最小？如果存在，求出所有满足条件的点Q 的坐标；如果不存在，请说明理由．FEDCBA（第26题）28．（本题满分10分）如图，在矩形ABCD 中，AD =a cm ，AB =b cm （a ＞b ＞4），半径为2cm 的⊙O 在矩形内且与AB 、AD 均相切．现有动点P 从A 点出发，在矩形边上沿着A →B →C →D 的方向匀速移动，当点P 到达D 点时停止移动；⊙O 在矩形内部沿AD 向右匀速平移，移动到与CD 相切时立即沿原路按原速返回，当⊙O 回到出发时的位置（即再次与AB 相切）时停止移动．已知点P 与⊙O 同时开始移动，同时停止移动（即同时到达各自的终止位置）．（1）如图①，点P 从A →B →C →D ，全程共移动了 ▲ cm （用含a 、b 的代数式表示）；（2）如图①，已知点P 从A 点出发，移动2s 到达B 点，继续移动3s ，到达BC 的中点．若点P 与⊙O 的移动速度相等，求在这5s 时间内圆心O 移动的距离；（3）如图②，已知a =20，b =10．是否存在如下情形：当⊙O 到达⊙O 1的位置时（此时圆心O 1在矩形对角线BD 上），DP 与⊙O 1恰好相切？请说明理由．2015年苏州市初中毕业暨升学考试数学试题答案一、选择题 1．C 2．B 3．A 4．C 5．D 6．B7．C8．D9．A10．B 二、填空题 11．3a 12．55 13．60 14．()()22a b a b +- 15．1416．317．2718．16（第28题）（图②）（图①）三、解答题19.解：原式＝3+5?1 ＝7．20.解：由12x+≥，解得1x≥，由()315x x-+＞，解得4x＞，∴不等式组的解集是4x＞．21.解：原式＝()21122xxx x++÷++＝()2121211x xx xx++⨯=+++．当1x==．22.解：设乙每小时做x面彩旗，则甲每小时做（x+5）面彩旗．根据题意，得60505x x=+．解这个方程，得x=25．经检验，x=25是所列方程的解．∴x+5=30．答：甲每小时做30面彩旗，乙每小时做25面彩旗．23.解：（1）1．（2）用表格列出所有可能的结果：由表格可知，共有12种可能出现的结果，并且它们都是等可能的，其中“两次都摸到红球”有2种可能．∴P（两次都摸到红球）=212=16．24.证明：（1）由作图可知BD=CD．在△ABD和△ACD中，∴△ABD≌△ACD（SSS）．∴∠BAD＝∠CAD，即AD平分∠BAC．解：（2）∵AB=AC，?BAC=50°，∴∠ABC＝∠ACB=65°．∵BD= CD = BC，∴△BDC为等边三角形．∴∠DBC＝∠DCB=60°．∴∠DBE＝∠DCF=55°．∵BC=6，∴BD= CD =6．∴DE的长度=DF的长度=556111806ππ⨯⨯=．∴DE 、DF 的长度之和为111111663πππ+=． 25．解：（1）∵点B （2，2）在ky x=的图像上， ∴k =4，4y x=． ∵BD ⊥y 轴，∴D 点的坐标为（0，2），OD =2．∵AC ⊥x 轴，AC =32OD ，∴AC =3，即A 点的纵坐标为3． ∵点A 在4y x=的图像上，∴A 点的坐标为（43，3）．∵一次函数y =ax +b 的图像经过点A 、D ， ∴43,3 2.a b b ⎧+=⎪⎨⎪=⎩ 解得3,42.a b ⎧=⎪⎨⎪=⎩ （2）设A 点的坐标为（m ，4m），则C 点的坐标为（m ，0）． ∵BD ∥CE ，且BC ∥DE ，∴四边形BCED 为平行四边形． ∴CE = BD =2．∵BD ∥CE ，∴∠ADF =∠AEC ．∴在Rt △AFD 中，tan ∠ADF =42AF mDF m -=，在Rt △ACE 中，tan ∠AEC =42AC mEC =， ∴4422m m m -=，解得m =1． ∴C 点的坐标为（1，0），BC．26．证明：（1）∵AD 是△ABC 的角平分线， ∴∠BAD =∠DAC ．∵∠E=∠BAD ，∴∠E =∠DAC ． ∵BE ∥AD ，∴∠E =∠EDA ． ∴∠EDA =∠DA C ． ∴ED ∥AC ．解：（2）∵BE ∥AD ，∴∠EBD =∠ADC ．∵∠E =∠DAC ，∴△EBD ∽△ADC ，且相似比2BDk DC==． ··················· ∴2124S k S ==，即124S S =． ∵2121640S S -+=，∴222161640S S -+=，即()22420S -=．∴212S =． ∵233ABC S BC BD CD CD S CD CD CD +====，∴32ABCS=． 27．解：（1）45．理由如下：令x =0，则y =-m ，C 点坐标为（0，-m ）．令y =0，则()210x m x m +--=，解得11x =-，2x m =．∵0＜m ＜1，点A 在点B 的左侧，∴B 点坐标为（m ，0）．∴OB =OC =m ．∵∠BOC ＝90°，∴△BOC 是等腰直角三角形，∠OBC ＝45°．（2）解法一：如图①，作PD ⊥y 轴，垂足为D ，设l 与x 轴交于点E ，由题意得，抛物线的对称轴为12mx -+=．设点P 坐标为（12m-+，n ）． ∵P A = PC ， ∴P A 2= PC 2，即AE 2+ PE 2=CD 2+ PD 2．∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭．解得12m n -=．∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．解法二：连接PB ．由题意得，抛物线的对称轴为12mx -+=． ∵P 在对称轴l 上，∴P A =PB ． ∵P A =PC ，∴PB =PC ．∵△BOC 是等腰直角三角形，且OB =OC ， ∴P 在BC 的垂直平分线y x =-上．∴P 点即为对称轴12mx -+=与直线y x =-的交点． ∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．（3）解法一：存在点Q 满足题意．∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭， ∴P A 2+ PC 2=AE 2+ PE 2+CD 2+ PD 2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． ∵AC 2=21m +，∴P A 2+ PC 2=AC 2．∴∠APC ＝90°． ∴△P AC 是等腰直角三角形．∵以Q 、B 、C 为顶点的三角形与△P AC 相似， ∴△QBC 是等腰直角三角形．∴由题意知满足条件的点Q 的坐标为（-m ，0）或（0，m ）． ①如图①，当Q 点的坐标为（-m ，0）时，若PQ 与x 轴垂直，则12mm -+=-，解得13m =，PQ =13．若PQ 与x 轴不垂直，则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭．∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ ．＜13， ∴当25m =，即Q 点的坐标为（25-，0）时， PQ 的长度最小．②如图②，当Q 点的坐标为（0，m ）时，若PQ 与y 轴垂直，则12mm -=，解得13m =，PQ =13．若PQ 与y 轴不垂直，则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ ．＜13， ∴当25m =，即Q 点的坐标为（0，25）时， PQ 的长度最小．综上：当Q 点坐标为（25-，0）或（0，25）时，PQ 的长度最小．解法二：如图①，由（2）知P 为△ABC 的外接圆的圆心． ∵∠APC 与∠ABC 对应同一条弧AC ，且∠ABC ＝45°，∴∠APC ＝2∠ABC ＝90°．下面解题步骤同解法一．28．解：（1）a +2b ．（2）∵在整个运动过程中，点P 移动的距离为()2a b +cm ，圆心O 移动的距离为()24a -cm ，由题意，得()224a b a +=-． ①∵点P 移动2s 到达B 点，即点P 用2s 移动了b cm ，点P 继续移动3s ，到达BC 的中点，即点P 用3s 移动了12a cm ．∴1223a b =． ② 由①②解得24,8.a b =⎧⎨=⎩∵点P 移动的速度与⊙O 移动的速度相等，∴⊙O 移动的速度为42b=（cm/s ）． ∴这5s 时间内圆心O 移动的距离为5×4=20（cm ）．（3）存在这种情形．解法一：设点P 移动的速度为v 1cm/s ，⊙O 移动的速度为v 2cm/s ，由题意，得()()1222021052422044v a b v a ++⨯===--．如图，设直线OO 1与AB 交于点E ，与CD 交于点F ，⊙O 1与AD 相切于点G ．若PD 与⊙O 1相切，切点为H ，则O 1G =O 1H ．易得△DO 1G ≌△DO 1H ，∴∠ADB =∠BDP ． ∵BC ∥AD ，∴∠ADB =∠CBD ． ∴∠BDP =∠CBD ．∴BP =DP ．设BP =x cm ，则DP =x cm ，PC =（20-x ）cm ，在Rt △PCD 中，由勾股定理，可得222PC CD PD +=，即()2222010x x -+=，解得252x =．∴此时点P 移动的距离为25451022+=（cm ）． ∵EF ∥AD ，∴△BEO 1∽△BAD ． ∴1EO BE AD BA =，即182010EO =．∴EO 1=16cm ．∴OO 1=14cm ．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ， ∴此时点P 与⊙O 移动的速度比为454521428=．∵455284≠， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ）， ∴此时点P 与⊙O 移动的速度比为45455218364==．∴此时PD 与⊙O 1恰好相切．解法二：∵点P 移动的距离为452cm （见解法一）， OO 1=14cm （见解法一），1254v v =， ∴⊙O 应该移动的距离为4541825⨯=（cm ）． ①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ≠18 cm ， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ），∴此时PD 与⊙O 1恰好相切．解法三：点P 移动的距离为452cm ，（见解法一） OO 1=14cm ，（见解法一）由1254v v =可设点P 的移动速度为5k cm/s ，⊙O 的移动速度为4k cm/s ， ∴点P 移动的时间为459252k k=（s ）． ①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的时间为1479422k k k =≠， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的时间为2(204)14942k k⨯--=， ∴此时PD 与⊙O 1恰好相切．。

2015年江苏省中考数学真题试卷(含答案解析)

【考点】扇形统计图. 【分析】设被调查的总人数是x人，根据最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，即可列方程求解. 【解答】解：设被调查的总人数是x人，则40%x﹣30%x=6，解得：x=60. 故答案是：60. 【点评】本题考查的是扇形统计图的综合运用，读懂统计图，从统计图中得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小.
A.4km B.(2+ )km C.2 km D.(4﹣ )km 【考点】解直角三角形的应用-方向角问题. 【分析】根据题意在CD上取一点E，使BD=DE，进而得出EC=BE=2，再利用勾股定理得出DE的长，即可得出答案. 【解答】解：在CD上取一点E，使BD=DE，可得：∠EBD=45°，AD=DC， ∵从B测得船C在北偏东22.5°的方向， ∴∠BCE=∠CBE=22.5°， ∴BE=EC， ∵AB=2， ∴EC=BE=2， ∴BD=ED=
菁优网版权所有
=2，得b=﹣4，解x2﹣4x=5即可. 【解答】解：∵对称轴是经过点(2，0)且平行于y轴的直线， ∴﹣ =2，解得：b=﹣4，解方程x2﹣4x=5，
解得x1=﹣1，x2=5，故选：D. 【点评】本题主要考查二次函数的对称轴和二次函数与一元二次方程的关系，难度不大. 9.(3分)(2015•苏州)如图，AB为⊙O的切线，切点为B，连接AO，AO与 ⊙O交于点C，BD为⊙O的直径，连接CD.若∠A=30°，⊙O的半径为2，则图中阴影部分的面积为( )
频数(通话 20 16 9 5 次数) 则通话时间不超过15min的频率为( ) A.0.1 B.0.4 C.0.5 D.0.9 【考点】频数(率)分布表. 【分析】用不超过15分钟的通话时间除以所有的通话时间即可求得通话时间不超过15分钟的频率. 【解答】解：∵不超过15分钟的通话次数为20+16+9=45次，通话总次数为20+16+9+5=50次， ∴通话时间不超过15min的频率为

江苏苏州中考数学试卷含答案

2015年苏州市初中毕业暨升学考试试卷数学本试卷由选择题、填空题和解答题三大题组成，共28小题，满分130分，考试时间120分钟．注意事项：1．答题前，考生务必将自己的姓名、考点名称、考场号、座位号用0.5毫米黑色墨水签字笔填写在答题卡相应位置上，并认真核对条形码上的准考号、姓名是否与本人的相符；2．答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，请用橡皮擦干净后，再选涂其他答案；答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题；3．考生答题必须答在答题卡上，保持卡面清洁，不要折叠，不要弄破，答在试卷和草稿纸上一律无效．一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将选择题的答案用2B铅笔涂在答题卡相应位置上．．．．．．．．．1．2的相反数是A．2 B．12C．?2 D．?122．有一组数据：3，5，5，6，7，这组数据的众数为A．3 B．5 C．6 D．73．月球的半径约为1738000m，1738000这个数用科学记数法可表示为A．1.738×106B．1.738×107C．0.1738×107D．17.38×1054．若()2m=-，则有A．0＜m＜1 B．-1＜m＜0 C．-2＜m＜-1 D．-3＜m＜-25．小明统计了他家今年5月份打电话的次数及通话时间，并列出了频数分布表：则通话时间不超过15min的频率为A．0.1 B．0.4 C．0.5 D．0.96．若点A（a，b）在反比例函数2yx=的图像上，则代数式ab-4的值为A．0 B．-2 C．2 D．-67．如图，在△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为A．35°B．45°C．55°D．60°8．若二次函数y =x 2+bx 的图像的对称轴是经过点（2，0）且平行于y 轴的直线，则关于x 的方程x 2+bx =5的解为A ．120,4xx == B ．121,5xx == C ．121,5x x ==- D ．121,5xx =-=9．如图，AB 为⊙O 的切线，切点为B ，连接AO ，AO 与⊙O 交于点C ，BD 为⊙O 的直径，连接CD ．若∠A =30°，⊙O 的半径为2，则图中阴影部分的面积为 A．43πB．43π-C．πD．23π10．如图，在一笔直的海岸线l 上有A 、B 两个观测站，AB =2km ，从A 测得船C 在北偏东45°的方向，从B 测得船C 在北偏东22.5°的方向，则船C 离海岸线l 的距离（即CD 的长）为 A ．4kmB．(2km C．D．(4km二、填空题：本大题共8小题，每小题3分，共24分．把答案直接填在答题卡相应位置上．．．．．．．．． 11．计算：2a a ⋅=▲．12．如图，直线a ∥b ，∠1=125°，则∠2的度数为▲°．DCBA（第7题）（第9（第10题）lba （第1320%10%30%40%其他乒乓球篮球羽毛球13．某学校在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘已知其中最喜欢羽毛球的人数比最人，则该校被调查的学生总人数为▲名． 14．因式分解：224ab -=▲．15．如图，转盘中8个扇形的面积都相等．任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为▲．16．若23a b -=，则924a b -+的值为▲． 17．如图，在△ABC 中，CD 是高，CE 是中线，CE =CB ，点A 、D 关于点F 对称，过点F 作FG ∥CD ，交AC 边于点G ，连接GE ．若AC =18，BC =12，则△CEG 的周长为▲． 18．如图，四边形ABCD 为矩形，过点D 作对角线BD 的垂线，交BC 的延长线于点E ，取BE 的中点F ，连接DF ，DF =4．设AB =x ，AD =y ，则()224x y +-的值为▲．三、解答题：本大题共10小题，共76分．把解答过程写在答题．．卡相应位置上．．．．．．，解答时应写出必要的计算过程、推演步骤或（第17GF E D CBA F EDC B A （第18（第15文字说明．作图时用2B 铅笔或黑色墨水签字笔． 19．（本题满分5分） (052--．20．（本题满分5分）解不等式组：()12,31 5.x x x +≥⎧⎪⎨-+⎪⎩＞21．（本题满分6分）先化简，再求值：2121122x x x x ++⎛⎫-÷⎪++⎝⎭，其中1x =． 22．（本题满分6分）甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问甲、乙每小时各做多少面彩旗？ 23．（本题满分8分）一个不透明的口袋中装有2个红球（记为红球1、红球2）、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．（1）从中任意摸出1个球，恰好摸到红球的概率是▲；（2）先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．24．（本题满分8分）如图，在△ABC 中，AB =AC ．分别以B 、C为圆心，BC 长为半径在BC 下方画弧，设两弧交于点D ，与AB 、AC 的延长线分别交于点E 、F ，连接AD 、BD 、CD ．（1）求证：AD 平分∠BAC ；（2）若BC =6，∠BAC ＝50?，求»DE、»DF 的长度之和（结果保留π）．25．（本题满分8分）如图，已知函数k y x=（x ＞0）的图像经过点A 、B ，点B 的坐标为（2，2）．过点A 作AC ⊥x 轴，垂足为C ，过点B 作BD⊥y 轴，垂足为D ，AC 与BD 交于点F ．一次函数y=ax +b 的图像经过点A 、D ，与x 轴的负半轴交于点E ．（1）若AC =32OD ，求a 、b 的值；（2）若BC ∥AE ，求BC 的长． 26．（本题满分10分）如图，已知AD 是△ABC 的角平分线，⊙O 经过A 、B 、D 三点，过点B 作BE ∥AD ，交⊙O 于点E ，连接ED ．（1）求证：ED ∥AC ；（2）若BD =2CD ，设△EBD 的面积为1S ，△ADC 的面积为2S ，且2121640S S -+=，求△ABC 的面积．27．（本题满分10分）如图，已知二（第24FEDCBA（第26题）次函数()21=+--（其中0＜m＜1）的图像与x轴交于y x m x mA、B两点（点A在点B的左侧），与y轴交于点C，对称轴为直线l．设P为对称轴l上的点，连接PA、PC，PA=PC．（1）∠ABC的度数为▲°；（2）求P点坐标（用含m的代数式表示）；（3）在坐标轴上是否存在点Q（与原点O不重合），使得以Q、B、C为顶点的三角形Array与△PAC相似，且线段PQ的长度最小？如果存在，求出所有满足条件的点Q的坐标；如果不存在，请说明理由．28．（本题满分10分）如图，在矩形ABCD中，AD=a cm，AB=b cm（a＞b＞4），半径为2cm的⊙O在矩形内且与AB、AD均相切．现有动点P从A点出发，在矩形边上沿着A→B→C→D的方向匀速移动，当点P到达D点时停止移动；⊙O在矩形内部沿AD向右匀速平移，移动到与CD相切时立即沿原路按原速返回，当⊙O回到出发时的位置（即再次与AB相切）时停止移动．已知点P与⊙O同时开始移动，同时停止移动（即同时到达各自的终止位置）．（1）如图①，点P从A→B→C→D，全程共移动了▲cm（用含a、b的代数式表示）；（2）如图①，已知点P从A点出发，移动2s到达B点，继续移动3s ，到达BC 的中点．若点P 与⊙O 的移动速度相等，求在这5s 时间内圆心O 移动的距离；（3）如图②，已知a =20，b =10．是否存在如下情形：当⊙O 到达⊙O 1的位置时（此时圆心O 1在矩形对角线BD 上），DP与⊙O 1恰好相切？请说明理由．2015年苏州市初中毕业暨升学考试数学试题答案一、选择题 1．C 2．B 3．A 4．C 5．D 6．B 7．C8．D9．A10．B二、填空题 11．3a 12．55 13．60 14．()()22a b a b +- 15．1416．317．2718．16三、解答题19.解：原式＝3+5?1＝7． 20.解：由12x +≥，解得1x ≥，由()315x x -+＞，解得4x ＞， ∴不等式组的解集是4x ＞．（第28（图（图21.解：原式＝()21122x x x x ++÷++＝()2121211x x x x x ++⨯=+++．当1x ===．22.解：设乙每小时做x 面彩旗，则甲每小时做（x +5）面彩旗．根据题意，得60505x x=+．解这个方程，得x =25．经检验，x =25是所列方程的解．∴x +5=30．答：甲每小时做30面彩旗，乙每小时做25面彩旗．23.解：（1）1．（2）用表格列出所有可能的结果：由表格可知，共有12种可能出现的结果，并且它们都是等可能的，其中“两次都摸到红球”有2种可能． ∴P （两次都摸到红球）=212=16．24.证明：（1）由作图可知BD =CD ．在△ABD 和△ACD 中， ∴△ABD ≌△ACD （SSS ）．∴∠BAD ＝∠CAD ，即AD 平分∠BAC ．解：（2）∵AB =AC ，?BAC =50°，∴∠ABC ＝∠ACB=65°．∵BD =CD =BC ，∴△BDC 为等边三角形． ∴∠DBC ＝∠DCB=60°． ∴∠DBE ＝∠DCF=55°． ∵BC =6，∴BD =CD =6．∴»DE的长度=»DF 的长度=556111806ππ⨯⨯=． ∴»DE、»DF 的长度之和为111111663πππ+=．25．解：（1）∵点B （2，2）在k y x=的图像上，∴k =4，4y x=．∵BD ⊥y 轴，∴D 点的坐标为（0，2），OD =2． ∵AC ⊥x 轴，AC =32OD ，∴AC =3，即A 点的纵坐标为3．∵点A 在4y x=的图像上，∴A 点的坐标为（43，3）．∵一次函数y =ax +b 的图像经过点A 、D ，∴43,3 2.a b b ⎧+=⎪⎨⎪=⎩解得3,42.a b ⎧=⎪⎨⎪=⎩（2）设A 点的坐标为（m ，4m），则C 点的坐标为（m ，0）．∵BD ∥CE ，且BC ∥DE ，∴四边形BCED 为平行四边形．∴CE =BD =2．∵BD ∥CE ，∴∠ADF =∠AEC ． ∴在Rt △AFD 中，tan ∠ADF =42AF mDF m -=，在Rt △ACE 中，tan ∠AEC =42AC mEC =，∴4422m m m -=，解得m =1．∴C 点的坐标为（1，0），BC．26．证明：（1）∵AD 是△ABC 的角平分线，∴∠BAD =∠DAC ．∵∠E=∠BAD ，∴∠E =∠DAC ． ∵BE ∥AD ，∴∠E =∠EDA ． ∴∠EDA =∠DA C ． ∴ED ∥AC ．解：（2）∵BE ∥AD ，∴∠EBD =∠ADC ．∵∠E =∠DAC ，∴△EBD ∽△ADC ，且相似比2BD k DC==．∴2124S k S ==，即124S S =．∵2121640S S -+=，∴222161640S S -+=，即()22420S-=．∴212S =．∵233ABCS BC BD CD CD S CD CD CD +====V ，∴32ABC S =V ． 27．解：（1）45．理由如下：令x =0，则y =-m ，C 点坐标为（0，-m ）．令y =0，则()210x m x m +--=，解得11x =-，2x m =．∵0＜m ＜1，点A 在点B 的左侧， ∴B 点坐标为（m ，0）．∴OB =OC =m ．∵∠BOC ＝90°，∴△BOC 是等腰直角三角形，∠OBC ＝45°．（2）解法一：如图①，作PD ⊥y 轴，垂足为D ，设l与x 轴交于点E ，由题意得，抛物线的对称轴为12m x -+=．设点P 坐标为（12m -+，n ）．∵PA =PC ，∴PA 2=PC 2，即AE 2+PE 2=CD 2+PD 2．∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭．解得12m n -=．∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．解法二：连接PB ．由题意得，抛物线的对称轴为12m x -+=．∵P 在对称轴l 上，∴PA =PB ． ∵PA =PC ，∴PB =PC ．∵△BOC 是等腰直角三角形，且OB =OC ， ∴P 在BC 的垂直平分线y x =-上．∴P 点即为对称轴12m x -+=与直线y x =-的交点． ∴P点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．（3）解法一：存在点Q 满足题意．∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭， ∴PA 2+PC 2=AE 2+PE 2+CD 2+PD2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． ∵AC 2=21m +，∴PA 2+PC 2=AC 2．∴∠APC ＝90°． ∴△PAC 是等腰直角三角形．∵以Q 、B 、C 为顶点的三角形与△PAC 相似， ∴△QBC 是等腰直角三角形．∴由题意知满足条件的点Q 的坐标为（-m ，0）或（0，m ）．①如图①，当Q 点的坐标为（-m ，0）时，若PQ 与x 轴垂直，则12m m -+=-，解得13m =，PQ =13．若PQ 与x 轴不垂直，则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ．＜13，∴当25m =，即Q 点的坐标为（25-，0）时，PQ 的长度最小．②如图②，当Q 点的坐标为（0，m ）时，若PQ 与y 轴垂直，则12m m -=，解得13m =，PQ =13．若PQ 与y 轴不垂直，则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ．＜13，∴当25m =，即Q 点的坐标为（0，25）时，PQ 的长度最小．综上：当Q 点坐标为（25-，0）或（0，25）时，PQ的长度最小．解法二：如图①，由（2）知P 为△ABC 的外接圆的圆心．∵∠APC 与∠ABC 对应同一条弧»AC ，且∠ABC ＝45°，∴∠APC ＝2∠ABC ＝90°．下面解题步骤同解法一．28．解：（1）a +2b ．（2）∵在整个运动过程中，点P 移动的距离为()2a b +cm ，圆心O 移动的距离为()24a -cm ，由题意，得()224a b a +=-．①∵点P 移动2s 到达B 点，即点P 用2s 移动了b cm ，点P 继续移动3s ，到达BC 的中点，即点P 用3s移动了12a cm ．∴1223a b =．②由①②解得24,8.a b =⎧⎨=⎩∵点P 移动的速度与⊙O 移动的速度相等， ∴⊙O 移动的速度为42b =（cm/s ）．∴这5s 时间内圆心O 移动的距离为5×4=20（cm ）．（3）存在这种情形．解法一：设点P 移动的速度为v 1cm/s ，⊙O 移动的速度为v 2cm/s ，由题意，得()()1222021052422044v a b v a ++⨯===--．如图，设直线OO 1与AB 交于点E ，与CD 交于点F ，⊙O 1与AD 相切于点G ．若PD 与⊙O 1相切，切点为H ，则O 1G =O 1H ．易得△DO 1G ≌△DO 1H ，∴∠ADB =∠BDP ． ∵BC ∥AD ，∴∠ADB =∠CBD ． ∴∠BDP =∠CBD ．∴BP =DP ．设BP =x cm ，则DP =x cm ，PC =（20-x ）cm ，在Rt △PCD 中，由勾股定理，可得222PC CD PD +=，即()2222010x x -+=，解得252x =． ∴此时点P 移动的距离为25451022+=（cm ）． ∵EF ∥AD ，∴△BEO 1∽△BAD ． ∴1EO BE ADBA=，即182010EO =． ∴EO 1=16cm ．∴OO 1=14cm ．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ， ∴此时点P 与⊙O 移动的速度比为454521428=．∵455284≠，∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ）， ∴此时点P 与⊙O移动的速度比为45455218364==．∴此时PD 与⊙O 1恰好相切．解法二：∵点P 移动的距离为452cm （见解法一），OO 1=14cm （见解法一），1254vv =，∴⊙O 应该移动的距离为4541825⨯=（cm ）．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ≠18cm ，∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ），∴此时PD 与⊙O 1恰好相切．解法三：点P 移动的距离为452cm ，（见解法一）OO 1=14cm ，（见解法一）由1254v v =可设点P 的移动速度为5k cm/s ，⊙O 的移动速度为4k cm/s ，∴点P移动的时间为459252k k=（s ）．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的时间为1479422k k k=≠，∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的时间为2(204)14942kk⨯--=，∴此时PD 与⊙O 1恰好相切．。

2015年苏州市中考数学试卷及答案

2015年苏州市初中毕业暨升学考试试卷数学一、选择题：本大题共 小题，每小题分，共 分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将选择题的答案用 铅笔涂在答题卡相应位置上．．．．．．．．．．的相反数是✌．．12 ．  ． 12．有一组数据：，，，，，这组数据的众数为✌．．．．．月球的半径约为  ❍，  这个数用科学记数法可表示为✌． ×  ． ×  ． ×  ． × ．若()2m=-，则有✌．＜❍＜． ＜❍＜． ＜❍＜  ． ＜❍＜ ．小明统计了他家今年月份打电话的次数及通话时间，并列出了频数分布表：则通话时间不超过 ❍♓⏹的频率为✌．  ．  ．  ．  ．若点✌（♋，♌）在反比例函数2yx=的图像上，则代数式♋♌ 的值为✌．．  ．  ． ．如图，在△✌中，✌ ✌，为 中点，∠ ✌ °，则∠ 的度数为✌． °． ° ． ° ． °．若二次函数⍓ ⌧ ♌⌧的图像的对称轴是经过点（，）且平行于⍓轴的直线，则关于⌧的方程⌧ ♌⌧ 的解为 ✌．120,4x x ==．121,5x x == ．121,5x x ==- ．121,5x x =-=．如图，✌为⊙ 的切线，切点为，连接✌，✌与⊙ 交于点， 为⊙的直径，连接 ．若∠✌ °，⊙ 的半径为，则图中阴影部分的面积为✌．43π．．如图，在一笔直的海岸线●上有✌、两个观测站，✌ ❍，从✌测得船在北偏东 °的方向，从测得船在北偏东 °的方向，则船离海岸线●的距离（即 的长）为 ✌．4 ❍．(2 ❍ ．．(4 ❍二、填空题：本大题共小题，每小题分，共 分．把答案直接填在答题卡相应位置．．．．．．．DCB A（第题）（第题）（第 题）l上．． ．计算：2a a ⋅ ✧ ．．如图，直线♋∥♌，∠ °，则∠ 的度数为 ✧ °．．某学校在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少人，则该校被调查的学生总人数为 ✧ 名．．因式分解：224a b - ✧ ．．如图，转盘中个扇形的面积都相等．任意转动转盘次，当转盘停止转动时，指针指向大于的数的概率为 ✧ ．．若23a b -=，则924a b -+的值为 ✧ ．．如图，在△✌中， 是高， ☜是中线， ☜ ，点✌、关于点☞GCDA ba（第 题）20%10%30%40%其他乒乓球篮球羽毛球（第 题）对称，过点☞作☞☝∥ ，交✌边于点☝，连接☝☜．若✌ ，  ，则△☜☝的周长为 ✧ ．．如图，四边形✌为矩形，过点作对角线 的垂线，交 的延长线于点☜，取 ☜的中点☞，连接 ☞， ☞ ．设✌ ⌧，✌ ⍓，则()224x y +-的值为 ✧ ．三、解答题：本大题共 小题，共 分．把解答过程写在答题卡相应位置上．．．．．．．．，解答时应写出必要的计算过程、推演步骤或文字说明．作图时用 铅笔或黑色墨水签字笔．．（本题满分分）(052--．．（本题满分分）解不等式组：()12,31 5.x x x +≥⎧⎪⎨-+⎪⎩＞．（本题满分分）先化简，再求值：2121122x x x x ++⎛⎫-÷⎪++⎝⎭，其中1x =．．（本题满分分）甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做面彩旗，甲做 面彩旗与乙做 面彩旗所用时间相等，问甲、乙每小时各做多少面彩旗？．（本题满分分）一个不透明的口袋中装有个红球（记为红球、红球）、个白球、个黑球，这些球除颜色外都相同，将球摇匀．（）从中任意摸出个球，恰好摸到红球的概率是 ✧ ；（）先从中任意摸出个球，再从余下的个球中任意摸出个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．．（本题满分分）如图，在△✌中，✌ ✌．分别以、为圆心， 长为半径在 下方画弧，设两弧交于点，与✌、✌的延长线分别交于点☜、☞，连接✌、 、 ．（）求证：✌平分∠ ✌；（）若  ，∠ ✌＝ ，求DE 、DF 的长度之和（结果保留π）．．（本题满分分）如图，已知函数ky x=（⌧＞）的图像经过点✌、，点的坐标为（，）．过点✌作✌⊥⌧轴，垂足为，过点作 ⊥⍓轴，垂足为，✌与 交于点☞．一次函数⍓♋⌧ ♌的图像经过点✌、，与⌧轴的负半轴交于点☜．（第 题）FEDCBA（）若✌32，求♋、♌的值；（）若 ∥✌☜，求 的长．．（本题满分 分）如图，已知✌是△✌的角平分线，⊙ 经过✌、、三点，过点作 ☜∥✌，交⊙ 于点☜，连接☜．（）求证：☜∥✌；（）若   ，设△☜的面积为1S ，△✌的面积为2S ，且2121640S S -+=，求△✌的面积．．（本题满分 分）如图，已知二次函数()21y x m x m =+--（其中＜❍＜）的图像与⌧轴交于✌、两点（点✌在点的左侧），与⍓轴交于点，对称轴为直线●．设为对称轴●上的点，连接 ✌、 ， ✌ ．（第 题）（）∠✌的度数为 ✧ °；（）求点坐标（用含❍的代数式表示）；（）在坐标轴上是否存在点✈（与原点不重合），使得以✈、、为顶点的三角形与△ ✌相似，且线段 ✈的长度最小？如果存在，求出所有满足条件的点✈的坐标；如果不存在，请说明理由．．（本题满分 分）如图，在矩形✌中，✌ ♋♍❍，✌ ♌♍❍（♋＞♌＞），半径为 ♍❍的⊙ 在矩形内且与✌、✌均相切．现有动点从✌点出发，在矩形边上沿着✌→ → → 的方向匀速移动，当点到达点时停止移动；⊙ 在矩形内部沿✌向右匀速平移，移动到与 相切时立即沿原路按原速返回，当⊙ 回到出发时的位置（即再次与✌相切）时停止移动．已知点与⊙ 同时开始移动，同时停止移动（即同时到达各自的终止位置）．（）如图①，点从✌→ → → ，全程共移动了 ✧ ♍❍（用含♋、♌的代数式表示）；（）如图①，已知点从✌点出发，移动 ♦到达点，继续移动 ♦，到达 的中点．若点与⊙ 的移动速度相等，求在这 ♦时间内圆心移动的距离；（）如图②，已知♋ ，♌ ．是否存在如下情形：当⊙ 到达⊙ 的位置时（此时圆心在矩形对角线 上）， 与⊙ 恰好相切？请说明理由．年苏州市初中毕业暨升学考试数学试题答案一、选择题．．．✌ ．．．．．．✌．二、填空题 ．3a ．  ．  ．()()22a b a b +- ．14．． ． 三、解答题解：原式＝  ＝ ． 解：由12x +≥，解得1x ≥，由()315x x -+＞，解得4x ＞，不等式组的解集是4x ＞．解：原式＝()21122x x x x ++÷++ ＝()2121211x x x x x ++⨯=+++．当1x ===． 解：设乙每小时做⌧面彩旗，则甲每小时做（⌧ ）面彩旗．根据题意，得60505x x=+．解这个方程，得⌧ ．经检验，⌧ 是所列方程的解． ⌧ ．答：甲每小时做 面彩旗，乙每小时做 面彩旗．解：（）1．（）用表格列出所有可能的结果：由表格可知，共有 种可能出现的结果，并且它们都是等可能的，其中“两次都摸到红球”有种可能． ∴ （两次都摸到红球）212 16． 证明：（）由作图可知  ．在 ✌和 ✌中， ,,,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩✌≌ ✌（ ）．✌＝ ✌，即✌平分 ✌．解：（） ✌ ✌， ✌ ， ✌＝ ✌ °．  ，  为等边三角形． ＝  °． ☜＝ ☞ °．  ，   ．DE 的长度 DF 的长度 556111806ππ⨯⨯=． DE 、DF 的长度之和为111111663πππ+=． ．解：（）点（，）在ky x=的图像上，∴ ，4y x=． ⊥⍓轴，∴ 点的坐标为（，），  ．✌⊥⌧轴，✌32，∴✌ ，即✌点的纵坐标为．点✌在4y x=的图像上，∴✌点的坐标为（43，）．一次函数⍓ ♋⌧ ♌的图像经过点✌、， ∴43,3 2.a b b ⎧+=⎪⎨⎪=⎩ 解得3,42.a b ⎧=⎪⎨⎪=⎩ （）设✌点的坐标为（❍，4m），则点的坐标为（❍，）． ∥ ☜，且 ∥ ☜，∴四边形 ☜为平行四边形．∴ ☜  ．∥ ☜，∴∠✌☞ ∠✌☜．∴在 ♦✌☞中，♦♋⏹∠✌☞ 42AF mDF m -=，在 ♦✌☜中，♦♋⏹∠✌☜ 42AC mEC =， ∴4422m m m -=，解得❍ ．∴ 点的坐标为（，）， ．．证明：（）∵✌是△✌的角平分线，∴∠ ✌ ∠ ✌．∵∠☜∠ ✌，∴∠☜ ∠ ✌． ∵ ☜∥✌，∴∠☜ ∠☜✌． ∴∠☜✌ ∠ ✌ ． ∴☜∥✌．解：（）∵ ☜∥✌，∴∠☜ ∠✌．∵∠☜ ∠ ✌，∴△☜ △✌，且相似比2BDk DC==． ∴2124S k S ==，即124S S =． ∵2121640S S -+=，∴222161640S S -+=，即()22420S -=．∴212S =． ∵233ABC S BC BD CD CD S CD CD CD +====，∴32ABCS=． ．解：（） ．理由如下：令⌧ ，则⍓ ❍，点坐标为（， ❍）．令⍓ ，则()210x m x m +--=，解得11x =-，2x m =． ∵ ＜❍＜，点✌在点的左侧， ∴ 点坐标为（❍，）．∴   ❍．∵∠ ＝ °，∴△ 是等腰直角三角形，∠ ＝ °．（）解法一：如图①，作 ⊥⍓轴，垂足为，设●与⌧轴交于点☜，由题意得，抛物线的对称轴为12mx -+=．设点坐标为（12m-+，⏹）． ∵ ✌ ， ∴ ✌  ，即✌☜ ☜   ．∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭．解得12m n -=．∴ 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．解法二：连接 ．由题意得，抛物线的对称轴为12mx -+=． ∵ 在对称轴●上，∴ ✌ ． ∵ ✌ ，∴  ．∵△ 是等腰直角三角形，且  ， ∴ 在 的垂直平分线y x =-上．∴ 点即为对称轴12mx -+=与直线y x =-的交点． ∴ 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．图①图②（）解法一：存在点✈满足题意．∵ 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭， ∴ ✌  ✌☜ ☜  222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． ∵✌ 21m +，∴ ✌  ✌ ．∴∠✌＝ °． ∴△ ✌是等腰直角三角形．∵以✈、、为顶点的三角形与△ ✌相似， ∴△✈是等腰直角三角形．∴由题意知满足条件的点✈的坐标为（ ❍，）或（，❍）． ①如图①，当✈点的坐标为（ ❍，）时，若 ✈与⌧轴垂直，则12mm -+=-，解得13m =， ✈ 13．若 ✈与⌧轴不垂直，则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+⎪⎪ ⎪⎝⎭⎝⎭⎝⎭．∵ ＜❍＜，∴当25m =时，2PQ 取得最小值110， ✈．＜13， ∴当25m =，即✈点的坐标为（25-，）时， ✈的长度最小．②如图②，当✈点的坐标为（，❍）时，若 ✈与⍓轴垂直，则12mm -=，解得13m =， ✈ 13．若 ✈与⍓轴不垂直，则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭．∵ ＜❍＜，∴当25m =时，2PQ 取得最小值110， ✈．＜13， ∴当25m =，即✈点的坐标为（，25）时， ✈的长度最小．综上：当✈点坐标为（25-，）或（，25）时， ✈的长度最小．解法二：如图①，由（）知为△✌的外接圆的圆心． ∵∠✌ 与∠✌对应同一条弧AC ，且∠✌＝ °， ∴∠✌＝ ∠✌＝ °．下面解题步骤同解法一．．解：（）♋ ♌．（）∵在整个运动过程中，点移动的距离为()2a b +♍❍，圆心移动的距离为()24a -♍❍，由题意，得()224a b a +=-． ①∵点移动 ♦到达点，即点用 ♦移动了♌♍❍，点继续移动 ♦，到达 的中点，即点用 ♦移动了12a ♍❍．∴1223a b =． ② 由①②解得24,8.a b =⎧⎨=⎩∵点移动的速度与⊙ 移动的速度相等， ∴⊙ 移动的速度为42b=（♍❍♦）． ∴这 ♦时间内圆心移动的距离为 × （♍❍）．（）存在这种情形．解法一：设点移动的速度为❖ ♍❍♦，⊙ 移动的速度为❖ ♍❍♦，由题意，得()()1222021052422044v a b v a ++⨯===--．FE如图，设直线  与✌交于点☜，与 交于点☞，⊙ 与✌相切于点☝．若 与⊙ 相切，切点为☟，则 ☝ ☟．易得  ☝≌  ☟，∴∠✌ ∠ ． ∵ ∥✌，∴∠✌ ∠ ． ∴∠  ∠ ．∴  ．设  ⌧♍❍，则  ⌧♍❍，  （ ⌧）♍❍，在 ♦△ 中，由勾股定理，可得222PC CD PD +=，即()2222010x x -+=，解得252x =． ∴此时点移动的距离为25451022+=（♍❍）． ∵☜☞∥✌，∴△ ☜ ∽△ ✌． ∴1EO BE AD BA =，即182010EO =．∴☜ ♍❍．∴  ♍❍．①当⊙ 首次到达⊙ 的位置时，⊙ 移动的距离为 ♍❍， ∴此时点与⊙ 移动的速度比为454521428=．∵455284≠， ∴此时 与⊙ 不可能相切．②当⊙ 在返回途中到达⊙ 的位置时，⊙ 移动的距离为 ☎✆（♍❍），∴此时点与⊙ 移动的速度比为45455218364==． ∴此时 与⊙ 恰好相切．解法二：∵点移动的距离为452♍❍（见解法一），  ♍❍（见解法一），1254v v =，∴⊙ 应该移动的距离为4541825⨯=（♍❍）． ①当⊙ 首次到达⊙ 的位置时，⊙ 移动的距离为 ♍❍≠  ♍❍， ∴此时 与⊙ 不可能相切．②当⊙ 在返回途中到达⊙ 的位置时，⊙ 移动的距离为 ☎✆（♍❍），∴此时 与⊙ 恰好相切．解法三：点移动的距离为452♍❍，（见解法一） ♍❍，（见解法一）由1254v v =可设点的移动速度为 ♍❍♦，⊙ 的移动速度为 ♍❍♦， ∴点移动的时间为459252k k=（♦）．①当⊙ 首次到达⊙ 的位置时，⊙ 移动的时间为1479422k k k=≠， ∴此时 与⊙ 不可能相切．②当⊙ 在返回途中到达⊙ 的位置时，⊙ 移动的时间为2(204)14942k k⨯--=， ∴此时 与⊙ 恰好相切．。

2015年苏州市中考数学试卷及其规范标准答案

2015年苏州市初中毕业暨升学考试试卷数学一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将选择题的答案用2B 铅笔涂在答题卡相应位置上．．．．．．．．． 1．2的相反数是A ．2B ．12C ．-2D ．-122．有一组数据：3，5，5，6，7，这组数据的众数为A ．3B ．5C ．6D ．73．月球的半径约为1 738 000m ，1 738 000这个数用科学记数法可表示为 A ．1.738×106 B ．1.738×107 C ．0.1738×107 D ．17.38×1054．若()2m =-，则有 A ．0＜m ＜1 B ．-1＜m ＜0 C ．-2＜m ＜-1 D ．-3＜m ＜-25．小明统计了他家今年5月份打电话的次数及通话时间，并列出了频数分布表：则通话时间不超过15min 的频率为 A ．0.1B ．0.4C ．0.5D ．0.96．若点A （a ，b ）在反比例函数2y x=的图像上，则代数式ab -4的值为 A ．0 B ．-2C ． 2D ．-67．如图，在△ABC 中，AB =AC ，D 为BC 中点，∠BAD =35°，则∠C 的度数为 A ．35° B ．45°C ．55°D ．60°DCB A（第7题）8．若二次函数y =x 2+bx 的图像的对称轴是经过点（2，0）且平行于y 轴的直线，则关于x 的方程x 2+bx =5的解为 A ．120,4x x ==B ．121,5x x ==C ．121,5x x ==-D ．121,5x x =-=9．如图，AB 为⊙O 的切线，切点为B ，连接AO ，AO 与⊙O 交于点C ，BD 为⊙O 的直径，连接CD ．若∠A =30°，⊙O 的半径为2，则图中阴影部分的面积为 A．43πB．43π-C．π D．23π10．如图，在一笔直的海岸线l 上有A 、B 两个观测站，AB =2km ，从A 测得船C 在北偏东45°的方向，从B 测得船C 在北偏东22.5°的方向，则船C 离海岸线l 的距离（即CD 的长）为 A ．4kmB．(2+kmC．D．(4km二、填空题：本大题共8小题，每小题3分，共24分．把答案直接填在答题卡相应位置上．．．．．．．．． 11．计算：2a a ⋅= ▲ ．12．如图，直线a ∥b ，∠1=125°，则∠2的度数为 ▲ °．13．某学校在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛（第9题）（第10题）lba（第13题）20%10%30%40%其他乒乓球篮球羽毛球球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为 ▲ 名． 14．因式分解：224a b -= ▲ ．15．如图，转盘中8个扇形的面积都相等．任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为 ▲ ．16．若23a b -=，则924a b -+的值为 ▲ ．17．如图，在△ABC 中，CD 是高，CE 是中线，CE =CB ，点A 、D 关于点F 对称，过点F作FG ∥CD ，交AC 边于点G ，连接GE ．若AC =18，BC =12，则△CEG 的周长为 ▲ ．18．如图，四边形ABCD 为矩形，过点D 作对角线BD 的垂线，交BC 的延长线于点E ，取BE 的中点F ，连接DF ，DF =4．设AB =x ，AD =y ，则()224x y +-的值为 ▲ ．三、解答题：本大题共10小题，共76分．把解答过程写在答题卡相应位置上．．．．．．．．，解答时应写出必要的计算过程、推演步骤或文字说明．作图时用2B 铅笔或黑色墨水签字笔． 19．（本题满分5分）(052---． 20．（本题满分5分）解不等式组：()12,31 5.x x x +≥⎧⎪⎨-+⎪⎩＞（第17题）GF E D CBA F EDC B A （第18题）（第15题）21．（本题满分6分）先化简，再求值：2121122x xx x++⎛⎫-÷⎪++⎝⎭，其中1x．22．（本题满分6分）甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问甲、乙每小时各做多少面彩旗？23．（本题满分8分）一个不透明的口袋中装有2个红球（记为红球1、红球2）、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．（1）从中任意摸出1个球，恰好摸到红球的概率是▲ ；（2）先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．24．（本题满分8分）如图，在△ABC中，AB=AC．分别以B、C为圆心，BC长为半径在BC下方画弧，设两弧交于点D，与AB、AC的延长线分别交于点E、F，连接AD、BD、CD．（1）求证：AD平分∠BAC；（2）若BC=6，∠BAC＝50︒，求»DE、»DF的长度之和（结果保留π）．（第24题）FED CBA25．（本题满分8分）如图，已知函数ky x=（x ＞0）的图像经过点A 、B ，点B 的坐标为（2，2）．过点A 作AC ⊥x 轴，垂足为C ，过点B 作BD ⊥y 轴，垂足为D ，AC 与BD 交于点F ．一次函数y=ax +b 的图像经过点A 、D ，与x 轴的负半轴交于点E ．（1）若AC =32OD ，求a 、b 的值；（2）若BC ∥AE ，求BC 的长．26．（本题满分10分）如图，已知AD 是△ABC 的角平分线，⊙O 经过A 、B 、D 三点，过点B 作BE ∥AD ，交⊙O 于点E ，连接ED ．（1）求证：ED ∥AC ；（2）若BD =2CD ，设△EBD 的面积为1S ，△ADC 的面积为2S ，且2121640S S -+=，求△（第26题）ABC 的面积．27．（本题满分10分）如图，已知二次函数()21y x m x m =+--（其中0＜m ＜1）的图像与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，对称轴为直线l ．设P 为对称轴l 上的点，连接P A 、PC ，P A =PC ．（1）∠ABC 的度数为 ▲ °；（2）求P 点坐标（用含m 的代数式表示）；（3）在坐标轴上是否存在点Q （与原点O 不重合），使得以Q 、B 、C 为顶点的三角形与△P AC 相似，且线段PQ 的长度最小？如果存在，求出所有满足条件的点Q 的坐标；如果不存在，请说明理由．28．（本题满分10分）如图，在矩形ABCD 中，AD =a cm ，AB =b cm （a ＞b ＞4），半径为2cm的⊙O 在矩形内且与AB 、AD 均相切．现有动点P 从A 点出发，在矩形边上沿着A →B →C →D 的方向匀速移动，当点P 到达D 点时停止移动；⊙O 在矩形内部沿AD 向右匀速平移，移动到与CD 相切时立即沿原路按原速返回，当⊙O 回到出发时的位置（即再次与AB 相切）时停止移动．已知点P 与⊙O 同时开始移动，同时停止移动（即同时到达各自的终止位置）．（1）如图①，点P 从A →B →C →D ，全程共移动了 ▲ cm （用含a 、b 的代数式表示）；（2）如图①，已知点P 从A 点出发，移动2s 到达B 点，继续移动3s ，到达BC 的中点．若点P 与⊙O 的移动速度相等，求在这5s 时间内圆心O 移动的距离；（3）如图②，已知a =20，b =10．是否存在如下情形：当⊙O 到达⊙O 1的位置时（此时圆心O 1在矩形对角线BD 上），DP 与⊙O 1恰好相切？请说明理由．2015年苏州市初中毕业暨升学考试数学试题答案一、选择题 1．C2．B3．A4．C5．D（第28题）（图②）（图①）6．B7．C 8．D 9．A 10．B 二、填空题 11．3a 12．55 13．60 14．()()22a b a b +- 15．1416．317．2718．16三、解答题19.解：原式＝ 3+5-1 ＝ 7． 20.解：由12x +≥，解得1x ≥，由()315x x -+＞，解得4x ＞， ∴不等式组的解集是4x ＞．21.解：原式＝()21122x x x x ++÷++ ＝()2121211x x x x x ++⨯=+++．当1x==． 22.解：设乙每小时做x 面彩旗，则甲每小时做（x +5）面彩旗．根据题意，得60505x x=+．解这个方程，得x =25．经检验，x =25是所列方程的解． ∴x +5=30．答：甲每小时做30面彩旗，乙每小时做25面彩旗． 23.解：（1）1．（2）用表格列出所有可能的结果：到红球”有2种可能．∴P （两次都摸到红球）=212=16． 24.证明：（1）由作图可知BD =CD ．在△ABD 和△ACD 中，,,,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩∴△ABD≌△ACD（SSS）．∴∠BAD＝∠CAD，即AD平分∠BAC．解：（2）∵AB=AC，∠BAC=50°，∴∠ABC＝∠ACB=65°．∵BD= CD = BC，∴△BDC为等边三角形．∴∠DBC＝∠DCB=60°．∴∠DBE＝∠DCF=55°．∵BC=6，∴BD= CD =6．∴»DE的长度=»DF的长度=556111806ππ⨯⨯=．∴»DE、»DF的长度之和为111111 663πππ+=．25．解：（1）∵点B（2，2）在kyx=的图像上，∴k=4，4yx =．∵BD⊥y轴，∴D点的坐标为（0，2），OD=2．∵AC⊥x轴，AC=32OD，∴AC=3，即A点的纵坐标为3．∵点A在4yx=的图像上，∴A点的坐标为（43，3）．∵一次函数y=ax+b的图像经过点A、D，∴43,32.a bb⎧+=⎪⎨⎪=⎩解得3,42.ab⎧=⎪⎨⎪=⎩（2）设A点的坐标为（m，4m），则C点的坐标为（m，0）．∵BD∥CE，且BC∥DE，∴四边形BCED为平行四边形．∴CE= BD=2．∵BD∥CE，∴∠ADF=∠AEC．∴在Rt△AFD中，tan∠ADF=42 AF mDF m-=，在Rt△ACE中，tan∠AEC=42 AC m EC=，∴4422m mm-=，解得m=1．∴C点的坐标为（1，0），BC．26．证明：（1）∵AD是△ABC的角平分线，∴∠BAD =∠DAC．∵∠E=∠BAD，∴∠E =∠DAC．∵BE∥AD，∴∠E =∠EDA．∴∠EDA =∠DA C ． ∴ED ∥AC ．解：（2）∵BE ∥AD ，∴∠EBD =∠ADC ．∵∠E =∠DAC ，∴△EBD ∽△ADC ，且相似比2BDk DC==． ··················· ∴2124S k S ==，即124S S =． ∵2121640S S -+=，∴222161640S S -+=，即()22420S -=．∴212S =． ∵233ABC S BC BD CD CD S CD CD CD +====V ，∴32ABC S =V ．27．解：（1）45．理由如下：令x =0，则y =-m ，C 点坐标为（0，-m ）．令y =0，则()210x m x m +--=，解得11x =-，2x m =．∵0＜m ＜1，点A 在点B 的左侧，∴B 点坐标为（m ，0）．∴OB =OC =m ．∵∠BOC ＝90°，∴△BOC 是等腰直角三角形，∠OBC ＝45°．（2）解法一：如图①，作PD ⊥y 轴，垂足为D ，设l 与x 轴交于点E ，由题意得，抛物线的对称轴为12mx -+=．设点P 坐标为（12m-+，n ）． ∵P A = PC ， ∴P A 2= PC 2，即AE 2+ PE 2=CD 2+ PD 2．∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭．解得12m n -=．∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．解法二：连接PB ．由题意得，抛物线的对称轴为12m x -+=． ∵P 在对称轴l 上，∴P A =PB ． ∵P A =PC ，∴PB =PC ．∵△BOC 是等腰直角三角形，且OB =OC ， ∴P 在BC 的垂直平分线y x =-上．∴P 点即为对称轴12mx -+=与直线y x =-的交点． ∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．图①图②（3）解法一：存在点Q 满足题意．∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭， ∴P A 2+ PC 2=AE 2+ PE 2+CD 2+ PD 2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． ∵AC 2=21m +，∴P A 2+ PC 2=AC 2．∴∠APC ＝90°． ∴△P AC 是等腰直角三角形．∵以Q 、B 、C 为顶点的三角形与△P AC 相似， ∴△QBC 是等腰直角三角形．∴由题意知满足条件的点Q 的坐标为（-m ，0）或（0，m ）． ①如图①，当Q 点的坐标为（-m ，0）时，若PQ 与x 轴垂直，则12m m -+=-，解得13m =，PQ =13．若PQ 与x 轴不垂直，则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+⎪⎪ ⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ ．＜13， ∴当25m =，即Q 点的坐标为（25-，0）时， PQ 的长度最小．②如图②，当Q 点的坐标为（0，m ）时，若PQ 与y 轴垂直，则12m m -=，解得13m =，PQ =13．若PQ 与y 轴不垂直，则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ．＜13， ∴当25m =，即Q 点的坐标为（0，25）时， PQ 的长度最小．综上：当Q 点坐标为（25-，0）或（0，25）时，PQ 的长度最小．解法二：如图①，由（2）知P 为△ABC 的外接圆的圆心． ∵∠APC 与∠ABC 对应同一条弧»AC ，且∠ABC ＝45°， ∴∠APC ＝2∠ABC ＝90°．下面解题步骤同解法一．28．解：（1）a +2b ．（2）∵在整个运动过程中，点P 移动的距离为()2a b +cm ，圆心O 移动的距离为()24a -cm ，由题意，得()224a b a +=-． ①∵点P 移动2s 到达B 点，即点P 用2s 移动了b cm ，点P 继续移动3s ，到达BC 的中点，即点P 用3s 移动了12a cm ．∴1223a b =． ② 由①②解得24,8.a b =⎧⎨=⎩∵点P 移动的速度与⊙O 移动的速度相等，∴⊙O 移动的速度为42b=（cm/s ）． ∴这5s 时间内圆心O 移动的距离为5×4=20（cm ）．（3）存在这种情形．解法一：设点P 移动的速度为v 1cm/s ，⊙O 移动的速度为v 2cm/s ，由题意，得()()1222021052422044v a b v a ++⨯===--．FE如图，设直线OO 1与AB 交于点E ，与CD 交于点F ，⊙O 1与AD 相切于点G ．若PD 与⊙O 1相切，切点为H ，则O 1G =O 1H ．易得△DO 1G ≌△DO 1H ，∴∠ADB =∠BDP ． ∵BC ∥AD ，∴∠ADB =∠CBD ． ∴∠BDP =∠CBD ．∴BP =DP ．设BP =x cm ，则DP =x cm ，PC =（20-x ）cm ，在Rt △PCD 中，由勾股定理，可得222PC CD PD +=，即()2222010x x -+=，解得252x =．∴此时点P 移动的距离为25451022+=（cm ）． ∵EF ∥AD ，∴△BEO 1∽△BAD ． ∴1EO BE AD BA =，即182010EO =．∴EO 1=16cm ．∴OO 1=14cm ．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ， ∴此时点P 与⊙O 移动的速度比为454521428=．∵455284≠， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ）， ∴此时点P 与⊙O 移动的速度比为45455218364==． ∴此时PD 与⊙O 1恰好相切．解法二：∵点P 移动的距离为452cm （见解法一）， OO 1=14cm （见解法一），1254v v =，∴⊙O 应该移动的距离为4541825⨯=（cm ）． ①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ≠18 cm ， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ），∴此时PD 与⊙O 1恰好相切．解法三：点P 移动的距离为452cm ，（见解法一） OO 1=14cm ，（见解法一）由1254v v =可设点P 的移动速度为5k cm/s ，⊙O 的移动速度为4k cm/s ， ∴点P 移动的时间为459252k k=（s ）．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的时间为1479422k k k=≠， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的时间为2(204)14942k k⨯--=， ∴此时PD 与⊙O 1恰好相切．。

(高清版)2015年江苏省苏州市中考数学试卷

为对称轴 l 上的点,连接 PA 、 PC , PA PC .
(1) ABC 的度数为
；
(2)求 P 点坐标(用含 m 的代数式表示)；
(3)在坐标轴上是否存在点 Q (与原点 O 不重合),使得以 Q 、B 、C 为顶点的三角形
与 △PAC 相似,且线段 PQ 的长度最小？如果存在,求出所有满足条件的点 Q 的
B.1.738 107 D.17.38 105
4.若
,则有
()
A. 0＜m＜1
B. 1＜m＜0
答
C. 2＜m＜1
D. 3＜m＜ 2
5.小明统计了他家今年 5 月份打电话的次数及通话时间,并列出了频数分布表：
通话时间
0＜x≤5
5＜x≤10 10＜x≤15 15＜x≤20
频数(通话次数) 20
16
9
5
则通话时间不超过15 min 的频率
坐标；如果不存在,请说明理由.
28.(本小题满分 10 分)如图,在矩形 ABCD 中, AD a cm , AB b cm(a＞b＞4) ,半径为 2 cm 的 O 在矩形内且与 AB 、AD 均相切.现有动点 P 从 A点出发,在矩形边上沿着 A B C D 的方向匀速移动,当点 P 到达 D 点时停止移动； O 在矩形内部沿 AD 向右匀速平移,移动到与 CD 相切时立即沿原路按原速返回,当 O 回到出发时的位置(即再次与 AB 相切)时停止移动.已知点 P 与 O 同时开始移动,同时停止移
题
A. 0.1
B. 0.4
C. 0.5
() D. 0.9
6.若点 A（a，b）在反比例函数
的图像上,则代数式 ab 4 的值为
()
(第 7 题)

2015年江苏省苏州市中考数学试卷-答案

江苏省苏州市2015年中考数学试卷数学答案解析第Ⅰ卷一、选择题 1.【答案】C【解析】此题考查了相反数的含义以及求法，要熟练掌握，根据相反数的含义，可得2的相反数是：2-。

【提示】根据相反数的含义，可得求一个数的相反数的方法就是在这个数的前边添加“-”，据此解答即可。

【考点】相反数 2.【答案】B【解析】这组数据中5出现的次数最多，故众数为5。

【提示】本题考查了众数的概念：一组数据中出现次数最多的数据叫做众数。

【考点】众数 3.【答案】A【解析】科学记数法的表示形式为n a 10⨯的形式，其中1a 10≤＜，n 为整数。

确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同。

当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数。

将1738000用科学记数法表示为：61.73810⨯。

【提示】此题考查科学记数法的表示方法。

科学记数法的表示形式为n a 10⨯的形式，其中1a 10≤＜，n 为整数，表示时关键要正确确定a 的值以及n 的值。

【考点】科学记数法—表示较大的数4.【答案】C【解析】()m 22=-=∵12<，∴21-<-。

【提示】先把m 大小，即可解答。

【考点】二次根式的运算，估算无理数的大小 5.【答案】D【解析】∵不超过15分钟的通话次数为2016945++=次，通话总次数为20169550+++=次，∴通话时间不超过15min 的频率为450.950=。

【提示】用不超过15分钟的通话时间除以所有的通话时间即可求得通话时间不超过15分钟的频率。

【考点】频数（率）分布表6.【答案】B【解析】∵点()a b ,反比例函数2y x =上，∴2b a=，即ab 2=，∴原式=242-=。

【提示】先把点()a b ,代入反比例函数2y x=求出ab 的值，再代入代数式进行计算即可。

【考点】反比例函数图象上点的坐标特征，求代数式的值，有理数的减法运算及整体思想 7.【答案】C【解析】AB AC =，D 为BC 中点，∴AD 是BAC ∠的平分线，B C ∠=∠，∵BAD 35∠=︒，∴BAC 2BAD 70∠=∠=︒，∴1C 18070552∠=︒︒=︒（-）。

2015苏州中考数学试题及答案

2015苏州中考数学试题及答案2015年苏州市初中毕业暨升学考试试卷数学（2015年6月16日）一、选择题：（本大题共10小题，每小题3分，共30分）1. 2015年是抗日战争胜利70周年，下列年份中属于抗日战争胜利的年份是（）A. 1945年B. 1937年C. 1931年D. 1949年答案：A2. 一个数的绝对值是3，这个数是（）A. 3B. -3C. 3或-3D. 以上答案都不对答案：C3. 一个等腰三角形的两边长分别为5和8，这个三角形的周长是（）A. 18B. 21C. 26D. 234. 将下列各数从小到大排列：-2，-1，0，1，2，3，4，5，6，7，8，9（）A. -2＜-1＜0＜1＜2＜3＜4＜5＜6＜7＜8＜9B. -2＜-1＜0＜1＜2＜3＜4＜5＜6＜7＜8＜9C. -2＜-1＜0＜1＜2＜3＜4＜5＜6＜7＜8＜9D. -2＜-1＜0＜1＜2＜3＜4＜5＜6＜7＜8＜9答案：A5. 已知a，b，c是三个实数，且a＞b，c＞0，则下列不等式中一定成立的是（）A. ac＞bcB. a+c＞b+cC. ac＞bcD. a-c＞b-c答案：B6. 已知a，b，c是三个实数，且a＞b，c＜0，则下列不等式中一定成立的是（）A. ac＞bcB. a+c＞b+cC. ac＞bcD. a-c＞b-c7. 已知a，b，c是三个实数，且a＞b，c＞0，则下列不等式中一定成立的是（）A. ac＞bcB. a+c＞b+cC. ac＞bcD. a-c＞b-c答案：A8. 已知a，b，c是三个实数，且a＞b，c＜0，则下列不等式中一定成立的是（）A. ac＞bcB. a+c＞b+cC. ac＞bcD. a-c＞b-c答案：C9. 已知a，b，c是三个实数，且a＞b，c＞0，则下列不等式中一定成立的是（）A. ac＞bcB. a+c＞b+cC. ac＞bcD. a-c＞b-c答案：B10. 已知a，b，c是三个实数，且a＞b，c＜0，则下列不等式中一定成立的是（）A. ac＞bcB. a+c＞b+cC. ac＞bcD. a-c＞b-c答案：D二、填空题：（本大题共6小题，每小题3分，共18分）11. 已知一个角的补角是它的余角的3倍，则这个角的度数是60°。

20l5苏州中考数学试题及答案

20l5苏州中考数学试题及答案2015年苏州中考数学试题及答案一、选择题（本题共10小题，每小题3分，共30分）1. 下列哪个数是正数？A. -3B. 0C. 2D. -1答案：C2. 一个数的相反数是-5，这个数是：A. 5B. -5C. 0D. 1答案：A3. 绝对值等于它本身的数是：A. 0B. 负数C. 正数D. 正数和0答案：D4. 一个数的平方是9，这个数是：A. 3或-3B. 3C. -3D. 9答案：A5. 以下哪个选项是不等式？A. 2x + 3 = 7B. 2x + 3 > 7C. 2x + 3 < 7D. 2x + 3答案：B6. 以下哪个选项是二次方程？A. 2x + 3 = 0B. x^2 + 2x + 1 = 0C. x^2 + 2x = 0D. 2x + 1答案：B7. 一个等腰三角形的两边长分别为3和5，那么这个三角形的周长是：A. 11B. 13C. 16D. 无法确定答案：B8. 一个圆的半径是2，那么这个圆的面积是：A. 4πB. 8πC. 16πD. 32π答案：B9. 以下哪个选项是一次函数？A. y = 2x + 3B. y = x^2 + 3C. y = 2x^2 + 3D. y = 2x/3答案：A10. 以下哪个选项是反比例函数？A. y = 2/xB. y = x^2C. y = 2xD. y = 2x + 3答案：A二、填空题（本题共5小题，每小题3分，共15分）11. 一个数的立方是-8，这个数是 -2。

12. 一个数的倒数是2，这个数是 1/2。

13. 一个数的平方根是4，这个数是 16。

14. 一个数的立方根是8，这个数是 512。

15. 一个直角三角形的两个直角边长分别为3和4，那么这个三角形的斜边长是 5。

三、解答题（本题共4小题，共55分）16. （本题满分10分）解方程：3x - 5 = 2x + 4。

解：将2x移到左边，得x = 9。

苏州市2015年中考数学试卷

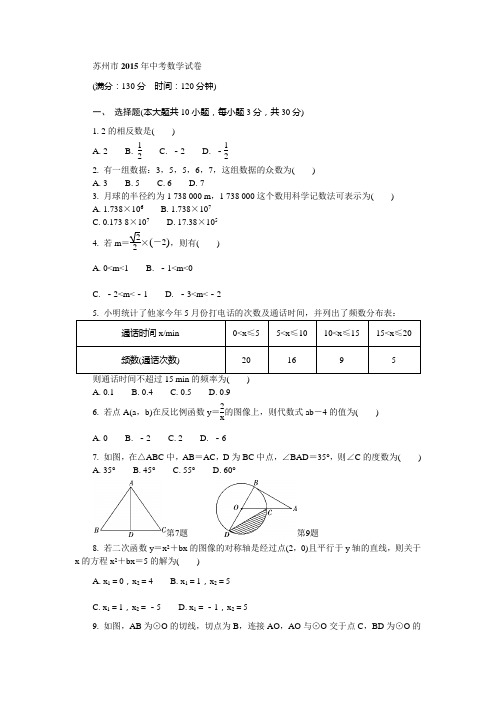
苏州市2015年中考数学试卷(满分：130分时间：120分钟)一、选择题(本大题共10小题，每小题3分，共30分)1. 2的相反数是()A. 2B. 12 C. －2 D. －122. 有一组数据：3，5，5，6，7，这组数据的众数为()A. 3B. 5C. 6D. 73. 月球的半径约为1 738 000 m，1 738 000这个数用科学记数法可表示为()A. 1.738×106B. 1.738×107C. 0.173 8×107D. 17.38×1054. 若m＝22×()－2，则有()A. 0<m<1B. －1<m<0C. －2<m<－1D. －3<m<－2则通话时间不超过15 min的频率为() A. 0.1 B. 0.4 C. 0.5 D. 0.96. 若点A(a，b)在反比例函数y＝2x的图像上，则代数式ab－4的值为()A. 0B. －2C. 2D. －67. 如图，在△ABC中，AB＝AC，D为BC中点，∠BAD＝35°，则∠C的度数为()A. 35°B. 45°C. 55°D. 60°第7题第9题8. 若二次函数y＝x2＋bx的图像的对称轴是经过点(2，0)且平行于y轴的直线，则关于x的方程x2＋bx＝5的解为()A. x1＝0，x2＝4B. x1＝1，x2＝5C. x1＝1，x2＝－5D. x1＝－1，x2＝59. 如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD.若∠A ＝30°，⊙O 的半径为2，则图中阴影部分的面积为( )A.4π3－3 B. 4π3－23 C. π－3 D. 2π3－3 10. 如图，在一笔直的海岸线l 上有A 、B 两个观测站，AB ＝2 km ，从A 测得船 C 在北偏东45°的方向，从B 测得船C 在北偏东22.5°的方向，则船C 离海岸线 l 的距离(即CD 的长)为( )第10题A. 4 kmB. (2＋2)kmC. 2 2 kmD. (4－2)km二、填空题(本大题共8小题，每小题3分，共24分) 11. 计算：a·a 2＝________．12. 如图，直线a ∥b ，∠1＝125°，则∠2的度数为________°.第12题第13题13. 某学校在“你最喜爱的球类运动”调查中，随机调查了若干名学生(每名学生分别选了一项球类运动)，并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为________名．14. 因式分解：a 2－4b 2＝________．15. 如图，转盘中8个扇形的面积都相等．任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为________．第15题第17题16. 若a －2b ＝3，则9－2a ＋4b 的值为________．17. 如图，在△ABC 中，CD 是高，CE 是中线，CE ＝CB ，点A 、D 关于点F 对称，过点F 作FG ∥CD ，交AC 边于点G ，连接GE.若AC ＝18，BC ＝12，则△CEG 的周长为________．18. 如图，四边形ABCD 为矩形，过点D 作对角线BD 的垂线，交BC 的延长线于点E ，取BE 的中点F ，连接DF ，DF ＝4.设AB ＝x ，AD ＝y ，则x 2＋()y －42的值为________．第18题三、解答题(本大题共10小题，共76分) 19. (本小题满分5分)计算：9＋|－5|－()2－30.20. (本小题满分5分)解不等式组：⎩⎪⎨⎪⎧x ＋1≥2，3（x －1）>x ＋5.21. (本小题满分6分)先化简，再求值：⎝ ⎛⎭⎪⎫1－1x ＋2÷x 2＋2x ＋1x ＋2，其中x ＝3－1.22. (本小题满分6分)甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问甲、乙每小时各做多少面彩旗？23. (本小题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．(1) 从中任意摸出1个球，恰好摸到红球的概率是________； (2) 先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法(画树状图或列表)求两次都摸到红球的概率．24. (本小题满分8分)如图，在△ABC 中，AB ＝AC.分别以B 、C 为圆心，BC 长为半径在BC 下方画弧，设两弧交于点D ，与AB 、AC 的延长线分别交于点E 、F ，连接AD 、BD 、CD.(1) 求证：AD 平分∠BAC ；(2) 若BC ＝6，∠BAC ＝50°，求DE ︵、DF ︵的长度之和(结果保留π)．第24题25. (本小题满分8分)如图，已知函数y ＝kx (x>0)的图像经过点A 、B ，点B 的坐标为(2，2)．过点A 作AC ⊥x 轴，垂足为C ，过点B 作BD ⊥y 轴，垂足为D ，AC 与BD 交于点F.一次函数y ＝ax ＋b 的图像经过点A 、D ，与x 轴的负半轴交于点E.(1) 若AC ＝32OD ，求a 、b 的值；(2) 若BC ∥AE ，求BC 的长．第25题26. (本小题满分10分)如图，已知AD 是△ABC 的角平分线，⊙O 经过A 、B 、D 三点，过点B 作BE ∥AD ，交⊙O 于点E ，连接ED. (1) 求证：ED ∥AC ；(2) 若BD ＝2CD ，设△EBD 的面积为S 1，△ADC 的面积为S 2，且S 21 －16S 2＋4 ＝0，求△ABC 的面积．第26题1－m x－m(其中0<m<1)的图像与27. (本小题满分10分)如图，已知二次函数y＝x2＋()x轴交于A、B两点(点A在点B的左侧)，与y轴交于点C，对称轴为直线l.设P为对称轴l上的点，连接PA、PC，PA＝PC.(1) ∠ABC的度数为________°；(2) 求P点坐标(用含m的代数式表示)；(3) 在坐标轴上是否存在点Q(与原点O不重合)，使得以Q、B、C为顶点的三角形与△PAC相似，且线段PQ的长度最小？如果存在，求出所有满足条件的点Q的坐标；如果不存在，请说明理由．第27题28. (本小题满分10分)如图，在矩形ABCD中，AD＝a cm，AB＝b cm(a>b>4)，半径为2 cm的⊙O在矩形内且与AB、AD均相切．现有动点P从A点出发，在矩形边上沿着A→B→C→D的方向匀速移动，当点P到达D点时停止移动；⊙O在矩形内部沿AD向右匀速平移，移动到与CD相切时立即沿原路按原速返回，当⊙O回到出发时的位置(即再次与AB相切)时停止移动．已知点P与⊙O同时开始移动，同时停止移动(即同时到达各自的终止位置)．(1) 如图①，点P从A→B→C→D，全程共移动了________cm(用含a、b的代数式表示)；(2) 如图①，已知点P从A点出发，移动2 s到达B点，继续移动3 s，到达BC的中点．若点P与⊙O的移动速度相等，求在这5 s时间内圆心O移动的距离；(3) 如图②，已知a＝20，b＝10.是否存在如下情形：当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上)，DP与⊙O1恰好相切？请说明理由．第28题苏州市2015年中考数学试卷1. C [解析]根据相反数的定义，给2 添上一个负号即可．2. B [解析]因为众数是一组数据中出现次数最多的数值，5 出现了两次，其他数均只出现一次，故选B.3. A [解析]科学记数法的表示结果应满足a ×10n (1≤a<10)的要求，故选A.4. C [解析]无理数的估算有不同的方法，比如近似值法，先化简为－2，－2≈－1.414.5. D [解析]不超过15 min 的通话次数为20＋16＋9＝45，通话的总次数为45＋5＝50，因此通话时间不超过15 min 的频率为45÷50＝0.9.6. B [解析]把点A(a ，b)代入y ＝2x中，得ab ＝2，再代入求值．7. C [解析]由AB ＝AC ，D 为BC 的中点，根据三线合一，可得AD 平分∠BAC ，AD ⊥BC.∴ ∠DAC ＝∠BAD ＝35°，∠ADC ＝90°.∴ ∠C ＝180°－(∠ADC ＋∠DAC)＝55°.8. D [解析]由题意，得二次函数的对称轴为直线x ＝2，∴ －b2＝2，解得b ＝－4.代入一元二次方程，得x 2－4x ＝5，解得x 1＝－1，x 2＝5.9. A [解析]先求出∠AOB ＝60°，则∠COD ＝120°，从而可求出扇形COD 的面积为4π3，再求出△COD 的面积为3，从而得出阴影部分的面积为4π3－ 3. 10. B [解析]如图，过点B 作BE ⊥AC ，交AC 于点E.在Rt △ABE 中，∠CAB ＝90°－45°＝45°，AB ＝2 km ，∴ BE ＝ 2 km.由题意可得∠ACD ＝45°，∠BCD ＝22.5°，∴ ∠BCA ＝22.5°.∴ ∠BCD ＝∠BCA.∴ BD ＝BE ＝ 2 km.∴ DC ＝AD ＝AB ＋BD ＝(2＋2)km.第10题11. a 3 [解析]由幂的运算性质，可得a·a 2＝a 1＋2＝a 3. 12. 55 [解析]由平行线的性质，可得∠2＝180°－∠1＝55°. 13. 60 [解析]由统计的概念，可得总人数为6÷(40%－30%)＝60(名)． 14. (a ＋2b)(a －2b) [解析]运用平方差公式分解因式即可．15. 14 [解析]总共有8种等可能的结果，其中指针指向大于6的数的结果有2种，∴ 指针指向大于6的数的概率为28＝14.16. 3 [解析]整体代入，把9－2a ＋4b 变形为9－2(a －2b)即可．17. 27 [解析]由题意可直接得到CE ＝CB ＝12.∵ F 是AD 的中点，FG ∥CD ，∴ FG 是△ADC 的中位线．∴ CG ＝12AC ＝9.∵ E 是AB 的中点，∴ EG 是△ABC 的中位线．∴GE ＝12BC ＝6.∴ △CEG 的周长为CE ＋GE ＋CG ＝12＋6＋9＝27.18. 16 [解析]在Rt △BDE 中，F 为BE 的中点，可得BE ＝2DF ＝8，BF ＝4.由矩形的性质，可得CD ＝AB ＝x ，BC ＝AD ＝y ，则CF ＝4－y.在Rt △CDF 中，CD 2＋CF 2＝DF 2，则有x 2＋(4－y)2＝42，即x 2＋(y －4)2＝16.19. [解析]根据数的开方、绝对值、零指数幂的法则先化简、再运算．解：原式＝3＋5－1＝7.20. [解析]分别解两个不等式，再确定解集的公共部分．解：由x ＋1≥2，解得x ≥1.由3(x －1)>x ＋5，解得x>4.∴ 不等式组的解集是x>4.21. [解析]先化简分式，再代入求值．解：原式＝x ＋1x ＋2÷（x ＋1）2x ＋2＝x ＋1x ＋2×x ＋2（x ＋1）2＝1x ＋1.当x ＝3－1时，原式＝13－1＋1＝13＝33.22. [解析]根据所用时间相等这个等量关系来构造分式方程，要注意最后的检验环节．解：设乙每小时做x 面彩旗，则甲每小时做(x ＋5)面彩旗．根据题意，得60x ＋5＝50x .解得x ＝25.经检验，x ＝25是原方程的解．∴ x ＋5＝30.∴ 甲每小时做30面彩旗，乙每小时做25面彩旗．23. [解析](1) 根据4个小球中红球的个数，即可确定出从中任意摸出1个球，恰好摸到红球的概率；(2) 列表得出所有等可能的结果数，找出两次都摸到红球的结果数，即可求出所求的概率．解：(1) 12；(2) 列表如下：由表格可知，共有12种等可能出现的结果，其中两次都摸到红球的结果有2种．∴ P(两次都摸到红球)＝212＝16.24. [解析](1) 本题的实质是角平分线的尺规作图，可依据“SSS ”证明全等，从而得证；(2) 关键是求出DE ︵、DF ︵所对的圆心角的度数及BD 、CD 的长，BD 、CD 分别是DE ︵、DF ︵所在圆的半径．解：(1) 由作图可知BD ＝CD.在△ABD 和△ACD 中，⎩⎪⎨⎪⎧AB ＝AC ，BD ＝CD ，AD ＝AD ，∴ △ABD ≌△ACD(SSS)．∴ ∠BAD ＝∠CAD ，即AD 平分∠BAC ；(2) ∵ AB ＝AC ，∠BAC ＝50°，∴ ∠ABC ＝∠ACB ＝180°－∠BAC2＝65°.∵ BD ＝CD ＝BC ，∴ △BDC 为等边三角形．∴ ∠DBC＝∠DCB ＝60°.∴ ∠DBE ＝∠DCF ＝180°－65°－60°＝55°.∵ BC ＝6，∴ BD ＝CD ＝6.∴ DE ︵的长度＝DF ︵的长度＝55×π×6180＝11π6.∴ DE ︵、DF ︵的长度之和为11π6＋11π6＝11π3.25. [解析](1) 关键是由条件“AC ＝32OD ”得出AC ＝3，这样就能得到点A 的坐标为⎝⎛⎭⎫43，3，再根据D(0，2)可求出直线AD 的解析式；(2) 设点A 的坐标为⎝⎛⎭⎫m ，4m ，则点C 的坐标为(m ，0)，在Rt △AFD 和Rt △ACE 中，利用 tan ∠ADF ＝tan ∠AEC 建立关于m 的方程，可以解出m ＝1，进而利用勾股定理可求出BC 的长．解：(1) ∵ 点B(2，2)在y ＝kx的图像上，∴ k ＝4.∴ y ＝4x .∵ BD ⊥y 轴，∴ 点D 的坐标为(0，2)，OD ＝2.∵ AC ⊥x 轴，AC ＝32OD ，∴ AC ＝3，即点A 的纵坐标为3.∵ 点A 在y ＝4x 的图像上，∴ 点A 的横坐标为43.∴ 点A 的坐标为⎝⎛⎭⎫43，3.∵ 一次函数y ＝ax ＋b 的图像经过点A 、D ，∴ ⎩⎪⎨⎪⎧43a ＋b ＝3，b ＝2，解得⎩⎪⎨⎪⎧a ＝34，b ＝2；(2) 设点A 的坐标为⎝⎛⎭⎫m ，4m ，则点C 的坐标为(m ，0)．∵ BD ∥CE ，BC ∥DE ，∴ 四边形BCED 为平行四边形．∴ CE ＝BD ＝2.∵ BD ∥CE ，∴ ∠ADF ＝∠AEC.∴ 在Rt △AFD 中，tan ∠ADF＝AF DF ＝4m －2m ；在Rt △ACE 中，tan ∠AEC ＝AC EC ＝4m 2.∴ 4m －2m ＝4m 2，解得m ＝1.∴ DF ＝OC ＝1.∴ BF ＝1.又∵ FC ＝OD ＝2，∴ BC ＝BF 2＋FC 2＝ 5.26. [解析](1) 利用BE ∥AD 可得∠E ＝∠EDA ，利用圆周角的性质有∠E ＝∠BAD ，再结合AD 是△ABC 的角平分线，可得∠DAC ＝∠EDA ，即可证明ED ∥AC ；(2) 先证△EBD ∽△ADC ，结合相似比k ＝BD DC ＝2得S 1S 2＝k 2＝4，即S 1＝4S 2，代入S 21－16S 2＋4＝0，消元，得16S 22－16S 2＋4＝0，解出S 2，再根据S 2和S △ABC 的关系求出S △ABC 即可．解：(1) ∵ AD 是△ABC 的角平分线，∴ ∠BAD ＝∠DAC.∵ ∠E ＝∠BAD ，∴ ∠E ＝∠DAC.∵ BE ∥AD ，∴ ∠E ＝∠EDA.∴ ∠EDA ＝∠DAC.∴ ED ∥AC ；(2) ∵ BE ∥AD ，∴ ∠EBD ＝∠ADC.又∵ ∠E ＝∠DAC ，∴ △EBD ∽△ADC.∴ BD DC ＝k ＝2.∴ S 1S 2＝k 2＝4，即S 1＝4S 2.∵ S 21－16S 2＋4＝0，∴ 16S 22－16S 2＋4＝0，即(2S 2－1)2＝0.∴ S 2＝12.∵ △ABC 在BC 边上的高和△ADC 在DC 边上的高相等，∴ S △ABC S 2＝BC CD ＝BD ＋CD CD ＝3CD CD ＝3.∴ S △ABC ＝32. 27. [解析](1) 由二次函数解析式的特点可以发现两根为x 1＝－1，x 2＝m ，与y 轴的交点C 的坐标为(0，－m)，即OB ＝OC ，从而可得△OBC 是等腰直角三角形，问题获解；(2) 如图①，作PD ⊥y 轴，垂足为D ，设l 与x 轴交于点E ，利用勾股定理或BC 的垂直平分线，结合抛物线的对称轴为直线x ＝－1＋m 2可以求解；(3) 由(2)知△PAC 是等腰直角三角形，所以△QBC 也是等腰直角三角形．分两种情况讨论：点Q 的坐标为(－m ，0)或(0，m)，再结合勾股定理分析最小值．解：(1) 45. 提示：令x ＝0，则y ＝－m ，∴ 点C 的坐标为(0，－m)．令y ＝0，则x 2＋(1－m)x －m ＝0，解得 x 1＝－1，x 2＝m.∵ 0<m<1，点A 在点B 的左侧，∴ 点B 的坐标为(m ，0)．∴ OB ＝OC ＝m.∵ ∠BOC ＝90°，∴ △BOC 是等腰直角三角形．∴ ∠ABC ＝45°；(2) 方法一：如图①，作PD ⊥y 轴，垂足为D ，设l 与x 轴交于点E.由题意，得抛物线的对称轴为直线x ＝－1＋m 2.设点P 的坐标为⎝ ⎛⎭⎪⎫－1＋m 2，n .∵ PA ＝PC, ∴ PA 2＝PC 2，即AE 2＋PE 2＝CD 2＋PD 2.∴ ⎝ ⎛⎭⎪⎫－1＋m 2＋12＋n 2＝(n ＋m)2＋⎝ ⎛⎭⎪⎫1－m 22.解得n ＝1－m 2.∴ 点P 的坐标为⎝ ⎛⎭⎪⎫－1＋m 2，1－m 2.方法二：如图①，连接PB.由题意，得抛物线的对称轴为直线x ＝－1＋m 2.∵ P 在对称轴l 上，∴ PA ＝PB.∵ PA ＝PC ，∴ PB ＝PC.由(1)的提示可知△BOC 是等腰直角三角形，且OB ＝OC ，∴ 点P 在BC 的垂直平分线y ＝－x 上．∴ 点P 即为对称轴直线x ＝－1＋m 2与直线y ＝－x 的交点．∴ 点P 的坐标为⎝ ⎛⎭⎪⎫－1＋m 2，1－m 2；(3) 存在点Q 满足题意．∵ 点P 的坐标为⎝ ⎛⎭⎪⎫－1＋m 2，1－m 2，∴ PA 2＋ PC 2＝AE 2＋ PE 2＋CD 2＋ PD 2＝⎝ ⎛⎭⎪⎫－1＋m 2＋12＋⎝ ⎛⎭⎪⎫1－m 22＋⎝ ⎛⎭⎪⎫1－m 2＋m 2＋⎝ ⎛⎭⎪⎫1－m 22＝1＋m 2.∵ AC 2＝1＋m 2，∴ PA 2＋ PC 2＝AC 2.∴ △PAC 是等腰直角三角形，且∠APC ＝90°.∵ 以Q 、B 、C 为顶点的三角形与△PAC 相似，∴ △QBC 是等腰直角三角形．∴ 由题意知满足条件的点Q 的坐标为(－m ，0)或(0，m)．① 如图①，当点Q 的坐标为(－m ，0)时，若PQ 与x 轴垂直，则－1＋m 2＝－m ，解得m ＝13，∴ PQ ＝13.若PQ 与x 轴不垂直，则PQ 2＝PE 2＋EQ 2＝⎝ ⎛⎭⎪⎫1－m 22＋⎝ ⎛⎭⎪⎫－1＋m 2＋m 2＝52m 2－2m ＋12＝52⎝⎛⎭⎫m －252＋110.∵ 0<m<1，∴ 当m ＝25时，PQ 2取得最小值110，即PQ 取得最小值1010.∵ 1010<13，∴ 当m ＝25，即点Q 的坐标为⎝⎛⎭⎫－25，0时， PQ 的长度最小；② 如图②，当点Q 的坐标为(0，m)时，若PQ 与y 轴垂直，则1－m 2＝m ，解得m ＝13，∴ PQ ＝13.若PQ 与y 轴不垂直，则PQ 2＝PD 2＋DQ 2＝⎝ ⎛⎭⎪⎫1－m 22＋⎝ ⎛⎭⎪⎫m －1－m 22＝52m 2－2m ＋12＝52⎝⎛⎭⎫m －252＋110.∵ 0<m<1，∴ 当m ＝25时，PQ 2取得最小值110，即PQ 取得最小值1010.∵ 1010<13，∴ 当m ＝25，即点Q 的坐标为⎝⎛⎭⎫0，25时，PQ 的长度最小．综上所述：当点Q 的坐标为⎝⎛⎭⎫－25，0或⎝⎛⎭⎫0，25时，PQ 的长度最小．第27题28. [解析](1) 根据矩形性质可以很快得出答案；(2) 首先是解读题干中的条件“已知点P 与⊙O 同时开始移动，同时停止移动(即同时到达各自的终止位置)”，这说明在整个运动过程中，点P 移动的距离为(a ＋2b)cm ，圆心O 移动的距离为2(a －4)cm ，且它们是相等的，即a ＋2b ＝2(a －4)．再结合(2)中的条件“移动2 s 到达B 点，继续移动3 s ，到达BC 的中点” 可得b 2＝12a 3，联立成二元一次方程组可求解；(3) 主要是分两种情况讨论，即⊙O 首次到达⊙O 1的位置、⊙O 在返回途中到达⊙O 1的位置，讨论后再进行取舍．解：(1) a ＋2b ；(2) ∵ 在整个运动过程中，点P 移动的距离为(a ＋2b)cm ，圆心O 移动的距离为2(a －4)cm ，由题意，得a ＋2b ＝2(a －4)．∵ 点P 移动2 s 到达B 点，即点P 用2 s 移动了b cm ；点P继续移动3 s ，到达BC 的中点，即点P 用3 s 移动了12a cm ，∴ b 2＝12a 3.由⎩⎪⎨⎪⎧a ＋2b ＝2（a －4），b 2＝12a 3，解得⎩⎪⎨⎪⎧a ＝24，b ＝8.∵ 点P 移动的速度与⊙O 移动的速度相等，∴ ⊙O 移动的速度为b 2＝4 cm/s.∴ 这5 s 时间内圆心O 移动的距离为5×4＝20(cm)；(3) 存在这种情形理由：设点P 移动的速度为v 1 cm/s ，⊙O 移动的速度为v 2 cm/s ，由题意，得v 1v 2＝a ＋2b 2（a －4）＝20＋2×102×（20－4）＝54. 第28题如图，设直线OO 1与AB 交于点E ，与CD 交于点F ，⊙O 1与AD 相切于点G.若PD 与⊙O 1相切，切点为H ，则O 1G ＝O 1H.又∵ ∠O 1HD ＝∠O 1GD ＝90°，O 1D ＝O 1D ，∴ Rt △DO 1G ≌△Rt △DO 1H(HL)．∴ ∠ADB ＝∠BDP.∵ BC ∥AD ，∴ ∠ADB ＝∠CBD.∴ ∠BDP ＝∠CBD.∴ BP ＝DP.设BP ＝x cm ，则DP ＝x cm ，PC ＝(20－x)cm.在Rt △PCD 中，由勾股定理，得PC 2＋CD 2＝PD 2，即(20－x)2＋102＝x 2，解得x ＝252.∴ 此时点P 移动的距离为10＋252＝452(cm)．∵ EF ∥AD ，∴ △BEO 1∽△BAD.∴ EO 1AD ＝BE BA ，即EO 120＝10－210.∴ EO 1＝16 cm.∴ OO 1＝14 cm. 方法一：① 当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14 cm ，∴ 此时点P 与⊙O 移动的速度比为45214＝4528.∵ 4528≠54，∴ 此时PD 与⊙O 1不可能相切；② 当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20－4)－14＝18(cm)，∴ 此时点P 与⊙O 移动的速度比为45218＝4536＝54.∴ 此时PD 与⊙O 1恰好相切．方法二：∵ 点P 移动的距离为452cm ，OO 1＝14 cm ，v 1v 2＝54，∴ ⊙O 应移动的距离为452×45＝18(cm)．① 当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14 cm ≠18 cm ，∴ 此时PD 与⊙O 1不可能相切；② 当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20－4)－14＝18(cm)，∴ 此时PD 与⊙O 1恰好相切．方法三：点P 移动的距离为452 cm ，OO 1＝14 cm ，由v 1v 2＝54可设点P 的移动速度为5k cm/s ，⊙O 的移动速度为4k cm/s.∴ 点P 移动的时间为4525k ＝92ks ．① 当⊙O 首次到达⊙O 1的位置时，⊙O 移动的时间为144k ＝72k (s)≠92ks ，∴ 此时PD 与⊙O 1不可能相切；② 当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的时间为2×（20－4）－144k＝92k(s)，∴ 此时PD 与⊙O 1恰好相切.。

20l5苏州中考数学试题及答案

20l5苏州中考数学试题及答案2015年苏州中学数学试题及答案第一部分：选择题1. 三角形ABC中，∠C=90°，AB=14，AC=12，则BC=（）A. 10B. 8C. 16D. 6答案：B2. 若3^x = 9^y, 则 x : y =（）A. 1 : 2B. 2 : 1C. 2 : 3D. 3 : 2答案：A3. 若a√2 + b = c - a√2, 则 a : b =（）A. -2 : 1B. -1 : 2C. 1 : -2D. 2 : -1答案：A4. 所有正数 a 的平均数是 5，a + b 的平均数是 7，则 b 的值为（）A. 4B. 5C. 6D. 7答案：A5. 已知 20% 的一个数等于 8，这个数是（）A. 30B. 32C. 34D. 40答案：C第二部分：填空题6. 解方程x^2 - 3x - n = 0（）（填整数）答案：-47. 已知二次函数 y = x^2 - 4x + 3 的图像与 x 轴相交于（）个点答案：28. 若 a:b = 5:2, b:c = 4:3, a + b + c = 84, 则 a 的值为（）（填整数）答案：309. 直线 l 与坐标轴相交于点 (4, 0)，与直线 x = 2y + 3 平行，则直线l 的方程为 y = （）答案：-210. 设 a 和 b 是两个不相等的正数，且满足 a/b = 3/2, 2a + b = 16，则a 的值为（）答案：6第三部分：解答题11. 计算：3 × 48 - 6 × 18 （答案写数值）答案：8412. 用45°角来画三角形 ABC（∠B = 90°, ∠C = 45°），若 AB = 5 cm, AC = 4 cm, 计算 BC 的长度。

（答案写数值）答案：3√2 cm13. 将一个小数 0.36 写成最简分数形式。

（答案写分数）答案：9/2514. 计算：(5/8) ÷ (25/32) （答案写分数）答案：4/515. 判断以下命题是否成立：若两条直线互相垂直，则两条直线的斜率互为相反数。