安徽省中考数学试卷-勾股定理专题

合集下载

中考数学专题复习《勾股定理之折叠问题分类讨论、存在性问题》测试卷(附带答案)

中考数学专题复习《勾股定理之折叠问题分类讨论存在性问题》测试卷（附带答案)学校:___________班级:___________姓名:___________考号:___________一单选题1．如图 ABC 中 90A ∠= 7AB = 24AC = 点D 为边AC 上一点将ABC 沿BD 折叠后点A 的对应点A '恰好落在BC 边上则线段AD 的长为（）A ．407B ．214C ．16825D ．3262．如图是一张直角三角形纸片已知6AC = 10AB = 将纸片沿AD 折叠使点C 落在AB 边上的点C '处则折痕AD 长为（）．A ．5B ．35C ．3D ．323．已知2OA = 2OB = 将AOB 沿着某直线CD 折叠后如图所示 CD 与x 轴交于点C 与AB 交于点D 则点C 坐标是（）A ．()0.4,0B ．()0.5,0C ．()0.6,0D ．()0.7,04．如图长方形纸片ABCD 中 6AB = 18AD = 将此长方形纸片折叠使点D 与点B 重合点C 落在点H 的位置折痕为EF 则ABE 的面积为（）A ．6B ．18C ．24D ．485．如图在平行四边形ABCD 中 60B ∠=︒ 4AB = 6AD = E 是AB 边的中点 F 是线段BC 上的动点将EBF 沿EF 所在直线折叠得到EB F ' 连接B D ' 则B D '的最小值是（）A ．4B ．6C ．2D ．26．将长方形纸片ABCD 如图折叠 B C 两点恰好重合在AD 边上的同一点P 处折痕分别是MH NG 若90MPN ∠=︒ 3PM = 5MN = 分别记PHM PNG PMN 的面积为1S 2S 3S 则1S 2S 3S 之间的数量关系是 ( )A ．312S S S =+B ．312322S S S =+C ．32155S S S =-D ．2123S S S =-7．如图直角ABC 中 90C ∠=︒ 3AC = 4BC = 将ABC 沿AB 折叠得ABD △ 点C 的对应点为点D 则点D 到BC 的距离为（）A ．125B ．245C ．9625D ．125或245 8．如图在Rt ABC △纸片中 9043A AB AC ∠=︒==，，将Rt ABC △纸片按图示方式折叠使点A 恰好落在斜边BC 上的点E 处 BD 为折痕则下列四个结论：①BD 平分ABC ∠①AD DE = ①DE EC = ①DEC 的周长为4 其中正确的个数有（）A ．1B ．2C ．3D ．4二填空题9．如图 Rt ABC △中 90ACB ∠=︒ 30B ∠=︒ 4AC = 点P 为AB 上一个动点以PC 为轴折叠APC △得到QPC 点A 的对应点为点Q 当点Q 落在ABC 内部（不包括边）上时 AP 的取值范围为 .10．如图在平面直角坐标系中长方形ABCO 的边OC OA 、分别在x 轴 y 轴上 3AB = 点E 在边BC 上将长方形ABCO 沿AE 折叠若点B 的对应点F 恰好是边OC 的三等分点则点E 的坐标是．11．如图有一个直角三角形纸片两直角边18cm AC = 24cm BC = 现将直角边AC 沿直线AD 折叠使它落在斜边AB 上且与AE 重合则BD = cm ．12．已知直线l 为长方形ABCD 的对称轴 5AD = 6AB = 点E 为射线DC 上一个动点把ADE 沿直线AE 折叠点D 的对应点D 恰好落在对称轴l 上．则点D 到边CD 的距离是．13．如图把长方形ABCD 沿直线BD 向上折叠使点C 落在C '的位置上 BC '交AD 于E 已知4CD = 8BC = 则EC D '的面积为．三解答题14．如图是一张直角三角形ABC 纸片 90C ∠=︒ 6AC = 8BC =．(1)在图1中将直角边AC 沿AD 折叠使点C 落在斜边AB 上的点E 处求CD 的长(2)在图2中将BFG 沿FG 折叠使点B 与点A 重合求BF 的长．15．一数学兴趣小组探究勾股定理在折叠中的应用如图将一张长方形纸片ABCD 放在平面直角坐标系中点A 与原点O 重合顶点B D 分别在x 轴 y 轴上 P 为边CD 上一动点连接BP 将BCP 沿BP 折叠点C 落在点C '处．(1)若4AB = 3AD = 如图1 连接BD 当点C '在线段BD 上时求点P 的坐标．(2)在（1）的条件下如图2 当点P 与点D 重合时沿BD 将BCD △折叠得BC D '△ DC '与x 轴交于E 点求BDE 的面积．(3)若8AB = 4BC = 当ADC '为等腰三角形时求点P 的坐标．16．如图1 ABC 中 90,BAC AB AC ∠=︒= D E 是直线BC 上两动点且45DAE =︒∠．探究线段BD DE EC 三条线段之间的数量关系：小明的思路是：如图2 将ABD △沿AD 折叠得ADF △ 连接EF 看能否将三条线段转化到一个三角形中 …请你参照小明的思路探究并解决下列问题：(1)猜想BD DE EC 三条线段之间的数量关系并证明(2)如图3 当动点E 在线段BC 上动点D 运动在线段CB 延长线上时其它条件不变（1）中探究的结论是否发生改变？请说明你的猜想并给予证明．17．已知ABC CDE △≌△ 且90B D ∠=∠=︒ 把ABC 和CDE 拼成如图所示的形状使点B C D 在同一条直线上若4AB = 3DE =．(1)求AE 的长(2)将ABC 沿AC 折叠点B 落在点F 处延长AF 与CE 相交于点G 求FG 的长．18．如图在ABC 中 90C ∠=︒ 把ABC 沿直线DE 折叠使ADE 与BDE 重合．(1)若38A ∠=︒ 则CBD ∠的度数为________(2)若6AC = 4BC = 求AD 的长(3)当(0)AB m m ABC =>，△的面积为24m +时求BCD △的周长．（用含m 的代数式表示）参考答案：1．B2．B3．B4．C5．C6．C7．C8．C9．234AP <<10．25⎛- ⎝⎭或2⎛- ⎝⎭11．1512．1或9/9或113．614．(1)3CD = (2)254BF15．(1)点P 的坐标为5,32⎛⎫ ⎪⎝⎭ (2)7516(3)当ADC '为等腰三角形时点P 的坐标为()44，或4⎫⎪⎪⎝⎭．16．(1)222DE BD EC =+(2)不变 222DE BD EC =+17．(1)AE =(2)9418．(1)14︒ (2)133AD =(3)BCD △的周长为4m +．。

中考数学勾股定理(讲义及答案)附解析

一、选择题1．如图，在ABC ∆中，,90︒=∠=AB AC BAC ，ABC ∠的平分线BD 与边AC 相交于点D ，DE BC ⊥，垂足为E ，若CDE ∆的周长为6，则ABC ∆的面积为（）.A ．36B ．18C ．12D ．9 2．如图所示，在中，，，.分别以，，为直径作半圆（以为直径的半圆恰好经过点，则图中阴影部分的面积是（）A ．4B ．5C ．7D ．63．如图，在等腰Rt ABC △中，908C AC ∠==°，，F 是AB 边上的中点，点D 、E 分别在AC 、BC 边上运动，且保持AD CE =．连接DE 、DF 、EF ．在此运动变化的过程中，下列结论：①DFE △是等腰直角三角形；②四边形CDFE 不可能为正方形；③DE 长度的最小值为4；④四边形CDFE 的面积保持不变；⑤△CDE 面积的最大值为8．其中正确的结论是（）A ．①④⑤B ．③④⑤C ．①③④D ．①②③4．如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD 、正方形EFGH 、正方形MNKT 的面积分别为S 1、S 2、S 3.若S 1+S 2+S 3=15，则S 2的值是( )A ．3B ．154C ．5D ．1525．若直角三角形的三边长分别为-a b 、a 、+a b ，且a 、b 都是正整数，则三角形其中一边的长可能为（）A ．22B ．32C ．62D ．826．如图,A 、B 两点在直线l 的两侧,点A 到直线l 的距离AC=4,点B 到直线l 的距离BD=2,且CD=6,P 为直线CD 上的动点, 则PA PB -的最大值是（）A ．62B ．22C ．210D ．67．如图，在△ABC 中，∠ACB ＝90°，AB 的中垂线交AC 于D ，P 是BD 的中点，若BC ＝4，AC ＝8，则S △PBC 为（）A ．3B ．3.3C ．4D ．4.58．将一根 24cm 的筷子，置于底面直径为 15cm ，高 8cm 的装满水的无盖圆柱形水杯中，设筷子浸没在杯子里面的长度为 hcm ，则 h 的取值范围是（）A ．h≤15cmB ．h≥8cmC ．8cm≤h≤17cmD ．7cm≤h≤16cm9．如图，在矩形ABCD 中，AB =8，BC =4，将矩形沿AC 折叠，点B 落在点B ′处，则重叠部分△AFC 的面积为（）A ．12B ．10C ．8D ．610．有下列的判断： ①△ABC 中，如果a 2＋b 2≠c 2，那么△ABC 不是直角三角形②△ABC 中，如果a 2－b 2＝c 2，那么△ABC 是直角三角形③如果△ABC 是直角三角形，那么a 2＋b 2＝c 2以下说法正确的是（）A ．①②B ．②③C ．①③D ．②二、填空题11．如图是一个三级台阶，它的每一级的长、宽和高分别为5 dm 、3 dm 和1 dm ，A 和B 是这个台阶两个相对的端点，A 点有一只蚂蚁，想到B 点去吃可口的食物．请你想一想，这只蚂蚁从A 点出发，沿着台阶面爬到B 点的最短路程是 dm ．12．如图所示的网格是正方形网格，则ABC ACB ∠+∠=__________°（点A ，B ，C 是网格线交点）．13．如图，在△ABC 中，OA ＝4，OB ＝3，C 点与A 点关于直线OB 对称，动点P 、Q 分别在线段AC 、AB 上(点P 不与点A 、C 重合)，满足∠BPQ ＝∠BAO.当△PQB 为等腰三角形时，OP 的长度是_____．14．如图，在ABC 中，D 是BC 边中点，106AB AC ==，，4=AD ，则BC 的长是_____________．15．在ABC ∆中，90BAC ∠=︒，以BC 为斜边作等腰直角BCD ∆，连接DA ，若22AB =，42AC =，则DA 的长为______．16．如图在三角形纸片ABC 中，已知∠ABC =90º，AC =5，BC=4，过点A 作直线l 平行于BC ，折叠三角形纸片ABC ，使直角顶点B 落在直线l 上的点P 处，折痕为MN ，当点P 在直线l 上移动时，折痕的端点M 、N 也随之移动，若限定端点M 、N 分别在AB 、BC 边上（包括端点）移动，则线段AP 长度的最大值与最小值的差为________________．17．如图,30AOB ∠=︒，点,M N 分别在,OA OB 上，且6,8OM ON ==，点,P Q 分别在,OB OA 上运动，则PM PQ QN ++的最小值为______．18．如图，△ABC 中，AB=AC=13，BC=10，AD 是BAC ∠的角平分线，E 是AD 上的动点，F 是AB 边上的动点，则BE+EF 的最小值为_____．19．在ABC 中，12AB AC ==，30A ∠=︒，点E 是AB 中点，点D 在AC 上，32DE =，将ADE 沿着DE 翻折，点A 的对应点是点F ，直线EF 与AC 交于点G ，那么DGF △的面积=__________．20．如图，在等腰△ABC 中，AB ＝AC ，底边BC 上的高AD ＝6cm ，腰AC 上的高BE ＝4m ，则△ABC 的面积为_____cm 2．三、解答题21．在等边ABC 中，点D 是线段BC 的中点，120,EDF DE ∠=︒与线段AB 相交于点,E DF 与射线AC 相交于点F ．()1如图1，若DF AC ⊥，垂足为,4,F AB =求BE 的长；()2如图2，将()1中的EDF ∠绕点D 顺时针旋转一定的角度，DF 仍与线段AC 相交于点F ．求证：12BE CF AB +=．()3如图3，将()2中的EDF ∠继续绕点D 顺时针旋转一定的角度，使DF 与线段AC 的延长线交于点,F 作DN AC ⊥于点N ，若,DN FN =设,BE x CF y ==，写出y 关于x 的函数关系式．22．如图1，在△ABC 中，AB ＝AC ，∠BAC ＝90°，D 为AC 边上一动点，且不与点A 点C 重合，连接BD 并延长，在BD 延长线上取一点E ，使AE ＝AB ，连接CE ．（1）若∠AED ＝20°，则∠DEC ＝度；（2）若∠AED ＝a ，试探索∠AED 与∠AEC 有怎样的数量关系？并证明你的猜想；（3）如图2，过点A 作AF ⊥BE 于点F ，AF 的延长线与EC 的延长线交于点H ，求证：EH 2+CH 2＝2AE 2．23．如图，在边长为2的等边三角形ABC 中，D 点在边BC 上运动（不与B ，C 重合），点E 在边AB 的延长线上，点F 在边AC 的延长线上，AD DE DF ==．（1）若30AED ∠=︒，则ADB =∠______．（2）求证：BED CDF △≌△．（3）试说明点D 在BC 边上从点B 至点C 的运动过程中，BED 的周长l 是否发生变化？若不变，请求出l 的值，若变，请求出l 的取值范围．24．在等腰Rt △ABC 中，AB ＝AC ，∠BAC ＝90°（1）如图1，D ，E 是等腰Rt △ABC 斜边BC 上两动点，且∠DAE ＝45°，将△ABE 绕点A 逆时针旋转90后，得到△AFC ，连接DF①求证：△AED ≌△AFD ；②当BE ＝3，CE ＝7时，求DE 的长；（2）如图2，点D 是等腰Rt △ABC 斜边BC 所在直线上的一动点，连接AD ，以点A 为直角顶点作等腰Rt △ADE ，当BD ＝3，BC ＝9时，求DE 的长．25．如图，△ACB 和△ECD 都是等腰直角三角形，∠ACB ＝∠ECD ＝90°，点D 在边AB 上，点E 在边AC 的左侧，连接AE ．（1）求证：AE ＝BD ；（2）试探究线段AD 、BD 与CD 之间的数量关系；（3）过点C 作CF ⊥DE 交AB 于点F ，若BD ：AF ＝1：2，CD 36，求线段AB 的长．26．如图， ABD 为边长不变的等腰直角三角形，AB AD =，90BAD ∠=︒，在 ABD外取一点 E ，以A 为直角顶点作等腰直角AEP △，其中 P 在 ABD 内部，90EAP ∠=︒，2AE AP ==，当E 、P 、D 三点共线时，7BP =．下列结论：①E 、P 、D 共线时，点B 到直线AE 的距离为5；②E 、P 、D 共线时， 13ADP ABP S S ∆∆+=+；=532ABD S ∆+③； ④作点 A 关于 BD 的对称点 C ，在 AEP 绕点 A 旋转的过程中，PC 的最小值为5+232-；⑤AEP △绕点A 旋转,当点E 落在AB 上，当点P 落在AD 上时，取BP 上一点N ，使得AN BN =，连接 ED ，则AN ED ⊥．其中正确结论的序号是___．27．如果一个三角形的两条边的和是第三边的两倍，则称这个三角形是“优三角形”，这两条边的比称为“优比”（若这两边不等，则优比为较大边与较小边的比），记为k . （1）命题：“等边三角形为优三角形，其优比为1”，是真命题还是假命题？（2）已知ABC 为优三角形，AB c =，AC b =，BC a =，①如图1，若90ACB ∠=︒，b a ≥，6b =，求a 的值.②如图2，若c b a ≥≥，求优比k 的取值范围.（3）已知ABC 是优三角形，且120ABC ∠=︒，4BC =，求ABC 的面积.28．（1）如图1，在Rt ABC ∆中，90ACB ∠=︒，60A ∠=︒，CD 平分ACB ∠.求证：CA AD BC +=.小明为解决上面的问题作了如下思考：作ADC ∆关于直线CD 的对称图形A DC '∆，∵CD 平分ACB ∠，∴A '点落在CB 上，且CA CA '=，A D AD '=.因此，要证的问题转化为只要证出A D A B ''=即可.请根据小明的思考，写出该问题完整的证明过程.（2）参照（1）中小明的思考方法，解答下列问题：如图3，在四边形ABCD 中，AC 平分BAD ∠，10BC CD ==，17AC =，9AD =，求AB 的长.29．已知ABC ∆中，90ACB ∠=︒，AC BC =，过顶点A 作射线AP .（1）当射线AP 在BAC ∠外部时，如图①，点D 在射线AP 上，连结CD 、BD ，已知21AD n =-，21AB n =+，2BD n =（1n >）.①试证明ABD ∆是直角三角形；②求线段CD 的长.（用含n 的代数式表示）（2）当射线AP 在BAC ∠内部时，如图②，过点B 作BD AP ⊥于点D ，连结CD ，请写出线段AD 、BD 、CD 的数量关系，并说明理由.30．定义：在△ABC 中，若BC ＝a ，AC ＝b ，AB ＝c ，若a ，b ，c 满足ac +a 2＝b 2，则称这个三角形为“类勾股三角形”，请根据以上定义解决下列问题：（1）命题“直角三角形都是类勾股三角形”是命题（填“真”或“假”）；（2）如图1，若等腰三角形ABC 是“类勾股三角形”，其中AB ＝BC ，AC ＞AB ，请求∠A 的度数；（3）如图2，在△ABC 中，∠B ＝2∠A ，且∠C ＞∠A ．①当∠A ＝32°时，你能把这个三角形分成两个等腰三角形吗？若能，请在图2中画出分割线，并标注被分割后的两个等腰三角形的顶角的度数；若不能，请说明理由； ②请证明△ABC 为“类勾股三角形”．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】利用角平分定理得到DE=AD ，根据三角形内角和得到∠BDE=∠BDA ，再利用角平分线定理得到BE=AB=AC ，根据CDE ∆的周长为6求出AB=6，再根据勾股定理求出218AB =，即可求得ABC ∆的面积.【详解】∵90BAC ︒∠=，∴AB ⊥AD,∵DE BC ⊥,BD 平分ABC ∠,∴DE=AD ，∠BED=90BAC ︒∠=，∴∠BDE=∠BDA ，∴BE=AB=AC ，∵CDE ∆的周长为6，∴DE+CD+CE=AC+CE=BC=6，∵,90︒=∠=AB AC BAC∴22236AB AC BC +==,∴2236AB =, 218AB =,∴ABC ∆的面积=211922AB AC AB ⋅⋅==, 故选：D.【点睛】此题考查角平分线定理的运用，勾股定理求边长，在利用角平分线定理时必须是两个垂直一个平分同时运用，得到到角两边的距离相等的结论. 2．D解析：D【解析】【分析】先利用勾股定理计算BC 的长度，然后阴影部分的面积=以AB 为直径的半圆面积+以BC 为直径的半圆面积+-以AC 为直径的半圆面积. 【详解】解：在中 ∵，, ∴, ∴BC=3,∴阴影部分的面积=以AB 为直径的半圆面积+以BC 为直径的半圆面积+-以AC 为直径的半圆面积=6.故选D. 【点睛】本题考查扇形面积的计算和勾股定理.在本题中解题关键是用重叠法去表示阴影部分的面积. 3．A解析：A【分析】作常规辅助线连接CF ，由SAS 定理可证△CFE 和△ADF 全等，从而可证∠DFE=90°，DF=EF ．所以△DEF 是等腰直角三角形；由割补法可知四边形CDFE 的面积保持不变；△DEF 是等腰直角三角形2DF ，当DF 与BC 垂直，即DF 最小时，DE 取最小值42，△CDE 最大的面积等于四边形CDEF 的面积减去△DEF 的最小面积．【详解】连接CF；∵△ABC是等腰直角三角形，∴∠FCB=∠A=45°，CF=AF=FB；∵AD=CE，∴△ADF≌△CEF；∴EF=DF，∠CFE=∠AFD；∵∠AFD+∠CFD=90°，∴∠CFE+∠CFD=∠EFD=90°，∴△EDF是等腰直角三角形.当D. E分别为AC、BC中点时，四边形CDFE是正方形.∵△ADF≌△CEF，∴S△CEF=S△ADF，∴S四边形CEFD=S△AFC.由于△DEF是等腰直角三角形，因此当DE最小时，DF也最小；即当DF⊥AC时,DE最小,此时DF=12BC=4.∴22当△CEF面积最大时，此时△DEF的面积最小.此时S△CEF=S四边形CEFD−S△DEF=S△AFC−S△DEF=16−8=8，则结论正确的是①④⑤.故选A.【点睛】本题考查全等三角形的判定与性质, 等腰直角三角形性质.要证明线段或者角相等，一般证明它们所在三角形全等，如果不存在三角形可作辅助线解决问题.4．C解析：C【解析】将四边形MTKN的面积设为x，将其余八个全等的三角形面积一个设为y，∵正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，S1+S2+S3=15，∴得出S1=8y+x，S2=4y+x，S3=x，∴S1+S2+S3=3x+12y=15，即3x+12y=15，x+4y=5，所以S2=x+4y=5，故答案为5．点睛：将四边形MTKN的面积设为x，将其余八个全等的三角形面积一个设为y，用x，y表示出S 1，S 2，S 3，再利用S 1+S 2+S 3=15求解是解决问题的关键．5．B解析：B【解析】由题可知（a-b ）2+a 2=（a+b ）2，解得a=4b ，所以直角三角形三边分别为3b ，4b ，5b ，当b=8时，4b=32，故选B ．6．C解析：C【解析】试题解析：作点B 关于直线l 的对称点B ',连接AB '并延长,与直线l 的交点即为使得PA PB -取最大值时对应的点.P此时.PA PB PA PB AB -=-'='过点B '作B E AC '⊥于点,E 如图,四边形B DCE '为矩形，6, 2.B E CD EC B D BD ∴=====''2.AE ∴=22210.AB AE B E ''+=PA PB -的最大值为：210.故答案为：210.7．A解析：A【分析】根据线段垂直平分线的性质得到DA=DB ，根据勾股定理求出BD ，得到CD 的长，根据三角形的面积公式计算，得到答案．【详解】解：∵点D在线段AB的垂直平分线上，∴DA＝DB，在Rt△BCD中，BC2+CD2＝BD2，即42+（8﹣BD）2＝BD2，解得，BD＝5，∴CD＝8﹣5＝3，∴△BCD的面积＝12×CD×BC＝12×3×4＝6，∵P是BD的中点，∴S△PBC＝12S△BCD＝3，故选：A．【点睛】本题考查的是线段垂直平分线的性质、直角三角形的性质、勾股定理，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．8．C解析：C【分析】筷子浸没在水中的最短距离为水杯高度，最长距离如下图，是筷子斜卧于杯中时，利用勾股定理可求得.【详解】当筷子笔直竖立在杯中时，筷子浸没水中距离最短，为杯高=8cmAD是筷子，AB长是杯子直径，BC是杯子高，当筷子如下图斜卧于杯中时，浸没在水中的距离最长由题意得：AB=15cm，BC=8cm，△ABC是直角三角形∴在Rt△ABC中，根据勾股定理，AC=17cm∴8cm≤h≤17cm故选：C【点睛】本题考查勾股定理在实际生活中的应用，解题关键是将题干中生活实例抽象成数学模型，然后再利用相关知识求解.9．B解析：B【分析】已知AD 为CF 边上的高，要求AFC △的面积，求得FC 即可，求证AFD CFB '△≌△，得B F DF '=，设DF x =，则在Rt AFD △中，根据勾股定理求x ，于是得到CF CD DF =-，即可得到答案．【详解】解：由翻折变换的性质可知，AFD CFB '△≌△，'DF B F ∴=，设DF x =，则8AF CF x ==-，在Rt AFD △中，222AF DF AD =+，即222(8)4x x -=+，解得：3x =，835CF CD FD ∴=-=-=， 1102AFC S AF BC ∴=⋅⋅=△．故选：B ．【点睛】本题考查矩形的性质、折叠的性质、勾股定理等内容，根据折叠的性质得到AFD CFB '△≌△是解题的关键．10．D解析：D【分析】欲判断三角形是否为直角三角形，这里给出三边的长，需要验证两小边的平方和等于最长边的平方即可．【详解】①c 不一定是斜边，故错误；②正确；③若△ABC 是直角三角形，c 不是斜边，则a 2＋b 2≠c 2，故错误，所以正确的只有②，故选D.【点睛】本题考查了勾股定理以及勾股定理的逆定理，熟练掌握勾股定理以及勾股定理的逆定理的内容是解题的关键.二、填空题11．【解析】试题分析：将台阶展开，如图，331312,5,AC BC =⨯+⨯==222169,AB AC BC ∴=+=13,AB ∴=即蚂蚁爬行的最短线路为13.dm考点：平面展开：最短路径问题．12．45【分析】如下图,延长BA 至网络中的点D 处,连接CD. ABC ACB DAC ∠+∠=∠，只需证△ADC 是等腰直角三角形即可【详解】如下图,延长BA 至网络中的点D 处,连接CD设正方形网络每一小格的长度为1则根据网络，555BC=5，∴5其中BD 、DC 、BC 边长满足勾股定理逆定理∴∠CDA=90°∵AD=DC∴△ADC 是等腰直角三角形∴∠DAC=45°故答案为：45°【点睛】本题是在网格中考察勾股定理的逆定理，解题关键是延长BA ，构造处△ABC 的外角∠CAD13．1或78【分析】分为三种情况：①PQ BP =，②BQ QP =，③BQ BP =，由等腰三角形的性质和勾股定理可求解．【详解】解：分为3种情况：①当PB PQ =时，4=OA ，3OB =，∴5BC AB ===， C 点与A 点关于直线OB 对称，BAO BCO ∴∠=∠，BPQ BAO ∠=∠，BPQ BCO ∴∠=∠，APB APQ BPQ BCO CBP ∠=∠+∠=∠+∠，APQ CBP ∴∠=∠，在APQ 和CBP 中，BAO BCP APQ B PQ B P C P ∠=∠⎧⎪∠=∠⎨=⎪⎩， ()APQ CBP AAS ∴△≌△，∴5AP BC ==，1OP AP OA ∴=-=；②当BQ BP =时，BPQ BQP ∠=∠，BPQ BAO ∠=∠，BAO BQP ∴∠=∠，根据三角形外角性质得：BQP BAO ∠>∠，∴这种情况不存在；③当QB QP =时，QBP BPQ BAO ∠=∠=∠，PB PA ∴=，设OP x =，则4PB PA x ==-在Rt OBP △中，222PB OP OB =+，222(4)3x x ∴-=+，解得：78x =； ∴当PQB △为等腰三角形时，1OP =或78；【点睛】本题考查了勾股定理，等腰三角形的性质，全等三角形的性质和判定的应用，解题的关键是熟练掌握所学的性质进行解题，注意分类讨论．14．【分析】延长AD至点E，使得DE＝AD＝4，结合D是中点证得△ADC≌△EDB，进而利用勾股定理逆定理可证得∠E＝90°，再利用勾股定理求得BD长进而转化为BC长即可．【详解】解：如图，延长AD至点E，使得DE＝AD＝4，连接BE，∵D是BC边中点，∴BD＝CD，又∵DE＝AD，∠ADC＝∠EDB，∴△ADC≌△EDB（SAS），∴BE＝AC＝6，又∵AB＝10，∴AE2＋BE2＝AB2，∴∠E＝90°，∴在Rt△BED中，2222=++=，BD BE DE64213∴BC＝2BD＝13故答案为：13【点睛】本题考查了全等三角形的判定及性质、勾股定理及其逆定理，正确作出辅助线是解决本题的关键．15．6或2.【分析】由于已知没有图形，当Rt△ABC固定后，根据“以BC为斜边作等腰直角△BCD”可知分两种情况讨论：①当D点在BC上方时，如图1，把△ABD绕点D逆时针旋转90°得到△DCE，证明A、C、E三点共线，在等腰Rt△ADE中，利用勾股定理可求AD长；②当D点在BC下方时，如图2，把△BAD绕点D顺时针旋转90°得到△CED，证明过程类似于①求解．【详解】解：分两种情况讨论：①当D点在BC上方时，如图1所示，把△ABD绕点D逆时针旋转90°，得到△DCE，则∠ABD=∠ECD，2，AD=DE，且∠ADE=90°在四边形ACDB中，∠BAC+∠BDC=90°+90°=180°，∴∠ABD+∠ACD=360°-180°=180°，∴∠ACD+∠ECD=180°，∴A、C、E三点共线．∴AE=AC+CE=42+22=62在等腰Rt△ADE中，AD2+DE2=AE2，即2AD2=（62）2，解得AD=6②当D点在BC下方时，如图2所示，把△BAD绕点D顺时针旋转90°得到△CED，则CE=AB=22，∠BAD=∠CED，AD=AE且∠ADE=90°，所以∠EAD=∠AED=45°，∴∠BAD=90°+45°=135°，即∠CED=135°，∴∠CED+∠AED=180°，即A、E、C三点共线．∴AE=AC-CE=42-22=22在等腰Rt△ADE中，2AD2=AE2=8，解得AD=2．故答案为：6或2.【点睛】本题主要考查了旋转的性质、勾股定理，解决这类等边（或共边）的两个三角形问题，一般是通过旋转的方式作辅助线，转化线段使得已知线段于一个特殊三角形中进行求解．1671【分析】分别找到两个极端,当M与A重合时，AP取最大值，当点N与C重合时，AP取最小，即可求出线段AP长度的最大值与最小值之差【详解】如图所示，当M 与A 重合时，AP 取最大值，此时标记为P 1，由折叠的性质易得四边形AP 1NB 是正方形，在Rt △ABC 中，2222AB=AC BC =54=3--，∴AP 的最大值为A P 1=AB=3如图所示，当点N 与C 重合时，AP 取最小，过C 点作CD ⊥直线l 于点D ，可得矩形ABCD ，∴CD=AB=3，AD=BC=4，由折叠的性质有PC=BC=4，在Rt △PCD 中，2222PD=PC CD =43=7--，∴AP 的最小值为AD PD=47-线段AP 长度的最大值与最小值之差为(1AP AP=347=71-- 71【点睛】本题考查勾股定理的折叠问题，可以动手实际操作进行探索.17．10【分析】首先作M 关于OB 的对称点M ′，作N 关于OA 的对称点N ′，连接M ′N ′，即为MP +PQ +QN 的最小值，易得△ONN ′为等边三角形，△OMM ′为等边三角形，∠N ′OM ′=90°，继而可以求得答案．【详解】作M 关于OB 的对称点M ′，作N 关于OA 的对称点N ′，连接M ′N ′，即为MP +PQ +QN 的最小值．根据轴对称的定义可知：∠N ′OQ =∠M ′OB =30°，∠ONN ′=60°，OM ′=OM =6，ON ′=ON =8，∴△ONN ′为等边三角形，△OMM ′为等边三角形，∴∠N ′OM ′=90°．在Rt △M ′ON ′中，M ′N 22''OM ON +．故答案为10．【点睛】本题考查了最短路径问题，根据轴对称的定义，找到相等的线段，得到直角三角形是解题的关键．18．12013【解析】 ∵AB=AC ，AD 是角平分线，∴AD ⊥BC ，BD=CD ， ∴B 点，C 点关于AD 对称，如图，过C 作CF ⊥AB 于F ，交AD 于E ，则CF=BE+FF 的最小值，根据勾股定理得，AD=12，利用等面积法得：AB ⋅CF=BC ⋅AD ，∴CF=BC AD AB ⋅=101213⨯=12013故答案为12013. 点睛：本题主要考查的是翻折的性质、垂线段最短、勾股定理的应用及三角形面积的等积法.明确当CF ⊥AB 时，CF 有最小值是解题的关键.19．39或639【分析】通过计算E 到AC 的距离即EH 的长度为3，所以根据DE 的长度有两种情况：①当点D 在H 点上方时，②当点D 在H 点下方时，两种情况都是过点E 作EH AC ⊥交AC 于点E ，过点G 作GQ AB ⊥交AB 于点Q ，利用含30°的直角三角形的性质和勾股定理求出AH,DH 的长度，进而可求AD 的长度，然后利用角度之间的关系证明AG GE =，再利用等腰三角形的性质求出GQ 的长度，最后利用2DGF AED AEG SS S =-即可求解．【详解】①当点D 在H 点上方时，过点E 作EH AC ⊥交AC 于点E ，过点G 作GQ AB ⊥交AB 于点Q ，12AB = ，点E 是AB 中点，162AE AB ∴== ． ∵EH AC ⊥，90AHE ∴∠=︒ ．30,6A AE ∠=︒=，132EH AE ∴== ， 22226333AH AE EH ∴=-=-=． 32DE =，2222(32)33DH DE EH ∴=-=-= ，DH EH ∴=，333AD AH DH =-=，45EDH ∴∠=︒，15AED EDH A ∴∠=∠-∠=︒ ．由折叠的性质可知，15DEF AED ∠=∠=︒，230AEG AED ∴∠=∠=︒ ，AEG A ∴∠=∠，AG GE ∴= ．又GQ AE ⊥ ，132AQ AE ∴== ． 30A ∠=︒ ， 12GQ AG ∴=． 222GQ AQ AG += ，即2223(2)GQ GQ +=， 3GQ ∴= ．2DGF AED AEG S S S =- ，112(333)36363922DGF S ∴=⨯⨯-⨯-⨯⨯=-； ②当点D 在H 点下方时，过点E 作EH AC ⊥交AC 于点E ，过点G 作GQ AB ⊥交AB 于点Q ，12AB = ，点E 是AB 中点，162AE AB ∴== ． ∵EH AC ⊥，90AHE ∴∠=︒．30,6A AE ∠=︒= ，132EH AE ∴== ， 22226333AH AE EH ∴=-=-=．3DE =，3DH ∴=== ，DH EH ∴=，3AD AH DH =+=，45DEH ∴∠=︒ ，90105AED A DEH ∴∠=︒-∠+∠=︒ ．由折叠的性质可知，105DEF AED ∠=∠=︒，218030AEG AED ∴∠=∠-︒=︒ ，AEG A ∴∠=∠，AG GE ∴= ．又GQ AE ⊥ ，132AQ AE ∴== ． 30A ∠=︒，12GQ AG ∴= ． 222GQ AQ AG += ，即2223(2)GQ GQ +=，GQ ∴= ．2DGF AED AEG S S S =- ，1123)36922DGF S ∴=⨯⨯⨯-⨯=，综上所述，DGF △的面积为9或9．故答案为：9或9．【点睛】本题主要考查折叠的性质，等腰三角形的判定及性质，等腰直角三角形的性质，勾股定理，含30°的直角三角形的性质，能够作出图形并分情况讨论是解题的关键．20．【分析】根据三角形等面积法求出32AC BC = ，在Rt△ACD 中根据勾股定理得出AC 2=14BC 2+36，依据这两个式子求出AC 、BC 的值.【详解】 ∵AD 是BC 边上的高，BE 是AC 边上的高， ∴12AC•BE＝12BC•AD， ∵AD＝6，BE ＝4，∴AC BC ＝32， ∴22AC BC ＝94， ∵AB＝AC ，AD⊥BC，∴BD＝DC ＝12BC ， ∵AC 2﹣CD 2＝AD 2，∴AC 2＝14BC 2+36， ∴221364BC BC +＝94，整理得，BC 2＝3648⨯，解得：BC＝∴△ABC 的面积为12×cm 2故答案为：【点睛】本题考查了三角形的等面积法以及勾股定理的应用，找出AC 与BC 的数量关系是解答此题的关键．三、解答题21．（1）BE ＝1；（2）见解析；（3）(2y x =【分析】（1）如图1，根据等边三角形的性质和四边形的内角和定理可得∠BED ＝90°，进而可得∠BDE =30°，然后根据30°角的直角三角形的性质即可求出结果；（2）过点D 作DM ⊥AB 于M ，作DN ⊥AC 于N ，如图2，根据AAS 易证△MBD ≌△NCD ，则有BM ＝CN ，DM ＝DN ，进而可根据ASA 证明△EMD ≌△FND ，可得EM ＝FN ，再根据线段的和差即可推出结论；（3）过点D 作DM ⊥AB 于M ，如图3，同（2）的方法和已知条件可得DM ＝DN ＝FN ＝EM ，然后根据线段的和差关系可得BE +CF ＝2DM ，BE ﹣CF ＝2BM ，在Rt △BMD 中，根据30°角的直角三角形的性质可得DMBM ，进而可得BE +CF（BE ﹣CF ），代入x 、y 后整理即得结果．【详解】解：（1）如图1，∵△ABC 是等边三角形，∴∠B ＝∠C ＝60°，BC ＝AC ＝AB ＝4．∵点D是线段BC的中点，∴BD＝DC＝12BC＝2．∵DF⊥AC，即∠AFD＝90°，∴∠AED＝360°﹣60°﹣90°﹣120°＝90°，∴∠BED＝90°，∴∠BDE=30°，∴BE＝12BD＝1；（2）过点D作DM⊥AB于M，作DN⊥AC于N，如图2，则有∠AMD＝∠BMD＝∠AND＝∠CND＝90°．∵∠A＝60°，∴∠MDN＝360°﹣60°﹣90°﹣90°＝120°．∵∠EDF＝120°，∴∠MDE＝∠NDF．在△MBD和△NCD中，∵∠BMD＝∠CND，∠B＝∠C，BD=CD，∴△MBD≌△NCD（AAS），∴BM＝CN，DM＝DN．在△EMD和△FND中，∵∠EMD＝∠FND，DM＝DN，∠MDE＝∠NDF，∴△EMD≌△FND（ASA），∴EM＝FN，∴BE+CF＝BM+EM+CN－FN＝BM+CN＝2BM＝BD＝12BC＝12AB；（3）过点D作DM⊥AB于M，如图3，同（2）的方法可得：BM＝CN，DM＝DN，EM＝FN．∵DN ＝FN ，∴DM ＝DN ＝FN ＝EM ，∴BE +CF ＝BM +EM +FN －CN ＝NF +EM ＝2DM =x +y ，BE ﹣CF ＝BM +EM ﹣（FN －CN ）＝BM +NC ＝2BM =x －y ，在Rt △BMD 中，∵∠BDM =30°，∴BD =2BM ，∴DM ＝22=3BD BM BM -，∴()3x y x y +=-，整理，得()23y x =-．【点睛】本题考查了等边三角形的性质、四边形的内角和定理、全等三角形的判定与性质、30°角的直角三角形的性质以及勾股定理等知识，具有一定的综合性，正确添加辅助线、熟练掌握上述知识是解题的关键．22．（1）45度；（2）∠AEC ﹣∠AED ＝45°，理由见解析；（3）见解析【分析】（1）由等腰三角形的性质可求∠BAE ＝140°，可得∠CAE ＝50°，由等腰三角形的性质可得∠AEC ＝∠ACE ＝65°，即可求解；（2）由等腰三角形的性质可求∠BAE ＝180°﹣2α，可得∠CAE ＝90°﹣2α，由等腰三角形的性质可得∠AEC ＝∠ACE ＝45°+α，可得结论；（3）如图，过点C 作CG ⊥AH 于G ，由等腰直角三角形的性质可得EH 2EF ，CH ＝2CG ，由“AAS ”可证△AFB ≌△CGA ，可得AF ＝CG ，由勾股定理可得结论．【详解】解：（1）∵AB ＝AC ，AE ＝AB ，∴AB ＝AC ＝AE ，∴∠ABE ＝∠AEB ，∠ACE ＝∠AEC ，∵∠AED ＝20°，∴∠ABE ＝∠AED ＝20°，∴∠BAE ＝140°，且∠BAC ＝90°∴∠CAE ＝50°，∵∠CAE +∠ACE +∠AEC ＝180°，且∠ACE ＝∠AEC ，∴∠AEC ＝∠ACE ＝65°，∴∠DEC ＝∠AEC ﹣∠AED ＝45°，故答案为：45；（2）猜想：∠AEC ﹣∠AED ＝45°，理由如下：∵∠AED ＝∠ABE ＝α，∴∠BAE ＝180°﹣2α，∴∠CAE ＝∠BAE ﹣∠BAC ＝90°﹣2α，∵∠CAE +∠ACE +∠AEC ＝180°，且∠ACE ＝∠AEC ，∴∠AEC ＝45°+α，∴∠AEC ﹣∠AED ＝45°；（3）如图，过点C 作CG ⊥AH 于G ，∵∠AEC ﹣∠AED ＝45°，∴∠FEH ＝45°，∵AH ⊥BE ，∴∠FHE ＝∠FEH ＝45°，∴EF ＝FH ，且∠EFH ＝90°，∴EH 2EF ，∵∠FHE ＝45°，CG ⊥FH ，∴∠GCH ＝∠FHE ＝45°，∴GC ＝GH ，∴CH 2CG ，∵∠BAC ＝∠CGA ＝90°，∴∠BAF +∠CAG ＝90°，∠CAG +∠ACG ＝90°，∴∠BAF ＝∠ACG ，且AB ＝AC ，∠AFB ＝∠AGC ，∴△AFB ≌△CGA （AAS ）∴AF ＝CG ，∴CH 2AF ，∵在Rt △AEF 中，AE 2＝AF 2+EF 2， 2AF ）2+2EF ）2＝2AE 2，∴EH 2+CH 2＝2AE 2．【点睛】本题是综合了等腰直角三角形的性质，全等三角形的性质与判定的动点问题，三个问题由易到难，在熟练掌握各个相关知识的基础上找到问题之间的内部联系，层层推进去解答是关键.23．（1）90°；（2）证明见解析；（3）变化，234l +≤<．（1）由等边三角形的性质可得∠ABC=∠ACB=60°，由等腰三角形的性质可求DAE=∠DEA=30°，由三角形内角和定理可求解；（2）根据等腰三角形的性质，可证得∠CDF=∠DEA 和∠EDB=∠DFA ，由此可利用“ASA”证明全等；（3）根据全等三角形的性质可得l =2+AD ，根据AD 的取值范围即可得出l 的取值范围．【详解】解：（1）∵△ABC 是等边三角形，∴AB=AC=BC=2，∠ABC=∠ACB=60°，∵AD=DE∴∠DAE=∠DEA=30°，∴∠ADB=180°-∠BAD-∠ABD=90°，故答案为：90°；（2）∵AD=DE=DF ，∴∠DAE=∠DEA ，∠DAF=∠DFA ，∵∠DAE+∠DAF=∠BAC=60°，∴∠DEA+∠DFA=60°，∵∠ABC=∠DEA+∠EDB=60°，∴∠EDB=∠DFA ，∵∠ACB=∠DFA+∠CDF=60°，∴∠CDF=∠DEA ，在△BDE 和△CFD 中∵CDF DEA DE DF EDB DFA ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△BDE ≌△CFD （ASA ）（3）∵△BDE ≌△CFD ，∴BE=CD ，∴l =BD+BE+DE=BD+CD+AD=BC+AD=2+AD ，当D 点在C 或B 点时，AD=AC=AB=2,此时B 、D 、E 三点在同一条直线上不构成三角形，2+AD=4；当D 点在BC 的中点时，∵AB=AC ，∴BD=112BC =，AD ==此时22l AD =+=综上可知24l +≤<．本题考查全等三角形的性质和判定，勾股定理，等边三角形的性质，等腰三角形的性质，三角形内角和定理．（1）掌握等腰三角形等边对等角是解决此问的关键；（2）中注意角之间的转换；（3）中注意临界点是否可取．24．（1）①见解析；②DE ＝297；（2）DE 的值为【分析】（1）①先证明∠DAE ＝∠DAF ，结合DA ＝DA ，AE ＝AF ，即可证明；②如图1中，设DE ＝x ，则CD ＝7﹣x ．在Rt △DCF 中，由DF 2＝CD 2+CF 2，CF ＝BE ＝3，可得x 2＝（7﹣x ）2+32，解方程即可；（2）分两种情形：①当点E 在线段BC 上时，如图2中，连接BE ．由△EAD ≌△ADC ，推出∠ABE ＝∠C ＝∠ABC ＝45°，EB ＝CD ＝5，推出∠EBD ＝90°，推出DE 2＝BE 2+BD 2＝62+32＝45，即可解决问题；②当点D 在CB 的延长线上时，如图3中，同法可得DE 2＝153．【详解】（1）①如图1中，∵将△ABE 绕点A 逆时针旋转90°后，得到△AFC ，∴△BAE ≌△CAF ，∴AE ＝AF ，∠BAE ＝∠CAF ，∵∠BAC ＝90°，∠EAD ＝45°，∴∠CAD +∠BAE ＝∠CAD +∠CAF ＝45°，∴∠DAE ＝∠DAF ，∵DA ＝DA ，AE ＝AF ，∴△AED ≌△AFD （SAS ）；②如图1中，设DE ＝x ，则CD ＝7﹣x ．∵AB ＝AC ，∠BAC ＝90°，∴∠B ＝∠ACB ＝45°，∵∠ABE ＝∠ACF ＝45°，∴∠DCF ＝90°，∵△AED ≌△AFD （SAS ），∴DE ＝DF ＝x ，∵在Rt △DCF 中， DF 2＝CD 2+CF 2，CF ＝BE ＝3，∴x 2＝（7﹣x ）2+32，∴x ＝297， ∴DE ＝297；（2）∵BD ＝3，BC ＝9，∴分两种情况如下：①当点E 在线段BC 上时，如图2中，连接BE ．∵∠BAC＝∠EAD＝90°，∴∠EAB＝∠DAC，∵AE＝AD，AB＝AC，∴△EAB≌△DAC（SAS），∴∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝9-3=6，∴∠EBD＝90°，∴DE2＝BE2+BD2＝62+32＝45，∴DE＝35；②当点D在CB的延长线上时，如图3中，连接BE．同理可证△DBE是直角三角形，EB＝CD＝3+9=12，DB＝3，∴DE2＝EB2+BD2＝144+9＝153，∴DE＝317，综上所述，DE的值为35或317．【点睛】本题主要考查旋转变换的性质，三角形全等的判定和性质以及勾股定理，添加辅助线，构造旋转全等模型，是解题的关键．25．（1）见解析；（2）BD2+AD2＝2CD2；（3）AB＝2+4．【分析】（1）根据等腰直角三角形的性质证明△ACE≌△BCD即可得到结论；（2）利用全等三角形的性质及勾股定理即可证得结论；（3）连接EF，设BD＝x，利用（1）、（2）求出EF=3x，再利用勾股定理求出x，即可得到答案.【详解】（1）证明：∵△ACB和△ECD都是等腰直角三角形∴AC＝BC，EC＝DC，∠ACB＝∠ECD＝90°∴∠ACB﹣∠ACD＝∠ECD﹣∠ACD∴∠ACE＝∠BCD，∴△ACE≌△BCD（SAS），∴AE＝BD．（2）解：由（1）得△ACE ≌△BCD ，∴∠CAE ＝∠CBD ，又∵△ABC 是等腰直角三角形，∴∠CAB ＝∠CBA ＝∠CAE ＝45°，∴∠EAD ＝90°，在Rt △ADE 中，AE 2+AD 2＝ED 2，且AE ＝BD ，∴BD 2+AD 2＝ED 2，∵ED ＝2CD ，∴BD 2+AD 2＝2CD 2，（3）解：连接EF ，设BD ＝x ，∵BD ：AF ＝1：2AF ＝2x ，∵△ECD 都是等腰直角三角形，CF ⊥DE ，∴DF ＝EF ，由（1）、（2）可得，在Rt △FAE 中，EF 22AF AE +22(22)x x +3x ， ∵AE 2+AD 2＝2CD 2，∴222(223)2(36)x x x ++=，解得x ＝1，∴AB ＝2+4．【点睛】此题考查三角形全等的判定及性质，等腰直角三角形的性质，勾股定理.26．②③⑤【分析】①先证得ABE ADP ≅，利用邻补角和等腰直角三角形的性质求得90PEB ∠=︒，利用勾股定理求出BE ，即可求得点B 到直线AE 的距离；②根据①的结论，利用APD ABP ABE APB S S S S ∆∆∆+=+AEP BEP S S ∆∆=+即可求得结论； ③在Rt AHB 中，利用勾股定理求得2AB ，再利用三角形面积公式即可求得ABD S ∆； ④当A P C 、、共线时，PC 最小，利用对称的性质，AB BC =的长，再求得AC 的长，即可求得结论；⑤先证得ABP ADE ≅，得到ABP ADE ∠=∠，根据条件得到ABP NAB ∠=∠，利用互余的关系即可证得结论．【详解】①∵ABD 与AEP 都是等腰直角三角形，∴90BAD ∠=︒，90EAP ∠=︒，AB AD =，AE AP =，45APE AEP ∠=∠=︒， ∴EAB PAD ∠=∠， ∴()ABE ADP SAS ≅，∴180********AEB APD APE ∠=∠=︒-∠=︒-︒=︒，∴1354590PEB AEB AEP ∠=∠-∠=︒-︒=︒，∴222PE BE PB +=，∵2AE AP ==，90EAP ∠=︒， ∴22PE AE ==，∴()22227BE +=，解得：3BE =，作BH ⊥AE 交AE 的延长线于点H ，∵45AEP ∠=︒，90PEB ∠=︒， ∴180180904545HEB PEB AEP ∠=︒-∠-∠=︒-︒-︒=︒，∴26sin 453HB BE =︒==， ∴点B 到直线AE 6，故①错误； ②由①知：ABE ADP ≅，2EP =，3BE =∴APD ABP ABE APB S S S S ∆∆∆∆+=+AEP BEP S S ∆∆=+1122AE AP PE EB =⨯⨯+⨯⨯ 11222322=⨯ 13=，故②正确；③在Rt AHB 中，由①知：6EH HB ==∴622 AH AE EH=+=+，22222256623AB AH BH⎛⎫⎛⎫=+=++=+⎪ ⎪⎪ ⎪⎭⎝⎭，21153222ABDS AB AD AB∆=⋅==+，故③正确；④因为AC是定值，所以当A P C、、共线时，PC最小，如图，连接BC，∵A C、关于BD的对称，∴523AB BC==+∴225231043AC BC==+=+∴minPC AC AP=-，10432=+⑤∵ABD与AEP都是等腰直角三角形，∴90BAD∠=︒，90EAP∠=︒，AB AD=，AE AP=，在ABP和ADE中，AB ADBAP DAEAP AE=⎧⎪∠=∠⎨⎪=⎩，∴()ABP ADE SAS≅，∴ABP ADE∠=∠，∵AN BN=，∴ABP NAB∠=∠，∴EAN ADE∠=∠，∵90EAN DAN∠+∠=︒，∴90ADE DAN∠+∠=︒，∴AN DE⊥，故⑤正确；综上，②③⑤正确，故答案为：②③⑤．【点睛】本题是三角形的综合题，主要考查了等腰直角三角形的性质，全等三角形的判定和性质，勾股定理的应用，三角形的面积公式，综合性强，全等三角形的判定和性质的灵活运用是解题的关键．27．（1）该命题是真命题，理由见解析；（2）①a 的值为92；②k 的取值范围为13k ≤<；（3）ABC ∆的面积为2033或1235．【分析】（1）根据等边三角形的性质、优三角形和优比的定义即可判断；（2）①先利用勾股定理求出c 的值，再根据优三角形的定义列出,,a b c 的等式，然后求解即可；②类似①分三种情况分析，再根据三角形的三边关系定理得出每种情况下,,a b c 之间的关系，然后根据优比的定义求解即可；（3）如图（见解析），设BD x =，先利用直角三角形的性质、勾股定理求出AC 、AB 的长及ABC ∆面积的表达式，再类似（2），根据优三角形的定义分三种情况分别列出等式，然后解出x 的值，即可得出ABC ∆的面积．【详解】（1）该命题是真命题，理由如下：设等边三角形的三边边长为a则其中两条边的和为2a ，恰好是第三边a 的2倍，满足优三角形的定义，即等边三角形为优三角形又因该两条边相等，则这两条边的比为1，即其优比为1故该命题是真命题；（2）①90,6CB b A ∠=︒=22236c a b a ∴=++根据优三角形的定义，分以下三种情况：当2a b c +=时，26236a a +=+，整理得24360a a -+=，此方程没有实数根。

2023年中考数学几何专题：勾股定理的应用(解析版)

2023中考数学几何专题：勾股定理的应用（解析版）1. 放学以后，小红和小颖从学校分手，分别沿东南方向和西南方向回家，若小红和小颖行走的速度都是40米/分，小红用15分钟到家，小颖20分钟到家，小红和小颖家的直线距离为（）A ．600米 B. 800米 C. 1000米 D. 不能确定【解析】速度一定且相同，路程比=时间比.再用勾股定理，直线距离应该是25分钟的路程.选C.【答案】C2. 一架25分米长的梯子，斜立在一竖直的墙上，这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米，那么梯足将滑动( )A. 9分米B. 15分米C. 5分米D. 8分米【解析】在初始和结束两个状态下,选定直角三角形,应用勾股定理. 初始时,经计算,可知,梯顶距墙底端24分米.结束时,经计算,可知,梯足距离墙底端15分米.选D. 【答案】D3. 如图,点P 是AOB ∠的角平分线上一点，过点P 作//PC OA 交OB 于点C .若60,4AOB OC ∠==,则点P 到OA 的距离PD 等于__________.【解析】过P 点作PE OB ⊥，并交OB 于点E .∵60,AOB OP ∠=是AOB ∠的角平分线， ∴630BOP ∠==. 又∵//PC OA ，∴60PCB AOB ∠=∠=.∴30OPC BOP BPC ∠==∠=∠.∴14,22PC OC EC PC ====.∴PB =.【答案】4. 将一根长为24cm 的筷子，置于底面直径为5cm ，高为12cm 的圆柱形水杯中，设筷子露在杯子外边的长度为cm h ，则h 的取值范围为PODC B A EP ODC BA【答案】2.3cm5. 如图，是一块直角三角形的土地，现在要在这块地上挖一个正方形蓄水池AEDF ，已知剩余的两直角三角形（阴影部分）的斜边长分别为20cm 和30cm ，则剩余的两个直角三角形（阴影部分）的面积和．．．为 2cm ．【解析】cm AE x =，cm BE a =，cm CF b =，在Rt BDE ∆中，22230900a x +== ① 在Rt CDF ∆中，22220400b x +== ②在Rt ABC ∆中，()()222502500a x b x +++==，即2222222500a ax x b bx x +++++= ③③-①-②得，221200ax bx +=，3002ax bx+=最简单的方法为两个小的直角三角形旋转合并成一个大的直角三角形（正方形的边重合）故130203002⨯⨯=．【答案】3006. 如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了步路（假设2步为1米），却踩伤了花草．【解析】直接应用勾股定理可知,少走了5m.又知2步为1米,所以少走了10步. 【答案】107. 蚂蚁沿图中的折线从A 点爬到D 点，一共爬了多少厘米？（小方格的边长为1厘米）【解析】把折线从A 到D,分三段计算.第1段长为5,第2段长为13,第3段长为10,进行加法计算,所以蚂蚁一共爬了28cm .【答案】28cm8. 在Rt ABC ∆中，90C ∠=︒，若54a b c +==，，则ABC S ∆= . 【解析】在Rt ABC ∆中,由勾股定理得，222a b c +=. 又有()2222a b a b ab +=++, 所以 ()222a b c ab +-=所以1924ABC S ab ∆==.【答案】94ABC S ∆=9. 如图，Rt ABC ∆中，90CAB ∠=︒，AB AC =，E 、F 为BC 上的点，且45EAF ∠=︒，求证：222EF BE FC =+．【解析】过点A 作线段AD ，使CAF BAD ∠=∠，且AD AF =．在ACF ∆和ABD ∆中， AC AB CAF BAD AF AD =⎧⎪∠=∠⎨⎪=⎩∴ACF ABD ∆∆≌ ∴CF BD =，DBA FCA ∠=∠90DBE DBA ABE FCA ABE ∠=∠+∠=∠+∠=︒ 在ADE ∆和AFE ∆中， 45AE AE EAF EAD AD AF =⎧⎪∠=∠=︒⎨⎪=⎩∴ADE AFE ∆∆≌ ∴ED EF =在Rt BDE ∆中，222DE BD BE =+，∴222EF BE FC =+．【答案】见解析F E C B ADF E CB ACBAD10. 如图，已知Rt △ABC 的周长为26+，其中斜边2AB =，求这个三角形的面积.【解析】在Rt △ABC 中，根据勾股定理，得2222a b +=，即2()24a b ab +-=。

中考数学复习《勾股定理》专项练习题-附带有答案

中考数学复习《勾股定理》专项练习题-附带有答案一、单选题1．线段a、b、c组成的三角形不是直角三角形的是（）A．a=7，b=24，c=25 B．Ba= √41，b=4，c=5C．a= 34，b=1，c= 54D．a=40，b=50，c=602．如图，在△ABC中，AB＝AC＝5，BC＝6，点M为BC的中点，MN⊥AC于点N，则MN等于（）A．65B．95C．125D．1653．如图，直线l上有三个正方形a，b，c，若a，c的面积分别为7和9，则b的面积为（）A．16 B．2 C．32 D．1304．如图，在5×5的正方形网格中，每个小正方形的边长为1，在图中找出格点C，使得△ABC是腰长为无理数的等腰三角形，点C的个数为（）A．3 B．4 C．5 D．75．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中S A=10，S B=8，S C=9，S D=4则下列判断不正确的是（）A．S E=18B．S F=13C．S M=31D．S M−S E=176．如图，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（）A．2.1B．√5C．2√2D．2√37．我国古代数学家赵爽“的勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示），如果大正方形的面积是25，小正方形的面积是1，直角三角形的两直角边分别是a、b，那么(a+b)2的值为（）.A．49 B．25 C．13 D．18．如图，在△ABC中∠C=60°，AC=4，BC=3 .分别以点A，B为圆心，大于12AB的长为半径作弧，两弧交于M、N两点，作直线MN交AC于点D，则CD的长为（）A．1 B．75C．32D．3二、填空题9．如图，△ABC中AB=AC=10，BC=16，△ABC的面积是.10．如图，在Rt△ABC中，∠C＝90°，AC＝3，以AB为一边向三角形外作正方形ABEF，正方形的中心为O，且OC＝4 √2，则BC＝．11．如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，点D在AB上，AD＝AC，AF⊥CD交CD于点E，交CB于点F，则CF的长是12．某小区两面直立的墙壁之间为安全通道，一架梯子斜靠在左墙DE时，梯子底端A到左墙的距离AE为0.7m，梯子顶端D到地面的距离DE为2.4m，若梯子底端A保持不动，将梯子斜靠在右墙BC上，梯子顶端C到地面的距离CB为2m，则这两面直立墙壁之间的安全通道的宽BE为m．13．活动探究：我们知道，已知两边和其中一边的对角对应相等的两个三角形不一定全等.如已知△ABC中∠A=30°，AC=3，∠A所对的边为√3，满足已知条件的三角形有两个（我们发现其中如图的△ABC是一个直角三角形），则满足已知条件的三角形的第三边长为三、解答题14．如图，点C在∠DAB内部，CD⊥AD于点D，CB⊥AB于点B，CD＝CB，若AD＝5，求AB的长．15．如图，在△ABC中，CD⊥AB，垂足为D．AD＝1，BD＝4，CD＝2．求证：∠ACB＝90°．16．如图，一只小鸟旋停在空中A点，A点到地面的高度AB=20米，A点到地面C点（B、C两点处于同一水平面）的距离AC=25米．若小鸟竖直下降12米到达D点（D点在线段AB上），求此时小鸟到地面C 点的距离．17．如图，在△ABC中，∠ACB的平分线CD交AB于点D，E为AC边上一点，且满足∠AED＝2∠DCB．（1）求证：DE∥BC；（2）若∠B＝90°，AD＝6，AE＝9，求CE的长．18．如图，在正△ABC的AC，BC上各取一点D，E，使AD=CE，AE，BD相交于点M（1）如图1，求∠BME的度数；（2）如图2，过点B作直线AE的垂线BH，垂足为H①求证：2MH+DM=AE；②若BE=2EC=2，求BH的长．答案1．D2．C3．A4．C5．D6．B7．A8．B9．4810．511．1.512．2.213．2√3或√314．解：解法一：连结AC∵CD⊥AD于点D，CB⊥AB于点B∴∠CDA=∠CBA=90°在Rt△ABC与Rt△ADC中有AC=AC，CD=CB∴Rt△ABC≌Rt△ADC（HL）∴AB=AD=5解法二：连结AC∵CD⊥AD于点D，CB⊥AB于点B∴∠CDA=∠CBA=90°∵CD=CB∴由勾股定理得：AB= √AC2−BC2 = √AC2−CD2 =AD=515．证明：∵CD是△ABC的高∴∠ADC=∠BDC=90°．∵AD=1，BD=4，CD=2∴AC2=AD2+CD2=12+22=5，BC2=BD2+CD2=42+22=20，AB2=（1+4）2=25．∴AC2+BC2=AB2．∴△ABC是直角三角形∴∠ACB=90°．16．解：由勾股定理得；BC2=AC2−AB2=252−202=225∴BC=15（米）∵BD=AB−AD=20−12=8（米）∴在Rt△BCD中，由勾股定理得CD=√DB2+BC2=√82+152=17∴此时小鸟到地面C点的距离17米．答；此时小鸟到地面C点的距离为17米．17．（1）证明：∵CD平分∠ACB∴∠ACD=∠DCB即∠ACB=2∠DCB又∵∠AED=2∠DCB∴∠ACB=∠AED∴DE//BC；（2）解：∵DE//BC∴∠EDC=∠BCD，∠B=∠ADE=90°∵∠BCD=∠ECD∴∠EDC=∠ECD∴ED=CE∵AD=6，AE=9∴DE=√AE2−AD2=√92−62=3√5∴CE=3√5．18．（1）解：∵△ABC是等边三角形∴AB=AC，∠BAC=∠C=60°又∵AD=CE ∴△ABD≌△CAE(SAS)∴∠BME=∠ABD+∠BAE=∠CAE+∠BAE=∠BAC=60°（2）解：①∵BH⊥AE ∠BME=60°∴∠HBM=30°∴BM=2MH∵△ABD≌△CAE ∴AE=BD=BM+MD=2MH+MD②过点E作EG⊥AB于点GBE=2EC=2 ∴AB=BC=3∴使用ABC=60°∴BG=1，AG=2，由勾股定理可得，GE= √3，AE= √7设HE=x，则AH= √7 -x由勾股定理得32-（√7 -x）2=22-x2解得x= √77再由勾般定理可得：BH= 3√21.7。

中考数学专项复习勾股定理含解析

中考数学专项复习勾股定理含解析一．选择题（共11小题）1．如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3．若S1+S2+S3=60，则S2的值是（）A．12 B．15 C．20 D．302．以下列各组数为边长，不能构成直角三角形的是（）A．3，4，5 B．9，12，15C．，，D．0.3，0.4，0.53．如图，有四个三角形，各有一边长为6，一边长为8，若第三边分别为6，8，10，12，则面积最大的三角形是A．B．C． D．4．下列条件中，不能判定△ABC为直角三角形的是（）A．a=1.5 b=2 c=2.5 B．a：b：c=5：12：13C．∠A+∠B=∠C D．∠A：∠B：∠C=3：4：55．如图，一棵大树在离地面3米处折断，树的顶端落在离树干底部4米处，那么这棵树折断之前的高度是（）A．8米B．12米C．5米D．5或7米6．如图所示，AB=BC=CD=DE=1，AB⊥BC，AC⊥CD，AD⊥DE，则AE=（）A．1 B． C． D．27．已知a，b，c为△ABC的三边长，且满足a2c2﹣b2c2=a4﹣b4，判定△ABC的形状（）A．等腰三角形B．直角三角形C．等腰直角三角形D．等腰三角形或直角三角形8．如图是由5个正方形和5个等腰直角三角形组成的图形，已知③号正方形的面积是1，那么①号正方形的面积是（）A．4 B．8 C．16 D．329．直角三角形的两边长分别是6，8，则第三边的长为（）A．10 B．2C．10或2 D．无法确定10．如图，在△ABC中，D、E分别是BC、AC的中点．已知∠ACB =90°，BE=4，AD=7，则AB的长为（）A．10 B．5C．2D．211．长方形台球桌ABCD上，一球从AB边上某处P击出，分别撞击球桌的边BC、DA各1次后，又回到动身点P处，每次球撞击桌边时，撞击前后的路线与桌边所成的角相等（例如图∠α=∠β）若AB=3，BC=4，则此球所走路线的总长度（不计球的大小）为（）A．不确定B．12 C．11 D．10二．填空题（共12小题）12．勾股定理a2+b2=c2本身确实是一个关于a，b，c的方程，满足那个方程的正整数解（a，b，c）通常叫做勾股数组．毕达哥拉斯学派提出了一个构造勾股数组的公式，依照该公式能够构造出如下勾股数组：（3，4，5），（5，12，13），（7，24，25），…．分析上面勾股数组能够发觉，4=1×（3+1），12=2×（5+1），24=3×（7+1），…分析上面规律，第5个勾股数组为．13．如图，在△ABC中，AB=AC=6，BC=7，E是BC上的一个动点（不与点B，C重合），△DEF≌△ABC，其中点A，B的对应点分别是点D，E．当点E运动时DE边始终通过点A．设EF与AC相交于点G，当△AEG是等腰三角形时，BE的长为．14．如图，OP=1，过P作PP1⊥OP且PP1=1，依照勾股定理，得OP 1=；再过P1作P1P2⊥OP1且P1P2=1，得OP2=；又过P2作P2P3⊥O P2且P2P3=1，得OP3=2；…依此连续，得OP2021=，OPn=（n为自然数，且n＞0）15．如图，已知点A（﹣1，0）和点B（1，2），在y轴正半轴上确定点P，使得△ABP为直角三角形，则满足条件的点P的坐标为．16．若一个三角形的三边长分别为3，4，x，则使此三角形是直角三角形的x的值是．17．直角三角形三边长分别为5，12，x，则x2=．若a，b为两个连续的正整数，且a＜＜b，则a+b=．18．有一棵9米高的大树，树下有一个1米高的小孩，假如大树在距地面4米处折断（未完全折断），则小孩至少离开大树米之外才是安全的．19．如图，分别以直角三角形三边向外作三个半圆，若S1=30，S2=40，则S3=．20．如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为．21．如图是由4个边长为1的正方形构成的“田字格”．只用没有刻度的直尺在那个“田字格”中最多能够作出以格点为端点、长度为的线段条．22．如图，所有的四边形差不多上正方形，所有的三角形差不多上直角三角形，其中最大的正方形的边长为10cm，正方形A2的边长为6cm，正方形B的边长为5cm，正方形C的边长为5cm，则正方形D的面积是cm2．23．设x＞0，则三个正数2x，3x，x+5，构成三角形三边的条件是；构成直角三角形、锐角三角形、钝角三角形的x的取值范畴分别是、、．三．解答题（共10小题）24．如图，有一艘货船和一艘客船同时从港口A动身，客船每小时比货船多走5海里，客船与货船速度的比为4：3，货船沿东偏南10°方向航行，2小时后货船到达B处，客船到达C处，若现在两船相距50海里．（1）求两船的速度分别是多少？（2）求客船航行的方向．25．从正面看一个底面直径为10cm的圆柱体饮料杯子如图所示，在它的正中间竖直插入一根吸管（吸管在杯口一端的位置固定不动），吸管露出杯子外1cm，当吸管伸向杯壁底部时，吸管顶端刚好与杯口高度平齐．求杯子的高度．26．先阅读下列一段文字，在回答后面的问题．已知在平面内两点P1（x1，y1）、P2（x2，y2），其两点间的距离公式P1P2=，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|．（1）已知A（2，4）、B（﹣3，﹣8），试求A、B两点间的距离；（2）已知A、B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为﹣1，试求A、B两点间的距离．（3）已知一个三角形ABC其中两个顶点坐标为A（0，﹣6）、B（﹣8，0）在坐标轴上是否存在点C，使三角形ABC中AB=AC或者AB=BC？若能请直截了当写出因此符合条件的点C的坐标；若不能，请说明理由．27．阅读下面的材料，然后解答问题：我们新定义一种三角形，两边的平方和等于第三边平方的2倍的三角形叫做奇特三角形．明白得：①依照奇特三角形的定义，请你判定：等边三角形一定是奇特三角形吗？（填“是”或“不是”）②若某三角形的三边长分别为1、、2，则该三角形（填“是”或“不是”）奇特三角形．探究：在Rt△ABC中，两边长分别是a、c，且a2=50，c2=100，则那个三角形是否是奇特三角形？请说明理由．拓展：在Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，且b＞a，若Rt△ABC是奇特三角形，求a2：b2：c2．28．如图，在△ABC中，∠ACB=90°，BC=15，AC=20，CD是高．（1）求AB的长；（2）求△ABC的面积；（3）求CD的长．29．阅读下列材料，并回答问题．事实上，在任何一个直角三角形中，两条直角边的平方之和一定等于斜边的平方，那个结论确实是闻名的勾股定理．请利用那个结论，完成下面活动：（1）一个直角三角形的两条直角边分别为6、8，那么那个直角三角形斜边长为．（2）如图1，AD⊥BC 于D，AD=BD，AC=BE，AC=3，DC=1，求B D的长度．（3）如图2，点A在数轴上表示的数是，请用类似的方法在图2数轴上画出表示数的B点（保留作图痕迹）．30．定义：如图，点M、N把线段AB分割成AM、MN、NB，若以A M、MN、NB为边的三角形是一个直角三角形，则称点M、N是线段AB 的勾股分割点．（1）已知M、N把线段AB分割成AM、MN、NB，若AM=1.5，MN =2.5，BN=2，则点M、N是线段AB的勾股分割点吗？请说明理由．（2）已知点M、N是线段AB的勾股分割点，且AM为直角边，若A B=24，AM=6，求BN的长．31．如图，将边长为a与b、对角线长为c的长方形纸片ABCD，绕点C顺时针旋转90°得到长方形FGCE，连接AF．通过用不同方法运算梯形ABEF的面积可验证勾股定理，请你写出验证的过程．32．在△ABC中，∠ABC=90°，D为平面内一动点，AD=a，AC=b，其中a，b为常数，且a＜b．将△ABD沿射线BC方向平移，得到△FCE，点A、B、D的对应点分别为点F、C、E．连接BE．（1）如图1，若D在△ABC内部，请在图1中画出△FCE；（2）在（1）的条件下，若AD⊥BE，求BE的长（用含a，b的式子表示）；（3）若∠BAC=α，当线段BE的长度最大时，则∠BAD的大小为；当线段BE的长度最小时，则∠BAD的大小为（用含α的式子表示）．33．如图，四边形ABCD中，∠ABC=135°，∠BCD=120°，AB=，BC=5﹣，CD=6，求AD．答案一．选择题（共11小题）1．如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3．若S1+S2+S3=60，则S2的值是（）A．12 B．15 C．20 D．30【分析】设每个小直角三角形的面积为m，则S1=4m+S2，S3=S2﹣4 m，依据S1+S2+S3=60，可得4m+S2+S2+S2﹣4m=60，进而得出S2的值．【解答】解：设每个小直角三角形的面积为m，则S1=4m+S2，S3=S2﹣4m，因为S1+S2+S3=60，因此4m+S2+S2+S2﹣4m=60，即3S2=60，解得S2=20．故选：C．【点评】此题要紧考查了勾股定理和正方形、全等三角形的性质的运用，证明勾股定理时，用几个全等的直角三角形拼成一个规则的图形，然后利用大图形的面积等于几个小图形的面积和化简整理得到勾股定理．2．以下列各组数为边长，不能构成直角三角形的是（）A．3，4，5 B．9，12，15C．，，D．0.3，0.4，0.5【分析】依照勾股定理的逆定理，一个三角形的三边满足两个较小边的平方和等于较大边的平方，那个三角形确实是直角三角形．【解答】解：A、因为32+42=52，故能构成直角三角形，此选项错误；B、因为92+122=152，能构成直角三角形，此选项错误；C、因为（）2+（）2≠（）2，不能构成直角三角形，此选项正确；D、因为0.32+0.42=0.52，能构成直角三角形，此选项错误．故选：C．【点评】本题考查勾股定理的逆定理，关键明白两个较小边的平方和等于较大边的平方，那个三角形确实是直角三角形．3．如图，有四个三角形，各有一边长为6，一边长为8，若第三边分别为6，8，10，12，则面积最大的三角形是A．B．C． D．【分析】过C作CD⊥AB于D，依据AB=6，AC=8，可得CD≤8，进而得到当CD与AC重合时，CD最长为8，现在，∠BAC=90°，△ABC 的面积最大．【解答】解：如图，过C作CD⊥AB于D，∵AB=6，AC=8，∴CD≤8，∴当CD与AC重合时，CD最长为8，现在，∠BAC=90°，△ABC的面积最大，∴BC==10，∴四个三角形中面积最大的三角形的三边长分别为6，8，10，故选：C．【点评】本题要紧考查了三角形的面积以及勾股定理的逆定理，关键在于正确的表示出斜边、直角边的长度，熟练运用勾股定理的逆定理进行分析．4．下列条件中，不能判定△ABC为直角三角形的是（）A．a=1.5 b=2 c=2.5 B．a：b：c=5：12：13C．∠A+∠B=∠C D．∠A：∠B：∠C=3：4：5【分析】依照勾股定理的逆定理以及三角形的内角和为180度，即可判定出三角形的形状．【解答】解：A、因为1.52+22=2.52符合勾股定理的逆定理，故△AB C为直角三角形；B、因为a：b：c=5：12：13，因此可设a=5x，b=12x，c=13x，则（5 x）2+（12x）2=（13x）2，故△ABC为直角三角形；C、因为∠A+∠B=∠C，∠A+∠B+∠C=180°，则∠C=90°，故△AB C为直角三角形；D、因为∠A：∠B：∠C=3：4：5，因此设∠A=3x，则∠B=4x，∠C= 5x，故3x+4x+5x=180°，解得x=15°，3x=15×3=45°，4x=15×4=60°，5x=15×5=75°，故此三角形是锐角三角形．故选：D．【点评】此题考查了解直角三角形的判定，依照勾股定理的逆定理、三角形的内角和定理结合解方程是解题的关键．5．如图，一棵大树在离地面3米处折断，树的顶端落在离树干底部4米处，那么这棵树折断之前的高度是（）A．8米B．12米C．5米D．5或7米【分析】由题意得，在直角三角形中，明白了两直角边，运用勾股定理即可求出斜边，从而得出这棵树折断之前的高度．【解答】解：∵一棵垂直于地面的大树在离地面3米处折断，树的顶端落在离树杆底部4米处，∴折断的部分长为=5，∴折断前高度为5+3=8（米）．故选：A．【点评】此题考查了勾股定理的应用，要紧考查学生对勾股定理在实际生活中的运用能力．6．如图所示，AB=BC=CD=DE=1，AB⊥BC，AC⊥CD，AD⊥DE，则AE=（）A．1 B． C． D．2【分析】依照勾股定理进行逐一运算即可．【解答】解：∵AB=BC=CD=DE=1，AB⊥BC，AC⊥CD，AD⊥DE，∴AC===；AD===；AE===2．故选：D．【点评】本题考查了利用勾股定明白得直角三角形的能力，即：直角三角形两直角边的平方和等于斜边的平方．7．已知a，b，c为△ABC的三边长，且满足a2c2﹣b2c2=a4﹣b4，判定△ABC的形状（）A．等腰三角形B．直角三角形C．等腰直角三角形D．等腰三角形或直角三角形【分析】第一把等式的左右两边分解因式，再考虑等式成立的条件，从而判定△ABC的形状．【解答】解：由a2c2﹣b2c2=a4﹣b4，得a4+b2c2﹣a2c2﹣b4=（a4﹣b4）+（b2c2﹣a2c2）=（a2+b2）（a2﹣b2）﹣c2（a2﹣b2）=（a2﹣b2）（a2+b2﹣c2）=（a+b）（a﹣b）（a2+b2﹣c2）=0，∵a+b＞0，∴a﹣b=0或a2+b2﹣c2=0，即a=b或a2+b2=c2，则△ABC为等腰三角形或直角三角形．故选：D．【点评】本题考查勾股定理的逆定理的应用、分类讨论．判定三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判定即可．8．如图是由5个正方形和5个等腰直角三角形组成的图形，已知③号正方形的面积是1，那么①号正方形的面积是（）A．4 B．8 C．16 D．32【分析】等腰直角三角形中，直角边长和斜边长的比值为1：，正方形面积为边长的平方；因此要求①号正方形的面积，求出①号正方形的边长即可．【解答】解：要求①号正方形的面积，求①号正方形的边长即可，题目中给出③号正方形的面积为1，即③号正方形的边长为1，依照勾股定理4号正方形的边长为=，以此类推，能够求得①号正方形边长为4，因此①号正方形面积为4×4=16．故选：C．【点评】本题考查的是在等腰直角三角形中勾股定理的运用，已知直角边求斜边边长，解本题的关键是正确的运用勾股定理．9．直角三角形的两边长分别是6，8，则第三边的长为（）A．10 B．2C．10或2 D．无法确定【分析】本题已知直角三角形的两边长，但未明确这两条边是直角边依旧斜边，因此两条边中的较长边既能够是直角边，也能够是斜边，因此求第三边的长必须分类讨论，即较长是斜边或直角边的两种情形，然后利用勾股定理求解．【解答】解：长为8的边可能为直角边，也可能为斜边．当8为直角边时，依照勾股定理，第三边的长==10；当8为斜边时，依照勾股定理，第三边的长==2．故选：C．【点评】此题易忽视的地点：长为8的边可能为直角边，也可能为斜边．10．如图，在△ABC中，D、E分别是BC、AC的中点．已知∠ACB =90°，BE=4，AD=7，则AB的长为（）A．10 B．5C．2D．2【分析】设EC=x，DC=y，则直角△BCE中，x2+4y2=BE2=16，在直角△ADC中，4x2+y2=AD2=49，解方程组可求得x、y，在直角△ABC中，AB=．【解答】解：设EC=x，DC=y，∠ACB=90°，∴在直角△BCE中，CE2+BC2=x2+4y2=BE2=16在直角△ADC中，AC2+CD2=4x2+y2=AD2=49，解得x=，y=1．在直角△ABC中，AB===2，故选：C．【点评】本题考查了勾股定理的灵活运用，考查了中点的定义，本题中依照直角△BCE和直角△ADC求DC．BC的长度是解题的关键．11．长方形台球桌ABCD上，一球从AB边上某处P击出，分别撞击球桌的边BC、DA各1次后，又回到动身点P处，每次球撞击桌边时，撞击前后的路线与桌边所成的角相等（例如图∠α=∠β）若AB=3，BC=4，则此球所走路线的总长度（不计球的大小）为（）A．不确定B．12 C．11 D．10【分析】要求球走过的总长度，就要求PQ+QR，依照运算得PQ+QR= BD=AC．依照此关系式能够解题．【解答】解：令PQ∥AC，则QR∥BD，∵撞击前后的路线与桌边所成的角相等∴图中所有三角形均相似；∴+==1，即PQ+QR=AC=BD，同理PS+SR=AC=BD，∴PQ+QR+RS+SP=AC+BD=2AC．∵AC==5，∴PQ+QR+RS+SP=AC+BD=2AC=10．故选：D．【点评】本题考查了直角三角形中勾股定理的运用，考查了相似三角形对应边比例相等的性质，本题中令PQ∥AC是解题的关键．二．填空题（共12小题）12．勾股定理a2+b2=c2本身确实是一个关于a，b，c的方程，满足那个方程的正整数解（a，b，c）通常叫做勾股数组．毕达哥拉斯学派提出了一个构造勾股数组的公式，依照该公式能够构造出如下勾股数组：（3，4，5），（5，12，13），（7，24，25），…．分析上面勾股数组能够发觉，4=1×（3+1），12=2×（5+1），24=3×（7+1），…分析上面规律，第5个勾股数组为（11，60，61）．【分析】由勾股数组：（3，4，5），（5，12，13），（7，24，25）…中，4=1×（3+1），12=2×（5+1），24=3×（7+1），…可得第5组勾股数中间的数为：5×（11+1）=60，进而得出（11，60，61）．【解答】解：由勾股数组：（3，4，5），（5，12，13），（7，24，25）…中，4=1×（3+1），12=2×（5+1），24=3×（7+1），…可得第4组勾股数中间的数为4×（9+1）=40，即勾股数为（9，40，41）；第5组勾股数中间的数为：5×（11+1）=60，即（11，60，61），故答案为：（11，60，61）．【点评】本题要紧考查了勾股定理的逆定理，关键是找出数据之间的关系，把握勾股定理逆定理．13．如图，在△ABC中，AB=AC=6，BC=7，E是BC上的一个动点（不与点B，C重合），△DEF≌△ABC，其中点A，B的对应点分别是点D，E．当点E运动时DE边始终通过点A．设EF与AC相交于点G，当△AEG是等腰三角形时，BE的长为1或．【分析】第一由∠AEF=∠B=∠C，且∠AGE＞∠C，可得AE≠AG，然后分别从AE=EG与AG=EG去分析，注意利用全等三角形与相似三角形的性质求解即可求得答案．【解答】解：∵∠AEF=∠B=∠C，且∠AGE＞∠C，∴∠AGE＞∠AEF，∴AE≠AG；当AE=EG时，则△ABE≌△ECG，∴CE=AB=6，∴BE=BC﹣EC=7﹣6=1，当AG=EG时，则∠GAE=∠GEA，∴∠GAE+∠BAE=∠GEA+∠CEG，即∠CAB=∠CEA，又∵∠C=∠C，∴△CAE∽△CBA，∴CE==，∴BE=7﹣=；∴BE=1或．故答案为：1或．【点评】此题考查了相似三角形的判定与性质、全等三角形的判定和性质、等腰三角形的性质，熟练把握性质定理是解题的关键．14．如图，OP=1，过P作PP1⊥OP且PP1=1，依照勾股定理，得OP 1=；再过P1作P1P2⊥OP1且P1P2=1，得OP2=；又过P2作P2P3⊥O P2且P2P3=1，得OP3=2；…依此连续，得OP2021=，OPn=（n为自然数，且n＞0）【分析】依照题意找出规律，依照规律解答．【解答】解：由题意得，OP1=；OP2=；OP3=，则OP2021=，OPn=，故答案为：；．【点评】本题考查的是勾股定理，假如直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．15．如图，已知点A（﹣1，0）和点B（1，2），在y轴正半轴上确定点P，使得△ABP为直角三角形，则满足条件的点P的坐标为（0，3）或（0，1+）．【分析】分两种情形进行讨论，过B作BP⊥AB，交y轴于P，过B作BD⊥CP于D，则∠ABP=90°，BD=1，依据△BCP是等腰直角三角形，即可得到点P的坐标；当∠APB=90°时，△ABP是直角三角形，依据C为AB的中点，AB=2，即可得到点P的坐标．【解答】解：如图，过B作BP⊥AB，交y轴于P，过B作BD⊥CP 于D，则∠ABP=90°，BD=1，∵点A（﹣1，0）和点B（1，2），∴直线AB的表达式为y=x+1，令x=0，则y=1，∴C（0，1），即OC=1=OA，∴△AOC是等腰直角三角形，∴∠ACO=45°=∠BCP，∴△BCP是等腰直角三角形，∴CP=2BD=2，∴OP=1+2=3，∴P（0，3）；如图，当∠APB=90°时，△ABP是直角三角形，∵点A（﹣1，0），点B（1，2），点C（0，1），∴C为AB的中点，AB=2，∴CP=AB=，∴OP=1+，∴P（0，1+），综上所述，点P的坐标为（0，3）或（0，1+）．故答案为：（0，3）或（0，1+）．【点评】本题要紧考查了坐标与图形的性质和直角三角形的判定．要把所有的情形都考虑到里面去，不要漏掉某种情形．16．若一个三角形的三边长分别为3，4，x，则使此三角形是直角三角形的x的值是5或．【分析】本题已知直角三角形的两边长，但未明确这两条边是直角边依旧斜边，因此两条边中的较长边4既能够是直角边，也能够是斜边，因此求第三边的长必须分类讨论，即4是斜边或直角边的两种情形，然后利用勾股定理求解．【解答】解：设第三边为x（1）若4是直角边，则第三边x是斜边，由勾股定理，得32+42=x2，因此x=5；（2）若4是斜边，则第三边x为直角边，由勾股定理，得32+x2=42，因此x=；因此第三边的长为5或．【点评】本题考查了利用勾股定明白得直角三角形的能力，当已知条件中没有明确哪是斜边时，要注意讨论，一些学生往往忽略这一点，造成丢解．17．直角三角形三边长分别为5，12，x，则x2=169或119．若a，b为两个连续的正整数，且a＜＜b，则a+b=9．【分析】分12为直角边和12为斜边两种情形，依照勾股定理运算；依照无理数的估算方法、算术平方根的概念解答．【解答】解：当12为直角边时，x2=52+122=169，当12为斜边时，x2=122﹣52=119；∵16＜20＜25，∴4＜＜5，∴a=4，b=5，∴a+b=9，故答案为：169或119；9．【点评】本题考查的是勾股定理，假如直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．18．有一棵9米高的大树，树下有一个1米高的小孩，假如大树在距地面4米处折断（未完全折断），则小孩至少离开大树4米之外才是安全的．【分析】依照题意构建直角三角形ABC，利用勾股定明白得答．【解答】解：如图，BC即为大树折断处4m减去小孩的高1m，则BC=4﹣1=3m，AB=9﹣4 =5m，在Rt△ABC中，AC===4．【点评】此题考查直角三角形的性质及勾股定理的应用，要依照题意画出图形即可解答．19．如图，分别以直角三角形三边向外作三个半圆，若S1=30，S2=40，则S3=70．【分析】依照勾股定理以及圆面积公式，能够证明：S1+S2=S3．故S3 =70．【解答】解：设直角三角形三边分别为a、b、c，如图所示：则S1=π（）2=，S2=π（）2=，S3=π（）2=．因为a2+b2=c2，因此+=．即S1+S2=S3．因此S3=70．【点评】注意发觉此图中的结论：S1+S2=S3．20．如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为16．【分析】依照已知及全等三角形的判定可得到△ABC≌△CDE，从而得到b的面积=a的面积+c的面积．【解答】解：∵∠ACB+∠ECD=90°，∠DEC+∠ECD=90°∴∠ACB=∠DEC∵∠ABC=∠CDE，AC=CE，在△ABC和△CDE中，∴△ABC≌△CDE（AAS），∴BC=DE∴（如上图），依照勾股定理的几何意义，b的面积=a的面积+c的面积∴b的面积=a的面积+c的面积=5+11=16．【点评】本题考查了对勾股定理几何意义的明白得能力，依照三角形全等找出相等的量是解答此题的关键．21．如图是由4个边长为1的正方形构成的“田字格”．只用没有刻度的直尺在那个“田字格”中最多能够作出以格点为端点、长度为的线段8条．【分析】如图，由于每个小正方形的边长为1，那么依照勾股定理容易得到长度为的线段，然后能够找出所有如此的线段．【解答】解：如图，所有长度为的线段全部画出，共有8条．【点评】此题是一个探究试题，第一探究如何找到长度为的线段，然后利用那个规律找出所有如此的线段．22．如图，所有的四边形差不多上正方形，所有的三角形差不多上直角三角形，其中最大的正方形的边长为10cm，正方形A2的边长为6cm，正方形B的边长为5cm，正方形C的边长为5cm，则正方形D的面积是14cm2．【分析】依照勾股定理的几何意义可直截了当解答．【解答】解：依照正方形的面积公式结合勾股定理，得正方形A2，B，C，D的面积和等于最大的正方形的面积，因此正方形D的面积=100﹣36﹣25﹣25=14cm2．【点评】此题注意依照正方形的面积公式以及勾股定理得到图中正方形的面积之间的关系：以直角三角形的两条直角边为边长的两个正方形的面积和等于以斜边为边长的面积．23．设x＞0，则三个正数2x，3x，x+5，构成三角形三边的条件是；构成直角三角形、锐角三角形、钝角三角形的x的取值范畴分别是x=或x=、＜x＜、＜x＜或x＞．【分析】依照三角形两边之和大于第三边，依照三边表达式列不等式求解；直角三角形两直角边平方和等于第三边平方，锐角三角形两边平方和大于第三边平方，钝角三角形两边平方和小于钝角所对应的边的平方．【解答】解：构成三角形则要满足2x+3x＞x+5，即4x＞5，则x＞，即可；①当三角形为直角三角形时，若x+5＞3x，即x＜（2x）2+（3x）2=（x+5）2解得x=，若3x＞x+5，即x＞（2x）2+（x+5）2=（3x）2解得x=②当构成锐角三角形时，即（2x）2+（3x）2＞（x+5）212x2﹣10x﹣25＞0解得x＞（2x）2+（x+5）2＞（3x）2﹣4x2+10x+25＞0x＜综上，构成锐角三角形的x的取值范畴是：＜x＜；③当构成钝角三角形时，若x+5＞3x，即x＜（2x）2+（3x）2＜（x+5）2解得＜x＜＜，若3x＞x+5，即x＞（2x）2+（x+5）2＜（3x）2解得x＞综上，构成钝角三角形的x的取值范畴是：＜x＜或x＞；故答案为x＞，x=或x=，＜x＜；＜x＜或x＞，【点评】本题考查了三角形成构成条件，考查了直角三角形中勾股定理的运用，本题中确定以x+5为第三边是解本题的关键．三．解答题（共10小题）24．如图，有一艘货船和一艘客船同时从港口A动身，客船每小时比货船多走5海里，客船与货船速度的比为4：3，货船沿东偏南10°方向航行，2小时后货船到达B处，客船到达C处，若现在两船相距50海里．（1）求两船的速度分别是多少？（2）求客船航行的方向．【分析】（1）设两船的速度分别是4x海里/小时和3x海里/小时，依据客船每小时比货船多走5海里，列方程求解即可；（2）依据AB2+AC2=BC2，可得△ABC是直角三角形，且∠BAC=90°，再依照货船沿东偏南10°方向航行，即可得到客船航行的方向为北偏东1 0°方向．【解答】解：（1）设两船的速度分别是4x海里/小时和3x海里/小时，依题意得4x﹣3x=5．解得x=5，∴4x=20，3x=15，∴两船的速度分别是20海里/小时和15海里/小时；（2）由题可得，AB=15×2=30，AC=20×2=40，BC=50，∴AB2+AC2=BC2，∴△ABC是直角三角形，且∠BAC=90°，又∵货船沿东偏南10°方向航行，∴客船航行的方向为北偏东10°方向．【点评】此题要紧考查了方向角以及勾股定理的应用，正确得出AB的长是解题关键．25．从正面看一个底面直径为10cm的圆柱体饮料杯子如图所示，在它的正中间竖直插入一根吸管（吸管在杯口一端的位置固定不动），吸管露出杯子外1cm，当吸管伸向杯壁底部时，吸管顶端刚好与杯口高度平齐．求杯子的高度．【分析】设杯子的高度为xcm，则吸管的长度为（x+1）cm，依照勾股定理可得出关于x的一元一次方程，解之即可得出结论．【解答】解：设杯子的高度为xcm，则吸管的长度为（x+1）cm，依照题意得：（x+1）2=52+x2，解得：x=12．答：杯子的高度为12cm．【点评】本题考查了勾股定理的应用以及解一元一次方程，在应用勾股定明白得决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．26．先阅读下列一段文字，在回答后面的问题．已知在平面内两点P1（x1，y1）、P2（x2，y2），其两点间的距离公式P1P2=，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|．（1）已知A（2，4）、B（﹣3，﹣8），试求A、B两点间的距离；（2）已知A、B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为﹣1，试求A、B两点间的距离．（3）已知一个三角形ABC其中两个顶点坐标为A（0，﹣6）、B（﹣8，0）在坐标轴上是否存在点C，使三角形ABC中AB=AC或者AB=BC？若能请直截了当写出因此符合条件的点C的坐标；若不能，请说明理由．【分析】（1）依照两点的距离公式运算即可；（2）关于平行于坐标轴的两点距离公式可利用|y2﹣y1|代入运算；（3）分别以A、B为圆心，以10为半径画圆与坐标轴的交点确实是C 点．【解答】解：（1）∵A（2，4）、B（﹣3，﹣8），∴AB==13…．（4分）答：A、B两点间的距离是13．（2）∵AB∥y轴，∴AB=5﹣（﹣1）=6，答：A、B两点间的距离是6．（8分）（3）如图所示：①AB=AC时，符合条件的点C的坐标为（8，0）、（0，4）、（0，﹣16）；②AB=BC时，符合条件的点C的坐标为：（0，6）、（2，0）、（﹣18，0）…．（1 2分）综上所述，符合条件的点C的坐标为：（2，0）、（8，0）（﹣18，0）、（0，4）、（0，﹣16）、（0，6）．【点评】本题考查了等腰三角形的判定、平面上两点的距离公式的明白得与应用，认真阅读材料，明白得两点间的距离公式，注意当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|．27．阅读下面的材料，然后解答问题：我们新定义一种三角形，两边的平方和等于第三边平方的2倍的三角形叫做奇特三角形．明白得：①依照奇特三角形的定义，请你判定：等边三角形一定是奇特三角形吗？是（填“是”或“不是”）②若某三角形的三边长分别为1、、2，则该三角形是（填“是”或“不是”）奇特三角形．探究：在Rt△ABC中，两边长分别是a、c，且a2=50，c2=100，则那个三角形是否是奇特三角形？请说明理由．那个工作可让学生分组负责收集整理,登在小黑板上,每周一换。

中考数学勾股定理专项练习题(附答案

中考数学勾股定理专项练习题（附答案）一、单选题（共15题；共30分）1.如图，在正方形网格中，将三角形ABC绕点A旋转后得到三角形ADE，则下列旋转方式中，符合题意的是( )（1题图）（2题图）A. 顺时针旋转90°B. 逆时针旋转90°C. 顺时针旋转45°D. 逆时针旋转45°2.如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3cm 至D点，则橡皮筋被拉长了（）A. 4cmB. 3cmC. 2cmD. 5cm3.以下列各组线段为边作三角形，不能构成直角三角形的是（）A. 1、、B. 5、12、13C. 2、3、4D. 9、40、414.如图，AB是⊙O的弦，半径OC⊥AB于点D，若⊙O的半径为5，AB=8，则CD的长是（）（4题图）（5题图）A. 2B. 3C. 4D. 55.如图，在△ABC中，CF⊥AB于F，BE⊥AC于E，D为BC的中点，EF=3，BC=8，则△DEF的周长是（）A. 7B. 10C. 11D. 146.如图，在平行四边形ABCD中，BD⊥AD，以BD为直径作圆，交于AB于E，交CD于F，若BD=12，AD：AB=1：2，则图中阴影部分的面积为（）（6题图）（7题图）A. 12B.C.D.7.如图，在正方形ABCD中∠DAE=25°，AE交对角线BD于E点，那么∠BEC等于（）A. 45°B. 60°C. 70°D. 75°8.如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=3，BC=5，将腰DC绕点D逆时针方向旋转90°至DE，连接AE，则△ADE的面积是（）（8题图）（9题图）A. 1B. 2C. 3D. 49.如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC=6，BC=5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图2所示的“数学风车”，则这个风车的外围周长是（）A. 76B. 72C. 68D. 5210.关于直角三角形，下列说法正确的是（）A. 所有的直角三角形一定相似；B. 如果直角三角形的两边长分别是3和4，那么第三边的长一定是5；C. 如果已知直角三角形两个元素（直角除外），那么这个直角三角形一定可解；D. 如果已知直角三角形一锐角的三角函数值，那么这个直角三角形的三边之比一定确定．11.如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B为（）（11题图）（12题图）A. 66°B. 104°C. 114°D. 124°12.如图，在矩形ABCD中，AB=4，BC=6，E是矩形内部的一个动点，且AE⊥BE，则线段CE的最小值为（）A. B. 2 ﹣2 C. 2 ﹣2 D. 413.下列各组长度的线段能组成直角三角形的是（）A. a=2，b=3，c=4B. a=4，b=4，c=5C. a=5，b=6，c=7D. a=5，b=12，c=1314.如图，半圆O的直径AB=4，与半圆O内切的动圆O1与AB切于点M，设⊙O1的半径为y，AM=x，则y 关于x的函数关系式是（）A. B.C. D.15.如图，将正方形纸片ABCD沿FH折叠，使点D与AB的中点E重合，则△FAE与△EBG的面积之比为（）A. 4：9B. 2： 3C. 3：4D. 9：16二、填空题（共6题；共14分）16.如图，在Rt△ABC中，E是斜边AB的中点，若AB＝10，则CE＝________．17.下列各组数：①1、2、3；②6、8、10；③0.3、0.4、0.5；④9、40、41；其中是勾股数的有________ (填序号)18.观察以下几组勾股数，并寻找规律：1）3，4，5；2）5，12，13；3）7，24，25；4）9，40，41；…请你写出有以上规律的第（n）组勾股数：________．19.一个图形无论经过平移变换还是旋转变换，下列结论一定正确的是________（把所有你认为正确的序号都写上）①对应线段平行；②对应线段相等；③对应角相等；④图形的形状和大小都不变．20.⊙O的半径为6，⊙O的一条弦AB长，以3为半径的同心圆与直线AB的位置关系是 ________．21.如图，在平面直角坐标系中，直线l：y=x+2交x轴于点A，交y轴于点A1，点A2，A3，…在直线l上，点B1，B2，B3，…在x轴的正半轴上．若△A1OB1，△A2B1B2，△A3B2B3依次均为等腰直角三角形，直角顶点都在x轴上，则第2017个等腰直角三角形A2017B2016B2017顶点B2017的横坐标为________．三、综合题（共5题；共56分）22.已知等腰Rt△ABC和等腰Rt△AED中，∠ACB=∠AED=90°，且AD=AC．（1）发现：如图1，当点E在AB上且点C和点D重合时，若点M、N分别是DB、EC的中点，则MN与EC的位置关系是________，MN与EC的数量关系是________．（2）探究：若把（1）小题中的△AED绕点A顺时针旋转45°得到的图2，连接BD和EC，并连接DB、EC 的中点M、N，则MN与EC的位置关系和数量关系仍然能成立吗？若成立，请给予证明，若不成立，请说明理由．（3）若把（1）小题中的△AED绕点A逆时针旋转45°得到的图3，连接BD和EC，并连接DB、EC的中点M、N，则MN与EC的位置关系和数量关系仍然能成立吗？若成立，请给予证明，若不成立，请说明理由．23.已知AB为⊙O的直径，BC⊥AB于B，且BC=AB，D为半圆⊙O上的一点，连接BD并延长交半圆⊙O的切线AE于E．（1）如图1，若CD=CB，求证：CD是⊙O的切线；（2）如图2，若F点在OB上，且CD⊥DF，求的值．24.在解决线段数量关系问题中，如果条件中有角平分线，经常采用下面构造全等三角形的解决思路．如：在图1中，若C是∠MON的平分线OP上一点，点A 在OM 上，此时，在射线ON上截取OB=OA，连结BC，根据三角形全等的判定方法(SAS)，容易构造出全等三角形△OBC 和△OAC，参考上面的方法，解答下列问题：（1）如图2，在△ABC 中，AD是∠BAC的平分线，E，F 分别为AB，AC上的点，且∠AED+∠AFD=180°．求证：DE=DF．（2）如图3，在非等边△ABC 中，∠B=60°，AD，CE 分别是∠BAC，∠BCA 的平分线，且AD，CE 交于点F，求证：AC=AE+CD．25.如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3．（1）求MP的值（2）在AB边上有一个动点F，且不与点A，B重合．当AF等于多少时，△MEF的周长最小？（3）若点G，Q是AB边上的两个动点，且不与点A，B重合，GQ=2．当四边形MEQG的周长最小时，求最小周长值．（计算结果保留根号）26.如图，O是菱形ABCD对角线AC与BD的交点，CD=5cm，OD=3cm；过点C作CE∥DB，过点B作BE∥AC，CE与BE相交于点E．（1）求OC的长；（2）求四边形OBEC的面积．答案一、单选题1. B2.C3. C4. A5. C6.C7. C8.C9. A 10.D 11. C 12.B 13. D 14. A 15.D二、填空题16. 5 17.②④ 18.2n+1，2n2+2n，2n2+2n+1 19.②③④ 20.相切21.22018﹣2三、综合题22.（1）MN⊥EC；MN= EC （2）解：如图2, 连接EM并延长交BC于F，∵∠AED=∠ACB=90°，∴DE∥BC，∴∠DEM=∠AFM，∠EDM=∠MBF，又BM=MD，在△EDM和△FBM中，，∴△EDM≌△FBM，∴BF=DE=AE，EM=FM，∴MN= FC= （BC﹣BF）= （AC﹣AF）= EC，且MN⊥EC（3）解：如图3, 延长ED交BC于点F，连接AF、MF，则AF为矩形ACFE对角线，所以必经过EC的中点N且AN=NF=EN=NC．在Rt△BDF中，M是BD的中点，∠B=45°，∴FD=FB，∴FM⊥AB，∴MN=NA=NF=NC，即MN= EC，∴∠NAM=∠AMN，∠NAC=∠NCA，∴∠MNF=∠NAM+∠AMN=2∠NAM，∠FNC=∠NAC+∠NCA=2∠NAC，∴∠MNC=∠MNF+∠FNC=2∠NAM+2∠NAC=2（∠NAM+∠NAC）=2∠DAC=90°，∴∠MNC=90°，即MN⊥FC且MN= EC23.（1）解：连接DO，CO，∵BC⊥AB于B，∴∠ABC=90°，在△CDO与△CBO中，，∴△CDO≌△CBO，∴∠CDO=∠CBO=90°，∴OD⊥CD，∴CD是⊙O的切线（2）解：连接AD，∵AB是直径，∴∠ADB=90°，∴∠ADF+∠BDF=90°，∠DAB+∠DBA=90°，∵∠BDF+∠BDC=90°，∠CBD+∠DBA=90°，∴∠ADF=∠BDC，∠DAB=∠CBD，∵在△ADF和△BDC中，，∴△ADF∽△BDC，∴= ，∵∠DAE+∠DAB=90°，∠E+∠DAE=90°，∴∠E=∠DAB，∵在△ADE和△BDA中，，∴△ADE∽△BDA，∴= ，∴= ，即= ，∵AB=BC，∴=124.（1）证明：如图1,在AB上截取AK=AF,连结KD∵AD是∠BAC的平分线,∴∠BAD=∠CAD. 在△AKD和△AFD中,∴△AKD≌△AFD(SAS)∴DK=DF,∠AKD=∠AFD ∵∠AED+∠AFD=180°∠EKD+∠AKD=180°∵,∠AED=∠EKD∴DE=DK ∴DE=DF（2）证明：如图2,在AC上截取AG=AE,连接FG∵AD是∠BAC的平分线,CE是∠BCA的平分线∴∠1=∠2,∠3=∠4在△AEF和△AGF中,∴△AEF≌△AGF(SAS),∴∠AFE=∠AFG∵∠B=60°∵.∠BAC+∠ACB=120°∵.∠2+∠3= (∠BAC+∠ACB)=60°,∵∠AFE=∠2+∠3,∴∠AFE=∠CFD=∠AFG=60°,∴∠CFG=180°-∠CFD-∠AFG=60°∴∠CFD=∠CFG,在△CFG和△CFD中∴△CFG≌△CFD(ASA)∴CG=CD,∴AC=AG+CG=AE+CD25.（1）解：∵四边形ABCD为矩形，∴CD=AB=4，∠D=90°，∵矩形ABCD折叠，使点C落在AD边上的点M处，折痕为PE，∴PD=PH=3，CD=MH=4，∠H=∠D=90°，∴MP==5；（2）解：如图1，作点M关于AB的对称点M′，连接M′E交AB于点F，则点F即为所求，过点E作EN⊥AD，垂足为N，∵AM=AD﹣MP﹣PD=12﹣5﹣3=4，∴AM=AM′=4，∵矩形ABCD折叠，使点C落在AD边上的点M处，折痕为PE，∴∠CEP=∠MEP，而∠CEP=∠MPE，∴∠MEP=∠MPE，∴ME=MP=5，在Rt△ENM中，MN===3，∴NM′=11，∵AF∥ME，∴△AFM′∽△NEM′，∴=，即=，解得AF=，即AF=时，△MEF的周长最小.（3）解：如图2，由（2）知点M′是点M关于AB的对称点，在EN上截取ER=2，连接M′R交AB于点G，再过点E作EQ∥RG，交AB于点Q，∵ER=GQ，ER∥GQ，∴四边形ERGQ是平行四边形，∴QE=GR，∵GM=GM′，∴MG+QE=GM′+GR=M′R，此时MG+EQ最小，四边形MEQG的周长最小，在Rt△M′RN中，NR=4﹣2=2，M′R==5，∵ME=5，GQ=2，∴四边形MEQG的最小周长值是7+5．26.（1）解：∵ABCD是菱形，∴AC⊥BD，∴直角△OCD中，OC= （cm）（2）解：∵CE∥DB，BE∥AC，∴四边形OBEC为平行四边形，又∵AC⊥BD，即∠COB=90°，∴平行四边形OBEC为矩形，∵OB=0D，∴S=OB•OC=4×3=12（cm2）矩形OBEC。

2023年中考数学高频考点专题训练--勾股定理及其应用原卷版

2023年中考数学高频考点专题训练--勾股定理及其应用原卷版一、综合题1．如图，在每个小正方形的边长为1的网格中，△ABC的顶点A、B、C均落在格点上．（1）△ABC的周长为．（2）请在如图所示的网格中，用无刻度的直尺在AC上确定一点M，使以点M为圆心，以MC为半径的⊙M与AB相切，并简要说明点M的位置是如何找到的（不要求证明）：▲ ．2．如图，已知：梯形ABCD中，∠ABC＝90°，∠DAB＝45°，AB∠DC，DC＝3，AB＝5，点P在AB边上，以点A为圆心AP为半径作弧交边DC于点E，射线EP于射线CB交于点F．（1）若AP=√13，求DE的长；（2）联结CP，若CP＝EP，求AP的长；（3）线段CF上是否存在点G，使得∠ADE与∠FGE相似？若相似，求FG 的值；若不相似，请说明理由．3．如图1，在Rt∠ABC中，∠ACB=90°，AB=10，BC=6，扇形纸片DOE的顶点O与边AB的中点重合，OD交BC于点F，OE经过点C，且∠DOE=∠B．（1）证明∠COF是等腰三角形，并求出CF的长；（2）将扇形纸片DOE绕点O逆时针旋转，OD，OE与边AC分别交于点M，N（如图2），当CM的长是多少时，∠OMN与∠BCO相似？4．如图矩形ABCO，点A，C分别在y轴与x轴的正半轴上，O为坐标原点，B 的坐标为（6，4），点D（1，0），点P为边AB上一个动点，过点D，P的圆∠M 与AB相切，∠M交x轴于点E，连接AM，（1）当P为AB的中点时，求DE的长及∠M的半径；（2）当AM∠DP时，求点P的坐标与∠M的半径；（3）是否存在一点P使∠M与矩形ABCO的另一条边也相切，若存在求出所有符合条件的点P的坐标．5．如图，AB是⊙O的直径，点C是弧AF的中点.（1）如图1，求证：AH=FH；（2）如图2，若CD⊥AB于点D，交AF于点E，求证：AE=CE；（3）如图3，在（2）的条件下，连接BC交AF于T，连接OT，CR∥AB 交AF于S、交⊙O于点R，已知∠OTB=45°，TH=1，求CR的长.6．如图，在矩形纸片ABCD中，已知ABBC = 23，将矩形沿EF对折（点E、F分别在边BC、AD上），使顶点D落在AB边上的点P处.（1）若AB=4，BC=6，①当AP=3时，求DF的长；②设AP=m，EQ=y，试求y与m之间函数表达式；（2）记四边形PQEF的面积为S，若APAB=k，试说明当k为何值时S的值最小？7．在∠ABC 中，∠BAC＝90°，AB<AC，M 是BC 边的中点，MN∠BC交AC 于点N，动点P 在线段BA 上以每秒√3cm 的速度由点B 向点A 运动.同时，动点Q 在线段AC 上由点N 向点 C 运动，且始终保持MQ∠MP. 一个点到终点时，两个点同时停止运动.设运动时间为t 秒(t>0).（1）∠PBM 与∠QNM 相似吗？请说明理由；（2）若∠ABC＝60°，AB＝4 √3cm.①求动点Q 的运动速度；②设∠APQ 的面积为s(cm2)，求S 与t 的函数关系式.（不必写出t 的取值范围）（3）探求BP²、PQ²、CQ² 三者之间的数量关系，请说明理由.)(a<0)是y轴负半轴上的一点，经过点C作直线，与抛8．如图，点C(0,1a物线y=ax2交于A、B两点（点A在点B的左侧），连接OA、OB，设点A的横坐标为m(m<0).（1）若点A的坐标为(−4,−2)，求点C的坐标；（2）若AC:BC=1:2，m=−1，求a的值，并证明：∠AOB=90°；（3）若AC:BC=1:k(k>1)，问“ ∠AOB=90°”这一结论还成立吗？试说明理由.9．在矩形ABCD中，AB＝4，AD＝8.（1）如图①若E从B到C运动，F从D到A运动且BE＝2DF，（i）当DF为何值时四边形ECDF是矩形.（ii）当DF为何值时EF＝2 √5.（2）如图②E在BC上，BE＝3，F在CD上，将∠ECF沿EF折叠，当C点恰好落在AD边上的G处时，求折痕EF的长.10．如图，在矩形ABCD中，AB＝4，AD＝3，连结BD．点P从点A出发，沿折线AB－BD－DC以每秒1个单位长度的速度向终点C运动．当点P不与矩形ABCD的顶点重合时，以AP为对角线作正方形AEPF（点F在直线AP的右侧）．设正方形AEPF的面积为S（平方单位），点P的运动时间为t（秒）．（1）当点P在线段BD上时，用含t的代数式表示PB的长，并写出t的取值范围；（2）当AP∠BD时，求t的值；（3）求S与t之间的函数关系式．（4）当直线BF将正方形AEPF分成的两部分图形面积相等时，直接写出t 的值．11．如图，平面直角坐标系中，O为原点，点A、B分别在y轴、x轴的正半轴的图象上．P A的上．∠AOB的两条外角平分线交于点P，P在反比例函数y=9x延长线交x轴于点C，PB的延长线交y轴于点D，连接CD．（1）求∠P的度数及点P的坐标；（2）求∠OCD的面积；（3）∠AOB的面积是否存在最大值？若存在，求出最大面积；若不存在，请说明理由．与y轴相交于点A，点12．如图，在平面直角坐标系xOy中，抛物线y=x2+ 14B与点O关于点A对称（1）填空：点B的坐标是；（2）过点B的直线y=kx+b（其中k＜0）与x轴相交于点C，过点C作直线l平行于y轴，P是直线l上一点，且PB=PC，求线段PB的长（用含k的式子表示），并判断点P是否在抛物线上，说明理由；（3）在（2）的条件下，若点C关于直线BP的对称点C′恰好落在该抛物线的对称轴上，求此时点P的坐标．13．（1）问题：如图①，在Rt∠ABC中，AB＝AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为；（2）探索：如图②，在Rt∠ABC与Rt∠ADE中，AB＝AC，AD＝AE，将∠ADE 绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；（3）应用：如图③，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°.若BD＝9，CD＝3，求AD的长.14．如图，点A在直线l上，点Q沿着直线l以3厘米/秒的速度由点A向右运，点C在点Q右侧，动，以AQ为边作Rt∠ABQ，使∠BAQ=90°，tan∠ABQ= 34CQ=1厘米，过点C作直线m∠l，过∠ABQ的外接圆圆心O作OD∠m于点D，CD，以DE、DF为交AB右侧的圆弧于点E．在射线CD上取点F，使DF= 13邻边作矩形DEGF．设运动时间为t秒．（1）直接用含t的代数式表示BQ、DF；（2）当0＜t＜1时，求矩形DEGF的最大面积；（3）点Q在整个运动过程中，当矩形DEGF为正方形时，求t的值．15．如图，在Rt△ABC中，∠ACB=90∘，AO是△ABC的角平分线．以O为圆心，OC为半径作⊙O．（1）求证：..是⊙O的切线；，（2）已知AO交⊙O于点E，延长AO交⊙O于点D，tanD=12的值．求AEAC（3）在（2）的条件下，设⊙O的半径为3，求AB的长．16．在四边形ABCD中，对角线AC、BD相交于点O，将ΔCOD绕点O按逆时针方向旋转得到ΔC1OD1，旋转角为θ（0°＜θ＜90°），连接AC1、BD1，AC1与BD1交于点P．（1）如图1，若四边形ABCD是正方形．①求证：ΔAOC1∠ ΔBOD1．②请直接写出AC1与BD1的位置关系．（2）如图2，若四边形ABCD是菱形，AC=6，BD=9，设AC1=kBD1．判断AC1与BD1的位置关系，说明理由，并求出k的值．（3）如图3，若四边形ABCD是平行四边形，AC=5，BD=10，连接DD1，设AC1=kBD1．请直接写出k的值和AC12+(kDD1)2的值．。

安徽省2024年中考数学试卷(解析版)

2024年安徽省中考数学试卷一、选择题（本大题共10小题，每小题4分，满分40分）1．（4分）（2024•安徽）（﹣2）×3的结果是（）A．﹣5 B．1C．﹣6 D．6考点：有理数的乘法．分析：依据两数相乘同号得正，异号得负，再把肯定值相乘，可得答案．解答：解：原式=﹣2×3=﹣6．故选：C．点评：本题考查了有理数的乘法，先确定积的符号，再进行肯定值的运算．2．（4分）（2024•安徽）x2•x3=（）A．x5B．x6C．x8D．x9考点：同底数幂的乘法．分析：依据同底数幂的乘法法则，同底数幂相乘，底数不变，指数相加，即a m•a n=a m+n计算即可．解答：解：x2•x3=x2+3=x5．故选A．点评：主要考查同底数幂的乘法的性质，娴熟驾驭性质是解题的关键．3．（4分）（2024•安徽）如图，图中的几何体是圆柱沿竖直方向切掉一半后得到的，则该几何体的俯视图是（）A．B．C．D．考点：简洁几何体的三视图．分析：俯视图是从物体上面看所得到的图形．解答：解：从几何体的上面看俯视图是，故选：D．点评：本题考查了几何体的三种视图，驾驭定义是关键．留意全部的看到的棱都应表现在三视图中．4．（4分）（2024•安徽）下列四个多项式中，能因式分解的是（）A．a2+1 B．a2﹣6a+9 C．x2+5y D．x2﹣5y考点：因式分解的意义．分析：依据因式分解是把一个多项式转化成几个整式积的形式，可得答案．解答：解：A、C、D都不能把一个多项式转化成几个整式积的形式，故A、C、D不能因式分解；B、是完全平方公式的形式，故B能分解因式；故选：B．点评：本题考查了因式分解的意义，把一个多项式转化成几个整式积的形式是解题关键．5．（4分）（2024•安徽）某棉纺厂为了解一批棉花的质量，从中随机抽取了20根棉花纤维进行测量，其长度x（单位：mm）的数据分布如下表所示，则棉花纤维长度的数据在8≤x＜32这个范围的频率为（）棉花纤维长度x频数0≤x＜8 18≤x＜16 216≤x＜24 824≤x＜32 632≤x＜40 3A．0.8 B．0.7 C．0.4 D．0.2考点：频数（率）分布表．分析：求得在8≤x＜32这个范围的频数，依据频率的计算公式即可求解．解答：解：在8≤x＜32这个范围的频数是：2+8+6=16，则在8≤x＜32这个范围的频率是：=0.8．故选A．点评：本题考查了频数分布表，用到的学问点是：频率=频数÷总数．6．（4分）（2024•安徽）设n为正整数，且n＜＜n+1，则n的值为（）A．5B．6C．7D．8考点：估算无理数的大小．分析：首先得出＜＜，进而求出的取值范围，即可得出n的值．解答：解：∵＜＜，∴8＜＜9，∵n＜＜n+1，∴n=8，故选；D．点评：此题主要考查了估算无理数，得出＜＜是解题关键．7．（4分）（2024•安徽）已知x2﹣2x﹣3=0，则2x2﹣4x的值为（）A．﹣6 B．6C．﹣2或6 D．﹣2或30考点：代数式求值．分析：方程两边同时乘以2，再化出2x2﹣4x求值．解答：解：x2﹣2x﹣3=02×（x2﹣2x﹣3）=02×（x2﹣2x）﹣6=02x2﹣4x=6故选：B．点评：本题考查代数式求值，解题的关键是化出要求的2x2﹣4x．8．（4分）（2024•安徽）如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A 点与BC的中点D重合，折痕为MN，则线段BN的长为（）A．B．C．4D．5考点：翻折变换（折叠问题）．分析：设BN=x，则由折叠的性质可得DN=AN=9﹣x，依据中点的定义可得BD=3，在Rt△ABC 中，依据勾股定理可得关于x的方程，解方程即可求解．解答：解：设BN=x，由折叠的性质可得DN=AN=9﹣x，∵D是BC的中点，∴BD=3，在Rt△ABC中，x2++32=（9﹣x）2，解得x=4．故线段BN的长为4．故选：C．点评：考查了翻折变换（折叠问题），涉及折叠的性质，勾股定理，中点的定义以及方程思想，综合性较强，但是难度不大．9．（4分）（2024•安徽）如图，矩形ABCD中，AB=3，BC=4，动点P从A点动身，按A→B→C的方向在AB和BC上移动，记P A=x，点D到直线P A的距离为y，则y关于x的函数图象大致是（）A．B．C．D．考点：动点问题的函数图象．分析：①点P在AB上时，点D到AP的距离为AD的长度，②点P在BC上时，依据同角的余角相等求出∠APB=∠P AD，再利用相像三角形的列出比例式整理得到y与x的关系式，从而得解．解答：解：①点P在AB上时，0≤x≤3，点D 到AP 的距离为AD的长度，是定值4；②点P在BC上时，3＜x≤5，∵∠APB+∠BAP=90°，∠P AD+∠BAP=90°，∴∠APB=∠P AD，又∵∠B=∠DEA=90°，∴△ABP∽△DEA，∴=，即=，∴y=，纵观各选项，只有B选项图形符合．故选B．点评：本题考查了动点问题函数图象，主要利用了相像三角形的判定与性质，难点在于依据点P的位置分两种状况探讨．10．（4分）（2024•安徽）如图，正方形ABCD的对角线BD长为2，若直线l满意：①点D到直线l的距离为；②A、C两点到直线l的距离相等．则符合题意的直线l的条数为（）A．1B．2C．3D．4考点：正方形的性质．分析：连接AC与BD相交于O，依据正方形的性质求出OD=，然后依据点到直线的距离和平行线间的距离相等解答．解答：解：如图，连接AC与BD相交于O，∵正方形ABCD的对角线BD长为2，∴OD=，∴直线l∥AC并且到D的距离为，同理，在点D的另一侧还有一条直线满意条件，故共有2条直线l．故选B．点评：本题考查了正方形的性质，主要利用了正方形的对角线相互垂直平分，点D到O的距离小于是本题的关键．czsx二、填空题（本大题共4小题，每小题5分，满分20分）11．（5分）（2024•安徽）据报载，2024年我国将发展固定宽带接入新用户25000000户，其中25000000用科学记数法表示为 2.5×107．考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的肯定值与小数点移动的位数相同．当原数肯定值＞1时，n是正数；当原数的肯定值＜1时，n是负数．解答：解：将25000000用科学记数法表示为2.5×107户．故答案为：2.5×107．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．12．（5分）（2024•安徽）某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y（元）关于x的函数关系式为y=a（1+x）2．考点：依据实际问题列二次函数关系式．分析：由一月份新产品的研发资金为a元，依据题意可以得到2月份研发资金为a×（1+x），而三月份在2月份的基础上又增长了x，那么三月份的研发资金也可以用x表示出来，由此即可确定函数关系式．解答：解：∵一月份新产品的研发资金为a元，2月份起，每月新产品的研发资金与上月相比增长率都是x，∴2月份研发资金为a×（1+x），∴三月份的研发资金为y=a×（1+x）×（1+x）=a（1+x）2．故填空答案：a（1+x）2．点评：此题主要考查了依据实际问题二次函数列解析式，此题是平均增长率的问题，可以用公式a（1±x）2=b来解题．13．（5分）（2024•安徽）方程=3的解是x=6．考点：解分式方程．专题：计算题．分析：分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．解答：解：去分母得：4x﹣12=3x﹣6，解得：x=6，经检验x=6是分式方程的解．故答案为：6．点评：此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程肯定留意要验根．14．（5分）（2024•安徽）如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中肯定成立的是①②④．（把全部正确结论的序号都填在横线上）①∠DCF=∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．考点：平行四边形的性质；全等三角形的判定与性质；直角三角形斜边上的中线．分析：分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF （ASA），得出对应线段之间关系进而得出答案．解答：解：①∵F是AD的中点，∴AF=FD，∵在▱ABCD中，AD=2AB，∴AF=FD=CD，∴∠DFC=∠DCF，∵AD∥BC，∴∠DFC=∠FCB，∴∠DCF=∠BCF，∴∠DCF=∠BCD，故此选项正确；延长EF，交CD延长线于M，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠A=∠MDE，∵F为AD中点，∴AF=FD，在△AEF和△DFM中，，∴△AEF≌△DMF（ASA），∴FE=MF，∠AEF=∠M，∵CE⊥AB，∴∠AEC=90°，∴∠AEC=∠ECD=90°，∵FM=EF，∴FC=FM，故②正确；③∵EF=FM，∴S△EFC=S△CFM，∵MC＞BE，∴S△BEC＜2S△EFC故S△BEC=2S△CEF错误；④设∠FEC=x，则∠FCE=x，∴∠DCF=∠DFC=90°﹣x，∴∠EFC=180°﹣2x，∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x，∵∠AEF=90°﹣x，∴∠DFE=3∠AEF，故此选项正确．故答案为：①②④．点评：此题主要考查了平行四边形的性质以及全等三角形的判定与性质等学问，得出△AEF≌△DME是解题关键．三、（本大题共2小题，每小题8分，满分16分）15．（8分）（2024•安徽）计算：﹣|﹣3|﹣（﹣π）0+2024．考点：实数的运算；零指数幂．专题：计算题．分析：原式第一项利用平方根定义化简，其次项利用肯定值的代数意义化简，第三项利用零指数幂法则计算，计算即可得到结果．解答：解：原式=5﹣3﹣1+2024=2024．点评：此题考查了实数的运算，娴熟驾驭运算法则是解本题的关键．16．（8分）（2024•安徽）视察下列关于自然数的等式：32﹣4×12=5 ①52﹣4×22=9 ②72﹣4×32=13 ③…依据上述规律解决下列问题：（1）完成第四个等式：92﹣4×42=17；（2）写出你猜想的第n个等式（用含n的式子表示），并验证其正确性．考点：规律型：数字的改变类；完全平方公式．分析：由①②③三个等式可得，被减数是从3起先连续奇数的平方，减数是从1起先连续自然数的平方的4倍，计算的结果是被减数的底数的2倍减1，由此规律得出答案即可．解答：解：（1）32﹣4×12=5 ①52﹣4×22=9 ②72﹣4×32=13 ③…所以第四个等式：92﹣4×42=17；（2）第n个等式为：（2n+1）2﹣4n2=2（2n+1）﹣1，左边=（2n+1）2﹣4n2=4n2+4n+1﹣4n2=4n+1，右边=2（2n+1）﹣1=4n+2﹣1=4n+1．左边=右边∴（2n+1）2﹣4n2=2（2n+1）﹣1．点评：此题考查数字的改变规律，找出数字之间的运算规律，利用规律解决问题．四、（本大题共2小题，每小题8分，满分16分）17．（8分）（2024•安徽）如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．（1）将△ABC向上平移3个单位得到△A1B1C1，请画出△A1B1C1；（2）请画一个格点△A2B2C2，使△A2B2C2∽△ABC，且相像比不为1．考点：作图—相像变换；作图－平移变换．分析：（1）利用平移的性质得出对应点位置，进而得出答案；（2）利用相像图形的性质，将各边扩大2倍，进而得出答案．解答：解：（1）如图所示：△A1B1C1即为所求；（2）如图所示：△A2B2C2即为所求．点评：此题主要考查了相像变换和平移变换，得出变换后图形对应点位置是解题关键．18．（8分）（2024•安徽）如图，在同一平面内，两条平行高速马路l1和l2间有一条“Z”型道路连通，其中AB段与高速马路l1成30°角，长为20km；BC段与AB、CD段都垂直，长为10km，CD段长为30km，求两高速马路间的距离（结果保留根号）．考点：解直角三角形的应用．分析：过B点作BE⊥l1，交l1于E，CD于F，l2于G．在Rt△ABE中，依据三角函数求得BE，在Rt△BCF中，依据三角函数求得BF，在Rt△DFG中，依据三角函数求得FG，再依据EG=BE+BF+FG即可求解．解答：解：过B点作BE⊥l1，交l1于E，CD于F，l2于G．在Rt△ABE中，BE=AB•sin30°=20×=10km，在Rt△BCF中，BF=BC÷cos30°=10÷=km，CF=BF•sin30°=×=km，DF=CD﹣CF=（30﹣）km，在Rt△DFG中，FG=DF•sin30°=（30﹣）×=（15﹣）km，∴EG=BE+BF+FG=（25+5）km．故两高速马路间的距离为（25+5）km．点评：此题考查了解直角三角形的应用，主要是三角函数的基本概念及运算，关键把实际问题转化为数学问题加以计算．五、（本大题共2小题，每小题10分，满分20分）19．（10分）（2024•安徽）如图，在⊙O中，半径OC与弦AB垂直，垂足为E，以OC为直径的圆与弦AB的一个交点为F，D是CF延长线与⊙O的交点．若OE=4，OF=6，求⊙O的半径和CD的长．考点：垂径定理；勾股定理；圆周角定理；相像三角形的判定与性质．专题：计算题．分析：由OE⊥AB得到∠OEF=90°，再依据圆周角定理由OC为小圆的直径得到∠OFC=90°，则可证明Rt△OEF∽Rt△OFC，然后利用相像比可计算出⊙O的半径OC=9；接着在Rt△OCF中，依据勾股定理可计算出C=3，由于OF⊥CD，依据垂径定理得CF=DF，所以CD=2CF=6．解答：解：∵OE⊥AB，∴∠OEF=90°，∵OC为小圆的直径，∴∠OFC=90°，而∠EOF=∠FOC，∴Rt△OEF∽Rt△OFC，∴OE：OF=OF：OC，即4：6=6：OC，∴⊙O的半径OC=9；在Rt△OCF中，OF=6，OC=9，∴CF==3，∵OF⊥CD，∴CF=DF，∴CD=2CF=6．点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理、圆周角定理和相像三角形的判定与性质．20．（10分）（2024•安徽）2024年某企业按餐厨垃圾处理费25元/吨、建筑垃圾处理费16元/吨的收费标准，共支付餐厨和建筑垃圾处理费5200元．从2024年元月起，收费标准上调为：餐厨垃圾处理费100元/吨，建筑垃圾处理费30元/吨．若该企业2024年处理的这两种垃圾数量与2024年相比没有改变，就要多支付垃圾处理费8800元．（1）该企业2024年处理的餐厨垃圾和建筑垃圾各多少吨？（2）该企业安排2024年将上述两种垃圾处理总量削减到240吨，且建筑垃圾处理量不超过餐厨垃圾处理量的3倍，则2024年该企业最少须要支付这两种垃圾处理费共多少元？考点：一次函数的应用；二元一次方程组的应用；一元一次不等式的应用．分析：（1）设该企业2024年处理的餐厨垃圾x吨，建筑垃圾y吨，依据等量关系式：餐厨垃圾处理费25元/吨×餐厨垃圾吨数+建筑垃圾处理费16元/吨×建筑垃圾吨数=总费用，列方程．（2）设该企业2024年处理的餐厨垃圾x吨，建筑垃圾y吨，须要支付这两种垃圾处理费共a元，先求出x的范围，由于a的值随x的增大而增大，所以当x=60时，a值最小，代入求解．解答：解：（1）设该企业2024年处理的餐厨垃圾x吨，建筑垃圾y吨，依据题意，得，解得．答：该企业2024年处理的餐厨垃圾80吨，建筑垃圾200吨；（2）设该企业2024年处理的餐厨垃圾x吨，建筑垃圾y吨，须要支付这两种垃圾处理费共a元，依据题意得，，解得x≥60．a=100x+30y=100x+30（240﹣x）=70x+7200，由于a的值随x的增大而增大，所以当x=60时，a值最小，最小值=70×60+7200=11400（元）．答：2024年该企业最少须要支付这两种垃圾处理费共11400元．点评：本题主要考查了二元一次方程组及一元一次不等式的应用，找准等量关系正确的列出方程是解决本题的关键；六、（本题满分12分）21．（12分）（2024•安徽）如图，管中放置着三根同样的绳子AA1、BB1、CC1；（1）小明从这三根绳子中随机选一根，恰好选中绳子AA1的概率是多少？（2）小明先从左端A、B、C三个绳头中随机选两个打一个结，再从右端A1、B1、C1三个绳头中随机选两个打一个结，求这三根绳子能连结成一根长绳的概率．考点：列表法与树状图法．专题：计算题．分析：（1）三根绳子选择一根，求出所求概率即可；（2）列表得出全部等可能的状况数，找出这三根绳子能连结成一根长绳的状况数，即可求出所求概率．解答：解：（1）三种等可能的状况数，则恰好选中绳子AA1的概率是；（2）列表如下：A B CA1（A，A1）（B，A1）（C，A1）B1（A，B1）（B，B1）（C，B1）C1（A，C1）（B，C1）（C，C1）全部等可能的状况有9种，其中这三根绳子能连结成一根长绳的状况有6种，则P==．点评：此题考查了列表法与树状图法，用到的学问点为：概率=所求状况数与总状况数之比．七、（本题满分12分）22．（12分）（2024•安徽）若两个二次函数图象的顶点、开口方向都相同，则称这两个二次函数为“同簇二次函数”．（1）请写出两个为“同簇二次函数”的函数；（2）已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5，其中y1的图象经过点A （1，1），若y1+y2与y1为“同簇二次函数”，求函数y2的表达式，并求出当0≤x≤3时，y2的最大值．考点：二次函数的性质；二次函数的最值．专题：新定义．分析：（1）只需任选一个点作为顶点，同号两数作为二次项的系数，用顶点式表示两个为“同簇二次函数”的函数表达式即可．（2）由y1的图象经过点A（1，1）可以求出m的值，然后依据y1+y2与y1为“同簇二次函数”就可以求出函数y2的表达式，然后将函数y2的表达式转化为顶点式，在利用二次函数的性质就可以解决问题．解答：解：（1）设顶点为（h，k）的二次函数的关系式为y=a（x﹣h）2+k，当a=2，h=3，k=4时，二次函数的关系式为y=2（x﹣3）2+4．∵2＞0，∴该二次函数图象的开口向上．当a=3，h=3，k=4时，二次函数的关系式为y=3（x﹣3）2+4．∵3＞0，∴该二次函数图象的开口向上．∵两个函数y=2（x﹣3）2+4与y=3（x﹣3）2+4顶点相同，开口都向上，∴两个函数y=2（x﹣3）2+4与y=3（x﹣3）2+4是“同簇二次函数”．∴符合要求的两个“同簇二次函数”可以为：y=2（x﹣3）2+4与y=3（x﹣3）2+4．（2）∵y1的图象经过点A（1，1），∴2×12﹣4×m×1+2m2+1=1．整理得：m2﹣2m+1=0．解得：m1=m2=1．∴y1=2x2﹣4x+3=2（x﹣1）2+1．∴y1+y2=2x2﹣4x+3+ax2+bx+5=（a+2）x2+（b﹣4）x+8∵y1+y2与y1为“同簇二次函数”，∴y1+y2=（a+2）（x﹣1）2+1=（a+2）x2﹣2（a+2）x+（a+2）+1．其中a+2＞0，即a＞﹣2．∴．解得：．∴函数y2的表达式为：y2=5x2﹣10x+5．∴y2=5x2﹣10x+5=5（x﹣1）2．∴函数y2的图象的对称轴为x=1．∵5＞0，∴函数y2的图象开口向上．①当0≤x≤1时，∵函数y2的图象开口向上，∴y2随x的增大而减小．∴当x=0时，y2取最大值，最大值为5（0﹣1）2=5．②当1＜x≤3时，∵函数y2的图象开口向上，∴y2随x的增大而增大．∴当x=3时，y2取最大值，最大值为5（3﹣1）2=20．综上所述：当0≤x≤3时，y2的最大值为20．点评：本题考查了求二次函数表达式以及二次函数一般式与顶点式之间相互转化，考查了二次函数的性质（开口方向、增减性），考查了分类探讨的思想，考查了阅读理解实力．而对新定义的正确理解和分类探讨是解决其次小题的关键．八、（本题满分14分）23．（14分）（2024•安徽）如图1，正六边形ABCDEF的边长为a，P是BC边上一动点，过P作PM∥AB交AF于M，作PN∥CD交DE于N．（1）①∠MPN=60°；②求证：PM+PN=3a；（2）如图2，点O是AD的中点，连接OM、ON，求证：OM=ON；（3）如图3，点O是AD的中点，OG平分∠MON，推断四边形OMGN是否为特别四边形？并说明理由．考点：四边形综合题．分析：（1）①运用∠MPN=180°﹣∠BPM﹣∠NPC求解，②作AG⊥MP交MP于点G，BH⊥MP于点H，CL⊥PN于点L，DK⊥PN于点K，利用MP+PN=MG+GH+HP+PL+LK+KN求解，（2）连接OE，由△OMA≌△ONE证明，（3）连接OE，由△OMA≌△ONE，再证出△GOE≌△NOD，由△ONG是等边三角形和△MOG是等边三角形求出四边形MONG是菱形．，解答：解：（1）①∵四边形ABCDEF是正六边形，∴∠A=∠B=∠C=∠D=∠E=∠F=120°又∴PM∥AB，PN∥CD，∴∠BPM=60°，∠NPC=60°，∴∠MPN=180°﹣∠BPM﹣∠NPC=180°﹣60°﹣60°=60°，故答案为；60°．②如图1，作AG⊥MP交MP于点G，BH⊥MP于点H，CL⊥PN于点L，DK⊥PN 于点K，MP+PN=MG+GH+HP+PL+LK+KN∵正六边形ABCDEF中，PM∥AB，作PN∥CD，∵∠AMG=∠BPH=∠CPL=∠DNK=60°，∴GM=AM，HL=BP，PL=PM，NK=ND，∵AM=BP，PC=DN，∴MG+HP+PL+KN=a，GH=LK=a，∴MP+PN=MG+GH+HP+PL+LK+KN=3a．（2）如图2，连接OE，∵四边形ABCDEF是正六边形，AB∥MP，PN∥DC，∴AM=BP=EN，又∵∠MAO=∠NOE=60°，OA=OE，在△ONE和△OMA中，∴△OMA≌△ONE（SAS）∴OM=ON．（3）如图3，连接OE，由（2）得，△OMA≌△ONE∴∠MOA=∠EON，∵EF∥AO，AF∥OE，∴四边形AOEF是平行四边形，∴∠AFE=∠AOE=120°，∴∠MON=120°，∴∠GON=60°，∵∠GON=60°﹣∠EON，∠DON=60°﹣∠EON，∴∠GOE=∠DON，∵OD=OE，∠ODN=∠OEG，在△GOE和∠DON中，∴△GOE≌△NOD（ASA），∴ON=OG，又∵∠GON=60°，∴△ONG是等边三角形，∴ON=NG，又∵OM=ON，∠MOG=60°，∴△MOG是等边三角形，∴MG=GO=MO，∴MO=ON=NG=MG，∴四边形MONG是菱形．点评：本题主要考查了四边形的综合题，解题的关键是恰当的作出协助线，依据三角形全等找出相等的线段．- 21 -。

中考数学复习----勾股定理知识点总结与专项练习题(含答案解)

中考数学复习----勾股定理知识点总结与专项练习题（含答案解）知识点总结1. 勾股民定理的内容：在直角三角形中，两直角边的平方的和等于斜边的平方。

若直角三角形的两直角边是b a ，，斜边是c ，则222b a c +=。

2. 勾股数：满足直角三角形勾股定理的三个正整数是一组勾股数。

3. 勾股定理的逆定理：若三角形的三条边分别是c b a ，，，且满足222b a c +=，则三角形是直角三角形，且∠C 是直角。

4. 特殊三角形三边的比：①含30°的直角三角形三边的比例为（从小打大）：2:3:1。

②45°的等腰直角三角形三边的比例为（从小到大）：2:1:1。

5. 两点间的距离公式：若点()11y x A ，与点()22y x B ，，则线段AB 的长度为：()()221221y y x x AB −+−=。

练习题 1、（2022•攀枝花）如图1是第七届国际数学教育大会（ICME ）的会徽，在其主体图案中选择两个相邻的直角三角形，恰好能够组合得到如图2所示的四边形OABC ．若OC ＝，BC ＝1，∠AOB ＝30°，则OA 的值为（）A ．3B ．23C ．2D ．1【分析】根据勾股定理和含30°角的直角三角形的性质即可得到结论．【解答】解：∵∠OBC＝90°，OC＝，BC＝1，∴OB＝＝＝2，∵∠A＝90°，∠AOB＝30°，∴AB＝OB＝1，∴OA＝＝＝，故选：A．2、（2022•荆门）如图，一座金字塔被发现时，顶部已经荡然无存，但底部未曾受损．已知该金字塔的下底面是一个边长为120m的正方形，且每一个侧面与地面成60°角，则金字塔原来高度为（）A．120m B．603m C．605m D．1203m【分析】根据底部是边长为120m的正方形求出BC的长，再由含30°角的直角三角形的性质求解AB的长，利用勾股定理求出AC的长即可．【解答】解：如图，∵底部是边长为120m的正方形，∴BC＝×120＝60m，∵AC⊥BC，∠ABC＝60°，∴∠BAC＝30°，∴AB ＝2BC ＝120m ，∴AC ＝＝m ．故选：B ．3、（2022•百色）活动探究：我们知道，已知两边和其中一边的对角对应相等的两个三角形不一定全等．如已知△ABC 中，∠A ＝30°，AC ＝3，∠A 所对的边为，满足已知条件的三角形有两个（我们发现其中如图的△ABC 是一个直角三角形），则满足已知条件的三角形的第三边长为（）A ．23B ．23﹣3C ．23或3D ．23或23﹣3【分析】根据题意知，CD ＝CB ，作CH ⊥AB 于H ，再利用含30°角的直角三角形的性质可得CH ，AH 的长，再利用勾股定理求出BH ，从而得出答案．【解答】解：如图，CD ＝CB ，作CH ⊥AB 于H ，∴DH ＝BH ，∵∠A ＝30°，∴CH ＝AC ＝，AH ＝CH ＝，在Rt △CBH 中，由勾股定理得BH ＝＝，∴AB ＝AH +BH ＝＝2，AD ＝AH ﹣DH ＝＝，故选：C ． 4、（2022•荆州）如图，在Rt △ABC 中，∠ACB ＝90°，通过尺规作图得到的直线MN 分别交AB ，AC 于D ，E ，连接CD ．若CE ＝31AE ＝1，则CD ＝．【分析】如图，连接BE ，根据作图可知MN 为AB 的垂直平分线，从而得到AE ＝BE ＝3，然后利用勾股定理求出BC ，AB ，最后利用斜边上的中线的性质即可求解．【解答】解：如图，连接BE ，∵CE ＝AE ＝1，∴AE ＝3，AC ＝4，而根据作图可知MN 为AB 的垂直平分线，∴AE ＝BE ＝3，在Rt △ECB 中，BC ＝＝2，∴AB ＝＝2， ∵CD 为直角三角形ABC 斜边上的中线，∴CD ＝AB ＝．故答案为：． 5、（2022•广元）如图，在△ABC 中，BC ＝6，AC ＝8，∠C ＝90°，以点B 为圆心，BC 长为半径画弧，与AB 交于点D ，再分别以A 、D 为圆心，大于21AD 的长为半径画弧，两弧交于点M 、N ，作直线MN ，分别交AC 、AB 于点E 、F ，则AE 的长度为（）A ．25B ．3C ．22D ．310 【分析】利用勾股定理求出AB ，再利用相似三角形的性质求出AE 即可．【解答】解：在Rt △ABC 中，BC ＝6，AC ＝8，∴AB ＝＝＝10， ∵BD ＝CB ＝6，∴AD ＝AB ﹣BC ＝4，由作图可知EF 垂直平分线段AD ，∴AF ＝DF ＝2，∵∠A ＝∠A ，∠AFE ＝∠ACB ＝90°，∴△AFE ∽△ACB ，∴＝， ∴＝，∴AE ＝，故选：A ．6、（2022•湖州）在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．如图，在6×6的正方形网格图形ABCD 中，M ，N 分别是AB ，BC 上的格点，BM ＝4，BN ＝2．若点P 是这个网格图形中的格点，连结PM ，PN ，则所有满足∠MPN ＝45°的△PMN 中，边PM 的长的最大值是（）A ．42B ．6C ．210D ．35【分析】在网格中，以MN 为直角边构造一个等腰直角三角形，使PM 最长，利用勾股定理求出即可．【解答】解：如图所示：∵BM＝NC＝4，BN＝CP＝2，且∠B＝∠C＝90°，∴△BMN≌△CNP（SAS），∴MN＝NP，∠BMN＝∠CNP，∵∠BMN+∠BNM＝90°，∴∠BNM+∠CNP＝90°，∴∠MNP＝90°，∴△NMP为等腰直角三角形，此时PM最长，在Rt△BMN和Rt△NCP中，根据勾股定理得：MN＝NP＝＝2，则PM＝＝2．故选：C．7、（2022•金华）如图是城市某区域的示意图，建立平面直角坐标系后，学校和体育场的坐标分别是（3，1），（4，﹣2），下列各地点中，离原点最近的是（）A．超市B．医院C．体育场D．学校【分析】根据题意可以画出相应的平面直角坐标系，然后根据勾股定理，可以得到点O到超市、学校、体育场、医院的距离，再比较大小即可．【解答】解：如右图所示，点O到超市的距离为：＝，点O到学校的距离为：＝，点O到体育场的距离为：＝，点O到医院的距离为：＝，∵＜＝＜，∴点O到超市的距离最近，故选：A．8、（2022•舟山）如图，在Rt△ABC和Rt△BDE中，∠ABC＝∠BDE＝90°，点A在边DE 的中点上，若AB＝BC，DB＝DE＝2，连结CE，则CE的长为（）A．14B．15C．4D．17【分析】方法一：根据题意先作出合适的辅助线，然后根据勾股定理可以得到AB和BC的长，根据等面积法可以求得EG的长，再根据勾股定理求得EF的长，最后计算出CE的长即可．方法二：延长ED到F，使得DE＝DF，连接CF，BF，然后根据全等三角形的判定和性质，以及勾股定理，可以求得CE的长．【解答】解：方法一：作EF⊥CB交CB的延长线于点F，作EG⊥BA交BA的延长线于点G，∵DB＝DE＝2，∠BDE＝90°，点A是DE的中点，∴BE＝＝＝2，DA＝EA＝1，∴AB＝＝＝，∵AB＝BC，∴BC＝，∵＝，∴，解得EG＝，∵EG⊥BG，EF⊥BF，∠ABF＝90°，∴四边形EFBG是矩形，∴EG＝BF＝，∵BE＝2，BF＝，∴EF＝＝＝，CF＝BF+BC＝+＝，∵∠EFC＝90°，∴EC＝＝＝，故选：D．方法二：延长ED到F，使得DE＝DF，连接CF，BF，如图所示，∵BD＝DE＝2，∠BDE＝90°，∴∠BDE＝∠BDF＝90°，EF＝4，∴△BDE≌△BDF（SAS），∴BE＝BF，∠BEA＝∠BF A＝45°，∵∠EBA+∠ABF＝90°，∠ABF+∠FBC＝90°，∴∠EBA＝∠FBC，∵BE＝BF，BA＝BC，∴△EBA≌△FBC（SAS），∴∠BEA＝∠BFC＝45°，AE＝CF，∴∠CFE＝∠BFC+∠AFB＝90°，∵点A为DE的中点，∴AE＝1，∴CF＝1，∴EC＝＝＝，故选：D．9、（2022•成都）若一个直角三角形两条直角边的长分别是一元二次方程x2﹣6x+4＝0的两个实数根，则这个直角三角形斜边的长是．【分析】设直角三角形两条直角边分别为a、b，斜边为c，由一元二次方程根与系数的关系可得a+b＝6，ab＝4，再由勾股定理即可求出斜边长．【解答】解：设直角三角形两条直角边分别为a、b，斜边为c，∵直角三角形两条直角边的长分别是一元二次方程x2﹣6x+4＝0的两个实数根，∴a+b＝6，ab＝4，∴斜边c＝＝＝＝2，故答案为：2．10、（2022•南充）如图，在Rt△ABC中，∠C＝90°，∠BAC的平分线交BC于点D，DE ∥AB，交AC于点E，DF⊥AB于点F，DE＝5，DF＝3，则下列结论错误的是（）A．BF＝1B．DC＝3C．AE＝5D．AC＝9【分析】根据角平分线的性质和和勾股定理，可以求得CD和CE的长，再根据平行线的性质，即可得到AE的长，从而可以判断B和C，然后即可得到AC的长，即可判断D；再根据全等三角形的判定和性质即可得到BF的长，从而可以判断A．【解答】解：∵AD平分∠BAC，∠C＝90°，DF⊥AB，∴∠1＝∠2，DC＝FD，∠C＝∠DFB＝90°，∵DE∥AB，∴∠2＝∠3，∴∠1＝∠3，∴AE＝DE，∵DE＝5，DF＝3，∴AE＝5，CD＝3，故选项B、C正确；∴CE＝＝4，∴AC＝AE+EC＝5+4＝9，故选项D正确；∵DE∥AB，∠DFB＝90°，∴∠EDF＝∠DFB＝90°，∴∠CDE+∠FDB＝90°，∵∠CDE+∠DEC＝90°，∴∠DEC＝∠FDB，∵tan∠DEC＝，tan∠FDB＝，∴，解得BF＝，故选项A错误；故选：A．11、（2022•通辽）在Rt△ABC中，∠C＝90°，有一个锐角为60°，AB＝6，若点P在直线AB上（不与点A，B重合），且∠PCB＝30°，则AP的长为．【分析】题中60°的锐角，可能是∠A也可能是∠B；∠PCB＝30°可以分为点P在在线段AB上和P在线段AB的延长线上两种情况；直角三角形中30°角所对的直角边等于斜边的一半，同时借助勾股定理求得AP的长度．【解答】解：当∠A＝30°时，∵∠C＝90°，∠A＝30°，∴∠CBA＝60°，BC＝AB＝×6＝3，由勾股定理得，AC＝3，①点P在线段AB上，∵∠PCB＝30°，∠CBA＝60°∴∠CPB＝90°，∴∠CP A＝90°，在Rt△ACP中，∠A＝30°，∴PC＝AC＝×3＝．∴在Rt△APC中，由勾股定理得AP＝．②点P在线段AB的延长线上，∵∠PCB＝30°，∴∠ACP＝90°+30°＝120°，∵∠A＝30°，∴∠CP A＝30°．∵∠PCB＝30°，∴∠PCB＝∠CP A，∴BP＝BC＝3，∴AP＝AB+BP＝6+3＝9．当∠ABC＝30°时，∵∠C＝90°，∠ABC＝30°，∴∠A＝60°，AC＝AB＝×6＝3，由勾股定理得，BC＝3，①点P在线段AB上，∵∠PCB＝30°，∴∠ACP＝60°，∴△ACP是等边三角形∴AP＝AC＝3．②点P在线段AB的延长线上，∵∠PCB＝30°，∠ABC＝30°，∴CP∥AP这与CP与AP交于点P矛盾，舍去．综上所得，AP的长为，9或3．故答案为：，9或3．12、（2022•武汉）如图，在Rt△ABC中，∠ACB＝90°，AC＞BC，分别以△ABC的三边为边向外作三个正方形ABHL，ACDE，BCFG，连接DF．过点C作AB的垂线CJ，垂足为J，分别交DF，LH于点I，K．若CI＝5，CJ＝4，则四边形AJKL的面积是．【分析】过点D作DM⊥CI于点M，过点F作FN⊥CI于点N，由正方形的性质可证得△ACJ≌△CDM，△BCJ≌△CFN，可得DM＝CJ，FN＝CJ，可证得△DMI≌△FNI，由直角三角形斜边上的中线的性质可得DI＝FI＝CI，由勾股定理可得MI，NI，从而可得CN，可得BJ与AJ，即可求解．【解答】解：过点D作DM⊥CI，交CI的延长线于点M，过点F作FN⊥CI于点N，∵△ABC为直角三角形，四边形ACDE，BCFG为正方形，过点C作AB的垂线CJ，CJ＝4，∴AC＝CD，∠ACD＝90°，∠AJC＝∠CMD＝90°，∠CAJ+∠ACJ＝90°，BC＝CF，∠BCF＝90°，∠CNF＝∠BJC＝90°，∠FCN+∠CFN＝90°，∴∠ACJ+∠DCM＝90°，∠FCN+∠BCJ＝90°，∴∠CAJ＝∠DCM，∠BCJ＝∠CFN，∴△ACJ≌△CDM（AAS），△BCJ≌△CFN（AAS），∴AJ＝CM，DM＝CJ＝4，BJ＝CN，NF＝CJ＝4，∴DM＝NF，∴△DMI≌△FNI（AAS），∴DI＝FI，MI＝NI，∵∠DCF＝90°，∴DI＝FI＝CI＝5，在Rt△DMI中，由勾股定理可得：MI＝＝＝3，∴NI＝MI＝3，∴AJ＝CM＝CI+MI＝5+3＝8，BJ＝CN＝CI﹣NI＝5﹣3＝2，∴AB＝AJ+BJ＝8+2＝10，∵四边形ABHL为正方形，∴AL＝AB＝10，∵四边形AJKL为矩形，∴四边形AJKL的面积为：AL•AJ＝10×8＝80，故答案为：80．13、（2022•内江）勾股定理被记载于我国古代的数学著作《周髀算经》中，汉代数学家赵爽为了证明勾股定理，创制了一幅如图①所示的“弦图”，后人称之为“赵爽弦图”．图②由弦图变化得到，它是由八个全等的直角三角形拼接而成．记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3．若正方形EFGH的边长为4，则S1+S2+S3＝．【分析】由勾股定理和乘法公式完成计算即可．【解答】解：设八个全等的直角三角形的长直角边为a，短直角边是b，则：S1＝（a+b）2，S2＝42＝16，S3＝（a﹣b）2，且：a2+b2＝EF2＝16，∴S1+S2+S3＝（a+b）2+16+（a﹣b）2＝2（a2+b2）+16＝2×16+16＝48．故答案为：48．14、（2022•永州）我国古代数学家赵爽创制了一幅“赵爽弦图”，极富创新意识地给出了勾股定理的证明．如图所示，“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．若大正方形的面积是25，小正方形的面积是1，则AE＝．【分析】根据题意得出AB＝BC＝CD＝DA＝5，EF＝FG＝GH＝HE＝1，设AF＝DE＝CH ＝BG＝x，结合图形得出AE＝x﹣1，利用勾股定理列方程求解．【解答】解：∵大正方形的面积是25，小正方形的面积是1，∴AB＝BC＝CD＝DA＝5，EF＝FG＝GH＝HE＝1，根据题意，设AF＝DE＝CH＝BG＝x，则AE＝x﹣1，在Rt△AED中，AE2+ED2＝AD2，∴（x﹣1）2+x2＝52，解得：x1＝4，x2＝﹣3（舍去），∴x﹣1＝3，故答案为：3．15、（2022•湖北）勾股定理最早出现在商高的《周髀算经》：“勾广三，股修四，径隅五”．观察下列勾股数：3，4，5；5，12，13；7，24，25；…，这类勾股数的特点是：勾为奇数，弦与股相差为1．柏拉图研究了勾为偶数，弦与股相差为2的一类勾股数，如：6，8，10；8，15，17；…，若此类勾股数的勾为2m（m≥3，m为正整数），则其弦是（结果用含m的式子表示）．【分析】根据题意得2m为偶数，设其股是a，则弦为a+2，根据勾股定理列方程即可得到结论．【解答】解：∵m为正整数，∴2m为偶数，设其股是a，则弦为a+2，根据勾股定理得，（2m）2+a2＝（a+2）2，解得a＝m2﹣1，∴弦是a+2＝m2﹣1+2＝m2+1，故答案为：m2+1．16、（2022•常州）如图，将一个边长为20cm的正方形活动框架（边框粗细忽略不计）扭动成四边形ABCD，对角线是两根橡皮筋，其拉伸长度达到36cm时才会断裂．若∠BAD＝60°，则橡皮筋AC断裂（填“会”或“不会”，参考数据：3≈1.732）．【分析】设AC与BD相交于点O，根据菱形的性质可得AC⊥BD，AC＝2AO，OD＝BD，AD＝AB＝20cm，从而可得△ABD是等边三角形，进而可得BD＝20cm，然后再在Rt△ADO中，利用勾股定理求出AO，从而求出AC的长，即可解答．【解答】解：设AC与BD相交于点O，∵四边形ABCD是菱形，∴AC⊥BD，AC＝2AO，OD＝BD，AD＝AB＝20cm，∵∠BAD＝60°，∴△ABD是等边三角形，∴BD＝AB＝20cm，∴DO＝BD＝10（cm），在Rt△ADO中，AO＝＝＝10（cm），∴AC＝2AO＝20≈34.64（cm），∵34.64cm＜36cm，∴橡皮筋AC不会断裂，故答案为：不会．17、（2022•常州）如图，在Rt△ABC中，∠C＝90°，AC＝9，BC＝12．在Rt△DEF中，∠F＝90°，DF＝3，EF＝4．用一条始终绷直的弹性染色线连接CF，Rt△DEF从起始位置（点D与点B重合）平移至终止位置（点E与点A重合），且斜边DE始终在线段AB上，则Rt△ABC的外部被染色的区域面积是．【分析】如图，连接CF交AB于点M，连接CF′交AB于点N，过点F作FG⊥AB于点H，过点F′作F′H⊥AB于点H，连接FF′，则四边形FGHF′是矩形，Rt△ABC的外部被染色的区域是梯形MFF′N．求出梯形的上下底以及高，可得结论．【解答】解：如图，连接CF交AB于点M，连接CF′交AB于点N，过点F作FG⊥AB于点H，过点F′作F′H⊥AB于点H，连接FF′，则四边形FGHF′是矩形，Rt△ABC的外部被染色的区域是梯形MFF′N．在Rt△DEF中，DF＝3，EF＝4，∴DE＝＝＝5，在Rt△ABC中，AC＝9，BC＝12，∴AB＝＝＝15，∵•DF•EF＝•DE•GF，∴FG＝，∴BG＝＝＝，∴GE＝BE﹣BG＝，AH＝GE＝，∴F′H＝FG＝，∴FF′＝GH＝AB﹣BG﹣AH＝15﹣5＝10，∵BF∥AC，∴＝＝，∴BM＝AB＝，同法可证AN＝AB＝，∴MN＝15﹣﹣＝，∴Rt△ABC的外部被染色的区域的面积＝×（10+）×＝21，故答案为：21．18、（2022•泰州）如图所示的象棋盘中，各个小正方形的边长均为1．“马”从图中的位置出发，不走重复路线，按照“马走日”的规则，走两步后的落点与出发点间的最短距离为．【分析】根据勾股定理即可得到结论．【解答】解：如图，第一步到①，第二步到②，故走两步后的落点与出发点间的最短距离为＝，故答案为：．。

中考数学专题复习《利用勾股定理求最短路径》测试卷-附带答案

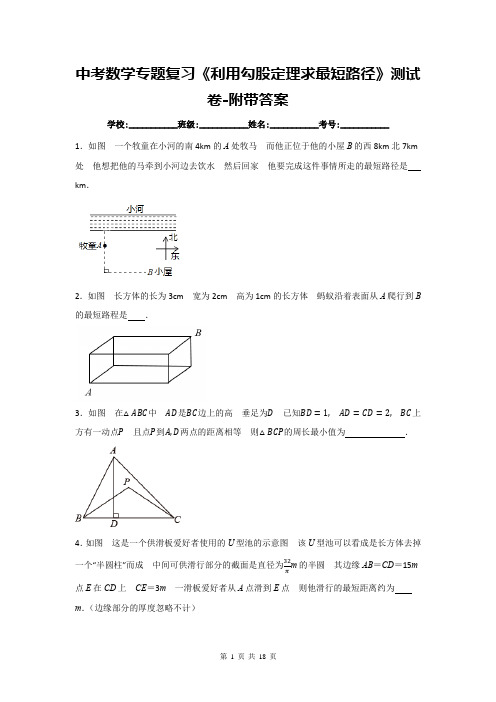
中考数学专题复习《利用勾股定理求最短路径》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________1．如图一个牧童在小河的南4km的A处牧马而他正位于他的小屋B的西8km北7km 处他想把他的马牵到小河边去饮水然后回家他要完成这件事情所走的最短路径是km．2．如图长方体的长为3cm 宽为2cm 高为1cm的长方体蚂蚁沿着表面从A爬行到B 的最短路程是．3．如图在△ABC中AD是BC边上的高垂足为D已知BD=1,AD=CD=2,BC上方有一动点P且点P到A,D两点的距离相等则△BCP的周长最小值为．4．如图这是一个供滑板爱好者使用的U型池的示意图该U型池可以看成是长方体去掉m的半圆其边缘AB＝CD＝15m 一个“半圆柱”而成中间可供滑行部分的截面是直径为32π点E在CD上CE＝3m一滑板爱好者从A点滑到E点则他滑行的最短距离约为m．（边缘部分的厚度忽略不计）5．如图四边形ABCD∠BAD＝60° ∠ADC＝150° 且BD∠DC已知AC的最大值是3 则BC＝．6．如图在一个长为5m宽为3m的长方形草地上放着一根长方体的木块它的棱和草地宽AD平行且棱长大于AD木块从正面看是边长为1m的正方形一只蚂蚁从点A处到达点C处需要走的最短路程约为m．（精确到1m）7．如图C为线段BD上一动点分别过B D作AB⊥BD ED⊥BD连接AC EC已知AB=5DE=1BD=8设CD=x．请用含x的代数式表示AC+CE的长为根据上述方法求出√x2+4+√(12−x)2+9的最小值为．8．如图四边形ABCD为矩形AD=3AB=4点E是AD所在直线的一个动点点F 是对角线BD上的动点且BF=DE则AF+BE的最小值是．9．如图长方形BCFG是一块草地折线ABCDE是一条人行道BC＝12米CD＝5米．为了避免行人穿过草地（走虚线BD践踏绿草管理部门分别在B D处各挂了一块牌子牌子上写着“少走米踏之何忍”．10．如图BD是RtΔABC的角平分线点F是BD上的动点已知AC=2AE=2√3−2∠ABC=30°则（1）BE=（2）AF+EF的最小值是．11．如图AB是半圆O的直径半圆的半径为4 点C D在半圆上OC⊥AB,BD=2CD 点P是OC上的一个动点则BP+DP的最小值为．12．如图一大楼的外墙面ADEF与地面ABCD垂直点P在墙面上若P A＝AB＝5米点P到AD的距离是4米有一只蚂蚁要从点P爬到点B它的最短行程是米13．如图在Rt∠AOB中∠AOB＝90° OA＝4 OB＝6 以点O为圆心3为半径的∠O与OB交于点C过点C作CD∠OB交AB于点D点P是边OA上的动点则PC+PD的最小值为．14．如图台阶阶梯每一层高20cm宽40cm长50cm．一只蚂蚁从A点爬到B点最短路程是．15．已知正方形ABCD的边长为1 点E F分别是边BC CD上的两个动点且满足BE= CF连接AE AF则AE+AF的最小值为．16．如图在菱形ABCD中AB=4∠ABC=60°M为AD中点P为对角线BD上一动点连接PA和PM则PA+PM的最小值是．17．如图圆柱形容器高为18cm 底面周长为24cm 在杯内壁离杯底4cm的点B处有乙滴蜂蜜此时一只蚂蚁正好在杯外壁离杯上沿2cm与蜂蜜相对的点A处则蚂蚁从外币A 处到达内壁B处的最短距离为．18．如图直线y＝﹣x+7与两坐标轴分别交于A B两点点C的坐标是（1 0）DE分别是AB OA上的动点当∠CDE的周长最小时点E的坐标是．19．如图菱形ABCD的边长为4 ∠BAD＝120° E是边CD的中点F是边AD上的一个动点将线段EF绕着点E顺时针旋转60°得到线段EF' 连接AF' BF' 则∠ABF'的周长的最小值是．20．如图已知矩形ABCD中AB＝4 AD＝3 E F分别为AB DC上的两个动点且EF∠AC则AF+FE+EC的最小值为．参考答案1．解：如图做出点A关于小河MN的对称点A` 连接A`B交MN于点P则A`B就是牧童要完成这件事情所走的最短路程长度．在Rt∠A`DB中由勾股定理求得A`B=√A`D2+DB2=√(7+4+4)2+82=17(km)．则他要完成这件事情所走的最短路程是17km．2．解：如图1AB= √52+12=√26（cm）如图2AB= √32+32=3√2（cm）如图3AB= √22+42=√20=2√5（cm）故沿长方体的表面爬到对面顶点B处只有图2最短其最短路线长为：3√2cm．故答案为：3√2.3．解：∠P到AD两点的距离相同∠P在线段AD的垂直平分线上取AD的中点H作HF//BC作B关于HF的对称点E连接CE与直线FH交于P点P 即为所求∠∠BFH=90° BF=EF EP=BP∠要使∠BCP的周长最小∠BP+CP最小即为CE长又∠EF//BC∠ADC=90°∠∠FHD=∠HDB=90°∠四边形BDHF是矩形AD=1∠FBD=90°∠BF=DH=EF=12∠BE=2∠CE=√BC2+BE2∠CE=√13∠BCP的周长最小值=BC+BP+CP=3+√13故答案为：3+√13．4．解：如图是其侧面展开图：AD=12π⋅32π=16（m）AB=CD=15m．DE=CD-CE=15-3=12（m）在Rt∠ADE中AE=√AD2+DE2=√162+122=20（m）．故他滑行的最短距离约为20m．故答案为：20．5．解：如图取BC的中点F以BC为边在∠BCD另一侧作等边三角形∠BCG连接DG DF FG∠∠ADC＝150° 且BD∠DC∠∠ADB＝150°﹣90°＝60°∠∠BAD＝60°∠∠ADB＝∠BAD＝60°∠∠ABD是等边三角形而∠BCG也是等边三角形∠AB＝DB BC＝BG∠ABD＝∠CBG＝60°∠∠ABD+∠DBC＝∠CBG+∠DBC即∠ABC＝∠DBG在∠ABC和∠DBG中{AB=DB ∠ABC=∠DBG BC=BG∠∠ABC∠∠DBG（S A S）∠AC＝DG∠AC 的最大值是3∠DG 的最大值也是3在∠DGF 中 DG ≤DF +FG∠当DF FG 在同一条直线上时 DG 取最大值3 即DG ＝DF +FG ＝3 ∠BD ∠DC BC 的中点F∠DF ＝BF ＝CF ＝12BC∠等边三角形∠BCG BC 的中点F∠GF ∠BC ∠BGF ＝∠CGF ＝12∠BGC ＝30°∠BF ＝CF ＝12BG ＝12BC∠设DF ＝BF ＝CF ＝x 则BC ＝BG ＝2x∠FG ＝√BG 2−BF 2=√(2x)2−x 2=√3x∠DF +FG ＝x +√3x ＝3解得：x ＝3√3−32∠BC ＝2x ＝2×3√3−32＝3√3﹣3故答案为3√3﹣3．6．解：由题意可知将木块展开如图长相当于是AB +2个正方形的宽∠长为5+2×1＝7m 宽为3 m ．于是最短路径为：√32+72=√58≈8 m ．故答案为8．7．解：AC +CE =√BC 2+AB 2+√CD 2+DE 2=√(8−x)2+25+√x 2+1 当A C E 三点共线时 AC +CE 的值最小如右图所示作BD =12 过点B 作AB ∠BD 过点D 作ED ∠BD 使AB =2 ED =3连接AE交BD于点C设BC=x则AE的长即为代数式√x2+4+√(12−x)2+9的最小值．过点A作AF∠BD交ED的延长线于点F得矩形ABDF则AB=DF=2 AF=BD=12 EF=ED+DF=3+2=5所以AE=√AF2+EF2=√122+52=13即√x2+4+√(12−x)2+9的最小值为13故答案为：√(8−x)2+25+√x2+113．8．解：如图延长BC至G使得BG=BD连接GF∵四边形ABCD是矩形∴∠DAB=∠ABC=90°,AD//CB∴∠EDB=∠FBC在△EDB与△FBG中{ED=BF ∠EDB=∠FBG BD=BG∴△EDB≌△FBG∴BE=GF∴AF+BE=AF+GF≥AG 在Rt△ABD中AD=3,AB=4BD=√AD2+AB2=5∴BG=5在Rt△ABG中BG=5,AB=4AG=√AB2+BG2=√42+52=√41∴AF+BE的最小值是√41．故答案为：√41．9．解：在Rt△BCD中∴BD=√BC2+CD2=13则BC+CD−BD=12+5−13=4（米）故答案为：410．解：（1）∠AC=2∠ABC=30°∠BAC=90°∠BC=2AC=4∠AB=√BC2−AC2=√42−22=2√3∠BE=AB−AE=2√3−(2√3−2)=2故答案为：2（2）如图所示作E点关于BD的对称点G连接EG AG GF∠BD是∠ABC的平分线∠点G在线段BC上∠根据对称性可得EF=GF BG=BE=2∠EF+AF=GF+AF≥AG∠当点A F G三点共线时GF+AF的长度最短即EF+AF的最小值为AG的长度．∠GC=BC-BG=4-2=2又∠∠ABC=30°∠BAC=90°∠∠C=60°又∠AC=2∠△AGC是等边三角形∠AG=AC=2．∠AF+EF的最小值是2．故答案为：2．11．解：作点D关于OC的对称点为D1连接BD1OD1过点D1作D1Q⊥AB由题知OC⊥AB BD=2CD∠BC=3CD可得CD对应的圆心角∠COD=30°又点D关于OC的对称点为D1∠∠COD1=30°∠AOD1=60°∠BD1长为BP+DP的最小值在RtΔQOD1中OD1=4∠OQ=2D1Q=2√3在RtΔQD1B中BQ=OQ+OB=6D1Q=2√3∠BD1=√62+(2√3)2=4√3故填：4√312．解：如图过P作PG∠BF于G连接PB∠AG=4 AP=AB=5∠PG=√AP2−AG2=3BG=9∠PB=√GB2+GP2=3√10故这只蚂蚁的最短行程应该是3√10故答案为：3√1013．解：延长CO交∠O于点E连接ED交AO于点P则PC+PD的值最小最小值为线段DE的长．∠CD∠OB∠∠DCB＝90°∠∠AOB＝90°∠∠DCB＝∠AOB ∠CD∠AO∠CD AO =BCBO∠CD 4=36∠CD＝2在Rt∠CDE中DE＝√CD2+CE2=√22+62=2√10∠PC+PD的最小值为2√10．故答案为：2√10．14．解：如图所示∠楼梯的每一级的高宽长分别为20cm宽40cm长50cm ∠AB=√502+[2(20+40)]2=130(cm)即蚂蚁从点A沿着台阶面爬行到点B的最短路程是130cm．故答案为：130cm．15．解：连接DE∠BE=CF且四边形ABCD为正方形∠CD-CF=BC-BE即DF=CE在△ADF和△DCE中{AD=DC ∠ADF=∠DCE DF=CE∴△ADF∠∠DCE∠AF=DE AE+AF=AE+DE以BC为对称轴作A点关于BC的对应点A′连接DA′与BC交点即为点E∠点A和点A′关于BC对称∠AE=A′EAE+DE=A′E+DE=A′D由勾股定理可得：A′D=√AD2+A′A2=√22+12=√5∠AE+AF的最小值为√5故答案为：√516．解：作点M关于BD的对称点N交CD于点N连接AN则AN就是P A+PM的最小值∠在菱形ABCD 中 AB =4 ∠ABC =60° M 为AD 中点 AC ∠BD∠∠ADC =60° DA =DC 点N 为CD 的中点∠∠DAC 是等边三角形 AN ∠CD∠AC =AD =AB =4∴AN =√AD 2−DN 2=√42−22=2√3故答案为：2√317．解∠如图将杯子侧面展开作A 关于EF 的对称点A ′ 连接A ′B 则A ′B 即为最短距离．根据勾股定理得A ′B =√A ′D 2+BD 2=√122+162=20m ．故答案为：20cm ．18．解：如图点C 关于OA 的对称点C ′（-1 0）点C 关于直线AB 的对称点C ″ ∠直线AB 的解析式为y =-x +7∠直线C C ″的解析式为y =x -1由{y =−x +7y =x −1得{x =4y =3∠F（4 3）∠F是C C″中点∠可得C″（7 6）．连接C′C″与AO交于点E与AB交于点D此时∠DEC周长最小∠DEC的周长=DE+EC+CD=E C′+ED+D C″=C′C″=√82+62=10．故答案为10．19．解：取AD中点G连接EG F'G BE作BH∠DC的延长线于点H∠四边形ABCD为菱形∠AB＝AD∠∠BAD＝120°∠∠CAD＝60°∠∠ACD为等边三角形又∠DE＝DG∠∠DEG也为等边三角形．∠DE＝GE∠∠DEG＝60°＝∠FEF'∠∠DEG﹣∠FEG＝∠FEF'﹣∠FEG即∠DEF＝∠GEF'由线段EF绕着点E顺时针旋转60°得到线段EF'所以EF＝EF'．在∠DEF和∠GEF'中{DE=GE∠DEF=∠GEF′EF=EF′∠∠DEF∠∠GEF'（SAS）．∠∠EGF'＝∠EDF＝60°∠∠F'GA＝180°﹣60°﹣60°＝60°则点F'的运动轨迹为射线GF'．观察图形可得A E关于GF'对称∠AF'＝EF'∠BF'+AF'＝BF'+EF'≥BE在Rt∠BCH中∠∠H＝90° BC＝4 ∠BCH＝60°∠CH=12BC=2,BH=2√3,在Rt∠BEH中BE＝√BH2+EH2＝√12+16＝2√7∠BF'+EF'≥2√7∠∠ABF'的周长的最小值为AB+BF'+EF'＝4+2√7故答案为：4+2√7．20．解：过B作BH∠EF交CD于H过A作AG∠EF且使AG＝EF连接GE∠四边形AGEF是平行四边形∠AF＝GE∠当G E C三点共线时AF+EC最小∠EF ∠AC∠BH ∠AC∠∠HBC +∠BCA ＝90° ∠BCA +∠ACH ＝90° ∠∠HBC ＝∠ACH∠tan∠HBC ＝tan∠ACD 即HC BC =AD CD∠AB ＝4 AD ＝3∠ HC 3=34∠HC ＝94∠BH =√BC 2+CH 2=√9+(94)2=154∠AF +EF +EC ≥GC +BH∠GA ∠AC∠∠ACG 为直角三角形∠AB ＝4 AD ＝3∠AC ＝5∠EF ＝BH ＝AG∠AG ＝154∠GC ＝√AG 2+AC 2=√52+(154)2=254∠GC +EF ＝254+154＝10∠AF +FE +EC 的最小值为10故答案为：10．。

2022年中考数学专题：勾股定理(二)

2022年中考数学专题：勾股定理（二）1．如图，每一小格的长度为1，点A，B都在格点上，若BC=2√133，则AC 的长为()A．√13B．4√133C．2√13D．3√132．如图，⊙O是RtΔABC的外接圆，OE⊥AB交⊙O于点E，垂足为点D，AE，CB的延长线交于点F．若OD=3，AB=8，则FC的长是( )A．10 B．8C．6D．43．如图，在RtΔABC中，∠ACB=90°，按以下步骤作图：①以B为圆心，任意长为半径作弧，分别交BA、BC于M、N两点；②分别以M、N为圆心，以大于12MN的长为半径作弧，两弧相交于点P；③作射线BP，交边AC于D点．若AB=10，BC=6，则线段CD的长为()A．3B．103C．83D．1654．如图，ΔABC中，∠ACB=90°，AC=8，BC=6，将ΔADE沿DE翻折，使点A与点B重合，则CE的长为()A．198B．2C．254D．745．在勾股定理的学习过程中，我们已经学会了运用如图图形，验证著名的勾股定理，这种根据图形直观推论或验证数学规律和公式的方法，简称为"无字证明"．实际上它也可用于验证数与代数，图形与几何等领域中的许多数学公式和规律，它体现的数学思想是()A．统计思想B．分类思想C．数形结合思想D．函数思想6．我国古代数学著作《九章算术》中记载了一个问题："今有池方一丈，葭(jiā )生其中，出水一尺．引葭赴岸，适与岸齐．问水深几何．"（丈、尺是长度单位，1丈=10尺）其大意为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面．水的深度是多少？则水深为()A．10尺B．11尺C．12尺D．13尺7．如图，在RtΔABC中，∠ACB=90°，AB=√5，BC=2，以点A为圆心，AC的长为半径画弧，交AB于点D，交AC于点C，以点B为圆心，AC的长为半径画弧，交AB于点E，交BC于点F，则图中阴影部分的面积为()A．8−πB．4−πC．2−π4D．1−π48．如图，在矩形ABCD中，AB=5，AD=3，点E为BC上一点，把ΔCDE 沿DE翻折，点C恰好落在AB边上的F处，则CE的长是()A．1B．43C．32D．539．如图，在RtΔABC纸片中，∠ACB=90°，AC=4，BC=3，点D，E分别在AB，AC上，连结DE，将ΔADE沿DE翻折，使点A的对应点F 落在BC的延长线上，若FD平分∠EFB，则AD的长为()A．259B．258C．157D．20710．如图，⊙O的直径AB=8，AM，BN是它的两条切线，DE与⊙O相切于点E，并与AM，BN分别相交于D，C两点，BD，OC相交于点F，若CD=10，则BF的长是()A．8√179B．10√179C．8√159D．10√15911．如图，在正方形ABCD中，点E、F分别在边BC、CD上，且∠EAF=45°，AE交BD于M点，AF交BD于N点．（1）若正方形的边长为2，则ΔCEF的周长是．（2）下列结论：① BM2+DN2=MN2；②若F是CD的中点，则tan∠AEF=2；③连接MF，则ΔAMF为等腰直角三角形．其中正确结论的序号是（把你认为所有正确的都填上）．12．已知菱形ABCD的面积为2√3，点E是一边BC上的中点，点P是对角线BD 上的动点．连接AE，若AE平分∠BAC，则线段PE与PC的和的最小值为，最大值为．13．如图，AB是⊙O的弦，C是AB^的中点，OC交AB于点D．若AB= 8cm，CD=2cm，则⊙O的半径为cm．14．如图，正方形ABCD的边长为4，对角线AC，BD相交于点O，点E，F分别在BC，CD的延长线上，且CE=2，DF=1，G为EF的中点，连接OE，交CD于点H，连接GH，则GH的长为．15．如图，已知⊙O的半径为1，点P是⊙O外一点，且OP=2．若PT是⊙O的切线，T为切点，连结OT，则PT=．16．在矩形ABCD中，AB=2cm，将矩形ABCD沿某直线折叠，使点B与点D重合，折痕与直线AD交于点E，且DE=3cm，则矩形ABCD的面积为cm2．17．在边长为4的正方形ABCD中，连接对角线AC、BD，点P是正方形边上或对角线上的一点，若PB=3PC，则PC=．18．如图，在▱ABCD中，对角线AC，BD交于点O，AB⊥AC，AH⊥BD 于点H，若AB=2，BC=2√3，则AH的长为．19．如图，正方形ABCD的边长为8，点M在DC上且DM=2，N是AC上的一动点，则DN+MN的最小值是．20．如图，在矩形ABCD中，AB=6，AD=8，将此矩形折叠，使点C与点A重合，点D落在点D′处，折痕为EF，则AD′的长为，DD′的长为．21．如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为P，过点D的⊙O的切线与AB延长线交于点E，连接CE．（1）求证：CE为⊙O的切线；（2）若⊙O半径为3，CE=4，求sin∠DEC．22．如图，以等边三角形ABC的BC边为直径画圆，交AC于点D，DF⊥AB 于点F，连接OF，且AF=1．（1）求证：DF是⊙O的切线；（2）求线段OF的长度．23．如图1，在ΔABC中，∠ACB=90°，AC=BC，点D是AB边上一点（含端点A、B)，过点B作BE垂直于射线CD，垂足为E，点F在射线CD上，且EF=BE，连接AF、BF．（1）求证：ΔABF∽ΔCBE；（2）如图2，连接AE，点P、M、N分别为线段AC、AE、EF的中点，连接PM、MN、PN．求∠PMN的度数及MN的值；PM（3）在（2）的条件下，若BC=√2，直接写出ΔPMN面积的最大值．24．已知：如图，矩形ABCD的对角线AC，BD相交于点O，∠BOC=120°，AB=2．（1）求矩形对角线的长；（2）过O作OE⊥AD于点E，连结BE．记∠ABE=α，求tanα的值．25．在一次数学探究活动中，李老师设计了一份活动单：已知线段BC=2，使用作图工具作∠BAC=30°，尝试操作后思考：（1）这样的点A唯一吗？（2）点A的位置有什么特征？你有什么感悟？“追梦”学习小组通过操作、观察、讨论后汇报：点A的位置不唯一，它在以BC为弦的圆弧上（点B、C除外），…．小华同学画出了符合要求的一条圆弧（如图1)．（1）小华同学提出了下列问题，请你帮助解决．①该弧所在圆的半径长为；② ΔABC面积的最大值为；（2）经过比对发现，小明同学所画的角的顶点不在小华所画的圆弧上，而在如图1所示的弓形内部，我们记为A′，请你根据图1证明∠BA′C>30°．（3）请你运用所学知识，结合以上活动经验，解决问题：如图2，已知矩形ABCD的边长AB=2，BC=3，点P在直线CD的左侧，且tan∠DPC=4．3①线段PB长的最小值为；SΔPAD，则线段PD长为．②若SΔPCD=2326．如图，圆O中两条互相垂直的弦AB，CD交于点E．（1）M是CD的中点，OM=3，CD=12，求圆O的半径长；（2）点F在CD上，且CE=EF，求证：AF⊥BD．27．在几何体表面上，蚂蚁怎样爬行路径最短？（1）如图①，圆锥的母线长为12cm，B为母线OC的中点，点A在底面圆周上，AC的长为4πcm．在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径，并标出它的长（结果保留根号）．（2）图③中的几何体由底面半径相同的圆锥和圆柱组成．O是圆锥的顶点，点A在圆柱的底面圆周上，设圆锥的母线长为l，圆柱的高为ℎ．①蚂蚁从点A爬行到点O的最短路径的长为l+ℎ（用含l，ℎ的代数式表示）．②设AD的长为a，点B在母线OC上，OB=b．圆柱的侧面展开图如图④所示，在图中画出蚂蚁从点A爬行到点B的最短路径的示意图，并写出求最短路径的长的思路．28．研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题．（1）阅读材料立体图形中既不相交也不平行的两条直线所成的角，就是将直线平移使其相交所成的角．例如，正方体ABCD−A′B′C′D′（图1)，因为在平面AA′C′C中，CC′//AA′，AA′与AB相交于点A，所以直线AB与AA′所成的∠BAA′就是既不相交也不平行的两条直线AB与CC′所成的角．解决问题如图1，已知正方体ABCD−A′B′C′D′，求既不相交也不平行的两直线BA′与AC所成角的大小．（2）如图2，M，N是正方体相邻两个面上的点；①下列甲、乙、丙三个图形中，只有一个图形可以作为图2的展开图，这个图形是；②在所选正确展开图中，若点M到AB，BC的距离分别是2和5，点N到BD，BC的距离分别是4和3，P是AB上一动点，求PM+PN的最小值．29．如图，在四边形ABCD中，对角线AC与BD交于点O，已知OA=OC，OB=OD，过点O作EF⊥BD，分别交AB、DC于点E，F，连接DE，BF．（1）求证：四边形DEBF是菱形：（2）设AD//EF，AD+AB=12，BD=4√3，求AF的长．30．如图，在正方形ABCD中，E，F为边AB上的两个三等分点，点A关于DE 的对称点为A′，AA′的延长线交BC于点G．（1）求证：DE//A′F；（2）求∠GA′B的大小；（3）求证：A′C=2A′B．参考答案1．B[※解析※]根据勾股定理先求出AB的长，由图可知AC=AB−BC，然后代入数据计算即可．解：由图可得，AB=√62+42=√36+16=√52=2√13，∵BC=2√133，∴AC=AB−BC=2√13−2√133=4√133，2．A[※解析※]先根据已知条件推出OD//BC，OD是ΔABC的中位线，OE是三角形AFC的中位线，再根据勾股定理求出圆的半径，根据中位线定理即可求出FC的长．解：由题知，AC为直径，∴∠ABC=90°，∵OE⊥AB，∴OD//BC，∵OA=OC，∴OD为三角形ABC的中位线，∴AD=12AB=12×8=4，又∵OD=3，∴OA=√AD2+OD2=√42+32=5，∴OE=OA=5，∵OE//CF，点O是AC中点，∴OE是三角形ACF的中位线，∴CF=2OE=2×5=10，3．A[※解析※]由尺规作图痕迹可知，BD是∠ABC的角平分线，过D点作DH⊥AB于H点，设DC=DH=x则AD=AC-DC=8-x，BC=BH=6，AH=AB-BH=4，在Rt△ADH中，由勾股定理得到(8−x)2=x2+42，由此即可求出x的值．解：由尺规作图痕迹可知，BD是∠ABC的角平分线，过D点作DH⊥AB于H点，∵∠C=∠DHB=90°，∴DC=DH，AC=√AB2−BC2=√102−62=8，设DC=DH=x，则AD=AC-DC=8-x，BC=BH=6，AH=AB-BH=4，在Rt△ADH中，由勾股定理：AD2=AH2+DH2，代入数据：(8−x)2=x2+42，解得x=3，故CD=3，4．D[※解析※]在RtΔBCE中，根据勾股定理得到方程(8−x)2=x2+62，即可求解．解：设CE=x，则AE=8−x=EB，在RtΔBCE中，BE2=CE2+BC2,即(8−x)2=x2+62，解得x=7，45．C[※解析※]掌握几种数学思想所包含的意义即可解决问题．解：这种根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明”，它体现的数学思想是数形结合思想，6．C[※解析※]根据勾股定理列出方程，再解方程即可求出水深．解：设水深为ℎ尺，则芦苇长为(ℎ+1)尺，根据勾股定理，得(ℎ+1)2−ℎ2=(10÷2)2，解得ℎ=12，∴水深为12尺，7．D[※解析※]先根据直角三角形中的勾股定理求得AC=1，再把不规则的阴影部分面积转化为求规则图形的面积：S阴影部分=SΔABC−(S扇形EBF+S扇形DAC)，把已知条件代入求解即可．解：根据题意可知AC=√AB2−BC2=√√52−22=1，则BE=BF=AD=AC= 1，设∠B=n°，∠A=m°，∵∠ACB=90°，∴∠B+∠A=90°，即n+m=90，∴S阴影部分=SΔABC−(S扇形EBF+S扇形DAC)=12×2×1−(nπ×12360+mπ×12360)=1−(n+m)π360=1−π4，8．D [※解析※]设CE=x，则BE=3−x由折叠性质可知，EF=CE=x，DF=CD=AB=5，求出AF=4，BF=AB−AF=1，在RtΔBEF中，BE2+BF2=EF2，即(3−x)2+12=x2，即可求解．解：设CE=x，则BE=3−x．由折叠性质可知，EF=CE=x，DF=CD=AB=5．在RtΔDAF中，AD=3，DF=5．∴AF=4．∴BF=AB−AF=1．在RtΔBEF中，BE2+BF2=EF2．即(3−x)2+12=x2．解得x=53．9．D[※解析※]先根据勾股定理求出AB，再根据折叠性质得出∠DAE=∠DFE，AD=DF，然后根据角平分线的定义证得∠BFD=∠DFE=∠DAE，进而证得∠BDF=90°，证明Rt△ABC∽Rt△FBD，可求得AD的长．【详解】解：∵ ∠ACB=90°,AC=4,BC=3，∴ AB=√AC2+BC2=√42+32=5，由折叠性质得：∠DAE=∠DFE，AD=DF，则BD=5﹣AD，∵ FD平分∠EFB，∴∠BFD=∠DFE=∠DAE，∵∠DAE+∠B=90°，∴∠BDF+∠B=90°，即∠BDF=90°，∴Rt△ABC∽Rt△FBD，∴ BDDF =BCAC即5−ADAD=34，解得：AD= 207，10． A[※解析※]构建平面直角坐标系，过点 D 作 DH ⊥BC 于 H ．想办法求出 C ， D 两点坐标，构建一次函数，根据方程组确定交点坐标即可．解：如图，构建如图平面直角坐标系，过点 D 作 DH ⊥BC 于 H ．∵AB 是直径， AB =8， ∴OA =OB =4，∵AD ， BC ， CD 是 ⊙O 的切线，∴∠DAB =∠ABH =∠DHB =90°， DA =DE ， CE =CB ， ∴四边形 ABHD 是矩形， ∴AD =BH ， AB =DH =8， ∴CH =√CD 2−DH 2=√102−82=6，设 AD =DE =BH =x ，则 EC =CB =x +6，∴x +x +6=10， ∴x =2，∴D(2,4)， C(8,−4)， B(0,−4)，∴直线 OC 的解析式为 y =−12x ，直线 BD 的解析式为 y =4x −4，由 {y =−12x y =4x −4，解得 {x =89y =−49， ∴F(89， −49)，∴BF =√(89)2+(−49+4)2=8√179，11．（1）4；（2）①③[※解析※](1)将AF绕点A顺时针旋转90°，F点落在G点处，证明ΔEAF≌ΔEAG(SAS)，ΔFAD≌ΔGAB(SAS)，进而得到EF=DF+BE，即可求出△CEF的周长；(2)对于①：将AM绕点A逆时针旋转90°，M点落在H点处，证明ΔBAM≌ΔDAH(SAS)，ΔMAN≌ΔHAN(SAS)即可判断；对于②：设正方形边长为2，BE=x，则EF=x+1，CE=2-x，在Rt△EFC中使用勾股定理求出x，在利用∠AEF=∠AEB 即可求解；对于③：证明A、M、F、D四点共圆，得到∠AFM=∠ADM=45°进而求解．解：(1)将AF绕点A顺时针旋转90°，F点落在G点处，如下图所示：∵ ∠EAF=45°，且∠FAG=90∘∴ ∠EAG=45∘，在ΔEAF和ΔEAG中：{AF=AG∠EAF=∠EAG=45∘AE=AE，∴ ΔEAF≌ΔEAG(SAS)，∴ EF=GE，又∠1+∠2=45°，∠3+∠2=45°， ∴∠1=∠3， ∵ABCD 为正方形， ∴AD =AB ，在 ΔFAD 和 ΔGAB 中： {AD =AB∠1=∠3AF =AG，∴ ΔFAD ≌ΔGAB(SAS)， ∴ ∠ABG =∠ADF =90∘∴ ∠ABG +∠ABE =90∘+90∘=180∘， ∴ G 、 B 、 E 三点共线， ∴ EF =GE =GB +BE =DF +BE ，∴ C ΔCEF =EF +EC +CF =(DF +BE)+EC +CF =(DF +CF)+(BE +EC)=CD +BC =4，故答案为： 4；(2)对于①：将AM 绕点A 逆时针旋转90°，M 点落在H 点处，如下图所示：∵∠1+∠2=45°，∠1+∠4=∠EAH -∠EAF =45°， ∴∠2=∠4，在 ΔBAM 和 ΔDAH 中： {BA =DA∠2=∠4AM =AH,∴ ΔBAM ≌ΔDAH(SAS)，∴ ∠ADH =∠ABM =45∘， BM =DH ， ∴ ∠NDH =∠ADH +∠ADN =45∘+45∘=90∘，∴在 RtΔHND 中，由勾股定理得： NH 2=DH 2+DN 2=BM 2+DN 2，在 ΔMAN 和 ΔHAN 中： {AN =AN∠MAN =∠HAN =45∘AM =AH,∴ ΔMAN ≌ΔHAN(SAS)， ∴ MN =NH ，∴ MN 2=NH 2=BM 2+DN 2，故①正确；对于②：由(1)中可知：EF=BE+DF ，设正方形边长为2，当F 为CD 中点时，GB=DF=1，CF=1，设BE=x ，则EF=x+1，CE =2-x ，在Rt△EFC 中，由勾股定理： EF 2=CF 2+CE 2， ∴ (x +1)2=12+(2−x)2，解得 x =23，即 BE =23， ∴ tan∠AEF =tan∠AEB =ABBE =2×32=3,故②错误；对于③：如下图所示：∵∠EAF=∠BDC=45°，∴A、M、F、D四点共圆，∴∠AFM=∠ADM=45°，∴△AMF为等腰直角三角形，故③正确；12．√3；2+√7[※解析※]根据点E是一边BC上的中点及AE平分∠BAC判定ΔABC是等边三角形，根据菱形ABCD的面积求出菱形的边长；求PE+PC的最小值，点E和点C是定点，点P是线段BD上动点，由轴对称最值问题，可求出最小值；求和的最大值，观察图形可知，当PE和PC的长度最大时，和最大，即点P和点D 重合时，PE+PC的值最大．解：根据图形可画出图形，如图所示，过点B作BF//AC交AE的延长线于点F，∴∠F=∠CAE，∠EBF=∠ACE，∵点E是BC的中点，∴ΔACE≅ΔFBE(AAS)，∴BF=AC，∵AE平分∠BAC，∴∠BAE=∠CAE，∴∠BAE=∠F，∴AB=BF=AC，在菱形ABCD中，AB=BC，∴AB=BC=AC，即ΔABC是等边三角形；∴∠ABC=60°，设AB=a，则BD=√3a，∴菱形ABCD的面积=12AC⋅BD=2√3，即12⋅a⋅√3a=2√3，∴a=2，即AB=BC=CD=2；∵四边形ABCD是菱形，∴点A和点C关于BD对称，∴PE+PC=AP+EP，当点A，P，E三点共线时，AP+EP的和最小，此时AE=√3；点P和点D重合时，PE+PC的值最大，此时PC=DC=2，过点D作DG⊥BC交BC的延长线于点G，连接DE，∵AB//CD，∠ABC=60°，∴∠DCG=60°，∴CG=1，DG=√3，∴EG=2，∴DE=√EG2+DG2=√22+(√3)2=√7，此时PE+PC=2+√7；即线段PE与PC的和的最小值为√3；最大值为2+√7．13． 5[※解析※]先根据圆心角、弧、弦的关系和垂径定理得出各线段之间的关系，再根据勾股定理求解出半径即可．解：如图，连接OA，∵C是AB的中点，∴D是弦AB的中点，∴OC⊥AB，AD==BD==4，∵OA==OC，CD==2，∴OD==OC−CD==OA−CD，在RtΔOAD中，OA2==AD2+OD2，即OA2==16+(OA−2)2，解得OA==5，14．√132[※解析※]先作辅助线构造直角三角形，求出CH 和MG 的长，再求出MH 的长，最后利用勾股定理求解即可．解:如图,作OK ⊥BC ，垂足为点K ， ∵正方形边长为4， ∴OK =2，KC =2， ∴KC =CE ，∴CH 是△OKE 的中位线 ∴ CH =12OK =1，作GM ⊥CD ，垂足为点M ， ∵G 点为EF 中点， ∴GM 是△FCE 的中位线，∴ GM =12CE =1， MC =12FC =12(CD +DF )=12×(4+1)=52， ∴ MH =MC −HC =52−1=32，在Rt △MHG 中， GH =√MH 2+MG 2=√(32)2+12=√132，15． √3[※解析※]根据圆的切线性质可得出 ΔOPT 为直角三角形，再根据勾股定理求得 PT 长度．解： ∵PT 是 ⊙O 的切线， T 为切点，∴OT ⊥PT ，在 Rt ΔOPT 中， OT =1， OP =2，∴PT =√OP 2−OT 2=√22−12=√3，16． (2√5+6)或 (6−2√5)[※解析※]有题中条件可得： BE =DE ，在直角 ΔABE 中，利用勾股定理求出 AE ，再根据矩形的面积即可求得．将此长方形折叠，使点 B 与点 D 重合，∴BE=ED=3cm．在RtΔABE中，AB2+AE2=BE2．∴22+AE2=32，解得AE=√5cm．∴AD=AE+ED=(√5+3)cm或AD=ED−AE=(3−√5)cm∴矩形ABCD的面积为为AD⋅AB=(2√5+6)cm2或(6−2√5)cm2．17．1或√2或−√2+√344[※解析※]按P在正方形的边上和对角线上分别画出图形，再逐个求解即可．解：如图1，∵四边形ABCD是正方形，AB=4，∴AC⊥BD，AC=BD，OB=OD，AB=BC=AD=CD=4，∠ABC=∠BCD=90°，在RtΔABC中，由勾股定理得：AC=√AB2+BC2=√42+42=4√2，∴OB=2√2，∵PB=3PC，∴设PC=x，则PB=3x，有三种情况：①点P在BC上时，如图2，∵AD=4，PB=3PC，∴PC=1；②点P在AC上时，如图3，在RtΔBPO中，由勾股定理得：BP2=BO2+OP2，(3x)2=(2√2)2+(2√2−x)2，解得：x=−√2+√34（负数舍去），4；即PC=−√2+√344③点P在CD上时，如图4，在RtΔBPC中，由勾股定理得：BC2+PC2=BP2，42+x2=(3x)2，解得：y=√2（负数舍去），即PC=√2；．综上，PC的长是1或√2或−√2+√34418．2√33[※解析※]根据勾股定理可求出AC和OB的长，又AH⊥OB，可根据等面积法求出AH的长．解：如图，∵AB⊥AC，AB=2，BC=2√3，∴AC=√(2√3)2−22=2√2，在▱ABCD中，OA=OC，OB=OD，∴OA=OC=√2，在RtΔOAB中，OB=√22+(√2)2=√6，又AH⊥BD，∴12OB⋅AH=12OA⋅AB，即12×√6⋅AH=12×2×√2，解得AH=2√33．19．10[※解析※]连接BM，用勾股定理求出BM的长，就是DN+MN的最小值.解：连接BM交AC于点P，∵点N为AC上的动点，由三角形两边和大于第三边，知当点N运动到点P时，BN+MN=BP+PM=BM，BN+MN的最小值为BM的长度，∵四边形ABCD为正方形，∴BC=CD=8，CM=8−2=6，BCM=90°，∴BM=√62+82=10，∴DN+MN的最小值是10．20．6[※解析※]根据折叠的性质即可求得AD′=CD=6；连接AC，根据勾股定理求得AC= 10，证得ΔBAE≅△ D′AF(AAS)，D′F=BE，根据勾股定理列出关于线段BE 的方程，解方程求得BE的长，即可求出D′FAE，然后根据相似三角形的性质即可求得DD′．∵四边形ABCD是矩形，∴CD=AB=6，∵AD′=CD，∴AD′=6；连接AC，∵AB=6，BC=AD=8，∠ABC=90°，∴AC=√AB2+BC2=√62+82=10，∵∠BAF=∠D′AE=90°，∴∠BAE=∠D′AF，在ΔBAE和△ D′AF中{∠BAE=∠D′AF∠B=∠AD′F=90°AB=AD′，∴ΔBAE≅△ D′AF(AAS)，∴D′F=BE，∠AEB=∠AFD′，∴∠AEC=∠D′FD，由题意知：AE=EC；设BE=x，则AE=EC=8−x，由勾股定理得：(8−x)2=62+x2，解得： x =74，∴BE =74， AE =8−74=254，∴BEAE =725， ∴D′F AE =725，∵∠AD′F =∠D′AF =90°， ∴D′F//AE ， ∵DF//EC ， ∴D′F AE =725，∴DD′AC=D′F AE =725，∴DD′=725×10=145，21．（1）见解析；（2） sin∠DEC =2425[※解析※]（1）连接 OC ， OD ，由等腰三角形的性质证得 ∠COE =∠DOE ，根据全等三角形判定证得 ΔCOE ≅ΔDOE ，得到 ∠OCE =∠ODE ，即可证得 CE 为 ⊙O 的切线；（2）作 DF ⊥CE 于 F ，根据勾股定理得到 OE =√OC 2+CE 2=√32+42=5，根据三角形的面积公式求出 CP 和 CD ，用勾股定理求出 PE ，根据切线长定理得到 DE =CE ，根据三角函数的定义即可得到结论．证明：（1）连接 OC ， OD ，∵OC =OD ， AB ⊥CD ，∴∠COE =∠DOE ，在 ΔCOE 和 ΔDOE 中，{OC =OD∠COE =∠DOE OE =OE ， ∴ΔCOE ≅ΔDOE(SAS)， ∴∠OCE =∠ODE ， ∵DE 是 ⊙O 的切线， ∴∠ODE =90°， ∴∠OCE =90°， ∵OD 是 ⊙O 的半径， ∴CE 为 ⊙O 的切线；（2）解：过 D 作 DF ⊥CE 于 F ，由（1）知， ∠OCE =90°，在 Rt ΔOCE 中， ∵CE =4， OC =3，∴OE =√OC 2+CE 2=√32+42=5， ∵AB ⊥CD ，∴S ΔOCE =12OC ⋅CE =12CP ⋅OE ，∴3×4=5CP ， ∴CP =125，∵OC =OD ， AB ⊥CD ， ∴CP =DP ， ∴CD =2CP =245，在 Rt ΔCPE 中， PE =√CE 2−CP 2=√42−(125)2=165， ∵CE ， DE 是 ⊙O 的切线， ∴DE =CE =4，∵S ΔCDE =12CE ⋅DF =12CD ⋅PE ， ∴4DF =245×165，∴DF=9625，在RtΔDEF中，sin∠DEC=DFDE =96254=2425．22．（1）见解析；（2）√7[※解析※]（1）连OD，根据等边三角形及圆性质求出OD//AB，再由DF⊥AB推出求出OD⊥DF，根据切线的判定推出即可；（2）根据∠A=60o，OD⊥DF，AF=1求出AD，AF，AB的长度，再根据中位线性质求出OD的长度，根据勾股定理即可求得OF的长．（1）证明：连接OD，∵ΔABC是等边三角形，∴∠C=∠A=60o，∵OC=OD，∴ΔOCD是等边三角形，∴∠CDO=∠A=60o，∴OD//AB，∵DF⊥AB，∴∠FDO=∠AFD=90°，∴OD⊥DF，∴DF是⊙O的切线；（2）解：∵OD//AB，OC=OB，∴OD是ΔABC的中位线，∵∠AFD=90°，∠A=60o，∴∠ADF=30°，∵AF=1∴CD=OD=AD=2AF=2，由勾股定理得：DF2=3，在RtΔODF中，OF=√OD2+DF2=√22+3=√7，∴线段OF的长为√7．23．（1）证明见解析；√2；（2）∠PMN=135∘；MNPM=（3）14[※解析※]（1）根据两边成比例夹角相等两三角形相似证明即可．（2）如图2中，延长PM交AF于T．证明四边形MNFT是平行四边形，推出∠TMN=∠AFC=45°，推出∠PMN=135°，再证明AF=√2EC，根据三角形的中位线定理可得结论．EC，所以当EC的值最大时，（3）因为MN=√2PM，∠PMN=135°，PM=12PM的值最大，此时ΔPMN的面积最大，（1）证明：如图1中，∵CA=CB，∠ACB=90°，EF=EB，∠BEF=90°，∴∠CBA=∠EBF=45°，AB=√2BC，BF=√2BE，∴∠CBE=∠ABF，ABBC =BFBE=√2，∴ΔABF∽ΔCBE．（2）解：如图2中，延长PM交AF于T．∵BE⊥CF，∴∠CEB=90°，∵ΔABF∽ΔCBE，∴∠CEB=∠AFB=90°，AFEC =ABBC=√2，∴AF=√2EC，∵∠EFB=45°，∴∠AFC=45°，∵AP=PC，AM=ME，∴PT//CF，PM=12EC，∵AM=ME，EN=NF，∴MN//AF，MN=12AF，∴四边形MNFT是平行四边形，MN=√2PM，∴∠TMN=∠AFC=45°，∴∠PMN=135°，∴MNPM=√2．（3）解：∵MN=√2PM，∠PMN=135°，PM=12EC，∴当EC的值最大时，PM的值最大，此时ΔPMN的面积最大，∵当点E与B重合时，EC的值最大，EC的最大值为√2，此时PM=√22，MN=√2PM=1，∴ΔPMN的面积的最大值为12×√22×1×√22=14．24．（1）4；（2）tanα=√32[※解析※]（1）根据矩形的性质求出AC=2AO，根据等边三角形的判定得出ΔAOB是等边三角形，求出AB=AO=2，求出BD；（2）根据勾股定理求出AD，然后根据等腰三角形的性质求得AE，然后解直角三角形求得tanα的值．解：（1）∵∠BOC=120°，∴∠AOB=60°，∵四边形ABCD是矩形，∴∠BAD=90°，AC=BD，AO=OC，BO=DO，∴AO=BO，∴ΔAOB是等边三角形，∴AB=AO=BO，∵AB=2，∴BO=2，∴BD =2BO =4， ∴矩形对角线的长为4；（2）由勾股定理得： AD =√BD 2−AB 2=√42−22=2√3，∵OA =OD ， OE ⊥AD 于点 E ， ∴AE =DE =12AD =√3，∴tanα=AEAB =√32．25．（1）①2；② √3+2；（2）见解析；（3）① √97−54；②7√24[※解析※]（1）①设 O 为圆心，连接 BO ， CO ，根据圆周角定理得到 ∠BOC =60°，证明 ΔOBC 是等边三角形，可得半径；②过点 O 作 BC 的垂线，垂足为 E ，延长 EO ，交圆于 D ，以 BC 为底，则当A 与 D 重合时， ΔABC 的面积最大，求出 OE ，根据三角形面积公式计算即可；（2）延长 BA′，交圆于点 D ，连接 CD ，根据三角形外角的性质和圆周角定理证明即可；（3）①根据，连接 PD ，设点 Q 为 PD 中点，以点 Q 为圆心， PD 为半径画圆，可得点 P 在优弧 CPD 上，连接 BQ ，与圆 Q 交于 P′，可得 BP′即为 BP 的最小值，再计算出 BQ 和圆 Q 的半径，相减即可得到 BP′；②根据 AD ， CD 和推出点 P 在 ∠ADC 的平分线上，从而找到点 P 的位置，过点 C 作 CF ⊥PD ，垂足为 F ，解直角三角形即可求出 DP ．解：（1）①设 O 为圆心，连接 BO ， CO ，∵∠BCA =30°，∴∠BOC =60°，又 OB =OC ， ∴ΔOBC 是等边三角形，∴OB =OC =BC =2，即半径为2；② ∵ΔABC 以 BC 为底边， BC =2，∴当点 A 到 BC 的距离最大时， ΔABC 的面积最大，如图，过点 O 作 BC 的垂线，垂足为 E ，延长 EO ，交圆于 D ，∴BE=CE=1，DO=BO=2，∴OE=√BO2−BE2=√3，∴DE=√3+2，∴ΔABC的最大面积为12×2×(√3+2)=√3+2；（2）如图，延长BA′，交圆于点D，连接CD，∵点D在圆上，∴∠BDC=∠BAC，∵∠BA′C=∠BDC+∠A′CD，∴∠BA′C>∠BDC，∴∠BA′C>∠BAC，即∠BA′C>30°；（3）①如图，当点P在BC上，且PC=32时，∵∠PCD=90°，AB=CD=2，AD=BC=3，∴tan∠DPC=CDPC =43，为定值，连接PD，设点Q为PD中点，以点Q为圆心，12PD为半径画圆，∴当点P在优弧CPD上时，tan∠DPC=43，连接BQ，与圆Q交于P′，此时BP′即为BP的最小值，过点Q作QE⊥BE，垂足为E，∵点Q是PD中点，∴点E为PC中点，即QE=12CD=1，PE=CE=12PC=34，∴BE =BC −CE =3−34=94， ∴BQ =√BE 2+QE 2=√974， ∵PD =√CD 2+PC 2=52， ∴圆 Q 的半径为 12×52=54， ∴BP′=BQ −P′Q =√97−54，即 BP 的最小值为 √97−54；② ∵AD =3， CD =2， S ΔPCD =23S ΔPAD ，则 CDAD =23，∴ΔPAD 中 AD 边上的高 =ΔPCD 中 CD 边上的高，即点 P 到 AD 的距离和点 P 到 CD 的距离相等，则点 P 到 AD 和 CD 的距离相等，即点 P 在 ∠ADC 的平分线上，如图，过点 C 作 CF ⊥PD ，垂足为 F ，∵PD 平分 ∠ADC ， ∴∠ADP =∠CDP =45°，∴ΔCDF 为等腰直角三角形，又 CD =2， ∴CF =DF =2√2=√2，∵tan∠DPC =CFPF =43， ∴PF =3√24， ∴PD =DF +PF =√2+3√24=7√24．26．（1）3√5；（2）见解析．[※解析※]（1）连接OD，如图：∵M是CD的中点，CD=12，∴DM=1CD=6，OM⊥CD，∠OMD=90°，2RtΔOMD中，OD=√OM2+DM2，且OM=3，∴OD=√32+62=3√5，即圆O的半径长为3√5；（2）连接AC，延长AF交BD于G，如图：∵AB⊥CD，CE=EF，∴AB是CF的垂直平分线，∴AF=AC，即ΔACF是等腰三角形，∵CE=EF，∴∠FAE=∠CAE，∵BC=BC，∴∠CAE=∠CDB，∴∠FAE=∠CDB，RtΔBDE中，∠CDB+∠B=90°，∴∠FAE+∠B=90°，∴∠AGB=90°，∴AG⊥BD，即AF⊥BD．27．（1）作图如图所示；（2）① h+ l；②见解析．[※解析※]（1）根据两点之间线段最短，即可得到最短路径；连接OA，AC，可以利用弧长与母线长求出∠AOC，进而证明出△OAC是等边三角形，利用三角函数即可求解；（2）①由于圆锥底面圆周上的任意一点到圆锥顶点的距离都等于母线长，因此只要蚂蚁从点A爬到圆锥底面圆周上的路径最短即可，因此顺着圆柱侧面的高爬行，所以得出最短路径长即为圆柱的高h加上圆锥的母线长l；②如图，根据已知条件，设出线段GC的长后，即可用它分别表示出OE、BE、GE、AF，进一步可以表示出BG、GA，根据B、G、A三点共线，在Rt△ABH中利用勾股定理建立方程即可求出GC的长，最后依次代入前面线段表达式中即可求出最短路径长．解：（1）如图所示，线段AB即为蚂蚁从点A爬行到点B最短路径；设∠AOC=n°，∵圆锥的母线长为12cm，AC⏜的长为4πcm，4π，∴ 12πn180=∴ n=60；连接OA、CA，∵ OA=OC=12，∴ △OAC是等边三角形，∵B为母线OC的中点，∴ AB⊥OC，∴ AB=OA×sin60°=6√3．（2）① 蚂蚁从点A爬行到点O的最短路径为：先沿着过A点且垂直于地面的直线爬到圆柱的上底面圆周上，再沿圆锥母线爬到顶点O上，因此，最短路径长为h+l② 蚂蚁从点A爬行到点B的最短路径的示意图如下图所示，线段AB即为其最短路径（G点为蚂蚁在圆柱上底面圆周上经过的点，图中两个C点为图形展开前图中的C点）；求最短路径的长的思路如下：如图，连接OG，并过G点作GF⊥AD，垂足为F，由题可知，OG=OC=l，GF=h， OB=b，由AD⏜的长为a，得展开后的线段AD=a，设线段GC的长为x，则GC⏜的弧长也为x，由母线长为l，可求出∠COG，作BE⊥OG，垂足为E，因为OB=b，可由三角函数求出OE和BE，从而得到GE，利用勾股定理表示出BG，接着由FD=CG=x，得到AF=a-x，利用勾股定理可以求出AG，将AF+BE即得到AH，将EG+GF即得到HB，因为两点之间线段最短，∴A、G、B三点共线，利用勾股定理可以得到：AB2=AH2+BH2,进而得到关于x的方程，即可解出x，将x的值回代到BG和AG中，求出它们的和即可得到最短路径的长．28．（1）两直线BA′与AC所成角为60°；（2）①丙；② PM+PN的最小值为10．[※解析※]（1）如图1中，连接BC′．证明△ A′BC′是等边三角形，推出∠BA′C′=60°，由题意可知∠C′A′B是两条直线AC与BA′所成的角．（2）①根据立方体平面展开图的特征，解决问题即可．②如图丙中，作点N关于AD的对称点K，连接MK交AD于P，连接PN，此时PM+PN的值最小，最小值为线段MK的值，过点M作MJ⊥NK于J．根据勾股定理求出MK即可．解：（1）如图1中，连接BC′．∵A′B=BC′=A′C′，∴△ A′BC′是等边三角形，∴∠BA′C′=60°，∵AC//A′C′，∴∠C′A′B是两条直线AC与BA′所成的角，∴两直线BA′与AC所成角为60°．（2）①观察图形可知，图形丙是图2的展开图，故答案为：丙．②如图丙中，作点N关于AD的对称点K，连接MK交AD于P，连接PN，此时PM+PN的值最小，最小值为线段MK的值，过点M作MJ⊥NK于J．由题意在RtΔMKJ中，∠MJK=90°，MJ=5+3=8，JK=8−(4−2)=6，∴MK=√MJ2+JK2=√82+62=10，∴PM+PN的最小值为10．29．（1）证明见解析；（2）4√330．（1）见解析；（2）45°；（3）见解析[※解析※]（1）设直线DE与AA′相交于点T，∵点A与A′关于DE对称，∴ DE垂直平分AA′，即DE⊥AA′,AT=TA′．∵E，F为AB边上的两个三等分点，∴ AE=EF，∴ ET是△AA′F的中位线，∴ ET∥A′F，即DE∥A′F．（2）连接FG，∵四边形ABCD是正方形，∴ AD=AB,∠DAB=∠ABG=90°,∠DAT+∠BAG=90°，∵ DE⊥AA′，∴ ∠DTA=90°，∴ ∠ADT+∠DAT=90°，∴ ∠ADT=∠BAG．∴ △DAE≌△ABG，∴ AE=BG，又AE=EF=FB，∴ FB=BG，∴ △FBG是等腰直角三角形，∴ ∠GFB=45°．∵ DE//A′F，∴ A′F⊥AA′，∴ ∠FA′G=90°．取FG的中点O，连接OA′,OB，在Rt△A′FG和Rt△BFG中，OA′=OF=OG=12FG,OB=OF=OG=12FG，∴ OA′=OF=OG=OB，∴点A′，F，B，G都在以FG为直径的⊙O上，∴ ∠GA′B=∠GFB=45°．（3）设AB=3a，则AD=BC=3a,AF=2a,AE=BF=a．由（2）得BG=AE=a，∴ tan∠BAG=BGAB =a3a=13，即tan∠A′AF=13，∴ A′FAA′=13．设A′F=k，则AA′=3k，在Rt△A′AF中，由勾股定理，得AF=√AA′2+A′F2=√10k，∴ √10k=2a,k=√10a5,A′F=√10a5．在Rt△ABG中，由勾股定理，得AG=√AB2+BG2=√10a．又∵ AA′=3k=3√10a5，∴ A′G=AG−AA′=√10a−3√10a5=2√10a5，∴ A′FA′G =√10a52√10a5=12．∵ CG=BC−CB=2a，∴ BFCG =a2a=12，∴ A′FA′G =BFCG=12．由（2）知，∠A′FB+∠A′GB=180°，又∵ ∠A′GC+∠A′GB=180°，∴ ∠A′FB=∠A′GC，∴ △A′FB∽△A′GC，∴ A′BA′C =BFCG=12，∴ A′C=2A′B．。

八年级数学勾股定理中考试题与答案

的长度为( B )
第6题图
数学
八年级下册
人教版
章末整合· 感知中考
B 第7题图
数学
八年级下册
人教版
章末整合· 感知中考
第8题图
数学
八年级下册
人教版
章末整合· 感知中考
9.(2021·岳阳)《九章算术》是我国古代数学名著，书中有下列问题：“今有户高多于广六尺八寸，两隅相去适一丈.问户高、广各几何?”其意思为：今有一门，高比宽多6尺8寸，门对
数学
八年级下册
人教版
章末整合· 感知中考
(3)①如图所示,直线PC即为所求;
②到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.(答案不唯一)
(1)求证：△ABC≌△ECD；
( 1 )证明:∵AB∥CD ∴∠ABC＝∠ECD, 又∵AB＝EC,BC＝CD, ∴△ABC≌△ECD(SAS).
数学
八年级下册
人教版
章末整合· 感知中考
解：(2)由(1)得△ABC≌△ECD, ∴∠CED＝∠A＝90°. 设BE＝x,∵AB＝CE＝3,则CD＝BC＝3＋x, 在Rt△BED中,DE2＝BD2－BE2, 在Rt△CED中,DE2＝CD2－CE2, ∴BD2－BE2＝CD2－CE2,
办法一：如图1，可利用一把有刻度的直尺在AB上量出CD ＝30 cm，然后分别以D，C为圆心，以50 cm与40 cm为半径画圆弧，两弧相交于点E，作直线CE，则∠DCE必为9 0 ° .
数学
八年级下册
人教版
章末整合· 感知中考
办法二：如图2，可以取一根笔直的木棒，用铅笔在木棒上
点出M，N两点，然后把木棒斜放在木板上，使点M与点C 重合，用铅笔在木板上将点N对应的位置标记为点Q.保持点 N不动，将木棒绕点N旋转，使点M落在AB上，在木板上将点 M对应的位置标记为点R.然后将RQ延长，在延长线上截取线段QS＝MN，得到点S，作直线SC，则∠RCS＝90°.

中考复习九年级数学三角形(勾股定理)专练(word版含答案)

（1）如图①,连接BE、CD,求证：BE＝CD；
（2）如图②,连接BD、CD,若∠BAC＝∠DAE＝60°,CD⊥AE,CD＝3 ,BD＝3 ,求△ACD的面积；
（3）如图③,若∠BAC＝∠DAE＝90°,且C点恰好落在DE上,试探究AB、CD、CE之间的数量关系,并证明．
参考答案
1．A
解：A、72+242=252,三边是整数,同时能构成直角三角形,故是勾股数,此选项符合题意；
B、 , 不是正整数,不是勾股数,此选项不合题意；
C、1.5,2.5,不是正整数,不是勾股数,此选项不合题意；
D、92+162≠252,不是勾股数,不合题意．
2．A
解：A、∵ ,∴三条线段不能组成直角三角形,故A选项符合题意；
B、∵ ,∴三条线段能组成直角三角形,故B选项不符合题意；
C、∵ ,∴三条线段能组成直角三角形,故C选项不符合题意；
17．如图,在中, , 是边上一点, , , ,则的长为（）
A． B． C．6D．8
18．如图,在正方形ABCD中,AB＝4,点M在CD边上,且DM＝1,△AEM与△ADM关于AM所在直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为（）
A．3B．4C．4.5D．5
4．C
解：如下图,在等腰三角形ABC中,底边长为BC=10 ,腰长为AB=13 ,
过点A作AD⊥BC于D,过点B作BE⊥AC于E,
∵AD⊥BC于D,
∴BD=DC,
∵BC=10 ,
∴BD=DC=5 ,
在Rt△ABD中, ,
由于 ,
∴ ,
5．A
解：设一条直角边为x,斜边为3x,依题意有
x2+（）2=（3x）2,

优质合肥市数学初中九年级勾股定理选择题中考专项复习训练

优质合肥市数学初中九年级勾股定理选择题中考专项复习训练一、易错易错压轴选择题精选：勾股定理选择题1．下列条件中，不能．．判定ABC 为直角三角形的是（） A ．::5:12:13a b c =B ．A BC ∠+∠=∠ C ．::2:3:5A B C ∠∠∠=D ．6a =，12b =，10c =2．如图是一块长、宽、高分别为6cm 、4cm 、3cm 的长方体木块，一只蚂蚁要从长方体木块的一个顶点A 处，沿着长方体的表面到长方体上和A 相对的顶点B 处吃食物，那么它需要爬行的最短路径的长是（）A ．cmB ．cmC ．cmD ．9cm3．已知：如图在△ABC ，△ADE 中，∠BAC=∠DAE=90°，AB=AC ，AD=AE ，点C ，D ，E 三点在同一条直线上，连接BD ，BE ，以下四个结论：①BD=CE ；②BD ⊥CE ；③∠ACE+∠DBC=45°；④BE 2=2（AD 2+AB 2），其中结论正确的个数是（）A ．1B ．2C ．3D ．44．如图，已知圆柱的底面直径6BC π=，高3AB =，小虫在圆柱侧面爬行，从C 点爬到A 点，然后再沿另一面爬回C 点，则小虫爬行的最短路程的平方为（）A ．18B ．48C ．120D ．725．如图，在长方形纸片ABCD 中，8AB cm =，6AD cm =. 把长方形纸片沿直线AC 折叠，点B 落在点E 处，AE 交DC 于点F ，则AF 的长为（）A ．254cmB ．152cmC ．7cmD ．132cm 6．如图，在ABC 中，90A ∠=︒，6AB =，8AC =，ABC ∠与ACB ∠的平分线交于点O ，过点O 作⊥OD AB 于点D ，若则AD 的长为( )A ．2B ．2C ．3D ．47．如图，等边ABC ∆的边长为1cm ，D ，E 分别是AB ，AC 上的两点，将ADE ∆沿直线DE 折叠，点A 落在点'A 处，且点'A 在ABC ∆外部，则阴影部分图形的周长为（）A ．1cmB ．1.5cmC ．2cmD ．3cm8．已知，如图，ABC ，点,P Q 分别是BAC ∠的角平分线AD ，边AB 上的两个动点，45C ︒∠=，6BC =，则PB PQ +的最小值是（）A ．3B ．23C ．4D ．329．如图，在Rt △ABC 中，∠C=90°，AC=4，BC=3，BD 平分∠ABC ，E 是AB 中点，连接DE ，则DE 的长为（）A ．102B ．2C ．512+D ．3210．如图，在△ABC 和△ADE 中，∠BAC =∠DAE =90°，AB =AC ，AD =AE ，点C ，D ，E 在同一条直线上，连接B ，D 和B ，E ．下列四个结论：①BD =CE ，②BD ⊥CE ，③∠ACE +∠DBC=30°，④()2222BE AD AB =+．其中，正确的个数是（）A ．1B ．2C ．3D ．411．如图，等腰直角三角形纸片ABC 中，∠C=90°，把纸片沿EF 对折后，点A 恰好落在BC 上的点D 处，若CE=1，AB=42，则下列结论一定正确的个数是（）①2；②BD>CE ；③∠CED+∠DFB=2∠EDF ；④△DCE 与△BDF 的周长相等； A ．1个 B ．2个 C ．3个 D ．4个12．为了庆祝国庆，八年级（1）班的同学做了许多拉花装饰教室，小玲抬来一架2.5米长的梯子，准备将梯子架到2.4米高的墙上，则梯脚与墙角的距离是（）A ．0.6米B ．0.7米C ．0.8米D ．0.9米13．已知直角三角形纸片ABC 的两直角边长分别为6，8，现将ABC 按如图所示的方式折叠，使点A 与点B 重合，则BE 的长是（）A ．72B ．74C ．254D ．15414．已知一个直角三角形的两边长分别为3和5，则第三边长是( )A ．5B ．4C ．34D ．4或34 15．下列各组数据，是三角形的三边长能构成直角三角形的是（）A ．2,3,4B ．4,5,6C ．2223,4,5D ．6,8,10 16．下列四组线段中，可以构成直角三角形的是（）A ．1、2、3B ．2、3、4C ．1、2、3D ．4、5、617．将一根 24cm 的筷子，置于底面直径为 15cm ，高 8cm 的装满水的无盖圆柱形水杯中，设筷子浸没在杯子里面的长度为 hcm ，则 h 的取值范围是（）A ．h≤15cmB ．h≥8cmC ．8cm≤h≤17cmD ．7cm≤h≤16cm18．如图，在ABC 中，13AB =，10BC =，BC 边上的中线12AD =，请试着判定ABC 的形状是（）A ．直角三角形B ．等边三角形C ．等腰三角形D ．以上都不对19．如图，在△ABC 中，AB=8，BC=10，AC=6，则BC 边上的高AD 为（）A ．8B ．9C ．245D ．1020．已知：△ABC 中，BD 、CE 分别是AC 、AB 边上的高，BQ ＝AC ，点F 在CE 的延长线上，CF ＝AB ，下列结论错误的是（）．A ．AF ⊥AQB ．AF=AQC ．AF=AD D ．F BAQ ∠=∠【参考答案】***试卷处理标记，请不要删除一、易错易错压轴选择题精选：勾股定理选择题1．D解析：D【分析】由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方或最大角是否是90︒即可．【详解】解：A 、22251213+=，ABC ∆∴是直角三角形，故能判定ABC ∆是直角三角形； B 、A B C ∠+∠=∠，90C ∴∠=︒，故能判定ABC ∆是直角三角形；C 、::2:3:5A B C ∠∠∠=，518090235C ∴∠=⨯︒=︒++，故能判定ABC ∆是直角三角形；D 、22261012+≠，ABC ∆∴不是直角三角形，故不能判定ABC ∆是直角三角形；故选：D ．【点睛】本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，可利用勾股定理的逆定理和直角三角形的定义判断．2．C解析：C【解析】【分析】本题中蚂蚁要跑的路径有三种情况，知道当蚂蚁爬的是一条直线时，路径才会最短．蚂蚁爬的是一个长方形的对角线．展开成平面图形，根据两点之间线段最短，可求出解．【详解】解：如图1，当爬的长方形的长是(4+6)=10，宽是3时，需要爬行的路径的长==cm ；如图2，当爬的长方形的长是(3+6)=9，宽是4时，需要爬行的路径的长==cm；如图3，爬的长方形的长是(3+4)=7时，宽是6时，需要爬行的路径的长==cm.所以要爬行的最短路径的长cm.故选C.【点睛】本题考查平面展开路径问题，本题关键知道蚂蚁爬行的路线不同，求出的值就不同，有三种情况，可求出值找到最短路线.3．C解析：C【解析】试题分析：①∵∠BAC=∠DAE=90°，∴∠BAC+∠CAD=∠DAE+∠CAD，即∠BAD=∠CAE．∵在△BAD和△CAE中，AB=AC，∠BAD=∠CAE，AD=AE，∴△BAD≌△CAE（SAS）．∴BD=CE．本结论正确．②∵△BAD≌△CAE，∴∠ABD=∠ACE．∵∠ABD+∠DBC=45°，∴∠ACE+∠DBC=45°．∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°．∴BD⊥CE．本结论正确．③∵△ABC为等腰直角三角形，∴∠ABC=∠ACB=45°．∴∠ABD+∠DBC=45°．∵∠ABD=∠ACE，∴∠ACE+∠DBC=45°．本结论正确．④∵BD⊥CE，∴在Rt△BDE中，利用勾股定理得：BE2=BD2+DE2．∵△ADE为等腰直角三角形，∴2，即DE2=2AD2．∴BE2=BD2+DE2=BD2+2AD2．而BD2≠2AB2，本结论错误．综上所述，正确的个数为3个．故选C．4．D解析：D【分析】要求最短路径，首先要把圆柱的侧面展开，利用两点之间线段最短，然后利用勾股定理即可求解．【详解】解：把圆柱侧面展开，展开图如图所示，点A ，C 的最短距离为线段AC 的长.∵已知圆柱的底面直径6BC π=， ∴623AD ππ=⋅÷=，在Rt ADC ∆中，90ADC ∠=︒ ，3CD AB ==，∴22218AC AD CD =+=，∴从C 点爬到A 点，然后再沿另一面爬回C 点，则小虫爬行的最短路程的平方为()222472AC AC ==.故选D.【点睛】本题考查了平面展开-最短路径问题，解题的关键是会将圆柱的侧面展开，并利用勾股定理解答．5．A解析：A【分析】由已知条件可证△CFE≌△AFD，得到DF=EF,利用折叠知AE=AB=8cm ，设AF=xcm ，则DF=(8-x)cm ，在Rt△AFD 中，利用勾股定理即可求得x 的值.【详解】∵四边形ABCD 是长方形，∴∠B=∠D=900，BC=AD,由翻折得AE=AB=8m ，∠E=∠B=900,CE=BC=AD又∵∠CFE=∠AFD∴△CFE≌△AFD∴EF=DF设AF=xcm ，则DF=（8-x ）cm在Rt△AFD 中，AF 2=DF 2+AD 2,AD=6cm ， 222(8)6x x =-+254x cm 故选择A.【点睛】此题是翻折问题，利用勾股定理求线段的长度.6．B解析：B【分析】过点O 作OE ⊥BC 于E ，OF ⊥AC 于F ，由角平分线的性质得到OD=OE=OF ，根据勾股定理求出BC 的长，易得四边形ADFO 为正方形，根据线段间的转化即可得出结果.【详解】解：过点O 作OE ⊥BC 于E ，OF ⊥AC 于F ，∵BO,CO 分别为∠ABC ，∠ACB 的平分线，所以OD=OE=OF ，又BO=BO,∴△BDO ≌△BEO,∴BE=BD.同理可得，CE=CF.又四边形ADOE 为矩形，∴四边形ADOE 为正方形.∴AD=AF.∵在Rt △ABC 中，AB=6，AC=8，∴BC=10.∴AD+BD=6①,AF+FC=8②，BE+CE=BD+CF=10③，①+②得，AD+BD+AF+FC=14，即2AD+10=14，∴AD=2.故选：B.【点睛】此题考查了角平分线的定义与性质，以及全等三角形的判定与性质，属于中考常考题型．7．D解析：D【分析】根据折叠的性质可得AD=A'D ，AE=A'E ，易得阴影部分图形的周长为=AB+BC+AC ，则可求得答案．解：因为等边三角形ABC 的边长为1cm ，所以AB=BC=AC=1cm ，因为△ADE 沿直线DE 折叠，点A 落在点A'处，所以AD=A'D ，AE=A'E ，所以阴影部分图形的周长=BD+A'D+BC+A'E+EC=BD+AD+BC+AE+EC=AB+BC+AC =1+1+1=3（cm ）．故选：D ．【点睛】此题考查了折叠的性质与等边三角形的性质．此题难度适中，注意掌握数形结合思想与转化思想的应用以及折叠前后图形的对应关系．8．D解析：D【分析】先根据等腰三角形的性质得出AD 是线段QE 垂直平分线，再根据垂直平分线的性质、两点之间线段最短得出PB PQ +最小值为BE ，最后根据垂线段最短、直角三角形的性质得出BE 的最小值即可得．【详解】如图，作QE AD ⊥，交AC 于点E ，∵AD 平分∠BAC ，∴∠BAD=∠CAD ，AD ∴是线段QE 垂直平分线（等腰三角形的三线合一）PQ PE ∴=PB PQ PB PE ∴+=+由两点之间线段最短得：当点,,B P E 共线时，PB PE +最小，最小值为BE 点,P Q 都是动点BE ∴随点,P Q 的运动而变化由垂线段最短得：当BE AC ⊥时，BE 取得最小值在Rt BCE ∆中，456,C C B ∠=︒= 2322BE CE BC ∴=== 即PB PQ +的最小值为32故选：D ．本题考查了等腰三角形的性质、垂直平分线的性质、两点之间线段最短等知识点，利用两点之间线段最短和垂线段最短确认PB PQ +的最小值是解题关键．9．A解析：A【解析】试题解析：如图，过D 作AB 垂线交于K ，∵BD 平分∠ABC ，∴∠CBD=∠ABD∵∠C=∠DKB=90°，∴CD=KD ，在△BCD 和△BKD 中，CD KD BD BD ⎧⎨⎩＝＝ ∴△BCD ≌△BKD ，∴BC=BK=3∵E 为AB 中点∴BE=AE=2.5，EK=0.5，∴AK=AE-EK=2，设DK=DC=x ，AD=4-x ，∴AD 2=AK 2+DK 2即（4-x ）2=22+x 2解得：x=32∴在Rt △DEK 中，2222310=+0.5=22DK KE +（）（）故选A ．10．B解析：B【分析】①由AB=AC ，AD=AE ，利用等式的性质得到夹角相等，利用SAS 得出三角形ABD 与三角形ACE 全等，由全等三角形的对应边相等得到BD=CE ；②由三角形ABD 与三角形ACE 全等，得到一对角相等，再利用等腰直角三角形的性质及等量代换得到BD 垂直于CE ；③由等腰直角三角形的性质得到∠ABD+∠DBC=45°，等量代换得到∠ACE+∠DBC=45°； ④由BD 垂直于CE ，在直角三角形BDE 中，利用勾股定理列出关系式，等量代换即可作出判断．【详解】解：如图，① ∵∠BAC=∠DAE=90°，∴∠BAC+∠CAD=∠DAE+∠CAD ，即∠BAD=∠CAE ，∵在△BAD 和△CAE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝∴△BAD ≌△CAE （SAS ），∴BD=CE ，故①正确；②∵△BAD ≌△CAE ，∴∠ABD=∠ACE ，∵∠ABD+∠DBC=45°，∴∠ACE+∠DBC=45°，∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=45°+45°=90°，∴∠BDC=90°，∴BD ⊥CE ，故②正确；③∵△ABC 为等腰直角三角形，∴∠ABC=∠ACB=45°，∴∠ABD+∠DBC=45°，∵∠ABD=∠ACE∴∠ACE+∠DBC=45°，故③错误；④∵BD ⊥CE ，∴在Rt △BDE 中，利用勾股定理得BE 2=BD 2+DE 2，∵△ADE 为等腰直角三角形，∴AE=AD ，∴DE 2=2AD 2，∴BE 2=BD 2+DE 2=BD 2+2AD 2，在Rt △BDC 中，BD BC <，而BC 2=2AB 2，∴BD 2<2AB 2，∴()2222BE AD AB <+ 故④错误，综上，正确的个数为2个．故选：B ．【点睛】此题考查了全等三角形的判定与性质，勾股定理，以及等腰直角三角形的性质，熟练掌握全等三角形的判定与性质是解本题的关键．11．D解析：D【分析】利用等腰直角三角形的相关性质运用勾股定理以及对应角度的关系来推导对应选项的结论即可.【详解】解：由2AC=BC=4，则AE=3=DE ，由勾股定理可得2 ①正确； 21>，②正确；由∠A=∠EDF=45°，则2∠EDF=90°，∠CED=90°-∠CDE=90°-（∠CDF-45°）= 135°-∠CDF=135°-（∠DFB+45°）= 90°-∠DFB ，故∠CED+∠DFB=90°=2∠EDF ，③正确； △DCE 的周长2，△BDF 的周长2224个，故选：D.【点睛】本题主要考查等腰直角三角形的相关性质以及勾股定理的运用,本题涉及的等腰直角三角形、翻折、勾股定理以及边角关系，需要熟练地掌握对应性质以及灵活的运用.12．B解析：B【解析】试题解析：依题意得：梯子、地面、墙刚好形成一直角三角形，梯高为斜边，利用勾股定（米）．故选B．13．C解析：C【分析】根据图形翻折变换的性质可知，AE=BE，设AE=x，则BE=x，CE=8-x，再在Rt△BCE中利用勾股定理即可求出BE的长度．【详解】解：∵△ADE翻折后与△BDE完全重合，∴AE＝BE，设AE＝x，则BE＝x，CE＝8﹣x，在Rt△BCE中，BE2＝BC2+CE2，即x2＝62+（8﹣x）2，解得，x＝254，∴BE＝254．故选：C．【点睛】本题考查了图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．14．D解析：D【详解】解：∵一个直角三角形的两边长分别为3和5，∴①当5是此直角三角形的斜边时，设另一直角边为x，则由勾股定理得到：x；②当5是此直角三角形的直角边时，设另一直角边为x，则由勾股定理得到：x故选：D15．D解析：D【分析】根据勾股定理的逆定理对各选项进行判断即可．【详解】解：A、∵22+32=13≠42，∴不能构成直角三角形，故本选项不符合题意；B 、∵42+52=41≠62，∴不能构成直角三角形，故本选项不符合题意；C 、∵222222(3)(4)337(5)+=≠，∴不能构成直角三角形，故本选项不符合题意；D 、∵62+82=100=102，∴能构成直角三角形，故本选项符合题意．故选：D ．【点睛】本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a ，b ，c 满足a 2+b 2=c 2，那么这个三角形就是直角三角形是解答此题的关键．16．A解析：A【分析】求出两小边的平方和、最长边的平方,看看是否相等即可.【详解】A 、12+2=2∴以1,故本选项正确;B 、22+32≠42 ∴以2、3、4为边组成的三角形不是直角三角形,故本选项错误; C 、12+22≠32 ∴以1、2、3为边组成的三角形不是直角三角形,故本选项错误;D 、 42+52≠62 ∴以4、5、6为边组成的三角形不是直角三角形,故本选项错误;故选A..【点睛】本题考查了勾股定理的逆定理应用，掌握勾股定理逆定理的内容就解答本题的关键.17．C解析：C【分析】筷子浸没在水中的最短距离为水杯高度，最长距离如下图，是筷子斜卧于杯中时，利用勾股定理可求得.【详解】当筷子笔直竖立在杯中时，筷子浸没水中距离最短，为杯高=8cmAD 是筷子，AB 长是杯子直径，BC 是杯子高，当筷子如下图斜卧于杯中时，浸没在水中的距离最长由题意得：AB=15cm ，BC=8cm ，△ABC 是直角三角形∴在Rt △ABC 中，根据勾股定理，AC=17cm∴8cm≤h≤17cm故选：C【点睛】本题考查勾股定理在实际生活中的应用，解题关键是将题干中生活实例抽象成数学模型，然后再利用相关知识求解.18．C解析：C【分析】利用勾股定理的逆定理可以推导出ABD △是直角三角形.再利用勾股定理求出A C ，可得出AB=AC ，即可判断.【详解】解：由已知可得CD=BD=5,22251213+=即222BD AD AB +=,ABD ∴是直角三角形，90ADB ∠=︒，90ADC ∴∠=︒222AD CD AC ∴+=2251213AC ∴=+=13AB AC ∴==故ABC 是等腰三角形.故选C【点睛】本题考查了勾股定理和它的逆定理，熟练掌握定理是解题关键.19．C解析：C【分析】本题根据所给的条件得知，△ABC 是直角三角形，再根据三角形的面积相等即可求出BC 边上的高.【详解】∵AB ＝8，BC ＝10，AC ＝6，∴62＋82＝102，∴△ABC 是直角三角形，∠BAC ＝90°，则由面积公式可知，S △ABC ＝12AB ⋅AC ＝12BC ⋅AD ， ∴AD ＝245.故选C. 【点睛】本题考查了勾股定理的逆定理，需要先证得三角形为直角三角形，再利用三角形的面积公式求得AD 的值.20．C解析：C 【分析】根据BD 、CE 分别是AC 、AB 边上的高，推导出EBH DCH ∠=∠；再结合题意，可证明FAC AQB △≌△，由此可得F BAQ ∠=∠,AF AQ =；再经90AEF ∠=得90F FAE ∠+∠=，从而证明AF ⊥AQ ；最后由勾股定理得222AQ AD QD =+，从而得到AF AD ≠，即可得到答案．【详解】如图，CE 和BD 相较于H∵BD 、CE 分别是AC 、AB 边上的高∴CE AB ⊥,BD AC ⊥∴90BEC BDC AEF ADQ ∠=∠=∠=∠=∴90EBH EHB DHC DCH ∠+∠=∠+∠=∵EHB DHC ∠=∠∴EBH DCH ∠=∠又∵BQ ＝AC 且CF ＝AB∴FAC AQB △≌△∴F BAQ ∠=∠,AF AQ =，故B 、D 结论正确；∵90AEF ∠=∴90F FAE ∠+∠=∴90BAQ FAE F FAE ∠+∠=∠+∠=∴AF ⊥AQ 故A 结论正确；∵90ADQ ∠=∴222AQ AD QD =+∵0QD ≠∴AQ AD ≠∴AF AD ≠故选：C ．【点睛】本题考查了全等三角形、直角三角形、勾股定理、三角形的高等知识；解题的关键是熟练掌握全等三角形、直角三角形、勾股定理、三角形的高的性质，从而完成求解．。

2024年安徽省中考数学试题含答案解析

数学试题注意事项：1．你拿到的试卷满分为150分，考试时间为120分钟．2．本试卷包括“试题卷”和“答题卷”两部分．“试题卷”共4页，“答题卷”共6页．3．请务必在“答题卷”上答题，在“试题卷”上答题是无效的．4、考试结束后，请将“试题卷”和“答题卷”一并交回．审核：魏敬德老师一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A ，B ，C ，D 四个选项，其中只有一个是符合题目要求的．1. ﹣5的绝对值是（）A. 5B. ﹣5C. 15− D. 15【答案】A【解析】【分析】根据负数的绝对值等于它的相反数可得答案．【详解】解：|﹣5|=5．故选A ．2. 据统计，2023年我国新能源汽车产量超过944万辆，其中944万用科学记数法表示为（）A. 70.94410×B. 69.4410×C. 79.4410×D. 694.410× 【答案】B【解析】【分析】本题考查了科学记数法，先把944万转化为9440000，再根据科学记数法：10na ×（110a ≤<，n 为整数），先确定a 的值，然后根据小数点移动的数位确定n 的值即可，根据科学记数法确定a 和n 的值是解题的关键．【详解】解：944万694400009.4410=×，故选：B ．3. 某几何体的三视图如图所示，则该几何体为（）A. B.C. D.【答案】D【解析】【分析】本题主要考查由三视图判断几何体，关键是熟悉三视图的定义．【详解】解：根据三视图的形状，结合三视图的定义以及几何体的形状特征可得该几何体为D 选项．故选：D ．4. 下列计算正确的是（）A. 356a a a +=B. 632a a a ÷=C. ()22a a −=D. a =【答案】C【解析】【分析】题目主要考查合并同类项、同底数幂的除法、积的乘方运算、二次根式的化简，根据这些运算法则依次判断即可【详解】解：A 、3a 与5a 不是同类项，不能合并，选项错误，不符合题意；B 、633a a a ÷=，选项错误，不符合题意；C 、()22a a −=，选项正确，符合题意；D a =，当0a ≥a =，当0a <a =−，选项错误，不符合题意；故选：C5. 若扇形AOB 的半径为6，120AOB ∠=°，则 AB 的长为（）A. 2πB. 3πC. 4πD. 6π【答案】C【解析】【分析】此题考查了弧长公式，根据弧长公式计算即可．【详解】解：由题意可得， AB 的长为12064180ππ×=, 故选：C ．6. 已知反比例函数()0k y k x=≠与一次函数2y x =−的图象的一个交点的横坐标为3，则k 的值为（） A. 3−B. 1−C. 1D. 3 【答案】A【解析】【分析】题目主要考查一次函数与反比例函数的交点问题，根据题意得出231y =−=−，代入反比例函数求解即可【详解】解：∵反比例函数()0k y k x=≠与一次函数2y x =−的图象的一个交点的横坐标为3， ∴231y =−=−， ∴13k −=，∴3k =−，故选：A 7. 如图，在Rt ABC △中，2AC BC ==，点D 在AB 的延长线上，且CD AB =，则BD 的长是（）A. B. C. 2− D. −【答案】B【解析】【分析】本题考查了等腰直角三角形的判定和性质，对顶角的性质，勾股定理，过点D 作DE CB ⊥的延长线于点E ，则90BED ∠=°，由90ACB ∠=°，2AC BC ==，可得AB =，45A ABC ∠=∠=°，进而得到CD =，45DBE ∠=°，即得BDE △为等腰直角三角形，得到DE BE =，设DE BE x ==，由勾股定理得()(2222x x ++，求出x 即可求解，正确作出辅助线是解题的关键．【详解】解：过点D 作DE CB ⊥的延长线于点E ，则90BED ∠=°，∵90ACB ∠=°，2AC BC ==，∴AB 45A ABC ∠=∠=°，∴CD =，45DBE ∠=°，∴BDE △为等腰直角三角形，∴DE BE =，设DEBE x ==，则2CE x =+，在Rt CDE △中，222CE DE CD +=，∴()(2222x x ++，解得11x =−，21x −（舍去），∴1DE BE ==−，∴BD ==，故选：B ．8. 已知实数a ，b 满足10a b −+=，011a b <++<，则下列判断正确的是（）A. 102a −<<B. 112b << C. 2241a b −<+<D. 1420a b −<+<【答案】C【解析】【分析】题目主要考查不等式的性质，根据等量代换及不等式的性质依次判断即可得出结果，熟练掌握不等式的性质是解题关键【详解】解：∵10a b −+=，∴1a b =−，∵011a b <++<， ∴0111b b <−++<，∴102b <<，选项B 错误，不符合题意； ∵10a b −+=，∴1b a =+，∵011a b <++<，∴0111a a <+++<， ∴112a −<<−，选项A 错误，不符合题意； ∵112a −<<−，102b <<， ∴221a −<<−，042b <<， ∴2241a b −<+<，选项C 正确，符合题意；∵112a −<<−，102b <<， ∴442a −<<−，021b <<， ∴4421a b −<+<−，选项D 错误，不符合题意；故选：C 9. 在凸五边形ABCDE 中，AB AE =，BC DE =，F 是CD 的中点．下列条件中，不能推出AF 与CD 一定垂直的是（）A. ABC AED ∠=∠B. BAF EAF ∠=∠C. BCF EDF ∠=∠D. ABD AEC ∠=∠ 【答案】D【解析】【分析】本题考查了全等三角形的判定和性质，等腰三角形“三线合一”性质的应用，熟练掌握全等三角形的判定的方法是解题的关键．利用全等三角形的判定及性质对各选项进行判定，然后根据等腰三角形“三线合一”的性质即可证得结论．【详解】解：A 、连结AC AD 、，∵ABC AED ∠=∠，AB AE =，BC DE =，∴()SAS ACB ADE ≌，∴AC AD =又∵点F 为CD 的中点∴AF CD ⊥，故不符合题意；B 、连结BF EF 、，∵AB AE =，BAF EAF ∠=∠，AF AF =，∴()SAS ABF AEF ≌，∴BF EF =， AFB AFE ∠=∠又∵点F 为CD 中点，∴CF DF =，∵BC DE =,∴()SSS CBF DEF ≌，∴CFB DFE ∠=∠， ∴90CFB AFB DFE AFE ∠+∠=∠+∠=°，∴AF CD ⊥，故不符合题意；C 、连结BF EF 、，∵点F 为CD 的中点，∴CF DF =，∵BCF EDF ∠=∠，BC DE =，∴()SAS CBF DEF ≌，的∴BF EF =， CFB DFE ∠=∠， ∵AB AE =，AF AF =，∴()SAS ABF AEF ≌，∴AFB AFE ∠=∠，∴90CFB AFB DFE AFE ∠+∠=∠+∠=°，∴AF CD ⊥，故不符合题意；D 、ABD AEC ∠=∠，无法得出相应结论，符合题意；故选：D ．10. 如图，在Rt ABC △中，90ABC ∠=°，4AB =，2BC =，BD 是边AC 上的高．点E ，F 分别在边AB ，BC 上（不与端点重合），且DE DF ⊥．设AE x =，四边形DEBF 的面积为y ，则y 关于x 的函数图象为（）A. B.C. D.【答案】A【解析】【分析】本题主要考查了函数图象的识别，相似三角形的判定以及性质，勾股定了的应用，过点E 作EH AC ⊥与点H ，由勾股定理求出AC ，根据等面积法求出BD ，先证明ABC ADB ∽，由相似三角形的性质可得出AB AC AD AB =，即可求出AD ，再证明AED BFD ∽，由相似三角形的性质可得出2AED BFD S AD S BD = ，即可得出4AED BFD S S = ，根据()ABC AED BDC BDF DEBF S S S S S =−−− 四边形，代入可得出一次函数的解析式，最后根据自变量的大小求出对应的函数值．【详解】解：过点E 作EH AC ⊥与点H ，如下图：∵90ABC ∠=°，4AB =，2BC =，∴AC ，∵BD 是边AC 上的高． ∴1122AB BC AC BD ⋅=⋅，∴BD = ∵BAC CAB ∠=∠，90ABC ADB ∠=∠=°，∴ABC ADB ∽△△， ∴AB AC AD AB=，解得：AD =，∴DC AC AD =−==， ∵90BDF BDE BDE EDA ∠+∠=∠+∠=°，90CBD DBA DBA A ∠+∠=∠+∠=°，∴DBC A ∠=∠，BDF EDA ∠=∠，∴AED BFD ∽，∴224AED BFD S AD S BD == ， ∴4AED BFD S S = ，∴()ABC AED BDC BDF DEBF S S S S S =−−− 四边形 1111sin 2224BFD AB BC AE AD A DC DB S ⋅−⋅∠−⋅+1311422422x =××−× 16355x =− ∵04x <<，∴当0x =时，165DEBF S =四边形，当4x =时，45DEBF S =四边形．故选：A ．二、填空题（本大题共4小题，每小题5分，满分20分）11. 若代数式14−x 有意义，则实数x 取值范围是_____．【答案】4x ≠【解析】【分析】根据分式有意义的条件，分母不能等于0，列不等式求解即可．【详解】解：分式有意义的条件是分母不能等于0，∴40x −≠∴4x ≠．故答案：4x ≠．【点睛】本题主要考查分式有意义的条件，解决本题的关键是要熟练掌握分式有意义的条件． 12.，祖冲之给出圆周率的一种分数形式的近似值为227．比较大______227（填“>”或“<”）．【答案】>【解析】【分析】本题考查的是实数的大小比较，先比较两个正数的平方，从而可得答案．【详解】解：∵222484749 =，24901049==，而4844904949<，∴22227 <，227>；故答案为：>13. 不透明的袋中装有大小质地完全相同的4个球，其中1个黄球、1个白球和2个红球．从袋中任取2个球，恰为2个红球的概率是______．的为【答案】16【解析】【分析】本题考查了用树状图或列表法求概率，画出树状图即可求解，掌握树状图或列表法是解题的关键．【详解】解：画树状图如下：由树状图可得，共有12种等结果，其中恰为2个红球的结果有2种，∴恰为2个红球的概率为21126=，故答案为：16． 14. 如图，现有正方形纸片ABCD ，点E ，F 分别在边,AB BC 上，沿垂直于EF 的直线折叠得到折痕MN ，点B ，C 分别落在正方形所在平面内的点B ′，C ′处，然后还原．（1）若点N 在边CD 上，且BEF α∠=，则C NM ′∠=______（用含α式子表示）；（2）再沿垂直于MN 的直线折叠得到折痕GH ，点G ，H 分别在边,CD AD 上，点D 落在正方形所在平面内的点D '处，然后还原．若点D '在线段B C ′′上，且四边形EFGH 是正方形，4AE =，8EB =，MN 与GH 的交点为P ，则PH 的长为______．【答案】 ①. 90α°− ②.【解析】【分析】①连接CC ′，根据正方形的性质每个内角为直角以及折叠带来的折痕与对称点连线段垂直的性质，再结合平行线的性质即可求解；②记HG 与NC ′交于点K ，可证：AEH BFE DHG CGF △≌△≌△≌△，则4AE CG DH ===，8DG BE ==，由勾股定理可求HG =，由折叠的性质得到：90NC B NCB ′∠=∠=°，89∠=∠，90D GD H ′∠=∠=°，NC NC ′=，8GD GD ′==，则NG NK =，4KC GC ′==，由的NC GD ′′∥，得HC K HD G ′′△∽，继而可证明HK KG =，由等腰三角形的性质得到PK PG =，故34PH HG ==．【详解】解：①连接CC ′，由题意得4C NM ′∠=∠，MN CC ′⊥，∵MN EF ⊥，∴CC FE ′∥，∴12∠=∠，∵四边形ABCD 是正方形，∴90B BCD ∠=∠=°，∴343290∠+∠=∠+∠=°，190BEF ∠+∠=°，∴24∠∠=，190α∠=°−， ∴490α∠=°−<∴90C NM α′∠=°−，故答案为：90α°−；②记HG 与NC ′交于点K ，如图：∵四边形ABCD 是正方形，四边形EFGH 是正方形，∴90A B C D ∠=∠=∠=∠=°，HE FE =，90HEF ∠=°，∴567690∠+∠=∠+∠=°，∴57∠=∠，∴AEH BFE △≌△，同理可证：AEH BFE DHG CGF △≌△≌△≌△，∴4AE CG DH ===，8DG BE ==，在Rt HDG △中，由勾股定理得HG =由题意得：90NC B NCB ′∠=∠=°，89∠=∠，90D GD H ′∠=∠=°，NC NC ′=，8GD GD ′==， ∴NC GD ′′∥，∴9NKG ∠=∠，∴8NKG ∠=∠，∴NG NK =，∴NC NG NC NK ′−=−，即4KC GC ′==，∵NC GD ′′∥，∴HC K HD G ′′△∽，∴12HKC K HGD G ′==′， ∴12HK HG =， ∴HK KG =，由题意得MN HG ⊥，而NG NK =，∴PK PG =，∴34PH HG ==故答案为：．【点睛】本题考查了正方形的性质，折叠的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，等腰三角形的判定与性质，熟练掌握知识点，正确添加辅助线是解决本题的关键．三、（本大题共2小题，每小题8分，满分16分）15. 解方程：223x x −=【答案】13x =，21x =−【解析】【分析】先移项，然后利用因式分解法解一元二次方程，即可求出答案．【详解】解：∵223x x −=，∴223=0x x −−，∴(3)(1)0x x −+=， ∴13x =，21x =−．【点睛】本题考查了解一元二次方程，解题的关键是掌握解一元二次方程的方法进行解题．16. 如图，在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy ，格点（网格线的交点）A 、B ，C 、D 的坐标分别为()7,8，()2,8，()10,4，()5,4．（1）以点D 为旋转中心，将ABC 旋转180°得到111A B C △，画出111A B C △；（2）直接写出以B ，1C ，1B ，C 为顶点四边形的面积；（3）在所给的网格图中确定一个格点E ，使得射线AE 平分BAC ∠，写出点E 的坐标．【答案】（1）见详解（2）40（3）()6,6E (答案不唯一)【解析】【分析】本题主要考查了画旋转图形，平行四边形的判定以及性质，等腰三角形的判定以及性质等知识，结合网格解题是解题的关键．（1）将点A ，B ，C 分别绕点D 旋转180°得到对应点，即可得出111A B C △．（2）连接1BB ，1CC ，证明四边形11BC B C 是平行四边形，利用平行四边形的性质以及网格求出面积即可．（3）根据网格信息可得出5AB =，5AC，即可得出ABC 是等腰三角形，根据三线合一的性质即可求出点E 的坐标．【小问1详解】解：111A B C △如下图所示：【小问2详解】连接1BB ，1CC ，的∵点B 与1B ，点C 与1C 分别关于点D 成中心对称，∴1DB DB =，1DC DC =，∴四边形11BC B C 是平行四边形， ∴1111122104402BC B C S CC B ==×××= ．【小问3详解】∵根据网格信息可得出5AB =，5AC， ∴ABC 是等腰三角形，∴AE 也是线段BC 的垂直平分线，∵B ，C 的坐标分别为，()2,8，()10,4 ∴点21084,22E ++，即()6,6E ．（答案不唯一）四、（本大题共2小题，每小题8分，满分16分）17. 乡村振兴战略实施以来，很多外出人员返乡创业．某村有部分返乡青年承包了一些田地．采用新技术种植A B ，两种农作物．种植这两种农作物每公顷所需人数和投入资金如表：农作物品种每公顷所需人数每公顷所需投入资金（万元） A4 8 B 3 9已知农作物种植人员共24位，且每人只参与一种农作物种植，投入资金共60万元．问A B ，这两种农作物的种植面积各多少公顷？【答案】A 农作物的种植面积为3公顷，B 农作物的种植面积为4公顷．【解析】【分析】本题考查了二元一次方程组的应用，设A 农作物的种植面积为x 公顷，B 农作物的种植面积为y 公顷，根据题意列出二元一次方程组即可求解，根据题意，找到等量关系，正确列出二元一次方程组是解题的关键．【详解】解：设A 农作物的种植面积为x 公顷，B 农作物的种植面积为y 公顷，由题意可得，43248960x y x y += +=，解得34x y = = ，答：设A 农作物的种植面积为3公顷，B 农作物的种植面积为4公顷．18. 数学兴趣小组开展探究活动，研究了“正整数N 能否表示为22x y −（x y ，均为自然数）”的问题．（1）指导教师将学生的发现进行整理，部分信息如下（n 为正整数）： N 奇数 4的倍数表示结果 22110=− 22420=−22321=−22831=− 22532=− 221242=−22743=− 221653=−22954=−222064=−一般结论()22211n n n −=−− 4n =______按上表规律，完成下列问题：（ⅰ）24=（）2−（）2；（ⅱ）4n =______；（2）兴趣小组还猜测：像261014 ，，，，这些形如42n −（n 为正整数）的正整数N 不能表示为22x y −（x y ，均为自然数）．师生一起研讨，分析过程如下：假设2242n x y −=−，其中x y ，均为自然数．分下列三种情形分析：①若x y ，均为偶数，设2x k =，2y m =，其中k m ，均为自然数，则()()()222222224x y k m k m −=−=−为4的倍数．而42n −不是4的倍数，矛盾．故x y ，不可能均为偶数．②若x y ，均为奇数，设21x k =+，21=+y m ，其中k m ，均为自然数，则()()22222121x y k m −=+−+=______为4的倍数．而42n −不是4的倍数，矛盾．故x y ，不可能均为奇数．③若x y ，一个是奇数一个是偶数，则22x y −为奇数．而42n −是偶数，矛盾．故x y ，不可能一个是奇数一个是偶数．由①②③可知，猜测正确．阅读以上内容，请在情形②的横线上填写所缺内容．【答案】（1）（ⅰ）7，5；（ⅱ）()()2211n n +−−；（2）()224k m k m −+−【解析】【分析】（1）（ⅰ）根据规律即可求解；（ⅱ）根据规律即可求解；（2）利用完全平方公式展开，再合并同类项，最后提取公因式即可；本题考查了平方差公式，完全平方公式，掌握平方差公式和完全平方公式的运算是解题的关键．【小问1详解】（ⅰ）由规律可得，222475=−，故答案为：7，5；（ⅱ）由规律可得，()()22411n n n =+−−，故答案为：()()2211n n +−−；【小问2详解】解：假设2242n x y −=−，其中x y ，均为自然数．分下列三种情形分析：①若x y ，均为偶数，设2x k =，2y m =，其中k m ，均为自然数，则()()()222222224x y k m k m −=−=−为4的倍数．而42n −不是4的倍数，矛盾．故x y ，不可能均为偶数．②若x y ，均为奇数，设21x k =+，21=+y m ，其中k m ，均为自然数，则()()()22222221214x y k m k m k m −=+−+=−+−为4的倍数．而42n −不是4的倍数，矛盾．故x y ，不可能均为奇数．③若x y ，一个是奇数一个是偶数，则22x y −为奇数．而42n −是偶数，矛盾．故x y ，不可能一个是奇数一个是偶数．由①②③可知，猜测正确．故答案为：()224k m k m −+−．五、（本大题共2小题，每小题10分，满分20分）19. 科技社团选择学校游泳池进行一次光的折射实验，如图，光线自点B 处发出，经水面点E 折射到池底点A 处．已知BE 与水平线的夹角36.9α=°，点B 到水面的距离 1.20BC =m ，点A 处水深为1.20m ，到池壁的水平距离 2.50m AD =，点B C D ，，在同一条竖直线上，所有点都在同一竖直平面内．记入射角为β，折射角为γ，求sin sin βγ的值（精确到0.1，参考数据：sin 36.90.60°≈，cos36.90.80°≈，tan 36.90.75°≈）．【答案】43【解析】【分析】本题考查了解直角三角形，勾股定理，三角函数，过点EF AD ⊥于F ，则90AFE ∠=°，DF CE =，由题意可得，36.9BEC α∠=∠=°，CBE β∠=∠， 1.2m =EF ，解Rt BCE 求出CE 、BE ，可求出sin β，再由勾股定理可得AE ，进而得到sin γ，即可求解，正确作出辅助线是解题的关键．【详解】解：过点EF AD ⊥于F ，则90AFE ∠=°，DF CE =，由题意可得，36.9BEC α∠=∠=°，CBE β∠=∠， 1.2m =EF ，在Rt BCE 中， 1.2 1.6m tan 0.75BC CE α=≈=， 1.22m sin 0.6BC BE α=≈=， ∴ 1.64sin 25CE BE β===， 1.6m DF =， ∴ 2.5 1.60.9m AF AD DF =−=−=，∴在Rt AFE， 1.5m AE ===， ∴0.93sin 1.55AF AEγ===， ∴4sin 453sin 35βγ==．20. 如图，O 是ABC 的外接圆，D 是直径AB 上一点，ACD ∠的平分线交AB 于点E ，交O 于另一点F ，FA FE =．（1）求证：CD AB ⊥；（2）设FM AB ⊥，垂足为M ，若1OM OE ==，求AC 的长．【答案】（1）见详解（2）【解析】【分析】本题主要考查了等腰三角形的性质，圆周角定理，勾股定理等知识，掌握这些性质以及定理是解题的关键．（1）由等边对等角得出FAE AEF ∠=∠，由同弧所对的圆周角相等得出FAE BCE ∠=∠，由对顶角相等得出AEF CEB ∠=∠，等量代换得出CEB BCE ∠=∠，由角角平分线的定义可得出ACE DCE ∠=∠，由直径所对的圆周角等于90°可得出90ACB ∠=°，即可得出90CEB DCE BCE ACE ACB ∠+∠=∠+∠=∠=°，即90CDE ∠=°．（2）由（1）知，CEB BCE ∠=∠，根据等边对等角得出BE BC =，根据等腰三角形三线合一的性质可得出MA ，AE 的值，进一步求出OA ，BE ，在利用勾股定理即可求出AC ．【小问1详解】证明：∵FA FE =，∴FAE AEF ∠=∠，又FAE ∠与BCE ∠都是 BF所对的圆周角， ∴FAE BCE ∠=∠，∵AEF CEB ∠=∠，∴CEB BCE ∠=∠，∵CE 平分ACD ∠，∴ACE DCE ∠=∠，∵AB 是直径，∴90ACB ∠=°，∴90CEB DCE BCE ACE ACB ∠+∠=∠+∠=∠=°，故90CDE ∠=°，即CD AB ⊥．【小问2详解】由（1）知，CEB BCE ∠=∠，∴BE BC =，又FA FE =，FM AB ⊥，∴2MA ME MO OE ==+=，4AE =，∴圆的半径3OA OB AE OE ==−=，∴2BE BC OB OE ==−=，在ABC 中．26AB OA ==，2BC =∴AC即AC 的长为六、（本题满分12分）21. 综合与实践【项目背景】无核柑橘是我省西南山区特产，该地区某村有甲、乙两块成龄无核柑橘园．在柑橘收获季节，班级同学前往该村开展综合实践活动，其中一个项目是：在日照、土质、空气湿度等外部环境基本一致的条件下，对两块柑橘园的优质柑橘情况进行调查统计，为柑橘园的发展规划提供一些参考．【数据收集与整理】从两块柑橘园采摘的柑橘中各随机选取200个．在技术人员指导下，测量每个柑橘的直径，作为样本数据．柑橘直径用x （单位：cm ）表示．将所收集的样本数据进行如下分组：组别 AB C D E x 3.5 4.5x ≤< 4.5 5.5x ≤< 5.5 6.5x ≤< 6.57.5x ≤< 7.58.5x ≤≤整理样本数据，并绘制甲、乙两园样本数据的频数直方图，部分信息如下：任务1 求图1中a 的值．【数据分析与运用】任务2 A ，B ，C ，D ，E 五组数据的平均数分别取为4，5，6，7，8，计算乙园样本数据的平均数．任务3 下列结论一定正确的是______（填正确结论的序号）．①两园样本数据的中位数均在C 组；②两园样本数据的众数均在C 组；③两园样本数据的最大数与最小数的差相等．任务4 结合市场情况，将C ，D 两组的柑橘认定为一级，B 组的柑橘认定为二级，其它组的柑橘认定为三级，其中一级柑橘的品质最优，二级次之，三级最次．试估计哪个园的柑橘品质更优，并说明理由．根据所给信息，请完成以上所有任务．【答案】任务1：40；任务2：6；任务3：①；任务4：乙园的柑橘品质更优，理由见解析【解析】【分析】题目主要考查统计表及频数分布直方图，平均数、中位数及众数的求法，根据图标获取相关信息是解题关键．任务1：直接根据总数减去各部分的数据即可；任务2：根据加权平均数的计算方法求解即可；任务3：根据中位数、众数及极差的计算方法求解即可；任务4：分别计算甲和乙的一级率，比较即可．【详解】解：任务1：2001570502540a =−−−−=；任务2：1545057065071586200×+×+×+×+×=，乙园样本数据的平均数为6；任务3：①∵1570100,157050101+++，∴甲园样本数据的中位数在C 组， ∵1550100,155070101+++，∴乙园样本数据的中位数在C 组，故①正确；②由样本数据频数直方图得，甲园样本数据的众数均在B 组，乙园样本数据的众数均在C 组，故②错误； ③无法判断两园样本数据的最大数与最小数的差是否相等，故③错误；故答案为：①；任务4：甲园样本数据的一级率为：5040100%45%200+×=，乙园样本数据的一级率为：7050100%60%200+×=， ∵乙园样本数据的一级率高于甲园样本数据的一级率，∴乙园的柑橘品质更优．七、（本题满分12分）22. 如图1，ABCD 的对角线AC 与BD 交于点O ，点M ，N 分别在边AD ，BC 上，且AM CN =．点E ，F 分别是BD 与AN ，CM 的交点．（1）求证：OE OF =；（2）连接BM 交AC 于点H ，连接HE ，HF ．（ⅰ）如图2，若HE AB ∥，求证：HF AD ∥；（ⅱ）如图3，若ABCD 为菱形，且2MD AM =，60EHF ∠=°，求AC BD的值．【答案】（1）见详解（2）（ⅰ）见详解，（ⅱ【解析】【分析】（1）利用平行四边形的性质得出AM CN ∥，再证明AMCN 是平行四边形，再根据平行四边形的性质可得出OAE OCF ∠=∠，再利用ASA 证明AOE COF △≌△，利用全等三角形的性质可得出OE OF =．（2）（ⅰ）由平行线截直线成比例可得出OH OE OA OB =，结合已知条件等量代换OH OF OA OD=，进一步证明HOF AOD ∽ ，由相似三角形的性质可得出OHF OAD ∠=∠，即可得出HF AD ∥．（ⅱ）由菱形的性质得出AC BD ⊥，进一步得出30EHO FHO ∠=∠=°，OH =，由平行线截直线成比例可得出13AH AM HC BC ==，进一步得出2OA OH =，同理可求出5OB OE =，再根据25AC OA OH BD OB OE ==即可得出答案．【小问1详解】证明：∵四边形ABCD 是平行四边形，∴AD BC ∥，OA OC =，∴AM CN ∥，又∵AM CN =，∴四边形AMCN 是平行四边形，∴∥AN CM ，∵OAE OCF ∠=∠．在AOE △与COF 中，OAE OCF OA OCAOE COF ∠=∠ = ∠=∠∴()ASA AOE COF ≌．∴OE OF =．【小问2详解】（ⅰ）∵HE AB ∥∴OH OE OA OB=，又OB OD =．OE OF =， ∴OH OF OA OD=， ∵HOF AOD ∠=∠，∴HOF AOD ∽ ，∴OHF OAD ∠=∠，∴HF AD ∥（ⅱ）∵ABCD 是菱形，∴AC BD ⊥，又OE OF =，60EHF ∠=°，∴30EHO FHO ∠=∠=°，∴OH =，∵AM BC ∥．2MD AM =， ∴13AHAM HC BC ==，即3HC AH =，∴()3OA AH OA OH +=−，∴2OA OH =，∵BN AD ∥，2MD AM =，AM CN =， ∴23BEBN ED AD ==，即32BE ED =，∴()()32OB OE OB OE −+∴5OB OE =，故25ACOA OH BD OB OE ===．【点睛】本题主要考查了平行四边形的判定以及性质，全等三角形判定以及性质，相似三角形的判定以及性质，平行线截线段成比例以及菱形的性质，掌握这些判定方法以及性质是解题的关键．八、（本题满分14分）23. 已知抛物线2y x bx =−+（b 为常数）的顶点横坐标比抛物线22y x x =−+的顶点横坐标大1．（1）求b 的值；（2）点()11,A x y 在抛物线22y x x =−+上，点()11,B x t y h ++在抛物线2y x bx =−+上．（ⅰ）若3h t =，且10x ≥，0t >，求h 的值；（ⅱ）若11x t =−，求h 的最大值．【答案】（1）4b =（2）（ⅰ）3；（ⅱ）103 【解析】【分析】题目主要考查二次函数的基本性质及化为顶点式，解一元二次方程，理解题意，熟练掌握运用二次根数的基本性质是解题关键．（1）根据题意求出22yx x =−+的顶点为()1,1，确定抛物线2y x bx =−+（b 为常数）的顶点横坐标为2，即可求解；（2）根据题意得出21112y x x =−+， 2111()4()y h x t x t +=−+++，然后整理化简211224h t x t x t =−−++；（ⅰ）将3h t =代入求解即可；（ⅱ）将11x t =−代入整理为顶点式，即可得出结果．【小问1详解】解：2222(21)1(1)1yx x x x x =−+=−−++=−−+， ∴22y x x =−+的顶点为()1,1，∵抛物线2y x bx =−+（b 为常数）的顶点横坐标比抛物线22y x x =−+的顶点横坐标大1， ∴抛物线2y x bx =−+（b 为常数）的顶点横坐标为2， ∴()221b −=×−， ∴4b =；【小问2详解】由（1）得224y x bx x x =−+=−+ ∵点()11,A x y 在抛物线22y x x =−+上，点()11,B x t y h ++在抛物线24y x x =−+上． ∴21112y x x =−+， 2111()4()y h x t x t +=−+++，整理得：211224h t x t x t =−−++ （ⅰ）∵3h t =， ∴2113224t t x t x t =−−++，整理得：()1122t t x t x +=+， ∵10x ≥，0t >， ∴1t =，∴3h =；（ⅱ）将11x t =−代入211224h t x t x t =−−++，整理得224103823()33h t t t =−+−=−−+， ∵30−<， ∴当43t =，即113x =时，h 取得最大值为103．。