单个交叉口模糊控制及Simulink仿真

合集下载

单交叉口交通灯信号模糊控制及其仿真

单交叉口交通灯信号模糊控制及其仿真The fuzzy algorithm control for Single road intersection traffic light and its simulation 摘要：本文采用模糊控制算法对四相位三车道单交叉口的交通灯进行控制。

首先通过离线计算机得到绿灯延时的模糊控制查询表，根据当前等待队列长与通行队列长查表和到绿灯延时。

通过使用同一随机种子产生随机数对该方法与传统定时控制方法进行仿真，仿真结果表明模糊控制方法在车辆延误时间上较之传统定时控制方法大为改善。

关键词：四相位;单交叉口;模糊控制;仿真Abstract: This paper uses the fuzzy control algorithm carries on the control to four phases three traffic lanes single road intersections traffic light. First obtains the green light time delay through the off-line computer the fuzzy control questionnaire. Is long and the general formation according to the current waiting formation long looks up the table and to the green light time delay. Has the random number through the use identical stochastic seed carries on the simulation to this method and the traditional timed control method, The simulation result indicates the fuzzy control method delays in the time in the vehicles compared with the traditional timed control method greatly is the improvement.Key words: Four phases；Single road intersection；Fuzzy control；Simulation1.引言传统单路口交通控制通常采用定时控制方案，预行人为分配好红绿灯的保持时间，其目的首先是协调好车辆的通行，其次是要尽量减少车辆的延误。

模糊控制simulink实例

模糊控制simulink实例一、模糊控制概述模糊控制是一种基于人工智能的控制方法，它模拟人类的思维方式进行控制决策。

模糊控制的核心思想是将模糊语言和模糊推理应用于控制系统中，通过建立模糊规则和模糊集合来实现对系统的控制。

模糊控制具有适应性强、处理非线性和复杂系统能力强等优点，在工业控制领域得到了广泛应用。

二、Simulink简介Simulink是MathWorks公司开发的一款基于MATLAB的通用仿真平台。

Simulink提供了一个直观的图形化界面，可以用于设计、模拟和实现各种系统模型。

Simulink 支持多领域的仿真，包括控制系统、信号处理、通信系统等，同时也提供了丰富的库函数和工具箱，方便用户进行系统建模与仿真。

三、模糊控制在Simulink中的应用模糊控制在Simulink中的应用可以通过Fuzzy Logic Toolbox来实现，该工具箱提供了一系列用于模糊控制设计和仿真的函数和模块。

下面介绍一个简单的模糊控制实例来说明模糊控制在Simulink中的应用。

3.1 系统建模首先，我们需要确定模糊控制系统的输入、输出和控制规则。

假设我们要设计一个小型的温度控制系统，系统的输入是环境温度（T），输出是加热器的电压（V）。

根据经验，我们可以定义几个模糊集合来描述温度和电压的状态，例如”冷”、“适中”和”热”。

然后，我们可以根据这些模糊集合定义一些模糊规则，例如”当温度冷时，增加电压”等。

3.2 模糊控制器设计在Simulink中，我们可以使用Fuzzy Logic Controller模块来设计模糊控制器。

该模块提供了一种快速且简单的方法来创建模糊控制器。

首先，我们需要定义输入和输出的模糊集合，以及模糊规则。

然后，我们可以将这些参数传递给Fuzzy Logic Controller模块，并设置输入输出的信号传递方式。

3.3 系统仿真在完成模糊控制器的设计后，我们可以进行系统的仿真。

在Simulink中，我们可以通过连接输入信号和模拟环境来模拟系统的行为。

模糊控制实例及simulink仿真实验报告

模糊控制实例及simulink仿真实验报告
一、背景介绍
模糊控制是一种基于模糊逻辑的控制方法，其优点在于可以很好地处理复杂的非线性和不确定性系统，而且不需要精确的数学模型和计算，能够快速实现控制的优化。

二、实例介绍
本次实例采用一个双轮小车为对象，实现小车在平面上向指定位置运动的控制。

通过小车的速度和转向角两个输入变量，输出一个模糊控制信号，控制小车前进和转向。

三、实验过程
1. 建立模糊控制系统模型
打开Simulink软件，建立一个新模型，模型中包括输入变量、输出变量和控制器。

2. 设计输入变量和输出变量
（1）设计输入变量
本实例选择小车速度和转向角两个输入变量，每个变量包含三个模糊集合，速度变量分别为“慢速”、“中速”、“快速”，转向角变量分别为“左转”、“直行”、“右转”。

（2）设计输出变量
模糊控制信号输出变量选择小车的前进和转向，每个变量包含三个模糊集合，分别为“慢行”、“中行”、“快行”、“左转”、“直行”、“右转”。

3. 建立控制器
建立模糊控制器，包含输入变量和输出变量的关系，建立控制规则库和模糊关系。

4. 仿真实验
在Simulink下进行仿真实验，调整控制器参数，观察小车运动状态，对比试验。

四、实验结果
经过多次试验和调整，得到最优的小车模糊控制参数，可以实现小车的平滑运动
和准确转向。

五、实验结论
本实验通过建立一个小车的模糊控制系统，可以有效实现小车的平滑运动和准确转向，控制效果优于传统的PID控制方法。

模糊控制可以很好地处理非线性、不确定性和模糊性的系统，适合许多需要快速优化控制的场合。

MATLAB设计模糊控制器并用simulink仿真

MATLAB设计模糊控制器并用simulink仿真
环境：MATLAB R2012a
目录
一、设计模糊控制器
1.1 创建项目文件夹
1.2 打开MATLAB
1.3 设计模糊控制器
二、设置控制系统
三、simulink仿真
一、设计模糊控制器
1.1 创建项目文件夹
在此路径如图
1.2 打开MATLAB
打开MATLAB R2012a切换当前目录为上一步路径，如图
1.3 设计模糊控制器
打开模糊控制器设计对话框
根据模糊控制器的输入输出设计模糊控制器，在此以二输入一输出为例。

完成后如图（左）所示，然后对每个输入输出变量设置隶属函数，如图（右）。

添加论域数量
设置隶属函数
完成后如图所示
设计模糊规则
保存刚刚设计的模糊控制器，如下图所示
加载模糊控制器到MATLAB中
二、设置控制系统
打开simulink仿真器
设计控制系统
设计完成如图所示
添加第一节中设计的模糊控制器，如下图
自此控制系统设计结束
三、simulink仿真
在仿真之前需要进行如下设置
开始仿真。

基于simulink的模糊控制仿真

基于simulink的模糊控制仿真已知系统的传递函数为：1/(10s+1)*e(-0.5s)。

假设系统给定为阶跃值r=30，系统初始值r0=0.试分别设计(1)常规的pid控制器；(2)常规的模糊控制器；（3）比较两种控制器的效果；(4)当通过改变模糊控制器的比例因子时，系统响应有什么变化？一、基于Simulink的PID控制器仿真与调试：调节后的kp，ki，kd分别为：10，1，0.05。

示波器观察到的波形为：二、基于Simulink的模糊控制器仿真与调试：（1）启动matlab后，在主窗口中键入fuzzy回车，屏幕上就会显现出如下图所示的“fiseditor”界面，即模糊推理系统编辑器。

（2）双击“输入数量”或“输出数量”模块框中的任意一个，弹出成员资格函数编辑器，缩写为MF编辑器。

（3）在fiseditor界面顺序单击菜单editor―rules出现模糊规则编辑器。

本设计采用双输入（偏差E和偏差变化EC）单输出（U）模糊控制器。

E的域为[-6,6]，EC的域为[-6,6]，u的域为[-6,6]。

它们的状态为负大（NB）、负中（nm）、负小（NS）、零（Zo）、正小（PS）、正中（PM）和正大（PB）。

语言值的隶属函数选择三角形的隶属函数。

选择Mamdani控制规则作为推理规则。

该控制器的控制规则表如图所示：Simulink仿真图如下：在调试过程中发现加入积分调节器有助于消除静差，通过试凑法得出量化因子，比例因子以及积分常数。

ke，kec，ku，ki分别是：3，2.5，3.5，0.27三、实验经验：通过比较pid控制器和模糊控制器，我们可知两个系统观察到的波形并没有太大的区别。

相对而言，对于给出精确数学模型的控制对象，pid控制器显得更具有优势，其一是操作简单，其二是调节三个参数可以达到满意的效果；对于给出给出精确数学模型的控制对象，模糊控制器并没有展现出太大的优势，其一是操作繁琐，其二是模糊控制器调节参数的难度并不亚于pid控制器。

模糊pidmatlab(simulink)仿真详细步骤

下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、范围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值范围，本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name中键入名称，在Type 中选择形状，在Params中键入范围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

模糊控制simulink实例

模糊控制simulink实例模糊控制是一种基于人类智能的控制方法，其能够克服传统控制方法中的困难和不足，使得控制系统能够更加稳定和灵活地进行控制。

在模糊控制中，模糊规则和模糊推理是非常关键的，而Simulink正是一款非常适合模拟和控制系统的MATLAB工具箱。

现在，我们就来看一个基于Simulink的模糊控制实例。

假设我们有一个小车可以沿着一条直线上下运动，并且需要通过模糊控制来控制小车的运动。

我们将小车的速度和位置分别作为系统的输入和输出，其中小车的速度可以在0-10m/s之间变化，而小车的位置则可以在0-50m之间变化。

需要注意的是，在这个系统中，小车的速度和位置都是模糊的，我们需要通过模糊规则和推理来确定小车应该如何移动。

首先，我们需要确定一组模糊规则来描述小车的运动。

这里我们设定了三个模糊规则，分别是：1. 如果小车位置很靠近上限，那么小车速度应该减缓。

2. 如果小车位置中间，那么小车速度应该保持不变。

3. 如果小车位置很靠近下限，那么小车速度应该加速。

然后，我们需要建立一组模糊推理机制来根据当前状态来确定小车的下一个状态。

这里我们选择了三个模糊推理机制：模糊最小性、模糊加法和模糊乘法。

其中，模糊最小性是用来确定模糊集合之间的交集，模糊加法是用来确定两个模糊集合之间的并集，而模糊乘法则是用来确定两个模糊集合之间的乘积。

最后，我们需要使用Simulink建立一个模糊控制系统，并将上述规则和推理机制应用到这个系统中。

在Simulink中，我们可以使用Fuzzy Logic Controller来实现这个过程。

首先，我们需要将输入和输出变量添加到Fuzzy Logic Controller中。

然后，我们需要为每个变量设置一个模糊集合，以便能够将当前状态转换为模糊状态。

接下来，我们需要将模糊规则添加到Fuzzy Logic Controller中，并为每个规则设置一些权重，以便能够决定规则的优先级。

Matlab模糊控制器的设计以及simulink下对模糊控制器系统的仿真(word文档良心出品)

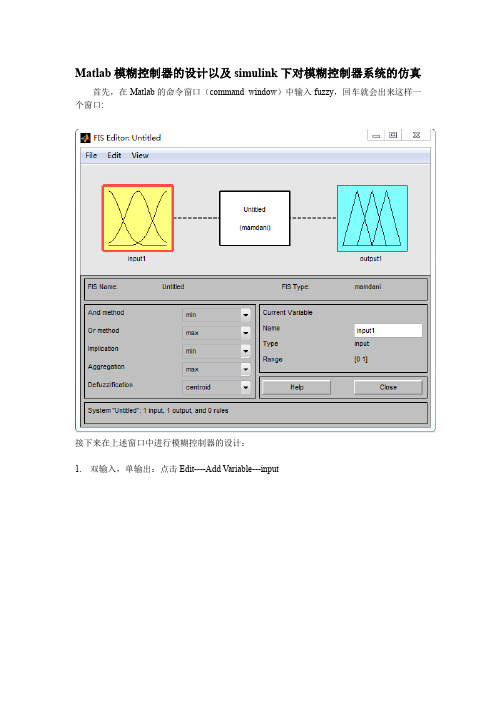
Matlab模糊控制器的设计以及simulink下对模糊控制器系统的仿真首先，在Matlab的命令窗口（command window）中输入fuzzy，回车就会出来这样一个窗口:接下来在上述窗口中进行模糊控制器的设计：1.双输入，单输出：点击Edit----Add Variable---input2.为E添加隶属度函数，E的论域为{-6，-5，-4，-3，-2，-1,0,1，2,3,4,5,6}，E的模糊集合为{NB,NM,NS,NZ,PZ,PS,PM,PB},Edit—Membership Function edit,如下图所示：3.为EB添加隶属度函数，EB的论域为{-6，-5，-4，-3，-2，-1,0,1，2,3,4,5,6}，EB的模糊集合为{NB,NM,NS,ZE,PS,PM,PB},Edit—Membership Function edit,如下图所示：4.为U添加隶属度函数，U的论域为{-6，-5，-4，-3，-2，-1,0,1，2,3,4,5,6}，U的模糊集合为{NB,NM,NS,ZE,PS,PM,PB},Edit—Membership Function edit,如下图所示：其中E,EB,U均为模糊量。

5.为模糊控制器设计模糊规则，由于E的语言变量有8个，EB的语言变量有7个，所以模糊控制器的模糊规则总共有8*7=56条，接下来为模糊控制器添加规则：双击untitled，则有下面的表格：制定完成后，会形成模糊规则矩阵，系统会根据模糊输入量E,EB，经过模糊控制规则[56条]，进而确定输出量U。

6.对输入量模糊化以及对输出量清晰化，我们采取最小最大重心法。

7.点击export—to file. ***#$.fis文件就是所设计的控制器。

8.下面对我们设计的模糊控制器进行检验，所构建的系统如下：系统分析：模糊控制器：双输入单输出，输入为误差以及误差的变化率的模糊量，输出为控制量的模糊量，模糊控制器中有56条规则。

模糊pid_matlab(simulink)仿真详细步骤

下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为 probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值围，本例中In_x和In_y的取值围均为[0 10], Out_x和Out_y的取值围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs 设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name 中键入名称，在Type 中选择形状，在Params中键入围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

模糊控制系统的MATLABSIMULINK仿真与分析

收稿日期:2000207203　基金项目:河南省教委自然科学基金项目(97465001)　作者简介:王东云(19642),男(汉族),湖南津市人,中原工学院电气工程系副教授、工学博士.　第11卷第4期郑州纺织工学院学报V ol.11　N o.42000年12月JOURNA L OF ZHENGZH OU TEXTI LE INSTITUTE Dec.,2000 文章编号:100724945(2000)0420001204模糊控制系统的MAT LAB ΠSI MULINK 仿真与分析王东云1,凌德麟2(1.中原工学院电气工程系;2.中原工学院院部,河南郑州　450007)摘要:　针对M AT LAB ΠSI M U LI NK 的模糊控制工具箱的使用方法和应用的相关文献尚未见到的情况,介绍了基于M AT 2LA B ΠSI M U LI NK 的模糊控制系统仿真分析的方法与步骤.在仿真的基础上,研究了量化因子、比例因子对模糊控制性能的影响.关　键　词:　M AT LAB ΠSI M U LI NK;模糊推理系统;模糊控制;隶属度函数中图分类号:TP273.5 文献标识码:A MAT LAB 软件自1984年由美国的Math W orks 公司推出以来,其应用范围越来越广泛.目前的MAT LAB 已经成为国际上最为流行的软件之一[1].它除了传统的交互式编程之外,还提供了丰富的矩阵运算、图形绘制、数据处理、图像处理、方便的Windows 编程等便利工具.另外,MAT LAB 有很强的开放性,针对不同的应用学科,在MAT LAB 上可以推出不同的工具箱,这样就大大扩展了MAT LAB 的运用范围.目前,已经推出了控制系统的工具箱、系统辨识工具箱、神经网络工具箱、信号处理工具箱及模糊推理系统工具箱等许多学科性的工具箱,但针对具体的学科性的工具箱的使用方法和应用的相关文献尚未见到.因此本文详细介绍了利用MAT LAB5.0模糊推理工具箱,进行模糊控制系统的仿真与分析的方法与步骤.1　MAT LAB ΠSIMU LINK 简介MAT LAB 语言是一种面向科学与工程计算的高级语言,基本语法单元是矩阵.变量的赋值采用:变量=表达式的形式,变量有全局变量和局部变量两种.MAT LAB 的数据结构非常简单,只有数据变量和字符变量两种.MAT LAB 语言有三种基本的程序结构:顺序结构、循环结构及分支结构.其中循环结构有FOR -E ND 循环和WHI LE -E ND 循环两种.FOR -E ND 循环的一般形式为:FOR x =表达式(形如x =起点:步长:终点)循环体E ND WHI LE -E ND 循环的一般形式为:WHI LE 表达式(表达式非零,则执行循环体)循环体E ND 分支、结构的一般形式为:IF (表达式(非零)) 语句体　1E LSE 语句体　2E NDMAT LAB 的M 文件在功能上可分为两种类型:文本文件和函数文件.这两种文件都是ASCII 码的文本格式.文本文件包含一系列专门的MAT LAB 语句,当运行一个文本文件时,将自动执行一系列命令直至给出最终结果,而不是交互地等待键盘输入,如M 文件的第一行包“FUNCTI ON ”,则这个文件就是函数文件.其一般形式:FUNCTI ON[输出函数1,输出函数2,…]=函数名(输入参数1,输入参数2,…).函数调用格式:[输出参数1,输出参数2,…]=函数名(输入参数1,输入参数2,…).M A T LA B 有很强的绘图功能,用命令plot ()实现.SI MU LI NK 子库是一个建模、分析各种物理和数学系统的软件.它用框图表示各系统的各个环节,用带方向的连线表示各环节的输入输出关系.SI M U LI NK 的启发十分丰富,只需在命令窗口键入“SI M U LI NK ”命令,此时出现一个SI M U LI NK 窗口,包含七个模型库和一个DE M OS ,分别是:信号源库、输出库、离散系统库、线性系统库、非线性系统库及扩展系统库.在这些库中你可以找到你所需的每个环节,必要时,你还可以建立自己的环节库.具体方法可参见文献[2].2　利用M A T LA B 建立模糊控制仿真系统2.1　利用图形编辑器编辑模糊推理系统(FIS )在MAT LAB 的命令状态下键入Fuzzy.模糊推理系统图形编辑器如图1所示.它显示了模糊推理系统的高层信息.在顶部有一标名为输入和输出的系统图表,通过双击输入或输出框,产生隶属函数编辑器;双击图表中心的模糊规则框,产生规则编辑器.图1　模糊推理系统图形编辑器图表的下方是显示当前FIS 名的文本区.窗口的左下角有一系列弹出菜单使你能定义用于模糊隐含程序的变量函数,右下方是提供关于当前变量信息的区域.通过单击输入或输出框来决定当前变量.如此我们构造了一个模糊推理系统,即建立了模糊控制器的输入输出变量名称、个数、变量的论域、分档、隶属度函数的形式、模糊运算方法、去模糊的方法、模糊规则集等.实际上我们可以利用show fis ()函数来查阅有关模糊推理系统的信息.另外还可以给刚刚建立的模糊推理系统取个名字,如:Firstfis.2.2　利用SIMU LINK 的图形编辑器构造模糊控制系统图2为一常规模糊控制系统.图2　常规的模糊控制系统结构其中:K 1、K 2为量化因子;K 3为比例因子.对如图2所示的模糊控制系统我们可以使用SI M 2U LI NK 的图形编辑器构造出,其步骤如下:(1)键入simulink ,进入SI MU LI NK 的图形编辑器.(2)在File ΠNew 下建立一个M odel 文件.(3)根据控制系统结构,利用SI MU LI NK 的图形编辑器,从SI MU LI NK 的模型库中“拖出”所需的各个环节,如在Blockets &T oolboxes 中的SI MU LI NK Fuzzy 库中,我们可以“拖出”Fuzzy logical controller ,在Linear 库或其它库中,我们可以设定控制对象.最后我们可以构造出所需的控制系统(见图3).图3　模糊控制系统控制框图注意在“拖出”所需的各个环节后,可以设置各环・2・郑州纺织工学院学报 2000年　第11卷　节的参数.如设置比例环节的比例系数等.注意在设置模糊控制器时,要把在第一步建立的模糊推理系统与之统一起来,这样就可以在仿真时使用.这时我们可以使用MAT LAB 命令:afuzzycontroller =readfis (‘firstfis ’)其中firstfis 为在第一步建立的模糊推理系统名,接下来我们可以开始仿真.3　基于MAT LAB 的模糊控制仿真分析实例对图2的一个经典的二维模糊逻辑控制器,比例因子K 1和K 2分别相当于模糊控制的比例作用和微分作用的系数,K 3则相当于总的放大倍数[3,4].K 1,K 2增大,相当于控制器的比例作用、微分作用增强;而K 3增大,相当于控制器的放大倍数加大.如图4为不同K 1时系统的阶跃响应.如图5为不同K 3时系统的阶跃响应.由以上仿真结果,我们不难分析出量化因子和比例因子对控制系统性能的影响:图4　K 1为不同值的系统响应图5　K 3为不同值的系统响应 (1)K 1越大,系统调节惰性越小,上升速率越快.(2)K 1过大,系统上升速率过大,产生的超调大,使调节时间增长,严重时还会产生振荡乃至系统不稳定.(3)K 1过小,系统上升速率较小,系统调节隋性变大,同时也影响系统的稳态性能,使稳态精度降低.(4)K 3增大,相当于系统总的放大倍数增大,系统的响应速度加快.(5)K 3过大,会导致系统输出上升速率过大,从而产生过大的超调乃至振荡和发散.(6)K 3过小,系统的前向增益很小,系统输出上升速率较小,快速性变差,稳态精度变差.4　结　语利用MAT LAB 来实现模糊控制器的仿真分析非常简便,为研究模糊控制理论、设计模糊控制器提供了有力的工具.如何利用MAT LAB 来实现自适应模糊控制器的仿真分析与设计,应是我们下一步要研究的问题.参考文献:[1]　张培强.M AT LAB 语言—演算纸式的科学工程计算语言[M].合肥:中国科技大学出版社,1995.228-327.[2]　施阳,李涛,许忻等.M AT LAB 语言精要及动态仿真工具S imulink[M].西安:西北工业大学出版社,1998.356-367.[3]　孙庚山,兰西柱.工程模糊控制[M].北京:机械工业出版社,1995.76-81.[4]　章正斌,吴汝善,于健.模糊控制工程[M].四川:重庆大学出版社,1995.288-290.(下转第7页)・3・　第4期王东云等:模糊控制系统的M AT LAB ΠSI M U LI NK 仿真与分析 (2)与静态冰蓄冷相比,动态冰蓄冷有以下特点:蓄冰槽内水温分布较均匀,不会出现温度不均及槽体的结构产生的“死区”.由于减少了管外冰壳造成的热阻,使水温下降较快,提高了整体结冰速度;且水流均匀冲刷盘管壁面,增大了管外的换热系数,充分利用了水的显热与潜热蓄冷的能力.(3)建议在冰蓄冷的过程中,采用动态的蓄冷过程.提高水的显热及潜热的利用能力.同时由于动态蓄冰时,槽体内水温低并且均匀,使释冷水温在较长时间保持稳定,提供较大的释冷速率,适应于短时间内需要大量的冷量的场合.国内一些公共建筑,如:体育馆、影剧院、会堂等均可采用动态冰蓄冷技术,提高经济效益.5　致谢本实验得到了中原工学院暖通空调教研室周光辉、范晓伟、王军及其专业实验室付光轩、刘寅等老师的大力帮助,在此表示感谢.参考文献:[1]　方贵银.蓄冷平板堆积床动态蓄冷性能研究[J ].制冷,1999,(2):1-6.[2]　华泽钊,刘道明.蓄冷技术及其在空调中的应用[M].北京:科学出版社,1997.48-64.[3]　张永铨.蓄冷空调系统[M].北京:中国建筑工业出版社,1998.20-38.[4]　W.D.马克劳斯基.陈义雄译.冰蓄冷与区域供冷[J ].暖通空调,1996,(1):71-73.Experimental R esearch of W ater T emperature Form ation in theCooling Storage T ank for Dynamic and Static Perform ance Cooling SystemsLI U Jian 1,G ONG Y i2(1.X i ′an University of Architecture &T echnology ,X i ′an 710049;2.Zhongyuan Institute of T echnology ,Zhenzhou 450007,China ) Abstract :　The purpose of this paper focuses specially on the experimental research on the water tem perature formation mechanism of the ice storage processes on the external melt ice 2on 2coil system in the ice storage tank ,in which the system op 2erats with different performance.Through the research of this system ,the characteristic of the initial tem perature of the cooling water with the time is studied.The result can be used by engineering designer.K ey w ords :　evaporator helical coil ;ice storage am ount ;cooling space(上接第3页)Simulation and Analysis for Fuzzy ControlSystem B ased on MAT LAB ΠSIMU LINKWANG Dong 2yun ,LI NG De 2lin(Zhongyuan Institute of T echnology ,Zhengzhou 450007,China ) Abstract :　Methods for simulating and analyzing fuzzy control system with MAT LAB ΠSI MU LI NK are introduced in thispaper ,for no relating references were published.Further m ore effect on performance of fuzzy control system by quantum factor and proportional factor is studied.K ey w ords :　MAT LAB ΠSI MU LI NK;fuzzy inference system (FIS );fuzzy control ;membership function・7・　第4期刘　建等:动、静态冰蓄冷蓄冷槽水温变化的实验分析。

如何使用Simulink模糊控制

如何使⽤Simulink模糊控制在⽤这个控制器之前，需要⽤readfis指令将fuzzy1.fis加载到matlab的⼯作空间，⽐如我们⽤这样的指令：fis1=readfis（‘fis1.fis’）；就创建了⼀个叫myFLC的结构体到⼯作空间，并在fuzzy logic controller中参数设为：fis1。

可以看到，在模糊控制器的输⼊和输出均有⼀个⽐例系数，我们叫它量化因⼦，它反映的是模糊论域范围与实际范围之间的⽐例关系，例如，模糊控制器输⼊输出的论域范围均为[-3，3]，⽽实际误差的范围是[-10，10]，误差变化率范围是[-100，100]，控制量的范围是[-24，24]，那么我们就可以算出量化因⼦分别为0.3，0.03，8。

量化因⼦的选取对于模糊控制器的控制效果有很⼤的影响，因此要根据实际情况认真选取哦。

好，现在我们可以设定仿真步长，⽐如定步长的10ms，就可以运⾏了。

运⾏后，产⽣这样⼀个错误：MinMax blocks do not accept 'boolean' signals. The input signal(s) of block 'test_fuzzy/Fuzzy Logic Controller/FISWizard/Defuzzification1/Max (COA)' must be one of the MATLAB 'uint8', 'uint16', 'uint32', 'int8', 'int16', 'int32', 'single', or 'double' data types 我想很多朋友做模糊控制的时候都会遇到这个情况。

没关系，这⾥提供两个解决办法：1．直接在Defuzzification1这个模块中的那个⽐较环节后加⼊数据类型转换模块，将boolean转化为double型，或者双击那个⽐较模块，选中show additional parameters，将输出数据类型改为specify via dialog，然后选uint(8)即可；但是在仿真之后，⼜会发现很多地⽅都存在这个问题，因此你不得不⼀个⼀个去修改，如果你不怕累的话。

Simulink模糊控制教程

发展
在20世纪70年代和80年代，模糊控制的理论框架逐渐形成，模糊集合、模糊逻辑和模糊推理等基本概念得到深入研究和应用。
应用
随着计算机技术的发展，模糊控制的应用领域不断扩大，涉及工业控制、智能家居、医疗等领域。
模糊控制的应用领域
01
工业控制
模糊控制在工业控制领域中得到了广泛应用，例如温度控制、压力控制、
最小值清晰化
将最小值推理得到的输出模糊集合映射到清晰输出上，通常采用中心平均法或中心最大值法。
04
模糊控制系统的仿真与实现
模糊控制系统的仿真
模糊逻辑工具箱
使用Simulink的模糊逻辑工具箱进行模糊控制系统的仿真，可以方便地创建模糊控制器并进行仿真分析。
模糊化与去模糊化
在仿真过程中，需要将输入信号模糊化，将输出信号去模糊化，以模拟实际模糊控制器的行为。
使用这个工具箱，用户可以轻松地构建和测试各种类型的模糊控制系统，包括单输入单输出（SISO）系统
和多输入多输出（MIMO）系统。
03
模糊控制器设计
模糊化方法
输入模糊化
将输入信号映射到对应的模糊集合上，通常采用三角形、梯形或任何可用的形状来表示模糊集合。
输出模糊化
根据系统输出和期望输出的偏差，调整模糊集合的中心和宽度，以实现输出模糊化。
模糊控制在液位控制系统中的应用
总结词
液位控制系统要求精确控制液位高度，同时要考虑到液体的流动性和容器的形状等因素，模糊控制能够实现高精度的液位控制。
详细描述
在液位控制系统中，模糊控制器可以根据液位传感器的实时数据和设定值，通过模糊逻辑推理快速调整进液或出液阀门的开度，实现液位的精确控制。同时，模糊控制器还可以根据液体的物理特性和容器的大小等因素对液位变化进行预测和控制。

单个交叉口两级模糊控制及仿真研究

第!"卷#第"$期#"%!"年&月!'(!!!&!)""%!"#"$*%%%%*%)#科#学#技#术#与#工#程+,-./,.0.,1/232456/78/4-/..9-/4#:23;!"#<2;"$#=>4?"%!"!#"%!"#+,-;0.,1;8/494;单个交叉口两级模糊控制及仿真研究刘小和"空军第一航空学院$信阳D'D%%%#摘#要#伴随着我国国民经济的高速发展和城市化进程的加快城市交通拥堵问题日趋严重交叉口作为城市交通网络的重要组成部分解决城市道路交叉口问题是解决城市交通的关键对其研究有着极其重要的意义在对现有国内外学者对交叉口信号模糊控制研究的基础之上对单个交叉口的模糊控制进行系统的分析阐述提出了一种新型的交叉口两级模糊控制方法对于模糊控制中复杂的逻辑推理和计算问题采用@=0I =Z 进行编程计算最后运用@=0I =Z 进行模糊控制器动态仿真结果表明模糊控制效果更好关键词#交叉口##模糊控制##仿真##@=0I =Z 中图法分类号#d DC!;)!%####文献标志码#="%!"年D 月!%日收到$D 月"%日修改作者简介&刘小和$河南人$研究方向&智能控制$信号优化'##随着交通拥堵问题日益严重$解决城市道路交叉口的问题是解决城市交通的关键$所以进行交叉口信号控制的研究具有重要的意义'交叉口信号控制有定时控制系统(感应控制和自适应控制)!*'定时控制和感应控制对于不同的环境下的变化交通流$其灵活性与适应性仍有所欠缺'自适应控制能够连续测量交通状态产生实时的控制$使控制效果达到最优或次优'自适应控制方法中模糊信号控制法作为一种重要的基于规则的控制方法$不需要建立被控对象的精确数学模型$能够模仿有经验的交警指挥交通时的思路$获得良好的控制效果)"$$*'本文基于国内外学者的研究$对单个交叉口的模糊控制进行系统的分析阐述$介绍两级模糊控制)D $)*'采用@=0I =Z 进行编程计算$运用@=0*I =Z 进行模糊控制器动态仿真'!"前提条件单个交叉口如图!所示$每条入口车道装两台车辆检测器$间距!)%J $分别检测各方向的排队长度和路段车辆数'路段车辆数定义为每条车道上两车辆检测器之间的车辆数'设交叉口车辆平均车速为!%J `M $使得在最小绿灯时间!)M 内$以平均速度为!%J `M 的车辆能在绿灯相位时间内顺利通过交叉口'根据检测器检测到的绿灯相的关键车流的路段车辆数以及红灯相的关键车流的排队长度信息$由模糊控制器可得到绿灯时间增量)'$(*'$"控制策略模糊控制方案&用路段车辆数的概念$通过添加绿灯相位进口交通流量与绿灯相位路段车辆数(红灯相位排队长度一道作为输入控制量$充分反映交叉口交通状态'输出量的控制思想&在最大绿灯时间的限制下$根据采集的交通信息$通过查询表得到具体的延长时间$使得延时更加合理有效'当延时为%时$代表的是转换相位'由于控制规则的复杂性$通过二级控制来减少控制规则数目)&*'控制策略为&首先开放东西向绿灯$并给予最小绿灯时间!)M %在最小绿灯时间结束前一时刻$检测到绿灯相位的进口流量和路段车辆数以及红灯相位的排队长度$从而得到绿灯相位和红灯相位的交通强度$进而推出具体的延长时间$但延时后的绿灯时间不超过最大绿灯时间'%M '当延长时间为%M 或超过最大绿灯时间$换绿灯相给南北向以最小绿灯时间$继续上述操作'$#!"模糊控制器的设计该两级模糊控制器系统组成如图"所示'图!#两相位交叉口的设计图"#两级模糊控制器结构图$#$"绿灯相位交通强度模块定义绿灯相位的交通强度"用0b 表示#是&6时间内的进口交通流量和路段车辆数的函数'绿灯相位的进口交通流量定义为&若绿灯相位是东西方向$则G $J 6S )G 6F "6#$G 69"6#*%若绿灯相位是南北方向$则G $J 6S )G 6F "6#$G 69"6#*'绿灯相位的路段车辆数定义为&若绿灯相位是东西方向$则+$J 6S )+6F "6#$+69"6#*'若绿灯相位是南北方向$则+$J 6S )+6E "6#$+6I "6#*'";";!#模糊推理的输入输出输入变量G $+%输出变量Q U 49../'";";"#模糊化处理G 的模糊化&基本论域&-%$%;!$%;"$%;$$%;D .%模糊词集&-很小$小$中$大$很大.'表!"$隶属函数赋值表隶属度G%%;!%;"%;$%;D 模糊词集很小!%?'%?"%%小%?'!%?'%?"%中%?"%?'!%?'%?"大%%?"%?'!%?'很大%%%?"%?'!##+的模糊化&基本论域&-%$"$D $'$&$!%$!"$!D $!'$!&$"%$""$"D $"'$"&.%模糊词集&-很短$短$中$长$很长.'表$"%隶属函数赋值表隶属度+%"D '&!%!"!D !'!&"%"""D "'"&模糊词集很短!%?&%?'%?D %?"%%%%%%%%%%短%?"%?D %?'%?&!%?&%?'%?D %?"%%%%%%中%%%%%?"%?D %?'%?&!%?&%?'%?D %?"%%长%%%%%%%%%?"%?D %?'%?&!%?&%?'很长%%%%%%%%%%%%%?"%?D%?'##Q U 49../的模糊化&的基本论域&-!$"$$$D $).%模糊词集&-很低$低$中$高$很高.'表%"&'J977-隶属函数赋值表隶属度Q U 49../!"$D )模糊词集很低!%?)%%%低%?)!%?)%%中%%?)!%?)%高%%%?)!%?)很高%%%%?)!";";$#模糊规则确定绿灯相位的模糊控制规则的原则是&如果绿灯相位的进口流量增大或路段车辆数增多$交通强度升高'通过总结实践和专家经验$建立模糊控制规则$如表D '";";D#模糊推理模糊决策有了各个模糊集合的隶属函数分布$就可以对每条模糊控制规则计算器模糊蕴涵关系'常用的模糊推理有两种方法&a 67.1法和@6J 76/-法'@6J 76/-推理法是一种模糊控制中普遍使用的方($!"$期刘小和&单个交叉口两级模糊控制及仿真研究法$其本质是一种合成推理方法'表+"模糊控制规则表Q U49../G很小小中大很大+很短很低很低低中高短很低低低中高中低低中高很高长中中高高很高很长中高高很高很高##模糊推理语句+N Q;6/7>G1./L,蕴含的关系为";.>(L#$根据@6J76/-模糊推理法$其关系矩阵U为U$";V>#0!V L%式中$";V>#0!为模糊关系矩阵";n>#Jn/构成的-V<列向量$0!为列向量转换$<和-分别为;和>论域元素的个数'";";)#控制量的去模糊化模糊推理总的输出实际上是多个控制规则推理结果的并集$需要进行去模糊化才能得到精确的推理结果'下面采用最大平均法进行去模糊化处理'由于计算的复杂性$在@=0I=Z中编写程序$运行得到结果如表)所示'表O"模糊控制查询表Q U49../+%"D'&!%!"!D!'!&"%"""D"'"&G%!!!!!!""""$$$$D%;!!!""""""""$$$$D%;"""""""$$$$$D D D)%;$$$$$$$$D D D D D D D)%;D$$D D D D D D D D))))) $#%"红灯相位定义红灯相位的交通强度"用Q U表示#是&6时间内的排队长度的函数'红灯相位的排队长度定义为&若红灯相位是东西方向$则Q U9.7RJ6S)+6F"6#$+69"6#*$若红灯相位是南北方向$则Q U9.7RJ6S)+6E"6#$+6!"6#*'";$;!#模糊推理的输入输出输入变量+%输出变量Q U9.7";$;"#模糊化处理+的模糊化&基本论域&-%$"$D$'$&$!%$!"$!D$ !'$!&$"%$""$"D$"'$"&.%模糊词集&-很短$短$中$长$很长.'表Q"%隶属函数赋值表隶属度+%"D'&!%!"!D!'!&"%"""D"'"&模糊词集很短!%?&%?'%?D%?"%%%%%%%%%%短%?"%?D%?'%?&!%?&%?'%?D%?"%%%%%%中%%%%%?"%?D%?'%?&!%?&%?'%?D%?"%%长%%%%%%%%%?"%?D%?'%?&!%?&%?'很长%%%%%%%%%%%%%?"%?D%?'##Q U9.7的模糊化&基本论域&-!$"$$$D$).%模糊词集&-很低$低$中$高$很高.'表T"&'97<隶属函数赋值表隶属度Q U49../!"$D)模糊词集很低!%?)%%%低%?)!%?)%%中%%?)!%?)%高%%%?)!%?)很高%%%%?)!";$;$#模糊规则确定红灯相位的模糊控制规则的原则是&如果红灯相位的排队长度增长$那么交通强度升高'通过总结实践经验$建立了模糊控制规则$如表&所示'表U"模糊控制规则表+很短短中长很长Q U9.7很低低中高很高";$;D#模糊推理模糊决策同绿灯相位模糊推理$根据各个模糊集合的隶属函数分布$就可以对每条模糊控制规则计算其模糊蕴涵关系'";$;)#控制量的去模糊化&$!科#学#技#术#与#工#程!"卷模糊推理总的输出实际上是多个控制规则推理结果的并集$需要进行去模糊化才能得到精确的推理结果'下面采用最大平均法进行去模糊化处理'在@=0I=Z中编写程序来计算$运行得到结果如表C所示'表V"模糊控制查询表+%"D'&!%!"!D!'!&"%"""D"'"& Q U9.7!!""""$$$$D D D D)$#+"决策模块模糊控制的第二级决定具体延长时间"如果延长时间为%$意思就是终止信号$进入下一相位#的信号相位'其输入级就是第一级的交通强度Q U49../和Q U9.7$其输出就是具体的延长时间'具体见表!%$控制规则表是通过专家经验及仿真实验而制定的'表!W"交通强度延时表&QQ U49../!"$D)Q U49../!%"D'& "%%"D' $%%%"D D%%%%" )%%%%%%"模糊控制器的仿真模糊控制器的最简单(最基本的实现方法是将一系列的模糊控制规则离线转化为一个查询表$存储在计算机中供在线控制时使用'对于两级模糊控制器$其第一级控制器由两个子模糊控制器组成'对于绿灯相位交通强度模糊控制器来说$采用的是@6J76/-模型)C*'其输入量&交通流量G和+$输出量为Q U49../'调用所编制的程序可得到控制表$并生成绿灯相位交通强度与进口车道交通流量(路段车辆数之间的三维关系图$如图$'对应于不同的交通流量G(路段车辆数+$其动态显示界面如图D所示'根据第一级的两个模糊控制器的控制表$我们就可以根据车辆检测器检测的数据进行查表处理$得到相应的延长时间'图$#三维关系图图D#模糊控制器动态仿真显示界面+"结论本文基于现有国内外学者对交叉口信号模糊控制研究的内容之上$对单个交叉口的模糊控制进行了系统的分析阐述'在模糊控制器的设计中$编写了独创性的计算方法$并运用@=0I=Z进行模糊控制器的动态仿真$仿真结果表明模糊控制比定时控制控制效果更佳'本文没有考虑混合交通的问题$仅考虑机动车流$这与国情不符'需进一步研究混合交通下的交叉口模糊控制问题'参考文献!#徐建闽;交通管理与控制;北京&人民交通出版社$"%%("#刘智勇;智能交通控制理论及其应用;北京&科学出版社$"%%$ $#I-K2/4;096Q Q-,676TG-W.,2/G923Q292W.9M6G>96G.7-M236G.7-/G.9M.,* G-2/M&@27.37.W.32TJ./G6/7M-J>36G-2/G.M G-/4;H2>9/632Q096/M T29* G6G-2/8/4-/..9-/4$"%%D%!$%")#&)CD!'%!C$!"$期刘小和&单个交叉口两级模糊控制及仿真研究D#a67.1I=;A>]]5M.G M;N/Q29J6G-2/k[2/G923$!C')%&&$$&!$)$ )#褚#静;模糊控制原理与应用;北京&机械工业出版社$"%%)'#陈#洪$陈森发;单路口交通实时模糊控制的一种方法;信息与控制$!CC(%"'"$#&""C!"$$(#刘智勇$朱#劲$李秀平$等;单交叉口的多相位模糊控制;信息与控制$!CCC%%'&D)$!D)&&#黄辉先$史忠科;城市单交叉路口交通流实时遗传算法优化控制?系统工程理论与实践$"%%!%%$&!%"!!%'C#徐建闽$舒#宁$尹宏宾;新型模糊控制算法在交叉口信号控制中的应用;华南理工大学学报"自然科学版#$"%%%%%'&!!)M A3(15.J7'8H H0;3-593/.-<=2>8/.523-.5=2-J/7K-57917:523-I N dP-62*1."A-9M G=W-6G-2/[233.4.2Q G1.=-9A29,.$P-/56/4D'D%%%$O?b?[1-/6#)*?159.:5*#V-G1G1.96T-77.W.32TJ./G2Q[1-/6g M/6G-2/63.,2/2J56/7G1.6,,.3.96G-2/2Q>9F6/-]6G-2/ T92,.M M$>9F6/G96Q Q-,,2/4.M G-2/-M492c-/4;N/G.9M.,G-2/-M6/-J T29G6/G T69G2Q G1.>9F6/G96Q Q-,/.G c29L$-Q G1./.G* c29L T92F3.J M16W.6F6716/73.7$G96Q Q-,,2/4.M G-2/c-33F..M T.,-6335T92J-/./G;02M23W.G1.T92F3.J2Q>9F6/ G96Q Q-,-/G.9M.,G-2/-M G1.L.52Q M23W-/4>9F6/G96Q Q-,$6/7-G16M49.6G M-4/-Q-,6/,.;Z6M.72/G1..S-M G-/472J.M G-, 6/7Q29.-4/M,12369M2/G1.-/G.9M.,G-2/M-4/63Q>]]5,2/G923$6Q G.97.M,9-F.7M-/43.-/G.9M.,G-2/2Q6M5M G.J6G-,6/635* M-M2Q Q>]]5,2/G923$6/2W.3J.G1272Q G1.-/G.9M.,G-2/2Q G c2*M G64.Q>]]5,2/G923-M T9.M./G.3;01.@=0I=ZT92* 496J J-/4G29.6M2/6/7,63,>36G.-M>M.7;A-/6335$G1.Q>]]5,2/G9233.9F5@=0I=Z-M M-J>36G.7;=/7G1.9.M>3G M M12cG16G Q>]]5,2/G923-M F.G G.9;)@70A39<1*#-/G.9M.,G-2/##Q>]]5,2/G923##M-J>36G-2/##@=0I=Z%D!科#学#技#术#与#工#程!"卷。

单点交叉口交通模糊控制仿真课件

模糊控制器设计源自010203
04
输入输出变量
选择合适的输入输出变量是模糊控制器设计的关键步骤。
模糊化
将输入变量的精确值映射到对应的模糊集合上。
规则库
基于专家知识和经验，制定一系列“if-then”规则。
去模糊化
将模糊集合的输出值映射回精确值。
模糊控制的优势与局限性
优势
能够处理不确定性和非线性问题；能够处理复杂的、难以建模的系统；能够处理多目标优化问题。
单点交叉口交通模糊控制仿真课件
目录
• 单点交叉口交通概述 • 模糊控制理论 • 单点交叉口交通模糊控制仿真模型 • 单点交叉口交通模糊控制实际应用 • 未来研究方向与展望
contents
01
单点交叉口交通概述
定义与特点
定义
单点交叉口是指只有一个交叉点的道路交汇点，是城市交通网络中的基本单元之一。
交叉口交通控制的优化策略包括智能化信号控制、自适应信号控制、多目标优化等，这些策略将有助于提高交叉口的运行效率和安全性。
THANKS
感谢观看
验证过程
对仿真模型进行多次运行，记录仿真结果，并对结果进行分析。
验证结论
根据验证结果，评估仿真模型的准确性和可靠性。
仿真结果分析
结果展示
将仿真结果以图表、数据等形式展示出来，以便于分析和比较。
结果分析
对仿真结果进行分析，探讨模糊控制在单点交叉口交通控制中的效果和优势。
结果总结
根据分析结果，总结模糊控制在单点交叉口交通控制中的适用性和局限性。
用规则。
实际应用效果评估
交通流量改善
通过模糊控制策略的优化，提高交叉口的通行效率，减少车辆等待时间和拥堵现象。

单点交叉口交通模糊控制仿真

Step2:在绿灯时间tGi马上完毕时,检测放行相位及下一个相位车道上的车辆排队长度。设其分别为Pi和Pi+1。
Step3:推断,假设Pi=0,或Pi≤m且ΔPi=Pi+1Pi≥n(m,n为依据交通量状况确定的常数)或者绿灯积存时间tGi=tGmax,则将通行权给下一相位,并回到step1;否则连续。
给出隶属度函数：
依据专家阅历,输入变量各个模糊子集的隶属度函数取高斯型曲线,其输出比较光滑。
模糊推理及反模糊化：
解模糊化的方法常用的有：重心法、最大隶属度法。
重心法(加权平均法)：重心法是指取模糊集隶属函数
曲线同根底变量轴所围而积的重心对应的根底变量值作为
清晰值的方法。 (μi))
I
I
公式u*=(∑ (uiμi)) /(∑
该种模糊掌握缺点： 1.此方法在相位固定的根底上再给出最优的当前相位绿灯
延时。这明显是存在了肯定的人为误差因素的，当固定的下一相位车流很小甚至为零时，依据这种掌握规章，要给出至少是最小绿灯时间，而且中间还包括绿灯转换所消耗的黄灯时长，假设下两相位或是更后的相位有很大的车流量，那么就必定会造成车辆平均延误较大了。 2. 仅依据单穿插口的相位的关键车流(同一相位中交通流量比大的一股车流)来打算交通信号配时,而无视了两相位的非关键车流对信号配时的影响。
μA： X→[0，1]， x→μA〔x〕式中，称μA为A的隶属度函数， μA〔x〕为x对A的隶属度。
由模糊集合的定义可知，论域X上的模糊集A完全由隶属度函数μA〔x〕来刻画。 μA〔x〕的取值范围为闭区间[0，1]， u的大小反映x对于模糊子集A的附属程度： μA〔x〕的值越接近1，表示x附属于A的程度越高； μA〔x〕的值越接近0，则表示x附属于A程度越低。

Simulink模糊控制教程

给出复杂模糊控制器设计实例和结果展示
实战演练三：模糊控制器优化与改进
模糊控制器优化方法：遗传算法、粒子群算法等改进模糊控制器性能的措施：调整隶属度函数、增加模糊规则数量等实际应用中模糊控制器的调试与测试案例分析：某工业过程控制中模糊控制器的应用与优化
实战演练四：模糊控制器在实时系统中的应用
更多可能性。
模糊控制理论的研究将更加注重实际应用，与工程实践的结合将更加紧密，推动工业自动化领域的进步与发展。
模糊控制在工业自动化领域的应用前景
工业自动化领域的现状和趋势
模糊控制技术的优势和特点
模糊控制在工业自动化领域的应用案例
模糊控制在工业自动化领域的未来发展前景
感谢观看
汇报人：XX
控制器性能评估
评估指标：准确性、稳定性、鲁棒性评估方法：仿真实验、实际测试评估工具：Simulink、Matlab/Simulink 评估步骤：设计控制器、搭建仿真模型、进行实验测试、分析实验结果
05
Simulink模糊控制应用实例
模糊控制在电机控制系统中的应用
模糊控制原理简介
模糊控制在电机控制中的应用实例
练
01
添加章节标题
02
Simulink模糊控制简介
模糊控制基本概念
模糊控制是一种基于模糊集合理论的控制方法，通过将输入变量模糊化，将模糊逻辑应用于控制
系统。
模糊控制的基本原理是通过模糊化、模糊推理和去模糊化三个步骤实
现控制。
模糊集合理论是模糊控制的基础，它通过模糊集合来表示输入和输出变量，并使用模糊逻辑规则进
去模糊化操作
定义：将模糊逻辑系统输出的模糊集合转换为清晰值的过程

模糊控制位置跟踪的SIMULINK仿真

智能控制作业二“模糊控制位置跟踪的SIMULINK 仿真一、题目设被控对象的传递函数为s s s G 252500)(2+=，输入信号为方波，周期为1秒，幅值为1，（可以用Pulse Generator 模块来产生）。

1）试设计两输入单输出模糊控制器，输入为偏差E 和偏差变化率EC ，输出为控制量U ，使系统输出能实时跟踪输入信号。

2）通过仿真理解并分析E 和EC 的参数选择对系统稳态误差和动态性能的影响，这些参数包括模糊子集的个数，论域的范围等。

作业中最好把不同参数下的仿真结果附上。

二、MATLAB 解决方案1、模糊控制模块的创建在MA TLAB 命令窗口中输入fuzzy 命令，会弹出模糊控制GUI 界面，打开隶属度函数编辑窗口，输入变量为E 和EC ，输出变量为U ，输入输出论域均设置为[-3 3]，每个变量都设置NB ，NM ，NS ，ZO ，PS ，PM ，PB 七个模糊子集，每个变量的隶属度函数均如图1所示，为了使输入误差在零附近反应敏感，这一部分隶属度函数设置得比较尖。

图1 隶属度函数编辑窗口根据如表1输入控制规则，如图2所示：表1 控制规则编辑完成后可以看到如图3所示的模糊输入与输出的三维示意图：图2 控制规则输入窗口图3 输出三维示意图2、simulink的仿真新建一个model，搭建如图4所示的控制框图，保存为fuc2文件夹中的fuz_ctrl.mdl。

其中增益模块用来控制将输入或输出与模糊控制器的论域相匹配。

图4 simulink控制框图3、调试后的仿真结果经过调试优化，最终得到的仿真波形如图5所示。

其中Ke=3，Kec=0.06，Ku=1.图5 最终运行结果三、控制参数对控制结果的影响1、论域对控制结果的影响这里采用Ke和Kec来起到控制输入变量的论域的作用，当增大量化因子，相当于缩小了输入变量的论域，当减小量化因子时，相当于增大了输入变量的论域。

在原来的基础上改变Ke，Kec的值，通过观察跟踪效果来说明论域对控制结果的影响。

城市单点交叉口信号灯模糊控制建模与仿真

城市单点交叉口信号灯模糊控制建模与仿真
牛虎;李桂萍;林磊
【期刊名称】《交通标准化》
【年(卷),期】2009(000)017
【摘要】从控制论的角度对城市单点交叉口信号灯的控制建立模糊控制模型,是通过模仿交通警察指挥疏导交通的决策过程而建模,设计详细的控制算法和模糊控制器,并利用Matlab和Simulink工具对模型进行仿真和分析。

与定时信号控制方案相比,该模型可减少交叉口平均车辆延误,具有较好的控制效果。

【总页数】5页(P32-36)
【作者】牛虎;李桂萍;林磊
【作者单位】北京交通大学交通运输学院,北京100044
【正文语种】中文
【中图分类】U491.51
【相关文献】
1.基于模糊控制的城市单交叉口信号灯配时优化
2.基于多智能体和模糊控制的道路交叉口建模与仿真
3.城市停车标志交叉口交通信号灯智能控制仿真
4.城市单点交叉口信号灯模糊控制建模与仿真
5.单点交叉口信号灯优化配时研究
因版权原因，仅展示原文概要，查看原文内容请购买。