2003年高考.全国卷.理科数学试题及答案

合集下载

2003年高考.江苏卷.数学试题及答案

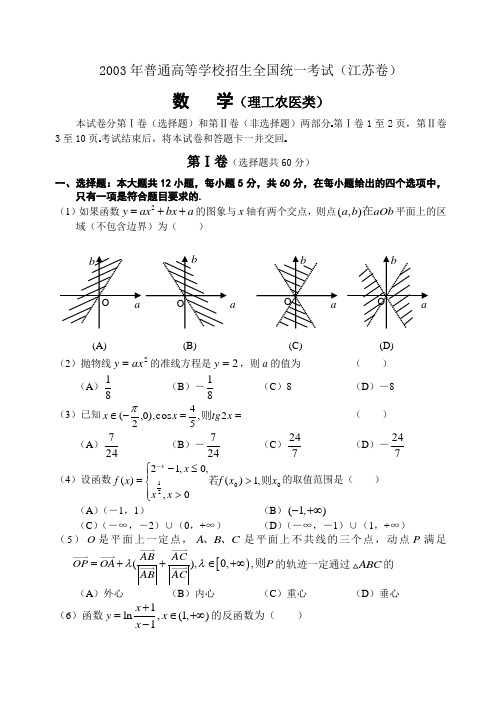
2003年普通高等学校招生全国统一考试（江苏卷）数学（理工农医类）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分1至2页，第Ⅱ卷3至10页考试结束后，将本试卷和答题卡一并交回第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的. （1）如果函数2y ax bx a =++的图象与x 轴有两个交点，则点(,)a b aOb 在平面上的区域（不包含边界）为（）（2）抛物线2ax y =的准线方程是2=y ，则a 的值为（）（A ）81 （B ）－81 （C ）8 （D ）－8 （3）已知==-∈x tg x x 2,54cos ),0,2(则π（）（A ）247 （B ）－247 （C ）724 （D ）－724 （4）设函数0021,1)(0,,0,12)(x x f x x x x f x 则若>⎪⎩⎪⎨⎧>≤-=-的取值范围是（）（A ）（－1，1）（B ）(1,)-+∞（C ）（－∞，－2）∪（0，+∞）（D ）（－∞，－1）∪（1，+∞）（5）O 是平面上一定点，A B C 、、是平面上不共线的三个点，动点P 满足[)(),0,,AB AC OP OA P ABACλλ=++∈+∞则的轨迹一定通过ABC 的（A ）外心（B ）内心（C ）重心（D ）垂心（6）函数1ln,(1,)1x y x x +=∈+∞-的反函数为（）a (A)(B) (C) (D)（A ）1,(0,)1x x e y x e -=∈+∞+ （B ）1,(0,)1x xe y x e +=∈+∞- （C ）1,(,0)1x x e y x e -=∈-∞+ （D ）1,(,0)1x xe y x e +=∈-∞- （7）棱长为a 的正方体中，连结相邻面的中心，以这些线段为棱的八面体的体积为（）（A ）33a （B ）34a （C ）36a （D ）312a（8）设20,()a f x ax bx c >=++，曲线()y f x =在点00(,())P x f x 处切线的倾斜角的取值范围为0,,4P π⎡⎤⎢⎥⎣⎦则到曲线()y f x =对称轴距离的取值范围为（）（A ）10,a ⎡⎤⎢⎥⎣⎦ （B ）10,2a ⎡⎤⎢⎥⎣⎦ （C ）0,2b a ⎡⎤⎢⎥⎣⎦ （D ）10,2b a ⎡-⎤⎢⎥⎣⎦（9）已知方程0)2)(2(22=+-+-n x x m x x 的四个根组成一个首项为41的的等差数列，则=-||n m （）（A ）1 （B ）43 （C ）21 （D ）83（10）已知双曲线中心在原点且一个焦点为F （7，0），直线1-=x y 与其相交于M 、N 两点，MN 中点的横坐标为32-，则此双曲线的方程是（）（A ）14322=-y x （B ）13422=-y x （C ）12522=-y x （D ）15222=-y x （11）已知长方形的四个顶点A （0，0），B （2，0），C （2，1）和D （0，1），一质点从AB 的中点0P 沿与AB 的夹角θ的方向射到BC 上的点1P 后，依次反射到CD 、DA 和AB 上的点2P 、3P 和4P （入射角等于反射角），设4P 的坐标为（4x ，0），若214<<x ，则tg θ的取值范围是（）（A ）（31，1）（B ）（31，32）（C ）（52，21）（D ）（52，32）（12）一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为（）（A ）π3（B ）4π（C ）π33（D ）π62003年普通高等学校招生全国统一考试（江苏卷）数学（理工农医类）第Ⅱ卷（非选择题共90分）二.填空题：本大题共4小题，每小题4分，共16分把答案填在题中横线上（13）92)21(xx -的展开式中9x 系数是（14）某公司生产三种型号的轿车，产量分别为1200辆，6000辆和2000辆为检验该公司的产品质量，现用分层抽样的方法抽取46辆进行检验，这三种型号的轿车依次应抽取___________，__________，___________辆（15）某城市在中心广场建造一个花圃，花圃分为6个部分（如图）现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有___________________种（以数字作答）（16）对于四面体ABCD ，给出下列四个命题①,,AB AC BD CD BC AD ==⊥若则②,,AB CD AC BD BC AD ==⊥若则③,,AB AC BD CD BC AD ⊥⊥⊥若则④,,AB CD AC BD BC AD ⊥⊥⊥若则其中真命题的序号是__________________.（写出所有真命题的序号）三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或或演算步骤（17）（本小题满分12分）有三种产品，合格率分别为0.90,0.95和0.95，各抽取一件进行检验（Ⅰ）求恰有一件不合格的概率；（Ⅱ）求至少有两件不合格的概率（精确到0.001）（18）（本小题满分12分）已知函数()sin()(0,0)f x x R ωϕωϕπ=+>≤≤是上的偶函数，其图象关于点3(,0)4M π对称，且在区间0,2π⎡⎤⎢⎥⎣⎦上是单调函数ωϕ和的值（19）（本小题满分12分）如图，在直三棱柱111C B A ABC -中，底面是等腰直角三角形，︒=∠90ACB ，侧棱21=AA ，D 、E 分别是1CC 与B A 1的中点，点E 在平面ABD 上的射影是△ABD 的重心G （Ⅰ）求B A 1与平面ABD 所成角的大小（结果用反三角函数值表示）（Ⅱ）求点1A 到平面AED 的距离E GD CBAC 1B 1A 1（20）（本小题满分12分）已知常数0,(0,),a c a i >==向量经过原点O 以c i λ+为方向向量的直线与经过定点(0,)2A a i c λ-以为方向向量的直线相交于P ，其中R λ∈试问：是否存在两个定点E 、F ，使得PE PF +为定值若存在，求出E 、F 的坐标；若不存在，说明理由（21）（本小题满分12分）已知0,a n >为正整数（Ⅰ）设()n y x a =-，证明1'()n y n x a -=-；（Ⅱ）设()()n nn f x x x a =--，对任意n a ≥，证明1'(1)(1)'(n n f n n f n ++>+（22）（本小题满分14分）设0a >，如图，已知直线:l y ax =及曲线2:,C y x C =上的点1Q 的横坐标为11(0).(1)n a a a C Q n <<≥从上的点作直线平行于x 轴，交直线11n n l P P ++于点，再从点作直线平行于y 轴，交曲线1.(1,2,3,n n C Q Q n +=于点 …）的横坐标构成数列{}n a（Ⅰ）试求1n n a a +与的关系，并求{}n a 的通项公式；（Ⅱ）当111,2a a =≤时，证明1211()32n k k k k a a a ++=-<∑ （Ⅲ）当1a =时，证明1211()3nk k k k a a a ++=-<∑2003年普通高等学校招生全国统一考试数学试题（江苏卷）答案一、选择题：本题考查基本知识和基本运算，每小题5分，满分60分.1．C 2．B 3．D 4．D 5．B 6．B 7．C 8．B 9．C 10．D 11．C 12．A 二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分. 13．221- 14．6,30,10 15．120 16．①④三、解答题17．本小题要主考查相互独立事件概率的计算，运用数学知识解决问题的能力，满分12分. 解：设三种产品各抽取一件，抽到合格产品的事件分别为A 、B 和C. （Ⅰ）95.0)()(,90.0)(===C P B P A P ， .05.0)()(,10.0)(===C P B P A P因为事件A ，B ，C 相互独立，恰有一件不合格的概率为176.095.095.010.005.095.090.02)()()()()()()()()()()()(=⨯⨯+⨯⨯⨯=⋅⋅+⋅⋅+⋅⋅=⋅⋅+⋅⋅+⋅⋅C P B P A P C P B P A P C P B P A P C B A P C B A P C B A P 答：恰有一件不合格的概率为0.176. 解法一：至少有两件不合格的概率为)()C ()B ()(C B A P B A P C A P C B A P ⋅⋅+⋅⋅+⋅⋅+⋅⋅012.005.010.095.005.010.0205.090.022=⨯+⨯⨯⨯+⨯= 解法二：三件产品都合格的概率为812.095.090.0)()()()(2=⨯=⋅⋅=⋅⋅C P B P A P C B A P由（Ⅰ）知，恰有一件不合格的概率为0.176，所以至有两件不合格的概率为.012.0)176.0812.0(1]176.0)([1=+-=+⋅⋅-C B A P答：至少有两件不合的概率为0.012.（18）在小题主要考查三角函数的图象和单调性、奇偶性等基本知识，以及分析问题和推理计算能力，满12分分。

2003年全国统一高考数学试卷(理科)

2003年全国统一高考数学试卷（理科）一、选择题（共12小题，每小题5分，满分60分）1．（5分）（2003•全国）已知x∈（﹣，0），cosx=，则tan2x等于（）A．B．﹣C．D．﹣2．（5分）（2003•全国）圆锥曲线的准线方程是（）A．ρcosθ=﹣2 B．ρcosθ=2 C．ρsinθ=﹣2 D．ρsinθ=23．（5分）（2003•全国）设函数若f（x0）＞1，则x0的取值范围是（）A．（﹣1，1）B．（﹣1，+∞）C．（﹣∞，﹣2）∪（0，+∞）D．（﹣∞，﹣1）∪（1，+∞）4．（5分）（2003•全国）函数y=2sinx（sinx+cosx）的最大值为（）A．B．C．D．25．（5分）（2003•全国）已知圆C：（x﹣a）2+（y﹣2）2=4及直线l：x﹣y+3=0，当直线l被C截得的弦长为时，则a等于（）A．B．C． D．6．（5分）（2003•全国）已知圆锥的底面半径为R，高为3R，在它的所有内接圆柱中，全面积的最大值是（）A．2πR2B．C．D．7．（5分）（2003•全国）已知方程（x2﹣2x+m）（x2﹣2x+n）=0的四个根组成一个首项为的等差数列，则|m﹣n|等于（）A．1 B．C．D．8．（5分）（2003•全国）已知双曲线中心在原点且一个焦点为F（，0），直线y=x﹣1与其相交于M、N两点，MN中点的横坐标为﹣，则此双曲线的方程是（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=19．（5分）（2003•全国）函数f（x）=sinx，x∈的反函数f﹣1（x）=（）A．﹣arcsinx，x∈[﹣1，1]B．﹣π﹣arcsinx，x∈[﹣1，1]C．﹣π+arcsinx，x∈[﹣1，1]D．π﹣arcsinx，x∈[﹣1，1]10．（5分）（2003•全国）已知长方形的四个项点A（0，0），B（2，0），C（2，1）和D（0，1），一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后，依次反射到CD．DA和AB上的点P2．P3和P4（入射角等于反射角），设P4坐标为（x4，0），若1＜x4＜2，则tanθ的取值范围是（）A．（，1）B．（，）C．（，）D．（，）11．（5分）（2003•全国）等于（）A．3 B．C．D．612．（5分）（2003•全国）棱长都为的四面体的四个顶点在同一球面上，则此球的表面积为（）A．3πB．4πC．3D．6π二、填空题（共4小题，每小题4分，满16分）13．（4分）（2003•全国）在的展开式中，x3的系数是（用数字作答）14．（4分）（2003•全国）使log2（﹣x）＜x+1成立的x的取值范围是．15．（4分）（2003•全国）如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色．现有4种颜色可供选择，则不同的着色方法共有种．（以数字作答）16．（4分）（2003•全国）下列五个正方体图形中，l是正方形的一条对角线，点M、N、P分别为其所在棱的中点，能得出l⊥面MNP的图形的序号是（写出所有符合要求的图形序号）．三、解答题（共6小题，满分74分）17．（12分）（2003•全国）已知复数z的辐角为60°，且|z﹣1|是|z|和|z﹣2|的等比中项．求|z|．18．（12分）（2003•全国）如图，直三棱柱ABC﹣A1B1C1中，底面是等腰直角三角形，∠ACB=90°，侧棱AA1=2，D、E分别是CC1与A1B的中点，点E在平面ABD 上的射影是△ABD的重心G．（Ⅰ）求A1B与平面ABD所成角的大小（结果用反三角函数值表示）；（Ⅱ）求点A1到平面AED的距离．19．（12分）（2003•全国）已知c＞0，设P：函数y=c x在R上单调递减，Q：不等式x+|x﹣2c|＞1的解集为R．如果P和Q有且仅有一个正确，求c的取值范围．20．（12分）（2003•全国）在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南方向300km的海面P处，并以20km/h的速度向西偏北45°方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大，问几小时后该城市开始受到台风的侵袭？21．（12分）（2003•全国）已知常数a＞0，在矩形ABCD中，AB=4，BC=4a，O 为AB的中点，点E、F、G分别在BC、CD、DA上移动，且，P为GE 与OF的交点（如图），问是否存在两个定点，使P到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由．22．（14分）（2003•全国）（1）设{a n}是集合{2s+2t|0≤s＜t且s，t∈Z}中所有的数从小到大排列成的数列，即a1=3，a2=5，a3=6，a4=9，a5=10，a6=12，…将数列{a n}各项按照上小下大，左小右大的原则写成如下的三角形数表：35 69 10 12﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣…①写出这个三角形数表的第四行、第五行各数；②求a100（2）设{b n}是集合{2r+2s+2t|0≤r＜s＜t，且r，s，t∈Z}中所有的数从小到大排列成的数列，已知b k=1160，求k．2003年全国统一高考数学试卷（理科）参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．（5分）（2003•全国）已知x∈（﹣，0），cosx=，则tan2x等于（）A．B．﹣C．D．﹣【考点】GS：二倍角的三角函数；GF：三角函数的恒等变换及化简求值．【专题】11 ：计算题．【分析】先根据cosx，求得sinx，进而得到tanx的值，最后根据二倍角公式求得tan2x．【解答】解：∵cosx=，x∈（﹣，0），∴sinx=﹣．∴tanx=﹣．∴tan2x===﹣×=﹣．故选：D．【点评】本题主要考查了三角函数中的二倍角公式．属基础题．2．（5分）（2003•全国）圆锥曲线的准线方程是（）A．ρcosθ=﹣2 B．ρcosθ=2 C．ρsinθ=﹣2 D．ρsinθ=2【考点】Q8：点的极坐标和直角坐标的互化．【专题】11 ：计算题．【分析】首先把圆锥曲线方程转化为直角坐标系的方程，然后根据抛物线的准线方程的公式求出准线方程，再转化为极坐标方程即得到答案．【解答】解：圆锥曲线由极坐标与直角坐标系的关系，可转化为直角坐标系上的方程，即为抛物线x2=8y，则准线方程为y=﹣2，再转化为极坐标方程为ρsinθ=﹣2．故选：C．【点评】此题主要考查极坐标与直角坐标系的转化，以及抛物线的准线方程的求解问题，属于综合性的问题有一定的难度．3．（5分）（2003•全国）设函数若f（x0）＞1，则x0的取值范围是（）A．（﹣1，1）B．（﹣1，+∞）C．（﹣∞，﹣2）∪（0，+∞）D．（﹣∞，﹣1）∪（1，+∞）【考点】3B：分段函数的解析式求法及其图象的作法．【专题】11 ：计算题．【分析】将变量x0按分段函数的范围分成两种情形，在此条件下分别进行求解，最后将满足的条件进行合并．【解答】解：当x0≤0时，，则x0＜﹣1，当x0＞0时，则x0＞1，故x0的取值范围是（﹣∞，﹣1）∪（1，+∞），故选：D．【点评】本题考查了分段函数已知函数值求自变量的范围问题，以及指数不等式与对数不等式的解法，属于常规题．4．（5分）（2003•全国）函数y=2sinx（sinx+cosx）的最大值为（）A．B．C．D．2【考点】GS：二倍角的三角函数；H4：正弦函数的定义域和值域．【分析】把函数式展开，可以看出要逆用正弦和余弦的二倍角公式，变为y=Asin（ωx+φ）的形式，在定义域是全体实数的条件下，根据正弦的值域求本题的最值．【解答】解：∵y=2sinx（sinx+cosx）∴y=2sin2x+2sinxcosx∴y=1﹣cos2x+sin2x=sin（2x﹣）+1∵当x∈R时，sin（2x﹣）∈[﹣1，1]∴y的最大值为+1，故选：A．【点评】三角函数是高中一年级数学教学中的一个重要内容，公式繁多应用灵活给学生的学习带来了一定的困难．为了学生掌握这一单元的知识，必须使学生熟练的掌握所有公式，在此基础上并能灵活的运用公式．5．（5分）（2003•全国）已知圆C：（x﹣a）2+（y﹣2）2=4及直线l：x﹣y+3=0，当直线l被C截得的弦长为时，则a等于（）A．B．C． D．【考点】J9：直线与圆的位置关系．【分析】弦心距、半径、半弦长满足勾股定理，半径是2，半弦长是，则弦心距是1，用点到直线的距离可以求解a．【解答】解：圆C：（x﹣a）2+（y﹣2）2=4的圆心（a，2），半径是2，半弦长是，则弦心距是1，圆心到直线的距离：1=∴故选：C．【点评】本题考查直线与圆的位置关系，弦心距、半径、半弦长满足勾股定理，是基础题．6．（5分）（2003•全国）已知圆锥的底面半径为R，高为3R，在它的所有内接圆柱中，全面积的最大值是（）A．2πR2B．C．D．【考点】7F：基本不等式及其应用．【分析】将全面积表示成底面半径的函数，用配方法求二次函数的最大值【解答】解：设内接圆柱的底面半径为r，高为h，全面积为S，则有∴h=3R﹣3r∴S=2πrh+2πr2=﹣4πr2+6πRr=﹣4π（r2﹣Rr）=﹣4π（r﹣）2+πR2∴当r=时，S取的最大值πR2．故选：B．【点评】考查实际问题的最值问题，常转化成函数的最值7．（5分）（2003•全国）已知方程（x2﹣2x+m）（x2﹣2x+n）=0的四个根组成一个首项为的等差数列，则|m﹣n|等于（）A．1 B．C．D．【考点】83：等差数列的性质；73：一元二次不等式及其应用．【专题】11 ：计算题．【分析】设4个根分别为x1、x2、x3、x4，进而可知x1+x2和x3+x4的值，进而根据等差数列的性质，当m+n=p+q时，a m+a n=a p+a q．设x1为第一项，x2必为第4项，可得数列，进而求得m和n，则答案可得．【解答】解：设4个根分别为x1、x2、x3、x4，则x1+x2=2，x3+x4=2，由等差数列的性质，当m+n=p+q时，a m+a n=a p+a q．设x1为第一项，x2必为第4项，可得数列为，，，，∴m=，n=．∴|m﹣n|=．故选：C．【点评】本题主要考查了等差数列的性质．解题的关键是运用了等差数列当m+n=p+q时，a m+a n=a p+a q的性质．8．（5分）（2003•全国）已知双曲线中心在原点且一个焦点为F（，0），直线y=x﹣1与其相交于M、N两点，MN中点的横坐标为﹣，则此双曲线的方程是（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=1【考点】KB：双曲线的标准方程．【分析】先设出双曲线的方程，然后与直线方程联立方程组，经消元得二元一次方程，再根据韦达定理及MN中点的横坐标可得a、b的一个方程，又双曲线中有c2=a2+b2，则另得a、b的一个方程，最后解a、b的方程组即得双曲线方程．【解答】解：设双曲线方程为﹣=1．将y=x﹣1代入﹣=1，整理得（b2﹣a2）x2+2a2x﹣a2﹣a2b2=0．由韦达定理得x1+x2=，则==﹣．又c2=a2+b2=7，解得a2=2，b2=5，所以双曲线的方程是．故选：D．【点评】本题主要考查代数方法解决几何问题，同时考查双曲线的标准方程与性质等．9．（5分）（2003•全国）函数f（x）=sinx，x∈的反函数f﹣1（x）=（）A．﹣arcsinx，x∈[﹣1，1]B．﹣π﹣arcsinx，x∈[﹣1，1]C．﹣π+arcsinx，x∈[﹣1，1]D．π﹣arcsinx，x∈[﹣1，1]【考点】HV：反三角函数；4R：反函数．【专题】11 ：计算题．【分析】先用诱导公式求出f（x）=sin（π﹣x），x∈，然后可以反函数的定义求解即可．【解答】解：函数f（x）=sinx，x∈所以：函数f（x）=sin（π﹣x），x∈可得π﹣x=arcsiny y∈[﹣1，1]∴f﹣1（x）=π﹣arcsinx，x∈[﹣1，1]故选：D．【点评】本题考查反函数的求法，是基础题．10．（5分）（2003•全国）已知长方形的四个项点A（0，0），B（2，0），C（2，1）和D（0，1），一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后，依次反射到CD．DA和AB上的点P2．P3和P4（入射角等于反射角），设P4坐标为（x4，0），若1＜x4＜2，则tanθ的取值范围是（）A．（，1）B．（，）C．（，）D．（，）【考点】IQ：与直线关于点、直线对称的直线方程．【专题】16 ：压轴题．【分析】先画草图，帮助理解，取BC上的点P1为中点，则P4和中点P0重合，tanθ=，用排除法解答．【解答】解：考虑由P0射到BC的中点上，这样依次反射最终回到P0，此时容易求出tanθ=，由题设条件知，1＜x4＜2，则tanθ≠，排除A．B．D，故选：C．【点评】由于是选择题，因而可以特殊值方法解答：排除验证法，也可以用动态观点判定答案．11．（5分）（2003•全国）等于（）A．3 B．C．D．6【考点】6F：极限及其运算；D5：组合及组合数公式．【专题】11 ：计算题；16 ：压轴题．【分析】利用组合数的性质对原式进行等价转化，得到．【解答】解：∵C22+C32+C42+…+C n2=C33+C32+C42++C n2=C43+C42+…+C n2═C n+13，，∴．故选：B．【点评】本题考查数列的极限，解题时要注意组合数的计算和应用．12．（5分）（2003•全国）棱长都为的四面体的四个顶点在同一球面上，则此球的表面积为（）A．3πB．4πC．3D．6π【考点】LG：球的体积和表面积．【专题】11 ：计算题；16 ：压轴题．【分析】本题考查的知识点是球的体积和表面积公式，由棱长都为的四面体的四个顶点在同一球面上，可求出内接该四面体的正方体棱长为1，又因为正方=4πR2，体的对角线即为球的直径，即球的半径R=，代入球的表面积公式，S球即可得到答案．【解答】解：借助立体几何的两个熟知的结论：（1）一个正方体可以内接一个正四面体；（2）若正方体的顶点都在一个球面上，则正方体的体对角线就是球的直径．则球的半径R=，∴球的表面积为3π，故选：A．【点评】棱长为a的正方体，内接正四面体的棱长为a，外接球直径等于长方体的对角线长a．二、填空题（共4小题，每小题4分，满16分）13．（4分）（2003•全国）在的展开式中，x3的系数是﹣（用数字作答）【考点】DA：二项式定理．【专题】11 ：计算题．【分析】首先根据题意，写出的二项展开式，可得9﹣2r=3，解可得r=3，将其代入二项展开式，计算可得答案．【解答】解：根据题意，对于，=C99﹣r•x9﹣r•（﹣）r=（﹣）r•C99﹣r•x9﹣2r，有T r+1令9﹣2r=3，可得r=3，当r=3时，有T4=﹣x3，故答案﹣．【点评】本题考查二项式定理的应用，注意系数与二项式系数的区别．14．（4分）（2003•全国）使log2（﹣x）＜x+1成立的x的取值范围是（﹣1，0）．【考点】4H：对数的运算性质；7E：其他不等式的解法．【专题】13 ：作图题；44 ：数形结合法．【分析】在坐标系中画出函数f（x）=log2（﹣x）和g（x）=x+1，图象，结合图象判定即可．【解答】解：利用作图法可以判断f（x）=log2（﹣x）和g（x）=x+1，相交于（﹣1，0）前者是单调递减，后者是单调递增．所以只有﹣1＜x＜0时，log2（﹣x）＜x+1成立故答案为：（﹣1，0）．【点评】本题考查对数函数的图象，数形结合法解不等式，是中档题．15．（4分）（2003•全国）如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色．现有4种颜色可供选择，则不同的着色方法共有72种．（以数字作答）【考点】D5：组合及组合数公式．【专题】11 ：计算题；16 ：压轴题；32 ：分类讨论．【分析】分类型，选3种颜色时，就是②④同色，③⑤同色；4种颜色全用，只能②④或③⑤用一种颜色，其它不相同，求解即可．【解答】解：由题意，选用3种颜色时：涂色方法C43•A33=24种4色全用时涂色方法：C21•A44=48种所以不同的着色方法共有72种．故答案为：72【点评】本题考查组合及组合数公式，考查分类讨论思想，避免重复和遗漏情况，是中档题．16．（4分）（2003•全国）下列五个正方体图形中，l是正方形的一条对角线，点M、N、P分别为其所在棱的中点，能得出l⊥面MNP的图形的序号是①④⑤（写出所有符合要求的图形序号）．【考点】LS：直线与平面平行．【专题】15 ：综合题；16 ：压轴题．【分析】能得出l⊥面MNP，关键是看平面MNP中有没有与1垂直的直线，逐一判断即可．【解答】解：如图，设正方体为ABCD﹣A1B1C1D1．在题图①中，连结AB1，则AB1⊥MN，又AB1是l在面ABB1A1内的射影，∴l⊥MN．同理，l⊥MP．∴l⊥平面MNP．故①符合．在题图②中，延长MP交C1D1的延长线于E，连结NE，若l⊥面MNP，则l ⊥NE．又C1D是l在平面CDD1C内的射影，CD1⊥C1D，∴l⊥CD1．∴l⊥平面CDD1C1，矛盾．∴②不符合．在题图③中，平面MNP与题图①中的平面MNP不是同一平面，它们又过同一点，∴题图③不符合．在题图④中，l⊥MP，l⊥MN，∴l⊥平面MNP．延长PM交AB于F，取CD的中点G，则GN∥MP，∴G∈平面MNP．连结FG交BC于H，则H∈平面MNP，可证H是BC的中点．∴题图④与题图⑤中的平面MNP实为同一平面．∴⑤也符合．答案：①④⑤【点评】点评：本题要先想象直观判断哪些图形符合，再加以推理，考查了空间想象能力、反证法、线面的位置关系等知识，通过这个试题可看出试题在向增加思维量、综合考查同学们的各种能力转化．三、解答题（共6小题，满分74分）17．（12分）（2003•全国）已知复数z的辐角为60°，且|z﹣1|是|z|和|z﹣2|的等比中项．求|z|．【考点】A1：虚数单位i、复数；87：等比数列的性质；A8：复数的模．【专题】11 ：计算题．【分析】本题考查的复数的基本概念及等比数列的性质，由复数z的辐角为60°，我们可以使用待定系数法设出复数Z，然后根据|z﹣1|是|z|和|z﹣2|的等比中项，结合等比数列的性质构造方程，解方程求出待定的系数，即可得到Z值，进而求出复数的模．【解答】解：设z=（rcos60°+rsin60°i），则复数z的实部为．由题设|z﹣1|2=|z|•|z﹣2|，即：（z﹣1）（﹣1）=|z|∴r2﹣r+1=r，整理得r2+2r﹣1=0．解得r=﹣1，r=﹣﹣1（舍去）．即|z|=﹣1．【点评】解决复数问题时，我们多使用待定系数法，即设出复数的值，然后根据题目中的其它条件，列出方程，解方程求出系数，即可得到未知复数的值．18．（12分）（2003•全国）如图，直三棱柱ABC﹣A1B1C1中，底面是等腰直角三角形，∠ACB=90°，侧棱AA1=2，D、E分别是CC1与A1B的中点，点E在平面ABD 上的射影是△ABD的重心G．（Ⅰ）求A1B与平面ABD所成角的大小（结果用反三角函数值表示）；（Ⅱ）求点A1到平面AED的距离．【考点】MI：直线与平面所成的角；L2：棱柱的结构特征；MK：点、线、面间的距离计算．【专题】11 ：计算题．【分析】（1）连接BG，则BG是BE在面ABD的射影，易证∠EBG是A1B与平面ABD所成的角，设F为AB中点，连接EF、FC，在三角形EBG中求出此角；（2）连接A1D，有，建立等量关系，求出点A1到平面AED的距离即可．【解答】解：（Ⅰ）连接BG，则BG是BE在面ABD的射影，即∠EBG是A1B与平面ABD所成的角．设F为AB中点，连接EF、FC，∵D，E分别是CC1，A1B的中点，又DC⊥平面ABC，∴CDEF为矩形，连接DE，G是△ADB的重心，∴G∈DF，在直角三角形EFD中，EF2=FG•FD=FD2，∵EF=1，∴FD=．于是ED=，EG=∵FC=，CD=1∴AB=2，A1B=2，EB=，∴A1B与平面ABD所成的角是arcsin；（Ⅱ）连接A1D，有∵ED⊥AB，ED⊥EF，又EF∩AB=F，∴ED⊥平面A1AB，设A1到平面AED的距离为h，则，，．∴，即A1到平面AED的距离为．【点评】本小题主要考查线面关系和直棱柱等基础知识，同时考查空间想象能力和推理运算能力．19．（12分）（2003•全国）已知c＞0，设P：函数y=c x在R上单调递减，Q：不等式x+|x﹣2c|＞1的解集为R．如果P和Q有且仅有一个正确，求c的取值范围．【考点】4B：指数函数的单调性与特殊点；R5：绝对值不等式的解法．【专题】11 ：计算题；15 ：综合题．【分析】函数y=c x在R上单调递减，推出c的范围，不等式x+|x﹣2c|＞1的解集为R，推出x+|x﹣2c|的最小值大于1，P和Q有且仅有一个正确，然后求出c 的取值范围．【解答】解：函数y=c x在R上单调递减⇔0＜c＜1．不等式x+|x﹣2c|＞1的解集为R⇔函数y=x+|x﹣2c|在R上恒大于1．∵x+|x﹣2c|=∴函数y=x+|x﹣2c|在R上的最小值为2c．∴不等式x+|x﹣2c|＞1的解集为R⇔2c＞1⇔c＞．如果P正确，且Q不正确，则0＜c≤．如果P不正确，且Q正确，则c＞1．∴c的取值范围为（0，]∪（1，+∞）．【点评】本题考查绝对值不等式的解法，指数函数单调性的应用，是中档题．20．（12分）（2003•全国）在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南方向300km的海面P处，并以20km/h的速度向西偏北45°方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大，问几小时后该城市开始受到台风的侵袭？【考点】JF：圆方程的综合应用．【专题】12 ：应用题；16 ：压轴题．【分析】建立坐标系：以O为原点，正东方向为x轴正向．设在时刻：t（h）台风中心P（x，y）的坐标进而可知此时台风侵袭的区域，根据题意可知其中r（t）=10t+60，若在t时，该城市O受到台风的侵袭，则有（0﹣x）2+（0﹣y）2≤（10t+60）2，进而可得关于t的一元二次不等式，求得t的范围，答案可得．【解答】解：如图建立坐标系：以O为原点，正东方向为x轴正向．在时刻：t（h）台风中心P（x，y）的坐标为令（x′，y′）是台风边缘线上一点，则此时台风侵袭的区域是（x′﹣x）2+（y′﹣y）2≤[r（t）]2，其中r（t）=10t+60，若在t时，该城市受到台风的侵袭，则有（0﹣x）2+（0﹣y）2≤（10t+60）2，即，即t2﹣36t+288≤0，解得12≤t≤24．答：12小时后该城市开始受到台风侵袭．【点评】本题主要考查了圆的方程的综合运用．考查了学生运用所学知识解决实际问题的能力．21．（12分）（2003•全国）已知常数a＞0，在矩形ABCD中，AB=4，BC=4a，O 为AB的中点，点E、F、G分别在BC、CD、DA上移动，且，P为GE 与OF的交点（如图），问是否存在两个定点，使P到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由．【考点】J3：轨迹方程；K4：椭圆的性质．【专题】11 ：计算题；16 ：压轴题．【分析】建立坐标系，按题意写出A，B，C，D四点的坐标，进而根据解出E，F，G三点的坐标参数表示，求出OF与GE两条直线的方程，两者联立即可求出点P的坐标满足的参数方程，消去参数，得到点P的轨迹方程．由于参数a的取值范围影响曲线的形状故按参数a的范围来对曲线进行分类．【解答】解：根据题设条件，首先求出点P坐标满足的方程，据此再判断是否存在两定点，使得点P到定点距离的和为定值．按题意有A（﹣2，0），B（2，0），C（2，4a），D（﹣2，4a）设=k（0≤k≤1），由此有E（2，4ak），F（2﹣4k，4a），G（﹣2，4a﹣4ak）．直线OF的方程为：2ax+（2k﹣1）y=0，①直线GE的方程为：﹣a（2k﹣1）x+y﹣2a=0．②从①，②消去参数k，得点P（x，y）坐标满足方程2a2x2+y2﹣2ay=0，整理得．当时，点P的轨迹为圆弧，所以不存在符合题意的两点；当时，点P轨迹为椭圆的一部分，点P到该椭圆焦点的距离的和为定长；当时，点P到椭圆两个焦点的距离之和为定值；当时，点P到椭圆两个焦点的距离之和为定值2a．【点评】考查解析法求点的轨迹方程，本题在做题时引入了参数k，故得到的轨迹方程为参数方程，需要消去参数得到轨迹方程，又当字母的取值范围对曲线的形状有影响时，要对其范围进行讨论以确定轨迹的具体性状．考查分类讨论的数学思想．22．（14分）（2003•全国）（1）设{a n}是集合{2s+2t|0≤s＜t且s，t∈Z}中所有的数从小到大排列成的数列，即a1=3，a2=5，a3=6，a4=9，a5=10，a6=12，…将数列{a n}各项按照上小下大，左小右大的原则写成如下的三角形数表：35 69 10 12﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣…①写出这个三角形数表的第四行、第五行各数；②求a100（2）设{b n}是集合{2r+2s+2t|0≤r＜s＜t，且r，s，t∈Z}中所有的数从小到大排列成的数列，已知b k=1160，求k．【考点】8B：数列的应用．【专题】11 ：计算题；15 ：综合题；16 ：压轴题．【分析】（1）①用（t，s）表示2t+2s，先利用前几个数找到其规律，是每一个的横坐标从0增加到对应的行数，而纵坐标为行数，就可求出第四行、第五行各数；②解法一：因为100=（1+2+3+4++13）+9，所以可以知道a100位于第14行第8列，即可求出a100．解法二：直接把设a100=2s0+2t0，再利用条件确定对应的正整数s0，t0即可．（2）利用上面的结论可以快速找到{b n}的规律，再结合组合数对其求解即可．【解答】（1）解：用（t，s）表示2t+2s，下表的规律为3（0，1）5（0，2）6（1，2）9（0，3）10（1，3）12（2，3）①第四行17（0，4）18（1，4）20（2，4）24（3，4）第五行33（0，5）34（1，5）36（2，5）40（3，5）48（4，5）②解法一：因为100=（1+2+3+4+…+13）+9，所以a100=（8，14）=28+214=16640解法二：设a100=2s0+2t0，只须确定正整数s0，t0．数列{a n}中小于2t0的项构成的子集为{2t+2s|0≤s＜t＜t0}，其元素个数为，依题意．满足等式的最大整数t0为14，所以取t0=14．因为100﹣C142=s0+1，由此解得s0=8，∴a100=214+28=16640．（2）解：b k=1160=210+27+23，令M={c∈B|C＜1160}（其中，B={2r+2s+2t|0≤r＜s＜t}）因M={c∈B|c＜210}∪{c∈B|210＜c＜210+27}∪{c∈B|210+27＜c＜210+27+23}．现在求M的元素个数：{c∈B|c＜210}={2r&+2s+2t|0≤r＜s＜t＜10}，其元素个数为C103：{c∈B|210＜c＜210+27}={210&+2s+2r|0≤r＜s＜7}．某元素个数为C72：{c∈B|210+27＜c＜210+27+23}={210+27+2r|0≤r＜3}某元素个数为C107：k=C103+C72+C32+1=145．另法：规定2r+2t+2s=（r，t，s），b k=1160=210+27+23=（3，7，10）则b1=20+21+22=（0，1，2）C22依次为（0，1，3）（0，2，3）（1，2，3）C32（0，1，4）（0，2，4）（1，2，4）（0，3，4）（1，3，4）（2，3，4）C42（0，1，9）（0，2，9）（6，8，9）（7，8，9）C92（0，1，10）（0，2，10）（0，7，10）（1，7，10）（2，7，10）（3，7，10）C72+4k=（C22+C32++C92）+C72+4=145．【点评】本题考查数列的应用是数列这一块的难题，适合做压轴题．考点卡片1．分段函数的解析式求法及其图象的作法【知识点的认识】分段函数是定义在不同区间上解析式也不相同的函数．若函数在定义域的不同子集上的对应法则不同，可用几个式子来表示函数，这种形式的函数叫分段函数．已知一个分段函数在某一区间上的解析式，求此函数在另一区间上的解析式，这是分段函数中最常见的问题．【解题方法点拨】求解函数解析式的几种常用方法主要有1、待定系数法，如果已知函数解析式的构造时，用待定系数法；2、换元法或配凑法，已知复合函数f[g（x）]的表达式可用换元法，当表达式较简单时也可用配凑法；3、消参法，若已知抽象的函数表达式，则用解方程组消参的方法求解f（x）；另外，在解题过程中经常用到分类讨论、等价转化等数学思想方法．分段函数是一类重要的函数模型．解决分段函数问题，关键抓住在不同的段内研究问题．【命题方向】分段函数是今后高考的热点题型．常考题型为函数值的求解，不等式有关问题，函数的图形相联系的简单问题．2．指数函数的单调性与特殊点【知识点归纳】1、指数函数单调性的讨论，一般会以复合函数的形式出现，所以要分开讨论，首先讨论a的取值范围即a＞1，0＜a＜1的情况．再讨论g（x）的增减，然后遵循同增、同减即为增，一减一增即为减的原则进行判断．2、同增同减的规律：（1）y=a x如果a＞1，则函数单调递增；（2）如果0＜a＜1，则函数单调递减．3、复合函数的单调性：（1）复合函数为两个增函数复合：那么随着自变量X的增大，Y值也在不断的增大；（2）复合函数为两个减函数的复合：那么随着内层函数自变量X的增大，内层函数的Y值就在不断的减小，而内层函数的Y值就是整个复合函数的自变量X．因此，即当内层函数自变量X的增大时，内层函数的Y值就在不断的减小，即整个复合函数的自变量X不断减小，又因为外层函数也为减函数，所以整个复合函数的Y值就在增大．因此可得“同增”若复合函数为一增一减两个函数复合：内层函数为增函数，则若随着内层函数自变量X的增大，内层函数的Y值也在不断的增大，即整个复合函数的自变量X不断增大，又因为外层函数为减函数，所以整个复合函数的Y值就在减小．反之亦然，因此可得“异减”．3．对数的运算性质【知识点的认识】对数的性质：①=N；②log a a N=N（a＞0且a≠1）．log a（MN）=log a M+log a N；log a=log a M﹣log a N；log a M n=nlog a M；log a=log a M．4．反函数【知识点归纳】【定义】一般地，设函数y=f（x）（x∈A）的值域是C，根据这个函数中x，y 的关系，用y把x表示出，得到x=g（y）．若对于y在中的任何一个值，通过x=g （y），x在A中都有唯一的值和它对应，那么，x=g（y）就表示y是自变量，x 是因变量是y的函数，这样的函数y=g（x）（x∈C）叫做函数y=f（x）（x∈A）的反函数，记作y=f（﹣1）（x）反函数y=f（﹣1）（x）的定义域、值域分别是函数y=f （x）的值域、定义域．【性质】反函数其实就是y=f（x）中，x和y互换了角色（1）函数f（x）与他的反函数f﹣1（x）图象关于直线y=x对称；函数及其反函数的图形关于直线y=x对称（2）函数存在反函数的重要条件是，函数的定义域与值域是一一映射；（3）一个函数与它的反函数在相应区间上单调性一致；（4）大部分偶函数不存在反函数（当函数y=f（x），定义域是{0}且f（x）=C （其中C是常数），则函数f（x）是偶函数且有反函数，其反函数的定义域是{C}，值域为{0}）．奇函数不一定存在反函数，被与y轴垂直的直线截时能过2个及以上点即没有反函数．若一个奇函数存在反函数，则它的反函数也是奇函数．（5）一切隐函数具有反函数；（6）一段连续的函数的单调性在对应区间内具有一致性；（7）严格增（减）的函数一定有严格增（减）的反函数【反函数存在定理】；（8）反函数是相互的且具有唯一性；（9）定义域、值域相反对应法则互逆（三反）；（10）原函数一旦确定，反函数即确定（三定）（在有反函数的情况下，即满足（2））．5．极限及其运算【知识点的知识】1．数列极限（1）数列极限的表示方法：（2）几个常用极限：③对于任意实常数，当|a|＜1时，a n=0，当|a|=1时，若a=1，则a n=1；若a=﹣1，则a n=（﹣1）n不存在当|a|＞1时，a n=不存在．（3）数列极限的四则运算法则：如果，那么特别地，如果C是常数，那么．（4）数列极限的应用：求无穷数列的各项和，特别地，当|q|＜1时，无穷等比数列的各项和为S=（|q|＜1）．（化循环小数为分数方法同上式）注：并不是每一个无穷数列都有极限．=a2．函数极限；（1）当自变量x无限趋近于常数x0（但不等于x0）时，如果函数f（x）无限趋进于一个常数a，就是说当x趋近于x0时，函数f（x）的极限为a．记作=a或当x→x0时，f（x）→a．注：当x→x0时，f（x）是否存在极限与f（x）在x0处是否定义无关，因为x→x0并不要求x=x0．（当然，f（x）在x0是否有定义也与f（x）在x0处是否存在极限无关．函数f（x）在x0有定义是存在的既不充分又不必要条件．）如P（x）=在x=1处无定义，但存在，因为在x=1处左右极限均等于零．（2）函数极限的四则运算法则：如果，那么。

2003年江苏高考数学试题及答案

2003年普通高等学校招生全国统一考试（江苏卷）数学（理工农医类）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分第Ⅰ卷1至2页，第Ⅱ卷3至10页考试结束后，将本试卷和答题卡一并交回第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．如果函数2y ax bx a =++的图象与x 轴有两个交点，则点(,)a b aOb 在平面上的区域（不包含边界）为（）2．抛物线2ax y =的准线方程是2=y ，则a 的值为（） A ．81 B ．－81 C ．8 D ．－8 3．已知==-∈x tg x x 2,54cos ),0,2(则π（）A ．247 B ．－247 C ．724 D ．－724 4．设函数0021,1)(0,,0,12)(x x f x x x x f x 则若>⎪⎩⎪⎨⎧>≤-=-的取值范围是（） A ．（－1，1）B ．(1,)-+∞a aAB C DC ．（－∞，－2）∪（0，+∞）D ．（－∞，－1）∪（1，+∞）5．O 是平面上一定点，A B C 、、是平面上不共线的三个点，动点P 满足[)(),0,,AB AC OP OA P ABACλλ=++∈+∞则的轨迹一定通过ABC 的A ．外心B ．内心C ．重心D ．垂心6．函数1ln,(1,)1x y x x +=∈+∞-的反函数为（） A ．1,(0,)1x xe y x e -=∈+∞+ B ．1,(0,)1x xe y x e +=∈+∞- C ．1,(,0)1x xe y x e -=∈-∞+ D ．1,(,0)1x xe y x e +=∈-∞- 7．棱长为a 的正方体中，连结相邻面的中心，以这些线段为棱的八面体的体积为（）A ．33aB ．34aC ．36aD ．312a8．设20,()a f x ax bx c >=++，曲线()y f x =在点00(,())P x f x 处切线的倾斜角的取值范围为0,,4P π⎡⎤⎢⎥⎣⎦则到曲线()y f x =对称轴距离的取值范围为（） A ．10,a ⎡⎤⎢⎥⎣⎦B ．10,2a ⎡⎤⎢⎥⎣⎦C ．0,2ba⎡⎤⎢⎥⎣⎦D ．10,2b a ⎡-⎤⎢⎥⎣⎦9．已知方程0)2)(2(22=+-+-n x x m x x 的四个根组成一个首项为41的的等差数列，则=-||n m （） A ．1B ．43C ．21D ．8310．已知双曲线中心在原点且一个焦点为F （7，0），直线1-=x y 与其相交于M 、N 两点，MN 中点的横坐标为32-，则此双曲线的方程是（） A ．14322=-y x B ．13422=-y x C ．12522=-y xD ．15222=-y x11．已知长方形的四个顶点A （0，0），B （2，0），C （2，1）和D （0，1），一质点从AB 的中点0P 沿与AB 的夹角θ的方向射到BC 上的点1P 后，依次反射到CD 、DA 和AB 上的点2P 、3P 和4P （入射角等于反射角），设4P 的坐标为（4x ，0），若214<<x ，则tg θ的取值范围是（） A ．（31，1）B ．（31，32） C ．（52，21） D ．（52，32） 12．一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为（） A ．π3B ．4πC ．π33D ．π62003年普通高等学校招生全国统一考试（江苏卷）数学（理工农医类）第Ⅱ卷（非选择题共90分）二.填空题：本大题共4小题，每小题4分，共16分把答案填在题中横线上13．92)21(xx -的展开式中9x 系数是14．某公司生产三种型号的轿车，产量分别为1200辆，6000辆和2000辆为检验该公司的产品质量，现用分层抽样的方法抽取46辆进行检验，这三种型号的轿车依次应抽取___________，__________，___________辆15．某城市在中心广场建造一个花圃，花圃分为6个部分（如图）4种不同的栽种方法有___________________种16．对于四面体ABCD ，给出下列四个命题①,,AB AC BD CD BC AD ==⊥若则②,,AB CD AC BD BC AD ==⊥若则③,,AB AC BD CD BC AD ⊥⊥⊥若则④,,AB CD AC BD BC AD ⊥⊥⊥若则其中真命题的序号是__________________.（写出所有真命题的序号）三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或或演算步骤17．（本小题满分12分）有三种产品，合格率分别为0.90,0.95和0.95，各抽取一件进行检验（Ⅰ）求恰有一件不合格的概率；（Ⅱ）求至少有两件不合格的概率（精确到0.001）18．（本小题满分12分）已知函数()sin()(0,0)f x x R ωϕωϕπ=+>≤≤是上的偶函数，其图象关于点3(,0)4M π对称，且在区间0,2π⎡⎤⎢⎥⎣⎦上是单调函数ωϕ和的值 19．（本小题满分12分）如图，在直三棱柱111C B A ABC -中，底面是等腰直角三角形，︒=∠90ACB ，侧棱21=AA ，D 、E 分别是1CC 与B A 1的中点，点E 在平面ABD 上的射影是△ABD 的重心G（Ⅰ）求B A 1与平面ABD 所成角的大小（结果用反三角函数值表示）（Ⅱ）求点1A 到平面AED 的距离E GD CBAC 1B 1A 120．（本小题满分12分）已知常数0,(0,),(1,0)a c a i >==向量经过原点O 以c i λ+为方向向量的直线与经过定点(0,)2A a i c λ-以为方向向量的直线相交于P ，其中λ∈试问：是否存在两个定点E 、F ，使得PE PF +为定值若存在，求出E 、F 的坐标；若不存在，说明理由21．（本小题满分12分）已知0,a n >为正整数（Ⅰ）设()n y x a =-，证明1'()n y n x a -=-；（Ⅱ）设()()n nn f x x x a =--，对任意n a ≥，证明1'(1)(1)'(n n f n n f n ++>+22．（本小题满分14分）设0a >，如图，已知直线:l y ax =及曲线2:,C y x C =上的点1Q 的横坐标为作直线平行于x 轴，交直线11n n l P P ++于点，再从点作直线平行于y 轴，交曲线1.(1,2,3,n n C Q Q n +=于点 …）的横坐标构成数列{}n a（Ⅰ）试求1n n a a +与的关系，并求{}n a 的通项公式；（Ⅱ）当111,2a a =≤时，证明1211()32n k k k k a a a ++=-<∑ （Ⅲ）当1a =时，证明1211()3nk k k k a a a ++=-<∑2003年普通高等学校招生全国统一考试数学试题（江苏卷）答案一、选择题：本题考查基本知识和基本运算，每小题5分，满分60分.1．C 2．B 3．D 4．D 5．B 6．B 7．C 8．B 9．C 10．D 11．C 12．A 二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分. 13．221- 14．6,30,10 15．12016．①④三、解答题17．本小题要主考查相互独立事件概率的计算，运用数学知识解决问题的能力，满分12分. 解：设三种产品各抽取一件，抽到合格产品的事件分别为A 、B 和C. （Ⅰ）95.0)()(,90.0)(===C P B P A P ， .50.0)()(,10.0)(===C P B P A P因为事件A ，B ，C 相互独立，恰有一件不合格的概率为176.095.095.010.005.095.090.02)()()()()()()()()()()()(=⨯⨯+⨯⨯⨯=⋅⋅+⋅⋅+⋅⋅=⋅⋅+⋅⋅+⋅⋅C P B P A P C P B P A P C P B P A P C B A P C B A P C B A P 答：恰有一件不合格的概率为0.176. 解法一：至少有两件不合格的概率为)()()()(C B A P C B A P C B A P C B A P ⋅⋅+⋅⋅+⋅⋅+⋅⋅012.005.010.095.005.010.0205.090.022=⨯+⨯⨯⨯+⨯= 解法二：三件产品都合格的概率为812.095.090.0)()()()(2=⨯=⋅⋅=⋅⋅C P B P A P C B A P由（Ⅰ）知，恰有一件不合格的概率为0.176，所以至有两件不合格的概率为.012.0)176.0812.0(1]176.0)([1=+-=+⋅⋅-C B A P答：至少有两件不合的概率为0.012.（18）在小题主要考查三角函数的图象和单调性、奇偶性等基本知识，以及分析问题和推理计算能力，满12分分。

2003全国高考理科综合试题及答案

2003年普通高等学校招生全国统一考试（全国卷）理科综合能力测试第I卷（选择题共22题每题6分共132分）在下列各题的四个选项中，只有一个选项是符合题目要求的。

以下数据可供解题时参考：原子量：H 1 Li 7 Be 9 C 12 O 16 Na 23 Mg 24 P 31 Cl 35.5 K 39 Ca 401．取适量干重相等的4份种子进行不同处理：（甲）风干，（乙）消毒后浸水萌发，（丙）浸水后萌发，（丁）浸水萌发后煮熟冷却、消毒。

然后分别放入4个保温瓶中。

一段时间后，种子堆内温度最高的是：A 甲B 乙C 丙D 丁2．植物叶片从幼到老的整个生命活动过程中A 有机物输出也输入，矿质元素只输入B 有机物只输出，矿质元素只输入C 有机物只输出，矿质元素输入也输出D 有机物与矿质元素都既输入，又输出3．下列关于叶绿素合成和功能的叙述，错误的是A 光是叶绿素合成的必要条件B 低温抑制叶绿素的合成C 矿质元素影响叶绿素的合成D 提取的叶绿素溶液，给予适宜的温度、光照和CO2，可进行光合作用4．一只成年雄狗仍然保持幼年的体态，且精神萎靡、反应迟钝、行动呆笨，无求偶行为，其原因是A 睾丸发育不全B 甲状腺功能低下C 生长激素分泌不足D 生长激素分泌不足、睾丸发育不全5．据图判断，下列叙述不符合生态学原理的是A 物质经过多级利用，实现了良性循环B 每一级生产环节都获得产品，提高了生态经济效益C 由于食物链延长，能量逐级损耗，系统总能量利用效率降低D 由于各级产物都可以利用，减少了废物和污染6．人类探测月球发现，在月球的土壤中含有较丰富的质量数为3的氦，它可以作为未来核聚变的重要原料之一。

氦的该种同位素应表示为A 43He B 32He C 42He D 33e7．在两个容积相同的容器中，一个盛有HCl气体，另一个盛有H2和Cl2的混合气体。

在同温同压下，两容器内的气体一定具有相同的A 原子数B 密度C 质量D 质子数第1 页共11 页8．某无色混合气体可能由CH4、NH3、H2、CO、CO2和HCl中的某几种气体组成。

2003年高考数学试题(全国文)及答案

2003年普通高等学校招生全国统一考试（全国卷）数学（文史类）注意事项：1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上．2. 每小题选出答案后，用铅笔把答题卡上对应答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．3. 考试结束，监考人将本试卷和答题卡一并收回．参考公式：三角函数的积化和差公式：正棱台、圆台的侧面积公式)]sin()[sin(21cos sin βαβαβα-++=⋅ l c c S )(21+'=台侧其中c '、c 分别表示)]sin()[sin(21sin cos βαβαβα--+=⋅ 上、下底面周长，l 表示斜高或母线长.)]cos()[cos(21cos cos βαβαβα-++=⋅ 球体的体积公式：334R V π=球，其中R)]cos()[cos(21sin sin βαβαβα--+-=⋅ 表示球的半径.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分第Ⅰ卷1至2页，第Ⅱ卷3至10页考试结束后，将本试卷和答题卡一并交回第Ⅰ卷（选择题共60分）一.选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的 1．直线2y x x =关于对称的直线方程为（）（A ）12y x =- （B ）12y x = （C ）2y x =- （D ）2y x =2．已知,02x π⎛⎫∈- ⎪⎝⎭，54cos =x ，则2tg x = （）（A ）247 （B ）247- （C ）724 （D ）724-3．抛物线2y ax =的准线方程是2,y a =则的值为（）（A ）18 （B ）18- （C ）8 （D ）8- 4．等差数列{}n a 中，已知1251,4,33,3n a a a a n =+==则为（）（A ）48 （B ）49 （C ）50 （D ）515．双曲线虚轴的一个端点为M ，两个焦点为1212,,120F F F MF ∠=︒，则双曲线的离心率为（）（A （B （C （D6．设函数⎪⎩⎪⎨⎧-=-2112)(xx f x 00>≤x x ，若1)(0>x f ，则0x 的取值范围是（）（A ）（1-，1）（B ）（1-，∞+）（C ）（∞-，2-）⋃（0，∞+）（D ）（∞-，1-）⋃（1，∞+） 7．已知5()lg ,(2)f x x f ==则（）（A ）lg 2 （B ）lg32 （C ）1lg32（D ）1lg 258．函数sin()(0)y x R ϕϕπϕ=+≤≤=是上的偶函数，则（）（A ）0 （B ）4π （C ）2π（D ）π 9．已知(,2)(0):-30a a l x y a >+==点到直线的距离为1，则（）（A （B ）2 （C 1 （D 1 10．已知圆锥的底面半径为R ，高为3R ，它的内接圆柱的底面半径为34R ，该圆柱的全面积为（）（A ）22R π （B ）249R π （C ）238R π （D ）252R π11．已知长方形的四个顶点A （0，0），B （2，0），C （2，1）和D （0，1），一质点从AB 的中点0P 沿与AB 夹角为θ的方向射到BC 上的点1P 后，依次反射到CD 、DA 和AB 上的点2P 、3P 和4P （入射角等于反射角）若40P P 与重合，则tg θ= （）（A ）31 （B ）52 （C ）21（D ）1 12．一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为（）（A ）π3 （B ）π4 （C ）π33 （D ）π62003年普通高等学校招生全国统一考试数学（文史类）第Ⅱ卷（非选择题共90分）二.填空题：本大题共4小题，每小题4分，共16分把答案填在题中横线上13x <的解集是____________________.14．92)21(xx -的展开式中9x 系数是 ________ .15．在平面几何里，有勾股定理：“设222,,ABC AB AC AB AC BC +=的两边互相垂直则”拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面面积与底面面积间的关系，可以得出的正确结论是：“设三棱锥A BCD-的三个侧面A B C A C 、、两两互相垂直，则______________________________________________.” 16．如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有种_______________________（以数字作答）三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或或演算步骤 17．（本小题满分12分）已知正四棱柱111111112ABCD A B C D AB AA E CC F BD -==，，，点为中点，点为点中点（Ⅰ）证明11EF BD CC 为与的公垂线（Ⅱ）求点1D BDE 到面的距离 18．（本小题满分12分）已知复数z 的辐角为︒60，且|1|-z 是||z 和|2|-z 的等比中项，求||z . 19．（本小题满分12分）已知数列{}n a 满足1111,3(2).n n n a a a n --==+≥ （Ⅰ）求23,a a ；（Ⅱ）证明312n n a -=20．（本小题满分12分）已知函数()2sin (sin cos )f x x x x =+ （Ⅰ）求函数()f x 的最小正周期和最大值；()y f x =在（Ⅱ）在给出的直角坐标系中，画出函数区间,22ππ⎡⎤-⎢⎥⎣⎦上的图象 21．（本小题满分12分）在某海滨城市附近海面有一台风，据监测，当前台风中(cos 10θθ=方心位于城市O （如图）的东偏南EDBACBD CAFMx向300km 的海面P 处，并以20km/h 的速度向西偏北︒45方向移动，台风侵袭的范围为圆形区域，当前半径为60km ，并以10km/h 的速度不断增大，问几小时后该城市开始受到台风的侵袭？ 22．（本小题满分14分）已知常数0>a ，在矩形ABCD 中，4=AB ，a BC 4=，O 为AB 的中点，点E 、F 、G 分别在BC 、CD 、DA 上移动，且DA DC CD CF BC BE ==，P 为GE 与OF 的交点（如图），问是否存在两个定点，使P 到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由2003年普通高等学校招生全国统一考试数学试题（文）参考解答及评分标准说明：一. 本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生物解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二. 对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定部分的给分，但不得超过该部分正确解答得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．三. 解答右端所注分数，表示考生正确做到这一步应得的累加分数．四. 只给整数分数．选择题和填空题不给中间分．一、选择题：本题考查基本知识和基本运算. 每小题5分，满分60分.1．C 2．D 3．B 4．C 5．B 6．D 7．D 8．C 9．C 10．B 11．C 12．A 二、填空题：本题考查基本知识和基本运算.每小题4分,满分16分. 13．]4,2( 14．221-15．2222BCD ADB ACD ABC S S S S ∆∆∆∆=++ 16．72 三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤. 17．（I ）证明：取BD 中点M ，连结MC ，FM ，∵F 为BD 1中点， ∴FM ∥D 1D 且FM=21D 1D 又EC=21CC 1，且EC ⊥MC ， ∴四边形EFMC 是矩形 ∴EF ⊥CC 1 又CM ⊥面DBD 1 ∴EF ⊥面DBD 1 ∵BD 1⊂面DBD 1，∴EF ⊥BD 1 故EF 为BD 1与CC 1的公垂线（II ）解：连结ED 1，有V由（I ）知EF ⊥面DBD 1，设点D 1到面BDE 的距离为d ，则S △DBC ·d=S △DCD 1·EF. ∵AA 1=2·AB=1.22,2====∴EF ED BE BD 23)2(2321,2222121=⋅⋅==⋅⋅=∴∆∆DBC DBD S S 故点D 1到平面BDE 的距离为332. 18．解：设z=2),60sin 60(cos r z i r 的实邻为则复数+ 2,r z z r z z ==+∴由题设|2||||1|2-⋅=-z z z即||)1)(1(=--z z 42122+-=+-r r r r r12120122--=-==-+r r r r 解得（舍去）即|z|=12-19．（I ）解∵1343,413,12321=+==+=∴=a a a（II ）证明：由已知故,311--=-n n n a a112211)()()(a a a a a a a a n n n n n +-++-+-=--- =.213133321-=++++--n n n所以213-=n n a20．解（I ）x x x x x x f 2sin 2cos 1cos sin 2sin 2)(2+-=+= )42sin(21)4sin 2cos 4cos 2(sin 21πππ-+=-⋅+=x x x所以函数)(x f 的最小正周期为π，最大值为21+.故函数)(x f y =在区间]2,2[ππ-上的图象是21．解：如图建立坐标系：以O 为原点，正东方向为x 轴正向. 在时刻：t （h ）台风中心),(y x P 的坐标为⎪⎪⎩⎪⎪⎨⎧⨯+⨯-=⨯-⨯=.22201027300,2220102300t y t x 此时台风侵袭的区域是222)]([)()(t r y y x x ≤-+-，其中10)(=t r t+60，若在t 时，该城市O 受到台风的侵袭，则有,)6010()0()0(222+≤-+-t y x即,)6010()22201027300()2220102300(222+≤⨯+⨯-+⨯-⨯t t t 即0288362≤+-t t ，解得2412≤≤t .答：12小时后该城市开始受到台风气侵袭22．解：根据题设条件，首先求出点P 坐标满足的方程，据此再判断是否存在两定点，使得点P 到定点距离的和为定值.按题意有A （－2，0），B （2，0），C （2，4a ），D （－2，4a ）设)10(≤≤===k k DADCCD CF BC BE ，由此有E （2，4ak ），F （2－4k ，4a ），G （－2，4a －4ak ）.直线OF 的方程为：0)12(2=-+y k ax ， ① 直线GE 的方程为：02)12(=-+--a y x k a . ②从①，②消去参数k ，得点P （x ，y ）坐标满足方程022222=-+ay y x a ，整理得1)(21222=-+a a y x .当212=a 时，点P 的轨迹为圆弧，所以不存在符合题意的两点. 当212≠a 时，点P 轨迹为椭圆的一部分，点P 到该椭圆焦点的距离的和为定长.当212<a 时，点P 到椭圆两个焦点),21(),,21(22a a a a ---的距离之和为定值2.当212>a 时，点P 到椭圆两个焦点)21021,0(22-+--a a a a ，），（的距离之和为定值a 2.。

2003年全国统一高考理综真题试题及答案

2003年江苏省高考综合考试理科综合试卷本试卷分第I卷(选择题)和第11卷(非选择题)两部分，第1卷1至6页，第Ⅱ卷7至14页。

满分150分。

考试用时120分钟。

第1卷(选择题共75分)注意事项：1．答第1卷前，考生务必将自己的姓名、考试号、考试科目涂写在答题卡上。

考试结束，将试题卷和答题卡一并交回。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，不能答在试题卷上。

一、本卷共25题，每题3分，共75分．在下列各题的四个选项中，只有一个选项是符合题目要求的．1．生物的生命活动都要消耗能量，这些能量由呼吸作用提供．活细胞内进行有氧呼吸的主要场所是A.高尔基体 B．线粒体C.叶绿体D.核糖体2．如果—个人多食少动，即摄人的食物过多，消耗的物质过少，容易导致身体的肥胖，其主要原因是体内的A.有机物氧化分解成C02和H20 B．葡萄糖合成肝糖元C.非脂肪类有机物转变脂肪D.葡萄糖合成肌糖元3.用0.3g/mL的蔗糖溶液可以使洋葱表皮细胞发生质壁分离，在发生质壁分离的原生质层和细胞壁之间充满的物质是A.蔗糖溶液B.水C.细胞液D.空气4.某园艺场经过长期精心选育，培养出一株形态优美的兰花.如果要保持每本的优良性状，并尽快大规模繁殖，最适合的繁殖方式是A.分裂生殖B.有性生殖C.孢子生殖D.组织培养5.下面是—个草原生态系统食物网的模式图，该食物网中共有食物链A.3条B.4条C.5条D.6条6.2002年诺贝尔化学奖授予利用“质谱分析法”和“核磁共振技术”等对生物大分子进行研究并作出重大贡献的科学家.下列物质中属于生物大分子的是 A.乙醇 B.葡萄糖 C.氨基酸 D.蛋白质7．136C N M R - (核磁共振)可以用于含碳化合物的结构分析．有关136C N M R -的说法正确的是A ．质子数为6B ．电子数为13C ．中子数为6D ．质量数为68．环境污染已成为人类社会面临的重大威胁之—．下列气体的排放不会造成大气污染的是 A ．S02 B ．N 2 C ．N02 D ．CO9．下列物质不属于有机物的是 A.CH 4 B ．CH 3CHO C ．NaCl D ．C 6H 610．不属于碱金属元素的是 A ．Li B ．Na C ．K D ．A111．下列说法正确的是A ．绿色食品是指不含任何化学物质的食品B ．纳米材料是一种称为“纳米”的新物质制成的材料C ．光导纤维是以二氧化硅为主要原料制成的高性能通讯材料D ．废旧干电池必须集中回收，目的是调剂给贫困地区使用 12．下列物质中既能跟盐酸反应，又能跟氢氧化钠溶液反应的是 A.Al(OH)3 B ．NaCl 溶液 C. K 2S04溶液 D ．稀H 2S0413.下列化合物中，不能由单质直接化合而得到的是 A.NH 3 B.Na 202C.FeCl 2D.FeCl 314.a g 的铜丝灼烧变黑，立即放人下列的某种物质中发生反应，铜丝变红且反应后铜丝质量仍为a g.则该物质是 A.稀H 2S04 B.C 2H 5OHC.CuS04溶液D.NaOH 溶液15.在O.1mol ／L 的CH 3COOH 溶液中存在如下电离平衡： CH 3COOH CH3COO -+H +对于该平衡，下列叙述正确的是A.加入少量NaOH 固体，平衡向正反应方向移动B.加水，反应速率增大，平衡向逆反应方向移动 C 滴加少量0.1mol ／LHCl 溶液，溶液中C(H +)减少 D.加入少量CH 3COONa 固体，平衡向正反应方向移动16.已知C 4H 10的同分异构体有两种:CH 3-CH 2-CH 2—CH 3、CH 3-CH(CH 3)-CH 3则C 4H 9OH 属于醇类的同分异构体共有A.1种B.2种C.3种D.4种 17.以下关于力的几种说法中，错误的是 A.力是物体间的相互作用 C.力是维持物体运动的原因 B.力能使物体发生形变 D.力是物体产生加速度的原因18.已知C 4H 10的同分异构体有两种:CH 3-CH 2-CH 2—CH 3、CH 3-CH(CH 3)-CH 318．如图所示，某质点沿半径为厂的半圆弧由口点运动到凸点，则它通过的位移和路程分别是 A ．0；0B ．2r ，向东； πrC ．r ，向东； πrD ．2r ，向东 2r19．下列涉及分子动理论的表述中，正确的是 A ．物质是由大量分子组成的B ．物体内分子的无规则运动，在通常条件下也可能停止C ．物体内分子之间的作用力一定表现为引力D ．物体内分子之间的作用力一定表现为斥力20．相隔—段距离的两个点电荷，它们之间的静电力为F ，现使其中—个点电荷的电量变为原来的2倍，同时将它们间的距离也变为原来的2倍，则它们之间的静电力变为 A ．2F B ．4F C ．2F D ．4F21．光导纤维在信息传递方面有很多应用．利用光导纤维进行光纤通信所依据的原理是 A.光的折射 B ．光的全反射 C 光的干涉 D ．光的色散 22．下列衰变中，属于。

2003年上海高考数学真题试卷及答案解析(理科)

绝密★启用前 2003年普通高等学校招生全国统一考试（上海卷）数学试卷（理工农医类）（满分150分，考试时间120分钟）考生注意1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页.2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答题纸指定位置.3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题.第Ⅰ卷（共110分）一、填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个空格填对得4分，否则一律得零分1．函数)4sin(cos )4cos(sin ππ+++=x x x x y 的最小正周期T= . 2．若=∈=+=απααπ则其中的解是方程),2,0(,1)cos(23x x .3．在等差数列}{n a 中，a 5=3, a 6=－2,则a 4+a 5+…+a 10= 4．在极坐标系中，定点A ),2,1(π点B 在直线0sin cos =+θρθρ上运动，当线段AB 最短时，点B 的极坐标是5．在正四棱锥P —ABCD 中，若侧面与底面所成二面角的大小为60°，则异面直线PA 与BC所成角的大小等于 .（结果用反三角函数值表示） 6．设集合A={x ||x |<4},B={x |x 2－4x +3>0}, 则集合{x |x ∈A 且}B A x ∉= . 7．在△ABC 中，sinA;sinB:sinC=2:3:4,则∠ABC= .（结果用反三角函数值表示） 8．若首项为a 1，公比为q 的等比数列}{n a 的前n 项和总小于这个数列的各项和，则首项a 1，公比q 的一组取值可以是（a 1，q ）= .9．某国际科研合作项目成员由11个美国人、4个法国人和5个中国人组成.现从中随机选出两位作为成果发布人，则此两人不属于同一个国家的概率为 .（结果用分数表示）10．方程x 3+lg x =18的根x ≈ .（结果精确到0.1） 11．已知点),0,24(),2,0(),2,0(nC n B n A +-其中n 的为正整数.设S n 表示△ABC 外接圆的面积，则n n S ∞→lim = .12．给出问题：F 1、F 2是双曲线201622y x -=1的焦点，点P 在双曲线上.若点P 到焦点F 1的距离等于9，求点P 到焦点F 2的距离.某学生的解答如下：双曲线的实轴长为8，由 ||PF 1|－|PF 2||=8，即|9－|PF 2||=8，得|PF 2|=1或17.该学生的解答是否正确？若正确，请将他的解题依据填在下面空格内，若不正确，将正确的结果填在下面空格内.二、选择题（本大题满分16分）本大题共4题，每题都给出代号为A 、B 、C 、D 的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分. 13．下列函数中，既为偶函数又在（0，π）上单调递增的是（） A ．y=tg|x |. B ．y=cos(－x ).C ．).2sin(π-=x y D ．|2|xctgy =. 14．在下列条件中，可判断平面α与β平行的是（）A ．α、β都垂直于平面r .B ．α内存在不共线的三点到β的距离相等.C ．l ，m 是α内两条直线，且l ∥β，m ∥β.D ．l ，m 是两条异面直线，且l ∥α，m ∥α, l ∥β，m ∥β.15．a 1、b 1、c 1、a 2、b 2、c 2均为非零实数，不等式a 1x 2+b 1x +c 1>0和a 2x 2+b 2x +c 2>0的解集分别为集合M 和N ，那么“212121c c b b a a ==”是“M=N ”的（）A ．充分非必要条件.B ．必要非充分条件.C ．充要条件D ．既非充分又非必要条件.16．f (x )是定义在区间[－c,c]上的奇函数，其图象如图所示：令g （x ）=af （x ）+b ，则下列关于函数g （x ）的叙述正确的是（）A ．若a <0,则函数g （x ）的图象关于原点对称.B ．若a =－1，－2<b<0,则方程g （x ）=0有大于2的实根.C ．若a ≠0,b=2,则方程g （x ）=0有两个实根.D ．若a ≥1,b<2,则方程g （x ）=0有三个实根.三、解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤. 17．（本题满分12分）已知复数z1=cosθ－i，z2=sinθ+i，求| z1·z2|的最大值和最小值.18．（本题满分12分）已知平行六面体ABCD—A1B1C1D1中，A1A⊥平面ABCD，AB=4，AD=2.若B1D⊥BC，直线B1D 与平面ABCD所成的角等于30°，求平行六面体ABCD—A1B1C1D1的体积.19．（本题满分14分）本题共有2个小题，第1小题满分5分，第2小题满分9分. 已知数列}{n a （n 为正整数）是首项是a 1，公比为q 的等比数列.（1）求和：;,334233132031223122021C a C a C a C a C a C a C a -+-+-（2）由（1）的结果归纳概括出关于正整数n 的一个结论，并加以证明.20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.如图，某隧道设计为双向四车道，车道总宽22米，要求通行车辆限高4.5米，隧道全长2.5千米，隧道的拱线近似地看成半个椭圆形状. （1）若最大拱高h 为6米，则隧道设计的拱宽l 是多少？（2）若最大拱高h 不小于6米，则应如何设计拱高h 和拱宽l ，才能使半个椭圆形隧道的土方工程量最最小？（半个椭圆的面积公式为lh S 4π=，柱体体积为：底面积乘以高.本题结果精确到0.1米）21．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分5分，第3小题满分7分.在以O 为原点的直角坐标系中，点A （4，－3）为△OAB 的直角顶点.已知|AB|=2|OA|，且点B 的纵坐标大于零.（1）求向量AB 的坐标；（2）求圆02622=++-y y x x 关于直线OB 对称的圆的方程；（3）是否存在实数a ，使抛物线12-=ax y 上总有关于直线OB 对称的两个点？若不存在，说明理由：若存在，求a 的取值范围.22．（本题满分18分）本题共有3个小题，第1小题满分5分，第2小题满分6分，第3小题满分7分.已知集合M是满足下列性质的函数f(x)的全体：存在非零常数T，对任意x∈R，有f(x+T)=T f(x)成立.（1）函数f(x)= x是否属于集合M？说明理由；（2）设函数f(x)=a x（a>0,且a≠1）的图象与y=x的图象有公共点，证明：f(x)=a x∈M；（3）若函数f(x)=sin kx∈M ,求实数k的取值范围.2003年普通高等学校招生全国统一考试（上海卷）数学（理工农医类）答案一、（第1题至第12题）1．π. 2．π34. 3．－49 . 4．)43,22(π. 5．arctg2. 6．[1,3]. 7．.611arccos8．10,0)(21,1(1<<>q a 的一组数）. 9．19011910．2.6 . 11．4π 12．|PF 2|=17.二、（第13题至第16题）题号 13 14 15 16 代号CDDB三、（第17题至第22题） 17．[解].2sin 412cos sin 2)sin (cos )cos sin 1(|)sin (cos cos sin 1|||2222221θθθθθθθθθθθ+=+=-++=-++=⋅i z z故||21z z ⋅的最大值为,23最小值为2.18．[解]连结BD ，因为B 1B ⊥平面ABCD ，B 1D ⊥BC ，所以BC ⊥BD.在△BCD 中，BC=2，CD=4，所以BD=32.又因为直线B 1D 与平面ABCD 所成的角等于30°，所以 ∠B 1DB=30°，于是BB 1=31BD=2.故平行六面体ABCD —A 1B 1C 1D 1的体积为S ABCD ·BB 1=38. 19．[解]（1）.)1(33,)1(231312111334233132031212111223122021q a q a q a q a a C a C a C a C a q a q a q a a C a C a C a -=-+-=-+--=+-=+-（2）归纳概括的结论为：若数列}{n a 是首项为a 1，公比为q 的等比数列，则nnn n n n n n n n nnn nnnn n nn n n n n n n n n n n n n n n q a C q C q C q qC C a C q a C q a C q a qC a C a C a C a C a C a C a n q a C a C a C a C a C a )1(])1([)1()1(:.,)1()1(133********122111011342312011134231201-=-++-+-=-++-+-=-++-+--=-++-+-++ 证明为正整数20．[解]（1）如图建立直角坐标系，则点P （11，4.5），椭圆方程为12222=+by a x .将b=h =6与点P 坐标代入椭圆方程，得3.3377882,7744≈===a l a 此时.因此隧道的拱宽约为33.3米.（2）[解一]由椭圆方程12222=+by a x ，得.15.4112222=+b a4.6,1.312222229,211,215.411,.29924,,2,995.41125.41122222222≈=≈======≥====≥⨯⨯≥+b h a l b a b a S ab lh S b h a l ab ab b a 此时得有取最小值时当所以且即因为πππ故当拱高约为6.4米、拱宽约为31.1米时，土方工程量最小.[解二]由椭圆方程12222=+b y a x ，得.15.4112222=+b a 于是,121481222-⋅=a a b ,121121121,,99,12181)2421212(481)242121121121(481222222222-=-≥⨯=+≥+-+-=a a S ab a a b a 有取最小值时当即得.229,211==b a 以下同解一.21．[解]（1）设⎩⎨⎧=-=+⎪⎩⎪⎨⎧=⋅==,034100,0||||||2||},,{22v u v u v u AB 即则由得},3,4{.86,86-+=+=⎩⎨⎧-=-=⎩⎨⎧==v u v u v u 因为或所以v －3>0,得v =8,故={6，8}.（2）由OB ={10，5}，得B （10，5），于是直线OB 方程：.21x y =由条件可知圆的标准方程为：(x －3)2+y(y+1)2=10, 得圆心（3，－1），半径为10.设圆心（3，－1）关于直线OB 的对称点为（x ,y ）则,31,231021223⎩⎨⎧==⎪⎪⎩⎪⎪⎨⎧-=-+=-⋅-+y x x y y x 得故所求圆的方程为(x －1)2+(y －3)2=10. （3）设P (x 1,y 1), Q (x 2,y 2) 为抛物线上关于直线OB 对称两点，则.23,022544,02252,,2252,202222222212212121212121>>-⋅-=∆=-++⎪⎪⎩⎪⎪⎨⎧-=-=+⎪⎪⎩⎪⎪⎨⎧-=--=+-+a a a a aa x a x x x a a x x a x x x x y y y y x x 得于是由的两个相异实根为方程即得故当23>a 时，抛物线y=ax 2－1上总有关于直线OB 对称的两点. 22．[解]（1）对于非零常数T ，f (x +T)=x +T, T f (x )=T x . 因为对任意x ∈R ，x +T= T x 不能恒成立，所以f (x )=.M x ∉（2）因为函数f (x )=a x （a >0且a ≠1）的图象与函数y=x 的图象有公共点，所以方程组：⎩⎨⎧==xy a y x有解，消去y 得a x =x ,显然x =0不是方程a x =x 的解，所以存在非零常数T ，使a T =T.于是对于f (x )=a x 有)()(x Tf a T a a a T x f x x T T x =⋅=⋅==++ 故f (x )=a x ∈M.（3）当k=0时，f (x )=0，显然f (x )=0∈M.当k ≠0时，因为f (x )=sin kx ∈M ，所以存在非零常数T ，对任意x ∈R ，有f (x +T)=T f (x )成立，即sin(kx +k T)=Tsin kx .因为k ≠0，且x ∈R ，所以kx ∈R ，kx +k T ∈R ，于是sin kx ∈[－1，1]，sin(kx +k T) ∈[－1，1]，故要使sin(kx +k T)=Tsin kx .成立，只有T=1±，当T=1时，sin(kx +k )=sin kx 成立，则k =2m π, m ∈Z .当T=－1时，sin(kx－k)=－sin kx成立，即sin(kx－k+π)= sin kx成立，则－k+π=2mπ, m∈Z ，即k=－2(m－1)π, m∈Z . 综合得，实数k的取值范围是{k|k= mπ, m∈Z}。

2011年山东高考专题-2003年理科数学真题及答案(全国卷)

阅读使人充实，会谈使人敏捷，写作使人精确。

——培根2003年普通高等学校招生全国统一考试（全国卷）数学（理工农医类）注意事项：1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上．2. 每小题选出答案后，用铅笔把答题卡上对应答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．3. 考试结束，监考人将本试卷和答题卡一并收回．参考公式：三角函数的积化和差公式：正棱台、圆台的侧面积公式)]sin()[sin(21cos sin βαβαβα-++=⋅ l c c S )(21+'=台侧其中c '、c 分别表示)]sin()[sin(21sin cos βαβαβα--+=⋅ 上、下底面周长，l 表示斜高或母线长.)]cos()[cos(21cos cos βαβαβα-++=⋅ 球体的体积公式：334R V π=球，其中R)]cos()[cos(21sin sin βαβαβα--+-=⋅ 表示球的半径.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分第Ⅰ卷（选择题共60分）一.选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的1．已知2(π-∈x ，0），54c o s =x ，则2tg x = （）A ．247B ．247-C ．724D ．724-2．圆锥曲线θθρ2cos sin 8=的准线方程是（） A ．2cos -=θρB ．2cos =θρC ．2sin =θρD ．2sin -=θρ3．设函数⎪⎩⎪⎨⎧-=-2112)(xx f x 00>≤x x ，若1)(0>x f ，则0x 的取值范围是（）A ．（1-，1）B ．（1-，∞+）C ．（∞-，2-）（0，∞+） D ．（∞-，1-）（1，∞+）4．函数)cos (sin sin 2x x x y +=的最大值为（）A ．21+B ．12-C ．2D ．25．已知圆C ：4)2()(22=-+-y a x （0>a ）及直线l ：03=+-y x ，当直线l 被C 截得的弦长为32时，则a 为（） A ．2B ．22-C ．12-D ．12+6．已知圆锥的底面半径为R ，高为3R ，在它的所有内接圆柱中，全面积的最大值是（）A ．22R πB ．249R πC ．238R πD ．223R π7．已知方程0)2)(2(22=+-+-n x x m x x 的四个根组成一个首项为41的的等差数列，则=-||n m （）A ．1B ．43C ．21D ．838．已知双曲线中心在原点且一个焦点为F （7，0），直线1-=x y 与其相交于M 、N 两点，MN 中点的横坐标为32-，则此双曲线的方程是（） A ．14322=-y xB ．13422=-y xC ．12522=-y xD ．15222=-y x9．函数x x f sin )(=，]23,2[ππ∈x 的反函数=-)(1x f（）A ．x arcsin - 1[-∈x ，1]B ．x arcsin --π 1[-∈x ，1]C ．x arcsin +π 1[-∈x ，1]D ．x arcsin -π 1[-∈x ，1]10．已知长方形的四个顶点A （0，0），B （2，0），C （2，1）和D （0，1），一质点从AB 的中点0P 沿与AB 的夹角θ的方向射到BC 上的点1P 后，依次反射到CD 、DA 和AB 上的点2P 、3P 和4P （入射角等于反射角），设4P 的坐标为（4x ，0），若214<<x ，则tg θ的取值范围是（） A ．（31，1）B ．（31，32）C ．（52，21） D ．（52，32）11．=++++++++∞→)(lim 11413122242322nnn C C C C n C C C C （）A ．3B ．31C ．61D ．612．一个四面体的所有棱长都为2，四个顶点在同一球面上，则些球的表面积为（）A ．π3B ．π4C ．π33D ．π62003年普通高等学校招生全国统一考试（全国卷）数学（理工农医类）第Ⅱ卷（非选择题共90分）二.填空题：本大题共4小题，每小题4分，共16分把答案填在题中横线上13．92)21(xx -的展开式中9x 系数是14．使1)(log 2+<-x x 成立的x 的取值范围是15．如图，一个地区分为5个行政区域，现给地图着色，要求相邻地区不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有种（以数字作答）16．下列5个正方体图形中，l 是正方体的一条对角线，点M 、N 、P 分别为其所在棱的中点，能得出⊥l 面MNP 的图形的序号是（写出所有符合要求的图形序号）① ② ③ ④ ⑤三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或或演算步骤17．（本小题满分12分）已知复数z 的辐角为︒60，且|1|-z 是||z 和|2|-z 的等比中项，求||z18．（本小题满分12分）如图，在直三棱柱111C B A ABC -中，底面是等腰直角三角形，︒=∠90ACB ，侧棱21=AA ，D 、E 分别是1CC 与B A 1的中点，点E 在平面ABD 上的射影是△ABD 的重心G（Ⅰ）求B A 1与平面ABD 所成角的大小（结果用反三角函数值表示）（Ⅱ）求点1A 到平面AED 的距离19．（本小题满分12分）已知0>c ，设P ：函数x c y =在R 上单调递减 Q ：不等式1|2|>-+c x x 的解集为R 如果P 和Q 有且仅有一个正确，求c 的取值范围20．（本小题满分12分）在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O （如图）的东偏南102arccos (=θθ）方向300km 的海面P处，并以20km/h 的速度向西偏北︒45方向移动，台风侵袭的范围为圆形区域，当前半径为60km ，并以10km/h 的速度不断增大，问几小时后该城市开始受到台风的侵袭？东O21．（本小题满分14分）已知常数0>a ，在矩形ABCD 中，4=AB ，a BC 4=，O 为AB 的中点，点E 、F 、G 分别在BC 、CD 、DA 上移动，且BE CF DG BC CD DA ==，P 为GE 与OF 的交点（如图），问是否存在两个定点，使P 到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由22．（本小题满分12分，附加题4 分）（I ）设}{n a 是集合|22{ts+ t s <≤0且Z t s ∈,}中所有的数从小到大排列成的数列，即31=a ，52=a ，63=a ，94=a ，105=a ，126=a ，…将数列}{n a 各项按照上小下大，左小右大的原则写成如下的三角形数表：35691012⑴写出这个三角形数表的第四行、第五行各数；⑵求100a（II ）（本小题为附加题，如果解答正确，加4 分，但全卷总分不超过150分）设}{n b 是集合t s r t s r <<≤++0|222{，且},,Z t s r ∈中所有的数从小到大排列成的数列，已知1160=k b ，求k .2003年普通高等学校招生全国统一考试(全国卷)数学（理工农医类）答案一、选择题：本题考查基本知识和基本运算. 每小题5分，满分60分.1．D 2．C 3．D 4．A 5．C 6．B 7．C 8．D 9．D 10．C 11．B 12．A二、填空题：本题考查基本知识和基本运算.每小题4分,满分16分. x13．221-14．（-1，0） 15．72 16．①④⑤ 三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤. 17．解：设)60sin 60cosr r z +=，则复数.2r z 的实部为2,r z z r z z ==-由题设.12||).(12,12:.012,421,)2)(2(||)1)(1(:|2||||1|2222-=--=-==-++-=+-∴--=---⋅=-z r r r r r r r r r z z z z z z z z 即舍去解得整理得即 18．（Ⅰ）解：连结BG ，则BG 是BE 在ABD 的射影，即∠EBG 是A 1B 与平面ABD 所成的角.设F 为AB 中点，连结EF 、FC ，.32arcsin.323136sin .3,32,22,2.36321,2)4(.3,1,31.,,,,,,112211所成的角是与平面于是分中在直角三角形的重心是连结为矩形平面又的中点分别是ABD B A EB EG EBG EB B A AB CD FC EG ED FD EF FD FD FG EF EFD DF G ADB G DE CDEF ABC DC B A CC E D ∴=⋅==∠∴===∴===⨯===∴==⋅=∈∴∆∴⊥（Ⅱ）解：,,,ED AB ED EF EF AB F ⊥⊥=又111111*********,.,.,.,.26,.ED A AB ED AED AED A AB AED A AB AE A K AE K A K AED A K A AED A A A B A AB A K A AED AB ∴⊥⊂∴⊥=⊥∴⊥⋅∆===面又面平面平面且面面作垂足为平面即是到平面的距离在中到平面 19．解：函数xc y =在R 上单调递减.10<<⇔c不等式.1|2|1|2|上恒大于在函数的解集为R c x x y R c x x -+=⇔>-+22,2,|2|2,2,|2|2.1|2|121.21,,0.21,, 1.(0,][1,).2x c x c x x c c x c y x x c R c x x c R c c P Q c P Q c c -≥⎧+-=⎨<⎩∴=+-∴+->⇔>⇔><≤≥+∞函数在上的最小值为不等式的解集为如果正确且不正确则如果不正确且正确则所以的取值范围为（以上方法在新疆考区无一人使用，大都是用解不等式的方法，个别使用的图象法）20．解：如图建立坐标系以O 为原点，正东方向为x 轴正向.在时刻：（1）台风中心P （y x ,）的坐标为⎪⎪⎩⎪⎪⎨⎧⨯+⨯-=⨯-⨯=.22201027300,2220102300t y t x此时台风侵袭的区域是,)]([)()(22t r y y x x ≤-+-其中,6010)(+=t t r 若在t 时刻城市O 受到台风的侵袭，则有.)6010()0()0(222+≤-+-t y x 即22)22201027300()2220102300(t t ⨯+⨯-+⨯-⨯2412,028836,)6010(22≤≤≤+-+≤t t t t 解得即答：12小时后该城市开始受到台风的侵袭.21．根据题设条件，首先求出点P 坐标满足的方程，据此再判断是否存在的两定点，使得点P 到两点距离的和为定值.按题意有A （－2，0），B （2，0），C （2，4a ），D （－2，4a ）设(01)B E C F D Gk k BC CD DA===≤≤ 由此有E （2，4a k ），F （2－4k ，4a ），G （－2，4a －4ak ）直线OF 的方程为：0)12(2=-+y k ax① 直线GE 的方程为：02)12(=-+--a y x k a②从①，②消去参数k ，得点P （x,y ）坐标满足方程022222=-+ay y x a整理得1)(21222=-+a a y x 当212=a 时，点P 的轨迹为圆弧，所以不存在符合题意的两点.当212≠a 时，点P 轨迹为椭圆的一部分，点P 到该椭圆焦点的距离的和为定长当212<a 时，点P 到椭圆两个焦点（),21(),,2122a a a a ---的距离之和为定值2当212>a 时，点P 到椭圆两个焦点（0，)21,0(),2122-+--a a a a 的距离之和为定值2a .22．（本小题满分12分，附加题4分）（Ⅰ）解：用(,)t s 表示22t s +，下表的规律为013(0,1)225(0,2)6(1,2)9(0,3)10(1,3)12(2,3)=+（i ）第四行 17(0,4) 18(1,4) 20(2,4) 24(3,4) 第五行 33(0,5) 34(1,5) 36(2,5) 40(3,5) 48(4,5)（i i ）解法一：因为100＝（1+2+3+4+……+13）+9，所以100a =(8,14)＝81422+＝16640解法二：设0022100t s a +=，只须确定正整数.,00t s数列}{n a 中小于02t的项构成的子集为 },0|2{20t t t s s <<≤+其元素个数为.1002)1(,2)1(000020<--=t t t t C t 依题意满足等式的最大整数0t 为14，所以取.140=t因为100－.1664022,8s ,181410000214=+=∴=+=a s C 由此解得（Ⅱ）解：,22211603710++==k b令r {|1160}(,B {222|0}s t M c B c r s t =∈<=++≤<<其中因10101071071073{|2}{|222}{|22222}.M c B c c B c c B c =∈<∈<<+∈+<<++ 现在求M 的元素个数：},100|222{}2|{10<<<≤++=<∈t s r c B c t s r其元素个数为310C ： }.70|222{}222|{1071010<<≤++=+<<∈s r c B c r s某元素个数为}30|222{}22222|{:710371071027<≤++=++<<+∈r c B c C r某元素个数为.1451:2327310710=+++=C C C k C 另法：规定222r t s ++=（r,t,s ），10731160222k b ==++＝（3,7,10）则0121222b =++＝（0,1,2） 22C依次为（0,1,3）（0,2,3）（1,2,3）23C （0,1,4）（0,2,4）（1,2,4）（0,3,4）（1,3,4）（2,3,4）24C…………（0,1,9）（0,2,9）………… （ 6,8,9 ）（7,8,9） 29C（0,1,10）（0,2,10）.........（0,7,10）（ 1,7,10）（2,7,10）（3,7,10） (2)7C +422222397()4145.k C C C C =+++++=阅读使人充实，会谈使人敏捷，写作使人精确。

2003年高考试题——理综(全国卷)

欢迎下载！！！2003年普通高等学校招生全国统一考试（全国卷）理科综合能力测试一、在下列各题的四个选项中，只有一个选项是最符合题目要求的。

1．取适量干重相等的4份种子进行不同处理：（甲）风干，（乙）消毒后浸水萌发，（丙）浸水后萌发，（丁）浸水萌发后煮着冷却，消毒。

然后分别放入4个保温瓶中。

一段时间后，种子堆内温度最高的是（）A．甲B．乙C．丙D．丁2．植物叶片从幼到老的整个生命活动过程中（）A．有机物输出也输入，矿质元素只输入 B．有机物只输出，矿质元素只输入C．有机物只输出，矿质元素输入也输出 D．有机物与矿质元素都既输入，又输出3．下列关于叶绿素合成和功能的叙述。

错误的是（）A．光是叶绿素合成的必要条件B．低温抑制叶绿素的合成C．矿质元素影响叶绿素的合成D．提取的叶绿素溶液，给予适宜的温度、光照和CO2，可进行光合作用4．一只成年雄狗仍然保持幼年的体态，且精神萎靡、反应迟钝、行动呆笨，无求偶行为，其原因是（）A．睾丸发育不全B．甲状腺功能低下C．生长激素分泌不足D．生长激素分泌不足、睾丸发育不全5．据图判断，下列叙述不．符合生态学原理的是（）A．物质经过了多级利用，实现了良性循环B．每一级生产环节都获得产品，提高了生态经济效益C．由于食物链延长，能量逐级损耗，系统总能量利用效率降低D．由于各级产物都可以利用，减少了废物和污染6．人类探测月球发现，在月球的土壤中含有较丰富的质量数为3的氦，它可以作为未来核聚变的重要原料之一。

氦的该种同位素应表示为（） A ．He 43 B ．He 32 C ．He 42 D ．He 33 7．在两个容积相同的容器中，一个盛有HCl 气体，另一个盛有H 2和Cl 2的混合气体。

在同温同压下，两容器内的气体一定具有相同的（）A ．原子数B ．密度C ．质量D ．质子数8．某无色混合气体可能由CH 4、NH 3、H 2、CO 、CO 2和HCl 中的某几种气体组成。

2003年全国统一高考数学试卷(辽宁卷)

2003年普通高等学校招生全国统一考试（辽宁卷）一、选择题（共12小题，每小题5分，满分60分）1. （2003▪辽宁）与曲线11y x =-关于原点对称的曲线为 A.11y x =+ B.11y x =-+ C.11y x=- D.11y x =-- 2. （2003▪辽宁）已知(2x π∈-，0)，54cos =x ，则tan 2x = A.247 B.724- C.724 D.247- 3. （2003▪辽宁）=+-2)3(31i i A.i 4341+ B.i 4341--C.i 2321+D.i 2321-- 4. （2003▪辽宁）已知四边形ABCD 是菱形，点P 在对角线AC 上（不包括端点A 、C ），则AP =A.()AB AD λ+，(0λ∈，1)B.()AB BC λ+，(0λ∈，C.()AB AD λ-，(0λ∈，1)D.()AB BC λ-，(0λ∈，25. （2003▪辽宁）设函数⎪⎩⎪⎨⎧>≤-=-)0()0(12)(21x x x x f x ，若1)(0>x f ，则0x 的取值范围是A.1(-，)1B.1(-，)∞+C.-∞(，0()2 -，)∞+D.-∞(，1()1 -，)∞+6. （2003▪辽宁）等差数列{}n a 中，已知113a =，254a a +=，33n a =，则n 为 A.48 B.49 C.50 D.517. （2003▪辽宁）函数1ln1x y x +=-，1(∈x ，)∞+的反函数为 A.11x x e y e -=+，0(∈x ，)∞+ B.11x x e y e +=-，0(∈x ，)∞+ C.11x x e y e -=+，-∞∈(x ，)0 D.11x x e y e +=-，-∞∈(x ，)0 8. （2003▪辽宁）棱长为a 的正方体中，连结相邻面的中心，以这些线段为棱的八面体的体积为A.33a B.43a C.63a D.123a9. （2003▪辽宁）设0a >，2()f x ax bx c =++，曲线)(x f y =在点0(x P ，))(0x f 处的切线的倾斜角的取值范围为0[，]4π，则P 到曲线)(x f y =对称轴距离的取值范围为A.[0，1]aB.[0，1]2aC.[0，||]2b a D.[0，1||]2b a-10. （2003▪辽宁）已知双曲线中心在原点且一个焦点为F 0)，直线1y x =-与其相交于M N 、两点，MN 中点的横坐标为23-，则此双曲线的方程是 A.14322=-y x B.13422=-y x C.12522=-y x D.15222=-y x 11. （2003▪辽宁）已知长方形的四个顶点(0A ，0)，(2B ，0)，(2C ，1)和(0D ，1).一质点从AB 的中点0P 沿与AB 夹角为θ的方向射到BC 上的点1P 后，依次反射到CD 、DA 和AB 上的点2P ，3P 和4P （入射角等于反射角）.设4P 的坐标为4(x ，0)，若412x <<，则θtan 的取值范围是 A.1(3，1) B.1(3，23） C.2(5，1)2 D.2(5，2)312. （2003▪辽宁）一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为A.3πB.4πC.D.6π 二、填空题（共4小题，每小题4分，满分16分）13. （2003▪辽宁）92)21(xx -展开式中9x 的系数是________________. 14. （2003▪辽宁）某公司生产三种型号的轿车，产量分别为1200辆，6000辆和2000辆.为检验该公司的产品质量，现用分层抽样的方法抽取46辆进行检验，这三种型号的轿车依次应抽取______、__________、__________辆.15. （2003▪辽宁）某城市在中心广场建造一个花圃，花圃分为6个部分（如图）．现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有_________种．（以数字作答）16. （2003▪辽宁）对于四面体ABCD ，给出下列四个命题：①若AB AC =，BD CD =，则BC AD ⊥；②若AB CD =，AC BD =，则BC AD ⊥；③若AB AC ⊥，BD CD ⊥，则BC AD ⊥；④若AB CD ⊥，BD AC ⊥，则BC AD ⊥.其中真命题的序号是________．（写出所有真命题的序号）三、解答题（共6小题，满分12+12+12+12+14+12=74分）17. （2003▪辽宁）已知正四棱柱1111ABCD A BC D -，1AB =，12AA =，点E 为1CC 中点，点F 为1BD 中点.⑴证明EF 为1BD 与1CC 的公垂线；⑵求点1D 到面BDE 的距离.18. （2003▪辽宁）已知函数()sin()(0f x x ωϕω=+>，0)ϕπ≤≤是R 上的偶函数，其图象关于点3(4M π，0)对称，且在区间[0，]2π上是单调函数，求ϕ和ω的值.19. （2003▪辽宁）设0a >，求函数()ln()f x x a +，(0x ∈，)+∞的单调区间.20. （2003▪辽宁）A 、B 两个代表队进行乒乓球对抗赛，每队三名队员，A 队队员是1A ，2A ，3A ，B 队队员是1B ，2B ，3B ，按以往多次比赛的统计，对阵队员之间胜负分分别为ξ、η.⑴求ξ、η的概率分布；⑵求E ξ，E η.21. （2003▪辽宁）设0a 为常数，且1*132()n n n a a n N --=-∈. ⑴证明对任意1n ≥，11[3(1)5n n n a -=+-•2](1)n n +-•02n a ； ⑵假设对任意1≥n 有1->n n a a ，求0a 的取值范围. 22. （2003▪辽宁）已知常数0a >，向量(0c =，)a ，(1i =，0)，经过原点O 以c iλ+为方向向量的直线与经过定点(0A ，)a 以2i c λ-为方向向量的直线相交于点P ，其中R λ∈.试问：是否存在两个定点E F 、，使得||||PE PF +为定值.若存在，求出E F 、的坐标；若不存在，说明理由.2003年辽宁省高考数学试卷参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．（5分）（2003•辽宁）与曲线关于原点对称的曲线为（）A．B． C．D．【分析】题目中：“曲线关于原点对称的曲线”，只要将原函数式中的x换成﹣x，y换成﹣y，即可得到新曲线的函数解析式．【解答】解：∵曲线关于原点对称的曲线，∴只要将原函数式中的x换成﹣x，y换成﹣y，即可得到新曲线的函数解析式，即﹣y=，整理，得．故选A．【点评】本题考查函数图象的变换，由于使用了数形结合的方法，使问题便迎刃而解，且解法简捷．2．（5分）（2003•全国）已知x∈（﹣，0），cosx=，则tan2x等于（）A．B．﹣C．D．﹣【分析】先根据cosx，求得sinx，进而得到tanx的值，最后根据二倍角公式求得tan2x．【解答】解：∵cosx=，x∈（﹣，0），∴sinx=﹣．∴tanx=﹣．∴tan2x===﹣×=﹣．故选D．【点评】本题主要考查了三角函数中的二倍角公式．属基础题．3．（5分）（2003•天津）=（）A． B．C． D．【分析】化简复数的分母，然后复数的分子、分母同乘分母的共轭复数，即可求得结果．【解答】解：=故选B．【点评】复数代数形式的混合运算，是基础题．4．（5分）（2003•辽宁）已知四边形ABCD是菱形，点P在对角线AC上（不包括端点A、C），则=（）A．B．C．D．【分析】先过P分别作AD、AB的平行线，可得，，运用向量的加法运算可得=λ（+），λ∈（0，1）．【解答】解：设P是对角线AC上的一点（不含A、C），过P分别作AD、AB的平行线，则可得．设，则λ∈（0，1）且．于是=λ（+），λ∈（0，1）．故选A．【点评】本题主要考查向量的线性运算和向量加法的几何意义．属基础题．5．（5分）（2003•全国）设函数若f（x0）＞1，则x0的取值范围是（）A．（﹣1，1）B．（﹣1，+∞）C．（﹣∞，﹣2）∪（0，+∞） D．（﹣∞，﹣1）∪（1，+∞）【分析】将变量x0按分段函数的范围分成两种情形，在此条件下分别进行求解，最后将满足的条件进行合并．【解答】解：当x0≤0时，，则x0＜﹣1，当x0＞0时，则x0＞1，故x0的取值范围是（﹣∞，﹣1）∪（1，+∞），故选D．【点评】本题考查了分段函数已知函数值求自变量的范围问题，以及指数不等式与对数不等式的解法，属于常规题．6．（5分）（2003•天津）等差数列{an}中，已知a1=，a2+a5=4，an=33，则n为（）A．48 B．49 C．50 D．51【分析】先由等差数列的通项公式和已知条件解出d，进而写出an的表达式，然后令an=33，解方程即可．【解答】解：设{an}的公差为d，∵，a2+a5=4，∴+d++4d=4，即+5d=4，解得d=．∴an=+（n﹣1）=，令an=33，即=33，解得n=50．故选C．【点评】本题主要考查了等差数列的通项公式an=a1+（n﹣1）d，注意方程思想的应用．7．（5分）（2003•天津）函数，x∈（1，+∞）的反函数为（）A．，x∈（0，+∞）B．，x∈（0，+∞）C．，x∈（﹣∞，0）D．，x∈（﹣∞，0）【分析】本题考查反函数的概念、求反函数的方法、指数式与对数式的互化，求函数的值域等函数知识和方法；将，看做方程解出x，然后根据原函数的定义域x∈（1，+∞）求出原函数的值域，即为反函数的定义域．【解答】解：由已知，解x得，令，当x∈（1，+∞）时，m∈（1，+∞），则，∴函数，x∈（1，+∞）的反函数为，x∈（0，+∞）故选B．【点评】这是一个基础性题，解题思路清晰，求解方向明确，所以容易解答；解答时注意两点，一是借助指数式和对数式的互化求x，二是函数，x∈（1，+∞）值域的确定，这里利用”常数分离法“和对数函数的性质推得．8．（5分）（2003•天津）棱长为a的正方体中，连接相邻面的中心，以这些线段为棱的八面体的体积为（）A．B．C．D．【分析】画出图形，根据题意求出八面体的中间平面面积，然后求出其体积．【解答】解：画出图就可以了，这个八面体是有两个四棱锥底面合在一起组成的．一个四棱锥的底面面积是正方体的一个面的一半，就是，高为，所以八面体的体积为：．故选C．【点评】本题考查学生空间想象能力，逻辑思维能力，体积的计算公式，考查转化思想，是基础题．9．（5分）（2003•天津）设a＞0，f（x）=ax2+bx+c，曲线y=f（x）在点P（x0，f（x0））处切线的倾斜角的取值范围为[0，]，则P到曲线y=f（x）对称轴距离的取值范围为（）A．[0，] B．[0，] C．[0，||] D．[0，||]【分析】先由导数的几何意义，得到x0的范围，再求出其到对称轴的范围．【解答】解：∵过P（x0，f（x0））的切线的倾斜角的取值范围是[0，]，∴f′（x0）=2ax0+b∈[0，1]，∴P到曲线y=f（x）对称轴x=﹣的距离d=x0﹣（﹣）=x0+∴x0∈[，]．∴d=x0+∈[0，]．故选：B．【点评】本题中是对导数的几何意义的考查，计算时，对范围的换算要细心．10．（5分）（2003•全国）已知双曲线中心在原点且一个焦点为F（，0），直线y=x﹣1与其相交于M、N两点，MN中点的横坐标为﹣，则此双曲线的方程是（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=1【分析】先设出双曲线的方程，然后与直线方程联立方程组，经消元得二元一次方程，再根据韦达定理及MN中点的横坐标可得a、b的一个方程，又双曲线中有c2=a2+b2，则另得a、b的一个方程，最后解a、b的方程组即得双曲线方程．【解答】解：设双曲线方程为﹣=1．将y=x﹣1代入﹣=1，整理得（b2﹣a2）x2+2a2x﹣a2﹣a2b2=0．由韦达定理得x1+x2=，则==﹣．又c2=a2+b2=7，解得a2=2，b2=5，所以双曲线的方程是．故选D．【点评】本题主要考查代数方法解决几何问题，同时考查双曲线的标准方程与性质等．11．（5分）（2003•全国）已知长方形的四个项点A（0，0），B（2，0），C（2，1）和D（0，1），一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后，依次反射到CD．DA和AB上的点P2．P3和P4（入射角等于反射角），设P4坐标为（x4，0），若1＜x4＜2，则tanθ的取值范围是（）A．（，1） B．（，）C．（，）D．（，）【分析】先画草图，帮助理解，取BC上的点P1为中点，则P4和中点P0重合，tan θ=，用排除法解答．【解答】解：考虑由P0射到BC的中点上，这样依次反射最终回到P0，此时容易求出tanθ=，由题设条件知，1＜x4＜2，则tanθ≠，排除A．B．D，故选C．【点评】由于是选择题，因而可以特殊值方法解答：排除验证法，也可以用动态观点判定答案．12．（5分）（2003•全国）棱长都为的四面体的四个顶点在同一球面上，则此球的表面积为（）A．3πB．4πC．3D．6π【分析】本题考查的知识点是球的体积和表面积公式，由棱长都为的四面体的四个顶点在同一球面上，可求出内接该四面体的正方体棱长为1，又因为正方体的对角线即为球的直径，即球的半径R=，代入球的表面积公式，S球=4πR2，即可得到答案．【解答】解：借助立体几何的两个熟知的结论：（1）一个正方体可以内接一个正四面体；（2）若正方体的顶点都在一个球面上，则正方体的体对角线就是球的直径．则球的半径R=，∴球的表面积为3π，故答案选A．【点评】棱长为a的正方体，内接正四面体的棱长为a，外接球直径等于长方体的对角线长a．二、填空题（共4小题，每小题4分，满分16分）13．（4分）（2003•全国）在的展开式中，x3的系数是﹣（用数字作答）【分析】首先根据题意，写出的二项展开式，可得9﹣2r=3，解可得r=3，将其代入二项展开式，计算可得答案．【解答】解：根据题意，对于，有Tr+1=C99﹣r•x9﹣r•（﹣）r=（﹣）r•C99﹣r•x9﹣2r，令9﹣2r=3，可得r=3，当r=3时，有T4=﹣x3，故答案﹣．【点评】本题考查二项式定理的应用，注意系数与二项式系数的区别．14．（4分）（2003•天津）某公司生产三种型号的轿车，产量分别为1200辆、6000辆和2000辆，为检验该公司的产品质量，现用分层抽样的方法抽取46辆进行检验，这三种型号的轿车依次应抽取 6 辆、30 辆、10 辆．【分析】由题意先求出抽样比例即为，再由此比例计算出在三种型号的轿车抽取的数目．【解答】解：因总轿车数为9200辆，而抽取46辆进行检验，抽样比例为=，而三种型号的轿车有显著区别，根据分层抽样分为三层按比例，故分别从这三种型号的轿车依次应抽取6辆、30辆、10辆．故答案为：6，30，10．【点评】本题的考点是分层抽样，即保证样本的结构和总体的结构保持一致，按照一定的比例样本容量和总体容量的比值，在各层中进行抽取．15．（4分）（2003•天津）某城市在中心广场建造一个花圃，花圃分为6个部分（如图）．现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有120 种．（以数字作答）【分析】由题意来看6部分种4种颜色的花，又从图形看知必有2组同颜色的花，从同颜色的花入手分类求．②与⑤同色，则③⑥也同色或④⑥也同色，③与⑤同色，则②④或⑥④同色，②与④且③与⑥同色，根据分类计数原理得到结果．【解答】解：从题意来看6部分种4种颜色的花，又从图形看知必有2组同颜色的花，从同颜色的花入手分类求．（1）②与⑤同色，则③⑥也同色或④⑥也同色，所以共有N1=4×3×2×2×1=48种；（2）③与⑤同色，则②④或⑥④同色，所以共有N2=4×3×2×2×1=48种；（3）②与④且③与⑥同色，则共有N3=4×3×2×1=24种．∴共有N=N1+N2+N3=48+48+24=120种．故答案为：120【点评】这是一道理科的高考题，本题还可以这样解：记颜色为A，B，C，D四色，先安排1，2，3有A43种不同的栽法，不妨设1，2，3已分别栽种A，B，C，则4，5，6栽种方法共5种，由以下树状图清晰可见．根据分步计数原理，不同栽种方法有N=A43×5=120．16．（4分）（2003•辽宁）对于四面体ABCD，给出下列四个命题①若AB=AC，BD=CD，则BC⊥AD；②若AB=CD，AC=BD，则BC⊥AD；③若AB⊥AC，BD⊥CD，则BC⊥AD；④若AB⊥CD，BD⊥AC，则BC⊥AD．其中真命题的序号是①④．（写出所有真命题的序号）【分析】证明线线垂直一般采用线面垂直来证线线垂直．①的证明可转借化证明BC ⊥面AHD．④的证明可转化为证垂心，然后再证明BC⊥面AED来证明BC⊥AD．②③条件下不能求出两线的夹角，也无法保证一个线垂直于另一个线所在的平面，故不对．【解答】证明：如图对于①取BC的中点H，连接AH与DH，可证得BC⊥面AHD，进而可得BC⊥AD，故①对；对于②条件不足备，证明不出结论；对于③条件不足备，证明不出结论；对于④作AE⊥面BCD于E，连接BE可得BE⊥CD，同理可得CE⊥BD，证得E 是垂心，则可得出DE⊥BC，进而可证得BC⊥面AED，即可证出BC⊥AD．综上知①④正确，故应填①④．【点评】本题在判断时有一定的难度，需要构造相关的图形，在立体几何中，构造法是一个常用的方法，本题用其来将线线证明转化线面证明，三、解答题（共6小题，满分74分）17．（12分）（2003•天津）已知正四棱柱ABCD﹣A1B1C1D1．AB=1，AA1=2，点E为CC1中点，点F为BD1中点．（1）证明EF为BD1与CC1的公垂线；（2）求点D1到面BDE的距离．【分析】（1）欲证明EF为BD1与CC1的公垂线，只须证明EF分别与为BD1与CC1垂直即可，可由四边形EFMC是矩形→EF⊥CC1．由EF⊥面DBD1→EF⊥BD1．（2）欲求点D1到面BDE的距离，将距离看成是三棱锥的高，利用等体积法：VE﹣DBD1=VD1﹣DBE．求解即得．【解答】解：（1）取BD中点M．连接MC，FM．∵F为BD1中点，∴FM∥D1D且FM=D1D．又EC CC1且EC⊥MC，∴四边形EFMC是矩形∴EF⊥CC1．又FM⊥面DBD1．∴EF⊥面DBD1．∵BD1⊂面DBD1．∴EF⊥BD1．故EF为BD1与CC1的公垂线．（Ⅱ）解：连接ED1，有VE﹣DBD1=VD1﹣DBE．由（Ⅰ）知EF⊥面DBD1，设点D1到面BDE的距离为d．则．∵AA1=2，AB=1．∴，，∴．∴故点D1到平面DBE的距离为．【点评】本小题主要考查线面关系和四棱柱等基础知识，考查空间想象能力和推理能力．18．（12分）（2003•天津）已知函数f（x）=sin（ωx+φ）（ω＞0，0≤φ≤π）是R上的偶函数，其图象关于点对称，且在区间上是单调函数，求φ和ω的值．【分析】由f（x）是偶函数可得ϕ的值，图象关于点对称可得函数关系，可得ω的可能取值，结合单调函数可确定ω的值．【解答】解：由f（x）是偶函数，得f（﹣x）=f（x），即sin（﹣ωx+φ）=sin（ωx+φ），所以﹣cosφsinωx=cosφsinωx，对任意x都成立，且w＞0，所以得cosφ=0．依题设0≤φ≤π，所以解得φ=，由f（x）的图象关于点M对称，得，取x=0，得f（）=sin（）=cos，∴f（）=sin（）=cos，∴cos=0，又w＞0，得=+kπ，k=0，1，2，3，…∴ω=（2k+1），k=0，1，2，…当k=0时，ω=，f（x）=sin（）在[0，]上是减函数，满足题意；当k=1时，ω=2，f（x）=sin（2x+）=cos2x，在[0，]上是减函数，满足题意；当k=2时，ω=，f（x）=sin（x+）在[0，]上不是单调函数；所以，综合得ω=或2．【点评】本题主要考查三角函数的图象、单调性、奇偶性等基本知识，以及分析问题和推理计算能力．19．（12分）（2003•天津）设a＞0，求函数f（x）=﹣ln（x+a）（x∈（0，+∞））的单调区间．【分析】由题意函数f（x）=﹣ln（x+a），首先求出函数的导数，然后根据导数与函数单调区间的关系对a的大小进行分类讨论．【解答】解：由题意得，令f′（x）=0，即x2+（2a﹣4）x+a2=0，其中△=4（a﹣2）2﹣4a2=8﹣8a，（i）当a＞1时，△＜0成立，对所有x＞0，有x2+（2a﹣4）+a2＞0．即f′（x）＞0，此时f（x）在（0，+∞）内单调递增；（ii）当a=1时，△=0成立，对x≠1，有x2+（2a﹣4）x+a2＞0，即f′（x）＞0，此时f（x）在（0，1）内单调递增，且在（1，+∞）内也单调递增，又知函数f（x）在x=1处连续，因此，函数f（x）在（0，+∞）内单调递增；（iii）当0＜a＜1时，△＞0成立，令f′（x）＞0，即x2+（2a﹣4）x+a2＞0，解得x＜2﹣a﹣2或x＞2﹣a+2，因此，函数f（x）在区间，内也单调递增．令f′（x）＜0，即x2+（2a﹣4）x+a2＜0，解得，因此，函数f（x）在区间内单调递减．【点评】本题主要考查导数的概念和计算，应用导数研究函数单调性的方法及推理和运算能力．20．（12分）（2003•天津）A、B两个代表队进行乒乓球对抗赛，每队三名队员，A 队队员是A1，A2，A3，B队队员是B1，B2，B3，按以往多次比赛的统计，对阵队员分，设A队、B队最后所得总分分别为ξ、η．（1）求ξ、η的概率分布；（2）求Eξ，Eη．【分析】（1）由题意知本题两个变量之间具有特殊关系，根据相互独立事件同时发生的概率做出变量ξ的分布列，根据两者之间和为3，得到另一个变量的分布列．（2）由题意知本题两个变量之间具有特殊关系，两个变量的期望之间也有这种关系，两个变量的期望的和是3，解出一个，另一个用做差来解．【解答】解：（1）ξ、η的可能取值分别为3，2，1，0．，，．根据题意知ξ+η=3，∴P（η=0）=P（ξ=3）=，P（η=1）=P（ξ=2）=，P（η=2）=P（ξ=1）=，P（η=3）=P（ξ=0）=．（2），∵ξ+η=3，∴．【点评】本小题考查离散型随机变量分布列和数学期望等概念，考查运用概率知识解决实际问题的能力，求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题，题目做起来不难，运算量也不大．21．（14分）（2003•天津）设an为常数，且an=3n﹣1﹣2an﹣1（n∈N*）．（1）证明对任意n≥1，有；（2）假设对任意n≥1有an＞an﹣1，求a0的取值范围．【分析】（1）选择利用数学归纳法为妥，需要注意的是有归纳假设ak到ak+1的变形，利用归纳假设，注意目标的形式就能得到结果；另外可以利用递推数列来求得通项公式，当然需要对递推数列的an+1=pan+f（n）这种形式的处理要合适；这种形式的一般处理方法是：两边同时除以pn+1或者是构造一个等比数列，构造法有一定的技巧，如本题可设an﹣a3n=﹣2（an﹣1﹣a3n﹣1），（2）由（1）的结论可作差an﹣an﹣1＞0并代入运算，由于含有（﹣1）n的形式要注意对n=2k﹣1和n=2k进行讨论，只需取k=1，2时得到a0的取值范围即可，另外一个思路是只需取n=1，2时得到a0的范围，然后分n=2k﹣1和n=2k进行证明an﹣an﹣1＞0．具体解法参见参考答案．【解答】解：（1）证法一：（i）当n=1时，由已知a1=1﹣2a0，等式成立；（ii）假设当n=k（k≥1）等式成立，则，那么=．也就是说，当n=k+1时，等式也成立．根据（i）和（ii），可知等式对任何n∈N，成立．证法二：如果设an﹣a3n=﹣2（an﹣1﹣a3n﹣1），用an=3n﹣1﹣2an﹣1代入，可解出．所以是公比为﹣2，首项为的等比数列．∴．即．（2）解法一：由an通项公式．∴an＞an﹣1（n∈N）等价于．①（i）当n=2k﹣1，k=1，2，时，①式即为即为．②式对k=1，2，都成立，有．（ii）当n=2k，k=1，2时，①式即为．即为．③式对k=1，2都成立，有．综上，①式对任意n∈N*，成立，有．故a0的取值范围为．解法二：如果an＞an﹣1（n∈N*）成立，特别取n=1，2有a1﹣a0=1﹣3a0＞0．a2﹣a1=6a0＞0．因此．下面证明当．时，对任意n∈N*，an﹣an﹣1＞0．由an的通项公式5（an﹣an﹣1）=2×3n﹣1+（﹣1）n﹣13×2n﹣1+（﹣1）n5×3×2n﹣1a0．（i）当n=2k﹣1，k=1，2时，5（an﹣an﹣1）=2×3n﹣1+3×2n﹣1﹣5×3×2n﹣1a0＞2×2n﹣1+3×2n﹣1﹣5×3×2n﹣1=0（ii）当n=2k，k=1，2时，5（an﹣an﹣1）=2×3n﹣1﹣3×2n﹣1+5×3×2n﹣1a0＞2×3n﹣1﹣3×2n﹣1≥0．故a0的取值范围为．【点评】本题主要考查数列、等比数列的概念，考查数学归纳法，考查灵活综合运用数学知识分析问题和解决问题的能力．对递推数列的an+1=pan+f（n）这种形式的考查是一个难点，同时除以pn+1得到，然后用累加法得到的等式可得结果，或者是构造一个等比数列an+1+kf（n）=p（an+kf（n））（不具有普适性）．22．（12分）（2003•天津）已知常数a＞0，向量=（0，a），=（1，0），经过原点O以+λ为方向向量的直线与经过定点A（0，a）以﹣2λ为方向向量的直线相交于点P，其中λ∈R．试问：是否存在两个定点E、F，使得|PE|+|PF|为定值．若存在，求出E、F的坐标；若不存在，说明理由．【分析】根据和，求得+λ和﹣2λ进而可得直线OP和AP的方程，消去参数λ，得点P（x，y）的坐标满足方程，进而整理可得关于x和y的方程，进而看当时，方程为圆不符合题意；当时和当时，P的轨迹为椭圆符合两定点．【解答】解：∵=（0，a），=（1，0），∴+λ=（λ，a），﹣2λ=（1，﹣2λa）．因此，直线OP和AP的方程分别为λy=ax和y﹣a=﹣2λax．消去参数λ，得点P（x，y）的坐标满足方程y（y﹣a）=﹣2a2x2．整理得．①因为a＞0，所以得：（i）当时，方程①是圆方程，故不存在合乎题意的定点E和F；（ii）当时，方程①表示椭圆，焦点和为合乎题意的两个定点；（iii）当时，方程①也表示椭圆，焦点和为合乎题意的两个定点．【点评】本题主要考查平面向量的概念和计算，求轨迹的方法，椭圆的方程和性质，利用方程判定曲线的性质，曲线与方程的关系等解析几何的基本思想和综合解题能力．参与本试卷答题和审题的老师有：yhx01248；zhwsd；qiss；wsj1012；minqi5；jj2008；liuerq；rxl；wzj123；geyanli；danbo7801；gongjy；涨停；xintrl；zhiyuan；于其才（排名不分先后）菁优网2017年5月28日。

(完整版)湖南省_2003年_高考数学真题(理科数学)(附答案)_历年历届试题

2003年普通高等学校招生全国统一考试数学(理工农医类)-同湖南一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知（==-∈x tg x x 2,54cos ),0,2(则π）A ．B ．C ．D ．247247-724724-2．圆锥曲线（的准线方程是θθρ2cos sin 8=）A ．B ．C ．D ．2cos -=θρ2cos =θρ2sin -=θρ2sin =θρ3．设函数（的取值范围是则若0021,1)(,.0,,0,12)(x x f x x x x f x >⎪⎩⎪⎨⎧>≤-=-）A ．（－1，1）B ．（－1，+）∞C ．D ．),0()2,(+∞⋃--∞),1()1,(+∞⋃--∞4．函数的最大值为（)cos (sin sin 2x x x y +=）A ．B ．C ．D ．221+12-25．已知圆的截得被当直线及直线C l y x l a x a x C .03:)0(4)2()(:22=+->=-+-弦长为时，则a =32A ．B ．C ．D ．222-12-12+6．已知圆锥的底面半径为R ，高为3R ，在它的所有内接圆柱中，全面积的最大值是（）A ．B ．C ．D ．22Rπ249R π238R π223r π7．已知方程的四个根组成的一个首项为的等差数列，0)2)(2(22=+-+-n x x m x x 41则（）=-||n mA ．1B ．C ．D ．4321838．已知双曲线中心在原点且一个焦点为M 、N 两点，与其相交于直线1),0,7(-=x y F MN 中点的横坐标为则此双曲线的方程是（ ,32-）A ．B ．C ．14322=-y x 13422=-y x 12522=-yx D ．15222=-y x 9．函数（ =∈=-)(23,2[,sin )(1x f x x x f 的反函数ππ）A ．B ．]1,1[,arcsin -∈-x x ]1,1[,arcsin -∈--x x πC ．D ．]1,1[,arcsin -∈+-x x π]1,1[,arcsin -∈-x x π10．已知长方形的四个项点A （0，0），B （2，0），C （2，1）和D （0，1），一质点从AB的中点P 0沿与AB 夹角为的方向射到BC 上的点P 1后，依次反射到CD 、DA 和AB θ上的点P 2、P 3和P 4（入射解等于反射角），设P 4坐标为（的取值范围是θtg ,2x 1),0,44则若<<x （）A ．B ．C ．D ．)1,31(32,31(21,52()32,52(11．（=++++++++∞→)(lim 11413122242322nnn C C C C n C C C C ）A ．3B ．C ．D ．6316112．一个四面体的所有棱长都为，四个项点在同一球面上，则此球的表面积为（2）A ．3B ．4C ．3D ．6πππ3π二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上.13．展开式中的系数是 .92)21(xx -9x 14．使成立的的取值范围是.1)(log 2+<-x x x15．如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有种.（以数字作答）16．下列五个正方体图形中，是正方体的一条对角线，点M 、N 、P 分别为具所在棱的中l 点，能得出⊥面MNP 的图形的序号是 .（写出所有符合要求的图形序l 号）三、解答题：本大题共6小题，共74分. 解答应写出文字的说明，证明过程或演算步骤.17．（本小题满分12分）已知复数z 的辐角为60°，且是和的等比中项. 求.|1|-z ||z |2|-z ||z 18．(本小题满分12分)如图，在直三棱柱ABC —A 1B 1C 1中，底面是等腰直角三形，∠ACB=90°，侧棱AA 1=2，D 、E 分别是CC 1与A 1B 的中点，点E 在平面ABD 上的射影是△ABD 的重心G.（Ⅰ）求A 1B 与平面ABD 所成角的大小（结果用反三角函数值表示）；（Ⅱ）求点A 1到平面AED 的距离.19．（本小题满分12分）已知设.0>c P ：函数在R 上单调递减.xc y =Q ：不等式的解集为R ，如果P 和Q 有且仅有一个正确，求的取值1|2|>-+c x x c 范围.20．（本小题满分12分）在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O （如图）的东偏南方向300km 的海面P 处，并以20km/h 的速度向西偏北45°方向移动. 102arccos(=θθ台风侵袭的范围为圆形区域，当前半径为60km,并以10km/h 的速度不断增大. 问几小时后该城市开始受到台风的侵袭？s21．（本小题满分14分）已知常数在矩形ABCD 中，AB=4，BC=4，O 为AB 的中点，点E 、F 、G 分,0>a a 别在BC 、CD 、DA 上移动，且，P 为GE 与OF 的交点（如图），问是DADGCD CF BC BE ==否存在两个定点，使P 到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由.22．（本小题满分12分，附加题4分）（Ⅰ）设中所有的数从小到大排列成的数Z}t s,,0|2{2}{t∈<≤+且是集合t s a sn 列，即.,12,10,9,6,5,3654321 ======a a a a a a将数列各项按照上小下大，左小右大的原则写成如下的三角形数表：}{n a35 69 1012— — — —— — — ——（i ）写出这个三角形数表的第四行、第五行各数；（i i ）求.100a （Ⅱ）（本小题为附加题，如果解答正确，加4分，但全卷总分不超过150分）设中所有的数都是从小到大排Z}t s,r,,0|22{2}{r∈<<≤++且是集合t s r b stn 列成的数列，已知k.,1160求=k b 2003年普通高等学校招生全国统一考试数学(理工农医类)答案一、选择题1．D 2．C 3．D 4．A 5．C 6．B 7．C 8．D 9．D 10．C 11．B 12．A二、填空题13． 14．（-1，0）15．7216．①④⑤221-三、解答题：17．解：设，则复数由题设)60sin 60cos r r z+=.2r z 的实部为2,r z z r z z ==-.12||).(12,12:.012,421,)2)(2(||)1)(1(:|2||||1|2222-=--=-==-++-=+-∴--=---⋅=-z r r r r r r r r r z z z z z z z z 即舍去解得整理得即18．（Ⅰ）解：连结BG ，则BG 是BE 在ABD 的射影，即∠EBG 是A 1B 与平面ABD 所成的角.设F 为AB 中点，连结EF 、FC ，112211,,,,,,.1,1,(4)3sinD E CC A B DC ABC CDEFDE G ADB G DF EFDEF FG FD FD EF FDED EG FC CD AB A B EBEGEBG AB ABDEB⊥∴∆∴∈=⋅==∴=======∴∠==∴分别是的中点又平面为矩形连结是的重心在直角三角形中分于是与平面所成的角是（Ⅱ）解：,,,FABEFEFEDABED=⋂⊥⊥又.36236232222,.,.,.,.,111111111111111的距离为到平面中在的距离到平面是即平面垂足为作面且面平面平面面又面AEDAABBAAAKAABAAEDAKAAEDKAKAEKAAEABAAEDABAAEDAEDEDABAED∴=⨯=⋅=∆⊥∴⊥=⋂⊥∴⊂⊥∴19．解：函数在R上单调递减xcy=.10<<⇔c不等式.1|2|1|2|上恒大于在函数的解集为RcxxyRcxx-+=⇔>-+).,1[21,0(.1,,.21,,.21121|2|.2|2|,2,2,2,22|2|+∞⋃≥≤<>⇔>⇔>-+∴-+=∴⎩⎨⎧<≥-=-+的取值范围为所以则正确且不正确如果则不正确且正确如果的解集为不等式上的最小值为在函数ccQPcQPccRcxxcRcxxycxccxcxcxx20．解：如图建立坐标系以O为原点，正东方向为x轴正向.在时刻：（1）台风中心P（）的坐标为yx,⎪⎪⎩⎪⎪⎨⎧⨯+⨯-=⨯-⨯=.22201027300,2220102300tytx此时台风侵袭的区域是其中若在t时刻城市O受到,)]([)()(22t ryyxx≤-+-,6010)(+=tt r台风的侵袭，则有即.)6010()0()0(222+≤-+-tyx22)22201027300()2220102300(tt⨯+⨯-+⨯-⨯2412,028836,)6010(22≤≤≤+-+≤tttt解得即答：12小时后该城市开始受到台风的侵袭.21．根据题设条件，首先求出点P坐标满足的方程，据此再判断是否存在的两定点，使得点P到两点距离的和为定值.按题意有A（－2，0），B（2，0），C（2，4a），D（－2，4a）设)10(≤≤==kDADCCDCFBCBE由此有E（2，4a k），F（2－4k，4a），G（－2，4a－4ak）直线OF的方程为：①)12(2=-+ykax直线GE 的方程为：②02)12(=-+--a y x k a 从①，②消去参数k ，得点P （x,y ）坐标满足方程022222=-+ay y x a 整理得当时，点P 的轨迹为圆弧，所以不存在符合题意的两点.1)(21222=-+a a y x 212=a当时，点P 轨迹为椭圆的一部分，点P 到该椭圆焦点的距离的和为定长。

2003年高考数学试题(全国卷)评析

2003年高考数学试题（全国卷）评析海盐元济高级中学胡水林2003年高考，受到了社会各界从未有过的关注。

高考时间的提前，SARS 的突袭，新旧教材的交替，考后的强烈反应等等，将会在一段时间内给人留下一份挥之不去的记忆。

我们处于一个改革锐进的时代，教育的理念，思维的方式都在发生变化，2003年高考数学试题反映了这种变化，它向传统的教学方式提出了挑战。

本文着重评价03年试题特色和教学的启示。

一、03年高考教学试题的特点03年试题的题型结构，考题份量与近年历届的试题持平，各分科所占比例大致合理。

1．突出基础知识和数学思想方法的考查1．1 高中数学的主干知识构成试题的主体如同以往，今年的高考试题继续坚持“高中数学的主干知识构成试题的主体”，试题中保持了较高的比例，并达到了必要的深度。

代数着重考查函数、数列、不等式、三角等主要内容；立体几何着重考查线面关系、线线关系，特别是它们之间的垂直关系；解析几何着重考查圆锥曲线和直线，以及它们之间的位置关系。

如函数作为高中代数中最基本、最重要的内容，在理科试题第（1）、（3）、（4）、（9）、（14）、（19）、（22）题，文科试题第（2）、（6）、（7）、（8）、（13）、（20）中，从不同的侧面，对函数进行了全面考查。

又如文科第（17）题、理科第（18）题，考查的是立体几何中点在平面上的射影、斜线与平面所成的角、点到平面的距离、异面直线及其公垂线等概念，以及棱柱的概念与性质等重点知识，将空间问题转化为平面问题的思考等重点方法。

1．2 抓住知识网络的交汇点设计命题。

今年的高考命题提纲挈领地抓住知识网络的交汇点，设计出具有综合性的新颖的试题，以达到较全面地考查学生的数学基础和数学素养的目的。

如理科的第（19）题，以最基本的指数函数、含有绝对值的不等式为载体，考查了函数的概念、函数的单调性、函数的最值等性质，含有绝对值不等式的解法，集合的概念与运算，以及对“有且只有”严谨的数学语言的解读。

2003年高考试题——理综(全国卷)

欢迎下载!！！2003年普通高等学校招生全国统一考试（全国卷）理科综合能力测试一、在下列各题的四个选项中，只有一个选项是最符合题目要求的。

1．取适量干重相等的4份种子进行不同处理：（甲）风干，（乙）消毒后浸水萌发，（丙）浸水后萌发，（丁）浸水萌发后煮着冷却，消毒。

然后分别放入4个保温瓶中。

一段时间后，种子堆内温度最高的是（）A ．甲B ．乙C ．丙D ．丁2．植物叶片从幼到老的整个生命活动过程中（）A ．有机物输出也输入，矿质元素只输入B ．有机物只输出，矿质元素只输入C ．有机物只输出，矿质元素输入也输出D ．有机物与矿质元素都既输入，又输出3．下列关于叶绿素合成和功能的叙述。

错误的是（）A ．光是叶绿素合成的必要条件B ．低温抑制叶绿素的合成C ．矿质元素影响叶绿素的合成D ．提取的叶绿素溶液，给予适宜的温度、光照和CO 2,可进行光合作用4．一只成年雄狗仍然保持幼年的体态，且精神萎靡、反应迟钝、行动呆笨，无求偶行为，其原因是（）A ．睾丸发育不全B ．甲状腺功能低下C ．生长激素分泌不足D ．生长激素分泌不足、睾丸发育不全5．据图判断，下列叙述不．符合生态学原理的是（）A ．物质经过了多级利用，实现了良性循环B ．每一级生产环节都获得产品，提高了生态经济效益C ．由于食物链延长，能量逐级损耗，系统总能量利用效率降低D ．由于各级产物都可以利用，减少了废物和污染6．人类探测月球发现,在月球的土壤中含有较丰富的质量数为3的氦，它可以作为未来核聚变的重要原料之一。

氦的该种同位素应表示为（）A ．He 43B ．He 32C ．He 42D ．He 33 7．在两个容积相同的容器中，一个盛有HCl 气体，另一个盛有H 2和Cl 2的混合气体。

2003年高考全国卷.理科数学试题及答案

2003年普通高等学校招生全国统一考试（全国卷）数学（理工农医类）注意事项：1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上．2. 每小题选出答案后，用铅笔把答题卡上对应答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．3. 考试结束，监考人将本试卷和答题卡一并收回．参考公式：三角函数的积化和差公式：正棱台、圆台的侧面积公式)]sin()[sin(21cos sin βαβαβα-++=⋅ l c c S )(21+'=台侧其中c '、c 分别表示)]sin()[sin(21sin cos βαβαβα--+=⋅ 上、下底面周长，l 表示斜高或母线长.)]cos()[cos(21cos cos βαβαβα-++=⋅ 球体的体积公式：334R V π=球，其中R)]cos()[cos(21sin sin βαβαβα--+-=⋅ 表示球的半径.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分第Ⅰ卷（选择题共60分）一.选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的 1．已知2(π-∈x ，0），54cos =x ，则2tg x = （）（A ）247 （B ）247- （C ）724 （D ）724-2．圆锥曲线θθρ2cos sin 8=的准线方程是（）（A ）2cos -=θρ （B ）2cos =θρ （C ）2sin =θρ （D ）2sin -=θρ 3．设函数⎪⎩⎪⎨⎧-=-2112)(xx f x 00>≤x x ，若1)(0>x f ，则0x 的取值范围是（）（A ）（1-，1）（B ）（1-，∞+）（C ）（∞-，2-）⋃（0，∞+）（D ）（∞-，1-）⋃（1，∞+） 4．函数)cos (sin sin 2x x x y +=的最大值为（）（A ）21+ （B ）12- （C ）2 （D ）25．已知圆C ：4)2()(22=-+-y a x （0>a ）及直线l ：03=+-y x ，当直线l 被C 截得的弦长为32时，则a （）（A ）2 （B ）22- （C ）12- （D ）12+6．已知圆锥的底面半径为R ，高为3R ，在它的所有内接圆柱中，全面积的最大值是（）（A ）22R π （B ）249R π （C ）238R π （D ）223R π7．已知方程0)2)(2(22=+-+-n x x m x x 的四个根组成一个首项为41的的等差数列，则=-||n m （）（A ）1 （B ）43 （C ）21 （D ）838．已知双曲线中心在原点且一个焦点为F （7，0），直线1-=x y 与其相交于M 、N 两点，MN 中点的横坐标为32-，则此双曲线的方程是（）（A ）14322=-y x （B ）13422=-y x （C ）12522=-y x （D ）15222=-y x 9．函数x x f sin )(=，]23,2[ππ∈x 的反函数=-)(1x f （）（A ）x arcsin - 1[-∈x ，1] （B ）x arcsin --π 1[-∈x ，1] （C ）x arcsin +π 1[-∈x ，1] （D ）x arcsin -π 1[-∈x ，1]10．已知长方形的四个顶点A （0，0），B （2，0），C （2，1）和D （0，1），一质点从AB 的中点0P 沿与AB 的夹角θ的方向射到BC 上的点1P 后，依次反射到CD 、DA 和AB 上的点2P 、3P 和4P （入射角等于反射角），设4P 的坐标为（4x ，0），若214<<x ，则tg θ的取值范围是（）（A ）（31，1）（B ）（31，32）（C ）（52，21）（D ）（52，32）11．=++++++++∞→)(lim 11413122242322nnn C C C C n C C C C （）（A ）3 （B ）31 （C ）61（D ）6 12．一个四面体的所有棱长都为2，四个顶点在同一球面上，则些球的表面积为（）（A ）π3 （B ）π4 （C ）π33 （D ）π62003年普通高等学校招生全国统一考试（全国卷）数学（理工农医类）第Ⅱ卷（非选择题共90分）二.填空题：本大题共4小题，每小题4分，共16分把答案填在题中横线上13．92)21(xx -的展开式中9x 系数是14．使1)(log 2+<-x x 成立的x 的取值范围是15．如图，一个地区分为5个行政区域，现给地图着色，要求相邻地区不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有种（以数字作答）16．下列5个正方体图形中，l 是正方体的一条对角线，点M 、N 、P 分别为其所在棱的中点，能得出⊥l 面MNP 的图形的序号是（写出所有符合要求的图形序号）① ② ③ ④ ⑤三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或或演算步骤17．（本小题满分12分）已知复数z 的辐角为︒60，且|1|-z 是||z 和|2|-z 的等比中项，求||z 18．（本小题满分12分）如图，在直三棱柱111C B A ABC -中，底面是等腰直角三角形，︒=∠90ACB ，侧棱21=AA ，D 、E 分别是1CC 与B A 1的中点，点E 在平面ABD 上的射影是△ABD 的重心G（I ）求B A 1与平面ABD 所成角的大小（结果用反三角函数值表示）（II ）求点1A 到平面AED 的距离 19．（本小题满分12分）已知0>c ，设P ：函数x c y =在R 上单调递减 Q ：不等式1|2|>-+c x x 的解集为R 如果P 和Q 有且仅有一个正确，求c 的取值范围 20．（本小题满分12分）在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O （如图）的东偏南102arccos (=θθ）方向300km 的海面P 处，并以20km/h 的速度向西偏北︒45方向移动，台风侵袭的范围为圆形区域，当前半径为60km ，并以10km/h 的速度不断增大，问几小时后该城市开始受到台风的侵袭？ 21．（本小题满分14分）D E KBCABAFCG东已知常数0>a ，在矩形ABCD 中，4=AB ，a BC 4=，O 为AB 的中点，点E 、F 、G 分别在BC 、CD 、DA 上移动，且BE CF DG BC CD DA ==，P 为GE 与OF 的交点（如图），问是否存在两个定点，使P 到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由 22．（本小题满分12分，附加题4 分）（I ）设}{n a 是集合|22{ts + t s <≤0且Z t s ∈,}中所有的数从小到大排列成的数列，即31=a ，52=a ，63=a ，94=a ，105=a ，126=a ，…将数列}{n a 各项按照上小下大，左小右大的原则写成如下的三角形数表：35 69 10 12 — — — —…………⑴写出这个三角形数表的第四行、第五行各数；⑵求100a（II ）（本小题为附加题，如果解答正确，加4 分，但全卷总分不超过150分）设}{n b 是集合t s r t s r <<≤++0|222{，且},,Z t s r ∈中所有的数从小到大排列成的数列，已知1160=k b ，求k .2003年普通高等学校招生全国统一考试(全国卷)数学（理工农医类）答案一、选择题：本题考查基本知识和基本运算. 每小题5分，满分60分.1．D 2．C 3．D 4．A 5．C 6．B 7．C 8．D 9．D 10．C 11．B 12．A 二、填空题：本题考查基本知识和基本运算.每小题4分,满分16分. 13．221-14．（-1，0） 15．72 16．①④⑤ 三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤. 17．解：设)60sin 60cosr r z +=，则复数.2r z 的实部为2,r z z r z z ==-由题设 .12||).(12,12:.012,421,)2)(2(||)1)(1(:|2||||1|2222-=--=-==-++-=+-∴--=---⋅=-z r r r r r r r r r z z z z z z z z 即舍去解得整理得即 18．（Ⅰ）解：连结BG ，则BG 是BE 在ABD 的射影，即∠EBG 是A 1B 与平面ABD 所成的角. 设F 为AB 中点，连结EF 、FC ，.32arcsin.323136sin .3,32,22,2.36321,2)4(.3,1,31.,,,,,,112211所成的角是与平面于是分中在直角三角形的重心是连结为矩形平面又的中点分别是ABD B A EB EG EBG EB B A AB CD FC EG ED FD EF FD FD FG EF EFD DF G ADB G DE CDEF ABC DC B A CC E D ∴=⋅==∠∴===∴===⨯===∴==⋅=∈∴∆∴⊥（Ⅱ）解：,,,F AB EF EF ED AB ED =⋂⊥⊥又.36236232222,.,.,.,.,111111*********的距离为到平面中在的距离到平面是即平面垂足为作面且面平面平面面又面AED A AB B A A A K A AB A AED A K A AED K A K AE K A AE AB A AED AB A AED AED ED AB A ED ∴=⨯=⋅=∆⊥∴⊥=⋂⊥∴⊂⊥∴19．解：函数xc y =在R 上单调递减.10<<⇔c不等式.1|2|1|2|上恒大于在函数的解集为R c x x y R c x x -+=⇔>-+ 22,2,|2|2,2,|2|2.1|2|121.21,,0.21,, 1.(0,][1,).2x c x c x x c c x c y x x c R c x x c R c c P Q c P Q c c -≥⎧+-=⎨<⎩∴=+-∴+->⇔>⇔><≤≥⋃+∞函数在上的最小值为不等式的解集为如果正确且不正确则如果不正确且正确则所以的取值范围为（以上方法在新疆考区无一人使用，大都是用解不等式的方法，个别使用的图象法） 20．解：如图建立坐标系以O 为原点，正东方向为x 轴正向.在时刻：（1）台风中心P （y x ,）的坐标为⎪⎪⎩⎪⎪⎨⎧⨯+⨯-=⨯-⨯=.22201027300,2220102300t y t x 此时台风侵袭的区域是,)]([)()(22t r y y x x ≤-+-其中,6010)(+=t t r 若在t 时刻城市O 受到台风的侵袭，则有.)6010()0()0(222+≤-+-t y x 即22)22201027300()2220102300(t t ⨯+⨯-+⨯-⨯2412,028836,)6010(22≤≤≤+-+≤t t t t 解得即答：12小时后该城市开始受到台风的侵袭.21．根据题设条件，首先求出点P 坐标满足的方程，据此再判断是否存在的两定点，使得点P 到两点距离的和为定值. 按题意有A （－2，0），B （2，0），C （2，4a ），D （－2，4a ）设(01)BE CF DG k k BC CD DA===≤≤ 由此有E （2，4a k ），F （2－4k ，4a ），G （－2，4a －4ak ）直线OF 的方程为：0)12(2=-+y k ax ① 直线GE 的方程为：02)12(=-+--a y x k a ②从①，②消去参数k ，得点P （x,y ）坐标满足方程022222=-+ay y x a整理得1)(21222=-+a a y x 当212=a 时，点P 的轨迹为圆弧，所以不存在符合题意的两点. 当212≠a 时，点P 轨迹为椭圆的一部分，点P 到该椭圆焦点的距离的和为定长当212<a 时，点P 到椭圆两个焦点（),21(),,2122a a a a ---的距离之和为定值2当212>a 时，点P 到椭圆两个焦点（0，)21,0(),2122-+--a a a a 的距离之和为定值2a .22．（本小题满分12分，附加题4分）（Ⅰ）解：用(t,s)表示22ts+，下表的规律为3（(0,1)=0122+）5(0,2) 6(1,2)9(0,3) 10(1,3) 12(2,3) — — — —…………（i ）第四行17(0,4) 18(1,4) 20(2,4) 24(3,4)第五行 33(0,5) 34(1,5) 36(2,5) 40(3,5) 48(4,5)（i i ）解法一：因为100＝（1+2+3+4+……+13）+9，所以100a =(8,14)＝81422+＝16640解法二：设0022100t s a +=，只须确定正整数.,00t s数列}{n a 中小于02t的项构成的子集为 },0|2{20t t t s s <<≤+ 其元素个数为.1002)1(,2)1(000020<--=t t t t C t 依题意满足等式的最大整数0t 为14，所以取.140=t因为100－.1664022,8s ,181410000214=+=∴=+=a s C 由此解得（Ⅱ）解：,22211603710++==k b令}0|22{2B ,(}1160|{r t s r C B c M t s <<≤++=<∈=其中因}.22222|{}222|{}2|{37107107101010++<<+∈⋃+<<∈⋃<∈=c B c c B c c B c M 现在求M 的元素个数：},100|222{}2|{10<<<≤++=<∈t s r c B c t s r其元素个数为310C ： }.70|222{}222|{1071010<<≤++=+<<∈s r c B c r s某元素个数为}30|222{}22222|{:710371071027<≤++=++<<+∈r c B c C r某元素个数为.1451:2327310710=+++=C C C k C另法：规定222r t s ++=（r,t,s ），10731160222k b ==++＝（3,7,10）则0121222b =++＝（0,1,2） 22C依次为（0,1,3）（0,2,3）（1,2,3） 23C （0,1,4）（0,2,4）（1,2,4）（0,3,4）（1,3,4）（2,3,4） 24C…………（0,1,9）（0,2,9）………… （ 6,8,9 ）（7,8,9） 29C（0,1,10）（0,2,10）.........（0,7,10）（ 1,7,10）（2,7,10）（3,7,10） (2)7C +422222397()4145.k C C C C =+++++=。

高考理科数学试题--2003年山东卷

2003年普通高等学校招生全国统一考试理科数学注意事项：1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上．2. 每小题选出答案后，用铅笔把答题卡上对应答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．3. 考试结束，监考人将本试卷和答题卡一并收回．参考公式：三角函数的积化和差公式：正棱台、圆台的侧面积公式)]sin()[sin(21cos sin βαβαβα-++=⋅ lc c S )(21+'=台侧其中c '、c 分别表示)]sin()[sin(21sin cos βαβαβα--+=⋅ 上、下底面周长，l 表示斜高或母线长. )]cos()[cos(21cos cos βαβαβα-++=⋅ 球体的体积公式：334RV π=球，其中R)]cos()[cos(21sin sin βαβαβα--+-=⋅表示球的半径.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分第Ⅰ卷（选择题共60分）一.选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的 1．已知2(π-∈x ，0），54co s =x ，则2tg x = （） A ．247B ．247-C ．724D ．724-2．圆锥曲线θθρ2cos sin 8=的准线方程是（） A ．2cos -=θρB ．2cos =θρC ．2sin =θρD ．2sin -=θρ3．设函数⎪⎩⎪⎨⎧-=-2112)(xx f x00>≤x x ，若1)(0>x f ，则0x 的取值范围是（）A ．（1-，1）B ．（1-，∞+）C ．（∞-，2-）（0，∞+）D ．（∞-，1-）（1，∞+）4．函数)cos (sin sin 2x x x y +=的最大值为（） A ．21+B ．12-C ．2D ．25．已知圆C ：4)2()(22=-+-y a x （0>a ）及直线l ：03=+-y x ，当直线l 被C 截得的弦长为32时，则a 为（） A ．2B ．22-C ．12-D ．12+6．已知圆锥的底面半径为R ，高为3R ，在它的所有内接圆柱中，全面积的最大值是（） A ．22R πB ．249R πC ．238R πD ．223R π7．已知方程0)2)(2(22=+-+-n x x m x x 的四个根组成一个首项为41的的等差数列，则=-||n m （）A ．1B ．43C ．21D ．838．已知双曲线中心在原点且一个焦点为F （7，0），直线1-=x y 与其相交于M 、N 两点，MN 中点的横坐标为32-，则此双曲线的方程是（）A ．14322=-yxB ．13422=-yxC ．12522=-yxD ．15222=-yx9．函数x x f sin )(=，]23,2[ππ∈x 的反函数=-)(1x f （）A ．x arcsin - 1[-∈x ，1]B ．x arcsin --π 1[-∈x ，1]C ．x arcsin +π 1[-∈x ，1]D ．x arcsin -π 1[-∈x ，1]10．已知长方形的四个顶点A （0，0），B （2，0），C （2，1）和D （0，1），一质点从AB 的中点0P 沿与AB 的夹角θ的方向射到BC 上的点1P 后，依次反射到CD 、DA 和AB 上的点2P 、3P 和4P （入射角等于反射角），设4P 的坐标为（4x ，0），若214<<x ，则tg θ的取值范围是（） A ．（31，1）B ．（31，32）C ．（52，21）D ．（52，32）11．=++++++++∞→)(lim11413122242322n nn C C C C n C C C C （）A ．3B ．31C ．61 D ．612．一个四面体的所有棱长都为2，四个顶点在同一球面上，则些球的表面积为（） A ．π3 B ．π4C ．π33D ．π62003年普通高等学校招生全国统一考试（全国卷）数学（理工农医类）第Ⅱ卷（非选择题共90分）二.填空题：本大题共4小题，每小题4分，共16分把答案填在题中横线上13．92)21(xx -的展开式中9x 系数是14．使1)(log 2+<-x x 成立的x 的取值范围是 15．如图，一个地区分为5个行政区域，现给地图着色，要求相邻地区不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有种（以数字作答）16．下列5个正方体图形中，l 是正方体的一条对角线，点M 、N 、P 分别为其所在棱的中点，能得出⊥l 面MNP 的图形的序号是（写出所有符合要求的图形序号）① ② ③ ④ ⑤三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或或演算步骤 17．（本小题满分12分）已知复数z 的辐角为︒60，且|1|-z 是||z 和|2|-z 的等比中项，求||z 18．（本小题满分12分）如图，在直三棱柱111C B A ABC -中，底面是等腰直角三角形，︒=∠90ACB ，侧棱21=AA ，D 、E 分别是1CC 与B A 1的中点，点E 在平面ABD 上的射影是△ABD 的重心G（Ⅰ）求B A 1与平面ABD 所成角的大小（结果用反三角函数值表示）（Ⅱ）求点1A 到平面AED 的距离19．（本小题满分12分）已知0>c ，设P ：函数x c y =在R 上单调递减 Q ：不等式1|2|>-+c x x 的解集为R 如果P 和Q 有且仅有一个正确，求c 的取值范围20．（本小题满分12分）在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O （如图）的东偏南102arccos(=θθ）方向300km 的海面P 处，并以20km/h 的速度向西偏北︒45方向移动，台风侵袭的范围为圆形区域，当前半径为60km ，并以10km/h 的速度不断增大，问几小时后该城市开始受到台风的侵袭？21．（本小题满分14分）已知常数0>a ，在矩形ABCD 中，4=AB ，a BC 4=，O 为AB 的中点，点E 、F 、G 分别在BC 、CD 、DA 上移动，且B EC FD G B CC DD A==，P 为GE 与OF 的交点东O否存在两个定点，使P 到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由22．（本小题满分12分，附加题4 分）（I ）设}{n a 是集合|22{t s + t s <≤0且Z t s ∈,}中所有的数从小到大排列成的数列，即31=a ，52=a ，63=a ，94=a ，105=a ，126=a ，…将数列}{n a 各项按照上小下大，左小右大的原则写成如下的三角形数表：35691012⑴写出这个三角形数表的第四行、第五行各数；⑵求100a（II ）（本小题为附加题，如果解答正确，加4 分，但全卷总分不超过150分）设}{n b 是集合t s r t s r <<≤++0|222{，且},,Z t s r ∈中所有的数从小到大排列成的数列，已知1160=k b ，求k .2003年普通高等学校招生全国统一考试答案一、选择题：本题考查基本知识和基本运算. 每小题5分，满分60分.1．D 2．C 3．D 4．A 5．C 6．B 7．C 8．D 9．D 10．C 11．B 12．A 二、填空题：本题考查基本知识和基本运算.每小题4分,满分16分. 13．221-14．（-1，0） 15．72 16．①④⑤三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤. 17．解：设)60sin 60cosr r z +=，则复数.2r z 的实部为2,r z z r z z ==-由题设.12||).(12,12:.012,421,)2)(2(||)1)(1(:|2||||1|2222-=--=-==-++-=+-∴--=---⋅=-z r r r r r r r r r z z z z z z z z 即舍去解得整理得即18．（Ⅰ）解：连结BG ，则BG 是BE 在ABD 的射影，即∠EBG 是A 1B 与平面ABD 所成的角.设F 为AB 中点，连结EF 、FC ，.32arcsin .323136sin .3,32,22,2.36321,2)4(.3,1,31.,,,,,,112211所成的角是与平面于是分中在直角三角形的重心是连结为矩形平面又的中点分别是ABD B A EBEG EBG EB B A AB CD FC EG ED FD EF FD FD FG EFEFD DF G ADB G DE CDEF ABC DC B A CC E D ∴=⋅==∠∴===∴===⨯===∴==⋅=∈∴∆∴⊥（Ⅱ）解：,,,ED AB ED EF EF AB F ⊥⊥= 又111111111111111,.,.,.,.6,33ED A AB ED AED AED A AB AED A AB AE A K AE K A K AED A K A AED A A A B A AB A K A AED AB ∴⊥⊂∴⊥=⊥∴⊥⋅∆=== 面又面平面平面且面面作垂足为平面即是到平面的距离在中到平面的距离为19．解：函数x c y =在R 上单调递减.10<<⇔c不等式.1|2|1|2|上恒大于在函数的解集为R c x x y R c x x -+=⇔>-+22,2,|2|2,2,|2|2.1|2|121.21,,0.21,, 1.(0,][1,).2x c x c x x c c x c y x x c R c x x c R c c P Q c P Q c c -≥⎧+-=⎨<⎩∴=+-∴+->⇔>⇔><≤≥+∞ 函数在上的最小值为不等式的解集为如果正确且不正确则如果不正确且正确则所以的取值范围为（以上方法在新疆考区无一人使用，大都是用解不等式的方法，个别使用的图象法） 20．解：如图建立坐标系以O 为原点，正东方向为x 轴正向.在时刻：（1）台风中心P （yx ,）的坐标为⎪⎪⎩⎪⎪⎨⎧⨯+⨯-=⨯-⨯=.22201027300,2220102300t y t x此时台风侵袭的区域是,)]([)()(22t r y y x x ≤-+-其中,6010)(+=t t r 若在t 时刻城市O 受到台风的侵袭，则有.)6010()0()0(222+≤-+-t y x 即22)22201027300()2220102300(t t ⨯+⨯-+⨯-⨯2412,028836,)6010(22≤≤≤+-+≤t t t t 解得即答：12小时后该城市开始受到台风的侵袭.21．根据题设条件，首先求出点P 坐标满足的方程，据此再判断是否存在的两定点，使得点P 到两点距离的和为定值.按题意有A （－2，0），B （2，0），C （2，4a ），D （－2，4a ）设(01)B EC FD Gk k B C C D D A ===≤≤由此有E （2，4a k ），F （2－4k ，4a ），G （－2，4a －4ak ）直线OF 的方程为：0)12(2=-+y k ax① 直线GE 的方程为：02)12(=-+--a y x k a②从①，②消去参数k ，得点P （x,y ）坐标满足方程022222=-+ay y x a 整理得1)(21222=-+aa y x当212=a时，点P 的轨迹为圆弧，所以不存在符合题意的两点.当212≠a 时，点P 轨迹为椭圆的一部分，点P 到该椭圆焦点的距离的和为定长当212<a 时，点P 到椭圆两个焦点（),21(),,2122a a a a ---当212>a 时，点P 到椭圆两个焦点（0，)21,0(),2122-+--a a a a 的距离之和为定值2a .22．（本小题满分12分，附加题4分）（Ⅰ）解：用(,)t s 表示22t s +，下表的规律为13(0,1)225(0,2)6(1,2)9(0,3)10(1,3)12(2,3)=+（i ）第四行 17(0,4) 18(1,4) 20(2,4) 24(3,4)第五行 33(0,5) 34(1,5) 36(2,5) 40(3,5) 48(4,5)（i i ）解法一：因为100＝（1+2+3+4+……+13）+9，所以100a =(8,14)＝81422+＝16640解法二：设022100t s a +=，只须确定正整数.,00t s数列}{n a 中小于02t 的项构成的子集为 },0|2{20t t t s s <<≤+ 其元素个数为.1002)1(,2)1(00002<--=t t t t C t 依题意满足等式的最大整数0t 为14，所以取.140=t因为100－.1664022,8s ,181410000214=+=∴=+=a s C 由此解得（Ⅱ）解：,22211603710++==kb令r{|1160}(,B {222|0}stMc B c r s t =∈<=++≤<<其中因10101071071073{|2}{|222}{|22222}.M c B c c B c c B c =∈<∈<<+∈+<<++ 现在求M 的元素个数：},100|222{}2|{10<<<≤++=<∈t s r c B c ts r其元素个数为310C ： }.70|222{}222|{1071010<<≤++=+<<∈s r c B c rs某元素个数为}30|222{}22222|{:710371071027<≤++=++<<+∈r c B c C r某元素个数为.1451:2327310710=+++=C C C k C另法：规定222r t s ++=（r,t,s ），10731160222kb ==++＝（3,7,10）则0121222b =++＝（0,1,2） 22C依次为（0,1,3）（0,2,3）（1,2,3）23C （0,1,4）（0,2,4）（1,2,4）（0,3,4）（1,3,4）（2,3,4）24C…………（0,1,9）（0,2,9）………… （ 6,8,9 ）（7,8,9） 29C（0,1,10）（0,2,10）.........（0,7,10）（ 1,7,10）（2,7,10）（3,7,10） (2)7C +422222397()4145.k C C C C =+++++=。