山东省莱州一中2017级高三第二次质量检测 数学(理)(含答案)word版
山东省莱州市第一中学2017届高三物理上学期第二次质量检测试题

莱州一中2014级高三第二次学习质量检测物理试题第I卷(选择题,共42分)一、选择题(1-7单选,8-14多选,每题3分,漏选得2分,共42分)1.下列几种情况,不可能发生的是()A.位移和加速度反向B.速度不变,加速度在变C.速度和加速度反向D.加速度不变,速度在变2.下列关于作用力和反作用力的说法中,正确的是()A.物体相互作用时,先有作用力,后有反作用力B.作用力和反作用力的合力为零,即两个力的作用效果可以互相抵消C.鸡蛋碰石头时,鸡蛋对石头的作用力与石头对鸡蛋的作用力大小是相等的D.马能将车拉动.是因为马拉车的力大于车拉马的力3.洗衣机的甩干筒在转动时有一衣物附在筒壁上,如图,则此时()A.衣物受到重力、筒壁的弹力和摩擦力、向心力的作用B.筒壁的弹力随筒的转速增大而增大C.衣物随筒壁做圆周运动的向心力是由于摩擦的作用D.筒壁对衣物的摩擦力随转速增大而增大、B、C是三个完全相同的带正电小球,从同一高度开始自由下落,A球穿过一水平方向的匀强磁场;B 球下落过程中穿过水平方向的匀强电场;C球直接落地,如图所示,试比较三个小球下落过程中所需的时间t A、t B、t C的长短及三个小球到达地面的速率v A、v B、v C间的大小关系,下列说法正确的是()>t B=t C v B>v A=v C=t B>t C v A<v B=v C=t B=t C v A=v B>v C>t B>t C v A=v B<v C5.一物体做直线运动,其位移-时间图象如图所示,设向右为正方向,则在前4s内()A.物体先向左运动,2s后开始向右运动B.物体始终向右做匀速直线运动C.在t=2s时,物体距出发点最远D.前2s物体位于出发点的左方,后2s位于出发点的右方6.如图为某双线客运索道,其索线由静止不动的承载索和牵引缆车运动的牵引索组成。
运行过程中牵引索通过作用力F使缆车沿倾斜的承载索道斜向上加速移动,不计空气阻力,在缆车向上移动过程中,下列说法正确的是A.F对缆车做的功等于缆车增加的动能和克服摩擦力所做的功之和B.F对缆车做的功等于缆车克服摩擦力和克服重力所做的功之和C.缆车克服重力做的功小于缆车增加的重力势能D.F对缆车做的功等于缆车增加的机械能与缆车克服摩擦力做的功之和7.如图所示,一条形磁铁放在水平桌面上,在条形磁铁的左上方固定一根与磁铁垂直的长直导线,当导线中通以图示方向的电流时( )A.磁铁对桌面的压力减小,且受到向左的摩擦力作用B.磁铁对桌面的压力减小,且受到向右的摩擦力作用C.磁铁对桌面的压力增大,且受到向左的摩擦力作用D.磁铁对桌面的压力增大,且受到向右的摩擦力作用8.下列说法中正确的是()A.电阻的定义式写成U/I,也可写成∆U/∆IB.磁场的方向与放在该点的电流元的受力方向相同C.奥斯特最先发现电流的周围存在着磁场D.电场线必然和等势面垂直9.如图所示电路中,电源内阻不可忽略,L1、L2两灯均正常发光,R1为定值电阻,R 为一滑动变阻器,P为滑动片,若将滑动片向下滑动,则()A.L 1灯变亮B.L2灯变暗C.R1上消耗功率变大D.总电流变小10.如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点。
(完整word版)2017年高考数学山东理试题及解析

2017年高考数学山东理1.(2017年山东理)设函数y=4-x 2的定义域为A ,函数y=ln(1-x)的定义域为B,则A∩B=( ) A.(1,2) B.(1,2] C.(-2,1) D.[-2,1)1.D 【解析】由4-x 2≥0得-2≤x≤2,由1-x >0得x <1,故A∩B={x|-2≤x≤2}∩{x|-2≤x <1}.故选D.2. (2017年山东理)已知a ∈R,i 是虚数单位.若z=a+3i,z·-z =4,则a =( ) A.1或-1 B.7或-7 C.- 3 D. 32. A 【解析】由z=a+3i,z·-z =4得a 2+3=4,所以a=±1.故选A.3. (2017年山东理)已知命题p :∀x >0,ln (x+1)>0;命题q :若a >b ,则a 2>b 2,下列命题为真命题的是( )A.p ∧qB. p ∧¬qC. ¬p ∧qD. ¬p ∧¬q3. B 【解析】由x >0时,x+1>1,ln (x+1)>0,知p 是真命题,由-1>-2,但(-2)2>(-1)2可知q 是假命题,,则p ∧¬q 是真命题.故选B.4. (2017年山东理)已知x,y 满足约束条件⎩⎪⎨⎪⎧x-y+3≤0,3x+y+5≤0,x+3≥0,则z=x+2y 的最大值是( )A.0B.2C.5D.64. C 【解析】约束条件⎩⎪⎨⎪⎧x-y+3≤0,3x+y+5≤0,x+3≥0,表示的可行域如图中阴影部分所示,目标函数z=x+2y ,即y=-12x+z 2,平移直线y=-12x+z 2,可知当直线y=-12x+z2经过直线3x+y+5=0与x=-3的交点(-3,4)时,z=x+2y 取得最大值,为z max =-3+2×4=5.故选C.5. (2017年山东理)为了研究某班学生的脚长x (单位:厘米)和身高y (单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y 与x 之间有线性相关关系,设其回归直线方程为^y =^b x +^a .已知∑i=110x i =225,∑i=110y i =1 600,^b=4.该班某学生的脚长为24,据此估计其身高为( )A.160B.163C.166D.1705. C 【解析】由已知得-x =22.5, -y =160,则^a =160-4×22.5=70,当x=24时,^y =4×24+70=166.故选C.6. (2017年山东理)执行两次下图所示的程序框图,若第一次输入的x 的值为7,第二次输入的x 的值为9,则第一次、第二次输出的a 的值分别为( )A.0,0B.1,1C.0,1D.1,06. D 【解析】第一次输入x=7,22<7,否,否,b=3,32>7,是,a=1;第二次输入x=9,22<9,否,否,b=3,32=9,否,是,a=0.故选D.7. (2017年山东理)若a >b >0,且ab=1,则下列不等式成立的是( ) A.a+1b <b 2a <log 2(a+b ) B. b 2a <log 2(a+b )<a+1bC. a+1b <log 2(a+b )<b 2aD. log 2(a+b )<a+1b <b 2a7. B 【解析】因为a >b >0,且ab=1,所以a >1,0<b <1,所以b 2a <1,log 2(a+b )>log 22ab =1,2a+1b >a+1b>a+ba+1b >log 2(a+b ).故选B.8. (2017年山东理)从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张.则抽到的2张卡片上的数奇偶性不同的概率是( ) A.518 B.49 C.59 D.798. C 【解析】标有1,2,…,9的9张卡片中,标奇数的有5张,标偶数的有4张,所以抽到2张卡片上的数奇偶性不同的概率是2C 1 5C 149×8 1 4 ,9×8)=59.故选C.9. (2017年山东理)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若△ABC 为锐角三角形,且满足sin B(1+2cos C)=2sin Acos C+cos Asin C ,则下列等式成立的是( ) A.a=2b B.b=2a C.A=2B D.B=2A9. A 【解析】由题意知sin(A+C)+2sin Bcos C=2sin Acos C+cos Asin C ,所以2sin Bcos C=sin Acos C ⇒2sin B=sin A ⇒2b=a.故选A.10. (2017年山东理)已知当x ∈[0,1]时,函数y=(mx-1)2的图象与y=x +m 的图象有且只有一个交点,则正实数m 的取值范围是( )A.(0,1]∪[23,+∞)B.(0,1]∪[3,+∞)C. (0,2]∪[23,+∞)D. (0, 2]∪[3,+∞)10. B 【解析】当0<m≤1时,1m ≥1,y=(mx-1)2在[0,1]上单调递减,且y=(mx-1)2∈[(m-1)2,1],y=x +m 在x ∈[0,1]上单调递增,且y=x +m ∈[m ,1+m],此时有且仅有一个交点;当m >1时,0<1m <1,y=(mx-1)2在[1m ,1]上单调递增,所以要有且仅有一个交点,需(m-1)2≥1+m ⇒m≥3.故选B.11. (2017年山东理)已知(1+3x )n 的展开式中含有x 2项的系数是54,则n=_________.11. 4 【解析】(1+3x )n 的展开式的通项公式为T r+1=C r n (3x)r = C rn ·3r x r ,令r=2,得C 2 n ·32=54,解得n=4.12. (2017年山东理) 已知e 1,e 2是互相垂直的单位向量,若3e 1-e 2与e 1+λe 2的夹角为60°,则实数λ的值是_________.12. 33 【解析】∵(3e 1-e 2)·(e 1+λe 2)=3e 12+3e 1·λe 2- e 1·e 2-λe 22=3-λ,|3e 1-e 2|=(3e 1-e 2)2=3e 12-23e 1·e 2 +e 22=2,|e 1+λe 2|=(e 1+λe 2)2=e 12+2e 1·λe 2+λ2e 22=1+λ2,∴3-λ=21+λ2×cos 60°=1+λ2,解得λ=33.13. (2017年山东理) 由一个长方体和两个14圆柱体构成的几何体的三视图如图,则该几何体的体积为 .13. 2+π2 【解析】由三视图可知,长方体的长、宽、高分别为2,1,1,圆柱的高为1,底面圆半径为1,所以V=2×1×1+2×π×124×1=2+π2.14. (2017年山东理)在平面直角坐标系xOy 中,双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右支与焦点为F 的抛物线x 2=2py (p >0)交于A ,B 两点.若|AF |+|BF |=4|OF |,则该双曲线的渐近线方程为 .14. y=±22x 【解析】由抛物线定义可得:|AF|+|BF|=y A +p 2+y B +p 2=4×p2⇒y A +y B =p,因为⎩⎨⎧x 2a 2-y 2b 2=1,x 2=2py⇒a 2y 2-2pb 2y+a 2b 2=0,所以y A +y B =2pb 2a 2=p ⇒a=2b ⇒渐近线方程为y=±22x.15. (2017年山东理)若函数e x f (x ) (e=2.718 28是自然对数的底数)在f (x )的定义域上单调递增,则称函数f (x )具有M 性质.下列函数中所有具有M 性质的函数的序号为_________. ①f (x )=2-x②f (x )=3-x③f (x )=x 3④f (x )=x 2+215. 6 【解析】①e x f (x )=e x ·2-x =(e2)x 在R 上单调递增,故f (x )=2-x 具有M 性质;②e x f (x )=e x ·3-x =(e3)x 在R 上单调递减,故f (x )=3-x 不具有M 性质;③e x f (x )=e x ·x 3,令g (x )=e x ·x 3,则g′(x )= e x ·x 3+3e x ·x 2=x 2e x (x+3), 当x >-3时,g′(x )>0,当x <-3时,g′(x )<0,∴e x f (x )= e x ·x 3在(-∞,-3)上单调递减,在(-3,+∞)上单调递增,故f (x )=x 3不具有M 性质;④e x f (x )=e x (x 2+2),令g (x )= e x (x 2+2),则g′(x )= e x (x 2+2)+2xe x =e x [(x+1)2+1]>0,∴e x (x 2+2)在R 上单调递增,故f (x )=x 2+2具有M 性质.16. (2017年山东理)设函数f(x)=sin(ωx -π6)+sin(ωx -π2),其中0<ω<3.已知f(π6)=0.(1)求ω;(2)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移π4个单位,得到函数y=g(x)的图象,求g(x)在[-π4,3π4]上的最小值.16.解:(1)因为f(x)=sin(ωx -π6)+sin(ωx -π2), 所以f(x)=32sin ωx -12cos ωx -cos ωx =32sin ωx -32cos ωx =3(12sin ωx -32cos ωx ) =3sin (ωx -π3). 有题设知f(π6)=0, 所以ωπ6-π3=kπ,k ∈Z.故ω=6k+2,k ∈Z ,又0<ω<3, 所以ω=2.(2)由(1)得f(x)=3sin (2x-π3).所以g(x)= 3sin (x+π4-π3)=3sin (x-π12).因为x ∈[-π4,3π4],所以x-π12∈[-π3,2π3],当x-π12=-π3,即x=-π4时,g(x)取得最小值-32.17. (2017年山东理)如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120°得到的,G 是⌒DF 的中点. (1)设P 是⌒CE上的一点,且AP ⊥BE ,求∠CBP 的大小; (2)当AB=3,AD=2时,求二面角E-AG-C 的大小.17.解:(1)因为AP ⊥BE ,AB ⊥BE , AB ,AP ⊂平面ABP ,AB∩AP=A , 所以BE ⊥平面ABP , 又BP ⊂平面ABP ,所以BE ⊥BP ,又∠EBC=120°, 因此∠CBP=30°. (2)解法一:取⌒EC的中点H,连接EH,GH,CH.因为∠EBC=120°,所以四边形BEHC为菱形,所以AE=GE=AC=GC=32+22=13.取AG中点M,连接EM,CM,EC.则EM⊥AG,CM⊥AG,所以∠EMC为所求二面角的平面角.又AM=1,所以EM=CM=13-1=2 3.在△BEC中,由于∠EBC=120°,由余弦定理得EC2=22+22-2×2×2×cos 120°=12,所以EC=23,因此△EMC为等边三角形,故所求的角为60°.解法二:以B为坐标原点,分别以BE,BP,BA所在的直线为x,y,z轴,建立如图所示的空间直角坐标系.由题意得A(0,0,3),E(2,0,0),G(1, 3 ,3),C(-1, 3 ,1),故→AE=(2,0,-3),→AG =(1, 3 ,0),→CG =(2,0,3),设m=(x1,y1,z1)是平面AEG的一个法向量.由⎩⎨⎧m ·→AE =0,m ·→AG =0,可得⎩⎨⎧2x 1-3z 1=0,x 1+3y 1=0,取z 1=2,可得平面AEG 的一个法向量m =(3,-3,3). 设n =(x 2,y 2,z 2)是平面ACG 的一个法向量. 由⎩⎨⎧m ·→AG =0,m ·→CG =0,可得⎩⎨⎧x 2+3y 2=0,2x 2+3z 2=0,去z 2=-2,可得平面ACG 的一个法向量n =(3,-3,-2). 所以cos<m ,n >=m ·n |m |·|n |=12.因此所求的角为60°.18. (2017年山东理)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用.现有6名男志愿者A 1,A 2,A 3,A 4,A 5,A 6和4名女志愿者B 1,B 2,B 3,B 4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.(1)求接受甲种心理暗示的志愿者中包含A 1但不包含B 1的概率;(2)用X 表示接受乙种心理暗示的女志愿者人数,求X 的分布列与数学期望EX . 18.解:(1)记接受甲种心理暗示的志愿者中包含A 1但不包含B 1的事件为M ,则P(M)=C 4 8C 5105 10)=518. (2)由题意知X 可取的值为0,1,2,3,4.则 P(X=0)=C 5 6C 5 105 10)=142,P(X=1)=C 4 6C 14C 5 104 ,C 5 10)=521, P(X=2)=C 3 6C 24C 5 104 ,C 5 10)=1021, P(X=3)=C 2 6C 34C 5 104 ,C 5 10)=521, P(X=4)=C 1 6C 44C 5 104 ,C 5 10)=142, 因此X 的分布列为X 的数学期望是EX =0×P (X=0)+1×P (X=1)+2×P (X=2)+3×P (X=3)+4×P (X=4)=0×142+1×521+3×521+4×142=2.19. (2017年山东理)已知{x n }是各项均为正数的等比数列,且x 1+x 2=3,x 3-x 2=2. (1)求数列{x n }的通项公式;(2)如图,在平面直角坐标系xOy 中,依次连接点P 1(x 1, 1),P 2(x 2, 2),…,P n+1(x n+1, n +1)得到折线P 1P 2…P n+1,求由该折线与直线y =0,x=x 1,x=x n+1所围成的区域的面积n T .19.解:(1)(I)设数列{x n }的公比为q ,由已知q >0.由题意得⎩⎨⎧x 1+x 1q=3,x 1q 2-x 1q=2,所以3q 2-5q-2=0,因为q >0,所以q=2,x 1=1, 因此数列{x n }的通项公式为x n =2n-1(2)过P 1,P 2,P 3,…,P n+1向x 轴作垂线,垂足分别为Q 1,Q 2,Q 3,…,Q n+1, 由(1)得x n+1-x n =2n -2n-1=2n-1. 记梯形P n P n +1Q n +1Q n 的面积为b n . 由题意b n =(n+n+1)2×2n-1=(2n+1)×2n-2, 所以T n =b 1+b 2+b 3+…+b n=3×2-1+5×20+7×21+…+(2n-1)×2n-3+(2n+1)×2n-2,① 又2T n =3×20+5×21+7×22+…+(2n-1)×2n-2+(2n+1)×2n-1,②①-②得-T n =3×2-1+(2+22+…+2n-1)-(2n+1)×2n-1=32+2(1-2n-1)1-2-(2n+1)×2n-1. 所以T n =(2n-1)×2n +12.20. (2017年山东理)已知函数f(x)=x 2+2cos x ,g(x)=e x (cos x-sin x+2x-2),其中e=2.718 28…是自然对数的底数.(1)求曲线y=f(x)在点(π,f(π))处的切线方程;(2)令h(x)=g(x)-af(x)(a ∈R),讨论h(x)的单调性并判断有无极值,有极值时求出极值.20.解:(1)由题意f(π)= π2-2,又f′(x)=2x -2sin x ,所以f′(π)=2π,因此 曲线y=f(x)在点(π,f(π))处的切线方程为y-(π2-2)=2π(x-π),即222y x ππ=--.(2)由题意得h(x)=e x (cos x-sin x+2x-2)-a(x 2+2cos x),因为h′(x)=e x (cos x-sin x+2x-2)+ e x (-sin x-cos x+2)-a(2x-2sin x)=2e x (x-sin x)-2a(x-sin x)=2(e x -a)(x-sin x),令m(x)=x-sin x ,则m′(x)=1-cos x≥0,所以m(x)在R上单调递增.因为m(0)=0,所以当x>0时,m(x)>0,当x<0时,m(x)<0,(1)当a≤0时,e x-a>0,当x<0时,h′(x)<0,h(x)单调递减,当0x 时,h′(x)>0,h(x)单调递增,所以当x=0时h(x)取到极小值,极小值是h(0)=-2a-1;(2)当a>0时,h′(x)=2(e x-e ln a)(x-sin x),由h′(x)=0得x1=ln a,x2=0.①当0<a<1时,ln a<0,当x∈(-∞,ln a)时,e x-e ln a<0,h′(x)>0,h(x)单调递增;当x∈(ln a,0)时,e x-e ln a>0,h′(x)<0,h(x)单调递减;当x∈(0,+∞)时,e x-e ln a>0,h′(x)>0,h(x)单调递增.所以当x=ln a时h(x)取得极大值.极大值为h(ln a)=-a[ln2a-2ln a+sin(ln a)+cos(ln a)+2],当x=0时h(x)取到极小值,极小值是h(0)=-2a-1;②当a=1时,ln a=0,所以当x∈(-∞,+∞)时,h′(x)≥0,函数h(x)在(-∞,+∞)上单调递增,无极值;③当a>1时,ln a>0,所以当x ∈(-∞,0)时,e x -e ln a <0,h′(x)>0,h (x )单调递增;当x ∈(0,ln a )时,e x -e ln a <0,h′(x)<0,h (x )单调递减;当x ∈(ln a ,+∞)时,e x -e ln a >0,h′(x)>0,h (x )单调递增.所以当x=0时h (x )取到极大值,极大值是h (0)=-2a-1;当x=ln a 时h (x )取到极小值.极小值是h (ln a )=-a[ln 2a-2ln a+sin(ln a)+cos(ln a)+2]综上所述:当a≤0时,h (x )在(-∞,0)上单调递减,在(0,+∞)上单调递增,函数h (x )有极小值,极小值是h (0)=-2a-1;当0<a <1时,函数h (x )在(-∞,ln a )和(0,+∞)上单调递增,在(ln a ,0)上单调递减,函数h (x )有极大值,也有极小值,极大值是h (ln a )=-a[ln 2a-2ln a+sin(ln a)+cos(ln a)+2],极小值是h (0)=-2a-1;当a=1时,函数h (x )在(-∞,+∞)上单调递增,无极值;当a >1时,函数h (x )在(-∞,0)和(ln a ,+∞)上单调递增,在(0,ln a )上单调递减,函数h (x )有极大值,也有极小值,极大值是h (0)=-2a-1,极小值是h (ln a )=-a[ln 2a-2ln a+sin(ln a)+cos(ln a)+2].21. (2017年山东理)在平面直角坐标系xOy 中,椭圆E :x 2a 2+y 2b 2=1(a >b >0)的离心率为22,焦距为2.(1)求椭圆E 的方程;(2)如图,动直线l :y=k 1x-32交椭圆E 于A ,B 两点,C 是椭圆E 上一点,直线OC 的斜率为k 2,且k 1k 2=24,M 是线段OC 延长线上一点,且|MC|:|AB|=2:3,○·M 的半径为|MC|,OS ,OT 是○·M 的两条切线,切点分别为S ,T.求∠SOT 的最大值,并求取得最大值时直线l 的斜率.21.解:(1)由题意知e=c a =22,2c=2, 所以a=2,b=1,因此 椭圆E 的方程为x 22+y 2=1. (2)设A (x 1,y 1),B (x 2,y 2),联立方程⎩⎨⎧x 22 +y 2=1,y=k 1x-32, 得(4k 12+2)x 2-43k 1x-1=0,由题意知Δ>0,且x 1+x 2=23k 12k 12+1,x 1x 2=-12(2k 12+1), 所以|AB|=1+k 12|x 1-x 2|=21+k 121+8k 122k 12+1.由题意可知圆M 的半径r 为r=2231+k 121+8k 122k 12+1. 由题设知k 1k 2=24, 所以k 2=24k 1, 因此直线OC 的方程为y=24k 1x. 联立方程⎩⎨⎧x 22 +y 2=1, y=24k 1x , 得x 2=8k 121+4k 12,y 2=11+4k 12, 因此|OC|=x 2+y 2=1+8k 121+4k 12. 由题意可知sin ∠SOT 2=r r+|OC|=11+|OC|r, 而|OC|r =1+8k 121+4k 122231+k 121+8k 122k 12+1=3241+2k 121+4k 121+k 12, 令t=1+2k 12, 则t >1,1t∈(0,1), 因此|OC|r =32t 2t 2+t-1=3212+1t -1t 2=321-(1t -12)2+94≥1, 当且仅当1t =12,即t=2时等号成立,此时k 1=±22,所以sin ∠SOT 2≤12, 因此∠SOT 2≤π6, 所以∠SOT 最大值为π3. 综上所述:∠SOT 的最大值为π3,取得最大值时直线l 的斜率为k 1=±22.。
2017届高三第二次教学质量检测数学理试题(12页有答案)

高三年级第二次教学质量检测试题理科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共60分)一.选择题:本大题共12个小题,每小题5分,满分60分,在每小题给出的四个选项中,只有 一项是符合题目要求的.1.已知集合{-2-1012}{|22}A B x x A B ==-<≤= ,,,,,,则A .{-1012},,,B .{-101},, C .{-2-101},,, D .{-2-1012},,,,2.复数ii+1-2对应的点在 A .第一象限 B .第二象限 C .第三象限 D .第四象限3.已知向量(2,1),(3,)a b x =-=,若3a b ⋅= ,则x =A .3B .4C .5D .64.已知双曲线12222=-b y a x 的一条渐近线方程为x y 43=,则此双曲线的离心率为A .43B .54 C .53 D5.已知条件p :46x -≤;条件q :1x m ≤+,若p 是q 的充分不必要条件,则m 的取值范围是A . (]1,-∞-B .(]9,∞-C . []9,1D .[)∞+,9 6.运行如图所示的程序框图,输出的结果S =A .14B .30C .62D .1267.1()nx x-的展开式中只有第5项的二项式系数最大,则展开式中含2x 项的系数是A .56B .35C .-56D .-358.已知,αβ是两个不同的平面,,,l m n 是不同的直线,下列命题不正确...的是A .若,,,,l m l n m n αα⊥⊥⊂⊂则l α⊥B .若//,,,l m l m αα⊂⊂/则//l αC .若,,,,l m m l αβαβα⊥=⊂⊥ 则m β⊥D .若,,,m n αβαβ⊥⊥⊥,则m n ⊥9.已知)(cos 3sin )(R x x x x f ∈+=,函数)(ϕ+=x f y 的图象关于直线0=x 对称,则ϕ的 值可以是A .2π B .6π C .3π D .4π10.男女生共8人,从中任选3人,出现2个男生,1个女生的概率为1528,则其中女生人数是A .2人B .3人C .2人或3人D .4人11.已知抛物线24y x =,过焦点F 作直线与抛物线交于点A ,B (点A 在x 轴下方),点1A 与 点A 关于x 轴对称,若直线AB 斜率为1,则直线1A B 的斜率为A .3 B C .2D 12.下列结论中,正确的有①不存在实数k ,使得方程21ln 02x x x k -+=有两个不等实根; ②已知△ABC 中,,,a b c 分别为角,,A B C 的对边,且2222a b c +=, 则角C 的最大值为6π; ③函数y=ln与ln tan2xy =是同一函数; ④在椭圆22221(0)x y a b a b+=>>,左右顶点分别为A ,B ,若P 为椭圆上任意一点(不同于,A B ),则直线PA 与直线PB 斜率之积为定值.A .①④B .①③C .①②D .②④第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分.第13题~21题为必考题,每个试题考生都必须做答.第22题、第23题为选考题,考生根据要求做答. 二.填空题:本大题共4小题;每小题5分,共20分. 13.已知等比数列{}n a 的前n 项和为n S ,且132455,24a a a a +=+=,则6S = __________. 14.已知实数x 、y 满足约束条件⎪⎩⎪⎨⎧≤+≥≥622y x y x ,则y x z 42+=的最大值为______ .15.一个几何体的三视图如图所示,则这个几何体的外接球的半径为__________ .16.下列命题正确是 . (写出所有正确命题的序号) ①若奇函数()f x 的周期为4,则函数()f x 的图象关于(2,0)对称; ②若(0,1)a ∈,则111aaa a++<;③函数1()ln1xf x x+=-是奇函数; ④存在唯一的实数a 使()()12lg 2++=x ax x f 为奇函数.三.解答题:本大题共6小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分12分)在△ABC 中,角A 、B 、C 的对边分别为a ,b ,c ,且3a =,4b =,2B A π=+.(1)求cos B 的值; (2)求sin 2sin A C +的值. 18.(本小题满分12分)如图,三棱柱111C B A ABC -中,侧棱1AA ⊥平面ABC ,ABC ∆为等腰直角三角形,90=∠BAC ,且AB AA =1,F E ,分别是BC CC ,1的中点.(1)求证:平面1AB F ⊥平面AEF ; (2)求二面角F AE B --1的余弦值.19.(本小题满分12分)某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[]1000,,样本数据分组为第一组[)200,,第二组[)4020,,第 三组[)6040,,第四组[)8060,,第五组[]10080,. (1)求直方图中x 的值;(2)如果年上缴税收不少于60万元的企业可申请政策优惠,若共抽取企业1200家,试估计 有多少企业可以申请政策优惠;(3)从所抽取的企业中任选4家,这4家企业年上缴税收少于20万元的家数记为X ,求X 的 分布列和数学期望.(以直方图中的频率作为概率)20.(本小题满分12分)已知椭圆C :)0(12222>>=+b a by a x 经过点P ,离心率2e = ,直线l 的方程为4=x .(1)求椭圆C 的方程;(2)经过椭圆右焦点F 的任一直线(不经过点P )与椭圆交于两点A ,B ,设直线AB 与 l 相交于点M ,记PM PB PA ,,的斜率分别为321,,k k k ,问:是否存在常数λ,使得 321k k k λ=+?若存在,求出λ的值,若不存在,说明理由.21.(本小题满分12分)已知函数x ax x f ln )(+=,其中a 为常数,设e 为自然对数的底数. (1)当1a =-时,求()f x 的最大值;(2)若()f x 在区间(0,]e 上的最大值为3-,求a 的值;(3)设),()(x xf x g =若0,a >对于任意的两个正实数1212,()x x x x ≠, 证明:12122()()()2x x g g x g x +<+. 请考生在第22、23二题中任选一题做答,如果多做,则按所做的第一题记分.做答时,用2B 铅笔在答题卡上把所选题目对应的题号涂黑. 22.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧=+-=t y t x 54253 (t 为参数),以原点O 为极点,x轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为θρsin a =. (1)若2=a ,求圆C 的直角坐标方程与直线l 的普通方程; (2)设直线l 截圆C 的弦长等于圆C 的半径长的3倍,求a 的值. 23.(本小题满分10分)选修4-5:不等式选讲已知函数5212)(++-=x x x f ,且m x f ≥)(恒成立. (1)求m 的取值范围;(2)当m 取最大值时,解关于x 的不等式:8223-≤--m x x .高三第二次质量检测理科数学答案一.ADABD CCABC CA二.13.631614.20 15.61 16.①③ 17.解: (1)∵2B A π=+, ∴2π-=B A ,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅1分又3,4a b ==,所以由正弦定理得34sin sin A B=, 所以34cos sin B B=-,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅3分所以3sin 4cos B B -=,两边平方得229sin 16cos B B =,又22sin cos 1B B +=,所以3cos 5B =±,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅5分而2B π>,所以3cos 5B =-.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅6分(2)∵3cos 5B =-,∴4sin 5B =,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅7分∵2B A π=+,∴22A B π=-, ∴sin 2sin(2)sin 2A B B π=-=-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅8分432sin cos 2()55B B =-=-⨯⨯-=分又A B C π++=,∴322C B π=-, ∴27sin cos 21cos 25C B B =-=-=.∴24731sin 2sin 252525A C +=+=. (12)分18.解答: (1)证明:∵F 是等腰直角三角形ABC ∆斜边BC 的中点, ∴AF BC ⊥.又∵侧棱ABC AA 平面⊥1,∴面ABC ⊥面11BB C C ...........2分 ∴AF ⊥面11BB C C ,1AF B F ⊥.…3分 设11AB AA ==,则,EF=,.∴22211B F EF B E +=,∴1B F EF ⊥............4分 又AF EF F ⋂=,∴1B F ⊥平面AEF .…而1B F ⊂面1AB F ,故:平面1AB F ⊥平面AEF .⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅5分(2)解:以F 为坐标原点,FA ,FB 分别为x ,y 轴建立空间直角坐标系如图, 设11AB AA ==,则(0,0,0)F ,(2A ,1(0,2B -,1(0,)22E -,1()2AE = ,1(AB = .…⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅6分由(1)知,1B F ⊥平面AEF ,取平面AEF 的法向量:1(0,,1)2m FB == .⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅7分设平面1B AE 的法向量为(,,)n x y z =,由,取3x =,得(3,1,n =- (10)分设二面角1B AE F --的大小为θ,则cos θ=|cos <>|=||=.由图可知θ为锐角,∴所求二面角1B AE F --的余弦值为.…⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅12分19.解答: 解:(I )由直方图可得:20(x 0.0250.00650.0032)1⨯+++⨯=解得0.0125x =. ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅2分 (II )企业缴税收不少于60万元的频率0.0032200.12=⨯⨯=, ∴12000.12144⨯=.∴1200个企业中有144个企业可以申请政策优惠. ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅4分 (III )X 的可能取值为0,1,2,3,4.由(I )可得:某个企业缴税少于20万元的概率10.0125200.254=⨯== .............5分25681)43()41()0(4004===C X P 6427)43()41()1(3114===C X P6427)43()41()2(2224===C X P 643)43()41()3(1334===C X P2561)43()41()4(0444===C X P .......................................10分..............11分∴12561464336427264271256810)(=⨯+⨯+⨯+⨯+⨯=X E . ....12分 20.解:(1)由点P 在椭圆上得,22421a b +=①22c e a ==又所以② 由 ①②得2224,8,4c a b ===,故椭圆C 的方程为22184x y +=……………………..4分 (2)假设存在常数λ,使得123k k k λ+=.由题意可设,AB k AB 的斜率为则直线的方程为(2)y k x =-③代入椭圆方程22184x y +=并整理得2222(12)8880k x k x k +-+-= 设1122(,),(,)A x y B x y ,则有22121222888,1212k k x x x x k k -+==++④ ……………6分在方程③中,令4x =得,(4,2)M k,从而2121k k ==32422k k k ==--.又因为B F A 、、共线,则有BF AF k k k ==,即有121222y yk x x ==--……………8分 所以=+21kk 121222y y x x +=--121212112()2222y y x x x x ++----=2k 12121242()4x x x x x x +--++⑤ ……………10分将④代入⑤得=+21kk 2k22222284122888241212k k k k k k k -+=--+++32k k =-, 所以=+21k k 32k . 故存在常数2=λ符合题意…………12分 21.【解答】解:(1)易知()f x 定义域为(0,)+∞,当1a =-时,()ln f x x x =-+,'11()1x f x x x-=-+=, 令'()0f x =,得1x =.当01x <<时,'()0f x >;当1x >时,'()0f x <. ................2分∴()f x 在(0,1)上是增函数,在(1,)+∞上是减函数.max ()(1)1f x f ==-.∴函数()f x 在(0,)+∞上的最大值为1-.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅4分 (2)∵'111(),(0,],[,)f x a x e x x e=+∈∈+∞. ①若1a e≥-,则'()0f x ≥,从而()f x 在(0,]e 上是增函数, ∴max ()()10f x f e ae ==+≥,不合题意.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅5分②若1a e <-,则由'1()00f x a x>⇒+>,即10x a <<-由'1()00f x a x <⇒+<,即1x e a-<≤.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅6分从而()f x 在1(0,)a -上增函数,在1(,)e a-为减函数 ∴max 11()()1ln()f x f a a=-=-+- 令11ln()3a -+-=-,则1ln()2a -=- ∴21e a --=,即2a e =-.∵21e e -<-,∴2a e =-为所求⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅8分 (3)法一:即证221212*********()2()ln()ln ln 222x x x x x x a ax ax x x x x ++++≤+++ 22222212121212()2()[]22x x x x a ax ax a x x ++--=⋅-- 212()02x x a -=-<⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅9分 另一方面,不妨设12x x <,构造函数11111()()ln()ln ln ()2x x k x x x x x x x x x +=+--> 则1()0k x =,而'1()ln ln 2x x k x x +=-=分 由10x x <<易知1012x x x+<< , 即'()0k x <,()k x 在1(,)x +∞上为单调递减且连续, 故()0k x <,即1111()ln()ln ln 2x x x x x x x x ++<+ 相加即得证 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅12分法二:'''1()21ln ,()20g x ax x g x a x =++=+> ..........9分 故'()g x 为增函数,不妨令21x x >令111()()()2()()2x x h x g x g x g x x +=+-> ''1()'()()2x x h x g x g +=-..........10分 易知12x x x +>,故''1()'()()02x x h x g x g +=-> .........11分而1()0h x =,知1x x >时,()0h x >故2()0h x >,即12122()()()2x x g g x g x +<+ .........12分22.解 (1)2a =时,圆C 的直角坐标方程为22(y 1)1x +-=;直线l 的普通方程为4380x y +-=.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅4分(2)圆C :42222a a y x =⎪⎭⎫ ⎝⎛-+,直线:4380l x y +-=,∵直线l 截圆C 的弦长等于圆C⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅7分 ∴圆心C 到直线的距离3812522aad -==⨯,得32a =或3211a =.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅10分 23.解 (1)544,251(x)6,22144,2x x f x x x ⎧--<-⎪⎪⎪=-≤≤⎨⎪⎪+>⎪⎩⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅2分 当5122x -≤≤时,函数有最小值6,所以6m ≤.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅5分 另解:∵2125(2x 1)(2x 5)66x x -++≥--+=-=.∴6m ≤.(2)当m 取最大值6时,原不等式等价于324x x --≤, ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅6分 等价于3324x x x ≥⎧⎨--≤⎩,或3324x x x <⎧⎨--≤⎩,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅8分 可得3x ≥或133x -≤<. 所以,原不等式的解集为13x x ⎧⎫≥-⎨⎬⎩⎭. ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅10分。
山东省莱州市第一中学2017届高三上学期第二次质量检测数学(文)试题 含答案

2014级高三第二次质量检测文科数学试题命题人:王桂萍 审核人:张建伟一.选择题:本大题共10小题。
每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}210,24x M x x x N x ⎧⎫=+≤=>⎨⎬⎩⎭,则M ∪N=( )A .[]1,0-B .(-1,0)C .(-2,+ ∞)D .(-2,0)2.若等差数列{}n a 的前7项和S 7=21,且2a =-1,则6a =( ) A .5 B .6 C .7 D .83.已知34,,cos 25αππα⎛⎫∈=- ⎪⎝⎭,则tan 4πα⎛⎫- ⎪⎝⎭等于 A .7 B .17 C .17- D .-7 4.已知如图所示的向量中,43AP AB =,用OA OB 、表示OP ,则OP 等于( ) A .1433OA OB - B .1433OA OB + C .1433OA OB -+ D .1433OA OB -- 5.设x ,y 满足约束条件32000,0x y x y x y --≤⎧⎪-≥⎨⎪≥≥⎩,若目标函数z =ax +2by (a 〉0,b >0)的最大值为1,则11a b +的最小值为( )A .322+B .322-C .8D .106.某三棱锥的三视图如图所示,则该三棱锥的体积为A .23B .16C .1D .137.在△ABC 中,内角A ,B,C 的对边分别是a ,b ,c ,12,sin sin sin ,2c a b B a A a C =-=则cos B 等于( ) A .34 B .23 C .13 D .128.已知数列是321121,,,,n n a a aa a a a -…,…是首项为1,公比为2的等比数列,则下列数中是数列{}na 中的项的是( ) A .16 B .12 C .32 D .649.已知函数()2sin sin 3f x x x πϕ⎛⎫=++ ⎪⎝⎭是奇函数,其中()0,ϕπ∈,则函数的图象( )A .关于点,012π⎛⎫ ⎪⎝⎭对称 B .可由函数()f x 的图象向右平移3π个单位得到 C .可由函数()f x 的图象向左平移6π单位得到 D .可由函数()f x 的图象向左平移12π个单位得到 10.已知数列{}na 满足()()1log 2n n a n n N *+=+∈,定义:试乘积123k a a a a …为正整数的()k k N *∈叫做“期盼数",则在区间[]1,2016所有的“期盼数”的和为( )A .2026B .2036C .4072D .4076二.填空题:(本大题共5小题,每小题5分,共25分,把答案填在答卷纸的相应位置上)11.已知函数()2211,1x x f x x ax x ⎧+<⎪=⎨+≥⎪⎩,,若()()04f f a =,则实数a 等于______ 12.已知αβ、均为锐角,()111cos ,cos 714ααβ=+=-,则角β为_______13.已知函数()()()200x x f x x x x ≤⎧⎪=⎨->⎪⎩,若函数()()g x f x m =-有三个不同的零点,则实数m 的取值范围是___________14.已知数列{}n a 满足()1111,2,2nn n a a a n +⎛⎫=+=≥ ⎪⎝⎭212222n n n S a a =⋅+⋅+⋅…+a 类比课本中推导等比数列前n 项和公式的方法,可求得132n n n S a +-⋅=_________15.已知函数()y f x =是定义在R 上的偶函数,对于x ∈R ,都有()()()42f x f x f +=+成立,当[]120,2x x ∈、且12x x ≠时,都有()()12120f x f x x x -<-。
2017届高三第二次模拟考试 数学理 (含答案)word版

2017年高考考前适应性训练数学(理工农医类)本试卷共4页,分第I 卷(选择题)和第II 卷(非选择题)两部分.共150分.考试时间120分钟.第I 卷(选择题 共60分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再改涂其它答案标号.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.复数ii ++113的虚部是A.i -B.1-C.iD.12.设集合⎭⎬⎫⎩⎨⎧=+=143422y x x A ,{}2x y y B ==,则B A ⋂=A.[]2,2-B.[]2,0C.0.4D.0.83.在某项测量中,测量结果ξ服从正态分布()(σσ2,1N >)0,若ξ在(0.2)内取值的概率为0.8,则ξ在()1,0内取值的概率为 A.0.1B.0.2C.0.4D.0.84. 已知两条直线 a ,b 与两个平面α、αβ⊥b ,,则下列命题中正确的是 ①若,//αa 则b a ⊥;②若b a ⊥,则a//α;③若β⊥b ,则βα// ; ④若βα⊥,则b//β. A. ①③B.②④C.①④D.②③5.已知点P 在圆522=+y x 上,点Q (0,—1),则线段PQ 的中点的轨迹方程是 A.022=-+x y xB.0122=-++y y x C.0222=--+y y xD.022=+-+y x y x6.已知a x x p ≥-+-910:的解集为R ,aq 1:<1,则⌝p 是q 的 A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.为了普及环保知识,增强环保意识,某大学从理工类专业的A 班和文史类专业的B 班各抽取20名同学参加环保知识测试.统计得到成绩与专业的列联表: 附:参考公式及数据: (1)卡方统计量()()()()()22122111222112112211222112n n n n n n n n n n n n n x ++++-=(其中)22211211n n n n n +++=;(2)独立性检验的临界值表:则下列说法正确的是A.有99%的把握认为环保知识测试成绩与专业有关B.有99%的把握认为环保知识测试成绩与专业无关C.有95%的把握认为环保知识测试成绩与专业有关D.有95%的把握认为环保知识测试成绩与专业无关8.函数()(()⎩⎨⎧≤++-=0142ln 2x x x x x x x f 的零点个数为A.0B.1C.2D.39.如图为某个几何体的三视图,则该几何体的侧面积为 A.π416+ B.π412+ C.π816+ D.π812+10.已知函数()x f 的图象向左平移1个单位后关于y 轴对称,当x 2>x 1>1时,()()[]()1212x x x f x f --<0恒成立,设()()3,2,21f c f b f a ==⎪⎭⎫ ⎝⎛-=,则a 、b 、c 的大小关系为 A.c >a >bB.c >b >aC.a >c >bD.b >a >c11.已知双曲线154:22=-y x C 的左、右焦点分别为F 1、F 2,P 为C 的右支上一点,且212F F PF =,则21PF ⋅等于A.24B.48C.50D.5612.对于定义域为D 的函数()x f ,若存在区间[](a D b a M ⊆=,<)b ,使得(){}M M x x f y y =∈=,,则称区间M 为函数()x f 的“等值区间”.给出下列四个函数:①();2xx f =②();3x x f =③();sin x x f =④().1log 2+=x x f则存在“等值区间”的函数的个数是A.1个B.2个C.3个D.4个>)0第II 卷(非选择题 共90分)注意事项:1.将第II 卷答案用0.5mm 的黑字签字笔答在答题纸的相应位置上。
2017高考数学山东卷理(附参考答案及详解)
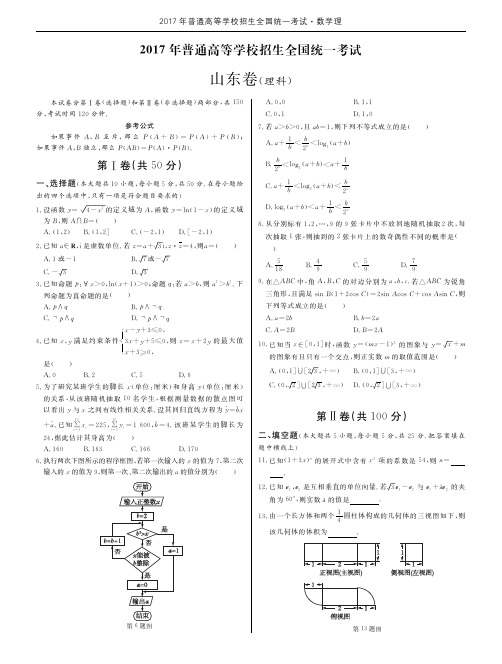
) /?$*%' 0*0" '"0* 0*0! '"0* '8@"' 0*0" '"0* $!.*8@
"%###
) /$*%\$!#.6%]^_`!
)
/$*%#/$!%#M"+*
#
! "
!
&
*.
! +
'*.*'"*.*.+.89:"$*.+%#
)
+ "*
#89:"$*.+%#*.
! +
!
(?, )¿(, )NSÁÂ!
!3!$本小题满 分 !$ 分%已 知 !#*"是 各 项 均 为 正 数 的 等 比 数 列#且 #! /#$ '(##( 0#$ '$! $!%求 数 列 !#* "的 通 项 公 式 ' $$%如图#在平面直角坐标系 #4- 中#依次连接点 6!$#!#!%#6$ $#$#$%#, #6*/! $#*/!#*/!%得 到 折 线 6!6$ ,6*/!#求 由 该 折 线 与 直 线 -'###'#!##'#*/!所 围 成 的 区 域 的 面 积 K*!
$$%当 "$'(#"&'$时#求二面角 07"J7% 的大小!
第 !2 题 图
年 普 通 高 等 学 校 招 生 全 国 统 一 考 试 数 学 理
!.!$本小题满分 !$ 分%在 心 理 学 研 究 中#常 采 用 对 比 试 验 的 方 法 评价不同心理暗 示 对 人 的 影 响#具 体 方 法 如 下&将 参 加 试 验 的 志愿者随机分成 两 组#一 组 接 受 甲 种 心 理 暗 示#另 一 组 接 受 乙 种心理暗示#通过对比这两组志 愿 者 接 受 心 理 暗 示 后 的 结 果 来 评 价 两 种 心 理 暗 示 的 作 用 !现 有 & 名 男 志 愿 者 "!#"$#"(#"-# ""#"& 和 - 名 女 志 愿 者 $!#$$#$(#$-#从 中 随 机 抽 取 " 人 接 受 甲 种 心 理 暗 示 #另 " 人 接 受 乙 种 心 理 暗 示 ! $!%求接受 甲 种 心 理 暗 示 的 志 愿 者 中 包 含 "! 但 不 包 含 $! 的 概率' $$%用 8 表示接受乙种心理暗 示 的 女 志 愿 者 人 数#求 8 的 分 布 列与数学期望08 !
2017年高考(252)山东省莱州一中2017届高三第二次质量检测

2017年高考(252)山东省莱州一中2017届高三第二次质量检测山东省莱州一中2017届高三第二次质量检测语文试题塑造自我:不断学习,不轻易放弃,保持热情,始终有昂扬的姿态,你就是那个既有活力又青春满格的自己。
第I卷(共36分)一、阅读下面一段文字,完成1-3题。
(每小题3分,共15分)齐白石授徒时有一句名言:学我者生,似我者死。
李苦禅谨记老师的这句话,因此他学的是老师独到的艺术匠心,而不是简单地描摩老师的艺术样式。
在绘画(题材/体裁)上,齐白石一生为万虫写照、百鸟传神,万虫百鸟寄托了齐白石对自然生活的思念。
而李苦禅则有意避开老师常画的风物,更强调对象的象征意义,(赋予/付与)对象某些人格内涵。
如综合了鹰、鹫等多种猛禽特点的雄鹰形象,是阳刚的化身;风中伫立的劲竹是刚正不阿的人格写照;雪侮霜欺芳益烈的白梅则表现了坚贞不屈的品格……在艺术修养方面,齐白石是诗、书、画、印四全,自谓印第一,诗第二,书第三,画第四;李苦禅未着意印学,诗不及齐,书法过之,较之老师又增武术戏曲之功。
李苦禅认为:齐老师治印是以金石艺术融入大写意,我把要这功夫尽用在读碑贴和欣赏铜器图文和砖石刻画的拓片上——体会它的金石味道,融进自己的书画里,习得齐派治印的真精神。
此外,李苦禅对《易经》很感兴趣,他在绘画中追求一种禅境,齐白石赞扬他能将有法为无法。
齐白石爱画暮鸦归林,从鸟的朝飞暮还中(领悟/领略)人生的真谛:李苦禅每临自然生机景象,往往喃喃念叨陶渊明的诗句此中有真意,欲辨已忘言。
1.文中加点的字的注音和加点词语的文字,都正确的一项是()A.授徒伫(ch)立B.描摩劲(jng)竹C.念叨着(zhu)意D.碑贴拓(t)片2.依次选用文中括号里的词语,最恰当的一项是()A.题材付与领略B.体裁付与领略C.题材赋予领悟D.体裁赋予领悟3.文中画线处的标点,使用错误的一项是()A.B.C.D.4.下列各句中加点成语的使用,全部正确的一项是()伴随着老龄化程度逐步加深,人社部新闻发言人李昌民明确表示,人社部将进行长期护理保险制度的顶层设计和实践探索,子女带薪护理方案呼之欲出。
2017年高考山东理科数学试题及答案(word解析版)

2017年普通高等学校招生全国统一(tǒngyī)考试(山东(shān dōnɡ)卷)数学(shùxué)(理科(lǐkē))第Ⅰ卷(共50分)一、选择题:本大题共10小题,每小题5分,在每小题给出的四个选项中,只有(zhǐyǒu)一项是符合题目要求的.(1)【2017年山东,理1,5分】设函数的定义域为,函数的定义域为,则()(A)(B)(C)(D)【答案】D【解析】由得,由得,,故选D.(2)【2017年山东,理2,5分】已知,是虚数单位,若,,则()(A)1或(B)或(C)(D)【答案】A【解析】由得,所以,故选A.(3)【2017年山东,理3,5分】已知命题:,;命题:若,则,下列命题为真命题的是()(A)(B)(C)(D)【答案】B【解析】由时有意义,知p是真命题,由可知q是假命题,即p,均是真命题,故选B.(4)【2017年山东,理4,5分】已知、满足约束条件,则的最大值是()(A)0 (B)2 (C)5 (D)6【答案】C【解析】由画出可行域及直线如图所示,平移20x y+=发现,当其经过直线与的交点时,2=+最大为z x y,故选C.(5)【2017年山东,理5,5分】为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,设其回归直线方程为,已知,,,该班某学生的脚长为24,据此估计其身高为()(A)160 (B)163 (C)166 (D)170【答案】C【解析】,故选C.(6)【2017年山东(shān dōnɡ),理6,5分】执行(zhíxíng)两次如图所示的程序框图,若第一次输入的x值为7,第二次输入(shūrù)的x值为9,则第一次、第二次输出(shūchū)的值分别(fēnbié)为()(A)0,0 (B)1,1 (C)0,1 (D)1,0【答案】D【解析】第一次;第二次,故选D.(7)【2017年山东,理7,5分】若,且,则下列不等式成立的是()(A)(B)(C)(D)【答案】B【解析】,故选B.(8)【2017年山东,理8,5分】从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到在2张卡片上的数奇偶性不同的概率是()(A)(B)(C)(D)【答案】C【解析】,故选C.(9)【2017年山东,理9,5分】在中,角A、B、的对边分别为a、、,若ABC∆为锐角三角形,且满足,则下列等式成立的是()(A)(B)(C)(D)【答案】A【解析】所以,故选A.(10)【2017年山东,理10,5分】已知当时,函数的图象与的图象有且只有一个交点,则正实数的取值范围是()(A)(B)(C)(D)【答案】B【解析】当时,,2=+单调递=-单调递减,且,y x m(1)y mx增,且,此时有且仅有一个交点;当时,,2=-在y mx(1)上单调递增,所以要有且仅有一个交点,需,故选B.第II卷(共100分)二、填空题:本大题共5小题,每小题5分(11)【2017年山东,理11,5分】已知的展开式中含有的系数是54,则.【答案】4【解析】,令得:,解得.(12)【2017年山东,理12,5分】已知、是互相垂直的单位向量,若与的夹角为,则实数的值是 . 【答案(dá àn)】【解析(jiě xī)】,,,,解得:.(13)【2017年山东(shān dōnɡ),理13,5分】由一个(yī ɡè)长方体和两个圆柱体构成(gòuchéng)的几何体的三视图如图,则该几何体的体积为 . 【答案】【解析】该几何体的体积为.(14)【2017年山东,理14,5分】在平面直角坐标系中,双曲线(,)的右支与焦点为的抛物线()交于A 、B 两点,若,则该双曲线的渐近线方程为 .【答案】【解析】,因为,所以渐近线方程为22y x =±. (15)【2017年山东,理15,5分】若函数(是自然对数的底数)在的定义域上单调递增,则称函数()f x 具有M 性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
烟台莱州一中 2017级高三第二次质量检测数学试题(理)一、选择题(本大题共12小题,每题5分,共60分。
在每小题给出的四个选项中选择一个符合题目要求的选项)1.设集合S {x ||x 2|3},T {x |a x a 8},S T R =->=<<+⋃=,则a 的取值范围是( ) A.3a 1-<<- B.3a 1-≤≤- C.a 3a 1≤-≥-或 D.a 3a 1<->-或2.若f (x)是幂函数,且满足f (4)3f (2)=,则1f ()2= .A.3B.-3C.13D.13-3.已知正三棱柱111ABC A B C -的棱长与底面边长相等,则1AB 与侧面11ACC A 所成角的正弦值等于( )4.如右图,在平行四边形ABCD 中,O 是对角线AC ,BD 的交点,N 是线段OD 的中点,AN 的延长线与CD 交于点E ,则下列说法 错误的是( )A.AC AB AD =+B.BD AD AB =-C.11AO AB AD 22=+D.5AE AB AD 3=+5.实数m 满足方程x 122log x 0-=,则有A.m 21m <<B.m m 12<<C.m 1m 2<<D.m 12m <<6.某几何体的三视图如图所示,则它的体积是A.283π-B.8-3πC.82π-D.23π 7.在等比数列n {a }中,56a a a(a 0)+=≠,15165a a b +=,则2526a a +等于( )A.b aB.22b aC.2b aD.2ba8.曲线x y e =在点2(2,e )处的切线与坐标轴所围三角形的面积( )A.29e 4B.22aC.2e D.2e 29.各项均不为零的等差数列n {a }中2n n 1n 1a a a 0(n N*,n 2)-+--=∈≥,则2009S 等于( ) A.4018 B.2009 C.2 D.010.已知a 、b 、l 表示三条不同的直线,αβγ、、表示三个不同的平面,有下列四个命题: ①若,b αβαβγ⋂=⋂=且a //b,则//αγ;②若a 、b 相交,且都在αβ、外,a //,a //,b //,b //αβαβ,则//αβ;③若αβ⊥,a,b ,a b αββ⋂=⊂⊥,则b α⊥; ④若a ,b ,l a,l b,αα⊂⊂⊥⊥则l α⊥. 其中正确的是( )A.①②B.②③C.①④D.③④.11.在ABC ∆中,AB 2==,若O 为ABC ∆内部的一点,且满足OA OB OC 0++=,则AO BC ⋅=( )A.12B.25C.13D.1412.若函数a f (x)log (x b)=+的图象如下图,其中a,b 为常数,则函数2g(x)a b =+的大致图象是( )二、填空题(本大题共4小题,共16分) 13.积分2e112x ()dx x+⎰的值是14.设x,y 满足约束条件x y 3x y 12x y 3+≥⎧⎪-≥-⎨⎪-≤⎩,若目标函数x y z (a 0,b 0)a b =+>>的最大值为10,则5a 4b +的最小值为 .15.设n S 表示等差数列n {a }的前n 项和,且9n S 18,S 240==,若n 4a 30(n 9)-=>,则n= . 16.关于函数2x 1f (x)lg (x 0,x R)|x |+=≠∈有下列命题:①函数y f (x)=的图象关于y 轴对称;②在区间(-∞,0)上,函数y f (x)=是减函数; ③函数f (x)的最小值为lg 2;④在区间(1,+∞)上,函数f (x)是增函数。
其中正确命题序号为 三、解答题(本大题共6小题,共74分。
应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)若函数2f (x)2x 2cos x m =++在区间[0,2π]上的最大值为6, (1)求常数m 的值(2)作函数f (x)关于y 轴的对称图象得函数1f (x)的图象,再把1f (x)的图象向右平移4π个单位得2f (x)的图象,求函数2f (x)的单调递减区间.18.(本小题满分12分)如图,在直三棱柱ABC-111A B C 中,A B A C 5==,D ,E 分别为BC ,1BB 的中点,1BB 的中点,四边形11B BCC 是边长为6的正方形. (1)求证:1A B //平面1AC D ; (2)求证:CE ⊥平面1AC D ;(3)求二面角1C AC D --的余弦值.19.(本小题满分12分)某商场销售某种商品的经验表明,该商品每日的销售量y (单位一:千克)与销售价格x (单位:元/千克)满足关系式2ay 10(x 6)x 3=+--其中3x 6<<,a 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
(1)求a 的值(2)若该商品的成本为3元/千克,试确定销售价格x 的值,使商场每日销售该商品所获得的利润最大。
20.(本小题满分12分)在ABC ∆中,若向量m (sin A sin B sin C),n (2sin A sin C,sin A sin B)=--=-+且m 与n 共线 (1)求角B ;(2)若3sin A 5=,求cosC 的值.21.(本小题满分12分)已知数列{n a }的前n 项和为n S ,数列n {b }的前n 项和为n T ,n {b }为等差数列且各项均为正数,*1n 1n 123a 1,a 2S 1(n N ),b b b 15+==+∈++= (1)求数列{n a }的通项公式;(2)若112233a b ,a b ,a b +++成等比数列,求12n111T T T ++…+22.(本小题满分14分)已知函数ln(1x f (x)x+=)(1)确定y f (x)=在(0,+∞)上的单调性;(2)设3h(x)xf (x)x ax =--在(0,2)上有极值,求a 的取值范围.第二次质量检测数学试题(理)答案1.A2.C3.B4.D5.B6.A7.C8.D9.A 10.B 11.C 12.D 13.2e 14.8 15.15 16.①③④17.解:f (x)2x cos 2x 1m +++ (1)=2sin(2x )1m 6π+++ (2)∵72x 666πππ≤+≤∴1sin(2x )126π-≤+≤ (3)∴m f (x)3m ≤≤+ (4)∴3+m=6 (5)∴m=3,f (x)2sin(2x )46π=++ (6)(2)12f (x)2sin(2x )46f (x)2sin(2x )462f (x)2sin(2(x ))42sin(2x )4946322k 2x 2k 232ππππππππππ=++=-++=--++=--+-+≤-≤+…………………………………… (11)2f (x )的单调递减区间是7k ,k k Z 1212ππππ⎡⎤++∈⎢⎥⎣⎦………………12 18.(1)证明:连结1A C ,与1AC 交于O 点,连结OD. 因为O ,D 分别为1A C 和BC 的中点, 所以OD//1A B 。
又OD 1AC D ⊂平面, 11A B AC D ⊄平面,所以11A B //AC D 平面.…………………………4分 (2)证明:在直三棱柱111ABC A B C -中, 1B B A B C ,A B C ⊥⊂平面又A D 平面, 所以1BB AD ⊥.因为AB AC,D =为BC 中点, 所以AD BC .⊥又1BC BB B ⋂=, 所以11AD B BCC ⊥平面. 又11CE B BCC ,AD CE ⊂⊥平面所以因为四边形11B BCC 为正方形,D ,E 分别为BC ,1BB 的中点, 所以11Rt CBE Rt C CD ,CC D BCE ∆≅∆∠=∠. 所以1BCE C DC 90∠+∠=. 所以1C D CE ⊥11AD C D D CE AC D⋂=⊥又所以平面 ………………………………8分(3)解:如图,以11B C 的中点G 为原点,建立空间直角坐标系, 则A (0,6,4),E (3,3,0) ,C (-3,6,0) ,1C (3,0,0)-.由(Ⅱ)知1CE AC D,CE=63,0⊥-平面所以(,)为平面1AC D 的一个法向量。
设n (x,y,z)=为平面1ACC 的一个法向量, 1AC (3,0,4),CC (0,6,0).=--=- 由1n AC 0,3x+4z=0-6y=0.n CC 0,⎧⋅=-⎧⎪⎨⎨⋅=⎩⎪⎩,可得令x 1=,则3y 0,z 4==-. 所以3n (1,0,)4=-.从而CE n cos CE n |CE ||n |⋅〈⋅〉==⋅.因为二面角1C AC D --为锐角, 所以二面角1C AC D --.……………………12分 19.解:(1)因为x=5时,y=11,所以a 1011,a 22+== (2)由(1)可知,该商品每日的销售量22y 10(x 6)x 3=+--, 所以商场每日销售该商品所获得的利润 222f (x)(x 3)[10(x 6)]210(x 3)(x 6),3x 6x 3=-+-=+--<<- 从而,2f '(x)10[(x 6)2(x 3)(x 6)]30(x 4)(x 6)=-+--=-- 于是,当x 变化时,f '(x),f (x)的变化情况如下表:由上表可得,x=4是函数f (x )在区间(3,6)内的极大值点,也是最大值点;所以, 当x=4时,函数f(x)取得最大值,且最大值等于42。
答:当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大。
20.(1)依题意得22sin Asin B sin(A A sin C)-=+-2Asin C sin C -,由正弦定理得:222a b c -=-, 222a c b ∴+-=由余弦定理知:222a c b cos BB 2ac 4π+-==∴=.(2)∵3sin A ,sin A A B 5=∴∴<又4B ,A ,cosA 445ππ=∴<∴=, ∴cosC=333cos(A)cos cos A sin sin A 444πππ-=+=21.解:(1)211a 2S 133a =+==当n 2≥时,n 1n n n 1n a a (2S 1)(2S 1)2a +--=+-+=………………………………3分 ∴n 12n 1n,2n 1a aa 3a 3a 33a a ++====即又 ∴数列{}n a 是首项a 1=,公比为3的等比数列…………………………4分从而得:n 1n a 3-= …………………………6分 (2)设数列{}n b 的公差为d(d 0)>∵32T 15,b 5=∴= 依题意有2221133(a b )(a b )(a b ),64(5d 1)(5d 9)+=++∴=-+++ d 2d 10(==-解之得或舍去) ……………………………………8分故2n n(n 1)T 3n 22n 2n 2-=+⨯=+ ……………………………………10分 12n 1111111111=()()T T T 212n 34n 1111132n 3()=12212n 1n 242(n 1)(n 2)⎡⎤++++-++⎢⎥⎣⎦⎡⎤+⎛⎫+-+- ⎪⎢⎥++++⎝⎭⎣⎦所以…+…+…++2…………分22.解:(1)由题知2xln(1x)x 1f '(x)x -++=.设xg x ln(1x)(x 0),x 1=-+>+() 则2211xg '(x)0x 1(x 1)(x 1)-=-=<+++在(0,+∞)恒成立, ∴g(x)在(0,+∞)上单调递减, ∴g(x)<g(0)=0, ∴f '(x)0<.因此f (x)在(0,+∞)上单调递减。
