算法设计与分析1
算法设计与分析-习题参考答案

算法设计与分析基础习题1.15..证明等式gcd(m,n)=gcd(n,m mod n)对每一对正整数m,n都成立.Hint:根据除法的定义不难证明:●如果d整除u和v, 那么d一定能整除u±v;●如果d整除u,那么d也能够整除u的任何整数倍ku.对于任意一对正整数m,n,若d能整除m和n,那么d一定能整除n和r=m mod n=m-qn;显然,若d能整除n和r,也一定能整除m=r+qn和n。
数对(m,n)和(n,r)具有相同的公约数的有限非空集,其中也包括了最大公约数。
故gcd(m,n)=gcd(n,r)6.对于第一个数小于第二个数的一对数字,欧几里得算法将会如何处理?该算法在处理这种输入的过程中,上述情况最多会发生几次?Hint:对于任何形如0<=m<n的一对数字,Euclid算法在第一次叠代时交换m和n, 即gcd(m,n)=gcd(n,m)并且这种交换处理只发生一次.7.a.对于所有1≤m,n≤10的输入, Euclid算法最少要做几次除法?(1次)b. 对于所有1≤m,n≤10的输入, Euclid算法最多要做几次除法?(5次)gcd(5,8)习题1.21.(农夫过河)P—农夫W—狼G—山羊C—白菜2.(过桥问题)1,2,5,10---分别代表4个人, f—手电筒4. 对于任意实系数a,b,c, 某个算法能求方程ax^2+bx+c=0的实根,写出上述算法的伪代码(可以假设sqrt(x)是求平方根的函数)算法Quadratic(a,b,c)//求方程ax^2+bx+c=0的实根的算法//输入:实系数a,b,c//输出:实根或者无解信息If a≠0D←b*b-4*a*cIf D>0temp←2*ax1←(-b+sqrt(D))/tempx2←(-b-sqrt(D))/tempreturn x1,x2else if D=0 return –b/(2*a)else return “no real roots”else //a=0if b≠0 return –c/belse //a=b=0if c=0 return “no real numbers”else return “no real roots”5.描述将十进制整数表达为二进制整数的标准算法a.用文字描述b.用伪代码描述解答:a.将十进制整数转换为二进制整数的算法输入:一个正整数n输出:正整数n相应的二进制数第一步:用n除以2,余数赋给Ki(i=0,1,2...),商赋给n第二步:如果n=0,则到第三步,否则重复第一步第三步:将Ki按照i从高到低的顺序输出b.伪代码算法DectoBin(n)//将十进制整数n转换为二进制整数的算法//输入:正整数n//输出:该正整数相应的二进制数,该数存放于数组Bin[1...n]中i=1while n!=0 do {Bin[i]=n%2;n=(int)n/2;i++;}while i!=0 do{print Bin[i];i--;}9.考虑下面这个算法,它求的是数组中大小相差最小的两个元素的差.(算法略) 对这个算法做尽可能多的改进.算法MinDistance(A[0..n-1])//输入:数组A[0..n-1]//输出:the smallest distance d between two of its elements习题1.31.考虑这样一个排序算法,该算法对于待排序的数组中的每一个元素,计算比它小的元素个数,然后利用这个信息,将各个元素放到有序数组的相应位置上去.a.应用该算法对列表‖60,35,81,98,14,47‖排序b.该算法稳定吗?c.该算法在位吗?解:a. 该算法对列表‖60,35,81,98,14,47‖排序的过程如下所示:b.该算法不稳定.比如对列表‖2,2*‖排序c.该算法不在位.额外空间for S and Count[] 4.(古老的七桥问题)习题1.41.请分别描述一下应该如何实现下列对数组的操作,使得操作时间不依赖数组的长度. a.删除数组的第i 个元素(1<=i<=n)b.删除有序数组的第i 个元素(依然有序) hints:a. Replace the i th element with the last element and decrease the array size of 1b. Replace the ith element with a special symbol that cannot be a value of the array ’s element(e.g., 0 for an array of positive numbers ) to mark the i th position is empty. (―lazy deletion ‖)第2章 习题2.17.对下列断言进行证明:(如果是错误的,请举例) a. 如果t(n )∈O(g(n),则g(n)∈Ω(t(n)) b.α>0时,Θ(αg(n))= Θ(g(n)) 解:a. 这个断言是正确的。
第1章 算法设计与分析 绪论

• 求gcd(m,n)的原理: (结构化的描述) • 第一步:如果n=0,返回m的值作为结果,结束;否则进 入第二步。 • 第二步:用n除m,余数赋值给r,进入第三步。 • 第三步:将n的值赋给m,将r的值赋给n,返回第一步。
例: gcd(60,24)=? 1-1、m=60, n=24 1-2、60 mod 24=12, r=12, 1-3、m=24, n=12 2-1、24 mod 12=0,r=0 2-2、m=12, n=0 2-3、条件“n=0”满足,返回gcd(m, n)=m=12
• 算法二:连续整数检测法
第一步:将min{m,n}赋值给t。 第二步:m除以t,如果余数为0,进入第三步,否则进入第 四步。 第三步:n除以t,如果余数为0,返回t的值;否则进入第四 步。 第四步:把t的值减1,返回第三步。 例:gcd(60, 24) t=min{60, 24}=24, m=60, n=24 60mod24=12≠0, t=23, 24 mod 23=1 ≠0 t=22, 24 mod 22=2 ≠0 t=21, 24 mod 21=3 ≠0 ….. t=12, 24 mod 12=0, 返回gcd(m, n)=t=12
第1章 绪论
1.1 什么是算法 1.2 算法问题求解基础 1.3 重要问题类型 1.4 基本数据结构 本章小结
1.1 算法的概念
• 没有一个统一的严谨的定义。一般而言, 对于计算机算法的概念是这样描述的:算 法是在有限步骤内求解某一问题所使用的 一组定义明确的指令。 • 本书采用的定义:An algorithm is a sequence of unambiguous instructions for solving a problem=算法是求解某一 问题所使用的一系列清晰的指令。
算法设计与分析实验报告三篇

算法设计与分析实验报告一实验名称统计数字问题评分实验日期2014 年11 月15 日指导教师姓名专业班级学号一.实验要求1、掌握算法的计算复杂性概念。
2、掌握算法渐近复杂性的数学表述。
3、掌握用C++语言描述算法的方法。
4.实现具体的编程与上机实验,验证算法的时间复杂性函数。
二.实验内容统计数字问题1、问题描述一本书的页码从自然数1 开始顺序编码直到自然数n。
书的页码按照通常的习惯编排,每个页码都不含多余的前导数字0。
例如,第6 页用数字6 表示,而不是06 或006 等。
数字计数问题要求对给定书的总页码n,计算出书的全部页码中分别用到多少次数字0,1,2, (9)2、编程任务给定表示书的总页码的10 进制整数n (1≤n≤109) 。
编程计算书的全部页码中分别用到多少次数字0,1,2, (9)三.程序算法将页码数除以10,得到一个整数商和余数,商就代表页码数减余数外有多少个1—9作为个位数,余数代表有1—余数本身这么多个数作为剩余的个位数,此外,商还代表1—商本身这些数出现了10次,余数还代表剩余的没有计算的商的大小的数的个数。
把这些结果统计起来即可。
四.程序代码#include<iostream.h>int s[10]; //记录0~9出现的次数int a[10]; //a[i]记录n位数的规律void sum(int n,int l,int m){ if(m==1){int zero=1;for(int i=0;i<=l;i++) //去除前缀0{ s[0]-=zero;zero*=10;} }if(n<10){for(int i=0;i<=n;i++){ s[i]+=1; }return;}//位数为1位时,出现次数加1//位数大于1时的出现次数for(int t=1;t<=l;t++)//计算规律f(n)=n*10^(n-1){m=1;int i;for(i=1;i<t;i++)m=m*10;a[t]=t*m;}int zero=1;for(int i=0;i<l;i++){ zero*= 10;} //求出输入数为10的n次方int yushu=n%zero; //求出最高位以后的数int zuigao=n/zero; //求出最高位zuigaofor(i=0;i<zuigao;i++){ s[i]+=zero;} //求出0~zuigao-1位的数的出现次数for(i=0;i<10;i++){ s[i]+=zuigao*a[l];} //求出与余数位数相同的0~zuigao-1位中0~9出现的次数//如果余数是0,则程序可结束,不为0则补上所缺的0数,和最高位对应所缺的数if(yushu==0) //补上所缺的0数,并且最高位加1{ s[zuigao]++;s[0]+=l; }else{ i=0;while((zero/=10)>yushu){ i++; }s[0]+=i*(yushu+1);//补回因作模操作丢失的0s[zuigao]+=(yushu+1);//补回最高位丢失的数目sum(yushu,l-i-1,m+1);//处理余位数}}void main(){ int i,m,n,N,l;cout<<"输入数字要查询的数字:";cin>>N;cout<<'\n';n = N;for(i=0;n>=10;i++){ n/=10; } //求出N的位数n-1l=i;sum(N,l,1);for(i=0; i<10;i++){ cout<< "数字"<<i<<"出现了:"<<s[i]<<"次"<<'\n'; }}五.程序调试中的问题调试过程,页码出现报错。
《算法设计与分析》实验报告实验一...

《算法设计与分析》实验报告实验一递归与分治策略应用基础学号:**************姓名:*************班级:*************日期:2014-2015学年第1学期第九周一、实验目的1、理解递归的概念和分治法的基本思想2、了解适用递归与分治策略的问题类型,并能设计相应的分治策略算法3、掌握递归与分治算法时间空间复杂度分析,以及问题复杂性分析方法二、实验内容任务:以下题目要求应用递归与分治策略设计解决方案,本次实验成绩按百分制计,完成各小题的得分如下,每小题要求算法描述准确且程序运行正确。
1、求n个元素的全排。
(30分)2、解决一个2k*2k的特殊棋牌上的L型骨牌覆盖问题。
(30分)3、设有n=2k个运动员要进行网球循环赛。
设计一个满足要求的比赛日程表。
(40分)提交结果:算法设计分析思路、源代码及其分析说明和测试运行报告。
三、设计分析四、算法描述及程序五、测试与分析六、实验总结与体会#include "iostream"using namespace std;#define N 100void Perm(int* list, int k, int m){if (k == m){for (int i=0; i<m; i++)cout << list[i] << " ";cout << endl;return;}else{for (int i=m; i<k; i++){swap(list[m], list[i]);Perm(list, k, m+1);swap(list[m], list[i]);}}}void swap(int a,int b){int temp;temp=a;a=b;b=temp;}int main(){int i,n;int a[N];cout<<"请输入排列数据总个数:";cin>>n;cout<<"请输入数据:";for(i=0;i<n;i++){cin>>a[i];}cout<<"该数据的全排列:"<<endl;Perm(a,n,0);return 0;}《算法设计与分析》实验报告实验二递归与分治策略应用提高学号:**************姓名:*************班级:*************日期:2014-2015学年第1学期一、实验目的1、深入理解递归的概念和分治法的基本思想2、正确使用递归与分治策略设计相应的问题的算法3、掌握递归与分治算法时间空间复杂度分析,以及问题复杂性分析方法二、实验内容任务:从以下题目中任选一题完成,要求应用递归与分治策略设计解决方案。
算法设计和分析习题答案解析1_6章

习题11. 图论诞生于七桥问题。
出生于瑞士的伟大数学家欧拉(Leonhard Euler ,1707—1783)提出并解决了该问题。
七桥问题是这样描述的:一个人是否能在一次步行中穿越哥尼斯堡(现在叫加里宁格勒,在波罗的海南岸)城中全部的七座桥后回到起点,且每座桥只经过一次,图1.7是这条河以及河上的两个岛和七座桥的草图。
请将该问题的数据模型抽象出来,并判断此问题是否有解。
七桥问题属于一笔画问题。
输入:一个起点输出:相同的点1, 一次步行2, 经过七座桥,且每次只经历过一次3, 回到起点该问题无解:能一笔画的图形只有两类:一类是所有的点都是偶点。
另一类是只有二个奇点的图形。
2.在欧几里德提出的欧几里德算法中(即最初的欧几里德算法)用的不是除法而是减法。
请用伪代码描述这个版本的欧几里德算法1.r=m-n2.循环直到r=02.1 m=n2.2 n=r2.3 r=m-n3 输出m3.设计算法求数组中相差最小的两个元素(称为最接近数)的差。
要求分别给出伪代码和C++描述。
//采用分治法//对数组先进行快速排序//在依次比较相邻的差#include <iostream>using namespace std;int partions(int b[],int low,int high) {图1.7 七桥问题int prvotkey=b[low];b[0]=b[low];while (low<high){while (low<high&&b[high]>=prvotkey)--high;b[low]=b[high];while (low<high&&b[low]<=prvotkey)++low;b[high]=b[low];}b[low]=b[0];return low;}void qsort(int l[],int low,int high){int prvotloc;if(low<high){prvotloc=partions(l,low,high); //将第一次排序的结果作为枢轴 qsort(l,low,prvotloc-1); //递归调用排序由low 到prvotloc-1qsort(l,prvotloc+1,high); //递归调用排序由 prvotloc+1到 high}}void quicksort(int l[],int n){qsort(l,1,n); //第一个作为枢轴,从第一个排到第n个}int main(){int a[11]={0,2,32,43,23,45,36,57,14,27,39};int value=0;//将最小差的值赋值给valuefor (int b=1;b<11;b++)cout<<a[b]<<' ';cout<<endl;quicksort(a,11);for(int i=0;i!=9;++i){if( (a[i+1]-a[i])<=(a[i+2]-a[i+1]) )value=a[i+1]-a[i];elsevalue=a[i+2]-a[i+1];}cout<<value<<endl;return 0;}4.设数组a[n]中的元素均不相等,设计算法找出a[n]中一个既不是最大也不是最小的元素,并说明最坏情况下的比较次数。
算法设计与分析-王-第1章-算法设计基础

2)有没有已经解决了的类似问题可供借鉴?
1.4 算法设计的一般过程
在模型建立好了以后,应该依据所选定的模型对问 题重新陈述,并考虑下列问题: (1)模型是否清楚地表达了与问题有关的所有重要
的信息?
(2)模型中是否存在与要求的结果相关的数学量? (3)模型是否正确反映了输入、输出的关系? (4)对这个模型处理起来困难吗?
程序设计研究的四个层次:
算法→方法学→语言→工具
理由2:提高分析问题的能力
算法的形式化→思维的逻辑性、条理性
1.2 算法及其重要特性
一、算法以及算法与程序的区别
例:欧几里德算法——辗转相除法求两个自然数 m 和 n 的最大公约数
m n
欧几里德算法
r
1.2 算法及其重要特性
欧几里德算法
① 输入m 和nห้องสมุดไป่ตู้如果m<n,则m、n互换;
对不合法的输入能作出相适应的反映并进行处理。 (2) 健壮性(robustness): 算法对非法输入的抵抗能力, 即对于错误的输入,算法应能识别并做出处理,而不是 产生错误动作或陷入瘫痪。 (3)可读性:算法容易理解和实现,它有助于人们对算 法的理解、调试和修改。 (4) 时间效率高:运行时间短。 (5) 空间效率高:占用的存储空间尽量少。
算法设计与分析
Design and Analysis of Computer Algorithms
高曙
教材:
算法设计与分析(第二版),清华大学出版社,王红梅, 胡明 编著
参考书目:
Introduction to Algorithms, Third Edition, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest,机械工 业出版社,2012
算法设计与分析(第2版) 郑宗汉 第1章-1

8
Байду номын сангаас
学习要求
深刻理解每一类算法的思想及其实现
能熟练运用所学知识解决实际问题
培养提高计算思维能力
9
考核方式
Homework and Reading: 20%
Final Exam (Written Test): 80%
10
第1章 算法的基本概念
1.1 引言
1.1.1 算法的定义和特性
c %3 0
(1.1.3)
16
1.1.2 算法的设计和复杂性分析
百鸡问题的穷举法
输入:所购买的3种鸡的总数目n 输出:满足问题的解的数目k,公鸡,母鸡,小鸡的只数g[],m[],s[]
1. void chicken_question(int n, int &k, int g[], int m[], int s[]) 2. { 3. int a,b,c; 分析发现:只能买到n/5 4. k = 0; 只公鸡,n/3只母鸡,将 5. for (a = 0; a <= n; a++) { 算法进行改进。 6. for ( b = 0; b <= n; b++) { 7. for (c = 0; c <= n; c++) { 8. if ((a + b + c == n) && (5 * a + 3 * b + c / 3 == n) && (c%3 == 0)) { 9. g[k] = a; 10. m[k] = b; 11. s[k] = c; 12. k++; 13. } 14. } 15. } 16. } 17. }
北航计算机研究生课程_算法设计与分析__Assignment_1

一、解:设第k月的需求量为Nk(k=1,2,3,4)状态变量Xk:第k月初的库存量,X1=X5=0,0≤Xk≤Nk+…+N4决策变量Uk:第k月的生产量,max{0,Nk-Xk}≤Uk≤min{6,Nk+…+N4 - Xk}状态转移方程:X k+1 = Uk + Xk – Nk第k月的成本Vk = 0.5*(Xk - Nk) Uk=03 + Uk + 0.5*(Uk + Xk - Nk) Uk≠0设F k(Xk)是由第k月初的库存量Xk开始到第4月份结束这段时间的最优成本则F k(Xk) = min{Vk + F k+1(X k+1)} 1≤k≤4= min{ 3 + Uk + 0.5*(Uk + Xk - Nk) + F k+1(Uk + Xk - Nk) } Uk≠0min{ 0.5*(Xk - Nk) + F k+1(Xk - Nk) } Uk=0 F5(X5)=0四个月内的最优成本为F1(X1)=F1(0)详细计算步骤如下:(1)k=4时4(2)k=3时(3)k=2时(4)k=1时由以上计算可得,4个月的总最优成本为F1(0) = 20.5(千元)二、解:1、变量设定阶段k:已遍历过k个结点,k=1,2…6,7。
K=1表示刚从V1出发,k=7表示已回到起点V1状态变量Xk=(i,Sk):已遍历k个结点,当前位于i结点,还未遍历的结点集合为Sk。
则X1=(1,{2,3,4,5,6}),X6=(i,Φ),X7=(1,Φ)决策变量Uk=(i,j):已遍历k个结点,当前位于i结点,下一个结点选择j。
状态转移方程:X k+1 = T(Xk,Uk) = (j,Sk-{j})第k阶段的指标函数Vk = D[i,j]。
最优指标函数Fk(Xk) = Fk(i,Sk):已遍历k个结点,当前从i结点出发,访问Sk中的结点一次且仅一次,最后返回起点V1的最短距离。
则Fk(i,Sk) = min{ D[i,j] + F k+1(j,Sk-{j}) } 1≤k≤6F7(X7) = F7(1,Φ) = 02、分析:(1)k=6时,F6(i,Φ) = min{D[i,1] + F7(X7)} = D[i,1] i=2,3,4,5,63、伪代码和时间复杂度为方便计算,结点编号改为0到5.(1)用一张二维表格F[][]表示F(i,Sk),行数是n,列数是2n-1。
(陈慧南 第3版)算法设计与分析——第1章课后习题答案

第一章课后习题
姓名:赵文浩 学号:16111204082 班级:2016 级计算机科学与技术
1-4 证明等式 gcd(m,n)=gcd(n mod m, m) 对每对正整数 m 和 n,m>0 都成立。
1-13 写一个递归算法和一个迭代算法计算二项式系数:
#include<stdio.h> int Coef_recursive(int n,int m);//递归算法 int Coef_iteration(int n,int m);//迭代算法 int Factorial(int n);//计算 n 的阶乘 int main() { int n,m;
1-12 试用归纳法证明程序 1-7 的排列产生器算法的正确性。
证明:主函数中,程序调用 perm(a,0,n),实现排列产生器。 ① 当 n=1 时,即数组 a 中仅包含一个元素。函数内 k=0,与(n-1)=0 相等,因此函 数内仅执行 if(k==n-1)下的 for 语句块,且只执行一次。即将 a 数组中的一个元 素输出,实现了对一个元素的全排列。因此当 n=1 时,程序是显然正确的; ② 我们假设程序对于 n=k-1 仍能够满足条件, 将 k-1 个元素的全排列产生并输出; ③ 当 n=k 时,程序执行 else 下语句块的内容。首先执行 swap(a[0],a[0]),然后执 行 Perm(a,1,n),根据假设②可知,该语句能够产生以 a[0]为第一个元素,余下 (k-1)个元素的全排列; 然后再次执行 swap(a[0],a[0]), 并进行下一次循环。 此时 i=1, 即在本次循环中, 先执行 swap(a[0],a[1]), 将第二个元素与第一个元素互换, 下面执行 Perm(a,1,n), 根据假设②可知, 该语句产生以 a[1]为第一个元素, 余下(k-1)个元素的全排列; 以此类推,该循环每一次将各个元素调到首位,通过执行语句 Perm(a,1,n)以及 基于假设②,能够实现产生 k 个元素的全排列。 因此 n=k 时,程序仍满足条件。 ④ 综上所述,该排列器产生算法是正确的,证毕。
计算机算法设计与分析(第5版)第1章
算法渐近复杂性
• T(n) , as n ; • (T(n) - t(n) )/ T(n) 0 ,as n; • t(n)是T(n)的渐近性态,为算法的渐近复杂性。 • 在数学上, t(n)是T(n)的渐近表达式,是T(n)略去低阶
问题求解(Problem Solving)
理解问题 精确解或近似解
选择数据结构 算法设计策略
设计算法 证明正确性
分析算法 设计程序
算法复杂性分析
• 算法复杂性 = 算法所需要的计算机资源 • 算法的时间复杂性T(n); • 算法的空间复杂性S(n)。 • 其中n是问题的规模(输入大小)。
算法的时间复杂性
项留下的主项。它比T(n) 简单。
渐近分析的记号
• 在下面的讨论中,对所有n,f(n) 0,g(n) 0。 • (1)渐近上界记号O • O(g(n)) = { f(n) | 存在正常数c和n0使得对所有n n0有:
0 f(n) cg(n) } • (2)渐近下界记号 • (g(n)) = { f(n) | 存在正常数c和n0使得对所有n n0有:
• (1)最坏情况下的时间复杂性 • Tmax(n) = max{ T(I) | size(I)=n } • (2)最好情况下的时间复杂性 • Tmin(n) = min{ T(I) | size(I)=n } • (3)平均情况下的时间复杂性
• Tavg(n) = p(I )T (I ) size(I )n
•
for x > -1,
x ln(1 x) x 1 x
•
for any a > 0,
Hale Waihona Puke log b nlim
算法分析与设计作业(一)及参考答案

《算法分析与设计》作业(一)本课程作业由两部分组成。
第一部分为“客观题部分”,由15个选择题组成,每题1分,共15分。
第二部分为“主观题部分”,由简答题和论述题组成,共15分。
作业总分30分,将作为平时成绩记入课程总成绩。
客观题部分:一、选择题(每题1分,共15题)1、递归算法:(C )A、直接调用自身B、间接调用自身C、直接或间接调用自身D、不调用自身2、分治法的基本思想是将一个规模为n的问题分解为k个规模较小的字问题,这些子问题:(D )A、相互独立B、与原问题相同C、相互依赖D、相互独立且与原问题相同3、备忘录方法的递归方式是:(C )A、自顶向下B、自底向上C、和动态规划算法相同D、非递归的4、回溯法的求解目标是找出解空间中满足约束条件的:(A )A、所有解B、一些解C、极大解D、极小解5、贪心算法和动态规划算法共有特点是:( A )A、最优子结构B、重叠子问题C、贪心选择D、形函数6、哈夫曼编码是:(B)A、定长编码B、变长编码C、随机编码D、定长或变长编码7、多机调度的贪心策略是:(A)A、最长处理时间作业优先B、最短处理时间作业优先C、随机调度D、最优调度8、程序可以不满足如下性质:(D )A、零个或多个外部输入B、至少一个输出C、指令的确定性D、指令的有限性9、用分治法设计出的程序一般是:(A )A、递归算法B、动态规划算法C、贪心算法D、回溯法10、采用动态规划算法分解得到的子问题:( C )A、相互独立B、与原问题相同C、相互依赖D、相互独立且与原问题相同11、回溯法搜索解空间的方法是:(A )A、深度优先B、广度优先C、最小耗费优先D、随机搜索12、拉斯维加斯算法的一个显著特征是它所做的随机选性决策有可能导致算法:( C )A、所需时间变化B、一定找到解C、找不到所需的解D、性能变差13、贪心算法能得到:(C )A、全局最优解B、0-1背包问题的解C、背包问题的解D、无解14、能求解单源最短路径问题的算法是:(A )A、分支限界法B、动态规划C、线形规划D、蒙特卡罗算法15、快速排序算法和线性时间选择算法的随机化版本是:( A )A、舍伍德算法B、蒙特卡罗算法C、拉斯维加斯算法D、数值随机化算法主观题部分:二、写出下列程序的答案(每题2.5分,共2题)1、请写出批处理作业调度的回溯算法。
算法设计与分析 第1章

例1 f(n) = 2n + 3 = O(n) 当n≥3时,2n+3≤3n,所以,可选c = 3,n0 = 3。对于n≥n0,f(n) = 2n + 3≤3n,所以,f(n) = O(n),即2n + 3O(n)。这意味着,当n≥3 时,例1的程序步不会超过3n,2n + 3 = O(n)。
例2 f(n) = 10n2 + 4n + 2 = O(n2) 对于n≥2时,有10n2 + 4n + 2≤10n2 + 5n,并 且当n≥5时,5n≤n2,因此,可选c = 11, n0 = 5;对于n≥n0,f(n) = 10n2 + 4n + 2≤11n2,所 以f(n) = O(n2)。
算法设计与分析
湖南人文科技学院计算机系 授课:肖敏雷
邮箱:minlei_xiao@
关于本课程
课程目的:计算机算法设计与分析导引
不是一门试验或程序设计课程 也不是一门数学课程
教材:计算机算法设计与分析-王晓东 前导课:数据结构+程序设计 参考资料:
算法设计与分析—C++语言描述 陈慧南编 电子工业出版社 计算机算法基础(第三版) 余祥宣 华中科技大学
渐近时间复杂度 使用大O记号及下面定义的几种渐近表示法 表示的算法时间复杂度,称为算法的渐近时间复 杂度(asymptotic complexity)。 只要适当选择关键操作,算法的渐近时间复 杂度可以由关键操作的执行次数之和来计算。一 般地,关键操作的执行次数与问题的规模有关, 是n的函数。 关键操作通常是位于算法最内层循环的语句。
当 n≥n0 时 , 有 f(n)≥cg(n) , 则 记 做 f(n)=Ω
计算机算法设计与分析--第1章 算法概述

③确认算法。算法确认的目的是使人们确信这一算 法能够正确无误地工作,即该算法具有可计算性。 正确的算法用计算机算法语言描述,构成计算机程 序,计算机程序在计算机上运行,得到算法运算的 结果; ④ 分析算法。算法分析是对一个算法需要多少计算 时间和存储空间作定量的分析。分析算法可以预测 这一算法适合在什么样的环境中有效地运行,对解 决同一问题的不同算法的有效性作出比较; ⑤ 验证算法。用计算机语言描述的算法是否可计算、 有效合理,须对程序进行测试,测试程序的工作由 调试和作时空分布图组成。
16
算法描述
1. 从第一个元素开始,该元素可以认为已 经被排序 2. 取出下一个元素,在已经排序的元 素序列中从后向前扫描 3. 如果该元素(已排序)大于新元素, 将该元素移到下一位置 4. 重复步骤3,直到找到已排序的元素 小于或者等于新元素的位置 5. 将新元素插入到该位置中 6. 重复步骤2
15
1.3 算法示例—插入排序算法
算法的思想:扑克牌游戏
a0,...,n-1 a0,...,n-1 a0,...,n-1 a0,...,n-1 a0,...,n-1 a0,...,n-1 a0,...,n-1
= = = = = = =
5,2,4,6,1,3 5,2,4,6,1,3 2,5,4,6,1,3 2,4,5,6,1,3 2,4,5,6,1,3 1,2,4,5,6,3 1,2,3,4,5,6
8
算法≠程序
算法描述:自然语言,流程图,程序设计
语言,伪代码 用各种算法描述方法所描述的同一算法, 该算法的功用是一样的,允许在算法的描述 和实现方法上有所不同。
本书中采用类C++伪代码语言描述算法
9
人们的生产活动和日常生活离不开算法, 都在自觉不自觉地使用算法,例如人们到 商店购买物品,会首先确定购买哪些物品, 准备好所需的钱,然后确定到哪些商场选 购、怎样去商场、行走的路线,若物品的 质量好如何处理,对物品不满意又怎样处 理,购买物品后做什么等。以上购物的算 法是用自然语言描述的,也可以用其他描 述方法描述该算法。
算法设计与分析(第2版)-郑宗汉-第1章-1

2021/3/10
5
第1章 算法的基本概念
References
1973. 5. A. V. Aho, J. D. Ullman等. The Design and Analysis of Computer Algorithms.
Addison-Wesley, 1974. 6. A. V. Aho, J. D. Ullman等. Data Structures and Algorithms. Addison-Wesley,
1983.4. 7. S. Baase. Computer Algorithms: Introduction to Design and Analysis.
Addison-Wesley, second edition, 1988. 8. E. Horowitz and Sartaj Sahni. Fundamentals of Computer Algorithms.
2021/3/10
12
第1章 算法的基本概念 1.1.1 算法的定义和特性
最大公约数问题:求两个正整数m和n的最大公约数
设计:
确可定行性性::
输入: 输出: 第一步: 第二步:
2021/3/10
8
第1章 算法的基本概念
学习要求
深刻理解每一类算法的思想及其实现 能熟练运用所学知识解决实际问题 培养提高计算思维能力
2021/3/10
9
第1章 算法的基本概念
东北大学《算法设计与分析( 一)》期末考试必备通关指导

东北大学继续教育学院算法设计与分析(一)复习题一、选择题1.算法的复杂性是()的度量,是评价算法优劣的重要依据。
A.时间效率B.算法效率C.空间效率D.输出效率2.衡量一个算法好坏的标准是()。
A.运行速度快B.占用空间少C.时间复杂度低D.代码短3.算法分析的两个主要方面是()。
A.空间复杂度和时间复杂度B.正确性和简单性C.可读性D.程序复杂度4.计算机算法指的是()。
A.计算方法B.排序方法C.解决问题的方法和过程D.调度方法5.多阶段决策问题就是要在可以选择的那些策略中间选取一个()策略使在预定的标准下达到最好的效果。
A.最优B.最差C.平衡D.任意6.下列关于算法的说法中正确的有()个。
(1)求解某一类问题的算法是唯一的;(2)算法必须在有限步操作后停止;(3)算法的每一步操作是明确的,不能有歧义或含义模糊;(4)算法执行后一定产生确定的结果。
7.( )是指算法执行时所需计算机资源的多少,包括运行时间和存储空间两个方面的要求。
A.正确性B.可读性C.效率D.健壮性8.对于简单的输入,输出和赋值语句,执行时间为()。
(1) (n) (n*n) D.都不对9.算法点的空间复杂度是指()。
A.算法在执行过程中所需的计算机存储空间B.算法所处理的数据量C.算法程序中的语句或指令的条数D.算法在执行过程中所需要的临时工作单元数10.算法点的时间复杂度是指()。
A.算法的执行时间B.算法所处理的数据量C.算法程序中的语句或指令的条数D.算法在执行过程中所需要的基本运算次数11.下列哪一种算法不是随机化算法()。
A.遗传算法B.模拟退火算法C.动态规划算法D.模特卡罗算法12.下面不是动态规划算法基本步骤的是()。
A.找出最优解的性质B.构造最优解C.算出最优解D.定义最优解13.下列是动态规划算法基本要素的是()。
A.定义最优解B.构造最优解C.算出最优解D.子问题重叠性质14.采用广度优先策略搜索的算法是()。
算法设计与分析习题答案1-6章

习题11. 图论诞生于七桥问题。
出生于瑞士的伟大数学家欧拉(LeonhardEuler ,1707—1783)提出并解决了该问题。
七桥问题是这样描述的:一个人是否能在一次步行中穿越哥尼斯堡(现在叫加里宁格勒,在波罗的海南岸)城中全部的七座桥后回到起点,且每座桥只经过一次,图是这条河以及河上的两个岛和七座桥的草图。
请将该问题的数据模型抽象出来,并判断此问题是否有解。
七桥问题属于一笔画问题。
输入:一个起点输出:相同的点1, 一次步行2, 经过七座桥,且每次只经历过一次3, 回到起点该问题无解:能一笔画的图形只有两类:一类是所有的点都是偶点。
另一类是只有二个奇点的图形。
图 七桥问题南2.在欧几里德提出的欧几里德算法中(即最初的欧几里德算法)用的不是除法而是减法。
请用伪代码描述这个版本的欧几里德算法=m-n2.循环直到r=0m=nn=rr=m-n3 输出m3.设计算法求数组中相差最小的两个元素(称为最接近数)的差。
要求分别给出伪代码和C++描述。
编写程序,求n至少为多大时,n个“1”组成的整数能被2013整除。
#include<iostream>using namespace std;int main(){double value=0;for(int n=1;n<=10000 ;++n){value=value*10+1;if(value%2013==0){cout<<"n至少为:"<<n<<endl;break;}}计算π值的问题能精确求解吗编写程序,求解满足给定精度要求的π值#include <iostream>using namespace std;int main (){double a,b;double arctan(double x);圣经上说:神6天创造天地万有,第7日安歇。
为什么是6天呢任何一个自然数的因数中都有1和它本身,所有小于它本身的因数称为这个数的真因数,如果一个自然数的真因数之和等于它本身,这个自然数称为完美数。
北航研究生 算法设计与分析大作业一
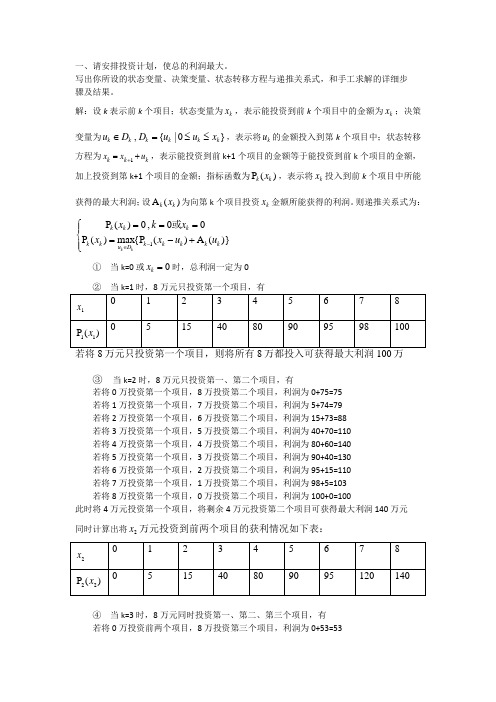
一、请安排投资计划,使总的利润最大。
写出你所设的状态变量、决策变量、状态转移方程与递推关系式,和手工求解的详细步 骤及结果。
解:设k 表示前k 个项目;状态变量为k x ,表示能投资到前k 个项目中的金额为k x ;决策变量为}0|{ , k k k k k k x u u D D u ≤≤=∈,表示将k u 的金额投入到第k 个项目中;状态转移方程为k k k u x x +=+1,表示能投资到前k+1个项目的金额等于能投资到前k 个项目的金额,加上投资到第k+1个项目的金额;指标函数为)(P k k x ,表示将k x 投入到前k 个项目中所能获得的最大利润;设)(A k k x 为向第k 个项目投资k x 金额所能获得的利润。
则递推关系式为:⎪⎩⎪⎨⎧+-====-∈)}(A )({P max )(P 00 , 0)(P 1k k k k k D u kk k k k u u x x x k x k k 或① 当k=0或0=k x 时,总利润一定为0③ 当k=2时,8万元只投资第一、第二个项目,有若将0万投资第一个项目,8万投资第二个项目,利润为0+75=75若将1万投资第一个项目,7万投资第二个项目,利润为5+74=79 若将2万投资第一个项目,6万投资第二个项目,利润为15+73=88 若将3万投资第一个项目,5万投资第二个项目,利润为40+70=110 若将4万投资第一个项目,4万投资第二个项目,利润为80+60=140 若将5万投资第一个项目,3万投资第二个项目,利润为90+40=130 若将6万投资第一个项目,2万投资第二个项目,利润为95+15=110 若将7万投资第一个项目,1万投资第二个项目,利润为98+5=103 若将8万投资第一个项目,0万投资第二个项目,利润为100+0=100此时将4万元投资第一个项目,将剩余4万元投资第二个项目可获得最大利润140万元 同时计算出将2x 万元投资到前两个项目的获利情况如下表:④ 当k=3时,8万元同时投资第一、第二、第三个项目,有 若将0万投资前两个项目,8万投资第三个项目,利润为0+53=53若将1万投资前两个项目,7万投资第三个项目,利润为5+52=57若将2万投资前两个项目,6万投资第三个项目,利润为15+51=66若将3万投资前两个项目,5万投资第三个项目,利润为40+50=90若将4万投资前两个项目,4万投资第三个项目,利润为80+45=125若将5万投资前两个项目,3万投资第三个项目,利润为90+40=130若将6万投资前两个项目,2万投资第三个项目,利润为95+26=121若将7万投资前两个项目,1万投资第三个项目,利润为120+4=124若将8万投资前两个项目,0万投资第三个项目,利润为140+0=140此时将4万元投资第一个项目,将剩余4万元投资第二个项目,第三个项目投资0元,可获得最大利润140万元。
算法设计与分析习题答案1

算法设计与分析习题答案1算法设计与分析习题答案1习题1 1. 图论诞生于七桥问题。
出生于瑞士的伟大数学家欧拉提出并解决了该问题。
七桥问题是这样描述的:北区一个人是否能在一次步行中穿越哥尼斯堡城中全部岛区的七座桥后回到起点,且每座桥只经过一次,南区图是这条河以及河上的两个岛和七座桥的图七桥问题草图。
请将该问题的数据模型抽象出来,并判断此问题是否有解。
七桥问题属于一笔画问题。
输入:一个起点输出:相同的点1,一次步行2,经过七座桥,且每次只经历过一次3,回到起点该问题无解:能一笔画的图形只有两类:一类是所有的点都是偶点。
另一类是只有二个奇点的图形。
2.在欧几里德提出的欧几里德算法中用的不是除法而是减法。
请用伪代码描述这个版本的欧几里德算法=m-n 2.循环直到r=0 m=n n=r r=m-n 3 输出m 3.设计算法求数组中相差最小的两个元素的差。
要求分别给出伪代码和C++描述。
//采用分治法//对数组先进行快速排序//在依次比较相邻的差#include using namespace std; int partions(int b,int low,int high) { int prvotkey=b[low]; b[0]=b[low]; while (low while (low=prvotkey)--high; b[low]=b[high]; while (low b[high]=b[low]; } b[low]=b[0]; return low; } void qsort(int l,int low,int high) { int prvotloc; if(low prvotloc=partions(l,low,high);//将第一次排序的结果作为枢轴qsort(l,low,prvotloc-1); //递归调用排序low 到prvotloc-1 qsort(l,prvotloc+1,high); //递归调用排序prvotloc+1到high } } void quicksort(int l,int n) { qsort(l,1,n); // 第一个作为枢轴,从第一个排到第n个} int main() { int a[11]={0,2,32,43,23,45,36,57,14,27,39};int value=0;//将最小差的值赋值给value for (int b=1;b quicksort(a,11); for(int i=0;i!=9;++i) { if( (a[i+1]-a[i]) value=a[i+2]-a[i+1]; } cout return 0; } 4.设数组a[n]中的元素均不相等,设计算法找出a[n]中一个既不是最大也不是最小的元素,并说明最坏情况下的比较次数。
北航计算机研究生课程-算法设计与分析-HomeWork-1

北航计算机研究生课程-算法设计与分析-HomeWork-1一、已知下列递推式:C(n) = 1 若n =1= 2C (n/2) + n – 1 若n ≥ 2请由定理1 导出C(n)的非递归表达式并指出其渐进复杂性。
定理1:设a,c 为非负整数,b,d,x 为非负常数,并对于某个非负整数k, 令n=c k , 则以下递推式f(n) =d 若 n=1=af(n/c)+bn x 若 n>=2的解是f(n)= bn x log c n + dn x 若 a=c x f(n)= x x xa x xn c a bc n c a bc d c ???? ??--???? ??-+log若a ≠c x解:令F(n) = C(n) – 1则 F(n) = 0 n=1F(n) = 2C(n/2) + n – 2 n>=2= 2[F(n/2) + 1] + n – 2= 2F(n/2) + n利用定理1,其中:d=0,a=2,c=2,b=1,x=1,并且a=c x所以 F(n) = nlog 2n所以 C(n) = F(n) + 1 = nlog 2n + 1C(n)的渐进复杂性是O(nlog 2n)二、由于Prim 算法和Kruskal 算法设计思路的不同,导致了其对不同问题实例的效率对比关系的不同。
请简要论述:1、如何将两种算法集成,以适应问题的不同实例输入;2、你如何评价这一集成的意义?答:1、Prim 算法基于顶点进行搜索,所以适合顶点少边多的情况。
Kruskal 从边集合中进行搜索,所以适合边少的情况。
根据输入的图中的顶点和边的情况,边少的选用kruskal 算法,顶点少的选用prim 算法2、没有一个算法是万能的,没有一个算法是对所有情况都适合的。
这一集成体现了针对具体问题选用最适合的方法,即具体问题具体分析的哲学思想。
三、分析以下生成排列算法的正确性和时间效率:HeapPermute (n )//实现生成排列的Heap 算法//输入:一个正正整数n和一个全局数组A[1..n]//输出:A中元素的全排列if n = 1write Aelsefor i ←1 to n doHeapPermute(n-1)if n is oddswap A[1]and A[n]else swap A[i]and A[n]解:n=1时,输出a1n=2时,输出a1a2,a2a1n=3时,(1)第一次循环i=1时,HeapPermute(2)将a1a2做完全排列输出,记为[a1a2]a3,并将A变为a2a1a3,并交换1,3位,得a3a1a2(2)第二次循环i=2时,HeapPermute(2)输出[a3a1]a2,并将A 变为a1a3a2,交换1,3位,得a2a3a1(3)第三次循环i=3时,HeapPermute(2)输出[a2a3]a1,并将A 变为a3a2a1,交换1,3位,得a1a2a3,即全部输出完毕后数组A回到初始顺序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在时间、空间、优性和简单可理解方面权衡。
由于图1.2中包含完全子图,故该解就是最优解。
什么是算法
● 算法是有限步内解一个数学问题的过程;
●算法满足有穷性、确定性、可行性、输入和输出条件; ●算法是对任意有效输入能够停机的图灵机。
算法与问题
●算法是用来解决问题的; ●问题是无穷多个实例组成的类; ●实例是问题定义域上的某个实体以及对该实体的提问。
四色猜想:(美大学生F.Guthrie 1852 )用四种颜色可以为所有地图着色。
1976年,美国依利若大学(W.Haken & K.Appel)通过改进算法并借助计算机(1200机时)证 明了该猜想的正确性。(为此,当地信封角标注四色是足够的,以示自豪。) 平面图着色问题的形式定义: 已知 n 点无向图 G=(V, E) ||V||=n, 求G的最小色数 k , 使得用 k 种颜色对G 的顶点着色, 可使 G 的任意两个相邻顶点着色不同。 五叉路口信号灯问题的对应无向图见 图1.2 p2 其中:点描述路线,边描述交叉关系, 最小色数 k 描述最小分组。(同一线路可能在多个组)
此时,若L为递增序列,需n-1次比较,若L为递减序列,需2n-2次比较,平 均比较次数界于两者之间。
该算法是最好的吗?
下面用分治法给出另一种新解,改进算法3。 Template<class Type > void MAXMIN3(Type L[ ], int n, Type M1, Type M2) { if (n= =2) If (L[1]> L[2] { M1=L[ 1]; M2=L[ 2]; } else { M1=L[ 2]; M2=L[ 1]; } else{ //把L分为长为n/2的L1, L2; MAXMIN(L1, n/2, M11, M21); MAXMIN(L2, n/2, M12, M22); M1=MAX(M11, M12); //MAX (a,b)为a,b中较大者 M2=MIN(M21, M22); //MIN (a,b)为a,b中较小者 } return; } 易见这个算法是正确的,下面分析其时间复杂性,为了简单起见,设 n=2k 由程序有: 0 n=1 T(n)= 1 n=2 T(n/2)+T(n/2)+2 n>2 也即, T(n)= 2 T(n/2)+2 = 2 (2T(n/4)+2)+2= 22 T(n/22)+ 22 +2=…… =2 k-1T(2)+21+22+…+2 k-1 =2 k-1+2k – 2=3n/2-2 这个结果比 2n-3 好多了。下面证明它在许多情况下是最好的。
所有比较可以分成六类:
S1、比较双方都是初次参加比较;
S2、一方是初次,另一方是胜者; S3、一方是初次,另一方是败者;
S4、比较双方都是胜者;
S5、比较双方都是败者; S6、其他情况。(例如,一方胜,一方败) 易见,S1 ∪ S2 ∪ S4 是求最大元的充分必要条件, S1 ∪ S3 ∪ S5 是求最 小元的充分必要条件,由此有求最大最小元总的比较次数 S≥|S1|+ |S2|+ |S4|+ |S1|+ |S3|+ |S5|- |S1|=n -1+n -1- |S1|
if(j==i) color[i]=k; } j=2; while(color[j]>0)&&(j<=n))j++; k++; } while(j<=n); return k-1; }
讨论:
1、权衡
2、最优性 求一个问题的最优解是一件困难的事情,上面五叉路口的一个解为: ab,ac,ad,ba,dc,ed; bc,bd,ea, ba,dc,ed; da,db, ba,dc,ed; eb,ec, ba,dc,ed;
下面分几种情况来讨论: ① d(n)=const, a≠1 此时有 T(n)= cak+cˊ
n a d (b j ) j 0
j
k 1
a
j 0
k 1
j
= cak+cˊ(ak -1)/(a-1) = O( ak ) = O(
n logb a
)
② d(n)=const, a=1 此时有 T(n)= c+cˊ logb n ③ d(n)=cˊ n 此时有
算法的研究与Moore定律
计算机速度每18个月翻一番。算法的研究仍十分必要,原因为:
■ 应用问题不断变化; ■ 应用问题的范围不断加大; ■ 应用问题的复杂程度不断加大。 如地球末日问题当 n>50就无法解决。 下面是计算机速度的提高和算法复杂度之间的关系 T(n)=n T(n)=n2 T(10n)=10n T(10 ½ n)=10n2
算法设计与分析: 科学出版社,刘瑾编著
算法的研究是计算机科学的核心问题,是人类难度最大最富创造性的活动之一。 程序设计=算法+数据结构 程序设计=算法+方法学+语言与工具 孙子算法,欧几里德算法。串行算法,并行算法,概率算法,近似算法,算法设计几乎无出不在。
算法的研究50年代以前占10%,60年代30%,其余60产生于70年代以后。
T(n)=2n T(10+n)=2 10+n =210*2n 这说明速度扩大1024倍,问题处理能 力仅扩大10而已。
MAXMIN问题
求n个元素中的最大元和最小元 若按前面求最大元算法显然有算法是正确的且: T(n)=W(n)=A(n)=2n-3 S(n)=O(1)
然而请问上述算法是解决MAXMIN问题的最优算法吗?回答是否定的。 这是 因为此算法独立地求出MAX和MIN,而MAX和MIN是相关的,当比较得到 L[i]>L[j] 时,就应该得到信息, L[i]决不是最小元,而L[j]决不是最大元,而 这些在上述算法中并没有反映出来。 改进算法1
算法理论的基本概念
●基本操作 随着问题规模增大而增加的操作;
算法的时间度量应独立于机器、程序设计风格、指令条数等。
●问题实例长度
算法复杂度与实例长度有关
T(n)
●复杂度的渐进性质 算法的优劣是根据其对应复杂度函数的渐进性质来度
量的,见图 1.5。
●最坏情形、最好情形和平均情形
最好情形价值不大,一般不用。 W(n)=MAX{ T(I) } I∈Dn , A(n)=∑P(I)T(I) , ∑P(I) =1 例、在数组L[1..n]中搜索 X Template<class Type> while((j<=n)&&(L[j]!=X)) j++; I∈Dn
但可发现循环体中的不合理处:如果MAX<L[i]为真,则 MIN>L[i]必为假, 无须再比较,故有改进算法二。
# include<iostream.h> Template<class Type> void MAXMIN2 (Type L[], int n) {Type MAX=L[1]; Type MIN=L[1]; For (int i=2; i<=n; i++) { if (MAX<L[i]) MAX=L[i]; else if (MIN>L[i]) MIN=L[i]; } cout<<”MAX=”<<MAX<<”,MIN=”<<MIN<<endl; return; }
例:整数乘法问题A;语言识别问题B; 旅行商问题C。
算法的评估
解决同一问题有多个算法,如何评价其优劣?一般评价准则是: 1、正确性 2、时间代价 3、空间代价 4、最优性 Template<class Type> Type Max(Type S[], int n) { Type max=S[0]; int i=1; while (i<n) {if (max<S[i]) max=S[i]; i++;} return max; } 易证,这就是一个在 n 个元素中求最大元的最优算法。 5、可理解性
易见,其最坏复杂度为:W(n)= n,即 x=xn 或 x 不在表中的情况。
复杂度函数的表示
●解析表示,一种精确表示,如:T(n)=n-1 ●阶表达式表示,如:2n2 + n-1和n2 +1是同阶的。 符号O(n), (n), (n) 。 定义1 、 T(n)=O(f(n)),如果存在常数 c>0与n0,使得当n> n0时有, T(n) ≤cf(n)。 定义2、 T(n)= (f(n)),如果存在常数 c>0与n0,使得当n> n0时有, T(n) ≥cf(n)。 定义3、 T(n)= (f(n)),如果存在常数 c1>0,c2>0与n0,使得当n> n0时有, c1f(n) ≥ T(n) ≥c2f(n)。 ●多项式函数和指数函数
其中, P(I)为实例I作为输入出现的概率, T(I) 为算法A以I为输入的耗费。
int Search(Type L[ ], Type X, int n)
{ int j=1;
return j;
}
分析:
X在L中共有 n 种情况,I1,I2,…… In , X不在L中统记为In+1 ,由此有: ∪Ii =Dn , i=1…n +1,T(Ii)=i,假设X在L中的概率为q,则有X不在L中的概 率为1-q,又假设X为L中某一元素的概率相等,即P( Ii )= q/n ,i=1…n。 现在可求得:A(n)=∑ P(Ii)T(Ii) i=1…..n+1 =q/n ∑i+(1-q)n=q/2(n+1)+(1-q)n 当q=1时,A(n)=(n+1)/2,当q=1/2时,A(n)=3n/4+1/4
