求解线性方程组SOR-k方法的一个注记
数值分析6-用SOR方法求解线性方程组

程序 clear;clc; A=[4,3,0;3,4,-1;0,-1,4]; b=[24,30,-24]'; N=length(b); %解向量的维数 fprintf('库函数计算结果:'); x=inv(A)*b %库函数计算结果 x=[1;1;1];%迭代初始值 %-----(A=D-E-F)-----D=diag(diag(A)); E=-tril(A,-1);%下三角 F=-triu(A,1);%上三角 w=1.5; %松弛因子,一般 0<w<2 B=inv(D-w*E)*[(1-w)*D+w*F];g=w*inv(D-w*E)*b; eps=1e-8;%相邻解的距离小于该数时,结束迭代 %--------开始迭代------for k=1:100 %最大迭代次数为 100 fprintf('第%d 次迭代:',k); y=B*x+g; if abs(x-y)<eps break; end x=y end x
程序结果
当比较松弛因Biblioteka 取 1.0 时当比较松弛因子取 1.25 时
当比较松弛因子取 1.5 时
作业七:编写用 SOR 方法求解线性方程组 Ax=B 的标准程序,并求下 列方程组的解, 并比较松弛因子取 1.0、 1.25、 1.5 时所需迭代的次数。 可取初始向量 X(0) =(1,1,1)’;迭代终止条件||x(k+1)-x(k)||<=10e-8
4 30 ������1 24 3 4 − 1 x2 = 30 0 − 14 x3 −24
解线性方程组的直接方法

解线性方程组的直接方法一、高斯消元法高斯消元法是解线性方程组最常用的方法之一、它通过一系列的消元操作,将线性方程组转化为阶梯型方程组,从而求解未知数的值。
1.确定线性方程组的阶数和未知数的个数。
设线性方程组中有n个未知数。
2.将线性方程组写成增广矩阵的形式。
增广矩阵是一个n行n+1列的矩阵,其中前n列是线性方程组的系数矩阵,第n+1列是等号右边的常数。
3.通过初等行变换(交换行、数乘行、行加行)将增广矩阵化为阶梯型矩阵。
具体步骤如下:a.首先,找到第一个非零元素所在的列,将它所在的行视为第一行。
b.将第一行的第一个非零元素(主元)变成1,称为主元素。
c.将主元所在列的其他元素(次元素)变为0,使得主元所在列的其他元素只有主元素是非零的。
d.再找到第一个非零元素所在的列,将它所在的行视为第二行,并重复上述步骤,直到将增广矩阵化为阶梯型矩阵。
4.根据阶梯型矩阵求解未知数的值。
具体步骤如下:a.从最后一行开始,依次求解每个未知数。
首先,将最后一行中非零元素所在的列作为含有该未知数的方程,将该未知数的系数设为1b.将含有该未知数的方程中其他未知数的系数设为0,并对其他方程进行相应的变换,使得该未知数所在列的其他元素都为0。
c.重复上述步骤,直到求解出所有未知数的值。
高斯消元法的优点是简单易懂、容易实现,但当线性方程组的系数矩阵接近奇异矩阵时,计算精度可能会降低。
二、矩阵求逆法矩阵求逆法是解线性方程组的另一种直接方法。
它通过对系数矩阵求逆,然后与常数矩阵相乘,得到未知数的值。
1.确定线性方程组的阶数和未知数的个数。
设线性方程组中有n个未知数。
2.将线性方程组写成矩阵方程的形式,即Ax=b,其中A是一个n阶方阵,x和b分别是n维列向量。
3.求系数矩阵A的逆矩阵A^-1a. 首先,计算系数矩阵A的行列式det(A)。
b. 判断det(A)是否为0,如果det(A)=0,则该线性方程组无解或有无穷多解;如果det(A)≠0,则系数矩阵A可逆。
奥数之解线性方程组

奥数之解线性方程组解奥数线性方程组奥数是小学生学习的一门课程,其中包括解线性方程组。
线性方程组是由一系列线性方程组成的方程组。
解决线性方程组的问题是找到一个或一组变量的值来使得方程组成立。
解决线性方程组的方法有很多,其中包括矩阵法、高斯消元法、克莱姆法等多种方法。
矩阵法矩阵法是解决线性方程组的一种方法。
矩阵法是将所有方程的系数和常数写成一个矩阵,然后通过对矩阵进行一些变换,最终得到方程组的解。
当方程的个数和未知数的个数相等时,利用矩阵法解决线性方程组是最常用的方法。
例如,有线性方程组:2x - 3y = -54x + y = 29将系数和常数写成矩阵的形式,得到:| 2 -3 | |x| |-5|| 4 1 | x |y| = |29|通过高斯消元法或其他方法对矩阵进行变换后,得到解x=7,y=3。
高斯消元法高斯消元法是解决线性方程组的另一种方法。
高斯消元法先将线性方程组进行初等变换,将其转化为一个上三角矩阵,然后再通过回代,求出方程组的解。
例如,有线性方程组:2x - 3y = -54x + y = 29通过初等变换,将方程组转化为上三角矩阵的形式:| 2 -3 | |x| |-5|| 0 13 | x |y| = |39|通过回代,求出解x=7,y=3。
克莱姆法克莱姆法是解决线性方程组的一种方法。
克莱姆法利用向量的概念,通过求出方程组系数矩阵的行列式和各个未知数的系数矩阵的行列式,最终求出方程组的解。
例如,有线性方程组:2x - 3y = -54x + y = 29通过克莱姆法,求出方程组的解:x = | -5 -3 | | 29 -3 || 29 1 | / | 2 4 | = 7y = | 2 -5 | | 2 29 || 4 1 | / | -5 1 | = 3需要注意的是,克莱姆法只适用于未知数个数等于方程个数的线性方程组。
综上所述,解决线性方程组的方法有很多种,包括矩阵法、高斯消元法、克莱姆法等。
sor方法

sor方法
SOR方法是一种迭代数值解法,主要被用于求解线性系统Ax=b,其中A是系数矩阵,b是右端向量。
SOR方法的全称为"Successive Over-Relaxation Method",意为迭代超松弛法。
在使用SOR方法求解线性方程组时,首先需要将系数矩阵A分解为L、D和U 三个部分,其中L是A的严格下三角矩阵,D是A的对角线矩阵,U是A的严格上三角矩阵。
同时,SOR方法还需要一个松弛因子w。
SOR方法的迭代公式为:
x(k+1) = (1-w)x(k) + w(D-wL)^(-1)(b-Ux(k))
其中x(k)表示第k次迭代求得的解向量,x(k+1)表示x(k)的下一次迭代,^(−1)表示逆矩阵。
可以发现,SOR方法是基于Gauss-Seidel方法的改进,它在每一次迭代中添加了一个松弛因子w,从而使得解向量的迭代更快、更稳定。
在实际应用中,我们需要选择一个合适的松弛因子w,以使得SOR方法能够收敛并且收敛速度较快。
一般来说,选择一个小于1的w能够保证SOR方法的收敛性,而选择一个大于1的w能够加快SOR方法的收敛速度。
需要注意的是,SOR方法只能够求解特定条件下的线性方程组,如系数矩阵为对称正定矩阵、对角占优矩阵等。
当系数矩阵不满足这些条件时,SOR方法可能出现发散的情况。
总的来说,SOR方法是一种简单而有效的数值解法,被广泛应用于工程计算等领域。
在使用时,需要根据具体问题选择合适的松弛因子w,并且注意其收敛性和收敛速度。
线性方程组的解法与计算方法

线性方程组的解法与计算方法线性方程组是高中数学中的重要内容,它与矩阵、向量等概念密不可分。
解决线性方程组的问题是很多科学和工程领域中必不可少的基础技能,因此,学习线性方程组的解法和计算方法也是至关重要的。
一、高斯消元法高斯消元法是解决线性方程组的经典方法,其核心思想是通过初等行变换将系数矩阵化为一个上三角矩阵,再采用回代法求解,具体步骤如下:(1)将系数矩阵A和右端向量b合并成一个增广矩阵[ A | b]。
(2)通过初等行变换将增广矩阵消元为一个上三角矩阵U。
(3)利用回代法求解上三角矩阵U的解x。
高斯消元法的优点是能够对任意的线性方程组进行求解,但其缺点是可能会出现浮点数舍入误差,影响求解精度。
二、列主元高斯消元法列主元高斯消元法是在高斯消元法基础上改进而来的,在消元时每次选择列主元,即系数矩阵A中以列为单位元素的绝对值最大的所在行,并将该行交换到当前的行数,然后再进行消元操作。
这样选择列主元能够减小误差,提高求解的精度,具体步骤如下:(1)选取列主元所在的行,并将其与当前行交换。
(2)用当前行的第一个元素除以主元,将主元所在列下面的元素消成0。
(3)进行下一次迭代,直到将系数矩阵化成上三角矩阵。
(4)通过回代法求解上三角矩阵的解x。
列主元高斯消元法在提高求解精度的同时也增加了计算量,因此在实际应用中需要根据具体的情况选择合适的方法。
三、LU分解LU分解是将系数矩阵A分解成一个下三角矩阵L与一个上三角矩阵U的乘积,即A=LU。
通过LU分解可以将求解x的过程分解为两个步骤:先求解Ly=b,再求解Ux=y。
具体步骤如下:(1)分别求解下三角矩阵L与上三角矩阵U。
(2)用LU分解求解方程Ax=b相当于先求解Ly=b,再求解Ux=y。
LU分解的优点是可以减少误差,提高求解精度,并且在计算某些特定的矩阵时比高斯消元法更加高效,但其缺点是需要较大的存储空间。
综上所述,线性方程组的解法和计算方法有多种,选择合适的方法需要根据具体问题的不同来进行选择。
用sor法解方程组

用SOR法解方程组引言方程组是数学中常见的问题,解决方程组可以帮助我们理解和预测各种实际问题。
解方程组的方法有很多种,其中一种常用的方法是SOR(Successive Over Relaxation)法。
SOR法是一种迭代法,通过不断迭代逼近解的过程来求解方程组。
本文将对SOR法进行详细的介绍和分析。
SOR法概述SOR法是一种求解线性方程组的迭代算法,其基本思想是通过引入松弛因子来加速收敛速度。
对于线性方程组Ax=b,SOR法的迭代公式为:x^(k+1) = (1-w)x^(k) + w * D^(-1) * (b - L * x^(k+1) - U * x^(k))其中,x(k)表示第k次迭代的解向量,x(k+1)表示第k+1次迭代的解向量,w为松弛因子(0 < w< 2),A被分解为下三角矩阵L、上三角矩阵U和对角矩阵D。
算法流程SOR法的算法流程如下:1.初始化解向量x^(0)2.对于每次迭代k = 0, 1, 2, …–计算下一次迭代的解向量x^(k+1): x^(k+1) = (1-w)x^(k) + w * D^(-1) * (b - L * x^(k+1) - U * x^(k))–判断迭代是否收敛:如果迭代误差小于预设的阈值就停止迭代,否则继续迭代3.返回最终的解向量x^(k+1)SOR法特点SOR法具有以下几个特点:1.相对于传统的迭代法,SOR法引入了松弛因子,能够加速迭代的收敛速度。
2.当松弛因子w=1时,SOR法等价于高斯-赛德尔迭代法。
3.大部分情况下,SOR法是收敛的。
收敛速度与松弛因子w有关,一般来说,选择一个合适的松弛因子可以加快算法的收敛速度。
4.SOR法对于对角占优的线性方程组具有较好的收敛性能,但对于一般的线性方程组效果可能不理想。
SOR法的数值实验为了验证SOR法的性能,我们进行了一系列的数值实验。
我们选取了不同规模的线性方程组,通过对比SOR法的迭代次数和收敛速度来评估其性能。
SOR迭代法求解线性方程组

SOR迭代法求解线性方程组一实验名称:实验四:逐次超松弛迭代法。
二实验题目:求解下面的三元一次线性方程组:2x-y+2z=4;x+2y+3z=9;2x-2y-3z=-3;要求选取不同的松弛因子进行计算,并估计最优松弛因子的大小。
三实验目的:1.熟悉掌握逐次超松值迭代法的基本原理和基本方法。
2.学会用逐次超松弛迭代法解简单的方程组。
3.选取不同的w值(0<w<2)进行试探性的计算,从中摸索出近似的最佳松弛因子。
四基础理论:超松弛迭代法以及所涉及的主要算法为:Xi^(k+1)←(1-w)*Xi^(k)+w*Xi的共轭的(k+1)次幂。
五实验环境:Visual C++6.0。
六实验过程:1. 在程序中输入不同的数据时,会得到不同的结果。
2.大于1的时候的松弛因子,被称作超松弛法。
小于则被称做低松弛法。
由于松弛因子对方程组的收敛速度影响很大,所以在一定的误差范围内,选择不同的松弛因子时,迭代次数也会不同。
3. 按照实验题目中的数据输入时,比较结果当w=0.6时,会出现下面的结果:当w=0.7时得当w=0.8时得当w=0.9时,会出现下面的结果当w=1.0时得七结果分析:当在一定的误差范围内,有以上运行结果可以得出答案,最优松弛因子的范围为0.8。
八逐次超松弛迭代法程序代码:#include<iostream.h>#include<stdlib.h>#include<stdio.h>#include<math.h>void SOR(double w, double a[3][3], double b[3], double x[3], double esp) {double t[3];int flag=0;int n=0;while(!flag){flag=1;n++;t[0]=x[0]; t[1]=x[1]; t[2]=x[2];for(int i=0;i<3;i++){double m=b[i];for(int j=0;j<3;j++){m-=(a[i][j]*x[j]);}x[i]=x[i]+w*m/a[i][i];}for(int k=0;k<3;k++){if(fabs(x[k]-t[k])>=esp){flag=0;break;}}}printf("%d\n",n);}void main(){double a[3][3];double b[3];double x[3];double w,esp;a[0][0]=2; a[0][1]=-1; a[0][2]=2;a[1][0]=1; a[1][1]=2; a[1][2]=3;a[2][0]=2; a[2][1]=-2; a[2][2]=-3;b[0]=4; b[1]=9; b[2]=-3;x[0]= x[1]= x[2]=0;w=0.6;esp=0.0001;SOR(w,a,b,x,esp);for(int i=0;i<3;i++)printf("%f\n",x[i]);}。
线性方程组解法归纳总结

线性方程组解法归纳总结在数学领域中,线性方程组是一类常见的方程组,它由一组线性方程组成。
解决线性方程组是代数学的基础知识之一,广泛应用于各个领域。
本文将对线性方程组的解法进行归纳总结。
一、高斯消元法高斯消元法是解决线性方程组的基本方法之一。
其基本思想是通过逐步消元,将线性方程组转化为一个上三角形方程组,从而求得方程组的解。
具体步骤如下:1. 将线性方程组写成增广矩阵的形式,即将系数矩阵和常数向量合并成一个矩阵。
2. 选取一个非零的主元(通常选取主对角线上的元素),通过初等行变换将其它行的对应位置元素消为零。
3. 重复上述步骤,逐步将系数矩阵转化为上三角形矩阵。
4. 通过回代法,从最后一行开始求解未知数,逐步得到线性方程组的解。
高斯消元法的优点是理论基础牢固,适用于各种规模的线性方程组。
然而,该方法有时会遇到主元为零或部分主元为零的情况,需要进行特殊处理。
二、克拉默法则克拉默法则是一种用行列式求解线性方程组的方法。
它利用方程组的系数矩阵和常数向量的行列式来求解未知数。
具体步骤如下:1. 求出系数矩阵的行列式,若行列式为零则方程组无解。
2. 对于每个未知数,将系数矩阵中对应的列替换为常数向量,再求出替换后矩阵的行列式。
3. 用未知数的行列式值除以系数矩阵的行列式值,即可得到该未知数的解。
克拉默法则的优点是计算简单,适用于求解小规模的线性方程组。
然而,由于需要计算多次行列式,对于大规模的线性方程组来说效率较低。
三、矩阵法矩阵法是一种将线性方程组转化为矩阵运算的方法。
通过矩阵的逆运算或者伴随矩阵求解线性方程组。
具体步骤如下:1. 将线性方程组写成矩阵的形式,其中系数矩阵为A,未知数矩阵为X,常数向量矩阵为B。
即AX=B。
2. 若系数矩阵A可逆,则使用逆矩阵求解,即X=A^(-1)B。
3. 若系数矩阵A不可逆,则使用伴随矩阵求解,即X=A^T(ATA)^(-1)B。
矩阵法的优点是适用于各种规模的线性方程组,且运算速度较快。
线性方程组求解方法回顾

Journal of Computational and Applied Mathematics 123(2000)1–33www.elsevier.nl/locate/camIterative solution of linear systems in the 20th centuryYousef Saad a ;1,Henk A.van der Vorst b ;∗a Department of Computer Science and Engineering,University of Minnesota,Minneapolis,USAb Department of Mathematics,Utrecht University,P.O.Box 80.010,3508TA Utrecht,NetherlandsReceived 23January 2000;received in revised form 2March 2000AbstractThis paper sketches the main research developments in the area of iterative methods for solving linear systems during the 20th century.Although iterative methods for solving linear systems ÿnd their origin in the early 19th century (work by Gauss),the ÿeld has seen an explosion of activity spurred by demand due to extraordinary technological advances in engineering and sciences.The past ÿve decades have been particularly rich in new developments,ending with the avail-ability of large toolbox of specialized algorithms for solving the very large problems which arise in scientiÿc and industrial computational models.As in any other scientiÿc area,research in iterative methods has been a journey characterized by a chain of contributions building on each other.It is the aim of this paper not only to sketch the most signiÿcant of these contributions during the past century,but also to relate them to one another.c 2000Elsevier Science B.V.All rights reserved.Keywords:ADI;Krylov subspace methods;Multigrid;Polynomial acceleration;Preconditioning;Relaxation methods;SOR;Sparse approximate inverse1.IntroductionNumerical linear algebra is an exciting ÿeld of research and much of this research has been triggered by a problem that can be posed simply as:given A ∈C m ×n ;b ∈C m ,ÿnd solution vector(s)x ∈C n such that Ax =b .Many scientiÿc problems lead to the requirement to solve linear systems of equations as part of the computations.From a pure mathematical point of view,this problem can be considered as being solved in the sense that we explicitly know its solution in terms of determinants.The actual computation of the solution(s)may however lead to severe complications,when carried out in ÿnite precision and when each basic arithmetic operation takes ÿnite time.Even ∗Corresponding author.E-mail addresses:saad@ (Y.Saad),vorst@math.uu.nl (H.A.van der Vorst).1Work supported by NSF =CCR and by the Minnesota Supercomputer Institute.0377-0427/00/$-see front matter c 2000Elsevier Science B.V.All rights reserved.PII:S 0377-0427(00)00412-X2Y.Saad,H.A.van der Vorst/Journal of Computational and Applied Mathematics123(2000)1–33the“simple”case when n=m and A is nonsingular,which is a trivial problem from a mathematical point of view,may become very complicated,from a computational point of view,and may even turn out to be impossible.The traditional way to solve a nonsingular linear system is to employ Gaussian elimination,and, with all its enhancements,to overcome numerical instabilities.This process can be carried out in O(n3)basic oating point operations(additions and multiplications,assuming n=m).Many applications lead to linear systems with a large n(where the notion of“large”depends,of course, on the capacity of the available computer),and it became soon evident that one has to exploit speciÿc properties of the A at hand in order to make solution of the system feasible.This has led to variants of Gaussian elimination in which the nonzero structure of A is exploited,so that multiplications with zero result are avoided and that savings in computer storage could be realized.Another direction of approach was based on the solution of a nearby linear system,with a ma-trix that admits a computationally inexpensive process(in terms of computing time and computer storage),and to embed this in an iterative process.Both approaches aim at making the impos-sible possible,and for the novice in thisÿeld this may seem to be just a collection of clever programming tricks:“in principle solving the problem is well understood but one has to be well organized to make the computational process a little faster”.For this novice it will certainly come as a big surprise that a whole,still incomplete,mathematical framework had to be developed with deep and elegant results.As a result,relevant systems could be solved many orders of magnitude faster(and also often more accurate)than by a straightforward Gaussian elimination approach.In this paper,we will sketch the developments and progress that has taken place in the20th century with respect to iterative methods alone.As will be clear,this subÿeld could not evolve in isola-tion,and the distinction between iterative methods and Gaussian elimination methods is sometimes artiÿcial–and overlap between the two methodologies is signiÿcant in many instances.Neverthe-less,each of the two has its own dynamics and it may be of interest to follow one of them more closely.It is likely that future researchers in numerical methods will regard the decade just passed as the beginning of an era in which iterative methods for solving large linear systems of equations started gaining considerable acceptance in real-life industrial applications.In looking at past literature,it is interesting to observe that iterative and direct methods have often been in competition for solving large systems that arise in applications.A particular discovery will promote a given method from one camp only to see another discovery promote a competing method from the other camp.For example,the1950s and1960s saw an enormous interest in relaxation-type methods–prompted by the studies on optimal relaxation and the work by Young,Varga,Southwell,Frankel and others.A little later,sparse direct methods appeared that were very competitive–both from the point of view of robustness and computational cost.To this day,there are still applications dominated by direct solvers and others dominated by iterative solvers.Because of the high memory requirement of direct solvers,it was sometimes thought that these would eventually be replaced by iterative solvers,in all applications.However,the superior robustness of direct solvers prevented this.As computers have become faster,very large problems are routinely solved by methods from both camps.Iterative methods were,even halfway in the20th century,not always viewed as promising.For instance,Bodewig[23,p.153],in1956,mentioned the following drawbacks of iterative methods: nearly always too slow(except when the matrix approaches a diagonal matrix),for most problemsY.Saad,H.A.van der Vorst/Journal of Computational and Applied Mathematics123(2000)1–333 they do not converge at all,they cannot easily be mechanised2and so they are more appropriate for computing by hand than with machines,and do not take advantage of the situation when the equations are symmetric.The only potential advantage seen was the observation that Rounding errors do not accumulate,they are restricted to the last operation.It is noteworthy that Lanczos’method was classiÿed as a direct method in1956.The penetration of iterative solvers into applications has been a slow process that is still ongoing. At the time of this writing for example,there are applications in structural engineering as well as in circuit simulation,which are dominated by direct solvers.This review will attempt to highlight the main developments in iterative methods over the past century.It is clear that a few pages cannot cover an exhaustive survey of100years of rich devel-opments.Therefore,we will emphasize the ideas that were successful and had a signiÿcant impact. Among the sources we used for our short survey,we would like to mention just a few that are notable for their completeness or for representing the thinking of a particular era.The books by Varga[188]and Young[205]give a complete treatise of iterative methods as they were used in the 1960s and1970s.Varga’s book has several excellent historical references.These two masterpieces remained the handbooks used by academics and practitioners alike for three decades.Householder’s book[102]contains a fairly good overview of iterative methods–speciÿcally oriented towards projection methods.Among the surveys we note the outstanding booklet published by the National Bureau of Standards in1959which contains articles by Rutishauser[150],Engeli[68]and Stiefel [170].Later Birkho [21],who supervised David Young’s Ph.D.thesis in the late1940s,wrote an excellent historical perspective on the use of iterative methods as he experienced them himself from1930to1980.The more recent literature includes the books by Axelsson[7],Brezinski[29], Greenbaum[88],Hackbusch[97],and Saad[157],each of which has a slightly di erent perspective and emphasis.2.The quest for fast solvers:a historical perspectiveIterative methods have traditionally been used for the solution of large linear systems with diag-onally dominant sparse matrices.For such systems the methods of Gauss–Jacobi and Gauss–Seidel could be used with some success,not so much because of the reduction in computational work, but mainly because of the limited amount of memory that is required.Of course,reduction of the computational work was also a serious concern,and this led Jacobi(1846)to apply plane rotations to the matrix in order to force stronger diagonal dominance,giving up sparsity.Jacobi had to solve many similar systems in the context of eigenvalue computations;his linear systems were rather small:of order7.In this century,simple iterative methods were predominantly applied for solving discretized elliptic self-adjoint partial di erential equations,together with a local parameter for accelerating the iteration process.Theÿrst and simplest of these methods in Richardson’s method[146].Actually,this method2This remark was removed from the second edition(in1959);instead Bodewig included a small section on methods for automatic machines[24,Chapter9].The earlier remark was not as puzzling as it may seem now,in view of the very small memories of the available electronic computers at the time.This made it necessary to store intermediate data on punched cards.It required a regular ow of the computational process,making it cumbersome to include techniques with row interchanging.4Y.Saad,H.A.van der Vorst/Journal of Computational and Applied Mathematics123(2000)1–33was later viewed as a polynomial method and many authors have sought to optimize it by selecting its parameters so that the iteration polynomials became the Chebyshev polynomials;this was work done in the period1950–1960by Young,Lanczos and others.In the second half of this decade it became apparent that using the explicit three-term recurrence relation between Chebyshev polynomials,which led to three-term recurrence iteration methods(rather than the classical methods that are two-term iterations),were numerically superior in terms of stability[87].The acceleration of the slightly more di cult to analyze Gauss–Seidel method led to point succes-sive overrelaxation techniques introduced simultaneously by Frankel[78]and by Young[203].It was shown,for rather simple Dirichlet problems,that a suitably chosen relaxation parameter could lead to drastic improvements in convergence.Young showed that these improvements could be expected for a larger class of matrices,characterized by his property A[203].Successive overrelaxation methods, and numerous variants,became extremely popular and were the methods of choice in computer codes for large practical problems,such as nuclear reactor di usion,oil reservoir modeling and weather prediction.Although their popularity has been overshadowed later,around after1980,by more pow-erful techniques,they are still used in some applications either as the main iterative solution method or in combination with recent techniques(e.g.as smoothers for multigrid or as preconditioners for Krylov methods).The successive over-relaxation(SOR)methods made it possible to solve e ciently systems within the order of20,000unknowns by1960[188],and by1965systems of the order of 100,000could be solved in problems related to eigenvalue computations in nuclear di usion codes. The success of the SOR methods has led to a rich theory for iterative methods;this could be used fruitfully for the analysis of later methods as well.In particular,many methods,including SOR, could be viewed as simple Richardson iterations for speciÿc splittings of the matrix of the linear system.In1955,Peaceman and Rachford[141]suggested a splitting that was motivated by the observation that the matrix for a three-pointÿnite di erence stencil for a one-dimensional second-order PDE is tridiagonal and this system can easily be solved.Their suggestion was to view theÿve-pointÿnite di erence approximation for a two-dimensional problem as the direct sum of two one-dimensional approximations.This led to an iteration in which alternatingly a tridiagonal associated with one of the two directions was split o ,and this became popular as the alternating direction iteration(ADI). With the inclusion of iteration parameters,that steered the inclusion of a diagonal correction to the iteration matrices,the resulting ADI iterations could be tuned into a very e ective method.Varga [188]gives a good overview of the theory for understanding ADI methods.He,as well as Birkho [21]mentions that ADI was initially derived as a by-product of numerical methods for parabolic equations(the correction to the diagonal was motivated by the e ect of the time derivative in these methods).Sheldon and Wachspress,in1957,gave an early proof for the convergence of ADI for ÿxed parameters[192].Wachspress discusses these ADI methods in his book[193]and considers also other grid-oriented acceleration techniques.One of these techniques exploits approximations obtained on coarser grids and can be viewed as a primitive predecessor to multigrid.Theÿrst half of the century begins also with simple local projection methods,in which one attempts to solve a set of equations by solving each separate equation by a correction that is small in some norm.These methods could be used for over-or underdetermined linear systems,such as those that arise in tomography problems.This has led to the methods of Cimmino[44]and Kaczmarz[106],which were later identiÿed as instances of Gauss–Jacobi and or Gauss–Seidel for related systems with A T A or AA T.Modern variants of these methods,under the name of ART andY.Saad,H.A.van der Vorst/Journal of Computational and Applied Mathematics123(2000)1–335 SIRT are very popular,for instance in medical and seismic tomography.ART and SIRT can be related to SOR and Block SOR.Spakman and Nolet[168]report on the solution of292,451by 20,070systems related to structures of the upper earth mantle,with these methods(and with LSQR). The second half of the century was marked by the invention(paper published in1952)of the conjugate gradient method by Hestenes and Stiefel[101]and the Lanczos algorithm for linear systems [117].This started the era of Krylov iterative methods.Initially,these were not viewed as truly iterative techniques,but rather as direct solution algorithms since they terminated in exact arithmetic in fewer than n steps,if n is the order of the matrix(see,for instance,Householder’s book where conjugate gradients is discussed in the chapter on direct methods[102,Chapter5.7]).Hestenes and Stiefel already recognized that the method behaves as an iterative method,in the sense that the norm of the residual often decreases quite regularly,and that this might lead for some systems to acceptable approximations for the solution within n steps.A little earlier,papers by Lanczos[115] and by Arnoldi[2]had addressed the issue of transforming a matrix into simpler form for the purpose of diagonalizing it.These four papers together set the foundations of many methods that were developed later.A famous publication by Engeli et al.[69]considered the method as a truly iterative process and showed that in rounding precision arithmetic,the conjugate gradient method did not terminate in the expected number of iteration steps(equal to at most the order of the matrix).This was shown for a matrix of order64,a discretized biharmonic problem.Convergence occurred only after a few hundred steps.Notwithstanding this apparent failure,the method appeared later in the famous Wilkinson and Reinsch collection[202]as a kind of memory-friendly direct technique.It was mentioned that actual convergence might occur only after m iterations,where m could be3up toÿve times the order of the matrix.Because of this not well-understood behavior in rounded arithmetic,the method did not make it to theÿrst universal linear algebra package LINPACK(mid-1970s).In the early to mid-1960s it became clear that the convergence of the conjugate gradient method depends on the distribution of the eigenvalues of the matrix,and not so much on the order of the matrix,as was,for example, explained in a paper by Kaniel[109].Daniel[50,51]studied the conjugate gradient method as an iterative method for the minimization of functionals in(inÿnite dimensional)Hilbert spaces.This is a natural consequence of the observation that conjugate gradients,like other Krylov subspace methods, requires the action of the matrix as a linear operator and does not exploit the actual representation of the matrix(that is,the method does not require knowledge of the individual entries of the matrix). Also,Daniel expressed concerns about the convergence behavior of the method inÿnite precision, and he discussed modiÿcations with guaranteed convergence[51,p.134].Note also that much of the convergence theory developed for the conjugate gradient and the Lanczos methods was almost invariably set in the context of operators on inÿnite-dimensional spaces,see,for example[109].It was Reid[145]who suggested to use the conjugate gradient method again as an iterative technique,but now for large sparse linear systems arising in the discretization of certain PDEs. Soon after this,the notion of preconditioning(already proposed in the Hestenes and Stiefel paper) became quite popular.Thus,the incomplete Choleski decompositions of Meijerink and van der Vorst [125]led to the ICCG process,which became the de facto iterative solver for SPD systems. Hence,it took about25years for the conjugate gradient method to become the method of choice for symmetric positive-deÿnite matrices(the incomplete Choleski decompositions were shown to exist for M matrices).A good account of theÿrst25years of the history of the CG method was given by Golub and O’Leary[86].6Y.Saad,H.A.van der Vorst/Journal of Computational and Applied Mathematics123(2000)1–33The unsymmetric variants of the Krylov methods required a similar amount of time to mature. The late1960s and early1970s,saw the roots for such methods.Techniques named ORTHODIR, ORTHOMIN,FOM,and others,were introduced but in their original formulations,these methods su ered from breakdowns and numerical instabilities.The GMRES variant,introduced by Saad and Schultz[158],was designed to avoid these undesirable features and became the de facto standard for unsymmetric linear systems.However,it su ered from the disadvantage of requiring increasing computational resources for increasing numbers of iterations.Bi-CG,the unsymmetric variant of con-jugate gradients,did not have these disadvantages.The method,based on the unsymmetric Lanczos method(1952),was introduced by Fletcher in1976[76],but it is mathematically equivalent to a technique that had already been described in Lanczos’paper.Bi-CG,however,su ered from other practical problems,known as breakdowns of theÿrst and second kind,which prevented early success. Moreover,the occurrence of nonorthogonal transformations led to much suspicion among numerical analysts.Nevertheless,the method became quite popular in a variant known as CGS(Sonneveld, 1984)[166]which,for virtually equal cost could essentially apply Bi-CG twice,leading often to a twice as fast convergence,but also amplifying the problems of Bi-CG.In the1980s,Parlett and co-authors[140]and later Freund and Nachtigal[81]have shown how to repair the deÿciencies in the Bi-CG method so that rather reliable software could be constructed.More recently,we have seen hybrids of the Bi-CG and GMRES approaches,with Bi-CGSTAB[186]as one of the most popular ones.Originally,the usage of iterative methods was restricted to systems related to elliptic partial di er-ential equations,discretized withÿnite di erence techniques.Such systems came from oil reservoir engineering,weather forecasting,electronic device modeling,etc.For other problems,for instance related to variousÿnite element modeling,practitioners preferred the usage of direct solution tech-niques,mainly e cient variants of Gaussian elimination,because of the lack of robustness of iterative methods for large classes of matrices.Until the end of the1980s almost none of the big commercial packages forÿnite element problems included iterative solution techniques.Simon[164]presented results,obtained for matrices of the order of55,000,for direct solution techniques.On the then fastest supercomputers,this required in the order of a few minutes of computing time.He claimed that direct sparse solvers would remain the method of choice for irregularly structured problems. Although this is certainly true if the structure of the matrix allows for an e cient elimination pro-cess,it became clear that for many PDE-related problems,the complexity of the elimination process increased too much to make realistic three-dimensional modeling feasible.Irregularly structuredÿ-nite element problems of order1,000,000,as foreseen by Simon,may be solved by direct methods –given a large enough computer(memory wise)but at tremendous cost and di culty.However, some of them can be solved with iterative techniques,if an adequate preconditioning can be con-structed.In the last decade of this century,much e ort was devoted to the identiÿcation of e ective preconditioners for classes of matrices.For instance,Pomerell[142]in1994reports on successful application of preconditioned Krylov methods for very ill-conditioned unstructuredÿnite element systems of order up to210,000that arise in semiconductor device modeling.While using iterative methods still requires know-how,skill,and insight,it can be said that enormous progress has been made for their integration in real-life applications.Still,linear systems arising from many relevant problems,for instance large electric and electronic circuits,are not easy to solve in an e cient and reliable manner by iterative methods.Steady progress is being made but theÿeld as a whole can still be viewed as being in its infancy.Y.Saad,H.A.van der Vorst/Journal of Computational and Applied Mathematics123(2000)1–337 3.Relaxation-based methodsThe Gauss–Seidel iteration was the starting point for the successive over-relaxation methods which dominated much of the literature on iterative methods for a big part of the second half of this century. The method was developed in the19th century,originally by Gauss in the mid-1820s and then later by Seidel in1874(see references in[102]).In fact,according to Varga[188],the earliest mention on iterative methods is by Gauss(1823).Indeed,on December26,1823,Gauss writes a letter to Gerling,in which he describes an iterative technique for the accurate computation of angles occurring in geodesy[84,p.278].The corrections for the four angles in a quadrangle,determined by four church towers,were computed from a singular linear systems of four equations with four unknowns(the singularity comes from the observation that the four angles sum up to360◦).The technique that Gauss describes is what we now know as the Gauss–Seidel algorithm.The order of processing of the equations was determined by the unknown that helped to reduce the residual most.Gauss recognized that the singularity of the system led to convergence to the solution modulo a vector in the null space,for which he could easily make a correction.The three pages of his letter are full of clever tricks.He concludes by recommending the new method to Gerling,arguing that the method is self correcting,and that one can easily determine how far to go and then ends his letter with the remark that the computations were a pleasant entertainment for him.He said that one could do this even half asleep,or one could think of other things during the computations.In view of this remark it may hardly be a surprise that the method became so popular in the era of electronic computing.The method as it was developed in the19th century was a relaxation technique,in which relaxation was done by“hand”.It was therefore natural to eliminate the largest components,see for example [55,118].This method is referred to as Nekrasov’s method in the Russian literature[130].Referring to the more modern method in which relaxation was done in a cyclic manner,Forsythe is quoted as having stated that“the Gauss–Seidel method was not known to Gauss and not recommended by Seidel”,see[102,p.115].However,the blossoming of overrelaxation techniques seems to have been initiated by the Ph.D. work of David Young[203].Young introduced important notions such as consistent ordering and property A,which he used for the formulation of an elegant theory for the convergence of these methods.Generalizations of Young’s results to other relevant classes of matrices were due to Varga, who published his book on Matrix Iterative Analysis in1962.For decades to come this book was the standard text for iterative methods for linear systems.It covered important notions such as regular splittings,a rather complete theory on Stieltjes and M-matrices,and a treatment of semi-iterative methods,including the Chebyshev semi-iteration method.The latter method,analyzed by Golub and Varga[87],also became more widely known,especially in the period when inner products were relatively expensive.The accelerated Gauss–Seidel methods have motivated important developments in the theory of matrix linear algebra.In particular,relevant properties for M-matrices,introduced by Ostrowski [135],were uncovered and convergence results for so-called regular splittings,introduced by Varga [189]were established.A cornerstone in the convergence theory was the theorem of Stein–Rosenberg (1948)[169]which proved relations between the asymptotic rates of convergence for the successive overrelaxation methods,including the Gauss–Seidel method,and the Gauss–Jacobi method.The concept of irreducibility of a matrix,a natural property for grid-oriented problems,helped to extend8Y.Saad,H.A.van der Vorst/Journal of Computational and Applied Mathematics123(2000)1–33 results for strongly diagonally dominant matrices to matrices for which the strict diagonal dominance inequality is required to hold only for one single equation at least.Another important notion is the concept of cyclic matrices:an irreducible matrix with k eigenvalues of modulus (A)is said to be of index k.Varga[188]gives a good overview of the relevant theory and the implications of this concept for iterative methods.It has a close relationship with Young’s property A[188,p.99], and provides the basis for the convergence theory of the SOR methods.Su cient conditions for the convergence of the SOR methods were given by theorems of Ostrowski[136]and Reich[144]. Lower bounds for the spectral radius of the SOR iteration matrix were derived by Kahan[107].This together provided the basis for a theory for iterative methods,published in Varga’s book[188]from which many new methods ter,in the1970s major part of this theory served well in the development of preconditioners for Krylov methods.The following is a quotation from Varga’s book(page1)“As an example of the magnitude of problems that have been successfully solved on digital computers by cyclic iterative methods,the Bettis Atomic Power laboratory of the Westinghouse Electric Corporation had in daily use in1960 a two-dimensional program which would treat as a special case,Laplacean-type matrix equations of order20,000”.So the state of the art in1960was a20;000×20;000Laplace equation.In the late1960s and early1970s a number of methods appeared in which the order of re-laxation was not prescribed or even deterministic.These were appropriately termed“chaotic”or “asynchronous”relaxations.It was established that if a variable is relaxed an inÿnite number of times,the global method would always converge for any order in which the relaxation takes place.A few of the main contributions were by Chazan and Miranker[41],Miellou[128],Robert[147] and Robert et al.[148].These methods were motivated by parallelism and were essentially ahead of their time for this reason.4.Richardson and projection methodsAnother line of development started with Richardson’s method[146].x k+1=x k+!r k=(I−!A)x k+!b;which can be viewed as a straightforward iteration associated with the splitting A=K−R,with K=(1=!)I,R=(1=!)I−A.Here r k is the residual vector of the current iterate: r k=b−Ax k:For the residual at the(k+1)th step,one obtainsr k+1=(I−!A)k+1r0=P k+1(A)r0;where P k+1(A)is a k+1degree polynomial in A,with P k+1(t)=(1−t)k+1.It is easy to see that for symmetric positive-deÿnite matrices the process will converge for!in the open interval 0¡!¡2= max where max is the largest eigenvalue of A.In addition the best!is known to be 2=( min+ max),see,e.g.,[188,157]for details.The original Richardson iteration is readily generalized by taking a di erent!=!k for each iteration,which leads to the generalized Richardson iterationx k+1=x k+!k r k:(1)。
数值计算 SOR方法
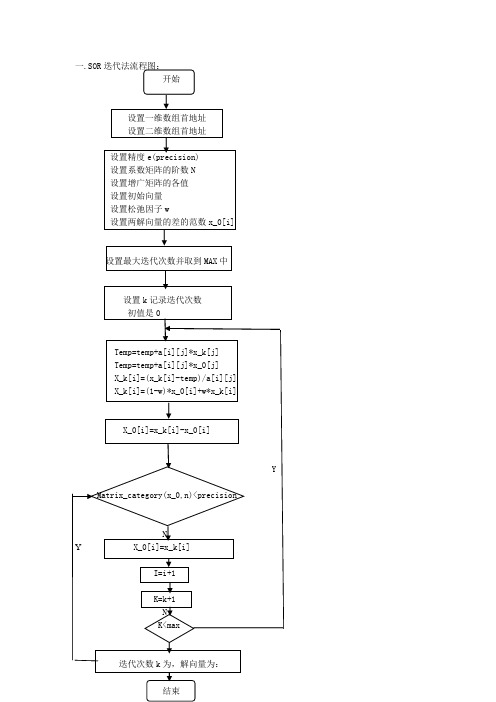
一.SOR迭代法流程图:开始设置一维数组首地址设置二维数组首地址设置精度e(precision)设置系数矩阵的阶数N设置增广矩阵的各值设置初始向量设置松弛因子w设置两解向量的差的范数x_0[i]设置最大迭代次数并取到MAX中设置k记录迭代次数初值是0Temp=temp+a[i][j]*x_k[j]Temp=temp+a[i][j]*x_0[j]X_k[i]=(x_k[i]-temp)/a[i][j]X_k[i]=(1-w)*x_0[i]+w*x_k[i]X_0[i]=x_k[i]-x_0[i]YMatrix_category(x_0,n)<precisionNY X_0[i]=x_k[i]I=i+1K=k+1NK<max实验名称: 松弛法实验解题小组成员(班级:09医软(1)班):姚飞 :09713047 参与程序的编写闫化晴 :09713046 参与搜集资料与编写程序余雷 :09713049 参与搜集资料与后期运行调试张珊 :09713051 参与程序的编写实验内容:二.SOR 迭代法理论:松弛法是 Gauss -Seidel 迭代 迭代法的一种加速方法.若记△X = X (K+1) - X (K) = LX (K+1) + UX (K) + f - X (K)则X (K+1) = X (K) + △X ,这样X (K+1) 可以看作是 X (K)加上修正项 △X 而得到.若在修正项△X 前面添加一个因子ω= 1,就是Gauss -Seidel 迭代.通过选择ω可使迭代法收敛的更快.松弛法简称SOR 方法,它的计算格式为:(1)()()()111122111(1)()(1)()()222211233222(1)()(1)()1111(1)(),(1)(),(1)(),k k k k n n k k k k k n n k k k k n n n n nn n nn x x b a x a x a x x b a x a x a x a x x b a x a x a ωωωωωω+++++--=-+---=-+----=-+---这里ω称为松弛因子.当ω< 1时称为低松弛迭代,当1 < ω <2时称为超松弛迭代.实验素材及结果:三、SOR 迭代法例1、用SOR 迭代法求解线性方程组:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----------74.012.018.168.072.012.006.016.012.001.103.014.006.003.088.001.016.014.001.076.04321x x x x取初始点T x )0,0,0,0()0(=,松弛因子05.1=ω,精度要求610-=ε.解 :根据上面程序运行结果如下:例2、用SOR迭代法求解方程组:8X1 + X2- 2X3 = 9,3X1 - 10X2 +X3 = 19,5X1 - 2X2 +20X3 = 72,取初始点X(0) = (0,0,0)T,松弛因子ω= 1,精度要求ε= 10-5.解:根据上面程序运行结果如下:。
SOR迭代法

aij x(jk )
3.1
若记
i1
n
r(k)
i
(bi
a x(k 1) ij j
aij
x
(k j
)
),
j 1
j i
i 1,2,L ,n
则 3.1 式可写为
x( k 1) i
x(k) i
1 aii
r(k)
i
3.2
由此可以看出, Gauss Seidel 迭代法的第 k 1
步 ,相当于在第 k 步的基础上每一个分量增加
SOR迭代法常以这种形式进行计算。
格式(3.4)的矩阵形式为
X (k1) (1 ) X k D1 b LX k UX (k) ,
3.5
其中
a11
D
a22
O
0
0
,
ann
0 a12 L
U
0O
O
0
a1n
an1,n
0
显然,A D L U.
0
0
L
a21
O
OO
上述定理说明,对于任何系数矩阵 A,若要 SOR
法收敛,必须选取松弛因子 0,2 , 然而,当松
弛因子满足条件 0 2 时,并不是对所有系数矩 阵 A 来说,SOR 法都是收敛的。但是,对一些特殊矩 阵来说,这一条件是充分的。
定理7 如果矩阵 A 是对称正定的,则 SOR 法 对于0 2 是收敛的。
其 Gauss Seidel 迭 代 格 式 可写为 (aii 0) :
x(k1) i
x(k) i
1 aii
bi
a x(k1) i1 1
L
a x(k1) i,i1, i1
大学数学(解线性方程组)

大学数学(解线性方程组)大学数学(解线性方程组)在大学数学课程中,解线性方程组是一个基础而重要的内容。
线性方程组是由一系列线性方程组成的方程组,其中每个方程都是未知数的线性组合。
解线性方程组的过程涉及到找到使得方程组中的所有方程都成立的未知数的值。
本文将介绍解线性方程组的常用方法和技巧。
一、高斯消元法高斯消元法是一种常用且有效的解线性方程的方法。
它的基本思想是通过使用一系列列变换将线性方程组化为上三角形式,从而使得方程求解更加简单。
首先,将线性方程组写成增广矩阵的形式,其中未知数的系数构成一个矩阵,等号右边的常数构成一个列矩阵。
然后,我们可以使用以下步骤来进行高斯消元法:1. 选定一个主元素:选择一个非零的系数作为主元素,通常选择系数绝对值最大的行作为主元素所在的行。
2. 行变换:将主元素所在的行除以主元素的值,使主元素变为1。
然后,将该主元素所在列上的其他元素通过适当的倍数相减,使得主元素下方的元素都变为0。
3. 重复步骤1和步骤2:重复选定主元素和行变换的过程,直到将线性方程组化为上三角形式。
4. 回代求解:从最后一行开始,逐个求解未知数的值。
对于每一行来说,已知未知数的值可以直接代入该行的方程,从而得到下一个未知数的值,直到求解出所有的未知数。
二、矩阵方法矩阵方法是另一种常用于解线性方程组的方法。
通过将线性方程组的系数矩阵和常数矩阵相乘,可以得到一个新的矩阵。
然后,通过对新的矩阵进行逆矩阵或者伴随矩阵运算,可以求解出未知数的值。
具体步骤如下:1. 构造增广矩阵:将线性方程组的系数矩阵和常数矩阵合并成一个增广矩阵。
2. 行变换:使用矩阵的初等行变换将增广矩阵化为行最简形式,即将其变为上三角矩阵。
3. 回代求解:从最后一行开始,逐个求解未知数的值,通过代入法可得到每个未知数的值。
三、矩阵的逆如果线性方程组的系数矩阵是可逆矩阵,那么可以通过求逆矩阵的方式直接得到未知数的值。
逆矩阵与原系数矩阵的乘积即为单位矩阵。
初中数学 线性方程组的解如何计算

初中数学线性方程组的解如何计算计算线性方程组的解可以使用多种方法,下面我将详细介绍三种常用的解法:高斯消元法、矩阵法和克莱姆法。
1. 高斯消元法:高斯消元法是一种基于矩阵变换的解线性方程组的方法,其主要步骤如下:- 将线性方程组写成增广矩阵的形式,即将系数矩阵和常数项列组合成一个矩阵。
- 通过矩阵变换,将增广矩阵化简为行阶梯形矩阵或行最简形矩阵。
- 根据化简后的矩阵,判断方程组的解的情况:- 如果矩阵中的某一行全为0,且对应的常数项不为0,则方程组无解。
- 如果方程组中的未知数的个数等于矩阵中非零行的个数,则方程组有唯一解。
- 如果方程组中的未知数的个数大于矩阵中非零行的个数,则方程组有无穷多解,可以引入自由变量。
2. 矩阵法:矩阵法是一种利用矩阵运算求解线性方程组的方法,其主要步骤如下:- 将线性方程组的系数和常数项组成系数矩阵和常数矩阵。
- 计算系数矩阵的逆矩阵(如果存在)。
- 如果逆矩阵存在,方程组有唯一解,可以通过矩阵运算求解。
- 如果逆矩阵不存在,可以使用矩阵的秩来判断方程组的解的情况:- 如果系数矩阵的秩小于常数矩阵的秩,则方程组无解。
- 如果系数矩阵的秩等于常数矩阵的秩且等于未知数的个数,则方程组有唯一解。
- 如果系数矩阵的秩等于常数矩阵的秩小于未知数的个数,则方程组有无穷多解,可以引入自由变量。
3. 克莱姆法:克莱姆法是一种利用行列式求解线性方程组的方法,适用于未知数的个数与方程组的个数相等的情况。
其主要步骤如下:- 将线性方程组的系数和常数项组成系数矩阵和常数矩阵。
- 计算系数矩阵的行列式。
- 如果系数矩阵的行列式不为0,则方程组有唯一解,可以通过计算行列式的余子式和代数余子式求解。
- 如果系数矩阵的行列式为0,则方程组无解或者有无穷多解,需要进行进一步的计算来判断解的情况。
通过掌握这三种解线性方程组的方法,我们可以根据方程组的具体形式和求解的要求来选择合适的方法,以求得方程组的解或者判断方程组是否有解。
数学线性方程组的解法

数学线性方程组的解法数学线性方程组是数学中的重要概念,广泛应用于各个领域,包括物理、经济、工程等。
解决线性方程组可以帮助我们更好地理解和处理现实生活中的问题。
本文将介绍几种常见的线性方程组的解法,帮助读者更好地掌握和运用相关知识。
一、高斯消元法高斯消元法是求解线性方程组的经典方法之一。
它的基本思想是通过一系列的行变换将线性方程组转化为简化的行阶梯形式,从而求得方程组的解。
下面以一个简单的二元线性方程组为例进行说明:```math2x + 3y = 43x - y = 5```首先,我们将方程组写成增广矩阵的形式:```math[2 3 | 4][3 -1 | 5]```接下来,通过行变换,目标是将矩阵的主元素以及主元素以下的元素都变为0。
具体步骤如下:1. 交换行以使得主对角线上的元素不为0;2. 用第一行的倍数加到其他行上,使得第一列的元素都变为0;3. 用第二行的倍数加到第一行上,使得第二行的首元素变为0;4. 若还有多个变量,继续重复上述步骤。
经过一系列的行变换,我们可以得到如下的简化行阶梯形式:```math[1 0 | 2][0 1 | 1]```这样,我们就得到了方程组的解为x=2,y=1。
当然,这只是一个简单的示例,对于复杂的线性方程组,可能需要更多的行变换才能得到解。
二、克拉默法则克拉默法则是另一种解线性方程组的方法。
它的基本思想是利用方程组的系数矩阵的行列式以及常数矩阵与系数矩阵的代数余子式之间的关系来求解方程组的解。
对于一个包含n个方程和n个未知数的线性方程组,可以表示为Ax=b的形式,其中A为系数矩阵,x为未知数向量,b为常数向量。
根据克拉默法则,方程组的解可以由以下公式给出:```mathx_i = \frac{{\det(A_i)}}{{\det(A)}}, \quad i=1,2,\ldots,n```其中,`A_i`为将系数矩阵A的第i列换成常数矩阵b所得到的矩阵,`det(A)`表示系数矩阵A的行列式。
数学实验“线性方程组的j迭代,gs迭代,sor迭代解法”实验报告(内含matlab程序代码)【最新精

西京学院数学软件实验任务书实验四实验报告一、实验名称:线性方程组的J-迭代,GS-迭代,SOR-迭代。
二、实验目的:熟悉线性方程组的J-迭代,GS-迭代,SOR-迭代,SSOR-迭代方法,编程实现雅可比方法和高斯-赛德尔方法求解非线性方程组12123123521064182514x x x x x x x x +=⎧⎪++=⎨⎪++=-⎩的根,提高matlab 编程能力。
三、实验要求:已知线性方程矩阵,利用迭代思想编程求解线性方程组的解。
四、实验原理:1、雅可比迭代法(J-迭代法):线性方程组b X A =*,可以转变为:迭代公式(0)(1)()k 0,1,2,....k k J XXB X f +⎧⎪⎨=+=⎪⎩ 其中b M f U L M A M I B J 111),(---=+=-=,称J B 为求解b X A =*的雅可比迭代法的迭代矩阵。
以下给出雅可比迭代的分量计算公式,令),....,()()(2)(1)(k n k k k X X X X =,由雅可比迭代公式有b XU L MXk k ++=+)()1()(,既有i ni j k i iji j k iij k iij b X aXa X a +--=∑∑+=-=+1)(11)()1(,于是,解b X A =*的雅可比迭代法的计算公式为⎪⎩⎪⎨⎧--==∑∑-=+=+)(1),....,(111)()()1()0()0(2)0(1)0(i j n i j k j ij k j ij i ii k iTn X a X a b a X X X X X 2、 高斯-赛德尔迭代法(GS-迭代法):GS-迭代法可以看作是雅可比迭代法的一种改进,给出了迭代公式:⎪⎩⎪⎨⎧--==∑∑-=+=+++)(1),....,(111)1()1()1()0()0(2)0(1)0(i j n i j k j ij k j ij i ii k iTn X a X a b a X X X X X 其余部分与雅克比迭代类似。
线性方程组的J-迭代,GS-迭代,SOR-迭代,SSOR-迭代方法

西京学院数学软件实验任务书课程名称数学软件实验班级数0901学号0912020119姓名王震实验课题雅克比迭代、高斯—赛德尔迭代、超松弛迭代实验目的熟悉雅克比迭代、高斯—赛德尔迭代、超松弛迭代实验要求运用Matlab/C/C++/Java/Maple/Mathematica等其中一种语言完成实验内容雅克比迭代法高斯—赛德尔迭代法、超松弛迭代法成绩教师【实验课题】雅克比迭代、高斯—赛德尔迭代、超松弛迭代【实验目的】学习和掌握线性代数方程组的雅克比迭代、高斯—赛德尔迭代、超松弛迭代法,并且能够熟练运用这些迭代法对线性方程组进行求解。
【实验内容】1、问题重述:对于线性方程组,即:A b X = (1),1111221n 12112222n 21122nn n n n n n na x a x a xb a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩ 其中,111212122111 0 - - 0 - 0 0 () - - - 0 n ij n nn n nn nn a a a a a a a a a a ⨯--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥A ==--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ 0n D L U ⎡⎤⎢⎥⎢⎥≡--⎢⎥⎢⎥⎣⎦()1,n b b b T= 如何运用雅克比迭代、高斯—赛德尔迭代、超松弛迭代法对线性方程组进行求解。
2、方法原理:2.1雅克比迭代迭代思想:首先通过构造形如的等式,然后给定一个初值A b X =()x f x =,再通过进行迭代。
(0)(0)(0)(0)12(,,)n x x x X = (1)()()k k f +X =X step1 :对(1)相应第行中的用其它元素表示为:i i x11111121111122,12211111()()11()()11()()n nj j j j j j n ni i ij j i j j j i j i j ii n nn n nj j n n nj j j j nn nn x b a x x b a x a a x b a x x b a x a a x b a x x b a x a a ===≠=-==⎧=-=+-⎪⎪⎪⎪⎨=-=+-⎪⎪⎪=-=+-⎪⎩∑∑∑∑∑∑ 即:()D b L U X =-+XStep 2 :进行迭代,,(0)(0)(0)(0)12(1)11()(,,)()n k k x x x D b D L U +--⎧X =⎨X =-+X ⎩0,1,2k = 取它的判断条件为小于一个确定的误差值,跳出循环。
解线性方程组知识点归纳总结

解线性方程组知识点归纳总结一、线性方程组的概念线性方程组是由一系列线性方程组成的方程集合。
每个线性方程都是一次方程,其变量的次数为1。
二、解线性方程组的方法1. 列主元消元法(高斯消元法):通过消元和代入的方式逐步求解方程组,将其转化为阶梯形方程组来求解。
2. 矩阵法(向量法):使用矩阵的运算方式来求解线性方程组,转化为求解矩阵方程的问题。
3. 克拉默法则:使用行列式的性质来求解线性方程组。
通过计算各个未知数的系数行列式和常数项行列式的比值来求解每个未知数的值。
三、线性方程组的解的情况1. 唯一解:当方程组的系数行列式不为0,且方程组的秩等于未知数的个数时,方程组存在唯一解。
2. 无解:当方程组的系数行列式为0,而常数项行列式不为0时,方程组无解。
3. 无穷解:当方程组的系数行列式为0,且常数项行列式为0时,方程组存在无穷多个解。
四、注意事项1. 线性方程组中的未知数个数应该与方程的个数相等,否则方程组可能没有解或存在无穷多个解。
2. 在使用列主元消元法求解时,需要注意零元素不可作为主元,否则可能会出现错误。
3. 克拉默法则适用于系数矩阵的行列式不为0的情况,否则无法使用该方法求解。
五、示例假设有如下线性方程组:2x + 3y = 74x - 5y = 2使用列主元消元法进行求解:2x + 3y = 7 (方程1)4x - 5y = 2 (方程2)首先将方程组转化为阶梯形方程组:2x + 3y = 7 (方程1)0x - 11y = -12 (方程2)由第二个方程可得到 `y` 的解为 `-12/(-11) = 12/11` ,将其代入第一个方程,可求得 `x` 的解为 `(7 - 3*(12/11))/2`。
因此,该线性方程组的解为 `x = 4/11,y = 12/11`。
六、结论解线性方程组是数学中的重要内容,掌握线性方程组的解法能帮助我们解决实际问题,加深对数学知识的理解和运用。
求解线性方程组的方法

6
(1) (1) (1) (1) (1) A ( a ) ( a ), b b. A x b 将原方程组记为 其中 i j i j
则第一步(k=1),若a11不等于0,则可以计算乘数
(1) mi1 ai(1) / a (i 2,3,, m) 1 11
(k ) kk
0 计算乘数 mik a
(k ) ik
/a
(k ) kk
(i k 1,, m)
用-mik乘上面的线性方程组的第k个方程加到第i个方程,可 以消去xk元,得到同解方程组 A( k 1) x b( k 1) ( k 1) (k ) (k ) 其中 a a m a i j i j ik k j (i k 1,, m, j k 1, n).
3 n 高斯消去法总的乘除运算量为: n2 n 3 3
10
定理2 约化的主元素 akk
(k )
0(k 1,2,, n) 的充要条件是
矩阵A的顺序主子式 Di 0(i 1, 2,, k ). 即
D1 a11 0 a11 a1i Di
证明略
推论 如果矩阵A的顺序主子式 Di 0(i 1, 2,, k ). 则
(1)
x1 0.1 x2 0.2 x3 0.72 x2 0.1 x1 0.2 x3 0.83 x 0.2 x 0.2 x 0.84 1 2 3
(2)
19
2 例题分析:
考虑解方程组 建立与式(1)相等价的形式:
10 x1 x2 2 x3 7.2 x1 10 x2 2 x3 8.3 x x 5 x3 4.2 2 1
线性方程组数值解法总结

好久没来论坛,刚刚发现以前的帖子现在那么火很欣慰,谢谢大家支持!今天趁着不想做其他事情,把线性方程组的数值解法总结下,有不足的地方希望大神指教!数学建模中也会用到线性方程组的解法,你会发现上10个的方程手动解得话把你累个半死,而且不一定有结果,直接用matlab的函数,可以,关键是你不理解用着你安心吗?你怎么知道解得对不对?我打算开个长久帖子,直到讲完为止!这是第一讲,如有纰漏请多多直接,大家一起交流!线性方程组解法有两大类:直接法和迭代法直接法是解精确解,这里主要讲一下Gauss消去法,目前求解中小型线性方程组(阶数不超过1000),它是常用的方法,一般用于系数矩阵稠密,而有没有特殊结构的线性方程组。
首先,有三角形方程组的解法引入Gauss消去法,下三角方程组用前代法求解,这个很简单,就是通过第一个解第二个,然后一直这样直到解出最后一个未知数,代码如下:前代法:function [b]= qiandai_method(L,b)n=size(L,1); %n 矩阵L的行数for j=1:n-1 %前代法求解结果存放在b中b(j)=b(j)/L(j,j);b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j);endb(n)=b(n)/L(n,n);上三角方程组用回代法,和前面一样就是从下面开始解x,代码:后代法:function [y]=houdai_method(U,y)n=size(U,1); %n 矩阵L的行数for j=n:-1:2 %后代法求解结果存放在y中y(j)=y(j)/U(j,j);y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);endy(1)=y(1)/U(1,1);Gauss消去的前提就是这两个算法:具体思想是把任何一个线性方程组的系数矩阵A,分解为一个上三角和一个下三角的乘积,即A=LU,其中L为下三角,U为上三角。
那么具体怎么做呢?有高斯变换,什么是高斯变换?由于时间有限我不可能去输入公式,所以我用最平白的话把它描述出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关键词 :线性方程组 ;S R k方法 ; P 循环矩阵 O—
中图分类号:2 1 O 4. 6 文献标识码: A
1 引 言
考虑线性方程组 A = x b, () 1
其 中系数矩阵 A∈R 是 P ” 循环的非奇异矩阵, b∈R 是 已知的列向量.
维普资讯
第 3 卷第 4 4 期
文章编 号:03 8320) — 5—3 10- 4(080 0 30 2 46
西南民族大学学报 ・ 自然科学版
J u n l f o t we t i e st r t n l isNa u a ce c d t n o r a u h s v r i f i a i e . t r l in eE i o o S Un y o Na o t S i
P一
mn ( = ) mn ( ) k J . ipL ) rk < ip , < P  ̄ pL) r (, 2
E as L 在假定 1 vn 和 i 中并未给出隐函数 g x 可定义 陛和可微性的证明, () 为了定理 2的完整和准确性, 下面将
给 出其证 明 .
间【, ] 2P 上连续, 在开区问 (, ) 2P 内可微. 对 V o 【, ] x ∈ 2P , 考虑Tii e  ̄g 关于 的连续函数, iU
q Y =X ,( ) (o 1 ) 0 Y 1 ( ) o Y ry =b x 一 一 , 很容易证得 g O <,O,( >,1. () () 1 ( 口) ) 这是由于 q O =0< (o 1 =rO ; () bx 一 ) () g1 = ( ) =(
用于线性方程组() S R方法称为 S R P 1 的 O O . 方法, 其迭代格式为
‘ = ’‘ ( c p ¨’ + 一o ) L
b , .
其中 ’ I o e~ ( -c I cU, L, ’,U, =(-c ) ( L I o +o ,,, ) ) = E, , , =
维普资讯
64 5 பைடு நூலகம்
西南民族大学学报 - 自然科学版
第 3 卷 4
其 ∑ = , = — Jl 中 』 p J l m+ _ j
jl =
在新 的划 分下 , 线性方 程组() S 用于 1的 OR方法 称为 S . ORk方法 .
把 记为 A在新划分下相应的块 Jcb矩阵, 3 e m 3 ̄ ( )和 ( )有相I的非零特征值, aoi 从[ L m a] l P , f 司 特别有 (( ) ) ( p) . =( B ) P
一
)g =62 () ,
P定义, 其中0<b — ) <( 为常数, 时 I 刮
P —
l 2I ) 一
假设函数 g x 是可微的. (
他 们在 上述假 定 的条件 下证 明了定理 2 .
定理 2¨如果 ( )仅有非正特征值, p B ) . P  ̄R ( <— , 则
( ( 1 等, ) i < ) 【 ・
( mn ( ’ t咄, ( 11 ’这 优 满足 i pL ) pL,= 一)一 ) 里最 参数 . i  ̄ = 、p) 1 ( ) ( ,
( ( ) ) p=(
‘
—
)( ) 一 , 一1 1 , (
l
) ,
矩阵 称为 S R p O - 迭代矩阵.
V ra a 在文献[ 40给出了如下定理. g 3] ,
定理 1 A为 P循环的非奇异矩阵, 为 . 若
的特征值, 为 B 的特征值, 和 满足方程: / a p 则
( 一1 + ) p=
/ . a
此外, ( )的所有特征值非正, 若 p 并且 ( ) — , <— 则
2 假定 1 的证 明
证明. 0 取 <b<( ),
P—Z
令 F( , =xY— ( 一1 ), x ) bx 一 2 P 0<Y<1 , . () 3 下面将充分证 明隐函数 Y=g x 在 F( , ) , x P 0<Y<1 () x Y =O2 , 的条件T -  ̄()式定义, n 3 - f 并且在闭区
A g2 8 u 00
.
。
求 解 线 性 方 程组 S R k方法 的一 个 注 记 O .
张伟,畅大为
( 陕西师范大学数 学与信息科学学院,陕西西安 7 0 6 10 2)
摘 要: 考虑将p 循环矩阵划 分为k 循环矩阵 ( k P ) 解决P循环系 A = (> ) S Rk方法Eas 2 来 统 x bp 2 的 O — . n v 和L在隐函 i 数存在和可微的假定下, 较了S Rk 比 O .选代矩阵 ’ k ) ( 2 的最优谱半径. Eas i 给出 但是, n和L 并未 v
收稿 日期 :2 0 _31 0 80 .1
作者 简介 : 张伟 (9 1), 18一 男, 山东枣庄 人, 陕西j范大 学硕 J i 1 j 线性代数.
基金项 目:国家 自然科学基金资助项 N(0 70 8. 10 14 )
究 ; 畅大为 (93), 陕西西安人 ,副教授, 16. 男, 硕士研究生导 , 究方 向: 数优
若使 =L +U , 和 分别为严格的块下三角矩阵和严格的块上三角矩阵, k k其中 则相关的 S Rk迭代 O-
矩阵为 =( 一oD一 (一c I , c L ( o + , )
E as L 做了以下假定: vn 和 i
) .
假定 1 . 【 假设函数 g x 由等式 ( ¨ () —
∈( 旦
,
1. )
—l
将线性方程组() 1的系数矩阵 A划分为 k 循环矩阵, 假设
2 k P 一1P > 2 , . () 2
并使整数 , , , 满足: ,
,
,, =1 = P, =12 … , . ,m1 , , , k
, =, +1 =12 … , + 1 , , , , k一1 .
