人教版八年级数学上册第16章_分式复习课1
八年级上册第16章分式精品课件-8.ppt

范例 例2.计算:
a 3b a b a b ba
两个分母该怎么处理?
巩固
3、填空:
9 x (1) x 3 3 x 3 3x (2) 2 2 x 1 1 x
2
小结
1.同分母分式的加减法则:
同分母分式相加减,分母不变,把 分子相加减。
a b a b 2.同分母分式的加减法公式: c c c 分式运算结果要求:
检查分子分母是否可以约分,使 结果化为最简分式(整式)。
范例 例1.计算:
5x 3 y 2x 2 2 2 2 x y x y
结果要注意什么?
归纳 分式运算结果要求: 检查分子分母是否可以约分,使 结果化为最简分式(整式)。
巩固 1.填空:
3a 4a (1) m m
x y (2) x y x y
巩固 2.计算:
x 1 1 (1) x x
探究
Ⅱ、类比同分母分数的加减,你能进行 下列分式的加减吗?
a b ab (1) c c c
a b a b (2) c c c
请用自己的语言归纳同分母 分式的加减法则。
归纳 同分母分式的加减法则:
同分母分式相加减,分母不变,把 分子相加减。 同分母分式的加减法公式:
a b ab c c c
引入 问题1:甲工程队完成一项工程需n天,乙 工程队比甲队多用3天完成这项工程, 两队共同工作一天完成这项工程的几分 之几?
1 1 n n3
引入 问题2:2001年, 2002年, 2003年某地 的森林面积(单位:公顷)分别是S1, S2, S3,2003年与2002年相比,森林面积 增长率提高了多少?
2020-2021学年人教版八年级数学第十六章《分式》考点提要+精练精析

2020-2021学年第十六章《分式》提要:分式的四则运算是整式四则运算的进一步发展,是有理式恒等变形的重要内容之一,所以,分式的四则运算是本章的重点.分式的四则混合运算,是整式运算、因式分解和分式运算的综合运用,由于运用了较多的基础知识,运算步骤增多,解题方法多样灵活,又容易产生符号和运算方面的错误,所以是分式的难点.同时列分式方程解应用题和列整式方程解应用题相比较,虽然涉及到的基本数量关系有时是相同的,但由于含有未知数的式子不受整式的限制,所以更为多样而灵活.习题:一、填空题1.使分式234x a x +-的值等于零的条件是_________. 2.在分式2242x x x ---中,当x _____________时有意义,当x _________时分式值为零. 3.在括号内填入适当的代数式,使下列等式成立:2xy =22()2ax y ; 322()x xy x y --=()x x y-. 4.某农场原计划用m 天完成A 公顷的播种任务,如果要提前a 天结束,那么平均每天比原计划要多播种_________公顷.5.函数y =221(3)x x -++-中,自变量x 的取值范围是___________. 6.计算1201(1)5(2004)2π-⎛⎫-+-÷- ⎪⎝⎭的结果是_________. 7.已知u=121s s t -- (u≠0),则t=___________. 8.当m =______时,方程233x m x x =---会产生增根. 9.用科学记数法表示:12.5毫克=________吨.10.用换元法解方程222026133x x x x+-=+ ,若设x 2+3x =y ,,则原方程可化为关于y 的整式方程为____________.11.计算(x +y )·2222x y x y y x +-- =____________. 12.若a ≠b ,则方程a b +x a =x b -b a的解是x = ____________; 13.当x _____________时,||3x x -与3x x -互为倒数. 14.约分:34522748a bx a b x =____________;22923a a a ---=_____________. 15.当 x __________________时,分式325x --12x +有意义. 16.若分式123x -- 的值为正,则x 的取值范围是_______________. 17.如果方程5422436x x k x x -+=--有增根,则增根是_______________. 18.已知x y =32;则x y x y -+= __________. 19.m ≠±1时,方程m (mx -m +1)=x 的解是x =_____________.20.一个工人生产零件,计划30天完成,若每天多生产5个,则在26 天完成且多生产15个.求这个工人原计划每天生产多少个零件?若设原计划每天生产x 个,由题意可列方程为____________.二、选择题21.下列运算正确的是( )A .x 10÷x 5=x 2;B .x -4·x =x -3;C .x 3·x 2=x 6;D .(2x -2)-3=-8x 622.如果m 个人完成一项工作需要d 天,则(m +n )个人完成这项工作需要的天数为( )A .d +nB .d -nC .md m n + D .d m n + 23.化简a b a b a b--+等于( ) A .2222a b a b +- B .222()a b a b +- C .2222a b a b -+ D .222()a b a b+- 24.若分式2242x x x ---的值为零,则x 的值是( ) A .2或-2 B .2 C .-2 D .425.不改变分式52223x y x y -+的值,把分子、分母中各项系数化为整数,结果是( )A .2154x y x y -+B .4523x y x y -+C .61542x y x y-+ D .121546x y x y -+ 26.分式:①223a a ++,②22a b a b --,③412()a a b -,④12x -中,最简分式有( ) A .1个 B .2个 C .3个 D .4个27.计算4222x x x x x x ⎛⎫-÷⎪-+-⎝⎭的结果是( ) A .12x + B .-12x + C .-1 D .1 28.若关于x 的方程x a c b x d-=- 有解,则必须满足条件( ) A .c ≠d B .c ≠-d C .bc ≠-ad D .a ≠b29.若关于x 的方程ax =3x -5有负数解,则a 的取值范围是( )A .a <3B .a >3C .a ≥3D .a ≤330.一件工作,甲独做a 小时完成,乙独做b 小时完成,则甲、乙两人合作完成需要( )小时.A .11a b +B .1abC .1a b +D .ab a b+ 三、解答题31.23651x x x x x+----; 32.2424422x y x y x x y x y x y x y ⋅-÷-+-+.33.11322x x x--=---.34.先化简,再求值:)12(122+-÷++x x x x x ,其中,2=x .35.已知:b ab a b ab a b a -+--=-22,211求的值.。
八年级上册第16章分式精品课件ppt

巩固
2.甲、乙两个工程队共同完成一项工 程,乙队先单独做1天,再由两队合 作2天就完成全部工程,已知甲队与 乙队的工作效率之比是3︰2,求甲、 乙两队单独完成此项工程各需多少 天?
Copyright 2004-2009 版权所有 盗版必究
范例
例2.为加快西部大开发,西部某省决定 新修一条高速公路。甲、乙两工程队承 包此项工程。如果甲工程队单独施工, 则刚好如期完成;如果乙工程队单独施 工,就要超过6个月才能完成。现在由 甲、乙两队先共同施工4个月,剩下的 由乙队单独施工,则刚好如期完成。 问原来规定修好这条公路需要多长时间?
Copyright 2004-2009 版权所有 盗版必究
巩固
1.甲、乙两个工程队共同完成一项工 程,乙队先单独做1天,再由两队合 作2天就完成全部工程,已知甲队与 乙队单独完成工程的时间之比是2︰3, 求甲、 乙两队单独完成此项工程各需 多少天?
Copyright 2004-2009 版权所有 盗版必究
Copyright 2004-2009 版权所有 盗版必究
复习
ⅰ. 一项工程甲单独做3天完成ቤተ መጻሕፍቲ ባይዱ乙单独做6 天完成,如果两队合作,需多少天完成?
问题:1.这项工程看作 单位1 ;
2.甲队的工作效率是
乙队的工作效率是
1 6
1 3
,
,
两队合作效率是
1 3
1 6
。
Copyright 2004-2009 版权所有 盗版必究
Copyright 2004-2009 版权所有 盗版必究
小结
列分式方程解应用题的一般步骤: 1.审:分清已知和未知,明确数量关系; 2.设:设出未知数; 3.找:找出相等关系; 4.列:列出方程; 5.解:解出方程; 6.验:验方程,验实际; 7.答:写出答案。
人教版八上第16章分式复习优秀课件教材

换元法化简思想:
设
1.已知
xy 2=3 =
=k
Z ,试求 4
则x=2k,y=3k,z=4k
代入换元
x+y-z
x+y+z
的值.
=1/9
例1.已(知 x +1x)2 =32,
求
1
x2 +x2
的值.
x2
1 x2
2
9
变: 已知 x2 – 3x+1=0 ,求 x2+
1
x2
的值.
x
x
变:已知 x+ 1 =3 ,求
3.分式值为 0 的条件: A=0且 B ≠0 A
4.分式 B > 0 的条件: A>0 ,B>0 或 A<0, B<0 分式 A < 0 的条件: A>0 ,B<0 或 A<0 ,B>0 B
【例1】下列代数式中:,是分式的有:
1
x , 1 x y, a b , x2 y2 , x y
2
ab x y x y
例析
将下列各组分别进行通分:
(1)(单单式) 1 , 1 ; 4a 2b 6a3b2c
(2)(单多式)
3 6x2
,
4x2
5 8x3
(3( ) 多多式) 1 , 1
;
x2 y 2 xy y 2
(4)
1 x2
x
,
x2
1 2x
1
整体代入法化简思想:
【例1】已知:1x
1 y
5
,求 2x 3xy 2y 的值.
5mnp 3q
1/2n2
(7)
人教版-数学-八年级上册--第16章《15.1.1 分式》学案

八年级数学下册第16章《15.1.1 分式》学案学习目标: 1.了解分式、有理式的概念. 2.能熟练地求出分式有意义的条件,分式的值为零的条件. 学习重难点重点:理解分式有意义的条件,分式的值为零的条件.难点:能熟练地求出分式有意义的条件,分式的值为零的条件. 学习过程一、自学导读1.长方形面积10cm 2,长为7cm ,宽应 ;长方形面积S,长为a ,宽应 2.把体积 200cm 3的水倒入底面积为 33cm 2 的圆柱形容器中,水面高度为 cm ;把体积 V 的水倒入底面积为 S 的圆柱形容器中,水面高度为3.一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?设江水的流速为v 千米/时.轮船顺流航行100千米所用的时间为 小时,逆流航行60千米所用时间 小时,以上式子有什么共同点?它们与分数有什么相同点和不同点?二、合作探究归纳:分式定义: 一般地,A B ÷可以写成 ,其中A 和B 均为整式,如果分母B 中 ,则式子AB叫做分式。
1. 下列各式中,哪些是整式?哪些是分式? (1)x 1; (2)2x ; (3)π213-x (4)y x xy +2; (5)33yx -.2.下列各式中,哪些是分式?哪些不是?(1)x 4 (2)4a (3)yx -1 (4)43x (5)21x 2 (6)1x x 2-;3. 分式有意义、分式值为零、分式无意义的条件 例1 当x 取什么值时,下列分式有意义? (1)2-x x ; (2)141+-x x (2)221x +练一练: 当x 取何值时,下列分式有意义?(1)44+-x x (2)232+x x (3)122-x(4)3||6--x x(5)xx 11-例2:当x 是什么数时,分式:⑴225x x +- (2)()()23156x x x x -+--的值是零?例3:x 取何值时,分式(1)225x x +- (2)()()23156x x x x -+--无意义归纳:(1)分式AB 有意义的条件是: ; ⑵分式0AB =的条件是: 。
八年级第16章分式复习

期末总复习
x 1 1、分式 ( x 1)(x 3) 有意义的条件是 x≠1且x≠3 ; 值为零的条件是 。
2
2、若分式 若分式
x x 1
x 2
2
x 1
无意义,则x=
1 。
2
。
x x2
的值为0,则x=
八年级 数学
期末总复习
2 1 x 3、在代数式 、 、x y 、 x 中,分式共有 3 (A)1个 (B)2个 (C)3个 (D)4个
2 2
(3 x ) 4 x ( x 2) ( x 4)( x 4) x 3 ( 2 x )(2 x )
2 2
( x 3)( x 2) ( x 4)( x 2)
x2 x 6 2 x 2x 8
八年级 数学
期末总复习
A、扩大2倍 C、扩大3倍
1 1 3, (12)已知 x y
八年级 数学
期末总复习
负整数指数幂 与科学记数法
八年级 数学
期末总复习
1、某种感冒病毒的直径是0.00000012米, 用科学记数法表示为 。 2、计算: (1) 2-3;
(2)(2a b ) (a b )
2 3 2
3 1 3
八年级 数学
期末总复习
( x 3)( x 3) x 9 x3 x( x 3) x( x 3) x 200 3 203 当 x = 200 时,原式= 200 200
2
八年级 数学
期末总复习
9 6x x2 x 3 x2 4x 4 (8) 2 2 x 16 4 x 4 x 9 6x x x 3 x 4x 4 解: x 2 16 4 x 4 x 2
八年级16章分式知识点

八年级16章分式知识点在数学学科中,分式是一个重要的概念。
在初中阶段,分式的具体内容通常在高年级进行学习,比如八年级第16章就是分式知识点的学习内容。
在这一章节中,学生将学习如何理解分式的概念,如何用分式解决实际问题,以及分式的简化和运算等知识点。
本文将详细介绍八年级第16章分式知识点的内容。
1. 章节概述在八年级第16章,学生需要掌握以下四个方面的内容:1.1 分式的概念分式是一个形如“a/b”的表达式,其中“a”和“b”是数。
分式的意义是将一个数“a”分为“b”份。
例如,“3/4”表示将数3分成4份,每一份为“3/4”。
1.2 分式的运算对于两个分式“a/b”和“c/d”,我们可以进行加、减、乘、除这四种运算。
具体来说,加法和减法可以通过通分实现,乘法可以直接相乘分子和分母,而除法则通过取倒数来实现。
1.3 分式的简化当分子和分母没有公因数时,分式就已经简化了。
但如果存在公因数,则需要通过约分来简化分式。
约分的过程是将分子和分母同时除以它们的最大公因数。
1.4 分式的应用分式在实际生活中有着广泛的应用,比如在化学中用于计算化学反应中物质的量,或者在经济学中用于计算利率等。
2.分式的概念分式是数学中非常重要的一个概念。
在具体的表达式中,分式通常表示将一个整体分为若干份的比例关系。
在八年级的16章中,学生需要掌握分式的基本概念,包括如何理解分式的意义,以及如何将分式表示为最简形式等。
3.分式的运算分式的运算分为四种,包括加法、减法、乘法和除法。
4种运算的具体规则如下:3.1 加法和减法在分式加法和减法中,需要先使两个分母相同,然后再将两个分式的分子进行相加或相减,最后化简得到最简分式。
具体来说,假设分式为a/b和c/d,则它们的和为(ad+bc)/bd,差为(ad-bc)/bd。
3.2 乘法分式的乘法比较简单,只需要将两个分式的分子和分母分别相乘,然后约分即可。
具体来说,假设分式为a/b和c/d,则它们的积为ac/bd。
八年级数学上册 16.3分式方程复习课件 新人教版

解分式方程的一般思路 去分母 分式方程
两边都乘以最简公分母
整式方程
【解分式方程】
10 1 解分式方程 x-5 = x2-25 解: 在方程两边都乘以最简公分母(x+5)(x-5)得, x+5=10 解这个整式方程,得x=5 检验:把x = 5 代入原方程中,发现x-5和x2-25的 值都为0,相应的分式无意义,因此x=5虽是方 程x+5=10的解,但不是原分式方程 1 = 10 x-5 x2-25 的解.实际上,这个分式方程无解.
4. 写出原方程的根.
布置作业 : 习题16.3第1题(单,双
号) 《课堂练习》P课时 A组 B组选做
盐场中学
赵建敏
温故知新
(1)方程? (2)一元一次方程? 解一元一次方 (3) 程的一般步骤
是什么?
解方程
() 1-3 8-x)=-2(15-2x) 1 (
x x 1 (2) 2 3
学过的方程
(1)2 x 5 7 1 (2)2( x 1) 3 x 2 2 y 1 y2 (3) 1 3 4 2x 1 x 1 (4) 3 2
【分式方程的解】
60 100 上面两个分式方程中,为什么 20+V = 20-V 去分母后得到的整式方程的解就是它的解,而 10 去分母后得到的整式方程的解却不 1 x-5 = x2-25 是原分式方程的解呢? 我们来观察去分母的过程 60 两边同乘(20+v)(20-v)100(20-v)=60(20+v) 100 = 20-V 当v=5时,(20+v)(20-v)≠0 20+V 分式两边同乘了不为0的式子,所得整式方程的解与 分式方程的解相同. 两边同乘(x+5)(x-5) 10 1 = x2-25 当x=5时, (x+5)(x-5)=0 x+5=10 x-5 分式两边同乘了等于0的式子,所得整式方程的解使 分母为0,这个整式方程的解就不是原分式方程的解
人教版八年级数学《分式》期末复习一

分式复习一1、分式的概念:形如BA ,其中A ,B 都是整式, 且B 中含有字母。
.例1:下列式子:(1)b a b a +- (2)π32-x (3)14-x (4)2x属于分式的有(1)(3} 。
例2:有理式x2,)(31y x +,3-πx ,x a -5,42yx -中,分式有( B )。
(A )1个 (B )2个 (C )3个 (D )4个小练习: 1.下列各式:x 2、22+x 、x xyx -、33yx +、23+πx 、()()1123-++x x x 中,分式有(C )A 、1个 B 、2个 C 、3个 D 、4个 2.下列各式:()xx x x y x x x 2225 ,1,2 ,34 ,151+---π中,分式有 。
2、分式是否有意义:对于分式A B来说,当分母B ≠0时,分式A B有意义;当分母B=0时,分式A B无意义。
例3、分式322--x x 有意义,则x 取值为( C )。
(A )2≠x (B )3≠x (C )23≠x (D )23-≠x例4、当x 时,分式42-x x无意义。
小练习:1、当x ≠ 3时,代数式32-x 有意义.当38-时,分式8x 32x +-无意义;2、当x 时分式xx2121-+有意义。
3、使分式24xx -有意义的x 的取值范围是(B) A. 2x = B.2x ≠ C.2x =- D.2x ≠-4、列分式中,一定有意义的是(D )(A )152--x x (B )yy 312+ (C )12+x x (D )112+-y y3、分式A B等于0,则分子A=0,且B ≠0。
例5、若分式xx-+44的值为0,则x 值为( a )。
(A )4-=x (B )4=x (C )0=x (D )0≠x例6、若分式293x x-+的值为0,则x 的值为( B )。
(A )3=x (B )3-=x (C )3x =± (D )不存在小练习:1、若分式112+-x x 的值为0,则x 的取值为( A )A 、1=xB 、1-=xC 、1±=xD 、无法确定2、分式392--x x 当x = -3 时分式的值为零。
人教版八年级数学上册15.分式复习课(共24张)

注:负整数次幂:任何不等于零的数的负整数 次幂,等于这个数的正整数次幂的倒数。
a-p=
1 ap
(a≠0,p为正整数)
15. 不改变分式的值,使下列分式的分子和分母都不含有
“-”号:
⑴ 5y 25 x 2
;
⑵ x . 2y
分式的符号变化规律:分式的分子、分母与分子本身的符
号,改变其中任何两个,分式的值不变,简称“三变二,
注:1、分式的值为零,实质上是一个分式方程的问题, 因此求得的整式方程的解必须验根! 2、分式的值为零、分式有意义、分式无意义是分式概 念中的三个常见的基本问题。
解题要领是; 分式的值为零 分子=0,且分母≠0 分式有意义 分母≠0 分式无意义 分母=0
练习:当 x=__2_____时,分式
x2-4 x+2
二、探索题
例 5 :( 2005 年 绍 兴 ) 已 知 : P=
x2 x-y -
y2 x-y
,
Q=(x+y)2-2y(x+y) ,小明、小聪两人在=2,=-1 的条件下
分别计算了 P 和 Q 的值,小明说 P 的值比 Q 大,小聪说
Q 的值比 P 大。请你判断谁的结论正确,并说明理由。
例 6:(2005 年河南实验区)有一道题:“先化简,再求值:
=
A•M B•M
,
A B=
A÷M B÷M
(其中
M
是不等于零的整式)
例 3:(2005 湖南湘潭)下列分式中,是最简分式的是( A)
A、
2x x2+1
B、
.4 2x
C、
.x-1 x2-1
D、
1-x x-1
注:1、如果分式的分子和分母还可以约分,那它就不是最简
八年级数学第16章分式复习教案

(1) 1
;
(2) x
2 .
x-1
2x 3
分析 要使分式有意义,必须且只须分母不等于零 .
解 (1)分母 x-1 ≠0,即 x ≠1.
所以,当 x ≠1时,分式 1 有意义 . x-1
(2)分母 2 x 3 ≠0,即 x ≠- 3 . 2
第 1页 共 4页
所以,当 x ≠- 3 时,分式 x 2 有意义 .
第 2页 共 4页
= 3x 12 = 3(x 4) = 3 (x 4)( x 4) ( x 4)( x 4) x 4
例 6 购一年期债券,到期后本利只获 2700 元,如果债券年利率 12.5%, &127; 那么利息是多少元 ?
解:(1)设利息为 x 元,则本金为( 2700-x)元,依题意列分式方程为:
例 5 计算: 3 x4
24
x2
. 16
分.析. 这里两个加项的分母不同,要先通分
.为此,先找出它们的最简公分
母.
注意到
2
x
16 = (x
4)( x
4) ,所以最简公分母是 (x
4)( x
4)
解
3
24
x 4 x2 16
=3
24
= 3( x 4)
24
= 3( x 4) 24
x 4 (x 4)( x 4) (x 4)( x 4) (x 4)( x 4) ( x 4)( x 4)
2、某一工程,在工程招标时,接到甲、乙两个工程队的投标书 .施工一天, 需付甲工程队工程款 1.5 万元 , 乙工程队工程款 1.1 万元 .工程领导小组根据甲、 乙两队的投标书测算:
(1)甲队单独完成这项工程刚好如期完成; (2)乙队单独完成这项工程要比规定日期多用 5 天; (3)若甲、乙两队合做 4 天,余下的工程由乙队单独做也正好如期完成 . 在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?
八年级数学 第16章《分式》知识要点复习及典型练习 新人教版

第16章《分式》知识要点复习一、本章主要内容本章主要内容是分式的概念;分式的基本性质;分式混合运算和可化为一元一次方程的分式方程及其应用,这些内容在今后进一步学习方程、函数等知识时占有重要地位和作用. ★(一)概念1、分式的概念:BA (注明:A 、B 都是整式,并且B 中都含有字母) 说明:分式比分数更具有一般性,如分式B A 可以表示为两个整式相除的商(除式不能为零),其中包括所有的分数。
2、分式的表示:B A (注明: B ≠0才有意义) 3、分式的值:⑴0=B A 时,A=0且B ≠0;⑵1=BA 时,A=B 且B ≠0。
4、最简分式: ★(二)分式的基本性质(类似分数的性质,运用类比数学思想)1.分式的基本性质是分式恒等变形的依据,•正确理解和熟练掌握这一性质是学好分式的关键,因此学习中要注意以下几点:(1)基本性质中的字母表示整数,(,A A M A A M B B M B B M⨯÷==⨯÷,M ≠0) (2)要特别强调M ≠0,且是一个整式,由于字母的取值可以是任意的,所以M•就有等于零的可能性,因此,应用基本性质时,重点要考查M 的值是否为零.2.运用分式的基本性质进行约分、通分.值得注意的是:约分是要找准分子和分母的公因式,最后的结果要是最简分式;通分是要正确地确定各个分母的最简公分母,一般的取系数的最小公倍数,以及所有因式的最高次幂的积,作为最简公分母.(三)分式运算(最后的结果要是最简分式,转化数学思想)1、分式的乘除法 分式乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
分式除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
分式乘方法则: 分式乘方要把分子、分母分别乘方。
(1)约分,约分的目的是化简,关键是找分子和分母的最高公因式,•即系数的最大公约数、相同因式的最低次幂.(2)如何找分子和分母的最高公因式n n n ba b a =)(bcad c d b a d c b a bd ac d c b a =⋅=÷=⋅;(3)分式的乘除法本质就是:①因式分解,②约分。
最新人教版初中八年级上册数学【分式全章复习(第一课时)】教学课件

4 1
当a=0,
a 2+3 (a+2)(a 2) = a 2 ∙ (a+1)(a 1)
0+2 原式= 0-1
(a+1)(a+2)(a 2) = (a 2)(a+1)(a 1)
= 2.
a+2 =a 1 .
练习
如果
a2+2a
1=0 ,求代数式 (a
4 a2 a )∙ a 2
的值.
解:原式
=(
a2 a
4 a2 a )∙ a 2
例
3 a2 先化简 (1+ a 2 )÷a2
1 4
,再选一个你喜欢的值,
代入求出代数式的值.
解:原式
=(
a a
2 3 a2 2 + a 2 ) ∙ a2
4 1
分式混合运算的运算顺序:
先乘方,再乘除,最后加减, 有括号时先算括号内的运算.
a 2+3 (a+2)(a 2)
= a 2 ∙ (a+1)(a 1)
∴a2+2a=1. 整体代入
∴原式=1.
∵ a2+2a 1=0, ∴a2=1 2a. 或 2a=1 a2.
=a(a+2)
∴原式=a2+2a
=a2+2a .
=(1 2a)+2a =1.
分式的运算
分式乘方运算:
(
a b
)n=
an bn
.
如:(
4 2 42 16 a ) = a2 = a2
.
分式的运算
分式的运算
例
计算:
4n 3m
a ÷6m2
.
数学人教版八年级上册分式复习——周艺雄
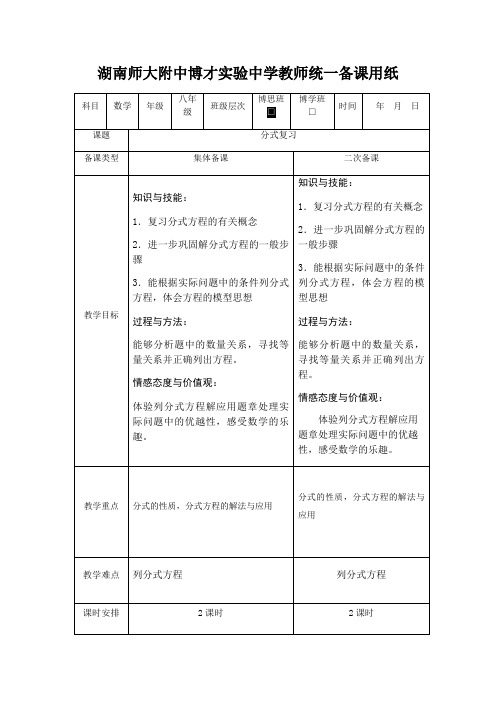
二、分式的基本性质
1.若把分式 的x和y都扩大两倍,则分式的值( )
A.扩大2倍B不变C缩小2倍D.缩小2倍
A.扩大3倍B.扩大9倍C.扩大4倍D.不变
3、填空:
例1:化简求值
练习:
三、分式方程
解分式方程步骤:
例2.如果整数A、B满足等式
求A与B的值。
练习:
注意:不要漏乘不含分母项。
2、解这个整式方程。
3、把整式方程的根代入最简公分母,看结果是否是零,使最简公分母为零的根,是原方程的增根,必须舍去。
4、写出结论
板书设计
学生收获
学生复习了分式相关知识,会用分式知识解决实际问题
教学反思
本节课在分式复习过程中,运算比较多,要注意时间把控。同时要注意到关注全体学生,把好计算关。博思班要争取人人过关,并且拓宽思维。
例3、如果下列关于x的方程有增根,求a的值。
练习:
1、如果下列关于x的方程有正数解,
求m的取值范围;
2、如果关于x的方程无解,求k的值,
四、列方程解应用题:
例4、甲、乙两人分别从相距36千米的A、B两地同时相向而行,甲从A地出发到1千米时发现有一物品遗忘在A地,立即返回,取过物品后又立即从A地向B地行进,这样两人恰好在A、B两地中点处相遇,又知甲比乙每小时多走0.5千米,求甲、乙两人的速度。
湖南师大附中博才实验中学教师统一备课用纸
科目
数学
Hale Waihona Puke 年级八年级班级层次
博思班□
博学班□
时间
年月日
课题
分式复习
备课类型
集体备课
二次备课
教学目标
人教版八年级数学第十六章分式知识点总结

第十六章 分式知识点及典型例子一、分式的定义:如果A 、B 表示两个整式,且B 中含有未知数,那么式子BA 叫做分式。
二、在分式中,如果________,则分式AB 有意义;如果________,则分式A B无意义;如果________且_________不为零时,则分式A B的值为零;如果__________,则分式0A B > 如果____________,则分式0A B <; 例1.下列各式a π,11x +,15x+y ,22a b a b --,-3x 2,0•中,是分式的有( )个。
例2.下列分式,当x 取何值时有意义。
(1)2132x x ++; (2)2323x x +-。
例3. 当x________时,分式2134x x +-的值为正数,当x________时,分式2134x x +-的值为负数 例4.当x______时,分式2134x x +-无意义。
当x_______时,分式2212x x x -+-的值为零。
当x_________时,分式2361x x -+的值为负数。
三、分式的基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变,用字母表示为_________________________________.分式的分子、分母和分式本身的符号改变其中任何____个,分式的值不变.四、约分:把分式的分子与分母的公因式约去,这样的分式变形叫做分式的约分,约分的理论依据是分式的___________________。
约分的方法:分式的分子与分母同除以他们的公因式,如果分式的分子、分母都是单项式,就直接约去分子、分母的__________;如果分式的分子或分母是多项式,就先__________,再判断公因式进行约分。
最简分式:分子与分母没有____________的分式,叫做最简分式。
(注意约分一定要彻底)五、通分:利用分式的基本性质把几个异分母的分式化为_________的分式,这样的分式变形叫做分式的通分。
人教版八年级数学上册第十六章 分式复习 教学案
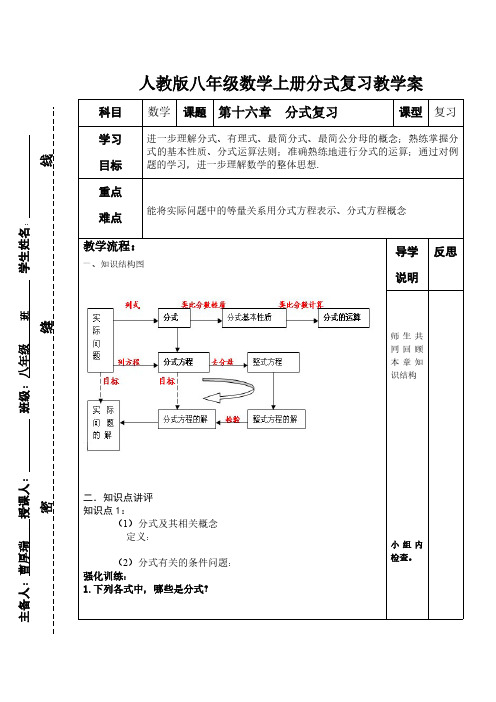
2 ( 2( x - x -1 x -1
知识点 4
(1)整数指数幂
a n
( 2)科学记数法 :
1 ( a 0, n是正整数) an
强化训练: 由科学记数法得N 3.25 105 则原数N为 ______ 填空: 1. 2 计算: 1 -1 3 0
(1) 16 (-2) - (
人教版八年级数学上册分式复习教学案
科目 学习 数学 课题 第十六章
分式复习
课型 复习
目标 重点
进一步理解分式、有理式、最简分式、最简公分母的概念;熟练掌握分 式的基本性质、分式运算法则;准确熟练地进行分式的运算;通过对例 题的学习,进一步理解数学的整体思想.
线
学生姓名:
难点 教学流程:
一、知识结构图
5x 3 y , 3
导学说明
每 组 2 名学 生 展示。
反思
2.⑴已知分式
x 1 ( x 1 )( x 2 )
,当 x
___
时,
分式有意义 当 xx ___ x ,3 9 ⑵若分式
x5
时,分式无意义.
x7
有意义,则 x 2 4 x 应满足的条件是___
⑶当 x= ___
学 生 展 示 , 其 他 成 员 组 内 互 批。
1 1 2 3.解方程: . 6 x 2 2 1 3x
我 有 问 题 教 学 反 思
问 老 师
密
缝
线
3
)
(
3 - 1)
每 组 2 名学 生 展示
(2)
1 ( 2 )0 ( ) 2 (2) 2 2
知识点 5:分式方程
强化训练: 解方程:
八年级数学课件 第16章 分式 期中复习

D.不变
2.下列各式正确的是( D )
A ab ab c c
C ab ab
c
c
B ab ab c c
D ab ab
c
c
3.下列等式成立的是( )
n n2
A. m m 2
B. n n a (a 0)
m ma
C.
n m
na ma
D.
n m
mn m2
4.①
x 1 y 2
1xy
2x y ② x 2y
期中复习之 第十六章 分式
知识结构
分式的定义
分式的基本概念 分式有意义的条件
分式值为零的条件
分式的基本性质
分 式
分式的运算 约分、通分
分式的乘除、加减运算
整数指数幂
分式方程 分式方程及应用
分式方程的应用
分式的定义
1.在下列式子中,分式的个数是( A )
1 ,
2xy ,
4a 2b 3c,
5 xy
10 x2
, , 9x ,
a
6 x 7 8
yx
A.5
B.4
C.3
D.2
分式有意义的条件
1.当x为任意实数时,下列分式一定有意义的是( C ) x1 x1 x1 x1
A. x2 B. x2 1 C. x2 1 D. x 分式值为零的条件 2. ①当x__=_3__时,分式 x2 9 的值为零.
b
b
89
则分式 a2 2ab b2 =____9_9_0_____.
ab2 a2b
科学家发现一种病毒的直径为0.00001962米, 用科学记数法表示为____________。 (保留2个有效数字).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
27a ya 1 1 - x a -12 2ab
b
2015-1-9
9
分式的运算
强化训练:
2 2 2 x y x - x -1 ( 2 ) 2. 计算:(1) x -1 x- y y- x 2 2 2 y x x 1 x ( 1 )原式 解:(2)原式 x- x y -1 x- y 1 2 - y2 2 x - x 1) ( x -1) x ( x- y x -1 ( x y )( x - y ) 1 x -1 x - y
⑵若分式 有意义,则x应满足的 条件是_______ x≠5、x≠7且x≠-9
x3 x9 x5 x7
B
{ B≠0 .
⑶当x= -2 时,分式
2015-1-9
x 2 4 x 2 5 x 14
的值为0.
2
分式的性质及应用
(1)分式的基本性质:
分式的分子与分母都乘以(或除以)同一个不为0的整式 , 分式的值 不变 用式子表示:
分式及其相关概念
(1)分式:如果A、B表示两个整式,并且B中含有 A (B≠0)叫做分式. 强化训练: 字母,那么代数式 B 1.下列各式中,哪些是分式?
m m 1 2 5 a b xy ( 1) , , x , , , 8 a 3 x 6 2 A 5x 2y
2 2
注意:分式
中,分母 B 中一定要有字
然后再约分. 注意: 通分的关键是找最简公分母(即各分母所有因式 的最高次幂的积).如果分式的分母是多项式,为便于确 定最简公分母,通常先分解因式.
2015-1-9
4
强化训练:
1.请写出下列等式中未知的分子或分母:
(1) 2 ( 2xy ) = xy x 2y2 (2) 3x x+y 15x(x+y) = ( 5(x+y)2 )
分式的概念
{
A 的形式 B
{
分式有意义 分式无意义
B≠0
{ B≠0
B=0 A=0
B BM B BM
a n an b bn
分 分式的乘方 式 a 的 分式的运算 同分母相加减 运 c 算 分式的加减
最简分式或整式
{
2015-1-9
b ab c c a c ad bc ad bc 异分b ab c c c
异分母分式相加减,先通分,变为同分母的分式, 再加减. a c ad bc ad bc
2015-1-9
b d bd bd bd
8
分式的运算
x 1 强化训练: 1. 计算: ( 1) x
b2
y x
a -a 2 a a 1 2 2b 3ab ( 3 ) ( 2) 2 a -1 a -1 3 4 9 a a 1 - 27a b 2 2 -b ay ( a -1 1) ( a 1 ) a 1 9 a 3 ab ( 3 )原式 ( 1)原式 x a 解: ( 2 -1) a ( ax 1)( 3 x 2b 4 (a -1)2
强化训练:
3.不改变分式的值,使下列分式的分子和分母 中最高次项的系数都是正数. x 3y 7y ( 1) ( 2) 2 57y y 1 2x x 2 m 3 m x 2 1 ⑵ 4.约分: ⑴ 2 2
2 2
x 2 x 1
9m
5.通分:
2015-1-9
x 与 y ( 1) 2 6a b 9ab 2c
A B
=
AXM (B X M )
A B
=
A÷M ( B÷M )
(其中M为
不为0
的整式).
A B
( -A )
(2)分式的符号法则:
= =
A
( -B )
=
-A ( -B )
B A ( B )
-A
2015-1-9
=
=
( -A ) B
=
-A ( B )
3
-B
⑶约分: 把一个分式的分子与分母的 公因式 约去, 叫做分式的约分. ⑷通分: 把几个异分母的分式化成 同分母 的分式, 注意: 分式的分子、分母是多项式的,应先分解因式, 叫做分式的通分.
2015-1-9
5
强化训练:
2.不改变分式的值,把下面分式的分子和分 母的各项系数都化成整数.
2 a 3 b 2
2ab 3
3 3 2a b ( 2a b) 6 12a 9b 2 2 解: 2 2 4a 6b ab ( a b) 6 3 3
2015-1-9 6
2015-1-9
x y
10
中考演练:
x 1 1 ( ) (2010· 鄂州)先化简 ,然 x -1 x 1 2 x 2 -2
后从-1、1、2中选取一个数作为x的值代入求值.
2015-1-9
11
分 式
{{
分式的值为0 B中含有字母 且B≠0 A AM , A AM (M 0) 分式的基本性质 分式的乘除 约分
通分
2 2 a 1 1 a ( a ) , 1.(2010· 黑龙江绥化)先化简 a 2 a a
然后给a选择一个你喜欢的数代入求值. 2. 已知
1 1 2a 3ab 2b 3 ,求分式 的值。 a b a ab b
13
2015-1-9
2015-1-9
14
5 a 1 (2) , ,a a b
2015-1-9
2
母。 温馨提示:
B
是圆周率,它代表的是一个
常数而不是字母。
1
(2)分式有关的条件问题:
A 有意义的条件 分式 强化训练: B
B≠0
A B= 0 分式 无意义的条件 x 1 2.⑴已知分式 B( x 1 )( x 2 ) ,当x ≠1且x≠-2 时, A,当x =1或x=-2 时,分式无意义 A=0 . 分式有意义 分式 的值为0的条件
a1 与 6 ( 2) 2 a 2a1 a2 1
7
分式的运算
分式的乘除、乘方及加减
分式乘以分式 分式除以分式 分式的乘方 a n an b n b
a c ac b d bd
a c a d ad b d b c bc
同分母分式相加减,分母不变,把分子相加减.
