第10章静电场中的介质电容器
2024秋季人教版高中物理必修第三册第十章静电场中的能量《电容器的电容》

教学设计:2024秋季人教版高中物理必修第三册第十章静电场中的能量《电容器的电容》一、教学目标(核心素养)1.物理观念:理解电容器的构造、工作原理及电容的概念,掌握电容的定义式及其物理意义。
2.科学思维:通过分析电容器充电、放电过程,培养学生的逻辑推理能力和问题解决能力,理解电容是描述电容器储存电荷本领的物理量。
3.科学探究:通过实验观察电容器充放电现象,体验科学探究的过程,学习使用实验仪器测量电容的方法。
4.科学态度与责任:培养学生的实验安全意识,尊重实验数据,形成实事求是的科学态度,同时了解电容器在现实生活中的应用及其重要性。
二、教学重点•电容器的构造、工作原理及电容的概念。
•电容的定义式及其物理意义。
三、教学难点•理解电容是描述电容器储存电荷本领的物理量,而非储存电荷的多少。
•分析电容器充放电过程中电场能的变化,理解电容与电压、电荷量的关系。
四、教学资源•多媒体课件(包含电容器构造展示、充放电过程模拟、电容定义及公式推导等)。
•实验器材(电容器、电源、开关、导线、电压表、电流表等,视条件可增减)。
•教科书、教辅资料及学生预习材料。
•实验报告模板。
五、教学方法•讲授法:讲解电容器的构造、工作原理及电容的概念。
•演示法:通过多媒体或实物演示电容器充放电过程。
•实验法:组织学生进行电容器充放电实验,观察现象并记录数据。
•讨论法:引导学生讨论电容的物理意义及其与电压、电荷量的关系。
六、教学过程导入新课•生活实例引入:展示手机电池、相机闪光灯电容器等生活中的电容器应用实例,提问“这些设备中的电容器是如何工作的?它们有什么共同特点?”引导学生思考电容器的作用。
•知识回顾:简要回顾静电场的基本概念和性质,为引入电容器做铺垫。
新课教学1.电容器的构造与工作原理:•展示电容器实物或图片,介绍电容器的基本构造,包括两个彼此绝缘又相互靠近的导体(极板)和中间的绝缘介质。
•通过多媒体演示或实物展示,说明电容器的工作原理——当电容器两极板间存在电势差时,极板上的电荷会重新分布,形成电场,储存电能。
第十章 静电场中的导体和电介质习题解答
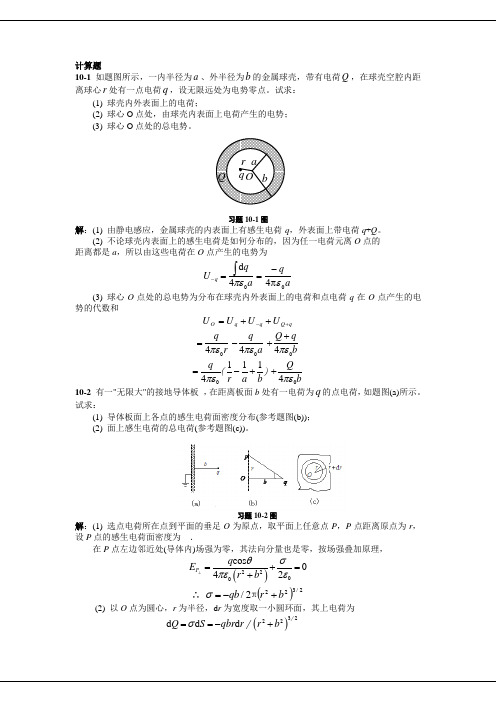
10-1 如题图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q ,设无限远处为电势零点。
试求: (1) 球壳内外表面上的电荷;(2) 球心O 点处,由球壳内表面上电荷产生的电势;(3) 球心O 点处的总电势。
习题10-1图解:(1) 由静电感应,金属球壳的内表面上有感生电荷-q ,外表面上带电荷q +Q 。
(2) 不论球壳内表面上的感生电荷是如何分布的,因为任一电荷元离O 点的 距离都是a ,所以由这些电荷在O 点产生的电势为0d 4q qU aπε-=⎰aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和q Q q q O U U U U +-++=04qr πε=04qa πε-04Q qb πε++01114()q r a bπε=-+04Q bπε+ 10-2 有一"无限大"的接地导体板 ,在距离板面b 处有一电荷为q 的点电荷,如题图(a)所示。
试求:(1) 导体板面上各点的感生电荷面密度分布(参考题图(b)); (2) 面上感生电荷的总电荷(参考题图(c))。
习题10-2图解:(1) 选点电荷所在点到平面的垂足O 为原点,取平面上任意点P ,P 点距离原点为r ,设P 点的感生电荷面密度为.在P 点左边邻近处(导体内)场强为零,其法向分量也是零,按场强叠加原理,()220cos 024P q E r b θσεπε⊥=+=+ ∴ ()2/3222/b r qb +-=πσ (2) 以O 点为圆心,r 为半径,d r 为宽度取一小圆环面,其上电荷为 ()3222d d d //Q S qbr r r bσ==-+q Q a bO r()q brrr qb S Q S-=+-==⎰⎰∞2322d d /σ10-3 如题图所示,中性金属球A ,半径为R ,它离地球很远.在与球心O 相距分别为a 与b 的B 、C 两点,分别放上电荷为A q 和B q 的点电荷,达到静电平衡后,问: (1) 金属球A 内及其表面有电荷分布吗?(2) 金属球A 中的P 点处电势为多大?(选无穷远处为电势零点)B C R AP Oq A q Bba习题10-3图解:(1) 静电平衡后,金属球A 内无电荷,其表面有正、负电荷分布,净电荷为零. (2) 金属球为等势体,设金属球表面电荷面密度为. ()()000d 4=4////AP A B S U U S R q a q a σπεπε==⋅+⎰⎰∵d 0AS S σ⋅=⎰⎰∴ ()()04///P A B U q a q a πε=+10-4 三个电容器如题图联接,其中C 1 = 10×10-6 F ,C 2 = 5×10-6 F ,C 3 = 4×10-6 F ,当A 、B 间电压U =100 V 时,试求:(1) A 、B 之间的电容;(2) 当C 3被击穿时,在电容C 1上的电荷和电压各变为多少?ABC 1C 2 C 3U习题10-4图解:(1) =+++=321321)(C C C C C C C 3.16×10-6 F(2) C 1上电压升到U = 100 V ,电荷增加到==U C Q 111×10-3 C10-5 一个可变电容器,由于某种原因所有动片相对定片都产生了一个相对位移,使得两个相邻的极板间隔之比为2:1,问电容器的电容与原来的电容相比改变了多少?(a) (b)习题10-5图解:如图所示,设可变电容器的静片数为n ,定片数为1-n ,标准情况下,极板间的距离为d (图a ),极板相对面积为S 。
高中三年级物理10-4 第1课时 电容器的电容

4 电容器的电容第1课时 电容器的电容1.知道什么是电容器及电容器的主要构造.2.理解电容的概念及其定义式.一、电容器1.电容器:储存电荷和电能的装置.任何两个彼此绝缘又相距很近的导体,都可以看成一个电容器.2.电容器的充放电(1)充电:把电容器的两极板分别与电池组的两极相连,两个极板分别带上等量的异种电荷的过程,充电过程中,由电源获得的能量储存在电容器中.(2)放电:用导线把充电后的电容器的两极板接通,两极板上的电荷中和的过程,放电过程中,电容器把储存的能量通过电流做功转化为电路中其他形式的能量.二、电容1.定义:电容器所带电荷量Q 与电容器两极板间的电势差U 的比值.2.定义式:C =Q U. 3.单位:电容的国际单位是法拉,符号为F ,常用的单位还有微法和皮法,1 F =106 μF =1012 pF.4.物理意义:电容器的电容是表示电容器容纳电荷本领的物理量,在数值上等于使两极板间的电势差为1 V 时电容器需要带的电荷量.5.击穿电压与额定电压(1)击穿电压:电介质不被击穿时加在电容器两极板上的极限电压,若电压超过这一限度,电容器就会损坏.(2)额定电压:电容器外壳上标的工作电压,也是电容器正常工作所能承受的最大电压,额定电压比击穿电压低.三、平行板电容器1.结构:由两个平行且彼此绝缘的金属板构成.2.电容的决定因素:电容C 与两极板间电介质的相对介电常数εr 成正比,跟极板的正对面积S 成正比,跟极板间的距离d 成反比.3.电容的决定式:C =εr S 4πkd ,εr 为电介质的相对介电常数,k 为静电力常量.当两极板间是真空时,C =S 4πkd. 四、常用电容器1.分类:分为固定电容器和可变电容器两类.2.固定电容器有:聚苯乙烯电容器、电解电容器等.3.可变电容器由两组铝片组成,固定的一组叫定片,可动的一组叫动片.转动动片,两组铝片的正对面积发生变化,电容就随着变化.一、电容器 电容1.电容器的充电过程,电源提供的能量转化为电容器的电场能;电容器的放电过程,电容器的电场能转化为其他形式的能.2.电容器的充、放电过程中,电路中有充电、放电电流,电路稳定时,电路中没有电流.3.C =Q U 是电容的定义式,由此也可得出:C =ΔQ ΔU. 4.电容器的电容决定于电容器本身,与电容器的电荷量Q 以及电势差U 均无关.二、平行板电容器1.C =Q U 与C =εr S 4πkd的比较 (1)C =Q U 是电容的定义式,对某一电容器来说,Q ∝U 但C =Q U不变,反映电容器容纳电荷本领的大小; (2)C =εr S 4πkd 是平行板电容器电容的决定式,C ∝εr ,C ∝S ,C ∝1d,反映了影响电容大小的因素. 2.平行板电容器动态问题的分析方法抓住不变量,分析变化量,紧抓三个公式:C =Q U 、E =U d 和C =εr S 4πkd3.平行板电容器的两类典型问题(1)开关S 保持闭合,两极板间的电势差U 恒定,Q =CU =εr SU 4πkd ∝εr S d, E =U d ∝1d. (2)充电后断开S ,电荷量Q 恒定,U =Q C =4πkdQ εr S ∝d εr S, E =U d =4πkQ εr S ∝1εr S.1.如图所示为一次心脏除颤器的模拟治疗,该心脏除颤器的电容为15μF,充电至9.0kV电压,如果电容器在2.0ms时间内完成放电(电荷定向移动形成电流qIt),下列说法正确的是()A.放电之后,电容器的电容为零B.该电容器的击穿电压为9kVC.放电之前,电容器存储的电荷量为135C D.该次通过人体的电流为67.5A2.照相机的闪光灯,在不到1s1000的短暂时间内发出强烈闪光,瞬时电流很大,该过程的发生是利用了()A.电池的放电B.电池的充电C.电容器的放电D.电容器的充电3.超级电容器又叫双电层电容器是一种新型储能装置,它不同于传统的化学电源,是一种介于传统电容器与电池之间、具有特殊性能的电源。
第十章静电场中的导体和电介质

第⼗章静电场中的导体和电介质第⼗章静电场中的导体和电介质在上⼀章中,我们讨论了真空中的静电场。
实际上,在静电场中总有导体或电介质存在,⽽且在静电的应⽤中也都要涉及导体和电介质的影响,因此,本章主要讨论静电场中的导体和电介质。
本章所讨论的问题,不仅在理论上有重⼤意义,使我们对静电场的认识更加深⼊,⽽且在应⽤上也有重⼤作⽤。
§10-1 静电场中的导体⼀、静电平衡条件1、导体与电介质的区别:(1)宏观上,它们的电导率数量级相差很⼤(相差10多个数量级,⽽不同导体间电导率数量级最多就相差⼏个数量级)。
(2)微观上导体内部存在⼤量的⾃由电⼦,在外电场下会发⽣定向移动,产⽣宏观上的电流⽽电介质内部的电⼦处于束缚状态,在外场下不会发⽣定向移动(电介质被击穿除外)。
2、导体的静电平衡条件(1)导体内部任何⼀点处的电场强度为零;(2)导体表⾯处的电场强度的⽅向,都与导体表⾯垂直.导体处于静电平衡状态的必要条件:0=i E(当导体处于静电平衡状态时,导体内部不再有⾃由电⼦定向移动,导体内电荷宏观分布不再随时间变化,⾃然其内部电场(指外场与感应电荷产⽣的电场相叠加的总电场)必为0。
⼆、静电平衡时导体上的电荷分布1、导体内部没有净电荷,电荷(包括感应电荷和导体本⾝带的电荷)只分布在导体表⾯。
这个可以由⾼斯定理推得:ii sq E ds ε?=,S 是导体内“紧贴”表⾯的⾼斯⾯,所以0i q =。
2、导体是等势体,导体表⾯是等势⾯。
显然()()0b a b i a V V E dl -=?=?,a,b 为导体内或导体表⾯的任意两点,只需将积分路径取在导体内部即可。
3、导体表⾯以处附近空间的场强为:0E n δε=,δ为邻近场点的导体表⾯⾯元处的电荷密度,?n 为该⾯元的处法向。
简单的证明下:以导体表⾯⾯元为中截⾯作⼀穿过导体的⾼斯柱⾯,柱⾯的处底⾯过场点,下底⾯处于导体内部。
由⾼斯定理可得:12i s s dsE ds E ds δε?+?=,1s ,2s 分别为⾼斯柱⾯的上、下底⾯。
张三慧《大学物理学:力学、电磁学》(第3版)(B版)(课后习题 静电场中的电介质)【圣才出品】

第10章 静电场中的电介质10.1 在HCl 分子中,氯核和质子(氢核)的距离为0.128 nm ,假设氢原子的电子完全转移到氯原子上并与其他电子构成一球对称的负电荷分布而其中心就在氯核上。
此模型的电矩多大?实测的HCl 分子的电矩为3.4×10-30C·m ,HCl 分子中的负电分布的“重心”应在何处?(氯核的电量为17e )解:按假设模型计算,HCl 分子的电矩为此结果比实测数值大。
设如图10-1所示,在HCl分子中负电分布的“重心”在氯核与质子中间离氯核l 距离处。
这时HCL 分子的电矩应为图10-110.2 两个同心的薄金属球壳,内、外球壳半径分别为R1=0.02 m 和R2=0.06m 。
球壳间充满两层均匀电介质,它们的相对介电常量分别为εr1=6和εr2=3。
两层电介质的分界面半径R =0.04 m 。
设内球壳带电量Q =﹣6×10-8 C ,求:(1)D 和E 的分布,并画D-r ,E-r 曲线;(2)两球壳之间的电势差;(3)贴近内金属壳的电介质表面上的面束缚电荷密度。
解:(1)由D 的高斯定律可得再由,可得D-r 和E-r曲线如图10-2所示。
图10-2(2)两球壳之间的电势差为(3)10.3 两共轴的导体圆筒的内、外筒半径分别为R1和R2,R2<2R1。
其间有两层均匀电介质,分界面半径为r0。
内层介质相对介电常量为εr1,外层介质相对介电常量为εr2,εr2=εr1/2。
两层介质的击穿场强都是Emax 。
当电压升高时,哪层介质先击穿?两筒间能加的最大电势差多大?解:设内筒带电的线电荷密度为λ,则可导出在内外筒的电压为U 时,内层介质中的最大场强(在r =R L处)为而外层介质中的最大场强(在r =r 0处)为两结果相比由于r 0<R 2,且R 2<2R 1,所以总有E 2/E 1>0,因此当电压升高时,外层介质中先达到E max 而被击穿。
而最大的电势差可由E 2=Emax 求得为10.4 一平板电容器板间充满相对介电常量为εr 的电介质而带有电量Q 。
川师大学物理第十章 静电场中的导体和电介质习题解

第十章 静电场中的导体和电介质10–1 如图10-1所示,有两块平行无限大导体平板,两板间距远小于平板的线度,设板面积为S ,两板分别带正电Q a 和Q b ,每板表面电荷面密度σ1= ,σ2= ,σ3= ,σ4= 。
解:建立如图10-2所示坐标系,设两导体平板上的面电荷密度分别为σ1,σ2,σ3,σ4。
由电荷守恒定律得12a S S Q σσ+= (1)34b S S Q σσ+= (2)设P ,Q 是分别位于二导体板内的两点,如图10-2所示,由于P ,Q 位于导板内,由静电平衡条件知,其场强为零,即3124000002222P E σσσσεεεε=---= (3)3124000002222Q E σσσσεεεε=++-= (4) 由方程(1)~(4)式得142abQ Q Sσσ+== (5) 232a bQ Q Sσσ-=-= (6) 由此可见,金属平板在相向的两面上(面2,3),带等量异号电荷,背向的两面上(面1,4),带等量同号电荷。
10–2 如图10-3所示,在半径为R 的金属球外距球心为a 的D 处放置点电荷+Q ,球内一点P 到球心的距离为r ,OP 与OD 夹角为θ,感应电荷在P 点产生的场强大小为 ,方向 ;P 点的电势为 。
解:(1)由于点电荷+Q 的存在,在金属球外表面将感应出等量的正负电荷,距+Q 的近端金属球外表面带负电,远端带正电,如图10-4所示。
P 点的场强是点电荷+Q 在P 点产生的场强E 1,与感应电荷在P 点产生的场强E 2的叠加,即E P =E 1+E 2,当静电平衡时,E P =E 1+E 2=0,由此可得21r 2204π(2cos )Qa r ar εθ=-=-+-E E e其中e r 是由D 指向P 点。
因此,感应电荷在P 点产生的场强E 2的大小为图10–4xσ2 4σQQ aQ b 图10-2σ1σ2 σ4σ3 Q a Q b图10-1图10-322204π(2cos )QE a r ar εθ=+-方向是从P 点指向D 点。
10.4 电容器的电容(练习题)(解析版)

第十章静电场中的能量10.4 电容器的电容一、单选题:1.一个电容器带电荷量为Q时,两极板间电压为U,若使其带电荷量增加4.0×10-7 C 时,它两极板间的电势差增加20 V,则它的电容为( )A.1.0×10-8 F B.2.0×10-8 FC.4.0×10-8 F D.8.0×10-8 F答案 B解析C=ΔQΔU=4.0×10-720F=2.0×10-8 F,故选B.2.传感器是自动控制设备中不可缺少的元件,已经渗透到宇宙开发、环境保护、交通运输以及家庭生活等各种领域.下列为几种电容式传感器,其中通过改变电容器两板间距离而引起电容变化的是( )【解析】A选项改变的是介质,B、D选项改变的是正对面积,C选项改变的是两板间距离,故C正确.【答案】 C3.对于两个电容不同的电容器,下列说法正确的是( )A.电容大的电容器带电荷量一定比较多B.电容大的电容器两板间的电势差一定比较大C.由C=QU知,电容器所带电荷量Q只要不断增大,U可无限增大D .在相同电压作用下,带电荷量多的电容器的电容比较大 答案 D解析 电容的大小与电容器两端的电压及电容器所带的电荷量无关,故A 错误;根据公式C =Q U 得,电势差U =QC ,因此电容大的电容器两板间的电势差不一定比较大,故B 错误;超过击穿电压,电容器将被损坏,故C 错误;根据公式C =QU ,在相同电压作用下,带电荷量多的电容器的电容比较大,故D 正确.4.如图所示,先接通S 使电容器充电,然后断开S 。
当增大两极板间距离时,电容器所带电荷量Q 、电容C 、两极板间电势差U 、两极板间场强E 的变化情况是( )A.Q 变小,C 不变,U 不变,E 变小B.Q 变小,C 变小,U 不变,E 不变C.Q 不变,C 变小,U 变大,E 不变D.Q 不变,C 变小,U 变小,E 变小解析 电容器充电后再断开S ,其所带电荷量Q 不变,由C ∝εr Sd可知,d 增大时,C 变小,又U =Q C ,所以U 变大;由于E =U d ,U =Q C =4πkdQ εr S ,所以E =4πkQεr S,故d 增大时,E不变。
大学物理下册第10章课后题答案

习题10-3图第10章 静电场中的导体和电介质习 题一 选择题10-1当一个带电导体达到静电平衡时,[ ] (A) 表面上电荷密度较大处电势较高 (B) 表面曲率较大处电势较高(C) 导体内部的电势比导体表面的电势高(D) 导体内任一点与其表面上任一点的电势差等于零 答案:D解析:处于静电平衡的导体是一个等势体,表面是一个等势面,并且导体内部与表面的电势相等。
10-2将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,导体B 的电势将[ ](A) 升高 (B)降低 (C)不会发生变化 (D)无法确定 答案:A解析:不带电的导体B 相对无穷远处为零电势。
由于带正电的带电体A 移到不带电的导体B 附近的近端感应负电荷;在远端感应正电荷,不带电导体的电势将高于无穷远处,因而正确答案为(A )。
10-3将一带负电的物体M 靠近一不带电的导体N ,在N 的左端感应出正电荷,右端感应出负电荷。
若将导体N 的左端接地(如图10-3所示),则[ ](A) N 上的负电荷入地 (B) N 上的正电荷入地 (C) N 上的所有电荷入地 (D) N 上所有的感应电荷入地 答案:A解析:带负电的带电体M移到不带电的导体N附近的近端感应正电荷;在远端感应负电荷,不带电导体的电势将低于无穷远处,因此导体N的电势小于0,即小于大地的电势,因而大地的正电荷将流入导体N,或导体N的负电荷入地。
故正确答案为(A)。
10-4 如图10-4所示,将一个电荷量为q电的导体球附近,点电荷距导体球球心为d。
设无穷远处为零电势,则在导体球球心O点有[ ](A)0E,4πε=qVd(B)24πε=qEd,4πε=qVd(C) 0E,0V(D)24πε=qEd,4πε=qVR答案:A解析:导体球处于静电平衡状态,导体球内部电场强度为零,因此0E。
导体球球心O点的电势为点电荷q及感应电荷所产生的电势叠加。
感应电荷分布于导体球表面,至球心O的距离皆为半径R,并且感应电荷量代数和q∑为0,因此4qVRπε==∑感应电荷。
高中物理人教必修三第10章第4节 电容器的电容教学设计

教版高中物理必修3电容器的电容教学设计出示图片:平行板电容器实验:观察电容器的充、放电现象1.实验器材:把直流电源、电阻、电容器、电流表、电压表以及单刀双掷开关2. 实验电路电容器的充、放电实验步骤1.把开关S接1,此时电源给电容器充电,观察实验现象。
出示:电源给电容器充电动画视频(1)现象:通过观察电流表可以知道,充电时电流由电源的正极流向电容器的正极板。
同时,电流从电容器的负极板流向电源的负极。
随着两极板之间电势差的增大,充电电流逐渐减小至0,此时电容器两极板带有一定的等量异种电荷。
另外,在充电过程中,还可以看到电压表示数迅速增大,随后逐渐稳定在某一数值,表示电容器两极板具有一定的电势差。
出示电容器的充电完成的电路图(2)充电:使原本不带电的两板带上等量异种电荷的过程两板分别带等量异种电荷,每个极板带电量的绝对值叫电容器的带电量。
出示图片:平行板电容器注意:即使断开电源,两极板上的电荷由于相互吸引而仍然被保存在电容器中。
2.把开关S接2,电容器对电阻R放电。
学生观看动画了解实验器材、实验电路、实验步骤并动手操作,观察实验现象锻炼学生的实验动手操作能力和总结能力出示电容器放电动画视频(1)现象:观察电流表可以知道,放电电流由电容器的正极板经过电阻R流向电容器的负极板,正负电荷中和。
此时两极板所带的电荷量减小,电势差减小,放电电流也减小,最后两极板电势差以及放电电流都等于0。
出示电容器的放电完成的电路图(2)放电:用导线将充电后的电容器两极接通,两极失去电荷的过程,叫电容器的放电。
出示电容器用导线将充电后的电容器两极接通的图片解释:电容器两极正负电荷通过导线中和。
电容器的充、放电现象视频总结:电容器充电的过程中,两极板的电荷量增加,极板间的电场强度增大,电源的能量不断储存在电容器中;放电的过程中,电容器把储存的能量通过电流做功转化为电路中其他形式的能量。
拓展学习用传感器观察电容器的放电过程1.实验电路和器材如图实验步骤(1)照图连接电路。
人教版(2019)高中物理必修第三册第十章第4节电容器的电容

典题剖析
典题剖析
例1 下列说法中正确的是( CD ) A. 电容器所带的电荷越多,电容就越大 B. 电容器两极板间电压越高,电容就越大 C. 电容器所带电荷增加一倍,则两极间的电压也一定增加一倍 D. 电容表征电容器容纳电荷的本领的物理量 E. 平行板电容器保持带电量不变而增大板距时,两板间电压要减小 F. 平行板电容器一板带电+Q,另一板带电-Q,则此电容器不带电
A.两极板间的电压不变,极板上的电荷量变小 B.两极板间的电压不变,极板上的电荷量变大 C.极板上电荷量几乎不变,两极板间电压变小 D.极板上电荷量几乎不变,两极板间电压变大
课堂小结
课堂小结
再见
四、常用电容器
超级电容器
超级电容器是介于传统电容器和充电电池之间的一种新型储能装置,是 通过电极与电解质之间形成的界面双层来存储能量的新型器件。
超级电容器的出现使电容器的容量得 到了巨大的提升。超级电容器的充电时间 短,储存电能多,放电功率大,使用寿命 长。这些优点展现了它作为新型动力电源 的广阔发展前景。
(2)电容器充电后断开和电源连接,在这种情况下,如果增大d, 则U、Q、 E如何变化?
ห้องสมุดไป่ตู้ 三、平行板电容器
不变量 自变量
始终与电源连接 U不变 d
充电后与电源断开 Q不变 S
因变量
E=U/d,d变大,E变小;d 变小,E变大
三、平行板电容器
分析电容器动态变化问题的步骤
四、常用电容器
电容器铭牌
三、平行板电容器
理解:电容C与Q、U无关,由电容器本身决定。
二、电容
3.物理意义:表征电容器容纳电荷本领的大小。 4.单位:国际制单位为法拉,简称法,符号为F。
1 F=1 C/V 常用单位有微法(μF)、皮法(pF)
新教材-人教版高中物理必修第三册-第10章-静电场中的能量-知识点考点重点难点提炼汇总

第10章静电场中的能量1.电势能和电势 (1)2.电势差 (5)3.电势差与电场强度的关系 (11)4.电容器的电容 (14)5.带电粒子在电场中的运动 (21)1.电势能和电势一、静电力做功的特点1. 特点: 静电力做的功与电荷的起始位置和终止位置有关, 与电荷经过的路径无关。
2.在匀强电场中静电力做功:WAB =qE ·LABcos θ, 其中θ为静电力与位移间的夹角。
二、电势能1. 概念: 电荷在静电场中具有的势能。
用Ep 表示。
2. 静电力做功与电势能变化的关系静电力做的功等于电势能的减少量, WAB =EpA -EpB 。
⎩⎨⎧ 电场力做正功,电势能减少;电场力做负功,电势能增加。
3. 电势能的大小: 电荷在某点的电势能, 等于静电力把它从该点移到零势能位置时所做的功。
4.零势能点:电场中规定的电势能为零的位置, 通常把离场源电荷无限远处或大地处的电势能规定为零。
三、电势1. 定义: 电荷在电场中某一点的电势能与它的电荷量的比值。
2. 定义式: φ=。
3.单位:国际单位制中, 电势的单位是伏特, 符号是V,1 V =1 J/C 。
4. 特点(1)相对性: 电场中各点电势的大小, 与所选取的零电势的位置有关, 一般情况下取离场源电荷无限远或大地为零电势位置。
(2)标矢性:电势是标量, 只有大小, 没有方向, 但有正负。
5. 与电场线关系:沿电场线方向电势逐渐降低。
考点1: 静电力做功和电势能的变化1. 电场力做功正、负的判定(1)若电场力是恒力, 当电场力方向与电荷位移方向夹角为锐角时, 电场力做正功;夹角为钝角时, 电场力做负功;夹角为直角时, 电场力不做功。
(2)根据电场力和瞬时速度方向的夹角判断。
此法常用于判断曲线运动中变化电场力的做功情况。
夹角是锐角时, 电场力做正功;夹角是钝角时, 电场力做负功;电场力和瞬时速度方向垂直时, 电场力不做功。
(1)做功判定法: 无论是哪种电荷, 只要是电场力做了正功, 电荷的电势能一定是减少的;只要是电场力做了负功(克服电场力做功), 电荷的电势能一定是增加的。
大学物理答案第10章

第十章 静电场中的导体与电介质10-1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,则导体B 的电势将( )(A ) 升高 (B ) 降低 (C ) 不会发生变化 (D ) 无法确定分析与解 不带电的导体B 相对无穷远处为零电势.由于带正电的带电体A 移到不带电的导体B 附近时,在导体B 的近端感应负电荷;在远端感应正电荷,不带电导体的电势将高于无穷远处,因而正确答案为(A ).10-2 将一带负电的物体M 靠近一不带电的导体N ,在N 的左端感应出正电荷,右端感应出负电荷.若将导体N 的左端接地(如图所示),则( ) (A ) N 上的负电荷入地 (B )N 上的正电荷入地 (C ) N 上的所有电荷入地 (D )N 上所有的感应电荷入地题 10-2 图分析与解 导体N 接地表明导体N 为零电势,即与无穷远处等电势,这与导体N 在哪一端接地无关.因而正确答案为(A ).10-3 如图所示将一个电量为q 的点电荷放在一个半径为R 的不带电的导体球附近,点电荷距导体球球心为d ,参见附图.设无穷远处为零电势,则在导体球球心O 点有( ) (A )d εq V E 0π4,0== (B )dεqV d εq E 020π4,π4== (C )0,0==V E (D )RεqV d εq E 020π4,π4==题 10-3 图分析与解 达到静电平衡时导体内处处各点电场强度为零.点电荷q 在导体球表面感应等量异号的感应电荷±q′,导体球表面的感应电荷±q′在球心O 点激发的电势为零,O 点的电势等于点电荷q 在该处激发的电势.因而正确答案为(A ).10-4 根据电介质中的高斯定理,在电介质中电位移矢量沿任意一个闭合曲面的积分等于这个曲面所包围自由电荷的代数和.下列推论正确的是( )(A ) 若电位移矢量沿任意一个闭合曲面的积分等于零,曲面内一定没有自由电荷 (B ) 若电位移矢量沿任意一个闭合曲面的积分等于零,曲面内电荷的代数和一定等于零 (C ) 若电位移矢量沿任意一个闭合曲面的积分不等于零,曲面内一定有极化电荷 (D ) 介质中的高斯定律表明电位移矢量仅仅与自由电荷的分布有关 (E ) 介质中的电位移矢量与自由电荷和极化电荷的分布有关分析与解 电位移矢量沿任意一个闭合曲面的通量积分等于零,表明曲面内自由电荷的代数和等于零;由于电介质会改变自由电荷的空间分布,介质中的电位移矢量与自由电荷与位移电荷的分布有关.因而正确答案为(E ). 10-5 对于各向同性的均匀电介质,下列概念正确的是( )(A ) 电介质充满整个电场并且自由电荷的分布不发生变化时,电介质中的电场强度一定等于没有电介质时该点电场强度的1/εr倍(B ) 电介质中的电场强度一定等于没有介质时该点电场强度的1/εr倍(C ) 在电介质充满整个电场时,电介质中的电场强度一定等于没有电介质时该点电场强度的1/εr倍(D ) 电介质中的电场强度一定等于没有介质时该点电场强度的εr倍分析与解 电介质中的电场由自由电荷激发的电场与极化电荷激发的电场迭加而成,由于极化电荷可能会改变电场中导体表面自由电荷的分布,由电介质中的高斯定理,仅当电介质充满整个电场并且自由电荷的分布不发生变化时,在电介质中任意高斯面S 有()∑⎰⎰=⋅=⋅+ii S S εχq 01d d 1S E S E 即E =E 0/εr,因而正确答案为(A ).10-6 不带电的导体球A 含有两个球形空腔,两空腔中心分别有一点电荷q b 、q c ,导体球外距导体球较远的r 处还有一个点电荷q d (如图所示).试求点电荷q b 、q c 、q d 各受多大的电场力.题 10-6 图分析与解 根据导体静电平衡时电荷分布的规律,空腔内点电荷的电场线终止于空腔内表面感应电荷;导体球A 外表面的感应电荷近似均匀分布,因而近似可看作均匀带电球对点电荷q d 的作用力.()20π4rεq q q F dc bd +=点电荷q d 与导体球A 外表面感应电荷在球形空腔内激发的电场为零,点电荷q b 、q c 处于球形空腔的中心,空腔内表面感应电荷均匀分布,点电荷q b 、q c 受到的作用力为零.10-7 一真空二极管,其主要构件是一个半径R 1=5.0×10-4m 的圆柱形阴极和一个套在阴极外、半径R 2=4.5×10-3m 的同轴圆筒形阳极.阳极电势比阴极电势高300 V ,阴极与阳极的长度均为L =2.5×10-2 m .假设电子从阴极射出时的速度为零.求:(1) 该电子到达阳极时所具有的动能和速率;(2)电子刚从阳极射出时所受的力.题 10-7 图分析 (1) 由于半径R 1<<L ,因此可将电极视作无限长圆柱面,阴极和阳极之间的电场具有轴对称性.从阴极射出的电子在电场力作用下从静止开始加速,电子所获得的动能等于电场力所作的功,也即等于电子势能的减少.由此,可求得电子到达阳极时的动能和速率. (2) 计算阳极表面附近的电场强度,由F =q E 求出电子在阴极表面所受的电场力. 解 (1) 电子到达阳极时,势能的减少量为J 108.4Δ17ep -⨯-=-=eV E由于电子的初始速度为零,故J 108.4ΔΔ17ep ek ek -⨯-=-==E E E因此电子到达阳极的速率为1-7ek s m 1003.122⋅⨯===meVm E v (2) 两极间的电场强度为r rελe E 0π2-= 两极间的电势差1200ln π2d π2d 2121R R r r V R R R R ελελ-=-=⋅=⎰⎰r E负号表示阳极电势高于阴极电势.阴极表面电场强度r r R R R V R ελe e E 12110ln π2=-=电子在阴极表面受力r e e E F N)1037.414-⨯=-=(这个力尽管很小,但作用在质量为9.11×10-31kg 的电子上,电子获得的加速度可达重力加速度的5×1015倍.10-8 一导体球半径为R 1 ,外罩一半径为R 2 的同心薄导体球壳,外球壳所带总电荷为Q ,而内球的电势为V 0 .求此系统的电势和电场的分布. 分析 若200π4R εQV =,内球电势等于外球壳的电势,则外球壳内必定为等势体,电场强度处处为零,内球不带电.若200π4R εQV ≠,内球电势不等于外球壳电势,则外球壳内电场强度不为零,内球带电.一般情况下,假设内导体球带电q ,导体达到静电平衡时电荷的分布如图所示.依照电荷的这一分布,利用高斯定理可求得电场分布.并由⎰∞⋅=pp V l E d 或电势叠加求出电势的分布.最后将电场强度和电势用已知量V 0、Q 、R 1、R 2表示.题 10-8 图解 根据静电平衡时电荷的分布,可知电场分布呈球对称.取同心球面为高斯面,由高斯定理()()∑⎰⋅=⋅=⋅02/π4d εq r E r r E S E ,根据不同半径的高斯面内的电荷分布,解得各区域内的电场分布为 r <R 1时, ()01=r E R 1<r <R 2 时,()202π4r εqr E =r >R 2 时, ()202π4r εqQ r E +=由电场强度与电势的积分关系,可得各相应区域内的电势分布. r <R 1时,20103211π4π4d d d d 2211R Q R q V R R R R r r εε+=⋅+⋅+⋅=⋅=⎰⎰⎰⎰∞∞lE l E l E l ER 1<r <R 2 时,200322π4π4d d d 22R Q r q V R R r r εε+=⋅+⋅=⋅=⎰⎰⎰∞∞lE l E l Er >R 2 时,rqQ V r 03π4d ε+=⋅=⎰∞l E 3也可以从球面电势的叠加求电势的分布:在导体球内(r <R 1)20101π4π4R εQR εq V +=在导体球和球壳之间(R 1<r <R 2 )2002π4π4R εQr εq V +=在球壳外(r >R 2)为rqQ V 03π4ε+=由题意102001π4π4R εQR εq V V +==得Q R R V R q 21010π4==ε 于是可求得各处的电场强度和电势的分布: r <R 1时,01=E ;01V V =R 1<r <R 2 时,22012012π4r R εQR r V R E -=;rR Q R r r V R V 201012π4)(ε-+= r >R 2 时,220122013π4)(r R Q R R r V R E ε-+=;rR QR R r V R V 2012013π4)(ε-+= 10-9 地球和电离层可当作球形电容器,它们之间相距约为100 km ,试估算地球-电离层系统的电容.设地球与电离层之间为真空.解 由于地球半径R 1=6.37×106m ;电离层半径R 2=1.00×105m +R 1 =6.47×106m ,根据球形电容器的电容公式,可得F 1058.4π4212210-⨯=-=R R R RεC10-10 两线输电线,其导线半径为3.26 mm ,两线中心相距0.50 m ,导线位于地面上空很高处,因而大地影响可以忽略.求输电线单位长度的电容.分析 假设两根导线带等量异号电荷,电荷在导线上均匀分布,则由长直带电线的电场叠加,可以求出两根带电导线间的电场分布,-++=E E E再由电势差的定义求出两根导线之间的电势差,就可根据电容器电容的定义,求出两线输电线单位长度的电容解 建立如图坐标,带等量异号电荷的两根导线在P 点激发的电场强度方向如图,由上述分析可得P 点电场强度的大小为)11(π20xd x E --=ελ 电场强度的方向沿x 轴,电线自身为等势体,依照定义两导线之间的电势差为x xd x l E U lRd Rd )11(π2d 0--=⋅=⎰⎰-ελ 上式积分得RR d ελU -=ln π0 因此,输电线单位长度的电容Rd εR R d εU λC ln /πln /π00≈-==代入数据 F 1052.512-⨯=C题 10-10 图10-11 电容式计算机键盘的每一个键下面连接一小块金属片,金属片与底板上的另一块金属片间保持一定空气间隙,构成一小电容器(如图).当按下按键时电容发生变化,通过与之相连的电子线路向计算机发出该键相应的代码信号.假设金属片面积为50.0 mm 2,两金属片之间的距离是0.600 mm .如果电路能检测出的电容变化量是0.250 pF ,试问按键需要按下多大的距离才能给出必要的信号?题 10-11 图分析 按下按键时两金属片之间的距离变小,电容增大,由电容的变化量可以求得按键按下的最小距离:解 按下按键时电容的变化量为⎥⎦⎤⎢⎣⎡-=0011Δd d S εC按键按下的最小距离为mm 152.0ΔΔΔ00200min =+=-=SC d Cd d d d ε10-12 一片二氧化钛晶片,其面积为1.0 cm 2,厚度为0.10 mm .把平行平板电容器的两极板紧贴在晶片两侧.(1) 求电容器的电容;(2) 当在电容器的两极间加上12 V 电压时,极板上的电荷为多少? 此时自由电荷和极化电荷的面密度各为多少? (3) 求电容器内的电场强度.解 (1) 查表可知二氧化钛的相对电容率εr =173,故充满此介质的平板电容器的电容F 1053.190-⨯==dSεεC r (2) 电容器加上U =12V 的电压时,极板上的电荷C 1084.18-⨯==CU Q极板上自由电荷面密度为2-80m C 1084.1⋅⨯==-SQσ 晶片表面极化电荷密度2-400m C 1083.111⋅⨯=⎥⎦⎤⎢⎣⎡-='-σεσr (3) 晶片内的电场强度为1-5m V 102.1⋅⨯==dUE 10-13 如图所示,半径R =0.10 m 的导体球带有电荷Q =1.0 ×10-8C ,导体外有两层均匀介质,一层介质的εr =5.0,厚度d =0.10 m ,另一层介质为空气,充满其余空间.求:(1) 离球心为r =5cm 、15 cm 、25 cm 处的D 和E ;(2) 离球心为r =5 cm 、15 cm 、25 cm 处的V ;(3) 极化电荷面密度σ′.题 10-13 图分析 带电球上的自由电荷均匀分布在导体球表面,电介质的极化电荷也均匀分布在介质的球形界面上,因而介质中的电场是球对称分布的.任取同心球面为高斯面,电位移矢量D 的通量与自由电荷分布有关,因此,在高斯面上D 呈均匀对称分布,由高斯定理⎰∑=⋅0d qS D 可得D (r ).再由r εε0/D E =可得E (r ).介质内电势的分布,可由电势和电场强度的积分关系⎰∞⋅=rV l E d 求得,或者由电势叠加原理求得.极化电荷分布在均匀介质的表面,其极化电荷面密度n P ='σ.解 (1) 取半径为r 的同心球面为高斯面,由高斯定理得 r <R 0π421=⋅r D01=D ;01=ER <r <R +d Q r D =⋅22π422π4r QD =;202π4r εεQ E r = r >R +d Q r D =⋅23π423π4r QD =;203π4rQ E ε= 将不同的r 值代入上述关系式,可得r =5 cm 、15 cm 和25 cm 时的电位移和电场强度的大小,其方向均沿径向朝外. r 1 =5 cm ,该点在导体球内,则01=r D ;01=r Er 2 =15 cm ,该点在介质层内,εr =5.0,则2822m C 105.3π42--⋅⨯==r Q D r 12220m V 100.8π42-⋅⨯==r εεQE r r r 3 =25 cm ,该点在空气层内,空气中ε≈ε0 ,则2823m C 103.1π43--⋅⨯==r QD r ; 13220m V 104.1π43-⋅⨯==r Q E r ε (2) 取无穷远处电势为零,由电势与电场强度的积分关系得 r 3 =25 cm ,V 360π4d 0r 331==⋅=⎰∞rεQV r Er 2 =15 cm ,()()V480π4π4π4d d 0020r3222=+++-=⋅+⋅=⎰⎰+∞+dR Qd R Q r Q V r r dR d R εεεεεrE r E r 1 =5 cm ,()()V540π4π4π4d d 000321=+++-=⋅+⋅=⎰⎰+∞+d R εQd R εεQ R εεQ V r r dR RdR rE r E(3) 均匀介质的极化电荷分布在介质界面上,因空气的电容率ε=ε0 ,极化电荷可忽略.故在介质外表面;()()()20π411d R εQ εE εεP r r n r n +-=-=()()282m C 106.1π41--⋅⨯=+-==d R εQεP σr r n在介质内表面:()()20π411R εQ εE εεP r r n r n -=-=()282m C 104.6π41--⋅⨯-=-=-='R εQ εP σr r n介质球壳内、外表面的极化电荷面密度虽然不同,但是两表面极化电荷的总量还是等量异号. 10-14 人体的某些细胞壁两侧带有等量的异号电荷.设某细胞壁厚为5.2 ×10-9m ,两表面所带面电荷密度为±5.2 ×10 -3C /m 2,内表面为正电荷.如果细胞壁物质的相对电容率为6.0,求(1) 细胞壁内的电场强度;(2) 细胞壁两表面间的电势差. 解 (1)细胞壁内的电场强度V /m 108.960⨯==rεεσE ;方向指向细胞外. (2) 细胞壁两表面间的电势差V 101.52-⨯==Ed U .10-15 如图(a )所示,有两块相距为0.50 的薄金属板A 、B 构成的空气平板电容器被屏蔽在一金属盒K 内,金属盒上、下两壁与A 、B 分别相距0.25 mm ,金属板面积为30 mm ×40 mm .求(1) 被屏蔽后电容器的电容变为原来的几倍;(2) 若电容器的一个引脚不慎与金属屏蔽盒相碰,问此时的电容又为原来的几倍?题 10-15 图分析 薄金属板A 、B 与金属盒一起构成三个电容器,其等效电路图如图(b)所示,由于两导体间距离较小,电容器可视为平板电容器,通过分析等效电路图可以求得A 、B 间的电容.解 (1) 由等效电路图可知13232123C C C C C C C C ++⋅=+=由于电容器可以视作平板电容器,且32122d d d ==,故1322C C C == ,因此A 、B 间的总电容12C C =(2) 若电容器的一个引脚不慎与金属屏蔽盒相碰,相当于2C (或者3C )极板短接,其电容为零,则总电容13C C =10-16 在A 点和B 点之间有5 个电容器,其连接如图所示.(1) 求A 、B 两点之间的等效电容;(2) 若A 、B 之间的电势差为12 V ,求U A C 、U CD 和U D B .题 10-16 图解 (1) 由电容器的串、并联,有μF 1221=+=C C C AC μF 843=+=C C C CD51111C C C C CD AC AB ++= 求得等效电容C AB =4 μF .(2) 由于AB DB CD AC Q Q Q Q ===,得V 4==AB ACABAC U C C U V 6==AB CDABCD U C C U V 2==AB DBABDB U C C U 10-17 如图,有一个空气平板电容器,极板面积为S ,间距为d .现将该电容器接在端电压为U 的电源上充电,当(1) 充足电后;(2) 然后平行插入一块面积相同、厚度为δ(δ <d )、相对电容率为εr 的电介质板;(3) 将上述电介质换为同样大小的导体板.分别求电容器的电容C ,极板上的电荷Q 和极板间的电场强度E .题 10-17 图分析 电源对电容器充电,电容器极板间的电势差等于电源端电压U .插入电介质后,由于介质界面出现极化电荷,极化电荷在介质中激发的电场与原电容器极板上自由电荷激发的电场方向相反,介质内的电场减弱.由于极板间的距离d 不变,因而与电源相接的导体极板将会从电源获得电荷,以维持电势差不变,并有()δSεεQ δd S εQU r 00+-=相类似的原因,在平板电容器极板之间,若平行地插入一块导体板,由于极板上的自由电荷和插入导体板上的感应电荷在导体板内激发的电场相互抵消,与电源相接的导体极板将会从电源获得电荷,使间隙中的电场E 增强,以维持两极板间的电势差不变,并有()δd SεQU -=0 综上所述,接上电源的平板电容器,插入介质或导体后,极板上的自由电荷 均会增加,而电势差保持不变. 解 (1) 空气平板电容器的电容dSεC 00=充电后,极板上的电荷和极板间的电场强度为U dS εQ 00=d U E /0=(2) 插入电介质后,电容器的电容C 1 为()()δd εδS εεδS εεQ δd SεQ Q C r r r -+=⎥⎦⎤⎢⎣⎡+-=0001/ 故有()δd εδSUεεU C C r r -+==011介质内电场强度()δd εδUS εεQ E r r -+=='011 空气中电场强度()δd εδU εS εQ E r r -+==011 (3) 插入导体达到静电平衡后,导体为等势体,其电容和极板上的电荷分别为δd SεC -=02 U δd S εQ -=02导体中电场强度 02='E 空气中电场强度δd UE -=2 无论是插入介质还是插入导体,由于电容器的导体极板与电源相连,在维持电势差不变的同时都从电源获得了电荷,自由电荷分布的变化同样使得介质内的电场强度不再等于E 0/εr.10-18 为了实时检测纺织品、纸张等材料的厚度(待测材料可视作相对电容率为εr 的电介质),通常在生产流水线上设置如图所示的传感装置,其中A ,B 为平板电容器的导体极板,d 0 为两极板间的距离.试说明检测原理,并推出直接测量量电容C 与间接测量量厚度d 之间的函数关系.如果要检测钢板等金属材料的厚度,结果又将如何?题 10-18 图分析 导体极板A 、B 和待测物体构成一有介质的平板电容器,关于电容C 与材料的厚度的关系,可参见题10-17 的分析. 解 由分析可知,该装置的电容为()d d d SC r r -+=00εεε则介质的厚度为()()C εSεεd εεC εS εεC d εd r r r r r r r 1110000---=--=如果待测材料是金属导体,其等效电容为dd SεC -=00导体材料的厚度CSεd d 00=-= 实时地测量A 、B 间的电容量C ,根据上述关系式就可以间接地测出材料的厚度.通常智能化的仪表可以实时地显示出待测材料的厚度.10-19 有一电容为0.50 μF 的平行平板电容器,两极板间被厚度为0.01 mm 的聚四氟乙烯薄膜所隔开,(1) 求该电容器的额定电压;(2) 求电容器存贮的最大能量. 分析 通过查表可知聚四氟乙烯的击穿电场强度E b =1.9 ×107 V /m ,电容器中的电场强度E ≤E b ,由此可以求得电容器的最大电势差和电容器存贮的最大能量. 解 (1) 电容器两极板间的电势差V 190b max ==d E U(2) 电容器存贮的最大能量J 1003.92132max e -⨯=CU W10-20 半径为0.10 cm 的长直导线,外面套有内半径为1.0 cm 的共轴导体圆筒,导线与圆筒间为空气.略去边缘效应,求:(1) 导线表面最大电荷面密度;(2) 沿轴线单位长度的最大电场能量.分析 如果设长直导线上单位长度所带电荷为λ,导线表面附近的电场强度0π2εσR ελE ==查表可以得知空气的击穿电场强度E b =3.0 ×106(V /m ),只有当空气中的电场强度E ≤E b 空气才不会被击穿,由于在导线表面附近电场强度最大,因而可以求出σ的极限值.再求得电场能量密度,并通过同轴圆柱形体元内电场能量的积分求得单位长度的最大电场强度.解 (1) 导线表面最大电荷面密度250max m C 1066.2--⋅⨯==b E εσ显然导线表面最大电荷面密度与导线半径无关.(2) 由上述分析得b E R ελ10max π2=,此时导线与圆筒之间各点的电场强度为()1210m π2R r R rR r E <<==ελ0=E (其他)222102m 0m 2121rE R E w b εε==沿轴线单位长度的最大电场能量r rER r r w W R Rb d 1πd π2212210m ⎰⎰⎰⎰Ω=⋅=ε 14122210mm J 1076.5lnπ--⋅⨯==R R E R W b ε 10-21 一空气平板电容器,空气层厚1.5 cm ,两极间电压为40 k V ,该电容器会被击穿吗? 现将一厚度为0.30 cm 的玻璃板插入此电容器,并与两极平行,若该玻璃的相对电容率为7.0,击穿电场强度为10 MV· m -1.则此时电容器会被击穿吗?分析 在未插入玻璃板时,不难求出空气中的电场强度小于空气的击穿电场强度,电容器不会被击穿.插入玻璃后,由习题10-17 可知,若电容器与电源相连,则极板间的电势差维持不变,电容器将会从电源获取电荷.此时空气间隙中的电场强度将会增大.若它大于空气的击穿电场强度,则电容器的空气层将首先被击穿.此时40 k V 电压全部加在玻璃板两侧,玻璃内的电场强度如也大于玻璃击穿电场强度的值,则玻璃也将被击穿.整个电容器被击穿.解 未插入玻璃时,电容器内的电场强度为16m V 107.2/-⋅⨯==d U E因空气的击穿电场强度16m V 100.3-⋅⨯=b E ,b E E <,故电容器不会被击穿.插入玻璃后,由习题6 -26 可知,空气间隙中的电场强度()16m V 102.3-⋅⨯=+-=δδd εVεE r r此时,因b E E > ,空气层被击穿,击穿后40 k V 电压全部加在玻璃板两侧,此时玻璃板内的电场强度17m V 103.1/-⋅⨯==δV E由于玻璃的击穿电场强度1bm MV 10-⋅='E ,b E E '> ,故玻璃也将相继被击穿,电容器完全被击穿.10-22 某介质的相对电容率 2.8r ε=,击穿电场强度为611810V m -⨯⋅ ,如果用它来作平板电容器的电介质,要制作电容为0.047 μF ,而耐压为4.0 k V 的电容器,它的极板面积至少要多大. 解 介质内电场强度16m V 1018-⋅⨯=≤b E E电容耐压U m =4.0 k V ,因而电容器极板间最小距离m 1022.2/4-⨯==b m E U d要制作电容为0.047 μF 的平板电容器,其极板面积210m 42.0==εεCdS 显然,这么大的面积平铺开来所占据的空间太大了,通常将平板电容器卷叠成筒状后再封装. 10-23 一平行板空气电容器,极板面积为S ,极板间距为d ,充电至带电Q 后与电源断开,然后用外力缓缓地把两极板间距拉开到2d .求:(1) 电容器能量的改变;(2) 此过程中外力所作的功,并讨论此过程中的功能转换关系.分析 在将电容器两极板拉开的过程中,由于导体极板上的电荷保持不变,极板间的电场强度亦不变,但电场所占有的空间增大,系统总的电场能量增加了.根据功能原理,所增加的能量应该等于拉开过程中外力克服两极板间的静电引力所作的功. 解 (1) 极板间的电场为均匀场,且电场强度保持不变,因此,电场的能量密度为20220221SεQ E εw e == 在外力作用下极板间距从d 被拉开到2d ,电场占有空间的体积,也由V 增加到2V ,此时电场能量增加SεdQ V w W e e 022ΔΔ== (2) 两导体极板带等量异号电荷,外力F 将其缓缓拉开时,应有F =-F e ,则外力所作的功为SεdQ QEd 02e 2ΔA ==⋅-=r F 外力克服静电引力所作的功等于静电场能量的增加.。
大学物理学 第十章 静电场中的电介质

2021/8/10
8
单位矢若量面元en
dS
endS
取在电介质的表面上,面元法线方向
由电介质指向真空,则电介质表面上的极化电
荷面密度为
d q出 dS
P
en
P cos
Pn
即 P • en P cos Pn
讨论 1)当θ = 0 0 时,P与n同向,σ 最大(正电荷)。
2)当θ< 90 0 时, 介质表面上将出现一层正极化电荷。
D4r 2 q
D
q
rˆ
E
D
0 r
4r 2
4
q
0
r
r
2
rˆ
-+
q' +q
-+ +-
-+
R
+
-
+r
+-
+
-
P E
D
r
E
q
4 0 r r 2
E0
q
4 0r 2
2021/8/10
为什么?
16
P 0(r 1)E
0 ( r
1)
q
4 0 r
r
2
rˆ
(1
1
r
)
q
4 r
2
rˆ
-
q' +q
-+
+
+-
-
+
E0
F
F
③在外电场作用下,分子固有电矩不同程度地转向和外电
场方向一致而发生的极化,称为取向极化 。
2021/8/10
5
3)极化结果 ①电介质从原来处处电中性变成出现了宏观的极化电荷。
第十章电荷和静电场(导体和电介质)

导体
证明: 设有两个相距很远的带电导体球,如图: 证明: 设有两个相距很远的带电导体球,如图: 用很长的细导线连接两导体球, 用很长的细导线连接两导体球, 忽略两球间的静电感应, 导体球上的电荷仍均匀分布。 忽略两球间的静电感应, 导体球上的电荷仍均匀分布。 Q 整个导体系统是等势体。 整个导体系统是等势体。 R 1 Q σA R q A 球:UA = = 4π ε0 R ε0 r A B 1 q σB r = B 球: UB = q + + ε 4π ε r
σ1 σ2σ3 σ4
σ1 σ2 σ3 σ4 r r r r a点 − − − =0 E4 E3 E2 E 1 2ε0 2ε0 2ε0 2ε0
a
σ1 σ2 σ3 σ4 + + − =0 b点 σ1 σ2σ3 σ4 2ε0 2ε0 2ε0 2ε0
由电荷守恒定律: 由电荷守恒定律:
A板 B板
σ1S +σ2S = Q
导体球表面: q 导体球表面: 内表面: 内表面:−q 电荷守恒) (电荷守恒) 导体球壳: 导体球壳: 外表面:Q+ q + (2) 先用高斯定理求场强分布,再用积分求电势。 先用高斯定理求场强分布,再用积分求电势。
q
q
R3
R1
Q +q
R2
0 q
由高斯定理: 由高斯定理:
(r < R ) 1
2
E = 4π ε0r
0
0
Q UA =UB , ∴
结论: ★ 结论:
第十章静电场中的导体与电介质(标准答案)

一、选择题[ B ]1(基础训练2) 一“无限大”均匀带电平面A ,其附近放一与它平行的有一定厚度的“无限大”平面导体板B ,如图所示.已知A 上的电荷面密度为+σ ,则在导体板B 的两个表面1和2上的感生电荷面密度为: (A) σ 1 = - σ, σ 2 = + σ. (B) σ 1 = σ21-, σ 2 =σ21+. (C) σ 1 = σ21-, σ 1 = σ21-. (D) σ 1 = - σ, σ 2 = 0. 【提示】“无限大”平面导体板B 是电中性的:σ 1S+σ 2S=0,静电平衡时平面导体板B 内部的场强为零,由场强叠加原理得:022202010=-+εσεσεσ联立解得: 1222σσσσ=-=,[ C ]2(基础训练4)、三个半径相同的金属小球,其中甲、乙两球带有等量同号电荷,丙球不带电。
已知甲、乙两球间距离远大于本身直径,它们之间的静电力为F ;现用带绝缘柄的丙球先与甲球接触,再与乙球接触,然后移去,则此后甲、乙两球间的静电力为:(A) 3F / 4. (B) F / 2. (C) 3F / 8. (D) F / 4. 【提示】设原来甲乙两球各自所带的电量为q ,则2204q F rπε=;丙球与它们接触后,甲带电2q ,乙带电34q ,两球间的静电力为:203324'48q q F F r πε⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭==[ C ]3(基础训练6)半径为R 的金属球与地连接。
在与球心O 相距d =2R 处有一电荷为q 的点电荷。
如图所示,设地的电势为零,则球上的感生电荷q '为:(A) 0. (B)2q . (C) -2q. (D) -q . 【提示】静电平衡时金属球是等势体。
金属球接地,球心电势为零。
球心电势可用电势叠加法求得:000'044q dq q R d πεπε'+=⎰, 00'01'44q q dq R d πεπε=-⎰, 'q q R d =-,其中d = 2R ,'2qq ∴=-[ C ]4(基础训练8)两只电容器,C 1 = 8 μF ,C 2 = 2 μF ,分别把它们充电到 1000 V ,然后将它们反接(如图所示),此时两极板间的电势差为:A+σ2(A) 0 V . (B) 200 V . (C) 600 V . (D) 1000 V【提示】反接,正负电荷抵消后的净电量为661212(82)101000610Q Q Q C U C U C --=-=-=-⨯⨯=⨯这些电荷重新分布,最后两个电容器的电压相等,相当于并联。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空气
r1 1
Q CU
绝缘陶瓷
Q2 6Q1
大部分电荷储存在下部
r2 6
U
空气部分用来产生火花 陶瓷部分避免产生火花,用来储存电荷
另外一种分路表面放 电式火花塞,本质上也是 一个圆柱形电容器,可产 生数厘米的火花深入发动 机燃烧室
与空气间隙式火花塞相比, 结构类似,但它不是以强电场 直接击破空气分子产生火花, 半导体表面放电,打破空气分 子而产生火花,所需放电电压 约为空气间隙式的五分之一
1 1 W CU 2 r C0U 2 rW0 2 2 1 A W W0 ( r 1)W0 ( r 1)C0U 2 2 (2)电路断开,Q 不变,插入介质后电容器的能量为 W Q2 Q2 W 0 2C 2 r C0 r 1 1 1 1W0 r A W W0 C0U 2 2 r r
D dS Q0i
i
根据旋转对称性,忽略边缘效应,电位移 线是垂直轴向向外辐射状
电位移通量
电位移线(绿色) D
底面
D
D dS
S
D dS
侧面
D dS
h
r
闭合曲面以向外为正方向
底面
D dS cos 90 D dS cos 0
孤立导体可作为电容器,例如一个金属球, 如果带电荷 Q ,
电势为(U = 0)
U R
Q 4 0 r
2
dr
Q 4 0 R
孤立导体球的电容
C Q U 40 R
这代表金属球储存电荷的能力 可见 球的半径越大,储存电荷能力越大。
金属之间通常还有 电介质,两个电极能够 绝缘分离; 另外一个作用:?
飞机发动机 点火系统
圆柱型电容器 产生强电场,将空 气分子击破,使其 电离,电场推动离 子和电子运动、碰 撞,发热发光,产 生一个高温“闪 电”,燃油和空气 的混合气体被点燃
空气间隙式点火器的原理示意图
上部 C C C 1 r1 0 0 下部 C2 r2C0 6C0 U相同
D
U R
R E dr R
R2 dr ln 2 0 r r 2 0 r R1
Q/ L R2 U ln 2 0 r R1
圆柱型电容器电容
*若金属电极之间是真空 r 1 表示真空没有产生极化电荷能力,空间电场由自由 电荷贡献 2 0 L C0 真空电容
E 40 r 2 0 Q
rR rR
2
R r Q
dr
半径为 r r + dr 的球壳内的电场能量为
1 1 Q Q 2 dr 2 2 dWe 0 E dV 0 4 r 2 4r dr 8 r 2 2 2 0 0
V
[例] 一平空气行板电容器,电容为 C0 ,接入充电电路充电至电压为 U , 此后(1)保持电路接通;(2)断开电路。今在极板间插入一块相对介电常数 为 r 的均匀各向同性介质,使介质充满极板间隙。求此过程中外力所做的功。 解:无介质时电容器的储能 W0 为 Q2 1 W0 C0U 2 2C0 2 插入介质后电容器的电容板为 C r C0 (1)电路接通,U 不变,插入介质后电容器的能量为
D2rh h
得到电位移
D 2r
方向沿半径向外
电位移矢量
D 0 r E
均匀各向同性的电介质
r
表示电介质产生极化电荷能力的一个参数,参数越 大,对自由电荷的电场削弱越厉害 电场矢量 电极之间电势差
E
R2
1
er 0 r 2 0 r r
2 1
Q 2 dr Q2 We dWe R 8 r 2 80 R 0 r R
结束学习之后的问题
谁? 什么会变化? 电荷、电压、电场 高斯定理、电场积分 如何描述? 为什么会变化? 电场、电压与电荷
量相关 电容器结构确定,U1 U 2 U
Q1 Q2 Q1 Q2 C C1 C2 U AB U U
C2
§10-5 电容器的能量
Energy of a Capacitor
考察电容的充电过程: 充电过程的实质,是把正电荷从电势低的负极板移到电势高 的正极板,静电场力做负功。因此外力必须克服静电场力对电荷 做功,使电容器获得能量并储存在电容器中。
§10-4 电容和电容器
Capacitance and Capacitors
开始学习之前的问题
谁? 什么会变化? 如何描述? 为什么会变化?
什么可以充当水容器?
任何固态物体都可以作为储存水的容器,即使是 一片树叶,一块海绵
什么可以充当电容器?
任何的状态物体都可以作为储存电的容器, 即使是一片云,一棵树,或者是一片金属片
汽车的点火器---圆柱形电容器
电容器的串并联
串联
A
1 1 1 1 C C1 C2 Cn
B Q QQ Q U1 U2
C1
C2
Q1 Q2 Q
并联
1 U AB U1 U 2 1 1 C Q Q Q C1 C2
Q1 C1
C C1 C2 Cn
1 1 1 1 2 we D E ( 0 E P) E 0 E P E 2 2 2 2
有介质时总电 场的能量密度 E E0 E
§5-5 电场的能量
介质中束缚电荷 的静电能密度
[例] 求半径为 R ,带电量为 Q 的导体球所产生电场的能量。 解:导体外电场强度分布为
侧面 侧面
0
D dS 底面没有电位移线出入,贡献是0
D dS
S
侧面
D dS D dS DS侧面
侧面
S
D
D dS D 2rh D dS Q0i h
S i
电位移通量只与闭合曲面内自由电荷相关
C0
Q不变
C rC0
Q UC0 1 U' U C C r
电场被削弱
电压减小了
发动机是飞机 的核心,是一 个极其精巧、 复杂的系统
发动机是如何开始工作的?
点火系统
功用:产生电花,点燃燃气混合气。 点火系统是短时间工作的,后续喷入的燃油 可由燃烧室的热量点燃。 连续点火-当外界条件可能导致燃烧室熄火时, 发动机也需要点火系统工作。
r
L
通过高斯定理求得电场 电场积分求得电势差U 应用定义,消去而且
必须消去Q,求得电容:
Q C U
Q 假设电容器带电Q, L 轴向单位长度带电量称为电荷线密度
电容器有绝缘的电介质存在, 空间电场由自由电荷Q和极 化电荷共同激发
R1
Q
R2 Q
r
h
L
D E U
做半径r(R1<r<R2),高度为 h,圆柱形高斯面,根据电 位移的高斯定理 有介质时的高斯定理
energy density of electric field
注:在忽略边缘效应的情况下,场强被局限在两平行极板之 间,且电场是均匀的,we We Sd 。
可以证明,上式对任意电场(包括非静电场)都成立,是 电场能量密度的普遍表达式。
如果考虑充有均匀各向同性电介质的平行板电容器,它的能 量可以用场强表示: 1 Q2 1 We 0 r E 2 Sd 2 C 2 We 1 1 2 故有 we 0 r E DE Sd 2 2 1 对任意电场和任 介质的总能量密度的普遍表达式: we D E 意介质普遍成立 2
Q 2 0 r L C R2 U ln R1
*有介质存在的时候
R2 ln R1 C rC0 C0
储存电荷能力增大
平行板电容器
D
s
d
A
S
Q Q
r
D E 0 r 0 r B d Qd U E dl E d A 0 r 0 r s
S
D dS DS S
D
B
Q 0 r S 0S C r U d d
同样有
r 1
C0
0S
L
d C rC0 C0
课后作业:证明球形电容器电容
球形电容器
R1R2 C 4 r 0 R2 R1
R1 r
例题:一圆柱型电容器,电极之间原为真空,用电 动势为U的电源充电后,断开电源。在电极之间充 入电介质(ε r),电容器两极间电压变为多少?
+ + + + +
-
- - - -
为了方便地存储电荷
和
利用电荷
用两个邻近导体制成电容器,利用电池或者电路中的电势差 U给两个导体加上电压,从而让电容器两个电极分别带电+Q和-Q
以Q作为电容器带电量 引入电容:
+Q
Q C U
U
-Q
电容:储存电荷的能力。这个能力与存储了多少电荷没有关 系,只决定于两导体的大小、形状、相对位置等因素。
典型电容器
平行板电容器
球形电容器
R1 r
电容器的应用:滤波、震荡、储能等等
收音机调台的旋钮就是在调节一 个电容的大小,以实现电路和不 同的频率的电磁波共振
电路中常见的电容
以圆柱形电容器为例,长度L,内径R1,外径R2, 电介质(ε r),说明如何确定电容器电容
假设电容器带电Q,
电容器的能量是指:电容器上电荷建立的
