2019-2020学年重庆市七校联盟高二上学期联考数学(文)试题 Word版
2019-2020学年重庆市七校联盟高二上学期联考数学(文)试题(解析版)

2019-2020学年重庆市七校联盟高二上学期联考数学(文)试题一、单选题1.设i 为虚数单位,则复数()2z i i =-对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】A【解析】利用复数的乘法将()2z i i =-化为a bi +的形式,则它在复平面对应的点为(),a b ,判断点所在的象限即可【详解】由题,()212z i i i =-=+,则在复平面上对应的点为()1,2,在第一象限, 故选:A 【点睛】考查复数与复平面的对应关系,考查复数的乘法,属于基础题 2.下列图中的两个变量是相关关系的是( )A .①②B .①③C .②④D .②③【答案】D【解析】①是函数关系,②③④由散点图的形状进行判定 【详解】①具有确定的函数关系;散点图上所有的点在一条直线附近波动,则为线性相关,则②符合; 若散点图上所有的点在一条曲线附近波动,则为非线性相关,则③符合; 故选:D 【点睛】本题考查由散点图反应变量的相关性,属于基础题3.已知回归直线斜率的估计值为1.32,样本点的中心为点()23,,则回归直线的方程为( ) A .$1.324y x =+ B .$1.325y x =+ C .$1.320.36y x =+D .$0.08 1.32y x =+【答案】C【解析】由回归直线恒过样本点的中心,则将点()2,3代入ˆˆ1.32yx a =+中求解即可 【详解】由题,设回归直线方程为ˆˆ1.32yx a =+, 因为点()2,3在直线上,所以ˆ3 1.322a =⨯+,即ˆ0.36a =, 所以回归直线方程为ˆ 1.320.36yx =+, 故选:C 【点睛】本题考查回归直线方程,属于基础题 4.设103iz i=+,则z 的共轭复数为 A .13i -+ B .13i --C .13i +D .13i -【答案】D【解析】试题分析:()()()1031013,333i i i z i z i i i -===+∴++-的共轭复数为13i -,故选D . 【考点】1.复数的四则运算;2.共轭复数的概念.5.用三段论推理命题:“任何实数的平方都大于,因为是实数,所以”你认为这个推理( ). A .大前提错误 B .小前提错误C .推理形式错误D .结论正确【答案】A【解析】:任何实数的平方大于0,这句话是错误的,所以导致后面的结论是错误的,因此大前提错误。
2019-2020学年重庆市三峡名校联盟高二上学期联合考试数学试题(解析版)

2019-2020学年重庆市三峡名校联盟高二上学期联合考试数学试题一、单选题1.将选项中所示的三角形绕直线l 旋转一周,可以得到下图所示的几何体的是( )A .B .C .D .【答案】B【解析】由几何体的轴截面特征直接判断即可。
【详解】由题可得:该几何体的轴截面是关于直线l 对称的, 并且l 的一侧是选项B 中的三角形形状。
故选:B 【点睛】本题主要考查了空间思维能力及关于直线旋转的几何体特征,属于基础题。
2.设k 为实数,则方程()1y k x =+表示的图形是( ) A .通过点()1,0的所有直线 B .通过点()1,0-的所有直线C .通过点()1,0且不与y 轴平行的所有直线D .通过点()1,0-且不与y 轴平行的所有直线 【答案】D【解析】由直线方程的斜截式判断,再由直线方程得到过定点判断。
【详解】由直线方程的斜截式可知,直线斜率为k ,故直线不能与y 轴平行。
再由直线方程得到过定点()1,0-,【点睛】本题考查了直线方程的斜截式及过定点问题。
3.已知命题:,(0,1)∀∈P x y ,2x y +<,则命题 P 的否定为( ) A .,(0,1)∀∈x y ,2x y +≥ B .,(0,1)∀∉x y ,2x y +≥ C .00,(0,1)∃∉x y ,002+≥x y D .00,(0,1)∃∈x y ,002+≥x y【答案】D【解析】根据全称命题的否定是特称命题,可直接得出结果. 【详解】命题:,(0,1)∀∈P x y ,2x y +<的否定为“00,(0,1)∃∈x y ,002+≥x y ”。
故选D 【点睛】本题主要考查全称命题的否定,只需改写量词与结论即可,属于基础题型.4.如图,正方形O A C B ''''的边长为1cm ,它是水平放置的一个平面图形的直观图,则它的原图形面积( )A .22B 2C .2(13)D .6【答案】A【解析】由题意求出直观图中O B ''的长度,根据斜二测画法,求出原图形平行四边形的底和高,求出面积即可. 【详解】由正方形O A C B ''''的边长为1cm ,所以2O B ''=O A C B ''''是水平放置的一个平面图形的直观图,所以它对应的原图为平行四边形高为222''=O B 1,所以原图形的面积为12222⨯=故选:A 【点睛】本题主要考查斜二测画法,属于基础题.5.已知m ,n 为两条直线,,αβ为两个平面,下列命题中正确的是( ) A .若n αP ,n βP ,则αβ∥ B .若m αP ,n αP ,则m n P C .若m α⊥,n β⊥,则αβ∥ D .若m α⊥,m β⊥,则αβ∥【答案】D【解析】A 项中,当直线平行于两相交平面的交线时,则直线与两平面都平行;B 项中,平行于同一平面的两直线可能平行,可能相交,也可能异面;C 项中,因为m 与n 关系不确定,所以由m α⊥,n β⊥无法确定α与β间关系;D 项中,垂直于同一直线的两平面平行,即可得出结论. 【详解】A 项中,若n αP ,n βP ,则α与β平行或相交,故A 错;B 项中,若m αP ,n αP ,则m 与n 平行、相交、异面均有可能,故B 错;C 项中,若m α⊥,n β⊥,因为m 与n 关系不确定,所以无法确定α与β间关系,故C 错;D 项中,若m α⊥,m β⊥,由垂直于同一直线的两平面平行可得αβ∥,故D 正确. 故选:D 【点睛】本题主要考查直线与直线、直线与平面、平面与平面间的位置关系,解题的关键熟练掌握空间中线、面关系.6.过点(12)A ,的直线在两坐标轴上的截距之和为零,则该直线方程为( ) A .10x y -+=B .30x y +-=C .20x y -=或+30x y -=D .20x y -=或10x y -+=【答案】D【解析】设直线方程为(1)2y k x =-+,计算截距得到2210k k--+=,计算得到答案. 【详解】易知斜率不存在时不满足;设直线方程为(1)2y k x =-+,则截距和为:2210k k--+=解得1k =或2k = 故直线方程为:1y x =+和2y x = 故选:D 【点睛】本题考查了直线方程,意在考查学生的计算能力.7.在ABC ∆中,“0AB AC ⋅<u u u r u u u r”是“ABC ∆为钝角三角形”的( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既非充分又非必要条件 【答案】A【解析】由0AB AC ⋅<u u u r u u u r可得出角A 为钝角,然后再利用充分条件、必要条件定义得出两条件之间的关系.【详解】cos 0AB AC AB AC A ⋅=⋅<u u u r u u u r u u u r u u u rQ ,cos 0A ∴<,则A 为钝角,∴“0AB AC ⋅<u u u r u u u r”⇒“ABC ∆是钝角三角形”,另一方面,“ABC ∆是钝角三角形”⇒“A 是钝角”.因此,“0AB AC ⋅<u u u r u u u r”是“ABC ∆为钝角三角形”的充分非必要条件. 故选:A. 【点睛】本题考查充分不必要条件的判断,要结合充分条件与必要条件的定义来判断,考查推理能力,属于中等题. 8.圆台上底半径为2,下底半径为6,母线长为5,则圆台的体积为( ) A .40π B .52πC .50πD .2123π 【答案】B【解析】作出圆台的轴截面,由圆台的上、下底面半径分别为2,6,构造直角三角形,结合母线长 为5,由勾股定理求出圆台的高.再求圆台的体积. 【详解】作出圆台的轴截面如图所示:上底面半径2MD =,下底面半径6NC =,过D 做DE 垂直NC , 则624EC =-= 由5CD = 故3DE = 即圆台的高为3, 所以圆台的体积为222213(2626)523V πππππ=⋅⋅⋅+⋅+⋅⋅⋅=. 故选B . 【点睛】本题考查的知识点是旋转体及其体积的计算,圆台的几何特征,其中画出轴截面,将空间问题转化为平面问题是解答的关键.9.已知圆心(,)a b (0,0)a b ><在直线21y x =-+上,且与x 轴相切,在y 轴上截得的弦长为5程为( )A .22(3)(5)25x y -++=B .22(2)(3)9x y -++=C .22(1)(1)1x y -++=D .222749339x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭ 【答案】B【解析】由题意可分析出圆的半径为b ,圆心到y 轴的距离为a ,y 轴上截得的弦长为25弦长的一半和半径正好构成直角三角形,由勾股定理可列出等式2225=+b a ,再由圆心(,)a b 在直线21y x =-+上,所以21b a =-+,联立方程求出a ,b 的值,写出椭圆方程即可.【详解】因为圆心(,)a b (0,0)a b ><在直线21y x =-+上,所以将圆心(,)a b 代入直线方程可得21b a =-+①,因为圆与x 轴相切,所以圆的半径为b ,圆心到y 轴的距离为a ,又因为在y 轴上截得的弦长为25可得2225=+b a ②,联立①②可得222215b a b a =-+⎧⎪⎨=+⎪⎩,又因为0,0a b ><,所以可解得2a =,3b =-,所以圆心为(2,3)-,半径为3,所以圆的方程为22(2)(3)9x y -++=. 故选:B 【点睛】本题主要考查直线与圆的位置关系,解题的关键是运用数形结合的思想解题.10.若圆()()22235x y r -++=上有且只有两个点到直线432x y -=的距离等于1,则半径r 的范围是( ) A .(]4,6 B .[)4,6C .()4,6D .[]4,6【答案】C【解析】先求出圆心到直线的距离d ,再根据有且只有两个点到直线432x y -=的距离等于1得到半径的范围为()1,1d d -+.【详解】圆心坐标为()3,5-,它到直线432x y -=的距离为2234532543d ⨯+⨯-==+,因为有且只有两个点到直线432x y -=的距离等于1,故半径()1,1R d d ∈-+, 所以()4,6R ∈.故选C . 【点睛】若圆的圆心到直线的距离为d ,圆的半径为r ,(1)若圆上有且仅有四个点到直线的距离为m ,则0d r m ≤<-; (2)若圆上有且仅有三个点到直线的距离为m ,则d r m =-; (3)若圆上有且仅有四个点到直线的距离为m ,则r m d r m -<<+; (4)若圆上有且仅有一个点到直线的距离为m ,则d r m =+.11.如果底面是菱形的直棱柱(侧棱与底面垂直的棱柱)1111ABCD A B C D -的所有棱长都相等,60ABC ︒∠=,E ,M ,N 分别为,AB ,BC 1CC 的中点,现有下列四个结论:①CE ⊥平面11CC D D ②1A B MN ∥③1AD ∥平面1A MN ④异面真线1D C 与MN 所成的角的余弦值为34,其中正确结论的个数为( )A .1个B .2个C .3个D .4个【答案】C【解析】根据线面垂直的性质可判断①正确;由1MN BC P 可知1A B 与MN 为异面直线,故②错误;根据线面平行的性质可判断③正确;根据异面直线1D C 与MN 所成的角即为11A BC ∠,可求出其余弦值. 【详解】如图,①连接AC ,CE ,因为60ABC ︒∠=,AB BC =,所以ABC ∆为等边三角形,又E 为AB 的中点,所以CE AB ⊥,因为1111ABCD A B C D -为底面是菱形的直棱柱,所以AB CD ∥,所以CE CD ⊥,因为1CC ⊥底面ABCD ,又CE ⊂底面ABCD ,所以1⊥CC CE ,又因为1=I CC CD C ,所以CE ⊥平面11CC D D ,故①正确; ②连接1A B ,MN ,1C B ,因为M ,N 分别为BC ,1CC 的中点,所以1MN BC P ,又11A B BC B ⋂=,所以1A B 与MN 为异面直线,故②错误;③连接1AD ,所以11AD BC P ,又1MN BC P ,所以1∥MN AD ,又因为MN ⊂平面1A MN ,1AD ⊄平面1A MN ,,所以1AD ∥平面1A MN ,故③正确;④连接1A B ,所以11D C A B P ,又1MN BC P ,所以异面真线1D C 与MN 所成的角即为11A BC ∠,设1111ABCD A B C D -的所有棱长都为1,则112=A BC B 111=AC ,由余弦定理可知113cos 4222==⨯⨯∠BC A ,故④正确.所以正确的有①③④.故选:C 【点睛】本题主要考查空间几何体中线面关系,要重点考查线面垂直、线面平行的性质,以及异面直线所成角的求法. 12.阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德并称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M 与两定点Q 、P 的距离之比||||MQ MP λ=(0,1)λλ>≠,那么点M 的轨迹就是阿波罗尼斯圆.已知动点M 的轨迹是阿波罗尼斯圆,其方程为221x y +=,定点Q 为x 轴上一点,1,02P ⎛⎫- ⎪⎝⎭且2λ=,若点(1,1)B ,则2||||MP MB +的最小值为( ) A 6 B 7C 10D 11【答案】C【解析】设(),0Q a ,(),M x y ,根据||||MQ MP λ=和221x y +=求出a 的值,由2||||||||+=+MP MB MQ MB ,两点之间直线最短,可得2||||MP MB +的最小值为BQ ,根据坐标求出BQ 即 【详解】设(),0Q a ,(),M x y ,所以()22=-+MQ x a y 1,02P ⎛⎫- ⎪⎝⎭,所以2212⎛⎫=++ ⎪⎝⎭PQ x y ,因为||||MQ MP λ=且2λ=()2222212-+=⎛⎫++ ⎪⎝⎭x a y x y,整理可得22242133+-++=a a x y x ,又动点M 的轨迹是221x y +=,所以24203113a a +⎧=⎪⎪⎨-⎪=⎪⎩,解得2a =-,所以()2,0Q -,又=2||MQ MP 所以2||||||||+=+MP MB MQ MB ,因为(1,1)B ,所以2||||MP MB +的最小值为()()22121010=++-=BQ .故选:C 【点睛】本题主要考查圆上动点问题,考查两点间直线最短.二、填空题13.若“x a >”是“2x >”的充分不必要条件,则实数a 的取值范围是________. 【答案】(2,)+∞【解析】根据“x a >”是“2x >”的充分不必要条件,可知{}x x a >是{}2x x >的子集,由集合间关系即可求出. 【详解】因为“x a >”是“2x >”的充分不必要条件,所以2>⇒>x a x ,所以2a >. 故答案为:(2,)+∞ 【点睛】本题主要考查充分、必要条件,解题的关键是会分析充分必要条件与集合间关系.14.已知12,F F 为椭圆221259x y += 的两个焦点,过1F 的直线交椭圆于A B , 两点,若2212F A F B += ,则||AB = ________【答案】8【解析】运用椭圆的定义,可得三角形ABF 2的周长为4a =20,再由周长,即可得到AB 的长. 【详解】椭圆22259x y +=1的a =5,由题意的定义,可得,|AF 1|+|AF 2|=|BF 1|+|BF 2|=2a ,则三角形ABF 2的周长为4a =20, 若|F 2A |+|F 2B |=12, 则|AB |=20﹣12=8. 故答案为:8 【点睛】本题考查椭圆的方程和定义,考查运算能力,属于基础题. 15.过点(3,1)P 且与圆224x y +=相切的直线方程 ___. 340x y +-=【解析】解:因为点3,1)P 在圆上,则过圆上点的切线方程为00434xx yy x y +=∴+=340x y +-=16.已知底面边长为a 的正三棱柱111ABC A B C -(底面是等边三角形的直三棱柱)的六个顶点在球1O 上,且球2O 与此正三棱柱的5个面都相切,则球1O 与球2O 的表面积之比为________. 【答案】5: 1【解析】设球1O 与球2O 的半径分别为R ,r ,由题意分析球2O 的半径等于正三棱柱底面正三角形内切圆的半径,且等于正三棱柱高的一半,求出其半径r ,再由球1O 的球心在上下底面中心连线的中点上,求出半径R ,再由球的表面积公式求出比值即可. 【详解】设球1O 与球2O 的半径分别为R ,r ,因为球2O 与此正三棱柱的5个面都相切,所以球2O 的半径等于正三棱柱底面正三角形内切圆的半径,且等于正三棱柱高的一半,如图所示,因为正三棱柱111ABC A B C -底面边长为a 的正三棱柱,所以AB a =,所以233323=⨯=AE a a ,133236===⨯=r DE OE a a ,因为正三棱柱111ABC A B C -的六个顶点在球1O 上,所以球1O 的球心在上下底面中心连线的中点上,所以222222233512⎫⎫==+=+=⎪⎪⎪⎪⎝⎭⎝⎭R OA OE AE a ,所以球1O 与球2O 的表面积之比为22222254125436ππ===⎛⎫⎪⎝⎭aR Rr r a ,所以表面积之比为5: 1.故答案为:5: 1 【点睛】本题以三棱柱为依托,考查正三棱柱外接球及内切球的性质,考察了空间想象能力,逻辑推理能力和运算求解能力.三、解答题17.已知:,p x R ∀∈cos x m >,q :方程22184x ym m+=+-表示焦点在x 轴上的椭圆,(1)若命题p 为假命题,求实数m 的取值范围;(2)若命题p 和命题q 中有一个为真命题且另一个为假命题,求实数m 的取值范围. 【答案】(1)1m ≥-(2)2m ≤-或14m -≤<【解析】(1)令p 为真命题,求出m 的范围,则命题p 为假命题时,取补集即可;(2)令命题q 为真命题,求出对应的m 范围,由命题p 和命题q 中有一个为真命题且另一个为假命题,则分情况p 真q 假和p 假q 真讨论,求出m 的取值范围即可. 【详解】(1)若p 真;则cos x m >恒成立,所以1m <-; 则当P 为假时,1m ≥-.(2)若q 真,方程22184x y m m +=+-表示焦点在x 轴上的椭圆,则8440m m m +>-⎧⎨->⎩, 即:24m -<<则m 的取值范围是(2,4)-.若p 真q 假,则142m m m <-⎧⎨≥≤-⎩或,所以2m ≤-;若p 假q 真,则124m m ≥-⎧⎨-<<⎩,所以14m -≤<;综上,2m ≤-或14m -≤<. 【点睛】本题主要考查真假命题,熟练掌握命题的真假与集合补集间关系. 18.已知圆221:1C x y +=与圆222:60C x y x m +-+=. (1)若圆1C 与圆2C 外切,求实数m 的值;(2)在(1)的条件下,若直线l 与圆2C 的相交弦长为23(2,1),求直线l 的方程. 【答案】(1)5m =;(2)直线l 方程为:2x =或1y =【解析】(1)先根据圆的方程求出圆心坐标和半径,再由由圆1C 与圆2C 外切,可知两圆心的距离等于两圆半径之和,代入数据求解即可;(2)分析可知弦的垂直平分线过圆心,由勾股定理可求出圆心到直线的距离,再由直线l 过点(2,1),可设出直线方程,分斜率存在和不存在两种情况,求出方程即可. 【详解】(1)221x y +=Q ,1(0,0),C ∴11r =,2260x y x m +-+=Q ,22(3)9x y m ∴-+=-,2(3,0)C ∴,29r m -,Q 圆1C 与圆2C 外切,1212C C r r ∴=+,319m ∴=-5m ∴=;(2)由(1)得5m =,圆2C 的方程为22(3)4,x y -+=2(3,0),C 22r =,设圆心2C 到直线l 的距离d ,因为直线l 与圆2C 的相交弦长为23则有22223=+r d ,代入数据解得1d =,当直线l 无斜率时:直线方程为2x =.符合题意. 当直线l 斜率为k 时,则直线方程为1(2)y k x -=-, 化为一般形式为210kx y k --+=, 则圆心(3,0)到直线l 的距离211d k ==+,解得0k =.综上,直线l 方程为:2x =或1y =.【点睛】本题主要考查圆与圆的位置关系,圆与直线的位置关系,求直线方程时要分析斜率是否存在.19.如图,已知三棱锥A -BPC 中,,AP PC ⊥AC BC ⊥,M 为AB 的中点,D 为PB 的中点,且PMB △为正三角形.(1)求证:DM P 平面APC ;(2)若4BC =,10AB =,求三棱锥D -BCM 的体积. 【答案】(1)证明见解析;(253【解析】(1)因为M 为AB 的中点,D 为PB 的中点,由中位线定理可得MD AP P ,再由线面平行的判定定理即可证明;(2)根据题意得M 到平面BCD 的距离为MD 的长,由三棱锥D -BCM 的体积即为三棱锥M -BCD 的体积,由题设条件求出MD 的长,及三角形BCD 的面积,由椎体体积公式代入数据求解即可. 【详解】(1)证明:因为M 为AB 的中点,D 为PB 的中点, 所以MD 是ABP △的中位线,MD AP P . 又MD Ë平面APC ,AP ⊂平面APC , 所以MD P 平面APC .(2)在等边三角形PMB 中,D 为PB 的中点,MD PB ∴⊥,AP PB ∴⊥,又AP PC ⊥,PB PC ⊂、平面PBC ,PB PC P ⋂=,AP ∴⊥平面PBC ,MD ∴⊥平面PBC , BC ⊂Q 平面PBC ,AP BC ∴⊥,又BC AC ⊥Q ,PA AC ⊂、平面P AC ,PA AC A =I ,BC ∴⊥平面P AC ,∴⊂PC 平面PBC ,BC PC ∴⊥.MD ⊥Q 平面PBC ,即MD 是三棱锥M -DBC 的高.又因为10AB =,M 为AB 的中点,PMB △为正三角形,所以5PB MB ==,532=MD , 由BC ⊥平面APC ,可得BC PC ⊥,在直角三角形PCB 中,由5,PB =4BC =,可得3PC =. 于是111433222∆∆==⨯⨯⨯=BCP BCD S S , 所以M D B BCM D C V V --=13∆=⋅BCD S MD 153332=⨯⨯53=. 【点睛】本题主要考查线面平行的判定及椎体的体积,解题的关键时对三棱锥体积的转化.20.已知椭圆222:1x C y m+=(常数1m >),P 是曲线C 上的动点,M 是曲线C 的右顶点,定点A 的坐标为(2,0).(1)若M 与A 重合,求曲线C 的焦距. (2)若3m =,求||PA 的最大值与最小值.【答案】(1)23(2)||PA 的最大值为5,最小值为22. 【解析】(1)由M 与A 重合,可得椭圆的右顶点的坐标为(2,0),即2m =,再由222c a b =-即可求出c 的值,从而求出焦距2c ;(2)设(),P x y ,利用两点间的距离公式及点P 坐标满足椭圆方程,得到||PA 关于x 的一元二次方程,根据二次函数的性质求出||PA 的最大值与最小值即可. 【详解】(1)根据题意,若M 与A 重合,即椭圆的右顶点的坐标为(2,0),则2m =,所以椭圆的方程为:2214x y +=,其焦点在x 轴上,设焦距为2c ,所以有2413=-=c 则3c =,所以椭圆焦距为3(2)若3m =,则椭圆的方程为2219x y +=,变形可得2219x y =-,设(),P x y ,则222||(2)PA x y =-+228894125994⎛⎫=-+=- +⎪⎝⎭x x x (33)x -≤≤根据二次函数的性质,可得3x =-时,2||PA 取得最大值25,当94x时,2||PA 取得最小值12, 所以||PA 的最大值为5,最小值为22. 【点睛】本题主要考查椭圆知识的综合应用,解题的关键是熟练掌握并应用椭圆的有关性质. 21.如图,在直角梯形中,,,且,点是中点,现将沿折起,使点到达点的位置.(Ⅰ)求证:平面平面;(Ⅱ)若与平面所成的角为,求平面与平面所成锐二面角的余弦值.【答案】(Ⅰ)见证明;(Ⅱ) 【解析】第(Ⅰ)问先证平面,由线面垂直证明面面垂直;第(Ⅱ)问先找垂直关系后建立空间直角坐标系,利用向量法求出两面的法向量,进而求所成二面角的余弦值. 【详解】解:(Ⅰ)证明:∵,,点是中点,∴,,∴四边形为平行四边形,∴, 又,∴, ∴,,∴平面,∴平面, 又∵平面,∴平面平面;(Ⅱ)由(Ⅰ)知平面,∴即为与平面所成的角,∴, ∵平面,∴,∴为等腰直角三角形,∴,故为等边三角形, 取的中点,连结,则,∵平面,又平面,∴平面平面,又平面,∴平面,以为坐标原点,过点与平行的直线为轴,所在的直线为轴,所在的直线为轴建立空间直角坐标系如图,设,则,,,,从而,,设平面的一个法向量为,则由得,令得,又平面的一个法向量,则,所以,平面与平面所成锐二面角的余弦值为.【点睛】本题是一道立体几何综合题,考查面面垂直的证明及二面角的求解。
2019-2020学年重庆市高二上学期联考数学(文)试题及答案

①,由于 0,2 ,2,所以“ 0 x 2”是“ x 2 ”成立的充分不 必要条件,所以①错误. ②,根据否命题的知识可知,②正确. ③,特称命题的否定是全称命题,注意到要否定结论,所
以③错误. ④,由于“ p ”与命题“ pq”都是真命题,所以 p 假 q 真,所 以④正确. 综上所述,真命题的个数是 2 个. 故选:C.
当 x2,0时, f x 2x2 ,则 f 10 =(
)
A. 2
B.2
C. 98
D.98
【答案】A
【解析】利用已知条件,化简求得 f 10 的值.
【详解】
由于 f x 是定义在 R 上的偶函数,且 f x 3 f x ,当 x2,0时, f x 2x2 ,所以
f 10 f 7 3 f 43 f 4 f 1 3 f 1 f 2 3 f 2
第 4 页 共 21 页
真命题,那么命题 q 一定是真命题;其中为真命题的个数
是( )
A.4 个
B.3 个
C.2 个
D.1 个
【答案】C
【解析】根据充分、必要条件的知识,判断①的正确性;
根据否命题的知识,判断②的正确性;根据特称命题的否
定是全称命题的知识,判断③的正确性;根据含有逻辑联
结词命题真假性的知识,判断④的正确性. 【详解】
A. 1,
B. 0,3
C. 1, 3
D. 1,3
【答案】C
【解析】利用配方法化简函数解析式,根据二次函数的性
质,求得函数在区间 1,4上的值域.
【详解】
由于 y x 22 1,函数的对称轴为 x 2 ,开口向上,所以 当 x 2时函数有最小值为 1,当 x 4时,函数有最大值为 3 ,
直.
重庆市主城区七校2019-2020学年高二下学期期末联考数学试题

2019—2020学年度第二学期期末七校联考高二数学试题本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟. 注意事项:1.答题前,务必将自己的姓名.准考证号等填写在答题卷规定的位置上.2.答选择题时,必须使用2B铅笔将答题卷上对应题目的答案标号涂黑.3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卷规定的位置上.4.考试结束后,将答题卷交回.第Ⅰ卷(选择题共60分)一、选择题.(本大题共12小题,每小题5分,共60分.在每小题列出的四个选项中,选出符合题目要求的一项)1.若21izi=+(其中i是虚数单位),则z=()A. 1B. 22 D. 4【答案】C【解析】【分析】化简求出z再根据模长公式求解z即可.【详解】()()()2121111i iiz ii i i-===+++-,故22112z=+=故选:C【点睛】本题主要考查了复数的基本运算以及模长公式.属于基础题.2.为对某组数据进行分析,建立了四种不同的模型进行拟合,现用回归分析原理,计算出四种模型的相关指数R2分别为0.97,0.86,0.65,0.55,则拟合效果最好的回归模型对应的相关指数R2的值是()A. 0.97B. 0.86C. 0.65D. 0.55 【答案】A【解析】【分析】在回归分析中,模型的相关指数R2越接近于1,其拟合效果就越好,即可求解.【详解】由题意,四种模型的相关指数R 2分别为0.97,0.86,0.65,0.55, 根据在回归分析中,模型的相关指数R 2越接近于1,其拟合效果就越好, 可得拟合效果最好的回归模型对应的相关指数R 2的值是0.97. 故选:A .【点睛】本题考查了用相关指数拟合模型效果的应用问题,其中解答中熟记回归分析中,模型的相关指数R 2越接近于1,其拟合效果就越好是解答的关键,属于基础题.3.在某次联考数学测试中,学生成绩ξ服从正态分布2(100,)(0)σσ>,若ξ在(80,120)内的概率为0.8,则任意选取一名学生,该生成绩不高于80的概率为( ) A. 0.05 B. 0.1C. 0.15D. 0.2【答案】B 【解析】1(80120)(80)(120)0.12P X P X P X -<<≤=≥== ,选B.4.曲线2y x lnx =+在点()1,1处的切线方程为( ) A. 320x y --=B. 320x y -+=C. 340x y +-=D.340x y +-=【答案】A 【解析】 【分析】 由题求得12y x x'=+,进而求得1|3x k y =='=,根据直线的点斜式方程求得在点()1,1处的切线方程即可.【详解】解:由题知12y x x'=+,故1|3x k y =='=, 故在点()1,1处的切线方程为()131y x -=-,化简整理得320x y --=. 故选:A.【点睛】本题主要考查用导数求曲线在某点处的切线方程,属于基础题.5.某市汽车牌照号码可以上网自编,但规定从左到右第二个号码只能从字母B 、C 、D 中选择,其他四个号码可以从0~9这十个数字中选择(数字可以重复),某车主第一个号码(从左到右)只想在数字3、5、6、8、9中选择,其他号码只想在1、3、6、9中选择,则他车牌号码可选的所有可能情况有( ) A. 180种 B. 360种 C. 720种 D. 960种【答案】D 【解析】 【分析】根据题意,依次分析牌照的第一个号码、第二个号码以及最后三个号码的选法数目,进而由分步计数原理计算可得答案.【详解】根据题意,车主第一个号码在数字3、5、6、8、9中选择,共5种选法, 第二个号码只能从字母B 、C 、D 中选择,有3种选法,剩下的3个号码在1、3、6、9中选择,每个号码有4种选法,则共有4×4×4=64种选法, 则共有5×3×64=960种, 故选:D.【点睛】本题考查排列、组合的应用,需要注意汽车牌照号码中数字可以重复,故最后三位号码有4×4×4种选法,而不是A 43种,属于基础题.6.从装有除颜色外完全相同的3个白球和m 个黑球的布袋中随机摸取一球,有放回的摸取5次,设摸得白球数为X ,已知()3E X =,则()(D X = ) A.85B.65C.45D.25【答案】B 【解析】 【分析】由题意知,3~(5,)3X B m +,由3533EX m =⨯=+,知3~(5,)5X B ,由此能求出()D X . 【详解】由题意知,3~(5,)3X B m +, 3533EX m ∴=⨯=+,解得2m =,3~(5,)5X B ∴,336()5(1)555D X ∴=⨯⨯-=.故选:B .【点睛】本题考查离散型随机变量的方差的求法,解题时要认真审题,仔细解答,注意二项分布的灵活运用.7.某产品的广告费用x 与销售额y 的统计数据如下表: 广告费用(万元) 4 2 3 5 销售额(万元)49263954根据上表可得回归方程ˆˆˆybx a =+中的ˆb 为9.4,据此模型预报广告费用为6万元时销售额为 A. 63.6万元 B. 65.5万元C. 67.7万元D. 72.0万元【答案】B 【解析】【详解】试题分析:4235492639543.5,4244x y ++++++====,∵数据的样本中心点在线性回归直线上,回归方程ˆˆˆybx a =+中的ˆb 为9.4, ∴42=9.4×3.5+a ,∴ˆa=9.1, ∴线性回归方程是y=9.4x+9.1,∴广告费用为6万元时销售额为9.4×6+9.1=65.5 考点:线性回归方程8. 我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰.如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( ) A. 12种 B. 18种C. 24种D. 48种【答案】C 【解析】试题分析:先将甲、乙两机看成一个整体,与另外一机进行全排列,共有种排列方法,且留有三个空;再从三个位置中将丙、丁两机进行排列,有种方法;由分步乘法计数原理,得不同的着舰方法有种.考点:排列组合.9.下图是相关变量,x y 的散点图,现对这两个变量进行线性相关分析,方案一:根据图中所有数据,得到线性回归方程:11ˆyb x a =+,相关系数为1r ;方案二:剔除点(10,32),根据剩下数据,得到线性回归方程:22ˆyb x a =+,相关系数为2r ;则( )A. 1201r r <<<B. 2101r r <<<C. 1210r r -<<<D. 2110r r -<<<【答案】A 【解析】 【分析】由散点图可判断正负相关,得出12,r r 为正,再结合剔除点前后的回归直线,即可比较出12,r r . 【详解】由散点图分布图可知,变量x 和y 成正相关,所以1201,01r r <<<< , 在剔除点(10,32)之后,且可看出回归直线22ˆyb x a =+的线性相关程度更强,2r 更接近1. 所以1201r r <<< . 故选:A.【点睛】本题主要考查散点图的正负相关以及变量的相关性,相关系数r 的意义:①当散点分布呈正相关,0r >;负相关,0r <;②0||1,||r r <<越接近1,说明两个变量越具有线性相关关系,即线性关系越强.10.设函数()f x 在定义域内可导,()y f x =的图像如图所示,则导函数()y f x '=的图像可能为( )A. B.C. D.【答案】D 【解析】 【分析】通过原函数的单调性可确定导函数的正负,结合图象即可选出答案.【详解】由函数()f x 的图象可知,当(0,)x ∈+∞时,()f x 单调递减,所以(0,)x ∈+∞时,()0f x '< ,符合条件的只有D 选项,故选D.【点睛】本题主要考查了函数的单调性与导函数的符号之间的对应关系,属于中档题. 11.有6名医生到3个医院去作新冠肺炎治疗经验交流,则每个医院至少去一名的不同分派方法种数为( ) A. 216 B. 729 C. 540 D. 420【答案】C 【解析】 【分析】首先确定各医院所去医生人数,先分类:1,1,4;1,2,3;2,2,2,这样第一步把6名医生按这个数字分组,然后三组分到三个医院,分组中要注意平均分组和不平均分组有. 【详解】人数进行分组共有三种情况:1,1,4;1,2,3;2,2,2,若分组分1,1,4,共有4113621132290C C C N A A ⋅⋅=⋅=;若分组分1,2,3,共有321326313360N C C C A =⋅⋅⋅=;若分组分2,2,2,共有2223642333390C C C N A A ⋅⋅=⋅=.∴不同分派方法种数为540N =. 故选:C.【点睛】本题考查排列组合的综合应用,考查平均分组和不平均分组问题,实际解题中还要注意分组后组与组之间有无区别.12.已知函数2()35f x x x =-+,()ln g x ax x =-,若对(0,)x e ∀∈,12,(0,)x x e ∃∈且12x x ≠,使得()()(1,2)i f x g x i ==,则实数a 的取值范围是( ) A. 16,e e ⎛⎫ ⎪⎝⎭B. 741,e e ⎡⎫⎪⎢⎣⎭C. 74160,,e e e ⎡⎫⎛⎤⎪⎢ ⎥⎝⎦⎣⎭ D. 746,e e ⎡⎫⎪⎢⎣⎭【答案】D 【解析】 【分析】先求出()f x 的值域,再利用导数讨论函数()g x 在区间()0,e 上的单调性,结合函数值域,由方程有两个根求参数范围即可. 【详解】因为()g x ax lnx =-,故()1ax g x x='-, 下面讨论()g x 的单调性:当0a ≤时,()0g x '<,故()g x 在区间()0,e 上单调递减;当10,a e ⎛⎫∈ ⎪⎝⎭时,()0,x e ∈时,()0g x '<,故()g x 在区间()0,e 上单调递减; 当1a e >时,令()0g x '=,解得1x a=,故()g x 在区间10,a ⎛⎫ ⎪⎝⎭单调递减,在区间1,e a ⎛⎫ ⎪⎝⎭上单调递增. 又()11,1a g lna g e a e ⎛⎫=+=-⎪⎝⎭,且当x 趋近于零时,()g x 趋近于正无穷; 对函数()f x ,当()0,x e ∈时,()11,54f x ⎡⎫∈⎪⎢⎣⎭; 根据题意,对(0,)x e ∀∈,12,(0,)x x e ∃∈且12x x ≠,使得()()(1,2)i f x g x i ==成立, 只需()111,54g g e a ⎛⎫<≥⎪⎝⎭, 即可得111,154lna ae +<-≥, 解得746,a e e ⎡⎫∈⎪⎢⎣⎭.故选:D.【点睛】本题考查利用导数研究由方程根的个数求参数范围的问题,涉及利用导数研究函数单调性以及函数值域的问题,属综合困难题.第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每小题题5分,共20分,请把答案填在答题卡相应位置) 13.若复数()32z i i =-(i 是虚数单位),则z 的虚部为______. 【答案】3- 【解析】 【分析】利用复数的乘法法则可得出复数z 的一般形式,进而可得出复数z ,由此可得出结果. 【详解】因为()3223z i i i =-=+,所以23z i =-,故z 的虚部为3-. 故答案为:3-.【点睛】本题考查共轭复数虚部的求解,同时也考查了复数乘法法则的应用,考查计算能力,属于基础题.14.篮子里装有2个红球,3个白球和4个黑球.某人从篮子中随机取出两个球,记事件A =“取出的两个球颜色不同”,事件B =“取出一个红球,一个白球”,则()|P B A =________________.【答案】313【解析】 【分析】先分别求出事件A 、B 选法种数,由古典概率和条件概率公式可求得答案.【详解】事件A 的选法有11111123243426C C C C C C ++=种,事件B 的选法有11236C C =种,所以292626()45P A C ==,2962()15P AB C ==,()()3()13P AB P B A P A ==∣.故答案为:313. 【点睛】本题考查古典概率和条件概率公式,属于基础题. 15.若()()7280128112x x a a x a x a x +-=++++,则127a a a +++的值为__.【答案】125 【解析】分析:令0x =可得01a =;令1x =,可得01282a a a a ++++=-;又78(2)a =-128=-,故可得127a a a +++的值.详解:在()()7280128112x x a a x a x a x +-=++++中,令0x =,可得01a =; 令1x =,可得01282a a a a ++++=-;又78(2)128a =-=-,∴12721281125a a a +++=-+-=.点睛:对形如(ax +b )n ,(ax 2+bx +c )m (a ,b ∈R )的式子求其展开式的各项系数之和,常用赋值法,只需令x =1即可;对形如(ax +by )n (a ,b ∈R )的式子求其展开式各项系数之和,只需令x =y =1即可.解题时如何赋值,要观察所求和式与差式的特点,根据所求值的式子的特征选择适合的方法.16.已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡,若顾客甲只带了现金,顾客乙只用支付宝或微信付款,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中三种结账方式,则他们结账方式的可能情况有________种. 【答案】20 【解析】 【分析】由题意,根据乙的支付方式进行分类,根据分类与分步计数原理即可求出.【详解】当乙选择支付宝时,丙丁可以都选银联卡,或者其中一人选择银联卡,另一人只能选支付宝或现金,故有1+C 21C 21=5,而乙选择支付宝时,丙丁也可以都选微信,或者其中一人选择微信,另一人只能选支付宝或现金,故有1+C 21C 21=5,此时共有5+5=10种,当乙选择微信时,丙丁可以都选银联卡,或者其中一人选择银联卡,另一人只能选微信或现金,故有1+C 21C 21=5,而乙选择微信时,丙丁也可以都选支付宝,或者其中一人选择支付宝,另一人只能选微信或现金,故有1+C 21C 21=5,此时共有5+5=10种, 综上故有10+10=20种, 故答案为20.【点睛】本题考查了分步计数原理和分类计数原理,考查了转化思想,属于难题.三、解答题(本大题共6小题,共70分,解答题应写出必要的文字说明、证明过程或演算步骤)17.已知二项式1nx ⎫⎪⎭的展开式中各项的系数和为256.(1)求n ;(2)求展开式中的常数项. 【答案】(1)8;(2)28. 【解析】 【分析】⑴观察1nx ⎫⎪⎭可知,展开式中各项系数的和为256,即112...256nn n n n C C C C ++++=,解出得到n 的值⑵利用二次展开式中的第1r +项,即通项公式11rn rrr nT C x -+⎛⎫= ⎪⎝⎭,将第一问的n 代入,并整理,令x 的次数为0,解出r ,得到答案【详解】(1)由题意,得112...256nn n n n C C C C ++++=,即2n =256,解得n =8.(2)该二项展开式中的第1r +项为T r +1=()84833881rr rr r Cx C x x --⎛⎫⋅=⋅ ⎪⎝⎭,令843r-=0,得r =2,此时,常数项为238T C ==28.【点睛】本题主要考的是利用赋值法解决展开式的系数和问题,考查了利用二次展开式的通项公式解决二次展开式的特定项问题.18. 某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定,小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定. (Ⅰ)求当天小王的该银行卡被锁定的概率;(Ⅱ)设当天小王用该银行卡尝试密码次数为X ,求X 的分布列和数学期望. 【答案】(Ⅰ)12;(Ⅱ)分布列见解析,期望52. 【解析】(Ⅰ)设“当天小王的该银行卡被锁定”的事件为A , 则5431()=6542P A =⨯⨯ (Ⅱ)依题意得,X 所有可能的取值是1,2,3 又1511542(X=1),(X=2),(X=3)1=.6656653P P P ==⨯==⨯⨯ 所以X 的分布列为所以1125E()1236632X =⨯+⨯+⨯=. 考点:1、古典概型;2、离散型随机变量的分布列和期望.19.已知函数2()()4x f x e ax b x x =+--,曲线()y f x =在点(0,(0))f 处切线方程为44y x =+.(1)求,a b 的值;(2)讨论()f x 的单调性,并求()f x 的极大值. 【答案】(1)4a b ==;(2)见解析. 【解析】【详解】试题分析:(1)求导函数,利用导数的几何意义及曲线()y f x =在点()()0,0f 处切线方程为44y x =+,建立方程,即可求得a ,b 的值;(2)利用导数的正负,可得()f x 的单调性,从而可求()f x 的极大值.试题解析:(1)()()24x f x e ax a b x =++--'.由已知得()04f =,()04f '=. 故4b =,8a b +=. 从而4a =,4b =. (2)由(1)知,()()2414xf x ex x x =+--,()()()14224422x x f x e x x x e ⎛⎫=+--=+- ⎝'⎪⎭.令()0f x '=得,ln2x =-或2x =-. 从而当()(),2ln 2,x ∈-∞--+∞时,()0f x '>;当()2,ln 2x ∈--时,()0f x '<.故()f x 在(),2-∞-,()ln 2,-+∞上单调递增,在()2,ln 2--上单调递减. 当2x =-时,函数()f x 取得极大值,极大值为()()2241f e--=-.考点:利用导数研究曲线上某点切线方程;利用导数研究函数的单调性;利用导数研究函数的极值.【方法点晴】本题考查了利用导数研究曲线上某点切线方程;利用导数研究函数的单调性;利用导数研究函数的极值.求极值的步骤是:(1)确定函数的定义域;(2)求导数()f x ';(3)解方程()0f x '=,求出函数定义域内的所有根;(4)列表检验()f x '在()0f x '=的根0x 左右两侧值的符号,如果左正右负,那么()f x 在0x 处取极大值,如果左负右正,那么()f x 在0x处取极小值.20.对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,作出甲的得分频率分布直方图如图所示,列出乙的得分统计表如表所示:分值[)0,10 [)10,20 [)20,30 [)30,40场数 10204030(1)估计甲在一场比赛中得分不低于20分的概率.(2)判断甲、乙两名运动员哪个成绩更稳定.(结论不要求证明)(3)在甲所进行的100场比赛中,以每场比赛得分所在区间中点的横坐标为这场比赛的得分,试计算甲每场比赛的平均得分.【答案】(1)0.72;(2)甲更稳定;(3)2380.. 【解析】 【分析】(1)根据频率分布直方图直接计算,即可得出结果;(2)根据频率分布直方图与统计表,分析成绩的集中程度,即可得出结论;(3)根据频率分布直方图,由每组中间值乘以该组的频率,再求和,即可得出平分值. 【详解】(1)根据频率分布直方图可知,甲在一场比赛中得分不低于20分的频率为0.048100.024100.480.240.72⨯+⨯=+=;即甲在一场比赛中得分不低于20分的概率为0.72;(2)根据甲的频率分布直方图可知,甲的成绩主要集中在[)20,30,由乙的得分统计表可得,乙的成绩比较分散,所以甲更稳定; (3)因为组距为10,所以甲在区间[)[)[)[)0,10,10,20,20,30,30,40上得分频率值分别为8100,20100,48100,24100. 设甲的平均得分为S , 则()5815202548110035242380S ⨯+⨯+⨯+==⨯.. 【点睛】本题主要考查由频率分布直方图求概率,以及求平均值等问题,属于基础题型. 21.随着网络和智能手机的普及与快速发展,许多可以解答各学科问题的搜题软件走红.有教育工作者认为:网搜答案可以起到拓展思路的作用,但是对多数学生来讲,容易产生依赖心理,对学习能力造成损害.为了了解网络搜题在学生中的使用情况,某校对学生在一周时间内进行网络搜题的频数进行了问卷调查,并从参与调查的学生中抽取了男、女学生各50人进行抽样分析,得到如下样本频数分布表:将学生在一周时间内进行网络搜题频数超过20次的行为视为“经常使用网络搜题”,不超过20次的视为“偶尔或不用网络搜题”.(1)根据已有数据,完成下列22⨯列联表(单位:人)中数据的填写,并判断是否在犯错误的概率不超过1%的前提下有把握认为使用网络搜题与性别有关?(2)将上述调查所得到的频率视为概率,从该校所有参与调查的学生中,采用随机抽样的方法每次抽取一个人,抽取4人,记经常使用网络搜题的人数为X,若每次抽取的结果是相互独立的,求随机变量X的分布列和数学期望.参考公式:()()()()()22n ad bcxa b c d a c b d-=++++,其中n a b c d=+++.参考数据:【答案】(1)填表见解析,在犯错误的概率不超过1%的前提下有把握认为使用网络搜题与性别有关;(2)分布列见解析,()12 5E X=.【解析】【分析】(1)根据题意填写列联表,计算观测值,对照临界值得出结论;(2)由题意34,5X B⎛⎫⎪⎝⎭,由此求出随机变量X的分布列和数学期望.【详解】(1)根据题意填写22⨯列联表如下:计算观测值()2210022123828326.635505060403K ⨯-⨯==>⨯⨯⨯, 所以在犯错误的概率不超过1%的前提下有把握认为使用网络搜题与性别有关.(2)将上述调查所得到的频率视为概率,从该校所有参与调查的学生中,采用随机抽样的方法抽取一人,抽到经常使用网络搜题的学生的概率为6031005=. 由题意34,5XB ⎛⎫ ⎪⎝⎭. ()040433160155625P X C ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭, ()31433961155625P X C ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭, ()2224332162155625P X C ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭, ()334332163155625P X C ⎛⎫⎛⎫==-= ⎪ ⎪⎝⎭⎝⎭, ()44433814155625P X C ⎛⎫⎛⎫==-= ⎪ ⎪⎝⎭⎝⎭. X 的分布列为:()312455E X ∴=⨯=.【点睛】本题考查独立性检验,考查离散型随机变量的分布列和数学期望,属于中档题. 22.已知函数()ln(1)(1)1(R)f x x k x k =---+∈. (1)求函数()f x 的单调区间;(2)若()0f x ≤在定义域内恒成立,求实数k 的取值范围;(3)证明:()2*ln 2ln 3ln 4ln 2,N 34514n n nn n n -+++⋯+<≥∈+. 【答案】(1)函数()f x 的递增区间为1(1,)k k+,函数()f x 的递减区间为1(1,)k ++∞;(2)1k ;(3)见解析.【解析】试题分析:(1)对函数()f x 求导得1()1k kxf x x +-'=-,对k 进行分类讨论,即可得到函数的单调区间;(2)由(1)可得,0k ≤时,()f x 在(0)+∞,上是增函数,而(2)0f >,()0f x ≤不成立,故0k >,由(1)可得max 1()(1)f x f k=+,即可求出k 的取值范围;(3)由(2)知,当1k =时,有()0f x ≤在(1)+∞,恒成立,即ln(1)2x x -<-,进而换元可得22ln 1n n <-,所以ln 112n n n -<+,即可得证. 试题解析:(1)定义域为()1,+∞,()1111k kx f x k x x +-=-='-- 若0k ≤,()101f x k x =-≥-',()f x 在()1,+∞上单调递增 若0k >,()11k k x k f x x +⎛⎫-- ⎪⎝⎭'=-, 所以,当()0f x '>时,111x k <<+,当()0f x '<时,11x k>+ 综上:若0k ≤,()f x 在()1,+∞上单调递增; 若0k >,()f x 在11,1k ⎛⎫+ ⎪⎝⎭上单调递增,在11,k ⎛⎫++∞ ⎪⎝⎭上单调递减 (2)由(1)知,0k ≤时,()210f k =->不可能成立;若0k >,()0f x ≤恒成立()max 110f x f k ⎛⎫⇔=+≤ ⎪⎝⎭,11ln 0f k k ⎛⎫+=-≤ ⎪⎝⎭,得1k ≥综上,1k ≥.(3)由(2)知,当1k =时,有()0f x ≤在()1,+∞上恒成立,即()ln 12x x -<- 令()2*1N ,1x nn n -=∈>,得22ln 1nn <-,即ln 112n n n -<+ln2ln3ln4ln 3451n n +++++ ()1123122224n n n --<++++=,得证. 点睛:(1)导数综合题中对于含有字母参数的问题,一般用到分类讨论的方法,解题时要注意分类要不重不漏;(2)对于恒成立的问题,直接转化为求函数的最值即可;(3)对于导数中,数列不等式的证明,解题时常常用到前面的结论,需要根据题目的特点构造合适的不等式,然后转化成数列的问题解决,解题时往往用到数列的求和.。
重庆市主城区七校2019-2020学年度高二第二学期期末联考试题 数学【含解析】

重庆市主城区七校2019-2020学年度高二第二学期期末联考试题数学【含解析】第Ⅰ卷(选择题共60分)一、选择题.(本大题共12小题,每小题5分,共60分.在每小题列出的四个选项中,选出符合题目要求的一项)1.若21izi=+(其中i是虚数单位),则z=()A. 1B. 22 D. 4【答案】C【解析】【分析】化简求出z再根据模长公式求解z即可.【详解】()()()2121111i iiz ii i i-===+++-,故22112z=+.故选:C【点睛】本题主要考查了复数的基本运算以及模长公式.属于基础题.2.为对某组数据进行分析,建立了四种不同的模型进行拟合,现用回归分析原理,计算出四种模型的相关指数R2分别为0.97,0.86,0.65,0.55,则拟合效果最好的回归模型对应的相关指数R2的值是()A. 0.97 B. 0.86 C. 0.65 D. 0.55【答案】A【解析】【分析】在回归分析中,模型的相关指数R2越接近于1,其拟合效果就越好,即可求解.【详解】由题意,四种模型的相关指数R2分别为0.97,0.86,0.65,0.55,根据在回归分析中,模型的相关指数R2越接近于1,其拟合效果就越好,可得拟合效果最好的回归模型对应的相关指数R2的值是0.97.故选:A.【点睛】本题考查了用相关指数拟合模型效果应用问题,其中解答中熟记回归分析中,模型的相关指数R 2越接近于1,其拟合效果就越好是解答的关键,属于基础题.3.在某次联考数学测试中,学生成绩ξ服从正态分布2(100,)(0)σσ>,若ξ在(80,120)内的概率为0.8,则任意选取一名学生,该生成绩不高于80的概率为( ) A. 0.05 B. 0.1C. 0.15D. 0.2【答案】B 【解析】1(80120)(80)(120)0.12P X P X P X -<<≤=≥== ,选B.4.曲线2y x lnx =+在点()1,1处的切线方程为( ) A. 320x y --= B. 320x y -+=C. 340x y +-=D. 340x y +-=【答案】A 【解析】 【分析】由题求得12y x x'=+,进而求得1|3x k y =='=,根据直线的点斜式方程求得在点()1,1处的切线方程即可. 【详解】解:由题知12y x x'=+,故1|3x k y =='=,故在点()1,1处的切线方程为()131y x -=-,化简整理得320x y --=. 故选:A.【点睛】本题主要考查用导数求曲线在某点处的切线方程,属于基础题.5.某市汽车牌照号码可以上网自编,但规定从左到右第二个号码只能从字母B 、C 、D 中选择,其他四个号码可以从0~9这十个数字中选择(数字可以重复),某车主第一个号码(从左到右)只想在数字3、5、6、8、9中选择,其他号码只想在1、3、6、9中选择,则他车牌号码可选的所有可能情况有( ) A. 180种 B. 360种C. 720种D. 960种【答案】D 【解析】 【分析】根据题意,依次分析牌照的第一个号码、第二个号码以及最后三个号码的选法数目,进而由分步计数原理计算可得答案.【详解】根据题意,车主第一个号码在数字3、5、6、8、9中选择,共5种选法, 第二个号码只能从字母B 、C 、D 中选择,有3种选法,剩下的3个号码在1、3、6、9中选择,每个号码有4种选法,则共有4×4×4=64种选法, 则共有5×3×64=960种, 故选:D.【点睛】本题考查排列、组合的应用,需要注意汽车牌照号码中数字可以重复,故最后三位号码有4×4×4种选法,而不是A 43种,属于基础题.6.从装有除颜色外完全相同的3个白球和m 个黑球的布袋中随机摸取一球,有放回的摸取5次,设摸得白球数为X ,已知()3E X =,则()(D X = ) A.85B.65C.45D.25【答案】B 【解析】 【分析】由题意知,3~(5,)3X B m +,由3533EX m =⨯=+,知3~(5,)5X B ,由此能求出()D X . 【详解】由题意知,3~(5,)3X B m +, 3533EX m ∴=⨯=+,解得2m =,3~(5,)5X B ∴,336()5(1)555D X ∴=⨯⨯-=.故选:B .【点睛】本题考查离散型随机变量的方差的求法,解题时要认真审题,仔细解答,注意二项分布的灵活运用.7.某产品的广告费用x 与销售额y 的统计数据如下表: 广告费用(万元) 4 2 3 5 销售额(万元)49263954根据上表可得回归方程ˆˆˆy bx a =+中的ˆb为9.4,据此模型预报广告费用为6万元时销售额为A. 63.6万元B. 65.5万元C. 67.7万元D. 72.0万元【答案】B 【解析】【详解】试题分析:4235492639543.5,4244x y ++++++====,∵数据的样本中心点在线性回归直线上,回归方程ˆˆˆy bx a =+中的ˆb为9.4, ∴42=9.4×3.5+a ,∴ˆa=9.1, ∴线性回归方程是y=9.4x+9.1,∴广告费用为6万元时销售额为9.4×6+9.1=65.5 考点:线性回归方程8. 我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰.如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( ) A. 12种 B. 18种C. 24种D. 48种【答案】C 【解析】试题分析:先将甲、乙两机看成一个整体,与另外一机进行全排列,共有种排列方法,且留有三个空;再从三个位置中将丙、丁两机进行排列,有种方法;由分步乘法计数原理,得不同的着舰方法有种.考点:排列组合.9.下图是相关变量,x y 的散点图,现对这两个变量进行线性相关分析,方案一:根据图中所有数据,得到线性回归方程:11ˆyb x a =+,相关系数为1r ;方案二:剔除点(10,32),根据剩下数据,得到线性回归方程:22ˆyb x a =+,相关系数为2r ;则( )A. 1201r r <<<B. 2101r r <<<C. 1210r r -<<<D. 2110r r -<<<【答案】A 【解析】 【分析】由散点图可判断正负相关,得出12,r r 为正,再结合剔除点前后的回归直线,即可比较出12,r r .【详解】由散点图分布图可知,变量x 和y 成正相关,所以1201,01r r <<<< , 在剔除点(10,32)之后,且可看出回归直线22ˆyb x a =+的线性相关程度更强,2r 更接近1. 所以1201r r <<< . 故选:A.【点睛】本题主要考查散点图的正负相关以及变量的相关性,相关系数r 的意义:①当散点分布呈正相关,0r >;负相关,0r <;②0||1,||r r <<越接近1,说明两个变量越具有线性相关关系,即线性关系越强.10.设函数()f x 在定义域内可导,()y f x =的图像如图所示,则导函数()y f x '=的图像可能为( )A. B.C. D.【答案】D 【解析】 【分析】通过原函数的单调性可确定导函数的正负,结合图象即可选出答案.【详解】由函数()f x 的图象可知,当(0,)x ∈+∞时,()f x 单调递减,所以(0,)x ∈+∞时,()0f x '< ,符合条件的只有D 选项,故选D.【点睛】本题主要考查了函数的单调性与导函数的符号之间的对应关系,属于中档题.11.有6名医生到3个医院去作新冠肺炎治疗经验交流,则每个医院至少去一名的不同分派方法种数为( ) A. 216 B. 729 C. 540 D. 420【答案】C 【解析】 【分析】首先确定各医院所去医生人数,先分类:1,1,4;1,2,3;2,2,2,这样第一步把6名医生按这个数字分组,然后三组分到三个医院,分组中要注意平均分组和不平均分组有. 【详解】人数进行分组共有三种情况:1,1,4;1,2,3;2,2,2,若分组分1,1,4,共有4113621132290C C C N A A ⋅⋅=⋅=;若分组分1,2,3,共有321326313360N C C C A =⋅⋅⋅=; 若分组分2,2,2,共有2223642333390C C C N A A ⋅⋅=⋅=.∴不同分派方法种数为540N =.故选:C.【点睛】本题考查排列组合的综合应用,考查平均分组和不平均分组问题,实际解题中还要注意分组后组与组之间有无区别.12.已知函数2()35f x x x =-+,()ln g x ax x =-,若对(0,)x e ∀∈,12,(0,)x x e ∃∈且12x x ≠,使得()()(1,2)i f x g x i ==,则实数a 的取值范围是( )A. 16,e e ⎛⎫ ⎪⎝⎭B. 741,e e ⎡⎫⎪⎢⎣⎭C. 74160,,e e e ⎡⎫⎛⎤⎪⎢ ⎥⎝⎦⎣⎭ D. 746,e e ⎡⎫⎪⎢⎣⎭【答案】D 【解析】 【分析】先求出()f x 的值域,再利用导数讨论函数()g x 在区间()0,e 上的单调性,结合函数值域,由方程有两个根求参数范围即可.【详解】因为()g x ax lnx =-,故()1ax g x x='-, 下面讨论()g x 的单调性:当0a ≤时,()0g x '<,故()g x 在区间()0,e 上单调递减;当10,a e ⎛⎫∈ ⎪⎝⎭时,()0,x e ∈时,()0g x '<,故()g x 在区间()0,e 上单调递减;当1a e >时,令()0g x '=,解得1x a=, 故()g x 在区间10,a ⎛⎫ ⎪⎝⎭单调递减,在区间1,e a ⎛⎫ ⎪⎝⎭上单调递增. 又()11,1a g lna g e a e ⎛⎫=+=-⎪⎝⎭,且当x 趋近于零时,()g x 趋近于正无穷; 对函数()f x ,当()0,x e ∈时,()11,54f x ⎡⎫∈⎪⎢⎣⎭; 根据题意,对(0,)x e ∀∈,12,(0,)x x e ∃∈且12x x ≠,使得()()(1,2)i f x g x i ==成立, 只需()111,54g g e a ⎛⎫<≥⎪⎝⎭,即可得111,154lna ae +<-≥, 解得746,a e e ⎡⎫∈⎪⎢⎣⎭.故选:D.【点睛】本题考查利用导数研究由方程根的个数求参数范围的问题,涉及利用导数研究函数单调性以及函数值域的问题,属综合困难题.第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每小题题5分,共20分,请把答案填在答题卡相应位置) 13.若复数()32z i i =-(i 是虚数单位),则z 的虚部为______. 【答案】3- 【解析】 【分析】利用复数的乘法法则可得出复数z 的一般形式,进而可得出复数z ,由此可得出结果. 【详解】因为()3223z i i i =-=+,所以23z i =-,故z 的虚部为3-. 故答案为:3-.【点睛】本题考查共轭复数虚部的求解,同时也考查了复数乘法法则的应用,考查计算能力,属于基础题. 14.篮子里装有2个红球,3个白球和4个黑球.某人从篮子中随机取出两个球,记事件A =“取出的两个球颜色不同”,事件B =“取出一个红球,一个白球”,则()|P B A =________________. 【答案】313【解析】 【分析】先分别求出事件A 、B 选法种数,由古典概率和条件概率公式可求得答案.【详解】事件A 的选法有11111123243426C C C C C C ++=种,事件B 的选法有11236C C =种, 所以292626()45P A C ==,2962()15P AB C ==,()()3()13P AB P B A P A ==∣.故答案为:313.【点睛】本题考查古典概率和条件概率公式,属于基础题.15.若()()7280128112x x a a x a x a x +-=++++,则127a a a +++的值为__.【答案】125 【解析】分析:令0x =可得01a =;令1x =,可得01282a a a a ++++=-;又78(2)a =-128=-,故可得127a a a +++的值.详解:在()()7280128112x x a a x a x a x +-=++++中,令0x =,可得01a =; 令1x =,可得01282a a a a ++++=-;又78(2)128a =-=-, ∴12721281125a a a +++=-+-=.点睛:对形如(ax +b )n ,(ax 2+bx +c )m (a ,b ∈R )的式子求其展开式的各项系数之和,常用赋值法,只需令x =1即可;对形如(ax +by )n (a ,b ∈R )的式子求其展开式各项系数之和,只需令x =y =1即可.解题时如何赋值,要观察所求和式与差式的特点,根据所求值的式子的特征选择适合的方法.16.已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡,若顾客甲只带了现金,顾客乙只用支付宝或微信付款,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中三种结账方式,则他们结账方式的可能情况有________种. 【答案】20 【解析】 【分析】由题意,根据乙的支付方式进行分类,根据分类与分步计数原理即可求出.【详解】当乙选择支付宝时,丙丁可以都选银联卡,或者其中一人选择银联卡,另一人只能选支付宝或现金,故有1+C 21C 21=5,而乙选择支付宝时,丙丁也可以都选微信,或者其中一人选择微信,另一人只能选支付宝或现金,故有1+C 21C 21=5,此时共有5+5=10种,当乙选择微信时,丙丁可以都选银联卡,或者其中一人选择银联卡,另一人只能选微信或现金,故有1+C 21C 21=5,而乙选择微信时,丙丁也可以都选支付宝,或者其中一人选择支付宝,另一人只能选微信或现金,故有1+C 21C 21=5,此时共有5+5=10种, 综上故有10+10=20种,故答案为20.【点睛】本题考查了分步计数原理和分类计数原理,考查了转化思想,属于难题.三、解答题(本大题共6小题,共70分,解答题应写出必要的文字说明、证明过程或演算步骤)17.已知二项式31nx x ⎫⎪⎭的展开式中各项的系数和为256. (1)求n ;(2)求展开式中的常数项. 【答案】(1)8;(2)28. 【解析】 【分析】⑴观察31nx x ⎫⎪⎭可知,展开式中各项系数的和为256,即112...256nn n n n C C C C ++++=,解出得到n 的值⑵利用二次展开式中的第1r +项,即通项公式(311rn rrr nT C x x -+⎛⎫= ⎪⎝⎭,将第一问的n 代入,并整理,令x 的次数为0,解出r ,得到答案【详解】(1)由题意,得112...256nn n n n C C C C ++++=,即2n =256,解得n =8. (2)该二项展开式中的第1r +项为T r +1=84833881rr rrr C x C x x --⎛⎫⋅=⋅ ⎪⎝⎭,令843r-=0,得r =2,此时,常数项为238T C ==28.【点睛】本题主要考的是利用赋值法解决展开式的系数和问题,考查了利用二次展开式的通项公式解决二次展开式的特定项问题.18. 某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定,小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定. (Ⅰ)求当天小王的该银行卡被锁定的概率;(Ⅱ)设当天小王用该银行卡尝试密码次数为X ,求X 的分布列和数学期望. 【答案】(Ⅰ)12;(Ⅱ)分布列见解析,期望52. 【解析】(Ⅰ)设“当天小王的该银行卡被锁定”的事件为A , 则5431()=6542P A =⨯⨯ (Ⅱ)依题意得,X 所有可能的取值是1,2,3 又1511542(X=1),(X=2),(X=3)1=.6656653P P P ==⨯==⨯⨯ 所以X 的分布列为所以1125E()1236632X =⨯+⨯+⨯=. 考点:1、古典概型;2、离散型随机变量的分布列和期望.19.已知函数2()()4x f x e ax b x x =+--,曲线()y f x =在点(0,(0))f 处切线方程为44y x =+. (1)求,a b 的值;(2)讨论()f x 的单调性,并求()f x 的极大值. 【答案】(1)4a b ==;(2)见解析. 【解析】【详解】试题分析:(1)求导函数,利用导数的几何意义及曲线()y f x =在点()()0,0f 处切线方程为44y x =+,建立方程,即可求得a ,b 的值;(2)利用导数的正负,可得()f x 的单调性,从而可求()f x 的极大值.试题解析:(1)()()24xf x eax a b x =++--'.由已知得()04f =,()04f '=. 故4b =,8a b +=. 从而4a =,4b =. (2)由(1)知,()()2414xf x ex x x =+--,()()()14224422x x f x e x x x e ⎛⎫=+--=+- ⎝'⎪⎭.令()0f x '=得,ln 2x =-或2x =-. 从而当()(),2ln 2,x ∈-∞--+∞时,()0f x '>;当()2,ln2x ∈--时,()0f x '<.故()f x 在(),2-∞-,()ln 2,-+∞上单调递增,在()2,ln 2--上单调递减.当2x =-时,函数()f x 取得极大值,极大值为()()2241f e --=-.考点:利用导数研究曲线上某点切线方程;利用导数研究函数的单调性;利用导数研究函数的极值. 【方法点晴】本题考查了利用导数研究曲线上某点切线方程;利用导数研究函数的单调性;利用导数研究函数的极值.求极值的步骤是:(1)确定函数的定义域;(2)求导数()f x ';(3)解方程()0f x '=,求出函数定义域内的所有根;(4)列表检验()f x '在()0f x '=的根0x 左右两侧值的符号,如果左正右负,那么()f x 在0x 处取极大值,如果左负右正,那么()f x 在0x 处取极小值.20.对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,作出甲的得分频率分布直方图如图所示,列出乙的得分统计表如表所示:分值[)0,10 [)10,20 [)20,30 [)30,40场数 10204030(1)估计甲在一场比赛中得分不低于20分的概率.(2)判断甲、乙两名运动员哪个成绩更稳定.(结论不要求证明)(3)在甲所进行的100场比赛中,以每场比赛得分所在区间中点的横坐标为这场比赛的得分,试计算甲每场比赛的平均得分.【答案】(1)0.72;(2)甲更稳定;(3)2380.. 【解析】【分析】(1)根据频率分布直方图直接计算,即可得出结果;(2)根据频率分布直方图与统计表,分析成绩的集中程度,即可得出结论;(3)根据频率分布直方图,由每组的中间值乘以该组的频率,再求和,即可得出平分值. 【详解】(1)根据频率分布直方图可知,甲在一场比赛中得分不低于20分的频率为0.048100.024100.480.240.72⨯+⨯=+=;即甲在一场比赛中得分不低于20分的概率为0.72;(2)根据甲的频率分布直方图可知,甲的成绩主要集中在[)20,30,由乙的得分统计表可得,乙的成绩比较分散,所以甲更稳定; (3)因为组距为10,所以甲在区间[)[)[)[)0,10,10,20,20,30,30,40上得分频率值分别为8100,20100,48100,24100. 设甲的平均得分为S , 则()5815202548110035242380S ⨯+⨯+⨯+==⨯.. 【点睛】本题主要考查由频率分布直方图求概率,以及求平均值等问题,属于基础题型.21.随着网络和智能手机的普及与快速发展,许多可以解答各学科问题的搜题软件走红.有教育工作者认为:网搜答案可以起到拓展思路的作用,但是对多数学生来讲,容易产生依赖心理,对学习能力造成损害.为了了解网络搜题在学生中的使用情况,某校对学生在一周时间内进行网络搜题的频数进行了问卷调查,并从参与调查的学生中抽取了男、女学生各50人进行抽样分析,得到如下样本频数分布表: 一周时间内进行网络搜题的频数区间男生频数 女生频数 []0,10 184(]10,20 108(]20,30 1213(]30,40 615(]40,50410将学生在一周时间内进行网络搜题频数超过20次的行为视为“经常使用网络搜题”,不超过20次的视为“偶尔或不用网络搜题”.(1)根据已有数据,完成下列22⨯列联表(单位:人)中数据的填写,并判断是否在犯错误的概率不超过1%的前提下有把握认为使用网络搜题与性别有关?经常使用网络搜题偶尔或不用网络搜题合计男生女生合计(2)将上述调查所得到的频率视为概率,从该校所有参与调查的学生中,采用随机抽样的方法每次抽取一个人,抽取4人,记经常使用网络搜题的人数为X,若每次抽取的结果是相互独立的,求随机变量X的分布列和数学期望.参考公式:()()()()()22n ad bcxa b c d a c b d-=++++,其中n a b c d=+++.参考数据:()2P x m≥0.050 0.010 0.001m 3.841 6.635 10.828【答案】(1)填表见解析,在犯错误的概率不超过1%的前提下有把握认为使用网络搜题与性别有关;(2)分布列见解析,()12 5E X=.【解析】【分析】(1)根据题意填写列联表,计算观测值,对照临界值得出结论;(2)由题意34,5X B⎛⎫⎪⎝⎭,由此求出随机变量X的分布列和数学期望.【详解】(1)根据题意填写22⨯列联表如下:经常使用网络搜题 偶尔或不用网络搜题 合计 男生 22 28 50 女生 38 12 50 合计 6040100计算观测值 ()2210022123828326.635505060403K ⨯-⨯==>⨯⨯⨯, 所以在犯错误的概率不超过1%的前提下有把握认为使用网络搜题与性别有关.(2)将上述调查所得到的频率视为概率,从该校所有参与调查的学生中,采用随机抽样的方法抽取一人,抽到经常使用网络搜题的学生的概率为6031005=. 由题意34,5XB ⎛⎫ ⎪⎝⎭. ()040433160155625P X C ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭, ()31433961155625P X C ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭, ()2224332162155625P X C ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭, ()334332163155625P X C ⎛⎫⎛⎫==-= ⎪ ⎪⎝⎭⎝⎭, ()44433814155625P X C ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭. X 的分布列为:X 0 1 2 3 4P16625 96625 216625 216625 81625()312455E X ∴=⨯=.【点睛】本题考查独立性检验,考查离散型随机变量的分布列和数学期望,属于中档题. 22.已知函数()ln(1)(1)1(R)f x x k x k =---+∈. (1)求函数()f x 的单调区间;(2)若()0f x ≤在定义域内恒成立,求实数k 的取值范围;(3)证明:()2*ln 2ln 3ln 4ln 2,N 34514n n nn n n -+++⋯+<≥∈+. 【答案】(1)函数()f x 的递增区间为1(1,)k k+,函数()f x 的递减区间为1(1,)k ++∞;(2)1k;(3)见解析. 【解析】试题分析:(1)对函数()f x 求导得1()1k kxf x x +-'=-,对k 进行分类讨论,即可得到函数的单调区间;(2)由(1)可得,0k ≤时,()f x 在(0)+∞,上是增函数,而(2)0f >,()0f x ≤不成立,故0k >,由(1)可得max 1()(1)f x f k=+,即可求出k 的取值范围;(3)由(2)知,当1k =时,有()0f x ≤在(1)+∞,恒成立,即ln(1)2x x -<-,进而换元可得22ln 1n n <-,所以ln 112n n n -<+,即可得证. 试题解析:(1)定义域为()1,+∞,()1111k kx f x k x x +-=-='-- 若0k ≤,()101f x k x =-≥-',()f x 在()1,+∞上单调递增 若0k >,()11k k x k f x x +⎛⎫-- ⎪⎝⎭'=-, 所以,当()0f x '>时,111x k <<+,当()0f x '<时,11x k>+ 综上:若0k ≤,()f x 在()1,+∞上单调递增; 若0k >,()f x 在11,1k ⎛⎫+ ⎪⎝⎭上单调递增,在11,k ⎛⎫++∞ ⎪⎝⎭上单调递减 (2)由(1)知,0k ≤时,()210f k =->不可能成立; 若0k >,()0f x ≤恒成立()max 110f x f k ⎛⎫⇔=+≤⎪⎝⎭,11ln 0f k k ⎛⎫+=-≤ ⎪⎝⎭,得1k ≥综上,1k ≥.(3)由(2)知,当1k =时,有()0f x ≤在()1,+∞上恒成立,即()ln 12x x -<- 令()2*1N ,1x nn n -=∈>,得22ln 1nn <-,即ln 112n n n -<+ ln2ln3ln4ln 3451n n +++++ ()1123122224n n n --<++++=,得证. 点睛:(1)导数综合题中对于含有字母参数的问题,一般用到分类讨论的方法,解题时要注意分类要不重不漏;(2)对于恒成立的问题,直接转化为求函数的最值即可;(3)对于导数中,数列不等式的证明,解题时常常用到前面的结论,需要根据题目的特点构造合适的不等式,然后转化成数列的问题解决,解题时往往用到数列的求和.。
重庆市七校联盟2019-2020学年高二上学期联考数学(文)试卷
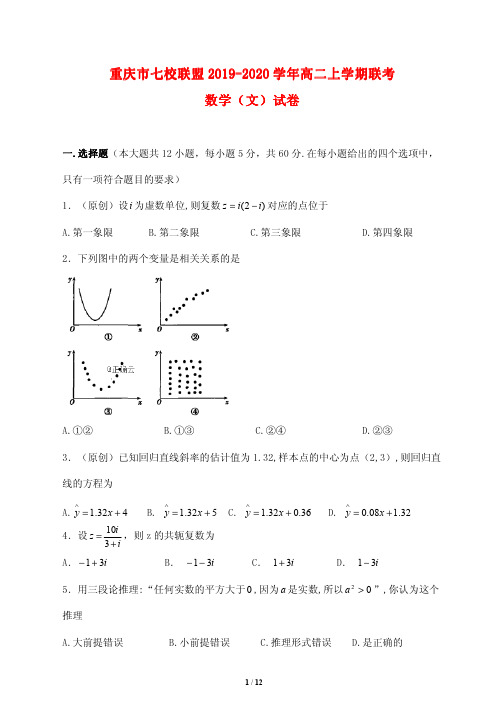
一.选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,
只有一项符合题目的要求) 1.(原创)设 i 为虚数单位,则复数 z = i(2 − i) 对应的点位于
A.第一象限
B.第二象限
C.第三象限
有 16 种,则 P( A) = 16 = 4 . 20 5
………………………12 分
20.(本小题满分 12 分)
解:(1)因 f (x) = 2x3 + ax 2 + bx + 1 ,故 f ' (x) = 6x 2 + 2ax + b ,
……2 分
从而 f ' (x) = 6(x + a )2 + b − a 2 ,即 y = f ' (x) 关于直线 x = − a 对称,
数.
………………………………12 分
18. (本小题满分 12 分) 解:(1)因为 x = 80 + 75 + 70 + 65 + 60 = 70 ,
5
…………………1 分
y = 70 + 66 + 68 + 64 + 62 = 66 , …………………2 分 5
∑5
xi yi = 80 × 70 + 75 × 66 + 70 × 68 + 65 × 64 + 60 × 62 = 23190 ,…3 分
(1)请根据上表提供的数据,用最小二乘法求出 y 关于 x 的线性回归方程
∧∧
∧
y = b x + a ;(参考数值: 80 × 70 + 75 × 66 + 70 × 68 + 65× 64 + 60 × 62 = 23190 ,
重庆市七校联盟2019-2020学年高二上学期联考数学(理)试卷

重庆市七校联考高二数学理科试题一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(原创)在复平面内,复数)21(i i z -=的共轭复数为 A .i --2 B.i -2 C.i +-2 D. i +22.(原创)若2017201722102017)21(x a x a x a a x ++++=- ,则=+++2017321a a a aA .2 B. 1 C.1- D. 2-3.用反证法证明命题“若022=+b a ,则b a ,全为0(R b a ∈,)”,假设的内容是 A.b a ,至少有一个不为0 B.b a ,至少有一个为0 C.b a ,全不为0 D.b a ,中只有一个为04.命题“有些有理数是无限循环小数,整数是有理数,所以整数是循环小数”是假命题,推理错误的原因是A.使用了归纳推理B.使用了类比推理C.使用了“三段论”,但推理形式错误D.使用了“三段论”,但小前提错误5.(原创)已知随机变量ξ服从正态分布),3(2σN ,68.0)4(=≤ξP ,则)2(≥ξP = A.84.0 B.68.0 C.32.0 D.16.0 6.(原创)已知函数2ln )(+=x a x f ,2)('=e f ,则a 的值为 A .1- B.1 C.e 2 D.2e7.观察下列各式:1=+b a ,322=+b a ,433=+b a ,744=+b a ,1155=+b a ,…,则=+1010b aA .28 B.76 C.123 D.1998.从1、2、3、4、5中任取2个不同的数,事件A 为“取到的2个数之和为偶数”,事件B 为“取到的2个数均为偶数”,则)|(A B P 等于A.81B.41C.21D.529. (原创)小王有70元钱,现有面值分别为20元和30元的两种IC 电话卡,若他至少购买一张卡,则不同的买法共有A.6种B.7种C.8种D.9种 10.设甲、乙两人每次射击命中目标的概率分别为34和45,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是 A.920 B.925 C.380 D.1940011.某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是A.72B.120C.144D.168 12.已知函数)(x f 的定义域为]5,1[-,部分对应值如下表)(x f 的导函数)('x f y =的图象如图所示下列关于函数)(x f 的命题: ①函数)(x f y =是周期函数; ②函数)(x f 在[0,2]是减函数;③如果当],1[t x -∈时,)(x f 的最大值是2,那么t 的最大值为4; ④当21<<a 时,函数a x f y -=)(有4个零点. 其中真命题的个数是A .1 B.2 C.3 D.4二、填空题(本大题共4小题,每小题5分,共20分.)13.(原创)4)2(y x +展开式中二项式系数最大的项的系数为 .(用数字作答)14.(原创)dx x x ⎰--222)sin 3(= .15.将甲、乙等5位同学分别保送到北京大学、上海交通大学、浙江大学三所大学就读,则每所大学至少保送一人的不同保送的方法数为 种.(用数字作答)16.给出下列命题:①用反证法证明命题“设,,a b c 为实数,且0,0,a b c ab bc ca ++>++>则0,0,0a b c >>>”时,要给出的假设是:,,a b c 都不是正数;②若函数()()2f x x x a =+在2x =处取得极大值,则2a =-或-6;③用数学归纳法证明*1111...(1,)2321n n n n N ++++<>∈-,在验证2n =成立时,不等式的左边是11123++; ④数列}{n a 的前n 项和c S n n -=3,则1=c 是数列}{n a 为等比数列的充要条件; 上述命题中,所有正确命题的序号为 .三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17.(本小题满分10分)(原创)当m 为何实数时,复数i m m m m m z )82(4622--+---=是 (Ⅰ)实数; (Ⅱ)纯虚数. 18.(本小题满分12分)已知函数x x x f 12)(3+-= (Ⅰ)求函数)(x f 的单调区间;(Ⅱ)求函数[]1,3)(-∈x x f 当时的最大值与最小值.19.(本小题满分12分)(原创)中秋节吃月饼是我国的传统习俗,设一礼盒中装有9个月饼,其中莲蓉月饼2个,伍仁月饼3个,豆沙月饼 4个,这三种月饼的外观完全相同,从中任意选取3个.(Ⅰ)求三种月饼各取到1个的概率;(Ⅱ)设X 表示取到伍仁月饼的个数,求X 的分布列与数学期望. 20.(本小题满分12分)数列}{n a 满足)(2*∈-=N n a n S n n .(Ⅰ)计算4321,,,a a a a ,并由此猜想通项公式n a ; (Ⅱ)用数学归纳法证明(Ⅰ)中的猜想. 21.(本小题满分12分)某校为全面推进新课程改革,在高一年级开设了研究性学习课程,某班学生在一次研究活动课程中,一个小组进行一种验证性实验,已知该种实验每次实验成功的概率为12.(Ⅰ)求该小组做了5次这种实验至少有2次成功的概率;(Ⅱ)如果在若干次实验中累计有两次成功就停止实验,否则将继续下次实验,但实验的总次数不超过5次,求该小组所做实验的次数ξ的概率分布列和数学期望. 22.(本小题满分12分)设函数),(ln )(2x x b ax x f -+=.)1(21)(2x b x x g -+-=已知曲线)(x f y =在点(1,)1(f )处的切线与直线01=+-y x 垂直.(Ⅰ)求a 的值;(Ⅱ)求函数)(x f 的极值点;(Ⅲ)若对于任意的),,1(+∞∈b 总存在],,1[,21b x x ∈使得m x g x g x f x f +->--)()(1)()(2121成立,求实数m 的取值范围.重庆市七校联考高二数学理科参考答案13. 24 14. 16 15. 150 16.③④ 三.解答题17. (本小题满分10分)解:(Ⅰ)当⎩⎨⎧=--≠-082042m m m ………………………………3分即2-=m 时,z 是实数; ………………………………5分(Ⅱ)当⎪⎩⎪⎨⎧≠--=---08204622m m m m m ………………………………7分⎩⎨⎧≠-≠-=⇒4223m m m 且或 ………………………………9分3=∴m 时,z 是纯虚数. ………………………………10分 18. (本小题满分12分)解:(Ⅰ) 由x x x f 12)(3+-=可得123)(2'+-=x x f ………………………2分令0)('>x f 即得22<<-x∴)(x f 的单调递增区间为)2,2(- …………………………4分令0)('<x f 即得22>-<x x 或∴)(x f 单调递减区间为)2,(--∞,),2(+∞.综上所述:)(x f 的单调递增区间为)2,2(-,单调递减区间为)2,(--∞,),2(+∞. …………………………6分(Ⅱ) 由(Ⅰ)可知:)(x f 在[]2,3--上单调递减,在[]1,2-上单调递增 ………………………8分又9)3(12)3()3(3-=-⨯+--=-f ……………………………9分16)2(12)2()2(3-=-⨯+--=-f ……………………………10分 111121)1(3=⨯+-=f ……………………………11分∴)(x f 在[]1,3-上的最大值为11,最小值为16- ………………………12分19. (本小题满分12分)解:(Ⅰ) 设三种月饼各取到一个的概率为P ,则 7239141312==C C C C P ………………………………5分 (Ⅱ)由题意可得:X 可能的取值为3,2,1,0 ………………………………6分215)0(3936===C C X P 2815)1(392613===C C C X P 143)2(391623===C C C X P 841)3(3933===C C X P10分X 的数学期望138412143184450215)(=⨯+⨯+⨯+⨯=ξE ………………12分 20. (本小题满分12分)解:(Ⅰ) n n a n S -=21121111=⇒-⨯==∴a a S n 时,当 ……………………………1分23222222=⇒-⨯==a a S n 时,当 ……………………………2分 47323333=⇒-⨯==a a S n 时,当 ……………………………3分815424444=⇒-⨯==a a S n 时,当……………………………4分由此猜想)(2121*-∈-=N n a n n n . ……………………………6分(Ⅱ) 证明①当1=n 时,11=a ,结论成立. ……………………………7分②假设)1(*∈≥=N k k k n 且时,结论成立,即1212--=k k k a ………………8分那么1+=k n 时,111122)1(2++++-+=+--+=-=k k k k k k k a a a k a k S S a ………………10分k k a a +=∴+221kk k k k k a a 2122212222111-=-+=+=∴+-+ …………………………11分 所以当1+=k n 时,结论成立,综上所述)(2121*-∈-=N n a n n n 成立. ………………………………12分21. (本小题满分12分)解:(Ⅰ)记“该小组做了5次实验至少有2次成功”为事件A ,“只成功一次”为事件1A ,“一次都不成功”为事件2A ,则:1613)21()21(1)()(1)(1)(5055152121=--=--=+-=C C A P A P A A P A P故该小组做了5次这种实验至少有2次成功的概率为1316.………………6分 (Ⅱ)ξ的可能取值为2,3,4,5.则41)21()2(2===ξP ;41)21()3(312===C P ξ,163)21()4(413===C P ξ,165)21()21()21()5(514515505=++==C C C P ξ.………………10分 ∴ξ的分布列为:11分∴ξ的数学期望:)(ξE =113557234544161616⨯+⨯+⨯+⨯=. ………………12分 22. (本小题满分12分)解:(Ⅰ)由题可知,函数)(x f 的定义域为),0(+∞ …………………………1分)11(2)(-+='x b ax x f∴a b a f 2)111(2)1(=-+=' ………………………………3分因为曲线)(x f y =在点(1,)1(f )处的切线与直线01=+-y x 垂直,故112-=⋅a ∴21-=a ………………………………4分(Ⅱ)由(I )得x bbx x x b x x f +--=-+-='2)11()((0>x )00)(2=-+='b bx x x f 得令(*)b b 42+=∆①时或时,即当04-042><>+=∆b b b b (*)式有两个根.24,242221b b b x b b b x ++-=+--=当4-<b 时,.0,021>>x x)上单调递增,,()上单调递减,在区间,在区间(1220)(x x x x f )上单调递减,在区间(∞+1x .此时为极大值点为极小值点,12x x x x == 当0>b 时,.0,021<>x x)上单调递减,()上单调递增,在区间,在区间(∞+110)(x x x f ,此时点为极大值点,无极小值1x x = ……………………6分 ②时时,即当04-042≤≤≤+=∆b b b 无极值点。
2019—2020学年度第二次联考:高2020级文科数学试题

重庆市名校联盟2019~2020学年度第二次联合考试文科数学试题(高2020级)【命题:重庆市名校联盟命题组】(本试卷共4页,总分150分,考试时间120分钟)注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,并认真核对条形码上的姓名、准考证号、座位号及科类名称。
2.请将准考证条形码粘贴在右侧的[考生条形码粘贴处]的方框内。
3.选择题必须使用2B 铅笔填涂;非选择题必须用0.5毫米黑色字迹的签字笔填写,字体工整、笔迹清楚。
4.请按题号顺序在各题的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效。
5.保持答题卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀。
第Ⅰ卷一、选择题:本大题共12个小题,每小题5分,共60分. 在每小题给出的四个备选项中,只有一项是符合题目要求的.1. 不等式0)1)(6(>+-x x 的解集是A .()6,1-B .()1,6-C .()(),16,-∞-+∞D .()(),61,-∞-+∞2. 下列说法正确的是A .方向相同的向量叫相等向量B .单位向量的长度为1C .若||||=,则 =D .若//,//a b b c ,则//a c 3. 数列1,41,91,161,…的一个通项公式为 A .n a n 1=B .21na n =C .1(2)n a n n =+D .na n 21=4. 已知)1,(),2,6(x b a =-=,且//,则x 等于A .13B .13-C .3D .3-5. 在等差数列{}n a 中,已知11=a ,55=a ,则=3aA .1B .2C .3D . 46. 在ABC ∆中,45,60==B A ,23=a ,则=bA.B.CD7. 满足不等式组⎪⎩⎪⎨⎧≥≤-+≥+-00301y y x y x 的点(),x y 组成的图形的面积是A .4B .5C .7D .88. 已知2|||==,2)()2(-=-⋅+,则a 与b 的夹角为A .6πB .3π C .23π D .56π 9. 在等比数列}{n a 中,,4,24231=+=+a a a a 则=+86a aA .16B .32C .64D .12810.b a ,为非零实数,已知0>ab 且b a >,则下列不等式恒成立的是A .ba 11< B .22b a > C .b a >D .bc ac >11.已知数列}{n a 中,,4,221==a a ,12n n n a a a -=++则=2018aA .4B .-4C .2D .-212.如图所示,在ABC ∆中,D 为AB 的中点,E 在边AC 上且满足→→=AC AE 31,CD 与BE 交于点P ,若→→→+=AC y AB x AP ,则=+y xA .51 B .52 C .53 D .54第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.13.已知数列{}n a 满足:287n a n n =-+,则数列{}n a 中最小项是第________项.14.若)1,2(=a ,)3,1(-=b,则||b a -= .15.在ABC △中,角C B A ,,对的边分别为,,,c b a 若b C a =cos 2,则ABC ∆的形状一定是三角形.16.已知02,0,0=-+>>xy y x y x ,则2x y +的最小值为_________.三、解答题:本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)已知向量)1,3(),3,1(--==. (Ⅰ)求b a ⋅;(Ⅱ)若)(λ+⊥,求λ的值.18.(本小题满分12分)设等差数列{}n a 的前n 项和为n S ,已知95=a ,93=S . (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列{}n a 的前n 项和n S .19.(本小题满分12分)在ABC ∆中,,,a b c 分别为角,,A B C 的对边,且满足2cos cos a c bC B-=. (Ⅰ)求角B 的大小;(Ⅱ)若b =4a c +=,求ABC ∆的面积.20.(本小题满分12分)已知,x y 满足不等式组00224x y x y t x y ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩表示的平面区域是D ,(Ⅰ)当4t =时,在下图中画出平面区域D ,并求y x z -=的取值范围; (Ⅱ)若目标函数96z x y =+的最大值的变化范围是[20,22],求t 的取值范围.21.(本小题满分12分)已知数列}{n a 的前n 项和为n S ,且).(23*∈-=N n a S n n (Ⅰ)求数列}{n a 的通项公式;(Ⅱ)设,1log 223+=n n a b 求数列⎭⎬⎫⎩⎨⎧+11n n b b 的前n 项和n T .22.(本小题满分10分)2()f x x bx c =++(b 、c 为常数),方程()f x x =的两个实数根为1x ,2x 且满足1210,1x x x >->.(Ⅰ)若实数0x 满足,)(00x x f =则称0x 为函数)(x f 的一个不动点.设,8,5=-=c b 求)(x f 的不动点;(Ⅱ)设10t x <<,比较()f t 与1x 的大小.重庆市名校联盟2019~2020学年度第二次联合考试文科数学答案(高2020级)一、选择题:本大题共12个小题,每小题5分,共60分. 在每小题给出的四个备选项中,只有一项是符合题目要求的.1—12:CBBDC BABCA AC12.由CD 与BE 交于点P 可设→→=BE BP λ,→→=DC DP μ,D 为AB 的中点,→→=ACAE 31则→→→→→→→→→→→+-=-+=-+=+=AC AB AB AC AB AB AE AB BE AB AP 3)1()31()(λλλλλ→→→→→→→→→→+-=-+=-+=+=AC AB AD AC AD AC AD DC AD AP μμμμμμ21)1()(∴⎪⎪⎩⎪⎪⎨⎧=-=-μλμλ3211 ∴ ⎪⎪⎩⎪⎪⎨⎧==5153μλ ∴→→→+=AC AB AP 5152∴51,52==y x ∴ 53=+y x二、填空题:本大题共4小题,每小题5分,共20分.13. 415.等腰 16.8 16. 02=-+xy y x ∴121=+yx ∴844424422)21()2(2=+=⋅+≥+++=+⋅+=+xyy x x y y x y x y x y x当且仅当xyy x =4即4,2==y x 时取等 三、解答题:本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)(I )b a⋅=33--=32- ……………………………………(6分) (II ) )(b a b λ+⊥∴0432)(2=+-=+⋅=+⋅λλλb a b b a b∴23=λ………………………………………………(12分)18. (本小题满分12分) (I ) {}n a 为等差数列∴9415=+=d a a 9332233113=+=⨯+=d a d a S ∴2,11==d a ………………………………………………(4分) ∴12-=n a n ………………………………………………(6分)(II )22)121(n nn S n =⋅-+=………………………………………………(12分)19. (本小题满分12分) (I )2cos cos a c bC B-= ∴C b B c B a cos cos cos 2=-∴C B B C B A cos sin cos sin cos sin 2=-………………(3分) ∴A C B B A sin )sin(cos sin 2=+=∴ 21cos =B∴3π=B ………………………………………………(6分)(II) B ab b a b cos 2222-+=∴3cos 22)(82πac ac c a --+=∴38=ac ………………………………………………(10分) ∴232233821sin 21=⨯⨯==∆B ac S ABC ………………(12分)20. (本小题满分12分)(I )当4t =时,平面区域D 如图所示…………………(3分)如图,画出直线0=-y x ,然后进行平行移动和可行域相交,可知在)0,2(A 和)2,0(C 分别取得最大值和最小值,所以y x z -=的取值范围]2,2[-………………(6分) (II )设1:24l x y +=与2:2l x y t +=交于点B ,联立1l 和2l 的方程824(,)33t t B --∴……………………………………………………………(9分) 当96z x y =+经过B 点时,z 取最大值3(8)2(24)16[20,22]max Z t t t ∴=-+-=+∈[4,6]t ∴∈………………………………………………………………(12分)21.(本小题满分12分) 解:(I )当1=n 时,,23111-==a S a .11=∴a由)(23*∈-=N n a S n n 可得),2(2311≥-=--n a S n n 两式相减可得:),23()23(11---=-=--n n n n n a a S S a 即:,231-=n n a a ∴数列}{n a 是以1为首项,23为公比的等比数列, .)23(1-=∴n n a ............6分 (II )由(1)得,121log 223-=+=n a b n n=n T 1b 1b 2+1b 2b 3+…+1b n -1b n 11++n n b b =11×3+13×5+…+1(2n -3)(2n -1) +)12)(12(1+-n n =12[(1-13)+(13-15)+… +(12n -3-12n -1)+)121121(+--n n ] =12+n n.....................................................12分 22.(本小题满分10分)证明:(I )由x x x x f =+-=85)(2可得2=x 或,4=x故)(x f 的不动点为2和4..............................................................................4分 (II )22111()()f t x t bt c x bx c -=++-++11()()t x t x b =-++,又121211x x b x b x +=-∴+=-,而111212,1,1x t b x t x x x x -<++∴-<-∴>-11110()()0()t x t x t x b f t x -<∴-++>∴>...............................10分(其它解法酌情给分)。
2019-2020学年重庆市七校联盟高二上学期联考数学(理)试题(解析版)

2019-2020学年重庆市七校联盟高二上学期联考数学(理)试题一、单选题1.在复平面内,复数()12z i i =-的共轭复数为 () A .2i -- B .2i -C .2i -+D .2i +【答案】B【解析】利用复数代数形式的乘除运算化简,再由共轭复数的概念得答案. 【详解】()122z i i i =-=+, 2z i ∴=-.故选:B. 【点睛】本题考查复数代数形式的乘除运算,考查复数的基本概念,属于基础题.2.若2017220170122017(12)x a a x a x a x-=+++⋯⋯+,则1232017a a a a ++⋯+=() A .2 B .1C .1-D .2-【答案】D【解析】在所给的等式中,分别令0x =,1x =,可得要求式子的值. 【详解】2017220170122017(12)x a a x a x a x -=+++⋯⋯+,令0x =,可得01a =. ∴再令1x =,可得012320171a a a a a +++⋯+=-,则12320172a a a a ++⋯+=-. 故选:D. 【点睛】本题主要考查二项式定理的应用,是给变量赋值问题,属于基础题.3.用反证法证明“若,a b ∈R ,220a b +=,则a ,b 全为0”时,假设正确的是( ) A .a ,b 中只有一个为0 B .a ,b 至少一个为0 C .a ,b 全不为0 D .a ,b 至少有一个不为0【答案】D【解析】分析:根据反证法的概念,把要证的结论否定后,即可得到所求的反设. 详解:由题意可知,由于“22,,0a b R a b ∈+=,则,a b 全为0”的否定为“,a b 至少有一个不为0”,故选D.点睛:本题主要考查了反证法的定义的理解与应用,正确理解反证法的基本概念是解答的关键,着重考查了推理与论证能力.4.命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是 () A .使用了归纳推理 B .使用了类比推理C .使用了“三段论”,但推理形式错误D .使用了“三段论”,但小前提错误 【答案】C【解析】有理数包含有限小数,无限不循环小数,以及整数,故有些有理数是无限循环小数,这个说法是错误的,即大前提是错误的. 【详解】大前提的形式:“有些有理数是无限循环小数”,不是全称命题,∴不符合三段论推理形式, ∴推理形式错误.故选:C. 【点睛】本题考查演绎推理的基本方法,解题的关键是理解演绎推理的三段论原理,在大前提和小前提中,若有一个说法是错误的,则得到的结论就是错误的. 5.已知随机变量ξ服从正态分布()23,N σ,()40.68P ξ≤=,则()2P ξ≥=( )A .0.84B .0.68C .0.32D .0.16【答案】B【解析】直接利用正态分布的应用和密度曲线的对称性的应用求出结果. 【详解】根据随机变量ξ服从正态分布()23,N σ,所以密度曲线关于直线3x =对称,由于()40.68P ξ≤=,所以()410.680.32P ξ≥=-=, 所以()20.32P ξ≤=,则()2410.320.320.36P ξ≤≤=--=, 所以()20.360.320.68P ξ≥=+=. 故选:B. 【点睛】本题考查的知识要点:正态分布的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.6.已知函数()2f x alnx =+,()'2f e =,则a 的值为 () A .1- B .1C .2eD .2e【答案】C【解析】根据题意,求出函数的导数,将x e =代入可得2ae=,变形可得答案. 【详解】根据题意,函数()ln 2f x a x =+,则()a f x x'=, 若()2af e e'==,则2a e =. 故选:C. 【点睛】本题考查函数的导数计算,关键是掌握导数的计算公式,属于基础题.7.观察下列各式:a+b=1.a 2+b 2=3,a 3+b 3=4 ,a 4+b 4=7,a 5+b 5=11,…,则a 10+b 10=( ) A .28 B .76C .123D .199【答案】C 【解析】【详解】 由题观察可发现,347,4711,71118+=+=+=, 111829,182947+=+=, 294776,4776123+=+=,即1010123a b +=, 故选C.【考点】观察和归纳推理能力.8.从1,2,3,4,5中任取2个不同的数,事件A =“取到的2个数之和为偶数”,事件B =“取到两个数均为偶数”,则()|P B A =( )A .18B .14C .25D .12【答案】B【解析】先求得()P A 和()P AB 的值,然后利用条件概率计算公式,计算出所求的概率. 【详解】依题意()22322542105C C P A C +===,()22251=10C P AB C =,故()|P B A =()()1110245P AB P A ==.故选B. 【点睛】本小题主要考查条件概型的计算,考查运算求解能力,属于基础题.9.小王有70元钱,现有面值分别为20元和30元的两种IC 电话卡.若他至少买一张,则不同的买法共有( ) A .7种 B .8种 C .6种 D .9种 【答案】A【解析】要完成的一件事是“至少买一张IC 电话卡”,分三类完成:买1张IC 卡,买2张IC 卡,买3张IC 卡.而每一类都能独立完成“至少买一张IC 电话卡”这件事.买1张IC 卡有2种方法,即买一张20元面值的或买一张30元面值的;买2张IC 卡有3种方法,即买两张20元面值的或买两张30元面值的或20元面值的和30元面值的各买一张,买3张IC 卡有2种方法,即买两张20元面值的和一张30元面值的或3张20元面值的,故共有2+3+2=7(种)不同的买法. 10.设甲、乙两人每次射击命中目标的概率分别为34和45,且各次射击相互独立,若按甲、乙、甲、乙的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是 A .920 B .925 C .380 D .19400【答案】D【解析】试题分析:击中目标时甲射击了两次包括甲乙第一次均未击中、甲第二次击中,及甲前两次均未击中、乙第二次才击中,所以其概率为11311143119454454580100400P=⨯⨯+⨯⨯⨯=+=,故选D.【考点】独立重复试验的概率.11.某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是A.72 B.120 C.144 D.168【答案】B【解析】试题分析:将所有的安排方法分成两类,第一类:歌舞类节目中间不穿插相声节目,有32132262224A A A=⨯⨯=(种);第二类:歌舞类节目中间穿插相声节目,有31113224622496A A A A=⨯⨯⨯=(种);根据分类加法计数原理,共有96+24=120种不同的排法.故选B.【考点】1、分类加法计数原理;2、排列.12.已知函数的定义域为,部分对应值如下表:的导函数的图象如图所示,则下列关于函数的命题:①函数是周期函数;②函数在是减函数;③如果当时,的最大值是2,那么的最大值为4;④当时,函数有4个零点。
2019-2020学年重庆市主城区七校高二下学期期末联考数学试题 Word版

绝密★启用前重庆市主城区七校2019-2020学年下学期期末联考高二数学试题学校:___________姓名:___________班级:___________考号:___________ 注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上第Ⅰ卷(选择题 共60分)一、选择题.(本大题共12小题,每小题5分,共60分.在每小题列出的四个选项中,选出符合题目要求的一项)1.(改编)若21i z i =+(其中i 是虚数单位),则z =( )A .4B .2C .1 D2.为对某组数据进行分析,建立了四种不同的模型进行拟合,现用回归分析原理,计算出四种模型的相关指数R 2分别为0.97,0.86,0.65,0.55,则拟合效果最好的回归模型对应的相关指数R 2的值是( )A .0.55B .0.86C .0.65D .0.973.在某次数学测试中,学生成绩ξ服从正态分布N (100,σ2)(σ>0),若ξ在(80,120)内的概率为0.8,则ξ在(0,80)内的概率为( )A .0.05B .0.1C .0.15D .0.24.(改编)曲线y =x 2+ln x 在点(1,1)处的切线方程为( )A .3x -y -2=0B .x -3y +2=0C .3x +y -4=0D .x +3y -4=05.(改编)某市汽车牌照号码可以上网自编,但规定从左到右第二个号码只能从字母B ,C ,D 中选择,其他四个号码可以从0~9这十个数字中选择(数字可以重复),有车主第一个号码(从左到右)只想在数字3,5,6,8,9中选择,其他号码只想在1,3,6,9中选择,则他的车牌号码可选的所有可能情况有( )A .180种B .360种C .720种D .960种6.从装有除颜色外完全相同的3个白球和m 个黑球的布袋中随机摸取一球,有放回地摸取5次,设摸得白球数为X ,已知E (X )=3,则D (X )=( )A .85B .65C .45D .257.(改编)某产品的广告费用x 与销售额y 的统计数据如下表:广告费用x(万元)4 2 35 销售额y(万元)49 26 39 54根据上表可得回归方程+=a x b y 中的b 为9.4,据此模型预报广告费用为6万元时销售额为( )A .63.6万元B .65.5万元C .67.7万元D .72.0万元8.(改编)我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰。
重庆市七校联盟2019_2020学年高二数学上学期联考试题理(含解析)

重庆市七校联盟2019-2020学年高二数学上学期联考试题理(含解析)一、选择题(本大题共12小题)1.在复平面内,复数的共轭复数为A. B. C. D.2.若,则A. 2B. 1C.D.3.用反证法证明命题“若,则a、b全为、”,其反设正确的是A. a、b至少有一个不为0B. a、b至少有一个为0C. a、b全不为0D. a、b中只有一个为04.命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是A. 使用了归纳推理B. 使用了类比推理C. 使用了“三段论”,但推理形式错误D. 使用了“三段论”,但小前提错误5.已知随机变量服从正态分布,,则A. B. C. D.6.已知函数,,则a的值为A. B. 1 C. 2e D.7.观察下列各式:,,,,,,则A. 28B. 76C. 123D. 1998.从1,2,3,4,5中任取2个不同的数,事件A:“取到的2个数之和为偶数”,事件B:“取到的2个数均为偶数”,则A. B. C. D.9.小王有70元钱,现有面值分别为20元和30元的两种IC电话卡,若他至少买一张,则不同的买法共用A. 7种B. 8种C. 6种D. 9种10.设甲、乙两人每次射击命中目标的概率分别为,且各次射击相互独立,若按甲、乙、甲、乙的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是A. B. C. D.11.某次联欢会要安排3个歌舞类节目,2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是A. 72B. 120C. 144D. 16812.的导函数的图象如图所示.下列关于函数的命题:函数是周期函数;函数在是减函数;如果当时,的最大值是2,那么t的最大值为4;当时,函数有4个零点.其中真命题的个数是A. 4个B. 3个C. 2个D. 1个二、填空题(本大题共4小题)13.展开式中二项式系数最大的项的系数为______用数字作答14.______.15.将5位同学分别保送到北京大学,上海交通大学,清华大学这3所大学就读,每所大学至少保送1人,则不同的保送方法共有______种16.给出下列命题:用反证法证明命题“设a,b,c为实数,且,,则,,”时,要给出的假设是:a,b,c都不是正数;若函数在处取得极大值,则或;用数学归纳法证明,在验证成立时,不等式的左边是;数列的前n项和,则是数列为等比数列的充要条件;上述命题中,所有正确命题的序号为______.三、解答题(本大题共6小题)17.当m为何实数时,复数是Ⅰ实数;Ⅱ纯虚数.18.已知函数判断函数的单调性求函数当时的最大值与最小值.19.中秋节吃月饼是我国的传统习俗,设一礼盒中装有9个月饼,其中莲蓉月饼2个,伍仁月饼3个,豆沙月饼4个,这三种月饼的外观完全相同,从中任意选取3个.Ⅰ求三种月饼各取到1个的概率;Ⅱ设X表示取到伍仁月饼的个数,求X的分布列与数学期望.20.数列满足Ⅰ计算,,,,并由此猜想通项公式;Ⅱ用数学归纳法证明Ⅰ中的猜想.21.某校为全面推进新课程改革,在高一年级开设了研究性学习课程,某班学生在一次研究活动课程中,一个小组进行一种验证性实验,已知该种实验每次实验成功的概率为.求该小组做了5次这种实验至少有2次成功的概率.如果在若干次实验中累计有两次成功就停止实验,否则将继续下次实验,但实验的总次数不超过5次,求该小组所做实验的次数的概率分布列和数学期望.22.设函数,,已知曲线在点处的切线与直线垂直.Ⅰ求a的值;Ⅱ求函数的极值点;Ⅲ若对于任意,总存在,,使得成立,求实数m的取值范围.答案和解析1.【答案】B【解析】解:,.故选:B.利用复数代数形式的乘除运算化简,再由共轭复数的概念得答案.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.2.【答案】D【解析】解:,令,可得.再令,可得,则,故选:D.在所给的等式中,分别令,,可得要求式子的值.本题主要考查二项式定理的应用,是给变量赋值问题,属于基础题.3.【答案】A【解析】解:由于“a、b全为、”的否定为:“a、b至少有一个不为0”,故选:A.把要证的结论否定之后,即得所求的反设.本题考查用反证法证明数学命题,得到“a、b全为、”的否定为:“a、b至少有一个不为0”,是解题的关键.4.【答案】C【解析】解:大前提的形式:“有些有理数是无限循环小数”,不是全称命题,不符合三段论推理形式,推理形式错误,故选:C.本题考查的知识点是演绎推理的基本方法及整数的,在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是推理形式错误,我们分析的其大前提的形式:“有些”,不难得到结论.演绎推理的主要形式就是由大前提、小前提推出结论的三段论推理.三段论推理的依据用集合论的观点来讲就是:若集合M的所有元素都具有性质P,S是M的子集,那么S 中所有元素都具有性质三段论的公式中包含三个判断:第一个判断称为大前提,它提供了一个一般的原理;第二个判断叫小前提,它指出了一个特殊情况;这两个判断联合起来,揭示了一般原理和特殊情况的内在联系,从而产生了第三个判断结论.演绎推理是一种必然性推理,演绎推理的前提与结论之间有蕴涵关系.因而,只要前提是真实的,推理的形式是正确的,那么结论必定是真实的,但错误的前提可能导致错误的结论.5.【答案】B【解析】解:根据随机变量服从正态分布,所以密度曲线关于直线对称,由于,所以,所以,则,所以.故选:B.直接利用正态分布的应用和密度曲线的对称性的应用求出结果.本题考查的知识要点:正态分布的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.6.【答案】C【解析】解:根据题意,函数,则,若,则;故选:C.根据题意,求出函数的导数,将代入可得,变形可得答案.本题考查函数的导数计算,关键是掌握导数的计算公式,属于基础题.7.【答案】C【解析】解:观察可得各式的值构成数列1,3,4,7,11,,其规律为从第三项起,每项等于其前相邻两项的和,所求值为数列中的第十项.继续写出此数列为1,3,4,7,11,18,29,47,76,123,,第十项为123,即,.故选:C.观察可得各式的值构成数列1,3,4,7,11,,所求值为数列中的第十项.根据数列的递推规律求解.本题考查归纳推理,实际上主要为数列的应用题.要充分寻找数值、数字的变化特征,构造出数列,从特殊到一般,进行归纳推理.8.【答案】B【解析】解:事件“取到的2个数之和为偶数”所包含的基本事件有:、、、,,事件“取到的2个数均为偶数”所包含的基本事件有,.故选:B.用列举法求出事件“取到的2个数之和为偶数”所包含的基本事件的个数,求,同理求出,根据条件概率公式即可求得结果.此题是个基础题.考查条件概率的计算公式,同时考查学生对基础知识的记忆、理解和熟练程度.9.【答案】A【解析】解:要完成的“一件事”是“至少买一张IC电话卡”,分3类完成:买1张IC卡、买2张IC卡、买3张IC卡.而每一类都能独立完成“至少买一张IC电话卡”这件事.买l张IC卡有2种方法,买2张IC卡有3种方法,买3张IC卡有2种方法.不同的买法共有种.故选:A.利用已知条件,分类列出不同的买法种数即可.本题考查排列组合的实际应用,考查计算能力.10.【答案】C【解析】解:设A表示甲命中目标,B表示乙命中目标,则A、B相互独立,停止射击时甲射击了两次包括两种情况:第一次射击甲乙都未命中,甲第二次射击时命中,此时的概率,第一次射击甲乙都未命中,甲第二次射击未命中,而乙在第二次射击时命中,此时的概率,故停止射击时甲射击了两次的概率;故选:C.根据题意,分析可得:停止射击时甲射击了两次包括两种情况:第一次射击甲乙都未命中,甲第二次射击时命中,第一次射击甲乙都未命中,甲第二次射击未命中,而第二次射击时命中,分别由相互独立事件概率的乘法公式计算其概率,再由互斥事件的概率的加法公式计算可得答案.本题考查互斥事件、相互独立事件概率的计算,关键是要根据题意将事件是分类互斥事件或分步相互独立事件,然后再利用加法原理和乘法原理进行求解.11.【答案】B【解析】解:分2步进行分析:1、先将3个歌舞类节目全排列,有种情况,排好后,有4个空位,2、因为3个歌舞类节目不能相邻,则中间2个空位必须安排2个节目,分2种情况讨论:将中间2个空位安排1个小品类节目和1个相声类节目,有种情况,排好后,最后1个小品类节目放在2端,有2种情况,此时同类节目不相邻的排法种数是种;将中间2个空位安排2个小品类节目,有种情况,排好后,有6个空位,相声类节目有6个空位可选,即有6种情况,此时同类节目不相邻的排法种数是种;则同类节目不相邻的排法种数是,故选:B.根据题意,分2步进行分析:、先将3个歌舞类节目全排列,、因为3个歌舞类节目不能相邻,则分2种情况讨论中间2个空位安排情况,由分步计数原理计算每一步的情况数目,进而由分类计数原理计算可得答案.本题考查计数原理的运用,注意分步方法的运用,既要满足题意的要求,还要计算或分类简便.12.【答案】D【解析】解:由导函数的图象和原函数的关系得,原函数的大致图象如图:由图得:为假命题,与上单调性相反,但原函数图象不一定对称.为真命题.因为在上导函数为负,故原函数递减;为假命题,当时,也满足时,的最大值是2;为假命题,当a离1非常接近时,对于第二个图,有2个零点,也可以是3个零点.综上得:真命题只有.故选D.先由导函数的图象和原函数的关系画出原函数的大致图象,再借助与图象和导函数的图象,对四个命题,一一进行验证,对于假命题采用举反例的方法进行排除即可得到答案.本题主要考查导函数和原函数的单调性之间的关系.二者之间的关系是:导函数为正,原函数递增;导函数为负,原函数递减.13.【答案】24【解析】解:展开式中的通项公式为,故第项的二项式系数为,故当时,二项式系数最大,故二项式系数最大的项的系数为,故答案为:24.由题意利用二项式展开式的通项公式、二项式系数的性质,求得二项式系数最大的项的系数.本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.14.【答案】16【解析】解:,故答案为:16.由定积分的定义进而求解.考查定积分的计算,属于基础题.15.【答案】150【解析】【分析】每所大学至少保送一人,可以分类来解,当5名学生分成2,2,1时,当5名学生分成3,1,1时根据分类计数原理得到结果.本题考查了分组分配问题,关键是如何分组,属于中档题.【解答】解:当5名学生分成2,2,1或3,1,1两种形式,当5名学生分成2,2,1时,共有种结果,当5名学生分成3,1,1时,共有种结果,根据分类计数原理知共有种,故答案为:150.16.【答案】【解析】解:假设是a,b,c不都是正数;所以不正确;函数,则,若在处取得极大值,则时方程的根,所以,解得或,当时,时,时,,所以是极小值点,与题意矛盾,所以不正确;时,左边加到,所以正确;由题意,时,,若是等比数列,则,,即,所以是必要条件;当时,,时,,是等比数列,所以是充分条件,所以正确.故答案为:.对每个命题逐个分析,判断它的正确与否.考查本题考查了命题的真假判断与应用,属于简单题.17.【答案】解:Ⅰ当,即时,z为实数;Ⅱ当,即,得时,z是纯虚数.【解析】Ⅰ由虚部为0求解m的值;Ⅱ由实部为0且虚部不为0列式求解.本题考查复数的基本概念,是基础题.18.【答案】解:,令得,当或时,,当时,,在上单调递减,在上单调递增,在上单调递减;由可知在上是减函数,在上是增函数,且,,,函数在上的最大值为11,最小值为.【解析】本题考查了导数与函数单调性,函数最值的关系,属于中档题.令求出极值点,判断的符号得出单调性;根据的单调性和区间端点函数值计算最值.19.【答案】解:Ⅰ设三种月饼各取到一个的概率为P,则;Ⅱ由题意可得:X可能的取值为0,1,2,3,所以,,,.所以的数学期望.【解析】Ⅰ直接利用组合数的应用求出概率的值.Ⅱ首先求出X的分布列,进一步求出X的数学期望.本题考查的知识要点:组合数的应用,数学期望的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题型.20.【答案】解:Ⅰ当时,,所以.当时,,所以.同理:,.由此猜想.Ⅱ证明:当时,左边,右边,结论成立.假设且时,结论成立,即,那么时,,所以,所以,这表明时,结论成立.由知对一切猜想成立.【解析】本题考查归纳推理,用数学归纳法证明等式,证明故当时,猜想也成立,是解题的难点和关键.Ⅰ通过,2,3,4,直接计算,,,,并由此猜想通项公式;Ⅱ直接利用数学归纳法证明.检验n取第一个值时,等式成立,假设,证明.21.【答案】解:Ⅰ记“该小组做了5次实验至少有2次成功”为事件A,“只成功一次”为事件,“一次都不成功”为事件,则:.故该小组做了5次这种实验至少有2次成功的概率为分Ⅱ的可能取值为2,3,4,5.则;,,每对一个得1 分分2 3 4 5P分分【解析】Ⅰ记“该小组做了5次实验至少有2次成功”为事件A,“只成功一次”为事件,“一次都不成功”为事件,则:由此能求出该小组做了5次这种实验至少有2次成功的概率.Ⅱ的可能取值为2,3,4,分别求出,,,的值,由此能求出的分布列和.本题考查离散型随机变量的分布列和数学期望,是历年高考的必考题型.解题时要认真审题,仔细解答,注意概率知识的灵活运用.22.【答案】解:Ⅰ,所以,所以分Ⅱ,其定义域为,,令,当时,,有,即,所以在区间上单调递减,故在区间无极值点;当时,,令,有,,,当时,,即,得在上递减;当时,,即 0'/>,得在上递增;当时,,即,得在上递减.此时有一个极小值点和一个极大值点.当时,,令,有,,当时,,即 0'/>,得在上递增;当时,,即,得在上递减.此时唯一的极大值点,无极小值点.综上可知,当时,函数有一个极小值点和一个极大值点.当时,函数在上有无极值点;当时,函数有唯一的极大值点,无极小值点;分令,,则若总存在,,使得成立,即总存在,,使得成立,即总存在,,使得成立,即,因为,所以,即在上单调递增,所以,即对任意成立,即对任意成立.构造函数:,,,当时,,在上单调递增,对于任意,.所以分【解析】Ⅰ求出函数的导数,得到,求出a的值即可;Ⅱ求出的导数,结合二次函数的性质,通过讨论b的范围,确定函数的单调区间,求出函数的极值点即可;Ⅲ令,,求出的导数,得到,问题转化为即对任意成立.构造函数:,,通过讨论函数的单调性,求出m的范围即可.本题考查了函数的单调性、最值、极值问题,考查导数的应用以及函数恒成立问题,考查分类讨论思想,是一道综合题.。
2019-2020学年重庆市七校联盟高二上学期联考数学(理)试题(解析版)

2019-2020学年重庆市七校联盟高二上学期联考数学(理)试题一、单选题1.在复平面内,复数()12z i i =-的共轭复数为 () A .2i -- B .2i -C .2i -+D .2i +【答案】B【解析】利用复数代数形式的乘除运算化简,再由共轭复数的概念得答案. 【详解】()122z i i i =-=+Q , 2z i ∴=-.故选:B. 【点睛】本题考查复数代数形式的乘除运算,考查复数的基本概念,属于基础题. 2.若2017220170122017(12)x a a x a x a x -=+++⋯⋯+,则1232017 a a a a ++⋯+=()A .2B .1C .1-D .2-【答案】D【解析】在所给的等式中,分别令0x =,1x =,可得要求式子的值. 【详解】2017220170122017(12)x a a x a x a x -=+++⋯⋯+Q ,令0x =,可得01a =. ∴再令1x =,可得012320171a a a a a +++⋯+=-,则12320172a a a a ++⋯+=-. 故选:D. 【点睛】本题主要考查二项式定理的应用,是给变量赋值问题,属于基础题.3.用反证法证明“若,a b ∈R ,220a b +=,则a ,b 全为0”时,假设正确的是( ) A .a ,b 中只有一个为0 B .a ,b 至少一个为0 C .a ,b 全不为0 D .a ,b 至少有一个不为0【答案】D【解析】分析:根据反证法的概念,把要证的结论否定后,即可得到所求的反设. 详解:由题意可知,由于“22,,0a b R a b ∈+=,则,a b 全为0”的否定为“,a b 至少有一个不为0”,故选D.点睛:本题主要考查了反证法的定义的理解与应用,正确理解反证法的基本概念是解答的关键,着重考查了推理与论证能力.4.命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是 () A .使用了归纳推理 B .使用了类比推理C .使用了“三段论”,但推理形式错误D .使用了“三段论”,但小前提错误 【答案】C【解析】有理数包含有限小数,无限不循环小数,以及整数,故有些有理数是无限循环小数,这个说法是错误的,即大前提是错误的. 【详解】Q 大前提的形式:“有些有理数是无限循环小数”,不是全称命题,∴不符合三段论推理形式, ∴推理形式错误.故选:C. 【点睛】本题考查演绎推理的基本方法,解题的关键是理解演绎推理的三段论原理,在大前提和小前提中,若有一个说法是错误的,则得到的结论就是错误的. 5.已知随机变量ξ服从正态分布()23,N σ,()40.68P ξ≤=,则()2P ξ≥=( )A .0.84B .0.68C .0.32D .0.16【答案】B【解析】直接利用正态分布的应用和密度曲线的对称性的应用求出结果. 【详解】根据随机变量ξ服从正态分布()23,N σ,所以密度曲线关于直线3x =对称,由于()40.68P ξ≤=,所以()410.680.32P ξ≥=-=, 所以()20.32P ξ≤=,则()2410.320.320.36P ξ≤≤=--=, 所以()20.360.320.68P ξ≥=+=. 故选:B. 【点睛】本题考查的知识要点:正态分布的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.6.已知函数()2f x alnx =+,()'2f e =,则a 的值为 () A .1- B .1C .2eD .2e【答案】C【解析】根据题意,求出函数的导数,将x e =代入可得2ae=,变形可得答案. 【详解】根据题意,函数()ln 2f x a x =+,则()a f x x'=, 若()2af e e'==,则2a e =. 故选:C. 【点睛】本题考查函数的导数计算,关键是掌握导数的计算公式,属于基础题.7.观察下列各式:a+b=1.a 2+b 2=3,a 3+b 3=4 ,a 4+b 4=7,a 5+b 5=11,…,则a 10+b 10=( ) A .28 B .76C .123D .199【答案】C 【解析】【详解】 由题观察可发现,347,4711,71118+=+=+=, 111829,182947+=+=, 294776,4776123+=+=,即1010123a b +=, 故选C.【考点】观察和归纳推理能力.8.从1,2,3,4,5中任取2个不同的数,事件A =“取到的2个数之和为偶数”,事件B =“取到两个数均为偶数”,则()|P B A =( )A .18B .14C .25D .12【答案】B【解析】先求得()P A 和()P AB 的值,然后利用条件概率计算公式,计算出所求的概率. 【详解】依题意()22322542105C C P A C +===,()22251=10C P AB C =,故()|P B A =()()1110245P AB P A ==.故选B. 【点睛】本小题主要考查条件概型的计算,考查运算求解能力,属于基础题.9.小王有70元钱,现有面值分别为20元和30元的两种IC 电话卡.若他至少买一张,则不同的买法共有( ) A .7种 B .8种 C .6种 D .9种 【答案】A【解析】要完成的一件事是“至少买一张IC 电话卡”,分三类完成:买1张IC 卡,买2张IC 卡,买3张IC 卡.而每一类都能独立完成“至少买一张IC 电话卡”这件事.买1张IC 卡有2种方法,即买一张20元面值的或买一张30元面值的;买2张IC 卡有3种方法,即买两张20元面值的或买两张30元面值的或20元面值的和30元面值的各买一张,买3张IC 卡有2种方法,即买两张20元面值的和一张30元面值的或3张20元面值的,故共有2+3+2=7(种)不同的买法. 10.设甲、乙两人每次射击命中目标的概率分别为34和45,且各次射击相互独立,若按甲、乙、甲、乙的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是 A .920 B .925 C .380 D .19400【答案】D【解析】试题分析:击中目标时甲射击了两次包括甲乙第一次均未击中、甲第二次击中,及甲前两次均未击中、乙第二次才击中,所以其概率为11311143119454454580100400P=⨯⨯+⨯⨯⨯=+=,故选D.【考点】独立重复试验的概率.11.某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是A.72 B.120 C.144 D.168【答案】B【解析】试题分析:将所有的安排方法分成两类,第一类:歌舞类节目中间不穿插相声节目,有32132262224A A A=⨯⨯=(种);第二类:歌舞类节目中间穿插相声节目,有31113224622496A A A A=⨯⨯⨯=(种);根据分类加法计数原理,共有96+24=120种不同的排法.故选B.【考点】1、分类加法计数原理;2、排列.12.已知函数的定义域为,部分对应值如下表:的导函数的图象如图所示,则下列关于函数的命题:①函数是周期函数;②函数在是减函数;③如果当时,的最大值是2,那么的最大值为4;④当时,函数有4个零点。
重庆市九校联盟高二上学期联考数学(文)试题解析版

2019-2020学年重庆市九校联盟高二上学期联考数学(文)试题一、单选题1.已知集合A ={1,2},B ={2,3},则A B I =( ) A .{}1,3 B .{}2 C .∅ D .{}1,2,3【答案】B【解析】根据交集的概念和运算,求得两个集合的交集. 【详解】交集是两个集合的公共元素组成,所以{}2A B ⋂=. 故选:B 【点睛】本小题主要考查交集的概念和运算,属于基础题. 2.极坐标方程化为直角坐标方程是( ) A . B .C .D .【答案】A【解析】试题分析:原极坐标方程可化为,所以其化为直角坐标方程是,即,故答案选.【考点】极坐标方程和平面直角坐标方程之间的关系.3.若复数满足12z i =+,则z 在复平面内对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】D【解析】求得z ,由此求得z 在复平面内对应的点以及对应的象限. 【详解】依题意12z i =-,对应的点为()1,2-,位于第四象限.故选:D 【点睛】本小题主要考查共轭复数,考查复数对应点所在象限,属于基础题.4. “因为四边形ABCD 是菱形,所以四边形ABCD 的对角线互相垂直”,补充以上推理的大前提正确的是( ) A .菱形都是四边形 B .四边形的对角线都互相垂直 C .菱形的对角线互相垂直 D .对角线互相垂直的四边形是菱形【答案】C【解析】根据三段论的知识确定正确选项. 【详解】根据小前提和结论可知,大前提为菱形的对角线互相垂直. 故选:C 【点睛】本小题主要考查三段论的理解,属于基础题.5.曲线323y x x =-+在1x =处的切线方程为( ) A .10x y -+= B .10x y --= C .10x y ++= D .10x y +-=【答案】A【解析】求得曲线在1x =处的切线斜率和切点坐标,由此求得切线方程. 【详解】依题意,'2'132,|321x y x y ==-=-=,且切点为()1,2,所以切线方程为21y x -=-,化简得10x y -+=. 故选:A. 【点睛】本小题主要考查曲线在某点处切线方程的求法,属于基础题. 6.二次函数243y x x =-+ 在区间(]1,4 上的值域是( )A .[)1,-+∞B .(]0,3C .[]1,3-D .(]1,3-【答案】C【解析】利用配方法化简函数解析式,根据二次函数的性质,求得函数在区间(]1,4上的值域. 【详解】由于()221y x =--,函数的对称轴为2x =,开口向上,所以当2x =时函数有最小值为1-,当4x =时,函数有最大值为3,所以函数在区间(]1,4 上的值域为[]1,3-. 故选:C 【点睛】本小题主要考查二次函数在给定区间上的值域的求法,属于基础题. 7.运行如图的程序框图,则输出s 的结果是( )A .16B .2524C .34D .1112【答案】B【解析】试题分析:210n =<成立,第一次循环,12s =,224n =+=; 410n =<成立,执行第二次循环,113244s =+=,426n =+=; 610n =<成立,执行第三次循环,,628n =+=;810n =<成立,执行第四次循环,1112512824s =+=,8210n =+=; 1010n =<不成立,输出s 的值为2524,故选B. 【考点】算法与程序框图8.给出下列四个命题:①“02x <<”是“2x <”成立的必要不充分条件②命题“若0a =,则0ab =”的否命题是:“若0a ≠,则0ab ≠”;③命题“0R x ∃∈,使得20010x x ++<”的否定是:“R x ∀∈,均有210x x ++>”④如果命题“p ⌝”与命题“p q ∨”都是真命题,那么命题q 一定是真命题;其中为真命题的个数是( ) A .4个 B .3个 C .2个 D .1个【答案】C【解析】根据充分、必要条件的知识,判断①的正确性;根据否命题的知识,判断②的正确性;根据特称命题的否定是全称命题的知识,判断③的正确性;根据含有逻辑联结词命题真假性的知识,判断④的正确性. 【详解】①,由于()()0,2,2-∞Ü,所以“02x <<”是“2x <”成立的充分不必要条件,所以①错误.②,根据否命题的知识可知,②正确.③,特称命题的否定是全称命题,注意到要否定结论,所以③错误. ④,由于“p ⌝”与命题“p q ∨”都是真命题,所以p 假q 真,所以④正确. 综上所述,真命题的个数是2个. 故选:C. 【点睛】本小题主要考查充分、必要条件,考查否命题,考查全称命题与特称命题,考查含有逻辑联结词命题真假性,属于基础题.9.若0.52a =,3log 2b =,2log 0.2c =,则 ( ) A .a b c >> B .b a c >> C .c a b >> D .b c a >>【答案】A【解析】利用“0,1分段法”判断出三者的大小关系. 【详解】 由于0.503322221,0log 2log 31,log 0.2log 10a b c =>=<=<==<=,所以a b c >>.故选:A 【点睛】本小题主要考查指数式、对数式比较大小,属于基础题.10.已知()f x 是定义在R 上的偶函数,且()()3f x f x +=-,当()2,0x ∈-时,()22f x x =,则()10f =( )A .2-B .2C .98-D .98【答案】A【解析】利用已知条件,化简求得()10f 的值. 【详解】由于()f x 是定义在R 上的偶函数,且()()3f x f x +=-,当()2,0x ∈-时,()22f x x =,所以()()()()()()()()1073434131232f f f f f f f f =+=-+==+=-=--+=-()()()()22131212f f f ==-+=--=-⨯-=-.故选:A 【点睛】本小题主要考查根据函数的性质求函数值,属于基础题.11. ()2()log 3a f x x ax =-+在()3,+∞上是增函数,则实数a 的取值范围是( )A .(),1-∞B .()1,2C .(]1,3D .(]1,4 【答案】D【解析】根据二次函数的性质,结合复合函数单调性同增异减列不等式组,解不等式组求得a 的取值范围. 【详解】 函数23y xax =-+的开口向上,对称轴为2a x =,在,2a ⎡⎫+∞⎪⎢⎣⎭上递增.根据复合函数单调性同增异减可知21323330a a a >⎧⎪⎪≤⎨⎪-+≥⎪⎩,解得14a <≤,所以实数a 的取值范围是(]1,4.故选:D 【点睛】本小题主要考查对数型复合函数的单调性,属于中等题.12.已知()f x 是R 上的可导函数,且对x R ∀∈均有()()f x f x '>,则以下说法正确的是( ) A .()()201820180f e f >B .()()201820180f e f <C .()()201820180f e f = D .()2018f 与()20180e f 的大小无法确定 【答案】A【解析】构造函数()()x f x g x e=,利用导数研究()g x 的单调性,由此判断出正确选项. 【详解】构造函数()()x f x g x e =,依题意()()()''0xf x f xg x e-=>,所以()g x 在R 上递增,所以()()20180g g >,即()()2018020180f f e e>,即()()201820180f e f >⋅. 故选:A 【点睛】本小题主要考查利用导数比较大小,属于基础题.二、填空题13.函数()()lg 1f x x =+的定义域为______. 【答案】(]1,3-【解析】根据偶次方根的被开方数为非负数,对数真数大于零列不等式组,解不等式组求得函数的定义域. 【详解】依题意29010x x ⎧-≥⎨+>⎩,解得331x x -≤≤⎧⎨>-⎩,解得13x -<≤,所以函数()f x 的定义域为(]1,3-.故答案为:(]1,3- 【点睛】本小题主要考查函数定义域的求法,属于基础题.14.i 是虚数单位,复数20171+ii z =,则复数z =______.【解析】根据复数乘方运算、复数除法运算以及复数模的运算,求得正确结果. 【详解】依题意,()()() 201720161111111111222i ii i i iz ii i i i i+-+======+++++-,所以22112222z⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭.故答案为:22【点睛】本小题主要考查复数运算,属于基础题.15.图,,,分别包含,,和个互不重叠的单位正方形,按同样的方式构造图形,则第个图包含个互不重叠的单位正方形.【答案】【解析】图1中包含1个单位正方形,图2在图1的基础上增加了4个单位正方形,有1+4=5个单位正方形,图3在图2的基础上增加了2×4=8个单位正方形,有5+5=13个单位正方形,图4在图3的基础上增加了3×4=12个单位正方形,有13+12=25个单位正方形.由此规律可知,第n个图在第1n-个图的基础上增加了4(1)n-个单位正方形,所以第n个图中有211141424(1)4(1)12212nn n n n+-+⨯+⨯++-=⨯⨯-+=-+L个单位正方形16.已知()2xf x=,()()212,3122,11x xg xg x x⎧-+-≤≤-⎪=⎨--<≤⎪⎩,则在区间()3,1-上方程()()0f xg x-=有______个实数解.【答案】4【解析】求得()g x在()3,1-上的解析式,画出()f x和()g x的图象,根据图象判断()()0f xg x-=的实数解的个数.【详解】当11x-<≤时,321x-<-≤-,所以()()22221g x g x x=-=-所以()()2212,3121,11x x g x x x ⎧-+-≤≤-⎪=⎨⎪--<≤⎩.注意到()()21231y x x =-+-≤≤-可化为()()222131x y x ++=-≤≤-,表示的图象是圆的上半部分.而()22111y x x =--<≤可化为()221114y x x +=-<≤,表示的图象是椭圆的上半部分.由此画出()f x 和()g x 的图象如下图所示,由图可知,两个函数图象有4个交点,所以()()0f x g x -=的实数解有4个.. 故答案为:4【点睛】本小题主要考查函数解析式的求法,考查方程的根的个数判断,考查数形结合的数学思想方法,属于中档题.三、解答题17.实数m 取什么数值时,复数z =()2221i 1m m z m m +-=+-+分别是:(1)实数? (2)纯虚数?【答案】(1)1m =;(2)2m =-.【解析】(1)复数为实数,则虚部为零,由此列方程,结合分式分母不为零,求得m 的值.(2)复数为纯虚数,则实部为零,虚部不为零,由此列式求得m 的值. 【详解】(1)由210m -=且10m +≠得,1m =. 所以,当1m =时,z 是实数;(2)由222011010m m m m m ⎧+-=⎪+⎪⎪+≠⎨⎪-≠⎪⎪⎩得,2m =-.当2m =-时,z 是纯虚数. 【点睛】本小题主要考查根据复数的类型求参数的值,属于基础题.18.随着中国教育改革的不断深入,越来越多的教育问题不断涌现.“衡水中学模式”入驻浙江,可以说是应试教育与素质教育的强烈碰撞.这一事件引起了广大市民的密切关注.为了了解广大市民关注教育问题与性别是否有关,记者在北京,上海,深圳随机调查了100位市民,其中男性55位,女性45位.男性中有45位关注教育问题,其余的不关注教育问题;女性中有30位关注教育问题,其余的不关注教育问题. (1)根据以上数据完成下列2×2列联表;(2)能否在犯错误的概率不超过0.025的前提下认为是否关注教育与性别有关系?参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.【答案】(1)见解析;(2)不能【解析】(1)根据表格所提供数据,补全2×2列联表. (2)计算2K 的值,对比题目所给数据,判断不能出在犯错误的概率不超过0.025的前提下认为关注教育与性别有关系. 【详解】(1)根据以上数据建立一个2×2列联表:(2)将2×2列联表将的数据代入公式()()()()()22n ad bc K a b c d a c b d -=++++得()221003010451575254555K ⨯⨯-⨯=⨯⨯⨯ 1003.03033=≈ 因为3.030<5.024,所以不能在犯错误的概率不超过0.025的前提下认为关注教育与性别有关系. 【点睛】本小题主要考查22⨯列联表独立性检验,属于基础题.19.假设某设备的使用年限x (年)和所支出的维修费用y (万元)有如下的统计资料,试求:(1221ni ii nii x y nx yb xnx ==-⋅=-∑∑,a y bx =-)y2.23.8 5.5 6.5 7.0(1)y 与x 之间的线性回归方程;(2)当使用年限为10年时,估计维修费用是多少?【答案】(1) 1.2308ˆ.0yx =+(2)12.38万元 【解析】(1)根据回归直线方程计算公式,计算出回归直线方程. (2)令10x =,代入回归直线方程,由此求得维修费用的估计值. 【详解】 (1)由已知得:()12345645x =++++=, ()12.23.8 5.5 6.57.055y =++++=, 512 2.23 3.84 5.55 6.567.0112.3i ii x y=⨯+=⨯+⨯+⨯+⨯=∑,222225122345690ii x==++++=∑,所以51522215112.3545ˆ 1.2390545i ii i i x y x ybx x ==-⋅-⨯⨯===-⨯-∑∑,$ˆ5 1.2340.08ay bx =-=-⨯=, ∴线性回归方程为$1.230.08y x =+.(2)当10x =时,$1.23100.0812.38y =⨯+=(万元), 即当使用10年时,估计维修费用是12.38万元. 【点睛】本小题主要考查回归直线方程的计算,并利用回归直线方程进行预测,属于基础题. 20.已知函数在处有极小值.(1)求、的值; (2)求出函数的单调区间.【答案】单调增区间为和,函数的单调减区间为.【解析】(1)由已知,可得f (1)=1-3a +2b =-1,①又f ′(x )=3x 2-6ax +2b ,∴f ′(1)=3-6a +2b =0.②由①②解得(2)由(1)得函数的解析式为f (x )=x 3-x 2-x . 由此得f ′(x )=3x 2-2x -1. 根据二次函数的性质, 当x <-或x >1时,f ′(x )>0; 当-<x <1时,f ′(x )<0. 因此,在区间和(1,+∞)上,函数f (x )为增函数;在区间上,函数f (x )为减函数.21.已知函数()ln f x x ax =-在2x =处的切线l 与直线230x y +-=平行. (1)求实数a 的值;(2)若函数()22y f x m x x =+-+在1,22⎡⎤⎢⎥⎣⎦上恰有两个零点,求实数m 的取值范围.(3)记函数()()212g x f x x bx =+-,设()1212,x x x x <是函数()g x 的两个极值点,若32b ≥,且()()12g x g x k -≥恒成立,求实数k 的最大值. 【答案】(1)1a =;(2)5ln 224m +≤<;(3)152ln 28- 【解析】(1)利用导数和切线的斜率列方程,解方程求得a 的值. (2)由(1)求得()f x 的解析式.构造函数()()()220h x f x m x xx =+-+>,利用导数研究()h x 的单调性,以及极值,结合()h x 在1,22⎡⎤⎢⎥⎣⎦上恰有两个零点列不等式组,解不等式组求得m 的取值范围.(3)利用导数,结合根与系数关系,求得()g x 两个极值点的关系式,将()()12g x g x -表示为只含1x 的表达式,由此利用导数求得()()12g x g x -的最小值,由此求得k 的取值范围.【详解】 (1)1()f x a x'=-, ∵函数()ln f x x ax =-在2x = 处的切线l 与直线230x y +-=平行, ∴()11222k f a '==-=-,解得1a =; (2)由(1)得()ln f x x x =-,∴函数()()2223ln 0y f x m x x x x x m x =+-+=-++>,令()()23ln 0h x x x x m x =-++>,则()()()211123x x h x x x x--'=-+=, 令()0h x '=得11x =,21x =,列表得:∴当1x =时,()h x 的极小值为()12h m =-,又15ln 224h m ⎛⎫=--⎪⎝⎭,()22ln 2h m =-+∵函数()22y f x m x x =+-+在1,22⎡⎤⎢⎥⎣⎦上恰有两个零点∴102(1)0(2)0h h h ⎧⎛⎫≥ ⎪⎪⎝⎭⎪⎪<⎨⎪≥⎪⎪⎩即5ln 204202ln 20m m m ⎧--≥⎪⎪-<⎨⎪-+≥⎪⎩,解得5ln 224m +≤<.(3)Q ()()21ln 12g x x x b x =+-+,∴()()()21111x b x g x x b x x-++'=+-+=,令()0g x '=得()2110x b x -++=,∵1x ,2x 是()g x 的极值点,∴121x x b +=+,121=x x ,∴211x x =, ∵32b ≥,∴121215210x x x x x ⎧+≥⎪⎪⎨⎪<<=⎪⎩解得:1102x <≤,∴()()()()()22112121221ln12x g x g x x x b x x x -=+--+-, ()2221121112111112ln 2ln ,0222x x x x x x x ⎛⎫⎛⎫=--=--<≤ ⎪ ⎪⎝⎭⎝⎭ 令()221112ln ,022F x x x x x ⎛⎫⎛⎫=--<≤ ⎪ ⎪⎝⎭⎝⎭,则()()22331210x F x x x xx --'=--=<,∴()F x 在10,2⎛⎤⎥⎝⎦上单调递减;∴当12x =时()min 1152ln 228F x F ⎛⎫==- ⎪⎝⎭,∴k 的最大值为152ln 28-. 【点睛】本小题主要考查利用导数研究函数的单调性和极值,考查利用导数研究函数的零点,考查利用导数研究不等式恒成立问题,考查化归与转化的数学思想方法,属于难题.22.已知直线l 的参数方程:12x ty t=⎧⎨=+⎩(t 为参数)和圆C 的极坐标方程:2sin ρθ=(1)将直线l 的参数方程化为普通方程,圆C 的极坐标方程化为直角坐标方程; (2)已知点()1,3M ,直线l 与圆C 相交于A 、B 两点,求MA MB +的值. 【答案】(1)l : 21y x =+, C :()2211x y +-=;(2)【解析】(1)消去参数t 求得直线l 的普通方程,将2sin ρθ=两边同乘以ρ,化简求得圆C 的直角坐标方程.(2)求得直线l 的标准参数方程,代入圆的直角坐标方程,化简后写出韦达定理,根据直线参数的几何意义,求得MA MB +的值. 【详解】(1)消去参数t ,得直线l 的普通方程为21y x =+,将2sin ρθ=两边同乘以ρ得22sin ρρθ=,()2211x y +-=,∴圆C 的直角坐标方程为()2211x y +-=;(2)经检验点()1,3M 在直线l 上,12x t y t =⎧⎨=+⎩可转化为51253x t y t⎧=+⎪⎪⎨⎪=+⎪⎩①, 将①式代入圆C 的直角坐标方程为()2211x y +-=得22525121t t ⎛⎫⎛⎫+++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 化简得22540t t ++=,设12,t t 是方程22540t t ++=的两根,则1225t t +=-,124t t =, ∵1240t t =>,∴1t 与2t 同号,由t 的几何意义得121225MA MB t t t t +=+=+=. 【点睛】本小题主要考查参数方程化为普通方程、极坐标方程化为直角坐标方程,考查利用直线参数的几何意义求解距离问题,属于中档题. 23.已知函数()|2|f x x a a =-+.(1)当a=2时,求不等式()6f x ≤的解集;(2)设函数()|21|g x x =-.当x ∈R 时,()()3f x g x +≥,求a 的取值范围. 【答案】(1){|13}x x -≤≤;(2)[2,)+∞. 【解析】试题分析:(1)当2a =时⇒()|22|2f x x =-+⇒|22|26x -+≤⇒13x -≤≤;(2)由()()|2||12|f x g x x a a x +=-++-|212|x a x a ≥-+-+|1|a a =-+⇒()()3f x g x +≥等价于|1|3a a -+≥,解之得2a ≥.试题解析: (1)当2a =时,()|22|2f x x =-+. 解不等式|22|26x -+≤,得13x -≤≤. 因此,()6f x ≤的解集为.(2)当x ∈R 时,()()|2||12|f x g x x a a x +=-++-|212|x a x a ≥-+-+|1|a a =-+,当12x =时等号成立, 所以当x ∈R 时,()()3f x g x +≥等价于|1|3a a -+≥. ① 当1a ≤时,①等价于13a a -+≥,无解. 当1a >时,①等价于13a a -+≥,解得2a ≥. 所以a 的取值范围是[2,)+∞. 【考点】不等式选讲.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆市七校联盟2019-2020学年高二上学期联考文科数学试题一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目的要求)1.(原创)设i 为虚数单位,则复数)2(i i z -=对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限 2.下列图中的两个变量是相关关系的是A.①②B.①③C.②④D.②③3.(原创)已知回归直线斜率的估计值为1.32,样本点的中心为点(2,3),则回归直线的方程为A.432.1+=∧x y B. 532.1+=∧x y C. 36.032.1+=∧x y D. 32.108.0+=∧x y4.设iiz +=310,则z 的共轭复数为 A .i 31+- B . i 31-- C . i 31+ D . i 31-5.用三段论推理:“任何实数的平方大于0,因为a 是实数,所以02>a ”,你认为这个推理 A.大前提错误 B.小前提错误 C.推理形式错误 D.是正确的6.用反证法证明命题时,对结论:“自然数c b a ,,中至少有一个是偶数”正确的假设为 A .c b a ,,都是奇数 B .c b a ,,都是偶数C .c b a ,,中至少有两个偶数D .c b a ,,中至少有两个偶数或都是奇数7.(原创)若图1的框图所给的程序运行结果为20S =,那么判断框中应填入的关于k 的条件是A .9k =?B .8k >?C .?2>kD .8k ≤?8.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是A.若2k 的观测值为6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;C.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系,是指有5% 的可能性使得推判出现错误;D.以上三种说法都不正确 9.设z y x ,,都是正实数,,1,1,1xz c z y b y x a +=+=+=则c b a ,,三个 A.至少有一个不大于2 B.都小于2 C.至少有一个不小于2 D.都大于210.观察x x 2)('2=,3'44x x =)(,x x sin )cos ('-=,由归纳推理可得:若定 义在R 上的函数)(x f 满足)()(x f x f =-,记)(x g 为)(x f 的导函数,则=-)(x g A.)(x f B.)(x f - C.)(x g D.)(x g -11.复数21,z z 满足i m m z )4(21-+=,i z )sin 3(cos 22θλθ++=),,(R m ∈θλ,并且21z z =,则λ的取值范围是A. ]1,1[-B. ]1,169[-C. ]7,169[-D. ]7,169[12.已知定义在R 上的可导函数)(x f 的导函数为)('x f ,满足)()('x f x f <,且)2(+x f 为偶函数, 1)4(=f ,则不等式xe xf <)(的解集为A. ),2(+∞-B. ),0(+∞C. ),1(+∞D. ),4(+∞ 二.填空题(本大题共4小题,每小题5分,共20分)13.(原创)要证明“1035>+”可选择的方法有以下几种,其中最合理的是 .(填序号)①反证法 ②分析法 ③综合法.14.甲、乙、丙三名同学中只有一人考了满分,当他们被问到谁考了满分时,回答如下.甲说:丙没有考满分;乙说:是我考的;丙说:甲说的是真话.事实证明:在这三名同学中,只有一人说的是假话,那么得满分的同学是 .15.若不等式042≥++ax x 对一切]1,0(∈x 恒成立,则a 的取值范围是 .16. (原创)如图,它满足第n 行首尾两数均为n ,则第n 行(n≥2)第2个数是 .三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17.(本小题满分12分)(原创)当m 为何实数时,复数i m m m m m z )82(4622--+---=是 (1)实数; (2)纯虚数.18.(本小题满分12分)(原创)A 、B 、C 、D 、E 五位学生的语文成绩x 与英语成绩y (单位:分)如下表:(1)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程∧∧∧+=a x b y ;(参考数值:2319062606465687066757080=⨯+⨯+⨯+⨯+⨯,24750606570758022222=++++)(2)若学生F 的语文成绩为90分,试根据(1)求出的线性回归方程,预测其英语成绩(结果保留整数).(参考公式:∧∧∧+=a x b y ,其中∑∑==∧--=ni ini ii xn xyx n y x b 1221)19.(本小题满分12分)“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金。
在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示:(1)列出2×2列联表;判断是否有90%的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(下面的临界值表供参考)(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中至少有一人在20~30岁之间的概率.(参考公式: ))()()(()(22b d dc c a b a bc ad n K ++++-=.其中d c b a n +++=.)20.(本小题满分12分)设12)(23+++=bx ax x x f 的导函数为)('x f ,若=y )('x f 的图像关于直线21-=x 对称,且0)1('=f (1)求实数b a ,的值; (2)求函数)(x f 的极值.21.(本小题满分12分)已知函数xx k x g x x f )1()(,ln )(-==. (1)当k=e 时,求函数)()()(x g x f x h -=的单调区间; (2) 若)()(x g x f ≥恒成立,求实数k 的值.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分。
作答时请写清题号22.(本小题满分10分)选修4-4:坐标系与参数方程选讲 已知直线l 的方程为4y x =+,圆C 的参数方程为2cos 22sin x y θθ=⎧⎨=+⎩(θ为参数),以原点为极点,x 轴正半轴为极轴,建立极坐标系. (1)求直线l 与圆C 的交点的极坐标;(2) 若P 为圆C 上的动点,求P 到直线l 的距离d 的最大值.23.(本小题满分10分)选修4-1:几何证明选讲在△ABC 中,CD 是∠ACB 的平分线,△ACD 的外接圆交BC 于点E ,AB=2AC . (1)求证:BE=2AD ;(2)当AC=1,EC=2时,求AD 的长.24.(本小题满分10分)选修4-5:不等式选讲 设函数122)(+--=x x x f . (1)求不等式x x f ≤)(的解集;(2)若不等式t t x f -≥2)(在x ∈[-2,-1]时恒成立,求实数t 的取值范围.重庆市七校联考高二数学文科参考答案一.选择题(每题5分,共60分)二.填空题(每题5分,共20分)13、② 14、甲15、[)+∞-,5 16、222+-n n三、解答题17. (本小题满分12分)解:(1)当⎩⎨⎧=--≠-082042m m m ………………………………3分即2-=m 时,z 是实数; ………………………………6分(2)当⎪⎩⎪⎨⎧≠--=---08204622m m m m m (8)分⎩⎨⎧≠-≠-=⇒4223m m m 且或 ………………………………10分3=∴m 时,z 是纯虚数. ………………………………12分18. (本小题满分12分) 解:(1)因为7056065707580=++++=x , …………………1分6656264686670=++++=y , …………………2分231906260646568706675708051=⨯+⨯+⨯+⨯+⨯=∑=ii i yx ,…3分24750606570758022222512=++++=∑=i ix……………4分所以36.0705247506670523190552512251=⨯-⨯⨯-=--=∑∑==∧i ii ii xxy x yx b ,……6分 8.407036.066=⨯-=-=∧∧x b y a . ……8分故所求线性回归方程为8.4036.0+=∧x y . ………………9分(2)由(1),当x=90时, 732.738.409036.0≈=+⨯=∧y , ………11分 答:预测学生F 的英语成绩为73分. ………………12分 19. (本小题满分12分) 解 :(1)22⨯列联表:则706.23100804020)30107010(120))()()(()(222>=⨯⨯⨯⨯-⨯⨯=++++-=b d dc c a b a bc ad n K …5分 所以有%90的把握认为猜对歌曲名称与否和年龄有关. ……6分(2)设事件A 为3名幸运选手中至少有一人在20~30岁之间,由已知得20~30岁之间的人数为2人,30~40岁之间的人数为4人,从6人中取3人的结果有20种,事件A 的结果有16种,则542016)(==A P . ………………………12分 20.(本小题满分12分)解:(1)因12)(23+++=bx ax x x f ,故b ax x x f ++=26)(2', ……2分从而6)6(6)(22'a b a x x f -++=,即)('x f y =关于直线6a x -=对称,从而由题设条件知216-=-a ,解得3=a ………………4分 又由于0)1('=f ,即026=++b a ,解得12-=b . …………5分 (2)由(1)知11232)(23+-+=x x x x f ,)2)(1(61266)(2'+-=-+=x x x x x f ………………6分令0)('=x f ,即0)2)(1(6=+-x x ,解得1,221=-=x x . ………………7分 当)2,(--∞∈x 时, 0)('>x f ,故)(x f 在)2,(--∞∈x 上为增函数; …………9分 当)1,2(-∈x 时, 0)('<x f ,故)(x f 在)1,2(-∈x 上为减函数; ……………10分 当),1(+∞∈x 时, 0)('>x f ,故)(x f 在),1(+∞∈x 上为增函数; …………11分 ∴函数)(x f 极大值为21)2(=-f ,极小值为6)1(-=f . ………12分 21.(本小题满分12分) 解:(1)当e k =时, 22'1)(xex x e x x h -=-=, ……………2分 若e x <<0,则0)('<x h ;若e x >,则0)('>x h .所以)(x h 是),0(e 上的减函数,是),(+∞e 上的增函数,故函数)(x h 的减区间为),0(e ,增区间为),(+∞e …5分 (2)解:由⑴知22'1)(xk x x k x x h -=-=, 当0≤k 时, 0)('>x h 对0>x 恒成立,所以)(x h 是),0(+∞上的增函数, 注意到0)1(=h ,所以10<<x 时, 0)(<x h 不合题意. ……………7分 当0>k 时,若k x <<0,0)('<x h ;若k x >,0)('>x h .所以)(x h 是),0(k 上的减函数,是),(+∞k 上的增函数, ……………8分 故只需01ln )()(min ≥+-==k k k h x h . ………………………9分 令)0(1ln )(>+-=x x x x u ,xxx x u -=-=111)(', 当10<<x 时,0)('>x u ; 当1>x 时,0)('<x u . 所以)(x u 是)1,0(上的增函数,是),1(+∞上的减函数. 故0)1()(=≤u x u 当且仅当1=x 时等号成立.所以当且仅当1=k 时,0)(≥x h 成立,即1=k 为所求.……………12分 22.(本小题满分10分) 解:(1)直线l:4y x =+,圆C :()2224x y +-=, …………………1分联立方程组()22424y x x y =+⎧⎪⎨+-=⎪⎩,解得22x y =-⎧⎨=⎩或4x y =⎧⎨=⎩, …………………3分 对应的极坐标分别为34π⎛⎫⎪⎝⎭,4,2π⎛⎫⎪⎝⎭…………………………………5分 (2)[方法1]设()2cos ,22sin P θθ+,则14d πθ⎛⎫==++ ⎪⎝⎭,当cos 14πθ⎛⎫+= ⎪⎝⎭时,d取得最大值2+…………………………………10分[方法2]圆心()0,2C 到直线l=,圆的半径为2,所以P 到直线l 的距离d的最大值为2+…………………………………10分23.(本小题满分10分)证明:(1)连接DE ,由于四边形DECA 是圆的内接四边形,所以:∠BDE=∠BCA …………………………………1分∠B 是公共角, ……………………………2分则:△BDE ∽△BCA . ……………………………3分 则:ACDE AB BE =, 又:AB=2AC所以:BE=2DE ,CD 是∠ACB 的平分线,所以:AD=DE , ……………………………………………………4分则:BE=2AD . ………………………………………………5分(2)由于AC=1,所以:AB=2AC=2. …………………………………………6分利用割线定理得:BD •AB=BE •BC , ……………………………………………8分由于:BE=2AD ,设AD=t ,则:2(2﹣t )=(2+2t )•2t ………………………………………9分解得:t=21, 即AD 的长为21. …………………………………………10分 24.(本小题满分10分)解:(1)=)(x f 2,3,221,13213≥--<<-+--≤+x x x x x x , x x f ≤)(由, ………………2分解得, x x x ≤+-≤321 ,或 x x x ≤+-<<-13221 ,或 x x x ≤--≥32 ,………………4分 故解集为⎪⎭⎫⎢⎣⎡+∞,41: ………………………………5分(2)依题意得,不等式[]1,2)(2--∈-≥x t t x f 在时恒成立t t x f -≥⇔2min )(, [],3)(,1,2+=--∈x x f x 且)(x f 在[]1,2--∈x 上单调递增, 所以2512511,1)2()(2min +≤≤-⇒≤-=-=t t t f x f 则 ………………10分。
