《直线与圆的位置关系》练习题

合集下载

直线与圆的位置关系经典例题

直线与圆的位置关系经典例题一、点与圆的位置关系结合图形认识直线与圆的位置关系，比较OA 与r 的大小关系若点A 在⊙O 内OA r 若点A 在⊙O 上OA r 若点A 在⊙O 外OA r小练习：1.在△ABC 中，90C ∠=︒,AC=2,BC=4,如果以点A 为圆心，AC 为半径作⊙A，那么斜边中点D 与⊙A 的位置关系是（）（A）D 在圆外（B）D 在圆上（C）D 在圆内（D）无法确定二、直线与圆的位置关系（1）实验创境：用移动的观点认识如果我们把太阳看作一个圆，那么太阳在升起的过程中，太阳和海平面就有图中的几种位置关系。

（可让学生用硬币自己操作演示）根据直线与圆公共点的个数可以得到三种位置关系：、、。

（2）用数量关系判断从以上的一个例子，可以看到，直线与圆的位置关系只有以下三种，如下图所示：若要判断圆与直线的位置关系，可以将______与_____进行比较大小，由比较的结果得出结论。

典型例题：例1、已知圆的半径等于5厘米，圆心到直线MN 的距离是：（1）4厘米；（2）5厘米；（3）6厘米。

分别说出直线MN 与圆的位置关系以及直线MN 和圆分别有几个公共点？例2.Rt △ABC 中，∠C=90°，AC=3，BC=4，若以C 为圆心，r 为半径作圆，当3,4.2,2===r r r 时，⊙C 与直线AB 分别是怎样的位置关系？★①直线l 和⊙O 相交d r ②直线l 和⊙O 相切d r ③直线l 和⊙O 相离d r1、如果⊙O 的直径为10厘米，圆心O 到直线AB 的距离为10厘米，那么⊙O 与直线AB有怎样的位置关系是2、已知：⊙A 的直径为6，点A 的坐标为)4,3(--，则⊙A 与x 轴的位置关系是；⊙A 与y 轴的位置关系是。

三、切线的判定实验探究：在练习纸上画⊙O ，在⊙O 上任取一点A ，连结OA ，过A 点作直线l ⊥OA ，判断直线l 是否与⊙O 相切？为什么？当直线和圆有唯一公共点时，直线是圆的切线；当直线和圆的距离等于该圆半径时，直线是圆的切线；那么，直接从直线和圆的位置上观察，具备什么条件的直线也是圆的切线呢？两个条件缺一不可（1）经过半径外端（2）垂直于这条半径切线判定定理：经过直径外端并且于这条直径的直线是圆的切线。

(附答案)《直线与圆的位置关系》典型例题

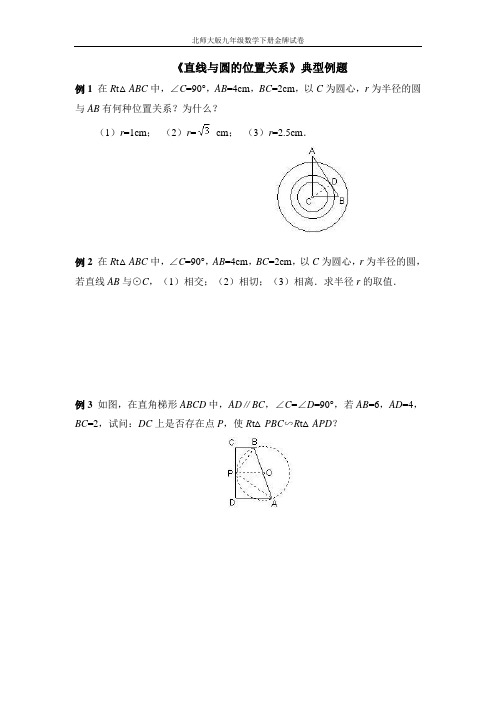
《直线与圆的位置关系》典型例题例1在R t△ABC中，∠C=90°，AB=4cm，BC=2cm，以C为圆心，r为半径的圆与AB有何种位置关系？为什么？（1）r=1cm；（2）r=cm；（3）r=2.5cm．例2 在R t△ABC中，∠C=90°，AB=4cm，BC=2cm，以C为圆心，r为半径的圆，若直线AB与⊙C，（1）相交；（2）相切；（3）相离．求半径r的取值．例3如图，在直角梯形ABCD中，AD∥BC，∠C=∠D=90°，若AB=6，AD=4，BC=2，试问：DC上是否存在点P，使R t△PBC∽R t△APD？例4如图，直角梯形中，，，，为上的一点，平分，平分.求证：以为直径的圆与相切.例5已知中，，于，，，以为圆心，为半径画圆.求证直线和⊙相离.参考答案例1分析如图，欲判定⊙C与直线AB的关系，只需先求出圆心C到直线AB的距离CD的长，然后再与r比较即可．解：过C点作CD⊥AB于D，在R t△ABC中，∠C=90°，AB=4，BC=2，∴AC=2，∴AB·CD=AC·BC，∴，（1）当r =1cm时CD＞r，∴圆C与AB相离；（2）当r=cm时，CD=r，∴圆C与AB相切；（3）当r=2.5cm时，CD＜r，∴圆C与AB相交．说明：从“数”到“形”，判定圆与直线位置关系．例2 解：过C点作CD⊥AB于D，在R t△ABC中，∠C=90°，AB=4，BC=2，∴AC=2，∴AB·CD=AC·BC，∴，（1）∵直线AB与⊙C相离，∴0r<CD，即0<r<；（2）∵直线AB与⊙C相切，∴r =CD，即r=；（3）∵直线AB与⊙C相交，∴r>CD，即r>．说明：从“形”到“数”，由圆与直线位置关系来确定半径．例3 分析：若R t△PBC∽R t△APD，则∠APD+∠BPC=90°，可知∠APB=90°，所以P点为以AB为直径的圆O与DC的交点，由条件可知为⊙O与DC相切，所以存在一点P，使R t△PBC∽R t△APD．解：设以AB为直径的圆为⊙O，OP⊥DC，则：OP为直角梯形ABCD的中位线，∴OP=（AD+BC）/2=（4+2）/2=3，又∵OA=OB=AB/2=3，∴OP=OA，∴⊙O与DC相切，∴∠APB=90°，∴∠APD+∠BPC=90°．又∵∠PBC+∠BPC=90°，∴∠APD=∠PBC，又∵∠C=∠D=90°，∴R t△PBC∽R t△APD．因此，DC上存在点P，使R t△PBC∽R t△APD．说明：①直线与圆位置关系的应用；②此题目可以变动数值，使DC与⊙O 相交、相离．例4 分析：要证以为直径的圆与相切，只需证明的中点到的距离等于.证明：过点作于，同理可证：为的中点，即：以为直径的圆与相切.说明：在判定直线是圆的切线时，若条件没有告诉它们有公共点，常用的方法就是“距离判定”法，即先由圆心到该直线作垂线，证明圆心到该直线的距离恰好等于半径，从而得出直线是圆的切线的结论.例5 分析：欲证直线和⊙相离，只需计算点到的距离的长，若，则判定与⊙相离（如图）证明于，是圆心到的距离∽.又⊙的半径为，故与⊙相离.学习要有三心:一信心；二决心；三恒心.知识+方法=能力,能力+勤奋=效率,效率×时间=成绩. 宝剑锋从磨砺出,梅花香自苦寒来.。

直线与圆的位置关系练习题及参考答案

直线与圆的位置关系练习题及参考答案一、选择题1. 在平面上，已知点A(4,-2)，圆心O(1,3)，半径R=5. 则点A与圆的位置关系是：A. A在圆内B. A在圆上C. A在圆外答案： A. A在圆内2. 已知直线L的方程为2x - 3y = 6，圆C的方程为x^2 + y^2 = 25.则直线L与圆C的位置关系是：A. 直线L与圆C相切B. 直线L与圆C相交于两点C. 直线L与圆C不相交答案： B. 直线L与圆C相交于两点3. 在平面上，已知两个圆C1与C2，圆C1的半径为3，圆心坐标为(1,1)，圆C2的半径为2，圆心坐标为(-2,-3). 则两个圆的位置关系是：A. 两个圆相交于两点B. 两个圆内切C. 两个圆相离答案： C. 两个圆相离二、填空题1. 已知圆C的半径为2，圆心坐标为(3,5). 则圆心到原点的距离是______.答案： sqrt(3^2 + 5^2) = sqrt(34)2. 在平面上，已知直线L的方程为y = 2x + 1，圆C的半径为4，圆心坐标为(-1,2). 则直线L与圆C的位置关系可以表示为______.答案： (x+1)^2 + (y-2)^2 = 16三、解答题1. 如图所示，在平面上有一个圆C，其圆心坐标为(2,3)，半径为4. 请写出圆C的方程，并确定点A(-3,4)与圆C的位置关系。

解答：圆C的方程为：(x-2)^2 + (y-3)^2 = 16点A(-3,4)与圆C的位置关系可以通过计算点A到圆心的距离来判断。

点A到圆心的距离为：distance = sqrt((-3-2)^2 + (4-3)^2) = sqrt(25) = 5比较点A到圆C的距离与圆的半径的关系：若 distance < 4，则点A在圆内；若 distance = 4，则点A在圆上；若 distance > 4，则点A在圆外。

因为 distance = 5 > 4，所以点A在圆外。

九年级直线与圆的位置关系练习(含答案)

直线与圆的位置关系练习(含答案)一．选择题（共19小题）1．如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠BAC的大小是（）A．70°B．40°C．50°D．20°2．已知⊙O的半径为4cm，如果圆心O到直线l的距离为3.5cm，那么直线l与⊙O的位置关系是（）A．相交B．相切C．相离D．不确定3．如图，PA、PB切⊙O于点A、B，PA=10，CD切⊙O于点E，交PA、PB于C、D两点，则△PCD的周长是（）A．10 B．18 C．20 D．224．已知⊙O的半径为3，圆心O到直线L的距离为2，则直线L与⊙O的位置关系是（）A．相交B．相切C．相离D．不能确定5．如图，AB是⊙O的直径，PA切⊙O于点A，OP交⊙O于点C，连接BC．若∠P=20°，则∠B的度数是（）A．20°B．25°C．30°D．35°6．如图，⊙O过正方形ABCD的顶点A、B，且与CD相切，若正方形ABCD的边长为2，则⊙O的半径为（）A．1 B．C．D．7．如图，已知⊙O的直径AB与弦AC的夹角为35°，过C点的切线PC与AB的延长线交于点P，则∠P等于（）A．15°B．20°C．25°D．30°8．如图，PA和PB是⊙O的切线，点A和B是切点，AC是⊙O的直径，已知∠P=40°，则∠ACB的大小是（）A．60°B．65°C．70°D．75°9．如图，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA=5，则△PCD的周长为（）A．5 B．7 C．8 D．1010．如图，⊙C与∠AOB的两边分别相切，其中OA边与⊙C相切于点P．若∠AOB=90°，OP=6，则OC的长为（）A．12 B．C．D．11．如图，已知直线AD是⊙O的切线，点A为切点，OD交⊙O于点B，点C在⊙O上，且∠ODA=36°，则∠ACB的度数为（）A．54°B．36°C．30°D．27°12．AB是⊙O的直径，PA切⊙O于点A，PO交⊙O于点C；连接BC，若∠P=40°，则∠B等于（）A．20°B．25°C．30°D．40°13．把直尺、三角尺和圆形螺母按如图所示放置于桌面上，∠CAB=60°，若量出AD=6cm，则圆形螺母的外直径是（）A．12cm B．24cm C．6cm D．12cm14．如图，AB是⊙O的直径，PA切⊙O于点A，连结PO并延长交⊙O于点C，连结AC，AB=10，∠P=30°，则AC的长度是（）A．B．C．5 D．15．已知⊙O的半径是5，直线l是⊙O的切线，P是l上的任一点，那么（）A．0＜OP＜5 B．OP=5 C．OP＞5 D．OP≥516．如图，△ABC的边AC与⊙O相交于C，D两点，且经过圆心O，边AB与⊙O相切，切点为B．如果∠A=34°，那么∠C等于（）A．28°B．33°C．34°D．56°17．如图，AB是⊙O的直径，点C在⊙O上，过点C作⊙O的切线交AB的延长线于点D，连接OC，AC．若∠D=50°，则∠A的度数是（）A．20°B．25°C．40°D．50°18．如图，PA、PB是⊙O的切线，切点分别是A，B，如果∠P=60°，那么∠AOB 等于（）A．60°B．90°C．120° D．150°19．如图，AB、AC是⊙O的两条弦，∠A=25°，过点C的切线与OB的延长线交于点D，则∠D的度数（）A．25°B．30°C．40°D．50°二．填空题（共16小题）20．如图，⊙M与x轴相切于原点，平行于y轴的直线交⊙M于P、Q两点，P 点在Q点的下方．若点P的坐标是（2，1），则圆心M的坐标是．21．如图，Rt△ABC中，∠C=90°，若AC=4，BC=3，则△ABC的内切圆半径r=．22．如图，AB与⊙O相切于点C，∠A=∠B，⊙O的半径为6，AB=16，则OA的长为．23．如图，PA、PB分别与⊙O相切于A、B两点，若∠C=65°，则∠P的度数为．24．如图，平面直角坐标系中，⊙P与x轴分别交于A、B两点，点P的坐标为（3，﹣1），AB=2．若将⊙P向上平移，则⊙P与x轴相切时点P的坐标为．25．一直角三角形的两条直角边长分别为6和8，则它的内切圆半径为．26．若⊙O的直径是4，圆心O到直线l的距离为3，则直线l与⊙O的位置关系是．27．如图，在平面直角坐标系中，⊙M与x轴相切于点A（8，0），与y轴分别交于点B（0，4）和点C（0，16），则圆心M的坐标为．28．如图，线段AB与⊙O相切于点B，线段AO与⊙O相交于点C，AB=12，AC=8，则⊙O的半径长为．29．如图，AC是⊙O的切线，切点为C，BC是⊙O的直径，AB交⊙O于点D，连接OD，若∠A=50°，则∠COD的度数为．30．在平面直角坐标系中，O是坐标原点，A、B两点的坐标分别为（3，0）、（0，4），则△AOB的内心与外心之间的距离是．31．P是⊙O的直径AB的延长线上一点，PC与⊙O相切于点C，∠APC的平分线交AC于Q，则∠PQC=．32．如图，AB、AC、BD是⊙O的切线，P、C、D为切点，如果AB=5，AC=3，则BD的长为．33．如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=50°，则∠BAC=．34．如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC，∠P=40°，则∠ABC的度数为．35．如图，已知⊙O的外切△PCD切⊙O于A、B、E三点，（1）若PA=5，则PB=；（2）若∠P=40°，则∠COD=度．三．解答题（共15小题）36．如图，CD是⊙O的直径，并且AC=BC，AD=BD．求证：直线AB是⊙O的切线．37．如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE丄AB，交AB的延长线于点E．（1）求证：CB平分∠ACE；（2）若BE=3，CE=4，求⊙O的半径．38．在Rt△ABC中，∠ACB=90°，BE平分∠ABC，D是边AB上一点，以BD为直径的⊙O经过点E，且交BC于点F．（1）求证：AC是⊙O的切线；（2）若BF=6，⊙O的半径为5，求CE的长．39．如图，在Rt△ABC中，∠ABC=90°，以AB为直径的⊙O与AC边交于点D，过点D作⊙O的切线交BC于点E，连接OE（1）证明OE∥AD；（2）①当∠BAC=°时，四边形ODEB是正方形．②当∠BAC=°时，AD=3DE．40．如图所示，AB是⊙O的直径，AD与⊙O相切于点A，DE与⊙O相切于点E，点C为DE延长线上一点，且CE=CB．（1）求证：BC为⊙O的切线；（2）若AB=4，AD=1，求线段CE的长．41．如图△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．（1）求证：PA是⊙O的切线；（2）若PD=，求⊙O的直径．42．如图，四边形ABCD 内接于⊙O，BD是⊙O的直径，过点A作⊙O的切线AE交CD的延长线于点E，DA平分∠BDE．（1）求证：AE⊥CD；（2）已知AE=4cm，CD=6cm，求⊙O的半径．43．如图，已知AB为⊙O的弦，C为⊙O上一点，∠C=∠BAD，且BD⊥AB于B．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为3，AB=4，求AD的长．44．如图所示，以Rt△ABC的直角边AB为直径作圆O，与斜边交于点D，E为BC边上的中点，连接DE．（1）求证：DE是⊙O的切线；（2）连接OE，AE，当∠CAB为何值时，四边形AOED是平行四边形？并在此条件下求sin∠CAE的值．45．已知：如图，△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D 作DE⊥AC于点E，交BC的延长线于点F．求证：（1）AD=BD；（2）DF是⊙O的切线．46．如图，AC是⊙O的直径，PA切⊙O于点A，点B是⊙O上的一点，且∠BAC=30°，∠APB=60°．（1）求证：PB是⊙O的切线；（2）若⊙O的半径为2，求弦AB及PA，PB的长．47．如图，AB为⊙O的直径，D为的中点，连接OD交弦AC于点F，过点D 作DE∥AC，交BA的延长线于点E．（1）求证：DE是⊙O的切线；（2）连接CD，若OA=AE=4，求四边形ACDE的面积．48．如图，在Rt△ABC中，∠C=90°，以BC为直径的⊙O交AB于点D，切线DE 交AC于点E．（1）求证：∠A=∠ADE；（2）若AD=16，DE=10，求BC的长．49．如图，已知AB是⊙O的直径，CD与⊙O相切于C，BE∥CO．（1）求证：BC是∠ABE的平分线；（2）若DC=8，⊙O的半径OA=6，求CE的长．50．如图，AB是⊙O的直径，点D在AB的延长线上，点C在⊙O上，CA=CD，∠CDA=30°．（1）试判断直线CD与⊙O的位置关系，并说明理由；（2）若⊙O的半径为4，求点A到CD所在直线的距离．直线与圆的位置关系练习参考答案一．选择题（共19小题）1．D；2．A；3．C；4．A；5．D；6．D；7．B；8．C；9．D；10．C；11．D；12．B；13．D；14．A；15．D；16．A；17．A；18．C；19．C；二．填空题（共16小题）20．（0，2.5）；21．1；22．10；23．50°；24．（3，2）；25．2；26．相离；27．（8，10）；28．5；29．80°；30．；31．45°；32．2；33．25°；34．25°；35．5；110；三．解答题（共15小题）36．；37．；38．；39．45；30；40．；41．；42．；43．；44．；45．；46．；47．；48．；49．；50．；。

初中直线与圆的位置关系经典练习题

圆与直线的基本性质一、定义[例1]在ABCRt∆中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆与AB有何位置关系？为什么？（1）r=2cm；（2）r=2.4cm；（3）r=3cm。

[例2]在ABC∆中，BC=6cm，∠B=30°，∠C=45°，以A为圆心，当半径r多长时所作的⊙A与直线BC相切？相交？相离？[变式题]已知⊙O的半径为2，直线l上有一点P满足PO=2，则直线l与⊙O的位置关系是【】A．相切B．相离C．相离或相切D．相切或相交二、性质例1：如图，AB是⊙O的直径，C．D是⊙O上一点，∠CDB=20°，过点C作⊙O的切线交AB的延长线于点E，则∠E等于【】A．40°B．50°C．60°D．70°变式1：如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于D，且CO=CD，则∠ACP=【】A．30B．45C．60D．67.5例3：如图，PA、PB是⊙O的切线，A、B是切点，点C是劣弧AB上的一个动点，若∠P＝40°，则∠ACB的度数是【】A．80° B．110°C．120° D．140°变式2：如图，圆周角∠BAC＝55°，分别过B，C两点作⊙O的切线，两切线相交与点P，则∠BPC ＝°．1 / 4例5：如图，在Rt△ABC中，∠B=90°，AB=6，BC=8，以其三边为直径向三角形外作三个半圆，矩形EFGH的各边分别与半圆相切且平行于AB或BC，则矩形EFGH的周长是．变式3：如图，在以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若AB的长为8cm，则图中阴影部分的面积为cm2．例7：如图，PA、PB分别与⊙O相切于点A、B，点M在PB上，且OM∥AP，MN⊥AP，垂足为N．（1）求证：OM=AN；（2）若⊙O的半径R=3，PA=9，求OM的长．变式4：如图，AB为⊙O的直径，EF切⊙O于点D，过点B作BH⊥EF 于点H，交⊙O于点C，连接BD．(1)求证：BD平分∠ABH；(2)如果AB＝12，BC＝8，求圆心O到BC的距离．2 / 4三、切线的判定定理：例1：如图，AB是⊙O的直径，AC和BD是它的两条切线，CO平分∠ACD．（1）求证：CD是⊙O的切线；（2）若AC=2，BC=3，求AB的长．例2：如图，已知AB=AC，∠BAC=120º，在BC上取一点O，以O 为圆心OB为半径作圆，①且⊙O过A点，过A作AD∥BC交⊙O于D，求证：（1）AC是⊙O的切线；（2）四边形BOAD是菱形。

高考数学专题《直线与圆的位置关系》习题含答案解析

专题9.2 直线与圆的位置关系1．（福建高考真题（理））直线:1l y kx =+与圆22:1O x y +=相交于,A B 两点，则"1"k =是“OAB ∆的面积为12”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分又不必要条件【答案】A 【解析】由1k =时,圆心到直线:1l y x =+的距离d =..所以1122OAB S ∆==.所以充分性成立,由图形的对成性当1k =-时,OAB ∆的面积为12.所以不要性不成立.故选A.2.（2018·北京高考真题（理））在平面直角坐标系中，记d 为点()cos ,sin P θθ到直线20x my --=的距离，当θ、m 变化时，d 的最大值为（）A ．1B ．2C ．3D ．4【答案】C 【解析】22cos sin 1θθ+=∴Q ，P 为单位圆上一点，而直线20x my --=过点()2,0A ，所以d 的最大值为1213OA +=+=，选C.3．（2021·全国高二单元测试）已知直线l 与直线1y x =+垂直，且与圆221x y +=相切，切点位于第一象限，则直线l 的方程是（）．A．0x y +=B ．10x y ++=C ．10x y +-=D．0x y +=【答案】A 【分析】根据垂直关系，设设直线l 的方程为()00x y c c ++=<，利用直线与圆相切得到参数值即可.【详解】由题意，设直线l 的方程为()00x y c c ++=<．练基础圆心()0,0到直线0x y c ++=1，得c =c =，故直线l 的方程为0x y +=．故选：A4．（2020·北京高考真题）已知半径为1的圆经过点(3,4)，则其圆心到原点的距离的最小值为（）．A ．4B ．5C ．6D ．7【答案】A 【分析】求出圆心C 的轨迹方程后，根据圆心M 到原点O 的距离减去半径1可得答案.【详解】设圆心(),C x y 1=，化简得()()22341x y -+-=，所以圆心C 的轨迹是以(3,4)M 为圆心，1为半径的圆，所以||1||OC OM +≥5==，所以||514OC ≥-=，当且仅当C 在线段OM 上时取得等号，故选：A.5.【多选题】（2021·吉林白城市·白城一中高二月考）若直线0x y m ++=上存在点P ，过点P 可作圆O ：221x y +=的两条切线PA ，PB ，切点为A ，B ，且60APB ∠=︒，则实数m 的取值可以为（）A ．3B ．C ．1D ．-【答案】BCD 【分析】先由题意判断点P 在圆224x y +=上，再联立直线方程使判别式0∆≥解得参数范围，即得结果.【详解】点P 在直线0x y m ++=上，60APB ∠=︒，则30APO OPB ∠=∠=︒，由图可知，Rt OPB V 中，22OP OB ==，即点P 在圆224x y +=上，故联立方程224x y x y m ⎧+=⎨++=⎩，得222240x mx m ++-=，有判别式0∆≥，即()2244240m m -⨯-≥，解得m -≤≤A 错误，BCD 正确.故选：BCD.6．（2022·江苏高三专题练习）已知大圆1O 与小圆2O 相交于(2,1)A ，(1,2)B 两点，且两圆都与两坐标轴相切，则12O O =____【答案】【分析】由题意可知大圆1O 与小圆2O 都在第一象限，进而设圆的圆心为(,)(0)a a a >，待定系数得5a =或1a =，再结合两点间的距离求解即可.【详解】由题知，大圆1O 与小圆2O 都在第一象限，设与两坐标轴都相切的圆的圆心为(,)(0)a a a >，其方程为222()()x a y a a -+-=，将点(1,2)或(2,1)代入，解得5a =或1a =，所以221:(5)(5)25O x y -+-=，222:(1)(1)1O x y -+-=，可得1(5,5)O ，2(1,1)O ，所以12||O O ==故答案为：7．（江苏高考真题）在平面直角坐标系xOy 中，圆C 的方程为228150x y x +-+=，若直线2y kx =-上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值为__________．【答案】43【解析】∵圆C 的方程为x 2+y 2-8x+15=0，整理得：（x-4）2+y 2=1，即圆C 是以（4，0）为圆心，1为半径的圆；又直线y=kx-2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，∴只需圆C ′：（x-4）2+y 2=4与直线y=kx-2有公共点即可．设圆心C （4，0）到直线y=kx-2的距离为d，2d 即3k 2≤4k，∴0≤k≤43，故可知参数k 的最大值为43.8.（2018·全国高考真题（文））直线1y x =+与圆22230x y y ++-=交于A B ，两点，则AB =________．【答案】【解析】根据题意，圆的方程可化为22(1)4x y ++=，所以圆的圆心为(0,1)-，且半径是2，根据点到直线的距离公式可以求得d ==，结合圆中的特殊三角形，可知AB ==，故答案为.9．（2021·湖南高考真题）过圆2240x y x +-=的圆心且与直线20x y +=垂直的直线方程为___________【答案】220x y --=【分析】根据圆的方程求出圆心坐标，再根据两直线垂直斜率乘积为1-求出所求直线的斜率，再由点斜式即可得所求直线的方程.【详解】由2240x y x +-=可得()2224x y -+=，所以圆心为()2,0，由20x y +=可得2y x =-，所以直线20x y +=的斜率为2-，所以与直线20x y +=垂直的直线的斜率为12，所以所求直线的方程为：()1022y x -=-，即220x y --=，故答案为：220x y --=.10.（2020·浙江省高考真题）设直线:(0)l y kx b k =+>与圆221x y +=和圆22(4)1x y -+=均相切，则k =_______；b =______．【解析】设221:1C x y +=，222:(4)1C x y -+=，由题意，12,C C到直线的距离等于半径，即1=1=，所以||4b k b =+，所以0k =（舍）或者2b k =-，解得k b ==.1．（2020·全国高考真题（理））若直线l 与曲线y和x 2+y 2=15都相切，则l 的方程为（）A ．y =2x +1B ．y =2x +12C ．y =12x +1D ．y =12x +12【答案】D 【分析】根据导数的几何意义设出直线l 的方程，再由直线与圆相切的性质，即可得出答案.【详解】设直线l在曲线y =(0x ，则00x >，函数y =y '=l的斜率k =，设直线l的方程为)0y x x =-，即00x x -+=，由于直线l 与圆2215x y +==两边平方并整理得2005410x x --=，解得01x =，015x =-（舍），则直线l 的方程为210x y -+=，即1122y x =+.练提升故选：D.2.【多选题】（2021·全国高考真题）已知点P 在圆()()225516x y -+-=上，点()4,0A 、()0,2B ，则（）A ．点P 到直线AB 的距离小于10B ．点P 到直线AB 的距离大于2C ．当PBA ∠最小时，PB =D ．当PBA ∠最大时，PB =【答案】ACD 【分析】计算出圆心到直线AB 的距离，可得出点P 到直线AB 的距离的取值范围，可判断AB 选项的正误；分析可知，当PBA ∠最大或最小时，PB 与圆M 相切，利用勾股定理可判断CD 选项的正误.【详解】圆()()225516x y -+-=的圆心为()5,5M ，半径为4，直线AB 的方程为142xy+=，即240x y +-=，圆心M 到直线AB 4=>，所以，点P 到直线AB 42-<，410<，A 选项正确，B 选项错误；如下图所示：当PBA ∠最大或最小时，PB 与圆M 相切，连接MP 、BM ，可知PM PB ⊥，=，4MP =CD 选项正确.故选：ACD.3．【多选题】（2021·肥城市教学研究中心高三月考）已知圆22:230A x y x +--=，则下列说法正确的是（）A ．圆A 的半径为4B ．圆A 截y 轴所得的弦长为C ．圆A 上的点到直线34120x y -+=的最小距离为1D ．圆A 与圆22:88230B x y x y +--+=相离【答案】BC 【分析】将圆的一般方程转化为标准方程即可得半径可判断A ；利用几何法求出弦长可判断B ；求出圆心A 到直线的距离再减去半径可判断C ；求出圆B 的圆心和半径，比较圆心距与半径之和的大小可判断D ，进而可得正确选项.【详解】对于A ：由22230x y x +--=可得()2214x y -+=，所以A 的半径为2r =，故选项A 不正确；对于B ：圆心为()1,0到y 轴的距离为1d =，所以圆A 截y 轴所得的弦长为==B 正确；对于C ：圆心()1,0到直线34120x y -+=3，所以圆A 上的点到直线34120x y -+=的最小距离为3321r -=-=，故选项C 正确；对于D ：由2288230x y x y +--+=可得()()22449x y -+-=，所以圆心()4,4B ，半径3R =，因为5AB r R ===+，所以两圆相外切，故选项D 不正确；故选：BC.4．（2021·全国高三专题练习）在平面直角坐标系xOy 中，圆C 的方程为228150x y x +-+=，若直线2y kx =-上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的取值范围是_______.【答案】403k ≤≤【分析】求出圆C 的圆心和半径，由题意可得圆心到直线的距离小于或等于两圆的半径之和即可求解.【详解】由228150x y x +-+=可得22(4)1x y -+=，因此圆C 的圆心为(4,0)C ，半径为1，若直线2y kx =-上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，只需点(4,0)C 到直线2y kx =-的距离112d =≤+=，即22(21)1k k -≤+，所以2340k k -≤，解得403k ≤≤，所以k 的取值范围是403k ≤≤，故答案为：403k ≤≤.5．（2021·富川瑶族自治县高级中学高一期中（理））直线()20y kx k =+>被圆224x y +=截得的弦长为________．【答案】60 【分析】由已知求得圆心到直线的距离，再由点到直线的距离公式列式求得k ，然后利用斜率等于倾斜角的正切值求解．【详解】直线()20y kx k =+>被圆224x y +=截得的弦长为所以，圆心()0,0O 到直线20kx y -+=的距离1d ==，1=，解得)0k k =>．设直线的倾斜角为()0180θθ≤<，则tan θ=，则60θ= ．因此，直线()20y kx k =+>的倾斜角为60 ．故答案为：60 ．6．（2021·昆明市·云南师大附中高三月考（文））已知圆O : x 2+y 2=4，以A (1,为切点作圆O 的切线l 1，点B 是直线l 1上异于点A 的一个动点，过点B 作直线l 1的垂线l 2，若l 2与圆O 交于D ， E 两点，则V AED 面积的最大值为_______.【答案】2【分析】由切线性质得2//OA l ，O 到直线2l 的距离等于A 到2l 的距离，因此ADEODE S S =!!，设O 到2l 距离为d ，把面积用d 表示，然后利用导数可得最大值．【详解】根据题意可得图，1OA l ⊥，所以2//OA l ，因此O 到直线2l 的距离等于A 到2l 的距离，ADEODE S S =!!，过点(00)O ，作直线2l 的垂线，垂足为F ，记||(20)OF d d =>>，则弦||DE =角形ADE 的面积为S ，所以12S d =g g ，将S 视为d 的函数，则S '=+ 1(2)2d d -当0d <<时，0S '>，函数()S d 2d <<时，0S '<，函数()S d 单调递减，所以函数()S d 有最大值，当d =max ()2S d =，故AED V 面积的最大值为2．故答案为：2．7．（2021·全国高三专题练习）已知ABC V 的三个顶点的坐标满足如下条件：向量(2,0)OB →=，(2,2)OC →=，,CA α→=)α，则AOB ∠的取值范围是________【答案】5,1212ππ⎡⎤⎢⎥⎣⎦【分析】先求出点A 的轨迹是以(2,2)C . 过原点O 作此圆的切线，切点分别为M 、N ，如图所示，连接CM ，CN ，得到MOB NOB θ∠∠…….所以15BOM ∠=︒，75BON ∠=︒，即得解.【详解】由题得||CA →=所以点A 的轨迹是以(2,2)C .过原点O 作此圆的切线，切点分别为M 、N ，如图所示，连接CM ，CN ，则向量OA →与OB →的夹角θ的范围是MOB NOB θ∠∠…….由图可知45COB ∠=︒.∵||OC →=1||||||2CM CN OC →→→==知30COM CON ∠=∠=︒，∴453015BOM ∠=︒-︒=︒，453075BON ∠=︒+︒=︒.∴1575θ︒︒…….故AOB ∠的取值范围为{}1575θθ︒≤≤︒丨.故答案为：{}π5π15751212θθ⎡⎤︒≤≤︒⎢⎥⎣⎦丨或，8．（2021·全国高三专题练习）已知x 、y R ∈，2223x x y -+=时，求x y +的最大值与最小值．【答案】最小值是1，最大值是1+【分析】根据2223x x y -+=表示圆()2214x y -+=，设x y b +=表示关于原点、x 轴、y 轴均对称的正方形，然后由直线与圆的位置关系求解.【详解】2223x x y -+=的图形是圆()2214x y -+=，既是轴对称图形，又是中心对称图形．设x y b +=，由式子x y +的对称性得知x y b +=的图形是关于原点、x 轴、y 轴均对称的正方形．如图所示：当b 变化时，图形是一个正方形系，每个正方形四个顶点均在坐标轴上，问题转化为正方形系中的正方形与圆有公共点时，求b 的最值问题．当1b <时，正方形与圆没有公共点；当1b =时，正方形与圆相交于点()1,0-，若令直线y x b =-+与圆()2214x y -+=相切，2，解得1b =±所以当1b =+当1b >+故x y +的最小值是1，最大值是1+．9．（2021·黑龙江哈尔滨市·哈尔滨三中）已知ABC V 的内切圆的圆心M 在y 轴正半轴上，半径为1，直线210x y +-=截圆M （1）求圆M 方程；（2）若点C 的坐标为()2,4，求直线AC 和BC 的斜率；（3）若A ，B 两点在x 轴上移动，且AB 4=，求ABC V 面积的最小值.【答案】（1）22(1)1y x +-=；（2）2；（3）163.【分析】（1）设ABC V 的内切圆的圆心()0,M b ，先求得圆心到直线210x y +-=的距离，再根据直线截圆M （2）当直线AC 和BC 的斜率不存在时，设直线方程为2x =，易知不成立；当直线AC 和BC 的斜率存在时，设直线方程为()42y k x -=-，然后由圆心到直线的距离等于半径求解；（3）根据AB 4=，设()()(),0,4,040A t B t t +-<<，进而得到直线AC 和直线 BC 的斜率，写出直线AC 和BC 的方程，联立求得点C 的坐标，进而得到坐标系的最小值求解.【详解】（1）设ABC V 的内切圆的圆心()0,,0M b b >，圆心到直线210x y +-=的距离为d又因为直线截圆M21+=，解得1b =，所以圆M 方程()2211x y +-=；（2）当直线AC 和BC 的斜率不存在时，设直线方程为2x =，则圆心到直线的距离 0221d r =-=≠=，不成立，当直线AC 和BC 的斜率存在时，设直线方程为()42y k x -=-，即 240kx y k --+=，圆心到直线的距离d ，解得2k =（3）因为AB 4=，设()()(),0,4,040A t B t t +-<<，所以直线AC 的斜率为：2222tan 2111ACt t k MAO t t-=∠==---，同理直线BC 的斜率为： ()()222241411BCt t k t t --+==+-- ，所以直线AC 的方程为：()221ty x t t =---，直线BC 的方程为：()()()224441t y x t t -+=--+- ，由()()()()222124441t y x t t t y x t t ⎧=--⎪-⎪⎨-+⎪=--⎪+-⎩，解得 22224412841t x t t t t y t t +⎧=⎪⎪++⎨+⎪=⎪++⎩，即2222428,4141t t t C t t t t ⎛⎫++ ⎪++++⎝⎭，又 ()2222282222414123t t y t t t t t +==-=-+++++-，当2t =-时，点C 的纵坐标取得最小值83，所以ABC V 面积的最小值.18164233ABC S =⨯⨯=V .10．（2021·新疆乌鲁木齐市·乌市八中高二期末（文））已知直线l ：43100x y ++=，半径为2的圆C 与l 相切，圆心C 在x 轴上且在直线l 的上方（1）求圆C 的方程；（2）过点()1,0M 的直线与圆C 交于A ，B 两点（A 在x 轴上方），问在x 轴正半轴上是否存在点N ，使得x 轴平分ANB ∠？若存在，请求出点N 的坐标；若不存在，请说明理由．【答案】（1）224x y +=；（2）存在，()4,0N .【分析】（1）设出圆心坐标(),0C a ，根据直线与圆相切可得圆心到直线的距离等于半径，由此求解出a 的值（注意范围），则圆C 的方程可求；（2）当直线AB 的斜率不存在时，直接根据位置关系分析即可，当直线AB 的斜率存在时，设出直线方程并联立圆的方程，由此可得,A B 坐标的韦达定理形式，根据AN BN k k =-结合韦达定理可求点N 的坐标.【详解】解：（1）设圆心(),0C a ，∵圆心C 在l 的上方，∴4100a +>，即52a >-，∵直线l ：43100x y ++=，半径为2的圆C 与l 相切，∴d r =，即41025a +=，解得：0a =或5a =-（舍去），则圆C 方程为224x y +=；（2）当直线AB x ⊥轴，则x 轴平分ANB ∠，当直线AB 的斜率存在时，设AB 的方程为()1y k x =-，(),0N t ，()11,A x y ，()22,B x y ，由224(1)x y y k x ⎧+=⎨=-⎩得，()22221240k x k x k +-+-=，所以212221k x x k +=+，212241k x x k -=+若x 轴平分ANB ∠，则AN BN k k =-，即()()1212110k x k x x tx t--+=--，整理得：()()12122120x x t x x t -+++=，即()()222224212011k k t t k k -+-+=++，解得：4t =，当点()4,0N ，能使得ANM BNM ∠=∠总成立．1．（2021·山东高考真题）“圆心到直线的距离等于圆的半径”是“直线与圆相切”的（）A ．充分没必要条件B ．必要不充分条件C ．充要条件D ．既不充分也没必要条件【答案】C 【分析】由直线与圆相切的等价条件，易判断【详解】由于“圆心到直线的距离等于圆的半径”⇒“直线与圆相切”，因此充分性成立；“直线与圆相切”⇒“圆心到直线的距离等于圆的半径”，故必要性成立；可得“圆心到直线的距离等于圆的半径”是“直线与圆相切”的充要条件故选：C2．（2021·北京高考真题）已知直线y kx m =+（m 为常数）与圆224x y +=交于点M N ，，当k 变化时，若||MN 的最小值为2，则m = A ．±1B．C．D ．2±【答案】C 【分析】先求得圆心到直线距离，即可表示出弦长，根据弦长最小值得出m 【详解】由题可得圆心为()0,0，半径为2，则圆心到直线的距离d =则弦长为||MN =则当0k =时，弦长|MN取得最小值为2=，解得m =故选：C.3.（2020·全国高考真题（理））已知⊙M ：222220x y x y +---=，直线l ：220x y ++=，P 为l 上的动点，过点P 作⊙M 的切线,PA PB ，切点为,A B ，当||||PM AB ⋅最小时，直线AB 的方程为（）练真题A ．210x y --=B ．210x y +-=C ．210x y -+=D ．210x y ++=【答案】D 【解析】圆的方程可化为()()22114x y -+-=，点M 到直线l的距离为2d >，所以直线l 与圆相离．依圆的知识可知，四点,,,A P B M 四点共圆，且AB MP ⊥，所以14442PAM PM AB S PA AM PA ⋅==⨯⨯⨯=V，而PA =，当直线MP l ⊥时，min MP =，min 1PA =，此时PM AB ⋅最小．∴()1:112MP y x -=-即1122y x =+，由1122220y x x y ⎧=+⎪⎨⎪++=⎩解得，10x y =-⎧⎨=⎩．所以以MP 为直径的圆的方程为()()()1110x x y y -++-=，即2210x y y +--=，两圆的方程相减可得：210x y ++=，即为直线AB 的方程．故选：D.4．【多选题】（2021·全国高考真题）已知直线2:0l ax by r +-=与圆222:C x y r +=，点(,)A a b ，则下列说法正确的是（）A ．若点A 在圆C 上，则直线l 与圆C 相切B ．若点A 在圆C 内，则直线l 与圆C 相离C ．若点A 在圆C 外，则直线l 与圆C 相离D ．若点A 在直线l 上，则直线l 与圆C 相切【答案】ABD 【分析】转化点与圆、点与直线的位置关系为222,a b r +的大小关系，结合点到直线的距离及直线与圆的位置关系即可得解.【详解】圆心()0,0C 到直线l的距离d =若点(),A a b 在圆C 上，则222a b r +=，所以d =则直线l 与圆C 相切，故A 正确；若点(),A a b 在圆C 内，则222a b r +<，所以d =则直线l 与圆C 相离，故B 正确；若点(),A a b 在圆C 外，则222a b r +>，所以d =则直线l 与圆C 相交，故C 错误；若点(),A a b 在直线l 上，则2220a b r +-=即222=a b r +，所以d =l 与圆C 相切，故D 正确.故选：ABD.5.（2021·山东高考真题）已知椭圆的中心在坐标原点，右焦点与圆22670x my m +--=的圆心重合，长轴长等于圆的直径，那么短轴长等于______．【答案】【分析】由于22670x my m +--=是圆，可得1m =，通过圆心和半径计算,,a b c ，即得解【详解】由于22670x my m +--=是圆，1m ∴=即：圆22670x y x +--=其中圆心为()3,0，半径为4那么椭圆的长轴长为8，即3c =，4a =，b ==那么短轴长为故答案为：6．（2019·北京高考真题（文））设抛物线y 2=4x 的焦点为F ，准线为l .则以F 为圆心，且与l 相切的圆的方程为__________．【答案】(x -1)2+y 2=4.【解析】抛物线y 2=4x 中，2p =4，p =2，焦点F （1,0），准线l 的方程为x =-1，以F 为圆心，且与l 相切的圆的方程为 (x -1)2+y 2=22,即为(x -1)2+y 2=4.。

直线与圆的位置关系练习(含参考答案)

直线与圆的位置关系习题课班级学号姓名-----------------------------------------------------【基础训练】-------------------------------------------------------1．直线y ＝kx ＋1与圆x 2＋y 2－2y ＝0的位置关系是（）A ．相交B ．相切C ．相离D ．取决于k 的值解析由y ＝kx ＋1知直线过定点(0,1)，由x 2＋y 2－2y ＝0得x 2＋(y －1)2＝1.∴直线经过圆的圆心，∴直线与圆相交．答案 A2．若直线x －y ＋1＝0与圆(x －a )2＋y 2＝2有公共点，则实数a 的取值范围是（）A ．[－3，－1]B ．[－1,3]C ．[－3,1]D ．(－∞，－3]∪[1，＋∞) 解析由题意可得，圆的圆心为(a,0)，半径为2，∴|a －0＋1|12＋(－1)2≤2，即|a ＋1|≤2，解得－3≤a ≤1. 答案 C3．若直线y ＝kx 与圆(x －2)2＋y 2＝1的两个交点关于直线2x ＋y ＋b ＝0对称，则k ，b 的值分别为（）A ．k ＝12，b ＝－4B ．k ＝－12，b ＝4C ．k ＝12，b ＝4D ．k ＝－12，b ＝－4 解析因为直线y ＝k x 与圆(x －2)2＋y 2＝1的两个交点关于直线2x ＋y ＋b ＝0对称，则y ＝k x与直线2x ＋y ＋b ＝0垂直，且2x ＋y ＋b ＝0过圆心，所以解得k ＝12，b ＝－4. 答案 A4．过点A (2,4)向圆x 2＋y 2＝4所引切线的方程为．解析显然x ＝2为所求切线之一；另设直线方程为y －4＝k (x －2)，即kx －y ＋4－2k ＝0，那么|4－2k |k 2＋1＝2，解得k ＝34，即3x －4y ＋10＝0. 答案 x ＝2或3x －4y ＋10＝05．若圆x 2＋y 2＋2x －4y ＋m ＝0(m ＜3)的一条弦AB 的中点为P (0,1)，则垂直于AB 的直径所在直线的方程为 .解析由圆的方程得该圆圆心为C (－1,2)，则CP ⊥AB ，直线CP 的斜率为－1，故垂直于AB 的直径所在直线的方程为y －1＝－x ，即x ＋y －1＝0.6．过点1(,1)2M 的直线l 与圆C ：(x －1)2＋y 2＝4交于A ，B 两点，C 为圆心，当∠ACB 最小时，直线l 的方程为．解析由题意得，当CM ⊥AB 时，∠ACB 最小，从而直线方程y －1＝－1－120－1⎝⎛⎭⎫x －12，即2x －4y ＋3＝0.答案 2x －4y ＋3＝07．已知直线x －y ＋a ＝0与圆心为C 的圆x 2＋y 2＋2x －4y －4＝0相交于A ，B 两点，且AC ⊥BC ，求实数a 的值.解析：圆C ∶x 2＋y 2＋2x －4y －4＝0的标准方程为(x ＋1)2＋(y －2)2＝9，所以圆心为C (－1,2)，半径为3.因为AC ⊥BC ，所以圆心C 到直线x －y ＋a ＝0的距离为322，即|－1－2＋a |2＝322，所以a ＝0或6.8．已知：圆C ：x 2＋y 2－8y ＋12＝0，直线l ：ax ＋y ＋2a ＝0.(1)当a 为何值时，直线l 与圆C 相切；(2)当直线l 与圆C 相交于A ，B 两点，且|AB |＝22时，求直线l 的方程．解析将圆C 的方程x 2＋y 2－8y ＋12＝0化成标准方程为x 2＋(y －4)2＝4，则此圆的圆心为(0,4)，半径为2.(1)若直线l 与圆C 相切，则有|4＋2a |a 2＋1＝2，解得a ＝－34. (2)过圆心C 作CD ⊥AB ，则根据题意和圆的性质，得⎩⎨⎧ |CD |＝|4＋2a |a 2＋1，|CD |2＋|DA |2＝|AC |2＝22，|DA |＝12|AB |＝ 2.解得a ＝－7或－1.故所求直线方程为7x －y ＋14＝0或x －y ＋2＝0.-------------------------------------------------------【能力提升】-----------------------------------------------------9．过点P (1,1)的直线，将圆形区域{(x ，y )|x 2＋y 2≤4}分为两部分，使得这两部分的面积之差最大，则该直线的方程为（）A ．x ＋y －2＝0B ．y －1＝0C ．x －y ＝0D ．x ＋3y －4＝0解析选A 两部分面积之差最大，即弦长最短，此时直线垂直于过该点的直径．因为过点P (1,1)的直径所在直线的斜率为1，所以所求直线的斜率为－1，方程为x ＋y －2＝0.10．已知点P (x 0，y 0)，圆O ：x 2＋y 2＝r 2(r ＞0)，直线l ：x 0x ＋y 0y ＝r 2，有以下几个结论：①若点P在圆O 上，则直线l 与圆O 相切；②若点P 在圆O 外，则直线l 与圆O 相离；③若点P 在圆O 内，则直线l 与圆O 相交；④无论点P 在何处，直线l 与圆O 恒相切，其中正确的个数是（）A ．1B ．2C ．3D ．4解析根据点到直线的距离公式有d ＝r 2x 20＋y 20，若点P 在圆O 上，则x 20＋y 20＝r 2，d ＝r ，相切；若点P 在圆O 外，则x 20＋y 20＞r 2，d ＜r ，相交；若点P 在圆O 内，则x 20＋y 20＜r 2，d ＞r ，相离，故只有①正确．答案 A11．已知圆O ：x 2＋y 2＝5，直线l ：x cos θ＋y sin θ＝1（0<θ<π2）.设圆O 上到直线l 的距离等于1的点的个数为k ，则k ＝ .解析圆O 的圆心(0,0)到直线l ：x cos θ＋y sin θ＝1的距离d ＝1.而圆的半径r ＝5，且r －d ＝5－1>1，∴圆O 上在直线l 的两侧各有两点到直线l 的距离等于1.答案：412．已知直线l ：y ＝－3(x －1)与圆O ：x 2＋y 2＝1在第一象限内交于点M ，且l 与y 轴交于点A ，则△MOA 的面积等于．解析依题意，直线l ：y ＝－3(x －1)与y 轴的交点A 的坐标为(0，3)．由22131x y y x +==--⎧⎪⎨⎪⎩，得点M 的横坐标x M ＝12，所以△MOA 的面积为S ＝12|OA |×x M ＝12×3×12＝34. 答案 3413．过直线x ＋y －22＝0上点P 作圆x 2＋y 2＝1的两条切线，若两条切线的夹角是60°，则点P的坐标是．解析法一如图所示，|OP |＝|OA |sin ∠OP A＝2，易得P 为CD 中点，故P (2，2)．法二设P (x ，y )，由法一可得⎩⎨⎧ x 2＋y 2＝2，x ＋y －22＝0⇒⎩⎨⎧x ＝2，y ＝2，故P (2，2)．答案 (2，2)14．半径为5的圆C 过点A )4,2(-，且以)3,1(-M 为中点的弦长为34，求圆C 的方程.解析设圆方程为22()()25x ay b -+-=，依题意，2222(2)(4)2525a b ⎧--+-=⎪⎨+=⎪⎩，解得10a b =⎧⎨=⎩或21a b =⎧⎨=⎩. 所以圆C 方程为：22(1)25x y -+=或22(2)(1)25x y -+-=. 15. 已知实数x 、y 满足方程x 2＋y 2－4x ＋1＝0，求下列各式的最大值与最小值：（1）y x；（2）y －x ；（3）(x +1)2＋y 2．解析 (1)原方程可化为(x －2)2＋y 2＝3，表示以(2,0)为圆心，3为半径的圆，y x的几何意义是圆上一点与原点连线的斜率，所以设y x＝k ，即y ＝kx . 当直线y ＝kx 与圆相切时，斜率k 取最大值或最小值，此时|2k －0|k 2＋1＝3，解得k ＝±3. 所以y x的最大值为3，最小值为－ 3. (2)y +x 可看作是直线y ＝-x ＋b 在y 轴上的截距，当直线y ＝-x＋b 与圆相切时，纵截距b 取得=，解得b ＝2±6. 所以y +x 的最大值为2＋6，最小值为2－ 6.(3)x 2＋y 2表示圆上的一点与点(-1,0)距离的平方，由平面几何知识知，在点(-1,0)与圆心连线与圆的两个交点处取得最大值和最小值．3=，所以x 2＋y 2的最大值是(3＋3)2＝12＋63，x 2＋y 2的最小值是(3－3)2＝12－6 3.16．已知圆M ：x 2＋(y －2)2＝1，Q 是x 轴上的动点，QA ，QB 分别切圆M 于A ，B 两点．（1）若Q (1,0)，求切线QA ，QB 的方程；（2）求四边形QAMB 面积的最小值；（3）若|AB |＝423，求直线MQ 的方程．解析 (1)设过点Q 的圆M 的切线方程为x ＝my ＋1，则圆心M 到切线的距离为1，∴|2m ＋1|m 2＋1＝1，∴m ＝－43或0， ∴QA ，QB 的方程分别为3x ＋4y －3＝0和x ＝1.(2)∵MA ⊥AQ ，∴S 四边形MAQB ＝|MA |·|QA |＝|QA |＝|MQ |2－|MA |2＝|MQ |2－1≥|MO |2－1＝ 3. ∴四边形QAMB 面积的最小值为 3.(3)设AB 与MQ 交于P ，则MP ⊥AB ，MB ⊥BQ ，∴|MP |＝ 1－⎝⎛⎭⎫2232＝13. 在Rt △MBQ 中，|MB |2＝|MP ||MQ |，即1＝13|MQ |，∴|MQ |＝3，∴x 2＋(y －2)2＝9. 设Q (x,0)，则x 2＋22＝9，∴x ＝±5，∴Q (±5，0)，∴MQ 的方程为2x ＋5y －25＝0或2x －5y ＋25＝0.。

九年级数学直线与圆的位置关系练习题及答案

九年级数学直线与圆的位置关系练习题及答案一、单选题1. 给定直线l ：3x-4y=12，圆C：(x-1)^2+(y+3)^2=25，则l与C的位置关系是:A. 相切B. 相离C. 相交于两点D. 相交于一个点2. 若直线l的方程为x-2y+1=0，圆C的方程为(x-3)^2+(y+4)^2=16，则l与C的位置关系是:A. 相切B. 相离C. 相交于两点D. 相交于一个点3. 在直角坐标系中，直线l：y=2x+1与圆C：(x-4)^2+(y+2)^2=36的位置关系是:A. 相切B. 相离C. 相交于两点D. 相交于一个点二、填空题1. 直线y=3x+2与圆(x-1)^2+(y-3)^2=16的位置关系可以用___________表示。

2. 若直线l ：2x+3y=6与圆C：(x-2)^2+(y-3)^2=9相交于点A(1,2)，则点A到直线l的距离为_________。

三、解答题1. 已知直线l的方程为y=2x-1，圆C的方程为(x-2)^2+(y-1)^2=r^2，求当r=3时，l与C的位置关系。

2. 某圆C的圆心坐标为(3,-2)，半径为4，直线l的方程为2x-y=5，则求l与C的位置关系并证明。

答案：一、单选题1. C2. A3. D二、填空题1. 相交于两点2. 3三、解答题1. 当r=3时，圆C的方程为(x-2)^2+(y-1)^2=9。

将直线l的方程代入圆C的方程，得到4x^2-4x+1+4x-4+y^2-2y+1=9，简化后为4x^2+y^2-2y-3=0。

该方程与圆C相交于两个点，故位置关系为相交于两点。

2. 圆C的圆心坐标为(3,-2)，半径为4。

直线l的斜率为2，l的方程可以改写为y=2x-5，将直线l的方程代入圆C的方程，得到(x-3)^2+(2x-5+2)^2=16。

化简后得到5x^2-35x+60=0，解得x=2和x=6。

将x的值代入直线l的方程，得到相应的y值，分别为y=-1和y=7。

高中数学-《直线与圆的位置关系》单元测试题

高中数学-《直线与圆的位置关系》单元测试题高中数学-《直线与圆的位置关系》单元测试题班级：__________姓名：__________成绩：__________ 一．选择题（每题5分，共12题，共60分）1.直线3x + 4y + 12 = 0 与圆(x + 1)^2 + (y + 1)^2 = 9的位置关系是A。

过圆心 B。

相切 C。

相离 D。

相交2.直线l将圆x^2 + y^2 - 2x - 4y = 0 平分，且与直线x + 2y = 0 垂直，则直线l的方程为A。

y = 2x B。

y = 2x - 2 C。

y = x + 1 D。

y = x - 13.若圆C半径为1，圆心在第一象限，且与直线4x - 3y = 0 和x轴都相切，则该圆的标准方程是A。

(x - 2)^2 + (y - 1)^2 = 1 B。

(x - 2)^2 + (y + 1)^2 = 1 C。

(x + 2)^2 + (y - 1)^2 = 1 D。

(x - 3)^2 + (y - 1)^2 = 14.若直线ax + by = 1与圆x^2 + y^2 = 1相交，则点P(a，b)的位置是A。

在圆上 B。

在圆外 C。

在圆内 D。

都有可能5.由直线y = x + 1上的一点向圆(x - 3)^2 + y^2 = 1引切线，则切线长的最小值为A。

1 B。

2 C。

3 D。

46.圆x^2 + y^2 + 2x + 4y - 3 = 0 上到直线l：x + y + 1 = 0的距离为2的点有A。

1个 B。

2个 C。

3个 D。

4个7.两圆x^2 + y^2 - 6x = 0 和x^2 + y^2 + 8y + 12 = 0 的位置关系是A。

相离 B。

外切 C。

相交 D。

内切8.两圆x + y = r,(x-3)+(y+1)=r外切，则正实数r的值是A。

10 B。

5 C。

2 D。

229.半径为6的圆与x轴相切,且与圆x+(y-3)^2=1内切,则此圆的方程是A。

高中数学直线与圆位置关系练习题

高中数学直线与圆位置关系练习题1．若直线2x＋y＋a＝0与圆x2＋y2＋2x－4y＝0相切，则a的值为( )A．± 5 B．±5C．3 D．±32．圆O1：x2＋y2－2x＝0和圆O2：x2＋y2－4y＝0的位置关系是( )A．相交B．外切C．相离D．内切3．(2020·敦化期末)与圆x2＋y2＋4x－4y＋7＝0和x2＋y2－4x－10y＋13＝0都相切的直线共有( )A．1条B．2条C．3条D．4条4．在平面直角坐标系内，过点P(0,3)的直线与圆心为C的圆x2＋y2－2x－3＝0相交于A，B两点，则△ABC面积的最大值是( )A．2 B．4C. 3 D．2 35．[逻辑推理、直观想象]已知过原点的直线l与圆C：x2＋y2－6x＋5＝0相交于不同的两点A，B，且线段AB的中点坐标为D(2，2)，则弦长为( )A．2 B．3C．4 D．56．[多选题]若直线l：ax＋y＋2a＝0被圆C：x2＋(y－4)2＝4截得的弦长为22，则a的值为( )A．－7 B．－1C．7 D．17．[多选题]已知圆C：(x－3)2＋(y－3)2＝72，若直线l：x＋y－m＝0垂直于圆C的一条直径，且经过这条直径的一个三等分点，则直线l的方程是( ) A．x＋y－2＝0 B．x＋y－4＝0C．x＋y－8＝0 D．x＋y－10＝08．已知圆C的圆心坐标是(0，m)，半径长是r.若直线2x－y＋3＝0与圆C相切于点A(－2，－1)，则m＝________，r＝________.9．已知AB为圆C：x2＋y2－2y＝0的直径，点P为直线y＝x－1上任意一点，则|PA|2＋|PB|2的最小值为________．10．已知直线l过点(1,1)，过点P(－1，3)作直线m⊥l，垂足为M，则点M到点Q(2,4)距离的取值范围为________．11．过点M(1,2)的直线l与圆C：(x－3)2＋(y－4)2＝25交于A，B两点，C为圆心，当∠ACB最小时，直线l的方程是________________．12．在直角坐标系xOy中，曲线y＝x2＋mx－2与x轴交于A，B两点，点C的坐标为(0,1)．当m变化时，解答下列问题：(1)能否出现AC⊥BC的情况？说明理由；(2)证明过A，B，C三点的圆在y轴上截得的弦长为定值．13．已知圆C：x2＋y2－8x－6y＋F＝0与圆O：x2＋y2＝4相外切，切点为A，过点P(4,1)的直线与圆C交于点M，N，线段MN的中点为Q.(1)求点Q的轨迹方程；(2)若|AQ|＝|AP|，点P与点Q不重合，求直线MN的方程及△AMN的面积．14．已知圆C：x2＋(y－a)2＝4，点A(1,0)．(1)当过点A的圆C的切线存在时，求实数a的取值范围；(2)设AM，AN为圆C的两条切线，M，N为切点，当|MN|＝455时，求MN所在直线的方程．。

高考数学真题练习——直线与圆的位置关系

直线与圆的位置关系一．选择题（共16小题）1．（2015•重庆）已知直线10x ay +-=是圆22:4210C x y x y +--+=的对称轴，过点(4,)A a -作圆C 的一条切线，切点为B ，则||(AB = )A ．2B ．6C ．D ．2．（2014•全国）若直线21y x =+与圆222(3)(2)x y r -+-=相切，则2(r = )A ．8B ．5C ．D3．（2014•福建）已知直线l 过圆22(3)4x y +-=的圆心，且与直线10x y ++=垂直，则l 的方程是( ) A ．20x y +-=B ．20x y -+=C ．30x y +-=D ．30x y -+=4．（2014•北京）已知圆22:(3)(4)1C x y -+-=和两点(,0)A m -，(B m ，0)(0)m >，若圆C 上存在点P ，使得90APB ∠=︒，则m 的最大值为( )A ．7B ．6C ．5D ．45．（2014•安徽）过点(P 1)-的直线l 与圆221x y +=有公共点，则直线l 的倾斜角的取值范围是( ) A ．(0，]6πB ．(0，]3πC ．[0，]6πD ．[0，]3π6．（2014•浙江）已知圆22220x y x y a ++-+=截直线20x y ++=所得弦的长度为4，则实数a 的值是( ) A ．2-B ．4-C ．6-D ．8-7．（2014•江西）在平面直角坐标系中，A ，B 分别是x 轴和y 轴上的动点，若以AB 为直径的圆C 与直线240x y +-=相切，则圆C 面积的最小值为( )A ．45πB ．34πC ．(6π-D ．54π8．（2013•重庆）设P 是圆22(3)(1)4x y -++=上的动点，Q 是直线3x =-上的动点，则||PQ 的最小值为( ) A ．6B ．4C ．3D ．29．（2013•陕西）已知点(,)M a b 在圆22:1O x y +=外，则直线1ax by +=与圆O 的位置关系是( ) A ．相切B ．相交C ．相离D ．不确定10．（2013•江西）过点引直线l 与曲线y =A ，B 两点，O 为坐标原点，当ABO ∆的面积取得最大值时，直线l 的斜率等于( )A B ．C ． D ． 11．（2013•天津）已知过点(2,2)P 的直线与圆22(1)5x y -+=相切，且与直线10ax y -+=垂直，则(a = ) A ．12-B ．1C ．2D ．1212．（2013•安徽）直线250x y +-=被圆22240x y x y +--=截得的弦长为( )A ．1B ．2C ．4 D．13．（2012•天津）设m ，n R ∈，若直线(1)(1)20m x n y +++-=与圆22(1)(1)1x y -+-=相切，则m n +的取值范围是( )A．[11+ B ．(-∞，1[13+，)+∞C．[2-2+D ．(-∞，2[222-+，)+∞14．（2012•重庆）对任意的实数k ，直线1y kx =+与圆222x y +=的位置关系一定是( ) A ．相离B ．相切C ．相交但直线不过圆心D ．相交且直线过圆心15．（2012•陕西）已知圆22:40C x y x +-=，l 为过点(3,0)P 的直线，则( ) A ．l 与C 相交 B ．l 与C 相切C ．l 与C 相离D ．以上三个选项均有可能16．（2012•安徽）若直线10x y -+=与圆22()2x a y -+=有公共点，则实数a 取值范围是( ) A ．[3-，1]-B ．[1-，3]C ．[3-，1]D ．(-∞，3][1-，)+∞二．填空题（共10小题）17．（2018•天津）已知圆2220x y x +-=的圆心为C，直线13x y ⎧=-⎪⎪⎨⎪=-⎪⎩，(t 为参数）与该圆相交于A ，B 两点，则ABC ∆的面积为．18．（2017•全国）直线20x -=被圆2220x y x +-=截得的线段长为．19．（2017•上海）若P 、Q 是圆222440x y x y +-++=上的动点，则||PQ 的最大值为．20．（2016•上海）在平面直角坐标系xOy 中，点A ，B 是圆22650x y x +-+=上的两个动点，且满足||AB =则||OA OB +的最小值为．21．（2014•湖北）直线1:l y x a =+和2:l y x b =+将单位圆22:1C x y +=分成长度相等的四段弧，则22a b += ． 22．（2014•上海）已知曲线:C x =，直线:6l x =，若对于点(,0)A m ，存在C 上的点P 和l 上的Q 使得0AP AQ +=，则m 的取值范围为．23．（2014•江苏）在平面直角坐标系xOy 中，直线230x y +-=被圆22(2)(1)4x y -++=截得的弦长为． 24．（2013•湖北）已知圆22:5O x y +=，直线:cos sin 1(0)2l x y πθθθ+=<<．设圆O 上到直线l 的距离等于1的点的个数为k ，则k = ．25．（2013•浙江）直线23y x =+被圆22680x y x y +--=所截得的弦长等于． 26．（2013•山东）过点(3,1)作圆22(2)(2)4x y -+-=的弦，其中最短的弦长为．三．解答题（共4小题）27．（2017•上海）某景区欲建造两条圆形观景步道1M 、2M （宽度忽略不计），如图所示，已知AB AC ⊥，60AB AC AD ===（单位：米），要求圆1M 与AB 、AD 分别相切于点B 、D ，圆2M 与AC 、AD 分别相切于点C 、D ；（1）若60BAD ∠=︒，求圆1M 、2M 的半径（结果精确到0.1米）（2）若观景步道1M 与2M 的造价分别为每米0.8千元与每米0.9千元，如何设计圆1M 、2M 的大小，使总造价最低？最低总造价是多少？（结果精确到0.1千元）28．（2015•陕西）如图，AB 切O 于点B ，直线AO 交O 于D ，E 两点，BC DE ⊥，垂足为C ．（Ⅰ）证明：CBD DBA ∠=∠；（Ⅱ）若3AD DC =，BC =，求O 的直径．29．（2013•江苏）在平面直角坐标系xOy 中，点(0,3)A ，直线:24l y x =-，设圆C 的半径为1，圆心在l 上．（1）若圆心C 也在直线3y x =-上，过点A 作圆C 的切线，求切线方程；（2）若圆C 上存在点M ，使||2||MA MO =，求圆心C 的横坐标的取值范围．30．（2013•四川）已知圆C 的方程为22(4)4x y +-=，点O 是坐标原点．直线:l y kx =与圆C 交于M ，N 两点．（Ⅰ）求k 的取值范围；（Ⅱ）设(,)Q m n 是线段MN 上的点，且222211||||||OQ OM ON =+．请将n 表示为m 的函数．直线与圆的位置关系参考答案与试题解析一．选择题（共16小题）1．（2015•重庆）已知直线10x ay +-=是圆22:4210C x y x y +--+=的对称轴，过点(4,)A a -作圆C 的一条切线，切点为B ，则||(AB = )A ．2B ．6C ．D ．【解答】解：圆22:4210C x y x y +--+=，即22(2)(1)4x y -+-=，表示以(2,1)C 为圆心、半径等于2的圆．由题意可得，直线:10l x ay +-=经过圆C 的圆心(2,1)，故有210a +-=，1a ∴=-，点(4,1)A --．(AC ==2CB R ==，∴切线的长||6AB ===．故选：B ．2．（2014•全国）若直线21y x =+与圆222(3)(2)x y r -+-=相切，则2(r = )A ．8B ．5C ．D【解答】解：直线21y x =+与圆222(3)(2)x y r -+-=相切，∴圆心(3,2)C 到直线的距离d r ===，25r ∴=．故选：B ．3．（2014•福建）已知直线l 过圆22(3)4x y +-=的圆心，且与直线10x y ++=垂直，则l 的方程是( ) A ．20x y +-=B ．20x y -+=C ．30x y +-=D ．30x y -+=【解答】解：由题意可得所求直线l 经过点(0,3)，斜率为1，故l 的方程是30y x -=-，即30x y -+=，故选：D ．4．（2014•北京）已知圆22:(3)(4)1C x y -+-=和两点(,0)A m -，(B m ，0)(0)m >，若圆C 上存在点P ，使得90APB ∠=︒，则m 的最大值为( )A ．7B ．6C ．5D ．4【解答】解：圆22:(3)(4)1C x y -+-=的圆心(3,4)C ，半径为1，圆心C 到(0,0)O 的距离为5，∴圆C 上的点到点O 的距离的最大值为6．再由90APB ∠=︒可得，以AB 为直径的圆和圆C 有交点，可得12PO AB m ==，故有6m ，故选：B ．5．（2014•安徽）过点(P 1)-的直线l 与圆221x y +=有公共点，则直线l 的倾斜角的取值范围是( )A ．(0，]6πB ．(0，]3πC ．[0，]6πD ．[0，]3π【解答】解：由题意可得点(P 1)-在圆221x y +=的外部，故要求的直线的斜率一定存在，设为k ，则直线方程为1(y k x +=，即10kx y -+-=．1，即22311k k -++，解得03k ，故直线l 的倾斜角的取值范围是[0，]3π，故选：D ．6．（2014•浙江）已知圆22220x y x y a ++-+=截直线20x y ++=所得弦的长度为4，则实数a 的值是( ) A ．2-B ．4-C ．6-D ．8-【解答】解：圆22220x y x y a ++-+= 即22(1)(1)2x y a ++-=-，故弦心距d =再由弦长公式可得224a -=+，4a ∴=-，故选：B ．7．（2014•江西）在平面直角坐标系中，A ，B 分别是x 轴和y 轴上的动点，若以AB 为直径的圆C 与直线240x y +-=相切，则圆C 面积的最小值为( )A ．45πB ．34πC ．(6π-D ．54π【解答】解：如图，设AB 的中点为C ，坐标原点为O ，圆半径为r ，由已知得||||OC CE r ==，过点O 作直线240x y +-=的垂直线段OF ，交AB 于D ，交直线240x y +-=于F ，则当D 恰为OF 中点时，圆C 的半径最小，即面积最小此时圆的直径为(0,0)O 到直线240x y +-=的距离为：d ==此时12r d ==∴圆C 的面积的最小值为：245min S ππ=⨯=．故选：A ．8．（2013•重庆）设P 是圆22(3)(1)4x y -++=上的动点，Q 是直线3x =-上的动点，则||PQ 的最小值为( ) A ．6B ．4C ．3D ．2【解答】解：过圆心A 作AQ ⊥直线3x =-，与圆交于点P ，此时||PQ 最小，由圆的方程得到(3,1)A -，半径2r =，则||||624PQ AQ r =-=-=．故选：B ．9．（2013•陕西）已知点(,)M a b 在圆22:1O x y +=外，则直线1ax by +=与圆O 的位置关系是( ) A ．相切B ．相交C ．相离D ．不确定【解答】解：(,)M a b 在圆221x y +=外， 221a b ∴+>，∴圆(0,0)O 到直线1ax by +=的距离1d r <=，则直线与圆的位置关系是相交．故选：B ．10．（2013•江西）过点引直线l 与曲线y =A ，B 两点，O 为坐标原点，当ABO ∆的面积取得最大值时，直线l 的斜率等于( )A B ．C ． D ．【解答】解：由y =221(0)x y y +=．所以曲线y =x 轴上方的部分（含与x 轴的交点），设直线l 的斜率为k ，要保证直线l 与曲线有两个交点，且直线不与x 轴重合，则10k -<<，直线l 的方程为0(y k x -=-，即0kx y -=．则原点O 到l 的距离d =，l则2211ABO k S k ∆-==+==令211t k =+，则ABO S ∆=34t =，即21314k =+时，ABOS ∆有最大值为12．此时由21314k =+，解得k = 故选：D ．11．（2013•天津）已知过点(2,2)P 的直线与圆22(1)5x y -+=相切，且与直线10ax y -+=垂直，则(a = ) A ．12-B ．1C ．2D ．12【解答】解：因为点(2,2)P 满足圆22(1)5x y -+=的方程，所以P 在圆上，又过点(2,2)P 的直线与圆22(1)5x y -+=相切，且与直线10ax y -+=垂直，所以切点与圆心连线与直线10ax y -+=平行，所以直线10ax y -+=的斜率为：20221a -==-．故选：C ．12．（2013•安徽）直线250x y +-=被圆22240x y x y +--=截得的弦长为( )A ．1B ．2C ．4D ．【解答】解：由22240x y x y +--=，得22(1)(2)5x y -+-=，所以圆的圆心坐标是(1,2)C ，半径r =圆心C 到直线250x y +-+=的距离为1d ===．所以直线直线250x y +-=被圆22240x y x y +--=截得的弦长为4．故选：C ．13．（2012•天津）设m ，n R ∈，若直线(1)(1)20m x n y +++-=与圆22(1)(1)1x y -+-=相切，则m n +的取值范围是( )A ．[11+B ．(-∞，1[13+，)+∞C ．[2-2+D ．(-∞，2[222-+，)+∞【解答】解：由圆的方程22(1)(1)1x y -+-=，得到圆心坐标为(1,1)，半径1r =，直线(1)(1)20m x n y +++-=与圆相切，∴圆心到直线的距离1d ==，整理得：21()2m n m n mn +++=，设m n x +=，则有214x x +，即2440x x --，2440x x --=的解为：12x =+22x =-∴不等式变形得：(220x x ---+，解得：222x +或222x -，则m n +的取值范围为(-∞，2[222-+，)+∞．故选：D ．14．（2012•重庆）对任意的实数k ，直线1y kx =+与圆222x y +=的位置关系一定是( ) A ．相离B ．相切C ．相交但直线不过圆心D ．相交且直线过圆心【解答】解：对任意的实数k ，直线1y kx =+恒过点(0,1)，且斜率存在 (0,1)在圆222x y +=内∴对任意的实数k ，直线1y kx =+与圆222x y +=的位置关系一定是相交但直线不过圆心故选：C ．15．（2012•陕西）已知圆22:40C x y x +-=，l 为过点(3,0)P 的直线，则( ) A ．l 与C 相交 B ．l 与C 相切C ．l 与C 相离D ．以上三个选项均有可能【解答】解：将圆的方程化为标准方程得：22(2)4x y -+=，∴圆心(2,0)C ，半径2r =，又(3,0)P与圆心的距离12d r ==<=，∴点P 在圆C 内，又直线l 过P 点，则直线l 与圆C 相交．故选：A ．16．（2012•安徽）若直线10x y -+=与圆22()2x a y -+=有公共点，则实数a 取值范围是( ) A ．[3-，1]-B ．[1-，3]C ．[3-，1]D ．(-∞，3][1-，)+∞【解答】解：直线10x y -+=与圆22()2x a y -+=有公共点∴圆心到直线10x y -+=2|1|2a ∴+31a ∴-故选：C ．二．填空题（共10小题）17．（2018•天津）已知圆2220x y x +-=的圆心为C，直线13x y ⎧=-⎪⎪⎨⎪=-⎪⎩，(t 为参数）与该圆相交于A ，B 两点，则ABC ∆的面积为12．【解答】解：圆2220x y x +-=化为标准方程是22(1)1x y -+=，圆心为(1,0)C ，半径1r =；直线13x y ⎧=-⎪⎪⎨⎪=-⎪⎩化为普通方程是20x y +-=，则圆心C到该直线的距离为d ==弦长||22AB =⨯=， ABC ∴∆的面积为111||2222S AB d ==⨯=．故答案为：12． 18．（2017•全国）直线20x -=被圆2220x y x +-=【解答】解：圆2220x y x +-=化为22(1)1x y -+=，设直线20x --=与圆22(1)1x y -+=的交点为A 、B ，圆心为(1,0)O ，线段AB 的中点为D ，半径为1r =则由圆的几何性质可知，OD AB ⊥，且1||2OD ==，||1OA r ==，||2||AB AD ∴===19．（2017•上海）若P 、Q 是圆222440x y x y +-++=上的动点，则||PQ 的最大值为 2 ．【解答】解：圆222440x y x y +-++=，可化为22(1)(2)1x y -++=，P 、Q 是圆222440x y x y +-++=上的动点，||PQ ∴的最大值为2，故答案为2．20．（2016•上海）在平面直角坐标系xOy 中，点A ，B 是圆22650x y x +-+=上的两个动点，且满足||AB =则||OA OB +的最小值为 4 ．【解答】解：设1(A x ，1)y ，2(B x ，2)y ，AB 中点(,)M x y ''． 122x x x +'=，122y y y +'=， ∴12(OA OB x x +=+，12)2y y OM +=，圆22:650C x y x +-+=，22(3)4x y ∴-+=，圆心(3,0)C ，半径2CA =．点A ，B 在圆C 上，AB = 2221()2CA CM AB ∴-=，即1CM =．点M 在以C 为圆心，半径1r =的圆上．312OM OC r ∴-=-=．||2OM ∴，∴||4OA OB +，∴||OA OB +的最小值为4．故答案为：4．21．（2014•湖北）直线1:l y x a =+和2:l y x b =+将单位圆22:1C x y +=分成长度相等的四段弧，则22a b += 2 ．【解答】解：由题意可得，圆心(0,0)到两条直线的距离相等，且每段弧长都是圆周的14，∴cos 452==︒=，222a b ∴+=，故答案为：2．22．（2014•上海）已知曲线:C x =，直线:6l x =，若对于点(,0)A m ，存在C 上的点P 和l 上的Q 使得0AP AQ +=，则m 的取值范围为 [2，3] ．【解答】解：曲线:C x =，是以原点为圆心，2 为半径的圆，并且[2P x ∈-，0]，对于点(,0)A m ，存在C 上的点P 和l 上的Q 使得0AP AQ +=，说明A 是PQ 的中点，Q 的横坐标6x =， 6[22Px m +∴=∈，3]．故答案为：[2，3]．23．（2014•江苏）在平面直角坐标系xOy 中，直线230x y +-=被圆22(2)(1)4x y -++=截得的弦长为．【解答】解：圆22(2)(1)4x y -++=的圆心为(2,1)C -，半径2r =，点C 到直线直线230x y +-=的距离d ，∴根据垂径定理，得直线230x y +-=被圆22(2)(1)4x y -++=截得的弦长为==． 24．（2013•湖北）已知圆22:5O x y +=，直线:cos sin 1(0)2l x y πθθθ+=<<．设圆O 上到直线l 的距离等于1的点的个数为k ，则k = 4 ．【解答】解：由圆的方程得到圆心(0,0)O ，半径r =圆心O 到直线l 的距离1d ==，且11r d d -=->=，∴圆O 上到直线l 的距离等于1的点的个数为4，即4k =．故答案为：425．（2013•浙江）直线23y x =+被圆22680x y x y +--=所截得的弦长等于【解答】解：圆22680x y x y +--=的圆心坐标(3,4)，半径为5，=因为圆心距，半径，半弦长满足勾股定理，所以直线23y x =+被圆22680x y x y +--=所截得的弦长为：2=故答案为：26．（2013•山东）过点(3,1)作圆22(2)(2)4x y -+-=的弦，其中最短的弦长为【解答】解：根据题意得：圆心(2,2)，半径2r =，2，(3,1)∴在圆内，圆心到此点的距离d ，2r =，∴最短的弦长为=故答案为：三．解答题（共4小题）27．（2017•上海）某景区欲建造两条圆形观景步道1M 、2M （宽度忽略不计），如图所示，已知AB AC ⊥，60AB AC AD ===（单位：米），要求圆1M 与AB 、AD 分别相切于点B 、D ，圆2M 与AC 、AD 分别相切于点C 、D ；（1）若60BAD ∠=︒，求圆1M 、2M 的半径（结果精确到0.1米）（2）若观景步道1M 与2M 的造价分别为每米0.8千元与每米0.9千元，如何设计圆1M 、2M 的大小，使总造价最低？最低总造价是多少？（结果精确到0.1千元）【解答】解：（1）1M 半径60tan3034.6=︒≈，2M 半径60tan1516.1=︒≈；（2）设2BAD α∠=，则总造价0.8260tan 0.9260tan(45)y παπα=+︒-，设1tan x α+=，则1812(817)84y x x ππ=+-，当且仅当32x =，1tan 2α=时，取等号，1M ∴半径30，2M 半径20，造价263.8千元．28．（2015•陕西）如图，AB 切O 于点B ，直线AO 交O 于D ，E 两点，BC DE ⊥，垂足为C ．（Ⅰ）证明：CBD DBA ∠=∠；（Ⅱ）若3AD DC =，BC =，求O 的直径．【解答】证明：（Ⅰ）DE 是O 的直径，则90BED EDB ∠+∠=︒， BC DE ⊥，90CBD EDB ∴∠+∠=︒，即CBD BED ∠=∠，AB 切O 于点B ，DBA BED ∴∠=∠，即CBD DBA ∠=∠；（Ⅱ）由（Ⅰ）知BD 平分CBA ∠，则3BA ADBC CD ==， 2BC =AB ∴=4AC =，则3AD =，由切割线定理得2AB AD AE =，即26AB AE AD==，故3DE AE AD =-=，即可O 的直径为3．29．（2013•江苏）在平面直角坐标系xOy 中，点(0,3)A ，直线:24l y x =-，设圆C 的半径为1，圆心在l 上．（1）若圆心C 也在直线3y x =-上，过点A 作圆C 的切线，求切线方程；（2）若圆C 上存在点M ，使||2||MA MO =，求圆心C 的横坐标的取值范围．【解答】解：（1）由题设，圆心C 在3y x =-上，也在直线24y x =-上，设切点的横坐标为a ， 243a a -=-，1a ∴=，(1,2)C ∴-．22:(1)(2)1C x y ∴-++=，由题，当斜率存在时，过A 点切线方程可设为3y kx =+，即30kx y -+=1=，解得：125k =-，⋯（4分）又当斜率不存在时，也与圆相切，∴所求切线为0x =或1235y x =-+，即0x =或125150x y +-=；（2）设点(,)M x y ，由||2||MA MO =，化简得：22(1)4x y ++=，∴点M 的轨迹为以(0,1)-为圆心，2为半径的圆，可记为圆D ，又点M 在圆C 上，∴圆C 与圆D 的关系为相交或相切，1||3CD ∴，其中||CD221(23)3a a ∴+-，解得：1205a． 30．（2013•四川）已知圆C 的方程为22(4)4x y +-=，点O 是坐标原点．直线:l y kx =与圆C 交于M ，N 两点．（Ⅰ）求k 的取值范围；（Ⅱ）设(,)Q m n 是线段MN 上的点，且222211||||||OQ OM ON =+．请将n 表示为m 的函数．【解答】解：（Ⅰ）将y kx =代入22(4)4x y +-=中，得：22(1)8120(*)k x kx +-+=，根据题意得：△22(8)4(1)120k k =--+⨯>，即23k >，则k 的取值范围为(-∞，⋃，)+∞；（Ⅱ）由M 、N 、Q 在直线l 上，可设M 、N 坐标分别为1(x ，1)kx ，2(x ，2)kx ，2221||(1)OM k x ∴=+，2222||(1)ON k x =+，22222||(1)OQ m n k m =+=+，代入222211||||||OQ OM ON =+得：22222212211(1)(1)(1)k m k x k x =++++，即21212222221212()2211x x x x m x x x x +-=+=，由(*)得到12281kx x k +=+，122121x x k =+，代入得：222222824()211144(1)k kk m k -++=+，即223653m k =-，点Q 在直线y kx =上，n km ∴=，即n k m =，代入223653m k =-，化简得225336n m -=，由223653m k =-及23k >，得到203m <<，即(m ∈0)(0⋃，根据题意得点Q 在圆内，即0n >，n ∴=则n 与m的函数关系式为(n m =∈0)(0⋃．。

中职数学基础模块下册《直线与圆的位置关系》word练习题

中职数学基础模块下册《直线与圆的位置关系》word练习题1.直线的倾斜角是指：直线l与x轴的夹角。

倾斜角的正切叫做直线的斜率。

90度的斜率是不存在，0度的斜率是0.2.已知直线过点A（1，3）和B（4，8），则直线的倾斜角是：45度，斜率是1.3.已知直线过点A（1，3），倾斜角α=45度，则该直线的点斜式方程是y-3=x-1.4.已知直线的斜率是K=-1，则直线的倾斜角是：-45度。

5.点A（2，5），B（-1，1），则A、B两点的距离是√26.6.已知直线过点A（3，5），直线的斜率是-2，则直线的点斜式方程是y-5=-2(x-3)；直线方程是y=-2x+11.7.填表中空格：直线的倾斜角α 斜率K=tanα30度 0.57745度 1120度 -1.732150度 -0.577 不存在8.过点A（3，5），倾斜角是60度的直线方程是y-5=√3(x-3)。

9.直线x=2过点（2，0），与y轴平行。

10.直线y=2x+5的斜率是2，在Y轴上的截距是5.11.倾斜角是120度，在x轴上的截距是2的直线方程是y=-√3x+2.12.直线3x+y-6=0的斜率是-3，在y轴上的截距是-6，在x轴上的截距是2.13.两条直线如果k1=k2且b1=b2，则这两条直线重合；如果k1=k2且b1≠b2，则这两条直线平行；如果k1≠k2，则这两条直线相交；如果k1×k2=-1，则这两条直线垂直。

二、选择填空：1.角α的终边过点P（2，3），则sinα=0.2.与X轴平行的直线的斜率K=0.3.与Y轴平行的直线的斜率K不存在。

4.直线的斜率K=1，则倾斜角α=45度。

5.数轴上点A的坐标是3，点B的坐标是5，则AB的距离是2.6.已知点A（3，-2），点B（5，2），则AB的距离是4.7.已知直线方程是y=3，则直线与x轴相交。

8.与y轴平行的直线的倾斜角是不存在。

9.已知直线方程是y=3x-5，则直线的倾斜角是71.57度。

(word版)高中数学直线与圆的位置关系练习题

高中数学直线与圆的位置关系一、单选题1.已知圆x2+y2−6x=0，过点(1,2)的直线被该圆所截得的弦的长度的最小值为()A. 1B. 2C. 3D. 42.从点P(m,3)向圆C：(x+2)2+(y+2)2=1引切线，则切线长的最小值为()A. 2√6B. √26C. 4+√2D. 53.圆x2+y2−4x+2y+1=0与圆x2+y2+4x−4y−1=0的公切线有()A. 1条B. 2条C. 3条D. 4条4.过点P(−2,4)作圆O：(x−2)2+(y−1)2=25的切线l，直线m：ax−3y=0与直线l平行，则直线l与m的距离为()A. 4B. 2C. 85D. 1255.已知圆C:x2−6x+y2+2ay+7+a2=0关于直线3x+y−1=0对称，则a=()A. 4B. 6C. 8D. 106.在坐标平面内，与点A(1,2)距离为1，且与点B(3,1)距离为2的直线共有()A. 1条B. 2条C. 3条D. 4条7.设O为原点直线y=kx+2与圆x2+y2=4相交于A，B两点，当▵ABO面积最大值时，k=()A. ±√22B. ±1C. ±√2D. ±28.圆C1：(x+1)2+(y+2)2=4与圆C2：(x−1)2+(y+1)2=9的位置关系是()A. 内切B. 相交C. 外切D. 相离9.直线l：y=x+1上的点到圆C：x2+y2+2x+4y+4=0上的点的最近距离为()A. √2B. 2−√2C. 1D. √2−110.若点P(1,1)为圆C：x2+y2−6x=0的弦MN的中点，则弦MN所在的直线方程为()A. 2x+y−3=0B. x−2y+1=0C. x+2y−3=0D. 2x−y−1=011. 已知圆C 的圆心为原点O ，且与直线x +y +4√2=0相切．点P 在直线x =8上，过点P 引圆C 的两条切线PA ，PB ，切点分别为A ，B ，如图所示，则直线AB 恒过定点的坐标为( )A. (2,0)B. (0,2)C. (1,0)D. (0,1)12. 若圆C 的半径为1，圆心在第一象限，且与直线4x −3y =0和x 轴都相切，则该圆的标准方程是( )A. (x −2)2+(y −1)2=1B. (x −2)2+(y +1)2=1C. (x +2)2+(y −1)2=1D. (x −3)2+(y −1)2=1二、多选题（本大题共2小题，共10.0分） 13. 已知圆M:x 2+y 2−4x −1=0，点P (x,y )是圆M 上的动点，则下列说法正确的有( )A. 圆M 关于直线x +3y −2=0对称B. 直线x +y =0与M 的相交弦长为√3C. t =y x+3的最大值为12D. x 2+y 2的最小值为9−4√514. 已知A (−2,0)，B (2,0)，若圆(x −2a +1)2+(y −2a −2)2=1上存在点M 满足MA →⋅MB →=0，实数a 可以是( ) A. −1 B. −0.5 C. 0D. 1三、单空题15. 已知点P 是直线y =x 上一个动点，过点P 作圆(x +2)2+(y −2)2=1的切线，切点为T ，则线段PT 长度的最小值为．16. 若过点P(1,√3)作圆O:x 2+y 2=1的两条切线，切点分别为A 和B ，则|AB |= ．17. 与直线y =x +3平行且与圆(x −2)2+(y −3)2=8相切的直线的方程为________________________．18.已知坐标原点为O，过点P(2,6)作直线2mx−(4m+n)y+2n=0(m,n不同时为零)的垂线，垂足为M，则|OM|的取值范围是______．19.若P(2,1)是圆(x−1)2+y2=25的弦AB的中点，则直线AB的方程为．20.已知直线x−√3y+8=0和圆x2+y2=r2(r>0)相交于A，B两点．若|AB|=6，则r的值为______．21.已知点P在直线x−y+4=0上，由点P向圆x 2+y 2=4作两条切线，切点分别为A，B，则∠APB的最大值为__________．四、多空题（本大题共1小题，共5.0分）22.已知圆C1:x2+y2=4与圆C2:x2+y2−8x+6y+m=0外切，则m=(1)，此时直线l:x+y=0被圆C2所截的弦长为(2)．五、解答题23.已知点M(3,1)，圆O1：(x−1)2+(y−2)2=4．(1)若直线ax−y+4=0与圆O1相交于A，B两点，且弦AB的长为2√3，求a的值；(2)求过点M的圆O1的切线方程．24.已知圆C1：x2+y2−2x=0和圆C2：x2+y2−6x−4y+4=0相交于A,B两点．(1)求公共弦AB的垂直平分线方程．(2)求ΔABC2的面积。

圆与直线的位置关系练习题

圆与直线的位置关系练习题圆与直线是几何学中常见的图形，它们之间的位置关系有着多种情况。

本文将通过一些练习题来深入探讨圆与直线的位置关系，帮助读者更好地理解和运用相关知识。

练习题一：圆内一点到圆的位置关系设有一个圆C，圆心为O，半径为r。

点P在圆C内部，距离圆心O的距离为d。

现在要画一条直线l通过点P，使得直线l与圆C相交于点A、B两个不同的点。

请问，在给定的条件下，直线l与圆C的位置关系有哪些可能性，并给出相应的解释。

解析：根据给定的条件，直线l必然与圆C相交于两个不同的点。

具体的位置关系取决于点P与圆心O之间的距离d与圆的半径r之间的关系。

以下是三种可能的情况：1. d > r：此时，点P与圆心O的距离大于圆的半径，直线l将穿过圆C的内部，与圆C相交于两个不同的点A、B。

2. d = r：此时，点P与圆心O的距离等于圆的半径，直线l刚好与圆C相切于点P。

3. d < r：此时，点P与圆心O的距离小于圆的半径，直线l将不会与圆C相交，即没有解。

练习题二：圆外一点到圆的位置关系现在考虑一个不同的情况，点P位于圆C的外部，距离圆心O的距离为d。

同样地，画一条直线l通过点P，使得直线l与圆C相交于点A、B两个不同的点。

请问，在给定的条件下，直线l与圆C的位置关系有哪些可能性，并给出相应的解释。

解析：与练习题一类似，直线l与圆C的位置关系取决于点P与圆心O之间的距离d与圆的半径r之间的关系。

以下是三种可能的情况：1. d > r：此时，点P与圆心O的距离大于圆的半径，直线l将与圆C相交于两个不同的点A、B。

2. d = r：此时，点P与圆心O的距离等于圆的半径，直线l将切割圆C并与圆相切于点P。

3. d < r：此时，点P与圆心O的距离小于圆的半径，直线l将穿过圆C的外部，无法与圆C相交。

练习题三：圆与平行直线的位置关系给定一条平行于$x$轴的直线$l$，圆C的圆心为O，半径为r。

27.4 直线与圆的位置关系(作业)(解析版)

27.4 直线与圆的位置关系（作业）一、单选题1．（2020·上海市建平中学西校九年级月考）下列命题中真命题是（）A．平分弦的半径垂直于弦B．垂直平分弦的直线必经过圆心C．相等的圆心角所对的弦相等D．经过半径一端且垂直于这条半径的直线是圆的切线【答案】B【分析】根据垂径定理，圆心角、弧、弦的关系定理，切线的判定定理判断即可．【详解】A.平分弦（不是直径）的半径垂直于弦，本选项说法是假命题；B.垂直平分弦的直线必经过圆心，本选项说法是真命题；C.在同圆或等圆中，相等的圆心角所对的弦相等，本选项说法是假命题；D.经过半径外端且垂直于这条半径的直线是圆的切线，本选项说法是假命题；故选：B．【点睛】本题主要考查了圆中相关命题正误的判断，熟练掌握垂径定理，圆心角、弦、弧的关系定理，切线的判定定理等知识是解决本题的关键．2．（2020·上海大学附属学校九年级三模）下列说法中，正确的是（）A．垂直于半径的直线是圆的切线；B．经过半径的外端且垂直于半径的直线是圆的切线；C．经过半径的端点且垂直于半径的直线是圆的切线；D．到圆心的距离等于直径的直线是圆的切线．【答案】B【分析】根据切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线，逐项分析即可．【详解】由切线的判定定理得：经过半径的外端且垂直于这条半径的直线是圆的切线，得出只有答案B符合，故选：B．【点睛】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线，属于基础性题目，难度不大．3．（2020·上海九年级一模）已知在矩形ABCD中，AB＝5，对角线AC＝13．⊙C的半径长为12，下列说法正确的是（）A．⊙C与直线AB相交B．⊙C与直线AD相切C．点A在⊙C上D．点D在⊙C内【答案】D【分析】根据点和圆的位置关系及直线和圆的位置关系判断即可．【详解】解：∵在△ABC中，∠ACB＝90°，AC＝13，AB＝5，∴BC＝12，∵⊙C的半径长为12，∴⊙C与直线AB相切，故A选项不正确，∵CD＝AB＝5＜12，∴⊙C与直线AD相交，故B选项不正确，∵AC＝13＞12，∴点A在⊙C外，故C选项不正确，∵CD＝5＜12，∴点D在⊙C内，故D选项正确，故选：D．【点睛】本题考查了点与圆的位置关系，直线与圆的位置关系，熟练掌握切线的判定及点与圆的位置关系是解题的关键．4．（2020·上海九年级一模）下列四个选项中的表述，一定正确的是（）A．经过半径上一点且垂直于这条半径的直线是圆的切线B．经过半径的端点且垂直于这条半径的直线是圆的切线C．经过半径的外端且垂直于这条半径的直线是圆的切线D．经过一条弦的外端且垂直于这条弦的直线是圆的切线【答案】C【分析】根据切线的判定对各个选项进行分析，从而得到答案．【详解】由切线的判定定理可知：经过半径外端点且与这条半径垂直的直线是圆的切线，故A，B，D选项不正确，C选项正确，故选：C．【点睛】此题主要考查了圆中切线的判定，熟练掌握切线的判定定理是解题的关键．5．（2020·上海九年级一模）下列四个选项中的表述，一定正确的是（）A．经过半径上一点且垂直于这条半径的直线是圆的切线；B．经过半径的端点且垂直于这条半径的直线是圆的切线；C．经过半径的外端且垂直于这条半径的直线是圆的切线；D．经过一条弦的外端且垂直于这条半径的直线是圆的切线.【答案】C【分析】逐一对选项进行分析即可.【详解】A选项中圆的切线不是经过半径上任一点，而是经过半径的非圆心一端且垂直于这条半径的直线是圆的切线.故该选项错误；B选项中，必须经过半径的非圆心的一端并且垂直于这条半径的直线，就是这个圆的一条切线.故该选项错误；C选项中经过半径的外端且垂直于这条半径的直线是圆的切线，故该选项正确；D选项中，不是经过任一条弦的外端且垂直于这条半径的直线就是圆的切线.故该选项错误.故选C【点睛】本题主要考查切线的意义和性质，掌握切线的性质是解题的关键.6．（2020·上海九年级专题练习）如图，在梯形ABCD中，AD∥BC，∠B＝90°，AD＝2，AB＝4，BC＝6，点O是边BC上一点，以O为圆心，OC为半径的⊙O，与边AD只有一个公共点，则OC的取值范围是（）A．4＜OC≤133B．4≤OC≤133C．4＜OC143£D．4≤OC143£【答案】B【分析】作DE⊥BC于E，当⊙O与边AD相切时，圆心O与E重合，即OC＝4；当OA＝OC时，⊙O与AD交于点A，设OA＝OC＝x，则OB＝6﹣x，在Rt△ABO中，由勾股定理得出方程，解方程得出OC＝133；即可得出结论．【详解】作DE⊥BC于E，如图所示：则DE＝AB＝4，BE＝AD＝2，∴CE＝4＝DE，当⊙O与边AD相切时，切点为D，圆心O与E重合，即OC＝4；当OA＝OC时，⊙O与AD交于点A，设OA＝OC＝x，则OB＝6﹣x，在Rt△ABO中，由勾股定理得：42+（6﹣x）2＝x2，解得：x＝133；∴以O为圆心，OC为半径的⊙O，与边AD只有一个公共点，则OC的取值范围是4≤x≤133；故选B．【点睛】本题考查了直线与圆的位置关系、直角梯形的性质、勾股定理等知识；熟练掌握直角梯形的性质，分情况讨论是解题的关键．7．（2020·上海九年级专题练习）在直角坐标平面内，已知点M(4，3)，以M 为圆心，r 为半径的圆与x 轴相交，与y 轴相离，那么r 的取值范围为( )A ．0r 5<<B ．3r 5<<C ．4r 5<<D ．3r 4<<【答案】D【分析】先求出点M 到x 轴、y 轴的距离，再根据直线和圆的位置关系得出即可．【详解】解：∵点M 的坐标是（4，3），∴点M 到x 轴的距离是3，到y 轴的距离是4，∵点M （4，3），以M 为圆心，r 为半径的圆与x 轴相交，与y 轴相离，∴r 的取值范围是3＜r ＜4，故选：D ．【点睛】本题考查点的坐标和直线与圆的位置关系，能熟记直线与圆的位置关系的内容是解此题的关键．8．（2020·上海九年级专题练习）已知⊙O 1与⊙O 2内切于点A ，⊙O 1的半径等于5，O 1 O 2=3,那么O 2A 的长等于（）A ．2B ．3C ．8D ．2或8【答案】D【分析】根据题意可知分两种情况讨论即可求解.【详解】根据题意可知分两种情况讨论：①O 1A ＞O 2A ，∵O 1A =5，O 1 O 2=3,∴O 2A= O 1A-O 1 O 2=2①O 2A ＞O 1A ，∵O 1A =5，O 1 O 2=3,∴O 2A= O 1A+O 1 O 2=8故选D.【点睛】此题主要考查圆与圆的位置关系，解题的关键是根据题意分情况讨论.9．（2019·上海江湾初级中学九年级三模）如图，O e 的半径为4，点A ，B 在O e 上，点P 在O e 内，3sin APB 5Ð=，AB PB ^，如果OP OA ^，那么OP 的长为( )A ．53B ．3C ．95D ．43【答案】D【分析】如图，连接OB ，作BM OP ^交OP 的延长线于M ，作AN MB ^交MB 的延长线于N.则四边形AOMN 是矩形，推出A 、O 、P 、B 四点共圆，根据圆周角定理得到BOP BAP ÐÐ=，根据三角函数的定义设BM 4k =，OM 3k =，根据勾股定理得到4k (5=负根已经舍弃)，根据相似三角形的性质即可得到结论．【详解】解：如图，连接OB ，作BM OP ^交OP 的延长线于M ，作AN MB ^交MB 的延长线于N.则四边形AOMN 是矩形，AOP ABP 90ÐÐ==o Q ，A \、O 、P 、B 四点共圆，BOP BAP ÐÐ\=，3sin APB 5Q Ð=，4tan BAP 3Ð\=，4BM tan BOM tan BAP 3OM ÐÐ===，设BM 4k =，OM 3k =，在Rt OMB V 中，222(4k)(3k)4+=，解得4k (5=负根已经舍弃)，16BM 5\=，12OM 5=，4BN MN BM 5=-=，MBP BPM 90o Q ÐÐ+=，MBP ABN 90ÐÐ+=o ，BPM ABN ÐÐ\=，BMP ANB 90ÐÐ==o Q ，BMP \V ∽ANB V ，PB PM AB BN\=，4PM 435\=，16PM 15\=，4OP OM PM 3\=-=．故选D ．【点睛】本题考查点与圆的位置关系，圆周角定理，相似三角形的判定和性质，矩形的判定和性质，勾股定理，锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造相似三角形，特殊四边形解决问题．二、填空题10．（2020·上海市建平中学西校九年级月考）在Rt ABC V 中，∠C ＝90°，AC ＝BC ，若以点C 为圆心，以2cm 长为半径的圆与斜边AB 相切，那么BC 的长等于_____．【答案】【分析】如图（见解析），先根据圆的切线的性质可得CD AB ^，再根据等腰直角三角形的判定与性质可得45B Ð=°，然后在Rt BCD V 中，根据等腰直角三角形的判定与性质即可得．【详解】如图，设圆与斜边AB 的切点为点D ，连接CD ，则2CD cm=由圆的切线的性质得：CD AB^90,C AC BCÐ=°=Q Rt ABC \V 是等腰直角三角形，45B Ð=°Rt BCD \V 是等腰直角三角形2,CD BD cm BC \====故答案为：．【点睛】本题考查了圆的切线的性质、等腰直角三角形的判定与性质，掌握理解圆的切线的性质是解题关键．11．（2020·上海九年级一模）两圆的半径之比为3:1，当它们外切时，圆心距为4，那么当它们内切时，圆心距为__________．【答案】2【分析】只需根据两圆的半径比以及两圆外切时，圆心距等于两圆半径之和，列方程求得两圆的半径；再根据两圆内切时，圆心距等于两圆半径之差求解．【详解】设大圆的半径为R，小圆的半径为r，则有r：R＝1：3；又R＋r＝4，解，得R＝3，r＝1，∴当它们内切时，圆心距＝3−1＝2．故答案为：2．【点睛】此题考查了两圆的位置关系与数量之间的联系．解题的关键是正确的求出两个半径．12．（2020·上海九年级专题练习）已知在Rt△ABC中，∠C=90º，AC=3，BC=4，⊙C与斜边AB相切，那么⊙C的半径为______.【答案】12 5【分析】首先根据勾股定理求出AB，然后根据圆相切的性质得出CD⊥AB，CD即为⊙C的半径，然后根据三角形面积列出等式，即可解得CD.【详解】设切点为D，连接CD，如图所示∵∠C=90º，AC=3，BC=4，∴AB5 ===又∵⊙C与斜边AB相切，∴CD⊥AB，CD即为⊙C的半径∴1122ABCS BC AC AB CD =×=×△∴125 CD=故答案为12 5 .【点睛】此题主要考查圆相切的性质以及勾股定理的运用，熟练掌握，即可解题.13．（2019·上海九年级其他模拟）在△ABC中，AB = AC = 5，tanB =43. 若⊙O的半径为，且⊙O经过点B与C，那么线段OA的长等于________.【答案】3或5【分析】根据题意可得△ABC为等腰三角形，且∠A为顶角，根据tanB的值可以得出BC=8，经过B、C两点的圆的圆心在BC的中垂线上，然后根据圆心在三角形内和三角形外两种情况进行分类讨论．【详解】解：分两种情况考虑：（i）如图1所示，∵AB＝AC，OB＝OC，∴AO垂直平分BC，∴OA⊥BC，D为BC的中点，在Rt△ABD中，AB＝5，tan∠ABC＝43＝ADBD，设AD＝4x，BD＝3x，由勾股定理得：（3x）2＋（4x）2＝52，解得x＝1，∴BD＝3，AD＝4，在Rt△BDO中，OD1=，BD＝3，则AO＝AD＋OD＝4＋1＝5；（ii）如图2所示，AO＝AD−OD＝4−1＝3；综合上述，OA的长为3或5．故答案为：3或5．【点睛】此题考查了垂径定理，勾股定理，等腰三角形的性质，以及直角三角形的性质，熟练掌握定理及性质是解本题的关键．三、解答题14．（2020·上海九年级二模）如图，已知AB、AC是⊙O的两条弦，且AO平分∠BAC．点M、N分别在弦AB、AC上，满足AM＝CN．（1）求证：AB＝AC；（2）联结OM 、ON 、MN ，求证：MN OM AB OA=．【分析】（1）过点O 作OD ⊥AB 于点D ，OE ⊥AC 于点E ，利用角平分线的性质和垂径定理即可得出答案；（2）联结OB ，OM ，ON ，MN ，首先证明BOM AON @V V ，然后再证明NOM BOA V :V ，根据相似三角形的性质即可得出答案．【详解】证明：（1）过点O 作OD ⊥AB 于点D ，OE ⊥AC 于点E ，如图所示：∵AO 平分∠BAC ．∴OD ＝OE ．222222,AD AO OD AE AO OE =-=-Q ，AD AE \=．,OD AB OE AC ^^Q ，2,2AB AD AC AE \==，∴AB ＝AC ；（2）联结OB ，OM ，ON ，MN ，如图所示，∵AM＝CN，AB＝AC∴BM＝AN．∵OA＝OB，∴∠B＝∠BAO．∵∠BAO＝∠OAN，∴∠B＝∠OAN，∴△BOM≌△AON（SAS），∴∠BOM＝∠AON，OM＝ON，∴∠AOB＝∠MON，∴△NOM∽△BOA，∴MN OM AB OA=．【点睛】本题主要考查相似三角形的判定及性质，全等三角形的判定及性质及圆的有关性质，熟练掌握相关性质及定理是解题的关键．。

直线与圆的位置关系 - 拔高 - 习题

直线与圆位置关系一、选择题（共12小题；共60分）1. 圆与曲线 ()____A. B. C. D.2. 已知点在圆()D_Dd__________ʲĝϨϨA. 相切B. 相交C. 相离D. 不确定3. 已知圆()D_Dd__________ʲĝϨϨA. B. C. D.4. 平行于直线 ^^ ()D_Dd__A. 或B. 2C. 或D. 或5. 已知圆()D_Dd__________ʲĝϨϨ________________ ^^_ 的方程为A. B.C. D.6. 已知圆 (观察点，要使视线不被圆()___________A.B.C.D.7. 圆上的点到直线 ()D_DdA. B. C. D.8. 已知圆截直线√_D_Dd，则实数 ()A. B. C. D.9. 已知直线与圆()D_Dd__________ʲĝA. B. C. D.10. 已知两点，，若点 ^ 上的动点，则 ()D_DdA. B. C. D.11. 要在边长为()__________________________________________________________________A. B. C. D.12. 已知圆 (__在直线〖〗^_D_Dd__________（__D_Dd_的取值范围是A. B. C. D.二、填空题（共5小题；共25分）13. 直线√__________，则圆 ()^()^_______________________14. 圆 ()^^D_Dd__________ ．15. 已知圆(√且与圆D_Dd__________иðϨϨ_____16. 如果直线 ^ _(√)_D_Dd__________αŊϨϨ________________ ^^D_Dd__17. 过点作圆∣∣D_Dd__________ѴҒϨϨ__等于．三、解答题（共5小题；共65分）18. 已知，直线 (所截得的弦长为，且∣∣D_Dd____（1）求的最大值与最小值；（2）圆 ()^()^__________篘_篚_篜_篠_繄_繆_繈19. 已知圆 ()D_Dd__．（1）若 D_Dd_______ 的方程；（2）若 D_Dd__________ððϨϨ________________ √_D_Dd__________-ðϨϨ_____20. 已知圆．（1）求圆 ()D_（2）已知两定点，，∣∣^∣∣^D_Dd_的取值范围．21. 已知圆（1）直线∣∣D_Dd__________ѴҒϨ；（2）如图，设，是圆__D_Dd__________ŊĝϨϨ，点__D_Dd_____，如果直线，与 ()D_和，问()^()^D_Dd__________௴Է22. 已知圆 (（（1）证明：不论 D_Dd__________ððϨϨ（2）求直线被圆D_Dd__________ĝð答案第一部分1. D2. B 【解析】由点在圆外，得，所以圆心到直线的距离，则直线与圆相交．3. B 【解析】由圆可知圆心为，圆的半径．所以圆心到直线的距离．因为圆截直线得弦长为，所以，即，所以．4. A 【解析】设所求直线方程为，则，所以，所以，所以所求直线方程为：或 .5. D【解析】设圆的圆心坐标为，则，或（舍），于是圆心为，所以圆的方程为．6. D7. A 【解析】将圆的方程化为，即圆心坐标为，半径为，则圆心到直线的距离，故圆上的点到直线距离的最大值为．8. B9. C10. B【解析】由过点，的直线为，圆心到直线的距离为，则圆上的点到直线最短的距离为，所以面积的最小值为．11. C12. B 【解析】计算知，直线与圆相离，过直线上一点作圆的两条切线，记该点对圆的张角为，则圆上存在点使得．由此知只需在直线上寻找对圆的张角等于的两点，，则线段即是符合题意的点所形成的轨迹．事实上，张角等于时，点与圆心及切点构成的四边形为正方形，．记，则解得或．第二部分13. （答案不唯一）14.【解析】的圆心为，由点到直线的距离公式可得：．15.16.17.【解析】如图所示：易知，，所以．，求出．第三部分18. （1）因为直线被圆所截得的弦长为，所以圆心到直线的距离，因为，所以，所以．所以的最大值与最小值分别为，．（2）由（）可得圆的方程：，令，则，令，则，所以圆与坐标轴相交于三点，，，所以为直角三角形，斜边，内切圆的半径为．19. （1）直线无斜率时，直线的方程为，此时直线和圆相切．直线有斜率时，设方程为，即，因为与圆相切，所以圆心到直线的距离等于半径，即，解得，所以直线的方程为．综上所述：当直线无斜率时，直线的方程为；当直线有斜率时，直线的方程为．（2）面积最大时，，，即是等腰直角三角形，由半径，得：圆心到直线的距离为，设直线的方程为：，即，则，所以或，所以直线的方程为：，．20. （1）由已知可设圆心，则．圆心到直线的距离，则，解得，从而所求圆的标准方程为或．（2）设，则，要求的取值范围，只需求的取值范围，而的几何意义为圆上的点到原点的距离的平方．由圆心到原点的距离，知点到原点的距离的最大值、最小值分别为，，则的取值范围为，故的取值范围为．21. （1）圆心到直线的距离．圆的半径，所以．（2）设，则，，，．得，得所以22. （1）直线的方程可变形为．，由得即直线恒过定点．圆心，（半径），点在圆内，从而直线与圆恒交于两点．（2）弦长最小时，．，直线的方程为．。