2013中考数学 重点班实数计算题
2013年中考数学专题复习第2讲:实数有关计算

0
【重点考点例析】
【解析】
例3:计算: 3 1 0 1 ( 3) cos 30 12 2 2
1
3 1 2 3 1 2
3 3 解:原式=2 1 2 3 (1 ) 2 2 3 3 =2 1 2 3 1 2 2
=2 3Biblioteka 5 6例1 :阅读材料:对于任何实数,我们规定符号
a b c d
的意义是
1 2 1 4 2 3 2 , =ad-bc.例如: c d 3 4
2 4 3 5 (2) 5 4 3 22
a b
(2)按照这个规定, 若
x 1 2x x 1 2x 3
=2,求x的值.
(2)估算 13的整数部分.
解: 9 13 16
3 13 4 13的整数部分为3.
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a 30° 三角函数 sin a 45°
2 2
60°
3 2
1 2
cos a tan a
3 2
3 3
2 2
1 2
1
3
1 例1:计算:2 2 (3) 3
(2)估算 13的整数部分.
解: 9 13 16
3 13 4 13的整数部分为3.
2
【重点考点例析】 考点一:实数的混合运算。
【解析】
1
例2:计算:
2
解:原式=4 6 3 1
1 1 3 1 3 1 3
1
解:原式= 2 1 1 2
1 (-2) 1 (2013 ) 2
0
2013-2014中考数学专题复习学生版第二讲 实数的运算

第二讲实数的运算【重点考点例析】考点一:实数的大小比较。
A.6个B.5个C.4个D.3个点评:本题主要考查了无理数的估算和数轴,根据数轴的特点,我们把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.对应训练1.(2013•内江)下列四个实数中,绝对值最小的数是()A.-5 B.C.1 D.4考点二:估算无理数的大小A.1与2之间B.2与3之间C.3与4之间D.4与5之间点评:此题主要考查了根式的计算和估算无理数的大小,解题需掌握二次根式的基本运算技能,灵活应用.“夹逼法”是估算的一般方法,也是常用方法.对应训练考点三:有关绝对值的运算例3 (2013•咸宁)在数轴上,点A(表示整数a)在原点的左侧,点B(表示整数b)在原点的右侧.若|a-b|=2013,且AO=2BO,则a+b的值为-671.点评:本题考查了数轴、绝对值以及两点间的距离.根据已知条件得到a<0<b是解题的关键.对应训练.考点四:实数的混合运算。
点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负零指数幂、负指数幂、特殊角的三角函数值、绝对值等考点的运算.对应训练考点五:实数中的规律探索。
例5 (2013•永州)我们知道,一元二次方程x2=-1没有实数根,即不存在一个实数的平方等于-1.若我们规定一个新数“i”,使其满足i2=-1(即方程x2=-1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=-1,i3=i2•i=(-1)•i=-i,i4=(i2)2=(-1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4n•i=(i4)n•i=i,同理可得i4n+2=-1,i4n+3=-i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013的值为()A.0 B.1 C.-1 D.i点评:本题考查了实数的运算,解答本题的关键是计算出前面几个数的值,发现规律,求出一个循环内的和再计算,有一定难度.对应训练【聚焦山东中考】A.- B.- C.-2 D.-1A.5B.-5C.6D.-63.(2013•日照)计算-22+3的结果是()A.7 B.5 C.-1 D.-5 4.(2013•聊城)(-2)3的相反数是()A.-6 B.8 C.- 16D.165.(2013•菏泽)如果a的倒数是-1,那么a2013等于()A.1 B.-1 C.2013 D.-2013 【备考真题过关】一、选择题1.(2013•广州)比0大的数是()A.-1 B.-12C.0 D.12.(2013•重庆)在-2,0,1,-4这四个数中,最大的数是()A.-4 B.-2 C.0 D.1 3.(2013•天津)计算(-3)+(-9)的结果等于()A.12 B.-12 C.6 D.-6 4.(2013•河北)气温由-1℃上升2℃后是()A.-1℃B.1℃C.2℃D.3℃5.(2013•自贡)与-3的差为0的数是()A.3 B.-3 C.13D.-136.(2013•温州)计算:(-2)×3的结果是()A.-6 B.-1 C.1 D.6 7.(2013•厦门)下列计算正确的是()A.-1+2=1 B.-1-1=0 C.(-1)2=-1 D.-12=1 8.(2013•南京)计算:12-7×(-4)+8÷(-2)的结果是()A.-1 B.1 C.D.710.(2013•南京)设边长为3的正方形的对角线长为a.下列关于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③3<a<4;④a是18的算术平方根.其中,所有正确说法的序号是()A.①④B.②③C.①②④D.①③④二、填空题...20.(2013•天河区一模)我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2,(1011)2换算成十进制数应为:(101)2=1×22+0×21+1×20=4+0+1=5;(1011)2=1×23+0×22+1×21+1×20=11按此方式,将二进制(1101)2换算成十进制数的结果是13.三、解答题。
中考数学专题复习《实数的运算》测试卷-附带答案

中考数学专题复习《实数的运算》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.下列说法中正确的是()A.√25的值是±5B.两个无理数的和仍是无理数C.-3没有立方根.D.√a2−b2是最简二次根式.2.实数m,n在数轴上的对应点的位置如图所示,下列结论中正确的是()A.|m|<|n|B.m+n>0C.m−n<0D.mn>0 3.计算:|−2|+3sin30°−2−1−(2022−π)0等于()A.-2B.−12C.2D.04.观察下列各式:√1+112+122=1+11×2√1+122+132=1+12×3√1+132+142=1+13×4…请利用你所发现的规律计算√1+112+122+√1+122+132+√1+132+142+⋯⋯+√1+192+1102其结果为()A.8910B.9910C.989D.8895.估计√2(√23−√2)的值应在()A.2和3之间B.3和4之间C.4和5之间D.5和6之间.6.秦兵马俑的发现被誉为“世界第八大奇迹” 兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比为√5−12下列各数中最接近于√5−12的是()A.25B.12C.35D.347.若x为实数在“(√3+1)◯ x”的“◯”中添上一种运算符号(在“+-× ÷”中选择)后其运算的结果为有理数则不可能是()A.√3−1B.1−√3C.3√3D.1+√38.计算sin60°⋅tan30°−sin45°⋅cos30°的结果是()A.−12+√62B.√32+12C.−√32+12D.12−√649.下列运算正确的是()A .√3+√2=√5B .|3.14−π|=π−3.14C .a 2⋅a 3=a 6D .(a −1)2=a 2−2a −110.今年“十一”期间 广州部分公园举行游园活动 据统计 天河公园早晨6时30分有2人进入公园 接下来的第一个30分钟内有4人进去1人出来 第二个30分钟内有8人进去2人出来 第三个30分钟内有16人进去3人出来 第四个30分钟内有32人进去4人出来.按照这种规律进行下去 到上午11时30分公园内的人数是( )A .211−47B .212−57C .213−68D .214−80二 填空题11.(√3−1.732)0+(−14)−2= .12.【中考变形】已知a =(12)−1+(−√3)0,b =(√3+√2)(√3−√2) 则√a +b = .13.计算:|−5|+(3−π)0−6×3−1+√3−1−2sin60°= 。
2013中考全国100份试卷分类汇编:实数运算(含答案)

2013中考全国100份试卷分类汇编:实数运算(含答案)。
cnXXXX年河北)在下面的计算中,正确的是+B1+的结果是()C.4﹣3 7 D。
cn13-a9 = 3B-8 = 2C .(-2)0 = 0D . 21 =2答案:d3分析:9是9的算术平方根,9 = 3,所以A是错误的;-8 =-2,b错了,(-2) 0 = 1,c也错了,选择d。
(XXXX年京5: 14)计算:(1?3)0??2?2cos45??()?1 .分辨率:1428,(13年山东青岛,8年)计算:2?1?回答:在XXXX,安徽省得了8分,计算:2 sin 300+(1) 2-2?231.(XXXX佛山)计算:2?5?(?2)?(??4?2)。
分析:根据负整数指数幂、绝对值和幂运算的性质,先计算幂,再计算乘除,最后计算加法解决方案:2×[5+(2)]﹣| | ﹣4 | > 2 = 2×(5-8)﹣4÷= ﹣6-﹣8)= 2。
备注:本主题主要考察实数运算。
本主题中需要注意的知识点是:当负整数指数为幂时,a=35.(XXXX深圳)计算:|-8|+()?1-4英寸45英寸?-(XXXX,湛江,广东)计算:-6+9???1?..解决方案:原始形式?6?3?12?837.(XXXX黄石公园)计算:3?3?tan30??38岁?(XXXX) (1)计算:2?1?1??sin45?8?2;?解决方案:原始公式=-1 1|×2(2 +1) 2 +|1- 2 2 21= - +(2 -1) ×2(2 +1)41= - +2[(2 )2 -12]41= 2-47= 465.(XXXX德阳市)计算:12013+(分析:一,一,二1 | 3 1 27 |+3 Tan 60 2。
2013中考试题汇编:实数

2013年全国各地中考数学解析汇编:实数(分2个考点精选92题)8.1 平方根与立方根1. (2013江苏盐城,3,3分)4的平方根是( )A.2B.16C.2±D.±16【解析】本题考查了平方根的概念.掌握有平方根的定义是关键.选项A 是4的算术平方根;选项B 是4的平方, 选项C 是4的平方根,表示为:24±=±【答案】4的平方根是2±,故选C【点评】本题主要考查平方根的定义,解决本题的关键是正确区分一个非负数的算术平方根与平方根.8.2. 实数1. (2013江苏盐城,5,3分)下列四个实数中,是无理数的为( )A.0B. C.-2 D. 27【解析】本题考查了无理数的概念,掌握无理数的三种构成形式是解答本题的关键.无限不循环小数称为无理数,无理数有三种构成形式:①开放开不尽的数;②与π有关的数;③构造性无理数.5属于开放开不尽的数,是无理数;【答案】 选项A,C 是整数,而D 是分数,它们都是有理数,应选B.【点评】本题主要考查了无理数的概念,要注意区分有理数和无理数2.(2013山东泰安,2,3分)下列运算正确正确的是( )5=- B.21()164--= C.632x x x ÷= D.325()x x = 【解析】因为180n r l π=|5|5=-=,2211()1614()4--==-,63633x x x x -÷==,32326()x x x ⨯==,所以B 项为正确选项。
【答案】B【点评】本题主要考查了非负数的算术平方根||a =,负指数幂1(0)p pa a a -=≠,同底数幂的除法m n m n a a a -÷=,幂的乘方()m n mn a a =,掌握这些相关运算的基本性质是解题的基础。
3.(2013山东德州中考,1,3,) 下列运算正确的是( )A.42=B.()23-=9-C.328-=D.020= 【解析】根据算术平方根的定义,4的算术平方根为4,故A 正确;负数的偶次方为正数,()23-=9,故B 错误;根据公式1p pa a -=(a≠0),3128-=,故C 错误; 021=,故D 错误. 【答案】A .【点评】正数的算术平方根为正数,0的算术平方根为0,负数的偶次方为正数,奇次方为负数,任何不等于0的数的负指数幂等于这个数的正指数幂的倒数;任何不等于0的数的0次方都为1.4.(2013山东省聊城,10,3分)如右图所示的数轴上,点B 与点C 关于点A 对称,A 、B 两点对应的实数是3和-1,则点C 所对应的实数是( )A. 1+3B. 2+3C. 23-1D. 23+1 解析:因为点B 与点C 关于点A 对称,所以B 、C 到点A 的距离相等.由于点C 在x 轴正半轴上,所以c 对应的实数是3+3+1=23+1.答案:D点评:根据实数与数轴上的点“一一对应”及点对称的性质即可解决问题.注意任容易分析失误而选A 情形.5. ( 2013年浙江省宁波市,6,3)下列计算正确的是(A )a 6÷a 2=a 3 (B)(a 3)2=a 5 (C)25 =±5 (D) 3-8 =-2【解析】根据幂的运算性质可排除A 和B,由算术平方根的定义可排除C,而D 计算正确,故选D【答案】D【点评】本题考查幂的运算性质、算术平方根、立方根的性质掌握情况,是比较基础的题目.6. ( 2013年浙江省宁波市,7,3)已知实数x,y 满足x-2 +(y+1)2=0,则x-y 等于 (A)3 (B)-3 (C)1 (D) -1【解析】由算术平方根及平方数的非负性,两个非负数之和为零时,这两个非负数同时为零,易得x-2=0,y+1=0,解得x=2,y= -1.【答案】A【点评】本题是一个比较常见题型,考查非负数的一个性质: “两个非负数之和为零时,这两个非负数同时为零.”7. (2013浙江丽水4分,11题)写出一个比-3大的无理数是_______.【解析】:只要比-3大的无理数均可.【答案】:答案不唯一,如-2、3、π等【点评】:无理数是无限不循环小数,其类型主要有三种:①开方开不尽的数,如2;②含π型,如π,2π;③无限不循环小数,如-0.1010010001···. 8.(2013广州市,6, 3分)已知,170a b -++=则a+b=( )A.-8B.-6C. 6D.8【解析】根据非负数的性质,得到两个代数式的值均为0.从而列出二元一次方程组,求出a,b 的值。
2013年全国各地中考数学考点分类汇编实数

学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的 0
的个数所决定. 解答:解:0.000 0025=2.5×10-6;故选:D. 点评:本题考查了用科学记数法表示较小的数,一般形式为a×10-n,其中 1≤|a|<10,n为由
原数左边起第一个不为零的数字前面的 0 的个数所决定.
等号.
3.(2013 浙江湖州,1,3 分)实数 π, 1 ,0,-1 中,无理数是( ) 5
A.π
1
B.
C.0
5
D.-1
【答案】A
【解析】A、是无理数;B、是分数,是有理数,故选项错误;C、是整数,是有理数,选项
错误;D、是整数,是有理数,选项错误.故选 A.
【方法指导】此题主要考查了无理数的定义,无理数就是无限不循环小数.理解无理数的概
即对原不等式两边进行加、减、乘、除运算,让学生根据不等式基本性质作出正确判断,解
决这类题,基本方法就是先弄清不等号两边进行了什么运算,然后再看这种运算是否符合不
等式的基本性质;第二种形式是设计为填空题,先给定一个不等式,然后对这个不等式的不
等号两边进行四则运算,要学生根据这个运算确定不等号方向是否发生改变,要求学生填不
【方法指导】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π 等;
开方开不尽的数;以及像 0.1010010001…,等有这样规律的数.
2013中考数学50个知识点专练1 实数及其运算

2013中考数学50个知识点专练1 实数及其运算一、选择题1.(2012·金华)下列各组数中,互为相反数的是( ) A .2和-2 B .-2和12 C .-2和-12 D.12和2 2.(2012·台州)在12、0、1、-2这四个数中,最小的数是( ) A.12B .0C .1D .-2 3.(2012·温州)计算:(-1)+2的结果是( )A .-1B .1C .-3D .34.(2012·日照)观察图中正方形四个顶点所标的数字规律,可知数2012应标在( )A .第502个正方形的左下角B .第502个正方形的右下角C .第503个正方形的左上角D .第503个正方形的右下角5.(2012·襄阳)下列说法正确的是( )A .(π2)0是无理数 B.33是有理数 C.4是无理数 D.3-8是有理数二、填空题6.(2012·杭州)写出一个比-4大的负无理数________.7.(2012·宁波)实数27的立方根是________.8.(2012·连云港)在日本核电站事故期间,我国某监测点监测到极微量的人工放射性核素碘-131,其浓度为0.0000963贝克/立方米.数据“0.0000963”用科学记数法可表示为________.9.(2012·乐山)数轴上点A 、B 的位置如图所示,若点B 关于点A 的对称点为C ,则点C 表示的数为_________.10.(2012·常德)先找规律,再填数:11+12-1=12,13+14-12=112,15+16-13=130,17+18-14=156,……则12011+12012-__________=12011×2012. 三、解答题11.(2012·衢州)计算:|-2|-(3-π)+2cos 45°12.(2012·东莞)计算:(2011-1)0+18sin45°-2-113.(2012·邵阳)为庆祝建党90周年,某学校欲按如下规则组建一个学生合唱团参加我市的唱红歌比赛.规则一:合唱队的总人数不得少于50人,且不得超过55人.规则二:合唱队的队员中,九年级学生占合唱团总人数的12,八年级学生占合唱团总人数的14,余下的为七年级学生. 请求出该合唱团中七年级学生的人数.14.(2012·广东)阅读下列材料:1×2=13×(1×2×3-0×1×2), 2×3=13×(2×3×4-1×2×3), 3×4=13×(3×4×5-2×3×4), 由以上三个等式相加,可得1×2+2×3+3×4=13×3×4×5=20. 读完以上材料,请你计算下列各题:(1) 1×2+2×3+3×4+…+10×11(写出过程);(2) 1×2+2×3+3×4+…+n ×(n +1)=_________;(3) 1×2×3+2×3×4+3×4×5+…+7×8×9=_________________.15.在数1,2,3,…,1998前添符号“+”和“-”,并依次运算,所得可能的最小非负数是多少?四、选做题16.已知数14的小数部分是b ,求b 4+12b 3+37b 2+6b -20的值.。
实数的有关计算问题(真题10道+模拟30道)-中考数学重难题型押题培优导练案【解析版】

实数的有关计算问题(北京真题10道+模拟30道)【方法归纳】题型概述,方法小结,有的放矢1.实数的运算(1)实数的运算和在有理数范围内一样,值得一提的是,实数既可以进行加、减、乘、除、乘方运算,又可以进行开方运算,其中正实数可以开平方.(2)在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.2.实数运算的“三个关键”(1).运算法则:乘方和开方运算、幂的运算、指数(特别是负整数指数,0指数)运算、根式运算、特殊三角函数值的计算以及绝对值的化简等.(2).运算顺序:先乘方,再乘除,后加减,有括号的先算括号里面的,在同一级运算中要从左到右依次运算,无论何种运算,都要注意先定符号后运算.(3).运算律的使用:使用运算律可以简化运算,提高运算速度和准确度.【典例剖析】典例精讲,方法提炼,精准提分【例1】(2021·北京·中考真题)计算:2sin60°+√12+|−5|−(π+√2)0.【答案】3√3+4【解析】【分析】根据特殊三角函数值、零次幂及二次根式的运算可直接进行求解.【详解】+2√3+5−1=3√3+4.解:原式=2×√32【点睛】本题主要考查特殊三角函数值、零次幂及二次根式的运算,熟练掌握特殊三角函数值、零次幂及二次根式的运算是解题的关键.【例2】(2022·北京·中考真题)计算:(π−1)0+4sin45∘−√8+|−3|.【答案】4【解析】【分析】根据零次幂、特殊角的正弦值、二次根式和去绝对值即可求解.【详解】解:(π−1)0+4sin45∘−√8+|−3|.=1+4×√22−2√2+3=4.【点睛】本题考查了实数的混合运算,掌握零次幂、特殊角的正弦值、二次根式的化简及去绝对值是解题的关键.【真题再现】必刷真题,关注素养,把握核心1.(2013·北京·中考真题)计算:.【答案】5【解析】【分析】针对零指数幂,绝对值,特殊角的三角函数值,负整数指数幂4个考点分别进行计算,然后根据实数的运算法则求得计算结果.【详解】解:原式=1+√2−2×√22+4=5.2.(2014·北京·中考真题)计算:(6−π)0+(−15)−1−3tan30°+|−√3|.【答案】-4【解析】【详解】特殊角的三角函数值,按顺序计算即可试题解析:原式=1+(−5)−√3+√3=-4考点:1、零指数幂;2特殊角的三角函数值;3、绝对值;4、负指数幂3.(2015·北京·中考真题)计算:(12)−2−(π−√7)0+|√3−2|+4sin60°.【答案】5+√3【解析】【分析】先根据一个数的负指数幂等于正指数幂的倒数,一个不等于零的数的零指数幂为1,一个数的绝对值是非负数,特殊角三角函数值sin60°=√32,求出各项的值即可. 【详解】解:原式=4−1+2−√3+4×√32=5−√3+2√3 =5+√3 【点睛】本题考查实数的混合运算;特殊角三角函数值.4.(2016·北京·中考真题)计算:(3−π)0+4sin45∘−√8+|1−√3|. 【答案】√3.【解析】【分析】根据实数的运算顺序,首先计算乘方、开方和乘法,然后从左向右依次计算即可.【详解】解:原式=1+4×√22−2√2+√3−1=√3. 5.(2017·北京·中考真题)计算:4cos30°+(1−√2)°−√12+|−2|.【答案】3.【解析】【详解】试题分析:利用特殊三角函数值,零指数幂,算术平方根,绝对值计算即可.试题解析:原式=4×√32 +1-2√3+2=2√3+1-2√3+2=3 . 6.(2018·北京·中考真题)计算:4sin45°+(π−2)0−√18+|−1|.【答案】2−√2【解析】【分析】按照实数的运算顺序进行运算即可.【详解】原式=4×√22+1−3√2+1=2−√2.【点睛】本题考查实数的运算,主要考查零次幂,绝对值,特殊角的三角函数值以及二次根式,熟练掌握各个知识点是解题的关键.7.(2019·北京·中考真题)计算:|−√3|−(4−π)0−2sin60∘+(14)−1.【答案】3【解析】【分析】根据绝对值、零指数幂、特殊角的三角函数值、负指数幂法则计算即可【详解】原式=√3−1+2×√32+4=√3−1−√3+4=3【点睛】本题考查零指数幂、特殊角的三角函数值,负指数幂,熟练掌握相关的知识是解题的关键.8.(2020·北京·中考真题)计算:(13)−1+√18+|−2|−6sin45°【答案】5【解析】【分析】分别计算负整数指数幂,算术平方根,绝对值,锐角三角函数,再合并即可得到答案.【详解】解:原式=3+3√2+2−6×√22=3+3√2+2−3√2=5.【点睛】本题考查的是负整数指数幂,算术平方根,绝对值,锐角三角函数,以及合并同类二次根式,掌握以上的知识是解题的关键.【模拟精练】押题必刷,巅峰冲刺,提分培优1.(2022·北京房山·二模)计算:tan60°+(3−π)0+|1−√3|+√27.【答案】5√3【解析】【分析】分别计算三角函数值、零指数幂,化简绝对值和二次根式,再进行加减即可.【详解】解:原式=√3+1+√3−1+3√3=5√3.【点睛】本题考查特殊角三角函数、零指数幂以及绝对值和二次根式的化简,属于基础题,熟练掌握上述基本知识是解题的关键.2.(2022·北京朝阳·二模)计算√18+2sin45∘−(12)−1+|√2−2|.【答案】3√2【解析】【分析】分别根据二次根式的性质,45°角的三角函数值,负整数指数幂及绝对值的性质进行化简,最后再由二次根式的运算法则合并即可.【详解】解:原式=3√2+2×√22−2+2−√2 =3√2.故答案为:3√2.【点睛】 此题考查了实数的混合运算,正确掌握二次根式的性质,45°角的三角函数值,负整数指数幂定义及绝对值的性质是解题的关键.3.(2022·北京平谷·二模)计算:√83+(13)−1−2cos30°+|1−√3|.【答案】4【解析】【分析】先利用负整数指数幂,特殊角锐角三角函数值,绝对值的性质,立方根的性质化简,再合并,即可求解.【详解】 解:√83+(13)−1−2cos30°+|1−√3|=2+3−2×√32+√3−1=2+3−√3+√3−1 =4.【点睛】本题主要考查了负整数指数幂,特殊角锐角三角函数值,绝对值的性质,立方根的性质,熟练掌握相关运算法则是解题的关键是解题的关键.4.(2022·北京北京·二模)计算:(12)−1−4cos30∘+√12+|−2|.【答案】4【解析】【分析】先计算乘方和化简二次根式,并把特殊角的三角函数值代入,去值符号,再计算乘法,最后计算加减即可.【详解】解:原式=2−4×√32+2√3+2 =2-2√3+2√3+2=4.【点睛】本题考查实数的混合运算,熟练掌握实数的运算法则,负整指数幂的运算,熟记特殊角的三角函数值是解题的关键.5.(2022·北京丰台·二模)计算:|−3|−2sin45∘+√8+(π+√3)0【答案】4+√2【解析】【分析】原式第一项利用绝对值的意义化简,第二项利用特殊角的三角函数值计算,第三项化为最简二次根式,第四项利用零指数幂法则计算即可得到结果.【详解】解:原式 = 3−2×√22+2√2+1 =3−√2+2√2+1=4+√2.【点睛】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.6.(2022·北京西城·二模)计算:|−√2|+2cos45°−√8+(13)−2. 【答案】9【解析】【分析】先去绝对符号,把特殊角三角函数值代入,化简二次根式并计算乘方,再进行乘法运算,最后计算加减即可.【详解】解:原式=√2+2×√22-2√2+9 =√2+√2-2√2+9=9.【点睛】本题考查实数的混合运算,熟练掌握特殊角的三角函数值、二次根式化简、负整指数幂的运算是解题的关键.7.(2022·北京顺义·二模)计算:√18−4cos45°+|−2|−(1−√2)0. 【答案】√2+1【解析】【分析】根据二次根式的性质化简,代入特殊角的三角函数值,化简绝对值,求零次幂,进行实数的计算即可求解.【详解】解:原式=3√2−4×√22+2−1 =3√2−2√2+2−1 =√2+1.【点睛】本题考查了实数的混合运算,掌握二次根式的性质化简,代入特殊角的三角函数值,化简绝对值,求零次幂是解题的关键.8.(2022·北京市十一学校二模)计算:√3tan30°+|√2−2|−√83+(π−3)0【答案】2−√2【解析】【分析】先根据特殊角锐角三角函数值,绝对值的性质,立方根,零指数幂化简,再合并,即可求解.【详解】 解:√3tan30°+|√2−2|−√83+(π−3)0 =√3×√33+2−√2−2+1=1+2−√2−2+1=2−√2【点睛】本题主要考查了特殊角锐角三角函数值,绝对值的性质,立方根,零指数幂,熟练掌握相关运算法则是解题的关键.9.(2022·北京大兴·一模)计算:2sin30°+√8+|−5|−(−12)−1. 【答案】8+2√2【解析】【分析】先计算锐角三角函数、算术平方根、绝对值和负整数指数幂,再利用实数的加减法法则计算即可.【详解】解:原式=2×12+2√2+5−(−2)=1+2√2+5+2=8+2√2.【点睛】本题考查特殊三角函数值、负整数指数幂、算术平方根等内容,掌握运算法则是解题的关键.10.(2022·北京东城·二模)计算:(−1)2022+√83−(13)−1+√2sin45°.【答案】1【解析】【分析】先计算乘方和开方运算,并把特殊角的三角函数值代入,再计算乘法,最后计算加减即可求解.【详解】解:原式=1+2-3+√2×√22=1+2-3+1=1【点睛】本题考查实数的混合运算,熟练掌握负整指数幂的运算法则和熟记特殊角的三角函数值是解题的关键. 11.(2022·北京丰台·一模)计算:(12)﹣1﹣2cos30°+|﹣√12|﹣(3.14﹣π)0. 【答案】√3+1【解析】【分析】分别根据负整数指数幂、特殊角的三角函数值、绝对值的性质、零指数幂计算出各数,再根据混合运算的法则进行计算;【详解】解:(12)﹣1﹣2cos30°+|﹣√12|﹣(3.14﹣π)0=2﹣2×√32+2√3﹣1 =2﹣√3+2√3﹣1 =√3+1【点睛】此题考查了负整数指数幂、特殊角的三角函数值、绝对值的性质、零指数幂,掌握相关运算法则是解题的关键.12.(2022·北京一七一中一模)计算:3tan30°+(13)−1+20220+|√3−2|.【答案】6【解析】【分析】根据特殊角三角函数值,负整数指数幂,零指数幂,绝对值的计算法则求解即可.【详解】解:3tan30°+(13)−1+20220+|√3−2|=3×√33+3+1+2−√3 =√3+3+1+2−√3=6.【点睛】本题主要考查了特殊角三角函数值,负整数指数幂,零指数幂,绝对值,实数的混合计算,熟知相关计算法则是解题的关键.13.(2022·北京平谷·一模)计算:√12+(15)−1−3tan30°−|−2|.【答案】3+√3【解析】【分析】根据特殊角三角函数值,负整数指数幂,绝对值,以及二次根式的性质进行求解即可.【详解】 解:√12+(15)−1−3tan30°−|−2|=2√3+5−3×√33−2 =2√3+5−√3−2=3+√3.【点睛】本题主要考查了特殊角三角函数值,负整数指数幂,绝对值,以及二次根式的性质,实数的运算,熟知相关计算法则是解题的关键.14.(2022·北京·东直门中学模拟预测)计算:2cos30°+√12−|−√3|−(π+√2)°.【答案】2√3−1【解析】【分析】根据0指数幂运算法则、绝对值的性质及特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可.【详解】解:原式=2×√32+2√3−√3−1=√3+2√3−√3−1=2√3−1.【点睛】本题考查的是实数的运算,熟知0指数幂的运算法则、绝对值的性质及特殊角的三角函数值是解答此题的关键.15.(2022·北京市第一六一中学分校一模)计算:2sin45°+|√2−3|−(π−2022)0+(13)−2.【答案】11【解析】【分析】原式第一项利用特殊角的三角函数值计算,第二项利用绝对值的代数意义化简,第三项利用零指数幂法则计算,最后一项利用负整数指数幂法则计算即可得到结果.【详解】解:2sin45°+|√2−3|−(π−2022)0+(13)−2=2×√22+3−√2−1+32=√2+3−√2−1+9=11.【点睛】此题考查了实数的运算、特殊角的三角函数值、零指数幂和负整数指数幂,熟练掌握运算法则是解本题的关键.16.(2022·北京朝阳·一模)计算:2cos30°+|−√3|−(π−√3)0−√12.【答案】-1【解析】【分析】根据实数的计算,把各个部分的值求出来进行计算即可.【详解】解:原式=2×√32+√3−1−2√3 =√3+√3−1−2√3=-1.【点睛】本题考查了实数的混合运算,准确记忆特殊角的锐角三角函数值、绝对值化简、零指数幂、二次根式的化简是解题的关键.17.(2022·北京顺义·一模)计算:2tan60°−√27+(12)−2+|1−√3|.【答案】3【解析】【分析】直接利用二次根式的性质、绝对值的性质、特殊角的三角函数值、负整数指数幂的性质分别化简得出答案.【详解】解:原式=2×√3−3√3+4+√3−1=3【点睛】此题主要考查了特殊角的三角函数值、实数运算,正确化简各数是解题关键.18.(2022·北京·中国人民大学附属中学朝阳学校一模)计算:4cos45°+(√3−1)0−√8+2−1. 【答案】32【解析】【分析】先分别根据特殊角的三角函数值、零指数幂、二次根式的化简、负指数幂计算,然后根据实数混合运算法则计算即可求得结果.【详解】解:原式=4×√22+1−2√2+12 =2√2+32−2√2 =32. 【点睛】本题考查了特殊角的三角函数值、零指数幂、二次根式的化简、负指数幂,熟练掌握相关运算法则和熟记特殊角的三角函数值是解题的关键.19.(2022·北京·模拟预测)计算:cos 230°+|1﹣√2|﹣2sin45°+(π﹣3.14)0 【答案】34【解析】【分析】根据cos30°=√32,|1−√2|=√2−1,sin45°=√22,(π−3.14)0=1,再计算即可. 【详解】解:原式=(√32)2+√2−1−2×√22+1 =34+√2−√2 =34【点睛】本题主要考查了实数的运算,掌握特殊角三角函数值,零指数次幂,绝对值的性质是解题的关键. 20.(2022·北京市师达中学模拟预测)计算:(15)−1−(π−2022)0+|√3−1|−3tan30°【答案】3【解析】【分析】先根据负指数幂、零指数幂、绝对值的意义和特殊角的三角函数值分别计算,然后再根据实数的混合运算法则计算即可求得结果.【详解】解:原式=5−1+√3−1−3×√33=3+√3−√3=3【点睛】本题主要考查负指数幂、零指数幂、绝对值的意义和特殊角的三角函数值,熟练掌握相关运算法则和熟记特殊角的三角函数值是解题的关键.21.(2022·北京朝阳·模拟预测)计算:(﹣1)2020﹣√9﹣(3﹣π)0+|3﹣√3|+(tan30°)﹣1.【答案】0【解析】【分析】计算乘方、算术平方根、零指数幂、去绝对值符号、代入三角函数值并计算负整数指数幂,再计算加减可得;【详解】解:原式=1﹣3﹣1+3﹣√3+(√33)-1=1﹣3﹣1+3﹣√3+√3=0.【点睛】本题考查了实数的运算,解决此类题目的关键是熟练掌握零指数幂、负整数指数幂、特殊角的三角函数值、绝对值等考点的运算.22.(2022·北京·一模)计算√2cos45°+(1−π)0+√14+|1−√2|.【答案】32+√2【解析】【分析】根据特殊角的三角函数值,零指数幂,二次根式的性质,化简绝对值进行计算即可.【详解】原式=√2×√22+1+12+(√2−1)=1+1+12+√2−1=32+√2【点睛】本题考查了实数的混合运算,掌握特殊角的三角函数值,零指数幂,二次根式的性质,化简绝对值是解题的关键.23.(2022·北京·北理工附中模拟预测)计算:−√274−(1−π)0+2tan 30°−|√32−(√32)−1| 【答案】−√3−1【解析】【分析】根据二次根式的性质化简,零指数幂,特殊角的三角函数值,负整数指数幂,化简绝对值,进行计算即可【详解】解:−√274−(1−π)0+2tan 30°−|√32−(√32)−1| =−3√32−1+2×√33−|√32−2√33| =−3√32+2√33−(2√33−√32)−1 =−√3−1 【点睛】本题考查了实数的混合运算,掌握二次根式的性质化简,零指数幂,特殊角的三角函数值,负整数指数幂,化简绝对值是解题的关键.24.(2022·北京师大附中模拟预测)计算:√8+(−12)−1−4cos45°+|−2|【答案】0【解析】【分析】根据二次根式的性质、负整数指数幂、特殊角的三角函数值分别计算各项,即可求解.【详解】解:原式=2√2−2−4×√22+2 =0.【点睛】本题考查实数的混合运算,掌握二次根式的性质、负整数指数幂、特殊角的三角函数值是解题的关键. 25.(2022·北京四中模拟预测)计算:(13)−1−√12+3tan30°+|√3−2|.【答案】5−2√3【解析】【分析】直接利用特殊角的三角函数值以及负指数幂的性质和绝对值的性质化简得出答案.【详解】解:原式=3−2√3+3×√33+2−√3 =5−2√3.【点睛】本题主要考查了实数的运算,正确化简各数是解题的关键.26.(2021·北京平谷·二模)计算:|−√2|−2cos45°+(π−1)0+(12)−1【答案】3【解析】【分析】根据绝对值的性质、特殊角的三角函数值、零指数幂以及负整指数幂进行运算即可【详解】解:|−√2|−2cos45°+(π−1)0+(12)−1 =√2−2×√22+1+2 =3【点睛】本题考查了实数的混合运算,涉及到绝对值的性质、特殊角的三角函数值、零指数幂以及负整指数幂,熟练掌握法则是解题的关键27.(2021·北京朝阳·二模)计算:√12+(√5−2)0−(13)−1+tan60°. 【答案】3√3−2【解析】【分析】直接根据无理数的运算,零指数幂,负整数指数幂和特殊角的三角函数值计算即可.【详解】解:原式=2√3+1−3+√3=3√3−2.【点睛】本题主要考查实数的运算,掌握无理数的运算,零指数幂,负整数指数幂的运算法则和特殊角的三角函数值是关键.28.(2021·北京顺义·二模)计算:(2−π)0+3−1+|√2|−2sin45°.【答案】43【解析】【分析】根据混合运算公式运算即可【详解】解:原式=1+13+√2−2×√22=43【点睛】本题主要考查实数混合运算内容,注意运算中的易错点,避免犯错,属于常考题.29.(2021·北京房山·二模)计算:(13)−1−2sin60°+|−√3|−(π−2021)0【答案】2【解析】【分析】根据负整数指数幂,绝对值的化简,零指数幂定义依次化简及特殊角的三角函数值代入计算即可.【详解】解:原式=(13)−1−2sin60°+|−√3|−(π−2021)0=3−√3+√3−1=2.【点睛】此题考查实数的计算,正确掌握负整数指数幂,绝对值的化简,零指数幂定义依次化简及特殊角的三角函数值是解题的关键.30.(2021·北京海淀·二模)计算:(12)−1+√8+|√3−1|−2sin60°.【答案】1+2√2【解析】【分析】原式利用负整数指数幂法则、二次根式的性质、绝对值的性质以及特殊角的三角函数值计算即可求出值.【详解】原式=2+2√2+√3−1−2×√32=1+2√2.【点睛】此题考查了实数的运算,负整数指数幂,绝对值的性质以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.。
2013年中考数学专题复习第1讲:实数(含答案)

2013年中考数学专题复习第一讲 实数【基础知识回顾】 一、实数的分类:1、按实数的定义分类: 实数2、按实数的正负分类:实数【名师提醒:1、正确理解实数的分类。
如:2π是 数,不是 数,722是 数,不是 数。
2、0既不是 数,也不是 数,但它是自然数】 二、实数的基本概念和性质1、数轴:规定了 、 、 的直线叫做数轴, 和数轴上的点是一一对应的,数轴的作用有 、 、 等。
2、相反数:只有 不同的两个数叫做互为相反数,a 的相反数是 ,0的相反数是 ,a 、b 互为相反数⇔3、倒数:实数a 的倒数是 , 没有倒数,a 、b 互为倒数⇔4、绝对值:在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。
a =⎪ ⎪ ⎪⎪⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪⎨ ⎧ 正无理数无理数 负分数 _ 零 正整数 整数 有理数无限不循环小数⎩⎨⎧⎩⎨⎧负有理数负零正无理数正实数实数(a >0)(a <0)0 (a =0)有限小数或无限循环数因为绝对值表示的是距离,所以一个数的绝对值是 数,我们学过的非负数有三个: 、 、 。
【名师提醒:a +b 的相反数是 ,a -b 的相反数是 ,0是唯一一个没有倒数的数,相反数等于本身的数是 ,倒数等于本身的数是 ,绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。
1、科学记数法:把一个较大或较小的数写成 的形式叫做科学记数法。
其中a 的取值范围是 。
2、近似数和有效数字:一般的,将一个数四舍五入后的到的数称为这个数的近似数,这时,从 数字起到近似数的最后一位止,中间所有的数字都叫这个数的有效数字。
【名师提醒:1、科学记数法不仅可以表示较大的数,也可以表示较小的数,其中a 的取值范围一样,n 的取值不同,当表示较大数时,n 的值是原整数数位减一,表示较小的数时,n 是负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数数位上的零)。
全国各地名校2013年中考数学5月试卷分类汇编 实数的运算

实数的运算一、选择题1、(2013年某某模拟二)为了逐步改善人民的居住条件,国家一方面大力遏制房价的过快增长,另一方面不断加大对保障性安居住房建设的投入力度.2011年全国保障性安居工程住房建设规模或将高达1000万套,投资将超过1万亿元人民币,1万亿用科学记数法表示正确的是 ( ). A .10110⨯ B . 11110⨯ C .12110⨯ D .13110⨯ 答案:C2.4月8日万用科学记数法表示为( )A .1.975×106B .1.975×107C .0.1975×107D .1.975×105答案:A3.股市有风险,投资需谨慎。
截至五月底,我国股市开户总数约95000000,正向1亿挺进,95000000用科学计数法表示为( )×106B. 9.5×107C. 9.5×108D. 9.5×109答案:B4.(2013年顺义区一模)若x y ,为实数,且30x +=,则2013y x ⎛⎫ ⎪⎝⎭的值为 A .1B . 1-C . 2D . 2-答案:B5、(2013年某某省模拟七)下列运算正确的是………………………………【 】A .236·a a a =B .1122-⎛⎫=- ⎪⎝⎭C 4=±D .|6|6-=答案:D6、(2013某某省某某模拟题)下列计算正确的是A .(x 2)3=x 6B .x 2+x 2=x 4C .(3x )·(2x )2=6x D .3x -x =3 答案:A7.(2013某某市景山中学模拟题)13-等于( ◆ )A .3B .31-C .-3D .31 答案:D8、(2013年某某某某一模)下列算式结果为2-的是()A .()12--B .()02-C .()2--D .2--答案:D9、(2013年某某某某一模)下面的数中,与2-的和为0的是 ( ▲ )A.2B.2-C.21D. 21- 答案:A10、 (2013年某某某某一模)下列运算正确的是( ▲ )A .328-=B .()23-=9-C2=D .020=答案:C11、(2013年某某某某一模)某优质袋装大米有A 、B 、C 三种包装,分别装有5千克、10千克、15千克大米,每袋售价分别为35元、65元、90元,每袋包装费用(含包装袋成本)分别为4元、5元、6元.超市销售A 、B 、C 三种包装的大米各60千克,获得利润最大的是A .A 种包装的大米B .B 种包装的大米C .C 种包装的大米D .三种包装的大米都相同答案:A12、(2013某某江干区模拟)要使算式“35-45”的结果最小,在“”中应填的运算符号是A .加号B .减号C .乘号D .除号 【答案】C13、(2013年某某省某某市一模)下列计算正确的是A . ﹣1+1=0 B . ﹣2﹣2=0C . 3÷=1D . 52=10答案:A14、(2013北仑区一模)5.我国第六次人口普查显示,全国人口为1370536875人,将这个总人口数(精确到千万位)用科学计数法表示为 ( ▲ ).A .8104.1⨯B.9104.1⨯C.81037.1⨯D.91037.1⨯ 【答案】D15、(2013某某模拟)2.2010年5月1日,举世瞩目的某某世博会正式开园. 截至当天19:00,约有204000名中外游客进世博园区参观,参观人数用科学记数法表示为(▲) A .420.410⨯人 B .52.0410⨯人 C .520.410⨯人 D .62.0410⨯人 【答案】B16、(2013某某永嘉一模)2.某某市拟在某某汽车东站、汽车西站间建造约10公里的空中轨道,总造价预计需要人民币2000 000 000元,将这个造价用科学记数法表示应为( ▲ ) A .2×107元 B .2×108元 C .2×109元 D. 2×1010元 【答案】C17.(2013年某某静安区二摸)下列方程中,有实数根的是(A )11-=+x (B )x x -=-1 (C ) 033=+x (D )044=+x 答案:C18.(2013年某某闵行区二摸)下列运算一定正确的是(A (B 1;(C )2a =; (D 2-答案:D19.(2013某某某某一模)文文设计了一个关于实数运算的程序,按此程序,输入一个数后,输出的数比输入的数的平方小1,则输出的结果为( ) A .5 B .6 C .7 D .8 答案:B20. (2013某某五校联考一模) 若n 满足(n-2011)2+(2012-n )2=1,则(2012-n )(n-2011)等于 ( ) A 、-1B 、0C 、12D 、1答案:B21.(2013某某五校联考一模)若对于所有的实数x ,22x ax b -+-恒为负数,且()()22222123M b b a b a b =++-++---,则M 的值为 ( )A .3-B .3C .223a b -+-D .47b + 答案:A22. (2013某某五校联考二模) 设213a a +=,213b b +=,且a b ≠,则代数式2211a b +的值为 ()A 5B 7C 9D 11 答案:B23、(2013某某某某特长展示)下列运算中,正确的是( )A . 144-=-B .140=C .24±=D . 4-=4-B24、(2013凤阳县县直义教教研中心)如果a 的倒数是1-,那么2013a 等于 (A )1; (B )1-; (C )2013; (D )2013-. B25、(2013年某某市初中毕业班质量检查)计算-3+3的结果是 ( ) A .0 B .-6 C .9 D .-9 A26、(2013某某沁阳市九年级第一次质量检测)下列等式成立的是 ( ) A . B.C .D . =9A二、填空题1、(2013年某某荆州模拟题)计算:()0232cos 45π---+︒=▲.答案:122、(2013年某某荆州模拟5)计算:︒60sin 2321(0+﹣+)-= ▲.答案: 33、(2013年某某某某一模)计算(2+1)(2-2)= ▲ . 答案: 24、(2013年某某某某一模)计算答案: 65、(2013年某某某某一模)=+-0122▲. 答案:326、(2013年某某某某一模)计算:2+8=▲. 答案:3 27、(2013某某勐捧中学二模)()0201212=-++y x ,则x=【答案】18、(2013某某一中一模)我国2012年国内生产总值约为7298000000000美元,世界排位第二,将7298000000000用科学计数法应表示为__________. 【答案】1210298.7⨯9、(2013年某某东台第二学期阶段检测))2的结果为__________. 答案:-2 ;10.(2013年某某东台第二学期阶段检测)某人用24000元买进甲、乙两种股票,在甲股票升值15%,乙股票下跌10%时卖出,共获利1350元,则此人买甲股票的钱比买乙股票的钱多_______元. 答案:600011. (2013某某黄浦二摸)计算:36a a ÷=▲.答案:3a12.(2013年某某静安区二摸)计算:212-= ▲ .答案:22 13.(2013年某某闵行区二摸)计算:124=▲. 答案:214.(2013x =的实数根是▲. 答案:2x =15.(2013年某某浦东新区二摸)计算:()=32x ▲.答案:6x16.(2013年某某徐汇区二摸)计算:=-)13(2a a _______▲_________. 答案:a a 262-17. (2013某某饶鹰中考模拟)已知3,2=-=b a ab ,则=+-32232ab b a b a . 答案:1818.(2013某某五校联考二模),a b 为实数,且满足2280,150ab a b a b ab ++-=+-=,则2()a b -= 答案:26三、解答题1、(2013年某某模拟二)101|sin 45(2π-⎛⎫+-+ ⎪⎝⎭°解:原式2112⨯+=. 2、(2013年某某凤阳模拟题二)计算:1- 2 -(12)-1+( 2 )0+ 4 ..解:原式=2-1-2+1+2= 23. (2013年某某凤阳模拟题三) 计算:(31)-1+16÷(-2)3+(2013—23)0—3tan 600解:—14.(201313(3)sin 45(2)2π----. 15. (2013年房山区一模)计算:1212312-⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-+tan 60︒. 答案:解:1212312-⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-+tan 60︒. =32132+----------------------------------------------------------4分=333---------------------------------------------------------5分6.(2013年龙文教育一模)计算:-1022cos30(π 3.14)++-.答案:解:原式=1212+-分=112+-32-...5分7.(2013年平谷区一模)计算:011()20132sin 602--+︒-.解:011()20132sin602--+︒--212=-+……………………………………………………………………4分1=1=………………………………………………………………………………5分8.(2013年顺义区一模)计算:101()4sin 60( 3.14)123π-+︒---.答案:解:原式=3341232+⨯-- …………………………………………4分 =2 ……………………………………………… 5分9、(2013年某某省模拟六)(实数的运算) 计算:()tan π-201⎛⎫30⨯1-3-5+2013⨯- ⎪2⎝⎭答案:解:原式=()3⨯3-1-1⨯43(4分)=31--43(6分) =3-3-3(8分) 10、(2013年聊城莘县模拟)计算:答案:解:原式=1+2-1-3=-11、(2013年某某奉贤区二模)计算:︒+--+--30tan 3)31(20132310;答案:解:原式=3333132⨯+++- -------------------------------------(每个值得2分,共8分)6=---------------------------------------------------------------------------------------------(2分) 12、(2013年某某长宁区二模)计算:()32230tan 31212+-︒⎪⎭⎫ ⎝⎛+-.答案:解:原式=)32(23332--⨯+(8分,每个化简结果2分)=32432++-=233-(结果正确,2分)13、(2013某某东阳吴宇模拟题)(本题6分)计算: O --+-45cos 2)21()12(10-9 答案:-214、(2013某某省某某模拟题)(本题6分)计算:0(21)4cos30223o-+-- 答案:解:15.(1)(2013某某市景山中学模拟题)计算:9-(- 1 5)0+(-1)2012. 答案: 316、计算:(31)-1+16÷(-2)3+(2007—23)0—3tan600解:—117、(2013某某勐捧中学一模)(本小题4分)计算:3(3–π)0–20–155– (–1)2012【答案】解:原式=3⨯1–(2–3)–1 = 318、(2013某某勐捧中学二模)(本小题5分)计算: -12012+12+121-⎪⎭⎫⎝⎛-2cos60°.【答案】解:原式=﹣1+2+2﹣2×=﹣1+2+2﹣1=2.19、(20131142sin 30(2012)3-⎛⎫+- ⎪⎝⎭10142sin 30(2012)3-⎛⎫+- ⎪⎝⎭ (4分)122132=-⨯+- (6分)314(223)1232233=++-=+-=原式1=-. (7分)20、(2013年某某市惠城区模拟)计算:1318245sin 2-⎪⎭⎫⎝⎛+--+︒解: 原式=3222222+-+⨯…………………3分 =3 ………………………………5分21、(2013年某某省某某市一模)计算:()10112 3.14tan 603π-⎛⎫+---︒ ⎪⎝⎭.解:解: 原式=23+3 -1 -3……………………… 4分 =3+2 ……………………… 5分 22、(2013年某某省某某市一模)计算:.解:原式=3﹣1+4=6.23、(2013北仑区一模)19(本题6分) 计算:313)6()2010(32---+-π 【答案】解:原式 ---------------------------4分(每个一分)------------------------------------------------6分24、(2013某某某某二模)17.(1)计算:13132760sin 2-⎪⎭⎫⎝⎛+-o【答案】 解:(1)原式=3333232+-⨯……3分 =3 ……1分25、(2013某某模拟)17.(本题10分) (1)计算:01)21(30tan 3)21(-+︒---; 【答案】53613-=--+=解:(1)原式132+--=……………3分 (注:每项计算1分)31--=……………2分(注:没有过程而答案正确的只给1分)26、(2013某某永嘉一模)17.(1)计算:()()0201320131-+-【答案】(1)解:()()8120132013--+-2211--=……………3分(每化对一个给1分) 22-=…………………2分27、(2013某某一中一模)19.计算:︒---+-----+-60cos 22721)15()1()21(3052. 【答案】解:原式=1312114--+---.................6分 =12--.................7分 28、(2013年某某东台第二学期阶段检测)(8分)计算:2114cos30223-⎫⎛⎫︒+-⎪ ⎪⎪⎝⎭⎝⎭.答案:.原式=8.(8分)92.(2013年某某某某崇安一模)(本题满分8分)(1)计算:(12)-1-38-20130;答案:2.(共8分)(1)解:原式=2-2-1………………(3分)=-1 ……………… (4分)30、 (2013某某市文园中学一模)计算:()()|1|3311321----⎪⎭⎫⎝⎛+--答案: 解:原式=1+3—3—1 (4分) =0 ( 2分)31.(2013年某某某某市四模)计算:()()()011π201060---+-°+2.解:()()()011π201060---+- °+2=1112+……………………………………………………………(4分) =1232-+…………………………………………………………………………(5分)=12-………………………………………………………………………………(6分)32.(2013年某某某某地区一模)计算:︒+-+-6022310sin )(, 解:()23232160sin 223100⋅+-+=+-+-……3分 =3 ………6分 33.(2013年某某徐汇区二摸)(本题满分10分)计算:20)21(23130cot )2(---+︒--π. 答案:. 解:原式 42331-++-=…………………………………………………(8分)32-=……………………………………………………………………(2分)34. (2013某某黄浦二摸)(本题满分10分)计算:))210212013tan 601-+-︒-.答案:原式=)3131+-----------------------------------------------------------(8分)----------------------------------------------------------------------------------(2分)35.(2013年某某浦东新区二摸)(本题满分10分)计算:()2113332318+-+⎪⎭⎫⎝⎛---π.答案: 19.解:原式=33-23-1++…………………………………………………… (8分)=0.………………………………………………………………………(2分)36.(2013某某饶鹰中考模拟)计算:︒++-+--60tan 2)31(412212 答案:解:33233244=++-+-=原式37.(2013某某某某一模)计算:02112sin30( 3.14)()2π---︒+-+.答案:解:原式=11214=52-⨯++.………………………4分 38.(2013年某某市初中毕业班质量检查) (每小题7分,共14分)(1) 计算:(π+3)0―|―2013|+64×18解: 原式=1-2013+8×18……3分=1-2013+1……4分 =-2011……7分(2) 已知a 2+2a =-1,求2a (a +1)-(a +2)(a -2)的值. 解:原式=2a 2+2a -a 2+4……3分= a 2+2a +4……4分∵a 2+2a =-1∴原式=-1+4=3……7分另解:∵a 2+2a =-1 ∴a 2+2a +1=0 ∴(a +1)2=0∴a =-1 ……3分原式=2×(-1)×(-1+1)-(-1+2)×(-1-2)=3 ……7分。
2013版中考总复习数学(人教版 全国通用)基础讲练 第1讲 实数(含答案点拨)
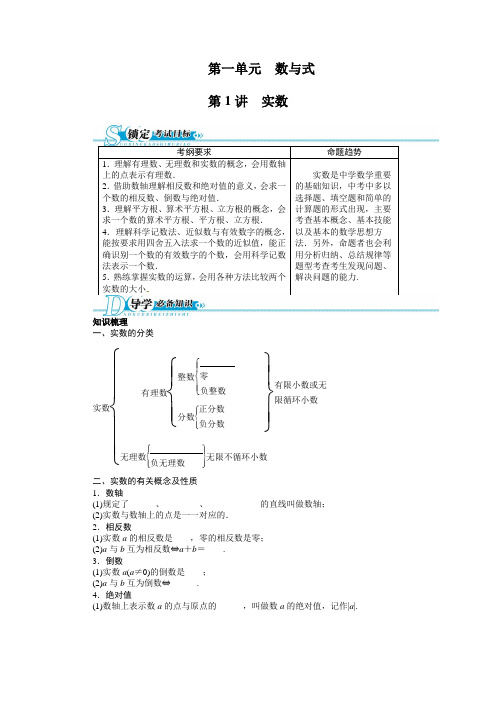
第一单元数与式第1讲实数考纲要求命题趋势1.理解有理数、无理数和实数的概念,会用数轴上的点表示有理数.2.借助数轴理解相反数和绝对值的意义,会求一个数的相反数、倒数与绝对值.3.理解平方根、算术平方根、立方根的概念,会求一个数的算术平方根、平方根、立方根.4.理解科学记数法、近似数与有效数字的概念,能按要求用四舍五入法求一个数的近似值,能正确识别一个数的有效数字的个数,会用科学记数法表示一个数.5.熟练掌握实数的运算,会用各种方法比较两个实数的大小.实数是中学数学重要的基础知识,中考中多以选择题、填空题和简单的计算题的形式出现,主要考查基本概念、基本技能以及基本的数学思想方法.另外,命题者也会利用分析归纳、总结规律等题型考查考生发现问题、解决问题的能力.知识梳理一、实数的分类实数⎩⎪⎪⎨⎪⎪⎧⎭⎪⎬⎪⎫有理数⎩⎪⎨⎪⎧整数⎩⎪⎨⎪⎧零负整数分数⎩⎪⎨⎪⎧正分数负分数有限小数或无限循环小数无理数⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫负无理数无限不循环小数二、实数的有关概念及性质1.数轴(1)规定了______、________、____________的直线叫做数轴;(2)实数与数轴上的点是一一对应的.2.相反数(1)实数a的相反数是____,零的相反数是零;(2)a与b互为相反数⇔a+b=____.3.倒数(1)实数a(a≠0)的倒数是____;(2)a与b互为倒数⇔______.4.绝对值(1)数轴上表示数a的点与原点的______,叫做数a的绝对值,记作|a|.(2)|a |=⎩⎪⎨⎪⎧(a >0), (a =0), (a <0).5.平方根、算术平方根、立方根(1)平方根①定义:如果一个数x 的平方等于a ,即x 2=a ,那么这个数x 叫做a 的平方根(也叫二次方根),数a 的平方根记作______.②一个正数有两个平方根,它们互为________;0的平方根是0;负数没有平方根. (2)算术平方根①如果一个正数x 的平方等于a ,即x 2=a ,那么这个正数x 叫做a 的算术平方根,a 的算术平方根记作____.零的算术平方根是零,即0=0.②算术平方根都是非负数,即a ≥0(a ≥0).③(a )2=a (a ≥0),a 2=|a |=⎩⎪⎨⎪⎧a (a ≥0),-a (a <0).(3)立方根①定义:如果一个数x 的立方等于a ,即x 3=a ,那么这个数x 叫做a 的立方根(也叫三次方根),数a 的立方根记作______.②任何数都有唯一一个立方根,一个数的立方根的符号与这个数的符号相同. 6.科学记数法、近似数、有效数字 (1)科学记数法把一个数N 表示成______(1≤a <10,n 是整数)的形式叫做科学记数法.当N ≥1时,n 等于原数N 的整数位数减1;当N <1时,n 是一个负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数位上的零).(2)近似数与有效数字一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位,这时从______第1个不为0的数字起,到末位数字止,所有的数字都叫做这个近似数的有效数字.三、非负数的性质 1.常见的三种非负数|a |≥0,a 2≥0,a ≥0(a ≥0). 2.非负数的性质(1)非负数的最小值是零;(2)任意几个非负数的和仍为非负数;(3)几个非负数的和为0,则每个非负数都等于0. 四、实数的运算 1.运算律(1)加法交换律:a +b =______.(2)加法结合律:(a +b )+c =________. (3)乘法交换律:ab =____.(4)乘法结合律:(ab )c =______.(5)乘法分配律:a (b +c )=__________. 2.运算顺序(1)先算乘方,再算乘除,最后算加减;(2)同级运算,按照从____至____的顺序进行;(3)如果有括号,就先算小括号里的,再算中括号里的,最后算大括号里的.3.零指数幂和负整数指数幂(1)零指数幂的意义为:a 0=____(a ≠0);(2)负整数指数幂的意义为:a -p =______(a ≠0,p 为正整数). 五、实数的大小比较 1.实数的大小关系在数轴上表示两个数的点,右边的点表示的数总比左边的点表示的数____.正数大于零,负数小于零,正数大于一切负数;两个负数比较,绝对值大的反而小. 2.作差比较法(1)a -b >0⇔a >b ;(2)a -b =0⇔a =b ;(3)a -b <0⇔a <b . 3.倒数比较法 若1a >1b ,a >0,b >0,则a <b . 4.平方法因为由a >b >0,可得a >b ,所以我们可以把a 与b 的大小问题转化成比较a 和b 的大小问题.(提示:本书[知识梳理]栏目答案见第122~123页) 自主测试1.-2的倒数是( )A .-12B ..12C .-2D .22.-2的绝对值等于( )A .2B .-2C .12D .-123.下列运算正确的是( )A .-|-3|=3B .⎝⎛⎭⎫13-1=-3 C .9=±3 D .3-27=-34.2012年世界水日主题是“水与粮食安全”.若每人每天浪费水0.32 L ,那么100万人每天浪费的水,用科学记数法表示为( )A .3.2×107 LB .3.2×106 LC .3.2×105 LD .3.2×104 L5.已知实数m ,n 在数轴上的对应点的位置如图所示,则下列判断正确的是( )A .m >0B .n <0C .mn <0D .m -n >0 6.计算:|-5|+16-32.考点一、实数的分类【例1】四个数-5,-0.1,12,3中为无理数的是( )A .-5B .-0.1C .12D . 3解析:因为-5是整数属于有理数,-0.1是有限小数属于有理数,12是分数属于有理数,3开不尽方是无理数,故选D. 答案:D方法总结 一个数是不是无理数,应先计算或者化简再判断.有理数都可以化成分数的形式.常见的无理数有四种形式:(1)含有π的式子;(2)根号内含开方开不尽的式子;(3)无限且不循环的小数;(4)某些三角函数式.触类旁通1 在实数5,37,2,4中,无理数是( )A .5B .37C . 2D . 4考点二、相反数、倒数、绝对值与数轴【例2】(1)-15的倒数是__________;(2)(-3)2的相反数是( )A .6B .-6C .9D .-9(3)实数a ,b 在数轴上的位置如图所示,化简|a +b |+(b -a )2=__________.解析:(1)-15的倒数为1-15=-5;(2)因为(-3)2=9,9的相反数是-9,故选D ;(3)本题考查了绝对值,平方根及数轴的有关知识. 由图可知,a <0,b >0,|a |>|b |,所以a +b <0,b -a >0,原式=-a -b +b -a =-2a . 答案:(1)-5 (2)D (3)-2a方法总结 1.求一个数的相反数,直接在这个数的前面加上负号,有时需要化简得出. 2.解有关绝对值和数轴的问题时常用到字母表示数的思想、分类讨论思想和数形结合思想.3.相反数是它本身的数只有0;绝对值是它本身的数是0和正数(即非负数);倒数是它本身的数是±1.触类旁通2 下列各数中,相反数等于5的数是( ) A .-5 B .5C .-15D .15考点三、平方根、算术平方根与立方根 【例3】(1)(-2)2的算术平方根是( )A .2B .±2C .-2D . 2 (2)实数27的立方根是__________.解析:(1)(-2)2的算术平方根,即(-2)2=|-2|=2; (2)27的立方根是327=3. 答案:(1)A (2)3方法总结 1.对于算术平方根,要注意:(1)一个正数只有一个算术平方根,它是一个正数;(2)0的算术平方根是0;(3)负数没有算术平方根;(4)算术平方根a 具有双重非负性:①被开方数a 是非负数,即a ≥0;②算术平方根a 本身是非负数,即a ≥0.2.(3a )3=a ,3a 3=a .触类旁通3 4的平方根是( ) A .2 B .±2 C .16 D .±16考点四、科学记数法、近似数、有效数字【例4】2012年安徽省有682 000名初中毕业生参加中考,按四舍五入保留两位有效数字,682 000用科学记数法表示为( )A .0.69×106B .6.82×105C .0.68×106D .6.8×105解析:用科学记数法表示的数必须满足a ×10n (1≤|a |<10,n 为整数)的形式;求近似数时注意看清题目要求和单位的换算;查有效数字时,要从左边第1个非零数查起,到精确到的数为止.682 000=6.82×105≈6.8×105.答案:D方法总结 1.用科学记数法表示数,当原数的绝对值大于或等于1时,n 等于原数的整数位数减1;当原数的绝对值小于1时,n 是负整数,它的绝对值等于原数中左起第一位非零数字前零的个数.2.取一个数精确到某一位的近似数时,应对“某一位”后的第一个数进行四舍五入,而之后的数不予考虑.3.用科学记数法表示的近似数,乘号前面的数(即a )的有效数字即为该近似数的有效数字;而这个近似数精确到哪一位,应将用科学记数法表示的数还原成原来的数,再看最后一个有效数字处于哪一个数位上.触类旁通4 某种细胞的直径是5×10-4毫米,这个数是( ) A .0.05毫米 B .0.005毫米 C .0.000 5毫米 D .0.000 05毫米 考点五、非负数性质的应用【例5】若实数x ,y 满足x -2+(3-y )2=0,则代数式xy -x 2的值为__________. 解析:因为x -2≥0,(3-y )2≥0,而x -2+(3-y )2=0,所以x -2=0,3-y =0,解得x =2,y =3,则xy -x 2=2×3-22=2.答案:2方法总结 常见的非负数的形式有三种:|a |,a (a ≥0),a 2,若它们的和为零,则每一个式子都为0.触类旁通5 若|m -3|+(n +2)2=0,则m +2n 的值为( ) A .-4 B .-1 C .0 D .4 考点六、实数的运算【例6】计算:(1)2-1+3cos 30°+|-5|-(π-2 011)0.(2)(-1)2 011-⎝⎛⎭⎫12-3+⎝⎛⎭⎫cos 68°+5π0+|33-8sin 60°|. (1)分析:2-1=12,cos 30°=32,|-5|=5,(π-2 011)0=1.解:原式=12+3×32+5-1=12+32+5-1=6.(2)分析:⎝⎛⎭⎫12-3=(2-1)-3=23=8,⎝⎛⎭⎫cos 68°+5π0=1,sin 60°=32. 解:原式=-1-8+1+⎪⎪⎪⎪33-8×32=-8+ 3.点拨:(1)根据负整数指数幂的意义可把负整数指数幂转化为正整数指数幂运算,即a -p =1ap (a ≠0).(2)a 0=1(a ≠0). 方法总结 提高实数的运算能力,首先要认真审题,理解有关概念;其次要正确、灵活地应用零指数、负整数指数的定义、特殊角的三角函数、绝对值、相反数、倒数等相关知识及实数的六种运算法则,根据运算律及顺序,选择合理、简捷的解题途径.要特别注意把好符号关.考点七、实数的大小比较【例7】比较2.5,-3,7的大小,正确的是( ) A .-3<2.5<7 B .2.5<-3<7 C .-3<7<2.5 D .7<2.5<-3 解析:由负数小于正数可得-3最小,故只要比较2.5和7的大小即可,由2.52<(7)2,得2.5<7,所以-3<2.5<7. 答案:A方法总结 实数的各种比较方法,要明确应用条件及适用范围.如:“差值比较法”用于比较任意两数的大小,而“商值比较法”一般适用于比较符号相同的两个数的大小,还有“平方法”、“倒数法”等.要依据数值特点确定合适的方法.触类旁通6在-6,0,3,8这四个数中,最小的数是( ) A .-6 B .0 C .3 D .81.(2012湖北黄石)-13的倒数是( )A .13B .3C .-3D .-132.(2012江苏南京)下列四个数中,负数是( )A .|-2|B .(-2)2C .- 2D .(-2)23.(2012北京)首届中国(北京)国际服务贸易交易会(京交会)于2012年6月1日闭幕,本届京交会期间签订的项目成交总金额达60 110 000 000美元.将60 110 000 000用科学记数法表示应为( )A .6.011×109B .60.11×109C .6.011×1010D .0.6011×10114.(2012四川南充)计算2-(-3)的结果是( ) A .5 B .1 C .-1 D .-55.(2012四川乐山)计算:⎪⎪⎪⎪-12=__________. 6.(2012重庆)计算:4+(π-2)0-|-5|+(-1)2 012+⎝⎛⎭⎫13-2.1.下列各数中,最小的数是( )A .0B .1C .-1D .- 2 2.若|a |=3,则a 的值是( )A .-3B .3C .13D .±33.下列计算正确的是( )A .(-8)-8=0B .⎝⎛⎭⎫-12×(-2)=1 C .-(-1)0=1 D .|-2|=-24.如图,数轴上A ,B 两点对应的实数分别为1和3,若点A 关于点B 的对称点为C ,则点C 所表示的实数是( )A .23-1B .1+ 3C .2+ 3D .23+15.(1)实数12的倒数是____.(2)写出一个比-4大的负无理数__________.6.若将三个数-3,7,11表示在数轴上,其中能被如图所示的墨迹覆盖的数是__________.7.定义一种运算☆,其规则为a ☆b =1a +1b,根据这个规则,计算2☆3的值是__________.8.如图,物体从点A 出发,按照A →B (第1步)→C (第2步)→D →A →E →F →G →A →B →…的顺序循环运动,则第2 012步到达点________处.9.计算:|-2|+(-1)2 012-(π-4)0.参考答案导学必备知识 自主测试1.A 1-2=-12.2.A3.D A 中-|-3|=-3,B 中⎝⎛⎭⎫13-1=3,C 中9=3.4.C 0.32×100万=320 000=3.2×105.5.C 因为从数轴可知:m 小于0,n 大于0,则mn <0,m -n <0. 6.解:|-5|+16-32=5+4-9=0. 探究考点方法触类旁通1.C 因为5是整数,37是分数,4=2是整数.触类旁通2.A 因为5的相反数是-5,-15的相反数是15,15的相反数是-15.触类旁通3.B触类旁通4.C 因为0.05=5×10-2,0.005=5×10-3,0.000 5=5×10-4,0.000 05=5×10-5,故选C.触类旁通5.B 因为|m -3|≥0,且(n +2)2≥0,又因为|m -3|+(n +2)2=0,所以m -3=0且n +2=0.所以m =3,n =-2,所以m +2n =3+2×(-2)=-1.触类旁通6.A 因为根据正数大于0,0大于负数,正数大于负数,解答即可. 品鉴经典考题1.C ∵-3×⎝⎛⎭⎫-13=1,∴-13的倒数是-3. 2.C A 中,|-2|=2,是正数,故本选项错误;B 中,(-2)2=4,是正数,故本选项错误;C 中,-2<0,是负数,故本选项正确;D 中,(-2)2=4=2,是正数,故本选项错误.3.C 因为科学记数法的形式为a ×10n ,用科学记数法表示较大的数,其规律为1≤a <10,n 是比原数的整数位数小1的正整数,所以60 110 000 000=6.011×1010.4.A 原式=2+3=5.5.12根据负数的绝对值是它的相反数,得⎪⎪⎪⎪-12=12. 6.解:原式=2+1-5+1+9=8. 研习预测试题1.D 因为正数和0都大于负数,2>1,两个负数比较大小,绝对值大的反而小,所以-2最小.2.D 绝对值为3的数有+3和-3两个,且互为相反数.3.B (-8)-8=-16,⎝⎛⎭⎫-12×(-2)=1,-(-1)0=-1,|-2|=2. 4.A 因为数轴上A ,B 两点对应的实数分别为1和3, 所以OA =1,OB = 3.所以AB =OB -OA =3-1. 由题意可知,BC =AB =3-1.所以OC =OB +BC =3+(3-1)=23-1. 5.(1)2 (2)-4+2(答案不唯一)6.7 因为-3<0,11>3,1<7<3. 7.56 因为2☆3=12+13=36+26=56. 8.A 由题意知,每隔8步物体到达同一点,因为2 012÷8=251余4,所以第2 012步到达A 点.9.解:原式=2+1-1=2.。
(完整版)山东省潍坊市2013年中考数学真题试题(解析版)

2013年潍坊市初中学业水平考试数学试题一、选择题(本题共 12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确 的选项选出来•每小题选对得3分,选错、不选或选出的答案超过一个均记 0分.)1.实数0.5的算术平方根等于()•A.2B. 2C. —D. 12 2答案:C.考点:算术平方根。
点评:理解算术平方根的意义,把二次根式化成最简形式是解答本题的关键 2.下面的图形是天气预报中的图标,其中既是轴对称图形又是中心对称图形的是()答案:A.考点:轴对称图形与中心对称图形的特征。
点评:此题主要考查了轴对称图形与中心对称图形的概念,二者既有联系又有区别。
. 3.2012年,我国财政性教育经费支出实现了占国内生产总值比例达 务教育均衡发展方面,安排义务教育教育经费保障教育机制改革资金达 “865.4亿元”用科学记数法可表示为()元.答案:B.考点:根据实物原型画出三视图。
点评:本题考查了俯视图的知识,注意俯视图是从上往下看得到的视图.5.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同 . 其中的一名学生想要知道自己能否进入前 5名,不仅要了解自己的成绩, 还要了解这9名学 生成绩的(). A.众数 B.方差 C. 平均数 D. 中位数 答案:D.D.4%的目标.其中在促进义865.4亿元.数据89A. 865 10B. 8.65 10C. 8.65 101011D. 0.865 10答案:C.考点:科学记数法的表示。
点评:此题考查了科学记数法的表示方法•科学记数法的表示形式为 1w |a| v 10, n 为整数,表示时关键要正确确定a 的值以及n 的值.4.如图是常用的一种圆顶螺杆,它的俯视图正确的是().a x 10n 的形式,其中B.考点:统计量数的含义•点评:本题要求学生结合具体情境辨析不同的集中量数各自的意义和作用 ,从而选择恰当的统计量为给定的题意提供所需的集中量数,进而为现实问题的解决提供理论支撑 •与单纯考查统计量数的计算相比较,这样更能考查出学生对统计量数的意义的认识程度 k6.设点A x 1, y 1和B x 2, y 2是反比例函数y图象上的两个点,当x 1 v x 2 v 0时,y 1 vxy ,则一次函数y 2x k 的图象不经过的象限是()考点:变量间的关系,函数及其图象 •点评:容器上粗下细,杯子里水面的高度上升应是先快后慢。
中考数学《实数》专题含解析

实数一、选择题1.某年哈尔滨市一月份的平均气温为﹣18℃,三月份的平均气温为2℃,则三月份的平均气温比一月份的平均气温高()A.16℃B.20℃C.﹣16℃D.﹣20℃2.下列计算正确的是()A.B.(a+b)2=a2+b2C.(﹣2a)3=﹣6a3D.﹣(x﹣2)=2﹣x3.下列计算正确的是()A.(﹣1)﹣1=1 B.(﹣3)2=﹣6 C.π0=1 D.(﹣2)6÷(﹣2)3=(﹣2)24.数字,,π,,cos45°,中是无理数的个数有()个.A.1 B.2 C.3 D.45.据报道,苏州市政府有关部门将在市区完成130万平方米老住宅小区综合整治工作.130万(即1300000)这个数用科学记数法可表示为()A.1.3×104B.1.3×105C.1.3×106D.1.3×1076.数轴上的点A表示的数是﹣1,点B表示的数是﹣,则点B关于点A的对称点B′点表示的数为()A.﹣2 B.﹣﹣2 C.﹣﹣1 D.07.下列计算结果正确的是()A.(﹣a3)2=a9B.a2•a3=a6 C.D.(sin60°﹣)0=08.28cm接近于()A.珠穆朗玛峰的高度B.三层楼的高度C.姚明的身高D.一张纸的厚度9.实数a、b在数轴上的位置如图所示,下列式子错误的是()A.a<b B.|a|>|b|C.﹣a<﹣b D.b﹣a>0二.填空题10.地球与太阳之间的距离约为149 600 000千米,用科学记数法表示(保留2个有效数字)约为千米.11.化简:=.12.若将三个数表示在数轴上,其中能被如图所示的墨迹覆盖的数是.13.已知a、b为两个连续的整数,且,则a+b=.14.已知互为相反数,则a:b=.15.若的值在x与x+1之间,则x=.16.,则x y=.17.计算:=.18.化简二次根式:=.19.一个自然数的算术平方根是a,则相邻的下一个自然数的算术平方根是.三.计算题20.计算:﹣+|1﹣|+()﹣1.21.计算:﹣2sin30°﹣(﹣)﹣2+(﹣π)0﹣+(﹣1).22..23.计算:.24.若x是不等于1的实数,我们把称为x的差倒数,如3的差倒数为,﹣5的差倒数为.现已知x1=﹣,x1的差倒数是x2,x2的差倒数是x3,…,以此类推,x的值是多少?实数参考答案与试题解析一、选择题1.某年哈尔滨市一月份的平均气温为﹣18℃,三月份的平均气温为2℃,则三月份的平均气温比一月份的平均气温高()A.16℃B.20℃C.﹣16℃D.﹣20℃【考点】有理数的减法.【专题】应用题.【分析】根据题意用三月份的平均气温气温减去一月份的平均气温气温,再根据有理数的减法运算法则“减去一个数等于加上这个数的相反数”计算求解.【解答】解:2﹣(﹣18)=2+18=20℃.故选B.【点评】本题考查有理数的减法运算法则.2.下列计算正确的是()A.B.(a+b)2=a2+b2C.(﹣2a)3=﹣6a3D.﹣(x﹣2)=2﹣x【考点】完全平方公式;去括号与添括号;幂的乘方与积的乘方;二次根式的加减法.【分析】利用完全平方公式、去括号与添括号法则、幂的乘方与积的乘方及二次根式的加减法等性质进行计算后即可确定答案.【解答】解:A、不是同类二次根式,因此不能进行运算,故本答案错误;B、(a+b)2=a2+b2+2ab,故本答案错误;C、(﹣2a)3=﹣8a3,故本答案错误;D、﹣(x﹣2)=﹣x+2=2﹣x,故本答案正确;故选D.【点评】本题考查了完全平方公式、去括号与添括号法则、幂的乘方与积的乘方及二次根式的加减法等性质,属于基本运算,要求学生必须掌握.3.下列计算正确的是()A.(﹣1)﹣1=1 B.(﹣3)2=﹣6 C.π0=1 D.(﹣2)6÷(﹣2)3=(﹣2)2【考点】负整数指数幂;同底数幂的除法;零指数幂.【专题】计算题.【分析】根据平方根,负指数幂的意义,同底数的幂的除法的意义,分别计算出各个式子的值即可判断.【解答】解:A、(﹣1)﹣1=﹣1,故A错误;B、(﹣3)2=9,故B错误;C、任何非0实数的零次幂等于1,故C正确;D、(﹣2)6÷(﹣2)3=(﹣2)3,故D错误.故选C.【点评】解决此题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、同底数的幂的除法等考点的运算.4.数字,,π,,cos45°,中是无理数的个数有()个.A.1 B.2 C.3 D.4【考点】无理数;特殊角的三角函数值.【分析】根据无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数,结合所给的数据判断即可.【解答】解:=2,cos45°=,所以数字,,π,,cos45°,中无理数的有:,π,cos45°,共3个.故选C.【点评】此题考查了无理数的定义,属于基础题,关键是掌握无理数的三种形式.5.据报道,苏州市政府有关部门将在市区完成130万平方米老住宅小区综合整治工作.130万(即1300000)这个数用科学记数法可表示为()A.1.3×104B.1.3×105C.1.3×106D.1.3×107【考点】科学记数法—表示较大的数.【专题】应用题.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于1时,n是正数;当原数的绝对值小于1时,n是负数.【解答】解:130万=1 300 000=1.3×106.故选C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.6.数轴上的点A表示的数是﹣1,点B表示的数是﹣,则点B关于点A的对称点B′点表示的数为()A.﹣2 B.﹣﹣2 C.﹣﹣1 D.0【考点】实数与数轴.【分析】先求出A、B之间的距离,然后根据对称的性质得出A、B′之间的距离,再设点B′表示的数为x,列出关于x的方程,解方程即可.【解答】解:∵数轴上的点A表示的数是﹣1,点B表示的数是﹣,∴AB=﹣1,∵点B和点B′关于点A对称,∴AB′=AB=﹣1.设点B′表示的数为x,则x+1=﹣1,x=﹣2.∴B′点表示的数为﹣2.故选A.【点评】本题考查了实数与数轴上的点的对应关系,以及对称的有关性质.7.下列计算结果正确的是()A.(﹣a3)2=a9B.a2•a3=a6 C.D.(sin60°﹣)0=0【考点】负整数指数幂;同底数幂的乘法;幂的乘方与积的乘方;零指数幂.【分析】根据有理数的幂的乘方和同底数幂的乘法及负指数幂的运算法则计算.【解答】解:A、平方取正值,指数相乘,应为a6,故A错误;B、a2•a3=a5,故B错误;C、,故C正确;D、(sin60°﹣)0=1≠0,故D错误.故选C.【点评】本题主要考查了有理数的有关运算法则,解答此题时要注意任何非0数的0次幂等于1.8.28cm接近于()A.珠穆朗玛峰的高度B.三层楼的高度C.姚明的身高D.一张纸的厚度【考点】有理数的乘方.【分析】根据有理数的乘方运算法则,计算出结果,然后根据生活实际来确定答案.【解答】解:28=24×24=16×16=256(cm)=2.56(m).A、珠穆朗玛峰峰的高度约8848米,错误;B、三层楼的高度20米左右,错误;C、姚明的身高是2.23米,接近2.56米,正确;D、一张纸的厚度只有几毫米,错误.故选C.【点评】解答这样的题目有两个要点需要注意,一是有理数的乘方运算法则要记牢;二是根据生活实际情况来做出选择.9.实数a、b在数轴上的位置如图所示,下列式子错误的是()A.a<b B.|a|>|b|C.﹣a<﹣b D.b﹣a>0【考点】实数与数轴.【分析】根据数轴表示数的方法得到a<0<b,数a表示的点比数b表示点离原点远,则a<b;﹣a>﹣b;b﹣a>0,|a|>|b|.【解答】解:根据题意得,a<0<b,∴a<b;﹣a>﹣b;b﹣a>0,∵数a表示的点比数b表示点离原点远,∴|a|>|b|,∴选项A、B、D正确,选项C不正确.故选C.【点评】本题考查了实数与数轴:数轴上的点与实数一一对应;数轴上原点左边的点表示负数,右边的点表示正数;右边的点表示的数比左边的点表示的数要大.二.填空题10.地球与太阳之间的距离约为149 600 000千米,用科学记数法表示(保留2个有效数字)约为 1.5×108千米.【考点】科学记数法与有效数字.【专题】计算题.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值是易错点,由于1 048 576有7位,所以可以确定n=7﹣1=6.有效数字的计算方法是:从左边第一个不是0的数字起,后面所有的数字都是有效数字.用科学记数法表示的数的有效数字只与前面的a有关,与10的多少次方无关.【解答】解:149 600 000=1.496×108≈1.5×108.故答案为1.5×108.【点评】此题考查科学记数法的表示方法,以及用科学记数法表示的数的有效数字的确定方法.11.化简:=.【考点】算术平方根.【分析】根据开平方的意义,可得答案.【解答】解:原式==,故答案为:.【点评】本题考查了算术平方根,先化成分数,再开方运算.12.若将三个数表示在数轴上,其中能被如图所示的墨迹覆盖的数是.【考点】实数与数轴.【专题】图表型.【分析】首先利用估算的方法分别得到﹣,,前后的整数(即它们分别在那两个整数之间),从而可判断出被覆盖的数.【解答】解:∵﹣2<﹣<﹣1,2<<3,3<<4,且墨迹覆盖的范围是1﹣3,∴能被墨迹覆盖的数是.【点评】本题考查了实数与数轴的对应关系,以及估算无理数大小的能力.13.已知a、b为两个连续的整数,且,则a+b=11.【考点】估算无理数的大小.【分析】根据无理数的性质,得出接近无理数的整数,即可得出a,b的值,即可得出答案.【解答】解:∵,a、b为两个连续的整数,∴<<,∴a=5,b=6,∴a+b=11.故答案为:11.【点评】此题主要考查了无理数的大小,得出比较无理数的方法是解决问题的关键.14.已知互为相反数,则a:b=.【考点】立方根.【分析】根据立方根互为相反数,可得被开方数互为相反数,根据互为相反数的两数的和为0,可得答案.【解答】解:互为相反数,∴(3a﹣1)+(1﹣2b)=0,3a=2b,故答案为:.【点评】本题考查了立方根,先由立方根互为相反数得出被开方数互为相反数,再求出的值.15.若的值在x与x+1之间,则x=2.【考点】估算无理数的大小.【分析】先估算的整数部分是多少,即可求出x的取值.【解答】解:∵2<<3,∴x=2.故答案为:2.【点评】此题主要考查了估算无理数的大小,确定无理数的整数部分即可解决问题.16.,则x y=﹣1.【考点】非负数的性质:算术平方根;非负数的性质:偶次方.【分析】首先根据非负数的性质,两个非负数的和是0,这两个数都是0求得x,y的值,代入即可求解.【解答】解:根据题意得:,解得:,∴x y=(﹣1)=﹣1.故答案是:﹣1.【点评】本题主要考查了非负数的性质,以及负指数幂的意义,正确求得x,y的值是解题的关键.17.计算:=.【考点】实数的运算;负整数指数幂;特殊角的三角函数值.【专题】计算题.【分析】根据负指数幂、二次根式化简、特殊角的三角函数3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:原式=3+0.5﹣6×=,故答案为.【点评】本题是基础题,考查了实数的有关运算,还涉及了零指数幂、负指数幂、二次根式化简、绝对值等考点.18.化简二次根式:=﹣2.【考点】二次根式的混合运算.【分析】首先进行各项的化简,然后合并同类项即可.【解答】解:=3﹣()﹣2=﹣2,故答案为﹣2.【点评】本题主要考查二次根式的化简、二次根式的混合运算,解题的关键在于对二次根式进行化简,然后合并同类项.19.一个自然数的算术平方根是a,则相邻的下一个自然数的算术平方根是.【考点】算术平方根.【分析】首先利用算术平方根求出这个自然数,然后即可求出相邻的下一个自然数的算术平方根.【解答】解:∵一个自然数的算术平方根是a,∴这个自然数是a2,∴相邻的下一个自然数为:a2+1,∴相邻的下一个自然数的算术平方根是:,故答案为:.【点评】此题主要考查算术平方根的定义及其应用,比较简单.三.计算题20.计算:﹣+|1﹣|+()﹣1.【考点】实数的运算;负整数指数幂.【专题】计算题.【分析】原式第一项化为最简二次根式,第二项分母有理化,第三项利用绝对值的代数意义化简,最后一项利用负指数幂法则计算即可得到结果.【解答】解:原式=3﹣+﹣1+2=3+1.【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.21.计算:﹣2sin30°﹣(﹣)﹣2+(﹣π)0﹣+(﹣1).【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.【专题】计算题.【分析】本题涉及零指数幂、乘方、特殊角的三角函数值、立方根等考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:原式=﹣2×﹣+1﹣(﹣2)+1=﹣1﹣9+1+2+1=﹣6.【点评】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是掌握零指数幂、乘方、特殊角的三角函数值、立方根等考点的运算.22..【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.【专题】计算题.【分析】根据零指数幂、负整数指数幂和特殊角的三角函数值得到原式=4+(1﹣)﹣1+2×+,再去括号和进行乘法运算,然后合并即可.【解答】解:原式=4+(1﹣)﹣1+2×+=4+1﹣﹣1++=4+.【点评】本题考查了实数的运算:先算乘方或开方,再算乘除,然后进行加减运算;有括号先算括号.也考查了零指数幂、负整数指数幂和特殊角的三角函数值.23.计算:.【考点】实数的运算;零指数幂;特殊角的三角函数值.【专题】计算题.【分析】本题涉及零指数幂、特殊角的三角函数值、二次根式化简、去绝对值4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:原式=2+×﹣(﹣1)﹣1,=2+1﹣+1﹣1,=+1.【点评】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握特殊角的三角函数值、零指数幂、二次根式、绝对值等考点的运算.24.若x是不等于1的实数,我们把称为x的差倒数,如3的差倒数为,﹣5的差倒数为.现已知x1=﹣,x1的差倒数是x2,x2的差倒数是x3,…,以此类推,x的值是多少?【考点】规律型:数字的变化类.【分析】根据差倒数的定义分别计算出x1=﹣,x2=;x3=4,x4=﹣,则得到从x1开始每3个值就循环,而÷3=671,即可得出答案.【解答】解:∵x1=﹣,∴x2==;x3==4;x4==﹣;…,∴三个数一个循环,∵÷3=671,∴x=x3=4.【点评】此题考查了数字的变化类,是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.。
中考数学试题分类解析 专题1 实数

【2013版中考12年】广东省广州市2002-2013年中考数学试题分类解析 专题1 实数一、选择题1. (2002年广东广州2分)0.000000108这个数,用科学记数法表示为【 】(A )91.0810-⨯ (B )81.0810-⨯ (C )71.0810-⨯ (D )61.0810-⨯2.(2002年广东广州2分)计算()210.25712-⎛⎫⨯-+- ⎪⎝⎭所得的结果是【 】(A )2 (B )54 (C )0 (D )17163. (2004年广东广州3分)2003年广州市完成国内生产总值(GDP )达3466.53亿元,用四舍五入法取近似值,保留3个有效数字并用科学记数法表示为【 】A .3.47×103亿元 B .3.47×104亿元 C .3.467×103亿元 D .3.467×104亿元 【答案】A 。
【考点】科学记数法,有效数字,近似数。
4. (2005年广东广州3分)下列四个数中,在-2和1之间的数是【 】A.–3B.0C.2D.35. (2005年广东广州3分)已知a 21b 21=+=-,,则a 与b 的关系是【 】A.a=bB.ab=1C.a=-bD.ab=-16. (2006年广东广州3分)某市某日的气温是一2℃~6℃,则该日的温差是【 】. (A)8℃ (B)6℃ (C)4℃ (D)一2℃7. (2007年广东广州3分)下列各数中,最小..的数是【 】 A .-2 B .-1 C .0 D 2 【答案】A 。
8. (2008年广东广州3分)计算3(2)-所得结果是【 】 A 6- B 6 C 8- D 89. (2008年广东广州3分)若实数a 、b 互为相反数,则下列等式中恒成立的是【 】 A a b 0-= B a b 0+= C ab 1= D ab 1=-10. (2009年广东广州3分) 实数a 、b 在数轴上的位置如图所示,则a 与b 的大小关系是【 】(A )a b < (B )a b = (C )a b > (D )无法确定11. (2010年广东广州3分)如果+10%表示“增加10%”,那么“减少8%”可以记作【 】A .-18%B .-8%C .+2%D .+8%【答案】B 。
2013年广东省各市中考数学分类解析专题1实数

A a 2.5B 2.5 aC a 2.5D a 2.5广东各市2山3年中考数学试题分类解析汇编专题实数一、选择题1. (2013年广东佛山3分) 2的相反数是【】C. 12【答案】A. 1考点】相反数口【分析】相反数的定义杲!如果两个数只有苻号不同,我们称苴中一个数为另一千数的相反数,特别地・o e 数还是0.囲!K-2的相反数是二故选亠 2. (2013年广东佛山3分)化简22[的结果是【 】A . 2 2 1 B- 2 2 C . 1 2 D . 2 23. (2013年广东广州3分)比0大的数是【 】1 A -1 B C 0 D 12【答案】D.【考点】实数的大小比簽,【分析】根据实数的夫小比较法顽 正数大于0*于负数,两个负数相比,绝对直走的反而小口因1匕T-Z-lcW 二比。
大的数是1・故选D ・23分)实数a 在数轴上的位置如图所示,则 |a 2.5 =【A . 2D .【分析】分子、分母同时乗以血+1即可:4. (2013年广东广州T^iTS+ii| — L11 + 11【看亞】绝对值和数轴.【分析】由数轴可知.a< 2.5 * §Pa- 2.5< 0 .'. a-2 5 =-*a-2 51= 2 5-a -故选弓-5. (2013年广东茂名3分)下列实数中,最小的数是【】A .—3B . 3 C. 1 D . 03【答案】2・【若点】冥数的大『卜比较.【分祈】很据实数的大小比较法駅正数大于E Q大于员航两牛负歎相比絶对值大的反而小.因此,-3<0<1<3,贵卜的数是7A・36. (2013年广东茂名3分)PM2.5是指大气中直径小于或等于 2.5 叩(0.0000025m)的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物.将0.0000025用科学记数法表示为【】A . 25 X10「7B . 2.5 X0「6C. 0.25 X0「5 D . 2.5 氷06【答案】缶【萼亘】科学记敎法x匕分析】根抿斜学谨t法的走义,科学记数法的袁示册式为凶仇其中1WKW・n为整甑表示时关键里确定请的值限矗11的值.在确定口的值时.看该数是大于或等干1还是T于1-当删犬于或等干I时•口城数位元薮减h当该敕小于1时,一口为它第一个有效数字前C的个数(剖盼前的1牛0)■ 0.0000025虽有JS数字前育行个3冶小数点前的1个①,从而0.0000025= 25xl0_\故选弐7. (2013年广东梅州3分)四个数-1 , 0, 1, 2中为无理数的是【】2A . —1B . 0 C. 1 D . . 22【答案】)【考点】无理数•【分折】无理颈就是无限不循环小驗有理数是整数与分数的统称.即有限小赦和无隈循环小数是苞理数,而不循环小数是无理裁.由此@卩可判定选择项;-h o是整^ 是有理轨丄是分熱是有理驗无理数孫JT •故选口28. (2013年广东深圳3分)—3的绝对值是【】A.3B. 一3 C・〔D・[3 3【答案】瓜【者点】相反数.【分析】相反数的走义杲;如果两个数貝有符号不同,我们称其中一^対另一个数的相長数,持别地「洱数还是丄因此一3的相反教是3.故选A.鼻<2013 3分)臬活动中,共募得捐款32000000元■将第血罠00用科学记数注表卞两【]A.032xlp3 C3.2X1C D32X1Q'【答案】G【专点】科学记数袪口【分析】根据科学记数法的定义科学记敌法的表示形式为护1”具中Ka<lC, zi为整紀表示时关键理确宦a的值以圧昭的值.在确宦n的值时,看臓是大于或等于1还是可于1.当该数尢于或等于1时心曲数位元数减1;当该較小于1时,-11沖它第一个肓舱数孚前0的个敎(舍卜数点前的1个P •耳曲口贺一共从而32000000=3,2^ 10\ 故选C・10. (2013年广东省3分)2的相反数是【】A. 1B. 1C—2 D.22 2【甞案】C・【肴点】相反数.【分析】相反频的定义是’如果两个数只有符号不1司,我们称其中一6数为另一个馥的相反数.特别地,D的数还是h 因此:的相反数是一h抜选U11. (2013年广东省3分)据报导,2013年第一季度,广东省实现地区生产总值约 1 260 000 000000元,用科学记数法表示为【】A. 0.126 X121 元B. 1.26 X ft元C. 1.26 X 10元D. 12.6 X 10元【答案】玄【苕盘】科学记数法.【分析】根摇科学记数法的定义,科学记数法的表示形式为旳只其中iwxia 口为整如表示时关蘿轟定盘的值以及"的值.衽确定n的值时,看该数是大于或等于1还是4吁L当该数大于或等于1时小尙数位元数减b当该数小于1时.一宜为它第一个有效数字前:〕的个数(含小薮点前的1个汨・1⑷:烦j 一共W 位,从而1 260 OOO OOaOOO=L26«1012H 故选B・12. (2013年广东省3分)下列等式正确的是【】A. ( 1) 3 1B. ( 4)0 1C. 26D. 52【答案】氏【考点】负整数指数嶽同底数幕的乘法和险法,零簸鼠【分折】棍捉负整数指数黑同底数幕的秉法和除法,零扌旨数黑运算法刚逐一作出判断:A. Jl)T=-h故此遥项错误;Bs (-4)°=1,故此选项正關:C* | -2 F x 4 -2』=卜-2 P = -2’,故Lt选项错误$Ds 1-5/ -r<-5(2= »-513= 52> 故此选匝错i吴口故选B P13. (2013年广东湛江4分)下列各数中,最小的数是【】A. 1B. 1 C .0 D. 1【答案】Do【澹点】实数的大小上肉t,【分析】根据实数田大小比靈法则,正敎大于h。
2013年中考数学实数复习题及答案

第2讲 实数一级训练1.||-9的平方根是( )A .81B .±3C .3D .-32.(2011年广东中山)下列各式中,运算正确的是( ) A.4=±2 B .-||-9=-()-9C.()x 32=x 6D.()2-π2=2-π3.计算:()-12+()-13=( )A .-2B .-1C .0D .24.由四舍五入法得到的近似数8.8×103,下列说法正确的是( )A .精确到十分位B .精确到个位C .精确到百位D .精确到千位5.下列计算正确的是( ) A.20=2 10 B.2·3= 6 C.4-2= 2 D.(3)2=-36.计算13-12的结果( ) A .-73 3 B.33 C. 3 D .-533 7.(2012年广东珠海)使x -2有意义的x 的取值范围是______.8.(2012年广东肇庆)计算20·15的结果是______. 9.(2012年广东)若x ,y 为实数,且满足||x -3+y -3=0,则⎝⎛⎭⎫x y 2 012的值是______.10.(2010年河南)若将三个数-3,7,11表示在数轴上,其中能被如图1-2-2所示的墨迹覆盖的数是__________.图1-2-211.(2012年广东珠海)计算:()-22-||-1+()2 012-π0-⎝⎛⎭⎫12-1.二级训练12.(2011年贵州贵阳)如图1-2-3,矩形OABC 的边OA 长为2,边AB 长为1,OA 在数轴上,以原点O 为圆心,对角线OB 的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )图1-2-3A .2.5B .22 C.3 D.5 X| k |B| 1 . c|O |m13.设a =20,b =(-3)2,c =3-27,d =12⎛⎫ ⎪⎝⎭-1,则a ,b ,c ,d 按由小到大的顺序排列正确的是( )A .c <a <d <bB .b <d <a <cC .a <c <d <bD .b <c <a <d14.(2011年湖南湘潭)规定一种新的运算:a ⊗b =1a +1b,则1⊗2=________. 15.使12n 是整数的最小正整数n =__________.16.(2012年广东深圳)计算:||4+⎝⎛⎭⎫12-1-(3-1)0-8cos45°.三级训练17.(2010年山东莱芜)已知:C 23=3×21×2=3,C 35=5×4×31×2×3=10,C 46=6×5×4×31×2×3×4=15,…. 观察上面的计算过程,寻找规律并计算C 610=____________.18.(2011年江苏盐城)如图1-2-4,将1,2,3,6按下列方式排列.若规定(m ,n )表示第m 排从左向右第n 个数,则(5,4)与(15,7)表示的两数之积是__________.图1-2-4第2讲 实数【分层训练】1.B 2.C 3.C 4.C 5.B 6.D7.x ≥2 8.2 9.1 10.711.解:原式=2-1+1-2=0.12.D 13.A 14.11215.3 16.解:原式=4+2-1-2 2·22=4+2-1-2=3. 17.210 解析:C 610=10×9×8×7×6×51×2×3×4×5×6=210. 18.2 3。
