大学物理 切向,法向加速度(精选)
合集下载
第三讲-切向加速度与法向加速度
2、伽利略速度变换关系≠运动的合成与分解；
运动的合成是在一个参考系中，总能成立； 伽利略速度变换则应用于两个参考系之间。
—— 质点运动学 ——
伽利略变换、绝对时空理论
例1 某人骑自行车以速率 υ 向正西方行使，遇到由 北向南刮的风(设风速大小也为 υ )，则他感到风是从
哪个方向吹来的？
—— 质点运动学 ——
例1、作曲线运动的质点,下列说法正确的是
（A）切向加速度必不为零； （B）法向加速度必不为零（拐点处除外）； （C）由于速度沿切线方向，法向分速度必为 零，因此法向加速度必为零； （D）物体作匀速率运动，其加速度必为零； （E）若物体的加速度为恒矢量，它一定作匀 变速率运动 .
—— 质点运动学 ——
切向加速度、法向加速度
例2 一质点作圆周运动，其路程与时间的关系为
υ0 和b 都是正的常数，圆周半径为r.
(1) 求质点在 t 时刻的速度; (2) t 为何值时，质点的切向加速度和法向加速度
的大小相等。
—— 质点运动学 ——
切向加速度、法向加速度
例3 一质点作半径为0.1 m 的圆周运动，已知
▲线量与角量之间的关系
Δs(弧长) RΔθ
υ Rω
aτ Rα
an
υ2 R
Rω2
—— 质点运动学 ——
切向加速度、法向加速度
•匀变速直线运动的几个运动学公式
比 较
•质点作匀变速率圆周运动的运动学公式
用角量描述平面圆周运动可转化为一维运动形式， 从而简化问题。
—— 质点运动学 ——
切向加速度、法向加速度
a
dυ
dt
υ2 an R
大学物理期中复习 二
（D）1 = 2 ，1 = 2 ，一个在地球上作竖直振动，另一个在月球上作竖直振动
例13：（补2）一弹簧振子，当把它水平放置时，它作简谐振动。若把它
竖直放置或放在光滑斜面上，试判断下列情况正确的是
（A）竖直放置作简谐振动，在光滑斜面上
不作简谐振动
（B）竖直放置不作简谐振动，在光滑斜面
上作简谐振动
（C）刚体所受的合外力和合外力矩均为零
（D）刚体的转动惯量和角速度均保持不变
例10：（补4）关于刚体有以下几种说法：
（1）对某个定轴而言，内力矩不会改变刚体的角动量
（2）作用力和反作用力对同一定轴的力矩之和必为零
（3）刚体角动量守恒的充分必要条件是刚体不受外力矩的作用
（A）只有(2)是正确的
（B）(1)、(2)是正确的
例24：（选1）一质点沿轴运动，运动方程 = ()，当满足下列哪个条
件时，质点向坐标原点O运动？
Τ
A
>0
B
<0
2
C
<0
2
D
>0
Τ
例25：（选3）根据瞬时速度的定义及其坐标表示，它的大小
റ
റ 可表
示为
1
4
റ +
റ +
+ =
则该质点运动轨迹方程是 ____________________
（SI），
它描述的轨迹是______________________。
半径为 的圆
例22：（补10）质点P在直线上运动，其坐标与时间有如下关系：
大学物理3切向法向加速度
01
车辆行驶过程中的转弯
在转弯过程中，车辆的切向加速度和法向加速度共同作用，使车辆按照
预定的轨迹行驶。
02
投掷物体的运动
在投掷物体时，出手的瞬间切向加速度和法向加速度达到最大值，共同
决定了物体的飞行轨迹。
03
天体运动
在天体运动中，行星绕太阳运动的轨迹是一个椭圆，切向加速度和法向
加速度的大小和方向不断变化，共同决定了行星的运动状态。
03
当物体沿着抛物线轨道运动时 ，法向加速度的计算公式为： an = v^2 / p，其中p表示抛 物线的焦距。
法向加速度的物理意义
法向加速度的物理意义在于描述 物体运动方向改变的快慢程度。
法向加速度越大，表示物体运动 方向的改变越快，物体运动的曲
率越大。
在圆周运动中，法向加速度的大 小决定了物体运动的角速度和周 期，其值越大则角速度和周期越
在车辆设计过程中，需要考虑轮胎与地面的摩擦力、悬挂系统的设计以及轮胎的弹性等因素，以确保 车辆在行驶过程中的稳定性和安全性。
飞行器飞行中的切向法向加速度
飞行器飞行中的切向法向加速度
在飞行器飞行过程中，由于气流的压力和摩擦力作用，会产生切向加速度，使飞行器产生偏航或滚转动作。同时 ，由于飞行器的翼型设计和气动布局，会产生法向加速度，使飞行器在飞行过程中保持稳定。
小。
03
CATALOGUE
切向法向加速度的关系
切向法向加速度的关联性
切向法向加速度是描述物体运 动状态的两个重要参数，它们
之间存在一定的关联性。
当物体做曲线运动时，切向 加速度决定物体运动轨迹的 弯曲程度，法向加速度则与 物体偏离轨迹的方向有关。
切向加速度和法向加速度的大 小和方向共同决定了物体的运
大学物理切向加速和法向加速
•切向坐标 沿运动
轨迹的切线方向； •法向坐标 n 沿运动 轨迹的法线方向。
二、切向加速度、 法向加速度
nn
物体沿平面作曲线运动，速度变化为 v 建立自然坐标系。
§2切向加速度、法向加速度/二、a、an
将 v 分解为 v 和 vn
v v0 vnn0 （1）
vA
vA
vn v
其中
AnB
vτ
vB
v 为速度增量在切线方向的分量；
vn 为速度增量在法线方向的分量； 0 切线方向的单位矢量；
n0 法线方向的单位矢量。
§2切向加速度、法向加速度/二、a、an
将（1）式两边同除 t 后取极限，
lim v
Δt 0 t
lim
Δ t 0
v t
0
lim
Δ t 0
vn t
n0
有
dv dt
dv dt
0
dv n dt
一、自然坐标系
•问题的提出： 在直角坐标系中，加速度公式无法看
出哪一部分是由速度大小变化产生的加速 度，哪一部分是由速度方向变化产生的加 速度，所以引入自然坐标系来描写。 1.自然坐标系
自然坐标系是建立在物体运动的轨 迹上的，有两个坐标轴，切向坐标和法 向坐标。
§2切向加速度、法向加速度/一、自然坐标系
方向：与过P点运动平面上半径为R的圆相切。
P点只有运动平面上的向心加速度，其大小为
a 2r n
2R cos
(7.27 105 )2 6.7310/ s2 )
P点加速度的方向在运动平面上由P指向地轴。
例如:已知北京、上海和广州三地的纬度分别 是北纬3957、3112和 2300，则三地的v 和 an 分别为：
切向加速度和法向加速度
r τ (t)
τ
r
θ
θ + θ
x
r τ r θ ： 大小 τ = 2sin 2 ≈ θ
dτ dτ dθ dτ dθ ds dτ r ds = ρ ds =V = = , =n , dθ , dt dt dθ dt dθ ds dt dθ
r τ ≈ θ n r r r dτ r τ θ n r lim θ →0, θlim θ = θ →0 θ = n dθ = n →0
α
r a
an
dV 2 V 2 2 2 a = at2 + an = ( ) + ( ) , tgα = an / at dt ρ
讨论：（1 直线运动， 讨论：（1）直线运动，ρ = ∞, an = 0 ：（ dV V2 a = 0, an = 匀速率圆周运动， （2）匀速率圆周运动， t = ：向心加速度 R dt 一般曲线运动及变速率圆周运动， （3）一般曲线运动及变速率圆周运动，at ≠ 0, an ≠ 0 V2 V2 （4） an = ρ= ：计算曲率半径
θ = 63.4o
第6节 节
圆周运动的角量表示
角坐标， s = Rθ θ ：角坐标，rad θ = θ (t) s = s(t)
y
r P r s θ A R O
V = ωR,
dω d 2θ ：角加速度， 角加速度， rad / s2 β= = 2 dt dt V 2 ω2 R2 = = ω2 R at = Rβ, an = R R
第5 节
相对运动
P
r r
S
O
静系
r r0
S′
O′
动系
r r′
r r r r = r ′ + r0 r r r dr dr ′ dr0 = + dt d = r′ + r0
第三讲切向加速度与法向加速度
质点运动学中，切向加速度和角加速度是两个重要概念。切向加速度反映速度大小变化的快慢，而角加速度则描述角速度变化的快慢。文档通过引入曲率圆和相似三角形的概念，深入解释了切向加速度和法向加速度的物理意义。特别地，在曲线运动中，质点的速度沿切线方向，因此法向分速度为零，但法向加速度不为零，它反映了速度方向变化的快慢。进一步地，文档给出了线量与角量之间的关系，其中切向加速度与角加速度的关系为aτ=Rα，即切向加速度等于角加速度与半径的乘积。这一关系式在质点作圆周运动时尤为重要，它连接了质点的线性运动和角运动。此外，文档还通过多个例题展示了如何应用这些概念解决实际问题，如的运动分析等。
加速度 切向和法向加速度
解：（1） v v0 et
y
dv v 2 v0 2 a et en en dt r (2)如图,设质点在 t=0 时位于 x=r , y=0 v0 v0 x r cos t , y r sin t r rer r r
v0 dx vx v0 sin t dt r v0 dy , v y v0 cos t dt r
a an
2 . at c , an 0 匀变速直线运动
3 . at 0 , an c
匀速率圆周运动 变速曲线运动
4
4 . at 0 , an 0
例2、设一质点在半径为r的圆周上以速率v0运动， 试写 出：（1）在自然坐标系中质点的速度、切向和法向加 速度；（2）在直角坐标系中质点的速度和加速度分量。
加速度 切向加速 度和法向加速度
1
一、加速度
v 平均加速度：a t
2 d r v dv 加速度： lim a t 0 t d t2 dt dvx dvy dvz a i j k axi a y j az k dvy dt dt
加速度大小：a a ax 2 ay 2 az 2
A
加速度方向？加速度方向 为速度变化的方向，指向 运动轨迹的凹的一侧。
vA
B
vA
v
vB
2
二、切向和法向加速度
在自然坐标系中
det dv d (vet ) dv 加速度：a et v dt dt dt dt det et d d
et (t dt) d源自det3 dv v 2 a et en at et an en dt
第三讲 切向加速度与法向加速度
ቤተ መጻሕፍቲ ባይዱ
—— 质点运动学 ——
伽利略变换、 伽利略变换、绝对时空理论
二船都以2m/s 3、在相对地面静止的坐标系内，A、B二船都以 在相对地面静止的坐标系内， 二船都以 的速率匀速行驶， 船沿 轴正向， 船沿 轴正向， 船沿x轴正向 船沿y轴正向 的速率匀速行驶，A船沿 轴正向， B船沿 轴正向， 今在A船上设置与地面坐标系方向相同的坐标系， 今在 船上设置与地面坐标系方向相同的坐标系，那 船上设置与地面坐标系方向相同的坐标系 么在A船上的坐标系中 船上的坐标系中， 船的速度为 么在 船上的坐标系中，B船的速度为 。 4、一飞机相对空气的速度大小为200km/h，风速为 一飞机相对空气的速度大小为 ， 56km/h，方向从西向东，地面雷达测得飞机的速率为 ，方向从西向东， 192km/h，则飞机相对地面运动的方向为 ， 。
o O′ z x z′ z
x
t′ = t
∗
z′ = z
—— 质点运动学 —— 伽利略变换、 伽利略变换、绝对时空理论
x′ = x − υt y′ = y
轴方向上。 设两参考系间的相对运动只发生在 x 轴方向上。 S系 S ′系 事件A 事件A ( x 1 , t 1 ) ′ ′ ( x1 , t1 ) 事件B 事件B ( x 2 , t 2 ) ′ ( x′ , t2 ) 2
1– 4
如何度量曲线弯曲程度？ 如何度量曲线弯曲程度？ P∆s P′
∆θ
ρ
ρ
曲率圆
∆θ dθ = 曲率： 曲率： k = lim ∆s→0 ∆ s ds ds 1 = 曲率半径： 曲率半径： ρ = dθ k
—— 质点运动学 —— 切向加速度、 切向加速度、法向加速度
v τ ( t + dt )
—— 质点运动学 ——
伽利略变换、 伽利略变换、绝对时空理论
二船都以2m/s 3、在相对地面静止的坐标系内，A、B二船都以 在相对地面静止的坐标系内， 二船都以 的速率匀速行驶， 船沿 轴正向， 船沿 轴正向， 船沿x轴正向 船沿y轴正向 的速率匀速行驶，A船沿 轴正向， B船沿 轴正向， 今在A船上设置与地面坐标系方向相同的坐标系， 今在 船上设置与地面坐标系方向相同的坐标系，那 船上设置与地面坐标系方向相同的坐标系 么在A船上的坐标系中 船上的坐标系中， 船的速度为 么在 船上的坐标系中，B船的速度为 。 4、一飞机相对空气的速度大小为200km/h，风速为 一飞机相对空气的速度大小为 ， 56km/h，方向从西向东，地面雷达测得飞机的速率为 ，方向从西向东， 192km/h，则飞机相对地面运动的方向为 ， 。
o O′ z x z′ z
x
t′ = t
∗
z′ = z
—— 质点运动学 —— 伽利略变换、 伽利略变换、绝对时空理论
x′ = x − υt y′ = y
轴方向上。 设两参考系间的相对运动只发生在 x 轴方向上。 S系 S ′系 事件A 事件A ( x 1 , t 1 ) ′ ′ ( x1 , t1 ) 事件B 事件B ( x 2 , t 2 ) ′ ( x′ , t2 ) 2
1– 4
如何度量曲线弯曲程度？ 如何度量曲线弯曲程度？ P∆s P′
∆θ
ρ
ρ
曲率圆
∆θ dθ = 曲率： 曲率： k = lim ∆s→0 ∆ s ds ds 1 = 曲率半径： 曲率半径： ρ = dθ k
—— 质点运动学 —— 切向加速度、 切向加速度、法向加速度
v τ ( t + dt )
大学物理-速度与加速度
dt
dt
d2x d2 y d2z dt 2 i dt 2 j dt 2 k
axi ay j azk
加速度的大小：
a a
d2 (
dt
x
2
)2
(
d2 dt
y
2
)2
(
d 2z dt 2
)2
三、切向加速度与法向加速度
质点在平面自然坐标系中的速度
v
v
o
根据加速度的定义，有：
a
d dt
d( dt
v
l0
h
l (t )
O
x
随堂练习
例2: 一质点作圆周运动(顺时针运动)，其路程与 时间的关系为
0 和b 都是正的常数，圆周半径为r. (1) 求质点在t 时刻的速度大小; (2) t 为何值时，质点的切向加速度和法向加速
度的大小相等。
υB
υA
B
υdBBBddn
A υA
dθ
dθ A
OR
O
d n ——速度方向改变量 d ——速度大小改变量
t 时刻， A点；t +dt 时刻，B点
a
a
ann
d dt
2 R
n
a
——速度大小变化率
an ——速度方向改变量
三、切向加速度与法向加速度
3、一般平面曲线运动中的加速度
分析思路：
曲率加速度
设运动质点经 t 时间，从A点运动到B点。
速度增量 v vB vA vA
1、平均加速度
vB
a
v
t
2、瞬时加速度
A
B
Δv
vB
a
lim
Δt 0
圆周运动的切向加速度和法向加速度 角加速度
如 t 0 时, 0, 0
0 0t 12t2
2
2 0
2 (
0)
对于作曲线运动的物体，以下几种说法中哪一 种是正确的：
（A）切向加速度必不为零；
（B）法向加速度必不为零（拐点处除外）；
（C）由于速度沿切线方向，法向分速度必为零， 因此法向加速度必为零；
（D）若物体作匀速率运动，其总加速度必为零；
周运动 , 若不计重力加速度的影响, 求: (1) 飞机在点B
的加速度; (2)飞机由点A 到点B 所经历的路程 .
A
v A
解（1）因飞机作匀变速率
运动所以 at 和 为常量 .
r an
o
a
B
at
v B
at
dv dt
分离变量有
vB dv
vA
t
0 atdt
已知：vA 1940km h1 vB 2192km h1
an
已知： vA 1940km h1 vB 2192km h1
（2）在时间
t 3s
t 内矢径
r
AB 3.5km
所转过的角度
为
A
v A
At
1t 2
2
飞机经过的路程为
r an
o
B
a
at
v B
s
r
v At
1 2
att
2
代入数据得
s 1722m
v
ds dt
et
vet
ret
质点作a 变 速ddvt率圆d周dvt运e动t 时v
det dt
切向加速度
v2 et2
o
r
evt11
at
dv dt
0 0t 12t2
2
2 0
2 (
0)
对于作曲线运动的物体，以下几种说法中哪一 种是正确的：
（A）切向加速度必不为零；
（B）法向加速度必不为零（拐点处除外）；
（C）由于速度沿切线方向，法向分速度必为零， 因此法向加速度必为零；
（D）若物体作匀速率运动，其总加速度必为零；
周运动 , 若不计重力加速度的影响, 求: (1) 飞机在点B
的加速度; (2)飞机由点A 到点B 所经历的路程 .
A
v A
解（1）因飞机作匀变速率
运动所以 at 和 为常量 .
r an
o
a
B
at
v B
at
dv dt
分离变量有
vB dv
vA
t
0 atdt
已知：vA 1940km h1 vB 2192km h1
an
已知： vA 1940km h1 vB 2192km h1
（2）在时间
t 3s
t 内矢径
r
AB 3.5km
所转过的角度
为
A
v A
At
1t 2
2
飞机经过的路程为
r an
o
B
a
at
v B
s
r
v At
1 2
att
2
代入数据得
s 1722m
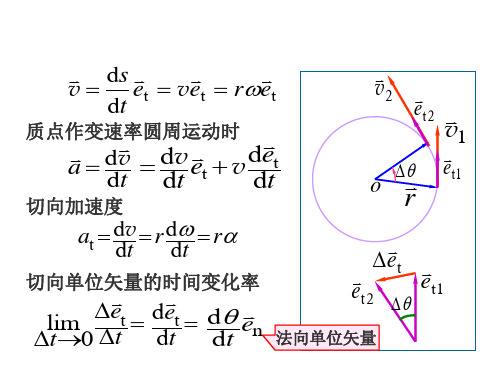
v
ds dt
et
vet
ret
质点作a 变 速ddvt率圆d周dvt运e动t 时v
det dt
切向加速度
v2 et2
o
r
evt11
at
dv dt
大学物理切向加速度和法向加速度
科研探索
在物理学、天文学、生物学等科研领域，切向加速度和法向加速度的应用对于探索物体运动规律和现象 具有重要作用，能够促进科学研究的深入开展和创新。
THANKS FOR WATCHING
感谢您的观看
曲线运动中的切向加速度
在曲线运动中，切向加速度等于物体速率对时间 的变化率，即$a_{t} = frac{dv}{dt}$。
3
匀速圆周运动中的切向加速度
在匀速圆周运动中，切向加速度的大小为$a_{t} = omega^{2}r$，方向始终指向圆心。
切向加速度在现实生活中的应用
车辆转弯
汽车在转弯时，由于离心力作用， 车轮与地面之间产生侧向摩擦力，
工程设计和优化
在机械、航空、交通等领域，切向加速度和法向加速度的应用对于工程设计和优化至关重要，能够帮助工程师更好地 分析物体的运动特性和受力情况，提高设计质量和安全性。
体育科技
在体育领域，切向加速度和法向加速度的应用对于运动分析和技术优化具有重要意义，能够帮助教练和运动员更好地 理解运动过程中的技术细节和改进方向。
使汽车产生切向加速度，影响车 辆行驶稳定性。
旋转机械
旋转机械在运转过程中，由于摩擦 力或外部扰动作用，会产生切向加 速度，影响机械的正常运转。
投掷运动
在投掷运动中，如标枪、铁饼等， 运动员通过施加切向力使器械产生 切向加速度，从而影响器械飞行的 轨迹和距离。
03 法向加速度
法向加速度的概念
法向加速度是描述物体在圆周运动或 曲线运动中速度方向变化快慢的物理 量。
在不同运动状态下的表现
01
02
03
匀速圆周运动
切向加速度为零，法向加 速度不为零，物体做匀速 圆周运动。
在物理学、天文学、生物学等科研领域，切向加速度和法向加速度的应用对于探索物体运动规律和现象 具有重要作用，能够促进科学研究的深入开展和创新。
THANKS FOR WATCHING
感谢您的观看
曲线运动中的切向加速度
在曲线运动中，切向加速度等于物体速率对时间 的变化率，即$a_{t} = frac{dv}{dt}$。
3
匀速圆周运动中的切向加速度
在匀速圆周运动中，切向加速度的大小为$a_{t} = omega^{2}r$，方向始终指向圆心。
切向加速度在现实生活中的应用
车辆转弯
汽车在转弯时，由于离心力作用， 车轮与地面之间产生侧向摩擦力，
工程设计和优化
在机械、航空、交通等领域，切向加速度和法向加速度的应用对于工程设计和优化至关重要，能够帮助工程师更好地 分析物体的运动特性和受力情况，提高设计质量和安全性。
体育科技
在体育领域，切向加速度和法向加速度的应用对于运动分析和技术优化具有重要意义，能够帮助教练和运动员更好地 理解运动过程中的技术细节和改进方向。
使汽车产生切向加速度，影响车 辆行驶稳定性。
旋转机械
旋转机械在运转过程中，由于摩擦 力或外部扰动作用，会产生切向加 速度，影响机械的正常运转。
投掷运动
在投掷运动中，如标枪、铁饼等， 运动员通过施加切向力使器械产生 切向加速度，从而影响器械飞行的 轨迹和距离。
03 法向加速度
法向加速度的概念
法向加速度是描述物体在圆周运动或 曲线运动中速度方向变化快慢的物理 量。
在不同运动状态下的表现
01
02
03
匀速圆周运动
切向加速度为零，法向加 速度不为零，物体做匀速 圆周运动。
自然坐标系--切向加速度和法向加速度
自然坐标系中反映速度方向的变化法向加速度的变化反映速度大小速率切向加速度圆周运动的角量描述这部分可用类比的方法自学在刚体一章将有详细介绍和应用
第二节
自然坐标系 切向加速度 法向加速度
一、自然坐标系
自然坐标系是建立在物体运动 轨迹上的，有两个坐标轴，
切向坐标和法向坐标。
自然坐标系是动坐系标。
nv
nv
v
v
•向切一向致坐, 标v0
v沿运动轨迹的切线方向，正方向与运动方
为切线方向的单位矢量。
•线法凹向侧坐，标nv0n为v沿法运线动方轨向迹的的单法位线矢方量向。，正方向指向曲
§2切向加速度、法向加速度/二、a、an
二、切向加速度、法向加速度
自然坐标系中
因为 v v
a dv dv v d dv v2 n
(1Fra bibliotek2tv )i
t
2
v j (SI
)，求t=1s时的切向加速度，
法向加速度和曲率半径。
另解：t
1s,
vv
v 2i
2
v j,
av
2
v j,
解：vv
v 2i
v 2tj ,
av
2
v j,
可知a an 2m / s2，
v 2 1t2 , a 2
v2 8 4 2m,
解：
v ds 10 t dt
t=5s时
v 5m s-1
a
dv dt
1m s-2
an
v2 R
0.5m s-2
a a2 an2 1.1m s-2
第二节
自然坐标系 切向加速度 法向加速度
一、自然坐标系
自然坐标系是建立在物体运动 轨迹上的，有两个坐标轴，
切向坐标和法向坐标。
自然坐标系是动坐系标。
nv
nv
v
v
•向切一向致坐, 标v0
v沿运动轨迹的切线方向，正方向与运动方
为切线方向的单位矢量。
•线法凹向侧坐，标nv0n为v沿法运线动方轨向迹的的单法位线矢方量向。，正方向指向曲
§2切向加速度、法向加速度/二、a、an
二、切向加速度、法向加速度
自然坐标系中
因为 v v
a dv dv v d dv v2 n
(1Fra bibliotek2tv )i
t
2
v j (SI
)，求t=1s时的切向加速度，
法向加速度和曲率半径。
另解：t
1s,
vv
v 2i
2
v j,
av
2
v j,
解：vv
v 2i
v 2tj ,
av
2
v j,
可知a an 2m / s2，
v 2 1t2 , a 2
v2 8 4 2m,
解：
v ds 10 t dt
t=5s时
v 5m s-1
a
dv dt
1m s-2
an
v2 R
0.5m s-2
a a2 an2 1.1m s-2
03运动学圆周运动 (自然坐标系、角速度、角加速度、切向加速度、法向加速度)
令： τ为圆周的切向上的单位矢量
sin i cosj
切向加速度为 a R R d d ( R ) dv
dt dt dt
n为圆周法向上的单位矢量
法向加速度为
n (cosi sin j )
2 2 ( R ) v an R 2 R R
解法：用积分或求解微分方程的Biblioteka 法求解。x x0 vdt
t0
t
v v0 adt
t0
t
12
α与ω方向相反。质点作减速圆周运动。
α等于恒量时作匀角加速度运动。
3
对匀角加速运动有： ω=ω0+ α t
1 2 0 0t t 2
0 ( 0 )t
2 2 0 2 ( 0 )
1 2
4
2 线量与角量的关系：质点做圆周运动时也可以用速 度、加速度来描述。 由于位置矢量可以表示为 r xi yj R cosi R sin j
第一章 质点运动学
1
§1-3 圆周运动
1 圆周运动的角量描述：质点做圆周运动时，轨道上 的任意点到圆心距离为R,用一个变量θ即可描述其运动。
Y
r
r =R
θ确定后：x=Rcosθ y=Rsinθ θ 单位 rad 弧度
t
θ=θ(t)
X
定义：角位置
角位移△θ=θ（t+ △t) -θ(t) 平均角速度 瞬时角速度 (SI)单位：rad/s 弧度/秒 工程单位 rev/min(转/分）
d lim t 0 t dt
2
平均角加速度 t
圆的加速度公式法向和切向
圆的加速度公式法向和切向在物理学中，圆是一个非常常见的几何形状。
当一个物体在圆形路径上运动时，我们可以使用加速度来描述其运动状态。
在圆的运动中，加速度可以分解为法向加速度和切向加速度。
我们来了解一下什么是加速度。
加速度是描述物体在单位时间内速度变化的物理量。
它的单位是米每秒平方(m/s^2)。
当物体在圆形路径上运动时，它的速度方向会不断改变。
根据牛顿第二定律，物体的加速度与作用在物体上的合力成正比，与物体的质量成反比。
在圆的运动中，合力可以被分解为法向力和切向力。
法向加速度是指物体在圆形路径上向内的加速度。
它是由向心力产生的。
向心力是指物体受到的指向圆心的力。
根据牛顿第二定律，向心力与物体的质量和法向加速度成正比。
向心力的大小等于质量乘以法向加速度。
切向加速度是指物体在圆形路径上沿切线方向的加速度。
它是由切向力产生的。
切向力是指物体受到的与切线方向相切的力。
根据牛顿第二定律，切向力与物体的质量和切向加速度成正比。
切向力的大小等于质量乘以切向加速度。
在圆的运动中，法向加速度和切向加速度的方向是不同的。
法向加速度的方向指向圆心，切向加速度的方向与切线方向相同。
由于速度的方向不断改变，物体在圆的运动中会不断受到向心力和切向力的作用，从而产生法向加速度和切向加速度。
法向加速度和切向加速度的大小可以根据下面的公式计算：法向加速度 = 速度的平方 / 半径切向加速度 = 半径乘以角度的二阶导数其中，速度的平方是物体在圆形路径上的速度的平方，半径是圆的半径，角度的二阶导数是角度关于时间的二阶导数。
通过计算法向加速度和切向加速度，我们可以更好地理解物体在圆的运动中的加速度变化。
法向加速度决定了物体在圆形路径上的向心力大小，而切向加速度决定了物体在圆形路径上的切向力大小。
总结一下，圆的加速度可以分解为法向加速度和切向加速度。
法向加速度是指物体在圆形路径上向内的加速度，由向心力产生；切向加速度是指物体在圆形路径上沿切线方向的加速度，由切向力产生。
角加速度切向加速度和法向加速度关系
角加速度切向加速度和法向加速度关系角加速度、切向加速度和法向加速度是三个密切相关的物理量，在运动学和动力学中都有着重要的作用。
它们之间存在着一定的关系，下面我们来具体了解一下。
首先，角加速度是描述物体旋转状态的物理量，它表示单位时间内，物体旋转角速度的变化率。
在平面运动中，若物体绕固定点做匀速圆周运动，则其角加速度大小为零。
若物体绕固定点做变速圆周运动，则其角加速度大小为非零值，且方向始终与物体运动方向垂直，根据右手定则可知，角加速度方向遵循“向内加速”的方向规律。
其次，切向加速度是描述物体在圆周运动中速度变化的物理量，它表示单位时间内物体在圆周方向上速度的变化率。
在匀速圆周运动中，物体速度大小不变，因此其切向加速度大小为零。
而在非匀速圆周运动中，物体速度大小随时间变化，因此其切向加速度大小不为零，且方向始终沿着物体运动方向。
切向加速度的大小可以通过求导物体速度关于时间的变化率来计算。
最后，法向加速度是描述物体在圆周运动中方向变化的物理量，它表示单位时间内物体在圆周垂直方向上速度的变化率。
在匀速圆周运动中，物体速度方向始终沿着圆周切线方向，因此其法向加速度大小为零。
而在非匀速圆周运动中，物体速度方向发生变化，因此其法向加速度大小不为零，且方向垂直于切向加速度方向，向圆心方向。
法向加速度的大小可以通过求导物体速度关于时间的方向变化率来计算。
综上所述，角加速度、切向加速度和法向加速度三者之间的关系可以用以下公式表示：a = √(aT + aN)其中，a表示合加速度，aT表示切向加速度，aN表示法向加速度。
这个公式说明了，物体在圆周运动中所受到的合加速度大小等于切向加速度和法向加速度的平方和的开方。
同时，切向加速度和法向加速度方向也分别与合加速度方向垂直和水平。