2020年广东财经大学考研试题601数学分析
广东财经大学金融学综合2012--2020年考研初试真题

欢迎报考广东财经大学硕士研究生,祝你考试成功!(第 1 页共 12 页)
广东财经大学硕士研究生入学考试试卷
考试年度:2020年考试科目代码及名称:431-金融学综合(自命题)适用专业:025100 金融硕士
[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!]
一、名词解释(6题,每题5分,共30分)
1.金融市场
2.流动性
3.一价定律
4.贴现现金流量
5.经营杠杆
6.股东价值最大化
二、判断题(10题,每题2分,共20分)
1.财政和货币政策属于需求转换型政策。
()
2.欧洲货币市场的资金来源最初是石油美元。
()
3.固定汇率制度下,外汇储备和本国货币供应量的变化方向相同。
()
4.货币市场和资本市场的划分是以资金的用途为标准的。
()
5.资金盈余部门的一部分资金通过银行等金融中介机构流向资金短缺
部门,称为直接金融转化机制。
()
6.有违约风险的公司债券风险溢价必须为负,违约风险越大,风险溢价越低。
()
7.凯恩斯强调了利率对交易性货币需求的影响。
()
8.弗里德曼认为货币的流通速度稳定可测。
()
9.中央银行具有发行的银行、银行的银行和政府的银行等三大职能。
()
10.通货膨胀有利于固定收入者而不利于可变收入者。
()
三、简答题(5题,每题8分,共40分)
1.简述资产证券化的作用。
1。
广东财经大学数学分析2020年考研专业课初试大纲

《数学分析》
《数学分析》考试大纲概述:
本科目要求考生系统掌握数学分析的基本知识、基础理论和基本方法,理解数学分析中反映出的数学思想与方法,并能运用相关理论和方法分析、解决具有一定实际背景的数学问题。
第一数列极限
1 数列极限概念
2 收敛数列的定理
3 数列极限存在的条件
第二函数极限
1 函数极限概念
2 函数极限的定理
3 两个重要极限
4 无穷大量与无穷小量
第三函数的连续性
1 连续性概念
2 连续函数的性质
第四导数与微分
1 导数的概念
2 求导法则
3 微分
4 高阶导数与高阶微分
第五中值定理与导数应用
1 微分学基本定理
2 函数的单调性与极值
第六不定积分
1 不定积分概念与基本积分公式
2 换元法积分法与分部积分法
第七定积分
1 定积分概念
2 可积条件
3 定积分的性质
4 定积分的计算
第八定积分的应用
1 平面图形的面积
2 旋转体的侧面积
第九级数
1 正项级数。
广东财经大学2020年管理学原理考研真题试题

欢迎报考广东财经大学硕士研究生,祝你考试成功!(第 1 页共 3 页)广东财经大学硕士研究生入学考试试卷考试年度:2020年 考试科目代码及名称:806-管理学原理(自命题)适用专业:120201会计学、120202 企业管理、120203 旅游管理、120204 技术经济及管理、1202Z1企业文化与伦理[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!]一、问题论述(3题,每题20分,共60分)1. 什么是价值链?成功的价值链管理有哪些要求?(20分)2. 什么是控制?控制在管理中有何作用?(20分)3. 共享的价值观有何作用?如何建立共享价值观? (20分)二、观点辨析(1题,共30分)1.面对飞速变化的管理环境,许多企业的管理者都觉得计划赶不上变化。
因此,他们认为制定长期计划是无用的。
你同意这个观点吗?三、案例分析(2题,每题30分,共60分)案例1 海底捞的员工激励实践四川海底捞餐饮股份有限公司成立于1994年,是一家以经营川味火锅为主,融汇各地火锅特色于一体的大型跨省直营餐饮民营企业。
2018年9月26日,海底捞(新上市编号:06862)正式登陆香港资本市场。
海底捞虽然是一家火锅店,但它的核心业务却不是餐饮,而是服务。
在将员工的主观能动性发挥到极致的情况下,“海底捞特色”日益丰富。
海底捞的员工激励措施与效果主要概括为以下几点:1)良好的晋升通道。
海底捞为员工设计好在本企业的职业发展路径,并清晰地向他们表明该发展途径及待遇。
每位员工入职前都会得到这样的承诺。
“海底捞现有的管理人员全部是从服务员、传菜员等最基层的岗位做起,公司会为每一位员工提供公平公正的发展空间,如果你诚实与勤奋,并且相信:用自己的双手可以改变命运。
那么,海底捞将成就你的未来!”该措施满足了职工对自我实现的需要,激励了员工对更好未来的追求。
2)独特的考核制度。
海底捞对管理人员的考核非常严格,除了业务方面的内容之外,还有创新、员工激情、顾客满意度、后备干部的培养等,每项内容都必须达到规定的标准。
广东财经大学601-数学分析2020年考研真题

1 广东财经大学硕士研究生入学考试试卷
考试年度:2020年 考试科目代码及名称:601-数学分析(自命题) 适用专业:071400 统计学
[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!]
一、计算题(6题,每题10分,共60分)
1.求极限!lim n n n n
→∞。
2.求极限lim arctan 41x x x x π→∞⎛⎫- ⎪+⎝⎭。
3.求极限21cos 20
lim t x x e dt x -→⎰。
4.
判断级数()1n x ∞=-∞<<+∞的一致收敛性。
5.设,x y z xyf y x ⎛⎫= ⎪⎝⎭,求 z x ∂∂和z
y ∂∂。
6.设()f x 是(),-∞+∞上的连续函数,且满足:
0()1cos x
tf x t dt x -=-⎰,求()f x 。
二、应用题(4题,每题15分,共60分)
7.计算由抛物线21y x =-+与2y x x =-所围成图形的面积。
8. 应用定积分的定义计算积分10x a dx ⎰。
9. 在底为a 高为h 的三角形中作内接矩形,矩形的一条边与三角形的底边重合,求此矩形的最大面积。
10.求sin ,0y x x π= ≤≤,绕x 轴旋转所成的曲面面积。
三、证明题(2题,每题15分,共30分)
11.证明方程sin (0,0)x a x b a b =+ >>至少有一个不超过a b +的正根。
12.若()f x 在区间X 中具有有界的导数,即|()|f x M '≤,试证()f x 在X 上一致连续。
广东财经大学数学分析考研真题试题2018、2019年

欢迎报考广东财经大学硕士研究生,祝你考试成功!(第 1 页 共 1 页) 广东财经大学硕士研究生入学考试试卷考试年度:2018年 考试科目代码及名称:614-数学分析(自命题)适用专业:071400 统计学[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!] 《数学分析》 [共150分]一、计算题(6题,每题10分,共60分)1.求极限()21sin 1lim 1x x x →-- 。
2.设函数()f x 在a 可导,求极限()()02lim 2t f a t f a t t →+-+ 。
3.求不定积分 。
4.求极限230lim 1nn x dx x→∞+⎰ 。
5.判别级数12!n n n n n ∞=∑的敛散性。
6.求复合函数的偏导数:(),,,u f x y x s t y st ==+= 。
二、应用题(4题,每题15分,共60分)1.已知圆柱形罐头盒的体积是V (定数),问它的高与底半径多大才能使罐头盒的表面积达到最小?2.求一条平面曲线方程,该曲线通过点(1,0)A ,并且曲线上每一点(,)P x y 的切线斜率是22,x x R -∈。
3.求以下曲线绕指定轴旋转所成旋转体的侧面积:2,06y x x =≤≤,绕x 轴。
4.已知矩形的周长为24cm ,将它绕其一边旋转而成一圆柱体,试求所得圆柱体体积最大时的矩形面积。
三、证明题(2题,每题15分,共30分)1.证明:若存在常数c ,n N ∀∈,有21321||||||n n x x x x x x c --+-++-< ,则数列{}n x 收敛。
2.证明:方程2sin (0)x x a a -=>至少有一个正实根。
欢迎报考广东财经大学硕士研究生,祝你考试成功!(第 1 页 共 1 页)广东财经大学硕士研究生入学考试试卷考试年度:2019年 考试科目代码及名称:601-数学分析(自命题) 适用专业:071400 统计学[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!]一、计算题(6题,每题10分,共60分)1.求数列极限();!)!2(!)!22(lim 1n n n n n -+++∞→2.求函数极限 ();sin 1ln sin tan lim 20x x x x x +-→3.设是可微函数,由所确定函数.求φ0),=--bz cy az cx (φ),(y x f z =. yz b x z a ∂∂+∂∂4.求函数级数的和函数和收敛域.∑+∞=-12n nx xe 5.设,确定使得满足方程 y x ex y x f 42),(-=ααf .122⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂x f x x x y f 6.设.求全微分xyz u =.3u d 二、应用题(4题,每题15分,共60分)1.已知满足求的取值范围.,x y ()22+21.x y -=w =2.曲线在点处得切线与轴得正向所夹得角度是多⎪⎩⎪⎨⎧=+=4222y y x z )5,4,2(x 少?3.求由方程确定的隐函数的二阶导数012=-+y x e xy )(x y y =).(''x y 4.求不定积分.⎰xdx e x sin 三、证明题(2题,每题15分,共30分)1. 已知在区间上连续. 求证)(x f ],[b a ().)()()(2122⎪⎭⎫ ⎝⎛-≤⎪⎭⎫ ⎝⎛⎰⎰-b a n n b a dx x f a b dx x f n2. 已知证明存在唯一使得 .,0为自然数n x >),(10∈θ.11lim 00+==+→⎰n xe dt e x x x t n n θθ且。
广东财经大学601-数学分析2018 - 2020年考研真题汇编

广东财经大学硕士研究生入学考试试卷考试年度:2019年 考试科目代码及名称:601-数学分析(自命题) 适用专业:071400 统计学[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!]一、计算题(6题,每题10分,共60分)1.求数列极限();!)!2(!)!22(lim 1n n n n n -+++∞→2.求函数极限();sin 1ln sin tan lim2xx xx x +-→ 3.设φ是可微函数,由0),=--bz cy az cx (φ所确定函数),(y x f z =.求yz b x z a∂∂+∂∂. 4.求函数级数∑+∞=-12n nx xe 的和函数和收敛域.5.设yx e x y x f 42),(-=α,确定α使得f 满足方程.122⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂x f x x x y f 6.设xyz u =.求全微分.3u d二、应用题(4题,每题15分,共60分) 1.已知,x y 满足()22+2 1.x y -=求w =的取值范围.2.曲线⎪⎩⎪⎨⎧=+=4222y y x z 在点)5,4,2(处得切线与x 轴得正向所夹得角度是多少?3.求由方程012=-+y x e xy 确定的隐函数)(x y y =的二阶导数).(''x y4.求不定积分⎰xdx e x sin .三、证明题(2题,每题15分,共30分) 1. 已知)(x f 在区间],[b a 上连续. 求证().)()()(2122⎪⎭⎫ ⎝⎛-≤⎪⎭⎫ ⎝⎛⎰⎰-b a n n ba dx x f ab dx x f n2. 已知.,0为自然数n x >证明存在唯一),(10∈θ使得.11lim 0+==+→⎰n xe dt e x x xt nn θθ且广东财经大学硕士研究生入学考试试卷考试年度:2020年 考试科目代码及名称:601-数学分析(自命题) 适用专业:071400 统计学[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!]一、计算题(6题,每题10分,共60分) 1.求极限!limn n n n→∞。
广东财经大学20年研究生入学考试
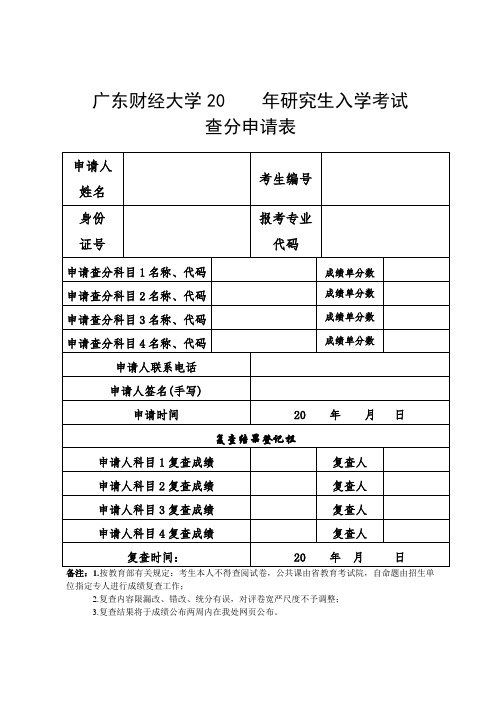
申请人科目2复查成绩
复查人
申请人科目查成绩
复查人
申请人科目4复查成绩
复查人
复查时间:
20年 月日
备注:1.按教育部有关规定:考生本人不得查阅试卷,公共课由省教育考试院,自命题由招生单位指定专人进行成绩复查工作;
2.复查内容限漏改、错改、统分有误,对评卷宽严尺度不予调整;
3.复查结果将于成绩公布两周内在我处网页公布。
广东财经大学20年研究生入学考试
查分申请表
申请人姓名
考生编号
身份
证号
报考专业
代码
申请查分科目1名称、代码
成绩单分数
申请查分科目2名称、代码
成绩单分数
申请查分科目3名称、代码
成绩单分数
申请查分科目4名称、代码
成绩单分数
申请人联系电话
申请人签名(手写)
申请时间
20年 月日
复查结果登记栏
申请人科目1复查成绩
广东财经大学金融学综合2012--2020年考研初试真题

广东财经大学硕士研究生入学考试试卷考试年度:2020年考试科目代码及名称:431-金融学综合(自命题)适用专业:025100 金融硕士[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!]一、名词解释(6题,每题5分,共30分)1.金融市场2.流动性3.一价定律4.贴现现金流量5.经营杠杆6.股东价值最大化二、判断题(10题,每题2分,共20分)1.财政和货币政策属于需求转换型政策。
()2.欧洲货币市场的资金来源最初是石油美元。
()3.固定汇率制度下,外汇储备和本国货币供应量的变化方向相同。
()4.货币市场和资本市场的划分是以资金的用途为标准的。
()5.资金盈余部门的一部分资金通过银行等金融中介机构流向资金短缺部门,称为直接金融转化机制。
()6.有违约风险的公司债券风险溢价必须为负,违约风险越大,风险溢价越低。
()7.凯恩斯强调了利率对交易性货币需求的影响。
()8.弗里德曼认为货币的流通速度稳定可测。
()9.中央银行具有发行的银行、银行的银行和政府的银行等三大职能。
()10.通货膨胀有利于固定收入者而不利于可变收入者。
()三、简答题(5题,每题8分,共40分)1.简述资产证券化的作用。
2.票据市场具有哪些作用?3.简述特里芬难题的基本内容。
4.简述商业银行超额准备金率的影响因素。
5.公司金融中为什么要进行敏感性分析和场景分析?试分析两种分析法的区别。
四、计算题(2题,每题10分,共20分)1.某人刚大学毕业,打算在5年后买一套70平方米的房子,目前房价是3万/平方米,并预计房价将每年以10%的幅度上涨。
买房要求支付3成首付,市场利率一直保持为6%,请问该人每年年初需要存多少钱,才能在第5年末存够首付所需资金?2.A公司发展很快。
股利预期在接下来的3年里将以24%的速度增长,之后将以6%的速度稳定增长。
如果必要报酬率是11%,且公司刚刚支付的股利为每股1.90美元,那么股票现在的价格为多少?五、论述题(2题,每题20分,共40分)1.试联系实际比较一般性货币政策工具。
北京邮电大学2020年《601数学分析》考研专业课真题试卷

北京邮电大学
2020年硕士研究生招生考试试题
考试科目:601数学分析
请考生注意:CD 所有答案(包括选择题和填空题)一律写在答题纸上,否则不计成绩。
@不允许使用计算器
一、计算题(8分)
求极限lim
1-(c o s x )'i n x 二、计算题(8分)
判断尸sin(x 2)dx 的符号.
三、计算题(8分)
设f(x)存在连续导数,f(O)= 0, f'(O) * 0, F(x) = ,b (x 2 -!2订(t)dt I 且x ➔0时,F'(x)与X k
为同阶
无穷小量,求k的值.四、计算题(8分)
判别积分r;11nx 『d x 的敛散性.
五、计算题(8分)
1 p 判别级数区(e-(1+-r)的敛散性.n
六、计算题(10分)
求级数2(-lf(n 2 -n+l)n=O 2n 的和
七、证明题(10分)
I 设a n =I+—+ .. ·+上-2✓n ,nEN 十,证明:包}收敛.五五
八、证明题(10分)
n oo a 设a n > 0 , n = I, 2, …·La n 发散,凡=Ia k , n=I,2, …证明:级数I.....!!.收敛.s2 考试科目:601数学分析k=I n=I n 第1页共2页。
广东财经大学2020年《612马克思主义基本原理概论(自命题)》考研专业课真题试卷

欢迎报考广东财经大学硕士研究生,祝你考试成功!(第 1 页共 2 页)
广东财经大学硕士研究生入学考试试卷
考试年度:2020年考试科目代码及名称:612-马克思主义基本原理概论(自命题)
适用专业:030500 马克思主义理论
[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!](1)名词解释(6题,每小题5分,共30分)
1.马克思主义体系
2.意识的能动性
3.矛盾分析法
4.价值规律
5.真理的客观性、绝对性和相对性
6.资本主义意识形态
(2)辨析题(5题,每小题6分,共30分)
1.哲学就是世界观。
2.任何量变都会引起质变。
3.在社会主义社会中,生产关系的公有化程度越高,越能促进生产力的发展。
4.剩余价值的产生,不在流通领域,与流通领域无关。
5.工人的工资是劳动的价值或价格。
(3)简答题(5题,每小题10分,共50分)
1.简述人民群众推动历史发展的决定性作用的表现。
2.简述物质资料的生产方式是社会发展的决定力量。
3.简述社会意识的相对独立性。
4.简述如何正确把握科学社会主义一般原则。
1。
广东财经大学501-专题设计(设计学)2020年考研真题

广东财经大学硕士研究生入学考试试卷
考试年度:2020年考试科目代码及名称:501-专题设计(设计学)
适用专业:130500设计学
[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!](1)设计题(1题,每题150分,共150分,6小时)
考试题目:
选取生活中的一个空间设计或产品设计或视觉形象设计(根据自己的专业方向选定),进行改良再设计。
考试要求:
1、深刻理解试题,根据自己所报考的专业方向考虑设计内容和表现形式。
充分发挥想象力,创意独特、形式感强。
2、在试卷内先做5个黑白草图方案,然后从中选取2个完成彩色放大稿。
尺寸、方法、绘图工具均不限。
3、对2个彩色放大稿分别给出200字以内的文字说明。
文字内容应言简意赅、表述清晰。
1。
2020年全国硕士研究生入学统一考试(高等数学二)真题及答案解析

x = −1: lim f (x) = ∞ ,则 x = −1 为第二类间断点; x→−1
1
1
x=
0 : lim x→0
f (x) =
lim
x→0
e1− (ex
x ln(1+ x) −1)(x − 2)
=
lim e1−x ⋅ x x→0 x(x − 2)
=
−1 2e
,则 x = 0 为可 = ∞ ,则 x = 1 为第二类间断点; x→1+
1
2 arcsin
xd arcsin
x
0 x(1− x)
0 1− ( x)2
0
=
(arcsin
x= )2 |10
(= π )2 2
π2 4
故应选(A)
(4)已知函数= f (x) x2 ln(1− x) ,当 n ≥ 3 时, f (n) (0) = ( )
(A) − n! n−2
【答案】A 【解析】
(D)
sin3 tdt= , m
3= , n
2 ,则 n(m +1) =5
0
2
故应选(D)
1
(2)函数
f
(x)
=
e x−1 ln |1+ x | (ex −1)(x − 2)
的第二类间断点的个数为(
)
(A)1
(B)2
(C)3
(D)4
【答案】C
【解析】由 f (x) 的表达式可知, f (x) 共有四个间断点,分别为
(B) n! n−2
(C) − (n − 2)! n
(D) (n − 2)! n
由 ln(1+ x) =x − x2 + x3 − + (−1)n−1 xn + ο (xn ) 2 3 n
广东财经大学2020年《809数据结构(自命题)》考研专业课真题试卷

欢迎报考广东财经大学硕士研究生,祝你考试成功!(第 1 页共 3 页)广东财经大学硕士研究生入学考试试卷考试年度:2020年考试科目代码及名称:809-数据结构(自命题)适用专业:085400电子信息[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!]一、单项选择题(10题,每题2分,共20分)1、设n是描述问题规模的非负整数。
下面的算法1是将一维数组a中的n个数逆序存放到原数组中,该算法的空间复杂度是________(要求用大O符号表示)。
A.O(1) B.O(n) C.O(2n) D.O(n2)算法1:for(i=0; i<n; i++)b[i]=a[n-(i+1)];for(i=0; i<n; i++)a[i]=b[i];图1图22、在n个结点的顺序表中,算法的时间复杂度是O(1)的操作是________。
A.访问第i个结点(1<=i<=n)和求第i个结点的直接前驱B.在第i个结点后插入一个新结点(1<=i<=n)C.删除第i个结点(1<=i<=n)D.将n个结点从小到大排序3、在双向链表中,删除结点p的操作是________。
A.p->prior->next=p->next; p->next->prior=p->prior;B.p->next=p->next->next; p->next->prior=p;C.p->priort=p->next->next; p->next=p->prior->prior;D.p->prior-next=p; p->prior=p->prior->prior;4、最大容量为n的循环队列,队尾指针是rear,队头是front,则队空的条件是________。
A. (rear+1)%n==frontB. rear==front C.rear+1==front D. (rear-l)%n==front5、若让元素1,2,3,4,5依次进栈,则出栈次序不可能出现在________种情况。
2020年广西民族大学601数学分析(试卷B卷)考研真题硕士研究生专业课考试试题

考试科目代码及名称:601 数学分析
第 1 页 共 2 页
2020年硕士研究生招生考试试题
【B 】卷
科目代码及名称:601 数学分析
考生须知
1. 答案须写在答题纸密封线内, 写在试卷、草稿纸等均无效.
2. 答题时一律使用蓝或黑色钢笔、签字笔书写.
3. 交卷时, 请本人将试卷、答题纸放入试题袋内, 密封后在封条与试卷袋骑缝处亲笔签名.
一、计算题(每小题15分, 共4小题, 共60分)
1.求极限n
2.计算曲面积分S
dS I z =⎰⎰,S 为球面2222x y z a ++=被平面(0)z h h a =<<所截的顶部. 3.计算⎰+L
ydx xdy ,其中L :沿抛物线22x y =从(0,0)到)2,1(. 4.计算dxdy y x D
⎰⎰+)(,积分区域}),{(22y x y x y x D +≤+=. 二、求解下面题目(每小题20分, 共3小题, 共60分)
1. (i) 设)(x f 在开区间),(b a 可微,且)(x f '在),(b a 有界. 证明)(x f 在),(b a 一致连续. (ii) 设)(x f 在开区间),(b a )(+∞<<<-∞b a 可微且一致连续,试问)(x f '在),(b a 是否一定有界.
2. 证明:函数 ⎪⎩⎪⎨⎧=+≠+++=0,
0,0,1sin )(),(22222222y x y x y x y x y x f 在原点)0,0(连续、存
在偏导数且可微. 3. 设 ()f x 在[1,)+∞上可微,()f x '单调增加且大于零.证明:当x →+∞ 时()f x 为正无穷大量.。
2023年广东财经大学《808高等代数 (数学)》考研真题

2023年广东财经大学《808高等代数 (数学)》考研真题一、计算题(6题,每题5分,共30分)1、试求7次多项式f(x)使得f (x )+1被 (x −1)4整除,而f (x )−1被(x +1)4整除.2、计算行列式 nn n D ⨯------=211200000000000210121012.3、设f(x)=x 100+x 99+⋯+x +1, A =(100001000), 求f(A)和f(A)−1.4、二次型 f (x 1,x 2)=x T Ax 经正交变换 x =Qy 化为标准形 y 12+3y 22. 若Q 的第一列是[√2√2]T ,求Q .5、解矩阵方程 ⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--011211021101110012112201111X .6、求方程组 ⎪⎩⎪⎨⎧=+++=-++=+-+322212432143214321x x x x x x x x x x x x的一般解.二、解答题(3题,每题15分,共45分)1、 设向量空间V 的线性变换σ在基123,,ααα下的矩阵为122212221A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,问σ能否对角化? 如果可以,求出可逆矩阵X ,使1X AX -为对角矩阵.2、 设A,B 均为n 阶矩阵,且AB=A+B ,则(1)A-E 与B-E 均可逆;(2)AB=BA ;(3)当⎪⎪⎪⎭⎫ ⎝⎛=221243121A 时,求B.3、设A 为数域K 上n 维线性空间V 的线性变换,满足A 2=A . 求A 的特征值,并说明A 可对角化.三、证明题(5题,每题15分,共75分)1、设,A B 分别是m n ⨯和n m ⨯矩阵. 证明:BA E AB E E A B E m n n m -=-=.2、设A, B 为n 阶方阵,则 (1) (AB )∗=B ∗A ∗; (2) 若n ≥2,(A T )∗=(A ∗)T .3、设A 是n 阶方阵,若存在n 维列向量α和正整数k ,使得0,01≠=-ααk k A A ,证明:向量组αααα12,,,,-k A A A 线性无关.4、设AX X x x f n T 1),...,(=是一个实二次型,若有实n 维向量21,X X 使0,02211<>AX X AX X T T . 证明:必存在实n 维向量00≠X 使000=AX X T .5、 设V 是数域F 上的向量空间,)},,2,1,),,,{(i m 21m i V U =∈=αααα也是F 上的向量空间.证明:(1)V 是无限维时,U 也是无限维的;(2)当V 为n 维时,求U 的维数和一组基.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东财经大学硕士研究生入学考试试卷
考试年度:2020年考试科目代码及名称:601-数学分析(自命题)
适用专业:071400统计学
[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!]
一、计算题(6题,每题10分,共60分)1.求极限!lim n n n n
→∞。
2.求极限lim arctan 41x x x x π→∞⎛⎫- ⎪+⎝⎭。
3.求极限21cos 20
lim t x x e dt x -→⎰。
4.判断级数()n x ∞=-∞<<+∞的一致收敛性。
5.设,x y z xyf y x ⎛⎫
= ⎪⎝⎭,求z x ∂∂和z y ∂∂。
6.设()f x 是(),-∞+∞上的连续函数,且满足:0()1cos x
tf x t dt x -=-⎰,求()f x 。
二、应用题(4题,每题15分,共60分)
7.计算由抛物线21y x =-+与2y x x =-所围成图形的面积。
8.应用定积分的定义计算积分1
0x a dx ⎰。
9.在底为a 高为h 的三角形中作内接矩形,矩形的一条边与三角形的底边重合,求此矩形的最大面积。
10.求sin ,0y x x π= ≤≤,绕x 轴旋转所成的曲面面积。
三、证明题(2题,每题15分,共30分)
11.证明方程sin (0,0)x a x b a b =+ >>至少有一个不超过a b +的正根。
12.若()f x 在区间X 中具有有界的导数,即|()|f x M '≤,试证()f x 在X 上一致连续。
