周易和排列组合
教你看懂《易经》的奥秘

教你看懂《易经》的奥秘教你看懂《易经》的奥秘《易经》的构成及内容《易经》的成书年代及作者是历代易学家争论的地方,据文字记载,在时间上经历了夏、商、周、春秋。
在成书的过程上,她由《连山易》、《归藏易》、到目前的《周易》。
据说《连山易》、《归藏易》早已失传,这三种《易》的差别仅仅在于六十四种卦的起点不同,即卦序的差异,而无本质的差异。
为了能够理解《易经》,就要知道《易经》是如何构成的,现今的《易经》,是由三部分组成:一是六十四个卦象、卦名;二是卦辞和爻辞;三是注语解说(古人读《易》的心得)。
古人将一、二合称为《易经》,三称为《易传》,后世人将经与传的合本统称为《周易》。
对《易经》成书有杰出贡献的两个人不得不提:一个是西周时期的周武王,他对《易经》的贡献是给出了一套完整的卦辞及爻辞(准确说从周文王开始为《易经》加卦辞及爻辞,至周武王结束,客观上二人的贡献更像是补充、完善了卦辞及爻辞)。
从这一时期开始,《易经》被后人称作《周易》。
这种说法被易学大家们所普遍接受。
一个是东周时期也就是春秋时期的孔圣人。
他给出了以《系辞》为代表的多种版本的心得体会,也就是人们常说的“十翼”(事实上对于十翼的作者同样存在很大的争议),为后人认识《易经》提供了方便。
八八六十四卦为《易经》的内容,卦辞与爻辞是对《易经》的文字表述,《易传》部分即包括《系辞》在内的十翼为注解,应不属于《易经》的内容。
客观上讲关于《易经》的所有说法,有些是有考古为依据,有些是通过并不完整、并不权威的文字记载为例证,但都由于其局限性存在牵强的感觉,好在不管如何,《易经》的内容本身确严谨、完整,可供人类来研究、应用的,这一点则是属于人类的幸运,可以说已经足够了。
至于《易经》那些悬而未决、似是而非的疑问,应该交给专业研究《易经》出处以及演变过程的史学家们来操心,因为这决不是我们这些普通人所能为之事。
用文字对《易》的叙述为(文字对于《易》的描述不属于《易经》内容):无极生太极,太极生两仪,两仪生四象,四象生八卦,八卦演变(排列组合)为六十四卦,每卦有其特定的卦辞及爻辞。
周易的结构组成

《周易》的结构组成——摘录于兴让著《周易研究》第三章节任何事物都有它的结构组成,《周易》自然也不例外,更何况《周易》本身乃由符号错综而成,其结构就显得更为复杂。
就简略而论,《周易》的结构乃是阴阳符号变易而成。
还有,《周易》的结构乃是《乾》(☰)、《坤》(☷)、《巽》(☴)、《震》(☳)、《坎》(☵)、《离》(☲)、《艮》(☶)、《兑》(☱)八卦相摩相荡重叠而成。
如果再往详细一点,就是《周易》中的原始八卦各代表一种物象;两种物象又各互相重叠组成了新的事物象征。
也有两个原始八卦相重叠组成了新的事物象征,这种事物又由六个爻位组成;这六个爻位的容变易又赋予了这个事物的一个特定容。
就一般情况而言,这是人们所共知的常识。
《周易》的研究到了宋代,一个叫邵雍的易学大师的研究颇令人关注。
在《周易》的占卜方面,他发明了“数字起卦”法,对占卜术来说,可以说是一次变革。
除此以外,他对《周易》的卦形结构组成也颇有研究,并推出了《伏羲八卦次序图》、《伏羲八卦方位图》、《伏羲六十四卦次序图》、《伏羲六十四卦方位图》、《文王八卦次序图》、《文王八卦方位图》六种图形(见图二、图三、图四、图五、图六、图七)。
我们先来看看邵雍所谈的这些结构。
这些图形被朱熹首次列入他的《周易本义》之首,并加了注译。
其图形(二)下注为:《系辞转》曰:“《易》有太极,是生两仪,两仪生四象,四象生八卦。
”邵子曰:“一分为二,二分为四,四分为八也。
”《说卦传》曰:“《易》,逆数也。
”《邵子》曰“《乾》一、《兑》二、《离》三、《震》四、《巽》五、《坎》六、《艮》七、《坤》八。
自《乾》至《坤》,皆未得生之卦,若逆推四时之比也。
”后六十四卦次序放此。
其图形(三)下注为:《说卦传》曰:“天地定位,山泽通气,雷风相薄,水火不相射,八卦相错,数往者顺,知来者逆。
”邵子曰:“《乾》南《坤》北,《离》东《坎》西,《震》东北,《兑》东南,《巽》西南,《艮》西北。
自《震》至《乾》为顺,自《巽》至《坤》为逆。
《周易》64卦的排列顺序有什么内在规律?

《周易》64卦的排列顺序有什么内在规律?对于《周易》64卦排序原理,孔子在《易传》中专门有一篇《序卦传》作专门论述。
笔者在研读《周易》的过程中,也发现了64卦的一些排列规律,借这个题目奉献给大家,供大家参考。
一,为什么64卦排序以乾坤两卦为首而以既济、未济两卦为尾?这个课题涉及到交互卦的问题。
每个卦都有自己的交互卦,交互卦反映本卦的本质与内涵。
每个卦都有交互卦,交互时,舍弃本卦的初爻与上爻,而取其中爻,以其上下互卦组成新卦即为交互卦。
《系辞传》云:“《易》之为书也,原始要终,以为质也。
六爻相杂,唯其时物也。
其初难知,其上易知,本末也。
初辞拟之,卒成之终。
若夫杂物撰德,辩是与非,则非其中爻不备。
噫!亦要存亡吉凶,则居可知矣。
”交互卦取本卦之中爻,故可辩其是与非,知其存亡吉凶之道,所以交互卦能反映本卦的本质与内涵。
每个卦都有交互卦,交互卦还会有交互卦,但是交互卦的交互卦最终就会归结为4个卦,这4个卦就是《乾》、《坤》、《既济》、《未济》。
也就是说《周易》64卦,或其交互卦直接就是这4个卦,或其交互卦的交互卦就是这4个卦(具体交互卦规律见附表),这4个卦就是所有卦的交互卦的最终结果。
《乾卦》的交互卦还是《乾坤》、《坤卦》的交互卦还是《坤卦》。
《乾》、《坤》两卦的交互卦都是其自身,已经不再发生变化。
《既济卦》的交互卦是《未济卦》,《未济卦》的交互卦为《既济卦》,两卦互为交互卦,所以也不再有别的变化。
“既济”、“未济”表示事物所处的两种状态,但《既济卦》的交互卦是《未济卦》,《未济卦》的交互卦是《既济卦》,说明这两种状态是相互转换的,也就是说,事物永远处于不断的运动变化之中,始而有终,终而又始。
《周易》64卦推演了天地万物之间的一切道理和规律,而这些道理和规律的内涵和实质归根到底就是一个道理和规律,这就是万物生于天地父母,永远处于始而有终,终则又始的运动变化之中。
这是宇宙间最基本的道理和规律。
《乾》、《坤》两卦代表天地父母,是万物的本源,故《周易》以《乾》、《坤》两卦为开头;《既济》、《未济》两卦代表事物发展的两种状态,揭示事物不断运动变化的规律,故《周易》以《既济》、《未济》两卦为结束。
周易(易经)64卦数学排列规律图
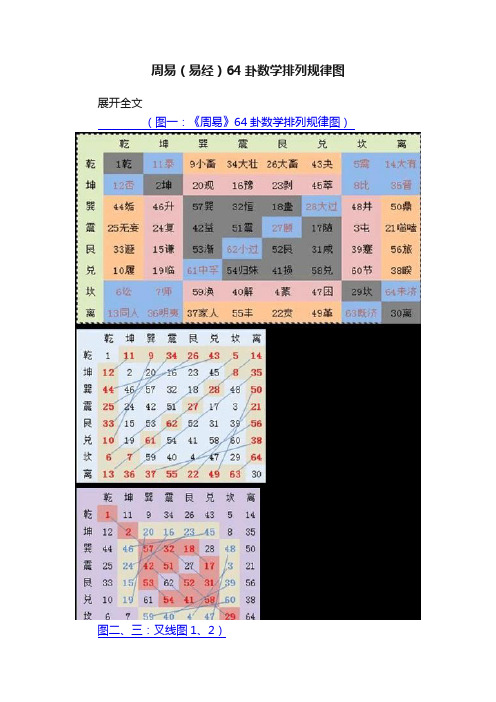
周易(易经)64卦数学排列规律图展开全文(图一:《周易》64卦数学排列规律图)图二、三:叉线图1、2)1.图2-5的规律都包含在图1中,《易经》64卦在数学排列上,有着严密的对称性;2.“64卦规律图”的存在,证明了流传至今的“通行本《易经》”在卦序排列上是正确传承的。
任何不同于“通行本《易经》”的卦序都是有问题的;3.《易经》64卦不仅在数学排列上具有此严密的对称规律,在内容上,也是前后卦相连贯的(请参见鄙人作品“易说《易经》”)。
这非常神奇,肯定消耗了作者n多的脑细胞。
这也说明“通行本《易经》”的作者极有可能是一个人,最多是几位要好的史官相互合作写的,不大可能是几代人前后续写的; 4.图1否定了若干不正确的64卦规律图,其实什么“河图”“洛书”根本就是数学问题,跟《易经》毫不沾边; 5.图1的规律由“8卦”顺序决定。
我本来拟定的顺序有二,一是乾坤巽震艮兑坎离,二是乾坤艮兑巽震坎离。
我们知道乾qian代表天,坤kun代表地,巽xun代表风,震zhen代表雷,兑dui代表泽,坎kan代表水,离li代表火。
图1说明8卦的顺序必然是这两者之一,先天八卦、后天八卦都有问题,按它们画图1的话,都不能得到最简单,最简洁的图形;6.图1有助于《易经》的初学者;7.图1不能说成是“卦序图”,其实除非是从1到64按顺序排,实在找不到“卦序图”。
而图4只在局部存在卦序规律,图4可以得出图5。
8.给图1添上两条“对角轴线”,可以发现除了4组卦外,都能以某一条“对角轴线”形成“翼式对称”;而1、2;29、30;27、28;61、62等4组,不能以这两条“对角轴线”形成“翼式对称”(它们踩在某一条“对角轴线”上,按此轴线折叠后,相对的两卦不是分布于轴线两侧)。
ok,“翼式对称”的各卦,其卦符旋转180度,就是其奇偶数的卦符,如第25卦的卦符旋转180度得到第26卦的卦符;“非翼式对称”的8卦,其卦符自身上下卦相对称。
ok,这便是图5中巽和兑、震和艮同步出现的原因。
周易 六十四卦

八卦代表八种基本物象: 乾为天、 坤为地、 震为雷、 巽为风、 艮为山、 兑为泽、 坎为水、 离为 火、 总称为经卦。 由八个经卦中的两个为一组的排列组 合、 则构成六十四卦。八卦符号两 两相重,构成了《周易》六十四卦 卦画,8×8=64。64×6=384
第一节、 第一节、六十四卦的卦序和卦画 排列特点
咸恒遁兮及大壮, 咸恒遁兮及大壮, 晋与明夷家人睽, 晋与明夷家人睽, 蹇解损益夬姤萃, 蹇解损益夬姤萃, 升困井革鼎震继, 升困井革鼎震继, 艮渐归妹丰旅巽, 艮渐归妹丰旅巽, 兑涣节兮中孚至, 兑涣节兮中孚至, 小过既济兼未济, 小过既济兼未济, 是为下经三十四。 是为下经三十四。
四、六十四卦卦画排列的特点
巽为风,风天小畜,风火家人, 巽为风,风天小畜,风火家人,风 雷益,天雷无妄,火雷噬嗑,山雷 雷益,天雷无妄,火雷噬嗑, 山风蛊。 颐,山风蛊。 坎为水,水泽节,水雷屯, 坎为水,水泽节,水雷屯,水火既 泽火革,雷火丰,地火明夷, 济,泽火革,雷火丰,地火明夷, 地水师。 地水师。
离为火,火山旅,火风鼎, 离为火,火山旅,火风鼎,火水 未济,山水蒙,风水涣,天水讼, 未济,山水蒙,风水涣,天水讼, 天火同人。 天火同人。 艮为山,山火贲.山天大畜, 艮为山,山火贲.山天大畜,山泽 火泽睽,天泽履,风泽中孚, 损,火泽睽,天泽履,风泽中孚, 风山渐。 风山渐。 兑为泽,泽水困,泽地萃,泽山咸, 兑为泽,泽水困,泽地萃,泽山咸, 水山蹇,地山谦,雷山小过, 水山蹇,地山谦,雷山小过,雷泽 归妹。 归妹。
为了记住六十四卦,以两个 经卦卦象称呼一别卦。如天地否 即看成由天地组成的卦画 称为 否卦。天山遁可看成由天山组成 的卦画 可称为遁卦。
卦的这种称谓方法,出自西汉 《京房易传》,叫做八宫卦序。 这种卦序排法不同于今本《周易》 (也产生于汉代),它是按照八 卦相重的原则,把《周易》六十 四卦分成八组,叫八宫,六十四 卦分属于八宫。
错综复杂——周易卦序的排布规律

错综复杂——周易卦序的排布规律易经是⼀门关于时(时间)和位(空间)的学问,讲究得时得位,即在正确的时间出现在正确的位置,这就是所谓的吉,反之就是凶。
因此易经特别强调秩序(顺序),包括易经万物⽣成模型的演化顺序、先阳后阴的阴阳⼆分顺序、天地⼈三才的顺序、四象相推的先后顺序、五⾏⽣克的循环顺序以及⼋卦的先天和后天顺序等等。
今天我们来了解六⼗四卦的顺序。
六⼗四卦的排序⽅法有很多,包括连⼭易序、归藏易序、帛书易序等等,⽬前最为流⾏的排序⽅法主要有三种,分别是周易卦序、先天卦序和⼋宫卦序。
我们先来介绍周易卦序。
周易卦序是《周易》⼀书中六⼗四卦的排列顺序。
为⽅便记忆,朱熹总结出了《六⼗四卦卦序歌》,将六⼗四卦分为上经三⼗卦和下经三⼗四卦。
《六⼗四卦卦序歌》内容如下:上经乾坤屯蒙需讼师,⽐⼩畜兮履泰否,同⼈⼤有谦豫随,蛊临观兮噬嗑贲,剥复⽆妄⼤畜颐,⼤过坎离三⼗备。
下经咸恒遁兮及⼤壮,晋与明夷家⼈睽,蹇解损益夬姤萃,升困井⾰⿍震继,⾉渐归妹丰旅巽,兑涣节兮中孚⾄,⼩过既济兼未济,是为下经三⼗四。
六⼗四卦卦序图如下:周易卦序《序卦传》中按照万物⽣成衍化的顺序对周易卦序做了说明:有天地,然后万物⽣焉。
盈天地之间者,唯万物,故受之以屯;屯者盈也,屯者物之始⽣也。
物⽣必蒙,故受之以蒙;蒙者,蒙也,物之稚也。
物稚不可不养也,故受之以需;需者饮⾷之道也。
饮⾷必有讼,故受之以讼。
讼必有众起,故受之以师;师者,众也。
众必有所⽐,故受之以⽐;⽐者,⽐也。
……不过对周易卦序我们要有清醒的认识,这个卦序不⼀定是周⽂王所定。
从周⽂王到孔⼦的⼏百年间,六⼗四卦的顺序可能有很多排法,直到孔⼦(或其门⼈弟⼦)做《序卦传》,这个卦序才被固定下来并⼀直沿⽤⾄今。
周易卦序⾃提出后就⼀直众说纷纭,没有⼈能猜透其排序依据,《说卦传》是按照事物的发展衍化的⾃然顺序来解释,其中不免有牵强附会之处。
唐代的孔颖达在《周易本义》中提出了'⼆⼆相偶,⾮覆即变'的观点,也只是对这个排序做出了部分解释,⽽未能完全解释。
易经中的数学原理和应用

易经中的数学原理和应用1. 引言作为中国古代经典之一,易经是一部充满智慧和哲学思想的书籍。
尽管易经本身并非数学著作,但在其中我们可以发现一些与数学相关的原理和应用。
本文将探讨易经中涉及的数学概念,并介绍其在现代数学中的应用。
2. 列点介绍易经中的数学原理•阴阳概念:易经的核心概念之一是阴阳。
阴阳代表了一对对立而又相互依存的概念,如阴阳、太阳、月亮等。
在数学中,这种对立双重性也存在于许多概念中,如正负数、奇偶数等。
•八卦图与三元组:易经中的八卦图由三条连续和三条间断的直线组成,分别代表了阴阳的变化。
这样的结构与数学中的三元组有些相似,三元组是指由3个元素组成的有序集合。
八卦图的三条连续直线可以看作是一个三元组,代表了一种状态或变化。
•二进制系统:易经中的虚实二分法与计算机科学中的二进制系统有些相似。
在易经中,阴阳可以看作是一种二进制的表示形式,0代表阴性,1代表阳性。
而在计算机科学中,二进制系统也是由0和1两个元素组成,用于表示计算机中的数字和信息。
•经卦数:易经的卦数可以看作是一种排列组合的数学方法。
在易经中,卦数由爻的排列组合形成,爻有两种状态,阴和阳,通过这些排列组合可以生成卦数。
这种排列组合的理念在数学中也有广泛的应用,如组合数学、概率等。
3. 易经数学原理的现代应用•密码学:二进制系统在密码学中有着广泛的应用。
由于易经中的虚实二分法与二进制系统相似,因此易经中的数学原理可以为密码学的研究提供一定的启示。
例如,可以利用易经中的阴阳概念设计出基于二进制的加密算法。
•组合数学:易经中的排列组合理念与组合数学有着密切的联系。
组合数学是研究离散结构的数学分支,涉及到排列、组合、集合等概念。
易经中的经卦数可以看作是一种排列组合的方法,因此易经中的数学原理可以为组合数学的研究提供一种参考和借鉴。
•数理逻辑:易经中的阴阳概念与数理逻辑中的对偶性有着相似之处。
数理逻辑是研究命题、推理和证明的数学分支,其中对偶性是一种非常重要的概念。
易经排列知识点总结

易经排列知识点总结1. 64卦爻的排列组合在易经中,有八卦(乾、坤、震、巽、坎、离、艮、兑),每个卦爻有6条线,每一条线可以是阴爻(Yin)或阳爻(Yang)。
这样一共可以有2的6次方,即64种排列组合。
这64卦爻又可以分成上下两部分,即“先天卦”和“后天卦”。
其中,先天卦是由上乾下坤和下坤上乾两个卦来确定的,而后天卦则是在先天卦的基础上通过叠卦的方法得到的。
通过64卦爻的排列组合,易经构成了丰富的“六十四卦”体系。
2. 各卦的含义和解释不同的卦爻排列组合形成了不同的卦。
每个卦都有其特定的含义和解释,这些含义和解释反映了宇宙和人生的种种不同方面。
比如,乾卦象征着天,坤卦象征着地,震卦象征雷,巽卦象征风,坎卦象征水,离卦象征火,艮卦象征山,兑卦象征泽。
每个卦都有其特定的象征意义和传统解释,这些含义和解释源于易经所表达的哲学和宇宙观念。
3. 易经的应用易经作为一部哲学著作,不仅仅是用来探讨宇宙和人生的哲理,它还可以用来预测未来和指导决策。
在易经中,卦爻可以被用来预测未来的发展趋势,也可以用来指导个人的生活和决策。
通过对卦爻的排列组合进行推演,可以得到有关人生和事物发展的种种信息。
在中国传统文化中,易经也被广泛应用于农业、医学、政治、军事等方面,成为了一种重要的智慧资源。
总之,易经的排列知识涉及了64卦爻的排列组合、各卦的含义和解释,以及易经的应用等多个方面。
通过对这些知识点的深入了解和学习,可以帮助我们更好地理解易经的哲学内涵和应用价值。
易经不仅仅是一部古老的经典著作,它还是一种灵活的思维工具,可以帮助我们更好地理解宇宙和人生,并指导我们在现实生活中做出更好的决策和选择。
因此,对易经的排列知识的深入了解和学习具有重要的价值和意义。
浅谈排列组合中的站队问题

浅谈排列组合中的站队问题作者:齐航来源:《中学生理科应试》2015年第01期排列与组合是《普通高中数学课程标准(实验)》中“数与代数”学习领域的一部分内容.在古代春秋时期就已经有了组合数学思想的萌芽,由《周易》中对卦符问题的研究——“易生太极,是生两仪,两仪生四象,四象生八卦”可见,排列组合是一个名副其实的古老数学问题 .解答排列组合应用问题时,我们应首先弄清楚是排列(有序)问题,还是组合(无序)问题,或者是排列与组合的混合问题.其次,我们要准确的确定哪一步是“分类”,哪一步是“分步”.排列组合应用到实际生活中,常常令情景变得千头万绪,但其中仍蕴含着不变的解题规律.本文通过一道带有7个小问的例题全面且详细的列举出此类问题的解答策略.常用的方法有“直接法”和“间接法”(即剔除不符合限制条件的情况,因而间接法又称为排除法).如果问题的正面分的类较多或正面问题计算较复杂,而反面问题分的类较少或计算较简便,则用“直接法”较麻烦,往往采用“间接法”.用“直接法”来解决这类有限制条件的排列问题的基本方法有:特殊元素优先排——即以元素为主,优先考虑特殊元素的要求,再考虑其他元素;特殊位置优先放——即以位置为主,优先考虑特殊位置的要求,再考虑其他位置.例(1)7位同学站成两排(前3后4),共有多少种不同的排法?(2)7位同学站成一排,其中甲站在中间的位置,共有多少种不同的排法?(3)7位同学站成一排,甲不能站排头,乙不能站排尾的排法共有多少种?(4)7位同学站成一排,其中甲不站在中间的位置,共有多少种不同的排法?(5)7位同学站成一排,甲、乙只能站在两端的排法共有多少种?(6)7位同学站成一排,A、B、C三人互不相邻共有多少种不同的排法?(7)7位同学站成一排,A、B、C三人相邻共有多少种不同的排法?1. 两个原理的应用(1)7位同学站成两排(前3后4),共有多少种不同的排法?解法一首先,判断“分类”还是“分步”;其次,确定“分步”之后,第一步:从7个不同的元素中取出3个元素,按照一定的顺序排成一列,即A37种排法.第二步:剩下的4个元素进行全排列,即A44种排法;最后,利用“分步乘法计数原理”,即A37×A44种排法.解法二分排问题直排处理.把n个元素排成若干排的排列问题,若没有其他特殊要求,可采取统一排成一排的方法处理.因7名同学可在前3后4的位置中随意站位,再无其他条件,所以两排可看做一排来处理,其不同站法种数为A77.2.直接法(2) 7位同学站成一排,其中甲站在中间的位置,共有多少种不同的排法?解本题正面计算简便,故用“直接法”.甲站在中间已经固定,让剩余的6个元素进行全排列即可,即A66种排法.(3) 7位同学站成一排,甲不能站排头,乙不能站排尾的排法共有多少种?解本题考虑直接法时首先要选择分类的标准.若以甲为研究对象,因为乙不能站在排尾,所以甲是否站在排尾要受乙的影响.进而分为两类,第一类:甲站在排尾——由于甲站在排尾,所以同时满足了甲不站排头和乙不站排尾这两个条件.从除甲之外的6个人中任取1人站在排头,有A16种排法,剩下的5个人在中间的5个位置进行全排列,有A55种排法.由分步乘法计数原理共有A16×A55种排法;第二类:甲不站在排尾——此时考虑首位的特殊性,从除甲、乙外的5个人中任选1人站在排尾,有A15种排法,再从除甲和站在排尾的人之外的5个人中任选1人站在排头,有A15种排法,最后将剩余的5个人在中间的5个位置进行全排列,有A55种排法.由分步乘法计数原理共有A15×A15×A55种排法.最后根据分类加法计数原理共有A16×A55+A15A15×A55排法.3.间接法(3)7位同学站成一排,甲不能站排头,乙不能站排尾的排法共有多少种?解“间接法”.正面计算此题时,分类之后每一类下又会有分步情况,情况复杂,不易解决,可考虑从反面入手,将其等价转化成一个较为简单的问题来处理,故采用“间接法”.不妨取名记为“正难则反”.计算甲站排头的排法,有A66种,同理乙站排尾也有A66种,用7个元素全排列减去甲站排头和乙站排尾的情况,即A77-2A66种.此时,很容易遗漏甲站排头和乙站排尾两种条件下,有一种情况重复了,即甲站排头同时乙站排尾的情况,有A55种排法.这一种情况我们减掉了两次,故应该在其基础上再加回一次,即A77-2A66+A55种排法.(4)7位同学站成一排,其中甲不站在中间的位置,共有多少种不同的排法?解甲不站在中间,则有6种可能的站法,正面分类复杂,计算繁琐,故采用“正难则反”的方法.由例(2)知,7个元素全排列减去甲站在中间的排法即得到甲不在中间的排法,即A77-A66种排法.4.特殊元素(位置)优先法(4) 7位同学站成一排,其中甲不站在中间的位置,共有多少种不同的排法?解安排甲时要求其不站在中间的位置,所以这是有限制条件的排列问题,应先考虑特殊元素——甲,或者特殊位置——中间,再考虑其他情况.解法一特殊元素优先排——因甲不能站在中间,故第一步先让甲站在除了中间的任一位置上,有A16种排法;第二步再让剩下的6个人站在剩余的六个位置上,有A66种排法,由分步乘法计数原理共有A16×A66种排法.解法二特殊位置优先放——因中间不能站甲,故第一步先从甲以外的6个人中任选一人站在中间,有A16种排法;第二步再让剩下的6个人站在除中间外的六个位置上,有A66种排法,由分步乘法计数原理共有A16×A66种排法.(5) 7位同学站成一排,甲、乙只能站在两端的排法共有多少种?解法一特殊元素优先排——首先考虑特殊元素,让甲、乙站在两端,有A22种排法;再让其他5个人在中间的五个位置上做全排列,有A55种排法,由分步乘法计数原理共有A22×A55种排法.解法二特殊位置优先放——首先考虑两端2个位置,让甲、乙站在两端,有A22种排法;再考虑中间5个位置,由剩下的5个人去站,有A55种排法,由分步乘法计数原理共有A22×A55种排法.5.插空法(6)7位同学站成一排,A、B、C三人互不相邻共有多少种不同的排法?解“插空法”——对于某几个元素不相邻的排列问题,可先将其他元素排好,然后再将不相邻的元素在这些排好的元素之间及两端的空隙中插入.首先将除A、B、C三人之外的4个人进行全排列,有A44种排法.四个人排列之后产生了5个空位,再从5个位置中任选3个位置,将A,B,C进行全排列,有A35种排法.根据分步乘法计数原理共有A44×A35种排法.6.捆绑法(7)7位同学站成一排,A、B、C三人相邻共有多少种不同的排法?解“捆绑法”——对于某几个元素要求相邻的排列问题,可先将相邻的元素“捆绑”起来看作一个元素与其他元素排列然后再对相邻元素之间进行排列.首先将A、B、C三人进行全排列,有A33种排法.再将三人看成一个整体,与剩余的四个人进行全排列,有A55种排法.根据分步乘法计数原理共有A33×A55种排法.通过几例“站队”问题映射出了排列应用题的六种解题策略.其中,应用分步排位的方法计算排列数时,应注意以下三个方面:①在题设条件制约下,每一步排位,哪些元素可取,哪些元素不能取;②在某一步排位后,下一步排位可取元素的个数,应视具体情况而定;③若某一步必须分类,则分类后各步都必须按各类分别计算.例(4)和例(5)都是带有限制条件的排列问题,此类问题应对特殊的元素或者特殊的位置进行优先考虑.例(6)和例(7)是典型的“邻不邻”问题.对于有些元素必须要安排在一起,我们常用“捆绑法”.把它们视为一个整体,即先排整体内部的元素,再把整体视为一个个体,一个大“元素”与其他元素一起排列即可.对于有些元素不能安排在一起,也就是需要间隔,我们把这类有部分元素不能相邻的排列问题称为间隔排列问题.解决间隔排列问题的有效方法是“插空法”,也就是先排不需要间隔(可以相邻)的元素,再将需要间隔的元素用插空方式插进来即可.三、总结解决排列组合问题的基本规律可以用16个字来概括:分类相加,分步相乘,有序排列,无序组合.“站队”问题的解题方法特殊,抽象性强,思维方法新颖.在解这类题时,往往会出现对题设认识不够,题设中的内涵关系理解不透,题设结论之间的联系分析不尽而出现解题思路受限,条件应用考虑不周,导致结果出现重复、遗漏甚至答非所问的情况 .本文通过对两类问题的解题规律和解题方法进行探究,从千差万别的实际问题中探究出数学模型,方便理解和记忆排列组合题型中的多种分类标准和解题方法.排列组合的内容虽然在高中数学教学中所占比重不大,但却是今后学习概率统计的基础.而且通过排列组合的学习,可以变换学生的思维方法,这也是培养学生思维品质、优化思维过程的一个重要方面.(收稿日期:2014-11-10)。
这道高考数学《易经》题,非常有意思,出题人将美好祝福深藏其中

这道高考数学《易经》题,非常有意思,出题人将美好祝福深藏其中每年高考季,都会祝愿所有参加高考的孩子们都能旗开得胜,跨入自己梦想的大学殿堂,并就读自己喜欢的学科专业。
我最近一直在写《易经》的文章,大家都知道,《易经》是我国古代流传下来的一本了不起的古籍,被称之大道之源。
2019年,《易经》相关的内容出现在了全国高考理科试卷中,也就是说《易经》也是众多莘莘学子需要了解的内容。
众所周知,迄今为止高考题目涉及的范围越来越广,《易经》作为我们传统文化的重要内容,出现在高考题目中,也算是稀松平常了。
考试原题内容如下:《周易》里面的基础常识非常重要,需要大家了解从这道题目来看,如果想要准确解答,至少要了解几个关于《易经》的基础概念。
首先,《周易》是一本古代典籍。
这个知识点其实是很简单的,因为几乎所有人都知道四书五经,其中五经包括《诗经》、《尚书》、《礼记》、《周易》、《春秋》,而《周易》正是其中之一。
其次,知道“卦”的说法。
占卜,算卦、八卦,对于“卦”这个字,其实对普通人来说也并不陌生。
卦到底是什么?这道题中的解释是描述万物的变化。
可以说,这个解读是非常精准的,当然这与我们日常生活中对“卦”的理解有很大的不同。
按我的理解来说,如果把《周易》与当代数学发生联系,我更愿意把“卦”解释为一种象数系统,类似于计算机系统里的二进制。
而与高中数学的联系,就是排列组合、概率。
第三,知道“阳爻”、“阴爻”两个概念,知道“重卦”的概念。
直横代表“阳爻”,断横代表了“阴爻”。
如果和数学联系,那就相当于概率里面的白球与黑球。
每一个“重卦”都是由6个爻组成。
“重卦”按照概率解读,就是从一个球袋(内有黑白两种球)里随机取球,共取6次。
每次取都是两种可能,或黑或白,共6次,所以是6个2相乘,也就是64种,由此对应《周易》里面共有64个重卦。
当然,假设对《周易》有基本了解,这个计算基本上就省了,因为《周易》共有64卦是常识。
这是一道5分的选择题,高考素来有“1分一操场”的说法,因此《周易》的一些基础常识还是很有必要了解和学习的。
09 排列组合问题的来源

凤凰初中数学配套教学软件_知识拓展
排列组合问题的来源
排列组合问题,最早见于我国的《易经》一书.所谓“四象”就是每次取两个爻的排列,“八卦”是每次取三个爻的排列.在汉代数学家徐岳的《数术记遗》(公元2世纪)中,也曾记载有与占卜有关的“八卦算”,即把卦按不同的方法在八个方位中排列起来.它与“八个人围一张圆桌而坐,问有多少种不同坐法”这一典型的排列问题类似.11世纪时,邵雍还进一步研究了六十四卦的排列问题.
唐朝僧人一行曾经研究过围棋布局的总数问题.古代的棋盘共有17路,289个点,后来发展到19路361个点.一行曾计算过一切可能摆出的棋局总数.后来,17世纪,北宋时期沈括在《梦溪笔谈》中,进一步讨论了围棋布局总数问题.他利用一些排列、组合的办法对一行的计算作了分析.沈括指出,当361个棋子全用上时,棋局总数达到1000052的数量级.。
排列组合问题的来源

排列组合问题的来源
排列组合问题,最早见于我国的《易经》一书.所谓“四象”就是每次取两个爻的排列,“八卦”是每次取三个爻的排列.在汉代数学家徐岳的《数术记遗》(公元2世纪)中,也曾记载有与占卜有关的“八卦算”,即把卦按不同的方法在八个方位中排列起来.它与“八个人围一张圆桌而坐,问有多少种不同坐法”这一典型的排列问题类似.11世纪时,邵雍还进一步研究了六十四卦的排列问题.
唐朝僧人一行曾经研究过围棋布局的总数问题.古代的棋盘共有17路,289个点,后来发展到19路361个点.一行曾计算过一切可能摆出的棋局总数.后来,17世纪,北宋时期沈括在《梦溪笔谈》中,进一步讨论了围棋布局总数问题.他利用一些排列、组合的办法
对一行的计算作了分析.沈括指出,当361个棋子全用上时,棋局总数达到的数量级.。
排列组合的数学历史小故事

排列组合的数学历史小故事虽然数数始于结绳计数的远古时代,由于那时人的智力的发展尚处于低级阶段,谈不上有什么技巧。
随着人们对于数的了解和研究,在形成与数密切相关的数学分支的过程中,如数论、代数、函数论以至泛函的形成与发展,逐步地从数的多样性发现数数的多样性,产生了各种数数的技巧。
同时,人们对数有了深入的了解和研究,在形成与形密切相关的各种数学分支的过程中,如几何学、拓扑学以至范畴论的形成与发展,逐步地从形的多样性也发现了数形的多样性,产生了各种数形的技巧。
近代的集合论、数理逻辑等反映了潜在的数与形之间的结合。
而现代的代数拓扑和代数几何等则将数与形密切地联系在一起了。
这些,对于以数的技巧为中心课题的近代组合学的形成与发展都产生了而且还将会继续产生深刻的影响。
由此观之,组合学与其他数学分支有着必然的密切联系。
它的一些研究内容与方法来自各个分支也应用于各个分支。
当然,组合学与其他数学分支一样也有其独特的研究问题与方法,它源于人们对于客观世界中存在的数与形及其关系的发现和认识。
例如,中国古代的《易经》中用十个天干和十二个地支以六十为周期来记载月和年,以及在洛书河图中关于幻方的记载,是人们至今所了解的最早发现的组合问题甚或是架构语境学。
于11和12世纪间,贾宪就发现了二项式系数,杨辉将它整理记载在他的《续古抉奇法》一书中。
这就是中国通常称的杨辉三角。
事实上,于12世纪印度的婆什迦罗第二也发现了这种组合数。
13世纪波斯的哲学家曾讲授过此类三角。
而在西方,布莱士·帕斯卡发现这个三角形是在17世纪中期。
这个三角形在其他数学分支的应用也是屡见不鲜的。
同时,帕斯卡和费马均发现了许多与概率论有关的经典组合学的结果。
因此,西方人认为组合学开始于17世纪。
组合学一词是德国数学家莱布尼茨在数学的意义下首次应用。
也许,在那时他已经预感到了其将来的蓬勃发展。
然而只有到了18世纪欧拉所处时代,组合学才可以说开始了作为一门科学的发展,因为那时,他解决了柯尼斯堡七桥问题,发现了多面体(首先是凸多面体,即平面图的情形)的顶点数、边数和面数之间的简单关系,被人们称为欧拉公式。
周易体系的两个系列

周易体系的两个系列
周易体系的两个系列
J.M.九宫格
周易的基本单元是卦,卦由六爻构成。
爻有爻位,周易规定的六爻顺序是“下初上上”,即爻位顺序方向自下而上。
人们熟知的先天方图和爻位方图是周易众多卦图中唯一一对整体按爻位顺序排列的卦图。
就爻位顺序而言,先天方图的整体顺序与六爻顺序方向逆反,爻位方图的整体顺序与六爻顺序方向顺同。
对本经卦序做数理逻辑解析可知它与爻位方图有渊源关系,可以得到易平方图、易经幻方、复合幻方、本经格局等一系列卦图,这是周易“本经系列”的一套组合。
借鉴爻位方图研究方法对先天方图进行类比推导同样可以得到包括“推论卦序”在内的一系列卦图,这是“本经推论系列”的一套组合。
以上由本经卦序解析、推导得到的“本经系列”和“本经推论系列”可以认为是周易体系的两个特例,事实上只要六十四卦整体按照
易平方图的制式呈现错综覆變双轴对称形态应用本篇的数理模型就能得到对应的一系列卦图包括一例“两两相耦非覆即變”的“骨构卦序”一般式。
上述两个特例是六十四卦整体按爻位顺序排列的结果,而本经卦序更是六十四卦整体爻位顺序与六爻顺序方向契合条件下的一例特别卦序。
排列组合问题的来源

初中数学配套教学软件_知识拓展
排列组合问题的来源
排列组合问题,最早见于我国的《易经》一书.所谓“四象”就是每次取两个爻的排列,“八卦”是每次取三个爻的排列.在汉代数学家徐岳的《数术记遗》(公元2世纪)中,也曾记载有与占卜有关的“八卦算”,即把卦按不同的方法在八个方位中排列起来.它与“八个人围一张圆桌而坐,问有多少种不同坐法”这一典型的排列问题类似.11世纪时,邵雍还进一步研究了六十四卦的排列问题.
唐朝僧人一行曾经研究过围棋布局的总数问题.古代的棋盘共有17路,289个点,后来发展到19路361个点.一行曾计算过一切可能摆出的棋局总数.后来,17世纪,北宋时期沈括在《梦溪笔谈》中,进一步讨论了围棋布局总数问题.他利用一些排列、组合的办法对一行的计算作了分析.沈括指出,当361个棋子全用上时,棋局总数达到1000052的数量级.。
周易组合卦研究

周易组合卦研究周易组合卦研究(一)【原创】Sniper 2010周易预测不仅对单个卦进行研究,对一组卦也要进行研究。
近来我对连升三天以上的卦作了统计(1991年-2009年),现公布这组数据如下。
有两组统计数据。
第一组,我称其为“K线卦推升组合”,就像K线组合一样。
第一个卦是跌卦,之后用连接号连接的一组卦都是升卦的。
推升组合前的第一个卦是跌卦,可以视为一个“转折信号”卦。
以后看到这个转折信号卦出现,就要密切留意后面的状况,一旦出现推升组合的头一,二个卦后,可以跟进。
第二个卦开始就是组合卦了,由四个以上的卦组成。
组合卦后面的统计数据是这个组合卦对大盘的推升点数。
天卦后面的数字是表示这个卦连续出现的次数。
K线卦推升组合(升400点以上)姤:同人-履-小畜-大有-夬-天8 972.36蹇:节-大畜-大壮-夬-天 574.71萃:益-损-泰-大壮-夬-天2 538.12渐:噬嗑-节-大畜-大壮-夬-天2 506.08晋:屯-损-泰-大壮 488.36风:火-泽-小畜-大有-夬-天 453.54下面的“K线卦推跌组合”的第一个卦是升卦,但也是一个“转折信号”卦,意味着后面会出现下跌走势。
一旦出现推跌组合的头一,二个卦后,就要撤离,第二个卦开始就是组合卦了,也是由四个以上的卦组成,组合卦后面的统计数据时这个组合对大盘的推跌点数。
地卦后面的数字是表示这个卦连续出现的次数。
K线卦推跌组合(跌400点以上)泽:风-旅-萃-观-剥-地3 -590.24雷:水-山-豫-比-剥 -496.98归妹:井-旅-萃-观 -471.76颐:师-谦-豫-比 -443.66履:风-旅-萃-观 -424.73大有:大过-遁-否-观 -418.20数据统计是准确的,但操作就要看实际情况而定了。
希望对大家有点点的帮助。
仅此而已。
周易组合卦研究(二)传统中,对八卦的阴阳属性的定义是:乾坎艮震为阳卦,巽离坤兑为阴卦。
如果我们对“阳”的理解在股市中表现为升,而对“阴”的理解在股市中表现为跌的话,那么,经过对两市大盘历年数据(1991-2009)的统计,我们发现:乾出现: 245次,推升:3380.04点兑出现: 95次,推升:2423.56点离出现: 79次,推升:1556.11点震出现: 72次,推升:1750.32点巽出现: 89次,推跌:-1757.09点坎出现: 60次,推跌:-1432.04点艮出现: 72次,推跌:-2131.90点坤出现: 109次,推跌:-1184.64点对照这些实际数据,我们就不得不对卦的阴阳属性做点修改了:乾兑离震为阳卦,巽坎艮坤为阴卦。
周易卦序结构分析

张清宇内容提要:易卦是一类古老而又神奇的符号,可以有种种解释。
采用内涵格解释,把卦的交错和交综解释成内涵格中的代数运算,由此引出错综不变组的概念并用于分析周易卦序结构。
64卦或两个一组,或四个一组,阴阳平衡,循环往复,形成20个错综不变组。
卦有主从之别(从卦也叫散卦)。
主卦6组16卦,上下篇各3组,统散卦而立其体,决定周易卦序的基本结构。
上篇3组象天而圆,先正后交,以乾坤为始,统8散卦,继之以乾坤之交泰否,统16散卦,终之以坎离。
下篇3组法地而方,先交后正,以震艮巽兑之交咸恒损益为始,统16散卦,继之以震艮巽兑,统8散卦,终之以坎离之交既济未济。
散卦14组48卦,按错综组、跨篇组、跨区组、自综组四部分从左至右定一大序,又按10小区(上下篇各有正二区和交三区)从上至下成另一大序,观之散乱,法象实存。
序卦的总原则为以阳馭阴,以刚制柔,首乾而主长男。
整个卦序井然森然杂而不乱,逆顺错综,处处对称,一往一复,妙趣无穷,呈现出一种两向(从左至右、从上至下)多层次(篇、区、组、卦)的平面结构,见文中周易卦序结构图。
This paper is a successive one of the author's preceding papers. It consists of three parts. The author associates eight trigrams with eight elements of the intensinal lattice 8 in terms of their ordering determined in Chou I, and constructs a sequence of hexagrams, which is arranged into a figure of 8 squares. For any hexagram(x, y), its left coordinate x and right coordinate y have either same signs or different signs; the former is called the "Class-corresponding hexagram", and the latter the "non-Class-corresponding hexagram". And, the absolute values of x and y are either same or not. If they are same, then (x, y) is called the "Main hexagram", otherwise the "Secondary hexagram". Main hexagrams have determined the basic hexagram-ordering structure. The author analyzes the hexagram-ordering by applying some concepts from the figure of eight squares. The 64 hexagrams are divided into 20 groups. Each group forms a set closing for both the opposite operation and the inversw operation. The author determins the order among the groups and the order among hexagrams in each group, and therefore clarifies the order among hexagrams thoroughly with some principles which are embodiments of Shen you-ding principle of deriving Yin by Yang. The hexagram-ordering structure of Chou I is shown on figure 2 in the paper.关键词:周易;卦序结构;内涵格;主卦;从卦;散卦Chou I;Hexagram;Main Hexagram;Secondary Hexagram;Hexagram-ordering Structure;Intensional Lattice周易卦序,错综复杂,不呈线性序,而显两向多层次的平面结构。
周易小成图的排盘逻辑

周易小成图的排盘逻辑
无极,就是你的业力推动,推动到这里。
有算卦的想法。
生太极,你的念头,比如,求官,求财,求子,求合作,求学业。
看忧患,看病,看婚姻。
太极生两仪,用起卦方式排出的上卦和下卦,比如取数3,4。
上离,下震(双数和除六,余1,这个一爻动,是它的内部逻辑)。
两仪生四象,由上离和下震,组合为四个卦,主卦(火雷噬嗑),主互(水山蹇),变互(水山蹇),变卦火地晋,即四象。
在梅花易数中,表示事物发展的三个阶段,开始,过程,结局。
六壬中的初传,中传,末传。
四象生八卦,落实在九宫的排盘,
主卦上卦(阳)在离九宫,上为阳;
主卦下卦(阴)在坎一宫,下为阴。
主互上卦在巽四宫,左为阳;
主互下卦在坤二宫,右为阴。
变卦上卦在震三宫,左为阳;
变卦下卦在兑七宫,右为阴
变互上卦在艮八宫,左为阳
变互下卦在乾六宫,右为阴
九宫小成图排盘八卦定吉凶。
吉凶生大业。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《周易》与排列组合
例1:从甲城到乙城,可以乘飞机、火车、汽车或轮船。
一天中午飞机有2班,火车有4班,汽车有1班,轮船有3班。
问从甲城到乙城一天中共有多少中不同的走法?
分析与解:
从甲城到乙城共有四种不同的交通工具,每种交通工具都有不同的班次,无论乘哪种交通工具的任何班次都能从甲城到达乙城。
由已知条件可知,一共有2+4+1+3=10(种)。
答:从甲城到乙城在一天种有10种不同的走法。
方法点拨:
这道十分简单的题目,包含了一种应用非常广泛的数学原理——加法原理。
如果完成一件工作有几类方法,每一类又分别有m1,m2,m3,--------种不同的方法,那么完成这种工作的方法总数就等于各类完成这种工作的方法的和,即n=m1+m2+m3+--------(n表示完成这件工作方法的总数)
试一试:
书架上有10本故事书,3本历史书,12本科技书,黄刚要任意从书架上取一本,有多少种不同的取法?
例2:某班要派出一对选手参加乒乓球混合双打比赛,男选手在王刚,李健,张明三人中产生;女选手在薛红,章芸,顾芬,沈华四人中产生。
问共有多少种不同的组成方式?
分析与解:
要选出一对双打选手要分两个步骤:第一步选一名男生,有三种选法;第二步再选一名女生,有四种选法。
一旦两步完成,双打选手即产生。
当我们选出
任一名男生后,都可以组成4种不同的双打选手,一共有3名男生,故有3×4= 12(种)。
答:共有12种不同的方法。
这道题目也比较简单,但同样也包含了一个应用非常广泛的数学原理——乘法原理。
如果一件工作,要分几步完成,每一步又分别各有m1,m2,m3…种不同的方法,那么完成这件工作的方法总数就等于完成各步的方法数的乘机,即N=m1×m2×m3…(N表示完成这件工作的方法总数)
加法原理和乘法原理是计数种应用十分广泛的两个原理。
再运用时,关键要分析问题的具体情况,准确地确定用哪条原理,也就是说加法原理和乘法原理的区别在于:完成工作的几类方法是独立的,一步即可(如任何一种交通工具的任何班次都能从甲城到达乙城)就用加法原理;如果做事需分步骤,各步均做完才算完成整件事(如必须选好男生后再选好女生,两名选手都选好才完成任务),就用乘法原理。
拓展训练营:
书架上有4本故事书,7本科技书,王刚想要从书架上任意取一本故事书和一本科技书,共有多少种不同的取法?
史料链接
《周易》
在道家之外,借助于老子的思维方法,用宇宙的道理来解释人世道理的第一批代表人物,是旧中国时期的《周易》学者。
《周易》是成书于周代的一部算卦书,它用“——”和“-”两种符号六层相叠、排列组合的方法,得出了六十四个复合符号,人称六十四卦的卦象,用六十四卦的卦象象征自然界及人世各种事物,用六十四卦卦象之间的异同象征事物之间的变化。
算卦时,根据所得卦象之间的转换,来判断事物的好坏和吉凶。
后人将《周易》作为一门学问来研究,于是形成了易学。
到了战国时期,这
种研究取得了划时代的成就,一批学者对《周易》做出了一整套带有宇宙论性质的解说,从而奠定了易学的理论基础。
他们的代表作共有10篇,即《文言传》、《彖传》上下、《象传》上下、《系辞传》上下、《说卦传》、《序卦传》、《杂卦传》,总称为《易传》。
由此,原本的《周易》也就有了《易经》的称谓。
“传”有传授的意思,《易传》意为传授、解说《周易》的书;“经”有恒久不变的意思,它是相对于“传”而言的,因为“传”是传授、解说之作,有许多种,各有各的说法,而原本《周易》只有一种,是各种“传”所遵从的恒久不变的依据,所以称为《易经》。
《易传》的作者们认为:《易经》中六十四卦之间的转换,尝示着宇宙中的一切变化,而六十四卦的转换,都基于每卦之中的两个最基本的符号“——”和“-”的相互更替,所以宇宙中事物的变化也一定是基于两种最基本的因素的相互更替。
六十四卦中这相互更替的两个基本符号是形象相反的两种符号,那么宇宙中相互更替的两种因素也一定是笥质相反的两种因素。
他们将六十四卦中这形象相反的两种符号分别用太阳照不到的阴面和太能
照射到的阳面来比喻,称“——”为阴,称“-”为阳,并将这种称谓推广到宇宙之中,将宇宙中具有柔弱、阴冷、退守、低下性质的因素称为阴,将宇宙中具有刚强、温暖、进取、尊贵性质的因素称为阳。
在他们看来,六十四卦之间的转换都基于阴阳两种符号的替,所以阴阳两种符号的交替是整个易卦变化的法则;与此相应,宇宙间一切事物的变化都基于阴阳两种因素的交替,所以阴阳两种因素的交替是整个宇宙变化的法则。
