2010年新疆中考数学试卷及答案
2010年新疆维吾尔自治区新疆生产建设兵团年初中学业水平考试(有答案).docx

2010 年新疆维吾尔自治区新疆生产建设兵团年初中学业水平考试(有答案 )数 学 试 题 卷考生须知: 1.本试卷分为试题卷和答题卷两部分 .2.试题卷共 4 页,满分 150 分 .考试时间 120 分钟 .3.答题卷共 4 页,所有答案必须写在答题卷上 ,写在试题卷上的无效 ............. ......... 4.答题前,考生应先在答题卷密封区内认真填写准考证号、姓名、考场号、座位号、地(州、市、师) 、县(市、区、团场)和学校.5.答题时可以使用科 学计算器 ...... ....一、精心选择 (本大题共 8 小题,每小题 5 分,共 40 分 .每小题所给四个选项中,只有一个是正确的 . )1.8 的相反数是A. 8B.8C.1D.18 82.计算 ( a 2 )3 的结果是A. a 5B. a 6C. a 6D. a 53.如右图,小明课间把老师的三角板的直角顶点放在黑板的两条平行线 a 、b上,已知 155°2的度数为,则A. 45°B. 35°C. 55°D.125°4.今年我区约有202 000名应届初中毕业生参加学业水平考试,202 000第 3 题图用科学记数法表示为A. 0.202 106B. 202 103C.20.2 104D. 2.02 10 55.如果从小军等 10 名大学生中任选 1 名作为“世博会”志愿者,那么小军被选中的概率是A.1B. 1C.1D. 1A11 1096.如图( 1)是一张 Rt △ ABC 纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图( 2),那么在 Rt △ ABC 中, sin B 的值是13D.3BCA. B.C.1图( 1)图( 2)2227.若点 A(x 1, y 1)、 B(x 2,y 2 ) 在反比例函数 y3 的图象上,且 x 1 0 x 2 ,则 y 1、 y 2 和x0 的大小关系是A. y 1 y 2 0B. y 1 y 2 08mCC. y 1 0 y 2D. y 1 0 y 2D8.如右图,王大爷家屋后有一块长12m ,宽 8m 的矩形空地,O 12mPAB他在以 BC 为直径的半圆内种菜,他家养的一只羊平时拴在A 处,为了不让羊吃到菜,拴羊的绳长可以选用来源学*科 * 网Z*X*X*K]A.3mB.5mC.7mD.9m二、合理填空(本大题共 6 个小题,每小题 5 分,共30 分)9.化简188___________.10.写出右图中所表示的不等式组的解集:____________.11.甲、乙两位棉农种植的棉花,连续五年的单位面积产量(千克 / 亩)统计如下图,则产量较稳定的是棉农_________(.填甲或乙)(第 11 题图)(第 12 题图)12.利用 1 个a a的正方形, 1 个b b 的正方形和2 个a b 的矩形可拼成一个正方形(如图所示),从而可得到因式分解的公式__________.13.长方体的主视图和左视图如下图所示(单位:cm ),则其俯视图的面积是 _________cm 2.y31 O1x(第 13 题图)(第 14 题图)14.抛物线y x2bx c 的部分图象如图所示,若y 0,则 x 的取值范围是__________.三、准确解答(本大题共有10 题,共 80 分)15.(6 分)解方程:2 x27x 6016.( 6 分)先化简,再求值x22x x,其中 x3 1x 1 1 x x1。
乌鲁木齐中考数学试题及答案

2010年新疆乌鲁木齐市初中毕业生学业水平测试数学试卷一、选择题(本大题共10小题,每小题4分,共40分)每题的选项中只有一项符合题目要求. 1.在0,2-,1,2-这四个数中负整数是 A.2- B. 0 C.22- D. 12.如图1是由五个相同的小正方体组成的几何体,则它的左视图是3.“十二五”期间,新疆将建成横贯东西、沟通天山的“十”字形高速公路主骨架,全疆高 速公路总里程突破4 000km ,交通运输条件得到全面改善,将4 000用科学记数法可以表 示为A.24010⨯B. 3410⨯C. 40.410⨯ D. 4410⨯4.阳光公司销售一种进价为21元的电子产品,按标价的九折销售,仍可获得20%,则这种 电子产品的标价为A. 26元B. 27元C. 28元D. 29元 5.已知整式252x x -的值为6,则2256x x -+的值为 A. 9 B. 12 C. 18 D. 246.如图2,在平面直角坐标系中,点A B C 、、的坐标为 (1,4)、(5,4)、(1、2-),则ABC △外接圆的圆心 坐标是A.(2,3)B.(3,2)C.(1,3)D.(3,1)7.有若干张面积分别为22a b ab 、、的正方形和长方形纸片,阳阳从中抽取了1张面积为2a的正方形纸片,4张面积为ab 的长方形纸片,若他想拼成一个大正方形,则还需要抽取 面积为2b 的正方形纸片A. 2张B.4张C.6张D.8张8.某校九年级(2)班50名同学为玉树灾区献爱心捐款情况如下表:捐款(元) 10 15 30 40 50 60人数3611 11 136则该班捐款金额的众数和中位数分别是A. 13,11B. 50,35C. 50,40D. 40,509.如图3,四边形OABC 为菱形,点A B 、在以点O 为圆心的DE 上,若312OA =∠=∠,,则扇形ODE 的面积为A.3π2 B. 2π C.5π2D. 3π 10.将边长为3cm 的正三角形各边三等分,以这六个分点为顶点构 成一个正六边形,则这个正六边形的面积为 A.332cm 2 B.334cm 2 C.338cm 2D.33cm 2 图2 ADO ECB图3二、填空题(本大题共5小题,每小题4分,共20分)把答案直接填在答题卡的相应位置处. 11.计算:18322-+=_____________.12.如图4,AB 是O ⊙的直径,C D 、为O ⊙上的两点, 若35CDB ∠=°,则ABC ∠的度数为__________. 13.在数轴上,点A B 、对应的数分别为2,51x x -+,且A B 、 两点关于原点对称,则x 的值为___________.14.已知点1(1)A y -,,2(1)B y ,,3(2)C y ,在反比例函数(0)k y k x=<的图象上,则 123y y y 、、的大小关系为_________(用“>”或“<”连接).15.暑假期间,瑞瑞打算参观上海世博会.她要从中国馆、澳大利亚馆、德国馆、英国馆、日本馆和瑞士馆中预约两个馆重点参观,想用抽签的方式来作决定,于是她做了分别写有以上馆名的六张卡片,从中任意抽取两张来确定预约的场馆,则他恰好抽中中国馆、澳大利亚馆的概率是___________.三、解答题(本大题Ⅰ—Ⅴ,共9小题,共90分)解答时对应在答题卡的相应位置处写出文字说明、证明过程或演算过程.Ⅰ.(本题满分15分,第16题6分,第17题9分)16.解不等式组1(4)223(1) 5.x x x ⎧+<⎪⎨⎪-->⎩,17.先化简,再求值:21111211a a a a a a ++-÷+-+-,其中 2.a = 四.(本题满分30分,第18题8分,第19题、20题,每题11分)18.如图5,在平行四边形ABCD 中,BE 平分ABC ∠交AD 于点E ,DF 平分∠ADC 交 BC 于点F . 求证:(1)ABE CDF △≌;(2)若BD EF ⊥,则判断四边形EBFD 是什么特殊四边形,请证明你的结论.19.如图6,在平面直角坐标系中,直线4:43l y x =-+分别交x 轴、y 轴于点A B 、,将AOB △绕点O 顺时针旋转90°后得到A OB ''△. (1)求直线A B ''的解析式;(2)若直线A B ''与直线l 相交于点C ,求A BC '△的面积.CO图4BDAFD 图5E C AB 图6CA y x OlA 'B '20.某过街天桥的截面图为梯形,如图7所示,其中天桥斜面CD 的坡度为1:3i =(1:3i =是指铅直高度DE 与水平宽度CE 的比),CD 的长为10m ,天桥另一斜面AB 坡角ABG ∠=45°.(1)写出过街天桥斜面AB 的坡度; (2)求DE 的长;(3)若决定对该过街天桥进行改建,使AB 斜面的坡度变缓,将其45°坡角改为30°, 方便过路群众,改建后斜面为AF .试计算此改建需占路面的宽度FB 的长(结果精确0.01)Ⅲ.(本题满分23分,第21题11分,第22题12分)21.2010年5月中央召开了新疆工作座谈会,为实现新疆跨越式发展和长治久安,作出了重 要战略决策部署.为此我市抓住机遇,加快发展,决定今年投入5亿元用于城市基础设施 维护和建设,以后逐年增加,计划到2012年当年用于城市基础设施维护与建设资金达到 8.45亿元.(1)求从2010年至2012年我市每年投入城市基础设施维护和建设资金的年平均增长率; (2)若2010年至2012年我市每年投入城市基础设施维护和建设资金的年平均增长率相同, 预计我市这三年用于城市基础设施维护和建设资金共多少亿元?22.2010年6月4日,乌鲁木齐市政府通报了首府2009年环境质量公报,其中空气质量级别分布统计图如图8所示,请根据统计图解答以下问题:(1)写出2009年乌鲁木齐市全年三级轻度污染天数:(2)求出空气质量为二级所对应扇形圆心角的度数(结果保留到个位);(3)若到2012年,首府空气质量良好(二级及二级以上)的天数与全年天数(2012年是闰年,全年有366天)之比超过85%,求2012年空气质量良好的天数要比2009年至少增加多少天?Ⅳ.(本题满分10分)23.已知二次函数2(0)y ax bx c a =++≠的图象经过(00)(1)O M ,,,1和()(0)N n n ≠,0 三点.(1)若该函数图象顶点恰为点M ,写出此时n 的值及y 的最大值;(2)当2n =-时,确定这个二次函数的解析式,并判断此时y 是否有最大值; (3)由(1)、(2)可知,n 的取值变化,会影响该函数图象的开口方向.请你求出n 满足 什么条件时,y 有最小值?F AB G D E C图7图8Ⅴ.(本题满分12分)24.如图9,边长为5的正方形OABC 的顶点O 在坐标原点处,点A C 、分别在x 轴、y 轴 的正半轴上,点E 是OA 边上的点(不与点A 重合),EF CE ⊥,且与正方形外角平分 线AC 交于点P .(1)当点E 坐标为(30),时,试证明CE EP =;(2)如果将上述条件“点E 坐标为(3,0)”改为“点E 坐标为(t ,0)(0t >)”,结论 CE EP =是否仍然成立,请说明理由;(3)在y 轴上是否存在点M ,使得四边形BMEP 是平行四边形?若存在,用t 表示点M 的坐标;若不存在,说明理由.数学试题参考答案及评分标准一、选择题(本大题共10小题,每小题4分,共40分)题号 1 2 3 4 5 6 7 8 9 10 答案 ADBCCDBCDA二、填空题(本大题共5小题,每小题4分,共20分)11.0 12.55° 13. 1 14. 231y y y <<或132y y y >> 15.115三、解答题(本大题1-V 题,共9小题,共90分) 16.解:由(1)得:440x x +<<, ··························································································· 2′由(2)得:3351x x x -+><-, ·················································································· 4′ ∴不等式组的解集是:1x <- ··························································································· 6′ 17.解:原式=()2111111a a a a a +--++-································································································ 3′ =1111a a -+- ············································································································· 4′ =221a -- ···················································································································· 7′当2a =时,原式=()22221-=-- ····································································· 9′ 18. 证明:(1)∵四边形ABCD 是平行四边形,∴A C AB CD ABC ADC ∠=∠=∠=∠,,∵BE 平分ABC ∠,DF 平分ADC ∠,∴ABE CDF ∠=∠ ································ 2′ ∴()ABE CDF ASA △≌△ ·················································································· 4′ (2)由ABE CDF △≌△,得AE CF = ····································································· 5′ 在平行四边形ABCD 中,AD BC AD BC =∥,∴DE BF DE BF =∥,∴四边形EBFD 是平行四边形 ··············································································· 6′ 若BD EF ⊥,则四边形EBFD 是菱形 ··································································· 8′19.解:(1)由直线l :443y x =-+分别交x 轴、y 轴于点A B 、,可知;()()3004A B ,,,∵AOB △绕点O 顺时针旋转90°而得到A OB ''△ ∴AOB A OB ''△≌△故()()0340A B ''-,,, ······································································································· 2′ 设直线A B ''的解析式为y kx b =+(0k k b ≠,,为常数)∴有340b k b =-⎧⎨+=⎩解之得:343k b ⎧=⎪⎨⎪=-⎩∴直线A B ''的解析式为334y x =- ·················································································· 5′ (2)由题意得:334443y x y x ⎧=-⎪⎪⎨⎪=-+⎪⎩解之得:84251225x y ⎧=⎪⎪⎨⎪=-⎪⎩∴84122525C ⎛⎫- ⎪⎝⎭, ··················································· 9′ 又7A B '=∴184294722525A CB S =⨯⨯=△′ ···························································································· 11′ 20.解:(1)在Rt AGB △中,45ABG ∠=° ∴AG BG =∴AB 的坡度=1AGBG= ······································································································· 2′ (2)在Rt DEC △中,∵3tan 3DE C EC ∠==∴30C ∠=° 又∵10CD = ∴()15m 2DE CD == ······································································· 5′ (3)由(1)知,5AG BG ==,在Rt AFG △中,30AFG ∠=°tan AGAFG FG∠=,即3535FB =+ ········································································· 7′ 解得535 3.66FB =-≈ ························································································ 10′答:改建后需占路面宽度约为3.66m. ···································································· 11′21.解:(1)设从2010至2012年我市每年投入城市基础设施维护和建设资金的年平均增长率为x ,由题意得:()2518.45x += ······························································································ 3′解得,1230% 2.3x x ==-,(不合题意舍去) ····························································· 6′答:从2010至2012年我市每年投入城市基础设施维护和建设资金的年平均增长率为30%. ··························································································································································· 7′(2)这三年共投资()5518.45x +++()5510.38.4519.95=+++=(亿元) ······························································· 10′ 答:预计我市这三年用于城市建设基础设施维护和建设资金共19.95亿元 ··············· 11′ 22. 解:(1)21.6%36578.8479⨯=≈(天) ······································································ 2′(2)()19.0% 2.7% 3.9%21.6%360-+++⨯⎡⎤⎣⎦°226.08=°226≈° ···················································································································· 5′ (3)设到2012年首府空气质量良好的天数比2009年增加了x 天,由题意得:()9.0%36562.8%36585%365x +⨯+⨯>···························································· 8′49.03x > ············································································································ 10′ 由题意知x 应为正整数,∴50x ≥ ································································ 11′答:2012年首府空气质量良好的天数比2009年首府空气质量良好的天数至少增加50天. ················································································································ 12′23.解:(1)由二次函数图象的对称性可知2n =;y 的最大值为1. ··································· 2′(2)由题意得:1420a b a b +=⎧⎨-=⎩,解这个方程组得:1323a b ⎧=⎪⎪⎨⎪=⎪⎩故这个二次函数的解析式为21233y x x =+ ···························································· 5′ ∵103> ∴y 没有最大值. ·················································································· 6′ (3)由题意,得210a b an bn +=⎧⎨+=⎩,整理得:()210an a n +-= ·································· 8′∵0n ≠ ∴10an a +-=故()11n a -=,而1n ≠ 若y 有最小值,则需0a > ∴10n -> 即1n <∴1n <时,y 有最小值. ························································································· 10′24.解:(1)过点P 作PH x ⊥轴,垂足为H∴2190∠=∠=° ∵EF CE ⊥ ∴34∠=∠ ∴COE EHP △∽△ARHOM Cy BGPFx∴CO EHOE HP=················································· 2′ 由题意知:5CO = 3OE = 2EH EA AH HP =+=+ ∴523HP HP += 得3HP = ∴5EH = ·························································································································· 3′ 在Rt COE △和Rt EHP △中∴2234CE CO OE =+= 2234EP EH PH =+=故CE EP = ······················································································································· 5′ (2)CE EP =仍成立.同理.COE EHP △∽△ ∴CO EHOE HP=········································································ 6′ 由题意知:5CO = OE t = 5EH t HP =-+ ∴55t HP t HP-+= 整理得()()55t HP t t -=- ∵点E 不与点A 重合 ∴50t -≠ ∴HP t = 5EH = ∴在Rt COE △和Rt EHP △中225CE t =+ 225EP t =+ ∴CE EP = ··························································· 5′ (3)y 轴上存在点M ,使得四边形BMEP 是平行四边形. ············································· 9′过点B 作BM EP ∥交y 轴于点M ∴590CEP ∠=∠=° ∴64∠=∠在BCM △和COE △中64BC OCBCM COE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BCM COE △≌△ ∴BM CE = 而CE EP = ∴BM EP =由于BM EP ∥ ∴四边形BMEP 是平行四边形. ················································ 11′ 故BCM COE △≌△可得CM OE t == ∴5OM CO CM t =-=-故点M 的坐标为()05t -, ···························································································· 12′。
2010年新疆中考数学试卷综合解读与评析---2011.3.28

2010新疆数学中考试卷综合解读与评析2010年的新疆中考数学试题遵循《数学课程标准》中有关评价的基本理念,既重视对学生数学知识与技能的结果和过程的评价,也重视对学生运用数学解决日常生活中问题能力的评价。
充分体现以学生为本的精神,努力实现数学学科的基础性,着眼于全体学生的发展。
试卷的编制较好地考查了学生对基础知识和基本技能和基本数学思想方法的理解和掌握情况;整份试卷体现了素质教育的要求,体现出了“重视基础,关注思想,加强应用,发展能力”的试题特征;体现出了与学业考试的目标指向“有利于课改,有利于减负,有利于教育均衡”一致.一、卷面分析1、试卷结构分析2010年新疆中考数学学业考试试题有客观性和主观性试题两部分组成,满分150分。
考试时间120分钟。
共三道大题,24道小题。
就考试内容分布来看,试题以初中学段的知识与技能为基准,选取的内容有较好的代表性;试题的设计充分考虑了整卷阅读量的合理性;试卷的语言、图形、文字能关注学生特点;试题的背景突出公平性;试题的难易呈现一定的坡度,既考虑到了衡量学生是否达到课程标准所规定的水平,又起到了升学考试的选拔功能。
2、试题特征⑴重视对数学核心内容的考查表三:2010新疆中考数学考查内容分布表⑵重视思想方法、数学能力的考查数学思想、数学方法是数学的灵魂,是知识转化为能力的桥梁,是培养学生数学思维能力、分析问题解决问题能力和继续学习能力的重要环节。
今年试题重视对这部分内容的考查,很好地突出了试题的选拔功能。
如:第19题体现方程思想;第19、21题体现化归思想;第7、10、12、14、22、24题体现数形结合思想;第22题体现分类讨论思想;第19、22、24题体现建模思想。
第7题需要学生结合条件画出符合题目的草图考查学生的数形结合思想,或采用特殊值法。
第10题需要学生根据所给出的数轴得出不等式的解集,体现了数形结合的数学思想。
第12题需要学生根据所给图形的面积等量关系转化为完全平方公式,体现了数形结合的数学思想。
新疆自治区中考数学试题含答案

年新疆中考数学试卷一、选择题(每小题分,共分).(分)如图所示,点表示的数是().(分)(•柳州)若分式有意义,则的取值范围是()能使得△的面积为的概率为()的人数比甲班的人数多人;③甲班每人植树数是乙班每人植树数的.若设甲班人数为人,求两班人数分二、填空题(每小题分,共分).(分)分解因式:﹣..(分)(•新疆)请你写出一个主视图与左视图相同的立体图形是..(分)(•绥化)当时,二次函数﹣有最小值..(分)(•嘉兴)如图,∠∠°,,,,则..(分)(•新疆)某校九年级一班班长统计去年~月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,这组数据的中位数是..(分)(•新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积,π,则是.三、解答题(共分).(分)(•新疆)计算:..(分)(•新疆)先化简,然后从﹣≤≤的范围内选择一个合适的整数作为的值代入求值..(分)(•新疆)如图,一次函数﹣的图象与反比例函数的图象交于(,).()求,的值;()根据图象,请写出当取何值时,一次函数的值小于反比例函数的值..(分)如图,在矩形中,以顶点为圆心、边长为半径作弧,交边于点,连接,过点作⊥于.猜想线段与图中现有的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.猜想:..(分)(•新疆)如图,跷跷板的一端碰到地面时,与地面的夹角为°,且.()求此时另一端离地面的距离(精确到);()若跷动,使端点碰到地面,请画出点运动的路线(不写画法,保留画图痕迹),并求出点运动路线的长.(参考数据:°≈,°≈,°≈).(分)(•新疆)为了解“阳光体育”活动情况,我市教育部门在市三中名学生中,随机抽取了若干学生进行问卷调查(要求每位学生只能填写一种自己喜欢的活动),并将调查的结果绘制成如图的两幅不完整的统计图:根据以上信息解答下列问题:()参加调查的人数共有人;在扇形图中,表示“”的扇形的圆心角为度;()补全条形统计图,并计算扇形统计图中的;()若要从该校喜欢“”项目的学生中随机选择名,则喜欢该项目的小华同学被选中的概率是多少?.(分)(•新疆)某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的,两种长方体形状的无盖纸盒.现有正方形纸板张,长方形纸板张,刚好全部用完,问能做成多少个型盒子?多少个型盒子?()根据题意,甲和乙两同学分别列出的方程组如下:甲:;乙:,根据两位同学所列的方程组,请你分别指出未知数,表示的意义:甲:表示,表示;乙:表示,表示;()求出做成的型盒子和型盒子分别有多少个(写出完整的解答过程)?.(分)(•新疆)如图,圆内接四边形,是⊙的直径,⊥于.()请你写出四个不同类型的正确结论;()若,,求..(分)(•新疆)库尔勒某乡,两村盛产香梨,村有香梨吨,村有香梨吨,现将这些香梨运到,两个冷藏仓库.已知仓库可储存吨,仓库可储存吨,从村运往,两处的费用分别为每吨元和元;从村运往,两处的费用分别为每吨元和元.设从村运往仓库的香梨为吨,,两村运香梨往两仓库的运输费用分别为元,元.()请问怎样调运,才能使两村的运费之和最小?求出最小值..(分)(•新疆)如图,在直角坐标系中,已知△的两个顶点坐标分别为(,),(,).()请你以的中点为对称中心,画出△的中心对称图形△,此图与原图组成的四边形的形状是,请说明理由;()如图,已知(,),过,,的抛物线与()所得的四边形的边交于点,求抛物线的解析式及点的坐标;()在问题()的图形中,一动点由抛物线上的点开始,沿四边形的边从﹣﹣向终点运动,连接交于,若运动所经过的路程为,试问:当为何值时,△为等腰三角形(只写出判断的条件与对应的结果)?年新疆中考数学试卷参考答案与试题解析一、选择题(每小题分,共分).(分)如图所示,点表示的数是().(分)(•柳州)若分式有意义,则的取值范围是()﹣,故本选项正确;析:能使得△的面积为的概率为()÷.的人数比甲班的人数多人;③甲班每人植树数是乙班每人植树数的.若设甲班人数为人,求两班人数分甲班每人植树数是乙班每人植树数的根据题意得×.(分)(•嘉兴)如图,∠∠°,,,,则.绘制了如图所示的折线统计图,这组数据的中位数是.故这组数据的中位数..(分)(•新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积,π,则是.,变形后得到,将已知的与代入,,即()π(π(,﹣π故答案为:.(分)(•新疆)计算:..(分)(•新疆)先化简,然后从﹣≤≤的范围内选择一个合适的整数作为的(﹣÷÷•,若时,原式;若﹣时,原式﹣..(分)(•新疆)如图,一次函数﹣的图象与反比例函数的图象交于(,).()求,的值;()根据图象,请写出当取何值时,一次函数的值小于反比例函数的值.)代入,得;图中现有的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.猜想:...(分)(•新疆)如图,跷跷板的一端碰到地面时,与地面的夹角为°,且.()求此时另一端离地面的距离(精确到);()若跷动,使端点碰到地面,请画出点运动的路线(不写画法,保留画图痕迹),并求出点运动路线的长.(参考数据:°≈,°≈,°≈)的长.是的中点,.问卷调查(要求每位学生只能填写一种自己喜欢的活动),并将调查的结果绘制成如图的两幅不完整的统计图:根据以上信息解答下列问题:()参加调查的人数共有人;在扇形图中,表示“”的扇形的圆心角为度;()补全条形统计图,并计算扇形统计图中的;故所表示的扇形的圆心角为××人,.纸盒.现有正方形纸板张,长方形纸板张,刚好全部用完,问能做成多少个型盒子?多少个型盒子?()根据题意,甲和乙两同学分别列出的方程组如下:甲:;乙:,根据两位同学所列的方程组,请你分别指出未知数,表示的意义:甲:表示型盒个数,表示型盒个数;乙:表示型纸盒中正方形纸板的个数,表示型纸盒中正方形纸板的个数;()求出做成的型盒子和型盒子分别有多少个(写出完整的解答过程)?()设型盒有个,型盒子有个,解得:()请你写出四个不同类型的正确结论;()若,,求.为的中点,即,;.(分)(•新疆)库尔勒某乡,两村盛产香梨,村有香梨吨,村有香梨吨,现将这些香梨运到,两个冷藏仓库.已知仓库可储存吨,仓库可储存吨,从村运往,两处的费用分别为每吨元和元;从村运往,两处的费用分别为每吨元和元.设从村运往仓库的香梨为吨,,两村运香梨往两仓库的运输费用分别为元,元.()请你以的中点为对称中心,画出△的中心对称图形△,此图与原图组成的四边形的形状是正方形,请说明理由;()如图,已知(,),过,,的抛物线与()所得的四边形的边交于点,求抛物线的解析式及点的坐标;()在问题()的图形中,一动点由抛物线上的点开始,沿四边形的边从﹣﹣向终点运动,连接交于,若∴四边形是正方形;(,解得﹣,,∴点的坐标为(,∴∵,∴﹣﹣.此时点运动的路程为:﹣﹣(﹣)﹣;.此时点到达终点,综上所述,当,﹣利于基础扎实的考生获得好成绩.。
2010年新疆建设兵团中考数学试卷(全解全析)

2010年新疆建设兵团中考数学试卷(全解全析)[键入文字]一、选择题(共8小题,每小题5分,满分40分)1、(2010•新疆)﹣8的相反数是()A、8B、﹣8C 、D 、﹣考点:相反数。
分析:根据相反数的概念,互为相反数的两个数和为0,即可得出答案.解答:解:根据概念可知﹣8+(﹣8的相反数)=0,所以﹣8的相反数是8.故选A.点评:主要考查相反数概念.相反数的定义:只有符号不同的两个数互为相反数,0的相反数是0.2、(2010•新疆)化简(﹣a2)3的结果是()A、﹣a5B、a5C、﹣a6D、a6考点:幂的乘方与积的乘方。
分析:根据积的乘方,把每一个因式分别乘方,再把所得的幂相乘;幂的乘方,底数不变指数相乘,计算后直接选取答案.解答:解:(﹣a2)3=(﹣1)3•(a2)3=﹣a6.故选C.点评:本题考查积的乘方的性质和幂的乘方的性质,熟练掌握性质是解题的关键.3、(2010•新疆)如图,顽皮的小聪课间把教师的直角三角板的直角顶点放在黑板的a两条平行线a,b上,已知∠1=55°,则∠2的度数为()A、35°B、45°C、55°D、125°考点:平行线的性质。
分析:如图,由a∥b得到∠1=∠3,而∠ACB=90°,由此可以求出∠2的度数.解答:解:∵a∥b,∴∠1=∠3=55°,∵∠ACB=90°,∴∠2=180°﹣∠3﹣∠ACB=180﹣55°﹣90°=35°.故选A.A、1B、C、D、考点:概率公式。
分析:从十名学生中选一名参加世博会,小军被选中的概率是.解答:解:把这十名学生排列序号1,2,3,4,5,6,7,8,9,10,学生选一名有十种情况,选一名就是;故选C.点评:本题考查概率的计算公式,用到的知识点为:概率等于所求情况数与总情况数之比.6、(2010•新疆)如图1是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图2,那么在Rt△ABC中,sin∠B 的值是()A、B、C、1D、考点:解直角三角形;等边三角形的性质。
2010年新疆初中毕业生升学文化课考试数学模拟试卷.doc

2010年新疆初中毕业生升学文化课考试数学模拟试卷本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题. 本试卷满分为120分,考试时间为120分钟.卷Ⅰ(选择题,共20分)注意事项:1.答卷Ⅰ前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上,考试结束,监考人员将试卷和答题卡一并收回.2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(08河北)8-的倒数是( ) A .8B .8-C .18D .18-2.(08河北)计算223a a +的结果是( ) A .23aB .24aC .43aD .44a3.(08河北)把某不等式组中两个不等式的解集表示在数轴上,如图1则这个不等式组可能是( ) A .41x x >⎧⎨-⎩,≤B .41x x <⎧⎨-⎩,≥C .41x x >⎧⎨>-⎩,D .41x x ⎧⎨>-⎩≤,4.(08河北)据河北电视台报道,截止到2008年5月21日,河北慈善总会已接受支援汶川地震灾区的捐款15 510 000元.将15 510 000用科学记数法表示为( ) A .80.155110⨯ B .4155110⨯C .71.55110⨯D .615.5110⨯5.(08河北)图2中的两个三角形是位似图形,它们的位似中心是( A .点P B .点O C .点M D .点N6.(08河北)某县为发展教育事业,加强了对教育经费的投入,2007年投入3 000万元,预计2009年投入5 000万元.设教育经费的年平均增长率为x ,根据题意,下面所列方程正确的是( ) A .23000(1)5000x += B .230005000x =C .23000(1)5000x +=%D .23000(1)3000(1)5000x x +++=7.(08河北)如图3,已知O 的半径为5,点O 到弦AB 的距离为3,则到弦AB 所在直线的距离为2的点有( )A .1个B .2个C .3个D .4个8.(08河北)同时抛掷两枚质地均匀的正方体骰子(骰子每个面上的点数分别为1,2,3,4,5,6).下列事件中是必然事件的是( )图1图2 图3A .两枚骰子朝上一面的点数和为6B .两枚骰子朝上一面的点数和不小于2C .两枚骰子朝上一面的点数均为偶数D .两枚骰子朝上一面的点数均为奇数 9.(08河北)如图4,正方形ABCD 的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上,且它们的各边与正方形ABCD 各边平行或垂直.若小正方形的边长为x ,且010x <≤,阴影部分的面积为y ,则能反映y 与x 之间函数关系的大致图象是( )10.(08河北)有一个四等分转盘,在它的上、右、下、左的位置分别挂着“众”、“志”、“成”、“城”四个字牌,如图5-1.若将位于上下位置的两个字牌对调,同时将位于左右位置的两个字牌对调,再将转盘顺时针旋转90,则完成一次变换.图5-2,图5-3分别表示第1次变换和第2次变换.按上述规则完成第9次变换后,“众”字位于转盘的位置是( )A .上B .下C .左D .右2008年河北省初中毕业生升学文化课考试数学试卷卷Ⅱ(非选择题,共100分)注意事项:1.答卷Ⅱ前,将密封线左侧的项目填写清楚.2.答卷Ⅱ时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题(本大题共8个小题;每小题3分,共24分.把答案写在题中横线上)11.(08河北)如图6,直线a b ∥,直线c 与a b , 相交.若170∠=, 则2_____∠=.12.(08河北)当x = 时,分式31x -无意义. 13.(08河北)若m n ,互为相反数,则555m n +-= . 14.(08河北)如图7,AB 与O 相切于点B ,AO 的延长线交O 连结BC .若36A ∠=,则______C ∠=.15.(08河北)某班学生理化生实验操作测试成绩的统计结果如下表:图4 x A . x B . x C . xD . 图5-1图5-2 图5-3 …1 2 ba图6 c图7则这些学生成绩的众数为 . 16.(08河北)图8每个果冻的质量也相等,则一块巧克力的质量是 g.17.(08河北)点(231)P m -,在反比例函数1y x=的图象上,则m =18.(08河北)图9-1全等的直角三角形围成的.若6AC =,5BC =,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图9-2所示的“数学风车”三、解答题(本大题共8个小题;共76分.解答应写出文字说明、证明过程或演算步骤) 19.(08河北)(本小题满分7分)已知2x =-,求21211x x x x -+⎛⎫-÷ ⎪⎝⎭的值.20.(08河北)(本小题满分8分)某种子培育基地用A ,B ,C ,D 四种型号的小麦种子共2 000粒进行发芽实验,从中选出发芽率高的种子进行推广.通过实验得知,C 型号种子的发芽率为95%,根据实验数据绘制了图10-1和图10-2两幅尚不完整的统计图.(1)D 型号种子的粒数是 ; (2)请你将图10-2的统计图补充完整;(3)通过计算说明,应选哪一个型号的种子进行推广;(4)若将所有已发芽的种子放到一起,从中随机取出一粒,求取到B 型号发芽种子的概率.21.(08河北)(本小题满分8分)ABC图9-1 图8A35% B20% C 20% D 各型号种子数的百分比 图10-1 图10-2如图11,直线1l 的解析表达式为33y x =-+,且1l 与x 轴交于点D ,直线2l 经过点A B ,,直线1l ,2l 交于点C .(1)求点D 的坐标; (2)求直线2l 的解析表达式; (3)求ADC △的面积;(4)在直线2l 上存在异于点C 的另一点P ,使得ADP △与ADC △的面积相等,请直接..写出点P 的坐标.22.(08河北)(本小题满分9分)气象台发布的卫星云图显示,代号为W 的台风在某海岛(设为点O )的南偏东45方向的B 点生成,测得OB =.台风中心从点B 以40km/h 的速度向正北方向移动,经5h 后到达海面上的点C 处.因受气旋影响,台风中心从点C 开始以30km/h 的速度向北偏西60方向继续移动.以O 为原点建立如图12所示的直角坐标系.(1)台风中心生成点B 的坐标为 ,台风中心转折点C 的坐标为 ;(结果保留根号)(2)已知距台风中心20km 的范围内均会受到台风的侵袭.如果某城市(设为点A )位于点O 的正北方向且处于台风中心的移动路线上,那么台风从生成到最初..侵袭该城要经过多长时间?23.(08河北)(本小题满分10分)在一平直河岸l 同侧有A B ,两个村庄,A B ,到l 的距离分别是3km 和2km ,km AB a =(1)a >.现计划在河岸l 上建一抽水站P ,用输水管向两个村庄供水.方案设计某班数学兴趣小组设计了两种铺设管道方案:图13-1是方案一的示意图,设该方案中管道长度为1d ,且1(km)d PB BA =+(其中BP l ⊥于点P );图13-2是方案二的示意图,设该方案中管道长度为2d ,且2(km)d PA PB =+(其中点A '与点A 关于l 对称,A B '与l 交于点P ).图11C 6045观察计算(1)在方案一中,1d = km (用含a 的式子表示);(2)在方案二中,组长小宇为了计算2d 的长,作了如图13-3所示的辅助线,请你按小宇同学的思路计算,2d = km (用含a 的式子表示). 探索归纳(1)①当4a =时,比较大小:12_______d d (填“>”、“=”或“<”); ②当6a =时,比较大小:12_______d d (填“>”、“=”或“<”);(2)请你参考右边方框中的方法指导,就a (当1a >时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?24.(08河北)(本小题满分10分)如图14-1,ABC △的边BC 在直线l 上,AC BC ⊥,且AC BC =;EFP △的边FP 也在直线l 上,边EF 与边AC 重合,且EF FP =.(1)在图14-1中,请你通过观察、测量,猜想并写出AB 与AP 所满足的数量关系和位置关系; (2)将EFP △沿直线l 向左平移到图14-2的位置时,EP 交AC 于点Q ,连结AP ,BQ .猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;(3)将EFP △沿直线l 向左平移到图14-3的位置时,EP 的延长线交AC 的延长线于点Q ,连结AP ,BQ .你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.图13-1 图13-2图13-3可以对它们的平方进行比较:2m n 2-=22()m n ∴-当22m n -当22m n -25.(08河北)(本小题满分12分)研究所对某种新型产品的产销情况进行了研究,为投资商在甲、乙两地生产并销售该产品提供了如下成果:第一年的年产量为x (吨)时,所需的全部费用y (万元)与x 满足关系式2159010y x x =++,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p 甲,p 乙(万元)均与x 满足一次函数关系.(注:年利润=年销售额-全部费用)(1)成果表明,在甲地生产并销售x 吨时,11420p x =-+甲,请你用含x 的代数式表示甲地当年的年销售额,并求年利润w 甲(万元)与x 之间的函数关系式; (2)成果表明,在乙地生产并销售x 吨时,110p x n =-+乙(n 为常数),且在乙地当年的最大年利润为35万元.试确定n 的值;(3)受资金、生产能力等多种因素的影响,某投资商计划第一年生产并销售该产品18吨,根据(1),(2)中的结果,请你通过计算帮他决策,选择在甲地还是乙地产销才能获得较大的年利润?参考公式:抛物线2(0)y ax bx c a =++≠的顶点坐标是2424b ac b aa ⎛⎫-- ⎪⎝⎭,.26.(08河北)(本小题满分12分)如图15,在Rt ABC △中,90C ∠=,50AB =,30AC =,D E F ,,分别是AC AB BC ,,的中点.点P 从点D 出发沿折线DE EF FC CD ---以每秒7个单位长的速度匀速运动;点Q 从点B 出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q 作射线QK AB ⊥,交折线BC CA -于点G .点P Q ,同时出发,当点P 绕行一周回到点D 时停止运动,点Q 也随之停止.设点P Q ,运动的时间是t 秒A (E )BC (F ) PllB FC 图14-1图14-2图14-3(0t >).(1)D F ,两点间的距离是 ;(2)射线QK 能否把四边形CDEF 分成面积相等的两部分?若能,求出t 的值.若不能,说明理由; (3)当点P 运动到折线EF FC -上,且点P 又恰好落在射线QK 上时,求t 的值; (4)连结PG ,当PG AB ∥时,请直接..写出t 的值.图152008年河北省初中毕业生升学文化课考试数学试题参考答案11.70; 12,1; 13.5-; 14.27;15.9分(或9);16.20; 17.2; 18.76. 三、解答题 19.解:原式21(1)x xx x -=⨯- 11x =-. 当2x =-时,原式13=-.20.解:(1)500; (2)如图1;(3)A 型号发芽率为90%,B 型号发芽率为92.5%, D 型号发芽率为94%,C 型号发芽率为95%. ∴应选C 型号的种子进行推广. (4)3701(B )6303703804705P ==+++取到型号发芽种子.21.解:(1)由33y x =-+,令0y =,得330x -+=.1x ∴=.(10)D ∴,. (2)设直线2l 的解析表达式为y kx b =+,由图象知:4x =,0y =;3x =,32y =-. 4033.2k b k b +=⎧⎪∴⎨+=-⎪⎩,326.k b ⎧=⎪∴⎨⎪=-⎩,∴直线2l的解析表达式为362y x =-. (3)由333 6.2y x y x =-+⎧⎪⎨=-⎪⎩,解得23.x y =⎧⎨=-⎩,(23)C ∴-,. 3AD =,193322ADC S ∴=⨯⨯-=△.(4)(63)P ,. 22.解:(1)B -,C -; 图1(2)过点C 作CD OA ⊥于点D ,如图2,则CD =. 在Rt ACD △中,30ACD ∠=,CD =,3cos302CD CA ∴==.200CA ∴=. 20020630-=,5611+=, ∴台风从生成到最初侵袭该城要经过11小时.23.观察计算 (1)2a +; (2. 探索归纳(1)①<;②>;(2)222212(2)420d d a a -=+-=-.①当4200a ->,即5a >时,22120d d ->,120d d ∴->.12d d ∴>; ②当4200a -=,即5a =时,22120d d -=,120d d ∴-=.12d d ∴=; ③当4200a -<,即5a <时,22120d d -<,120d d ∴-<.12d d ∴<.综上可知:当5a >时,选方案二; 当5a =时,选方案一或方案二;当15a <<(缺1a >不扣分)时,选方案一. 24.解:(1)AB AP =;AB AP ⊥. (2)BQ AP =;BQ AP ⊥.证明:①由已知,得EF FP =,EF FP ⊥,45EPF ∴∠=. 又AC BC ⊥,45CQP CPQ ∴∠=∠=.CQ CP ∴=.在Rt BCQ △和Rt ACP △中,BC AC =,90BCQ ACP ∠=∠=,CQ CP =,Rt Rt BCQ ACP ∴△≌△,BQ AP ∴=.②如图3,延长BQ 交AP 于点M .Rt Rt BCQ ACP △≌△,12∴∠=∠./kmC6045lAB FC Q 图3M12 34 EP在Rt BCQ △中,1390∠+∠=,又34∠=∠,241390∴∠+∠=∠+∠=. 90QMA ∴∠=.BQ AP ∴⊥.(3)成立. 证明:①如图4,45EPF ∠=,45CPQ ∴∠=.又AC BC ⊥,45CQP CPQ ∴∠=∠=.CQ CP ∴=.在Rt BCQ △和Rt ACP △中,BC AC =,90BCQ ACP ∠=∠=,CQ CP =,Rt Rt BCQ ACP ∴△≌△.BQ AP ∴=.②如图4,延长QB 交AP 于点N ,则PBN CBQ ∠=∠.Rt Rt BCQ ACP △≌△,BQC APC ∴∠=∠.在Rt BCQ △中,90BQC CBQ ∠+∠=,90APC PBN ∴∠+∠=.90PNB ∴∠=. QB AP ∴⊥.25.解:(1)甲地当年的年销售额为211420x x ⎛⎫-+ ⎪⎝⎭万元; 2399020w x x =-+-甲. (2)在乙地区生产并销售时, 年利润222111590(5)9010105w x nx x x x n x ⎛⎫=-+-++=-+-- ⎪⎝⎭乙. 由214(90)(5)535145n ⎛⎫⨯-⨯--- ⎪⎝⎭=⎛⎫⨯- ⎪⎝⎭,解得15n =或5-. 经检验,5n =-不合题意,舍去,15n ∴=. (3)在乙地区生产并销售时,年利润2110905w x x =-+-乙, lABQP EF图4N C将18x =代入上式,得25.2w =乙(万元);将18x =代入2399020w x x =-+-甲, 得23.4w =甲(万元).w w >乙甲,∴应选乙地.26.解:(1)25. (2)能.如图5,连结DF ,过点F 作FH AB ⊥于点H , 由四边形CDEF 为矩形,可知QK 过DF 的中点O 时,QK 把矩形CDEF 分为面积相等的两部分(注:可利用全等三角形借助割补法或用中心对称等方法说明),此时12.5QH OF ==.由20BF =,HBF CBA △∽△,得16HB =. 故12.5161748t +==. (3)①当点P 在EF 上6(25)7t ≤≤时,如图6.4QB t =,7DE EP t +=,由PQE BCA △∽△,得7202545030t t--=. 21441t ∴=. ②当点P 在FC 上6(57)7t ≤≤时,如图7. 已知4QB t =,从而5PB t =,由735PF t =-,20BF =,得573520t t =-+. 解得172t =. (4)如图8,213t =;如图9,39743t =. (注:判断PG AB ∥可分为以下几种情形:当6027t <≤时,点P 下行,点G 上行,可知其中存在PG AB ∥的时刻,如图8;此后,点G 继续上行到点F 时,4t =,而点P 却在下行到点E 再沿EF 上行,发现点P 在EF 上运动时不存在PG AB ∥;当6577t ≤≤时,点P G ,均在FC 上,也不存在PG AB ∥;由于点P 比点G 先到达点C 并继续沿CD 下行,所以在6787t <<中存在PG AB ∥的时刻,如图9;当810t ≤≤时,点P G ,均在CD 上,不存在PG AB ∥)E B图5B图6E B图7B图8B图9情感语录1.爱情合适就好,不要委屈将就,只要随意,彼此之间不要太大压力2.时间会把最正确的人带到你身边,在此之前,你要做的,是好好的照顾自己3.女人的眼泪是最无用的液体,但你让女人流泪说明你很无用4.总有一天,你会遇上那个人,陪你看日出,直到你的人生落幕5.最美的感动是我以为人去楼空的时候你依然在6.我莫名其妙的地笑了,原来只因为想到了你7.会离开的都是废品,能抢走的都是垃圾8.其实你不知道,如果可以,我愿意把整颗心都刻满你的名字9.女人谁不愿意青春永驻,但我愿意用来换一个疼我的你10.我们和好吧,我想和你拌嘴吵架,想闹小脾气,想为了你哭鼻子,我想你了11.如此情深,却难以启齿。
2010年中考数学试卷分析

• 2、科学训练、规范解题过程 • 在帮助学生梳理课本知识点,形成知识体系 的基础上,要进行一定量的做题训练,加强知 识的应用。在解题训练时,教师应该运用变式 训练,改变问题呈现方式的方法,将学生从思 维定式中解脱出来,养成学生多角度多侧面分 析问题的思路,以培养学生思维的广阔性,缜 密性和创新性,同时要重视对学生解题步骤和 格式的规范要求,以保证考试时会做的题目不 失分。
• 2、突出数学本质,关注数学思想 • 去年的试卷突出考查了学生在学习数学和 运用数学解决问题过程中最为重要的,必须 掌握的思想方法和基本概念和常用技能,如 试卷第14小题 24小题的第三问,充分考查 了函数中的数形结合思想,利用所给图象及 根据题意所得函数简图可以直接得到正确答 案。第23、24题是综合性较强的题目,考查 动点问题及函数解析式的求法,考查分类讨 论思想,数形结合思想,方程思想,对学生 的能力是一个集中的考查。
• 二O一O年新疆中考数学考查内容分布表
考查内容
实数及其运算
数与代数 整式运算 方程与不等式 函数问题
题号
1 、4 、9、
2 、12、16、 10、15、 19、 7、5、6、 5、6、8 5、5、10
总计
15
16 19 20
几何视图与投影
几何图形的对称 三角形中角度计算 空间与图形
13、
17、 3
5、
6、 5
5
6 5
三角形全等的判断与性质
三角形相似的条件探索 特殊四边形的判定 解直角三角形的应用 圆中的证明与计算
21、
23、 0 6 8、21、 1、18、 11、20、
4、
10、 0 5 5、4、 5 、 6、 5、8、
4
10 0 5 9 11 13
2010年新疆中考数学试题及答案
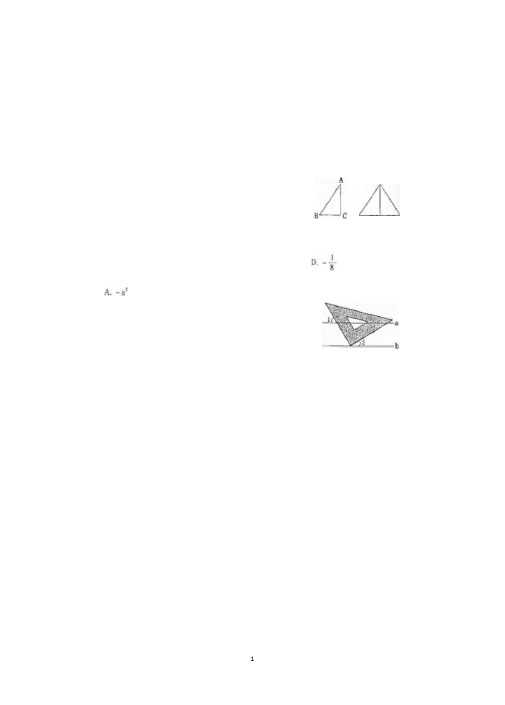
如们图,王大亡家屋后有一块怅宽8m的矩形空地,他在氏BC 处直径的半圆内种突,他家养的一只羊平时拴在A赴’为了不让羊吃到菜'拴羊的绳长可以选用A-3ni B.5m C.7m D.9m二、合理填空(左丸题共6小题,每小題5旅共30分)乩化简vis = _D 2写出右图中所表示的不等式组的解集: _______ 。
一人「丄11■甲、乙两位梶农种植的棉花■连续五年的单检面积产量~ 2 ^ o ! z (千克/亩)统计如下启,则产敖较稳定的是棉农 ____ o(填甲戎乙)1匕列用1个axa的正方形J个b xb的正方形和2个axb的雄彫可拼成一个正方形(如图所示人从而可得到因式分解的公式 _____ 。
13.长方体的主视图和左视图如下閤胖示(单・见1其俯视图的面积是______ 凹化14.抛物裁y = d +bx + c的部分图象如图所示•若y则x的取值范围是-------- 0三、准鳩黑答(本尢题共有⑴题,共閃沁15.(6分)解方程:釜"-7x +6 =016.(6分)先化简,再求值«右■芒)骨三I’其中―再+ 1(第L3题图》(第12起主視14171筒分)用四埃如下图(】)斯示的正方形卡片密成一个就的正方形,便拼咸的图案是一个轴对称圏形,清你在图(2)、图(3)、图(4)中各同出_种拼法(粪求三样彥法各不栢zoio^dtaE.朗刊中字我松苇试或爹试暫老鄴臾知虫他(6分)小王将一黑一白两双祎同号码的袜子一只一只地扔进捕屉里占他随愆从抽曜 里拿出两只袜子时,恰好成取与不成双的机会是芬少?请你用树影图求解。
19-(8分)2010年4月14日我国讶海玉树地区发生强烈地震,急需大益歸灾帐篷。
某帐篷主产企业按到任务后,加大生产投人謳高生产效率•实际每天生产祗瘵比原计划各 200顶,现在生产2000顶帐篷所用的时间与原计划生产2000顶的时间相同。
现在该 金业每夭能生产多少顶帐遥?2広(&分)某瓜果销售公司去年3月至X 月销售库尔勒香梨、哈巒瓜的情况见下坯:3月4月 5月 6月 7月 塔月 1库尔勒香梨(吨)4 85 S 2 13 喑密瓜(吨)8797107(1(阴谭你瑕据下面两个要求跨迪两种几果在去年3月儉至8月份的甫售情况进行分折:① 根据平均数和方差为析;② 根摇折线图上两种瓜祟销售樂的趋势分圻. 21. 〈8分)匮心角都是90°的堀形AOB 与扇形COD 如图所示那样衽放在一起,连结AC.BD (1)求证:AAOC iABOD ;(Z )若AO =3cm OG “cm 求阴影部分的面积口22.(1D 分)如图(1)「其灌魁设备的哽头B 高出地面L25m,^i±的挝舫线形水流在与喷 头底部A 的距藹为lm 处达到距定面最大髙度£ 25m,试在恰当绝直角坐标系中求出 与该菟物线水流对应的二次画数关系式*学生小龙在解答圏(1〉折示的间题吋,具体解答如下:及氷淀的蛊高点为恿点,迂原点們加平线为横轴,辻原点的辂矗统为埶軸,建止平均数 方差—库尔勒香梨89 哈密瓜t 1(2)卄全右面折统统计图;B(第n 題图) 1.25m如图(2)迥0年自怡区、兵団初中栄业水圧序试散学试题卷第頊拒1风斯示的平面主角坐祎系;② 设相物践水流甘应的二决岳数关系式为y = ax';③ 楹提題意可得B 点与x 轴旳証离为lm,^B A 的坐林为(-XI ); ④ i 弋入 y = d4?-l*・l,^Uti = * 1 ;⑤ 所以抛物线水廉对应的二次晶数关.系式为y= -x 20 数学老师看了小龙的站題过程说广小龙的辭答是错误的”。
2010年中考数学试题及答案

2010年中考数 学 试 卷*考试时间120分钟 试卷满分150分一、选择题(本大题共7小题,每小题4分,共28分)每题所给的四个选项中只有一项是符合题目要求的,请将所选项的代号字母填在答卷的相应位置处. 1) A. BC.-D2.反比例函数23m y x--=的图象位于( )A .第一、三象限B .第二、四象限C .第二、三象限D .第一、二象限3.从2、3、4、5这四个数中,任取两个数()p q p q ≠和,构成函数2y px y x q =-=+和,并使这两个函数图象的交点在直线2x =的右侧,则这样的有序数对()p q ,共有( ) A .12对 B .6对 C .5对 D .3对4.把多项式2288x x -+分解因式,结果正确的是( ) A .()224x -B .()224x -C .()222x -D .()222x +5.某等腰三角形的两条边长分别为3cm 和6cm ,则它的周长为( ) A .9cm B .12cm C .15cm D .12cm 或15cm6.一次函数y kx b =+(k b ,是常数,0k ≠)的图象如图所示,则不等式0kx b +>的解集是A .2x >-;B .0x >;C .2x <-;D .0x <7.若0a >且2x a =,3y a =,则x ya -的值为( )A .1-B .1C .23D .32二、填空题(本大题共6小题,每小题4分,共24分)把答案直接填在答卷的相应位置处.xb +8.将点(12),向左平移1个单位,再向下平移2个单位后得到对应点的坐标是 .9.幼儿园把新购进的一批玩具分给小朋友.若每人3件,那么还剩余59件;若每人5件,那么最后一个小朋友分到玩具,但不足4件,这批玩具共有 件.10.李师傅随机抽查了本单位今年四月份里6天的日用水量(单位:吨)结果如下:7,8,8,7,6,6,根据这些数据,估计四月份本单位用水总量为 吨.11.我们知道利用相似三角形可以计算不能直接测量的物体的高度,阳阳的身高是1.6m ,他在阳光下的影长是 1.2m ,在同一时刻测得某棵树的影长为 3.6m ,则这棵树的高度约为 m . 12.如图所示的半圆中,AD 是直径,且3AD =,2AC =,则sin B 的值是 .13.某个圆锥的侧面展开图形是一个半径为6cm ,圆心角为︒120的扇形,则这个圆锥的底面半径为______________cm .三、解答题(本大题Ⅰ—Ⅴ题,共10小题,共98分)解答时应在答卷的相应位置处写出文字说明、证明过程或演算过程. Ⅰ.(本题满分12分,第14题6分,第15题6分)14.计算:230116(2)(πtan60)3-⎛⎫--÷-+-- ⎪⎝⎭.15.先化简,再求值:221111121x x x x x +-÷+--+,其中1x =. Ⅱ.(本题满分28分,第16题7分,第17题10分,第18题11分)C BD A16.如图,线段AB 与⊙O 相切于点C ,连结OA ,OB ,OB 交⊙O 于点D ,已知6OA OB ==,AB =(1)求⊙O 的半径; (2)求图中阴影部分的面积.17.响应“家电下乡”的惠农政策,某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台,其中甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超..过.132 000元.已知甲、乙、丙三种电冰箱的出厂价格分别为:1 200元/台、1 600元/台、2 000元/台.(1)至少购进乙种电冰箱多少台?(2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数,则有哪些购买方案?18.甲、乙两名运动员进行长跑训练,两人距终点的路程y (米)与跑步时间x (分)之间C OABD的函数图象如图所示,根据图象所提供的信息解答问题:(1) 他们在进行 米的长跑训练,在0<x <15的时段内,速度较快的人是 ;(2) 求甲距终点的路程y (米)和跑步时间 x (分)之间的函数关系式; (3) 当x =15时,两人相距多少米?在15<x <20的时段内,求两人速度之差.Ⅲ.(本题满分36分,第19题12分,第20题12分,第21题12分)19.把一副扑克牌中的3张黑桃牌(它们的正面牌面数字分别是3、4、5)洗匀后正面朝下放在桌面上.(1)如果从中随机抽取一张牌,那么牌面数字是4的概率是多少?(2)小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽出一张牌,记下牌面数字.当2张牌面数字相同时,小王赢;当2张牌面数字不相同时,小李赢.现请你利用树状图或列表法分析游戏规则对双方是否公平?并说明理由.20.如图,河流两岸a b ,互相平行,C D ,是河岸a 上间隔50m 的两个电线杆.某人在河分)岸b 上的A 处测得30DAB ∠= ,然后沿河岸走了100m 到达B 处,测得60CBF ∠=,求河流的宽度CF 的值(结果精确到个位).21.三个生产日光灯管的厂家在广告中宣称,他们生产的日光灯管在正常情况下,灯管的使用寿命为12个月.工商部门为了检查他们宣传的真实性,从三个厂家各抽取11只日光灯管进行检测,灯管的使用寿命(单位:月)如下:试问:(1)这三个厂家的广告,分别利用了统计中的哪一个特征数(平均数、中位数、众数)进行宣传?(2)如果三种产品的售价一样,作为顾客的你选购哪个厂家的产品?请说明理由.Ⅳ(本题满分8分)BED CFab A22.如图, 已知等边三角形ABC 中,点D ,E ,F 分别为边AB ,AC ,BC 的中点,M 为直线BC 上一动点,△DMN 为等边三角形(点M 的位置改变时, △DMN 也随之整体移动) . (1)如图①,当点M 在点B 左侧时,请你判断EN 与MF 有怎样的数量关系?点F 是否在直线NE 上?都请直接....写出结论,不必证明或说明理由; (2)如图②,当点M 在BC 上时,其它条件不变,(1)的结论中EN 与MF 的数量关系是否仍然成立?若成立,请利用图②证明;若不成立,请说明理由;(3)若点M 在点C 右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN 与MF 的数量关系是否仍然成立?若成立?请直接写出结论,不必证明或说明理由.Ⅴ(本题满分14分)图① 图② 图③A·BCD EF··N MFEDCB ANMF EDCBA·23.如图,在平面直角坐标系中,以点(11)C ,为圆心,2为半径作圆,交x 轴于A B ,两点,开口向下的抛物线经过点A B ,,且其顶点P 在C 上.(1)求ACB 的大小;(2)写出A B ,两点的坐标; (3)试确定此抛物线的解析式;(4)在该抛物线上是否存在一点D ,使线段OP 与CD 互相平分?若存在,求出点D 的坐标;若不存在,请说明理由.2010年中考数学试题参考答案及评分标准二、填空题(本大题共6小题,每小题4分,共24分) 8.(00),;9.152;10.210;11.4.8;12.23;13.4 三、解答题(本大题Ⅰ—Ⅴ题,共10小题,共98分) Ⅰ.(本题满分12分,第14题6分,第15题6分) 14.解:原式=9-16÷(-8)+1-23×23……………………2分 =9+2+1-3.……………………………………4分 =9 ………………………………6分15.解:原式211(1)1(1)(1)1x x x x x -=-++-+······································································ 2分 2211(1)(1)1(1)(1)x x x x x x -+--=-=+++ ······························································· 4分 22(1)x =+ ········································································································ 5分当1x =时,原式23== ··································································· 6分 Ⅱ.(本题满分28分,第16题7分,第17题10分,第18题11分)16.(1)连结OC ,则 OC AB ⊥. …………………………………………………1分∵OA OB =,∴1122AC BC AB ===⨯ ………………………………………2分在Rt AOC △中,3OC ===.∴ ⊙O 的半径为3. …………………………………………………………3分 (2)∵ OC =12OB , ∴ ∠B =30o , ∠COD =60o . ……………………………………5分 ∴扇形OCD 的面积为OCD S 扇形=260π3360⨯⨯=32π. …………………………………5分阴影部分的面积为:Rt Δ=OBC OCD S S S -阴影扇形=12OC CB ⋅-3π2-3π2.…………………………7分 17.解:(1)设购买乙种电冰箱x 台,则购买甲种电冰箱2x 台,丙种电冰箱(803)x -台,根据题意,列不等式: ································································ 1分120021600(803)2000132000x x x ⨯++-⨯≤. ···························································· 3分解这个不等式,得14x ≥. ·································································································· 4分 ∴至少购进乙种电冰箱14台. ····························································································· 5分 (2)根据题意,得2803x x -≤. ····················································································· 6分 解这个不等式,得16x ≤. ·································································································· 7分 由(1)知14x ≥. 1416x ∴≤≤. 又x 为正整数, 141516x ∴=,,. ···················································································································· 8分 所以,有三种购买方案:方案一:甲种电冰箱为28台,乙种电冰箱为14台,丙种电冰箱为38台; 方案二:甲种电冰箱为30台,乙种电冰箱为15台,丙种电冰箱为35台; 方案三:甲种电冰箱为32台,乙种电冰箱为16台,丙种电冰箱为32台. ··················· 10分 18.解:(1)5000…………………………………2分甲 ………………………………4分(2)设所求直线的解析式为:y =kx +b (0≤x ≤20), ………5分由图象可知:b =5000,当x =20时,y =0, ∴0=20k +5000,解得k = -250. …7分即y = -250x +5000 (0≤x ≤20) ……………7分(3)当x =15时,y = -250x +5000= -250×15+5000=5000-3750=1250. ………8分 两人相距:(5000 -1250)-(5000-2000)=750(米)………………9分 两人速度之差:750÷(20-15)=150(米/分)……………11分Ⅲ.(本题满分36分,第19题12分,第20题12分,第21题12分) 19解:(1)P (抽到牌面数字是4)13=; ········································································ 2分(2)游戏规则对双方不公平. ················································································· 5分 理由如下:由上述树状图或表格知:所有可能出现的结果共有9种. P (抽到牌面数字相同)=3193=, P (抽到牌面数字不相同)=6293=.∵1233<,∴此游戏不公平,小李赢的可能性大. ············································ 12分 (说明:答题时只需用树状图或列表法进行分析即可)20.解:过点C 作CE AD ∥,交AB 于E CD AE ∥,CE AD ∥ ····································································································· 2分∴四边形AECD 是平行四边形 ······························································································ 4分 50AE CD ∴==m ,50EB AB AE =-=m ,30CEB DAB ∠=∠= ···························· 6分又60CBF ∠=,故30ECB ∠=,50CB EB ∴==m ···················································· 8分∴在Rt CFB △中,sin 50sin 6043CF CB CBF =∠=≈m ········································ 11分 答:河流的宽度CF 的值为43m . ······················································································ 12分21.答:(1)甲厂的广告利用了统计中的平均数. ····························································· 2分乙厂的广告利用了统计中的众数. ············································································ 4分 丙厂的广告利用了统计中的中位数. ············································································ 7分分…………………………8分11F B C (2) 选用甲厂的产品. 因为它的平均数较真实地反映灯管的使用寿命 ······················· 10分 或选用丙厂的产品.因为丙厂有一半以上的灯管使用寿命超过12个月 ··························· 10分Ⅳ.(本题满分8分)22.(1)判断:EN 与MF 相等 (或EN=MF ),点F 在直线NE 上, ········ 2分(2)成立. ······························ 3分 证明:法一:连结DE ,DF .∵△ABC 是等边三角形, ∴AB =AC =BC .又∵D ,E ,F 是三边的中点,∴DE ,DF ,EF 为三角形的中位线.∴DE =DF =EF ,∠FDE =60°.又∠MDF +∠FDN =60°, ∠NDE +∠FDN =60°,∴∠MDF =∠NDE .在△DMF 和△DNE 中,DF =DE ,DM =DN , ∠MDF =∠NDE ,∴△DMF ≌△DNE . 8∴MF =NE . ·························· 6分法二:延长EN ,则EN 过点F .∵△ABC 是等边三角形, ∴AB =AC =BC .又∵D ,E ,F 是三边的中点, ∴EF =DF =BF .∵∠BDM +∠MDF =60°, ∠FDN +∠MDF =60°,∴∠BDM =∠FDN .又∵DM =DN , ∠ABM =∠DFN =60°,∴△DBM ≌△DFN .∴BM =FN .∵BF =EF , ∴MF =EN . ·························· 6分(3)画出图形(连出线段NE ), 6MF 与EN 相等的结论仍然成立(或MF =NE 成立). ·············· 8分Ⅴ.(本题满分14分)23.解:(1)作CHN C A B F M D E NC A B F MD E12 1CH = ,半径2CB = ·························································· 1分60BCH ∠= ,120ACB ∴∠= ········································· 3分(2)1CH = ,半径2CB =HB ∴=(1A ,················································ 5分(1B ··············································································· 6分 (3)由圆与抛物线的对称性可知抛物线的顶点P 的坐标为(13), ······································· 7分 设抛物线解析式2(1)3y a x =-+ ·························································································· 8分把点(1B 代入上式,解得1a =- ·············································································· 9分 222y x x ∴=-++ ·············································································································· 10分 (4)假设存在点D 使线段OP 与CD 互相平分,则四边形OCPD 是平行四边形 ·········· 11分 PC OD ∴∥且PC OD =.PC y ∥轴,∴点D 在y 轴上. ····················································································· 12分又2PC = ,2OD ∴=,即(02)D ,. 又(02)D ,满足222y x x =-++, ∴点D 在抛物线上 ··············································································································· 13分 所以存在(02)D ,使线段OP 与CD 互相平分. ·································································· 14分。
2010年新疆内初班招生数学试卷(解析版)

8. (1 分)把红、黄、白、绿、蓝五种颜色的球 10 个放在一个袋子里,至少取 可以保证取到两个颜色相同的球. 9. (2 分)11 和 31 的最小公倍数是 10. (5 分) 2.5 时= 分 8 元 6 角= 元 5 吨 30 千 克 = 7.09 升= 千克 11. (3 分) :12= ÷8=0.75=
2
,14 和 84 的最大公因数是
.
升
毫升. = %
12. (1 分)将一个面积为 12.56cm 的圆等分成若干份,拼成一个近似的长方形,这个长方 形的长是 (π 取 3.14) .
2 2 2
13. (1 分)将表面积分别是 54dm 、96dm 、150dm 的三个正方体铁块,熔铸成一个大的正 方体铁块,这个大正方体的表面积是 . .
14. (1 分)一个两位数既是 2 和 5 的倍数,又是 3 的倍数,这个数最大是 15. (1 分)5 个连续奇数的平均数是 17,这五个数中最大的数是 16. (3 分)下面是六(1)班第一组 9 名同学身高情况统计表: 姓名 李华 丁怡 1.60 古丽 1.58 王田 1.62 张军 1.60 孙小明 吐尔逊 高卫 1.52 1.65 1.48 .
二、判断对错. (对的打“√” ,错的打“×” . ) (每题 2 分,共 12 分. ) 18. (2 分)因为 2.5×4=10,所以 10 是 2.5 的倍数. 19. (2 分)2100 年全年有 365 天. 20. (2 分)圆的周长与半径成正比例. 21. (2 分)质数都是奇数,合数都是偶数. . . (判断对错) . (判断对错) . (判断对错) . . (判断对错) .
第 3 页(共 14 页)
3800 吨货物,需要多少时间? 39. (5 分)为庆祝国庆节,公园里摆了 300 盆菊花,比月季花盆数的 2 倍少 20 盆,月季花 有多少盆?(用方程解) 40. (9 分)希望小学六年级同学参加兴趣班情况如图. (1)参加小记者班的人数占百分之几? (2)书法班人数是美术班人数的几分之几? (3)如果六年级有 240 人参加兴趣班,那么参加乒乓球班的人数比舞蹈班的人数多多少 人?
2010-2017新疆中考分析

【2010年】X1数相反数5【2011年】X1数科学记数法—表示较大的数55 3.33%【2010年】X4数科学记数法—表示较大的数5【2011年】X5式完全平方公式、幂的乘方与积的乘方5【2010年】X2式幂的乘方与积的乘方5【2011年】X6式实数大小比较、零指数幂、负整数指数幂、特殊角的三角函数值5【2010年】T9式二次根式的加减法5【2011年】T9式二次根式有意义的条件5【2010年】T12式因式分解-运用公式法5【2011年】J15式分式的化简求值6【2010年】J16式分式的混合运算、化简求值6【2011年】X2方程与方程组解一元一次方程5【2010年】J15方程方程组一元二次方程-因式分解法6【2011年】T10 方程与方程组解分式方程5【2010年】J19方程与方程组分式方程的应用8【2011年】T12 方程与方程组一元二次方程根的判别式5【2010年】T10不等式与不等式组在数轴上表示不等式的解集55 3.33%【2011年】J23方程与方程组一元二次方程的应用(商品利润问题)、待定系数法求一次函数解析式10【2010年】X7一次函数与反比列函数反比例函数性质、图象上点的坐标特征55 3.33%【2011年】J16不等式与不等式组解一元一次不等式组、在数轴上表示不等式的解集66 4.00%【2010年】T14二次函数二次函数的图象、二次函数与不等式5【2011年】X7一次函数与反比列函数反比例函数的性质55 3.33%【2010年】J22二次函数二次函数的应用10【2011年】J19二次函数抛物线与x轴的交点、不等式、二次函数的图象、二次函数图象与几何变换88 5.33%【2010年】T11统计方差5【2011年】X4统计方差5【2010年】J20统计折线统计图、算术平均数、方差8【2011年】J17统计扇形统计图;加权平均数;中位数8【2010年】X5概率一步完成事件的概率5【2011年】J18概率游戏公平性;列表法与树状图法66 4.00%【2010年】J18概率两步完成事件的概率6【2011年】X3线与角平行线的性质55 3.33%【2010年】X3线与角平行线的性质55 3.33%【2011年】T11三角形等边三角形的性质;勾股定理55 3.33%【2010年】X8三角形勾股定理的应用55 3.33%【2011年】J21四边形平行四边形的判定、反证法88 5.33%【2010年】J21圆扇形面积的计算、全等三角形的判定8【2011年】T13圆圆周角定理;解直角三角形5【2010年】J23圆切线的性质、平行线的判定、相似三角形的判定与性质10【2011年】J22圆切线的性质、勾股定理、相似三角形的判定与性质10【2010年】X6锐角三角函数解直角三角形、等边三角形的性质55 3.33%【2011年】X8视图与投影圆锥的计算;由三视图判断几何体55 3.33%【2010年】T13视图与投影由三视图判断几何体55 3.33%【2011年】T14图形的变换利用轴对称设计图案55 3.33%【2010年】J17图形的变换利用旋转设计图案、利用轴对称设计图案66 4.00%【2011年】J20图形的变换图-旋转变换;锐角三角函数的定义88 5.33%【2010年】J24开放探究题一次函数的应用综合探究12128.00%【2011年】J24开放探究题等腰梯形的性质、二次函数的最值、菱形的性质、解直角三角形综合探究1010 6.67%10 6.67% 2114.00%189.33%10.00%12.00%138.67%2114.00%2516.67%8.67%10.67%141513161510.00%2014年-----2017年新疆中考数学各考点分布及所占比重统计表。
2010年全国各地中考数学选择题、填空题答案及参考答案
★2010年全国各地中考数学选择题、填空题答案及参考解答第一部分 选择题1.C解:设抛物线的对称轴与x 轴交于点E如图1,当∠CAD =60°时,则DE =1,BE =3 ∴B (1+3,0),C (1,-1)将B (1+3,0),C (1,-1)代入y =a (x -1)2+k ,解得k =-1,a =31∴y =31(x -1)2-1如图2,当∠ACB =60°时,由菱形性质知A (0,0),C (1,3) 将A (0,0),C (1,3)代入y =a (x -1)2+k ,解得k =-3,a =3 ∴y =3(x -1)2-3同理可得:y =-31(x -1)2+1,y =-3(x -1)2+3所以符合条件的抛物线的解析式共4个3.D解:设DE =x ,则EC =x 2,BD =x 6,BC =x +x 8 由△AGF ∽△ABC 得:xx x 22+=xx x 8+,∴x4=16,x =2,∴正方形DEFG 的面积为4∴S △ABC =1+1+3+4=94.C解:如图,过A 作BC 的垂线交CB 的延长线于H ,则HD =AH ,HC =3AH∴HC -HD =(3-1)AH =3,∴AH =23(3+1),HB =23(3+1)-3=23(3-1) ∴AB =22HB AH+=235.B6.D∠ACD 、∠BAD 、∠ODA 、∠ODE 、∠OED7.D解:如图,则有⎩⎨⎧a2+1=r2(2-a )2+(21)2=r2解得:a =1613,r =161758.A解:如图,连结BD S 1=21π×32-S △ABD -S 弓形=2π,S 2=21AB ·BC -S △ABD -S 弓形 S 1-S 2=21π×32-21AB ·BC =2π,AB ·BC =8π,BC =34π9.B解:由已知得:AB +AC +BC =2CD +AC +BC =2+AC +BC =52+,∴AC +BC =5 ∴(AC +BC )2=AC 2+BC 2+2AC ·BC =5又AC 2+BC 2=AB 2=(2CD )2=4,∴2AC ·BC =1∴S △ABC =21AC ·BC =4110.C解:如图,延长AD 至E ,使DE =AD ,连结BE 、CE ,则四边形ABEC是平行四边形 ∴BE =AC =13,∴AB 2+AE 2=52+122=169=132=BE 2∴△ABD 是直角三角形∴BD =22AD AB+=2265+=61,∴BC =61211.A解:如图,延长MN 交BC 的延长线于点E∵∠AMB =∠NMB ,∠AMB =∠MBC ,∠NMB =∠MBC ,∴BE =ME 易知△NDM ≌△NCE ,∴CE =MD ,MN =NE ,∴ME =2MN 设正方形边长为2,MD =x ,则AM =2- x ,DN =1,BE =x +2在直角三角形DMN 中,由勾股定理得:MN =12+x ,∴ME =122+x∴x +2=122+x ,解得:x =0(不合题意,舍去),或x =34B AD CAB CD EDBCAMNE∴AM =2-34=32,AM :AB =3112.A解:设正方形DEFG 的边长为x ,△ABC 的BC 边上的高为h由△AGF ∽△ABC 得:a x =h x h -,∴x =h a ah +,∴S 2=2)(h a ah +又S 1=ah 21,∴212S S =222221)(h a h a ah+=ah h a 2)(+·41≥ah h a 22)(·41=1 ∴S 1≥2S 213.B解:由△BEM ∽△AED 得:边上的高边上的高AD BM =AD BM =21,∴BM 边上的高=31AB =31∴S 阴影=2(21-31)=3114.C 解:如图,连结OE 、OF 、OC 、OD 、OG∵AE 、BF 为半圆的切线,∴OE ⊥AE ,OF ⊥BF ,又AE =BF ,OE =OF ∴△AOE ≌△BOF ,∴∠AOE =∠BOF∵CD 切半圆于G ,∴CF =CG .仿上可得∠COF =∠COG ,同理∠DOE =DOG ∵∠AOE +∠DOE +∠DOG +∠COG +∠COF +∠BOF =180°,∴∠AOE +∠DOE +∠COF =90° ∴∠BCO =90°-∠COF =∠AOE +∠DOE =∠AOD同理∠BOC =∠ADO ,∴△BCO ∽△AOD ,∴BC/AO =BO/AD设AO =BO =a ,则y =xa 215.B解:用排除法:从函数图象可以看出:①的支出费用减少,反映了建议(1);③的支出费用没改变,提高了车票价格,反映了建议(2);②、④不符合题意。
2010年新疆建设兵团中考数学试卷及解析
数 学 试 题 卷考生须知:1.本试卷分为试题卷和答题卷两部分.2.试题卷共4页,满分150分.考试时间120分钟.3.答题卷共4页,所有答案必须写在答题卷上............,写在试题卷上的无效..........4.答题前,考生应先在答题卷密封区内认真填写准考证号、姓名、考场号、 座位号、地(州、市、师)、县(市、区、团场)和学校.5.答题时可以使用科学计算器.......... 一、精心选择(本大题共8小题,每小题5分,共40分.每小题所给四个选项中,只有一个是正确的.) 1.8-的相反数是A.8B.8-C.18D.18- 2.计算23()a -的结果是A.5a - B.6a C.6a - D.5a3.如右图,小明课间把老师的三角板的直角顶点放在黑板的两 条平行线a b 、上,已知155∠=°,则2∠的度数为 A.45° B.35° C.55° D.125°4.今年我区约有202 000名应届初中毕业生参加学业水平考试, 202 000用科学记数法表示为 A.60.20210⨯ B.320210⨯ C.420.210⨯ D.52.0210⨯5.如果从小军等10名大学生中任选1名作为“世博会”志愿者,那么小军被选中的概率是A.1B.111 C. 110 D. 196.如图(1)是一张Rt ABC △纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图(2),那 么在Rt ABC △中,sin B ∠的值是A.12B.32C.1D.327.若点1122()()A x y B x y ,、,在反比例函数3y x=-的图象上,且120x x <<,则12y y 、和0的大小关系是A.120y y >>B.120y y <<C.120y y >>D.120y y <<新疆维吾尔自治区 新疆生产建设兵团2010年初中学业水平考试第3题图AB C图(1)图(2)8.如右图,王大爷家屋后有一块长12m,宽8m 的矩形空地, 他在以BC 为直径的半圆内种菜,他家养的一只羊平时拴在 A 处,为了不让羊吃到菜,拴羊的绳长可以选用 A.3m B.5m C.7m D.9m二、合理填空(本大题共6个小题,每小题5分,共30分) 9.化简188-=___________.10.写出右图中所表示的不等式组的解集:____________. 11.甲、乙两位棉农种植的棉花,连续五年的单位面积产量 (千克/亩)统计如下图,则产量较稳定的是棉农_________.(填甲或乙)12.利用1个a a ⨯的正方形,1个b b ⨯的正方形和2个a b ⨯的矩形可拼成一个正方形(如图所示),从而可得到因式分解的公式__________.13.长方体的主视图和左视图如下图所示(单位:cm),则其俯视图的面积是_________cm 2.14.抛物线2y x bx c =-++的部分图象如图所示,若0y >,则x 的取值范围是__________. 三、准确解答(本大题共有10题,共80分) 15.(6分)解方程:22760x x -+=16.(6分)先化简,再求值22111x x xx x x ⎛⎫-÷ ⎪---⎝⎭,其中31x =+ ABC 8m12mDPO (第11题图)(第12题图) (第13题图)(第14题图) O x y 1-1 317.(6分)用四块如下图(1)所示的正方形卡片拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形)18.(6分)小王将一黑一白两双相同号码的袜子一只一只地扔进抽屉里,当他随意从抽屉里拿出两只袜子时,恰好成双与不成双的机会是多少?请你用树形图求解.19.(8分)2010年4月14日我国青海玉树地区发生强烈地震,急需大量赈灾帐篷.某帐篷生产企业接到任务后,加大生产投入,提高生产效率,实际每天生产帐篷比原计划多200顶,现在生产3 000顶帐篷所用的时间与原计划生产2 000顶的时间相同.现在该企业每天能生产多少顶帐篷?3月 4月 5月 6月 7月 8月 库尔勒香梨(吨) 4 8 5 8 10 13 哈密瓜(吨)8797107平均数 方差 库尔勒香梨 8 9 哈密瓜(2)补全右面折线统计图;(3)请你根据下面两个要求对这两种瓜果在去年3月份至8月份的销售情况进行分析: ①根据平均数和方差分析;②根据折线图上两种瓜果销售量的趋势分析.21.(8分)圆心角都是90°的扇形AOB 与扇形COD 如图所示那样叠放在一起,连结AC BD 、.(1)求证:AOC BOD △≌△;(2)若3AO cm,OC =1cm,求阴影部分的面积.(第20题图)A B CD O (第21题图) (2) (3) (4)(1)22.(10分)如图(1),某灌溉设备的喷头B 高出地面1.25m,喷出的抛物线形水流在与喷头底部A 的距离为1m 处达到距地面最大高度2.25m,试在恰当的直角坐标系中求出与该抛物线水流对应的二次函数关系式.学生小龙在解答图(1)所示的问题时,具体解答如下:①以水流的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴,建立如图(2)所示的平面直角坐标系;②设抛物线水流对应的二次函数关系式为2y ax =;③根据题意可得B 点与x 轴的距离为1m,故B 点的坐标为(1-,1); ④代入2y ax =得11a -=·,所以1a =-;⑤所以抛物线水流对应的二次函数关系式为2y x =-.数学老师看了小龙的解题过程说:“小龙的解答是错误的”.(1)请指出小龙的解答从第_________步开始出现错误,错误的原因是什么? (2)请你写出完整的正确解答过程.23.(10分)如图是一个量角器和一个含30°角的直角三角形放置在一起的示意图,其中点B 在半圆O 的直径DE 的延长线上,AB 切半圆O 于点F ,且.BC OE = (1)求证:DE CF ∥;(2)当2OE =时,若以O B F 、、为顶点的三角形与ABC △相似,求OB 的长.(3)若2OE =,移动三角板ABC 且使AB 边始终与半圆O 相切,直角顶点B 在直径DE 的延长线上移动,求出点B 移动的最大距离.24.(12分)张师傅在铺地板时发现,用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形,如图(1).然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个边长为1的小图(1) 图(2) A B C O (第23题图) DF E正方形(阴影部分),假设长方形的长为y ,宽为x ,且.y x(1)请你求出图(1)中y 与x 的函数关系式; (2)求出图(2)中y 与x 的函数关系式;(3)在图(3)中作出两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;(4)根据以上讨论完成下表,观察x 与y 的关系,回答:如果给你任意8个相同的长方形,你能否拼出类似图(1)和图(2)的图形?说出你的理由.图(2)中小正方形边长1 2 3 4 … x 6 y10…图(1) 图(2) 图(3)数学试卷参考答案及评分标准(满分150分)说明:本参考答案供阅卷教师评卷时使用.阅卷中,考生如有其它解法,只要正确、合理,均可得相应分值.二、合理填空(本大题共6小题,每小题5分,共30分)10.32x -<≤ 11.乙 12.2222()a ab b a b ++=+ 13.12 14.31x -<<三、准确解答(本大题共10小题,共80分) 15.(6分)解法不唯一. 例解:27302x x -+= 274949321616x x -+=-+ ····································································2′ 271()416x -= ··················································································4′ 7144x -=± ····················································································5′12x = 232x = ·········································································6′16.(6分)解:2222111111x x x x x x x x x x x x⎛⎫⎛⎫--÷=+ ⎪ ⎪-----⎝⎭⎝⎭· =2211x x x x x+--· ················································2′ =(2)11x x x x x+--· ················································3′ =2x + ····························································4′当1x =时,原式123+= ···················································6′17.(6分)解法不唯一,例解如下:新疆维吾尔自治区 新疆生产建设兵团2010年初中学业水平考试每个图形2′,共6′18.(6分)··············································································································3′()13P=成双································································································5′()23P=不成双·····························································································6′19.(8)分例解:设现在该企业每天生产x顶帐篷,则原计划每天生产(200)x-顶帐篷 ·············1′由题意得:3 000 2 000200x x=-·········································································4′解得600x= ····························································································6′经检验600x=是原方程的解 ·······································································7′即该企业现在每天生产600顶帐篷 ································································8′20.(8分)平均数方差库尔勒香梨8 9哈密瓜843··············································································································3′(2)如图··············································································································6′(1)(2)(3)24.(12分)解法不唯一解:(1)由图(1)得:35y x = 53y x =·····························································2′ (2)由图(2)得281(2)xy x y +=+ ····································································3′ 整理得:2(2)1x y -=21x y -=±53y x = 5213x x ∴-=- 30x =-<21x y ∴-=-不成立 ·················································································4′ 即21y x =- ·····························································································5′ (3) ··············································································································7′ 交点坐标(3,5) ····························································································8′ 实际意义解答不唯一例①:瓷砖的长为5,宽为3时,能围成图(1),图(2)的图形 ········································9′ 例②:当瓷砖长为5,宽为3时,围成图(2)的正方形中的小正方形边长为1. 图(2)中小正方形边长1 2 3 4 … x 3 6 9 12 … y5101520…············································································································ 11′ 情况①:不能,长方形的长与宽若不能满足53y x =,则不能 情况②:能,长方形的长与宽只要满足53y x =即可 情况③:综合上述两种说法只要符合其中一种情况均给分 ···································································· 12′。
2010年新疆中考数学试卷和答案

2010年新疆中考数学试卷和答案一、选择题1. 若多项式f(x)除以x-3所得的余式为4,求f(3)的值。
A. 1B. 2C. 3D. 42. 已知一组数据:4,5,7,10,14,19……,其中每个数都是它前面连续的几个数的和。
求第15项的值。
A. 117B. 112C. 105D. 1003. 设集合A={A | A<2},集合A={A | A≥0},则A∩B等于A. {A | A < 0}B. {A | A≤ 2}C. {A | 0 ≥ A < 2}D. {A | 0 ≤ A < 2}4. 如图,求阴影部分的面积。
(图略)A. 82平方厘米B. 80平方厘米C. 78平方厘米D. 76平方厘米5. 设函数y=2x-3,若x = 2,则y = ()。
A. 1B. 2C. 3D. 46. 化简:2a+3a-5a-(-a) = ()。
A. -5aB. -3aC. -4aD. -2a7. 小红跑步比小帅多跑30米,若小红跑了150米,则小帅跑了()米。
A. 90B. 120C. 150D. 1808. 若甲数比乙数大5,且两数的和是36,求甲、乙两数分别是多少。
A. 15、20B. 18、23C. 21、26D. 24、299. 计算:0.5^2 × 0.5^3 = ()。
A. 0.025B. 0.125C. 0.5D. 0.5^610. 一个三位数的各位数字之和为12,若该三位数是12的倍数,则该三位数是()。
A. 252B. 372C. 486D. 594二、解答题1. 根据等比数列的性质求解:已知等比数列的首项是2,公比是3,求该等比数列的首项和前4项的和。
解:首项a₁ = 2公比q = 3前4项和S₄ = a₁(1-q⁴)/(1-q) = 2(1-3⁴)/(1-3) = 2(1-81)/(-2) = 80答:该等比数列的前4项和为80。
2. 试求二次函数y = -2x² + 4x - 1的最值点以及开口方向。
2010年新疆普通高中学业水平模拟考试数学试题及参考答案

(A) p
3
p
(B) 4
10
(C) arcsin 4
6
(D) arcsin 4
12.设 f ¢( x) 是函数 f(x)的导函数,y= f ¢( x) 的图象 如图所示,则 y= f(x)的图象最有可能的是
二、填空题:本大题共4 小题,每小题4 分,共 16 分,把答案填写在答题卡的相应位置
13.设常数 a
M
BO = D O , BC = C D ,\ C O ^ BD.
D
O C
在 D A O C 中,由已知可得 A O = 1, C O = 3 .
B
E
2
2
2
而 AC = 2, \ AO + CO = AC ,
\ ÐAOC = 90o, 即 AO ^ OC.
BD O C = O , \ A O ^ 平面 B C D
2010 年新疆普通高中学业水平模拟考试数学试题及
参考答案
一、选择题(5 分×12=60 分)
3x2
1 函数 f ( x) =
+ lg(Βιβλιοθήκη x + 1) 的定义域是
1- x
1
A (- ,+ ¥) B
3
1
(- ,1) 3
11
C (- , )
33
2 若复数 z 满足方程 z 2 + 2 = 0 ,则 z 3 =
-
p
, kp
+
p
ù ú,k
Î
Z.
ë
3
6û
(II)方法一:
p
先把 y = sin 2 x 图象上所有点向左平移
p
个单位长度,得到 y = sin(2 x + ) 的图象,再把所得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年新疆建设兵团中考数学试卷一、精心选择(本大题共8小题,每小题5分,共40分.每小题所给四个选项中,只有一个是正确的.) 1.8-的相反数是A.8B.8-C.18D.18- 2.计算23()a -的结果是A.5a -B.6aC.6a -D.5a3.如右图,小明课间把老师的三角板的直角顶点放在黑板的两 条平行线a b 、上,已知155∠=°,则2∠的度数为 A.45° B.35° C.55° D.125°4.今年我区约有202 000名应届初中毕业生参加学业水平考试, 202 000用科学记数法表示为 A.60.20210⨯ B.320210⨯ C.420.210⨯ D.52.0210⨯5.如果从小军等10名大学生中任选1名作为“世博会”志愿者,那么小军被选中的概率是A.1B.111 C. 110 D. 196.如图(1)是一张Rt ABC △纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图(2),那 么在Rt ABC △中,sin B ∠的值是A.12B.32C.1D.327.若点1122()()A x y B x y ,、,在反比例函数3y x=-的图象上,且120x x <<,则12y y 、和0的大小关系是A.120y y >>B.120y y <<C.120y y >>D.120y y << 8.如右图,王大爷家屋后有一块长12m ,宽8m 的矩形空地, 他在以BC 为直径的半圆内种菜,他家养的一只羊平时拴在 A 处,为了不让羊吃到菜,拴羊的绳长可以选用 A.3m B.5m C.7m D.9m二、合理填空(本大题共6个小题,每小题5分,共30分) 9.化简188-=___________.10.写出右图中所表示的不等式组的解集:____________. 11.甲、乙两位棉农种植的棉花,连续五年的单位面积产量第3题图AB C图(1)图(2)ABC 8m12mDPO(千克/亩)统计如下图,则产量较稳定的是棉农_________.(填甲或乙)12.利用1个a a ⨯的正方形,1个b b ⨯的正方形和2个a b ⨯的矩形可拼成一个正方形(如图所示),从而可得到因式分解的公式__________. 13.长方体的主视图和左视图如下图所示(单位:cm ),则其俯视图的面积是_________cm 2.14.抛物线2y x bx c =-++的部分图象如图所示,若0y >,则x 的取值范围是__________. 三、准确解答(本大题共有10题,共80分) 15.(6分)解方程:22760x x -+=16.(6分)先化简,再求值22111x x xx x x ⎛⎫-÷ ⎪---⎝⎭,其中31x =+ 17.(6分)用四块如下图(1)所示的正方形卡片拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形)(第11题图)(第12题图) (第13题图)(第14题图) O x y 1-1 3 (2) (3) (4)(1)18.(6分)小王将一黑一白两双相同号码的袜子一只一只地扔进抽屉里,当他随意从抽屉里拿出两只袜子时,恰好成双与不成双的机会是多少?请你用树形图求解.19.(8分)2010年4月14日我国青海玉树地区发生强烈地震,急需大量赈灾帐篷.某帐篷生产企业接到任务后,加大生产投入,提高生产效率,实际每天生产帐篷比原计划多200顶,现在生产3 000顶帐篷所用的时间与原计划生产2 000顶的时间相同.现在该企业每天能生产多少顶帐篷?3月 4月 5月 6月 7月 8月 库尔勒香梨(吨) 4 8 5 8 10 13 哈密瓜(吨)8797107(平均数 方差 库尔勒香梨 8 9 哈密瓜(2)补全右面折线统计图;(3)请你根据下面两个要求对这两种瓜果在去年3月份至8月份的销售情况进行分析: ①根据平均数和方差分析;②根据折线图上两种瓜果销售量的趋势分析.21.(8分)圆心角都是90°的扇形AOB 与扇形COD 如图所示那样叠放在一起,连结AC BD 、.(1)求证:AOC BOD △≌△;(2)若3AO cm ,OC =1cm ,求阴影部分的面积.22.(10分)如图(1),某灌溉设备的喷头B 高出地面1.25m ,喷出的抛物线形水流在与喷头底部A 的距离为1m 处达到距地面最大高度2.25m ,试在恰当的直角坐标系中求出与该抛物线水流对应的二次函数关系式.学生小龙在解答图(1)所示的问题时,具体解答如下:(第20题图)A B CD O (第21题图) 图(1)图(2)①以水流的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴,建立如图(2)所示的平面直角坐标系;②设抛物线水流对应的二次函数关系式为2y ax =;③根据题意可得B 点与x 轴的距离为1m ,故B 点的坐标为(1-,1); ④代入2y ax =得11a -=·,所以1a =-;⑤所以抛物线水流对应的二次函数关系式为2y x =-.数学老师看了小龙的解题过程说:“小龙的解答是错误的”.(1)请指出小龙的解答从第_________步开始出现错误,错误的原因是什么? (2)请你写出完整的正确解答过程.23.(10分)如图是一个量角器和一个含30°角的直角三角形放置在一起的示意图,其中点B 在半圆O 的直径DE 的延长线上,AB 切半圆O 于点F ,且.BC OE = (1)求证:DE CF ∥;(2)当2OE =时,若以O B F 、、为顶点的三角形与ABC △相似,求OB 的长.(3)若2OE =,移动三角板ABC 且使AB 边始终与半圆O 相切,直角顶点B 在直径DE 的延长线上移动,求出点B 移动的最大距离.24.(12分)张师傅在铺地板时发现,用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形,如图(1).然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个边长为1的小正方形(阴影部分),假设长方形的长为y ,宽为x ,且.y x >A B C O (第23题图) DFE(1)请你求出图(1)中y与x的函数关系式;(2)求出图(2)中y与x的函数关系式;(3)在图(3)中作出两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;(4)根据以上讨论完成下表,观察x与y的关系,回答:如果给你任意8个相同的长方形,你能否拼出类似图(1)和图(2)的图形?说出你的理由.图(2)中小正方形边长1234…x6y10…新疆维吾尔自治区2010年初中学业水平考试新疆生产建设兵团数学试卷参考答案及评分标准(满分150分)说明:本参考答案供阅卷教师评卷时使用.阅卷中,考生如有其它解法,只要正确、合理,均可得相应分值.题号 1 2 3 4 5 6 7 8 选项ACBDCBCA二、合理填空(本大题共6小题,每小题5分,共30分)9.2 10.32x -<≤ 11.乙 12.2222()a ab b a b ++=+ 13.12 14.31x -<<三、准确解答(本大题共10小题,共80分) 15.(6分)解法不唯一. 例解:27302x x -+= 274949321616x x -+=-+ ····································································2′ 271()416x -= ··················································································4′ 7144x -=± ····················································································5′12x = 232x = ·········································································6′16.(6分)解:2222111111x x x x x x x x x x x x⎛⎫⎛⎫--÷=+ ⎪ ⎪-----⎝⎭⎝⎭· =2211x x x x x +--· ················································2′ =(2)11x x x x x+--·················································3′ =2x + ····························································4′当31x =+时,原式=31233++=+ ·················································6′17.(6分)解法不唯一,例解如下:(1) (2) (3)每个图形2′,共6′ 18.(6分)··············································································································3′()13P =成双 ································································································5′ ()23P =不成双 ·····························································································6′ 19.(8)分例解:设现在该企业每天生产x 顶帐篷,则原计划每天生产(200)x -顶帐篷 ·········1′由题意得:3 000 2 000200x x =- ·······································································4′ 解得600x = ····························································································6′ 经检验600x =是原方程的解 ·······································································7′即该企业现在每天生产600顶帐篷 ································································8′ 20.(8分) 平均数 方差 库尔勒香梨 8 9哈密瓜843··············································································································3′ (2)如图 ··············································································································6′24.(12分)解法不唯一解:(1)由图(1)得:35y x = 53y x =··················································2′ (2)由图(2)得281(2)xy x y +=+ ····························································3′整理得:2(2)1x y -=21x y -=±53y x =5213x x ∴-=- 30x =-< 21x y ∴-=-不成立 ·················································································4′ 即21y x =- ·····························································································5′ (3) ··············································································································7′ 交点坐标(3,5)······················································································8′ 实际意义解答不唯一例①:瓷砖的长为5,宽为3时,能围成图(1),图(2)的图形 ························9′ 例②:当瓷砖长为5,宽为3时,围成图(2)的正方形中的小正方形边长为1. 图(2)中小正方形边长1 2 3 4 … x 3 6 9 12 … y5101520…············································································································ 11′ 情况①:不能,长方形的长与宽若不能满足53y x =,则不能 情况②:能,长方形的长与宽只要满足53y x =即可 情况③:综合上述两种说法 只要符合其中一种情况均给分 ···································································· 12′。
