海拔与大气密度和温度间的换算关系
海拔高度与大气压换算公式

海拔高度与大气压换算公式引言:在地球上,大气压力随着海拔的增加而逐渐减小,这是因为海拔高度的增加导致大气层的厚度减小,空气分子的密度减小,从而导致大气压力的降低。
为了准确地了解海拔高度与大气压力之间的关系,科学家们推导出了海拔高度与大气压力之间的换算公式。
一、大气压力的定义:大气压力是指单位面积上空气分子对该面积的压力。
通常使用帕斯卡(Pa)作为大气压力的单位,1帕斯卡等于1牛顿/平方米。
在实际应用中,常使用帕斯卡的倍数千帕(kPa)或百帕(hPa)来表示大气压力。
二、海拔高度与大气压力的关系:根据理想气体状态方程,大气压力与温度、空气密度及海拔高度之间存在着一定的关系。
在一定范围内,可以通过近似的计算方法来估算海拔高度与大气压力之间的关系。
三、换算公式:根据国际标准大气模型,可以使用以下换算公式来估算海拔高度与大气压力之间的关系:P = P0 * (1 - L * h / T0)^(g * M / R * L)其中,P为海拔高度为h时的大气压力,P0为海平面上的标准大气压力(通常取为101.325kPa),L为温度随海拔变化的温度梯度(通常取为0.0065K/m),T0为海平面上的标准温度(通常取为288.15K),g为地球表面重力加速度(通常取为9.80665m/s^2),M 为空气的平均摩尔质量(通常取为0.02896kg/mol),R为气体常数(通常取为8.31447J/(mol·K))。
四、应用举例:以海平面上的标准大气压力P0为101.325kPa为例,假设温度梯度L为0.0065K/m,标准温度T0为288.15K,重力加速度g为9.80665m/s^2,空气的平均摩尔质量M为0.02896kg/mol,气体常数R为8.31447J/(mol·K)。
则可以利用上述换算公式计算不同海拔高度处的大气压力。
例如,我们想知道海拔高度为5000米时的大气压力。
带入换算公式可得:P = 101.325 * (1 - 0.0065 * 5000 / 288.15)^(9.80665 * 0.02896 / (8.31447 * 0.0065))通过计算可以得出,海拔高度为5000米时的大气压力约为56.699kPa。
大气压与海拔高度关系公式推导

大气压与海拔高度关系公式推导海拔高度是指点位于海平面的垂直高度。
随着海拔的增加,温度、密度和大气压都会发生变化。
根据理想气体状态方程,大气压与温度和密度有关。
PV=nRT其中,P表示压力,V表示体积,n表示物质的量,R表示气体常数,T表示温度。
此方程表明,在一定温度和物质有限的情况下,压力与体积呈正比。
现在,我们开始推导大气压与海拔高度之间的关系。
步骤1:假设在一些高度上方有一小段厚度为dz的大气层,其压力为P。
这个大气层的上表面与下一个小段厚度为dz的大气层的下表面之间存在一个平衡。
步骤2:根据大气压力的传递原理,上表面的压力P可以分解为P+dP,其中dP为上表面与下表面之间存在的压力差。
步骤3:根据理想气体状态方程PV = nRT,可以得到dP = -ρgdz,其中ρ表示大气层的密度,g表示重力加速度,dz表示大气层的厚度。
步骤4:将dP = -ρgdz代入P + dP,可以得到P + (-ρgdz) = P,即P = P + ρgdz。
步骤5:将压力表示为单位面积上的压力,即P=F/A,其中F表示单位面积上的力,A表示面积。
并假设在上表面施加一个力F,下表面施加一个力F+dF。
步骤6:假设单位面积上的质量为m,则F = mg,其中m = ρAdz,g 表示重力加速度。
将F = mg代入F + dF,得到mg + dF。
步骤7:根据牛顿第二定律F = ma,其中a表示加速度。
将F = ma 代入mg + dF,得到mg + dF = ma。
步骤8:根据动力学定律mg + dF = ma,可以得到mg - ma = -dF,即mg - ma = -d(mg),即mg - ma = -mgdm。
步骤9:将dP = -ρgdz代入mg - ma = -mgdm,可以得到ρgdz - ρg(dz/ds)ds = -ρgdz,其中s表示海拔高度。
步骤10:化简得,dz/ds = -1,即dz = -ds。
海拔与大气密度和温度间的换算关系

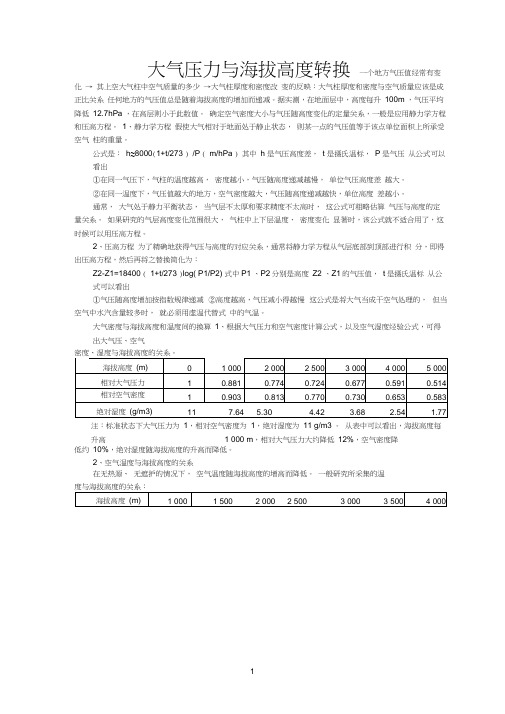
海拔高度与大气密度和温度间的换算关系1根据大气压力和空气密度计算公式,以及空气湿度经验公式,可得出大气压、空气密度、湿度与海拔高度的关系。
注:标准状态下大气压力为1,相对空气密度为1,绝对湿度为11g/m0从表中可以看出,海拔高度每升高1000m,相对大气压力大约降低12%,空气密度降低约10%,绝对湿度随海拔高度的升高而降低。
绝对湿度是指每单位容积的气体所含水分的重量,用mg/L或g/m3表示;相对湿度是指绝对湿度与该温度饱和状态水蒸气含量之比用百分数表达。
2、空气温度与海拔高度的关系在无热源、无遮护的情况下,空气温度随海拔高度的增高而降低。
一般研究所采集的温度与海从表中可以看出:空气温度在一般情况下,海拔高度每升高1000m,最高温度会降低5C,平均温度也会降低5C。
大气密度(atmosphericdensity )单位容积的大气质量。
空气密度在标准状况( 0°C( 273k),101KPa)下为1.293g L-1 o空气的密度大小与气温等因素有关,我们一般采用的空气密度是指在0摄氏度、绝对标准指标下,密度为1.297千克每立方米(1.297kg/m3).大气压力随海拔高度而变化,由经验公式P=P0( 1-0.02257h ) 5.256 (kPa)式中h —海拔高度(kn).用上面公式,算出压力,然后根据密度二P*29/(8314*T),其中P的单位是帕,T的单位是K,通常也就是273.15+t不同温度下干空气算公式:空气密度=1.293(实际压力/标准物理大气压)*(273/实际绝对温度),绝对温度=+273 通常情况下,即30摄氏度时,取1.165KG/M3-60摄氏度时,取1.65KG/M3。
大气压和海拔的换算参考资料
大气压力与海拔高度转换一个地方气压值经常有变化→ 其上空大气柱中空气质量的多少→大气柱厚度和密度改变的反映:大气柱厚度和密度与空气质量应该是成正比关系任何地方的气压值总是随着海拔高度的增加而递减。
据实测,在地面层中,高度每升100m ,气压平均降低12.7hPa ,在高层则小于此数值。
确定空气密度大小与气压随高度变化的定量关系,一般是应用静力学方程和压高方程。
1、静力学方程假使大气相对于地面处于静止状态,则某一点的气压值等于该点单位面积上所承受空气柱的重量。
公式是:h≈8000(1+t/273 ) /P ( m/hPa ) 其中h 是气压高度差,t 是摄氏温标,P 是气压从公式可以看出①在同一气压下,气柱的温度越高,密度越小,气压随高度递减越慢,单位气压高度差越大。
②在同一温度下,气压值越大的地方,空气密度越大,气压随高度递减越快,单位高度差越小。
通常,大气处于静力平衡状态,当气层不太厚和要求精度不太高时,这公式可粗略估算气压与高度的定量关系。
如果研究的气层高度变化范围很大,气柱中上下层温度、密度变化显著时,该公式就不适合用了,这时候可以用压高方程。
2、压高方程为了精确地获得气压与高度的对应关系,通常将静力学方程从气层底部到顶部进行积分,即得出压高方程,然后再将之替换简化为:Z2-Z1=18400 ( 1+t/273 )log( P1/P2) 式中P1 、P2分别是高度Z2 、Z1的气压值,t是摄氏温标从公式可以看出①气压随高度增加按指数规律递减②高度越高,气压减小得越慢这公式是将大气当成干空气处理的,但当空气中水汽含量较多时,就必须用虚温代替式中的气温。
大气密度与海拔高度和温度间的换算1、根据大气压力和空气密度计算公式,以及空气湿度经验公式,可得出大气压、空气注:标准状态下大气压力为1,相对空气密度为1,绝对湿度为11 g/m3 。
从表中可以看出,海拔高度每升高 1 000 m,相对大气压力大约降低12%,空气密度降低约10%,绝对湿度随海拔高度的升高而降低。
大气压力与海拔的关系

一个地方气压值经常有变化→其上空大气柱中空气质量的多少→大气柱厚度和密度改变的反映:大气柱厚度和密度与空气质量应该是成正比关系任何地方的气压值总是随着海拔高度的增加而递减。
据实测,在地面层中,高度每升100m,气压平均降低12.7hPa,在高层则小于此数值。
确定空气密度大小与气压随高度变化的定量关系,一般是应用静力学方程和压高方程。
1、静力学方程具体太长,我简单说明下:假使大气相对于地面处于静止状态,则某一点的气压值等于该点单位面积上所承受空气柱的重量。
公式是:h≈8000(1+t/273)/P(m/hPa)其中h是气压高度差,t是摄氏温标,P是气压从公式可以看出①在同一气压下,气柱的温度越高,密度越小,气压随高度递减越慢,单位气压高度差越大。
②在同一温度下,气压值越大的地方,空气密度越大,气压随高度递减越快,单位高度差越小。
通常,大气处于静力平衡状态,当气层不太厚和要求精度不太高时,这公式可粗略估算气压与高度的定量关系。
如果研究的气层高度变化范围很大,气柱中上下层温度、密度变化显著时,该公式就不适合用了,这时候可以用压高方程。
2、压高方程为了精确地获得气压与高度的对应关系,通常将静力学方程从气层底部到顶部进行积分,即得出压高方程,然后再将之替换简化为:Z2-Z1=18400(1+t/273)log( P1/P2)式中P1、P2分别是高度Z2、Z1的气压值,t是摄氏温标从公式可以看出①气压随高度增加按指数规律递减②高度越高,气压减小得越慢这公式是将大气当成干空气处理的,但当空气中水汽含量较多时,就必须用虚温代替式中的气温。
这就不详细再说了,太复杂了,你应该也不需要用到这么复杂的公式吧!呵呵,我没看清楚你的真正题意,给你一个相关的链接,可能比较准确。
大气压力与海拔高度关系表大气压力与海拔高度关系表(1mmHg=133.32Pa)大气压力(mmHg)海拔高度(m)PO2(mmHg)768760752745737730728714707699 692 684 676 669 661 654 646 638-84 085 170 256 343 431 519 608 698 789 880 9721066116012541350 1447160159157154151146138135 155.6152.4149.5147.7144.5142.8141.3139.7136.5133.3631623616608600593585570 562 555 547 5401544 1643 1743 1843 1945 2047 2151 2256 2362 2469 2577 2687 2797 2908 3020 313233603472358436953806131.8130.2128.6127125.4123.8122.3120.6119117.5116114112.7 111109108106105103 101.6100983916 403096.8 95。
海拔高度大气压计算

海拔高度大气压计算海拔高度与大气压力之间存在着密切的关系。
了解和计算海拔高度与大气压力的关系对于气象学、地理学等学科具有重要意义。
本文将探讨海拔高度与大气压力之间的计算方法,并进一步深入讨论这两者之间的关系。
首先,我们需要了解大气压力与海拔高度的基本概念。
大气压力是指空气对单位面积的垂直作用力,以帕(Pa)为单位。
海拔高度是指地球表面以上的高度,以米(m)为单位。
从现实角度而言,我们可以观测到大气压力随着海拔高度的增加而减小。
这是因为随着海拔高度的增加,空气的密度和质量逐渐减小。
根据理想气体状态方程,大气压力与空气密度及温度有关,可以通过以下公式计算:P=ρ*g*h其中,P代表大气压力,单位为帕;ρ代表空气密度,单位为千克/立方米;g代表重力加速度,单位为米/平方秒;h代表海拔高度,单位为米。
在计算大气压力时,我们需要知道空气密度和重力加速度的数值。
空气密度通常可以通过气象学或地理学相关的表格或手册进行查询。
而重力加速度的数值可以用地球表面的标准重力加速度9.8米/平方秒来估算。
通过上述公式计算,我们可以得到特定海拔高度的大气压力。
举个例子,假设在海拔1000米的地方,空气密度为1.1千克/立方米,那么我们可以计算得到该海拔高度的大气压力:这样,我们就可以得到对应海拔高度的大气压力数值。
除了上述方法外,我们还可以使用其他的公式来计算海拔高度与大气压力之间的关系。
例如,国际标准大气模型(ISA)提供了一种常用的计算方法。
根据ISA模型,海拔高度与大气压力的关系可以用以下公式表示:P=P0*(1-L*h/T0)^(gM/(RL))其中,P0代表地面上的大气压力;L代表温度梯度,即大气温度随高度变化的速率;T0代表地表温度;g代表重力加速度;M代表空气的平均分子质量;R代表气体常数;h代表海拔高度。
通过这种方式,我们可以通过给定的参数计算出对应海拔高度的大气压力。
这种方法更加精确,但计算过程也更加复杂。
大气压和海拔的换算参考资料

大气压力与海拔高度转换一个地方气压值经常有变化→其上空大气柱中空气质量的多少→大气柱厚度和密度改变的反映:大气柱厚度和密度与空气质量应该是成正比关系任何地方的气压值总是随着海拔高度的增加而递减。
据实测,在地面层中,高度每升100m,气压平均降低12.7hPa,在高层则小于此数值。
确定空气密度大小与气压随高度变化的定量关系,一般是应用静力学方程和压高方程。
1、静力学方程假使大气相对于地面处于静止状态,则某一点的气压值等于该点单位面积上所承受空气柱的重量。
公式是:h≈8000(1+t/273)/P(m/hPa)其中h是气压高度差,t是摄氏温标,P是气压从公式可以看出①在同一气压下,气柱的温度越高,密度越小,气压随高度递减越慢,单位气压高度差越大。
②在同一温度下,气压值越大的地方,空气密度越大,气压随高度递减越快,单位高度差越小。
通常,大气处于静力平衡状态,当气层不太厚和要求精度不太高时,这公式可粗略估算气压与高度的定量关系。
如果研究的气层高度变化范围很大,气柱中上下层温度、密度变化显著时,该公式就不适合用了,这时候可以用压高方程。
2、压高方程为了精确地获得气压与高度的对应关系,通常将静力学方程从气层底部到顶部进行积分,即得出压高方程,然后再将之替换简化为:Z2-Z1=18400(1+t/273)log( P1/P2)式中P1、P2分别是高度Z2、Z1的气压值,t是摄氏温标从公式可以看出①气压随高度增加按指数规律递减②高度越高,气压减小得越慢这公式是将大气当成干空气处理的,但当空气中水汽含量较多时,就必须用虚温代替式中的气温。
大气密度与海拔高度和温度间的换算1、根据大气压力和空气密度计算公式,以及空气湿度经验公式,可得出大气压、空气密度、湿度与海拔高度的关系。
从表中可以看出,海拔高度每升高1 000 m,相对大气压力大约降低12%,空气密度降低约10%,绝对湿度随海拔高度的升高而降低。
2、空气温度与海拔高度的关系在无热源、无遮护的情况下,空气温度随海拔高度的增高而降低。
空气密度和海拔高度的关系(一)

空气密度和海拔高度的关系(一)空气密度和海拔高度的关系密度的定义和计算方法•密度是指单位体积内物质的质量,通常用公式ρ = m/V计算,其中ρ表示密度,m表示质量,V表示体积。
空气密度的定义和影响因素•空气密度是指单位体积内大气所含的空气分子数量,通常用公式ρ = n/V计算,其中ρ表示空气密度,n表示空气分子数量,V 表示体积。
•空气密度的主要影响因素有温度、压力和湿度。
海拔高度对空气密度的影响•随着海拔高度的增加,空气密度会逐渐减小。
•海拔较低的地方,大气压力较大,空气分子较为密集,所以空气密度较大;而海拔较高的地方,大气压力较小,空气分子较为稀疏,所以空气密度较小。
空气密度和海拔高度关系的原因•空气密度和海拔高度的关系主要是由大气压力随海拔高度变化所导致的。
•大气压力随着海拔高度的增加逐渐减小,这是因为在地球表面上方,大气的重力作用逐渐减弱,导致大气分子相互撞击的频率减小,从而降低了空气分子的密度和压力。
空气密度和海拔高度关系的应用•空气密度和海拔高度的关系在许多领域有着重要的应用,例如航空航天、气象学和山地运动等。
•在航空航天领域,对空气密度和海拔高度关系的研究可以用于飞机的设计和性能评估,以及导航和气象预报等方面。
•在气象学中,空气密度和海拔高度的关系对于预测天气、气候模拟和气象灾害的研究非常重要。
•在山地运动中,空气密度和海拔高度的关系影响着人们在高海拔地区的呼吸和身体适应能力,对于登山、滑雪和攀岩等运动的安全和表现有着重要的影响。
总结•空气密度和海拔高度有着密切的关系,随着海拔高度的增加,空气密度逐渐减小。
这是由于海拔较高的地方大气压力较小,导致空气分子相互撞击的频率减小,降低了空气分子的密度和压力。
这一关系在航空航天、气象学和山地运动等领域有着广泛的应用。
大气压与海拔高度的计算公式

大气压与海拔高度的计算公式大气压力梯度方程可以通过理想气体状态方程和重力加速度来推导。
首先,我们先回顾一下理想气体状态方程:PV=nRT其中,P表示气体的压力,V表示气体的体积,n表示气体的摩尔数,R表示气体常数,T表示气体的温度。
另外,我们知道气体的压力与其密度直接相关。
密度可以表示为:ρ=m/V其中,ρ表示气体的密度,m表示气体的质量,V表示气体的体积。
根据理想气体状态方程和密度公式,我们可以推导出:P=ρRT现在我们考虑海拔高度对大气的影响。
随着海拔高度的增加,大气的压强会逐渐减小。
这是因为在较低的海拔高度,上方的大气重量会对下方的气体产生较大的压力。
而随着海拔的升高,上方的大气重量减小,因此压力也会减小。
为了表达大气压力随着海拔高度变化的关系,我们可以引入压力梯度。
压力梯度表示在垂直方向上单位距离内的压力变化。
假设压力梯度为dp/dh,其中p表示压力,h表示高度。
根据物理学定律,压力梯度与重力场的作用呈正比,即:dp/dh = -ρg其中,g表示重力加速度。
代入前面推导出的P=ρRT公式,我们可以得到:dp/dh = -Pg/RT我们可以把这个微分方程进行求解,从而得到大气压力与海拔高度之间的关系。
这个关系被称为大气压力与高度的指数函数关系,也称为大气压力高度公式。
P=P₀*(1-L*h/T₀)^(gM/RL)其中,P₀表示参考海平面处的大气压力,L表示温度下降率,h表示海拔高度,T₀表示参考温度,M表示大气的平均分子量,R表示气体常数。
这个公式使用了各种常数和参数,这些参数的确切数值取决于所考虑的大气条件和位置。
但是,通过选择适当的参数值,我们可以将这个公式应用于各种情况下的大气压力与海拔高度的计算。
总结起来,大气压力与海拔高度之间的关系可以由大气压力梯度方程得到。
这个方程给出了大气压力与海拔高度之间的指数函数关系。
通过选择适当的参数值,我们可以将这个公式应用于各种情况下的大气压力与海拔高度的计算。
空气的温度与密度

空气的温度与密度
答案:
空气的密度与温度之间存在反比关系,即温度升高时,空气密度减小;温度降低时,空气密度增大。
空气的密度受到多种因素的影响,其中温度是一个重要的因素。
一般而言,一定质量的气体,当温度升高时,气体分子运动加快,分子间的平均距离增加,导致气体体积膨胀,密度变小。
相反,当温度降低时,分子运动减慢,平均距离减小,气体体积收缩,密度变大。
这种密度变化不仅影响空气,也适用于所有气体。
具体到空气密度与温度的关系,可以这样理解:在标准条件下(0℃, 1个标准大气压(1atm)),空气密度约为1.29kg/m³。
但随着温度的变化,空气密度会相应调整。
例如,在20℃时,空气密度取1.205kg/m³。
这种变化可以通过空气密度换算关系式来描述:空气密度=1.293*(实际压力/标准物理大气压)*(273/实际绝对温度),其中绝对温度=摄氏温度+273。
这个公式考虑了气温、海拔等因素对空气密度的影响,海拔越高密度越低。
此外,空气的组成也对密度产生影响。
空气是由氧气、氮气和惰性气体等多种气体组成的混合物,其中氮气的体积分数约为78%,氧气的体积分数约为21%。
这些成分的相对含量在一定温度和压力下决定了空气的整体密度。
了解空气密度与温度的关系有助于理解一些自然现象,如风的形成。
由于一定质量的空气受热后体积膨胀,密度变小而上升,周围的冷空气流过来补充,形成了对流,这就是风的形成原理。
这种对流现象在自然界中广泛存在,影响着气候和天气模式。
不同海拔高度机械真空表的读数

不同海拔高度机械真空表的读数
摘要:
一、海拔高度与大气压力的关系
二、海拔高度与空气密度的关系
三、海拔高度对真空表读数的影响
四、如何根据海拔高度调整真空表读数
五、结论
正文:
在不同海拔高度下,机械真空表的读数会受到大气压力和空气密度等因素的影响。
为了更好地理解和应用这些规律,我们首先来了解一下海拔高度与大气压力、空气密度之间的关系。
一、海拔高度与大气压力的关系
大气压力是由于空气分子做无规则运动而产生的。
海拔高度越高,大气压力越低。
根据分子动理论,当温度不变时,某点的压强与单位体积内的分子数成正比。
在海拔高度变化时,大气压力也会相应改变。
二、海拔高度与空气密度的关系
空气密度受到大气压力、温度和海拔高度等因素的影响。
随着海拔高度的升高,空气密度会逐渐降低。
当海拔高度发生变化时,空气密度也会相应改变。
三、海拔高度对真空表读数的影响
真空表读数受到大气压力和空气密度的影响。
随着海拔高度的升高,大气
压力和空气密度都会降低,从而导致真空表读数偏低。
四、如何根据海拔高度调整真空表读数
1.了解所处地区的海拔高度和大气压力、空气密度等参数。
2.根据海拔高度和大气压力、空气密度的关系,计算出实际的大气压力和空气密度。
3.使用真空表的校正公式,将海拔高度引起的读数偏差进行修正。
五、结论
海拔高度对机械真空表的读数有显著影响。
了解海拔高度与大气压力、空气密度之间的关系,并采取相应的校正方法,可以确保真空表读数的准确性。
8000米空气密度

8000米空气密度1. 简介在大气科学中,空气密度是指单位体积的空气质量。
当海拔高度增加时,由于大气压力的减小,空气密度也会随之下降。
本文将探讨8000米海拔处的空气密度及其影响因素。
2. 海拔高度与大气压力2.1 海拔高度对空气密度的影响海拔高度越高,大气压力越低,空气密度也随之下降。
这是因为在大气层中,由于重力的作用,大气分子越往下会受到更多的分子压力,因此近地面处的大气密度较高。
随着海拔高度的增加,大气分子的数量减少,每个单位体积内的分子数目相应减少,从而导致空气密度的降低。
2.2 大气压力与海平面标准大气压海平面标准大气压是指在海平面上的标准大气状态下的气压值,约等于101325帕斯卡(Pa)。
然而,随着海拔高度的增加,大气压力逐渐减小。
根据国际标准大气模型,当海拔达到8000米时,大气压力约为35600帕斯卡(Pa)。
3. 空气密度的计算方法空气密度可以通过以下公式计算:密度 = 质量 / 体积对于理想气体(近似于大气中的气体),根据理想气体状态方程可得:密度 = 压力 / (气体常数× 温度)其中,压力是指大气压力,气体常数是一个与气体特性相关的常数,而温度是指大气的温度。
4. 8000米海拔处的空气密度根据公式计算,可以得到8000米处的空气密度。
假设温度为摄氏零下30度(-30℃),将大气压力代入公式,可得到空气密度约为0.371千克/立方米。
5. 空气密度对气象和航空的影响5.1 气象方面的影响空气密度对气象有着重要的影响。
随着空气密度的降低,大气中的气压梯度减小,风速变慢。
此外,空气密度的变化也会影响气候和天气的变化,如降水量、湿度等。
5.2 航空方面的影响空气密度对飞行器的性能有着重要的影响。
在较高的海拔上,空气密度降低会导致飞机的升力减小,所需的飞行速度也会增加。
这意味着在高海拔处飞行时,飞机需要更长的起飞和着陆距离,以及更高的爬升速度。
6. 总结本文探讨了8000米海拔处的空气密度及其影响因素。
海拔与大气密度和温度间的换算关系

海拔与大气密度和温度间的换算关系Modified by JEEP on December 26th, 2020.海拔高度与大气密度和温度间的换算关系1、根据大气压力和空气密度计算公式,以及空气湿度经验公式,可得出大气压、空气密度、湿度与海拔高度的关系。
注:标准状态下大气压力为1,相对空气密度为1,绝对湿度为11 g/m3。
从表中可以看出,海拔高度每升高1000 m,相对大气压力大约降低12%,空气密度降低约10%,绝对湿度随海拔高度的升高而降低。
绝对湿度是指每单位容积的气体所含水分的重量,用mg/L或g/m3表示;相对湿度是指绝对湿度与该温度饱和状态水蒸气含量之比用百分数表达。
2、空气温度与海拔高度的关系在无热源、无遮护的情况下,空气温度随海拔高度的增高而降低。
一般研究所采集的温度与海拔高度的关系:从表中可以看出:空气温度在一般情况下,海拔高度每升高1000 m,最高温度会降低5 ℃,平均温度也会降低5 ℃。
大气密度(atmospheric density)单位容积的大气质量。
空气密度在标准状况(0℃(273k),101KPa)下为·L-1。
空气的密度大小与气温等因素有关,我们一般采用的空气密度是指在0摄氏度、绝对标准指标下,密度为千克每立方米m3).大气压力随海拔高度而变化,由经验公式 P=P0()(kPa)式中 h一海拔高度(km). 用上面公式,算出压力,然后根据密度= P *29/(8314*T),其中 P的单位是帕,T的单位是K,通常也就是+t不同温度下干空气算公式:空气密度 =(实际压力 /标准物理大气压) *(273/实际绝对温度),绝对温度 = + 273通常情况下,即 30摄氏度时,取 M3-60摄氏度时,取 M3。
[指导]大气压和海拔的换算
![[指导]大气压和海拔的换算](https://img.taocdn.com/s3/m/12a047c648649b6648d7c1c708a1284ac850056d.png)
大气压力与海拔高度怎么转换000标准大气压强Po= Pa= cmHg= mmHg000Po=1.01325×10^5 Pa=76cmHg=760mmHg000一个地方气压值经常有变化→其上空大气柱中空气质量的多少→大气柱厚度和密度改变的反映:大气柱厚度和密度与空气质量应该是成正比关系000任何地方的气压值总是随着海拔高度的增加而递减。
据实测,在地面层中,高度每升100m,气压平均降低12.7hPa,在高层则小于此数值。
000确定空气密度大小与气压随高度变化的定量关系,一般是应用静力学方程和压高方程。
0001、静力学方程000假使大气相对于地面处于静止状态,则某一点的气压值等于该点单位面积上所承受空气柱的重量。
000公式是:h≈8000(1+t/273)/P(m/hPa)000其中h是气压高度差,t是摄氏温标,P是气压000从公式可以看出000①在同一气压下,气柱的温度越高,密度越小,气压随高度递减越慢,单位气压高度差越大。
000②在同一温度下,气压值越大的地方,空气密度越大,气压随高度递减越快,单位高度差越小。
000通常,大气处于静力平衡状态,当气层不太厚和要求精度不太高时,这公式可粗略估算气压与高度的定量关系。
如果研究的气层高度变化范围很大,气柱中上下层温度、密度变化显著时,该公式就不适合用了,这时候可以用压高方程。
0002、压高方程000为了精确地获得气压与高度的对应关系,通常将静力学方程从气层底部到顶部进行积分,即得出压高方程,然后再将之替换简化为:000Z2-Z1=18400(1+t/273)log( P1/P2) 000式中P1、P2分别是高度Z2、Z1的气压值,t是摄氏温标000从公式可以看出000①气压随高度增加按指数规律递减000②高度越高,气压减小得越慢000这公式是将大气当成干空气处理的,但当空气中水汽含量较多时,就必须用虚温代替式中的气温。
000大气密度与海拔高度和温度间的换算0001、根据大气压力和空气密度计算公式,以及空气湿度经验公式,可得出大气压、空气密度、湿度与海拔高度的关系。
[精彩]大气压和海拔的换算
![[精彩]大气压和海拔的换算](https://img.taocdn.com/s3/m/823844e44793daef5ef7ba0d4a7302768e996ff8.png)
大气压力与海拔高度转换一个地方气压值经常有变化→其上空大气柱中空气质量的多少→大气柱厚度和密度改变的反映:大气柱厚度和密度与空气质量应该是成正比关系00任何地方的气压值总是随着海拔高度的增加而递减。
据实测,在地面层中,高度每升100m,气压平均降低12.7hPa,在高层则小于此数值。
0确定空气密度大小与气压随高度变化的定量关系,一般是应用静力学方程和压高方程。
001、静力学方程0假使大气相对于地面处于静止状态,则某一点的气压值等于该点单位面积上所承受空气柱的重量。
00公式是:h≈8000(1+t/273)/P(m/hPa)0其中h是气压高度差,t是摄氏温标,P是气压00从公式可以看出00①在同一气压下,气柱的温度越高,密度越小,气压随高度递减越慢,单位气压高度差越大。
00②在同一温度下,气压值越大的地方,空气密度越大,气压随高度递减越快,单位高度差越小。
00通常,大气处于静力平衡状态,当气层不太厚和要求精度不太高时,这公式可粗略估算气压与高度的定量关系。
如果研究的气层高度变化范围很大,气柱中上下层温度、密度变化显著时,该公式就不适合用了,这时候可以用压高方程。
002、压高方程0为了精确地获得气压与高度的对应关系,通常将静力学方程从气层底部到顶部进行积分,即得出压高方程,然后再将之替换简化为:00Z2-Z1=18400(1+t/273)log( P1/P2) 0式中P1、P2分别是高度Z2、Z1的气压值,t是摄氏温标0从公式可以看出00①气压随高度增加按指数规律递减00②高度越高,气压减小得越慢00这公式是将大气当成干空气处理的,但当空气中水汽含量较多时,就必须用虚温代替式中的气温。
00大气密度与海拔高度和温度间的换算1、根据大气压力和空气密度计算公式,以及空气湿度经验公式,可得出大气压、空气密度、湿度与海拔高度的关系。
注:标准状态下大气压力为1,相对空气密度为1,绝对湿度为11 g/m3。
从表中可以看出,海拔高度每升高1 000 m,相对大气压力大约降低12%,空气密度降低约10%,绝对湿度随海拔高度的升高而降低。
海拔高度与大气压换算公式

海拔高度与大气压换算公式
海拔高度与大气压之间存在着一定的关系,这种关系可以用一定的公式进行换算。
一般而言,海拔高度越高,大气压就越低,而且这种关系并不是线性的,因为大气的密度随着高度的增加而逐渐降低。
在海拔高度较低的地方,可以使用国际标准大气模型来计算海拔高度和大气压的关系。
这种模型假设大气是均匀、静止的,并且按照一定的温度和压力分布来计算大气的密度。
根据这个模型,可以使用下面的公式来计算海拔高度和大气压之间的关系:
P = P0 * e^(-M*g*h / R*T)
其中,P表示海拔高度为h时的大气压,P0表示海平面上的大气压,M表示大气的平均分子质量,g表示重力加速度,R表示气体常数,T表示大气的平均温度。
这个公式中的指数函数表示了海拔高度和大气压之间的非线性关系,其中指数的值随着海拔高度的增加而逐渐减小。
使用这个公式可以方便地计算出不同海拔高度处的大气压,从而更好地进行高度计算和气象预报等工作。
- 1 -。
地球 大气密度 温度

地球大气密度温度地球的大气密度与温度是与我们的生活息息相关的重要参数。
地球是宇宙中唯一被发现本身拥有大气层的行星,这使得地球成为了生命能够存在的独特环境。
在地球上,大气层主要由氮气(约占78%)、氧气(约占21%)和少量的其他气体组成。
大气密度和温度是大气层的两个基本属性,它们会随着海拔和季节的变化而变化。
首先,大气密度是指单位体积空气中分子(或原子)数目的多少,通常以千克/立方米表示。
大气密度随着海拔的升高而逐渐减小,这是因为随着海拔的增加,大气层中的气体分子数目变少,导致单位体积中气体的质量减小。
换句话说,海拔越高,大气压力越低,大气密度也相应减小。
这也是高山上气温较低和氧气含量较少的原因之一。
其次,温度是指物质中分子的热运动程度的度量,通常以摄氏度或开尔文度表示。
地球的大气温度随着海拔的升高和纬度的变化而不同。
总体来说,随着海拔的增加,气温会下降,这是因为气压下降会导致气体的膨胀并吸收大量的热量。
此外,地球的极地地区温度较低,而赤道地区温度较高。
这是因为太阳辐射在赤道附近更直接,而在极地地区因为太阳高度角较低而散射较多,导致辐射热量减少。
大气密度和温度的变化对我们的生活有着重要的影响。
首先,在航空领域,大气密度和温度是飞机起飞和飞行的重要参考因素。
随着海拔的升高,飞机的升力减小,所以在高海拔上,飞机需要更长的起飞跑道或者减少载荷。
而温度的变化也会对飞机的性能产生影响,高温会导致空气稀薄,进而降低发动机的功率和提供的升力。
其次,在气象学中,大气密度和温度对天气和气候的形成也有重要影响。
大气层中的气体运动和温度分布是形成气压系统、风和降水的基础。
冷暖气团的相互作用会引发气象现象,比如冷暖锋面上的降雨、台风等等。
通过研究大气密度和温度分布,我们可以更好地预测和理解天气变化。
此外,大气密度和温度的变化还会对环境和生物产生影响。
例如,高温和较高的大气密度会影响农作物的生长,而在寒冷的地区,则可能限制某些植物的范围。
海拔对高低压柜的影响

海拔高度对中压开关设备的影响1.高海拔对电器产品的要求1)高海拔地区的主要特征是大气压力和空气密度的降低。
在此首先对低气压下的一些物理机理进行简单分析。
根据气体状态方式求得空气密度与海拔高度的关系为:ρH=ρ0(1-αΗ/Τ0)4.26式中:ρH为海拔高度为 H 时的空气密度;ρ0 为标准状态下空气密度,海平面在摄氏零度气温条件下的空气密度是 1292g/m3;H为海拔高度(m);Τ0 为绝对温度,为 273K;α为空气温度梯度,约为0.0065K/m。
通过上述方程式,计算出的结果见表1表 1 海拔高度与大气压力、空气密度、绝对湿度的关系海拔高度(m) 0 1000 2000 2500 3000 4000 5000相对大气压 1 0.881 0.774 0.724 0.677 0.591 0.514相对空气密度 1 0.903 0.813 0.770 0.730 0.653 0.583绝对湿度(g/m3) 11 7.64 5.30 4.42 3.68 2.54 1.77从表 1 中可以看出,海拔高度每升高 1000m,相对大气压大约降低12%,空气密度降低约 10%,绝对湿度随海拔高度的升高而降低。
另外,随着海拔高度的升高,空气温度也在降低,每升高 1000m,温度降低 6.5K。
空气密度降低后对中压电器产品带来的直接影响表现在两个方面;一是空气稀薄后在电场中更容易发生电离,从而导致绝缘性能的下降;二是空气稀薄后对流散热能力下降导致载流体载流能力的下降。
因此就对在高海拔地区使用的中压电器提出了一些特殊要求。
关于空气的电离,电离度和空气密度并不是线性的关系,在空气密度较大和接近真空的空气密度下都不利于气体分子的电离。
在空气密度较大的情况下,电子或自由电子附着在气体分子上形成的离子在电场中加速运动,由于气体分子间的间隙很小,分子间碰撞频繁,离子无法加速到足够的动能去碰撞其它分子使其电离。
而在接近真空的情况下,尽管在电场中荷能电子或离子可以加速到足够的动能,但与气体分子的碰撞概率大大降低,同样不利于气体介质的电离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海拔与大气密度和温度
间的换算关系
The manuscript was revised on the evening of 2021
海拔高度与大气密度和温度间的换算关系
1、根据大气压力和空气密度计算公式,以及空气湿度经验公式,可得出大气压、空气密度、湿度与海拔高度的关系。
注:标准状态下大气压力为1,相对空气密度为1,绝对湿度为11 g/m3。
从表中可以看出,海拔高度每升高1000 m,相对大气压力大约降低12%,空气密度降低约10%,绝对湿度随海拔高度的升高而降低。
绝对湿度是指每单位容积的气体所含水分的重量,用mg/L或g/m3表示;相对湿度是指绝对湿度与该温度饱和状态水蒸气含量之比用百分数表达。
2、空气温度与海拔高度的关系
在无热源、无遮护的情况下,空气温度随海拔高度的增高而降低。
一般研究所采集的温度与海拔高度的关系:
从表中可以看出:空气温度在一般情况下,海拔高度每升高1000 m,最高温度会降低5℃,平均温度也会降低5 ℃。
大气密度(atmospheric density)
单位容积的大气质量。
空气密度在标准状况(0℃(273k),101KPa)下为·L-1。
空气的密度大小与气温等因素有关,我们一般采用的空气密度是指在0摄氏度、绝对标准指标下,密度为千克每立方米m3).
大气压力随海拔高度而变化,由经验公式 P=P0()(kPa)式中 h一海拔高度(km). 用上面公式,算出压力,然后根据密度= P *29/(8314*T),其中 P的单位是帕,T的单位是K,通常也就是+t
不同温度下干空气算公式:
空气密度 =(实际压力 /标准物理大气压) *(273/实际绝对温度),绝对温度= + 273通常情况下,
即 30摄氏度时,取 M3
-60摄氏度时,取 M3。
