数学实验(1)
【精选】数学实验一矩阵运算与Matlab命令24

运行
17
矩阵的运算(矩阵的加减、数乘、乘积)
C=A1+B1 D=A1-B1 syms c, cA=c*A1 A2=A1(:,1:3), B1 G=A2*B1
18
矩阵的运算(矩阵的加减、数乘、乘积)
求解方程组Ax=b x=A\b 若A为可逆方阵, 输出原方程的解x; 若A为nxm(n>m)阵, 且A’A可逆,输出
原方程的最小二乘解x.
21
矩阵的运算(求解线性方程组)
求矩阵方程:
设A、B满足关系式:AB=2B+A,求B。 其中A=[3 0 1; 1 1 0; 0 1 4]。
取出A的1、3行和1、3列的交叉处元素 构成新矩阵A1
程序
A=[1 0 1 1 2;0 1 -1 2 3;
3 0 5 1 0;2 3 1 2 1],
vr=[1, 3];vc=[1, 3];
A1=A(vr, vc)
观察结果
26
分块矩阵(矩阵的标识)
将A分为四块,并把它们赋值到矩阵B 中,观察运行后的结果。
3
2
2
35 20 60 45
, B 10
15
50
40
20 12 45 20
将 表 格 写 成 矩 阵 形 式
6
计算
输入下面Matlab指令 A=[4 2 3;1 3 2;1 3 3;3 2 2], B=[35 20 60 45;10 15 50 40;20
3 0 5 1 0;2 3 1 2 1]
数学建模实验报告(一)MATLAB中矩阵的基本操作

1.5270
j =
2 3 2 5 1 4
>> min(a,[],1)
ans =
Columns 1 through 5
-2.3299 -0.1303 -1.3617 -1.1176 -0.3031
Column 6
0.0230
>> min(a,[],2)
ans =
-0.4762
-0.0679
-2.3299 -0.1303 0.4550 -1.1176 -0.2176
-1.4491 0.1837 -0.8487 1.2607 -0.3031
Column 6
0.0230
0.0513
0.8261
1.5270
0.4669
>> size(a)
ans =
5 6
>> [i,j]=find(a==max(max(a)))
-1.0000 2.5000 1.0000
3.5000 5.5000 2.5000
>> X=D
X =
4.0000 1.5000 -1.0000
-1.0000 2.5000 1.0000
3.5000 5.5000 2.5000
5、利用randn(5,6)命令生成一个随机矩阵T,求T的矩阵大小,每一行、每一列的最大值和最小值,整个矩阵的最大值与最小值;然后将整个矩阵的最大值所在位置的元素换为100,将最小值所在位置的元素取为-100。
(2):>> a=[2 5 8;7 1 9]
a =
2 5 8
7 1 9
>> b=[4 2 1 3;0 7 6 2;-3 5 9 -1]
复变函数实验课(一)

湖北民族学院理学院2014年春季学期数学与应用数学专业复变函数实验课(一)计算部分上课教师:汪海玲Matlab中复变函数命令集定义符号变量Syms虚单位z=Sqrt(-1)复数表示z=x+y*i指数表示z=r*exp(i*a)求实部Real(z)求虚部Imag(z)求共轭Conj(z)求模Abs(z)求幅角Angle(z)三角函数z=sin(z)z=cos(z)指数函数z=exp(z)对数函数z=log(z)幂函数z=z^a解方程expr=‘方程式’;Solve(expr)泰劳展开Taylor(e,z)求留数[r,p,k]=residue(p,q)傅立叶变换Fourier(e,z,w)逆傅立叶变换Ifourier(e,w,z)拉普拉斯变换Laplace(e,w,t)逆拉普拉斯变换Ilaplace(e,t,x)一复数的运算1.复数的实部和虚部复数的实部和虚部的提取可由函数real和imag实现。
调用形式real返回复数x的实部(x)(ximag返回复数x的虚部)2.共轭复数复数的共轭可由函数conj实现。
调用形式conj返回复数x的共轭复数(x)3.复数的模和辐角复数的模和辐角的求解由功能函数abs和angle实现。
调用形式abs复数x的模)(xangle复数x的辐角)(x上机操作:课本例题1.2、例题1.4、课后习题(一)1.4.复数的乘除法复数的乘除法运算由“/”和“ ”实现。
5.复数的平方根复灵敏的平方根运算由函数sprt实现。
调用形式)sprt返回复数x的平方根值(x6.复数的幂运算x^,结果返回复数x的n次幂。
复数的幂运算的形式为n上机操作:课本例题1.87.复数的指数和对数运算复数的指数和对数运算分别由函数exp和log实现。
调用形式exp(x返回复数x的以e为底的指数值)log(x返回复数x的以e为底的对数值)上机操作:课本例题2.17、 2.188.复数的三角函数运算复数的三角函数运算函数参见下面的复数三角函数复数三角函数表9.复数方程求根复数方程求根或实方程的复数根求解也由函数solve实现。
数学实验报告 (1)

(1)参数方程:z=2^2^/2^2^sin y x y x ++(-8<=x<=8,-8<=y<=8) (2)程序:[X,Y]=meshgrid(-8::8);r=sqrt(x.^2+y.^2)+eps;Z=sin(r)./r;Mesh(x,y,z)Axis square(3)程序的输出结果:3:球面,椭球面,双叶双曲面,单叶双曲面1球面: (4):参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *R z R y R x 0π<=θ<2* 0<=ϕ<π (5)程序:u=[0:pi/60:2*pi];v=[0:pi/60:pi];[U,V]=meshgrid(u,v);R=3;X=R*sin(v).*cos(u);Y=R*sin(v).*sin(u);Z=R*cos(v);Surf(x,y,z);axis equal;(3)程序输出结果:2椭球面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *c z b y a x 0<=θ<2*π 0<=ϕ<=π (2)程序:ezsurf(‘3*sin(u)*cos(v) ,’3*sin(u)*sin(v)’,’1*cos(u)’,[0,pi,0,2*pi]);(3)程序的输出结果:3单叶双曲面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕtan sin *sec *cos *sec *z a y a x 0<=θ<2*π -π/2<ϕ<π/2 (2)程序:ezsurf(‘3*sec(u)*cos(v),’3*sec(u)*sin(v)’,’5*tan(u)’,[-pi/2,pi/2,0,2*pi]);axis auto(3)输出程序结果:4双叶双曲面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕsec *sin *tan *cos *tan *c z b y a x 0<=θ<2*π -π<ϕ<3*π/2,ϕ≠π/2(2)程序:ezsurf(‘3*tan(u)*cos(v)’,’3*tan(u)*sin(v)’,’5*sec(u)’,[-pi/2,3*pi/2,0,2*pi]);axis auto(4) (3)输出程序结果:抛物螺线: (1)参数方程:⎪⎩⎪⎨⎧===2^*sin **cos **t c z t t b y t t a x 0<T<+∞ (2)程序:ezplot3(‘2*t*cos(t)’,’2*t*sin(t)’,’t.^2/3’,[0,50]);(3)输出程序结果:(5)马鞍面: (1)参数方程:z=x^2/9-y^2/4 (-25<=x<=25,-25<=y<=25)(2)程序:[X,Y]=meshgrid(-25:1:25);Z=X.^2/9-Y.^2/4;Surf(X,Y,Z)Title(‘马鞍面’)grid off(3)输出程序结果:(6)黎曼函数:(1)程序:n=100;x=[];y=[];k=1;for q=2:nfor p=1:q-1if gcd(q,p)==1 %利用函数gcd(m,n)可求m和n的最大公约数x(k)=p/q;y(k)=1/q;k=k+1;endendendplot(x,y,’.b’); axis([0,1,0,1])(2)程序输出结果:。
北京工业大学工程数学-实验1-数学建模入门

d1100101010011000过河的方式有两种过河次数为奇数时船从此岸划向彼岸过河次数为偶数时船从彼岸划向此岸所以则状态ks随决策kd变化的规律为??kdkksks11????因此设计安全过河方案归结为求决策序列21ddddn??使状态ssk?按状态转移律由初始状态??11111?s经n步达到??00001??ns
我们将人,猫,鸡,米在岸上的情况,依次用四维向量S表示,即S(人,猫,鸡,米),并将这些向量称为状态,则第k次渡河前的状态记为 。
当一物在此岸时,相应分量记为1,在彼岸时记为0。例如(1,1,1,1)表示它们都在此岸,(0,1,1,0)表示猫和鸡在此岸,人和米在彼岸。由于问题中的限制条件,有些状态是允许的,有些状态是不允许的。安全渡河条件下的状态称为允许状态。对本问题而言,允许状态集合为:
(1,0,0,0)
(1,0,0,1)
(1,0,1,0)
(1,1,0,0)
(1,0,0,0)
(1,0,1,0)
1
2
3
4
5
6
7
8
(1,1,1,1)
(0,1,0,1)
(1,1,0,1)
(0,0,0,1)
(1,1,0,1)
(0,0,1,0)
(1,0,1,0)
(0,0,0,0)
(1,0,1,0)
(1,0,0,0)
(2)甲乙两站之间有汽车想通,每隔10分钟甲乙两站相互发一趟车,但发车时刻不一定相同。甲乙两站之间有一中间站丙,某人每天在随机时刻到达丙站,并搭乘最先经过丙站的那趟车,结果发现100天中约有90天到达甲站,大约10天到达乙站。问开往甲乙两站的汽车经过两站的时刻表是如何安排的?
三年级数学题实验

三年级数学题实验本实验旨在探索适合三年级学生的数学题形式,以提高他们的数学学习兴趣和能力。
下面将介绍实验设计、实验过程和实验结果。
实验设计:实验对象:三年级学生实验目的:通过设计合适的数学题,激发学生对数学的兴趣,提高他们的数学学习能力。
实验时间:根据学校课程安排,安排每周一次课外实验活动。
实验过程:1. 实验前准备:教师根据教学大纲和学生的实际情况,设计一系列适合三年级学生的数学题目。
2. 实验活动:每周一次,教师在课堂上向学生分发实验题,并组织学生独立完成。
3. 实验规则:学生在限定的时间内完成数学题,可以自行参考教材或向教师寻求帮助。
4. 实验记录:学生将答案写在答题纸上,并在课后交给教师批改。
5. 实验讨论:教师在批改后,组织学生讨论答案,澄清疑惑,解释题目中的知识点。
6. 实验总结:每次实验结束后,教师和学生共同总结实验的效果和不足之处,并根据学生的反馈不断优化数学题的设计。
实验结果:经过一学期的实验活动,学生们对数学的兴趣明显增加,数学学习能力也得到提升。
他们在独立解答数学题和理解数学概念方面表现出更大的自信和积极性。
此外,在实验讨论环节中,学生之间的互动和合作也得到了增强。
结论:通过本实验,得出了对三年级学生进行数学题实验的可行性。
这种实验活动不仅可以提高学生对数学的兴趣,还能够锻炼他们的逻辑思维和解决问题的能力。
但在今后的实验中,需要进一步完善题目的难易程度和相关辅导材料的配套,以更好地帮助学生提高数学学习水平。
总之,本实验通过设计合适的数学题目,激发学生对数学的兴趣,提高他们的数学学习能力。
实验结果表明,这种实验形式对三年级学生的数学学习具有积极的促进作用。
希望将来有更多的学校和教师能够在课堂教学中引入这样的实验活动,以提升学生的数学素养。
数学实验1-3章习题答案
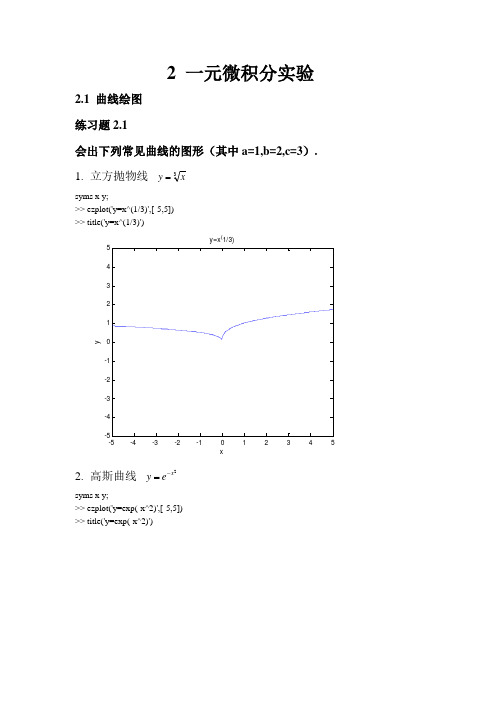
ans =
18.3287
函数的单调区间为:
(1)单调递增区间:-2<x<-1.5326 -0.7315<x<0以及1.5951<x<2;
(2)单调递减区间:-1.5326<x<-0.7315以及0<x<1.5951.
(2)
函数的图形为:
clear
>> fplot('3*x^5-20*x^3+10',[-3,3])
ans =
-3
最值2:
x=1:0.1:3;
>> y=3.*x.^5-20.*x.^3+10;
>> [m k]=max(y)
m =
199
k =
21
>> x(k)
ans =
3
驻点1及相应的二阶导数值:
clear
>> syms x y
>> y=3*x^5-20*x^3+10;
>> yxx=diff(y,x,2);
>> grid on
f=inline('100*acos(1-1/200*(r^2))+r^2*acos(1/20*r)-10*sqrt(r^2-1/400*r^4)-50*pi','r');
>> y=fzero(f,12)
y =
11.5873
3.求解下列非线性方程组在远点附近的根:
clear
>> syms x y z
>> [x y z]=solve('9*x^2+36*y^2+4*z^2-36','x^2-2*y^2-20*z','16*x-x^3-2*y^2-16*z^2',x,y,z)
数学实验1 MATLAB操作基础

1.1.2 MATLAB命令形式 命令形式
在工作空间或MATLAB命令窗口中输入 命令窗口中输入MATLAB 在工作空间或 命令窗口中输入 认可的任何命令,按回车键都可执行其操作. 认可的任何命令,按回车键都可执行其操作 如“4+7”、“4-7”、“4*7”、“4/7”、 “4^5”, 、 、 、 、 , 等按回车键后可显示其结果. “sqrt(5)”等按回车键后可显示其结果 等按回车键后可显示其结果
随机抽取10 名学生的高等数学课程成绩, 例1.2.2 随机抽取 名学生的高等数学课程成绩, 并统计他们中的最高分、 并统计他们中的最高分、最低分以及他们的平均 成绩。 成绩。
math=[88,90,77,69,92,80,74,66,95,85]; %产生 维向量 产生10维向量 产生 mathaver=sum(math)/10 %计算平均成绩 计算平均成绩 h=max(math) l=min(math) %求出最高分 求出最高分 %求出最低分 求出最低分
第一章 MATLAB使用说明 1.1 MATLAB窗口环境与命令形式
1.1.1 Matlab 的窗口环境
当前工 作目录 当前工 作空间 命令 提示符 命令窗口 输入命令的 历史记录
运行MATLAB创建一个或多个窗口
a) 命令区 命令区(Command Window)是用户使用的主 是用户使用的主 要场所,此时,可以输入变量、 要场所,此时,可以输入变量、数组及运算命 进行一些简单的运算; 键搜索、 令,进行一些简单的运算;用↑↓←→键搜索、 键搜索 修改以前使用过的命令操作, 清除窗口; 修改以前使用过的命令操作 用 clc清除窗口 清除窗口 寻求有关帮助; 用help sqrt ( help input …)寻求有关帮助 寻求有关帮助 b) 编辑区 编辑区(Editor\Debugger Window)编制各种 编制各种 M-文件,存盘 文件, 文件 存盘(Save)、运行(Run)等. 、运行( )
重庆大学-数学实验-1MATLAB软件入门

其各位数字的立方和等于该数本身。例如,153是一个水仙花数,因为153=1 计算程序
for a=1:1:9 for b=0:1:9 for c=0:1:9 A=a*100+b*10+c; if A==a^3+b^3+c^3 disp(A)
end end end end 最终结果: 153 370 371 407 分析:此题使我进一步熟悉了循环语句for、while等的基本格式和应用方法, 得注意的是每一个循环语句或条件语句的出现,必定要对应的出现一个end,这 点很容易忽视。 6.编写函数M-文件sq.m:用迭代法求的值。求平方根的迭代公式为 程序: function f=sq(a) a>=0 x=eps; y=1/2*(x+a/x); while (abs(x-y)>=10^(-5)) x=y y=1/2*(x+a/x) end f=x else disp('their exist errors') end 运行结果 调用sq(16),输出结果是4.0000 分析:此题要求掌握利用循环语句进行迭代,实现开方方程的求解,另外x的取
分析在表达乘方的时候要用“y1=x.^2”的形式,在表达x分量的时候可以用 linspace和直接用 生成数组的形式。主要函数:plot:生成图片;hold on和old off用来在同一幅图 描图;text:用程序对图片加标注;gtext:用鼠标在图中加字符;title:用于对 加标题。
1数学建模实验-圆周率的计算

11-23π
1 1 = 4 arctan − arctan (Machin公式) 公式) 公式 4 5 239
此式求得了π的第 位小数且全部正确 此式求得了 的第100位小数且全部正确 的第
12-23
方法1 利用幂级数表达式
1 2 4 n−1 2n−2 =1− x + x −L+ (−1) x +L 2 1+ x
4-23
古 典 方 法 分 析 方 法 其 它 方 法 Ä 概率方法 Ä 数值积分方法
5-23
古典方法
的近似值呢?显然, 用什么方法来计 算π的近似值呢?显然,不可能仅根 据圆周率的定义,用圆的周长去除以直径。起先, 据圆周率的定义,用圆的周长去除以直径。起先,人们 采用的都是用圆内接正多边形和圆外切正多边形来逼近 的古典方法。 的古典方法。
19-23
设计方案
在正方形 0< x <1, 0< y<1 上随机的投大量的点,那么 落在四分之一园内的点数 数m与在正方形内的点数n 之比m/n应为这两部分图形 面积之比=π/4,故 π=4 m/n 计算机模拟:产生区间[0,1]上数目为n的一组 随机数(x,y),计算满足x2+y2<1的点数m
3.1415926535897932384626433832795028841971 6939937510582097494459230781640628620899 8628034825342117068 但是你会计算π的值吗?你又能用几种 方法计算π的值?
3-23
π的计算 的计算
Ä 圆周率是人类获得的最古老的数学概念 之一,早在大约3700年前(即公元前1700 之一,早在大约3700年前(即公元前1700 3700年前 年左右) 256/81( 年左右)的古埃及人就已经在 用256/81( 约3.1605)作为π的近似值了。几千年来 3.1605)作为π的近似值了。 ,人们一直没有停止过求π的努力。 人们一直没有停止过求π的努力。
数学实验报告(新)1-6

实验报告课程名称:院系:专业班级:学号:学生姓名:指导教师:开课时间:至学年第学期一、学生撰写要求按照实验课程培养方案的要求,每门实验课程中的每一个实验项目完成后,每位参加实验的学生均须在实验教师规定的时间内独立完成一份实验报告,不得抄袭,不得缺交。
学生撰写实验报告时应严格按照本实验报告规定的内容和要求填写。
字迹工整,文字简练,数据齐全,图表规范,计算正确,分析充分、具体、定量。
二、教师评阅与装订要求1.实验报告批改要深入细致,批改过程中要发现和纠正学生实验报告中的问题,给出评语和实验报告成绩,签名并注明批改日期。
实验报告批改完成后,应采用适当的形式将学生实验报告中存在的问题及时反馈给学生。
2.实验报告成绩用百分制评定,并给出成绩评定的依据或评分标准(附于实验报告成绩登记表后)。
对迟交实验报告的学生要酌情扣分,对缺交和抄袭实验报告的学生应及时批评教育,并对该次实验报告的分数以零分处理。
对单独设课的实验课程,如学生抄袭或缺交实验报告达该课程全学期实验报告总次数三分之一以上,不得同意其参加本课程的考核。
3.各实验项目的实验报告成绩登记在实验报告成绩登记表中。
本学期实验项目全部完成后,给定实验报告综合成绩。
4.实验报告综合成绩应按课程教学大纲规定比例(一般为10-15%)计入实验课总评成绩;实验总评成绩原则上应包括考勤、实验报告、考核(操作、理论)等多方面成绩;5.实验教师每学期负责对拟存档的学生实验报告按课程、学生收齐并装订,按如下顺序装订成册:实验报告封面、实验报告成绩登记表、实验报告成绩评定依据、实验报告(按教学进度表规定的实验项目顺序排序)。
装订时统一靠左侧按“两钉三等分”原则装订。
数学实验基础 实验报告(1)常微分方程

实验一 常微分方程1. 分别用Euler 法和ode45解下列常微分方程并与解析解比较: (1) ,(0)1,13y x y y x '=+=<<Euler 法:function [t,y]=euler(Fun,tspan,y0,h) t=tspan(1):h:tspan(2); y(1)=y0;for i=1:length(t)-1y(i+1)=y(i)+h.*feval(Fun,t(i),y(i)); end t=t'; y=y';function f=Fun(x,y) % 常微分方程的右端函数 f=x+y;>> [x,y]=euler('Fun',[0,3],1,0.1)>> [x,y] ans =0 1.0000 0.1000 1.1000 0.2000 1.2200 0.3000 1.3620 0.4000 1.5282 0.5000 1.7210 0.6000 1.9431 0.7000 2.1974 0.8000 2.4872 0.9000 2.8159 1.0000 3.1875 1.1000 3.6062 1.2000 4.0769 1.3000 4.6045 1.4000 5.1950 1.5000 5.8545 1.6000 6.5899 1.7000 7.4089 1.8000 8.3198 1.9000 9.3318 2.0000 10.4550 2.1000 11.7005 2.2000 13.0805 2.3000 14.6086 2.4000 16.2995 2.5000 18.1694 2.6000 20.2364 2.7000 22.5200 2.8000 25.0420 2.9000 27.8262 3.0000 30.8988ode45:>> [x,y]=ode45('Fun',[0,3],1) ans =0 1.0000 0.0502 1.0528 0.1005 1.1109 0.1507 1.17460.2010 1.2442 0.2760 1.3596 0.3510 1.4899 0.4260 1.63610.5010 1.7996 0.5760 1.9817 0.6510 2.1838 0.7260 2.4074实验一 常微分方程0.8010 2.6544 0.8760 2.9264 0.9510 3.2254 1.0260 3.55351.1010 3.9131 1.1760 4.3065 1.2510 4.7364 1.3260 5.20561.4010 5.7172 1.4760 6.2744 1.5510 6.8810 1.6260 7.54061.7010 8.2574 1.7760 9.0359 1.8510 9.8808 1.9260 10.79742.0010 11.7912 2.0760 12.8683 2.1510 14.0351 2.2260 15.29862.3010 16.6664 2.3760 18.1466 2.4510 19.7478 2.5260 21.47962.6010 23.3522 2.6760 25.3764 2.7510 27.5641 2.8260 29.92812.9010 32.4820 2.9257 33.3694 2.9505 34.2796 2.9752 35.21343.0000 36.1711解析解:>> y=dsolve('Dy=x+y','y(0)=1','x') y =2*exp(x) - x - 1(2) 20.01()2sin(),(0)0,(0)1,05y y y t y y t ''''-+===<< Euler 法:实验一常微分方程function f=Fun(t,y)% 常微分方程的右端函数f=[y(2);0.01*y(2)^2-2*y(1)+sin(t)];>> [t,y]=euler('Fun',[0,5],[0,1],0.2)ode45:>> [t,y]=ode45('Fun',[0,5],[0,1])t =0 0.0001 0.0001 0.0002 0.0002 0.0005 0.0007 0.0010 0.0012 0.00250.0037 0.0050 0.0062 0.0125 0.0188 0.0251 0.0313 0.0627 0.0941 0.12550.1569 0.2819 0.4069 0.5319 0.6569 0.7819 0.9069 1.0319 1.1569 1.28191.4069 1.5319 1.6569 1.7819 1.90692.0319 2.1569 2.2819 2.4069 2.53192.6569 2.7819 2.90693.0319 3.1569 3.2819 3.4069 3.5319 3.6569 3.78193.90694.0319 4.1569 4.2819 4.4069 4.5319 4.6569 4.7427 4.8285 4.91425.0000y =0 1.0000 0.0001 1.0000 0.0001 1.0000 0.0002 1.0000 0.0002 1.00000.0005 1.0000 0.0007 1.0000 0.0010 1.0000 0.0012 1.0000 0.0025 1.00000.0037 1.0000 0.0050 1.0000 0.0062 1.0000 0.0125 1.0000 0.0188 1.00000.0251 0.9999 0.0313 0.9998 0.0627 0.9987 0.0941 0.9965 0.1253 0.99340.1564 0.9893 0.2786 0.9632 0.3966 0.9220 0.5085 0.8662 0.6126 0.79670.7072 0.7146 0.7908 0.6210 0.8620 0.5176 0.9198 0.4058 0.9632 0.28760.9915 0.1647 1.0043 0.0392 1.0013 -0.0869 0.9826 -0.2117 0.9485 -0.33310.8996 -0.4490 0.8365 -0.5578 0.7605 -0.6577 0.6725 -0.7471 0.5742 -0.8246实验一 常微分方程0.4669 -0.8889 0.3525 -0.9393 0.2327 -0.9748 0.1095 -0.9950 -0.0154 -0.9996-0.1398 -0.9887 -0.2619 -0.9624 -0.3798 -0.9212 -0.4916 -0.8657 -0.5957 -0.7970-0.6904 -0.7161 -0.7742 -0.6242 -0.8460 -0.5228 -0.9046 -0.4134 -0.9491 -0.2978-0.9789 -0.1777 -0.9934 -0.0549 -0.9945 0.0300 -0.9883 0.1146 -0.9748 0.1985-0.9543 0.28092. 求一通过原点的曲线,它在(,)x y 处的切线斜率等于22,0 1.57.x y x +<<若x 上限增为1.58,1.60会发生什么?function f=Fun(x,y) % 常微分方程的右端函数 f=2*x+y.^2;>> [x,y]=ode45('Fun',[0,1.57],0) x =0 0.0393 0.0785 0.1178 0.1570 0.1963 0.2355 0.2748 0.3140 0.3533 0.3925 0.4318 0.4710 0.5103 0.5495 0.5888 0.6280 0.6673 0.7065 0.7458 0.7850 0.8243 0.8635 0.9028 0.9420 0.9813 1.0205 1.0598 1.0990 1.1383 1.1775 1.2168 1.2560 1.2953 1.3345 1.3738 1.4130 1.4248 1.4367 1.4485 1.4604 1.4722 1.4840 1.4959 1.5077 1.5140 1.5203 1.5265 1.5328 1.5376 1.5424 1.5472 1.5519 1.5543 1.5567 1.5591 1.5614 1.5631 1.5647 1.5664 1.5681 1.5685 1.5690 1.5695 1.5700 y =实验一 常微分方程0 0.0015 0.0062 0.0139 0.0247 0.0386 0.0556 0.0758 0.09920.1259 0.1559 0.1895 0.2266 0.2675 0.3124 0.3615 0.4152 0.4738 0.5378 0.6076 0.6841 0.7679 0.8601 0.9620 1.0751 1.2014 1.3434 1.5045 1.6892 1.9037 2.1557 2.4577 2.8282 3.3003 3.9056 4.7317 5.9549 6.4431 7.0116 7.6832 8.4902 9.4821 10.7170 12.3090 14.4551 15.9220 17.7080 19.9390 22.8164 25.6450 29.2282 33.9673 40.5910 44.9434 50.3088 57.1229 66.1087 74.3108 84.7123 98.4901 117.7875 124.9206 132.9699 142.1268 152.641500.20.40.60.81 1.2 1.4 1.6若x 上限增为1.58,1.60,则超出运算的范围,发生溢出。
实验1单容水箱液位数学模型的测定实验

实验1 单容水箱液位数学模型的测定实验一、实验目的1、熟练掌握液位测量方法。
2、熟练掌握调节阀流量调节特性。
3、获得单容水箱液位数学模型。
二、实验设备A3000-FS/FBS 常规现场系统,任意控制系统。
三、实验原理与介绍1、实验结构介绍水流入量Qi 由调节阀u 控制,流出量Qo 则由用户通过闸板开度来改变。
被调量为水位H 。
分析水位在调节阀开度扰动下的动态特性。
直接在调节阀上加定值电流,从而使得调节阀具有固定的开度。
(可以通过智能调节仪手动给定,或者AO 模块直接输出电流。
)调整水箱出口到一定的开度。
突然加大调节阀上所加的定值电流观察液位随时间的变化,从而可以获得液位数学模型。
通过物料平衡推导出的公式:μμk Q H k Q i O ==,那么 )(1H k k Fdt dH -=μμ,给定值 图4-1单容水箱液位数学模型的测定实验其中,F 是水槽横截面积。
在一定液位下,考虑稳态起算点,公式可以转换成μμR k H dtdH RC =+。
公式等价于一个RC 电路的响应函数,C=F 就是水容,k H R 02=就是水阻。
如果通过对纯延迟惯性系统进行分析,则单容水箱液位数学模型可以使用以下S 函数表示:)1()(0+=TS S KR S G 。
相关理论计算可以参考清华大学出版社1993年出版的《过程控制》,金以慧编著。
2、控制系统接线表3参考结果单容水箱水位阶跃响应曲线,如图4-2所示:图4-2 单容水箱液位飞升特性此时液位测量高度184.5 mm ,实际高度184.5 mm -3.5 mm =181 mm 。
实际开口面积5.5x49.5=272.25 mm²。
此时负载阀开度系数:s m x H Q k /1068.6/5.24max -==。
水槽横截面积:0.206m²。
那么得到非线性微分方程为(标准量纲)::H H dt dH 24003.000138.0206.0/)668000.0000284.0(/-=-=进行线性简化,可以认为它是7一阶惯性环节加纯延迟的系统)1/()(+=-Ts Ke s G s τ。
高等数学实验(1稿)

录
实验 1 MATLAB 环境 ........................................................................................................................ 1 1.1 MATLAB 窗口 .......................................................................................................................... 1 1.2 MATLAB 的在线帮助系统 .......................................................................................................3 1.3 MATLAB 的运行方式 ..............................................................................................................4 实验 2 MATLAB 的数组及其运算 .....................................................................................................5 2.1 变量 ......................................................................................................................................5 2.2 一维数组............................................................................................................................... 5 2.2.1 一维数组的创建...........................................................................................................5 2.2.2 一维数组的子数组寻访和赋值 .................................................................................... 6 2.3 二维数组............................................................................................................................... 6 2.3.1 二维数组的创建...........................................................................................................6 2.3.2 二维数组的寻访和赋值 ............................................................................................... 6 2.4 数组运算............................................................................................................................... 7 2.5 向量运算............................................................................................................................... 8 2.6 集合运算............................................................................................................................... 9 实验 3 MATLAB 的程序设计 ........................................................................................................... 10 3.1 MATLAB 的关系运算和逻辑运算.......................................................................................... 10 3.1.1 MATLAB 的关系运算 .................................................................................................... 10 3.1.2 MATLAB 的逻辑运算 .................................................................................................... 10 3.2 MATLAB 的流程控制 ............................................................................................................ 11 3.2.1 MATLAB 的循环结构 .................................................................................................... 11 3.2.2 MATLAB 的分支结构 .................................................................................................... 13 3.2.3 MATLAB 的控制语句 .................................................................................................... 14 3.3 MATLAB 的 M 函数 ................................................................................................................ 15 实验 4 一元函数图形绘制............................................................................................................ 17
高等数学实验-1

图1-9 八次拟合Βιβλιοθήκη 第1章函数与极限—设计性实验
实验二
复利问题
【实验目的】 1.加深对函数极限概念的理解 2.讨论极限在实际问题中的应用 3.会用Matlab命令求函数极限 【实验要求】 掌握极限概念,Matlab软件求函数极限的命 令limit
第1章函数与极限—设计性实验
【实验内容】
复利,即利滚利。不仅是一个经济问题,而且是 一个古老又现代的经济社会问题。随着商品经济 的发展,复利计算将日益普遍,同时复利的期限 将日益变短,即不仅用年息、月息,而且用旬息、 日息、半日息表示利息率。现在我们已进入电子 商务时代,允许储户随时存款或取款,如果一个 储户连续不断存款和取款,结算本息的频率趋于 无穷大,每次结算后将本息全部存入银行,这意 味着银行不断地向储户支付利息,称为连续复利 问题。
第1章函数与极限--验证性实验
【实验内容】 1.求下列函数的复合函数 (1) f 1 , g sin y ,求
1 x2
f ( g ( y))
【实验过程】 1.(1)>>syms x y >> f=1/(1+x^2); >> g=sin(y); >> compose(f,g) 运行结果: ans = 1/(sin(y)^2+1) 由上述结果可知:
本金+利息= p(1+r/n)+ p(1+r/n)*r/n =p(1+r/n)2 ……,
第n期到期后的本利和是 p(1+r/n)n 存期为t年(事实上是有tn期),到期后的本利和为 p(1+r/n)tn 随着结算次数的无限增加,即在上式中n→∞,t=1 年后本息共计 n lim100000 r/n) ≈10.6184(万元) (1+ n 随着结算次数的无限增加,一年后本息总和将稳 定于10.6184万元,储户并不能通过该方法成为百 万富翁。
离散数学实验1

“离散数学”实验报告(实验1)专业班级学号姓名目录一.实验目的; ....................................... - 1 -二.实验内容; ....................................... - 2 -1. 逻辑联接词的运算 ..................................................................................................... - 2 -2. 求任意一个命题公式的真值表 ................................................................................. - 2 -三.实验环境; ....................................... - 2 -四. 实验原理和实现进程(算法描述);................. - 2 -1.实验原理 ....................................................................................................................... - 2 -2.实验进程 ....................................................................................................................... - 3 -五.实验数据及结果分析;.............................. - 7 -题A:................................................................................................................................ - 7 - B,C题:............................................................................................................................ - 9 - 六. 源程序清单; ................................... - 13 -A题部份源代码: .......................................................................................................... - 13 - tt:printf("***************************************\n");其他收成和体会。
以数学实验促概念理解——《角的初步认识》教学设计(一)

小学教学计·数学2022/04【教学内容】苏教版二年级下册第84、85页。
【教学过程】●实验一:建立角的概念。
1.激活经验。
师:两位同学正在做手工,他们已经做成了什么?师:为什么叫五角星和三角形?大家提到了角,这就是今天要研究的内容———角的初步认识。
2.实验示范。
师:什么是角呢?来进行今天师:请一组同桌来示范一下。
生1:来看看材料袋里有什么?生2:第一个要求是找角,看,我找到的角就在这里。
生1:我也来再框一个角。
生2:我们再来摸一摸角吧。
生1:(边摸边说)这里是尖尖的,两边是直直的。
生2:是的,这个角也是这样。
生1:那我们把“角”描下来吧。
生2:我先把刚才摸的尖尖的点画出来。
再描两条直直的线,这个角就描好了。
【设计意图:一个有效的数学实验应该具备以下几点:1.明确的实验目标;2.相对规范的实验步骤;3.带有思考的具身参与。
这个实验的内容比较丰富,包含了找一找、摸一摸、描一描三个环节,因此示范很重要。
实验示范也有两个目的:一是如何找一找、摸一摸、描一描。
找是为了让学生的活动聚焦于角;摸是要让学生切身感知角的特征,如前文所述,由于学生会误以为角的顶点就是角,所以实验用“框”的办法让学生“看”到角的全貌,再通过“摸”引导学生感受角尖尖的点以及两条直直的边;而“描”则是将实物第一次抽象出角的过程,让学生对角的认识从形象逐步到抽象。
有了这些实验示范,学生才能进行有效的实验活动,且每一个实验活动都能够指向角概念的感知。
二是在实验中如何合作,实验者如何清楚地表达自己的感受,而实验伙伴如何倾听,双方如何相互启发学习等,这样才能提高合作的效率,最终充分地、高效地完成数学实验。
】3.展开实验。
(学生实验,教师巡视指导,实验结束后请学生汇报实验成果)师:我们得到了这么多角,它们开口的方向不同,形状也不同,却都是角,它们有什么共同点吗?生:它们都有一个尖尖的点。
生:它们还有两条直直的边。
生:那两条边正好靠到这一个点上,组成了一个角。
