相交线与平行线单元测试题

合集下载

(完整word版)相交线与平行线单元测试卷(含答案)

12345678（第4题）ab cABCD （第7题）第五章《相交线与平行线》测试卷姓名 _______ 成绩 _______一、选择题（每小题4分，共 40 分） 1、如图所示,∠1和∠2是对顶角的是（）ABC D121212122、如图,在正方体中和AB 垂直的边有（）条。

A.1 B 。

2 C.3 D 。

43、如图AB ∥CD,∠ABE=120°，∠ECD=25°,则∠E=（ )A.75°B.80°C.85° D 。

95°4、如图所示，直线a 、b 被直线c 所截，现给出下列四种条件： ①∠2＝∠6 ②∠2＝∠8 ③∠1＋∠4＝180° ④∠3＝∠8，其中能判断是a ∥b 的条件的序号是( ）A 、①②B 、①③C 、①④D 、③④ 5、某人在广场上练习驾驶汽车,两次拐弯后，行驶方向与原来相同，这两次拐弯的角度可能是（ ) A 、第一次左拐30°，第二次右拐30° B 、第一次右拐50°，第二次左拐130° C 、第一次右拐50°，第二次右拐130° D 、第一次向左拐50°，第二次向左拐130° 6、下列哪个图形是由左图平移得到的（）A B CDE(第10题)水面入水点运动员(第14题)ABCDEF G H 第13题A BCD7、如图,在一个有4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD 面积的比是（）A 、3：4B 、5:8C 、9:16D 、1：2 8、下列现象属于平移的是( ）① 打气筒活塞的轮复运动，② 电梯的上下运动，③ 钟摆的摆动,④ 转动的门,⑤ 汽车在一条笔直的马路上行走A 、③B 、②③C 、①②④D 、①②⑤ 9、下列说法正确的是（ )A 、有且只有一条直线与已知直线平行B 、垂直于同一条直线的两条直线互相垂直C 、从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离。

相交线与平行线单元测试题总集完整含答案

B E DA CF87654321DCBA第五章相交线与平行线测试题一、选择题(每题3分,共30分)1、如图1，直线a ，b 相交于点O ，若∠1等于40°，则∠2等于（）A ．50°B ．60°C ．140°D ．160°图1 图2 图3 2、如图2，已知AB ∥CD ，∠A ＝70°，则∠1的度数是（）A ．70°B ．100°C ．110°D ．130°3、已知：如图3，AB CD ⊥，垂足为O ，EF 为过点O 的一条直线，则1∠ 与2∠的关系一定成立的是（）A ．相等B ．互余C ．互补D ．互为对顶角4、如图4，AB DE ∥，65E ∠=，则B C ∠+∠=（）A ．135B ．115C ．36D ．65图4 图5 图65、如图5，小明从A 处出发沿北偏东60°方向行走至B 处，又沿北偏西20方向行走至C 处，此时需把方向调整到与出发时一致，则方向的调整应是（）A ．右转80°B ．左转80°C ．右转100°D ．左转100° 6、如图6，如果AB ∥CD ，那么下面说法错误的是（）A ．∠3=∠7；B ．∠2=∠6C 、∠3+∠4+∠5+∠6=1800D 、∠4=∠87、如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30，那么这两个角是（）A ． 42138、；B ．都是10；C ． 42138、或4210、；D ．以上都不对8、下列语句：①三条直线只有两个交点，则其中两条直线互相平行；②如果两条平行线被第三条截，同旁内角相等，那么这两条平行线都与第三条直线垂直；③过一点有且只有一条直线与已知直线平行，其中（）A ．①、②是正确的命题；B ．②、③是正确命题；C ．①、③是正确命题；D ．以上结论皆错DB A C1ab1 2OABCD EF 2 1Oa b M P N 1 2 3A B C a b1 23 B E9、下列语句错误的是（）A ．连接两点的线段的长度叫做两点间的距离；B ．两条直线平行，同旁内角互补C ．若两个角有公共顶点且有一条公共边，和等于平角，则这两个角为邻补角D ．平移变换中，各组对应点连成两线段平行且相等10、如图7，a b ∥，M N ，分别在a b ，上，P 为两平行线间一点，那么123∠+∠+∠=（）A ．180B ．270C ．360D ．540二、填空题(每题3分,共18分)11、如图8，直线a b ∥，直线c 与a b ，相交．若170∠=，则2_____∠=．图7 图8 图9 图1012、如图9，已知170,270,360,∠=︒∠=︒∠=︒则4∠=______︒．13、如图10，已知AB ∥CD ，BE 平分∠ABC ，∠CDE ＝150°，则∠C ＝______14、如图11，已知a b ∥，170∠=，240∠=，则3∠ 图11 1315、如图12的一个条件．16、如图13，已知AB CD //，∠α=____________ 三、解答题（共52分）17、推理填空：(每空1分,共12分)如图： ① 若∠1=∠2，则 ∥ （）若∠DAB+∠ABC=1800，则∥ （）②当 ∥ 时，∠ C+∠ABC=1800 （）当 ∥ 时，∠3=∠C （）18、如图，∠1＝30°，AB ⊥CD ，垂足为O ，EF 经过点O .求∠2、∠3的度数. (8分)12 bac b ac d1 2 3 4 A BCDE 321DCBAABCDO123EF19、已知：如图AB ∥CD ，EF 交AB 于G ，交CD 于F ，FH 平分∠EFD ，交AB 于H ，∠AGE=500，求：∠BHF 的度数．(8分)20、(10分（1）如图a ，图中共有＿＿＿对对顶角；（2）如图b ，图中共有＿＿＿对对顶角；（3）如图c ，图中共有＿＿＿对对顶角.（4）研究（1）～（3）小题中直线条数与对顶角的对数之间的关系，若有n 条直线相交于一点，则可形成多少对对顶角？（5）若有2008条直线相交于一点，则可形成多少对对顶角？21、(6分)如图，AD 是∠EAC 的平分线，AD ∥BC ，∠B ＝30º，求∠EAD ，∠DAC ，∠C 的度数。

平行线与相交线单元测试题

平行线与相交线单元测试题一、选择题（每题2分，共10分）1. 平行线的定义是什么？A. 永远不会相交的直线B. 相交于一点的直线C. 垂直于同一条直线的直线D. 相交于一个点但角度不同的直线2. 如果两条直线相交，它们的角度和是多少度？A. 90度B. 180度C. 360度D. 45度3. 以下哪项不是平行线的性质？A. 平行线在任何地方都不相交B. 平行线之间的距离处处相等C. 平行线可以相交D. 通过平行线之一可以画出无数条平行线4. 两条平行线被第三条直线所截，所形成的内错角的特点是？A. 内错角相等B. 内错角互补C. 内错角和为90度D. 内错角和为180度5. 同位角的定义是什么？A. 两条平行线被第三条直线所截，同侧的角B. 两条直线相交形成的角C. 两条平行线被第三条直线所截，异侧的角D. 两条直线相交形成的同侧角二、填空题（每题2分，共10分）6. 当两条直线相交时，它们形成的角中，____角相等。

7. 如果两条直线相交，且其中一个角是90度，则这两条直线是____。

8. 平行线之间的距离在任何地方都是____。

9. 两条平行线被第三条直线所截，同旁内角的和是____。

10. 如果两条直线相交，且其中一个角是锐角，则这个角的对顶角是____。

三、判断题（每题1分，共5分）11. 平行线永远不会相交。

（）12. 垂直线是相交线的一种特殊形式。

（）13. 两条平行线之间的夹角总是90度。

（）14. 同旁内角互补，即它们的和为180度。

（）15. 如果两条直线相交形成的角是钝角，那么这个角的对顶角是锐角。

（）四、简答题（每题5分，共10分）16. 解释什么是“对应角”，并给出一个例子。

17. 描述如何使用三角板来测量两条直线是否平行。

五、计算题（每题5分，共10分）18. 如果两条平行线被一条直线所截，形成的内错角分别为40度和140度，请计算同旁内角的度数。

19. 在一个直角三角形中，如果一个锐角是30度，求另一个锐角的度数。

相交线与平行线单元测试题(含答案)

相交线与平行线一、选择题（本大题共8小题，每小题只有一个正确选项，每小题3分，共24分）1．在下面各图中，∠1与∠2是对顶角的是（）A．B．C．D．2．如图，直线a、b相交于点O，若∠1＝30°，则∠2等于（）A．60°B．30°C．140°D．150°3．如图，直线a，b相交于点O，若∠1＝40°，则∠2＝（）A．40°B．50°C．60°D．140°4．如图，点P在直线l外，点A，B在直线l上，PA＝3，PB＝7，点P到直线l的距离可能是（）A．2 B．4 C．7 D．85．如图，直线a∥b，∠1＝50°，则∠2的度数为（）A．40°B．50°C．55°D．60°6．如图，工人师傅用角尺画出工件边缘AB的垂线a和b，得到a∥b．理由是（）A．连接直线外一点与直线上各点的所有线段中，垂线段最短B．在同一平面内，垂直于同一条直线的两条直线互相平行C．在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线D．经过直线外一点，有且只有一条直线与这条直线平行7．如图，已知ON丄a，OM丄a，所以OM与ON重合的理由是（）A．两点确定一条直线B．经过一点有且只有一条线段垂直于己知直线C．过一点只能作一条垂线D．垂线段最短8．如图，直线AB∥CD，∠A＝70°，∠E＝30°，则∠C等于（）A．30°B．40°C．60°D．70°二、填空题（本大题共6小题，每小题3分，共18分）9．如图所示，在铁路旁边有一李庄，现要建一火车站，为了使李庄人乘火车最方便（即距离最近），请你在铁路旁选一点来建火车站（位置已选好），说明理由：．10．如图，已知O是直线AB上一点，∠1＝30°，OD平分∠BOC，则∠2＝．11．如图，直线AB、CD相交于点O，EO⊥AB，∠AOC＝25°。

《相交线与平行线》单元测试题

《相交线与平行线》单元测试题一．选择题（共10小题）1．下列图形中，∠1与∠2是对顶角的是（）A．B．C．D．2．下列句子中不是命题的是（）A．明年是2020年B．延长线段EFC．三角形的内角和是360度D．对顶角相等3．在同一平面内，已知点P在直线l上，过点P画直线l的垂线，可以画出多少条（）A．1条B．2条C．3条D．4条4．如图，下列判断正确的是（）A．∠3与∠6是同旁内角B．∠2与∠4是同位角C．∠1与∠6是对顶角D．∠5与∠3是内错角5．如图，点P是直线l外一点，从点P向直线l引P A，PB，PC，PD四条线段，其中只有PC与l垂直，这四条线段中长度最短的是（）A．P A B．PB C．PC D．PD6．下面推理正确的是（）A．∵a∥b，b∥c，∴c∥d B．∵a∥c，b∥d，∴c∥dC．∵a∥b，a∥c，∴b∥c D．∵a∥b，c∥d，∴a∥c7．如图，在下列给出的条件中，不能判定AB∥CD的是（）A．∠BAD+∠ADC＝180°B．∠ABD＝∠BDCC．∠ADB＝∠DBC D．∠ABE＝∠DCE8．如图，△ABC沿射线BC方向平移到△DEF（点E在线段BC上），如果BC＝7cm，EC ＝4cm，那么平移距离为（）A．3cm B．5cm C．8cm D．13cm9．如图，AC∥BD，AE∥BF，下列结论错误的是（）A．∠A＝∠B B．∠A+∠B＝180°C．∠B＝∠DPE D．∠A＝∠APB 10．某同学的作业如下框，其中横线处应填的依据是（）如图所示，当∠1＝∠2时，∠3＝∠4吗？为什么？请完成下面的说理过程．解，∵∠1＝∠2（已知）．∴直线a∥b（______________）．∴∠3＝∠4（两直线平行，同位角相等）A．两直线平行，内错角相等B．内错角相等，两直线平行C．两直线平行，同位角相等D．同位角相等，两直线平行二．填空题（共6小题）11．如图所示，△EFG是由△ABC沿水平方向平移得到的，如果∠ABC＝90°，AB＝3cm，BC＝2cm，则EF＝，FG＝，EG＝．12．将命题“互为补角的两个角都是锐角”改写成“如果……，那么……”的形式是．13．如图，在三角形ABC中，∠C＝90°，AC＝3，BC＝4，AB＝5，则点A到BC的距离等于．14．如图，在长方体中，与棱AB平行的棱有条．15．如图，一个弯形管道ABCD，若它的两个拐角∠ABC＝120°，∠BCD＝60°，则管道AB∥CD．这里用到的推理依据是．16．如图，已知∠1＝∠2＝32°，∠D＝78°，则∠BCD＝．三．解答题（共8小题）17．如图，直线AB，CD相交于点O，OA平分∠EOC，若∠EOD＝88°，求∠BOD的度数．18．指出下列命题的题设和结论，并判断其真假，如果是假命题，请举出一个反例．（1）邻补角互补；（2）同旁内角互补．19．如图，△ABC，△A1B1C1的顶点都在边长为1个单位长度的小正方形组成的网格线交点上．（1）将△ABC向右平移4个单位得到△A2B2C2，请画出△A2B2C2．（2）试描述△A1B1C1经过怎样的平移可得到△A2B2C2．20．如图，在直角三角形ABC中，∠C＝90°，DE⊥AC交AC于点E，交AB于点D．（1）请分别写出当BC，DE被AB所截时，∠B的同位角、内错角和同旁内角．（2）试说明∠1＝∠2＝∠B的理由．21．如图，已知AB∥CD，射线AH交BC于点F，交CD于点D，从D点引一条射线DE，若∠B+∠CDE＝180°，求证：∠AFC＝∠EDH．证明：∵AB∥CD（已知）∴∠B＝（两直线平行，内错角相等）∵∠B+∠CDE＝180°（已知）∴∠BCD+∠CDE＝180°（等量代换）∴BC∥（同旁内角互补，两直线平行）∴＝∠EDH（）∵＝∠BFD（对顶角相等）∴∠AFC＝∠EDH（等量代换）22．如图是两个重叠的直角三角形，将其中一个直角三角形沿着BC方向平移BE的长度就得到该图形，求阴影部分的面积（单位：厘米）23．如图，点O在直线AB上，OC⊥OD，∠D与∠1互余，F是DE上一点，连结OF．（1）ED是否平行于AB，请说明理由；（2）若OD平分∠BOF，∠OFD＝80°，求∠1的度数．24．如图，图①是一种网红弹弓的实物图，在两头上系上皮筋，拉动皮筋可形成平面示意图如图②和图③，弹弓的两边可看成是平行的，即AB∥CD，各活动小组探索∠APD与∠A，∠C之间数量关系时，有如下发现：（1）在图②所示的图形中，若∠A＝30°，∠D＝35°，则∠APD＝；（2）在图③中，若∠A＝150°，∠APD＝60°，则∠D＝；（3）有同学在图②和图③的基础上，画出了图④所示的图形，其中AB∥CD，请判断∠α，∠β，∠γ之间的关系，并说明理由．。

(完整版)《相交线与平行线》单元测试卷含答案

第4章相交线与平行线单元测试卷一、选择题(每题2分,共20分)1.如图,直线a,b被直线c所截,∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角D.对顶角2.如图,AB∥CD,AD平分∠BAC,若∠BAD=65°,那么∠ACD的度数为()A.40°B.35°C.50°D.45°1 2 33.如图,AB∥EC,下列说法不正确的是()A. ∠B=∠ECDB. ∠A=∠ECDC. ∠B+∠ECB=180°D. ∠A+∠B+∠ACB=180°4.如图,在俄罗斯方块游戏中,出现一小方块拼图向下运动,通过平移运动拼成一个完整的图案,最终所有图案消失,则对小方块进行的操作为()A.向右平移1格再向下B.向右平移3格再向下C.向右平移2格再向下D.以上答案均可5.如图所示,3块相同的三角尺拼成一个图形,图中有很多对平行线,其中不能由下面的根据得出两直线平行的是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.平行于同一直线的两直线平行D.垂直于同一直线的两直线平行6.如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是()A.40°B.70°C.80°D.140°7.同一平面内的四条互不重合的直线满足a⊥b,b⊥c,c⊥d,则下列各选项中关系能成立的是()A.a∥dB.a⊥cC.a⊥dD.b⊥d8.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=()A.120 °B.130°C.140°D.150°9.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为()A.30°B.60°C.80°D.120°10.如图,把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是()6 8 9 10二、填空题(每题3分,共21分)11.如图所示,某地一条小河的两岸都是直的,小明和小亮分别在河的两岸,他们拉紧了一根细绳,当测出∠1和∠2满足关系________时,河岸的两边才是平行的.12.同一个平面内的三条直线两两相交,最多有a个交点,最少有b个交点,则a+b=________.13.在测量跳远成绩时,从落地点到起跳线所拉的皮尺应当与起跳线________.14.如图,在三角形ABC中,BC=5 cm,将三角形ABC沿BC方向平移至三角形A'B'C'的位置时,B'C=3 cm,则三角形ABC平移的距离为cm.11 14 1515.如图是我们常用的折叠式小刀,刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图所示的∠1与∠2,则∠1与∠2的度数和是度.16.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=°.17.如图所示,第1个图案是由黑白两种颜色的六边形地面砖组成的,第2个,第3个图案可以看成是第1个图案经过平移而得,那么第2015个图案中有白色六边形地面砖块.三、解答题(22~24题每题9分,其余每题8分,共59分)18.如图,在一条公路l的两侧有A,B两个村庄.(1)现在镇政府为民服务,沿公路开通公共汽车,同时修建A,B两个村庄到公路的道路,要使两个村庄村民乘车最为方便,请你设计道路路线,在图中画出(标明①),并标出公共汽车停靠点的位置,说出你这样设计的理由;(2)为方便两村物流互通,A,B两村计划合资修建一条由A村到达B村的道路,要使两个村庄物流、通行最为方便,请你设计道路路线,在图中画出(标明②),说出你这样设计的理由.19.如图所示,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.20.如图,CD⊥AB,EF⊥AB,∠E=∠EMC,说明:CD是∠ACB的平分线.21.如图,已知点A,O,B在同一直线上,OC是从点O出发的任意一条射线,OD是∠AOC的平分线,OE是∠COB的平分线,试确定OD和OE的位置关系,并说明理由.22.如图,∠E=∠3,∠1=∠2,试说明:∠4+∠BAP =180°.23.如图所示,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射时,入射光线与平面镜的夹角等于反射光线与平面镜的夹角(∠1=∠2,∠3=∠4).请说明为什么进入潜望镜的光线和离开潜望镜的光线是平行的.24.如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①②③④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(1)当动点P落在第①部分时,如图①,试说明:∠APB=∠PAC+∠PBD;(2)当动点P落在第②部分时,如图②,∠APB=∠PAC+∠PBD是否成立?若不成立,请说明理由.参考答案一、1.【答案】B 2.【答案】C3.【答案】B解：根据两直线平行,同位角相等,得出A正确;根据两直线平行,同旁内角互补,得出C正确;根据两直线平行,内错角相等,得出∠A=∠ACE,而∠ACE+∠B+∠ACB=180°,则∠A+∠B+∠ACB=180°.得出D正确.故选B.4.【答案】C5.【答案】C6.【答案】B7.【答案】C8.【答案】C9.【答案】A10.【答案】B二、11.【答案】∠1=∠212.【答案】4解：a=3,b=1.13.【答案】垂直14.【答案】215.【答案】9016.【答案】14017.【答案】8062三、18.解:(1)画图如图,P,Q即为公共汽车停靠点的位置垂线段最短;(2)画图如图,两点之间,线段最短.19.解:因为AB∥CD,所以∠ECD=∠A=37°,又因为DE⊥AE,所以∠CED=90°,所以∠D=180°-90°-37°=53°.20.解:因为CD⊥AB,EF⊥AB,所以CD∥EF(垂直于同一直线的两直线平行).相等),又因为∠E=∠EMC,所以∠BCD=∠ACD(等量代换).所以CD是∠ACB的平分线(角平分线定义).21.解:OD和OE互相垂直,即OD⊥OE.理由如下:因为点A,O,B在同一直线上,所以∠AOB=180°.又因为OD是∠AOC的平分线,OE是∠COB的平分线,所以∠DOC=∠AOC,∠COE=∠COB.所以∠DOE=∠DOC+∠COE=(∠AOC+∠COB)=∠AOB=×180°=90°,所以OD⊥OE.22.解:因为∠ENM=∠3(对顶角相等),∠E=∠3(已知),所以∠ENM=∠E(等量代换),所以AE∥HM(内错角相等,两直线平行).所以∠EAM=∠AMH(两直线平行,内错角相等).又因为∠1=∠2,所以∠EAM+∠1=∠AMH+∠2(等式性质),即∠BAM=∠AMC.所以AB∥CD(内错角相等,两直线平行).所以∠AMD+∠BAP=180°(两直线平行,同旁内角互补).因为∠4=∠AMD(对顶角相等),所以∠4+∠BAP=180°(等量代换).23.解:根据题意,作出如图所示的几何图形,已知:AB∥CD,∠1=∠2,∠3=∠4.试说明:EF∥GH.说明过程:因为AB∥CD(已知),所以∠2=∠3(两直线平行,内错角相等).又因为∠1=∠2,∠3=∠4,所以∠1=∠2=∠3=∠4.因为∠5=180°-(∠1+∠2),∠6=180°-(∠3+∠4),所以∠5=∠6,所以EF∥GH(内错角相等,两直线平行).即进入潜望镜的光线和离开潜望镜的光线是平行的.24.解:(1)如图①:过点P作MP∥AC,则MP∥BD,因为MP∥AC,所以∠APM=∠PAC,因为MP∥BD,所以∠BPM=∠PBD,所以∠APM+∠BPM =∠PAC+∠PBD,①②(2)不成立.理由如下:如图②,过点P作MP∥AC,则MP∥BD, 因为MP∥AC,所以∠APM=∠PAC,因为MP∥BD,所以∠BPM=∠PBD,所以∠APM+∠BPM =∠PAC+∠PBD,即:360°-∠APB=∠PAC+∠PBD.所以∠APB=∠PAC+∠PBD不成立.。

《相交线与平行线》单元测试题及答案

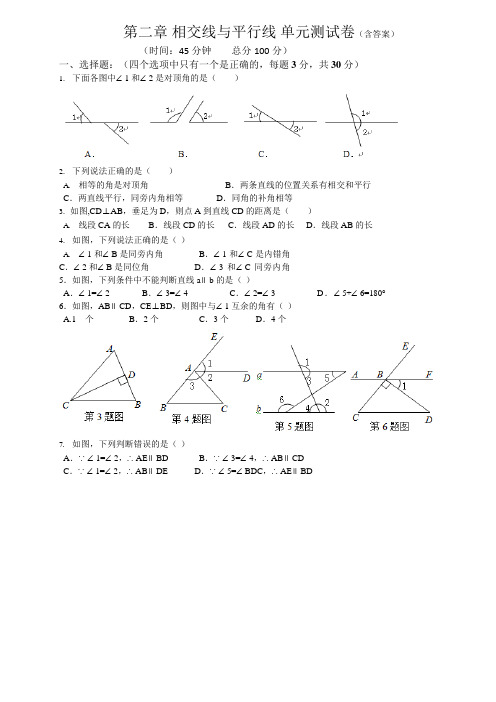
第二章相交线与平行线单元测试卷（含答案）（时间：45 分钟总分 100 分）一、选择题：（四个选项中只有一个是正确的，每题3 分，共30 分）1.下面各图中∠1 和∠2 是对顶角的是（）2.下列说法正确的是（）A.相等的角是对顶角B．两条直线的位置关系有相交和平行C．两直线平行，同旁内角相等D．同角的补角相等3.如图,CD⊥AB，垂足为D，则点A 到直线CD 的距离是（）A.线段CA 的长B．线段CD 的长C．线段AD 的长D．线段AB 的长4.如图，下列说法正确的是（）A.∠1 和∠B 是同旁内角B．∠1 和∠C 是内错角C．∠2 和∠B 是同位角D．∠3 和∠C 同旁内角5．如图，下列条件中不能判断直线a∥b 的是（）A．∠1=∠2 B．∠3=∠4 C．∠2=∠3 D．∠5+∠6=180°6．如图，AB∥CD，CE⊥BD，则图中与∠1 互余的角有（）A.1个B．2 个C．3 个D．4 个7.如图，下列判断错误的是（）A．∵∠1=∠2，∴AE∥BD B．∵∠3=∠4，∴AB∥CDC．∵∠1=∠2，∴AB∥DE D．∵∠5=∠BDC，∴AE∥BD8.如图，AB∥CD∥EF，BC∥DE，则∠B 与∠E 的关系是（）A．相等B．互余C．互补D．不能确定9．如图，AB∥CD，∠1=58°，FG 平分∠EFD，则∠FGB 的度数等于（）A．122°B．151°C．116°D．97°10．如图，直线a∥b，直角三角形ABC 的顶点B 在直线a 上，∠C=90°，∠β=55°，则∠α的度数为（）A．15°B．25°C．35°D．55°二．填空题：（将答案填在题目的横线上，每空3 分，共18 分）11．如图，∠1=∠2，∠4=58°，则∠3= 度；12.如图，AB∥CD，EF⊥CD 于点F，射线FN 交AB 于点M，∠NMB=57°，则∠EFN=；13.若一个角的余角是它的3 倍，则这个角的度数为；14．如图，已知AB∥DE，∠ABC=80°，∠CDE=140°，则∠BCD= ；15.如图，把矩形（长方形）ABCD 沿EF 对折，若∠1=40°，则∠AEF= ；16.老师在黑板上随便画了两条直线AB，CD 相交于点0，还作了∠BOC 的平分线OE 和CD 的垂线OF（如图），若∠DOE 被OB 分成2：3 两部分，则∠AOF 等于度；三、解答题：（写出必要的说明过程、解答步骤，共52 分）17.尺规作图：已知∠ABC，求作一个角等于∠ABC；（保留作图痕迹）（6 分）18.已知：如图，BE∥DF，∠B=∠D；试说明AD∥BC；（8 分）19.如图，直线EF，CD 相交于点O，OA⊥OB，且OC 平分∠AOF；若∠AOE=40°，求∠BOD 的度数；（9 分）20.推理填空：（9 分）如图，已知DG⊥BC，BC⊥AC，EF⊥AB，∠1=∠2，试判断CD 与AB 的位置关系；解：∵DG⊥BC，BC⊥AC（已知）∴∠DGB=∠=90°（）∴DG∥，∴∠2=∠，∵∠1=∠2（已知）∴∠1=∠（）∴EF∥，∴∠AEF=∠（）∵EF⊥AB，∴∠AEF=90°∴∠ADC=90°即：CD⊥AB．21.如图，BE 平分∠ABD，DE 平分∠BDC，DG 平分∠CDF，且∠1+∠2=90°，试说明BE∥DG；（9 分）22.已知一个角的两边与另一个角的两边分别平行，请结合图①②探索这两个角之间的关系；(11 分)(1)如图①，AB∥CD，BE∥DF，则∠1 与∠2 的关系是；(2)如图②，AB∥CD，BE∥DF，则∠1 与∠2 的关系是；并说明理由；(3)由此得出结论，如果两个角的两边分别平行，那么这两个角；(4)若两个角的两边分别平行，且一个角比另一个角的3 倍少60°，则这两个角分别为多少度？参考答案：1~10 CDCDB ACBBA 11．58；12．33°；13．22.5°；14．40°；15．110°；16．45°或90度；717.略；（参考课本P56 步骤5 的图）18.方法一：（利用同旁内角互补，两直线平行）∵BE∥DF（已知），∴∠B+∠BCD=180°（两直线平行，同旁内角互补）∵∠B=∠D（已知）∴∠D+∠BCD=180°(等量代换)∴AD∥BC (同旁内角互补,两直线平行)方法二：（利用三角形内角和等于180°）(略)19.∵OA⊥OB（已知）∴∠AOB=90°(垂直的定义)∵∠AOE=40°（已知）∴∠BOE=∠AOB-∠AOE=90°-40°=50°∵OC 平分∠AOF(已知)∴∠AOC = 1 ∠AOF =1 (∠EOF -∠AOE) =1 (1800- 400 ) = 7002 2 2∴∠BOD = ∠COD -∠AOC -∠AOB = 1800- 700- 900= 200∴∠BOD=20°20.按顺序分别填：BCA，垂直的定义，AC，ACD，ACD，等量代换，CD，ADC，两直线平行，同位角相等；21.方法一：通过证明∠E=∠EDG 得到；∵∠1+∠2=90°（已知）∴△BDE 中，∠E=180°-(∠1+∠2)=90°∵DE 平分∠BDC，DG 平分∠CDF(已知)∴∠EDG=∠EDC+∠CDG= 1 ∠BDC+ 1 ∠CDF =1 ∠BDF =1 ⨯1800= 9002 2 2 2∴∠E=∠EDG(等量代换)∴BE∥DG （内错角相等，两直线平行）方法二：通过证明∠1=∠3 得到；（略）22．（1）相等；（2）互补；∵AB∥CD（已知）∴∠1=∠3（两直线平行，内错角相等）∵BE∥DF（已知）∴∠2+∠3=180°（两直线平行，同旁内角互补）∴∠1+∠2=180°（等量代换）（3）相等或互补；（4）30°，30°；或60°，120°；解：设一个角为x，则另一个角为3x-60°，①由x=3x-60°得：x=30°，3x-60°=30°②由x+3x-60°=180°得：x=60°，3x-60°=120°∴这两个角分别30°，30°或60°，120°；。

相交线与平行线单元测试题含答案

相交线与平行线单元测试题含答案相交线与平行线单元测试题一、选择题1、下列说法正确的是（） A. 相交的两条直线一定有一个交点 B. 同位角相等 C. 两直线平行，对角线一定相等 D. 相等的两个角一定是对顶角2、以下不能说明直线AB与CD平行的是（） A. AB//CD，A与B在同一方向，C与D在同一方向 B. $\angle 3 = \angle 4$ C. $\angle A = \angle C$ D. $\angle A + \angle B = 180^{\circ}$，$\angleC + \angleD = 180^{\circ}$3、下列说法正确的是（） A. 过一点有且只有一条直线与已知直线平行 B. 两直线平行，同位角相等 C. 内错角相等，两直线平行 D. 如果两条直线都与第三条直线平行，那么这两条直线也互相平行4、下列说法正确的是（） A. 两条直线被第三条直线所截，同位角相等 B. 相等的两个角是对顶角 C. 两直线平行，同旁内角互补 D. 互补的两个角不一定是邻补角5、下列说法正确的是（） A. 同位角相等 B. 互补的角是邻补角 C. 两直线平行，同旁内角相等 D. 两直线平行，内错角相等二、填空题1、同一平面内，如果两条直线都与第三条直线平行，那么这两条直线互相________，简述为________.2、两直线平行，同位角________；两直线平行，内错角________；两直线平行，同旁内角________．3、两条直线的位置关系有________、________．4、若三条直线两两相交，则共有________个交点．5、在同一平面内，若两直线都垂直于第三条直线，那么这两条直线________．6、如图所示，若$\angle A + \angle B = 180^{\circ}$，$\angle A = \angle D$，则$\angle B =$________．7、如图所示，若$\angle A = \angle B$，则$\angle C =$________．8、如图所示，若$\angle A + \angle B = 90^{\circ}$，$\angle B + \angle C = 90^{\circ}$，则$\angle A =$________．9、若一个角的两边分别和另一个角的两边分别平行，则这两个角的关系是________．10、如图所示，若AB//CD，则$\angle A + \angle B + \angle C=$________．三、解答题1、已知两条平行线被第三条直线所截，则形成的同位角的数量是多少？这些同位角还具有什么性质？2、利用所给图形探究规律。

人教版七年级数学下册第五章相交线与平行线单元检测卷(共6套)

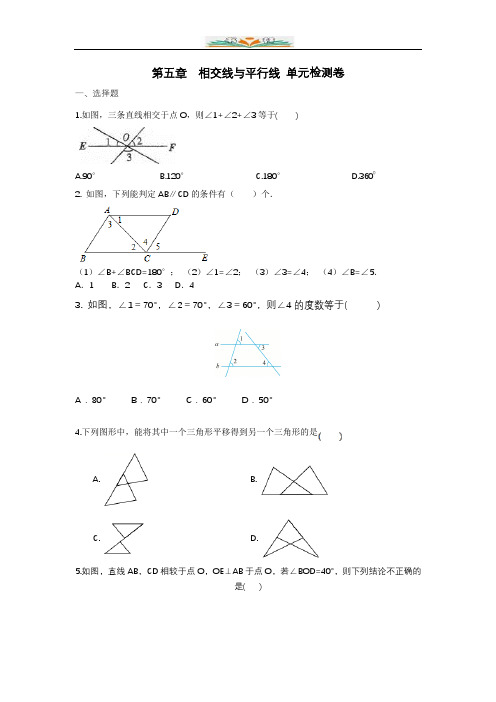
第五章相交线与平行线单元检测卷一、选择题1.如图，三条直线相交于点O，则∠1+∠2+∠3等于( )A.90°B.120°C.180°D.36002. 如图，下列能判定AB∥CD的条件有（）个．（1）∠B+∠BCD=180°；（2）∠1=∠2；（3）∠3=∠4；（4）∠B=∠5．A．1 B．2 C．3 D．43. 如图，∠1＝70°，∠2＝70°，∠3＝60°，则∠4的度数等于( )A．80°B．70°C．60°D．50°4.下列图形中，能将其中一个三角形平移得到另一个三角形的是A. B.C. D.5.如图，直线AB，CD相较于点O，OE⊥AB于点O，若∠BOD=40°，则下列结论不正确的是( )A.∠AOC=40°B.∠COE=130°C.∠EOD=40°D.∠BOE=90°6.如图，直线a,b被c,d所截，且a∥b，则下列结论中正确的是( )A.∠1=∠2 C.∠3+∠4=180°B.∠3=∠4 D.∠1+∠4=180°7.如图，点A在直线BG上,AD∥BC，AE平分∠GAD，若∠CBA=80°,则( )A.60°B.50°C.40°D.30°8.下列各图中，∠1与∠2互为邻补角的是( )9.对于图中标记的各角，下列条件能推理得到a∥b的是（）A．∠1=∠2 B．∠2=∠4 C．∠3=∠4 D．∠1+∠4=18010．下列说法正确的是( )A.一个角的补角一定比这个角大B.一个角的余角一定比这个角小C.一对对顶角的两条角平分线必在同一条直线上D.有公共顶点并且相等的两个角是对顶角二、填空题11.如图，直线AB，CD相交于点O, EO⊥AB于点O，∠EOD=50°，则∠BOC的度数为______.12. 如图是由五个形状、大小完全相同的三角形组成的图案，三角形的三个角分别为36°，72°，72°，则图中共有_____对平行线．13.如图，，则的度数等于14．如图，点0是直线AB上一点平分，图中与互余的角有______ ．图中与互补的角有______ ．15. 说明命题“x>－4，则x2>16”是假命题的一个反例可以是x＝____________．16.如图，现要从村庄A修建一条连接公路PQ的最短小路，过点A作AH⊥PQ于点H，沿AH修建公路，则这样做的理由是三、解答题17.如图，直线AB，CD 相交于点O，∠AOD=3∠BOD+20°.(1)求∠BOD的度数；(2)以O为端点引射线OE,OF ,射线OE平分∠BOD，且∠EOF= 90°，求∠BOF的度数.18．已知：如图，AB∥CD，∠1=∠2，∠3=∠4．（1）求证：AD∥BE；（2）若∠B=∠3=2∠2，求∠D的度数．19.如图，D，E，F是线段AB的四等分点.(1)过点D画DH∥BC交于点H,过点E画EG∥BC交AC于点G，过点F画FM∥BC交AC 于点M;(2)量出线段AH,HG,GM,MC的长度，你有什么发现？(3)量出线段HD,EG,FM,BC的长度，你又有什么发现？20.请写出命题“两直线平行，同位角相等”的题设和结论：题设：，结论：．21.观察下图，寻找对顶角：(1)如图1，图中共有对对顶角(2)如图2，图中共有对对顶角(3)如图3，图中共有对对顶角(4)若有n条直线相交于一点，则可形成多少对对顶角？22.如图，已知直线AB∥DF,∠D+∠B=180°.(1)试说明DE∥BC；(2)若∠AMD=75°，求∠AGC的度数.【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

相交线与平行线单元测试题(含答案)

相交线与平行线单元测试题一、选择题（每小题3分，共30分）1. 如图，直线AB 、CD 相交于O 点，若︒=∠301，则∠2、∠3的度数分别为（）第3题图A. 120°、60°B. 130°、50°C. 140°、40°D. 150°、30°2. 已知同一平面内的直线l 1、l 2、l 3，如果l 1⊥l 2，l 2∥l 3，那么l 1与l 3的位置关系是( ).A.平行B.相交C.垂直D.以上均不对3.如图，AB ∥CD ，若∠1=45°，则∠2的度数是（） A. 45° B. 90° C. 30° D. 135°4. 下列说法中，正确的是（）A ．同一平面内，两条直线的位置关系只有相交、平行两种；B ．同一平面内，不相交的两条线段互相平行；C ．不相交的两条直线是平行线；D ．同一平面内，不相交的两条射线互相平行．5.如图，AOC ∠和BOD ∠都是直角，且︒=∠30DOC ，则=∠AOB ( ). A ．︒30 B ．︒60C ．︒120D ．︒1506. 以下判定中，正确的个数有（）（1）若a ∥b ，b ∥c ，则a ∥c （2）若a ⊥b ，b ⊥c ，则a ⊥cA B CD12 123A BCD O 第1题图AODCBDC B A 1（3）若同旁内角相等，则两直线平行（4）若同位角相等，则两直线平行 A ．1个 B ．2个 C ．3个 D ．4个7.将含300角的三角板ABC 如图放置，使其三个顶点分别落在三条平行直线上，其中∠ACB=900，当∠1=600时，图中等于300的角的个数是（）A.6个B.5个C.4个D.3个 8. 如图，若∠1=70°，∠2=110°，∠3=70°，则有（）Ａ．a ∥b Ｂ．c ∥dＣ．a ⊥d Ｄ．任两条都无法判定是否平行bcda3217题图 8题图 9题图9. 如图，直线AB ∥CD ，∠A ＝70︒，∠C ＝40︒，则∠E 等于（） A ．30° Ｂ．40° C ．60° Ｄ．70°10. Rt ABC △中， 90ACB ∠=°，DE 过点C ，且DE AB ∥，若 55ACD ∠=°，则∠B 的度数是（）A ．35°B ．45°C ．55°D ．65° 二、填空题（每小题3分，共30分）1. 如图，AB ∥CD ，则与∠1相等的角(∠1除外)共有个．2.如图，直线l 1与l 2相交于点O ，1OM l ⊥，若44α∠=︒，则β∠等于．A B CD EACBDEFEDCB A12N MG F EDC BA GF EDCB A 12第2题图第3题图3.如图，l ∥m ，矩形ABCD 的顶点B 在直线m 上，则∠α= 度.4. 如图，如果DE ∥AB ，那么∠A + =180°，或∠B + =180°，根据是；如果∠CED =∠FDE ，那么 ∥ ．根据是内错角相等，两直线平行．F E DCBA第4题图第5题图第6题图第7题图 5. 如图，已知AB ∥CD ，∠1=65°，∠2=45°，则∠ADC =________． 6．如图，若AB ∥EF ，BC ∥DE ，则∠B +∠E =________．7.如图，BC ⊥AE ，垂足为C ，过C 作CD ∥AB ．若∠ECD =48°，则∠BAC 的度数是．8．如图，已知直线AB ，CD 被直线EF 所截，若∠1=∠2，•则∠AEF+∠CFE =________．第8题图第9题图第10题图9.如图，已知AB ∥CD ，直线EF 分别交AB ，CD 于E ，F ，EG •平分∠BEF ，若∠1=72°，则∠2=_______．10. 如图所示，把一张长方形纸片ABCD 沿EF 折叠，若∠EFG =50°，则∠DEG 的度数为 .三、解答题55DαAC BlmO l 2l 1βα1. 读句画图：如图，直线CD 与直线AB 相交于C ，根据下列语句画图：（1）过点P 作PQ ∥CD ，交AB 于点Q ；（2）过点P 作PR ⊥CD ，垂足为R ．2.已知以下基本事实：①对顶角相等；②一条直线截两条平行直线所得的同位角相等；③两条直线被第三条直线所截，若同位角相等，则这两条直线平行； (1)在利用以上基本事实作为依据来证明命题“两直线平行，内错角相等”时，必须要用的基本事实有 (填入序号即可)；(2)根据在(1)中的选择，结合所给图形，请你证明命题“两直线平行，内错角相等”．已知：如图，_____________________．求证：_____ ______．cb a123.如图，AB 与CD 相交于点O ，OE ⊥CD ，∠BOE =54°，求∠AOC 的度数．4. 如图，在网格图中，平移三角形ABC 使点A 平移到点D ．FE21DCBA（1）画出平移后的三角形DEF ；（2）三角形DEF 与三角形ABC 有什么关系？5.如图，已知B 、E 分别是AC 、DF 上的点，∠1=∠2，∠C =∠D ． (1)∠ABD 与∠C 相等吗?为什么? (2)∠A 与∠F 相等吗?请说明理由．6. 如图，MN 、EF 是两面互相平行的镜面，根据镜面反射规律，若一束光线AB 照射到镜面MN 上，反射光线为BC ，则一定有∠1=∠2．试根据这一规律：（1）利用直尺和量角器作出光线BC 经镜面EF 反射后的反射光线CD ；（2）试判断AB 与CD 的位置关系，并说明理由．7.有一天李小虎同学用《几何画板》画图，他先画了两条平行线线AB 、CD ，然后在平行线间画了一点E ，连结BE 、CE 后（如图①），它用鼠标左键点住点E ，拖动后，分别得到如图②、③、④等图形，这时它突然一想，∠B 、∠D 与∠BED 之间的度数有没有某种联系呢？接着小虎同学通过利用《几何画板》的“度量角度”和“计算”的功能，找到了这三个角之间的关系。

相交线与平行线单元测试题

相交线与平行线单元测试题一、选择题（每题2分，共20分）1. 下列说法中，正确的是：A. 经过直线外一点，有且只有一条直线与已知直线平行B. 经过直线外一点，有且只有一条直线与已知直线相交C. 经过直线外一点，可以画无数条直线与已知直线平行D. 经过直线外一点，可以画无数条直线与已知直线相交2. 如果两直线相交，那么它们相交所成的角是：A. 锐角B. 直角C. 钝角D. 任意角3. 两条直线被第三条直线所截，如果同侧的内错角相等，那么这两条直线：A. 平行B. 相交C. 垂直D. 无法判断4. 平行线的性质中，下列说法不正确的是：A. 平行线之间的距离处处相等B. 平行线永不相交C. 两条平行线可以确定一个平面D. 平行线之间的夹角是锐角5. 对于两条平行线，下列说法正确的是：A. 它们之间的距离在任何地方都是相同的B. 它们可以相交C. 它们之间的夹角可以是任意角D. 它们可以确定一个平面二、填空题（每题2分，共10分）6. 如果两条直线相交成直角，则称这两条直线互相______。

7. 两条直线相交，如果其中一个角是锐角，则其他三个角分别是______。

8. 平行线之间的距离是指______。

9. 两条直线相交所成的角中，最大的角是______。

10. 如果两条直线被第三条直线所截，那么内错角相等的条件是这两条直线______。

三、判断题（每题1分，共10分）11. 两条直线相交所成的角都是锐角。

（）12. 平行线在任何地方的距离都是相等的。

（）13. 两条直线相交，形成的对顶角相等。

（）14. 两条平行线之间的夹角是直角。

（）15. 如果两条直线被第三条直线所截，同位角相等，则这两条直线平行。

（）四、简答题（每题5分，共20分）16. 解释什么是“同位角”、“内错角”和“同旁内角”，并说明它们在判断两条直线是否平行时的作用。

17. 描述如何使用直角三角板来检验两条直线是否平行。

18. 给出两条直线相交的几何图形，并说明如何确定它们相交所成的角的大小。

第五章《相交线与平行线》单元测试卷(含答案)

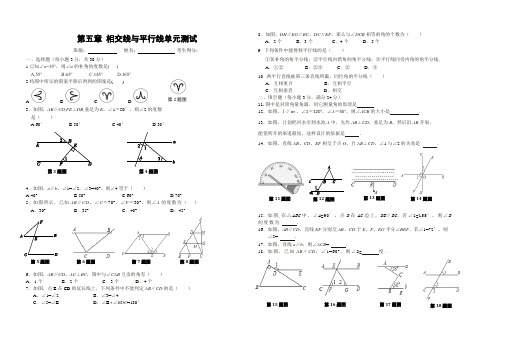
第五章相交线与平行线单元测试班级：姓名：考生得分：一、选择题（每小题3分，共30分） 1.已知∠α=35°，则∠α的补角的度数是( ) A.55° B.65° C.145° D.165° 2.将图中所示的图案平移后得到的图案是( )A. B. C. D.3．如图，AB ∥CD ,FE ⊥DB ,垂足为E ，∠1＝50°，则∠2的度数是（）A.60°B.50°C.40°D.30°4．如图，a ∥b ，∠1=∠2，∠3=40°，则∠4等于（） A.40° B.50° C.60° D.70° 5．如图所示，已知AB ∥CD ，∠C ＝70°，∠F ＝30°，则∠A 的度数为（） A ．30° B ．35° C ．40° D ．45°6．如图，AB ∥CD ，AC ⊥BC ，图中与∠CAB 互余的角有（） A ．1个 B ．2个 C ．3个 D ．4个7．如图，点E 在CD 的延长线上，下列条件中不能判定AB ∥CD 的是（） A ．∠1=∠2 B ．∠3=∠4 C ．∠5=∠B D ．∠B +∠BDC =180°8．如图，DH ∥EG ∥BC ，DC ∥EF ，那么与∠DCB 相等的角的个数为（） A ．2个 B ．3个 C ．4个 D ．5个 9. 下列条件中能得到平行线的是（）①邻补角的角平分线；②平行线内错角的角平分线；③平行线同旁内角的角平分线． A ．①② B ．②③ C ．② D ．③10. 两平行直线被第三条直线所截，同位角的平分线（） A ．互相重合 B ．互相平行 C ．互相垂直 D ．相交二、填空题（每小题3分，满分24分） 11.图中是对顶角量角器，用它测量角的原理是 .12．如图，l ∥m ，∠1＝120°，∠A ＝55°，则∠ACB 的大小是 . 13．如图，计划把河水引到水池A 中，先作AB ⊥CD ，垂足为B ，然后沿AB 开渠，能使所开的渠道最短，这样设计的依据是．14．如图，直线AB ，CD ，EF 相交于点O ，且AB ⊥CD ，∠1与∠2的关系是．15．如图,在△ABC 中，∠A =90°，点D 在AC 边上，DE ∥BC ，若∠1=155°，则∠B 的度数为．16．如图，AB ∥CD ，直线EF 分别交AB 、CD 于E 、F ，EG 平分∠BEF ，若∠1=72°，则∠2= ．1718第2题图第6题图第7题图第8题图第11题图第13题图第14题图第15题图第16题图第17题图第18题图第3题图三、解答题（共46分）19．（7分）读句画图：如图，直线CD与直线AB相交于C，根据下列语句画图：（1）过点P作PQ∥CD，交AB于点Q；（2）过点P作PR⊥CD，垂足为R；（3）若∠DCB=120°，猜想∠PQC是多少度？并说明理由．20．（7分）如图，方格中有一条美丽可爱的小金鱼．（1）若方格的边长为1，则小鱼的面积为；（2）画出小鱼向左平移3格后的图形．（不要求写作图步骤和过程）21．（8分）已知：如图，∠BAP+∠APD =180°，∠1 =∠2.求证：∠E =∠F．22．（8分）已知：如图，∠1 =∠2，∠3 =∠4，∠5 =∠6.求证：ED∥FB．23．（8分）如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠EDC的度数．24．（9分）如图，已知AB∥CD，∠B=65°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数．25．（10分）如图，直线EF，CD相交于点0，OA⊥OB，且OC平分∠AOF，（1）若∠AOE=40°，求∠BOD的度数；（2）若∠AOE=α，求∠BOD的度数；（用含α的代数式表示）（3）从（1）（2）的结果中能看出∠AOE和∠BOD有何关系？第19题图第五章相交线与平行线检测题参考答案1.C 解析：∵∠α=35°，∴∠α的补角的度数为180°35°=145°,故选C.2. C 解析：根据平移的性质可知C正确.3. C 解析：因为FE⊥DB，所以∠FED=90°，由∠1=50°可得∠FDE=90°-50°=40°.因为AB∥CD，由两直线平行，同位角相等，可得∠2=∠FDE=40°.4. D 解析：因为a∥b，所以∠2=∠4.又∠2=∠1，所以∠1=∠4.因为∠3=40°，所以∠1=∠4==70°.5. C 解析：由AB∥CD可得，∠FEB＝∠C＝70°，∵∠F＝30°，又∵∠FEB＝∠F+∠A，∴∠A＝∠FEB∠F＝70°30°＝40°.故选项C是正确的.6. C 解析：∵AB∥CD，∴∠ABC=∠BCD.设∠ABC的对顶角为∠1，则∠ABC=∠1.又∵AC⊥BC，∴∠ACB=90°，∴∠CAB+∠ABC=∠CAB+∠BCD=∠CAB+∠1=90°，因此与∠CAB互余的角为∠ABC，∠BCD，∠1．故选C．7. A 解析：选项B中，∵∠3=∠4，∴AB∥CD（内错角相等，两直线平行），故正确；选项C中，∵∠5=∠B，∴AB∥CD（内错角相等，两直线平行），故正确；选项D中，∵∠B+∠BDC=180°，∴AB∥CD（同旁内角互补，两直线平行），故正确；而选项A中，∠1与∠2是直线AC、BD被直线AD所截形成的内错角，∵∠1=∠2，∴AC∥BD，故A错误．选A．8. D 解析：如题图所示，∵DC∥EF，∴∠DCB=∠EFB.∵DH∥EG∥BC，∴∠GEF=∠EFB，∠DCB=∠HDC，∠DCB=∠CMG=∠DME，故与∠DCB相等的角共有5个．故选D．9. C 解析：结合已知条件，利用平行线的判定定理依次推理判断．10. B 解析：∵两条平行直线被第三条直线所截，同位角相等，∴它们角的平分线形成的同位角相等，∴同位角相等的平分线平行．故选B．11.对顶角相等解析：根据图形可知量角器测量角的原理是：对顶角相等.12. 65°解析：∵l∥m，∴∠ABC=180°-∠1=180°-120°=60°.在△ABC中，∠ACB=180°-∠ABC-∠A=180°-60°-55°=65°.13. 垂线段定理：直线外一点与直线上所有点的连线中，垂线段最短解析：根据垂线段定理，直线外一点与直线上所有点的连线中，垂线段最短，∴沿AB开渠，能使所开的渠道最短．14. ∠1+∠2=90°解析：∵直线AB、EF相交于O点，∴∠1=∠DOF.又∵AB⊥CD，∴∠2+∠DOF=90°，∴∠1+∠2=90°．15. 65°解析：∵∠1=155°，∴∠EDC=180°-155°=25°.∵DE∥BC，∴∠C=∠EDC=25°.∵在△ABC中，∠A=90°，∠C=25°，∴∠B=180°-90°-25°=65°．故答案为65°．16. 54°解析：∵AB∥CD，∴∠BEF=180°∠1=180°72°=108°，∠2=∠BEG.又∵EG平分∠BEF，∴∠BEG=∠BEF=×108°=54°，故∠2=∠BEG=54°．17. 78°解析：延长BC与直线a相交于点D，∵a∥b，∴∠ADC=∠DBE=50°. ∴∠ACB=∠ADC +28°=50°+28°=78°.故应填78°.18. 120 解析：∵AB∥CD，∴∠1=∠3，而∠1=60°，∴∠3=60°.又∵∠2+∠3=180°，∴∠2=180°-60°=120°．故答案为120．19．解：（1）（2）如图所示.第19题答图（3）∠PQC=60°.理由：∵PQ∥CD,∴∠DCB+∠PQC=180°.∵∠DCB=120°,∴∠PQC=180°120°=60°．20. 解：（1）小鱼的面积为7×621×5×621×2×521×4×221××121×21×11=16.（2）将每个关键点向左平移3个单位，连接即可．第20题答图21.证明：∵ ∠BAP +∠APD = 180°，∴ AB ∥CD .∴ ∠BAP =∠APC . 又∵ ∠1 =∠2,∴ ∠BAP −∠1 =∠APC −∠2.即∠EAP =∠APF .∴ AE ∥FP .∴ ∠E =∠F .22．证明：∵ ∠3 =∠4,∴ AC ∥BD .∴ ∠6+∠2+∠3 = 180°. ∵ ∠6 =∠5，∠2 =∠1,∴ ∠5+∠1+∠3 = 180°. ∴ ED ∥FB .23. 解：∵ DE ∥BC ，∠AED =80°，∴ ∠EDC =∠BCD ，∠ACB=∠AED=80°.∵ CD 平分∠ACB ，∴ ∠BCD = 21∠ACB =40°，∴ ∠EDC =∠BCD =40°．24. 解：∵ AB ∥CD ，∴ ∠B +∠BCE =180°（两直线平行，同旁内角互补）.∵ ∠B =65°，∴ ∠BCE =115°.∵ CM 平分∠BCE ，∴ ∠ECM =21∠BCE =57.5°. ∵ ∠ECM +∠MCN +∠NCD =180°，∠MCN =90°，∴ ∠NCD =180°-∠ECM -∠MCN =180°-57.5°-90°=32.5°．25、解：（1）∵∠AOE +∠AOF =180°（互为补角），∠AOE =40°，∴∠AOF =140°；又∵OC 平分∠AOF ，∴∠FOC =∠AOF =70°，∴∠EOD =∠FOC =70°（对顶角相等）；而∠BOE =∠AOB ﹣∠AOE =50°，∴∠BOD =∠EOD ﹣∠BOE =20°； (2)(3)略。

相交线与平行线单元测试题

相交线与平行线单元测试题一、选择题（每题2分，共10分）1. 两条直线在同一平面内，且不相交，这两条直线叫做平行线。

以下哪项描述不正确？A. 平行线在任何情况下都不会相交B. 平行线之间的距离处处相等C. 平行线可以无限延伸D. 平行线可以相交2. 根据平行线的性质，以下哪个命题是正确的？A. 同位角相等B. 内错角相等C. 同旁内角互补D. 以上都是3. 如果两条直线相交成30度角，那么这两条直线的对顶角是：A. 30度B. 60度C. 90度D. 120度4. 已知直线AB与CD相交于点O，那么OA与OB的关系是：A. OA=OBB. OA垂直于OBC. OA平行于OBD. 无法确定5. 在平面几何中，以下哪个条件不能判定两直线平行？A. 同位角相等B. 内错角相等C. 同旁内角互补D. 两直线没有交点二、填空题（每题2分，共10分）6. 如果两条直线相交所构成的同位角不相等，则这两条直线_________。

7. 平行于同一条直线的两条直线_________。

8. 两条直线相交，如果其中一个角是直角，则这两条直线_________。

9. 如果直线a与直线b相交，且a垂直于直线b，则直线a与直线b所成的角是_________度。

10. 两条平行线被第三条直线所截，同旁内角的度数之和为_________。

三、判断题（每题1分，共5分）11. 两条直线相交所形成的角中，对顶角相等。

（）12. 平行线的性质可以推出同位角相等，内错角相等，同旁内角互补。

（）13. 如果两条直线相交，那么它们一定在某一点相交。

（）14. 两条直线相交所形成的角中，邻角互补。

（）15. 平行线之间的距离处处相等，这是平行线的一个性质。

（）四、简答题（每题5分，共10分）16. 解释什么是“相交线”，并给出相交线的基本性质。

17. 解释什么是“平行线”，并说明平行线的性质有哪些。

五、解答题（每题15分，共15分）18. 在平面直角坐标系中，已知直线L1: y = 2x + 3 和直线L2: y = -x + 5，请判断这两条直线是否平行或相交，并给出证明。

(完整版)相交线与平行线单元测试题

相交线与平行线单元测试题一、填空题(每小题3分，共30分)1、如图,AB⊥CD,垂足为B，EF是过点B的一条直线,已知∠EBD=135°,则∠CBE=_____, ∠ABF=______.(1) (5) (6)2、把命题“锐角的补角是钝角”改写成“如果……，那么……”的形式是__________.3、平移线段AB，使点A移动到点C的位置，若AB=3cm，AC=4cm，则点B移动的距离是______.4、过钝角的顶点向它的一边作垂线，将此钝角分成两个度数之比为1:6的角，则此钝角的度数为______.5、如图，两条直线a、b被第三条直线c所截，如果a∥b，∠1=70°，则∠2=______.6、如图,直线l1、l2分别和l3、l4相交,若∠1与∠3互余,∠2与∠3的余角互补,∠4 =110°，那么∠3=______.7、如图，把一张平行四边形纸片ABCD沿BD对折，使C点落在E处，BE与AD相交于点O，若∠DBC=15°，则∠BOD=______.(7) (8) (9)8、如图，已知∠ABC＋∠ACB=110°，BO、CO分别是∠ABC和∠ACB的平分线，EF 过点O与BC平行，则∠BOC=______.9、如图，AB∥CD，直线EF分别交AB、CD分于点E、F，FH平分∠EFD，若∠1=110°，则∠2=______.10、在同一平面内，1个圆把平面分成0×1＋2=2个部分，2个圆把平面最多分成1×2＋2=4个部分，3个圆把平面最多分成2×3＋2=8个部分，4个圆把平面最多分成3×4＋2=14个部分，那么10个圆把平面最多分成_____________个部分．二、选择题(每小题3分，共18分)11、如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC =70°，则∠BOD 的度数等于（）A．30°B．35 C．20°D．40°(11) (13) (14)12、如图，将四个完全相同的矩形分别等分成四个相同的小矩形，其中阴影部分面积相等的是（）A．只有①和②相等B．只有③和④相等C．只有①和④相等D．①和②，③和④分别相等13、如图，直线a、b被直线c所截，若a∥b，∠1=130°，则∠2等于（）A．30°B．40°C．50°D．60°14、如图，直线l1∥l2，l3⊥l4，有三个命题：①∠1＋∠3=90°；②∠2＋∠3=90°；③∠2=∠4．下列说法中，正确的是（）A．只有①正确B．只有②正确C．①和③正确D．①②③都正确15、如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°,∠D=120°，则∠C的度数为（）A．120°B．100°C．140°D．90°(15) (17) (19)三、解答题(共72分)17、(7分)如图，已知∠BAP与∠APD互补，∠1=∠2，在括号中填上理由．因为∠BAP与∠APD互补() 所以AB∥CD()从而∠BAP=∠APC() 又∠1=∠2()所以∠BAP－∠1=∠APC－∠2 () 即∠3=∠4从而AE∥PF() 所以∠E=∠F()18、作图题(9分)(1)如图，小刚准备在C处牵牛到河边AB饮水：①请用三角板作出小刚行走的最短路线(不考虑其他因素)；②如图，若小刚在C处牵牛到河边AB饮水，并且必须到河边D处观察河水的水质情况，请指出小刚行走的最短路线．19、(8分)如图,已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF =25°．求：∠AOC与∠EOD的度数．20、(6分)如图，依据图形，找出能使AD∥BC成立的条件(至少6个)．(20) (21) (22)21、(8分)已知：如图，DE⊥AC，∠AGF=∠ABC，∠1＋∠2=180°，试判断BF与AC 的位置关系，并说明理由．22、(8分)如图所示，已知直线a∥b，直线c和直线a、b交于C、D两点，在C、D之间有一点M，如果点M在C、D之间运动，问∠1、∠2、∠3之间有怎样的关系？这种关系是否发生变化？23、(12分)已知AD与AB、CD交于A、D两点,EC、BF与AB、CD交于E、C、B、F,且∠1=∠2,∠B=∠C(如图)．(1)你能得出CE∥BF这一结论吗？(2)你能得出∠B=∠3和∠A=∠D这两个结论吗？若能，写出你得出结论的过程．24、(14分)如图a)，已知直线m∥n，A、B为直线n上的两点，C、P为直线m上的两点，其中A、B、C为三个定点，点P在m上移动，我们知道，无论P点移动到任何位置总有△ABP与△ABC的面积相等，其理由是：______________________________________。

相交线与平行线单元测试卷(含答案)

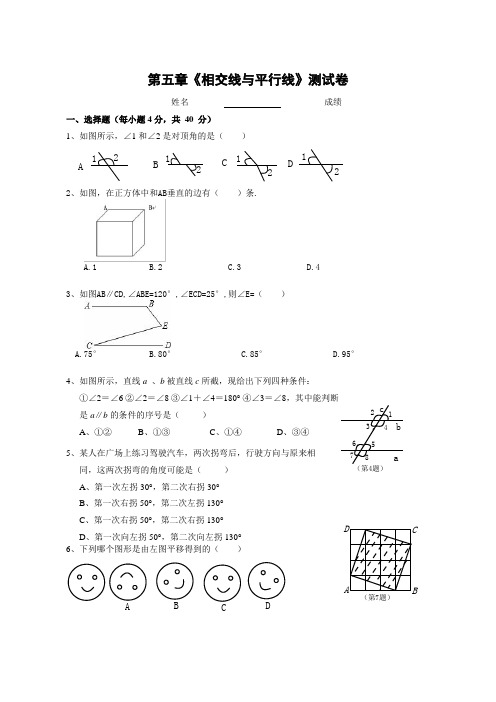
12345678（第4题）ab cABCD （第7题）第五章《相交线与平行线》测试卷姓名 _______ 成绩 _______一、选择题（每小题4分，共 40 分） 1、如图所示，∠1和∠2是对顶角的是（）ABC D121212122、如图，在正方体中和AB 垂直的边有（）条.A.1B.2C.3D.4 3、如图AB ∥CD,∠ABE=120°,∠ECD=25°,则∠E=（）A.75°B.80°C.85°D.95°4、如图所示，直线a 、b 被直线c 所截，现给出下列四种条件：①∠2＝∠6 ②∠2＝∠8 ③∠1＋∠4＝180° ④∠3＝∠8，其中能判断是a ∥b 的条件的序号是（）A 、①②B 、①③C 、①④D 、③④5、某人在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来相同，这两次拐弯的角度可能是（） A 、第一次左拐30°，第二次右拐30° B 、第一次右拐50°，第二次左拐130° C 、第一次右拐50°，第二次右拐130° D 、第一次向左拐50°，第二次向左拐130°6、下列哪个图形是由左图平移得到的（）BDA BCDE(第10题)水面入水点运动员(第14题)ABC D EFG H第13题7、如图，在一个有4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD 面积的比是（）A 、3：4B 、5：8C 、9：16D 、1：2 8、下列现象属于平移的是（）① 打气筒活塞的轮复运动，② 电梯的上下运动，③ 钟摆的摆动，④ 转动的门，⑤ 汽车在一条笔直的马路上行走A 、③B 、②③C 、①②④D 、①②⑤ 9、下列说法正确的是（）A 、有且只有一条直线与已知直线平行B 、垂直于同一条直线的两条直线互相垂直C 、从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离。

相交线与平行线单元测试卷(附答案)

相交线和平行线单元检测卷时间：90分钟满分：120分班级：__________ 姓名：__________ 得分：__________一、选择题(每小题3分，共30分)1．如图，直线a，b被直线c所截，∠1和∠2的位置关系是( )A．同位角B．内错角C．同旁内角D．对顶角2．下列图形中，不能通过其中一个四边形平移得到的是( )3．如图，直线a，b被直线c所截，下列说法正确的是( )A．当∠1＝∠2时，一定有a∥bB．当a∥b时，一定有∠1＝∠2C．当a∥b时，一定有∠1＋∠2＝90°D．当∠1＋∠2＝180°时，一定有a∥b4．O为直线l外一点，A，B，C三点在直线l上，OA＝4cm，OB＝5cm，OC＝1.5cm.则点O到直线l的距离( )A．大于1.5cm B．等于1.5cmC．小于1.5cm D．不大于1.5cm5．某商品的商标可以抽象为如图所示的三条线段，其中AB∥CD，∠EAB＝45°，则∠FDC的度数是（）A．30° B．35°C．40° D．45°6．如图，AB∥CD，DA⊥AC，垂足为A.若∠ADC＝35°，则∠1的度数为( )A．65° B．55° C．45° D．35°7．如图，下列说法正确的个数有( )①过点A有且只有一条直线AC垂直于直线l；②线段AC的长是点A到直线l的距离；③线段AB，AC，AD中，线段AC最短，根据是两点之间线段最短；④线段AB，AC，AD中，线段AC最短，根据是垂线段最短．A．1个 B．2个C．3个 D．4个8．如图，已知a∥b，直角三角板的直角顶点在直线b上，若∠1＝60°，则下列结论错误的是( )A．∠2＝60° B．∠3＝60°C．∠4＝120° D．∠5＝40°第8题图第9题图9．如图，在甲、乙两城市之间要修建一条笔直的城际铁路，从甲地测得公路的走向是北偏东42°，现在甲、乙两城市同时开工，为使若干天后铁路能准确在途中接通，则乙城市所修铁路的走向应是( )A．南偏西42° B．北偏西42° C．南偏西48° D．北偏西48°10．如图，AB∥EF，则∠A，∠C，∠D，∠E满足的数量关系是BA．∠A＋∠C＋∠D＋∠E＝360°B．∠A＋∠D＝∠C＋∠EC．∠A－∠C＋∠D＋∠E＝180°D．∠E－∠C＋∠D－∠A＝90°二、填空题(每小题3分，共24分)11．如图，若剪刀中的∠AOB＝30°时，则∠COD＝________.12．如图，直线AB，CD被直线AE所截，AB∥CD，∠A＝110°，则∠1＝________度．第11题图第12题图第13题图13．如图，把河水引入试验田P灌溉，沿过P作河岸l的垂线开沟引水的理由是：．14．如图，直线AB∥CD，CA平分∠BCD，若∠1＝50°，则∠2＝________．第14题图第15题图第16题图15．如图，直线AB，CD被BC所截，若AB∥CD，∠1＝45°，∠2＝35°，则∠3＝度．16．如图，若∠1＝40°，∠2＝40°，∠3＝116°30′，则∠4＝ .17．对于同一平面内的三条直线a，b，c，给出下列五个结论：①a∥b；②b∥c；③a ⊥b；④a∥c；⑤a⊥c.请以其中两个作为已知条件，一个作为结论，组成一个正确的语句 (用数学语言作答)．18．如图，a∥b，c⊥a，∠1＝130°，则∠2等于________.三、解答题(共66分)19．(8分)如图，有一条小船，若把小船平移，使点A平移到点B，请你在图中画出平移后的小船．20．(10分)推理填空：如图，已知∠B＝∠CGF，∠DGF＝∠F，试说明∠B＋∠F＝180°.解：∵∠B＝__ __(已知)，∴AB∥CD( )．∵∠DGF＝____________(已知)，∴CD∥EF( )．∴AB∥EF(___________________)．∴∠B＋______＝180°(____ )．21．(10分)如图，直线AB，CD，EF交于点O，OG平分∠BOF，且CD⊥EF，∠AOE＝60°，求∠DOG的度数．22．(12分)如图，AD∥BC，∠1＝60°，∠B＝∠C，DF为∠ADC的平分线．(1)求∠ADC的度数；(2)试说明DF∥AB.23．(12分)如图，BD⊥AC，ED∥BC，∠1＝∠2，AC＝9cm，且点D为AF的中点，点F为DC 的中点．(1)试说明BD∥GF；(2)求BD与GF之间的距离．24．(14分)已知BC∥OA，∠B＝∠A＝100°，试回答下列问题：(1)如图①所示，试说明OB∥AC；(2)如图②，若点E，F在BC上，且满足∠FOC＝∠AOC，并且OE平分∠BOF.则∠EOC的度数等于________(在横线上填上答案即可)；(3)在(2)的条件下，若平行移动AC，如图③，那么∠OCB∶∠OFB的值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值；(4)在(3)的条件下，在平行移动AC的过程中，若使∠OEB＝∠OCA，此时∠OCA的度数等于________(在横线上填上答案即可).参考答案与解析1．B 2.D 3.D 4.D 5.D 6.B 7.C 8.D 9.A 10．C 解析：如图，过点C 作CG ∥AB ，过点D 作DH ∥EF ，则∠A ＝∠ACG ，∠EDH ＝180°－∠E .∵AB ∥EF ，∴CG ∥DH ，∴∠CDH ＝∠DCG ，∴∠ACD ＝∠ACG ＋∠DCG ＝∠A ＋∠CDH ＝∠A ＋∠CDE －(180°－∠E )，∴∠A －∠ACD ＋∠CDE ＋∠E ＝180°.故选C.11．30° 12.70 13.垂线段最短 14．65° 15.80 16.63°30′17．若a ∥b ，b ∥c ，则a ∥c (答案不唯一) 18.40° 19．解：平移后的小船如图所示．(8分)20．解：∠CGF 同位角相等，两直线平行(2分) ∠F 内错角相等，两直线平行(6分) 平行于同一直线的两直线平行(8分) ∠F 两直线平行，同旁内角互补(10分)21．解：∵∠AOE ＝60°，∴∠BOF ＝∠AOE ＝60°(2分)．∵OG 平分∠BOF ，∴∠BOG ＝12∠BOF ＝30°.(4分)∵CD ⊥EF ，∴∠COE ＝90°，∴∠AOC ＝90°－60°＝30°，∴∠BOD ＝30°，(8分)∴∠DOG ＝∠BOD ＋∠BOG ＝60°.(10分)22．解：(1)∵AD ∥BC ，∴∠B ＝∠1＝60°，∠C ＋∠ADC ＝180°.(3分)∵∠B ＝∠C ，∴∠C ＝60°，∴∠ADC ＝180°－60°＝120°.(6分)(2)∵DF 平分∠ADC ，∴∠ADF ＝12∠ADC ＝12×120°＝60°.(8分)又∵∠1＝60°，∴∠1＝∠ADF ，∴AB ∥DF .(12分)23．解：(1)∵ED ∥BC ，∴∠1＝∠DBC .(2分)∵∠1＝∠2，∴∠DBC ＝∠2，(4分)∴BD ∥GF .(6分)(2)∵AC ＝9cm ，D 为AF 的中点，F 为DC 的中点，∴AD ＝DF ＝FC ＝9÷3＝3(cm)．(9分)∵DF ⊥BD ，BD ∥GF ，∴BD 与GF 之间的距离为3cm.(12分)24．解：(1)∵BC ∥OA ，∴∠B ＋∠O ＝180°.∵∠A ＝∠B ，∴∠A ＋∠O ＝180°，∴OB ∥AC .(3分)(2)40°(6分) 解析：∵∠A ＝∠B ＝100°，由(1)得∠BOA ＝180°－∠B ＝80°.∵∠FOC ＝∠AOC ，OE 平分∠BOF ，∴∠EOF ＝12∠BOF ，∠FOC ＝12∠FOA ，∴∠EOC ＝∠EOF ＋∠FOC＝12(∠BOF ＋∠FOA )＝12∠BOA ＝40°. (3)∠OCB ∶∠OFB 的值不发生变化．(8分)理由如下：∵BC ∥OA ，∴∠OFB ＝∠FOA ，∠OCB ＝∠AOC .又∵∠FOC ＝∠AOC ，∴∠FOC ＝∠OCB ，∴∠OFB ＝∠FOA ＝∠FOC ＋∠AOC ＝2∠OCB，(10分)∴∠OCB∶∠OFB＝1∶2.(11分)(4)60°(14分) 解析：由(1)知OB∥AC，∴∠OCA＝∠BOC，由(2)可设∠BOE＝∠EOF ＝α，∠FOC＝∠AOC＝β，∴∠OCA＝∠BOC＝2α＋β.∵BC∥OA，∴∠OEB＝∠EOA＝α＋2β.∵∠OEB＝∠OCA，∴2α＋β＝α＋2β，∴α＝β.∵∠AOB＝80°，∴α＝β＝20°，∴∠OCA＝2α＋β＝40°＋20°＝60°.。

《相交线与平行线》单元测试卷含答案

第4章相交线与平行线单元测试卷一、选择题(每题２分,共2０分)1、如图,直线a,b被直线c所截,∠1与∠2得位置关系就是()Ａ、同位角ﻩB、内错角ﻩＣ、同旁内角D。

对顶角2、如图,ＡＢ∥ＣD,ＡD平分∠BAC,若∠BAD=6５°,那么∠ACＤ得度数为() Ａ.40°B、35°ﻩＣ。

5０°ﻩD。

4５°12 33.如图,AＢ∥EC,下列说法不正确得就是()A。

∠B=∠ECＤ B.∠Ａ＝∠ＥＣDC、∠Ｂ+∠ECB=1８0°ﻩ D. ∠A+∠B+∠ＡCB=180°4。

如图,在俄罗斯方块游戏中,出现一小方块拼图向下运动,通过平移运动拼成一个完整得图案,最终所有图案消失,则对小方块进行得操作为( )Ａ.向右平移1格再向下ﻩＢ、向右平移3格再向下C。

向右平移２格再向下ﻩD。

以上答案均可5。

如图所示,3块相同得三角尺拼成一个图形,图中有很多对平行线,其中不能由下面得根据得出两直线平行得就是()A、同位角相等,两直线平行ﻩB。

内错角相等,两直线平行C.平行于同一直线得两直线平行ﻩD、垂直于同一直线得两直线平行6。

如图,直线AB∥ＣD,AＥ平分∠CAB,AＥ与CD相交于点E,∠ＡCD=４0°,则∠ＢＡE得度数就是( )Ａ、４0°B。

７0°C。

80°D、1４0°7。

同一平面内得四条互不重合得直线满足a⊥ｂ,ｂ⊥c,c⊥d,则下列各选项中关系能成立得就是( )A。

ａ∥d B。

ａ⊥ｃﻩC、a⊥d D.b⊥d8。

如图,AB∥ＥF,CＤ⊥EF,∠BAC=５0°,则∠ACD=()A.12０°B。

130°ﻩＣ.14０° D.１50°９。

如图,AD就是∠EＡC得平分线,ＡＤ∥BC,∠B=30°,则∠C为( )Ａ。

30°B。

6０°ﻩ C.８0°ﻩＤ、1２0°１0、如图,把一块含有45°角得直角三角尺得两个顶点放在直尺得对边上。

(完整版)《相交线与平行线》单元测试卷含答案

第4章相交线与平行线单元测试卷一、选择题(每题2分,共20分)1。

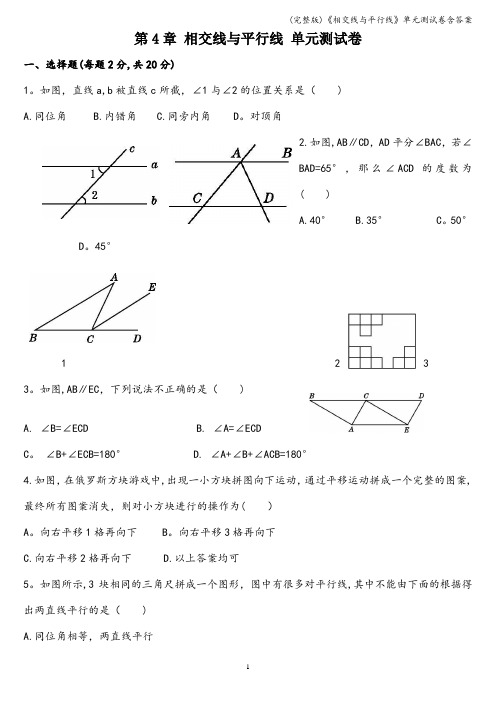
如图，直线a,b被直线c所截，∠1与∠2的位置关系是（)A.同位角B.内错角C.同旁内角D。

对顶角2.如图,AB∥CD，AD平分∠BAC，若∠BAD=65°，那么∠ACD的度数为( )A.40°B.35° C。

50°D。

45°31 2 3。

如图,AB∥EC，下列说法不正确的是（)A. ∠B=∠ECDB. ∠A=∠ECDC。

∠B+∠ECB=180° D. ∠A+∠B+∠ACB=180°4.如图，在俄罗斯方块游戏中,出现一小方块拼图向下运动，通过平移运动拼成一个完整的图案,最终所有图案消失，则对小方块进行的操作为( ）A。

向右平移1格再向下 B。

向右平移3格再向下C.向右平移2格再向下D.以上答案均可5。

如图所示,3块相同的三角尺拼成一个图形，图中有很多对平行线,其中不能由下面的根据得出两直线平行的是（)A.同位角相等，两直线平行B.内错角相等，两直线平行C.平行于同一直线的两直线平行D。

垂直于同一直线的两直线平行6。

如图，直线AB∥CD，AE平分∠CAB，AE与CD相交于点E，∠ACD=40°,则∠BAE的度数是( ）A.40°B.70°C.80° D。

140°7。

同一平面内的四条互不重合的直线满足a⊥b,b⊥c，c⊥d，则下列各选项中关系能成立的是( )A。

a∥d B。

a⊥c C。

a⊥d D。

b⊥d8。

如图,AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD=( )A.120 ° B。

130° C.140° D。

150°9。

如图，AD是∠EAC的平分线,AD∥BC,∠B=30°，则∠C为( )A。

30° B.60° C。

80° D。

相交线与平行线单元测试题

(完整word版)相交线与平行线单元测试卷(含答案)

相交线与平行线单元测试题总集完整含答案

平行线与相交线单元测试题

相交线与平行线单元测试题(含答案)

《相交线与平行线》单元测试题

(完整版)《相交线与平行线》单元测试卷含答案

《相交线与平行线》单元测试题及答案

相交线与平行线单元测试题含答案

人教版七年级数学下册第五章相交线与平行线单元检测卷(共6套)

相交线与平行线 单元测试题(含答案)

相交线与平行线单元测试题

第五章《相交线与平行线》单元测试卷(含答案)

相交线与平行线单元测试题

(完整版)相交线与平行线单元测试题

相交线与平行线单元测试卷(含答案)

相交线与平行线单元测试卷(附答案)

《相交线与平行线》单元测试卷含答案

(完整版)《相交线与平行线》单元测试卷含答案

相交线与平行线单元测试题(含答案)