2016-2017年江苏省南京师大附中高三(上)期中数学试卷及参考答案(文科)
江苏省南师附中高2020届高2017级高三年级第二学期期初检测试卷数学参考答案及评分标准

南师附中2020届高三年级第二学期期初检测试卷数学试题参考答案及评分标准第Ⅰ卷(必做题,160分)一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.[]2,4-2.二3.64.55.()2,06.58 7.38.252 9.12 10.120,5⎡⎤⎢⎥⎣⎦11.[)4,+∞ 12.19 13.[]1,11- 14.3ln 2,02⎛⎫-- ⎪⎝⎭二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分) 解:(1)由正弦定理a sin A =b sin B =c sin C=2R ,得a =2R sin A ,b =2R sin B ,c =2R sin C , 代入a cos B +b cos A =c cos Acos C ,得 (sin A cos B +sin B cos A ) cos C =sin C cos A ,…………2分即sin(A +B )cos C =sin C cos A .因为A +B =π-C ,所以sin(A +B )=sin C , 所以sin C cos C =sin C cos A ,…………4分因为C 是△ABC 的内角,所以sin C ≠0,所以cos C =cos A .又因为A ,C 是△ABC 的内角,所以A =C .…………6分(2)由(1)知,因为A =C ,所以a =c ,所以cos B =a 2+c 2-b 22ac =a 2-2a 2.…………8分因为BA →·BC →=1,所以a 2cos B =a 2-2=1,所以a 2=3.…………10分 所以cos B =13.…………12分因为B △(0,π),所以sin B =1-cos 2B =223.…………14分16.(本小题满分14分)解:(1)因为AD △平面BCC 1B 1,AD ⊂平面ABCD ,平面BCC 1B 1∩平面ABCD =BC , 所以AD △BC .…………4分又因为BC ⊄平面ADD 1A 1,AD ⊂平面ADD 1A 1, 所以BC △平面ADD 1A 1.…………6分(2)由(1)知AD △BC ,因为AD △DB ,所以BC △DB ,…………8分 在直四棱柱ABCD -A 1B 1C 1D 1中DD 1△平面ABCD ,BC ⊂底面ABCD , 所以DD 1△BC ,…………10分又因为DD 1⊂平面BDD 1B 1,DB ⊂平面BDD 1B 1,DD 1∩DB =D , 所以BC △平面BDD 1B 1,…………12分 因为BC ⊂平面BCC 1B 1,所以平面BCC 1B 1△平面BDD 1B 1.…………14分 17.(本小题满分14分)解:(1)连接AB ,因为正方形边长为10米,所以10OA OB AB ===,则3AOB π∠=,所以»103AB π=,…………2分所以广场的面积为2211050(1010)10100233ππ⋅⋅+=+-答:广场的面积为501003π+-.…………6分 (2)作OG CD ⊥于G ,OK AD ⊥于K G ,记OAK α∠=, 则2220sin AD DG OK α===,…………8分 由余弦定理得2222cos OD OA AD OA AD α=+-⋅221cos 210(20sin )21020sin cos 100400200sin 22ααααα-=+-⨯⨯=+⨯-230045)1)α=-+≥o ,…………12分所以1)OD ≥,当且仅当22.5α=o时取等号,所以201)OA OB OC OD +++≤+=因此求4条小路的总长度的最小值为.答:4条小路的总长度的最小值为.…………14分 18.(本小题满分14分)解:(1)设椭圆的焦距为2c (c >0). 依题意,c a =12,且a 2c =4,解得a =2,c =1.故b 2=a 2-c 2=3.所以椭圆C 的标准方程为x 24+y 23=1.…………4分(2)设点M (x 1,y 1),N (x 2,y 2),则x 124+y 123=1,x 224+y 223=1.两式相减,得(x 1-x 2)(x 1+x 2)4+(y 1-y 2)(y 1+y 2)3=0,14+13·y 1-y 2x 1-x 2·y 1+y 2x 1+x 2=0,所以14+13·k ·(-12)=0,得k =32.…………8分(3)由题意,S 1S 2=32,即12·|AF |·|y 1|12·|BF |·|y 2|=32,整理可得|y 1||y 2|=12,…………10分所以→NF =2→FM .代入坐标,可得⎩⎨⎧1-x 2=2(x 1-1)-y 2=2y 1,即⎩⎨⎧x 2=3-2x 1y 2=-2y 1.…………12分又点M ,N 在椭圆C 上,所以⎩⎨⎧x 124+y 123=1 (3-2x 1)24+(-2y 1)23=1,解得⎩⎨⎧x 1=74y =38 5.所以M 的坐标为(74,358).…………16分19.(本小题满分16分)解:(1)f ′(x )=1x -a x 2,则f ′(1)=1-a =2,解得a =-1,则f (x )=ln x -1x +1,此时f (1)=ln1-1+1=0,则切点坐标为(1,0), 代入切线方程,得b =-2, 所以a =-1,b =-2.…………2分(2)g (x )=f (x )+ax =ln x +a x +ax +1,g ′(x )=1x -ax 2+a =ax 2+x -a x 2.△当a =0时,g ′(x )=1x >0,则g (x )在区间(0,12)上为增函数,则g (x )在区间(0,12)上无最小值.…………4分△当a ≠0时,方程ax 2+x -a =0的判别式Δ=1+4a 2>0, 则方程有两个不相等的实数根,设为x 1,x 2,由韦达定理得x 1x 2=-1,则两根一正一负,不妨设x 1<0<x 2. 设函数m (x )=ax 2+x -a (x >0), (i )若a >0,若x 2△(0,12) ,则m (0)=-a <0 ,m (12)=a 4+12-a >0 ,解得0<a <23.此时x △(0,x 2)时,m (x )<0,则g (x )递减;x △(x 2,12)时,m (x )>0,则g (x )递增,当x =x 2时,g (x )取极小值,即为最小值.若x 2≥12,则x △(0,12),m (x )<0,g (x )在(0,12)单调减,无最小值.…………6分(ii )若a <0,此时x △(0,x 2)时,m (x )>0,则g (x )递增;x △(x 2,+∞)时,m (x )<0,则g (x )递减, 在区间(0,12)上,g (x )不会有最小值.所以a <0不满足条件.综上,当0<a <23时,g (x )在区间(0,12)上有最小值.…………8分(3)当a =0时,由方程f (x )=bx 2,得ln x +1-bx 2=0,记h (x )=ln x +1-bx 2,x >0,则h ′(x )=1x -2bx =-2bx 2+1x.△当b ≤0时,h ′(x )>0恒成立,即h (x )在(0,+∞)上为增函数,则函数h (x )至多只有一个零点,即方程f (x )=bx 2至多只有一个实数根, 所以b ≤0不符合题意.…………10分△当b >0时,当x △(0,12b)时,h ′(x )>0,所以函数h (x )递增; 当x △(12b,+∞)时,h ′(x )<0,所以函数h (x )递减, 则h (x )max =h (12b)=ln 12b +12. 要使方程f (x )=bx 2有两个不相等的实数根,则h (12b)=ln 12b +12>0,解得0<b <e2.…………12分 (i )当0<b <e 2时,h (1e )=-be 2<0.又(1e)2-(12b )2=2b -e 22b e 2<0,则1e<12b, 所以存在唯一的x 1△(1e ,12b),使得h (x 1)=0.…………14分 (ii )h (1b )=ln 1b +1-1b =-ln b +1-1b ,记k (b )=-ln b +1-1b ,0<b <e2,因为k ′(b )=-1b +1b 2=1-b b 2,则k (b )在(0,1)上为增函数,在(1,e2)上为减函数,则k (b )max =k (1)=0,则h (1b )≤0.又(1b)2-(12b )2=2-b 2b 2>0,即1b>12b, 所以存在唯一的x 2△(12b ,1b],使得h (x 2)=0, 综上,当0<b <e2时,方程f (x )=bx 2有两个不相等的实数根.…………16分20.(本小题满分16分)解:(1)△若1λ=,因为111n n n n n n a S a S a a λ+++-=-,则()()1111n n n n S a S a +++=+,111a S ==. 又△0n a >,0n S >,△1111n n n nS a S a +++=+,△3131221212111111n n n nS S a a S a S S S a a a +++++⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅+++, 化简,得1112n n S a +++=.△ △当2n ≥时,12n n S a +=.△△-△,得12n n a a +=,即()122n na n a +=≥. △当1n =时,22a =,1n =时上式也成立,△数列{}n a 是首项为1,公比为2的等比数列,12n n a -=.…………4分△因为()1n n b n a =+,△()112n n b n -=+⋅.所以012212232422(1)2n n n T n n --=⨯+⨯+⨯++⨯++⨯L ,所以123122232422(1)2n nn T n n -=⨯+⨯+⨯++⨯++⨯L ,所以1212222(1)2n nn T n --=++++-+⨯L 12(12)2(1)2212n n n n n --=+-+⨯=-⨯-,所以2nn T n =⋅.…………8分(2)令1n =,得21a λ=+.令2n =,得()231a λ=+.要使数列{}n a 是等差数列,必须有2132a a a =+,解得0λ=. 当0λ=时,()111n n n n S a S a ++=+,且211a a ==.…………10分 当2n ≥时,()()()1111n n n n n n S S S S S S +-+-=+-,整理,得2111n n n n n S S S S S +-++=+,1111n n n nS S S S +-+=+, 从而3312412123111111n n n nS S S S S S S S S S S S +-+++⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅+++, 化简,得11n n S S ++=,所以11n a +=.…………14分综上所述,()*1Nn a n =∈,所以0λ=时,数列{}n a 是等差数列.…………16分第△卷(选做题,40分)21.【选做题】在A 、B 、C 三小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤. A.选修4—2:矩阵与变换解:(1) M 2=⎣⎡⎦⎤ 2 1 1 2 ⎣⎡⎦⎤ 2 1 1 2 =⎣⎡⎦⎤5445 .…………4分 (2)矩阵M 的特征多项式为f (λ)=⎪⎪⎪⎪⎪⎪λ-2 -1-1 λ-2=(λ-1)(λ-3).令f (λ)=0,解得M 的特征值为λ1=1,λ2=3.…………6分 △当λ=1时,⎣⎡⎦⎤ 2 1 1 2 ⎣⎡⎦⎤x y =⎣⎡⎦⎤x y ,得⎩⎨⎧x +y =0,x +y =0.令x =1,则y =-1,于是矩阵M 的一个特征向量为⎣⎡⎦⎤1-1.…………8分△当λ=3时,⎣⎡⎦⎤ 2 1 1 2 ⎣⎡⎦⎤x y =3⎣⎡⎦⎤xy ,得⎩⎨⎧x -y =0,x -y =0.令x =1,则y =1,于是矩阵M 的一个特征向量为⎣⎡⎦⎤11. 因此,矩阵M 的特征值为1,3,分别对应一个特征向量为⎣⎡⎦⎤1-1,⎣⎡⎦⎤11.…………10分 B.选修4—4:坐标系与参数方程解:分别化为普通方程得直线1x =与圆22(1)1x y +-=,…………4分易得直线1x =与圆22(1)1x y +-=切于点Q ()1 1,,…………6分 所以交点Q 的极坐标是)π4,.…………10分【必做题】第22题、第23题,每题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)解:(1)因为l 过M (2,0),且当l 垂直于x 轴时,AB =4, 所以抛物线经过点(2,2),代入抛物线方程,得4=2p ×2,解得p =1.…………2分 (2)设直线l 方程为:y =k (x -2)(k ≠0),A (x 1,y 1),B (x 2,y 2).联立⎩⎨⎧y 2=2x ,y =k (x -2),消去x ,得ky 2-2y -4k =0,则y 1+y 2=2k ,y 1y 2=-4.…………4分因为C 为AB 中点,所以y C =y 1+y 22=1k, 则直线l 1方程为:y =1k.…………6分因为直线l 2过点M 且与l 垂直,则l 2方程为:y =-1k(x -2),联立⎩⎨⎧y =1k ,y =-1k (x -2),…………8分解得⎩⎪⎨⎪⎧x =1,y =1k ,即P (1,1k),所以,点P 在定直线x =1上.…………10分 23.(本小题满分10分)解:(1)0111111101=-=+=a a S ;231121111112102=+-=++=a a a S ;011313111111132103=-+-=+++=a a a a S ;35114161411111111432104=+-+-=++++=a a a a a S .…………4分(2)由二项式定理得,(1),,k kk na k n k =-∈C N ≤, 因为!()!1!C k nk n k n -=)!1(])!(!)][1()1[(21+-+++-⋅++=n k n k k k n n n )!1()!()!1()!1(!21+-+++-⋅++=n k n k k n k n n ⎥⎦⎤⎢⎣⎡+-++++-⋅++=)!1()!()!1()!1()!1(!21n k n k n k n k n n ⎥⎦⎤⎢⎣⎡+⋅++=+++111C 1C 121k n k n n n ,…………8分 所以∑==nk kn a S 01011211111111111111(1)2C C C C C C n n n n n n n n n n n +++++++⎡⎤⎛⎫⎛⎫⎛⎫+=⋅+-+++-+⎢⎥ ⎪ ⎪ ⎪+⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦L高三数学参考答案 第 11 页 共 11 页 0111111(1)2C C n n n n n n +++⎛⎫+=⋅+- ⎪+⎝⎭()n n n )1(121-+⋅++=.…………10分。
2016-2017学年江苏省南京师大附中高三(上)期中数学试卷和答案(文科)
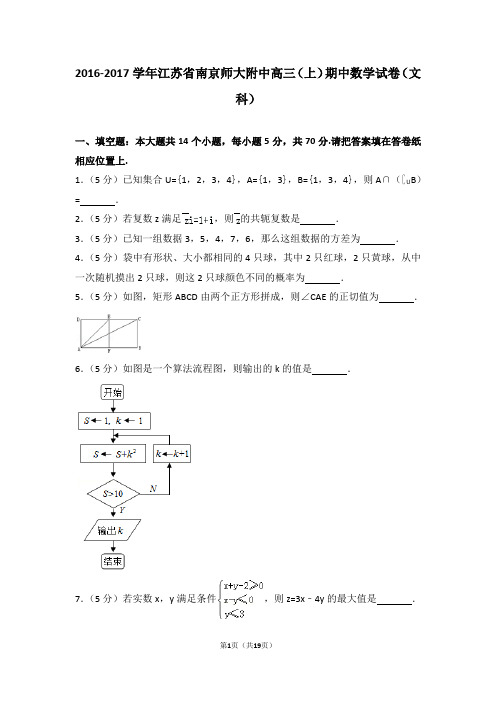
2016-2017学年江苏省南京师大附中高三(上)期中数学试卷(文科)一、填空题:本大题共14个小题,每小题5分,共70分.请把答案填在答卷纸相应位置上.1.(5分)已知集合U={1,2,3,4},A={1,3},B={1,3,4},则A∩(∁U B)=.2.(5分)若复数z满足,则的共轭复数是.3.(5分)已知一组数据3,5,4,7,6,那么这组数据的方差为.4.(5分)袋中有形状、大小都相同的4只球,其中2只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为.5.(5分)如图,矩形ABCD由两个正方形拼成,则∠CAE的正切值为.6.(5分)如图是一个算法流程图,则输出的k的值是.7.(5分)若实数x,y满足条件,则z=3x﹣4y的最大值是.8.(5分)若双曲线﹣=1的一条渐近线经过点(3,﹣4),则此双曲线的离心率为.9.(5分)已知cos()=,则cos()﹣sin2(α﹣)=.10.(5分)在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°,点E和F分别在线段BC和DC上,且=,=,则•的值为.11.(5分)等比数列{a n}的首项为2,公比为3,前n项和为S n,若log3[a n (S4m+1)]=9,则+的最小值是.12.(5分)在平面直角坐标系xOy中,点A(1,0),B(4,0),若直线x﹣y+m=0上存在点P,使得2PA=PB,则实数m的取值范围是.13.(5分)已知函数f(x)=,g(x)=kx+1,若方程f(x)﹣g(x)=0有两个不同实根,则实数k的取值范围为.14.(5分)已知不等式(ax+3)(x2﹣b)≤0对任意x∈(0,+∞)恒成立,其中a,b是整数,则a+b的取值的集合为.二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.(14分)在△ABC中,角A,B,C的对边分别为a,b,c,且=.(1)求角A的值;(2)若△ABC的面积为,且a=,求△ABC的周长.16.(14分)在四棱锥P﹣ABCD中,∠ACD=90°,∠BAC=∠CAD,PA⊥平面ABCD,E为PD的中点.(1)求证:平面PAC⊥平面PCD;(2)求证:CE∥平面PAB.17.(14分)如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).(1)若要求圆柱体罐子的侧面积最大,应如何截取?(2)若要求圆柱体罐子的体积最大,应如何截取?18.(16分)如图,在平面直角坐标系xOy中,已知A,B,C是椭圆=1(a>b>0)上不同的三点,,B(﹣2,﹣2),C在第三象限,线段BC的中点在直线OA上.(1)求椭圆的标准方程;(2)求点C的坐标;(3)设动点P在椭圆上(异于点A,B,C)且直线PB,PC分别交直线OA于M,N两点,证明为定值并求出该定值.19.(16分)已知数列{a n}和{b n}满足a1a2a3…a n=(n∈N*).若{a n}为等比数列,且a1=2,b3=6+b2.(Ⅰ)求a n和b n;(Ⅱ)设c n=(n∈N*).记数列{c n}的前n项和为S n.(i)求S n;(ii)求正整数k,使得对任意n∈N*均有S k≥S n.20.(16分)已知函数f(x)=x2﹣2alnx(a∈R),g(x)=2ax.(1)求函数f(x)的极值;(2)若a>0,函数h(x)=f(x)﹣g(x)有且只有一个零点,求实数a的值;(3)若0<a<1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f (x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,求a的取值范围.2016-2017学年江苏省南京师大附中高三(上)期中数学试卷(文科)参考答案与试题解析一、填空题:本大题共14个小题,每小题5分,共70分.请把答案填在答卷纸相应位置上.1.(5分)已知集合U={1,2,3,4},A={1,3},B={1,3,4},则A∩(∁U B)=∅.【解答】解:∵集合U={1,2,3,4},B={1,3,4},∴∁U B={2},∵A={1,3},∴A∩(∁U B)=∅,故答案为:∅2.(5分)若复数z满足,则的共轭复数是1+i.【解答】解:∵,∴﹣i•i=﹣i(1+i),则=1﹣i则的共轭复数是1+i.故答案为:1+i.3.(5分)已知一组数据3,5,4,7,6,那么这组数据的方差为2.【解答】解:一组数据3,5,4,7,6,这组数据的平均数==5,这组数据的方差S2=[(3﹣5)2+(5﹣5)2+(4﹣5)2+(7﹣5)2+(6﹣5)2]=2.故答案为:2.4.(5分)袋中有形状、大小都相同的4只球,其中2只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为.【解答】解:袋中有形状、大小都相同的4只球,其中2只红球,2只黄球,从中一次随机摸出2只球,基本事件总数n==6,这2只球颜色不同,包含的基本事件个数m=C=4,∴这2只球颜色不同的概率p==.故答案为:.5.(5分)如图,矩形ABCD由两个正方形拼成,则∠CAE的正切值为.【解答】解:因为矩形ABCD由两个正方形拼成,设正方形的边长为1,则在Rt△CAD中,=2,,所以⇔⇒.故答案为:6.(5分)如图是一个算法流程图,则输出的k的值是3.【解答】解:模拟程序的运行,可得S=1,k=1S=2,不满足条件S>10,k=2,S=6不满足条件S>10,k=3,S=15满足条件S>10,退出循环,输出k的值为3.故答案为:3.7.(5分)若实数x,y满足条件,则z=3x﹣4y的最大值是﹣1.【解答】解:不等式组对应的平面区域如图:由z=3x﹣4y得y=,平移直线y=,则由图象可知当直线y=,当经过点A时,直线的截距最小,此时z最大.由,解得,即A(1,1),此时最大值z=3×1﹣4×1=﹣1,故答案为:﹣18.(5分)若双曲线﹣=1的一条渐近线经过点(3,﹣4),则此双曲线的离心率为.【解答】解:双曲线﹣=1的渐近线方程为y=±x,由渐近线过点(3,﹣4),可得﹣4=﹣,即b=a,c===a,可得e==.故答案为:.9.(5分)已知cos()=,则cos()﹣sin2(α﹣)=.【解答】解:cos()=cos[π﹣(﹣α)]=﹣cos(﹣α)=﹣sin2(α﹣)=sin2[﹣(﹣α)]=1﹣cos2(﹣α)=1﹣(﹣)2=∴cos()﹣sin2(α﹣)=﹣﹣=﹣.故答案为:﹣10.(5分)在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°,点E和F分别在线段BC和DC上,且=,=,则•的值为.【解答】解:∵AB=2,BC=1,∠ABC=60°,∴BG==,CD=2﹣1=1,∠BCD=120°,∵=,=,∴•=(+)•(+)=(+)•(+)=•+•+•+•=2×1×cos60°+×2×1×cos0°+×1×1×cos60°+××1×1×cos120°=1+=,故答案为:11.(5分)等比数列{a n}的首项为2,公比为3,前n项和为S n,若log3[a n (S4m+1)]=9,则+的最小值是 2.5.【解答】解:∵等比数列{a n}的首项为2,公比为3,前n项和为S n,∴a n=2•3n﹣1;S n=3n﹣1,∵log3[a n•(S4m+1)]=9,∴(n﹣1)+4m=9,∴n+4m=10,∴+=(n+4m)(+)=(17+)≥(17+8)=2.5,当且仅当m=n=2时取等号,∴+的最小值是2.5.故答案为:2.5.12.(5分)在平面直角坐标系xOy中,点A(1,0),B(4,0),若直线x﹣y+m=0上存在点P,使得2PA=PB,则实数m的取值范围是[﹣2,2] .【解答】解:设P(x,x+m),∵2PA=PB,∴4|PA|2=|PB|2,∴4(x﹣1)2+4(x+m)2=(x﹣4)2+(x+m)2,化为(x+m)2=4﹣x2,∴4﹣x2≥0,解得x∈[﹣2,2],∴m=﹣x±,令x=2cosθ,θ∈[0,π],∴m=﹣2cosθ±2sinθ=±2sin(θ±)∈[﹣2,2],实数m的取值范围是[﹣2,2],故答案为[﹣2,2].13.(5分)已知函数f(x)=,g(x)=kx+1,若方程f(x)﹣g (x)=0有两个不同实根,则实数k的取值范围为(,1)∪(1,e﹣1];.【解答】解:∵g(x)=kx+1,∴方程f(x)﹣g(x)=0有两个不同实根等价为方程f(x)=g(x)有两个不同实根,即f(x)=kx+1,则等价为函数f(x)与函数y=kx+1有两个不同的交点,当1<x≤2,则0<x﹣1≤1,则f(x)=f(x﹣1)=e x﹣1,当2<x≤3,则1<x﹣1≤2,则f(x)=f(x﹣1)=e x﹣2,当3<x≤4,则2<x﹣1≤3,则f(x)=f(x﹣1)=e x﹣3,…当x>1时,f(x)=f(x﹣1),周期性变化;函数y=kx+1的图象恒过点(0,1);作函数f(x)与函数y=kx+1的图象如下,C(0,1),B(2,e),A(1,e);故k AC=e﹣1,k BC=;在点C处的切线的斜率k=e0=1;结合图象可得,当k∈(1,e一1]时,k取中间值,交点在f(x)=e x上两点,定点(0,1),另一点在第一象限A点下方.当k∈(,1)时,任取k为中间值,则交点过C,另一点在笫二象限,点c 的左下方.当k∈(0,],交点有3点以上,与f(x)、f(x一1)都有交点.当k∈(一∞,e一1)时,与f(x)只交于点C.综上要使两个函数有两个交点,则实数k的取值范围为(,1)∪(1,e﹣1];故答案为:(,1)∪(1,e﹣1];14.(5分)已知不等式(ax+3)(x2﹣b)≤0对任意x∈(0,+∞)恒成立,其中a,b是整数,则a+b的取值的集合为{﹣2,8} .【解答】解:当b≤0 时,由(ax+3)(x2﹣b)≤0得到ax+3≤0 在x∈(0,+∞)上恒成立,则a不存在;当b>0 时,由(ax+3)(x2﹣b)≤0,可设f(x)=ax+3,g(x)=x2﹣b,又g(x)的大致图象如下,那么由题意可知:再由a,b 是整数得到或因此a+b=8或﹣2.故答案为{﹣2,8}二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.(14分)在△ABC中,角A,B,C的对边分别为a,b,c,且=.(1)求角A的值;(2)若△ABC的面积为,且a=,求△ABC的周长.【解答】解:(1)由=,利用正弦定理可得2sinBcosA﹣sinCcosA=sinAcosC,化为2sinBcosA=sin(C+A)=sinB,∵sinB≠0,∴cosA=,∵A∈(0,π),∴A=.(2)∵A=,△ABC的面积为=bcsinA=bc×,∴bc=2,∵a=,由余弦定理a2=b2+c2﹣2bccosA,可得:5=b2+c2﹣bc=(b+c)2﹣3bc=(b+c)2﹣6,∴解得:b+c=,∴△ABC的周长l=a+b+c=+.16.(14分)在四棱锥P﹣ABCD中,∠ACD=90°,∠BAC=∠CAD,PA⊥平面ABCD,E为PD的中点.(1)求证:平面PAC⊥平面PCD;(2)求证:CE∥平面PAB.【解答】证明:(1)因为PA⊥平面ABCD,CD⊂平面ABCD,所以PA⊥CD,…(2分)又∠ACD=90°,则CD⊥AC,而PA∩AC=A,所以CD⊥平面PAC,因为CD⊂平面ACD,…(4分)所以,平面PAC⊥平面PCD.…(7分)(2)证法一:取AD中点M,连EM,CM,则EM∥PA.因为EM⊄平面PAB,PA⊂平面PAB,所以EM∥平面PAB.…(9分)在Rt△ACD中,AM=CM,所以∠CAD=∠ACM,又∠BAC=∠CAD,所以∠BAC=∠ACM,则MC∥AB.因为MC⊄平面PAB,AB⊂平面PAB,所以MC∥平面PAB.…(12分)而EM∩MC=M,所以平面EMC∥平面PAB.由于EC⊂平面EMC,从而EC∥平面PAB.…(14分)(2)证法二:延长DC,AB交于点N,连PN.因为∠NAC=∠DAC,AC⊥CD,所以C为ND的中点.而E为PD中点,所以EC∥PN.因为EC⊄平面PAB,PN⊂平面PAB,所以EC∥平面PAB.…(14分)17.(14分)如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).(1)若要求圆柱体罐子的侧面积最大,应如何截取?(2)若要求圆柱体罐子的体积最大,应如何截取?【解答】解:(1)连接OC,设BC=x,则AB=2,(其中0<x<30),∴S=2x=2 ≤x2+(900﹣x2)=900,当且仅当x2=900﹣x2,即x=15时,S取最大值900;∴取BC=15cm时,矩形ABCD的面积最大,最大值为900cm2.(2)设圆柱底面半径为r,高为x,则AB=2=2πr,解得r=,∴V=πr2h=(900x﹣x3),(其中0<x<30);∴V′=(900﹣3x2),令V′(x)=0,得x=10;因此V(x)=(900x﹣x3)在(0,10 )上是增函数,在(10,30)上是减函数;∴当x=10时,V(x)取得最大值V(10)=,∴取BC=10cm时,做出的圆柱形罐子体积最大,最大值为cm3.18.(16分)如图,在平面直角坐标系xOy中,已知A,B,C是椭圆=1(a>b>0)上不同的三点,,B(﹣2,﹣2),C在第三象限,线段BC的中点在直线OA上.(1)求椭圆的标准方程;(2)求点C的坐标;(3)设动点P在椭圆上(异于点A,B,C)且直线PB,PC分别交直线OA于M,N两点,证明为定值并求出该定值.【解答】解:(1)由已知,将,B(﹣2,﹣2)代入椭圆方程:,解得,∴椭圆的标准方程为;…(4分)(2)解:设点C(m,n)(m<0,n<0),则BC中点为(,).由已知,求得直线OA的方程:x﹣2y=0,从而m=2n﹣2.①又∵点C在椭圆上,∴m2+4n2=20.②由①②,解得:n=2(舍),n=﹣1,从而m=﹣4.∴点C的坐标为(﹣4,﹣1).…(8分)(3)证明:设P(x0,y0),M(2y1,y1),N(2y2,y2).∵P,B,M三点共线,则=整理得y1=.…(10分)∵P,C,N三点共线,则=,整理得y2=.…(12分)∵点C在椭圆上,∴x02+4y02=20,x02=20﹣4y02,从而y1y2===2×=.…(14分)∴•=5y1y2=.∴•为定值,定值为.…(16分)19.(16分)已知数列{a n}和{b n}满足a1a2a3…a n=(n∈N*).若{a n}为等比数列,且a1=2,b3=6+b2.(Ⅰ)求a n和b n;(Ⅱ)设c n=(n∈N*).记数列{c n}的前n项和为S n.(i)求S n;(ii)求正整数k,使得对任意n∈N*均有S k≥S n.【解答】解:(Ⅰ)∵a1a2a3…a n=(n∈N*)①,当n≥2,n∈N*时,②,由①②知:,令n=3,则有.∵b3=6+b2,∴a3=8.∵{a n}为等比数列,且a1=2,∴{a n}的公比为q,则=4,由题意知a n,∴q>0,∴q=2.>0∴(n∈N*).又由a1a2a3…a n=(n∈N*)得:,,∴b n=n(n+1)(n∈N*).(Ⅱ)(i)∵c n===.∴S n=c1+c2+c3+…+c n====;(ii)因为c1=0,c2>0,c3>0,c4>0;当n≥5时,,而=>0,得,所以,当n≥5时,c n<0,综上,对任意n∈N*恒有S4≥S n,故k=4.20.(16分)已知函数f(x)=x2﹣2alnx(a∈R),g(x)=2ax.(1)求函数f(x)的极值;(2)若a>0,函数h(x)=f(x)﹣g(x)有且只有一个零点,求实数a的值;(3)若0<a<1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f (x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,求a的取值范围.【解答】解:(1)f′(x)=,当a≤0时,f′(x)>0,f(x)在(0,+∞)递增,f(x)无极值,当a>0时,x∈(0,)时,f′(x)<0,f(x)递减,x∈(,+∞)时,f′(x)>0,f(x)递增,∴f(x)有极小值f()=a﹣alna,综上:a≤0时,f(x)无极值,a>0时,f(x)极小值=a﹣alna,无极大值;(2)令h(x)=x2﹣2alnx﹣2ax,则h′(x)=,∵a>0,令h′(x)=0,解得x0=,∴h(x)在(0,)递减,在(,+∞)递增,∴h(x)在x0处取得极小值h(x0)=0,∴﹣2alnx0﹣2ax0=0且2﹣2ax0﹣2a=0,联立可得:2lnx0+x0﹣1=0,令m(x)=2lnx+x﹣1得m′(x)=+1>0,故m(x)在(0,+∞)递增又m(1)=0,x0=1,即=1,解得:a=;(3)不妨令1≤x1<x2≤2,则由(1)得f(x1)<f(x2)∴|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)⇔f(x2)﹣f(x1)>g(x2)﹣g(x1)⇔f(x2)﹣g(x2)>f(x1)﹣g(x1),则h(x)在[1,2]递增,∴h′(x)=≥0在[1,2]恒成立,即2x2﹣2ax﹣2a≥0在[1,2]恒成立,∴a≤在[1,2]恒成立,令t=x+1∈[2,3],则=t+﹣2≥,∴0<a≤,∴a的范围是(0,].。
南京师范大学附属中学-上学期高三数学期中试卷

南师大附中2007-2008学年度高三第一学期期中考试数学试题(满分160分,考试用时120分钟)一、填空题:本大题共14小题,每小题5分,共70分1已知a与b均为单位向量,它们的夹角为60°,那么|a+b|等于____________.2向量OA=(1,2),OB=(2,-1),OC=(1+m,3),若点A、B、C三点共线,则实数m应满足的条件为___. 3条件p:a>1;条件q:存在x∈[0,2],使a>x.p是q的_______________条件(填“充要”、“充分不必要”、“必要不充分”或“既不充分也不必要”)4若-π/3<x<π/6,要使cos x=2m-1成立,则实数m的取值范围是___________5A={x||x-1|<2},B={x|(x+1)(x-a)<0},且A∩B=B,则实数a的取值范围是_________ 6等比数列{a n}的前n项和为S n=x·3n-1/6,则常数x的值为_________7已知函数f(x)=lg(1-x)/(1+x),若f(a)=1/2,则f(-a)=____________8设x≥1,则函数y=(x+2)(x+3)/(x+1)的最小值是______________9函数f(x)=√3·sinωx cosωx+cos2ωx(其中0<ω<2),若函数f(x)图像的一条对称轴为x=π/3,那么ω=____________10已知数列{a n}中,a1=1,a2=2,a n=a n-1-a n-2(n∈N*n≥3),则a2007=__________11已知函数f(x)=-x2+ax+b2-b+1(a∈R,b∈R),对任意实数x都有f(1-x)=f(1+x)成立,若当x∈[-1,1]时,f(x)>0恒成立,则b的取值范围是___________a,(a≤b)12定义运算a*b=b,(a>b) ,例如,1*2=1,则函数f(x)=x2*(1-|x|)的最大值为________ 13估测函数f(x)=e x-1/x的零点所在的区间是_________(要求区间长度不超过0.25,e ≈2.71)14数列{a n}是正项等差数列,若b n=(a1+2a2+3a3+…+na n)/(1+2+3+…+n),则数列{b n}也为等差数列.类比上述结论,若{c n}为正项等比数列,写出d n=________,则数列{d n}也为等比数列.二、解答题:本大题共6小题,共90分15(本小题满分12分)解关于x的不等式:(1-a)/(x-1)>a(a≥0)16(本小题满分14分)已知A、B、C的坐标分别为A(3,0),B(0,3),C(cosα,sinα),α∈(π/2,3π/2) .(1)若|AC|=|BC|,求角α的值;(2)若AC·BC=-1,求(2sin2α+sin2α)/(1+tanα)的值.17(本小题满分14分)已知数列{a n}的前n项和S n=9-6n,且a n+1=2n·b n(n∈N*(1)求数列{a n}与{b n}的通项公式;1(2)求数列{n(2-log2|b n|) }的前n项和T n3某市原水价为1.5元/吨,从2006年5月1日起执行新的水价标准,实行分段计量水价:当家庭人口数不超过4人时,月用水量如表1所示;当家庭人口数超过4人时,人均月用水量如表2所示,水费由第一级别开始逐级计算,月用水量超出第一级别的部分按第二级别水价收取水费,月用水量超出第二级别的3所示.表1:表2:表3:(1)某家庭有3口人,5月份的用水量为35吨,求该家庭在5月份的水费比实施新的水价标准之前多少元?(2)如果按新的水价标准收费,试写出某人口数为n(n∈N*且n≥4)的家庭某月的用水水费总额y(元)关于月用水量x(吨)的函数设函数f(x)的定义域是(0,+∞),对任意正实数m,n恒有f(mn)=f(m)+f(n)x>1时,f(x)>0.f(2)=1 (1)求f(1/2)的值;(2)求证:f(x)在(0,+∞)上是增函数;(3)求方程4sinx=f(x)的根的个数20(本小题满分18分)已知数列{a n}、{b n}、{c n}的通项公式满足b n=a n+1-a n,c n=b n+1-b n(n∈N*b n}是一个非零常数列,则称数列{a n}是一阶等差数列;若数列{c n}是一个非零常数列,则称数列{a n}是二阶等差数列(1)试写出满足条件a 1=1,b1=1,c n=1(n∈N*a n}的前五项;(2)求满足条件(1)的二阶等差数列{a n}的通项公式a n;(3)若数列{a n}首项a1=2,且满足c n-b n+1+3a n=-2n+1(n∈N*a n}的通项公式数学参考答案一、填空题:本大题共14小题,每小题5分,共70分1.√32.m=-1/33.充分不必要条件4.(3/4,1 ]5.[-1,3]6. 1/67. -1/28. 69. 1/2 10. 1 11.b<-1或b>2 12.(3-√5)/2 13.(0.5,0.75)不唯一14.(c1·c22·c33·…·c n n)1/(1+2+3+…+n)二、解答题:本大题共6小题,共90分15(本小题满分12分)不等式可化为(ax-1)/(x-1)<0,即(x-1)(ax-1)<0,(2分)(1)若a=0,则不等式的解集是{x|x>1}.(4分)(2)若a>0,则不等式可化为(x-1)(x-1/a)<0,(6分)①当0<a<1时,1<1/a,不等式的解集为{x|1<x<1/a};(8分)②当a>1时,1>1/a,不等式的解集为{x|1/a<x<1};(10分)③当a=1时,不等式的解集为∮(12分)16(本小题满分14分)(1)∵AC=(cosα-3,sinα),BC=(cosα,sinα-3),(2分)∴|AC|=√(cosα-3)2+sin2α=√10-6cosα,|BC|=√cosα2+(sinα-3)2=√10-6sinα4分)由|AC|=|BC|得sinα=cosα又∵α∈(π/2,3π/2),∴α=5π/4.(6分)(2)由AC·BC=-1,得(cosα-3)cosα+sinα(sinα-3)=-1∴sinα+cosα=2/39分)又(2sin2α+sin2α)/(1+tanα)=(2sin2α+2sinαcosα)/(1+sinα/cosα)=2sinαcosα12分)由①式两边平方得1+2sinαcosα=4/9,∴2sinαcosα=-5/9∴(2sin2α+sin2α)/(1+tanα)=-5/914分)17(本小题满分14分)(1)当n=1时,a1=S1=3,(2分)当n≥2时,a n=S n-S n-1=-6,(4分)即数列的通项公式为a n=3(n=1),-6(n≥2).(6分)b n=a n+1/2n=-6/2n.(8分)(2)1/{n〔2-log2(|b n|/3) 〕}=1/〔n(n+1)〕=1/n-1/(n+1)11分)故T n=(1-1/2)+(1/2-1/3)+…+(1/n-1/n+1)=n/(n+1)14分)18(本小题满分16分)(1)如果按原来的水价,水费为35×1.5=52.5元,(3分)如果按新标准则∵35>25,∴水费按三个级别来收取,25×1.9+(33-25)×2.5+(35-33)×3=73.5元,(6分)相差73.5-52.5=21元答:该家庭在5月份的水费比实施新的水价标准之前多21元8分)(2)若n≥5时,当月用水量0≤x≤6n时,水费y=1.9x;(10分)当月用水量6n<x≤8n时,水费y=1.9×6n+2.5×(x-6n);(12分)当月用水量x>8n时,y=1.9×6n+2.5×(8n-6n)+3(x-8n),(14分)综上所述:若n≥5时,某家庭某月的用水水费总额y(元)关于月用水量x(吨)的函数为1.9x 0≤x≤6n,y= 2.5x-3.6n 6n<x≤8n,(16分)3x-7.6n x>8n.19(本小题满分16分)(1)令m=n=1,则f(1×1)=f(1)+f(1(1)=0令m=2,n=1/2,则f(1)=f(2×1/2)=f(2)+f(1/2)2分)∴f(1/2)=f(1)-f(2)= -14分)(2)设0<x1<x2,则x2/x1>1,∵当x>1时,f(x)>0,∴f(x2/x1)>06分)f(x2)=f(x1×x2/x1)=f(x1)+f(x2/x1)>f(x1).(8分)∴f(x)在(0,+∞)上是增函数10分)(3)∵y=4sinx的图像如下所示,由图可知y最大值为4,又∵f(4)=f(2×2)=2f(2)=2,f(16)=f(4×4)=2f(4)=412分)由y=f(x)在x>0单调递增,且f(1)=0,f(16)=4可得f(x)的图像大致形状如上所示,由图可知,y=4sinx的图像与y=f(x)的图像在[0,2π]内有一个交点,在(2π,4π]内有两个交点,在(4π,5π]内有两个交点,又5π<16<6π,所以总共有5个交点∴方程4sinx=f(x)的根的个数是516分)20(本小题满分18分)(1)a1=1,a2=2,a3=4,a4=7,a5=114分)(2)依题意b n+1-b n=c n=1,n=1,2,3,…所以b n=(b n-b n-1)+(b n-1-b n-2)+(b n-2-b n-3)+…+(b2-b1)+b1=1+1+1+…+1=n6分)又a n+1-a n=b n=n,n=1,2,3,…所以a n=(a n-a n-1)+(a n-1-a n-2)+(a n-2-a n-3)+…+(a2-a1)+a1=(n-1)+(n-2)+…+2+1+1=n(n-1)/2+1=(n2-n+2)/210分)(3)由已知c n-b n+1+3a n= -2n+1,可得b n+1-b n-b n+1+3a n=-2n+1,即b n-3a n=2n+1,∴a n+1=4a n+2n+1.(12分)解法一:整理得:a n+1+2n+1=4(a n+2n),(15分)因而数列{a n+2n}是首项为a1+2=4,公比为4的等比数列,∴a n+2n=4·4n-1=4n,即a n=4n-2n.(18分)解法二:在等式a n+1=4a n+2n+1两边同时除以2n+1得:a n+1/2n+1=2·a n/2n+1.(15分)令k n=a n/2n,则k n+1=2k n+1,即k n+1+1=2(k n+1)故数列{k n+1}是首项为2,公比为2的等比数列所以k n+1=2·2n-1=2n,即k n=2n-1.∴a n=2n k n=2n(2n-1)=4n-2n.(18分)解法三:∵a1=2,∴a2=12=22×(22-1),a3=56=23×(23-1),a4=32=24×(24-1)猜想:a n=2n(2n-1)=4n-2n.(15分)下面用数学归纳法证明如下:(i)当n=1时,a1=2=4-2,猜想成立;(ii)假设n=k时,猜想成立,即a k=4k-2k.那么当n=k+1时,a k+1=4a k+2k+1=4(4k-2k)+2k+1=4 k+1-2 k+1,结论也成立∴由(i)、(ii)可知,a n=4n-2n.(18分)。
江苏省南京师范大学附属中学2015-2016学年高一上学期期中考试数学试题(word版含答案)

高一年级期中考试数学试卷一、填空题:本大题共14小题,每小题3分,共计42分.请把答案填写在答卷纸相应位置.......上.. 1. 若{}103A =-,,,{}1123B =-,,,,则A B =∩ .2. 函数lg(4)3x y x -=-的定义域...是 .3. 若(]A a =-∞,,(]12B =,,A B B =∩,则a 的取值范围是 .4. 若真函数()y f x =的图像过点(42),,则(9)f = . 5. 若函数2()2f x x mx m =-++是偶函数,则m =.6. 已知0.70.8a =,0.90.8b =,0.81.2c =,则a 、b 、c 按从小到大....的顺序排列为.7. 已知函数2y a b =+(0a >且1a ≠)的图象如下图所示,则a b -的值是.8. 已知函数31() 1.x x f x x x ⎧=⎨->⎩,,,≤若()2f x =,则x =.9. 函数222()2xx f x -+=的值域为 .10.函数()log (1)x a f x a x =++(0a >且1a ≠)在[]01,上的最大值与最小值之和为a ,则a 的值为.11.函数212log (2)y x x =-+的单调递增....区间是.12.二次函数()f x 满足(3)(3)f x f x -=+,又()f x 是[]03,上的增函数,且()(0)f a f ≥,那么实数a 的取值范围是.13.已知函数()f x m 的取值范围是 . 14.函数2()2f x x ax a =-+的定义域为[]11-,,值域为[]22-,,则a 的值为.二、解答题:本大题共6小题,共计58分.请在答题纸指定区域内作答,解答时应用出文字说明、证明过程或演算步骤.15.(本小题满分8分)已知R U =,{}11A x x =-<<,{}21x B x =>. ⑴求A B ∪;⑵求U A B ∩ð. 16.(本小题满分10分)计算:⑴122302927(9.6)(1.5)48--⎛⎫⎛⎫---+ ⎪ ⎪⎝⎭⎝⎭;⑵2log 3423log 9log 232-+. 17.(本小题满分10分) ⑴已知函数1()log 1axf x x -=+(0a >且1a ≠)的图象经过点325P ⎛⎫- ⎪⎝⎭,.求函数()y f x =的解析式;⑵设1()1xg x x-=+,用函数单调性的定义证明:函数()y g x =在区间(11)-,上单调递减. 18.(本小题满分10分)某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能往返16次(去程加返程算往返一次),如果每次拖7节车厢,则每日能往返10次.⑴若每日往返的次数y 是每次拖挂车厢节数x 的一次函数,求这个函数的解析式,并指出定义域.⑵在⑴有条件下,若每节车厢能载乘客110人.问这列火车每天往返多少次才能使运营人数最多?并求出每天最多运营人数. 19.(本小题满分10分)已知定义域为R 的函数12()2x x b f x a+-+=+是奇函数.⑴求a ,b 的值;⑵已知()f x 在定义域上为减函数,若对任意的R t ∈,不等式22(2)(2)0f t t f t k -+-<(k 为常数)恒成立.求k 的取值范围. 20.(本小题满分10分)已知二次函数2()21(0)g x mx mx n m =-++>在区间[]03,上有最大值4,最小值0. ⑴求函数()g x 的解析式;⑵设()2()g x xf x x-=.若(2)20k xf k -⋅≤(k 为常数)在[]33x ∈-,时恒成立,求k 的取值范围.1.{}13-, 2.()()334-∞,,∪3.[)2+∞, 4.3 5.06.b a c << 7.68.23log9.[)2+∞, 10.1211.(12),或写成[)12, 12.[]06, 13.[]04,14.1-15.⑴由题(11)A =-,,(0)B =+∞, (1)A B =-+∞,∪ ⑵(]0U R C B C B ==-∞, (](11)0U A C B =--∞,,∩∩ (]10=-,16.⑴原式2333341229-⎡⎤⎛⎫=--+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦14412992=-+= ⑵原式2232232log log 33=++ 322232log log 323=⋅++ 232log 333⎛⎫=⨯+ ⎪⎝⎭538=+= 17.⑴由题325f ⎛⎫-= ⎪⎝⎭即315log log 42315a a ⎛⎫-- ⎪⎝⎭==⎛⎫+- ⎪⎝⎭即24a =,又0a > ∴2a =∴21()log 1xf x x -=+⑵证明:12()111x g x x x -==-+++ 任取1x ,2(11)x ∈-,且12x x <, 则121222()()1111g x g x x x ⎛⎫⎛⎫-=-+--+ ⎪ ⎪++⎝⎭⎝⎭21122()(1)(1)x x x x -=++∵1211x x -<<<∴210x x ->,110x +>,210x +> ∴12()()0g x g x -> 即12()()g x g x > ∴()g x 在(11)-,上单调递减. 18.⑴设(0)y kx b k =+≠则164210724k b k k b b =+=-⎧⎧⇒⎨⎨=+=⎩⎩即224(111)y x x x N +=-+∈,≤≤⑵设每次拖鞋车厢x 节,则每天能往返(224)x -+次,且运营人数为w 人. 110(224)w x x =⋅⋅-+ 2220(12)x x =--2220(6)7920x =--+ (111)x x N +∈,≤≤ 当6x =,即22412x -+=时,w 取得最大值7920.答:⑴略⑵每天往返12次,最多运营人数为7920人. 19.⑴∵()f x 是定义在R 的奇函数∴()()f x f x -=-令0x =,(0)(0)f f =-,(0)0f = 令1x =,(1)(1)f f -=-,∴1102222222bab ba a-⎧-+=⎪⎪'+⎨-+-+⎪=-⎪++⎩解得:21 ab=⎧⎨=⎩经检验,当2a=,1b=时,()f x为奇函数.⑵22(2)(2)f t t f t k-<--∵()f x是奇函数∴22(2)(2)f t t f k t-<-∵()f x在R上单调减∴2222t t k t->-即2320t t k-->在R上恒成立∴4430k=+⋅<△∴13 k<-即k的取值范围是13⎛⎫-∞-⎪⎝⎭,20.⑴2()(1)1g x m x n m=-+-+∵03x≤≤∴112x--≤≤∴20(1)4x-≤≤∵0m>∴1()31 n m g x m n-+++≤≤即3141100 m n mn m n++==⎧⎧⇒⎨⎨-+==⎩⎩∴2()21g x x x=-+⑵2411()4x xf x xx x-+==+-令2xt=,[]33x∈-,,则188t⎡⎤∈⎢⎥⎣⎦,∴()0f t kt-≤在188t⎡⎤∈⎢⎥⎣⎦,上恒成立即140t ktt+--≤恒成立∵0t>∴21411t t +-+在188t ⎡⎤∈⎢⎥⎣⎦,上恒成立 又22141123t t t ⎛⎫-+=-- ⎪⎝⎭,1188t ⎡⎤∈⎢⎥⎣⎦,∴当18t =时,2max14133t t ⎛⎫-+= ⎪⎝⎭,∴33k ≥即k 的取值范围是[]33+∞,。
南师大附中数学答案

1 1 AB , 由 题 意 CD// AB , 2 2
a 2 b 2 c 2 a 5 3 5 (1) 由题意,得 2 1 b 1 2 4b 4a c 2 c 2 5 5 a
所以椭圆 C 的标准方程为
………………
3分
MN //CD 所以四边形 MNDC 是平行四边形,所以 CM//DN,
……………………12 分
又S
当r
S ( ) 在 [45, ) 上单调减,当 r 45 时,S 最大 337.5 平方米,此时
18.(本小题满分 16 分)
1 . ……………14 分 3
S
1 7 ac sin B 2 4
………14 分
16.(本小题满分 14 分) (1)取 AP 的中点 N,连结 MN 和 DN,由因为 M 是 PB 的中点, 所 以 MN 是 △ PAB 的 中 位 线 , 所 以 MN //
②当直线 AB 的斜率存在时,设 A( x1 , y1 ) , B( x2 , y 2 ) 直线 AB 为 y k ( x 2)
试卷第 1 页 共 8 页
试卷第 2 页 共 8 页
y k ( x 2) 由 2 2 x 5 y 5
消去 y 后整理得 (1 5k ) x 20k x 20k 5 0
② …………11 分
2 (c a ) b c a 1 c a 1 a 1 (2) b 2 ……8 分 a2 c2 b2 3 2 2 a c 5 c 2 ca 3 2ac 2 BA BC ca cos B 2 cos B 3 7 sin B , 4 4
2016-2017学年江苏省南京师范大学附属中学上学期高三期中考试文数(详细答案版)

2016-2017学年江苏省南京师范大学附属中学上学期高三期中考试文数一、填空题:共14题1.已知集合,,,则__________.【答案】{1,2,3}【解析】本题考查集合的运算;由题意,得;故填{1,2,3}.2.若复数满足,则的共轭复数是__________.【答案】【解析】本题考查复数的运算和复数的概念;因为,所以,则;故填.3.已知一组数据,那么这组数据的方差为__________.【答案】2【解析】本题考查样本的数字特征;由题意,得该组数据的平均数为5,则方差为;故填2.4.袋中有形状、大小都相同的4只球,其中有2只红球,2只白球,若从中随机一次摸出2只球,则这2只球颜色不同的概率为__________.【答案】【解析】本题考查古典概型、排列组合应用题;若从4个小球中随机一次摸出2只球,共有种不同的摸法,其中这2只球颜色不同有种摸法,则这2只球颜色不同的概率为;故填.5.如下图,矩形由两个正方形拼成,则的正切值为__________.【答案】【解析】本题考查正切函数的定义、两角差的正切公式;设正方形的边长为1,则;故填.6.下图是一个算法流程图,则输出的的值是__________.【答案】5【解析】本题考查程序框图中的循环结构;由题意,得;故填5.7.若实数满足条件,则目标函数的最大值是__________. 【答案】【解析】本题考查简单的线性规划问题;将化为,作出可行域和目标函数基准直线(如图所示),当直线向左上方平移时,直线在轴上的截距增大,即减小,由图象,得当直线过点时取得最大值,联立,得,;故填.8.若双曲线)的一条渐近线经过点,则此双曲线的离心率为__________.【答案】【解析】本题考查双曲线的几何性质;因为双曲线)的一条渐近线经过点,所以,则此双曲线的离心率为;故填.9.若,则__________.【答案】【解析】本题考查同角三角函数基本关系式和诱导公式;因为,所以;故填.10.在等腰梯形中,已知,,,,点和点分别在线段和上,且,,则的值为__________.【答案】【解析】本题考查平面向量的线性运算和数量积运算;由平面几何知识,得在等腰梯形中,,,,,,,因为,,所以;故填.11.等比数列的首项为2,公比为3,前项的和为,若,则的最小值为__________.【答案】【解析】本题考查等比数列、对数运算、基本不等式;因为等比数列的首项为2,公比为3,前项和为,所以,因为,所以,即,则=(当且仅当取等号),所以的最小值为;故填.12.在平面直角坐标系数中,点,,若直线上存在点,使得,则实数的取值范围是__________.【答案】【解析】本题考查点到直线的距离公式、三角代换;设,因为,所以4,所以可化为,则,即,令,则,即实数的取值范围为;故填.13.已知函数,,若方程有两个不同的实根,则实数的取值范围是__________.【答案】【解析】本题考查分段函数、函数的零点以及数形结合思想的应用;方程有两个不同的实根,即函数和函数的图象有两个不同的交点,当时,,函数成周期变化,函数的图象恒过点,在同一坐标系中作出两函数图象(如图所示),且,在点处的切线斜率,由图象得,实数的取值范围为;故填.14.已知不等式对于任意的恒成立,其中是整数,则的取值集合为__________.【答案】【解析】本题考查不等式恒成立问题;当时,由得,在上恒成立,则不存在;当时由,可设,则,又因为是整数,所以或,即或;故填.二、解答题:共6题15.在中,角的对边分别为,且.(1)求角的值;(2)若的面积为,且,求的周长.【答案】因为,由正弦定理得,即因为,所以所以.因为B∈(0,π),所以sin B≠0,所以,因为,所以.(2)△ABC的面积为,且由,.所以周长【解析】本题考查正弦定理、余弦定理、三角形的面积公式和两角和的正弦公式;(1)先利用正弦定理将边角关系转化为角角关系,再利用两角和的正弦公式进行求解;(2)利用三角形的面积公式、余弦定理得到关于另外两边的方程组进行求解.16.在四棱锥中,,,平面,点为的中点.(1)求证:平面平面;(2)求证:平面.【答案】证明: (1)因为PA⊥平面ABCD,CDÌ平面ABCD,所以PA⊥CD,又∠ACD=90°,则,而PA∩AC=A,所以CD⊥平面PAC,因为CDÌ平面ACD,所以,平面PAC⊥平面PCD.(2)证法一:取AD中点M,连EM,CM,则EM∥PA.因为EM平面PAB,PA平面PAB,所以EM∥平面PAB.在Rt△ACD中,AM=CM,所以∠CAD=∠ACM,又∠BAC=∠CAD,所以∠BAC=∠ACM, 则MC∥A B.因为MC平面PAB,AB平面PAB,所以MC∥平面PAB.而EM∩MC=M,所以平面EMC∥平面PAB.由于EC平面EMC,从而EC∥平面PAB.证法二:延长DC,AB交于点N,连PN.因为∠NAC=∠DAC,AC⊥CD,所以C为ND的中点.而E为PD中点,所以EC∥PN.因为EC平面PAB,PN平面PAB,所以EC∥平面PAB【解析】本题考查空间中垂直关系的转化、平行关系的转化;(1)先分别利用线面垂直的性质和直角证明线线垂直,再利用线面、面面垂直的判定定理进行证明;(2)构造三角形,利用三角形的中位线性质得到线线平行,再利用线面平行的判定定理进行证明.17.如图,在半径为30的半圆形铁皮上截取一块矩形材料(点在直径上,点在半圆周上),并将其卷成一个以为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).(1)若要求圆柱体罐子的侧面积最大,应如何截取?(2)若要求圆柱子罐子的体积最大,应如何截取?【答案】(1)如图,设圆心为O,连结,设,法一易得,,故所求矩形的面积为==≤=)(当且仅当,)时等号成立) 此时;法二设,; 则,,所以矩形的面积为,当,即时,)此时;当截取的矩形铁皮的一边为为时,圆柱体罐子的侧面积最大.(2)设圆柱的底面半径为,体积为,由得,,所以,其中,由得,此时,在上单调递增,在上单调递减, 故当时,体积最大为,当截取的矩形铁皮的一边为为时,圆柱体罐子的体积最大.【解析】本题考查圆柱的侧面积和体积公式、基本不等式及导数在研究函数最值中的应用;(1)设出有关变量,利用函数表达式,利用基本不等式或三角代换求其最值;(2) 设出圆柱的底面半径,列出其体积关于半径的函数表达式,再利用导数求其最值.18.如图,在平面直角坐标系中,已知是椭圆)上不同的三点,,,在第三象限,线段的中点在直线上.(1)求椭圆的标准方程;(2)求点的坐标;(3)设动点在椭圆上(异于点)且直线分别交直线于两点,证明为定值并求出该定值.【答案】(1)由已知,得解得所以椭圆的标准方程为.(2)设点,则中点为.由已知,求得直线的方程为,从而.①又∵点在椭圆上,∴.②由①②,解得(舍),,从而.所以点的坐标为.(3)设,,.∵三点共线,∴,整理,得.∵三点共线,∴,整理,得.∵点在椭圆上,∴,.从而===.所以.∴为定值,定值为.【解析】本题考查椭圆的标准方程、直线和椭圆的位置关系以及平面向量的数量积运算;(1)设出椭圆方程,代点利用待定系数法进行求解;(2)利用线段的中点坐标公式和点在椭圆上进行求解;(3)利用三点共线设出直线的两点式方程,求出相关点的纵坐标,再利用点在椭圆上和平面向量的数量积进行求解.19.已知数列{a n}和{b n}满足a1a2a3…a n=((n∈N*).若{a n}为等比数列,且a1=2,b3=6+b2. (Ⅰ)求a n与b n;(Ⅱ)设c n=-(n∈N*).记数列{c n}的前n项和为S n.(ⅰ)求S n;(ⅱ)求正整数k,使得对任意n∈N*均有S k≥S n.【答案】(Ⅰ)由题意a1a2a3…a n=(,b3-b2=6,知a3=(=8.又由a1=2,得公比q=2(q=-2,舍去),所以数列{a n}的通项为a n=2n(n∈N*).所以,a1a2a3…a n==()n(n+1).故数列{b n}的通项为b n=n(n+1)(n∈N*).(Ⅱ)(ⅰ)由(Ⅰ)知c n=-=-(-)(n∈N*),所以S n=-(n∈N*).(ⅱ)因为c1=0,c2>0,c3>0,c4>0;当n≥5时,c n=[-1],而-=>0,得≤<1,所以,当n≥5时,c n<0.综上,对任意n∈N*恒有S4≥S n,故k=4.【解析】本题主要考查等差数列与等比数列的概念、通项公式、求和公式、不等式性质等基础知识,同时考查运算求解能力.20.已知函数,.(1)求函数的极值;(2)若时,函数有且只有一个零点,求实数的值;(3)若,对于区间上的任意两个不相等的实数,都有>成立,求的取值范围.【答案】(1),当时,,f(x)在上递增,f(x)无极值当时,时,,f(x)递减;时,,f(x)递增,所以f(x)有极小值综上,当时,f(x)无极值;当时,f(x)有极小值,无极大值(2),则因为,令,得,故h(x)在上递减,在上递增,所以h(x)有极小值,.且,联立可得令,得,故m(x)在上递增又m(1) = 0,所以,即,(3)不妨令,因为0<a<1,则,由(1)可知,因为所以>>.所以=在[1,2]上递增所以在[1,2]上恒成立,即在[1,2]上恒成立,令,则,所以.【解析】本题考查导数在研究函数中的应用、导数在研究不等式恒成立问题中的应用;(1)求导,利用导数的符号变换确定函数的单调性和极值点;(2) 求导,利用导数的符号变换确定函数的单调性和极值,再利用极值的符号确定函数零点的个数;(3)合理构造函数,利用导数研究函数的单调性和最值即可求解.。
师大附中高三期中考试数学试卷及答案

命题人:江卫兵 审题人:孙居国一、填空题:(本大题共14小题,每小题5分,共70分)1.设集合{}{}{}1,2,3,4,5,1,2,1,3U A B ===,则()U A B =U ð ▲ ; 2.已知α为第三象限角,则2tanα的符号为 ▲ (填“正”或“负”);3.设ABC ∆的三个内角A 、B 、C 所对边的长分别是a 、b 、c ,且CcA a sin cos =, 那么A ∠= ▲ ;4.在等差数列{}n a 中,1815360a a a ++=,则9102a a -的值为 ▲ ; 5.若函数)0)(sin(3)(>+=ωϕωx x f 的图象的相邻两条对称轴的距离是π2,则ω的值为 ▲ ;6.若函数2()lg(1)f x mx mx =++的定义域为R ,则m 的取值范围是 ▲ ;7.设复数2(,)1i a bi a b R i-=+∈+,则a b += ▲ ;8.已知变量x 、y 满足条件⎪⎩⎪⎨⎧≤-+≤-≥09201y x y x x 则z x y =+的最大值是 ▲ ;9.函数2sin y x x =-在(0,π2)内的单调增区间为 ▲ ;10.若ΔABC 的三个内角C B A 、、所对边的长分别为c b a 、、,向量()a b c a m -+=,,),(b c a n -=,若⊥,则∠C 等于 ▲ ; 11.已知等比数列{}n a 中,363,24a a ==,则该数列的通项n a = ▲ ; 12.已知函数)(x f 是R 上的减函数,)2,3(),2,0(--B A 是其图象上的两点,那么不等式|2|)2(>-x f 的解集是 ▲ ;13.若()f n 为21n +*()n N ∈的各位数字之和,如2141197+=,19717++=,则(14)17f =;记1()()f n f n =,21()(())f n f f n =,…,1()(())k k f n f f n +=,*k N ∈,则2008(8)f = ▲ ;14请将错误的一个改正为lg ▲ = ▲ ;南京师大附中2008—2009学年度第1学期高三年级期中考试数学答题卷班级 学号 ______ 姓名 得分 一、填空题:(本大题共14小题,每小题5分,共70分) 1. ;2. ;3. ;4. ; 5. ;6. ;7. ;8. ; 9. ;10. ;11. ;12. ; 13. ;14.lg = .二、解答题:(本大题共6小题,共90分) 15.(本小题满分14分)已知20πα<<,且3sin 5α=(1)求αααα2cos cos 2sin sin 22++的值; (2)求⎪⎭⎫⎝⎛-πα45tan 的值.16.(本小题满分14分)如图,ACD △是等边三角形,ABC △是等腰直角三角形,90ACB =o ∠,BD 交AC 于E ,2AB =.BAC DE(Ⅰ)求CBE ∠cos 的值; (Ⅱ)求AE .17.(本小题满分14分)已知函数421,0()3,1c ccx x c f x x x c x +<<⎧=⎨+≤<⎩ 满足29()8f c =; (1)求常数c 的值; (2)解不等式()2f x <.18.(本题满分16分)某市旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售a 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为x ()01x <<,那么月平均销售量减少的百分率为2x . 记改进工艺后,旅游部门销售该纪念品的月平均利润是y(元).(1)写出y与x的函数关系式;(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.19. (本小题满分16分)把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设(,)ij a i j N *∈是位于这个三角形数表中从上往下数第i 行、从左往右数的第j 个数(如428a =).⑴试用i 表示ii a (不要求证明); ⑵若2008ij a =,求,i j 的值;⑶记三角形数表从上往下数第n 行的各数之和为n b ,令1,(1),(2)n n n c n n b n=⎧⎪=⎨≥⎪-⎩,若数列{}n c 的前n 项和为n T ,求n T .1 2 3 4 5 6 7 8 9 10…………20.(本题满分16分)已知函数()ln f x x =,)0(21)(2≠+=a bx ax x g (I )若2-=a 时,函数)()()(x g x f x h -=在其定义域内是增函数,求b 的取值范围;(II )在(I )的结论下,设]2ln ,0[,)(2∈+=x be e x x x ϕ,求函数)(x ϕ的最小值; (III )设函数)(x f 的图象1C 与函数)(x g 的图象2C 交于点P 、Q ,过线段PQ 的中点R 作x 轴的垂线分别交1C 、2C 于点M 、N ,问是否存在点R ,使1C 在M 处的切线与2C 在N 处的切线平行?若存在,求出R 的横坐标;若不存在,请说明理由.南京师大附中2008—2009学年度第1学期 高三年级期中考试数学试卷(解答)一、填空题:(本大题共14小题,每小题5分,共70分)1.设集合{}{}{}1,2,3,4,5,1,2,1,3U A B ===,则()U C A B =U ▲ ;{4,5}2.已知α为第三象限角,则2tan α的符号为 ▲ (填“正”或“负”);负3.设ABC ∆的三个内角A 、B 、C 所对边的长分别是a 、b 、c ,且CcA a sin cos =, 那么=A ▲ ;4π 4.在等差数列{}n a 中,1815360a a a ++=,则9102a a -的值为 ▲ ; 12 5.若函数)0)(sin(3)(>+=ωϕωx x f 的图象的相邻两条对称轴的距离是π2,则ω的值为 ▲ ;216.若函数2()lg(1)f x mx mx =++的定义域为R ,则m 的取值范围是 ▲ ;[0,4)7.设复数2(,)1i a bi a b R i-=+∈+,则a b += ▲ ; 18.已知变量x 、y 满足条件⎪⎩⎪⎨⎧≤-+≤-≥09201y x y x x 则z x y =+的最大值是 ▲ ; 69.函数2sin y x x =-在(0,π2)内的单调增区间为 ▲ ;)35,3(ππ10.若ΔABC 的三个内角C B A 、、所对边的长分别为c b a 、、,向量()a b c a -+=,,),(b c a -=,若n m ⊥,则∠C 等于 ▲ ;π311.已知等比数列{a n }中,a 3=3,a 6=24,则该数列的通项a n =______3·2n -3________.12.已知函数)(x f 是R 上的减函数,)2,3(),2,0(--B A 是其图象上的两点,那么不等式|2|)2(>-x f 的解集是 ▲ ; ),2()1,(+∞--∞Y13.若()f n 为21n +*()n N ∈的各位数字之和,如2141197+=,19717++=, 则(14)17f =;记1()()f n f n =,21()(())f n f f n =,…,1()(())k k f n f f n +=,*k N ∈,则2008(8)f = ▲ ; 1114.下列表中的对数值有且仅有一个是错误的:15 = 3a-b+c二、解答题:(本大题共6小题,共90分) 15.(本小题满分14分)已知20πα<<,且3sin 5α=(1)求αααα2cos cos 2sin sin 22++的值;(2)求⎪⎭⎫ ⎝⎛-πα45tan 的值.解:(1)由sin α=53又 0<α<2π ∴cos α=54,tan α=43∴ααααααααα22222sin cos 2cos sin 2sin 2cos cos 2sin sin -⋅+=++ =2333)43(2432)43(tan 2tan 2tan 2222=-⨯+=-+ααα (2)tan(71431143tan 11tan 45tan tan 145tan tan )45-=+-=+-=⋅+-=-ααπαπαπα16.(本小题满分14分)如图,ACD △是等边三角形,ABC △是等腰直角三角形,90ACB =o ∠,BD 交AC于E ,2AB =.(Ⅰ)求CBE ∠cos 的值; (Ⅱ)求AE .解:(Ⅰ)因为9060150BCD=+=o o o ∠,CB AC CD ==,所以15CBE=o ∠.所以cos cos(4530)CBE =-=o o ∠. (Ⅱ)在ABE △中,2AB =,由正弦定理2sin(4515)sin(9015)AE =-+o o o o. 故2sin 30cos15AE =oo 124⨯== 17.(本小题满分14分)已知函数421,0()3,1c ccx x c f x x x c x +<<⎧=⎨+≤<⎩ 满足29()8f c =; (1)求常数c 的值; (2)解不等式()2f x <.B AC DE解:(1)因为01c <<,所以2c c <; 由29()8f c =,即3918c +=,12c = (2)由(1)得211122()31x x f x x x x ⎧⎛⎫+0<< ⎪⎪⎪⎝⎭=⎨1⎛⎫⎪+< ⎪⎪2⎝⎭⎩,,≤由()2f x <得,当102x <<时,解得102x <<,当112x <≤时,2320x x +-<解得1223x <≤, 所以()2f x <的解集为203x x ⎧⎫<<⎨⎬⎩⎭.18.(本题满分16分)某市旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售a 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为x ()01x <<,那么月平均销售量减少的百分率为2x .记改进工艺后,旅游部门销售该纪念品的月平均利润是y (元).(1)写出y 与x 的函数关系式;(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大. 18、(1)改进工艺后,每件产品的销售价为()201x +,月平均销售量为()21a x -件,则月平均利润()()2120115y a x x =-⋅+-⎡⎤⎣⎦(元),∴y 与x 的函数关系式为()235144y a x x x =+-- ()01x << (2)由()2542120y a x x '=--=得112x =,23x =-(舍) 当102x <<时0y '>;112x <<时0y '<,∴函数()235144y a x x x =+-- ()01x <<在12x =取得最大值.故改进工艺后,产品的销售价为12012⎛⎫+ ⎪⎝⎭30=元时,旅游部门销售该纪念品的月平均利润最大.19. (本小题满分16分)把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设(,)ij a i j N *∈是位于这个三角形数表中从上往下数第i 行、从左往右数的第j 个数(如428a =).12 3 4 5 6 7 8 9 10…………⑴试用i 表示ii a (不要求证明); ⑵若2008ij a =,求,i j 的值;⑶记三角形数表从上往下数第n 行的各数之和为n b ,令1,(1),(2)n n n c n n b n=⎧⎪=⎨≥⎪-⎩,若数列{}n c 的前n 项和为n T ,求n T .解:(1)∵三角形数表中前n 行共有(1)122n n n ++++=L 个, 即第i 行的最后一个数是(1)2i i + ∴ii a =(1)2i i + (2)由题意,先求使得i 是不等式(1)20082i i +≥的最小正整数解.由(1)20082i i +≥,得240160i i +-≥∵*i N ∈,∴11112662.5222i -+-+-+≥>==,∴63i = (另解:∵626363641953,201622⨯⨯== ∴63i =)于是,第63行的第一个数是6263119542⨯+=, 故(20081954)155j =-+=(3)前n 行的所有自然数的和为21(1)(1)(1)(2)[1]2222n n n n n n n n n S +++++=⨯+=则21(1)2n n n n n b S S -+=-=,所以,当2n ≥时,2211111n n n c b n n n n ===----+, 111111111()()()()132435111115115211121212(1)n T n n n n n n n n n =+-+-+-++--++=++--=--=-+++L当1n =时,1n T =也适合,521()2(1)n n T n N n n *+∴=-∈+ 20.(本题满分16分)已知函数()ln f x x =,)0(21)(2≠+=a bx ax x g(I )若2-=a 时,函数)()()(x g x f x h -=在其定义域内是增函数,求b 的取值范围;(II )在(I )的结论下,设]2ln ,0[,)(2∈+=x be e x x x ϕ,求函数)(x ϕ的最小值; (III )设函数)(x f 的图象1C 与函数)(x g 的图象2C 交于点P 、Q ,过线段PQ 的中点R 作x 轴的垂线分别交1C 、2C 于点M 、N ,问是否存在点R ,使1C 在M 处的切线与2C 在N 处的切线平行?若存在,求出R 的横坐标;若不存在,请说明理由.解:(I )依题意:.ln )(2bx x x x h -+=()h x Q 在(0,+∞)上是增函数,1()20h x x b x '∴=+-≥对x ∈(0,+∞)恒成立, 12,0b x x x ∴≤+>Q ,则12x x+≥ b ∴的取值范围是(,-∞.(II )设].2,1[,,2∈+==t bt t y e t x 则函数化为 22().24b b y t =+-∴Q 当12b-≤,即2b -≤≤y 在[1,2]上为增函数,当1t =时,min 1y b =+;,]2,1[4,22;42,24,2212min 上是减函数在函数时即当时当时即当y ,b bb ,y b t b b -≤≥--=-=-<<-<-< 当2t =时,min 42y b =+.综上所述:21,2(),42442, 4.b b bx b b b ϕ⎧+-≤≤⎪⎪=--<<-⎨⎪+≤-⎪⎩(III )设点P 、Q 的坐标是.0),,(),,(212211x x y x y x <<且则点M 、N 的横坐标为.221x x x += C 1在点M 处的切线斜率为.2|1212121x x x k x x x +==+= C 2在点N 处的切线斜率为.2)(|212221b x x a b ax k x x x ++=+=+= 假设C 1在点M 处的切线与C 2在点N 处的切线平行,则.21k k =即1212()2.2a x xb x x +=++则 22222121212211122212112()()()()()222ln ln ln,x x a x x a ab x x x bx x bx x x x y y x x x --=+-=+-++=-=-=22211211212(1)2()ln 1x x x x x x x x x x --∴==++ 设211,x u x =>则2(1)ln ,1,1u u u u -=>+ (1)令2(1)()ln ,11u r u u u u-->+,则22214(1)()(1)(1)u r u u u u u -'=-=++,1,()0u r u '>∴>Q ,所以 ()r u 在[1,)+∞上单调递增,故()(1)0r u r >=,则2(1)ln 1u u u ->+,与(1)矛盾!。
江苏省南师大附中2019届高三年级第一学期期中考试数学试题含附加题(含答案)

江苏省南师大附中2019届高三年级第一学期期中考试数学试题(总分160分,考试时间120分钟)一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上.)1.已知集合A ={﹣2,﹣1,3,4},B ={﹣1,2,3},则集合A B 为 . 2.若(2i)i i a b -=-,其中a 、b ∈R ,i 是虚数单位,则a +b = . 3.函数2ln(4)y x =-的定义域为 .4.如图是某算法的流程图,则算法运行后输出的结果S 是 .5.某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则在抽测的100根中,有 根棉花纤维的长度小于20mm . 6.等比数列{}n a 的各项均为正数,其前n 项和为n S ,已知234S =,4154S =,则6a = . 7.函数Asin()y x ωϕ=+(A >0,0ω>,22ππϕ-<<)的部分图象如图所示,则函数的解析式为 .第5题第7题 第4题8.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和大于9的概率是 .9.在平面直角坐标系xOy 中,双曲线22221x y a b-=的一条渐近线方程为20x y -=,则它的离心率为 .10.若将一个圆锥的侧面沿一条母线剪开,其展开图是半径为2cm 的半圆,则该圆锥的体积为 cm 3.11.在平面直角坐标系xOy 中,己知圆C 过点A(0,﹣8),且与圆22660x y x y +--=相切于原点,则圆C 的方程为 .12.在△ABC 中,D ,E 分别是AC ,AB 的中点,BA BC 6⋅=,CA CB 3⋅=,BD CE ⋅=4-,则BA CA ⋅的值是 .13.己知实数x ,y ,z ∈[0,4],如果x 2,y 2,z 2是公差为2的等差数列,则x y y z-+-的最小值为 .14.已知函数()33x x f x -=-,3313(12log )(3log 1)log f t f t t -+-≥,则t 的取值范围是.二、解答题(本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.) 15.(本小题满分14分)在△ABC 中,已知AB =2,AC =3,BC (1)求角A 的大小;(2)求cos(B ﹣C)的值.16.(本小题满分14分)如图,在四棱锥P —ABCD 中,AP ⊥CD ,AD ∥BC ,AB =BC =1,AD =2,E ,F 分别为AD ,PC 的中点.求证:(1)AP ∥平面BEF ;(2)平面BEF ⊥平面PAC .17.(本小题满分14分)为美化城市环境,相关部门需对一半圆形中心广场进行改造出新,为保障市民安全,施工队对广场进行围挡施工.如图,围挡经过直径的两端点A ,B 及圆周上两点C ,D 围成一个多边形ABPQR ,其中AR ,RQ ,QP ,PB 分别与半圆相切于点A ,D ,C ,B .已知该半圆半径OA 长30米,∠COD 为60°,设∠BOC 为θ.(1)求围挡内部四边形OCQD 的面积; (2)为减少对市民出行的影响,围挡部分面积要尽可能小.求该围挡内部多边形ABPQR 面积的最小值?并写出此时θ的值.18.(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆E :22221(0)x y a b a b +=>>的离心率为2,点A(2,1)是椭圆E 上的点.(1)求椭圆E 的方程;(2)过点A 作两条互相垂直的直线l 1,l 2分別与椭圆E 交于B ,C 两点,己知△ABC 的面积为209,求直线BC 的方程.19.(本小题满分16分)已知函数()ln 1f x x x ax =++,直线2y x =是曲线()y f x =的一条切线. (1)求实数a 的值;(2)若对任意的x ∈(0,+∞),都有()(1)f x k x >-,求整数k 的最大值. 20.(本小题满分16分)已知{}n a ,{}n b 都是各项为正数的数列,且11a =,1b =n ,都有n a ,2n b ,1n a -成等差数列,n b ,1n b +成等比数列.(1)求数列{}n a 和{}n b 的通项公式;(2)若存在p >0,使得集合M ={}n n n a p n N λ*≥∈,恰有一个元素,求实数λ的取值范围.南京师大附中2018~2019学年度第一学期 高三年级数学期中试卷(数学Ⅰ)参考答案1、{-1,3}.2、1.3、(-2,2).4、12.5、30.6、8.7、f (x )=2sin(2x -π3).8、16.9、 52.10、 33π.11、x 2+y 2+8x +8y =0.12、2.13、4-2 3.14、[1,+∞). 15.解:(1)由余弦定理得:cos A =AB 2+AC 2-BC 22AB ·AC =22+32-(7)22·2·3=12,……………2分因为A ∈(0,π),所以A =π3.……………5分(漏掉A ∈(0,π)扣1分) (2)由正弦定理得:BC sin A =AB sin C ,所以sin C =AB sin A BC =2·32 7= 217.又因为AB <BC ,所以C <A即0<C <π3,所以cos C = 1-sin 2C =1-(217)2 =277.……………8分所以sin2C =2 sin C cos C =2·217·2 77=437,cos2C =2cos 2C -1=2(2 77)2-1=17.…11分因为A +B +C =π,A =π3.所以B +C =2π3,所以B =2π3-C ,所以cos(B -C )=cos(2π3-2C )=cos 2π3cos2C +sin 2π3sin2C =(-12)·17+ 32·4 37=1114.…14分 (说明:算出cos B =714,sin B =32114…11分,cos(B -C )=cos B cos C +sin B sin C =714·2 77+3 2114·217=1114…14分)16.证明:(1)连接AC 交BE 于点O ,连接OF ,连接CE .因为AE =BC =1,AD ∥BC ,所以四边形ABCE 为平行四边形.所以点O 为AC 的中点,又因为点F 为PC 的中点.所以OF ∥AP .……3分又因为OF ⊂平面BEF ,AP ⊄平面BEF 所以AP ∥平面BEF ……7分 (2)因为AD ∥BC ,ED =BC =1,所以四边形BCDE 为平行四边形.所以BE ∥CD . 因为AP ⊥CD ,所以AP ⊥BE .又因为四边形ABCE 为平行四边形,AB =BC ,所以四边形ABCE 为菱形.所以AC ⊥BE . ……3分 又因为AP ⊥BE ,AP ∩AC =A ,AP ⊂平面APC ,AC ⊂平面APC . 所以BE ⊥平面APC .…5分因为BE ⊂平面BEF .所以平面BEF ⊥平面PAC . ……7分 17.解:(1)连接OQ ,因为QD ,QC 为圆O 的切线,所以QD =QC ,OD =OC =30, OQ =OQ ,所以△ODQ ≌△OCQ ,所以∠DOQ =∠COQ =30°,又因为OD ⊥DQ ,所以DQ OD =tan30°=33,所以DQ =103,所以S △ODQ =12OD ·DQ =1503,所以S OCQD =2S △ODQ即围挡内部四边形OCQD 的面积为……4分(2)BP =OB tan 2θ,S OBPC =2S △OBP =900 tan 2θ,同理S OARD =2S △OAR =900 tan(3π-2θ), S ABPQR =900[tan 2θ+ tan(3π-2θ)]+2(0,)3πθ∈ ……9分 (漏掉2(0,)3πθ∈扣1分) 即求 tan 2θ+ tan(3π-2θ)的最小值,tan 2θ+ tan(3π-2θ)= tan 2θ+tan 212θθ+=2)212θθ(*)令12x θ+=,由2(0,)3πθ∈得x ∈(1,4) 则(*)42)x x +-x =2时取等号,此时3πθ=, 故S min=900×3答:围挡内部多边形ABPQR 面积的最小值为3πθ=……14分注:(*)也可令tan 2x θ=,转化成函数求导,进而求最值.18.解:(1) 因为椭圆E 的离心率为 22,所以c 2a 2=12,又因为a 2=b 2+c 2=2c 2,所以a 2=2b 2=2c 2,因为点A (2,1)是椭圆E 上的点,所以 42b 2+1b 2=1 ……2分解得b 2=3,a 2=6,所以椭圆E 的标准方程是 x 26+y 23=1. ……4分(2)当AB 的斜率不存在或为0时,AB =4或2,此时△ABC 的面积为4,不合题意舍去; ……6分 当AB 的斜率存在且不为0时,设AB 的斜率为k ,则直线AB 方程为y -1=k (x -2),由⎩⎨⎧x 26+y 23=1 ,y -1=k (x -2),解得⎩⎪⎨⎪⎧x = 2, y = 1,或⎩⎪⎨⎪⎧x =4k 2-4k -21+2k 2y =-2k 2-4k+11+2k2. ……8分AB =1+k 2| 4k 2-4k -21+2k 2-2|=1+k 2|4k +41+2k2|,同理将上式中的k 用-1k 替换,得AC =1+k 2|4k -4k 2+2|,因为△ABC 的面积为 209,所以12 ⋅AB ⋅ AC =121+k 2|4k +41+2k 2|⋅1+k 2|4k -4k 2+2|=209,……10分 化简得(1+k 2)|k 2-1|( 1+2k 2)( k 2+2)=518, 当k 2≥1时,原方程可化为8k 4-25k 2-28=0,解得k 2=4,……12分当k 2≤1时,解得k 2=14,即k =2或-2或12或-12,当AB 的斜率2时,AC 的斜率-12,此时B 点坐标(23,-53),C 点坐标(23,53),此时直线BC 的方程为x =23, ……14分当AB 的斜率-2时,AC 的斜率12,此时B 点坐标(229,19),C 点坐标(-2,-1),此时直线BC 的方程为x -4y -2=0, ……16分 综上,直线BC 的方程为x =23或x -4y -2=0.19. 解:(1)设切点P (m ,m ln m +am +1),由f ′(x )=ln x +1+a ……2分 知 f (m )=ln m +1+a .则在点P 处的切线l 方程为:y =(ln m +1+a )x -m +1.若与题目中的切线重合,则必有⎩⎨⎧ln m +1+a =21-m =0, ……4分解得a =m =1,所以a 的值为1. ……6分 (2) 令F (x )=f (x )-k (x -1),则根据题意,等价于F (x )>0对任意的正数x 恒成立. F ′(x )=ln x +2-k ,令F ′(x )=0,则x =e k -2.当0<x <e k -2 ,则F ′(x )<0,F (x )在(0,e k -2)上单减;当x >e k -2 ,则F ′(x )>0,F (x )在(e k -2,+∞)上单增. 所以有F (x )min =F (ek -2) >0,即ek -2-k -1<0.当k =3,容易验证,e k -2-k -1<0; ……10分下证:当k ≥4,e k -2-k -1>0成立. ……13分令h (x )=e x -2-x -1,x ≥4,则h ′(x )=e x -2-1≥0,对任意的x ≥4恒成立。
2016届南京师大附中高三年级校模拟考试数学含参考答案

7 5
(第 4 题)
5.将甲、乙两个不同的球随机放入编号为 1,2,3 的 3 个盒子中,每个盒子的放球数量不限,则 1,2 号盒子中各有 1 个球的概率为 ▲ . ▲ .
x-1≤0, 6.设变量 x,y 满足约束条件 x+y+1≥0,则目标函数 z=2x+y 的最小值是 x-y+3≥0,
高三数学答案 第 1 页 共 14 页
高三数学答案 第 3 页 共 14 页
18.(本小题满分 16 分) 如图,在平面直角坐标系 xOy 中,已知点 F1、F2 分别是椭圆 E: x2 y2 + 2=1(a>b>0)的左、右焦点, 2 a b π 时, 4
过点 F1、 F2 分别作倾斜角都为α(α≠0)的两条直线 AB、 DC, 分别交椭圆 E 于点 A、 B 和 D、 C. 当α= 点 B 坐标为(0,1). (1)求椭圆 E 的方程; (2)当α变化时,讨论线段 AD 与 BC 长度之间的关系,并给出证明; (3)当α变化时,求四边形 ABCD 面积的最大值及对应的α值. y B C F2 D (第 18 题) 19.(本小题满分 16 分) 1 已知函数 f(x)=ln( x+1)+ ,g(x)=lnx. 2x (1)求函数 f(x)的单调区间; 1 (2)设 k 是实数,若关于 x 的不等式 f(x)- ≤kx 在[1,+∞)上恒成立,求 k 的取值范围; 2x (3)是否存在正实数 c,使得关于 x 的方程 f(x)=cg(x)有两个不同的实数根?并说明理由.
π 7.已知函数 y=Asin(ωx+φ)(A>0,ω>0,|φ|< ),则φ=________ ▲ . 2
(第 7 题) 8.已知一圆柱的若底面直径和高相等,其侧面积是π,则这个圆柱的体积是________ ▲ . 9.设 a 为实数,若函数 f(x)= 3-x- 1+x-a 存在零点,则实数 a 的取值范围是________ ▲ . x2 y2 10.在平面直角坐标系 xOy 中,已知点 F1、F2 分别是双曲线 C: - 2=1(a>0,b>0)的左、右焦点, 2 a_x001F_ b P 是右支上一点.若△PF F 是顶角为 120°的等腰三角形,则双曲线 C 的离心率是________ ▲ .
师大附中高三期中考试数学试卷及答案

江苏省南京师大附中2008—2009学年度第1学期高三期中考试数学试卷命题人:江卫兵审题人:孙居国一、填空题:(本大题共14小题,每小题5分,共70分)1.设集合,则▲;2.已知为第三象限角,则的符号为▲ (填“正”或“负”);3.设的三个内角、、所对边的长分别是、、,且,那么▲;4.在等差数列中,,则的值为▲;5.若函数的图象的相邻两条对称轴的距离是,则的值为▲;6.若函数的定义域为,则的取值范围是▲;7.设复数,则▲;8.已知变量、满足条件则的最大值是▲;9.函数在(0,)内的单调增区间为▲;10.若ΔABC的三个内角所对边的长分别为,向量,,若,则∠等于▲;11.已知等比数列中,,则该数列的通项= ▲;12.已知函数是上的减函数,是其图象上的两点,那么不等式|的解集是▲;13.若为的各位数字之和,如,,则;记,,…,,,则▲;14.下列表中的对数值有且仅有一个是错误的:358915请将错误的一个改正为▲= ▲;南京师大附中2008—2009学年度第1学期高三年级期中考试数学答题卷班级学号______姓名得分一、填空题:(本大题共14小题,每小题5分,共70分)1.;2.;3.;4.;5.;6.;7.;8.;9.;10.;11.;12.;13.;14.= .二、解答题:(本大题共6小题,共90分)15.(本小题满分14分)已知,且(1)求的值;(2)求的值.16.(本小题满分14分)如图,是等边三角形,是等腰直角三角形,,交于,.(Ⅰ)求的值;(Ⅱ)求.BAC DE17.(本小题满分14分)已知函数满足;(1)求常数的值;(2)解不等式.18.(本题满分16分)某市旅游部门开发一种旅游纪念品,每件产品的成本是元,销售价是元,月平均销售件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为,那么月平均销售量减少的百分率为. 记改进工艺后,旅游部门销售该纪念品的月平均利润是(元).(1)写出与的函数关系式;(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.19. (本小题满分16分)把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设是位于这个三角形数表中从上往下数第行、从左往右数的第个数(如).⑴试用表示(不要求证明);⑵若,求的值;⑶记三角形数表从上往下数第行的各数之和为,令,若数列的前项和为,求.12345678910…………20.(本题满分16分)已知函数,(I)若时,函数在其定义域内是增函数,求b的取值范围;(II)在(I)的结论下,设,求函数的最小值;(III)设函数的图象与函数的图象交于点、,过线段的中点作轴的垂线分别交、于点、,问是否存在点,使在处的切线与在处的切线平行?若存在,求出的横坐标;若不存在,请说明理由.南京师大附中2008—2009学年度第1学期高三年级期中考试数学试卷(解答)一、填空题:(本大题共14小题,每小题5分,共70分)1.设集合,则▲;{4,5}2.已知为第三象限角,则的符号为▲ (填“正”或“负”);负3.设的三个内角、、所对边的长分别是、、,且,那么▲;4.在等差数列中,,则的值为▲ ; 12 5.若函数的图象的相邻两条对称轴的距离是,则的 值为 ▲ ;6.若函数的定义域为,则的取值范围是 ▲ ;7.设复数,则▲ ; 18.已知变量、满足条件则的最大值是▲ ; 6 9.函数在(0,)内的单调增区间为 ▲ ;10.若ΔABC 的三个内角所对边的长分别为,向量,,若,则∠等于▲ ;π311.已知等比数列{a n }中,a 3=3,a 6=24,则该数列的通项a n =______3·2n -3________.12.已知函数是上的减函数,是其图象上的两点,那么不等式|的解集是 ▲ ;13.若为的各位数字之和,如,, 则;记,,…,,,则▲ ; 1114.下列表中的对数值有且仅有一个是错误的:358915请将错误的一个改正为 15 = 3a-b+c二、解答题:(本大题共6小题,共90分)15.(本小题满分14分)已知,且(1)求的值;(2)求的值.解:(1)由sin=又0<<∴cos=,tan=∴=(2)tan(16.(本小题满分14分)如图,是等边三角形,是等腰直角三角形,,交于,.(Ⅰ)求的值;(Ⅱ)求.解:(Ⅰ)因为,,所以.所以.(Ⅱ)在中,,由正弦定理BACDE.故.17.(本小题满分14分)已知函数满足;(1)求常数的值;(2)解不等式.解:(1)因为,所以;由,即,(2)由(1)得由得,当时,解得,当时,解得,所以的解集为.18.(本题满分16分)某市旅游部门开发一种旅游纪念品,每件产品的成本是元,销售价是元,月平均销售件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为,那么月平均销售量减少的百分率为.记改进工艺后,旅游部门销售该纪念品的月平均利润是(元).(1)写出与的函数关系式;(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.18、(1)改进工艺后,每件产品的销售价为,月平均销售量为件,则月平均利润(元),∴与的函数关系式为(2)由得,(舍)当时;时,∴函数在取得最大值.故改进工艺后,产品的销售价为元时,旅游部门销售该纪念品的月平均利润最大.19. (本小题满分16分)把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设是位于这个三角形数表中从上往下数第行、从左往右数的第个数(如).⑴试用表示(不要求证明);⑵若,求的值;⑶记三角形数表从上往下数第行的各数之和为,令,若数列的前项和为,求.解:(1)∵三角形数表中前行共有个,即第行的最后一个数是 ∴=(2)由题意,先求使得是不等式的最小正整数解. 由,得∵,∴,∴12 3 4 5 6 7 8 9 10…………(另解:∵∴)于是,第63行的第一个数是,故(3)前行的所有自然数的和为则,所以,当时,,当时,也适合,20.(本题满分16分)已知函数,(I)若时,函数在其定义域内是增函数,求b的取值范围;(II)在(I)的结论下,设,求函数的最小值;(III)设函数的图象与函数的图象交于点、,过线段的中点作轴的垂线分别交、于点、,问是否存在点,使在处的切线与在处的切线平行?若存在,求出的横坐标;若不存在,请说明理由.解:(I)依题意:在(0,+)上是增函数,对∈(0,+)恒成立,,则的取值范围是.(II)设当,即时,函数在[1,2]上为增函数,当时,;当时,.综上所述:(III)设点P、Q的坐标是则点M、N的横坐标为C1在点M处的切线斜率为C2在点N处的切线斜率为假设C1在点M处的切线与C2在点N处的切线平行,则即则设则 (1)令,则,,所以在上单调递增,故,则,与(1)矛盾!。
2023-2024学年江苏省南京师范大学附属中学高三上学期期中考试数学试卷

2023-2024学年江苏省南京师范大学附属中学高三上学期期中考试数学试卷1.设集合,则()A.B.C.D.2.已知复数,则的虚部为()A.B.C.1D.-13.设α,β是两个平行平面,若α内有3个不共线的点,β内有4个点(任意3点不共线),从这些点中任取4个点最多可以构成四面体的个数为()A.34B.18C.12D.74.在宋代《营造法式》一书中,记载着我国古代一项兼具屋面排水与檐下采光,且美观好看的建筑技术——举折,其使屋面呈一条凹形优美的曲线,近似物理学中的最速曲线.如图,“举”是屋架的高度,点是屋宽的五等分点,连接,在处下“折”安置第一榑,连接,在处下“折”安置第一榑,依次类推,每次下“折”高度是前一次下“折”高度的一半,则第四榑的高度为()A.B.C.D.5.已如是表面积为的球的球面上的三个点,且,则三棱锥的体积为()A.B.C.D.6.若直线与曲线和圆都相切,则的方程可能为()A.B.C.D.7.已知椭圆,为两个焦点,O为原点,P为椭圆上一点,,则()A.B.C.D.8.已知函数,若对任意的,当时,恒成立,则实数的取值范围()A.B.C.D.9.已知数列,记数列的前项和为,下列结论正确的是()A.若“”是“为递增数列”的充分不必要条件B.“为等差数列”是“为等差数列”的必要不充分条件C.若为等比数列,则成等比数列D.若为等比数列,则可能是等差数列10.已知函数,则在区间上可能()A.单调递增B.有零点C.有最小值D.有极值点11.已知抛物线的焦点为F,过原点O的动直线l交抛物线于另一点P,交抛物线的准线于点Q,下列说法正确的是()A.若O为线段中点,则B.若,则C.存在直线l,使得D.△PFQ面积的最小值为212.已知点A,B是函数图象上不同的两点,则下列结论正确的是()A.若直线AB与y轴垂直,则a的取值范围是B.若点A,B分别在第二与第四象限,则a的取值范围是C.若直线AB的斜率恒大于1,则a的取值范围是D.不存在实数a,使得A,B关于原点对称13.在中,已知点满足,若,则__________.14.已知分别为内角的对边.若,则的最小值为__________.15.已知双曲线:的右焦点为,过分别作的两条渐近线的平行线与交于,两点,若,则的离心率为________16.若函数存在极大值点,且对于的任意可能取值,恒有极大值,则的最大值为__________.17.已知的三内角所对的边分别是分别为,且.(1)求;(2)若,求周长的最大值.18.如图,矩形所在平面与所在平面垂直,,(1)证明:平面;(2)若平面与平面的夹角的余弦值是,求异面直线与所成角的余弦值.19.已知等比数列公比为2,数列满足,若数列的前项和为.(1)求数列和的通项公式;(2)是否存在正整数,使得成等差数列,若存在,请求出所有满足条件的正整数,如不存在,请说明理由.20.随着“双十一购物节”的来临,某服装店准备了抽奖活动回馈新老客户,活动规则如下:奖券共3张,分别可以再店内无门槛优惠10元、20元和30元,每人每天可抽1张奖券,每人抽完后将所抽取奖券放回,以供下一位顾客抽取.若某天抽奖金额少于20元,则下一天可无放回地抽2张奖券,以优惠金额更大的作为所得,否则正常抽取.(1)求第二天获得优惠金额的数学期望;(2)记“第天抽取1张奖券”的概率为,写出与的关系式并求出.21.设双曲线的方程为,直线过抛物线的焦点和点.已知的焦距为且一条渐近线与平行.(1)求双曲线的方程;(2)已知直线过双曲线上的右焦点,若与交于点(其中点在第一象限),与直线交于点,过作平行于的直线分别交直线轴于点,求.22.已知函数.(1)求曲线在处的切线方程;(2)已知实数,设.(i)若,求的极值;(ii)若有3个零点,求的值.。
【南京师范大学附属中学】2017届期中考试数学试卷-答案

南京师范大学附属中学2017届期中考试数学试卷答 案1.{1,2,3}2.1i +3.24.235.136.5 7.1-8.539.2310.291811.5212.[-13.e 1(,1)(1,e 1]2-- 14.{2,8}- 15.(本小题满分14分)解:(1)因为2cos cos b c C a A-=(2)cos cos b c A a C -=,由正弦定理得: (2sin sin )cos sin cos B C A A C -=,………………2分即2sin cos sin cos sin cos B A A C C A =+=()sin A C +.………………4分因为πB A C --=,所以()sin sin B A C =+,所以2sin cos sin B A B =.因为π()0,B ∈,所以sin 0B ≠, 所以1cos 2A =,因为0πA <<,所以3A π=.………………7分(2)ABC △,且a =由22222131sin 2212cos 522bc S bc A a b c bc A b c bc ⎧==⎪⇒⎨⎨⎪⎪=+-=+-⎩⎪⎩2222(b c)7417bc b c =⎧⇒+=+=⎨+=⎩. 所以b c +a b c ++=14分16.(本小题满分14分)证明:(1)因为PA ABCD ⊥平面,CD ABCD ⊥平面,所以PA CD ⊥,………………2分 又90ACD ︒∠=,则CD AC ⊥,而PA AC A =,所以CD PAC ⊥平面,因为CD ACD ⊥平面,………………4分所以,平面PAC PCD ⊥平面.………………7分证法一:取AD 中点M ,连EM ,CM ,则EM ∥PA .因为EM ⊄平面PAB ,PA ⊂PAB 平面,所以EM PAB ∥平面.………………9分在Rt ACD △中,AM CM =,所以CAD ACM ∠=∠,又BAC CAD ∠∠=,所以BAC ACM ∠∠=,则MC AB ∥.因为MC ⊄平面PAB ,AB ⊂平面PAB ,所以MC PAB ∥平面.………………12分而EM MC M =,所以平面EMC PAB ∥平面.由于EC ⊂平面EMC ,从而EC PAB ∥平面.………14分证法二:延长DC ,AB 交于点N ,连PN .因为NAC DAC ∠∠=,AC CD ⊥,所以C ND 为的中点.而E PD 为中点,所以EC PN ∥.因为EC ⊄平面PAB ,PN ⊂平面PAB ,所以EC PAB ∥平面………………14分17.(本小题满分14分)解:(1)如图,设圆心为O ,连结OC ,设BC =x ,法一:易得AB =(0,30)x ∈,故所求矩形ABCD 的面积为()2S x =3分=()22900x x ≤+-900=(2cm )(当且仅当22900x x =-,x =(cm )时等号成立)此时BC =;……6分 法二设COB θ∠=,0 θπ⎛⎫∈ ⎪2⎝⎭,;则30sin BC θ=,30cos OB θ=, 所以矩形ABCD 的面积为()230sin 30cos 900sin 2S θθθθ=⨯⨯=,………3分当sin 21θ=,即θπ=4时,max ()900S θ=(2cm )此时BC =;………6分(2)设圆柱的底面半径为r ,体积为V ,由2AB r ==π得,r =所以()231900V r x x x =π=-π,其中(0,30)x ∈,………9分由()2190030V x '=-=π得x =()31900V x x =-π在(上单调递增,在()上单调递减,故当x =3cm ,………13分答:(1)当截取的矩形铁皮的一边BC 为为时,圆柱体罐子的侧面积最大.(2)当截取的矩形铁皮的一边BC为为时,圆柱体罐子的体积最大.………14分 18.(本小题满分16分)解:(1)由已知,得2222101041,441,a b ab ⎧⎪+=⎪⎨⎪+=⎪⎩解得2220,5.a b ⎧=⎨=⎩ 所以椭圆的标准方程为221205x y +=.………………4分 (2)设点(,)C m n (0,0)m n <<,则BC 中点为22(,)22m n --. 由已知,求得直线OA 的方程为20x y -=,从而22m n =-.①又∵点C 在椭圆上,∴22420m n +=.②由①②,解得2n =(舍),1n =-,从而4m =-.所以点C 的坐标为(4,1)--.…8分 (3)设00(,)P x y ,11(2,)M y y ,22(2,)N y y .∵,,P B M 三点共线,∴011022222y y y x ++=++,整理,得001002()22x y y y x -=+-.………………10分 ∵,,P C N 三点共线,∴022011244y y y x ++=++,整理,得00200422x y y y x -=--.………………12分 ∵点C 在椭圆上,∴2200420x y +=,2200204x y =-. 从而2200000012220000002(45)2(205)55244416442x y x y x y y y x y x y x y +--===⨯=+---.…………………14分 所以122552OM ON y y ==.∴OM ON 为定值,定值为252.………………16分 19.(本小题满分16分) 解:(1)由题意123n a a a a=n b ,326b b -=,知3328a b b -==.设数列{}n a 的公比为q ,又由 1a =2,得2314a q a ==,)22(q q -==舍去,所以数列{}n a 的通项为(2)n a n n *∈N =.…3分 所以,123n a a a a ⋯=(1)22n n +=()1n n +. 故数列{}bn 的通项为1()()n b n n n *∈N =+.…………6分 (2)(i )由(1)知11111()21n n n n c n a b n n *⎛⎫---∈ ⎪+⎝⎭N ==.所以1112()n S n n n*-∈+N =.…10分(ii )因为12300040c c c c >>>=,,,,当5n ≥时,1(1)1(1)2n n n c n n n +⎡⎤=-⎢⎥+⎣⎦, 而(1)(1)(2)(1)(2)022121n n n n n n n n n ++++--=>++, 得(1)5(51)1225n n n +⨯+≤<,所以,当5n ≥时,0n c <. 综上,若对任意n *∈N 恒有k n S S ≥,则4k =.…………16分20.(本小题满分16分)(1)2222()2a x a f x x x x-'=-= 当0a ≤时,()0f x '>,()f x 在(0,)+∞上递增,()f x 无极值…………2分当0a >时,x ∈时,()0f x '<,()f x 递减;)x ∈+∞时,()0f x '>,()f x 递增,所以()f x 有极小值ln f a a a =- 综上,当0a ≤时,()f x 无极值;当0a >时,()f x 有极小值ln f a a a =-,无极大值…………4分(2)2()2ln 2h x x a x ax =--,则22222'()22a x ax a h x x a x x --=--=因为0a >,令()0h x '=,得0x =,故()h x 在0(0,)x 上递减,在0(,)x +∞上递增,所以()h x 有极小值0()0h x =,20002ln 20x a x ax --=…………6分且2002220x ax a --=联立可得002ln 10x x +-=令()2ln 1m x x x =+-,得2()11m x x'=+>,故()m x 在(0,)+∞上递增又(1)0m =,所以01x =112a =⇒=…………10分 (3)不妨令1212x x ≤<≤,因为01a <<,则12()()g x g x <由(1)可知12()()f x f x <,因为1212()()()()f x f x g x g x ->-所以21212211()()()()()()()()f x f x g x g x f x g x f x g x ->-⇒->-所以2()()()2ln 2h x f x g x x a x ax =-=--在[1]2,上递增所以2()220ah x x ax'=--≥在[1]2,上恒成立,…………12分即21xax≤+在[1]2,上恒成立令1[2,3]t x=+∈,则211212xtx t=+-≥+,……14分所以1(0,]2a∈…………16分。
南京师范大学附属中学2017届高三考前模拟考试数学试题(附答案)

2017届南京师范大学附中高三考前模拟考试数学第Ⅰ卷(共60分)一、填空题:本大题共14个小题,每小题5分,共70分.不需要写出解答过程,请把答案写在答题纸指定的位置上.1.已知集合2{1,2,3,4},{|20}A B x x x ==-->,则AB =2. 已知复数z 满足(1)3z i i +=-,其中i 为虚数单位,则复数z 的模z =3.某时段内共有100辆汽车经过某一雷达测速区域,将测得的汽车时速绘制成如图所示的频率分布直方图,根据图形推断,该时段的时速超过50/km h 的车辆数为 辆. ( )4. 如下图所示的流程图中,输出的S 为5.函数()f x =的定义域是6. 袋中有形状、大小相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为7.已知正四棱锥的底面边长为4cm,则该四棱锥的侧面积是2cm8. 设变量,x y 满足约束条件41x y y x x +≤⎧⎪≥⎨⎪≥⎩,若目标函数z ax y =+的最小值为2-,则a =9. 设函数()2sin cos (0)f x wx wx wx w =->,且()y f x =的图象的一个对称中心到最近的对称轴的距离为4π,则()f x 在区间[,0]4π-上的最大值为10. 设n S 是等比数列{}n a 的前n 项和,若满足41130a a +=,则2114S S = 11. 若1b a >>且3log 6log 11a b b a +=,则321a b +-的最小值为 12.已知P 是圆221x y +=上的一动点,AB 是圆22(5)(12)4x y -+-=的一条动弦(,A B 是直径的两个端点),则PA PB ⋅的取值范围是13. 设()34f x ax x =-,对[1,1]x ∀∈-总有()1f x ≤,则a 的取值范围是14.在ABC ∆中,已知边,,a b c 所对的角分别为,,A B C ,若2222sin 3sin 2sin sin sin sin B C A B C A +=+,则tan A =第Ⅱ卷(共80分)二、解答题 (本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.) 15. 在ABC ∆中,角,,A B C 的对边分别为,,a b csin )sin C A B -=. (1)求bc a-的值; (2)若32b BA BC =⋅=,求ABC ∆的面积. 16. 如图,在四棱锥P ABCD -中,1//,2CD AB AD DC AB ==.(1)若M 是PB 的中点,求证://CM 平面PAD ; (2)若,CD AB BC PC ⊥⊥,求证:平面PAC ⊥平面PBC .17.园林管理处拟在公园某区域规划建设一半径为r 米圆心角为θ(弧度)的扇形景观水池,其中O 为扇形AOB 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过24万元,水池造价为每平方米400元,步道造价为每米1000元. (1)当r 和θ分别为多少时,可使广场面积最大,并求出最大值; (2)若要求步道长为105米,则可设计出水池最大面积是多少.18. 平面直角坐标系中,椭圆2222:1(0)x y C a b a b +=>>过点(1)求椭圆C 的标准方程;(2)过点(2,0)K 作一直线与椭圆C 交于,A B 两点,过,A B 点作椭圆右准线的垂线,垂足分别为11,A B ,试问直线1AB 与1A B 的交点是否为定点,若是,求出定点的坐标;若不是,请说明理由.19.设()sin ,[0.2](xf x e x ax x a π=⋅+∈为常数).(1)当0a =时,求()f x 的单调区间;(2)若()f x 在区间(0.2)π的极大值、极小值各有一个,求实数a 的取值范围. 20.设{}n a 是各项均不相等的数列,n S 为它的前n 项和,满足11(,)n n na S n N R λλ++=+∈∈.(1)若11a =,且123,,a a a 成等差数列,求λ的值; (2)若{}n a 的各项均不相等,问当且仅当λ为何值时,23,,,,n a a a 成等差数列?试说明理由. 21.选做题A.如图,AB 为O 的直径,D 为O 上一点,过D 作O 的切线交AB 的延长线于点C , 若DA DC = ,求证:2AB BC =.B.已知矩阵111A a -⎡⎤=⎢⎥⎣⎦,其中a R ∈,若点(1,1)P 在矩阵A 的变换下得到点(0,1)P -, 求矩阵A 的两个特征值. C.已知点P是曲线2cos :(x C y θθθ=⎧⎪⎨=⎪⎩为参数,2πθπ≤≤)上一点,O 为原点,若直线OP 的倾斜角3π,求点P 的直角坐标. D.已知实数,,x y z 满足2x y z ++=,求22223x y z ++的最小值.[必做题]第22题、第23题,每题10分,共计20分,请在答题卡指定区域内作答,解答应写出文字说明、证明过程或演算步骤.22.某小组共10人,利用暑假参加义工活动,已知参加义工活动此时为1,2,3的人数分别为3,3,4,现从10人中学车2人作为该组参加座谈会.(1)记“选出2人参加义工活动的次数之和为4”为事件A ,求事件A 的发生的概率; (2)设X 为选出2人参加义工活动次数之差的绝对值,求随机变量X 的分布列和数学期望.23.(1)设23260126(1)x x a a x a x a x ++=++++,求23,a a .(2)设2017(25(25x =+++,其x 的整数部分的个位数字.试卷答案一、填空题1. {}3,43 .774 .25125 .3(,2]26 .567 .248 .2- 9.1 10 7611.112 .[]140,192 13{}3 14.1- 二、解答题15.解:(1)bc a b c a-=⇒=- (2)22222)111325322cos 2c a b c a c a a b a c b c a c ca ac BA BC ca B -=-=⎧-==⎧⎧⎪=⇒⇒⇒⎨⎨⎨⎨+-=+=⋅=⎩⎩⎪⎪⎩⎪⋅==⎩,所以3cos sin 44B B =⇒=,所以1sin 24S ac B ==. 16.解(1)取AP 的中点N ,连接MN 和DN ,由因为M 是PB 的中点, 所以MN 是PAB ∆的中位线,所以1//,2MN AB MN AB =, 由题意1//,2CD AB CD AB =,所以,//MN CD MN CD =, 所以四边形MNDC 是平行四边形,所以//CM DN .(2)由题意,在直角梯形ABCD 中,经计算可证得BC AC ⊥,又,,BC PC AC PC ⊥⊂面ACP , ACPC C =,BC ⊥面ACP ,又BC ⊂面PBC ,所以平面PAC ⊥平面PBC.17.解:(1)由题意,输出弧长AB 为r θ,扇形面积为212S r θ=, 由题意2414001000(2)24102r r r θθ⨯++≤⨯,即25(2)1200r r r θθ++≤,即2r r θ+≥所以21200r θ+≤,所以t 0t >,则2101200402t t t +≤⇒≤,所以当240r r θ==时,面积212S r θ=的最大值为400. (2)即105210522r r rθθπ+=⇒=-<,1052r r θ=-代入可得 215(1052)51051200210567502r r r r r -+⨯≤⇒-+≥⇒≤或45r ≥,又222211105105105(1052)()222416S r r r r r r θ==-=-+=--+,当1510510522122152()2r r θπ≤=-≥-=>与2θπ<不符,()S θ在[45,)+∞上单调,当45r =时,S 最大337.5平方米,此时13θ=. 18.解(1)由题意得2222253114425a b c a b a b c c a⎧⎪=+⎧=⎪⎪⎪+=⇒=⎨⎨⎪⎪=⎩⎪=⎪⎩,所以椭圆的标准方程为2215x y +=. (2)①当直线AB 的斜率不存在时,准线15:,2l x AB =与1A B 的交点是9(,0)4; ②当直线AB 的斜率存在时,设1122(,),(,)A x y B x y ,直线AB 为(2)y k x =-, 由222222(2)(15)20205055y k x k x k x k x y =-⎧⇒+-+-=⎨+=⎩,所以2212122220205,1515k k x x x x k k-+==++,1255(,),(,)22A y B y , 所以121215:()522AB y y l y x y x -=-+- ,121125:()522A B y y l y x y x -=-+- 联立解得2212222122205252545(1)9154420520(1)4515k x x k k x k x x k k----++====+--+-+, 代入上式可得222221122121112020594()9()42015150104410410k k k k k x x k x x kx x k k k y y x x x --⋅+⋅--+++++=+===-+--,综上,直线1AB 与1A B 过定点9(,0)4.19.解:(1)当0a =时,()(sin cos )sin()4xx f x e x x x π'=+=+,令()0f x '>,则()370,2,44x x f x πππ<<<<单调增; 令()0f x '<,则()37,44x f x ππ<<单调增, 所以()f x 的单调递增区间为37(0,),(,2)44πππ,单调递减区间为37(,)44ππ. (2)设()()(sin cos )xg x f x e x x a '==++,则()22cos g x e x '=,令()0g x '>,则3cos 0,0,222x x x πππ><<<<,令()0g x '<,则3cos 0,22x x ππ<<<,所以()g x 的单调递增区间为3(0,),(,2)22πππ,单调递减区间为3(,)22ππ. 故()g x 在2x π=处取得极大值,在32x π=处取得极小值,()3222301,(),(),(2)22g a g a e g a e g a e ππππππ=+=+=-=+,所以()32()(0)()22g g g g πππ>>> ①若3()02g π≥,则()()0,f x f x '≥在(0,2)π上单调增,故()f x 在(0,2)π无极值,所以3()02g π<; ②若3()02g π≤,则()f x 在(0,2)π内至多有一个极值点,从而()20,()02g g ππ>>,于是在区间33(,),(,2)222ππππ内()f x 分别有极大值、极小值各一个, 则在(0,)2π内无极值点,从而()00g ≥3223210(0)0()001230()02a g g a e a e a e g πππππ⎧+≥⎧⎪≥⎪⎪⎪⎪>⇒+>⇒-≤<⎨⎨⎪⎪⎪⎪-<⎩<⎪⎩ ,所以的取值范围是321a e π-≤<. 20.解:(1)令1,2n =,得21321212211a a a S a a λλ=+=⎧⎨=+=++⎩,又由123,,a a a 成等差数列,所以213321a a a a =+=+,解得λ=. (2)当且仅当12λ=时,23,,,,n a a a 成等差数列,证明如下:由已知11n n na S λ+=+,当2n ≥时,1(1)1n n n a S λ--=+,两式相减得1n n n n n na na na a a λλλλ+-++=,即1()(1)n n n n a a a λλ+-=-, 由于{}n a 个各项均不相等,所以1,(2)1n n na n n a a λλ+=≥--, 当3n ≥时,所以11(1)1n n n a n a a λλ---=-- 两式相减可得1111n n n n n n a a a a a a λλ-+-=----, ①当12λ=,得111n n n n n n a a a a a a -+-=--,当3n ≥时,所以11111n n nn n n n n n a a a a a a a a a -+--=+=---, 0n a ≠,所以11112(3)n n n n n n n a a a a a a a n +-+--=-⇒=+≥,故23,,,,n a a a 成等差数列.②再证当23,,,,n a a a 成等差数列,时,12λ=,因为23,,,,n a a a 成等差数列,所以11(3)n n n n a a a a n +--=-≥,可得11111111n n n n n n n n n n n n a a a a a a a a a a a a λλ--+----=-==-----, 所以12λ=, 所以当且仅当12λ=时,23,,,,n a a a 成等差数列.22.A 解:连接OD ,因为DC 为切线且点D 为切点,所以BDC BAD ∠=∠, 因为OA OD =, 所以OAD ODA ∠=∠ 又因为AD DC = 所以BCD OAD ∠=∠故OAD BDC ∆≅∆,所以BC OD R ==,从而2AB BC =. B.解:111001111a a -⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦,所以11a +=,即2a =-, 特征方程211(1)2021λλλ-⎡⎤=--=⎢⎥-⎣⎦,因此1λ=C.解:由题意得,曲线C 的普通方程为22143x y +=, 2sin 00y πθπθ≤≤⇒≤⇒≤,直线OP的方程为y =,联立得x y ⎧=⎪⎪⎨⎪=⎪⎩(舍去)或5x y ⎧=⎪⎪⎨⎪=-⎪⎩,所以点P的坐标为(. D.解:由柯西不等式可知:2222221)1](23)z x y z ++⋅≤++++,所以2222()24231111123x y z x y z ++++≥=++,当且仅当6412,,111111x y z ===时取等号. 22.解:(1)有已知得1123432101()3C C C P A C +==,所以事件A 的发生的概率为13. (2)随机变量X 的所有可能的取值为0,1,2,2221111334333422101047(0),(1)1515C C C C C C C P X P X C C +++======, 11342104(2)15C C P X C ===, 所以随机变量X 的分布列为数学期望为()1E X =.23.解:(1)因为23230312224333333(1)((1))(1)(1)(1)x x x x C x C x x C x x C x ++=++=++++++, 所以2121123313326,7a C C a C C C =+==+=.(2)令2017(25(25y =-+-,则20172017(25(25(25(25x y y +==++++-+-20201717[(25(25][(25(25]=++-+++-201818202017215168202017172(2525620(620)2(2525620(620))C C C C =+⨯++++⨯++,已知x y +为整数且个位数为0,而50250.225<-=<=,所以201720170(25(250.20.21<-+-<+<,所以x 的各位为9.。
数学---江苏省南京市南师附中2017届高三上学期期中试卷

江苏省南京市南师附中2017届高三上学期学期中试卷一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置 上)1. 函数113x y -⎛⎫= ⎪⎝⎭的单调增区间为 .2.在ABC ∆中,若a cos A =b cos B =c cos C,则ABC ∆的形状是_________三角形. 3.已知n m ,为直线,βα,为空间的两个平面,给出下列命题:①αα//,n n m m ⇒⎩⎨⎧⊥⊥;②n m n m //,//⇒⎪⎩⎪⎨⎧⊂⊂βαβα;③βαβα//,⇒⎩⎨⎧⊥⊥m m ;④n m n m //,⇒⎩⎨⎧⊥⊥ββ.其中的正确命题 为 .4.已知||2a =,||3b =,,a b 的夹角为60°,则|2|a b -= .5.数列{}n a 满足:2123()n a a a a n n N *⋅⋅⋅⋅⋅=∈,则通项公式是:n a = _ ____.6. 定义:区间[],()m n m n <的长度为n m -,已知函数12log y x =的定义域为[],,a b 值域为[]0,2,则区间[],a b 长度的最大值与最小值的差为 .7.已知)(),(x g x f 均为R 上的奇函数且0>)x (f 解集为(4,10),0>)x (g 解集为(2,5),则0)()(>⋅x g x f 的解集为 . 8.设函数)0(sin >=ωωx y 在区间⎥⎦⎤⎢⎣⎡-4,5ππ上是增函数,则ω的取值范围为 ____. 9.已知()1,5x ∈,则函数2115y x x=+--的最小值为 . 10.设实数b y x ,,满足⎪⎩⎪⎨⎧+-≥≥≥-b x y x y y x ,,02若y x z +=2的最小值为3,则实数b 的值为 .11.已知ABC ∆中,AB 边上的高与AB 边的长相等,则ACBC AB AC BC BC AC ⋅++2的最大值为 .12.在棱长为1的正方体1111ABCD A B C D -中,E 为1AB 的中点,在面ABCD 中取一点F ,使1EF FC +最小,则最小值为__________. 13.设{}n a 是等比数列,公比2=q ,n S 为{}n a 的前n 项和,记)(1712*+∈-=N n a S S T n nn n ,设0n T 为数列{}n T 的最大值,则0n = .14.当n 为正整数时,函数()N n 表示n 的最大奇因数,如(3)3,(10)5,N N ==⋅⋅⋅,设(1)(2)(3)(4)...(21)(2)n nn S N N N N N N =+++++-+,则n S = .二、解答题:(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)15. (本题满分14分) 在ABC ∆中,a 、b 、c 分别是角A 、B 、C 的对边,且cos Bcos C=-b2a +c. (1)求角B 的大小;(2)若b =13,a +c =4,求ABC ∆的面积.16.(本题满分14分) 如图,在四棱锥ABCD P -中,BC AD //,且AD BC 2=,CD PB CD AD ⊥⊥,,点E 在棱PD 上,且ED PE 2=. (1)求证:平面⊥PCD 平面PBC ; (2)求证://PB 平面AEC .17.(本题满分15分) 设不等式⎪⎩⎪⎨⎧+-≤>>n nx y y x 300所表示的平面区域为n D ,记n D 内的整点个数为n a (n ∈*N ),(整点即横坐标和纵坐标均为整数的点) (1)求数列{a n }的通项公式; (2)记数列{a n }的前项和为S n ,且123-⋅=n nn s T ,若对于一切正整数n ,总有≤n T m ,求实数m 的取值范围.18.(本题满分15分)如图,半径为1,圆心角为3π2的圆弧AB 上有一点C . (1)若C 为圆弧AB 的中点,点D 在线段OA 上运动,求|→OC +→OD |的最小值;(2)若D ,E 分别为线段OA ,OB 的中点,当C 在圆弧AB 上运动时,求→CE •→CD 的取值范围.19.(本题满分16分)对于定义域为D 的函数)(x f y =,如果存在区间[m ,n ]⊆D ,同时满足:①)(x f 在[m ,n ]内是单调函数;②当定义域是[m ,n ]时,)(x f 的值域也是[m ,n ].则称[m ,n ]是该函数的“和谐区间”.(1)证明:[0,1]是函数)(x f y ==2x 的一个“和谐区间”.(2)求证:函数xx g y 53)(-==不存在“和谐区间”. (3)已知:函数xa x a a x h y 221)()(-+==(∈a R ,0≠a )有“和谐区间”[m ,n ],当a 变化时,求出n ﹣m 的最大值.20. (本题满分16分)已知首项为1的正项数列{}n a 满足221152n n n n a a a a +++<,n *∈N .(1)若232a =,3a x =,44a =,求x 的取值范围; (2)设数列{}n a 是公比为q 的等比数列,n S 为数列{}n a 前n 项的和.若1122n n n S S S +<<,n *∈N ,求q 的取值范围;(3)若1a ,2a ,⋅⋅⋅,k a (3k ≥)成等差数列,且12120k a a a ++⋅⋅⋅+=,求正整数k 的最小值,以及k 取最小值时相应数列1a ,2a ,⋅⋅⋅,k a 的公差.参考答案1.(,0)-∞(亦可写成(,0]-∞) 2.等边 3.③④ 45.21(1)(2,)1n n n n N n *=⎧⎪⎨⎛⎫≥∈⎪⎪-⎝⎭⎩ 6.3 7.(5,4)(4,5)-- 8.(0,2]9.34+ 10.9411. 12.2 13.4 14.423n +15.解:(1)由余弦定理知:cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab .将上式代入cos B cos C =-b 2a +c 得:a 2+c 2-b 22ac ·2ab a 2+b 2-c 2=-b2a +c, 整理得:a 2+c 2-b 2=-ac .∴cos B =a 2+c 2-b 22ac =-ac 2ac =-12.∵B 为三角形的内角,∴B =23π.(2)将b =13,a +c =4,B =23π代入b 2=a 2+c 2-2ac cos B ,得b 2=(a +c )2-2ac -2ac cos B ,∴13=16-2ac ⎝⎛⎭⎫1-12,∴ac =3.∴S △ABC =12ac sin B =334. 16.证明:(1)因为,//AD CD AD BC ⊥, 所以CD BC ⊥ 。
2016年江苏省南京师大附中高考数学模拟试卷(一)

2016年江苏省南京师大附中高考数学模拟试卷(一)一.填空题1.(5分)已知边长为6的正三角形ABC ,=,=,AD 与BE 交于点P ,则?的值为.2.(5分)设函数f (x )的定义域为R ,且为奇函数,当x >0时,f (x )=﹣x 2+2x .若f (x )在区间[﹣1,a ﹣2]上是单调递增函数,则a 的取值范围是.3.(5分)已知曲线y=(x ∈R ,e 是自然对数的底数)在x=﹣1处的切线和它在x=x 0(x 0≠0)处的切线互相垂直,设x 0∈(,),m 是整数,则m=.4.(5分)在△ABC 中,角A ,B ,C 所对的边分别是a 、b 、c ,已知b=2,且cos2B+cosB+cos(A ﹣C )=1,当a+2c 取得最小值时,最大边所对角的余弦值是.5.(5分)设集合A={(x ,y )|x 2+y 2+2x ﹣1=0},B={(x ,y )|(x+t )2≥y 2},若A ?B ,则实数t 的取值范围为.6.(5分)已知函数f (x )=a 2x+ma x﹣n (a >0且a ≠1),若存在实数x 使得f (x )+f (﹣x )=﹣2,则m 2+4n 2的最小值为.二、解答题7.如图,在平面直角坐标系xOy 中,已知椭圆E :+=1(a >b >0)的离心率为,点A (,)在椭圆E 上,射线AO 与椭圆E 的另一交点为B ,点P (﹣4t ,t )在椭圆E内部,射线AP ,BP 与椭圆E 的另一交点分别为C ,D .(1)求椭圆E 的方程;(2)求证:CD ∥AB .8.如图,某城市有一个五边形的地下污水管通道ABCDE ,四边形BCDE 是矩形,其中CD=8km ,BC=3km ;△ABE 是以BE 为底边的等腰三角形,AB=5km .现欲在BE 的中间点P 处建地下污水处理中心,为此要过点P 建一个“直线型”的地下水通道MN 接通主管道,其中接口处M 点在矩形BCDE 的边BC 或CD 上.(1)若点M在边BC上,设∠BPM=θ,用θ表示BM和NE的长;(2)点M设置在哪些地方,能使点M,N平分主通道ABCDE的周长?请说明理由.9.数列{a n}的前n项和为S n,且满足a1=1,2a n+1=2a n+p(p为常数,n=1,2,3,…).(Ⅰ)若S3=12,求S n;(Ⅱ)若数列{a n}是等比数列,求实数p的值.(Ⅲ)是否存在实数p,使得数列{}满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的p的值;若不存在,说明理由.10.设f(x)=lnx﹣x﹣k,x∈(0,+∞).(1)若f[f(1)]<0,求实数k的取值范围;(2)设函数g(x)=f(x)﹣kx2的单调递增区间为D,对任意给定的k>0,均有D?(0,a](a为与k无关的常数),求证:a的最小值为1.(3)求证:f(x)在区间(0,e)上有两个零点的充要条件为k∈(1﹣e,﹣1).三、理科加试11.某班从6名干部中(其中男生4人,女生2人)选3人参加学校的义务劳动.(1)设所选3人中女生人数为ξ,求ξ的分布列及Eξ;(2)求男生甲或女生乙被选中的概率;(3)在男生甲被选中的情况下,求女生乙也被选中的概率.12.设整数n≥3,集合P={1,2,3,…,n},A,B是P的两个非空子集.记a n为所有满足A中的最大数小于B中的最小数的集合对(A,B)的个数.(1)求a3;(2)求a n.2016年江苏省南京师大附中高考数学模拟试卷(一)参考答案与试题解析一.填空题1.(5分)(2016?南京校级模拟)已知边长为6的正三角形ABC,=,=,AD与BE交于点P,则?的值为.【考点】平面向量数量积的运算.【专题】综合题;数形结合;数形结合法;平面向量及应用.【分析】由题意以BC为x轴,以BC的垂直平分线为y轴,建立坐标系,根据等边三角形的性质,得到点的坐标,根据三等分点坐标公式求出点E的坐标,再根据两点式,求出直线直线BE的方程,令x=0,得到P点的坐标,再根据向量的数量积即可求出答案.【解答】解:∵等边三角形ABC的边长为6,=,=,∴以BC为x轴,以BC的垂直平分线为y轴,∴B(﹣3,0),C(3,0),A(0,3),D(0,0),∴E(,)=(1,2),∴直线BE的方程为=,即y=(x+3),令x=0,得y=,∴P(0,),∴=(﹣3,﹣),=(0,﹣),∴?=﹣3×0+(﹣)×(﹣)=.故答案为:2.(5分)(2016?南京校级模拟)设函数f(x)的定义域为R,且为奇函数,当x>0时,f (x)=﹣x2+2x.若f(x)在区间[﹣1,a﹣2]上是单调递增函数,则a的取值范围是1<a ≤3.【考点】奇偶性与单调性的综合.【专题】数形结合;转化法;函数的性质及应用.【分析】利用函数奇偶性的性质作出对应的图象,利用函数单调性的性质进行求解即可.【解答】解:因为f(x)为R上的奇函数,所以f(x)的图形关于原点成中心对称,图形如图.由图象可知函数f(x)在区间[﹣1,1]上为单调递增函数,所以,解得1<a≤3.故答案为:1<a≤33.(5分)(2016?南京校级模拟)已知曲线y=(x∈R,e是自然对数的底数)在x=﹣1处的切线和它在x=x0(x0≠0)处的切线互相垂直,设x0∈(,),m是整数,则m=2.【考点】利用导数研究曲线上某点切线方程.【专题】方程思想;分析法;导数的概念及应用.【分析】求出x<0的函数的导数,可得在x=﹣1处的切线斜率,由两直线垂直的条件:斜率之积为﹣1,可得在x=x0(x0≠0)处的切线斜率,求出x>0的函数的导数,可得切线的斜率,构造函数g(t)=te t﹣,求出导数,运用零点存在定理,即可判断m=2.【解答】解:当x<0时,y=﹣的导数为y′=,可得在x=﹣1处的切线斜率为﹣2e,由在x=﹣1处的切线和它在x=x0(x0≠0)处的切线互相垂直,可得在x=x0(x0≠0)处的切线斜率为,即有x0>0,则y=的导数为y′=﹣,即有=,即(1﹣x0)e1﹣x0=,设t=1﹣x0,即有te t=,令g(t)=te t﹣,g′(t)=(1+t)e t,当m=0时,x0∈(0,),t∈(,1);当m=1时,x0∈(,),t∈(,);当m=2时,x0∈(,),t∈(,);由g()=e﹣<0,g()=e﹣>0,g()=e﹣>0,g(1)=e﹣>0,且g(t)在(,1)递增,可得g(t)在(,)内只有一解,故m=2成立.故答案为:2.4.(5分)(2016?南京校级模拟)在△ABC中,角A,B,C所对的边分别是a、b、c,已知b=2,且cos2B+cosB+cos(A﹣C)=1,当a+2c取得最小值时,最大边所对角的余弦值是﹣.【考点】余弦定理;三角函数中的恒等变换应用.【专题】对应思想;综合法;解三角形.【分析】使用二倍角公式和两角和的余弦函数公式化简,借助于正弦定理得出a,b,c成等比数列,利用基本不等式得出a+2c取得最小值时的条件,代入余弦定理即可求出.【解答】解:在△ABC中,∵cos2B+cosB+cos(A﹣C)=1,∴cosB+cos(A﹣C)=1﹣cos2B,∵cosB=﹣cos(A+C),cos2B=1﹣2sin2B,∴cos(A﹣C)﹣cos(A+C)=2sin2B,∴﹣2sinAsin(﹣C)=2sin2B,即sinAsinC=sin2B,∴ac=b2=4.即c=.∴a+2c=a+≥2=4,当且仅当a=即a=2时取等号.∴当a+2c取得最小值时,a=2,c=.∴最大边对的角为A,由余弦定理得cosA===﹣.故答案为:﹣.5.(5分)(2016?南京校级模拟)设集合A={(x,y)|x 2+y2+2x﹣1=0},B={(x,y)|(x+t)2≥y2},若A?B,则实数t的取值范围为t≤﹣1或t≥3.【考点】集合的包含关系判断及应用.【专题】计算题;数形结合;数形结合法;集合.【分析】由题意可得:集合A为以(﹣1,0)为圆心,为半径的圆上的点,集合B表示两条相交直线所成区域内的点,利用直线与圆相切,求出t的值,即可得出结论.【解答】解:由题意可得:集合A为以(﹣1,0)为圆心,为半径的圆上的点,集合B 表示两条相交直线所成区域内的点,如图所示:当直线x±y+t=0与圆相切时,d==,∴t=3或﹣1.若A?B,则t 的范围为t≤﹣1或t≥3,故答案为:t≤﹣1或t≥3.6.(5分)(2016?南京校级模拟)已知函数f (x )=a 2x +ma x﹣n (a >0且a ≠1),若存在实数x 使得f (x )+f (﹣x )=﹣2,则m 2+4n 2的最小值为.【考点】函数的最值及其几何意义.【专题】计算题;转化思想;整体思想;换元法;函数的性质及应用.【分析】换元令t=a x,t >0;从而可得(t+)2+m (t +)﹣2n=0,再令u=t+,则u ≥2;从而可得u 2+mu ﹣2n=0,从而化简m 2+4n 2=m 2+(u 2+mu )2=(u 2+1)m 2+2u 3m+u 4,从而求最值即可.【解答】解:令t=a x,t >0;则f (x )=g (t )=t 2+mt ﹣n ,f (﹣x )=g ()=()2+m﹣n ,故f (x )+f (﹣x )=t 2+mt ﹣n+()2+m﹣n=﹣2,即(t+)2+m (t+)﹣2n=0,令u=t+,则u ≥2;则u 2+mu ﹣2n=0,故2n=u 2+mu ,故m 2+4n 2=m 2+(u 2+mu )2=m 2+u 4+2mu 3+m 2u2=(u 2+1)m 2+2u 3m+u 4,△=4u 6﹣4(u 2+1)u 4=﹣4u 4<0,∴当m=﹣时,取最小值;故最小值为==(u 2+1)+﹣2,∵u ≥2,∴u 2+1≥5,∴(u 2+1)+≥5+,∴(u 2+1)+﹣2≥3+=,故答案为:.二、解答题7.(2016?南京校级模拟)如图,在平面直角坐标系xOy中,已知椭圆E:+=1(a>b>0)的离心率为,点A(,)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(﹣4t,t)在椭圆E内部,射线AP,BP与椭圆E的另一交点分别为C,D.(1)求椭圆E的方程;(2)求证:CD∥AB.【考点】直线与圆锥曲线的关系;椭圆的标准方程.【专题】转化思想;综合法;圆锥曲线的定义、性质与方程.【分析】(1)将点A代入椭圆方程,e==,联立求得a和b的值,求得椭圆方程;(2)根据对称性求得B点坐标,,,求得x1和y1,代入椭圆方程,求得,同理求得(λ2+1)?18t2=λ2﹣1,两式相减求得λ1=λ2,因此可证明CD∥AB.【解答】解:(1)将点A代入椭圆方程得:,且e==,解得:a2=1,,所以,椭圆E的方程为:x2+2y2=1.(2)∵,∴.设C(x1,y1),D(x2,y2),,,其中:λ1,λ2∈(0,1),则,代入椭圆方程并整理得,,同理得,(λ2+1)?18t2=λ2﹣1,两式相减得:(λ1﹣λ2)?(18t2﹣1)=0.∵点P(﹣4t,t)在椭圆E内部,∴18t2<1,∴λ1=λ2,从而CD∥AB.8.(2016?南京校级模拟)如图,某城市有一个五边形的地下污水管通道ABCDE,四边形BCDE是矩形,其中CD=8km,BC=3km;△ABE是以BE为底边的等腰三角形,AB=5km.现欲在BE的中间点P处建地下污水处理中心,为此要过点P建一个“直线型”的地下水通道MN接通主管道,其中接口处M点在矩形BCDE的边BC或CD上.(1)若点M在边BC上,设∠BPM=θ,用θ表示BM和NE的长;(2)点M设置在哪些地方,能使点M,N平分主通道ABCDE的周长?请说明理由.【考点】已知三角函数模型的应用问题;正弦定理.【专题】方程思想;三角函数的图像与性质;解三角形.【分析】(1)根据条件结合三角形的边角公式建立函数关系即可.(2)根据正弦定理结合三角函数的性质进行求解.【解答】解:(1)当点M在边BC上,设∠BPM=θ,在Rt△BPM中,BM=BP?tanθ=4tanθ.在△PEN中,不妨设∠PEN=α,其中,则,即;(2)当点M在边BC上,由BM+AB+AN=MC+CD+DE+EN,BM﹣NE=2;即;即8tan2θ﹣8tanθ﹣3=0,解得.∵与矛盾,点只能设在CD上.当点M在边CD上,设CD中点为Q,由轴对称不妨设M在CQ上,此时点N在线段AE 上;设∠MPQ=θ,在Rt△MPQ中,MQ=PQ?tanθ=3tanθ;在△PAN中,不妨设∠PAE=β,其中;则,即;由MC+CB+BA+AN=MQ+QD+DE+EN,得AN=MQ,即;解得tanθ=0或;故当CM=4,或者时,符合题意.答:当点M位于CD中点Q处,或点M到点C的距离为3km时,才能使点M,N平分地下水总通道ABCDE的周长.9.(2016?南京校级模拟)数列{a n}的前n项和为S n,且满足a1=1,2a n+1=2a n+p(p为常数,n=1,2,3,…).(Ⅰ)若S3=12,求S n;(Ⅱ)若数列{a n}是等比数列,求实数p的值.(Ⅲ)是否存在实数p,使得数列{}满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的p的值;若不存在,说明理由.【考点】等差数列的性质;数列递推式.【专题】综合题;等差数列与等比数列.【分析】(Ⅰ)利用a1=1,2a n+1=2a n+p,求出2a2=2+p,2a3=2+2p,利用S3=12,求出p,即可求S n;(Ⅱ)若数列{a n}是等比数列,则a22=a1a3,求出实数p的值,再验证;(Ⅲ)利用反证法进行证明即可得出结论.【解答】解:(Ⅰ)∵a1=1,2a n+1=2a n+p,∴2a2=2+p,2a3=2+2p,∵S3=12,∴2+2+p+2+2p=6+3p=24,∴p=6,∴a n+1﹣a n=3,∴数列{a n}是以1为首项,3为公差的等差数列,∴S n=n+=;(Ⅱ)若数列{a n}是等比数列,则a22=a1a3,∴(1+)2=1×(1+p),∴p=0,∴a n+1=a n,此时,数列{a n}是以1为首项,1为公比的等比数列;(Ⅲ)p=0时,a n=1,数列{}是等差数列,满足题意;p≠0时,a n+1﹣a n=,∴数列{a n}是以1为首项,为公差的等差数列,∴a n=n+1﹣.假设存在p0≠0,满足题意,数列记为{b n}.①p0>0,a n>0,数列{b n}是各项均为正数的递减数列,∴d<0.∵b n=b1+(n﹣1)d,∴n<1﹣时,b n=b1+(n﹣1)d<b1+(1﹣﹣1)d=0,与b n>0矛盾;②p0<0,令<0,∴n>1﹣,a n<0,数列{b n}是各项均为负数的递增数列,∴d>0.∵b n=b1+(n﹣1)d,∴n>1﹣时,b n=b1+(n﹣1)d>b1+(1﹣﹣1)d=0,与b n<0矛盾,综上所述,p=0是唯一满足条件的p的值.10.(2016?南京校级模拟)设f(x)=lnx﹣x﹣k,x∈(0,+∞).(1)若f[f(1)]<0,求实数k的取值范围;(2)设函数g(x)=f(x)﹣kx2的单调递增区间为D,对任意给定的k>0,均有D?(0,a](a为与k无关的常数),求证:a的最小值为1.(3)求证:f(x)在区间(0,e)上有两个零点的充要条件为k∈(1﹣e,﹣1).【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性;利用导数研究函数的极值.【专题】计算题;分类讨论;转化思想;综合法;导数的综合应用.【分析】(1)利用f[f(1)]<0,推出k的不等式,求解即可.(2)求出,求出g(x)的单调递增区间,讨论0<a<1,当给定的时,D?(0,a]不成立.得到a≥1,然后推出a的最小值.(3)设f(x)=lnx﹣x﹣k,x∈(0,e),求出导数,得到函数的单调区间,利用f(x)在区间(0,e)上有两个零点的必要条件为,转化求解k的取值范围.【解答】解:(1)f[f(1)]<0,即f(﹣1﹣k)<0,即ln(﹣1﹣k)﹣(﹣1﹣k)﹣k<0,即ln(﹣1﹣k)<﹣1,所以.(2)得2kx2+x﹣1<0,注意到,所以g(x)的单调递增区间为.若0<a<1,则令,得,这说明当给定的时,D?(0,a]不成立.所以a≥1,又a=1时,,这显然正确,所以a=1满足条件,故a的最小值为1.(3)证明:设f(x)=lnx﹣x﹣k,x∈(0,e),则,所以f(x)在(0,1)上单调递增,在(1,e)上单调递减,f(1)=﹣1﹣k,f(e)=1﹣e﹣k,因此f(x)在区间(0,e)上有两个零点的必要条件为,即1﹣e<k<﹣1.当,即1﹣e<k<﹣1时,因为f(e k)=﹣e k<0,e k<1,结合f(x)在(0,1)上单调递增,得在区间f(x)在(0,1)上存在唯一零点,而,及f(x)在(1,e)上单调递减,得f(x)在区间(1,e)上存在唯一零点,故f(x)在区间(0,e)上有两个零点的充要条件为1﹣e<k<﹣1.故所求的k的取值范围为(1﹣e,﹣1).三、理科加试11.(2012?惠州模拟)某班从6名干部中(其中男生4人,女生2人)选3人参加学校的义务劳动.(1)设所选3人中女生人数为ξ,求ξ的分布列及Eξ;(2)求男生甲或女生乙被选中的概率;(3)在男生甲被选中的情况下,求女生乙也被选中的概率.【考点】离散型随机变量的期望与方差;等可能事件的概率.【专题】计算题.【分析】(1)ξ的所有可能取值为0,1,2,再根据题意分别求出其概率即可得到其分布列,进而求出其期望.(2)根据题意求出其对立事件的概率,进而根据有关公式求出答案.(3)记“男生甲被选中”为事件A,“女生乙被选中”为事件B,再求出事件A与事件A、B 共同发生的概率,进而根据条件概率的公式求出答案.【解答】解:(1)ξ的所有可能取值为0,1,2,所以依题意得:P(ξ=0)==,P(ξ=1)==,P(ξ=2)==所以ξ的分布列为ξ01 2P所以Eξ=.(2)设“甲、乙都不被选中”为事件C,则P(C)==,所以所求概率为.(3)记“男生甲被选中”为事件A,“女生乙被选中”为事件B,所以P(A)==,所以P(B|A)=.所以在男生甲被选中的情况下,女生乙也被选中的概率为.12.(2016?江苏模拟)设整数n≥3,集合P={1,2,3,…,n},A,B是P的两个非空子集.记a n为所有满足A中的最大数小于B中的最小数的集合对(A,B)的个数.(1)求a3;(2)求a n.【考点】数列的求和;子集与真子集.【专题】等差数列与等比数列.【分析】(1)当n=3时,P={1,2,3 },由此能求出a3=5.(2)设A中的最大数为k,其中1≤k≤n﹣1,整数n≥3,则A中必含元素k,另元素1,2,…,k﹣1,可在A中,B中必不含元素1,2,…,k;元素k+1,k+2,…,k可在B中,但不能都不在B中.由此能求出a n.【解答】解:(1)当n=3时,P={1,2,3 },其非空子集为:{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3},则所有满足题意的集合对(A,B)为:({1},{2}),({1},{3}),({2},{3}),({1},{2,3}),({1,2},{3})共5对,∴a3=5.…(3分)(2)设A中的最大数为k,其中1≤k≤n﹣1,整数n≥3,则A中必含元素k,另元素1,2,…,k﹣1,可在A中,故A的个数为:,…(5分)B中必不含元素1,2,…,k,另元素k+1,k+2,…,n可在B中,但不能都不在B中,故B的个数为:=2n﹣k﹣1,…(7分)从而集合对(A,B)的个数为2k﹣1?(2n﹣k﹣1)=2n﹣1﹣2k﹣1,∴a n=(2n﹣1﹣2k﹣1)=n﹣1+1.…(10分)=(n﹣2)?2参与本试卷答题和审题的老师有:whgcn;maths;双曲线;zhczcb;lcb001;炫晨;铭灏2016;刘长柏;qiss;haichuan;zlzhan(排名不分先后)菁优网2016年11月9日。
江苏省南大附中2015-2016学年度高三数学第一学期期中试卷(无答案)

南大附中2015-2016学年度高三数学第一学期期中试卷一、填空题:(本大题共14小题,每小题5分,共计70分)1、设全集U =R ,集合A ={x |1≤x ≤3},则C U A =_______2、函数f (x )=ln (2—x )的定义域为_________3、已知m ,n 为实数,若关于x 的不等式x 2+mx +n <0的解集为(—1,3),则m +n 的值为_______4、过点P (1,0)且与直线2x +y —5=0平行的直线的方程为________5、已知a ,b 是夹角为60°的两个单位向量,则|a +b |=_______6、若曲线f (x )=2ln —xm 在x =1处的切线的斜率为3,则实数m 的值为________ 7、已知2x +3y =6,则4x +8y 的最小值为________8、函数f (x )=2xe (e 为自然对数的底数)的单调减区间为_______9、若实数x ,y 满足条件0,0,3250,2.x y x y x y ≥⎧⎪≥⎪⎨+-≤⎪⎪+≤⎩ 则z =5x +4y 的最大值为_______ 10、用半径为r的圆锥筒,则r 的值为_______11、已知函数f (x )=3sin (2x —3π),若函数y =f (x +a )(0<a <2π)为偶函数,则a 的值为_______12、在等腰梯形ABCD 中,已知AB //DC ,∠ABC =60°,BC =12AB =2,动点E 和F 分别在线段BC 和DC 上,且BE =λBC ,DF =λ21DC ,则AE ·BF 的最小值为_______A B(第12题)13、已知圆C :(x +1)2+(y —1)2=1,直线l :y =2x —4上存在点P ,使得过点P 可作一条射线与圆依次交于点A ,B ,满足P A =2AB ,则点P 的横坐标的取值范围是________14、已知e 为自然对数的底数,若方程|xlnx —ex +e |=mx 在区间[e1,e 2]上有三个不同实数根,则实数m 的取值范围是________二、解答题:(本大题共6小题,共计90分)15、(本小题满分14分) F在∆ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若2asinB =3b ,cosC =135. (1)求sinA 的值;(2)求cosB 的值.16、(本小题满分14分)如图,在正三棱柱ABC —A 1B 1C 1中,点D 为为边BC 的中点,AB =4,AA 1=2.(1)若点E 是B 1C 1的中点,求证A 1E //平面ADB 1;(2)求证:平面ADC 1⊥平面ADB 1.(第16题)ABC A 1 B 1 C 1E D17、(本小题满分14分)设函数f (x )=ax —sinx(1)若函数f (x )在R 上是单调增函数,求实数a 的取值范围;(2)当a =21时,求函数f (x )在区间[0,2π]上的最大值与最小值.18、(本小题满分16分)一幅广告印刷品的画面(矩形,如图①阴影部分)面积6m 2,它的两边都留有宽为0.15m 的空白,顶部和底部都留有宽为0.1m 的空白(1)如何选择纸张的尺寸,才能使纸张的用量最少?(2)如图②,将此广告张贴在墙上,其画面(不包含空白)的最高点A 处离地面4m ,最低点B 处离地面2m ,若从地面1.5m 的C 处观赏它,则离墙多远是,视角θ 最大?A B C 4m 1.5m 2m ① ② (第18题)19、(本小题满分16分)已知∆ABC 的三个顶点A (0,2),B (0,4),C (1,3),其外接圆为圆M(1)求圆M 的方程;(2)若直线l 过点D (12,2),且被圆M ,求直线l 的方程; (3)设点P 为圆M 上异于A ,B 的任意一点,直线P A 交x 轴于点E ,直线PB 交x 轴于点F ,问以EF 为直径的圆N 是否过定点?若过定点,求出定点坐标;若不过定点,说明理由.20、(本小题满分16分)设函数f (x )=|x —m |,其中m 为实数(1)若方程f (x )=|m |有两个不同的非负实数解,求m 的取值范围;(2)设函数g (x )=xf (x )+m 2—7m ,若对任意x 1∈(—∞,4] ,均存在x 2∈[3,+∞),使得f (x 1)>g (x 2)成立,求m 的取值范围;(3)设m ,函数h (x )=xf (x )在区间(s ,t )上既有最大值又有最小值,试分别求出实数s ,t 的取值范围(用m 表示)。
江苏省南京市南京师范大学附属中学2017届高三数学考前模拟考试试题(含解析)

2017届南京师范大学附中高三考前模拟考试数学第Ⅰ卷(共60分)一、填空题:本大题共14个小题,每小题5分,共70分.不需要写出解答过程,请把答案写在答题纸指定的位置上.1. 已知集合,则 ______________【答案】【解析】,所以2. 已知复数满足,其中为虚数单位,则复数的模 ______________ 【答案】【解析】因为,所以3. 某时段内共有100辆汽车经过某一雷达测速区域,将测得的汽车时速绘制成如图所示的频率分布直方图,根据图形推断,该时段的时速超过的车辆数为______________辆.【答案】【解析】试题分析:根据频率分布直方图,得时速超过的汽车的频率为;所以时速超过的汽车辆数为.所以答案应填:77.考点:频率分布直方图.4. 如图所示的流程图中,输出的为______________【答案】【解析】由题意输出点睛:算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项.5. 函数的定义域是______________【答案】【解析】由题意得,即定义域是6. 袋中有形状、大小相同的只球,其中只白球,只红球,只黄球,从中一次随机摸出只球,则这只球颜色不同的概率为______________【答案】【解析】试题分析:根据题意,记白球为A,红球为B,黄球为,则一次取出2只球,基本事件为、、、、、共6种,其中2只球的颜色不同的是、、、、共5种;...所以所求的概率是.考点:古典概型概率7. 已知正四棱锥的底面边长为,高为,则该四棱锥的侧面积是______________【答案】【解析】四棱锥的侧面积是8. 设变量满足约束条件,若目标函数的最小值为,则___________【答案】【解析】可行域为一个三角形ABC及其内部,其中 ,因为目标函数的最小值为,所以,因此,解得点睛:线性规划的实质是把代数问题几何化,即数形结合的思想.需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最大或最小值会在可行域的端点或边界上取得.9. 设函数,且的图象的一个对称中心到最近的对称轴的距离为,则在区间上的最大值为______________【答案】【解析】,由题意得,因此,则在区间上的最大值为1.点睛:三角恒等变换的综合应用主要是将三角变换与三角函数的性质相结合,通过变换把函数化为的形式再借助三角函数图象研究性质,解题时注意观察角、函数名、结构等特征.10. 设是等比数列的前项和,若满足,则_________【答案】【解析】因为,所以,因此11. 若且,则的最小值为______________【答案】【解析】因为,所以;因为,所以,即因此当且仅当时取等号12. 已知是圆上的一动点,是圆的一条动弦(是直径的两个端点),则的取值范围是______________【答案】【解析】设圆圆心为C.则,又,因此13. 设,对总有,则的取值范围是______________ 【答案】【解析】由题意得当时,;当时,;当时,;令,则,因此当时,;当时,当时,,综上的取值范围是14. 在中,已知边所对的角分别为,若,则 _________________【答案】...【解析】由正弦定理得,由余弦定理得,即因为所以点睛:三角形中问题,一般先根据正、余弦定理及三角形面积公式结合已知条件灵活转化边和角之间的关系,利用基本不等式或三角函数有界性求取值范围. 最后根据等号取法确定函数值.第Ⅱ卷(共80分)二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15. 在中,角的对边分别为,已知.(1)求的值;(2)若,求的面积.【答案】(1)(2)【解析】试题分析:(1)根据正弦定理将角的关系转化为边的关系:,即得的值;(2)根据向量数量积得,再利用余弦定理得,结合,解方程组可得,代得,即得,最后根据三角形面积公式求面积.试题解析:解:(1)由正弦定理,;(2),所以,所以.16. 如图,在四棱锥中,.(1)若是的中点,求证:平面;(2)若,求证:平面平面.【答案】(1)见解析(2)见解析【解析】试题分析:(1)取的中点,利用平几知识证明四边形是平行四边形,即得.最后根据线面垂直判定定理得平面;(2)由平均知识计算,再由,根据线面垂直判定定理得面,最后根据面面垂直判定定理得平面平面.试题解析:解(1)取的中点,连接和,由因为是的中点,所以是的中位线,所以,由题意,所以,所以四边形是平行四边形,所以.因为,所以平面;(2)由题意,在直角梯形中,经计算可证得,又面,,面,又面,所以平面平面.点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.(1)证明线面、面面平行,需转化为证明线线平行.(2)证明线面垂直,需转化为证明线线垂直....(3)证明线线垂直,需转化为证明线面垂直.17. 园林管理处拟在公园某区域规划建设一半径为米圆心角为(弧度)的扇形景观水池,其中为扇形的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过万元,水池造价为每平方米元,步道造价为每米元.(1)当和分别为多少时,可使广场面积最大,并求出最大值;(2)若要求步道长为米,则可设计出水池最大面积是多少.【答案】(1)最大值为400.(2)当时,最大平方米,此时.【解析】试题分析:(1)步道长为扇形周长,利用弧长公式及扇形面积公式可得不等式,利用基本不等式将不等式转化为关于的一元不等式,解得的范围,确定最大值为400.(2)由条件得,消得,由及,解出,根据二次函数最值取法得到当时,最大试题解析:解:(1)由题意,弧长为,扇形面积为,由题意,即,即,所以,所以,,则,所以当时,面积的最大值为400.(2)即,代入可得或,又,当与不符,在上单调,当时,最大平方米,此时.18. 平面直角坐标系中,椭圆过点,离心率为.(1)求椭圆的标准方程;(2)过点作一直线与椭圆交于两点,过点作椭圆右准线的垂线,垂足分别为,试问直线与的交点是否为定点,若是,求出定点的坐标;若不是,请说明理由.【答案】(1)(2)直线与过定点.【解析】试题分析:(1)由离心率得,由椭圆过点得,解方程组可得(2)先根据对称性得定点必在x轴上,再利用特殊位置确定定点为.最后证明直线与皆过定点.试题解析:解(1)由题意得,所以椭圆的标准方程为.(2)①当直线的斜率不存在时,准线与的交点是;②当直线的斜率存在时,设,直线为,由,所以,,所以,联立解得,...代入上式可得,综上,直线与过定点.点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现.19. 设为常数).(1)当时,求的单调区间;(2)若在区间的极大值、极小值各有一个,求实数的取值范围.【答案】(1)单调递增区间为,单调递减区间为.(2)【解析】试题分析:(1)先求导数,再根据导函数大于零得三角不等式,解得单调增区间;同理根据导函数小于零得三角不等式,解得单调减区间,注意单调区间不可用并集连接,(2)导函数必有两个不等的零点,利用导数分析导函数图像得:先增后减再增,比较两个端点及两个极值点知,,解不等式可得实数的取值范围.试题解析:解:(1)当时,,令,则单调增;令,则单调增,所以的单调递增区间为,单调递减区间为.(2)设,则,令,则,令,则,所以的单调递增区间为,单调递减区间为.故在处取得极大值,在处取得极小值,,所以①若,则在上单调增,故在无极值,所以;②若,则在内至多有一个极值点,从而,于是在区间内分别有极大值、极小值各一个,则在内无极值点,从而,所以的取值范围是.20. 设是各项均不相等的数列,为它的前项和,满足.(1)若,且成等差数列,求的值;(2)若的各项均不相等,问当且仅当为何值时,成等差数列?试说明理由.【答案】(1)(2)当且仅当时,成等差数列【解析】试题分析:(1)根据解出(用表示),再根据成等差数列,得,代入解出的值;(2)先研究成等差数列时为何值,同(1)根据解出,(用表示),再根据成等差数列解出的值;再证明时,成等差数列,实际上求出这个关系式.试题解析:解:(1)令,得,...又由成等差数列,所以,解得.(2)当且仅当时,成等差数列,证明如下:由已知,当时,,两式相减得,即,由于个各项均不相等,所以,当时,所以两式相减可得,①当,得,当时,所以,,所以,故成等差数列.②再证当成等差数列时,,因为成等差数列,所以,可得,所以,所以当且仅当时,成等差数列.21. 如图,为的直径,为上一点,过作的切线交的延长线于点,若,求证:.【答案】见解析【解析】试题分析:根据弦切角定理得,而可得,因此,即得,因此.试题解析:解:连接,因为为切线且点为切点,所以,因为,所以又因为所以故,所以,从而.22. 已知矩阵,其中,若点在矩阵的变换下得到点,...求矩阵的两个特征值.【答案】【解析】试题分析:由矩阵变换得,解得,再利用特征多项式求特征值试题解析:解:,所以,即,特征方程,因此.23. 已知点是曲线为参数,)上一点,为原点,若直线的倾斜角,求点的直角坐标.【答案】点的坐标为.【解析】试题分析:先根据同角三角函数平方关系消去参数得曲线的普通方程,再根据点斜式得直线的方程,最后联立方程组解出点的直角坐标.试题解析:解:由题意得,曲线的普通方程为, ,直线的方程为,联立得(舍去)或,所以点的坐标为.24. 已知实数满足,求的最小值.【答案】 【解析】略25. 某小组共10人,利用暑假参加义工活动,已知参加义工活动此时为的人数分别为,现从10人中学车2人作为该组参加座谈会.(1)记“选出2人参加义工活动的次数之和为4”为事件,求事件的发生的概率; (2)设为选出2人参加义工活动次数之差的绝对值,求随机变量的分布列和数学期望. 【答案】(1).(2),分布列见解析【解析】试题分析:(1)借助题设条件运用概率公式求解;(2)借助题设条件运用概率公式和数学期望公式求解. 试题解析:由题得:的可能取值为,,∴的分布列为:∴考点:概率公式及数学期望的计算公式等有关知识的综合运用.26. (1)设,求.(2)设,求的整数部分的个位数字.【答案】(1)(2)的个位为.【解析】试题分析:(1)利用二项式定理分别求项系数得.(2)取对偶关系式,的整数部分的个位数字利用二项式定理证明为整数且个位数为0,根据范围确定,从而得到试题解析:解:(1)因为,所以.(2)令,则,已知为整数且个位数为0,而,所以,所以的个位为.。
江苏省南京师大附中高三上学期期中考试数学试题(扫描版,无答案).pdf

集备部分自备部分第二章陆地和海洋第一节 大洲和大洋教学目标 课时:一课时 教学手段:多媒体课件、展示台教学过程: 【问题引入】宇航员加加林指着从人造地球卫星上拍摄的地球照片说:“我看到的地球更像水球。
”那同学们认为自己所居住的星球,是该叫“地球”呢,还是该叫“水球”呢? 【活动】1:学生讨论自己所居住的星球是应叫“地球”还是应叫“水球”? 2:学生发表自己的观点并说明理由; 3:引导学生旋转地球仪,用右手食指随机点出是陆地还是海洋,并作概率统计。
【演示】课件(水半球和陆半球图、世界海陆面积比较图)说明地球表面的海洋和陆地的比例:“七分海洋、三分陆地”。
【转承】同学们是生活在陆地上还是海洋里哪?(陆地上)那么,陆地都有哪些表现形式呢?那海洋呢? 【演示】课件(中国东部沿海分布图) 【活动】1、请学生根据学过的有关的地图知识,找出自己熟悉的岛屿、半岛和大陆; 2、请学生在图中找出自己熟悉的海、洋、海峡; 【展示】“大陆、半岛、岛屿与海洋”素描图,让学生巩固陆地和海洋的各种表现形式。
【转承】教师点评学生的谈话,同时引出“大陆与它周围的岛屿合起来称为大洲”。
那同学们知道全球分为哪些大洲吗? 【演示】课件(大洲、大洋的分布图) 【活动】1、请一位同学带领全班学生认识七大洲轮廓和大小; 2、请学生观察课本 “世界政治地图”,完成拼图游戏? ? 3、让全体同学根据所拼世界地图,观察地图仪说出主要大洲的分界线。
【演示】课件(亚洲与欧洲、非洲分界图) 【转承】在熟悉七大洲的位置时,我们发现各大洲基本上被海洋包围,那如果从海洋的角度去观察,你会发现什么特点呢? 【活动】1、学生讨论后认为海洋是彼此相连的,并且被陆地分隔成相对独立的四部分,即上面提到的四大洋。
? 2、让学生看图思考四大洋各被哪些大洲所包围。
【课堂训练】:根据拼图模板提问: 1、面积由大到小排序? “亚非北南美、南极欧大洋” 2、它们的轮廓大致有什么特点? 3、全球共有哪几个大陆? 4、赤道横穿哪几个洲的大陆? 5、哪些大洲全部或大部分在北半球?那南半球呢? 6、练一练:在全球图、东西半球图、南北半球图中填填写 七大洲四大洋 大陆 地球:陆地29% 表现形式 半岛 大洲 七大洲 水球:海洋71% 表现形式 洋 大洋 四大洋 【课堂小结】: 初中学习网,资料共分享!我们负责传递知识!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年江苏省南京师大附中高三(上)期中数学试卷(文科)一、填空题:本大题共14个小题,每小题5分,共70分.请把答案填在答卷纸相应位置上.1.(5分)已知集合U={1,2,3,4},A={1,3},B={1,3,4},则A∩(∁U B)=.2.(5分)若复数z满足,则的共轭复数是.3.(5分)已知一组数据3,5,4,7,6,那么这组数据的方差为.4.(5分)袋中有形状、大小都相同的4只球,其中2只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为.5.(5分)如图,矩形ABCD由两个正方形拼成,则∠CAE的正切值为.6.(5分)如图是一个算法流程图,则输出的k的值是.7.(5分)若实数x,y满足条件,则z=3x﹣4y的最大值是.8.(5分)若双曲线﹣=1的一条渐近线经过点(3,﹣4),则此双曲线的离心率为.9.(5分)已知cos()=,则cos()﹣sin2(α﹣)=.10.(5分)在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°,点E和F分别在线段BC和DC上,且=,=,则•的值为.11.(5分)等比数列{a n}的首项为2,公比为3,前n项和为S n,若log3[a n (S4m+1)]=9,则+的最小值是.12.(5分)在平面直角坐标系xOy中,点A(1,0),B(4,0),若直线x﹣y+m=0上存在点P,使得2PA=PB,则实数m的取值范围是.13.(5分)已知函数f(x)=,g(x)=kx+1,若方程f(x)﹣g(x)=0有两个不同实根,则实数k的取值范围为.14.(5分)已知不等式(ax+3)(x2﹣b)≤0对任意x∈(0,+∞)恒成立,其中a,b是整数,则a+b的取值的集合为.二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.(14分)在△ABC中,角A,B,C的对边分别为a,b,c,且=.(1)求角A的值;(2)若△ABC的面积为,且a=,求△ABC的周长.16.(14分)在四棱锥P﹣ABCD中,∠ACD=90°,∠BAC=∠CAD,PA⊥平面ABCD,E为PD的中点.(1)求证:平面PAC⊥平面PCD;(2)求证:CE∥平面PAB.17.(14分)如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).(1)若要求圆柱体罐子的侧面积最大,应如何截取?(2)若要求圆柱体罐子的体积最大,应如何截取?18.(16分)如图,在平面直角坐标系xOy中,已知A,B,C是椭圆=1(a>b>0)上不同的三点,,B(﹣2,﹣2),C在第三象限,线段BC的中点在直线OA上.(1)求椭圆的标准方程;(2)求点C的坐标;(3)设动点P在椭圆上(异于点A,B,C)且直线PB,PC分别交直线OA于M,N两点,证明为定值并求出该定值.19.(16分)已知数列{a n}和{b n}满足a1a2a3…a n=(n∈N*).若{a n}为等比数列,且a1=2,b3=6+b2.(Ⅰ)求a n和b n;(Ⅱ)设c n=(n∈N*).记数列{c n}的前n项和为S n.(i)求S n;(ii)求正整数k,使得对任意n∈N*均有S k≥S n.20.(16分)已知函数f(x)=x2﹣2alnx(a∈R),g(x)=2ax.(1)求函数f(x)的极值;(2)若a>0,函数h(x)=f(x)﹣g(x)有且只有一个零点,求实数a的值;(3)若0<a<1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f (x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,求a的取值范围.2016-2017学年江苏省南京师大附中高三(上)期中数学试卷(文科)参考答案与试题解析一、填空题:本大题共14个小题,每小题5分,共70分.请把答案填在答卷纸相应位置上.1.(5分)已知集合U={1,2,3,4},A={1,3},B={1,3,4},则A∩(∁U B)=∅.【解答】解:∵集合U={1,2,3,4},B={1,3,4},∴∁U B={2},∵A={1,3},∴A∩(∁U B)=∅,故答案为:∅2.(5分)若复数z满足,则的共轭复数是1+i.【解答】解:∵,∴﹣i•i=﹣i(1+i),则=1﹣i则的共轭复数是1+i.故答案为:1+i.3.(5分)已知一组数据3,5,4,7,6,那么这组数据的方差为2.【解答】解:一组数据3,5,4,7,6,这组数据的平均数==5,这组数据的方差S2=[(3﹣5)2+(5﹣5)2+(4﹣5)2+(7﹣5)2+(6﹣5)2]=2.故答案为:2.4.(5分)袋中有形状、大小都相同的4只球,其中2只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为.【解答】解:袋中有形状、大小都相同的4只球,其中2只红球,2只黄球,从中一次随机摸出2只球,基本事件总数n==6,这2只球颜色不同,包含的基本事件个数m=C=4,∴这2只球颜色不同的概率p==.故答案为:.5.(5分)如图,矩形ABCD由两个正方形拼成,则∠CAE的正切值为.【解答】解:因为矩形ABCD由两个正方形拼成,设正方形的边长为1,则在Rt△CAD中,=2,,所以⇔⇒.故答案为:6.(5分)如图是一个算法流程图,则输出的k的值是3.【解答】解:模拟程序的运行,可得S=1,k=1S=2,不满足条件S>10,k=2,S=6不满足条件S>10,k=3,S=15满足条件S>10,退出循环,输出k的值为3.故答案为:3.7.(5分)若实数x,y满足条件,则z=3x﹣4y的最大值是﹣1.【解答】解:不等式组对应的平面区域如图:由z=3x﹣4y得y=,平移直线y=,则由图象可知当直线y=,当经过点A时,直线的截距最小,此时z最大.由,解得,即A(1,1),此时最大值z=3×1﹣4×1=﹣1,故答案为:﹣18.(5分)若双曲线﹣=1的一条渐近线经过点(3,﹣4),则此双曲线的离心率为.【解答】解:双曲线﹣=1的渐近线方程为y=±x,由渐近线过点(3,﹣4),可得﹣4=﹣,即b=a,c===a,可得e==.故答案为:.9.(5分)已知cos()=,则cos()﹣sin2(α﹣)=.【解答】解:cos()=cos[π﹣(﹣α)]=﹣cos(﹣α)=﹣sin2(α﹣)=sin2[﹣(﹣α)]=1﹣cos2(﹣α)=1﹣(﹣)2=∴cos()﹣sin2(α﹣)=﹣﹣=﹣.故答案为:﹣10.(5分)在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°,点E和F分别在线段BC和DC上,且=,=,则•的值为.【解答】解:∵AB=2,BC=1,∠ABC=60°,∴BG==,CD=2﹣1=1,∠BCD=120°,∵=,=,∴•=(+)•(+)=(+)•(+)=•+•+•+•=2×1×cos60°+×2×1×cos0°+×1×1×cos60°+××1×1×cos120°=1+=,故答案为:11.(5分)等比数列{a n}的首项为2,公比为3,前n项和为S n,若log3[a n (S4m+1)]=9,则+的最小值是 2.5.【解答】解:∵等比数列{a n}的首项为2,公比为3,前n项和为S n,∴a n=2•3n﹣1;S n=3n﹣1,∵log3[a n•(S4m+1)]=9,∴(n﹣1)+4m=9,∴n+4m=10,∴+=(n+4m)(+)=(17+)≥(17+8)=2.5,当且仅当m=n=2时取等号,∴+的最小值是2.5.故答案为:2.5.12.(5分)在平面直角坐标系xOy中,点A(1,0),B(4,0),若直线x﹣y+m=0上存在点P,使得2PA=PB,则实数m的取值范围是[﹣2,2] .【解答】解:设P(x,x+m),∵2PA=PB,∴4|PA|2=|PB|2,∴4(x﹣1)2+4(x+m)2=(x﹣4)2+(x+m)2,化为(x+m)2=4﹣x2,∴4﹣x2≥0,解得x∈[﹣2,2],∴m=﹣x±,令x=2cosθ,θ∈[0,π],∴m=﹣2cosθ±2sinθ=±2sin(θ±)∈[﹣2,2],实数m的取值范围是[﹣2,2],故答案为[﹣2,2].13.(5分)已知函数f(x)=,g(x)=kx+1,若方程f(x)﹣g (x)=0有两个不同实根,则实数k的取值范围为(,1)∪(1,e﹣1];.【解答】解:∵g(x)=kx+1,∴方程f(x)﹣g(x)=0有两个不同实根等价为方程f(x)=g(x)有两个不同实根,即f(x)=kx+1,则等价为函数f(x)与函数y=kx+1有两个不同的交点,当1<x≤2,则0<x﹣1≤1,则f(x)=f(x﹣1)=e x﹣1,当2<x≤3,则1<x﹣1≤2,则f(x)=f(x﹣1)=e x﹣2,当3<x≤4,则2<x﹣1≤3,则f(x)=f(x﹣1)=e x﹣3,…当x>1时,f(x)=f(x﹣1),周期性变化;函数y=kx+1的图象恒过点(0,1);作函数f(x)与函数y=kx+1的图象如下,C(0,1),B(2,e),A(1,e);故k AC=e﹣1,k BC=;在点C处的切线的斜率k=e0=1;结合图象可得,当k∈(1,e一1]时,k取中间值,交点在f(x)=e x上两点,定点(0,1),另一点在第一象限A点下方.当k∈(,1)时,任取k为中间值,则交点过C,另一点在笫二象限,点c 的左下方.当k∈(0,],交点有3点以上,与f(x)、f(x一1)都有交点.当k∈(一∞,e一1)时,与f(x)只交于点C.综上要使两个函数有两个交点,则实数k的取值范围为(,1)∪(1,e﹣1];故答案为:(,1)∪(1,e﹣1];14.(5分)已知不等式(ax+3)(x2﹣b)≤0对任意x∈(0,+∞)恒成立,其中a,b是整数,则a+b的取值的集合为{﹣2,8} .【解答】解:当b≤0 时,由(ax+3)(x2﹣b)≤0得到ax+3≤0 在x∈(0,+∞)上恒成立,则a不存在;当b>0 时,由(ax+3)(x2﹣b)≤0,可设f(x)=ax+3,g(x)=x2﹣b,又g(x)的大致图象如下,那么由题意可知:再由a,b 是整数得到或因此a+b=8或﹣2.故答案为{﹣2,8}二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.(14分)在△ABC中,角A,B,C的对边分别为a,b,c,且=.(1)求角A的值;(2)若△ABC的面积为,且a=,求△ABC的周长.【解答】解:(1)由=,利用正弦定理可得2sinBcosA﹣sinCcosA=sinAcosC,化为2sinBcosA=sin(C+A)=sinB,∵sinB≠0,∴cosA=,∵A∈(0,π),∴A=.(2)∵A=,△ABC的面积为=bcsinA=bc×,∴bc=2,∵a=,由余弦定理a2=b2+c2﹣2bccosA,可得:5=b2+c2﹣bc=(b+c)2﹣3bc=(b+c)2﹣6,∴解得:b+c=,∴△ABC的周长l=a+b+c=+.16.(14分)在四棱锥P﹣ABCD中,∠ACD=90°,∠BAC=∠CAD,PA⊥平面ABCD,E为PD的中点.(1)求证:平面PAC⊥平面PCD;(2)求证:CE∥平面PAB.【解答】证明:(1)因为PA⊥平面ABCD,CD⊂平面ABCD,所以PA⊥CD,…(2分)又∠ACD=90°,则CD⊥AC,而PA∩AC=A,所以CD⊥平面PAC,因为CD⊂平面ACD,…(4分)所以,平面PAC⊥平面PCD.…(7分)(2)证法一:取AD中点M,连EM,CM,则EM∥PA.因为EM⊄平面PAB,PA⊂平面PAB,所以EM∥平面PAB.…(9分)在Rt△ACD中,AM=CM,所以∠CAD=∠ACM,又∠BAC=∠CAD,所以∠BAC=∠ACM,则MC∥AB.因为MC⊄平面PAB,AB⊂平面PAB,所以MC∥平面PAB.…(12分)而EM∩MC=M,所以平面EMC∥平面PAB.由于EC⊂平面EMC,从而EC∥平面PAB.…(14分)(2)证法二:延长DC,AB交于点N,连PN.因为∠NAC=∠DAC,AC⊥CD,所以C为ND的中点.而E为PD中点,所以EC∥PN.因为EC⊄平面PAB,PN⊂平面PAB,所以EC∥平面PAB.…(14分)17.(14分)如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).(1)若要求圆柱体罐子的侧面积最大,应如何截取?(2)若要求圆柱体罐子的体积最大,应如何截取?【解答】解:(1)连接OC,设BC=x,则AB=2,(其中0<x<30),∴S=2x=2 ≤x2+(900﹣x2)=900,当且仅当x2=900﹣x2,即x=15时,S取最大值900;∴取BC=15cm时,矩形ABCD的面积最大,最大值为900cm2.(2)设圆柱底面半径为r,高为x,则AB=2=2πr,解得r=,∴V=πr2h=(900x﹣x3),(其中0<x<30);∴V′=(900﹣3x2),令V′(x)=0,得x=10;因此V(x)=(900x﹣x3)在(0,10 )上是增函数,在(10,30)上是减函数;∴当x=10时,V(x)取得最大值V(10)=,∴取BC=10cm时,做出的圆柱形罐子体积最大,最大值为cm3.18.(16分)如图,在平面直角坐标系xOy中,已知A,B,C是椭圆=1(a>b>0)上不同的三点,,B(﹣2,﹣2),C在第三象限,线段BC的中点在直线OA上.(1)求椭圆的标准方程;(2)求点C的坐标;(3)设动点P在椭圆上(异于点A,B,C)且直线PB,PC分别交直线OA于M,N两点,证明为定值并求出该定值.【解答】解:(1)由已知,将,B(﹣2,﹣2)代入椭圆方程:,解得,∴椭圆的标准方程为;…(4分)(2)解:设点C(m,n)(m<0,n<0),则BC中点为(,).由已知,求得直线OA的方程:x﹣2y=0,从而m=2n﹣2.①又∵点C在椭圆上,∴m2+4n2=20.②由①②,解得:n=2(舍),n=﹣1,从而m=﹣4.∴点C的坐标为(﹣4,﹣1).…(8分)(3)证明:设P(x0,y0),M(2y1,y1),N(2y2,y2).∵P,B,M三点共线,则=整理得y1=.…(10分)∵P,C,N三点共线,则=,整理得y2=.…(12分)∵点C在椭圆上,∴x02+4y02=20,x02=20﹣4y02,从而y1y2===2×=.…(14分)∴•=5y1y2=.∴•为定值,定值为.…(16分)19.(16分)已知数列{a n}和{b n}满足a1a2a3…a n=(n∈N*).若{a n}为等比数列,且a1=2,b3=6+b2.(Ⅰ)求a n和b n;(Ⅱ)设c n=(n∈N*).记数列{c n}的前n项和为S n.(i)求S n;(ii)求正整数k,使得对任意n∈N*均有S k≥S n.【解答】解:(Ⅰ)∵a1a2a3…a n=(n∈N*)①,当n≥2,n∈N*时,②,由①②知:,令n=3,则有.∵b3=6+b2,∴a3=8.∵{a n}为等比数列,且a1=2,∴{a n}的公比为q,则=4,,∴q>0,∴q=2.由题意知a n>0∴(n∈N*).又由a1a2a3…a n=(n∈N*)得:,,∴b n=n(n+1)(n∈N*).(Ⅱ)(i)∵c n===.∴S n=c1+c2+c3+…+c n====;(ii)因为c1=0,c2>0,c3>0,c4>0;当n≥5时,,而=>0,得,所以,当n≥5时,c n<0,综上,对任意n∈N*恒有S4≥S n,故k=4.20.(16分)已知函数f(x)=x2﹣2alnx(a∈R),g(x)=2ax.(1)求函数f(x)的极值;(2)若a>0,函数h(x)=f(x)﹣g(x)有且只有一个零点,求实数a的值;(3)若0<a<1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f (x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,求a的取值范围.【解答】解:(1)f′(x)=,当a≤0时,f′(x)>0,f(x)在(0,+∞)递增,f(x)无极值,当a>0时,x∈(0,)时,f′(x)<0,f(x)递减,x∈(,+∞)时,f′(x)>0,f(x)递增,∴f(x)有极小值f()=a﹣alna,综上:a≤0时,f(x)无极值,a>0时,f(x)极小值=a﹣alna,无极大值;(2)令h(x)=x2﹣2alnx﹣2ax,则h′(x)=,∵a>0,令h′(x)=0,解得x0=,∴h(x)在(0,)递减,在(,+∞)递增,∴h(x)在x0处取得极小值h(x0)=0,∴﹣2alnx0﹣2ax0=0且2﹣2ax0﹣2a=0,联立可得:2lnx0+x0﹣1=0,令m(x)=2lnx+x﹣1得m′(x)=+1>0,故m(x)在(0,+∞)递增又m(1)=0,x0=1,即=1,解得:a=;(3)不妨令1≤x1<x2≤2,则由(1)得f(x1)<f(x2)∴|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)⇔f(x2)﹣f(x1)>g(x2)﹣g(x1)⇔f(x2)﹣g(x2)>f(x1)﹣g(x1),则h(x)在[1,2]递增,∴h′(x)=≥0在[1,2]恒成立,即2x2﹣2ax﹣2a≥0在[1,2]恒成立,∴a≤在[1,2]恒成立,令t=x+1∈[2,3],则=t+﹣2≥,∴0<a≤,∴a的范围是(0,].。
