全微分方程及积分因子
全微分方程与积分因子法

已构成全微分的项分出再把剩下的项凑成全微分.但这种方法
要求熟记一些简单二元函数的全微分,如
ydx+xdy=d(x,y)
ydx-xdy y2
=d(
x y
)
-ydx+xdy x2
=d(
x y
)
ydx-xdy =d(ιn| x |)
xy
y
ydx-xdy x2+y2
=d(arctg
x y
)
| | ydx-xdy x2-y2
的通解为
μ(x,y)=∫x0xP(x,y)dx+∫y0xQ(x,y)dy=C
(7)
其中点(x0,y0)可在与路径无关的单连通区域 G 内 任 意 取
得.很 多 情 况 下 都 选 (0,0)为 (x0,y0),只 有 当 点 (0,0)不 在 上 述
单连通区域 G 内,才考虑其他点作为曲线积分的始点.
坠p - 坠Q 坠y 坠x
-P
这里 φ 仅为 y 的函数.从而求得方程 (1)的一个积分因子 μ=
e 。 ∫φ(y)dy
例 4 试用公式法解线性微分方程(8)
解 : 将 (8)式 改 写 成 [Q(x)-P(X)Y]DX-DY=0
(10)
这时由公式,μ(x)=e∫p(x)dx.以 μ(x)=e∫p(x)dx 乘上(10)式得到
或 y=e-∫p(x)dx[∫Q(x)e∫p(x)dxdx+C]
2.公 式 法
由同一个方程
ydx-xdy=0
可以有不同的积分因子 1 y2
,
1 x2
,
1和 1 xy x2±y2
.可以证明,只要方程有解,则必有积分因子存在,
并且不是唯一的.因此,在具体解题过程中,由于求出的积分因
如何求解全微分方程

全微分方程是一类常见的偏微分方程,它描述了函数的某些性质。
求解全微分方程通常需要使用一些特定的方法,如分离变量法、变量代换法、积分因子法等。
以下是一个求解全微分方程的步骤:
确定方程的形式:首先需要确定全微分方程的形式,以便了解方程中包含哪些未知函数和它们的导数。
寻找积分因子:积分因子是使全微分方程成为恰当方程的函数。
通过寻找积分因子,可以将全微分方程转化为恰当方程,从而更容易求解。
变量代换:如果全微分方程的形式比较复杂,可以考虑使用变量代换,将方程中的未知函数和导数转换为更简单的形式。
分离变量:如果全微分方程中包含多个未知函数,可以考虑使用分离变量的方法,将方程中的未知函数分离出来,分别求解。
求解方程:根据具体情况选择适当的方法求解全微分方程。
如果方程是恰当方程,可以使用直接积分法求解;如果方程不是恰当方程,可以考虑使用其他方法,如常数变异法、参数法等。
验证解的正确性:最后需要验证求解得到的解是否正确。
可以通过将解代入原方程进行验证,或者使用其他方法验证解的正确性。
需要注意的是,求解全微分方程的方法并不是唯一的,具体的方法需要根据具体情况选择。
同时,全微分方程的解可能存在多种形式,需要根据问题的实际背景选择适当的解的形式。
微分方程的积分因子

在求解某些类型的微分方程时,可以使用积分因子(integrating factor)来简化方程的求解过程。
积分因子是一个乘法因子,可以乘以微分方程的两边,使其变为可积分的形式。
对于形如dy/dx + P(x)y = Q(x) 的一阶线性常微分方程,其中P(x) 和Q(x) 是已知函数,可以使用积分因子来求解。
积分因子的计算步骤如下:
1.将方程写成标准形式:dy/dx + P(x)y = Q(x)。
2.计算积分因子μ(x) = exp(∫P(x)dx)。
3.将积分因子乘以原方程的两边,得到μ(x)dy/dx + μ(x)P(x)y = μ(x)Q(x)。
4.左侧的第一项可以通过链式法则化简为d(μ(x)y)/dx。
5.整理得到d(μ(x)y)/dx = μ(x)Q(x)。
6.对上述等式两边同时积分,得到μ(x)y = ∫μ(x)Q(x)dx。
7.最后,解出y = (1/μ(x)) ∫μ(x)Q(x)dx。
通过引入积分因子,原本的一阶线性常微分方程可以转化为可积分的形式。
积分因子的选择依赖于方程中的函数P(x) 和Q(x),使得乘以积分因子后,方程的左侧可以写成导数的形式,从而方便求解。
需要注意的是,不是所有的一阶线性常微分方程都可以使用积分因子法求解,这种方法适用于特定类型的方程。
在具体求解时,还需要根据具体方程形式和条件进行判断和处理。
全微分方程与积分因子

全微分方程与积分因子在数学中,微分方程是研究自然现象的一种重要工具,它是描述自然现象变化的一种数学模型。
而全微分方程是其中的一种重要类型,它在物理、工程、经济等领域中都有广泛应用。
全微分方程的定义全微分方程指的是能够写成下面形式的方程:M(x,y)dx+N(x,y)dy=0其中,M(x,y)和N(x,y)是定义在平面区域D上的连续函数。
dx 和dy分别表示x和y的微小变化量,而该式的解y=f(x)就是D中的一个隐函数。
当该式满足以下条件时,被称作全微分方程:∂M/∂y=∂N/∂x换言之,就是该式的两个偏导数相等。
全微分方程的求解对于全微分方程,求解的方法非常简单,只需要对其进行积分,就得到了y=f(x)的通解。
以一个简单的例子来说明:设M(x,y)=3x^2y, N(x,y)=x^3,则上式就变成了:3x^2ydx+x^3dy=0对该式两边同时积分,得到:x^3y+θ=y^2/2其中,θ是一个常数。
积分因子积分因子是用于求解非全微分方程的一种技巧,它能够将非全微分方程转化成全微分方程从而求解。
设非全微分方程为:M(x,y)dx+N(x,y)dy=0称一个与M(x,y)和N(x,y)有关的非零函数μ(x,y)为该非全微分方程的积分因子,当且仅当以下条件成立时:μ(x,y)M(x,y)dx+μ(x,y)N(x,y)dy=0是一个全微分方程。
在实际应用中,常常可以通过以下步骤求解积分因子:1.检查M(x,y)和N(x,y)的偏导数是否满足条件∂M/∂y≠∂N/∂x。
2.令μ(x,y)=exp(Q(x,y)),其中Q(x,y)是希望得到的积分因子。
3.代入μ(x,y)和求导后的积分因子到M(x,y)和N(x,y)的总和中,判断是否为全微分方程,如果是,则可得到积分因子。
例如,考虑非全微分方程:(2y^3 +3x^2y)dx+(3x^2+y^2)dy=0通过检查偏导数条件可知:∂M/∂y=6y^2+3x^2≠∂N/∂x=6x所以该方程不是全微分方程。
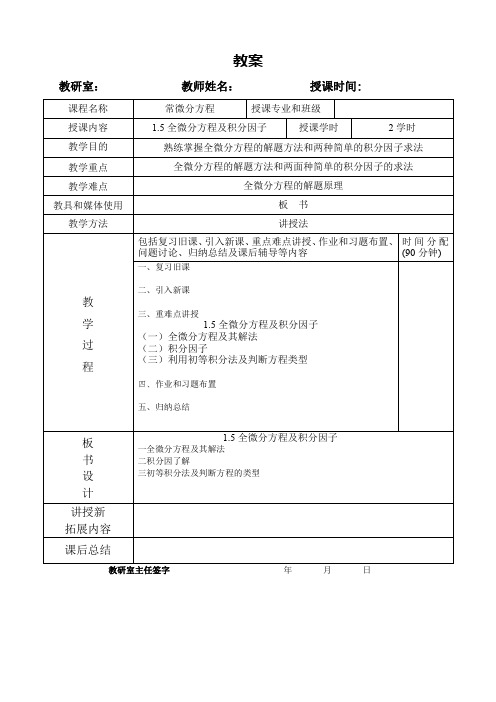
1.5全微分方程及积分因子.
②求原函数,按公式 M ( x, y )dx [N
x
x0
M ( x, y )dx N ( x 0 , y )dy u ( x, y ) (10)
y0 x y x0 y0
证明: (略) 问题: (1) 如何判断(1)是恰当微分方程? (2) 如果(1)是恰当微分方程,如何求得函数 u u ( x, y ) ? (3)如果(1)是恰当微分方程,函数 M ( x, y ), N ( x, y ) 应有什么性质? 定理 2:如果(1)中的 M ( x, y ), N ( x, y ) 在矩形区域 R:|x-x0|≤a,|y-y0|≤b 上 连续可微,那么方程(1)是恰当微分方程的充要条件是:
0
1 1 1 即有通解为 x 4 x 2 y 2 x 3 C 4 2 3
2) (2xy4e y 2xy3 y)dx ( x2 y4e y x2 y2 3x)dy 0 解:由于
M N 2 xy 4 e y 8 xy 3e y 6 xy 2 1 y x 2 xy 4 e y 2 xy 2 3 8 xy 3e y 8 xy 2 4 4 M y
M N (5) y x
且此时恰当微分方程(2)的通解是
M ( x, y )dx [N y M ( x, y)dx]dy = c (9)或
x
x0
M ( x, y )dx N ( x, y )dy u ( x, y ) (10)
y0
y
证明: (略) 3、全微分方程的解题方法 ①由
微分方程的积分因子求解法

微分方程的积分因子求解法常微分方程的积分因子求解法内容摘要:本文给出了几类特殊形式的积分因子的求解方法,并推广到较一般的形式。
关键词:全微分方程,积分因子。
—、基本知识定义1、1对于形如M(x. y)dx + N(x. y)dy = 0 (l x 1)的微分方程,如果方程的左端恰就是X , y的一个可微函数(7(x,y)的全微分,即d U(x, y) = M (x, y)dx + N(x, y)dy 1 s 1)为全微分方程、易知上述全微分方程的通解为U^y) = C, (C为任意常数).定理k 1 (全微分方程的判别法)设M(x,y),N(x,y)在x*平面上的单连通区域G内具有连续的一阶偏导数,则(1、1)就是全微分方程的充要条件为OM (x, y) = 6N(x, y) (1 2) dy dx证明见参考文献[1]、定义1、2对于微分方程(1、1),如果存在可微函数“(a),使得方程“(x, y) M (x, y)clx + “(x, y)N(x, y)dy = 0 (1、3)就是全微分方翟则称“(x, y)为微分方程(1、1)的积分因子、定理1、2 可微函数“(x,y)为微分方程(1.1)的积分因子的充要条件为Ng y )別】"(")_ M (X y ) 6 In “g )二 6M (x, y ) _ 4V (x,y )dx , dy dy dx证明:由定理1.1得/心y )为微分方程(1、1)的积分因子的充要条件为0(“ (俎刃N (x 』))ax展开即得:上 证毕Ng 严小-M (3)沁也」竺』一空y (料).dxdy I dy dx 丿式整理即得(1.4)注1、1 若“(3)工0,则(1、3)与(1、1)同解。
所以,欲求(1.1)的通解,只须求出(1. 3 )的通解即可,而(1、3 )就是全微分方程,故关键在于求积分因子“(X, y )。
为了求解积分因子A (x,y )z 必须求解方程(1、4)。
积分因子与全微分方程

积分因子与全微分方程1 微分方程的用途镭是一种放射性物质,它的原子不停地向外放射出氦原子和其它的射线.从而自身的原子量减少,这样就变成了其它的物质(如常见的铅).一定质量的镭随着时间的变化,它的质量就会减少.现在已经发现镭的裂变速度(即单位时间裂变的质量)与它的剩余量成正比,设一块镭在时刻0t t =时,其质量0R R =,请确定这块镭在时刻t 的质量R .分析:时刻t 时镭的剩余量R 是t 的函数,由于R 将随时间t 的流逝而减少.故镭的裂变速度dRdt应该是负值,于是按照镭的裂变规律可列出方程dRkR dt=-,其中k 为一正的比例常数. 1.1 微分方程 定义1[]()1P 1 联系着自变量、未知函数以及它的导数的方程叫做微分方程.上式是一个关于未知函数R 的微分方程,上述的问题就是要从这个式子中求出未知函数()R R t =来.不仅镭的质量满足这样的规律,其它的放射性物质也都满足这一规律,不同的只是各种放射性物质具有各自不同的系数k .从这个关系式出发,可以利用放射性物资来测定某种物体的绝对年龄,实际上,火箭的升空,弹道的计算,自动控制,化学反应过程中稳定性的研究等都要用到微分方程.微分方程其实就是联系着自变量,未知函数以及它的导数的关系式,它的本质也是一个方程.像上面这些例子都可以建立成微分方程的的模型.我们了解了什么是微分方程,和微分方程在现实中的应用.那么解这样的方程就是理所应当该首先考虑的问题了.2 全微分方程的定义我们可以将一阶方程(),dyf x y dx=写成微分的形式(),0f x y dx dy -=,写成具有对称形式的一阶微分方程()(),,0M x y dx N x y dy +=.其中(),M x y ,(),N x y 在某矩形域内是x , y 的连续且具有连续的一阶偏导数. 2.1 全微分方程 定义2[]()139P 如果微分方程()(),,0M x y dx N x y dy +=的左边恰好是某个二元函数(),u x y 的全微分,即()()(),,,M x y dx N x y dy du x y +≡u u dx dy x y∂∂≡+∂∂ 则称()(),,0M x y dx N x y dy +=为全微分方程.3 全微分方程的求解知道了什么是全微分方程,自然会提出一些问题,①如何来判断方程是全微分方程,②判断了方程为全微分方程,那如何来求全微分方程的通解呢?下面我们来给一些结论:方程()(),,0M x y dx N x y dy +=为全微分方程的冲要条件为:M Ny x∂∂=∂∂. 一般求解全微分方程通解的过程我们用一个例题来演示一下: 例1 求()()222336640x xy dx x y y dy +++=的通解. 解 这里2236M x xy =+,2364N x y y =+, 这时12M xy y ∂=∂,12N xy x∂=∂, 因此方程是全微分方程.现在求u ,使它满足如下两个方程2236ux xy x∂=+∂, 2364ux y y y∂=+∂, 由2236ux xy x∂=+∂,对x 积分,得到 ()3223u x x y y ϕ=++.为了确定()y ϕ,将()3223u x x y y ϕ=++对y 求导数,并且使它满足2364ux y y y∂=+∂,即得到()223664d y ux y x y y y dyϕ∂=+=+∂, 于是()34d y y dyϕ=,积分后得()4y y ϕ=, 将()y ϕ代入()3223u x x y y ϕ=++,得到32243u x x y y =++因此,方程的通解为32243x x y y c ++=,这里c 为任意常数.4 积分因子当方程()(),,0M x y dx N x y dy +=不是全微分方程时,则M Ny x∂∂=∂∂不成立. 4.1 积分因子 定义3[]()241P 如果存在连续可微的函数(),0x y μμ=≠,使得非全微分方程()(),,0M x y dx N x y dy +=两边同时乘以(),x y μ并且使得()()()(),,,,0x y M x y dx x y N x y dy μμ+=变为一个全微分方程,即存在函数(),x y ν使()()()(),,,,x y M x y dx x y N x y dy d μμν+≡则称(),x y μ为方程()(),,0M x y dx N x y dy +=的积分因子.这时(),x y c ν=是()()()(),,,,x y M x y dx x y N x y dy d μμν+≡的通解.因而就是()(),,0M x y dx N x y dy +=的通解.全微分方程可以通过积分求出它的通解.因此能否将一个非全微分方程化为全微分方程就有很大的意义.积分因子是在考虑将非全微分方程化为全微分方程进行求解这一问题上引进的.对于某些简单的微分方程,可以通过“凑微分”的方法来找到它的积分因子.所以熟悉的掌握一些基本地二元函数的全微分是必要的.例如[]()143P :()ydx xdy d xy += 2ydx xdyx d y y ⎛⎫-= ⎪⎝⎭2ydx xdy y d x x -+⎛⎫= ⎪⎝⎭ln ydx xdy y d xy x -⎛⎫= ⎪⎝⎭22ydx xdy y d arcty x y x -⎛⎫= ⎪+⎝⎭ 221ln2ydx xdy x yd x y x y⎛⎫--= ⎪-+⎝⎭例 2 方程0ydx xdy -=不是全微分方程,而21y 是它的积分因子,在方程两边同时乘以21y 后,即得到全微分方程20ydx xdy y -=解它得到:0x d y ⎛⎫= ⎪⎝⎭.即这个方程的通解为xc y =. 5 求积分因子一般情况下用方程来求解积分因子比求这个微分方程本身都困难,但是有一些特殊的微分方程还是比较适合求得它的积分因子的.5.1 积分因子不唯一定理 定理1[]()36P 如果方程()(),,0M x y dx N x y dy +=存在解,则该方程必有积分因子存在,且不唯一.5.2 只与x 或y 有关的积分因子对于方程()(),,0M x y dx N x y dy +=如果存在只与x 有关的积分因子的()x μμ=,则0y μ∂=∂.这时方程M N N M x y y x μμμ⎛⎫∂∂∂∂-=- ⎪∂∂∂∂⎝⎭变成了d M N N dx y x μμ⎛⎫∂∂=- ⎪∂∂⎝⎭,即M Nd y xdx Nμμ∂∂-∂∂=.由此可知,方程()(),,0M x y dx N x y dy +=有只与x 有关的积分因子的充要条件是()M N y x x N ψ∂∂-∂∂=,这里()x ψ仅是x 的函数.假如条件()M Ny xx Nψ∂∂-∂∂=成立,则根据方程M Nd y xdx Nμμ∂∂-∂∂=可以求得方程()(),,0M x y dx N x y dy +=的一个积分因子()x dxe ψμ⎰=同样,假如()(),,0M x y dx N x y dy +=有只于y 有关的积分因子的充要条件是()M Ny xy Mϕ∂∂-∂∂=-,这里()y ϕ仅是关于y 的函数.从而求得方程()(),,0M x y dx N x y dy +=的一个积分因子.例3 求解方程()4430x y dx xy dy +-= 解 因为M= 44x y +,N= 3xy -,所以34M y y ∂=∂,3Ny x∂=-∂,显然M N y x ∂∂≠∂∂,从而原方程不是全微分方程.考虑到33345y y xy x+=--,从而方程有只与x 有关的积分因子551dx x ex μ⎛⎫- ⎪⎝⎭⎰==. 原方程两边乘以积分因子μ,变为435410y y dx dx dy x x x+-=,整理得()44ln 04y d x d x ⎛⎫+-= ⎪⎝⎭,所以原方程的通解为44ln 4y x c x -=,(这里c 为任意的常数). 例4 求解方程()0ydx y x dy +-= 解 因为M y =,N y x =-,所以1M y ∂=∂,1Nx∂=-∂也容易看出原方程不是全微分方程,所以方程有只与y 有关的积分因子221dy y eyμ⎛⎫- ⎪⎝⎭⎰==. 原方程两边都乘以积分因子μ,变成了2110xdx dy dy y y y+-=,整理得()ln 0x d y d y ⎛⎫+= ⎪⎝⎭,所以通解为ln xy c y +=(这里c 为任意常数).另外,此方程还有0y =一个解.5.3 用分项组合的方法求积分因子下面我们再介绍一种用分项的方法求积分因子的方法. 当方程()(),,0M x y dx N x y dy +=不是全微分方程时,则M Ny x∂∂=∂∂不成立.但如果存在不恒为零的连续可微函数(),x y μμ=使方程()(),,0M x y dx N x y dy μμ+=成为全微分方程的积分因子.5.3.1 积分因子扩展定理 定理2[]()43132P - 如果(),x y μ是微分方程()(),,0M x y dx N x y dy +=的积分因子,即存在可微函数(),x y μμ=使得()(),,M x y dx N x y dy du μμ+=那么(),x y μ也是方程()(),,0M x y dx N x y dy +=的积分因子的充要条件是()(),x y u μμφ=,这里()u φ是u 的可微函数.证明 充分性.()()()()()()u Mdx Ndy u Mdx Ndy u du d u μφφμμφ+=+==Φ,这里()u Φ是()u φ的一个原函数,这就说明了()()0u Mdx Ndy μφ+=是全微分方程,其通解就是()u c Φ=(c 任意的常数).必要性.因为(),x y μ是方程()(),,0M x y dx N x y dy +=的积分因子,所以存在可微函数(),u u x y =,使得Mdx Ndy du μμ+=,两边都乘以μ,得()Mdx Ndy du du μμμμμ+==,所以()du u du μμμ==Φ,这里令()duu duΦ=为可微函数,得证. 5.3.2 分组求积分因子 定理3[]540P 如果μ是微分方程()(),,0M x y dx N x y dy +=的积分因子,即Mdx Ndy du μμ+=,那么()u μϕ也是方程()(),,0M x y dx N x y dy +=的积分因子,这里()u ϕ是u 的任何连续函数.证明 ()()()()()()u Mdx Ndy u Mdx Ndy u du d u μϕϕμϕ+=+==Φ,这里()u Φ是()u ϕ的一个原函数.对于比较复杂的微分方程,可以通过观察进行“分项组合”而求得积分因子.例如在分项组合的情况下,有()()11220M dx N dy M dx N dy +++=.然后,分别找出两组的积分因子1μ以及2μ,也就是说,存在函数()11,x y μμ=和()22,x y μμ=,使得11111M dx N dy du μμ+=,22222M dx N dy du μμ+=,再借助1μ以及2μ来求微分方程()()11220M dx N dy M dx N dy +++=的积分因子.这样,对于上述“分项组合”的情形,如果能够选取适当的函数()1u ϕ以及()2u ϕ,使得()()1122u u μμϕμϕ==,那么,μ即使第一组的积分因子,也是第二组的积分因子,因而也就是方程()()11220M dx N dy M dx N dy +++=的积分因子.例5 求微分方程()20xy y dx xdy ++=的通解.解 把它的左边“分项组合”成()20xy dx ydx xdy ++=.现在21μ=,2u xy =,于是(),x y φ是第二组的积分因子,只要适当选取(),x y φ,使(),x y φ也是第一组的积分因子即可.为此,取()221,x y x y φ=.在所给方程的两边乘以221x y得到()220d xy dx x x y +=, 积分得所给方程的通解为1ln x C xy-=,(这里C 为常数). 5.4 积分因子是含x ,y 的关系式 连续可微函数(),x y μ为()(),,0M x y dx N x y dy +=式的积分因子即当()()()(),,,,0x y M x y dx x y N x y dy μμ+=时,存在函数(),x y ν,使()()()(),,,,x y M x y dx x y N x y dy d μμν+≡函数(),x y μ为()(),,0M x y dx N x y dy +=的积分因子的充要条件是()()M N y xμμ∂∂=∂∂ 即:M N NM x y y x μμμ⎛⎫∂∂∂∂-=- ⎪∂∂∂∂⎝⎭, 若方程()(),,0M x y dx N x y dy +=具有形式(),x y μμ=Φ⎡⎤⎣⎦的积分因子,应有()(){}()(){},,,,x y M x y x y N x y y xμμ∂Φ∂Φ⎡⎤⎡⎤⎣⎦⎣⎦=∂∂ 即M Nd y xd N M x yμμ∂∂-∂∂=Φ∂Φ∂Φ-∂∂, 从而()(),,0M x y dx N x y dy +=具有形式(),x y μμ=Φ的积分因子的充要条件为(),M Ny xf x y N M x y∂∂-∂∂=Φ⎡⎤⎣⎦∂Φ∂Φ-∂∂, 此时()f d e μΦΦ⎰=.例如(1):当(),x y x y Φ=+时1x∂Φ=∂,1y ∂Φ=∂,从而()(),,0M x y dx N x y dy +=具有形如()x y μ+的积分因子的充要条件为()M Ny xf x y N M∂∂-∂∂=+-,()f d e μΦΦ⎰=其中(),x y x y Φ=Φ=+,例如(2):当(),x y xy Φ=时,y x∂Φ=∂,x y ∂Φ=∂,从而()(),,0M x y dx N x y dy +=具有形如()xy μμ=的积分因子的充要条件是()M N y xf xy yN xM∂∂-∂∂=-, ()f d e μΦΦ⎰=,其中 (),x y xy Φ=Φ=.利用(),M Ny x f x y N M x y∂∂-∂∂=Φ⎡⎤⎣⎦∂Φ∂Φ-∂∂和()f d e μΦΦ⎰=两个式子还可以求出方程()(),,0M x y dx N x y dy +=还具有以下特殊形式:()x μ,()y μ,()x y μ-,()22x y μ-,()22x y μ+等好多的积分因子,相关证明请读者根据上述例题自己完成.参考文献[1] 王高雄,周之铭,朱思铭,王寿松.常微分方程[M].北京:高等教育出版社,2000[2] 东北师范大学数学系微分方程教研室.常微分方程[M].北京:高等教育出版社,2004[3] 滕文凯.积分因子的分组求法[J].承德民族师专学报,2004.5,2期[4] 龚雅玲.求解微分方程的积分因子法[J].南昌教育学院学报,2007,1期[5] 李振东,张永珍.求积分因子的新方法[J].唐山学院报,2003,6期[6] (美)Dennis G.Zill,(美)Michael R.Cullen编.陈启宏,张凡,郭凯旋译.微分方程与边界值问题[M].北京:机械工业出版社,2005[7] 徐安农,段复建.全微分方程与积分因子法[J].桂林电子工业学院学报,2002.4,2期[8] Walter W. Ordinary differential equations. New york :springer-verlag, 1998。
全微分方程及积分因子

1.5 全微分方程及积分因子一、全微分方程的定义及条件则它的全微分为是一个连续可微的函数设,),(y x U U =dy yU dx x U dU ¶¶+¶¶=如果我们恰好碰见了方程0),(),(=¶¶+¶¶dy yy x U dx x y x U 就可以马上写出它的通积分.),(c y x U=定义1使得若有函数),,(y x U dyy x N dx y x M y x dU ),(),(),(+=则称微分方程)1(,0),(),(=+dy y x N dx y x M 是全微分方程..),()1(c y x U =的通积分为此时如0=+ydx xdy 0)2()3(322=+++dy xy x dx y y x 0)()(=+dy y g dx x f 是全微分方程.=)(xy d =+)(23xy y x d =+òò))()((y d y g x d x f d 1.全微分方程的定义需考虑的问题(1) 方程(1)是否为全微分方程?(2) 若(1)是全微分方程,怎样求解?(3) 若(1)不是全微分方程,有无可能转化为全微分方程求解?2 方程为全微分方程的充要条件定理1则方程偏导数中连续且有连续的一阶域在一个矩形区和设函数,),(),(R y x N y x M )1(,0),(),(=+dy y x N dx y x M 为全微分方程的充要条件是).2(,),(),(x y x N y y x M ¶¶=¶¶)1(,0),(),(=+dy y x N dx y x M证明“必要性”设(1)是全微分方程,使得则有函数),,(y x U dy yU dx x U y x dU ¶¶+¶¶=),(dy y x N dx y x M ),(),(+=故有),,(y x M xU =¶¶),(y x N y U =¶¶从而从而有都是连续的和由于,22y x U x y U ¶¶¶¶¶¶,22y x U x y U ¶¶¶=¶¶¶故.),(),(xy x N y y x M ¶¶=¶¶yx U y N x y U y M ¶¶¶=¶¶¶¶¶=¶¶22,“充分性”,xy x N y y x M ¶¶=¶¶),(),(若解这个方程得看作参数把出发从,,)5(y 满足则需构造函数),,(y x U )4(,),(),(),(dy y x N dx y x M y x dU +=即应满足)5(),,(y x M x U =¶¶)6(),,(y x N yU =¶¶ò+=).(),(),(y dx y x M y x U j,)(的任意可微函数是这里y y j =¶¶y U 因此ò¶¶-=)7(),()(dx y x M y N dy y d j ,)7(无关的右端与下面证明x 的偏导数常等于零即对x 事实上]),([ò¶¶-¶¶dx y x M y N x ]),([ò¶¶¶¶-¶¶=dx y x M yx x N )6(),,(y x N y U =¶¶即同时满足使下面选择),6(),(U y j ò+¶¶dy y d dx y x M y )(),(j N =ò+=).(),(),(y dx y x M y x U j]),([ò¶¶¶¶-¶¶=dx y x M x y x N yM x N ¶¶-¶¶=.0º积分之得右端的确只含有于是,)7(,y ,]),([)(dy dx y x M y N y òò¶¶-=j 故ò=dx y x M y x U ),(),(,]),([dy dx y x M yN òò¶¶-+(8)。
全微分方程及积分因子

全微分⽅程及积分因⼦1.5 全微分⽅程及积分因⼦⼀、全微分⽅程的定义及条件则它的全微分为是⼀个连续可微的函数设,),(y x U U =dy yU dx x U dU ??+??=如果我们恰好碰见了⽅程0),(),(=??+??dy yy x U dx x y x U 就可以马上写出它的通积分.),(c y x U=定义1使得若有函数),,(y x U dyy x N dx y x M y x dU ),(),(),(+=则称微分⽅程)1(,0),(),(=+dy y x N dx y x M 是全微分⽅程..),()1(c y x U =的通积分为此时如0=+ydx xdy 0)2()3(322=+++dy xy x dx y y x 0)()(=+dy y g dx x f 是全微分⽅程.=)(xy d =+)(23xy y x d =+òò))()((y d y g x d x f d 1.全微分⽅程的定义需考虑的问题(1) ⽅程(1)是否为全微分⽅程?(2) 若(1)是全微分⽅程,怎样求解?(3) 若(1)不是全微分⽅程,有⽆可能转化为全微分⽅程求解?2 ⽅程为全微分⽅程的充要条件定理1则⽅程偏导数中连续且有连续的⼀阶域在⼀个矩形区和设函数,),(),(R y x N y x M )1(,0),(),(=+dy y x N dx y x M 为全微分⽅程的充要条件是).2(,),(),(x y x N y y x M ??=??)1(,0),(),(=+dy y x N dx y x M证明“必要性”设(1)是全微分⽅程,使得则有函数),,(y x U dy yU dx x U y x dU ??+??=),(dy y x N dx y x M ),(),(+=故有),,(y x M xU =??),(y x N y U =??从⽽从⽽有都是连续的和由于,22y x U x y U ,22y x U x y U ???=???故.),(),(xy x N y y x M ??=??yx U y N x y U y M =??=??22,“充分性”,xy x N y y x M ??=??),(),(若解这个⽅程得看作参数把出发从,,)5(y 满⾜则需构造函数),,(y x U )4(,),(),(),(dy y x N dx y x M y x dU +=即应满⾜)5(),,(y x M x U =??)6(),,(y x N yU =??ò+=).(),(),(y dx y x M y x U j,)(的任意可微函数是这⾥y y j =??y U 因此ò??-=)7(),()(dx y x M y N dy y d j ,)7(⽆关的右端与下⾯证明x 的偏导数常等于零即对x 事实上]),([ò??-??dx y x M y N x ]),([ò-??=dx y x M yx x N )6(),,(y x N y U =??即同时满⾜使下⾯选择),6(),(U y j ò+??dy y d dx y x M y )(),(j N =ò+=).(),(),(y dx y x M y x U j]),([ò-??=dx y x M x y x N yM x N ??-??=.0o积分之得右端的确只含有于是,)7(,y ,]),([)(dy dx y x M y N y òò??-=j 故ò=dx y x M y x U ),(),(,]),([dy dx y x M yN òò??-+(8)。
全微分方程与积分因子

全微分⽅程与积分因⼦全微分⽅程定义如果⽅程M(x,y)dx+N(x,y)dy=0$的左端恰好是某个⼆元函数u(x,y)的全微分,即M(x,y)dx+N(x,y)dy≡du(x,y)则⽅程为全微分⽅程,u(x,y)称为⽅程的⼀个原函数定理⽅程是全微分⽅程的充要条件是:设函数M(x,y),N(x,y)在xoy平⾯上的单连通域D内连续可微,那么在D内恒成⽴∂(M(x,y))∂y=∂(N(x,y))∂x成⽴则函数u(x,y)=∫x x0M(x,y0)dx+∫y yN(x,y)dy或u(x,y)=∫x x0M(x,y)dx+∫y yN(x0,y)dy是⽅程原函数,其中(x0,y0)∈D全微分⽅程求解⽅法①线积分法如上述定理u(x,y)=c②不定积分法du(x,y)=M(x,y)dx+N(x,y)dy 由此得到:∂u∂x=M(x,y),∂u∂y=N(x,y)所以u(x,y)=∫M(x,y)dx+φ(y)另⼀⽅⾯∂u(x,y)∂y=∂∂y∫M(x,y)dx+φ′(y)=N(x,y)由此确定φ′(y),积分求得φ(y)把φ(y)代⼊u(x,y)=∫M(x,y)dx+φ(y)即得u(x,y)所以通解为u(x,y)=c③观察法常⽤的全微分⽅程表达式xdx+ydy=d(x2+y2 2)xdx+ydy x2+y2=12dln(x2+y2)xdy−ydxx2=d(y x)xdy+ydxxy=dln(xy)xdy−ydxx2+y2=d(arctan y x)xdy−ydx x2−y2=12dlnx+yx−y例题例12xydx+(x2−y2)dy=0∂M(x,y)∂y=2x=∂N(x,y)∂x所以⽅程是全微分⽅程取x0=0,y0=0得u(x,y)=∫x00dx+∫y0(x2−y2)dy=x2y−y3 3于是通解为x2y−y33=c例22x(1+√x2−y)dx−√x2−ydy=0∂M(x,y)∂y=−x√x2−y=∂N(x,y)∂x所以⽅程是全微分⽅程2xdx+(2x√x2−ydx−√x2−ydy)=0即dx2+d(23(x2−y)32)=0所以⽅程通解为x2+23(x2−y)32=c积分因⼦定义:若存在可微函数µ=µ(x,y)使µM(x,y)dx+µN(x,y)dy=0是全微分⽅程,则称µ(x,y)为⽅程的积分因⼦定理1:µ(x,y)是⽅程积分因⼦的充要条件是∂(µM)∂y=∂(µM)∂x定理2:若µ(x,y)是⽅程的⼀个积分因⼦,且µMdx+µNdy=dU则µφ(U)也是⽅程的积分因⼦,其中φ(U)是U的任⼀连续函数积分因⼦求法①观察法常⽤积分因⼦−1x2,1y2,1xy,1x2+y2,1x2−y2②公式法若⽅程M(x,y)dx+N(x,y)dy=0中的M(x,y),N(x,y)满⾜Ⅰ、1 N(∂M∂y−∂N∂x)=φ(x)(仅是x的函数)则它有积分因⼦µ(x)=e∫φ(x)dx Ⅱ、−1M(∂M∂y−∂N∂x)=φ(y)(仅是y的函数)则它有积分因⼦µ(y)=e∫φ(y)dyⅢ、分组求积分因⼦法(M1dx+N1dy)+(M2dx+N2dy)=0分别求得各组的积分因⼦µ1和µ2于是就可找到u1,u2使µ1M1dx+µ1N1dy=du1µ2M2dx+µ2N2dy=du2选适当函数Φ1(u1),Φ2(u2)使µ1Φ1(u1)=µ2Φ2(u2)可求得⽅程积分因⼦为µ1Φ1(u1)(x4+y4)dx−xy3dy=0∂M∂y=4y3,∂N∂x=−y3所以∂M ∂y−∂N ∂xN=5−x所以µ(x)=e∫5−x dx=1x5⽅程两边乘1x5得dxx+y4x5dx−y3x4dy=0即d(ln|x|)−d(y44x4)=0⽅程通解为ln|x|−y44x4=cProcessing math: 100%。
常微分方程初等积分法解法研究常微分方程及积分因子

常微分方程初等积分法解法研究常微分方程及积分因子初等积分法解常微分方程的关键在于求解不定积分。
不定积分是解微分方程的主要手段,通过找到合适的积分因子,可以将一个一阶微分方程转化为一个可积的方程。
在本文中,将对常微分方程及积分因子进行研究。
dy/dx = f(x, y)其中,f(x,y)是已知函数。
解这个方程的方法之一就是通过积分来找到y。
我们需要将这个方程转化成一个可积的形式。
考虑一个形式为 dy/dx + P(x)y = Q(x) 的一阶常微分方程。
要将这个方程转化为可积的形式,需要找到一个因子M(x),使得通过乘以M(x)可以使得原方程的左侧变为一个可积的形式。
这个因子M(x)被称为积分因子。
要找到积分因子,通常通过求解方程 M(x) = 1/M dM/dx = P(x) 来确定。
最常见的积分因子是指数函数,即M(x) = e^(∫P(x)dx)。
通过乘以这个积分因子,原方程可以变为积分形式:d/dx (M(x)y) = M(x)Q(x)通过对上式两边进行不定积分,可以求解出y。
举个例子来说明。
考虑一阶常微分方程 dy/dx + xy = x^2、我们需要找到一个积分因子。
通过解方程 M(x) = 1/M dM/dx = x,可以得到M(x) = e^(1/2 x^2)。
d/dx (e^(1/2 x^2) y) = x e^(1/2 x^2)对上式两边不定积分,得到:e^(1/2 x^2) y = ∫x e^(1/2 x^2) dx通过不定积分求解上式,可以得到y。
通过求解积分因子,我们可以将一阶常微分方程转化为可积的形式。
这种方法适用于一阶线性常微分方程。
对于高阶常微分方程,可以通过转化为一组一阶微分方程来求解。
总结起来,常微分方程及积分因子的研究是通过寻找积分因子来将一阶常微分方程转化为可积的形式。
通过解不定积分,可以求解出未知函数。
初等积分法解常微分方程是一种常用的方法,对于一阶线性常微分方程特别适用。
常微分方程中常用的解题方法

常微分方程中常用的解题方法1、变量分离法,一阶常微分方程求解有两个重要的方法:一是变量分离方法,二是全微分方程及积分因子的方法。
其中前者是通过适当的变形及变换,将自变量、自变量的微分和因变量的微分分别置于方程的两端,然后分别进行积分即可得方程的通解后者则是寻求适当的积分因子,将方程化为通解的恰当方程,进一d步得通解。
如求方程的通解。
ddyy=0是解,若y?0,分离变量,得所以原方程通解(c?R) ?,两端分别积分,得ln|y|=x^2+c。
y2、积分因子的方法,形如M(x,y)dx+N(x,y)dy=0 的一阶微分方程,因为其dy中X和Y的地位对等性,所以较之于一阶微分方程的常见形式?dx ??更具有一般性。
若该方程中有? 则存在u(x,y),使得 ?du(x,y)=M(x,y)dx+N(x,y)dy,此时,该方程称为恰当微分方程,其通解为u(x,y) =c。
当然大部分的方程并不是恰当微分方程,但是我们可以寻求与其通解的恰当微分方程,即可以寻求积分因子?(x,y) ,使得通解方程?M(x,y)dx+?N(x,y)dy=0为恰当方程。
积分因子的方法为求解一般的一阶微分方程提供了一种全新的思路。
例?m?y??如求解ydx+(y-x)dy=0 解:m只与Y有关,所以可以寻求形如?(y)的积分因子,代入,得1ydx?,故与原方程通解的恰当方程为xyln1ydyx,求其通解为y??????。
3、待定系数的方法,待定系数的方法是大学数学分析类学科中应用较为广泛的一种方法。
在常微分方程中,该方法主要体现在已利用定性分析、解的结构或其他方法确定了解的形式,但是其中具体系数未定,这时我们往往将形式解代入微分方程,进一步求得系数或系数函数。
应用该方法的关键在与确定的形式。
d2x例如,求解方程dt2 解:相应齐次线性方程的特征根为? =+-1 ,因为i 不是特征根,所以可以寻找形如 x'(t)=Acost+Bsint 的特解,代入原方程,得-2Acost-2Bsint=cost ,解得而原方程通解为xt?c1etc2et??911A? 所以2x't? ,从??p?,从而4、参数的方法,参数解法是常微分方程中重要而常用的方法之一,参数解法是一种变量变化的方法,即在常微分方程中引人一个或几个新的变量,并用该变量表示方程中未知函数,表达式即为方程的参数解,新变量即称参变量,参数解法往往能解决一些基本方法不能解决的问题。
微分方程的积分因子法

微分方程是数学中重要的研究对象,它通过描述变量之间的关系,可以用来解释许多自然现象和物理规律。
微分方程的求解是数学分析的重要方法之一,其中积分因子法是一种常用且有效的求解微分方程的方法。
首先,我们来了解什么是微分方程。
微分方程是包含未知函数及其导数的方程,一般形式为dy/dx = f(x,y),其中y是未知函数,f(x,y)是已知的函数。
微分方程可以分为常微分方程和偏微分方程两类,常微分方程中只包含一个自变量,而偏微分方程中包含多个自变量。
解微分方程要找出满足方程的函数形式,而积分因子法是一种特殊的方法用来解决一类形式为M(x,y)dx + N(x,y)dy = 0的一阶常微分方程。
积分因子法的思想是通过引入一个适当的积分因子来改变微分方程的形式,从而使其变得可积。
具体步骤如下:1.将方程化为其标准形式:M(x,y)dx + N(x,y)dy = 0,其中M(x,y)和N(x,y)为已知函数。
2.判断方程是否是恰当微分方程。
若满足∂M/∂y = ∂N/∂x,则该方程为恰当微分方程,直接求解即可;若不满足,则进行下一步。
3.求取积分因子。
积分因子可以通过通解公式I(x) = e^(∫P(x)dx),其中P(x)为方程的系数。
4.将积分因子乘到方程上,得到恰当微分方程:I(x)M(x,y)dx +I(x)N(x,y)dy = 0。
5.求解恰当微分方程。
由于恰当微分方程是可积的,可以直接求出其解。
通过这样的步骤,利用积分因子法可以将一些常见的非恰当微分方程转化为恰当微分方程,从而能够更方便地求解微分方程。
需要指出的是,积分因子法并不适用于所有的微分方程,只适用于一些具有特定形式的微分方程。
对于其他形式的微分方程,可能需要使用其他的求解方法。
总结来说,积分因子法是一种求解常微分方程的有效方法,它通过引入适当的积分因子,将非恰当微分方程转化为恰当微分方程,从而更容易求解。
使用积分因子法需要熟悉方程的形式及其特点,才能正确选择和应用积分因子。
1.5 全微分方程及积分因子

1. ydx ( y 2 x )dy 0 2. xy 3dx ( x 2 y 2 1)dy 0
高 等 数 学
[例4] 解方程 ydx ( y x )dy 0
2
哈 尔 滨 工 程 大 学
1 2 [解] ( 2 ) [ ydx xdy y dy] 0 y 2 2 y y
1) 方程M ( x , y )dx N ( x , y ) 0存在仅与x有关的 积分因子 ( x , y ) ( x )的充要条件为
高 等 数 学
1 M N ( ) N y x
仅与x有关,这时该方程的积分因子为
1 M N ( x ) dx ) ( x) e , 这里 ( x ) ( N y x
积分因子的确定
高 等 数 学
( x , y )是方程M ( x , y )dx N ( x , y ) 0的积分因子的
充要条件是 : ( x , y ) M ( x , y ) ( x , y ) N ( x , y ) y x
即
哈 尔 滨 工 程 大 学
M N N M ( ) x y y x
2)微分方程M ( x , y )dx N ( x , y ) 0有一个仅依赖
哈 尔 滨 工 程 大 学
于y的积分因子的充要条件是
1 M N ( ) M y x
仅与y有关,这时该方程的积分因子为
高 等 数 学
( y ) dy ( y) e ,
1 M N 这里 ( y ) ( ). M y x
高 等 数 学
1 2 (2xydx x dy ) de d ( y ) 0 2 1 2 2 d(x y y ex ) 0 2 1 2 2 x 所以 x y y e c 2
全微分方程

1.5.2 积分因子
(2 xy x2 y y3 / 3)dx ( x2 y 2 )dy 0 ex (2xy x2 y y3 / 3)dx ex ( x2 y 2 )dy 0
M N d y x dx N
M N d y x dy M
求 e y dx ( xe y 2 y )dy 0 满足初始条件 y(2) 3 的解。
ห้องสมุดไป่ตู้(2x sin y 3x2 y)dx ( x3 x2 cos y y2 )dy 0
练习1.
( x2 4xy 2 y2 )dx ( y2 4xy 8)dy 0 e y dx ( xe y 3 y 2 )dy 0 ( x3 xy2 )dx ( x2 y y3 )dy 0 y dx ( y 3 ln x)dy 0 x
分组求积分因子
(3x3 y)dx (2x2 y x)dy 0
例12. ( x4 x2 y2 x)dx ydy 0
例13. ydx ( x x2 y y3 )dy 0
例14. 例15.
( x3 y 2 y 2 )dx x4dy 0
( x y)dx ( x y)dy 0
( x)
( y )
例8. 例9. 例10.
xdy ydx 0
(2 xy x 2 y 1 3 y )dx ( x 2 y 2 )dy 0 3
M N d y x dx N
M N d y x dy M
(3x3 y)dx (2x2 y x)dy 0
例11. (3x 6xy 3 y 2 )dx (2x2 3xy)dy 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全微分方程及积分因子
全微分方程及积分因子
内容:凑微分法,全微分方程的判别式,全微分方程的公式解,积分因子的微分方程,只含一个变量的积分因子和其他特殊形式的积分因子。
由于有数学分析多元微积分的基础,本节的定理1可以简化处理。
对课本中第三块知识即全微分方程的物理背景可以留到后面处理,对第四块知识增解和失解的情况要分散在本章各小节,每次都要重视这个问题。
关于初等积分法的局限性可归到学习近似解法时一起讲解。
重点:全微分方程的公式解和积分因子的计算,难点为凑微分法和积分因子的计算。
习题1(1,3,5),2,3
思考题:讨论其他特殊形式的积分因子。
方程:0),(),(=+dy y x N dx y x M
判定:全微分⇔x
N
y M ∂∂≡∂∂ 解法:C
dy y x N dx y x M y
y x
x =+⎰⎰
),(),(0
初值问题0=C
积分因子:x
N y M y M x N ∂∂-∂∂=⎭
⎬⎫⎩
⎨⎧∂∂-∂∂μμμ1
)(x μ: N
x
N
y M dx d ∂∂-
∂∂=μμ1 )(y μ:
M
x
N
y M dy d ∂∂-
∂∂-=μμ1
1.解下列方程: 1)0
)(222
=-+dy y x
xydx
解:x
N y M ∂∂≡∂∂=x 2 ⎰
⎰=-+x
y
C
dy y xydx 0
2)0(2既 C
y y x =-3/32
2)0
)2(=+---dy xe y dx e
y y
解:x
N y M ∂∂≡∂∂=y
e -- ⎰⎰
=-+-y
x
y
C
dy y dx e 0
)2(既C
y xe
y
=--2
3)0
)1(222=---+
dy y x dx y x x
解:x
N y M ∂∂≡∂∂=y
x --2
21
⎰
⎰
=---+x
y C
dy y dx y x x 0
2)1(2 C
y y y x x =-+---+23
2
32322
)(32)(32)(32
既
C
y x x =-+23
2
2
)(32 4)0
)ln (3
=++dy x y dx x
y
解:x N y M ∂∂≡∂∂=x
1 C
dy y dx x
y
y x
=+⎰⎰
030
既C
y
x y =+4/||ln 4
5)
05233
3222=+-+dy y y
x dx y y x
解:
x
N y M ∂∂≡∂∂=3
2
6--y x
⎰
⎰=-+-x
y C dy y dx y
y x 0
02
22253
C
y x y x =++-/523
6)0
2cos )2sin 1(2
=-+xdy y dx x y
解:x
N y M ∂∂≡∂∂=x y 2sin 2 C
ydy dx x y x
y
=-+⎰
⎰0
2)2sin 1( C y y x y x =-+-
2222
1
212cos 21
C x y x =-
2cos 2
12
2.求下列方程的积分因子和积分: 1)0
)(22
=+++xydy dx x y x
解:N x y y y x N y M
1
2==-=∂∂-∂∂ 1let 1
1==⇒=C Cx x
dx d μμμ既
x x =)(μ
C
dy dx x xy x y
x
=+++⎰⎰
2
230)(
C x y x x =++3
2243
12141
2)0
)3()22(224234=--+++dy x y x e y x dx y xy e
xy y y
解:1
682234+++=∂∂-∂∂xy e xy e xy x
N y M
y y
M y
xy e xy xy e xy y y 4
488 322 2324=
++=++-
y
dy d 4
1-=μμ4
)(-=⇒y y μ ⎰
⎰=+++-x
y
y C
dy dx y y x xe 0
30)/22(
C
xy y x e x y =++-322/
3)0
)(344
=-+dy xy dx y x
解:N
x
y y x N y M
5
433
-=+=∂∂-∂∂
5
)(5
1-=⇒-=x x x
dx d μμμ
C
dx yx x x
=+⎰
--0
51)(既C
x
y
x =-4
4ln
4)0)(2)2242(2
3
4
2
2
2
3=+++++++dy x y x y dx y xy xy y x y x
解:2444432
3
++++=∂∂-∂∂xy xy x y x x
N y M
2
4--xy
xN
xy x y x 2444323=++=
2
)(21x e x x dx
d =⇒=μμμ
⎰⎰=+++++y x x C
dy y dx y xy xy y x y x e
304
2
2
2
32)2242(2
{}
{
}
{}
{}{}
C
y dx ye y e y y e
y dx
ye xye y e y e y x x
x x x x
x x x x =++
⎭⎬⎫⎩⎨⎧-+-+-++-⎰⎰2/2212
1
2240
4422
2222
2
22
2
2
2
2
C e y xy y x x =⎪⎭⎫
⎝
⎛++242
2212
3.求下列方程的积分因子: 1)0)()()()(=+dy y Q x P dx y N x M 解:)()(1),(y N x P y x =μ 2)dx x f y x p dy )]()([+=
解:N x p x N y M
)(-=∂∂-∂∂ 所以⎰=⇒-=-dx
x p e x x p dx
d )()()(1μμ
μ
3))1,0( ])()([≠+=n dx y x q y x p dy n
解:⎰
=-dx
x p n n
e
y u x )()1(1),(μ
4.设)(),(2
1
z f z f 连续可微,
)]()([),(21≠-=xy xy f xy f y x ϕ,求证:
)
,(1y x ϕ是方程
)()(21=+xdy xy f ydx xy f 的一个积分因子。
证明:
)()()()(2211xy f xy xy f xy f xy xy f x
N y M -'
-+'=∂∂-∂∂
⎭
⎬⎫⎩⎨⎧∂∂-∂∂y M x N μμμ1=
⎭
⎬
⎫
⎩⎨⎧∂∂-∂∂--y M x N 11ϕϕϕ
=⎭
⎬⎫⎩⎨⎧∂∂-∂∂--y M x N ϕϕϕ
1
}}
)]()([ )]()({[)( })]()([ )]()({[)({2212112212121y x xy f xy f x
xy f xy f y xy f xy xy f xy f y
xy f xy f x xy f '
-'+--'
-'+--=-ϕ
x
N
y M ∂∂-∂∂=
5.设y
f
y x f ∂∂ , ),(连续,试证方程
),(=-dx y x f dy 为线性方程的充要条件是它有仅
依赖于x 的积分因子。
证明:方程有仅依赖于x 的积分因子等价于
N x p x
N
y M )(=∂∂-∂∂)()(x p xy f y =⇔
)
()(),(x q y x p y x f +=⇔
既方程为线性的。
