2005年高考题分章节汇编_3
05年各地高考题

高考语文真题分专题讲解第一讲——2005各地基础部分试题汇编一、字音——121、下列词语中加点的字,每对的读音完全相同的一组是全国2A.强求 / 牵强纤夫 / 纤尘不染来日方长 / 拔苗助长B.宿仇 / 宿将落笔 / 失魂落魄差可告慰 / 差强人意C.解嘲 / 押解蹊跷 / 另辟蹊径一脉相传 / 名不虚传D.卡片 / 关卡度量 / 置之度外方兴未艾 / 自怨自艾2、下列词语中,加点字的读音完全相同的一组足湖北卷A、羚羊邻居可怜孤苦伶仃B、质问桎梏幼稚炙手可热C、喉咙宠罩垄断得陇望蜀D、楼盘搂抱头颅光怪陆离3、下列词语中加点的字,读音全都正确的一组是湖南卷A.娴熟(xián) 辗转(niǎn) 踽踽独行(yǔ) 信手拈来(niān)B.惬意(xiá) 延宕(dàng) 通衙广陌(mò) 掎角之势(qǐ)C.膏腴(yú) 围歼(qiān) 矢志不渝(yù) 斐然成章(fěi)D.拓本(tà ) 饯别(jiàn) 鸠形鹄面(hú ) 并行不悖(bèi)4、下列词语中加点字的读音完全相同的一组是江苏卷A.眩晕舷梯炫耀武力改弦更张 B.羡慕募捐幕天席地蓦然回首C.剽悍漂泊虚无缥缈飘忽不定 D.舟楫逻辑开门揖盗缉拿归案5、下列词语的读音有两处错误的一组是辽宁卷A.塑料sùliào暂时zànshí纸屑zhǐxiè胳臂gēbeiB.擦拭cāshì察觉chájué撺掇cuànduo串珠chuànzhūC.血压xuèyā档次dǎngcì鲫鱼jìyú体己tījiD.处理chùlǐ掠夺lüèduó享受xiǎngshòu 尽快jìnkuài6、下列词语中加点字的读音全都相同的一组是北京卷A.舷梯娴熟悬崖勒马弦外之音 B.按捺纳税刚毅木讷方凿圆枘C.静谧猕猴弥天盖地所向披靡 D.皎洁缴纳狡兔三窟矫揉造作7、下列词语中加点字的读音完全相同的一组是广东卷A.奇数通缉豆萁放荡不羁犄角之势B.商榷雀跃官阙声名鹊起生性怯懦C.茁壮琢磨浑浊着手成春擢发难数D.谚语笑靥砚台狼吞虎咽雁过拔毛8、下列依次给出的加点字的注音,正确的一项是山东卷角色露骨力能扛鼎量体裁衣拾级而上A.júe lòu kāng liàng shíB.jiāo lùkāng liáng shè C.jiāo lòu gāng liáng shí D.júe lùgāng liàng shè 9、下列词语中加点的字的读音完全相同的一项是天津卷A.暂且砧板颤栗明修栈道技艺精湛B.与会峪口熨帖瑕不掩瑜钟灵毓秀C.陌路蓦然病殁拐弯抹角没齿不忘D.强劲根茎颈椎大相径庭不胫而走10、下列词语中加点的字的读音全都正确的一组是浙江卷A.粘贴(zhān)玷污(zhān) 龌龊(wò)运筹帷幄(wò)B.蹉跎(cuō)磋商(cuō)遭殃(yāng)怏怏不乐(yāng)C.飞镖(biāo) 剽悍(biāo) 绯红(fēi)妄自菲薄(fēi)D.蜿蜒(yán)筵席(yán) 市侩(kuài)脍炙人口(kuài)11、下列词语中加点的字的读音完全相同的一组是重庆卷A.承担呈献惩罚乘风破浪成人之美B.靓丽体谅酝酿量力而行歌声嘹亮C.谨慎景观瓶颈紧锣密鼓锦衣玉食D.抒怀酥糖苏醒殊途同归书香门第12、下列词语中加点的字,读音全都正确的一组是()江西卷A.悖(bèi)谬翎(lín)毛赧(nǎn)然咬文嚼(jiáo)字B.脉(mò)脉提(dī)防吮(shǔn)吸模棱(léng)两可C.福祉(zhǐ) 重(zhòng)听怔(zhèng)怔虚与委蛇(shé)D.游说(suì) 破绽(zhàn) 斡(wò)旋少不更(gēng)事二、字形——131、下列词语中没有错别字的一组是全国1A.忌讳砥砺蜚然成章流水不腐,户枢不蠹B.刍议安详自鸣得意愚者千虑,必有一得C.烦躁闲暇焚膏继晷金玉其外,败絮其中D.徇私编纂坚如磐石盛名之下,其实难负2、下列词语中没有错别字的一组是全国3A.切磋洽谈会悬梁刺骨覆水难收B.气概水笼头风雨如晦落荒而逃C.招募度假村有恃无恐试目以待D.怅惘挖墙脚功亏一篑矫枉过正3、下列词语中,没有错别字的一组是湖北卷A.边陲船仓放空炮高朋满座无心插柳柳成阴B.沟通赋与唱双簧有恃无恐有缘千里来相会C.稼穑皇历跑龙套记忆尤新壶里没酒难留客D.通缉砂糖碰钉子披星戴月有一利必有一弊4、下列词语中投有错别字的一组是湖南卷A.福祉梗概耳提面命钟灵毓秀B.箴言幅射蜂拥而上博闻强识C.摄取颓唐金壁辉煌夙兴夜寐D.恪守荧屏厚积薄发异曲同功5、下列各句中没有错别字的一句是江苏卷A.联合国维和部队进驻后,这一地区箭拔弩张的局势才得以缓和,冲突双方终于坐到了谈判桌前。
2005年高考试题分类汇编(数列)

2005年高考试题分类汇编(数列)考法1等差数列1.(2005·山东卷·文科){}n a 是首项11a =,公差3d =的等差的数列,如果2005n a =,则序号n 等于A.667B.668C.669D.6702.(2005·福建卷·文理科)已知等差数列{}n a 中,7916a a +=,41a =,则12a 的值是A .15B .30C .31D .64 3.(2005·辽宁卷·文理科)若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m ,则m 的范围是A .(1,2)B .(2,)+∞C .[3,)+∞D .(3,)+∞ 4.(2005·全国卷Ⅱ·理科)如果数列1a ,2a ,,n a 是各项都大于零的等差数列,公差0d ≠,则A.1845a a a a ⋅>⋅B.1845a a a a ⋅<⋅C.5481a a a a +>+D.5481a a a a =5.(2005·全国卷Ⅱ·文科)如果数列}{n a 是等差数列,则 A.5481a a a a +<+ B.5481a a a a +=+ C.5481a a a a +>+ D.5481a a a a =考试2等比数列11.(2005·全国卷Ⅱ·文科)在22738和之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为 .1.(2005·全国卷Ⅰ·理科)设等比数列{}n a 的公比为q ,前n 项和0n S >(1,2,n =).(Ⅰ)求q 的取值范围;(Ⅱ)设1223++-=n n n a a b ,记{}n b 的前n 项和为n T ,试比较n S 与n T 的大小.1.(2005·天津卷·文科)若公比为c 的等比数列{}n a 的首项1a 且满足122n n n a a a --+=(3,4,5,n =,0c >).(Ⅰ)求c 的值;(Ⅱ)求数列{}n na 的前n 项和n S .考法3等差数列与等比数列的综合应用15.(2005·湖北卷·理科)设等比数列}{n a 的公比为q ,前n 项和为n S ,若1n S +,n S ,2n S +成等差数列,则q 的值为 .2.(2005·福建卷·文科)已知{}n a 是公比为q 的等比数列,且1a ,3a ,2a 成等差数列.(Ⅰ)求q 的值;(Ⅱ)设{}n b 是以2为首项,q 为公差的等差数列,其前n 项和为n S ,当2n ≥时,比较n S 与n b 的大小,并说明理由.15.(2005·湖北卷·文科)设数列}{n a 的前n 项和为22n S n =,}{n b 为等比数列,且11a b =,2211()b a a b -=. (Ⅰ)求数列}{n a 和}{n b 的通项公式; (Ⅱ)设nnn b a c =,求数列}{n c 的前n 项和n T . 1.(2005·全国卷Ⅰ·文科)设正项等比数列{}n a 的首项211=a ,前n 项和为n S ,0)12(21020103010=++-S S S .(Ⅰ)求{}n a 的通项; (Ⅱ)求{}n nS 的前n 项和n T .1.(2005·全国卷Ⅲ·文理科)在等差数列{}n a 中,公差0d ≠,2a 是1a 与4a 的等比中项.已知数列1a ,3a ,1k a ,2k a ,3k a ,,n k a ,,成等比数列,求数列{}n k 的通项n k .11.(2005·全国卷Ⅱ·文理科)已知{}n a 是各项均为正数的等差数列,1lg a ,2lg a ,4lg a 成等差数列.又21nn b a =,1,2,3,n =.(Ⅰ)证明:{}n b 为等比数列; (Ⅱ)如果数列{}n b 前3项的和等于724,求数列{}n a 的首项1a 和公差d . 考法4 其它13.(2005·天津卷·理科)在数列{}n a 中,11a =,22a =,且21(1)n n n a a +-=+-( n N *∈),则100S = .1.(2005·北京卷·文科)数列{}n a 的前n 项和为n S ,且11a =,113n n a S +=,1,2,3,n =,求:(Ⅰ)2a ,3a ,4a 的值及数列{}n a 的通项公式; (Ⅱ)2462n a a a a ++++的值.1.(2005·江西卷·理科)已知数列{}n a 的各项都是正数,且满足:01a =,11(4)2n n n a a a +=-(n N ∈). (Ⅰ)证明12n n a a +<<,n N ∈ (Ⅱ)求数列}{n a 的通项公式n a .1.(2005·山东卷·文理科)已知数列{}n a 的首项15a =,前n 项和为n S ,且15n n S S n +=++(*n N ∈).(Ⅰ)证明数列{}1n a +是等比数列; (Ⅱ)令212()n n f x a x a x a x =+++,求函数()f x 在点1x =处的导数(1)f '并比较2(1)f '与22313n n -的大小.1.(2005·重庆卷·文科)数列{}n a 满足11a =,且11816250n n n n a a a a ++-++=(1n ≥),记112n n b a =-(1n ≥),(Ⅰ)求1b 、2b 、3b 、4b 的值;(Ⅱ)求数列}{n b 的通项公式及数列}{n n b a 的前n 项和.n S。
2005年全国各地高考试题分类解析2005年高考全国试题分类解析(三角函数部分)

2005年全国高考数学试题(三角函数部分)选择题1.(北京卷)对任意的锐角α,β,下列不等关系中正确的是 D (A )sin(α+β)>sin α+sin β (B )sin(α+β)>cos α+cos β (C )cos(α+β)<sinα+sinβ (D )cos(α+β)<cosα+cosβ2.(北京卷)函数f (x )=cos xA(A )在[0,),(,]22πππ上递增,在33[,),(,2]22ππππ上递减 (B )在3[0,),[,)22πππ上递增,在3(,],(,2]22ππππ上递减 (C )在3(,],(,2]22ππππ上递增,在3[0,),[,)22πππ上递减 (D )在33[,),(,2]22ππππ上递增,在[0,),(,]22πππ上递减 3.(全国卷Ⅰ)当20π<<x 时,函数xxx x f 2sin sin 82cos 1)(2++=的最小值为 D(A)2(B)32(C)4(D)344.(全国卷Ⅰ)在ABC ∆中,已知C BA sin 2tan=+,给出以下四个论断: B ① 1cot tan =⋅B A② 2sin sin 0≤+<B A③ 1cos sin 22=+B A④ C B A 222sin cos cos =+其中正确的是 (A)①③ (B)②④ (C)①④ (D)②③ 5.(全国卷Ⅱ)函数f (x ) = | sin x +cos x |的最小正周期是 C(A) 4π (B)2π(C)π (D)2π 6.(全国卷Ⅱ)已知函数y =tan x ω 在(-2π,2π)内是减函数,则 B(A)0 <ω ≤ 1 (B)-1 ≤ ω < 0 (C)ω≥ 1 (D)ω≤ -17.(全国卷Ⅱ)锐角三角形的内角A 、B 满足tan A -A2sin 1= tan B,则有(A)sin 2A –cos B = 0 (B)sin 2A + cos B = 0 (C)sin 2A – sin B = 0 (D) sin 2A + sin B = 0 8.(全国卷Ⅲ)已知α为第三象限角,则2α所在的象限是 D(A)第一或第二象限 (B)第二或第三象限(C)第一或第三象限 (D)第二或第四象限9.(全国卷Ⅲ)设02x π≤≤,sin cos x x =-,则 C(A) 0x π≤≤ (B)744x ππ≤≤(C) 544x ππ≤≤ (D) 322x ππ≤≤10.(全国卷Ⅲ)22sin 2cos 1cos 2cos 2⋅=+ααααB (A) tan α (B) tan 2α (C) 1 (D)1211.(浙江卷)已知k <-4,则函数y =cos2x +k (cos x -1)的最小值是( A ) (A) 1 (B) -1 (C) 2k +1 (D) -2k +1 12.(浙江卷)函数y =sin(2x +6π)的最小正周期是( B ) (A)2π(B) π (C) 2π (D)4π 13.(江西卷)已知==ααcos ,32tan 则( B )A.54B.-54 C.154 D.-53 14.(江西卷)设函数)(|,3sin |3sin )(x f x x x f 则+=为( A )A.周期函数,最小正周期为32π B.周期函数,最小正周期为3π C.周期函数,数小正周期为π2D.非周期函数15.(江西卷)在△OAB 中,O 为坐标原点,]2,0(),1,(sin ),cos ,1(πθθθ∈B A ,则当△OAB 的面积达最大值时,=θ( D )A.6π B.4π C.3π D.2π 16、(江苏卷)若316sin =⎪⎭⎫⎝⎛-απ,则⎪⎭⎫ ⎝⎛+απ232cos =( A ) A.97-B.31-C.31D.97 17.(湖北卷)若∈<<=+απαααα则),20(tan cos sin( C )A.)6,0(πB.)4,6(ππ C.)3,4(ππ D.)2,3(ππ 18.(湖南卷)tan600°的值是( D )A.33-B.33C.3-D.319.(重庆卷)=+-)12sin12)(cos12sin12(cos ππππ( D )A.23-B.21-C.21D.23 20.(福建卷)函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图,则 ( C )A.4,2πϕπω== B.6,3πϕπω==C.4,4πϕπω==D.45,4πϕπω==21.(福建卷)函数x y 2cos =在下列哪个区间上是减函数 ( C )A.]4,4[ππ-B.]43,4[ππ C.]2,0[πD.],2[ππ22.(山东卷)已知函数)12cos()12sin(π-π-=x x y ,则下列判断正确的是( B )(A)此函数的最小正周期为π2,其图象的一个对称中心是)0,12(π(B)此函数的最小正周期为π,其图象的一个对称中心是)0,12(π(C)此函数的最小正周期为π2,其图象的一个对称中心是)0,6(π(D)此函数的最小正周期为π,其图象的一个对称中心是)0,6(π23(山东卷)函数⎪⎩⎪⎨⎧≥<<-π=-0,01),sin()(12x e x x x f x ,若2)()1(=+a f f ,则a 的所有可能值为( B )(A)1 (B)22,1-(C)22- (D)22,1 24.(天津卷)要得到函数x y cos 2=的图象,只需将函数)42sin(2π+=x y 的图象上所有的点的(C)(A)横坐标缩短到原来的21倍(纵坐标不变),再向左平行移动8π个单位长度 (B)横坐标缩短到原来的21倍(纵坐标不变),再向右平行移动4π个单位长度(C)横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动4π个单位长度(D)横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动8π个单位长度 25(天津卷)函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示,则函数表达式为( A )(A))48sin(4π+π-=x y (B))48sin(4π-π=x y (C))48sin(4π-π-=x y (D))48sin(4π+π=x y填空题:1.(北京卷)已知tan2α=2,则tanα的值为-34,tan ()4πα+的值为-712.(全国卷Ⅱ)设a 为第四象限的角,若513sin 3sin =a a ,则tan 2a =___43-___________. 3.(上海卷)函数[]π2,0|,sin |2sin )(∈+=x x x x f 的图象与直线k y =有且仅有两个不同的交点,则k 的取值范围是__________。
2005年高考题分章节汇编

2005年高考题分章节汇编 第七章 直线与圆的方程一、选择题1.(2005年春考·北京卷·文6)直线1)1(02322=+-=-+y x y x 被圆所截得的线段的长为 ( C )A .1B .2C .3D .22.(2005年高考·北京卷·理2文3) “21=m ”是“直线03)2()2(013)2(=-++-=+++y m x m my x m 与直线相互垂直”的( B )A .充分必要条件B .充分而不必要条件C .必要而不充分条件D .既不充分也不必要条件3.(2005年高考·北京卷·理4)从原点向圆0271222=+-+y y x 作两条切线,则该圆夹在两条切线间的劣弧长为(B )A .πB .2πC .4πD .6π4.(2005年高考·北京卷·文5)从原点向圆0271222=+-+y y x 作两条切线,则这两条切线的夹角的大小为( B )A .6π B .3π C .2π D .32π 5.(2005年高考·湖南卷·理4)已知点P (x ,y )在不等式组⎪⎩⎪⎨⎧≥-+≤-≤-022,01,02y x y x 表示的平面区域上运动,则z =x -y 的取值范围是( C )A .[-2,-1]B .[-2,1]C .[-1,2]D .[1,2]6.(2005年高考·辽宁卷9)若直线02=+-c y x 按向量)1,1(-=平移后与圆522=+y x 相切,则c 的值为( A )A .8或-2B .6或-4C .4或-6D .2或-87.(2005年高考·江西卷·理3) “a =b ”是“直线相切与圆2)()(222=++-+=b y a x x y ”的 ( A ) A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分又不必要条件8.(2005年高考·重庆卷·理1文1)圆5)2(22=++y x 关于原点(0,0)对称的圆的方程为( A )A .5)2(22=+-y xB .5)2(22=-+y xC .5)2()2(22=+++y xD .5)2(22=++y x9.(2005年高考·浙江卷·理2文3)点(1,-1)到直线x -y +1=0的距离是 ( D )A .21 B .32CD10.(2005年高考·浙江卷·理7)设集合{}(,)|,,1A x y x y x y --=是三角形的三边长,则A 所表示的平面区域(不含边界的阴影部分)是( A )A .B .C .D .11.(2005年高考·浙江卷·文10)设集合A ={(x ,y )|x ,y ,1-x -y 是三角形的三边长},则A 所表示的平面区域(不含边界的阴影部分)是 ( A ) A . B . C . D .12.(2005年高考·天津卷·理3文7)给出下列三个命题①若1->≥b a ,则bb aa +≥+11②若正整数m 和n 满足n m ≤,则2)(n m n m ≤-③设),(11y x P 为圆9:221=+y x O 上任一点,圆O 2以),(b a Q 为圆心且半径为 1.当1)()(2121=-+-y b x a 时,圆O 1与圆O 2相切2005年高考数学试题分类汇编(春考3套,秋考29套) 湖北省枝江一中时爱华收集整理第七章 直线与圆的方程第87页其中假命题的个数为 ( B ) A .0 B .1 C .2 D .313.(2005年高考·天津卷·文4)将直线2x-y+λ=0沿x 轴向左平移1个单位,所得直线与圆x 2+y 2+2x-4y=0相切,则实数λ的值为 (A ) A .-3或7 B .-2或8 C .0或10 D .1或11 14.(2005年高考·全国卷Ⅰ·理3)已知直线l 过点(-2,0),当直线l 与圆x y x 222=+有两个交点时,其斜率k 的取值范围是( B )A .)22,22(-B .)2,2(-C .)42,42(D .)81,81(-15.(2005年高考·全国卷Ⅰ·理9文9)在坐标平面上,不等式组⎩⎨⎧+-≤-≥1||3,1x y x y 所表示的平面区域面积为 ( C )A .2B .23C .223 D .216.(2005年高考·全国卷Ⅰ·文12)设直线l 过点(-2,0),且与圆x 2+y 2=1相切,则l 的斜率是 ( D )A .±1B .±21C .±33 D .±317.(2005年高考·全国卷Ⅲ·理2文2)已知过点A(-2,m)和B(m ,4)的直线与直线2x +y -1=0平行,则m 的值为 ( B )A .0B .-8C .2D .10二、填空题1.(2005年春考·北京卷·理11)若圆04122=-++mx y x 与直线1-=y 相切,且其圆心在y 轴的左侧,则m 的值为__________.32.(2005年高考·上海卷·理6)将参数方程⎩⎨⎧=+=θθsin 2cos 21y x (θ为参数)化为普通方程,所得方程是__________.4)1(22=+-y x3.(2005年高考·上海卷·文3)若y x ,满足条件⎩⎨⎧≤≤+xy y x 23,则y x z 43+=的最大值是__________.114.(2005年高考·上海卷·文9)直线x y 21=关于直线1=x 对称的直线方程是__________. x +2y -2=05.(2005年高考·福建卷·理14文15)非负实数x 、y 满足y x y x y x 3,03042+⎩⎨⎧≤-+≤-+则的最大值为 . 96.(2005年高考·湖北卷·理16文16)某实验室需购某种化工原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元. 在满足需要的条件下,最少要花费 元. 500 7.(2005年高考·湖南卷·理13)已知直线ax +by +c =0与圆O :x 2+y 2=1相交于A 、B 两点,且|AB|=3,则⋅ = . 21-8.(2005年高考·湖南卷·文11)设直线0132=++y x 和圆03222=--+x y x 相交于点A 、B ,则弦AB 的垂直平分线方程是 . 0323=--y x 9.(2005年高考·江西卷·理14文14)设实数x , y满足的最大值是则x y y y x y x ,03204202⎪⎩⎪⎨⎧≤->-+≤-- . 23 10.(2005年高考·重庆卷·文14)若y x y x -=+则,422的最大值是 . 2211.(2005年高考·山东卷·理15文15)设x 、y 满足约束条件5,3212,03,0 4.x y x y x y +≤⎧⎪+≤⎪⎨≤≤⎪⎪≤≤⎩则使得目标函数65z x y =+的最大的点(,)x y 是 .()2,312.(2005年高考·全国卷II ·理13文14)圆心为(1,2)且与直线5x -12y -7=0相切的圆的方程为 . 22(1)(2)4x y -+-=三、解答题1. (本题满分16分) (2005年春考·上海卷21)本题共有3个小题,第1小题满分3分, 第2小题满分6分,第3小题满分7分. 已知函数xax x f +=)(的定义域为),0(∞+,且222)2(+=f . 设点P 是函数图象上的2005年高考数学试题分类汇编(春考3套,秋考29套) 湖北省枝江一中时爱华收集整理第七章 直线与圆的方程第89页任意一点,过点P 分别作直线x y =和y 轴的垂线,垂足分别为N M 、. (1)求a 的值;(2)问:||||PN PM ⋅是否为定值?若是,则求出该定值,若不是,则说明理由;(3)设O 为坐标原点,求四边形OMPN 面积的最小值.[解](1)∵ 22222)2(+=+=a f ,∴ 2=a . …… 3分(2)设点P 的坐标为),(00y x ,则有002x x y +=,00>x ,由点到直线的距离公式可知:0000||,12||||x PN x y x PM ==-=, 故有1||||=⋅PN PM ,即||||PN PM ⋅为定值,这个值为1. …… 9分 (3)由题意可设),(t t M ,可知),0(0y N .∵ PM 与直线x y =垂直,∴ 11-=⋅PM k ,即100-=--tx ty ,解得 )(2100y x t +=,又0002x x y +=,∴ 0022x x t +=. ∴22212+=∆x S OPM ,222120+=∆x S OPN , ∴ 212)1(212020+≥++=+=∆∆x x S S S OPN OPM OMPN , 当且仅当10=x 时,等号成立.∴ 此时四边形OMPN 面积有最小值21+. …… 16分 2.(本小题满分14分)(2005年高考·广东卷20)在平面直角坐标系中,已知矩形ABCD 的长为2,宽为1,AB、AD 边分别在x 轴、y 轴的正半轴上,A 点与坐标原点重合(如图5所示).将矩形折叠,使A 点落在线段DC 上.(Ⅰ)若折痕所在直线的斜率为k ,试写出折痕所在直线的方程; (Ⅱ)求折痕的长的最大值. 解:设点A 关于拆痕的对称点E ,由于点E 在线段DC 上,故可设点E 的坐标为(t ,1)(02t ≤≤).(Ⅰ)若0t =,则“拆痕”所在的直线为线段AD 的中垂线,它的方程为12y =; 若02t <≤,由1AE K k ⋅=-,则11k t k t⋅=-⇔=-,从而线段AE 的中点M 的坐标为1(,)22k -,故“拆痕”所在直线的方程为 1()22k y k x -=+. 综上所述,“拆痕”所在直线的方程为1()22ky k x -=+. (Ⅱ)设“拆痕”的长为l .(1)当“折痕”过AD 的中点时(如图3),0k =;当“折痕”过点B 时(如图4),由于10,k-<<求得2k =20k ≤≤时,“折痕”与y 轴及2x =均有交2005年高考数学试题分类汇编(春考3套,秋考29套) 湖北省枝江一中时爱华收集整理第七章 直线与圆的方程第91页点,分别求得为21(0,)2k +、241(2,)2k k ++. 此时,l ==由于l 是关于k的函数,它在2,0]上是减函数,所以,当2k =时,max l =.(2)当“折痕”过点D 时(如图5),1k =-.所以,当12k -≤≤时,“折痕”与y 轴及x 轴均有交点,分别求得为21(0,)2k +、1(,0)22k k --. 此时,l == 设 232(1)()k f k k +=,则22232(1)(21)()k k f k k+-'=,由此得:当12k -≤<-时,()0f k '<;当2k =-时,()0f k '=;当22k -<≤时,()0f k '>.所以,max ()(1)f k f =-,或max ()2)f k f =.由于2)(1)1200f f --=->,所以,max l ===.(3)当“折痕”过AC 的中点时(如图6),求得2k =-.所以,当21k -≤≤-时,“折痕”与1y =及x 轴均有交点,分别求得为21(,1)2k k-、1(,0)22k k --. 此时,l == 由于l 是关于k 的函数,它在[2,1]--上是增函数,所以,当1k =-时,max l =由于.3.(本小题满分12分)(2005年高考·江苏卷19)如图,圆1O 与圆2O 的半径都是1,1O 2O =4,过动点P 分别作圆1O 、圆2O 的切线PM 、PN (M 、N 分别为切点),使得PN 2PM =,试建立适当的坐标系,并求动点P 的轨迹方程。
2005年全国各地高考数学试题及解答分类汇编大全(09解三角形)

2005年全国各地高考数学试题及解答分类汇编大全(09解三角形)一、选择题:1、(2005春招北京文、理)在ABC ∆中,已知C B A sin cos sin 2=,那么ABC ∆一定是( B )A .直角三角形B .等腰三角形C .等腰直角三角形D .正三角形2. (2005春招上海)在△ABC 中,若CcB b A a cos cos cos ==,则△ABC 是 [答] ( ) (A )直角三角形. (B )等边三角形. (C )钝角三角形. (D )等腰直角三角形.3. (2005江苏)△ABC 中,,3,3A BC π==则△ABC 的周长为(A))33B π++ (B))36B π++ (C )6sin()33B π++ (D )6sin()36B π++ [评述]:本题考查了在三角形正弦定理的的运用,以及三角公式恒等变形、化简等知识的运用。
[解析]:在ABC ∆中,由正弦定理得:,233sin =B AC 化简得AC=,sin 32B 233)3(sin[=+-ππB AB ,化简得AB=)32sin(32B -π, 所以三角形的周长为:3+AC+AB=3+B sin 32+)32sin(32B -π=3+.3)6sin(6cos 3sin 33++=+πB B B 故选D.4.(2005江西文、理)在△OAB 中,O 为坐标原点,]2,0(),1,(sin ),cos ,1(πθθθ∈B A ,则当△OAB 的面积达最大值时,=θ ( )A .6π B .4π C .3π D .2π 【思路点拨】运用图形,根据图形表示ABC ∆的面积,将实际问题转化成数学问题.【正确解答】1111sin cos (1cos )(1sin )222ABC S θθθθ∆=----- 11sin cos 22θθ=-11sin 224θ=-当2θπ=即2πθ=时,面积最大.【解后反思】运用三角函数解决相应的实际问题,首先应根据题目的要求将面积的表达式写出来,然后在表达式中,根据自变量的取值范围,最终求出答案,所要注意的是,解决此类问题时不能仅凭函数的表达式,应考虑实际情况,例如,在函数的自变量中,可以取负数,而如果在实际题目中,自变量表示的是天数,那么这相自变量必须为正数,且为整数等等.二、填空题:1. (2005北京文)在△ABC 中,AC=3,∠A=45°,∠C=75°,则BC 的长为 . 【答案】2【详解】060120180)C A (180B =-=∠+∠-=∠,由正弦定理得sinBACsinA BC =, 所以223223sinBsinAAC BC =⨯=⋅=【名师指津】凡是关于三角形的边角关系的问题,一般要考虑是否能用正弦定理、余弦定理2、(2005上海文、理)在ABC ∆中,若︒=120A ,AB=5,BC=7,则AC=__________. 【思路点拨】本题主要考查解斜三角形的相关知识和运算能力.可画出草图,设法求出AC. 【正确解答】由余弦定理︒⨯⨯-+=120cos 2222AC BC AC BC AB 解得8AC =-(舍)或AC=3,因此ABC ∆的面积4315120sin 21S =︒⨯⨯⨯=AC AB 【解后反思】要注意正、余弦定理的灵活运用.本题可视为关于AC 的方程,求出AC 的目的,在于求ABC ∆的面积,若利用正弦定理求AC 就较繁了.最优解总是我们追求的目标.三、解答题:1.(2005湖北文)(本小题满分12分)在△ABC 中,已知63,31cos ,3tan ===AC C B ,求△ABC 的面积.1.本小题主要考查正弦定理、余弦定理和三角形面积公式等基础知识,同时考查利用三角公式进行恒等变形的技能和运算能力.解法1:设AB 、BC 、CA 的长分别为c 、a 、b ,.21cos ,23sin ,60,3tan ==∴==B B B B 得由 应用正弦定理得又,322cos 1sin 2=-=C C 8232263sin sin =⨯==B C b c ..3263332213123sin cos cos sin )sin(sin +=⨯+⨯=+=+=∴C B C B C B A 故所求面积.3826sin 21+==∆A bc S ABC 解法3:同解法1可得c=8. 又由余弦定理可得.64,,364,32321236330sin sin sin sin ,sin sin .12030,900,60.64,64.0108,21826454,cos 222122222+=<-=>=⋅=⋅>⋅==<<∴<<=-=+==+-∴⨯⨯-+=-+=a a B b A B b a B b A a A C B a a a a a a B ac c a b 故舍去而得由所得即故所求面积.3826sin 21+==∆B ac S ABC2.(2005湖北理)(本小题满分12分)在△ABC 中,已知AC B AB ,66cos ,364==边上的中线BD=5,求sinA 的值. 2.本小题主要考查正弦定理、余弦定理等基础知识,同时考查利用三角公式进行恒等变形的技能和运算能力.解法1:设E 为BC 的中点,连接DE ,则DE//AB ,且DE=,,36221x BE AB ==设 在△BDE 中利用余弦定理可得: BD 2=BE 2+ED 2-2BE ·EDcosBED ,,6636223852x x ⨯⨯++= ,328cos 2,2),(37,1222=⋅-+==-==B BC AB BC AB AC BC x x 从而故舍去解得.1470sin ,6303212sin 2,630sin ,3212====A AB AC 故又即 解法2:以B 为坐标原点,x 轴正向建立直角坐标系,且不妨设点A 位于第一象限.).(314,2.5)352()634(||).352,634(),0,(),354,34()sin 364,cos 364(,630sin 22舍去从而由条件得则设则由-===++=+=====x x x x BD x BC B B B ),354,32(-=故.1470cos 1sin ,141439809498091698098||||cos 2=-=∴=+++-==A A CA BA A 于是 解法3:过A 作AH ⊥BC 交BC 于H ,延长BD 到P 使BD=DP ,连接AP 、PC , 过P 作PN ⊥BC 交BC 的延长线于N ,则HB=ABcosB=,354,34=AH .1470sin ,6303212sin 2.3212,32,2,34,310)354()52(22222222=∴==+===-=∴===-=-=-=A A HC AH AC HC CN BN BC HB CN AH BP PN BP BN 故由正弦定理得而3.(2005全国Ⅲ理)(本小题满分12分)△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知a ,b ,c 成等比数列,.43cos =B (Ⅰ)求cotA+cotC 的值; (Ⅱ)设c a +=⋅求,23的值. 【思路点拨】本题考查:1.三角式的化简、求值;2.向量法的应用.解决问题1.应该注意先整理所求三角式,再利用公式、性质等进行化简,最后将已知条件(可能要在整理之后)代入化简后的三角式求值.解决问题2.则应该注意使用数形结合的思想方法并注意随时与问题的具体情境相结合.【正确解答】(Ⅰ)由,47)43(1sin ,43cos 2=-==B B 得由b 2=a c 及正弦定理得 .s i n s i n s i n 2C A B =于是BC A CA A C A C CC AA CAC A 2sin )sin(sin sin sin cos cos sin sin cos sin cos tan 1tan 1cot cot +=+=+=+=+.774sin 1sin sin 2===B B B (Ⅱ)由.2,2,43cos ,23cos 232====⋅=⋅b ca B B ca 即可得由得 由余弦定理 b 2=a 2+c 2-2a c+cosB 得a 2+c 2=b 2+2a c ·cosB=5. 3,9452)(222=+=+=++=+c a ac c a c a【解后反思】当问题中出现三角形边、角之间的比例关系时,应首先考虑采用正弦定理,因为所有三角基本公式中只有它涉及边与角之间的比例关系.利用正弦定理求角时,注意有可能出现多解情况,要好好讨论,防止出现漏解或多解情况.4. (2005天津理)(本小题满分12分)在ABC ∆中,,,A B C ∠∠∠所对的边长分别是,,a b c .设,,a b c 满足条件222b c bc a +-=和12c b =+tan A B ∠和的值. 【思路点拨】本题考查余弦定理、正弦定理、两角差的正弦公式、同角三角函数的基本关系等基础知识,考查基本运算能力,把握住这些定理的结构,进行边角互化即可求得.【正确解答】解法一:由余弦定理212cos 222=-+=bc a c b A , 因此,︒=∠60A 在△ABC 中,∠C=180°-∠A -∠B=120°-∠B.由已知条件,应用正弦定理BB BC b c sin )120sin(sin sin 321-︒===+ ,21cot 23sin sin 120cos cos 120sin +=︒-︒=B B B B解得,2cot =B 从而.21tan =B解法二:由余弦定理212cos 222=-+=bc a c b A , 因此,︒=∠60A ,由222a bc c b =-+,得.41532133411)(1)(22=--+++=-+=b c b c b a所以.215=b a ① 由正弦定理5123152sin sin =⋅==A a b B . 由①式知,b a >故∠B<∠A ,因此∠B 为锐角,于是152sin 1cos 2=-=B B ,从而.21cos sin tan ==B B B 解法3:()22222221cos 222b c b c bc b c a A bc bc +-+-+-=== 所以:60B ∠=︒由:180120C A B B ∠=︒-∠-∠=︒-∠()sin 1201sin sin120cos cos120sin 12sin sin sin 2B cC B B b B B B ︒-︒-︒====+所以:1tan 2B =【解后反思】解斜三角形问题时,一是要观察差异(或角、或函数、或运算),寻找联系(借助于熟知的公式、方法和技巧)分析综合(由因导果或执果索因),实现转化.二是要尽可能统一,即统一到角(解法1)或统一到边(解法2)便于问题的解决.。
2005年高考试题分类汇编(解析几何)

2005年高考试题分类汇编(解析几何)考点1直线与圆的方程1.(2005·北京卷·文理科)“12m =”是“直线(2)310m x my +++=与直线(2)(2)30m x m y -++-=相互垂直”的A.充分必要条件B.充分而不必要条件C.必要而不充分条件D.既不充分也不必要条件2.(2005·全国卷Ⅲ·文理科)已知过点(2,)A m -和(,4)B m 的直线与直线 210x y +-=平行,则m 的值为A .0B .8-C .2D .103.(2005·北京卷·文理科)从原点向圆2212270x y x +-+=作两条切线,则该圆夹在两条切线间的劣弧长为A.πB.2πC.4πD.6π4.(2005·江西卷·文理科)“a b =”是“直线2y x =+与圆22()()2x a y b -++= 相切”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件5.(2005·全国卷Ⅰ·理科)已知直线l 过点(2,0)-,当直线l 与圆x y x 222=+有两个交点时,其斜率k 的取值范围是A.(-B.(C.(44-,D.11()88-, 6.(2005·全国卷Ⅱ·理科)圆心为(1,2)且与直线51270x y --=相切的圆的方程为 .考点2椭圆1.(2005·全国卷Ⅲ·文理科)设椭圆的两个焦点分别为1F 、2F ,过2F 作椭圆长轴的垂线交椭圆于点P ,若12F PF ∆为等腰直角三角形,则椭圆的离心率是A.2B.12C.212.(2005·天津卷·理科)设双曲线以椭圆192522=+y x 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为A.2±B.34±C.21±D.43± 3.(2005·湖北卷·理科)设A 、B 是椭圆λ=+223y x 上的两点,点(1,3)N 是线段AB 的中点,线段AB 的垂直平分线与椭圆相交于C 、D 两点.(Ⅰ)确定λ的取值范围,并求直线AB 的方程;(Ⅱ)试判断是否存在这样的λ,使得A 、B 、C 、D 四点在同一个圆上?并说明理由.考点3 抛物线1.(2005·北京卷·文科)抛物线24y x =的准线方程是 ;焦点坐标是 .2.(2005·江西卷·理科)如图,设抛物线C :2y x =的焦点为F ,动点P 在直线l :20x y --=上运动,过P 作抛物线C 的两条切线PA 、PB ,且与抛物线C 分别相切于A 、B 两点.(Ⅰ)求APB ∆的重心G 的轨迹方程.(Ⅱ)证明PFA PFB ∠=∠.3.(2005·江西卷·文科)M 是抛物线上2y x =上的一点,动弦ME 、MF 分别 交x 轴于A 、B 两点,且MA MB =.(Ⅰ)若M 为定点,证明:直线EF 的斜率为定值;(Ⅱ)若M 为动点,且90EMF ∠=,求EMF ∆的重心G 的轨迹方程.4.(2005·全国卷Ⅲ·文理科)设11(,)A x y ,22(,)B x y 两点在抛物线22y x =上,l 是AB 的垂直平分线.(Ⅰ)当且仅当12x x +取何值时,直线l 经过抛物线的焦点F ?证明你的结论; (Ⅱ)当11x =,23x =-时,求直线l 的方程.考点4 双曲线1.(2005·辽宁卷·理科)已知双曲线的中心在原点,离心率为3.若它的一条准线与抛物线x y 42=的准线重合,则该双曲线与抛物线24y x =的交点到原点的距离是A .23+6B .21C .21218+D .212.(2005·全国卷Ⅱ·文科)双曲线19422=-y x 的渐近线方程是 A.x y 32±= B.x y 94±= C.x y 23±= D.x y 49±= 3.(2005·全国卷Ⅱ·理科)已知双曲线22163x y -=的焦点为1F 、2F ,点M 在双曲线上且1MF x ⊥轴,则1F 到直线2F M 的距离为C.65D.564.(2005·全国卷Ⅲ·文理科)已知双曲线2212y x -=的焦点为1F 、2F ,点M 在双曲线上且120MF MF ⋅=,则点M 到x 轴的距离为A.43B.53C.35.(2005·福建卷·理科)已知1F 、2F 是双曲线22221x y a b-=(0,0a b >>)的两焦点,以线段12F F 为边作正三角形12MF F ,若边1MF 的中点在双曲线上,则双曲线的离心率是A .324+B .13-C .213+ D .13+6.(2005·湖北卷·文理科)双曲线221x y m n-=(0mn ≠)离心率为2,有一个焦点与抛物线x y 42=的焦点重合,则mn 的值为A .163B .83C .316D .38 7.(2005·全国卷Ⅰ·理科)已知双曲线2221x y a-=(0a >)的一条准线与抛物线26y x =-的准线重合,则该双曲线的离心率为 A.23 B.23 C.26 D.332 8.(2005·山东卷·理科)设双曲线22221x y a b-=(0a >,0b >)的右焦点为F ,右准线l 与两条渐近线交于P 、Q 两点,如果PQF ∆是直角三角形,则双曲线的离心率e = .9.(2005·江西卷·文理科)以下同个关于圆锥曲线的命题中①设A 、B 为两个定点,k 为非零常数,PA PB k -=,则动点P 的轨迹为双曲线;②设定圆C 上一定点A 作圆的动点弦AB ,O 为坐标原点,若1()2OP OA OB =+,则动点P 的轨迹为椭圆;③方程22520x x -+=的两根可分别作为椭圆和双曲线的离心率;④双曲线13519252222=+=-y x y x 与椭圆有相同的焦点. 其中真命题的序号为 .(写出所有真命题的序号)。
2005年高考全国试题分类解析(极限)

2005年全国高考数学试题分类汇编——极限1.(全国卷Ⅲ理第5题)22112lim 3243x x x x x →⎛⎫-= ⎪-+-+⎝⎭ ( ) A 12- B 12 C 16- D 162.(辽宁卷第2题)极限)(lim 0x f x x →存在是函数)(x f 在点0x x =处连续的( )A .充分而不必要的条件B .必要而不充分的条件C .充要条件D .既不充分也不必要的条件3.(浙江卷理第1题)limn →∞2123nn++++=( ) (A) 2 (B) 4 (C) 21(D)04.(广东卷第3题)233lim 9x x x →-+=-( )(A)16-(B)0(C)16(D)135. (湖北卷理第8题)若1)11(lim 21=---→xbx a x ,则常数b a ,的值为 ( )A .4,2=-=b aB .4,2-==b aC .4,2-=-=b aD .4,2==b a6.(重庆卷理第14题):3213223lim 23n n n n n +→∞-+= _________。
7. (上海卷理第7题)计算:112323lim -+∞→+-n n nn n =__________。
8. (湖南卷理第3题)已知数列{log 2(a n -1)}(n ∈N *)为等差数列,且a 1=3,a 2=5,则lim 21321111()n n na a a a a a →∞++++---=( )A .2B .23C .1D .219.(福建卷理第15题) 若常数b 满足|b|>1,则=++++-∞→n n n bb b b 121lim .10. (山东卷理第13题)2222lim__________(1)n n nn C C n -→∞+=+.11.(江西卷理第8题) 11(1)1lim1,lim 1(22)x x f x x x f x →→--==--若则( ) A .-1 B .1C .-21D .2112.(广东卷第10题)已知数列{}n x 满足212x x =,)(2121--+=n n n x x x ,,4,3=n .若2lim =∞→n x x ,则=1x A .23B .3C .4D .5参考答案1. A2. B 3.C 4.A 5. C 6.-3 7. 3 8. C 9.11-b 10. 32 11. C 12. B12. 解法一:特殊值法,当31=x 时,3263,1633,815,49,2365432=====x x x x x 由此可推测2lim =∞→n x x ,故选B . 解法二:∵)(2121--+=n n n x x x ,∴)(21211-----=-n n n n x x x x ,21211-=-----n n n nx x x x 即, ∴{}n n x x -+1是以(12x x -)为首项,以21-为公比6的等比数列, 令n n n x x b -=+1,则11111211)21()21(2)21)((x x x x q b b n n n n n -=-⋅-=--==---+-+-+=)()(23121x x x x x x n …)(1--+n n x x+-+-+-+=121211)21()21()2(x x x x …11)21(x n --+3)21(32)21(1)21(12111111xxxx nn---+=--⎥⎦⎤⎢⎣⎡---+=∴2323)21(321111limlim==⎥⎦⎤⎢⎣⎡-+=-∞→∞→xxxx nxnx,∴31=x,故选B.解法三:∵)(2121--+=nnnxxx,∴0221=----nnnxxx,∴其特征方程为0122=--aa,解得211-=a,12=a,nnnacacx2211+=,∵11xx=,212xx=,∴3211xc-=,3212xc=,∴3)21(3232)21(3211111xxxxx nnn--+=+-⋅-=,以下同解法二.解法四:∵()121212n n n n n n nx x x x x x x----=+⇔-=-将上列各式叠加,并将122xx=代入,整理得1122n nx x x-=-对上式两边同时取极限,设limnnx A→∞=,则1limnnx A-→∞=(这是此法的关键点)∴122A x A=-解得1332322Ax⨯===.。
2005年全国高考数学试题分类汇编集合与简易逻辑

2005年全国高考数学试题分类汇编——集合与简易逻辑注:本汇编只收录了高一新生适合做的题目;而将集合、简易逻辑与其它章节的综合题,收录在其它相关的分类汇编专题中。
1.(全国卷Ⅰ理第2题,文第2题)设I 为全集,321S S S 、、是I 的三个非空子集,且I S S S =⋃⋃321,则下面论断正确的是(A )Φ=⋃⋂)(321S S S C I(B )123I I S C S C S ⊆⋂()(C )123I I I C S C S C S ⋂⋂=Φ(D )123I I S C S C S ⊆⋃()2.(全国卷Ⅱ文第10题)已知集合2{|47},{|60}M x x N x x x =-≤≤=-->则N M ⋂为 (A){|4237}x x x -≤<-<≤或 (B){|4237}x x x -<≤-≤<或 (C){|23}x x x ≤->或 (D){|23}x x x <-≥或3.(全国卷Ⅱ理第9题)已知集合M={x∣2x -3x -28 ≤0},N = {x|2x -x-6>0},则M∩N 为(A ){x|- 4≤x< -2或3<x≤7} (B ){x|- 4<x≤ -2或 3≤x<7 } (C ){x|x≤ - 2或 x> 3 } (D ){x|x<- 2或x≥3}4.(北京卷文第1题)设集合M ={x | x >1,P ={x | x 2>1},则下列关系中正确的是 (A )M =P (B )P ÜM (C )M ÜP ( D )M P R = 5.(北京卷理第1题)设全集U =R ,集合M ={x | x >1,P ={x | x 2>1},则下列关系中正确的是(A ) M =P (B )P ÜM (C )M ÜP ( D )U M P =∅ ð6.(上海卷理第14题,文第14题)已知集合{}R x x x M ∈≤-=,2|1||,⎭⎬⎫⎩⎨⎧∈≥+=Z x x x P ,115|,则P M 等于( ) A .{}Z x x x ∈≤<,30| B .{}Z x x x ∈≤≤,30| C .{}Z x x x ∈≤≤-,01| D .{}Z x x x ∈<≤-,01|7.(2005天津卷文第1题)设集合∈<≤=x x x A 且30{N}的真子集...的个数是( ) (A) 16(B) 8; (C) 7 (D) 48.(2005天津卷理第1题)设集合{}R x x x A ∈≥-=,914, ⎭⎬⎫⎩⎨⎧∈≥+=R x x xxB ,03, 则A∩B= (A)]2,3(-- (B)]25,0[]2,3(⋃-- (C)),25[]3,(+∞⋃--∞ (D)),25[)3,(+∞⋃--∞9.(2005福建卷文第1题)已知集合∈≤-=x x x P ,1|1|||R|,Q P N x x Q 则},|{∈=等于 ( )A .PB .QC .{1,2}D .{0,1,2}10.(2005福建卷文第8题)已知q p ab q a p 是则,0:,0:≠≠的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件11.(2005福建卷理第7题)已知p :,0)3(:,1|32|<-<-x x q x 则p 是q 的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件12.(2005广东卷第1题)若集合{}2M x x =≤,{}230N x x x =-=,则M N =(A){}3 (B){}0 (C){}0,2 (D){}0,313.(2005湖北卷理第1题,文第1题)设P 、Q 为两个非空实数集合,定义集合P+Q=},5,2,0{},,|{=∈∈+P Q b P a b a 若 }6,2,1{=Q ,则P+Q 中元素的个数是( )A .9B .8C .7D .614.(2005湖北卷理第2题,文第2题)对任意实数a ,b ,c ,给出下列命题: ①“b a =”是“bc ac =”充要条件;②“5+a 是无理数”是“a 是无理数”的充要条件③“a >b ”是“a 2>b 2”的充分条件; ④“a <5”是“a <3”的必要条件. 其中真命题的个数是 ( )A .1B .2C .3D .415.(2005江苏卷第1题)设集合{}2,1=A ,{}3,2,1=B ,{}4,3,2=C ,则()C B A =( ) A .{}3,2,1 B .{}4,2,1 C .{}4,3,2 D .{}4,3,2,116、(2005江苏卷第13题)命题“若b a >,则122->b a ”的否命题为__________。
2005年高考试题——理综(全国卷+III)

2005年普通高等学校招生全国统一考试理科综合能力测试以下数据可供解题时参考:相对原子质量(原子量):H:1 He:4 C:12 N:14 O:16第I卷一、选择题(本题包括13小题。
每小题只有一个....选项符合题意)1.连续分裂的动物体细胞的生长即体积增大,发生在细胞周期的()A.分裂间期B.分裂前期C.分裂中期D.分裂后期2.右图表示在适宜的温度、水分和CO2条件下,两种植物光合作用强度的变化情况。
下列说法错误..的是()A.当光照强度增加到一定程度时,光合作用强度不再增加,即达到饱和B.C3植物比C4植物光合作用强度更容易达到饱和C.C4植物比C3植物光能利用率高D.水稻是阴生植物,玉米是阳生植物3.当人体处于饥饿状态时()A.肾上腺素分泌减少,胰高血糖素分泌增加B.肾上腺素分泌增加,胰高血糖素分泌增加C.肾上腺素分泌减少,胰高血糖素分泌减少D.肾上腺素分泌增加,胰高血糖素分泌减少4.关于抗体的产生、特性和作用等的叙述,错误..的是()A.抗毒素是抗体B.抗体都能被蛋白酶分解C.淋巴细胞都能产生抗体D.抗体在某些特殊情况下会对自身成分起免疫反应5.科学家通过基因工程的方法,能使马铃薯块茎含有人奶主要蛋白。
以下有关该基因工程的叙述,错误..的是()A.采用反转录的方法得到的目的基因有内含子B.基因非编码区对于目的基因在块茎中的表达是不可缺少的C.马铃薯的叶肉细胞可作为受体细胞D.用同一种限制酶,分别处理质粒和含目的基因的DNA,可产生黏性末端而形成重组DNA分子6.现有以下几种措施:①对燃烧煤时产生的尾气进行除硫处理,②少用原煤做燃料,③燃煤时鼓入足量空气、,④开发清洁能源。
其中能减少酸雨产生的措施的是()A.①②③B.②③④C.①②④D.①③④7.下列气体的制备可采用右图装置的是()A.铜与浓硝酸反应制NO2B.铜与稀硝酸反应制SOC.乙醇与浓硫酸反应制乙烯D.氯化钠与浓硫酸反应制HCl8.在体积可变的密闭容器中,反应mA(气)+nB (固)pC(气)达到平衡后,压缩容器的体积,发现A的转化率随之降低。
2005年全国各地高考试卷总汇

绝密★启用前试卷类型:A 2005年普通高等学校招生全国统一考试(广东卷)生物本试卷分选择题和非选择题两部分,共10页.满分150分:考试用时120分钟。
注意事项:l.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卡上、用2B铅笔将答题卡试卷类型(A)填涂在答题卡上,并在答题卡右上角的“试室号”和“座位号”栏填写试室号、座位号,将相应的试室号、座位号信息点涂黑。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液:不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回。
第一部分选择题(共70分)一.选择题:本题共26小题,每小题2分,共52分。
每小题给出的四个选项中,只有一选项最符合题目要求。
1.细胞有丝分裂完成后.平均分配到两个子细胞的物质是A.线粒体DNA B.细胞核DNA c.核糖体RNA D.叶绿体DNA2.下列选项中,全部属于植物必需的大量矿质元素是A.P、N、Mn、K B.N、S、H、P C.Fe、S、P、N D.Ca、N、P、K3.甲(〇)乙(●)两种物质在细胞膜两侧的分布情况如右图(颗粒的多少表示浓度的高低),在进行跨膜运输时,下列说法正确的是A.乙进入细胞一定有载体蛋白的参与B.乙运出细胞一定有载体蛋白的参与c.甲进入细胞一定需要能量D.甲运出细胞一定不需要能量4.叶绿体色素的纸层析结果显示.叶绿素b位于层析滤纸的最下端,原因是A.分子量最小 B.分子量最大C.在层祈液中的溶解度最小 D.在层析液中的溶解度最大5.关于单克隆抗体,下列叙述不正确的是A.可以制成诊断盒.用于疾病的珍断 B.可以与药物结合,用于病变细胞的定向治疗c.可以利用基因工程技术生产 D.可以在生物体内生产,不能体外生产6.植物扦插繁殖时,需要对插枝进行去除成熟叶片、保留芽和幼叶等处理,这样可以促进插枝成活。
2005年高考数学试题分章汇编:圆锥曲线方程

2005年高考题分章节汇编 第八章 圆锥曲线方程一、选择题1.(2005年春考·北京卷·理5)设0≠abc ,“0>ac ”是“曲线c by ax =+22为椭圆”的( B )A .充分非必要条件B .必要非充分条件C .充分必要条件D .既非充分又非必要条件2.(2005年春考·北京卷·理6)已知双曲线的两个焦点为)0,5(1-F ,)0,5(2F ,P 是此双曲线上的一点,且21PF PF ⊥,2||||21=∙PF PF ,则该双曲线的方程是 ( C )A .13222=-y x B .12322=-y x C .1422=-y x D .1422=-y x 3.(2005年春考·北京卷·文5) “ab <0”是“曲线ax 2+by 2=1为双曲线”的( C )A .充分非必要条件B .必要非充分条件C .充分必要条件D .既非充分又非必要条件4.(2005年高考·上海卷·理15)过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B两点,它们的横坐标之和等于5,则这样的直线( B )A .有且仅有一条B .有且仅有两条C .有无穷多条D .不存在5.(2005年高考·福建卷·理10)已知F 1、F 2是双曲线)0,0(12222>>=-b a by a x 的两焦点,以线段F 1F 2为边作正三角形MF 1F 2,若边MF 1的中点在双曲线上,则双曲线的离心率是( D )A .324+B .13-C .213+ D .13+6.(2005年高考·福建卷·文9)已知定点A 、B 且|AB|=4,动点P 满足|PA|-|PB|=3,则|PA|的最小值是 ( C )A .21B .23 C .27 D .57.(2005年高考·广东卷5)若焦点在x 轴上的椭圆1222=+my x 的离心率为21,则m=( B )A .3B .23 C .38 D .32 8.(2005年高考·湖北卷·理5文6)双曲线)0(122≠=-mn ny m x 离心率为2,有一个焦点与抛物线x y 42=的焦点重合,则mn 的值为( A )A .163B .83 C .316 D .38 9.(2005年高考·湖南卷·理7文8)已知双曲线22a x -22b y =1(a >0,b >0)的右焦点为F ,右准线与一条渐近线交于点A ,△OAF 的面积为22a (O 为原点),则两条渐近线的夹角为( D )A .30ºB .45ºC .60ºD .90º10.(2005年高考·辽宁卷11)已知双曲线的中心在原点,离心率为3.若它的一条准线与抛物线x y 42=的准线重合,则该双曲线与抛物线x y 42=的交点到原点的距离是 ( B )A .23+6B .21C .21218+D .2111.(2005年高考·重庆卷·理9文9)若动点(y x ,)在曲线)0(14222>=+b by x 上变化,则y x 22+的最大值为 ( A )A .⎪⎩⎪⎨⎧≥<<+)4(2),40(442b b b bB .⎪⎩⎪⎨⎧≥<<+)2(2),20(442b b b bC .442+bD .2b12.(2005年高考·江苏卷6)抛物线24x y =上的一点M 到焦点的距离为1,则点M 的纵坐标是 (B )A .1617 B .1615 C .87 D .013.(2005年高考·江苏卷11)点P (-3,1)在椭圆)0(12222>>=+b a by a x 的左准线上,过点P 且方向为)5,2(-=的光线,经直线2-=y 反射后通过椭圆的左焦点,则这个椭圆的离心率为 (A )A .33B .31 C .22 D .21 14.(2005年高考·山东卷·理12文12)设直线:220l x y ++=关于原点对称的直线为l ',若l '与椭圆2214y x +=的交点为A 、B 、,点P 为椭圆上的动点,则使PAB ∆的面积为12的点P 的个数为( B )A .1B .2C .3D .415.(2005年高考·天津卷·理5文6)设双曲线以椭圆192522=+y x 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为 ( C )A .2±B .34±C .21±D .43±16.(2005年高考·全国卷Ⅰ·理5)已知双曲线)0(1222>=-a y ax 的一条准线与抛物线x y 62-=的准线重合,则该双曲线的离心率为( A )A .23 B .23 C .26 D .332 17.(2005年高考·全国卷Ⅰ·文5)已知双曲线)0(1222>=-a y ax 的一条准线为23=x ,则该双曲线的离心率为( A )A .23B .23 C .26 D .33218.(2005年高考·全国卷II ·理6)已知双曲线13622=-y x 的焦点为F 1、F 2,点M 在双曲线上且MF 1⊥x 轴,则F 1到直线F 2M 的距离为( C )A .563 B .665 C .56 D .65 19.(2005年高考·全国卷II ·文5)抛物线y x 42=上一点A 的纵坐标为4,则点A 与抛物线焦点的距离为( D )A .2B .3C .4D .520.(2005年高考·全国卷II ·文6)双曲线19422=-y x 的渐近线方程是 ( C )A .x y 32±= B .x y 94±= C .x y 23±= D .x y 49±= 21.(2005年高考·全国卷Ⅲ·理9文9)已知双曲线1222=-y x 的焦点为F 1、F 2,点M 在双曲线上且120,MF MF ⋅=则点M 到x 轴的距离为( C )A .43B .53C D 22.(2005年高考·全国卷Ⅲ·理10文10)设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是 ( D )A .2 B C .2 D 1二、填空题1.(2005年春考·北京卷·文10)192522=+y x 的离心率是 ,准线方程是 .42554±=x2. (2005年春考·上海卷7)双曲线116922=-y x 的焦距是 .653.(2005年高考·北京卷·文9)抛物线x y 42=的准线方程是 ,焦点坐标是 . )0,1(1-=x4.(2005年高考·上海卷·理5)若双曲线的渐近线方程为x y 3±=,它的一个焦点是()0,10,则双曲线的方程是__________.1922=-y x 5.(2005年高考·上海卷·文7)若椭圆长轴长与短轴长之比为2,它的一个焦点是()0,152,则椭圆的标准方程是__________.1208022=+y x 6.(2005年高考·江西卷·理16文16)以下同个关于圆锥曲线的命题中 ①设A 、B 为两个定点,k 为非零常数,k =-||||,则动点P 的轨迹为双曲线;②设定圆C 上一定点A 作圆的动点弦AB ,O 为坐标原点,若),(21+=则动点P 的轨迹为椭圆;③方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率;④双曲线13519252222=+=-y x y x 与椭圆有相同的焦点. 其中真命题的序号为 (写出所有真命题的序号)③④7.(2005年高考·重庆卷·理16)连接抛物线上任意四点组成的四边形可能是 (填写所有正确选项的序号).②③⑤ ①菱形 ②有3条边相等的四边形 ③梯形 ④平行四边形 ⑤有一组对角相等的四边形 8.(2005年高考·重庆卷·文16)已知B A ),0,21(-是圆F y x F (4)21(:22=+-为圆心)上一动点,线段AB 的垂直平分线交BF 于P ,则动点P 的轨迹方程为 .13422=+y x 9.(2005年高考·浙江卷·理13文13)过双曲线22221x y a b-=(a >0,b >0)的左焦点且垂直于x 轴的直线与双曲线相交于M 、N 两点,以MN 为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________. 210.(2005年高考·山东卷·理14文14)设双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,右准线l 与两条渐近线交于P 、Q 两点,如果PQF ∆是直角三角形,则双曲线的离心率___________e =.e =三、解答题1.(本小题满分14分)(2005年春考·北京卷·理18)如图,O 为坐标原点,直线l 在x 轴和y 轴上的截距分别是a 和b ,且交抛物线)0(22>=p px y 于),(11y x M 、),(22y x N 两点.(1)写出直线l 的截距式方程; (2)证明:by y 11121=+; (3)当p a 2=时,求MON ∠的大小.本小题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题和解决问题的能力,满分14分. (Ⅰ)解:直线l 的截距式方程为.1=+bya x ① (Ⅱ)证明:由①及y 2=2px 消去x 可得0222=-+pab pay by ②点M ,N 的纵坐标y 1, y 2为②的两个根,故.12211.2,22121212121b pa b pay y y y y y pa y y bpay y =--=+=+-=-=+所以 (Ⅲ)解:设OM ,ON 的斜率分别为k 1,k 2,.90,,144,44)4(4)(,4)(2,2,42,)(,2.,2221212122222212*********2121221222111 =∠⊥-=-========-=-====MON ON OM p p x x y y k k p p p p y y x x x x p y y px y px y p pa y y II p a x y k x y k 即所以因此相乘得由知由时当则2.(本小题满分14分)(2005年春考·北京卷·文18)如图,O 为坐标原点,过点P (2,0)且斜率为k 的直线l 交抛物线y 2=2x 于M (x 1,y 1),N(x 2, y 2)两点. (1)写出直线l 的方程; (2)求x 1x 2与y 1y 2的值; (3)求证:OM ⊥ON .本小题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题和解决问题的能力,满分14分. (Ⅰ)解:直线l 的方程为 )0()2(≠-=k x k y ①(Ⅱ)解:由①及y 2=2x 消去y 可得.04)1(22222=++-k x k x k ②点M ,N 的横坐标x 1与 x 2是②的两个根, 由韦达定理得22212122212,2.44x y x y k k x x ====由.4,0,16444)(212121221-=<=⨯==y y y y x x y y 所以注意到得(Ⅲ)证明:设OM ,ON 的斜率分别为k 1, k 2,.,144.,212121222111ON OM x x y y k k x y k x y k ⊥-=-====所以相乘得则 3. (本题满分18分) (2005年春考·上海卷22)本题共有3个小题,第1小题满分5分,第2小题满分8分. 第3小题满分5分.(1)求右焦点坐标是)0,2(,且经过点)2,2(--的椭圆的标准方程;(2)已知椭圆C 的方程是12222=+by a x )0(>>b a . 设斜率为k 的直线l ,交椭圆C 于A B 、两点,AB 的中点为M . 证明:当直线l 平行移动时,动点M 在一条过原点的定直线上;(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.[解](1)设椭圆的标准方程为12222=+b y a x ,0>>b a ,∴ 422+=b a ,即椭圆的方程为142222=++b y b x , ∵ 点(2,2--)在椭圆上,∴ 124422=++bb , 解得 42=b 或22-=b (舍),由此得82=a ,即椭圆的标准方程为14822=+y x . …… 5分 (2)设直线l 的方程为m kx y +=, …… 6分与椭圆C 的交点A (11,y x )、B (22,y x ),则有⎪⎩⎪⎨⎧=++=12222b y a x m kx y , 解得 02)(222222222=-+++b a m a kmx a x k a b ,∵ 0>∆,∴ 2222k a b m +<,即 222222k a b m k a b +<<+-.则 222221212222212,2k a b mb m kx m kx y y k a b kma x x +=+++=++-=+,∴ AB 中点M 的坐标为⎪⎪⎭⎫⎝⎛++-22222222,k a b m b k a b km a . …… 11分∴ 线段AB 的中点M 在过原点的直线 022=+y k a x b 上. …… 13分(3)如图,作两条平行直线分别交椭圆于A 、B 和D C 、,并分别取AB 、CD 的中点N M 、,连接直线MN ;又作两条平行直线(与前两条直线不平行)分别交椭圆于1A 、1B 和11D C 、,并分别取11B A 、11D C 的中点11N M 、,连接直线11N M ,那么直线MN 和11N M 的交点O 即为椭圆中心. …… 18分 4.(本小题共14分)(2005年高考·北京卷·理18文20)如图,直线l 1:)0(>=k kx y 与直线l 2:kx y -=之间的阴影区域(不含边界)记为W ,其左半部分记为W 1,右半部分记为W 2.(Ⅰ)分别用不等式组表示W 1和W 2;(Ⅱ)若区域W 中的动点P (x ,y )到l 1,l 2的距离之积等于d 2,求点P 的轨迹C 的方程;(Ⅲ)设不过原点O 的直线l 与(Ⅱ)中的曲线C 相交于M 1,M 2两点,且与l 1,l 2分别交于M 3,M 4两点. 求证△OM 1M 2的重心与△OM 3M 4的重心重合. 解:(I )},0,|),{(1<-<<=x kx y kx y x W }.0,|),{(2><<-=x kx y kx y x W(II )直线.0:,0:21=+=-y kx l y kx l 直线由题意得.0)1(0)1(,1,0,),(,1||,1||1||22222222222222222222222222=+--=+--=+->-∈=+-=++⋅+-d k y x k C P d k y x k d k y x k y x k W y x P d k y x k d k y kx k y kx 的方程为的轨迹所以动点即所以知由即(III )当直线l 与x 轴垂直时,可设直线l 的方程为)0(≠=a a x . 由于直线l ,曲线C 关于x 轴对称,且l 1与l 2关于x 轴对称,于是M 1M 2,M 3M 4的中点坐标都为(a ,0),所以△OM 1M 2,△OM 3M 4的重心坐标都为)0,32(a,即它们的重心重合.当直线l 与x 轴不垂直时,设直线l 的方程为).0(≠+=n n mx y由.02)(,0)1(222222222222=-----⎩⎨⎧+==+--d d k n mnx x m k nmx y d k y x k 得由直线l 与曲线C 有两个不同交点,可知且,022≠-m k),,(),,(,.2)(2),,(),,(,,0)()(4)2(443343212122212211212222222y x y x M M n x x m y x m k mn x x y x y x M M d d k n m k mn x的坐标分别为设则的坐标分别为设++=+-=+>++⨯-+=∆,3030,3030,2)(2)(,2,,,,432143212121434321224343y y y y x x x x y y n x x m n x x m y y x x m k mnx x m k nx m k n x nmx y kx y n mx y kx y ++=++++=+++=++=++=++=-=++-=-=⎩⎨⎧+=-=⎩⎨⎧+==所以所以从而得及由 于是△OM 1M 2的重心与△OM 3M 4的重心也重合. 5.(本题满分14分)(2005年高考·上海卷·理19)本题共有2个小题,第1小题满分6分,第2小题满分8分.如图,点A 、B 分别是椭圆1203622=+y x 长轴的左、右端点,点F 是椭圆的右焦点,点P 在椭圆上,且位于x 轴上方,PF PA ⊥.(1)求点P 的坐标;(2)设M 是椭圆长轴AB 上的一点,M 到直线AP 的距离等于||MB ,求椭圆上的点到点M 的距离d 的最小值.[解](1)由已知可得点A (-6,0),F (4,0)设点P 的坐标是},4{},,6{),,(y x y x y x -=+=则,由已知得.623,018920)4)(6(120362222-===-+⎪⎩⎪⎨⎧=+-+=+x x x x y x x y x 或则 由于).325,23(,325,23,0的坐标是点于是只能P y x y ∴==> (2)直线AP 的方程是.063=+-y x设点M 的坐标是(m ,0),则M 到直线AP 的距离是2|6|+m , 于是,2,66|,6|2|6|=≤≤--=+m m m m 解得又 椭圆上的点),(y x 到点M 的距离d 有,15)29(94952044)2(222222+-=-++-=+-=x x x x y x d 由于.15,29,66取得最小值时当d x x =∴≤≤- 6.(本题满分16分)(2005年高考·上海卷·文21)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.已知抛物线)0(22>=p px y 的焦点为F ,A 是抛物线上横坐标为4、且位于x 轴上方的点,A 到抛物线准线的距离等于5.过A 作AB 垂直于y 轴,垂足为B ,OB 的中点为M.(1)求抛物线方程;(2)过M 作FA MN ⊥,垂足为N ,求点N 的坐标;(3)以M 为圆心,MB 为半径作圆M ,当)0,(m K 是x 轴上一动点时,讨论直线AK 与圆M 的位置关系.解:(1)抛物线.2,524,222=∴=+-==p pp x px y 于是的准线为 ∴抛物线方程为y 2= 4x .(2)∵点A 的坐标是(4,4), 由题意得B (0,4),M (0,2),又∵F (1,0), ∴,43,;34-=∴⊥=MN FA k FA MN k 则FA 的方程为y=34(x -1),MN 的方程为.432x y -=-解方程组).54,58(5458,432)1(34N y x x y x y ∴⎪⎪⎩⎪⎪⎨⎧==⎪⎪⎩⎪⎪⎨⎧-=--=得(3)由题意得,圆M 的圆心是点(0,2),半径为2.当m=4时,直线AK 的方程为x =4,此时,直线AK 与圆M 相离, 当m ≠4时,直线AK 的方程为),(44m x my --=即为,04)4(4=---m y m x 圆心M (0,2)到直线AK 的距离2)4(16|82|-++=m m d ,令1,2>>m d 解得1>∴m 当时,直线AK 与圆M 相离;当m=1时,直线AK 与圆M 相切; 当1<m 时,直线AK 与圆M 相交. 7.(本小题满分12分)(2005年高考·福建卷·理21文22)已知方向向量为v =(1,3)的直线l 过点(0,-23)和椭圆C :)0(12222>>=+b a by a x 的焦点,且椭圆C 的中心关于直线l 的对称点在椭圆C 的右准线上.(Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在过点E (-2,0)的直线m 交椭圆C 于点M 、N ,满足634=⋅OM , cot ∠MON ≠0(O 为原点).若存在,求直线m 的方程;若不存在,请说明理由.本小题主要考查直线、椭圆及平面向量的基本知识,平面解析几何的基本方法和综合解题能力.满分14分.(I )解法一:直线323:-=x y l , ①过原点垂直l 的直线方程为x y 33-=, ② 解①②得.23=x ∵椭圆中心(0,0)关于直线l 的对称点在椭圆C 的右准线上,.32322=⨯=∴c a∵直线l 过椭圆焦点,∴该焦点坐标为(2,0)..2,6,222===∴b a c 故椭圆C 的方程为.12622=+y x ③ 解法二:直线333:-=x y l .设原点关于直线l 对称点为(p ,q ),则⎪⎪⎩⎪⎪⎨⎧-=⋅-⋅=.1332232p q p q 解得p=3. ∵椭圆中心(0,0)关于直线l 的对称点在椭圆C 的右准线上,.32=∴c a ∵直线l 过椭圆焦点,∴该焦点坐标为(2,0)..2,6,222===∴b a c 故椭圆C 的方程为.12622=+y x ③ (II )解法一:设M (11,y x ),N (22,y x ).当直线m 不垂直x 轴时,直线)2(:+=x k y m 代入③,整理得,061212)13(2222=-+++k x k x k ,13612,131222212221+-=⋅+-=+∴k k x x k k x x ,13)1(62136124)1312(14)(1||22222222212212++=+-⋅-+-+=-++=k k k k k k kx x x x kMN点O 到直线MN 的距离21|2|kk d +=,cot 634MON ON OM ∠=⋅ 即 ,0sin cos 634cos ||||≠∠∠=∠⋅MONMON MON OM ,634||.632,634sin ||||=⋅∴=∴=∠⋅∴∆d MN S MON ON OM OMN即).13(6341||6422+=+k k k 整理得.33,312±=∴=k k当直线m 垂直x 轴时,也满足632=∆OMN S .故直线m 的方程为,33233+=x y或,33233--=x y 或.2-=x经检验上述直线均满足0≠⋅. 所以所求直线方程为,33233+=x y 或,33233--=x y 或.2-=x 解法二:设M (11,y x ),N (22,y x ).当直线m 不垂直x 轴时,直线)2(:+=x k m 代入③,整理得,061212)13(2222=-+++k x k x k ,13122221+-=+∴k k x x∵E (-2,0)是椭圆C 的左焦点,∴|MN|=|ME|+|NE|=.13)1(6262)1312(622)()()(2222212212++=++-⋅=++=+++k k k k a x x a c x c a e x c a e 以下与解法一相同.解法三:设M (11,y x ),N (22,y x ).设直线2:-=ty x m ,代入③,整理得.024)3(22=--+ty y t,32,34221221+-=+=+∴t y y t t y y.)3(242438)34(4)(||222222212121++=+++=-+=-t t t t t y y y y y y,cot 634MON OM ∠=⋅ 即 ,0sin cos 634cos ||||≠∠∠=∠⋅MONMON MON ON OM.632,634sin ||||=∴=∠⋅∴∆OMN S MON OM=-⋅=+=∆∆∆||||2121y y OE S S S OENOEM OMN .)3(2424222++t t∴222)3(2424++t t =632,整理得.324t t =解得,3±=t 或.0=t故直线m 的方程为,33233+=x y 或,33233--=x y 或.2-=x经检验上述直线方程为.0≠⋅所以所求直线方程为,33233+=x y 或,33233--=x y 或.2-=x 8.(本小题满分14分)(2005年高考·广东卷17)在平面直角坐标系x Oy 中,抛物线y=x 2上异于坐标原点O 的两不同动点A 、B 满足AO ⊥BO (如图4所示).(Ⅰ)求△AOB 的重心G (即三角形三条中线的交点)的轨迹方程;(Ⅱ)△AOB 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.解:(I )设△AOB 的重心为G(x,y),A(x 1,y 1),B(x 2,y 2), 则1212,3.3x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩...(1) ∵OA ⊥OB ,即12120x x y y +=, (2)又点A ,B 在抛物线上,有221122,y x y x ==,代入(2)化简得121-=x x ∴222221212121211122()[()2](3)3333333y y y x x x x x x x x +==+=+-=⨯+=+, 所以重心为G 的轨迹方程为3232+=x y .(II)1||||2AOB S OA OB ∆===由(I)得AOB S ∆==12 1.2=≥==⨯= 当且仅当2212x x =即121x x =-=-时,1AOB S ∆=. 所以△AOB 的面积存在最小值,且最小值为1. 9.(本小题满分12分)(2005年高考·湖北卷·理21文22)设A 、B 是椭圆λ=+223y x 上的两点,点N (1,3)是线段AB 的中点,线段AB 的垂直平分线与椭圆相交于C 、D 两点.(Ⅰ)确定λ的取值范围,并求直线AB 的方程;(Ⅱ)试判断是否存在这样的λ,使得A 、B 、C 、D 四点在同一个圆上?并说明理由. (此题不要求在答题卡上画图) 本小题主要考查直线、圆和椭圆等平面解析几何的基础知识以及推理运算能力和综合解决问题的能力. (Ⅰ)解法1:依题意,可设直线AB 的方程为λ=++-=223,3)1(y x x k y 代入,整理得 .0)3()3(2)3(222=--+--+λk x k k x k ① 设212211,),,(),,(x x y x B y x A 则是方程①的两个不同的根, ∴,0])3(3)3([422>--+=∆k k λ ②且,3)3(2221+-=+k k k x x 由N (1,3)是线段AB 的中点,得.3)3(,12221+=-∴=+k k k x x解得k=-1,代入②得,λλ即,12>的取值范围是(12,+∞). 于是,直线AB 的方程为.04),1(3=-+--=-y x x y 即 解法2:设),,(),,(2211y x B y x A 则有.0))(())((332121212122222121=+-++-⇒⎪⎩⎪⎨⎧=+=+y y y y x x x x y x y x λλ依题意,.)(3,212121y y x x k x x AB ++-=∴≠∵N (1,3)是AB 的中点, ∴.1,6,22121-==+=+AB k y y x x 从而 又由N (1,3)在椭圆内,∴,1231322=+⨯>λ∴λ的取值范围是(12,+∞). 直线AB 的方程为y -3=-(x -1),即x +y -4=0.(Ⅱ)解法1:∵CD 垂直平分AB ,∴直线CD 的方程为y -3=x -1,即x -y+2=0,代入椭圆方程,整理得 .04442=-++λx x又设),,(),,(4433y x D y x C CD 的中点为4300,),,(x x y x C 则是方程③的两根, ∴).23,21(,232,21)(21,10043043-=+=-=+=-=+M x y x x x x x 即且 于是由弦长公式可得 .)3(2||)1(1||432-=-⋅-+=λx x kCD ④将直线AB 的方程x +y -4=0,代入椭圆方程得016842=-+-λx x ⑤同理可得 .)12(2||1||212-=-⋅+=λx x k AB ⑥∵当12>λ时,||||,)12(2)3(2CD AB <∴->-λλ假设存在λ>12,使得A 、B 、C 、D 四点共圆,则CD 必为圆的直径,点M 为圆心.点M 到直线AB 的距离为 .2232|42321|2|4|00=-+-=-+=y x d ⑦ 于是,由④、⑥、⑦式和勾股定理可得.|2|2321229|2|||||22222CD AB d MB MA =-=-+=+==λλ 故当λ>12时,A 、B 、C 、D 四点匀在以M 为圆心,2||CD 为半径的圆上.(注:上述解法中最后一步可按如下解法获得:)A 、B 、C 、D 共圆⇔△ACD 为直角三角形,A 为直角⇔|AN|2=|CN|·|DN|,即 ).2||)(2||()2||(2d CD d CD AB -+= ⑧ 由⑥式知,⑧式左边,212-=λ 由④和⑦知,⑧式右边,2122923)2232)3(2)(2232)3(2(-=--=--+-=λλλλ ∴⑧式成立,即A 、B 、C 、D 四点共圆.解法2:由(Ⅱ)解法1及λ>12,∵CD 垂直平分AB , ∴直线CD 方程为13-=-x y ,代入椭圆方程,整理得.04442=-++λx x ③将直线AB 的方程x +y -4=0,代入椭圆方程,整理得.016842=-+-λx x ⑤解③和⑤式可得 .231,21224,32,1-±-=-±=λλx x不妨设)233,231(),233,231(),12213,12211(-+-+---------+λλλλλλD C A∴)21233,23123(---+-+-+=λλλλCA)21233,23123(-------+=λλλλ计算可得0=⋅,∴A 在以CD 为直径的圆上. 又B 为A 关于CD 的对称点,∴A 、B 、C 、D 四点共圆. (注:也可用勾股定理证明AC ⊥AD ) 10.(本小题满分14分)(2005年高考·湖南卷·理19文21)已知椭圆C :22a x +22by =1(a >b >0)的左.右焦点为F 1、F 2,离心率为e. 直线l :y =e x +a 与x 轴.y 轴分别交于点A 、B ,M 是直线l 与椭圆C 的一个公共点,P 是点F 1关于直线l 的对称点,设=λ. (Ⅰ)证明:λ=1-e 2; (Ⅱ)若43=λ,△PF 1F 2的周长为6;写出椭圆C 的方程;(理科无此问) (Ⅲ)确定λ的值,使得△PF 1F 2是等腰三角形.(Ⅰ)证法一:因为A 、B 分别是直线l :a ex y +=与x 轴、y 轴的交点,所以A 、B 的坐标分别是2222222.,,1,).,0(),0,(b a c a b y c x b y ax a ex y a e a +=⎪⎩⎪⎨⎧=-=⎪⎩⎪⎨⎧=++=-这里得由. 所以点M 的坐标是(a b c 2,-). 由).,(),(2a eaa b e a c AB AM λλ=+-=得即221e a ab e ac e a-=⎪⎪⎩⎪⎪⎨⎧==-λλλ解得证法二:因为A 、B 分别是直线l :a ex y +=与x 轴、y 轴的交点,所以A 、B 的坐标分别是).,0(),0,(a e a -设M 的坐标是),,(),(),,(0000a eay e a x AM y x λλ=+=得由 所以⎪⎩⎪⎨⎧=-=.)1(00a y ea x λλ 因为点M 在椭圆上,所以 ,1220220=+b y a x 即.11)1(,1)()]1([22222222=-+-=+-ee b a a e aλλλλ所以,0)1()1(2224=-+--λλe e 解得.1122e e -=-=λλ即(Ⅱ)当43=λ时,21=c ,所以.2c a = 由△MF 1F 2的周长为6,得.622=+c a所以.3,1,2222=-===c a b c a 椭圆方程为.13422=+y x (Ⅲ)解法一:因为PF 1⊥l ,所以∠PF 1F 2=90°+∠BAF 1为钝角,要使△PF 1F 2为等腰三角形,必有|PF 1|=|F 1F 2|,即.||211c PF = 设点F 1到l 的距离为d ,由,1||1|0)(|||21221c eec a e a c e d PF =+-=+++-==得.1122e e e =+- 所以.321,3122=-==e e λ于是即当,32时=λ△PF 1F 2为等腰三角形. 解法二:因为PF 1⊥l ,所以∠PF 1F 2=90°+∠BAF 1为钝角,要使△PF 1F 2为等腰三角形,必有|PF 1|=|F 1F 2|,设点P 的坐标是),(00y x ,则⎪⎪⎩⎪⎪⎨⎧+-=+-=⎪⎪⎩⎪⎪⎨⎧+-=+-=+-.1)1(2,13.220102202200000e a e y c e e x a c x e y e cx y 解得 由|PF 1|=|F 1F 2|得,4]1)1(2[]1)3([2222222c e a e c e c e =+-+++- 两边同时除以4a 2,化简得.1)1(2222e e e =+- 从而.312=e 于是32112=-=e λ. 即当32=λ时,△PF 1F 2为等腰三角形. 11.(本小题满分14分)(2005年高考·辽宁卷21)已知椭圆)0(12222>>=+b a by a x 的左、右焦点分别是F 1(-c ,0)、F 2(c ,0),Q 是椭圆外的动点,满足.2||1a F =点P 是线段F 1Q 与该椭圆的交点,点T 在线段F 2Q 上,并且满足.0||,022≠=⋅TF TF PT (Ⅰ)设x 为点P 的横坐标,证明x aca F +=||1; (Ⅱ)求点T 的轨迹C 的方程;(Ⅲ)试问:在点T 的轨迹C 上,是否存在点M , 使△F 1MF 2的面积S=.2b 若存在,求∠F 1MF 2的正切值;若不存在,请说明理由.本小题主要考查平面向量的概率,椭圆的定义、标准方程和有关性质,轨迹的求法和应用,以及综合运用数学知识解决问题的能力.满分14分.(Ⅰ)证法一:设点P 的坐标为).,(y x 由P ),(y x 在椭圆上,得.)()()(||222222221x aca xa b b c x y c x F +=-++=++=由0,>+-≥+≥a c x a c a a x 知,所以 .||1x aca F +=………………………3分 证法二:设点P 的坐标为).,(y x 记,||,||2211r P F r P F ==则.)(,)(222221y c x r y c x r ++=++=由.||,4,211222121x a ca r P F cx r r a r r +===-=+得 证法三:设点P 的坐标为).,(y x 椭圆的左准线方程为.0=+x aca由椭圆第二定义得a c ca x P F =+||||21,即.||||||21x a c a c a x a c F +=+=由0,>+-≥+-≥a c x a c a a x 知,所以.||1x aca P F +=…………………………3分 (Ⅱ)解法一:设点T 的坐标为).,(y x当0||=时,点(a ,0)和点(-a ,0)在轨迹上.当|0||0|2≠≠TF PT 且时,由0||||2=⋅TF PT ,得2TF PT ⊥. 又||||2PF PQ =,所以T 为线段F 2Q 的中点. 在△QF 1F 2中,a F ==||21||1,所以有.222a y x =+ 综上所述,点T 的轨迹C 的方程是.222a y x =+…………………………7分 解法二:设点T 的坐标为).,(y x 当0||=时,点(a ,0)和点(-a ,0)在轨迹上. 当|0||0|2≠≠TF PT 且时,由02=⋅TF PT ,得2TF PT ⊥.又||||2PF PQ =,所以T 为线段F 2Q 的中点.设点Q 的坐标为(y x '',),则⎪⎪⎩⎪⎪⎨⎧'=+'=.2,2y y cx x因此⎩⎨⎧='-='.2,2y y c x x ①由a F 2||1=得.4)(222a y c x ='++' ② 将①代入②,可得.222a y x =+综上所述,点T 的轨迹C 的方程是.222a y x =+……………………7分(Ⅲ)解法一:C 上存在点M (00,y x )使S=2b 的充要条件是⎪⎩⎪⎨⎧=⋅=+.||221,2022020b y c a y x由③得a y ≤||0,由④得.||20c b y ≤所以,当cb a 2≥时,存在点M ,使S=2b ; ③ ④当cb a 2<时,不存在满足条件的点M.………………………11分当cb a 2≥时,),(),,(002001y xc MF y x c MF --=---=, 由2222022021b c a y c x MF MF =-=+-=⋅,212121cos ||||MF F MF MF MF MF ∠⋅=⋅,22121sin ||||21b MF F MF MF S =∠⋅=,得.2tan 21=∠MF F 解法二:C 上存在点M (00,y x )使S=2b 的充要条件是⎪⎩⎪⎨⎧=⋅=+.||221,2022020b y c a y x 由④得.||20c b y ≤ 上式代入③得.0))((2224220≥+-=-=c b a c b a cb a x 于是,当cb a 2≥时,存在点M ,使S=2b ;当cb a 2<时,不存在满足条件的点M.………………………11分当c b a 2≥时,记cx y k k c x y k k M F M F -==+==00200121,,由,2||21a F F <知︒<∠9021MF F ,所以.2|1|tan 212121=+-=∠k k k k MF F …………14分12.(本小题满分14分)(2005年高考·江西卷·理22)如图,设抛物线2:x y C =的焦点为F ,动点P 在直线02:=--y x l 上运动,过P 作抛物线C 的两条切线PA 、PB ,且与抛物线C 分别相切于A 、B 两点. (1)求△APB 的重心G 的轨迹方程. (2)证明∠PFA=∠PFB.解:(1)设切点A 、B 坐标分别为))((,(),(0121120x x x x x x ≠和,③ ④∴切线AP 的方程为:;02200=--x y x x 切线BP 的方程为:;02211=--x y x x解得P 点的坐标为:1010,2x x y x x x P P =+=所以△APB 的重心G 的坐标为 P PG x x x x x =++=310,,343)(3321021010212010pP P G y x x x x x x x x x y y y y -=-+=++=++=所以243G G p x y y +-=,由点P 在直线l 上运动,从而得到重心G 的轨迹方程为:).24(31,02)43(22+-==-+--x x y x y x 即(2)方法1:因为).41,(),41,2(),41,(2111010200-=-+=-=x x FB x x x x FP x x FA 由于P 点在抛物线外,则.0||≠∴||41)1)(1(||||cos 102010010FP x x x x x x x x FA FP AFP +=--+⋅+==∠同理有||41)1)(1(||||cos 102110110FP x x x x x x x x FB FP BFP +=--+⋅+==∠ ∴∠AFP=∠PFB.方法2:①当,0,0,,0000101==≠=y x x x x x 则不妨设由于时所以P 点坐标为)0,2(1x ,则P 点到直线AF 的距离为:,4141:;2||12111x x x y BF x d -=-=的方程而直线即.041)41(1121=+--x y x x x 所以P 点到直线BF 的距离为:2||412||)41()()41(|42)41(|1211212122111212x x x x x x x x x d =++=+-+-=所以d 1=d 2,即得∠AFP=∠PFB.②当001≠x x 时,直线AF 的方程:,041)41(),0(041410020020=+-----=-x y x x x x x x y 即 直线BF 的方程:,041)41(),0(041411121121=+-----=-x y x x x x x x y 即 所以P 点到直线AF 的距离为:2||41)41)(2|)41(|41)2)(41(|1020201020220012010201x x x x x x x x x x x x x x d -=++-=+-+-+-=,同理可得到P 点到直线BF 的距离2||012x x d -=,因此由d 1=d 2,可得到∠AFP=∠PFB. 13.(本小题满分12分)(2005年高考·江西卷·文21)如图,M 是抛物线上y 2=x 上的一点,动弦ME 、MF 分别交x 轴于A 、B 两点,且MA=MB.(1)若M 为定点,证明:直线EF 的斜率为定值;(2)若M 为动点,且∠EMF=90°,求△EMF 的重心G 的轨迹方程.解:(1)设M (y 20,y 0),直线ME 的斜率为k(l>0)则直线MF 的斜率为-k ,).(200y x k y y ME -=-∴的方程为直线⎪⎩⎪⎨⎧=-=-∴xy y x k y y 2200)(由消0)1(002=-+-ky y y ky x 得2200)1(,1kky x k ky y F F -=∴-=解得).(2142)1()1(1102022022000定值y k ky k k ky k ky k ky k ky x x y y k F E F E EF-=-=+---+--=--=∴所以直线EF 的斜率为定值(2),1,45,90==∠=∠k MAB EMF 所以时当).(200y x k y y ME -=-∴的方程为直线 ).1,)1((,0202200y y E xy y x y y --⎪⎩⎪⎨⎧=-=-得由 同理可得)).1(,)1((020y y F +-+设重心G (x , y ),则有⎪⎪⎩⎪⎪⎨⎧-=+--+=++=+=++-+=++=33)1()1(33323)1()1(3000020202020y y y y x x x x y y y y x x x x F E M F E M).32(2729120>-=x x y y 得消去参数 14.(本小题满分12分)(2005年高考·重庆卷·理21)已知椭圆C 1的方程为1422=+y x ,双曲线C 2的左、右焦点分别为C 1的左、右顶点,而C 2的左、右顶点分别是C 1的左、右焦点. (Ⅰ)求双曲线C 2的方程;(Ⅱ)若直线2:+=kx y l 与椭圆C 1及双曲线C 2都恒有两个不同的交点,且l 与C 2的两个交点A 和B 满足6<⋅(其中O 为原点),求k 的取值范围.解:(Ⅰ)设双曲线C 2的方程为12222=-by a x ,则.1,31422222==+=-=b c b a a 得再由故C 2的方程为.1322=-y x (II )将.0428)41(1422222=+++=++=kx x k y x kx y 得代入 由直线l 与椭圆C 1恒有两个不同的交点得,0)14(16)41(16)28(22221>-=+-=∆k k k即 .412>k ① 0926)31(1322222=---=-+=kx x k y x kx y 得代入将.由直线l 与双曲线C 2恒有两个不同的交点A ,B 得.131.0)1(36)31(36)26(,0312222222<≠⎪⎩⎪⎨⎧>-=-+-=∆≠-k k k k k k 且即)2)(2(,66319,3126),,(),,(22+++=+<+<⋅--=⋅-=+B A B A B A B A B A B A BA B A B B A A kx kx x x y y x x y y x x k x x k k x x y x B y x A 而得由则设.1373231262319)1(2)(2)1(222222-+=+-⋅+--⋅+=++++=k k kk k k k x x k x x k B A B A .0131315,613732222>--<-+k k k k 即于是解此不等式得 .31151322<>k k 或 ③ 由①、②、③得.11513314122<<<<k k 或 故k 的取值范围为)1,1513()33,21()21,33()1513,1( ---- 15.(本小题满分12分)(2005年高考·重庆卷·文21)已知中心在原点的双曲线C 的右焦点为(2,0),右顶点为)0,3( (1)求双曲线C 的方程;(2)若直线2:+=kx y l 与双曲线C 恒有两个不同的交点A 和B ,且2>⋅(其中O 为原点). 求k 的取值范围.解:(Ⅰ)设双曲线方程为12222=-by a x ).0,0(>>b a由已知得.1,2,2,32222==+==b b a c a 得再由故双曲线C 的方程为.1322=-y x (Ⅱ)将得代入13222=-+=y x kx y .0926)31(22=---kx x k 由直线l 与双曲线交于不同的两点得⎪⎩⎪⎨⎧>-=-+=∆≠-.0)1(36)31(36)26(,0312222k k k k即.13122<≠k k 且 ① 设),(),,(B B A A y x B y x A ,则,22,319,312622>+>⋅--=-=+B A B A B A B A y y x x OB OA kx x k k x x 得由 而2)(2)1()2)(2(2++++=+++=+B A B A B A B A B A B A x x k x x k kx kx x x y y x x.1373231262319)1(22222-+=+-+--+=k k k k k k k 于是解此不等式得即,01393,213732222>-+->-+k k k k.3312<<k ② 由①、②得 .1312<<k故k 的取值范围为).1,33()33,1(⋃-- 16.(2005年高考·浙江卷·理17文19)如图,已知椭圆的中心在坐标原点,焦点12,F F 在x 轴上,长轴12A A 的长为4,左准线l 与x 轴的交点为M ,|MA 1|∶|A 1F 1|=2∶1.(Ⅰ)求椭圆的方程;(Ⅱ)(理)若直线1l :x =m (|m |>1),P 为1l 上的动点,使12F PF ∠最大的点P 记为Q ,求点Q 的坐标(用m 表示).(Ⅱ)(文)若点P 为l 上的动点,求∠F 1PF 2最大值.解:(Ⅰ)设椭圆方程为()222210x y a b a b+=>>,半焦距为c ,则2111,a MA a A F a c c =-=-()2222224a a a c c a abc ⎧-=-⎪⎪⎪=⎨⎪=+⎪⎪⎩由题意,得2,1a b c ∴=== 221.43x y +=故椭圆方程为(Ⅱ)(理) 设()0,,||1P m y m >, 当00y >时,120F PF ∠=;当00y ≠时,22102F PF PF M π<∠<∠<,∴只需求22tan F PF ∠的最大值即可设直线1PF 的斜率011y k m =+,直线2PF 的斜率021y k m =-,x =021********||tan 11y k k F PF k k m y-∴∠==≤=+-+ 0||y =时,12F PF ∠最大,(,,||1Q m m ∴>(Ⅱ)(文)()004,,0P y y -≠设001122121102112212000121212350,22tan 115tan y yPF k PF k F PF PF M F PF y k k F PF k k y y y F PF F PF F PF π=-=-<∠<∠<∴∠-∴∠==≤=++=±∠∠∠ 设直线的斜率,直线的斜率 为锐角。
2005年高考题之导数
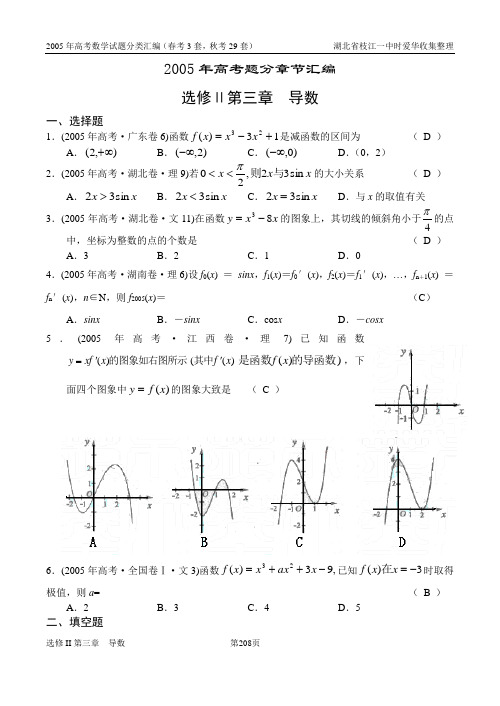
2005年高考题分章节汇编 选修Ⅱ第三章 导数一、选择题1.(2005年高考·广东卷6)函数13)(23+-=x x x f 是减函数的区间为 ( D )A .),2(+∞B .)2,(-∞C .)0,(-∞D .(0,2)2.(2005年高考·湖北卷·理9)若x x x sin 32,20与则π<<的大小关系( D )A .x x sin 32>B .x x sin 32<C .x x sin 32=D .与x 的取值有关3.(2005年高考·湖北卷·文11)在函数x x y 83-=的图象上,其切线的倾斜角小于4π的点中,坐标为整数的点的个数是( D )A .3B .2C .1D .04.(2005年高考·湖南卷·理6)设f 0(x ) = sinx ,f 1(x )=f 0′(x ),f 2(x )=f 1′(x ),…,f n +1(x ) = f n ′(x ),n ∈N ,则f 2005(x )=(C )A .sinxB .-sinxC .cos xD .-cosx5.(2005年高考·江西卷·理7)已知函数)(()(x f x f x y ''=其中的图象如右图所示))(的导函数是函数x f ,下面四个图象中)(x f y =的图象大致是 ( C )6.(2005年高考·全国卷Ⅰ·文3)函数,93)(23-++=x ax x x f 已知3)(-=x x f 在时取得极值,则a =( B )A .2B .3C .4D .5二、填空题1.(2005年高考·北京卷·理12)过原点作曲线x e y =的切线,则切点的坐标为 ,切线的斜率为 .(1,e ) e2.(2005年高考·重庆卷·理12)曲线)0)(,(33≠=a a a x y 在点处的切线与x 轴、直线a x =所围成的三角形的面积为a 则,61= . 1± 3.(2005年高考·重庆卷·文12)曲线3x y =在点(1,1)处的切线与x 轴、直线2=x 所围成的三角形的面积为 .38 4.(2005年高考·江苏卷14)曲线13++=x x y 在点(1,3)处的切线方程是_____________________。
2005年高考题分类汇编

2005年高考题分类汇编1.力物体的平衡1.(2005上海)对如图所示的皮带传动装置,下列说法中正确的是BDA.A轮带动B轮逆时针方向旋转B.B轮带动A轮逆时针方向旋转C.C轮带动D轮顺时针方向旋转D.D轮带动C轮顺时针方向旋转2.(2005天津)如图所示,表面粗糙的固定斜面顶端安有滑轮,两物块P、Q用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦),P悬于空中,Q放在斜面上,均处于静止状态。
当用水平向左的恒力推Q时,P、Q仍静止不动,则 DA.Q受到的摩擦力一定变小B.Q受到的摩擦力一定变大C.轻绳上拉力一定变小D.轻绳上拉力一定不变3.(2005江苏)(10分)某同学用如图所示的装置做探究弹力和弹簧伸长关系的实验。
他先测出不挂砝码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上砝码,并逐个增加砝码,测出指针所纸的标尺刻度,所得数据列表如下:(重力加速度g=9.8m/s2)(1)根据所测数据,在答题卡的坐标纸上作出弹簧指针所指的标尺刻度x与砝码质量m的关系曲线。
(2)根据所测得的数据和关系曲线可以判断,在______N范围内弹力大小与弹簧伸长关系满足胡克定律。
这种规格弹簧的劲度系数为______N/m。
(1)如右图(2)0~4.9,25.04.(2005全国)在“验证力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,另一端系上两根细绳,细绳的另一端都有绳套(如图)。
实验中需用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条。
某同学认为在此过程中必须注意以下几项:A.两根细绳必须等长。
B.橡皮条应与两绳夹角的平分线在同一直线上。
C.在使用弹簧秤时要注意使弹簧秤与木板平面平行。
其中正确的是________。
(填入相应的字母) c5.(2005全国)用游标为50分度的卡尺(测量值可准确到0.02mm)测定某圆柱的直径时,卡尺上的示数如图。
可读出圆柱的直径为_________mm。
42.126.(2005全国)⑴用螺旋测微器测圆柱体的直径时,示数如图所示,此示数为__________mm。
2005年全国高考数学试题分类汇编函数与导数解答题参考答案

2005年全国高考数学试题分类汇编函数与导数解答题参考答案——函数与导数解答题参考答案(注:打▲标记的为导数应用试题)▲ 9.(2005辽宁卷第22题,本小题满分12分)本小题考查导数概念的几何意义,函数极值、最值的判定以及灵活运用数形结合的思想判断函数之间的大小关系.考查学生的学习能力、抽象思维能力及综合运用数学基本关系解决问题的能力.满分12分(Ⅰ)解:).()(000x f x x f m '-=…………………………………………2分 (Ⅱ)证明:令.0)(),()()(),()()(00=''-'='-=x h x f x f x h x f x g x h 则 因为)(x f '递减,所以)(x h '递增,因此,当0)(,0>'>x h x x 时;当0)(,0<'<x h x x 时.所以0x 是)(x h 唯一的极值点,且是极小值点,可知)(x h 的最小值为0,因此,0)(≥x h 即).()(x f x g ≥…………………………6分(Ⅲ)解法一:10≤≤b ,0>a 是不等式成立的必要条件,以下讨论设此条件成立. 0)1(,122≥-+-+≥+b ax x b ax x 即对任意),0[+∞∈x 成立的充要条件是 .)1(221b a -≤另一方面,由于3223)(x x f =满足前述题设中关于函数)(x f y =的条件,利用(II )的结果可知,3223x b ax =+的充要条件是:过点(0,b )与曲线3223x y =相切的直线的斜率大于a ,该切线的方程为.)2(21b x b y +=-于是3223x b ax ≥+的充要条件是.)2(21b a ≥…………………………10分综上,不等式322231x b ax x ≥+≥+对任意),0[+∞∈x 成立的充要条件是.)1(2)2(2121b a b -≤≤- ①显然,存在a 、b 使①式成立的充要条件是:不等式.)1(2)2(2121b b -≤- ②有解、解不等式②得.422422+≤≤-b ③因此,③式即为b 的取值范围,①式即为实数在a 与b 所满足的关系.…………12分(Ⅲ)解法二:0,10>≤≤a b 是不等式成立的必要条件,以下讨论设此条件成立.0)1(,122≥-+-+≥+b ax x b ax x 即对任意),0[+∞∈x 成立的充要条件是 .)1(221b a -≤………………………………………………………………8分令3223)(x b ax x -+=φ,于是3223x b ax ≥+对任意),0[+∞∈x 成立的充要条件是 .0)(≥x φ 由.0)(331--==-='a x xa x 得φ当30-<<a x 时;0)(<'x φ当3->a x 时,0)(>'x φ,所以,当3-=a x 时,)(x φ取最小值.因此0)(≥x φ成立的充要条件是0)(3≥-a φ,即.)2(21-≥b a ………………10分综上,不等式322231x b ax x ≥+≥+对任意),0[+∞∈x 成立的充要条件是.)1(2)2(2121b a b -≤≤-①显然,存在a 、b 使①式成立的充要条件是:不等式2121)1(2)2(b b -≤- ②有解、解不等式②得.422422+≤≤-b因此,③式即为b 的取值范围,①式即为实数在a 与b 所满足的关系.…………12分▲10.(2005北京卷理第15题,本小题共13分;文第19题,满分14分) 解:(I ) f ’(x )=-3x 2+6x +9.令f ‘(x )<0,解得x <-1或x >3, 所以函数f (x )的单调递减区间为(-∞,-1),(3,+∞). (II )因为f (-2)=8+12-18+a =2+a ,f (2)=-8+12+18+a =22+a ,所以f (2)>f (-2).因为在(-1,3)上f ‘(x )>0,所以f (x )在[-1, 2]上单调递增,又由于f (x )在[-2,-1]上单调递减,因此f (2)和f (-1)分别是f (x )在区间[-2,2]上的最大值和最小值,于是有 22+a =20,解得 a =-2.故f (x )=-x 3+3x 2+9x -2,因此f (-1)=1+3-9-2=-7, 即函数f (x )在区间[-2,2]上的最小值为-7.11.(2005北京卷理第20题,本小题共14分)(I )证明:设x *为f (x ) 的峰点,则由单峰函数定义可知,f (x )在[0, x *]上单调递增,在[x *, 1]上单调递减.当f (x 1)≥f (x 2)时,假设x *∉(0, x 2),则x 1<x 2<x *,从而f (x *)≥f (x 2)>f (x 1), 这与f (x 1)≥f (x 2)矛盾,所以x *∈(0, x 2),即(0, x 2)是含峰区间.当f (x 1)≤f (x 2)时,假设x *∉( x 2, 1),则x *<≤x 1<x 2,从而f (x *)≥f (x 1)>f (x 2), 这与f (x 1)≤f (x 2)矛盾,所以x *∈(x 1, 1),即(x 1, 1)是含峰区间. (II )证明:由(I )的结论可知:当f (x 1)≥f (x 2)时,含峰区间的长度为l 1=x 2; 当f (x 1)≤f (x 2)时,含峰区间的长度为l 2=1-x 1; 对于上述两种情况,由题意得 210.510.5x rx r+⎧⎨-+⎩≤≤ ①由①得 1+x 2-x 1≤1+2r ,即x 1-x 1≤2r. 又因为x 2-x 1≥2r ,所以x 2-x 1=2r, ② 将②代入①得x 1≤0.5-r, x 2≥0.5-r , ③ 由①和③解得 x 1=0.5-r , x 2=0.5+r .所以这时含峰区间的长度l 1=l 1=0.5+r ,即存在x 1,x 2使得所确定的含峰区间的长度不大于0.5+r .(III )解:对先选择的x 1;x 2,x 1<x 2,由(II )可知 x 1+x 2=l , ④在第一次确定的含峰区间为(0, x 2)的情况下,x 3的取值应满足 x 3+x 1=x 2, ⑤由④与⑤可得2131112x x x x =-⎧⎨=-⎩,当x 1>x 3时,含峰区间的长度为x 1.由条件x 1-x 3≥0.02,得x 1-(1-2x 1)≥0.02,从而x 1≥0.34. 因此,为了将含峰区间的长度缩短到0.34,只要取x 1=0.34,x 2=0.66,x 3=0.32.12.[ 2005浙江卷理第16题(前2问),文第20题(共3问) ]理科数学:本题主要考查函数图象的对称、中点坐标公式、解不等式等基础知识,以及运算和推理能力满分14分文科数学:本题主要考查函数图象的对称、二次函数的基本性质与不等式的应用等基础知识,以及综合运用所学知识分析和解决问题的能力14分解:(Ⅰ)设函数()y f x =的图象上任意一点()00,Q x y 关于原点的对称点为(),P x y ,则0000,,2.0,2x xx x y y y y +⎧=⎪=-⎧⎪⎨⎨+=-⎩⎪=⎪⎩即 ∵点()00,Q x y 在函数()y f x =的图象上∴()22222,2y x x y x x g x x x -=-=-+=-+,即 故(Ⅱ)由()()21210g x f x x x x ≥----≤, 可得当1x ≥时,2210x x -+≤,此时不等式无解当1x <时,2210x x +-≤,解得12x -≤≤因此,原不等式的解集为11,2⎡⎤-⎢⎥⎣⎦(Ⅲ)()()()21211h x x x λλ=-++-+①()[]1411,1h x x λ=-=+-当时,在上是增函数, 1λ∴=-②11.1x λλλ-≠-=+当时,对称轴的方程为 ⅰ)111, 1.1λλλλ-<-≤-<-+当时,解得ⅱ)111,10.1λλλλ->-≥--<≤+当时,解得0.λ≤综上,▲13.(2005浙江卷理第20题)本题主要考查二次函数的求导、导数的应用、等差数列、数学归纳法等基础知识,以及综合运用所学知识分析和解决问题的能力14分解:(Ⅰ)由题意得()21111,0,:7A C y x x b =-+, 设点(),P x y 是1C 上任意一点,则1||A P ==令()()()222117f x x x x b =-+-+则()()()()21212727f x x x x b x '=-+-+-由题意得()20f x '=,即()()()222122127270x x x b x-+-+-=又()22,2P x 在1C 上,222127x x b∴=-+ 解得213,14x b ==故1C 的方程为2714y x x =-+ (Ⅱ)设点(),P x y 是n C 上任意一点,则||n A P ==令()()()222n n ng x x x x a x b =-+++则()()()()2222n n nng x x x x a x b x a '=-++++由题意得()10n g x +'=即()()()21112220n n n n nn n x x x a x b xa +++-++++=又1212n n n n n x a x b ++=++ ,()()()112201n n n n n x x x a n ++∴-++=≥,即()()111220*n n n n n x x a +++-+=下面用数学归纳法证明21n x n =-,①当1n =时,11x =,等式成立;②假设当n k =时,等式成立,即21k x k =-,则当1n k =+时,由()*知()111220k k k k k x x a +++-+=, 又11242k k a k -=---,1122112k k k k k x a x k ++-∴==++, 即1n k =+时,等式成立由①②知,等式对*n N ∈成立, 故{}n x 是等差数列▲ 14.(2005湖北卷理第17题,文第17题,本小题满分12分)本小题主要考查平面向量数量积的计算方法、利用导数研究函数的单调性,以及运用基本函数的性质分析和解决问题的能力。
2005年高考试题分类解析(数列,数学归纳法)

2005年全国高考数学试题分类汇编——数列·数学归纳法1. (2005全国卷II 文科第7题)如果数列{}n a 是等差数列,则( )(A)1845a a a a +<+(B) 1845a a a a +=+ (C) 1845a a a a +>+ (D) 1845a a a a =2. (2005全国卷II 文科第13题)在83和272之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为_______.3. (全国卷II 理科第11题)如果128,,,a a a 为各项都大于零的等差数列,公差0d ≠,则( ) (A)1845a a a a > (B) 1845a a a a < (C) 1845a a a a +>+ (D) 1845a a a a =4.(2005湖南卷文科第5题)已知数列}{n a 满足)(133,0*11N n a a a a n n n ∈+-==+,则20a =( )A .0B .3-C .3D .235.(2005湖南卷理科第3题)已知数列{log 2(a n -1)}(n ∈N *)为等差数列,且a 1=3,a 2=5,则lim 21321111()n n na a a a a a →∞++++---=( )A .2B .23C .1D .216. (2005湖北卷理科第15题)设等比数列}{n a 的公比为q ,前n 项和为S n ,若S n+1,S n ,S n+2成等差数列,则q 的值为 . 7.(2005江苏卷第3题)在各项都为正数的等比数列{a n }中,首项a 1=3 ,前三项和为21,则a 3+ a 4+ a 5=( ) ( A ) 33 ( B ) 72 ( C ) 84 ( D )189 8.(2005山东卷文科第1题){}n a 是首项1a =1,公差为d =3的等差数列,如果n a =2005,则序号n 等于( )(A )667 (B )668 (C )669 (D )6709.(2005福建卷理科第2题)已知等差数列}{n a 中,12497,1,16a a a a 则==+的值是 ( ) A .15B .30C .31D .6410.(2005天津卷文科第14题)在数列{a n }中, a 1=1, a 2=2,且)( )1(12*+∈-+=-N n a a n n n ,则10S =_ ___.11.(2005天津卷理科第13题)在数列{a n }中, a 1=1, a 2=2,且)( )1(12*+∈-+=-N n a a n n n ,则100S =__ .12.(2005辽宁卷第12题)一给定函数)(x f y =的图象在下列图中,并且对任意)1,0(1∈a ,由关系式)(1n n a f a =+得到的数列}{n a 满足)(*1N n a a n n ∈>+,则该函数的图象是 ( )(A ) (B ) (C ) (D )13.(2005广东卷第10题)已知数列{}n x 满足122x x =,()1212n n n x x x --=+,3,4,n =….若lim 2n n x →∞=,则( )(A)32(B)3 (C)4 (D)514. (2005广东卷第14题)设平面内有n条直线(3)n ≥,其中有且仅有两条直线互相平行,任意三角形不过同一点.若用()f n 表示这n条直线交点的个数,则(4)f _______;当n>4时,()f n =_______.15. (2005北京卷第14题)已知n 次多项式1011()n n n n n P x a x a x a x a --=++++,如果在一种算法中,计算0kx (k =2,3,4,…,n )的值需要k -1次乘法,计算30()P x 的值共需要9次运算(6次乘法,3次加法),(文科)那么计算100()P x 的值共需要 次运算. (理科)那么计算0()n P x 的值共需要 次运算. 下面给出一种减少运算次数的算法:0011(),()()k k k P x a P x xP x a ++==+ (k =0, 1,2,…,n -1).利用该算法,计算30()P x 的值共需要6次运算, (文科)计算100()P x 的值共需要 次运算. (理科)计算0()n P x 的值共需要 次运算.16. [ 2005上海理科第12题,文科第16题(选择题)]用n 个不同的实数n a a a ,,,21 可得到!n 个不同的排列,每个排列为一行写成一个!n 行的数阵。
2005年高考试题分类解析(高三概率与统计)
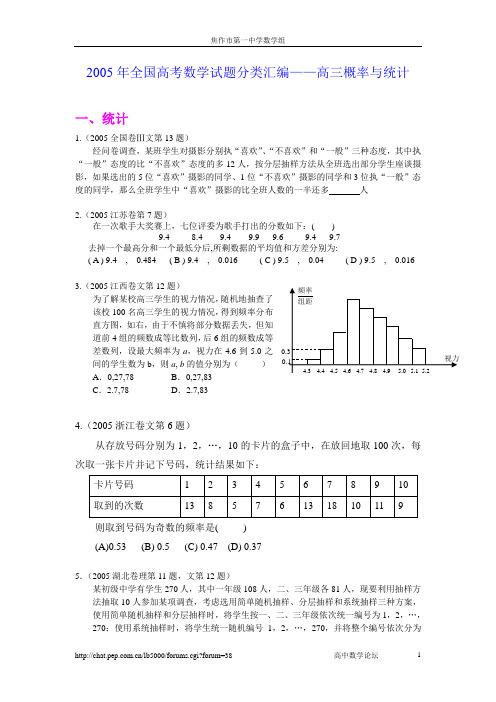
2005年全国高考数学试题分类汇编——高三概率与统计一、统计1.(2005全国卷Ⅲ文第13题)经问卷调查,某班学生对摄影分别执“喜欢”、“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”态度的多12人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的5位“喜欢”摄影的同学、1位“不喜欢”摄影的同学和3位执“一般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多 人2.(2005江苏卷第7题)在一次歌手大奖赛上,七位评委为歌手打出的分数如下:( )9.4 8.4 9.4 9.9 9.6 9.4 9.7去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为:( A ) 9.4 , 0.484 ( B ) 9.4 , 0.016 ( C ) 9.5 , 0.04 ( D ) 9.5 , 0.0163.(2005江西卷文第12题) 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a ,视力在4.6到5.0之间的学生数为b ,则a , b 的值分别为( ) A .0,27,78 B .0,27,83 C .2.7,78 D .2.7,834.(2005浙江卷文第6题)从存放号码分别为1,2,…,10的卡片的盒子中,在放回地取100次,每次取一张卡片并记下号码,统计结果如下:则取到号码为奇数的频率是( ) (A)0.53 (B) 0.5 (C) 0.47 (D) 0.375.(2005湖北卷理第11题,文第12题)某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:①7,34,61,88,115,142,169,196,223,250; ②5,9,100,107,111,121,180,195,200,265; ③11,38,65,92,119,146,173,200,227,254; ④30,57,84,111,138,165,192,219,246,270; 关于上述样本的下列结论中,正确的是 ( )A .②、③都不能为系统抽样B .②、④都不能为分层抽样C .①、④都可能为系统抽样D .①、③都可能为分层抽样6.(2005湖南卷理第11题,文第12题)一工厂生产了某种产品16800件,它们来自甲.乙.丙3条生产线,为检查这批产品的质量,决定采用分层抽样的方法进行抽样,已知甲.乙.丙三条生产线抽取的个体数组成一个等差数列,则乙生产线生产了________件产品.7. (2005山东文第13题)某学校共有教师490人,其中不到40岁的有350人,40岁及以上的有140人。
2005年普通高等学校招生全国统一考试

2005年普通高等学校招生全国统一考试数学(理工农医类)分类整理 三角函数、解三角形与平面向量(全国卷Ⅰ)(6)当20π<<x 时,函数xxx x f 2sin sin 82cos 1)(2++=的最小值为(A )2(B )32(C )4(D )34(10)在ABC ∆中,已知C BA sin 2tan =+,给出以下四个论断: ①1cot tan =⋅B A②2sin sin 0≤+<B A③1cos sin 22=+B A④C B A 222sin cos cos =+其中正确的是 (A )①③(B )②④ (C )①④ (D )②③(15)ABC ∆的外接圆的圆心为O ,两条边上的高的交点为H ,)(m ++=,则实数m = (17)(本大题满分12分)设函数)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ图像的一条对称轴是直线8π=x 。
(Ⅰ)求ϕ;(Ⅱ)求函数)(x f y =的单调增区间;(Ⅲ)证明直线025=+-c y x 与函数)(x f y =的图像不相切。
(全国卷Ⅱ)1.函数f (x )=|sin x +cos x |的最小正周期是( )A .4πB .2πC .πD .2π 4.已知函数)2,2(tan ππω-=在x y 内是减函数,则( )A .0<ω≤1B .-1≤ω<0C .ω≥1D .ω≤-17.锐角三角形的内角A 、B 满足tanA -A2sin 1=tanB ,则有( )A .sin2A -cosB=0B .sin2A+cosB=0C .sin2A -sinB=0D .sin2A+sinB=08.已知点A (3,1),B (0,0)C (3,0).设∠BAC 的平分线AE 与BC 相交于E , 那么有λλ其中,CE BC =等于( )A .2B .21 C .-3 D .-3110.点P 在平面上作匀速直线运动,速度向量v =(4,-3)(即点P 的运动方向与v 相同,且每秒移动的距离为|v |个单位.设开始时点P 的坐标为(-10,10),则5秒后点P 的坐标为 ( ) A .(-2,4) B .(-30,25) C .(10,-5) D .(5,-10) (全国卷Ⅲ)(1)已知α为第三象限角,则2α所在的象限是(A )第一或第二象限 (B )第二或第三象限 (C )第一或第三象限 (D )第二或第四象限(7)设02x π≤≤,sin cos x x =-,则 (A) 0x π≤≤ (B)744x ππ≤≤(C) 544x ππ≤≤ (D) 322x ππ≤≤(8)αααα2cos cos 2cos 12sin 22⋅+(A) tan α (B) tan 2α (C) 1 (D)12(14)已知向量(,12),(4,5),(,10)OA k OB OC k ===-,且A 、B 、C 三点共线,则k= (16)已知在△ABC 中,∠ACB=90°,BC=3,AC=4,P 是AB 上的点,则点P 到AC 、BC 的距离乘积的最大值是 (19)(本小题满分12分)△ABC 中,内角A ,B ,C 的对边分别是a ,b,c ,已知a ,b,c 成等比数列,且cosB =34。
2005年全国各地高考数学试题及解答分类汇编大全-导数

f 3 ( x) f 2 ( x) cos x, f 4 ( x) f 3 ( x) sin x, .
由此继续求导下去,四个一循环, f n ( x ) 的周期为 4
第 1页 (共 21页)
又 2005 4 501 余1,所以f 2005 ( x ) f 1( x ) sinx. 故选 B. 【解后反思】 我们在解决一些比较庞大的数学问题或项数比较多的时候,大部分同学可能也意识到其 中可能存在周期性或其他规律性的东西.可以总是找不出,或没有头绪,这个时候我们不能怕麻烦,就 用列举法,多写几项,就可以把握住这种类型的题目.
2
选 A. 【解后反思】 在求函数某一点极限的过程中,总是先化简,再代入的思路,不要先随便代入或不加思 索的用极限计算的运算法则进行分离.
10. (2005 天津理)若函数 f ( x ) log a ( x ax )(a 0, a 1) 在区间 ( 值范围是
3
1 则 a 的取 , 0) 内单调递增, 2
(A) [ ,1) (B) [ ,1) (C) [ , ) 当 0 a 1 时,由 f ( x ) log a ( x ax ) 区间 (
3
1 4
3 4
9 4
g ( x) 0 1 对一切 , 0) 内单调递增的充要条件是 2 g ( x ) 0
2 1 1 3 a x x ( , 0) 恒成立,即 对一切 x ( , 0) 恒成立,解得 a [ ,1) , 2 2 2 4 a 3x
3 1 当 a 1 时,要使得 f x 是增数,则需有 g ' x 0 恒成立,所以 a 3 。矛盾。排除 C、 4 2 D 3 1 当 0 a 1 时,要使得 f x 是增数,则需有 g ' x 0 恒成立,所以 a 3 。 4 2 排除 A 本题答案选 B 【解后反思】一般地, m f ( x ) 对 x [a , b ] 上的一切 x 恒成立的充要条件是 m f max ( x ) ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2005年高考题分章节汇编 第一章 集合与简易逻辑
一、选择题
1. (2005年春考·上海卷15)若c b a 、、是常数,则“0402<->c a b a 且”是“对任意R ∈x ,有02>++c x b x a ” 的
( A )
A .充分不必要条件.
B .必要不充分条件.
C .充要条件.
D .既不充分也不必要条件.
2.(2005年高考·北京卷·理1文1)设合集U=R ,集合}1|{},1|{2>=>=x x P x x M ,则下列关系中正确的是 ( C )
A .M=P
B .P M
C .M P
D .( U M)∩P=Φ
3. (2005年高考·上海卷·理14文14)已知集合{}R x x x M ∈≤-=,2|1||,⎭⎬⎫⎩⎨⎧∈≥+=Z x x x P ,115|
,则P M 等于
( B )
A .{}Z x x x ∈≤<,30|
B .{}Z x x x ∈≤≤,30|
C .{}Z x x x ∈≤≤-,01|
D .{}Z x x x ∈<≤-,01|
4.(2005年高考·上海卷·文15)条件甲:“1>a ”是条件乙:“a a >”的
( B )
A .既不充分也不必要条件
B .充要条件
C .充分不必要条件
D .必要不充分条件
5.(2005年高考·福建卷·文1)已知集合∈≤-=x x x P ,1|1|||R|,Q P N x x Q 则},|{∈=等于
( D ) A .P
B .Q
C .{1,2}
D .{0,1,2}
6.(2005年高考·福建卷·文2)不等式01
31
2>+-x x 的解集是 ( A )
A .}2
131|{>-<x x x 或 B .}2
1
31|{<<-x x
C .}2
1|{>
x x
D .}3
1
|{->x x
7.(2005年高考·福建卷·文8)已知q p ab q a p 是则,0:,0:≠≠的 ( B )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
8.(2005年高考·福建卷·理7)已知p :,0)3(:,1|32|<-<-x x q x 则p 是q 的( A ) A .充分不必要条件 B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
9.(2005年高考·广东卷1)若集合}03|{},2|||{2
=-=≤=x x x N x x M ,则M ∩N=( B )
A .{3}
B .{0}
C .{0,2}
D .{0,3}
10.(2005年高考·湖北卷·理1文1)设P 、Q 为两个非空实数集合,定义集合P+Q=},5,2,0{},,|{=∈∈+P Q b P a b a 若}6,2,1{=Q ,则P+Q 中元素的个数是
( B )
A .9
B .8
C .7
D .6
11.(2005年高考·湖北卷·理2文1)对任意实数a ,b ,c ,给出下列命题: ①“b a =”是“bc ac =”充要条件; ②“5+a 是无理数”是“a 是无理数”的充要条件③“a >b ”是“a 2>b 2”
的充分条件;④“a <5”是“a <3”的必要条件. 其中真命题的个数是 ( B )
A .1
B .2
C .3
D .4
12.(2005年高考·湖南卷·文1)设全集U={-2,-1,0,1,2},A={-2,-1,0},B={0,1,2},则( U A )∩B= ( C ) A .{0} B .{-2,-1} C .{1,2} D .{0,1,2} 13.(2005年高考·湖南卷·理8)集合A ={x |1
1
+-x x <0=,B ={x || x -b|<a },若“a =1”是“A ∩B ≠φ”的充分条件,则b 的取值范围是
( D )
A .-2≤b <0
B .0<b ≤2
C .-3<b <-1
D .-1≤b <2
14.(2005年高考·湖南卷·文6)设集合A ={x |1
1
+-x x <0},B ={x || x -1|<a },若“a =1”是“A ∩B ≠φ”的
( A )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分又不必要条件
15.(2005年高考·江西卷·理1文1)设集合⋃--==∈<=A B A Z x x x I 则},2,1,2{},2,1{},,3|||{(C I B )=
( D )
A .{1}
B .{1,2}
C .{2}
D .{0,1,2}
16.(2005年高考·江苏卷1)设集合A={1,2},B={1,2,3},C={2,3,4},则()A B C = (D)
A .{1,2,3}
B .{1,2,4}
C .{2,3,4}
D .{1,2,3,4}
17.(2005年高考·浙江卷·文2)设全集U ={1,2,3,4,5,6,7},P ={1,2,3,4,5},Q ={3,4,5,6,7},则P ∩C U Q = ( A )
A .{1,2}
B .{3,4,5}
C .{1,2,6,7}
D .{1,2,3,4,5}
18.(2005年高考·浙江卷·理9)设f(n)=2n +1(n ∈N ),P ={1,2,3,4,5},Q ={3,4,5,6,7},记P ∧
={n ∈N |f (n )∈P },Q ∧
={n ∈N |f (n )∈Q },则(P ∧∩C N Q ∧)∪(Q ∧∩C N P ∧
)=( A )
A .{0,3}
B .{1,2}
C .{3,4,5}
D .{1,2,6,7}
19.(2005年高考·山东卷·理10文11)设集合A 、B 是全集U 的两个子集,则A B ⊂是()U C A B U ⋃=的 ( A )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
19.(2005年高考·天津卷·理1)设集合{}R x x x A ∈≥-=,914, ⎭
⎬⎫⎩⎨
⎧∈≥+=R x x x x B ,03, 则A ∩B=
( D )
A .]2,3(--
B .]2
5
,0[]2,3(⋃-- C .),25[]3,(+∞⋃--∞
D .),2
5[)3,(+∞⋃--∞
20.(2005年高考·天津卷·文1)设集合∈<≤=x x x A 且30{N}的真子集...
的个数是( C)
A .16
B .8
C .7
D .4
21.(2005年高考·全国卷Ⅰ·理1文1)设I 为全集,S 1、S 2、S 3是I 的三个非空子集且S 1∪S 2∪S 3=I ,则下面论断正确的是 ( C )
A .C I S I ∩(S 2∪S 3)=φ
B .S 1⊆(
C I S 2∩C I S 3)
C .C I S I ∩C I S 2 ∩C I S 3=φ
D .S 1⊆(C I S 2∪C I S 3)
22.(2005年高考·全国卷II ·理9)已知集合M={x |x 2-3x -28≤0},|N={x |x 2-x -6>0},则M ∩N 为
( A )
A .|x |-4≤x <-2或3<x ≤7|
B .|x |-4<x ≤-2或3≤x <7|
C .|x |x ≤-2或x >3|
D .|x |x <-2或x ≥3|
23.(2005年高考·全国卷II ·文10)已知集合为则N M x x x N x x M ⋂>--=≤≤-=},06|{|},74|{2 ( A )
A .}7324|{≤<-<≤-x x x 或
B .}7324|{≤<-<≤-x x x 或
C .}32|{>-≤x x x x 或
D .}32|{≥-<x x x x 或
24.(2005年高考·全国卷Ⅲ·理12)计算机中常用十六进制是逢16进1的计数制,采用数字0~9和字母A ~F 共
例如,用十六进制表示:E+D=1B ,则A ×B=
( A )
A .6E
B .72
C .5F
D .B0
二、填空题
1.(2005年高考·重庆卷·理11)集合∈=<--∈=x B x x R x A {},06|{2R| }2|2|<-x ,则B A = .
}30|{<<x x
2.(2005年高考·重庆卷·文11)若集合}0)5)(2(|{},034|{2<--∈=<+-∈=x x R x B x x R x A ,则=B A . }32|{<<x x。
