迪杰斯特拉算法
迪杰斯特拉算法案例

迪杰斯特拉算法案例摘要:1.迪杰斯特拉算法简介2.算法案例分析3.算法的优点与应用场景正文:一、迪杰斯特拉算法简介迪杰斯特拉算法(Dijkstra"s Algorithm)是一种用于寻找两点间最短路径的算法,由荷兰计算机科学家艾兹赫尔·迪杰斯特拉于1956 年提出。
该算法主要适用于有向图和无向图中的单源最短路径问题,即从某个特定点出发,寻找到达其他所有点的最短路径。
它适用于实际生活中的许多场景,如导航系统、物流运输等。
二、算法案例分析以一个简单的例子来说明迪杰斯特拉算法的工作原理。
假设有一个无向图,包含4 个顶点A、B、C、D 和3 条边(A-B、B-C、C-D)。
我们需要从顶点A 出发,找到到达顶点D 的最短路径。
1.初始化:将源顶点A 与起点的距离设为0,其他顶点的距离设为无限大(表示还未到达)。
此时,距离值为:A: 0B: ∞C: ∞D: ∞2.迭代:从距离值最小的顶点A 开始,遍历相邻顶点B,计算从A 到B 的距离,并与当前已知的从A 到B 的距离进行比较。
如果从A 到B 的距离更小,则更新距离值。
此时,距离值为:A: 0B: 1C: ∞D: ∞3.迭代:从距离值最小的顶点B 开始,遍历相邻顶点C,计算从B 到C 的距离,并与当前已知的从B 到C 的距离进行比较。
如果从B 到C 的距离更小,则更新距离值。
此时,距离值为:A: 0B: 1C: 2D: ∞4.迭代:从距离值最小的顶点C 开始,遍历相邻顶点D,计算从C 到D 的距离,并与当前已知的从C 到D 的距离进行比较。
如果从C 到D 的距离更小,则更新距离值。
此时,距离值为:A: 0B: 1C: 3D: 35.重复迭代过程,直到所有顶点的距离值都更新完毕,此时,从A 到D 的最短路径为A-B-C-D,总距离为3。
三、算法的优点与应用场景迪杰斯特拉算法具有以下优点:1.可以处理大规模的图结构,适用于各种复杂的网络环境。
Dijkstra算法

Dijkstra算法1.定义概览Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
Dijkstra算法是很有代表性的最短路径算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
注意该算法要求图中不存在负权边。
问题描述:在无向图G=(V,E) 中,假设每条边E[i] 的长度为w[i],找到由顶点V0 到其余各点的最短路径。
(单源最短路径)2.算法描述1)算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径, 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S 中。
在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U 中任何顶点的最短路径长度。
此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2)算法步骤: a.初始时,S只包含源点,即S={v},v的距离为0。
U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
迪杰斯特拉算法详解

迪杰斯特拉算法详解简述 迪杰斯特拉算法是⼀种基于贪⼼法求有向图或⽆向图单源最短路的算法,其本质就是把顶点集划分为两部分,已求出最短路径的集合S和未求出最短路径的集合U,U集⾥⾯每个点都有⼀个边权,代表源点通过S集⾥的点到达U集的那个点的最短路径(注意这⾥的最短不⼀定是全局最短),S⼀开始只有源点,U⾥⾯和源点的边权为路径本⾝,不相邻的边权为inf,通过贪⼼不断地把U集合⾥⾯的顶点加⼊S,直到求完源点到所有顶点的最短路径。
暴⼒时间复杂度为O(n⽅),经过堆优化可为O(nlogn)。
思想过程 如何将集合U⾥的点⼀个⼀个加⼊集合S呢? 我们发现,我们可以确定,U⾥⾯顶点的最⼩边权就是源点到该路径的最短路径。
例如该图: A和B直接和源点相邻,那么U集中最⼩边权对应的顶点就是源点到该顶点的最短路径,在此图就是源点到B点的最短路径为2,因为A点的边权5不是最⼩边权,所以在这⼀步还不能确定是不是最短路径。
那为什么U集⾥的最⼩边权就是源点到该点的最短路径呢?我们⽤反证法,假设最⼩边权不是源点到该点设为y的最⼩路径,那么必然存在⼀个点设为x,使得源点到x的距离加x到y的距离⼩于U⾥的最⼩边权,那么源点到x的距离就要⼩于这个最⼩边权,⽭盾!所以结论得证! 在加⼊S集后,该点要对其他点的边权进⾏松弛,什么意思呢?U集合⾥⾯的边权是源点到该顶点的路径距离嘛,⼀开始只有和源点相邻的边,但随着S集合新点的加⼊,源点到其他点的距离会被改变,因为S集合有新的点x 加⼊,那么源点到其他的点的距离可能会被更⼩的源点到x的距离加x到其他点的距离取代,即如上图:B加⼊S之后,U集⾥⾯A的边权就可以更新为 源点-B+B-A,为4,4⽐5⼩,故更新。
所以每当有点加⼊S集的时候,都要对U⾥⾯的其他点的边权进⾏松弛。
于是不断地加⼊,松弛,加⼊,松弛,直到全部点都在S⾥⾯,就能跑出源点S到其余所有点的最短路径了。
算法模拟 因为S集和U集没有相同的部分,所以我们⽤⼀个集合加个标记就可以区分两个集合。
Dijkstra算法描述

Dijkstra算法描述目录一、算法概述1二、算法原理及计算12.1算法原理12.2计算过程22.3改良的算法〔Dijkstra-like〕分析5三、源码分析6四、接口调用7一、算法概述Dijkstra〔迪杰斯特拉〕算法是典型的单源最短路径计算算法,用于解决源点到所有结点最短路径计算的问题,它采用了分治和贪心〔动态规划的特殊形式〕的思想搜索全局最优解。
本系统采用了主流、开源的JAVA图论库——Jgrapht来解决源点到终点间所有可能路径输出的问题,它的核心计算引擎采用了一种Dijkstra-like算法,由经典的Dijkstra〔迪杰斯特拉〕算法演化和改良而来。
二、算法原理及计算2.1算法原理Dijkstra算法思想为:设(,)= 是带权有向图,V代表图中顶点集合,E代G V E表图中含权重的边集合。
将全部顶点集合V分成两组,第一组为已求出最短路径的顶点集合,用S表示〔初始时S中只有一个源点,以后每求得一条最短路径,就将该路径的终点参加到集合S中〕;第二组为其余待确定最短路径的顶点集合,用U表示。
按最短路径长度的递增次序依次把U集合的顶点逐个参加到S集合中,约束条件是保持从源点v到S中各顶点的最短路径长度不大于从源点v到U 中任何顶点的最短路径长度。
算法的终止条件是集合U为空集,即集合U的顶点全部参加到集合S中。
2.2计算过程以图1为例讨论Dijkstra算法的计算过程,即计算某源点到网络上其余各结点的最短路径,设源点为①,逐步搜索,每次找出一个结点到源点①的最短路径,直至完成所有结点的计算。
图1 带权有向图记()D v为源点①到某终点v的距离,是源点①到终点v某条路径的所有链路长度之和。
记(,)l w v 是源点w到终点v的距离。
Dijkstra算法归纳如下:S=,U是其余未确〔1〕初始化,令S是已求出最短路径的顶点集合,{}U=,可写出:定最短路径的顶点集合,{}(1,)()l v D v ⎧=⎨∞⎩(1-1) 公式1-1中,(1,)l v 是源点①与终点v 的直连路径长度,而∞代表源点①与终点v 不相连,初始化结果如表1所示;〔2〕遍历集合U 中的所有结点v 并计算[]min (),()(,)D v D w l w v + 。
迪杰斯特拉算法介绍

迪杰斯特拉算法介绍迪杰斯特拉(Dijkstra)算法是典型最短路径算法,⽤于计算⼀个节点到其他节点的最短路径。
它的主要特点是以起始点为中⼼向外层层扩展(⼴度优先搜索思想),直到扩展到终点为⽌。
基本思想通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
此外,引进两个集合S和U。
S的作⽤是记录已求出最短路径的顶点(以及相应的最短路径长度),⽽U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。
然后,从U中找出路径最短的顶点,并将其加⼊到S中;接着,更新U中的顶点和顶点对应的路径。
然后,再从U中找出路径最短的顶点,并将其加⼊到S中;接着,更新U中的顶点和顶点对应的路径。
... 重复该操作,直到遍历完所有顶点。
操作步骤(1) 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
(2) 从U中选出"距离最短的顶点k",并将顶点k加⼊到S中;同时,从U中移除顶点k。
(3) 更新U中各个顶点到起点s的距离。
之所以更新U中顶点的距离,是由于上⼀步中确定了k是求出最短路径的顶点,从⽽可以利⽤k来更新其它顶点的距离;例如,(s,v)的距离可能⼤于(s,k)+(k,v)的距离。
(4) 重复步骤(2)和(3),直到遍历完所有顶点。
单纯的看上⾯的理论可能⽐较难以理解,下⾯通过实例来对该算法进⾏说明。
迪杰斯特拉算法图解以上图G4为例,来对迪杰斯特拉进⾏算法演⽰(以第4个顶点D为起点)。
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!第1步:将顶点D加⼊到S中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。
dijkstra算法

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。
是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。
迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
定义Dijkstra算法一般的表述通常有两种方式,一种用永久和临时标号方式,一种是用OPEN, CLOSE表的方式,这里均采用永久和临时标号的方式。
注意该算法要求图中不存在负权边。
迪克斯特拉算法原理1.首先,引入一个辅助数组(vector)D,它的每个元素D表示当前所找到的Dijkstra算法运行动画过程从起始点(即源点)到其它每个顶点的长度。
例如,D[3] = 2表示从起始点到顶点3的路径相对最小长度为2。
[1] 这里强调相对就是说在算法执行过程中D的值是在不断逼近最终结果但在过程中不一定就等于长度。
[3]2.D的初始状态为:若从到有弧(即从到存在连接边),则D为弧上的权值(即为从到的边的权值);否则置D为∞。
显然,长度为D = Min{ D | ∈V } 的路径就是从出发到顶点的长度最短的一条路径,此路径为()。
3.那么,下一条长度次短的是哪一条呢?也就是找到从源点到下一个顶点的最短路径长度所对应的顶点,且这条最短路径长度仅次于从源点到顶点的最短路径长度。
假设该次短路径的终点是,则可想而知,这条路径要么是(),或者是()。
它的长度或者是从到的弧上的权值,或者是D加上从到的弧上的权值。
4.一般情况下,假设S为已求得的从源点出发的最短路径长度的顶点的集合,则可证明:下一条次最短路径(设其终点为)要么是弧(),或者是从源点出发的中间只经过S中的顶点而最后到达顶点的路径。
因此,下一条长度次短的的最短路径长度必是D = Min{ D | ∈V-S },其中D要么是弧()上的权值,要么是D(,∈S)和弧(,)上的权值之和。
最短路径算法比较

最短路径算法比较最短路径算法是计算两个顶点之间最短路径的一种常用算法。
在图论中,最短路径表示在图中从一个顶点到另一个顶点经过的边的权重之和最小的路径。
本文将比较三种常用的最短路径算法:迪杰斯特拉算法、贝尔曼-福特算法和弗洛伊德算法。
一、迪杰斯特拉算法迪杰斯特拉算法是一种解决单源最短路径问题的算法,即从一个顶点到其他所有顶点的最短路径。
它采用了广度优先搜索和贪心策略,每次选择当前最短路径的顶点作为下一个顶点进行松弛操作。
该算法的时间复杂度为O(V^2),其中V为顶点数。
迪杰斯特拉算法的优点在于对于有向图和无向图均适用,并且可以处理存在负权边的情况。
然而,该算法的缺点是对于大规模图来说效率较低,因为需要对每个顶点进行遍历。
二、贝尔曼-福特算法贝尔曼-福特算法是一种解决单源最短路径问题的算法,与迪杰斯特拉算法相似,但可以处理存在负权边的情况。
该算法采用了动态规划的思想,在每一轮迭代中对所有的边进行松弛操作,共进行V-1轮迭代,其中V为顶点数。
贝尔曼-福特算法的优点在于可以处理负权边,而迪杰斯特拉算法不可以。
然而,该算法的缺点在于时间复杂度较高,为O(V*E),其中E 为边数,可能导致在规模较大的图中运行时间过长。
三、弗洛伊德算法弗洛伊德算法是一种解决多源最短路径问题的算法,可以计算任意两个顶点之间的最短路径。
该算法采用了动态规划的思想,通过中间顶点的遍历,不断更新路径长度矩阵,直到所有顶点之间的最短路径计算完成。
弗洛伊德算法的优点是可以处理由负权边引起的环路问题,并且可以计算任意两个顶点之间的最短路径。
然而,该算法的缺点在于时间复杂度较高,为O(V^3),其中V为顶点数,在规模较大的图中可能运行时间过长。
综上所述,最短路径算法有迪杰斯特拉算法、贝尔曼-福特算法和弗洛伊德算法三种常用的方法。
其中,迪杰斯特拉算法适用于单源最短路径问题,贝尔曼-福特算法适用于单源最短路径问题且允许存在负权边,而弗洛伊德算法适用于多源最短路径问题。
迪杰斯特拉(dijkstra)算法

初 始 时
dist path
1 0 C1
2 4 C1,C2
3 8 C1,C3
4 maxint
5 maxint
6 maxint
第一次:选择m=2,则s=[c1,c2],计算比较dist[2]+GA[2,j]与dist[j]的大小(3<=j<=6)dist path源自1 02 43 7
4 8
5 10
6 maxint
求从C1到各顶点的最短路径
9 4 2
C3
C6
4 2 6
C5
C4
4 3
8
C2
4
C1
Procedure dijkstra(GA,dist,path,i); {表示求Vi到图G中其余顶点的最短路
径,GA为图G的邻接矩阵,dist和path为变量型参数,其中path的基类型为集合} begin for j:=1 to n do begin {初始化} if j<>i then s[j]:=0 else s[j]:=1; dist[j]:=GA[i,j]; if dist[j]<maxint then path[j]:=[i]+[j] else path[j]:=[ ]; end; for k:=1 to n-2 do begin w:=maxint; m:=i; for j:=1 to n do {求出第k个终点Vm} if (s[j]=0) and (dist[j]<w) then begin m:=j;w:=dist[j];end; if m<>i then s[m]:=1 else exit; {若条件成立,则把Vm加入到s中,否则 退出循环,因为剩余的终点,其最短路径长度均为maxint,无需再计算下去}
dijkstra最短路径算法

图解迪杰斯特拉(Dijkstra)最短路径算法目录前言一、最短路径的概念及应用二、Dijkstra迪杰斯特拉1.什么是Dijkstra2.逻辑实现总结前言无论是什么程序都要和数据打交道,一个好的程序员会选择更优的数据结构来更好的解决问题,因此数据结构的重要性不言而喻。
数据结构的学习本质上是让我们能见到很多前辈在解决一些要求时间和空间的难点问题上设计出的一系列解决方法,我们可以在今后借鉴这些方法,也可以根据这些方法在遇到具体的新问题时提出自己的解决方法。
(所以各种定义等字眼就不用过度深究啦,每个人的表达方式不一样而已),在此以下的所有代码都是仅供参考,并不是唯一的答案,只要逻辑上能行的通,写出来的代码能达到相同的结果,并且在复杂度上差不多,就行了。
一、最短路径的概念及应用在介绍最短路径之前我们首先要明白两个概念:什么是源点,什么是终点?在一条路径中,起始的第一个节点叫做源点;终点:在一条路径中,最后一个的节点叫做终点;注意!源点和终点都只是相对于一条路径而言,每一条路径都会有相同或者不相同的源点和终点。
而最短路径这个词不用过多解释,就是其字面意思:在图中,对于非带权无向图而言,从源点到终点边最少的路径(也就是BFS广度优先的方法);而对于带权图而言,从源点到终点权值之和最少的路径叫最短路径;最短路径应用:道路规划;我们最关心的就是如何用代码去实现寻找最短路径,通过实现最短路径有两种算法:Dijkstra迪杰斯特拉算法和Floyd弗洛伊德算法,接下来我会详细讲解Dijkstra迪杰斯特拉算法;二、Dijkstra迪杰斯特拉1.什么是DijkstraDijkstra迪杰斯特拉是一种处理单源点的最短路径算法,就是说求从某一个节点到其他所有节点的最短路径就是Dijkstra;2.逻辑实现在Dijkstra中,我们需要引入一个辅助变量D(遇到解决不了的问题就加变量[_doge]),这个D我们把它设置为数组,数组里每一个数据表示当前所找到的从源点V开始到每一个节点Vi的最短路径长度,如果V到Vi有弧,那么就是每一个数据存储的就是弧的权值之和,否则就是无穷大;我们还需要两个数组P和Final,它们分别表示:源点到Vi的走过的路径向量,和当前已经求得的从源点到Vi的最短路径(也就是作为一个标记表示该节点已经加入到最短路径中了);那么对于如下这个带权无向图而言,我们应该如何去找到从V0到V8的最短路径呢;在上文中我们已经描述过了,在从V0到V8的这一条最短路径中,V0自然是源点,而V8自然是终点;于是我根据上文的描述具现化出如下的表格;在辅助向量D中,与源点V0有边的就填入边的权值,没边就是无穷大;构建了D、P和Final,那么我们要开始遍历V0,找V0的所有边中权值最短的的边,把它在D、P、Final中更新;具体是什么意识呢?在上述带权无向图中,我们可以得到与源点有关的边有(V0,V1)和(V0,V2),它们的权值分别是1和5,那么我们要找到的权值最短的的边,就是权值为1 的(V0,V1),所以把Final[1]置1,表示这个边已经加入到最短路径之中了;而原本从V0到V2的距离是5,现在找到了一条更短的从V0 -> V1 -> V2距离为4,所以D[2]更新为4,P[2]更新为1,表示源点到V2经过了V1的中转;继续遍历,找到从V0出发,路径最短并且final的值为0的节点。
迪杰斯特拉算法

迪杰斯特拉算法迪杰斯特拉算法是一种用于在无向图或有向图中找到从一个节点到另一个节点的最短路径的算法,也称为最短路径算法。
它是由著名的科学家爱迪生发明的,后来被保罗迪杰斯特拉命名。
迪杰斯特拉算法是一种基于动态规划的算法,旨在在给定的有向图中找到最短路径。
它的主要特点是将一个大问题分成若干小问题,然后一个个地解决它们,最终获得最优解。
迪杰斯特拉算法的步骤如下:1.始化:根据图的拓扑构造表,确定出发节点和目的节点;2.算:从出发节点开始,逐一计算每个节点到目的节点的最短路径距离;3.踪:跟踪每个节点到目的节点的最短路径;4. 优化:检查每个节点的最短路径距离,如果存在更优的路径,则更新最短路径距离;5.成:当所有节点的最短路径距离都计算出来后,算法结束。
迪杰斯特拉算法虽然很简单,但是却非常有效,只要图是联通的,就能够找到每个节点到目的节点的最短路径,却不必考虑太多复杂性。
迪杰斯特拉算法可以用于许多领域,如交通和物流,电路设计,社会网络分析,计算机网络和银行的交易处理等。
例如,在交通和物流领域,迪杰斯特拉算法可以用来规划最佳路线,即找到从一个地点到另一个地点的最短路径,以便节省旅行时间并最大化出行费用。
对于物流行业,可以使用迪杰斯特拉算法来优化货物快递系统,可以利用它来规划最佳路线,以便尽可能快地将货物运输到指定地点。
此外,迪杰斯特拉算法还可以用于解决计算机网络中的路由问题,如在大型网络内如何转发信息,在多个回路之间如何寻找最短路径等。
它能够有效地处理小延迟和大延迟等不同类型的网络服务。
最后,迪杰斯特拉算法可以用作银行的结算系统,以最快的时间将款项从发件人转移到收件人,以最少的费用和最少的时间。
为此,迪杰斯特拉算法可以提供一种方便快捷的解决方案,通过此方法,可以有效地缩短支付时间,降低银行费用。
以上就是迪杰斯特拉算法的基本原理以及它的应用场景,它在我们的日常生活中发挥着重要的作用,是一种非常有效的算法,值得我们去学习和研究。
迪杰斯特拉算法(戴克斯特拉算法)(Dijkstra算法)-贪心、最短路径问题
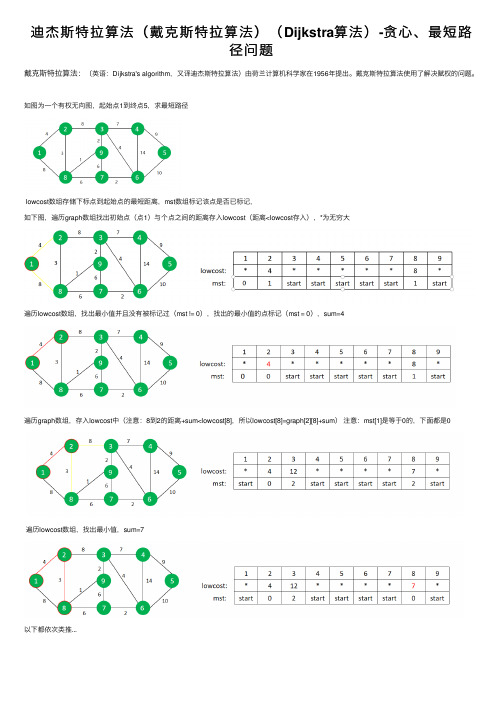
迪杰斯特拉算法(戴克斯特拉算法)(Dijkstra算法)-贪⼼、最短路径问题戴克斯特拉算法:(英语:Dijkstra's algorithm,⼜译迪杰斯特拉算法)由荷兰计算机科学家在1956年提出。
戴克斯特拉算法使⽤了解决赋权的问题。
如图为⼀个有权⽆向图,起始点1到终点5,求最短路径lowcost数组存储下标点到起始点的最短距离,mst数组标记该点是否已标记,如下图,遍历graph数组找出初始点(点1)与个点之间的距离存⼊lowcost(距离<lowcost存⼊),*为⽆穷⼤遍历lowcost数组,找出最⼩值并且没有被标记过(mst != 0),找出的最⼩值的点标记(mst = 0),sum=4遍历graph数组,存⼊lowcost中(注意:8到2的距离+sum<lowcost[8],所以lowcost[8]=graph[2][8]+sum)注意:mst[1]是等于0的,下⾯都是0遍历lowcost数组,找出最⼩值,sum=7以下都依次类推...输⼊:9 14 1 5 1 2 41 8 82 8 32 3 88 9 18 7 63 9 29 7 63 4 73 6 47 6 24 6 144 5 96 5 10输出:24代码:#include <iostream>#include <bits/stdc++.h>using namespace std;#define MAX 100#define MAXCOST 0x7fffffff //int型最⼤值void prim(int graph[][MAX],int n,int start,int end){int lowcost[MAX];int mst[MAX];int sum=0;for(int i=1;i<=n;i++)//将与各点与起始点的距离存⼊lowcost中{lowcost[i]=graph[start][i];mst[i]=1;}mst[start]=0; //起始点被标记for(int i=1;i<=n;i++){if(mst[end]==0)//终点被标记结束{cout<<sum;break;}int min=MAXCOST;int minid=0;for(int j=1;j<=n;j++)//遍历lowcost数组,找最⼩值{if(lowcost[j]<min && mst[j]!=0){min=lowcost[j]; //最⼩值minid=j; //最⼩值下标}}//cout<<"V"<<mst[minid]<<"-V"<<minid<<"="<<min<<endl;sum=min;//cout<<sum<<endl;mst[minid]=0; //最⼩值下标点被标记for(int j=1;j<=n;j++)//找最⼩值点与各点的距离{if(graph[minid][j]==MAXCOST)//如果此点与最⼩值点没有联系(距离为最⼤值)则lowcost不变,跳过{continue;}else if(graph[minid][j]+sum<lowcost[j] && mst[j]!=0)//此点与最⼩点有联系,并且+sum<lowcost 并且此点没有被标记,则赋值给lowcost {lowcost[j]=graph[minid][j]+sum;}}}}int main(){int n,m;int start,end;int graph[MAX][MAX];cin>>n>>m>>start>>end;//初始化图Gfor(int i=1;i<=n;i++){for(int j=1;j<=n;j++){graph[i][j]=MAXCOST;}}//构建图Gfor(int k=1;k<=m;k++){int i,j,cost;cin>>i>>j>>cost;graph[i][j]=cost;graph[j][i]=cost;}prim(graph,n,start,end); return0;}。
最短路问题迪杰斯特拉算法

min {d23,d25,c47,d67}=min {2+6,2+5,1+2,3+4}=min {8,7,3,7}=3
X={1,2,4,6,7}, p7=3
X={1,2,4,6,7}
p1=0
p2=2
2
6
1
2
3
1
10
p4=1
5
9
p5=6
3
4
7
5
6
5
2
3
4
6
7
8
4
8
p6=3
p7=3
min {d23,d25,d75,d78}=min {2+6,2+5,3+3,3+8}=min {8,7,6,11}=6
X={1,4}
p1=0
p2=2
2
6
1
2
3
1
10
p4=1
5
9
3
4
7
5
6
5
2
3
4
6
7
4
8 8
min {d12,d16,d42,d47}=min {0+2,0+3,1+10,1+2}=min {2,3,11,3}=2 X={1,2,4}, p2=2
X={1,2,4}
p1=0
p2=2
2
6
1
2
3
1
10
p4=1
② v j 具有T 标号,即v j s ,s 为T 标号点集.
修改 v j 的T标号为 min{T (v j ), p(v1) l1 j} ,并将结
果仍记为T(vj)。= l1j
迪杰斯特拉(Dijkstra)算法描述及理解

迪杰斯特拉(Dijkstra)算法描述及理解Dijkstra算法是⼀种计算单源最短⽆负边路径问题的常⽤算法之⼀,时间复杂度为O(n2)算法描述如下:dis[v]表⽰s到v的距离,pre[v]为v的前驱结点,⽤以输出路径,vis[v]表⽰该点最短路径是否已经确认初始化:dis[v]=INT dis[s]=0 pre[s]=0 执⾏n次 在没有确定的点中找到⼀个路径最短的,并修改为已经确认 通过这个点修改其他所有没有确定的点 直到所有点已经确认为最短路径,退出循环现在证明算法的正确性:⾸先,我们说明两条性质:1.确定任何⼀个点为最短路径时,前驱p⼀定已经是最短路径(假设源点的前驱是它本⾝)。
2.任意时刻在还没有确定最短路径的点的集合中路径最短的点就是可以被确定的点。
稍微证明⼀下这两条性质(反证法):证明1:假如前驱p还不是最短路径,那么显然当p是最短路径时到当前节点的路径更短,即不是最短路径的节点所确定的节点⼀定不是最短路径(好像很显然)证明2:为了⽅便描述,我们定义已经确定的点为⽩点,没有确定的点为蓝点。
若是蓝点中路径最短x还不能确定为⽩点,那么x的最短路径上必定存在⼀个蓝点y。
即dis[x]>dis[y]+edge[y][x]。
⽽dis[y]处于两种状态:(1)dis[y]已经是y点的最短路径,那么显然与dis[x]为蓝点中最短的相⽭盾。
(2)dis[y]还不是y点的最短路径,那么它的前驱显然是另外⼀个蓝点,即dis[y]>=dis[x](这⾥省略了⼀些步骤,不过⾃⼰稍微想⼀下,我觉得挺显然的),也⽭盾。
综上,性质2得证。
回过头再看我们的算法:在刚开始的时候,⾸先确定的最短路(就是直接和源点相连的点)进⼊⽩点集合,满⾜性质1,2。
此后每个过程都满⾜以上两个性质,所以算法正确。
算法实现:1 memset(vis,0,sizeof(vis));2 vis[s]=1;3 dis[s]=0;4 for(int i=1;i<n;i++)5 {6 int m=INT_MAX;7 int k=0;8 for(int j=1;j<=n;j++)9 {10 if(!vis[j] && dis[j]<m)11 {12 m=dis[j];13 k=j;14 }15 }16 if(k==0)17 break;18 vis[k]=1;19 for(int j=1;j<=n;j++)20 {21 if(dis[k]+e[k][j]<dis[j])22 dis[j]=dis[k]+e[k];23 }24 }View Code。
简述迪杰斯特拉算法

简述迪杰斯特拉算法
迪杰斯特拉算法是一种用于解决最短路径问题的算法。
最短路径问题指的是在图中从一个起点到一个终点找到一条路径,使得路径上的边权之和最小。
迪杰斯特拉算法的思路是从起点开始,逐步扩展出离起点越来越远的节点。
对于每个扩展出来的节点,算法会记录当前到达该节点的路径的长度,并和之前记录的路径长度进行比较,从而更新最短路径。
具体步骤如下:
1. 将起点到自身的路径长度设为0,将起点到其它所有节点的路径长度设为无穷大。
2. 从起点开始,选择距离起点最近的节点,并将该节点标记为已访问。
3. 对于该节点的每个邻居节点,计算从起点到该邻居节点的路径长度,并和之前记录的路径长度进行比较,从而更新最短路径。
4. 重复步骤2和步骤3,直到所有节点都被访问过。
通过这个算法,我们可以得到从起点到所有节点的最短路径。
迪杰斯特拉算法的时间复杂度为O(n^2),其中n为节点数。
在实际应用中,可以通过使用优先队列等数据结构来优化算法的效率。
- 1 -。
迪杰斯特拉 算法

迪杰斯特拉算法
迪杰斯特拉算法,也称为狄克斯特拉算法,是一种常用的图算法,用于在带有权重的图中找到最短路径。
该算法采用贪心策略,从一个起点开始,逐步扩展到其他顶点。
在算法运行过程中,维护两个集合S和V-S,其中S表示已找到最短路径的顶点集合,V-S表示未找到最短路径的顶点集合。
算法的具体实现中,每次从V-S中选择距离起点最近的顶点,加入S集合。
然后更新以该顶点为起点的所有边的权重,如果存在更短的路径,则进行更新。
这个过程循环执行,直到所有顶点都加入S集合,最终得到起点到各个顶点的最短路径。
迪杰斯特拉算法的时间复杂度为O(n^2),其中n为图中顶点的个数。
对于稠密图而言,该算法表现良好。
同时,该算法也可以用堆优化的方式实现,使时间复杂度降为O(nlogn),在处理稀疏图时表现更优。
- 1 -。
迪杰特斯拉算法

迪杰特斯拉算法⼀. 迪杰特斯拉算法迪杰斯特拉算法的基本思路迪杰斯特拉算法的基本思路:1. 找出最便宜的顶点,即距离出发顶点距离最近的顶点,作为新的出发顶点2. 更新该顶点的邻居的开销3. 重复(1)(2)步骤,直到对每个顶点都做了此操作4. 计算最终路径如何对下⾯的图使⽤迪杰斯特拉算法每条边上标识的数字都表⽰,两个顶点之间的距离。
⼆. 算法详解假设要求从 A 到 D 的最短路径,步骤如下:准备⼯作:在计算前,需要做⼀些准备⼯作,列出每个节点的开销:在执⾏迪杰斯特拉算法的过程中,将不断的更新这个表。
为了计算最终路径,还需要在表中添加表⽰⽗顶点(前驱顶点)的列第⼀步:找出最便宜的顶点,作为新的出发顶点(红⾊标识表⽰该顶点已经被访问过,选择新的出发顶点是不再考虑该顶点)站在出发顶点A,与A直连的顶点有:C(A到C的距离为7)B(A到B的距离为5)G(A到G的距离为2)显然,A到G的距离最近,则G为最便宜的顶点。
此时,由于你还不知道从A出发到其它⾮直连的顶点的距离是多少,因此,我们都将他们暂时设为⽆穷⼤第⼆步:更新顶点G的邻居的开销计算从出发顶点A出发,经过G顶点,到G的各个邻居(与G直连的顶点)的开销G顶点的邻居有:顶点A(A被访问过)顶点B(G到B的距离为3)顶点E(G到E的距离为4)顶点F(G到F的距离为6)再执⾏第⼀步:下⼀个最便宜的顶点是B 第⼆步:更新顶点B的邻居的开销B顶点的邻居有:- 顶点A (A被访问过)- 顶点G(G被访问过)- 顶点D (B到D的距离为9)再执⾏第⼀步:下⼀个最便宜的顶点是E 第⼆步:更新顶点E的邻居的开销E顶点的邻居有:- 顶点C(E到C的距离为8)- 顶点G(G被访问过)- 顶点F (E到F的距离为5)再执⾏第⼀步:下⼀个最便宜的顶点是C 第⼆步:更新顶点C的邻居的开销C顶点的邻居有:- 顶点A(A被访问过)- 顶点E(G被访问过)再执⾏第⼀步:下⼀个最便宜的顶点是F 第⼆步:更新顶点F的邻居的开销F顶点的邻居有:- 顶点E(E被访问过)- 顶点G(G被访问过)- 顶点D(F到D的距离为4)再执⾏第⼀步:下⼀个最便宜的顶点是D 第⼆步:更新顶点D的邻居的开销D顶点的邻居有:- 顶点B(B被访问过)- 顶点F(F被访问过)三. 计算最终路径(求从 A 到 D 的最短路径)过程如下:顶点D的前驱顶点为F顶点F的前驱顶点为G顶点G的前驱顶点为A(A为出发顶点,⾄此得出最短路径)所以:A到D的最短路径长度为12;最短路径为:A——>G——>F——>D代码`package com.dyt.algorithmdemo.dijkstra;import java.util.*;/**迪杰特斯拉算法*/public class DijkstraAlgorithm {public static void main(String[] args) {//顶点数组String[] vertex = {"A", "B", "C", "D", "E", "F", "G"};//邻接矩阵int[][] matrix = new int[vertex.length][vertex.length];final int N = 65535; //表⽰不可连接,没有路//初始化邻接矩阵matrix[0] = new int[]{N, 5, 7, N, N, N, 2};matrix[1] = new int[]{5, N, N, 9, N, N, 3};matrix[2] = new int[]{7, N, N, N, 8, N, N};matrix[3] = new int[]{N, 9, N, N, N, 4, N};matrix[4] = new int[]{N, N, 8, N, N, 5, 4};matrix[5] = new int[]{N, N, N, 4, 5, N, 6};matrix[6] = new int[]{2, 3, N, N, 4, 6, N};//创建图对象Graph graph = new Graph(vertex, matrix);graph.showGraph();graph.djs(0);graph.showDijkstra();//输出路径graph.printPath(0, 3);}}/**图*/class Graph {//顶点数组private String[] vertex;//邻接矩阵private int[][] matrix;//访问过的顶点private VisitedVertex visitedVertex;public Graph(String[] vertex, int[][] matrix) {this.vertex = vertex;this.matrix = matrix;}//显⽰图public void showGraph() {for (int[] link : matrix) {System.out.println(Arrays.toString(link));}}/**迪杰特斯拉算法核⼼代码@param index*/public void djs(int index) {visitedVertex = new VisitedVertex(vertex.length, index);update(index); //更新index顶点到周围顶点的距离和前驱顶点for (int j = 1; j < vertex.length; j++) {index = visitedVertex.updateArr();//选择并返回新的访问顶点update(index);// 更新index顶点到周围顶点的距离和前驱顶点}}//更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点public void update(int index) {int len = 0;//遍历我们的邻接矩阵matrix[index]⾏for (int j = 0; j < matrix[index].length; j++) {//len : 出发顶点到index顶点的距离 + 从index顶点到j顶点距离的和len = visitedVertex.getDis(index) + matrix[index][j];//如果j顶点没有被访问过 && 距离⼩于从出发顶点到j点的距离if (!visitedVertex.in(j) && len < visitedVertex.getDis(j)) {visitedVertex.updatePre(j, index);//更新j顶点的前驱为index顶点visitedVertex.updateDis(j, len); //更新出发点到顶点j的距离}}}/**输出路径@param startIndex 起点索引@param endIndex 终点索引*/public void printPath(int startIndex, int endIndex) {int[] dis = visitedVertex.getDis();int[] pre_visited = visitedVertex.getPre_visited();String startVertex = this.vertex[startIndex];String endVertex = this.vertex[endIndex];//距离System.out.println(startVertex + "到" + endVertex + "的最短距离为:" + dis[endIndex]);//路径List path = new ArrayList<>();path.add(vertex[endIndex]);while (true) {endIndex = pre_visited[endIndex];path.add(vertex[endIndex]);if (endIndex == startIndex) {break;}}Collections.reverse(path);String pathInfo = "";for (int i = 0; i < path.size(); i++) {pathInfo = path.get(i);if (i != path.size() - 1) {pathInfo = pathInfo + "——>";}System.out.print(pathInfo);}System.out.println();}public void showDijkstra() {visitedVertex.show();}}/**已访问过的顶点*/class VisitedVertex {//记录各个顶点是否访问过。
矩阵最短路径算法

矩阵最短路径算法矩阵最短路径算法是一种用于寻找两个点之间最短路径的算法。
在计算机科学中,路径指的是从一个点到另一个点经过的一系列边或节点。
而最短路径则是指路径上边或节点的权重之和最小的路径。
矩阵最短路径算法常用于图论和网络分析等领域。
它可以帮助我们找到网络中最短的路径,从而优化网络通信、物流运输等问题。
以下将介绍两种常用的矩阵最短路径算法:迪杰斯特拉算法和弗洛伊德算法。
一、迪杰斯特拉算法迪杰斯特拉算法是一种用于解决单源最短路径问题的算法,即给定一个起始点,求解该点到其他所有点的最短路径。
该算法使用了贪心策略,每次选择当前距离最短的点作为中间节点,更新其他点的距离。
迪杰斯特拉算法的基本步骤如下:1. 初始化距离矩阵,将起始点到其他点的距离初始化为无穷大。
2. 将起始点的距离设为0,并将其加入已访问节点集合。
3. 对于起始点的相邻节点,更新其距离矩阵中的值,即将起始点到相邻节点的距离设为起始点到当前节点的距离加上当前节点到相邻节点的距离。
4. 从未访问节点中选择距离最短的节点,将其加入已访问节点集合。
5. 重复步骤3和4,直到所有节点都被访问。
二、弗洛伊德算法弗洛伊德算法是一种用于解决多源最短路径问题的算法,即给定任意两个点,求解它们之间的最短路径。
该算法采用动态规划的思想,通过逐步迭代更新路径矩阵,得到最终的最短路径。
弗洛伊德算法的基本步骤如下:1. 初始化路径矩阵,将任意两个节点之间的路径长度初始化为无穷大。
2. 对于每个节点,将其直接相邻的节点之间的路径长度更新为它们之间的实际路径长度。
3. 对于每个节点对(i, j),以节点k作为中间节点,如果路径(i, k) + (k, j)的长度小于路径(i, j)的长度,则更新路径矩阵中(i, j)的值为路径(i, k) + (k, j)的长度。
4. 重复步骤3,直到路径矩阵不再更新。
矩阵最短路径算法在实际应用中具有广泛的意义。
例如,在物流运输中,我们可以将城市视为节点,将城市间的距离视为路径长度,通过矩阵最短路径算法,可以找到从一个城市到另一个城市的最短路径,从而优化物流运输的时间和成本。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章图迪杰斯特拉算法如下:SHORTEST—PATH(intcost[][n],intv,intn,intdist[],intpath[)){ihti,N,u,count,pos[n];for(i=0;i<n;i++){s[i]=0;/x标记数组置0 x/dist[i]=cost[V][i];/。
将邻接矩阵第v行元素依次送dist数组xpath[i][0]=v;/x源点v到各顶点的路径置初值。
/pos[i]=0;/。
第i条路径的位置计数器置初值x/} /x对辅助数组进行初始化。
/s[v]=l;count=1; /x计数器赋初值1 x/while(count<n){ /‘以下过程执行n-1次x/u=MINDIST(s,dist);/x利用s和dist在尚未找到最短路径的顶点中确定一个与v最近的顶点u。
/s[u]=1;/‘置u的标记为1●/path[u)C++pos[u]]=u;/x将u添加到v到u的最短路径中。
/count++;/,计数器累力n1 x/while(1){ /。
根据u更新v到所有尚未确定最短路径的顶点的路径长度。
/if((w=SEARCH_VER(s,dist,u))==-1)/,找到通过u可以直接到达、且尚未确定最短路径的一个顶点。
/break;/x未找到,路径长度更新过程结束。
/else{if(dist[u]+cost[u][w]<dist[w]]{dist[N]=dist[u]+cost[u][w];/x更新路径长度●/for[i=0;i<pos[u];i++)path[w][i]=path[u][i];/。
用源点v到顶点u的路径替换源点v到w的路径。
/}} } .习题8.1 判断题(在你认为正确的题后的括号中打√,否则打X)。
(1)没有顶点的图称为空图。
( )(2)图的度是图中所有顶点的度的最大值。
( )(3)边上带权值的图称为网(络)。
( )(4)图中一个顶点的度应该是它的出度与人度之和。
( )(5)n个顶点的无向图最多有n(n-1)条边。
( )(6)在有向图中,所有顶点的人度之和等于所有顶点的出度之和。
( )(7)在无向图中,若顶点i到顶点j有路径,则这两个顶点之间是连通的。
( )(8)在有向图中,若顶点i到顶点j有路径,则这两个顶点之间是连通的。
( )(9)连通图的最小生成树是惟一的。
( )(10)邻接矩阵主要用来表示顶点之间的关系。
( )(u)若表示某图的邻接矩阵不是对称矩阵,则该图一定是有向图。
( )(12)若表示某图的邻接矩阵中出现了全零行或者全零列,则该图一定是非连通图或者非强连通图。
( )(13)对于同一个有向图,邻接表中的边结点数目与逆邻接表中边结点数目相等。
( )(14)无向图的邻接表中边结点数目一定为偶数。
( )(15)邻接表中边结点数目为奇数的图一定是有向图。
( )(16)邻接表中边结点数目为偶数的图一定是无向图。
( )(17)对图进行广度优先搜索的过程中要用到队列。
( )(18)对图进行深度优先搜索的过程中要用到堆栈。
( )(19)带权连通图的最小生成树是惟一的。
( )(20)最短路径一定是简单路径。
( )(21)求源点到各点的最短路径的迪杰斯特拉算法不适用于存在回路的有向网络。
( )(22)不能对强连通图进行拓扑排序。
( )(23)若AOV网中存在拓扑序列,则一般情况下,拓扑序列不是惟一的。
( )(24)关键路径是由权值最大的边构成的。
( )(25)给定的AOE网的关键路径一定是惟一的。
( )8.2单项选择题。
(1)在一个图中,所有顶点的度数之和等于所有边数的——倍。
A.1/2 B.1 C.2 D.4(2)一个具有n个顶点的无向图最多有——条边。
A.n(n-1)/2 B.n(n-1) C.n(n+1)/2 D.n(2)(3)一个具有n个顶点的有向图最多有——条边。
A.n(n-1)/2 B.n(n-1) C.n(n+1)/2 D.n(2)(4)在一个具有n个顶点的无向图中,要连通全部顶点至少需要——条边。
A.n B.n+1 C.n-1 D.2n(5)具有n个顶点的连通图的生成树一定有——条边。
A.n B.n+1 C.n-1 D.2n(6)若一个非连通的无向图最多有28条边,则该无向图至少有——个顶点。
,A.6 B.7 C.8 D.9(7)在带权图中,两个顶点之间的路径长度是——。
A.路径上的顶点数目B.路径上的边的数目C.路径上顶点和边的数目D.路径上所有边上的权值之和(8)若具有n个顶点的无向图采用邻接矩阵存储方法,该邻接矩阵一定为一个——。
A.一般矩阵B.对称矩阵C.对角矩阵D.稀疏矩阵(9)若图的邻接矩阵中主对角线上的元素均为0,其余元素全为1,则可以断定该图一定_____.A.是无向图B.是有向图C.是完全图D.不是带权图(10)有向图的邻接表的第i个链表中的边结点数目是第i个顶点的——。
A.度数B.出度C.人数D.边数(11)若某图的邻接表中的边结点数目为奇数,则该图——。
A.一定有奇数个顶点B.一定有偶数个顶点C.一定是有向图D。
可能是无向图(12)若某图的邻接表中的边结点数目为偶数,则该图——。
A.一定是无向图B。
可能是有向图C.可能是无向图,也可能是有向图D.一定有偶数个顶点(13)若无向图有k条边,则相应的邻接表中就有——个边结点。
A.k-1 B.k C.2k D.K(2)(14)若有向图有k条边,则相应的邻接表中就有——个边结点。
A.k-1 B.k C.2k D.K(2)(15)对于一个不带权的无向图的邻接矩阵而言,——。
A.矩阵中非零元素的数目等于图中边的数目B.矩阵中非全零的行的数目等于图中顶点的数目巴第i行的非零元素的数目与第i列的非零元素的数目相等D。
第i行与第i列的非零元素的总数等于第i个顶点的度数(16)导致图的遍历序列不惟一的因素有——。
A.出发点不同、遍历方法不同B,出发点不同、存储结构不同C,遍历方法不同、存储结构不同D.出发点不同、存储结构不同、遍历方法不同(17)若从无向图的任意一个顶点出发进行一次深度优先搜索便可以访问该图的所有顶点,则该图一定是一个——图。
A.非连通B.连通C.强连通D.完全(18)可以进行拓扑排序的图一定是——。
A.连通图B.带权连通图C.无回路的图D.无回路的有向图(19)已知某有向图G=(V,E),其中V={v1,v2,v3,v4,v5,v6},E={{v1,v2),(v1,v4),{v2,v6),(v3,v1),(v3,v4),(v4,v5),{v5,v2),{v5,v6)},G的拓扑序列是——A.v3,v1,v4,v5,v2,v6 B.v3,v4,v1,v5,v2,v6C.v1,v3,v4,v5,v2,v6 D.v1,v4,v3,v5,v2,v6(20)下面关于AOE网的叙述中,不正确的是———。
A.若所有关键活动都提前完成,则整个工程一定能够提前完成B.即使所有非关键活动都未按时完成,整个工程仍有可能按时完成C.任何一个关键活动的延期完成,都会导致整个工程的延期完成D.任何一个关键活动的提前完成,都会导致整个工程的提前完成8.3 设一有向图为G=(V,E),其中,V={vl,v2,v3,v4},E={<v2,v1>,<v3,v2>,<v4,v3>,<v4,v2>,<v1,v4>},请画出该有向图。
8.4 已知给定有向图如图8。
26所示。
(1)分别写出每个顶点的人度与出度;(2)画出相应的邻接矩阵与邻接表;(3)画出强连通分量。
8.5 已知给定无向图如图8.27所示。
(1)画出相应邻接矩阵;(2)画出相应邻接表。
8.6 证明n个顶点的无向图的边数达到的最大值为n(n—1)/2。
8.7 具有n个顶点的强连通图至少有多少条边?这样的图的形状有何特点?8.8 已知一无向图如图8.28所示,请写出其邻接表表示,然后根据该邻接表分别写出从顶v1出发进行深度优先搜索与广度优先搜索时得到的顶点序列。
8.9 已知某带权连通无向图采用邻接矩阵存储方法,邻接矩阵以三元组表形式给出,不包括主对角线元素在内的下三角形部分元素对应的各三元组分别为(2,1,7),(3,1,6),(3,2,8),(4,1,9),(4,2,4),(4,3,6),(5,1,oo),(5,2,4),(5,3,oo),(5,4,2)。
该连通图的最小生成树的权值之和是多少?8.10 试编写一构造无向图邻接表结构的算法,设该无向图G=(V,E)以V={v1,v2,…,vn}与E={(Vi,Vj)|Vi,Vj属于V,i≤n,j≤n}作为输入。
8.11 设计一个算法,将一个已知图的邻接矩阵存储形式转换为邻接表的存储形式。
8.12 已知一个具有n个顶点的无向图采用邻接表存储方法。
试设计一个算法,删除图中一条边(u,v)。
8.13 一个带权连通图的最小生成树是否一定惟一?什么情况下有可能不惟一?8.14 已知一带权连通图如图8.29所示。
请首先写出其邻接矩阵,然后再按Prim算法求出其所有可能的最小生成树。
8.15 根据SHORTEST PA TH算法,求出给定有向图(如图8.30所示)从顶点v1到其他各顶点长度递增的最短路径,并分别写出执行算法过程中各个数组的变化状态。
8.16 源点到图中其他各顶点的所有最短路径构成一棵生成树,该生成树是否为最小生成树?为什么?8.17 某航空公司在六个城市设有分公司v1,v2,v3,v4,v5,v6;矩阵A中元素A[i][j]表示vi到vj的飞机票价(A[i][j]=+oo表示vi与vj之间不直接通航)。
请为该航空公司制作一张由vl到各分公司去的最便宜的通航线路图。
8.18 已知一AOE网采用邻接矩阵存储方式,其邻接矩阵为一稀疏矩阵,并采用三元组表形式给出(见图8.31)。
(1)画出该AOE网;(2)分别说明各顶点、有向边表示什么,边上权值代表什么。
8.19 设计出一种求AOE网关键路径的算法。
8.20 对给定AOE网(如图8.32所示)。
(1)分别求出各活动的最早开始时间与最晚开始时间;(2)求出所有关键路径;(3)该工程完成的最短时间是多少?历年考试题1.若<v i, v j>是有向图的一条边,则称()A.v i邻接于v j B.v j邻接于v iC.v i和v j相互邻接D.v i与v j不相邻接2.在一个带权连通图G中,权值最小的边一定包含在G的()A.最小生成树中B.深度优先生成树中C.广度优先生成树中D.深度优先生成森林中3.下列数据组织形式中,()的各个结点可以任意邻接。
A.集合B.树形结构C.线性结构D.图状结构4.邻接表是图的一种()A.顺序存储结构B.链式存储结构C.索引存储结构D.散列存储结构5.如果无向图G必须进行二次广度优先搜索才能访问其所有顶点,则下列说法中不正确的是()A.G肯定不是完全图B.G一定不是连通图C.G中一定有回路D.G有2个连通分量6.一个带权的无向连通图的最小生成树()A.有一棵或多棵B.只有一棵C.一定有多棵D.可能不存在7.下列有关图遍历的说法中不正确的是()A.连通图的深度优先搜索是一个递归过程B.图的广度优先搜索中邻接点的寻找具有“先进先出”的特征C.非连通图不能用深度优先搜索法D.图的遍历要求每一顶点仅被访问一次8.n个顶点的有向完全图中含有向边的数目最多为( )A.n-1B.nC.n(n-1)/2D.n(n-1)9.已知一个有向图如右所示,则从顶点a出发进行深度优先偏历,不可能得到的DFS序列为( )A.a d b e f cB.a d c e f bC.a d c b f eD.a d e f c b10.顶点数为n、边数为n(n-1)/2的无向图称为_____________。
