习题与作业1-4
理论综合题物业管理员(国家职业资格证四级)复习题(练习题1-4有答案)

C、商务文件和技术文件
D、投标函和技术文件
14、物业管理投标的过程包括:①准备投标文件②获取招标信息③登记并取得招标文件④项目评估与
风险防范⑤接受资格审查⑥送交投标文件⑦签订并执行合同⑧参加开标、现场答辩会议。正确的投标
步骤是(
)
A、②-③-④-⑤-①-⑥-⑧-⑦
B、④-③-⑤-②-⑦-①-⑥-⑧
C、③-②-⑤-④-①-⑥-⑧-⑦
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力通根1保据过护生管高产线中工敷资艺设料高技试中术卷0资配不料置仅试技可卷术以要是解求指决,机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料试荷试卷下卷问高总题中2体2资配,料置而试时且卷,可调需保控要障试在各验最类;大管对限路设度习备内题进来到行确位调保。整机在使组管其高路在中敷正资设常料过工试程况1卷下中安与,全过要,度加并工强且作看尽下护可1都能关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编.工写保况复护进杂层行设防自备腐动与跨处装接理置地,高线尤中弯其资曲要料半避试径免卷标错调高误试等高方,中案要资,求料编技试5写术卷、重交保电要底护气设。装设备管置备4高线动调、中敷作试电资设,高气料技并中课3试术且资件、卷中拒料中管试包绝试调路验含动卷试敷方线作技设案槽,术技以、来术及管避系架免统等不启多必动项要方高案式中;,资对为料整解试套决卷启高突动中然过语停程文机中电。高气因中课此资件,料中电试管力卷壁高电薄中气、资设接料备口试进不卷行严保调等护试问装工题置作,调并合试且理技进利术行用,过管要关线求运敷电行设力高技保中术护资。装料线置试缆做卷敷到技设准术原确指则灵导:活。在。对分对于线于调盒差试处动过,保程当护中不装高同置中电高资压中料回资试路料卷交试技叉卷术时调问,试题应技,采术作用是为金指调属发试隔电人板机员进一,行变需隔压要开器在处组事理在前;发掌同生握一内图线部纸槽故资内障料,时、强,设电需备回要制路进造须行厂同外家时部出切电具断源高习高中题中资电资料源料试,试卷线卷试缆切验敷除报设从告完而与毕采相,用关要高技进中术行资资检料料查试,和卷并检主且测要了处保解理护现。装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2020部编版五年级语文下册1-4单元同步练习题带答案

第一单元一、下列加点字的读音无误的一项是()。
(3分)A.涟漪(yí)逛街(guàng)B.萌动(méng) 倭瓜(wěi)C.葬身(zàng) 点缀(zhuì)D.秉性(bǐng)公顷(qīng)二、看拼音,写词语。
(6分)sāng shù() chéngrèn( ) yuán gǔn gǔn( ) bái zhòu( ) húdié( ) míng huǎnghuǎng( )三、补全下列词语,并给加点字选择正确的解释。
(写序号)(6分)1.()()胜数①查点,逐个说出。
②列举,责备。
③数目。
2.()()大悟①了解,领会。
②见面。
③感觉。
3.能()善()①善良,慈善。
②熟悉。
③擅长,长于。
四、选择恰当的词语填空。
(8分)阴凉阴暗1. 我玩累了,就在房子底下找个()的地方睡着了。
2.地下室光线(),空气潮湿。
五、解释下列加点的词语,并用自己的话说一说诗句的意思。
(12分)1. 童孙未解供耕织,也傍桑阴学种瓜。
供:傍:诗句的意思:2. 稚子金盆脱晓冰,彩丝穿取当银钲。
稚子:钲:诗句的意思:3. 牧童归去横牛背,短笛无腔信口吹。
腔:信口:诗句的意思:六、在“浓浓的乡情、美好的童年”班级主题活动中,你和陈佳被推选为主持人,下面是活动主持稿中的一部分,请你仿照陈佳的话,将主持稿补充完整。
(9分)陈佳:人是家乡的好,月是故乡的明。
我:________________________________________________陈佳:故乡的歌是一支清远的笛,总在有月亮的晚上响起。
我:________________________________________________陈佳:童年是一幅画,一幅天真童稚的画,珍藏在我们的心中。
我:________________________________________________七、课内阅读。
北京某大学马克思主义基本原理概论1-4作业考试复习题
L380 作业4-1单选题1、马克思主义产生的经济根源是()(5 分)2、马克思主义是时代的产物,马克思主义产生的社会历史条件中最重要的是()(5 分)3、马克思主义从产生到发展,表现出强大的生命力,这种强大生命力的根源在于它的()(5 分)4、唯物主义同唯心主义对立的根本点在于()(5 分)5、在哲学上,主张思维和存在具有同一性,属于()(5 分)6、马克思主义崇高的社会理想是()(5 分)7、从广义上说,马克思主义是()(5 分)8、唯心主义的基本类型区分为()(5 分)9、马克思主义产生的阶级基础是()(5 分)10、唯物主义和唯心主义这两个专门的哲学术语有着特定的含义,划分唯物主义和唯心主义的根据是()(5 分)11、否认思维与存在的同一性必然导致()(5 分)12、在哲学史上第一次明确提出哲学基本问题是思维和存在的关系问题的哲学家是()(5 分)多选题13、思维和存在的关系问题之所以是哲学的基本问题,这是由哲学的性质和特点所决定的。
思维和存在的关系问题()(8 分)14、把握马克思主义的基本原理,要突出的三个方面是()(8 分)15、哲学基本问题包括两个方面的内容,它们是()(8 分)16、马克思主义的哲学基础指的是()(8 分)17、马克思主义的三个主要的理论来源是()(8 分)L380 作业4-2(新)单选题1、我们常说“失败是成功之母”,西方人还说“失败教会成功”,说的都是同一个意思,即失败总是与成功相生相伴,没有失败,就不会有成功。
上述观点给我们的启示是()(5 分)2、老子曰:合抱之木,生于毫末;九层之台,起于垒土;千里之行,始于足下。
这句话体现的哲理是()(5 分)3、“盲人摸象”与“管中窥豹,可见一斑”告诉我们的哲理是()(5 分)4、发挥人的主观能动性的前提是()(5 分)5、在辩证法范畴中,因果关系是对于客观事物及其发展过程中()(5 分)6、唯物辩证法是一个完整的科学体系,作为一个理论体系,其核心是()(5 分)7、在唯物辩证法的范畴体系中,偶然性是必然性的()(5 分)8、《荀子》中《天论篇》说道:“天行有常,不为尧存,不为桀亡。
线性代数课后习题1-4作业答案(高等教育出版社)

第一章 行列式1. 利用对角线法则计算下列三阶行列式:(1)381141102---;解381141102--- =2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4.(3)222111c b a cb a ;解222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).4. 计算下列各行列式:(1)7110025*******214; 解 7110251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---=143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-;解 2605232112131412-260503212213041224--=====cc 041203212213041224--=====rr000003212213041214=--=====r r .(3)efcf bf decd bd ae ac ab ---;解 ef cf bf de cd bd ae ac ab ---e c b ec b e c b ad f ---=a b c d e fa d fbc e 4111111111=---=.(4)dc b a 100110011001---.解dc b a100110011001---dc b a ab ar r 10011001101021---++=====d c a ab 101101)1)(1(12--+--=+01011123-+-++=====cdc ad a ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 6. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213ab a b a a b a ab ac c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)yx z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=yx z x z y zy x b a )(33+=.8. 计算下列各行列式(D k 为k 阶行列式):(1)aaD n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解a a a a a D n 0 0010 000 00 0000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n行展开))1()1(10 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a a n n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1 )1()1(=an-a n -2=a n -2(a 2-1).(2)xa a a x aa a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得ax x a ax x a a x x a aa a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0 ,再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 000 00 )1(=[x +(n -1)a ](x -a )n 第二章 矩阵及其运算 1. 计算下列乘积: (5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.2. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B ,求3AB -2A 及A T B .解⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T.3.已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4.设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A , ⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A , 而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.5. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0.(2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y . 解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y . 7.设⎪⎪⎭⎫⎝⎛=λλλ001001A ,求A k .解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ,⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫.用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.8. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵.证明 因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵. 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫⎝⎛5221;解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为⎪⎭⎫⎝⎛--=⎪⎭⎫⎝⎛=1225*22122111A A A A A , 故 *||11A A A =-⎪⎭⎫⎝⎛--=1225.(3)⎪⎪⎭⎫ ⎝⎛---145243121;解⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A ,所以*||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解⎪⎪⎪⎭⎫ ⎝⎛=n a a a A0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=-n a a a A 10011211 .12. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x ,从而有⎪⎩⎪⎨⎧===001321x x x . 19.设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 20. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511,求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)]=diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫ ⎝⎛=1111111114.21. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ).另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.22. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或 E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或 E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1, )3(41)2(1A E E A -=+-.第三章 矩阵的初等变换与线性方程组 1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫ ⎝⎛--340313021201;解⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. ) ~⎪⎪⎭⎫ ⎝⎛100001000001.(3)⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311;解⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011.3. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z , 所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫ ⎝⎛323513123;解⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫ ⎝⎛---101011001200410123~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001 故逆矩阵为⎪⎪⎪⎪⎭⎫⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解⎪⎪⎪⎭⎫⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321~⎪⎪⎪⎭⎫ ⎝⎛----------10612631110`1022111000010000100021~⎪⎪⎪⎭⎫ ⎝⎛-------106126311101042111000010********* 故逆矩阵为⎪⎪⎪⎭⎫ ⎝⎛-------10612631110104211.5. (2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫⎝⎛-=132321B , 求X 使XA =B .解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫ ⎝⎛---411007101042001 ~r ,所以⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X ,从而 ⎪⎭⎫⎝⎛---==-4741121BA X . 9. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量. 12.设⎪⎪⎭⎫⎝⎛----=32321321k k k A ,问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3. 解⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r .(1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3. P106/ 1.已知向量组A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ;B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T , 证明B 组能由A 组线性表示, 但A 组不能由B 组线性表示. 证明 由⎪⎪⎪⎭⎫⎝⎛-=312123111012421301402230) ,(B A ⎪⎪⎪⎭⎫ ⎝⎛-------971820751610402230421301~r⎪⎪⎪⎭⎫ ⎝⎛------531400251552000751610421301~r ⎪⎪⎪⎭⎫ ⎝⎛-----000000531400751610421301~r知R (A )=R (A , B )=3, 所以B 组能由A 组线性表示. 由⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=000000110201110110220201312111421402~~r r B 知R (B )=2. 因为R (B )≠R (B , A ), 所以A 组不能由B 组线性表示. 4. 判定下列向量组是线性相关还是线性无关: (1) (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; (2) (2, 3, 0)T , (-1, 4, 0)T , (0, 0, 2)T .解 (1)以所给向量为列向量的矩阵记为A . 因为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=000110121220770121101413121~~r r A ,所以R (A )=2小于向量的个数, 从而所给向量组线性相关. (2)以所给向量为列向量的矩阵记为B . 因为022200043012||≠=-=B ,所以R (B )=3等于向量的个数, 从而所给向量组线性相无关.5. 问a 取什么值时下列向量组线性相关? a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T . 解 以所给向量为列向量的矩阵记为A . 由)1)(1(111111||+-=--=a a a aa a A知, 当a =-1、0、1时, R (A )<3, 此时向量组线性相关.9.设b 1=a 1+a 2, b 2=a 2+a 3, b 3=a 3+a 4, b 4=a 4+a 1, 证明向量组b 1, b 2, b 3, b 4线性相关.证明 由已知条件得a 1=b 1-a 2, a 2=b 2-a 3, a 3=b 3-a 4, a 4=b 4-a 1,于是 a 1 =b 1-b 2+a 3 =b 1-b 2+b 3-a 4 =b 1-b 2+b 3-b 4+a 1, 从而 b 1-b 2+b 3-b 4=0,这说明向量组b 1, b 2, b 3, b 4线性相关.11.(1) 求下列向量组的秩, 并求一个最大无关组:(1)a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T , a 3=(-2, -4, 2, -8)T ; 解 由⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛----=000000010291032001900820291844210141002291) , ,(~~321r r a a a ,知R (a 1, a 2, a 3)=2. 因为向量a 1与a 2的分量不成比例, 故a 1, a 2线性无关, 所以a 1, a 2是一个最大无关组.12.利用初等行变换求下列矩阵的列向量组的一个最大无关组: (1)⎪⎪⎪⎭⎫⎝⎛4820322513454947513253947543173125;解 因为⎪⎪⎪⎭⎫ ⎝⎛482032251345494751325394754317312513121433~r r r r r r ---⎪⎪⎪⎭⎫ ⎝⎛531053103210431731253423~r r r r --⎪⎪⎪⎭⎫ ⎝⎛00003100321043173125, 所以第1、2、3列构成一个最大无关组.(2)⎪⎪⎪⎭⎫⎝⎛---14011313021512012211. 解 因为⎪⎪⎪⎭⎫ ⎝⎛---1401131302151201221113142~r r r r --⎪⎪⎪⎭⎫ ⎝⎛------222001512015120122112343~r r r r +↔⎪⎪⎪⎭⎫ ⎝⎛---00000222001512012211, 所以第1、2、3列构成一个最大无关组. 13. 设向量组(a , 3, 1)T , (2, b , 3)T , (1, 2, 1)T , (2, 3, 1)T的秩为2, 求a , b .解 设a 1=(a , 3, 1)T , a 2=(2, b , 3)T , a 3=(1, 2, 1)T , a 4=(2, 3, 1)T . 因为⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=52001110311161101110311131********) , , ,(~~2143b a a b a b a r r a a a a ,而R (a 1, a 2, a 3, a 4)=2, 所以a =2, b =5. 20.求下列齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x ;解 对系数矩阵进行初等行变换, 有 ⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=00004/14/3100401 2683154221081~r A ,于是得⎩⎨⎧+=-=43231)4/1()4/3(4x x x x x .取(x 3, x 4)T =(4, 0)T , 得(x 1, x 2)T =(-16, 3)T ; 取(x 3, x 4)T =(0, 4)T , 得(x 1, x 2)T =(0, 1)T . 因此方程组的基础解系为ξ1=(-16, 3, 4, 0)T , ξ2=(0, 1, 0, 4)T .(2)⎪⎩⎪⎨⎧=-++=-++=+--03678024530232432143214321x x x x x x x x x x x x . 解 对系数矩阵进行初等行变换, 有 ⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛----=000019/719/141019/119/201 367824531232~r A ,于是得⎩⎨⎧+-=+-=432431)19/7()19/14()19/1()19/2(x x x x x x . 取(x 3, x 4)T =(19, 0)T , 得(x 1, x 2)T =(-2, 14)T ; 取(x 3, x 4)T =(0, 19)T , 得(x 1, x 2)T =(1, 7)T . 因此方程组的基础解系为ξ1=(-2, 14, 19, 0)T , ξ2=(1, 7, 0, 19)T .26. 求下列非齐次方程组的一个解及对应的齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=+++=+++=+3223512254321432121x x x x x x x x x x ;解 对增广矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛=2100013011080101 322351211250011~r B . 与所给方程组同解的方程为⎪⎩⎪⎨⎧=+=--=213 843231x x x x x . 当x 3=0时, 得所给方程组的一个解η=(-8, 13, 0, 2)T . 与对应的齐次方程组同解的方程为⎪⎩⎪⎨⎧==-=043231x x x x x . 当x 3=1时, 得对应的齐次方程组的基础解系ξ=(-1, 1, 1, 0)T .(2)⎪⎩⎪⎨⎧-=+++-=-++=-+-6242163511325432143214321x x x x x x x x x x x x . 解 对增广矩阵进行初等行变换, 有 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛-----=0000022/17/11012/17/901 6124211635113251~r B . 与所给方程组同解的方程为⎩⎨⎧--=++-=2)2/1((1/7)1)2/1()7/9(432431x x x x x x . 当x 3=x 4=0时, 得所给方程组的一个解η=(1, -2, 0, 0)T .与对应的齐次方程组同解的方程为⎩⎨⎧-=+-=432431)2/1((1/7))2/1()7/9(x x x x x x . 分别取(x 3, x 4)T =(1, 0)T , (0, 1)T , 得对应的齐次方程组的基础解系ξ1=(-9, 1, 7, 0)T . ξ2=(1, -1, 0, 2)T .。
通信电路原理习题课1-4章共29页文档
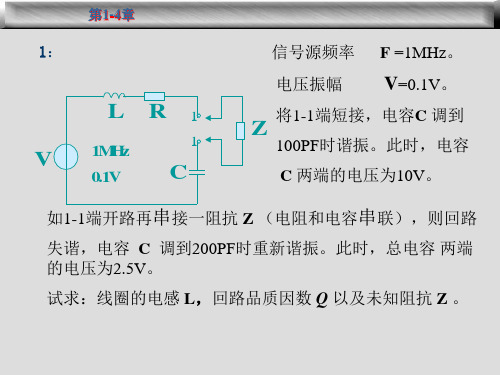
1) 应采用哪一个可变电容器,为什么?
2) 回路电感应该等于多少?
3) 绘出实际的并联回路图。
解:
1)根据已知条件, 535kHz, 1605kHz均为
谐振频率,且比值为3,即:
1
H LCmin 3LFra bibliotek1 LCmax
C max 9 C min
第1-4章
【习题】
在两个可变电容当中, 100/12<9,不满足要求, 450/15=30>9,满足要求,
L2与C则构成并联谐振,在负载上能构产 生压降,因此:
R1
C R2
1 2 L2C
L1
1 C
L2
计算结果:
L1 =375μH, L2 =125μH
第1-4章
【习题】
2.有一并联回路在某频段内工作,频段最低频率为535kHz,最高 频率为1605kHz。现有两个可变电容器,一个电容器的最小电容 量是12pF,最大电容量是100pF;另一个电容器的最小电容量是 15pF,最大电容量是450pF。试问:
第1-4章
【习题】
1. 有一双电感复杂并联回路如图所示,已知L1+L2=500uH,C=500pF,为了使 电源中的二次谐波能被回路消除,应如何分配L1和L2 ?
解: 假设在该图上并联一个负载(如图示),
则要使二次谐波消除,则应该不让二次谐
波在负载上产生压降,因此对于二次谐波 L1
L2
要求 L2与C构成串联谐振,而对于基频L1 、
b. 作图
P1
n
P2
P3
n-1 P4
y1
Ω
如果点P4落在n与n -1的衰减线之间,则选择n
第1-4章
2) 选择电路: 满足同一要求的低通滤波器电路有两种结构, 它们互为对偶,一般选择电感少的电路;
1-4章习题讲解、练习题、内存实验(操作系统)

一个状态转换的发生,是否一定导致另一 个转换发生,列出所有的可能。
解答:不一定。可能的情况如下: 1.就绪执行 导致 执行就绪 2.执行阻塞 导致 就绪执行(就绪队列不空) 3.执行就绪 导致 就绪执行(就绪队列不空) 4.阻塞就绪 可能导致 就绪执行 (在抢占方式下,该进程优先级高于当前进程和 就绪队列中的所有进程) 作业问题:认为阻塞就绪一定导致就绪执行。
31.(c)(e)会发生死锁。
34.(a)不是死锁状态,(b)是死锁状 态。
P1
R1 P1
R2
14.在一个请求分页系统中,采用LRU页面置换算法,假如 一个页面的页面走向为4、3、2、1、4、3、5、4、3、2 、1、5,当分配给作业的物理块数为3和4时,试计算在访 问过程中所发生的缺页次数和缺页率,并比较所得结果
选择题
1、在计算机系统中配置操作系统的主要目的是(A),操作系 统的主要功能是管理计算机系统中的(B),其中包括(C)管 理和(D)管理,以及设备管理和文件管理。这里的(C)管理 主要是对进程进行管理。 A:(1)增强计算机系统的功能;(2)提高系统资源的利用 率;(3)提高系统的运行速度;(4)合理地组织系统的工作 流程,以提高系统吞吐量。 B:(1)程序和数据;(2)进程;(3)资源;(4)作业 ;(5)任务。 C、D:(1)存储器;(2)虚拟存储器;(3)运算器; (4)处理机;(5)控制器。
8、对于记录型信号量,在执行一次P操作时,信号量的值应 当 A ;当其值为 B 时,进程应阻塞。在执行V操作时 ,信号量的值应当 C ;当其值为 D 时,应唤醒阻塞队 列中的进程。 A,C:(1)不变; (2)加1; (3)减1; (4)加指定数值; (5)减指定数值。 B,D:(1)大于0; (2)小于0; (3)大于等于 0; (4)小于等于0。
1-4章复习题

则以每一车组为一批。
练一练:
7.零担货物和使用集装箱运输的货物,
以每张运单为一批;使用集装箱的货物,每批必
须是同一箱型,最多不超过铁路一辆货
车所装运的箱数。
8.西瓜与手机可按一批托运。(X)
9.冻肉与大米可按一批托运。(X)
10.铁块可用集装箱装运。(X)
A.保证金B.罚款C.违约金D.费用
21.铁路货物运输的长远计划通常都在(B)年以上。
A.3 B.5 C.10 D.15
22.下列各组货物中,以按一批托运的是(B)。
A.1个l0t集装箱和1个5t集装箱B.2个10t集装箱C.8个
10t集装箱D.2个40英尺集装箱
23.1t集装箱一般用(B)装运。
A.棚车B.敞车
练一练
23.承运人按铁路有关规定运单,若符合运输条件,并在运单上签证货物搬入日期或装车日期,即为(承运)。
24.货运员对搬入货场的货物进行检查核对,确认符合运输要求并同意进入场库指定货位,叫(验收)。
25.货票乙联的作用是(报告联,由发站送交发局,是各项统计工作的依据)。
26.到站在收货人办完货物领取手续和缴清应交费用后,货物运单(交托运人报销用)。
⑵A站托运一整车牲骨,麻袋包装,要求B、D两站分卸。
⑶A站托运一整车炭黑,麻袋包装,要求C、D两站分卸
⑷A站托运一整车冻猪肉,纸箱包装,要求B、C两站分
卸。
D
A F
B
C E
练一练:
1.下列十种货物可否按零担办理,并简要说明理由。
⑴活牛(1头,重500kg/件)
⑵冻肉(2箱,25kg/件)
⑶硝化甘油炸药(1箱,50kg/件)
线性代数课后习题1-4作业答案(高等教育出版社)

第一章 行列式1. 利用对角线法则计算下列三阶行列式: (1)381141102---;解 381141102---=2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4. (3)222111c b a c b a ; 解 222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).4. 计算下列各行列式:(1)71100251020214214; 解 7110251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-;解 2605232112131412-260503212213041224--=====c c 041203212213041224--=====r r 000003212213041214=--=====r r . (3)efcf bf de cd bd aeac ab ---;解 ef cf bf de cd bd ae ac ab ---e c b e c b ec b adf ---=abcdef adfbce 4111111111=---=.(4)dc b a 100110011001---. 解d c b a 100110011001---dc b aab ar r 10011001101021---++===== dc a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ada ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 6. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)y x z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=yx z x z y zy x b a )(33+=.8. 计算下列各行列式(D k 为k 阶行列式): (1)aa D n 1 1⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解aa a a a D n 0 0010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 000 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a an n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1)1()1(=a n -a n -2=a n -2(a 2-1).(2)xa a a x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得 ax x a ax x a a x x a a a a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(=[x +(n -1)a ](x -a )n 第二章 矩阵及其运算 1. 计算下列乘积:(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.2. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A TB .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503, ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T . 3.已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4.设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问: (1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.5. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k .解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫⎝⎛=222002012λλλλλ,⎪⎪⎭⎫⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.8. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵.证明 因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵. 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为 ⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (3)⎪⎪⎭⎫⎝⎛---145243121; 解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A ,所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 利用逆矩阵解下列线性方程组: (1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x ,从而有 ⎪⎩⎪⎨⎧===001321x x x .19.设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 20. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.21. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ).另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.22. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或 E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或 E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1, )3(41)2(1A E E A -=+-.第三章 矩阵的初等变换与线性方程组 1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫⎝⎛--340313021201;解 ⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫⎝⎛100001000001.(3)⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; 解 ⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011. 3. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫⎝⎛323513123;解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫⎝⎛---101011001200410123~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫⎝⎛----------10612631110`1022111000010000100021 ~⎪⎪⎪⎭⎫⎝⎛-------106126311101042111000010000100001 故逆矩阵为⎪⎪⎪⎭⎫⎝⎛-------10612631110104211. 5. (2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B . 解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫⎝⎛---411007101042001 ~r ,所以 ⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X ,从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X . 9. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.12. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3. P106/ 1.已知向量组A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ;B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T , 证明B 组能由A 组线性表示, 但A 组不能由B 组线性表示.证明 由 ⎪⎪⎪⎭⎫⎝⎛-=312123111012421301402230) ,(B A ⎪⎪⎪⎭⎫ ⎝⎛-------971820751610402230421301~r ⎪⎪⎪⎭⎫⎝⎛------531400251552000751610421301 ~r ⎪⎪⎪⎭⎫ ⎝⎛-----000000531400751610421301~r 知R (A )=R (A , B )=3, 所以B 组能由A 组线性表示.由⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=000000110201110110220201312111421402~~r r B 知R (B )=2. 因为R (B )≠R (B , A ), 所以A 组不能由B 组线性表示. 4. 判定下列向量组是线性相关还是线性无关: (1) (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; (2) (2, 3, 0)T , (-1, 4, 0)T , (0, 0, 2)T .解 (1)以所给向量为列向量的矩阵记为A . 因为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=000110121220770121101413121~~r r A ,所以R (A )=2小于向量的个数, 从而所给向量组线性相关. (2)以所给向量为列向量的矩阵记为B . 因为022200043012||≠=-=B ,所以R (B )=3等于向量的个数, 从而所给向量组线性相无关.5. 问a 取什么值时下列向量组线性相关? a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T . 解 以所给向量为列向量的矩阵记为A . 由)1)(1(111111||+-=--=a a a aa a A知, 当a =-1、0、1时, R (A )<3, 此时向量组线性相关.9.设b 1=a 1+a 2, b 2=a 2+a 3, b 3=a 3+a 4, b 4=a 4+a 1, 证明向量组b 1, b 2, b 3, b 4线性相关.证明 由已知条件得a 1=b 1-a 2, a 2=b 2-a 3, a 3=b 3-a 4, a 4=b 4-a 1,于是 a 1 =b 1-b 2+a 3 =b 1-b 2+b 3-a 4 =b 1-b 2+b 3-b 4+a 1, 从而 b 1-b 2+b 3-b 4=0,这说明向量组b 1, b 2, b 3, b 4线性相关.11.(1) 求下列向量组的秩, 并求一个最大无关组:(1)a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T , a 3=(-2, -4, 2, -8)T ; 解 由⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛----=000000010291032001900820291844210141002291) , ,(~~321r r a a a , 知R (a 1, a 2, a 3)=2. 因为向量a 1与a 2的分量不成比例, 故a 1, a 2线性无关, 所以a 1, a 2是一个最大无关组.12.利用初等行变换求下列矩阵的列向量组的一个最大无关组:(1)⎪⎪⎪⎭⎫⎝⎛4820322513454947513253947543173125;解 因为⎪⎪⎪⎭⎫ ⎝⎛482032251345494751325394754317312513121433~r r r r r r ---⎪⎪⎪⎭⎫ ⎝⎛531053103210431731253423~rr r r --⎪⎪⎪⎭⎫ ⎝⎛00003100321043173125, 所以第1、2、3列构成一个最大无关组.(2)⎪⎪⎪⎭⎫⎝⎛---140113*********12211. 解 因为⎪⎪⎪⎭⎫ ⎝⎛---1401131302151201221113142~rr r r --⎪⎪⎪⎭⎫ ⎝⎛------222001512015120122112343~rr r r +↔⎪⎪⎪⎭⎫ ⎝⎛---00000222001512012211, 所以第1、2、3列构成一个最大无关组. 13. 设向量组(a , 3, 1)T , (2, b , 3)T , (1, 2, 1)T , (2, 3, 1)T的秩为2, 求a , b .解 设a 1=(a , 3, 1)T , a 2=(2, b , 3)T , a 3=(1, 2, 1)T , a 4=(2, 3, 1)T . 因为⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=52001110311161101110311131********) , , ,(~~2143b a a b a b a r r a a a a ,而R (a 1, a 2, a 3, a 4)=2, 所以a =2, b =5. 20.求下列齐次线性方程组的基础解系: (1)⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x ;解 对系数矩阵进行初等行变换, 有⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=00004/14/3100401 2683154221081~r A ,于是得⎩⎨⎧+=-=43231)4/1()4/3(4x x x x x .取(x 3, x 4)T =(4, 0)T , 得(x 1, x 2)T =(-16, 3)T ; 取(x 3, x 4)T =(0, 4)T , 得(x 1, x 2)T =(0, 1)T . 因此方程组的基础解系为ξ1=(-16, 3, 4, 0)T , ξ2=(0, 1, 0, 4)T .(2)⎪⎩⎪⎨⎧=-++=-++=+--03678024530232432143214321x x x x x x x x x x x x .解 对系数矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛----=000019/719/141019/119/201 367824531232~r A ,于是得⎩⎨⎧+-=+-=432431)19/7()19/14()19/1()19/2(x x x x x x .取(x 3, x 4)T =(19, 0)T , 得(x 1, x 2)T =(-2, 14)T ; 取(x 3, x 4)T =(0, 19)T , 得(x 1, x 2)T =(1, 7)T . 因此方程组的基础解系为ξ1=(-2, 14, 19, 0)T , ξ2=(1, 7, 0, 19)T .26. 求下列非齐次方程组的一个解及对应的齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=+++=+++=+3223512254321432121x x x x x x x x x x ;解 对增广矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛=2100013011080101 322351211250011~r B . 与所给方程组同解的方程为⎪⎩⎪⎨⎧=+=--=213 843231x x x x x . 当x 3=0时, 得所给方程组的一个解η=(-8, 13, 0, 2)T . 与对应的齐次方程组同解的方程为⎪⎩⎪⎨⎧==-=043231x x x x x . 当x 3=1时, 得对应的齐次方程组的基础解系ξ=(-1, 1, 1, 0)T .(2)⎪⎩⎪⎨⎧-=+++-=-++=-+-6242163511325432143214321x x x x x x x x x x x x . 解 对增广矩阵进行初等行变换, 有⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-----=0000022/17/11012/17/901 6124211635113251~r B . 与所给方程组同解的方程为⎩⎨⎧--=++-=2)2/1((1/7)1)2/1()7/9(432431x x x x x x . 当x 3=x 4=0时, 得所给方程组的一个解η=(1, -2, 0, 0)T .与对应的齐次方程组同解的方程为⎩⎨⎧-=+-=432431)2/1((1/7))2/1()7/9(x x x x x x . 分别取(x 3, x 4)T =(1, 0)T , (0, 1)T , 得对应的齐次方程组的基础解系ξ1=(-9, 1, 7, 0)T . ξ2=(1, -1, 0, 2)T .。
线性代数课后习题1-4作业答案(高等教育出版社)

= 1 2 −2 ====== 0 0 − 2 =0.
10
3
14
c1
+
1 2
c3
17
17
14
2 1 41
(2)
3 1
−1 2
2 3
1 2
;
5 0 62
解
2 3 1
1 −1 2
4 2 3
1 1 2
c4 − c2 =====
2 3 1
1 −1 2
4 2 3
0 2 0
r4 − r2 =====
2 3 1
2 2
52⎟⎠⎞⎜⎝⎛00
12 ⎟⎠⎞ = ⎜⎝⎛ 00
96⎟⎠⎞ ,
而
A2
−
B2
=
⎜⎝⎛
3 4
181⎟⎠⎞ − ⎜⎝⎛13
40⎟⎠⎞ = ⎜⎝⎛ 12
78⎟⎠⎞ ,
故(A+B)(A−B)≠A2−B2.
5. 举反列说明下列命题是错误的:
(1)若 A2=0, 则 A=0;
解 取 A=⎜⎝⎛00 01⎟⎠⎞ , 则 A2=0, 但 A≠0. (2)若 A2=A, 则 A=0 或 A=E;
4. 计算下列各行列式:
4 124
(1)1 10Fra bibliotek2 5
0 2
2 0
;
0 117
解
4 1 10 0
1 2 5 1
2 0 2 1
4 2 0 7
=cc=42=−−=7c=c33=10140
−1 2 3 0
2 0 2 1
−10 2
−14 0
4 =1
10
−1 2 3
−10 2 ×(−1)4+3
管理信息系统习题1-4

第一章:管理信息系统概论一、选择题1、管理信息是( )A 管理者的指令B 客观世界的实际记录C 数据处理的基础D加工后反映和控制管理活动的数据2、现代管理信息系统是()A 手工管理系统B 计算机系统C 人和计算机等组成的系统D 通信网络系统3、管理信息系统由四大部件组成,它们是()A信息源、信息处理器、信息用户和信息管理者B信息源、信息收集器、信息处理器和信息管理者C信息收集器、信息处理器、信息用户和信息管理者D以上说法都不对4、管理信息系统的应用离不开一定的环境和条件,环境具体指的是()A 组织所处的自然环境B 组织所处的社会环境C 组织内外各种因素的综合D 组织所处的自然环境和社会环境的综合5、运行控制层上的决策多属于()A 结构化B 半结构化C 非结构化D 以上都有6、ERP是( )进步一步发展的结果A EDPB MPRC MISD MRPⅡ7、决策支持系统(DSS)有三个技术层次,它们分别是()A 语言子系统、知识子系统、问题处理系统B 模型库系统、语言子系统、问题处理系统C 模型库系统、知识库于系统、决策支持系统工具D 专用DSS、DSS生成器和DSS工具8、电子商务中企业对企业的形式可称作()A B to GB B to BC B to CD C to C9、企业资源计划的核心是()A MPRB MPRⅡC JITD CAM10、下列不属于管理信息系统范畴的是()A 管理信息系统B 决策支持系统C 专家系统D 事务处理系统11、在管理信息系统的金字塔型结构中,处于最下层的是()A 业务处理系统B 财务系统C 数据处理系统D 决策支持系统12、管理信息系统的功能不包括下面哪一项A 信息处理功能B 预测功能C 决策功能D 计划功能13、系统方法的主要原则是( )A 整体性原则B 目标优化原则C 分解协调原则D 以上均是14、下列人员不属于管理信息系统用户的是( )A 总经理B 系统分析员C 部门经理D 数据输入员15、管理信息系统学科属于( )A 计算机学科B 管理学科C 工程学科D综合型学科二、判断题1、管理信息系统涉及到管理和信息两个方面。
建筑构造作业(1-4)习题和答案

质发生化学反应。 ④保温材料的机械强度要与使用环境相适应。 ⑤保温材料的寿命要与被保温主体的正常维修期基本相适应。 ⑥保温材料应选择吸水率小的材料。 ⑦按照防火的要求,保温材料应选用不燃或难燃的材料。 ⑧保温材料应有合适的单位体积价格和良好的施工性能。 2、什么情况下应设置防震缝? 答:①建筑物平面体型复杂,凹角长度过大或突出部分较多,应用防震缝将其分开,使其形成几个简
4、什么是现浇整体式钢筋混凝土楼板?其有何特点? 答: 现浇整体式钢筋混凝土楼板是在施工现场经支模、扎筋、浇筑混凝土等施工工序,再养护达到 一定强度后拆除模板而成型的楼板结构。由于楼板为整体浇筑成型,因此,结构的整体性强、刚度好,有 利于抗震,但现场湿作业量大,施工速度较慢,施工工期较长,主要适用于平面布置不规则,尺寸不符合 模数要求或管道穿越较多的楼面,以及对整体刚度要求较高的高层建筑。随着高层建筑的日益增多,施工 技术的不断革新和组合式钢模板的发展,现浇钢筋混凝土楼板的应用逐渐增多。 现浇钢筋混凝土楼板按其结构类型不同,可分为板式楼板、梁板式楼板、井式楼板、无梁楼板。此外, 还有压型钢板混凝土组合楼板。 1)板式楼板:将楼板现浇成一块平板,并直接支承在墙上,这种楼板称为板式楼板。 2)梁板式楼板:当房间的跨度较大时,若仍采用板式楼板,会因板跨较大而增加板厚。
-2-
ofrualdinkgwtesc,pbyhm
建筑构造作业 3
3、块瓦屋面中块瓦的固定加强措施有哪些? 答:1)水泥砂浆卧瓦者,用双股 18 号铜丝将瓦与Φ6 钢筋绑牢;
2)钢挂瓦条钩挂者,用双股 18 号铜丝将瓦与钢挂瓦条绑牢; 3)木挂瓦条钩挂者,用 40 圆钉(或双股 18 号铜丝)将瓦与木挂瓦条钉(绑)牢。 4、屋顶的排水方式有哪几种?简述各自的优缺点和适用范围。 答: 屋顶排水方式分为无组织排水和有组织排水两大类。 1)无组织排水:无组织排水又称自由落水,是指屋面雨水直接从檐口落至室外地面的一种排水方式。 这种做法具有构造简单、造价低廉的优点,但屋面雨水自由落下会溅湿墙面,外墙墙脚常被飞溅的雨水侵 蚀,影响到外墙的坚固耐久性,并可能影响人行道的交通。无组织排水方式主要适用于少雨地区或一般低 压建筑,不宜用于临街建筑和高度较高的建筑。 2)有组织排水:有组织排水是指屋面雨水通过排水系统,有组织地排至室外地面或地下管沟的一种 排水方式。这种排水方式具有不妨碍人行交通、不易溅湿墙面的优点,因而在建筑工程中应用非常广泛。 但与无组织排水相比,其构造复杂,造价相对较高。 有组织排水方案可分为外排水和内排水两种基本形式,常用外排水方式有女儿墙外排水、挑檐沟外排 水、女儿墙檐沟外排水三种。 5、简述铝合金窗的安装要点。 答:为了便于铝合金窗的安装,一般先在窗框外侧用螺钉固定钢质锚固件,安装时与洞口四周墙中的 预埋铁件焊接或锚固在一起,玻璃是嵌固在铝合金窗料中的凹槽内,并加密封条。窗框固定铁件,除四周 离边角 150mm 设一点外,一般间距不大于 400~500mm。其连接方法有:①采用墙上预埋铁件连接;②墙上 预留孔洞埋入燕尾铁脚连接;③采用金属膨胀螺栓连接;④采用射钉固定,锚固铁件用厚度不小于 1.5mm 的镀锌铁片。窗框固定好后窗洞四周的缝隙一般采用软质保温材料填塞,如泡沫塑料条、泡沫聚氨脂条、 矿棉毡条和玻璃丝毡条、聚氨脂发泡剂等。填实处用水泥砂浆抹留 5~8mm 深的弧形槽,槽内嵌密封胶。
电大形成性考核作业:数控电气控制作业1-4

数控机床电气控制课程习题(一)1.按钮开关和行程开关的作用分别是什么?如何确定按钮开关的选用原则?答:按钮开关通常用作短时接通或断开小电流控制电路的开关,用于控制电路中发出起动或停止等指令,通过接触器、继电器等控制电器接通或断开主电路。
行程开关又称限位开关,是根据运动部件位置而切换电路的自动控制电器。
动作时,由挡块与行程开关的滚轮相碰撞,使触头接通或断开用来控制运动部件的运动方向、行程大小或位置保护。
按钮开关的选用原则①根据用途选择开关的形式,如紧急式、钥匙式、指示灯式等。
②根据使用环境选择按钮开关的种类,如开启式、防水式、防腐式等。
③按工作状态和工作情况的要求,选择按钮开关的颜色。
2.低压断路器在电路中的作用是什么?答:低压断路器又称自动空气开关,它不但能用于正常工作时不频繁接通和断开电路,而且当电路发生过载、短路或失压等故障时,能自动切断电路,有效地保护串接在它后面的电气设备,因此,低压断路器在机床上使用得越来越广泛。
3.接触器的用途是什么?它由哪几部分组成?答:接触器是一种用来频繁地接通或分断带有负载(如电动机)的主电路自动控制电器。
接触器按其主触头通过电流的种类不同,分为交流、直流两种,机床上应用最多的是交流接触器。
它由电磁机构、触头系统、灭弧装置及其他部件等四部分组成。
4.接近开关与行程开关相比有哪些优点?若接近开关为三线制输出,一般为哪三根输出线?答:接近开关又称无触点行程开关。
与行程开关相比,接近开关具有工作稳定可靠、使用寿命长、重复定位精度高、操作频率高等优点。
接近开关多为三线制。
三线制接近开关有二根电源线(通常为24V)和一根输出线,输出有常开、常闭两种状态。
5..中间继电器的作用是什么?它和交流接触器有何区别?答:中间继电器实质上是电压继电器的一种,其触点数量多(多至6对或更多),触点电流容量大(额定电流5~10A),动作时间不大于0.05s。
其主要用途是当其他继电器的触头数量或触点容量不够时,可借助中间继电器来扩大它们的触点数或触点容量,起到中间转换和放大作用。
中级财务会计(二)作业1-4参考标准答案

《中级财务会计(二)》形成性考核作业1习题一参考答案1、借:原材料 902 000应交税费—应交增值税(进项税额) 153 000贷:银行存款 1 0550002、借:应收账款 1 170 000贷:主营业务收入1 000 000应交税费——应交增值税(销项税额) 170 000借:营业税金及附加 100 000贷:应交税费——应交消费税 100 000同时,借:主营业务成本750 000贷:库存商品 750 0003、借:银行存款15000累计摊销75 000贷:无形资产 80000应交税费——应交营业税 750营业外收入 9 2504、借:原材料69 600应交税费—应交增值税(进项税额) 10 400贷:银行存款 80 0005、借:委托加工物资100 000贷:原材料 100 000•借:委托加工物资 27 500•应交税费—应交增值税(进项税额)4 250•贷:银行存款 31 750•借:原材料 127 500•贷:委托加工物资 1275006、借:固定资产180000应交税费—应交增值税(进项税额) 30 600贷:银行存款 210 6007、借:在建工程 58 500贷:原材料50 000应交税费—应交增值税(进项税额转出) 8 5008、借:待处理财产损溢——待处理流动资产损溢 4 000贷:原材料 4 000习题二参考答案甲公司债务重组的处理:债务重组利得=重组债务的账面价值350-转让的非现金资产公允价值(180+30.6+30)=109.4万转让的非现金资产的账面价值=(200-15)+(15+10)=210万转让的非现金资产的公允价值210万-转让的非现金资产的账面价值210=0,则计入当期损益的金额为0。
借:应付账款——乙公司3500000贷:主营业务收入1800000应交税费——应交增值税(销项税额) 306000可供出售金融资产—A公司股票(成本) 150000—A公司股票(公允价值变动) 100000投资收益 50000营业外收入—债务重组利得1094000借:主营业务成本1850000存货跌价准备150000贷:库存商品 2000000借:资本公积—其他资本公积 10万贷:投资收益—股票投资收益 10万乙公司债务重组的处理:受让非现金资产按其公允价值入账,公允价值金额=180+30.6+30==240.6万重组债权的账面余额=350万元债务重组损失=重组债权的账面余额-受让的非现金资产的公允价值=350-240.6=109.4万将该差额冲减减值准备105万(350*30%),再将其差额4.4万计入营业外支出。
(高等教育出版社)线性代数课后习题1-4作业答案

第一章 行列式1. 利用对角线法则计算下列三阶行列式: (1)381141102---;解 381141102---=2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4. (3)222111c b a c b a ; 解 222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).4. 计算下列各行列式: (1)7110025*******214; 解 71100251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-;解 2605232112131412-260503212213041224--=====c c 041203212213041224--=====r r 0000003212213041214=--=====r r . (3)efcf bf de cd bd aeac ab ---;解 ef cf bf de cd bd aeac ab ---e c b e c b e c b adf ---=abcdef adfbce 4111111111=---=.(4)dc b a 100110011001---. 解d c b a 100110011001---dc b aab ar r 10011001101021---++===== d c a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ada ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 6. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)y x z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=yx z x z y zy x b a )(33+=.8. 计算下列各行列式(D k 为k 阶行列式):(1)aaD n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解aa a a a D n 0 0010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 00 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a an n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1)1()1(=a n -a n -2=a n -2(a 2-1).(2)xa aa x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得 ax x a ax x a a x x a a a a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 000 00 )1(=[x +(n -1)a ](x -a )n 第二章 矩阵及其运算 1. 计算下列乘积:(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.2. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫ ⎝⎛--=150421321B , 求3AB -2A 及A TB .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T.3. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4.设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问: (1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.5. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k .解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫⎝⎛=222002012λλλλλ,⎪⎪⎭⎫⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA k k kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.8. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵.证明 因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵. 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为 ⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (3)⎪⎪⎭⎫⎝⎛---145243121; 解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A ,所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x ,从而有 ⎪⎩⎪⎨⎧===001321x x x .19.设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 20. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112 ⎪⎪⎭⎫⎝⎛=1111111114.21. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ).另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.22. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或 E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或 E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1, )3(41)2(1A E E A -=+-.第三章 矩阵的初等变换与线性方程组 1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫⎝⎛--340313021201;解 ⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫⎝⎛100001000001.(3)⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; 解 ⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011. 3. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫⎝⎛323513123;解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫⎝⎛---101011001200410123~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫⎝⎛----------10612631110`1022111000010000100021 ~⎪⎪⎪⎭⎫⎝⎛-------106126311101042111000010000100001 故逆矩阵为⎪⎪⎪⎭⎫⎝⎛-------10612631110104211. 5. (2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B . 解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫⎝⎛---411007101042001 ~r ,所以 ⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X ,从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X . 9. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.12. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3. P106/ 1.已知向量组A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ;B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T , 证明B 组能由A 组线性表示, 但A 组不能由B 组线性表示. 证明 由 ⎪⎪⎪⎭⎫⎝⎛-=312123111012421301402230) ,(B A ⎪⎪⎪⎭⎫ ⎝⎛-------971820751610402230421301~r ⎪⎪⎪⎭⎫⎝⎛------531400251552000751610421301 ~r ⎪⎪⎪⎭⎫ ⎝⎛-----000000531400751610421301~r 知R (A )=R (A , B )=3, 所以B 组能由A 组线性表示. 由⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=000000110201110110220201312111421402~~r r B 知R (B )=2. 因为R (B )≠R (B , A ), 所以A 组不能由B 组线性表示. 4. 判定下列向量组是线性相关还是线性无关: (1) (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; (2) (2, 3, 0)T , (-1, 4, 0)T , (0, 0, 2)T .解 (1)以所给向量为列向量的矩阵记为A . 因为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=000110121220770121101413121~~r r A ,所以R (A )=2小于向量的个数, 从而所给向量组线性相关. (2)以所给向量为列向量的矩阵记为B . 因为022200043012||≠=-=B ,所以R (B )=3等于向量的个数, 从而所给向量组线性相无关.5. 问a 取什么值时下列向量组线性相关? a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T . 解 以所给向量为列向量的矩阵记为A . 由)1)(1(111111||+-=--=a a a aa a A知, 当a =-1、0、1时, R (A )<3, 此时向量组线性相关.9.设b 1=a 1+a 2, b 2=a 2+a 3, b 3=a 3+a 4, b 4=a 4+a 1, 证明向量组b 1, b 2, b 3, b 4线性相关.证明 由已知条件得a 1=b 1-a 2, a 2=b 2-a 3, a 3=b 3-a 4, a 4=b 4-a 1,于是 a 1 =b 1-b 2+a 3 =b 1-b 2+b 3-a 4 =b 1-b 2+b 3-b 4+a 1, 从而 b 1-b 2+b 3-b 4=0,这说明向量组b 1, b 2, b 3, b 4线性相关.11.(1) 求下列向量组的秩, 并求一个最大无关组:(1)a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T , a 3=(-2, -4, 2, -8)T ; 解 由⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛----=000000010291032001900820291844210141002291) , ,(~~321r r a a a ,知R (a 1, a 2, a 3)=2. 因为向量a 1与a 2的分量不成比例, 故a 1, a 2线性无关, 所以a 1, a 2是一个最大无关组.12.利用初等行变换求下列矩阵的列向量组的一个最大无关组: (1)⎪⎪⎪⎭⎫⎝⎛4820322513454947513253947543173125;解 因为⎪⎪⎪⎭⎫ ⎝⎛482032251345494751325394754317312513121433~r r r r r r ---⎪⎪⎪⎭⎫ ⎝⎛531053103210431731253423~rr r r --⎪⎪⎪⎭⎫ ⎝⎛00003100321043173125, 所以第1、2、3列构成一个最大无关组.(2)⎪⎪⎪⎭⎫⎝⎛---14011313021512012211. 解 因为⎪⎪⎪⎭⎫ ⎝⎛---1401131302151201221113142~rr r r --⎪⎪⎪⎭⎫ ⎝⎛------222001512015120122112343~rr r r +↔⎪⎪⎪⎭⎫ ⎝⎛---00000222001512012211, 所以第1、2、3列构成一个最大无关组. 13. 设向量组(a , 3, 1)T , (2, b , 3)T , (1, 2, 1)T , (2, 3, 1)T的秩为2, 求a , b .解 设a 1=(a , 3, 1)T , a 2=(2, b , 3)T , a 3=(1, 2, 1)T , a 4=(2, 3, 1)T . 因为⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=5200111031116110111031113111332221) , , ,(~~2143b a a b a b a r r a a a a ,而R (a 1, a 2, a 3, a 4)=2, 所以a =2, b =5. 20.求下列齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x ;解 对系数矩阵进行初等行变换, 有⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=00004/14/3100401 2683154221081~r A ,于是得⎩⎨⎧+=-=43231)4/1()4/3(4x x x x x .取(x 3, x 4)T =(4, 0)T , 得(x 1, x 2)T =(-16, 3)T ; 取(x 3, x 4)T =(0, 4)T , 得(x 1, x 2)T =(0, 1)T . 因此方程组的基础解系为ξ1=(-16, 3, 4, 0)T , ξ2=(0, 1, 0, 4)T .(2)⎪⎩⎪⎨⎧=-++=-++=+--03678024530232432143214321x x x x x x x x x x x x .解 对系数矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛----=000019/719/141019/119/201 367824531232~r A ,于是得⎩⎨⎧+-=+-=432431)19/7()19/14()19/1()19/2(x x x x x x .取(x 3, x 4)T =(19, 0)T , 得(x 1, x 2)T =(-2, 14)T ; 取(x 3, x 4)T =(0, 19)T , 得(x 1, x 2)T =(1, 7)T . 因此方程组的基础解系为ξ1=(-2, 14, 19, 0)T , ξ2=(1, 7, 0, 19)T .26. 求下列非齐次方程组的一个解及对应的齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=+++=+++=+3223512254321432121x x x x x x x x x x ;解 对增广矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛=2100013011080101 322351211250011~r B . 与所给方程组同解的方程为⎪⎩⎪⎨⎧=+=--=213 843231x x x x x . 当x 3=0时, 得所给方程组的一个解η=(-8, 13, 0, 2)T . 与对应的齐次方程组同解的方程为⎪⎩⎪⎨⎧==-=043231x x x x x . 当x 3=1时, 得对应的齐次方程组的基础解系ξ=(-1, 1, 1, 0)T .(2)⎪⎩⎪⎨⎧-=+++-=-++=-+-6242163511325432143214321x x x x x x x x x x x x . 解 对增广矩阵进行初等行变换, 有⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-----=0000022/17/11012/17/901 6124211635113251~r B . 与所给方程组同解的方程为⎩⎨⎧--=++-=2)2/1((1/7)1)2/1()7/9(432431x x x x x x . 当x 3=x 4=0时, 得所给方程组的一个解η=(1, -2, 0, 0)T .与对应的齐次方程组同解的方程为⎩⎨⎧-=+-=432431)2/1((1/7))2/1()7/9(x x x x x x . 分别取(x 3, x 4)T =(1, 0)T , (0, 1)T , 得对应的齐次方程组的基础解系ξ1=(-9, 1, 7, 0)T . ξ2=(1, -1, 0, 2)T .。
部编版五年级语文下册全册课时作业本一课一练习题1-4单元

部编版五年级语文下册全册课时作业本一课一练习题(1-4单元)1 古诗三首课时练第一课时一、默写古诗《四时田园杂兴(其三十一)》,并完成后面练习。
四时田园杂兴(其三十一)昼出耘田,村庄儿女各当家。
,也傍学种瓜。
1.选择下列加点词语的正确意思。
耘田()①在田里锄草②犁地傍()①靠近②并排2.用自己的话写出这首诗后两行的意思。
二、查资料,抄写一首自己喜欢的其他田园诗。
【答案】一、1.夜绩麻童孙未解供耕织桑阴 2.①①3. 儿童不明白怎么耕田织布,但也在桑树下学着大人的样子种瓜。
二、乡村四月作者:翁卷(宋) 绿遍山原白满川,子规声里雨如烟。
乡村四月闲人少,才了蚕桑又插田。
第二课时一、写出加点词语的意思。
稚子弄冰宋代:杨万里稚子金盆脱晓冰,彩丝穿取当银钲。
敲成玉磬穿林响,忽作玻璃碎地声。
1.稚子:。
2.钲:。
3.磬(qìng):。
4.玻璃:。
二、用自己的话写出《稚子弄冰》前两句的意思。
【答案】一、1.稚子:指幼稚、天真的孩子。
2.钲:一种金属打击乐器。
3.磬(qìng):一种用玉或石制成的击乐器。
4.玻璃:一种天然玉石,也叫水玉,并不是现在的玻璃。
二、清晨,满脸稚气的小孩,将夜间冻结在盘中的冰块脱下,用彩线穿取,当做银钲。
第三课时一、把诗句补充完整,并用自己的话写出所填字词的意思。
村晚宋代:雷震草满池塘水满(),山衔落日()寒漪。
牧童()横牛背,短笛无腔()吹。
1. 。
2. 。
3. 。
4. 。
二、用自己的话写出《村晚》后两句的情景。
【答案】一、陂浸归去信口1.陂(bēi):池塘。
2.浸:淹没。
3.归去:回去。
4.信口:随口。
二、那小牧童横骑在牛背上,缓缓地回家去,他拿着一支短笛,随口吹着,也没有固定的曲调。
2祖父的园子课时练第一课时一、读拼音,写汉字。
春天到了,爷爷把我家院子后面的空地上的杂草bá()掉,用来种菜。
我用脚把那下了种的土窝一个一个地溜平,还东一脚西一脚地xiā()闹。
人教版七年级地理上册《1-4 地形图的判读》作业同步练习题及参考答案

第四节地形图的判读下图为我国东南沿海某地区等高线地形图(单位:米)。
读图,完成第1~2 题。
1.该地区的地形类型主要是( )A.山地和丘陵B.高原和平原C.山地和高原 D.平原和丘陵2.M 村和N 村所在地区的地形类型是( )A.山地B.高原C.平原D.丘陵小敏班上准备组织一次登山活动,同学们个个都兴高采烈。
为了安全,老师拿出一张等高线地形图(下图)说:“这是我们要登的山,它比较高,大家注意……”接着,强调了安全事项,顺便复习了等高线地形图的有关知识,要求同学们上山后留心观察这些地形部位。
据此完成第3~5 题。
3.从图中可以看出,最高的山峰海拔是( )A.900 米B.1 200 米C.900 米以上1 200 米以下D.1 200 米以上1 500 米以下4.老师强调图中有一个陡崖很危险,希望大家上山时一定要注意。
判断该陡崖在( )A.甲地B.丙地C.丁地D.戊地5.老师告诉同学们:“图上甲、丙、丁、戊四处等高线形态不一样,分别表示不同地形部位,上山后一定要留心观察,看它们在地形上有什么区别。
”图中甲、丙、丁、戊依次是指( )A.山峰、山脊、山谷、陡崖B.山峰、陡崖、山脊、山谷C.山峰、陡崖、山谷、山脊D.山峰、山谷、山脊、陡崖下图为某岛国不同海拔的陆地面积所占比例统计图。
读图,完成第6~7 题。
6.该岛国的主要地形类型是( )A.高原B.平原C.丘陵D.山地7.在分层设色地形图上,该岛国的颜色大部分是( )A.白色B.黄色C.褐色D.绿色8.图甲为某同学所画的一幅地形景观图,其最有可能与图乙中等高线地形图相对应的是( )图甲图乙9.读某地区等高线图(单位:米),完成下列各题。
(1)图中A 地山峰的海拔为500~ 米。
(2)图中B 所在地形部位名称是。
(3)图中甲城镇位于乙城镇的( )方向。
A.正西 B.正东C.西南D.西北(4)若C 地到D 地的图上距离是1.2 厘米,则两地的水平距离是千米。
操作系统复习题及参考答案1-4

中南大学网络教育课程考试复习题及参考答案操作系统1一、判断题:1.资源共享是现代操作系统的一个根本特征。
〔〕2.信号量机制中,P、V操作必须成对出现。
〔〕3.假设进程资源分配图中含有环,那么一定有进程处于死锁状态。
〔〕4.绝对装入方式需要对内存地址进行重定位。
〔〕5.“分页对换〞和“分段对换〞是为了支持虚拟存储系统。
〔〕6.通道没有自己的内存,通道所执行的通道程序是放在主机的内存中的。
〔〕7.程序的并行执行是现代操作系统的一个根本特征。
〔〕8.一个进程被唤醒意味着重新占有了CPU。
〔〕9.进程在运行过程中,请问和释放资源顺序不当,同样可以引起死锁。
〔〕10.分段存储管理的引入是为了满足用户〔程序员〕在编程和使用上多方面的要求。
〔〕11.系统中的各个部件,如CPU、存储设备等的连接都是由总线设备来实现的。
〔〕12.在文件的索引存取方法中,允许随意存取文件中的一个记录。
〔〕13.程序在并发执行时会失去封闭性。
〔〕14.由于用户的响应时间要求,因此要求设置大的时间片长度。
〔〕15.预防死锁是指在资源动态分配过程中,用某种方法去防止系统进入不平安状态。
〔〕16.内存的单一连续分配模式只能用在单用户、单任务的OS中。
〔〕17.虚拟存储器的“虚拟〞是指用户可使用的内存容量比实际的内存容量大的多。
〔〕18.在文件系统支持下,用户也需知道文件存放的物理地址。
〔〕19.在单CPU环境下可以实现“多道程序系统〞。
〔〕20.程序与进程最主要的区别在于程序是静态实体,而进程是动态实体。
〔〕21.死锁与程序的死循环一样。
〔〕22.内存固定分区分配模式只能用在单用户、单任务的OS中。
〔〕23.采用LRU置换算法时,当驻留集增大时,页故障率一定不会增加。
〔〕24.通道与CPU共享内存。
〔〕二、填空题:1.操作系统的根本任务是( )。
2.从资源分配的角度看,P(wait)操作意味着向系统( )一个资源,V(signal)操作意味着( )一个资源。
建筑构造作业(1-4)习题和答案(永久免费)

三、简答题答:1)满足建筑使用功能的要求;2)确保结构安全;3)适应建筑工业化和建筑施工的需要;4)注重社会、经济和环境效益;5)注重美观。
答:建筑剖面图是用一假想的垂直剖切面将房屋剖开,移去观察与剖切平面之间的房屋部分,作出剩余部分的房屋的正投影图,简称剖面图。
建筑剖面图主要表示房屋的内部结构、分层情况、各层高度、楼面和地面的构造以及各配件在垂直方向上的相互关系等内容。
在施工中,可作为进行分层、砌筑内墙、铺设楼板和屋面板以及内装修等工作的依据,是与平、立面图相互配合的不可缺少的重要图样之一。
答:特级:1)列为国家重点项目或以国际性活动为主的特高级大型公共建筑;2)有全国性历史意义或技术要求特别复杂的中小型公共建筑;3)30层以上建筑;4)高大空间有声、光等特殊要求的建筑物。
一级:1)高级大型公共建筑;2)有地区性历史意义或技术要求复杂的中、小型公共建筑;3)16层以上、29层以下或超过50m高的公共建筑。
答:1)色彩处理要注意统一与变化,并掌握好尺度。
2)色彩运用应符合建筑性格。
3)色彩运用要与环境有机结合,既要与周围相邻建筑、环境气氛相协调,又要适应各地的气候条件与文化背景。
答:1)地基应具有足够的承载能力和均匀程度。
2)基础应具有足够的强度和耐久性。
3)经济技术要求。
四、构造图示题答:答:三、简答题答:①所选用的保温材料在正常使用条件下,不会有较大的变形损坏,以保证保温效果和使用寿命。
②在相同保温效果的前提下,导热系数小的材料其保温层厚度和保温结构所占的空间就更小。
但在高温状态下,不要选用密度太小的保温材料,因为此时这种保温材料的导热系数可能会很大。
③保温材料要有良好的化学稳定性,在有强腐蚀性介质的环境中,要求保温材料不会与这些腐蚀性介质发生化学反应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题与作业第一章绪论思考题1、冬天,经过在白天太阳底下晒过的棉被,晚上盖起来感到很暖和,并且经过拍打以后,效果更加明显。
试解释原因。
答:棉被经过晾晒以后,可使棉花的空隙里进人更多的空气。
而空气在狭小的棉絮空间里的热量传递方式主要是导热,由于空气的导热系数较小(20℃,1.01325×105Pa时,空气导热系数为0.0259W/(m·K),具有良好的保温性能。
而经过拍打的棉被可以让更多的空气进入,因而效果更明显。
2、夏季在维持20℃的室内工作,穿单衣感到舒适,而冬季在保持22℃的室内工作时,却必须穿绒衣才觉得舒服。
试从传热的观点分析原因。
答:首先,冬季和夏季的最大区别是室外温度的不同。
夏季室外温度比室内气温高,因此通过墙壁的热量传递方向是出室外传向室内。
而冬季室外气温比室内低,通过墙壁的热量传递方向是由室内传向室外。
因此冬季和夏季墙壁内表面温度不同,夏季高而冬季低。
因此,尽管冬季室内温度(22℃)比夏季略高(20℃),但人体在冬季通过辐射与墙壁的散热比夏季高很多。
根据上题人体对冷感的感受主要是散热量的原理,在冬季散热量大,因此要穿厚一些的绒衣。
3、试分析室内暖气片的散热过程,各环节有哪些热量传递方式?以暖气片管内走热水为例。
答:有以下换热环节及热传递方式(1)由热水到暖气片管到内壁,热传递方式是对流换热(强制对流);(2)由暖气片管道内壁至外壁,热传递方式为导热;(3)由暖气片外壁至室内环境和空气,热传递方式有辐射换热和对流换热。
4、冬季晴朗的夜晚,测得室外空气温度t高于0℃,有人却发现地面上结有—层簿冰,试解释原因(若不考虑水表面的蒸发)。
解:如图所示。
假定地面温度为了T e,太空温度为T sky,设过程已达稳态,空气与地面的表面传热系数为h,地球表面近似看成温度为T c的黑体,太空可看成温度为T sky的黑体。
则由热平衡:,由于T a>0℃,而T sky<0℃,因此,地球表面温度T e有可能低于0℃,即有可能结冰。
课后习题1-1对于附图所示的两种水平夹层,试分析冷、热表面间热量交换的方式有何不同?如果要通过实验来测定夹层中流体的导热系数,应采用哪一种布置?解:(a)中热量交换的方式主要有热传导和热辐射。
(b)热量交换的方式主要有热传导,自然对流和热辐射。
所以如果要通过实验来测定夹层中流体的导热系数,应采用(a )布置。
1-7一炉子的炉墙厚13cm ,总面积为20m 2,平均导热系数为1.04w/m ·k ,内外壁温分别是520℃及50℃。
试计算通过炉墙的热损失。
如果所燃用的煤的发热量是2.09×104kJ/kg ,问每天因热损失要用掉多少千克煤? 解:根据傅利叶公式kw t A Q 2.7513.0)50520(2004.1=-⨯⨯=∆=δλ 每天用煤d kg /9.3101009.22.753600244=⨯⨯⨯1-9在一次测定空气横向流过单根圆管的对流换热实验中,得到下列数据:管壁平均温度t w =69℃,空气温度t f =20℃,管子外径d=14mm ,加热段长80mm ,输入加热段的功率8.5w ,如果全部热量通过对流换热传给空气,试问此时的对流换热表面传热系数多大? 解:根据牛顿冷却公式c m w t A Q ︒∙=-⨯⨯⨯=∆=2/3.49)2069(08.0014.014.35.8α1-14宇宙空间可近似的看作0K 的真空空间。
一航天器在太空中飞行,其外表面平均温度为250K ,表面发射率为0.7,试计算航天器单位表面上的换热量? 解:航天器单位表面上的换热量2484241/155)250(1067.57.0)(m w T T Q =⨯⨯⨯=-=-εσ1-27附图所示的空腔由两个平行黑体表面组成,孔腔内抽成真空,且空腔的厚度远小于其高度与宽度。
其余已知条件如图。
表面2是厚δ=0.1m 的平板的一侧面,其另一侧表面3被高温流体加热,平板的平均导热系数λ=17.5w/m •K ,试问在稳态工况下表面3的t w3温度为多少? 解:表面1到表面2的辐射换热量=表面2到表面3的导热量δλσ2341420)(w w t t T T -=-c T T t t w w ︒=⨯-⨯+=-+=7.1325.171.0)34(67.5127)(444142023δλσt w3 ε=1.0 t w2=127℃t w1=27℃δ第二章 导热理论基础及稳态导热部分思考题1、一维无内热源、平壁稳态导热的温度场如图所示。
试说明它的导热系数λ是随温度增加而增加,还是随温度增加而减小?答:由傅立叶里叶定律,图中随x 增加而减小,因而随2增加x 而增加,而温度t 随x 增加而降低,所以导热系数随温度增加而减小。
2、在寒冷的北方地区,建房用砖采用实心砖还是多孔的空心砖好?为什么? 答:在其他条件相同时,实心砖材料如红砖的导热系数约为0.5W/(m·K)(35℃),而多孔空心砖中充满着不动的空气,空气在纯导热(即忽略自然对流)时,其导热系数很低,是很好的绝热材料。
因而用多孔空心砖好。
3、两种几何尺寸完全相同的等截面直肋,在完全相同的对流环境(即表面传热系数和流体温皮均相同)下,沿肋高方向温度分布曲线如图所示。
请判断两种材料导热系数的大小和肋效率的高低?答:对一维肋片,导热系数越高时,沿肋高方向热阻越小,因而沿肋高方向的温度变化(降落或上升)越小。
因此曲线1对应的是导热系数大的材料.曲线2对应导热系数小的材料。
而且,由肋效率的定义知,曲线1的肋效率高于曲线2。
4、用套管温度计测量容器内的流体温度,为了减小测温误差,套管材料选用铜还是不锈钢?答:由于套管温度计的套管可以视为一维等截面直助,要减小测温误差(即使套管顶部温度t H 尽量接近流体温度t f ),应尽量减小沿套管长度流向容器壁面的热量,即增大该方向的热阻。
所以,从套管树料上说应采用导热系数更小的不锈钢。
5、工程中应用多孔性材料作保温隔热,使用时应注意什么问题?为什么?答:应注意防潮。
保温材料的一个共同特点是它们经常呈多孔状,或者具有纤维结构,其中的热量传递是导热、对流换热、热辐射三种传热机理联合作用的综合过程。
如果保温材料受潮,水分将替代孔隙中的空气,这样不仅水分的导热系数高于空气,而且对流换热强度课后习题2-4一烘箱的炉门由两种保温材料A 和B 做成,且δA =2δB (见附图)。
已知λA =0.1 w/m •K ,λB =0.06 w/m •K 。
烘箱内空气温度t f1=400℃,内壁面的总表面传热系数h 1=50 w/m 2•K 。
为安全起见,希望烘箱炉门的外表面温度不得高于50℃。
设可把炉门导热作为一维导热问题处理,试决定所需保温材料的厚度。
环境温度t f2=25℃,外表面总表面传热系数h 2=9.5 w/m 2•K 。
解:按热平衡关系,有:)(1221f w BB A A wf t t t t -=++-αλλαh 1 t f1h 2 t f2 t wδA δ B)2550(5.906.01.0250150400-=++-B B δδ由此得,δB =0.0396m δA =2δB =0.0792 m2-8在如图所示的平板导热系数测定装置中,试件厚度δ远小于直径d 。
由于安装制造不好,试件与冷、热表面之间存在着一厚度为Δ=0.1mm 的空气隙。
设热表面温度t 1=180℃,冷表面温度t 2=30℃,空气隙的导热系数可分别按t 1、t 2查取。
试计算空气隙的存在给导热系数的测定带来的误差。
通过空气隙的辐射换热可以忽略不计。
(Φ=58.2w d=120mm)解:不考虑空气隙时侧得的导热系数记为λ0,则02915.02.58150420=⨯=∆=d t A πφλδ已知空气隙的平均厚度Δ1、Δ2均为0.1mm ,并设导热系数分别为λ1、λ2,则试件实际的导热系数应满足: φλλλδtA ∆=∆+∆+21110 所以21110λλλδλδ∆+∆=- 即92.2102915.003745.002646.002915.000267.00001.000378.00001.0021110=+=+=∆+∆=-λδλλλλλ%2-11一根直径为3mm 的铜导线,每米长的电阻为2.22×10-3Ω。
导线外包有1mm 、导热系数0.15w/m.k 的绝缘层。
限定绝缘层的最高温度为65℃,最低温度0℃,试确定这种条件下导线中允许通过的最大电流。
解:最大允许通过电流发生在绝缘层表面温度为65℃,最低温度0℃的情形。
此时每米导线的导热量:m W d d t l Q /9.11935ln 6515.014.3ln 212=⨯⨯=∆=πλ最大允许通过电流满足9.1192=R I mt 1t 2δ所以A I m 4.232=2-14一直径为30mm 、壁温为100℃的管子向温度为20℃的环境散热,热损失率为100W/m 。
为把热损失减小到50W/m ,有两种材料可以同时被利用。
材料A 的导热系数为0.5 w/m •K ,可利用度为3.14×10-3m 3/m ;材料B 的导热系数为0.1 w/m •K ,可利用度为4.0×10-3m 3/m 。
试分析如何敷设这两种材料才能达到上要求。
假设敷设这两种材料后,外表面与环境间的表面传热系数与原来一样。
解:对表面的换热系数α应满足下列热平衡式: 10003.014.3)20100(=⨯⨯-α由此得α=13.27 w/m 2•K每米长管道上绝热层每层的体积为)(4221i i d d V -=+π。
当B 在内,A 在外时,B 与A 材料的外径为d 2、d 3可分别由上式得出。
0774.003.0785.0104785.023212=+⨯=+=-d V d m1.00774.0785.01014.3785.023223=+⨯=+=-d Vd m此时每米长度上的散热量为:7.431.014.327.1315.028.6)4.77100ln(1.028.6)304.77ln(20100=⨯⨯+⨯+⨯-=l QW/m当A 在内,B 在外时,A 与B 材料的外径为d 2、d 3可分别由上式得出。
07.003.0785.01014.3785.023212=+⨯=+=-d V d m1.007.0785.0104785.023223=+⨯=+=-d Vd m此时每米长度上的散热量为:2.741.014.327.1311.028.6)70100ln(5.028.6)3070ln(20100=⨯⨯+⨯+⨯-=l Q W/m绝热性能好的材料B 在内才能实现要求。
2-35:一具有内热源∙φ,外径为r 0的实心长圆柱,向周围温度为t ∞的环境散热,表面传热系数为h ,试列出圆柱体中稳态温度场的微分方程式和边界条件,并对=∙φ常数的情形进行求解。
