菁才中学2012年八年级下学期期末测试
2012学年初二年级第二学期数学期末考试试卷

2012学年初二年级第二学期数学期末考试试卷一、选择题(本大题共6题,每题2分,满分12分)1.一次函数y=kx+k ,不论k 取何值,函数图像一定会经过定点 ( ) A. (1, -1 ) B. (1,0 ) C. (-1,0 ) D. C. (-1,1 ) 2.下列方程中,有实数根的方程是 ( )(A )01=+x ; (B )012=+x ; (C )x x =; (D )01=++x x . 3.在函数y=kx(k>0)的图象上有三点A 1(x 1,y 1),A 2(x 2,y 2),A 3(x 3,y 3),已知x 1<x 2<0<x 3,则下列各式中,正确的是( ) A .y 1<y 2<y 3 B .y 3<y 2<y 1 C .y 2<y 1<y 3 D .y 3<y 1<y 24.如图所示,已知△ABC 中,∠ABC=∠BAC ,D 是AB 的中点,EC ∥AB ,DE ∥BC ,AC 与DE 交于点O ,则下列结论中,不一定成立的是 ( )A. AC=DE B. AB=AC C. AD ∥EC 且AD=EC D. OA=OE5.在下列命题中,是真命题的是 ( )A .两条对角线相等的四边形是矩形B .两条对角线互相平分的四边形是平行四边形C .两条对角线互相垂直的四边形是菱形D .两条对角线互相垂直且相等的四边形是正方形 6.下列说法正确的是 ( )A .任何事件发生的概率为1; B .随机事件发生的概率可以是任意实数; C .可能性很小的事件在一次实验中有可能发生;D .不可能事件在一次实验中也可能发生。
二、填空题(本大题共12题,每题2分,满分24分) 7. 已知一次函数221)(--=x x f ,则=)2(f . 8. 如果关于x 的方程x k x =-25有实数根2x =,那么 . 9.已知12y y y =+,1y 与1x -成正比,2y 与x 成正比;当=2x 时,4y =,当=1x -时, -5y =,则y 与x 的函数10. 已知平面直角坐标系内,O (0,0), A (2,6), C (6,0)若以O ,A ,C ,B 为顶点的四边形是平行四边形,则点B 不可能在第 象限。
2012012学年第二学期八年级语文期末试卷答案.doc

2011-2012学年第二学期八年级语文期末试卷答案1.ní、qǐ、谧、璀2.(1)举杯销愁愁更愁(2)殷勤谢红叶(3)何当共剪西窗烛(4)燕然未勒归无计(5)且教桃李闹春风(6)江山代有才人出(7)沉舟侧畔千帆过,病树前头万木春(8)春蚕到死丝方尽,蜡炬成灰泪始干.3.(1)李逵、两把板斧、李鬼(一空1分)(2)鲁智深(1分),见义勇为、嫉恶如仇、好打抱不平、急躁莽撞、粗中有细等等(答出二个词语得1分)4.第一句:将讨论并阅读改为阅读并讨论第二句:将不但我改为我不但第三句:将激励着我战胜困难的动力改为激励着我战胜困难5.考古学家将挖掘《蒙娜丽莎》原型的骸骨,并试图复原那神秘微笑。
6.近窗病人:心地善良、乐于助人、无私等(1分)远窗病人:本性善良(1分)但嫉妒心强、心胸狭隘、自私冷漠等(1分)7.窗是本文的线索(1分),且窗这个词一语双关:既指实物窗,又指心灵之前窗。
(1分)与中心相扣。
8.只要……就……在文中强调了,救助近窗病人对于远窗病人来说轻而易举,是举手之劳(1分);然而他却纹丝不动,以此衬托他的自私、冷漠。
(1分)9.这一结尾既在意料之外又在情理之中(1分)墙,一语双关,以光秃秃、毫无生气的窗外之景衬托远窗病人被嫉妒心蒙蔽的卑劣心灵(1分)并从中透露出之前窗外的美景都是近窗病人善意的谎言,表现出近窗病人美好的心灵。
(1分)10.言之有理即可11.特别爱好;光彩耀眼的样子;之于;挂在腰间(或腰间挂着)12.D13.(1)因此人们大多愿意把书借给我,我于是能够博览群书。
(2)因为心中有足以快乐的事,不是觉得吃得、穿得不如别人。
(3)朝廷每天有米粮供给,父母每年有冬夏的衣服给予。
14.盖余之勤且艰若此。
(1分)写同舍生的衣着、装扮,是为了和我的生活状况形成对比(1分),突出我的生活条件艰苦。
(1分)15.形成对比(1分)是为了说明一个道理:学习能否有所成就,关键在于是否专心刻苦。
(2分)16.线索:情感---人们对于希特勒的仇恨。
2012八年级下期末综合检测试题(三)3

密封 线学校 班级姓名 学号密 封 线 内 不 得 答 题2011—2012年第二学期八年级数学期末质量检测试题(三)时间:90分钟 满分:100分 得分一、选择题:(每小题3分,共30分)每小题只有一个选符合题目的要求,请你把你认为正确的选项的代号填入题后所给的括号内。
1.若分式34922+--x x x 的值为0,则x 的值为( )A . 3-B .3或3-C .3D .无法确定2.已知反比例函数ky x=的图象经过点(3)m m ,,则此反比例函数的图象在( ) A .第一、二象限 B .第一、三象限 C .第二、四象限 D .第三、四象限 3.下列分式运算错误的是( )A .)0(≠=c bc ac b aB .1-=+--b a b aC .ba ba b a b a 321053.02.05.0-+=-+ D .x y x y y x y x +-=+- 4.如图,四边形ABCD 中,cm DA cm BC cm AB 13,4,3===,cm CD 12=,且090=∠ABC ,则四边形ABCD 的面积为( )A .84B .36C .251D .无法确定5.在平面直角坐标系中,C B A ,,三点的坐标分别为)2,2(),5,0(),0,0(---,以这三点为平行四边形的三个顶点,则第四个顶点不可能在( )A .第一象限B .第二象限C .第三象限D .第四象限 6.已知一组数据54321,,,,a a a a a 的平均数为8,则另一组数据101+a ,102-a ,103+a ,10,1054+-a a 的平均数为( ) A .6 B .8 C .10 D .127.将n 个边长都为cm 1的正方形按如图1所示的方法摆放,点,,21A A ……,n A 分别是正方形的中心,则n 个这样的正方形重叠部分(阴影部分)的面积和为( )A .241cmB .24cm n C.241cm n - D .24cm n8.如图2,四边形ABCD 的对角线互相平分,可供添加的条件有①BC AB ⊥;②BC AB =;③BD AC ⊥;④BD AC =,其中能使它变为矩形的是( )A .①②B .②④C .③④D .①④9.边长为4的正方形ABCD 的对称中心是坐标原点x AB O //,轴,y BC //轴, 反比例函数x y 2=与xy 2-=的图象均与正方形ABCD 的边相交,则图4中的阴影部分的面积是( ) A .2 B .4 C .8 D .6 10.在一次科技知识竞赛中,两组学生成绩统计如下表,通过计算可知两组的方差为2S 172甲=,2S 256乙=。
2012年八年级(下)期末教学质量监测数学试题(含答案)

2011-2012学年度下学期期末教学质量监测八年级数学试题一、确的,请把正确的答案写在下面的答题栏中)1A .31B .3.0C .3a 2+D .2ab2、甲、乙两地六月上旬各天的平均气温如下表所示(单位:℃)甲地:27 25 22 26 24 23 21 19 22 28 乙地:30 29 28 31 32 29 27 28 26 24要判断两地这10天气温的波动程度,你认为用什么数据来表达比较合适? A .极差 B .平均数 C .方差 D .中位数 3、将一副三角板按图中的方式叠放,则角α等于 A .75B .60C .45D .304、如图,在直角坐标系中,OB=OD ,AB=CD ,若点A 的坐标为A (0,3),则点C 的坐标是A .(0,3)B .(0,-3)C .(-3,0)D .(3,0)5、在正方形网格中,AOB ∠如图放置,则sin AOB ∠的值是 A .32 B .13132 C .13133 D .无法确定 OBA第4题图 α 第3题图6、下列各式中正确的是 A .552±=B5=-C.25=- D.5=-7、下列命题①同旁内角互补;②各角对应相等的两个三角形全等;③两组角对应相等的两个三角形相似;④有两角相等的三角形是等腰三角形,其中真命题有 A .1个 B .2个 C .3个 D .4个 8、下列各组二次根式不是..同类二次根式的是 A .21与8 B .2.0与8.0 C .753与45 D .x 与3x9、如果一组数据x 1,x 2,x 3,…,x n 的方差s 2=5,那么x 1-3, x 2-3, x 3-3, …, x n -3的方差是 A .5B .2C .8D .510、如图,在△ABC 中,DE ∥BC ,若AD =3,BD =4,BC =5,则DE 的长为A .154B .157C .125D .5211、如图,AB//CD ,点E 在CB 的延长线上,若∠ABE =60°,则=∠ECD A .120° B .100° C .60° D .20° 12、如图,D 、E 分别是ABC ∆的边AB 、AC 上的点, DE ∥BC ,并且32=AB AD ,则ADE ∆的面积与四边形DECB 的面积之比是A .2∶1B .2∶3C .4∶9D .4∶513、若一组数据2,4,6,8,x 的平均数是6,则这组数据的标准差是 A .22 B .8C .102D .4014、如图,沿坡度1i =:3的山坡植树,要求相邻两棵树之间的水平距离AC =2m ,那么相邻两棵树间的斜坡距离AB 为 A .4m B .334m C .22m D .32m第10题图DE CBA第12题图ABCDE第11题图第5题图ABCDE15、如图所示,将直角三角形ABC 绕顶点A 顺时针旋转60°后,得到直角三角形AB′C′,且C′为BC 的中点,则C′D ∶DB′的值为 A .1∶2 B .1∶22C .1∶3D .1∶3二、填空(请将答案直接填写在横线上)16、某校八年级(一班)班长统计了去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,根据折线图我们可以发现这组数据的极差是 .17、如图,CAE BAD ∠=∠,要使ABC ∆∽ADE ∆,还需添加一个条件,这个条件可以是 (只需写出一个).18、在用反证法证明“在ABC ∆中,A ∠和B ∠不可能都是直角”时,第一步应为. 19、要使式子x2x -有意义,则x 的取值范围为 . 20、命题“等边三角形的各个内角相等”的逆命题写成“如果……,那么……。
2012学年第二学期期末考试八年级语文试卷

2012学年第二学期期末考试八年级语文试卷第一部分阅读(90分)一、文言文阅读(42分)(一)默写(18分)1.神龟虽寿,犹有竟时。
__________,__________。
2._______________,坐我潇湘洞庭。
3.王于兴师,修我甲兵。
_______________。
4.__________________,笑谈渴饮匈奴血。
5.青山绿水,__________________。
6.复投之,__________________。
(二)古诗词阅读理解(4分)四块玉·别情关汉卿自送别,心难舍,一点相思几时绝? 凭阑袖拂杨花雪。
溪又斜,山又遮,人去也!7.本曲的曲牌名是_______________。
(2分)8.下列理解正确的一项是____(2分)A.“杨花雪”指的是如杨花般飞舞的雪。
B.“斜”指的是溪流歪斜着向远处伸展。
C.“凭阑”指的是主人公正在倚栏远眺。
D.本曲写出友人间依依不舍的离别之情。
(三)阅读下文,完成9——11题(8分)黔之驴①黔无驴,有好事者船载以入。
至则无可用,放之山下。
虎见之,庞然大物也,以为神,蔽林间窥之,稍出近之,慭慭然,莫相知。
①他日,驴一鸣,虎大骇,远遁;以为且噬己也,甚恐。
然往来视之,觉无异能者;益习其声,又近出前后,终不敢搏。
稍近,益狎,荡倚冲冒。
驴不胜怒,蹄之。
虎因喜,计之曰:“技止此耳!”因跳踉大㘎,断其喉,尽其肉,乃去。
9.本文作者是_________,我们还学过他写的一篇山水游记,篇名是《_________》。
(2分)10.用现代汉语翻译文中的画线句,注意加点词的意思。
(3分)因跳踉大㘎,断其.喉,尽其肉,乃去。
_____________________________11.下列理解正确的一项是____(3分)A.本文详略分明,重点刻画的是驴的形象B.本文以描写为主,主要采取了肖像描写。
C.本文讽刺那些外强中干、无才无德的人。
D.“黔驴技穷”、“虎视眈眈”均出自本文。
2012—2013学年下期期末考试

1 2012—2013学年下期期末考试
八年级 物理 参考答案
一、1.相互的 具有惯性 2.力的作用点 竖直向下 3..小 瓶内水面上方的气压比瓶外大气压小 4. 大于 甲 5.变大 变大 6. 弹 200 7. 变小 不变 支持力 8.3 杠杆自重
二、 9.B 10.B 11.A 12.D 13.C 14.C 15.D 16.B 17.D 18.A 三、
四、21. ( l ) 1.6 0 ( 2 )木块做加速运动(或测力计不在水平方向上)
22.(1)竖直 匀速 (2)71% 74% (3)其它条件一定时,物重越大,机械效率越高 (4)没有摩擦力的作用
23.(1)2、3 (2)下落的高度 地面材料 球的型号 (3)篮球受到空气阻力(或能量转化过程中有损耗) (4)物体间力的作用是相互的(或重力势能转化为动能,只要合理即可)
五、
24.(1)运动状态 重 (4分)
(2)F=G=mg=60kg ×10N/kg=600N (2分)
P=F/S=600N/150×10-4m 3=4×104Pa (2分)
(3)V=m/ρ=60kg/1.0×103m 3=0.06 m 3 (2分)
V 排=0.9V=0.054 m 3 (2分)
F 浮=ρ水
g V 排=540N (2分) 25. (1)小于 mg kv 3t (6分)
(2)P=Fv=8.16×107W (2分)
(3)W=Pt=4.896×1010J (3分)
F G F
L 2。
2012年下学期八年级数学期末试卷(1)

2012年下学期八年级数学期末综合试卷(1)一.选择题(本题共8个小题,每小题3分,满分24分) 1. 9的平方根是A .没有平方根B .3C .3-D .3± 2.在实数23-,0,35,πA .1个B .2个C .3个D .4个 3.一个正方形的面积是18,估计它的边长的大小在A .2与3之间B .3与4之间C .4与5之间D .5与6之间 4.函数y=中,自变量x 的取值范围是A .1x ≥-B .12x -≤≤C .2x ≥-D .21x x ≥-≠且5.在一个暗箱里放有若干个除颜色外其他完全相同的球,其中红球只有3个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱,通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出这个暗箱这大约有球A.12个B.9个C.4个D.3个 6. 如图所示,△ABC 与△A ′B ′C ′关于直线l 对称,则∠B 的度数为 A .100oB .90oC .50oD . 30o7.甲、乙两人赛跑,所跑路程S 与时间t 之间的函数关系如下图所示,小王根据图象得到如下四个信息,其中错误的是A .这是一次1500m 赛跑;B .甲、乙两人同时起跑;C .甲、乙两人中先到达终点的是乙;D .甲在这次赛跑中的速度为5m/s 。
8. 如图,已知ABC △中,45ABC ∠= , F 是高AD 和BE 的交点,4CD =,则线段DF 的长度为 ( ) A.. 4 C..二.填空题(本题共8个小题,每小题3分,满分24分) 9.的相反数是 .第6题图CB ′l第8题图10.在直角坐标系中,点(32)P --,关于y 轴的对称点坐标是 . 11.一次函数24y x =-+不经过第 象限。
12.将直线2y x =+3向下平移5个单位,所得直线的函数解析式为 。
13.若一组数据 1、1、2、3、x 的平均数是3,则数1在这组数据中出现的频率是 .14.已知函数y kx b =+和y mx n =+的图象如图所示,则关于x y ,的方程组y kx b y mx n =+⎧⎨=+⎩的解是 .15.如图所示,已知A D ∠=∠,请添加一个条件,使△ABC ≌△DCB ,那么你添加的条是 。
2012学年第二学期期末考试

2012学年第二学期八年级期终考试数学试卷(时间90分钟,满分100分)考生注意:1.本试卷含四个大题,共26题;2.答题时,考生务必按答题要求在答题纸的规定位置上作答,在草稿纸、本试卷上答题无效;3.除一、二大题外,其余各题如无特殊说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题(本大题共6题,每题2分,满分12分) 1.一次函数21y x =-的图像不经过( )A.第一象限;B.第二象限;C.第三象限;D.第四象限.2.若一次函数y kx b =+的函数值y 随x 的增大而减小,且图像与x 轴负半轴相交,那么对k 与b 的符号判断正确的是( )A.第一象限;B.第二象限;C.第三象限;D.第四象限. 3.用换元法解分式方程2211x x x x --=-时,如果设1x y x =-,将原方程化为关于x 的整式方程,那么这个整式方程是( )A.2210y y -+=; B.2210y y --=; C.220y y +-=; D.220y y --=. 4.下列图形中,是中心对称图形的是( )A.平行四边形;B.等边三角形;C.直角梯形;D.等腰梯形5.如图1,E 是梯形ABCD 底边BC 上一点,且ABED 为菱形,下列向量中与BE相等的向量是( )A.AB; B.EC ; C.AD ; D.DA .6.下列事件中,随机事件是( )A.从长度为3,4,5,6的四条线段中任取3条,这三条线段能构成三角形;B.任取一个反比例函数,它的图像与x 轴有交点;C.任取一个一元二次方程,该方程有两个实数根;D.将一个实数平方,所得的结果小于0.二、填空题(本大题共12题,每题3分,满分36分) 7.直线3y x =-与y 轴的交点坐标是 .8.若一次函数2y x b =+的图像向上平移四个单位后经过点()2,1-,则b 的值为 .图1CDBA E9.关于x 的方程:21ax x =-的解是 . 10.0x =的解是 .11.在平面直角坐标系xOy 中,在直线21y x =-+上,位于x 轴下方的所有点的横坐标的取值范围是 .12.某航空公司规定,旅客乘机需付旅行费y (元)与所携带行李的重量x (公斤)的关系在平面直角坐标系中可以表示成一条射线,如图2所示,如果某旅客携带35公斤行李登机,那么他需付行李费 元. 13布袋里有2个红球和3个黄球,它们除颜色外其他都相同,从布袋里同时取出2个球恰好都是黄球的概率是 .14.若某个多边形的内角和为1260o,则它的边数为 .15.如果一个梯形的中位线长是6,高是4,那么它的面积等于 .16.如果一个等腰梯形的一个底角为60o ,它的上、下底长分别为3和5,那么其腰长为 . 17.如果把正方形ABCD 绕点C 旋转得到正方形'''A B CD ,点'B 落在对角线AC 上,点'A 落在CD 的延长线上,那么''AA B ∠= .18.如图3,平行四边形ABCD 中,对角线AC 和BD 交与点O ,过点O 作OE AB ⊥,垂足为E ,如果6,53AD AE BE ===,,那么BO 的长为 .三、解答题(本大题共6题,每题6分,满分36分) 19.(本题满分6分) 解方程:262122x x x +=+-+20.(本题满分6分)解方程组:2233221x y x x y ⎧-=-⎪⎨-=⎪⎩L L L L L ①②图2E OCDBA图321.(本题满分6分)如图4,在ABC △中,AB a = ,AC b =.(1)BC = ;(用含有a ,b的式子表示) (2)在答题卷上求作:AB AC +(不要求写出作法)(3)若1,2,90AB AC A ==∠=,则AB AC += .22.(本题满分6分)如图5,E 、F 是平行四边形ABCD 对角线上的两点,且BE DF =. 求证:四边形AECF 是平行四边形.23.(本题满分6分)如图6,在梯形ABCD 中,AD BC =,AB ∥DC ,2DC AB =,分别在对角线CA ,DB 延长线上取点E 、F ,使得,EA OA FB OB ==,依次联结DE 、EF 、FC .(1)求证:BDC ACD ∠=∠; (2)求证:四边形DCFE 是矩形.24.(本题满分6分)某校原有一个面积为48平方米的矩形花坛,现因学校改建,花坛的其中一边长需减少2米,为了使改建后的花坛仍为矩形且面积不变,因此另一边长需增加四米,问改建后花坛的周长是多少米?CAB图4BAOFECD图6EDAFC B 图5四、综合题(本大题共2题,每题8分,满分16分) 25.(本题满分8分)如图7,在平面直角坐标系xOy 中,点A 的坐标为()3,0,点B 的坐标为()0,4. (1)求直线AB 的解析式;(2)点C 是线段AB 上一点,O 为坐标原点,点D 在第二象限,且四边形BCOD 为菱形,求点D 坐标; (3)在(2)的条件下,点E 在x 轴上,点P 在直线AB 上,且以B 、D 、E 、P 为顶点的四边形是平行四边形,请将所有满足的点P 的坐标直接写在答题卷指定位置.备用图图726.(本题满分8分)如图8,正方形ABCD 中,1AB =,E 为边AB 上一点(点E 不与端点A 、B 重合),F 为BC 延长线 上一点,且AE CF =,联结EF 交对角线AC 于点G(1)设,AE x AG y ==,求y 关于x 的函数解析式及定义域; (2)联结DG ,求证:DG EF ⊥图8GDAB EF备用图GD AB EF。
2012~2013学年度第二学期八年级期末测试卷

2012~2013学年度第二学期八年级期末测试卷数 学一、选择题(每小题2分,共12分)1.函数1y x=-的图像位于( )A .第一、三象限B .第二、四象限C .第一、二象限D .第三、四象限 2.下列命题中,真命题是( ) A .内错角相等 B .面积相等的三角形全等 C .任何数的平方都大于0 D .两点之间线段最短3.一个不透明的盒子里装有1个白球,一个红球,若干个黄球,这些球除了颜色外,没有任何其他区别.若从这个盒子中随机摸出一个是黄球的概率是35,则盒子中黄球的个数是( )A .1B .2C .3D .44.从下列不等式中选择一个与12x +≥组成不等式组,若要使该不等式组的解集为1x ≥,则可以选择的不等式是( ) A .0x > B .2x > C .0x < D .2x < 5.如图,已知12∠=∠,那么添加下列一个条件后,仍无法判定ABC ADE ⊿⊿的是( )A .AB AC AD AE = B .AB BC AD DE =C .BD ∠=∠ D .C AED ∠=∠21DAB CE6.某班四个小组进行辩论比赛,赛前甲、乙、丙三位同学预测比赛结果如下: 甲说:“第二组得第一,第四组得第三”; 乙说:“第一组得第四,第三组得第二”; 丙说:“第三组得第三,第四组得第一”;赛后得知,三人各猜对一半,则冠军是( ) A .第一组 B .第二组 C .第三组 D .第四组 二、填空题(每小题2分,共20分)7.当x =__________时,分式23x x-+没有意义.8.已知23a b =,则3ba bα+=-___________.9.在比例尺为18000000∶的地图上,南京与徐州的图上距离是4.4cm ,则南京与徐州的实际距离是__________km .10.已知小明同学身高1.5米,经太阳光照射,在地面的影长为2米,若此时测得一塔在同一地面的影长为60米,则塔高应为__________米.11.ABC △的三条边之比为2∶5∶6,与其相似的三角形最大边长为12cm ,则最小边的长为__________cm .12.对于反比例函数2y x-=,下列说法:①点(-2,-1)在它的图象上;②它的图象在第一、三象限;③当0x >时,y 随x 的增大而增大;④当0x <时,y 随x 的增大而减小.上述说法中,正确的序....号.是__________.(填上所有你认为正确的序号)13.若关于x 的方程1011m xx x --=--有增根,则m 的值是__________. 14.如图,将三角尺与直尺贴在一起,使三角尺的直角顶点()90C ACB ∠=︒在直尺的一边上,若130∠=︒,则2∠=__________.(第14题)15.如图,以数轴上的原点为位似中心,将边长为32的正方形ABCD 放大为原来的2倍,若A B 、两点均在数轴上,且A 点对应的实数是2,则B '点对应的实数是__________.(第15题)C '16.如图,矩形AOCB 的两边OC OA 、分别位于x 轴、y 轴上,点B 的坐标为2053B ⎛⎫- ⎪⎝⎭,,D 是AB 边上的一点.将ADO △沿直线OD 翻折,使A 点恰好落在对角线OB 上的点E 处,若点E 在一反比例函数的图像上,那么该函数的关系式是__________.(第16题)三、解答题:(本大题共12小题,共88分)17.(7分)解不等式组()2322122x x x x +≥+⎧⎪⎨-⎪⎩,<,并写出不等式组的整数解.18.(6分)先化简,再求值:2121a a a a a -+⎛⎫-÷ ⎪⎝⎭,其中2a =.19.(6分)解分式方程:11222x x x-+=--. 20.(6分)下表反映了x 与y 之间存在某种函数关系,现给出了几种可能的函数关系式:61751y x y x y y x =+=-=-=-,,,(2)请说明你选择这个函数表达式的理由.21.(7分)把一个可以自由转动的均匀转盘3等分,并在各个扇形内分别标上数字(如图).小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之积是偶数,小明获胜,否则小亮获胜.你认为游戏是否公平?请说明理由.(第21题)22.(8分)如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO 表示直立在广场上的灯杆,点P表示照明灯的位置.(第22题)P(1)在小亮由B处沿BO所在的方向行走到达O处的过程中,他在地面上的影子长度的变化情况为__________________;(2)请你在图中画出小亮站在AB处的影子;(3)当小亮离开灯杆的距离 4.2mOB=时,身高(AB)为1.6m的小亮的影长为1.6m,问当小亮离开灯杆的距离6mOD=时,小亮的影长是多少m?23.(4分)阅读材料,解答问题:观察下列方程:①23xx+=;②65xx+=;③127xx+=;…;(1)按此规律写出关于x的第4个方程为____________________,第n个方程为____________________;(2)直接写出第n个方程的解,并检验此解是否正确.24.(6分)如图,一条4m宽的道路将矩形花坛分为一个直角三角形和一个直角梯形,根据图中数据,求这条道路的占地面积.(第24题)D C25.(9分)某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.(1)甲、乙工程队每天各能铺设多少米?(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工作量(以百米为单位)的方案有几种?请你帮助设计出来.26.(8分)如图,在直角坐标系中,O 为坐标原点.已知反比例函数()0ky k x=>的图像经过点()4A m ,,过点A 作AB x ⊥轴于点B ,AOB △的面积是2. (1)求k 和m 的值;(2)过原点O 的直线y nx =(n 为常数,且0n ≠)与反比例函数ky x=的图像交于P Q 、两点,当线段PQ 长度取最小值时,求点P 和点Q 的坐标;(3)请你直接根据图像写出使得knx x>成立x 的取值范围.27.(9分)【问题提出】规定:四条边对应相等,四个角对应相等的两个四边形全等.我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究. 【初步思考】在两个四边形中,我们把“一条边对应相等或一个角对应相等”称为一个条件.满足4个条件的两个四边形不一定全等,如边长相等的正方形与菱形就不一定全等.类似地,我们容易知道两个四边形全等至少需要5个条件. 【深入探究】(1)小莉所在学习小组进行了研究,她们认为5个条件可分为以下四种类型,小莉写出其中的两种类型,请你写出剩下的两种类型: Ⅰ一条边和四个角对应相等; Ⅱ______________________; Ⅲ______________________; Ⅳ四条边和一个角对应相等.(2)现对Ⅰ、Ⅳ两种类型进行深入研究,请你用“八下证明(一)”全等三角形知识解决以下问题: ①小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等,请你举例说明.②小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等,请你结合下图进行证明(不需要写出每一步推导的理由).已知:如图,______________. .求证: ______________. . 证明:(第27题)DACA 1B 1C 1D 1【联想迁移】(3)类比以上小红判断两个四边形全等的方法,你能得出“要使得两个四边形相似,需要满足的条件是________________________________________”. 28.(12分)我们曾“利用一张不等边三角形纸片折出一个矩形”(如图①),矩形的四个顶点在三角形的三边上,那么称这个矩形叫做三角形的内接矩形.(第28题)D GACE F图③图②图①【画法初探】 (1)如图②,在ABC △内任作一矩形DEFG ,点D 在边AB 上,点E F 、在边BC 上,借助矩形DEFG ,利用位似作图,画出ABC △内接矩形(画图工具不限,保留画图痕迹或有必要的说明);(2)按照以上作图方法,你觉得一个三角形存在__________个内接矩形,要使得作出的内接矩形为正方形,四边形DEFG 的形状是__________形; 【特例探究】(3)若ABC △为锐角三角形,则存在__________个内接正方形, 若ABC △为直角三角形,则存在__________个内接正方形, 若ABC △为钝角三角形,则存在__________个内接正方形;(4)如图③,若用一个不等边锐角ABC △(a b c >>)纸板制造面积尽可能大的正方形,则正方形两个顶点应都在__________条边上. 【拓展应用】(5)如图④,ABC △的高AD 为3,BC 为4,过AD 上任一点G 作ABC △的内接矩形EPQF ,以EF 为斜边作等腰直角三角形HEF (点H 与点A 在直线EF 的异侧),设EF 为x ,EFH △与四边形EPQF 重合部分的面积为y . ①求线段AG (用x 表示);②求y 与x 的函数关系式,并求x 的取值范围.第28题④D GAB CE FPQ。
2012-2013学期2期末答案

2012—2013学年度第二学期终结性检测八年级数学参考答案及评分标准一、选择题(每题3分,共30分)二、填空题(每题3分) 11、5312、 613、(1)43(2) 7 (3)220y t =- 15、8 16、 96 1922n三、解答题17、∵四边形ABCD 是正方形,∴AD=AB , 90DAB ∠= …………………………………………1分 ∴90DAF DAB ∠=∠=……………………………………… 2分 ∵E 是AD 的中点,∴12AE AD =∵AF =21AB ∴AE =AF ………………………………………………………3分 ∴DAF BAE △≌△ ………………………………………… 5分 ∴BE =DF ………………………………………………………6分18、(1)(31)(03)A B ,,,-…………………………………………2分设一次函数的表达式为y kx b =+,依题意得13,3k b b =+⎧⎨-=⎩ ∴4,33k b ⎧=⎪⎨⎪=-⎩所求一次函数的表达式为433y x =-(2)设(0,)P p ∵12ABP AOB S S ∆∆=∴12BP OB = ………………………………………………………4分∵(03)B ,- ∴32BP =∴39(0,)(0,)22P --或…………………………………………………6分 19、∵∠ACD =∠B ,∠A =∠A ,∴△ACD ∽△ABC ………………………………………………1分 ∴AC ADAB AC=…………………………………………………2分 ∴2AC AD AB =⋅ ………………………………………3分 又∵AB =4,D 为AB 中点 ∴AD =2∴2248AC AD AB =⋅=⨯= ……………………………4分 ∴AC =……………………………………………5分20、过点A 作AE DC ∥ …………………………………………1分 又∵AD ∥BC , ∴AECD 是平行四边形∴AD =EC ,AE =DC ………………………………………………… 2分 ∵AD =3,BC =7∴BE =4 ……………………………………………3分∵AB =DC , AE =DC ∴AB =AE 又∵∠ABC =60°∴△ABE 是等边三角形…………………………………………… 4分 ∴4AB = ………………………………………………………5分21、(1)400 , 0.31 …………………………………2分(2)略 …………………………………4分 (3) 500 ………………………………………………5分22、(1)5 ………………………………………………2分(2)(0,0),(4,2),(4,4),(3,3),(3,2),(0,1)………………………………………………6分注:(2)题写对2个给1分,写对3个给2分,写对4个给3分, 写对6个给4分23、取BE 中点H ,连结FH …………………………………1分 ∵ F 是AE 的中点∴ FH 为△EAB 的中位线∴11=22FH AB FH AB ∥, ………………………………2分EA BD CA 又∵ABCD∴ ,DC AB DC AB =∥∴ FH ∥EC∴ ∠CEG =∠FHG ,∠ECG =∠HFG 又∵ E 为DC 中点∴ 1122EC DC AB FH === …………………………3分∴ △ECG ≌△HFG …………………………4分 ∴ GF =GC ……………………………………5分24.(1)作CF ⊥AD 交AD 的延长线于F . ……………………1分 ∵ ∠ADC =120°, ∴ ∠CDF=60°.在Rt △CDF 中,3.FC CD === …………………………3分 即点C 到直线AD 的距离为3. (2)∵ ∠BED=135°,BE = ∴ ∠AEB =45°. ∵ 90A ∠=︒, ∴ ∠ABE =45°.∴ 2.AB AE == ……………………………………………4分 作BG ⊥CF 于G .可证四边形ABGF 是矩形. ∴ FG =AB =2,CG =CF -FG =1.H∵ 12DF CD ==∴ 22 4.BG AF AE ED DF ==++=+= ………………5分∴ BC === ………………………………6分 25.(1) 不是; 是. ………………………………2分 (2)如图所示:∵点P (a ,3)在y =-x +b 上 ∴3=-a +b ∴a =b -3则P (b -3,3) …………………………………………………3分 ∴OA =PB =3,PA =OB =|b -3| ∵和谐点P 在y =-x +b 上 ∴2OA +2PA =OA ·PA即2×3+2·|b -3|=3 ·|b -3| ∴|b -3|=6解得:b =9或-3 ∴a =6或-6∴a =6,b =9或a =-6,b =-3…………………………4分(3)如图所示∵点Q 在直线y =x +4上,∴设点Q 坐标为(x ,x +4) ∴OA =|x |,QA =|x +4| 由题意得2|x |+2|x +4|=|x |·|x +4|① 当x >0时,2x +2(x +4)=x整理得,x 2=8解得,x =(舍负)此时,和谐点Q 坐标为(+4) ……………………6分○2当-4<x <0时,-2x+2(x+4)=-x ·(x+4) 整理得,x 2+4x+8=0, 此方程无解○3当x <-4时,-2x -2(x+4)=(-x )·[-(x+4)] 整理得,x 2+8x+8=0解得,x =-4-4+此时,和谐点Q 坐标为(-4-8分 综上:点Q 坐标为()或(-4-,-。
-2012学年八年级下学期期末试卷(人教版,附答案)

2011—2012学年(下)期末调研抽测试卷八年级历史(考试时间60分钟,满分100分)题号一二三总分分数一、选择题:本大题共25小题,每题2分,共50分。
以下各题中只有一个选项最符合题目要求,请将其字母代号填入下表中。
题号 1 2 3 4 5 6 7 8 9答案题号10 11 12 13 14 15 16 17 18答案题号19 20 21 22 23 24 25答案1.黄继光是“最可爱的人”的代表,他牺牲于()A.渡江战役B.百团大战C.上甘岭战役D.孟良崮战役2.我国存在了两千多年的封建剥削土地制度被彻底废除的标志是()A.土地改革基本完成B.1950年《中华人民共和国土地改革法》的颁布C.中华人民共和国的成立D.对农业的社会主义改造基本完成3.第一个五年计划期间,以鞍山钢铁公司为中心的工业基地位于我国()A.华北地区B.东南沿海地区C.东北地区D.西北地区4.1954年第一届全国人民代表大会胜利召开具有里程碑意义。
这次会议的最重要成果是()A.选举了国家领导人B.强调了坚持民主集中制C.通过了《中华人民共和国宪法》D.宣告中华人民共和国成立5.创作于1948的《暴风骤雨》中关于分马有这样的一段描写:“……郭全海和老初带领积极分子们,忙着分牲口。
……整个场子里,有二百七八十匹骡马,还有二三十头牛,外加五条小毛驴。
牲口都标出等次,人都按着排号的次序,重新分配,他们计算了,全屯没马的小户,都能摊上一个顶用的牲口。
”这样的场景应该是在()A.抗日战争时期B.解放战争时期C.土地改革时期D.三大改造时期6.在中国进行的社会主义改造中,最主要的创举是()A.实现农业合作化B.对农业的社会主义改造C.对资本主义工商业的赎买政策D.没收官僚资本,建立社会主义国营经济7.我国进入社会主义初级阶段的标志是()A.中华人民共和国成立B.三大改造的基本完成C.土地改革的完成D.《中华人民共和国宪法》的制定8.中国结束了靠“洋油”的时代始于()A.新中国成立后B.三大改造完成后C.大庆油田的建成D.改革开放以后9.下图反映的是1958年某日出版的《人民日报》,它报道了福建花生的产量,出现这种报道的主要原因是()A.农村生产力有了很大的提高B.《人民日报》凭空虚构C.当地群众弄虚作假D.当时浮夸风盛行10.下列均是为我国社会主义建设事业作出卓越贡献而成为全国人民楷模的人物,其中为我国核武器的研究作出了卓越贡献的是()A.焦裕禄B.王进喜C.雷锋D.邓稼先11.“文化大革命”的十年是指()A.1959-1969年B.1966-1976年C.1968-1978年D.1957-1967年12.中共十一届三中全会是建国以来党的历史上的伟大转折。
2012年八年级(下)期末质量抽测数学试题(含答案).doc

八年级数学试卷1. 下列各代数式中,属于分式的是( ▲ )A. 13B. 3xC. 1aD. 232xy2. 最近科学家们研制出了目前世界上最小的有机发光装置,这个装置只有0.0000002m 长, 这样小的光源可制作很小的电子设备.把0.0000002用科学记数法表示为( ▲ ) A .2×10-6 B .2×10-7 C .0.2×10-8 D .200×10-93. 下列各式与33x x -+相等的是( ▲ )A.(3)5(3)5x x -+++B. 222233x x -+ C . 2323x x -+ D. 222(3)3x x -- 4. 下列计算正确的是( ▲ )A .3)3(2= B .3)3(2-=- C .39±= D=5. 一鞋店试销一种新款凉鞋,试销期间销售情况如下表:尺码(cm ) 22 23 24 25 数量(双)310222则下列统计量对鞋店经理来说最有意义的是( ▲ )A. 平均数B. 众数C. 中位数D. 方差 6. 顺次连结四边形各边中点所得到的四边形一定是( ▲ ) A .平行四边形 B .矩形 C .菱形 D .正方形7. 在△ABC 中,∠A ,∠B ,∠C 的对边分别是a ,b ,c ,满足下列条件的△ABC ,不是..直角三角形的是( ▲ )A. ∠A ∶∠B ∶∠C = 1∶1∶2B. a ∶b ∶c =1∶1C. 222a b c -= D. ∠A+∠B=2∠C 8.下列图象中,是函数1||y x =的图象是( ▲ )9.如图,平面内4条直线l 1、l 2、l 3、l 4是一组平行线,相邻2条平行线的距离都是1个单位长度,正方形ABCD 的4个顶点A 、B 、C 、D ( ▲ )都在这些平行线上,则这个正方形的面积不可能...是A .1 B .3 C .5 D .9(第9题图)10.根据图(1)所示的程序,得到了y 与x 的函数,其图象如图(2)所示.若点M 是y 轴正半轴上任意一点,过点M 作PQ ∥x 轴交图象于点P ,Q ,连接OP ,OQ .以下结论: ① x <0 时,2y x=-; ② x < 0时,y 随x 的增大而减小 ; ③ PQ =3PM .④ ∠POQ 可以等于90° 则其中正确结论有( ▲ ) A .1个 B .2个 C .3个 D .4个二、填空题(本题有8小题,每小题4分,共32分) 11.若有意义,则x 的取值范围 ▲ ;12.数-2,1,3,6,7的平均数是 ▲ ;13. 请写出一个反比例函数解析式,使图象在每一象限内,函数值y 随x 的增大而增大 ▲ ; 14.一个直角三角形的三边长分别为6,8,x ,则x = ▲ ;15.如图,等腰梯形ABCD 中,AD ∥BC , AD =AB =5,且∠ABC =45°,则BC 等于____▲____;16.如图,依次连接第一个菱形各边的中点得到一个矩形,再依次连接矩形各边的中点得到第二个菱形,按照此方法继续下去.已知第一个菱形的面积为1,则第5个菱形的面积 为 ▲ ;17.如图,矩形纸片ABCD 中,已知AD =8,折叠纸片使AB 边与对角线AC 重合,点B 落在点F 处,折痕为AE ,且EF =3, 则AB 的长为 ▲ ;18.设max {x ,y }表示x ,y 两个数中的最大值,例如max {0,2}=2,max {12,8}=12,max {2-,2-}=2-,已知一次函数1y ax b =+的图象与反比例函数2ky x=的图象交于点M(2 ),m 和点N (1 4)--,,则当max {1y ,2y }=1y 时,x 的取值范围为 ▲ ; 三、解答题(第19、20、21题每题5分,第22、23题每题7分,第24题8分,第25题9分,第26题12分,共58分) 1911(2012)()2-+--+20.先化简221224x x x x -÷-+-(),再从2-,0,2三个数中,选择一个你认为合适..的数作为x 的值代入求值.图(1) 图(2)C(第10题图)(第15题图) (第16题图)21.解分式方程:xxx --=-222322.小明每天骑自行车到15km 的学校上学.最近一条新路开通,路程缩短为12km ,路况也变好了,于是骑车的平均速度比原来提高了20%,这样比以前提前20分钟到达学校.试求小明原来骑车的速度为每小时多少千米?23.如图,ABC ∆和DCE ∆都是边长为4的等边三角形,点B 、C 、E 在同一条直线上,连接BD ,求BD 的长.24.某校为了迎接中考,老师安排了五次数学模拟考试,对李明、王亮两位同学的成绩进行统计后,绘制成图①、图②的统计图.(1)在图②中画出表示王亮这5次数学成绩的变化情况的折线统计图; (2)填写表格:图 ①图 ②(3)请你根据上述统计情况,从“平均成绩、折线走势、方差”三方面进行分析,估计谁在中考中会取得较好的成绩?25.如图,反比例函数xky 的图象经过点 A (2,m ),过点 A 作AB 垂直y 轴于点 B , △AOB 的面积为5. (1)求 k 和m 的值;(2)已知点C (-5,-2)在反比例函数图象上,直线AC 交x 轴于点M ,求△AOM 的面积; (3)过点C 作CD ⊥x 轴于点D ,连结BD ,试证明四边形ABDC 是梯形.26.如图,已知在Rt △ABC 中,∠ABC =90°,∠C =30°,AC =12cm ,点E 从点A 出发沿AB 以每秒1cm 的速度向点B 运动,同时点D 从点C 出发沿CA 以每秒2cm 的速度向点A 运动,运动时间为t 秒(0<t <6),过点D 作DF ⊥BC 于点F .(1)试用含t 的式子表示AE 、AD 的长;(2)如图①,在D 、E 运动的过程中,四边形AEFD 是平行四边形,请说明理由; (3)连接DE ,当t 为何值时,△DEF 为直角三角形?(4)如图②,将△ADE 沿DE 翻折得到△A ′DE ,试问当t 为何值时,四边形 AEA ′D 为菱形?并判断此时点A 是否在BC 上?请说明理由.图① 图② 备用图温岭市2011学年第二学期期末质量抽测试卷八年级数学试卷答案及评分标准一、选择题(本题有10小题,每小题3分,共30分)题号 1 2 3 4 5 6 7 8 9 10 答案 CBDABADBBC二、填空题(本题有8小题,每小题4分,共32分)11.x ≥1(答x >1给1分) 12.3 13. 1y x=-(k < 0即可)14.10或2分 ) 15. 5+ 16.4811142256(答案为或均正确) 17. 6 18.-1≤x <0或x ≥2(答对一个给2分,无等号扣1分)三、解答题:(本题有8小题,共58分)19.解:原式=12++---4分(答对一个给1分)= 1 --------- 5分20.解:原式=2241(2)(2)4x x x x +÷-+--------1分=24(2)(2)(2)(2)x x x x x +∙+--+------2分 =24x + -------------3分 当x =0时 --------------4分 原式=2044+=----------5分21.解:3=2(x -2)+ x ---2分 3x =7x =73 --------4分 经检验:x =73是原方程的解.--------5分22.解:设小明原来骑车的速度为每小时x 千米 ------------- 1分由题意得151220(120%)60x x =++ ---------- 3分 解得 x =15 ----- 5分经检验 x =15是原方程的解 -------- 6分答:小明原来骑车的速度为每小时15千米. ----------- 7分 23.解:∵ABC ∆和DCE ∆都是边长为4的等边三角形 ∴ CB =CD ----------------2分∴∠BDC =∠DBC =30°-----------------3分 又∠CDE =60°∴∠BDE =90°------------5分 在Rt BDE ∆中,DE =4 BE =8∴BD ===7分(注:其它正确解法相应给分)24.(1)(2)----- 5分(评分标准:表中数据1个正确给1分,2个或3个正确给2分,全部正确给3分)(3)从平均成绩看,两人都是90分;从折线走势看,李明成绩呈上升趋势,王亮成绩呈下降趋势;从方差来看,李明比王亮稳定.综合分析结果,李明在本次中考中会取得较高的成绩.---8分(评分标准:只要回答有理均给3分)25.(1)12552AOB S m m ∆=⨯⋅=∴= ------------- 1分2510k ∴=⨯= -------------- 2分(2)设直线AC 的解析式为y =kx +b由2552k b k b +=⎧⎨-+=-⎩ 得13k b =⎧⎨=⎩ ---- 3分∴y =x +3 令y =0 得x =-3 ∴M (-3,0) ------- 4分1357.52AOM S ∆∴=⨯⨯= --------- 5分(3)证明:∵AB ⊥y 轴,DM ⊥y 轴 ∴DM ∥AB又DM =5-3=2 AB =2 ∴DM = AB∴四边形ABDM 是平行四边形 ---------- 7分 ∴AC ∥BD --- 8分 又AB ∥x 轴 CD ⊥x 轴 ∴AB 与CD 不平行∴四边形ABDC 是梯形。
2012年八年级下学期期末考试数学卷(有答案)

2012年八年级下学期期末考试数学卷(有答案)2012年八年级下学期期末考试数学卷(有答案)注意事项:1.本试卷共3大题,29小题,满分130分,考试时间120分钟;2.答题前,考生务必将自己的学校、班级、姓名、考试号用0.5毫米黑色墨水签字笔填写在答题卡相应的位置上,并用2B铅笔将考试号所对应的标号涂黑;3.答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,请用橡皮擦干净后,再选涂其它答案;答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上,不在答题区域内的答案一律无效,不得用其他笔答题(作图可用铅笔);4.考生答题必须答在答题卡上,答在试卷和草稿纸上一律无效.一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.在函数中,自变量x必须满足的条件是(▲)A.x≠1B.x≠-1C.x≠0D.x>12.分式的计算结果是(▲)A.B.C.D.3.以下说法正确的是(▲)A.在367人中至少有两个人的生日相同;B.一次摸奖活动的中奖率是l%,那么摸100次奖必然会中一次奖;C.一副扑克牌中,随意抽取一张是红桃K,这是必然事件;D.一个不透明的袋中装有3个红球,5个白球,任意摸出一个球是红球的概率是.4.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则AC的长是(▲)A.2B.4C.2D.45.已知反比例函数的图象过点P(1,3),则该反比例函数的图象位于(▲) A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限6.小宸同学的身高为1.8m,测得他站立在阳光下的影长为0.9m,紧接着他把手臂竖直举起,测得影长为1.2m,那么小宸举起的手臂超出头顶的高度为(▲)A.0.3mB.0.5mC.0.6mD.2.1m7.高跟鞋的奥秘:当人肚脐以下部分的长m与身高,的比值越接近0.618时,越给人以一种匀称的美感,如图,某女士身高170cm,脱去鞋后量得下半身长为97cm,则建议她穿的高跟鞋高度大约为(▲)A.4cmB.6cmC.8cmD.10cm8.为了早日实现“绿色太仓,花园之城”的目标,太仓对4000米长的城北河进行了绿化改造.为了尽快完成工期,施工队每天比原计划多绿化10米,结果提前2天完成.若原计划每天绿化x米,则所列方程正确的是(▲)A.B.C.D.9.如图是反比例函数和(k1线AB//y轴,并分别交两条曲线于A、B两点,若S△AOB=4,则k2-k1的值是(▲)A.1B.2C.4D.810.如图,已知DE是直角梯形ABCD的高,将△ADE沿DE翻折,腰AD恰好经过腰BC的中点,则AE:BE等于(▲)A.2:1B.1:2C.3:2D.2:3二、填空题(本大题共8小题,每小题3分.共24分)11.画在比例尺为1:20的图纸上的某个零件的长是32cm,这个零件的实际长是▲cm.12.当x=▲时,分式的值为0.13.若一次函数y=(m-1)x+2的图象,y随x的增大而减小,则m的取值范围是▲.14.若,则=▲.15.如图,在△ABC中,已知DE∥BC,AB=8,BD=BC=6,则DE=▲.16.使分式的值为整数的所有整数m的和是▲.17.如图,已知两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3把线段AB缩小,则点A的对应点坐标是▲.18.如图,将三角形纸片的一角折叠,使点B落在AC边上的F处,折痕为DE.已知AB=AC=3,BC=4,若以点E,F,C为顶点的三角形与△ABC相似,那么BE的长是▲.三、解答题(本大题共11小题,共76分,应写出必要的计算过程、推理步骤或文字说明)19.(本题共5分)解方程:.20.(本题共5分)先化简,再求值:,其中.21.(本题共6分)解不等式组:,并判断是否为该不等式组的解.22.(本题共6分)如图,在正方形ABCD中,已知CE⊥DF于H.(1)求证:△BCE≌△CDF:(2)若AB=6,BE=2,求HF的长.23.(本题共6分)有两堆背面完全相同的扑克,第一堆正面分别写有数字1、2、3、4,第二堆正面分别写有数字1、2、3.分别混合后,小玲从第一堆中随机抽取一张,把卡片上的数字作为被减数;小惠从第二堆中随机抽取一张,把卡片上的数字作为减数,然后计算出这两个数的差.(1)请用画树状图或列表的方法,求这两数差为0的概率;(2)小玲与小惠作游戏,规则是:若这两数的差为非负数,则小玲胜;否则,小惠胜.你认为该游戏规则公平吗?如果公平,请说明理由.如果不公平,请你修改游戏规则,使游戏公平.24.(本题共7分)教材第97页在证明“两边对应成比例且夹角对应相等的两个三角形相似”(如图,已知(AB>DE),∠A=∠D,求证:△ABC∽△DEF)时,利用了转化的数学思想,通过添设辅助线,将未知的判定方法转化为前两节课已经解决的方法(即已知两组角对应相等推得相似或已知平行推得相似).请利用上述方法完成这个定理的证明.25.(本题共7分)如图,某一时刻垂直于地面的大楼AC的影子一部分在地上(BC),另一部分在斜坡上(BD).已知坡角,∠DBE=45°,BC =20米,BD=2米,且同一时刻竖直于地面长1米的标杆的影长恰好也为1米,求大楼的高度AC.26.(本题共8分)如图,在平面直角坐标系内,已知OA=OB=2,∠AOB =30°.(1)点A的坐标为(▲,▲);(2)将△AOB绕点O顺时针旋转a度(0①当a=30时,点B恰好落在反比例函数y=(x>0)的图象上,求k的值;②在旋转过程中,点A、B能否同时落在上述反比例函数的图象上,若能,求出a的值;若不能,请说明理由.27.(本题共8分)如图1,已知直线y=-2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连结BC,作BC的中垂线分别交OB、AB交于点D、E.(l)当点C与点O重合时,DE=▲;(2)当CE∥OB时,证明此时四边形BDCE为菱形;(3)在点C的运动过程中,直接写出OD的取值范围.28.(本题共9分)如图①,将直角梯形OABC放在平面直角坐标系中,已知OA=5,OC=4,BC∥OA,BC=3,点E在OA上,且OE=1,连结OB、BE.(1)求证:∠OBC=∠ABE;(2)如图②,过点B作BD⊥x轴于D,点P在直线BD上运动,连结PC、P、PA和CE.①当△PCE的周长最短时,求点P的坐标;②如果点P在x轴上方,且满足S△CEP:S△ABP=2:1,求DP的长.29.(本题共9分)探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K字形是非常重要的基本图形,可以建立如下的“模块”(如图①):(1)请就图①证明上述“模块”的合理性;(2)请直接利用上述“模块”的结论解决下面两个问题:①如图②,已知点A(-2,1),点B在直线y=-2x+3上运动,若∠AOB =90°,求此时点B的坐标;②如图③,过点A(-2,1)作x轴与y轴的平行线,交直线y=-2x +3于点C、D,求点A关于直线CD的对称点E的坐标.。
浙江省衢州市菁才中学-学八年级英语第二学期期末检测

菁才中学2011-2012学年度第二学期八年级期末检测英语试卷考生须知:1.全卷共七大题,82小题,满分120分。
考试时间为100分钟。
2.全卷分为试卷I (选择题)和试卷II(非选择题)两部分。
卷Ⅰ的答案必须用2B铅笔填涂在机读卡上,非选择题必须做在答题卷的相对应的位置上,答在试题卷上无效。
3.请用黑色钢笔或签字笔在答题卷密封区填写考生相关信息。
卷Ⅰ说明:本卷共有四大题,65小题,共85分。
请用2B铅笔在“机读卡”上将你认为正确的选项对应的小方框涂黑、涂满。
一、听力(共15小题,第1~10小题每题1分,第11~15小题每题2分, 共20分)第一节:听小对话,从A、B、C三个选项中选择符合对话内容的选项,回答问题。
1.What does the boy usually do in his free time?A. B. C.2. What’s the man’s hobby?A. B. C.3. How much did the woman pay for the skirt?. . .A B C4. Why will the boy be late for the party?A. B. C.5. What did the boy’s uncle send him on his twelfth birthday?A. B. C. 第二节:听长对话,从A、B、C三个选项中选择符合对话内容的选项,回答问题。
听下面一段较长的对话,回答第6~7小题。
6. What does John want to be when he grows up?A. To be a teacher.B. To be a football player.C. To be an astronaut.7. What would John like to do if he wants to be stronger?A. He’d like to have more healthy food.B. He’d like to play football every day.C. He’d like to do morning exercise.听下面一段较长的对话,回答第8~10小题。
2012年八年级下册期末试题
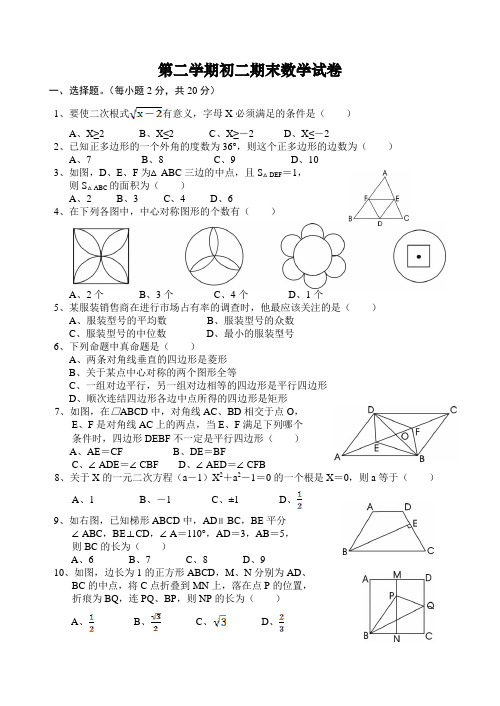
第二学期初二期末数学试卷一、选择题。
(每小题2分,共20分)1、要使二次根式有意义,字母X必须满足的条件是()A、X≥2B、X≤2C、X≥-2D、X≤-22、已知正多边形的一个外角的度数为36°,则这个正多边形的边数为()A、7B、8C、9D、103、如图,D、E、F为△ABC三边的中点,且S △DEF=1,则S△ABC的面积为()A、2B、3C、4D、64、在下列各图中,中心对称图形的个数有()A、2个B、3个C、4个D、1个5、某服装销售商在进行市场占有率的调查时,他最应该关注的是()A、服装型号的平均数B、服装型号的众数C、服装型号的中位数D、最小的服装型号6、下列命题中真命题是()A、两条对角线垂直的四边形是菱形B、关于某点中心对称的两个图形全等C、一组对边平行,另一组对边相等的四边形是平行四边形D、顺次连结四边形各边中点所得的四边形是矩形7、如图,在□ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形()A、AE=CFB、DE=BFC、∠ADE=∠CBFD、∠AED=∠CFB8、关于X的一元二次方程(a-1)X2+a2-1=0的一个根是X=0,则a等于()A、1B、-1C、±1D、9、如右图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为()A、6B、7C、8D、910、如图,边长为1的正方形ABCD,M、N分别为AD、BC的中点,将C点折叠到MN上,落在点P的位置,折痕为BQ,连PQ、BP,则NP的长为()A、B、C、D、二、填空题。
(每小题2分,共20分)11、化简=;12、△ABC中,AB=AC,∠A=40°,则∠ACB的外角度数是;13、已知直角三角形的两条直角边长分别是3cm和4cm,则斜边上的高线长是;14、某校八年级共有学生400人,为了解这些学生的视力情况,抽查了20名学生的视力,对所得数据进行整理,在得到的频数分布表中,若数据在0.95~1.15这一小组频数为6,则可以估计该校八年级学生视力在0.95~1.15范围内的人数约为人;15、当X=时,X(X-8)的值与-16的值相等;16、等腰梯形的上底长为2cm,下底长为10cm,高为3cm,则它的腰长为cm;17、下列命题:①对顶角相等;②等腰梯形同一底边上的两底角相等;③菱形的对角线相等;④两直线平行,同位角相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
菁才中学2012年八年级下学期期末测试
科 学 答 案 2012.6
一、选择题(每小题只有一个正确答案,每小题3分,共60分) 1 2 3 4 5 6 7 8 9 10 C B D A D B B C D C 11 12 13 14 15 16 17 18 19 20 B
C
C
B
B
C
C
C
B
C
二、简答题(每空2分,共40分)
21、 220 卢瑟福 22、(1) 3NO 3- (2) Al 2O 3 23、 C +1 24、(1) 吸气 (2) 减小 (3) 甲 25、(1) 导管 (2) 乙 蒸腾 26、 不偏转 发电机
27、 高 (1) 石灰水变浑浊 (2) 烧杯内的液面升高 28、(1) 物理 (2) 2H 2S+3O 2===2SO 2+2H 2O (3) S 三、实验探究题(每空2分,共30分)
29、(1) 7→4→6 (2) 光照 (3) 不变蓝 (4) 不合理 因为土壤中含有钾元素 30、(1) B D 、E
① 催化剂 ② 5% ③ 2H 2O 2====2H 2O+O 2↑
31、(1)为什么会晃动?(符合即可)(2)钨丝通电后产生了磁场(意思对即可) (1) S (2) 0.2 (3) A 、C
四、分析计算题(8+8+6+8,共30分) 32、(1) 4 (2分)
解:(2)C :H :O=(12×12):(1×22):(16×14)=72:11:112 (3分)
点燃
Fe 2O 3
(3)Zn%=Zn/C12H22O14Zn×100%=65/(12×12+1×22+16×14+65)×100%=14.3%答:……
注:(2)(3)小题格式正确才能得满分(3分)
33、(1)12.0 (2)40% (各2分)
解:设20克稀硫酸中含溶质X克
Zn+H2SO4==ZnSO4+H2↑(1分)
65 98
20-17.4 X
65:2.6克=98:X
X=3.92克(2分)
H2SO4%=3.92克/20克×100%=19.6% (1分)
答:……
34、(1)6O2(2)0.6 (3) B (各2分)
35、(1)A、B (2)变小(各2分)
解:U2=U-U1=9V-6V=3V (1分)
I2=U2/R2=3V/100Ω=0.03A (1分)
R1=U1/I1=6V/0.03A=200Ω(1分)
查表可知此时B=0.08T (1分)(说明,其他方法参照此标准评分)
答:……。
