FGI-7DE
型月九宫格阵营定义

型月九宫格阵营定义标题:型月九宫格阵营定义:开启虚构世界的奇幻之旅【导语】在当代的虚构作品中,无论是电影、动画还是游戏,都不乏以虚构的世界为背景的故事。
而在这样的世界中,人们常常会被各种不同的阵营、势力和角色所吸引。
其中,型月九宫格阵营作为Fate系列作品中的核心概念之一,既展示了创作者的丰富想象力,又吸引了无数粉丝进行深入探索。
本文将从深度和广度两个方面对型月九宫格阵营进行综合评估,并探讨其背后的意义和个人理解。
【第一部分】深度探讨:型月九宫格阵营的定义与来源1. 型月九宫格阵营概述在Fate系列作品中,型月九宫格阵营(也称为“凛、衛宮、間桐、杜立德、游戏、劍之、居住區、聖杯、法螺”)是游戏剧情中的核心元素之一,同时也是创作者奈须蘑菇先生独创的概念。
它以一个九格方阵的形式展示了不同角色、势力和故事之间的复杂联系。
2. 九个阵营的定义与特点- 凛:代表着冷静理智、聪明机敏的角色和势力。
他们通常以策略家、谋士的身份出现,善于推理和分析。
- 衛宮:代表着忠诚、勇气和坚持的角色和势力。
他们通常以正义的使者、英雄的身份出现,守护正义与和平。
- 間桐:代表着阴暗、狡诈和复仇的角色和势力。
他们以自私自利、冷酷无情的形象阐述着自己的立场和目标。
- 杜立德:代表着追求力量、掌握命运的角色和势力。
他们通常以魔法师、能力者的身份出现,追求真理和实现自己的野心。
- 游戏:代表着玩家、读者的角色和势力。
他们作为角色的外部存在,用他们的选择和干预推动着故事的发展。
- 劍之:代表着传奇、英雄与刀剑之力的角色和势力。
他们以剑士、战士的形象出现,体现着力量和战斗的本质。
- 居住區:代表着平凡、普通人的角色和势力。
他们通常身不由己、无法干预故事的发展,却在其中扮演着见证者和支持者的角色。
- 聖杯:代表着神秘、超自然的力量源泉。
它是型月九宫格阵营中的至高存在,同时也是故事发展的核心和驱动力。
- 法螺:代表着干预、改变故事的奇妙手段。
五年级奥数专题组合图形面积

五年级奥数专题组合图形面积(一)1、一根铁丝长12厘米,要围成两个整厘米数的正方形,这两个正方形的面积分别是多少?1、有两个相同的长方形,长7厘米,宽3厘米,把它们按下图的样子重叠在一起,这个图形的面积是多少?3、有一个梯形,它的上底是6厘米,下底8厘米,如果只把上底增加4厘米,那么面积就增加6平方厘米。
求原来梯形的面积。
4、求下图长方形ABCD的面积。
(单位:厘米)5、如图,已知四条线段的长度分别是:AB=4厘米,CE=12厘米,CD=10厘米,AF=8厘米,并且有两个直角。
求四边形ABCD的面积。
6、图中BC=10厘米,EC=8厘米,且阴影部分面积比三角形EFG的面积大10平方厘米。
求平行四边形的面积。
7、图中,ABCD是长方形,E、F分别是AB、DA的中点,G是BF和DE的交点,四边形BCDG的面积是40平方厘米,那么ABCD的面积是多少平方厘米?组合图形面积(二)【一】一个正方形被分成3个大小、形状完全一样的长方形,每个小长方形的周长都是24厘米,求这个正方形的面积。
练习1、一个正方形被分成6个大小、形状完全一样的长方形,每个长方形的周长都是14厘米。
原来正方形的面积是多少?2、一块长方形布,周长是18米,长比宽多1米。
这块布的面积是多少?【二】下图是由6个相等的三角形拼成的图形,求这这图像的面积。
练习1、ABCD是正方形,求阴影部分的面积。
(单位:厘米)2、下图中,E、F分别是长和宽的中点,求阴影部分的面积。
(单位:厘米)【三】如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)练习1、求下图中阴影部分的面积和。
2、求下图中阴影部分的面积。
(单位:厘米)【四】下图中,边长为10和15的两个正方形并放在一起,求三角形ABC(阴影部分)的面积。
练习1、下图中,三角形ABC的面积是72平方厘米,三角形ABE与三角形AEC面积相等,如果AB=18厘米,FB=FE,求三角形AFE的面积。
甘肃省兰州市天庆实验中学2022年数学九年级第一学期期末学业质量监测试题含解析

2022-2023学年九上数学期末模拟试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)1.如图,□ABCD 的对角线AC ,BD 交于点O ,CE 平分∠BCD 交AB 于点E ,交BD 于点F ,且∠ABC =60°,AB =2BC ,连接OE .下列结论:①EO ⊥AC ;②S △AOD =4S △OCF ;③AC :BD =21:7;④FB 2=OF •DF .其中正确的是( )A .①②④B .①③④C .②③④D .①③2.在矩形ABCD 中,B 的角平分线BE 与AD 交于点E ,BED ∠的角平分线EF 与DC 交于点F ,若7AB =,34DF FC =,则BC 的长为( )A .721B .432C .225D .423 3.把二次函数243y x x =---化成2()y a x h k =-+的形式是下列中的 ( )A .2(2)1y x =--B .2(2)1=---y xC .2(2)1y x =-++D .2(2)1y x =-+- 4.已知抛物线24y x bx =-++经过(2,)n -和(4, )n 两点,则n 的值为( )A .﹣2B .﹣4C .2D .4 5.对于反比例函数y=k x(k≠0),下列所给的四个结论中,正确的是( ) A .若点(3,6)在其图象上,则(﹣3,6)也在其图象上B .当k >0时,y 随x 的增大而减小C .过图象上任一点P 作x 轴、y 轴的线,垂足分别A 、B ,则矩形OAPB 的面积为kD .反比例函数的图象关于直线y=﹣x 成轴对称6.下列事件中必然发生的事件是( )A .一个图形平移后所得的图形与原来的图形不全等B .不等式的两边同时乘以一个数,结果仍是不等式C .200件产品中有5件次品,从中任意抽取6件,至少有一件是正品D .随意翻到一本书的某页,这页的页码一定是偶数7.三角形的一条中位线将这个三角形分成的一个小三角形与原三角形的面积之比等于( )A .1:2B .1:2C .1:4D .1:1.68.已知圆锥的底面半径为3cm ,母线为5cm ,则圆锥的侧面积是 ( )A .30πcm 2B .15πcm 2C .152π cm 2D .10πcm 29.已知23x y =,则下列比例式成立的是( )A .23x y =B .23x y =C .32x y =D .52x y x += 10.对于二次函数y =4(x +1)(x ﹣3)下列说法正确的是( )A .图象开口向下B .与x 轴交点坐标是(1,0)和(﹣3,0)C .x <0时,y 随x 的增大而减小D .图象的对称轴是直线x =﹣1二、填空题(每小题3分,共24分)11.如图,平行四边形ABCD 的一边AB 在x 轴上,长为5,且∠DAB =60°,反比例函数y =23x和y =33x -分别经过点C ,D ,则AD =_____.12.已知△ABC 与△DEF 相似,相似比为 2:3,如果△ABC 的面积为 4,则△DEF 的面积为_____.13.如图,在平面直角坐标系xoy 中,矩形EFGO 的两边在其坐标轴上,以y 轴上的某一点为位似中心作矩形ABCD ,使它与矩形EFGO 位似,且点B ,F 的坐标分别为()4,4-,()2,1,则点D 的坐标为__________.14.将方程257x x +=化为一元二次方程的一般形式,其中二次项系数为1,则一次项系数、常数项分别为____.15.在ABC 中,若211sin (cos )022A B -+-=,则C ∠的度数是______. 16.一元二次方程x 2﹣2x=0的解是 .17.在直角坐标系中,点A (-7,5)关于原点对称的点的坐标是_____.18.工厂质检人员为了检测其产品的质量,从同一批次共1000件产品中随机抽取50件进行检检测出次品1件,由此估计这一批产品中的次品件数是_____.三、解答题(共66分)19.(10分)天空中有一个静止的广告气球C ,从地面A 点测得C•点的仰角为45°,从地面B 测得仰角为60°,已知AB=20米,点C 和直线AB 在同一铅垂平面上,•求气球离地面的高度.(结果精确到0.1米)20.(6分)如图,矩形ABCD 中,点E 为AD 边上一点,过点E 作CE 的垂线交AB 于点F .(1)求证:CDE EAF ∆∆∽;(2)若 1.5,0.5,3AF BF AE ===,求DE 的长.21.(6分)如图,在平面直角坐标系中,抛物线2323333y x x =--x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,对称轴与x 轴交于点D ,点()4,E n 在抛物线上.(1)求直线AE 的解析式.(2)点P 为直线CE 下方抛物线上的一点,连接PC ,PE .当PCE ∆的面积最大时,连接CD ,CB ,点K 是线段CB 的中点,点M 是线段CP 上的一点,点N 是线段CD 上的一点,求KM MN NK ++的最小值.(3)点G 是线段CE 的中点,将抛物线2323333y x x =--与x 轴正方向平移得到新抛物线y ',y '经过点D ,y '的顶点为点F ,在新抛物线y '的对称轴上,是否存在点Q ,使得FGQ ∆为等腰三角形?若存在,直接写出点Q 的坐标;若不存在,请说明理由.22.(8分)甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球,记下标号后放回口袋中,充分摇匀后,再从口袋中随机摸出一个小球,记下该小球的标号,两次记下的标号分别用x 、y 表示.若x y +为奇数,则甲获胜;若x y +为偶数,则乙获胜. 请你运用所学的概率的相关知识通过计算说明这个游戏对甲、乙双方是否公平.23.(8分)如图,已知⊙O 的半径长为R=5,弦AB 与弦CD 平行,它们之间距离为5,AB=6,求弦CD 的长.24.(8分)如图,反比例函数y =k x(x >0)和一次函数y =mx +n 的图象过格点(网格线的交点)B 、P .(1)求反比例函数和一次函数的解析式;(2)观察图象,直接写出一次函数值大于反比例函数值时x 的取值范围是: .(3)在图中用直尺和2B 铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:①四个顶点均在格点上,且其中两个顶点分别是点O ,点P ;②矩形的面积等于k 的值.25.(10分)如图,AB 是O 的直径,AC 是弦,D 是弧BC 的中点,过点D 作EF 垂直于直线,AC 垂足为F ,交AB 的延长线于点E .()1求证:EF 是O 的切线;()2若6,8AF EF ==,求O 的半径. 26.(10分)如图,F 是ABC ∆中AB 边上的中点,//FM AC 交BC 于点M ,C 是BDF ∆中BD 边上的中点,且AC与DF 交于点E .(1)求EC AC的值. (2)若,AB m BF CE ==,求AC 的长. (用含m 的代数式表示)参考答案一、选择题(每小题3分,共30分)1、B【分析】①正确.只要证明EC=EA=BC ,推出∠ACB=90°,再利用三角形中位线定理即可判断.②错误.想办法证明BF=2OF ,推出S △BOC =3S △OCF 即可判断.③正确.设BC=BE=EC=a ,求出AC ,BD 即可判断.④正确.求出BF ,OF ,DF (用a 表示),通过计算证明即可.【详解】解:∵四边形ABCD 是平行四边形,∴CD ∥AB ,OD=OB ,OA=OC ,∴∠DCB+∠ABC=180°,∵∠ABC=60°,∴∠DCB=120°,∵EC 平分∠DCB ,∴∠ECB=12∠DCB=60°, ∴∠EBC=∠BCE=∠CEB=60°,∴△ECB 是等边三角形,∴EB=BC ,∵AB=2BC ,∴EA=EB=EC ,∴∠ACB=90°, ∵OA=OC ,EA=EB ,∴OE ∥BC , ∴∠AOE=∠ACB=90°,∴EO ⊥AC ,故①正确,∵OE ∥BC ,∴△OEF ∽△BCF ,∴12OE OF BC FB == , ∴OF=13OB , ∴S △AOD =S △BOC =3S △OCF ,故②错误,设BC=BE=EC=a ,则AB=2a ,3,223(72)a a +=,∴BD=7a,∴AC:BD=3a:7a=21:7,故③正确,∵OF=13OB=76a,∴BF=73a,∴BF2=79a2,OF•DF=76a•777269a a⎛⎫+=⎪⎪⎝⎭a2,∴BF2=OF•DF,故④正确,故选:B.【点睛】此题考查相似三角形的判定和性质,平行四边形的性质,角平分线的定义,解直角三角形,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题.2、D【分析】先延长EF和BC,交于点G,再根据条件可以判断三角形ABE为等腰直角三角形,并求得其斜边BE的长,然后根据条件判断三角形BEG为等腰三角形,最后根据△EFD∽△GFC得出CG与DE的倍数关系,并根据BG=BC +CG进行计算即可.【详解】延长EF和BC,交于点G,∵3DF=4FC,∴34 CFDF=,∵矩形ABCD中,∠ABC的角平分线BE与AD交于点E,∴∠ABE=∠AEB=45°,∴AB=AE=7,∴直角三角形ABE中,BE227772+=,又∵∠BED的角平分线EF与DC交于点F,∴∠BEG=∠DEF,∵AD ∥BC ,∴∠G =∠DEF ,∴∠BEG =∠G ,∴BG =BE =∵∠G =∠DEF ,∠EFD =∠GFC ,∴△EFD ∽△GFC , ∴3 4CG CF DE DF ==, 设CG =3x ,DE =4x ,则AD =7+4x =BC ,∵BG =BC +CG ,∴7+4x +3x =,解得x −1,∴BC =7+4x =7+−4=3+,故选:D .【点睛】本题主要考查了矩形、相似三角形以及等腰三角形,解决问题的关键是掌握矩形的性质:矩形的四个角都是直角,矩形的对边相等.解题时注意:有两个角对应相等的两个三角形相似.3、C【分析】先提取二次项系数,然后再进行配方即可.【详解】22243(44)34(2)1y x x x x x =---=-++-+=-++.故选:C .【点睛】考查了将一元二次函数化成y=a (x-h )2+k 的形式,解题关键是正确配方.4、B【分析】根据(2, )n -和(4, )n 可以确定函数的对称轴=1x ,再由对称轴的2b x =即可求解; 【详解】解:抛物线24y x bx =-++经过(2, )n -和(4, )n 两点,可知函数的对称轴=1x , 12b ∴=, 2b ∴=;224y x x ∴=-++,将点(2, )n -代入函数解析式,可得=-4n ;故选B .【点睛】本题考查二次函数图象上点的坐标;熟练掌握二次函数图象上点的对称性是解题的关键.5、D【解析】分析:根据反比例函数的性质一一判断即可;详解:A .若点(3,6)在其图象上,则(﹣3,6)不在其图象上,故本选项不符合题意;B .当k >0时,y 随x 的增大而减小,错误,应该是当k >0时,在每个象限,y 随x 的增大而减小;故本选项不符合题意;C .错误,应该是过图象上任一点P 作x 轴、y 轴的线,垂足分别A 、B ,则矩形OAPB 的面积为|k |;故本选项不符合题意;D .正确,本选项符合题意.故选D .点睛:本题考查了反比例函数的性质,解题的关键是熟练掌握反比例函数的性质,灵活运用所学知识解决问题,属于中考常考题型.6、C【分析】直接利用随机事件、必然事件、不可能事件分别分析得出答案.【详解】A 、一个图形平移后所得的图形与原来的图形不全等,是不可能事件,故此选项错误;B 、不等式的两边同时乘以一个数,结果仍是不等式,是随机事件,故此选项错误;C 、200件产品中有5件次品,从中任意抽取6件,至少有一件是正品,是必然事件,故此选项正确;D 、随意翻到一本书的某页,这页的页码一定是偶数,是随机事件,故此选项错误;故选C .【点睛】此题主要考查了随机事件、必然事件、不可能事件,正确把握相关定义是解题关键.7、C【分析】中位线将这个三角形分成的一个小三角形与原三角形相似,根据中位线定理,可得两三角形的相似比,进而求得面积比.【详解】根据三角形中位线性质可得,小三角形与原三角形相似比为1:2,则其面积比为:1:4,故选C .【点睛】本题考查了三角形中位线的性质,比较简单,关键是知道面积比等于相似比的平方. 8、B【解析】试题解析:∵底面半径为3cm ,∴底面周长6πcm ∴圆锥的侧面积是12×6π×5=15π(cm 2), 故选B .9、C【分析】依据比例的性质,将各选项变形即可得到正确结论.【详解】解:A .由23x y =可得,2y=3x ,不合题意; B .由23x y =可得,2y=3x ,不合题意; C .由32x y =可得,3y=2x ,符合题意; D .由52x y x +=可得,3x=2y ,不合题意; 故选:C .【点睛】本题主要考查了比例的性质,解决问题的关键是掌握:内项之积等于外项之积. 10、C【解析】先把解析式化为顶点式的二次函数解析式,再利用二次函数的性质求解即可.【详解】()()413y x x =+-A. ∵a=4>0,图象开口向上,故本选项错误,B. 与x 轴交点坐标是(-1,0)和(3,0),故本选项错误,C. 当x <0时,y 随x 的增大而减小,故本选项正确,D.图象的对称轴是直线x=1,故本选项错误,故选C.【点睛】本题主要考查了二次函数的性质,解题的关键是理解并灵活运用二次函数的性质.二、填空题(每小题3分,共24分)11、1【分析】设点C (23,x x ),则点D (3,2x -23x ),然后根据CD 的长列出方程,求得x 的值,得到D 的坐标,解直角三角形求得AD .【详解】解:设点C (23,x x ),则点D (3,2x -23x ), ∴CD =x ﹣(32x -)=52x ∵四边形ABCD 是平行四边形,∴CD =AB =5,∴52x =5,解得x =1, ∴D (﹣3,3),作DE ⊥AB 于E ,则DE =3,∵∠DAB =60°,32sin 6032DE AD ∴===︒故答案为:1.【点睛】本题考查的是平行四边形的性质、反比例性质、特殊角的三角函数值,利用平行四边形性质和反比例函数的性质列出等式是解题的关键.12、1【解析】由△ABC 与△DEF 的相似,它们的相似比是2:3,根据相似三角形的面积比等于相似比的平方,即可得它们的面积比是4:1,又由△ABC 的面积为4,即可求得△DEF 的面积.【详解】∵△ABC 与△DEF 的相似,它们的相似比是2:3,∴它们的面积比是4:1,∵△ABC 的面积为4,∴△DEF 的面积为:4×94=1.故答案为:1.【点睛】本题考查的知识点是相似三角形的性质,解题关键是掌握相似三角形的面积比等于相似比的平方定理.13、()0,6【分析】首先求出位似图形的位似中心坐标,然后即可得出点D 的坐标.【详解】连接BF 交y 轴于P ,如图所示:∵矩形EFGO 和矩形ABCD ,点B ,F 的坐标分别为()4,4-,()2,1,∴点C 的坐标为()0,4∵BC ∥GF ∴2142GP GF PC BC === ∴GP=1,PC=2,OP=3∴点P 即为其位似中心∴OD=6∴点D 坐标为()0,6故答案为:()0,6.【点睛】此题主要考查位似图形的性质,熟练掌握,即可解题.14、5,7-.【分析】一元二次方程化为一般形式后,找出一次项系数与常数项即可.【详解】解:方程整理得:2570x x +-=,则一次项系数、常数项分别为5,7-;故答案为:5,7-.【点睛】此题考查了一元二次方程的一般形式,其一般形式为20(a 0)++=≠ax bx c .15、90 【分析】先根据非负数的性质求出1sinA 2=,1cosB 2=,再由特殊角的三角函数值求出A ∠与B ∠的值,根据三角形内角和定理即可得出结论. 【详解】在ABC 中,211sinA (cosB )022-+-=, 1sinA 2∴=,1cosB 2=, A 30∠∴=,B 60∠=,C 180306090∠∴=--=,故答案为90.【点睛】本题考查了非负数的性质以及特殊角的三角函数值,熟练掌握特殊角的三角函数值是解题的关键.16、12x 0x 2==,【分析】方程整理后,利用因式分解法求出解即可.【详解】方程整理得:x (x ﹣1)=0,可得x=0或x ﹣1=0,解得:x 1=0,x 1=1.故答案为x 1=0,x 1=1.17、(7,.【分析】直接利用关于原点对称点的性质得出答案.【详解】解:点A (-7关于原点对称的点的坐标是:(7,.故答案为:(7,.【点睛】此题主要考查了关于原点对称点的性质,正确记忆横纵坐标的符号是解题关键.18、1【分析】求出次品所占的百分比,即可求出1000件中次品的件数.【详解】解:1000×150=1(件), 故答案为:1.考查样本估计总体,求出样本中次品所占的百分比是解题的关键.三、解答题(共66分)19、47.3米【解析】试题分析:过点C 作CD ⊥AB ,交AB 于点D ;设AD=x .本题涉及到两个直角三角形△ADC 、△BDC ,应利用其公共边CD 构造等量关系,解三角形可得AD 、BD 与x 的关系;借助AB=AD-BD 构造方程关系式,进而可求出答案.试题解析:过点C 作CD ⊥AB ,交AB 于点D ;设CD=x ,在Rt △ADC 中,有AD=45CD tan ︒=CD=x , 在Rt △BDC 中,有BD=360CD tan ︒x , 又有AB=AD-BD=20;即3, 解得:x=10(3)≈47.3(米).答:气球离地面的高度CD 为47.3米.20、(1)证明见解析;(2)1DE =【分析】(1)根据同角的余角相等推出∠=∠AFE CED ,结合90A D ∠=∠=︒即可判定相似;(2)根据条件可得CD=2,再利用相似三角形对应边成比例,建立方程即可求出DE.【详解】解:(1)⊥CE EF ,90∴∠+∠=︒CED AEF又90∠+∠=︒AEF AFEAFE CED ∴∠=∠90A D ∠=∠=︒CDE EAF ∴∆∆∽(2) 1.5,0.5==AF BFCDE EAF ∆∆∽,AF AE DE DC∴= 1.532DE ∴= 1DE =∴【点睛】本题考查了相似三角形的判定与性质,熟练掌握“一线三垂直”模型的证明方法是解题的关键.21、(1)33y x =+;(2)3;(3)存在,点Q 的坐标为或或(3,或(3,5-. 【解析】 【分析】(1)求出点A 、B 、 E 的坐标,设直线AE 的解析式为y kx b =+ ,将点A 和点E 的坐标代入即可;(2)先求出直线CE 解析式,过点P 作//y P F 轴,交CE 与点F ,设点P 的坐标为 (,3322333)x x x --,则点F 3(,x x - ,从而可表示出△E PC 的面积,利用二次函数性质可求出x 的值,从而得到点 P 的坐标,作点K 关于CD 和CP 的对称点G 、H ,连接G 、 H 交CD 和CP 与N 、M ,当点O 、N 、 M 、H 在一条直线上时,KM+MN+NK 有最小值,最小值= GH ,利用勾股定理求出GH 即可;(3)由平移后的抛物线经过点D ,可得到点F 的坐标,利用中点坐标公式可求得点 G 的坐标,然后分为FG FQ GF GQ QG QF =、=、= 三种情况讨论求解即可.【详解】解:(1)22323)1)(3)3y x x x x x x ==--=+- (1,0),(3,0)A B ∴-当4x =时,164y ==E ∴设直线AE 的解析式为y kx b =+ ,将点A 和点E 的坐标代入得05343k b k b -+=⎧⎪⎨+=⎪⎩解得3333k b ⎧=⎪⎪⎨⎪=⎪⎩ 所以直线AE 的解析式为3333y x =+ . (2)设直线CE 的解析式为3y mx =- ,将点E 的坐标代入得:53433m -=解得:233m = ∴直线CE 的解析式为2333y x =- 如图,过点P 作//y PF 轴,交 CE 与点F设点P 的坐标为2(3323x x x ,则点F 233(x x 则FP 22233233433(3)x x x x x -+= 2234323831)2(4EPCx x x S x ∴=⨯⨯= ∴当8332232()x ===⨯- 时,△EPC 的面积最大,此时232343433333333x x --=--=- (2,3)P ∴-如图2所示:作点K 关于CD 和CP 的对称点G 、H ,连接G 、H 交CD 和CP 与N 、MK 是CB 的中点,33(,2K ∴ 3tan KCP ∴∠= OD =1, OC =333tan OCD ∴∠= 30OCD KCP ∴∠∠︒==30KCD ∴∠︒=K 是BC 的中点,∠OCB =60°OC CK ∴=∴点O 与点K 关于CD 对称∴点G 与点O 重合∴点G(0,0)点H 与点K 关于CP 对称∴点H 的坐标为333(,22- KM MN NK MH MN GN +----∴当点O 、N 、 M 、H 在条直线上时,KM+MN+NK 有最小值,最小值=GH22333()()322GH ∴=+=KM MN NK ∴++的最小值为 3.(3)如图'y 经过点D ,'y 的顶点为点F ∴点43(3,)F 点G 为 CE 的中点,3(2,)2G ∴ 22532211()33FG ∴=+-= 当FG =FQ 时,点 (3,432213)Q -+或'43221Q -- 当GF =GQ 时,点 F 与点''Q 关于直线33y = 对称 ∴点''(3,23)Q当QG =QF 时,设点 1Q 的坐标为(3)a , 由两点间的距离公式可得:224331()3a a =+- ,解得23a = ∴点1Q 的坐标为23(3, 综上所述,点Q 的坐标为43221)-+ 或43221-- 或(3,23) 或23(3,)【点睛】本题考查了二次函数的图像与性质的应用,涉及的知识点主要有待定系数法求一次函数的解析式、三角函数、勾股定理、对称的坐标变换、两点间的距离公式、等腰三角形的性质及判定,综合性较强,灵活利用点坐标表示线段长是解题的关键.22、公平,见解析【分析】画树状图展示所有16种等可能的结果数,然后根据概率公式求解.【详解】画树状图如图所示,由图知共有16种等可能结果,其中x y +为奇数的可能有8种,为偶数也有8种可能,故x y +结果为奇数或偶数的概率都是12, 甲乙获胜的概率相同,故游戏公平.【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n ,再从中选出符合事件A 或B 的结果数目m ,然后利用概率公式计算事件A 或事件B 的概率.23、6【分析】如图所示作出辅助线,由垂径定理可得AM=3,由勾股定理可求出OM 的值,进而求出ON 的值,再由勾股定理求CN 的值,最后得出CD 的值即可.【详解】解:如图所示,因为AB ∥CD ,所以过点O 作MN ⊥AB 交AB 于点M ,交CD 于点N ,连接OA ,OC , 由垂径定理可得AM=132AB =, ∴在Rt △AOM 中,2222534OM OA AM =-=-=,∴ON=MN-OM=1,∴在Rt △CON 中,2222512426CN OC ON =-=-== ∴246CD CN ==, 故答案为:46【点睛】本题考查勾股定理及垂径定理,作出辅助线,构造直角三角形是解题的关键.24、(1)y=4x,y =﹣12x+3;(2)2<x<1;(3)见解析【分析】(1)利用待定系数法即可求出反比例函数和一次函数的解析式;(2)根据图象即可求得;(3)根据矩形满足的两个条件画出符合要求的两个矩形即可.【详解】(1)∵反比例函数y=kx(x>0)的图象过格点P(2,2),∴k=2×2=1,∴反比例函数的解析式为y=4x,∵一次函数y=mx+n的图象过格点P(2,2),B(1,1),∴2241m nm n+=⎧⎨+=⎩,解得123mn⎧=-⎪⎨⎪=⎩,∴一次函数的解析式为y=﹣12x+3;(2)一次函数值大于反比例函数值时x的取值范围是2<x<1,故答案为2<x<1.(3)如图所示:矩形OAPE、矩形ODFP即为所求作的图形.【点睛】此题是一道综合题,考查待定系数法求函数解析式、矩形的性质,(3)中画矩形时把握矩形特点即可正确解答.25、(1)详见解析;(2)⊙O的半径为154.【分析】(1)证明EF是O的切线,可以连接OD,证明OD⊥EF;(2)要求O的半径,即线段OD的长,在证明△EOD∽△EAF的基础上,利用对应线段成比例可得ODAF=OEEA,其中AF=6,AE可利用勾股定理计算出来,OE可用含半径的代数式表示出,这样不难计算出半径OD的长.【详解】(1)证明:连接OD.∵EF⊥AF,∴∠F=90°.∵D是BC的中点,∴=BD CD.∴∠EOD=∠DOC=12∠BOC,∵∠A=12∠BOC,∴∠A=∠EOD,∴OD∥AF.∴∠EDO=∠F=90°.∴OD⊥EF,∴EF是⊙O的切线;(2)解:在Rt△AFE中,∵AF=6,EF=8,∴22AE AF EF=+2268+10,设⊙O半径为r,∴EO=10﹣r.∵∠A=∠EOD,∠E=∠E,∴△EOD∽△EAF,∴ODAF=OEEA,∴10610r r-=.∴r=154,即⊙O的半径为154.【点睛】本题考查的知识点有切线的性质与判定,相似三角形的性质与判定,解题中添加过切点与圆心的辅助线是关键点,也是难点.26、(1)13EC AC =;(2)32m 【分析】(1)通过证明FMD ECD ∆∆,再根据相似三角形对应边成比例即可求出;(2)设AB=m ,由F 是ABC ∆中AB 边上的中点,可得1122FB AB m ==,进而得出12EC m =,根据题意,进而得出332AC EC m == 【详解】解:(1)∵F 为AB 的中点,//FM AC , ∴M 为BC 的中点,12FM AC =, ∴,CED MFD ECD FMD ∠=∠∠=∠,∴FMDECD ∆∆, ∴23DC EC DM FM ==, ∴22113323EC FM AC AC ==⨯=, ∴13EC AC =. (2)∵AB m =,∴1122FB AB m ==. ∵FB EC =,∴12EC m =. ∵13EC AC =, ∴332AC EC m ==.【点睛】本题考查了相似三角形的判定及性质和三角形的中位线定理,熟练掌握相关性质结合题目条件论证是解题的关键.。
型月知识点

型月知识点型月(TYPE-MOON)是一家日本成人游戏和动画制作公司,成立于2000年。
该公司以其知名的作品《Fate/stay night》系列而闻名于世。
本文将以“型月知识点”为标题,为您介绍一些与型月相关的知识。
一、Fate系列Fate系列是型月公司最为知名的作品,包括游戏、小说、漫画和动画等多种形式。
其中,《Fate/stay night》是该系列的首部作品,讲述了一场召唤英灵(Servant)与魔术师(Master)对抗的战斗,故事充满了魔法、英雄和命运等元素。
二、剧情分支在《Fate/stay night》中,玩家可以选择不同的剧情分支,决定主角的命运走向。
主要分为“Fate”、“Unlimited Blade Works”和“Heaven’s Feel”三条路线。
每条路线都有自己的故事和角色发展,为整个系列增添了更多的情节和复杂性。
三、Servant类型在Fate系列中,Servant是英灵的称呼,他们是历史上伟大战士、英雄或传奇人物的灵魂投射。
Servant被召唤到现实世界中,为魔术师提供力量和战斗能力。
根据召唤的方式和英灵的类型,Servant可分为七个不同的职阶:Saber(剑士)、Lancer(枪兵)、Archer(弓兵)、Rider(骑兵)、Caster(术师)、Assassin(刺客)和Berserker(狂战士)。
四、魔术系统型月作品中的魔术系统是一个重要的元素,魔术师们通过施展魔术来获得超自然的力量。
魔术系统包括了各种咒语、符咒和仪式等,有着严格的规则和限制。
在《Fate/stay night》中,主要的魔术系统是由魔术师家族“间桐”所掌握的间桐式魔术。
五、Holy Grail WarHoly Grail War(圣杯战争)是《Fate/stay night》系列的核心背景。
它是一场由七位魔术师和他们各自召唤的Servant之间展开的战斗。
他们的目标是为了夺取圣杯,圣杯被认为可以实现获胜者的任何愿望。
【硬核闲扯】fate系列宝具真名解析(合集·上)

主,也有称之为“EA(埃阿)”的说法。
马尔杜克神杀死了提亚马特,埃阿神杀死了阿勃祖。
(这对⽗⼦简直灭世双煞)宝具名:祈祷之⼸持有者:罗宾汉宝具真名:Yew Bow真名解析:Yew→凯尔特的圣树·紫衫⽊,剧毒。
Bow→⼸,也有低下头的意思,低下头有为了做祈祷准备的感觉。
翻译过来⼤概就是「垂⾸的紫衫⽊」或「紫衫⽊⼸」宝具名:诉状的箭书持有者:阿塔兰忒宝具真名:Phoibos Catastrophe真名解析:Phoibos→⾳译是福玻斯,⽤希腊语写则是Φοίβος,是与阿波罗对应的罗马太阳神,意思是「光」。
Catastrophe→⼤灾难。
简单来说就是「阿波罗之灾」,接地⽓的说法就是「阿波罗⼜双叒要搞⼤事情了」宝具名:神罚之野猪持有者:阿塔兰忒宝具真名:Agrius Metamorphose真名解析:Agrius→Ἄγριος野蛮者,⾳译为阿格⾥俄斯。
乌拉诺斯与盖亚的⼉⼦,种族为“癸⼲忒斯(巨⼈)”。
Metamorphose→变形/变质即「变质为野蛮者」。
根据宝具的描述,若是有⼈披上这块⽪,那么变成的就是魔⼈⽽⾮魔兽。
宝具名:流星⼀条持有者:阿拉什宝具真名:Stella真名解析:拉丁语的「星星」,那个英雄⼜化作了星星吗?宝具名:鲜⾎魔娘持有者:伊丽莎⽩·巴托⾥宝具真名:Báthory Erzsébet宝具真名:Bellerophon真名解析:Bellerophon→「柏勒洛丰」,驾驭了从美杜莎⾎液中诞⽣的天马珀伽索斯(Pegasus)的⼈类英雄。
宝具名:他者封印·鲜⾎神殿持有者:美杜莎宝具真名:Blood Fort·Andromeda真名解析:Blood Fort→鲜⾎堡垒Andromeda→珀尔修斯的妻⼦安德罗墨达,死后升为仙⼥座。
「仙⼥座·鲜⾎堡垒」注:在原版波德星图(Uranographia)中,仙⼥座双⼿是被铁链缚著的,所以才是「封印」吧。
小学五年级数学思维专题训练—等积变形(含答案解析)
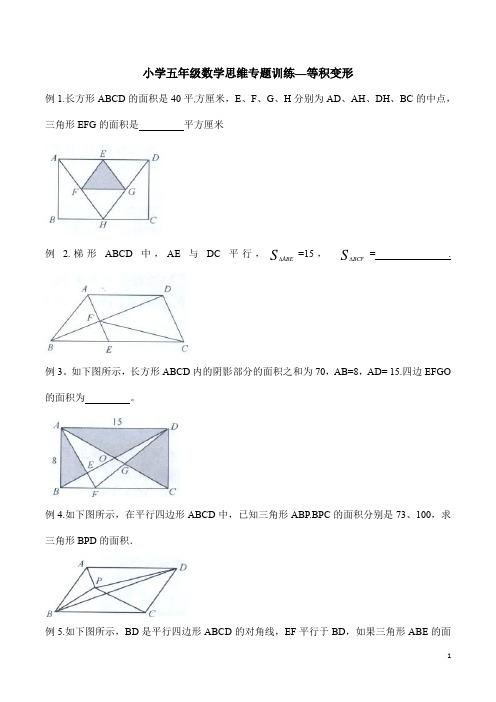
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
圣杯战争

自古便管理着冬木之地的灵脉的魔术名家。擅长于将力量转移到宝石上。向圣杯战争关系者提供土地的就是 远坂。虽然是日本的家系,但咒文的咏唱和仪礼却使用德语。起因是教授远坂魔术的老师是泽尔里奇。还有,远 坂家的人具备一种让人困扰的特质,常常在致命的时机上发动的“那个”,用通俗言语来表示的话就是“不留 神”。远坂凛之父——远坂时臣,即拜此所赐而失去生命。
随后,他们与日本本土的魔术家族远坂家接触,并一同开始了实现“圣杯”降世,达到“根源”的行动。
擅长于炼金术的魔术名家,构筑出冬木市的圣杯战争的系统的御三家之一。实际上是第三魔法使的弟子们制 作的人造人。在制作者纷纷离开后,还在为实现制作者的理念继续运行。在贵金属的操作上无比强大。由于在擅 长领域的研究上加以特化,因而在魔术战斗的应用这一点上稍有逊色。构筑圣杯战争的系统时,一起创造出小圣 杯和大圣杯的就是爱因兹贝伦。启动大圣杯,使用其力量固定前往“根源”的孔,到达“那一边”。为此而被使 用的手段,就是爱因兹贝伦家所流传的“第三魔法”。
历次斗争
01
第一次
02
第二次
03
第三次
04
亚种
06
圣杯大战
05
第四次
第五次 Fate/Grand Order
夜之 解体
伪
月
圣杯探索——冠位
指定
约1810年代,最初的圣杯战争打响。
最开始时,这第一次的圣杯召唤仪式以“合作召唤”的形式进行的。然而在圣杯打开了与魔力源泉的接连之 后,事态却演变成远坂和爱因兹贝伦家族、玛奇里家族相互争夺独占的权力,结果立刻以失败告终。从此三大家 族组成圣杯盟约,立下沿用至今的规则,叫来其他的魔术师,然后让他们以圣杯为目的相互残杀——除了自己以 外,能够召唤出英灵的魔术师全部都是妨碍者,让他们在战斗中死去就行了——如果一开始抱有的是这样的想法 的话,整个运作过程的效率也会更好;而以三大家族的立场来看,能够合法的收拾掉自己以外的魔术师未尝不是 件好事。
型月的七曜魔法使

型月的七曜魔法使《型月的七曜魔法使》我国最著名的视觉小说公司之一,TYPE-MOON,创下了许多深受粉丝喜爱的作品。
其中,《Fate/stay night》系列更是风靡全球,成为日本次文化的重要组成部分。
而这个系列中最令人痴迷的元素之一,便是“七曜魔法使”。
在《Fate/stay night》的世界观中,魔法是一种能力,七曜魔法使便是拥有这种能力的特殊存在。
七曜——我们平时所熟知的太阳、月亮、火星、水星、木星、金星和土星。
在传说中,七曜被赋予了特殊的意义和能力,被魔法使们视作极其重要的存在。
每位魔法使都与特定的七曜之一相对应,他们通过与之建立契约,可以获得特殊的魔力。
这些魔法使分别掌握着不同的魔法,例如太阳魔法使可以利用太阳的力量释放强大的火焰;月亮魔法使则可以借助月亮的力量进行追踪和侦察。
七曜魔法使的魔法能力是多样而强大的,他们经常成为故事的关键人物。
在《Fate/stay night》的剧情中,主角——英灵使——与七个不同的七曜魔法使展开了一场残酷的战斗。
他们为了获得“圣杯”的力量,相互争夺,展开了一场生死搏斗。
在这个世界中,魔法是一种力量的象征,而通过与七曜建立契约,魔法使们能够超越常人的能力限制。
然而,魔法并非唯一的力量。
在《Fate/stay night》中,英灵的存在也对故事的发展起到了重要作用。
英灵作为历史上的英雄或传说中的人物,拥有与众不同的力量。
与魔法使相对立的是英灵使,而他们之间的对抗也是剧情中的核心。
《Fate/stay night》系列通过将魔法和英灵融合在一起,创造了一个独特而引人入胜的故事世界。
七曜魔法使们的存在,使得这个世界更加神秘和多样化。
他们的能力给予了剧情更多的可能性,也为粉丝们带来了更多的悬念和期待。
通过《Fate/stay night》这一作品,我们可以见识到TYPE-MOON作品的独特魅力。
七曜魔法使们不仅是战斗的象征,也是对于魔法和人类力量的思考。
他们所承载的神秘力量,与现实世界中的科技进步形成了鲜明的对比,给人们带来了一种愉悦的沉浸式体验。
FGO英灵统计
双围最大值 24857 17093 26371 21837 18358 21202 22346 17092 26250 17113 22021 20919 25377 16902 21109 16538 12938 16832 20992 14950 17180 14542 17122 16137 14436 14095 16419 16104 15996 20641 21082 16061 16020 14242 13878 16055 12324 24857 16184 11955 13874 20503 15500 13765 14047 11942 19881 20982 20804 16421 12795 24862 25269
生命最大值 14259 10302 15150 11589 10632 11753 14165 9595 13907 10498 13256 11521 13097 Байду номын сангаас0187 12476 9506 7122 9593 11870 9149 10098 7959 9883 8937 9200 7907 10130 9028 8640 12348 13068 8643 9506 8484 8080 9216 7129 14259 9604 6220 7594 11518 8293 8309 8393 6565 10473 10327 10327 8302 7722 12150 13770
6604 7303 8763 9166 7688 11458 16500 14553 11404 14259 8643 10200 12830 11286 13070 13225 11637 14825 10098 9786 11286 11882 12696 14680 13825 11761 9506 10887 8592 10687 14259 13230 13632 12696 12750 14825 10327 14248 15453 11055 14107 11172 8731 12177 15221 12210 13968 11882 11993 11360 11882 9123 9506 11761
六年级奥数优胜教育第3讲:等积变形含答案

第三讲等积变形例1:如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为.例2:长方形ABCD的面积为36cm2,E、F、G为各边中点,H为AD边上任意一点,问阴影部分面积是多少?A H DE GB F C例3:如图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD=15,四边形EFGO的面积为.A DE OGB F C例4:已知ABC为等边三角形,面积为400,D、E、F分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC)例5:如图,已知CD=5,DE=7,EF=15,FG=6,线段AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是.A AC D E F G C D E FGB B例6:如图在△ABC中,D,E分别是AB,AC上的点,且AD:AB=2:5,AE:AC=4:7,△S ADE=16平方厘米,求△ABC的面积.AAD DE EB C B C例7:如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△S ADE=12平方厘米,求△ABC的面积.DAEB CDAEB C例8:如图,平行四边形ABCD,BE=AB,C F=2CB,G D=3DC,HA=4A D,平行四边形ABCD的面积是2,求平行四边形ABCD与四边形EFGH的面积比.H HA B E A B EG D C G D CF例9:如图所示的四边形的面积等于多少?FC O131213D1312131212AB例10:如图所示,∆ABC中,∠ABC=90︒,AB=3,BC=5,以AC为一边向∆ABC外作正方形ACDE,中心为O,求∆OBC的面积.EEO DODA3B5CA3B5C F A1.如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?_E_E_A_B_A_B_F_F_D_G_C_D_G_C2.在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.A D A(P)D A DP PB C B C B CC C甲乙3.如图,长方形ABCD的面积是36,E是AD的三等分点,AE=2ED,则阴影部分的面积为.A E DA E DMNO OB B4.如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?A AD E DEB C B C5.如图,三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC=4,B E=3,AE=6,乙部分面积是甲部分面积的几倍?A AE B甲乙D C BED CB6.如图,以正方形的边AB为斜边在正方形内作直角三角形ABE,∠AEB=90︒,AC、B D 交于O.已知AE、BE的长分别为3cm、5cm,求三角形OBE的面积.C B C BO E OEFD A D A7.如下图,六边形ABCDEF中,AB=ED,AF=CD,BC=EF,且有AB平行于ED,AF 平行于CD,BC平行于EF,对角线FD垂直于BD,已知F D=24厘米,BD=18厘米,请问六边形ABCDEF的面积是多少平方厘米?B G BAC ACF D F DE E角形 BCD 的面积的 ,且 AO = 2 ,DO = 3 ,那么 CO 的长度是 DO 的长度的_________倍.EBE8.如图,三角形 ABC 的面积是 1 , E 是 AC 的中点,点 D 在 BC 上,且 BD : DC = 1: 2 , AD 与 BE 交于点 F .则四边形 DFEC 的面积等于 .AEBDFC9.如图,长方形 ABCD 的面积是 2 平方厘米, EC = 2DE , F 是 DG 的中点.阴影部分的面积是多少平方厘米?AD ADBGFECBxF x y Gy EC10.四边形 ABCD 的对角线 AC 与 BD 交于点 O (如图所示).如果三角形 ABD 的面积等于三13ADOBCC11.如图,平行四边形 ABCD 的对角线交于 O 点,△CEF 、△OEF 、△ODF 、△BOE 的面 积依次是 2、4、4 和 6.求:⑴求 △OCF 的面积;⑵求 △GCE 的面积.ADOF GBEC12.如图,长方形 ABCD 中, BE : EC = 2:3 , DF : FC = 1: 2 ,三角形 DFG 的面积为 2 平方 厘米,求长方形 ABCD 的面积.AGDFAGDFBCC13.如图,正方形ABCD面积为3平方厘米,M是AD边上的中点.求图中阴影部分的面积.B CGA M D14.在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是平方厘米.A DFB E C15.已知ABCD是平行四边形,BC:CE3:2,三角形ODE的面积为6平方厘米.则阴影部分的面积是平方厘米.A DA DO OB C E B C E1.右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米.A D A D992121O44B E B E CCDA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数 ,那么,2.右图中 ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米), 阴影部分的面积是 平方厘米.AD AD881616O 2 2BEC BEC3.如图,长方形 ABCD 被 CE 、 DF 分成四块,已知其中 3 块的面积分别为 2、5、8 平方厘 米,那么余下的四边形 OFBC 的面积为___________平方厘米.A EFB A EFB225O ?5O ?88DC D C4.如图, ∆ABC 是等腰直角三角形, DEFG 是正方形,线段 AB 与 CD 相交于 K 点.已知正 方形 DEFG 的面积 48, AK : KB = 1:3 ,则 ∆BKD 的面积是多少?DA G DA GKKBEF C B E M F C5.下图中,四边形 ABCD 都是边长为 1 的正方形,E 、F 、G 、H 分别是 AB ,BC ,CD ,mn(m + n ) 的值等于.AH D A H DEG E GBFC BFC1.用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.2.用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及 1∶3∶4.3.如右图,在梯形 ABCD 中,AC 与 BD 是对角线,其交点 △O ,求证:AOB 与△COD 面积相等.4.如右图,把四边形 ABCD 改成一个等积的三角形.5.如右图,已知在△ABC 中,BE=3AE ,CD=2AD .若△ADE 的面积为 1 平方厘米.求三角形 ABC的面积.6.如下页图,在△ABC 中,BD=2AD ,AG=2CG ,BE=EF=FC=面积的几分之几?1 3BC ,求阴影部分面积占三角形 A BC7.如右图,ABCD 为平行四边形,EF 平行 △A C ,如果 ADE 的面积为 4 平方厘米.求三角形 CDF的面积.8.如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.9.如右图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若△S ADE=1,求△BEF的面积.△S ACD = △S BCD ,则可知直线 AB 平行于 CD .E第三讲 等积变形1.等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图 S : S = a : b12③夹在一组平行线之间的等积变形,如图 △S ACD = △S BCD ;反之,如果④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于 它们的高之比. 2.鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在 △ABC 中,D , E 分别是 AB, AC 上的点如图 ⑴(或 D 在 BA 的延长线上, 在 AC 上),则S△ABC :S△ADE=(AB⨯AC):(AD⨯AE)3.蝶形定理任意四边形中的比例关系(“蝶形定理”):①S:S=S:S或者S⨯S=S⨯S②AO:OC=(S+S):(S+S)124313241243蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.DAS2S1OS4S3B C梯形中比例关系(“梯形蝶形定理”):①S:S=a2:b213②S:S:S:S=a2:b2:ab:ab;1324③S的对应份数为(a+b)2.4.相似模型(一)金字塔模型(二)沙漏模型A E F DAD F EB GC B G C①AD AE DE AF===AB AC BC AG;②:=AF2:AG2.△S ADE△S ABC所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.5.共边定理(燕尾模型和风筝模型)共边定理:若直线AO和BC相交于D(有四种情形),则有S∆ABO :S∆ACO=BD:DC在三角形ABC中,AD,BE,CF相交于同一点O,那么S:S=BD:DC.∆ABO∆ACO上述定理给出了一个新的转化面积比与线段比的手段,因为∆ABO和∆ACO的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.AFEBOD C1.了解三角形的底、高与面积的关系,会通过分析以上关系解题。
南京市鼓楼区2021-2022学年九年级上学期期中考试数学试卷

江苏省南京市鼓楼区2021-2022学年九年级(上)期中考试数学试卷 一、选择题(本大题共6小题,每小题2分,共12分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)2分)一元二次方程x 2=x 1.(的根为()A .0B .1C .0或1D .0或﹣12分)平面内,若⊙O 的半径为2,OP 2.(=A .内,则点P 在⊙O (CB .上.外)D .内或外 3.(2分)某商品单价经过两次降价从144元降至81元,设平均每次降价的百分率为x ,则可列方程()A .144(1+x )2=81C .81(1+x )2=1441﹣x )2=811﹣x )2=B .144(D .81(144 4.(2分)在某次比赛中,有10位同学参加了“10进5”的淘汰赛,他们的比赛成绩各不相同.其中一位同学要知道自己能否晋级,不仅要了解自己的成绩,还需要了解10位参赛同学成绩的(A ).平均数B .加权平均数C .众数D .中位数2分)如图,△ABC 内接于⊙O ,DE ,FG 是⊙O 的弦,AB =DE ,FG =AC 5.(.下列结论: ①DE +FG =BC ;②+;③∠DOE +∠FOG =∠BOC ;④∠DEO +∠FGO =∠BAC =.其中所有正确结论的序号是()A .①②③④B .②③C .②④D .②③④6.(2分)如图,∠1是正九边形两条对角线的夹角,则∠1的度数是()A .45°B .54°C .60°D .72° 二、填空题(本大题共10小题,每小题2分,共20分。
不需写出解答过程,请把答案直接填写在答题卡相应的位置上) 7.(2分)写出一个一元二次方程,使它有两个不相等的实数根.8.(2分)已知扇形的圆心角为60°,半径为1,则扇形的弧长为.2分)已知⊙O 的半径为2,若点P 是⊙O 的切线l 上任一点,则OP 9.(长的取值范围是. 10.(2分)已知一个圆锥的底面半径为2,母线长为5,则这个圆锥的侧面积为(结果保留π).2分)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,AE =1,CD =4,则OC 11.(的长为.2分)一元二次方程x 2+kx ﹣3=0的一个根是x =1,则另一个根是. 12.(13.( 2分)某单位要招聘1名英语翻译,小亮参加招聘考试的各门成绩如表所示若把听、说、读、写的成绩按3:3:2:2计算平均成绩,则小亮的平均成绩为. 项目 听 说读写成绩(分)7090858514.(2分)如图,四边形ABCD 的各边都与圆相切,它的周长为18,若AB =5,则CD 的长为.15.(2分)如图,矩形ABCD 的四个顶点分别在扇形OEF 的半径和弧上,若∠O =60°,OB =BC ,OE =4,则AB 的长为.16.( 2分)在平面直角坐标系中,A (﹣2,0),B (4,0),若直线y =x +b 上存在点P 满足45°≤∠APB ≤90°且P A =PB ,则常数b 的取值范围是.三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.(8分)解下列一元二次方程 1)x ((x +2)=5(x +2);(2)x 2+5x +3=0.8分)一块矩形菜地的面积是130m 2,若将它的长、宽分别增加5m ,8m ,它恰成为18.(一块正方形菜地.求原矩形菜地的长和宽.19.(8分)如图,在以AB 为直径的圆中,弦CD ⊥AB ,M 是AB 上一点,射线DM ,CM 分别交圆于点E ,F ,连接EF ,求证EF ⊥AB.8分)已知关于x 的一元二次方程x 2+20.((k +4)x +k +3=0的两根是x 1,x 2.1)当k 为何值时,这个方程总有两个不相等的实数根(?(2)说明:无论k 为何值,方程总有一个不变的根.21.(8分)数学小组对当地甲、乙两家网约车公司司机的月收入情况进行了抽样调查.两家 公司分别随机抽取10名司机,他们的月收入(单位:千元)情况如图所示. 将以上信息整理分析如下: 平均数 中位数众数方差 甲公司a 7c d乙公司7b 57.6 1)填空:a (= ;b =;c =;d =; (2)某人计划从甲、乙公司中选择一家做网约车司机,你建议他选哪家公司?说明理由.22.(8分)利用圆的性质,证明定理“直角三角形斜边上的中线等于斜边的一半”.已知:如图,在△ABC 中,∠ACB =90°,CD 是斜边AB 上的中线.求证:CD =AB . 8分)若关于x 的方程x 2+bx +c =0有两个实数根,且其中一个根比另一个根大2,23.(那 么称这样的方程为“隔根方程”.例如,方程x 2+2x =0的两个根是x 1=0,x 2=﹣2,则方程x 2+2x =0是“隔根方程”.1)方程x 2﹣x ﹣20=0是“隔根方程”吗?判断并说明理由(; (2)若关于x 的方程x 2+mx +m ﹣1=0是“隔根方程”,求m 的值. 24.(8分)在方格纸中,仅用无刻度直尺过点A 画出圆的所有切线.1)如图1,点A (在圆上;(2)如图2,点A 在圆外. 25.( 8分)如图,在Rt △ABC 中,∠C =90°,AC =6cm ,BC =8cm ,点P 从点B 开始沿 BC 向点C 以1cm /s 的速度运动,点Q 从点C 开始沿CA 向点A 以2cm /s 的速度运动,P ,Q 同时出发,各自到达终点后停止运动.在整个运动过程中,设它们的运动时间为ts .1)下列说法(正确的是.(填写所有正确结论的序号)①PQ 可以平分△ABC的周长;②PQ 可以平分△ABC 的面积.(2)当t 为何值时,△PCQ 的面积等于7cm 2?26.(8分)如图,在正方形ABCD 中,E 是BD 上一点,射线AE 交CD 于点F ,交BC 的延长线于点G ,过点C ,F ,G 画圆,连接CE .求证:CE 是圆的切线.27.(8分)解题与遐想.如图,Rt △ABC 的内切圆与斜边AB 相切于点D ,AD =4,BD =5.求Rt △ABC 的面积.王小明:这道题算出来面积刚好是20,太凑巧了吧.刚好是4×5=20,有种白算的感觉…赵丽华:我把4和5换成m 、n 再算一遍,△ABC 的面积总是m •n !确实非常神奇了…数学刘老师:大家想一想,既然结果如此简单到极致,不计算能不能得到呢?比如,拼图?霍佳:刘老师,我在想另一个东西,这个图能不能尺规画出来啊感觉图都定了.我怎么想不出来呢?计算验证1)通过计算求出Rt △ABC (的面积.拼图演绎(2)将Rt△ABC分割放入矩形中(左图),通过拼图能直接“看”出“20”请在图中画出拼图后的4个直角三角形甲、乙、丙、丁的位置,作必要标注并简要说明.尺规作图(3)尺规作图:如图,点D在线段AB上,以AB为斜边求作一个Rt△ABC,使它的内切圆与斜边AB相切于点D.(保留作图的痕迹,写出必要的文字说明)江苏省南京市鼓楼区2021-2022学年九年级(上)期中考试数学试卷答案与解析一、选择题(本大题共6小题,每小题2分,共12分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)2分)一元二次方程x2=x1.(的根为()A.0B.1C.0或1D.0或﹣1【分析】先移项,再两边都除以3,分解因式,即可得出两个一元一次方程,求出方程的解即可.【解答】解:x2=x,x2﹣x=0,x(x﹣1)=0,∴x=0或x=1,故选:C.2分)平面内,若⊙O的半径为2,OP 2.(=A.内,则点P在⊙O(CB.上.外)D.内或外【分析】根据半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内,可得答案.【解答】解:由题意得,d=∵d<r,∴点P在⊙O内,故选:A ,r=2..3.(2分)某商品单价经过两次降价从144元降至81元,设平均每次降价的百分率为x,则可列方程()A.144(1+x)2=81 C.81(1+x)2=1441﹣x)2=811﹣x)2=B.144(D.81(1441﹣平均每次降价的百分率)2,即可得出【分析】利用经过两次降价后的价格=原价×(关于x的一元二次方程,此题得解.1﹣x )2=81.【解答】解:依题意得:144(故选:B . 4.(2分)在某次比赛中,有10位同学参加了“10进5”的淘汰赛,他们的比赛成绩各不相同.其中一位同学要知道自己能否晋级,不仅要了解自己的成绩,还需要了解10位参赛同学成绩的(A ).平均数B .加权平均数C .众数D .中位数【分析】10人成绩的中位数是第5名和第6名同学的成绩的平均数.参赛选手要想知道自己是否能晋级,只需要了解自己的成绩以及全部成绩的中位数,比较即可.【解答】解:由于总共有10个人,且他们的成绩各不相同,第5名和第6名同学的成绩的平均数是中位数,要判断是否能晋级,故应知道中位数的多少.故选:D .2分)如图,△ABC 内接于⊙O ,DE ,FG 是⊙O 的弦,AB =DE ,FG =AC 5.(.下列结论: ①DE +FG =BC ;②+;③∠DOE +∠FOG =∠BOC ;④∠DEO +∠FGO =∠BAC =.其中所有正确结论的序号是()A .①②③④B .②③C .②④D .②③④【分析】利用已知条件与三角形的任意两边之和大于第三边可以判定①错误;利用在同圆或等圆中,等弦对等弧,以及等式的性质可以判定②正确;利用在同圆或等圆中,等弦所对的圆心角相等以及等式的性质可以判定③正确;利用等腰三角形的性质以及③的结论可以判定④正确.【解答】解:∵AB +AC >BC ,AB =DE ,FG =AC ,∴DE +FG >BC .∴①错误;∵AB =DE ,FG =AC ,,∴∴∴.,+=.∴②正确;连接OA ,OB ,OC ,OD ,OE ,OF ,OG ,如图, ∵AB =DE ,FG =AC ,∴∠AOB =∠DOE ,∠AOC =∠FOG .∴∠AOB +∠AOC =∠DOE +∠FOG .即∠DOE +∠FOG =∠BOC .∴③正确;∵OA =OB ,∴∠OAB =∠OBA =同理可得:∠OAC =90°﹣∠AOC ,∠DEO =90°﹣∠DOE ,∠FGO =90°﹣∠FOG =90°﹣∠AOB ..∴∠OAB +∠OAC =180°﹣(∠AOB +∠AOC )=180°﹣∠BOC ,∠DEO +∠FGO =180°﹣(∠DOE +∠FOG ).由③知:∠DOE +∠FOG =∠BOC,∴∠OAB +∠OAC =∠DEO +∠FGO .即:∠DEO +∠FGO =∠BAC .∴④正确;∴正确的序号为:②③④.故选:D .6.(2分)如图,∠1是正九边形两条对角线的夹角,则∠1的度数是()A .45°B .54°C .60°D .72°【分析】根据正多边形与圆求出相应的圆心角度数,再根据圆周角定理和三角形外角的性质可得答案.【解答】解:如图,设这个正九边形的外接圆为⊙O ,则∠AOB ==40°,∠COD =2∠AOB =80°,∴∠ADB =∠AOB =20°,∠CBD =∠COD =40°,∴∠1=∠ADB +∠CBD =20°+40°=60°,故选:C .二、填空题(本大题共10小题,每小题2分,共20分。
fgo测试题及答案

fgo测试题及答案Fate/Grand Order(简称FGO)是一款基于TYPE-MOON出品的《Fate/stay night》视觉小说的角色扮演游戏。
以下是一份关于FGO 的测试题及答案,供玩家进行自我测试。
一、选择题1. FGO的故事背景中,英灵是由什么构成的?A. 神话传说B. 历史传说C. 人类愿望D. 以上都是答案:D2. 在游戏中,玩家扮演的组织名称是什么?A. 迦勒底B. 阿赖耶识C. 圣杯战争D. 冬木市答案:A3. 下列哪位英灵不是Saber职阶?A. 阿尔托莉雅·潘德拉贡B. 贞德·达尔克C. 赫拉克勒斯D. 弗拉德三世答案:C4. FGO中,圣杯战争的胜利者将获得什么?A. 无尽的财富B. 一个愿望C. 至高的力量D. 永生答案:B5. 下列哪项不是游戏中的职阶?A. SaberB. ArcherC. LancerD. Mage答案:D二、是非题1. 在FGO中,所有的英灵都是基于真实历史或神话传说中的人物。
()答案:错误。
虽然许多英灵是基于真实历史或神话传说中的人物,但也有一部分是虚构的,如原创角色。
2. 游戏中的职阶系统决定了英灵的性别。
()答案:错误。
职阶系统决定了英灵在圣杯战争中的战斗角色和能力,与性别无关。
3. 玩家在游戏过程中只能召唤一次英灵。
()答案:错误。
玩家可以通过游戏内的召唤系统多次召唤英灵。
三、简答题1. 描述一下FGO中的“令咒”系统是如何工作的。
答案:在FGO中,令咒是赋予Master的三个强大的命令符,可以用来强制命令从者执行特定的行动。
每个令咒都有不同的充能时间,一旦使用,需要等待一段时间才能再次使用。
令咒可以用于在战斗中强制从者攻击、防御或者执行其他特殊行动。
2. 解释一下什么是“技能强化本”。
答案:技能强化本是游戏中的一种特殊副本,玩家可以通过完成这些副本来提升从者的技能等级。
技能等级的提升可以增强从者的特定能力,如攻击力、防御力或者特殊技能效果。
莫徳雷德图法利斯的记忆材料

莫徳雷德图法利斯的记忆材料中文名莫德雷德外文名 Mordredモードレッド别名叛逆之骑士、小莫、莫仔、熊孩子饰演甲斐千寻(2017年舞台剧)配音日语:桑岛法子(2006Fsn)泽城美雪(FGO&FA)、英语:Erica Indbeck、德语:Ilena Gwisdalla、意大利语:Cristiana Rossi、西班牙语:Rocío Pereiras、葡萄牙语:Amanda Moreira(巴西)性别女登场作品《Fate/Apocrypha》《Fate/stay night》(阿尔托莉雅的回忆)即他是阿尔托莉雅和摩根的不贞之子的真相,以及“亚瑟王并不知道莫德雷德是自己的孩子,即使知道,她也不会承认自己有这么一个污秽的孩子”这种话。
莫德雷德在受到打击的同时,也沉浸在无上的喜悦之中。
虽然背负母亲如此的妄念,但莫德雷德对于亚瑟王的憧憬远超那份野心。
虽然自己并不是正常的人类,却和那位王留着相同的血脉。
作为王的继承人,自己可谓名副其实,深皆符。
但直到最后,阿尔托莉雅依旧是很明确地拒绝了莫德雷德。
在决战之地卡姆兰(Camlan)之丘上,莫德雷德最终被阿尔托莉雅杀死,而阿尔托莉雅自己也受到了致命一击——这场战争最终将王国引向灭亡。
莫德雷德 Fate/Apocrypha 人物设定出处:亚瑟王传说地区:英国属性:混沌·中庸性别:女性和阿尔托莉雅在体格方面完全一致。
莫德雷德是圆桌骑士的成员之一、也是亚瑟王的嫡子。
同时也是在剑栏之丘将亚瑟王杀死——为传说画上句点的叛逆之骑士。
莫德雷德是由亚瑟王的姐姐、同时也是其宿敌的魔女摩根以诡计所生下的人工生命——属于Homunculus的一种。
莫德雷德是为了讨伐亚瑟王、并且成为超越亚瑟的王者而诞生的。
身为Homunculus的莫德雷德有着惊人的成长速度,出生数年之后便开始以骑士的身份侍奉亚瑟王。
同时,借由完全模仿了亚瑟王的身体性能,很快地在众多骑士中脱颖而出。
fate里的部分名词解释

fate里的部分名词解释Fate是一部热门的日本动漫作品,该作品以其扣人心弦的剧情和精美的画面而深受观众喜爱。
在这部作品中,有许多名词以及概念需要解释以加深我们对Fate世界的理解和欣赏。
以下是对这些名词的解释,希望能为大家带来更丰富的观赏体验。
1. Holy Grail(圣杯)在Fate系列中,圣杯是众多魔术师为之争夺的目标。
据传,获得圣杯的人将被赋予实现任何愿望的能力。
因此,圣杯成为了各种势力之间争夺的焦点。
但是,在剧情中,圣杯往往并非如人们所期望的那样纯净善良,而是带有某种程度上的腐败和恶意。
2. Servant(从者)Servant是与圣杯战争相关的特殊存在,他们是历史上伟大英灵化身的精神投射体。
Servant被分为七个等级:S/A/B/C/D/E,其中S级是最高等级,能力最强大,而E级则是最低等级。
Servant的能力主要来源于他们有着丰富的传说和历史背景。
3. Command Spell(指令咒印)Command Spell是供Master(魔术师)支配Servant的特殊标记。
每位Master初始拥有三个Command Spell,这些标记允许Master下达三个无条件的命令给Servant。
这些命令一旦被用完,Master就会失去对Servant的控制权。
4. Noble Phantasm(宝具)Noble Phantasm是Servant的终极技能,每个Servant都有其独特的Noble Phantasm。
宝具通常代表着Servant的传说和历史起源,其威力通常是毁灭性的。
在战斗中,Servant可以使用宝具来提高自身的战斗力,但使用宝具需要耗费Servant自身的真名。
5. Grail War(圣杯战争)Grail War是为了争夺圣杯而举行的一场残酷的战斗。
圣杯战争通常由七名魔术师以及他们各自的Servant参与。
他们被放置在一个虚拟地图中,为了争夺圣杯而互相战斗。
在这个过程中,只有最后一位存活下来的Master和他的Servant才能获得圣杯。
(金手指)圣女贞德(日汉化版)[精彩]
![(金手指)圣女贞德(日汉化版)[精彩]](https://img.taocdn.com/s3/m/75f5a5fb4bfe04a1b0717fd5360cba1aa8118c80.png)
(金手指)圣女贞德(日汉化版) _G JEANNE D'ARC -圣女贞德-_S UCJS-10048_C0 金钱_N0 代码片段_L 0x002B476C 0x0098967F _C0 GEROGE_N0 代码片段_L 0x002BEEB8 0x00000063 _C0 GEORGE_N0 代码片段_L 0x002BEB00 0x00000063 _C0 经验值99_N0 代码片段_L 0x802B49F6 0x000D0140 _L 0x00000063 0x00000000_C0 无限变身时间_N0 代码片段_L 0x002B5E74 0x00000063 _C0 全技能购买_N0 代码片段_L 0x802CC2A0 0x018A0001 _L 0x00000063 0x00000000 _C0 盗贼用挖宝技能石_N0 代码片段_L 0x002BEEC4 0x00000000 _L 0x002BEECA 0x00000000 _C0 物攻+3_N0 代码片段_L 0x002BEB26 0x00000063 _C0 魔攻+3_N0 代码片段_C0 防御+3_N0 代码片段_C0 魔防+3_N0 代码片段_L 0x002BEB32 0x00000063 _C0 命中+5_N0 代码片段_L 0x002BEB36 0x00000063 _C0 回避+5_N0 代码片段_L 0x002BEB3A 0x00000063 _C0 无限移动_N0 代码片段_L 0x802B49F8 0x000F0140 _L 0x00000032 0x00000000_L 0x802B4A04 0x000F0140 _L 0x00000000 0x00000000 _C0 移动力_N0 代码片段_L 0x002B49BF 0x0000008C _L 0x002B4AFF 0x0000008C _L 0x002B4C3F 0x0000008C _L 0x002B4D7F 0x0000008C _L 0x002B4EBF 0x0000008C _L 0x002B4FFF 0x0000008C _L 0x002B513F 0x0000008C _L 0x002B527F 0x0000008C _L 0x002B53BF 0x0000008C _L 0x002B54FF 0x0000008C _C0 SP MAX_N0 代码片段_L 0x802B49F2 0x000F0140 _L 0x0000000A 0x00000000 _C0 SPMAX2_N0 代码片段_L 0x002B49F2 0x0000000A _L 0x002B58F2 0x0000000A _L 0x002B52B2 0x0000000A _C0 其他人的SP_N0 代码片段_L 0x002B4B32 0x0000000A _L 0x002B4C72 0x0000000A _L 0x002B4DB2 0x0000000A _L 0x002B4EF2 0x0000000A _L 0x002B5032 0x0000000A _L 0x002B5172 0x0000000A_L 0x002B52B2 0x0000000A _L 0x002B53F2 0x0000000A _L 0x002B5532 0x0000000A _C0 CT关键值_N0 代码片段_L 0x002B49E8 0x00000064 _L 0x002B4B28 0x00000064 _L 0x002B4C68 0x00000064 _L 0x002B4DA8 0x00000064 _L 0x002B4EE8 0x00000064 _L 0x002B5028 0x00000064 _L 0x002B5168 0x00000064 _L 0x002B52A8 0x00000064 _L 0x002B53E8 0x00000064 _L 0x002B5528 0x00000064 _C0 腕轮_N0 代码片段_L 0x002B49C8 0x00000001 _L 0x002B4B08 0x00000001 _L 0x002B4C48 0x00000001 _L 0x002B4D88 0x00000001 _L 0x002B4EC8 0x00000001 _L 0x002B5008 0x00000001 _L 0x002B5148 0x00000001 _L 0x002B5288 0x00000001 _L 0x002B53C8 0x00000001 _L 0x002B5508 0x00000001 _C0 MP上限_N0 代码片段_L 0x002B4998 0x000003E7 _L 0x002B4AD8 0x000003E7_L 0x002B4C18 0x000003E7 _L 0x002B4D58 0x000003E7 _L 0x002B4E98 0x000003E7 _L 0x002B4FD8 0x000003E7 _L 0x002B5118 0x000003E7 _L 0x002B5258 0x000003E7 _L 0x002B5398 0x000003E7 _L 0x002B54D8 0x000003E7 _C0 MP不减_N0 代码片段_L 0x102B49F0 0x000003E7 _L 0x102B4B30 0x000003E7 _L 0x102B4B30 0x000003E7 _L 0x102B4DB0 0x000003E7 _L 0x102B4EF0 0x000003E7 _L 0x102B5030 0x000003E7_L 0x102B5170 0x000003E7 _L 0x102B52B0 0x000003E7 _L 0x102B53F0 0x000003E7 _L 0x102B5530 0x000003E7 _L 0x102B5670 0x000003E7 _L 0x102B58F0 0x000003E7 _L 0x102B61B0 0x000003E7 _L 0x002BEEC4 0x0000000F _L 0x002BEECC 0x0000000F _L 0x00A110B8 0x0000000F _L 0x002BEEF8 0x0000000F _L 0x002BEEFE 0x0000000F _L 0x002BEEF2 0x0000000F _L 0x002BEF1E 0x0000000F _L 0x002BEF2A 0x0000000F_L 0x002BEF30 0x0000000F _L 0x002BEF34 0x0000000F _L 0x002BEEB4 0x0000000F _L 0x002BEEE8 0x0000000F _L 0x002BEFAA 0x0000000F _L 0x002BEFA8 0x0000000F _L 0x002BEEE6 0x0000000F _L 0x002BEFA4 0x0000000F _L 0x002BEF08 0x0000000F _L 0x002BEE38 0x0000000F _L 0x002BEE94 0x0000000F _L 0x002BEF8A 0x0000000F _L 0x002BEE60 0x0000000F _L 0x002BEE62 0x0000000F _L 0x002BEE5C 0x0000000F _L 0x002BEE5E 0x0000000F_L 0x002BEE64 0x0000000F _L 0x002BEF6E 0x0000000F _L 0x002BEAF4 0x0000000F _L 0x002BEAF2 0x0000000F _L 0x002BEA18 0x0000000F _L 0x002BEA04 0x0000000F _L 0x002BEA02 0x0000000F _L 0x002BE9F0 0x0000000F _L 0x002BE9D0 0x0000000F _L 0x002BE9CE 0x0000000F _L 0x002BE9CC 0x0000000F _L 0x002BE9A8 0x0000000F _L 0x002BE9A6 0x0000000F _L 0x002BE97E 0x0000000F _L 0x002BE980 0x0000000F_L 0x002BE97C 0x0000000F _L 0x002BEA6E 0x0000000F _L 0x002BEA86 0x0000000F _L 0x002BEA60 0x0000000F _L 0x002BEA7C 0x0000000F _L 0x002BEA76 0x0000000F _L 0x002BEA92 0x0000000F _L 0x002BEA48 0x0000000F _L 0x002BEA52 0x0000000F _L 0x002BEA54 0x0000000F _L 0x002BEAE0 0x0000000F _L 0x002BEAE4 0x0000000F _L 0x002BEB26 0x0000005A _C0 火球_N0 代码片段_L 0x002BEE22 0x0000005A_C0 慈光_N0 代码片段_L 0x002BEE3A 0x00000047 _C0 JH_N0 代码片段_L 0x002BEE42 0x00000051 _C0 闪光一击_N0 代码片段_L 0x002BEE72 0x0000003F _C0 隔山打牛_N0 代码片段_L 0x002BEE82 0x00000047 _C0 太阳精+1_N0 代码片段_L 0x002BEEEE 0x00000036_C0 劈柴刀_N0 代码片段_L 0x002BEF66 0x0000005C _C0 天空之箭_N0 代码片段_L 0x002BEE92 0x0000003C _C0 HP全回_N0 代码片段_L 0x202BEB04 0x000A000B _C0 范围补_N0 代码片段_L 0x002BEB12 0x00000032 _C0 MP全回_N0 代码片段_L 0x202BEB0C 0x001E0032 _C0 天使群补_N0 代码片段_L 0x202BEB10 0x005A005A _C0 一闪_N0 代码片段_L 0x002BEEAA 0x0000000D _C0 宝物侄爱_N0 代码片段_L 0x002BEECC 0x00000001 _C0 贤衣_N0 代码片段_L 0x002BEA46 0x0000001E _C0 鞭_N0 代码片段_L 0x202BEAF4 0x003C0033 _C0 手象_N0 代码片段_L 0x202BEA18 0x002A003C _C0 荣光赞歌_N0 代码片段_L 0x002BEE80 0x00000018 _C0 百战一夜_N0 代码片段_L 0x002BEE7E 0x00000019 _C0 2连击_N0 代码片段_L 0x002BEF86 0x00000015 _C0 大惨击_N0 代码片段_L 0x002BEE7E 0x00000019 _C0 扇攻_N0 代码片段_L 0x002BEE86 0x00000016 _C0 射击4_N0 代码片段_L 0x002BEF7A 0x0000001D _C0 复活_N0 代码片段_L 0x002BEE52 0x0000001C _C0 炸弹_N0 代码片段_L 0x002BEE6C 0x0000001B _C0 邪恶风暴_N0 代码片段_L 0x002BEE62 0x0000001A _C0 毁灭者_N0 代码片段_L 0x002BEE8A 0x00000014 _C0 满天飞舞_N0 代码片段_L 0x002BEE8C 0x00000013 _C0 乱射_N0 代码片段_L 0x002BEE92 0x00000010 _C0 死之引导_N0 代码片段_L 0x002BEED0 0x00000022 _C0 狂舞_N0 代码片段_L 0x002BEE96 0x00000012 _C0 瞬间毁灭_N0 代码片段_L 0x202BEEA0 0x000E000F_C0 暗黑之章_N0 代码片段_L 0x002BEEA2 0x0000000E _C0 赤心_N0 代码片段_L 0x202BEEAC 0x000B000C _C0 蓝心_N0 代码片段_L 0x002BEEAE 0x0000000B _C0 天空之手_N0 代码片段_L 0x002BEF58 0x00000014 _C0 神兽_N0 代码片段_L 0x002BEEBC 0x00000028_C0 JY4_N0 代码片段_L 0x002BEF30 0x00000035 _C0 移动1_N0 代码片段_L 0x002BEEE6 0x00000035。
初中数学几何题超难及答案分析-七年级几何题超难
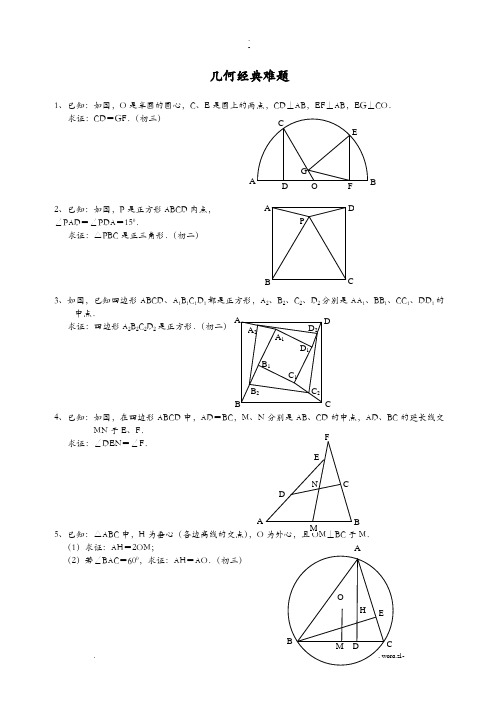
几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点) (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FGCE B O D D 2 C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E EP13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB C B D AFPDECBA. -18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH⊥AB,连接EO。
2023-2024学年江西省宜春市九年级(上)期中数学试卷(含解析)

2023-2024学年江西省宜春市九年级第一学期期中数学试卷一、选择题(本题共6小题,每小题3分,共18分)1.观察如图所示的月饼图案,下列说法正确的是( )A.它是轴对称图形,不是中心对称图形B.它是中心对称图形,不是轴对称图形C.它是轴对称图形,也是中心对称图形D.它既不是轴对称图形,也不是中心对称图形2.下列函数中不是二次函数的有( )A.y=(x﹣1)2B.C.y=3x2+2x﹣1D.y=(x+1)2﹣x23.抛物线的顶点坐标是( )A.(7,﹣5)B.(﹣7,﹣5)C.(7,5)D.(﹣7,5)4.如图,正方形ABCD和正方形EFGO的边长都是2,正方形EFGO绕点O旋转时,两个正方形重叠部分的面积是( )A.1B.2C.3D.45.已知关于x的一元二次方程(a﹣1)x2﹣4x﹣1=0有两个实数根,则a的取值范围是( )A.a≥﹣4B.a>﹣3C.a≥﹣3且a≠1D.a>﹣3且a≠1 6.如图,在△ABC中,∠BAC=120°,AB+AC=4,将BC绕点C顺时针旋转120°得到CD,则线段AD的长度的最小值是( )A.B.C.D.二、填空题(本大题共6小题,每小题3分,共18分)7.一种纪念品经过两次涨价,从原来每个76.8元涨至现在的120元,则平均每次涨价的百分率是 %.8.已知x1,x2是关于x的一元二次方程x2+3x+m=0的两个实数根,且,则m 的值为 .9.已知点A(a,1)与点B(﹣3,﹣1)关于原点对称,则a= .10.已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2、y3的大小关系是 .11.对于实数a,b定义运算“※”如下:a※b=ab2+2ab,例如1※2=1×22+2×1×2=8,则方程1※x=﹣1的解为 .12.已知矩形ABCD中,AD=5,AB=3,现将边AD绕它的一个端点旋转,当另一端点恰好落在边BC所在直线的点E处时,线段DE的长度为 .三、解答题(本大题共5小题,每小题6分,共30分)13.选择适当的方法解下列方程:(1)(x﹣2)2=4;(2)x2﹣3x+1=0.14.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,AC=4.(1)求A′A的长;(2)若∠1=15°,求∠BAA′的度数.15.已知抛物线与x轴的交点是A(﹣1,0),B(3,0),经过点C(0,3).(1)求该抛物线的函数解析式;(2)设该抛物线的顶点为M,求△ABM的面积.16.杭州亚运会期间,某商店销售一批亚运会吉祥物挂件,每个进价13元,规定销售单价不低于20元.试销售期间发现,当销售单价定为20元时,每月可售出200个,销售单价每上涨1元,每天销售量减少10个,现商店决定提价销售.(1)涨价多少时,利润为1620元;(2)将亚运会吉祥物挂件销售单价定为多少元时,商店每天销售亚运会吉祥物挂件获得的利润y最大?最大利润是多少元?17.如图1四边形ABCD是正方形;如图2四边形ABCD是矩形,△MAD是等腰三角形.请只用无刻度的直尺按要求画图.(1)在图1中,画出正方形ABCD的对称中心O;(2)在图2中,画出线段BC的中点N;四、解答题(本大题共3小题,每小题8分,共24分)18.已知函数y=是关于x的二次函数.(1)求m的值;(2)当m为何值时,该函数图象的开口向下?(3)当m为何值时,该函数有最小值?19.如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.(1)求证:BE=CF;(2)当四边形ACDE为菱形时,求BD的长.20.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:(1)求二次函数的解析式;(2)直接写出不等式ax2+bx+c>0的解集 ;(3)若方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围是 .五、解答题(本大题共2小题,每小题9分,共18分)21.已知关于x的一元二次方程x2﹣2kx+k2+k+1=0有两个实数根.(1)试求k的取值范围;(2)若,求k的值;(3)若此方程的两个实数根为x1,x2,且满足|x1|+|x2|=2,试求k的值.22.阅读以下材料,并解决相应问题:小明在课外学习时遇到这样一个问题:定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求函数y=2x2﹣3x+1的“旋转函数”,小明是这样思考的,由函数y=2x2﹣3x+1可知,a1=2,b1=﹣3,c1=1,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2就能确定这个函数的“旋转函数”.请思考小明的方法解决下面问题:(1)写出函数y=x2﹣4x+3的“旋转函数”;(2)若函数y=5x2+(m+1)x+n与y=﹣5x2﹣nx﹣3互为“旋转函数”,求(m+n)2023的值;(3)已知函数y=2(x﹣1)(x+3)的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C,点A,B,C关于原点的对称点分别是A1,B1,C1,试证明:经过点A1,B1,C1的二次函数与y=2(x﹣1)(x+3)互为“旋转函数”.六、解答题(本大题共12分)23.如图,在△ABC中,∠ABC=90°,BA=BC.将线段AB绕点A逆时针旋转90°得到线段AD,E是边BC上的一动点,连接DE交AC于点F,连接BF.(1)求证:FB=FD;(2)点H在边BC上,且BH=CE,连接AH交BF于点N.①判断AH与BF的位置关系,并证明你的结论;②连接CN.若AB=2,请直接写出线段CN长度的最小值.参考答案一、选择题(本题共6小题,每小题3分,共18分)1.观察如图所示的月饼图案,下列说法正确的是( )A.它是轴对称图形,不是中心对称图形B.它是中心对称图形,不是轴对称图形C.它是轴对称图形,也是中心对称图形D.它既不是轴对称图形,也不是中心对称图形【分析】把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.据此判断即可.解:该图是轴对称图形,也是中心对称图形.故选:C.【点评】此题主要考查了中心对称图形和轴对称图形,熟练掌握中心对称图形和轴对称图形的定义是解答本题的关键.2.下列函数中不是二次函数的有( )A.y=(x﹣1)2B.C.y=3x2+2x﹣1D.y=(x+1)2﹣x2【分析】根据二次函数的定义逐一判断即可.解:A.y=(x﹣1)2是二次函数,不符合题意;B.是二次函数,不符合题意;C.y=3x2+2x﹣1是二次函数,不符合题意;D.y=(x+1)2﹣x2=2x+1是一次函数,符合题意;故选:D.【点评】本题主要考查二次函数的定义:“形如y=ax2+bx+c(a≠0),y=a(x﹣h)2+k (a≠0),y=a(x﹣h)2(a≠0)的函数是二次函数.3.抛物线的顶点坐标是( )A.(7,﹣5)B.(﹣7,﹣5)C.(7,5)D.(﹣7,5)【分析】直接由抛物线解析式可求得答案.解:∵抛物线y=(x﹣7)2+5,∴抛物线的顶点坐标是:(7,5),故选:C.【点评】本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x﹣h)2+k中,顶点坐标为(h,k),对称轴为x=h.4.如图,正方形ABCD和正方形EFGO的边长都是2,正方形EFGO绕点O旋转时,两个正方形重叠部分的面积是( )A.1B.2C.3D.4【分析】根据正方形的性质得出OB=OC,∠OBA=∠OCB=45°,∠BOC=∠EOG=90°,推出∠BON=∠MOC,证出△OBN≌△OCM,即可求解.解:如图,设AB与OE交点N,BC与OG交点M,∵四边形ABCD和四边形EFGO都是正方形,∴OB=OC,∠OBA=∠OCB=45°,∠BOC=∠EOG=90°,∴∠BON=∠MOC.在△OBN与△OCM中,,∴△OBN≌△OCM(ASA),∴S△OBN=S△OCM,∴.故选:A.【点评】本题考查了正方形的性质,旋转的性质,全等三角形的性质和判定等知识,正确记忆相关知识点是解题关键.5.已知关于x的一元二次方程(a﹣1)x2﹣4x﹣1=0有两个实数根,则a的取值范围是( )A.a≥﹣4B.a>﹣3C.a≥﹣3且a≠1D.a>﹣3且a≠1【分析】利用一元二次方程的定义和判别式的意义得到a﹣1≠0且Δ=(﹣4)2﹣4(a ﹣1)×(﹣1)≥0,然后求出两不等式的公共部分即可.解:根据题意得a﹣1≠0且Δ=(﹣4)2﹣4(a﹣1)×(﹣1)≥0,解得a≥﹣3且a≠1.故选:C.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac 有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.也考查了一元二次方程的定义.6.如图,在△ABC中,∠BAC=120°,AB+AC=4,将BC绕点C顺时针旋转120°得到CD,则线段AD的长度的最小值是( )A.B.C.D.【分析】在AC的上方作∠ACM=120°,且使CM=CA,连接AM,DM.设AB=x,则AC=4﹣x=CM,根据ASA证明△BAC≌△DMC得出DM=BA=x,∠CMD=∠BAC=120°,得出∠AMD=90°,即可推出结论.解:如图,在AC的上方作∠ACM=120°,且使CM=CA,连接AM,DM.设AB=x,则AC=4﹣x=CM,∴,∵将BC绕点C顺时针旋转120°得到CD,∴∠BCA+∠ACD=120,又∵∠ACD+∠DCM=∠ACM=120°,∴∠ACB=∠DCM,∴△BAC≌△DMC(ASA),∴DM=BA=x,∠CMD=∠BAC=120°.∴∠AMD=90°,∴AD2=AM2+DM2=3(4﹣x)2+x2=4(x﹣3)2+12≥12,∵0<x<4,∴AD的最小值为.故选:C.【点评】本题考查了旋转的性质,全等三角形的判定与性质,正确作出辅助线是解题的关键.二、填空题(本大题共6小题,每小题3分,共18分)7.一种纪念品经过两次涨价,从原来每个76.8元涨至现在的120元,则平均每次涨价的百分率是 25 %.【分析】设平均每次涨价的百分率是x,根据增长率问题建立方程求出其解可以得出答案.解:设平均每次涨价的百分率是x,由题意,得,76.8(1+x)2=120,解得:x1=0.25,x2=﹣2.25(不符合题意,舍去),∴x=0.25=25%,故答案为:25.【点评】本题考查了增长率问题在实际问题中的运用及列一元二次方程解实际问题的能力.8.已知x1,x2是关于x的一元二次方程x2+3x+m=0的两个实数根,且,则m 的值为 ﹣3 .【分析】利用一元二次方程根与系数的关系得到x1+x2=﹣3,x1•x2=m,结合,即可求解.解:∵x1,x2是关于x的一元二次方程x2+3x+m=0的两个实数根,∴x1+x2=﹣3,x1•x2=m,∵,∴,解得:m=﹣3,经检验符合题意;故答案为:﹣3.【点评】本题主要考查了一元二次方程根与系数的关系,熟练掌握根与系数的关系是解答本题的关键.9.已知点A(a,1)与点B(﹣3,﹣1)关于原点对称,则a= 3 .【分析】直接利用关于原点对称点的性质得出a的值,进而得出答案.解:∵点A(a,1)与点B(﹣3,﹣1)关于原点对称,∴a=3.故答案为:3.【点评】此题主要考查了关于原点对称点的性质,正确记忆关于原点对称点的性质是解题关键.10.已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2、y3的大小关系是 y3>y1>y2 .【分析】分别计算出自变量为4,和﹣2时的函数值,然后比较函数值得大小即可.解:把A(4,y1),B(,y2),C(﹣2,y3)分别代入y=(x﹣2)2﹣1得:y1=(x﹣2)2﹣1=3,y2=(x﹣2)2﹣1=5﹣4,y3=(x﹣2)2﹣1=15,∵5﹣4<3<15,所以y3>y1>y2.故答案为y3>y1>y2.【点评】本题考查了二次函数图象上点的坐标特征,解题的关键是:明确二次函数图象上点的坐标满足其解析式.11.对于实数a,b定义运算“※”如下:a※b=ab2+2ab,例如1※2=1×22+2×1×2=8,则方程1※x=﹣1的解为 ﹣1 .【分析】此题主要考查了定义新运算,以及实数的运算,根据a※b=ab2+2ab,由1※x=﹣1,可得:x2+2x=﹣1,据此求出x的值为多少即可.解:∵a※b=ab2+2ab,由1※x=﹣1,得:x2+2x=﹣1,即x2+2x+1=0,∴(x+1)2=0,解得:x=﹣1,故答案为:﹣1.【点评】本题考查了实数的运算,掌握新定义的运算法则是解题的关键.12.已知矩形ABCD中,AD=5,AB=3,现将边AD绕它的一个端点旋转,当另一端点恰好落在边BC所在直线的点E处时,线段DE的长度为 或3或5 .【分析】分两种情形:绕A旋转或绕D旋转,利用勾股定理求解即可.解:如图,∵四边形ABCD是矩形,∴AB=CD=3,AD=BC=5,∠ABC=∠DCB=90°,当AD绕A旋转,AD=AE1=AE2=5时,BE1=BE2==4,∴CE1=1,CE2=9,∴DE1==,DE2==3,当AD绕D旋转时,DE3=DE4=5,综上所述,满足条件的DE的值为或3或5,故答案为:或3或5.【点评】本题考查旋转变换,矩形的性质,等腰三角形的性质,勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.三、解答题(本大题共5小题,每小题6分,共30分)13.选择适当的方法解下列方程:(1)(x﹣2)2=4;(2)x2﹣3x+1=0.【分析】(1)利用直接开方法解方程即可;(2)利用配方法解方程即可.解:(1)(x﹣2)2=4,x﹣2=±2,解得:x1=4,x2=0;(2)x2﹣3x+1=0,,,,解得:.【点评】此题考查了解一元二次方程﹣因式分解法,配方法,公式法,以及直接开方法.14.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,AC=4.(1)求A′A的长;(2)若∠1=15°,求∠BAA′的度数.【分析】(1)由旋转的性质可知:AC=CA′=4,∠ACA′=90°,利用勾股定理即可求出A′A;(2)由旋转的性质得到△CAA′是等腰直角三角形,且∠1=15°,求出∠CB′A′,∠CB′A′=∠CAB,即可解决问题.解:(1)由旋转的性质可知:AC=CA′=4,∠ACA′=90°,∴;(2)由旋转的性质可知:AC=CA′=4,∠ACA′=90°,∴∠CA′A=45°,∵∠1=15°,∴∠CA′B′=45°﹣15°=30°,∴∠CAB=∠CA′B′=30°,∴∠A′AB=45°+30°=75°.【点评】本题考查旋转的性质,三角形内角和定理,勾股定理等知识,解题的关键是掌握相关知识的灵活运算.15.已知抛物线与x轴的交点是A(﹣1,0),B(3,0),经过点C(0,3).(1)求该抛物线的函数解析式;(2)设该抛物线的顶点为M,求△ABM的面积.【分析】(1)由于已知抛物线与x轴的交点坐标,则可设交点式y=a(x+1)(x﹣3),然后把C点坐标代入求出a的值即可;(2)把(1)中的解析式配成顶点式得到M点的坐标,然后根据三角形面积公式△ABM 的面积.解:(1)设抛物线的解析式为y=a(x+1)(x﹣3),把C(0,3)代入得:(﹣1)×3a=3,解得a=﹣1.∴抛物线解析式为y=﹣(x+1)(x﹣3),即y=﹣x2+2x+3;(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴M(1,4),∵AB=4,∴.【点评】本题考查了利用待定系数法求二次函数的解析式和二次函数的性质,熟练运用待定系数法求函数解析式,勾股定理,函数图象的对称性是解题关键.16.杭州亚运会期间,某商店销售一批亚运会吉祥物挂件,每个进价13元,规定销售单价不低于20元.试销售期间发现,当销售单价定为20元时,每月可售出200个,销售单价每上涨1元,每天销售量减少10个,现商店决定提价销售.(1)涨价多少时,利润为1620元;(2)将亚运会吉祥物挂件销售单价定为多少元时,商店每天销售亚运会吉祥物挂件获得的利润y最大?最大利润是多少元?【分析】(1)设上涨x元,则每个纪念品利润为(20+x﹣13)元,销售量为(200﹣10x)个,根据“总利润=每个纪念品利润×销售量”列出关于x的方程,解之可得;(2)依据(1)中的相等关系列出函数解析式,配方成顶点式,再依据二次函数的性质求解可得.解:(1)设上涨x元,则每个纪念品利润为(20+x﹣13)元,销售量为(200﹣10x)个,由题意得:(20+x﹣13)(200﹣10x)=1620,整理得:x2﹣13x+22=0,即(x﹣2)(x﹣11)=0,解得:x1=11,x2=2,答:涨价11元或2元时,利润为1620元;(2)由(1)知当上涨x元,则每个纪念品利润为(20+x﹣13)元,销售量为(200﹣10x)个,则y=(20+x﹣13)(200﹣10x),即y=﹣10x2+130x+1400,∵,∴当时,y有最大值,最大值为,∵,∴售单价定为元时,商店每天销售亚运会吉祥物挂件获得的利润最大,最大利润是元.【点评】本题考查了二次函数的性质在实际生活中的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出函数关系式再求解.17.如图1四边形ABCD是正方形;如图2四边形ABCD是矩形,△MAD是等腰三角形.请只用无刻度的直尺按要求画图.(1)在图1中,画出正方形ABCD的对称中心O;(2)在图2中,画出线段BC的中点N;【分析】(1)依据正方形的对称中心为对角线的交点进行作图;(2)利用矩形的对称中心为对角线的交点,等腰三角形的轴对称图形,即可得到点N.解:(1)如图所示,连接AC,BD交于点O即为所求;(2)如图所示,连接AC,BD交于点O,连接MO并延长交BC于点N即为所求.【点评】此题主要考查了作图与应用作图,关键是掌握正方形、矩形的性质和中心对称图形的性质.首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.四、解答题(本大题共3小题,每小题8分,共24分)18.已知函数y=是关于x的二次函数.(1)求m的值;(2)当m为何值时,该函数图象的开口向下?(3)当m为何值时,该函数有最小值?【分析】(1)根据二次函数的定义求出m的值即可解决问题.(2)运用当二次项系数小于0时,抛物线开口向下;(3)运用当二次项系数大于0时,抛物线开口向上,图象有最低点,函数有最小值.解:(1)∵函数y=(m+3)x是关于x的二次函数,∴m2+3m﹣2=2,m+3≠0,解得:m1=﹣4,m2=1;(2)∵函数图象的开口向下,∴m+3<0,∴m<﹣3,∴当m=﹣4时,该函数图象的开口向下;(3)∵当m+3>0时,抛物线有最低点,函数有最小值,∴m>﹣3,又∵m=﹣4或1,∴当m=1时,y=4x2有最小值,最小值为0.【点评】该题主要考查了二次函数的定义及其性质的应用问题;牢固掌握定义及其性质是解题的关键.19.如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.(1)求证:BE=CF;(2)当四边形ACDE为菱形时,求BD的长.【分析】(1)先由旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则∠EAF+∠BAF =∠BAC+∠BAF,即∠EAB=∠FAC,利用AB=AC可得AE=AF,于是根据旋转的定义,△AEB可由△AFC绕点A按顺时针方向旋转得到,然后根据旋转的性质得到BE=CF;(2)由菱形的性质得到DE=AE=AC=AB=1,AC∥DE,根据等腰三角形的性质得∠AEB=∠ABE,根据平行线得性质得∠ABE=∠BAC=45°,所以∠AEB=∠ABE=45°,于是可判断△ABE为等腰直角三角形,所以BE=AC=,于是利用BD=BE﹣DE 求解.【解答】(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,∴AE=AB,AF=AC,∠EAF=∠BAC,∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,∵AB=AC,∴AE=AF,∴△AEB可由△AFC绕点A按顺时针方向旋转得到,∴BE=CF;(2)解:∵四边形ACDE为菱形,AB=AC=1,∴DE=AE=AC=AB=1,AC∥DE,∴∠AEB=∠ABE,∠ABE=∠BAC=45°,∴∠AEB=∠ABE=45°,∴△ABE为等腰直角三角形,∴BE=AC=,∴BD=BE﹣DE=﹣1.【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了菱形的性质.20.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:(1)求二次函数的解析式;(2)直接写出不等式ax2+bx+c>0的解集 x<1或x>3 ;(3)若方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围是 k>﹣2 .【分析】(1)把抛物线解析式设为顶点式求解即可;(2)根据不等式的解集即为二次函数图象在x轴上方时自变量的取值范围求解即可;(3)根据方程有两个不相等的实数根即二次函数y=ax2+bx+c(a≠0)与直线y=k有两个不同的交点进行求解即可.解:(1)由题意得,二次函数与x轴的交点坐标为(1,0),(3,0),顶点坐标为(2,﹣2),∴可设二次函数解析式为y=a(x﹣2)2﹣2,把(1,0)代入解析式得:0=a(1﹣2)2﹣2,解得a=2,∴二次函数解析式为y=2(x﹣2)2﹣2=2x2﹣8x+6;(2)由函数图象可知不等式ax2+bx+c>0的解集为x<1或x>3,故答案为:x<1或x>3;(3)由函数图象可知方程ax2+bx+c=k有两个不相等的实数根,即为二次函数y=ax2+bx+c(a≠0)与直线y=k有两个不同的交点,∴k>﹣2,故答案为:k>﹣2.【点评】本题主要考查了待定系数法求二次函数解析式,图象法解一元二次不等式,一元二次方程与二次函数综合等等,熟知二次函数的相关知识是解题的关键.五、解答题(本大题共2小题,每小题9分,共18分)21.已知关于x的一元二次方程x2﹣2kx+k2+k+1=0有两个实数根.(1)试求k的取值范围;(2)若,求k的值;(3)若此方程的两个实数根为x1,x2,且满足|x1|+|x2|=2,试求k的值.【分析】(1)根据方程的系数结合根的判别式Δ≥0,即可得出关于k的一元一次不等式,解之即可得出k的取值范围;(2)由根与系数的关系可得出x1+x2=2k,,结合可得出关于k的方程,解之即可得出k的值;(3)由(2)可知:x1+x2=2k,,根据,可得x1x2>0,即由|x1|+|x2|=2,可得,进而可得,则有,即(2k)2=4,问题得解.解:(1)∵关于x的一元二次方程x2﹣2kx+k2+k+1=0有两个实数根,∴Δ=b2﹣4ac=(﹣2k)2﹣4×1×(k2+k+1)≥0,解得:k≤﹣1;(2)∵方程x2﹣2kx+k2+k+1=0的两个实数根为x1,x2,∴x1+x2=2k,,∵,∴,∴(2k)2﹣2(k2+k+1)=10,整理得:k2﹣k﹣6=0,解得:k=3或者k=﹣2,∵根据(1)有k≤﹣1,即k=﹣2;(3)由(2)可知:x1+x2=2k,,∵,∴x1x2>0,∵|x1|+|x2|=2,∴,∴,∵x1x2>0,∴,∴,∴(2k)2=4,∴k=±1,∵根据(1)有k≤﹣1,即k=﹣1.【点评】本题考查了一元二次方程根的判别式,一元二次方程根与系数的关系,熟练掌握一元二次方程根的判别式和根与系数的关系,灵活运用完全平方公式的变形是解题的关键.22.阅读以下材料,并解决相应问题:小明在课外学习时遇到这样一个问题:定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求函数y=2x2﹣3x+1的“旋转函数”,小明是这样思考的,由函数y=2x2﹣3x+1可知,a1=2,b1=﹣3,c1=1,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2就能确定这个函数的“旋转函数”.请思考小明的方法解决下面问题:(1)写出函数y=x2﹣4x+3的“旋转函数”;(2)若函数y=5x2+(m+1)x+n与y=﹣5x2﹣nx﹣3互为“旋转函数”,求(m+n)2023的值;(3)已知函数y=2(x﹣1)(x+3)的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C,点A,B,C关于原点的对称点分别是A1,B1,C1,试证明:经过点A1,B1,C1的二次函数与y=2(x﹣1)(x+3)互为“旋转函数”.【分析】(1)由二次函数的解析式可得出a1,b1,c1的值,结合“旋转函数”的定义可求出a2,b2,c2的值,此问得解;(2)由函数y=5x2+(m+1)x+n与y=﹣5x2﹣nx﹣3互为“旋转函数”,可求出m,n 的值,将其代入(m+n)2023即可求出结论;(3)利用二次函数图象上点的坐标特征可求出点A,B,C的坐标,结合对称的性质可求出点A1,B1,C1的坐标,由点A1,B1,C1的坐标,利用交点式可求出过点A1,B1,C1的二次函数解析式,由两函数的解析式可找出a1,b1,c1,a2,b2,c2的值,再由a1+a2=0,b1=b2,c1+c2=0,可证出经过点A1,B1,C1的二次函数与函数y=2(x﹣1)(x+3)互为“旋转函数”.【解答】(1)解:由函数y=x2﹣4x+3知,a1=1,b1=﹣4,c1=3,∵a1+a2=0,b1=b2,c1+c2=0,∴a2=﹣1,b2=﹣4,c2=﹣3,∴函数y=x2﹣4x+3的“旋转函数”是y=﹣x2﹣4x﹣3;(2)解:根据题意得:,解得,∴(m+n)2023=[(﹣4)+3]2023=﹣1;(3)证明:令y=2(x﹣1)(x+3)=0,得x1=1,x2=﹣3;令x=0,则y=﹣6;∴A、B、C三点的坐标分别为A(1,0),B(﹣3,0),C(0,﹣6),∴A、B、C三点关于原点对称的点坐标分别为A1(﹣1,0),B1(3,0),C1(0,6),设经过A1,B1,C1三点的函数解析式为y=a(x+1)(x﹣3),将C1(0,6)代入y=a(x+1)(x﹣3),得:a×1×(﹣3)=6,解得:a=﹣2,∴经过A1,B1,C1三点的函数解析式为y=﹣2(x+1)(x﹣3),即y=﹣2x2+4x+6,∴y=﹣2x2+4x+6与原函数y=2(x﹣1)(x+3)是旋转函数.【点评】本题考查了二次函数综合运用,涉及到函数与x轴的交点、二次函数图象上点的坐标特征、对称的性质以及二次函数图象与几何变换,解题的关键是正确理解“旋转函数”的定义.六、解答题(本大题共12分)23.如图,在△ABC中,∠ABC=90°,BA=BC.将线段AB绕点A逆时针旋转90°得到线段AD,E是边BC上的一动点,连接DE交AC于点F,连接BF.(1)求证:FB=FD;(2)点H在边BC上,且BH=CE,连接AH交BF于点N.①判断AH与BF的位置关系,并证明你的结论;②连接CN.若AB=2,请直接写出线段CN长度的最小值.【分析】(1)证明△FAD≌△FAB(SAS)即可解决问题.(2)①首先证明四边形ABCD是正方形,再证明∠BAH=∠CBF即可解决问题.②如图3中,取AB的中点O,连接ON,OC.理由三角形的三边关系解决问题即可.【解答】(1)证明:如图1中,∵BA=BC,∠ABC=90°,∴∠BAC=∠ACB=45°,∵线段AB绕点A逆时针旋转90°得到线段AD,∴∠BAD=90°,BA=AD,∴∠FAD=∠FAB=45°,∵AF=AF,∴△FAD≌△FAB(SAS),∴BF=DF.(2)①解:结论:AH⊥BF.理由:如图2中,连接CD.∵∠ABC+∠BAD=180°,∴AD∥BC,∵AD=AB=BC,∴四边形ABCD是平行四边形,∵∠ABC=90°,∴四边形ABCD是矩形,∵AB=BC,∴四边形ABCD是正方形,∵BA=CD,∠ABH=∠DCE,BH=CE,∴△ABH≌△DCE(SAS),∴∠BAH=∠CDE,∵∠FCD=∠FCB=45°,CF=CF,CD=CB,∴△CFD≌△CFB(SAS),∴∠CDF=∠CBF,∴∠BAH=∠CBF,∵∠CBF+∠ABF=90°,∴∠BAH+∠ABF=90°,∴∠ANB=90°,∴AH⊥BF.②如图3中,取AB的中点O,连接ON,OC.∵∠ANB=90°,AO=OB,∴ON=AB=1,在Rt△OBC中,OC==,∵CN≥OC﹣ON,∴CN≥﹣1,∴CN的最小值为﹣1.【点评】本题属于几何变换综合题,考查了正方形的判定和性质,全等三角形的判断和性质,三角形的三边关系等知识,解题的关键是正确寻找全等三角形解决问题,学会利用三角形的三边关系解决最值问题,属于中考压轴题.。
