1、2 数的组成
10以内数的分解与组成[1]
![10以内数的分解与组成[1]](https://img.taocdn.com/s3/m/b9af251edaef5ef7ba0d3cec.png)
10以内数的分解与组成[1]数的组成数的组成:1和1可以组成21和2可以组成31和3可以组成4 2和2可以组成41和4可以组成5 2和3可以组成51和5可以组成6 2和4可以组成6 3和3可以组成61和6可以组成7 2和5可以组成7 3和4可以组成71和7可以组成8 2和6可以组成8 3和5可以组成8 4和4可以组成8 1和8可以组成9 2和7可以组成9 3和6可以组成9 4和5可以组成91 12 1 231 341 451 561 67 1 781 892 242 352 46 2 572 682 793 363 47 3 583 694 484 59完成以下练习:3 2 1 1 5 3 3 1 6 27 2 3 5 2 2 5 4 4 31 3 4 52 4 8 1 6 24 1 3 2 2 7 45 3 34 4 3 3 8 1 6 1 4 13 6 2 54 2 2 6 6 3完成以下练习:35 1258372526 3924484915 5627152347 3679563748 3989171438 57262967完成以下练习:4 2 15 58 372835 1 1 5 3 146927 16384 1 265 4 26 473 64 47 2 18 34584758 2469365 4数的分解:2可以分成1和13可以分成1和24可以分成1和3 4可以分成2和25可以分成1和4 5可以分成2和36可以分成1和5 6可以分成2和4 6可以分成3和37可以分成1和6 7可以分成2和5 7可以分成3和48可以分成1和7 8可以分成2和6 8可以分成3和5 8可以分成4和4 9可以分成1和8 9可以分成2和7 9可以分成3和6 9可以分成4和52 1 131 241 342 251 45 2 361 562 463 371 67 2 573 481 782 683 58 4 491 892 793 694 5完成以下练习:2 1314342545 2616463767 5738186832 1324342515 261626371完成以下练习:1 1 12 13 2 2 1 42 3 1 5 2 4 3 3 1 62 534 1 7 2 6 3 51 1 12 13 2 2 1 42 3 1 5 2 4 3 3 1 6完成以下练习:21 1 24142 1 452 1 564 3 3 1 67 274 1 786851 1 1 241425452 1 562 3 376。
2~10数的组成
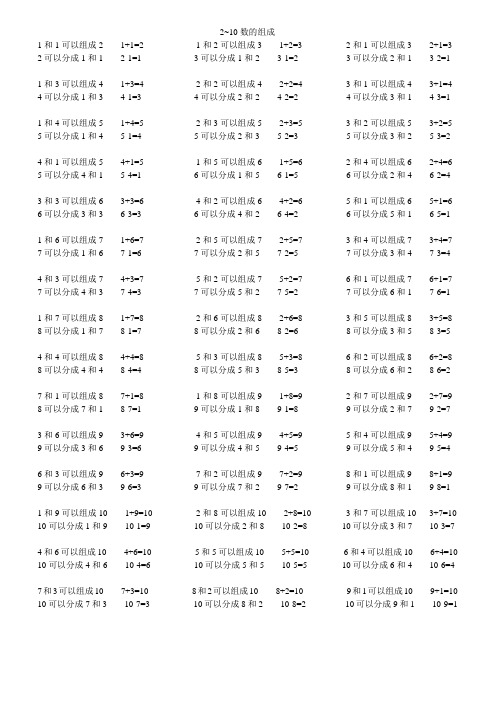
2~10数的组成1和1可以组成2 1+1=2 1和2可以组成3 1+2=3 2和1可以组成3 2+1=3 2可以分成1和1 2-1=1 3可以分成1和2 3-1=2 3可以分成2和1 3-2=11和3可以组成4 1+3=4 2和2可以组成4 2+2=4 3和1可以组成4 3+1=4 4可以分成1和3 4-1=3 4可以分成2和2 4-2=2 4可以分成3和1 4-3=11和4可以组成5 1+4=5 2和3可以组成5 2+3=5 3和2可以组成5 3+2=5 5可以分成1和4 5-1=4 5可以分成2和3 5-2=3 5可以分成3和2 5-3=24和1可以组成5 4+1=5 1和5可以组成6 1+5=6 2和4可以组成6 2+4=6 5可以分成4和1 5-4=1 6可以分成1和5 6-1=5 6可以分成2和4 6-2=43和3可以组成6 3+3=6 4和2可以组成6 4+2=6 5和1可以组成6 5+1=6 6可以分成3和3 6-3=3 6可以分成4和2 6-4=2 6可以分成5和1 6-5=11和6可以组成7 1+6=7 2和5可以组成7 2+5=7 3和4可以组成7 3+4=7 7可以分成1和6 7-1=6 7可以分成2和5 7-2=5 7可以分成3和4 7-3=44和3可以组成7 4+3=7 5和2可以组成7 5+2=7 6和1可以组成7 6+1=7 7可以分成4和3 7-4=3 7可以分成5和2 7-5=2 7可以分成6和1 7-6=11和7可以组成8 1+7=8 2和6可以组成8 2+6=8 3和5可以组成8 3+5=8 8可以分成1和7 8-1=7 8可以分成2和6 8-2=6 8可以分成3和5 8-3=54和4可以组成8 4+4=8 5和3可以组成8 5+3=8 6和2可以组成8 6+2=8 8可以分成4和4 8-4=4 8可以分成5和3 8-5=3 8可以分成6和2 8-6=27和1可以组成8 7+1=8 1和8可以组成9 1+8=9 2和7可以组成9 2+7=9 8可以分成7和1 8-7=1 9可以分成1和8 9-1=8 9可以分成2和7 9-2=73和6可以组成9 3+6=9 4和5可以组成9 4+5=9 5和4可以组成9 5+4=9 9可以分成3和6 9-3=6 9可以分成4和5 9-4=5 9可以分成5和4 9-5=46和3可以组成9 6+3=9 7和2可以组成9 7+2=9 8和1可以组成9 8+1=9 9可以分成6和3 9-6=3 9可以分成7和2 9-7=2 9可以分成8和1 9-8=11和9可以组成10 1+9=10 2和8可以组成10 2+8=10 3和7可以组成10 3+7=10 10可以分成1和9 10-1=9 10可以分成2和8 10-2=8 10可以分成3和7 10-3=74和6可以组成10 4+6=10 5和5可以组成10 5+5=10 6和4可以组成10 6+4=10 10可以分成4和6 10-4=6 10可以分成5和5 10-5=5 10可以分成6和4 10-6=47和3可以组成10 7+3=10 8和2可以组成10 8+2=10 9和1可以组成10 9+1=10 10可以分成7和3 10-7=3 10可以分成8和2 10-8=2 10可以分成9和1 10-9=1。
数的组成与分解

数的组成与分解数字是我们日常生活中重要的元素,它们组成了我们的年龄、电话号码、地址等等。
数字的组成与分解是数学中一个重要的概念,它不仅帮助我们理解数字的含义,还为我们解决实际问题提供了便利。
本文将深入探讨数的组成与分解的概念、方法和应用。
一、数的组成数的组成指的是将一个数字拆分为几个部分,这些部分的总和等于该数字本身。
例如,数字123可以拆分为100、20和3三个部分。
在这个例子中,100是这个数字的百位数字,20是该数字的十位数字,3是个位数字。
在数的组成中,我们经常遇到的是十进制系统,其中数字由0到9这十个数字组成。
每个数字的位数是由右至左递增的,分别是个位、十位、百位、千位等。
通过这种位次顺序,我们可以快速理解一个数字的大小和含义。
例如,数字365表示有三百六十五个单位。
数的组成也可以通过表格或图表来表示。
例如,我们可以用表格记录一个数字的各个位数,并将其分别列出。
这种方法可以帮助我们更好地理解数字的组成和含义。
二、数的分解数的分解指的是将一个数字分解为不同的部分,这些部分加起来等于该数字本身。
与数的组成相反,数的分解将一个较大的数字拆分为几个较小的数字。
例如,我们可以将数字245分解为200、40和5。
在数的分解中,我们可以使用不同的方法,如列式法和连加法。
列式法是将数字的各个位数以竖式的形式依次写下来,然后进行分解。
例如,我们可以将数字879分解为800+70+9。
连加法是将较大的数分解为不同的数,然后将这些数相加。
例如,我们可以将数字496分解为400+90+6。
数的分解不仅帮助我们更好地理解数字的结构,还可以在数学运算中起到便利的作用。
例如,在加法和减法中,我们可以将两个或多个数字分解为较小的数字,然后进行运算。
这种分解方法使得运算更加简单和高效。
三、数的组成与分解的应用数的组成与分解在生活中有着广泛的应用。
以下是一些常见的例子:1. 基础数学运算:在加法、减法、乘法和除法中,我们经常需要将数字进行组合和分解。
数字的组合与分解

数字的组合与分解1. 数字的组合数字的组合是指将不同的数字进行排列组合,形成新的数字。
组合的方式有很多,下面将介绍其中几种常见的组合方法。
1.1 两位数的组合两位数的组合是将十位和个位的数字进行排列组合。
例如,以数字1和2为例,可以组合成12和21。
1.2 三位数的组合三位数的组合是将百位、十位和个位的数字进行排列组合。
以数字1、2和3为例,可以组合成123、132、213、231、312和321等。
1.3 多位数的组合多位数的组合原理与两位数和三位数的组合类似,只是位数更多,例如四位数、五位数等。
以数字1、2、3和4为例,可以组合成1234、1243、1324、1342、1423、1432、2134、2143、2314、2341、2413、2431、3124、3142、3214、3241、3412、3421、4123、4132、4213、4231、4312和4321等。
2. 数字的分解数字的分解是将一个多位数按照位数分解为各个数字的和。
以下将介绍两种常见的数字分解方法。
2.1 十进制分解十进制分解是将一个多位数按照其位数逐一分解,每位上的数字乘以对应的权重再相加,得到最终的结果。
例如,将数字123分解,分别为1×100 + 2×10 + 3×1 = 100 + 20 + 3 = 123。
2.2 二进制分解二进制分解是将一个多位数按照二进制位上的权重逐一分解,每位上的数字乘以对应的权重再相加,得到最终的结果。
例如,将二进制数1101分解为1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 8 + 4 + 0 + 1 = 13。
3. 数字的应用数字的组合与分解在数学和计算机科学等领域有广泛的应用。
3.1 数字密码在密码学中,数字的组合与分解常用于生成密码。
通过组合不同的数字可以产生大量的密码的组合,提高密码的安全性。
用数字0,1,2组成的非零自然数

用数字0,1,2组成的非零自然数非零自然数是由数字0、1、2组成的数,它们在我们的日常生活中扮演着重要的角色。
每个数字都有自己的特点和意义,从个人生活到社会发展,都离不开这些数字的存在。
让我们一起来探索数字0、1、2的奥秘吧!首先,让我们谈谈数字0。
在数学中,0代表着“空”的概念,也常被称为“零值”。
它是一个非常特殊的数字,因为它与其他数字的运算有着独特的规则。
当我们将0与任何数相加或相乘时,结果都会是0。
这种特性使得0在数学中扮演着一种“中性”的角色。
在现实生活中,我们也经常遇到数字0。
当我们说“一分钱不值”时,实际上就是在表达某个物品或事物的价值接近于零。
而在计量中,0也被用来表示一个事物的数量为零。
无论是在购物时找零还是测量物体的重量,0都扮演着非常重要的角色。
接下来,让我们聊聊数字1。
在数学中,数字1有着特殊的地位。
它是自然数中最小的正整数,也被称为“单位”。
对于所有数字,1都是其自身的因数,这意味着任何数除以1都等于它本身。
因此,1在数学运算中经常被用作标准单位。
在日常生活中,数字1也扮演着重要的角色。
想象一下,如果没有数字1,我们将无法计数或测量任何东西。
在通信中,数字1经常用来表示信号的存在,而0表示信号的缺失。
例如,在电子设备中,我们会经常使用二进制代码,其中0表示关,而1表示开。
最后,我们来谈谈数字2。
数字2是最小的偶数,也是自然数中仅次于1的数字。
它是一个非常重要的数字,因为它在数学和科学中有着广泛的应用。
在分数中,我们经常会遇到数字2,它常常用来表示分子或分母的数量。
而在几何学中,数字2是定义直线和平面的基本要素。
在社会生活中,数字2也有着重要的意义。
例如,在合作与竞争之间,数字2往往代表着两个人或两个团体之间的关系。
分工合作和合伙生意都需要双方的共同努力,而竞争则需要双方之间的对抗和对比。
综上所述,数字0、1、2虽然看似简单,但它们在我们的生活中扮演着重要的角色。
数字0代表空、中性;数字1代表单位、整体;数字2代表偶数、对抗。
数字的组合和拆分

数字的组合和拆分数字是我们生活中常常接触到的元素,我们使用数字来计数、测量和表示不同的数量。
数字的组合和拆分是数学中常见的概念,它们在解决问题、计算和数论中扮演着重要的角色。
本文将探讨数字的组合和拆分,并讨论与之相关的一些概念和应用。
一、数字的组合数字的组合指的是用不同的数字构成一个数。
例如,数字1、2和3可以组成数字123,这是一个由三个数字组成的数。
组合的顺序是重要的,所以123和132是不同的组合。
在数字的组合中,有以下几个重要的概念:1. 排列:排列是一种有序的组合方式,其中重复使用同一个数字是允许的。
例如,对于数字1、2和3来说,它们可以组成的不同的三位数的排列有123、132、213、231、312和321。
2. 组合:组合是一种无序的组合方式,其中不允许重复使用同一个数字。
例如,对于数字1、2和3来说,它们可以组成的不同的三位数的组合有123、132、213和231。
数字的组合在实际生活中有很多应用。
例如,我们可以使用数字的组合来表示电话号码、车牌号码和密码等。
在计算中,数字的组合也常常出现,如代数、组合数学和概率论中。
二、数字的拆分数字的拆分指的是将一个数拆分成若干个数字的和。
例如,数字123可以拆分成1+2+3,这是一个由三个数字的和组成的拆分。
拆分的方式有很多种,每种方式都会得到不同的结果。
在数字的拆分中,有以下几个重要的概念:1. 分割:分割是一种将一个数划分成若干个非负整数之和的拆分方式。
例如,数字6可以分割成1+1+1+1+1+1,也可以分割成1+2+3。
2. 划分:划分是一种将一个数划分成若干个正整数之和的拆分方式。
例如,数字6可以划分成1+1+1+1+1+1,也可以划分成1+2+3和1+5。
数字的拆分在数学中有很多研究和应用。
例如,整数拆分是组合数学中的一个重要问题,它与分区数和斐波那契数列等数论概念相关联。
在实际生活中,数字的拆分也常常出现,如货币的拆分、资金的分配和物品的拆解等。
密码是1和2组成的两位数.ppt

从数学广角回到家中有几种走法?
4种:AC、AD、BC、BD
数学广角 Α Β
C
家
DБайду номын сангаас
E
三个人握手,每两人握一 次手,一共握几次手?
一共握3次手
为什么三个数字能组成6个两位数, 三个小动物有6种不同的跑道站法,
而三个人却只能握3次手呢?
两个人握手不存在调换位置的情况
买一块5角的本子,可以怎样付钱?
4种付法:①1个5角 ②5个1角 ③2个2角和1个1角 ④1个2角和3个1角
共四种穿法
密码是1和2组 成的两位数
12
• 1、2、3能组成几个两位数?
6个:12、21、13、31、23、32
小兔、小狗、小猫要进行跑步比赛了,有三条跑道, 它们可以有几种不同的站法呢?
6种:①小兔、小狗、小猫 ②小兔、小猫、小狗 ③小狗、小兔、小猫 ④小狗、小猫、小兔 ⑤小猫、小兔、小狗 ⑥小猫、小狗、小兔
小学数学中的数字排列组合

小学数学中的数字排列组合数字排列组合是小学数学中的一个重要概念。
它涉及到数字的排列和组合的情况,是数学中常见的一种问题类型。
通过数字排列组合的学习,小学生能够培养逻辑思维能力,提高解决问题的能力。
下面将对小学数学中的数字排列组合进行详细介绍。
一、排列排列是指从一组元素中按照一定的顺序选取若干元素的方式。
在排列中,元素的顺序是重要的。
1.1 重复排列重复排列是指从一组元素中选取若干元素,其中元素可以重复出现的情况。
例如,从数字1、2、3中选取两个数字进行重复排列,可以有以下情况:11、12、13、21、22、23、31、32、33。
1.2 不重复排列不重复排列是指从一组元素中选取若干元素,其中元素不能重复出现的情况。
例如,从数字1、2、3中选取两个数字进行不重复排列,可以有以下情况:12、13、21、23、31、32。
二、组合组合是指从一组元素中按照一定的顺序选取若干元素的方式,与排列不同的是,组合中元素的顺序不重要。
2.1 重复组合重复组合是指从一组元素中选取若干元素,其中元素可以重复出现的情况。
例如,从数字1、2、3中选取两个数字进行重复组合,可以有以下情况:11、12、13、22、23、33。
2.2 不重复组合不重复组合是指从一组元素中选取若干元素,其中元素不能重复出现的情况。
例如,从数字1、2、3中选取两个数字进行不重复组合,可以有以下情况:12、13、23。
三、应用场景数字排列组合在日常生活中有着广泛的应用。
例如,排列可以用来确定参加各种比赛的人员名单以及座位的安排;组合可以用来确定不同菜肴的搭配和选择。
三、归纳总结通过对小学数学中的数字排列组合的学习,我们可以培养小学生的逻辑思维能力和解决问题的能力。
在日常生活中,数字排列组合的应用也是无处不在的。
因此,对于小学生来说,深入理解和掌握数字排列组合的概念和应用是非常重要的。
以上是关于小学数学中的数字排列组合的简单介绍。
希望通过这篇文章能够帮助读者更好地理解和应用数字排列组合的知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、2 数的组成
教学目标:1、能够准确地说出数的组成
2、体会并理解数的组成
重点:知道几十几是由几个十和几个一组成的
难点:理解数的组成
教学流程:
一、复习导入
上一节课咱们学习了数100以内的数,那么请小朋友们告诉我到底是怎么数数的呢?
二、探究学习
1、同学们说的都很好,那么一起来数数黑板上有多少小棒?(5捆小棒和4根棒)
在数之前要求学生先安静地独立思考,是否能一个一个地数?
2、由同学展示说出黑板上小棒的数量,并引导他完成相应的填空,()个十和()个一组成()。
3、完成例3的填空,然后个别同学展示说说自己的答案
三、拓展提升
1、7个一和9个十组成()
()个一和()个十组成43
注:老师可以更改数字多出同类型的题,让学生快速回答
2、思考:黑板上画了一堆没有圈的五角星,怎样数数才能避免出错
引导学生说出可以先圈,而且是十个十个地圈,然后再数有多少。
或者是一个一个地数
四、课堂总结
教师针对黑板上的板书引导学生回顾本堂课所学的知识点。
五、达标检测
完成练习一的3、4、5题。
