九年级数学下册 第二十九章 投影与视图章节复习同步练习课件 新人教版
人教版新课标九年级下册第二十九章:视图与投影复习课件(共29张PPT)

Hale Waihona Puke ( D)A.△ACE D.△ABD
B.△BFD C.四边形BCED
4、如图(1),小明站在残墙前,小亮在残墙后面 活动,双不被小明看见.请在图(1)的俯视图(2) 中画出小亮的活动区域.
盲区
盲区
5、与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上 有一盆花和一棵树。晚上,幕墙反射路灯灯光形成了那盆 花的影子(如图所示),树影是路灯灯光形成的。你能确定
做一做
8、下列命题正确的是( C )
A、三视图是中心投影 B、小华观察牡丹花,牡丹花就是视点 C、球的三视图均是半径相等的圆 D、阳光从矩形窗子里照射到地面上得到的光区仍是矩形
9、右图是由一些相同的小正方体构成的几何体的三视
图,则构成这个几何体的小正方体的个数是( D )
A、5 B、6 C、7 D、8
2m, 当 AB 在 光 源 与 墙 壁 正 中 间 时 ,
画出AB在墙壁上的投影,当AB向光
E
源移动2.5m(CD的位置)时,画出此
M
时它在墙壁上的投影。
CA
P O
DB
分 别 求 出 木 棒 在 AB,CD 位 置 时
N
盲区的面积.
F
3、如图所示,在房子外的屋檐E处安有一台监视器, 房子前有一面落地的广告牌,那么监视器的盲区在
• 中心线或某些边线;
•
(3)一般从主视图画起,按投影规律,再画另两个视图;
•
(4)按线型要求,描粗加深物体轮廓线,完成三视图绘制.
•
2.连接物体顶点与其影子顶点,如果得到的是平行线,即为
人教版九年级下册数学 第29章 投影与视图 同步练习题(含答案)
人教版九年级下册数学第29章投影与视图同步练习题29.1 投影1.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是()2.小飞晚上到广场去玩,他发现有两人的影子一个向东,一个向西,于是他肯定地说,广场上的大灯泡一定位于两人.3.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中一定成立的是() A.AB=CD B.AB≤CDC.AB>CD D.AB≥CD4.如图,如果在阳光下你的身影的方向是北偏东60°方向,那么太阳相对于你的方向是()A.南偏西60°B.南偏西30°C.北偏东60° D.北偏东30°5.如图所示,右面水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是()6.如图,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD. (1)请你在图中画出路灯灯泡所在的位置(用点P表示);(2)画出小华此时在路灯下的影子(用线段EF表示).7.如图,已知线段AB=2 cm,投影面为P,太阳光线与地面垂直.(1)当AB垂直于投影面P时(如图1),请画出线段AB的投影;(2)当AB平行于投影面P时(如图2),请画出它的投影,并求出正投影的长;(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图3中画出线段AB的正投影,并求出其正投影长.29.2 三视图第1课时几何体的三视图1.下列立体图形中,主视图是圆的是()2.如图是由四个小正方体叠成的一个几何体,它的左视图是()3.如图,水平的讲台上放置的圆柱形笔筒和正方体形粉笔盒,其俯视图是()4.如图所示几何体的左视图是()5.将如图所示的两个平面图形绕轴旋转一周,对其所得的立体图形,下列说法正确的是()A.主视图相同B.左视图相同C.俯视图相同D.三种视图都不相同6.图中物体的一个视图(a)的名称为.7.画出如图所示圆柱的三视图.8.画出如图所示几何体三视图.9.下列四个几何体中,主视图与左视图相同的几何体有()A.1个 B.2个C.3个D.4个10.如图是一个空心圆柱体,其左视图正确的是()11.形状相同、大小相等的两个小木块放置于桌面,其俯视图如图,则其主视图是()12.如图,一个正方体切去一个三棱锥后所得几何体的俯视图是()13.一位美术老师在课堂上进行立体模型素描教学时,把由圆锥与圆柱组成的几何体(如图所示,圆锥在圆柱上底面正中间放置)摆在讲桌上,请你在指定的方框内分别画出这个几何体的三视图(从正面、左面、上面看得到的视图).14.一种机器上有一个进行转动的零件叫燕尾槽(如图),为了准确做出这个零件,请画出它的三视图.15.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为下列几何体中的哪一个?选择并说明理由.第2课时由三视图确定几何体1.如图是某几何体的三视图,则这个几何体是()A.棱柱 B.圆柱C.棱锥 D.圆锥2.一个几何体的三视图如图所示,这个几何体是()A.圆柱 B.棱柱C.圆锥 D.球3.如图所示,所给的三视图表示的几何体是()A.圆锥 B.正三棱锥C.正四棱锥 D.正三棱柱4.如图是由几个相同小正方体组成的立体图形的俯视图,图上的数字表示该位置上方小正方体的个数,这个立体图形的左视图是()5.图中的三视图所对应的几何体是()6.已知一个正棱柱的俯视图和左视图如图,则其主视图为()7.某几何体的三视图如图所示,则组成该几何体共用了小方块()A.12块B.9块C.7块D.6块8.如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体不可能是()A.6个B.7个 C.8个 D.9个第3课时由三视图确定几何体的表面积或体积1.如图是一个几何体的三视图,根据图中提供的数据(单位: cm)可求得这个几何体的体积为()A.2 cm3B.3 cm3C.6 cm3D.8 cm32.如图是一几何体的三视图,由图中数据计算此几何体的侧面积为.(结果保留π)3.如图是某工件的三视图,求此工件的全面积.4.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积,结果为 cm2.(结果可保留根号)5.一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.6.如图是一个几何体的三视图(单位:cm).(1)写出这个几何体的名称;(2)根据所示数据计算这个几何体的表面积;(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个路线的最短长度.参考答案:第二十九章投影与视图29.1 投影1.B2.中间的上方.3.D4.A5.D6.解:如图所示.7.解:(1)点C为所求的投影.(2)线段CD为所求的投影,CD=2 cm.(3)线段CD为所求的投影,CD=2cos30°= 3 cm.29.2 三视图第1课时几何体的三视图1.D2.A3.D4.A5.D6.主视图.7.解:如图所示.8.解:如图所示.9. D10.B11.D12.D13.解:如图.14.解:如图.15.解:比较各几何体的三视图,考虑是否有长方形,圆及三角形即可.对于A,三视图分别为长方形、三角形、圆(含直径),符合题意;对于B,三视图分别为三角形、三角形、圆(含圆心),不符合题意;对于C,三视图分别为正方形、正方形、正方形,不符合题意;对于D,三视图分别为三角形、三角形、矩形(含对角线),不符合题意;故选A.第2课时由三视图确定几何体1.D2.A3.D4.B5.B6.D7.D8.D 提示:如图,根据左视图可以推测d=e=1,a,b,c中至少有一个为2. 当a,b,c中一个为2时,小立方体的个数为:1+1+2+1+1=6;当a,b,c中两个为2时,小立方体的个数为:1+1+2+2+1=7;当a,b,c三个都为2时,小立方体的个数为:1+1+2+2+2=8.所以小立方体的个数可能为6个、7个或8个.故选D.第3课时由三视图确定几何体的表面积或体积1.B2.10π.3.解:由三视图可知,该工件为底面半径为10 cm、高为30 cm的圆锥体.圆锥的母线长为302+102=1010(cm),圆锥的侧面积为12×20π×1010= 10010π(cm 2),圆锥的底面积为102π=100π(cm 2),圆锥的全面积为100π+10010π=100(1+10)π(cm 2).45.解:该几何体的形状是直四棱柱,由三视图知,棱柱底面菱形的对角线长分别为 4 cm ,3 cm.∴菱形的边长为(32)2+22=52(cm ),棱柱的侧面积为52×8×4=80(cm 2). 6.解:(1)圆锥.(2)表面积S =S 扇形+S 圆=πrl +πr 2=12π+4π=16π(cm 2).(3)如图将圆锥侧面展开,线段BD 为所求的最短长度.由条件,得∠BAB ′=120°,C 为弧BB ′的中点,∴BD =33(cm ).。
人教版九年级数学下册第二十九章《29-1 投影(第1课时)》优课件

C
D
E AP
F QB
这一 样个 的人 人所 才受 有的 学教 问育 。超
过 了 自 己 的 智 力 ,
You made my day!
我们,还在路上……
第二十九章 投影与视图
29.1 投影
预习目标(课本100页,101页)
1 、什么叫做投影?什么叫做投影线?什么叫 做投影面?
2 、什么叫做平行投影?平行投影的投影线有 什么特征?
3、什么叫做中心投影?中心投影的投影线有 什么特征?
一般地,用光线照射物体,在某个平面(地面、墙壁等) 上得到的影子叫做物体的投影(projection)
照射光线叫做投影线 投影所在的平面叫做投影面.
投影线
投影
投影面
有时光线是一组互相平行的射线,例如太阳光或探照灯光 的一束光中的光线,由平行光线形成的投影是平行投影.
例如,物体在太阳光的照射下形成的影子(简称日影) 就是平行投影.日影的方向可以反映时间.
我国古代的计时器日晷,就是根据日影来观测时间的.
物体与影子有关系吗?
物体在日光或灯光的照射下,会在地面、 墙壁等处形成影子,影子与物体的形状有 密切的关系.
练习
把下列物体与它们的投影用线连接起来:
小试牛刀
1. 在太阳光照射下, 早晨太阳从东边 升起, 物体的影子偏向西 边;中午太阳在 南边, 物体的影子偏向北 边;下午太阳落 到 西 边, 物体的影子偏向 东 方.
P
2.如下图所示,小明在晚上由路灯A走向路
灯B,当他行到处P时,发现他在路灯B下
的影长为2米,且影子顶端与重合;接着他
又走了6.5米至Q处,已知小明身高为1.8米,
影子顶端与B重合,已知路灯B高9米,
九年级数学下册第二十九章投影与视图本章总结提升课件新版新人教版

本章总结提升
第二十九章 投影与视图
本章总结提升
知识框架 整合提升 专题阅读
本章总结提升
知识框架
本章总结提升
整合提升
问题1 投影的应用
什么是中心投影、平行投影?什么是正投影?当平面图形分别平 行、倾斜和垂直于投影面时,它的正投影有什么性质?
本章总结提升
例1 如图29-T-1(示意图),某同学想测量旗杆的高度,他在某 一时刻测得1米长的竹竿竖直放置时的影长为1.5米,在同一时 刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面 上,有一部分落在墙上,他测得落在地面上的影长为15米,留 在墙上的影高为2米,求旗杆的高度.
本章总结提升
问题5 由三视图求表面积和体积
三视图有何实际应用? 例5 如图29-T-5是一个物体的三视图,根 据设计图纸上标明的尺寸(单位:mm)计算该 物体的表面积和体积.
图29-T-5
本章总结提升
[解析]由三视图可以看出:物体是由上、下两个半径不同的圆柱组成 的,其立体图和展开图如图①,②所示.
[解析] 从正面看到的是正方形且右上角有三角形,从左面看是正方形(不 要忽略看不见的轮廓线),从上面看到的是正方形且右下角有三角形.
解:如图所示.
本章总结提升
【归纳总结】画三视图时要注意“长对正、高平齐、宽相等”, 看得见的轮廓线画成实线,看不见的轮廓线画成虚线.
本章总结提升
问题3 由三视图描述几何体
本章总结提升
【归纳总结】根据设计图纸中的三视图及其上所标尺寸求零件的 表面积和体积,这是三视图在实际生活中的主要应用,也是日常 生活中经常遇到的问题.解决这类问题时,首先由三视图想象出 几何体的形状,再画出其展开图,然后根据图中尺寸利用相应公 式进行计算或解决最优化问题.
人教版数学九年级下册第二十九章投影与视图单元复习课件可编辑图片版共19张PPT
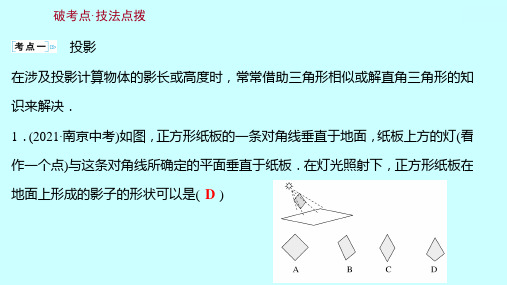
1.(2021·东营中考)已知某几何体的三视图如图所示,则该几何体的侧面展开图圆
心角的度数为( C )
A.214° B.215° C.216° D.217°
2.(2019·河北中考)图 2 是图 1 中长方体的三视图,若用 S 表示面积,S 主=x2+
2x,S 左=x2+x,则 S 俯=( A )
三视图 几何体的三视图的位置是有顺序的,同时画几何体的三视图,看得见部分的轮廓 线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
1.(2021·贺州中考)下列几何体中,左视图是圆的是( A )
2.(2021·黑龙江中考)由若干个完全相同的小立方块搭成的几何体的左视图和俯视
图如图所示,则搭成该几何体所用的小立方块的个数可能是( B )
A.4 个 B.5 个 C.7 个 D.8 个
【温馨提示】 1.画三视图的注意事项 (1)三视图的位置应该放在合适的位置; (2)画三视图时,三视图的大小也是有规定的,必须根据各个部分尺寸大小按照一 定的比例画出三视图. 2.根据三视图复原几何体的步骤 (1)根据三视图的形状,想象几何体的形状; (2)结合三视图的尺寸,确定几何体的尺寸.
【解析】见全解全析
【方法·技巧】 1.判断中心投影和平行投影的方法 物体和影子的对应点的连线是否平行,若平行,则为平行投影,否则为中心投影. 2.平行投影中的有关计算 在应用平行投影求物体的高度(或影长)时,注意在同一时刻的前提下,一般运用 三角形相似的判定和性质解答.
3.中心投影中的有关计算 在应用中心投影求物体的高度(或影长)时,一般也是运用三 同学们,皮影戏是中心投影还是平行投影,你知道吗? 【解析】皮影道具本身是很小的,但经光线投影后,皮影就能在幕布上投射出很 大的影子,它是中心投影.
九年级数学下册 第二十九章投影与视图(第1课时)复习课件 人教新课标版

第二页,编辑于星期五:十三点 四十八分。
灯光与影子
第三页,编辑于星期五:十三点 四十八分。
物体在光线 的照射下,会 在地面和墙壁 上留下它的影 子,这就是投 影( projection ) 现象.
烛光 照射
夜来幽梦忽还乡, 小轩窗,正梳妆。 相顾无言,
唯有泪千行……
第九页,编辑于星期五:十三点 四十八分。
例:确定图中路灯灯泡所在的位置.
O
怎样确定一个点?
解:过一根木杆及其影子的顶端作一条直线 ,再过另一根木杆及其影子的顶端作一条直 线,两直线交于一点O.点O就是路灯灯泡所 在的位置.
第十页,编辑于星期五:十三点 四十八分。
以以下图是两
棵小树在同一时刻
它们是
第二十页,编辑于星期五:十三点 四十八分。
想一想:
你会画出在路灯下树 和人的影子吗?
A
B
C B1
△ABC与△A1B1C1相似吗?
A1 C1
路 灯 光 可 以
路看 灯成 杆点
束 光 线
不相似
第二十一页,编辑于星期五:十三点 四十八分。
想一想:
你会画出在路灯下 树和人的影子吗?
路
灯
A
杆
B
C
△ABC与△A1B1C1相似吗?
⑵如果两棵小树的影子方向相反,能判断它们是中心 投影吗?与同伴进行交流.
⑶如果两棵小树的影子方向相同,且树高与影长不成比 例,能判断它们是中心投影吗?与同伴进行交流.
第十六页,编辑于星期五:十三点 四十八分。
灯光与影子
⑴小东在一路灯下行走,他的影长怎样变化?小
东在阳光照耀的道路上行走,他的影长怎样变 化? ⑵有人说,在同一路灯下,如果甲物体比乙物体的 影子长,那么就说明甲物体比乙物体高.你认为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精选
7
专题二 立体图形的三视图
【要点指导】 从正面、上面、左面三个方向观察立体图形, 可得到 立体图形的三个视图, 即主视图、俯视图、左视图.画 立体图形的三视 图时, 先画主视图, 然后在主视图右边画左视 图, 最后在主视图正下方画 俯视图.主视图和俯视图要“长对 正”, 主视图和左视图要“高平齐”, 左视图和俯视图要“宽相 等”.
物体在灯泡发出的 光的照射下 形成的 影子是中心投影
定义 类型 实例
投影
定义
当我们从某一方向观察 一个物体时, 所看到的 平面图形叫作物体的一 个视图
视 图
主 视 在正面内得到的 由前向后观察 图 物 体的视图
三 视 图
投影与视图 精选
俯 视 在水平面内得到 的由上向下观 图 察 物体的视图
左 视 在侧面内得到的 由左向右观察 图 物 体的视图
挡住该住户窗户约0.68米.
精选
6
相关题1 小明和小红想利用影子长 度测量操场上旗杆的高度. 在某一 时刻, 小明测得自 己的影子长为0.8米, 同一 时刻小红测得 旗杆的影子 长为5米. 已知小明的身高 为1.6米, 则旗杆的 高度为 多少米?
解 设旗杆的高度为x米,则x∶5=1.6∶0.8,解得x=10. 答:旗杆的高度为10米.
第二十九章 投影与视图
章末复习
精选
1
章末复习
知识框架
归纳整合
素养提升
中考链接
精选
2
知识框架
一般地, 用光线照射 物体, 在某个 平面(地 面、墙壁等)上得到的 影 子叫作物体的投影
平行投影:由平行 光线形成的 投影
中心投影:由同一点 (点光源)发 出的光线 形成的投 物体在太阳光的 照射下形成的 影 子是平行投影
精选
13
相关题3-2 [梧州中考]如图29-Z-8所 示, 计算所给三视图表示 的几何体的 体积是__1_3_6_π__.
精选
14
素养提升
专题 转化思想
【要点指导】转化思想是解决数学问题的一种重要思想, 通过 转化 可以将复杂的、生疏的问题转化为简单的、熟悉的问题, 把 非常规问题 常规化, 把不规则问题规则化, 从而使问题得到解决, 如在本章中通常将 立体图形的问题转化为平面图形的问题等. 学 习本章内容要对此加以体 会, 同时注意对空间的想象.
精选
16
解 图29-Z-10是圆柱的侧面展开图, 过点P作PE⊥BB1于点E, 连接PQ. PQ的长就是圆柱的侧面上P , Q两点的最短距离, 在Rt△PEQ中, ∵PE=10π cm, QE=80-30-40=10(cm),
精选
17
相关题 如图29-Z-11所示, A是高为10 cm的圆柱底面圆上
精选
15
例 如图29-Z-9所示, 已知圆柱的高为80 cm, 底面半径为 10 cm, 轴 截面上有两点P , Q, PA=40 cm, B1Q=30 cm, 则圆柱的侧面上P , Q两点的最短 距离是多少?
分析 利用圆柱的侧面展开图, 过点P作PE⊥BB1于 点E, 连接PQ, 在 Rt△PQE中利用勾股定理解决问题.
若影响, 挡住该住户窗户多高?
若不影响, 请说明理由.
(参考数据:
精选
5
解 如图29-Z-1所示, 设光线FE照射到B楼的E处, 点G,由题意知EG=MN=30米, ∠FEG=30°,
则MG=FM-FG≈20-17.32=2.68(米), 即EN≈2.68米. 因为DN=2米,
所以ED≈2.68-2=0.68(米). 即A楼的影子影响B楼一楼住户的采光,
3
归纳整合
专题一 投影在实际生活中的应用
【要点指导】投影包括平行投影和中心投影, 我们常见的平行
投影 是物体在太阳光的照射下形成的影子;物体由灯光照射形成 的影子是中 心投影. 这两种投影在实际生活中有非常广泛的应用,
如生活中测量物体 的高度问题、解决建楼时是否挡光的问题都要
用到投影的知识, 这类问 题一般需要结合相似三角形、解直角三
精选
20
链接1 [荆州中考]父亲节这天佳 佳送给父亲一个礼盒(如图 29-Z-13), 该礼盒的主视图是( C ).
精选
11
例3 如图29-Z-6是某几何体的三视图, 则该几何 体的表面积是 ( C ). A.36π B.60π C.96π D.120π
精选
12
相关题3-1 长方体的主视图和左视图 如图29-Z-7所示(单位: cm), 则其俯 视图的面积是___1_2 __cm2.
解析 由主视图和左视图可知,该长方体的长为4 cm, 宽为3 cm,高为2 cm,则其俯视图为矩形,且相邻两 边长分别为4 cm和3 cm,故其俯视图的面积为4×3= 12(cm2).
角形的知识来解决.
精选
4
例1 如图29-Z-1所示, 某居民小区内A, B 两楼之间的距离
MN=30米, 两楼的高都是20米, A楼在B楼正南方, B楼窗户朝
南. B楼内一楼住户 的窗台离小区地面的距离DN=2米, 窗户
高CD= 1.8米.当正午时刻太阳光线与地面成30°角时, A楼
的影子是否影响B楼一楼住户的采光?
19
考点:物体的三视图. 考情:判断常见物体的三视图是中考中常见的 考点之一. 策略: 三视图是分别从正面、左面、上面三个方 向看同一物体 所得到的平面图形, 主视图可以看作 是从前往后压缩物体得到 的平面图形, 左视图可以 看作是从左往右压缩物体得到的平面 图形, 俯视图 可以看作是从上往下压缩物体得到的平面图形.
一点, 一只蜗牛从点A出发, 沿30°角绕圆柱侧面爬行, 当它
爬到顶上时, 它沿圆柱侧面爬行的最短路程是(0 cm
C.30 cm
D.40 cm
精选
18
中考链接
母题1 (教材P101习题29.2第1题) 把图29-Z-12中的几何体与 它们对应的三视图用线连接起来.
精选
精选
8
例2 如图29-Z-2所示, 几何体上半部分为正三棱柱, 下半部 分为圆 柱, 其俯视图是( C ).
精选
9
相关题2 下列选项中是图29-Z-4 中几何体的俯视图的是 ( A ).
精选
10
专题三 由三视图求物体的体积、表面积问题
【要点指导】由三视图想象立体图形的形状, 先根据三种 视图所反 映出的长、宽、高来确定立体图形的相关数据, 由 此再代入体积、表面 积公式进行计算
