线性代数详细知识点
线性代数知识点总结完整
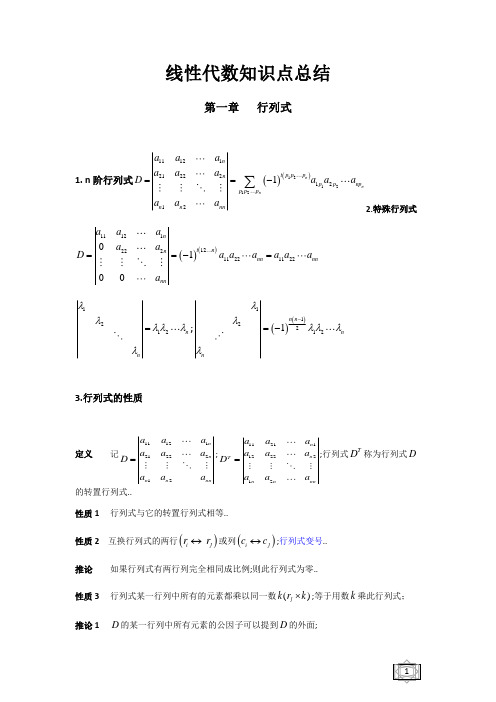
线性代数知识点总结第一章 行列式1. n 阶行列式()()121212111212122212121==-∑n nnn t p p p n p p np p p p n n nna a a a a a D a a a a a a 2.特殊行列式()()111211222211221122010n t n n nn nn nna a a a a D a a a a a a a ==-=1212n nλλλλλλ=;()()1122121n n n nλλλλλλ-=-3.行列式的性质定义 记111212122212n n n n nna a a a a a D a a a =;112111222212n n T nnnna a a a a a D a a a =;行列式TD 称为行列式D 的转置行列式.. 性质1行列式与它的转置行列式相等..性质2 互换行列式的两行()↔i j r r 或列()↔i j c c ;行列式变号.. 推论 如果行列式有两行列完全相同成比例;则此行列式为零..性质3 行列式某一行列中所有的元素都乘以同一数()⨯j k r k ;等于用数k 乘此行列式;推论1D 的某一行列中所有元素的公因子可以提到D 的外面;推论2 D 中某一行列所有元素为零;则=0D ..性质4若行列式的某一列行的元素都是两数之和;则1112111212222212()()()i i ni i n n n ni ninna a a a a a a a a a D a a a a a '+'+='+1112111112112122222122221212i n i ni n i n n n ninnn nninna a a a a a a a a a a a a a a a a a a a a a a a ''=+' 性质6 把行列式的某一列行的各元素乘以同一数然后加到另一列行对应的元素上去;行列式的值不变..算得行列式的值..4. 行列式按行列展开余子式 在n 阶行列式中;把元素ij a 所在的第i 行和第j 列划去后;留下来的1n -阶行列式叫做元素ij a 的余子式;记作ij M ..代数余子式 ()1i jij ij A M +=-记;叫做元素ij a 的代数余子式..引理一个n 阶行列式;如果其中第i 行所有元素除i;j (,)i j 元外ij a 都为零;那么这行列式等于ij a 与它的代数余子式的乘积;即ij ij D a A =..高阶行列式计算首先把行列上的元素尽可能多的化成0;保留一个非零元素;降阶定理n 阶行列式 111212122212=n n n n nna a a a a a D a a a 等于它的任意一行列的各元素与其对应的代数余子式的乘积之和;即1122i i i i in in D a A a A a A =+++;(1,2,,)i n =1122j j j j nj nj D a A a A a A =+++或;(1,2,,)j n =..第二章 矩阵1.矩阵111212122211n n m m mn a a a a a a A a a a ⎛⎫ ⎪ ⎪= ⎪⎪⎝⎭行列式是数值;矩阵是数表; 各个元素组成方阵 :行数与列数都等于n 的矩阵A .. 记作:A n.. 行列矩阵:只有一行列的矩阵..也称行列向量.. 同型矩阵:两矩阵的行数相等;列数也相等.. 相等矩阵:AB 同型;且对应元素相等..记作:A =B 零矩阵:元素都是零的矩阵不同型的零矩阵不同 对角阵:不在主对角线上的元素都是零..单位阵:主对角线上元素都是1;其它元素都是0;记作:E注意 矩阵与行列式有本质的区别;行列式是一个算式;一个数字行列式经过计算可求得其值;而矩阵仅仅是一个数表;它的行数和列数可以不同..2. 矩阵的运算矩阵的加法 111112121121212222221122n n n n m m m m mn mn a b a b a b a b a b a b A B a b a b a b +++⎛⎫⎪+++⎪+= ⎪⎪+++⎝⎭说明 只有当两个矩阵是同型矩阵时;才能进行加法运算.. 矩阵加法的运算规律()1A B B A +=+;()()()2A B C A B C ++=++()()1112121222113,()n n ij ij m nm n m m mn a a a a a a A a A a a a a ⨯⨯---⎛⎫⎪--- ⎪=-=-= ⎪⎪---⎝⎭设矩阵记;A -称为矩阵A 的负矩阵()()()40,A A A B A B +-=-=+-..数与矩阵相乘111212122211,n n m m mn a a a a a a A A A A A a a a λλλλλλλλλλλλλλ⎛⎫ ⎪ ⎪== ⎪⎪⎝⎭数与矩阵的乘积记作或规定为数乘矩阵的运算规律设A B 、为m n ⨯矩阵;,λμ为数()()()1A A λμλμ=;()()2A A A λμλμ+=+;()()3A B A B λλλ+=+..矩阵相加与数乘矩阵统称为矩阵的线性运算..矩阵与矩阵相乘 设(b )ij B =是一个m s ⨯矩阵;(b )ij B =是一个s n ⨯矩阵;那么规定矩阵A 与矩阵B的乘积是一个m n⨯矩阵(c )ij C =;其中()12121122j j i i is i j i j is sj sj b b a a a a b a b a b b ⎛⎫⎪ ⎪=+++ ⎪ ⎪ ⎪⎝⎭1sik kj k a b ==∑;()1,2,;1,2,,i m j n ==;并把此乘积记作C AB = 注意1..A 与B2..矩阵的乘法不满足交换律;即在一般情况下;AB BA ≠;而且两个非零矩阵的乘积可能是零矩阵..3..对于n 阶方阵A 和B;若AB=BA;则称A 与B 是可交换的..矩阵乘法的运算规律()()()1AB C A BC =; ()()()()2AB A B A B λλλ==()()3A B C AB AC +=+;()B C A BA CA +=+ ()4m n n n m m m n m n A E E A A ⨯⨯⨯⨯⨯==()5若A 是n 阶方阵;则称 A k 为A 的k 次幂;即kk A A AA =个;并且mk m kA A A+=;()km mk AA =(),m k 为正整数..规定:A 0=E 只有方阵才有幂运算注意 矩阵不满足交换律;即AB BA ≠;()kk k AB A B ≠但也有例外转置矩阵把矩阵A 的行换成同序数的列得到的新矩阵;叫做A 的转置矩阵;记作A T ;()()1TT A A =;()()2T T T A B A B +=+;()()3T T A A λλ=;()()4TT T AB B A =..方阵的行列式由n 阶方阵A 的元素所构成的行列式;叫做方阵A 的行列式;记作A注意 矩阵与行列式是两个不同的概念;n 阶矩阵是n 2个数按一定方式排成的数表;而n 阶行列式则是这些数按一定的运算法则所确定的一个数..()1T A A =;()2n A A λλ=;(3)AB A B B A BA ===对称阵 设A 为n 阶方阵;如果满足A =A T ;那么A 称为对称阵.. 伴随矩阵行列式A 的各个元素的代数余子式ij A 所构成的如下矩阵112111222212n n nnnn A A A A A A A A A A *⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭称为矩阵A 的伴随矩阵.. 性质 AA A A A E **==易忘知识点总结1只有当两个矩阵是同型矩阵时;才能进行加法运算..2只有当第一个矩阵的列数等于第二个矩阵的行数时;两个矩阵才能相乘;且矩阵相乘不满足交换律.. 3矩阵的数乘运算与行列式的数乘运算不同..逆矩阵:AB =BA =E;则说矩阵A 是可逆的;并把矩阵B 称为A 的逆矩阵..1A B -=即..说明1 A ;B 互为逆阵; A = B -12 只对方阵定义逆阵..只有方阵才有逆矩阵 3.若A 是可逆矩阵;则A 的逆矩阵是唯一的..定理1矩阵A 可逆的充分必要条件是0A ≠;并且当A 可逆时;有1*1AA A-=重要奇异矩阵与非奇异矩阵 当0A =时;A 称为奇异矩阵;当0A ≠时;A 称为非奇异矩阵..即0A A A ⇔⇔≠可逆为非奇异矩阵..求逆矩阵方法**1(1)||||021(3)||A A A A A A -≠=先求并判断当时逆阵存在;()求;求。
线性代数知识点全归纳

线性代数知识点全归纳线性代数是数学的一个重要分支,研究向量空间及其上的线性映射。
它广泛应用于物理、工程、计算机科学等领域。
下面将对线性代数的主要知识点进行全面归纳。
1.矩阵及其运算:矩阵是线性代数的基本概念之一,由若干行和列组成的方阵。
常见的矩阵运算有加法、减法、数乘、矩阵乘法和转置等。
2.向量及其运算:向量是一个有序数组,具有大小和方向。
常见的向量运算有加法、减法、数乘、点乘和叉乘等。
3.线性方程组:线性方程组是线性代数的核心内容之一、包括齐次线性方程组和非齐次线性方程组。
解线性方程组的方法有高斯消元法、克莱姆法则和矩阵求逆等。
4.向量空间与线性变换:向量空间是线性代数的基本概念之一,包含零向量、加法和数乘运算。
线性变换是一种保持向量空间结构的映射。
5.基与维度:基是向量空间的一组线性无关向量,可以由基线性组合得到向量空间中的任意向量。
维度是向量空间中基的数量。
6.线性相关与线性无关:向量组中的向量线性相关指存在非零的线性组合,其系数不全为零。
如果向量组中的向量线性无关,则任何线性组合的系数都为零。
7.线性变换与矩阵:线性变换可以用矩阵表示,矩阵的列向量表示线性变换作用于基向量上后的结果。
矩阵乘法可以将多个线性变换组合为一个线性变换。
8.特征值与特征向量:对于一个线性变换,如果存在一个非零向量,使得它在该线性变换下只发生伸缩而不发生旋转,那么这个向量称为该线性变换的特征向量,对应的伸缩比例为特征值。
9.二次型与正定矩阵:二次型是线性代数中的重要概念,是一个关于变量的二次函数。
正定矩阵是指二次型在所有非零向量上的取值都大于零。
10.内积与正交性:内积是向量空间中的一种运算,它满足线性性、对称性和正定性。
正交性是指两个向量的内积为零,表示两个向量互相垂直。
11.正交变换与正交矩阵:正交变换是指保持向量长度和向量之间夹角的变换。
正交矩阵是一种特殊的方阵,它的行向量和列向量两两正交,并且长度为112.奇异值分解与特征值分解:奇异值分解将一个矩阵分解为三个矩阵的乘积,其中一个是正交矩阵,另外两个是对角矩阵。
线性代数知识点归纳,超详细

线性代数知识点归纳,超详细线性代数复习要点第⼀部分⾏列式1. 排列的逆序数2. ⾏列式按⾏(列)展开法则3. ⾏列式的性质及⾏列式的计算⾏列式的定义1.⾏列式的计算:①(定义法)②(降阶法)⾏列式按⾏(列)展开定理:⾏列式等于它的任⼀⾏(列)的各元素与其对应的代数余⼦式的乘积之和.推论:⾏列式某⼀⾏(列)的元素与另⼀⾏(列)的对应元素的代数余⼦式乘积之和等于零.③(化为三⾓型⾏列式)上三⾓、下三⾓、主对⾓⾏列式等于主对⾓线上元素的乘积.④若都是⽅阵(不必同阶),则⑤关于副对⾓线:⑥范德蒙德⾏列式:证明⽤从第n⾏开始,⾃下⽽上依次的由下⼀⾏减去它上⼀⾏的倍,按第⼀列展开,重复上述操作即可。
⑦型公式:⑧(升阶法)在原⾏列式中增加⼀⾏⼀列,保持原⾏列式不变的⽅法.⑨(递推公式法) 对阶⾏列式找出与或,之间的⼀种关系——称为递推公式,其中,,等结构相同,再由递推公式求出的⽅法称为递推公式法.(拆分法) 把某⼀⾏(或列)的元素写成两数和的形式,再利⽤⾏列式的性质将原⾏列式写成两⾏列式之和,使问题简化以例计算.⑩(数学归纳法)2. 对于阶⾏列式,恒有:,其中为阶主⼦式;3. 证明的⽅法:①、;②、反证法;③、构造齐次⽅程组,证明其有⾮零解;④、利⽤秩,证明;⑤、证明0是其特征值.4. 代数余⼦式和余⼦式的关系:第⼆部分矩阵1.矩阵的运算性质2.矩阵求逆3.矩阵的秩的性质4.矩阵⽅程的求解1.矩阵的定义由个数排成的⾏列的表称为矩阵.记作:或①同型矩阵:两个矩阵的⾏数相等、列数也相等.②矩阵相等: 两个矩阵同型,且对应元素相等.③矩阵运算a. 矩阵加(减)法:两个同型矩阵,对应元素相加(减).b. 数与矩阵相乘:数与矩阵的乘积记作或,规定为.c. 矩阵与矩阵相乘:设, ,则,其中注:矩阵乘法不满⾜:交换律、消去律, 即公式不成⽴.a. 分块对⾓阵相乘:,b. ⽤对⾓矩阵○左乘⼀个矩阵,相当于⽤的对⾓线上的各元素依次乘此矩阵的○⾏向量;c. ⽤对⾓矩阵○右乘⼀个矩阵,相当于⽤的对⾓线上的各元素依次乘此矩阵的○列向量.d. 两个同阶对⾓矩阵相乘只⽤把对⾓线上的对应元素相乘.④⽅阵的幂的性质:,⑤矩阵的转置:把矩阵的⾏换成同序数的列得到的新矩阵,叫做的转置矩阵,记作.a. 对称矩阵和反对称矩阵:是对称矩阵.是反对称矩阵.b. 分块矩阵的转置矩阵:⑥伴随矩阵:,为中各个元素的代数余⼦式.,, .分块对⾓阵的伴随矩阵:,矩阵转置的性质:矩阵可逆的性质:伴随矩阵的性质:r(A)与r(A*)的关系若r(A)=n,则不等于0,A*=可逆,推出r(A*)=n。
线性代数知识点归纳

线性代数知识点归纳一、向量1. 向量的定义- 向量是具有大小和方向的量,用箭头表示,例如:$\vec{v}$。
2. 向量的加法- 两个向量相加,可以将它们的对应分量相加得到新向量的分量。
- 例如:$\vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3\end{bmatrix}$,$\vec{w} = \begin{bmatrix} w_1 \\ w_2 \\ w_3\end{bmatrix}$,则$\vec{v} + \vec{w} = \begin{bmatrix} v_1 + w_1\\ v_2 + w_2 \\ v_3 + w_3 \end{bmatrix}$。
3. 向量的数量乘法- 向量乘以一个标量,可以将向量的每个分量都乘以该标量。
- 例如:$\vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3\end{bmatrix}$,$c$为标量,则$c \cdot \vec{v} = \begin{bmatrix} c\cdot v_1 \\ c \cdot v_2 \\ c \cdot v_3 \end{bmatrix}$。
二、矩阵1. 矩阵的定义- 矩阵是一个按照矩形排列的数的集合,用方括号表示,例如:$A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix}$。
2. 矩阵的加法- 两个矩阵相加,可以将它们的对应元素相加得到新矩阵的元素。
- 例如:$A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} &a_{22} \end{bmatrix}$,$B = \begin{bmatrix} b_{11} & b_{12} \\b_{21} & b_{22} \end{bmatrix}$,则$A + B = \begin{bmatrix} a_{11} + b_{11} & a_{12} + b_{12} \\ a_{21} + b_{21} & a_{22} + b_{22}\end{bmatrix}$。
《线性代数》的主要知识点

《线性代数》的主要知识点第一部分 行列式概念:1. n 阶行列式展开式的特点:①共有n!项,正负各半;②每项有n 个元素相乘,且覆盖所有的行与列;③每一项的符号为(列)行)ττ+-()1(2. 元素的余子式以及代数余子式 ij j i ij M )1(A +-=3. 行列式的性质计算方法:1. 对角线法则2. 行列式的按行(列)展开 (另有异乘变零定理)第二部分 矩阵1. 矩阵的乘积注意:①不满足交换率(一般情况下B A A B ≠)②不满足消去率 (由AB=AC 不能得出B=C )③由AB=0不能得出A=0或B=0④若AB=BA ,则称A 与B 是可换矩阵2.矩阵的转置满足的法则:T T T B A )B A (+=+,T T T T T A B AB kA kA ==)(,)(3.矩阵的多项式 设n n x a x a a x +++=Λ10)(ϕ,A 为n 阶方阵,则n n A a A a E a A +++=Λ10)(ϕ称为A 的n 次多项式。
对与对角矩阵有关的多项式有结论如下:(1)如果 1-Λ=P P A ,则n n A a A a E a A +++=Λ10)(ϕ11110---Λ++Λ+=P Pa P Pa EP Pa n n Λ= 1)(-ΛP P ϕ(2)若),,(21n a a a diag Λ=Λ,则))(),(),(()(21n a a a diag ϕϕϕϕΛ=Λ4.逆矩阵:n 阶矩阵A,B ,若E BA AB ==,则A,B 互为逆矩阵。
n 阶矩阵A 可逆0A ≠⇔;n A r =⇔)( (或表示为n A R =)()即A 为满秩矩阵; ⇔A 与E 等价;⇔A 可以表示成若干个初等矩阵的乘积;⇔A 的列(行)向量组线性无关;⇔A 的所有的特征值均不等于零 求法:①伴随矩阵法:*11A AA ⋅=- ②初等变换法:()()1,,-−−−→−A E E A 初等行变换或⎪⎪⎭⎫⎝⎛−−−→−⎪⎪⎭⎫ ⎝⎛-1A E E A 初等列变换, E 是单位矩阵性质:(1)矩阵A 可逆,则A 的逆矩阵是唯一的(2)设A 是n 阶矩阵,则有下列结论 ①若A 可逆,则1-A 也可逆,且A A =--11)( ②若A 可逆,则T A 也可逆,且T T A A )()(11--=③若A 可逆,数0≠k ,则kA 可逆,且111)(--=A kkA ④若B A .为同阶矩阵且均可逆,则B A .也可逆,且111)(---=A B AB5.方阵A 的行列式:满足下述运算规律(设B A ,为n 阶方阵,λ为数) ①A A T = ②A A nλλ= ③B A AB =6.伴随矩阵:行列式A 的各个元素的代数余子式ij A 所构成的如下的矩阵 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=nn n n n n A A A A A A A A A A ΛM M M ΛΛ212221212111*,称为矩阵A 的伴随矩阵(注意行与列的标记的不同) 伴随矩阵具有性质:E A A A AA ==** 常见的公式有:①1*-=n A A ②1*-⋅=A A A ③A AA 1)(1*=- ④=-1*)(A *1)(-A 等 7.初等矩阵:由单位矩阵E 经过一次初等变换后所得的矩阵称为初等矩阵。
线性代数总结知识点

线性代数总结知识点线性代数是数学的一个分支,主要研究向量、向量空间(也称为线性空间)、线性变换以及线性方程组的理论。
它是现代数学的基础工具之一,广泛应用于物理学、工程学、计算机科学、经济学和社会科学等领域。
以下是线性代数的一些核心知识点总结:1. 向量与向量运算- 向量的定义:向量可以是有序的数字列表,用于表示空间中的点或方向。
- 向量加法:两个向量对应分量相加得到新的向量。
- 标量乘法:一个向量与一个标量相乘,每个分量都乘以该标量。
- 向量的数量积(点积):两个向量的对应分量乘积之和,用于计算向量的长度或投影。
- 向量的向量积(叉积):仅适用于三维空间,结果是一个向量,表示两个向量平面的法向。
2. 矩阵- 矩阵的定义:一个由数字排列成的矩形阵列。
- 矩阵加法和减法:对应元素相加或相减。
- 矩阵乘法:第一个矩阵的列数必须等于第二个矩阵的行数,结果矩阵的每个元素是两个矩阵对应行列的乘积之和。
- 矩阵的转置:将矩阵的行变成列,列变成行。
- 单位矩阵:对角线上全是1,其余位置全是0的方阵。
- 零矩阵:所有元素都是0的矩阵。
3. 线性相关与线性无关- 线性相关:如果一组向量中的任何一个可以通过其他向量的线性组合来表示,则这组向量是线性相关的。
- 线性无关:如果只有所有向量的零组合才能表示为零向量,则这组向量是线性无关的。
4. 向量空间(线性空间)- 定义:一组向量,它们在向量加法和标量乘法下是封闭的。
- 子空间:向量空间的子集,它自身也是一个向量空间。
- 维数:向量空间的基(一组线性无关向量)的大小。
- 基和坐标:向量空间的一组基可以用来表示空间中任何向量的坐标。
5. 线性变换- 定义:保持向量加法和标量乘法的函数。
- 线性变换可以用矩阵表示,矩阵的乘法对应线性变换的复合。
6. 特征值和特征向量- 特征值:对应于线性变换的标量,使得变换后的向量与原向量成比例。
- 特征向量:与特征值对应的非零向量,变换后的向量与原向量方向相同。
线性代数详细知识点

线性代数 第一章 行列式§1 二阶和三阶行列式一、二元一次线性方程组与二阶行列式结论:如果112212210a a a a -≠,则二元线性方程组 11112212112222a x a xb a x a x b +=⎧⎨+=⎩的解为122122*********b a a b x a a a a -=-,1121212112121a b b a x a b b a -=-。
定义:设11122122,,,a a a a ,记11221221a a a a -为11122122a a a a 。
称11122122a a a a 为二阶行列式有了行列式的符号,二元线性方程组的求解公式可以改写为112222111122122b a b a x a a a a =,111122211122122a b a b x a a a a =二、三阶行列式与三元一次线性方程组定义:111213212223313233a a a a a a a a a 112233122331132132132231122133112332a a a a a a a a a a a a a a a a a a =++---定理:如果1112132122233132330a a a D a a a a a a =≠,则***123(,,)x x x 是下面的三元线性方程组的解111122133121122223323113223333a x a x a xb a x a x a x b a x a x a x b ++=⎧⎪++=⎨⎪++=⎩当且仅当*1x =112132222333233/b a a b a a D b a a ,*2x =111132122331333/a b a a b a D a b a ,*3x =111212122231323/a a b a a b D a a b 其中111213212223313233a a a a a a a a a 为系数行列式。
线性代数知识点归纳

线性代数知识点归纳线性代数是一门研究向量、向量空间、线性变换以及有限维线性方程组的数学分支。
它广泛应用于各个领域,如物理、计算机科学、工程学等。
线性代数的核心概念和工具包括行列式、矩阵、向量组以及线性方程组等。
下面将详细介绍线性代数的相关知识点。
一、行列式1.1 行列式的概念:行列式是一个函数,它从n×n阶方阵到实数(或复数)的映射。
行列式记作|A|,其中A是一个n×n的方阵。
1.2 逆序数:在n×n阶方阵A中,将行列式中元素a_ij与a_ji互换,所得到的新的行列式称为原行列式的逆序数。
1.3 余子式:在n×n阶方阵A中,将第i行第j列的元素a_ij删去,剩下的(n-1)×(n-1)阶方阵的行列式称为原行列式的余子式,记作M_ij。
1.4 代数余子式:在n×n阶方阵A中,将第i行第j列的元素a_ij替换为它的相反数,然后计算得到的新的行列式,称为原行列式的代数余子式,记作A_ij。
1.5 行列式的性质:行列式具有以下性质:(1)交换行列式中任意两个元素的位置,行列式的值变号。
(2)行列式中某一行(列)的元素乘以常数k,行列式的值也乘以k。
(3)行列式中某一行(列)的元素与另一行(列)的元素相加,行列式的值不变。
(4)行列式某一行(列)的元素与另一行(列)的元素相减,行列式的值变号。
1.6 行列式的计算方法:行列式的计算方法有:降阶法、按行(列)展开法、克拉默法则等。
二、矩阵2.1 矩阵的概念:矩阵是一个由数组元素构成的矩形阵列,矩阵中的元素称为矩阵的项。
矩阵记作A,其中A是一个m×n的矩阵,A_ij表示矩阵A中第i行第j列的元素。
2.2 矩阵的线性运算:矩阵的线性运算包括加法、减法、数乘等。
2.3 矩阵的乘法:两个矩阵A和B的乘法,记作A×B,要求A是一个m×n的矩阵,B是一个n×p的矩阵。
矩阵的乘法满足交换律、结合律和分配律。
线性代数超强总结

考试重点第一章: 行列式的定义、行列式的计算;第二章: 1、求矩阵的逆阵(伴随矩阵法、初等变换法); 2.求矩阵的秩(用初等变换法);3.求矩阵方程: Ax=B, xA=B, AxB=C ; 第三章: 证明向量组的线性相关性; 第四章: 方程组Ax=0, Ax=b 求解; 第五章: 1、会求特征值与特征向量; 2.相似矩阵的性质;3.实对称矩阵的对角化; 第六章: 1.用正交变换把二次型化为标准形;2.二次型的秩, 二次型正定的定义; 3、矩阵正定的判断方法:(1)各阶顺序主子式都大于零;(2)每个特征值都大于零()0A r A n A Ax A A οο⎧⎪<⎪⎪=⇔=⎨⎪⎪⎪⎩不可逆 有非零解是的特征值的列(行)向量线性相关 12()0,,T s i nA r A n Ax A A A A A A A p p p p Ax οββ⎧⎪=⎪⎪=⎪⎪⎪≠⇔⎨⎪⎪⎪⎪=⋅⋅⋅⎪⎪∀∈=⎩可逆 只有零解 的特征值全不为零 的列(行)向量线性无关 是正定矩阵 与同阶单位阵等价 是初等阵总有唯一解⎫⎪−−−→⎬⎪⎭具有向量组等价相似矩阵反身性、对称性、传递性矩阵合同 √ 行列式的计算:① 若A B 与都是方阵(不必同阶),则(1)mn A A A A B B B B A A BB οοοοο*===**=-②上三角、下三角行列式等于主对角线上元素的乘积.③关于副对角线: √ 逆矩阵的求法:①1A A A*-=②1()()A E E A -−−−−→初等行变换③11a b d b c d c a ad bc --⎡⎤⎡⎤=⎢⎥⎢⎥--⎣⎦⎣⎦ TT T T T A B A C C D BD ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦④12111121n aa n a a a a -⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦21111211na a n a a a a -⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⑤11111221n n A A A A A A ----⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ 11121211n nA A A A A A ----⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦√ 设 , 对 阶矩阵 规定: 为 的一个多项式.√ 设 的列向量为 , 的列向量为 , 的列向量为 ,√ 用对角矩阵Λ左乘一个矩阵,相当于用Λ的对角线上的各元素依次乘此矩阵的行向量; 用对角矩阵Λ右乘一个矩阵,相当于用Λ的对角线上的各元素依次乘此矩阵的列向量. √ 两个同阶对角矩阵相乘只用把对角线上的对应元素相乘,与分块对角阵相乘类似,即:11112222kk kk A B A B AB A B οο⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦√ 判断 是 的基础解系的条件: ① 12,,,s ηηη线性无关; ② 12,,,s ηηη是0Ax =的解;③ ()s n r A =-=每个解向量中自由变量的个数.① 零向量是任何向量的线性组合,零向量与任何同维实向量正交. ② 单个零向量线性相关;单个非零向量线性无关.③ 向量组12,,,n ααα⋅⋅⋅线性相关⇔向量组中至少有一个向量可由其余1n -个向量线性表示. 向量组12,,,n ααα⋅⋅⋅线性无关⇔向量组中每一个向量i α都不能由其余1n -个向量线性表示. ④ m 维列向量组12,,,n ααα⋅⋅⋅线性相关()r A n ⇔<; m 维列向量组12,,,n ααα⋅⋅⋅线性无关()r A n ⇔=. ⑤ ()0r A A ο=⇔=.⑥ 若 线性无关, 而 线性相关,则 可由 线性表示,且表示法惟一. ⑦ 矩阵的行向量组的秩等于列向量组的秩. 阶梯形矩阵的秩等于它的非零行的个数.⑧ 矩阵的行初等变换不改变矩阵的秩,且不改变列 、行向量间的线性关系.⑨ 矩阵 与 等价 作为向量组等价,即: 秩相等的向量组不一定等价.矩阵A 与B 作为向量组等价⇔1212(,,,)(,,,)n n r r αααβββ⋅⋅⋅=⋅⋅⋅=1212(,,,,,,)n n r αααβββ⋅⋅⋅⋅⋅⋅⇒ 矩阵A 与B 等价.向量组 可由向量组 线性表示 ≤ .向量组 可由向量组 线性表示,且 , 则 线性相关.向量组12,,,s βββ⋅⋅⋅线性无关,且可由12,,,n ααα⋅⋅⋅线性表示,则s ≤n .⑩ 向量组12,,,s βββ⋅⋅⋅可由向量组12,,,n ααα⋅⋅⋅线性表示,且12(,,,)s r βββ⋅⋅⋅12(,,,)n r ααα=⋅⋅⋅,则两向量组等价;⑪ 任一向量组和它的极大无关组等价.⑫ 向量组的任意两个极大无关组等价,且这两个组所含向量的个数相等. ⑬ 若两个线性无关的向量组等价,则它们包含的向量个数相等. 若 是 矩阵,则 ,若 , 的行向量线性无关;若 , 的列向量线性无关,即:12,,,n ααα⋅⋅⋅线性无关.Ax β=1122n n x x x αααβ+++=1112111212222212,,n n m m mn n m a a a x b a a a x b A x a a a x b β⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 12,1,2,,j j jmj j n αααα⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦51212120,,,0,,,()(),,,A n A n n Ax Ax A nAx Ax A Ax r A r A n βοαααβοβαααββααα⇒⇔==−−−−−→=<<≠⇒⇒⇔==−−−−−→≠⇔=⇔=<≠=⇒当为方阵时当为方阵时有无穷多解有非零解线性相关 有唯一组解只有零解可由线性表示有解线性无关 12()(),,,()()()1()A n r A r A Ax r A r A r A r A ββαααβββ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪−−−−−→⎪⎩⇔≠⎧⎪⇔=⇔<⎨⎪⇔+=⎩当为方阵时 克莱姆法则 不可由线性表示无解6线性方程组解的性质:√ 设A 为m n ⨯矩阵,若()r A m =,则()()r A r A β=,从而Ax β=一定有解. 当m n <时,一定不是唯一解.⇒<方程个数未知数的个数向量维数向量个数,则该向量组线性相关.m 是()()r A r A β和的上限. √ 矩阵的秩的性质:① ()()()T T r A r A r A A == ② ()r A B ±≤()()r A r B + ③ ()r AB ≤{}min (),()r A r B④ ()0()00r A k r kA k ≠⎧=⎨=⎩若 若⑤ ()()A r r A r B B οο⎡⎤=+⎢⎥⎣⎦⑥0,()A r A ≠若则≥1⑦ ,,()0,()()m n n s A B r AB r A r B ⨯⨯=+若且则≤n ⑧ ,()()()P Q r PA r AQ r A ==若可逆,则 ⑨ ,()()A r AB r B =若可逆则,()()B r AB r A =若可逆则⑩ (),()(),r A n r AB r B ==若则且A 在矩阵乘法中有左消去律:0AB B AB AC B Cο=⇒==⇒=n 个n 维线性无关的向量,两两正交,每个向量长度为1.(,)0αβ=.1α==.√ 内积的性质: ① 正定性:② 对称性: ③ 双线性:1212(,)(,)(,)ααβαβαβ+=+ (,)(,)(,)c c c αβαβαβ==123,,ααα线性无关,112122111313233121122(,)()(,)(,)()()βααββαβββαβαββαββββββ=⎧⎪⎪⎪=-⎨⎪⎪=--⎪⎩正交化单位化: T AA E =.√ 是正交矩阵的充要条件: 的 个行(列)向量构成 的一组标准正交基.√ 正交矩阵的性质: ① ; ② T T AA A A E ==;③ A 是正交阵,则T A (或1A -)也是正交阵; ④ 两个正交阵之积仍是正交阵; ⑤ 正交阵的行列式等于1或-1.E A λ-.()E A f λλ-=.√ 上三角阵、下三角阵、对角阵的特征值就是主对角线上的n 各元素.√ 若0A =,则0λ=为A 的特征值,且0Ax =的基础解系即为属于0λ=的线性无关的特征向量. √ 12n A λλλ= 1ni A λ=∑tr√ 若 ,则 一定可分解为 = 、 ,从而 的特征值为: , .√ 若 的全部特征值 , 是多项式,则: ① ()f A 的全部特征值为12(),(),,()n f f f λλλ;② 当A 可逆时,1A -的全部特征值为12111,,,n λλλ,A *的全部特征值为12,,,n A AAλλλ.√ 1122,.m m Ak kA a b aA bEAA AA A λλλλλλλ-*⎧⎪++⎪⎪⎪⎨⎪⎪⎪⎪⎩是的特征值则:分别有特征值 √ 1122,m m Ak kAa b aA bEAx A x AA A λλλλλλλ-*⎧⎪++⎪⎪⎪⎨⎪⎪⎪⎪⎩是关于的特征向量则也是关于的特征向量.. 相似于对角阵的充要条件: 恰有 个线性无关的特征向量.这时, 为 的特征向量拼成的矩阵, 为对角阵,主对角线上的元素为 的特征值. √ 可对角化的充要条件: 为 的重数. √ 若n 阶矩阵A 有n 个互异的特征值,则A 与对角阵相似.1B P AP -= (P 为正交矩阵)√ 相似矩阵的性质: ① 若 均可逆 ② T T A B③ kk A B (k 为整数)④ E A E B λλ-=-,从而,A B 有相同的特征值,但特征向量不一定相同.即:x 是A 关于0λ的特征向量,1P x -是B 关于0λ的特征向量. ⑤ A B = 从而,A B 同时可逆或不可逆 ⑥ ()()r A r B = ⑦ ()()A B =tr tr√ 数量矩阵只与自己相似. √ 对称矩阵的性质:① 特征值全是实数,特征向量是实向量; ② 与对角矩阵合同;③ 不同特征值的特征向量必定正交;④ k 重特征值必定有k 个线性无关的特征向量;⑤ 必可用正交矩阵相似对角化(一定有n 个线性无关的特征向量,A 可能有重的特征值,重数=()n r E A λ--).12(,,,)T n f x x x X AX = A 为对称矩阵 12(,,,)T n X x x x =√ 用正交变换法化二次型为标准形:① 求出A 的特征值、特征向量; ② 对n 个特征向量单位化、正交化; ③ 构造C (正交矩阵),1C AC -=Λ; ④ 作变换X CY =,新的二次型为2121(,,,)nn i i f x x x d y =∑,Λ的主对角上的元素i d 即为A 的特征值.正定二次型对应的矩阵. √ 合同变换不改变二次型的正定性.① √ 成为正定矩阵的充要条件(之一成立):②正惯性指数为n;③A的特征值全大于0;④A的所有顺序主子式全大于0;⑤大于0).√成为正定矩阵的必要条件: ;.11。
线性代数知识点总结

线性代数知识点总结第一章 行列式一要点1、二阶、三阶行列式2、全排列和逆序数;奇偶排列可以不介绍对换及有关定理;n 阶行列式的定义3、行列式的性质4、n 阶行列式ij a D =;元素ij a 的余子式和代数余子式;行列式按行列展开定理5、克莱姆法则二基本要求1、理解n 阶行列式的定义2、掌握n 阶行列式的性质3、会用定义判定行列式中项的符号4、理解和掌握行列式按行列展开的计算方法;即+11j i A a +22j i A a ⎩⎨⎧≠==+j i j i D A a jn in 0 +j i A a 1122i j a A +⎩⎨⎧≠==+j i j i D A a nj ni0 5、会用行列式的性质简化行列式的计算;并掌握几个基本方法:归化为上三角或下三角行列式;各行列元素之和等于同一个常数的行列式;利用展开式计算6、掌握应用克莱姆法则的条件及结论会用克莱姆法则解低阶的线性方程组7、了解n 个方程n 个未知量的齐次线性方程组有非零解的充要条件第二章 矩阵一要点1、矩阵的概念n m ⨯矩阵n m ij a A ⨯=)(是一个矩阵表..当n m =时;称A 为n 阶矩阵;此时由A 的元素按原来排列的形式构成的n 阶行列式;称为矩阵A 的行列式;记为A .注:矩阵和行列式是两个完全不同的两个概念..2、几种特殊的矩阵:对角阵;数量阵;单位阵;三角形矩阵;对称矩阵3、矩阵的运算;矩阵的加减法;数与矩阵的乘法;矩阵的转置;矩阵的乘法1矩阵的乘法不满足交换律和消去律;两个非零矩阵相乘可能是零矩阵..如果两矩阵A 与B 相乘;有BA AB =;则称矩阵A 与B 可换..注:矩阵乘积不一定符合交换2方阵的幂:对于n 阶矩阵A 及自然数k ;个k k A A A A ⋅⋅= 规定I A =0;其中I 为单位阵 .3 设多项式函数k k k k a a a a ++++=--λλλλϕ1110)( ;A 为方阵;矩阵A 的多项式I a A a A a A a A k k k k ++++=--1110)( ϕ;其中I 为单位阵..4n 阶矩阵A 和B ;则B A AB =.5n 阶矩阵A ;则A A nλλ=4、分块矩阵及其运算5、逆矩阵:可逆矩阵若矩阵A 可逆;则其逆矩阵是唯一的;矩阵A 的伴随矩阵记为*A ; E A A A AA ==**矩阵可逆的充要条件;逆矩阵的性质..6、矩阵的初等变换:初等变换与初等矩阵;初等变换和初等矩阵的关系;矩阵在等价意义下的标准形;矩阵A 可逆的又一充分必要条件:A 可以表示成一些初等矩阵的乘积;用初等变换求逆矩阵..7、矩阵的秩:矩阵的k 阶子式;矩阵秩的概念;用初等变换求矩阵的秩8、矩阵的等价二要求1、理解矩阵的概念;矩阵的元素;矩阵的相等;矩阵的记号等2、了解几种特殊的矩阵及其性质3、掌握矩阵的乘法;数与矩阵的乘法;矩阵的加减法;矩阵的转置等运算及性质4、理解和掌握逆矩阵的概念;矩阵可逆的充分条件;伴随矩阵和逆矩阵的关系;当A 可逆时;会用伴随矩阵求逆矩阵5、了解分块矩阵及其运算的方法1在对矩阵的分法符合分块矩阵运算规则的条件下;其分块矩阵的运算在形式上与不分块矩阵的运算是一致的..2特殊分法的分块矩阵的乘法;例如n m A ⨯;l n B ⨯;将矩阵B 分块为) (21l b b b B =;其中j b l j 2, ,1=是矩阵B 的第j 列;则=AB ) (21l b b b A ) (21l Ab Ab Ab =又如将n 阶矩阵P 分块为) (21n p p p P =;其中j p n j 2, ,1=是矩阵P 的第j 列.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n P λλλ 0 0 00 0 00 0 0 21 ) (21n p p p = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n λλλ 0 0 00 0 00 0 0 21) (2211n n p p p λλλ = 3设对角分块矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=SS A A A A 2211 ;),2,1(s P A PP =均为方阵; A 可逆的充要条件是PP A 均可逆;s P ,2,1=;且⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=----11221111 ss A A A A6、理解和掌握矩阵的初等变换和初等矩阵及其有关理论;掌握矩阵的初等变换;化矩阵为行最简形;会用初等变换求矩阵的秩、求逆矩阵7、理解矩阵的秩的概念以及初等变换不改变矩阵的秩等有关理论8、若矩阵A 经过有限次初等变换得到矩阵B ;则称矩阵A 和矩阵B 等价;记为B A ≅. n m ⨯矩阵A 和B 等价当且仅当)()(B r A r =;在等价意义下的标准型:若r A r =)(;则r D A ≅;⎥⎦⎤⎢⎣⎡=000 r r I D ;r I 为r 阶单位矩阵.. 因此n 阶矩阵A 可逆的充要条件为n I A ≅..第三章 线性方程组一要点1、n 维向量;向量的线性运算及其有关运算律记所有n 维向量的集合为n R ;n R 中定义了n 维向量的线性运算;则称nR 为 n 维向量空间..2、向量间的线性关系1线性组合与线性表示;线性表示的判定2线性相关与线性无关;向量组的线性相关与无关的判定3、向量组的等价;向量组的秩;向量组的极大无关组及其求法;向量组的秩及其求法 1设有两个向量组,1α,2αs α )(A,1β,2βt β )(B向量组)(A 和)(B 可以相互表示;称向量组)(A 和)(B 等价..向量组的等价具有传递性..2一个向量组的极大无关组不是惟一的;但其所含向量的个数相同;那么这个相同的个数定义为向量组的秩..4、矩阵的秩与向量组的秩的关系5、线性方程组的求解1线性方程组的消元解法2线性方程组解的存在性和唯一性的判定3线性方程组解的结构4齐次线性方程的基础解系与全部解的求法5非齐次方程组解的求法二要求1、理解n 维向量的概念;掌握向量的线性运算及有关的运算律2、掌握向量的线性组合、线性表示、线性相关、线性无关等概念3、掌握线性表示、线性相关、线性无关的有关定理4、理解并掌握向量组的等价极大无关组、向量组的秩等概念;及极大无关组、向量组秩的求法5、掌握线性方程组的矩阵形式、向量形式的表示方法6、会用消元法解线性方程组7、理解并掌握齐次方程组有非零解的充分条件及其判别方法8、理解并掌握齐次方程组的基础解系、全部解的概念及其求法9、理解非齐次方程组与其导出组解的关系;掌握非齐次方程组的求解方法第四章 矩阵的特征值与特征向量一要点1、矩阵的特征值与特征向量的定义;特征方程、特征值与特征向量的求法与性质2、相似矩阵的定义、性质;矩阵可对角化的条件3、实对称矩阵的特征值和特征向量向量内积的定义及其性质;正交向量组;施密特正交化方法;正交矩阵;实对称矩阵的特征值与特征向量的性质;实对称矩阵的对角化二要求1、理解矩阵的特征值、特征向量的概念及有关性质2、掌握特征值与特征向量的求法3、理解并掌握相似矩阵的概念与性质4、掌握判断矩阵与对角矩阵相似的条件及对角化的方法5、会将实对称矩阵正交相似变换化为对角矩阵..第五章二次型一要点1、二次型与对称矩阵:二次型的定义;二次型与对称矩阵的对应关系2、二次型与对称矩阵的标准形配方法;初等变换法;正交变换法;合同矩阵;二次型及对称矩阵的标准形与规范形 3、二次型与对称矩阵的有定性二次型与对称矩阵的正定、负定、半正定、半负定二要求1、理解并掌握二次型的定义及其矩阵的表示方法..2、会用三种非退化线性替换:即配方法、初等变换法、正交变换法化二次型为标准形及规范型3、掌握二次型的正定、负定、半正定、半负定的定义;会判定二次型的正定性..。
线性代数知识点总结汇总

线性代数知识点总结1行列式(一)行列式概念和性质1、逆序数:所有的逆序的总数2、行列式定义:不同行不同列元素乘积代数和3、行列式性质:(用于化简行列式)(1)行列互换(转置),行列式的值不变(2)两行(列)互换,行列式变号(3)提公因式:行列式的某一行(列)的所有元素都乘以同一数k,等于用数k乘此行列式(4)拆列分配:行列式中如果某一行(列)的元素都是两组数之和,那么这个行列式就等于两个行列式之和。
(5)—行(列)乘k加到另一行(列),行列式的值不变。
(6)两行成比例,行列式的值为0。
(二)重要行列式4、上(下)三角(主对角线)行列式的值等于主对角线元素的乘积5、副对角线行列式的值等于副对角线元素的乘积乘6、Laplace展开式:(A是m阶矩阵,B是n阶矩阵),则★ 8对角线的元素为a ,其余元素为b 的行列式的值:(三)按行(列)展开 9、按行展开定理:(1)任一行(列)的各元素与其对应的代数余子式乘积之和等 于行列式的值(2)行列式中某一行(列)各个元素与另一行(列)对应元素 的代数余子式乘积之和等于 0 (四)行列式公式 10、行列式七大公式: (1) |kA|=kn|A|1 1…ik £…益■y (v)」IT=n厲-号)klXn7、n 阶(n 》2)范德蒙德行列式数学归纳法证明(2) |AB|=|A| • |B|(3) |AT|=|A|(4) |A-1|=|A|-1(5) |A*|=|A|n-1(6) 若A的特征值入1、入2、……入n,贝y P(7) 若A与B相似,则|A|=|B|(五)克莱姆法则11、克莱姆法则:(1 )非齐次线性方程组的系数行列式不为0,那么方程为唯解(2)如果非齐次线性方程组无解或有两个不同解,则它的系数行列式必为0(3 )若齐次线性方程组的系数行列式不为0,则齐次线性方程组只有0解;如果方程组有非零解,那么必有D=0b2矩阵(一)矩阵的运算1、矩阵乘法注意事项:(1)矩阵乘法要求前列后行一致;(2)矩阵乘法不满足交换律;(因式分解的公式对矩阵不适用,但若B=E,O,A-1,A*,f(A)时,可以用交换律)(3)AB=O不能推出A=O或B=O2、转置的性质( 5 条)( 1)( A+B) T=AT+BT( 2)( kA) T=kAT( 3)( AB) T=BTAT( 4) |A|T=|A|( 5)( AT) T=A(二)矩阵的逆3、逆的定义:B=A-1 AB=E或 BA=E成立,称A可逆,B是A的逆矩阵,记为注:A可逆的充要条件是|A|工04、逆的性质:( 5 条)(1)( kA) - 1=1/k ・A-1 (k 工0)(2)(AB)-仁B- 1 ・A-1(3)|A-1|=|A|-1( 4)( AT) -1= ( A-1 ) T( 5)( A-1 ) -1=A5、逆的求法:( 1 ) A 为抽象矩阵:由定义或性质求解(2) A为数字矩阵:(A|E初等行变换E|A-1 )(三)矩阵的初等变换6、初等行(列)变换定义:(1)两行(列)互换;(2)一行(列)乘非零常数c(3)一行(列)乘k 加到另一行(列)7、初等矩阵:单位矩阵E 经过一次初等变换得到的矩阵。
(完整版)线性代数知识点总结

线性代数知识点总结第一章 行列式二三阶行列式N 阶行列式:行列式中所有不同行、不同列的n 个元素的乘积的和 n nn nj j j j j j j j j nija a a a ...)1(21212121)..(∑-=τ(奇偶)排列、逆序数、对换行列式的性质:①行列式行列互换,其值不变。
(转置行列式TD D =) ②行列式中某两行(列)互换,行列式变号。
推论:若行列式中某两行(列)对应元素相等,则行列式等于零。
③常数k 乘以行列式的某一行(列),等于k 乘以此行列式。
推论:若行列式中两行(列)成比例,则行列式值为零; 推论:行列式中某一行(列)元素全为零,行列式为零。
④行列式具有分行(列)可加性⑤将行列式某一行(列)的k 倍加到另一行(列)上,值不变 行列式依行(列)展开:余子式ij M 、代数余子式ij j i ij M A +-=)1(定理:行列式中某一行的元素与另一行元素对应余子式乘积之和为零。
克莱姆法则:非齐次线性方程组 :当系数行列式0≠D 时,有唯一解:)21(n j DD x j j ⋯⋯==、齐次线性方程组 :当系数行列式01≠=D 时,则只有零解 逆否:若方程组存在非零解,则D 等于零 特殊行列式:①转置行列式:332313322212312111333231232221131211a a a a a a a a a a a a a a a a a a → ②对称行列式:ji ij a a =③反对称行列式:ji ij a a -= 奇数阶的反对称行列式值为零④三线性行列式:333122211312110a a a a a a a 方法:用221a k 把21a 化为零,。
化为三角形行列式 ⑤上(下)三角形行列式:行列式运算常用方法(主要)行列式定义法(二三阶或零元素多的) 化零法(比例)化三角形行列式法、降阶法、升阶法、归纳法、第二章 矩阵矩阵的概念:n m A *(零矩阵、负矩阵、行矩阵、列矩阵、n 阶方阵、相等矩阵) 矩阵的运算:加法(同型矩阵)---------交换、结合律 数乘n m ij ka kA *)(=---------分配、结合律乘法nm lkj ik n l kj l m ik b a b a B A *1**)()(*)(*∑==注意什么时候有意义一般AB=BA ,不满足消去律;由AB=0,不能得A=0或B=0 转置A A T T =)( TT T B A B A +=+)( T T kA kA =)( TT T A B AB =)((反序定理) 方幂:2121k k k kA AA +=2121)(k k k k A A +=几种特殊的矩阵:对角矩阵:若AB 都是N 阶对角阵,k 是数,则kA 、A+B 、 AB 都是n 阶对角阵数量矩阵:相当于一个数(若……)单位矩阵、上(下)三角形矩阵(若……) 对称矩阵 反对称矩阵阶梯型矩阵:每一非零行左数第一个非零元素所在列的下方 都是0分块矩阵:加法,数乘,乘法:类似,转置:每块转置并且每个子块也要转置 注:把分出来的小块矩阵看成是元素逆矩阵:设A 是N 阶方阵,若存在N 阶矩阵B 的AB=BA=I 则称A 是可逆的, B A=-1(非奇异矩阵、奇异矩阵|A|=0、伴随矩阵)初等变换1、交换两行(列)2.、非零k 乘某一行(列)3、将某行(列)的K 倍加到另一行(列)初等变换不改变矩阵的可逆性 初等矩阵都可逆 初等矩阵:单位矩阵经过一次初等变换得到的(对换阵 倍乘阵 倍加阵) 等价标准形矩阵⎪⎪⎭⎫ ⎝⎛=O OO I D rr矩阵的秩r(A):满秩矩阵 降秩矩阵 若A 可逆,则满秩 若A 是非奇异矩阵,则r (AB )=r (B ) 初等变换不改变矩阵的秩求法:1定义2转化为标准式或阶梯形矩阵与行列式的联系与区别:都是数表;行列式行数列数一样,矩阵不一样;行列式最终是一个数,只要值相等,就相等,矩阵是一个数表,对应元素相等才相等;矩阵n ij n ij a k ka )()(=,行列式nij n n ij a k ka =逆矩阵注:①AB=BA=I 则A 与B 一定是方阵 ②BA=AB=I 则A 与B 一定互逆; ③不是所有的方阵都存在逆矩阵;④若A 可逆,则其逆矩阵是唯一的。
线性代数知识点全面总结

线性代数知识点全面总结线性代数是数学的重要分支,广泛应用于各个领域,如物理学、计算机科学、经济学等。
本文将全面总结线性代数的知识点,帮助读者系统地了解和掌握该学科。
1. 线性代数的基本概念1.1 向量及其表示:向量是线性代数的基本概念,可以用有序数对、矩阵或列向量表示,具有方向和大小。
1.2 矩阵及其运算:矩阵是由数字排列成的矩形数组,可以进行加法、乘法、转置等运算。
1.3 线性方程组:线性方程组是由一组线性方程组成的方程组,可以用矩阵和向量的表示形式来求解。
2. 向量空间2.1 向量空间的定义:向量空间是由一组满足一定条件的向量构成的集合,满足加法和数乘运算的封闭性。
2.2 子空间:子空间是向量空间的子集,也是向量空间,满足加法和数乘运算的封闭性。
2.3 线性无关与生成子空间:线性无关是指向量组中的向量之间不存在线性关系,生成子空间是指向量组中所有向量的线性组合的集合。
3. 线性映射3.1 线性映射的定义:线性映射是一个将一个向量空间映射到另一个向量空间的映射,保持加法和数乘运算的性质。
3.2 线性映射的矩阵表示:线性映射可以用矩阵表示,将一个向量空间的向量转化为另一个向量空间的向量。
3.3 核与像:核是线性映射中被映射为零向量的向量集合,像是线性映射中所有被映射到的向量组成的集合。
4. 矩阵的特征值与特征向量4.1 特征值和特征向量的定义:特征值是一个矩阵对应的线性变换中不改变方向的标量因子,特征向量是在特征值下发生伸缩的向量。
4.2 特征值与特征向量的计算:特征值与特征向量可以通过求解特征方程来计算。
4.3 对角化与相似矩阵:若一个矩阵相似于一个对角矩阵,则称其可对角化,对角矩阵是一个形式为对角线非零、其余元素均为零的矩阵。
5. 线性代数的应用5.1 物理学中的应用:线性代数在量子力学、力学等物理学领域有广泛应用,如描述粒子的状态和变换等。
5.2 计算机科学中的应用:线性代数在计算机图形学、机器学习等领域起到重要作用,如图像处理、数据分析等。
大学线性代数知识点总结

大学线性代数知识点总结1. 向量与空间- 向量的定义与表示- 向量的加法与数乘- 向量的内积与外积- 向量的模、方向与单位向量- 向量空间的定义与性质- 基、维数与坐标表示- 子空间及其性质- 线性相关与线性无关的概念2. 矩阵- 矩阵的定义与表示- 矩阵的加法、数乘与转置- 矩阵的乘法规则- 矩阵的逆- 行列式的概念与性质- 行列式的计算方法- 秩的概念与求解- 矩阵的分块3. 线性方程组- 线性方程组的表示- 高斯消元法- 行列式法- 逆矩阵解法- 克拉默法则- 线性方程组的解的结构- 齐次与非齐次线性方程组 - 线性方程组的解空间4. 特征值与特征向量- 特征值与特征向量的定义 - 特征值与特征向量的计算 - 矩阵的对角化- 矩阵的Jordan标准形- 特征值与特征向量的应用5. 内积空间- 内积空间的定义- 正交与正交性- 正交基与正交矩阵- 格拉姆-施密特正交化过程 - 最小二乘法- 正交投影与正交补6. 线性变换- 线性变换的定义与性质- 线性变换的矩阵表示- 线性变换的核与像- 线性变换的不变子空间- 线性变换的复合与逆变换 - 线性变换的分类7. 广义逆矩阵- 广义逆矩阵的概念- 广义逆矩阵的计算方法- 广义逆矩阵的性质与应用8. 谱理论- 谱定理- 谱半径与谱半径估计- 谱聚类9. 线性代数在其他领域的应用- 计算机图形学- 数据分析与机器学习- 量子力学- 结构工程- 电路分析结语线性代数是数学的一个重要分支,它在科学、工程、经济等多个领域都有着广泛的应用。
掌握线性代数的基本概念、理论和方法是解决实际问题的关键。
本文总结了线性代数的核心知识点,旨在为学习和应用线性代数提供参考和指导。
线性代数知识点总结汇总

线性代数知识点总结1 行列式(一)行列式概念和性质1、逆序数:所有的逆序的总数2、行列式定义:不同行不同列元素乘积代数和3、行列式性质:(用于化简行列式)(1)行列互换(转置),行列式的值不变(2)两行(列)互换,行列式变号(3)提公因式:行列式的某一行(列)的所有元素都乘以同一数k,等于用数k 乘此行列式(4)拆列分配:行列式中如果某一行(列)的元素都是两组数之和,那么这个行列式就等于两个行列式之和。
(5)一行(列)乘k加到另一行(列),行列式的值不变。
(6)两行成比例,行列式的值为0。
(二)重要行列式4、上(下)三角(主对角线)行列式的值等于主对角线元素的乘积5、副对角线行列式的值等于副对角线元素的乘积乘6、Laplace展开式:(A是m阶矩阵,B是n阶矩阵),则7、n阶(n≥2)范德蒙德行列式数学归纳法证明★8、对角线的元素为a,其余元素为b的行列式的值:(三)按行(列)展开9、按行展开定理:(1)任一行(列)的各元素与其对应的代数余子式乘积之和等于行列式的值(2)行列式中某一行(列)各个元素与另一行(列)对应元素的代数余子式乘积之和等于0(四)行列式公式10、行列式七大公式:(1)|kA|=k n|A|(2)|AB|=|A|·|B|(3)|A T|=|A|(4)|A-1|=|A|-1(5)|A*|=|A|n-1(6)若A的特征值λ1、λ2、……λn,则(7)若A与B相似,则|A|=|B|(五)克莱姆法则11、克莱姆法则:(1)非齐次线性方程组的系数行列式不为0,那么方程为唯一解(2)如果非齐次线性方程组无解或有两个不同解,则它的系数行列式必为0(3)若齐次线性方程组的系数行列式不为0,则齐次线性方程组只有0解;如果方程组有非零解,那么必有D=0。
2 矩阵(一)矩阵的运算1、矩阵乘法注意事项:(1)矩阵乘法要求前列后行一致;(2)矩阵乘法不满足交换律;(因式分解的公式对矩阵不适用,但若B=E,O,A-1,A*,f(A)时,可以用交换律)(3)AB=O不能推出A=O或B=O。
线性代数知识点总结汇总

线性代数知识点总结1 行列式(一)行列式概念和性质1、逆序数:所有的逆序的总数2、行列式定义:不同行不同列元素乘积代数和3、行列式性质:(用于化简行列式)(1)行列互换(转置),行列式的值不变(2)两行(列)互换,行列式变号@(3)提公因式:行列式的某一行(列)的所有元素都乘以同一数k,等于用数k 乘此行列式(4)拆列分配:行列式中如果某一行(列)的元素都是两组数之和,那么这个行列式就等于两个行列式之和。
(5)一行(列)乘k加到另一行(列),行列式的值不变。
(6)两行成比例,行列式的值为0。
(二)重要行列式4、上(下)三角(主对角线)行列式的值等于主对角线元素的乘积5、副对角线行列式的值等于副对角线元素的乘积乘|6、Laplace展开式:(A是m阶矩阵,B是n阶矩阵),则7、n阶(n≥2)范德蒙德行列式数学归纳法证明★8、对角线的元素为a,其余元素为b的行列式的值:(三)按行(列)展开)9、按行展开定理:(1)任一行(列)的各元素与其对应的代数余子式乘积之和等于行列式的值(2)行列式中某一行(列)各个元素与另一行(列)对应元素的代数余子式乘积之和等于0(四)行列式公式10、行列式七大公式:(1)|kA|=k n|A|(2)|AB|=|A|·|B|/(3)|A T|=|A|(4)|A-1|=|A|-1(5)|A*|=|A|n-1(6)若A的特征值λ1、λ2、……λn,则(7)若A与B相似,则|A|=|B|(五)克莱姆法则11、克莱姆法则:。
(1)非齐次线性方程组的系数行列式不为0,那么方程为唯一解(2)如果非齐次线性方程组无解或有两个不同解,则它的系数行列式必为0(3)若齐次线性方程组的系数行列式不为0,则齐次线性方程组只有0解;如果方程组有非零解,那么必有D=0。
2 矩阵(一)矩阵的运算1、矩阵乘法注意事项:(1)矩阵乘法要求前列后行一致;'(2)矩阵乘法不满足交换律;(因式分解的公式对矩阵不适用,但若B=E,O,A-1,A*,f(A)时,可以用交换律)(3)AB=O不能推出A=O或B=O。
最完整的线代基础知识点

最完整的线代基础知识点第1章行列式1.1 n阶行列式1.1.1 二阶、三阶行列式起源:发现规律了,继续~从上述推倒可以看出,行列式说白了就是对方程求解的简化过程。
后续的所有变换也都是基于此的。
了解到根源了,就不难理解了。
知识点:(所有的知识其实都是不成体系的,体系都是人为归纳的,其实知识就是一个一个的点而已)1.对角线法则这个法则只能用在二阶和三阶,高阶有另外的算法,后面会介绍到,耐心往下看吧。
以后看到二三阶可以直接用这个算哦。
2.行列式应用(克莱姆法则)法则啥的就是别人先发现了,就是一个规律。
不用理解,直接记住。
(因为本来就是一个现象)小技巧:再算d1d2d3的时候默念一下d1换1(列)d2换2(列)d3换3(列)。
1.1.2 排列既逆序数起源:逆序数为奇数,为奇排列,偶数为偶排列。
知识点:1.任一排列经过对换后,必改变其奇偶性。
2.所有n阶排列中,奇排列与偶排列个数相同,各有n!/2个。
1.1.3 n阶行列式知识点:1.计算方法前面说了,n阶有其他方法,这个就是其中之一不过比较笨重难算一点。
只要看懂这个式子,这节就ok啦,看不懂的可以评论问我。
2.对角行列式对角行列式等于其对角元素的连乘,再加上一个逆序数。
因为除了去取对角之外但凡取到其他位置上的0,就会让这项变成0。
上三角行列式和下三角行列式与对角行列式类似,不能取0。
好题:1.对行列式中数字的选取规则理解如果不用分块矩阵的话,直接从定义出发,三行用两个书,必有一行选不到非零数。
1.2 行列式的性质知识点:1.行列式与它的转置行列式相同,即行与列为完全等价的。
2.互换行列式的两行或两列,行列式值变号3.若行列式有两行或两列元素相同则其行列式的值为04.行列式的某一行中所有元素都乘以k,等于用k数乘行列式5.如果行列式中某一行的元素都为0,则其值为06.若行列式有两列或两行元素成比例,则其为07.若两个行列式除了一行外相同,则可以相合。
相同的行不变,不同的行相加。
(完整版)线性代数知识点全归纳

1线性代数知识点1、行列式1.n 行列式共有2n 个元素,展开后有!n 项,可分解为2n 行列式;2. 代数余子式的性质:①、ij A 和ij a 的大小无关;②、某行(列)的元素乘以其它行(列)元素的代数余子式为0; ③、某行(列)的元素乘以该行(列)元素的代数余子式为A ; 3.代数余子式和余子式的关系:(1)(1)i j i j ij ijij ijM A A M ++=-=-4. 设n 行列式D :将D 上、下翻转或左右翻转,所得行列式为1D ,则(1)21(1)n n D D -=-; 将D 顺时针或逆时针旋转90,所得行列式为2D ,则(1)22(1)n n D D -=-;将D 主对角线翻转后(转置),所得行列式为3D ,则3D D =;将D 主副角线翻转后,所得行列式为4D ,则4D D =;5. 行列式的重要公式:①、主对角行列式:主对角元素的乘积;②、副对角行列式:副对角元素的乘积(1)2(1)n n -⨯ -;③、上、下三角行列式( = ◥◣):主对角元素的乘积; ④、 ◤和 ◢:副对角元素的乘积(1)2(1)n n -⨯ -;⑤、拉普拉斯展开式:A O A C AB CB O B==、(1)m n CA OA AB B OB C==-⑥、范德蒙行列式:大指标减小指标的连乘积; ⑦、特征值;6. 对于n 阶行列式A ,恒有:1(1)nnk n k k k E A S λλλ-=-=+-∑,其中k S 为k 阶主子式;7. 证明0A =的方法:①、A A =-; ②、反证法;③、构造齐次方程组0Ax =,证明其有非零解; ④、利用秩,证明()r A n <; ⑤、证明0是其特征值;22、矩阵1.A 是n 阶可逆矩阵:⇔0A ≠(是非奇异矩阵); ⇔()r A n =(是满秩矩阵) ⇔A 的行(列)向量组线性无关; ⇔齐次方程组0Ax =有非零解; ⇔n b R ∀∈,Ax b =总有唯一解;⇔A 与E 等价;⇔A 可表示成若干个初等矩阵的乘积; ⇔A 的特征值全不为0; ⇔T A A 是正定矩阵;⇔A 的行(列)向量组是n R 的一组基; ⇔A 是n R 中某两组基的过渡矩阵;2. 对于n 阶矩阵A :**AA A A A E == 无条件恒成立;3.1**111**()()()()()()T T T T A A A A A A ----===***111()()()T T T AB B A AB B A AB B A ---===4. 矩阵是表格,推导符号为波浪号或箭头;行列式是数值,可求代数和;5. 关于分块矩阵的重要结论,其中均A 、B 可逆:若12s A A A A ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭,则: Ⅰ、12s A A A A =;Ⅱ、111121s A A A A ----⎛⎫⎪⎪= ⎪ ⎪ ⎪⎝⎭; ②、111A O A O O B OB ---⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭;(主对角分块) ③、111O A O B B O A O ---⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭;(副对角分块) ④、11111A C A A CB O B OB -----⎛⎫-⎛⎫=⎪ ⎪⎝⎭⎝⎭;(拉普拉斯) ⑤、11111A O A O C B B CAB -----⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭;(拉普拉斯)33、矩阵的初等变换与线性方程组1. 一个m n ⨯矩阵A ,总可经过初等变换化为标准形,其标准形是唯一确定的:rm nEO F OO ⨯⎛⎫= ⎪⎝⎭; 等价类:所有与A 等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵; 对于同型矩阵A 、B ,若()()r A r B A B = ⇔ ;2. 行最简形矩阵:①、只能通过初等行变换获得;②、每行首个非0元素必须为1;③、每行首个非0元素所在列的其他元素必须为0;3. 初等行变换的应用:(初等列变换类似,或转置后采用初等行变换)①、若(,)(,)rA E E X ,则A 可逆,且1X A -=;②、对矩阵(,)A B 做初等行变化,当A 变为E 时,B 就变成1A B -,即:1(,)(,)cA B E A B - ~ ;③、求解线形方程组:对于n 个未知数n 个方程Ax b =,如果(,)(,)rA b E x ,则A 可逆,且1x A b -=;4. 初等矩阵和对角矩阵的概念:①、初等矩阵是行变换还是列变换,由其位置决定:左乘为初等行矩阵、右乘为初等列矩阵;②、12n ⎛⎫⎪⎪Λ= ⎪ ⎪⎝⎭λλλ,左乘矩阵A ,i λ乘A 的各行元素;右乘,iλ乘A 的各列元素;③、对调两行或两列,符号(,)E i j ,且1(,)(,)E i j E i j -=,例如:1111111-⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭;④、倍乘某行或某列,符号(())E i k ,且11(())(())E i k E i k-=,例如:1111(0)11kk k -⎛⎫⎛⎫⎪⎪⎪=≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭; ⑤、倍加某行或某列,符号(())E ij k ,且1(())(())E ij k E ij k -=-,如:11111(0)11k k k --⎛⎫⎛⎫ ⎪ ⎪=≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭;5. 矩阵秩的基本性质:①、0()min(,)m n r A m n ⨯≤≤;②、()()T r A r A =; ③、若AB ,则()()r A r B =;④、若P 、Q 可逆,则()()()()r A r PA r AQ r PAQ ===;(可逆矩阵不影响矩阵的秩) ⑤、max((),())(,)()()r A r B r A B r A r B ≤≤+;(※) ⑥、()()()r A B r A r B +≤+;(※) ⑦、()min((),())r AB r A r B ≤;(※)4⑧、如果A 是m n ⨯矩阵,B 是n s ⨯矩阵,且0AB =,则:(※) Ⅰ、B 的列向量全部是齐次方程组0AX =解(转置运算后的结论);Ⅱ、()()r A r B n +≤⑨、若A 、B 均为n 阶方阵,则()()()r AB r A r B n ≥+-;6. 三种特殊矩阵的方幂:①、秩为1的矩阵:一定可以分解为列矩阵(向量)⨯行矩阵(向量)的形式,再采用结合律;②、型如101001a c b ⎛⎫⎪⎪ ⎪⎝⎭的矩阵:利用二项展开式; 二项展开式:01111110()nn n n m n m mn n n n m m n mn n n n n n m a b C a C a b C a b C a b C b C a b-----=+=++++++=∑;注:Ⅰ、()n a b +展开后有1n +项;Ⅱ、0(1)(1)!1123!()!--+====-m n n n n n n n m n C C C m m n mⅢ、组合的性质:111102---+-===+==∑nmn m mm m r nr r nnn n nnn n r C C CC CCrC nC ;③、利用特征值和相似对角化:7. 伴随矩阵:①、伴随矩阵的秩:*()()1()10()1n r A n r A r A n r A n = ⎧⎪==-⎨⎪<-⎩; ②、伴随矩阵的特征值:*1*(,)AAAX X A A A A X X λλλ- == ⇒ =;③、*1A A A -=、1*n A A-=8. 关于A 矩阵秩的描述:①、()r A n =,A 中有n 阶子式不为0,1n +阶子式全部为0;(两句话)②、()r A n <,A 中有n 阶子式全部为0; ③、()r A n ≥,A 中有n 阶子式不为0;9. 线性方程组:Ax b =,其中A 为m n ⨯矩阵,则:①、m 与方程的个数相同,即方程组Ax b =有m 个方程;②、n 与方程组得未知数个数相同,方程组Ax b =为n 元方程;10. 线性方程组Ax b =的求解:①、对增广矩阵B 进行初等行变换(只能使用初等行变换);②、齐次解为对应齐次方程组的解; ③、特解:自由变量赋初值后求得;511. 由n 个未知数m 个方程的方程组构成n 元线性方程:①、11112211211222221122n n n n m m nm n na x a x a xb a x a x a x b a x a x a x b +++= ⎧⎪+++= ⎪⎨⎪⎪+++=⎩; ②、1112111212222212n n m m mn m m a a a x b a a a x b Ax b a a a x b ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪=⇔= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭(向量方程,A 为m n ⨯矩阵,m 个方程,n 个未知数)③、()1212n n x x aa a x β⎛⎫⎪ ⎪= ⎪⎪⎝⎭(全部按列分块,其中12n b b b β⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭); ④、1122n n a x a x a x β+++=(线性表出)⑤、有解的充要条件:()(,)r A r A n β=≤(n 为未知数的个数或维数)4、向量组的线性相关性1.m 个n 维列向量所组成的向量组A :12,,,m ααα构成n m ⨯矩阵12(,,,)m A =ααα;m 个n 维行向量所组成的向量组B :12,,,T TTm βββ构成m n ⨯矩阵12T T T m B βββ⎛⎫⎪ ⎪= ⎪ ⎪ ⎪⎝⎭;含有有限个向量的有序向量组与矩阵一一对应;2. ①、向量组的线性相关、无关 0Ax ⇔=有、无非零解;(齐次线性方程组)②、向量的线性表出 Ax b ⇔=是否有解;(线性方程组) ③、向量组的相互线性表示 AX B ⇔=是否有解;(矩阵方程)3. 矩阵m n A ⨯与l n B ⨯行向量组等价的充分必要条件是:齐次方程组0Ax =和0Bx =同解;(101P 例14)4.()()T r A A r A =;(101P 例15)5.n 维向量线性相关的几何意义:①、α线性相关⇔0α=; ②、,αβ线性相关 ⇔,αβ坐标成比例或共线(平行);③、,,αβγ线性相关 ⇔,,αβγ共面;6. 线性相关与无关的两套定理:若12,,,s ααα线性相关,则121,,,,s s αααα+必线性相关;若12,,,s ααα线性无关,则121,,,s ααα-必线性无关;(向量的个数加加减减,二者为对偶)若r 维向量组A 的每个向量上添上n r -个分量,构成n 维向量组B :6若A 线性无关,则B 也线性无关;反之若B 线性相关,则A 也线性相关;(向量组的维数加加减减) 简言之:无关组延长后仍无关,反之,不确定;7. 向量组A (个数为r )能由向量组B (个数为s )线性表示,且A 线性无关,则r s ≤; 向量组A 能由向量组B 线性表示,则()()r A r B ≤;向量组A 能由向量组B 线性表示AX B ⇔=有解; ()(,)r A r A B ⇔=向量组A 能由向量组B 等价()()(,)r A r B r A B ⇔ ==8. 方阵A 可逆⇔存在有限个初等矩阵12,,,l P P P ,使12l A P P P =;①、矩阵行等价:~rA B PA B ⇔=(左乘,P 可逆)0Ax ⇔=与0Bx =同解 ②、矩阵列等价:~cA B AQ B ⇔=(右乘,Q 可逆); ③、矩阵等价:~A B PAQ B ⇔=(P 、Q 可逆);9. 对于矩阵m n A ⨯与l n B ⨯:①、若A 与B 行等价,则A 与B 的行秩相等;②、若A 与B 行等价,则0Ax =与0Bx =同解,A 与B 的任何对应的列向量组有相同的线性相关性; ③、矩阵的初等变换不改变矩阵的秩; ④、矩阵A 的行秩等于列秩;10. 若m s s n m n A B C ⨯⨯⨯=,则:①、C 的列向量组能由A 的列向量组线性表示,B 为系数矩阵; ②、C 的行向量组能由B 的行向量组线性表示,T A 为系数矩阵;(转置)11. 齐次方程组0Bx =的解一定是0ABx =的解,【考试中可以直接作为定理使用,而无需证明】 ①、0ABx = 只有零解0Bx ⇒ =只有零解;②、0Bx = 有非零解0ABx ⇒ =一定存在非零解;12. 设向量组12:,,,n r r B b b b ⨯可由向量组12:,,,n s s A a a a ⨯线性表示为:1212(,,,)(,,,)r s b b b a a a K =(B AK =)其中K 为s r ⨯,且A 线性无关,则B 组线性无关()r K r ⇔=;(B 与K 的列向量组具有相同线性相关性)(必要性:()()(),(),()r r B r AK r K r K r r K r ==≤≤∴=;充分性:反证法)注:当r s =时,K 为方阵,可当作定理使用;13. ①、对矩阵m n A ⨯,存在n m Q ⨯,m AQ E = ()r A m ⇔=、Q 的列向量线性无关;②、对矩阵m n A ⨯,存在n m P ⨯,n PA E = ()r A n ⇔=、P 的行向量线性无关;14. 12,,,s ααα线性相关⇔存在一组不全为0的数12,,,s k k k ,使得11220s s k k k ααα+++=成立;(定义)⇔1212(,,,)0s s x xx ααα⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭有非零解,即0Ax =有非零解;⇔12(,,,)s r s ααα<,系数矩阵的秩小于未知数的个数;715. 设m n ⨯的矩阵A 的秩为r ,则n 元齐次线性方程组0Ax =的解集S 的秩为:()r S n r =-;16. 若*η为Ax b =的一个解,12,,,n r ξξξ-为0Ax =的一个基础解系,则*12,,,,n r ηξξξ-线性无关;5、相似矩阵和二次型1. 正交矩阵T A A E ⇔=或1T A A -=(定义),性质:①、A 的列向量都是单位向量,且两两正交,即1(,1,2,)0T i j i j a a i j n i j=⎧==⎨≠⎩;②、若A 为正交矩阵,则1T A A -=也为正交阵,且1A =±; ③、若A 、B 正交阵,则AB 也是正交阵;注意:求解正交阵,千万不要忘记施密特正交化和单位化;2. 施密特正交化:12(,,,)r a a a11b a =;1222111[,][,]b a b a b b b =-121121112211[,][,][,][,][,][,]r r r r r r r r r b a b a b a b a b b b b b b b b b ----=----;3. 对于普通方阵,不同特征值对应的特征向量线性无关;对于实对称阵,不同特征值对应的特征向量正交;4. ①、A 与B 等价 ⇔A 经过初等变换得到B ;⇔=PAQ B ,P 、Q 可逆; ()()⇔=r A r B ,A 、B 同型;②、A 与B 合同 ⇔=T C AC B ,其中可逆; ⇔T x Ax 与T x Bx 有相同的正、负惯性指数; ③、A 与B 相似 1-⇔=P AP B ;5. 相似一定合同、合同未必相似;若C 为正交矩阵,则T C AC B =⇒A B ,(合同、相似的约束条件不同,相似的更严格);6. A 为对称阵,则A 为二次型矩阵;7.n 元二次型T x Ax 为正定:A ⇔的正惯性指数为n ;A ⇔与E 合同,即存在可逆矩阵C ,使T C AC E =; A ⇔的所有特征值均为正数;A ⇔的各阶顺序主子式均大于0;0,0ii a A ⇒>>;(必要条件)8第一章 随机事件互斥对立加减功,条件独立乘除清; 全概逆概百分比,二项分布是核心; 必然事件随便用,选择先试不可能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性代数 第一章 行列式§1 二阶和三阶行列式一、二元一次线性方程组与二阶行列式结论:如果112212210a a a a -≠,则二元线性方程组 11112212112222a x a xb a x a x b +=⎧⎨+=⎩的解为122122*********b a a b x a a a a -=-,1121212112121a b b a x a b b a -=-。
定义:设11122122,,,a a a a ,记11221221a a a a -为11122122a a a a 。
称11122122a a a a 为二阶行列式有了行列式的符号,二元线性方程组的求解公式可以改写为112222111122122b a b a x a a a a =,111122211122122a b a b x a a a a =二、三阶行列式与三元一次线性方程组定义:111213212223313233a a a a a a a a a 112233122331132132132231122133112332a a a a a a a a a a a a a a a a a a =++---定理:如果1112132122233132330a a a D a a a a a a =≠,则***123(,,)x x x 是下面的三元线性方程组的解 111122133121122223323113223333a x a x a xb a x a x a x b a x a x a x b ++=⎧⎪++=⎨⎪++=⎩当且仅当*1x =112132222333233/b a a b a a D b a a ,*2x =111132122331333/a b a a b a D a b a ,*3x =111212122231323/a a b a a b D a a b 其中111213212223313233a a a a a a a a a 为系数行列式。
证明:略。
性质1:行列式行列互换,其值不变。
即111213112131212223122232313233132333a a a a a a a a a a a a a a a a a a =。
性质2:行列式某两行或列互换,其值变号。
例如111213212223212223111213313233313233a a a a a a a a a a a a a a a a a a =- 推论:行列式有两行相同,其值为零。
性质3:行列式某一行的所有数乘一常数等于行列式乘该常数。
例如111213111213212223212223313233313233a a a a a a ka ka ka k a a a a a a a a a = 推论:行列式某一行或列的公因数可以提到行列式外面。
推论:行列式有一行全为零,其值为零。
性质4:行列式有两行成比例时,其值为零。
性质5:行列式关于它的每一行和每一列都是线性的。
例如111213111213111213212122222323212223212223313233313233313233a a a a a a a a a ab a b a b a a a b b b a a a a a a a a a +++=+ 性质6:将行列式的某一行(列)的所有元素都乘以数k 后加到另一行(列)对应位置的元素上, 其值不变。
例如111213111213211122122313212223313233313233a a a a a a a ka a ka a ka a a a a a a a a a +++=性质7:行列式按某一行展开精品文档111213222321232122212223111213323331333132313233a a a a a a a a a a a a a a a a a a a a a a a a =-+定理的证明:用22233233a a a a 乘第一个方程1111221331a x a x a xb ++=,得222322232223222311112213313233323332333233a a a a a a a a a x a x a xb a a a a a a a a ++=①用12133233a a a a 乘第一个方程2112222332a x a x a x b ++=,得121312131213121321122223323233323332333233a a a a a a a a a x a x a x b a a a a a a a a ++=②;同理,有121312131213121331132233332223222322232223a a a a a a a a a x a x a xb a a a a a a a a ++=③。
①+(-1)②+③,得2223121312131121311323332332223()a a a a a a a a a x a a a a a a -+2223121312131222322323332332223()a a a a a a a a a x a a a a a a +-+2223121312131323333323332332223()a a a a a a a a a x a a a a a a +-+222312131213123323332332223a a a a a ab b b a a a a a a =-+利用性质7,得111213121213131213112132122231222223223222332222331323332323333323333233a a a a a a a a ab a a a a a x a a a x a a a x b a a a a a a a a a a a b a a ++=从而1112131121321222312222331323333233a a ab a a a a a x b a a a a a b a a =。
定理:111122133211222233311322333000a x a x a x a x a x a x a x a x a x ++=⎧⎪++=⎨⎪++=⎩有非零解当且仅当系数行列式0D =。
证明:必要性:若齐次方程组有非零解,如果0D ≠,由前面的定理,矛盾。
充分性:若0D =,注意111213212223313233a a a a a a a a a =222321232122111213323331333132aa a a a a a a a a a a a a a ⎛⎫+⋅-+ ⎪⎝⎭把222321232122323331333132(,,)a a a a a a a a a a a a -带入第2和第3个方程,容易验证它是方程组的解。
因此,如果222321232122323331333132,,a a a a a a a a a a a a -不全为零,则定理得证。
如果2223212321223233313331320,0,0a a a a a a a a a a a a ===,则232122313233a a a a a a ==。
原方程组实际上等价于11112213321122223300a x a x a x a x a x a x ++=⎧⎨++=⎩。
而该方程组一定有非零解(为什么?自己讨论)。
§2 全排列及其逆序数定义:1,2,,n ⋅⋅⋅的一个排列是指这n 个数组成的一个有序组。
定义(逆序与逆序数):设12n i i i ⋅⋅⋅是1,2,,n ⋅⋅⋅的一个排列,如果j k <,而j k i i >,则称(,)j k i i 构成一个逆序对,排列12n i i i ⋅⋅⋅的所有逆序对的个数叫做置换排列12n i i i ⋅⋅⋅的逆序数,记为12()n i i i π⋅⋅⋅。
12()(1)n i i i π⋅⋅⋅-叫做排列12n i i i ⋅⋅⋅的符号,记为12()n sgn i i i ⋅⋅⋅。
12()1n sgn i i i ⋅⋅⋅=的排列叫做偶排列,12()1n sgn i i i ⋅⋅⋅=-的排列12n i i i ⋅⋅⋅叫做奇排列。
定理 3.2.1:设12n i i i ⋅⋅⋅,12n j j j ⋅⋅⋅是1,2,,n ⋅⋅⋅的任意两个排列,那么总可以通过一系列对换把是12n i i i ⋅⋅⋅变成12n j j j ⋅⋅⋅。
例:排列7523146包含的逆序对有75、72、73、71、74、76; 52、53、51、54; 21;31。
故逆序数为12。
§3 n 阶行列式的定义 一、n 阶行列式的正式定义定义:数域K 上的n 阶行列式定义为nnn n n n a a a a a a a a a212222111211121212()12(1)n n nj j j j j nj j j j a a a π⋅⋅⋅∀⋅⋅⋅=-⋅⋅⋅∑。
其中对任意的,1,2,,i j n =⋅⋅⋅,ij a K ∈。
通常记之为A 。
例1:0001002012342403004000=⨯⨯⨯=。
例2:100010101=例3:121421243233430000?00000a a a a a a a =例4:。
123451234512121200000000a a a a ab b b b bc cd de e =。
例5:11121222112200n n nn nna a a a a a a a a =§5、行列式的性质性质1:行列式行列互换,其值不变。
即111212122212n n n n nna a a a a a a a a 112111222212n n nnnna a a a a a a a a =。
性质2:行列式某两行或列互换,其值变号。
推论:行列式有两行相同,其值为零。
性质3:行列式某一行的所有数乘一常数等于行列式乘该常数。
推论:行列式某一行或列的公因数可以提到行列式外面。
推论:行列式有一行全为零,其值为零。
性质4:行列式有两行成比例时,其值为零。
性质5:行列式关于它的每一行和每一列都是线性的。
性质6:将行列式的某一行(列)的所有元素都乘以数k 后加到另一行(列)对应位置的元素上, 其值不变。
§6 行列式按行展开定义1:在111212122212n n n n nna a a a a a a a a中,把位于i 行,j 列的元素划去后留下的1n -行列式叫做ij a 的余子式,记为ij M 。
