协同克里格
一种Markov模型在协同克里格中的新应用

一
种 Mak v r o 模型在协同克里格 中的新应用
张 挺 杜 奕 ,
ZHANG T n DU Yi i g,
1 . 上海电力学院 计算机与信息工程学院 , 上海 209 00 0
lr rs pp r h n t ep i r a a e a ge u o t a h rma v r bl . t y i Ke r :Cok i n M a k v mo l c e n n fe t had daa s t aa y wo ds rgig; r o de;s r e i g e f c ; r t ; of d t
Mak vMo e 2 MM2 frsc aei peetdt e tea o ec n io . h ro d l ( ) hacs rsne meth b v o dt n T eMM2sre igh p tei o u s o i cenn y oh s s
v r b ei d f e n amu h lr e p o t h n t e r r a a l , h M 1i n t p r p ae T e n i r v d a a l e n d o c g r u p r t a i i s i a s h p ma y v r b e t eM i s o p o r t . h n a a i mp o e
l 引言
在 一 些科 学技 术 领 域 , 值 方 法 被 广 泛 用 于 预 插
果表 明, 当硬数据定义在比软数据小的空间尺度 时, MM2 模型下的协同克里格方法有效 。
土壤养分含量的协同克里格法插值研究

Sp i ldit i uto t fe e a p i um b r fs i ut intusng C o r gng ata sr b i n wih dif r nts m lng n e s o o ln r e i k i i
L a . U D n — t I n X o gr .WU Y n -e N u a gj i
浙 江农 业 学 报 A t A r u ua hj n es , 0 l2 ( ) 10 —10 c gi h reZ eagni 2 1 ,3 5 :0 1 0 6 a c i s
h p/ w w  ̄ yb ( t :/ w . nx .: t n
李 楠 , 东 瑞 , 杨 洁 .土 壤 养 分 含 苣 的 协 同 克里 格 法 插 值 研 究 [ ] 浙 汀农 业 学报 ,0 ,3 5 :0 1—10 . 徐 吴 J. 2 1 2 ( ) 10 1 06
Ab ta t p t li tr oa in i i t o o b ann e s a il i r u i n o oln tin h c s a m— s r c :S ai n e p lt s aman meh d fr o ti i g t p t s i t fs i u r tw i h i n i a o h a d tb o e
( oeeo e uc a dE v om n Si c, ee N r a nvrt, h i h ag0 0 1 ,hn ) C lg R s r n ni n et c ne H bi om l i sy S i zu n 5 0 6 C ia l f o e r e U ei j a
空 间插 值 。 关键 词 : 土壤 养 分 ; 间插 值 ; 通 克 里 格 法 ; 同 克 里 格 方 法 ; 叉检 验 空 普 协 交
地球物理计算常用的插值方法-克里格法

克里格法(Kriging)是地统计学的主要内容之一,从统计意义上说,是从变量相关性和变异性出发,在有限区域内对区域化变量的取值进行无偏、最优估计的一种方法;从插值角度讲是对空间分布的数据求线性最优、无偏内插估计一种方法。
克里格法的适用条件是区域化变量存在空间相关性。
克里格法,基本包括普通克里格方法(对点估计的点克里格法和对块估计的块段克里格法)、泛克里格法、协同克里格法、对数正态克里格法、指示克里格法、折取克里格法等等。
随着克里格法与其它学科的渗透,形成了一些边缘学科,发展了一些新的克里金方法。
如与分形的结合,发展了分形克里金法;与三角函数的结合,发展了三角克里金法;与模糊理论的结合,发展了模糊克里金法等等。
应用克里格法首先要明确三个重要的概念。
一是区域化变量;二是协方差函数,三是变异函数一、区域化变量当一个变量呈空间分布时,就称之为区域化变量。
这种变量反映了空间某种属性的分布特征。
矿产、地质、海洋、土壤、气象、水文、生态、温度、浓度等领域都具有某种空间属性。
区域化变量具有双重性,在观测前区域化变量Z(X)是一个随机场,观测后是一个确定的空间点函数值。
区域化变量具有两个重要的特征。
一是区域化变量Z(X)是一个随机函数,它具有局部的、随机的、异常的特征;其次是区域化变量具有一般的或平均的结构性质,即变量在点X与偏离空间距离为h的点X+h处的随机量Z(X)与Z(X+h)具有某种程度的自相关,而且这种自相关性依赖于两点间的距离h与变量特征。
在某种意义上说这就是区域化变量的结构性特征。
二、协方差函数协方差又称半方差,是用来描述区域化随机变量之间的差异的参数。
在概率理论中,随机向量X与Y 的协方差被定义为:区域化变量在空间点x和x+h处的两个随机变量Z(x)和Z(x+h)的二阶混合中心矩定义为Z(x)的自协方差函数,即区域化变量Z(x) 的自协方差函数也简称为协方差函数。
一般来说,它是一个依赖于空间点x 和向量h 的函数。
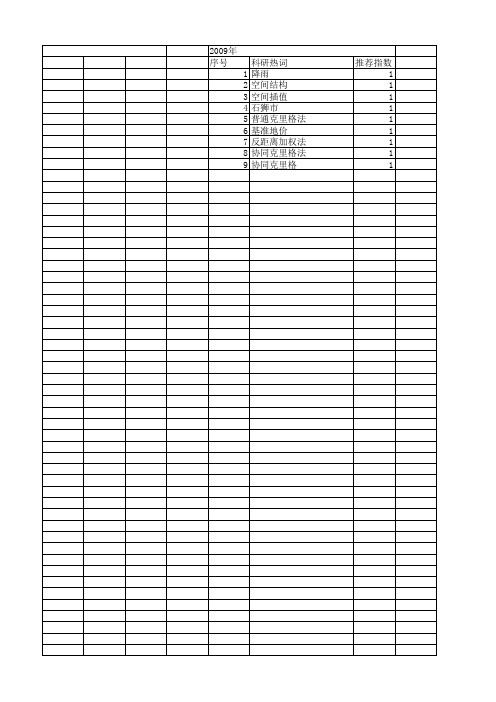
【国家自然科学基金】_协同克里格_基金支持热词逐年推荐_【万方软件创新助手】_20140731
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9
科研热词 空间插值 甘肃省 泛克里格 气象数据 普通克里格 土壤有机质 回归克里格 协同克里格 dem
推荐指数 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
2014年 序号 1 2 3 4 5 6 7 8
科研热词 黄河三角洲 辅助变量 土壤盐渍化 土壤养分 协同克里格 克里格 kriging cokring
推荐指数 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9
科研热词 降雨 空间结构 空间插值 石狮市 普通克里格法 基准地价 反距离加权法 协同克里格法 协同克里格
推荐指数 1 1 1 1 1 1 1 1 1
2010年 序号ቤተ መጻሕፍቲ ባይዱ1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词 空间插值 频率 降水 误差分析 气温 时空格局 日极端气温 年平均气温 年代际变化 安徽 天津 协同克里格法 交叉验证
科研热词 高光谱 风效指数 降水量 空间预测 空间插值 甘肃省 环境一号卫星 温湿指数 气温 权函数 时空变异 旅游气候舒适度 总磷 地理加权回归模型 土壤属性 协同克里格遗传算法 协同克里格法 协同克里格插值 华东地区 克里格插值 arcgis
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
森林碳储量空间统计学的协同克里格法

森林碳储量空间统计学的协同克里格法引言:森林碳储量是指森林生物量及其所包含的碳元素的总量。
准确估计森林碳储量对于了解森林生态系统的健康状况以及应对气候变化具有重要意义。
近年来,空间统计学在森林碳储量估计中得到了广泛应用,其中协同克里格法成为一种常用的方法。
本文将介绍森林碳储量的概念及其重要性,并详细描述协同克里格法在森林碳储量空间统计学中的应用。
一、森林碳储量的概念及重要性森林碳储量是指森林生态系统中储存的碳元素总量,包括活体碳、死体碳和土壤有机碳等。
森林碳储量的准确估计可以帮助我们了解森林生态系统的健康状况,评估生态系统对气候变化的响应能力,制定合理的森林管理政策,以及推动碳排放减少和生态保护。
二、空间统计学在森林碳储量估计中的应用空间统计学是指研究空间变量的分布及其随机性的一门学科。
在森林碳储量估计中,空间统计学可以帮助我们利用已知的样点数据来预测未知位置的碳储量,并揭示碳储量的空间分布规律。
协同克里格法是一种基于空间统计学的插值方法,它基于空间自相关原理,通过已知样点数据的空间相互关系来推断未知位置的碳储量。
协同克里格法利用了不同尺度的协方差函数,依据不同尺度下的变异性,进行合理的插值分析。
具体步骤如下:1. 数据收集与预处理:收集已知位置的样点数据,包括森林碳储量和与碳储量相关的环境因素。
对数据进行预处理,包括异常值处理、空间变换等。
2. 协同变异函数估计:计算已知样点数据之间的协方差函数,并根据不同尺度的变异性进行拟合和估计。
3. 变异函数模型选择:选择适当的变异函数模型,并进行参数估计和模型验证。
常用的变异函数模型包括球型模型、指数模型和高斯模型等。
4. 空间插值与预测:根据已估计的变异函数模型,对未知位置的碳储量进行插值分析,并得出空间预测结果。
常见的插值方法包括克里格法、逆距离加权法和径向基函数插值法等。
5. 空间插值结果评估:对插值结果进行评估,包括预测误差、模型拟合度和空间分布的一致性等。
基于协同克里格插值和地理加权回归模型的土壤属性空间预测比较

基于协同克里格插值和地理加权回归模型的土壤属性空间预测比较一、本文概述Overview of this article本文旨在比较协同克里格插值(Co-Kriging)和地理加权回归模型(Geographically Weighted Regression,GWR)在土壤属性空间预测中的应用效果。
土壤属性空间预测是农业、环境科学和地球科学等领域的重要研究内容,对于土地资源管理、生态环境保护以及农业可持续发展具有重要意义。
协同克里格插值和地理加权回归模型是两种常用的空间预测方法,它们各自具有独特的优点和适用范围。
This article aims to compare the application effects of Co Kriging interpolation and Geographically Weighted Regression (GWR) models in soil attribute spatial prediction. Soil attribute spatial prediction is an important research content in fields such as agriculture, environmental science, and earth science, which is of great significance for land resource management, ecological environment protection, and sustainable development of agriculture. Collaborative Kriginginterpolation and geographically weighted regression models are two commonly used spatial prediction methods, each with unique advantages and applicability.协同克里格插值是一种基于空间统计学的插值方法,它利用多个相关变量的空间分布信息,通过计算权重系数来预测未知点的属性值。
数字土壤制图方法及国内外研究进展

数字土壤制图方法及国内外研究进展数字土壤制图以土壤—景观模型理论为基础,通过地理信息系统、遥感、空间分析等技术手段来获取土壤发生环境信息,采用统计学、地统计学等其他数字定量方法来模拟土壤与其发生环境信息之间的定量关系,并在空间上扩展该关系,达到制图目的(Scull et al.,2003)。
数字化土壤图以及从中衍生的信息系统,可以提供高精度、高分辨率的土壤类型和土壤属性等信息,进而服务于现代农业生产实践和资源环境管理决策。
数字土壤制图已成为当前国内外土壤科学的研究热点。
传统制图程序一般分为野外土壤草图测绘、室内底图清绘、图面整饰三个步骤,因其耗时久、耗费人力物力、精度有限等缺点,逐渐被淘汰。
取而代之的数字化土壤制图,具有成本低廉、记载性强、更新快、效率高、精度高、制图美观等优点,已经成为土壤制图的主要方法(Carréet al.,2007)。
2009年,“全球土壤数字制图计划”在美国正式启动,该计划通过综合利用土壤学、地理学、遥感技术、地理信息系统、数据挖掘等多种理论和方法,最后建立具有高分辨率的全球土壤属性的三维网格数字土壤地图(蔡玉高,2011)。
国内外学者对数字化土壤制图做了大量扩展研究,试图寻找数字化土壤制图精度较高、制图效果较好的方法,其中地统计学、决策树、模糊聚类等方法都得到讨论验证,但是目前仍没有得到普遍认可的数字制图方法。
国内数字化土壤制图研究起步较晚,目前出现的方法主要有地统计法、模糊聚类、决策树、支持向量机、线性回归模型以及上述方法的组合等。
孙孝林等(2013)总结出数字化土壤制图五种理论基础:土壤发生学理论、地理学、数学,以及土壤学与地理学、地理学与数学,并对每种理论基础出现的模型、所需样本要求进行系统归纳,有效丰富了土壤数字制图的理论基础。
一、地统计学地统计学是利用原始数据和半方差函数的结构性特征,对未采样点的区域化变量进行无偏最优估计,它以地理学为理论基础,认为空间上任何事物都与其他事物相关,且其相关性与距离有关,是在国内数字化土壤制图方面得到广泛研究的方法。
GIS空间分析名词解释

:空间数据....拓扑分析、空间叠加、缓冲分析、网络分析P3数字地面模型(DTM):数字高程模型(DEM):不规则三角网(TIN):地质统计学:是利用空间变量的自相关特征研究空间随机场性质的一种统计理论。
它分为(1)结构分析理论;(2)克立格插值理论(插值理论);(3)条件模拟理论。
协方差、空间采样理论P9估计误差:是指实测值与真实值之间的误差。
估计方差:是指估计误差的离散程度。
数字高程模型DEM:是描述地面特性空间分布的有序数值阵列,所记地面特性是高程z,它的空间分布由x , y水平坐标系统来描述。
DEM派生信息:以数字地面模型为基础,通过数字地形分析(DTA)手段可提取出用于描述地表不同方面特征的参数,这些参数统称为DEM派生信息。
坡度、坡向、曲率P16地面曲率:地面曲率是对地形表面一点扭曲变化程度的定量化度量因子,地面曲率在垂直和水平两个方向上分量分别称为平面曲率和剖面曲率。
剖面曲率、平面曲率、坡形P18汇流量(汇流面积):一个栅格单元的汇流量是其上游单元向其输送的水流量的总和。
地形湿度指数:单位等高线上的汇流面积与坡度之比。
通视分析:就是利用DEM判断地形上任意点之间是否可以相互可见的技术方法,分为视线分析和视域分析。
缓冲区:地理空间目标的一种影响范围或服务范围,具体指在点. 线. 面实体周围自动建立的一定宽度的多边形。
叠置分析:是将同一地区的两组或两组以上的要素进行叠置,产生新的特征的分析方法。
合成叠置、统计叠置P30交、并、剪P31 差、识别P32距离分析:用于分析图像上每个点与目标的距离,如有多目标,则以最近的距离作为栅格值。
距离制图、直线距离分析P32密度分析:针对一些点要素(或线要素)的特征值(如人口数)并不是集中在点上(或线上)的特点,对要素的特征值进行空间分配,从而更加真实地反映要素分布。
密度制图:根据输入的要素数据集计算整个区域的数据聚集状况,从而产生一个连续的密度表面。
ArcGIS中几种空间插值方法

ArcGIS 中几种空间插值方法1. 反距离加权法(IDW)ArcGIS 中最常用的空间内插方法之一,反距离加权法是以插值点与样本点之间的距离为权重的插值方法,插值点越近的样本点赋予的权重越大,其权重贡献与距离成反比。
可表示为:1111()()n nip p i i i i Z Z D D ===∑∑其中Z 是插值点估计值,Z i (i=1Λn)是实测样本值,n 为参与计算的实测样本数,D i 为插值点与第i 个站点间的距离,p 是距离的幂,它显著影响内插的结果,它的选择标准是最小平均绝对误差。
2.多项式法多项式内插法(Polynomial Interpolation)是根据全部或局部已知值,按研究区域预测数据的某种特定趋势来进行内插的方法,属统计方法的范畴。
在GA 模块中,有二种类型的多项式内插方法,即全局多项式内插和局部多项式内插。
前者多用于分析数据的全局趋势;后者则是使用多个平面来拟合整个研究区域,能表现出区域内局部变异的情况。
3.样条函数内插法样条函数是一个分段函数,进行一次拟合只有少数点拟合,同时保证曲线段连接处连续,这就意味着样条函数可以修改少数数据点配准而不必重新计算整条曲线。
样条函数的一些缺点是:样条内插的误差不能直接估算,同时在实践中要解决的问题是样条块的定义以及如何在三维空间中将这些“块”拼成复杂曲面,又不引入原始曲面中所没有的异常现象等问题。
4.克里格插值法克里格法是GIS 软件地理统计插值的重要组成部分。
这种方法充分吸收了地理统计的思想,认为任何在空间连续性变化的属性是非常不规则的,不能用简单的平滑数学函数进行模拟,可以用随机表面给予较恰当的描述。
这种连续性变化的空间属性称为“区域性变量”,可以描述象气压、高程及其它连续性变化的描述指标变量。
地理统计方法为空间插值提供了一种优化策略,即在插值过程中根据某种优化准则函数动态的决定变量的数值。
Kriging 插值方法着重于权重系数的确定,从而使内插函数处于最佳状态,即对给定点上的变量值提供最好的线性无偏估计。
第5章克里格法

2、指示克里金法
• 设一区域化变量Z(x),对于任意 给定的阈值z,引入指示函数 I(x, z),表达式如下:
• 指示克立格法步骤如下:
• (1)确定一阈值,根据指示函 数将原数据转换为0或1;
• (2)利用转换的数据计算指示 变异函数,并进行拟合;
• (3)建立指示克立格方程组, 计算待估点值。若把指示函数 看做一普通区域化变量,也可 直接由简单或普通克立格方法 来计算待估点的值。
• 用矩阵表示为:
• 将简单克里金方程组表达式带入估计方差表达式得 简单克里金估计方差表达式:
1、简单克里金法
从简单克里金方程组的n个方程中便可求得n个权重系数λi,则YV(x)的简 单克里金估计量为:
简单克里金法的估计精度在很大程度上依赖于m值的准确度,但是通常情 况下很难正确估计m值,从而导致简单克里金估计精度降低。
• 所谓泛克里金法,就是在漂移的形式E[Z(x)]=m(x),和非平稳随机函数Z(x)的 协方差函数C(h)或变异函数γ(h)为已知的条件下,一种考虑到有漂移的无偏线 性估计量的地统计学方法,这种方法属于线性非平稳地统计学范畴。
(1)漂移和涨落
• 漂移:非平稳区域化变量Z(x)的数学
期望,在任一点x上的漂移就是该点 上区域化变量Z(x)的数学期望。
(2)非平稳区域化变量的协方差函数和变异函数
• 1)基本假设
• 假设Z(x)的增量[Z(x)-Z(y)]具有非平稳的数学期望[m(x)-m(y)]和非平稳的方差 函数,即假设下式存在:
• 2)协方差函数和变异函数 • 当Z(x)=m(x)+R(x)时,Z(x)的协方差函数C(x,y)为:
• Z(x)的变异函数γ(x,y)为:
第五章 克里金法
克里格法Kriging——有公式版

克里格法(Kriging)——有公式版二、克里格法(Kriging)克里格法(Kriging)是地统计学的主要内容之一,从统计意义上说,是从变量相关性和变异性出发,在有限区域内对区域化变量的取值进行无偏、最优估计的一种方法;从插值角度讲是对空间分布的数据求线性最优、无偏内插估计一种方法。
克里格法的适用条件是区域化变量存在空间相关性。
克里格法,基本包括普通克里格方法(对点估计的点克里格法和对块估计的块段克里格法)、泛克里格法、协同克里格法、对数正态克里格法、指示克里格法、折取克里格法等等。
随着克里格法与其它学科的渗透,形成了一些边缘学科,发展了一些新的克里金方法。
如与分形的结合,发展了分形克里金法;与三角函数的结合,发展了三角克里金法;与模糊理论的结合,发展了模糊克里金法等等。
应用克里格法首先要明确三个重要的概念。
一是区域化变量;二是协方差函数,三是变异函数一、区域化变量当一个变量呈空间分布时,就称之为区域化变量。
这种变量反映了空间某种属性的分布特征。
矿产、地质、海洋、土壤、气象、水文、生态、温度、浓度等领域都具有某种空间属性。
区域化变量具有双重性,在观测前区域化变量Z(X)是一个随机场,观测后是一个确定的空间点函数值。
区域化变量具有两个重要的特征。
一是区域化变量Z(X)是一个随机函数,它具有局部的、随机的、异常的特征;其次是区域化变量具有一般的或平均的结构性质,即变量在点X 与偏离空间距离为h的点X+h处的随机量Z(X)与Z(X+h)具有某种程度的自相关,而且这种自相关性依赖于两点间的距离h与变量特征。
在某种意义上说这就是区域化变量的结构性特征。
二、协方差函数协方差又称半方差,是用来描述区域化随机变量之间的差异的参数。
在概率理论中,随机向量X与Y的协方差被定义为:区域化变量在空间点x 和x+h处的两个随机变量Z(x) 和Z(x+h) 的二阶混合中心矩定义为Z(x) 的自协方差函数,即区域化变量Z(x) 的自协方差函数也简称为协方差函数。
地质统计学与随机建模原理3-克里格估值

式(4)是在确保估计方差最小的前提下推导出来的,它是克里格方差,
2 故记号为 K 。其中关键的区别在于λi (i=1,2,… ,n)在两个式中的
意义不一样。
从克里格方程组解出λi 后,即得到YV的简单克里格估计量:
Z m Y m jY j m j (Z j m)
其协方差函数为: E[Y(x) · Y( y) ]=C(x, y )
对ZV的估计转化为对YV* 的估计,且有:
YV 1 V
V
Y ( x)dx
1 V
Z ( x)dx m Z
V
V
m
所用的估计量为:
Y iYi
V i 1 n
其中: Y Z i m (i 1,2,, n)
' T
(v 1 ,v n ) 1 (v 2 ,v n ) 1
(v n ,v n ) 1 1 0
2 K
M (V ,V )
'
(4)信息样品为非点承载时的普通克里格方程组与普通克里格方差 若样品的承载不能看作是点承载,而是以x i为中心,其体积为v i
在无偏性条件 数法。 令:
i 1
n
i
1 下,要使得估计方差最小,从而求得诸权
系数λ i , (i=1,2,…,n),这是一个求条件极值的问题,要用拉格朗日乘
n F 2 i 1 ,为n个权系数λ 和μ 的(n+1)元函数。 i i 1
2 E
-2 μ是拉格朗日乘数。求出F对λ i , (i=1,2,…,n)以及F对μ的偏导数,并
基于光谱信息辅助的污灌区农田土壤镉协同克里格分析

摘
要
为 获取农 田土壤重金属 精确 空间 分布信 息 ,以某 污灌 区 5 2个土 壤全 量镉 、有效 镉含 量为 目标变
量 ,以土壤一阶微分光谱为辅助协 同变量 , 采用协 同克里格 法 , 进行空 间变异及插值研 究 。结果表 明 , 土壤 反射光谱相对有 机质 、 氧化铁 等单一 土壤环境变量 ,能反映更 多土壤 表面属性 信息 , 与土壤镉含量表现 出更 高显著相关性 ; 选择其一 阶微分 光谱作为协 同变量 , 进行 C o k r i g i n g 插值 , 与普通 Kr i g i n g和以有机质 、 氧化 铁等协 同变量 的 C o k r i g i n g插值结果相 比较 ,估测精度 明显提 高。以土壤 光谱作 为辅 助变量 , 能大 大提高土 壤重金属插 值精度 , 获取更精确 空间分布信息 , 而且相对常用协 同变量 , 具有测定简单 、省时 、 无损 等优 点 , 是提高土壤重金属 空间插 值的理想辅助 因子 。 关键词 土壤镉 ; 土壤反射光谱 ;协 同克里格 ;预测精度
基金项 目: 国家高技术研究发展计划( 8 6 3 计划) 项 目( 2 0 1 3 A A 1 0 2 4 0 1 ) , 国家科技支撑 计划项 目( 2 0 1 2 B A H2 9 B 0 4 ) , 国家教育部博 士点专项
第3 3 卷, 第8 期
2 0 1 3年 8月
光
谱
学
与
光
谱
分
析
S p e c t r o s c o p y a n d S p e c t r a l An a l y s i s
Vo 1 . 3 3 , No . 8 , p p 2 1 5 7 — 2 1 6 2 Au g u s t ,2 0 1 3
ArcGIS中几种空间插值方法

ArcGIS 中几种空间插值方法1. 反距离加权法(IDW)ArcGIS 中最常用的空间内插方法之一,反距离加权法是以插值点与样本点之间的距离为权重的插值方法,插值点越近的样本点赋予的权重越大,其权重贡献与距离成反比。
可表示为:1111()()n nip p i i i i Z Z D D ===∑∑其中Z 是插值点估计值,Z i (i=1Λn)是实测样本值,n 为参与计算的实测样本数,D i 为插值点与第i 个站点间的距离,p 是距离的幂,它显著影响内插的结果,它的选择标准是最小平均绝对误差。
2.多项式法多项式内插法(Polynomial Interpolation)是根据全部或局部已知值,按研究区域预测数据的某种特定趋势来进行内插的方法,属统计方法的范畴。
在GA 模块中,有二种类型的多项式内插方法,即全局多项式内插和局部多项式内插。
前者多用于分析数据的全局趋势;后者则是使用多个平面来拟合整个研究区域,能表现出区域内局部变异的情况。
3.样条函数内插法样条函数是一个分段函数,进行一次拟合只有少数点拟合,同时保证曲线段连接处连续,这就意味着样条函数可以修改少数数据点配准而不必重新计算整条曲线。
样条函数的一些缺点是:样条内插的误差不能直接估算,同时在实践中要解决的问题是样条块的定义以及如何在三维空间中将这些“块”拼成复杂曲面,又不引入原始曲面中所没有的异常现象等问题。
4.克里格插值法克里格法是GIS 软件地理统计插值的重要组成部分。
这种方法充分吸收了地理统计的思想,认为任何在空间连续性变化的属性是非常不规则的,不能用简单的平滑数学函数进行模拟,可以用随机表面给予较恰当的描述。
这种连续性变化的空间属性称为“区域性变量”,可以描述象气压、高程及其它连续性变化的描述指标变量。
地理统计方法为空间插值提供了一种优化策略,即在插值过程中根据某种优化准则函数动态的决定变量的数值。
Kriging 插值方法着重于权重系数的确定,从而使内插函数处于最佳状态,即对给定点上的变量值提供最好的线性无偏估计。
克里格空间插值法

其中,Z(si)是已测得的第i个位置的属性值,wi是在第i个位置上测 得值的权重,s0是待插值的位置,n是已知样点的数目。 距离倒数加权插值中,权重wi仅取决于样点到待插值点的距离。 在克里格插值中,权重不仅考虑了已知点与插值点间的距离,而且考 虑了己知点的位置和属性值整体的空间分布和格局。克里格插值中的 权重来自半方差函数模型(生成的表示地理现象连续表面的函数), 在半方差函数模型和邻近已知点的空间分布的基础上,对研究区内的 各个位置进行预测,权重wi取决于已知点的拟合模型、到插值点的距 离和插值点周围的已知样点的空间关系。
( 4) 成 层 随 机 采 样
( 5) 聚 集 采 样
( 6) 等 值 线 采 样
图1 各种不同的采样布置方式
1.7 区域变量
区域化变量 一个变量的空间分布称为该变量的区域化。
如果变量以三个空间坐标(x,y,z)为自变量, 那么该变量就是区域化变量。
区域化变量假定,在一定空间范围内,属性 指标的变异可以用一个连续的、空间上相关的随 机域来模拟。任何变量的空间变异可以表示为三 个主要组分之和:确定性成份、区域成分和随机 成分。
1.2.1整体插值方法
1 边界内插方法 边界内插方法假设任何重要的变化发生
在边界上,边界内的变化是均匀的,同质 的,即在各方向都是相同的。
2 趋势面分析
根据采样点的属性数据与地理坐标的关 系,进行多元回归分析得到平滑数学平面 方程的方法,称为趋势面分析。
1.2.2局部插值方法
只使用邻近的数据点来估计未知点的值, 包括几个步骤:
空间插值的理论假设是空间位置上越靠 近的点,越可能具有相似的特征值;而距离 越远的点,其特征值相似的可能性越小。
1.1空间插值法简述
协同克里格方法在东海表面温度场数据插值中的应用

时间 内获 取数 据 。将这 些来 源不 同、 精度 不一 的水 温 数据 转 化 为某 一 时 间段平 均 的格 网数 据是 水 温原 始调 查数 据转 化 为数据 产 品 的基 础 性 工作 。因 此 , 有必 要 对 原始 测 量 数
据进 行插 补或 插值 处理 以及 对 数据进 行 时 间段统 计处 理分 析 , 以期 在其 客观性 、 学性 和 科 完备 性上 作 出提升 。
区域 水 文数据 可 看成 由物 理机 理控 制 的趋势 场分 量和 受 随机 因素控 制 的剩余 场分 量 两部 分组 成 。物理 趋 势场分 量 可视 为确 定 因素 , 由理论模 拟 , 可 随机 场部 分这 里 引入地 质
统计 方法 进行 处理 。将 两个 分量 分别 进行 插 值 处 理 , 后求 和 得 到 最终 插 值 结果 。本研 然
1 技 术 流 程
技 术 流程分 为 以下几 部分 : 实验 数据 准备 、 平稳 检验 、 相关 性 检验 、 实验 变差 函数 计算 与拟合 、 N/ 通克 里格插 值 、 协 普 求得 海表 面温 度均估 计 值 、 计效 果分 析和 分析讨 论 得 出 估
结论 ( 1 。 图 )
学等许 多 方面 都有 成功 应用 的实 例 。本研 究 首次 将协 同 克里格 方法 引入 到海 洋水 文插 ]
收 稿 日期 : 0 10 — 6 2 1 - 6 2
作 者 简 介 : 庆 磊 (9 1) 男 , 面研 究 . — i sn q@ f . r. n 宋 18一, 硕 主 Ema :o gl i og c l o
普通克里格插值
剩余估计值
物理趋 势值
格网化空间数据 估 计效果 分析
克里格插值法

工程数学
提出了如下的平稳假设及内蕴假设: 提出了如下的平稳假设及内蕴假设:
{ 随机函数: 随机函数:Z (u ), u ∈ 研究范围} ,其空间分布律不因平移 而改变,即若对任一向量h, 而改变,即若对任一向量 ,关系式
F ( z1 , z2 , ⋅⋅⋅; x1 , ⋅⋅⋅) = F ( z1 , z2 , ⋅⋅⋅; x1 + h, x2 + h, ⋅⋅⋅)
D(ξ ) = Var (ξ ) = E[ξ − E (ξ )] = E (ξ ) − E (ξ )2 22来自工程数学工程数学
(3)协方差 ) 协方差是用来刻画随机变量之间协同变化程度的指标, 协方差是用来刻画随机变量之间协同变化程度的指标,其 大小反映了随机变量之间的协同变化的密切程度。 大小反映了随机变量之间的协同变化的密切程度。
σ ij = Cov(ξ1 , ξ 2 ) = E[(ξ1 − E (ξ1 ) (ξ 2 − E (ξ 2 ) ] ) )
= E (ξ1ξ 2 ) − E (ξ1 ) E (ξ 2 )
(4)相关系数 ) 协方差是有量纲的量,与随机变量分布的分散程度有关, 协方差是有量纲的量,与随机变量分布的分散程度有关,为 消除分散程度的影响,提出了相关系数这个指标。 消除分散程度的影响,提出了相关系数这个指标。
成立时,则该随机函数 成立时,则该随机函数Z(x)为平稳性随机函数。 为平稳性随机函数。 这实际上就是指,无论位移h多大,两个 维向量的随机变量 多大, 这实际上就是指,无论位移 多大 两个k维向量的随机变量
{ Z ( x1 ), Z ( x2 ),L , Z ( xk )} 和 { Z ( x1 + h), Z ( x2 + h),L , Z ( xk + h)}
MATLAB克里格工具箱中文翻译版

MATLAB克里格工具箱(4.0版:2001年7月)翻译:阿童木看星星伊夫格拉顿等加拉弗勒克里格工具箱是分布式的自由和技术支持。
规格克里格工具箱4.0版MATLAB 6.1兼容。
这是一个2.0版本的升级,已matlab下实现4.2编译,编译matlab下实现5.1和3.0版本。
请注意,此升级只使用2 - D矩阵,即使新的MATLAB版本支持更大的矩阵维数。
优化功能要求的Matlab优化工具箱。
然而,站在替代自我功能还提供了人,谁没有购买优化工具箱(参见“fitvario.m”)。
志工具箱正常的研究是必要的。
它是提供与克里格工具箱。
说明此工具箱的发展是基于使用2个或3个标量的客观分析的必要性在物理海洋学的尺寸。
这种类型的插值通常比标准更好的结果插值方法。
此外,它的不可忽略的优势,使插值误差的估计。
这个工具箱的功能几乎完全是从书Deutsch和Journel(1992)和Marcotte论文(1991)。
变差函数的功能是墨西哥文件编制前,而协同克里格法的功能发表后,在Matlab格式,在1991年Marcotte的论文。
所有的参数和例子可以发现,在英国,在该两本刊物。
Journel和Huijbregts(1992)的书是最好的书semivariograms。
一个完整的例子在物理海洋学的最优估计可以登曼和弗里兰(1985)发现的文件。
同时,kridemo显示2 - D目标的轮廓分析。
登曼,吉隆坡和HJ斐然,1985年。
相关秤,客观的测绘和统计检验Geostrophy超过大陆架。
研究月RES,43:517-539。
德语,C. V和AG Journel,1992年GSLIB:地统计的软件库和用户指南。
牛津牛津大学出版社,340页。
Journel,AG和Huijbregts终审法院首席法官,1992年,矿业统计学。
学术出版社,纽约,600页。
Marcotte,D. 1991。
Cokrigeage与MATLAB。
克里金差值法论文

基于Cokriging的空间插值算法研究与实现作者姓名:蒋鑫专业班级:信息与计算科学200807020104指导教师:白林摘要空间数据插值技术对于地表高程、地质属性等空间数据建模具有重要意义。
本文首先介绍了空间插值算法的相关理论和相关技术,然后以普通克里格插值算法为基础,着重研究协同克里格的空间插值算法,并且给出了两种算法的程序实现。
最后以河南省焦作市修武段地下水高程数值模拟为例,以地下水位高度为主区域化变量,以容易获取的节点地表高程信息作为协同区域化变量,计算了各自的实验变差函数和交互实验变差函数,分别进行普通克里格法插值和协同克里格插值,指出协同克里格法在进行松散多孔介质区域地下水位估值时能取得更为良好的效果。
论文以Visual C++ 6.0为开发工具实现算法编程,使用Matlab三维图形库函数进行三维曲面显示。
关键词:空间插值;区域化变量;协同克里格;变差函数The Research and Realization of Comparison Interpolation Algorithm Basedon CokrigingIntroduction of the author: Jiang Xin, whose instructor was Lecturer Bai Lin . He graduated from Chengdu University of Technology in Information and Computing Science major.Abstract The spatial data interpolation techniques for the surface elevation, geological properties, and spatial data modeling is important. This paper first introduces the relevant theory and technology of the spatial interpolation algorithm, then the ordinary kriging algorithm, focused on the co-kriging spatial interpolation algorithm, and gives the program of the two algorithms. Finally, numerical simulation of Jiaozuo City, Henan Province, the Xiuwu paragraph groundwater elevation, for example, that the height of the main regionalized variables to groundwater level, easy access to the node surface elevation information as collaborative regionalized variables to calculate the experimental variogram and interactive the experimental variogram, respectively, ordinary Kriging interpolation and co-kriging interpolation, that can achieve more good results during the regional groundwater valuation of loose porous media Cokriging. Thesis to the Visual C++ 6.0 development tools, algorithmic programming, Matlab 3D graphics library functions for three-dimensional surface display.Keywords: Comparison Interpolation;Regionalized variables;Cokriging;Variogram目录第1章绪论.................................................................. 错误!未定义书签。
地统计插值
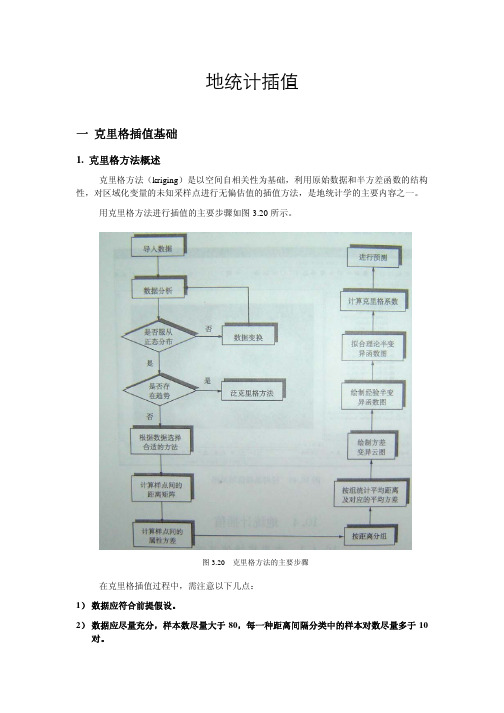
地统计插值一 克里格插值基础1. 克里格方法概述克里格方法(kriging )是以空间自相关性为基础,利用原始数据和半方差函数的结构性,对区域化变量的未知采样点进行无偏估值的插值方法,是地统计学的主要内容之一。
用克里格方法进行插值的主要步骤如图3.20所示。
在克里格插值过程中,需注意以下几点:1) 数据应符合前提假设。
2) 数据应尽量充分,样本数尽量大于80,每一种距离间隔分类中的样本对数尽量多于10对。
图3.20 克里格方法的主要步骤3)在具体建模过程中,很多参数是可调的,且每个参数对结果的影响不同。
A.块金值:误差随块金值的增大而增大。
B.基台值:对结果影响不大。
C.变程:存在最佳变程值。
D.拟合函数:存在最佳拟合函数。
4)当数据足够多时,各种插值方法的效果基本相同。
2. 克里格方法的分类及适用条件目前,克里格方法主要有以下几种类型:普通克里格(Ordinary Kriging)、简单克里格(Simple Kriging)、泛克里格(Universal Kriging)、协同克里格(Co-Kriging)、对数正态克里格(Logistic Normal Kriging)和析取克里格(Disjunctive Kriging)等。
下面简要介绍ArcGIS中常用的几种克里格方法的适用条件,其具体的算法、原理可查阅相关文献资料。
不同的方法有其适用的条件,按照图3.20所示步骤,当数据服从正态分布时,选用对数正态克里格;若不服从简单分布时,选用析取克里格;当数据存在主导趋势时,选用泛克里格;当只需了解属性值是否超过某一域值时,选用指示克里格;当同一事物的两种属性存在相关关系,且一种属性不易获取时,选用协同克里格方法,它借助另一属性实现该属性的空间内插;当假设属性值的期望值为某一已知常数时,选用简单克里格;当假设属性值的期望值是未知的,选用普通克里格。
下面只选取了普通克里格、泛克里格和协同克里格三种方法的操作步骤、注意事项作为示例,其余相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
where \^K(u) is the weight assigned to the primary datum z 1 (u a1 ), Xf^(u) is the weight assigned to the secondary datum z2(um2), and m1 and m2 are the primary and secondary means assumed known and constant within the study
21
0882-8121/98/0100-0021$15.00/1 © 1998 International Association for MathematicaБайду номын сангаас Geology
22
Goovaerts
most of the secondary data weights tend to be small and some of them are necessarily negative with a risk of getting unacceptable results such as negative concentration estimates. To reduce the occurrence of negative weights and avoid limiting artificially the impact of secondary data, Isaaks and Srivastava (1989, p. 416) proposed to use a single constraint that forces all primary and secondary data weights to sum to one. Unbiasedness of the estimator then is ensured by rescaling all secondary variables to the same mean as the primary variable, hence the term "rescaled" or "standardized" ordinary cokriging (Deutsch and Journel, 1992, p. 70). Another advantage of using a single contraint is that the secondary information can be limited to a single datum when the secondary variable is sampled at the estimated point (collocated cokriging; Almeida and Journel, 1994); under the traditional constraints that datum would get, by construction, a zero weight. In this paper, properties of traditional and rescaled ordinary cokriging estimators are compared and the impact of the unbiasedness constraints on the cokriging weights is investigated. Several authors (Stein and others, 1988; Hevesi, Istok, and Flint, 1992; Asli and Marcotte, 1995) have compared the prediction performances of simple and ordinary kriging or cokriging in the equally and undersampled situations. Using an environmental dataset, that comparison is here extended to rescaled ordinary cokriging and the situation of single collocated secondary data. Two performance criteria are considered: (1) the mean absolute error of prediction of heavy metal concentrations at 100 test locations, and (2) the proportion of test locations that are classified wrongly as safe or contaminated on the basis of cokriging estimates. SIMPLE COKRIGING Let (z1(ua1), «1 = 1, . . . , n1} be the values of the primary attribute z1 at n1 locations ua1. To alleviate notation consider the situation where there is only one secondary attribute z2 measured at, possibly different, locations ua2, {z2(uM2), a2= 1, ... ,n2}. The simple cokriging (SCK) estimator of z\ at location u is written:
Mathematical Geology, Vol. 30, No. 1, 1998
Ordinary Cokriging Revisited1 P. Goovaerts2
This paper sets up the relations between simple cokriging and ordinary cokriging with one or several unbiasedness constraints. Differences between cokriging variants are related to differences between models adopted for the means of primary and secondary variables. Because it is not necessary for the secondary data weights to sum to zero, ordinary cokriging with a single unbiasedness constraint gives a larger weight to the secondary information while reducing the occurrence of negative weights. Also the weights provided by such cokriging systems written in terms of covariances or correlograms are not related linearly, hence the estimates are different. The prediction performances of cokriging estimators are assessed using an environmental dataset that includes concentrations of five heavy metals at 359 locations. Analysis of reestimation scores at 100 test locations shows that kriging and cokriging perform equally when the primary and secondary variables are sampled at the same locations. When the secondary information is available at the estimated location, one gains little by retaining other distant secondary data in the estimation. KEY WORDS: cokriging, unbiasedness constraints, negative weights, standardization.
INTRODUCTION Depending on the model adopted for the random function, three kriging variants can be distinguished: simple kriging, ordinary kriging, and kriging with a trend model (universal kriging). Several authors (Matheron, 1970, p. 129; Journel and Rossi, 1989) showed that the latter two algorithms are but simple kriging with the stationary mean replaced by a local mean that is estimated within each search neighborhood. Similar relations exist in the multivariate situation and are developed here for the most frequently used simple and ordinary cokriging. Moreover, the cokriging system for estimating the local primary and secondary means implicitly used in ordinary cokriging is established. The unbiasedness of the ordinary cokriging estimator is ensured by forcing the primary data weights to sum to one whereas the weights of each secondary variable are constrained to sum to zero. Under these "traditional" constraints
